




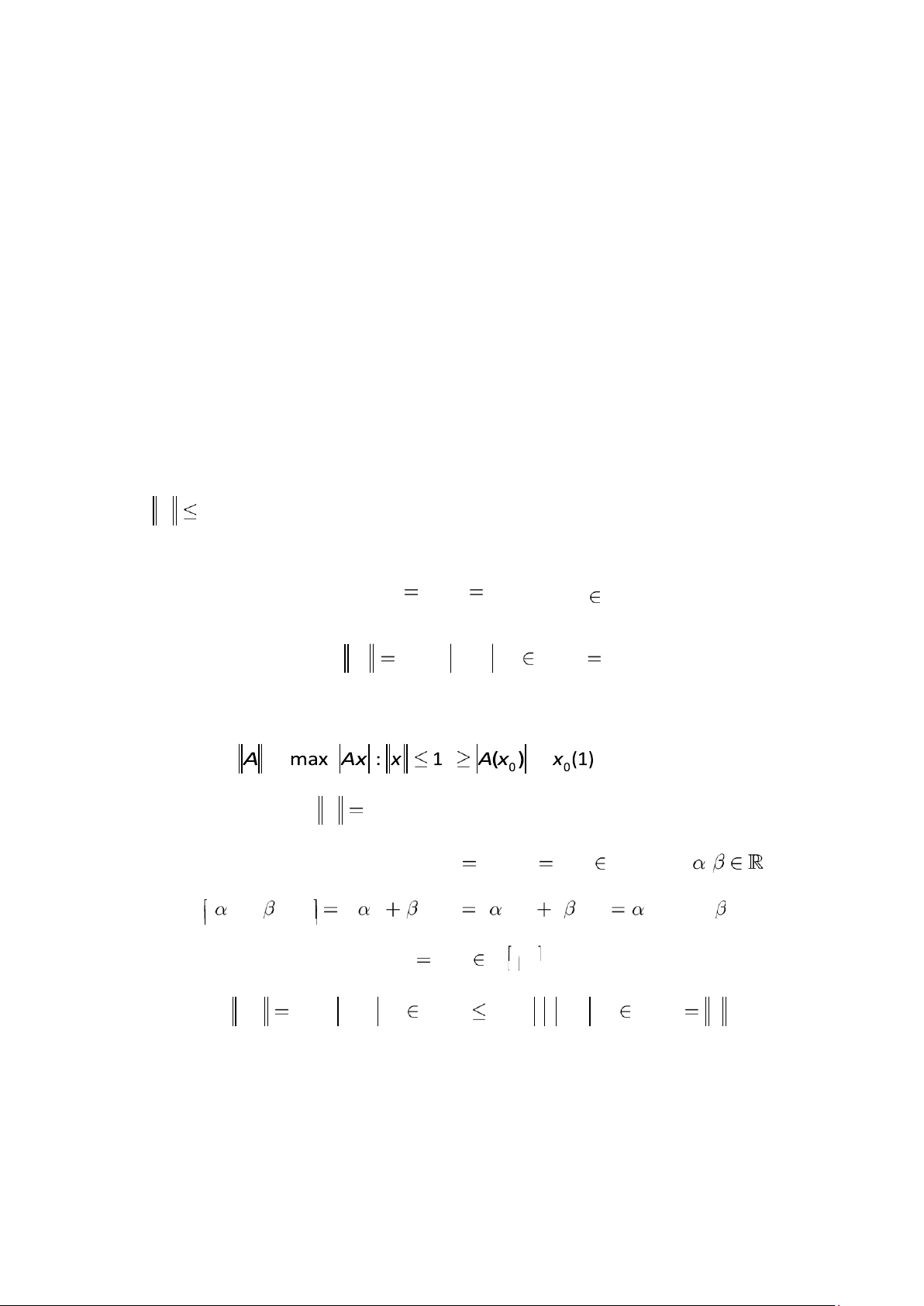








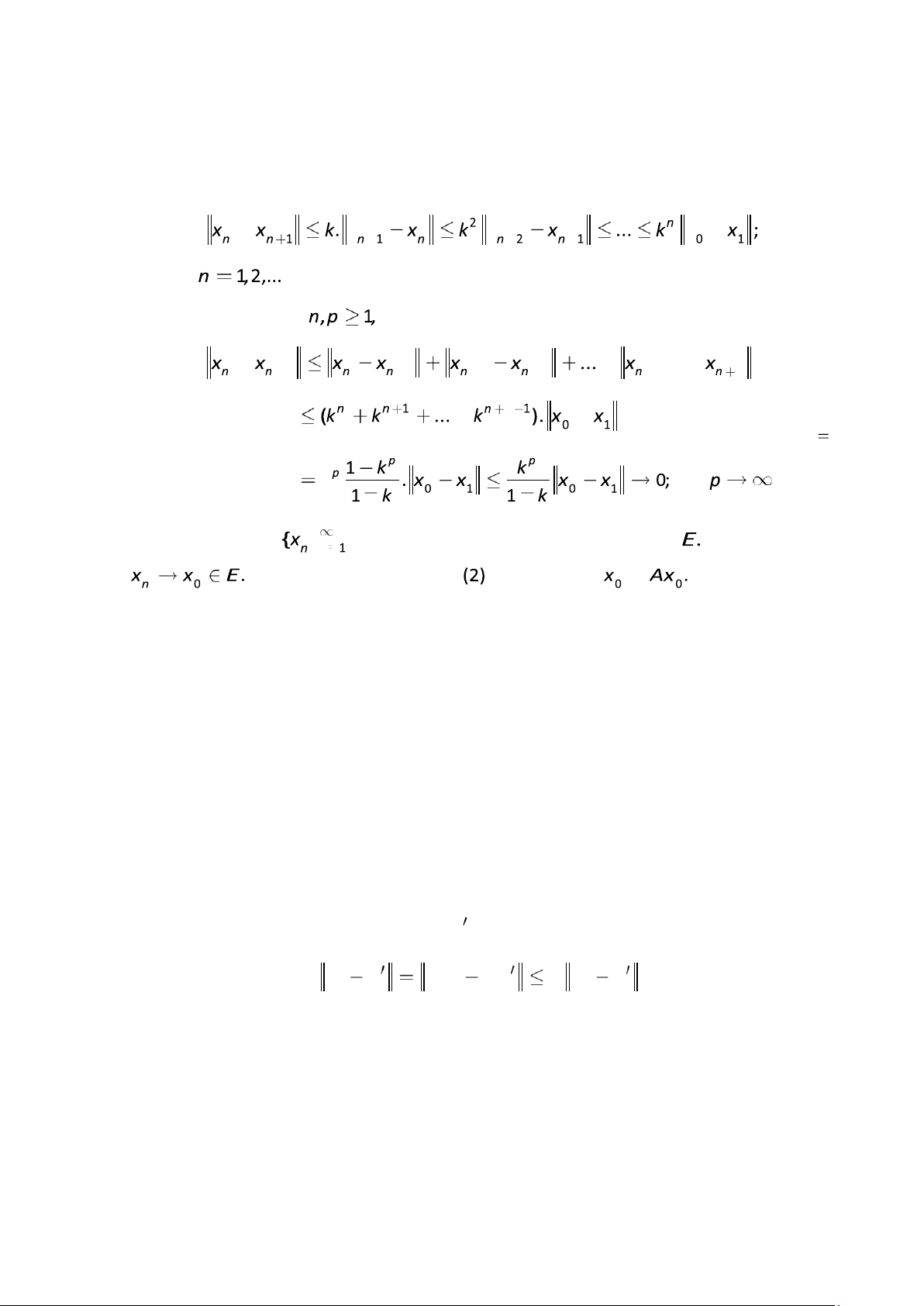


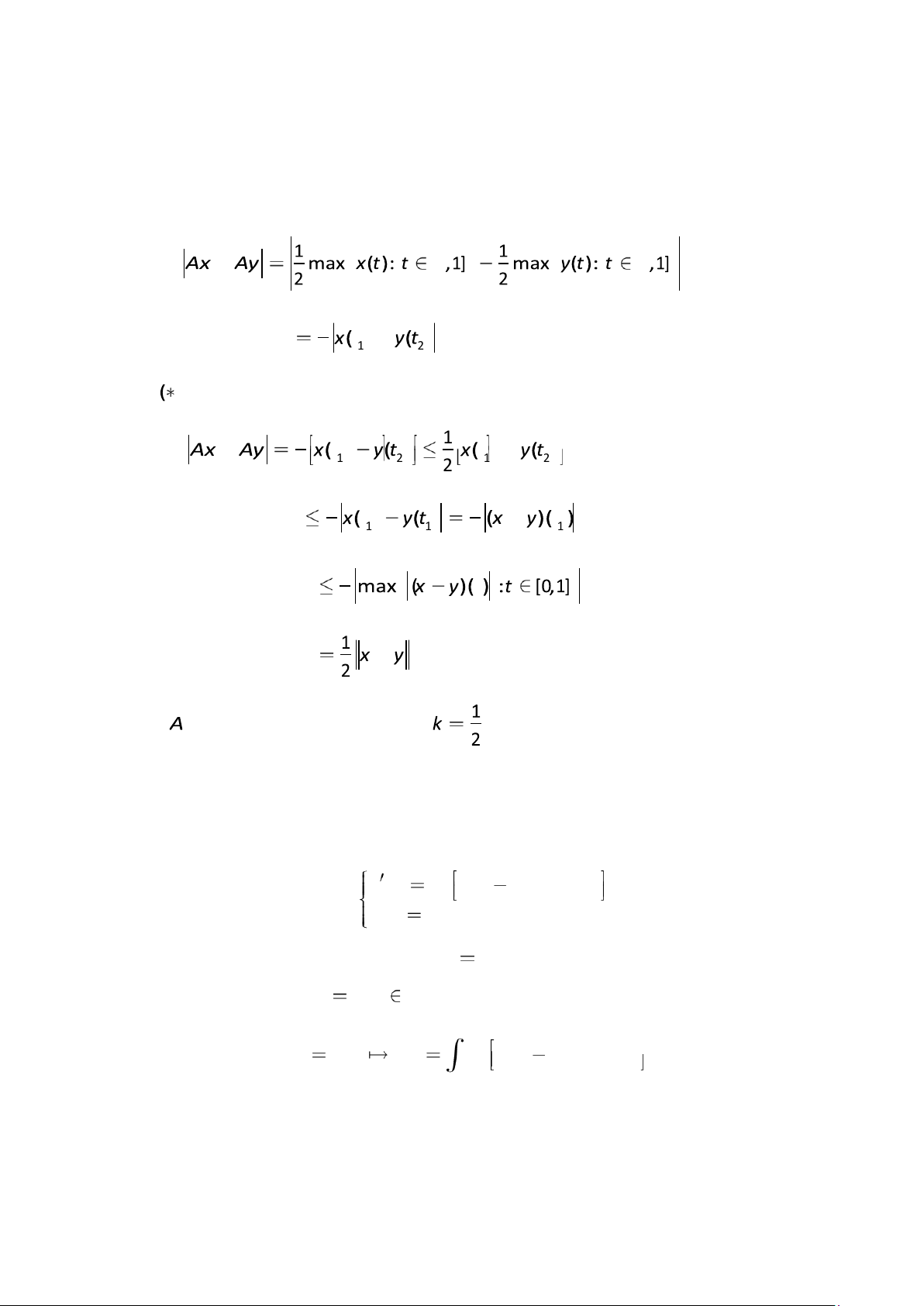

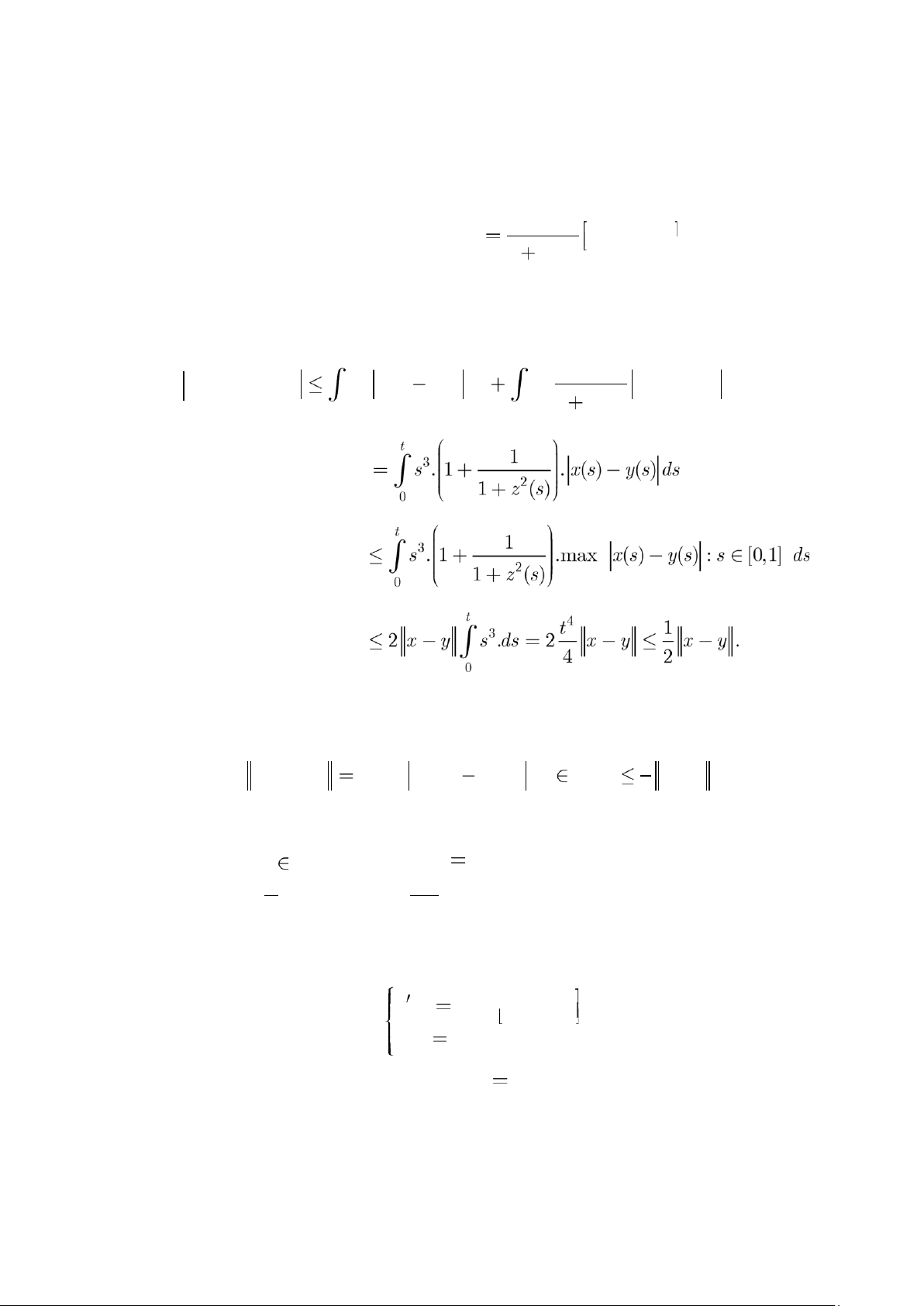
Preview text:
lOMoAR cPSD| 40551442
ÔN TẬP GIẢI TÍCH HÀM
Vấn đề I. Xác định được công thức chuẩn trên một số không gian và tính được
chuẩn của các vector trên không gian tương ứng. 1. Không gian C a b[ , ] với chuẩn được xác định bởi x max x t( ) :t
[a b, ] ; với x
x t( ) C a b[ , ].
Bài 1. Tính chuẩn của một vector trên không gian tương ứng
a) Trên không gian C[0,1] tính chuẩn của véc tơ x x t( ) t et; với t [0,1].
b) Trên không gian C[0, ] tính chuẩn của véc tơ x x t( ) sint cos ;t t [0, ]. Bài giải a) Ta có v ớ i m ọ i . Như v ậ y , hàm
đ ồ ng bi ế n trên đo ạ n Do đó, ta có b) Ta có x t( ) (cost sin );t t [0, ]. Khi đó Từ đó, ta nhận được lOMoAR cPSD| 40551442
2. Chuẩn trên không gian C a b1[ , ] gồm tất cả các hàm khả vi liên tục trên đoạn [a b, ] được xác định bởi x max x t( ) x t( ) :t
[a b, ] ; với x x t( ).
Bài 3. Trên C1[0,1] tìm chuẩn của vector x x t( ) t2. Ta có x t( ) x t( ) t2 2t t2
2t; với mọi t [0,1]. Do đó, ta nhận được t 2t : t B ở i vì , hàm
đ ồ ng bi ế n trên nên t 2t : t
Vấn đề 2. Xác định tích vô hướng trên một số không gian và tính tích vô hướng của
hai vector trên không gian tương ứng.
1. Không gian tuyến tính gồm tất cả các dãy số thực hoặc số phức khả tổng bậc p được ký hiệu là
xạ được xác định như dưới đây là một tích vô hướng trên không gian lp .
( )ii Xác định chuẩn sinh bởi tích vô hướng trên lOMoAR cPSD| 40551442 Không gian
v ớ i chu ẩ n dư ớ i đây là m ộ t không gian Banach : v ớ i x l
xác định hàm chuẩn bởi công thức 1 p p 1 2.
Không gian tuyến tính gồm tất cả các hàm nhận giá trị thực xác định trên đoạn
[a b, ] có bình phương khả tích được ký hiệu là V ớ i hai hàm và trong không gian
Ch ứ ng minh r ằ ng ánh x ạ được xác định như dư
ới đây là một tích vô hướng trên không gian L a b2[ , ]. 3.
Không gian tuyến tính gồm tất cả các hàm nhận giá trị phức xác định trên đoạn
[a b, ] có bình phương khả tích được ký hiệu là V ớ i hai hàm và trong không gian
Ch ứ ng minh r ằ ng ánh x ạ được xác định như dư
ới đây là một tích vô hướng trên không gian L a b2[ , ]. lOMoAR cPSD| 40551442
Bài 4. Xét tính trực giao của các vector dưới đây trên không gian tương ứng
a) Trên không gian tuyến tính L2[0,1] với hai vector x x t( ) t y, y t( ) et.
b) Trên không gian L2[ 1,1] với hai vector x
x t( ) t2025et2 và y y t( ) et2 Bài giải a) Ta có 1 1 1 te dt
Vậy hai vector đã cho không trực giao với nhau. b) Ta có 1
Hàm dưới dấu tích phân là hàm lẻ nên tích phân trên bằng 0. Như vậy hai vector trực giao.
Chứng minh trực tiếp như sau 1 0 1 2 2 2 1 1 0
Tính tích phân trong số hạng thứ nhất của tổng trên bằng phép đổi biến u t ta nhận được lOMoAR cPSD| 40551442 1 1 1 1 1 2025 2025 2025 2025 2025 e du
Vậy hai vector đã cho trực giao với nhau.
Vấn đề 3. Kiểm tra tính liên tục của toán tử trong không gian định chuẩn và tìm chuẩn của toán tử
Bài 5. Chứng minh tính liên tục và tìm chuẩn của các toán tử sau x b) A C: c) f C: lOMoAR cPSD| 40551442 d) f x( ) A 1. (1)
Như vậy, toán tử A là liên tục.
Tìm chuẩn của toán tử A: Lấy x x t 0 0( )
1; với mọi t [0,1]. Khi đó, ta có x0 max x t0( ) :t [0,1] 1. Mặt khác, ta có 1. (2) Từ (1) và 1 . (2) ta suy ra A
b) Chứng minh A tuyến tính: Với mọi x x t y( ), y t( ) C[0,1] và , ta có A ( x y t)( ) t x(
y t)( ) t x t( ) t y t( ) Ax t( ) Ay t( ).
Chứng minh A liên tục: Với mọi x x t( ) C 0,1 ta có Ax sup tx t( ) :t [0,1]
sup t x t. ( ) :t [0,1] x .
Như vậy, toán tử A là bị chặn và cũng liên tục. Ta cũng có A 1. (1) lOMoAR cPSD| 40551442
Tìm chuẩn của toán tử A: Lấy x x t 0 0( )
1; với mọi t [0,1]. Khi đó, ta có x0 max x t0( ) :t [0,1] 1.. Khi đó, ta có 1 0 0 T ừ (1) và ta suy ra 1 . 1 (2) và
c) Chứng minh f tuyến tính: Với mọi x ta có y t dt f( x 2 2 0 0
Chứng minh f là phiếm hàm bị chặn hay liên tục: Với mọi x
x t( ) C[0,1] ta có lOMoAR cPSD| 40551442 Như th ế , ta đư ợ c 1 . (1) 2 L ấ y v ớ i m ọ i . Khi đó . M ặ t khác, ta l ạ i có 2 1 1 0 . 2 0 T ừ (1) và ta nh ậ n đư ợ c Vấn đề 3
1. Nguyên lý đồ thị đóng
Khái niệm toán tử đóng. Cho hai không gian định chuẩn X và Y. Ta gọi đồ thị của ánh
xạ A X Y: là tập hợp ( )A (x Ax x X, ): X Y . lOMoAR cPSD| 40551442
Nếu đồ thị ( )A của toán tử A là tập đóng trong không gian định chuẩn tích X Y thì ta gọi
A là toán tử đóng.
Nguyên lý đồ thị đóng Banach. Cho X và Y là các không gian định chuẩn. Khi đó,
Ch ứ ng minh. Th ậ t v ậ y, l ấ y m ộ t dãy b ấ t k ỳ h
ộ i t ụ t ớ i ph ầ n t ử . T ứ c là . Khi đó, ta có Do đó và .
nếu toán tử tuyến tính A X Y: liên tục thì A có đồ thị đóng.
Từ tính liên tục của toán tử A và tính duy nhất của giới hạn trong không gian định chuẩn, ta suy ra y nlim Axn A nlim xn Ax. Nghĩa là (x y, ) (x Ax, )
( )A . Như vậy A là toán tử đóng trong X Y. Định lý được chứng minh.
2. Nguyên lý bị chặn đều
Khái niệm bị chặn đều của một họ toán tử tuyến tính từ không gian định chuẩn X
vào không gian định chuẩn Y. Cho X và Y là hai không gian định chuẩn. Họ các toán
tử A L(XY, ) được gọi là I
( )i Bị chặn tại điểm x X nếu tập hợp A x
là bị chặn trong Y. Tức là, tồn tại hằng số Mx 0 sao cho M A x Y x; với mọi lOMoAR cPSD| 40551442
( )ii Bị chặn đều nếu A
bị chặn trong không gian L(X Y, ). Tức là, tồn tại I hằng số M 0 sao cho A M; với mọi I.
Nguyên lý bị chặn đều Banach - Steinhauss. Giả sử X là không gian Banach và Y là
không gian tuyến tính định chuẩn. Giả sử A : I là các toán tử tuyến tính liên tục từ X vào
Y sao cho với mỗi x X tập hợp A x bị chặn trong Y. Khi đó, họ I A
là tập hợp bị chặn trong L(X Y,
); nghĩa là tồn tại hằng số dương M sao cho Khi đó, ta có 1 1 1 fn( x y) ( x y)cosn x cosn y cosn f xn( ) f yn( ). Ta có đánh giá 1 1 cos 1 1 v ớ i m ọ i Như v ậ y h ọ ánh x ạ b ị ch ặ n đ ề u. 1,2,... lOMoAR cPSD| 40551442 3. Ánh xạ mở
Khái niệm ánh xạ mở. Ánh xạ A từ không gian metric M ,
1 (X d X) vào không gian metric M ,
2 (Y d Y ) được gọi là ánh xạ mở tại điểm x0 X nếu A biến mỗi lân cận của
điểm x0 trong M1 thành lân cận của điểm Ax0 trong M2. Ánh xạ A được gọi là mở
nếu ánh xạ biến mỗi tập mở trong M1 thành tập mở trong M2.
Nguyên lý Banach về ánh xạ mở. Nếu ánh xạ A là toàn ánh tuyến tính liên tục từ
không gian Banach E lên không gian Banach F , thì A là ánh xạ mở.
Bài tập 6. Chứng minh ánh xạ f :
cho bởi f x( ) x có đồ thị đóng nhưng không phải là ánh xạ mở.
Ta chứng minh đồ thị của ánh xạ f là tập đóng. Giả sử x f x x n, (
n) ( )f hội tụ đến phần tử (
y0 0, ). Do ánh xạ f là liên tục nên ta có (x y0 0, )
nlim xn, (f xn)
nlim xn, limn f x( n) x f x0, ( 0) ( )f .
Như vậy, đồ thị của ánh xạ f là tập đóng. Ta có f( 1,1) [0,1).
Như vậy, ánh xạ đã cho không là ánh xạ mở.
4. Nguyên lý thác triển Hahn- Banach
Mọi phiếm hàm tuyến tính liên tục f xác định trên không gian tuyến tính con thực
sự X0 của không gian định chuẩn X . Khi đó, tồn tại phiếm hàm tuyến tính F xác định trên X sao cho X ( )i F x( )
f x( ); với mọi x 0. lOMoAR cPSD| 40551442 ( )ii F f X X0
Bài 7. Cho không gian định chuẩn X trên trường số thực cho phần tử x0 X khác Chứ
ng minh rằng tồn tại một phiếm hàm tuyến tính liên tục f trên X sao cho f x( và . 0) Đặt X 0
. Khi đó X0 là một không gian tuyến tính con của X . Xét ánh xạ f0 : X0 x tx0 f x0( ) t x0 .
là ánh xạ tuyến tính trên X x 0 có f x0 0( ) 0 và f x0( ) x do đó . f
Áp dụng nguyên lý thác triển Hahn-Banach, tồn tại phiếm hàm tuyến tính liên tục f trên X sao cho f x ( ) f x( ) và 0( ); với mọi x hay f x 0 và 1.
5. Định lý F. Riesz về dạng tổng quát của phiếm hàm tuyến tính liên tục trên
không gian Hilbert. Giả sử H là không gian Hilbert. Khi đó, ta có các khẳng định sau
( )i Với mọi a H phép tương ứng fa : H x x a,
xác định một phiếm hàm tuyến tính liên tục trên H và . f
( )ii Ngược lại, mọi phiếm hàm tuyến tính liên tục f trên H tồn tại duy nhất phần tử a H sao cho f x( ) f xa( )
x a, ; với mọi x H.
Bài 8. a) Phát biểu định lý Riesz về dạng tổng quát của phiếm hàm tuyến tính liên tục trên không gian Hilbert. lOMoAR cPSD| 40551442
b) Giả sử a là phần tử cố định tùy ý thuộc không gian Hilbert H chứng minh rằng fa x a,
là một phiếm hàm tuyến tính liên tục trên X và . f
( )i Trước hết, ta chứng minh công xác định fa như trên là một phiếm hàm tuyến tính
liên tục: Giả sử a là phần tử cố định tùy ý thuộc không gian H . Khi đó, với mọi x y H, và , ta có fa( x y) x y a, x a, y a, x a, x a, f x( ) f y( ).
Theo bất đẳng thức Cauchy - Schwarz, ta có f xa( ) x a, a . x .
Như vậy, phiếm hàm f là tuyến tính bị chặn và cũng liên tục trên H . Từ đó, ta cũng nhận được f a . Khi a 6. Ánh xạ co
Định nghĩa. Ánh xạ A từ không gian định chuẩn E vào không gian định chuẩn F được
gọi là một ánh xạ co nếu tồn tại hằng số k : 0 k 1 sao cho Ax Ay k x y. ; với mọi x y E, . F E lOMoAR cPSD| 40551442
Điểm x E gọi là một điểm bất động của ánh xạ A từ không gian định chuẩn E vào chính nó nếu Ax x.
Nguyên lý ánh xạ co Banach. Ánh xạ co từ không gian Banach E vào chính nó đều
có điểm bất động x .
0 duy nhất. Nghĩa là Ax0
Chứng minh. Giả sử E là một không gian Banach và A E E: là một ánh xạ co. Khi đó,
tồn tại hằng số k : 0 k 1 sao cho Ax Ay k x y.
; với mọi x y E, . (1)
Lấy điểm bất kỳ x x
0 E. Ta xây dựng dãy { } n n 1
E được xác định bởi x Ax n
n 1; với mọi n 1,2,... (2) Từ (1) và (2) ta suy ra
; với mọi n 1,2,...
Sử dụng điều này liên tiếp ta nhận được lOMoAR cPSD| 40551442 v ớ i m ọ i . T
ừ đó suy ra, v ớ i m ọ i ta có 1 1 2 1 khi
Đi ề u đó, ch ứ ng t ỏ
là dãy Cauchy trong không gian Banach Như th ế , dãy
L ấ y gi ớ i h ạ n hai v ế trong ta nh ậ n đư ợ c Như v ậ y, ph ầ n ; k .
tử x0 là một điểm bất động của ánh xạ A.
Giả sử, ánh xạ A còn có điểm bất động x0. Khi đó, ta có x0 x0 Ax0 Ax0 k x. 0 x0 . Từ đó, ta suy ra lOMoAR cPSD| 40551442
Như vậy, ta nhận được hay
x x . Điều đó, chứng tỏ điểm x0
là điểm bất động duy nhất. 1 1 . 3 3 Bài 7.
Tìm đi ể m b ấ t đ ộ ng c ủ a ánh x ạ 1 3 V ớ i m ọ i t a có
Như vậy A là ánh xạ co với hằng số co bằng k Giả sử x x t 0
0( ) là điểm bất động của ánh xạ A. Khi đó, ta có lOMoAR cPSD| 40551442 Ax t0( )
x t0( ); với mọi t [0,1].
Điều đó, tương đương với 1 x0(0)
x t0( ); với mọi t [0,1]. (1) 3 Tại t 0, ta nhận được
1 x0(0) x0(0). 3 Do đó, ta suy ra x 0(0) (2)
Từ (1) và (2) ta nhận được x0 x t0( )
C[0,1]; với mọi t [0,1].
Bài 8. Chứng minh ánh xạ được cho dưới đây là ánh xạ co và tìm hằng số co A C: [0,1] 1 x x t( ) Ax t( ) max x t( ):t [0,1] . 5
là ánh xạ co và tìm hằng số co của nó.
Bài giải. Với hai hàm x
x t y( ), y t( ) C[0,1] luôn tồn tại t t1 2, [0,1] tương ứng sao cho x t( )1 max x t( ):t [0,1] và y t( )2 max y t( ):t [0,1] .
Không mất tính tổng quát ta có thể giả sử ( ) ( )
x t 1 y t 2 . Khi đó, ta thấy x t( )1 y t( )2 max y t( ):t [0,1] y t( )1 . ( ) lOMoAR cPSD| 40551442 Do đó, ta nhận được [0 [0 1 1 2 2 T ừ ta nh ậ n đư ợ c 1 1 1 2 1 2 2 2 1 1 1 1 1 2 2 1 2
V ậ y là ánh x ạ co v ớ i h ằ ng s ố co là
Bài 9. Chứng minh phương trình Cauchy
x t( ) t3. ( )x t arctan ( )x t x(0) 0.
có nghiệm duy nhất trong lân cận điểm t 0.
Bài giải. Với mỗi hàm x x t( ) C[0,1] xét ánh xạ được xác định bởi công thức t x x t( ) Ax
s3. ( )x s arctan ( )x s ds. 0 lOMoAR cPSD| 40551442
Bởi vì đạo hàm của hàm theo cận trên bằng hàm dưới dấu tích phân, nên ta có vào chính nó.
Tiếp theo, với mọi x Ax t( ) t t
s x s3. ( ) y s ds( )
s3. arctan ( )y s arctan ( )x s ds 0 0 Hàm f w s( )
arctan ( )w s khả vi trên đoạn nằm giữa x s( ) và y s( ) với 1 f w s( ) . 1 w s2( )
Theo định lý Lagrange, tồn tại c s( ) trong khoảng nằm giữa x s( ) và y s( ) sao cho lOMoAR cPSD| 40551442 1 arctan ( ) arctan ( )y s x s
y s( ) x s( ) . 1 c s2( ) Do đó, ta có t t 1 Ax t( ) Ay t( )
s x s3. ( ) y s ds( ) s3.
x s( ) y s ds( ) 0 0 1 c s2( ) Từ đó, suy ra 1 Ax Ay max Ax t( )
Ay t( ) :t [0,1] x y . 2
Như vậy A là ánh xạ co từ không gian C[0,1] và chính nó. Theo nguyên lý điểm bất động,
tồn tại duy nhất x C[0,1] sao cho Ax x . Vậy phương trình có nghiệm duy nhất. Bài 10.
Chứng minh phương trình Cauchy x t( ) t2.ln 1 x t2( ) x(0) 0.
có nghiệm duy nhất trong lân cận của điểm t 0.



