Bài Tập Hình 8 Bài Diện Tích Hình Thoi Có Lời Giải

5. DIỆN TÍCH HÌNH THOI
I. KIẾN THỨC CƠ BẢN
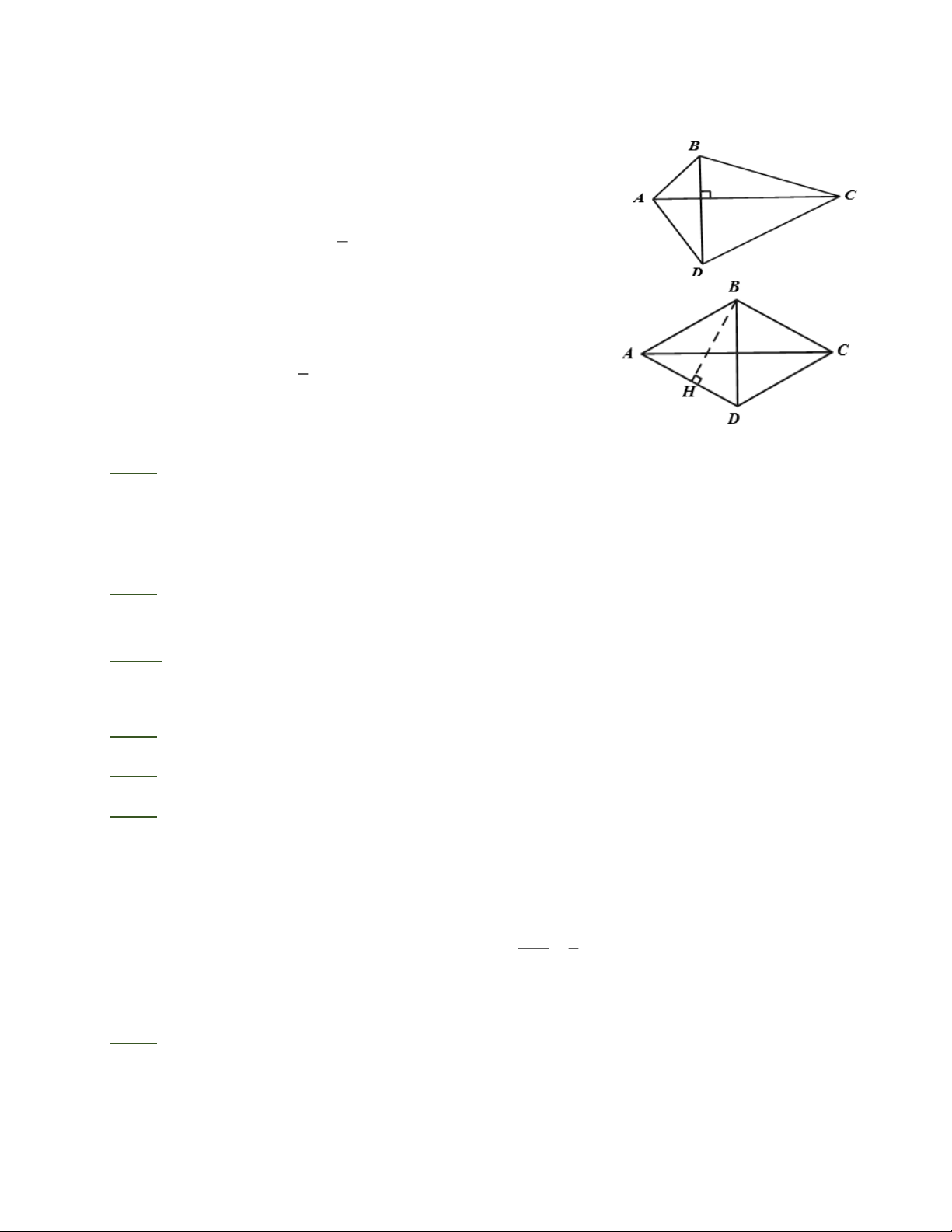
 Diện tích tứ giác có hai đường chéo vuông góc bằng nửa tích hai đường chéo. 1 S = AC. D B 2
 Diện tích hình thoi bằng nửa tích hai đường chéo hoặc
bằng tích của một cạnh với chiều cao. 1 S = A C .BD = AD.BH 2 III. BÀI TẬP
Bài 1: Cho hình thang ABCD ( AB//CD) có AB = 5 c ,
m CD = 12 cm, BD = 8 cm, AC = 15 . cm
a) Qua B kẻ đường thẳng song song với AC và cắt CD ở E. Tính DBE.
b) Tính diện tích hình thang ABC . D
Bài 2: Một hình chữ nhật có hai cạnh kề dài 8m và 5m. Tính diện tích tứ giác có đỉnh là
trung điểm các cạnh của hình chữ nhật.
Bài 3: Tứ giác ABCD có A C = BD . Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC,
CD, DA. Biết EG = 5cm , HF = 4 cm . Tính diện tích tứ giác EFGH .
Bài 4: Tính diện tích hình thoi có cạnh bằng a, góc tù của hình thoi bằng 1500.
Bài 5: Tính diện tích hình thoi có chu vi bằng 52 cm, một đường chéo bằng 24 cm.
Bài 6: Cho tam giác ABC vuông tại A ( AB  AC ). Gọi I là trung điểm của cạnh BC. Qua
I kẻ IM vuông góc với AB tại M và IN vuông góc với AC tại N. Lấy D đối xứng I qua N.
a) Tứ giác ADCI là hình gì? DK 1
b) Đường thẳng BN cắt DC tại K. Chứng minh = . DC 3
c) Cho AB = 12 c , m BC = 20 c .
m Tính diện tích hình ADCI.
Bài 7: Hình thang ABCD(AB//CD) có AB = 3cm, CD = 14cm, AC = 15cm, BD = 8cm.
a) Chứng minh rằng AC vuông góc với BD.
b) Tính diện tích hình thang. Trang 1
Bài 8: Tính diện tích hình thoi có cạnh bằng 4 cm, tổng hai đường chéo bằng 10 cm
Bài 9: Tính cạnh của hình thoi có diện tích bằng 2
24 cm , tổng hai đường chéo bằng 14 . cm Tự luyện:
Bài 10: Cho hình thang cân ABCD ( AB//CD) có AC vuông góc với BD tại O.
a) Chứng minh các tam giác OCD, OAB vuông cân.
b) Biết AB = 2 c ,
m CD = 8 cm, AD = 5 c .
m Tính diện tích hình thang ABC . D
Bài 11: Cho hình thoi ABCD có AC = 10 c ,
m BD = 6 c .
m Gọi E, F, G, H theo thứ tự là
trung điểm của AB, BC, CD, D . A
a) Tứ giác EFGH là hình gì? Vì sao?
b) Tính diện tích hình thoi ABC . D
c) Tính diện tích tứ giác EFGH .
Bài 12: So sánh diện tích của một hình thoi và một hình vuông có cùng chu vi.
KẾT QUẢ - ĐÁP SỐ Bài 1:
a) DE = 17cm ;BE = 15cm ;BD = 8cm 2 2 2 2 2 2
DE = BE + DB = 17 = 15 + 8 = 289   · DBE vuông tại B  DBE =  90 . 1
b) Theo câu a, có BD ^ A C Þ S = A × C B × D = 60 A BCD 2 2 cm .
Bài 2: Đáp số: (Tứ giác đó là hình thoi, diện tích bằng 20 m2. )
Bài 3: EF là đường trung bình của tam giác ABC nên 1 EF = AC 2 1 1 Tương tự: GH =
AC ; EH = FG = D B 2 2
Do A C = BD nên EF = FG = GH = EH suy ra EFGH là hình thoi Trang 2 1 1 2 S = EG.FH = 5.4 = 10(cm ) EFGH 2 2 B a
Bài 4: Kẻ BH ⊥ AD . Ta tính được ˆ A = 30 , BH= 2 30° C 2 = a a A S AD. B H = . a = ABCD 2 2 H D
Bài 5: Đáp số: 2 120cm Bài 6:
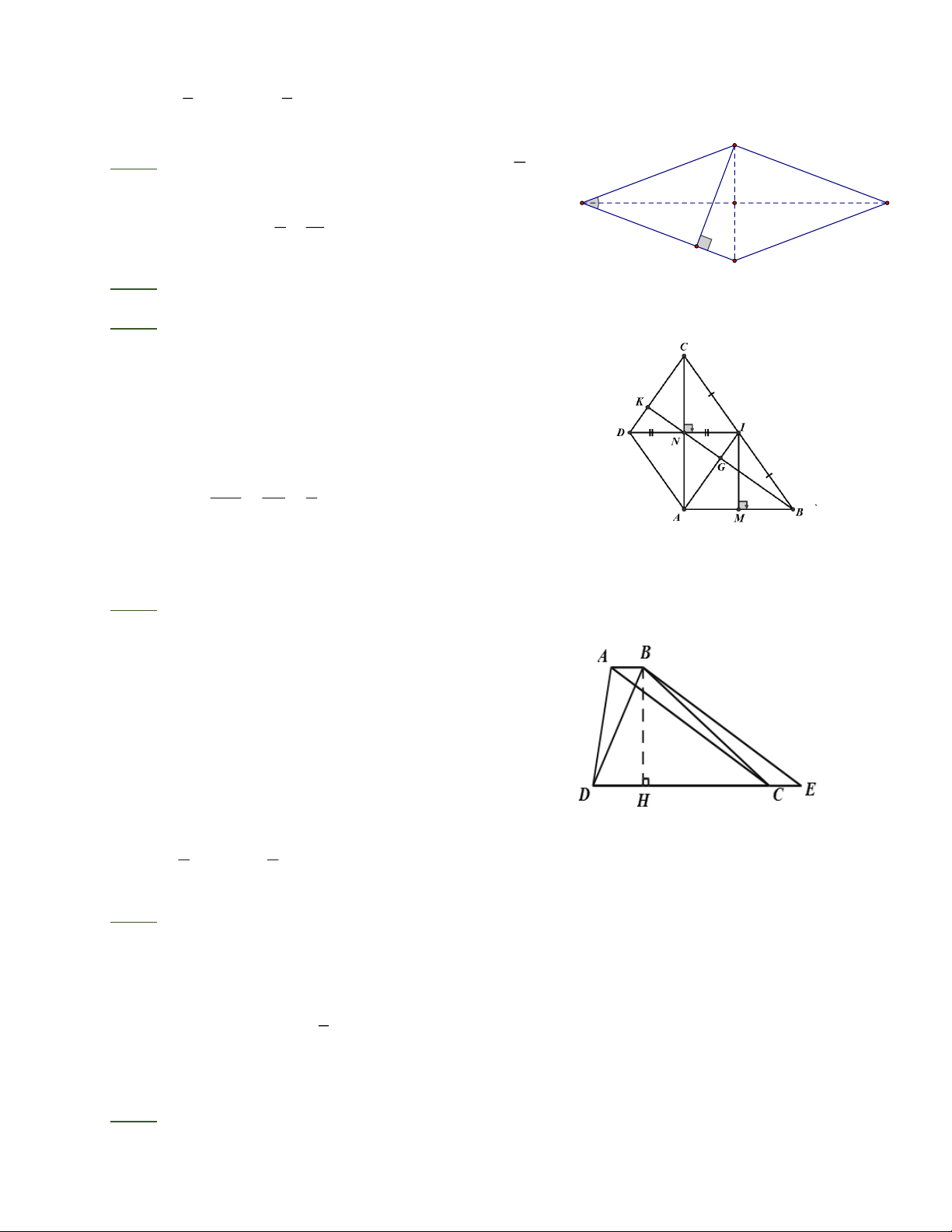
a) Chứng minh được ADCI là hình thoi.
b) Gọi AI  BN = G  G là trọng tâm ABC.
Ta chứng minh được DK = GI, lại có =  DK = GI = 1 DC AI . DC AI 3 c) S = 2S = S = 2 ADCI ACI ABC 96cm .
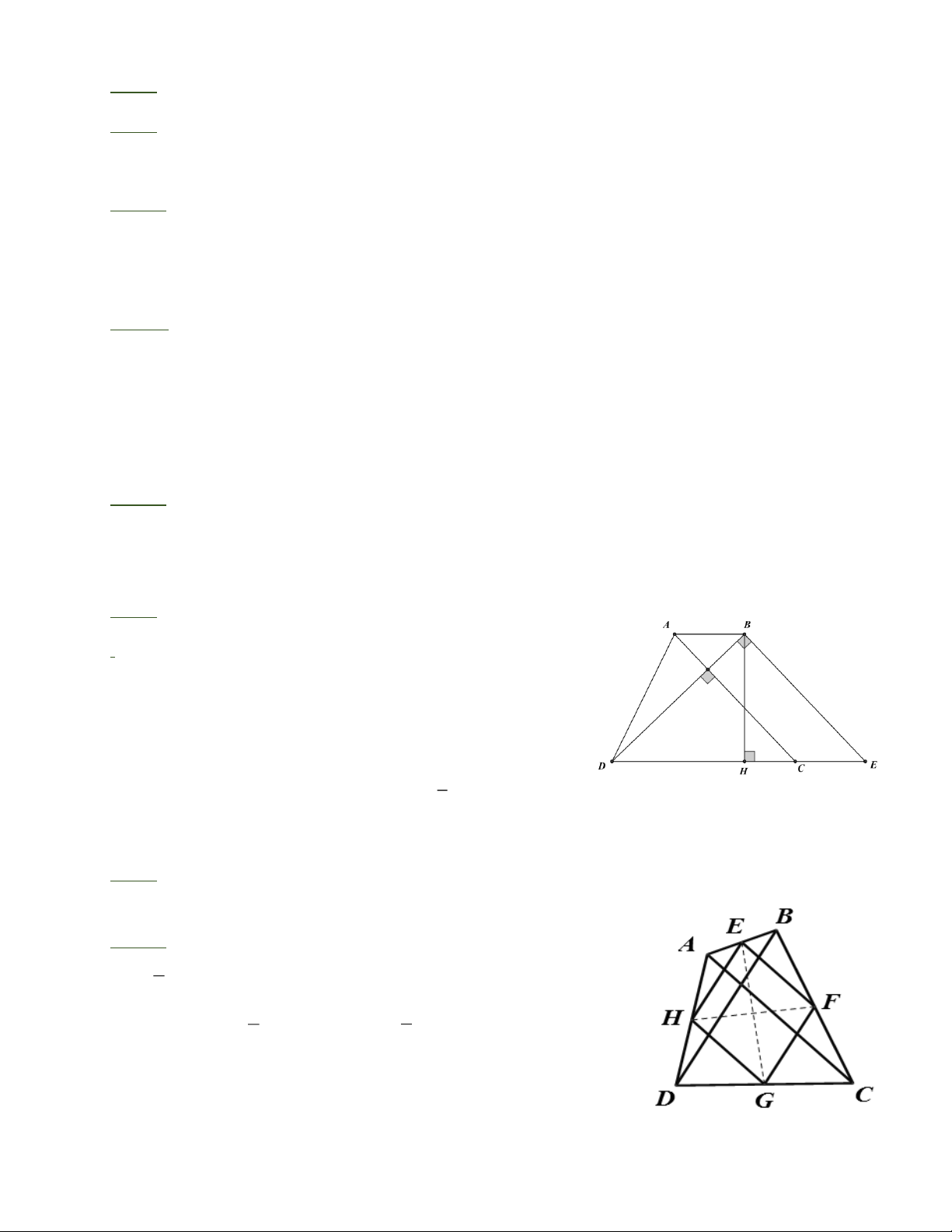
Bài 7: a) Kẻ BE//AC. Tứ giác ABEC là hình bình hành nên BE = AC = 15cm, CE = AB = 3 cm
suy ra DE = DC + CE = 14 + 3 =17 (cm) Tam giác BDE vuông vì có:
BD2 + BE2 = DE2 ( Vì 82 + 152 = 172)
Nên BD ⊥ BE . Ta lại có BE//AC nên
b) Hình thang ABCD có hai đường chéo vuông góc nên 1 1 2 S = AC. D B = .15.8 = 60(cm ) D ABC . 2 2
Bài 8: Gọi độ dài hai đường chéo là 2x và 2y , ta có 2x + 2y = 10 và 2 2 2 x + y = 4 . 2
Suy ra xy = (x + y ) ( 2 2 x + y ) 2 2 – = 5 - 16 = 9 1
Diện tích hình thoi bằng 2
.2x.2y = 2xy = 9(cm ) 2 Bài 9: Trang 3
Gọi độ dài hai đường chéo là 2x và 2y , ta có 2x2y = 48 Û xy = 12 và
2x + 2y = 14 Þ x + y = 7 Þ (x + y)2 2 2 2 2
= 49 = x + y + 2xy Û x + y = 49 - 24 = 25
Từ đó suy ra Cạnh hình thoi bằng 5. Trang 4