Bài Tập Hình Học 7 Định Lí Pitago Có Lời Giải

 ĐỊNH LÝ PITAGO
I. KIẾN THỨC CƠ BẢN
1. Định lý Py-ta-go:
Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông
D A B C vuông tại A 2 2 2
Þ BC = A B + A C . B
2. Định lý Py-ta-go đảo:
Nếu một tam giác có bình phương của một cạnh bằng tổng các bình
phương của hai cạnh kia thì tam giác đó là tam giác vuông. A C D A BC 2 2 2 · có 0
BC = A B + A C Þ BA C = 90 II. BÀI TẬP
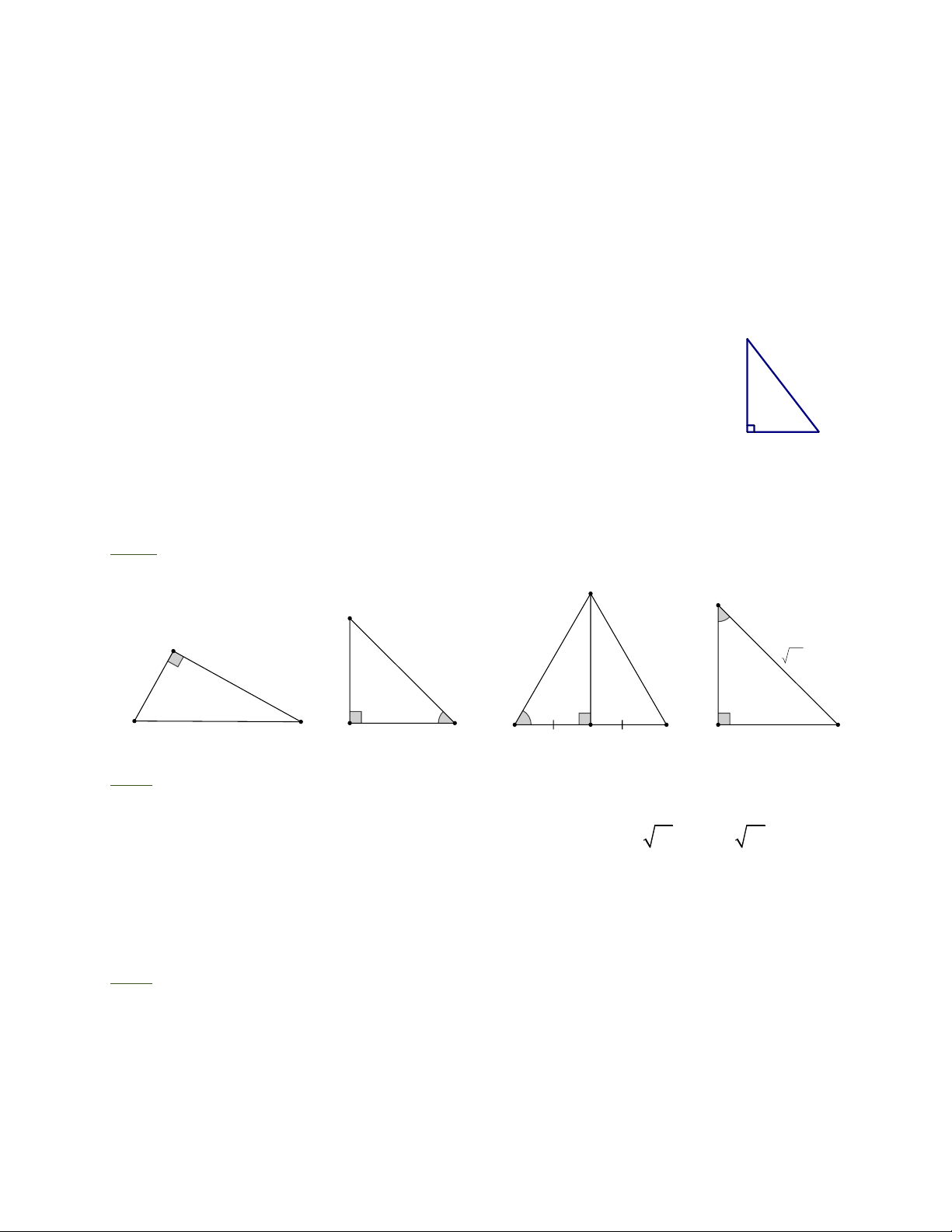
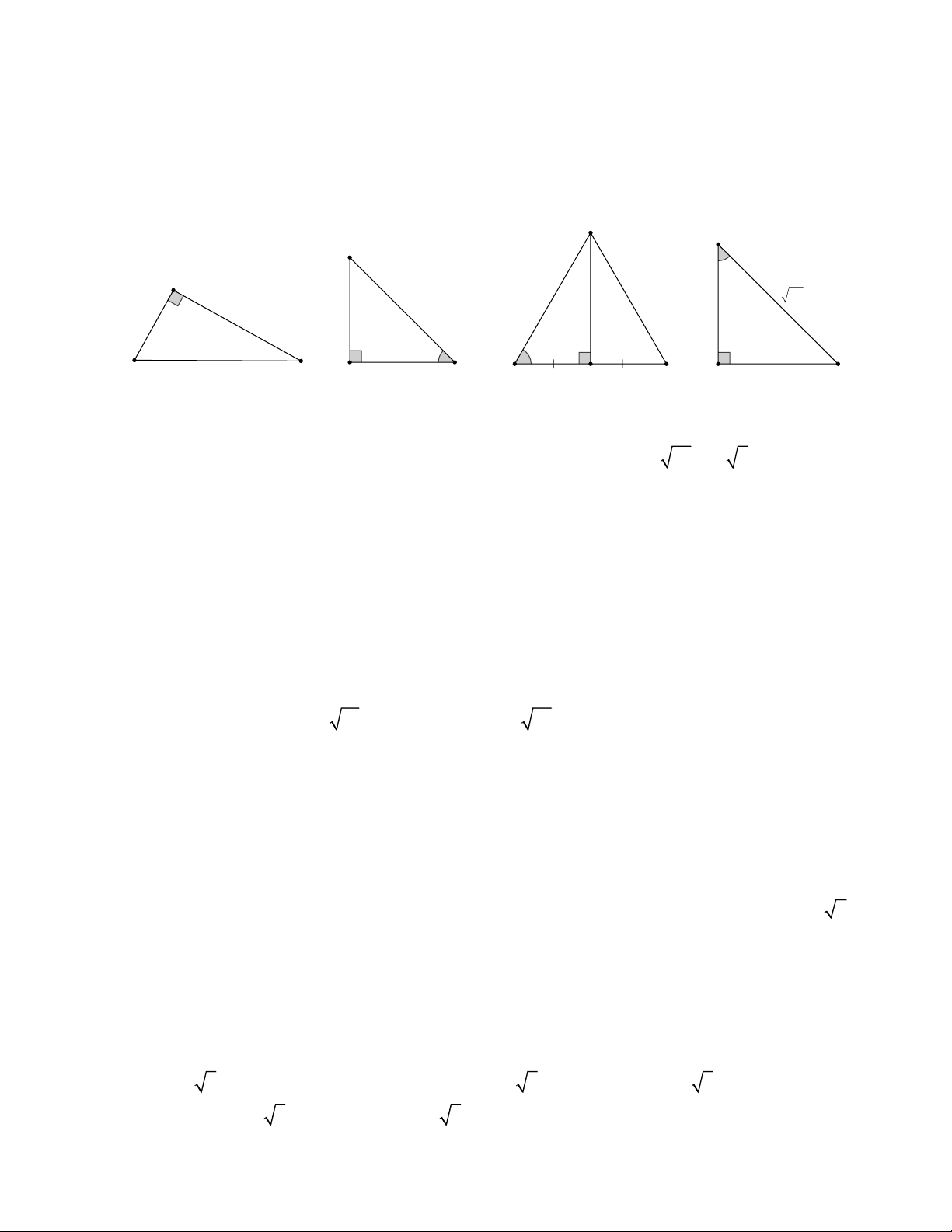
Bài 1: Tính độ dài đoạn thẳng trong các hình sau: G M E 45° A 4 4 32 3 12 9 45° C 60° B D F H K N P
Bài 2: Các tam giác cho dưới đây có phải là tam giác vuông không? Chứng minh.
Nếu tam giác là tam giác vuông hãy chỉ rõ vuông tại đỉnh nào?
a) A B = 25; BC = 7;CA = 24. b) DE = 2; EF = 11; FD = 15 c) GH = 5; HI = 6; IG = 7
d*) K L = 4a + 5 , LM = 9a + 12 , MK = 8a + 11 với a là độ dài cạnh huyền của tam giác
vuông cân có độ dài cạnh góc vuông là 1.
Bài 3: Cho tam giác ABC nhọn, cân tại .
A Kẻ BH vuông góc với AC tại H. Tính độ dài cạnh BC biết
a) HA = 7 cm, HC = 2 cm.
b) AB = 5 cm, HA = 4 cm. Trang 1
Bài 4: Cho D A B C có A B = 24, A C = 32, BC = 40 . Trên cạnh AC lấy điểm M sao
cho A M = 7 . Chứng minh rằng: a) D A B C vuông · µ b) A MB = 2C A B 8
Bài 5: D A B C vuông ở A có =
, BC = 51 . Tính A B, A C . A C 15
Bài 6: Cho D A B C vuông cân ở A; M là điểm tùy ý nằm giữa B và C. Vẽ đường cao AH của  ABC. BC a) Chứng minh A H = b*) Chứng minh 2 2 2
MB + MC = 2MA . 2
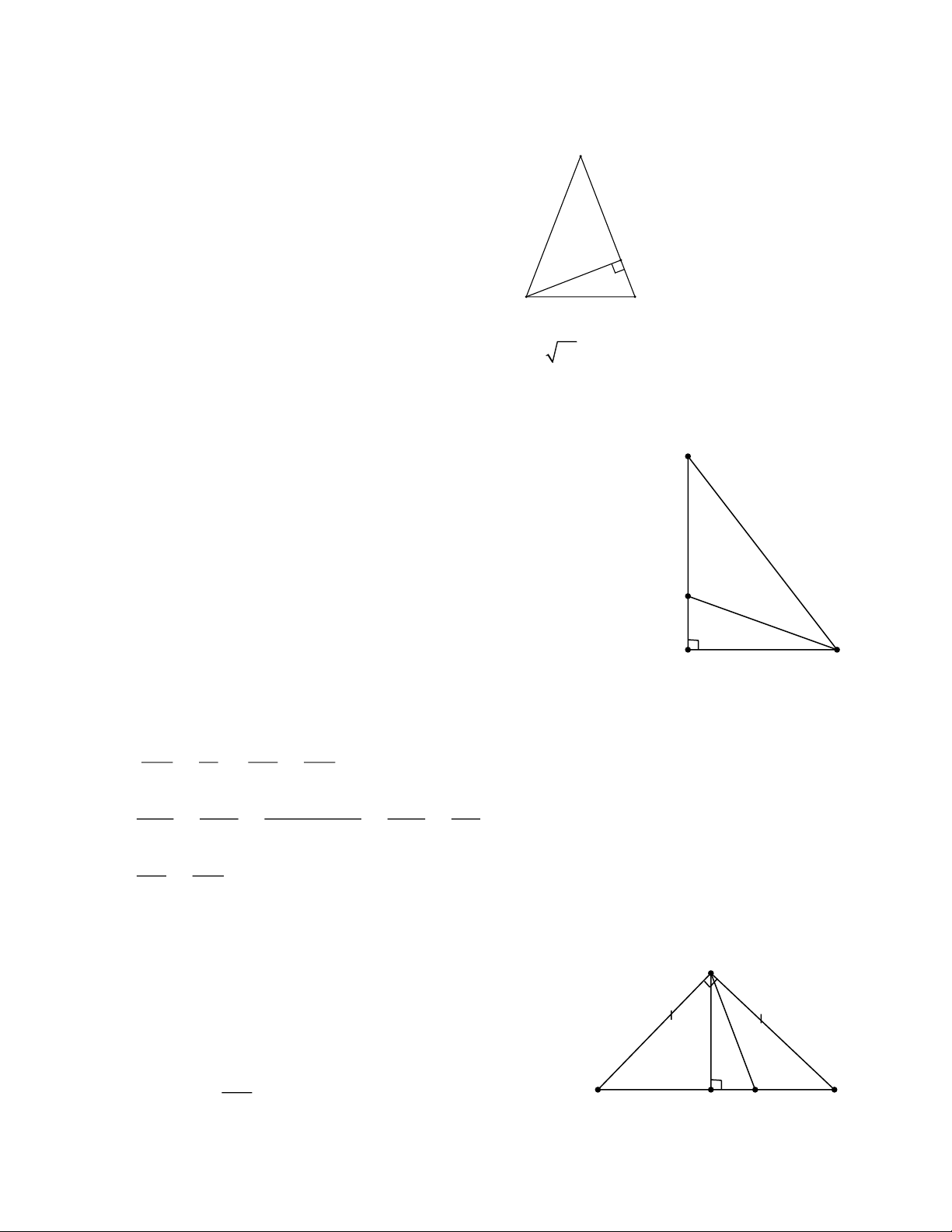
Bài 7: Cho hình vẽ bên, trong đó BC = 6cm , A D = 8cm . Chứng minh rằng AD vuông góc với BC. 3 A B 7 C D
Bài 8: a) D A B C có đường cao A H . Chứng minh : 2 2 2 2 2
A B + A C = BH + CH + 2A H .
b) Cho D A B C nhọn (AB > AC) có đường cao A H , E là điểm tùy ý trên A H Chứng minh: 2 2 2 2
A B – A C = EB – EC .
c) Cho D A B C có ba góc nhọn, A B = A C . Vẽ đường cao CH . Chứng minh 2 2 2 2 2 2
A B + BC + CA = BH + 2A H + 3CH . Hết Trang 2 HDG Bài 1: G M E 45° A 4 4 32 3 12 9 45° C 60° B D F H K N P a) 2 2 2
BC = A B + A C = 225 Þ BC = 15
b) D DEF cân tại D Þ DF = 3 . 2 2 2
EF = DE + DF = 18 Þ EF = 18 = 9 2
c) D HGK đều Þ GH = GK = HK = 4
d) D MNP cân tại N 2 2 2 2 2
MN + NP = MP Þ 2MN = 32 Þ MN = 16 Þ MN = 4 . Vậy MN = NP = 4 Bài 2: a) Có: 2 2 2 2 2 2
BC + CA = 7 + 24 = 49 + 576 = 625 = 25 = A B .
Vậy ABC vuông tại C (Định lý Pythagore đảo) 2 2 b) Có: 2 2 2 DE + EF = + ( ) = + = = ( ) 2 2 11 4 11 15 15 = FD .
Vậy DEF vuông tại E (Định lý Pythagore đảo) c) Ta có: 7  6  5 . Mà 2 2 2 2 2 2
GH + HI = 5 + 6 = 25 + 36 = 61 > 49 = 7 = IG .
Vậy GHI không phải là tam giác vuông.
d) KL = 4a + 5 , LM = 9a +12 , MK = 8a +11 .
a là độ dài cạnh huyền của tam giác vuông cân có độ dài cạnh góc vuông là 1 nên a = 2
KL < MK < LM Có:
KL + MK = ( a + )2 + ( a + )2 2 2 2 2 2 4 5 8
11 = 16a + 40a + 25 + 64a + 176a + 121 = 80a + 216a + 146 LM = ( a + )2 2 2 9
12 = 81a + 216a + 144 . Thay a = 2 . Ta được: 2 2
KL + MK = 80.2 + 216. 2 + 146 = 306 + 216 2 ; 2
LM = 81.2 + 216. 2 + 144 = 306 + 216 2 Trang 3 Vậy 2 2 2
KL + MK = LM nên KLM vuông tại K (Định lý Pythagore đảo) . Bài 3: A
a) AB = AC = HB + HC = 9 cm.
Dùng định lý Py-ta-go ta có 2 2 2
BC = BH + HC H 2 2 2
= AB − AH + HC Từ đó BC = 6 cm. B C
b) Làm tương tự câu a, tính được C H = c 1 m  BC = 10 cm. Bài 4: a) Có: 2 2 2 2 2 2
A B + A C = 24 + 32 = 576 + 1024 = 1600 = 40 = BC .
Vậy ABC vuông tại A (Định lý Pythagore đảo) C
b) Áp dụng định lý Pythagore cho ABM vuông tại A có: 2 2 2 2 2
BM = A B + A M = 24 + 7 = 576 + 49 = 625  MB = 25
Có A M + MC = A C nên MC = A C - A M = 32 - 7 = 25 .
MBC có MB = MC = 25 nên MBC cân tại M . · ˆ
Þ C = MBC (t/c tam giác cân) (1) M · · Lại có: ˆ
A MB = C + MBC (tính chất góc ngoài tam giác) (2) · µ
Từ (1) và (2) suy ra A MB = 2C . A B
Bài 5: Áp dụng định lý Pythagore cho ABC vuông tại A có: 2 2 2
BC = AB + AC A B 8 A B A C Có = Þ = A C 15 8 15 2 2 2 2 2 2 A B A C A B + A C BC 51 Þ = = = = = 9 64 225 64 + 225 289 289 A B A C Þ = = 3 | 8 15
Vậy A B = 24 ; A C = 45 . · ·
Bài 6: a) D A B C vuông cân nên A BC = A CB = 45° . A · ·
Chỉ ra HA B = HA C = 45° ,
D A HB vuông cân tại H nên A H = HB
D A HC vuông cân tại H nên A H = HC BC HB = HC = B C 2 H M Trang 4 BC Þ A H = 2
b) Có MB = MH + HB ; MC = HC – MH . 2 2 2 2
MB + MC = (MH + HB ) + (HC – HM ) 2 2 2 2
= MH + 2MH .HB + HB + HC - 2HC .HM + HM
Vì HA = HB = HC nên 2 2 2 2
MB + MC = MH + HA = ( 2 2 MH + HA ) 2 2 2 2 = 2MA
(Áp dụng ĐL Pythagore cho D HA M vuông tại H ). Vậy 2 2 2
MB + MC = 2MA Bài 7:
Qua B kẻ đường thẳng song song với AD, cắt CD ở E. 3
Ta chứng minh được DE = A B = 3 , BE = A D = 8 B A
Tam giác BCE có BC = 6, BE = 8, CE = 10 8 nên ta chứng minh được D 90O CB =
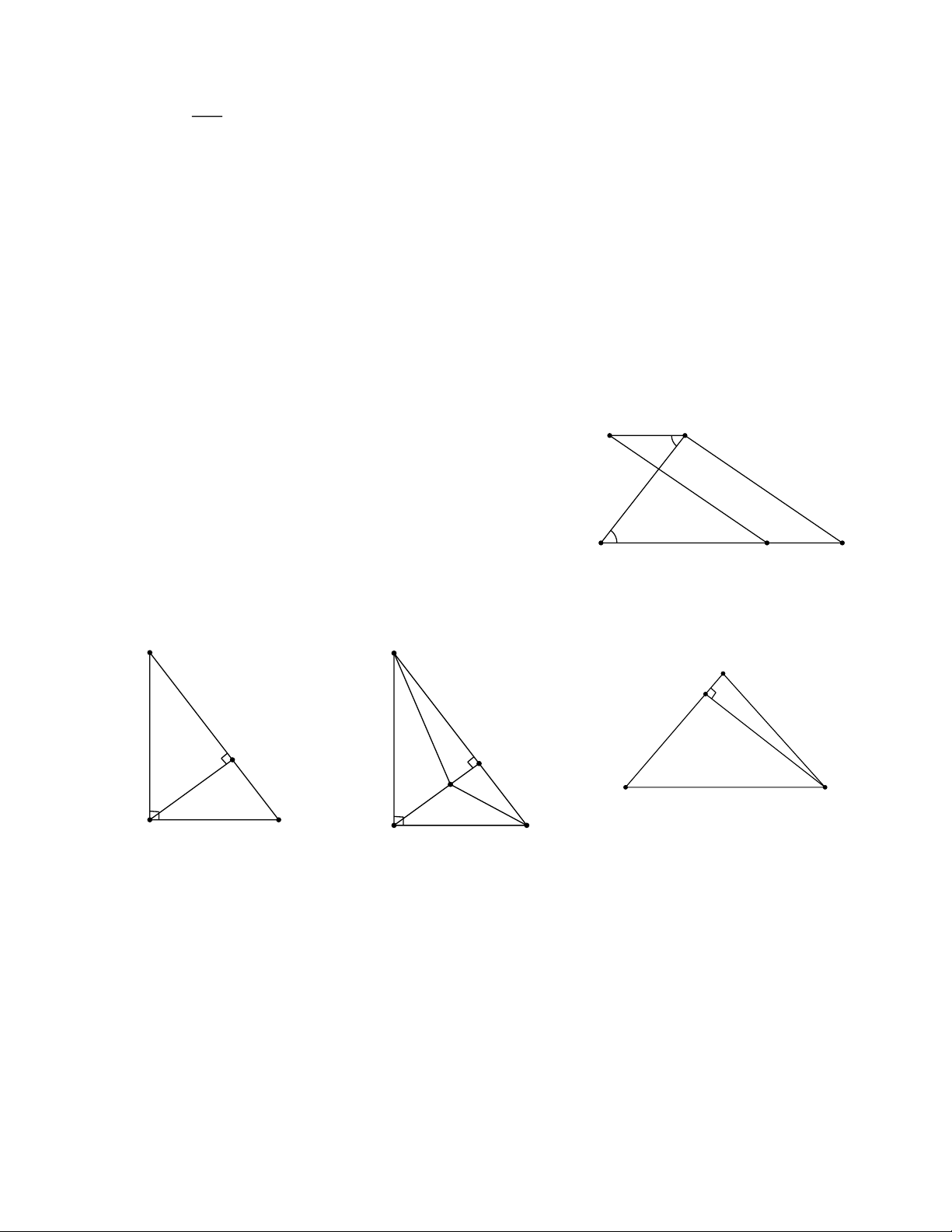
A D / / BE üïï E ý Þ BC ^ A D C 7 D 3 BC ^ BE ïïþ Bài 8: C C A H H H B C E A B A B
a) Áp dụng định lý Pythagore cho D HA B và D HA C vuông tại H có: 2 2 2
A B = HA + HB ; 2 2 2
A C = HA + HC Vậy 2 2 2 2 2 2 2 2 2
A B + A C = HA + HB + HA + HC = BH + CH + 2A H .
b) Áp dụng định lý Pythagore cho D HA B ; D HEB ; và D HEC vuông tại H có: 2 2 2
A B = HA + HB ; 2 2 2
A C = HA + HC ; 2 2 2
EB = HE + HB ; 2 2 2
EC = HE + HC Vậy 2 2 2 2
A B - A C = HA + HB - ( 2 2 HA + HC ) 2 2 = BH - CH . 2 2 2 2
EB - EC = HE + HB - ( 2 2 HE + HC ) 2 2 = BH - CH Vậy 2 2 2 2
A B – A C = EB – EC . Trang 5 C H
c) Áp dụng định lý Pythagore cho D HB C ; D HA C vuông tại H có: E 2 2 2
BC = HB + HC ; A B 2 2 2
A C = HA + HC Mà 2 2
A B = A C Þ A B = A C Nên : 2 2 2 2 2
A B + BC + CA = BC + 2A C 2 2 = HB + HC + ( 2 2 HA + HC ) 2 2 2 2
= BH + 2A H + 3CH . Trang 6