Bài Tập Hình Học 7 Hai Đường Thẳng Song Song Có Lời Giải

. HAI ĐƯỜNG THẲNG SONG SONG
I. KIẾN THỨC CƠ BẢN
1. Định nghĩa :
Hai đường thẳng song song (trong mặt phẳng ) là hai đường thẳng không có điểm chung .
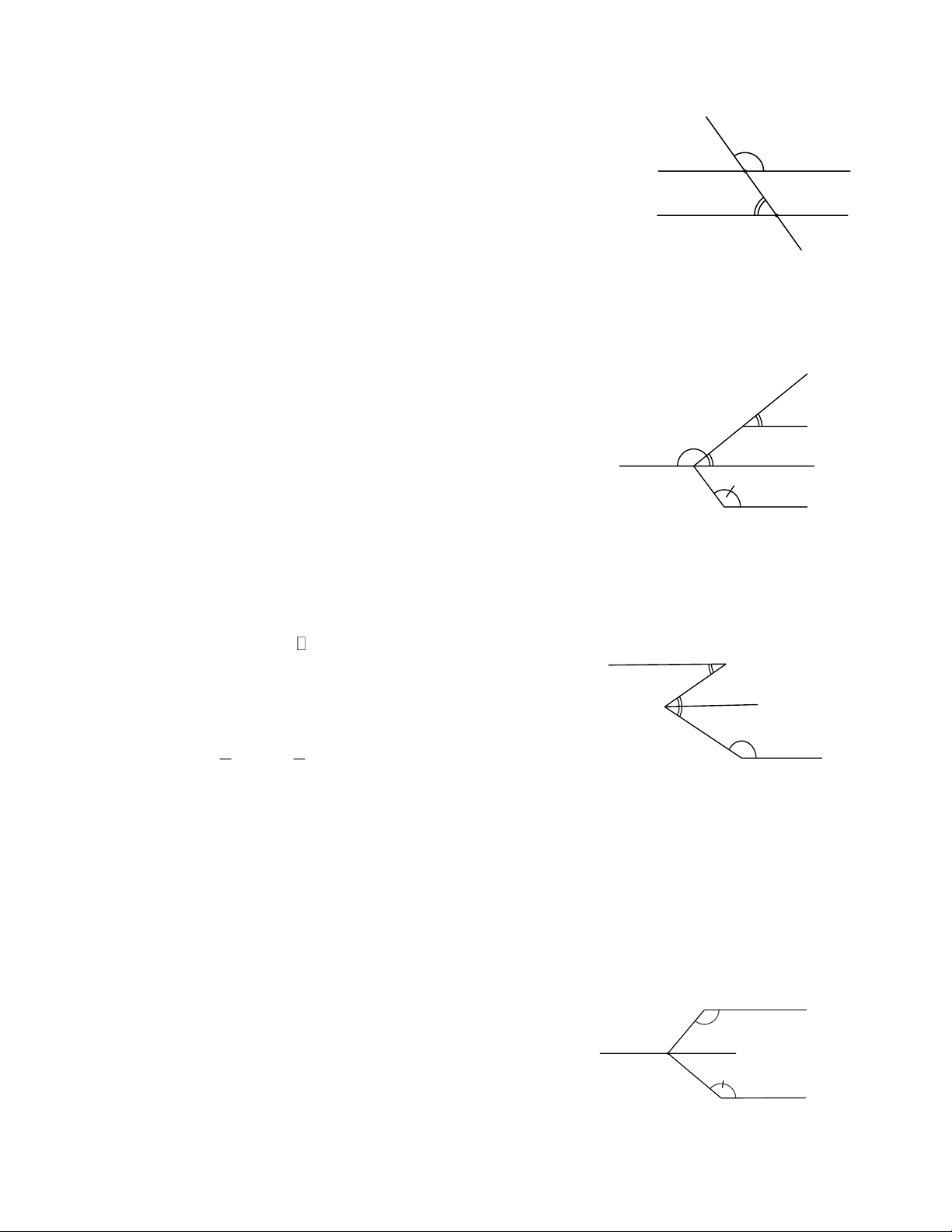
2. Dấu hiệu nhận biết hai đường thẳng song song:
Nếu đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le
trong bằng nhau (hoặc một cặp góc đồng vị bằng nhau) thì a và
b song song với nhau. c a A 3  µ µ
A1 = B 1 Þ a/ / b 1 2 µ µ  A b B 1
3 = B 1 Þ a/ / b µ µ  A o
2 + B 1 = 180 Þ a/ / b
 Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song. II. BÀI TẬP Bài 1: Bài 2:
Cho hình vẽ bên biết cAa' =  120 , ABb = 
60 . Tìm trên hình vẽ bên các cặp đường thẳng song song.
Hai đường thẳng aa’ và bb’ có song c a A a' b b' B c'
Bài 3: Cho hình vẽ bên biết yAt = 
40 , Bài 4: Cho hình vẽ bên biết OAx =  30 , xOy =  140 và OBz =  130 . OBy = 
150 và Ot là tia phân giác của
Chứng minh At // Bz. AOB = 
60 . Chứng minh ba đường thẳng y
Ax, By và Ot đôi một song song x A A t t O x O B z B y Trang 1 B x
Bài 5: Cho Bx // Ny // Oz, OBx =  130 và z O ONy = 14  0 . Tính BON. N y µ µ
Bài 6: Cho DEF có D = 60 ;
° E = 60° . Trên tia đối của tia DE lấy điểm G . Vẽ góc EGy so le · ·
trong với góc DEF và EGy = 60°. Vẽ Dx là tia phân giác của GDF . Chứng minh: a) Gy // Dx b) Dx // EF
Bài 7: Cho xOy = 
50 . Lấy điểm A trên tia Ox. Trên cùng nửa mặt phẳng bờ Ox chứa tia Oy vẽ
tia At sao cho At cắt Oy tại B và OAt = 
80 . Gọi At ' là tia phân giác của góc xAt. .
a) Chứng minh At ' // Oy;
b) Trên nửa mặt phẳng không chứa điểm A bờ là đường thẳng Oy vẽ tia Bn sao cho OBn =  50 . Chứng minh Bn // . Ox Trang 2 HDG c
Bài 1: Ta có: cAa + a AB = 0 ' ' 180 (hai góc kề bù) a A a'  a AB = 0 − cAa = 0 − 0 = 0 ' 180 ' 180 120 60  b b' a AB = ABb = 0 '
60 (hai góc so le trong bằng nhau) B  a // . b c'
Bài 2: a) a//b : xét cặp góc trong cùng phía.
b) b//c : xét cặp góc đồng vị.
c) a//c : xét cặp góc trong cùng phía. (hoặc y
Bài 3: Kẻ tia đối Ox’ của Ox  yOx = 0 ' 40 A
 yOx' = yAt (hai góc đồng vị bằng nhau)  Ox' // At ( ) 1 t
Mặt khác: OA ⊥ OB  AOB = 0 90 x O x'
 x OB = yOB − yOx = 0 − 0 = 0 ' ' 90 40 50 B z
 x OB + OBz = 0 + 0 = 0 ' 50 130
180 (hai góc trong cùng phía bù nhau) Ox' // . Bz (2) Từ ( )
1 và (2)suy ra At Bz . x A Bài 4: t
Vì Ot là phân giác AOB nên O
AOt = BOt = 1 AOB = 1  0 60 = 0 30 2 2 B y
 xAO = AOt (hai góc so le trong bằng nhau)  Ax // Ot ( ) 1
Lại có : tOA + OBy = 0 + 0 = 0 30 150
180 (hai góc trong cùng phía bù nhau)
 Ot // By (2) Từ ( )
1 và (2)ta có Ax // By // Ot. Bài 5:
Kẻ Oz ' là tia đối của tia Oz . B x · · 0
Bx / / Oz Þ xBO + BOz ' = 180 · 0 Þ BOz ' = 50 . z O z' · · 0
Oz / / Ny Þ z 'ON + ONy = 180 · 0 Þ z 'ON = 40 N y · 0 0 0
Þ BON = 50 + 40 = 90 . Bài 6: ¶ ·
a) Ta có D + FDG = 180° (2 góc kề bù) E 1 · ·
Þ 60° + FDG = 180° Þ FDG = 120° ·
Vì Dx là tia phân giác của FDG nên ¶ ¶ 1 · y D = D = FDG = 60° 1 2 3 2 D 2 F 3 · ¶
Ta có : DGy = D = 60° 3 G x
Mà hai góc nằm ở vị trí so le trong nên HG // Dx · ¶
DEF = D = 60° mà hai góc nằm ở vị trí so le trong nên 3 EF //Dx y t t' n B Bài 7: a) OAt = 0  xAt = 0 80 100 .
A t ' là tia phân giác của góc xA t O x A  xAt = 0 ' 50
Do đó xOy = xAt ' mà hai góc ở vị trí đồng vị  Oy // At '. b) xOy = OBn = 0 50  Ox // B . n