-
Thông tin
-
Quiz
Bài tập kèm đáp án Nhiệt học - Vật lý đại cương 1 | Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội
Bài tập kèm đáp án Nhiệt học - Vật lý đại cương 1 | Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Vật lý đại cương 1 (ĐHCN) 31 tài liệu
Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội 537 tài liệu
Bài tập kèm đáp án Nhiệt học - Vật lý đại cương 1 | Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội
Bài tập kèm đáp án Nhiệt học - Vật lý đại cương 1 | Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Môn: Vật lý đại cương 1 (ĐHCN) 31 tài liệu
Trường: Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội 537 tài liệu
Thông tin:
Tác giả:
Preview text:
!"#
$ %&'!()*+ !"#&
'
,-./012322245/6/% 789:
; !"&879:8<=>?
$ @/0!(A798%
; !"&87978<?
*B=!C/%"$0
!"#&
$ *.!(&D6!#$E<
!"#&.
; !"&879:8BB?
$ @/0!(A98%
; !"&898>?F68<=B,G
!C/%"$0=H,;-I6$0/
" -J % ) # K L /% $0 $E
=>M,% !"N!O0-J!'6/
,-./012322245/6/%%&/-)4D6
789:=789:= p p p − p 1 2 1 2 = = m m m − m 1 2 1 2
?&-J!'6A p ∆m = m − m = 1 2 − m = k 5 , 7 g 1 2 p 1 1
H% P . !( = &
-J/Q#$EM90 !"#& .
/-). 789: FG
P.789: p= ρ :9 (2) R6FG9FG m m T = = + = 2 T1 (t1 27 ) 3 1400K V ρ ρV >
S6 !"%=P.!(=
&0A
&/-)'
$ ; !"&'
?&-J/Q&/-)'
3 ?&-J/Q&'
/-)'A V = p µ / RT ≈ 2,4 1 1
$ ; !"'A8797 ≈H?
?&-J/Q#/-)'A m1 3 ρ = = 4 1 , 4kg / m 1 V1
3 ?&-J/Q#'A m1 3 ρ = = k 1 g / m 1 V2 M
1" $0T " U H%4D 0 #
!' " & -J % / + $0 4D !" L
S&)%
,-./012322245/6/% m p V = 1 RT µ T − T ∆ → p = p ≈ 19at m / 2 2 1 p V = R − ∆ 2 (T T ) 2T µ H
1"V;-I$.4D%V6!/N
3-)H>*;WX6$.!-J>0$%
X0$.S%Y
?&-JV$. µPV m = RT
IV$. m p µ V t = = ∆m ∆mRT
6
H>*8=>,=
8HZ8<?= 3 V = 300m =
:8B=[9%?=8=∆8>;\!-J ≈ << B
%3]*P4)!4N!-J !"
%4D**+-J!4N!'T ,^T
CaCO + H SO → CaSO + CO + H O 3 2 4 4 2 2
P&% CO /$E&%# CaCO ^T?& 2 3
-J# CaCO ^TA 3 pV m = n .M = n .100 = 100 CaCO CaCO CO 3 3 2 RT
6&8*8 ,133 1 . 05 Pa = −3 3 V = 3 , 1 . 2 10 m m ≈ 7 1 , g 8 <
$0V !-J&4) $E " & %= T _
"$0T$E>,=$0TD
M, 1` D ! $0N %% !"
N!O?!'X$E=$0D>,0
#$0VT=$#$0TD>
O&%/-)4DN!OF4D !"aN !OGQA p V p V p + 1 1 2 2 (V V 1 2 ) + = RT RT RT
7\6=#$0VT p − p 1 3 → V = V = d 5 m 2 1 p − p 2
$0TTN4)$E"&
#6#$0TD=#$0T
D Rb !V!= $0V -JD 4D
P!`D!$0N%%
!"4cN6!O # /%$0
N
-.C$D\<=A p V p V p + 1 1 2 2 (V V 1 2 ) + = RT RT RT p V + p V → p 1 1 2 2 = = , 1 6at V + V 1 2
1" & #6 3 !d= " !V " !V Rb !V
-Ib!V4D%"\-)%%-)/%4D%D
&$E=d%KL#&$EP!-I
/b&Q"!%LF0G*+T-) /%&3X
Q$%Q=$/E !"SeN!O4D
e6DHM*
fg!"%"-)/%&DS
/%&XQ p = (p − x o )(cmH O 2 )
hi\j..1/N%&$i p l = ( p l + 4 − x) = (p − ) x (l + 4− ) x o o S
6&A p = 760mmHg = 103 cm 3 H O = l = 20cm o 2 x 2 -105 x 7 + 4132 = 0 → x = 9 , 3 c 5 m kF x = 105 c 3 m lZ%LG
/%&%4a$"N=3%!
!d $0-ILmDH>*
0&-J/Q#N/%&
$Q/%%4a$ p'= p − p = 1 m 0 mHg = 1360Pa o
?&-J/Q# ( µ p − p 29 1 . 360 o ) 3 ρ = = ≈17g / m RT , 8 31.273 o
B NS6 W J 4) $% FG n !i &
-J#N%WJ!
?&-J#%WJ m µ = ( + + g / mo ) m m l 1 2 = (kg/ kmo) 8 22 l = = 4 k 0 g/ kmol n m m 1 2 8/ 32 +22/ 44 + µ µ 1 2
1"WJ=B;.4D=oS6 !"H%4D
>;90#WJ!
WJ
m m 1 2 2800 3200 + RT + . 3 , 8 1 ( . 273+ 1 ) 7 nRT µ µ 1 2 28 32 3 V = = = ≈ , 1 2m 5 p p . 4 10
> ? O D " W J p " V & -J 6!N 4D V
& -J oS6 *'6 S !i & -J /Q # O ! !d
-I
2%$D=&-J%#O m + m 1+ m / m m / m 8 2 1 = 1 + 8 1 2 2 1 µ = = = = 12g / mol m1 m2 1 m 2 / m 1 1/ 2 + 8 / 32 + + µ µ µ µ 1 2 1 2
?&-J/Q#WJ 5 p µ 1 . 2 0 , 1 . 1 10 o 3 ρ = = ≈ 534g / m RT 3 , 8 . 1 273 o
B M %S6 !-J q !" >% ! M% 0
-JD\!-J4D!"$Q"r#&/%
eb/0
h(k$h( A
@/0!( m m 5 160 5 Q ∆ = U ∆ = C T ∆ = R T ∆ = . .8 3 . 1 − ≈ ≈ V (.60 50) 1040J 25 c 0 al µ µ 2 32 2
$ @/0!(
h"$Q"r m U ∆ = C ∆ = V T 25 c 0 al µ
; -J\4D% m m Q ∆ = U ∆ + A = C ∆T + p∆V = + ∆ = ∆ V (C R V ) m 7 T R T µ µ µ 2 6& ∆@ 160 7 = . .8 3 . 1 ( . 60− 50)≈ 145 J 4 ≈ 350cal 32 2
B 0 3/QFG!(#"!6Qs=
$/E&-J/Q#!!d tD8H=<> 9
7)!6Qs= 3/Q%!(C = R 3 (J / molK) V
!d Qt m ρRTo p V = RT → µ = o o o µ po
; 3/Q!( CV po CV p 3 c o = = = ≈ 1400J / kgK V µ R ρ T T ρ
B 0 3/QFG!(#"=$/E&
-J#"N%!D89%* &,%SNFm&
!%L G8= A
; 3/Q%!(A C = C + R p V 7) Cp γR γ = 8l C = C p γ −1 V
; 3/Q!(A C γR , 1 . 4 3 , 8 1 c p p = = µ µ(γ − ) = = 1 30 1 . 0 −3 ( . , 1 4 − ) 969 5 , J /kgK 1
B 1"$0T;.4D !"HP
.=/%$0Q)>*+A
; !"#.Y
$ #$0Y
h"r"r#Y
@/0!(= !"&.D p 1 p 2 p = → T 2 = = 2 T1 1500K T1 T 2 p1
$0 mRT V 1 = = 12 7 , l 2 µp1
h"r"r#&A m ∆U = C (T −T ) m 5 p = R 2 − 1 T = 12 4 , 6kJ V 2 1 µ µ 2 p 1 1
F N D-u6Qs8>= C = R 5 / 2 G 2 V
B> ;U!(N0 +/$/E
&_$E9$!V
;6Q v T # !" C g= -J D & \ !-J ∆ Q = A' ∆ + U
@/0!( Q∆w8nC ∆T = V
; -JD&\!-J V V 2 2 dV V ∆ Q= A'= pdV = pV = p1V ln 2 V V 1 1 V 1 V1 4 −3 1 Q ∆ = 8 , 9 1 1 . 0 . 1 . 3 0 ln ≈ 6 − 76 J 10
xyzm//Ee/0CC+
BM 1"$0=!C. !"%P.
= / $0 Q ) * 0 -J D &
!'\!-J=$$0'U
j0'U=#$0N!O=e/0D!( {8
;6Qv| !"Cg m iR ∆ Q = A + ∆ U = ∆ U = (T T 2 − 1 ) µ 2 i m m i m ∆Q = RT − RT = p V RT 2 1 − 2 1 2 µ µ 2 µ
F N D-u6Qs8>= C = G V R 5 / 2 2
6&8*8=M ,=78=8B? Q ∆ =4 k 1 , J
BH *. M oS6/% " $0 ' U !"
H=q>;9Q)> ;90A
; !"#&.k
$ ; -J!'%&
j0='U=e/0!(= !"&.
D p1 p 2 p2 3 1 . 05 = → T = T = + = 2 1 (273 37) 930K T T p 10 5 1 2 1
$ ; -J !' % $E -J D \
!-J/%e/0!(/Q
m ∆Q = ∆U = C R − = − V (T T 2 1 ) m i p RT 2 1 µ µ 2 1 p 1 16 5 5 Q ∆ = . 3 , 8 . 1 (273 + 37) 3 1 . 0 −1 ≈ ,64kJ 32 2 105
BB P \ !-J -J @8>= !" # 8=
S r q 8M%)8%*+e/0 .!!-J
D/%!d D%Y
; -JD\!-J m µQ Q = C ∆T → C = x x µ ( m t − t 2 1) 3 . 2 150.4 1 , 8 C = = 2 , 0 7 J 7 / molK x 4 , 0 . 3 (40 −16)
; 3/Q%!(#SA iR 5. 3 , 8 1 C = = = 20 7 , J 7 / molK = C V x 2 2
;-4\6C = C =e/0D!( x V
B< M=> 6!/N !" H%= \ -J ' !N= /%
!d N!O
ND/
$ h"$Q"r#&
; -J!'%&
N/ A = ( p V − V = − = 2 1) p(2V1 1) m V RT1 µ , 6 5 A = . 3 , 8 1 ( . 273 + 27) ≈ 1 , 8 1 . 03 J 2
$ h"$Q"r#&A m ∆U = C − = − = 2 − = V(T2 T1) i m m i RT2 RT1 ( pV1 pV1) i m RT1 µ 2 µ µ 2 2 µ 5 , 6 5 U ∆ = . 3 , 8 . 1 ( . 273 + 27) 3 ≈ 2 , 0 2.10 J 2 2
; -J!'%&S$E -J
D\!-J2%6Qv| ∆Q = A+ ∆ U = . 1 , 8 103 + 2 , 0 2 1 . 03 = 28 3 , 1 . 03 J
Fh&4)6Qs6!/NF-u6QsG&$\C3%6Qs 8>G
B %S6%=>,P.!(=
r!0A
; -JD&\!-J
$ ;"r#&/-)4D.
2%6Qv|= -JD &\ !-J/% eb
/0!( m + + Q = A + U ∆ = C − = − = − p (T T 2 1 ) i 2 m m i 2 m RT RT pV RT µ 2 2 1 µ µ 2 2 1 µ 5+ 2 5 − 3 10 Q = . 3 10 1 . 0 1 . 0 − . 3 , 8 1 ( . 273 +10) ≈ , 7 9 1 . 0 3J 2 32
$ ;"r#&/-). m m i U = = 1 CV T1 RT µ µ 2 1 10 5 U = . . 3 , 8 1 + ≈ 1 (.273 1 ) 0 8 , 1 1 . 03 J 32 2
;"r#&. m m i i U = C T = RT = pV 2 V 2 µ µ 2 2 2 2 5 U = 3 . .10 5 1 . 0 1 . 0 −3 = 5 , 7 1 . 0 3J 2 2
Fh&4)6Qs%S6F-u6QsG&$\C3%6Qs8>G
B 1" #6 N 6 !" /% -) I N U /% $0
T##6N]/N3%/j/E
# $0 T D >= # N U q
^)
?]/DN/-I-)/)4D !"%-
N !O x% ! e /0 ' # #6 N /% -) % D e
/0!( FV!bD\iG
N3%/A p A = p V ln 1 = 1 9 . 81 , 10 . 4 .5 10 . − 3 ln100≈ 2 26 , 10 . 3 J 1 1 p 2
B % $%!-J . !(% ! !" r
Q>%0
h"$Q"r#&
$ N3%'/
; -J/6d%
h"$Q"r#& m iR 3 6. , 8 31 U ∆ = T ∆ = 2.10 .50 ≈ 2500kJ µ 2 2
FD!6QsFSDGQ&$\C3%#X sDMG
$ N3%'/ A = p(V − ) m V = ( R T − T ) 2 1 2 1 µ A = 2.10 . 3 3 , 8 1.50 ≈ 830kJ
; -J/6d%$E -JD\!-J Q = U ∆ + A = 2500 +830 =3330kJ
B H$%!-J.%) !"rQ%
/%!d 'C3%0N3%/4D!"$QQ
"r#
f'C3%}D!(F'/%e6=$E
e6G
N3%/' A = p( m m m V − V = RT − RT = R T − T 2 1 ) 2 1 ( 2 1 ) µ µ µ 7 A = . 3 , 8 1 1 . 0 ≈ 1 , 3 2J 44
h"$Q"r#& m iR 7 6. 3 , 8 1 U ∆ = T ∆ = . .10 ≈ 3 , 9 7J µ 2 44 2
FD!6QsFSDGQ&$\C3%#XsD MG
B %S6 4D !" % !-J . !( 4D
')0A
; -J%&
$ h"$QQ"r#&
N3%/'
; -J%$E -JD\4D% m i + 2 m m i + 2 m Q = A + ∆ U = C (T − T ) = RT − RT = pV RT p 2 1 2 1 − 2 1 µ 2 µ µ 2 µ 5 + 2 4 3 − 10 Q = 3. 8 , 9 1 1 . 0 1 . 0 1 . 0 − . 3 , 8 1 ( . 273 +1 ) 0 = 8 , 7 1 . 03 J 2 32
$ h"$Q"r m m C V i U ∆ = C − = − = = V (T2 T1) Cp (T2 T ) Q 5 , 5 .10 3 1 J µ µ C i + 2 p
N3%/'
A = Q − ∆U 2 3 , .103 = J
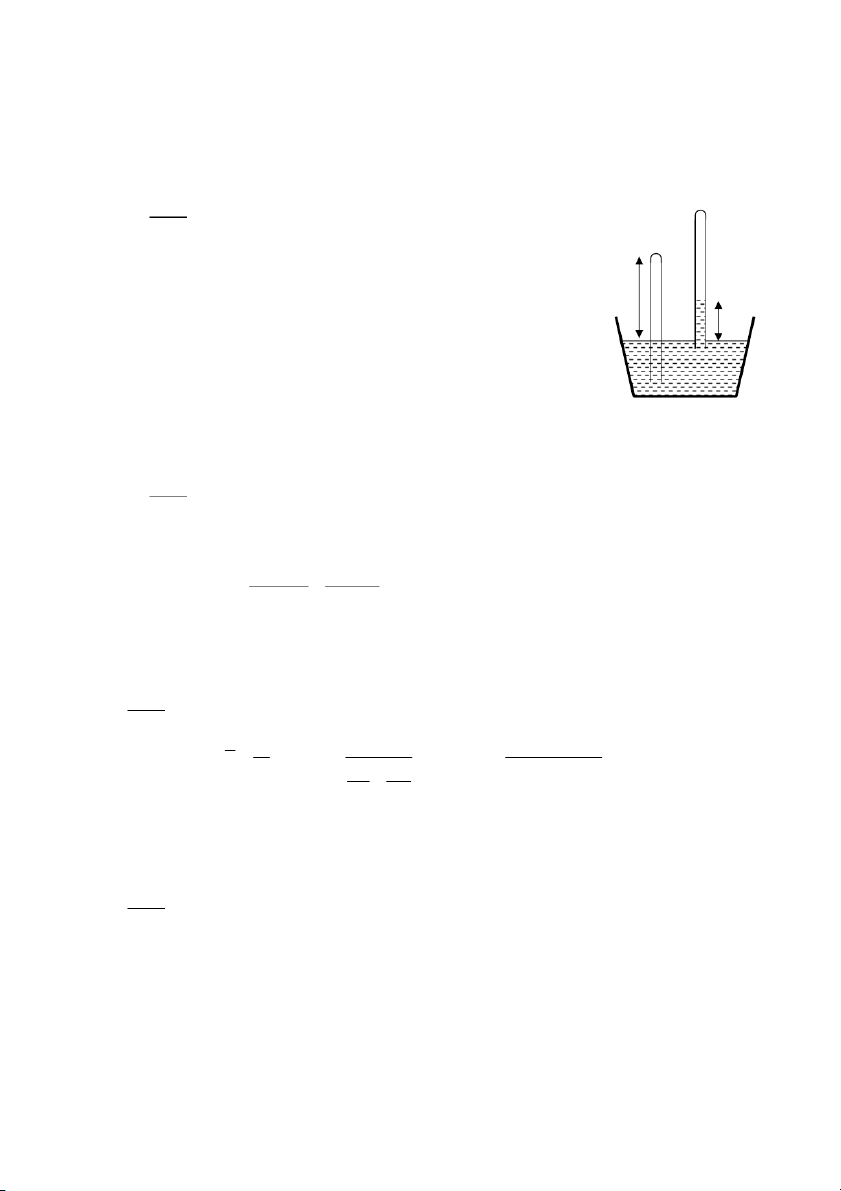
B> 1" !C /% " S !~ ( !T N &
-J N ! 3 !" !-J *+ V ^ C " N
$E$%Q!XNQ%Q"%^ h = 1 c 10 m
d%$!V#"ND h 1 = 5
=e6D o cm p = a
1 t = 3 ~ N 2
S = 10cm ; !" #%DN o
!O/%&e/0
N3%/ V h + h 1 o 1 A = p V ln = p V ln o o o o o V h o 0
*6=$!O\4D%"NA h − A = o p V ln o o o h + h o 1
N#e6A A = p Sh k o 1
NVC $%pN/6d%4DN•e6 h 1 A'= A − A = p S h h ln 1 k o − 1 o + ho 4 −4 −2 −2 10 A' = 1.9 8 , 1 . 0 1 . 0 1 . 0 1 . 0 10 −1 . 5 10 .ln 1 + ≈ 2 J 3 , 15
BM ' !( q 8> !
N 3% / 4D -J % /% e /0 '
2%6Qv| Q = A + ∆U U ∆ = 0 p V =p V V2 V 1 1 2 2 p 2 1 Q = A = pdV = p V ln = p V ln 1 1 1 1 V1 V p 1 2 4 5 Q = A = 2.5 9 . 8 , 1 1 . 0 . ln = 2,2.105J 4
BH 1"&;878!-J')
!N0&_4DN3%/' !DA h(
$ h(
h%L
@/0!(
& 88
N3%/ A = p ∆V = 1 9 . 8 , 1 1 . 04 − − − ≈ 1 (.2 1.0 1.0 3 10 1.0 3) 980J
$ @/0!(
& A V p V = p V → p 1 = p = a 5 , 0 t 1 1 2 2 2 1 V2
N3%/ V A = p V ln 2 = 4 − . 1 8 , 9 1 1 . 0 1 . 0 1 . 0 .3ln 2 = MB[ 1 1 V1
@/0!%L γ V γ γ p V = p V → p = p 1 1 2 2 2 1 1 V2
h&4);= i + 2 5 + 2 γ = = = , 1 4 i 2 ;Q p = = 2 1 / 2 ,14 3 , 0 8at
ZN3%/ m Q = A + U ∆ → A = −∆U = C − = − V (T1 T2 ) i m m RT 1 RT µ 2 2 µ µ γ γ −1 i A = (p − = − = − 1 V1 p2 V2 ) i V1 i V p1 V1 V 2 p V 1 1 1 1 2 2 V 2 2 V2 5 A = 8 , 9 1 1 . 04 1 . 0 1
. 0−3(1− 2−0,4 ) ≈ 590J 2
BB ;U%S6q!d Qt)0A
4D !" # & W e /0 U !(
4D!%L
$ N V ! U /% W /-I J q != 6 /
QU2%D%0J.
$!V 10 V = .2 , 2 4 = 7l 1 32
@/0U!( A
&e/0DA
V1 p V = p V → p = p 1 1 2 2 2 1 V2 5 7 p = ≈ 2 10 . 7 , 1 .105 Pa 4
*%~I-.0/LA m mRT p V = p V = RT → p 1 = 1 1 2 2 1 2 µ V µ 2 10 3 , 8 . . 1 273 p = ≈ 7 , 1 .105 Pa 2 3 . 2 4.10 3 −
; !"N!OT = = 2 T1 273K
NU$E4D-J34)N/ V 2 m V A = − = − = − 2 A p1V ln 1 RT ln 2 V 1 µ 1 V1 10 4 A = − . 3 , 8 . 1 273. ln ≈ 397 1 J 32 7 $
A γ V 1,4 γ γ 1 5 7 p = → = = = 1V1 p2V2 p2 p1 10 2 2 , .105 Pa V 2 4 ; !" γ −1 1 − V ,4 1 γ − γ − 1 1 1 7 T V = T V → T = T = 273 ≈ 34 K 1 1 1 2 2 2 1 V 4 2
NU$E4D-J34)N/ γ 1 − 5 −3 , 1 4− 1 p V V 10 7 . .10 7 1 1 1 A = − 1 − = − 1 − ≈ 439 J > A 2 1 γ −1 V , 1 4 −1 4 2
7\6U!( 0&.
B< ;-I & U N ! *+ Q U
!( 6U!%L Y
N U2% e/0!( F$E4D-J3 4) 4)N
D/GA V V A = − 2 p V ln = p V ln FG 1 1 1 1 1 1 V V 1 2
-.C=!&4)e/0!%L A
∆Q = A+ ∆U = 0 → A = −∆ U
NU/%/-IJD6=-.C-!'D4)$DBHA γ −1 i V1
A = −A = ∆U = − p V 1 − FG 2 1 1 2 V2 qFG4DFG
γ 1 − , 1 4 1 − A i (V / V ) − 1 5 − 2 1 2 (10/ 2) 1 = . = . ≈ , 1 4 > 1 A 2 1 ( ln V / V 1 2 ) 2 ( ln 10 / ) 2
7\6U2%e/0!( &N.=3%!J.
B f'!%L "&N%%#r
!N*'6 !"&N!&e/0=$/Eb
! !"%
,-./0%e/0!%L p γ = γ → γ − = γ − → γ − = γ − 1 V1 p2V2 (p1V1 )V 1 1 (p2V2 )V 1 2 T1V 1 1 T V 1 2 2 γ −1 − V 1 ,14 1 → T = = ≈ 2 T 1 1 273 207K V 2 2
B H=%S6!-JU!%L !=b!#
UDM*+$!VY
,-./0FS2]]G%e/0!%L γ 1,4 γ γ V 1 p V = p V → p = p 1 = 16. ≈ a 1 t 1 1 2 2 2 1 V 7,2 2
B N !"%4D =>!-J'!%L
!*+A
NrQ$%QVY
$ ; !"N'Y
N3%N/'Y
q-./0 1/γ 1/1,4 γ γ V p , 1 5 p V = p V 2 1 → = = ≈ 3 , 1 3 1 1 2 2 V p 1 1 2
r%^=V
$ ,-./0%e/0!g 1 γ − γ γ γ γ p 1−γ γ 1 −γ p V = p V → T p = T p → T = T 1 1 2 2 1 1 2 2 2 1 1 p2 1−1,4 1,4 T = + ≈ 2 (273 ) 5 , 1 30 270K 1
N3%/ m iR A = −∆U = (T − T ) 1 2 µ 2
h&4)N8<9%=$\C3%#Xs8> 103 . 5 31 , 8 A = (.303 − 270) ≈ , 2 4.10 4J 29 2
B T/E!&4)"v-S!i-./0A 2 pV = U i
wD"r#&6=D$\C3%
;"rv- i U = nRT 2
,-./012322245/6/% pV = nRT x%! 2 pV = U i
B 1" N% ; F8B9%G !d Q t ' !%L
%%#rQ>V0A
N3%C
$ h"$QQ"r#&
; !"UDA γ γ γ 1 − γ 1 − p V = p V → T V = T V 1 1 2 2 1 1 2 2 γ −1 1,4−1 V 1 → T = T 1 = 273. ≈14 , 3 4K 2 1 V 5 2
N3%C m iR A = −∆U = (T − T 1 2 ) µ 2 3 5 3 , 8 . 1 A = 10 . (273− 14 , 3 4)≈ 2 7 , 1 . 06 J 2
$ h"$Q"r#&$E4D-J34)N
3%/ ∆U = −A = , 2 7 1 . 06 − J
B> ?N/%S#"!".!&/%!-JU!g
q!> !"#&e/0
U$/E !"$!V#D o C
,-./0%e/0!%L
− 1 γ γ γ γ γ p 1−γ γ 1 −γ p V =p V →T p =T p →T =T 1 1 2 2 1 1 2 2 2 1 1 p2 1−1,4 1,4 T = + ≈ = 2 (273 ) 1 40 86 K 5 592o C 35
BM 1"&'!%L =#r!N=-
!"6 !&#^!=V0&$\C3%#X s!
q-./0 γ γ γ 1 − γ 1 ln(T / T 2 )1 p V = − p V → T V = T V →γ −1 = 1 1 2 2 1 1 2 2 ln (V / V 1 2 ) γ 1 − 2 = / i 2 l ( n V / V 1 2 ) . 2 ln (1/ 2 ) → i = = = 5 ln (T / T 2 1 ) l ( n 1/ 3 , 1 ) 2
P&$\C3%D>
BH 1"-u6QsV =
= p = $i 1 , 0 a 5 tm 1 , 0 l 5
U !%L ) 7 4D P ! -I €
6QV 4DDL) !"$!V?! 2
#D p = a 1 tm o
7•!pi#e/0!
$ 0 V 4D p 2 2
hpi#e/0A %
7 7 7
$ @/05!( QA p1 p V = p V → V = V = 2 , 0 l 5 = V o 3 1 1 3 1 2 po
@/05!%L QA γ γ γ γ V p p V = p V → p 1 = p o = p 1 1 2 2 2 V 1 p 1 2 1 p = 2 ,14 5 , 0 . ≈ 3 , 1 2at 2
F? -u 6Q s 8> Q , { x i + 2 5 +2 γ = = = , 1 4G i 5
BB ?U!%L %-u6Q , j
s=-I!'&NM[*+ !"
#rQ$%QY % 7 7 7
*0B
? \ " N {8M[ F N 5{8
M[G=!"r"r$EN\4D%# m iR U ∆ = A = T ∆ µ 2 2A 2 1 . 4 . 6 103 → ∆T = = ≈ 7K iRm / µ . 5 3 , 8 . 1 103
; !"rHo C
B< 1" -J %S6 7 o
4D
8 !" H C
8B=>, /L T = N & 78=> 4D
8M>,FG0 -JD/'=4D
!" $ Q " r # & f^ $D % /% /-I J
$!O&q/L)/L2%%!-IA {j $ {xj
@/0{j
{!(A m iR i m m Q = ∆ U = (T − T ) = RT RT AC C A − C A µ 2 2 µ µ i 5 Q = (p − p = − − = − 2 1 ) V 6 1 . 0 5 , 8 2 1 . 05 3 1 . 0 3 1650 AC 1 ( ) J 2 2
@/0j!(AC p = C V + R m i + 2 m m Q = (C + ) R (T −T ) = RT RT CB V B C − B C µ 2 µ µ i 2 + 5+ 2 Q = p − = − − = 2 (V2 V ) 6 1 . 05 1 ( , 4 5 3)10 3 3150J CB 2 2
^e/0 Q = Q + Q = 1 − 650 + 3150 = 1500J ACB AC CB
@/0{j\-J Q =1500J ACB
m U ∆ = C ( T − ) i T = (p V −p V ) AB V B A 2 2 1 1 µ 2 5 ∆U = − − − = AB (6.10 .54 5,.10 3 2, 8 .10 .53.10 3 ) 600J 2
!"#$% A = A = p (V −V ) ACB CB 2 2 1 A = 6.105. − − − = ACB (4 5,.10 3 3.10 3 ) 900J
$ @/0{xj &
@/0{x!( m i + 2 m m Q = C R T T RT RT AD ( + V )( − D A ) = − D A µ 2 µ µ i+ 2 + Q = p − = − − = AD (V V 1 2 ) 5 2 , 8 2.105 1 (4 5 , 3)10 3 4305J 2 2
xj!(A m iR i m m Q = ∆U = T T RT RT DB ( − B D ) = − A C µ 2 2 µ µ i Q = − = − − = − DB (p p 2 1 ) 5 V2 (6 1.05 ,8 .2105) ,4 .510 3 2475J 2 2
^e/0 Q = Q + Q = 4305 −2475 =1830J ADB AC CB
m U ∆ = C − = − AB V ( TB A ) i T (p V p V 2 2 1 1 ) µ 2 5 ∆U = − − − = AB (6.10 .54 5,.10 3 2, 8 .10 .53.10 3 ) 600J 2
!"# A = A = p − ADB AD 1 (V V 2 1 ) A = , 8 2.10 . 5 − − − = ADB ( 5, 4 .10 3 3.10 3 ) 1230J
B 1"% F& -J % G C " /0 {jx -
03-)=/%!{j=xDe/0!( =T4)
!" T 4DT =j4Dx{De/0!(T4) V 1 2 2 4DV 1
{ { x x j j 7 7 7
T/E p p A D = p p B C
$ N4D /%^/0
3]Q-./0#e/0!( A p V V p A B C D = = = F!G p V V p B A D C
$ N#/0$EN/Qe/0{j4Dx=
e/0KLN$EN m pV= RT V V µ m V 2 1 A= A + A = p V ln + p V ln = ( R T −T ln AB CD A A D D 2 ) 2 1 V V µ V 1 2 1
; \/%^/0A m Q = A = ( V R T −T ln 2 ) 2 1 µ V1
B 1"&C "/0-04•3-)=/%!4D
De/0!( T4) !"T 4DT =4D 1 2
De/0!%L % V =2 = =V = = p = 7 0A 1 atm 3 l 1 l,V 5 2 l 8
Q= A+∆ U = A
7 7 7 7 7
p , p , p ,V ,T 2 3 4 4 2
$ NC /%qe/04D/%%D/0
; D & \ !-J 6 + / /% q e /0 !( V p 1 = =
=%ND-u6QsA8>=A 2 p1 , 2 7atm V2 γ V p 2 = = 3 p , 1 4 2 a 5 tm V3 γ −1 1 − γ V γ 2 T T = = = = 2 T1 33 K 1 ; p 4 p 2 1 , 3 6atm V 3 T1 p V 3 = = 4 V , 3 3 l2 p4
$ NC /Qqe/0A V A = = 12 pV ln 2 1300 1 1 J V1 p 2V2 T A 2 = − = 23 1 620J γ 1 − T 1 V A = = − 34 p2V ln 4 1070 2 J V3 p V 2 2 T A 1 = − = − 41 1 62 J 0 γ − 1 T2
NC /%^/0A A= A + + + = 12 A23 A34 A 230 41 J
; D\/%qe/0!%L A
Q = =
=\ 12 A 1300 12 J Q = = −
=^ 34 A 107 J 0 34
B /%"$0;4D%S60!"$QQ"r#
WJ!DLS&B%
h"^"r m iR m iR U O ∆ = T N ∆ + T ∆ µ 2 µ 2 O N 32 20 5. , 8 3 ∆U = + ( 1 273+ 2 )8 ≈10000J 32 28 2
B f^!pN2%v6#"6U!-J4•/Q0B5
F^ !p C /K .G h%L {j T 4) e
/0U!( N=je/0!t6N4D%$0
TFN!OGkx5^!""/%S#
6U!4%4D4Lkx{5%N4D%
*'6 T /E N # 6 U "
/0 $E N !& 4) e /0 !( 4D !-J $ 3‚ $E
3 {jfƒ j , , x * { f ƒ 7 7 7 *0B
N{#6U$EN\!-J4D$E3 {jx A = dt(ABCDA) = dt (ABH ) A + d ( t BCDHB) dt (BCDHB) = (p − p = − = − = 2 1 )V p V p V p 2 1 1 1 2 1 (V V 1 2 ) dt (AFGH ) → A = dt(AB ) HA + d ( t AFG ) H = d ( t ABG ) F F!G
B 7•!pi#€e/0!(=!(=!( 4D%
!%L #^!p = =w $ =7 3 7=w
f^!p=
• @ /0 !( A 98%= !p i $ 3‚ D !-I
(e&L!"F!-IG
• @ /0 !( A N !O= !p i $ 3‚ D
!-I(%%4)F!-IG
• @ /0 !( A !" N!O= !pi$ 3‚D
!-I(%4)
• @/0!%L PC]"4D%%$-./0 γ γ − 1 p = const T . γ γ γ F403%pVγ = c (= const) (pV) → c = = (nR)γ T γ − 1 → p = const T . G 1 1 γ 1 − γ 1 p p −
,-./0D6!piFGD"!-I%!e&g!" $ f^!p=7 7
• @ /0 !( A N !O= !p i $ 3‚ D !-I
(%%4)F!-IG
• @/0!(A798%=!pi$3‚D!-I(e
&L%!"F!-IG
• @/0!( A8%=!pi$3‚D!-I(% 4)7
• @/0!%L PC]"74D%%$-./0 1 V = const T . γ −1 .
1 −
F403% pVγ = c(= const )→c = (pV ) γ−1 V = (nR ) γ−1 γ 1 TV → V = const T . − =lG
,-. /0 D6 !piFGD " !-I % 3L62$%
\4)/]g!"F!-IG
/%"e/0$„A m U =
RT =e/0!(=!( µ
=!%L !-I$3‚D!-I(e&g!"F!-I
==G=e/0!( !-J%$!-IEF!-IG w ==
3 f^ !p w=7 Fw " E & mC = 3% ! m V U% 3D V µ
Q "m& m C !&4)/] !pi=7 •\!-J !pi V µ w=7G 7 w
1" 6 . -) N =H…=Q ] B= /%
"I;r+ #DHB9; !"#
p%= !"#pLD>BoC 0
C # 6 P% ! 4) v - #
6 D4 2%/0N4)€p /Q
* C#6 Q 1 , 4 7 3 . 600 h coich = 10 % 0 = 10 % 0 ≈ 2 % 0 Q 1 , 8 7 . 80 . 0 1 , 4 8 toanphan
* v-2%/0N T − T 200− 58 h n l = 100% = 100% ≈ 30% lt T 200 + 273 n *6 2 h = h lt 3
%LC/%6DLv-C "N$E
$% Q ! 6 ! " -J >[ q $p D L=
!" # $p D M?= K !" # -) D L D B>?
* &DL#!". Q 2 ε = A
;6L62%/0N-J0A T2 ε = T − T 1 2 P6/ T 1 285 → A = −1 Q = − 1 1 05 ≈ 8365(J ) T 2 2 263
;p Q 1 16 A L Q 2 ;pL
1" !" . v - L6 2% /0 N= ^ %
pLB† -JD!-J#p;
-J!-J/%"/0D=>0A
* !".
$ ND!".//%"/0 ;p Q 1 h" . A Q 2 ;pL
* #!". A Q η = 100% = 1 2 − 100% = (1− ) 8 , 0 100% = 20% Q Q 1 1
ND!".//%"/0
{8@8==>8=8=>[
1"!". D4 2%/0N=W/0
" N {8H=>[ ; !" # p D o C=
!"#pLD%0A
* !".
$ ; -J\!-J#p"/0
; -J^%pL"/0
* #!".
T 273 η = 1 2 − 100% = 1 − 100% ≈ 26 8 , % T 100 + 273 1
$ ; -J\!-J#p"/0 Q = A /η = 7 3 , . 5 104 / , 0 268 ≈ 27 4 , 2 1 . 04 1 (J)
; -J^%pL"/0 Q = Q − A = 27 4 , 2 1 . 04 − 7 3 , 5 1 . 04 = 20 0 , 7 1 . 04 (J) 2 1
; !"#.-)qK.4D%6.-)D o
8H C =
!"#$0-D o
8H C *+&" -J@8
0!-J"NC!L2%v6$E$%QY
N C !L 2% v 6 !-J !" . D 4 2% /0
N\i4) v- T2 η = 1 − T1 1~ A T + 2 27 273 η = → A = 1− Q = 1 − 1 = 0 ( 4 , kca ) l = 6 , 1 7 ( 2 k ) J Q T 227+ 273 1
1" /0 N C € 6 !d !"
8%=8%I!C /0!D80
N F NG D 4 # !" .2% /0 6= $
XDN=&e/0' !(
$E !V e /0 U !%L % N
8<9% 7 7 7 7 7
; -J \ !-J#!"./% "/0 D \!-J
/%e/0F04•G m p1 Q = RT ln 1 1 µ p2
@/0!%L Q γ γ 1− γ γ 1− γ γ p V = p V → p T = p T 1 1 4 4 1 1 4 4
1" % v - C " /0 p e /0
!(4De/0!(?!#6!O
q78>!78> 4Dq8!8*+N
C $ /0 D6 + . $% Q VN C
$ /0 N !-I !( T 4) !" )
4D + # /0 /Q= ' !(
rQ!NY
NC /%^/0A A = (p − p )(V − V ) 2 1 2 1
/%/0N= !"pT4)!F7=G=pL 4)F7 V'2
=G/%"/0X\ p V ln
4) A 2 2 V'1 T − T p V − p V 2 1 2 2 1 1 η = = T p V 2 2 2
N//%"/0A V' A' =ηQ = p V − p V ln 1 ( 2 2 1 ) 2 1 V'1 (p V − p V ) V' ln 2 A' 2 2 1 1 V'1 → = = 2 1 , A (p − p )(V − V ) 1 2 2 1
1"6.-)D4 2%/0-04•< j , x , % { ˆ 7% 7 7 7 '(
%LQ.-)qp.4D%S=.-)E
q%)=N!O4D$E7%F{jG
$ *. -) ] ! 4D%= N 6 !" q / ^
F jG 4) . N !O D 4Dr Q 7
n!4L= N6!"]^
!S^6/e/0'!%L F;xGk
3 ?!4i/&_$Q^=0.-)/%S!4D%
pL=!.^S&%=KN
!O$E7 =FxˆG
2 ,N6!"-JL=!t6.-)KL/%S
/%D=!N!O$E%=^q7)
7%Fˆ{G
*'6 N D 6 / W /0= 7%8=>k
78=>k78k%8k84D &!%L D8=
NC /Qqe/0/Q$ A
Z@/0{j4Dxˆ!(=NN A = A = 0 AB DE
Z@/0j='!(=N A = p − = − − = BC 1 (V V 1 ) 12.9 8 , .10 4 o ( 5 , 1 5 , 0 ).10 3 117 ( 6 J)
Z@/0 x ' !g = 2% N T F,MGV ] ]=
N//%e/0'!%L A γ 1 − − p V V 1 . 2 9 1 . 8 , 04. 5 , 1 1 . 0−3 , 1 5 ,133 1 A 1 1 = 1 1 − = 1 − ≈1093 CD (J) γ − 1 V 3 , 1 3 −1 3 2
Z@/0ˆ{$!O!(=NC A = p (V − V ) = 8 , 9 .104 ( 5 , 0 − 3).10 3 − ≈ 2 − 45 (J ) EA o o 2
N D 6 / /% W /0 D 4 $E N
C $ A = A + + + + = + + + − = AB A BC A CD A DE A EA 0 1176 1093 0 245 202 ( 4 J)
*04• </0$D6^!pv 6 # !" .!&/%$& „
/%e/0!VQ=WJ6!-JL4D%S=
!%8%4Drq7)7F{jGk
$ /% e /0 T F jG= W C% 6 !-J U
!%L q7 )7?! !"rq%!
4Dq %!k x , ˆ , { % j 7 7 7 *0<
2%De/0!&6WJ6$E2s
! k!rq)=N!O4D$E
7 FxG= !"r)k
3 2% D e /0 ' !%L q 7 ) 7
FxˆG= !"^S&k
2 &_#NF!ˆG=4=%/%D=
b ^ ) %= N !O 4D $E 7 F ˆjG
‰ &_De/0U!(%Fj{G
*'6 #/0 &U ε 87978>4D &!%L
Dγ 8=
; X \ /% ^ /0 $E X \
/%e/0xA Q = Q = nC (T − T ) 1 CD V D C
/QˆjX+ F \4D%•3XGA Q = nC (T − T ) 2 V B E
* #!".A Q T − T nR T − T p V − p V V p − p 2 B E ( B E ) o 1 4 1 1 o 4 η = 1+ = 1 + =1 + =1 + = 1 + FG Q T − T nR(T − T ) p V − p V V p − p 1 D C D C 2 2 1 2 2 2 1 1~A γ γ γ γ p V = p V ; p
V = p V → p − p V = p − p V 1 2 o 1 2 2 4 1 ( 2 1 ) γ 2 ( 4 o ) γ 1 γ p − p V o 4 2 γ → = − = ε − − FG p − p V 2 1 1
6FG4D%FGA η = 1 1 − − γ ε = 1− 51− ,133 = 4 , 1 2%
0 # !" . !& /%= % $ & !%L D
=4D &U$EA
7 978k $7 97 8Mk7978Bk
2%$D<!-JV-J%e/0] η = 1 1 − −γ ε = 1 − 41− ,133 = 36 7 , % $ η =1 1 − − γ ε = 1 − 6 1− ,133 = 44 6 , % η = 1 1 − − γ ε =1 − 8 1− ,133 = 4 , 9 6%
/0#!".!2Š2$&„!-J/0$D6/Q0<
x ˆ j % { 7 7 7 7 '()
;{jT4)e/0LN= %8k
$ ;j5N!-JU!%L )b
&„U= Q !-J 4D% S= Q 6
/%N=!N6!"^=!V
QD!(FxG=!D!%L FxˆGk
3 &e/0!%L =4%=^S&% FˆjGk
2 ;j{T4)e/0!t6/+S
0 #!".32Š2
/%"/0=Xm\ /Qe/0xA Q = Q = nC (T − T ) 1 CD p D C ;^ A Q = Q = nC (T − T ) 2 EB V B E * A − − − Q 1 T T 1 p V p V 1 V p / p p / p η = 1 2 + = 1 B E + = 1 o 2 2 2 + = 1 2 o 1 2 1 + Q γ T − T γ p V − p V γ V V / V −1 1 D C 1 3 1 1 1 3 1 p p o 2 − ε p p η = 1 1 1 + FG γ β −1
/%! ε = V / V 2 1 1~ γ p V γ γ o 1 γ p V p V k o 2 = 1 1 → = ε − = p V 1 2 γ γ p V V V γ γ 2 3 3 1 γ γ p V = p V → = = β ε − = FG 2 2 1 3 p V V V 1 2 1 2 7) V3 β = V1
6FG4D%FG4D$!O\!-JA
γ β −1 η = 1 − γ−1 γε (β 1 − )
1"6.-)L62%/0pe/0!(
4De/0!(-0< #
/0!P% !4) /0N
_ !"#p4DpL 7 *0<
; \\!-J/%"/0D4 $%peb/0
54D5 Q = nC T − T 23 V ( 1 2 ) V Q = A = nRT ln 34 34 2 1 V1
NX/F$EN!"%/G/%"/0D 4 V V V A = A + A + A + A = nRT ln 0 nRT ln 0 nR T T ln 12 23 34 41 1 2 + + 2 1 + = ( − ) 1 2 2 V V V 2 1 1
* #!". A T − T T − T 1 2 1 2 η = = < η = Q + Q C T − T T 23 34 V ( 1 2 ) Carnot 1 T + 1 R ln (V / V 2 1 )
7\6!".D4 2%/0P +.D
4 2%/0/%
!"$Q2/Npy.!(M=>!/N=
r!N
h"$Q2/%6/%eb/0!( Q δ nC dT dS p = = T T
^e/02/%6$Q"-J T2 dT m i + 2 2 T ∆S = dS = nC = R ln p T1 T µ 2 T1
1~=e/0!(Q T V 2 2 = = 2 T V 1 1 7)*!/N8> 5 , 6 5 + 2 S = . , 8 . 31. ln(2)= 65 5 , 2(J / K) 2 2
!"r2/N6$!O-)%D.%
h"$Q2/%6-)!-JD)% δQ mCdT dT T dS = = → ∆S = dS = mC = 2 mCln 1 T T T T1 − + 3 100 273 ∆S = 10 .4180. ln = 3 , 1 1 0+ 273
h"$Q2/%6/%e/0-).% Q δ Lm , 2 26.10 . 6 10−3 ∆ S = = = ≈ 2 1 , 6 T T 373 2 2
h"$QQ2/%6/%^e/0 S ∆ = S ∆ + ∆ ≈ 1 S 2 , 7 4 (J / K )
!"$Q2/Npy'!( =>;.q
)> δ ∆ Q Q m V2 10 5 , ∆S = = = R ln = . 3 , 8 1.ln (5/ 2) ≈ 2,9(J / K) T T µ V 28 1
NS6 !-J . q 8>% ) 8>% !" $ Q
2/N6e/0.DA
h(k $!(
@/0!( δQ δA + dU m dT m i + 2 T ∆S = = = C = R ln 2 V T T µ T µ 2 T1 10 5 1 50 +273 ∆S = . , 8 31. ln ≈ 7 , 1 (J / K) 32 2 50 + 273 $ h(
δQ m dT m i + 2 T S ∆ = = C = p R ln 2 T µ T µ 2 T 1 10 5 + 2 150 + 273 ∆S = . 3 , 8 . 1 ln ≈ 2,4 (J / K ) 32 2 50 + 273
!" $ Q 2/N6 $ !O M 6!/N q
==>!M=
70!"$Q 2/%6 m]"4D%/L!V4D&Q
g%"$!O$„DN^-)e^
(L=%$!O!()=!'!()
M
Z7)e/0TFe/0!(GA δ Q dT m T m p ∆S = nC C ln C ln 1 = V = 2 = 2 V V T T µ T µ p 1 1
Z7)e/0TFe/0!(GA δQ dT m T m V ∆S = nC C ln C ln 2 = p = 2 = 2 p p T T µ T µ V 1 1
h"$Q2/%6#^e/0 m V p S ∆ = S ∆ + S ∆ = C ln 2 + C ln 2 1 2 p V µ V 1 p1 6 5 + 2 60 5 1 ∆S = . 3 , 8 . 1 ln + . 3 , 8 . 1 ln ≈ 7 ( 1 J / ) K 2 2 20 2 , 1 5
1" N% -u 6Q s !-J . = !" 6 !&
# !-J r Q => V !" $ Q 2/N6 e
/0.DA
h(k $h(
@/0!( δQ dT m T 2 m i T S ∆ = n = C = C ln = R ln 2 1 V V T T µ T µ 1 2 T1 3 5 ∆S = 10 . . 3 , 8 . 1 ln ≈ 1 ( 5 , 1 ) , 8 4 1 . 03 (J / K) 2
$ @/0!( Q dT T i 2 + T ∆S = δ n = C = nC ln 2 = n R ln 2 2 T p T p T 2 T 1 1 5 +2 ∆S = 103 ≈ 2 . , 8 . 31. ln( ) 5 , 1 11 1 . 8 , 03 (J / K) 2
.!-J.= !"6 !&#r=V
4D 2/N6 r Q =<9? nU S2 e /0 . D !r
6!(Y
f^s 3#e/0$!OD=! Q δ dT m T ∆S = n = C = C ln 2 T T µ T 1 µ S ∆ 2 . 8 1 , 4 9 → C = = ≈ ( 7 cal / K)≈ 2 ( 9 J / K) m ln(T / T 2 1 ) 22.ln ( 1 , 2 )
h&4);. iR + C = ≈ 2 = ≈ V ( 1 J / mo ) (i 2)R l ;C 29 p (J / mol) 2 2
7\6e/0.De/0!(
h"$Q2/N6/Q!%L€e/0!%L /%
/0N$E9!"* !"€!-I!(
D%*+ -J!'6DN/% /0D6
fg !"#!-I!( D4DFlG
N C /% /0 $E # \ 4D% C C 4D
+/CC/%"/0F$EO -J*
+, /%^/0G A = Q + Q 1 2
/%/0/% Q + Q T − T Q Q Q − Q A 1 2 1 2 1 2 1 2 η = = → = = = Q T T T T − T T −T 1 1 1 2 1 2 1 2
/% e /0 !( F€ e /0 !%L G= !" $ Q 2/%6D Q Q Q 1 2 S ∆ = δ = = T T T 1 2 ;Q A = (T − T )∆ S = 10 ( 0 kca ) l = 41 ( 8 k ) J 1 2
j+ -) ! % 4D% -) % /% " $0 4+
v - !" $ Q 2/N6 # /% e
/0/%!O q!6//E m/6dq4\
4\L%$ ^6/Q#-)!%D
8B9k 3/Q#-)D9!"
; !"X$E# /%!O S!iq-./0
X$E + −λ m λ + cm (t − t ) = cm (t − t) c(m t m t m 2 2 1 1 ) 1 → t = 1 1 1 2 2 c(m + m 1 2 ) ( 1 40 . 0 30 +100 ) 0 . − 80 1 . 00 t = = 8(oC) = 281(K ) ( 1 100 + 400)
h&4)-)!=!"r2/%6$%p!"r3%^64D!"r3%
r !" T δQ δQ Q dT m λ ∆ T ∆S cm cm ln 1 = + = + 1 = 1 + 1 1 2 T T T T 1 T T T 1 1 1
7)8BF?GD !"X$E#
h&4)-)$iL!=2/%6•^=!"$QD6D T Q δ dT T ∆S cm cm ln 2 = = 2 = 2 T T 2 T T1
h"$QQ2/%6# D m λ T T ∆S = ∆S + ∆S 1 = + cm ln + cm ln 1 2 1 2 T T T 1 1 2 8 . 0 1 , 0 281 281 ∆S = + 1. 1 , 0 . ln +1. , 0 4. ln ≈ 0 0 , 0 ( 2 kcal / K) (0 + 27 ) 3 0 + 273 30 + 273
6∆Pl=!d!T+ m/6dq4\4\ L
‹hT m/6dq4\4\L
D - A nU 4\ N \= r -J # $^% %D F e
/0SUmQe!C/6d 0 !-J$^%%DG Q = Q + Q = const → Q δ = − Q δ 1 2 1 2 /%! Q δ = Q δ
D!"$Q -J#4\4D 1 2
h"$Q2/%6 δ δ 1 Q Q2 dS = dS + dS = + 1 2 T T 1 2
2%F‹G 1 1 (T − T δ 2 1 ) Q dS = δ Q 1 − = > → − δ > 1 0 (T2 T1) Q1 0 T T T T 1 2 1 2
; l 0 @l T D 4\ \ 6 /6d q 4\
4\
;Œ0@ŒTD4\+ 6 /6dq4\ 4\
7\6 m/6dq4\4\L
!"$Q2/N6#"v-/L
#6!Oq{)jF0<>G2%A
, , { x , j 7 7 7
*0<> h-I{j $ h-I{xj %$A7 o
8k8B=>;9k78=>k 8H C =8M >;9
h"$Q2/%6N]"4D%e/0$!O-D%=
Dm]"4D%/L!V4D/L&=QA C dT B dT T T ∆ S = ∆ S S nC nC nC ln nC ln AC + ∆ CB = V + p = C V + B p A C T T T T A C
{4D5j!(Q T p T V C 2 = k B 2 = T p T V A 1 C 1 x%! i p i 2 V p V i p i 2 V 2 + 2 1 1 2 + 2 ∆S = n R ln + n R ln = ln + ln 2 p 2 V T 2 p 2 V 1 1 1 1 1 , 8 31.10 .5 . 3 10−3 6 6.105 6+ 2 4 5 , ∆S = ln + ln ≈ , 5 4(J / K ) ( 27 + 273 ) 2 ,831.105 2 3
$0=$0T78T;.
8=$0T78T
8>%$0N4)4D!~b/%"4+
v- !"$ Q 2/N6 # /"
c 4D% = $ !" $ !V /% $0 $E 4D $EH%
?'4D%NN= L$iQe
/0 !L !-J /L & _ !" N !OF- v= !X6 N
^De/0!%L \iGˆ/%66!O"-JF
$E%!-I!( G δQ Q δ ∆S = ∆ S + ∆S = 1 2 + 1 2 T T
@/0!(
V2 Q = A = pV ln V1 p V V + V p V V + V ∆S 1 1 = ln 1 2 2 2 + ln 1 2 T V T V 1 2 8 , 9 1 . 0 .42 1 . 0− 3 2 + 3 . 5 9 . 8 , 104 3 . .10− 3 2 + 3 ∆S = ln + ln ≈ ( 1 , 3 J / K) 273+ 27 2 273 + 27 3
•%!-J$+4D%" -JT-)
o C ˆ/N6# D66!O-D%X$E Y
P/%!O •X$E !"%,-./0X$E c m t + c m t c m t − t = c m t − t → t = 1 1 ( 1 ) 2 2 ( 2 ) 1 1 1 2 2 2 c m + c m 1 1 2 2 460. 2 , 0 .100 +418 . 0 , 0 . 3 12 t = 1 ( 8 o ≈ ) C 460 0 . ,2 + 418 . 0 , 0 3
h"$Q2/%6# $%pC^2/%6#•4DC
r2/%6#&-) dT dT T T ∆S = c m c m c m ln c m ln 1 1 + 2 2 = 1 1 + 2 2 T T T T 1 2 18 + 273 18 + 273 ∆ S = 460 , 0 . 2. ln + 4180 0 . 3 , . ln ≈ , 3 ( 3 J / K) 100 + 273 12 + 273
7\6X$E 2/%6# rQ"-J=F[9?G
!"#
*2B ;90
!"#/%/-IJ
%*2Dv-
$ %*2DC
? *2 v -= !" !-J S !i q -. /0
12!22245/6/% pV 108 1 . 0 . 0 10−6 T = = ≈ 48 ( 1 K ) (m / µ)R (10 / ) 4 . 3 , 8 1
$ ?*2C= !"!-JS!iq-./0732 … m 2 a m m 1 p µ m a m p + 2 2 V− b = RT → T = + 2 V − b µ V µ µ R m µ V µ 1 4.108 10 . 1 , 4 10 4 − 6 10 T − 5 = + − − ≈ , 8 31 10 4 ( 2 − 100.10 6 ) 100.10 3 , 2 .10 205K 4 h&4)*2
a = 4,121.10-4 Jm 3 / kmol 2; b = 2,3.10-5 m 3 / kmol
/%"$0T=>. !"H%
0m&€"4D3%3]QD$0
$ 0m&€"4D#$0
E&732…#;. a = 0,14 J 1 m3 / mol2 ; b 9 , 3 2 1 . 0 5 − = m3 / mol
,-./0732… 2 m a m m p + V− b = RT FG 2 µ V 2 µ µ
m&€"4D3%3]QD$0 2 ;" m a p'= 2 2 µ V
4#FG%‡A p m µV2 RT p RV 2T p' ma m + 1 V− b = → = → = FG 2 V − b p' µ am p' m m p R µ V T µ a V − b µ µ p' 25 . 0 0 1 , 41 250 − = . , 0 01− . 9 , 3 2.10 5 ≈ 4 9 , % p 28. , 8 31. , 0 012.300 28
! " #$ "% &' $( )* + , -. / 0 1 ( 23 45
$ m&€"4D#$0 " m V'= b µ m& −5 V' mb 25 . 0 9 , 3 . 2 10 = = = , 3 % 5 V µV 28. , 0 01 0
#$%%
$&-J/Q#
!"!D>>9
,-./0732… 2 2 m a m m ρ a ρ ρ p + V − b = RT → p + 1 − b = RT 2 2 2 µ V µ µ µ µ µ 2 RT ρ a → p = − (µ / ρ − b) 2 µ 6& 2 3 , 8 1 (.273 + 3) 550 p 8 = ( − ≈ , 0 028 / 550 − 9 , 3 . 2 10− 5 ) .0 1 , 41 , 1 4 1 . 0 (Pa) , 0 028
#%S6rq!>3n2%S6DC
0N#"C/%e/0'! ;" 2 m a p'= 2 µ V
N#"C 2 2 m V 2 adV m 1 1 A' = p'dV = = a − V 2 1 µ V µ V V 1 2 2 4 1 1 A' = 0 1 , 38 − ≈ , 1 ( 7 J) 32 , 0 001 , 0 005
" # $% b & -J /Q # D
>>9 % $ !& 4) $% A 8? 4D
8H=M;9
;"#$%
2 2 2 m a ρ 27RTk p' = = 2 µ V2 2 µ 64 pk ;-3% 2 27RT a = k 64 p k ;Q 2 550 2 . 7 3 , 8 . 1 3042 p'= ≈ 8 , 6 1 . 0 6 (Pa ) , 0 044 64.7,4 1 . 06
&-J-)V%4D%"$0 !
!)/L)L%D$"#$0
fg&-J -) V%4D% $0D ? ! )/L)
L=#$0D)L=Q m m V µ V = V = V = b 3 → m = k ok µ µ b 3
*E&732…#-)$8=>M9%=!-J8>=<
n !i&-J /Q# .-) !)L2%/i
"$8=9% " m m m µ , 0 018 V = V = b 3 → ρ = = = = 200 kg / m k ok k ( 3 −3 ) µ µ V b 3 3. 0 , 0 . 3 10 k
h&4)$%A8=M>[9%=$8=9%*+A
$%+)D$%QY
$ .$'%K)D$%QY
+ !"%D$%QY
3 V^U4)$E$%Q!D
+ !"%4D>%
) # $% + T 4 /L ) L
F6/q!-I!( 732…G m b 3 m 3. 0 , 0 4 . 3 10 3 − V = V = ≈ ≈ 9 , 2 3 1 . 0 3 − m3 / kg k ok µ µ 4 . 4 10−3
F$8=9%8=9%G
$ .$'%%DC!LT4)!$F6/q!-I
!( 732…G
a 0,364 p = = ≈ k 7,4 1 . 06 (Pa) 27b2 2 27(0,043.10-3)
F8=M>[9%8=M[9%G
; !"%D.K+T4) !"!$ a 8 8.0 3 , 64 T = = ≈ 304K = 31o k (C)( ) ! 27Rb 27. 3 , 8 . 1 , 0 043 1 . 0−3
3 $%+%VU)$E)L p = 7,4 1 . 0 6 k (Pa)
h a D !" ) D $% + g
7) !">%DNC %+4)$TD%
h QT/L)LD4\vg ;{7Q/6
3_""/%!!C"&T22!-JD
*."!e/L)L
%= Q2 -) ^ " $E $% Q V
/r#&!! !")L=&T!V6
Q2 /L ) LY j /E & -J % Q2 D
H9%= & -J /Q # Q2 % $E H9 h&
4)Q28<%=8>=<>;9k
$ ; #&)6+.Q2)L0•
S^6/ -J0 !"XQY
fg4D&-JQ2!O4D%&D74D=#
/L)LD7F3%!aD#&G m m m RTk V = V = b 3 = b 3 k ok µ µ µ 8p k m V 8 p µ 8. 0 , 0 7 . 4 34 9 , .10 5 V k = → = = ≈ ρ V 3 R ρ T . 3 71 . 4 3 , 8 1. + k k (273 193) 25%
$ ?#&+.70-!22Q)
/L)L22!'!V6&
?#&).70-!22Q)
/L)L22!'$6.
$
n!iN V !$ " g-) D -. _
F} D ! g -) ! D € g +G !-I
=x $d~ #g-) b!V%-N!
%4)O3 $d~#g-._
?&-J#"g-._ 4 3
m = πρr F/D$g-.G 3
P&g-.!-JL%Dqg-) M 3M N = = 3 m 4πρr
x $d~#"g 2
s = 4πr =4\63 $d~O" M 3 6M S = sN = =
F38/D!-Ig-.G r ρ d ρ
N V !$ g D -. _& $Er-J ~ %D 6σM A = S σ = ρd 6 0 . 0 , 73. , 0 001 A = = 2 1 , 9(J ) 100 . 0 2.10 6 −
* g #6 X 4) $ W g D \ L D
" g ) *+ !" # g #6 X r Q $% QY
% $ #6 X r ~ %D 8=>;9= & -J
/Q8=M9=`3/Q8B[9!"
fg$#g+D/=#g)!-JL%DD:A 4 3 4 3 3
πR ρ = 2 πr ρ → R = r 2 3 3
;\D"=3 ~%D#g)•+.O3 ~
%D # g+=r -J $d~ •^ h"^ r -J $d
~D6•$E -J#g)\!-J ( 4 2.4 r 2 π − 4 R 2 π )σ = mc∆t k 3 m = 2 π r ρ 3 x%! 3 3 4 3σ 4 3. , 0 5 t ∆ = 1 − = 1 − ≈ , 1 65 1 . 0−4 (o C) 2 c r ρ 2 138 1 . , 3 6. , 0 001
N V C ! O " $% $ SD K !L !
$/8HPr~%D#-)SDKD8
;9e6%8=>;9
% !" # /% e /0 O D N !O Fe /0 !(
GNVO$%$$ENL%/~%DF$Er-J
~%DG{=4DNU!( {#"-J!b$E-J
/%$%$&e/0qe64D% 2 2 A = 2.σ 4 r π = 8σ r π 1 p A = pV ln 2 po
%De6=D/%$%$
h = b v D SD K p ~ X = W ~ X
F~G•X6//]yUz4D%X4)/i2%
NTR2
p = 2σ / r ]O"3%DSDKX6/%$Q/% p
$%p3%~%%D4D~%/%F4)$
SSm$~%%DG4De6"LA 4σ p = + p o r x%! 4σ 4 σ σ σ 3 p + 4 / r 4 o 3 4 4 A = p + r π ln = π 2 o r po + 1 l n 1 + r 3 po 3 p r o p r o 703% 4σ x =
<<1 Q (1 + x)l ( n x + ) 1 ≈ (1+ )
x x ≈ x Q p r o 16σπr 2 A ≈ 2 3
7\6NO" 16σ r2 π σπ 2 40 r 2 A = A + A = 8σ r π + = 1 2 3 3 40. 0 , 0 . 4 1 , 3 . 4 , 0 07 2 A = ≈ , 8 2 1 . 0−2(J) 3
1" D$E€ !%L3X6 %L Th%L3X6
{j!"=3D8>?!-J#"DSDK
r~%D8=>;9FGNVC
!U%{j/"!%L∆S8
{ { j j () (-
RC&U%{j$ECr~%D3]Q{j=N#C
D6 Fa $E r -J ~ %D !' !-J r Q 3% r 3
$d~DG A = Fs = σl∆x = , 0 045. 1 , 0 . 5 , 0 04 = , 5 4 1 . 0−4(J)
" 0 € \d 3D 8 h%L 3X6 {j
!"!D+04NFG*+
!%L{j•3i64dD%4D3i6"!%L$E
$% Q 0 4N ! !-J # $E D
+ r ~ %D -. T DA
8=M;94D8=;9
nU4d~r-J=r-J~%D# $!VD (σ + σ FP 1 )S 2
D3 s0€\G* X$E4i/%%r-J~
%D# DSDKD+=}D3X6{j•6
!"4dDDSDKr~%D).?e^D
3X6{j•6 !"!\ _$QD Tr~ K ).
hS!iCr~%D#/-J-ID-A%
/-J /% " $0 ^6 + g / %D 2% " & +
(!T!-I38IgD6/.2%g
D8X6;-I6/EI8HBX60
8 /-J ^6 / r ~ %D # /-J %
W•#g/-J$•!V/.!-I$E!-I
#&+g
?&-J#"g/-J τ m ∆ m= FG t ∆
fgF$•!VG+S&A
(1) ∆ τ mg τ∆mg πσd = mg → σ = = t ∆ d π ∆t 3 − 6& 2 1 . . 0 10 . 8 , 9 σ = ≈ , 0 04N / m 1 , 3 4 2 . .10 3 − .780
1"J3X6$L!-I38=!-J/2%(!T?D
^6 !-J g $L 0 J 3X6 $L • ! " !%L
8=> n !i r # ~ %D $L +Y %
$&-J/Q#$L+D8<9 4DS2/E
W•#g$L$•!V/.!-I$E!-I
#J3X6$L 2
?&-J#$L!'%+ d π M = ρ h 4
?&-J#"g$L+ M d h 2 ρπ m = = FG k 4k
fgF$•!VG+S&A ( ) 1 2 ρπd h g ρ dh πσd = mg g →σ = = k 4 4k 6& 3 − g ρ dh 9300. 8 , 9 1 . 0 . , 0 205 σ = = ≈ 3 , 0 ( 9 N / m) 4k 4.12
" & % 3c !-I %D 38= " !V !-J $i
hV$i!!C"#6XF>G?&-J#
& % 3c 4D #6 X D = hV $i # & % 3c
/% -) n2 -) D -) %D %D & % 3c 4D -)
r ~ %D 8=H;9= & -J /Q 89
3
*05>
* F&%3cZ•XGi3]#Cr~%D4D/g
C-)S&=C{2-)Q=X$E0 d2 ( 4 π d σ + mg) σ d π + mg = ρπ h → h = 2 4 π g ρ d 4( 1 , 3 4. 0 , 0 73. , 0 003 + , 0 0002. 8 , 9 ) h = ≈ c 8 , 3 m 1 , 3 4.1000 9 . 8 , ( . , 0 00 ) 3 2
h T C r ~ %D= -I !O -) 4D% "
3X6$E-)•DJ-)!'!-J#")/‰W
#-)•3L0/K!-I38=*+d%
)#T-)!O4D%3X6D-)^6/2%W!Y
;-) K !g !-J /Q 3X6 D 3% C r ~ %D S L ~
% . Sb # 4K 3X6 4D -) ;-) • + S& T r
~%DNK!#T€€?! σ 2 4 4 0 . 0 , 73 g ρ h d π / 4 ≤ σ d π → h ≤ = ≈ 15(cm) ρgd 100 . 0 1 . 0 0 0 , 002
/%"&%3c!~(!T=!-I/%
"g-)*+&-J#g-)^-D%!
~$Q3-)#g-)DA~Ž=~(=~pY
!i D g -) • ! 3V ) !6 & % 3c h"
FŽG#~$Q3-)•yU.z~/QF~/QN
ND~V4)!-I$E!-I#&%3cG?&
-J#g-)D)!"%~$Q3-)D^=!
&-Jg-)!L)/i%D%!~D6•D~(=
)./iD6~/D~p πσd 1 , 3 . 4 , 0 073. , 0 001 m g = σ d π → m = = 3 , 2 4 1 . 0 5 − ≈ kg o o g 8 , 9 7\6QA • ?Œ 2 3 , 4 1 . 0 5
− kg ~$Q3-)D~Ž • ?8 2 3 , 4 1 . 0 5
− kg ~$Q3-)D~( • ?l 2 3 , 4 1 . 0 5
− kg ~$Q3-)D~p
* & % 3c !-I /% V -J D => 4D
b/%"$0!C+ T+
/%&%3cA
+!D-)
$ +!D#6X
?b&/%-)=-)•3XQh"3XQ#
-)/%q&D 4σ h = ρgd
* T+/%&%3cD σ 4 1 1 4. , 0 073 1 1 h ∆ = − = − ≈ ( 3 c ) m ρg d d 100 . 0 8 , 9 0 0 , 005 , 0 001 2 1
$ ?b & /%• X= • X /%&•L
S&h"LS&#•X/%q&DX$E
€ • } 4D ] %! $Q/%
+6L~ 2σ 4σ g ρ h = → h = d / 2 ρgd
* T+/%&%3cD 4σ 1 1 4. , 0 5 1 1 h ∆ = − = − ≈ , 1 5(cm) ρg d d 13600. 8 , 9 0 0 , 005 , 0 001 2 1
1"&!-Jb(!T/%"$03C+*+
d%#"-)/%&6!O-D%&%
3c4D$0!-JXQ3V!d4)&./Y*LS&
3V!d4)&./012 A
?$04D&!-JXQ4)&=#!$Q/%
& ~ % + %D & $% p e6=
•}#"-)=]X6$~4DX6/
3%CeD6/i$EL€!
$E4)%D& p p = p − p + o o ρ gh + ργ h → h = p p ρ (g + γ )
?&%3c4D$0N6!"Fγ = 0 G0 p p h = o ρg x%!A h g = h g +γ o
?XQγ = g h 1 = h 2 o
?LS&Aγ = g − / 2 h = 2 h o
& % 3c p 4D% = !p /]= b ( !T
4D%"$0-)h-I/%#&%3c+=$E$d
/"#2L%Q€&%3cj+e$d3D6#&
% 3c /% *+T + /% & D% % .=% .
$%QVY
h"3X#-)/%&%3c/% 4σ h =
F3D!-I/%#&%3c/%G 1 ρgd
h-I/%#&%3c%D2%^!-JD3h"
3X#-)/%&%3c%DD?X$EOCr~
%D !-I Sb € ~ % # -) 4) & % 3c
/%4D%DF(!T-)QG$E/gC#"-)3XQ
F(!T-)S&G 2 σ σ d π + σπ d 3 = (π( d 3 ) / 4 − d 2 π / 4) 2 h g ρ → h = 2 2 g ρ d x%! h1 = 2 h 2
7 8 9 ' : ; $< = >% & ? @A B )C 9 @ 0' & I& ργ " )J 8 A K :A LM 9 I& ργ " $< : 8 B' &' A
7\6 -) 3XQ /% & %3c /% % . V %4) !"3X
#y2z%3c€&
#6 ( !~ %% " %^
38== b ( !T 4D% /% " + n !i
&-J/Q#+!$/Ed%#&
+€#63XQ"!%L8=P
r ~%D#+D =H;9n2+D-)
%D%D#6
h"3X#T+/%&D= 2σ 2. , 0 027 2bσ = hdbρg → ρ = = ≈ 86 ( 3 1 kg / m ) ghd 8 , 9 . , 0 032. , 0 0002
* T#6X/%#&%3c0€w
!-I/%384D38D∆8n!i
r~%D##6X%$& -J/Q##6
XD=M 9
X$E%!63-)~X#) 4σ 4σ ρg∆hd d 1 2 = + ρg h ∆ →σ = d d 4 d − d 1 2 ( 2 1 ) 1360 . 0 8 , 9 . , 0 0 . 1 , 0 001. , 0 002 σ = ≈ , 0 67(N / m) 4(0 0 , 02 − , 0 001)
?&-J/Q#N/%"$%$3-)!6
#"p -)XM) >V &-J/Q#N
e6F !"$E !" !6pG n!i $
$%$
fg$#$%$D:=$Q/%$%$DA σ = + + ρ FG
q-./012!Q225Q/N6/&-J/Q#$Q
/%4D$Q%D$%$V-JD p µ p µ ρ = 4D o ρ = RT o RT q! ρ p n = = FG ρ p o o
6FG4D%FG 2σ g ρ h 2σ n 1 = + + →r = p r p (n− ) 1 p − ρgh o o o 6&A 2. , 0 073 r = = 0,4 m µ (5− ) 1 1 . 05 −1000. 8 , 9 .6
/Q~-)-I!"$N")u+F!
%+$i-)D-)G?!-I)D$%Q
!!-J€/Q~-)DN$i0S&3-)Y
%$&-J/Q#UDD8H=H9
h N $i 0 0 3%/% -J # L ~ Sb
€4D-)^+.X6/$~ %#-)4D
3%C!t6{23]Q S 2 ≤ rl σ mg − F − ρ / 2 ρ A mg ( m ) l r g ≥ ≥ FG r S rl 2
/%!33
TCD$=d3D=&-J/Q#4D 3
#-)K&-.#A m πr 2 = lρ r FG
6FG4D%FG 16σ 16. , 0 073 2r = d ≤ π( = ≈ 2ρ − ρ − r )g 1 , 3 4 (.2.7,7 ) , 1 6mm 1 9 . 8 , .103 l *
m m µp N pV = RT → ρ = = µ V RT
/%e/0!%L Q
δ = 0 → pdV + nC dT = 0 F,G V
* &!%L Cp C + R R R γ γ = = V → C = kC = F,G C C V γ − p γ − V V 1 1
4D%FG=4D-v-./012322245/6/%
pV = nRT → pdV + Vdp =nRdT % 1 pdV + (pdV + Vdp) = 0 γ − 1 → pdV + Vdp = 0 → d(pVγ γ )= 0 *6 pVγ = const
hX6D-./0%e/0!%L
*6a4 pV γ = (pV) γ−1 V = nR ( γ−1 TV ) → TVγ−1 = const F,G γ (pV)γ γ pV = (nR)γ Τ = → p1−γ Tγ = const F,G γ −1 γ −1 p p
N/%e/0!%L ( ) 2 1 A = − U ∆ = − nC T ∆ = − nR∆T V γ − 1 x% nR T ∆ = n ( R T − T ) = p V − p V 2 1 2 2 1 1 ;Q p V − p V A 1 1 2 2 = F,>G γ − 1
a4 γ − ( )3 1 1 T p V V 2 1 1 1 A = nRT 1 1 F,MG 1 − = − γ − 1 T γ − 1 V 1 2 •
!"#$ %&'( )'('
,-./0732…%"%C a RT a p + ( V − b) = RT → p = − V 2 2 V − b V L!$ RT a k p = − F,HG k 2 V − b V k k
p ∂ RT 2a RT 2a k k = 0 → − + = 0 → = F,BG ∂V = V − b V V − b V V 0 k ( k )2 3 k ( k )2 3 k 2 ∂ p 2RT 6a RT a 3 k k = 0 → − = 0 → = F,2 V ∂ (V − b V V − b V k )3 4 k ( k )3 4 k V =0 k F, V = F,G k b 3
F,G4D%F,HG\!-J RT a a k p = V − b − → p = F,G k ( k ) (V − b V 27b k ) k 2 2 2 k
qF,G4DF,BG\!-J a 8 T = F,G k 27bR
E&732…
qF,HG4DF,BG RT a 2 V RT k k k p = − → b = F,G k 3 V − b V 2 8p k k k
*E&!-J0qF,G4DF,G 2 2 2 27R Tk a = 27b p = F,G k 64pk ‹‹‹*‹‹‹