lOMoARcPSD| 40651217 lOMoAR cPSD| 40651217
Bài tập Kiến trúc máy tính
1. Cho hệ thống bn cache gồm 256 đường, sử dụng ánh xạ trực tiếp. Xác định khối 432
được ánh xạ vào đường nào? Giải:
Ánh xạ trực tiếp 256 đường, khối 432 sẽ được ánh xạ vào đường Li với: i = 432%256 => i = 176
2. Cho hệ thống bn cache gồm 256 đường, sử dụng ánh xạ tập kết hợp 4 đường. Xác
địnhkhối 267 được ánh xạ vào đường nào? Giải:
Ánh xạ tập kết hợp 4 đường => k = 4
=> số tập: v = 256/4 = 64
=> Khối 267 được ánh xạ vào tập: i = 267%64 = 11
=> khối 267 được ánh xạ vào tập 11 gồm các đường 44, 45, 46, 47
3. Cho hệ thống bn cache gồm 512 đường, kích thước mỗi đường là 64B. Tính dung lượng BN cache Giải: Dung lượng BN Cache: 512 x 64 = 32768B = 32kB
5. Cho chip RAM có 20 chân địa chỉ, kích thước ngăn nhớ là 2B. Tính dung lượng Chip RAM Giải:
(số ô nhớ = 2^N | N: số chân địa chỉ)
20 chân địa chỉ => 2^20 ô nhớ
Dung lượng BN: 2^20 x 2 = 2^21 B = 2048 kB = 2MB lOMoARcPSD| 40651217
6. Cho chip RAM có 30 chân địa chỉ, kích thước ngăn nhớ là 2B. Tính dung lượng Chip RAM Giải:
30 chân địa chỉ => 2^30 ô nhớ
Dung lượng BN: 2^30 x 2 = 2^31 B = 2GB
7. Với mã Hamming SEC, tính số bit mã K cho từ dữ liệu M 16bGiải:
từ mã K (k bit), k=log2m+1 k = 5 bit
8. Với mã Hamming SEC-DEC, tính số bit mã K cho từ dữ liệu M 32bGiải: k=log2m+2 => k = 7 bit 9. Ổ
cứng HDD gồm 4 đĩa 2 mặt, tính số đầu đọc/ghi Giải:
4 đĩa 2 mặt => 8 đầu đọc/ghi
10. Ổ cứng HDD gồm 6 đĩa 2 mặt, tính số track trong một cylinder.
11. Biểu diễn các số hệ 16 sau dưới dạng nhị phân
a. A125 -> 1010 0001 0010 0101
b. 125A.3 -> 1 0010 0101 1010. 0011
c. 1104.E -> 1 0001 0000 0100. 111
d. 54BCD -> 101 0100 1011 1100 1101 e. 1.AE -> 1. 1010 111
12. Biểu diễn số hệ nhị phân sau sang hệ 16: a. 1110.11101 -> E.E8 b. 10101.01 -> 15.4 c. 1110001101 -> 38D lOMoARcPSD| 40651217 d. 101011111.11 -> 15F.C 13.
Cho các số hệ nhị phân sau, tính trọng số của các chữ số đầu tiên và cuối cùng của các số đó
Trọng số: r^i (r: hệ đếm, i: vị trí) a. 1110.11101 2^3 = 8 2^(-5) = 0.03125 b. 10101.01 2^4 = 16 2^(-2) = 0.25 c. 1110001101 2^9 = 512 2^0 = 1 d. 101011111.11 2^8 = 256 2^(-2) = 0.25 14.
Cho các số hệ bát phân sau, tính trọng số của các chữ số đầu tiên và cuối cùng của cácsố đó a. 1325.7 8^3 = 512 8^(-1) = 0.125 b. 203.5 8^2 = 64 8^(-1) = 0.125 c. 2734 8^3 = 512 8^0 = 1 d. 11.65 8^1 = 8 8^(-1) = 0.015625 e. 2354.5 lOMoARcPSD| 40651217 8^3 = 512 8^(-1) = 0.125
15. Cho các số hệ thập lục phân sau, tính trọng số của các chữ số đầu tiên và cuối cùng của các số đó a. A125 16^3 = 4096 16^0 = 1 b. 125A.3 16^2 = 256 16^(-1) = 0.0625 c. 1104.E 16^3 = 4096 16^(-1) = 0.0625 d. 54BCD 16^4 = 65536 16^0 = 1 e. 1.AE 16^0 = 1 16^(-2) = 3.90625 x 10^(-3) 16.
Tính phạm vi biểu diễn (miền giá trị) của các dạng biểu diễn dấu độ lớn-nb và bù 2nb. Giải:
Miền giá trị của biểu diễn dấu độ lớn – n bit :
−(2n−1−1)→(2n−1−1) −(2^(n-1) - 1)
Miền giá trị của biểu diễn bù 2 – 10 đến +(2^(n-1) - 1)10 n bit: lOMoARcPSD| 40651217
−(2n−1)→(2n−1−1)
−(2^(n-1) )10 đến +(2^(n-1) - 1)10 17.
Mã Hamming SEC có syndrome khi đọc dữ liệu ra là: 0110. Hỏi dữ liệu đọc ra có
lỗi hay không và nếu có thì lỗi ở vị trí nào? Giải: Lỗi. Lỗi ở vị trí 6 18.
Mã Hamming SEC có syndrome khi đọc dữ liệu ra là: 0100. Hỏi dữ liệu đọc ra có
lỗi hay không và nếu có thì lỗi ở vị trí nào?
Giải: Lỗi ở bit check nên không cần sửa 19.
Mở rộng phạm vi biểu diễn của các số dạng dấu độ lớn 4b sau thành dạng biểu diễn 8b: a. 1101 Giải:
1101 (4b) -> 1000 0101 (8b) b. 0010 Giải:
0010 (4b) -> 0000 0010 (8b) c. 1111 Giải:
1111 (4b) -> 1000 0111 (8b) d. 0101 Giải:
0101 (4b) -> 0000 0101 (8b) e. 1110 Giải:
1110 (4b) -> 1000 0110 (8b) f. 1011 Giải:
1011 (4b) -> 1000 0011 (8b) lOMoARcPSD| 40651217
20. Mở rộng phạm vi biểu diễn của các số dạng bù 2 4b sau thành dạng biểu diễn 8b: a. 1101 Giải: Hộp giá trị: -8 4 2 1 1 1 0 1 => 1101 = -8 + 4 + 1 = -3 3 = 0000 0011 Bù 1: 1111 1100 Cộng 1: -3 = 1111 1101
Vậy: 1101(bù 2-4b) -> 1111 1101(bù 2-8b) b. 0010 Giải: Hộp giá trị: -8 4 2 1 0 0 1 0 => 1101 = 2 2 = 0000 0010
Vậy: 0010 (bù 2-4b) -> 0000 0010 (bù 2-8b) c. 1111 Giải: Hộp giá trị: -8 4 2 1 1 1 1 1
=> 1101 = -8 + 4 + 2 + 1 = -1 1 = 0000 0001 lOMoARcPSD| 40651217 Bù 1: 1111 1110 Cộng 1: -1 = 1111 1111
Vậy: 1111 (bù 2-4b) -> 1111 1111 (bù 2-8b) d. 0101 Giải: Hộp giá trị: -8 4 2 1 0 1 0 1 => 1101 = 4 + 1 = 5 5 = 0000 0101
Vậy: 0101 (bù 2-4b) -> 0000 0101 (bù 2-8b) e. 1110 Giải: Hộp giá trị: -8 4 2 1 1 1 1 0 => 1101 = -8 + 4 + 2 = -2 2 = 0000 0010 Bù 1: 1111 1101 Cộng 1: -2 = 1111 1110
Vậy: 1110 (bù 2-4b) -> 1111 1110 (bù 2-8b) f. 1011 Giải: Hộp giá trị: -8 4 2 1 lOMoARcPSD| 40651217 1 0 1 1 => 1101 = -8 + 2 + 1 = -5 5 = 0000 0101 Bù 1: 1111 1010 Cộng 1: -5 = 1111 1011
Vậy: 1011 (bù 2-4b) -> 1111 1011 (bù 2-8b)
21. Đổi dấu các số bù 2 8b sau: a. 1110 0101Giải: Bù 1: 0001 1010 Cộng 1: 0001 1011
=> Đổi dấu ta được: 0001 1011 b. 0111 0000Giải: Bù 1: 1000 1111 Cộng 1: 1001 0000
=> Đổi dấu ta được: 1001 0000 c. 1101 0001 Giải: Bù 1: 0010 1110 Cộng 1: 0010 1111
=> Đổi dấu ta được: 0010 1111 lOMoARcPSD| 40651217 d. 1000 0000Giải:
Số đối vượt quá phạm vi biểu diễn của phép bù 2-8b
1000 0000 (bù 2-8b) -> 1111 1111 1000 0000 (bù 2-16b) Bù 1: 0000 0000 0111 1111 Cộng 1: 0000 0000 1000 0000
=> Đổi dấu ta được: 0000 0000 1000 0000
22. Thực hiện phép toán của các số nguyên dạng bù 2 như sau: a. 1000 1000 – 0011 b. 1100 0001+1100 1111 c. 0110 1101-1000 1101
d. 0100 0001+0011 1111Giải: a. 1000 1000 – 0011 0011 -> 0000 0011 1000 1000 – 0000 0011 Xét: 0000 0011 Bù 1: 1111 1100 Cộng 1: 1111 1101 – 0000 0011 = 1111 1101
1000 1000 – 0000 0011 = 1000 1000 + 1111 1101 = 1000 0101
Vậy: 1000 1000 – 0011 = 1000 0101
b. 1100 0001+1100 1111 = 1001 0000 c. 0110 1101 - 1000 1101 Xét: 1000 1101 Bù 1: 0111 0010 lOMoARcPSD| 40651217 Cộng 1: 0111 0011 – 1000 1101 = 0111 0011
0110 1101 - 1000 1101= 0110 1101 + 0111 0011 = 1110 0000
Không có kết quả vì phép tính trả về giá trị có dấu ngược với 2 số hạng
d. 0100 0001+0011 1111 = 10000000
Không có kết quả vì phép tính trả về giá trị có dấu ngược với 2 số hạng
23. Tính giá trị của số biểu diễn dạng bù 2 sau: a. 1101Gi ải: Hộp giá trị: -8 4 2 1 1 1 0 1 => -8 + 4 + 1 = -3 Vậy: 1101 = -3 b. 1110 0001Giải: Hộp giá trị: -128 64 32 16 8 4 2 1 1 1 1 0 0 0 0 1
=> -128 + 64 + 32 + 1 = -31 Vậy: 1110 0001 = -33 c. 0000 1111 Giải: Hộp giá trị: -128 64 32 16 8 4 2 1 0 0 0 0 1 1 1 1 lOMoARcPSD| 40651217 => 8 + 4 + 2 + 1 = 15 Vậy: 0000 1111 = 15 d. 1000 1111Giải: Hộp giá trị: -128 64 32 16 8 4 2 1 1 0 0 0 1 1 1 1
=> -128 + 8 + 4 + 2 + 1 = -113
Vậy: 1000 1111 = -113 e. 0101Gi ải: Hộp giá trị: -8 4 2 1 0 1 0 1 => 4 + 1 = 5 Vậy: 0101 = 5
24. Biểu diễn các số sau sang dạng dấu độ lớn 8b và bù 2 8b a. 34 c. 101 e. 76 b. -23 d. -101 f. -73 Giải: a. 34
- Dấu- độ lớn 8b: 34 = 0010 0010 - Bù 2-8b: 34 = 0010 0010 b. -23
- Dấu- độ lớn 8b: lOMoARcPSD| 40651217 23 = 10111 -23 = 1001 0111 - Bù 2-8b:
23 = 10111 -> 0001 0111 (8b) Bù 1: 1110 1000 Cộng 1: 1110 1001 -23 = 1110 1001 c. 101
- Dấu- độ lớn 8b: 101 = 0110 0101 - Bù 2-8b: 101 = 0110 0101 d. -101
- Dấu- độ lớn 8b: 101 = 1100101 -101 = 1110 0101 - Bù 2-8b:
101 = 1100101 -> 0110 0101 (8b) Bù 1: 1001 1010 Cộng 1: 1001 1011 -101 = 1001 1011 e. 76
- Dấu- độ lớn 8b: 76 = 0100 1100 - Bù 2-8b: 76 = 0100 1100 f. -73
- Dấu- độ lớn 8b: 73 = 1001001 lOMoARcPSD| 40651217 -73 = 1100 1001 - Bù 2-8b:
73 = 1001001 -> 0100 1001 (8b) Bù 1: 1011 0110 Cộng 1: 1011 0111 -73 = 1011 0111
25. Phép nhân hai số bù 2-8b sử dụng thuật toán Booth cần bao nhiêu vòng lặp 8 vòng lặp
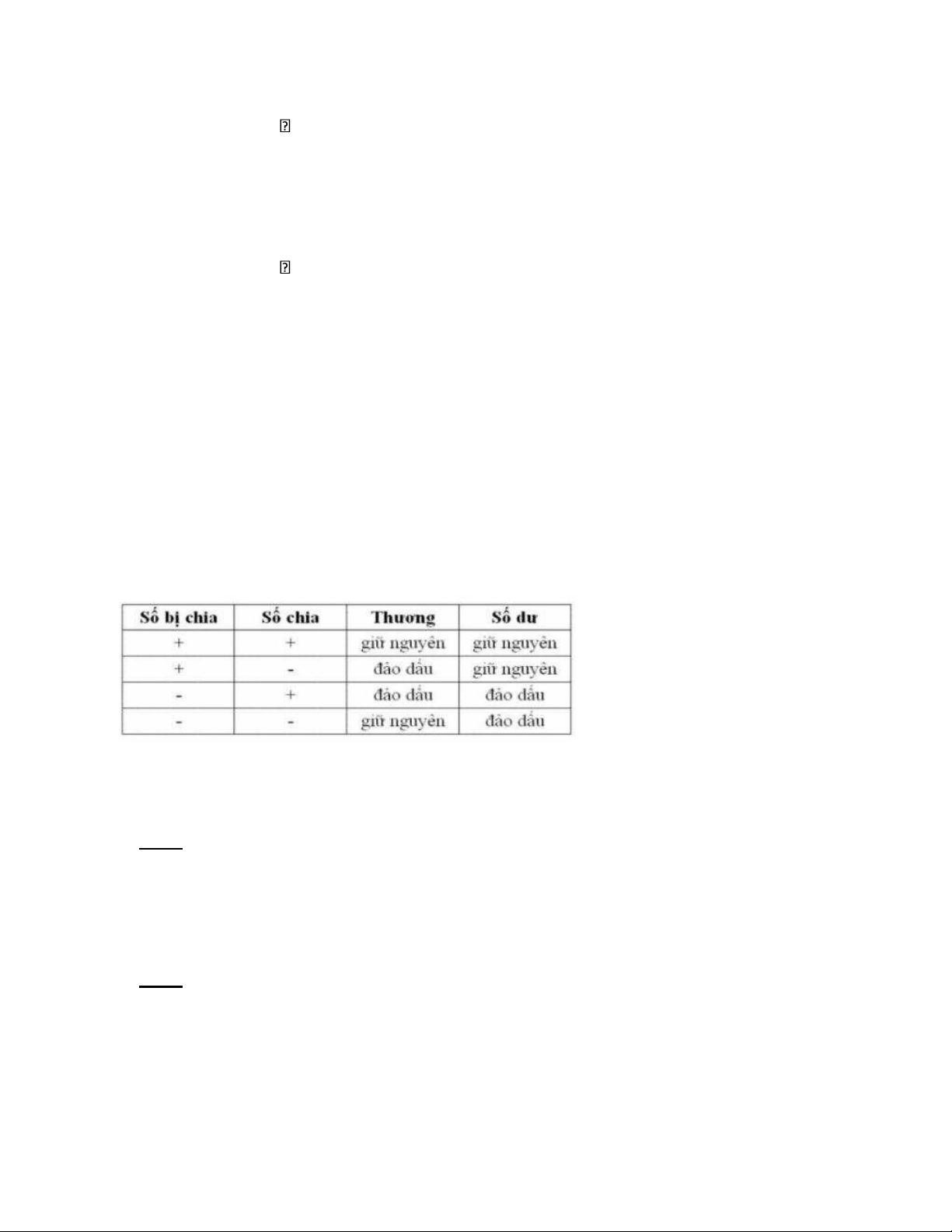
26. Phép chia hai số bù 2-8b cần hiệu chỉnh kết quả như thế nào trong các trường hợp sau:
a. Số bị chia dương, số chia âm
b. Số bị chia âm, số chia dương
c. Cả hai số cùng dương d. Cả hai số cùng âm
27. Tính toán độ lệch của dạng biểu diễn số nhị phân dấu chấm động 32b, với 8b phần mũ Giải: Độ lệch: 2^7 -1 = 127
28. Tính toán độ lệch của dạng biểu diễn số nhị phân dấu chấm động 64b, với 11b phần mũ Giải: Độ lệch: 2^10 -1 = 1023 lOMoARcPSD| 40651217
29. Tính toán độ lệch của dạng biểu diễn số nhị phân dấu chấm động 128b, với 15b phần mũ Giải: Độ lệch: 2^14 -1 = 16383
30. Biểu diễn các số sau dưới dạng số nhị phân dấu chấm động 32b a. 34.25 Giải:
34.25 = 100010.01 = 1.0001001 x 2^5 S: 0 E: 5 + 127 = 132 = 1000 0100 M: 00010010000000000000000
S E M: 0100 0010 0000 1001 0000 0000 0000 0000
Vậy: 34.25 = 0100 0010 0000 1001 0000 0000 0000 0000 b. 74.125 Giải:
74.125= 1001010.001= 1.001010001 x 2^6 S: 0 E: 6 + 127 = 133 = 1000 0101 M: 00101000100000000000000
S E M: 0100 0010 1001 0100 0100 0000 0000 0000
Vậy: 74.125= 0100 0010 1001 0100 0100 0000 0000 0000 c. 69.375 Giải:
69.375= 1000101.011= 1.000101011 x 2^6 lOMoARcPSD| 40651217 S: 0 E: 6 + 127 = 133 = 1000 0101 M: 00010101100000000000000
S E M: 0100 0010 1000 1010 1100 0000 0000 0000
Vậy: 69.375= 0100 0010 1000 1010 1100 0000 0000 0000 d. 112.5 Giải:
112.5 = 1110000.1= 1.1100001x 2^6 S: 0 E: 6 + 127 = 133 = 1000 0101 M: 11000010000000000000000
S E M: 0100 0010 1110 0001 0000 0000 0000 0000
Vậy: 112.5 = 0100 0010 1110 0001 0000 0000 0000 0000 e. 45.625 Giải:
45.625= 101101.101= 1.01101101 x 2^5 S: 0 E: 5 + 127 = 132 = 1000 0100 M: 01101101000000000000000
S E M: 0100 0010 0011 0110 1000 0000 0000 0000
Vậy: 45.625= 0100 0010 0011 0110 1000 0000 0000 0000
31. Xác định giá trị các số biểu diễn dạng nhị phân dấu chấm động 32b như sau:
a. 1100 0001 1110 1100 0000 0000 0000 0000Giải: lOMoARcPSD| 40651217 S E M 1 1000 0011 11011 - Dấu: -
- E: 1000 0011 = 131 => 132 -127 = 4 => Số mũ: 4
- M: 11011 . Số mũ = 4 => 1101.1
=> Giá trị: -11101.1 = -29.5
Vậy: 1100 0001 1110 1100 0000 0000 0000 0000 = -29.5
b. 0100 0001 1001 1100 0000 0000 0000 0000Giải: S E M 0 1000 0011 00111 - Dấu: +
- E: 1000 0011 = 131 => 132 -127 = 4 => Số mũ: 4
- M: 00111 . Số mũ = 4 => 0011.1
=> Giá trị: 10011.1 = 19.5
Vậy: 0100 0001 1001 1100 0000 0000 0000 0000 = 19.5
c. 1011 1101 1110 0100 0000 0000 0000 0000Giải: S E M 1 0111 1011 11001 - Dấu: -
- E: 0111 1011 = 123 => 123 -127 = -4 => Số mũ: -4 - M: 11011 . Số mũ = -4
=> Giá trị: -1.11001 x 2^-4 = -0.0001 1100 1000 = -0.111328125
Vậy: 1011 1101 1110 0100 0000 0000 0000 0000= -0.111328125
d. 0011 1110 0110 1100 0000 0000 0000 0000Giải: lOMoARcPSD| 40651217 S E M 0 0111 1100 11011 - Dấu: +
- E: 0111 1100 = 124 => 124 -127 = -3 => Số mũ: -3 - M: 00111 . Số mũ = -3
=> Giá trị: 1.00111 x 2^-3 = 0.0010 0111 = 0.15234375
Vậy: 0011 1110 0110 1100 0000 0000 0000 0000 = 0.15234375