















Preview text:
BÀI T P L N MÔN: TRÍ TU NHÂN T O
ĐỀ TÀI: AKT ĐỂ TÌM ĐƯỜNG ĐI TỐI ƯU CHO CẤU TRÚC CÂY Sinh viên thực hi n: 1. Trịnh Minh Châu. 2. Tr n Thị Minh Hải. 3. Nguy n Bá Nguy n. 4. Vũ Quý Thăng. 5. Ph m Trọng Toàn.
Giảng viên hư ng d n: Ths Tr n Hùng Cư ng. 1
L I NÓI Đ U....................................................................................................3
Phân tích bài toán................................................................................................4
Mục đích bài toán............................................................................................4
Cách làm. .......................................................................................................5
C u trúc dữ li u và cách biểu di n tr ng thái của bài toán .....................................7
L p khai báo đối tượng ...................................................................................7
Hàm t o m u chuỗi nh p vào ...........................................................................8
Hàm xử lý chuỗi nh p vào ..............................................................................9
Hàm xác định tọa đ cho các nút vẽ ............................................................... 11
Hàm vẽ đồ thị ............................................................................................... 12
Hàm giải thu t AKT ...................................................................................... 13
Các hàm cho giải thu t .................................................................................. 15
Giao di n chương trình...................................................................................... 19
Tài li u tham khảo ............................................................................................ 20 2 LỜI NÓI ĐẦU Trí tu là gì?
Theo từ điển Bách khoa toàn thư Webster: Trí tu là khả năng:
Phản ứng thích hợp l i những tình huống m i thông qua điều chỉnh hành vi m t cách thích hợp.
Hiểu rõ mối liên h giữa các sự ki n của thế gi i bên ngoài nhằm đưa ra
những hành vi phù hợp để đ t được mục đích.
V y trí tu nhân t o là gì?
Thu t ngữ trí tu nhân t o(Artifical Intel egence) được Jonh McCarthly đưa ra
trong h i thảo ở Darthouth vào mùa hè năm 1956. Đã có r t nhiều định nghĩa khác
nhau về trí tu nhân t o. V i trí tu nhân t o, máy tính đã giúp con ngư i giải
quyết các v n đề m t cách thông minh nh t. Ta sẽ tìm hiểu m t số phương pháp
giải quyết v n đề cơ bản. Cụ thể là phương pháp tìm kiếm trong không gian tr ng thái v i thu t giải AKT. 3
1. Phân tích bài toán.
1.1. Mục đích bài toán.
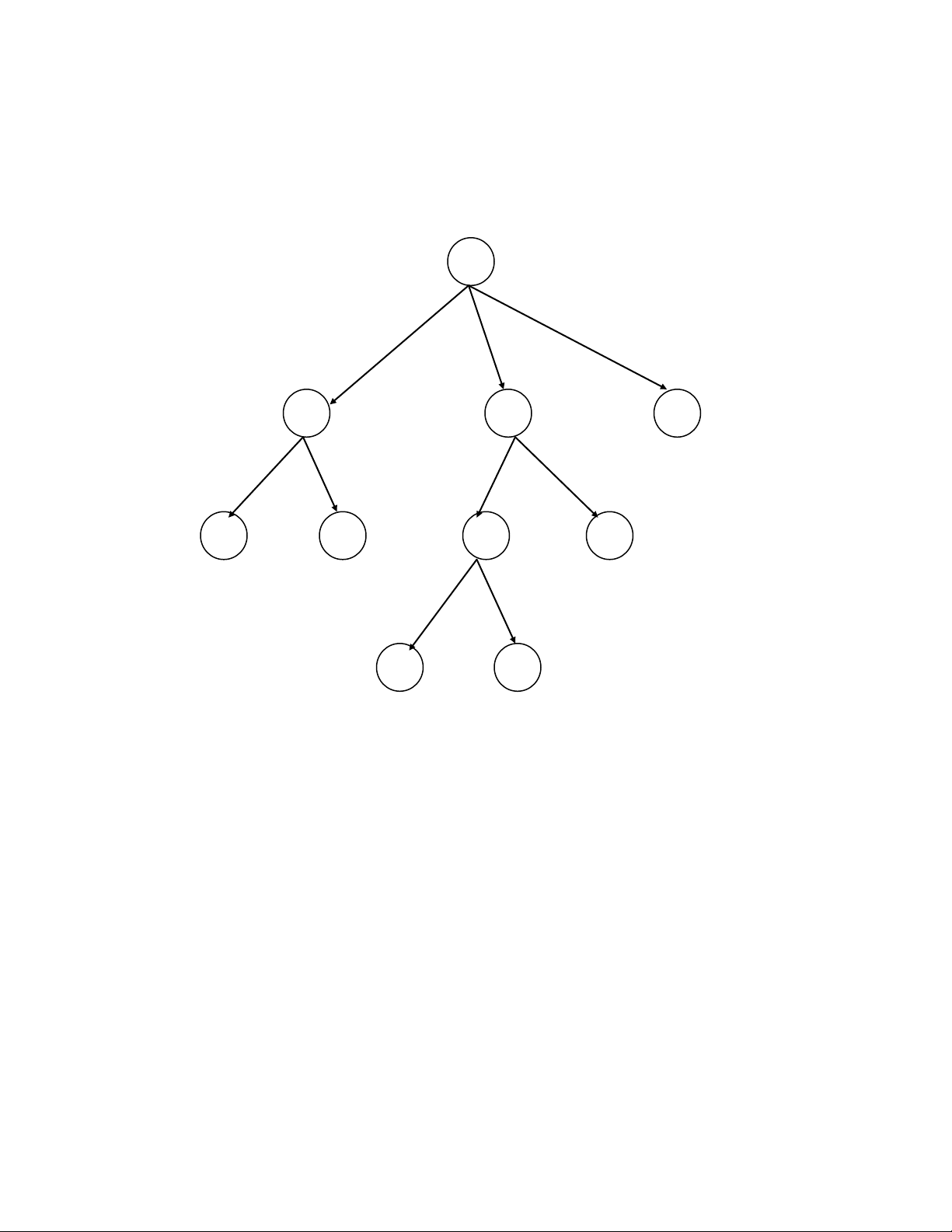
Giả sử ta có m t đồ thị d ng cây như hình vẽ: A B C D E F G H I J
Ta c n tìm đư ng đi từ điểm A J. Biết g(n) là chi phí thực từ n 0 n.
Thu t giải AKT là mở r ng của thu t giải AT bằng cách sử dụng thêm thông tin ư c lượng h(n).
Thu t giải AT là thu t giải tìm đư ng đi tối ưu mà nó chỉ xét đến đỉnh và giá của
chúng (g). Tuy nhiên giải thu t này không còn phù hợp khi gặp phải những bài
toán phức t p do phải tháo m t lượng nút l n(có kích thư c bài toán tăng theo hàm
mũ từ đó d n đến bùng nổ về tổ hợp) để khắc phục nhược điểm này ngư i ta sử
dụng thêm các thông tin bổ sung xu t phát từ bản thân bài toán để tìm ra các đỉnh
có triển vọng, tức là đư ng đi tối ưu sẽ t p trung xung quanh đư ng đi tốt nh t nếu
sử dụng các thông tin đặ tả về bài toán. 4
V y theo định nghĩa các thông tin này được gọi là các Heuristics: h(n) hay chính là
chi phí ư c lượng từ n G.
Các kỹ thu t sử dụng h(n) gọi là các mẹo giải, ta có thể đưa ra các mẹo giải sau:
- Chọn toán tử xây dựng cung sao cho có thể lo i b t các đỉnh không liên
quan và tìm ra các đỉnh có triển vọng.
- Sử dụng thêm các thông tin bổ sung nhắm xây dựng t p MO và cách l y các đỉnh trong t p MO.
Để làm được vi c này, ngư i ta phải đưa ra đ đo, tiêu chuẩn đề tìm ra các điểm
triển vọng. Các hàm sử dụng các kỹ thu t này gọi là hàm đánh giá. Sau đây, ta đưa
ra m t số phương pháp xây dựng hàm đánh giá:
- Dựa vào xác su t của đỉnh trên đư ng đi tối ưu.
- Dựa vào khoảng cách, sự sai khác của tr ng thái đang xét v i tr ng thái đích
hoặc các thông tin liên quan t i tr ng thái đích.
Để tìm được phương án tối ưu ta sử dụng đ i lượng hàm ư c lượng f(n) và
f(n)= g(n)+ h(n) là đ tốt của l i giải. 1.2. Cách làm. Thuật giải AKT Bước 1:
- Mọi đỉnh, cũng như các hàm g, h, f chưa biết.
- Mở đỉnh đ u tiên S, gán g(S) = 0
- Sử dụng tri thức bổ sung để ư c tính hàm h(S) - Tính f(S) = g(S) + h(S)
Bước 2: Chọn đỉnh mở có f là nhỏ nh t và gọi là đỉnh N
- Nếu N là đích: đư ng đi từ đỉnh ban đ u đến đỉnh N là ngắn nh t và
và bằng g(N). Dừng (Success).
- Nếu không tồn t i đỉnh mở nào: cây biểu di n v n đề không tồn t i
đư ng đi t i mục tiêu. Dừng (Fail).
Nếu có 2 đỉnh mở trở lên có cùng giá trị f nhỏ nh t: Chúng ta phải kiểm tra
xem những đỉnh đó có đỉnh nào là đích hay không. 5
o + Nếu có: đư ng đi từ đỉnh ban đ u đến đỉnh N là ngắn nh t và bằng g(N). Dừng (Success).
o + Nếu không có: chọn ng u nhiên m t trong các đỉnh đó và gọi đỉnh đó là N. Bước 3:
- Đóng đỉnh N, mở mọi đỉnh sau N. V i mỗi đỉnh S sau N, tính: - g(S) = g(N) + cost(SN)
- Sử dụng tri thức bổ sung để tính h(S) và f(S): f(S) = g(S) + h(S) Bước 4: - Quay l i bư c 2.
Thủ tục tìm kiếm: Vào:
- Đồ thị G =(N,A) trong đó N là t p đỉnh, A là t p cung.
- f : N R+ (f là hàm ư c lượng).
- Đỉnh đ u là n0 và t p các đỉnh ĐICH. Ra: - Đư ng đi p: n 0 nk ĐICH.
ư : Sử dụng 2 danh sách M và D NG
{MO = {n0}; tính f(n0) = g(n0) + h(n0) While M ≠ do
{n getmoi(MO) // L y đỉnh n sao cho f(n) min DONG = DONG U{n}
If n DICH then exit (“thành công”) If B(n) ≠ then For each m B(n) do 6 If m MO DONG then { MO =MO {m} Tính f(m) }
Else if fcu(m) >fmoi(m) then MO = MO {m} }
Write(“không thành công”) }
2. Cấu trúc dữ liệu và cách biểu diễn trạng thái của bài toán
1. Lớp khai báo đối tượng class Nut { protected string _Ten; private int _G; private int _H; protected int _ID; protected int _IDcha;
public Nut(int id, int idcha, string ten, int g, int h) { _ID = id; _IDcha = idcha; _G = g; _H = h; _Ten = ten; } public string Ten { get { return _Ten; } set { _Ten = value; } } public int G { get { return _G; } set { _G = value; } } public int H 7 { get { return _H; } set { _H = value; } } public int ID { get { return _ID; } set { _ID = value; } } public int IDcha { get { return _IDcha; } set { _IDcha = value; } } public Object Tag; }
Giải thích: class này dùng để khai báo các đối tượng của nút _Ten : Tên nút _ID : Mã nút _IDcha : Mã nút cha _G : g _H : h
2. Hàm tạo mẫu chuỗi nhập vào
//Tạo một mẫu mặc định
public string TaoCayGia(int maxLen, string title) { int ser = 0,ser1=0,ser2=1; string text = "";
text = "ID\tID Cha\tTên Nut\tG\tH";
text += "\r\n_______\t_______\t_______\t_______\t_______";
for (int i = 0; i < maxLen; i++) {
ser = rdNumber(maxLen, i, ser); ser1 = rdNumber(5, i, ser1);
ser2 = rdNumber(58, i, ser2);
text += string.Format("\r\n{0}\t{1}\t{2}{0}\t{3}\t{4}", i + 1, i > 0 && (i +
ser) <= 0 ? i : (i + ser), title, i > 0 && (i +
ser1) <= 0 ? i : (i + ser1), 8 i > 0 && (i +
ser2) <= 0 ? i : (i + ser2)); } return text; } //tạo lấy số
private int rdNumber(int max, int i, int last) { int avr = max / 2; int mod = i % avr; int range = (mod - i) / avr;
last += (range + (last % 2)); return last; }
3. Hàm xử lý chuỗi nhập vào
//Xử lý chuỗi nhập vào
public TreeNode TaoCayTuChuoi(string text) {
//loại bỏ các ký tự xuống dòng
string[] lines = text.Split(new char[] { '\r', '\n' },
StringSplitOptions.RemoveEmptyEntries);
//trả về mảng chuỗi vẫn còn các ký tự tab return TaoCayTuChuoi(lines); }
public TreeNode TaoCayTuChuoi(string[] lines) {
//Bỏ qua 2 dòng đầu chứa các tiêu đề if (lines.Length <= 2) return null;
TreeNode trNodes = new TreeNode();
SortedList sortnodes = new SortedList();
for (int id = 2; id < lines.Length; id++) { string line = lines[id]; char[] tab = { '\t' };
//cắt chuỗi ở vị trí tab
string[] chuoi = line.Split(tab, StringSplitOptions.RemoveEmptyEntries);
//cắt khoảng trắng ở đầu cuối các chuỗi
chuoi[0].Trim(); chuoi[1].Trim(); chuoi[2].Trim(); chuoi[3].Trim(); chuoi[4].Trim(); TreeNode curNode = null;
try { curNode = sortnodes[chuoi[0]]; }
catch (Exception) { curNode = null; } if (curNode == null) {
curNode = new TreeNode(chuoi[2]);
sortnodes.Add(chuoi[0], curNode); } curNode.Text = chuoi[2]; //them nut 9
curNode.Tag = new Nut(int.Parse(chuoi[0]), int.Parse(chuoi[1]),
curNode.Text, int.Parse(chuoi[3]), int.Parse(chuoi[4])); //kiểm tra trùng tên
//if (kiemtratennut(chuoi[2])) break; // thêm vào mảng
addnode(int.Parse(chuoi[0]), int.Parse(chuoi[1]), curNode.Text,
int.Parse(chuoi[3]), int.Parse(chuoi[4])); // TreeNode parentNode = null;
try { parentNode = sortnodes[chuoi[1]]; }
catch (Exception) { parentNode = null; } if (parentNode == null) {
parentNode = new TreeNode(chuoi[1]);
sortnodes.Add(chuoi[1], parentNode); }
parentNode.Nodes.Add(curNode); } IEnumerator> nodesEnum = sortnodes.GetEnumerator(); nodesEnum.Reset(); while (nodesEnum.MoveNext()) {
TreeNode node = (TreeNode)nodesEnum.Current.Value; if (node.Level == 0) trNodes.Nodes.Add(node); }
TreeNode lastNode = trNodes.Nodes.Count > 1 ? trNodes : trNodes.Nodes[0];
lastNode.Text = "Đồ thị"; return lastNode; }
//hàm kiểm tra trùng tên
//public bool kiemtratennut(string ten) //{
// for (int i = 0; i < ALLNut.Count; i++) // {
// ArrayList anut = ALLNut[i];
// string str = (string)anut[2]; // if (str == ten) // {
// MessageBox.Show("Tên nút trùng nhau, xin hãy kiểm tra lại!"); // return true; // break; // } // } // return false; //}
//them node vào arraylist chính
private void addnode(int ID, int IDcha, string ten, int g, int h) { 10 int f = 0;
ArrayList addn = new ArrayList(){ ID,IDcha,ten,g,h,f }; ALLNut.Add(addn); }
4. Hàm xác định tọa độ cho các nút vẽ //tọa độ public class ToaDo { public ToaDo(Object tag) { Tag = tag; } public Size sz;//text size public string Text;
public Object Tag;//Tham chiếu đến đối tượng liên quan
public static Font font = new Font("Times New Roman", 9);
public static int KCgiuaTang = 60;
public static int TangX = 10;
public static int TangY = 10;
public int delta = 0, kidsW = 0, prevW = 0;
public Point ViTri = new Point(0, 0);
public Rectangle vien//hcn kích thước của text { get { int w = sz.Width + delta;
return new Rectangle(ViTri.X + (w - sz.Width) / 2 - 1, ViTri.Y +
TangY, sz.Width + 1, sz.Height); } } public Point diemDau { get { Rectangle rect = vien;
return new Point(rect.Left + (rect.Width / 2), rect.Top); } } public Point diemCuoi { get { Rectangle rect = vien;
return new Point(rect.Left + (rect.Width / 2), rect.Bottom); } } } 11
5. Hàm vẽ đồ thị //Vẽ cây
//-----------------------------------------------------------------------------------
public Bitmap VeCay(TreeNode node) {
int tangX = ToaDo.TangX, kcachtang = ToaDo.KCgiuaTang, w = ToaDo.TangX, h = ToaDo.KCgiuaTang; Font fnt = ToaDo.font;
Bitmap bmp = new Bitmap(w, h);
Graphics gr = Graphics.FromImage(bmp); //vẽ nút
LayNutCay laynut = (tnode) => { Boolean first = true; ToaDo cb = new ToaDo(tnode); ((Nut)tnode.Tag).Tag = cb;
cb.Text = " g= " + ((Nut)tnode.Tag).G.ToString() + "\n " + tnode.Text +
"\n h= " + ((Nut)tnode.Tag).H.ToString();
cb.sz = Size.Ceiling(gr.MeasureString(cb.Text, fnt));
cb.delta = tangX;//tăng chiều rộng bởi thêm các nút con
cb.ViTri = new Point(tangX / 2, ((tnode.Level - 1) * kcachtang)); //vòng lặp
while (tnode.Parent != null && tnode.Parent.Tag != null) {
ToaDo b = (ToaDo)((Nut)tnode.Tag).Tag; TreeNode p = tnode.Parent;
ToaDo pb = (ToaDo)((Nut)p.Tag).Tag;
//Tăng chiều rộng của các nút cha bởi chiều rộng cung cấp
int pbw = pb.sz.Width + pb.delta;
int bw = b.sz.Width + b.delta;
pb.kidsW -= !first ? b.prevW : 0;
pb.delta += ((bw + pb.kidsW - pbw) + Math.Abs(bw + pb.kidsW - pbw)) / 2;
pbw = pb.sz.Width + pb.delta; pb.kidsW += bw; b.prevW = bw; //Điều chỉnh vị trí if (first) {
//các nút con được vẽ sau nút cha nên điều chỉnh sẽ chính xác
b.ViTri = new Point(pb.ViTri.X + pb.kidsW - bw, ((tnode.Level - 1) * kcachtang)); first = false; } //
w = Math.Max(pb.ViTri.X + pbw + ToaDo.TangX / 2, w);
h = Math.Max((((tnode.Level - 1) * kcachtang)) + kcachtang, h); // tnode = p; }
if (first && w > tangX) 12 { cb.ViTri.Offset(w, 0);
w = Math.Max(cb.ViTri.X + cb.sz.Width + cb.delta, w); } };
NutLap(node, laynut);//lặp lại các nút để lấy tọa độ các nút gr.Dispose(); bmp.Dispose(); bmp = new Bitmap(w, h);
gr = Graphics.FromImage(bmp);
LayNutCay draw = (tnode) => {
Brush mau_nut = new SolidBrush(Color.Ivory);
Brush mau_chu = new SolidBrush(Color.Black);
Brush mau_trang = new SolidBrush(Color.White);
Nut mpttNode = (Nut)tnode.Tag; int level = tnode.Level;
ToaDo b = (ToaDo)((Nut)tnode.Tag).Tag; Rectangle rect = b.vien; //Vẽ nhánh
if (tnode.Parent.Tag != null) {
gr.SmoothingMode = System.Drawing.Drawing2D.SmoothingMode.HighQuality;
Pen pen = new Pen(new SolidBrush(Color.Red), 1.0F);
gr.DrawLine(pen, ((ToaDo)((Nut)tnode.Parent.Tag).Tag).diemCuoi, b.diemDau); } //Vẽ nút
LinearGradientBrush brush = new LinearGradientBrush(rect, Color.White,
Color.DodgerBlue, LinearGradientMode.ForwardDiagonal); gr.FillEllipse(brush, rect);
gr.DrawEllipse(new Pen(new SolidBrush(Color.Brown)), rect); //viết tên nút, g,h
using (StringFormat sf = new StringFormat()) {
sf.Alignment = StringAlignment.Center;
sf.LineAlignment = StringAlignment.Center;
gr.DrawString(b.Text, fnt, mau_chu, rect, sf); } };
NutLap(node, draw);//lặp lại các nút trong cây gr.Dispose(); return bmp; }
6. Hàm giải thuật AKT
public List ALLNut = new List();//mảng chính List nodeBn = new List(); List MO = new List(); List DONG = new List(); 13 public int dem = 0;
public void akt_search(string root,string nodesearch,ListView lv) { if (dem == 0) { tinhF_Bn(); dem++; } ListViewItem itemlv; if (Tontainut(nodesearch)) {
if (root == "")//nếu chưa có nút nào mở thì thêm nút gốc { themMO(laygoc());
itemlv = new ListViewItem(root); lv.Items.Add(itemlv); itemlv.SubItems.Add("");
itemlv.SubItems.Add(layMO()); itemlv.SubItems.Add("");
akt_search(laynutMo(), nodesearch, lv); } else { if (root != nodesearch) {
daduyet(root);//xóa nút ra khỏi MO themBn(root); themMO(); themDONG(root);
itemlv = new ListViewItem(root); lv.Items.Add(itemlv);
itemlv.SubItems.Add(laybn());
itemlv.SubItems.Add(layMO());
itemlv.SubItems.Add(layDONG());
akt_search(laynutMo(), nodesearch, lv); } else { themDONG(root);
itemlv = new ListViewItem(root); lv.Items.Add(itemlv);
itemlv.SubItems.Add("Đích"); itemlv.SubItems.Add("");
itemlv.SubItems.Add(layDONG()); } } } else
MessageBox.Show("Không tồn tại nút này!"); } 14
7. Các hàm cho giải thuật //lấy nút gốc public ArrayList laygoc() { ArrayList goc = null;
for (int i = 0; i < ALLNut.Count; i++) { ArrayList node = ALLNut[i]; if ((int)node[1] == 0) return node; } return goc; }
//xóa nút đã duyệt khỏi MO
public void daduyet(string tennut) {
for (int i = 0; i < MO.Count; i++) { ArrayList ar = MO[i]; if ((string)ar[2]==tennut) MO.RemoveAt(i); } }
//Lấy tên nút có F nhỏ nhất trong MO public string laynutMo() { string st = "";
for (int j = 0; j < MO.Count; j++) { ArrayList arr1 = MO[j];
if ((int)arr1[5] == lay_min_f()) st=(string)arr1[2]; } return st; } public int lay_min_f() { int min = 1000000;
for (int i = 0; i < MO.Count; i++) { ArrayList arr1 = MO[i];
min = (int)arr1[5] <= min ? (int)arr1[5] : min; } return min; }
//lấy chuỗi để add vào listview // // //lay ten nut goc public string layten() 15 { string ten = ""; ArrayList ar = laygoc(); ten = (string)ar[2]; return ten; } //lay cac nut trong bn public string laybn() { string st="";
for (int i = 0; i < nodeBn.Count; i++) { ArrayList nut = nodeBn[i]; string ten = (string)nut[2];
st += ten + "(F= " + nut[5].ToString() + ")\r\n"; } return st; } //lay cac nut trong MO public string layMO() { string st = "";
for (int i = 0; i < MO.Count; i++) { ArrayList nut = MO[i]; string ten = (string)nut[2];
st += ten + "(F= " + nut[5].ToString() + ")\r\n"; } return st; } //lay cac nut trong DONG public string layDONG() { string st = "";
for (int i = 0; i < DONG.Count; i++) { ArrayList nut = DONG[i]; string ten = (string)nut[2];
st += ten + "(F= " + nut[5].ToString() + ") "; } return st; } //tính F của các nút
//------------------------------------------------ public void tinhF_Bn() {
for (int i = 0; i < ALLNut.Count; i++) { ArrayList root = ALLNut[i];
if ((int)root[1] == 0) root[5] = root[4];
for (int j = 0; j < ALLNut.Count; j++) {
ArrayList rootchild = ALLNut[j];
int idcha = (int)rootchild[1]; if (idcha == (int)root[0]) {
rootchild[3] = (int)root[3] + (int)rootchild[3]; 16
rootchild[5] = (int)rootchild[3] + (int)rootchild[4]; } } } }
//Thêm các phần tử vào các mảng con Bn,MO,DONG
public void themBn(string nut) { //xóa sạch bn nodeBn.Clear();
for (int i = 0; i < ALLNut.Count; i++) { //lấy nút n ArrayList anut = ALLNut[i];
string tennut = (string)anut[2];
if (tennut == nut)//nếu phần tử trong mảng có tên là n {
for (int j = 0; j < ALLNut.Count; j++)
{//thêm vào bn phần tử từ mảng gốc ArrayList node = ALLNut[j]; int idcha = (int)node[1]; if (idcha == (int)anut[0]) { nodeBn.Add(node); } } } } } public void themMO() { //MO sẽ thêm từ Bn
for (int i = 0; i < nodeBn.Count; i++) { MO.Add(nodeBn[i]); } }
//thêm phần tử vào MO nếu chưa có phần tử nào
public void themMO(ArrayList n) { MO.Add(n); }
public void themDONG(string nutduyet) {
for (int i = 0; i < ALLNut.Count; i++) { ArrayList ar = ALLNut[i];
if (nutduyet == (string)ar[2]) { DONG.Add(ar); } } } 17
//kiểm tra tồn tại nút //
public bool Tontainut(string nuttim) {
for (int i = 0; i < ALLNut.Count; i++) { ArrayList anut = ALLNut[i];
string str = (string)anut[2];
if (str == nuttim)//nếu có phần tử nào trong mảng đầu có tên trùng { return true; } } return false; }
//Hàm lấy đường đi và chi phí public int f=0; string st = "";
public string duongdi_chiphi(string nodesearch) { string s1=" --> "; string s = nodesearch; //ArrayList az;
for (int i = 0; i < ALLNut.Count; i++) { ArrayList nuts = ALLNut[i]; if (s == (string)nuts[2]) {
if (f == 0) f = (int)nuts[3];
for (int j = 0; j < ALLNut.Count; j++) { ArrayList az = ALLNut[j];
if ((int)az[0] == (int)nuts[1]) { if ((int)az[1] == 0) {
st = String.Concat(az[2].ToString(), s1, nuts[2].ToString(), st); } else {
st = String.Concat(s1, nuts[2].ToString(), st); } s = (string)az[2]; duongdi_chiphi(s); } } } } return st; } 18
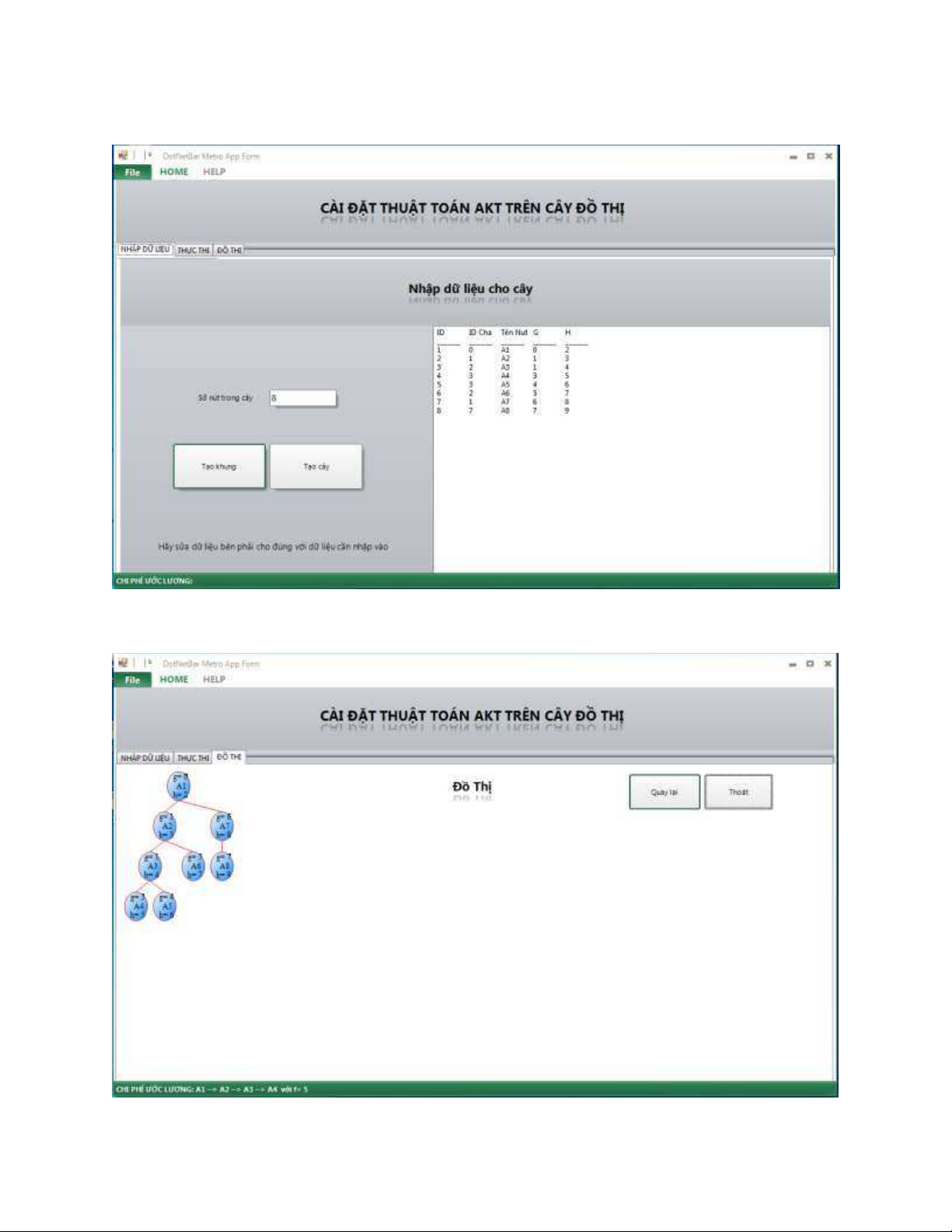
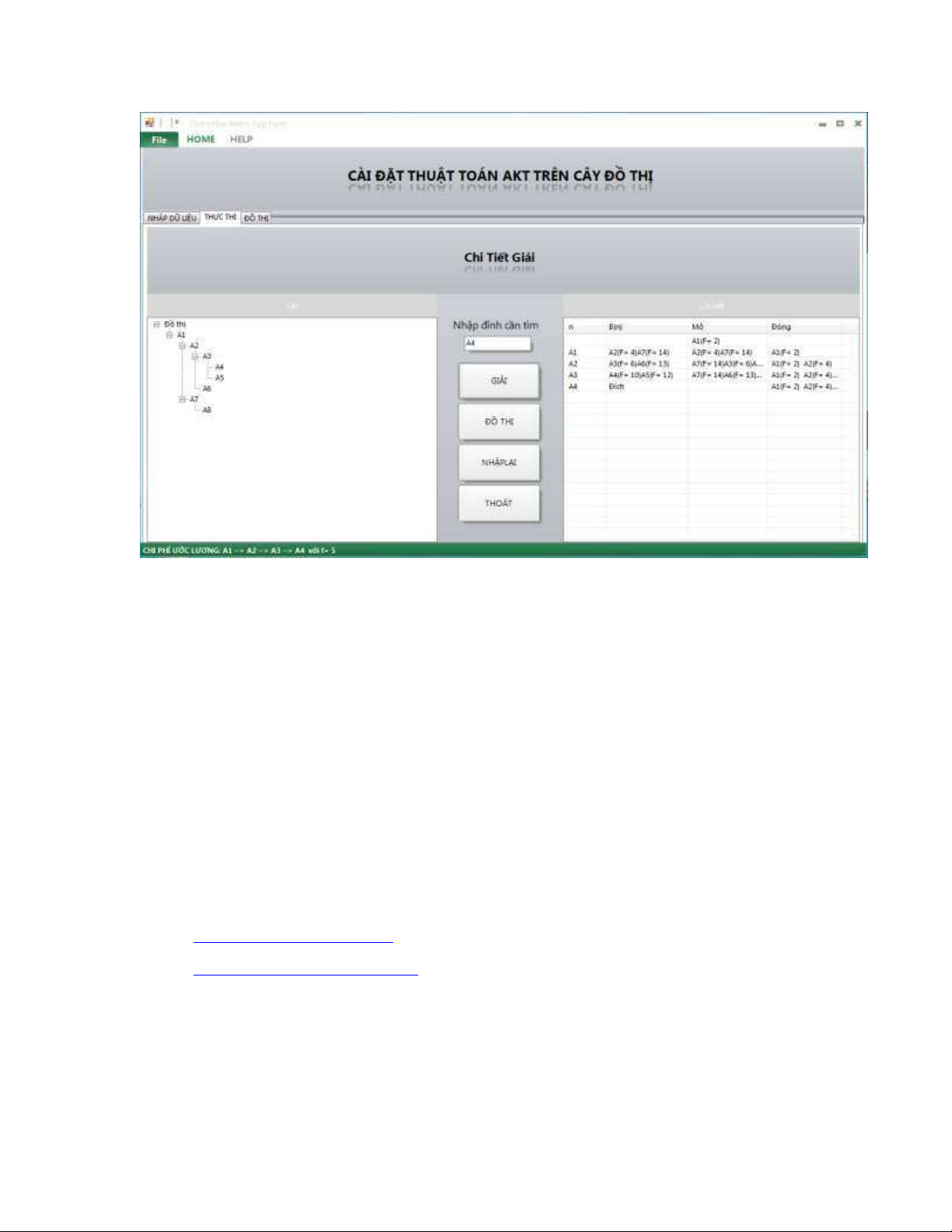
3. sGiao diện chương trình 19
Tài liệu tham khảo 1.
Tr n Hùng Cư ng_Giáo trình ậ slide TRÍ TU NHÂN T O(Artificial Intellegence ậ AI) 2.
Geogre F. Luger, William A. Stubblefield ậ Albuquerque ậ Artifical
Intelligence ậ Wesley Pubblishing Conpany, Inc ậ 1997 (Chapter 1) 3.
Bùi Xuân To i ậ Trương Gia Vi t (Biên dịch) ậ Trí tu nhân t o ậ Các c u
trúc và chi n lược giải quyết v n đề - NXB Thống kê, 2000 (Ph n 1) 4.
PTS. Nguy n Thanh Thủy ậ Trí tu nhân t o ậ Các phương pháp giải quyết
v n đề và kỹ thu t xử lí tri thức ậ NXB Giáo dục, 1995 (Chương 1) 5.
Wikipedia ậ Bách khoa toàn thư mở - Lịch sử ngành Trí tu nhân t o 6. www.codeproject.com 7. www.congdongcviet.com 20




