






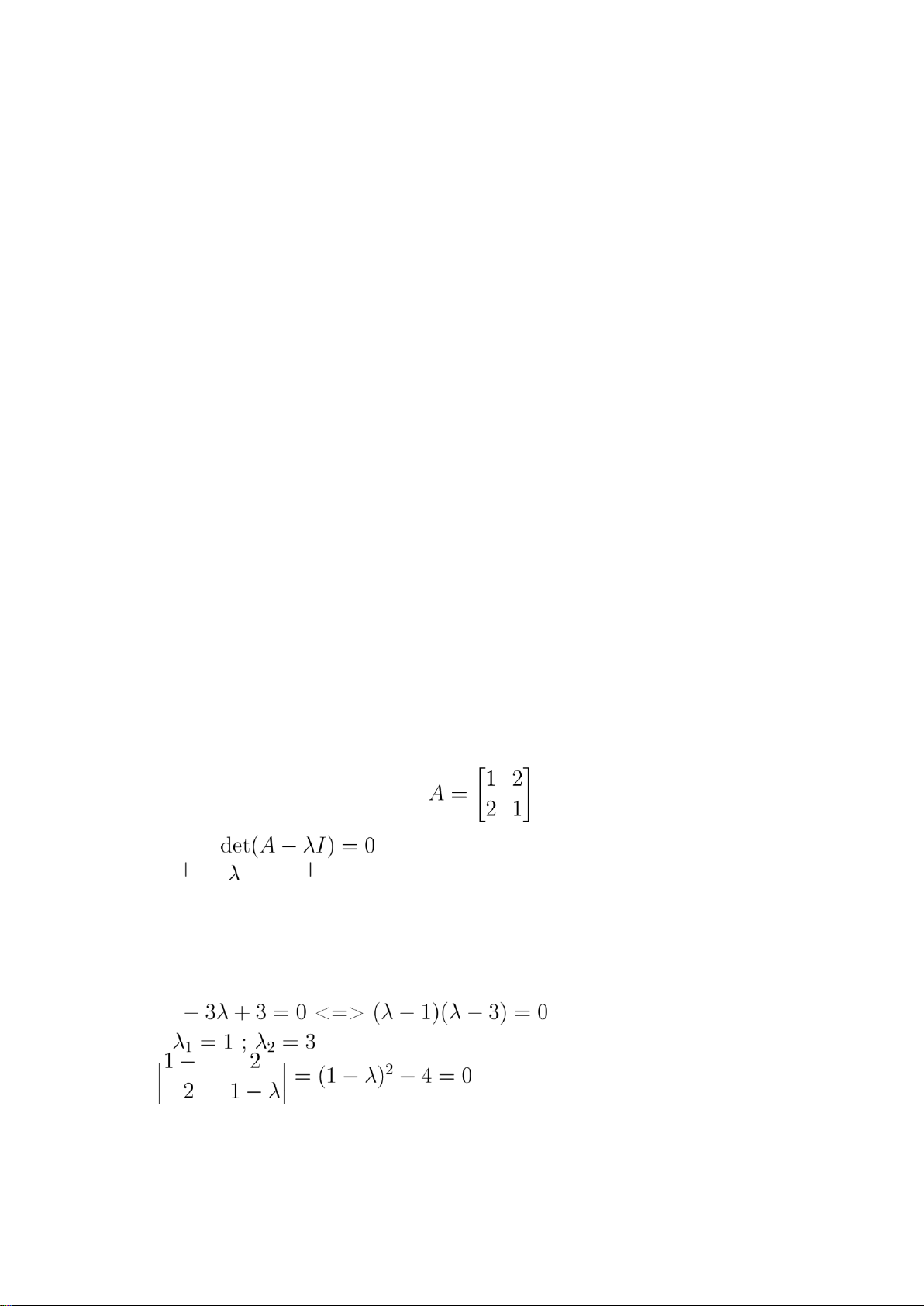




Preview text:
ĐẠI HỌC QUỐC GIA THÀNH PHỐ HỒ CHÍ MINH TRƯỜNG ĐẠI HỌC BÁCH KHOA
ĐẠI SỐ TUYẾN TÍNH (MT1015)
BÁO CÁO BÀI TẬP LỚN ĐỀ TÀI SỐ 4
Ứng Dụng SVD Giảm Chiều Dữ Liệu lOMoARcPSD| 36782889 Mục lục
1 Giới thiệu về đề tài ..................................................................................................................................... 2
2 CƠ SỞ LÝ THUYẾT ....................................................................................................................................... 2
2.1 Một số khái niệm cơ bản ................................................................................................................... 2
2.1.1 Trị riêng và vector riêng của ma trận vuông .......................................................................... 2
2.1.2 Ma trận trực giao ................................................................................................................... 4
2.1.3 Chéo hóa ma trận .................................................................................................................. 5
2.1.4 Singular Values ....................................................................................................................... 7
2.2 Phát biểu SVD .................................................................................................................................... 8
3 ÁP DỤNG SVD VÀO NÉN DỮ LIỆU ............................................................................................................... 9
3.1 Các bước cụ thể để giảm chiều dữ liệu ............................................................................................. 9
3.2 Ví dụ cụ thể ...................................................................................................................................... 10
3.3 Ứng dụng của SVD vào nén ảnh ...................................................................................................... 12
4 ÁP DỤNG TRÊN MATLAB .......................................................................................................................... 12
4.1 Phần code matlab ............................................................................................................................ 12
4.2 Ví dụ minh họa ................................................................................................................................ 13 lOMoARcPSD| 36782889 1
Giới thiệu về đề tài
Nén ảnh là một kỹ thuật mã hóa các ảnh, số hóa nhằm giảm số lượng các bit
dữ liệu để biểu diễn ảnh. Mục đích của việc nén ảnh số là mã hoá các dữ liệu
ảnh về một dạng thu gọn, tối thiểu hoá cả số bit dùng để biểu diễn ảnh, nhằm
giảm dung lượng lưu trữ và giảm tối thiểu thời gian truyền ảnh và đồng thời
chúng ta vẫn đảm bảo được chất lượng của ảnh. Có hai cách nén ảnh là nén
không mất thông tin (lossless image compression) và nén có mất thông tin
(lossy image compression). Trong thực tế, để có thể nén được nhiều ảnh số,
người ta thường áp dụng các phương pháp nén có mất mát thông tin vì việc
này không đồng nghĩa với việc làm mất nét của ảnh. SVD (Singular Value
Decomposition) là một phương pháp để phân tích một ma trận bất kỳ thành
tích của ba ma trận thành phần. Phương pháp này được phát triển dựa trên
những kiến thức đã biết từ ma trận trực giao và ma trận đường chéo để tìm
được một ma trận xấp xỉ mới ma trận gốc. Phân tích SVD thường được dùng
để trích chọn các đặc trưng bền vững và có nhiều ứng dụng trong lĩnh vực hình
học vi phân, hồi qui tuyến tính, khử nhiễu âm thanh, xử lý hình ảnh, các thuật
toán nén và giảm chiều dữ liệu. Hiện nay được ứng dụng phổ biến trong hệ
thống giao thông vận tải của nhiều nước nhằm đảm bảo truyền thông tin được
nhanh chóng, giảm độ trễ, tiết kiệm dung lượng cho các camera giám sát, nhận
diện biển số, kiểm soát ra vào bãi đỗ xe, nhận diện tắc nghẽn giao thông, đều
ứng dụng SVD để nén dữ liệu hình ảnh.
Ở đây, chúng ta sẽ nói về ứng dụng của SVD trong việc giảm chiều dữ liệu, đặc
biệt trong nén ảnh, nén file. 2 CƠ SỞ LÝ THUYẾT 2.1
Một số khái niệm cơ bản 2.1.1
Trị riêng và vector riêng của ma trận vuông
Cho A là một ma trận cấp n, nếu số vô hướng λ và vector x = 0̸ ∈ Rn thỏa mãn: Ax = λx
thì λ được gọi là **trị riêng** của A và x là **vector riêng** tương ứng với trị riêng đó. lOMoARcPSD| 36782889 Tính chất
1.Nếu x là một vector riêng của A ứng với λ thì kx, k = 0̸ cũng là vector riêng
ứng với trị riêng đó. Chứng minh. Ta có: Ax = λx kx ∗
Ax = kx ∗ λx
⇒ k ∗ λx = λ ∗ kx ⇒ λ ∗ kx = λx
Do k = 0̸ nên ta có:
λ ∗ kx = λx ⇒ kx = x
Vậy kx cũng là một vector riêng của A ứng với trị riêng λ.
2.Mọi ma trận vuông bậc n đều có n trị riêng (kể cả lặp) và có thể là các số phức.
Chứng minh. Ta có thể sử dụng định lý Cayley-Hamilton. Định lý này cho biết rằng: P(A) = 0
với P(x) là đa thức đặc trưng của A.
Mặt khác, đa thức đặc trưng của A có n hệ số. Do đó, P(A) có n nghiệm,
bao gồm nghiệm thực và nghiệm ảo.
x1,x2,...,xn
là các nghiệm của P(x). Nếu x1,x2,...,xm là các nghiệm thực và xm + 1,...,xn là
các nghiệm ảo, thì các nghiệm thực là các trị riêng của A. lOMoARcPSD| 36782889
Vậy mọi ma trận vuông bậc n đều có n trị riêng (kể cả lặp) và có thể là các số phức.
3.Với ma trận đối xứng, tất cả các trị riêng đều là các số thực.
Chứng minh. Ta có thể sử dụng định lý spectral cho ma trận đối xứng.
Định lý này cho biết rằng:
A = U · D · UT
với U là ma trận các vector riêng của A và D là ma trận đường chéo
chứa các trị riêng của A.
Do U là ma trận thực nên UT cũng là ma trận thực. Do đó, ma trận D cũng là ma trận thực.
Vậy tất cả các trị riêng của A đều là các số thực. 2.1.2 Ma trận trực giao
Ma trận vuông A bậc được gọi là ma trận trực giao nếu: AT = A−1 hoặc
ATA = AAT = I
Trong đó I là ma trận đơn vị bậc tương ứng với bậc của ma trận A.
Ma trận trực giao thể hiện phép xoay của một vectơ (phép xoay không làm
thay đổi tích vô hướng giữa 2 vector): Ví dụ, cho ma trận là ma trận trực giao. lOMoARcPSD| 36782889
bị xoay 90 độ theo chiều kim đồng hồ bởi ma trận A.
bị xoay 90 độ theo chiều ngược kim đồng hồ bởi ma trận A. Chứng minh:
Để chứng minh rằng A là ma trận trực giao, ta cần chứng minh rằng A thỏa mãn hai phương trình sau: AT = A−1 (1) và
ATA = AAT = I (2)
Chứng minh phương trình (1): Ta có:
AT = (AT)−1 = (A−1)T = A−1
Chứng minh phương trình (2): Ta có:
ATA = A(AT)A
= A(A−1)A = A2 = I
Như vậy, ta đã chứng minh được rằng A là ma trận trực giao. 2.1.3 Chéo hóa ma trận
Cho A là một ma trận vuông cấp n, xét ma trận khả nghịch P cấp n và ma trận đường chéo D, ta có:
D = PAP −1
P là ma trận làm chéo hóa ma trận A, còn D là dạng chéo của ma trận A. lOMoAR cPSD| 36782889
Quá trình chéo hóa là quá trình tìm các ma trận P và D ở trên. Trong đó,
* A là ma trận vuông cấp n * P là ma trận khả nghịch cấp n * D là ma trận
đường chéo cấp n Giải thích:
Phương trình D = PAP −1 được gọi là phương trình chéo hóa của ma trận A.
Ma trận P là ma trận làm chéo hóa ma trận A. Nó có các cột là các vector
riêng của ma trận A, được chuẩn hóa theo vectơ đơn vị.
Ma trận D là dạng chéo của ma trận A. Nó có các phần tử trên đường chéo
là các giá trị riêng của ma trận A. Quá trình chéo hóa:
Quá trình chéo hóa là quá trình tìm các ma trận P và D thỏa mãn phương
trình D = PAP −1.
Có nhiều cách để thực hiện quá trình chéo hóa. Một cách phổ biến là sử dụng phương pháp Jacobi. Phương pháp Jacobi:
- Phương pháp Jacobi được thực hiện như sau:
1. Khởi tạo ma trận P là ma trận đơn vị.
2. Lặp lại các bước sau cho đến khi ma trận A được chéo hóa: * Chọn
một giá trị riêng λi của ma trận A.
* Tìm vector riêng vi của ma trận A tương ứng với giá trị riêng λi.
* Cập nhật ma trận P theo công thức sau: nếu ij = 1 nếu lOMoARcPSD| 36782889 2.1.4 Singular Values
det(A−λI) = 0 Trong đó,
* A là ma trận vuông cấp n * λ là giá trị riêng của ma trận A * I là ma trận
đơn vị cùng bậc với ma trận A
Lấy căn bậc hai của λ, ta được các giá trị được gọi là Singular Value của ma trận A: σi = pλi Giải thích:
Phương trình detA − ΛI= 0 là phương trình đặc trưng của ma trận A. Nó có
n nghiệm, tương ứng với n giá trị riêng của ma trận A.
Lấy căn bậc hai của các giá trị riêng λi, ta được các giá trị σi. Các giá trị này
được gọi là các giá trị riêng của ma trận A. Ví dụ:
Giả sử ma trận A có dạng sau: Ta có: Giải phương trình: λ2 Vậy lOMoARcPSD| 36782889
σ1 = √λ 1 = √1 σ2 = √λ 2 = √3 2.2 Phát biểu SVD
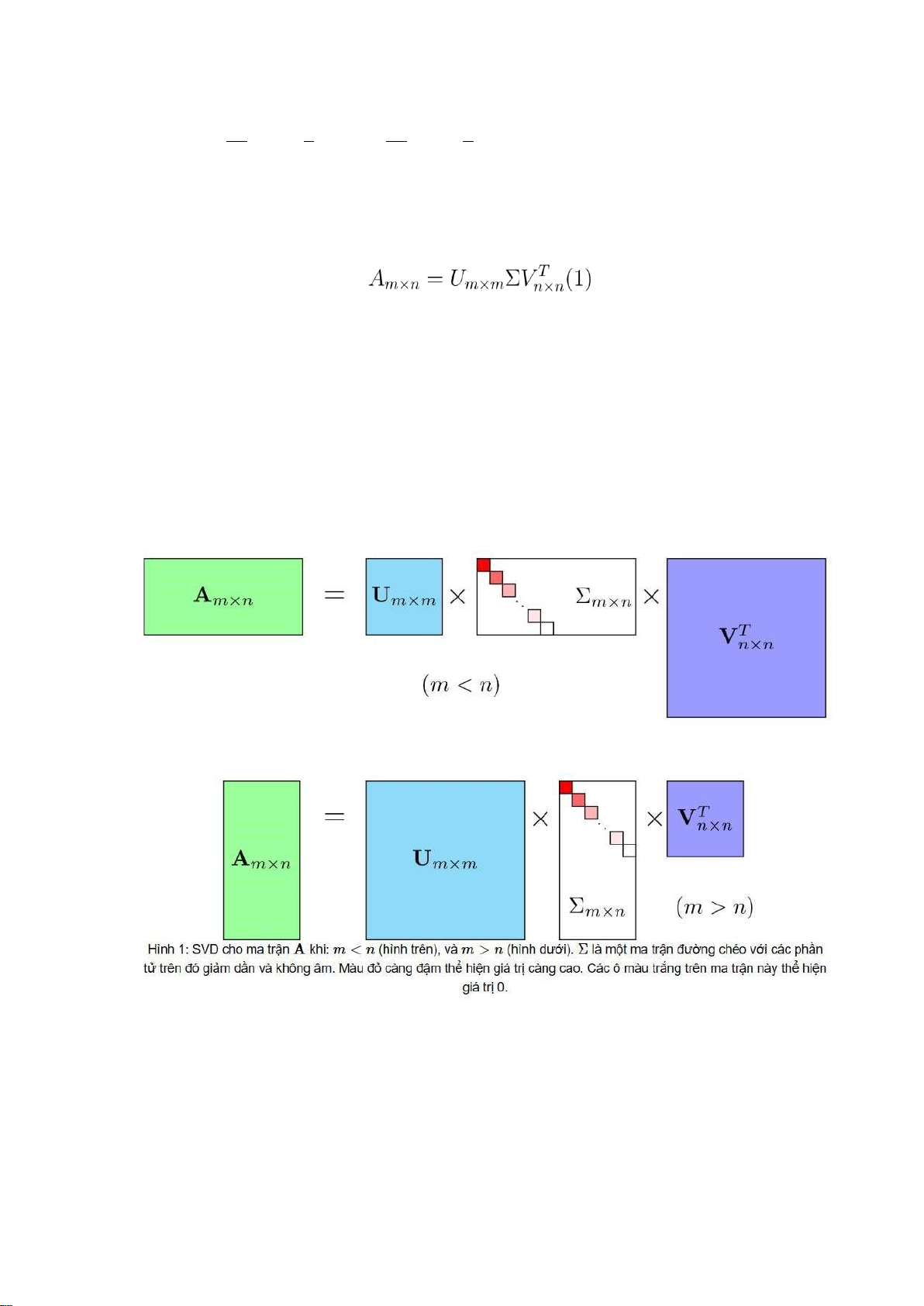
Một ma trận Am×n bất kỳ đều có thể được phân tích thành dạng: Trong đó:
• A là ma trận đầu vào bất kỳ.
• U và V là ma trận trực giao (từ phép tính AAT và ATA).
• Σ là ma trận đường chéo không vuông có cùng kích thước với ma trận A,
với các phần tử nằm trên đường chéo là Singular values của ma trận A.
Trong đó, σ1 ≥ σ2 ≥ ··· ≥ σr ≥ 0 (với r là rank của ma trận A). lOMoARcPSD| 36782889 3
ÁP DỤNG SVD VÀO NÉN DỮ LIỆU 3.1
Các bước cụ thể để giảm chiều dữ liệu
Ở đây chúng ta sẽ sử dụng phương pháp cắt ngắn ma trận (Truncated SVD)
được coi là phương pháp xấp xỉ hạng ma trận tốt nhất (Best lowrank Approximation).
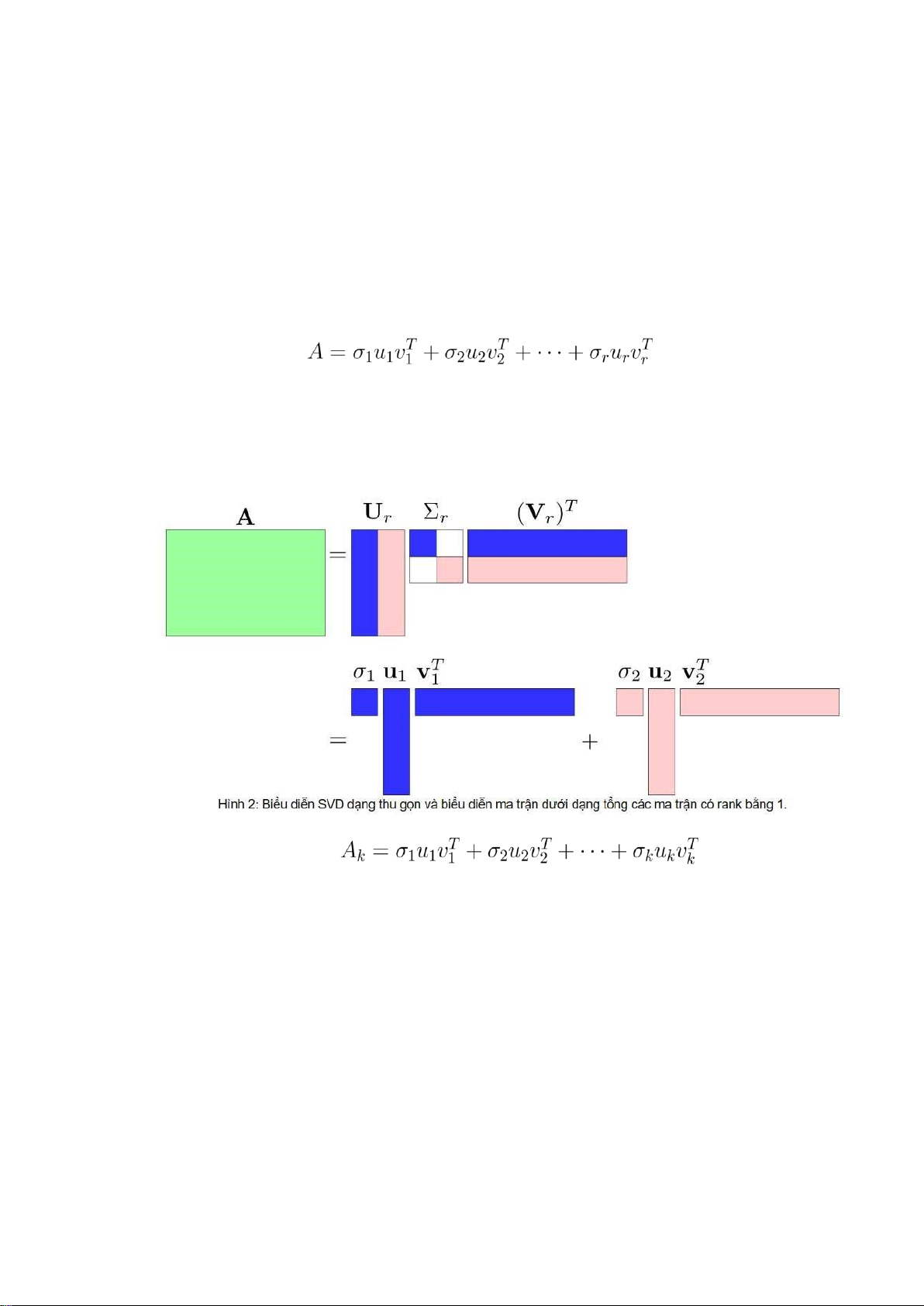
Viết lại biểu thức (1) dưới dạng tổng các ma trận:
với σ1 ≥ σ2 ≥ ··· ≥ σiriT≥, với0. 1 ≤ i ≤ r, là một ma trận có rank bằng 1.
Chú ý rằng mỗi u v
Với 1 ≤ k ≤ r, đặt
, các giá trị trên đường chéo là không âm. Chú ý rằng trong ma trận Σ
tích ma trậnvà có giá trị giảm dầnA σ1 ≥ σ2 ≥ ··· ≥iσmang giá trị lớn, các giá trị
cònr ≥ 0. Đa số khi chúng ta phân thì chỉ một lượng nhỏ σ
lại thường rất nhỏ và gần bằng 0. Khi chúng ta bỏ bớt một số giá trị σi (k < i <
r) rất bé phía sau thì giá trị của A gần như không thay đổi. Do đó ta có thể xấp
xỉ ma trận A bằng tổng của k (k < r) ma trận có rank bằng 1: lOMoARcPSD| 36782889
Như vậy ta thấy ta có thể chọn độ sai số của dữ liệu phụ thuộc vào k.
Với k càng lớn thì sai số của dữ liệu càng ít nhưng k vẫn bé hơn rank A. 3.2 Ví dụ cụ thể Cho ma trận:
SVD của ma trận A được xác định bởi A = UΣV T, trong đó U là ma trận trực
giao bên trái, Σ là ma trận chứa các singular values trên đường chéo chính, và
V T là ma trận trực giao bên phải.
Bước 1: Xây dựng ma trận U và V - Ma trận U: + Tính ATA
+ Tìm vectơ riêng của ATA **Trị riêng:
det(AT · A − λI) = 0
**Vector riêng tương ứng:
det(AT · A − λI)X = 0
Giải phương trình trên ta được 2 vector với các giá trị tương ứng: lOMoARcPSD| 36782889 Ma trận U: - Ma trận V: + Tính AAT
Tương tự, ta cũng tìm trị riêng và vectơ riêng của AAT Ma trận V:
Bước 2: Xây dựng ma trận Σ
Vì ma trận A có kích thước 2x2 nên ma trận Σ cũng có kích thước tương tự với
đường chéo là các singular values của AAT hoặc ATA
Chúng ta cần tính các singular values từ trị riêng của ATA hoặc AAT.
Do đó, các trị của ATA là λ1 = 53.07 và λ2 = 0.92.
Các singular values được tính bằng cách lấy căn bậc hai của các trị riêng này:
Vậy, ta có thể phân rã A bằng phương pháp SVD: lOMoARcPSD| 36782889 3.3
Ứng dụng của SVD vào nén ảnh
Chúng ta có thể nén ảnh vì thông tin trong bức ảnh sắp xếp ngẫu nhiên mà có
trật tự, có cấu trúc cụ thể tùy thuộc vào từng ảnh. Vì thế, nếu phân tích, số
hóa được tính trật tự, cấu trúc đó thì chúng ta có thể bỏ bớt những phần thông
tin kém quan trọng để biểu diễn và truyền đi với số lượng ít bit hơn so với ảnh
gốc mà vẫn đảm bảo tính đầy đủ cần thiết của ảnh. Khi nhận được thông tin
về ảnh, quá trình giải mã sẽ sắp xếp, tổ chức lại được bức ảnh xấp xỉ gần chính
xác so với ảnh gốc và vẫn thỏa mãn chất lượng yêu cầu. Nén ảnh (nén mất
thông tin) là phương pháp giảm dung lượng ảnh bằng cách loại bỏ các phần ít
quan trọng trong ảnh đã được số hóa. Phân tích SVD với đặc tính xác định
được các phần tử có sự tập trung thông tin cao của ảnh nên có thể được sử
dụng trong nén ảnh. Khi một hình ảnh được chuyển đổi bằng SVD, nó không
bị nén. Nhưng do dữ liệu sau khi phân tích thì những giá trị đầu tiên đã có một
lượng lớn thông tin hình ảnh, chúng ta có thể chỉ sử dụng một vài giá trị lớn
nhất để thể hiện hình ảnh thì kết quả đạt được cũng sẽ không có nhiều khác biệt so với bản gốc. 4 ÁP DỤNG TRÊN MATLAB 4.1 Phần code matlab
‘tenfile’ là tên của file ta nhập vào img = imread(’tenfile’); img_gray = rgb2gray(img); [U, S, V] = svd(double(img_gray));
k1 = 5; % Số lượng giá trị singular để giữ lại lần 1 k2 = 10; % Số
lượng giá trị singular để giữ lại lần 2 k3 = 20; % Số lượng giá trị
singular để giữ lại lần 3 U_approx1 = U(:, 1:k1);
S_approx1 = S(1:k1, 1:k1); V_approx1 = V(:, 1:k1); img_approx1 = U_approx1 * S_approx1 * V_approx1’;
approx_error1 = norm(double(img_gray) - img_approx1, ’fro’) / norm(double(img_gray) lOMoARcPSD| 36782889 U_approx2 = U(:, 1:k2);
S_approx2 = S(1:k2, 1:k2); V_approx2 = V(:, 1:k2); img_approx2 = U_approx2 * S_approx2 * V_approx2’;
approx_error2 = norm(double(img_gray) - img_approx2, ’fro’) / norm(double(img_gray) U_approx3 = U(:, 1:k3);
S_approx3 = S(1:k3, 1:k3); V_approx3 = V(:, 1:k3); img_approx3 = U_approx3 * S_approx3 * V_approx3’;
approx_error3 = norm(double(img_gray)-img_approx3,’fro’) / norm(double(img_gray),’f fprintf(’Sai số
xấp xỉ lần 1: %e\n’, approx_error1); fprintf(’Sai số xấp xỉ lần 2: %e\n’, approx_error2); fprintf(’Sai số xấp
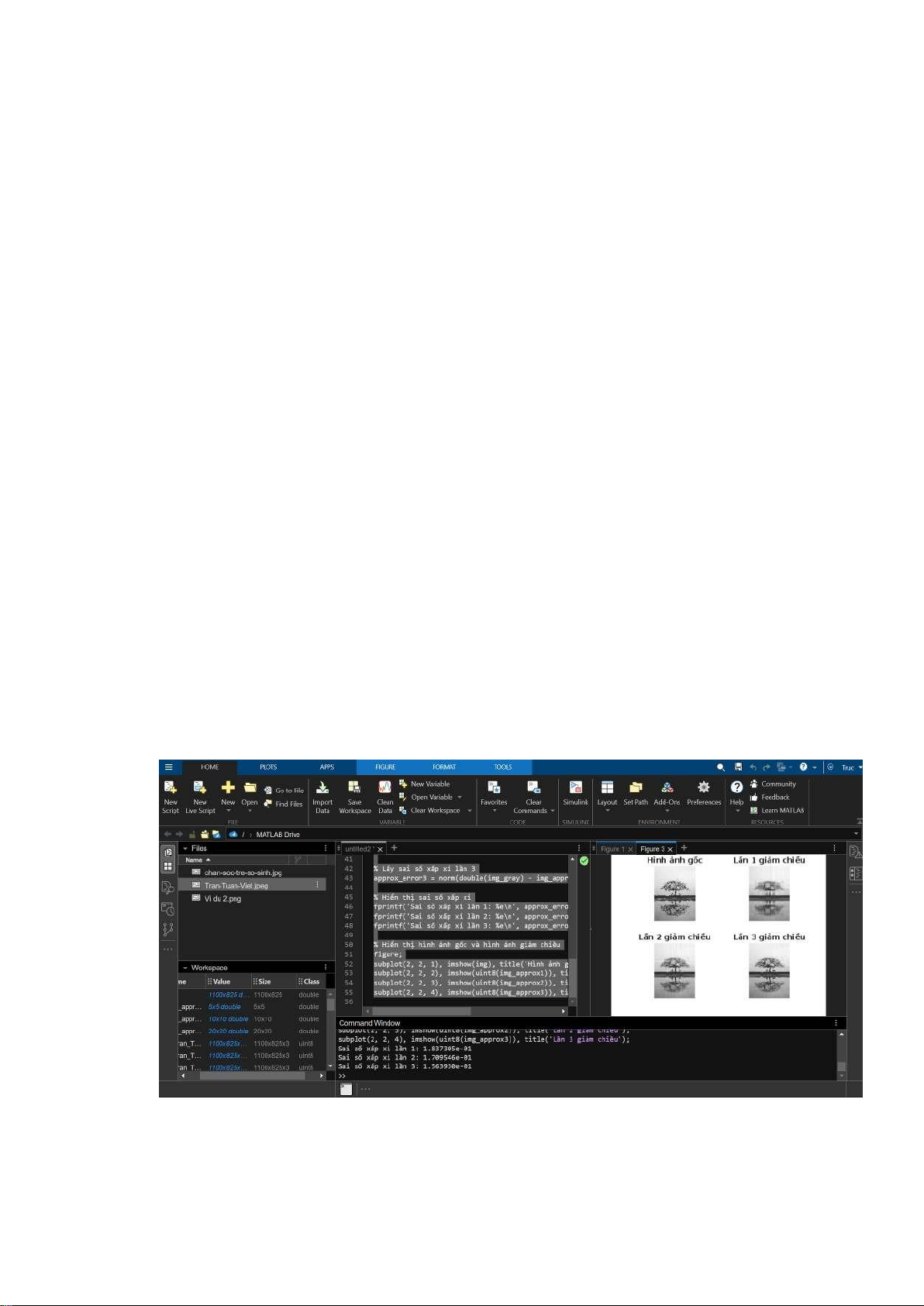
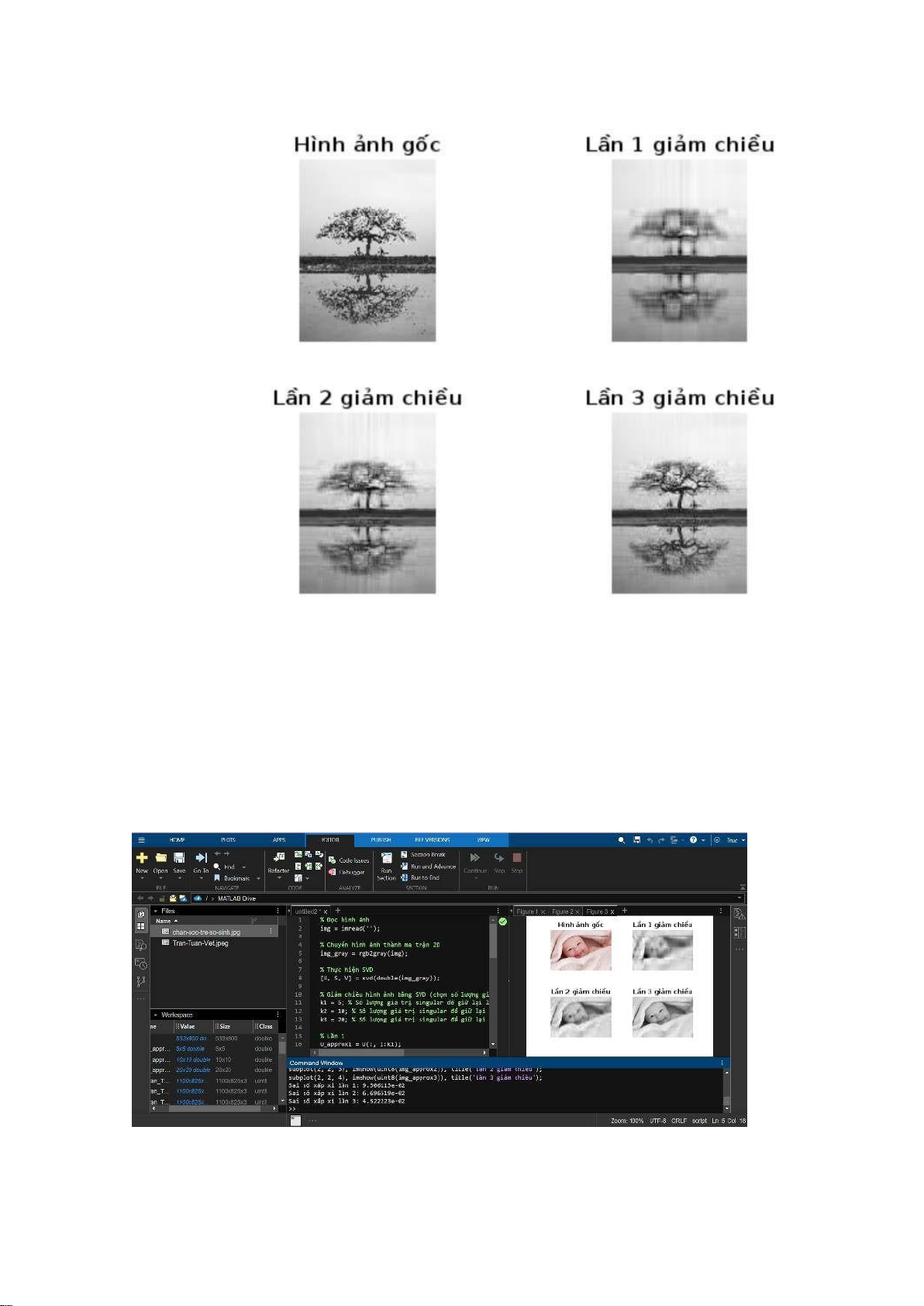
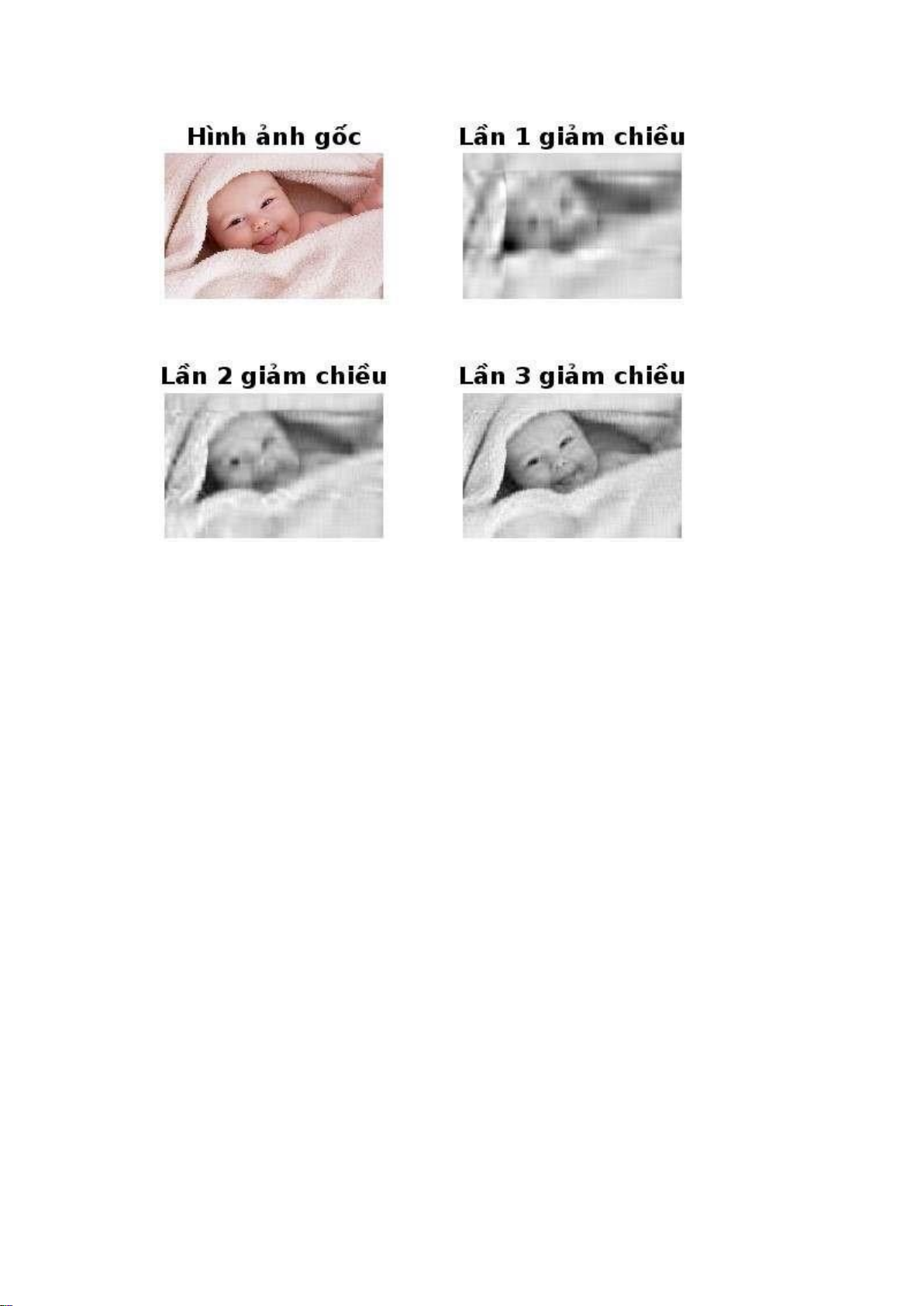
xỉ lần 3: %e\n’, approx_error3); figure;
subplot(2, 2, 1), imshow(img), title(’Hình ảnh gốc’); subplot(2, 2, 2),
imshow(uint8(img_approx1)), title(’Lần 1 giảm chiều’); subplot(2, 2, 3),
imshow(uint8(img_approx2)), title(’Lần 2 giảm chiều’); subplot(2, 2, 4),
imshow(uint8(img_approx3)), title(’Lần 3 giảm chiều’); 4.2 Ví dụ minh họa - Ví dụ 1: + Đánh giá sai số:
Sai số xấp xỉ lần 1: 1.837305e-01
Sai số xấp xỉ lần 2: 1.709546e-01
Sai số xấp xỉ lần 3: 1.563930e-01 + Tổng quát: lOMoARcPSD| 36782889 - Ví dụ 2: + Đánh giá sai số:
Sai số xấp xỉ lần 1: 9.306113e-02
Sai số xấp xỉ lần 2: 6.696519e-02
Sai số xấp xỉ lần 3: 4.522223e-02 + Tổng quát: lOMoARcPSD| 36782889 lOMoAR cPSD| 36782889




