Bài tập lớn môn Đại số tuyến tính đề tài "Ứng dụng biến đổi Fourier rời rạc để khử nhiễu âm thanh"

lOMoARcPSD| 36782889
M Ụ C L Ụ C
CHƯƠNG I: TÓM TẮT BÀI BÁO CÁO .................................................................. 2
CHƯƠNG II: NỘI DUNG BÀI BÁO CÁO ............................................................... 3
1. ĐẶT VẤN ĐỀ VÀ MỤC TIÊU ......................................................................... 3
2. CƠ SỞ LÝ THUYẾT ......................................................................................... 4
2.1. Một số khái niệm cơ bản liên quan ............................................................ 4
2.1.1 Định nghĩa ánh xạ tuyến tính .............................................................. 4
2.1.2 Nhân và ảnh của ánh xạ tuyến tính ..................................................... 4
2.2. Tổng quan về phương pháp biến ổi Fourier ............................................. 5
2.2.1 Giới thiệu khai triển Fourier rời rạc .................................................... 5
2.2.2 Mục ích ............................................................................................. 5
2.2.3 Định nghĩa ........................................................................................... 6
2.2.4 Ví dụ khai triển Fourier .................................................................... 6,7
2.3. Ứng dụng biến ổi Fourier hữu hạn trong khử nhiễu âm thanh. ............... 8
3. BIẾN ĐỔI FOURIER RỜI RẠC ĐỂ KHỬ NHIỄU ÂM THANH TRONG
MATLAB ................................................................................................................ 9
3.1. Các bước dùng phép biến ổi Fourier hữu hạn ể khử nhiễu ..................... 9
3.1.1 Các lệnh dùng trong matlab ............................................................. 10
3.1.2 Đoạn code trong matlab ................................................................... 10
3.2. Hình ảnh oạn code sử dụng trong Matlab ............................................... 12
3.3. Ví dụ minh họa .......................................................................................... 13
4. KẾT LUẬN ....................................................................................................... 14
TÀI LIỆU THAM KHẢO .......................................................................................... 15
LỜI CẢM ƠN ............................................................................................................. 16 Page | 0 lOMoARcPSD| 36782889
CHƯƠNG I: TÓM TẮT BÀI BÁO CÁO
Bài báo cáo của nhóm 1 sẽ thể hiện nội dung liên quan ến cách sử dụng biến ổi
Fourier rời rạc (DFT- Discrete Fourier Transform) ể khử nhiễu âm thanh cho file âm
thanh có chứa những tạp âm không mong muốn.
Bài viết chỉ ra cơ sở lí thuyết, cách sử dụng Fourier và các bước lập trình code ể
khử nhiễu âm thanh trên phần mềm MATLAB. Từ ó, rút ra những hiểu biết cần thiết
và những kinh nghiệm trong việc xử lí tình huống, cải thiện kỹ năng làm việc nhóm
và có ược những hiểu biết về công cụ MATLAB cũng như cách sử dụng công cụ
matlab diễn tả các bài toán một cách cụ thể, ngắn ngọn ể ứng dụng thực tế. Từ ó,
biết cách xử lí một oạn âm thanh bị nhiễu cũng như chứa các tập âm khó chịu Page | 1 lOMoARcPSD| 36782889
CHƯƠNG II: NỘI DUNG BÀI BÁO CÁO
1. ĐẶT VẤN ĐỀ VÀ MỤC TIÊU
Trong cuộc sống thường nhật hằng ngày, giải trí là nhu cầu tất yếu của mỗi người,
chẳng hạn như xem phim, nghe nhạc, …nó dường như ã là một phần trong cuộc
sống của chúng ta. Mà trong ó âm thanh là thứ không thể thiếu ược. Ví dụ như ể có
một bộ phim, không thể nào thiếu ược âm thanh của xe cộ, tiếng mưa rơi, tiếng ộng
vật, …Hay là những bài nhạc luôn phải ược thu âm sẵn những lời hát của các ca sĩ.
Nhưng trong quá trình tạo ra những âm thanh ó, luôn có những tiếng ồn không cần
thiết khiến ta khó có thể nghe ược và khiến âm thanh không còn ược hay nữa. Vì
vậy, ta phải loại bỏ i những tiếng ồn này, hay ược gọi là khử nhiễu âm thanh.
Nếu chúng ta có thể xử lý một tập tin âm thanh theo các tiêu chí : trọng tâm,
chính xác, hiệu quả và tiết kiệm thời gian. Trong nghiên cứu về âm thanh, sẽ giúp ta
tiết kiệm ược thời gian hơn, phục vụ và ứng dụng ược nhiều trong các mảng giải trí,
nghệ thuật. Trong doanh nghiệp về lĩnh vực truyền thông a phương tiện, nếu xử lí
tốt file âm thanh, sẽ tiết kiệm ược rất nhiều chi phí trong việc thiết kế một phần mềm
nào ó, hay chỉ ơn giản là tăng chất lượng âm thanh trong quá trình edit video chuyên
nghiệp. Từ ó sẽ hướng ến nhiều ối tượng khách hàng hơn với một trải nghiệm về
chất lượng âm thanh tuyệt vời, chân thật và ặc biệt là không còn tạp âm.
Và cách thường ược sử dụng nhiều ể khử nhiểu nhiễu âm thanh là dùng biến ổi
Fourier hữu hạn, là một biến ổi trong giải tích Fourier cho các tín hiệu thời gian rời rạc. Page | 2 lOMoARcPSD| 36782889
2. CƠ SỞ LÝ THUYẾT
2.1. Một số khái niệm cơ bản liên quan
2.1.1 Định nghĩa ánh xạ tuyến tính
Cho X, Y là hai tập hợp rỗng tuỳ ý. Ánh xạ f giữa X và Y là quy tắc cho tương
ứng mỗi phần tử một và chỉ một phần tử x ∈ X một và chỉ một phần tử y ∈ 끫뢘
Hay f : X  Y là ánh xạ, nếu ∀ 끫룊 ∈ 끫뢖, ∃! 끫료 ∈ 끫뢘, 끫료 = 끫뢦(끫룊)
2.1.2 Nhân và ảnh của ánh xạ tuyến tính
Định nghĩa 2.1.2.1 Cho ánh xạ tuyến tính 끫뢦: 끫뢒 → 끫뢔. Tập hợp tất cả các
vecto của 끫룊 của V sao cho 끫뢦(끫룊) = 0 ược gọi là nhân của ánh xạ tuyến tính
끫뢦, kí hiệu là 끫롼 끫뢤끫뢤 끫뢦 = {∀ 끫룊 끫븬 V , f(x) = 0}
Định nghĩa 2.1.2.2 Cho ánh xạ tuyến tính 끫뢦: 끫뢒 → 끫뢔. Tập hợp tất cả các
vectơ y của W, sao cho tồn tại 끫룊 ∈ 끫뢒 thoả 끫료 = 끫뢦(끫룊) ược gọi là ánh xạ tuyến
tính 끫뢦, ký hiệu là 끫롸끫롸끫뢦 = {끫료끫븬끫뢔|∃끫룊 ∈ 끫뢒, 끫료 = 끫뢦(끫룊)}
Định nghĩa 2.1.2.3 Cho ánh xạ tuyến tính 끫뢦: 끫뢒 → 끫뢔
1/ Nhân của 끫뢦 là không gian con của V
2/ Ảnh của 끫뢦 là không gian của 끫뢔
3/ dim(ker 끫뢦) + dim (끫롸끫롸끫뢦) = dim(끫뢒) Page | 3 lOMoARcPSD| 36782889
2.2. Tổng quan về phương pháp biến ổi Fourier
2.2.1 Giới thiệu khai triển Fourier rời rạc
Trong toán học, phép toán biển ổi Fourier rời rạc (Discrete Fourier Transfrom)
hay (DFT), ôi khi còn ược gọi là biến ổi Fourier hữu hạn, là một biến ổi trong giải tích
Fourier cho các tín hiệu thời gian rời rạc. Đầu vào của biến ổi này là một chuỗi hữu hạn
các số thực hoặc số phức, làm biến ổi này là một công cụ lý tưởng ể xử lý các thông tin
trên máy tính. Đặc biệt, biến ổi này ược sử dụng rộng rãi trong xử lí tín hiệu và các
ngành liên quan ến phân tích các tần số chứa trong một tín hiệu, ể giải phương trình ạo
hàm riêng, và ể làm các phép như tích chập. Biến ổi này có thể ược tính nhanh bởi thuật
toán biến ổi Fourier nhanh (DFT).
Biến ổi Fourier là một công thức toán học liên hệ một tín hiệu ược một mẫu trong
thời gian hoặc không gian với cùng một tí hiệu ược lẫy mẫu tần số. Trong xử lý tín hiệu,
thuyết biển ổi Fourier có thể tiết lộ các ặc tính quan trọng của tín hiệu cụ thể là các thành phần tần số
Biến ổi Fourier ược xác ịnh cho một vectơ x với n iểm ược lấy mẫu thống nhất qua công thức 2.2.2 Mục ích
Mục ích của biến ổi Fourier là tách tín hiệu dạng sóng thành các tần số riêng lẻ
tạo ra nó. Hay biến ổi Fourier giúp biến ổi tín hiệu từ miền thời gian sang miền tần số.
Cụ thể hơn, biến ổi Fourier tách hàm số thành tổng các hàm sin và cos, mỗi hàm có tần
số khác nhau. Từ các biến ổi này, ta có thể dễ dàng biết ược các ặc trưng của tín hiệu 2.2.3 Định nghĩa
DFT ối với tín hiệu tương tự Page | 4 lOMoARcPSD| 36782889
Với một hàm liên tục một biến F(t), phép biến ổi Fourier F(f) ược ịnh nghĩa: Và biến ổi ngược:
Với j là căn bậc 2 của -1, e biểu thị số mũ tự nhiên
DFT với tín hiệu rời rạc:
Giả sử một chuỗi phức X(k) với phép lấy mẫu gồm N mẫu: Với x là số phức
Phép biến ổi Fourier của chuỗi này ược biểu thị X(k) gồm N mẫu Phép
biến ổi ược ịnh nghĩa: với n=0,1,……..,N-1 Phép biến ổi ngược: với n=0,1,………,N-1
Với N là ộ dài của một chu kì
Chuỗi số thực tương tự phần ảo bằng 0.
2.2.4 Ví dụ khai triển Fourier
Ví dụ 1: Khai triển chuỗi Fourier cho tín hiệu rời rạc tuần hoàn:
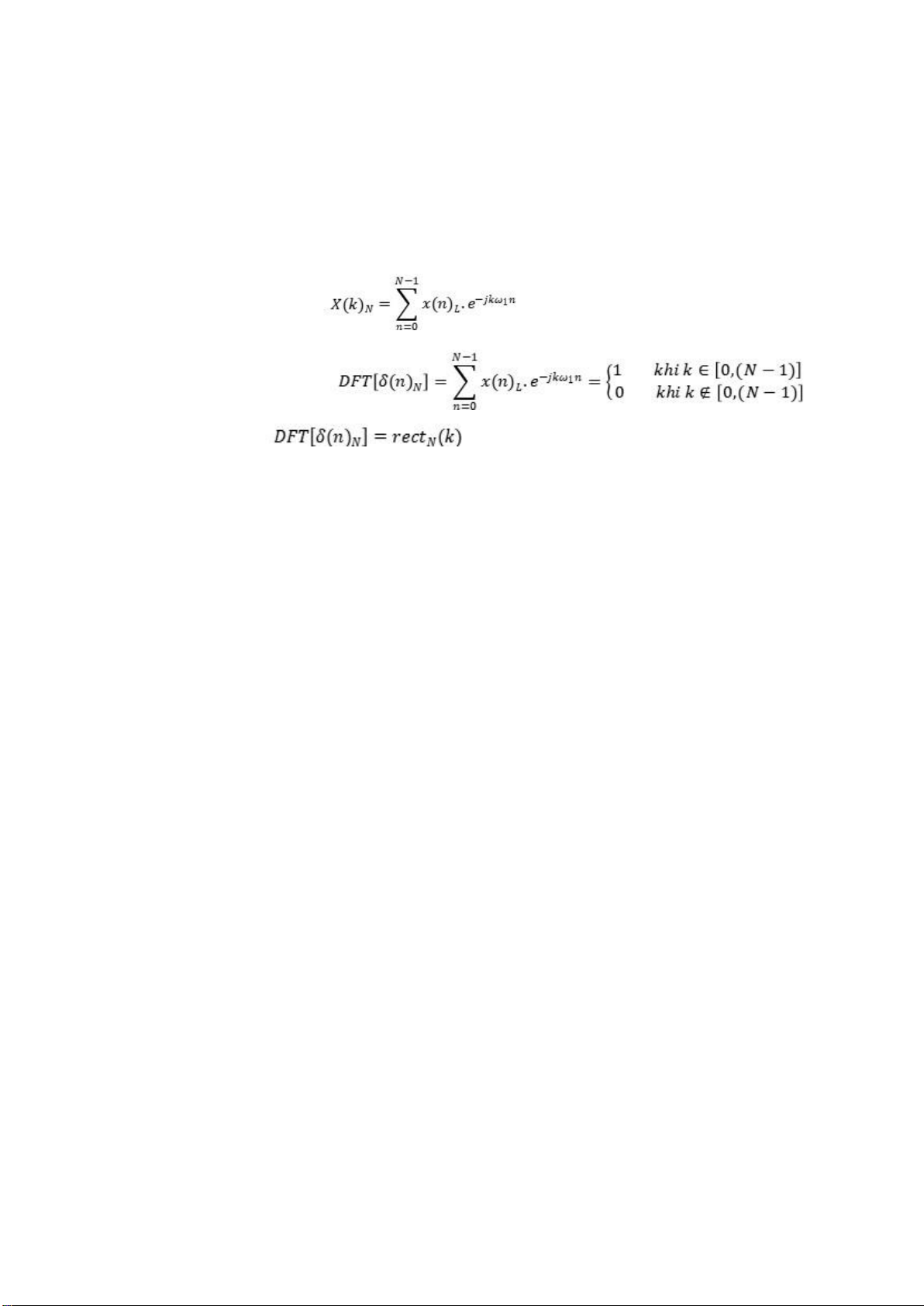
 Tìm DFT của dãy xung rời rạc sau: Giải Cuố cùng ta có: Page | 5 lOMoARcPSD| 36782889
Như vậy, DFT của dãy xung rời rạc là tập vô số xung rời rạc có chiều cao là
và có khoảng cách giữa hai xung cạnh nhau là  Xác ịnh của dãy tuần hoàn với chu kỳ Giải Tại Tại Tại Tại
Ví dụ 2: Biến ổi Fourier của tín hiệu rời rạc dài hữu hạn:
 Tính DFT của 끫룊(끫뢶) = 끫룄(끫뢶) − 끫룄(끫뢶 − 끫뢂) Giải
Suy ra DFT của 끫룊(끫뢶) = 1 với 끫뢶 = 0,1, … ,7 Giải Page | 6 lOMoARcPSD| 36782889
Có thể xem 끫뷾(끫뢶)끫뢂 là dãy 끫뷾(끫뢶)끫뢂 = 0 끫뢰ℎ 끫뢬 0 <1
끫뢰ℎ 끫뢬끫뢶 ≤ 끫뢶 = 0(끫뢂 − 1)
Theo biểu thức DFT thuận có hàm phố rời rạc: (Biến ổi thuận) Vậ y
2.3. Ứng dụng biến ổi Fourier hữu hạn trong khử nhiễu âm thanh.
Phép biến ổi 끫뢘 = 끫롲끫뢶끫뢖 gọi là phép biển ổi fourier rời rạc của vector X
+ Vector 끫뢘 = 끫롲끫뢶끫뢖 có dạng: 끫뢘 = 끫롨 + 끫뢬끫뢬
+ Vecto A chứa các hệ số 끫뷸끫뢬 trong
+ Vecto B chứa các hệ số 끫뷺끫뷺 trong.
Như vậy dùng phép biến ổi Fourier rời rạc, ta chuyển tín hiệu X ở miền thời gian
thành tín hiệu ở miền tần số gồm tổng các hàm 끫뢠끫뢠끫뢠 và 끫뢠끫뢬끫뢶
Giả sử tín hiệu gốc có dạng + nhiễu
Sau khi phân tích Fourier rời rạc 끫뢘 = 끫롲끫뢶. 끫뢖, so sánh với hình vẽ trước và
sau khi phân tích, ta có thể xác ịnh tần số tín hiệu chính và tần số nhiễu. Lọc bỏ tín hiệu
nhiễu, chỉ giữ lại tín hiệu chính, sau ó phân tích Fourier ngược ra sẽ thu ược tín hiệu ã khử nhiễu Page | 7 lOMoARcPSD| 36782889
3. BIẾN ĐỔI FOURIER RỜI RẠC ĐỂ KHỬ NHIỄU ÂM THANH TRONG MATLAB
3.1 Các bước dùng phép biến ổi Fourier hữu hạn ể khử nhiễu
Bước 1: Số hóa một file âm thanh, ta có một vector
[y, fs]=audioread('this.m4a');
Bước 2: Phân tích Fourier rời rạc vector y: Y = fft(y)
Bước 3: Vẽ tín hiệu ban ầu. Phân tích tần số của tín hiệu ể biết ược tần số của tín
hiệu chính và của tín hiệu bị nhiễu. plot(abs(Y),'r') M = max(abs(Y)); thresh = 0.1
Bước 4: Lọc bớt tần số của tín hiệu nhiễu chỉ giữ lại tần số tín hiệu chính.
Ythresh=(abs(Y)>thresh*M).*Y;
N = sum(abs(Ythresh)>0)/L
Bước 5: Biến ổi Fourier ngược lại;
Ythresh = real(ifft(Ythresh));
3.1.1. Các lệnh dùng trong bài matlab
Audioread(filename.m4a)
Đọc file âm thanh trong Matlab L=length(y)
Tính toán kích cỡ file âm thanh sound() Nghe âm thanh fft()
Biến đổi Fourier hữu hạn max()
Giá trị lớn nhất Page | 8 lOMoARcPSD| 36782889 Abs ()
Lấy giá trị tuyệt đối Ifft()
Biến đổi Fourier ngược lại Plot() Vẽ đồ thị
datathresh=(abs(y)>thresh.*M).*data Lọc nhiễu
3.1.2. Đoạn code trong matlab
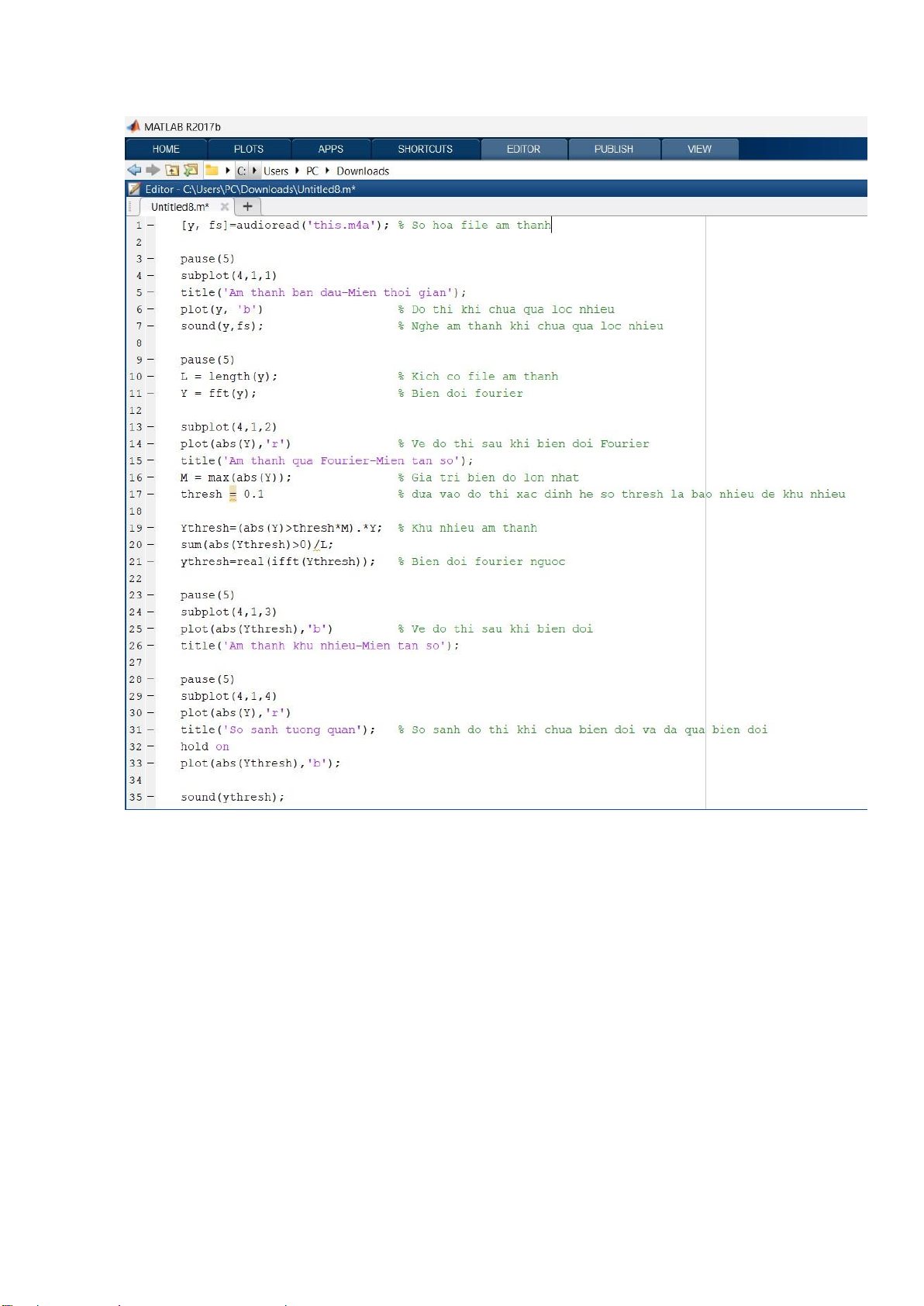
 [y, fs] = audioread('this.m4a'); % So hoa file am thanh  pause(5)  subplot(4,1,1)
 title('Am thanh ban dau-Mien thoi gian');
 plot(y, 'b') % Do thi khi chua qua loc nhieu
 sound(y,fs); % Nghe am thanh khi chua qua loc nhieu  pause(5)
 L = length(y); % Kich co file am thanh
 Y = fft(y); % Bien doi fourier  subplot(4,1,2)
 plot(abs(Y),'r') % Ve do thi sau khi bien doi Fourier
 title('Am thanh qua Fourier-Mien tan so');
 M = max(abs(Y)); % Gia tri bien do lon nhat
 thresh = 0.1 % dua vao do thi xac dinh he so thresh la bao nhieu de khu nhieu
 Ythresh=(abs(Y)>thresh*M).*Y; % Khu nhieu am thanh
 N = sum(abs(Ythresh)>0)/L; % Sau khi khu nhieu kich
thuoc file còn N lan so voi ban dau
 ythresh=real(ifft(Ythresh)); % Bien doi fourier nguoc  pause(5)  subplot(4,1,3)
 plot(abs(Ythresh),'b') % Ve do thi sau khi bien doi Page | 9 lOMoARcPSD| 36782889
 title('Am thanh khu nhieu-Mien tan so');  pause(5)  subplot(4,1,4)  plot(abs(Y),'r')
 title('So sanh tuong quan'); % So sanh do thi khi
chua bien doi va da qua bien doi  hold on  plot(abs(Ythresh),'b');  pause(5)  sound(ythresh);
3.2 Hình ảnh oạn code sử dụng trong Matlab Page | 10 lOMoARcPSD| 36782889
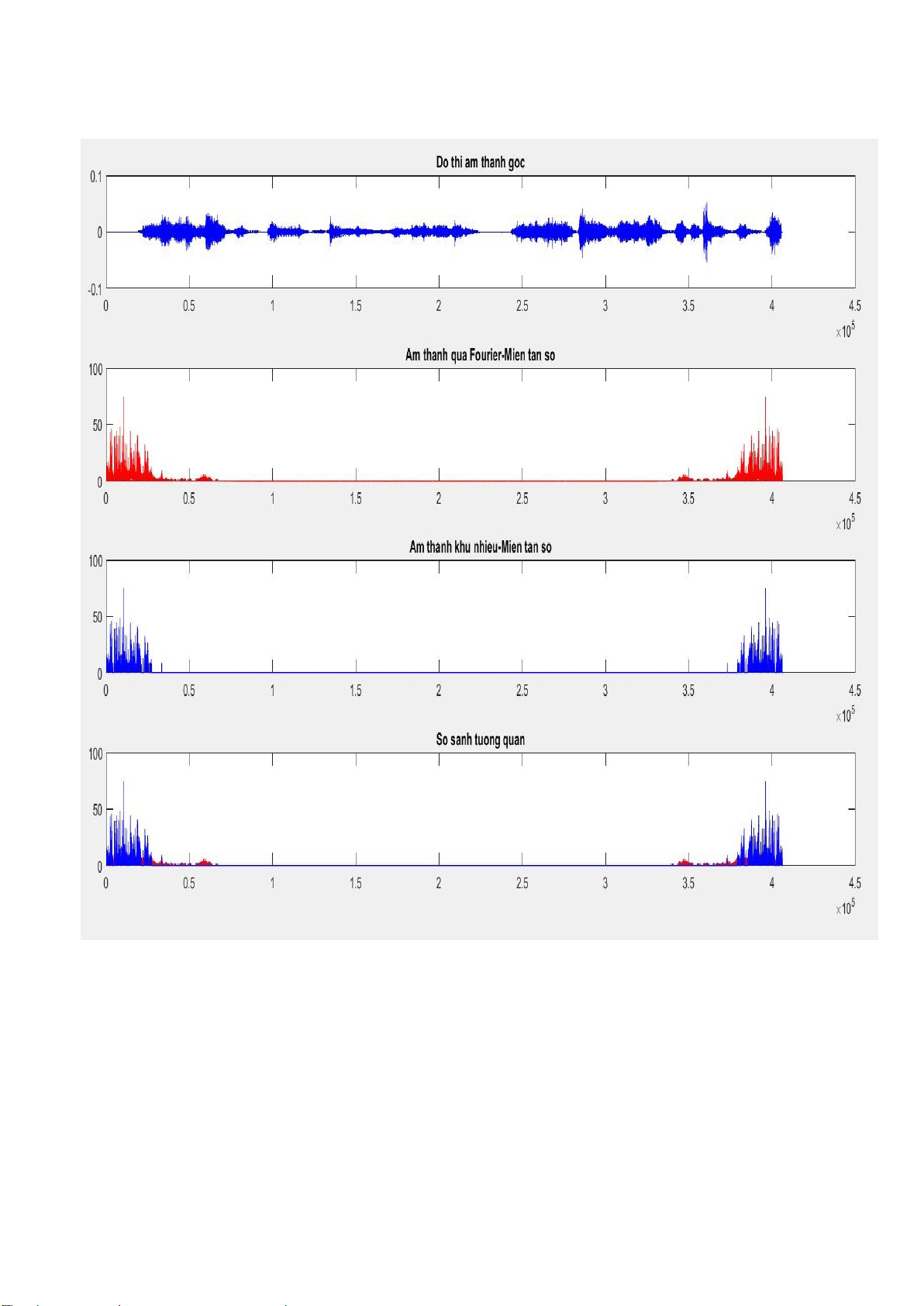
3.3 Ví dụ minh họa
Trong phần này ta sử dụng một file âm thanh ã chuẩn bị có lẫn tạp âm, sử dụng
lệnh fft trong Matlab, biến ổi Fourier từ miền thời gian sang miền tần số. Khử
những tần số nhiễu giữ lại tần số chinh. Dùng lệnh ifft biến ổi ngược lại, ta nghe
ược âm thanh sau khi khử nhiễu. Page | 11 lOMoARcPSD| 36782889 4. KẾT LUẬN
Phép biến ổi Fourier hữu hạn (DFT- Discrete Fourier Transform) là một phép biến
ổi sử dụng trong xử lí âm thanh và tín hiệu ể chuyển ổi một tín hiệu thời gian thành một tín hiệu tần số.
Thông qua bài tập lớn tìm hiểu ề tài này và với sự phân chia công việc hợp lý cho
từng thành viên trong nhóm, ý thức trách nhiệm của mỗi người mà nhóm em ã hoàn
thành ược bài tập với sự cố gắng chỉnh chu nhất. Page | 12 lOMoARcPSD| 36782889
- Hiểu ược cách lọc nhiễm một file âm thanh bất kì trên MATLAB
- Nắm rõ các ứng dụng của môn học, ặc biệt là Fourier hữu hạn trong khử nhiễu âm.
- Tăng khả năng nghiên cứu học tập có ý thức
- Biết các phối hợp hỗ trợ làm việc nhóm hiệu quả và tăng tính oàn kết của nhóm
- Ứng dụng môn học thực tiễn tạo sự hứng thú với môn học
TÀI LIỆU THAM KHẢO [1]
Đăng Văn Vinh, (2021). Giáo trình Đại số tuyến tính, Trường Đại học
Bách khoa ĐHQG.HCM – NXB Đại học Quốc gia Thành phố Hồ Chí Minh [2]
Meyer C.D, Matrix analysis and Applied linear algebra, SIAM, 2000, chapter 5, section 8 [3]
Isaac Amidror, Mastering the Discrete Fourier Transform in One, Two or
Several Dimensions: Pitfalls and Artifacts, Springer, 2013 Page | 13