


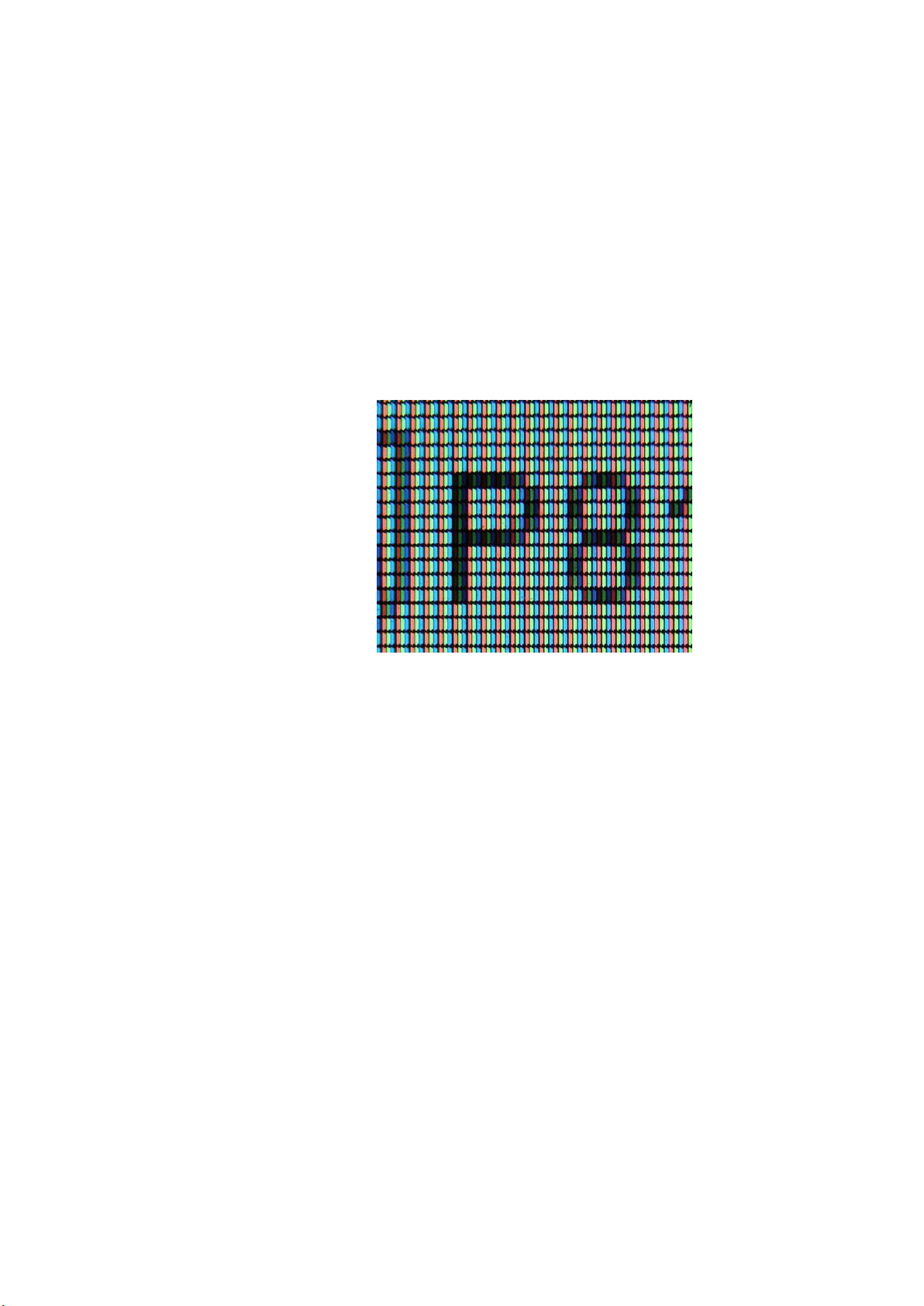










Preview text:
lOMoARcPSD| 36782889 LỜI MỞ ĐẦU
Trong sự phát triển của kỹ thuật hiện nay, hình thức xử lý tín hiệu ang dần
chiếm ưu thế về số lượng lớn ặc biệt trong việc xử lý ảnh, nén ảnh ... nhờ vào
các ưu iểm của nó ể thỏa mãn nhu cầu của con người. Điều này cho ta thấy yêu
cầu ngày càng cao trong việc xử lý tín hiệu, nén dữ liệu không bị nhiễu ồng thời
tiết kiệm dung lượng trên ường truyền tín hiệu ể có thể ưa ra tín hiệu với chất lượng tốt.
Trong các phương pháp xử lý tín hiệu, có rất nhiều phương pháp xử lý bằng
thuật toán, biến ổi toán học. Trong số ó, biến ổi Haar hiện nay ang ược xem là
phương pháp biến ổi mới có rất nhiều tiềm năng trong việc phát triển với nhiều
ưu iểm vượt trội. Biến ổi Haar cho phép phân tích tín hiệu cả trong miền tần số
và thời gian. Hiện nay, phương pháp biến ổi Haar ang ược sử dụng rộng rãi trong việc xử lý ảnh.
Hôm nay nhóm chúng em xin ược báo cáo ề tài “Nén ảnh bằng cách sử dụng
phép biến ổi Haar’’ ể cùng nhau tìm hiểu chi tiết. MỤC LỤC
CHƯƠNG I: CƠ SỞ LÝ THUYẾT .................................................................. 1
1.GIỚI THIỆU CHUNG ................................................................................. 1
1.1. SƠ LƯỢC VỀ THUẬT TOÁN HAAR ................................................. 1
1.2. TÁC DỤNG ........................................................................................... 1
1.3. ĐÔI NÉT VỀ ẢNH ................................................................................ 2
2. ỨNG DỤNG PHÉP BIẾN ĐỔI HAAR TRONG NÉN ẢNH .................. 2 lOMoARcPSD| 36782889
2.1. Giải thích thuật toán ............................................................................... 2
2.2. Nén mất dữ liệu ..................................................................................... 7
2.3. Nén không mất dữ liệu ........................................................................... 8
CHƯƠNG 2: MATLAB CODE VÀ GIẢI THÍCH ....................................... 12
1. Tổng quan về Matlab ................................................................................. 12
2. Các hàm Matlab cơ bản ược sử dụng trong bài toán ............................. 12
3. Giải bài toán trên Matlab .......................................................................... 13
3.1. Đoạn code hoàn chỉnh .......................................................................... 13
3.2. Hình ảnh chạy thuật toán trên Matlab .................................................. 14
3.3. Một số hình ảnh sau khi nén bằng biến ổi Haar: ................................. 14
4. Ưu iểm và nhược iểm của nén ảnh bằng phương pháp biến ổi Haar . 16
CHƯƠNG III TỔNG KẾT ............................................................................. 16
1. Kiến thức ..................................................................................................... 16
3. Kết luận ....................................................................................................... 17
DANH MỤC TÀI LIỆU THAM KHẢO ......................................................... 17 lOMoARcPSD| 36782889
CHƯƠNG I: CƠ SỞ LÝ THUYẾT 1.GIỚI THIỆU CHUNG
1.1. SƠ LƯỢC VỀ THUẬT TOÁN HAAR
− Alfred Haar (1885-1933) là một nhà toán học người Hungary ã làm việc
trong phân tích nghiên cứu các hệ thống trực giao của các hàm, phương trình vi
phân một phần, xấp xỉ Chebyshev và bất bình ẳng. Năm 1909, Haar giới thiệu lý
thuyết sóng Haar. Ở dạng rời rạc sóng Haar có liên quan ến một hoạt ộng toán
học ược gọi là biến ổi Haar.
− Hàm biến ổi nén Haar là một cách ơn giản ể thể hiện cả hai phương pháp
nén mất dữ liệu và nén không mất dữ liệu. Nó phụ thuộc vào trung bình và các
giá trị khác nhau trong ma trận hình ảnh ể mà tạo ra những ma trận thưa hoặc
gần thưa. Một ma trận thưa ược lưu trữ một cách hiệu quả, dẫn tới việc làm nhỏ
i kích cỡ của ma trận ó. 1.2. TÁC DỤNG
− Được sử dụng rộng rãi trong nhiều ứng dụng khác nhau, bao gồm nén
hình ảnh, phát hiện biên ộc lập với tỷ lệ, phân tích tín hiệu,....
− Với sự ra ời của máy ảnh kĩ thuật số, một trong những ứng dụng phổ
biến nhất là lưu trữ, thao tác và truyền hình ảnh kỹ thuật số. Tuy nhiên, các tệp
bao gồm những hình ảnh này có thể khá lớn và có thể nhanh chóng chiếm phần
lớn dung lượng bộ nhớ. Biến ổi Haar Wavelet ược sử dụng ể nén hình ảnh bằng
cách giảm kích thước của hình ảnh và loại bỏ các chi tiết không cần thiết.
− Biến ổi Haar wavelet ược tìm thấy hiệu quả trong các ứng dụng như nén
tín hiệu và hình ảnh trong kỹ thuật iện và máy tính vì nó cung cấp một cách tiếp
cận ơn giản và hiệu quả về mặt tính toán ể phân tích các khía cạnh ịa phương của
tín hiệu. Nó ã cung cấp phương tiện mà chúng ta có thể nén hình ảnh ể rằng nó
chiếm ít không gian lưu trữ hơn, và do ó truyền iện tử nhanh hơn và ở mức ộ chi tiết tăng dần. 1 lOMoARcPSD| 36782889
1.3. ĐÔI NÉT VỀ ẢNH
− Gốc của ảnh là ảnh liên tục về không gian và ộ sáng. Để xử lý bằng máy
tính, ảnh cần phải ược số hoá.Số hoá ảnh là sự biến ổi gần úng một ảnh liên tục
thành một tập iểm phù hợp với ảnh thật về vị trí (không gian) và ộ sáng (mức
xám). Khoảng cách giữa các iểm ảnh ó ược thiết lập sao cho mắt người không
phân biệt ược ranh giới giữa chúng. Mỗi một iểm như vậy gọi là iểm ảnh (PEL:
Picture Element) hay gọi là pixel. Trong khuôn khổ ảnh 2 chiều, mỗi pixel có tọa ộ là (x,y)
H椃nh 1: Ví dụ minh họa về Pixel(ảnh chụp các yếu tố hiển thị pixel trên màn
h椃nh LCD của máy tính)
− Mức xám: Mức xám của iểm ảnh là cường ộ sáng của nó ược gán bằng
giá trị số tại iểm ó. Mức xám của ảnh số là kết quả của sự mã hóa tương ứng
cường ộ ánh sangs của mỗi iểm ảnh với một giá trị số.
− Mật ộ pixel ược ấn ịnh trên một ảnh chính là ộ phân giải của ảnh. Độ
phân giải càng thấp thì hình ảnh hiển thị càng mờ, ngược lại ộ phân giải càng
cao thì ảnh càng sắc nét.
2. ỨNG DỤNG PHÉP BIẾN ĐỔI HAAR TRONG NÉN ẢNH
2.1. Giải thích thuật toán
− Ở phương pháp này, ta sẽ tập trung vào thước xám (Ảnh xám hay còn
gọi là ảnh ơn sắc (monochromatic), là ảnh mà tại mỗi iểm ảnh có một giá trị mức
xám. Ảnh 8 mức xám sẽ có giá trị mỗi iểm ảnh nằm trong oạn [0, 7]. Ảnh 256
mức xám sẽ có giá trị mỗi iểm ảnh nằm trong oạn [0, 255]). 2 lOMoARcPSD| 36782889
− Phương pháp bắt ầu với một ảnh A, ta có thể xem như là một ma trận cỡ
m x n , với giá trị từ 0 ến 255. Trong matlab, nó sẽ là một ma trận với 8-bit giá trị
nguyên. Chúng ta có thể chia nhỏ ảnh thành 8 x 8.
Ví Dụ: Dưới ây là hình ảnh thang ộ xám 512 x 512 pixel của các trụ bay
của Nhà Thờ Đức Bà Paris:
H椃nh 2: h椃nh ảnh thang ộ xám 512 x 512 pixel của các trụ bay của Nhà Thờ Đức Bà Paris
Và từ bức ảnh trên, ta có ma trận của các giá trị iểm ảnh như sau:
− Đầu tiên, chúng ta tập trung vào hàng ầu làm mẫu:
𝑟1 = ( 88 88 89 90 92 94 96 97 )
− Quá trình chuyển ổi bao gồm 3 bước: o Trước 3 lOMoARcPSD| 36782889
hết, nhóm các số theo cặp, ta có: o ([88,88]; [89,90]; [92,94]; [96,97])
o Tiếp theo, ta lấy trung bình cộng của 4 cặp thế vào 4 cột ầu tiên của r1
và nửa hiệu của 4 cặp thế vào 4 cột cuối cùng của r1 . Hàng mới có kí hiệu là:
𝑟1 ℎ1 = ( 88 89.5 93 96.5 0 − 0.5 − 1 − 0.5 ) o 4 mục ầu tiên
ược gọi là hệ số xấp xỉ và 4 mục cuối cùng ược gọi là hệ số chi tiết. Bước tiếp
theo, nhóm 4 cột ầu của hàng mới thành 2 cặp [88,89.5], [93,96.5] và thay thành
hàng mới với 2 cột ầu bằng nửa tổng của 2 cặp số và 2 cột sau bằng nửa hiệu
của 2 cặp số ó, các cột còn lại của r1 h1 ta giữ nguyên. Và biểu thị hàm mới thứ 2 này là:
𝑟1ℎ1ℎ2 = ( 88.75 94.75 − 0.75 0 − 0.5 − 1 − 0.5 ) o Cuối cùng, nhóm 2
mục ầu của r1 h1 h2 thành 1 cặp [88.75 94.75] và
thay hàng mới với cột ầu là nửa tổng và cột 2 là nửa hiệu của cặp số trên. Ta
giữ nguyên 6 cột cuối cùng. Ta ký hiệu hàng mới cuối cùng này là:
𝑟1ℎ1ℎ2ℎ3 = ( 91.75 − 3 0.75 − 1.75 0 − 0.5 − 1 − 0.5 )
− Tiếp tục lặp lại quy trình này cho các hàng còn lại của A. Sau ó, lặp lại
tương tự cho các cột của A, và nhóm các hàng theo cùng một cách với các cột, ma trận kết quả là:
− Giờ ta sẽ thảo luận về cách thực hiện quá trình trên bằng cách sử dụng
phép nhân ma trận dưới ây - ma trận biến ổi Haar wavelet. Nếu ban ầu ta xác ịnh:
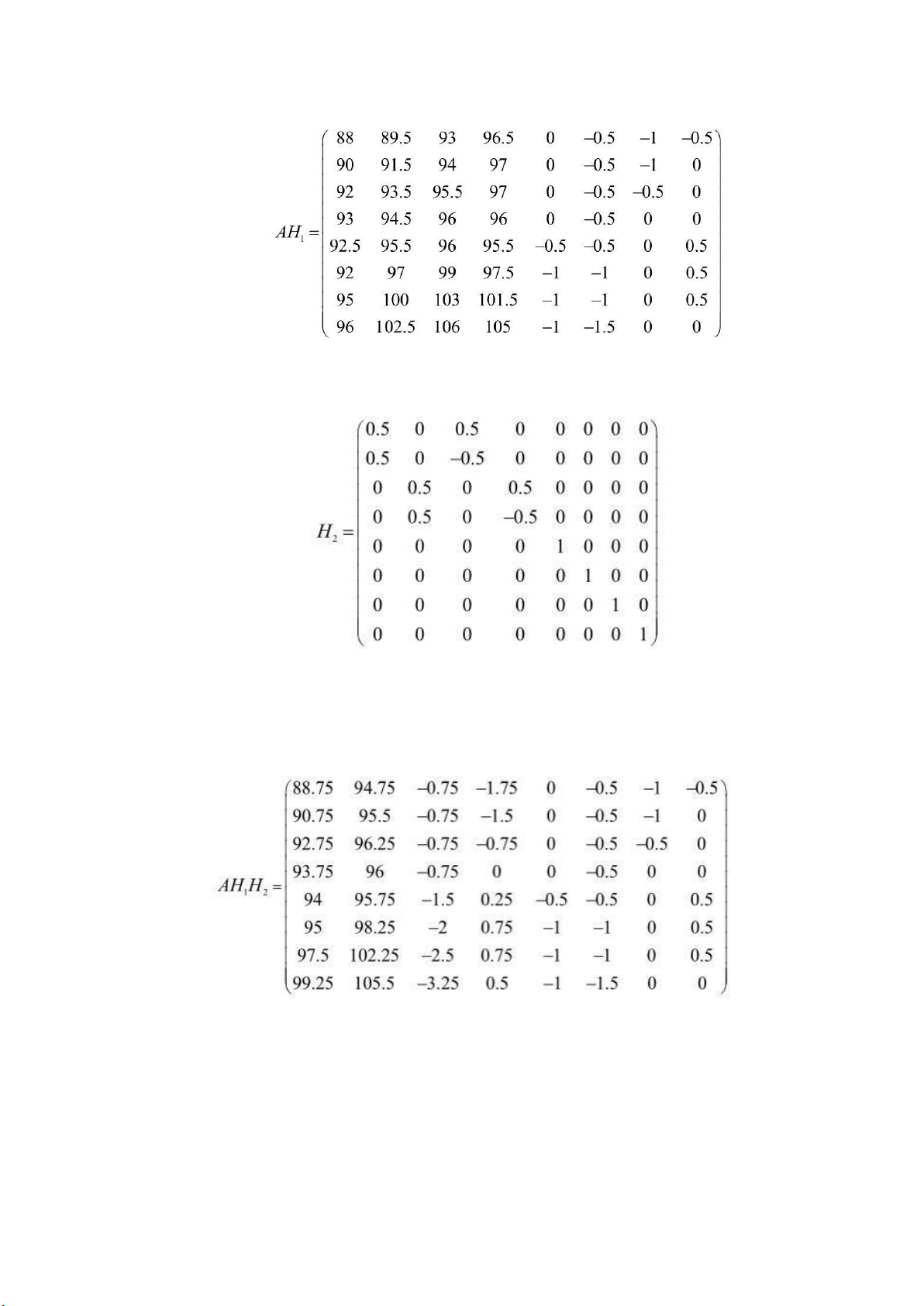
nếu lấy phép nhân ma trận A với H1 thì AH1 tương ứng với bước ầu tiên nhưng
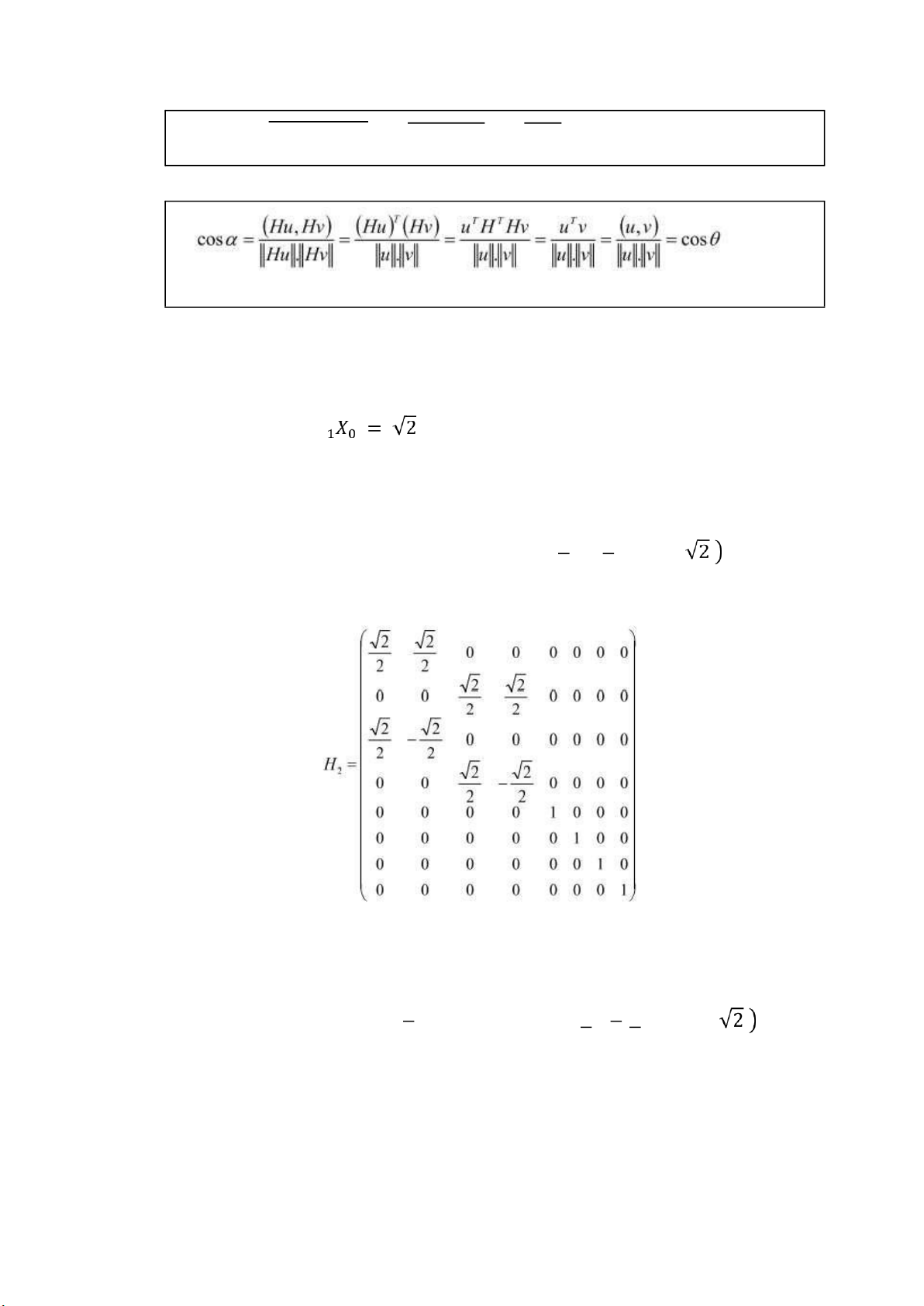
với tất cả các hàng của A. 4 lOMoARcPSD| 36782889 − Tương tự, ta có H2 :
− Sau ó AH1H2 tương ương với 2 bước trên và ược áp dụng cho tất cả các hàng của A:
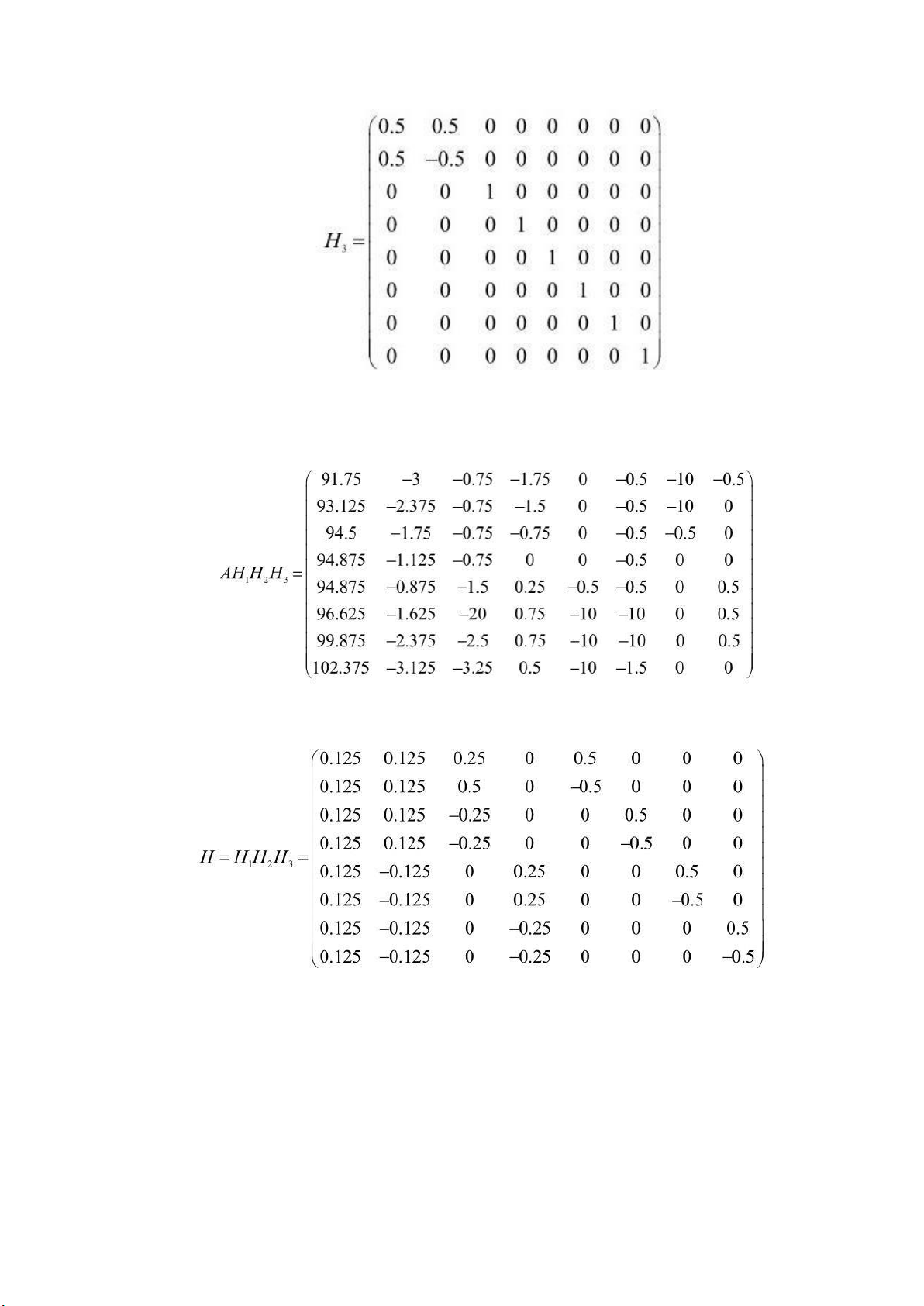
− Cuối cùng ta xác ịnh: 5 lOMoARcPSD| 36782889
− Sau ó AH1H2H3 tương ương với 3 bước trên ược áp dụng cho tất cả các
hàng của A. Cụ thể là:
− Ta ặt H là tích của 3 ma trận bên phải A, tức:
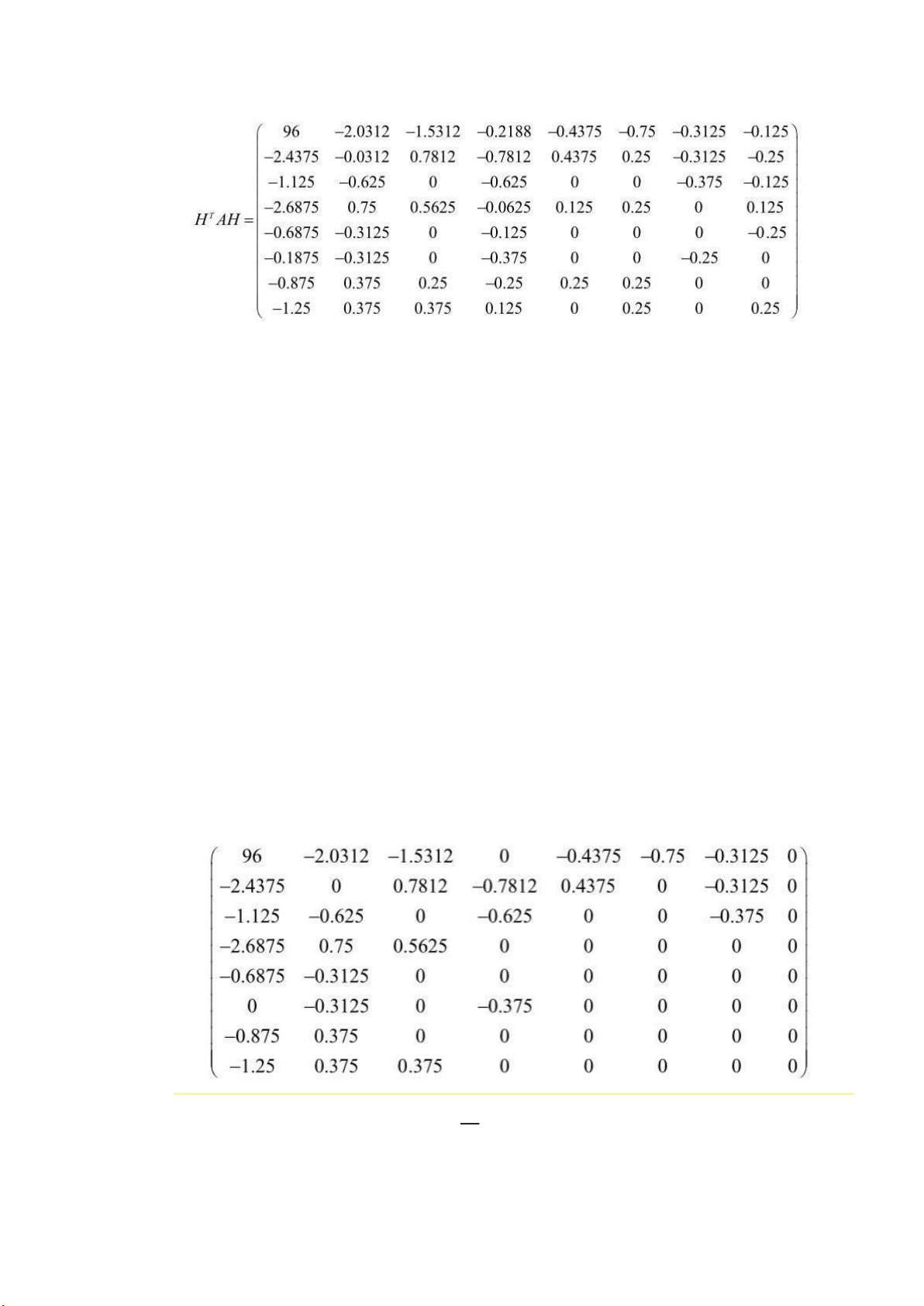
− Để áp dụng quy trình cho các cột, chỉ cần nhân A ở bên trái với HT. Ma trận kết quả là: 6 lOMoARcPSD| 36782889
− Nếu như ta có B = HT AH thì A = (HT )-1 BH-1 .
− Vì H là một ma trận khả nghịch và B chính là kết quả ảnh nén của A nên
ây ược gọi là phép nén không mất dữ liệu.
2.2. Nén mất dữ liệu.
− Phép biến ổi Haar có thể biểu diễn ma trận nén mất dữ liệu ể giữ lại chất
lượng hình ảnh khi chúng ta giải nén hình ảnh này bằng cách sử dụng biến ổi Haar wavelet ngược.
− Đầu tiên, xác ịnh tỷ lệ nén của hình ảnh là tỷ lệ của các phần tử khác 0
trong ảnh gốc với các phần tử khác 0 trong ảnh nén.
− Tiếp theo, áp dụng phép biến ổi Haar ngược, ta thu ược kết quả với một
hình ảnh ược giải nén gần giống với bản gốc. Với ma trận A lấy từ ví dụ, nếu
chọn 𝜀 = 0.25 (với những số có trị tuyệt ối từ 0 tới 𝜀 biến thành số 0), sẽ có kết quả với ma trận: − 48
Ma trận này có tỉ lệ nén là
=1 (7) với phần tử số 48 là một nửa của 27
số trên cùng 96 và phần mẫu là 27 số khác 0. 7 lOMoARcPSD| 36782889
− Một số ví dụ về hình ảnh ban ầu ược nén theo các tỷ lệ khác nhau:
H 椃 nh 3: Ảnh gốc
H 椃 nh 4: Tỷ lệ nØn 10:1
H 椃 nh 5: Tỷ lệ nØn 30:1
H 椃 nh 6: Tỷ lệ nØn 50:1
2.3. Nén không mất dữ liệu.
− Ví dụ: Xét một phép nén dữ liệu dựa trên biến ổi Haar. Giả sử ta có oạn dữ liệu
𝑋0 = ( 154 150 156 152 160 160 152 156 )𝑇 8 lOMoARcPSD| 36782889
− Ta tiếp tục chia dữ liệu thành từng cặp và tìm nửa tổng và nửa hiệu của
các cặp. Khi ó ta ược dãy:
𝑋1 = ( 152 154 160 154 2 2 0 − 2 )𝑇
với 4 số ầu tiên là nửa tổng và 4 số tiếp theo là nửa hiệu của các cặp.
− Ta sử dụng ma trận ể mô tả quá trình này như sau:
− Dễ dàng thấy các cột của A tạo nên 1 họ trực giao. Trực chuẩn hóa
chúng, ta chia mỗi cột cho ộ dài của A ( | A||= √ 2 ). 2
Ta ược 1 họ trực chuẩn và ma trận tương ứng là ma trận trực giao H :
− Khi ó nghịch ảo của H là HT . Ta dùng H ể nén dữ liệu thay cho A.
Ta có 𝑌1 = 𝐻𝑋0 . Giải nén dữ liệu ta ược 𝑋0 = 𝐻𝑇𝑌1 .
Phép biến ổi trực giao H có tính chất bảo toàn khoảng cách và góc. Chứng minh: 9 lOMoARcPSD| 36782889
| | 𝐻𝑋 | | = √ ( 𝐻𝑋 ) 𝑇 ( 𝐻𝑋 ) = √ 𝑋 𝑇 𝐻 𝑇 𝐻𝑋 = √ 𝑋 𝑇 𝑋 = | | 𝑋 | |
Qua phép biến ổi H, góc giữa hai vector H u và H v thỏa:
Với 2 tính chất trên, phép biến ổi không làm thay ổi hình dạng của ảnh trong quá trình nén.
Tiếp tục quá trình nén ở trên ta có: 𝑌1 = 𝐻
( 152 154 160 154 2 2 0 − 2 )𝑇
− Với H1 là ma trận H ở ví dụ trước, lấy 4 số ầu ta chia thành 2 cặp, tìm
nửa tổng và nửa hiệu của các cặp và giữ 4 số sau của dãy lại ta ược 𝑇
𝑌2 = 𝐻2𝑌1 = ( 306 314 − 2 6 2√ 2 2 √ 2 0 − 2 với:
− Tiếp tục quá trình trên và giữ 6 số cuối của Y2 lại. Hai số ầu ược thay
bởi nửa tổng và nửa hiệu của chúng, ta có 𝑇
𝑌3 = 𝐻3𝑌2 = ( 310√2 − 4√2 − 2 6 2√ 2 2 √ 2 0 − 2 với 10 lOMoARcPSD| 36782889
- Tóm lại ta có 𝑌3 = 𝐻3𝐻2 𝐻1 𝑌0 <=> 𝑌3 = 𝑄𝑋0
− Giải nén dãy dữ liệu Y3 tìm lại dãy X0 = Q-1 Y3 <=> X0 = QTY3 , với:
− Dưới ây là ảnh minh họa cho phép biến ổi nén không mất dữ liệu: 11 lOMoARcPSD| 36782889
H nh 7: H nh ảnh gốc
H nh 8: Ảnh sau một lần biến đổi
Hình 9: Ảnh sau hai lần biến ổi
Hình 10: Ảnh sau ba lần biến ổi
CHƯƠNG 2: MATLAB CODE VÀ GIẢI THÍCH
1. Tổng quan về Matlab
MATLAB là phần mềm cung cấp môi trường tính toán số và lập trình, do
công ty MathWorks thiết kế. MATLAB cho phép tính toán số với ma trận, vẽ ồ
thị hàm số hay biểu ồ thông tin, thực hiện thuật toán, tạo các giao diện người
dùng và liên kết với những chương trình máy tính viết trên nhiều ngôn ngữ lập trình khác.
2. Các hàm Matlab cơ bản ược sử dụng trong bài toán Lệnh
Ý nghĩa của lệnh 12 lOMoARcPSD| 36782889 clear all Xóa biến. imread(‘filename’)
Đọc hình ảnh từ tệp ồ họa. imresize(A,[NUMROWS
Thay ổi kích thước hình ảnh. NUMCOLS]) rgb2gray(image)
Chuyển ổi hình ảnh hoặc bản ồ màu RGB sang thang ộ xám. size(‘ ’) Tính kích thước mảng. round(‘ ’)
Làm tròn ến giá trị của biến. imshow(‘filename’)
Hiển thị hình ảnh từ tệp ô họa. xlabel(‘filename’)
Thêm nhãn text vào trục x. subplot(2,1,n) Chia figure window thành 2
phần theo chiều ngang, ảnh
hiển thị ở phần thứ n.
3. Giải bài toán trên Matlab
3.1. Đoạn code hoàn chỉnh clear all I = imread(['anh.jpg']); I = imresize(I, [128 128]);
I = rgb2gray(I); k = 1; for i = 1:2:size(I,2) I1(:,k) =
(I(:,i)+I(:,i+1))/2; k=k+1; end
for i = 1:2:size(I,2) I1(:,k) = (I(:,i)-I(:,i+1))/2; k=k+1;
end I1 = round(I1); k = 1; for i = 1:2:size(I,1) I2(k,:) = (I1(i,:)+I1(i+1,:))/2; k =
k+1; end for i = 1:2:size(I,1) 13 lOMoARcPSD| 36782889
I2(k,:) = (I1(i,:)-I1(i+1,:))/2; k = k+1; end I2 = round(I2); subplot(2,1,1) imshow(I) xlabel('Anh Ban Dau') subplot(2,1,2) imshow(I2) xlabel('Anh Sau Khi Nen')
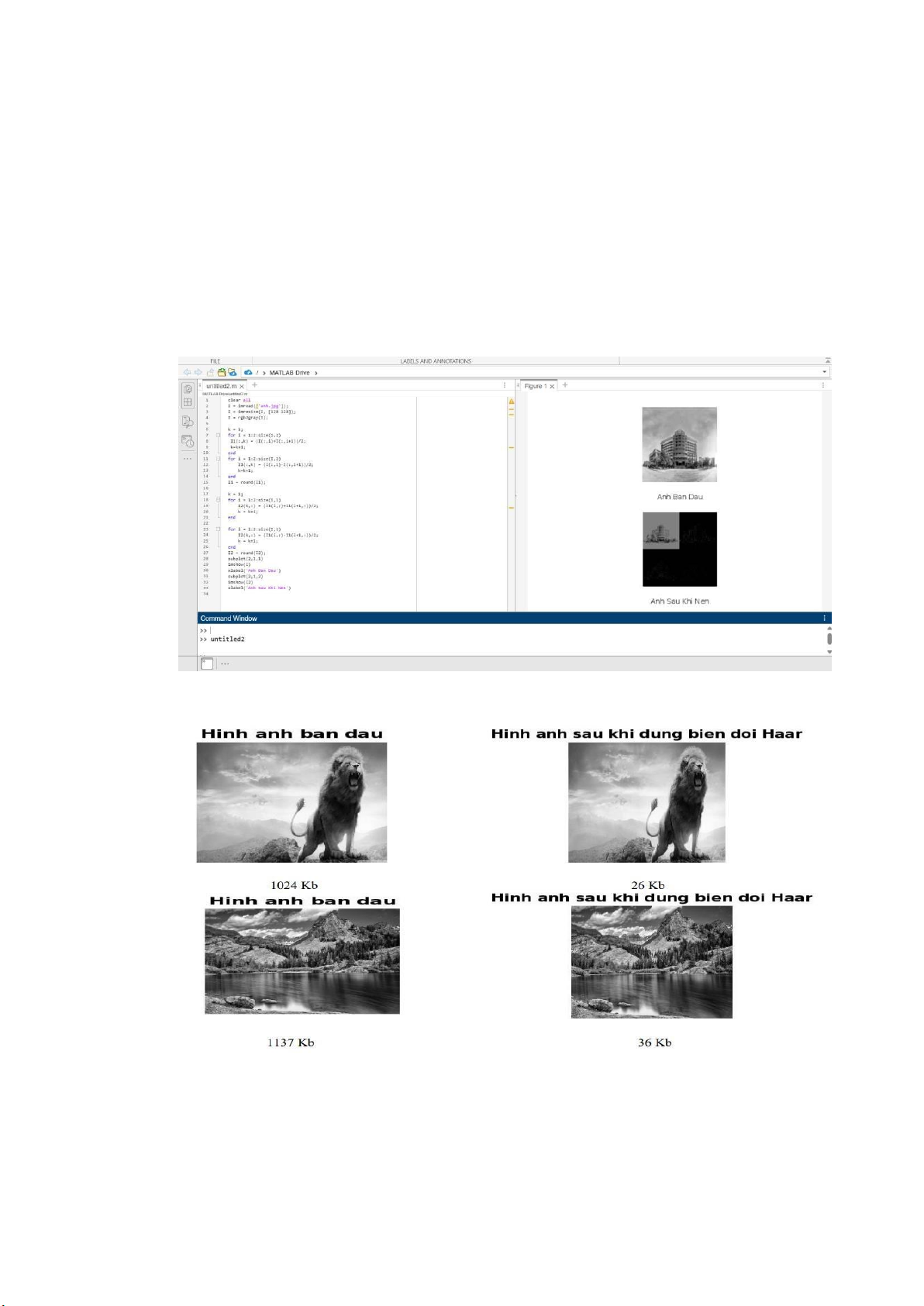
3.2. Hình ảnh chạy thuật toán trên Matlab
3.3. Một số hình ảnh sau khi nén bằng biến ổi Haar: 14 lOMoARcPSD| 36782889
Nhận xét về dung lượng khi nén ảnh:
− Dung lượng ảnh ban ầu ã bị giảm i rất nhiều.
− Chất lượng ảnh thấp, giảm dần sau mỗi lần nén.
− Sau lần nén ầu tiên : Ảnh có mờ i nhưng không áng kể.
− Lấy ảnh mới nén tiếp tục i nén thì ộ mờ giảm tiếp do dung lượng tiếp tục ược nén. 15 lOMoARcPSD| 36782889
4. Ưu iểm và nhược iểm của nén ảnh bằng phương pháp biến ổi Haar Ưu Điểm Nhược Điểm
-Hiệu quả nén cao
-Mất mát thông tin
Biến ổi Haar thường tạo ra một số
Quá trình giữ lại một lượng hệ số cao
lượng hệ số gần bằng 0 cho các tần số
hoặc thấp có thể dẫn ến mất mát thông
thhấp, giúp gảm kích thước dữ liệu hiệu
quả. Giúp tang khả năng nén ảnh vẫn
tin quan trọng và gây ra hiện tượng
giữ ược mức hình ảnh có thể chấp nhận ượ nhiễu. c.
-Khả năng iều chỉnh chất lượng
-Không hiệu quả ối với hình ảnh ộng
Có thể kiểm soát chất lượng hình ảnh
Biến ổi Haar thường không hiệu quả ối
thông qua việc giữ lại spố lượng hệ số
với việc nén hình ảnh ộng và videi, do
biến ổi cao hoặc thấp dẫn ến iều chỉnh
ược mức ộ nén và chất lượng hình ảnh.
không giữ ược thông tin thời gian và
không gian một cách hiệu quả.
-Thực hiện nhanh chóng và ơn giản
-Dễ bị ảnh hưởng bỡi nhiễu
Biến ổi Haar có thể ược thực hiện nhanh - Không linh hoạt
chóng và hiệu quả, ặc biệt là khi áp
Khả năng biểu diễn của biến ổi Haar
dụng thuật toán chia ể trị, phương pháp
nén hiệu quả với chi phí tính toán thâp.
giới hạn sao với một số phương pháp khác
CHƯƠNG III TỔNG KẾT 1. Kiến thức
− Dựa vào các kiến thức lí thuyết ã ược học ể thực hiện phép biến ổi Haar.
− Tìm hiểu và sử dụng phần mềm Matlab viết chương trình sử dụng phép
biển dổi Haar ể nén dữ liệu. 16 lOMoARcPSD| 36782889
− Phương pháp biến ổi Haar là một phương pháp biến ổi dùng ể phân tích
tín hiệu cả trong miền thời gian và tần số. Đây là một phương pháp biến ổi mới,
có rất nhiều tiềm năng, ang phát triển khá mạnh mẽ với các ưu iểm vượt trội so
với các phép biến ổi truyền thống. 2. Kỹ năng
− Sau thời gian làm việc chung, nhóm ã ạt ược kết quả sau:
o Nhóm hoạt ộng ổn ịnh, có tổ chức, tôn trọng lẫn nhau, thường xuyên
tương tác, trao ổi qua lại giữa các thành viên.
o Thành viên có trách nhiệm, tham gia tất cả các cuộc bàn luận và hoàn
thành nhiệm vụ ược phân công. o Mọi công việc ều rõ ràng nên nhóm ã hoạt
ộng một cách tối ưu và
ạt ược hiệu quả công việc cao.
o Các thành viên ã nâng cao ược kĩ năng làm việc nhóm như khả năng
giao tiếp, thảo luận với nhau, ưa ra quan iểm cá nhân,… o Giữa các thành viên
có sự thống nhất, mọi người ều có tính kỷ luật,
tuân theo nội quy của nhóm. 3. Kết luận
Với sự phân công chuẩn bị kĩ lưỡng và cố gắng hết mình nhóm ã hoàn
thành ề tài ược giao và Matlab ã cho ra những kết quả như mong muốn. Qua
phần bài tập lớn, nhóm ã biết ược những thao tác ể có thể nén dữ liệu bằng
phương pháp Haar và ứng dụng của của phép biến ổi Haar trong việc nén hình
ảnh. Ngoài ra còn nâng cao thêm ược sự hứng thú trong môn học, trau dồi tinh
thần trách nhiệm làm việc nhóm.
DANH MỤC TÀI LIỆU THAM KHẢO
[1] ĐẶNG VĂN VINH. GIÁO TRÌNH ĐẠI SỐ TUYẾN TÍNH
[2] ANTON, H. and C. RORRES. Elementary Linear Algebra: Applications
Version, 7th ed. New York: John Wiley & Sons, Inc., 1994.
[3] Meyer C.D, Matrix analysis and Applied linear algebra, SIAM, 2000.
[4] KOLMAN, B. Introductory Linear Algebra with Applications. New Jersey: 17 lOMoARcPSD| 36782889 Prentice Hall, Inc., 1997."
[5] GIÁO TRÌNH XỬ LÍ ẢNH- CHƯƠNG 8: NÉN DỮ LIỆU ẢNH
[6] http://kdientu.duytan.edu.vn/media/49753/thi-giac-may-va-anh-so.docx
[7] https://arxiv.org/ftp/arxiv/papers/1010/1010.4084.pdf
[8]https://www.researchgate.net/publication/328190353_IMAGE_COMPRES
SION_USING_HAAR_WAVELET_TRANSFORM 18




