Bài tập lớn Môn Động lực học công trình nâng cao | Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh

lOMoAR cPSD| 58702377 BÀI TẬP LỚN
MÔN ĐỘNG LỰC HỌC CÔNG TRÌNH NÂNG CAO
Lớp Cao học Kỹ thuật Xây dựng, Khóa 2019B Ngày giao: 27/7/2020 Ngày nộp: 10/8/2020 Yêu cầu :
- Mỗi học viên làm 1 báo cáo theo số liệu tương ứng của học viên - Báo cáo
trình bày dạng tiểu luận.
- Nộp file báo cáo dạng pdf Câu 1:
Cho hệ một bậc tự do như H nh vẽ 1. Hệ dao ộng cưỡng bức có cản với chuyển vị ban ầu u(0)
và vận tốc ban ầu u( )0 . Số liệu các ại lượng ược cho trong Bảng 1.
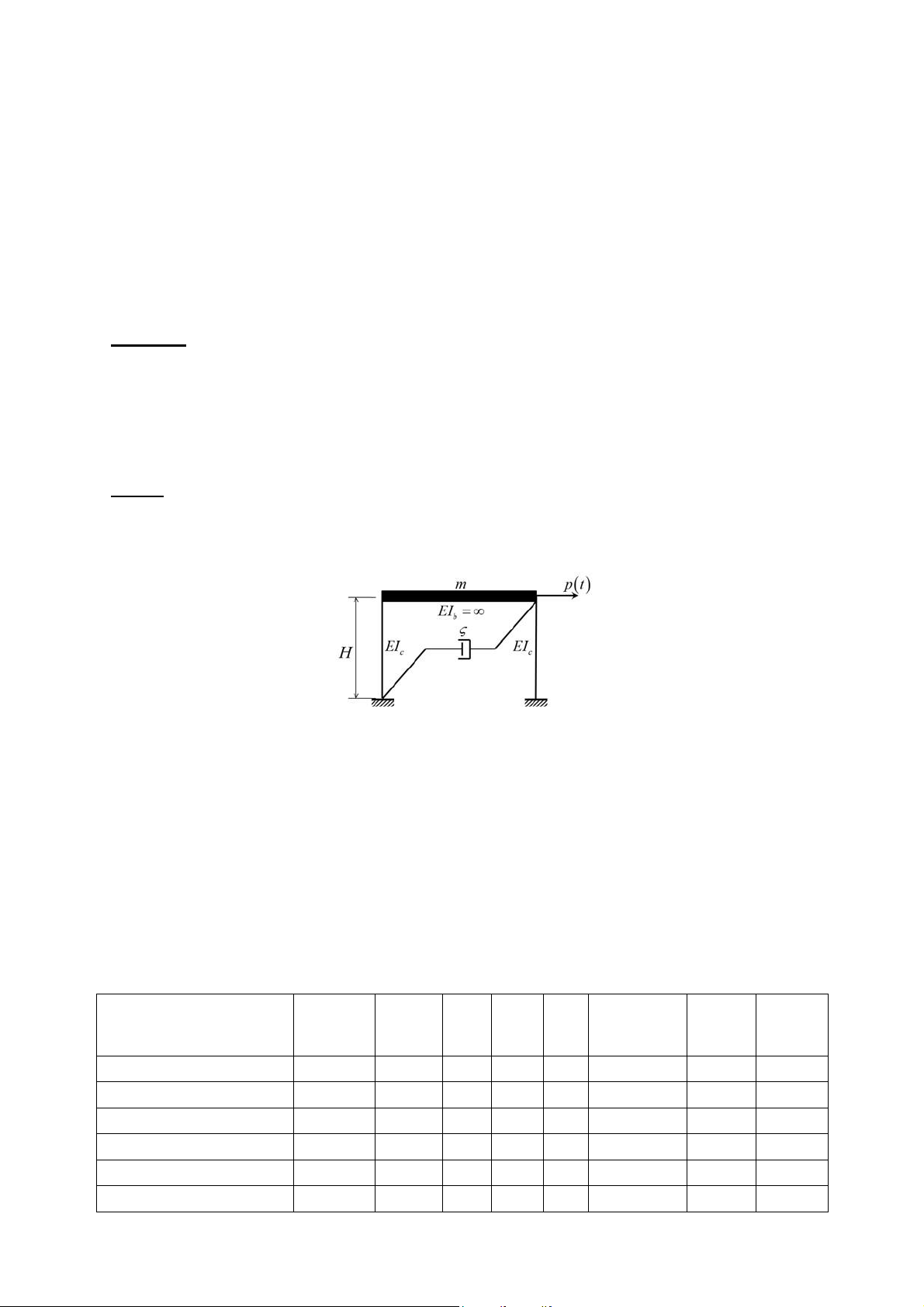
H nh vẽ 1: Khung 1 bậc tự do chịu tÆc dụng của ngoại lực p(t) a.
Dùng lời giải giải tích, xác ịnh chuyển vị ngang u(t) của khối lượng m tại các thời iểm
cho trong Bảng 2 (lấy 4 số thập phân). b.
Dùng phương pháp xấp xỉ lực kích thích, xác ịnh chuyển vị ngang u(t) của khối lượng
m tại các thời iểm cho trong Bảng 2 (lấy 4 số thập phân). c.
Dùng phương pháp sai phân trung tâm, xác ịnh chuyển vị ngang u(t) của khối lượng m
tại các thời iểm cho trong Bảng 2 (lấy 4 số thập phân). d.
Dùng phương pháp Newmark (γ = 1/2, β = 1/6), xác ịnh chuyển vị ngang u(t) của khối
lượng m tại các thời iểm cho trong Bảng 2 (lấy 4 số thập phân).
Bảng 1: Số liệu khung, tải trọng v iều kiện ban ầu I H m ζ u(0) u( )0 Họ và tên E c
p(t) (kN)
(kN/m2) (cm4) (m) (tấn) (%) (cm) (cm/s) Châu Thanh Bình 3,2x107 12000 4,1 6,2 4 610sin(11t) 2 1 Nguyễn Ánh Cao 3,1x107 13000 4,2 6,1 5 620sin(12t) 3 2 Lê Minh Chánh 3,0x107 14000 4,3 6,0 6 630sin(13t) 4 3 Phạm Duy Chung 2,9x107 15000 4,4 5,9 7 640sin(14t) 5 4 Nguyễn Khánh Duy 2,8x107 16000 4,5 5,8 8 650sin(15t) 6 5 Nguyễn Hoàng Dũng 2,7x107 17000 4,6 5,7 9 660sin(16t) 7 6 lOMoAR cPSD| 58702377 Nguyễn Thị Thu Hảo 3,2x107 13000 4,3 5,9 8 630sin(13t) 4 3 Nguyễn Công Hậu 3,1x107 14000 4,4 5,8 9 610sin(11t) 5 2 Phạm Vũ Minh Hoàng 3,0x107 15000 4,5 5,7 4 620sin(12t) 2 1 Trương Thanh Hòa 2,9x107 16000 4,6 6,2 5 630sin(13t) 3 2 Nguyễn Văn Khánh 2,8x107 17000 4,1 6,1 6 640sin(14t) 4 3 Nguyễn Việt Khánh 2,7x107 12000 4,2 6,0 7 650sin(15t) 5 3 Trần Chí Nghĩa 3,2x107 14000 4,3 5,8 9 660sin(16t) 6 1 Trần Mạnh Quân 3,1x107 15000 4,4 5,7 8 610sin(11t) 7 2 Nguyễn Quang Sĩ 3,0x107 16000 4,5 5,9 9 620sin(12t) 5 3 Lâm Ngọc Thiện 2,9x107 17000 4,6 5,8 4 630sin(13t) 6 4 Lê Ích Trọng 2,8x107 12000 4,3 5,7 5 640sin(14t) 2 5 Nguyễn Văn Ty 2,7x107 13000 4,4 6,2 6 650sin(15t) 3 6 Đoàn Đinh Thiên Vương 3,2x107 14000 4,1 5,7 7 660sin(16t) 4 5
Bảng 2: Kết quả chuyển vị theo thời gian t 0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 PP giải u(t) tích PP xấp xỉ u(t) lực kích thích PP sai u(t) phân trung tâm PP u(t) Newmark Câu 2:
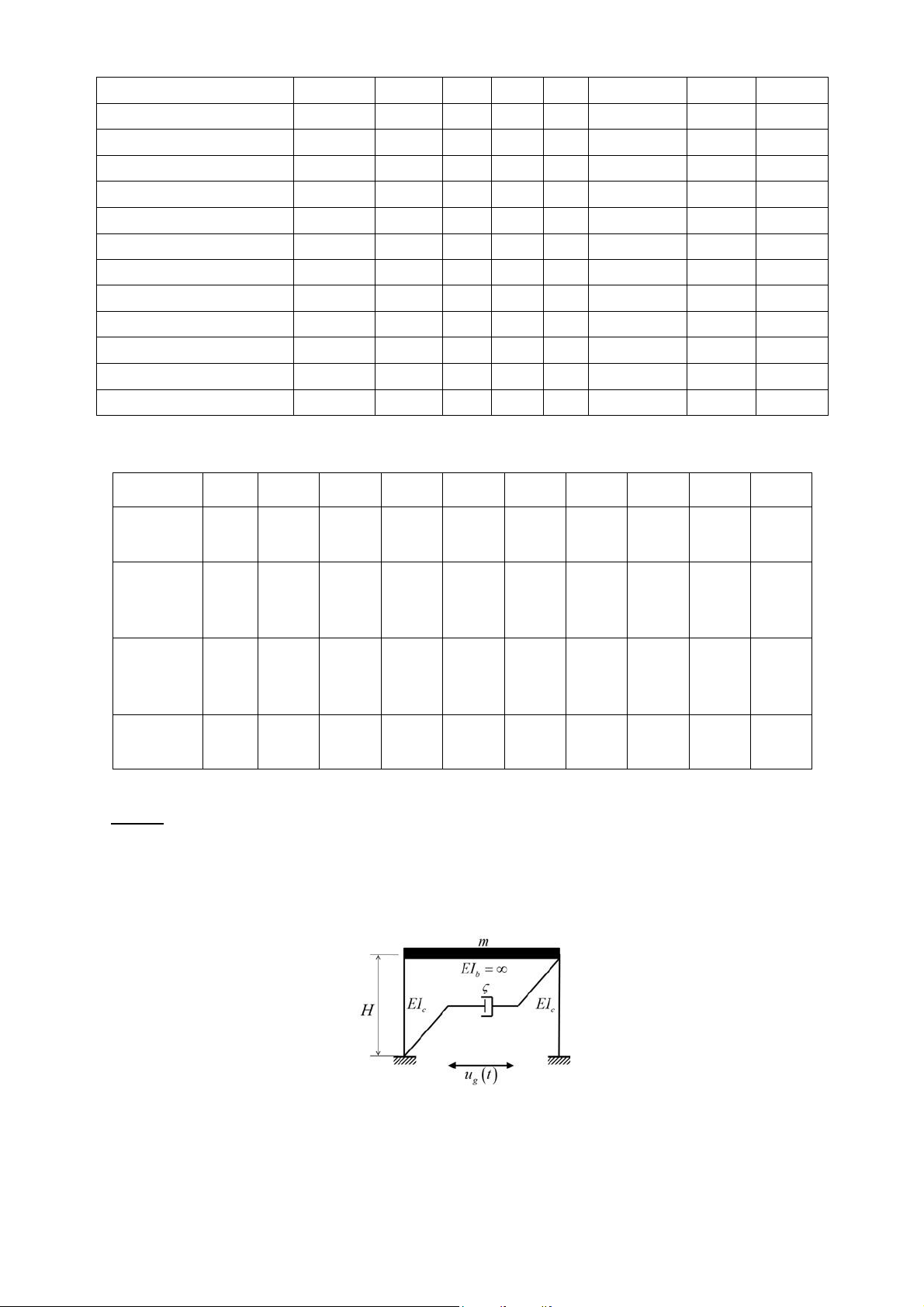
Cho hệ một bậc tự do như H nh vẽ 2. Hệ dao ộng có cản với chuyển vị ban ầu u(0) = 0 và vận
tốc ban ầu u( )0 = 0 do trận ộng ất El-Centro (file ính kèm). Số liệu các ại lượng ược cho trong Bảng 3.
H nh vẽ 1: Khung 1 bậc tự do
a. Dùng phương pháp xấp xỉ lực kích thích, xác ịnh chuyển vị ngang u(t) của khối lượng m tại
các thời iểm cho trong Bảng 4 (lấy 4 số thập phân).
b. Dùng phương pháp sai phân trung tâm, xác ịnh chuyển vị ngang u(t) của khối lượng m tại
các thời iểm cho trong Bảng 4 (lấy 4 số thập phân). lOMoAR cPSD| 58702377
c. Dùng phương pháp Newmark (γ = 1/2, β = 1/6), xác ịnh chuyển vị ngang u(t) của khối lượng
m tại các thời iểm cho trong Bảng 4 (lấy 4 số thập phân).
d. Vẽ phổ phản ứng chuyển vị của hệ một bậc tự do do chuyển ộng nền El-Centro.
Bảng 3: Số liệu khung E Ic H m ζ Họ và tên
(kN/m2) (cm4) (m) (tấn) (%) Châu Thanh Bình 3,2x107 12000 4,1 6,2 4 Nguyễn Ánh Cao 3,1x107 13000 4,2 6,1 5 Lê Minh Chánh 3,0x107 14000 4,3 6,0 6 Phạm Duy Chung 2,9x107 15000 4,4 5,9 7 Nguyễn Khánh Duy 2,8x107 16000 4,5 5,8 8 Nguyễn Hoàng Dũng 2,7x107 17000 4,6 5,7 9 Nguyễn Thị Thu Hảo 3,2x107 13000 4,3 5,9 8 Nguyễn Công Hậu 3,1x107 14000 4,4 5,8 9 Phạm Vũ Minh Hoàng 3,0x107 15000 4,5 5,7 4 Trương Thanh Hòa 2,9x107 16000 4,6 6,2 5 Nguyễn Văn Khánh 2,8x107 17000 4,1 6,1 6 Nguyễn Việt Khánh 2,7x107 12000 4,2 6,0 7 Trần Chí Nghĩa 3,2x107 14000 4,3 5,8 9 Trần Mạnh Quân 3,1x107 15000 4,4 5,7 8 Nguyễn Quang Sĩ 3,0x107 16000 4,5 5,9 9 Lâm Ngọc Thiện 2,9x107 17000 4,6 5,8 4 Lê Ích Trọng 2,8x107 12000 4,3 5,7 5 Nguyễn Văn Ty 2,7x107 13000 4,4 6,2 6 Đoàn Đinh Thiên Vương 3,2x107 14000 4,1 5,7 7
Bảng 4: Kết quả chuyển vị theo thời gian t 0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 PP xấp xỉ u(t) lực kích thích PP sai u(t) phân trung tâm PP u(t) Newmark Câu 3:
Cho kết cấu như H nh vẽ 3a. Bỏ qua khối lượng và biến dạng dọc trục của cột. a.
Viết phương trình vi phân chuyển ộng của kết cấu?
b. Xác ịnh các tần số riêng ωi và các véc-tơ dạng dao ộng riêng φi tương ứng của kết cấu? lOMoAR cPSD| 58702377
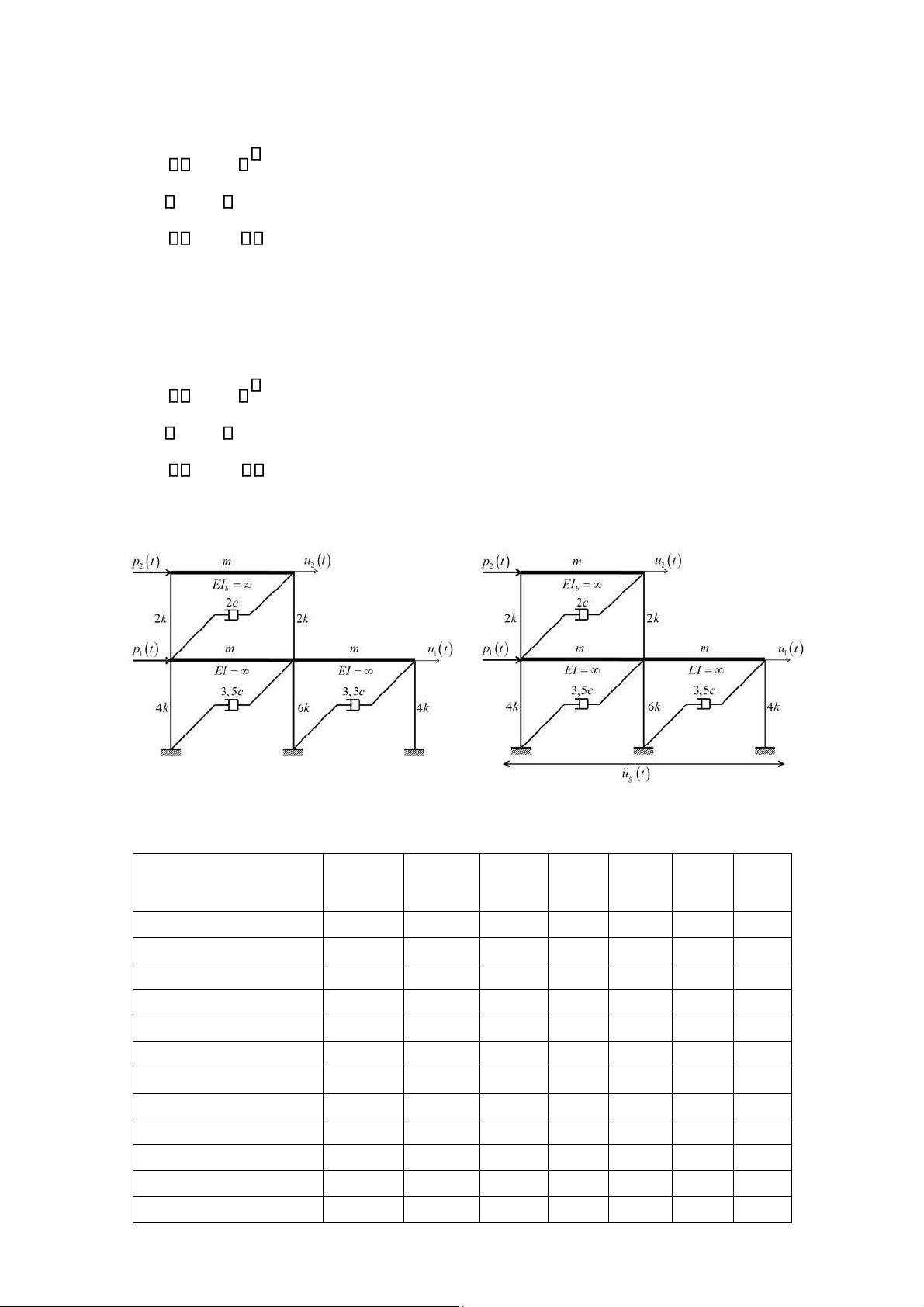
c. Biết p1(t) = p10cos(ωt) kN và p2(t) = p20cos(ωt) kN. Các giá trị m, c, k, p10, p20, ω cho trong Bảng 5. u t1( ) Giả sử
=φ1 1q t( ), với φ1 là véc-tơ dạng dao ộng riêng ứng với tần số riêng nhỏ nhất u ( ) 2 t
của kết cấu. Xác ịnh chuyển vị ở trạng thái ổn ịnh của u1 và u2 tại thời iểm t = 12 giây?
d. Giả sử kết cấu ở H nh vẽ 3a không chịu tác ộng của lực kích thích p1(t) và p2(t) mà chịu tác
ộng của gia tốc nền u ( ) g
t = ug0 cos(ωt) m/s2 như H nh vẽ 3b. u t1( ) Giả sử
=φ1 1q t( ), với φ1 là véc-tơ dạng dao ộng riêng ứng với tần số riêng nhỏ nhất u ( ) 2 t
của kết cấu. Với các giá trị của m, c và k cho ở câu 2c, xác ịnh chuyển vị
ở trạng thái ổn ịnh của u1 và u2 tại thời iểm t = 12 giây? H nh vẽ 3a H nh vẽ 3b Bảng 5 m c k p10 p20 ω
ug0 Họ và tên
(kNs2/m) (kNs/m) (kN/m) (kN)
(kN) (rad/s) (m/s2) Châu Thanh Bình 10 50 4000 15 25 25 5 Nguyễn Ánh Cao 12 55 4100 20 30 24 10 Lê Minh Chánh 14 60 4200 25 35 23 15 Phạm Duy Chung 16 65 4300 30 40 22 20 Nguyễn Khánh Duy 18 70 4400 35 45 21 25 Nguyễn Hoàng Dũng 20 75 4500 40 50 20 30 Nguyễn Thị Thu Hảo 12 60 4000 25 40 21 5 Nguyễn Công Hậu 14 65 4100 30 45 20 5 Phạm Vũ Minh Hoàng 16 70 4200 35 50 25 10 Trương Thanh Hòa 18 75 4300 40 25 24 15 Nguyễn Văn Khánh 20 50 4400 15 30 23 20 Nguyễn Việt Khánh 10 55 4500 20 35 22 25 lOMoAR cPSD| 58702377 Trần Chí Nghĩa 14 65 4000 25 40 21 30 Trần Mạnh Quân 16 70 4100 30 45 20 5 Nguyễn Quang Sĩ 18 75 4200 35 50 21 5 Lâm Ngọc Thiện 20 50 4300 40 40 20 10 Lê Ích Trọng 10 55 4400 15 45 25 15 Nguyễn Văn Ty 12 60 4500 20 50 24 20 Đoàn Đinh Thiên Vương 16 70 4000 25 25 23 25 Câu 4:
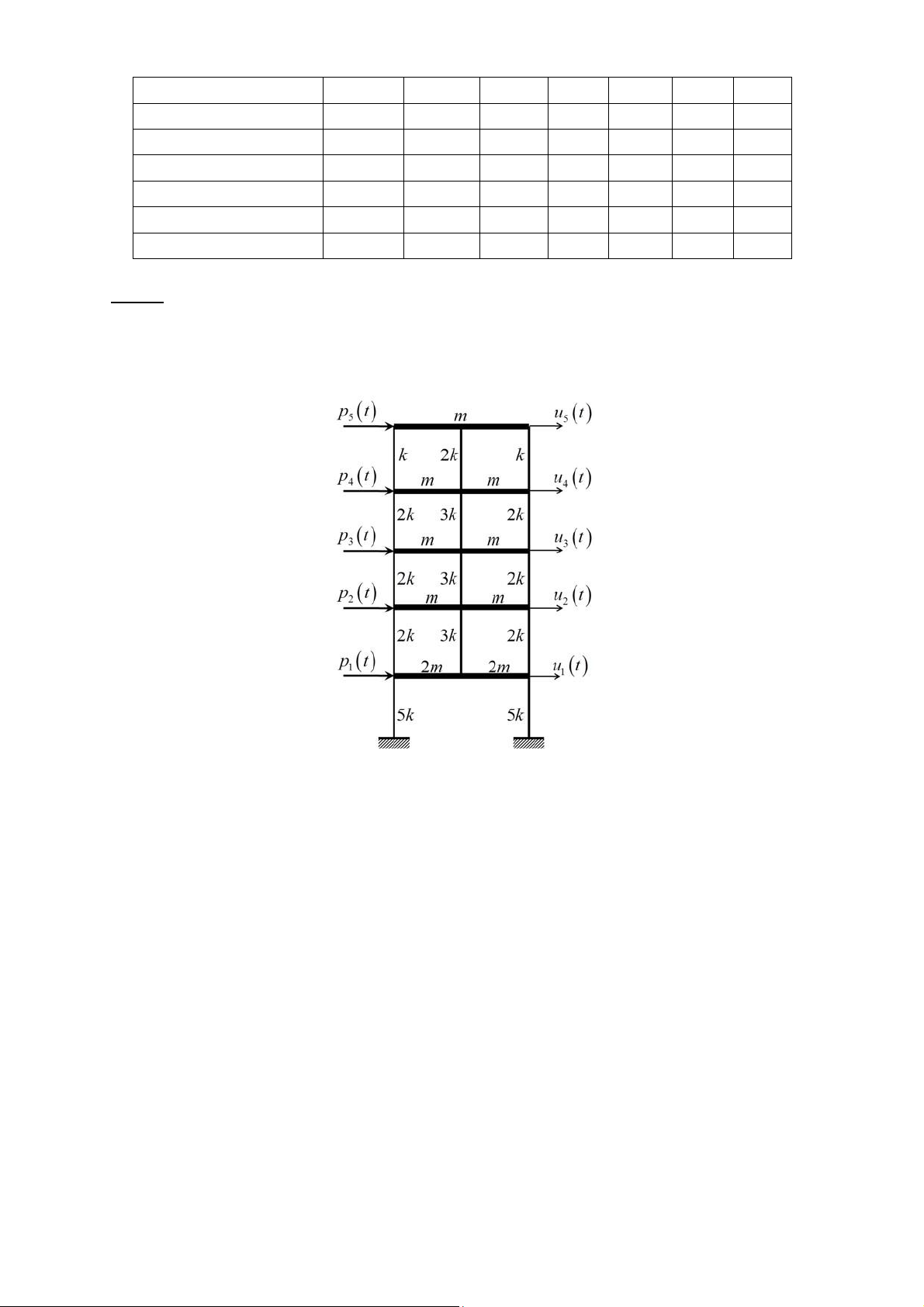
Cho kết cấu không cản như H nh vẽ 4. Kết cấu chịu tác ộng của các tải trọng iều hòa p1(t) =
p0cos(ωt) kN, p2(t) = 2p1(t) kN, p3(t) = 3p1(t) kN, p4(t) = 4p1(t) kN, p5(t) = 5p1(t) kN. Điều kiện ban ầu u ( (
0 t = =0) 0, u0 t = =0) 0 và các giá trị m, k, p0, ω cho trong Bảng 6. H nh vẽ 3
a. Thiết lập phương trình vi phân chuyển ộng của hệ theo m và k?
b. Tính tần số tự nhiên ωi và dạng dao ộng riêng φi tương ứng của hệ theo m và k?
c. Xác ịnh chuyển vị theo thời gian của các tầng trong các trường hợp xấp xỉ chuyển vị như sau: d1.
u( )t =φ1 1q ( )t d2. u( )t =φ1 1q ( )t +φ2 2q ( )t d3.
u( )t =φ1 1q ( )t +φ2 2q ( )t +φ3 3q ( )t d4. u( )t
=φ1 1q ( )t +φ2 2q ( )t +φ3 3q ( )t +φ4 4q ( )t d5. u( )t
=φ1 1q ( )t +φ2 2q ( )t +φ3 3q ( )t +φ4 4q ( )t +φ5 5q ( )t
Trong ó, φ1, φ2, φ3, φ4, φ5 lần lượt là các dạng dao ộng riêng ứng với các tần số ω1 < ω2 < ω3 < ω4 < ω5.
Vẽ các kết quả chuyển vị u5(t) theo thời gian trong 5 trường hợp d1, d2, d3, d4, d5 trên cùng 1
ồ thị và so sánh, nhận xét kết quả. lOMoAR cPSD| 58702377
Gợi : C thể lập tr nh bằng Matlab ể giải Bảng 6 m k p ω Họ và tên 0 (kNs2/m) (kN/m) (kN) (rad/s) Châu Thanh Bình 2.1 420 30 21 Nguyễn Ánh Cao 2.2 430 32 22 Lê Minh Chánh 2.3 440 34 23 Phạm Duy Chung 2.4 450 36 24 Nguyễn Khánh Duy 2.5 460 38 25 Nguyễn Hoàng Dũng 2.6 470 40 26 Nguyễn Thị Thu Hảo 2.1 430 32 23 Nguyễn Công Hậu 2.2 440 30 21 Phạm Vũ Minh Hoàng 2.3 450 32 22 Trương Thanh Hòa 2.4 460 34 23 Nguyễn Văn Khánh 2.5 470 36 24 Nguyễn Việt Khánh 2.6 420 38 25 Trần Chí Nghĩa 2.1 430 40 26 Trần Mạnh Quân 2.2 440 32 23 Nguyễn Quang Sĩ 2.3 450 30 21 Lâm Ngọc Thiện 2.4 460 32 22 Lê Ích Trọng 2.5 470 34 23 Nguyễn Văn Ty 2.6 430 36 24 Đoàn Đinh Thiên Vương 2.1 440 38 25