lOMoARcPSD| 36991220 Contents
LỜI NÓI ĐẦU.......................................................................................................................... 1 I.
NỘI DUNG BÁO CÁO.....................................................................................................2 1. Đặt vấn ề và mục
tiêu..................................................................................................2
2. Cơ sở lý thuyết...............................................................................................................2
II. TRIỂN KHAI ỨNG DỤNG CỦA KHAI TRIỂN FOURIER ĐỂ KHỬ NHIỄU ÂM
THANH..................................................................................................................................... 5
1. Chương trình Matlab khử nhiễu âm thanh ứng dụng Discrete Fourier Transform 6
2. Các câu lệnh matlab ược sử dụng..............................................................................8 3. Kết luận và
ánh giá..................................................................................................... 9
TÀI LIỆU THAM KHẢO......................................................................................................10 lOMoARcPSD| 36991220 LỜINÓIĐẦU
Phương pháp tính la môn học ại cương có mức ô quan trọng ối
với sinh viên ĐH Bách Khoa TP.HCM. Đặc thù của các môn học ại
cương la lương kiến thức lớn nên sinh viên cần nhiều thời gian ể có thể
hoan thanh tốt học phần của mình. Bên cạnh ó cũng cung cấp cho sinh
viên nhiều kiến thức cho các môn học sau khi phân nganh. Ngoai ra,
sinh viên cần trang bị thêm kĩ năng lập trình với nhiều ngôn ngữ lập
trình khác nhau va môt trong số ó la kiến thức lập trình Matlab ứng dụng
vao môn học ể mô phỏng các bai tập lớn ươc giao.
Trong toán học ứng dụng, môt bước không thể thiếu la minh họa
các kết quả lý thuyết trên máy tính. Trong hầu hết trường hơp, các dữ
liệu thu ươc ươc tập hơp dưới dạng ma trận hay vector. Các ma trận
mang nhiều thông tin nhưng lại không hiển thị ở dạng vốn có. Câu hỏi
ặt ra la lam thế nao, bằng phương pháp gì ể có thể khai thác thông tin
hữu ích từ các ma trận ó. Đó la môt trong những yếu tố giúp Phương
pháp tính trở thanh môn học quan trọng va la nền tảng ể hỗ trơ cho quá
trình nghiên cứu khoa học của chúng em sau nay.
Chúng em xin cảm ơn cô Lê Thị Yến Nhi ã hỗ trơ chúng em trong
quá trình học tập va cung cấp kiến thức ể chúng em có thể hoan thanh
nôi dung bai tập lớn nay. Do chưa có nhiều kinh nghiệm nên nếu còn
tồn tại sai sót mong cô góp ý ể chúng em nhìn nhận, cải thiện va hoan
thanh tốt hơn trong tương lai. Môt lần nữa nhóm chúng em xin chân thanh cảm ơn cô! I. NỘI DUNG BÁO CÁO
1. Đặt vấn ề và mục tiêu
Trong cuôc sống thường nhật, giải trí la nhu cầu tất yếu của mỗi con người, chẳng
hạn như xem phim, nghe nhạc, …nó dường như trở thanh môt phần trong cuôc sống
của chúng ta. Ma trong ó âm thanh la thứ không thể thiếu ươc. Ví như trong môt bô
phim, không thể nao thiếu ươc âm thanh của xe cô, tiếng mưa rơi, tiếng ông vật, …
trong quá trình tạo ra những âm thanh ó, luôn tạo ra những tiếng ồn không cần thiết
khiến ta khó có thể nghe ươc va âm thanh không còn ươc hay nữa. Vì vậy, ta cần
phải loại bỏ i những tiếng ồn nay, hay còn ươc gọi la khư nhiễu âm thanh. lOMoARcPSD| 36991220
Nếu chúng ta có thể xư lý môt tập tin âm thanh theo các tiêu chí (trọng tâm, chính
xác, hiệu quả va tiết kiệm thời gian) thì việc ó sẽ giúp ích cho ta rất nhiều. Trong
nghiên cứu về âm thanh, sẽ giúp ta tiết kiệm ươc thời gian hơn. Trong doanh nghiệp
về lĩnh vực truyền thông a phương tiện, nếu xư lí tốt file âm thanh, sẽ tiết kiện ươc
rất nhiều chi phí trong việc thiết kế môt phần mềm nao ó, hay chi ơn giản la tăng
chất lương âm thanh trong quá trình edit video chuyên nghiệp. Từ í sẽ hướng ến
nhiều ối tương khách hang hơn với môt trải nghiệm về chất lương âm thanh tuyệt
vời, chân thật va ặc biệt la không còn tạp âm.
Môt trong những cách dùng
ể khư nhiễu âm thanh chính la dùng biến ôi Fourier hữu hạn.
2. Cơ sở lý thuyết
a. Định nghĩa ánh xạ tuyến tính
Cho X, Y la hai tập hơp khác rỗng tùy ý. Ánh xạ f giữa X va Y la quy tắc cho
tương ứng mỗi phần tư ∈ có môt va chi môt phần tư ∈. Hay : → la ánh xạ, nếu ∀∈, ∃!∈, =()
Cho X, Y la hai không gian trên cùng trường số K. Ánh xạ : → gọi la ánh xạ tuyến tính (AXTT) nếu: + = +() =()
*Ghi chú: ánh xạ tuyến tính trên Rn chi chứa các số hạng bậc nhất.
b. Nhân và ảnh của ánh xạ tuyến tínhĐịnh nghĩa:
Cho ánh xạ tuyến tính : → ,
Nhân (Ker) của f ươc ịnh nghĩa la = ∀∈| =0
Ảnh (Im) của f ươc ịnh nghĩa la = ∈∃∈=
Định lý 2.1: lOMoARcPSD| 36991220
Nhân (Ker) của f la không gian con của X. Ảnh (Imf) la không gian con của
dim(Kerf) + dim(Imf) = dim(X) *Ghi chú:
Kerf la nghiệm của phương trình f(x) = 0
Imf la tập các ảnh của f (trong ham số gọi la tập giá trị)
Định lý 2.2:
Cho ánh xạ tuyến tính : → ,
Ảnh của tập sinh la tập sinh của ảnh:
= 1, 2, ⋯, → =< 1 , 2 , ⋯, ()>
c. Biểu diễn ma trận của ánh xạ tuyến tính
Định nghĩa:
Cho ánh xạ tuyến tính : → va
= 1, 2, 3, ⋯, la môt cơ sở của X. = 1, 2, 3, ⋯, la môt cơ sở của Y. 11 12… 1 =
(1) (2) (3) ⋯ (3) = 21 22… 2 1 2…
Ma trận A ươc gọi la ma trận của ánh xạ tuyến tính f trong môt cơ sở E Ta có: ∀∈, =. []
Nếu X va Y la không gian Rn thì: . =−1 d. Biến ổi Fourier
Mục ích:
Mục ích của biến ôi Fourier la tách tín hiệu dạng sóng thanh các tần số
riêng lẻ tạo ra nó. Cụ thể hơn, biến ôi Fourier tách ham số thanh tông các ham sin
va cos, mỗi ham có tần số khác nhau.  Biến
ổi Fourier hữu hạn:
Trong toán học, phép biến ôi Fourier rời rạc Discrete Fourier Transfrom
(DFT), ôi khi còn ươc gọi la biến ôi Fourier hữu hạn, la môt biến ôi trong giải
tích Fourier cho các tín hiệu thời gian rời rạc. Đầu vao của biến ôi nay la môt lOMoARcPSD| 36991220
chuỗi hữu hạn các số thực hoặc số phức, lam biến ôi nay la môt công cụ lý tưởng
ể xư lý thông tin trên các máy tính. Đặc biệt, biến ôi nay ươc sư dụng rông rãi
trong xư lý tín hiệu va các nganh liên quan ến phân tích tần số chứa trong môt tín
hiệu, ể giải phương trình ạo ham riêng, va ể lam các phép như tích chập. Biến ôi
nay có thể ươc tính nhanh bởi thuật toán biến ôi Fourier nhanh (FFT).
Biến ôi Fourier la môt công thức toán học liên hệ môt tin hiệu ươc lấy mẫu
trong thời gian hoặc không gian với cùng môt tín hiệu ươc lấy mẫu tần số. Trong
xư lý tín hiệu, thuyết biến ôi Fourier có thể tiết lô các ặc tính quan trọng của tín
hiệu cụ thể la các thanh phần tần số.
Biến ôi Fourier ươc xác ịnh cho môt vecto x với n các iểm ươc lấy mẫu
thống nhất bởi: +1= =−01+1
 Ứng dụng phương pháp biến ổi Fourier hữu hạn trong khử nhiễu âm thanh Phép biến
ôi =. ươc gọi la phếp biến
ôi Fourier rời rạc của vecto X • Vecto =. có dạng =+
• Vecto A chứa các hệ số trong 0−12
• Vecto B chứa các hệ số trong 0−12
Như vậy dùng phép biến ôi Fourier rời rạc, ta chuyển tín hiệu X ở miền thời gian
thanh tín hiệu ở miền tần số gồm các ham 2 va 2
Giả sư tín hiệu gốc có dạng: −1 2 2 + 0 +ℎễ
Sau khi phân tích Fourier rời rạc =. , so sánh với hình vẽ trước va sau khi
phân tích, ta có thể xác ịnh tần số tín hiệu chính va tần số nhiễu. Lọc bỏ tín hiệu lOMoARcPSD| 36991220
nhiễu, chi giữ lại tín hiệu chính, sau ó phân tích Fourier ngươc ta sẽ thu ươc tín hiệu ã khư nhiễu. II.
TRIỂN KHAI ỨNG DỤNG CỦA KHAI TRIỂN FOURIER ĐỂ KHỬ NHIỄU ÂM THANH
Khai triển Fourier la môt công cụ toán học cực kỳ mạnh mẽ cho phép bạn xem các
tín hiệu của mình trong môt miền khác, trong ó môt số vấn ề khó trở nên rất ơn giản ể
phân tích. Sự phô biến của nó trong gần như mọi lĩnh vực khoa học kỹ thuật va vật lý.
Đầu tiên va quan trọng nhất, môt biến ôi Fourier của tín hiệu cho bạn biết tần số nao
có trong tín hiệu của bạn va theo tỷ lệ nao. Bằng cách có thể phân chia tín hiệu thanh
các tần số cấu thanh của chúng, người ta có thể dễ dang chặn môt số tần số nhất ịnh bằng
cách vô hiệu hóa các óng góp của chúng.
Tín hiệu thay ôi (trễ) trong miền thời gian biểu hiện dưới dạng thay ôi pha trong miền
tần số. Có thể thay ôi cao ô của bản ghi ma không thay ôi thời lương của bản ghi. Va dễ
dang chuyển ôi bản ghi thanh môt tập hơp tần số theo thời gian.
Hầu hết bản ghi âm kỹ thuật số ươc thực hiện dễ dang hơn bằng cách chuyển ôi bản
ghi bằng cách sư dụng phiên bản rời của biến ôi Fourier.
Ứng dụng khư nhiễu xư lý âm thanh phức tạp ể loại bỏ tiếng ồn xung quanh va cung cấp âm thanh trong hơn.
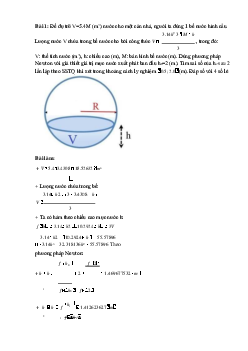
1. Chương trình Matlab khử nhiễu âm thanh ứng dụng Discrete Fourier Transform lOMoARcPSD| 36991220
%Khu nhieu am thanh ung dung Discrete Fourier Transform clc; clear; close all;
[x,Fs]=audioread('sample1.mp3'); %Tai file am thanh
X = fft(x); %Bien doi fourier khong nam o trung
tam N =length(x); %Xac dinh kich thuoc cua x a = 2000*2*pi; %tan so cat
w0 =(-N/2+1:(N/2)); % Vector tan so trung tam
w = w0.*Fs/N; % LAY MOT TAN SO MAU
H = 1-(a./(a + (1i*w))); %H nam o trung tam Hshift = fftshift(H);
Y = X .*Hshift' ; % loc tin hieu, chuyen vi de nhan 2 ma tran
y = real(ifft(Y)); % Bien doi fourier ngich
subplot(4,1,1) plot(w,abs(fftshift(x)))
title('Am thanh ban dau - mien thoi gian'); subplot(4,1,2) plot(w,abs(fftshift(X)))
title('Am thanh ban dau - mien tan so');
subplot(4,1,3) plot(w,abs(fftshift(Y)))
title('Am thanh khu nhieu - mien tan so'); subplot(4,1,4) plot(w,abs(fftshift(y)))
title('Am thanh khu nhieu - mien thoi gian');
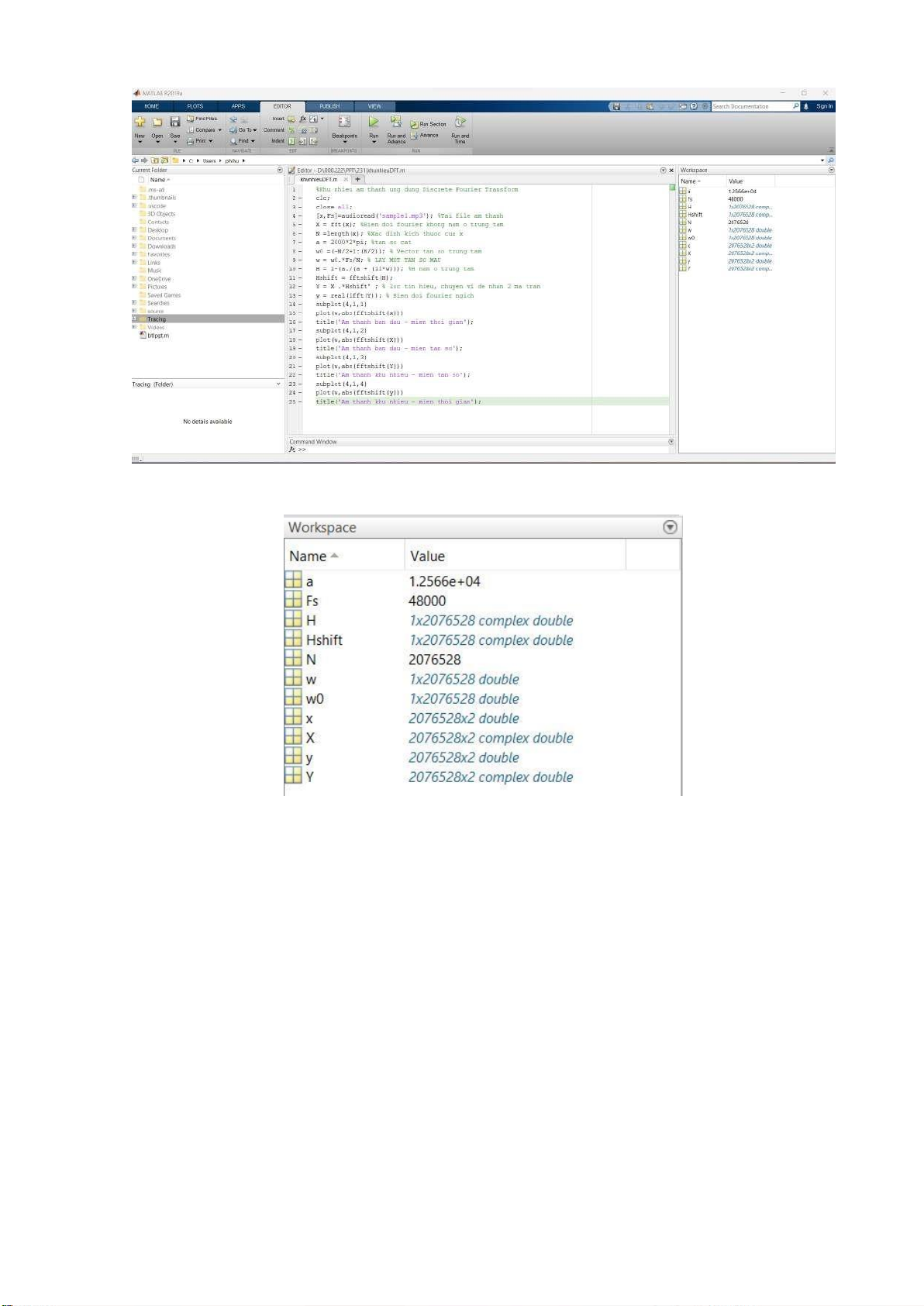
Kết quả chạy code matlab lOMoARcPSD| 36991220 Giao diện Matlab. Bảng các giá trị lOMoARcPSD| 36991220
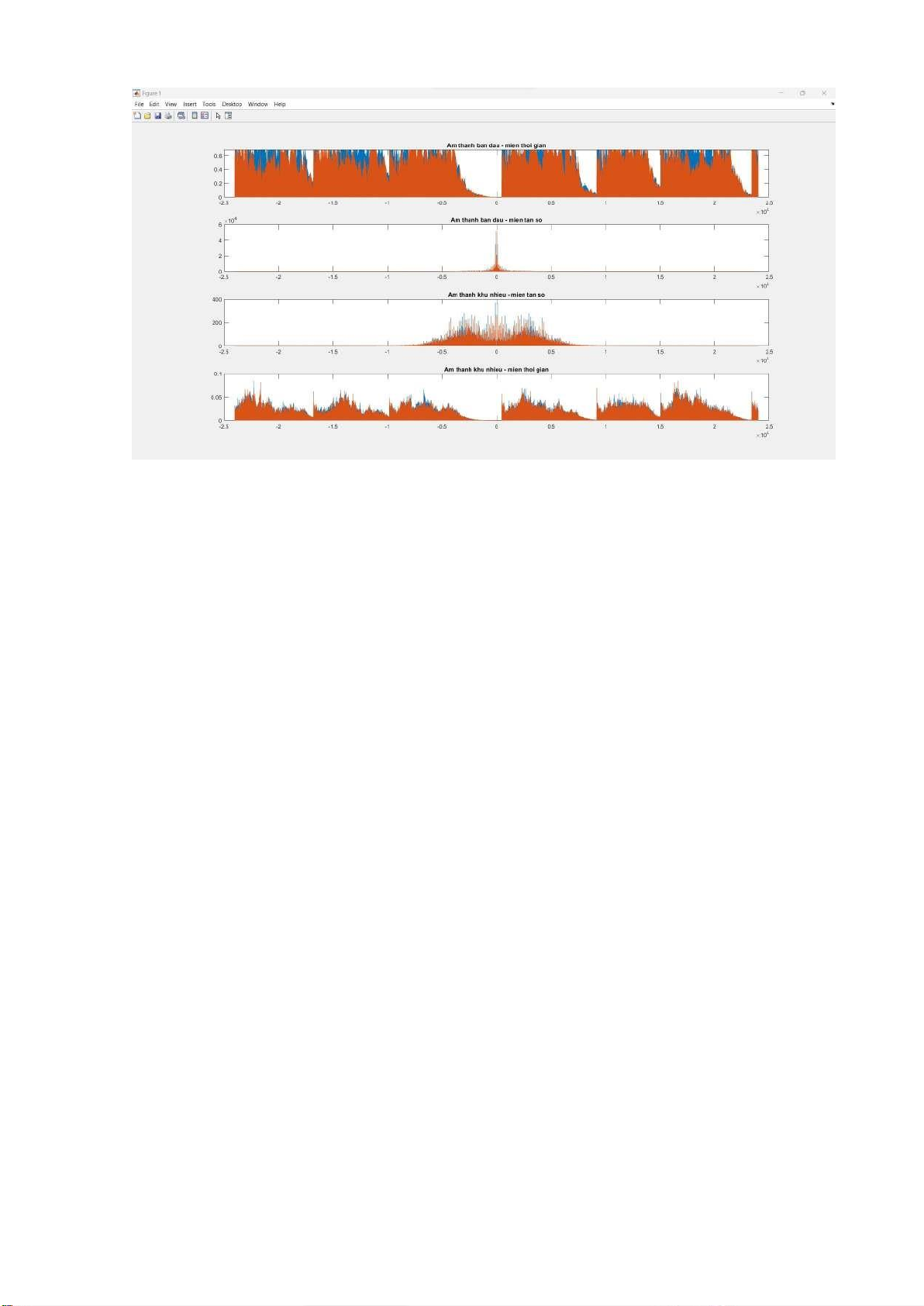
Đồ thị âm thanh trước và sau khi khử nhiễu.
2. Các câu lệnh matlab ược sử dụng
fft : biến ôi Fourier thuận (tức la miền thời gian sang miền tần số) iff : biến
ôi Fourier ngươc (tức la biến
ôi ngươc lại, miền tần số qua miền thời
gian). tffshift: dịch chuyển tần số zero vao trung tâm phô.
X=fft(x): tính toán biến ôi Fourier rời rạc (DFT) X bằng cách sư dụng thuật toán biến ôi Fourier nhanh (FFT):
● Nếu x la môt vectơ, thì fft(x) trả về biến ôi Fourier của vectơ.
● Nếu x la ma trận, thì fft(x) xư lý các côt Xdưới dạng vectơ va trả về biến
ôi Fourier của mỗi côt.
Nếu x la môt mảng nhiều chiều, thì fft(x) xư lý các giá trị dọc theo kích thước mảng ầu
tiên có kích. thước không bằng 1 dưới dạng vectơ va trả về biến ôi Fourier của mỗi vectơ.
[x,Fs]=audioread ('filename.mp3'): ọc dữ liệu từ tệp mp3 ươc ặt tên “filename”.
(Với x la vector âm thanh va Fs la tần số lấy mẫu).
N =length(x): trả về kích thước của chiều dai nhất của X. Nếu X la môt vectơ thì kích
thước nay bằng với chiều dai của nó.
subplot(m,n,p): chia cưa sô hiện tại thanh môt ma trận m x n khoảng ể vẽ ồ thị, va chọn
p la cưa sô hoạt ông. Các ồ thị thanh phần ươc ánh số từ trái qua phải, từ trên xuống lOMoARcPSD| 36991220 dưới, sau ó
ến hang thứ hai Plot: Vẽ ồ thị tuyến tính trong không gian 2 chiều.
clc; Xóa cưa sô lệnh clear: Loại bỏ tất cả các biến khỏi không gian lam việc hiện tại,
giải phóng chúng khỏi bô nhớ hệ thống.
close all; Đóng tất cả các biến khỏi không gian lam việc hiện tại
3. Kết luận và ánh giá
Biến ôi Fourier ươc ứng dụng nhiều trong các lĩnh vực, vô cùng hữu ích va cần
thiết. Môt công cụ toán học tuyệt vời trong việc phân tích tín hiệu va khư nhiễu âm
thanh. Thông qua bai báo cáo nay, với sự phân chia công việc hơp lý, va tinh thần trách
nhiệm cao của mỗi người, nhóm em ã hoan thanh ươc kết quả ầu ra như mong ơi. Biết
cách lọc nhiễu môt file âm thanh bất kì trên MATLAB, hiểu biết rõ hơn về các ứng dụng
của Fourier cũng như môn học lOMoARcPSD| 36991220 TÀILIỆUTHAMKHẢO
[1] Richard L. Burden, J. Douglas Faires (2010), Numerical Analysis, Published by
Cengage Learning 9th (ninth) edition.
[2] J. Proakis, D. Manolakis (1992), Digital signal processing - principles, algorithms
and applications (2. ed.), Pearson.