Bài Tập Lớn QHTT 26: Ứng Dụng Đại Số Tuyến Tính Vào Vận Tải | Đại số tuyến tính | Đại học Bách khoa TP Hồ Chí Minh

ĐẠI HỌC QUỐC GIA
ĐẠI HỌC BÁCH KHOA THÀNH PHỐ HỒ CHÍ MINH BÁO CÁO BÀI TẬP LỚN
ĐỀ TÀI 26 : ỨNG DỤNG ĐẠI SỐ TUYẾN TÍNH VÀO QUY HOẠCH TUYẾN TÍNH BÀI TOÁN VẬN TẢI Giảng viên hướng dẫn Nguyễn Anh Thi Lớp: L09 Nhóm:
Ngày nộp báo cáo : 03/12/2022 MỤC LỤC SINH VIÊN THỰC HIỆN MÃ SỐ SINH VIÊN ĐIỂM SỐ LÊ VŨ NHỰT TÂM 2213022 Contents
I) Cơ sở lý thuyết ………………………………………………………………1
1) Giới thiệu lý thuyết cơ bản của quy hoạch tuyến tính……2
2) Bài toán vận tải……………………………………………………………..3
II) Ứng dụng đại số tuyến tính trong quy hoạch tuyến tính trong
vận tải……………….4
1) Áp dụng toán vận tải vào thực tế…………………………………..5
2) Nêu các bước thực hiện…………………………………………………6
3) Cho ví dụ minh họa………………………………………………………..7
III) Chương trình Matlab…………………………………………………….8
IV) Nguồn tham khảo…………………………………………………………9 Đề tài 26
1/ Ứng dụng của đại số tuyến tính trong qui hoạch tuyến tính với bài toán vận tải.
2/ Viết chương trình để giải một bài toán cụ thể I. Giới thiệu 1. Đĩnh nghĩa .
- Trong toán học, quy hoạch tuyến tính (QHTT) (tiếng Anh: linear
programming - LP) là bài toán tối ưu hóa, trong đó hàm mục
tiêu (objective function) và các điều kiện ràng buộc đều là tuyến tính.
- Có thể tạm định nghũa quy hoạch tuyến tính là lĩnh vực toán học cứu các
bài toán tối ưu mà hàm mục tiêu( vấn đề được quan tâm) và các ràng buộc
(điều kiện của bài toán) đều là hàm và các phương trình hoặc bất phương trình
tuyến tính. Đây chỉ là một định nghĩa mơ hồ, bài toán quy hoạch tuyến tính sẽ
được xác định rõ ràng hơn thông qua các ví dụ.
VD1: nhận dạng bài toán quy hoạch tuyến tính . DẠNG TỔNG QUÁT
x1 + x2 +3x3 ->> max hoặc min ( HÀM MỤC TIÊU). x1 + x2 + x3 ≤ 40 x1 + x2 + x3 – x4 ≤ 20 x1 – x2 – 6x3 +x5 ≥ 60 ĐIỀU KIỆN RÀNG BUỘC x1 – x2 – x3 + x6 = 40
# Điều kiện xi > 0 (i=1,,,,4)
II).Bài toán vận tải.
- Là dạng đặc biệt của bài toán quy hoạch tuyến tính.(chiếm gần
85%) .Giải quyết vấn đề phân phối hàng hoá từ một số địa điểm cung cấp
(điểm nguồn) đến một số địa điểm tiêu thụ (điểm đích) sao cho: Tổng chi phí ít nhất.
Cự ly vận chuyển nhỏ nhất .
Hay tổng tiền lời là nhiều nhất
$ . NHẬN DẠNG BÀI TOÁN VẬN TẢI.
VD2. Bài toán vận tải vận chuyển hàng:
Người ta cần vận chuyển hàng hóa từ M kho đến N cửa hàng bán lẻ. Lượng
hàng hóa ở kho I là i và (i=1,2,….,M) và nhu cầu hang hóa của cửa hàng J và
(j=1,2,…,N). Cước vận chuyển một đơn vị hàng hóa từ kho i đến cứa hàng j là X đồng.
Bài toán đặt ra là lập kế hoạch vận chuyển để tiền cước là nhỏ nhất, với điều
kiện là mỗi cửa đều nhận đủ và mỗi kho đều trao hết hàng.
Gọi X là lượng hàng hóa phải vận chuyển từ kho I đến cửa hàng J. B1 B2 B3 Khả năng cung cấp A1 X11 X12 X13 D A2 X21 X22 X23 E A3 X31 X32 X33 F Nhu cầu tiêu thụ A B C
Tổng cung cấp và tiêu thụ
Cước vận chuyển hàng hóa I đến tất cả các kho J là : A1,A2,A3 là các nơi B1,B2,B3 là các KHO
Xij i,j(1,2,3) là SỐ TIỀN VẬN CHUỂN TIÊU THỤ CUNG CẤP
A, B, C, D, E, F LÀ TỔNG SỐ CÁC ĐƠN HÀNG NHẬN VÀ GIAO
- Giả sử tổng hàng hóa có ở các kho và tổng nhu cầu hàng hóa ở các cửa hàng là bằng nhau:
A + B + C = D + E + F (SỐ LƯỢNG ĐƠN HÀNG )
Yêu cầu bài toán Hãy xác định phương án vận chuyển đá từ nơi cung cấp
đến nơi tiêu thụ để tổng chi phí vận chuyển là thấp nhất và phải vận chuyển hết hàng trong kho ?
#. ĐÂY LÀ MỘT VÍ DỤ CƠ BẢN về BÀI TOÁN VẬN TẢI.
III.ỨNG DỤNG CỦA ĐẠI SỐ TUYẾN TÍNH TRONG QUY HOẠCH TUYẾN TÍNH BÀI TOÁN VẬN TẢI.
- CÁC bước GIẢI BÀI TOÁN BÊN QUY HOẠCH TUYẾN TÍNH.
 Bước 1: Tìm phương án xuất phát. (1 trong 3 quy tắc)
+ Qui tắc góc Tây Bắc (North – West Corner Rule);
+ Qui tắc chi phí nhỏ nhất (Least – Cost Rule); + Qui tắc Voghel.
 Bước 2: Kiểm tra tính tối ưu của một phương án, nếu:
+ Tối ưu: đi đến kết luận;
+ Chưa tối ưu: đi đến bước 3;
 Bước 3: Tìm phương án mới tốt hơn, quay lại bước 2. Gọi:
là lượng hàng vận chuyển từ điểm phát thứ i đến điểm thu thứ j.
là chi phí vận chuyển một đơn vị hàng từ điểm phát thứ i đến điểm thu thứ j. Ta có:
là chi phí vận chuyển từ điểm phát i đến điểm thu j.
là tổng chi phí vận chuyển (hàm mục tiêu).
-Nhiệm vụ của bài toán là tối ưu hóa chi phí vận chuyển bằng cách tìm min của hàm mục tiêu.
ĐÓ LÀ CÁC BƯỚC LÀM BÊN QUY HOẠCH TUYẾN TÍNH.
Ứng dụng của ĐẠI SỐ TUYẾN TÍNH VÀO QUY HOẠCH TUYẾN TÍNH TRONG BÀI TOÁN.
#1. ÁP DỤNG BẰNG CÁCH ĐƯA CÁC HÀM MỤC TIÊU, PHƯƠNG TRÌNH RÀNG BUỘC
TUYẾN TÍNH, ĐIỀU KIỆN RÀNG BUỘC VỀ DẠNG MA TRẬN CẤP M×N.
#2. DÙNG các phép biến đổi , xây dựng thuật toán để tính toán.
IV. GIẢI BÀI TOÁN THỰC TẾ. CÁC BƯỚC THỰC HIỆN. TÓM TẮT BÀI TOÁN.
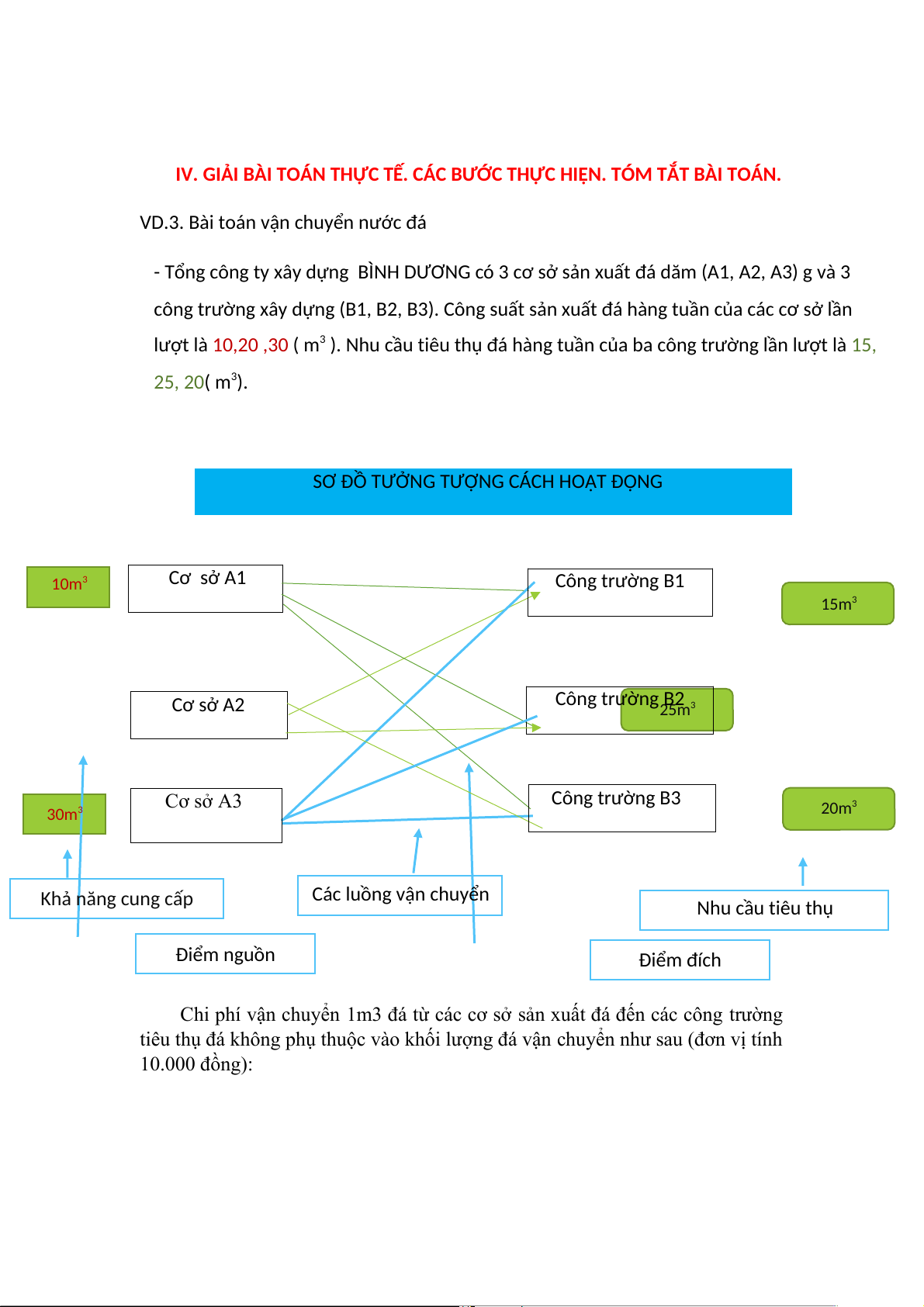
VD.3. Bài toán vận chuyển nước đá
- Tổng công ty xây dựng BÌNH DƯƠNG có 3 cơ sở sản xuất đá dăm (A1, A2, A3) g và 3
công trường xây dựng (B1, B2, B3). Công suất sản xuất đá hàng tuần của các cơ sở lần
lượt là 10,20 ,30 ( m3 ). Nhu cầu tiêu thụ đá hàng tuần của ba công trường lần lượt là 15, 25, 20( m3).
SƠ ĐỒ TƯỞNG TƯỢNG CÁCH HOẠT ĐỘNG Cơ sở A1 10m3 Công trường B1 15m3 Công trường B2 Cơ sở A2 25m3 Cơ sở A3 Công trường B3 30m3 20m3 Các luồng vận chuyển Khả năng cung cấp Nhu cầu tiêu thụ Điểm nguồn Điểm đích
Chi phí vận chuyển 1m3 đá từ các cơ sở sản xuất đá đến các công trường
tiêu thụ đá không phụ thuộc vào khối lượng đá vận chuyển như sau (đơn vị tính 10.000 đồng): B1 B2 B3 A1 2 1 5 A2 3 4 3 A3 4 6 6
Hãy xác định phương án vận chuyển đá từ cung cấp đến nơi tiêu thụ để tổng
chi phí vận chuyển là thấp nhất. Phải vận chuyển hết hàng trong kho ?
#. BÂY GIỜ THIẾT LẬP TOÀN BỘ BÀI TOÁN VẬN TẢI Ở 1 BẢN DUY NHẤT. Khả năng cung cấp Cơ sở nước B1 B2 B3 Khả năng giới hạn đá cung cấp của cơ sở A1 A1 2 1 5 15 A2 3 4 3 25 Lượng hàng vận chuyển từ điểm A3 4 6 6 20 nguồn đến điểm Nhu cầu tiêu 10 20 30 60 đích thụ Tổng lượng cung cấp và tiêu
Nhu cầu tiêu thụ của công trường thụ B2
Cước phí vận chuyển một m3 đá từ nơi cung cấp A3 đến công trường B1 PHÁT HỌA BÀI TOÁN TRÊN
- Gọi xij ( i = 1, 2, 3 và j 1, 2, 3 ) là LƯỢNG NƯỚC ĐÁ cần vận chuyển từ
Cơ sở sản xuất đến Các công trường xây dựng.
- Tổng chi phí vân chuyển là nhỏ nhất ( tìm hàm cực tiểu ) là . F(x) = 2x11 + x + 5x 12 13 3x21 + 4x + 3x 22 23 min 4x31 + 6x + 6x 32 33
- Điều kiện của các kho x11 + x + x 12 = 15 13 x21 + x +x 22 23 = 25 x31 + x + x 32 = 20 33
- Điều kiện của công trường x11 + x + x 12 = 10 13 x21 + x +x 22 23 = 20 x31 + x + x 32 = 30 33
xij > 0 (i = 1, 2, 3 và j = 1, 2, 3 ).
#. Giải bài toán bằng matlap cho ví dụ mình họa.
1. Đưa các chi phí vận chuyển, như cầu sản phẩm, số lượng sản phẩm cung cấp thành MA TRẬN.
2. Đặt ma trận A là ma trận biểu diễn chi phí 2 1 5 A = 3 4 3 4 6 6
Ma trận B là ma trận nhu cầu tiêu thụ (xếp nghang) B = 10 20 30
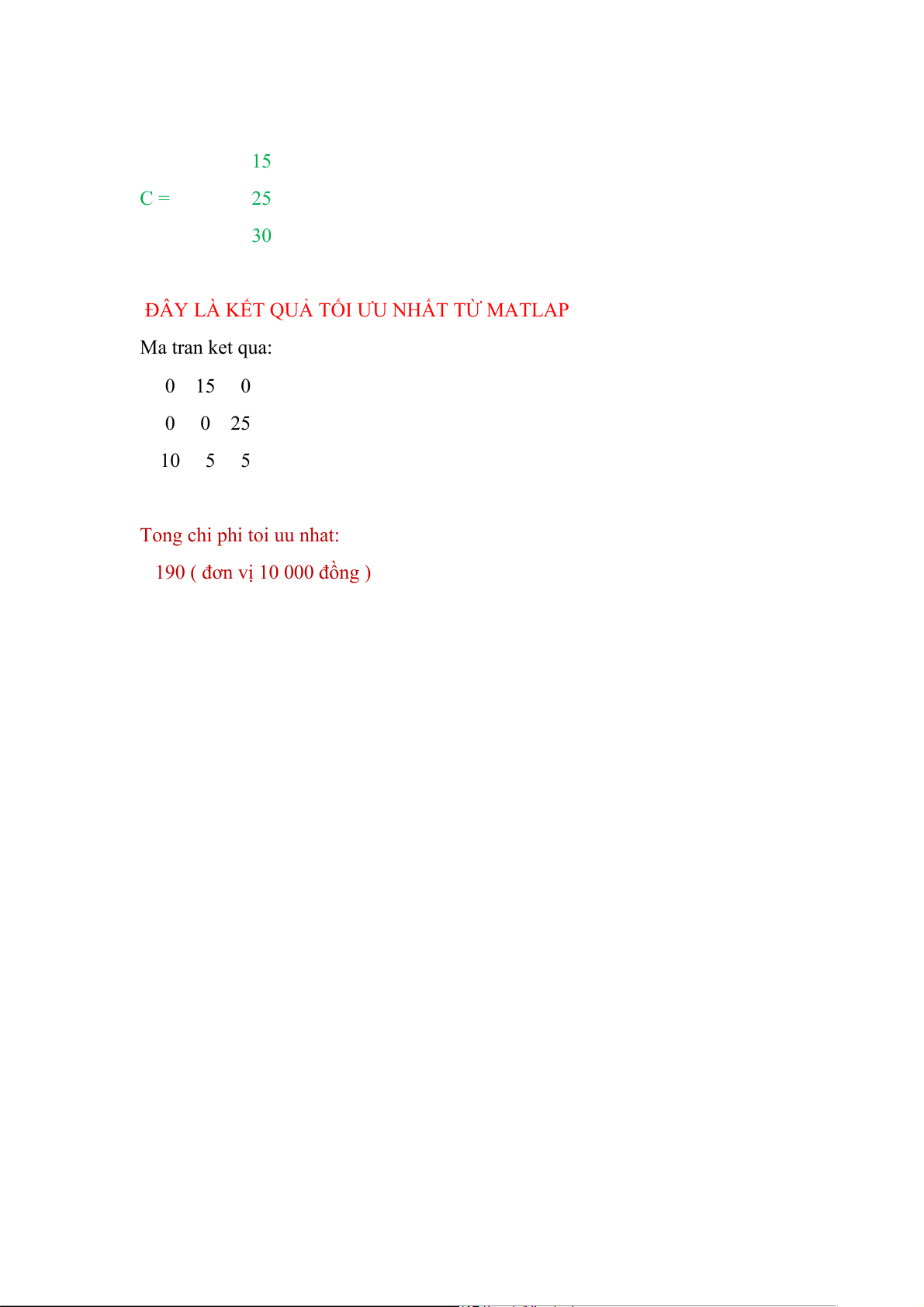
Ma trận C là ma trận khả năng cung cấp (xếp dọc) 15 C = 25 30
ĐÂY LÀ KẾT QUẢ TỐI ƯU NHẤT TỪ MATLAP Ma tran ket qua: 0 15 0 0 0 25 10 5 5 Tong chi phi toi uu nhat:
190 ( đơn vị 10 000 đồng ) VD.4
MỘT DOANH NGHIỆP có 10 tấn lúa trong kho quận 1, 30 tấn trong
kho quận 2, 32 tấn trong kho quận 3, 4 tấn trong kho quận 4, 12 tấn trong kho
quận 5. Muốn vận chuyển ra các tỉnh thành : quận 1 chuyển 14 tấn lúa ra BÌNH
DƯƠNG, quận 2 chuyển 4 tấn lúa ra VŨNG TÀU, quận 3 chuyển 2 tấn ra
ĐỒNG NAI, quận 4 chuyển 10 tấn lúa đến TIỀN GIANG, quận 5 cần chuyển
48 tấn lúa đến MIỀN BĂC TRUNG BỘ .CHI PHÍ vận chuyển( chục triệu / tấn hàng ): Cửa hàng các Quận1 Quận 2 Quận 3 Quận 4 Quận 5 tỉnh Kho chứa lúa Bình Dương 1 2 4 5 6 Vũng Tàu 2 4 7 9 4 Đồng Nai 4 3 1 6 4 Tiền Giang 3 9 8 4 1 Bắc Trung Bộ 3 4 8 4 9
Thiết lập bài toán như sau:
- Gọi xij ( i = 1, 2, 3, 4, 5 và j 1, 2, 3, 4, 5 ) là LƯỢNG TẤN LÚA cần vận
chuyển từ các kho đến nơi tiêu thụ.
- Tổng chi phí vân chuyển là nhỏ nhất ( tìm hàm cực tiểu ) là . 1x11 2 x12 4 x13 5 x14 6 x15 2x21 4 x22 7 x23 9 x24 4 x25 4x31 3x32 1 x33 6 x34 4 x35 MIN 3x41 9x42 8 x43 4 x44 1 x45 3x51 4 x52 8 x53 4 x54 9 x55
- Điều kiện của các kho hàng : x11 + x + x 12 +x 13 14 +x = 10 15 x21 + x +x 22 23 +x +x 24 = 30 25 x31 + x + x 32 +x 33 +x 34 = 32 35 x41 + x + x 42 + x 43 + x 44 = 4 45 x51 + x + x 52 + x 53 + x 54 = 12 55
- Điều kiện của các nơi tiêu thụ: x11 + x + x 12 +x 13 14 +x = 12 15 x21 + x +x 22 23 +x +x 24 = 4 25 x31 + x + x 32 +x 33 +x 34 = 2 35 x41 + x + x 42 + x 43 + x 44 = 10 45 x51 + x + x 52 + x 53 + x 54 = 48 55
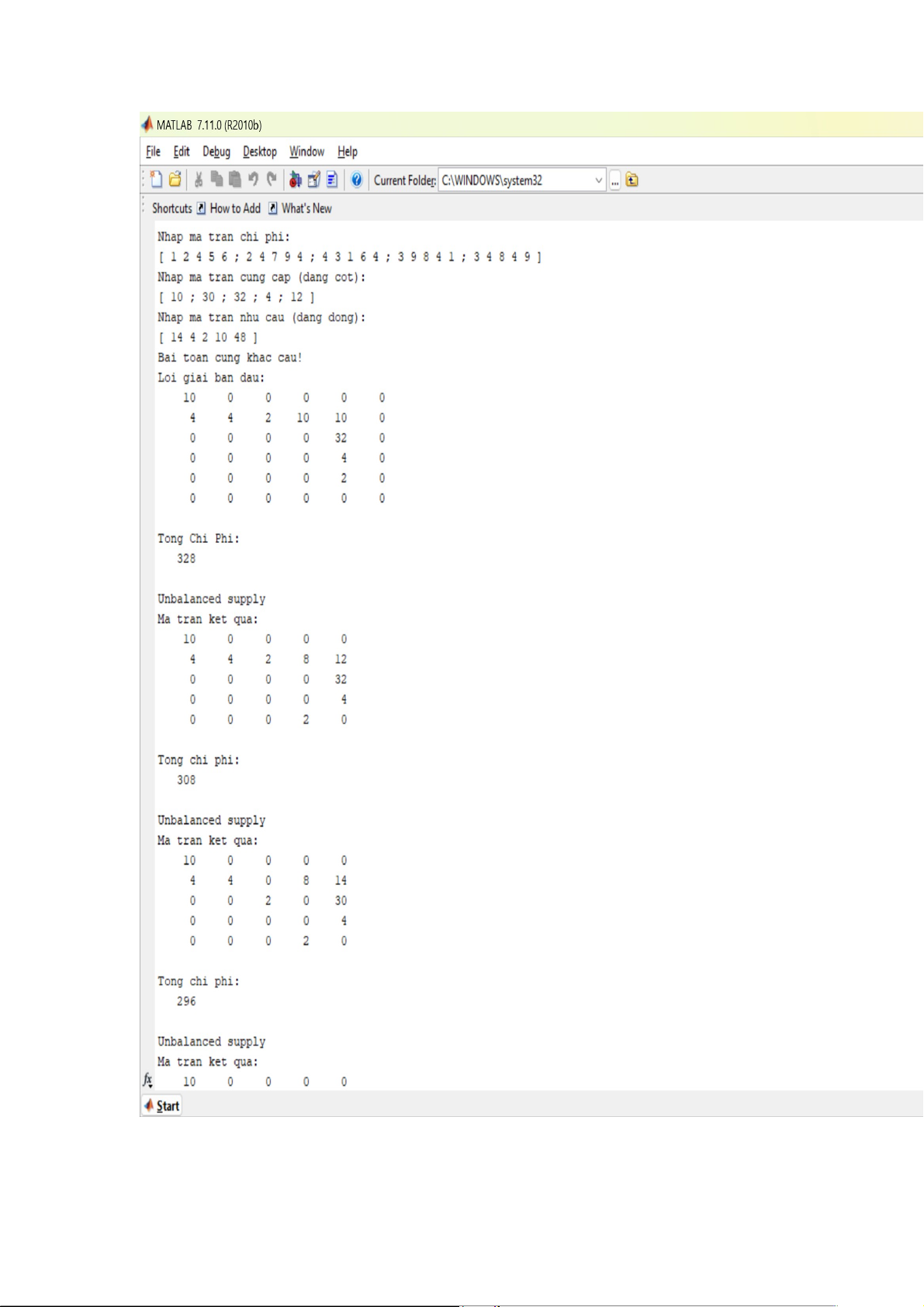
#. Từ các dữ kiện bài toán ở trên ta nhập
Ma trận A chi phí vào matlap 1 2 4 5 6 2 4 7 9 4 A = 4 3 1 6 4 3 9 8 4 1 3 4 8 4 9
Ma trận B cung cấp dạng cột ( dùng dấu ; để xuống dòng trong matlap ) B = 10 30 32 4 12
Ma trận C nhu cầu dang dòng: C = [ 14 4 2 10 48 ]
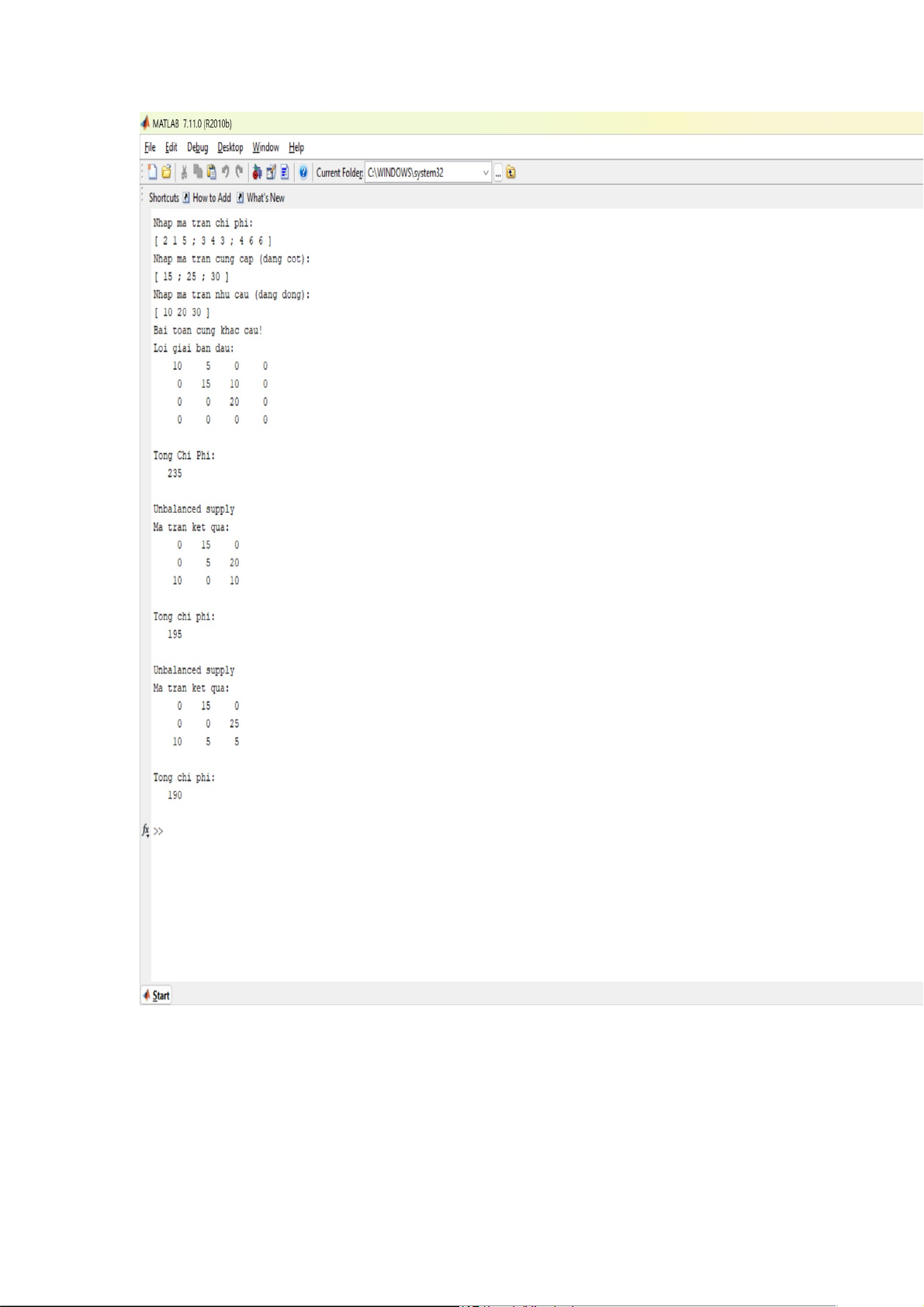
#. ĐÁP ÁN TỪ MATLAP:
Loi giai ban dau: ma tran ket qua 10 0 0 0 0 0 4 4 2 10 10 0 0 0 0 0 32 0 0 0 0 0 4 0 0 0 0 0 2 0 0 0 0 0 0 0 Tong Chi Phi:
328 ( đơn vị 1 000 000 đồng ) Ma tran ket qua: 10 0 0 0 0 4 4 0 0 22 0 0 2 8 22 0 0 0 0 4 0 0 0 2 0 Tong chi phi:
272 ( đơn vị 1 000 000 đồng )
#. Trong số các phương án thì PHƯƠNG ÁN NÀY LÀ TỐI ƯU NHẤT Ma tran ket qua: 10 0 0 0 0 4 0 0 0 26 0 4 2 8 18 0 0 0 0 4 0 0 0 2 0
Tong chi phi: 268 ( đơn vị 1 000 000 đồng ) V. TÀI LIỆU THAM KHẢO
1.https://www.academia.edu/21540412/Quy_ho%E1%BA%A1ch_tuy %E1%BA%BFn_t%C3%Adnh
2.https://tailieumienphi.vn/doc/tieu-luan-ve-bai-toan-quy-hoach-tuyen-tinh- cynotq.html
3.Allaire, Grégoire (2005). Analyse numérique et optimisation (bằng tiếng
Pháp). Ellipses. ISBN 9782730212557.