Bài tập mạch điện tử | Đại học Bách khoa Hà Nội

Một số bài tập Mạch điện tử ( có đáp án) về: Diode bán dẫn; Transistor hai lớp tiếp giáp; Thiết kế và phân tích tín hiệu nhỏ tần số thấp; Mạch Transistor ghép liên tầng; Mạch khuếch đại hồi tiếp;... giúp bạn ôn tập và đạt kết quả cao cuối học phần Mạch điện tử

183 92 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Mạch điện tử

Trường: Đại học Bách Khoa Hà Nội

Thông tin:

40 trang 6 tháng trước

Tác giả:

Profile VietJack
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
1
MOÄT SOÁ BAØI TAÄP MAÃU CHO QUYEÅN
“Giaùo trình maïch ñieän töû I”
Chöông I: DIODE BAÙN DAÃN.
I. Diode baùn daãn thoâng thöôøng:
1) Veõ daïng soùng chænh löu: (Baøi 1-1 trang 29)
Coâng thöùc toång quaùt tính V
L
:
L
Li
DS
L
R
RR
V
V
V
+
−
=
V
D
= 0,7V (Si) vaø V
D
= 0,2V (Ge)
a- Veõ V
L
(t) vôùi V
S
(t) daïng soùng vuoâng coù bieân ñoä 10 vaø 1V
Keát quaû vôùi giaû thieát: R
i
= 1Ω, R
L
= 9Ω, V
D
= 0,7V.
Vì Diode chænh löu chæ daãn ñieän theo moät chieàu neân:
∗ Trong
0T
2
1
>
, Diode daãn
→
i
D
≠
0
→
i
L
≠
0
→
V
L
≠
0.
V37,89
9
1
7
,
0
10
V
1L
=
+
−
= vaø V27,09
9
1
7
,
0
1
V
2L
=
+
−
=
∗
Trong 0T
2
1
< , Diode taét → i
D
= 0 → i
L
= 0 → V
L
= 0.
i
L
i
D
R
L
R
i
V
L
V
s
-
-
V
D
10
-
10
0
1
-
-
V
S
2
3
4
t(ms)
1
-
1
0
1
-
-
V
S
2
3
4
t(ms)
8,37
0
1
V
L1
2
3
4
t(ms)
0,27
0
1
V
L2
2
3
4
t(ms)
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
2
b- Veõ V
L
(t) vôùi V
S
(t) daïng soùng sin coù bieân ñoä 10 vaø 1V.
∗
Khi V
S
= 10sinω
o
t nghóa laø V
Sm
= 10V >> V
D
=0,7V ta coù:
99
91
10
R
RR
V
V
L
Li
Sm
1L
=
+
≈
+
≈
t
sin
9
V
01L
ω
≈
(Ta giaûi thích theo
0T
2
1
>
vaø
0T
2
1
<
)
∗
Khi V
S
= 1sinω
0
t
nghóa laø V
Sm
= 1V so saùnh ñöôïc vôùi 0,7V:
+
V
S
> 0,7V, Diode daãn, i
D
≠ 0, i
L
≠ 0, V
L
≠ 0.
6,0tsin9,09
9
1
7
,
0
t
sin
1
V
0
0
2L
−ω=
+
−
ω
=
Taïi sinω
0
t = 1, |V
L2
| = 0,27V.
+
V
S
< 0,7V, Diode taét, i
D
= 0, i
L
= 0, V
L
= 0.
Vôùi daïng soùng tam giaùc ta coù keát quaû töông töï nhö soùng sin.
2)
Baøi 1-3:
Ñeå coù caùc keát quaû roõ raøng ta cho theâm caùc giaù trò ñieän trôû: R
1
=
1KΩ, R
b
= 10KΩ, R
L
= 9KΩ.
a- Veõ V
L
(t) vôùi daïng soùng vuoâng coù bieân ñoä 10V vaø 1 V.
∗
0T
2
1
>
, Diode daãn, R
thD
≈ 0, doøng i
L
chaûy qua R
i
, D, R
L
neân ta coù:
V37,810.9.
10.910
7
,
0
10
R
RR
V
V
V
3
33
L
Li
DS
1L
=
+
−
=
+
−
=
V27,010.9.
10.910
7
,
0
1
R
RR
V
V
V
3
33
L
Li
DS
2L
=
+
−
=
+
−
=
i
L
R
L
9K
R
i
=1K
V
L
V
s
-
-
V
D
R
b
=10K
10
0
-
10
9
-
-
1
2
3
4
t(ms)
V
S
V
L1
0
1
2
3
4
t(ms)
1
0
-
1
1
2
3
4
t(ms)
V
S
V
L2
0
1
2
3
4
t(ms)
0,7
0,27
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
3
∗
0T
2
1
< , Diode taét, R
ng
= ∞, doøng i
L
chaûy qua R
i
, R
b
, R
L
neân ta coù.
V5,410.9.
10.91010
10
R
RRR
V
V
3
343
L
Lbi
S
1L
=
++
=
++
=
V45,010.9.
10.91010
1
R
RRR
V
V
3
343
L
Lbi
S
1L
=
++
=
++
=
b- Veõ V
L
(t) vôùi daïng soùng sin coù bieân ñoä 10V vaø 1 V.
∗
Ñeå ñôn giaûn khi V
Sm
= 10V (>>V
D
= 0,7V) ta boû qua V
D
. Khi ñoù:
+
0T
2
1
>
, Diode daãn, R
thD
≈ 0, doøng i
L
chaûy qua R
i
, D, R
L
neân ta
coù:
)V(tsin910.9.
10.910
tsin10
R
RR
V
V
0
3
33
0
L
Li
S
1L
ω=
+
ω
=
+
=
+
0T
2
1
<
, Diode taét, R
ng
= ∞, doøng i
L
chaûy qua R
i
, R
b
, R
L
neân ta coù.
)V(tsin5,410.9.
10.91010
t
sin
10
R
RRR
V
V
0
3
343
0
L
Lbi
S
1L
ω=
++
ω
=
++
=
∗
Khi V
S
= 1sinω
0
t so saùnh ñöôïc vôùi V
D
ta seõ coù:
+
0T
2
1
> , khi V
Sm
≥ 0,7, Diode daãn, R
thD
≈ 0, doøng i
L
chaûy qua R
i
,
D, R
L
neân ta coù:
)V(63,0tsin9,010.9.
10.910
7,0tsin1
R
RR
7,0tsin1
V
0
3
33
0
L
Li
0
2L
−ω=
+
−ω
=
+
−ω
=
Taïi
2
t
0
π
=ω
, sinω
0
t = 1, ta coù V
L2m
= 0,9 - 0,63 = 0,27V
+
0T
2
1
>
, khi V
Sm
< 0,7, Diode taét, R
ngD
= ∞, doøng i
L
chaûy qua R
i
,
R
b
, R
L
neân ta coù:
10
-
10
0
1
-
-
V
S
2
3
4
t(ms)
1
-
1
0
1
-
-
V
S
2
3
4
t(ms)
8,37
0
1
V
L1
2
3
4
t(ms)
0,27
0
1
V
L2
2
3
4
t(ms)
-
4,5
-
0,45
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
4
tsin315,010.9.
10.91010
tsin7,0
R
RRR
tsin7,0
V
0
3
343
0
L
Lbi
0
2L
ω=
++
ω
=
++
ω
=
+
0T
2
1
<
, Diode taét, R
ng
= ∞, doøng i
L
chaûy qua R
i
, R
b
, R
L
neân ta coù.
tsin45,010.9.
10.91010
tsin1
R
RRR
tsin1
V
0
3
343
0
L
Lbi
0
2L
ω=
++
ω
=
++
ω
=
2) Daïng maïch Thevenin aùp duïng nguyeân lyù choàng chaäp:
Baøi 1-20 vôùi V
i
(t) = 10sinω
0
t
a-
Veõ maïch Thevenin:
AÙp duïng nguyeân lyù xeáp choàng ñoái vôùi hai nguoàn ñieän aùp V
DC
vaø V
i
:
∗
Khi chæ coù V
DC
, coøn V
i
= 0 thì ñieän aùp giöõa hai ñieåm A-K:
V3
10.5,110
10.5,1
5
rR
r
VV
33
3
ii
i
DCAK
=
+
=
+
=
∗
Khi chæ coù V
i
, coøn V
DC
= 0 thì ñieän aùp giöõa hai ñieåm A-K laø:
)V(tsin4
10.5,110
10
tsin.10
rR
R
VV
0
33
3
0
ii
i
iAK
ω=
+
ω=
+
=
V
L
-
V
i
-
i
D
R
L
1,4K
R
i
=1K
V
DC
=5v
K
A
r
i
=1,5K
R
T
i
d
V
T
K
A
R
L
R
i
//r
i
i
L
V
T
K
A
10
0
-
10
9
-
-
t(ms)
V
S
V
L1
t(ms)
1
0
-
1
t(ms)
V
S
V
L2
t(ms)
0,7
0,315
-
-
-
4,5
-
4,5
0,585
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
5
∗
Vaäy khi taùc ñoäng ñoàng thôøi caû V
DC
vaø V
i
thì söùc ñieän ñoäng töông
ñöông Thevenin giöõa hai ñieåm A-K laø:
)V(tsin43
rR
R
V
rR
r
VV
0
ii
i
i
ii
i
DCT
ω+=
+
+
+
=
∗
Ñieän trôû töông ñöông Thevenin chính laø ñieän trôû töông ñöông cuûa
phaàn maïch khi Diode hôû maïch laø:
Ω=+
+
=+
+
= K210.4,1
10.5,110
10.5,1.10
R
rR
r.R
R
3
33
33
L
ii
ii
T
b-
Veõ ñöôøng taûi DC khi
2
,
3
,
2
,
3
,0t
0
π
−
π
−
π
π
=ω .
∗
Taïi
V
3
V
0
t
T0
=
⇒
=
ω
∗
Taïi
)V(46,6
2
3
43V
3
t
T0
=+=
⇒
π
=ω
∗
Taïi )V(71.43V
2
t
T0
=+=⇒
π
=ω
∗
Taïi
)V(46,0
2
3
43V
3
t
T0
−=−=
⇒
π
−=ω
∗
Taïi
)V(11.43V
2
t
T0
−=−=⇒
π
−=ω
Theo ñònh luaät Ohm cho toaøn maïch ta coù.
T
T
D
TT
DT
R
V
V.
R
1
R
V
V
i +−=
−
=
∗
Taïi )mA(15,1
10
.
2
3
7,0.
10
.
2
1
i0t
33
0
=+−=⇒=ω
∗
Taïi )mA(88,2
10
.
2
46
,
6
7,0.
10
.
2
1
i
3
t
33
0
=+−=⇒
π
=ω
i
D
(mA)
3,15
2,88
1,15
3
6,46
7
-
1
V
T
t
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
6
∗
Taïi )mA(15,3
10
.
2
7
7,0.
10
.
2
1
i
2
t
33
0
=+−=⇒
π
=ω
∗
Taïi )mA(58,0
10
.
2
46
,
0
7,0.
10
.
2
1
i
3
t
33
0
−=−−=⇒
π
−=ω
∗
Taïi )mA(85,0
10
.
2
1
7,0.
10
.
2
1
i
2
t
33
0
−=−−=⇒
π
−=ω
c- Veõ
( )
( )
)V(tsin8,21,2tsin437,0V7,0
10.2
V
10.4,1
Rr//R
V
R
R
V
.Ri.R)t(V
00T
3
T
3
Lii
T
L
T
T
LDLL
ω+=ω+==
=
+
===
II. Diode Zenner:
1)
Daïng doøng I
L
= const (baøi 1-40); 200mA ≤ I
Z
≤ 2A, r
Z
= 0
a-
Tìm R
i
ñeå V
L
= 18V = const.
I
min
= I
Zmin
+ I
L
= 0,2 + 1 = 1,2 A.
I
max
= I
Zmax
+ I
L
= 1 + 2 = 3 A.
Maët khaùc ta coù: V
imin
= 22V = I
Zmin
.R
i
+ V
Z
.
Suy ra:
Ω==
−
=
−
= 3,3
2,1
4
2,1
18
22
I
V
V
R
minZ
Zmini
i
V
imax
= 28V = I
Zmax
R
i
+ V
Z
Suy ra
Ω==
−
=
−
= 3,3
3
10
3
18
28
I
V
V
R
maxZ
Zmaxi
i
Vaäy R
i
= 3,3Ω.
b-
Tìm coâng suaát tieâu thuï lôùn nhaát cuûa Diode Zenner:
P
Zmzx
= I
Zmax
.V
Z
= 2.18 = 36W.
V
L
0
-
0,7
2,1
4,9V
t
R
L
=18
Ω
V
Z
=18v
22v<V
DC
<28v
R
i
I
Z
V
L
I
L
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
7
2)
Daïng doøng I
L
≠ const: (baøi 1-41), 10mA ≤ I
L
≤ 85mA.
I
Zmin
= 15mA.
a-
Tính giaù trò lôùn nhaát cuûa R
i
maxLminZ
Zi
i
minLmaxZ
Zi
II
V
V
R
II
V
V
+
−
≤≤
+
−
∗
Khi V
DC
= 13V ta coù
Ω=
+
−
≤ 30
085,0015,0
10
13
R
maxi
∗
Khi V
DC
= 16V ta coù
Ω=
+
−
≤ 60
085,0015,0
10
16
R
maxi
Vaäy ta laáy R
imax
= 30Ω.
b-
Tìm coâng suaát tieâu thuï lôùn nhaát cuûa Diode Zenner.
P
Zmax
= I
Zmax
.V
Z
.
Maët khaùc: V
imax
= I
Zmax
R
i
+ V
Z
⇒
mA200
30
10
16
R
V
V
I
i
Zmaxi
max
=
−
=
−
=
⇒
mA
190
19
,
0
01
,
0
2
,
0
I
I
I
minLmaxmaxz
=
=
−
=
−
=
⇒
W
9
,
1
10
19
,
0
P
maxz
=
×
=
3)
Daïng I
Z
≠ const; I
L
≠ const (Baøi 1-42)
30 ≤ I
L
≤ 50mA, I
Zmin
= 10mA.
r
Z
= 10Ω khi I
Z
= 30mA; P
zmax
=800mW.
a-
Tìm R
i
ñeå Diode oån ñònh lieân tuïc:
mA80
10
8
,
0
V
P
I
Z
maxZ
maxZ
===
Vaäy 10mA ≤ I
Z
≤ 80mA
Ta coù: I
min
= I
Zmin
+ I
Lmax
= 60mA
I
max
= I
Zmax
+ I
Lmin
= 110mA
R
L
V
Z
=10v
20v<V
DC
<25v
R
i
10Ω
I
Z
V
L
I
L
R
L
V
Z
=10v
13v<V
DC
<16v
R
i
I
Z
V
L
I
R
I
L
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
8
Maët khaùc: V
imin
= I
min
.R
i
+ V
Z
= 20V
⇒
Ω=
−
= 7,166
06,0
10
20
R
maxi
V
imax
= I
max
.R
i
+ V
Z
= 25V
⇒
Ω=
−
= 36,136
11,0
10
25
R
mini
Suy ra: 136,4Ω ≤ R
i
≤ 166,7Ω
Vaäy ta choïn R
i
=150Ω
b-
Veõ ñaëc tuyeán taûi:
Ta coù: V
Z
+ I
Z
R
i
= V
DC
– I
L
R
i
∗
Vôùi V
DC
= 20V ta coù:
==×−
==×−
=+
mA50IkhiV5,1215005,020
mA30IkhiV5,1515003,020
150IV
L
L
ZZ
∗
Vôùi DC = 25V ta coù:
==×−
==×−
=+
mA50IkhiV5,1715005,025
mA30IkhiV5,2015003,025
150IV
L
L
ZZ
Töông öùng ta tính ñöôïc caùc doøng I
Z:
mA7,36
150
10
5
,
15
I
1Z
=
−
= ; mA7,16
150
10
5
,
12
I
2Z
=
−
=
mA70
150
10
5
,
20
I
3Z
=
−
= ; mA50
150
10
5
,
17
I
4Z
=
−
= ;
I
Z
(mA)
V
Z
36,7
50
30
80
70
10
20,5
17,5
15,5
V
Z
=10V
0
r
Z
=10
Ω
16,7
12,5
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
9
Chöông II: TRANSISTOR HAI LÔÙP TIEÁP GIAÙP
I. Boä khueách ñaïi R-C khoâng coù C
C
vaø khoâng coù C
E
(E.C).
1)
Baøi 2-10: 20 ≤ β ≤ 60, suy ra I
CQ
khoâng thay ñoåi quaù 10%.
∗
Phöông trình taûi moät chieàu:
V
CC
= V
CEQ
+ I
CQ
(R
C
+ R
E
).
mA8
1010.5,1
525
RR
V
V
I
33
EC
CEQCC
CQ
=
+
−
=
+
−
=
⇒
Neáu coi ñaây laø doøng ñieän ban ñaàu khi β = 60 sao cho sau moät thôøi gian
β chæ coøn β = 20 thì yeâu caàu I
CQ
≥ 7,2mA.
∗
Ta giaûi baøi toaùn baøi toaùn moät caùch toång quaùt coi β
1
= 20; β
2
= 60.
E22bbE11b
R
10
1
RRR
10
1
R β=≤≤β=
Ω==≤≤Ω== K610.60.
10
1
RRK210.20.
10
1
R
3
2bb
3
1b
Vaäy 2KΩ ≤ R
b
≤ 6KΩ
∗
Maët khaùc
β
+
−
=
b
E
BB
CQ
R
R
7
,
0
V
I , neáu coi V
BB
≈ const thì ta coù:
9,0
R
R
R
R
I
I
1
b
E
2
b
E
2CQ
1CQ
≥
β
+
β
+
= (1)
∗
Coù theå tính tröïc tieáp töø baát phöông trình (1):
β
+
β
−≥
⇒
β
+≥
β
+
12
bE
1
b
E
2
b
E
9,01
RR1,0
R
R9,0
R
R
Ω==
+−
=
β
+
β
−
≤⇒
−
K53,3
10.3,28
100
20
9,0
60
1
10.1,0
9,01
R1,0
R
3
3
12
E
b
V
CEQ
= 5V
-
+25V
R
2
R
1
R
C
=1,5K
R
E
=1K
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
10
Choïn R
b
= 3,5KΩ.
∗
Neáu boû qua I
BQ
ta coù V
BB
≈ V
BE
+ I
EQ
R
E
= 0,7 + 8.10
-3
.10
3
= 8,7V.
Suy ra:
Ω≈Ω==
−
=
−
= K4,55368
652,0
10.5,3
25
7,8
1
1
10.5,3
V
V
1
1
RR
3
3
CC
BB
b1
Ω≈Ω=== K06,1010057
7,8
25
10.5,3
V
V
RR
3
BB
CC
b2
∗
Ta coù theå tính toång quaùt: Choïn R
b
= 4KΩ thay vaøo (1):
%9,88
1200
1067
20
10.4
10
60
10.4
10
I
I
3
3
3
3
2CQ
1CQ
==
+
+
=
, bò loaïi do khoâng thoûa maõn (1).
∗
Choïn R
b
=3KΩ thay vaøo (1):
91,0
1150
1050
20
10.3
10
60
10.3
10
I
I
3
3
3
3
2CQ
1CQ
==
+
+
=
thoûa
maõn baát phöông trình (1), ta tính tieáp nhö treân.
2)
Baøi 2-11: Vôùi hình veõ baøi (2-10) tìm giaù trò cho R
1
, R
2
sao cho doøng i
C
xoay
chieàu coù giaù trò cöïc ñaïi.
∗
Ñieåm Q toái öu ñöôïc xaùc ñònh nhö sau:
AC
ÖCQTTÖCEQ
ACDC
CC
TÖCQ
maxCm
R.IV
RR
V
II
=
+
==
Töø hình veõ: R
DC
= R
C
+ R
E
= 1,5.10
3
+ 10
3
= 2,5KΩ.
R
AC
= R
C
+ R
E
= 1,5.10
3
+ 10
3
= 2,5KΩ.
Suy ra:
mA5
10.5,210.5,2
25
I
33
TÖCQ
=
+
=
V
CEQTÖ
= 5.10
-3
.2,5.10
3
= 12,5V
∗
Choïn Ω==β= K1010.100.
10
1
R
10
1
R
3
Eb
(boû qua I
BQ
)
V
BB
≈ V
BE
+ I
CQTÖ
.R
E
= 0,7 + 5.10
-3
.10
3
= 5,7V
V
CE
(V)
i
C
(mA)
V
CEQTÖ
= 12,5
25
10
R
V
DC
CC
=
( )
5
RR2
V
EC
CC
=
+
−≡
3
10.5,2
1
ACLLDCLL
Q
TÖ
0
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
11
Ω≈Ω==
−
=
−
= K13K95,12
772,0
10
25
7,5
1
1
10.10
V
V
1
1
RR
4
3
CC
BB
b1
Ω≈Ω=== K44K85,43
7,5
25
10
V
V
RR
4
BB
CC
b2
Vì R
DC
= R
AC
neân phöông trìng taûi DC vaø AC truøng nhau.
3)
Baøi 2-14: Ñieåm Q
baát kyø
vì bieát V
BB
= 1,2V; β = 20. Tìm giaù trò toái ña cuûa dao
ñoäng coù theå coù ñöôïc ôû C vaø tính η.
Bieát β = 20, V
BEQ
= 0,7V.
Ta coù: mA3,3
50100
7,02,1
R
R
V
V
I
b
E
BEQBB
CQ
=
+
−
=
β
+
−
=
∗
Ñeå tìm giaù trò toái ña cuûa dao ñoäng coù theå coù ñöôïc ôû C ta phaûi veõ
phöông trình taûi DC, AC
V
CEQ
= V
CC
– I
CQ
(R
C
+ R
E
) = 6 – 3,3.10
-3
.1,1.10
3
= 2,37V
∗
Vaäy giaù trò toái ña cuûa dao ñoäng laø:
I
Cmmax
= i
Cmax
– I
CQ
= 5,45 – 3,3 = 2,15mA
Suy ra V
Lmax
= I
Cmmax
.R
C
= 2,15.10
3
.10
-3
= 2,15V
∗
P
CC
= I
CQ
.V
CC
= 3,3.10
-3
.6 = 19,8mW
+6V
R
b
= 1K
R
C
= 1K
R
E
= 100
Ω
V
BB
= 1,2V
45,5
R
V
DC
CC
=
I
CQ
= 3,3
i
C
(mA)
V
CE
(V)
2,37
3
6
0
2,725
Q
TÖ
Q
bk
−=
1100
1
ACLLDCLL
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
12
( )
(
)
mW31,210.10.15,2
2
1
R.I
2
1
P
3
2
3
C
2
maxCmL
===
−
Hieäu suaát:
%7,11
10.8,19
10.31,2
P
P
3
3
CC
L
===η
−
−
II. Boä KÑRC khoâng coù C
C
, C
E
(tuï bypass Emitter) (EC)
1)
Baøi 2-15: Ñieåm Q baát kyø.
a-
Tìm R
1
, R
2
ñeå I
CQ
= 01mA (R
b
<< βR
E
)
Vì R
b
<< βR
E
neân ta coù:
A10mA10
R
7
,
0
V
I
2
E
BB
CQ
−
==
−
≈
suy ra V
BB
= 0,7 + 100.10
-2
= 1,7V
Ω==β= K1100.100
10
1
R
10
1
R
Eb
Ω≈=
−
=
−
= K2,1
83,0
10
10
7,1
1
10
V
V
1
1
RR
33
CC
BB
b1
Ω=== K88,5
7,1
10
10
V
V
RR
3
BB
CC
b2
b-
Ñeå tìm I
Cmmax
vôùi R
1
, R
2
nhö treân ta phaûi veõ DCLL vaø ACLL:
C
E
→
∞
V
cc
=10V
R
2
R
1
R
C
=150
Ω
R
E
100Ω
β
=100; V
BEQ
=0,7v
i
C
(mA)
V
CE
(V)
Q
−
150
1
ACLL
−
250
1
DCLL
7,5
60
10
V
CEmax
= 9V
I
Cmmax
15
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
13
V
CEQ
= V
CC
– I
CQ
(R
C
+ R
E
) = 10 – 10
-2
.250 = 7,5V
Töø hình veõ ta nhaän thaáy ñeå I
Cm
lôùn nhaát vaø khoâng bò meùo thì I
Cmmax
=
10mA.
Ta coù theå tìm i
Cmax
vaø V
Cemax
theo phöông trình
( )
CEQCE
C
CQC
VV
R
1
Ii −−=−
Cho V
CE
= 0 ⇒
mA60
150
5,7
10
R
V
Ii
2
C
CEQ
CQmaxC
=+=+=
−
Cho i
C
= 0 ⇒ V95,7150.10VR.IV
1
CEQCCQmaxCE
=+=+=
−
2)
Baøi 2-16: Ñieåm Q toái öu (hình veõ nhö hình 2-15).
Ñeå coù dao ñoäng Collector cöïc ñaïi ta coù:
ACDC
CC
ÖCQT
maxCm
RR
V
II
+
== (1)
V
CEQTÖ
= R
AC
.I
CQTÖ
(2)
R
DC
= R
C
+ R
E
= 150 + 100 = 250Ω
R
AC
= R
C
= 150Ω
Thay vaøo (1) ta ñöôïc: mA25
150
250
10
I
ÖCQT
=
+
=
V75,310.25.150V
3
ÖCEQT
==
−
V
BB
≈ 0,7 + I
CQTÖ
.R
E
= 3,2V.
Ω==β= K1100.100.
10
1
R
10
1
R
Eb
Ω≈=
−
=
−
= K47,1
68,0
10
10
2,3
1
10
V
V
1
1
RR
33
CC
BB
b1
V
CE
(V)
i
C
(mA)
V
CEQTÖ
= 3,75
2I
CQTÖ
= 50
40
RR
V
EC
CC
=
+
−
150
1
ACLL
2V
CEQTÖ
=7
10
I
CQTÖ
= 25
−
250
1
DCLL
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
14
Ω≈Ω=== K1,33125
2,3
10
10
V
V
RR
3
BB
CC
b2
Ñeå veõ ACLL, raát ñôn giaûn ta chæ caàn xaùc ñònh:
i
Cmax
= 2I
CQTÖ
vaø V
Cemax
= 2V
CEQTÖ.
III. Boä KÑ R-C coù C
C
vaø C
E
(E.C).
1)
Baøi 2-20: Ñieåm Q toái öu
R
DC
= R
C
+ R
E
= 900 + 100 =1KΩ
Ω=
+
=
+
= 450
900900
900
.
900
RR
R
R
R
LC
LC
AC
mA9,6
RR
V
II
DCAC
CC
ÖCQT
maxCm
≈
+
==
V
CEQTÖ
= I
CQTÖ
.R
AC
= 6,9.10
-3
.450 = 3,1V
V
BB
= 0,7 + R
E
.I
CQTÖ
= 0,7 + 100.6,9.10
-3
= 1,4V
Ω==β= K1100.100.
10
1
R
10
1
R
Eb
C
E
→
∞
V
cc
=10V
R
2
R
1
R
C
=900
Ω
R
E
100Ω
C
C
→
∞
R
L
=900K
V
CE
(V)
i
C
(mA)
V
CEQTÖ
= 3,1
2I
CQTÖ
= 13,8
10
RR
V
EC
CC
=
+
−
450
1
ACLL
6,2
10
0
I
CTÖ
= 6,9
−
1000
1
DCLL
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
15
Ω≈=
−
=
−
= 1163
86,0
10
10
4,1
1
10
V
V
1
1
RR
33
CC
BB
b1
Ω=== 7143
4,1
10
10
V
V
RR
3
BB
CC
b2
Ta coù doøng xoay chieàu:
V1,3V
mA45,39,6
900900
900
I.
RR
R
I
Lm
Cm
LC
C
Lm
=⇒
=
+
=
+
=
2)
Vaãn baøi 2-20 neáu ta boû tuï C
E
thì ta seõ coù boä khueách ñaïi R.C coù C
C
maø khoâng
coù C
E
. Khi ñoù keát quaû tính toaùn seõ khaùc raát ít vì R
E
<< R
C
, R
L
R
DC
= R
C
+ R
E
= 900 + 100 = 1KΩ
Ω=
+
+=
+
+= 550
900900
900
.
900
100
RR
R
R
RR
LC
LC
EAC
mA45,6
55010
10
RR
V
II
3
ACDC
CC
maxCm
ÖCQT
=
+
=
+
==
V
CEQTÖ
= I
CQTÖ
.R
AC
= 6,45.10
-3
.550 = 3,55V
V
BB
= 0,7 + I
CQ
. R
E
= 0,7 + 6,45.10
-3
.100 = 1,345V
Ω==β= K1100.100.
10
1
R
10
1
R
Eb
Ω==
−
=
−
= 1155
8655,0
10
10
345,1
1
10
V
V
1
1
RR
33
CC
BB
b1
Ω=== 7435
345,1
10
10
V
V
RR
3
BB
CC
b2
mA225,310.45,6.
900900
900
I
RR
R
I
3
Cm
LC
C
Lm
=
+
=
+
=
−
V
Lm
= R
L
.I
Lm
= 900.3,225.10
-3
= 2,9V.
IV. Boä KÑ R.C maéc theo kieåu C.C.
1)
Baøi 2-22: Maïch coù thieân aùp Base.
* Ñaây laø daïng baøi ñieåm Q baát kyø vì ñaõ bieát R
1
, R
2
.
V525.
10.2010.5
10.5
V
RR
R
V
33
3
CC
21
1
BB
=
+
=
+
=
mA1,2
60
10.4
10.2
7
,
0
5
R
R
7
,
0
V
I
3
3
b
E
BB
CQ
=
+
−
=
β
+
−
=
R
b
= = =
4K
Ω
R
1
+ R
2
R
1
R
2
5.10
3
+ 20.10
3
5.10
3
.20.10
3
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
16
(Vì
β
>>
b
E
R
R
neân coù theå tính gaàn ñuùng theo coâng thöùc
E
BB
CQ
R
7
,
0
V
I
−
=
)
V
CEQ
= V
CC
– I
CQ
(R
C
+ R
E
) = 25 – 2,1.10
-3
.3.10
3
= 18,7V
Töø hình veõ ta thaáy: I
CQ
< I
CQTÖ
neân I
Cm
= I
CQ
= 2,1mA
mA05,110.1,2.
10.210.2
10.2
I
RR
R
I
3
33
3
Cm
LE
L
Lm
=
+
=
+
=
−
V
Lmmax
= R
L
.I
Lm
= 2.10
3
.1,05.10
-3
= 2,1V
* Caùch veõ DCLL vaø ACLL cuûa boä KÑ R.C maéc C.C töông töï nhö caùch maéc E.C
( )
CEQCE
AC
CQC
VV
R
1
Ii −−=−
vôùi
Ω=
+
+= k2
RR
R
R
RR
LE
LE
CAC
Cho V
CE
= 0 suy ra
mA45,11
10.2
7,18
10.1,2
R
V
Ii
3
3
AC
CEQ
CQC
=+=+=
−
Q
V
CE
(V)
i
C
(mA)
V
CEQ
= 18,7
I
Cmax
= 11,45
3,8
R
V
DC
CC
=
−
3
10.2
1
ACLL
10
0
I
CQTÖ
= 5
−
3
10.3
1
DCLL
22,9
25
I
CQ
= 2,1
V
L
C
C
→
∞
V
cc
=25V
R
2
20K
R
1
5K
R
C
=1K
R
E
=2K
R
L
2K
β
=60
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
17
i
C
= 0 suy ra
V9,2210.1,2.10.27,18IRVV
33
CQACCEQmaxCEQ
=+=+=
−
* Vôùi baøi toaùn treân neáu chöa bieát R
1
vaø R
2
ta coù theå thieát keá ñeå doøng ñieän ra lôùn
nhaát: R
DC
= R
C
+ R
E
= 10
3
+ 2.10
3
= 3KΩ.
Ta coù:
mA5
10.210.3
25
RR
V
I
33
ACDC
CC
ÖCQT
=
+
=
+
=
V
CEQTÖ
= I
CQTÖ
.R
AC
= 10V.
2)
Baøi 2-24: Maïch ñöôïc ñònh doøng Emitter.
Theo ñònh luaät K.II: ΣV
kín
= 0 ta coù
R
b
I
BQ
+ V
BEQ
+ R
E
.I
EQ
–V
EE
= 0
Suy ra
mA93
100
7
,
0
10
R
R
7
,
0
V
I
b
E
BB
EQ
=
−
≈
β
+
−
=
V
CEQ
= V
CC
+ V
EE
– I
CQ
(R
C
+ R
E
)
= 10 + 10 – 93.10
-3
.150 = 6,05V
∗
mA5,4610.93.
100100
100
I
RR
R
I
3
Em
LE
E
Lm
=
+
=
+
=
−
∗
V
Lm
= I
Lm
R
L
= 46,5.10
-3
.10
2
= 4,65V
∗
Ñaây laø ñieåm Q baát kyø neân ta coù:
( )
CEQCE
AC
CQC
VV
R
1
Ii −−=−
+
Cho V
CE
= 0 suy ra
mA214
R
V
Ii
AC
CEQ
CQmaxC
=+=
+
Cho i
C
= 0 suy ra
V675,1050.10.9305,6RIVV
3
ACCQCEQCE
=+=+=
−
i
L
I.
I
C
C
→
∞
V
L
C
E
→
∞
V
EE
=
-
10v
R
b
<<
β
R
E
R
C
=50
Ω
R
E
=100
Ω
R
L
=100
Ω
V
CC
=10v
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
18
∗
Neáu baøi naøy ñöôïc tính ôû cheá ñoä toái öu thì:
R
DC
= R
C
+ R
E
= 150Ω
Ω=
+
= 50
RR
R
R
R
LE
LE
AC
khi ñoù
mA100A1,0
50150
20
RR
V
I
DCAC
CC
ÖCQT
==
+
=
+
=
V
CEQTÖ
= I
CQTÖ
.R
AC
= 5V
V
CE
(V)
i
C
(mA)
V
CEQ
= 6,05
214
133
RR
V
V
EC
EECC
=
+
+
−
50
1
ACLL
10,675
20
0
I
CQ
= 93
−
150
1
DCLL
Q
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
19
Chöông IV
:
THIEÁT KEÁ VAØ PHAÂN TÍCH TÍN HIEÄU NHOÛ TAÀN SOÁ THAÁP.
I. Sô ñoà maéc Emitter chung E.C:
1)
Baøi 4-7: Q baát kyø.
a-
Cheá ñoä DC
K3
205,3
20
.
5
,
3
RR
R
R
R
21
21
b
≈
+
=
+
=
V320.
205,3
5
,
3
V
RR
R
V
CC
21
1
BB
≈
+
=
+
=
mA6,4
100
10.3
500
7
,
0
3
I
3
CQ
≈
+
−
=
V
CEQ
= V
CC
– I
CQ
(R
C
+ R
E
) = 20 – 4,6.10
-3
.2.10
3
= 10,8V
Ω==
−
−
760
10.6,4
10.25
h.4,1h
3
3
feie
b-
Cheá ñoä AC:
Z
o
i
C
Z
i
R
i
2K
i
b
R
b
3K
i
i
R
C
1,5K
i
L
R
L
=1,5K
h
ie
100i
b
1,2K
R
L
=1,5K
i
i
R
C
=1,5K
C
C2
→
∞
-
+V
CC
=20V
C
E
→∞
-
R
1
3,5K
i
L
R
2
=20K
R
i
=2K
R
E
1,5K
C
C1
→
∞
-
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
20
i
b
b
L
i
L
i
i
i
i
i
i
i
A ==
(1)
50100.
10.5,110.5,1
10.5,1
h.
RR
R
i
i
i
i
i
i
33
3
fe
LC
C
b
C
C
L
b
L
−=
+
−=
+
−==
( )
61,0
76010.2,1
10.2,1
hR//R
R//R
i
i
3
3
iebi
bi
i
b
=
+
=
+
=
Thay vaøo (1) ta coù: A
i
= -50.0,61 = -30,6
Z
i
= R
i
//R
b
//h
ie
= 1200//760 = 465Ω
Z
o
= R
C
= 1,5KΩ.
2)
Baøi 4-11: Q baát kyø vaø h
fe
thay ñoåi.
a-
Cheá ñoä DC:
∗
100R5010.50.
10
1
R
10
1
R
bE11b
=<Ω==β=
, khoâng boû qua I
BQ
.
∗
100R15010.150.
10
1
R
10
1
R
bE22b
=>Ω==β=
, boû qua I
BQ
.
mA83
50
100
10
7
,
0
7
,
1
R
R
7
,
0
V
I
1
b
E
BB
1EQ
=
+
−
=
β
+
−
=
mA100
10
7
,
0
7
,
1
R
7
,
0
V
I
E
BB
2EQ
=
−
=
−
≈
Ω≈=
−
−
21
10
.
83
10.25
.50.4,1h
3
3
1ie
Ω==
−
−
5,52
10
.
100
10.25
.150.4,1h
3
3
2ie
suy ra 21Ω ≤ h
ie
≤ 52,5Ω
R
L
=100
Ω
R
b
=100
Ω
V
BB
=1,7v
i
i
R
C
=100
Ω
C
C
→
∞
-
+V
CC
=20v
C
E
→∞
-
i
L
R
E
10Ω
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
21
b-
Cheá ñoä AC:
ieb
b
fe
LC
C
i
b
b
L
i
L
i
hR
R
.h.
RR
R
i
i
i
i
i
i
A
++
−===
66,20
21
100
100
.50.
100
100
100
A
1i
−=
++
−=
1,49
5,52100
100
.150.
100100
100
A
2i
−=
++
−=
Z
i
= R
b
//h
ie
suy ra Z
i1
= 100//21 = 17,36Ω
Z
i2
= 100//52,5 = 34,43Ω
Vaäy 20,66 ≤ A
i
≤ 49,18
17,36Ω ≤ Z
i
≤ 34,43Ω
3)
Baøi 4-12: Daïng khoâng coù tuï C
E
a-
Cheá ñoä DC:
mA5,4
100
10
10
7
,
0
7
,
5
h
R
R
7
,
0
V
I
4
3
fe
b
E
BB
CQ
=
+
−
=
+
−
=
(coù theå tính I
CQ
= 5 mA)
V
CEQ
= V
CC
– I
CQ
(R
C
+ R
E
) = 20 – 4,5.10
-3
.(3.10
3
) = 6,5V
Ω==
−
−
778
10.5,4
10.25
.100.4,1h
3
3
ie
R
b
=10K
V
BB
=5,7V
i
i
R
C
=2K
C
C
→
∞
-
+V
CC
=20V
i
L
R
E
=1K
R
L
=1
00
Ω
i
C
i
b
R
b
100Ω
i
i
R
C
100Ω
i
L
h
ie
h
fe
i
b
R
L
= 100
Ω
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
22
b-
Cheá ñoä AC:
i
b
b
L
i
L
i
i
i
i
i
i
i
A ==
(1)
24,95h.
RR
R
i
i
i
i
i
i
fe
LC
C
b
C
C
L
b
L
−=
+
−==
09,0
1077810
10
RhhR
R
i
i
54
4
Efeieb
b
i
b
=
++
=
++
=
Thay vaøo (1) ta ñöôïc A
i
= -95,24.0,09 = -8,6
[
]
Ω=≈+= K1,910//10Rhh//RZ
54
Efeiebi
II. Sô ñoà maéc B.C: Baøi 4-21, h
oe
=
4
10
1) Cheá ñoä DC:
91,0
11
10
h1
h
h
fe
fe
fb
==
+
=
Ω==
+
=
−
−
32
10
10.25
.10.4,1.
11
1
h1
h
h
3
3
fe
ie
ib
5
4
fe
oe
ob
10
11
10
h1
h
h
−
−
==
+
=
R
L
=100
Ω
i
b
R
b
10K
i
i
R
C
2K
i
L
h
fe
R
E
100i
b
h
ie
=778
Ω
V
CC
R
2
V
i
-
R
1
C
b
→
∞
r
i
=50
Ω
R
L
=10K
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
23
2) Cheá ñoä AC:
i
e
e
L
i
L
V
V
i
i
V
V
V
A ==
(1)
82791,0.
1010
10.10
h.
h
1
R
h
1
R
i
i
.
i
Ri
i
V
54
54
fb
ob
L
ob
L
e
C
C
LL
e
L
−=
+
−=
+
−==
012,0
3250
1
hR
1
hR
V
.
V
1
V
i
ibiibi
i
ii
e
−=
+
−=
+
−=
+
−
=
Thay vaøo (1) ta ñöôïc A
V
= (-827).(-0,012) = 10,085 ≈ 10
III. Sô ñoà maéc C.C: Baøi 4-23
1) Cheá ñoä DC
V
CC
= I
BQ
R
b
+ V
BEQ
+ R
E
I
EQ
mA65,4
100
10
10
7
,
0
10
R
R
7
,
0
V
I
5
3
b
E
CC
EQ
=
+
−
=
β
+
−
=
⇒
V
CEQ
= V
CC
– R
E
I
EQ
= 10 – 4,65.10
-3
.10
3
= 5,35 V
R
L
10KΩ
i
L
1/h
ob
10
5
Ω
i
C
h
fb
i
e
0,91i
b
h
ib
32Ω
i
e
R
i
50
Ω
V
i
-
R
L
1KΩ
V
i
-
R
E
1KΩ
Z
o
Z
i
C
c2
→∞
r
i
500
Ω
100K
Ω
R
b
C
c1
→∞
+V
CC
=10V
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
24
2) Cheá ñoä AC
Ω≈=
−
−
753
10.65,4
10.25
h4,1h
3
3
feie
i
b
b
L
i
L
v
V
V
V
V
V
V
A ==
(1)
(
)
( )
[ ]
985,0
000
.
50
753
500.100
R//Rhhi
R
//
R
h
.
i
V
V
LEfeieb
LEfeb
b
L
=
+
=
+
=
(2)
R
’
b
= R
b
//[h
ie
+ h
fe
(R
E
//R
L
)] = 33,3Ω
994,0
10.3,33500
K3,33
Rr
R
Rr
V
.R.
V
1
V
V
3'
bi
'
b
'
bi
i
'
b
ii
b
=
+
Ω
=
+
=
+
=
(3)
Thay (2), (3) vaøo (1) ta coù: A
V
= 0,985.0,994 = 0,979 ≈ 0,98
[ ]
Ω≈+≈
+= 37,12553,7//10
h
R//r
h//RZ
3
fe
bi
ibEo
(
)
[
]
Ω==+= K3,33RR//Rhh//RZ
'
bLEfeiebi
i
L
’
r
i
500
Ω
V
i
-
h
ie
753
Ω
i
b
R
b
100KΩ
R
e
.hfe
100KΩ
R
L
.hfe
100KΩ
V
b
V
L
Z
i
h
ie
/h
fe
7,53
Ω
i
e
R
E
1KΩ
r
i
/hfe
5Ω
R
b
/hfe
1KΩ
Z
o
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
25
Chöông VI: MAÏCH TRANSISTOR GHEÙP LIEÂN TAÀNG.
I. Transistor gheùp Cascading:
1) E.C – C.E
Baøi 6-1: Ñieåm Q baát kyø, 2 taàng hoaøn toaøn ñoäc laäp vôùi nhau.
a - Cheá ñoä DC
Ω==>Ω=
+
=
+
= 500R.h.
10
1
RK1,2
10.710.3
10.7.10.3
RR
R.R
R
Efeb
33
33
2111
2111
1b
suy ra, khoâng ñöôïc boû qua I
BQ1
;
V310.
10.710.3
10.3
V.
RR
R
V
33
3
CC
2111
11
1BB
=
+
=
+
=
mA2,16
50
2100
100
7
,
0
3
h
R
R
7
,
0
V
I
1fe
b
E
1BB
1EQ
1
1
=
+
−
=
+
−
=
V
CEQ1
= V
CC
– I
EQ1
(R
C1
+ R
E1
) = 10 – 16,2.10
-3
.300 = 5,14V
Ω===
−
−−
108
10.2,16
10.25
.50.4,1
I
10.25
.h4,1h
3
3
1EQ
3
1fe1ie
Ω==<Ω=
+
=
+
= 1250R.h.
10
1
RK9,0
10.910
10.9.10
RR
R.R
R
Efeb
33
33
2212
2212
2b
suy ra, ñöôïc boû qua I
BQ2
;
V110.
10.910
10
V.
RR
R
V
33
3
CC
2212
12
2BB
=
+
=
+
=
mA2,1
250
3
,
0
50
900
250
7
,
0
1
2
h
R
R
7
,
0
V
I
2b
2E
2BB
2EQ
=≈
+
−
=
+
−
=
V
CEQ2
= V
CC
– I
EQ2
(R
C2
+ R
E2
) = 10 – 1,2.10
-3
.2250 = 7,3V
Ω===
−
−−
1458
10.2,1
10.25
.50.4,1
I
10.25
.h4,1h
3
3
2EQ
3
2fe2ie
b - Cheá ñoä AC
i
1b
1b
2b
2b
L
i
i
i
.
i
i
.
i
i
A =
(1)
i
C2
V
L
Z
o
Z
i
R
b
2,1K
i
i
h
ie1
108
50i
b1
R
C1
200
R
b2
900
h
ie2
1458
50i
b2
R
C
2K
i
b1
i
b2
i
C1
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
26
50h.1
i
i
.
i
i
i
i
2fe
2b
2C
2C
L
2b
L
−=−==
(2)
( )
06,550.
1458
164
164
h.
hR//R
R
//
R
i
i
.
i
i
i
i
1fe
2ie2b1C
2b1C
1b
1C
1C
2b
1b
2b
−≈
+
−
≈
+
−
==
(3)
951,0
1082100
2100
hR
R
i
i
1ieb
b
i
1b
=
+
=
+
=
(4)
Thay (2), (3), (4) vaøo (1) ta coù
A
i
= (-50).(5,06).(0,951) ≈ 241
Z
i
= R
b
//h
ie1
= 2,1.10
3
//108 ≈ 103Ω
Z
o
= ∞
Ñeå tìm bieân ñoä ñænh ñoái xöùng cöïc ñaïi ta veõ DCLL vaø ACLL.
Töø
( )
CEQCE
AC
CQC
Vv
R
1
Ii −−=−
v
CE
= 0 suy ra, I
Cmax
= I
CQ
+V
CEQ
/R
AC
= 1,2.10
-3
+ 7,3/2.10
3
= 4,85mA
i
C
= 0 suy ra, v
Cemax
= V
CEQ
.R
AC
= 7,3 + 1,2.10
-3
.2.10
3
= 9,7V
Töø ñaëc tuyeán DCLL vaø ACLL ta coù I
Cmmax
= 1,2mA
Baøi 6-2: Ñieåm Q toái öu neân phaûi tính taàng thöù hai tröôùc, taàng 1 sau.
a- Cheá ñoä DC:
R
DC2
= R
C2
+ R
E2
= 2250Ω; R
AC2
= R
C
= 2KΩ.
mA35,2
20002250
10
RR
V
I
2AC2DC
CC
ÖT2CQ
=
+
=
+
=
V
CEQ2TÖ
= I
CQ2TÖ
.R
AC2
= 2,35010
-3
.2.10
3
= 4,7V
Q
V
CE
(V)
i
C
(mA)
7,3
i
Cmax
= 4,85
4,4
R
V
DC
CC
=
−
3
10.2
1
ACLL
0
−
250
1
DCLL
9,7
10
I
CQ
= 1,2
I
Cmmax
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
27
Ω===
−
−−
745
10.35,2
10.25
.50.4,1
I
10.25
.h4,1h
3
3
2EQ
3
2fe2ie
R
DC1
= R
C1
+ R
E1
= 200 + 100 = 300Ω;
R
AC1
= R
C1
//R
b2
//h
ie2
= 200//900//745 ≈ 134,4Ω
mA23
4,134300
10
RR
V
I
1AC1DC
CC
ÖT1CQ
=
+
=
+
=
Ω===
−
−−
76
10.23
10.25
.50.4,1
I
10.25
.h4,1h
3
3
1EQ
3
1fe1ie
b- Cheá ñoä AC: Sô ñoà töông ñöông tín hieäu nhoû nhö treân chæ coù h
ie1
vaø h
ie2
coù giaù trò khaùc. Ta aùp duïng luoân coâng thöùc (1) ôû treân:
( )
434
762100
2100
.
745164
164
.2500
hR
R
.
hR//R
R
//
R
h.hA
1ieb
b
2ie2b1C
2b1C
2fe1fei
≈
++
=
++
=
2) E.C – C.C:
Baøi 6-3 Ñieåm Q toái öu
a- Cheá ñoä DC:
Taàng 2:
R
DC2
= R
E2
= 1KΩ; R
AC2
= R
E2
//R
L
= 500Ω.
mA7,6
50010
10
RR
V
I
3
2AC2DC
CC
ÖT2CQ
=
+
=
+
=
V
CEQ2TÖ
= I
CQ2TÖ
.R
AC2
= 6,7.10
-3
.500 = 3,35V
Ω===
−
−−
522
10.7,6
10.25
.100.4,1
I
10.25
.h4,1h
3
3
2EQ
3
2fe2ie
Ω=Ω=== K101010.100.
10
1
R.h
10
1
R
43
2E2fe2b
V
BB
= 0,7 + I
CQ2TÖ
.R
E
= 0,7 + 6,7.10
-3
.10
3
= 7,4V
Ω==
−
=
−
= K46,38
26,0
10
10
4,7
1
10
V
V
1
R
R
44
CC
2BB
b
12
Ω=== K5,13
4,7
10
10
V
V
RR
4
2BB
CC
b22
Taàng 1:
R
DC1
= R
C1
+ R
E1
= 400 + 100 = 500Ω;
R
AC1
= R
C1
//R
b2
//[h
ie2
+ h
fe
(R
L
//R
E
)]
= 400//10
4
//[261 + 100.500] = 400//8333 ≈ 382Ω.
mA34,11
382500
10
RR
V
I
1AC1DC
CC
ÖT1CQ
=
+
=
+
=
V
CEQ1TÖ
= I
CQ1TÖ
.R
AC1
= 11,34.10
-3
.382 = 4,33V
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
28
Ω===
−−
309
34,11
10.25
.100.4,1
I
10.25
.h4,1h
3
2EQ
3
1fe1ie
Ω=== K1100.100.
10
1
R.h
10
1
R
1E1fe1b
V
BB1
= 0,7 + I
CQ1TÖ
.R
E1
= 0,7 + 11,34.10
-3
.100 = 1,834V
Ω==
−
=
−
= K25,12
8166,0
10
10
834,1
1
10
V
V
1
R
R
33
CC
1BB
1b
11
Ω=== K45,5
834,1
10
10
V
V
RR
3
1BB
CC
1b21
b- Cheá ñoä AC:
i
1b
1b
2b
2b
L
T
i
i
.
i
i
.
i
V
A =
(1)
( )( )
3
LEfe
2b
L
10.5,50R//Rh1
i
V
=+=
(2)
( ) ( )
75,0
51407
10.385
100.
50500
522
385
385
h.
R//Rh1hR//R
R
R
i
i
.
i
i
i
i
2
1fe
LEfe2ie2b1C
2b1C
1b
1C
1C
2b
1b
2b
−≈
−
=
+
+
−
=
+++
−
==
(3)
764,0
30910
10
hR
R
i
i
3
1ie1b
1b
i
1b
=
+
=
+
=
(4)
Thay (2), (3), (4) vaøo (1) ta coù
A
T
= (50,5.10
3
).(-0,75).(0,764) ≈ -29000
A
T
= -29000V/A = -29V/mA.
Z
i
= R
b
//h
ie1
= 10
3
//309 = 236Ω
[ ]
Ω≈=+=
+= 907,9//1085,322,5//10
h
R//R
h//RZ
33
2fe
2b1C
2ibEo
i
L
’
V
L
Z
o
Z
i
R
b1
2,1K
i
i
h
ie1
309
100i
b
R
C1
400
R
b2
10K
h
ie2
522
(1+h
fe
)R
L
101KΩ
i
b1
i
b2
i
C1
(1+h
fe
)R
E
101KΩ
R
E
1KΩ
Z
o
h
ib2
i
e2
R
c1
//R
b2
h
fe2
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
29
3) Daïng baøi hoãn hôïp E.C – C.C: Baøi 6-4
Tìm R ñeå
i
02
i
01
i
V
i
V
−=
(1)
i
1b
1b
2b
2b
01
i
01
i
i
.
i
i
.
i
V
i
V
=
(2)
i
1b
1b
2b
2E2fe
i
02
i
i
.
i
i
.R)h1(
i
V
+=
(3)
suy ra
2E2fe
2b
01
R).h1(
i
V
+−=
(4)
2b
2C
2C
3b
3b
01
2b
01
i
i
.
i
i
.
i
V
i
V
=
(5)
Töø (5) suy ra
2E2fe2fe
3E3fe3ie2C
2C
3E3fe
2b
01
R)h1(h
R)h1(hRR
R
.R)h1(
i
V
+−=
++++
+=
5050100.
5050
10
R
10
10
.5050
33
3
−=
+
+
+
−
(6)
10
5
= 7050 + R
R = 100KΩ - 7,05KΩ ≈ 93KΩ
Tìm
i
01
i
V
Töø (2) ta coù:
5050
5050
10
10
.
93
10
10.10.5050
R)h1(hRR
h
.
R
.
R
)
h
1
(
i
i
i
i
i
V
i
V
333
23
3E3fe3ie2C
2fe2C3E3fe
2b
2C
2C
3b
3b
01
2b
01
−≈
+
+
+
−=
++++
+
−==
(7)
(
)
( )
63,7
6550
10.5
5050
1000
500
100.500
h.
R)h1(hR//R
R
R
i
i
.
i
i
i
i
4
1fe
2E2fe2ie2b1C
2b1C
1b
1C
1C
2b
1b
2b
−=−=
+
+
−=
+++
−==
(8)
(
)
( )
5,0
1010
10
hR//R
R//R
i
i
33
3
1ie1bi
1bi
i
1b
=
+
=
+
=
(9)
Thay (7), (8), (9) vaøo (2) ta ñöôïc:
i
C2
h
ie1
1K
R
i
100K
i
i
h
ie2
1K
100i
b1
R
C1
1K
R
b2
1K
h
fe2
R
E2
5050
i
b2
i
b1
i
C1
R
b1
1K
V
o2
100i
b2
h
ie3
1K
R
C2
1K
h
fe3
R
E3
5050
i
b3
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
30
( )( )
mA
V
27,195,0.63,7.5050
i
V
i
01
≈−−=
Z
i
= R
i
//R
b1
//h
ie1
≈ 500Ω
[ ]
Ω≈++=
++= 5,471093010//50
h
R
h
R
h//RZ
3fe
2C
3fe
3ib3Eo
II. Transistor maéc vi sai vaø Darlingtôn
1) Baøi 6-23: E.C – E.C.
a- Cheá ñoä DC
V25,29.
10.310
10
V.
RR
R
VV
33
3
CC
2111
11
2BB1BB
=
+
=
+
==
mA55,1
42,710
7
,
0
25
,
2
h
R
R2
7
,
0
V
II
3
fe
b
E
1BB
2EQ1EQ
=
+
−
=
+
−
==
I
E
= 2I
E1
= 3,1mA
V
CEQ1
= V
CC
– 2R
E
.I
CQ1
= 9 – 2.500.1,55.10
-3
= 7,45V
V
CEQ2
= V
CC
– 2R
E
.I
CQ1
– R
C2
.I
CQ2
= 9 – 10
3
.1,55.10
-3
– 2,5.10
3
.1,55.10
-3
= 3,575V
R
E3
50Ω
Z
o
h
ib3
10
R/h
fe3
930
R
c2
h
fe3
=10
+V
CC
=9V
i
i
R
21
3K
i
L
i
b3
R
11
K
R
E1
500
T
1
T
2
R
C2
2,5K
R
22
3K
R
12
1K
T
3
T
4
R
C4
=R
L
60
R
E4
60
h
fe
=100
i
C4
h
ie1
h
fe2
i
b2
100i
b2
R
L
(1+h
fe
)R
E1
(1+h
fe
)i
b4
i
i
h
ie3
R
C2
2,5K
R
b2
750
h
2
fe
R
E4
i
b1
i
b2
h
fe3
h
ie4
R
b1
750
h
ie2
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
31
V
725
,
3
4
,
1
875
,
3
9
V
V
I
.
R
V
V
4BE3BE2CQ2CCCR
4E
=−−=−−−=
mA62
60
725,3
R
V
II
4E
R
4EQ4CQ
4E
≈===
mA62,0
10
10.62
h
I
III
2
3
fe
4CQ
4BQ3EQ3CQ
≈=≈==
−
V
CEQ4
= V
CC
– I
CQ4
(R
C4
+ R
E4
) = 9 – 62.10
-3
.120 = 9 – 7,44 = 1,56V
V
CEQ3
= V
CEQ4
– V
BE4
= 1,56 – 0,7 = 0,86V
Ω===
−
−−
2258
10.55,1
10.25
.100.4,1
I
10.25
.h4,1h
3
3
1EQ
3
1fe1ie
Ω===
−
−−
5645
10.62,0
10.25
.100.4,1
I
10.25
.h4,1h
3
3
1EQ
3
3fe3ie
Ω===
−
−−
45,56
10.62
10.25
.100.4,1
I
10.25
.h4,1h
3
3
1EQ
3
4fe4ie
b- Cheá ñoä AC
(
)
50500101.500h1RR
fe1E
'
E
==+=
(
)
[
]
(
)
[
]
Ω=+=+++= K76,617101.606045,56h1Rh1hR
3fe4E4fe4ie
'
4E
i
1b
1b
2c
2c
3b
3b
L
i
L
i
i
i
.
i
i
.
i
i
.
i
i
i
i
A ==
(1)
( )( )
10201101.101h1h1
i
i
4fe3fe
3b
L
==++=
(2)
( )
3
33
3
'
4E4iefe3ie2C
2C
2c
3b
10,4
605,631
5,2
10.76,6175700564510.5,2
10.5,2
Rhh1hR
R
i
i
−≈
−
=
+++
−
=
++++
−
=
(3)
( )
1001.h
i
i
i
i
i
i
2fe
1b
2b
2b
2c
1b
2c
−=−==
(4)
(Vì R’
E
raát lôùn neân coi i
b2
≈ i
b1
)
3
''
E1ieb
b
i
1b
10.4,128
28322258750
750
RhR
R
i
i
−
=
++
=
++
=
(5)
i
C2
h
ie1
2258
100i
b2
R
C
60Ω
R
’
E
50,5K
Z
o
(1+
h
fe
)
2
i
b3
10201i
b3
i
i
h
ie3
5645
R
C2
2,5K
R
b
750
R
’
E4
618K
i
b1
i
b2
h
ie4
(1+h
fe
)
5700
R
b1
750
h
ie2
2258
i
b3
i
L
Z
o
’
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
32
vôùi
[
]
Ω≈=+= 28323008//5050Rh//RR
b2ie
'
E
''
E
Thay (2), (3), (4), (5) vaøo (1) ta coù:
A
i
= 10201.(-4.10
-3
).(-100).128,4.10
-3
= 522,3 (laàn)
Z
i
= R
b1
//(h
ie1
+R’’
E
) ≈ 750//(2258 + 2832) = 654Ω
Z
o
= ∞ ⇒ Z’
o
= Z
o
//R
C
= R
C
= 60Ω
2) Baøi 6-24:
E.C – C.C
a- Cheá ñoä DC
AÙp duïng ñònh luaät K.II ΣV
kín
= 0 cho voøng 2 ta coù:
V
BE3
+ I
EQ3
R
E3
– V
EE
= 0 (1)
mA3,2
10
7
,
0
3
R
V
V
I
3
3E
3BEEE
3EQ
=
−
=
−
=
mA15,1
2
I
II
3EQ
2EQ1EQ
===
V
CE1
= V
CE2
= V
CC
– R
C1
I
CQ1
– V
E1
(2)
Maët khaùc aùp duïng ñònh luaät K.II ΣV
kín
= 0 cho voøng 1 ta coù:
-V
BB1
+ R
b
I
BQ1
+ V
BE1
+ V
E1
= 0 (3)
⇒ V
E
= V
BB1
– R
b
I
BQ1
– V
BE1
= 1 – 10
4
.1,15.10
-5
– 0,7 =0,185V
Thay vaøo (2) ta ñöôïc:
V
CE1
= V
CE2
= 6 – 10
3
.1,15. 10
-3
– 0,185 = 4,665V ≈ 4,67V
Ta coù V
E1
= V
CE3
+ R
E3
.I
EQ3
- V
EE
(4)
Suy ra V
CE3
= V
EE
+ V
E1
– R
E3
I
EQ3
= 3 + 0,185 – 10
3
.2,3.10
-3
= 0,885V
V
RE6
= V
CC
– R
C2
I
CQ2
– V
BE4
- V
BE5
- V
BE6
= 6 – 10
3
.1,15.10
-3
– 2,1 = 2,75V
mA275
10
75
,
2
R
V
I
6E
6RE
6EQ
===
V
CE6
= V
CC
– V
RE6
= 6 – 2,75 = 3,25V
V
CE5
= V
CE6
– V
BE6
= 3,25 – 0,7 = 2,55V
V
L
Z
o
Z
i
i
i
-
3V
R
b1
10K
R
C1
1K
R
b2
10K
R
E
1K
V
BB2
1V
T
4
T
5
R
C2
1K
V
BB1
1V
T
3
R
E6
10
T
6
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
33
V
CE4
= V
CE5
– V
BE5
= 2,55 – 0,7 = 1,85V
Ω===
−
−
−
−
3043
10.15,1
10.25
.100.4,1
10.15,1
10.25
.h4,1h
3
3
3
3
1fe1ie
mA75,2
h
I
I
6fe
6EQ
5EQ
==
;
A10.75,2
h
I
I
5
5fe
5EQ
4EQ
−
==
Ω===
−
−−
72,12
10.275
10.25
.100.4,1
I
10.25
.h4,1h
3
3
6EQ
3
6fe6ie
h
ie5
= 1272Ω; h
ie4
= 127.200Ω
b- Cheá ñoä AC
(
)
Ω≈≈+=
76
6E
3
fe6E
'
6E
1010.Rh1RR
i
2b
2b
4b
4b
L
i
L
T
i
i
.
i
i
.
i
V
i
V
A ==
(1)
Ω≈=
7'
6E
4b
L
10R
i
V
(2)
4
4
2
733
23
'
6E4ie2C
2fe2C
2b
2C
2C
4b
2b
4b
10.3,96
106,3811
10
1010.6,38110
10.10
Rh3R
h
.
R
i
i
.
i
i
i
i
−
−=
++
−=
++
−=
++
−==
(3)
485,0
1010.086,610
10
Rh2R
R
i
i
i
i
434
4
2b1ie1b
1b
i
1b
i
2b
−=
−+
−=
++
−=−=
(4)
Thay (2), (3), (4) vaøo (1) ta coù
A
T
= 10
7
.(-96,3).10
-4
.(-0,485) = 46728V/A = 46,7V/mA
Z
i
= R
b1
//[2h
ie1
+ R
b2
] ≈ 6,15KΩ
( )
Ω≈=
+= 37,0382,0//10
h
h3
h
R
//RZ
3
fe
4ie
3
fe
2C
6Eo
i
C2
h
ie1
3043
V
L
h
fe2
i
b2
100i
b2
Z
o
Z
i
i
i
h
ie4
127,2K
R
C2
1K
R
b2
10K
R
’
E6
i
b1
R
b1
10K
h
ie2
3043
i
b4
i
b2
h
ie5
.h
fe4
127,2K
h
ie5
.h
fe4
.h
fe5
127,2K
Z
o
R
E6
3h
ie4
h
3
fe
=0,381
R
c2
h
3
fe
≈
10
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
34
Chöông VII:
MAÏCH KHUEÁCH ÑAÏI HOÀI TIEÁP.
I. Hoài tieáp aùp, sai leäch doøng.
1) Baøi 7-4
=
Ω=
40h
K1h
GT
fe
ie
;
==
=
?
i
i
A
?T
KL
i
L
i
Ñaây laø daïng hoài tieáp aùp, sai leäch doøng.
a-
Tính ñoä lôïi doøng T: cho i
i
= 0
'
1
1b
1b
2b
2b
1
i
'
1
1
V
i
.
i
i
.
i
V
0i
V
V
T =
=
= (1)
( )
3
2fe22E
2b
1
10.41h1R
i
V
=+=
(2)
( ) ( )
941,0
85
80
10
.
41
10
.
41
10
10
.
2
40.10.2
h1Rh1RhR
h
.
R
i
i
.
i
i
i
i
3333
3
2fe22E2fe21E2ie1C
1fe1C
1b
1C
1C
2b
1b
2b
−=−=
+
+
+
−=
+++++
−==
(3)
6
34
1ief1ief
'
1
'
1
'
1
1b
10.91
1010
1
hR
1
hR
V
.
V
1
V
i
−
=
+
=
+
=
+
=
(4)
V
1
i
i
R
E22
1K
R
f
10K
R
C1
2K
R
C2
2K
i
L
R
L
100
+V
CC
R
E21
1K
T
1
V
L
i
C2
h
ie1
h
fe1
i
b1
40i
b1
R
E21
(h
fe2
+1)
41K
Z
o
Z
i
i
i
R
C1
2K
R
C2
2K
i
b1
i
c1
40i
b2
R
f
V
1
h
ie2
1K
i
b2
V
’
1
-
R
E22
(h
fe2
+1)
41K
R
L
100
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
35
Thay (2), (3), (4) vaøo (1) ta coù:
T = 41.10
3
.(-0,941).91.10
-6
= -3,51
b-
Tính
i
L
i
i
i
A
=
cho V’
1
= 0
i
1b
1b
2b
2b
L
i
L
i
i
i
.
i
i
.
i
i
i
i
A ==
(1)
6,3940.
1010.2
10.2
h.
RR
R
i
i
.
i
i
i
i
3
3
2fe
L2C
2C
2b
2C
2C
L
2b
L
−=
+
−=
+
−==
(2)
941,0
i
i
1b
2b
−=
(nhö (3) ôû phaàn treân) (3)
2
34
4
1ief
f
i
1b
10.91
1010
10
hR
R
i
i
−
=
+
=
+
=
(4)
Thay (2), (3), (4) vaøo (1) ta coù:
A
i
= (-39,6).(-0,941).91.10
-2
= 33,9 ≈ 34
c-
Tính A
if
, Z
if
, Z
of
.
54,7
51,31
34
T1
A
A
i
if
=
+
=
−
=
Z
i
= R
f
//h
ie1
= 10
4
//10
3
≈ 910Ω
Ω=
+
=
−
= 202
51,31
910
T1
Z
Z
i
if
Z
o
= R
C2
= 2KΩ
Ω=
+
=
−
= 443
51,31
10.2
T1
Z
Z
3
o
of
2) Baøi 7-11
∞→
Ω=
=
C
10h
100h
GT
ib
fe
;
=
==
?T
Z;Z
?
i
i
A
KL
oi
i
L
i
i
i
R
f
= R
b
=10K
R
C
2K
C
i
L
R
L
+V
CC
R
E
100
C
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
36
h
ie
= h
ib
.h
fe
= 10.100 = 1KΩ
a- Ñoä lôïi voøng T: cho i
i
= 0
'
L
b
b
L
i
'
L
L
V
i
.
i
V
0i
V
V
T =
=
=
(1)
4
33
233
fe
LC
C
L
b
C
C
L
b
L
10.5
1010
10.10.10
h.
RR
R
.R
i
i
.
i
V
i
V
−=
+
−=
+
−==
(2)
6
34
iefief
'
L
'
L
'
L
b
10.91
1010
1
hR
1
hR
V
.
V
1
V
i
−
=
+
=
+
=
+
=
(3)
Thay (2), (3) vaøo (1) ta coù:
T =(-5.10
4
).91.10
-6
= -4,55
b- Tính A
i
, Z
i
, Z
o
.
i
b
b
L
'
L
i
L
i
i
i
.
i
i
0V
i
i
A =
=
=
(1)
50100.
1010
10
h.
RR
R
i
i
.
i
i
i
i
3
3
fe
LC
C
b
C
C
L
b
L
−=
+
−=
+
−==
(2)
2
34
4
ief
f
i
b
10.91
1010
10
hR
R
i
i
−
=
+
=
+
=
(3)
Thay (2), (3) vaøo (1) ta coù:
A
i
= (-50).91.10
-2
= -45,45
Z
i
= R
f
//h
ie
= 10
4
//10
3
= 910Ω
Z
o
= R
C
= 10
3
Ω = 1KΩ
c- Tính A
if
, Z
if
, Z
of
.
2,8
55,41
50
T1
A
A
i
if
−=
+
−=
−
=
Ω=
+
=
−
= 164
55,41
910
T1
Z
Z
i
if
Ω=
+
=
−
= 180
55,41
10
T1
Z
Z
4
o
of
h
ie1
i
L
V
L
h
fe
i
b
100i
b
Z
o
i
i
R
C
1K
i
b
i
c
R
f
R
f
10K
V
’
L
-
R
L
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
37
II. Hoài tieáp aùp, sai leäch aùp:
1) Baøi 7-10
∞→
Ω=
=
C
50h
50h
GT
ib
fe
;
=
==
?T
Z;Z
?
i
i
A
KL
oi
i
L
i
a- Tính ñoä lôïi voøng T (cho i
i
= 0)
'
L
1b
1b
2b
2b
L
i
'
L
L
V
i
.
i
i
.
i
V
0i
V
V
T =
=
= (1)
33
34
34
2fe
2Cf
2Cf
2b
2C
2C
L
2b
L
10.5,8350.10.67,150.
10
.
2
10
10.2.10
h.
RR
R
.
R
i
i
.
i
V
i
V
−=−=
+
−=
+
−==
(2)
( )
46,12
10.5,210.83,0
50.10.83,0
h
hR//R
R
R
i
i
.
i
i
i
i
33
3
1fe
2ie2b1C
2b1C
1b
1C
1C
2b
1b
2b
−=
+
−=
+
−==
(3)
6
3533
3
1fef1E1fe1ie1b
1fe1E
'
L
1b
10.2,1
10.210.5
1
.
10.510.5,2890
10.5
'Rh.R
1
.
R.hhR
h
.
R
V
i
−
−=
+++
−
=
+++
−
=
(4)
V
L
i
i
R
f
=10K
C
+V
CC
R
21
8K
C
R
11
1K
R
C1
1K
R
E1
100
R
22
10K
R
12
10K
R
C2
2K
R
E2
1K
i
C1
h
fe1
i
b1
50i
b1
h
ie1
2,5K
h
ie2
2,5K
R
C2
2K
Z
o
i
i
R
C1
1K
R
b2
5K
R
f
10K
i
b2
i
b1
i
C2
h
fe2
i
b2
50i
b2
R
f
.h
fe1
5.10
5
R
E1
h
fe1
5K
V
’
L
-
R
b1
890
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
38
Thay (2), (3), (4) vaøo (1) ta coù:
T = (-83,5.10
3
).(-12,46).(1,2.10
-6
)= -1,25
b- Tính A
T
, Z
i
, Z
o
.
i
1b
1b
2b
2b
L
i
L
T
i
i
.
i
i
.
i
V
i
V
A ==
(1)
2b
L
i
i
vaø
1b
2b
i
i
tính nhö treân theo coâng thöùc (2), (3)
( )
107,0
10.95,410.5,2890
890
hRRhR
R
i
i
33
1fef1E1ie1b
1b
i
1b
=
++
=
+++
=
(4)
Thay (2), (3), (4) vaøo (1) ta coù:
A
i
= (-83,5.10
3
).(-12,46).(0,107) = 111.10
3
V/A = 111V/mA
Z
i
= R
b1
//[h
ie1
+ (R
E11
//R
f
)(1 + h
fe
)] = 890 //[2500 + 4950] = 795Ω
Z
o
= R
f
= 10KΩ
c- Tính A
Vf
, Z
of
, Z
if
.
mA
V
49
A
V
10.49
25,11
10.111
T1
A
A
3
3
T
Tf
==
+
=
−
=
(
)
Ω
=
+
=
−
=
1788
)
25
,
1
1
(
795
T
1
Z
Z
iif
Ω=
+
=
−
= 4444
25,11
10
T1
Z
Z
4
o
of
2) Baøi 7-12
∞→
Ω=
=
C
50h
20h
GT
ib
fe
;
=
=
?T
Z;Z
?A
KL
oi
V
V
L
V
i
-
r
i
1K
R
f
=1K
C
+V
CC
R
21
10K
C
R
11
1K
R
C1
500
R
E12
82
R
22
10K
R
12
1K
R
C2
500
R
E22
82
C
R
E11
22
C
R
E21
22
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
39
a- Tính ñoä lôïi voøng T (cho V
i
= 0)
'
L
1b
1b
2b
2b
L
i
'
L
L
V
i
.
i
i
.
i
V
0i
V
V
T =
=
=
(1)
( )
666720.500//10h.
RR
R
.
R
i
i
.
i
V
i
V
3
2fe
2Cf
2Cf
2b
2C
2C
L
2b
L
−=−=
+
−==
(2)
( ) ( )
52,3
1835
6460
462
1050
323
20.323
h
h1RhR//R
R
//
R
i
i
.
i
i
i
i
1fe
2fe21E2ie2b1C
2b1C
1b
1C
1C
2b
1b
2b
−=−=
+
+
−=
+++
−==
(3)
( )
(
)
(
)
( )( ) ( )
6
3
3
1bi1ie1fef11E
1fef11E
1fef
,
L
,
L
'
L
1b
10.88,10
4,41546
10.452
4,4761050452
452
.
10.21
1
R//rhh1R//R
h1R//R
.
h1R
V
.
V
1
V
i
−
−
−=−=
++
−=
+++
+
+
−=
(4)
Thay (2), (3), (4) vaøo (1) ta coù:
T = (-6667).(-3,52).(-10,88.10
-6
)= -0,255
b- Tính A
V
, Z
i
, Z
o
.
i
1b
1b
2b
2b
L
i
L
V
V
i
.
i
i
.
i
V
V
V
A ==
(1)
2b
L
i
V
vaø
1b
2b
i
i
tính nhö treân theo coâng thöùc (2), (3)
( ) ( )( )
5
3
3
1fef11E1ie1bi
1bi
i
i
ii
1b
10.24
4,1978
10.4,476
45210504,476
4,476
.
10
1
h1R//RhR//r
R
r
.
r
V
.
V
1
V
i
−
−
==
++
=
+++
=
(4)
h
fe1
i
b1
20i
b1
R
f
(h
fe1
+1)
21K
h
ie2
1050
V
i
-
Z
o
Z
i
R
b1
910
R
Cb2
910
i
b1
i
C2
R
E11
(1+h
fe1
)
462
i
C1
V
’
L
-
r
i
1K
R
C1
500
R
C2
500
i
b2
i
i
h
ie1
1050
R
E21
(1+h
fe2
)=462
Ω
20i
b2
R
f
1050
R
f
(h
fe1
+1)
21K
R
b1
910
i
b1
R
E11
(1+h
fe1
)
462
r
i
1K
h
ie1
1050
V
’
L
R
f
(1+h
fe1
)
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Moät soá baøi taäp maãu
40
Thay (2), (3), (4) vaøo (1) ta coù:
A
V
= (-6667)(-3,52).24.10
-5
= 5,63
Z
i
= R
b
//[h
ie1
+ (R
E11
//R
f
)(1 + h
fe1
)] = 10
3
//1502 ≈ 600Ω
Z
o
= R
f
= 1000Ω
c- Tính A
Vf
, Z
if
, Z
of
.
486,4
255,01
63
,
5
T1
A
A
V
Vf
=
+
=
−
=
(
)
Ω
=
+
=
−
=
753
)
255
,
0
1
(
600
T
1
Z
Z
iif
Ω=
+
=
−
= 797
255,01
1000
T1
Z
Z
o
of
| 1/40
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
MOÄT SOÁ BAØI TAÄP MAÃU CHO QUYEÅN
“Giaùo trình maïch ñieän töû I”
Chöông I: DIODE BAÙN DAÃN. I.
Diode baùn daãn thoâng thöôøng:
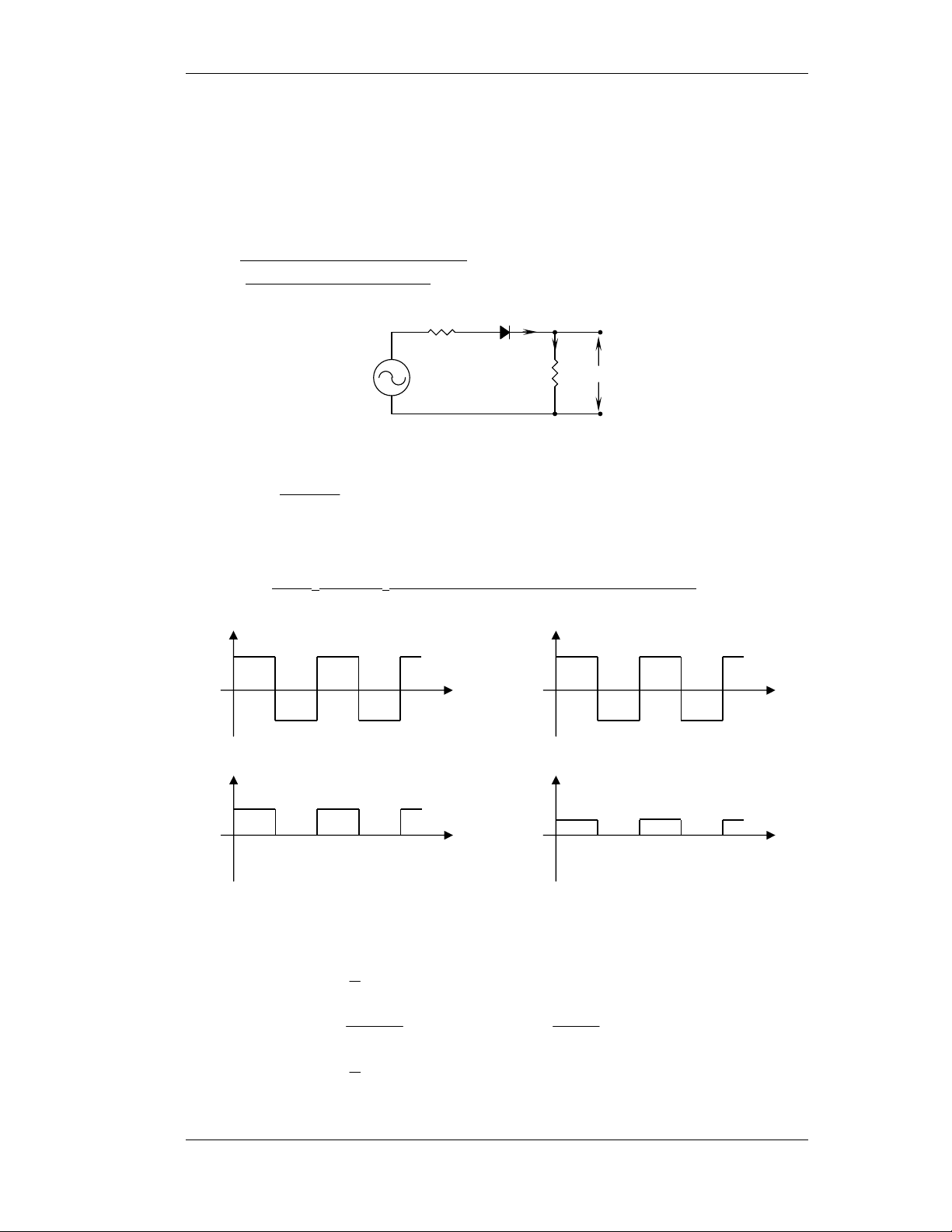
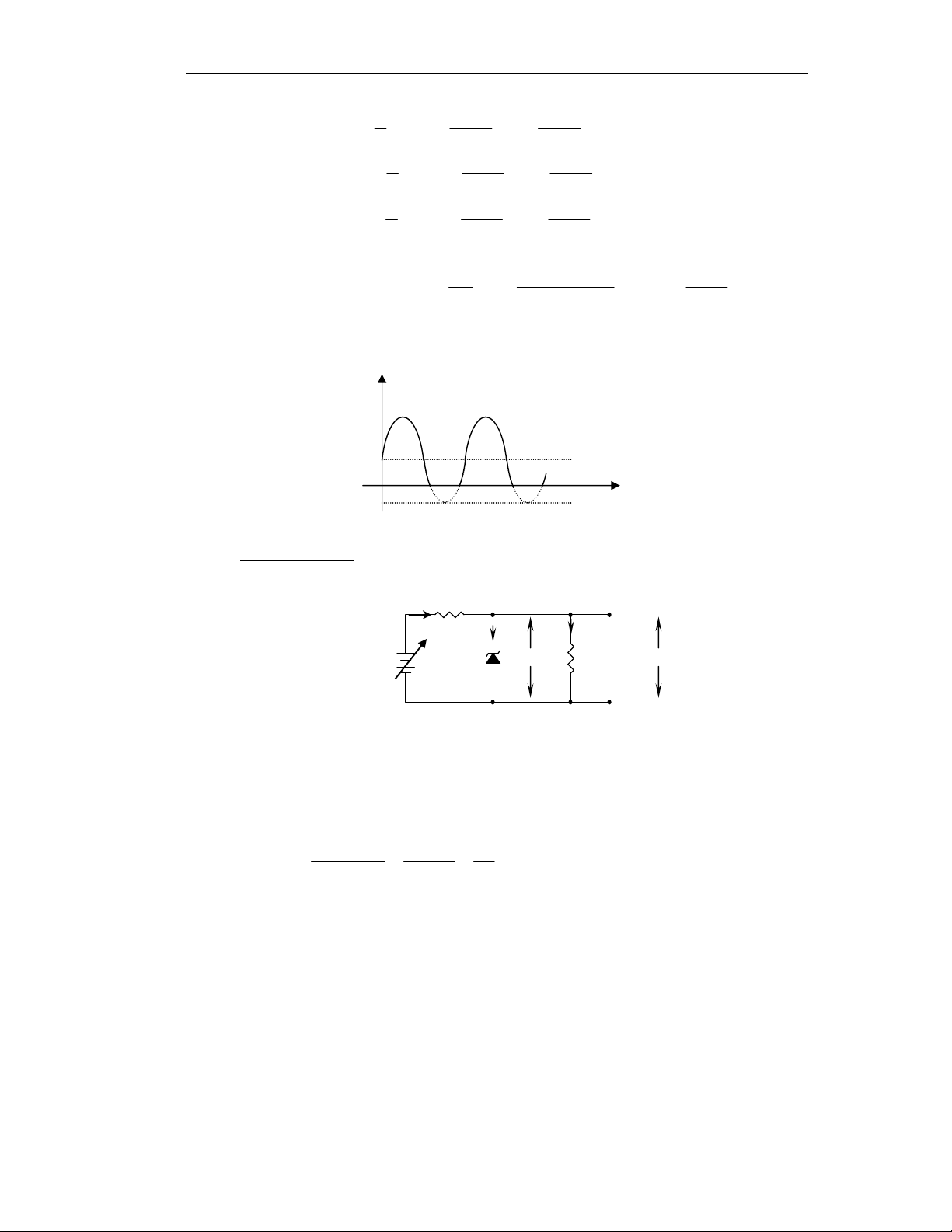
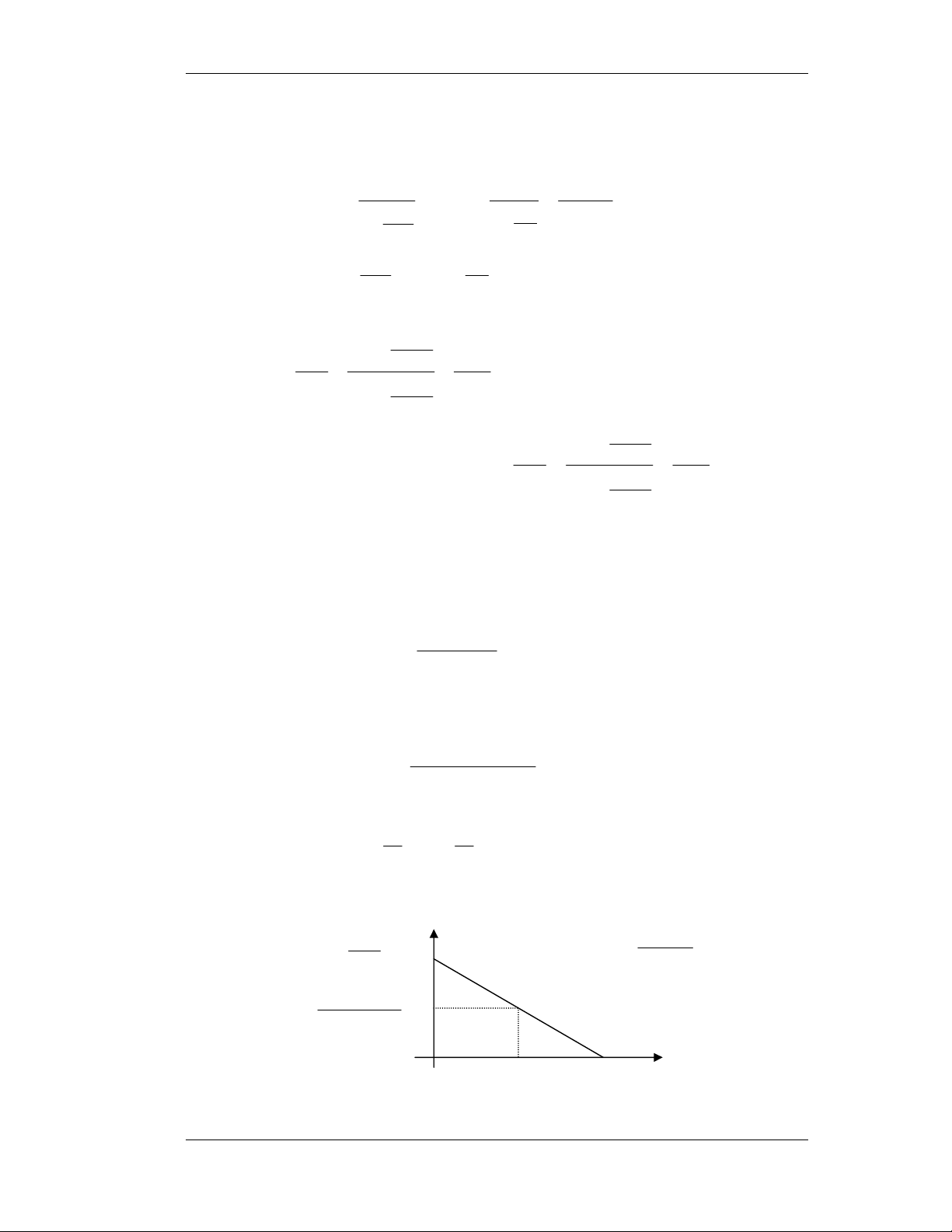
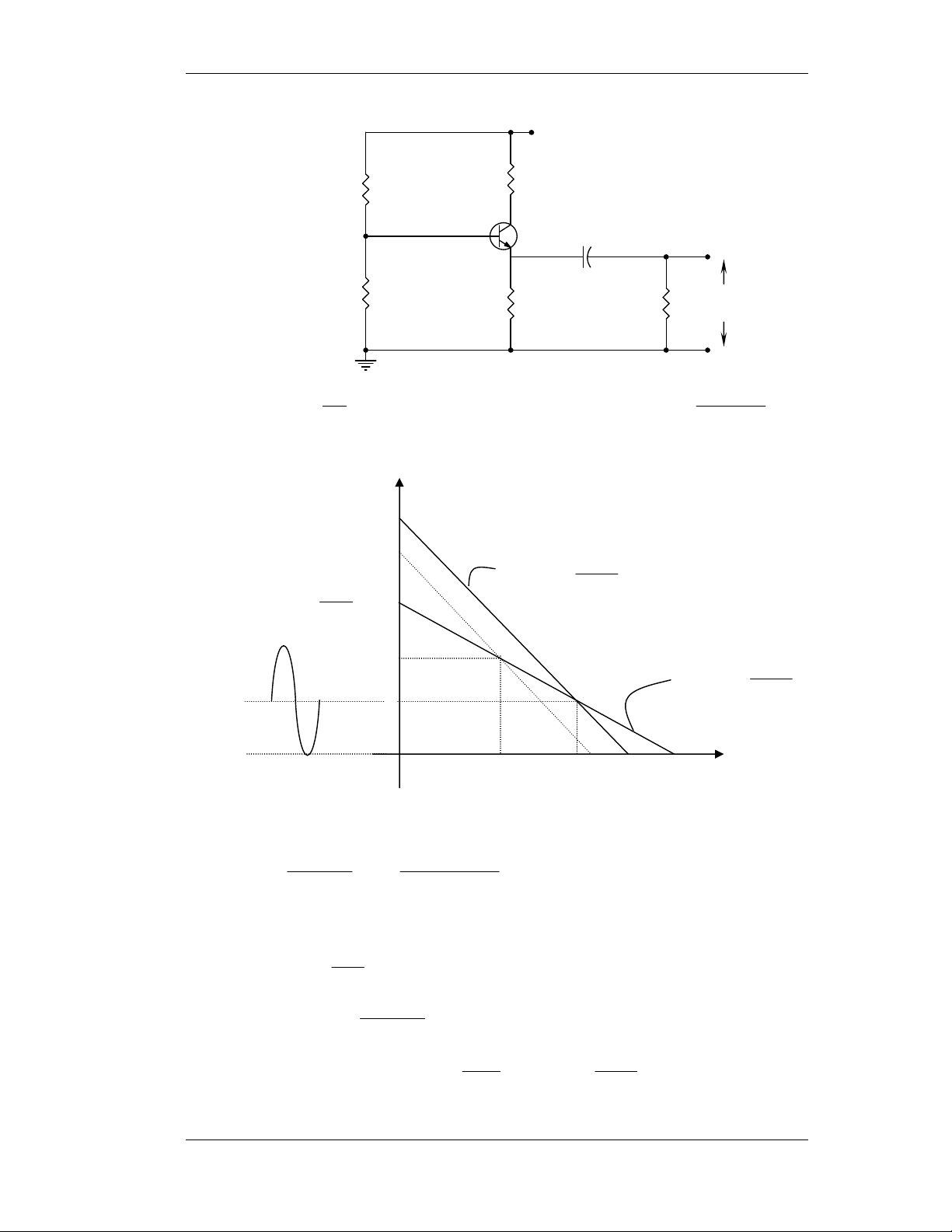
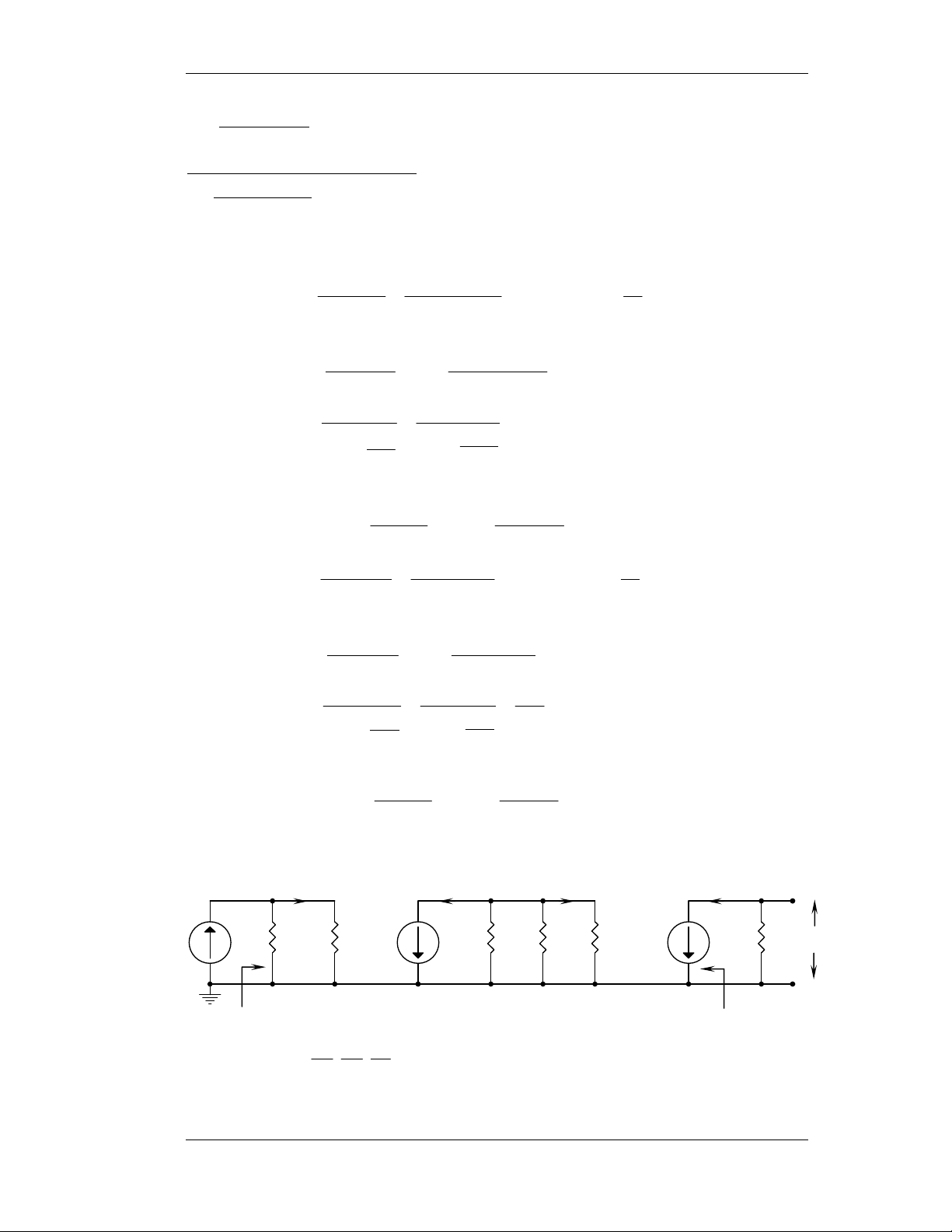
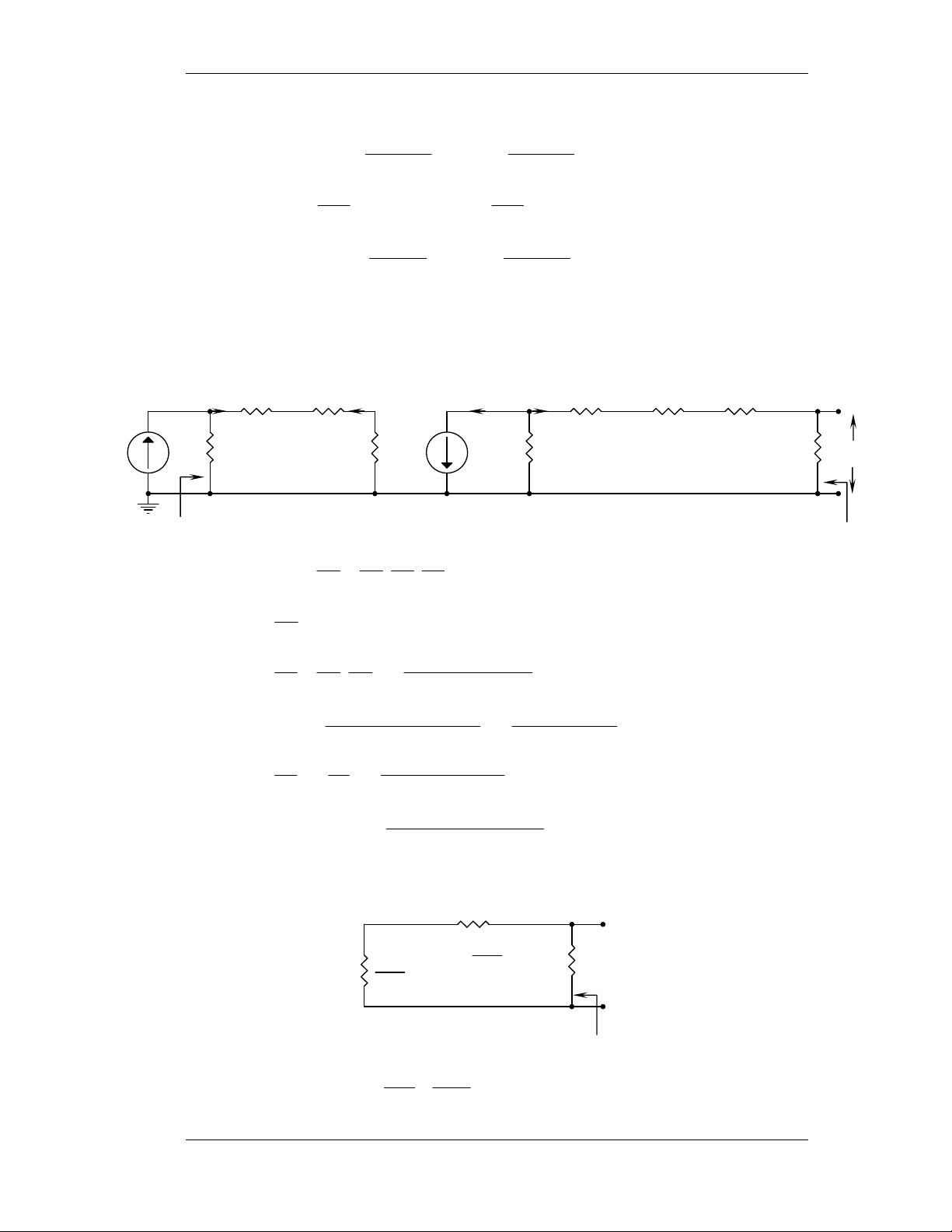
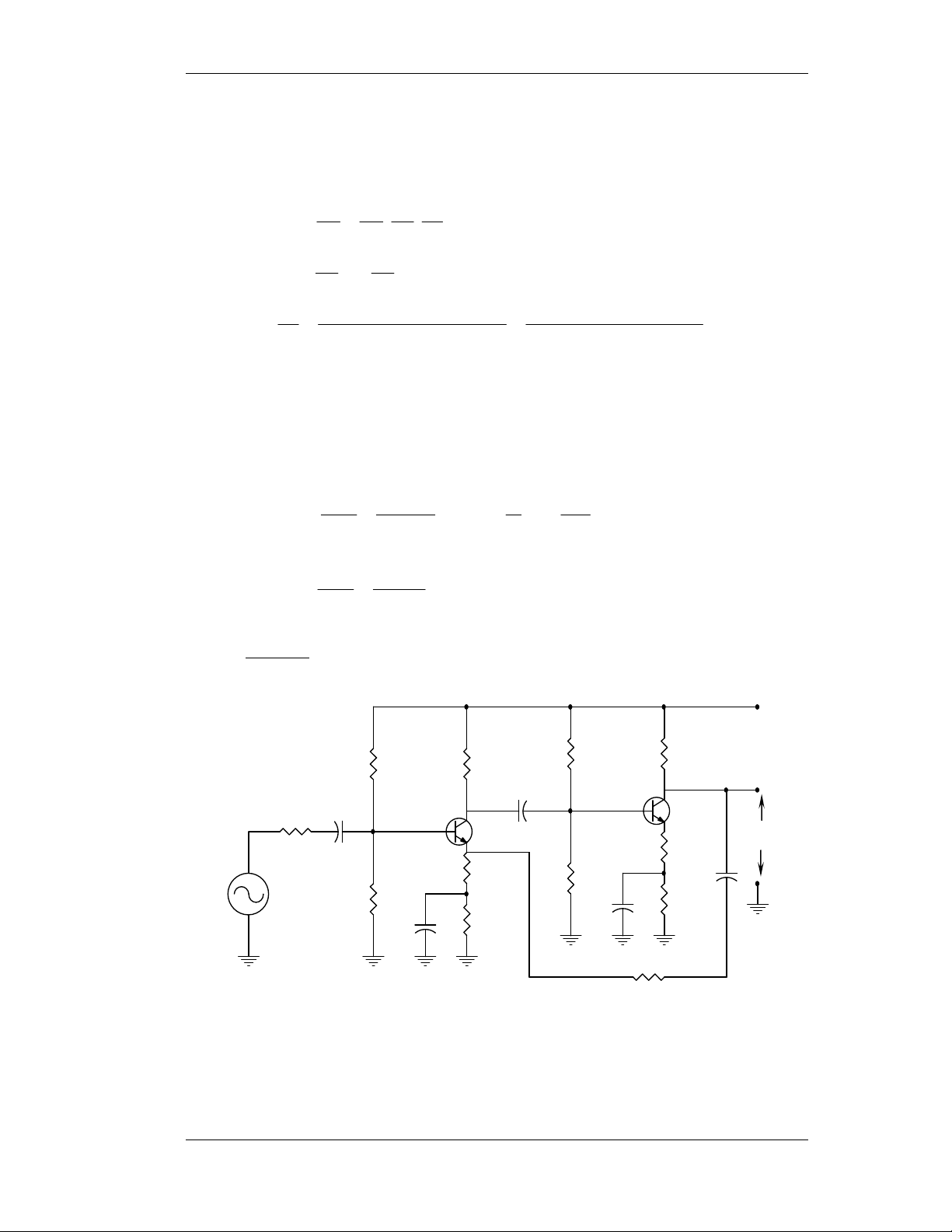
1) Veõ daïng soùng chænh löu: (Baøi 1-1 trang 29) iD Ri + - VD i L + RL VL Vs -
Coâng thöùc toång quaùt tính VL: V − V S D V = R L L R + R i L
VD = 0,7V (Si) vaø VD = 0,2V (Ge)
a- Veõ VL(t) vôùi VS(t) daïng soùng vuoâng coù bieân ñoä 10 vaø 1V VS VS 10 1 + + + + 0 1 - 2 3 - 4 t(ms) 0 1 2 3 4 t(ms) - - -10 -1 V V L1 L2 8,37 0,27 0 1 2 3 4 t(ms) 0 1 2 3 4 t(ms)
Keát quaû vôùi giaû thieát: Ri = 1Ω, RL = 9Ω, VD = 0,7V.
Vì Diode chænh löu chæ daãn ñieän theo moät chieàu neân: 1 ∗ Trong T 0
> , Diode daãn → iD ≠ 0 → iL ≠ 0 → VL ≠ 0. 2 10 − 7 , 0 V 1− 7 , 0 = 9 = V 37 , 8 vaø V = 9 = V 27 , 0 1 L 1 L2 + 9 1 + 9 1
∗ Trong T < 0 , Diode taét 2
→ iD = 0 → iL = 0 → VL = 0. Moät soá baøi taäp maãu 1
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
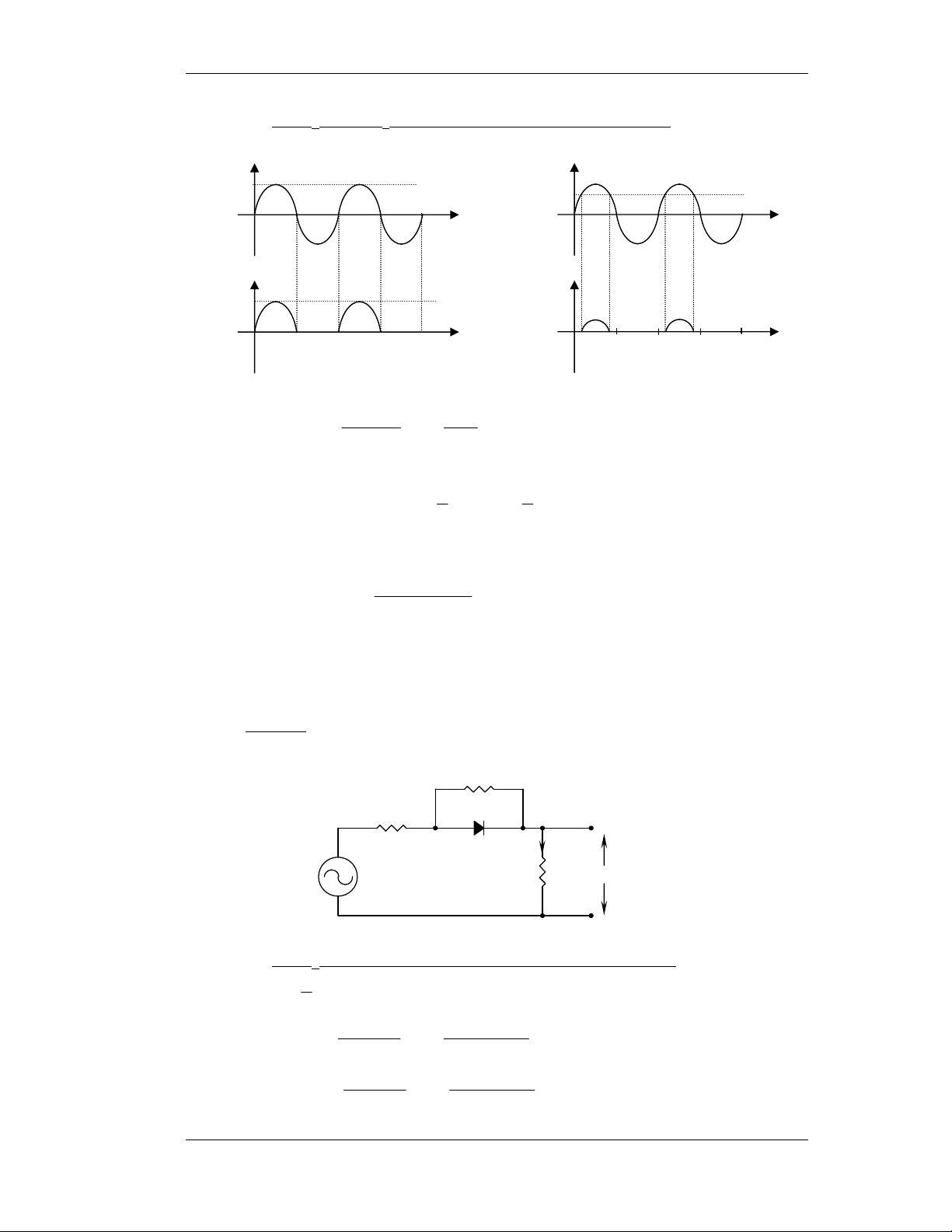
b- Veõ VL(t) vôùi VS(t) daïng soùng sin coù bieân ñoä 10 vaø 1V. VS VS 10 1 + + 2 3 0,7 2 3 0 0 1 - - 4 t(ms) 1 4 t(ms) -10 -1 VL1 VL2 9 0,27 0 1 2 3 4 t(ms) 0 1 2 3 4 t(ms)
∗ Khi VS = 10sinωot nghóa laø VSm = 10V >> VD =0,7V ta coù: V 10 V Sm ≈ R ≈ 9 = 9 1 L R + R L 1 + 9 i L V ≈ 9sin t 1 L ω0 (Ta giaûi thích theo 1 T 1 > 0 vaø T < 0 ) 2 2
∗ Khi VS = 1sinω0t nghóa laø VSm = 1V so saùnh ñöôïc vôùi 0,7V: +
VS > 0,7V, Diode daãn, iD ≠ 0, iL ≠ 0, VL ≠ 0. 1sin ω t − 7 , 0 V 0 = 9 = 9 , 0 sin ω t − 6 , 0 L2 1 + 9 0
Taïi sinω0t = 1, |VL2| = 0,27V. +
VS < 0,7V, Diode taét, iD = 0, iL = 0, VL = 0.
Vôùi daïng soùng tam giaùc ta coù keát quaû töông töï nhö soùng sin.
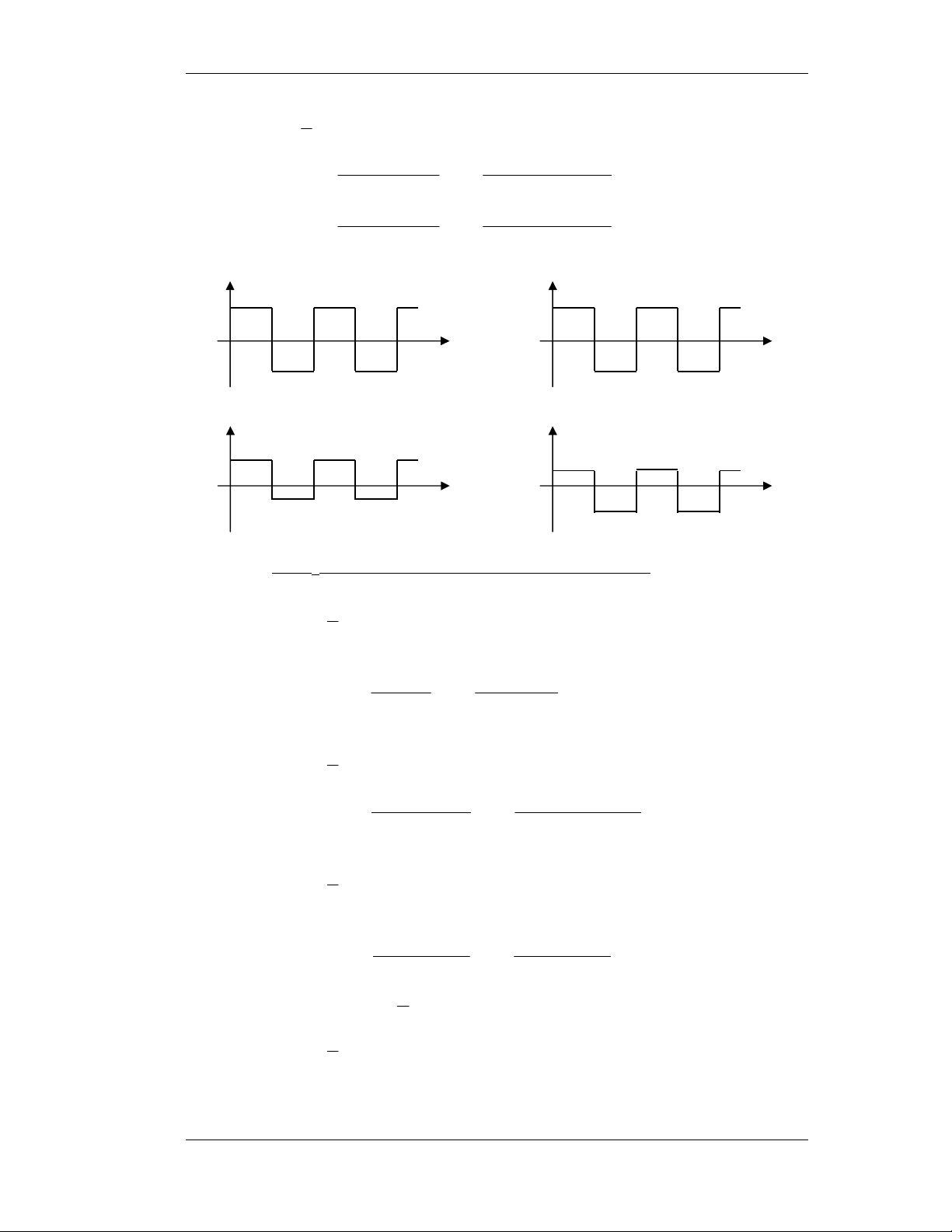
2) Baøi 1-3: Ñeå coù caùc keát quaû roõ raøng ta cho theâm caùc giaù trò ñieän trôû: R1 =
1KΩ, Rb = 10KΩ, RL = 9KΩ. Rb=10K Ri=1K + + - VD iL RL Vs V 9K L -
a- Veõ VL(t) vôùi daïng soùng vuoâng coù bieân ñoä 10V vaø 1 V. 1 ∗ T > 0 , Diode daãn, R 2
thD ≈ 0, doøng iL chaûy qua Ri, D, RL neân ta coù: V − V S D 10 − 7 , 0 V = R = .9.103 = 37 , 8 V 1 L R + R L i L 103 + 9.103 V − V S D 1 − 7 , 0 V = R = .9.103 = 27 , 0 V L2 R + R L i L 103 + 9.103 Moät soá baøi taäp maãu 2
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I 1 ∗ T < 0 , Diode taét, R 2
ng = ∞, doøng iL chaûy qua Ri, Rb, RL neân ta coù. VS 10 V = R = .9.103 = V 5 , 4 1 L R + R + R L i b L 103 + 104 + 9.103 VS 1 V = R = .9.103 = 45 , 0 V 1 L R + R + R L i b L 103 + 104 + 9.103 V V S S 10 1 + + + + 0 1 4 t(ms) - 2 3 - 4 t(ms) 0 1 - 2 3 - -10 -1 VL1 VL2 8,37 0 1 2 3 4 0,27 t(ms) 0 1 2 3 4 t(ms) -4,5 -0,45
b- Veõ VL(t) vôùi daïng soùng sin coù bieân ñoä 10V vaø 1 V.
∗ Ñeå ñôn giaûn khi VSm = 10V (>>VD = 0,7V) ta boû qua VD. Khi ñoù: 1 + T > 0 , Diode daãn, R 2
thD ≈ 0, doøng iL chaûy qua Ri, D, RL neân ta coù: V 10 sin ω t V S = R 0 = 9 . 10 . 3 = 9sin ω t(V) 1 L R + R L 103 + . 9 103 0 i L 1 + T < 0 , Diode taét, R 2
ng = ∞, doøng iL chaûy qua Ri, Rb, RL neân ta coù. V 10sin ω t V S = R 0 = .9.103 = 5 , 4 sinω t(V) 1 L R + R + R L i b L 103 +104 + 9.103 0
∗ Khi VS = 1sinω0t so saùnh ñöôïc vôùi VD ta seõ coù: 1 + T > 0 , khi V 2
Sm ≥ 0,7, Diode daãn, RthD ≈ 0, doøng iL chaûy qua Ri, D, RL neân ta coù: 1sin ω t − 7 , 0 1sin ω t − 7 , 0 V 0 = R 0 = .9.103 = 9 , 0 sinω t − ( 63 , 0 V) L2 R + R L i L 103 + 9.103 0 Taïi ω t π , sin 0 = 2
ω0t = 1, ta coù VL2m = 0,9 - 0,63 = 0,27V 1 + T > 0 , khi V 2
Sm < 0,7, Diode taét, RngD = ∞, doøng iL chaûy qua Ri, Rb, RL neân ta coù: Moät soá baøi taäp maãu 3
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I 7 , 0 sin ω t 7 , 0 sin ω t V 0 = R 0 = . . 9 103 = 315 , 0 sin ω t L2 R + R + R L i b L 103 + 104 + 9.103 0 1 + T < 0 , Diode taét, R 2
ng = ∞, doøng iL chaûy qua Ri, Rb, RL neân ta coù. 1sin ω t 1sin ω t V 0 = R 0 = .9.103 = 45 , 0 sin ω t L2 R + R + R L i b L 103 + 104 + 9.103 0 VS VS 10 1 + + 0,7 0 - - t(ms) 0 t(ms) -10 -1 VL1 VL2 9 0,585 + + 0,315 -4,5 - - t(ms) t(ms) -4,5
2) Daïng maïch Thevenin aùp duïng nguyeân lyù choàng chaäp:
Baøi 1-20 vôùi Vi(t) = 10sinω0t i Ri=1K D A K + r i=1,5K V + RL DC=5v VL V 1,4K i - - A K A Ri//ri iL R i T d RL VT VT K a- Veõ maïch Thevenin:
AÙp duïng nguyeân lyù xeáp choàng ñoái vôùi hai nguoàn ñieän aùp VDC vaø Vi:
∗ Khi chæ coù VDC, coøn Vi = 0 thì ñieän aùp giöõa hai ñieåm A-K: ri 5 , 1 .103 V = V = 5 = V 3 AK DC R + r i i 103 + 5 , 1 .103
∗ Khi chæ coù Vi, coøn VDC = 0 thì ñieän aùp giöõa hai ñieåm A-K laø: R 103 V = V i = 10.sin ω t = 4 sin ω t(V) AK i R + r 0 103 + 5 , 1 .103 0 i i Moät soá baøi taäp maãu 4
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
∗ Vaäy khi taùc ñoäng ñoàng thôøi caû VDC vaø Vi thì söùc ñieän ñoäng töông
ñöông Thevenin giöõa hai ñieåm A-K laø: r R V = V i + V i = 3 + 4 sin ω t(V) T DC R + r i R + r 0 i i i i
∗ Ñieän trôû töông ñöông Thevenin chính laø ñieän trôû töông ñöông cuûa
phaàn maïch khi Diode hôû maïch laø: R r. i i 103. . 5 , 1 103 R = + R = + . 4 , 1 103 = 2KΩ T R L + r i i 103 + . 5 , 1 103
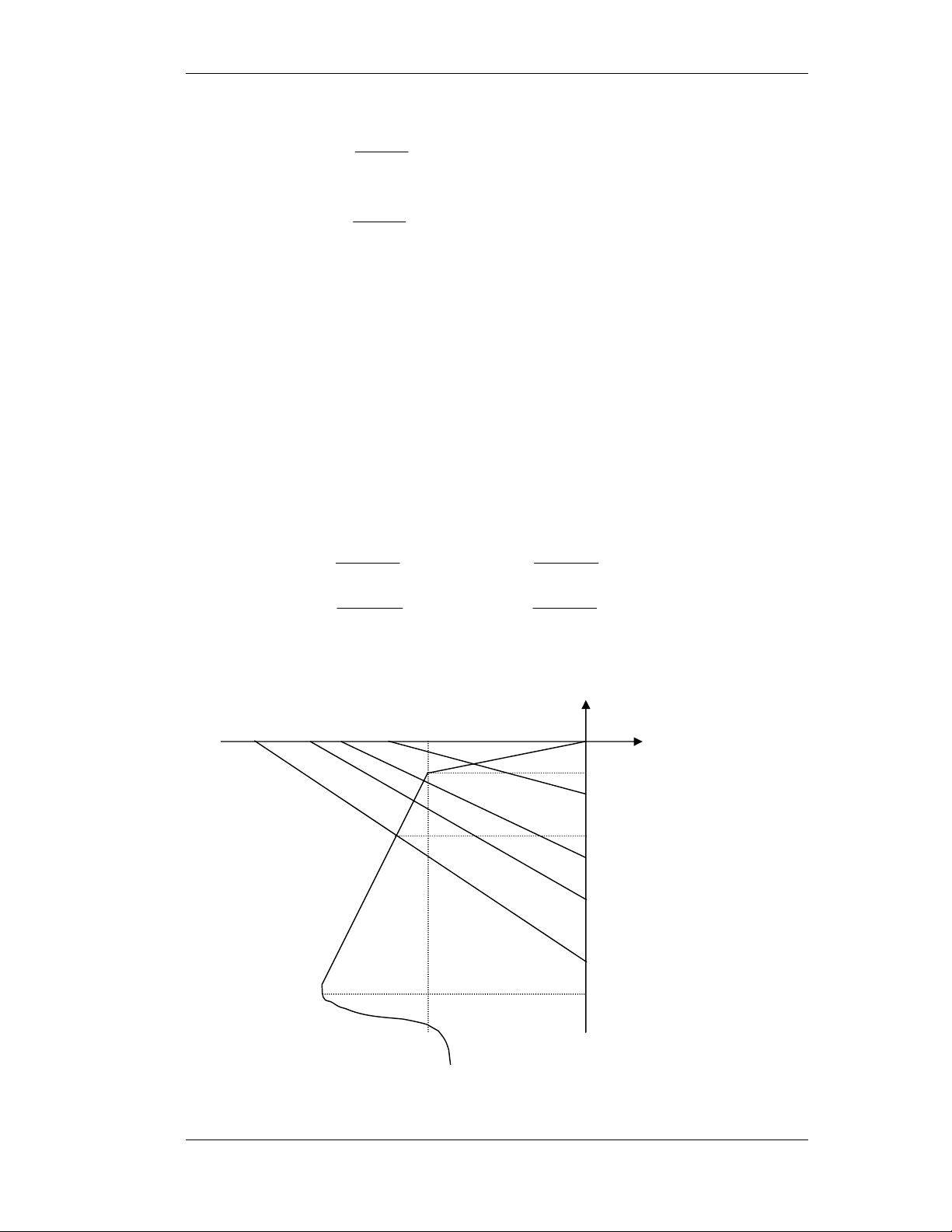
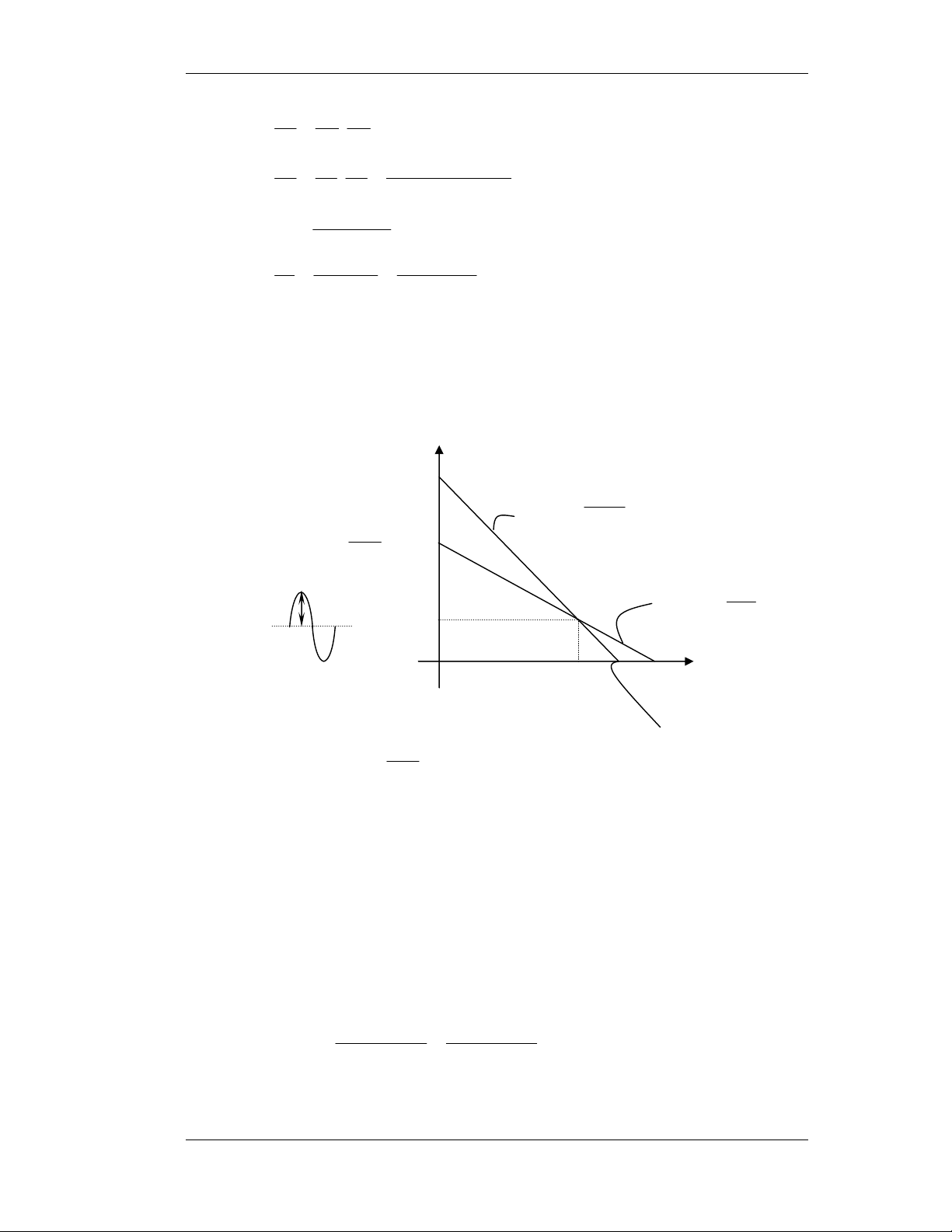
b- Veõ ñöôøng taûi DC khi ω t , 0 π = , π , π − , π . 0 3 2 3 − 2 ∗ Taïi ω t = 0 ⇒ V = V 3 0 T π 3 ∗ Taïi ω t = ⇒ V = 3 + 4 = ( 46 , 6 V) 0 3 T 2 π ∗ Taïi ω t = ⇒ V = 3 + 4.1 = ( 7 V) 0 2 T π 3
∗ Taïi ω t = − ⇒ V = 3 − 4 = − ( 46 , 0 V) 0 3 T 2 π
∗ Taïi ω t = − ⇒ V = 3 − 4.1 = − ( 1 V) 0 2 T iD (mA) 3,15 2,88 1,15 -1 3 6,46 7 VT t
Theo ñònh luaät Ohm cho toaøn maïch ta coù. V − V 1 V T D T i = = − V . D R R + R T T T 1 3 ∗ Taïi ω t = 0 ⇒ i = − . 7 , 0 + ( 15 , 1 mA) 0 = 2.103 2.103 π 1 46 , 6 ∗ Taïi ω t = ⇒ i = − . 7 , 0 + = ( 88 , 2 mA) 0 3 2.103 2.103 Moät soá baøi taäp maãu 5
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I π 1 7 ∗ Taïi ω t = ⇒ i = − . 7 , 0 + = ( 15 , 3 mA) 0 2 2.103 2.103 π 1 46 , 0
∗ Taïi ω t = − ⇒ i = − .0 7 , − = − ( 58 , 0 mA) 0 3 2.103 2.103 π 1 1 ∗ Taïi ω t = − ⇒ i = − 0 . 7 , − = 0 − ( 85 , mA) 0 2 2 10 . 3 2 10 . 3 c- Veõ V V T T 3 V V (t) = R i. = R . = R = 4 , 1 10 . T L L D L L 3 RT (R // r i i ) + R 2.10 L = 0 V 7 , T = ( 7 , 0 3 + 4sin ω t 0 ) = 1 , 2 + 2 8 , sin ω t (V) 0 VL 4,9V 2,1 0 t -0,7 II. Diode Zenner:
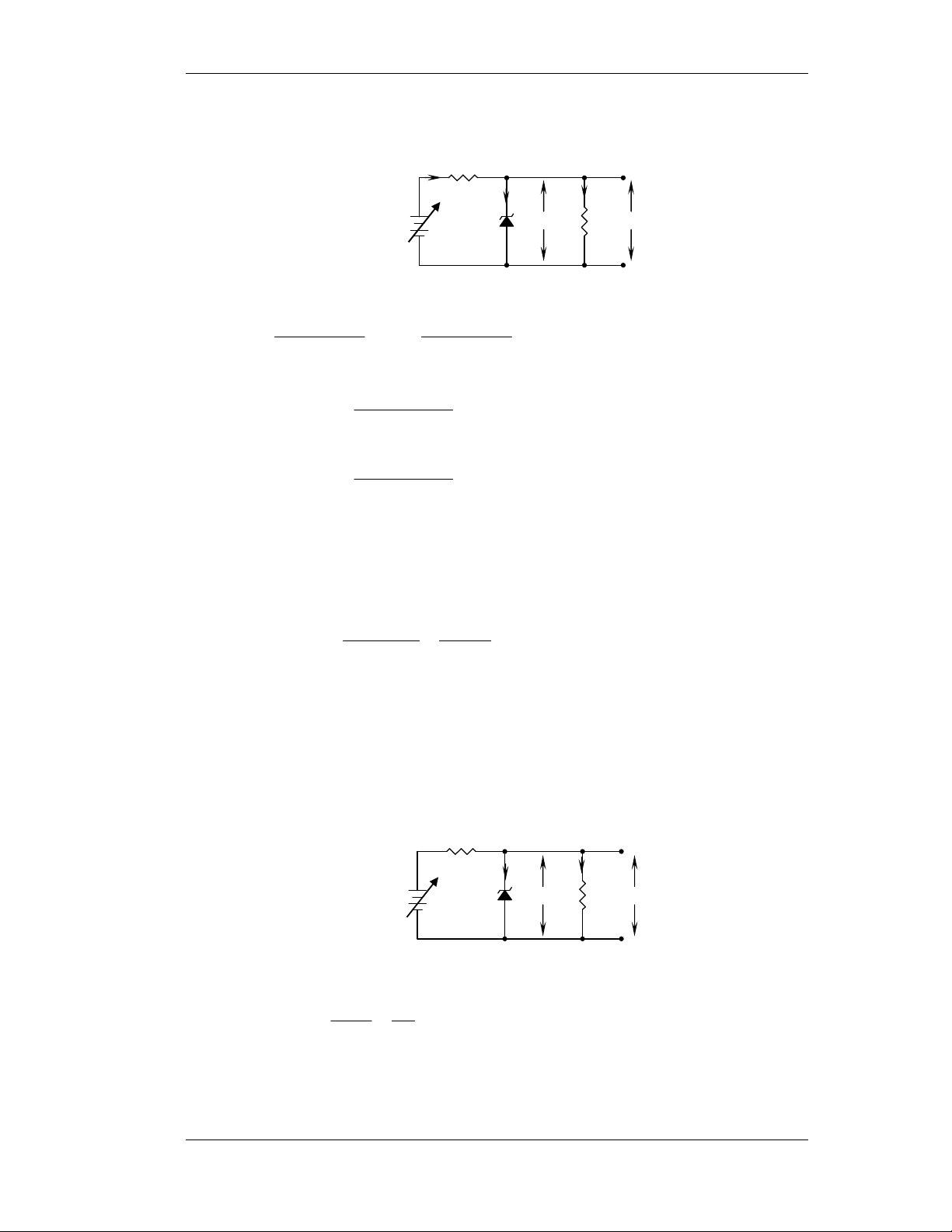
1) Daïng doøng IL = const (baøi 1-40); 200mA ≤ IZ ≤ 2A, rZ = 0 R IL i IZ V Z=18v 22vRL=18Ω DC<28v VL
a- Tìm Ri ñeå VL = 18V = const.
Imin = IZmin + IL = 0,2 + 1 = 1,2 A.
Imax = IZmax + IL = 1 + 2 = 3 A.
Maët khaùc ta coù: Vimin = 22V = IZmin.Ri + VZ. Suy ra: V − V i min Z 22 −18 4 R = = = = Ω 3 , 3 i I 2 , 1 2 , 1 Z min Vimax = 28V = IZmaxRi + VZ Suy ra V −V i max Z 28 −18 10 R = = = = Ω 3 , 3 i I 3 3 Z max Vaäy Ri = 3,3Ω.
b- Tìm coâng suaát tieâu thuï lôùn nhaát cuûa Diode Zenner:
PZmzx = IZmax.VZ = 2.18 = 36W. Moät soá baøi taäp maãu 6
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
2) Daïng doøng IL ≠ const: (baøi 1-41), 10mA ≤ IL ≤ 85mA. IZmin = 15mA. IR Ri I IL Z VZ=10v R L 13vV DC<16v L
a- Tính giaù trò lôùn nhaát cuûa Ri V − V V − V i Z i Z ≤ R i I + I ≤ I + I Z max L min Z min L max ∗ Khi VDC = 13V ta coù 13 −10 R ≤ = 30Ω i max 015 , 0 + 085 , 0 ∗ Khi VDC = 16V ta coù 16 −10 R ≤ = 60Ω i max 015 , 0 + 085 , 0 Vaäy ta laáy Rimax = 30Ω.
b- Tìm coâng suaát tieâu thuï lôùn nhaát cuûa Diode Zenner. PZmax = IZmax.VZ.
Maët khaùc: Vimax = IZmaxRi + VZ V − V 16 −10 ⇒ I i max Z = = = 200mA max R 30 i ⇒ I = I − I = 2 , 0 − 01 , 0 = 19 , 0 = 190mA z max max L min ⇒ P = 19 , 0 ×10 = 9 , 1 W z max
3) Daïng IZ ≠ const; IL ≠ const (Baøi 1-42)
30 ≤ IL ≤ 50mA, IZmin = 10mA.
rZ = 10Ω khi IZ = 30mA; Pzmax =800mW. Ri I I Z L 10Ω VZ=10v RL 20vVL DC<25v
a- Tìm Ri ñeå Diode oån ñònh lieân tuïc: PZmax 8 , 0 I = = = 80mA Z max V 10 Z Vaäy 10mA ≤ IZ ≤ 80mA
Ta coù: Imin = IZmin + ILmax = 60mA Imax = IZmax + ILmin = 110mA Moät soá baøi taäp maãu 7
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Maët khaùc: Vimin = Imin.Ri + VZ = 20V 20 10 ⇒ − R = = 166 Ω 7 , i max 06 , 0 Vimax = Imax.Ri + VZ = 25V 25 10 ⇒ − R = = 136 36 , Ω i min 0 11 ,
Suy ra: 136,4Ω ≤ Ri ≤ 166,7Ω Vaäy ta choïn Ri =150Ω b- Veõ ñaëc tuyeán taûi:
Ta coù: VZ + IZRi = VDC – ILRi ∗ Vôùi VDC = 20V ta coù: 20 − 03 , 0 ×150 = V 5 , 15 khi I = 30mA V + I 150 = Z  L Z 20 − 05 , 0 ×150 = V 5 , 12 khi I = 50mA L ∗ Vôùi DC = 25V ta coù: 25 − 03 , 0 ×150 = V 5 , 20 khi I = 30mA V + I 150 = Z  L Z 25 − 05 , 0 ×150 = V 5 , 17 khi I = 50mA L
Töông öùng ta tính ñöôïc caùc doøng IZ: 5 , 15 −10 I 12 5 , −10 = = 36 7 , mA ; I = = 16 7 , mA 1 Z 150 Z2 150 20 5 , −10 I 5 , 17 −10 = = 70mA ; I = = 50mA ; Z3 150 Z4 150 IZ(mA) 20,5 17,5 15,5 12,5 VZ =10V 0 VZ 10 16,7 30 rZ =10Ω 36,7 50 70 80 Moät soá baøi taäp maãu 8
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
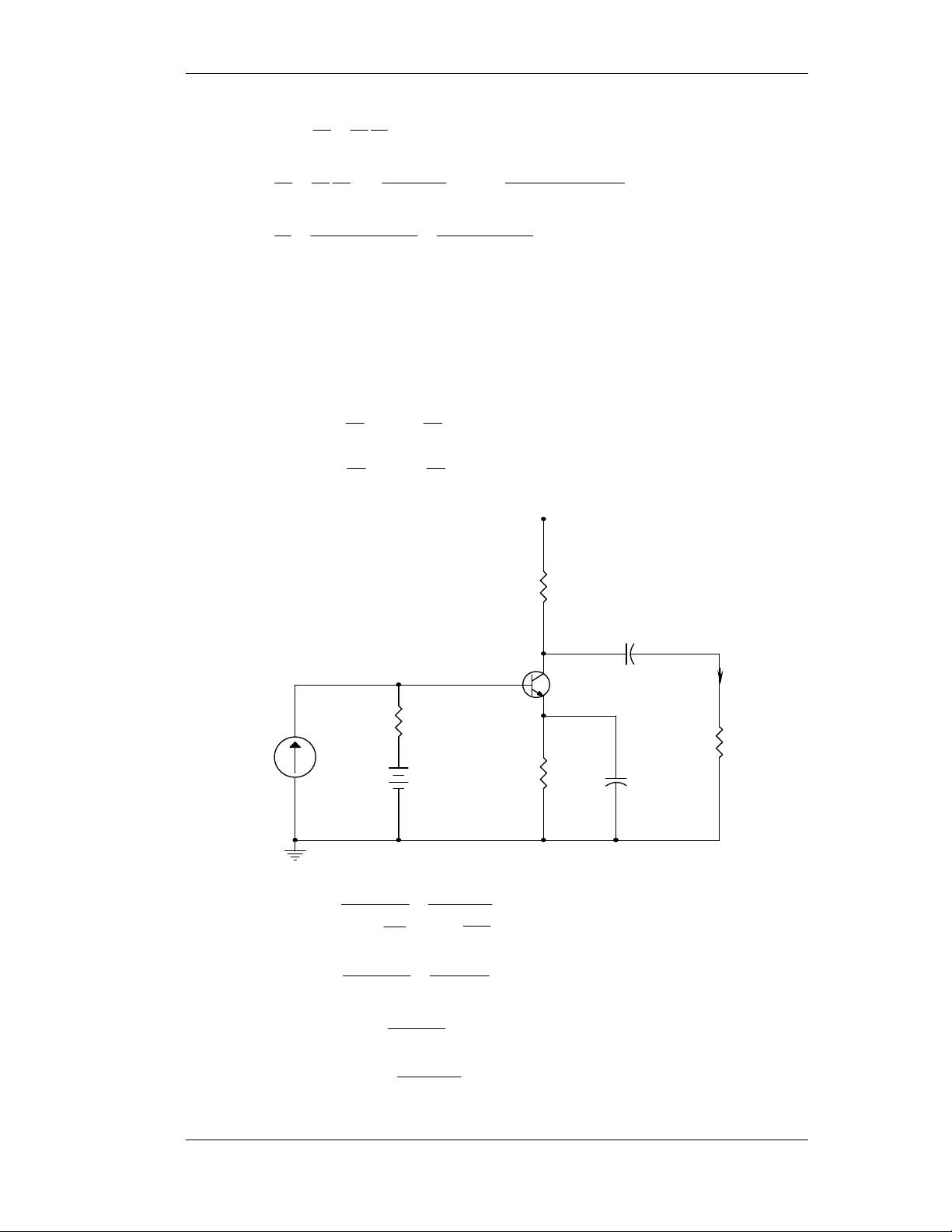
Chöông II: TRANSISTOR HAI LÔÙP TIEÁP GIAÙP I.
Boä khueách ñaïi R-C khoâng coù CC vaø khoâng coù CE (E.C).
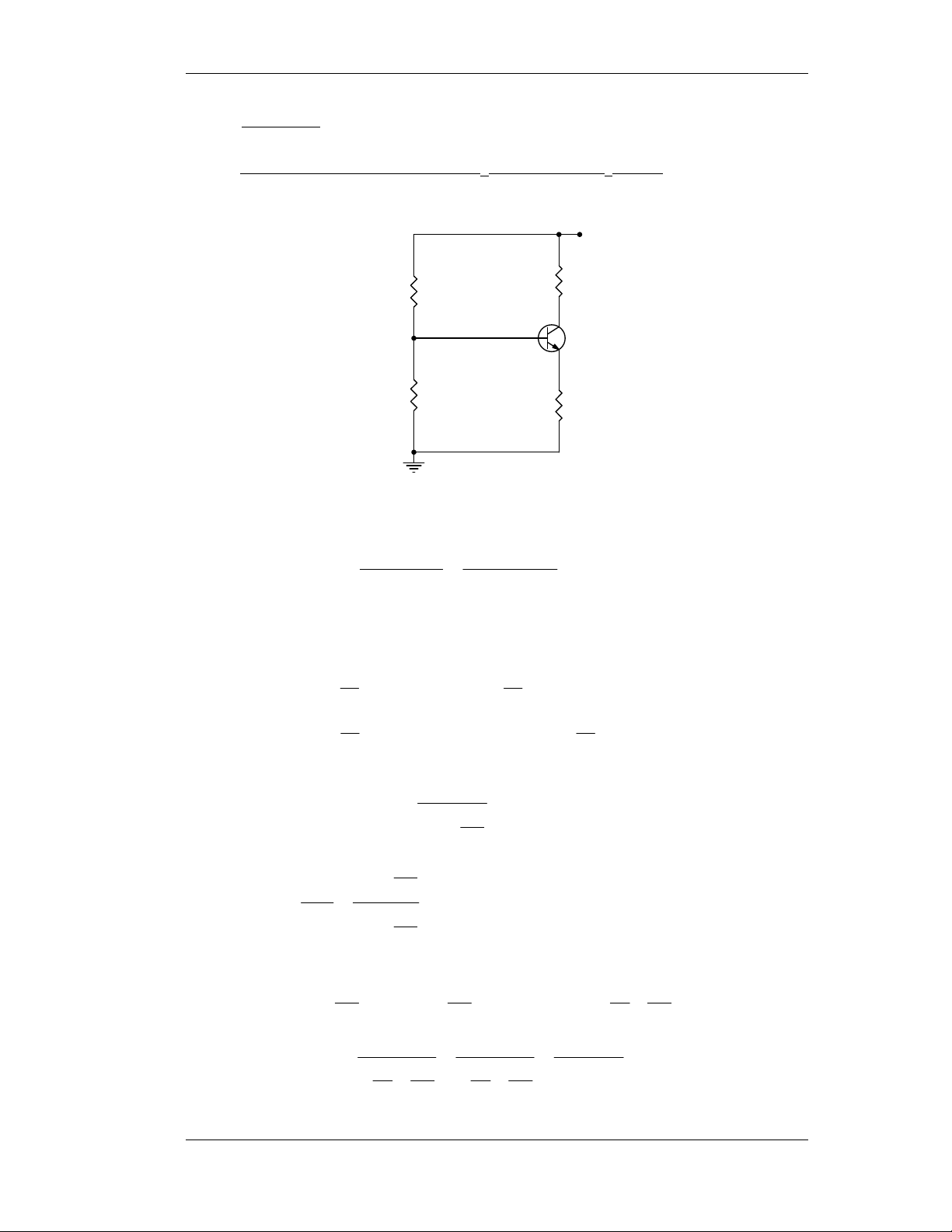
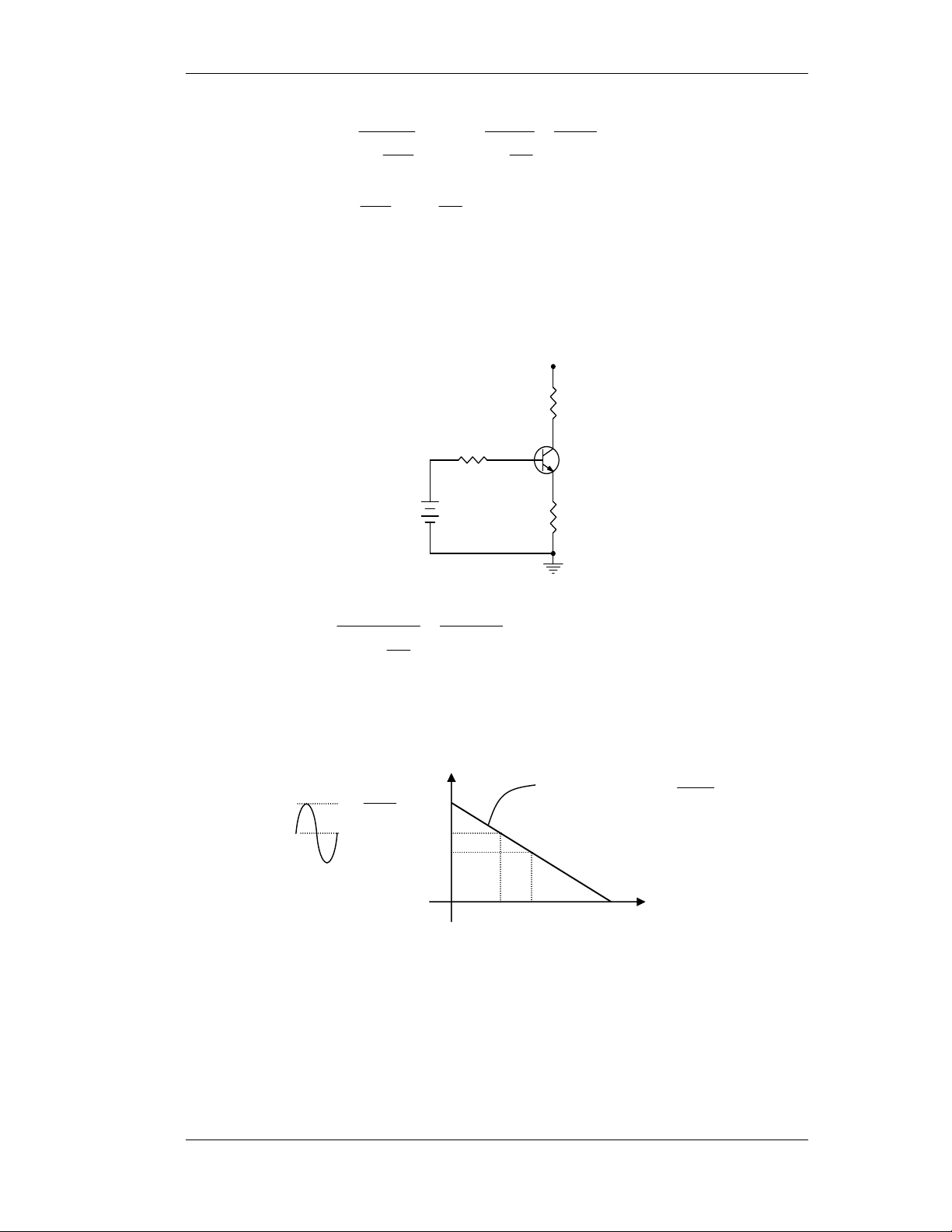
1) Baøi 2-10: 20 ≤ β ≤ 60, suy ra ICQ khoâng thay ñoåi quaù 10%. +25V R RC=1,5K 2 + VCEQ = 5V - R1 R E=1K
∗ Phöông trình taûi moät chieàu: VCC = VCEQ + ICQ(RC + RE). V − V CC CEQ 25 − 5 ⇒ I = = = mA 8 CQ R + R C 5 , 1 .103 E + 103
Neáu coi ñaây laø doøng ñieän ban ñaàu khi β = 60 sao cho sau moät thôøi gian
β chæ coøn β = 20 thì yeâu caàu ICQ ≥ 7,2mA.
∗ Ta giaûi baøi toaùn baøi toaùn moät caùch toång quaùt coi β1 = 20; β2 = 60. 1 1 R = β R ≤ R ≤ R = β R 1 b 1 E b b2 2 E 10 10 1 3 1 R = .20.10 = 2KΩ ≤ R ≤ R = .60.103 = 6KΩ b1 10 b b2 10 Vaäy 2KΩ ≤ Rb ≤ 6KΩ V − 7 , 0 ∗ Maët khaùc I = BB , neáu coi V CQ R BB ≈ const thì ta coù: R + b E β R R b I E + CQ1 β2 = ≥ 9 , 0 (1) I R CQ2 R b E + β1
∗ Coù theå tính tröïc tieáp töø baát phöông trình (1): R  R   1 9 , 0  R + b ≥ 9 , 0 R + b ⇒ R 1 , 0 ≥ R E  E  E b  − +  β2  β1   β β 2 1  0 R 1 , E 1 , 0 .103 100 ⇒ R ≤ = = = K 53 , 3 Ω b − 1 9 , 0 1 9 , 0 3 , 28 .10 3 − + − + β β 60 20 2 1 Moät soá baøi taäp maãu 9
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I Choïn Rb = 3,5KΩ.
∗ Neáu boû qua IBQ ta coù VBB ≈ VBE + IEQRE = 0,7 + 8.10-3.103 = 8,7V. Suy ra: 1 3 1 5 , 3 .103 R = R = 5 , 3 .10 = = Ω 5368 ≈ 4 , 5 KΩ 1 b V 7 , 8 BB 0 652 , 1 − 1 − V 25 CC VCC 3 25 R = R = 5 , 3 .10 = 10057Ω ≈ 06 , 10 KΩ 2 b V 7 , 8 BB
∗ Ta coù theå tính toång quaùt: Choïn Rb = 4KΩ thay vaøo (1): 3 4.103 10 I + CQ1 60 1067 = = = 9 ,
88 %, bò loaïi do khoâng thoûa maõn (1). ICQ2 4.103 3 1200 10 + 20 3 3.103 10 I + CQ1 60 1050
∗ Choïn Rb =3KΩ thay vaøo (1): = = = 91 , 0 thoûa ICQ2 3.103 3 1150 10 + 20
maõn baát phöông trình (1), ta tính tieáp nhö treân.
2) Baøi 2-11: Vôùi hình veõ baøi (2-10) tìm giaù trò cho R1, R2 sao cho doøng iC xoay
chieàu coù giaù trò cöïc ñaïi.
∗ Ñieåm Q toái öu ñöôïc xaùc ñònh nhö sau: VCC I = I Cm max TÖ CQ = R + R DC AC V = I R . TÖ CEQ CQTÖ AC
Töø hình veõ: RDC = RC + RE = 1,5.103 + 103 = 2,5KΩ.
RAC = RC + RE = 1,5.103 + 103 = 2,5KΩ. 25 Suy ra: I = = mA 5 CQTÖ 2 5 , .103 + 5 , 2 .103
VCEQTÖ = 5.10-3.2,5.103 = 12,5V 1 1 ∗ Choïn R = βR = .100.103 = 10KΩ (boû qua I b 10 E 10 BQ) i C(mA) V  1  CC = 10 DCLL ACLL ≡  −  3 5 , 2 .10 R   DC V Q CC TÖ = 5 2(R + R C E ) 0 VCEQTÖ = 12,5 25 V CE(V)
VBB ≈ VBE + ICQTÖ.RE = 0,7 + 5.10-3.103 = 5,7V Moät soá baøi taäp maãu 10
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I 1 3 1 104 R = R = 10.10 = = K 95 , 12 Ω ≈ K 13 Ω 1 b V 7 , 5 BB 772 , 0 1 − 1 − V 25 CC VCC 4 25 R = R = 10 = K 85 , 43 Ω ≈ 44KΩ 2 b V 7 , 5 BB
Vì RDC = RAC neân phöông trìng taûi DC vaø AC truøng nhau.
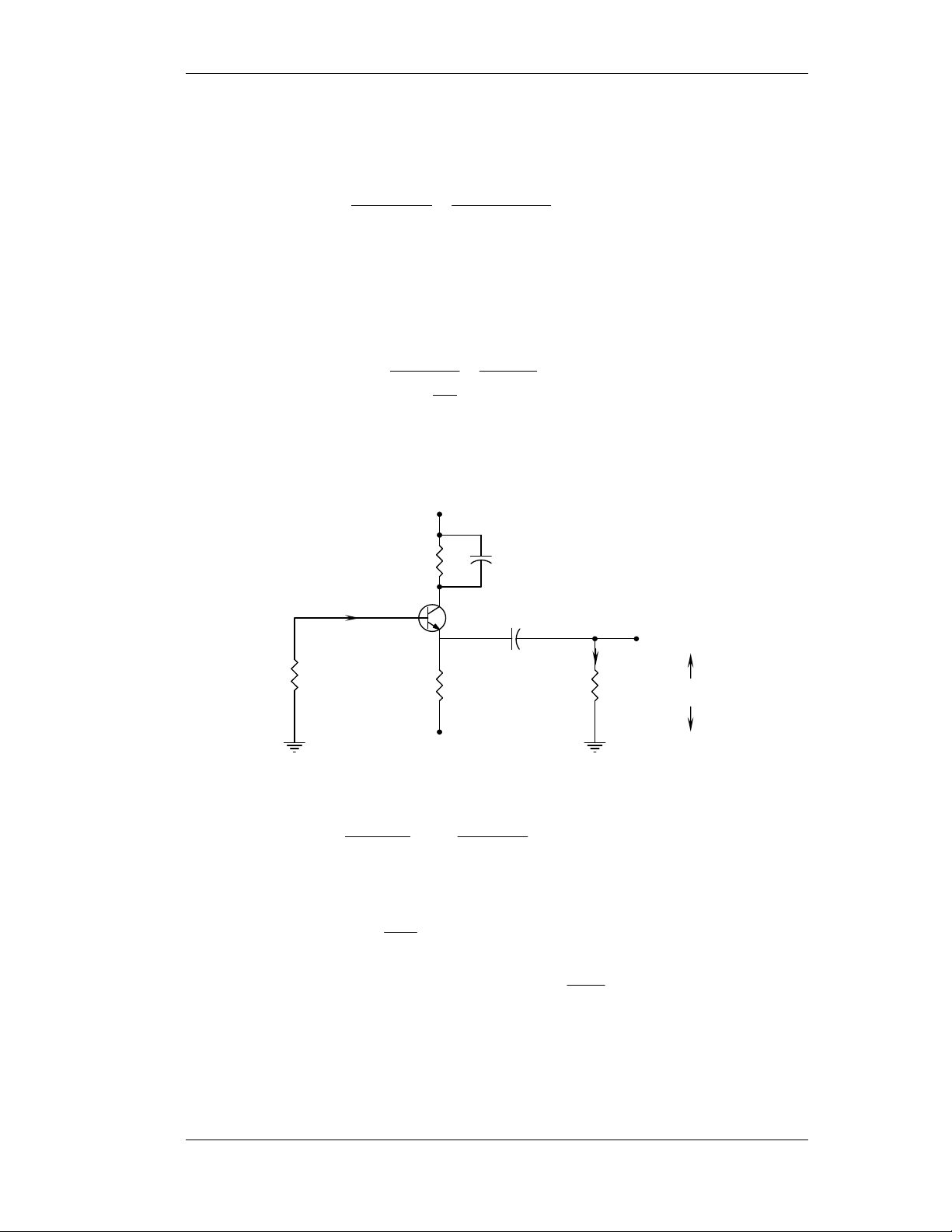
3) Baøi 2-14: Ñieåm Qbaát kyø vì bieát VBB = 1,2V; β = 20. Tìm giaù trò toái ña cuûa dao
ñoäng coù theå coù ñöôïc ôû C vaø tính η. +6V RC = 1K Rb = 1K VBB = 1,2V RE = 100Ω Bieát β = 20, VBEQ = 0,7V. V − V BB BEQ 2 , 1 − 7 , 0 Ta coù: I = = = mA 3 , 3 CQ Rb 100 + 50 RE + β
∗ Ñeå tìm giaù trò toái ña cuûa dao ñoäng coù theå coù ñöôïc ôû C ta phaûi veõ phöông trình taûi DC, AC iC (mA)  1  V DCLL = ACLL−  CC = 45 , 5  1100  R DC I Qbk CQ = 3,3 2,725 QTÖ 0 2,37 3 6 VCE(V)
VCEQ = VCC – ICQ(RC + RE) = 6 – 3,3.10-3.1,1.103 = 2,37V
∗ Vaäy giaù trò toái ña cuûa dao ñoäng laø:
ICmmax = iCmax – ICQ = 5,45 – 3,3 = 2,15mA
Suy ra VLmax = ICmmax.RC = 2,15.103.10-3 = 2,15V
∗ PCC = ICQ.VCC = 3,3.10-3.6 = 19,8mW Moät soá baøi taäp maãu 11
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I 1 2 1 P − L = (ICmmax ) R . C = ( 15 , 2 .10 )2 3 .103 = mW 31 , 2 2 2 P 3 − Hieäu suaát: L 31 , 2 .10 η = = = 7 , 11 % P − CC 19 8 , .10 3
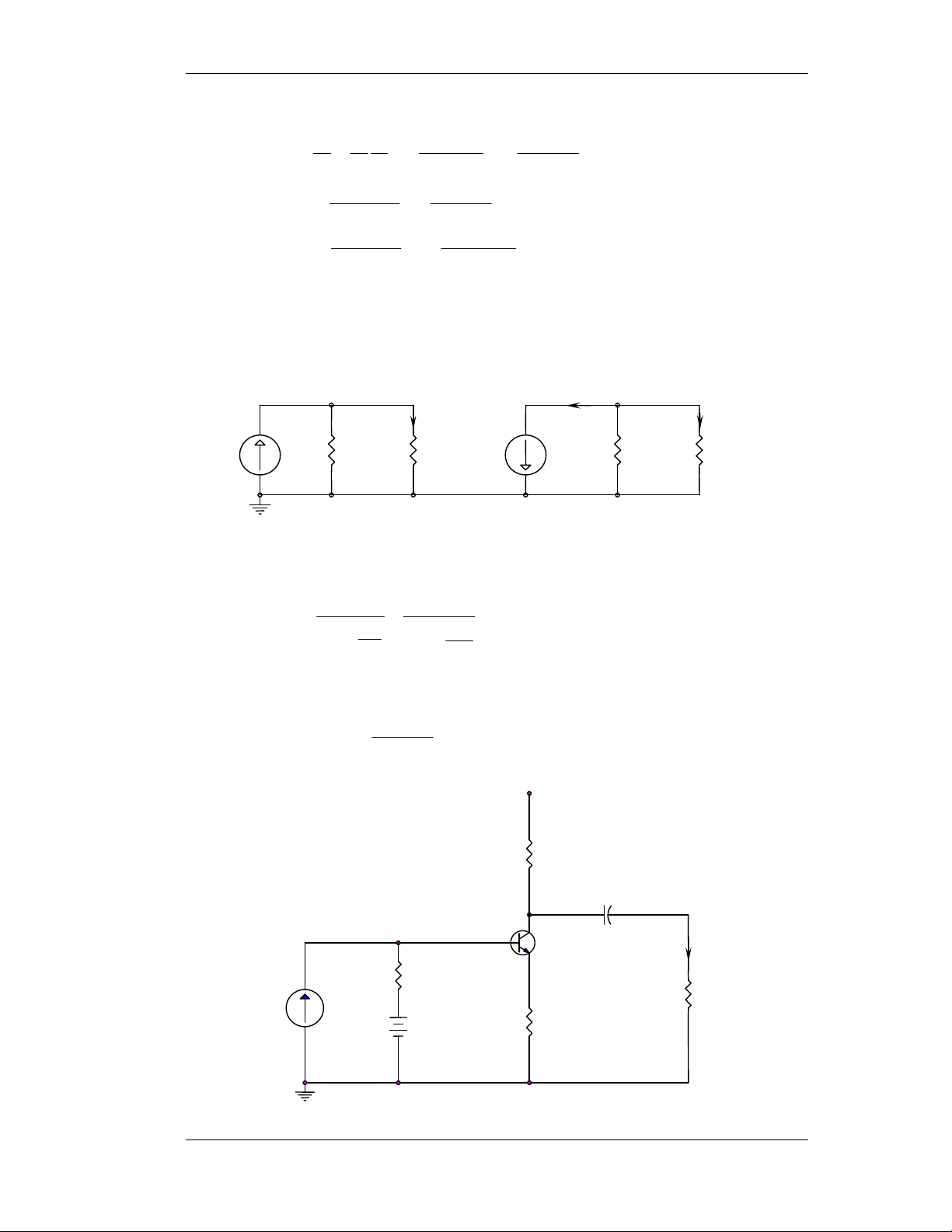
II. Boä KÑRC khoâng coù CC, CE (tuï bypass Emitter) (EC)
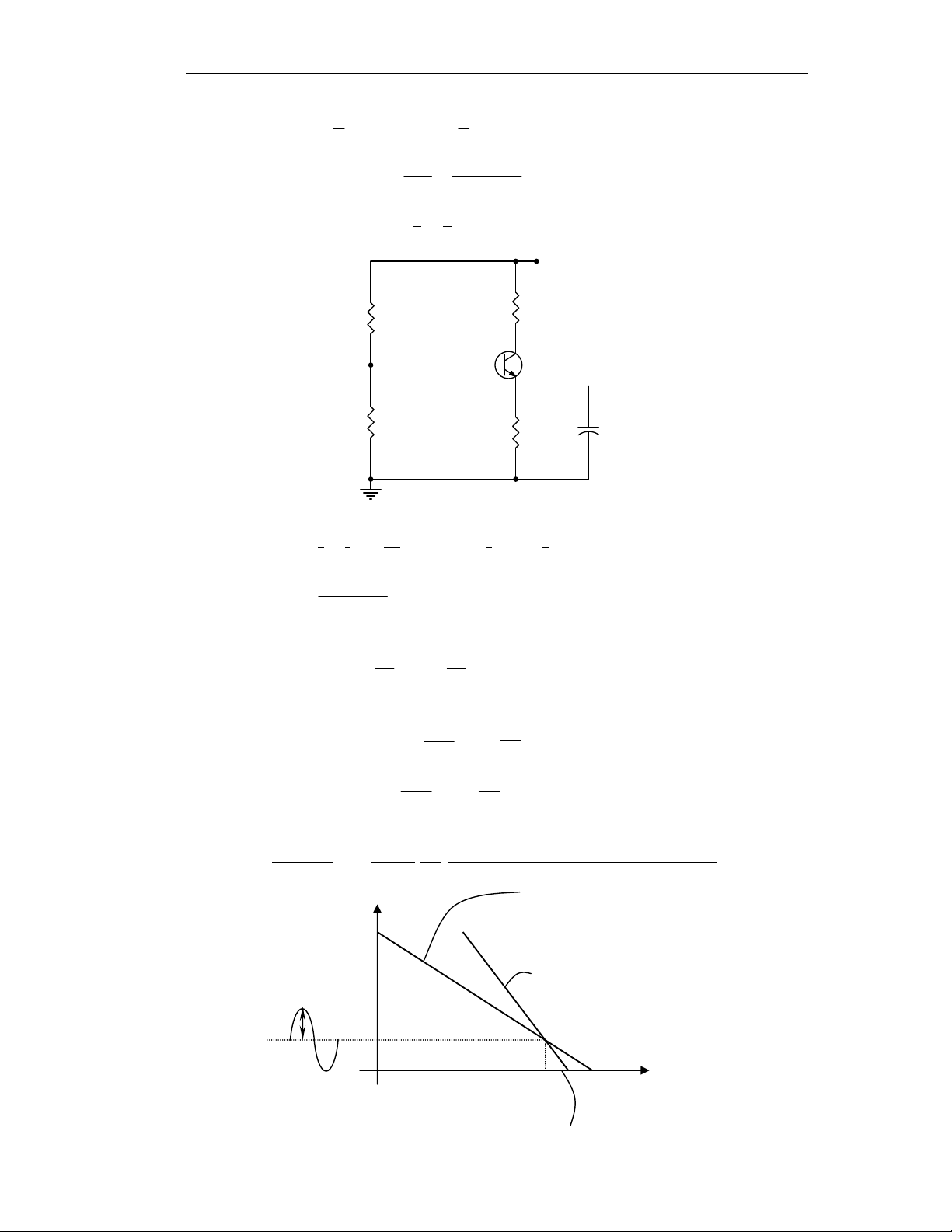
1) Baøi 2-15: Ñieåm Q baát kyø. Vcc=10V R RC=150Ω 2 β=100; VBEQ=0,7v R1 RE C E→ ∞ 100Ω
a- Tìm R1, R2 ñeå ICQ = 01mA (Rb << βRE)
Vì Rb << βRE neân ta coù: V − 7 , 0 I BB ≈ = 10mA = 10−2 A CQ RE
suy ra VBB = 0,7 + 100.10-2 = 1,7V 1 1 R = βR = 100.100 = K 1 Ω b 10 E 10 3 3 1 10 10 R = R = = ≈ 2 , 1 KΩ 1 b V 7 , 1 BB 83 , 0 1 − 1 − V 10 CC V CC 3 10 R = R = 10 = K 88 , 5 Ω 2 b V 7 , 1 BB
b- Ñeå tìm ICmmax vôùi R1, R2 nhö treân ta phaûi veõ DCLL vaø ACLL:  1  iC (mA) DCLL−   250  60 I Q  1  Cmmax ACLL−   150  15 7,5 10 VCE(V) VCEmax = 9V Moät soá baøi taäp maãu 12
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
VCEQ = VCC – ICQ(RC + RE) = 10 – 10-2.250 = 7,5V
Töø hình veõ ta nhaän thaáy ñeå ICm lôùn nhaát vaø khoâng bò meùo thì ICmmax = 10mA.
Ta coù theå tìm iCmax vaø VCemax theo phöông trình 1 i − I = − V − V C CQ ( CE CEQ ) RC V Cho V CEQ −2 5 , 7 CE = 0 ⇒ i = I + = 10 + = 60mA C max CQ R 150 C Cho i 1 − C = 0 ⇒ V = I R . + V = 10 .150 + 5 , 7 = 9V CE max CQ C CEQ
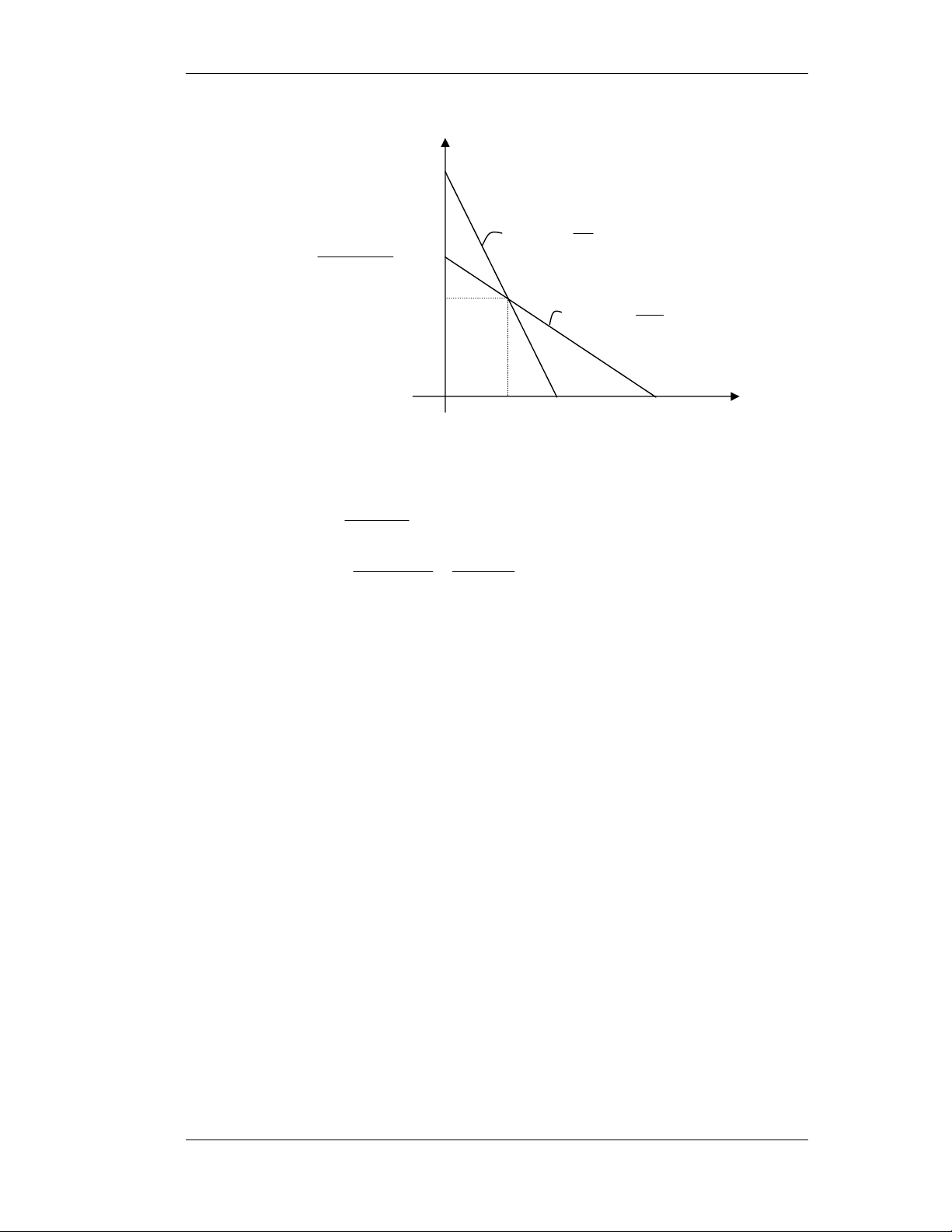
2) Baøi 2-16: Ñieåm Q toái öu (hình veõ nhö hình 2-15).
Ñeå coù dao ñoäng Collector cöïc ñaïi ta coù: VCC I = I (1) Cm max Ö CQT = R + R DC AC VCEQTÖ = RAC.ICQTÖ (2)
RDC = RC + RE = 150 + 100 = 250Ω RAC = RC = 150Ω Thay vaøo (1) ta ñöôïc: 10 I = = 25mA CQTÖ 250 + 150 V = 150.25.10 3 − V 75 , 3 Ö CEQT = iC(mA) 2ICQTÖ = 50 V  1  CC ACLL −  = 40 R  150  + R C E ICQTÖ = 25  1  DCLL−   250  VCEQTÖ 2VCEQTÖ 10 VCE(V) = 3,75 =7
VBB ≈ 0,7 + ICQTÖ.RE = 3,2V. 1 1 R = βR = .100.100 = K 1 Ω b 10 E 10 1 103 103 R = R = = ≈ 47 , 1 KΩ 1 b V 2 , 3 BB 68 , 0 1 − 1 − V 10 CC Moät soá baøi taäp maãu 13
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I VCC 3 10 R = R = 10 = Ω 3125 ≈ K 1 , 3 Ω 2 b V 2 , 3 BB
Ñeå veõ ACLL, raát ñôn giaûn ta chæ caàn xaùc ñònh:
iCmax = 2ICQTÖ vaø VCemax = 2VCEQTÖ.
III. Boä KÑ R-C coù CC vaø CE (E.C).
1) Baøi 2-20: Ñieåm Q toái öu
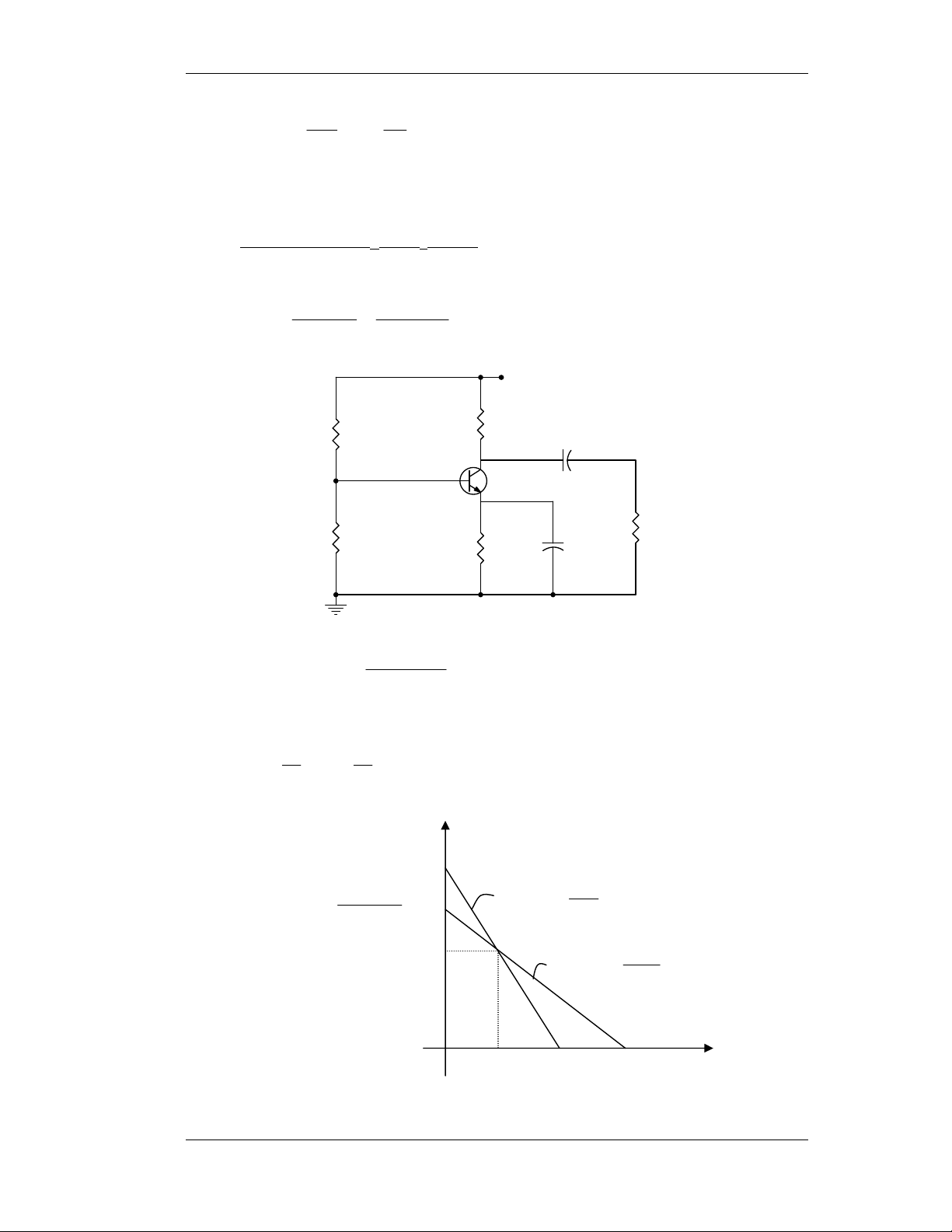
RDC = RC + RE = 900 + 100 =1KΩ R R C L 900.900 R = = = 450Ω AC RC + R 900 L + 900 Vcc=10V R R C=900Ω 2 CC→ ∞ RL=900K R1 RE CE→ ∞ 100Ω V I = I CC = ≈ 9 , 6 mA Cm max Ö CQT R + R AC DC
VCEQTÖ = ICQTÖ.RAC = 6,9.10-3.450 = 3,1V
VBB = 0,7 + RE.ICQTÖ = 0,7 + 100.6,9.10-3 = 1,4V 1 1 R = βR = .100.100 = K 1 Ω b 10 E 10 iC(mA) 2ICQTÖ = 13,8 V  1  CC ACLL = 10  −  R 450 + R   C E ICTÖ = 6,9  1  DCLL−   1000  0 V V CEQTÖ 6,2 10 CE(V) = 3,1 Moät soá baøi taäp maãu 14
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I 1 103 103 R = R = = ≈ Ω 1163 1 b V 4 , 1 BB 86 , 0 1 − 1 − V 10 CC VCC 3 10 R = R = 10 = Ω 7143 2 b V 4 , 1 BB Ta coù doøng xoay chieàu: RC 900 I = I. = 9 , 6 = mA 45 , 3 Lm R + R Cm 900 + 900 C L ⇒ V = V 1 , 3 Lm
2) Vaãn baøi 2-20 neáu ta boû tuï CE thì ta seõ coù boä khueách ñaïi R.C coù CC maø khoâng
coù CE. Khi ñoù keát quaû tính toaùn seõ khaùc raát ít vì RE << RC, RL
RDC = RC + RE = 900 + 100 = 1KΩ R R C L 900.900 R = R + = 100 + = 550Ω AC E R + R 900 + 900 C L VCC 10 I = I = = = mA 45 , 6 CQTÖ Cm max R + R DC 103 AC + 550
VCEQTÖ = ICQTÖ.RAC = 6,45.10-3.550 = 3,55V
VBB = 0,7 + ICQ. RE = 0,7 + 6,45.10-3.100 = 1,345V 1 1 R = βR = .100.100 = K 1 Ω b 10 E 10 1 103 103 R = R = = = Ω 1155 1 b V 345 , 1 BB 0 8655 , 1 − 1 − V 10 CC VCC 3 10 R = R = 10 = Ω 7435 2 b V 345 , 1 BB RC 900 I = I = . . 45 , 6 10−3 = mA 225 , 3 Lm R + R Cm 900 + 900 C L
VLm = RL.ILm = 900.3,225.10-3 = 2,9V.
IV. Boä KÑ R.C maéc theo kieåu C.C.
1) Baøi 2-22: Maïch coù thieân aùp Base.
* Ñaây laø daïng baøi ñieåm Q baát kyø vì ñaõ bieát R1, R2. R 5.103.20.103 R 1R2 b = = = 4KΩ R 5.103 + 20.103 1 + R2 R1 5.103 V = V = .25 = V 5 BB R + R CC 1 2 5.103 + 20.103 V − 0 7 , 5 − 7 , 0 I BB = = = 2 mA 1 , CQ Rb 3 4 10 . 3 RE + 2.10 + β 60 Moät soá baøi taäp maãu 15
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I Vcc=25V R2 RC=1K 20K β=60 CC→ ∞ R1 R 5K R L E=2K VL 2K R V 7 , 0
(Vì R >> b neân coù theå tính gaàn ñuùng theo coâng thöùc BB I − E CQ = ) β RE
VCEQ = VCC – ICQ(RC + RE) = 25 – 2,1.10-3.3.103 = 18,7V iC(mA) ICmax = 11,45  1  ACLL−  V  3 2.10  CC = 3 , 8 R DC ICQTÖ = 5  1  DCLL−  Q 3  3.10  ICQ = 2,1 0 10 VCEQ 22,9 V 25 CE(V) = 18,7
Töø hình veõ ta thaáy: ICQ < ICQTÖ neân ICm = ICQ = 2,1mA RL 2.103 I = I = . 1 , 2 .10−3 = mA 05 , 1 Lm R + R Cm E L 2.103 + 2.103
VLmmax = RL.ILm = 2.103.1,05.10-3 = 2,1V
* Caùch veõ DCLL vaø ACLL cuûa boä KÑ R.C maéc C.C töông töï nhö caùch maéc E.C 1 i − I = − V − V C CQ ( CE CEQ ) RAC R R vôùi R = R + E L = 2 Ω k AC C R + R E L V Cho V CEQ −3 7 , 18 CE = 0 suy ra i = I + = 1 , 2 .10 + = mA 45 , 11 C CQ RAC 2.103 Moät soá baøi taäp maãu 16
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I i 3 3 − C = 0 suy ra V = V + R I = 7 , 18 + . 2 10 . 1 , 2 .10 = 9 , 22 V CEQ max CEQ AC CQ
* Vôùi baøi toaùn treân neáu chöa bieát R1 vaø R2 ta coù theå thieát keá ñeå doøng ñieän ra lôùn
nhaát: RDC = RC + RE = 103 + 2.103 = 3KΩ. V Ta coù: CC 25 I = = = mA 5 CQTÖ R + R DC . 3 103 AC + 2.103 VCEQTÖ = ICQTÖ.RAC = 10V.
2) Baøi 2-24: Maïch ñöôïc ñònh doøng Emitter.
Theo ñònh luaät K.II: ΣVkín = 0 ta coù
RbIBQ + VBEQ + RE.IEQ –VEE = 0 V − 7 , 0 Suy ra BB 10 − 7 , 0 I = ≈ = mA 93 EQ Rb 100 RE + β
VCEQ = VCC + VEE – ICQ(RC + RE)
= 10 + 10 – 93.10-3.150 = 6,05V VCC=10v R C C→ ∞ C=50Ω I. I CE→ ∞ iL Rb<<βRE RE=100Ω RL=100Ω V L VEE=-10v RE 100 ∗ I = I = . . 93 10−3 = mA 5 , 46 Lm R + R Em 100 + 100 E L
∗ VLm = ILmRL = 46,5.10-3.102 = 4,65V
∗ Ñaây laø ñieåm Q baát kyø neân ta coù: 1 i − I = − V − V C CQ ( CE CEQ ) RAC VCEQ + Cho VCE = 0 suy ra i = I + = 214mA C max CQ RAC + Cho iC = 0 suy ra V = V + I R = 05 , 6 + 93.10 3 − .50 = V 675 , 10 CE CEQ CQ AC Moät soá baøi taäp maãu 17
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I iC(mA) 214  1  ACLL V  −  + V CC EE  50  = 133 R + R C E I Q CQ = 93  1  DCLL  −   150  0 VCEQ 10,675 20 VCE(V) = 6,05
∗ Neáu baøi naøy ñöôïc tính ôû cheá ñoä toái öu thì: RDC = RC + RE = 150Ω R R R = E L = 50Ω khi ñoù AC R + R E L VCC 20 I = = = A 1 , 0 = 100mA Ö CQT R + R 150 + 50 AC DC VCEQTÖ = ICQTÖ.RAC = 5V Moät soá baøi taäp maãu 18
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I Chöông IV:
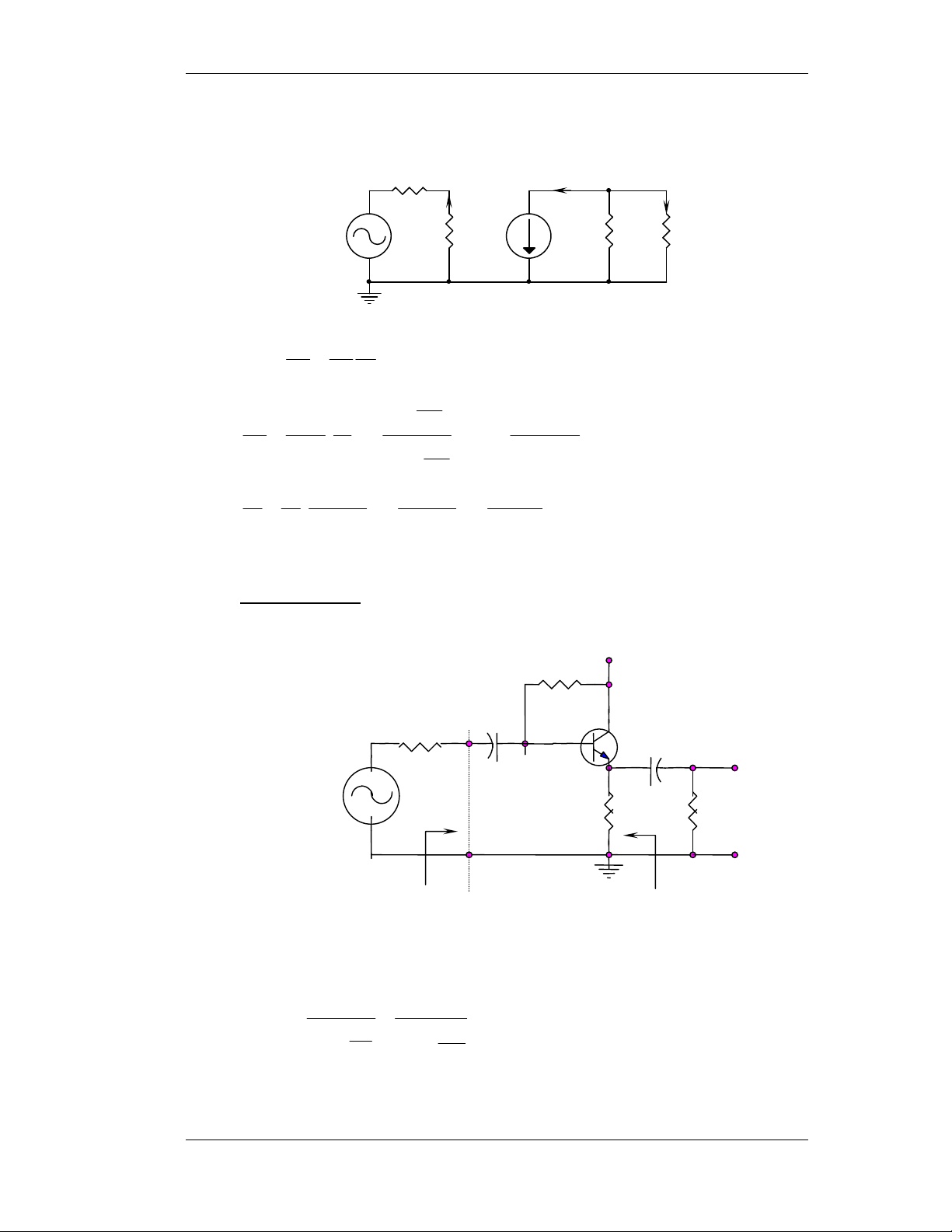
THIEÁT KEÁ VAØ PHAÂN TÍCH TÍN HIEÄU NHOÛ TAÀN SOÁ THAÁP. I.
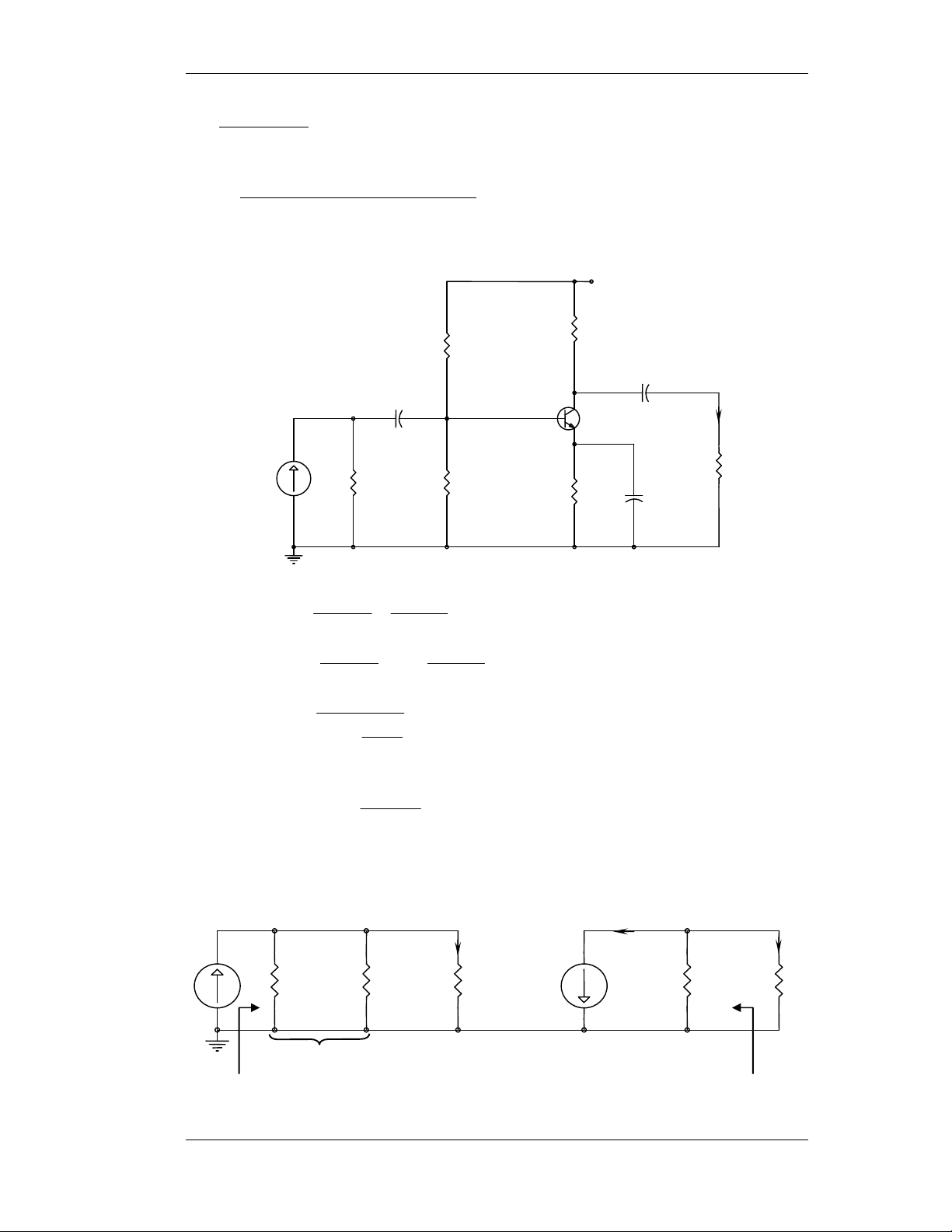
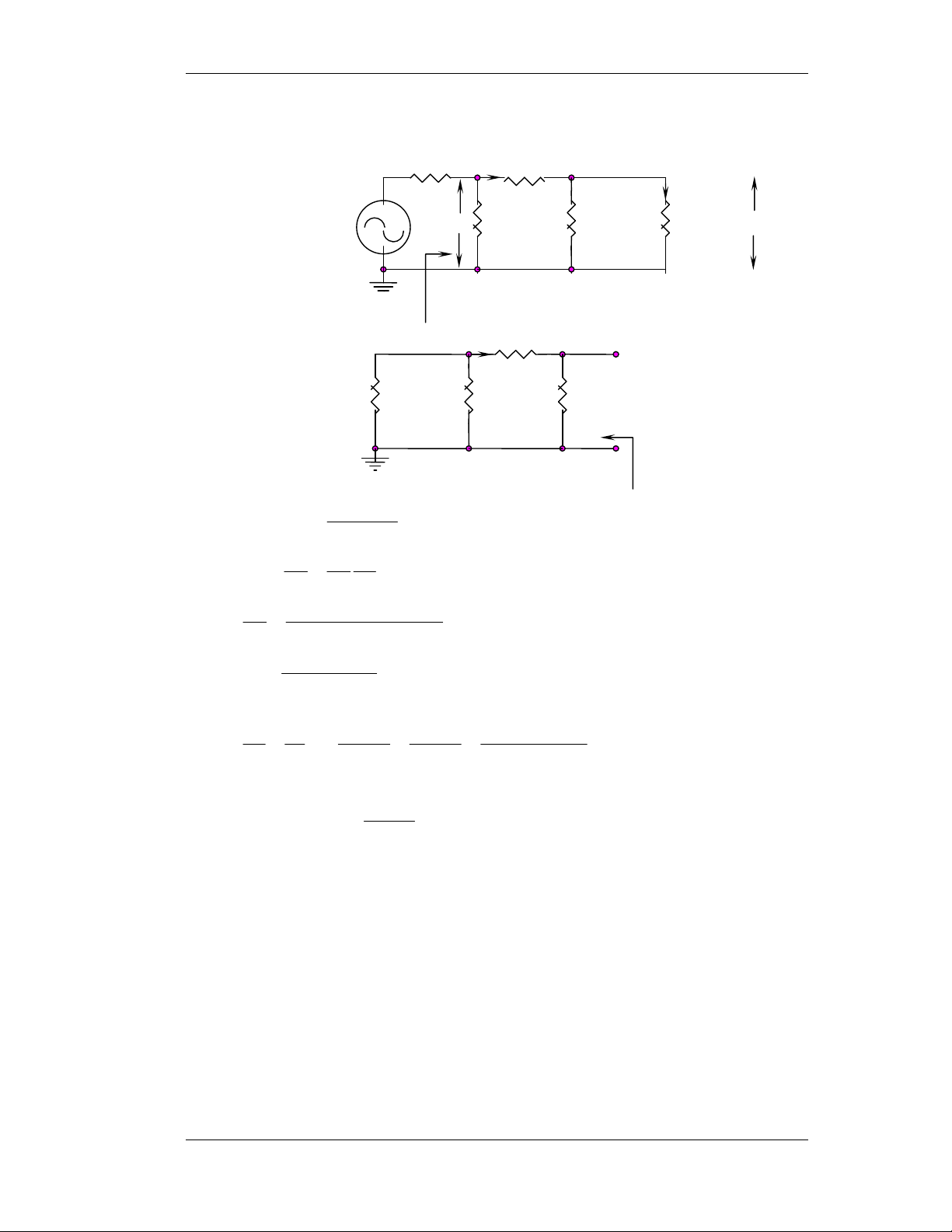
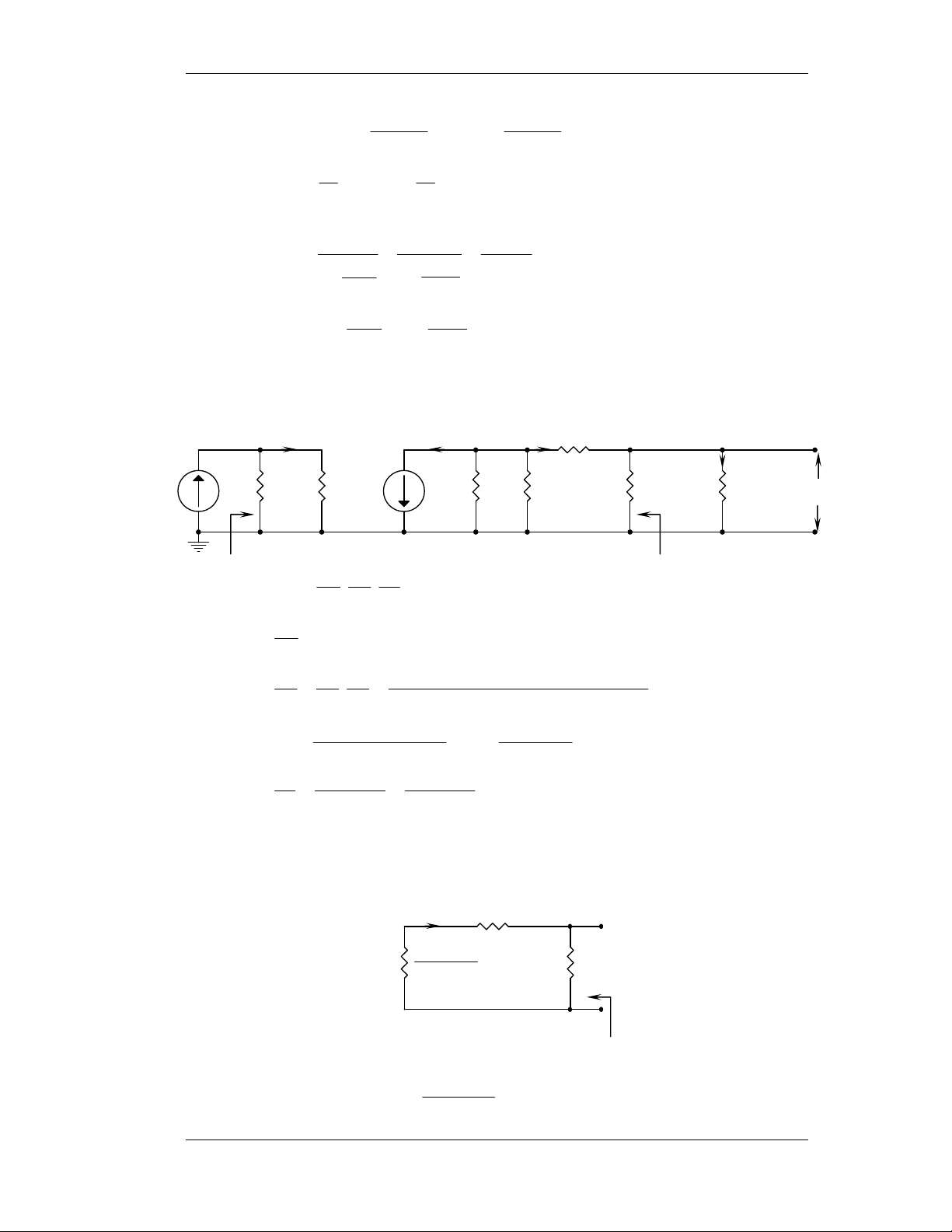
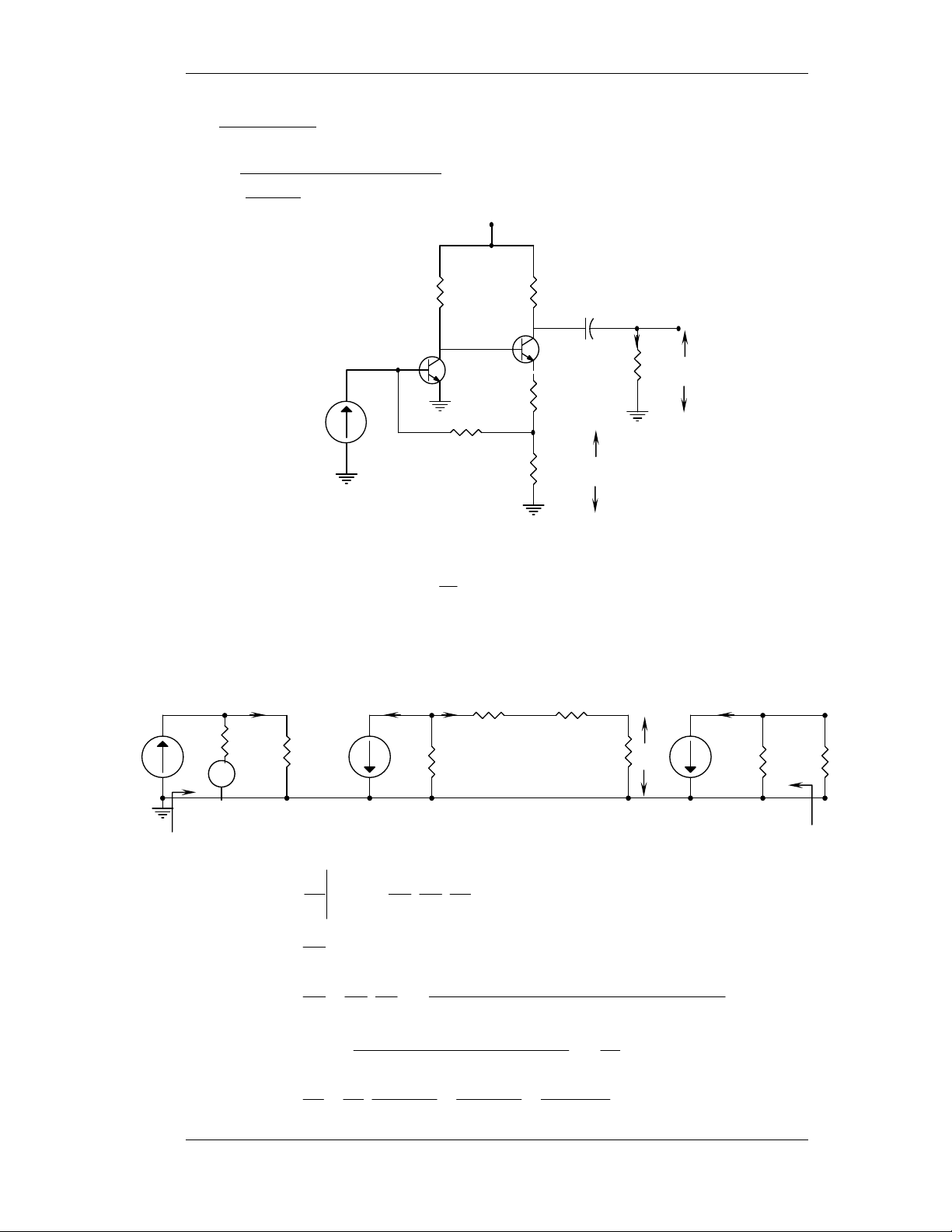
Sô ñoà maéc Emitter chung E.C: 1) Baøi 4-7: Q baát kyø. a- Cheá ñoä DC +VCC=20V RC=1,5K R2=20K CC2→ ∞ + - CC1→ ∞ + - iL RL=1,5K R1 + ii Ri=2K RE 3,5K 1,5K C E→∞ - R R 5 , 3 .20 R 1 2 = = ≈ K 3 b R + R 5 , 3 + 20 1 2 R 5 , 3 V 1 = V = .20 ≈ V 3 BB R + R CC 5 , 3 + 20 1 2 3 − 7 , 0 I = ≈ 6 , 4 mA CQ 3 10 . 3 500 + 100
VCEQ = VCC – ICQ(RC + RE) = 20 – 4,6.10-3.2.103 = 10,8V − 25 10 . 3 h = 4 , 1 h . = 760Ω ie fe − 4 6 , 10 . 3 b- Cheá ñoä AC: iC ib i L R R R i b hie C R 2K 3K L=1,5K i 1,5K i 100ib 1,2K Zi Zo Moät soá baøi taäp maãu 19
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I i i i L L b Ai = (1) i = i i i b i i i i R L L C C 5 , 1 10 . 3 = = − h . = − .100 = −50 i i i R + R fe b C b C L 5 , 1 10 . 3 + 5 , 1 10 . 3 i R // R b i b 2 , 1 .103 = = = 61 , 0 ii (R // R i b ) + h ie 2 , 1 .103 + 760
Thay vaøo (1) ta coù: Ai = -50.0,61 = -30,6
Zi = Ri//Rb//hie = 1200//760 = 465Ω Zo = RC = 1,5KΩ.
2) Baøi 4-11: Q baát kyø vaø hfe thay ñoåi. a- Cheá ñoä DC: 1 1 ∗ R = β R =
.50.10 = 50Ω < R = 100 , khoâng boû qua I 1 b 10 1 E 10 b BQ. 1 1 ∗ R = β R =
.150.10 = 150Ω > R = 100 , boû qua I b2 10 2 E 10 b BQ. +VCC=20v RC=100Ω C C→ ∞ + - iL R b=100Ω RL=100Ω + i RE i VBB=1,7v 10 C Ω E→∞ - V − 7 , 0 7 , 1 − 7 , 0 I BB = = = mA 83 1 EQ R 100 R b + 10 E + β 50 1 V − 0 7 , 7 , 1 − 7 , 0 I BB ≈ = = 100mA EQ2 R 10 E − 25.10 3 h = 4 , 1 .50. ≈ Ω 21 1 ie − 83 10 . 3 − 25.10 3 h = 4 , 1 150 . . = 52 Ω 5 , ie2 − 100.10 3
suy ra 21Ω ≤ hie ≤ 52,5Ω Moät soá baøi taäp maãu 20
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I b- Cheá ñoä AC: i i i R R L L b C b A = = = − h . . i fe i i i R + R R + h i b i C L b ie 100 100 A = − .50. = 20 − 66 , 1 i 100 + 100 100 + 21 100 100 A = − .150. = − 1 , 49 i2 100 +100 100 + 52 5 ,
Zi = Rb//hie suy ra Zi1 = 100//21 = 17,36Ω Zi2 = 100//52,5 = 34,43Ω Vaäy 20,66 ≤ Ai ≤ 49,18 17,36Ω ≤ Zi ≤ 34,43Ω iC ib iL Rb RC hie h RL = 100Ω 100Ω feib 100Ω ii
3) Baøi 4-12: Daïng khoâng coù tuï CE a- Cheá ñoä DC: V − 7 , 0 7 , 5 − , 0 7 I BB = = = mA 5 , 4 CQ Rb 3 104 RE + 10 h + fe 100 (coù theå tính ICQ = 5 mA)
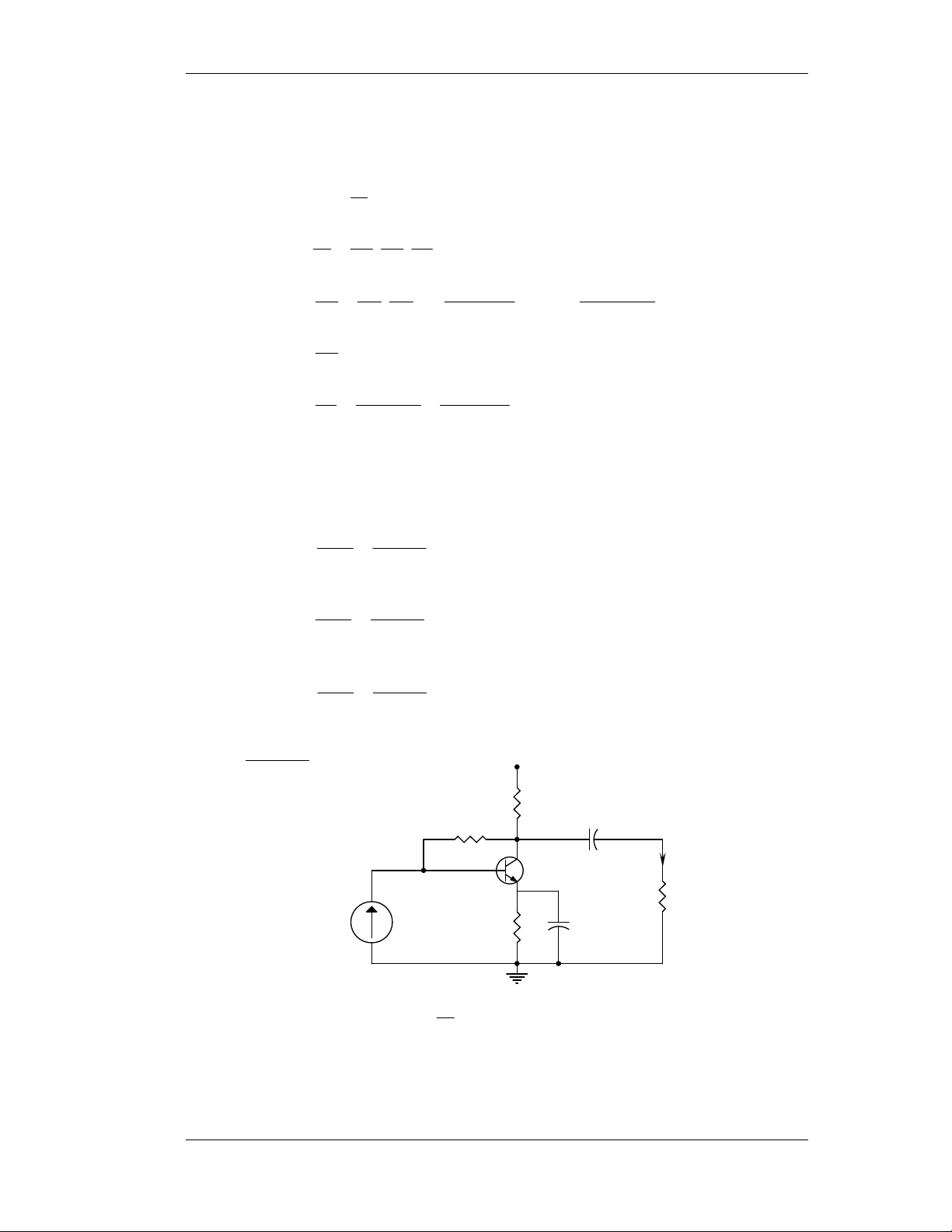
VCEQ = VCC – ICQ(RC + RE) = 20 – 4,5.10-3.(3.103) = 6,5V − 25.10 3 h = 4 , 1 .100. = Ω 778 ie − 5 , 4 .10 3 +V CC=20V R C=2K CC→ ∞ + - iL Rb=10K R i L=100Ω i V R BB=5,7V E=1K Moät soá baøi taäp maãu 21
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I b- Cheá ñoä AC: ib h ie=778Ω R i R L b C hfeRE RL=100Ω 10K i 100i 2K i b i i i L L b Ai = (1) i = i i i b i i i i R L L C C = = − h . = − 24 , 95 i i i R + R fe b C b C L i R b b 104 = = = 09 , 0 i R + h + h R i b ie fe E 104 + 778 +105
Thay vaøo (1) ta ñöôïc Ai = -95,24.0,09 = -8,6 Z = R // i b [h + h R ie fe E ] ≈ 10 4 // 10 5 = K 1 , 9 Ω
II. Sô ñoà maéc B.C: Baøi 4-21, hoe = 4 10 1) Cheá ñoä DC: r i=50Ω RL=10K R2 + V i - R1 V C CC b→ ∞ h 10 h fe = = = 0 91 , fb 1+ h 11 fe − h 1 25.10 3 h = ie = 4 , 1 . 10 . . = 32Ω ib 1 + − h 11 10 3 fe 4 h 10− oe −5 h = = = 10 ob 1+ h 11 fe Moät soá baøi taäp maãu 22
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I 2) Cheá ñoä AC: Ri 50Ω i C i e iL + hib 1/h ob RL Vi hfbie 32Ω 105 Ω - 10KΩ 0,91ib V V i L L e AV = (1) V = i V i e i 1 R V i R i L h L L L C ob 104.105 = . = − h . = − . 91 , 0 = 827 i i i 1 fb − e C e 104 +105 RL + hob i 1 − V 1 1 e = . i = − = − = −0 012 , V V R + h R + h 50 + 32 i i i ib i ib
Thay vaøo (1) ta ñöôïc AV = (-827).(-0,012) = 10,085 ≈ 10
III. Sô ñoà maéc C.C: Baøi 4-23 1) Cheá ñoä DC +VCC =10V 100KΩ R b r C i 500Ω c1→∞ Cc2→∞ + V RL i R E 1K - Ω 1KΩ Z i Zo VCC = IBQRb + VBEQ + REIEQ V − 7 , 0 10 − 7 , 0 ⇒ I CC = = = mA 65 , 4 EQ Rb 3 105 RE + 10 + β 100
VCEQ = VCC – REIEQ = 10 – 4,65.10-3.103 = 5,35 V Moät soá baøi taäp maãu 23
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I 2) Cheá ñoä AC r i i 500Ω b hie 753Ω i ’ L + Rb Re.hfe R V L.hfe V i b 100K V Ω 100K L Ω 100KΩ - Zi hie/hfe 7,53Ω ie ri/hfe Rb/hfe RE 5Ω 1KΩ 1KΩ Zo − 25.10 3 h = 4 , 1 h ≈ Ω 753 ie fe − 65 , 4 .10 3 V V V L L b Av = (1) V = V V i b i V i h . L b fe (R // R E L ) V = i b b [h + h ie fe (R // R E L )] (2) 100.500 = = 985 , 0 753 + 50.000
R’b = Rb//[hie + hfe(RE//RL)] = 33,3Ω Vb 1 ' V R' i b K 3 , 33 = R . . Ω = = = 994 , 0 (3) V V b i i r + R' r + R' 500 + 3 , 33 .103 i b i b
Thay (2), (3) vaøo (1) ta coù: AV = 0,985.0,994 = 0,979 ≈ 0,98  r // R  Z = R // i b 3 o E h + ib  ≈ 10 //[ 53 , 7 + ] 5 ≈ 12 Ω 37 ,  hfe  Z = R // i b [h + h ie fe (R // R E L )] = R ' = K 3 , 33 Ω b Moät soá baøi taäp maãu 24
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Chöông VI: MAÏCH TRANSISTOR GHEÙP LIEÂN TAÀNG.
I. Transistor gheùp Cascading: 1) E.C – C.E
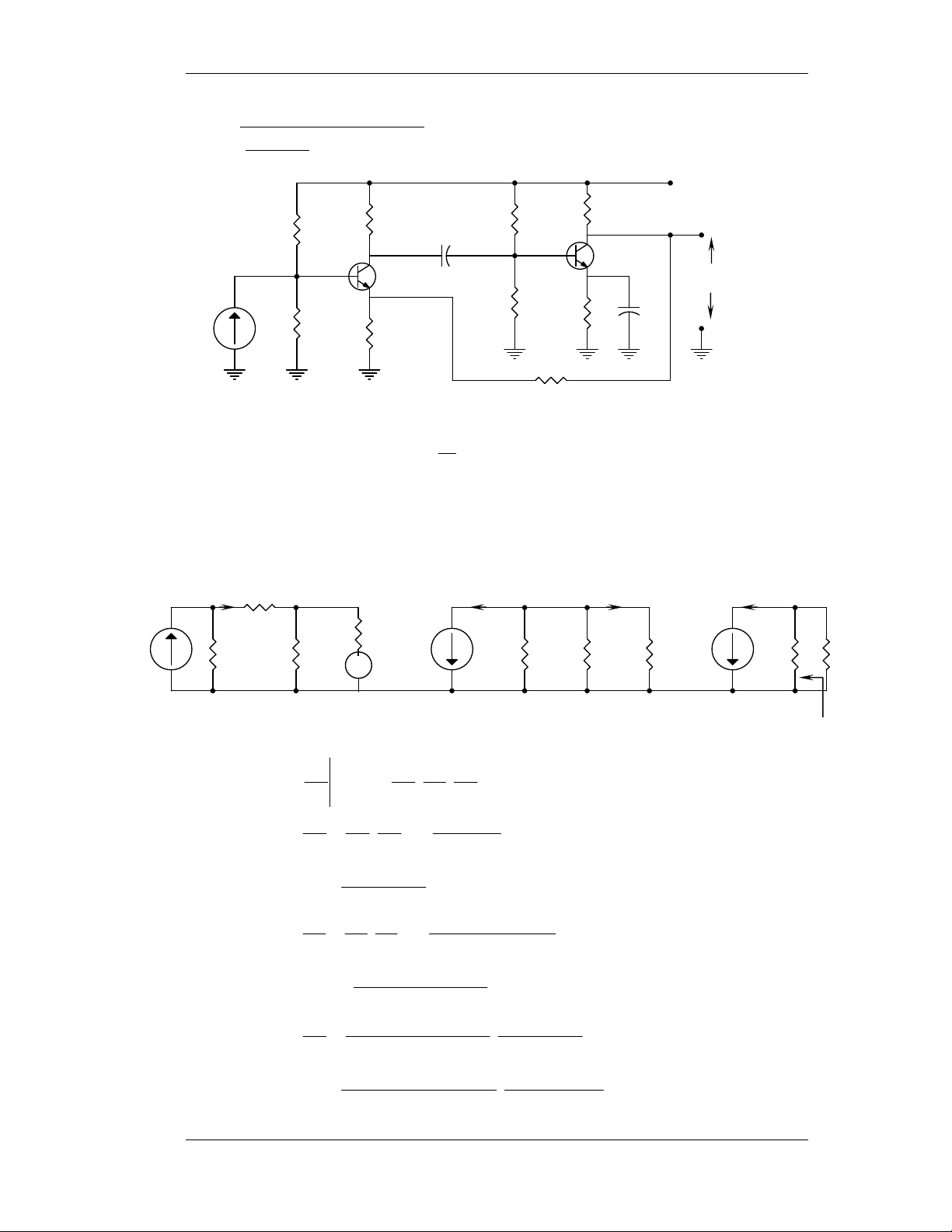
Baøi 6-1: Ñieåm Q baát kyø, 2 taàng hoaøn toaøn ñoäc laäp vôùi nhau. a - Cheá ñoä DC R R . 3 10 . 3 7 . 10 . 3 1 R = 11 21 = = K 1 , 2 Ω > R = h . R . = 500Ω 1 b R 3 3 b fe E + R 3.10 + 7 10 . 10 11 21
suy ra, khoâng ñöôïc boû qua IBQ1; R11 3.103 V = V . = .10 = V 3 1 BB R + R CC 11 21 3.103 + 7 10 . 3 V − 7 , 0 1 BB 3 − 7 , 0 I = = = 16 2 , mA 1 EQ R 2100 R b1 + 100 + E1 h 50 1 fe
VCEQ1 = VCC – IEQ1(RC1 + RE1) = 10 – 16,2.10-3.300 = 5,14V −3 − 25.10 25.10 3 h = 4 , 1 h . = 4 , 1 .50. = Ω 108 1 ie 1 fe − I 1 EQ 16 2 , .10 3 R R . 12 22 103.9.103 1 R = = = 9 , 0 KΩ < R = h . R . = 1250Ω b2 R 3 3 b fe E + R 12 22 10 + 9.10 10
suy ra, ñöôïc boû qua IBQ2; R12 103 V = V . = .10 = V 1 BB2 R + R CC 12 22 103 + 9.103 V − 7 , 0 BB2 1− 7 , 0 3 , 0 I = = ≈ = 2 , 1 mA EQ2 R 900 b2 250 R + 250 E2 + h2 50
VCEQ2 = VCC – IEQ2(RC2 + RE2) = 10 – 1,2.10-3.2250 = 7,3V −3 − 25.10 25.10 3 h = 4 , 1 h . = 4 , 1 .50. = Ω 1458 ie2 fe2 − IEQ2 2 , 1 .10 3 b - Cheá ñoä AC i iC1 i b1 ib2 C2 Rb hie1 RC1 Rb2 hie2 RC VL ii 2,1K 108 50ib1 200 900 1458 50ib2 2K Zi Zo i i i L b2 1 b A = . . (1) i i i i b2 1 b i Moät soá baøi taäp maãu 25
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I i i i L L = . C2 = −1 h . = −50 (2) i i i fe2 b2 C2 b2 i i i − R // R b2 b2 = . 1 C 1 C b2 = h . i i i 1 b 1 C 1 b (R // R 1 C b2 ) + h 1 fe ie2 (3) − 164 ≈ 50 . ≈ − 06 , 5 164 + 1458 i R 2100 1 b b = = = 951 , 0 (4) i R + h 2100 +108 i b 1 ie
Thay (2), (3), (4) vaøo (1) ta coù
Ai = (-50).(5,06).(0,951) ≈ 241
Zi = Rb//hie1 = 2,1.103//108 ≈ 103Ω Zo = ∞
Ñeå tìm bieân ñoä ñænh ñoái xöùng cöïc ñaïi ta veõ DCLL vaø ACLL. iC(mA) iCmax = 4,85  1  ACLL−  3 V  2 10 .  CC = 4 , 4 R DC  1  ICmmax DCLL Q  −   250  I CQ = 1,2 VCE(V) 0 7,3 10 9,7 Töø 1 i − I = − v − V C CQ ( CE CEQ ) RAC
vCE = 0 suy ra, ICmax = ICQ +VCEQ/RAC
= 1,2.10-3 + 7,3/2.103 = 4,85mA
iC = 0 suy ra, vCemax = VCEQ.RAC
= 7,3 + 1,2.10-3.2.103 = 9,7V
Töø ñaëc tuyeán DCLL vaø ACLL ta coù ICmmax = 1,2mA
Baøi 6-2: Ñieåm Q toái öu neân phaûi tính taàng thöù hai tröôùc, taàng 1 sau. a- Cheá ñoä DC:
RDC2 = RC2 + RE2 = 2250Ω; RAC2 = RC = 2KΩ. VCC 10 I = = = mA 35 , 2 CQ2 Ö T R + R 2250 + 2000 DC2 AC2
VCEQ2TÖ = ICQ2TÖ.RAC2 = 2,35010-3.2.103 = 4,7V Moät soá baøi taäp maãu 26
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I −3 − 25.10 25.10 3 h = 4 , 1 h . = 4 , 1 .50. = Ω 745 ie2 fe2 − IEQ2 35 , 2 .10 3
RDC1 = RC1 + RE1 = 200 + 100 = 300Ω;
RAC1 = RC1//Rb2//hie2 = 200//900//745 ≈ 134,4Ω VCC 10 I = = = 23mA 1 CQ TÖ R + R 300 +134 4 , 1 DC 1 AC −3 − 25.10 25.10 3 h = 4 , 1 h . = 4 , 1 .50. = 76Ω 1 ie 1 fe − I 1 EQ 23.10 3
b- Cheá ñoä AC: Sô ñoà töông ñöông tín hieäu nhoû nhö treân chæ coù hie1 vaø hie2
coù giaù trò khaùc. Ta aùp duïng luoân coâng thöùc (1) ôû treân: R // R R 1 C b2 b 164 2100 A = h h . . = 2500. . ≈ 434 i 1 fe fe2 (R // R 1 C b2 ) + h R + h 164 + 745 2100 + 76 ie2 b 1 ie 2) E.C – C.C: Baøi 6-3 Ñieåm Q toái öu a- Cheá ñoä DC: Taàng 2:
RDC2 = RE2 = 1KΩ; RAC2 = RE2//RL = 500Ω. VCC 10 I = = = 7 , 6 mA CQ2 Ö T R + R DC2 AC 103 2 + 500
VCEQ2TÖ = ICQ2TÖ.RAC2 = 6,7.10-3.500 = 3,35V −3 − 25.10 25.10 3 h = 4 , 1 h . = 4 , 1 .100. = 522Ω ie2 fe2 − IEQ2 7 , 6 .10 3 1 1 R = h R . = 100 . .103 = 104 Ω = 10KΩ b2 10 fe2 E2 10
VBB = 0,7 + ICQ2TÖ.RE = 0,7 + 6,7.10-3.103 = 7,4V Rb 104 104 R = = = = 46 , 38 KΩ 12 V 4 , 7 BB2 0 26 , 1− 1− V 10 CC VCC 4 10 R = R = 10 = K 5 , 13 Ω 22 b V 4 , 7 BB2 Taàng 1:
RDC1 = RC1 + RE1 = 400 + 100 = 500Ω;
RAC1 = RC1//Rb2//[hie2 + hfe(RL//RE)]
= 400//104//[261 + 100.500] = 400//8333 ≈ 382Ω. VCC 10 I = = = 34 , 11 mA CQ1 Ö T R + R 500 + 382 1 DC 1 AC
VCEQ1TÖ = ICQ1TÖ.RAC1 = 11,34.10-3.382 = 4,33V Moät soá baøi taäp maãu 27
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I −3 − 25.10 25.10 3 h = 4 , 1 h . = 4 , 1 .100. = 309Ω 1 ie 1 fe I 34 , 11 EQ2 1 1 R = h R . = .100 100 . = K 1 Ω 1 b 10 1 fe 1 E 10
VBB1 = 0,7 + ICQ1TÖ.RE1 = 0,7 + 11,34.10-3.100 = 1,834V R 1b 103 103 R = = = = K 25 , 12 Ω 11 V 834 , 1 1 BB 8166 , 0 1− 1− V 10 CC VCC 3 10 R = R = 10 = K 45 , 5 Ω 21 1 b V 834 , 1 1 BB b- Cheá ñoä AC: ib1 iC1 ib2 hie2 522 i ’ L Rb1 hie1 RC1 Rb2 (1+hfe)RE (1+hfe)RL V ii L 2,1K 309 100ib 400 10K 101KΩ 101KΩ Zi Zo V i i L b2 1 b A = . . (1) T i i i b2 1 b i VL = (1+ h R // R = 50 5,.10 (2) fe )( E ) 3 L ib2 i i i − R // R b2 b2 = . 1 C 1 C b2 = h . i i i 1 b 1 C 1 b (R // R 1 C
b2 ) + h ie2 + (1 + h fe )R // R 1 fe E L (3) − 385 − 385.102 = .100 = ≈ − 75 , 0 385 + 522 + 50500 51407 i R b1 1 b 103 = = = 764 , 0 (4) i R + h i b1 1 ie 10 + 309
Thay (2), (3), (4) vaøo (1) ta coù
AT = (50,5.103).(-0,75).(0,764) ≈ -29000 AT = -29000V/A = -29V/mA. ie2 h ib2 Rc1//Rb2 RE hfe2 1KΩ Zo
Zi = Rb//hie1 = 103//309 = 236Ω  R // R  Z = R // 1 C b2 3 3 o E h + ib2  = 10 //[ 22 , 5 + ] 85 , 3 = 10 // 07 , 9 ≈ 9Ω  hfe2  Moät soá baøi taäp maãu 28
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
3) Daïng baøi hoãn hôïp E.C – C.C: Baøi 6-4 ib1 iC1 ib2 h iC2 ie2 1K ib3 hie3 1K Ri R h b1 ie1 RC1 Rb2 RC2 100 K 1K 1K Vo2 i 1K 1K hfe2RE2 1K hfe3RE3 i 100i b1 5050 100ib2 5050 V V Tìm R ñeå 01 02 (1) i = − i i i V V i i 01 01 b2 b1 = . . (2) i i i i i b2 b1 i V i i 02 b2 1 b = 1 ( + h )R . . (3) fe2 E2 i i i i b1 i V suy ra 01 = − 1 ( + h R ). (4) fe2 E2 ib2 V V i i 01 01 b3 C2 = . . (5) i i i i b2 b3 C2 b2 Töø (5) suy ra V R 01 C2 = 1 ( + h R ) . h = − 1 ( + h )R fe3 E3 fe2 fe2 E2 i R + R + h + 1 ( + h R ) b2 C2 ie3 fe3 E3 103 − 5050. .100 = −5050 (6) 103 + R +103 + 5050 105 = 7050 + R
R = 100KΩ - 7,05KΩ ≈ 93KΩ V Tìm 01 ii Töø (2) ta coù: V V i i 1 ( + h R ) R . h . 01 01 b3 C2 fe3 E3 C2 fe2 i
= i i i = − R + R + h + 1(+ h )R b2 b3 C2 b2 C2 ie3 fe3 E3 (7) 5050.103.102 = − ≈ −5050 103 + 93.103 +103 + 5050 i i i b2 b2 1 C (R // R 1 C b2 ) = . = − h . i i i 1 b 1 C b1 (R // R 1 C b2 ) + h + 1 ( + h R ) 1 fe ie2 fe2 E2 (8) 500.100 5.104 = − = − = − 63 , 7 500 + 1000 + 5050 6550 ib1 (R // R i 1 b ) 103 = = = 5 , 0 (9) ii (R // R i 1 b ) + h 1 ie 103 +103
Thay (7), (8), (9) vaøo (2) ta ñöôïc: Moät soá baøi taäp maãu 29
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I V01 V = (− 5050) ( . − 63 , 7 ). 5 , 0 ≈ 27 , 19 i mA i R/hfe3 930 h ib3 10 Rc2 RE3 =10 h fe3 50Ω Zo Zi = Ri//Rb1//hie1 ≈ 500Ω  R R  Z = R // o E3 h + + C2 ib3  = 50 //[10 + 930 + 10] ≈ Ω 5 , 47  h h fe3 fe3 
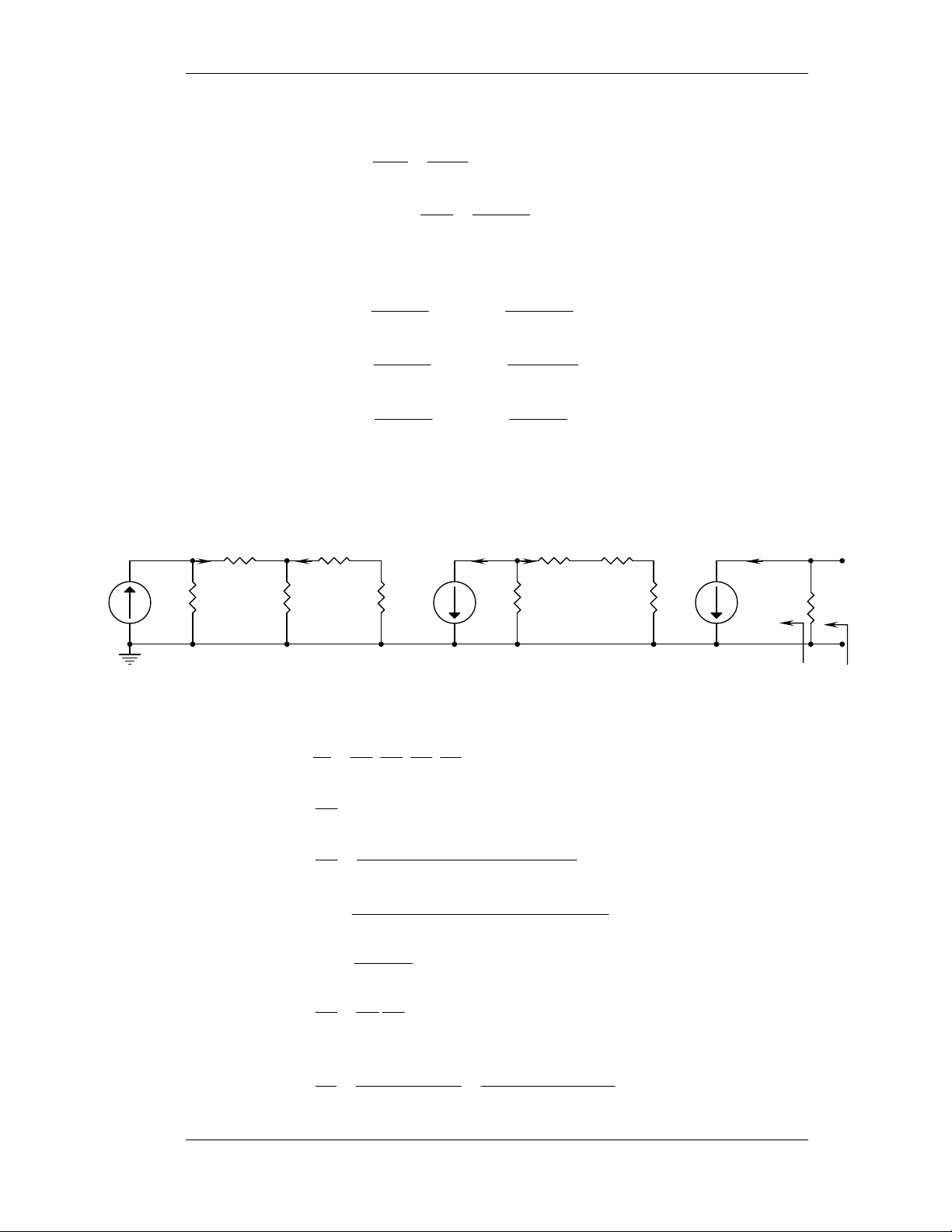
II. Transistor maéc vi sai vaø Darlingtôn 1) Baøi 6-23: E.C – E.C. +VCC =9V iL R R C2 21 R R 2,5K 22 C4=RL 3K 3K i 60 b3 T3 T 1 T2 hfe=100 T 4 i R R i 11 R 12 R E1 E4 K 500 1K 60 i i b1 i h b2 ie2 h h C4 hie1 ie3 fe3hie4 Rb1 Rb2 R R C2 L (1+h 7 fe)RE1 hfe2ib2 h2 50 750 feRE4 2,5K i i 100ib2 (1+hfe)ib4 a- Cheá ñoä DC R11 103 V = V = V . = .9 = V 25 , 2 1 BB BB2 R + R CC 11 21 103 + 3.103 V − 7 , 0 1 BB 25 , 2 − 7 , 0 I = I = = = mA 55 , 1 1 EQ EQ2 Rb 103 + 42 , 7 2RE + hfe IE = 2IE1 = 3,1mA
VCEQ1 = VCC – 2RE.ICQ1 = 9 – 2.500.1,55.10-3 = 7,45V
VCEQ2 = VCC – 2RE.ICQ1 – RC2.ICQ2
= 9 – 103.1,55.10-3 – 2,5.103.1,55.10-3 = 3,575V Moät soá baøi taäp maãu 30
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I V = V − R I. − V − V = 9 − 875 , 3 − 4 , 1 = 725 , 3 V R CC C2 CQ2 BE3 BE4 E 4 VRE4 725 , 3 I = I = = ≈ 62mA CQ4 EQ4 R 60 E4 I − CQ4 62.10 3 I = I = I ≈ = ≈ 62 , 0 mA CQ3 EQ3 BQ4 hfe 102
VCEQ4 = VCC – ICQ4(RC4 + RE4) = 9 – 62.10-3.120 = 9 – 7,44 = 1,56V
VCEQ3 = VCEQ4 – VBE4 = 1,56 – 0,7 = 0,86V −3 − 25.10 25.10 3 h = 4 , 1 h . = 4 , 1 .100. = Ω 2258 1 ie 1 fe − IEQ1 55 , 1 .10 3 −3 − 25.10 25.10 3 h = 4 , 1 h . = 4 , 1 .100. = Ω 5645 ie3 fe3 − IEQ1 62 , 0 .10 3 −3 − 25.10 25.10 3 h = 4 , 1 h . = 4 , 1 .100. = 56 Ω 45 , ie4 fe4 − IEQ1 62.10 3 b- Cheá ñoä AC hie3 hie4(1+hfe) ib1 h 58 ib2 h i i ie1 22 C2 ie2 2258 ib3 5645 5700 L R R’ R R’ b1 E b RC2 E4 RC i 750 50,5K 750 618K i 2,5K (1+hfe)2ib3 60 100i Ω b2 10201ib3 Z ’ o Zo R ' R = + = = E 1 E (1 h fe ) 500.101 50500 R' = E4 [h + ie4
(1+ hfe4 )RE4 ](1+ hfe3 ) = [ 45 , 56 + 6060].101 = 76 , 617 KΩ i i i i i L L b3 c2 1 b A = = . . . (1) i i i i i i i b3 c2 1 b i i L = (1+ h (2) fe3 )(1 + h fe4 ) = 101 101 . = 10201 ib3 i − R b3 C2 i = R + h + 1+ h h + R c2 C2 ie3 ( fe ) ' ie4 E4 3 − 2 5 , .10 = (3) 3 3 5 , 2 .10 + 5645 + 5700 + 76 , 617 .10 − 5 , 2 3 = ≈ 4 − 10 , 605 , 631 i i i c2 c2 b2 = = h (4) fe2 ( . − ) 1 = 100 i i i − 1 b b2 1 b
(Vì R’E raát lôùn neân coi ib2 ≈ ib1) i R 750 b1 b −3 = = = 4 , 128 .10 (5) '' i R + h + R 750 + 2258 + 2832 i b 1 ie E Moät soá baøi taäp maãu 31
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I vôùi R'' = R' // E E [h + R ie2 b ] = 5050 // 3008 ≈ 2832Ω
Thay (2), (3), (4), (5) vaøo (1) ta coù:
Ai = 10201.(-4.10-3).(-100).128,4.10-3 = 522,3 (laàn)
Zi = Rb1//(hie1 +R’’E) ≈ 750//(2258 + 2832) = 654Ω
Zo = ∞ ⇒ Z’o = Zo//RC = RC = 60Ω 2) Baøi 6-24: E.C – C.C RC1 RC2 1K 1K T4 T5 R T6 R b2 b1 10K 10K ii T3 R VBB1 VBB2 E6 VL 10 1V 1V Z RE i Zo 1K -3V a- Cheá ñoä DC
AÙp duïng ñònh luaät K.II ΣVkín = 0 cho voøng 2 ta coù: VBE3 + IEQ3RE3 – VEE = 0 (1) V − V EE BE3 3 − 7 , 0 I = = = 2 mA 3 , EQ3 RE 103 3 I I = I EQ3 = = mA 15 , 1 EQ1 EQ2 2
VCE1 = VCE2 = VCC – RC1ICQ1 – VE1 (2)
Maët khaùc aùp duïng ñònh luaät K.II ΣVkín = 0 cho voøng 1 ta coù:
-VBB1 + RbIBQ1 + VBE1 + VE1 = 0 (3)
⇒ VE = VBB1 – RbIBQ1 – VBE1 = 1 – 104.1,15.10-5 – 0,7 =0,185V Thay vaøo (2) ta ñöôïc:
VCE1 = VCE2 = 6 – 103.1,15. 10-3 – 0,185 = 4,665V ≈ 4,67V
Ta coù VE1 = VCE3 + RE3.IEQ3 - VEE (4)
Suy ra VCE3 = VEE + VE1 – RE3IEQ3
= 3 + 0,185 – 103.2,3.10-3 = 0,885V
VRE6 = VCC – RC2ICQ2 – VBE4 - VBE5 - VBE6
= 6 – 103.1,15.10-3 – 2,1 = 2,75V VRE6 75 , 2 I = = = 275mA EQ6 R 10 E6
VCE6 = VCC – VRE6 = 6 – 2,75 = 3,25V
VCE5 = VCE6 – VBE6 = 3,25 – 0,7 = 2,55V Moät soá baøi taäp maãu 32
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
VCE4 = VCE5 – VBE5 = 2,55 – 0,7 = 1,85V −3 − 25.10 25.10 3 h = 4 , 1 h . = 4 , 1 .100. = Ω 3043 1 ie 1 fe −3 − 15 , 1 .10 15 , 1 .10 3 I I I EQ6 EQ5 = = 75 , 2 mA ; I = = 75 , 2 .10−5 A EQ5 h EQ4 h fe6 fe5 −3 − 25.10 25.10 3 h = 4 , 1 h . = 4 , 1 .100. = 12 72 , Ω ie6 fe6 − IEQ6 275.10 3
hie5 = 1272Ω; hie4 = 127.200Ω b- Cheá ñoä AC hie4 hie5.hfe4 hie5.hfe4.hfe5 ib1 h h iC2 ie1 3043 ie2 3043 ib4 127,2K 127,2K 127,2K R ib2 b1 Rb2 h RC2 fe2ib2 R’ 10K E6 V 10K 1K L i 100ib2 i Zi ' 3 R Z = R 1 h R .10 10 o E6 E6 ( + fe ) ≈ 6 ≈ 7 Ω E6 V V i i L L b4 b2 A = = . . (1) T i i i i i b4 b2 i VL = 'R ≈ 7 10 Ω (2) E6 ib4 i i i R h . b4 b4 C2 C2 fe2 = . = − ' i i i R + 3h + R b2 C2 b2 C2 ie4 E6 (3) 3 2 2 10 .10 10 −4 = − = − = 96 − 3 , .10 3 3 7 4 10 + 6 , 381 .10 +10 1+ 6 , 381 +10 i i R b2 1 b 1 b i = − i = − R + 2h + R i i b1 1 ie b2 (4) 104 = − = − 485 , 0 104 + 086 , 6 10 . 3 −104
Thay (2), (3), (4) vaøo (1) ta coù
AT = 107.(-96,3).10-4.(-0,485) = 46728V/A = 46,7V/mA 3h ie4 =0,381 RE6 Rc2 h3 ≈10 fe h3fe Z Z o
i = Rb1//[2hie1 + Rb2] ≈ 6,15KΩ  R 3h  Z = R // o E6  C2 + ie4  = 10 //( 382 , 0 ) ≈ 37 , 0 Ω 3 3  h h fe fe  Moät soá baøi taäp maãu 33
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Chöông VII: MAÏCH KHUEÁCH ÑAÏI HOÀI TIEÁP. I.
Hoài tieáp aùp, sai leäch doøng. 1) Baøi 7-4 +V CC RC1 RC2 2K 2K T iL 1 R L R VL E21 100 1K ii R f 10K RE22 V 1 1K h  T ? = K 1 Ω = GT   ie ; KL i A L ?  h = 40 = = fe  i  ii
Ñaây laø daïng hoài tieáp aùp, sai leäch doøng. RE21(hfe2+1) i ib2 h i b1 ic1 C2 ie2 1K 41K Rf h R R C1 E22(hfe2+1) RC2 + V RL i ie1 1 41K i hfe1ib1 2K 2K V’ 100 1 40i - 40i b2 b1 Zi Zo
a- Tính ñoä lôïi doøng T: cho ii = 0 V V i i 1 1 b2 b1 T = = . . (1) ' ' V i = 0 i i V 1 i b2 1 b 1 V 1 = R 1+ h = 41 10 . (2) E22 ( fe ) 3 2 ib2 i i i R h . b2 b2 = . 1 C 1 C 1 fe i i i = − R + h + R 1+ h + R 1+ h 1 b 1 C 1 b 1 C ie2 E21 ( fe2 ) E22 ( fe2 ) (3) 2.103.40 80 = − = − = − 941 , 0 2.103 +103 + 41.103 + 41.103 85 ' i 1 V 1 1 1 b 1 −6 = . = = = 91.10 (4) ' ' 4 3 V V R + h R + h 10 +10 1 1 f 1 ie f 1 ie Moät soá baøi taäp maãu 34
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Thay (2), (3), (4) vaøo (1) ta coù:
T = 41.103.(-0,941).91.10-6 = -3,51 b- i Tính L A = cho V’1 = 0 i ii i i i i L L b2 1 b A = = . . (1) i i i i i i b2 1 b i i i i R 3 L L C2 C2 2.10 = . = − h . = − .40 = − 6 , 39 (2) i i i R + R fe2 b2 C2 b2 C2 L 2.103 +10 i b2 = − 941 , 0
(nhö (3) ôû phaàn treân) (3) i 1b 4 i R 10 1 b f −2 = = = 91.10 (4) 4 3 i R + h 10 + 10 i f 1 ie
Thay (2), (3), (4) vaøo (1) ta coù:
Ai = (-39,6).(-0,941).91.10-2 = 33,9 ≈ 34 c- Tính Aif, Zif, Zof. A 34 A i = = = 54 , 7 if 1− T 1+ 51 , 3
Zi = Rf//hie1 = 104//103 ≈ 910Ω Zi 910 Z = = = 202Ω if 1− T 1+ 51 , 3 Zo = RC2 = 2KΩ Zo 2 10 . 3 Z = = = Ω 443 of 1− T 1+ 51 , 3 2) Baøi 7-11 +VCC RC 2K Rf = Rb =10K C iL R L RE C ii 100  i A L ?  h = 100  = = i i  fe i GT  h = 10Ω ; KL Z ;Z ib  i o    C → ∞ T ?  =  Moät soá baøi taäp maãu 35
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
hie = hib.hfe = 10.100 = 1KΩ ib ic i L Rf hie1 RC Rf + R V ii h L feib L V’ 1K 10K L 100ib - Zo
a- Ñoä lôïi voøng T: cho ii = 0 V V i L L b T = = . (1) ' ' V i = 0 i V L i b L 3 3 2 V V i R 10 .10 10 . L L C C 4 = . = −R . h . = − = 5 − .10 (2) L fe 3 3 i i i R + R 10 +10 b C b C L ' i 1 V 1 1 b L −6 = . = = = 91.10 (3) ' ' 4 3 V V R + h R + h 10 + 10 L L f ie f ie
Thay (2), (3) vaøo (1) ta coù: T =(-5.104).91.10-6 = -4,55 b- Tính Ai, Zi, Zo. i i i L L b A = = . (1) i ' i V = 0 i i i L b i i i i R 3 L L C C 10 = . = − h . = − .100 = −50 (2) i i i R + R fe b C b C L 103 +10 4 i R 10 b f −2 = = = 91.10 (3) 4 3 i R + h 10 +10 i f ie
Thay (2), (3) vaøo (1) ta coù: Ai = (-50).91.10-2 = -45,45
Zi = Rf//hie = 104//103 = 910Ω Zo = RC = 103Ω = 1KΩ c- Tính Aif, Zif, Zof. A 50 A i = = − = − 2 , 8 if 1− T 1+ 55 , 4 Zi 910 Z = = = 164Ω if 1− T 1+ 55 , 4 Zo 104 Z = = = 180Ω of 1− T 1+ 55 , 4 Moät soá baøi taäp maãu 36
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
II. Hoài tieáp aùp, sai leäch aùp: 1) Baøi 7-10 +VCC R R C2 C1 R22 R 2K 21 1K C 10K 8K VL R 12 R 10K E2 C R 11 RE1 1K i 1K i 100 Rf =10K  i A L ?  h = 50  = = i i  fe i GT  h = 50Ω ; KL Z ; Z ib  i o    C → ∞ T ?  =  ib1 h iC1 i ie1 2,5K ib2 C2 R f.hfe1 RE1hfe1 R R 5.105 b1 R h f 5K + h ie2 RC1 b2 10K R fe1ib1 ii 2,5K C2 890 5K hfe2ib2 V’L 50i 1K 2K b1 - 50i b2 Zo
a- Tính ñoä lôïi voøng T (cho ii = 0) V V i i L L b2 1 b T = = . . (1) ' ' V i = 0 i i V L i b2 1 b L V V i R R . L L C2 f C2 = . = − h . fe2 i i i R + R b2 C2 b2 f C2 (2) 4 3 10 .2.10 3 3 = − .50 = − 67 , 1 .10 .50 = − 5 , 83 .10 4 3 10 + 2.10 i i i R // R b2 b2 = . 1 C 1 C b2 = − h i i i 1 b 1 C 1 b (R // R 1 C b2 ) + h 1 fe ie2 (3) 83 , 0 .103.50 = − = 12 − 46 , 83 , 0 .103 + 5 , 2 .103 i − R h . 1 b1 1 E fe1 = . ' V R + h + h R . R h . + R' L b1 1 ie 1 fe 1 E f 1 fe (4) 3 − 5.10 1 −6 = . = − 2 , 1 10 . 3 3 5 3 890 + 5 , 2 .10 + 5.10 5.10 + 2.10 Moät soá baøi taäp maãu 37
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Thay (2), (3), (4) vaøo (1) ta coù:
T = (-83,5.103).(-12,46).(1,2.10-6)= -1,25 b- Tính AT, Zi, Zo. V V i i L L b2 1 b A = = . . (1) T i i i i i b2 1 b i i i
L vaø b2 tính nhö treân theo coâng thöùc (2), (3) i i b2 1 b i R b1 1 b 890 = = = 107 , 0 (4) i R + h i b1 1 ie + (R + R 1 E f )h 890 + 5 , 2 10 . 3 1 fe + 95 , 4 .103
Thay (2), (3), (4) vaøo (1) ta coù:
Ai = (-83,5.103).(-12,46).(0,107) = 111.103V/A = 111V/mA
Zi = Rb1//[hie1 + (RE11//Rf)(1 + hfe)] = 890 //[2500 + 4950] = 795Ω Zo = Rf = 10KΩ c- Tính AVf, Zof, Zif. A 111 10 . 3 T 3 V V A = = = 49 10 . = 49 Tf 1− T 1+ 25 , 1 A mA Z = Z if i (1 − T) = 1 ( 795 + ) 25 , 1 = 1788Ω Zo 104 Z = = = 4444Ω of 1− T 1+ 25 , 1 2) Baøi 7-12 +V CC R R 21 RC1 R22 C2 10K 500 10K 500 ri 1K C RE21 VL 22 RE11 R C + 12 R 11 22 1K R V E22 i 1K C - 82 R E12 C 82 R f =1K  h = 20 A = ?  fe V GT  h = 50Ω ; KL Z ; Z ib  i o    C → ∞  T = ? Moät soá baøi taäp maãu 38
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I Rf(hfe1+1) ii r RC2 500 i 1 K ib1 hie1 1050 21K iC1 ib2 h i ie2 1050 C2 + h 20i fe1ib1 b2 V Rb1 + R 20i C1 RCb2 i b1 - 910 V’ 500 910 L - Z R i E11(1+hfe1) R Rf 1050 Z o 462 E21(1+hfe2)=462Ω
a- Tính ñoä lôïi voøng T (cho Vi = 0) ib1 hie1 1050 ri R R Rf(hfe1+1) b1 E11(1+hfe1) V’L 1K 462 21K 910 Rf(1+hfe1) V V i i L L b2 1 b T = = . . (1) ' ' V i = 0 i i V L i b2 1 b L V V i R R . L L = . C2 f C2 = − h . (2) fe2 = −(103 // 500) 20 . = 6667 i i i R + R − b2 C2 b2 f C2 i i i R // R b2 b2 = . 1 C 1 C b2 = − h 1 fe i i i 1 b 1 C 1 b (R // R 1 C b2 ) + h + R ie2 E21 (1 + h fe2 ) (3) 323.20 6460 = − = − = − 52 , 3 323 +1050 + 462 1835 , i 1 V R // R 1+ h 1 b L ( 11 E f )( 1 fe ) = − . . ' , V V R 1+ h R // R 1+ h + h + r // R L L f ( 1 fe ) ( 11 E f )( 1 fe ) 1 ie ( i 1 b ) (4) −3 1 452 452.10 −6 = − . = − = − 88 , 10 .10 3 21.10 452 +1050 + 476 4 , 41546 4 ,
Thay (2), (3), (4) vaøo (1) ta coù:
T = (-6667).(-3,52).(-10,88.10-6)= -0,255 b- Tính AV, Zi, Zo. V V i i L L b2 1 b A = = . . (1) V V i i V i b2 b1 i V i
L vaø b2 tính nhö treân theo coâng thöùc (2), (3) i i b2 1 b i 1 V r // R b1 i i 1 b = . . V V r r // R + h + R // R 1+ h i i i ( i 1 b ) 1 ie ( 11 E f )( 1 fe ) (4) −3 1 476 4 , 476 4 , .10 −5 = . = = 24.10 3 10 476 4 , +1050 + 452 4 , 1978 Moät soá baøi taäp maãu 39
Khoa Ñieän - Ñieän töû Vieãn thoâng Maïch Ñieän Töû I
Thay (2), (3), (4) vaøo (1) ta coù:
AV = (-6667)(-3,52).24.10-5 = 5,63
Zi = Rb//[hie1 + (RE11//Rf)(1 + hfe1)] = 103 //1502 ≈ 600Ω Zo = Rf = 1000Ω c- Tính AVf, Zif, Zof. A 63 , 5 A V = = = 486 , 4 Vf 1− T 1+ 0 255 , Z = Z if i (1 − T) = 600 1 ( + 255 , 0 ) = 753Ω Zo 1000 Z = = = 797Ω of 1− T 1+ 255 , 0 Moät soá baøi taäp maãu 40