Bài tập mệnh đề và tập hợp – Diệp Tuân

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 1-Mệnh Đề và Mệnh Đề Chứa Biến

1

Lớp Toán Thầy -Diệp Tuân Tel: 0935.660.880

1

MỆNH ĐỀ – TẬP HỢP

A – L THUY󰈸T

1. Định nghĩa.

Mệnh đề là một câu khẳng định đúng hoặc sai.

Một mệnh đề không thể vừa đúng hoặc vừa sai.

Ví dụ 1: Hà Nội là thủ đô của nước Việt Nam.

Lời giải

....................................................................................................................................................................................................................

Ví dụ 2: Hãy đi nhanh lên;

Lời giải

....................................................................................................................................................................................................................

2. Mệnh đề phủ định.

Cho mệnh đề

P

.

Mệnh đề

''

Không phải

P

''

gọi là mệnh đề phủ định của

P

.

Ký hiệu là

P

.

Nhận xét. Nếu

P

đúng thì

P

sai, nếu

P

sai thì

P

đúng.

Ví dụ 3:

12

là số nguyên tố.

Lời giải

....................................................................................................................................................................................................................

3. Mệnh đề kéo theo và mệnh đề đảo.

Cho hai mệnh đề

P

và

Q

.

Mệnh đề "nếu

P

thì

Q

" gọi là mệnh đề kéo theo.

Ký hiệu là

PQ

.

Nhận xét. Mệnh đề

PQ

chỉ sai khi

P

đúng

Q

sai.

Cho mệnh đề

PQ

. Khi đó mệnh đề

QP

gọi là mệnh đề đảo của

QP

Ví dụ 4: Cho tam giác

ABC

. Xét hai mệnh đề

P

:

''

Tam giác

ABC

cân

''

.

Q

:

''

Tam giác

ABC

có hai đường cao bằng nhau

''

Hãy phát biểu mệnh đề

PQ

và mệnh đề

QP

.

Lời giải.

....................................................................................................................................................................................................................

4. Mệnh đề tương đương.

Cho hai mệnh đề

P

và

Q

.

Mệnh đề "

P

nếu và chỉ nếu

Q

" gọi là mệnh đề tương đương.

§BI 1. MỆNH ĐỀ VÀ MỆNH ĐỀ CHỨA BIẾN

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 1-Mệnh Đề và Mệnh Đề Chứa Biến

2

Lớp Toán Thầy -Diệp Tuân Tel: 0935.660.880

Ký hiệu là

PQ

.

Mệnh đề

PQ

đúng khi cả

PQ

và

Q PA

cùng đúng.

Chú ý: "Tương đương" còn được gọi bằng các thuật ngữ khác như

"điều kiện cần và đủ

", "khi

và chỉ khi", "nếu và chỉ nếu".

Ví dụ 5. Cho tam giác

ABC

với trung tuyến

AM

.

Xét hai mệnh đề:

:"P

Tam giác

ABC

vuông tại

A

''

Q :"

Trung tuyến

AM

bằng một nữa cạnh

BC

"

,

Hãy phát biểu mệnh đề

PQ

. Mệnh đề này đúng hay sai.

Hãy phát biểu mệnh đề

QP

.

Mệnh đề này đúng hay sai. Hãy phát biểu mệnh đề

QP

. Mệnh đề này đúng hay sai.

Lời giải

....................................................................................................................................................................................................................

5. Mệnh đề chứa biến.

Mệnh đề chứa biến là một câu khẳng định chứa biến nhận giá trị trong một tập

X

nào đó mà

với mỗi giá trị của biến thuộc

X

ta được một mệnh đề.

Ví dụ 6:

 

:Pn

"

n

chia hết cho

5

" với

n

là số tự nhiên.

 

;P x y

:"

25xy

" Với

,xy

là số thực.

Lời giải

....................................................................................................................................................................................................................

6. Các kí hiệu



,



và mệnh đề phủ định của mệnh đề có chứa kí hiệu



,



.

a. Kí hiệu



: đọc là với mọi.

Cho mệnh đề chứa biến

 

Px

với

xX

. Khi đó khẳng định mệnh đề:

"Với mọi

x

thuộc

X

,

 

Px

đúng "

hay

"

 

Px

đúng với mọi

x

thuộc

X

"

Được ký hiệu là

 

'' , ''x X P x

Mệnh đề này đúng nếu với

0

x

bất kỳ thuộc

X

,

 

0

Px

là mệnh đề đúng.

Mệnh đề này sai nếu có một

0

x

thuộc

X

sao cho

 

0

Px

là mệnh đề sai.

Ví dụ 7. Cho mệnh đề

 

2

:'' , 4 5 0''    P x x x x

. Xét tính đúng sai của mệnh đề sau và nêu

mệnh đề phủ định của nó.

Lời giải

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 1-Mệnh Đề và Mệnh Đề Chứa Biến

3

Lớp Toán Thầy -Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

b. Kí hiệu



: đọc là tồn tại

Cho mệnh đề chứa biến

 

Px

với

xX

. Khi đó khẳng định mệnh đề:

"Tồn tại

x

thuộc

X

,

 

Px

đúng "

Được ký hiệu là

 

'' , ''x X P x

Mệnh đề này đúng nếu có

0

x

thuộc

X

,

 

0

Px

là mệnh đề đúng.

Ví dụ 8. Cho mệnh đề

 

2

:'' , 3''  P x x x

. Xét tính đúng sai của mệnh đề sau và nêu mệnh đề

phủ định của nó.

Lời giải.

....................................................................................................................................................................................................................

c. Mối quan hệ hai kí hiệu.

Phủ định của mệnh đề

 

'' , ''x X P x

là mệnh đề

'' , ( )''x X P x

.

Phủ định của mệnh đề

 

'' , ''x X P x

là mệnh đề

'' , ( )''x X P x

.

B. PHÂN DẠNG VÀ BÀI TẬP MINH HỌA

Dạng 1. MỆNH ĐỀ V TÍNH ĐÚNG SAI CỦA MỆNH ĐỀ

1. Phương pháp:

Khẳng định đúng là mệnh đề đúng, khẳng định sai là mệnh đề sai.

Câu không phải là câu khẳng định hoặc câu khẳng định mà không có tính đúng-sai đều

không phải là mệnh đề.

Tính đúng-sai có thể chưa xác định hoặc không biết nhưng chắc chắn hoặc đúng hoặc sai

cũng là mệnh đề.

Không có mệnh đề vừa đúng vừa sai hoặc không đúng cũng không sai.

Mệnh đề đúng, mệnh đề sai



P

đúng

 P

sai;



P

sai

 P

đúng



 

PQ

chỉ sai khi

P

đúng và

Q

sai.

Đặc biệt:

 Nếu

P

sai thì

 

PQ

luôn đúng dù

Q

đúng hoặc sai.

 Nếu

Q

đúng thì

 

PQ

luôn đúng dù

P

đúng hoặc sai.



 

PQ

chỉ đúng khi

P

và

Q

cùng đúng hoặc cùng sai.

Mệnh đề chứa dấu

,

.



 

,x X P x

đúng



mọi

 

00

,x X P x

đúng.



 

,x X P x

sai



có

 

00

,x X P x

sai.



 

,x X P x

đúng



có

 

00

,x X P x

đúng.



 

,x X P x

sai



mọi

 

00

,x X P x

sai.

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 1-Mệnh Đề và Mệnh Đề Chứa Biến

4

Lớp Toán Thầy -Diệp Tuân Tel: 0935.660.880

2. Bài tập minh họa.

Bài 1. Các câu sau đây, câu nào là mệnh đề, câu nào không phải là mệnh đề ? Nếu là mệnh đề hay

cho biết mệnh đề đó đúng hay sai.

a). Không được đi lối này! b). Bây giờ là mấy giờ ?

c). 7 không là số nguyên tố. d).

5

là số vô tỉ.

Lời giải

....................................................................................................................................................................................................................

Bài 2. Các câu sau đây, câu nào là mệnh đề, câu nào không phải là mệnh đề ? Nếu là mệnh đề hãy

cho biết mệnh đề đó đúng hay sai.

a). Số



có lớn hơn

3

hay không ?

b). Hai tam giác bằng nhau khi và chỉ khi chúng có diện tích bằng nhau.

c). Một tứ giác là hình thoi khi và chỉ khi nó có hai đường chéo vuông góc với nhau.

d). Phương trình

2

2015 2016 0  xx

vô nghiệm.

Lời giải

....................................................................................................................................................................................................................

Bài 3. Cho tam giác

ABC

. Xét hai mệnh đề

:P

''

tam giác

ABC

vuông

''

và

2 2 2

:" "Q AB AC BC

. Phát biểu và cho biết mệnh đề sau đúng hay sai

a).

PQ

. b).

QP

.

Lời giải

....................................................................................................................................................................................................................

Bài 4. Cho tam giác

ABC

. Lập mênh đề

PQ

và mệnh đề đảo của nó, rồi xét tính đúng sai của

chúng khi

a).

P

:

''

Góc

A

bằng

0

90

''

và

Q

:

''

Cạnh

BC

lớn nhất

''

.

b).

P

:

''

AB

''

và

Q

:

''

Tam giác

ABC

cân

''

.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 1-Mệnh Đề và Mệnh Đề Chứa Biến

5

Lớp Toán Thầy -Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Bài 5. Phát biểu mệnh đề

PQ

và phát biểu mệnh đề đảo, xét tính đúng sai của nó

a).

:P

"Tứ giác

ABCD

là hình chữ nhật" và

:Q

"Tứ giác

ABCD

có hai đường thẳng

AC

và

BD

vuông góc với nhau".

b).

: " 3 2"  P

và

   

33

: " 3 2 "  Q

.

c).

:P

"Tam giác

ABC

có

A B C

" và

:Q

"Tam giác

ABC

có

2 2 2

BC AB AC

".

d).

:P

"Tố Hữu là nhà Toán học lớn của Việt Nam" và

:Q

"Évariste Galois là nhà Thơ lỗi lạc

của Thế giới ".

Lời giải

....................................................................................................................................................................................................................

Bài 6. Phát biểu mệnh đề

PQ

và phát biểu mệnh đề đảo, xét tính đúng sai của nó

a).

:P

"Tứ giác

ABCD

là hình thoi" và

:Q

"Tứ giác

ABCD

AC

và

BD

cắt nhau tại trung

điểm mỗi đường".

b).

: "2 9"P

và

: "4 3"Q

.

c).

:P

"Tam giác

ABC

vuông cân tại

A

" và

:Q

"Tam giác

ABC

có

2AB

".

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 1-Mệnh Đề và Mệnh Đề Chứa Biến

6

Lớp Toán Thầy -Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Bài 7. Phát biểu mệnh đề

PQ

bằng hai cách và và xét tính đúng sai của nó

a).

:P

"Tứ giác

ABCD

là hình thoi" và

:Q

"Tứ giác

ABCD

là hình bình hành có hai đường

chéo vuông góc với nhau

''

.

b).

:P

"Bất phương trình

2

31xx

có nghiệm" và

:Q

   

2

'' 1 3. 1 1''   

.

Lời giải

....................................................................................................................................................................................................................

Bài 8. Lập mệnh đề kéo theo và mệnh đề tương đương của hai mệnh đề sau đây và cho biết tính

đúng, sai của chúng

:P

''

Điểm

M

nằm trên phân giác của góc

Oxy

''

và

:Q

''

Điểm

M

cách đều hai cạnh

Ox

,

''Oy

Lời giải

....................................................................................................................................................................................................................

Bài 9. Phát biểu hai mệnh đề sau bằng hai cách và và xét tính đúng sai của nó

a). Cho tứ giác

ABCD

.

Xét hai mệnh đề

:P

''

Tứ giác

ABCD

là hình vuông" và

:Q

''

Tứ giác

ABCD

là hình chữ

nhật có hai đường chéo bằng vuông góc với nhau

''

.

b).

:P

"Bất phương trình

2

3 1 0  xx

có nghiệm" và

:Q

"Bất PT

2

3 1 0  xx

vô nghiệm".

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 1-Mệnh Đề và Mệnh Đề Chứa Biến

7

Lớp Toán Thầy -Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

3. Câu hỏi trắc nghiệm

Mức độ 1. Nhận biết

Câu 1. Trong các câu sau, câu nào không phải là mệnh đề?

A. Buồn ngủ quá!

B. Hình thoi có hai đường chéo vuông góc với nhau.

C. 8 là số chính phương.

D. Băng Cốc là thủ đô của Mianma.

Lời giải

....................................................................................................................................................................................................................

Câu 2. Trong các câu sau, có bao nhiêu câu là không phải là mệnh đề?

a) Huế là một thành phố của Việt Nam.

b) Sông Hương chảy ngang qua thành phố Huế.

c) Hãy trả lời câu hỏi này!

d)

5 19 24.

e)

6 81 25.

f) Bạn có rỗi tối nay không?

g)

2 11.x

A. 1. B. 2. C. 3. D. 4.

Lời giải

....................................................................................................................................................................................................................

Câu 3. Trong các câu sau, có bao nhiêu câu là mệnh đề?

a). Hãy đi nhanh lên!

b). Hà Nội là thủ đô của Việt Nam.

c).

5 7 4 15.  

d). Năm

2018

là năm nhuận.

A.

4.

B.

3.

C.

1.

D.

2.

Lời giải

....................................................................................................................................................................................................................

Câu 4. Trong các câu sau, có bao nhiêu câu là mệnh đề?

a). Cố lên, sắp đói rồi!

b). Số 15 là số nguyên tố.

c). Tổng các góc của một tam giác là

180 .

d).

x

là số nguyên dương.

A.

3.

B.

2.

C.

4.

D.

1.

Lời giải

....................................................................................................................................................................................................................

Câu 5. Trong các câu sau, câu nào là mệnh đề?

A. Đi ngủ đi! B. Trung Quốc là nước đông dân nhất thế giới.

C. Bạn học trường nào? D. Không được làm việc riêng trong giờ học.

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 1-Mệnh Đề và Mệnh Đề Chứa Biến

8

Lớp Toán Thầy -Diệp Tuân Tel: 0935.660.880

Lời giải

....................................................................................................................................................................................................................

Câu 6. Trong các mệnh đề sau, mệnh đề nào là mệnh đề đúng?

A. Tổng của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn.

B. Tích của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn.

C. Tổng của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ.

D. Tích của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ.

Lời giải

....................................................................................................................................................................................................................

Câu 7. Trong các câu sau, câu nào là mệnh đề đúng?

A. Nếu

ab

thì

22

.ab

B. Nếu

a

chia hết cho 9 thì

a

chia hết cho 3.

C. Nếu em chăm chỉ thì em thành công.

D. Nếu một tam giác có một góc bằng

60

thì tam giác đó đều.

Lời giải

....................................................................................................................................................................................................................

Câu 8. Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?

A.

2

2 4.



    

B.

2

4 16.



  

C.

23 5 2 23 2.5.  

D.

23 5 2 23 2.5.    

Lời giải

....................................................................................................................................................................................................................

Câu 9. Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?

A. Hai tam giác bằng nhau khi và chỉ khi chúng đồng dạng và có một góc bằng nhau.

B. Một tứ giác là hình chữ nhật khi và chỉ khi chúng có 3 góc vuông

.

C. Một tam giác là vuông khi và chỉ khi nó có một góc bằng tổng hai góc còn lại

.

D. Một tam giác là đều khi và chỉ khi chúng có hai đường trung tuyến bằng nhau và có một

góc bằng

60 .

Lời giải

....................................................................................................................................................................................................................

Câu 10. Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?

A. Nếu số nguyên

n

có chữ số tận cùng là

5

thì số nguyên

n

chia hết cho

5.

B. Nếu tứ giác

ABCD

có hai đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác

ABCD

là hình bình hành.

C. Nếu tứ giác

ABCD

là hình chữ nhật thì tứ giác

ABCD

có hai đường chéo bằng nhau.

D. Nếu tứ giác

ABCD

là hình thoi thì tứ giác

ABCD

có hai đường chéo vuông góc với nhau.

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 1-Mệnh Đề và Mệnh Đề Chứa Biến

9

Lớp Toán Thầy -Diệp Tuân Tel: 0935.660.880

Lời giải

....................................................................................................................................................................................................................

Câu 11. Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?

A. Nếu số nguyên

n

có tổng các chữ số bằng

9

thì số tự nhiên

n

chia hết cho

3.

B. Nếu

xy

thì

22

.xy

C. Nếu

xy

thì

. . .t x t y

D. Nếu

xy

thì

33

.xy

Lời giải

....................................................................................................................................................................................................................

Câu 12. Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?

A.

"ABC

là tam giác đều



Tam giác

ABC

cân

".

B.

"ABC

là tam giác đều



Tam giác

ABC

cân và có một góc

60 ".

C.

"ABC

là tam giác đều



ABC

là tam giác có ba cạnh bằng nhau

".

D.

"ABC

là tam giác đều



Tam giác

ABC

có hai góc bằng

60 ".

Lời giải

....................................................................................................................................................................................................................

Câu 13. Phát biểu nào sau đây là một mệnh đề?

A. Mùa thu Hà Nội đẹp quá! B. Bạn có đi học không?

C. Đề thi môn Toán khó quá! D. Hà Nội là thủ đô của Việt Nam.

Lời giải

....................................................................................................................................................................................................................

Câu 14. Câu nào sau đây không là mệnh đề?

A. Tam giác đều là tam giác có ba cạnh bằng nhau.

B.

31

.

C.

4 5 1

.

D. Bạn học giỏi quá!

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 1-Mệnh Đề và Mệnh Đề Chứa Biến

10

Lớp Toán Thầy -Diệp Tuân Tel: 0935.660.880

Câu 15. Cho các phát biểu sau đây:

(I): “17 là số nguyên tố”

(II): “Tam giác vuông có một đường trung tuyến bằng nửa cạnh huyền”

(III): “Các em C14 hãy cố gắng học tập thật tốt nhé !”

(IV): “Mọi hình chữ nhật đều nội tiếp được đường tròn”

Hỏi có bao nhiêu phát biểu là một đề?

A.

4

. B.

3

. C.

2

. D.

1

Lời giải

....................................................................................................................................................................................................................

Câu 16. Cho các câu sau đây:

(I): “Phan-xi-păng là ngọn núi cao nhất Việt Nam”.

(II): “

2

9,86





”.

(III): “Mệt quá!”.

(IV): “Chị ơi, mấy giờ rồi?”.

Hỏi có bao nhiêu câu là mệnh đề?

A.

1

. B.

3

. C.

4

. D.

2

Lời giải

....................................................................................................................................................................................................................

Câu 17. Câu nào trong các câu sau không phải là mệnh đề?

A.



có phải là một số vô tỷ không?. B.

2 2 5

.

C.

2

là một số hữu tỷ. D.

4

2



Lời giải

....................................................................................................................................................................................................................

Câu 18.Trong các câu sau, có bao nhiêu câu là mệnh đề?

Hãy cố gắng học thật tốt!

Số

20

chia hết cho

6

.

Số

5

là số nguyên tố.

Số

x

là số chẵn.

A.

4

. B.

3

. C.

2

. D.

1

.

Lời giải

....................................................................................................................................................................................................................

Dạng 2. MỆNH ĐỀ CHỨA BI󰈸N

1. Phương pháp.

Mệnh đề chứa biến là một câu khẳng định chứa biến(

, ...xy

) nhận giá trị trong một tập

X

nào đó mà với mỗi giá trị của biến thuộc

X

ta được một mệnh đề.

Mệnh đề chưa biến có tính đúng sai phù thuộc vào biến số.

2. Bài tập minh họa.

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 1-Mệnh Đề và Mệnh Đề Chứa Biến

11

Lớp Toán Thầy -Diệp Tuân Tel: 0935.660.880

Bài 10. Cho mệnh đề chứa biến "

 

3

: P x x x

", xét tính đúng sai của các mệnh đề sau

a).

 

1P

. b).

1

3







P

.

c).

 

,x P x

. d).

 

,x P x

.

Lời giải

....................................................................................................................................................................................................................

Bài 11.

a). Với

n

, cho mệnh đề chứa biến

 

2

:" 2P n n

chia hết cho

4''

. Xét tính đúng sai của

mệnh đề

 

2015P

.

b). Xét tính đúng sai của mệnh đề

   

*

1

:'' , 1

2

  P n n n n

chia hết cho

11''

.

Lời giải

....................................................................................................................................................................................................................

Bài 12. Xét các mệnh đề chứa biến sau. Tìm một giá trị của biến để được mệnh đề đúng; mệnh đề

sai

a).

 

2

: " , 2 0"  P x x x x

. b).

 

:''Q n n

chia hết cho 3, với

n

".

Lời giải

....................................................................................................................................................................................................................

Bài 13. Dùng các kí hiệu để viết các câu sau

a). Tích của ba số tự nhiên liên tiếp chia hết cho sáu.

b). Với mọi số thực bình phương của là một số không âm.

c). Có một số nguyên mà bình phương của nó bằng chính nó.

d). Có một số hữu tỉ mà nghịch đảo của nó lớn hơn chính nó.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 1-Mệnh Đề và Mệnh Đề Chứa Biến

12

Lớp Toán Thầy -Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Bài 14. Xác định tính đúng - sai của các mệnh đề sau

a).

2

, 2 4     x x x

.

b).

2

, 2 4    x x x

.

c).

,,mn

m

và

n

là các số lẻ



22

mn

là số chẵn.

d).

2

, 4 2    x x x

.

Lời giải

....................................................................................................................................................................................................................

Bài 15. Xét tính đúng - sai của các mệnh đề sau

a).

a

,

2

2a

. b).

2

,1  nn

không chia hết cho

3

.

c).

33

,:      x y x y x y

. d).

, : 2     x y x y xy

.

Lời giải

....................................................................................................................................................................................................................

Bài 16. Cho số tự nhiên

n

. Xét hai mệnh đề chứa biến

 

:''A n n

là số chẵn

''

và

 

2

:''B n n

là số chẵn

''

.

a). Hãy phát biểu mệnh đề

   

A n B n

. Cho biết mệnh đề này đúng hay sai ?

b). Hãy phát biểu mệnh đề

   

'' , ''  n B n A n

.

c). Hãy phát biểu mệnh đề

   

'' , ''  n A n B n

.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 1-Mệnh Đề và Mệnh Đề Chứa Biến

13

Lớp Toán Thầy -Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Bài 17. Cho mệnh đề

:P

''

Với mọi số thực

x

, nếu

x

là số hữu tỉ thì

2x

là số hữu tỉ".

a). Dùng kí hiệu viết

P

và xác định tính đúng - sai của nó.

b.) Phát biểu mệnh đề đảo của

P

và chứng tỏ mệnh đề đó là đúng. Phát biểu mệnh đề dưới

dạng mệnh đề tương đương.

Lời giải

....................................................................................................................................................................................................................

Bài 18. Cho các mệnh đề sau

:''6A

là số nguyên tố

''

;

:"7 5"B

.

Phát biểu các mệnh đề

, ,   A B B A A B

.

Lời giải

....................................................................................................................................................................................................................

Bài 19. Tìm tất cả các cặp số

 

;xy

sao cho cả ba mệnh đề

, , P Q R

sau đây đều đúng

     

2 2 2

; :"2 9 0", ; :"2 81", :" ".     P x y x xy Q x y x y R x x

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 1-Mệnh Đề và Mệnh Đề Chứa Biến

14

Lớp Toán Thầy -Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

3. Câu hỏi trắc nghiệm

Mức độ 1. Nhận biết

Câu 19. Kí hiệu

X

là tập hợp các cầu thủ

x

trong đội tuyển bóng rổ,

 

Px

là mệnh đề chứa biến

''

x

cao trên

180 cm

''

. Mệnh đề

 

" , "x X P x

khẳng định rằng:

A. Mọi cầu thủ trong đội tuyển bóng rổ đều cao trên

180 .cm

B. Trong số các cầu thủ của đội tuyển bóng rổ có một số cầu thủ cao trên

180 .cm

C. Bất cứ ai cao trên

180 cm

đều là cầu thủ của đội tuyển bóng rổ.

D. Có một số người cao trên

180 cm

là cầu thủ của đội tuyển bóng rổ.

Lời giải

....................................................................................................................................................................................................................

Câu 20. Mệnh đề

2

" , 2"xx  

khẳng định rằng:

A. Bình phương của mỗi số thực bằng 2.

B. Có ít nhất một số thực mà bình phương của nó bằng 2.

C. Chỉ có một số thực mà bình phương của nó bằng 2.

D. Nếu

x

là một số thực thì

2

2.x 

Lời giải

....................................................................................................................................................................................................................

Câu 21. Trong các mệnh đề sau đây, mệnh đề nào đúng?

A. Không có số chẵn nào là số nguyên tố.

B.

2

, 0.xx   

C.

 

, 11 6n n n   

chia hết cho

11.

D. Phương trình

2

3 6 0x 

có nghiệm hữu tỷ.

Lời giải

....................................................................................................................................................................................................................

Câu 22. Trong các mệnh đề sau đây, mệnh đề nào sai?

A.

2

, 2 8 0.xx   

B.

 

2

, 11 2n n n   

chia hết cho

11.

C. Tồn tại số nguyên tố chia hết cho

5.

D.

 

2

,1nn  

chia hết cho

4.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 1-Mệnh Đề và Mệnh Đề Chứa Biến

15

Lớp Toán Thầy -Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Câu 23. Trong các mệnh đề sau đây, mệnh đề nào sai?

A.

2

, , 0.x y x y     

B.

2

, , 0.x y x y     

C.

2

, , 0.x y x y     

D.

2

, , 0.x y x y     

Lời giải

....................................................................................................................................................................................................................

Câu 24. Trong các mệnh đề sau đây, mệnh đề nào đúng?

A. Với mọi số thực

x

, nếu

2x 

thì

2

4.x 

B. Với mọi số thực

x

, nếu

2

4x 

thì

2.x 

C. Với mọi số thực

x

, nếu

2x 

thì

2

4.x 

D. Với mọi số thực

x

, nếu

2

4x 

thì

2.x 

Lời giải

....................................................................................................................................................................................................................

Câu 25. Trong các mệnh đề sau đây, mệnh đề nào đúng?

A.

2

,.x x x  

B.

2

,.x x x  

C.

, 1 1.x x x    

D.

2

,.x x x  

Lời giải

....................................................................................................................................................................................................................

Câu 26. Cho

x

là số thực, mệnh đề nào sau đây đúng?

A.

2

, 5 5x x x   

hoặc

5.x 

B.

2

, 5 5 5.x x x     

C.

2

, 5 5.x x x    

D.

2

, 5 5x x x   

hoặc

5.x 

Lời giải

....................................................................................................................................................................................................................

Câu 27. Mệnh đề nào sau đây đúng?

A.

2

,1xx



  

là bội số của

3.

B.

2

, 3.xx  

C.

, 2 1

x

x  

là số nguyên tố. D.

, 2 2.

x

xx   

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 1-Mệnh Đề và Mệnh Đề Chứa Biến

16

Lớp Toán Thầy -Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Câu 28. Cho mệnh đề chứa biến

 

2

:"3 5 "P x x x

với

x

là số thực.

Mệnh đề nào sau đây là đúng:

A.

 

3P

. B.

 

4P

. C.

 

1P

. D.

 

5P

Lời giải

....................................................................................................................................................................................................................

Câu 29. Mệnh đề nào dưới đây sai?

A.

 

1

1 2 ,

8

x x x  

. B.

2

15

2,

22

xx

x

   



.

C.

2

11

,

13

xx

x

xx







. D.

2

1

,

12

x





.

Lời giải

....................................................................................................................................................................................................................

Câu 30. Trong các mệnh đề sau, mệnh đề nào đúng?

A.

x

,

2

1x 



1x 

. B.

x

,

2

1x 



1x 

.

C.

x

,

1x 



2

1x 

. D.

x

,

1x 



2

1x 

Lời giải

....................................................................................................................................................................................................................

Câu 31. Trong các mệnh đề sau, mệnh đề nào đúng?

A.

62

là số hữu tỷ.

B. Phương trình

2

7 2 0xx  

có

2

nghiệm trái dấu.

C.

17

là số chẵn.

D. Phương trình

2

70xx  

có nghiệm.

Lời giải

....................................................................................................................................................................................................................

Câu 32. Cho định lí “Nếu hai tam giác bằng nhau thì diện tích chúng bằng nhau”.

Mệnh đề nào sau đây đúng?

A. Hai tam giác bằng nhau là điều kiện cần để diện tích chúng bằng nhau.

B. Hai tam giác bằng nhau là điều kiện cần và đủ để chúng có diện tích bằng nhau.

C. Hai tam giác có diện tích bằng nhau là điều kiện đủ để chúng bằng nhau.

D. Hai tam giác bằng nhau là điều kiện đủ để diện tích chúng bằng nhau.

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 1-Mệnh Đề và Mệnh Đề Chứa Biến

17

Lớp Toán Thầy -Diệp Tuân Tel: 0935.660.880

Lời giải

....................................................................................................................................................................................................................

Câu 33.Cho

PQ

là mệnh đề đúng. Khẳng định nào sau đây là sai?

A.

PQ

sai. B.

PQ

đúng. C.

QP

sai. D.

PQ

sai.

Lời giải

....................................................................................................................................................................................................................

Câu 34. Cho

P

là mệnh đề đúng,

Q

là mệnh đề sai, chọn mệnh đề đúng trong các mệnh đề sau.

A.

PP

. B.

PQ

. C.

PQ

. D.

QP

.

Lời giải

....................................................................................................................................................................................................................

Dạng 3. PHỦ ĐỊNH CỦA MỆNH ĐỀ

1. Phương pháp.

Phủ định của mệnh đề

P

là mệnh đề "không phải

P

".

 Tính chất

X

thành tính chất không

X

, và ngược lại.

 Quan hệ



thành quan hệ



, và ngược lại.

 Quan hệ



thành quan hệ



, và ngược lại.

 Quan hệ



thành quan hệ



, và ngược lại.

 Liên kết "và" thành liên kết "hoặc", và ngược lại.

Phủ định của mệnh đề có dấu

,

: đối nhau hai loại dấu

,

và phủ định thêm tính chất

 

Px



 

,x X P x

thành

 

,x X P x

.



 

,x X P x

thành

 

,x X P x

.

Mở rộng



 

, , ,   x X y Y P x y

thành

 

, , ,   x X y Y P x y

.



 

, , ,   x X y Y P x y

thành

 

, , ,   x X y Y P x y

.

Chú ý: Đôi khi xét tính đúng, sai của mệnh đề

P

phức tạp thì ta chuyển qua xét tính đúng sai

của mệnh đề phủ định

2. Bài tập minh họa.

Bài 20. Nêu mệnh đề phủ định của các mệnh đề sau và cho biết tính đúng sai của mệnh đề phủ

định đó

:A

"Hình thoi có hai đường chéo vuông góc với nhau";

:B

"Tổng hai cạnh của một tam giác nhỏ hơn cạnh còn lại";

:C

"Trong tam giác tổng ba góc không bằng 180

0

";

:D

"Tồn tại hình thang là hình vuông ".

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 1-Mệnh Đề và Mệnh Đề Chứa Biến

18

Lớp Toán Thầy -Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Bài 21. Nêu mệnh đề phủ định của các mệnh đề sau và cho biết tính đúng sai của mệnh đề phủ

định đó

:A

"6 là số nguyên tố";

:B

"

 

2

3 27

là số nguyên ";

:C

 

'' , 1  n n n

là một số chính phương

''

;

:D

42

'' , 1   n n n

là hợp số ".

Lời giải

....................................................................................................................................................................................................................

Bài 22. Nêu mệnh đề phủ định của các mệnh đề sau và cho biết tính đúng sai của mệnh đề phủ

định đó

:A

2

'' , 3  xn

chia hết cho

4''

;

:B

''x

,

x

chia hết cho

1''x

.

Lời giải

....................................................................................................................................................................................................................

Bài 23. Nếu mệnh đề phủ định của các mệnh đề sau và cho biết tính đúng sai của mệnh đề phủ

định đó

:A

"Phương trình

42

2 2 0  xx

có nghiệm";

:B

"Bất phương trình

2013

2030x

vô nghiệm";

:C

  

4 2 2 2

'' , 1 3 1 3 1 ''        x x x x x x x

;

:D

2

'' , 2 1 0''   qq

.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 1-Mệnh Đề và Mệnh Đề Chứa Biến

19

Lớp Toán Thầy -Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Bài 24. Nêu mệnh đề phủ định của các mệnh đề sau và cho biết tính đúng sai của mệnh đề phủ

định đó

A

:

32

'' , 1 0''    x x x

;

B

:

''

Tồn tại số thực

a

sao cho

1

1 2''

1

  



a

.

Lời giải

....................................................................................................................................................................................................................

Bài 25. Xét tính đúng sai của mệnh đề sau và nêu mệnh đề phủ định của nó

a).

 

2

:'' , 3''  P x x x

.

b).

 

*

:'' :2 3  

n

P n n

là một số nguyên tố

''

.

c).

 

2

:'' , 4 5 0''    P x x x x

.

d).

 

42

:'' , 2 2 0''     P x x x x x

.

Lời giải

....................................................................................................................................................................................................................

Bài 26. Hãy phát biểu mệnh đề kéo theo

PQ

,

QP

và xét tính đúng sai của mệnh đề này

a). Cho tứ giác

ABCD

và hai mệnh đề

:P

"Tổng hai góc đối của tứ giác lồi bằng 180

0

" và

:Q

"Tứ giác nội tiếp được đường tròn ".

b).

:P

"

2 3 1  

" và

:Q

"

 

2

2 3 1  

".

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 1-Mệnh Đề và Mệnh Đề Chứa Biến

20

Lớp Toán Thầy -Diệp Tuân Tel: 0935.660.880

3. Câu hỏi trắc nghiệm

Mức độ 1. Nhận biết

Câu 35. Mệnh đề nào sau đây là phủ định của mệnh đề

''

Mọi động vật đều di chuyển

''

?

A. Mọi động vật đều không di chuyển.

B. Mọi động vật đều đứng yên.

C. Có ít nhất một động vật không di chuyển.

D. Có ít nhất một động vật di chuyển.

Lời giải

....................................................................................................................................................................................................................

Câu 36. Phủ định của mệnh đề

''

Có ít nhất một số vô tỷ là số thập phân vô hạn tuần hoàn

''

là

mệnh đề nào sau đây?

A. Mọi số vô tỷ đều là số thập phân vô hạn tuần hoàn.

B. Có ít nhất một số vô tỷ là số thập phân vô hạn không tuần hoàn.

C. Mọi số vô tỷ đều là số thập phân vô hạn không tuần hoàn.

D. Mọi số vô tỷ đều là số thập phân tuần hoàn.

Lời giải

....................................................................................................................................................................................................................

Câu 37. Lập mệnh đề phủ định của mệnh đề: “ Số 6 chia hết cho 2 và 3”.

A. Số 6 chia hết cho 2 hoặc 3.

B. Số 6 không chia hết cho 2 và 3.

C. Số 6 không chia hết cho 2 hoặc 3.

D. Số 6 không chia hết cho 2 và chia hết cho 3.

Lời giải

....................................................................................................................................................................................................................

Câu 38. Viết mệnh đề phủ định

P

của mệnh đề

P

:

''

Tất cả các học sinh khối

10

của trường em

đều biết bơi

''

.

A.

P

:

''

Tất cả các học sinh khối

10

trường em đều biết bơi

''

.

B.

P

:

''

Tất cả các học sinh khối

10

trường em có bạn không biết bơi

''

.

C.

P

:

''

Trong các học sinh khối

10

trường em có bạn biết bơi

''

.

D.

P

:

''

Tất cả các học sinh khối

10

trường em đều không biết bơi

''

.

Lời giải

....................................................................................................................................................................................................................

Câu 39. Cho mệnh đề: “

2

, 3 5 0x x x    

”. Mệnh đề phủ định của mệnh đề trên là

A.

2

, 3 5 0x x x    

. B.

2

, 3 5 0x x x    

.

C.

2

, 3 5 0x x x    

. D.

2

, 3 5 0x x x    

.

Lời giải

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 1-Mệnh Đề và Mệnh Đề Chứa Biến

21

Lớp Toán Thầy -Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Câu 40. Cho mệnh đề “Có một học sinh trong lớp C4 không chấp hành luật giao thông”. Mệnh đề

phủ định của mệnh đề này là

A. Không có học sinh nào trong lớp C4 chấp hành luật giao thông.

B. Mọi học sinh trong lớp C4 đều chấp hành luật giao thông.

C. Có một học sinh trong lớp C4 chấp hành luật giao thông.

D. Mọi học sinh trong lớp C4 không chấp hành luật giao thông.

Lời giải

....................................................................................................................................................................................................................

Câu 41. Cho mệnh đề: “ Có một học sinh trong lớp 10A không thích học môn Toán”. Mệnh đề

phủ định của mệnh đề này là:

A. “ Mọi học sinh trong lớp 10A đều thích học môn Toán”.

B. “ Mọi học sinh trong lớp 10A đều không thích học môn Toán”.

C. “ Mọi học sinh trong lớp 10A đều thích học môn Văn”.

D. “ Có một học sinh trong lớp 10A thích học môn Toán”.

Lời giải

....................................................................................................................................................................................................................

Câu 42. Mệnh đề phủ định của mệnh đề “

2018

là số tự nhiên chẵn” là

A.

2018

là số chẵn. B.

2018

là số nguyên tố.

C.

2018

không là số tự nhiên chẵn. D.

2018

là số chính phương.

Lời giải

....................................................................................................................................................................................................................

Câu 43.Mệnh đề: “Mọi động vật đều di chuyển” có mệnh đề phủ định là

A. Có ít nhất một động vật di chuyển. B. Mọi động vật đều đứng yên.

C. Có ít nhất một động vật không di chuyển. D. Mọi động vật đều không di chuyển.

Lời giải

....................................................................................................................................................................................................................

Câu 44. Mệnh đề

 

2

:" , 7 0"P x x x x    

. Phủ định của mệnh đề

P

là

A.

2

, 7 0.x x x    

B.

2

, 7 0.x x x    

C.

2

, 7 0.x x x    

D.

2

, 7 0.x x x    

Lời giải

....................................................................................................................................................................................................................

Câu 45. Mệnh đề phủ định của mệnh đề

 

2

:" 3 1 0P x x x  

với mọi

"x

là

A. Tồn tại

x

sao cho

2

3 1 0.xx  

B. Tồn tại

x

sao cho

2

3 1 0.xx  

C. Tồn tại

x

sao cho

2

3 1 0.xx  

D. Tồn tại

x

sao cho

2

3 1 0.xx  

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 1-Mệnh Đề và Mệnh Đề Chứa Biến

22

Lớp Toán Thầy -Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Câu 46. Mệnh đề phủ định của mệnh đề

 

2

:" : 2 5P x x x x   

là số nguyên tố

"

là

A.

2

: 2 5x x x   

là hợp số. B.

2

: 2 5x x x   

là hợp số.

C.

2

: 2 5x x x   

là hợp số. D.

2

: 2 5x x x   

là số thực.

Lời giải

....................................................................................................................................................................................................................

Câu 47. Phủ định của mệnh đề

 

2

:" , 5 3 1"P x x x x   

là

A.

2

" , 5 3 1".x x x   

B.

2

" , 5 3 1".x x x   

C.

2

" , 5 3 1".x x x   

D.

2

" , 5 3 1".x x x   

Lời giải

....................................................................................................................................................................................................................

Câu 48. Cho mệnh đề

 

2

:" , 1 0"P x x x x    

. Mệnh đề phủ định của mệnh đề

 

Px

là

A.

2

" , 1 0"x x x    

. B.

2

" , 1 0"x x x    

.

C.

2

" , 1 0"x x x    

. D.

2

" , 1 0"x x x    

.

Lời giải

....................................................................................................................................................................................................................

Câu 49. Tìm mệnh đề phủ định của mệnh đề:

2

, 5 0x x x    

.

A.

2

, 5 0x x x    

. B.

2

, 5 0x x x    

.

C.

2

, 5 0x x x    

. D.

2

, 5 0x x x    

.

Lời giải

....................................................................................................................................................................................................................

Câu 50. Tìm mệnh đề phủ định của mệnh đề

2

" : "x x x  

.

A.

2

:x x x  

. B.

2

:x x x  

.

C.

2

:x x x  

. D.

2

:x x x  

.

Lời giải

....................................................................................................................................................................................................................

Câu 51. Cho

x

là số tự nhiên. Phủ định của mệnh đề “

x

chẵn,

2

xx

là số chẵn” là mệnh đề:

A.

x

lẻ,

2

xx

là số lẻ. B.

x

lẻ,

2

xx

là số chẵn.

C.

x

lẻ,

2

xx

là số lẻ. D.

x

chẵn,

2

xx

là số lẻ.

Lời giải

....................................................................................................................................................................................................................

Câu 52. Phủ định của mệnh đề

2

" :2 5 2 0"x x x    

là

A.

2

" :2 5 2 0"x x x    

. B.

2

" :2 5 2 0"x x x    

.

C.

2

" :2 5 2 0"x x x    

. D.

2

" :2 5 2 0"x x x    

.

Lời giải

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 1-Mệnh Đề và Mệnh Đề Chứa Biến

23

Lớp Toán Thầy -Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Câu 53. Tìm mệnh đề sai.

A.

2

" ; 2 3 0"x x x   

. B.

2

" ; "x x x

.

C.

2

" ; 5 6 0"x x x   

. D.

1

" ; "xx

x



.

Lời giải.

....................................................................................................................................................................................................................

Câu 54. Cho mệnh đề

2

“ , 7 0”    x x x

. Hỏi mệnh đề nào là mệnh đề phủ định của mệnh

đề trên?

A.

2

, 7 0    x x x

. B.

2

, 7 0    x x x

.

C.

2

, 7 0    x x x

. D.

2

, 7 0    x x x

.

Lời giải

....................................................................................................................................................................................................................

Câu 55. Mệnh đề nào sau là mệnh đề sai?

A.

2

:0xx  

. B.

2

:x x x  

C.

2

:n n n  

. D.

n

thì

2nn

.

Lời giải

....................................................................................................................................................................................................................

Câu 56. Chọn mệnh đề sai.

A. “

2

:0xx  

”. B. “

2

:n n n  

”.

C. “

:2n n n  

”. D. “

:1xx  

”.

Lời giải

....................................................................................................................................................................................................................

Câu 57. Cho mệnh đề:

x

;

2

20xa  

, với

a

là số thực cho trước.

Tìm

a

để mệnh đề đúng.

A.

2a 

. B.

2a 

. C.

2a 

. D.

2a 

.

Lời giải

....................................................................................................................................................................................................................

Câu 58. Mệnh đề phủ định của mệnh đề “

2

, 13 0x x x    

” là

A. “

2

, 13 0x x x    

”. B. “

2

, 13 0x x x    

”.

C. “

2

, 13 0x x x    

”. D. “

2

, 13 0x x x    

”.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 1-Mệnh Đề và Mệnh Đề Chứa Biến

24

Lớp Toán Thầy -Diệp Tuân Tel: 0935.660.880

Câu 59.Tìm mệnh đề phủ định của mệnh đề

2

:" ; 1 0"P x x x    

.

A.

2

:" ; 1 0"P x x x    

. B.

2

P:" ; 1 0"x x x    

.

C.

2

:" ; 1 0"P x x x    

. D.

2

:" ; 1 0"P x x x    

.

Lời giải

....................................................................................................................................................................................................................

Câu 60. Tìm mệnh đề đúng.

A.

2

" ; 3 0"xx  

B.

42

" ; 3x 2 0"xx   

C.

52

" ; x "xx  

. D.

 

2

" ; 2 1 1 4"nn   

Lời giải.

....................................................................................................................................................................................................................

Mức độ 2. Thông hiểu

Câu 61. Trong các mệnh đề sau, mệnh đề nào sai?

A.

n

,

2

11 2nn

chia hết cho

11

. B.

n

,

2

1n 

chia hết cho

4

.

C. Tồn tại số nguyên tố chia hết cho

5

. D.

n

,

2

2 8 0x 

.

Lời giải

....................................................................................................................................................................................................................

Câu 62. Trong các mệnh đề sau, mệnh đề nào đúng?

A.

x

,

 

2

11xx  

. B.

,3xx  

3x

.

C.

2

,1nn  

chia hết cho

4

. D.

2

,1nn  

không chia hết cho

3

.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 2. Áp Dụng Mệnh Đề Vào Suy Luận Toán Học

25

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

A. LÝ THUYẾT

I. Định lí và chứng minh định lí.

Trong toán học định lý là một mệnh đề đúng.

Nhiều định lý được phát biểu dưới dạng

   

'' , ''  x X P x Q x

với

   

, P x Q x

là các mệnh

đề chứa biến.

Để chứng minh một mệnh đề ta thường làm hai cách sau:

Cách 1: Chứng minh trực tiếp gồm các bước sau:

Lấy

xX

bất kỳ mà

 

Px

đúng.

Chứng minh

 

Qx

đúng (bằng suy luận và kiến thức toán học đã biết).

Ví dụ 1. Chứng minh với mọi

, xy

, ta có

a).

22

10   x xy y

. b).

22

4 4 6 3 4   x y x xy

.

Lời giải

....................................................................................................................................................................................................................

Ví dụ 2. Chứng minh rằng

a). Nếu

0ab

thì có ít nhất một số

a

hoặc

b

dương.

b). Nếu

a

và

b

là hai số dương thì

2a b ab

.

Lời giải

....................................................................................................................................................................................................................

II. Định lí đảo, điều kiện cần, điều kiện đủ, điều kiện cần và đủ.

1. Điều kiện cần, điều kiện đủ.

Cho định lí dưới dạng "

   

,   x X P x Q x

" (1). Khi đó

 

Px

là điều kiện đủ để có

 

Qx

.

 

Qx

là điều kiện cần để có

 

Px

.

§BI 2. ÁP DỤNG MỆNH ĐỀ VÀO SUY LUẬN TOÁN HỌC

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 2. Áp Dụng Mệnh Đề Vào Suy Luận Toán Học

26

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

Ví dụ 3. Sử dụng thuật ngữ

''

điều kiện cần

''

để phát biểu các định lí sau

a). Nếu một số tự nhiên chia hết cho 15 thì nó chia hết cho 5.

b). Nếu

ab

thì

22

ab

.

c). Trong mặt phẳng, nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ

ba thì hai đường thẳng ấy song song với nhau.

Lời giải

....................................................................................................................................................................................................................

Ví dụ 4. Sử dụng thuật ngữ

''

điều kiện đủ

''

để phát biểu các định lí sau

a). Nếu

a

và

b

là hai số hữu tỉ thì tổng

ab

là số hữu tỉ.

b). Nếu hai tam giác bằng nhau thì chúng có diện tích bằng nhau.

c). Nếu một số tự nhiên có chữ số tận cùng là chữ số 5 thì nó chia hết cho 5.

Lời giải

....................................................................................................................................................................................................................

2. Điều kiện cần và đủ.

Mệnh đề

   

,   x X Q x P x

đúng thì được gọi định lí đảo của định lí dạng (1).

Lúc đó (1) được gọi là định lý thuận và khi đó có thể gộp lại thành một định lí

   

'' , ''  x X Q x P x

.

Ta gọi là "

 

Px

là

điều kiện cần và đủ để

có

 

Qx

".

Ngoài ra còn nói "

 

Px

nếu và chỉ nếu

 

Qx

", "

 

Px

khi và chỉ khi

 

Qx

".

Ví dụ 5. Dùng thuật ngữ

''

điều kiện cần và đủ

''

để phát biểu định lí sau

a). Một tam giác là tam giác cân nếu và chỉ nếu nó có hai góc bằng nhau.

b). Tứ giác là hình bình hành khi và chỉ khi tứ giác có hai đường chéo cắt nhau tại trung điểm

của mỗi đường.

c). Tứ giác

MNPQ

là hình bình hành khi và chỉ khi

MN QP

.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 2. Áp Dụng Mệnh Đề Vào Suy Luận Toán Học

27

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

B. PHÂN DẠNG VÀ BÀI TẬP MINH HỌA.

Dạng 1. ĐIỀU KIỆN CẦN – ĐIỀU KIỆN ĐỦ

1. Phương pháp.

Cho định lí dưới dạng "

   

, x X P x Q x  

" (1). Khi đó

 

Px

là điều kiện đủ để có

 

Qx

.

 

Qx

là điều kiện cần để có

 

Px

.

Mệnh đề

   

, x X Q x P x  

đúng thì được gọi định lí đảo của định lí dạng (1).

Lúc đó (1) được gọi là định lý thuận và khi đó có thể gộp lại thành một định lí

   

'' , ''x X Q x P x  

.

Ta gọi là "

 

Px

là điều kiện cần và đủ để có

 

Qx

".

Ngoài ra còn nói "

 

Px

nếu và chỉ nếu

 

Qx

", "

 

Px

khi và chỉ khi

 

Qx

".

2. Bài tập minh họa.

Bài tập 1. Dùng thuật ngữ

''

điều kiện cần

''

để phát biểu các định lí sau

a). Nếu

MA MB

thì

M

thuộc đường tròn đường kính

AB

.

b).

0a

hoặc

0b

là điều kiện đủ để

22

0ab

.

Lời giải

....................................................................................................................................................................................................................

Bài tập 2. Cho định lí "Cho số tự nhiên

n

, nếu

5

n

chia hết cho 5 thì

n

chia hết cho 5". Định lí này

được viết dưới dạng

PQ

.

a). Hãy xác định các mệnh đề

P

và

Q

.

b). Phát biểu định lí trên bằng cách dùng thuật ngữ “điều kiện cần”.

c). Phát biểu định lí trên bằng cách dùng thuật ngữ “điều kiện đủ”.

d). Hãy phát biểu định lí đảo (nếu có) của định lí trên rồi dùng các thuật ngữ “điều kiện cần và

đủ” phát biểu gộp cả hai định lí thuận và đảo.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 2. Áp Dụng Mệnh Đề Vào Suy Luận Toán Học

28

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Bài tập 3. Phát biểu các định lý sau bằng cách sử dụng khái niệm "điều kiện cần", "điều kiện đủ"

a). Nếu trong mặt phẳng, hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì hai

đường thẳng đó song song với nhau.

b). Nếu số nguyên dương có chữ tận cùng bằng 5 thì chia hết cho 5.

c). Nếu tứ giác là hình thoi thì hai đường chéo vuông góc với nhau.

d). Nếu hai tam giác bằng nhau thì chúng có các góc tương ứng bằng nhau.

e). Nếu số nguyên dương

a

chia hết cho 24 thì chia hết cho 4 và 6.

Lời giải

....................................................................................................................................................................................................................

Bài tập 4. Sử dụng thuật ngữ “điều kiện cần”, “điều kiện đủ” để phát biểu định lí sau

a). Nếu một tứ giác là hình vuông thì nó có bốn cạnh bằng nhau.

Có định lí đảo của định lí trên không , vì sao ?

b). Nếu một tứ giác là hình thoi thì nó có hai đường chéo vuông góc.

Có định lí đảo của định lí trên không , vì sao ?

Lời giải

....................................................................................................................................................................................................................

Bài tập 5. Phát biểu các mệnh đề sau với thuật ngữ "điều kiện cần", "điều kiện đủ"

a). Nếu hai tam giác bằng nhau thì chúng có diện tích bằng nhau.

b). Nếu số nguyên dương chia hết cho 6 thì chia hết cho 3.

c). Nếu hình thang có hai đường chéo bằng nhau thì nó là hình thang cân.

d). Nếu tam giác

ABC

vuông tại

A

và

AH

là đường cao thì

2

.AB BC BH

.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 2. Áp Dụng Mệnh Đề Vào Suy Luận Toán Học

29

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Bài tập 6. Sử dụng thuật ngữ

''

điều kiện cần và đủ

''

để phát biểu các định lí sau

a). Một tứ giác nội tiếp được trong một đường tròn khi và chỉ khi tổng hai góc đối diện của nó

bằng

0

180

.

b).

xy

nếu và chỉ nếu

3

xy

.

c). Tam giác cân khi và chỉ khi có trung tuyến bằng nhau.

Lời giải

....................................................................................................................................................................................................................

Bài tập 7. Dùng thuật ngữ

''

điều kiện cần và đủ

''

để phát biểu định lí sau

a). Tam giác

ABC

vuông khi và chỉ khi

2 2 2

AB AC BC

.

b). Tứ giác là hình chữ nhật khi và chỉ khi nó có ba góc vuông.

c). Tứ giác là nội tiếp được trong đường tròn khi và chỉ khi nó có hai góc đối bù nhau.

d). Một số chia hết cho 2 khi và chỉ khi nó có chữ số tận cùng là số chẵn.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 2. Áp Dụng Mệnh Đề Vào Suy Luận Toán Học

30

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Dạng 2. PHƯƠNG PHÁP CHỨNG MINH MỆNH ĐỀ

1. Phương Pháp.

Chứng minh định lý

   

'' , ''x X P x Q x

Cách 1: Chứng minh trực tiếp gồm các bước sau:

Bước 1. Lấy

xX

bất kỳ mà

 

Px

đúng.

Bước 2. Chứng minh

 

Qx

đúng (bằng suy luận và kiến thức toán học đã biết).

Cách 2: Chứng minh bằng phản định lí gồm các bước sau:

Bước 1. Giả sử tồn tại

0

xX

sao cho

 

0

Px

đúng và

 

0

Qx

sai.

Bước 2. Dùng suy luận và các kiến thức toán học để đi đến mâu thuẫn.

2. Bài tập minh họa.

Bài tập 8. Chứng minh với mọi số tự nhiên

n

, ta có

a). Nếu

n

lẻ thì

3

n

lẻ.

b). Nếu

n

chia hết cho 3 thì

 

1nn

chia hết cho 6.

Lời giải

....................................................................................................................................................................................................................

Bài tập 9. Chứng minh rằng

a). Mọi số chính phương có dạng

4k

hoặc

41k

.

b). Mọi nguyên tố khác 2 đều là số lẻ.

Lời giải

....................................................................................................................................................................................................................

Bài tập 10. Chứng minh rằng

a). Nếu

2a

thì

32

4 5 2 0   a a a

.

b). Nếu

, a b A B

thì

.

2 2 2

  



aA bB a b A B

.

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 2. Áp Dụng Mệnh Đề Vào Suy Luận Toán Học

31

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

Lời giải

....................................................................................................................................................................................................................

Bài tập 11. Cho số tự nhiên

n

. Chứng minh rằng

a). Nếu

2

n

chẵn thì

n

chẵn.

b). Nếu

2

n

chia hết cho 5 thì

n

chia hết cho 5.

Lời giải

....................................................................................................................................................................................................................

Bài tập 12. Chứng minh rằng

a). Nếu

2ab

thì một trong hai số

a

và

b

phải nhỏ hơn 1.

b). Cho

n

là số tự nhiên, nếu

54n

lẻ thì

n

lẻ.

Lời giải

....................................................................................................................................................................................................................

Bài tập 13. Chứng minh rằng

a). Một tam giác không phải là tam giác đều thì nó có ít nhất một góc nhỏ hơn

0

60

.

b). Nếu

1x

và

1y

thì

1   x y xy

.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 2. Áp Dụng Mệnh Đề Vào Suy Luận Toán Học

32

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Bài tập 14. Chứng minh rằng

2

là số vô tỉ.

Lời giải

....................................................................................................................................................................................................................

Bài tập 15. Bằng phương pháp phản chứng, hãy chứng minh rằng

''

Nếu hai số nguyên dương có

tổng bình phương chia hết cho 3 thì cả hai số đó phải chia hết cho

3''

.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

33

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

A. LÍ THUYẾT.

I. Tập hợp và cách xác định tập hợp.

1. Tập hợp là một khái niệm cơ bản của toán học, không định nghĩa.

2. Cách xác định tập hợp:

Liệt kê các phần tử: viết các phần tử của tập hợp trong hai dấu móc

 

...

.

Chỉ ra tính chất đăc trưng cho các phần tử của tập hợp.

3. Tập rỗng: là tập hợp không chứa phần tử nào, kí hiệu



.

Ví dụ 1. Trong các tập hợp sau, tập hợp nào rỗng ?

a).

 

2

10    A x x x

. b).





2

4 2 0    B x x x

.

c).





2

6 7 1 0    C x x x

. d).





1  D x x

.

Lời giải

....................................................................................................................................................................................................................

Ví dụ 2. Viết mỗi tập hợp sau bằng cách liệt kê các phần tử

a).

  

 

22

2 2 3 2 0     A x x x x x

.

b).

 

32

2 3 5 0    B x x x x

.

c).

 

2

2 75 77 0    C x x x

.

Lời giải

....................................................................................................................................................................................................................

§BI 3. TẬP HỢP VÀ CÁC PHÉP TOÁN TRÊN TẬP HỢP

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

34

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Ví dụ 3. Viết mỗi tập hợp sau bằng cách nêu tính chất đặc trưng

a).

2 3 4 5 6

; ; ; ;

3 8 15 24 35









A

. b).

 

0;3;8;15;24;35B

.

c).

 

4;1;6;11;16C

. d).

 

1; 2;7D

.

Lời giải

....................................................................................................................................................................................................................

II. Tập hợp con–Tập hợp bằng nhau

1. Tập con:

     A B x A x B

.

2. Các tính chất:

,A A A

.

,  AA

.

,AB

, và

BC

suy ra

AC

.

Tập bằng nhau

  A B A B

và

     B A x A x B

.

Ví dụ 4. Tìm tất cả các tập hợp con cuả tập

a).

 

C

. b).

 

1;2;3B

.

c).

 

;A a b

. d).

 

; ; ;D a b c d

.

Lời giải

....................................................................................................................................................................................................................

3. Nhận xét: cho tập hợp gồm có

n

phần tử khi đó:

Số phần tử của tập con là

2

n

tập hợp.

Ví dụ 5. Tập có 3 phần tử thì số tập con là

3

28

tập con.

Số phần tử của tập con có 2 phần tử là

 

1

2

nn

.

Ví dụ 6. Tập có 5 phần tử thì số tập con có hai phần tử là

 

5 5 1

10

2





tập con.

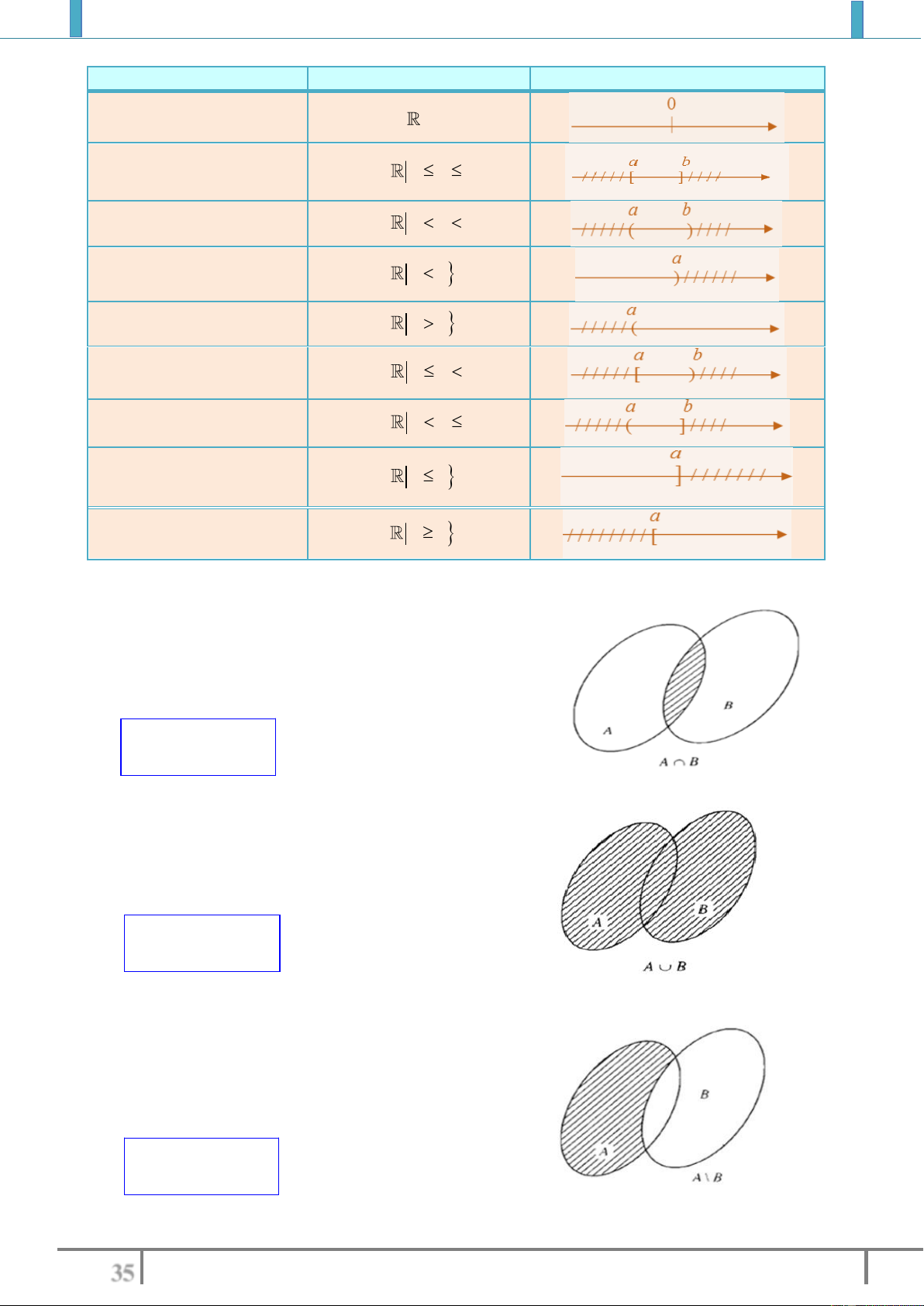
Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

35

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

3. Một số tập con của tập hợp số thực

Tên gọi, ký hiệu

Tập hợp

Hình biểu diễn

Tập số thực

 

; 

Đoạn

 

;ab

 

  x a x b

Khoảng

 

;ab

 

  x a x b

Khoảng

 

; a

 

x x a

Khoảng

 

;a

 

x x a

Nửa khoảng





;ab

 

  x a x b

Nửa khoảng





;ab

 

  x a x b

Nửa khoảng





; a

 

x x a

Nửa khoảng





;a

 

x x a

IV. Các phép toán tập hợp

1. Giao của hai tập hợp

Tập hợp

C

gồm các phần tử vừa thuộc

,A

vừa thuộc

B

được gọi là giao của

A

và

.B

Kí hiệu

C A B

(phần gạch chéo trong hình).

Vậy

 

|;   A B x x A x B

xA

x A B

xB





  







2. Hợp của hai tập hợp.

Tập hợp

C

gồm các phần tử thuộc

A

hoặc thuộc

B

được

gọi là hợp của

A

và

B

Kí hiệu

C A B

(phần gạch chéo trong hình).

Vậy

 

|   A B x x A hoac x B

xA

x A B

xB





  







3. Hiệu và phần bù của hai tập hợp

Hiệu: Tập hợp

C

gồm các phần tử thuộc

A

nhưng không

thuộc

B

gọi là hiệu của

A

và

.B

Kí hiệu

\C A B

(phần gạch chéo trong hình 7).

Vậy

 

\ | ;    A B A B x x A x B

\

xA

x A B

xB













Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

36

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

4. Phần bù:

Khi

BA

thì

\AB

gọi là phần bù của

B

trong

,A

kí

hiệu

.

A

CB

Ví dụ 7. Cho hai tập hợp

 

0;1;2;3;4A

và

 

2;3;4;5;6B

.

a). Tìm các tập

\ , \ , , A B B A A B A B

.

b). Tìm các tập

       

\ \ , \ \A B B A A B B A

.

Lời giải

....................................................................................................................................................................................................................

Ví dụ 8. Cho tập hợp

 

1;2;3;4;5;6;7;8;9E

và các tập hợp con

 

1;2;3;4A

,

 

2;4;6;8B

. Xác

định

E

CA

,

E

CB

,

 



E

C A B

,



EE

C A C B

.

Lời giải

....................................................................................................................................................................................................................

B. PHÂN DẠNG VÀ BÀI TẬP MINH HỌA.

Dạng 1. XÁC ĐỊNH TẬP HỢP

1. Phương pháp

Xác định một tập hợp ta thường mô tả theo 2 cách:

Liệt kê tất cả các phần tử của tập hợp.

Nêu tính chất đặc trưng.

2. Bài tập minh họa.

Bài tập 1. Viết mỗi tập hợp sau bằng cách liệt kê các phần tử

a).

 

*2

3 30   A n n

.

b).

 

3  B n x

.

c).



3C x x k

với

k

và



4 12  x

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

37

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

Lời giải

....................................................................................................................................................................................................................

Bài tập 2. Viết mỗi tập hợp sau bằng cách liệt kê các phần tử

a). Tập hợp các số chính phương.

b). Tập hợp các ước chung của 36 và 120.

c). Tập hợp các bội chung của 8 và 15.

Lời giải

....................................................................................................................................................................................................................

Bài tập 3. Viết mỗi tập hợp sau bằng cách nêu tính chất đặc trưng

a).

 

2;3;5;7A

. b).

 

3; 2; 1;0;1;2;3   B

.

c).

 

5;0;5;10C

. d).

 

1;2;3;4;6;9;12;18;36D

.

Lời giải

....................................................................................................................................................................................................................

Bài tập 4. Viết mỗi tập hợp sau đây theo cách nêu tính chất đặc trưng

a). Tập hợp các điểm

M

trên mặt phẳng

 

P

, thuộc đường tròn tâm

O

và đường kính

2R

.

b). Tập hợp các điểm

M

trên mặt phẳng

 

P

, thuộc hình tròn tâm

O

.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

38

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Bài tập 5. Viết lại các tập hợp sau bằng cách liệt kê các phần tử

a).



4   A x x x

là bội của



3

. b).



  



22

2 2 3 5 0     B x x x x x

.

c).

 

2

1

1 3 3 0

2







      











C x x x x

. d).

 

 

1 3 2 3 0     D x x x x

.

Lời giải

....................................................................................................................................................................................................................

Bài tập 6.

a). Cho

A

là tập hợp các số chẵn có hai chữ số. Hỏi

A

có bao nhiêu phần tử ?

b). Cho

B

là tập hợp các số lẻ có

3

chữ số. Hỏi

B

có bao nhiêu phần tử ?

c). Cho

C

là tập hợp các số nguyên dương bé hơn

500

và là bội của

3

. Hỏi

C

có bao nhiêu

phần tử ?

Lời giải

....................................................................................................................................................................................................................

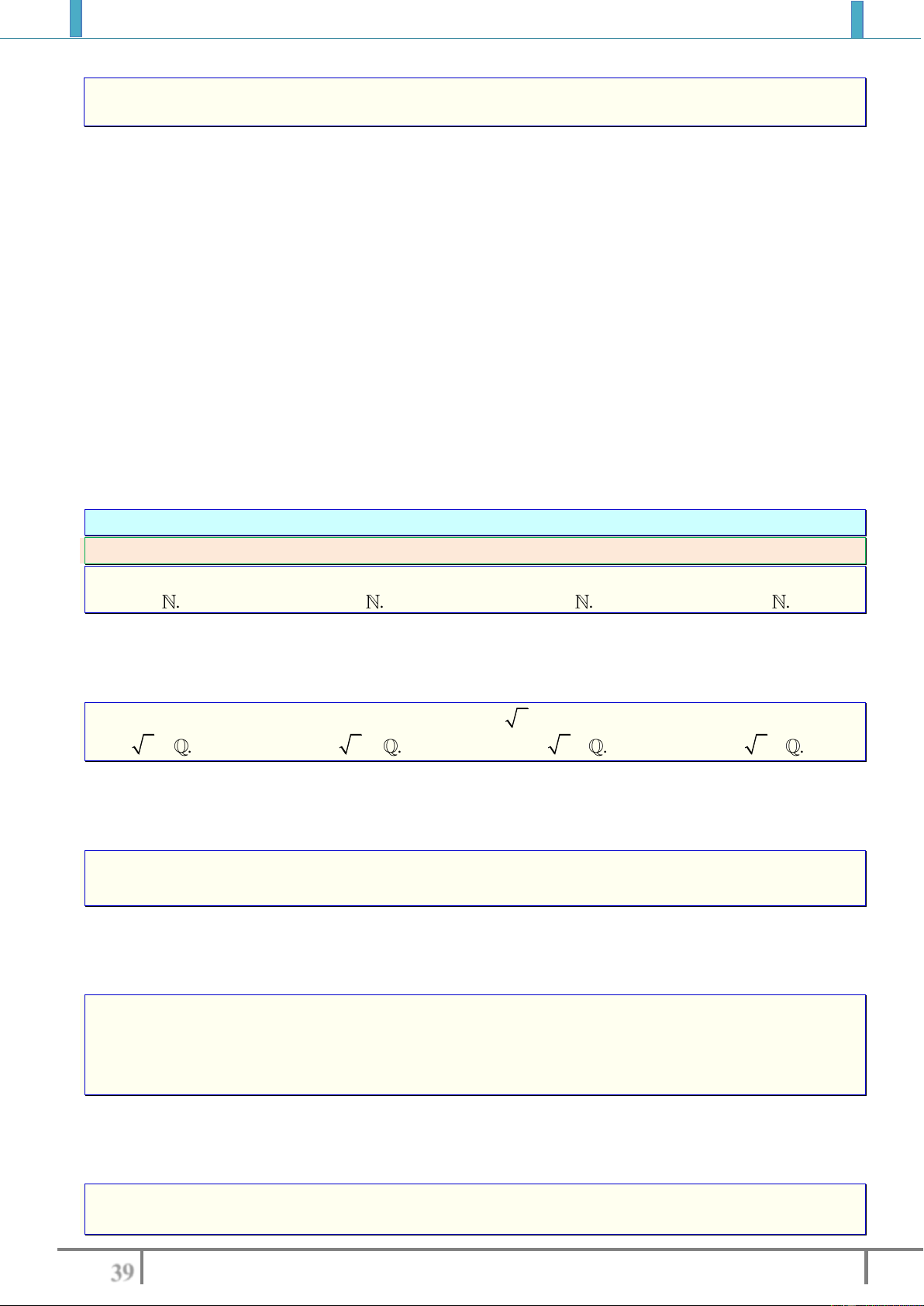
Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

39

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Bài tập 7. Cho hai tập

A

,

B

khác



;

AB

có

6

phần tử; số phần tử của

AB

bằng nửa số phần

tử của

B

. Hỏi

A

,

B

có thể có bao nhiêu phần tử?

Lời giải

....................................................................................................................................................................................................................

3. Câu hỏi trắc nghiệm

Mức độ 1. Nhận biết

Câu 1. Kí hiệu nào sau đây dùng để viết đúng mệnh đề

''

7

là số tự nhiên

''

?

A.

7 .

B.

7 .

C.

7 .

D.

7 .

Lời giải

....................................................................................................................................................................................................................

Câu 2. Kí hiệu nào sau đây dùng để viết đúng mệnh đề

''

2

không phải là số hữu tỉ

''

?

A.

2.

B.

2.

C.

2.

D.

2.

Lời giải

....................................................................................................................................................................................................................

Câu 3. Cho

A

là một tập hợp. Trong các mệnh đề sau, mệnh đề nào đúng

A.

.A A

B.

.A

C.

.AA

D.

 

.AA

Lời giải

....................................................................................................................................................................................................................

Câu 4. Cho

x

là một phần tử của tập hợp

.A

Xét các mệnh đề sau:

(I)

.x A

(II)

 

.x A

(III)

.x A

(IV)

 

.x A

Trong các mệnh đề trên, mệnh đề nào đúng?

A. I và II. B. I và III. C. I và IV. D. II và IV.

Lời giải

....................................................................................................................................................................................................................

Câu 5. Mệnh đề nào sau đây tương đương với mệnh đề

?A 

A.

,.x x A

B.

,.x x A

C.

,.x x A

D.

,.x x A

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

40

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

Lời giải

....................................................................................................................................................................................................................

Câu 6. Hãy liệt kê các phần tử của tập

 

2

5 3 0 .2X xxx 

A.

 

0.X 

B.

 

1.X 

C.

3

.

2

X









D.

3

1; .

2

X









Lời giải

....................................................................................................................................................................................................................

Câu 7. Cho

 

*

, 10, 3A x x x  

. Chọn khẳng định đúng.

A.

A

có

4

phần tử. B.

A

có

3

phần tử. C.

A

có

5

phần tử. D.

A

có

2

phần tử.

Lời giải

....................................................................................................................................................................................................................

Câu 8. Tập hợp

  

 

 

3

1 2 4 0A x x x x x     

có bao nhiêu phần tử?

A.

1

. B.

3

. C.

5

. D.

2

.

Lời giải

....................................................................................................................................................................................................................

Câu 9. Trong các tập hợp sau, tập nào là tập rỗng?

A.

 

2

1

| 3 4 0T x x x    

. B.

 

2

1

| 3 0T x x   

C.

 

2

1

|2T x x  

. D.

 

 

2

1

| 1 2 5 0T x x x    

.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

41

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Câu 10. Hãy liệt kê các phần tử của tập hợp:

 

2

, 1 0    X x x x

.

A.

 

0X

. B.

 

2X

. C.

X

. D.

0X

.

Lời giải

....................................................................................................................................................................................................................

Câu 11. Hãy liệt kê các phần tử của tập hợp

 

2

| 2 5 3 0X x x x    

.

A.

 

1X 

. B.

3

2

X









. C.

 

0X 

. D.

3

1;

2

X









.

Lời giải

....................................................................................................................................................................................................................

Câu 12. Trong các tập hợp sau, tập nào là tập rỗng?

A.

 

2

5 6 0x x x   

. B.

 

2

3 5 2 0x x x   

.

C.

 

2

10x x x   

. D.

 

2

5 1 0x x x   

.

Lời giải

....................................................................................................................................................................................................................

Câu 13. Tính chất đặc trưng của tập hợp

 

1;2;3;4;5 .X 

A.

 

5.xx

B.

 

*

5.xx

C.

 

5.xx

D.

 

5.xx

Lời giải

....................................................................................................................................................................................................................

Câu 14. Tính chất đặc trưng của tập hợp

 

3; 2; 1;0;1;2;3 .X    

A.

 

3.xx

B.

 

3.xx

C.

 

3.xx

D.

 

3 3 .xx   

Lời giải

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

42

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Mức độ 2. Thông hiểu

Câu 15. Cho tập

 

 

22

.4 1 2 7 3 0X xxxxx  

Tính tổng

S

các phần tử của tập

.X

A.

4.S 

B.

9

.

2

S 

C.

5.S 

D.

6.S 

Lời giải

....................................................................................................................................................................................................................

Câu 16. Ch tập

 

 

22

.9 . 1 2 02X xxx x







   





Hỏi tập

X

có bao nhiêu phần tử?

A.

1.

B.

2.

C.

3.

D.

4.

Lời giải

....................................................................................................................................................................................................................

Câu 17. Hãy liệt kê các phần tử của tập

  

 

22

6 5 0 .X x x x x   

A.

 

5;3 .X 

B.

 

5; 2; 5;3 .X   

C.

 

2;3 .X 

D.

 

5; 5 .X 

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

43

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Câu 18. Hãy liệt kê các phần tử của tập

 

2

1 0 .X xxx 

A.

0.X 

B.

 

0.X 

C.

.X 

D.

 

.X 

Lời giải

....................................................................................................................................................................................................................

Câu 19. Cho tập hợp

{A x x

là ước chung của

36 và120}

.

Hãy liệt kê các phần tử của tập hợp

A

.

A.

 

1;2;3;4;6;12 .A 

B.

 

1;2;4;6;8;12 .A 

C.

 

2;4;6;8;10;12 .A 

D.

 

1;36;120 .A 

Lời giải

....................................................................................................................................................................................................................

Câu 20. Hỏi tập hợp

 

2

1 , 2kAk k 

có bao nhiêu phần tử?

A.

1.

B.

2.

C.

3.

D.

5.

Lời giải

....................................................................................................................................................................................................................

Câu 21. Tập hợp nào sau đây là tập rỗng?

A.

 

.A 

B.

 

 

2

3 2 3 4 1 0 .B x x x x     

C.

 

 

2

3 2 3 4 1 0 .C x x x x     

D.

 

 

2

3 2 3 4 1 0 .D x x x x     

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

44

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

Câu 22. Cho tập

 



;,M x y x y

và



1.xy

Hỏi tập

M

có bao nhiêu phần tử ?

A.

0.

B.

1.

C.

2.

D.

4.

Lời giải

....................................................................................................................................................................................................................

Câu 23. Cho tập

 



;,M x y x y

và



22

0.xy

Hỏi tập

M

có bao nhiêu phần tử ?

A.

0.

B.

1.

C.

2.

D. Vô số.

Lời giải

....................................................................................................................................................................................................................

Câu 24. Cho ba tập hợp:

M

: tập hợp các tam giác có

2

góc tù.

N

: tập hợp các tam giác có độ dài ba cạnh là ba số nguyên liên tiếp.

P

: tập hợp các số nguyên tố chia hết cho

3

.

Tập hợp nào là tập hợp rỗng?

A. Chỉ

N

và

P

. B. Chỉ

P

và

M

. C. Chỉ

M

. D. Cả

M

,

N

và

P

.

Lời giải

....................................................................................................................................................................................................................

Câu 25. Xác định số phần tử của tập hợp

 

| 4, 2017X n n n  

.

A.

505

. B.

503

. C.

504

. D.

502

.

Lời giải

....................................................................................................................................................................................................................

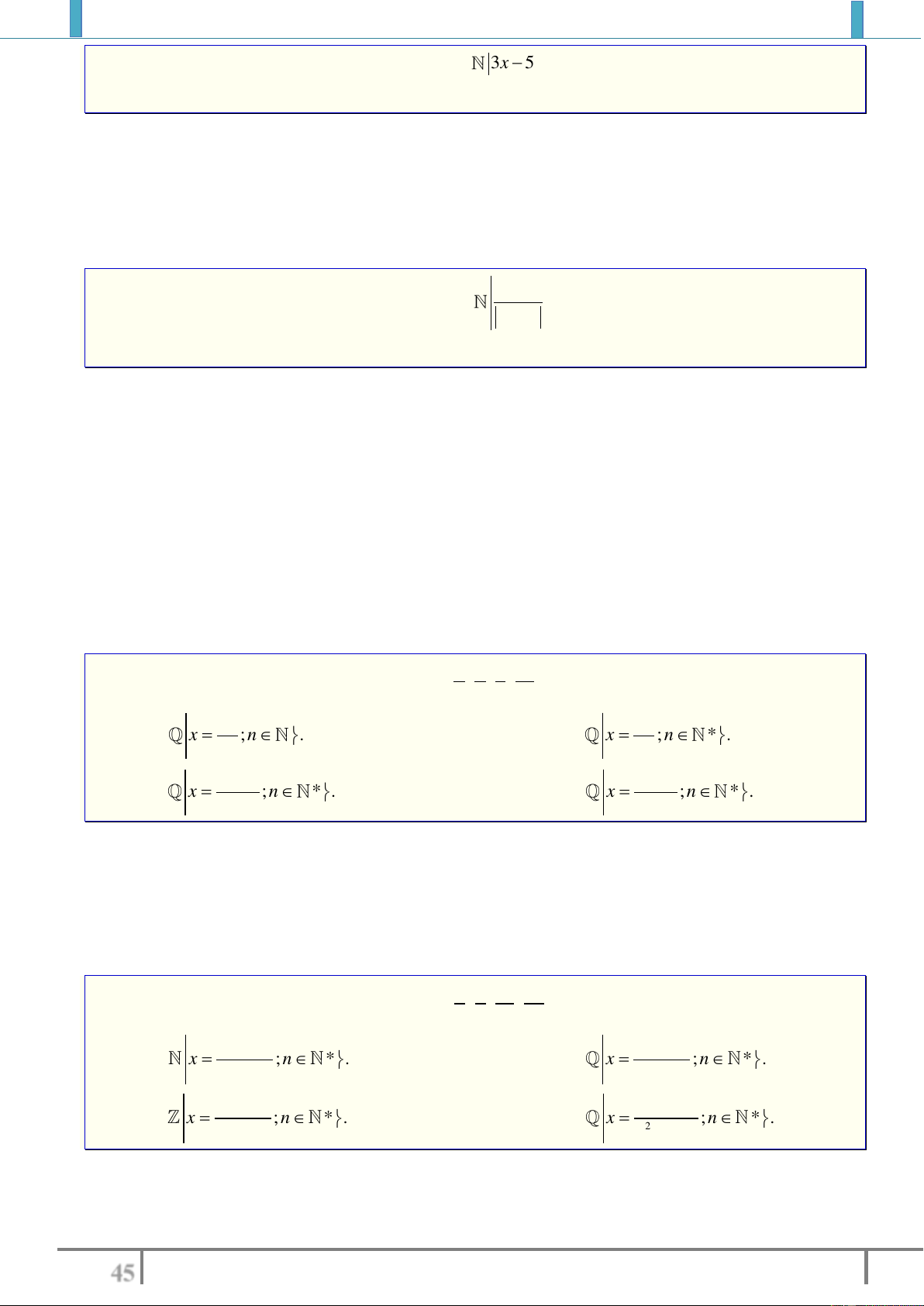
Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

45

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

Câu 26. Liệt kê các phần tử của tập hợp

 

3 5 .X x x x   

A.

 

1;2;3X 

. B.

 

1,2X 

. C.

 

0;1;2X 

. D.

X 

.

Lời giải

....................................................................................................................................................................................................................

Câu 27. Liệt kê các phần tử của tập hợp

5

2.

21

Xx

x





  









A.

 

0;1;2;3X 

. B.

 

0;1X 

. C.

 

0;1;2X 

. D.

X 

.

Lời giải

....................................................................................................................................................................................................................

Câu 28. Tính chất đặc trưng của tập hợp

1 1 1 1

; ; ; ;.... .

2 4 8 16

X









A.

1

;.

2

x x n

n



  





B.

1

; * .

2

x x n

n



  





C.

1

; * .

21

x x n

n



  







D.

1

; * .

21

x x n

n



  







Lời giải

....................................................................................................................................................................................................................

Câu 29. Tính chất đặc trưng của tập hợp

1 1 1 1

; ; ; ;.... .

2 6 12 20

X









A.

1

; * .

( 1)

x x n

nn



  







B.

1

; * .

( 1)

x x n

nn



  







C.

1

; * .

( 1)

x x n

nn



  







D.

2

1

; * .

( 1)

x x n

nn



  







Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

46

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Câu 30. Tính chất đặc trưng của tập hợp

 

2; 1;0;1;2;3 .X   

A.

 

2 3 .xx   

B.

 

2 3 .xx   

C.

 

2 3 .xx   

D.

 

2 1 6 .xx    

Lời giải

....................................................................................................................................................................................................................

Câu 31. Tính chất đặc trưng của tập hợp

 

0;1;4;9;16;25;36.... .X 

A.

 

2

;.x x n n  

B.

 

2*

;.x x n n  

C.

 

( 1); .x x n n n   

D.

 

( 1); .x x n n n   

Lời giải

....................................................................................................................................................................................................................

Câu 32. Tính chất đặc trưng của tập hợp

1 1 1 1 1

; ; ; ; .

2 4 8 16 32

X



   





A.

( 1)

;.

2

n

x x n

n







  







B.

( 1)

;.

2

n

x x n

n







  







C.

1

( 1)

;.

2

n

x x n

n









  







D.

*

( 1)

;.

2

n

x x n

n







  







Lời giải

....................................................................................................................................................................................................................

Câu 33. Tính chất đặc trưng của tập hợp

11

9; 3;1; ; ;... .

39

X



  





A.

*

1

9. ; .

3

n

x x n







   











B.

1

9. ; .

3

n

x x n







   











C.

1

9. ; .

3

n

x x n







   











D.

1

9. ; .

3

n

x x n







   











Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

47

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

Dạng 2. CÁC PHÉP TOÁN TRÊN TẬP HỢP

1. Phương Pháp.

Giao của hai tập hợp:

{|  A B x x A

và

}xB

: phần chung

Hợp của hai tập hợp:

{|  A B x x A

hoặc

}xB

: phần chung và phần riêng

Hiệu của hai tập hợp:

\ { |A B x x A

và

}xB

Phần bù: Cho

BA

thì

\

A

C B A B

.

2. Bài tập minh họa.

Bài tập 8. Cho

A

là tập hợp các học sinh lớp 10 đang học ở trường em,

B

là tập hợp học sinh đang

học tiếng Anh ở trường em. Hãy diễn đạt bằng lời các tập

a).

AB

. b).

\AB

. c).

AB

. d).

\BA

.

Lời giải

....................................................................................................................................................................................................................

Bài tập 9. Cho hai tập hợp

A

và

B

dưới đây. Viết tập

, A B A B

bằng hai cách

a)



A x x

là ước nguyên dương của



12

và



B x x

là ước nguyên dương của



18

.

b)



A x x

là bội nguyên dương của



6

và



B x x

là bội nguyên dương của



15

.

Lời giải

....................................................................................................................................................................................................................

Bài tập 10. Cho các tập hợp

     

1;2;3;4 , 2;4;6;8 , 3;4;5;6  A B C

.

Tìm

AB

,

AC

,

BC

,

AB

,

AC

,

BC

,

 

A B C

,

 

A B C

.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

48

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

Bài tập 11. Cho tập hợp

A

các ước số tự nhiên của 18 và tập hợp

B

các ước số tự nhiên của 30.

Xác định

, AB

,

AB

,

AB

,

\AB

,

\BA

.

Lời giải

....................................................................................................................................................................................................................

Bài tập 12. Cho





5  A x x

,





3 1, , 3     B x x k k k

.

Xác định tập

, , , , \ , \A B A B A B A B B A

.

Lời giải

....................................................................................................................................................................................................................

Bài tập 13. Cho

A

là tập các số tự nhiên chẵn không lớn hơn 10,





6  B n n

và





4 10   C n n

. Tìm

a).

 

A B C

. b).

     

\ \ \A B A C B C

.

Lời giải

....................................................................................................................................................................................................................

Bài tập 14. Cho các tập hợp sau

 

16    A x x

,

 

 

22

1 3 3 2 0     B x x x x

,

 

0;1;2;3;4;5;6C

.

a). Viết các tập hợp

, AB

dưới dạng liệt kê các phần tử.

b). Tìm

, , \ ,



  

BA

A B A B A B C A B

.

c). Chứng minh rằng

( ) .  A B C A

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

49

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Bài tập 15. Cho các tập hợp

  

 

22

7 6 4 0     A x x x x

,

 

28  B x x

và



21  C x x

và



24  x

.

a). Hãy viết lại các tập hợp

, , A B C

dưới dạng liệt kê các phần tử.

b). Tìm

AB

,

AB

,

\BC

,

 

\

AB

C B C

.

c). Tìm

 

\A C B

.

Lời giải

....................................................................................................................................................................................................................

Bài tập 16. Xác định hai tập

A

,

B

biết rằng

     

\ 1;5;7;8 , \ 2;10 , 3;6;9   A B B A A B

.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

50

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Bài tập 17. Cho hai tập hợp

 

1;2A

và

 

1;2;3;4B

.

Tìm tất cả các tập hợp

X

sao cho

A X B

.

Lời giải

....................................................................................................................................................................................................................

Bài tập 18. Cho các tập hợp:

 

|5  A x R x

và

 

| 3 7    B x R x

. Tìm

;AB

AB

Lời giải

....................................................................................................................................................................................................................

3. Câu hỏi trắc nghiệm

Mức độ 1. Nhận biết

Câu 34. Cho hai tập hợp

 

1;5A 

và

 

1;3;5 .B 

Tìm

.AB

A.

 

1.AB

B.

 

1;3 .AB

C.

 

1;3;5 .AB

D.

 

1;5 .AB

Lời giải

....................................................................................................................................................................................................................

Câu 35. Cho hai tập hợp

   

; ; ; ; , ; ; ; ;A a b c d m B c d m k l

. Tìm

AB

.

A.

 

;.A B a b

B.

 

; ; .A B c d m

C.

 

;.A B c d

D.

 

; ; ; ; ; ; .A B a b c d m k l

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

51

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Câu 36. Cho hai tập hợp

 

1;2;4;7;9X 

và

 

1;0;7;10X 

. Tập hợp

XY

có bao nhiêu phần

tử?

A.

9

. B.

7

. C.

8

. D.

10

.

Lời giải

....................................................................................................................................................................................................................

Câu 37. Cho

 

|3A x x  

,

 

0;1;2;3B 

. Tập

AB

bằng

A.

 

1;2;3

. B.

 

3; 2; 1;0;1;2;3  

. C.

 

0;1;2

. D.

 

0;1;2;3

.

Lời giải

....................................................................................................................................................................................................................

Câu 38. Gọi

n

B

là tập hợp các bội số của

n

trong . Xác định tập hợp

24

BB

?

A.

2

.B

B.

4

.B

C.

.

D.

3

.B

Lời giải

....................................................................................................................................................................................................................

Mức độ 2. Thông hiểu

Câu 39. Cho hai tập

  

 

22

2 2 3 2 0A x x x x x     

và

 

2

3 30B n n



   

. Tìm

.AB

A.

 

2;4 .AB

B.

 

2.AB

C.

 

4;5 .AB

D.

 

3.AB

Lời giải

....................................................................................................................................................................................................................

Câu 40. Cho các tập hợp

{M x x

là bội của

2}

,

{N x x

là bội của

6}

,

{P x x

là

ước của

2}

,

{Q x x

là ước của

6}.

Mệnh đề nào sau đây đúng?

A.

.MN

B.

.QP

C.

.M N N

D.

.P Q Q

Lời giải

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

52

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Câu 41. Cho hai tập hợp

   

1;3;5;8 , 3;5;7;9AB

. Xác định tập hợp

.AB

A.

 

3;5 .AB

B.

 

1;3;5;7;8;9 .AB

C.

 

1;7;9 .AB

D.

 

1;3;5 .AB

Lời giải

....................................................................................................................................................................................................................

Câu 42. Cho các tập hợp

 

; ; A a b c

,

 

; ; B b c d

,

 

; ; C b c e

. Khẳng định nào sau đây đúng?

A.

   

.A B C A B C    

B.

     

.A B C A B A C     

C.

     

.A B C A B A C     

D.

   

.A B C A B C    

Lời giải

....................................................................................................................................................................................................................

Câu 43. Gọi

n

B

là tập hợp các bội số của

n

trong . Xác định tập hợp

36

.BB

A.

36

.BB  

B.

3 6 3

.B B B

C.

3 6 6

.B B B

D.

3 6 12

.B B B

Lời giải

....................................................................................................................................................................................................................

Câu 44. Cho hai tập hợp

   

0;1;2;3;4 , 2;3;4;5;6AB

. Xác đinh tập hợp

\.AB

A.

 

\ 0 .AB

B.

 

\ 0;1 .AB

C.

 

\ 1;2 .AB

D.

 

\ 1;5 .AB

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

53

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Câu 45. Cho hai tập hợp

   

0;1;2;3;4 , 2;3;4;5;6AB

. Xác đinh tập hợp

\.BA

A.

 

\ 5 .BA

B.

 

\ 0;1 .BA

C.

 

\ 2;3;4 .BA

D.

 

\ 5;6 .BA

Lời giải

....................................................................................................................................................................................................................

Câu 46. Cho tập

 

0;2;4;6;8A 

;

 

3;4;5;6;7B 

. Tập

\AB

là

A.

 

0;6;8

. B.

 

0;2;8

. C.

 

3;6;7

. D.

 

0;2

.

Lời giải

....................................................................................................................................................................................................................

Câu 47. Cho hai tập hợp

   

0;1;2;3;4 , 2;3;4;5;6AB

. Tìm

   

\ \ .X A B B A

A.

 

0;1;5;6 .X 

B.

 

1;2 .X 

C.

 

5.X 

D.

.X 

Lời giải

....................................................................................................................................................................................................................

Câu 48. Cho hai tập hợp

   

0;1;2;3;4 , 2;3;4;5;6AB

.

Xác định tập hợp

   

\ \ .X A B B A

A.

 

0;1;5;6 .X 

B.

 

1;2 .X 

C.

 

2;3;4 .X 

D.

 

5;6 .X 

Lời giải

....................................................................................................................................................................................................................

Câu 49. Cho hai tập hợp

   

1;2;3;7 , 2;4;6;7;8AB

. Khẳng định nào sau đây đúng?

A.

 

2;7AB

và

 

4;6;8 .AB

B.

 

2;7AB

và

 

\ 1;3 .AB

C.

 

\ 1;3AB

và

 

\ 2;7 .BA

D.

 

\ 1;3AB

và

 

1;3;4;6;8 .AB

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

54

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

Câu 50. Cho

A

là tập hợp tất cả các nghiệm của phương trình

2

4 3 0xx  

;

B

là tập hợp các số

có giá trị tuyệt đối nhỏ hơn 4 Khẳng định nào sau đây đúng?

A.

.A B A

B.

.A B A B  

C.

\.AB

D.

\.BA

Lời giải

....................................................................................................................................................................................................................

Câu 51. Cho hai tập hợp

   

0;1;2;3;4 , 1;3;4;6;8 .AB

Mệnh đề nào sau đây đúng?

A.

.A B B

B.

.A B A

C.

 

\ 0;2 .AB

D.

 

\ 0;4 .BA

Lời giải

....................................................................................................................................................................................................................

Câu 52. Cho hai tập hợp

 

0;2A 

và

 

0;1;2;3;4 .B 

Có bao nhiêu tập hợp

X

thỏa mãn

.A XB

A.

2.

B.

3.

C.

4.

D.

5.

Lời giải

....................................................................................................................................................................................................................

Câu 53. Cho

, AB

là hai tập hợp được minh họa như hình vẽ.

Phần tô đen trong hình vẽ là tập hợp nào sau đây ?

A.

.AB

B.

.AB

C.

\.AB

D.

\.BA

Lời giải

....................................................................................................................................................................................................................

Câu 54. Cho

, AB

là hai tập hợp được minh họa như hình vẽ.

Phần không bị gạch trong hình vẽ là tập hợp nào sau đây ?

A.

.AB

B.

.AB

C.

\.AB

D.

\.BA

Lời giải

....................................................................................................................................................................................................................

Câu 55. Cho

, , A B C

là ba tập hợp được minh họa như hình vẽ

bên. Phần gạch sọc trong hình vẽ là tập hợp nào sau đây?

A.

 

\.A B C

B.

 

\.A B C

C.

   

\ \ .A C A B

D.

.A B C

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

55

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

Mức độ 3. Vận dụng

Câu 56. Lớp

1

10B

có

7

học sinh giỏi Toán,

5

học sinh giỏi Lý,

6

học sinh giỏi Hóa,

3

học sinh giỏi

cả Toán và Lý,

4

học sinh giỏi cả Toán và Hóa,

2

học sinh giỏi cả Lý và Hóa,

1

học sinh giỏi cả

3

môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) của lớp

1

10B

là

A.

9.

B.

10.

C.

18.

D.

28.

Lời giải

....................................................................................................................................................................................................................

Câu 57. Lớp

1

10A

có

7

học sinh giỏi Toán,

5

học sinh giỏi Lý,

6

học sinh giỏi Hóa,

3

học sinh giỏi

cả Toán và Lý,

4

học sinh giỏi cả Toán và Hóa,

2

học sinh giỏi cả Lý và Hóa,

1

học sinh giỏi cả

3

môn Toán, Lý, Hóa. Số học sinh giỏi đúng hai môn học của lớp

1

10A

là:

A.

6.

B.

7.

C.

9.

D.

10.

Lời giải

....................................................................................................................................................................................................................

Câu 58. Cho hai đa thức

 

fx

và

 

gx

.

Xét các tập hợp

 

 

|0A x f x  

,

 

 

|g 0B x x  

,

 

|0

fx

Cx

gx





  







. Mệnh đề nào

sau đây đúng?

A.

.C A B

B.

.C A B

C.

\ B.CA

D.

\.C B A

Lời giải

....................................................................................................................................................................................................................

Câu 59. Cho hai đa thức

 

fx

và

 

gx

.

Xét các tập hợp

 

 

|0A x f x  

,

 

 

|g 0B x x  

,

   

 

22

|0C x f x g x   

. Mệnh

đề nào sau đây đúng?

A.

.C A B

B.

.C A B

C.

\ B.CA

D.

\.C B A

Lời giải

....................................................................................................................................................................................................................

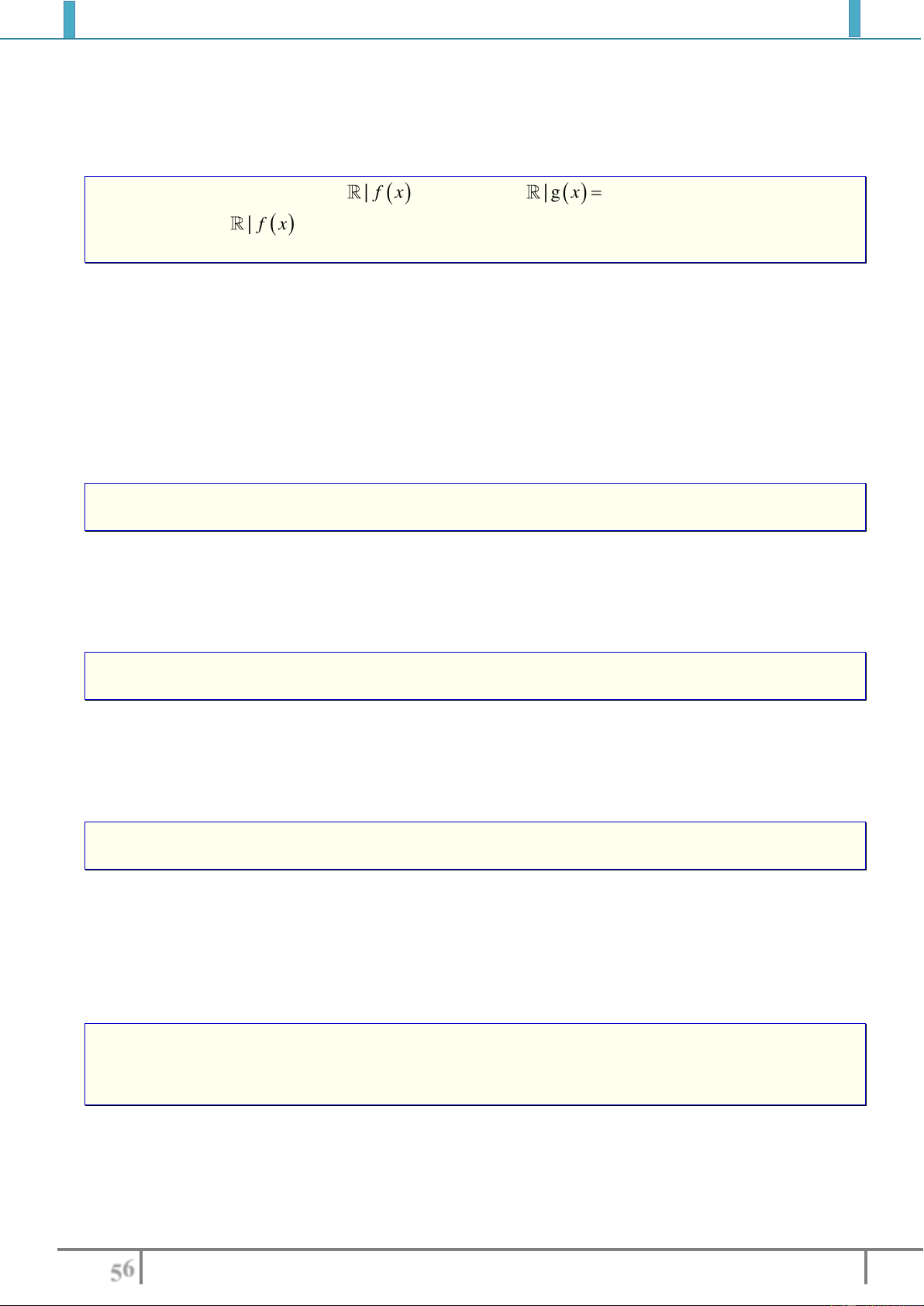
Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

56

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Câu 60. Cho hai tập hợp

 

 

|0E x f x  

,

 

 

|g 0F x x  

.

Tập hợp

   

 

|0H x f x g x  

. Trong các mệnh đề sau, mệnh đề nào đúng?

A.

.H E F

B.

.H E F

C.

\.H E F

D.

\.H F E

Lời giải.

....................................................................................................................................................................................................................

Câu 61. Cho tập hợp

A 

. Trong các mệnh đề sau, mệnh đề nào đúng?

A.

\.A   

B.

\.AA

C.

\.A  

D.

\.AA

Lời giải.

....................................................................................................................................................................................................................

Câu 62. Cho tập hợp

A 

. Trong các mệnh đề sau, mệnh đề nào sai?

A.

.A  

B.

.AA 

C.

.  

D.

.A A A

Lời giải.

....................................................................................................................................................................................................................

Câu 63. Cho tập hợp

A 

. Trong các mệnh đề sau, mệnh đề nào sai?

A.

.AA 

B.

.A  

C.

.  

D.

.A A A

Lời giải.

....................................................................................................................................................................................................................

Câu 64. Cho

, MN

là hai tập hợp khác rỗng. Mệnh đề nào sau đây đúng?

A.

\.M N N

B.

\.M N M

C.

 

\.M N N  

D.

\.M N M N

Lời giải.

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

57

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Câu 65. Tập hai tập hợp

, MN

thỏa mãn

MN

. Mệnh đề nào sau đây đúng?

A.

.M N N

B.

\.M N N

C.

.M N M

D.

\.M N M

Lời giải.

....................................................................................................................................................................................................................

Câu 66. Mệnh đề nào sau đây sai?

A.

.A B A A B   

B.

.A B A B A   

C.

\.A B A A B    

D.

\.A B A B     

Lời giải.

....................................................................................................................................................................................................................

Câu 67. Cho

 

33A x mx mx    

,

 

2

40B x x   

. Tìm

m

để

\B A B

.

A.

33

22

m  

. B.

3

2

m 

. C.

33

22

m  

. D.

3

2

m 

.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

58

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

Dạng 3. ĐOẠN – KHOẢNG – NỮA KHOẢNG

1. Phương Pháp

Nhớ tuyệt chiêu:

Giao gạch bỏ, hợp tô đậm.

\AB

là

A

tô đậm,

B

gạch bỏ.

\BA

là

B

tô đậm,

A

gạch bỏ.

Phần bù

A

CB

ta làm hai bước:

 Bước 1: Kiểm tra tập con

.BA

 Bước 2: Tính

\.AB

Nếu thỏa mãn hai bước trên thì gọi là phần bù của

B

trong

,A

kí hiệu

.

A

CB

2. Bài tập minh họa.

Bài tập 19. Cho đoạn

 

5;1A

và khoảng

 

3;2B

. Xác định

AB

,

AB

,

\AB

,

CB

.

Lời giải

....................................................................................................................................................................................................................

Bài tập 20. Cho hai nửa khoảng





1;0A

và





0;1B

. Xác định

, , , \ , \A B A B C A A B B A

.

Lời giải

....................................................................................................................................................................................................................

Bài tập 21. Cho hai nửa khoảng





0;2A

và





1;4B

. Xác định

   

, C A B C A B

.

Lời giải

....................................................................................................................................................................................................................

Bài tập 22. Cho các tập hợp

 

2

4  A x x

,

 

1  B x x

.

Viết các tập hợp sau đây

, , \ , A B A B A B C B

dưới dạng các khoảng, nửa khoảng, đoạn.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

59

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Bài tập 23. Xác định các tập hợp

, \ ,   A B A C A B C

, biết

a).

 

13    A x x

,

 

1  B x x

,

 

;1 C

.

b).

 

22    A x x

,

 

3  B x x

,

 

;0 C

.

Lời giải

....................................................................................................................................................................................................................

Bài tập 24. Cho các tập hợp

 

2

25 0   X x x

,

 

  A x x a

và

 

  B x x b

.

Tìm

a

,

b

để

AX

và

BX

là các đoạn có chiều dài lần lượt là

7

và

9

.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

60

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Bài tập 25. Có thể kết luận gì về số

a

, biết

a).

   

1;3 ;    a

. b).



  

3;12 \ ;  a

. c).

     

5; 2;8 2;8a

.

Lời giải

....................................................................................................................................................................................................................

Bài tập 26. Cho hai tập hợp

 

4;1A

,

 

3;Bm

. Tìm

m

để

a).

 

3;1  AB

. b).

A B A

.

Lời giải

....................................................................................................................................................................................................................

Bài tập 27. Cho hai tập hợp

 

1;5Am

và

 

3; B

. Tìm

m

để

\ AB

.

Lời giải

....................................................................................................................................................................................................................

Bài tập 28. Cho hai tập hợp

 

4;3A

và

 

7;B m m

. Tìm

m

để

BA

.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

61

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

Bài tập 29. Cho hai tập hợp





; Am

và

 

5; B

. Tùy theo

m

, tìm

AB

.

Lời giải

....................................................................................................................................................................................................................

Bài tập 30. Cho số thực

0a

và hai tập hợp

 

;9 Aa

,

4

;



 





B

a

. Tìm

a

để

  AB

.

Lời giải

....................................................................................................................................................................................................................

Bài tập 31. Cho hai tập khác rỗng





–1; 4Am

và

 

–2;2 2Bm

, với

m

. Xác định

m

để

a).

  AB

. b).

AB

.

c).

BA

. d)

   

1;3  AB

.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

62

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

3. Bài tập vận dụng.

Bài tập 32. Cho ba tập hợp





2;3A

,





3;2015B

và





2016;  C

.

Tính

, , , , , ,

A A A B B A B A B

B C C C

C C C C C C C

.

Lời giải

....................................................................................................................................................................................................................

Bài tập 33. Cho hai tập hợp

 

2 1; 3  A m m

,

 

4;5B

. Tìm

m

để

a).

AB

. b).

BA

.

c).

  AB

. d).

AB

là một khoảng.

Lời giải

....................................................................................................................................................................................................................

Bài tập 34. Cho hai tập hợp

 

2;Am

,





1;5B

. Tùy theo

m

, xác định tập

\BA

.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

63

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Bài tập 35. Cho hai tập hợp





3;5A

,





; Ba

. Tìm

a

để

a).

 

2;5  AB

. b).

AB

có đúng một phần tử.

Lời giải

....................................................................................................................................................................................................................

Bài tập 36. Cho hai tập hợp

 

4;2A

và

 

8; 2  Ba

. Tìm

a

để

AB

có vô số phần tử.

Lời giải

....................................................................................................................................................................................................................

Bài tập 37. Cho hai tập hợp

 

2; 1Am

và

1

;

2



 







B

. Tìm

m

để

AB

chỉ có đúng 1 phần tử.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

64

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

Bài tập 38. Cho hai tập hợp

 

;1A m m

,

 

3;5B

. Tìm

m

để

AB

là một khoảng.

Lời giải

....................................................................................................................................................................................................................

Bài tập 39. Cho các tập hợp

 

; Am

và

 

3 1;3 3  B m m

. Tìm

m

để

a).

A C B

. b).

  C A B

.

Lời giải

....................................................................................................................................................................................................................

Bài tập 40. Cho hai tập hợp





;1  Am

và

 

25   B x x m

.

a). Khi

5m

. Tính

AB

,

AB

. b). Tìm

m

để

  AB

.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

65

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

Bài tập 41. Cho hai tập hợp

 

; Aa

,





; Bb

. Tìm điều kiện đối với

a

,

b

để

a).

  AB

. b).

AB

.

c).

\ AB

. d).

   

\\  AB

.

Lời giải

....................................................................................................................................................................................................................

Bài tập 42. Cho các nửa khoảng





;1A a a

,





;2B b b

.

a). Gọi

C A B

. Với điều kiện nào của

, ab

thì

C

là một đoạn. Tính độ dài của

C

khi đó.

b). Gọi

C A B

. Với điều kiện nào của

, ab

thì

C

là một đoạn. Tính độ dài của

C

khi đó.

Lời giải

....................................................................................................................................................................................................................

Bài tập 43. Cho hai tập hợp

 

;2A a a

,

 

;1B b b

. Tìm điều kiện của

a

,

b

để

  AB

.

Lời giải

....................................................................................................................................................................................................................

Bài tập 44. Tìm các giá trị thực của tham số

a

sao cho

   

1

; ; 1 1;

2





    





a

.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

66

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

4. Câu hỏi trắc nghiệm

Mức độ 1. Nhận biết

Câu 68. Cho tập





 

;2 6; .X     

Khẳng định nào sau đây đúng?

A.





;2 .X  

B.

 

6; .X   

C.

 

;.X   

D.





6;2 .X 

Lời giải.

....................................................................................................................................................................................................................

Câu 69. Tập hợp

 





2011 2011; 

bằng tập hợp nào sau đây?

A.

 

2011

. B.





2011;

. C.



. D.





;2011

.

Lời giải.

....................................................................................................................................................................................................................

Câu 70. Cho tập

 

1;0;1;2 .A 

Khẳng định nào sau đây đúng?

A.





1;3 .A   

B.





1;3 .A   

C.





*

1;3 .A   

D.





1;3 .A   

Lời giải.

....................................................................................................................................................................................................................

Câu 71. Cho

 

   

1;4 ; 2;6 ; 1;2A B C  

. Khi đó,

A B C

là:

A.





1;6 .

B.





2;4 .

C.





1;2 .

D.

.

Lời giải.

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

67

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

Câu 72. Tập

 





; 3 5;2   

bằng

A.





5; 3

. B.





;5 

. C.

 

;2 

. D.

 

3; 2

.

Lời giải

....................................................................................................................................................................................................................

Câu 73. Hình vẽ sau đây (phần không bị gạch) là biểu diễn của tập hợp nào?

A.

 





; 2 5;   

. B.

   

; 2 5;   

.

C.





 

; 2 5;   

. D.



 



; 2 5;   

.

Lời giải

....................................................................................................................................................................................................................

Câu 74. Kết quả của



 



4;1 2;3  

là

A.

 

2;1

B.

 

4;3

C.





4;2

D.





1;3

Lời giải

....................................................................................................................................................................................................................

Câu 75. Cho hai tập hợp

 

2;3A 

và

 

1;B  

. Tìm

AB

.

A.





2;AB   

. B.





1;3AB

. C.

 

1;3AB

. D.

 

1;3AB

.

Lời giải

....................................................................................................................................................................................................................

Câu 76. Cho

 

1; 9A 

,





3;B  

, câu nào sau đây đúng?

A.





1;AB  

. B.

 

9;AB  

. C.

 

1;3AB

. D.





3;9AB

.

Lời giải

....................................................................................................................................................................................................................

Câu 77. Cho





;5A  

,

 

0;B  

. Tìm

AB

.

A.





0;5AB

. B.

 

0;5AB

.

C.





0;5AB

. D.

 

;AB   

.

Lời giải

5



2



Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

68

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Câu 78. Kết quả của phép toán

 





;1 1;2  

là

A.

 

1;2

. B.

 

;2

. C.





1;1

. D.

 

1;1

.

Lời giải

....................................................................................................................................................................................................................

Câu 79. Cho hai tập hợp

 

3;3A 

và

 

0;B   

. Tìm

AB

.

A.

 

3;AB    

. B.





3;AB    

. C.





3;0AB  

. D.

 

0;3AB

.

Lời giải

....................................................................................................................................................................................................................

Câu 11. Khẳng định nào sau đây sai?

A.

.

B.

**

.

C.

.

D.

*

.

Lời giải.

....................................................................................................................................................................................................................

Câu 80. Tập hợp nào sau đây chỉ gồm các số vô tỷ?

A.

*

\

. B.

\

. C.

\

. D.

 

\0

.

Lời giải

....................................................................................................................................................................................................................

Câu 81. Cho tập hợp

 

| 2 5M x x   

. Hãy viết tập

M

dưới dạng khoảng, đoạn.

A.





2;5M 

. B.

 

2;5M 

. C.

 

2;5M 

. D.





2;5M 

.

Lời giải

....................................................................................................................................................................................................................

Câu 82. Cho

 

1;3A 

;

 

2;5B 

. Tìm mệnh đề sai.

A.





\ 3;5BA

. B.





2;3AB

. C.

 

\ 1;2AB

. D.

 

1;5AB  

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

69

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

Câu 83.Cho





;2A  

và

 

0;B  

. Tìm

\AB

.

A.





\ ;0AB 

. B.

 

\ 2;AB 

. C.





\ 0;2AB

. D.

 

\ ;0AB 

.

Lời giải

....................................................................................................................................................................................................................

Mức độ 2. Thông hiểu

Câu 84. Cho tập hợp



3; 5A







. Tập hợp

CA

bằng

A.

  

; 3 5;



    



. B.

   

; 3 5;    

.

C.

 

; 3 5;



    



. D.

  

; 3 5;



    



.

Lời giải

....................................................................................................................................................................................................................

Câu 85. Phần bù của





2;1

trong là

A.





;1

. B.

 





; 2 1;   

. C.

 

;2 

. D.

 

2;

.

Lời giải

....................................................................................................................................................................................................................

Câu 86. Xác định phần bù của tập hợp

 

;2 

trong

 

;4

.

A.

 

2;4

. B.





2;4

. C.





2;4

. D.

 

2;4

.

Lời giải

....................................................................................................................................................................................................................

Câu 87. Mệnh đề nào sau đây sai?

A.

 

 

1;7 7;10 .   

B.







  

2;4 4; 2; .     

C.

 

 





1;5 \ 0;7 1;0 .  

D.





 

\ ;3 3; .  

Lời giải.

....................................................................................................................................................................................................................

Câu 88. Cho tập





3;2X 

. Phần bù của

X

trong là tập nào trong các tập sau?

A.

 

; 3 .A   

B.

 

3; .B  

C.





2; .C  

D.

 





; 3 2; .D     

Lời giải.

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

70

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Câu 89. Xác định phần bù của tập hợp

     

; 10 10; 0    

trong .

A.





10; 10

. B.

 

 

10; 10 \ 0

. C.









10; 0 0; 10

. D.



  

10; 0 0; 10

.

Lời giải

....................................................................................................................................................................................................................

Câu 90. Cho hai tập hợp

 

| 3 2A x x    

,

 

1; 3B 

.

Chọn khẳng định đúng trong các khẳng định sau:

A.





1; 2AB  

. B.

 

\ 3; 1AB  

.

C.

 





; 1 3;CB    

. D.

 

2; 1;0;1;2AB   

.

Lời giải

....................................................................................................................................................................................................................

Câu 91. Cho các tập

 

|1A x x   

,

 

|3B x x  

. Tập

 

\ AB

là :

A.

 





; 1 3;   

. B.





1;3

. C.





1;3

. D.





 

; 1 3;   

.

Lời giải

....................................................................................................................................................................................................................

Câu 92. Cho các khoảng

   

1

2;2 ; 1; ; ;

2

A B C



      





. Khi đó tập hợp

A B C

bằng:

A.

1

1.

2

xx



   





B.

1

2.

2

xx



   





C.

1

1.

2

xx



   





D.

1

1.

2

xx



   





Lời giải.

....................................................................................................................................................................................................................

Câu 93.Cho các tập hợp

 

3; 6M 

và

   

; 2 3;N      

. Khi đó

MN

là

A.

 

 

; 2 3; 6  

. B.

 





; 2 3;    

.

C.



 



3; 2 3; 6  

. D.

   

3; 2 3; 6  

.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

71

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Câu 94. Cho





;2A  

,





2;B  

,

 

0;3C 

. Chọn phát biểu sai.

A.





0;2AC

. B.

 

0;BC  

. C.

 

\2AB

. D.





2;3BC

.

Lời giải

....................................................................................................................................................................................................................

Câu 95. Cho





;2A   

,





3;B  

,

 

0;4 .C 

Khi đó tập

 

A B C

là

A.





 

; 2 3;   

. B.

 





; 2 3;   

. C.





3;4

. D.

 

3;4

.

Lời giải

....................................................................................................................................................................................................................

Câu 96. Cho các số thực

, , ,a b c d

và

a b c d  

. Khẳng định nào sau đây đúng?

A.

     

; ; ; .a c b d b c

B.

   

 

; ; ; .a c b d b c

C.

  

  

; ; ; .a c b d b c

D.

     

; ; ; .a c b d b d

Lời giải.

....................................................................................................................................................................................................................

Câu 97. Cho hai tập hợp

 

, 3 4 2A x x x    

và

 

, 5 3 4 1 .B x x x    

Tìm tất cả các số

tự nhiên thuộc cả hai tập

A

và

.B

A.

0

và

1.

B.

1.

C.

0.

D. Không có.

Lời giải.

....................................................................................................................................................................................................................

Câu 98. Cho tập

    



4;4 7;9 1;7A    

. Khẳng định nào sau đây đúng?

A.

 

4;9 .A 

B.

 

;.A   

C.

 

1;8 .A 

D.





6;2 .A 

Lời giải.

....................................................................................................................................................................................................................

Câu 99. Cho



 

  

; 2 ; 3; ; 0;4A B C     

. Khi đó,

 

A B C

là:

A.

 

3;4 .

B.





 

; 2 3; .   

C.





3;4 .

D.

 





; 2 3; .   

Lời giải.

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

72

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Câu 100. Cho hai tập hợp

 

4;7A 

và

   

; 2 3;B     

. Khi đó

AB

là:

A.





 

; 2 3; .   

B.



 



4; 2 3;7 .  

C.



  

4; 2 3;7 .  

D.

 





; 2 3; .   

Lời giải.

....................................................................................................................................................................................................................

Câu 101. Cho



 

  

5;1 ; 3; ; ; 2A B C      

. Khẳng định nào sau đây đúng?

A.

 

5; .AB   

B.

 

;.BC   

C.

.BC  

D.

 

5; 2 .AC   

Lời giải.

....................................................................................................................................................................................................................

Câu 102. Sử dụng kí hiệu khoảng để viết các tập hợp sau đây:

  



4; \ ;2E   

.

A.





4;9 .

B.

 

;. 

C.

 

1;8 .

D.

 

4; .

Lời giải.

....................................................................................................................................................................................................................

Câu 103. Cho

 

2

7 6 0A x x x    

và

 

4B x x  

. Khi đó:

A.

.A B A

B.

.A B A B  

C.

\.A B A

D.

\.BA

Lời giải.

....................................................................................................................................................................................................................

Câu 104. Cho

 

   

0;3 ; 1;5 ; 0;1A B C  

. Khẳng định nào sau đây sai?

A.

.A B C   

B.





0;5 .A B C  

C.

   

\ 1;5 .A C C

D.

  



\ 1;3 .A B C

Lời giải.

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

73

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Câu 105. Cho



 

 



;1 ; 1; ; 0;1A B C    

. Khẳng định nào sau đây sai?

A.

 

1.A B C  

B.

 

;.A B C    

C.

  



 

\ ;0 1; .A B C    

D.

 

\.A B C C

Lời giải.

....................................................................................................................................................................................................................

Câu 106. Cho các tập hợp

 

|3A x x  

,

 

|1 5B x x   

,

 

| 2 4C x x    

.

Khi đó

   

\B C A C

bằng

A.





2;3

. B.

 

3;5

. C.





;1

. D.

 

2;5

.

Lời giải

....................................................................................................................................................................................................................

Câu 107. Cho





;1A  

;





1;B  

;





0;1C 

. Câu nào sau đây sai?

A.

  



 

\C ;0 1;AB    

. B.

 

C1AB   

.

C.

 

C;AB    

. D.

 

\CAB  

.

Lời giải

....................................................................................................................................................................................................................

Câu 108. Cho hai tập hợp

 

2;A  

và

5

;

2

B



 









. Khi đó

   

\A B B A

là

A.

5

;2

2







. B.

 

2;

. C.

5

;

2













. D.

5

;

2









.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

74

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Câu 109. Cho

 

1;3A 

và

 

0;5B 

. Khi đó

   

\A B A B

là

A.

 

1;3

. B.

 

1;3

. C.

   

1;3 \ 0

. D.





1;3

.

Lời giải

....................................................................................................................................................................................................................

Câu 110. Cho hai tập hợp

X

,

Y

thỏa mãn

 

\ 7;15XY

và

 

1;2XY  

.

Xác định số phần tử là số nguyên của

X

.

A.

2

. B.

5

. C.

3

. D.

4

.

Lời giải

....................................................................................................................................................................................................................

Mức độ 3. Vận dụng

Câu 111. Tập hợp nào dưới đây là giao của hai tập hợp

 

: 1 3A x x    

,

 

:2B x x  

A.

 

1;2

. B.





0;2

. C.

 

2;3

. D.





1;2

.

Lời giải

....................................................................................................................................................................................................................

Câu 112. Cho ba tập hợp:

 

4;3X 

,

 

:2 4 0, 5Y x x x    

,

  

 

: 3 4 0Z x x x    

.

Chọn câu đúng nhất:

A.

XY

. B.

ZX

. C.

Z X Y

. D.

ZY

.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

75

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Câu 113. Cho





1;A  

,

 

2

| 1 0B x x   

,

 

0;4C 

. Tập

 

A B C

có bao nhiêu phần tử

là số nguyên.

A.

3

. B.

1

. C.

0

. D.

2

.

Lời giải

....................................................................................................................................................................................................................

Câu 114. Cho

 

5A x x   

. Tìm

C A

.

A.

 

C 5;5 .A 

B.

 

C 5;5 .A 

C.





C 5;5 .A 

D.



 



C ; 5 5; .A     

Lời giải.

....................................................................................................................................................................................................................

Câu 115. Cho tập hợp



C 3; 8A







và

 

C 5;2 3; 11B   

. Tập

 

C AB

là:

A.

 

3; 3 .

B.

.

C.

 

5; 11 .

D.

 

3;2 3; 8 .

Lời giải.

....................................................................................................................................................................................................................

Câu 116. Cho





;1A a a

. Lựa chọn phương án đúng.

A.



 



; 1;C A a a    

. B.

 





; 1;C A a a    

.

C.





 

; 1;C A a a    

. D.

   

; 1;C A a a    

.

Lời giải

....................................................................................................................................................................................................................

Câu 117. Cho hai tập hợp

 

4;3A 

và

 

7;B m m

. Tìm

m

để

BA

.

A.

3.m 

B.

3.m 

C.

3.m 

D.

3.m 

Lời giải.

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

76

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Câu 118. Cho các tập hợp

 

;Am 

và

 

3 1;3 3B m m  

. Tìm

m

để

A C B

.

A.

1

.

2

m 

B.

1

.

2

m 

C.

1

.

2

m 

D.

1

.

2

m 

Lời giải.

....................................................................................................................................................................................................................

Câu 119. Cho hai tập hợp

 

1;3A 

và

 

;1B m m

. Tìm tất cả giá trị của tham số

m

để

BA

.

A.

1m 

. B.

12m

. C.

12m

. D.

2m 

.

Lời giải

....................................................................................................................................................................................................................

Câu 120. Cho

 

2;A  

,

 

;Bm 

. Điều kiện cần và đủ của

m

sao cho

B

là tập con của

A

là

A.

2m 

. B.

2m 

. C.

2m 

. D.

2m 

.

Lời giải

....................................................................................................................................................................................................................

Câu 121. Cho số thực

0a 

và hai tập hợp

 

;9Aa 

,

4

;B

a



 





. Tìm

a

để

AB  

.

A.

2

.

3

a 

B.

2

0.

3

a  

C.

2

0.

3

a  

D.

2

.

3

a 

Lời giải.

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

77

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

Câu 122. Cho hai tập

 

0;5A 

;





2 ;3 1B a a

, với

1a 

.

Tìm tất cả các giá trị của

a

để

A.B  

A.

5

2

1

3

a













. B.

5

2

1

3

a













. C.

15

32

a  

. D.

15

32

a  

.

Lời giải

....................................................................................................................................................................................................................

Câu 123. Cho các tập hợp khác rỗng

3

1;

2

m











và

 





; 3 3;B     

.

Tập hợp các giá trị thực của

m

để

AB  

là

A.

 





; 2 3;   

. B.

 

2;3

.

C.

 





; 2 3;5  

. D.

   

; 9 4;   

.

Lời giải

....................................................................................................................................................................................................................

Câu 124. Cho

m

là một tham số thực và hai tập hợp

 

1 2 ; 3A m m  

,

 

| 8 5B x x m   

.

Tất cả các giá trị

m

để

AB  

là

A.

5

6

m 

. B.

2

3

m 

. C.

5

6

m 

. D.

25

36

m  

.

Lời giải

....................................................................................................................................................................................................................

Câu 125. Cho các tập hợp khác rỗng

 

;Am 

và

 

2 2;2 2B m m  

.

Tìm

m

để

R

C A B  

A.

2m 

. B.

2m 

. C.

2m 

. D.

2m 

.

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

78

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

Lời giải

....................................................................................................................................................................................................................

Câu 126. Cho hai tập hợp

 

4;1A 

,

 

3;Bm

. Tìm

m

để

A B A

.

A.

1.m 

B.

1.m 

C.

3 1.m  

D.

3 1.m  

Lời giải.

....................................................................................................................................................................................................................

Câu 127. Cho





;1Am  

;

 

1;B   

. Điều kiện để

 

AB

là

A.

1m 

. B.

2m 

. C.

0m 

. D.

2m 

.

Lời giải

....................................................................................................................................................................................................................

Câu 128. Cho hai tập hợp

 

1;5Am

và

 

3;B  

. Tìm

m

để

\AB

.

A.

4.m 

B.

4.m 

C.

4 6.m

D.

4 6.m

Lời giải.

....................................................................................................................................................................................................................

Dạng 4. TẬP CON – TẬP BẰNG NHAU

1. Phương pháp.

Tập con:

     A B x A x B

.



,A A A

.



,  AA

.



AB

và

BC

suy ra

AC

.

Tập bằng nhau

  A B A B

và

     B A x A x B

.

2. Bài tập minh họa.

Bài tập 45. Cho tập

 

1;2;3;4A

. Hãy viết các tập con gồm

a). 1 phần tử. b). 2 phần tử. c). 3 phần tử. d). 4 phần tử.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

79

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Bài tập 46. Cho tập

 

1;2;3;4;5A

. Viết tất cả các tập con của

A

có ít nhất 3 phần tử.

Lời giải

....................................................................................................................................................................................................................

Bài tập 47. Cho tập

 

1 ;2;3;4;5;6;7X

.

a). Hãy tìm tất cả các tập con của

X

có chứa các phần tử 1, 3, 5, 7.

b). Có bao nhiêu tập con của

X

chứa đúng 2 phần tử ?

Lời giải

....................................................................................................................................................................................................................

Bài tập 48. Cho hai tập hợp

 

0;2;4;6A

và

 

4;5;6B

.

a). Hãy xác định tất cả các tập con khác rỗng

, XY

của

A

biết rằng

X Y A

và

 

A B X

.

b). Hãy xác định tất cả các tập

P

biết rằng

   

   A B P A B

.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

80

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Bài tập 49. Cho các tập hợp

A

,

B

và

C

. Chứng minh rằng

a).

     

\ \ \  A B C A B A C

.

b).

     

\ \ \  A B C A B A C

.

c).

       

\ \ \   A B B A A B A B

.

Lời giải

....................................................................................................................................................................................................................

Bài tập 50. Tìm quan hệ bao hàm hay bằng nhau giữa các tập hợp sau đây

a).

 

2  A x x

và

 

22

( ) ( 2) 0    B x x x x

.

b).

 

14   A x x

và

 

2

90   B x x

.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

81

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Bài tập 51. Cho ba tập hợp

   

 

3 1 , 1 5 , 2 .            A x x B x x C x x

Chứng minh rằng

     

.  C A B C A C B

Lời giải

....................................................................................................................................................................................................................

Bài tập 52. Cho hai tập hợp

A

,

B

bất kì. Chứng minh rằng

    A B A B A B

.

Lời giải

....................................................................................................................................................................................................................

Bài tập 53. Tìm tập hợp

X

sao cho

   

; ; ; ;a b X a b c d

.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

82

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Bài tập 54. Cho hai tập hợp

 

; ; ; ;A a b c d e

và

 

; ; ;B a c e f

. Tìm tất cả các tập hợp

X

sao cho

XA

và

XB

.

Lời giải

....................................................................................................................................................................................................................

Bài tập 55. Cho ba tập hợp

 

2;5A

,

 

5;Bx

và

 

; ;5C x y

. Tìm các giá trị của

x

,

y

sao cho

A B C

.

Lời giải

....................................................................................................................................................................................................................

Bài tập 56. Cho các tập hợp

 

15   A x x

,

 

47   B x x

và

 

26   C x x

.

Gọi

 

   D x a x b

. Hãy xác định

a

,

b

để

 

  D A B C

.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

83

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

Bài tập 57. Cho hai tập hợp

 

0;3A

và

 

;2B a a

. Tìm

a

để

BA

.

Lời giải

....................................................................................................................................................................................................................

3. Câu hỏi trắc nghiệm

Mức độ 1. Nhận biết

Câu 129. Hình nào sau đây minh họa tập

A

là con của tập

B

?

A. B.

C. D.

Lời giải

....................................................................................................................................................................................................................

Câu 130. Cho tập

 

2;3;4 .X 

Hỏi tập

X

có bao nhiêu tập hợp con?

A.

3.

B.

6.

C.

8.

D.

9.

Lời giải

....................................................................................................................................................................................................................

Câu 131. Cho tập

 

1;2;3;4 .X 

Khẳng định nào sau đây đúng?

A. Số tập con của

X

là

16.

B. Số tập con của

X

có hai phần tử là

8.

C. Số tập con của

X

chứa số 1 là

6.

D. Số tập con của

X

chứa 4 phần tử là

0.

Lời giải

....................................................................................................................................................................................................................

Câu 132. Tập

 

0;2;4;6A 

có bao nhiêu tập hợp con có đúng hai phần tử?

A.

4.

B.

6.

C.

7.

D.

8.

Lời giải

....................................................................................................................................................................................................................

Câu 133. Tập

 

1;2;3;4;5;6A 

có bao nhiêu tập hợp con có đúng hai phần tử?

A.

30.

B.

15.

C.

10.

D.

3.

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

84

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

Lời giải

....................................................................................................................................................................................................................

Câu 134. Cho tập

 

; ; ; ; ; ; ; ; ;X

         



.

Số các tập con có ba phần tử trong đó có chứa

,



của

X

là

A.

8.

B.

10.

C.

12.

D.

14.

Lời giải

....................................................................................................................................................................................................................

Câu 135. Cho hai tập hợp

{X n n

là bội của

4 và 6}

,

{Y n n

là bội của

12}

. Mệnh đề

nào sau đây sai?

A.

.YX

B.

.XY

C.

:n n X

và

.nY

D.

.XY

Lời giải

....................................................................................................................................................................................................................

Câu 136. Trong các tập hợp sau, tập nào có đúng một tập hợp con ?

A.

.

B.

 

1.

C.

 

.

D.

 

;1 .

Lời giải

....................................................................................................................................................................................................................

Câu 137. Trong các tập hợp sau, tập nào có đúng hai tập hợp con ?

A.

.

B.

 

1.

C.

 

.

D.

 

;1 .

Lời giải

....................................................................................................................................................................................................................

Câu 138. Trong các tập hợp sau, tập nào có đúng hai tập hợp con ?

A.

 

;.xy

B.

 

.x

C.

 

;.x

D.

 

; ; .xy

Lời giải

....................................................................................................................................................................................................................

Câu 139. Cho tập hợp

 

, , , A a b c d

. Tập

A

có mấy tập con?

A.

15

. B.

12

. C.

16

. D.

10

.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

85

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

Câu 140. Tập hợp nào sau đây có đúng một tập hợp con?

A.



. B.

 

1

. C.

 



. D.

 

1; 

.

Lời giải

....................................................................................................................................................................................................................

Câu 141.Cho tập hợp

P

. Tìm mệnh đề sai trong các mệnh đề sau?

A.

PP

. B.

P

. C.

 

PP

. D.

PP

.

Lời giải

....................................................................................................................................................................................................................

Câu 142. Tập hợp nào sau đây có đúng hai tập hợp con?

A.

 

;x 

. B.

 

x

. C.

 

;;xy

. D.

 

;xy

.

Lời giải

....................................................................................................................................................................................................................

Câu 143. Cho

A

,

B

là các tập khác rỗng và

AB

. Khẳng định nào sau đây sai?

A.

A B A

. B.

A B A

. C.

\BA

. D.

\AB

.

Lời giải

....................................................................................................................................................................................................................

Câu 144. Cho

 

1;2;3A 

, số tập con của

A

là

A.

3

. B.

5

. C.

8

. D.



.

Lời giải

....................................................................................................................................................................................................................

Câu 145. Cho tập

 

,A a b

,

 

, , ,B a b c d

. Có bao nhiêu tập

X

thỏa mãn

A X B

?

A.

4

. B.

5

. C.

3

. D.

6

.

Lời giải

....................................................................................................................................................................................................................

Câu 146. Cho tập

X

có

1n 

phần tử (

n

). Số tập con của

X

có hai phần tử là

A.

 

1nn

.

B.

 

1

2

nn

. C.

1n 

. D.

 

1

2

nn

.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

86

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Câu 147. Cho hai tập hợp

 

1;2;3A 

và

 

1;2;3;4;5 .B 

Có tất cả bao nhiêu tập

X

thỏa

?A X B

A.

4.

B.

5.

C.

6.

D.

8.

Lời giải

....................................................................................................................................................................................................................

Câu 148. Cho hai tập hợp

 

1;2;5;7A 

và

 

1;2;3 .B 

Có tất cả bao nhiêu tập

X

thỏa

XA

và

?XB

A.

1.

B.

2.

C.

3.

D.

4.

Lời giải

....................................................................................................................................................................................................................

Câu 149. Cho các tập hợp sau:



M xx 

là bội số của



2

.



N xx 

là bội số của



6

.



P xx 

là ước số của



2

.



Q xx 

là ước số của



6

.

Mệnh đề nào sau đây đúng?

A.

.MN

B.

.NM

C.

.PQ

D.

.QP

Lời giải

....................................................................................................................................................................................................................

Câu 150. Cho ba tập hợp

, EF

và

.G

Biết

, E F F G

và

.GE

Khẳng định nào sau đây đúng.

A.

.EF

B.

.FG

C.

.EG

D.

.E F G

Lời giải

....................................................................................................................................................................................................................

Câu 151. Tìm

, xy

để ba tập hợp

   

2;5 , 5;A B x

và

 

; ;5C x y

bằng nhau.

A.

2.xy

B.

2xy

hoặc

2, 5.xy

C.

2, 5.xy

D.

5, 2xy

hoặc

5.xy

Lời giải

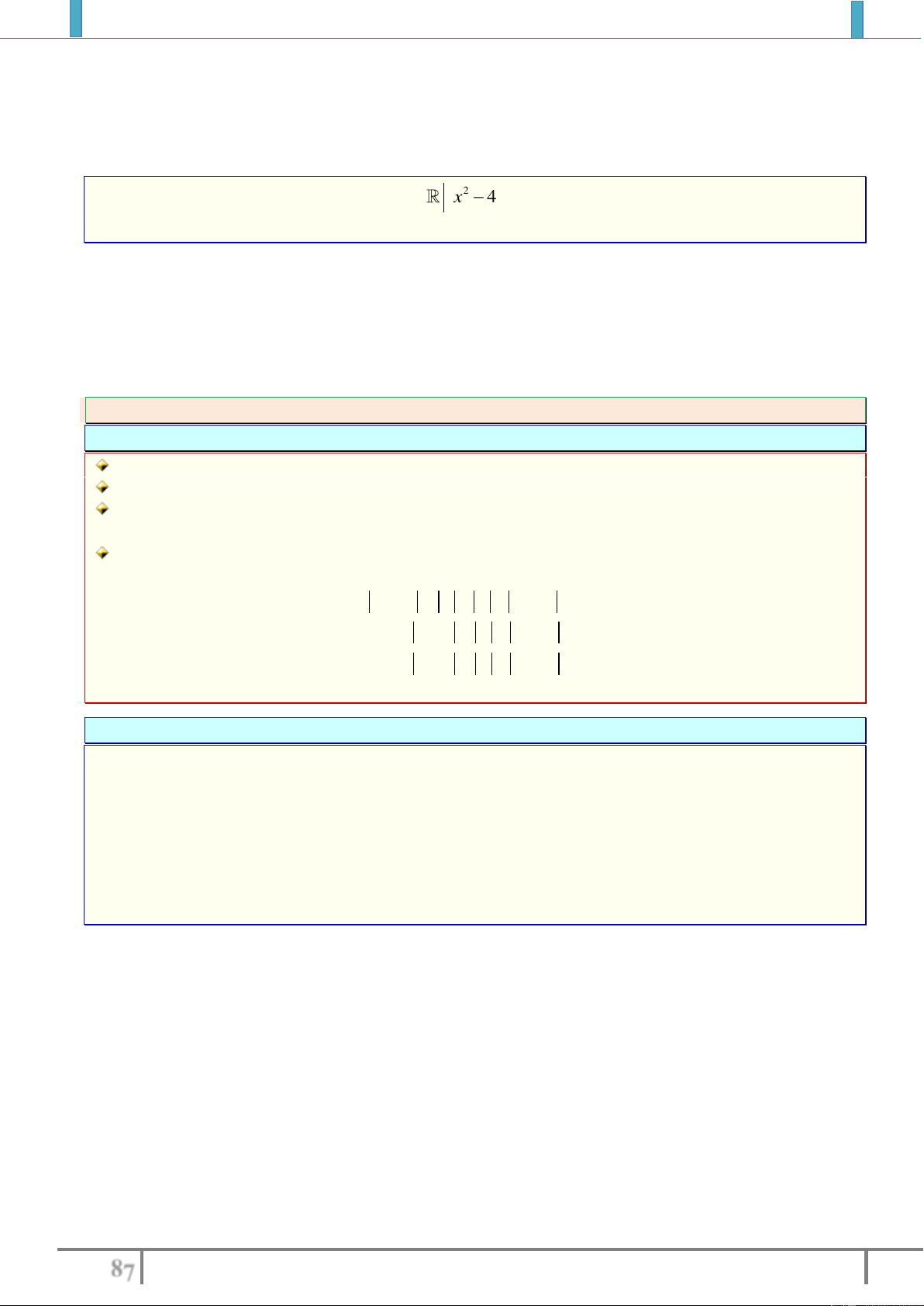
Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

87

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Câu 152. Cho tập hợp

 

 

 

2

1;3;m , 4 3 0B C x x x     

. Tìm

m

để

CB

A.

1.m 

B.

4.m 

C.

0.m 

D.

3.m 

Lời giải

....................................................................................................................................................................................................................

Dạng 5. SỬ DỤNG BIỂU ĐỒ VEN ĐỂ GIẢI TOÁN

1. Phương pháp.

Chuyển bài toán về ngôn ngữ tập hợp.

Sử dụng biểu đồ ven để minh họa các tập hợp.

Dựa vào biểu đồ ven ta thiết lập được đẳng thức(hoặc phương trình hệ phương trình) từ đó

tìm được kết quả bài toán.

Ta có thể sử dụng một số công thức sau:

 Nếu bài toán chỉ có hai tập hợp:

 Tổng số phần tử của tập hợp

.A B A B A B    

 Chỉ có số phần tử của tập hợp

A

là

\.A B A A B  

 Chỉ có số phần tử của tập hợp

B

là

\.B A B A B  

 Nếu bài toán chỉ có ba tập hợp:

2. Bài tập minh họa.

Bài tập 58. Trong lớp 10A có 25 học sinh khá các môn tự nhiên, 24 học sinh khá các môn xã hội,

10 học sinh khá các môn tự nhiên và xã hội, 3 học sinh không học khá các môn tự nhiên và xã hội.

Hỏi :

a). Lớp học đó có bao nhiêu học sinh học khá các môn tự nhiên nhưng không học khá các môn

xã hội.

b). Lớp học đó có bao nhiêu học sinh học khá các môn xã hội nhưng không học khá các môn tự

nhiên.

c). Lớp học đó có bao nhiêu học sinh.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

88

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Bài tập 58. Trong lớp 10A có 45 học sinh trong đó có 25 em thích môn Văn, 20 em thích môn Toán,

18 em thích môn Sử, 6 em không thích môn nào, 5 em thích cả ba môn. Hỏi số em thích chỉ một

môn trong ba môn trên.

Lời giải

....................................................................................................................................................................................................................

Bài tập 59. Trong lớp 11A có 16 học sinh giỏi môn Toán, 15 học sinh giỏi môn Lý và 11 học sinh

giỏi môn Hóa. Biết rằng có 9 học sinh vừa giỏi Toán và Lý (có thể giỏi thêm môn Hóa), 6 học sinh

vừa giỏi Lý và Hóa (có thể giỏi thêm môn Toán), 8 học sinh vừa giỏi Hóa và Toán (có thể giỏi thêm

môn Lý) và trong đó chỉ có đúng 11 học sinh giỏi đúng hai môn. Hỏi có bao nhiêu học sinh của lớp

a). Giỏi cả ba môn Toán, Lý, Hóa.

b). Giỏi đúng một môn Toán, Lý hoặc Hóa.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

89

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

3. Câu hỏi trắc nghiệm

Câu 153. Một lớp có 30 học sinh, trong đó mỗi học sinh giỏi ít nhất một trong hai môn Hóa và

Văn, biết rằng có

15

bạn học giỏi môn Hóa,

20

bạn học giỏi môn Văn. Hỏi lớp đó có bao nhiêu học

sinh giỏi cả hai môn

A.

25.

B.

20.

C.

10.

D.

5.

Lời giải

....................................................................................................................................................................................................................

Câu 154. Trong số

45

học sinh của lớp 10A có

15

bạn được xếp loại học lực giỏi,

20

bạn được xếp

loại hạnh kiểm tốt, trong đó có 10 bạn vừa được học sinh giỏi vừa được hạnh kiểm tốt. Khi đó lớp

10A có bao nhiêu bạn được khen thưởng, biết rằng muốn được khen thưởng bạn đó phải có học

lực giỏi hay hạnh kiểm tốt.

A.

25.

B.

20.

C.

35.

D.

40.

Lời giải

....................................................................................................................................................................................................................

Câu 155. Trong số

45

học sinh của lớp 10A có

15

bạn được xếp loại học lực giỏi,

20

bạn được xếp

loại hạnh kiểm tốt, trong đó có 10 bạn vừa được học sinh giỏi vừa được hạnh kiểm tốt. Khi đó lớp

10A có bao nhiêu bạn chưa được xếp loại học lực giỏi và chưa có hạnh kiểm tốt.

A.

25.

B.

20.

C.

35.

D.

40.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

90

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

Câu 156. Trong kì thi học sinh giỏi cấp trường, lớp 10A có

17

bạn được xếp công nhận học sinh

giỏi Văn,

25

bạn học sinh giỏi Toán. Tìm số học sinh giỏi cả Văn và Toán biết lớp 10A có

45

học

sinh và có

13

học sinh không đạt học sinh giỏi.

A.

10.

B.

32.

C.

30.

D.

15.

Lời giải

....................................................................................................................................................................................................................

Câu 157. Trong kì thi học sinh giỏi cấp trường, lớp 10A có

17

bạn được xếp công nhận học sinh

giỏi Văn,

25

bạn học sinh giỏi Toán. Tìm số học sinh giỏi cả Văn và Toán biết lớp 10A có

45

học

sinh và có

10

học sinh không đạt học sinh giỏi.

A.

7.

B.

32.

C.

12.

D.

15.

Lời giải

....................................................................................................................................................................................................................

Câu 158. Lớp 10A có

10

học sinh giỏi Toán,

10

học sinh giỏi Lý,

11

học sinh giỏi hóa,

6

học sinh

giỏi cả Toán và Lý,

5

học sinh giỏi cả Hóa và Lý,

4

học sinh giỏi cả Toán và Hóa,

3

học sinh giỏi cả

ba môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một trong ba môn (Toán, Lý, Hóa) của lớp 10A là

A.

19

. B.

18

. C.

31

. D.

49

.

Lời giải

....................................................................................................................................................................................................................

Câu 2. Lớp

10A

có

7

học sinh giỏi Toán,

5

học sinh giỏi Lý,

6

học sinh giỏi Hoá,

3

học sinh giỏi

cả Toán và Lý,

4

học sinh giỏi cả Toán và Hoá,

2

học sinh giỏi cả Lý và Hoá,

1

học sinh giỏi cả ba

môn Toán, Lý, Hoá. Số học sinh giỏi ít nhất một môn (Toán, Lý, Hoá ) của lớp

10A

là

A.

9

. B.

18

. C.

10

. D.

28

.

Lời giải

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 3. Tập Hợp Và Các Phép Toán Trên Tập Hợp

91

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 4. Số Gần Đúng Và Sai Số

92

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

A. LÝ THUYẾT

I. Giá trị đúng và giá trị gần đúng:

1. Định nghĩa. Gọi

a

là giá trị đúng,

a

là giá trị gần đúng của

a

, Khi đó:

Sai số tuyệt đối:

a

aa  

.

Sai số tương đối:

a

aa









.

Ví dụ 1. Cho số

2

7

x

và các giá trị gần đúng của

x

là

0,28 ; 0,29 ; 0,286

. Hãy xác định sai số

tuyệt đối trong từng trường hợp và cho biết giá trị gần đúng nào là tốt nhất.

Lời giải

....................................................................................................................................................................................................................

II. Độ chính xác:

1. Định nghĩa:

d

được gọi là độ chính xác của số gần đúng

a

nếu

a

d

.

Tức là

a

a a d d a a d        

a d a a d    

.

Quy ước: quy ước viết gọn là

a a d

.

Nhận xét: Từ đây ta có thể suy ra

a

aa

d

a a a







  

(

dùng để tính sai số tương đối)

Ví dụ 2. Độ dài của một cây cầu người ta đo được là

996m 0,5m

. Sai số tương đối tối đa trong

phép đo là bao nhiêu.

Lời giải

....................................................................................................................................................................................................................

3. Số quy tròn:

Nếu chữ số đầu tiên bỏ đi nhỏ hơn

5

thì ta giữ nguyên bộ phận còn lại.

Nếu chữ số đầu tiên bỏ đi lớn hơn hoặc bằng

5

thì ta cộng vào chữ số cuối cùng của bộ phận còn

lại một đơn vị.

Ví dụ 3. Dùng máy tính bỏ túi. Viết giá trị gần đúng của mỗi số sau, chính xác đến hàng phần trăm

và hàng phần nghìn

a).

3

. b).

2



.

Lời giải

....................................................................................................................................................................................................................

§BI 4. SỐ GẦN ĐÚNG VÀ SAI SỐ

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 4. Số Gần Đúng Và Sai Số

93

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

4. Chữ số chắc (chữ số đáng tin): Chữ số

k

của số gần đúng

a

là chữ số chắc, nếu sai số tuyệt đối



a

không vượt quá nửa đơn vị của hàng

(phần chục, phần trăm, phần nghìn..)

có chữ số

k

đó.

Ví dụ 4. Số dân của một tỉnh là

1034258 300A

(người). Hãy tìm các chữ số chắc và viết

A

dưới

dạng chuẩn.

Lời giải

....................................................................................................................................................................................................................

5. Dạng chuẩn của số gần đúng:

Cách viết chuẩn số gần đúng dưới dạng số thập phân là các chữ số đều là chữ số chắc.

Còn số nguyên thì dạng chuẩn của nó là

.10

k

A

, trong đó

A

là số nguyên và

k

là hàng thấp nhất

có chữ số chắc.

6. Kí hiệu khoa học của một số: Mọi số thập phân khác

0

đều viết dưới dạng

.10

n



với

1 10



và

n

nguyên.

Quy ước:

m

nguyên dương thì

1

10





m

.

A. PHÂN DẠNG VÀ VÍ DỤ MINH HỌA

Dạng 1. SAI SỐ TƯƠNG ĐỐI – SAI SỐ TUYỆT ĐỐI

1. Phương pháp.

Cho

a

là số gần đúng của

a

  

a

aa

là sai số tuyệt đối của số gần đúng

a

.

Nếu

a a d

thì

d

gọi là độ chính xác của số gần đúng

a

. Khi đó

a d a a d a a d      

Tỉ số

a

aa

d

a a a







  

gọi là sai số tương đối của số gần đúng



(thường viết dưới dạng

phần trăm)

Lưu ý:

Phân biệt cận trên của sai số tuyệt đối với sai số tuyệt đối.

Trên thực tế, ta không biết được sai số tuyệt đối (vì chưa biết giá trị của số gần đúng) nên

thường chỉ đánh giá được sai số tuyệt đối không vượt quá một số

d

nào đó.

Số

d

càng nhỏ chứng tỏ sai số giữa số gần đúng và số đúng càng nhỏ. Do đó,

d

được gọi là độ

chính xác của số gần đúng.

Chú ý rằng độ chính xác

d

của một số gần đúng không phải là duy nhất.

2. Bài tập minh họa.

Bài tập 1. Số

a

được cho bởi số gần đúng

5,7824a

với sai số tương đối không vượt quá

0,5%

.

Hãy đánh giá sai số tuyệt đối của

a

.

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 4. Số Gần Đúng Và Sai Số

94

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

Lời giải

....................................................................................................................................................................................................................

Bài tập 2. Một cái ruộng hình chữ nhật có chiều dài là

23m 0,01mx

và chiều rộng là

15m 0,01my

. Chứng minh

a). Chu vi của ruộng là

76m 0,04mP

.

b). Diện tích của ruộng là

345m 0,3801mS

Lời giải

....................................................................................................................................................................................................................

Bài tập 5. Cho tam giác

ABC

có độ dài ba cạnh đo được như sau

12cm 0,2cma

;

10,2cm 0,2cmb

;

8cm 0,1cmc

. Tính chu vi

P

của tam giác và đánh giá sai số tuyệt đối, sai

số tương đối của số gần đúng của chu vi qua phép đo.

Lời giải

....................................................................................................................................................................................................................

3. Câu hỏi trắc nghiệm

Mức độ 1. Nhận biết

Câu 1. Độ cao của một ngọn núi được ghi lại như sau

1372,5m 0,2mh 

. Độ chính xác

d

của

phép đo trên là

A.

0,1md 

. B.

1md 

. C.

0,2md 

. D.

2md 

.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 4. Số Gần Đúng Và Sai Số

95

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Câu 2. Chiều cao của một ngọn đồi là

347,13m 0,2mh 

. Độ chính xác

d

của phép đo trên là:

A.

347,33md 

. B.

0,2md 

. C.

347,13md 

. D.

346,93md 

.

Lời giải

....................................................................................................................................................................................................................

Câu 3. Đo chiều dài của một cây thước, ta được kết quả

45 0,3(cm)a 

.

Khi đó sai số tuyệt đối của phép đo được ước lượng là

A.

45

0,3

. B.

45

0,3

. C.

45

0,3  

. D.

45

0,3  

.

Lời giải

....................................................................................................................................................................................................................

Câu 4. Cho giá trị gần đúng của

8

17

là

0,47

. Sai số tuyệt đối của số

0,47

là

A.

0,001

. B.

0,003

. C.

0,002

. D.

0,004

.

Lời giải

....................................................................................................................................................................................................................

Dạng 2. SỐ GẦN ĐÚNG – CHỮ SỐ CHẮC

1. Phương pháp.

Cách quy tròn đến hàng đơn vị, hàng chục, hàng trăm,...hay đến hàng phần chục, phần trăm...

Nếu chữ số ngay sau hàng quy tròn nhỏ hơn

5

thì ta thay chữ số đó và các chữ bên phải nó

bởi số

0

.

Nếu chữ số ngay sau hàng quy tròn lớn hơn

5

thì ta cũng thay chữ số đó và các chữ bên phải

nó bởi số

0

nhưng cộng thêm

1

đơn vị vào chữ số ở hàng quy tròn.

Khi thay số đứng bởi số quy tròn, thì sai số tuyệt đối không vượt quá nửa đơn vị của hàng quy

tròn.

Nhận xét:

Nếu bài toán không nói rõ hàng đơn vị phải quy tròn mà cho dưới dạng độ chính xác

a a d

thì ta phải xác định hàng quy tròn bằng cách chỉ ra độ chính xác nhỏ hơn hàng đơn

vị nào đó.

Hàng đơn vị đó chính là hằng mà ta quy tròn.

Cách tìm các chữ số chắc: Trong số gần đúng

a

với độ chính xác

d

, một chữ số của

a

được gọi là

chữ số chắc nếu

d

không vượt quá nửa đơn vị của hàng có chữ số đó.

2. Bài tập minh họa.

Bài tập 6. Hãy viết số quy tròn của số a với độ chính xác

d

được cho sau đây

a).

17658 16a

. b).

15,318 0,056a

.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 4. Số Gần Đúng Và Sai Số

96

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Bài tập 7. Các nhà khoa học Mỹ đang nghiên cứu liệu một máy bay có thể có tốc độ gấp bảy lần tốc

độ ánh sáng. Với máy bay đó trong một năm (giả sử một năm có 365 ngày) nó bay được bao nhiêu

? Biết vận tốc ánh sáng là 300 nghìn km/s. Viết kết quả dưới dạng kí hiệu khoa học.

Lời giải

....................................................................................................................................................................................................................

Bài tập 8. Đo chiều dài của một con dốc, ta được số đo

192,55 ma

, với sai số tương đối không

vượt quá

0,3%

. Hãy tìm các chữ số chắc của

d

và nêu cách viết chuẩn giá trị gần đúng của

a

.

Lời giải

....................................................................................................................................................................................................................

Bài tập 9. Tìm số chắc và viết dạng chuẩn của số gần đúng

a

biết

a). Số người dân tỉnh Lâm Đồng là

3214056a

người với độ chính xác

100d

người.

b).

1,3462a

sai số tương đối của

a

bằng

1%

.

Lời giải

....................................................................................................................................................................................................................

Bài tập 10. Một hình lập phương có thể tích

33

180,57cm 0,05cmV

. Xác định các chữ số chắc

chắn của

V

.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 4. Số Gần Đúng Và Sai Số

97

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

Bài tập 11. Viết các số gần đúng sau dưới dạng chuẩn

a).

467346 12a

. b).

2,4653245 0,006b

.

Lời giải

....................................................................................................................................................................................................................

3. Câu hỏi trắc nghiệm

Mức độ 1. Nhận biết

Câu 5. Cho số gần đúng

23748023a 

với độ chính xác

101d 

. Hãy viết số quy tròn của số

.a

A.

23749000.

B.

23748000.

C.

23746000.

D.

23747000.

Lời giải.

....................................................................................................................................................................................................................

Câu 6. Cho giá trị gần đúng của



là

3,141592653589a 

với độ chính xác

10



. Hãy viết số quy

tròn của số

.a

A.

3,141592654.a 

B.

3,1415926536.a 

C.

3,141592653.a 

D.

3,1415926535.a 

Lời giải.

....................................................................................................................................................................................................................

Câu 7. Sử dụng máy tính bỏ túi, hãy viết giá trị gần đúng của

3

chính xác đến hàng phần nghìn.

A. 1,7320. B. 1,732. C. 1,733. D. 1,731.

Lời giải.

....................................................................................................................................................................................................................

Câu 8. Khi sử dụng máy tính bỏ túi với

10

chữ số thập phân ta được:

8 2,828427125

. Giá trị

gần đúng của

8

chính xác đến hàng phần trăm là

A.

2,81

. B.

2,80

. C.

2,82

. D.

2,83

.

Lời giải

....................................................................................................................................................................................................................

Câu 9. Sử dụng máy tính bỏ túi, hãy viết giá trị gần đúng của

2



chính xác đến hàng phần nghìn.

A. 9,873. B. 9,870. C. 9,872. D. 9,871.

Lời giải.

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 4. Số Gần Đúng Và Sai Số

98

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Câu 10. Hãy viết số quy tròn của số gần đúng

17658a 

biết

17658 16.a 

A. 17700. B. 17800. C. 17500. D. 17600.

Lời giải.

....................................................................................................................................................................................................................

Câu 11. Hãy viết số quy tròn của số gần đúng

15,318a 

biết

15,318 0,056.a 

A. 15,3. B. 15,31. C. 15,32. D. 15,4.

Lời giải.

....................................................................................................................................................................................................................

Câu 12. Đo độ cao một ngọn cây là

347,13m 0,2m.h 

Hãy viết số quy tròn của số gần đúng 347,13.

A. 345. B. 347. C. 348. D. 346.

Lời giải.

....................................................................................................................................................................................................................

Câu 13. Theo thống kê, dân số Việt Nam năm

2016

được ghi lại như sau

94 444 200 3000S 

(người). Số quy tròn của số gần đúng

94 444 200

là:

A.

94 440 000

. B.

94 450 000

. C.

94 444 000

. D.

94 400 000

.

Lời giải

....................................................................................................................................................................................................................

Câu 14. Đo độ cao một ngọn cây là

17,14m 0,3mh 

. Hãy viết số quy tròn của số

17,14

?

A.

17,1

. B.

17,15

. C.

17,2

. D.

17

.

Lời giải

....................................................................................................................................................................................................................

Câu 15. Cho số

4,1356 0,001a 

. Số quy tròn của số gần đúng

4,1356

là

A.

4,135

. B.

4,13

. C.

4,136

. D.

4,14

.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 4. Số Gần Đúng Và Sai Số

99

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Mức độ 2. Thông hiểu

Câu 16. Cho tam giác

ABC

có độ dài ba cạnh:

12cm 0,2cm;a 

10,2cm 0,2cm;b 

8cm 0,1cm.c 

Tính chu vi

P

của tam giác đã cho.

A.

30,2 cm 0,2 cm.P 

B.

30,2 cm 1 cm.P 

C.

30,2 cm 0,5 cm.P 

D.

30,2 cm 2 cm.P 

Lời giải.

....................................................................................................................................................................................................................

Câu 17. Một miếng đất hình chữ nhật có chiều rộng

43m 0,5mx 

và chiều dài

63m 0,5my 

.

Tính chu vi

P

của miếng đất đã cho.

A.

212m 4m.P 

B.

212m 2m.P 

C.

212m 0,5m.P 

D.

212m 1m.P 

Lời giải.

....................................................................................................................................................................................................................

Câu 18.

Một thửa ruộng hình chữ nhật có chiều dài là

23m 0,01mx 

và chiều rộng là

15m 0,01my 

.

Tính diện tích

S

của thửa ruộng đã cho.

A.

345m 0,001m.S 

B.

345m 0,38m.S 

C.

345m 0,01m.S 

D.

345m 0,3801m.S 

Lời giải.

....................................................................................................................................................................................................................

Câu 19. Độ dài các cạnh của một đám vườn hình chữ nhật là

7,8m 2cmx 

và

25,6m 4cmy 

.

Cách viết chuẩn của diện tích (sau khi quy tròn) là

A.

22

200m 0,9m

. B.

22

199m 0,8m

. C.

22

199m 1m

. D.

22

200m 1m

.

Lời giải

....................................................................................................................................................................................................................

Câu 20.Cho số

367 653 964 213a 

. Số quy tròn của số gần đúng

367 653 964

là

A.

367 653 960

. B.

367 653 000

. C.

367 654 000

. D.

367 653 970

.

Lời giải

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 4. Số Gần Đúng Và Sai Số

100

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Câu 21. Theo thống kê, dân số Việt Nam năm

2002

là

79715675

người. Giả sử sai số tuyệt đối của

số liệu thống kê này nhỏ hơn

10000

người. Hãy viết số quy tròn của số trên

A.

79710000

người. B.

79716000

người.

C.

79720000

người. D.

79700000

người.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 5. Ôn Tập Chương I

101

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

A. BÀI TẬP TỰ LUẬN.

Bài tập 1. Cho hai tập hợp



21

3

x

Ax

x





  







và

 

4;6;8;10B 

. Tìm

.AB

Lời giải

....................................................................................................................................................................................................................

Bài tập 2. Cho các tập hợp số

 

;4A  

và

 

2;B    

. Hãy xác định các tập hợp sau và biểu

diễn trên trục số:

a).

.AB

b).

.AB

c).

\.AB

d).

\.BA

Lời giải

....................................................................................................................................................................................................................

Bài tập 3. Cho các tập hợp số

 

;5A  

và





3;B    

. Hãy xác định các tập hợp sau và biểu

diễn trên trục số:

a).

.AB

b).

.AB

c).

\.AB

d).

\.BA

e).

.CA

f).

\.B

Lời giải

....................................................................................................................................................................................................................

§BI 5. TỔNG ÔN CHƯƠNG I

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 5. Ôn Tập Chương I

102

Bài tập 4. Cho các tập hợp số





;3A   

và

 





4;1 2; .B     

Hãy xác định các tập hợp sau và

biểu diễn trên trục số:

a).

.AB

b).

.AB

c).

\.AB

d).

\.BA

e).

\.B

Lời giải

....................................................................................................................................................................................................................

Bài tập 5. Cho tập hợp

 

1 5 .A x x   

a). Biểu diễn

A

trên trục số. b). Tìm phần bù của

A

trong

.

Lời giải

....................................................................................................................................................................................................................

Bài tập 6. Cho tập hợp

 

24A x x   

và

 

3 5 .B x x    

a). Biểu diễn

A

trên trục số.

b). Tìm phần bù của

A

trong

.

c). Tìm

,AB

AB

và biểu diễn trên trục số.

Lời giải

....................................................................................................................................................................................................................

Bài tập 7. Cho tập hợp

 

5.A x x  

a). Hãy biểu diễn

A

trên trục số.

b). Tìm phần bù của

A

trong

.

Lời giải

....................................................................................................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Bài 5. Ôn Tập Chương I

103

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

....................................................................................................................................................................................................................

Bài tập 8. Cho tập hợp

 

3 4 .A x x   

Hãy biểu diễn

A

trên trục số.

Lời giải

....................................................................................................................................................................................................................

Bài tập 9. Cho tập hợp

1

2

Ax

x





  









và

 

1 1 .B x x   

Hãy tìm

,AB

AB

và biểu diễn trên trục số.

Lời giải

....................................................................................................................................................................................................................

Bài tập 10. Cho tập hợp và

 

1 2 ,A x x   

 

3 4 .B x x   

Hãy tìm

,AB

AB

và biểu diễn trên trục số.

Lời giải

....................................................................................................................................................................................................................

.................................................................................................................................................................................................................

....................................................................................................................................................................................................................

B. CÂU HỎI TRẮC NGHIỆM

Bài tập mệnh đề và tập hợp – Diệp Tuân

Chương 1: Mệnh đề và tập hợp (KNTT) 31 tài liệu

Toán 10 2.8 K tài liệu

Bình luận

Bài tập mệnh đề và tập hợp – Diệp Tuân