Bài tập mô hình toán ứng dụng môn Toán kinh tế | Học viện Công Nghệ Bưu Chính Viễn Thông

Bài Tập Mô Hình Toán Ứng Dụng
Thầy giáo hướng dẫn: Ngô Văn Thứ
Nhóm sinh viên thực hiện: Nhóm 11 Nguyễn Thùy Linh Đồng Vĩnh Nga Nguyễn Hằng Nga Đỗ Thế Thành Lớp : Toán Kinh Tế 48 Khoa : Toán Kinh Tế Bài tập 2 Chương 3
Một cửa hàng kinh doanh một mặt hàng iện tử, nhu cầu về mặt hàng
này trong khu vực là 40000 ơn vị/năm. Giá mua mỗi ơn vị là 14$, chi phí bảo
quản mỗi ơn vị tính tỷ lệ với giá mua theo hệ số 0,05. Chi phí cho mỗi lần liên
hệ và hợp ồng mua hàng là 120$, Thời gian từ lúc bắt ầu làm hợp ồng mua ến
khi có hàng về ể bán là 2 tháng.
a) Tính lượng hàng ặt mỗi lần sao cho tổng chi phí bé nhất; xác ịnh thời
gian mỗi chu kỳ mua và tiêu thụ hàng; mức hàng còn lại trong kho vào
thời iểm cần tiến hành làm thủ tục mua hàng cho chu kỳ sau?
b) Vẽ ồ thị minh họa và dựa vào ồ thị mô tả hành vi hợp lý của cửa hàng
khi có hạ giá cho lô hàng lớn hơn hoặc bằng S ? 0
c) Giả sử S ược chọn trong câu b, nhưng kho của cửa hàng không cho 0
phép mở rộng hơn mức tối ưu ở câu a, việc thuê kho là tăng chi phí kho
với hệ số k= 0,2 thì nên hiệu chỉnh lượng hàng ặt như thế nào? Bài làm
a) Ta giải bài toán nhờ mô hình Wilson ( mô hình dự trữ tiêu thụ ều, bổ
sung tức thời). Theo bài ta có: Tổng nhu cầu Q = 40000
Chi phí ặt hàng mỗi lần A = 120$
Hệ số chi phí dự trữ I = 0,05 Đơn giá C = 14$
Thời gian ặt hàng T = 2 tháng =60 ngày =0,16438 năm
- Gọi q* là lượng hàng ặt tối ưu mỗi lần ể tổng chi phí bé nhất
Ta có công thức xác ịnh q* như sau: 2 AQ 2*120 *40000 q * IC 0,05*14 3703 ,28 ( ơn vị)
- Tổng chi phí bé nhất là: F(q*) = 562592,296 $
- Xác ịnh thời gian mỗi chu kỳ mua và tiêu thụ hàng t* Số lần ặt hàng n* Q 40000 10 , 8 q * 3703 ,28 1 1
Vậy thời gian mỗi chu kỳ t* 0 ,0926 (năm) = 33,8 (ngày) n * 10 ,8
- Xác ịnh mức hàng còn lại trong kho vào thời iểm cần tiến hành làm thủ
tục mua hàng cho kỳ sau. Đây thực chất là xác ịnh thời iểm ặt hàng.
B* = Q [T - t*.int(T / t*)] mà int(T / t*) = int 0 0 0
(0,16438/0,0926) = int(1,775) = 1 năm Vậy B* =
40000[0,16438 – 0,0926*1] = 2871,2 ( ơn vị)
b) Giả sử lấy mức khối lượng mốc là S và chủ hàng quy ịnh nếu lô hàng 0
nào lớn hơn hoặc bằng S thì giá hàng sẽ hạ ( 0 < <1 ) 0
Tức là : C’= C với q < S 0
C’= C(1- ) với q S q < S : ường chi phí 0 0
dự trữ sẽ không thay ổi
q S : ường chi phí dự trữ sẽ dịch chuyển xuống dưới Ta có 0 2 trường hợp sau:
❖ TH 1 : q* S 0 F(q) AQ q IC CQ min q 2 D(q) AQ q IC q 2
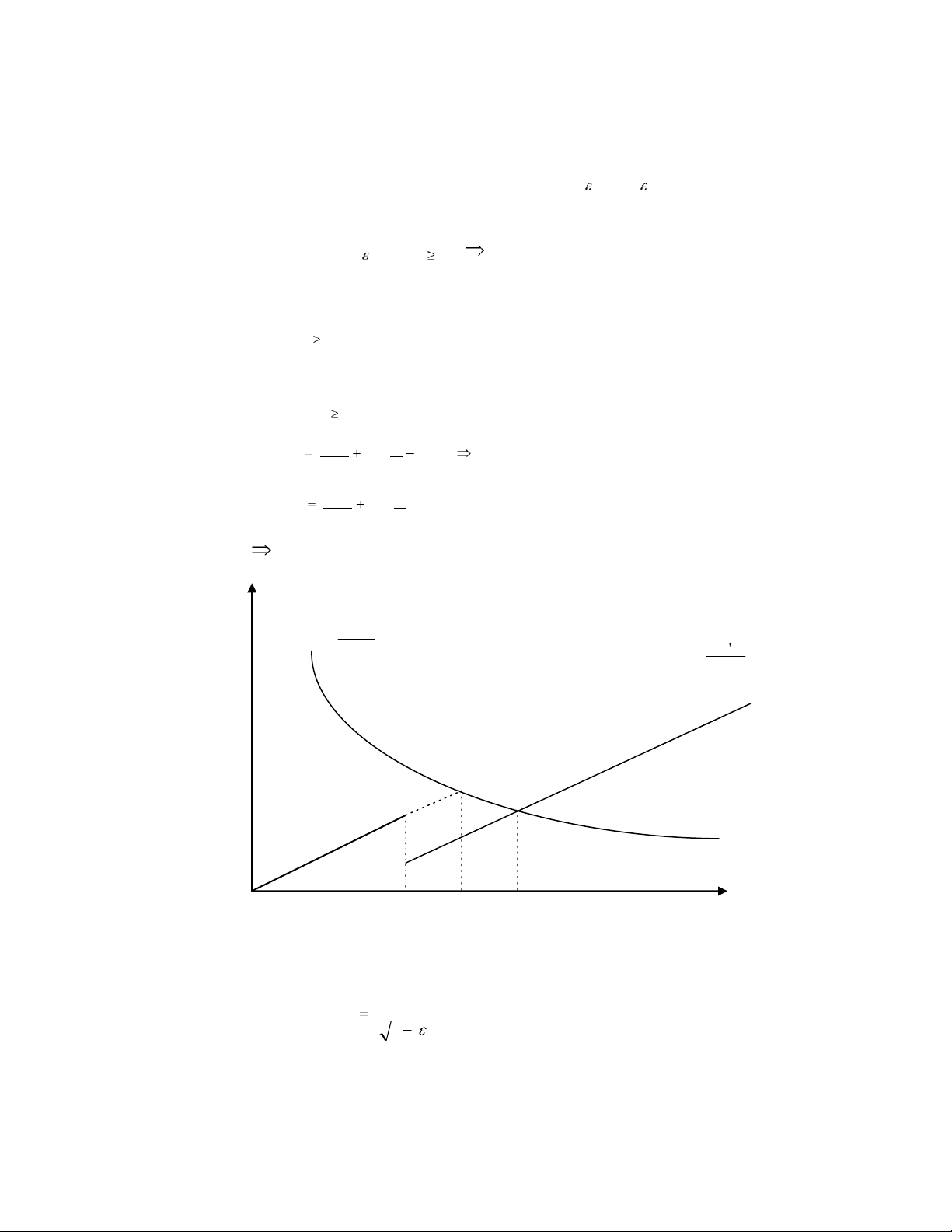
Đồ thị mô tả D(p) và lời giải của ồ thị như sau: Chi AQ phí ' ICq q 2 0 S q* q’* Lượng hàng 0
Nhìn trên ồ thị ta thấy q’* là lượng hàng ặt tối ưu mỗi lần và ược q * tính như sau: q ' * 1 ❖ TH : q* < S 2 0 q *
Ta vẫn tính: q ' * 1
Và khi ó có 2 khả năng xảy ra như sau: KN : q’* < S 1 0
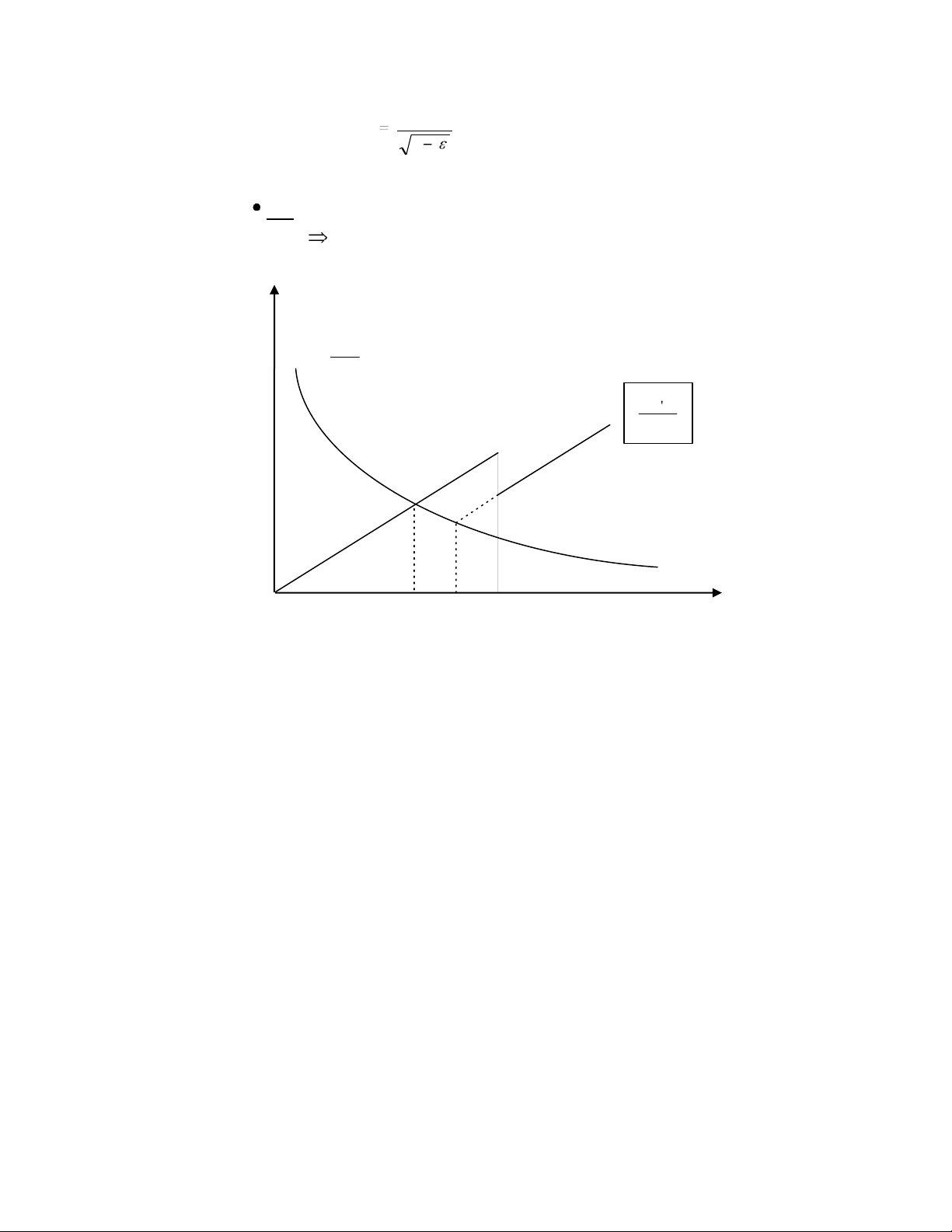
Đồ thị mô tả D(q) và lời giải của ồ thị như sau: Chi phí AQ q ICq' 2 0 q* q’* S Lượng hàng 0
Nhận xét: Với q < S thì F(q)min = F(q*) 0
Với q S thì F(q) min = F( S ) 0 0
Ta so sánh F(q*) và F( S 0 ) từ ó tìm ra lượng hàng ặt tối ưu mỗi lần.
KN 2 : q ’* S 0
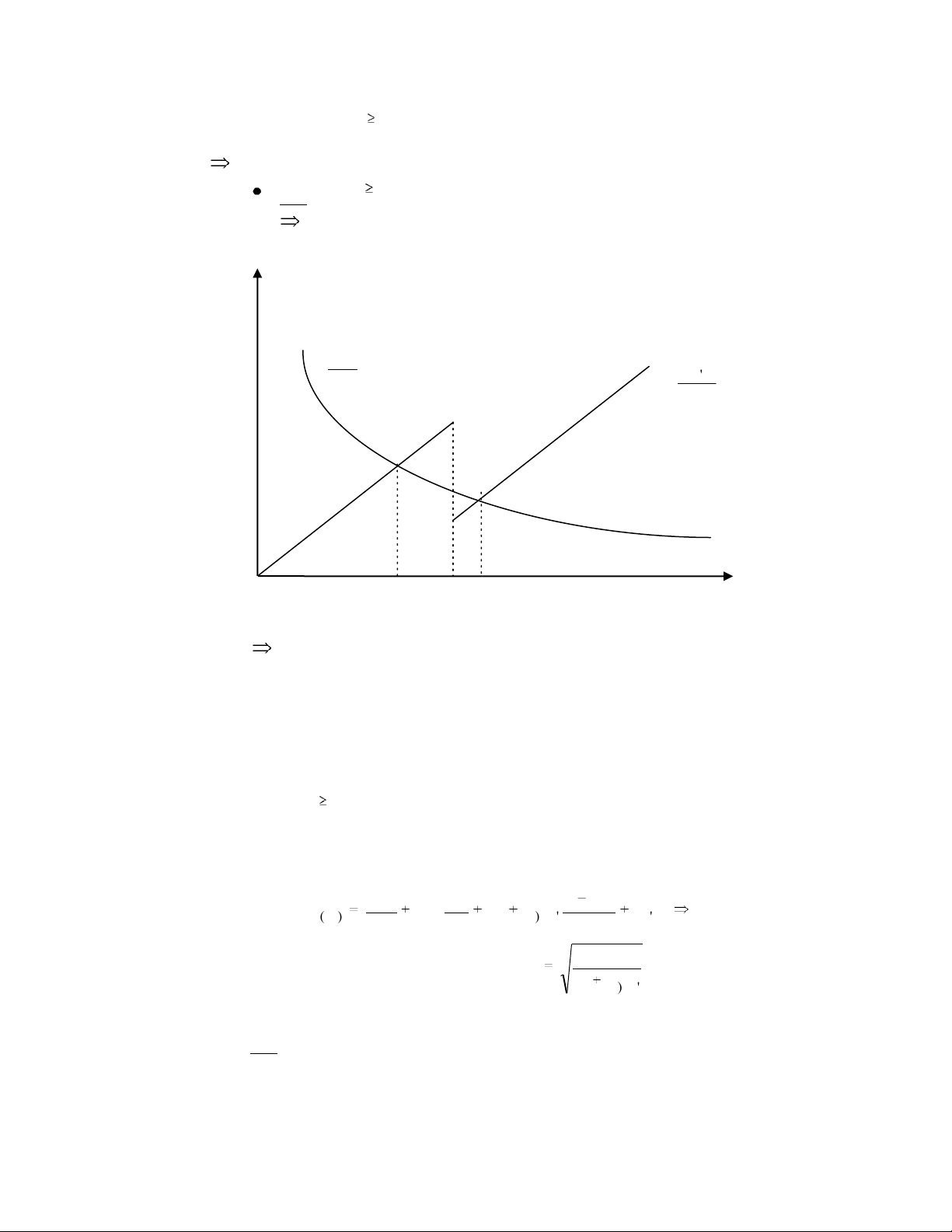
Đồ thị mô tả D(q) và lời giải của ồ thị như sau: Chi phí AQ ICq' q 2 0 q* So q’* Lượng hàng
q* là lượng hàng ặt tối ưu mỗi lần.
c) S ược chọn trong câu b, nhưng kho của cửa hàng không cho phép mở 0
rộng hơn mức tối ưu ở câu a. Như vậy ở ây q* óng vai trò là dung lượng
kho cố ịnh, và mỗi ơn vị hàng ở ầu chu kỳ dự trữ vượt quá q* phát sinh
một chi phí thuê kho với tỷ lệ k = 0,2. ❖ TH : q* S 1 0
Theo câu b trường hợp này cửa hàng nhận ược khuyến mãi. Đơn giá
của một ơn vị hàng lúc này là C’. Từ ây ta có thể lập hàm chi phí theo
lượng hàng ặt mỗi lần q như sau : AQ q * q q * Nq( ) IC ' ( I ) kC ' ' CQ min q 2 2
Lời giải tối ưu của bài toán này là: 2 AQ q * 0 ( I ) kC '
Khi ó ta thấy có 2 khả năng có thể xảy ra: KN : q* > q* 1 0 2 AQ 2 AQ > ( I k C) ' IC (I+k)(1- )C < IC 0,25(1- ) < 0,05 1- < 0,2 < 0,8
Cửa hàng phải thuê thêm kho và lượng tối ưu là q* 0 KN : q* q*
0,8 Cửa hàng không phải thuê thêm kho 2 0 ❖ TH :q* < S 2 0 KN : q’* 0 tính 1 ở câu b nếu q’* AQ q * q q * S IC ' ( I ) kC ' ' CQ Xét N q( )min q 2 2 Làm tương tự trên
KN : q’* tính trên ở câu b nếu q*< q’* < S Xét F(q*) và 2 0 N(S ) ta có: 0 F q( *) 2 AQIC CQ AQ q * S 0 q * N S( 0 ) IC ' ( I k C) ' C Q' S 0 2 2 Nếu F(q*) > N(S ) S là iểm tối ưu. 0 0 F(q*) < N(S ) q* là iểm tối ưu. 0 F(q*) = N(S )
Cả S và q* ều là tối ưu. 0 0 KN : q’* q* q* là tối ưu. 3