Bài tập nhóm môn Toán rời rạc phần 1 | Học viện Công nghệ Bưu chính Viễn thông
Bài tập nhóm môn Toán rời rạc phần 1 của Học viện Công nghệ Bưu chính Viễn thông với những kiến thức và thông tin bổ ích giúp sinh viên tham khảo, ôn luyện và phục vụ nhu cầu học tập của mình cụ thể là có định hướng ôn tập, nắm vững kiến thức môn học và làm bài tốt trong những bài kiểm tra, bài tiểu luận, bài tập kết thúc học phần, từ đó học tập tốt và có kết quả cao cũng như có thể vận dụng tốt những kiến thức mình đã học vào thực tiễn cuộc sống. Mời bạn đọc đón xem!
Tài liệu liên quan:
Preview text:
lOMoARcPSD| 37922327 lOMoARcPSD| 37922327 1.Ví dụ 2:
1.1. Đề bài: Liệt kê (duyệt) các xâu nhị phân có ộ dài n. 1.2. Sơ ồ thuật toán:
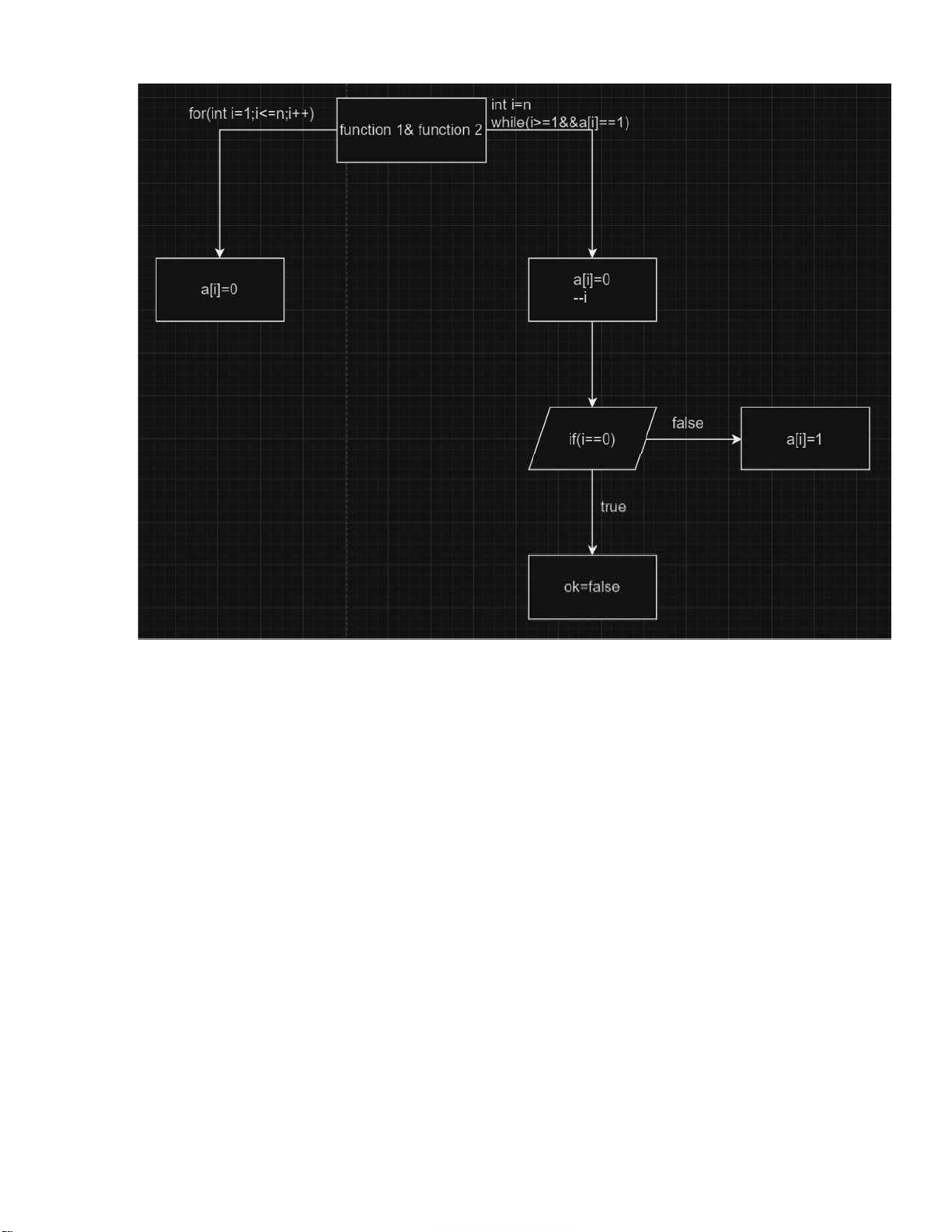
- Sơ ồ hàm sinh nhị phân: - Sơ ồ hàm main: lOMoARcPSD| 37922327 1.3. Viết code: - Hàm sinh nhị phân: lOMoARcPSD| 37922327 #include using namespace std; int n,k,a[100]; bool ok; void ktao(){ for(int i=1;i<=n;i++){ a[i]=0; } } void sinh(){ int i=n;
while(i>=1&&a[i]==1){ a[i]=0; --i; } if(i==0) ok=false; else a[i]=1; } 1.4. Kết quả: - Trường hợp n=4: lOMoARcPSD| 37922327 2.Bài tập 1:
2.1. Đề bài: Cho một hình chữ nhật gồm nxm hình vuông ơn vị. Hãy
liệt kê tất cả các ường i từ ỉnh cuối của ô vuông cuối cùng phía
bên trái ến ỉnh ầu của ô vuông trên cùng phía bên phải. Biết mỗi
bước i chỉ ược phép dịch chuyển sang bên phải hoặc lên trên
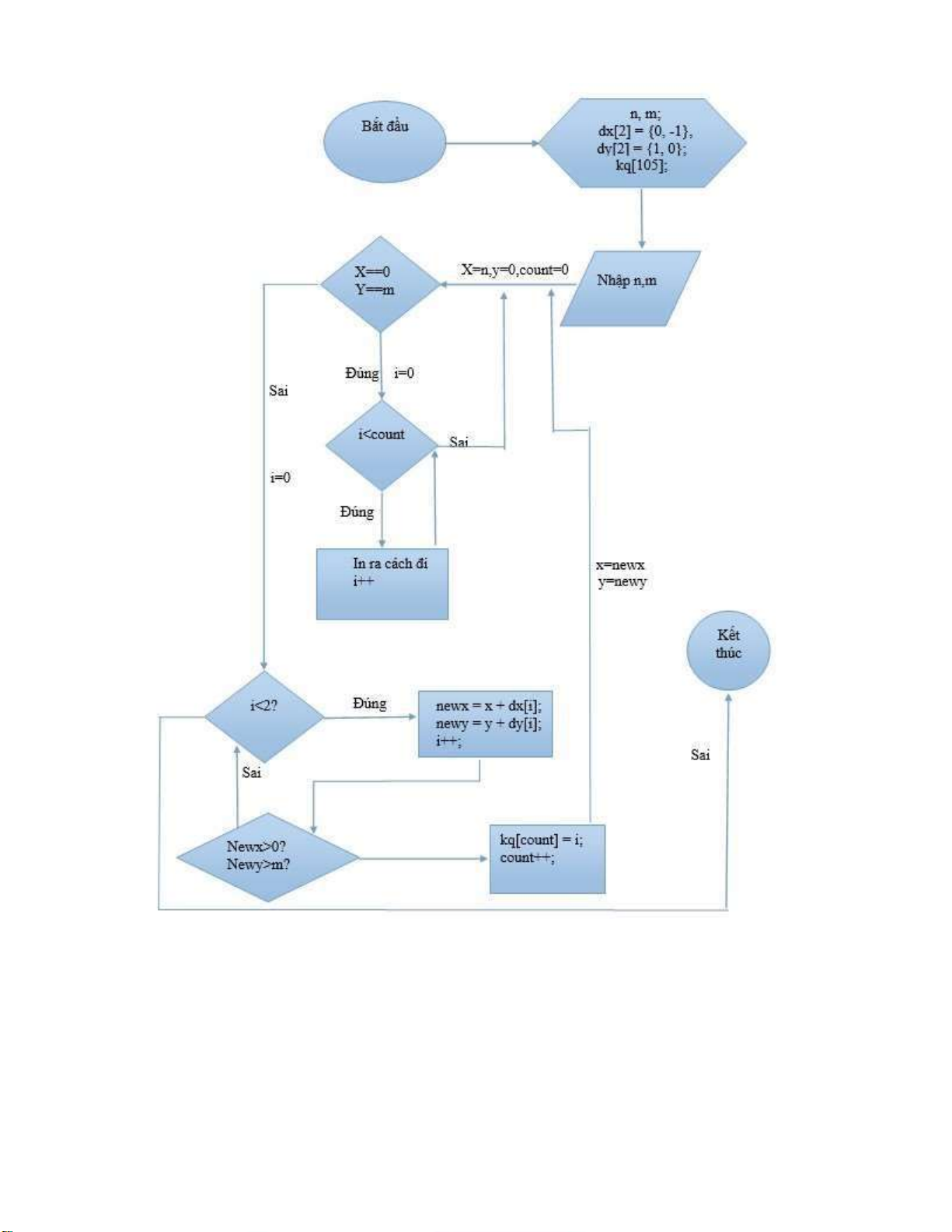
theo các cạnh của hình vuông ơn vị. 2.2. Sơ ồ thuật toán: lOMoARcPSD| 37922327 2.3. Viết code: - Hàm kiểm tra: lOMoARcPSD| 37922327 #include using namespace std; #define ll long long int n, m;
int dx[2] = {0, -1}, dy[2] = {1, 0}; int kq[105]; bool checkOut(int x, int y){ if
(x < 0 || y > m) return false; return true; } - Hàm xử lý: lOMoARcPSD| 37922327
void ql(int x, int y, int count){
if (x == 0 && y == m){ for
(int i = 0; i < count; i++){ if
(kq[i] == 1) cout << "L "; else cout << "P "; } cout << endl; return; }
for (int i = 0; i < 2; i++){ int newx = x + dx[i]; int newy = y + dy[i]; if (checkOut(newx, newy) == true){ kq[count] = i; count++; ql(newx, newy, count); count--; } } } - Hàm main: lOMoARcPSD| 37922327 int main(){
cin >> n >> m; ql(n, 0, 0); return 0; } 2.4. Kết quả: - Trường hợp n=4, m=4: 3. Bài tập 2:
3.1. Đề bài: Hãy liệt kê tất cả các xâu nhị phân có ộ dài n sao cho mỗi
xâu nhị phân có duy nhất một dãy k bit 1 liên tiếp. 3.2. Sơ ồ thuật toán:
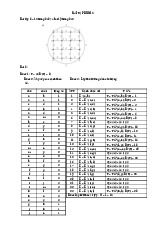
- Sơ ồ hàm sinh nhị phân: lOMoARcPSD| 37922327
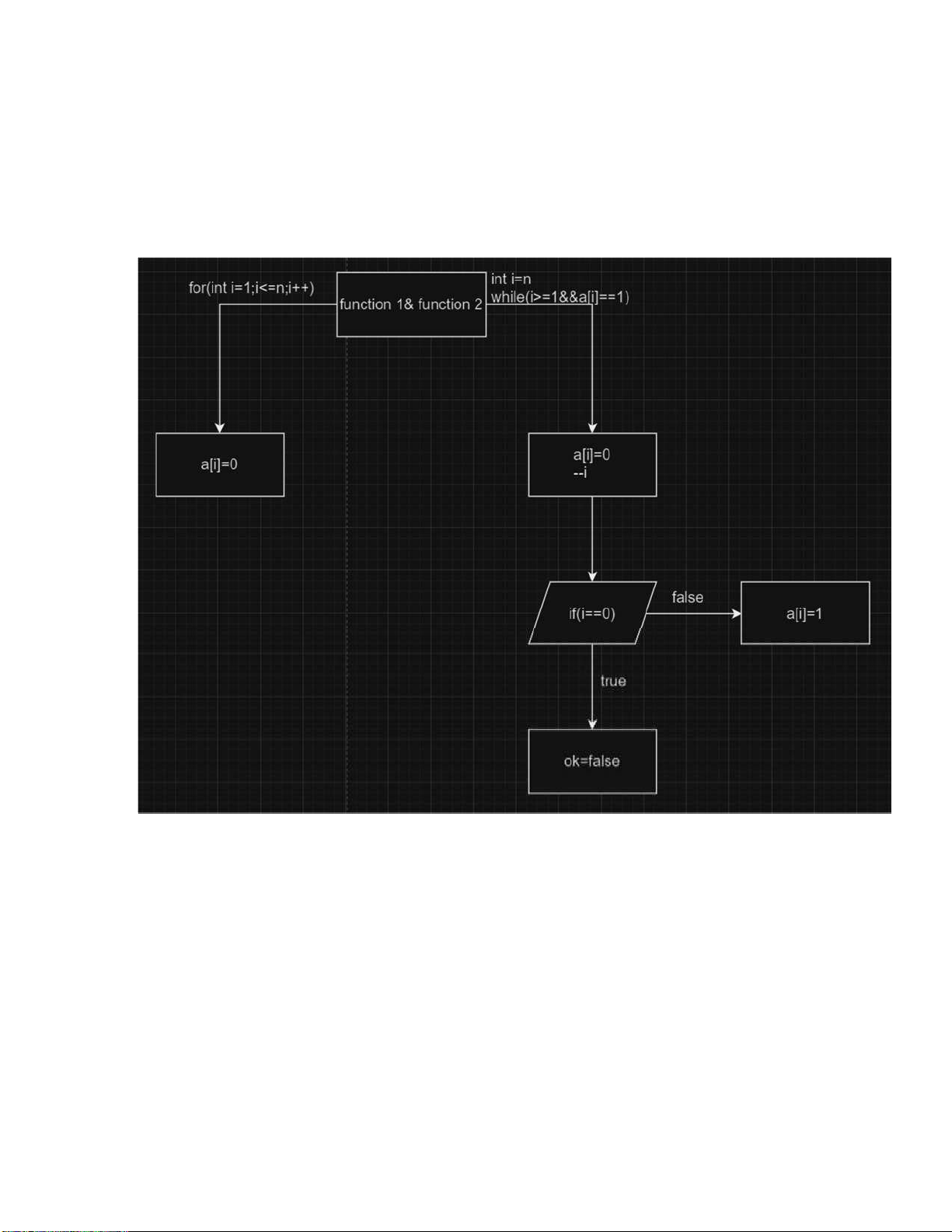
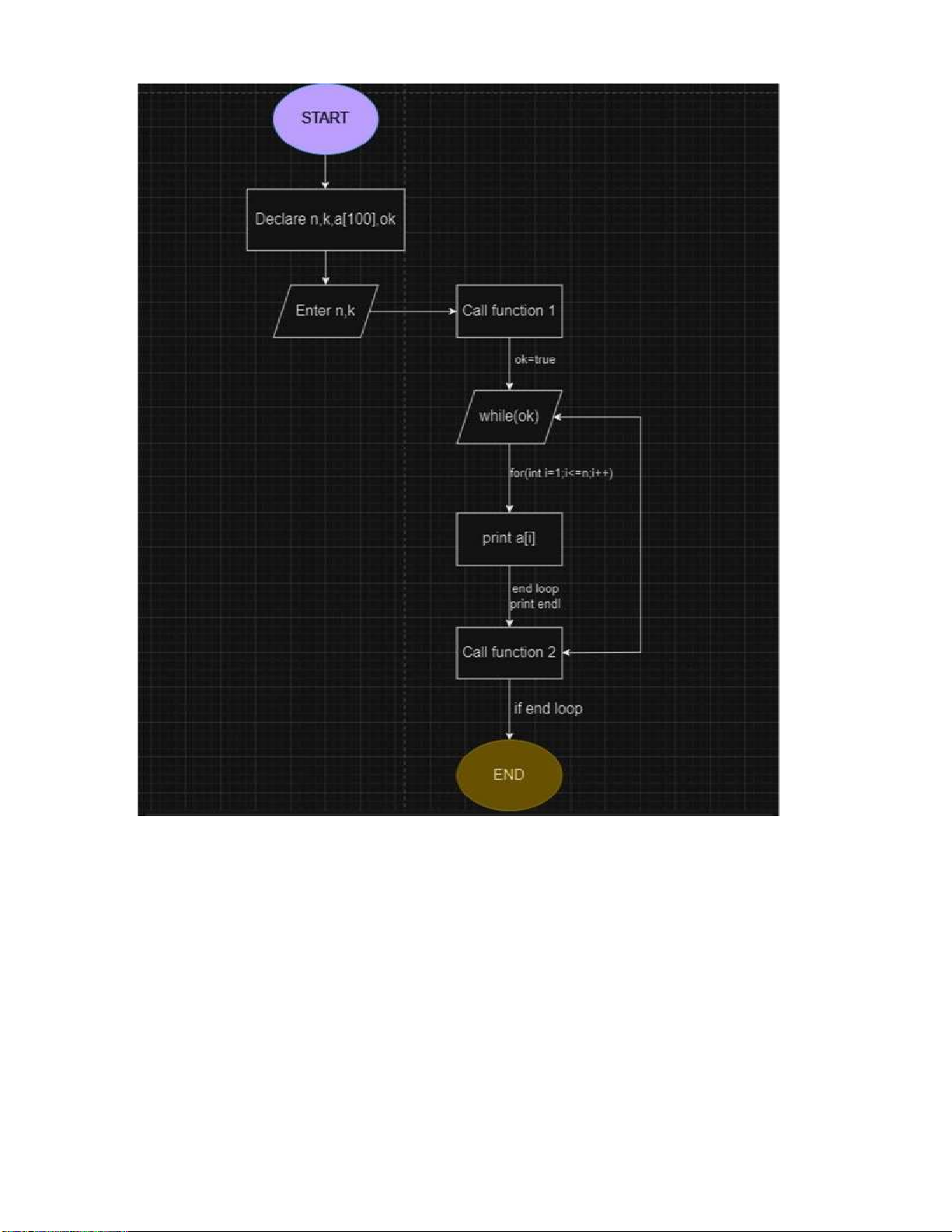
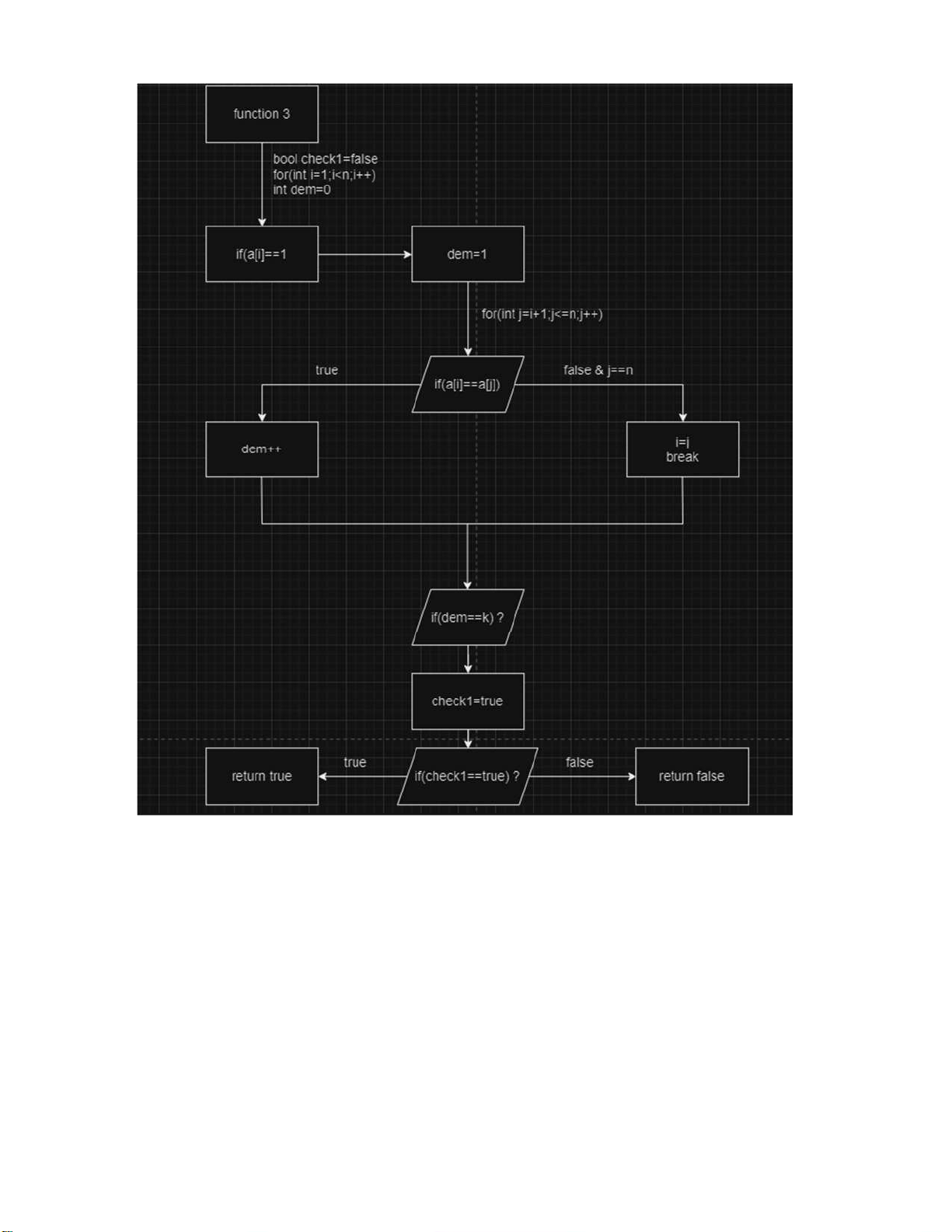
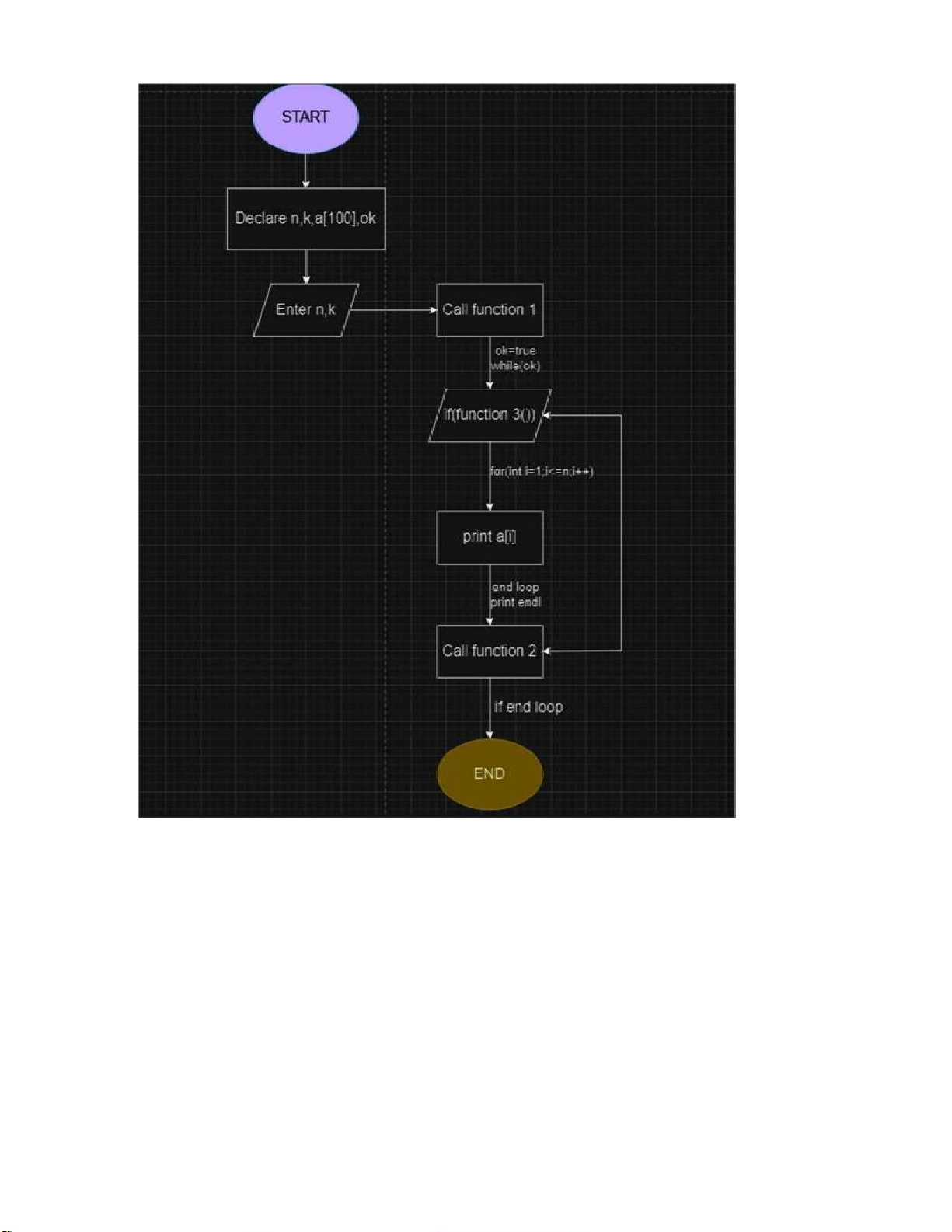
- Sơ ồ hàm kiểm tra k bit 1: lOMoARcPSD| 37922327 - Sơ ồ hàm main: lOMoARcPSD| 37922327 lOMoARcPSD| 37922327 Hàm sinh nhị phân: #include lOMoARcPSD| 37922327
- Hàm kiểm tra k bit 1 liên tiếp: bool check(){ bool check1=false; for(int i=1;i int dem=0; if(a[i]==1){ dem=1; for(int j=i+1;j<=n;j++){ if(a[i]==a[j]) dem++; if(a[i]!=a[j]||j==n){ i=j; break; } } } if(dem==k) check1=true; } if(check1) return true; else return false; } - Hàm main: lOMoARcPSD| 37922327 int main(){ cin >> n >> k; ktao(); ok=true; while(ok){ if(check()){ for(int i=1;i<=n;i++){ cout << a[i]; } cout << endl; } sinh(); } } lOMoARcPSD| 37922327 3.4. Kết quả:
- Trường hợp n=5 và k=3:
- Trường hợp n=6 và k=4: