Slide bài giảng môn học Toán rời rạc nội dung: Bài toán tìm đường ngắn nhất

lOMoARcPSD| 37922327
Học viện Công nghệ Bưu chính Viễn thông
Khoa Công nghệ thông tin 1 Toán rời rạc 2
Bài toán tìm đường đi ngắn nhất Ngô Xuân Bách
B ộ môn KHMT, Khoa CNTT1 Nội dung lOMoARcPSD| 37922327 
Phát biểu bài toán tìm ường i ngắn nhất  Thuật toán Dijkstra
 Thuật toán Bellman-Ford  Thuật toán Floyd lOMoARcPSD| 37922327
Bài toán tìm đường đi ngắn nhất (1/2)
 Khái niệm ộ dài ường i trên ồ thị
o Xét ồ thị 𝐺 =< 𝑉, 𝐸 > với tập ỉnh 𝑉 và tập cạnh 𝐸
o Với mỗi cạnh (𝑢, 𝑣) ∈ 𝐸, ta ặt tương ứng một số thực 𝑎(𝑢, 𝑣) ược
gọi là trọng số của cạnh, 𝑎(𝑢, 𝑣) = ∞ nếu (𝑢, 𝑣) ∉ 𝐸
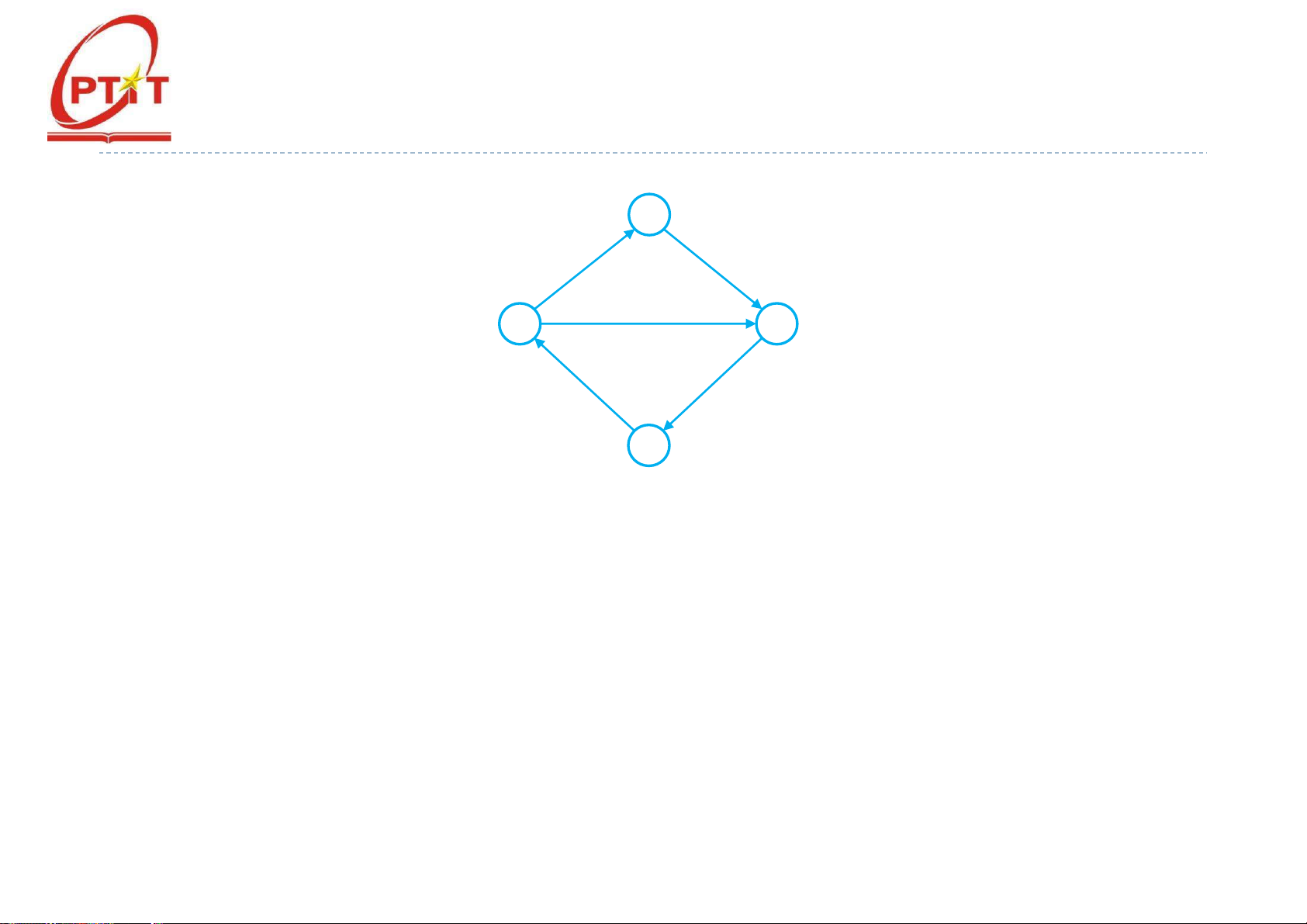
o Nếu dãy 𝑣0, 𝑣1, . . . , 𝑣𝑘 là một ường i trên 𝐺 thì σ𝑘𝑖=1 𝑎(𝑣𝑖−1, 𝑣𝑖) ược
gọi là ộ dài của ường i
 Bài toán dạng tổng quát
o Tìm ường i (có ộ dài) ngắn nhất từ một ỉnh xuất phát 𝑠 ∈ 𝑉 ( ỉnh
nguồn) ến ỉnh cuối 𝑡 ∈ 𝑉 ( ỉnh ích)?
o Đường i như vậy ược gọi là ường i ngắn nhất từ 𝑠 ến 𝑡, ộ dài của
ường i 𝑑(𝑠, 𝑡) ược gọi là khoảng cách ngắn nhất từ 𝑠 ến 𝑡
o Nếu không tồn tại ường i từ 𝑠 ến 𝑡 thì ộ dài ường i 𝑑(𝑠, 𝑡) = ∞ lOMoARcPSD| 37922327
Bài toán tìm đường đi ngắn nhất (2/2)
 Trường hợp 1: 𝑠 cố ịnh, 𝑡 thay ổi
o Tìm ường i ngắn nhất từ 𝑠 ến tất cả các ỉnh còn lại trên ồ thị ?
o Đối với ồ thị có trọng số không âm, bài toán luôn có lời giải bằng thuật toán Dijkstra
o Đối với ồ thị có trọng số âm nhưng không tồn tại chu trình âm,
bài toán có lời giải bằng thuật toán Bellman-Ford
o Trong trường hợp ồ thị có chu trình âm, bài toán không có lời giải
 Trường hợp 2: 𝑠 thay ổi và 𝑡 cũng thay ổi
o Tìm ường i ngắn nhất giữa tất cả các cặp ỉnh của ồ thị o Đối với ồ
thị có trọng số không âm, bài toán ược giải quyết bằng cách thực
hiện lặp lại 𝑛 lần thuật toán Dijkstra
o Đối với ồ thị không có chu trình âm, bài toán có thể giải quyết bằng thuật toán Floyd Nội dung lOMoARcPSD| 37922327
Phát biểu bài toán tìm ường i ngắn nhất  Thuật toán Dijkstra
 Thuật toán Bellman-Ford  Thuật toán Floyd lOMoARcPSD| 37922327 Thuật toán Dijkstra (1/2)  Mục ích
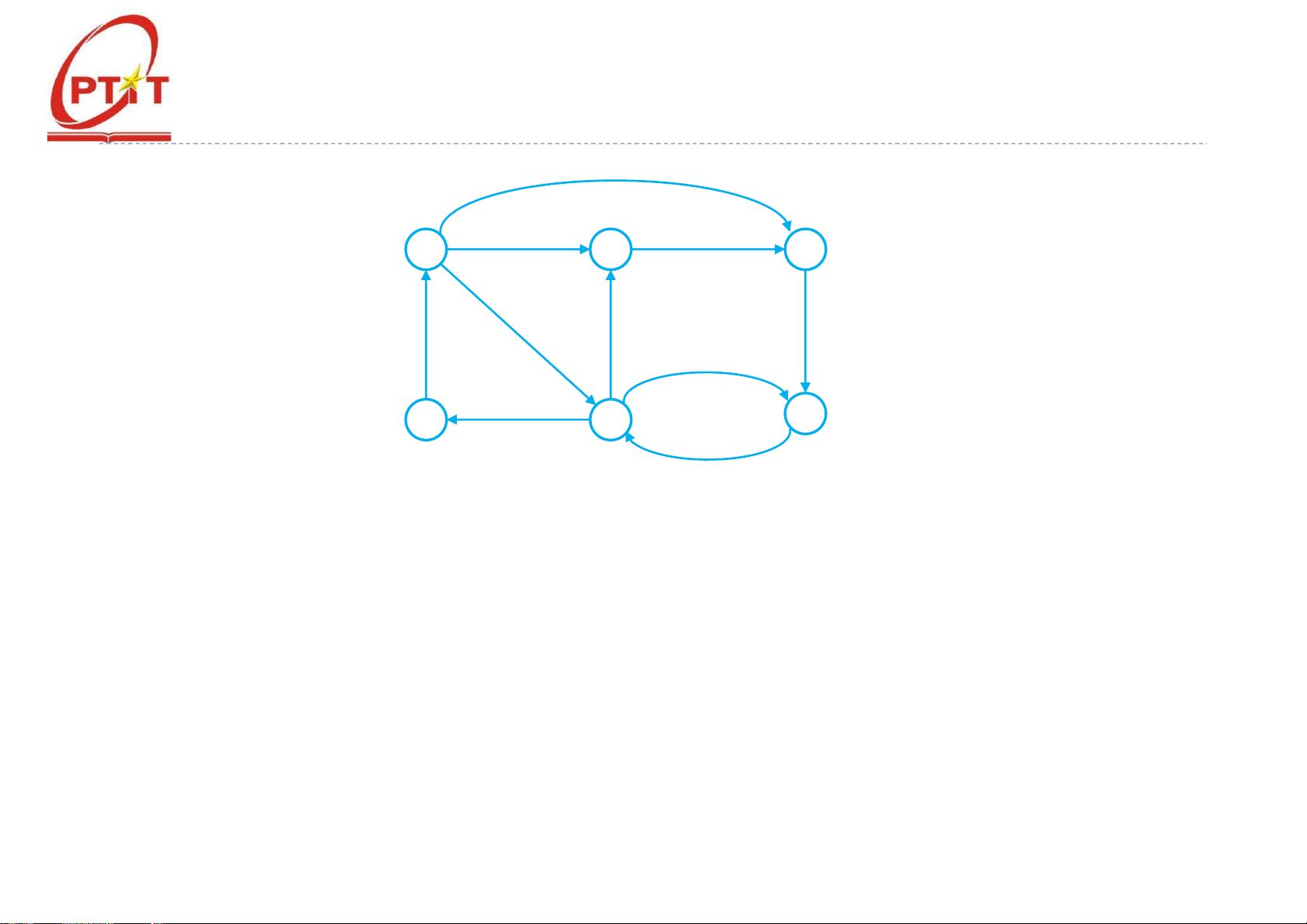
o Sử dụng ể tìm ường i ngắn nhất từ một ỉnh 𝑠 tới các ỉnh còn lại của ồ thị
o Áp dụng cho ồ thị có hướng với trọng số không âm  Tư tưởng
o Gán nhãn tạm thời cho các ỉnh
 Nhãn của mỗi ỉnh cho biết cận trên của ộ dài ường i ngắn nhất tới ỉnh ó
o Các nhãn này sẽ ược biến ổi (tính lại) nhờ một thủ tục lặp
 Ở mỗi một bước lặp sẽ có một nhãn tạm thời trở thành nhãn cố ịnh
(nhãn ó chính là ộ dài ường i ngắn nhất từ 𝑠 ến ỉnh ó) Thuật toán Dijkstra (2/2)
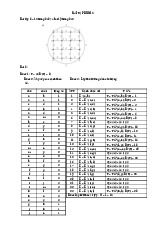
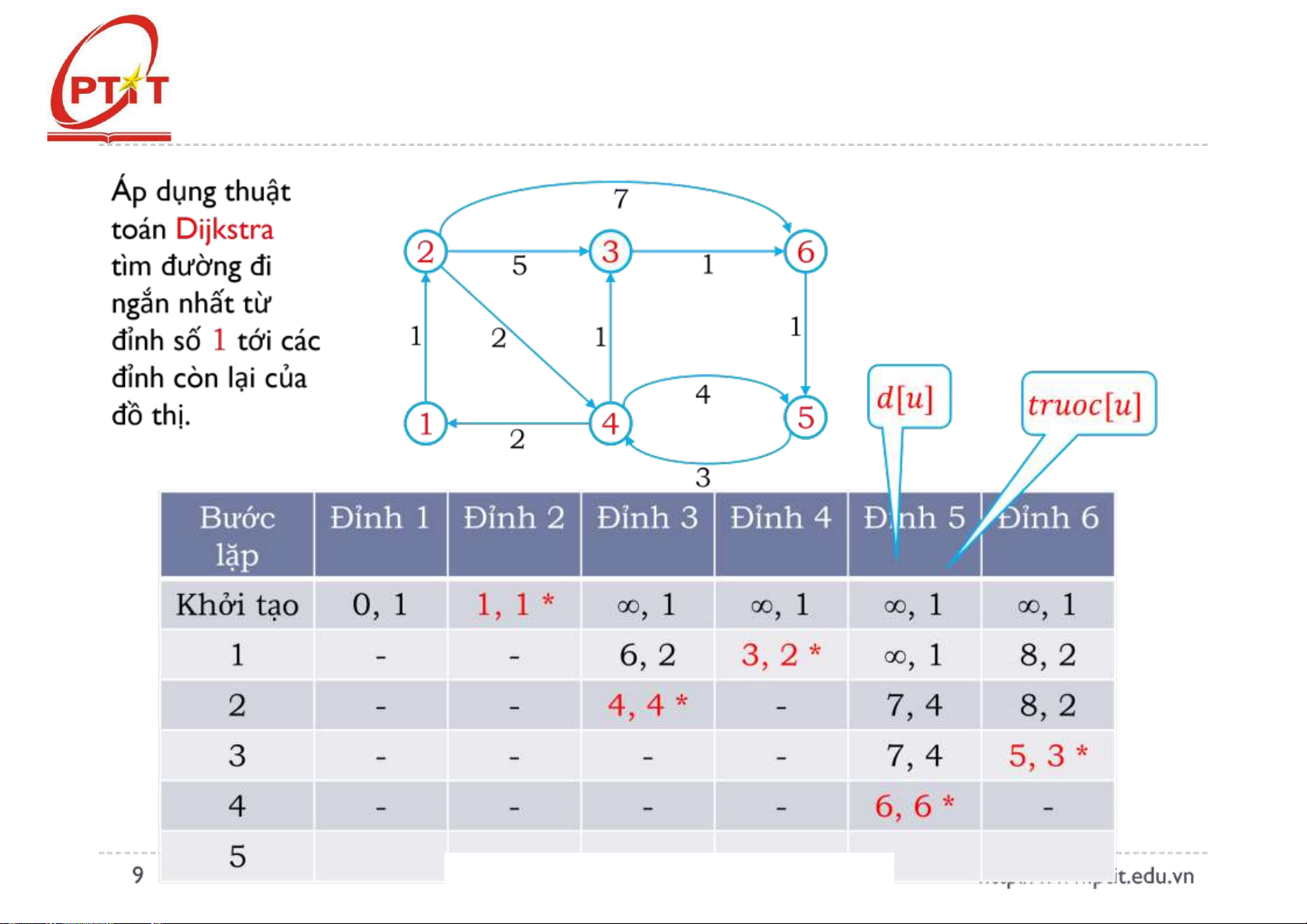
Dijkstra (𝑠){ lOMoARcPSD| 37922327 Bước 1 (Khởi tạo):
𝑑[𝑠] = 0; //Gán nhãn của ỉnh 𝑠 là 0 𝑇 = 𝑉\{𝑠}; // 𝑇 là
tập ỉnh có nhãn tạm thời for (𝑣 ∈ 𝑉){ //Sử dụng 𝑠 gán
nhãn cho các ỉnh còn lại
𝑑[𝑣] = 𝑎(𝑠, 𝑣);
𝑡𝑟𝑢𝑜𝑐[𝑣] = 𝑠; } Bước 2 (Lặp): while (𝑇 ≠ ∅ ){
Tìm ỉnh 𝑢 ∈ 𝑇 sao cho 𝑑[𝑢] = min{ 𝑑[𝑧] | 𝑧 ∈ 𝑇};
𝑇 = 𝑇\{𝑢}; //cố ịnh nhãn ỉnh 𝑢
for (𝑣 ∈ 𝑇){ //Sử dụng 𝑢, gán nhãn laị cho các ỉnh if
(𝑑[𝑣] > 𝑑[𝑢] + 𝑎(𝑢, 𝑣)){
𝑑[𝑣] = 𝑑[𝑢] + 𝑎(𝑢, 𝑣); //Gán lại nhãn cho ỉnh 𝑣;
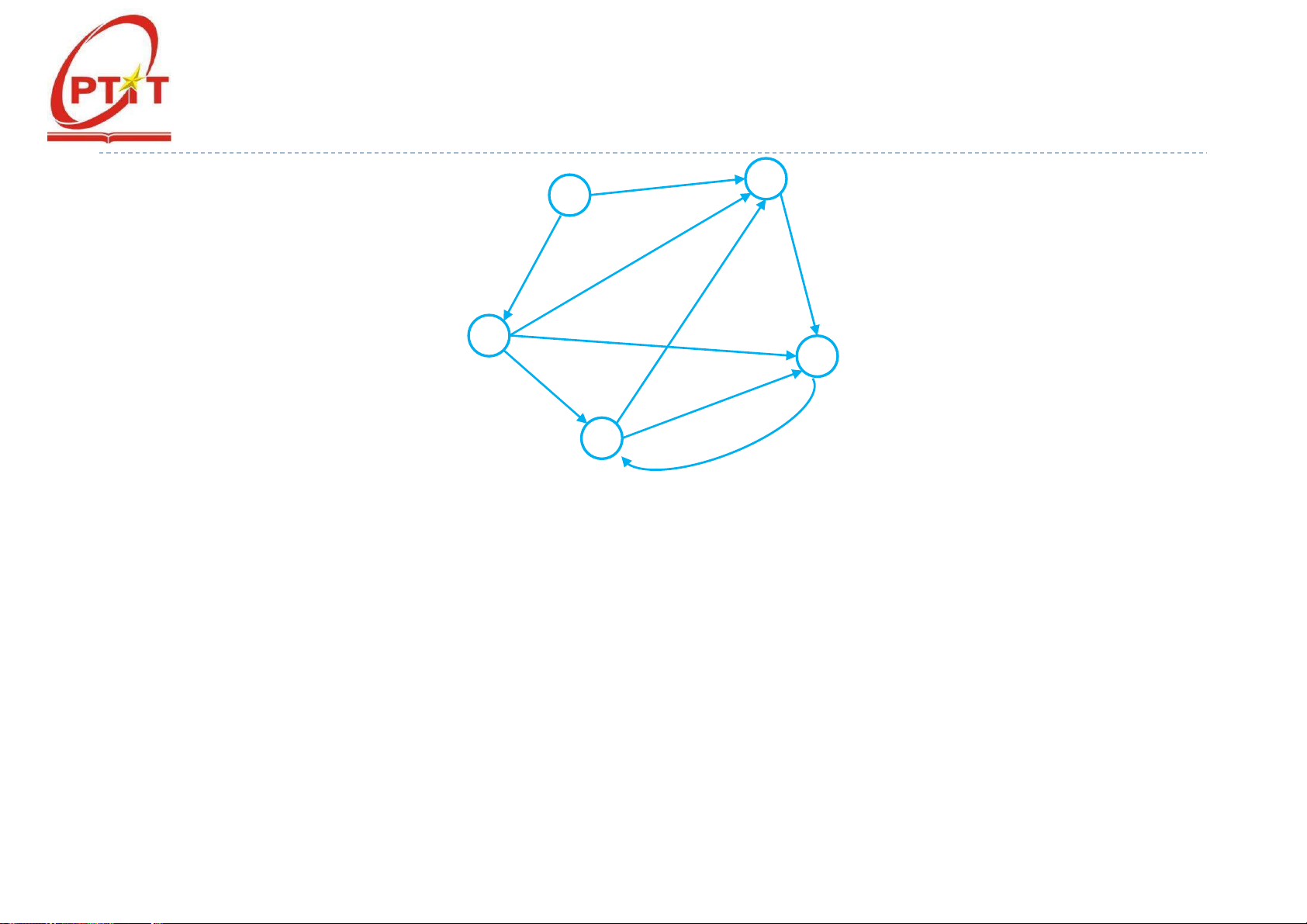
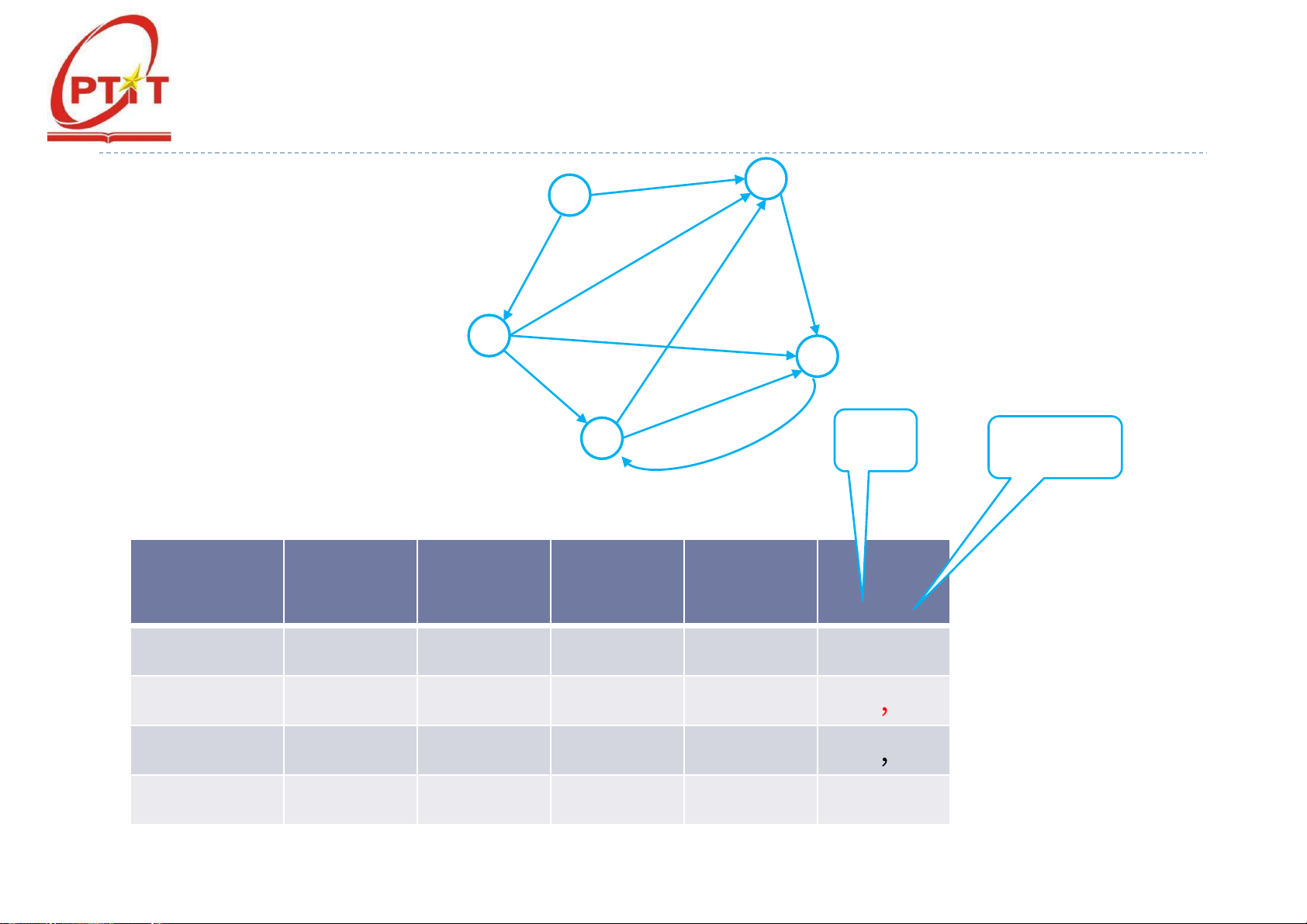
𝑡𝑟𝑢𝑜𝑐[𝑣] = 𝑢; } } } } lOMoARcPSD| 37922327 Ví dụ - Dijkstra (1/2) Áp d ụng thu t ậ 7 toán Dijkstra 2 3 6 tìm đ ng đi 5 1 ườ ng ắnnh tt ấ ừ đ nhs 1 t icác 1 1 2 1 ỉ ố ớ đ ỉnh cònl ic a ạ ủ 4 đ ồ th . ị 1 5 4 2 3 lOMoARcPSD| 37922327 Ví dụ - Dijkstra (2/2) lOMoARcPSD| 37922327 lOMoARcPSD| 37922327 Nội dung
Phát biểu bài toán tìm ường i ngắn nhất  Thuật toán Dijkstra
 Thuật toán Bellman-Ford  Thuật toán Floyd lOMoARcPSD| 37922327
Thuật toán Bellman-Ford (1/2)
 Mục ích o Sử dụng ể tìm ường i ngắn nhất từ một ỉnh 𝑠 tới các ỉnh còn lại của ồ thị
o Áp dụng cho ồ thị có hướng và không có chu trình âm (có thể có cạnh âm)  Tư tưởng
o Gán nhãn tạm thời cho các ỉnh
 Nhãn của mỗi ỉnh cho biết cận trên của ộ dài ường i ngắn nhất tới ỉnh ó
o Các nhãn này sẽ ược làm tốt dần (tính lại) nhờ một thủ tục lặp
 Mỗi khi phát hiện 𝑑[𝑣] > 𝑑[𝑢] + 𝑎(𝑢, 𝑣), cập nhật 𝑑 𝑣 = 𝑑[𝑢] + 𝑎(𝑢, 𝑣)
Thuật toán Bellman-Ford (2/2)
Bellman-Ford(𝑠){ lOMoARcPSD| 37922327 Bước 1 (Khởi tạo):
for (𝑣 ∈ 𝑉){ //Sử dụng 𝑠 gán nhãn cho các ỉnh còn lại
𝑑[𝑣] = 𝑎(𝑠, 𝑣);
𝑡𝑟𝑢𝑜𝑐[𝑣] = 𝑠; } Bước 2 (Lặp): 𝑑 𝑠 = 0;
for (𝑘 = 1; 𝑘 ≤ 𝑛 − 1; 𝑘 + + ){
for (𝑣 ∈ 𝑉\{𝑠}){
for (𝑢 ∈ 𝑉){ if (𝑑[𝑣] > 𝑑[𝑢] + 𝑎(𝑢, 𝑣)){
𝑑[𝑣] = 𝑑[𝑢] + 𝑎(𝑢, 𝑣);
𝑡𝑟𝑢𝑜𝑐[𝑣] = 𝑢; } } } } } lOMoARcPSD| 37922327 Ví dụ: Bellman-Ford (1/2) 3 Áp d ng thu t 1 5 ụ ậ toán Bellman- 1 8 Ford tìm đ ng -5 4 ườ đi ng ắnnh tt ấ ừ đ nhs t icác 2 3 ỉ 1 ố ớ 4 đ ỉnh cònl ic a ạ ủ 3 1 đ ồ th . ị 3 2 lOMoARcPSD| 37922327 Ví dụ: Bellman-Ford (2/2) 3 Áp d ng thu t 1 5 ụ ậ toán Bellman- 1 8 Ford tìm đ ng -5 4 ườ đi ng ắnnh tt ấ ừ đ nhs t icác 2 3 ỉ 1 ố ớ 4 đ ỉnh cònl ic a ạ ủ 3 1 đ ồ th . ị 3 𝑑[𝑢] 2 𝑡𝑟𝑢𝑜𝑐[𝑢] B ướ c
Đ ỉ nh 1 Đ ỉ nh 2 Đ ỉ nh 3 Đ ỉ nh 4 Đ ỉ nh 5 l ặ p Kh ở it ạ o 0 , 1 , 1 1 ∞, 1 ∞, 1 , 3 1 k=1 , 0 1 1 1 , 4 , 2 4 , 2 -1 3 , 2 0 , 1 1 , 1 4 2 , , 3 5 -1 3 , 3 Không , 0 1 , 1 1 4 2 , 3 , 5 -1 , 3 thay ổi giá trị lOMoARcPSD| 37922327 Nội dung
Phát biểu bài toán tìm ường i ngắn nhất  Thuật toán Dijkstra
 Thuật toán Bellman-Ford  Thuật toán Floyd lOMoARcPSD| 37922327 Thuậ t toán Floyd (1/3)
 Mục ích o Sử dụng ể tìm ường i ngắn nhất giữa tất cả các cặp ỉnh của ồ thị
o Áp dụng cho ồ thị có hướng và không có chu trình âm (có thể có cạnh âm)  Tư tưởng
o Thực hiện quá trình lặp
Xét từng ỉnh, với tất cả các ường i (giữa 2 ỉnh bất kỳ), nếu ường i
hiện tại lớn hơn ường i qua ỉnh ang xét, ta thay lại thành ường i qua ỉnh này lOMoARcPSD| 37922327 Thuậ t toán Floyd (2/3) Floyd( ){ Bước 1 (Khởi tạo):
for (𝑖 = 1, 𝑖 ≤ 𝑛; 𝑖 + +){ for( 𝑗 = 1, 𝑗 ≤ 𝑛; 𝑗 + +){ //Xét từng cặp đỉnh
𝑑[𝑖, 𝑗] = 𝑎(𝑖, 𝑗);
if(𝑎 𝑖, 𝑗 ! = ∞) 𝑛𝑒𝑥𝑡[𝑖, 𝑗] = 𝑗;
else 𝑛𝑒𝑥𝑡 𝑖, 𝑗 = 𝑛𝑢𝑙𝑙; } } Bước 2 (Lặp):
for (𝑘 = 1, 𝑘 ≤ 𝑛; 𝑘 + +){ for (𝑖 = 1, 𝑖 ≤ 𝑛; 𝑖
+ +){ for (𝑗 = 1, 𝑗 ≤ 𝑛; 𝑗 + +){
if (𝑑[𝑖, 𝑗] > 𝑑[𝑖, 𝑘] + 𝑑[𝑘, 𝑗]){
𝑑[𝑖, 𝑗] = 𝑑[𝑖, 𝑘] + 𝑑[𝑘, 𝑗];
𝑛𝑒𝑥𝑡[𝑖, 𝑗] = 𝑛𝑒𝑥𝑡[𝑖, 𝑘]; } lOMoARcPSD| 37922327 Thuậ } } } } t toán Floyd (3/3) Khôi phục ường i
Reconstruct-Path( 𝑢, 𝑣){
if ( 𝑛𝑒𝑥𝑡[𝑢][𝑣] == 𝑛𝑢𝑙𝑙) ; else{
𝑝𝑎𝑡ℎ = [𝑢]; // path bắt ầu từ 𝑢 while(𝑢 ≠ 𝑣){
𝑢 = 𝑛𝑒𝑥𝑡[𝑢][𝑣]; lOMoARcPSD| 37922327 Thuậ
𝑝𝑎𝑡ℎ. 𝑎𝑝𝑝𝑒𝑛𝑑(𝑢); //ỉnh tiếp theo trên ường i }
return 𝑝𝑎𝑡ℎ; } } lOMoARcPSD| 37922327 Kiểm nghiệm thuật toán Áp d ụng thu t ậ 1 toán Floyd tìm -2 đ ường đi ng n 4 ắ nh ất gi at tc 3 ữ ấ ả 2 cácc 3 ặp đ nhc a ỉ ủ đ ồ th . ị -1 2 4 lOMoARcPSD| 37922327 Tóm tắt
 Bài toán tìm ường i ngắn nhất trên ồ thị, các dạng của bài toán
 Thuật toán Dijkstra, áp dụng
 Thuật toán Bellman-Ford, áp dụng lOMoARcPSD| 37922327
 Thuật toán Floyd, áp dụng lOMoARcPSD| 37922327 Bài tập
Làm một số bài tập trong giáo trình