Học viện Công nghệ Bưu chính Viễn thông Khoa Công nghệ thông tin 1 Toán rời rạc 1
Một số kiến thức cơ bản Ngô Xuân Bách Nội dung  Lý thuyết tập hợp  Logic mệnh đề  Logic vị từ
 Thuật toán và độ phức tạp  Bài tập 2 http://www.ptit.edu.vn
Một số ký hiệu tập hợp
 Tập hợp: , , … , , , …
 Phần tử của tập hợp: , , … , , , …
 Phần tử thuộc (không thuộc) : ,
 Số phần tử của tập hợp : | | o
Một tập hợp có phần tử được gọi là một -tập  Tập hợp con: ⊆ o ⇒
 Tập hợp bằng nhau: nếu ⊆ và ⊆ thì =  Tập rỗng: ∅ o Không có phần tử nào o
Là con của mọi tập hợp 3 http://www.ptit.edu.vn
Các phép toán trên tập hợp  Phần bù của trong : ҧ = |
 Hợp của hai tập hợp: = | ℎ ặ
 Giao của hai tập hợp: = { | à }
 Hiệu của hai tập hợp: B = { | à }  Luật kết hợp: = =  Luật giao hoán: = , =  Luật phân bố: = =  Luật đối ngẫu: = ҧ ത, = ҧ ത
 Tích Đề các: × = { , | , } 4 http://www.ptit.edu.vn Quan hệ
 Quan hệ: một quan hệ hai ngôi trên tập , , là
một tập con của tích Đề các ×
 Tính chất của quan hệ: o
Phản xạ: mọi phần tử có quan hệ với chính nó o
Đối xứng: có quan hệ với kéo theo có quan hệ với o
Kéo theo: có quan hệ với và có quan hệ với kéo theo có quan hệ với  Ví dụ o = , , , o ,
, có quan hệ đối với nếu chia hết cho o
= { , , , , , , , , , , , , , , , }
 Phản xạ, kéo theo, nhưng không đối xứng 5 http://www.ptit.edu.vn
Quan hệ tương đương và phân hoạch
 Quan hệ tương đương: là một quan hệ có đủ ba tính
chất, phản xạ, đối xứng, và kéo theo
 Lớp tương đương: một quan hệ tương đương trên tập
hợp sẽ chia tập hợp thành các lớp tương đương o
Hai phần tử thuộc cùng một lớp có quan hệ với nhau o
Hai phần tử khác lớp không có quan hệ với nhau o
Các lớp tương đương phủ kín tập hợp ban đầu
 Phân hoạch: là một họ các lớp tương đương (các tập
con khác rỗng) của một tập hợp
Một quan hệ tương đương trên tập hợp sẽ xác định một phân hoạch trên
tập hợp, ngược lại một phân hoạch bất Kỳ trên tập hợp sẽ tương ứng với
một quan hệ tương đương trên nó. 6 http://www.ptit.edu.vn
Ví dụ quan hệ tương đương  Xét = , , … , , là số nguyên dương > 
là số nguyên dương, < <  Định nghĩa quan hệ trên như sau  Với , , aRb ⇔ ≡ o có quan hệ
với nếu và có cùng số dư khi chia cho  là quan hệ tương đương o
Phản xạ, đối xứng, kéo theo  Đặt � = ≡ � , � = , , … , − 
, , … , �− tạo thành một phân hoạch của 7 http://www.ptit.edu.vn Nguyên lý cộng  Nếu và là hai tập rời nhau thì = +  Nếu { ,
, … , �} là một phân hoạch của tập hợp thì = + + ⋯ + �
 Nếu A là một tập con của X ҧ = − | |  Ví dụ o
Một đoàn VĐV gồm 2 môn bắn súng và bơi. Nam có 10 người. Số
VĐV thi bắn súng là 14. Số nữ VĐV thi bơi bằng số nam VĐV thi
bắn súng. Hỏi toàn đoàn có bao nhiêu VĐV? 8 http://www.ptit.edu.vn Nguyên lý nhân
 Nếu mỗi thành phần � của bộ có thứ tự thành phần
, , … , � có � khả năng chọn, thì số bộ được tạo ra
sẽ là tích các khả năng … �  Hệ quả: o × × ⋯ × � = … � � o = | |�  Ví dụ o
Có bao nhiêu số nguyên dương có 5 chữ số được thành lập bởi các chữ số 0,1,2? 9 http://www.ptit.edu.vn Chỉnh hợp lặp
 Định nghĩa: Một chỉnh hợp lặp chập của phần tử là
một bộ có thứ tự gồm thành phần, lấy từ thành phần
đã cho. Các thành phần có thể được lặp lại.
 Theo nguyên lý nhân, số chỉnh hợp lặp chập của phần tử là �  Ví dụ o
Tính số tập con của một -tập 10 http://www.ptit.edu.vn Chỉnh hợp không lặp
 Định nghĩa: Một chỉnh hợp không lặp chập của
phần tử là một bộ có thứ tự gồm thành phần, lấy từ
thành phần đã cho. Các thành phần không được lặp lại.
 Theo nguyên lý nhân, số chỉnh hợp không lặp chập của phần tử là − … − +  Ví dụ o
Tính số đơn ánh từ một -tập vào một -tập 11 http://www.ptit.edu.vn Hoán vị
 Định nghĩa: Ta gọi một hoán vị của phần tử là một
cách xếp thứ tự các phần tử đó  Một hoán vị của
phần tử là một trường hợp riêng của
chỉnh hợp không lặp khi = o
Số hoán vị của n phần tử là . − … . = !  Ví dụ o
Cần bố trí việc thực hiện chương trình trên một máy vi tính. Biết
rằng các chương trình thực hiện độc lập (không phụ thuộc thứ
tự). Hỏi có bao nhiêu cách? 12 http://www.ptit.edu.vn Tổ hợp
 Định nghĩa: Một tổ hợp chập
của phần tử là một bộ không kể thứ tự gồm
thành phần khác nhau lấy từ phần tử đã cho. � ! � = ! − !  Một số tính chất � �−� o � = �� o � = � = � �− � o � = �− + �−  Nhị thức Newton � + �= � �− � � � �−� � � + � + ⋯ + � = ෍ � �= 13 http://www.ptit.edu.vn Bài tập 1
 Sử dụng định nghĩa chứng minh một số phép toán trên tập hợp 14 http://www.ptit.edu.vn Bài tập 2
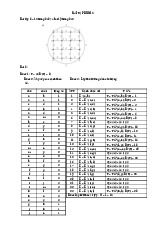
 Cho biết trong các hệ thức dưới đây hệ thức nào là đúng, hệ thức nào là sai? 1) ⊆ 2) ⊆ 3) ⊆ 4) = 5) \ = \B 15 http://www.ptit.edu.vn Bài tập 3  Ký hiệu
là tập hợp các số nguyên. Xét hai tập con của : = : = − ớ� ộ à đó = : = + ớ� ộ à đó Chứng minh rằng = . 16 http://www.ptit.edu.vn Bài tập 4  Cho = , , , , và xác định quan hệ trên bởi:
= { , , , , , , , , , , , , , , , , , , , , , , , , , }. 1)
có phải là một quan hệ tương đương hay không? 2)
Nếu câu 1) là đúng thì chỉ ra phân hoạch của thành
các lớp tương đương theo quan hệ . 17 http://www.ptit.edu.vn Nội dung  Lý thuyết tập hợp  Logic mệnh đề  Logic vị từ
 Thuật toán và độ phức tạp  Bài tập 18 http://www.ptit.edu.vn
Một số khái niệm của logic mệnh đề
 Mệnh đề: là một câu khẳng định hoặc đúng hoặc sai.  Ví dụ:
• “Hà Nội là thủ đô của Việt Nam” là một mệnh đề đúng.
• “(5 < 3)” là một mệnh đề sai, “(5 > 3)” là một mệnh đề đúng.
• “(a<7)” không phải là mệnh đề vì nó không biết khi nào đúng khi nào sai.
 Giá trị chân lý của mệnh đề: mỗi mệnh đề chỉ có một trong 2 giá
trị “đúng”, ký hiệu là “T”, giá trị “sai”, ký hiệu là “F”. Tập { T, F}
được gọi là giá trị chân lý của mệnh đề.
 Ký hiệu: ta ký hiệu mệnh đề bằng các chữ cái in thường
( , , , , , , . ỗ� mệnh đề còn được gọi là một công thức. Từ
khái niệm về mệnh đề, giá trị chân lý của mỗi mệnh đề, ta xây dựng
nên các mệnh đề phức hợp (được gọi là công thức) thông qua các
phép toán trên mệnh đề. 19 http://www.ptit.edu.vn
Các phép toán của logic mệnh đề (1/2) Cho và là hai mệnh đề  Phép phủ định o
¬ là ký hiệu mệnh đề, đọc là “Không phải ” o
Mệnh đề cho giá trị đúng nếu p sai và cho giá trị sai nếu p đúng  Phép hội o
là ký hiệu mệnh đề, đọc là “ và ” o
Mệnh đề có giá trị đúng khi cả và có giá trị đúng, có giá trị sai
trong các trường hợp khác còn lại  Phép tuyển o
là ký hiệu mệnh đề, đọc là “ hoặc ” o
Mệnh đề có giá trị sai khi cả và có giá trị sai, có giá trị đúng trong
các trường hợp khác còn lại 20 http://www.ptit.edu.vn