Bài Tập Ôn Tập Kinh Tế Vĩ Mô | Trường Đại học Thương Mại

NHÓM 2 Bài 1
a,Ptrinh đường cầu có dạng: QD = a-bP Ta chọn 2 điểm P = 10; QD = 40  40 = a -10b P = 12; QD = 36  36 = a -12b Ta có hệ phương trình 40 = a -10b 36 = a -12b  a=60; b =2
 Phương trình đường cầu có dạng: QD = 60 – 2P
Phương trình đường cung: QS = c + dP Ta ch n 2 i ọ ểm P = 10; QS = 40  40 = c + 10d P = 12; QS = 50  50 = c + 12d Ta có hệ phương trình 40 = c + 10d 50 = c + 12d  c = -10; d = 5  QS = -10 + 5P b, d,
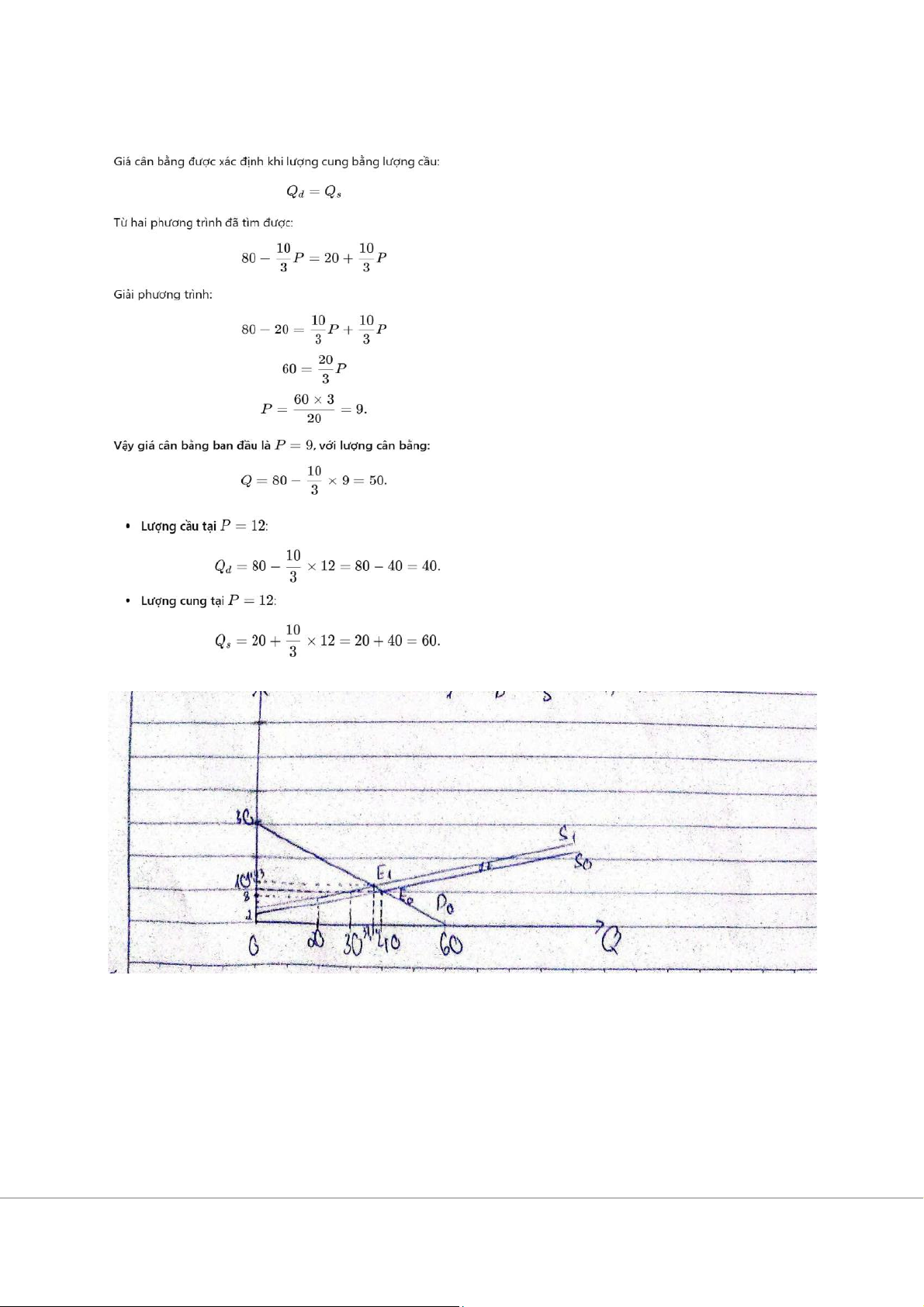
g, Phương trình cung ban đầu: Qs=20+10/3P
Khi lượng cung giảm 10 đơn vị ở mỗi mức giá, phương trình cung mới sẽ là:
Qs′=(20+10/3P)−10 =10+10/3P= 10 + 10/3P=10+ 10/3P
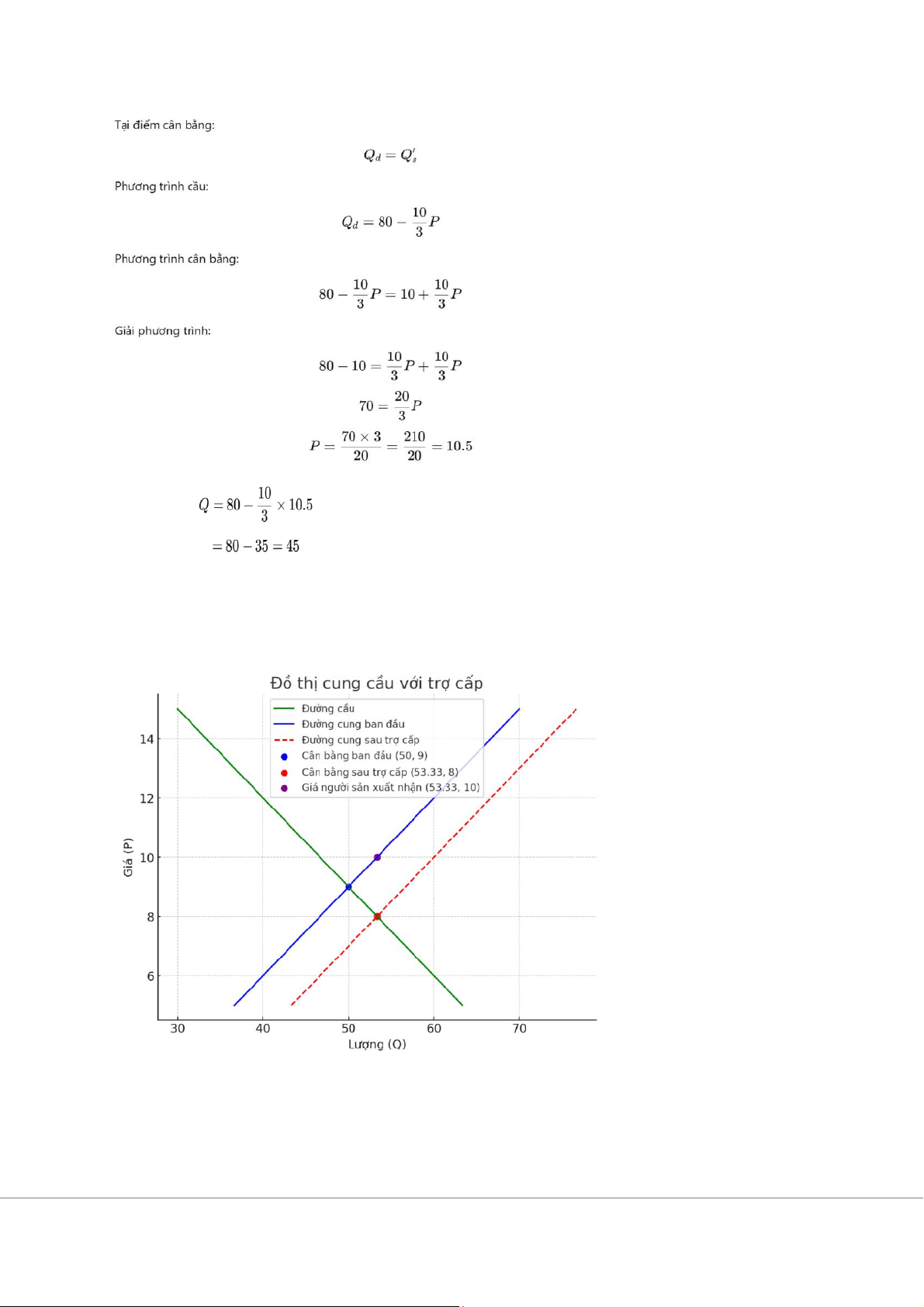
Vậy lượng cân bằng mới là 45
Giá cân bằng mới là 10,5 h,
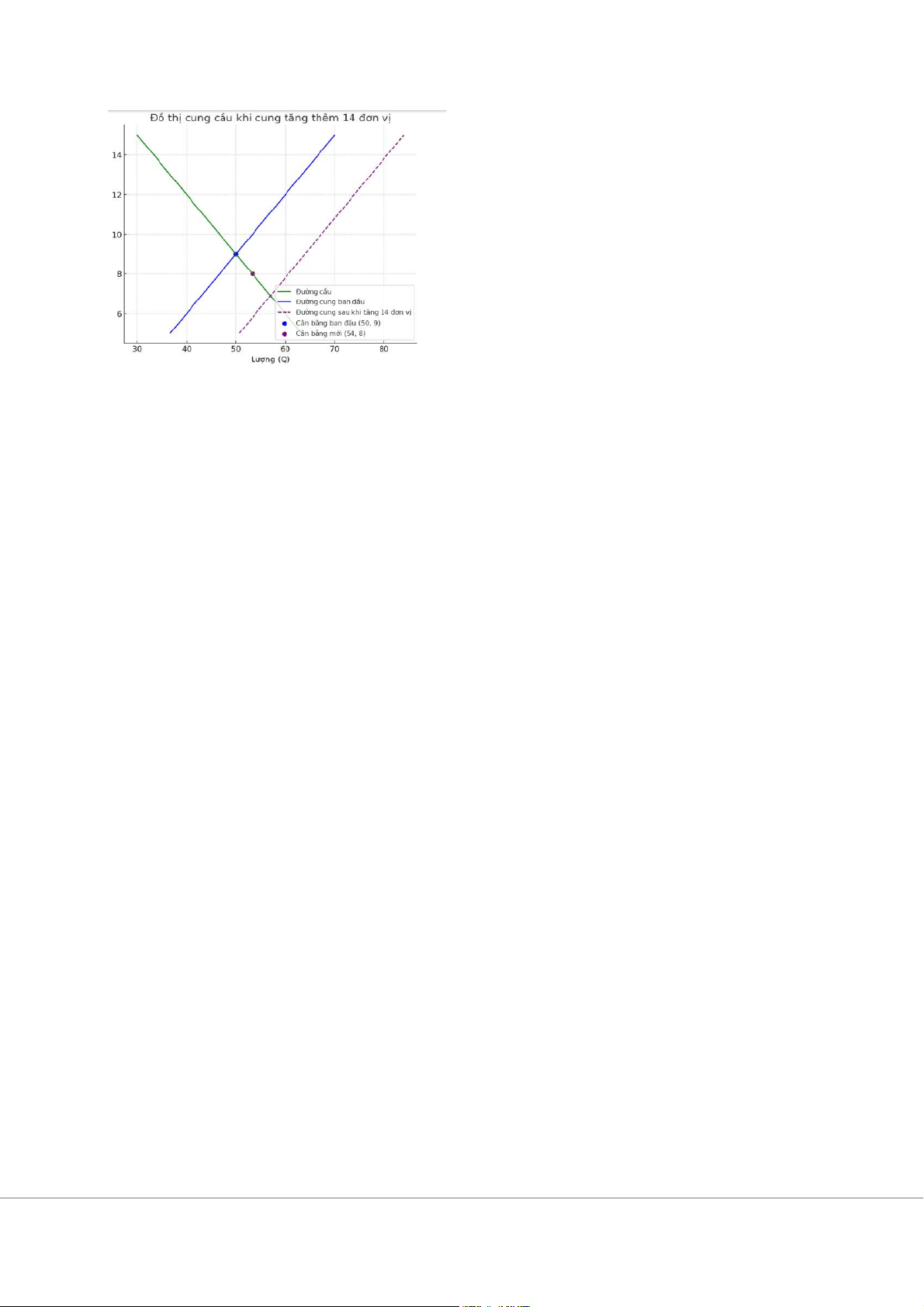
Phương trình cầu ban đầu: QD = 80 – 10/3P
Khi lượng cầu tăng 14 đơn vị ở mỗi mức giá, ta có phương trình mới Bài 2
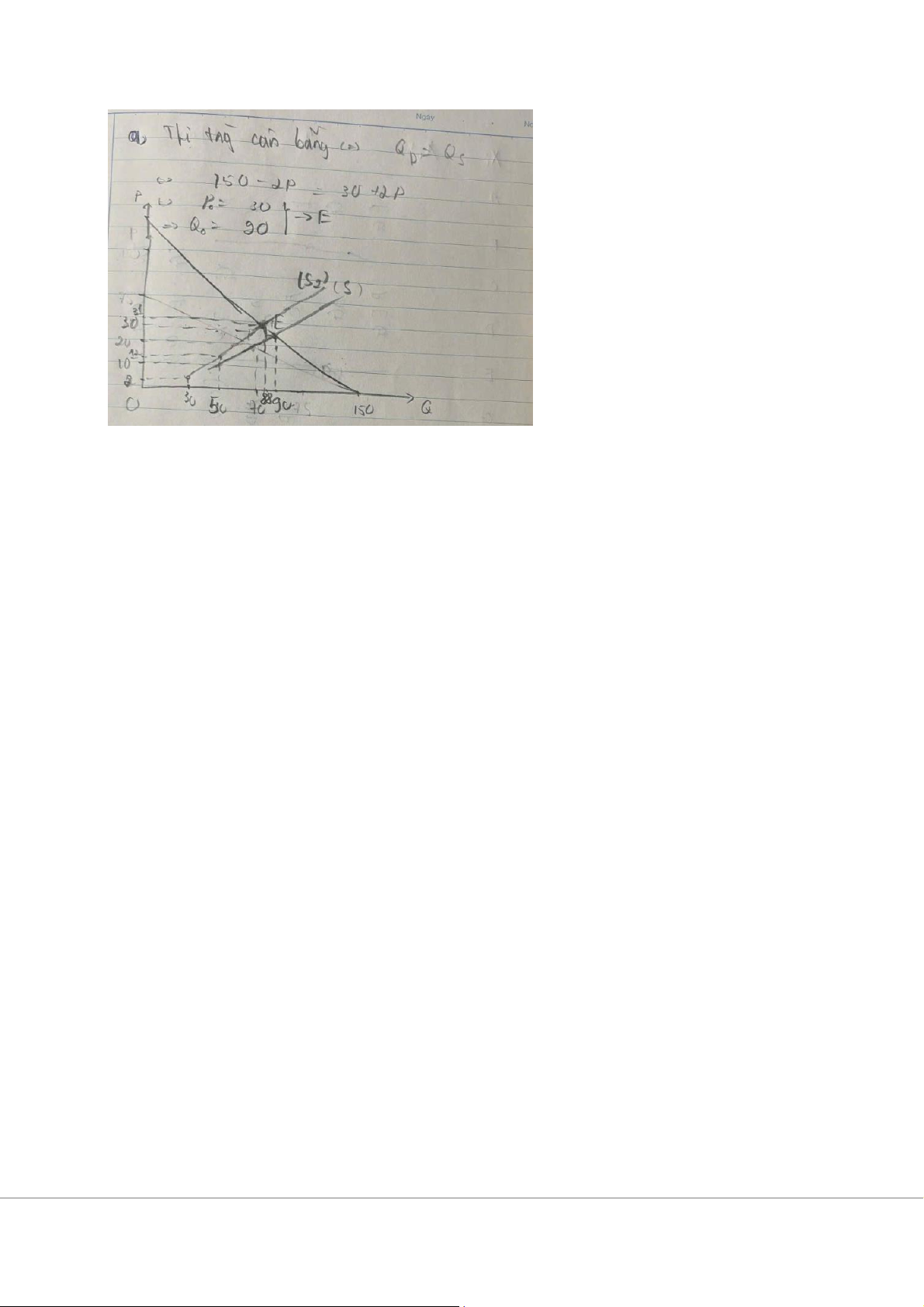
a) Xác định giá và lượng cân bằng trên thị trường của hàng hóa X và vẽ đồ thị minh họa.
Tại điểm cân bằng, lượng cầu bằng lượng cung: ( QD = QS ). ⇔150 - 2P = 30 + 2P ⇔120=4P ⇔P=30
=>Giá cân bằng: P = 30 (nghìn đồng).
Thay P = 30 vào hàm cầu ta được: QD = 150 - 2*30 = 150 - 60 = 90
=>Lượng cân bằng: Q = 90 (đơn vị hàng hóa).
b) Tính lượng dư thừa hoặc thiếu hụt tại các mức giá ( P = 10 ), ( P = 15 ), ( P = 20 ).
Tính độ co dãn của cầu theo giá tại các mức giá này và cho nhận xét về kết quả. • Tại ( P = 10 ):
o Lượng cầu: QD = 150 - 2*10 = 150 - 20 = 130 .
o Lượng cung: QS = 30 + 2*10 = 30 + 20 = 50 .
o So sánh: ( QD > QS ), Thiếu hụt= QD - QS = 130 - 50 = 80. • Tại ( P = 15 ):
o Lượng cầu: QD = 150 - 2*15 = 150 - 30 = 120.
o Lượng cung: QS = 30 + 2*15 = 30 + 30 = 60.
o So sánh: ( QD>QS ), Thiếu hụt= QD - QS = 120 - 60 = 60. • Tại ( P = 20 ):
o Lượng cầu: QD = 150 - 2*20 = 150 - 40 = 110.
o Lượng cung: QS = 30 + 2 *20 = 30 + 40 = 70.
o So sánh: ( QD > QS ),Thiếu hụt= QD - QS = 110 - 70 = 40.
Tính độ co dãn của cầu theo giá
Công thức ED=QD/QDP/P
Với phương trình cầu QD=150 - 2P, ta có QDP=2 => ED=QD/QDP/P=-2 PQD • Tại P=10, QD=130: ED=-210130=213 (ít co dãn) • Tại P=15, QD=120: ED=-215120=14 (ít co dãn) • Tại P=20, QD=110: ED=-220110=411 (ít co dãn) Nhận xét:
• Độ co dãn của cầu tại các mức giá ( P = 10 ), ( P = 15 ), ( P = 20 ) lần lượt là
(213), (14), (411), đều nhỏ hơn 1, nghĩa là cầu không co dãn . Điều này cho thấy
người tiêu dùng không nhạy cảm lắm với sự thay đổi giá ở các mức giá này.
• Độ co dãn tăng dần khi giá tăng, vì khi giá cao hơn, lượng cầu giảm, và sự thay
đổi giá có tác động tương đối lớn hơn đến lượng cầu.
c) Giả sử chính phủ đánh một mức thuế ( t = 2 ) triệu mỗi đơn vị sản phẩm bán ra,
khi đó giá và lượng cân bằng trên thị trường là bao nhiêu? Vẽ đồ thị minh họa.
Khi có thuế t=2, giá người mua trả (PB) và giá người bán nhận (PS) sẽ khác nhau PB=PS+t. => PB=PS+2.
• Phương trình cầu (theo giá người mua): QD=150-2PB.
• Phương trình cung (theo giá người bán): QS=30+2PS.
• Ở phương trình cầu, thay PB=PS+2 ta được: QD=150-2(PS+2)=146-2PS.
• Tại điểm cân bằng, lượng cầu bằng lượng cung: ( QD = QS ). ⇔ 146-2PS=30+2PS.
=> Giá người bán nhận: PS=29.
=> Giá người mua trả: PB= PS+2=29+2=31.
Lượng cân bằng: Q=30+2*29=88.
d) Giả sử chính phủ đánh một mức thuế ( t = 2 ) triệu mỗi đơn vị sản phẩm tiêu
dùng, khi đó giá và lượng cân bằng trên thị trường là bao nhiêu? Vẽ đồ thị minh họa.
• Trường hợp này giống hệt câu c), vì thuế đánh trên đơn vị sản phẩm tiêu dùng hay sản
phẩm bán ra không thay đổi bản chất kinh tế trong mô hình này (người mua và người bán cùng chịu thuế).
• Khi có thuế t=2, giá người mua trả (PB) và giá người bán nhận (PS) sẽ khác nhau PB=PS+t. => PB=PS+2.
• Phương trình cầu (theo giá người mua): QD=150-2PB.
• Phương trình cung (theo giá người bán): QS=30+2PS.
Ở phương trình cầu, thay PB=PS+2 ta được: QD=150-2(PS+2)=146-2PS.
Tại điểm cân bằng, lượng cầu bằng lượng cung: ( QD = QS ). ⇔ 146-2PS=30+2PS.
=> Giá người bán nhận: PS=29.
=> Giá người mua trả: PB= PS+2=29+2=31.
Lượng cân bằng: Q=30+2*29=88.
e) Giả sử chính phủ trợ cấp một mức ( s = 2 ) triệu mỗi đơn vị sản phẩm bán ra, khi
đó giá và lượng cân bằng trên thị trường là bao nhiêu? Vẽ đồ thị minh họa.
Khi có trợ cấp s=2, giá người mua trả (PB) và giá người bán nhận (PS) sẽ khác nhau: PB=PS-s. => PB=PS-2.
Phương trình cầu: QD=150-2PB.
Phương trình cung: QS=30+2PS.
Thay PB=PS-2 vào phương trình cầu ta được: QD=150-2(PS-2)=154-2PS.
Tại điểm cân bằng, lượng cầu bằng lượng cung: ( QD=QS ). ⇔ 154-2PS=30+2PS.
=> Giá người bán nhận: PS=31.
=> Giá người mua trả: PB=PS-2=31-2=29.
Lượng cân bằng: Q=30+2*31=92.
i) Giả sử lượng cung giảm đi 5 đơn vị trong ứng với mỗi mức giá, khi đó giá và
lượng cân bằng trên thị trường là bao nhiêu? Vẽ đồ thị minh họa.
Lượng cung giảm 5 đơn vị tại mỗi mức giá, nên phương trình cung mới là: QS=30+2P-5=25+2P.
Tại điểm cân bằng, lượng cầu bằng lượng cung: ( QD = QS ). ⇔ 150-2P=25+2P
=> Giá cân bằng: P=28,75
=> Lượng cân bằng: Q=25+2*28,75=92,5.
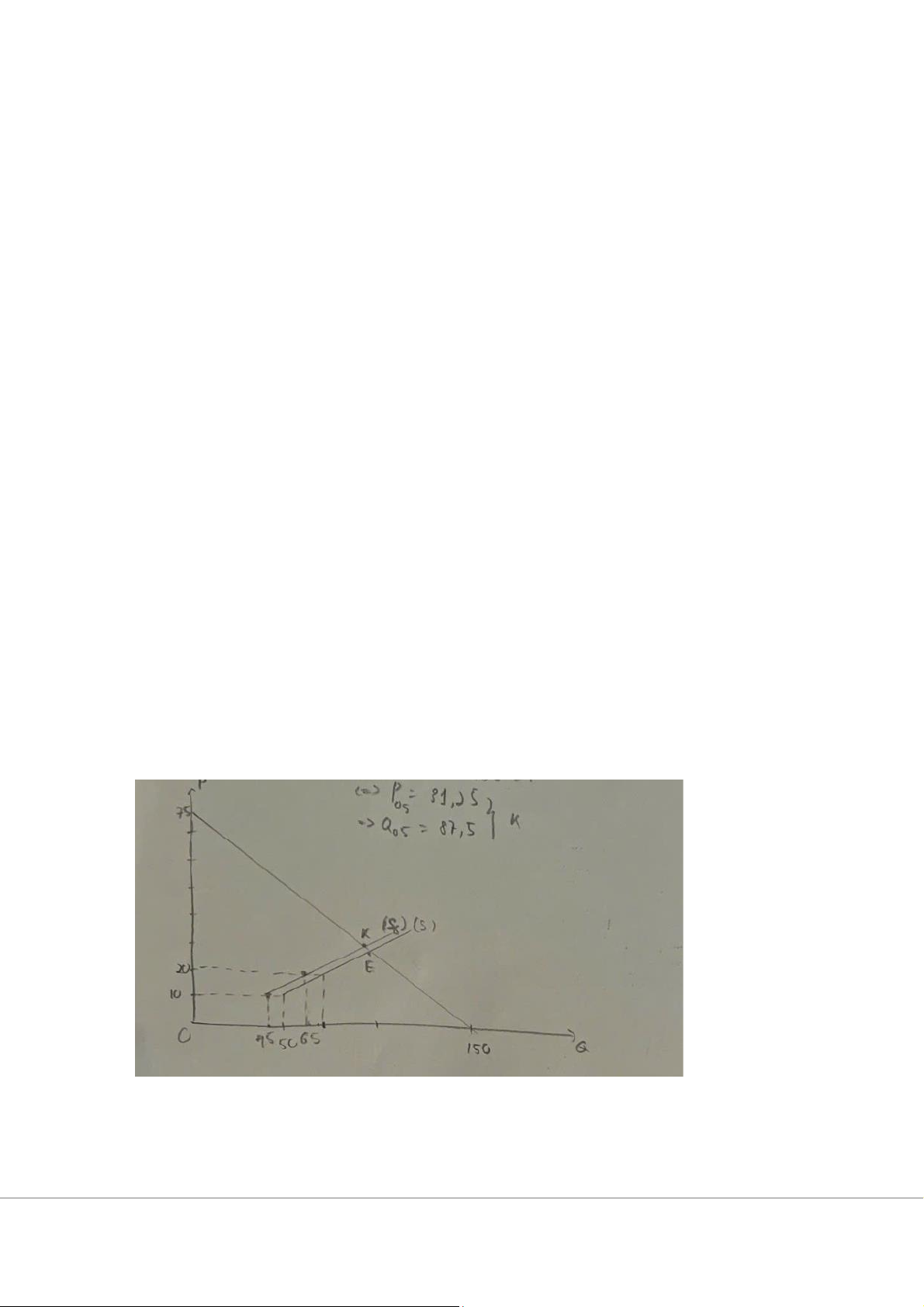
Bước 3: Vẽ đồ thị minh họa
• Đường cầu: Giữ nguyên ( Q_D = 150 - 2P ):
o Khi ( P = 0 ), ( Q_D = 150 ): Điểm (150, 0).
o Khi ( Q_D = 0 ), ( 0 = 150 - 2P ), ( P = 75 ): Điểm (0, 75).
• Đường cung mới: ( Q_S = 25 + 2P ):
o Khi ( P = 0 ), ( Q_S = 25 ): Điểm (25, 0).
o Khi ( P = 31.25 ), ( Q_S = 25 + 2 \times 31.25 = 25 + 62.5 = 87.5 ): Điểm (87.5, 31.25).
• Điểm cân bằng mới: Giao điểm của đường cầu và đường cung mới tại ( (Q = 87.5, P = 31.25) ).
• So sánh với đường cung cũ: Đường cung mới ( Q_S = 25 + 2P ) dịch chuyển song
song sang trái so với đường cung ban đầu ( Q_S = 30 + 2P ), vì lượng cung giảm 5
đơn vị tại mỗi mức giá. Bài 3
Một hãng cạnh tranh hoàn hảo có tổng chi phí là TC = Q2 +2Q + 64
a,Viết phương trình các hàm TFC = 64 TVC = TC – TFC = Q2 +2Q AVC = TVC/Q = Q +2 ATC = TC/Q = Q + 2 + 64/Q
MC = ∆TC/∆Q = Q2 +2Q + 64)’ = 2Q + 2
b,Xác định mức giá hòa vốn và mức giá đóng cửa sản xuất của hãng Giá hòa vốn: P = ATCmin ATCmin  ATC = MC  Q +2 + 64/Q = 2Q + 2  Q2 -64 = 0  Q = 8  P = 2.8 + 2 = 18
Mức giá đóng cửa  P = AVCmin  AVC = MC  Q2 + 2 = 2Q + 2  Q = 0  P = 0
c,Nếu giá thị trường là P = 10 thì lợi nhuận tối đa của hãng  MC = P  2Q + 2 = 10  Q = 4
Lợi nhuận tối đa: ∏ = TR – TC = P.Q – Q2 - 2Q – 64
= 40 - Q2 – 2Q – 64 = 40 – 16 – 8 -64 = -48
Ta thấy P > AVCmin (10>2)
 Hãng nên tiếp tục sản xuất để bù đắp 1 phần chi phí cố định
d,Nếu giá thị trường là P = 35
Điều kiện để đạt lợi nhuận tối đa : MC = P  2Q + 2 = 35  Q = 16,5
Lợi nhuận tối đa: ∏ = TR – TC
= P.Q – Q2 -2Q – 64 = 35.16,5 – 16,52 – 2.16 – 64 = 208,25 Nhóm 4 Câu 4: a, TFC = 16 TVC = 2Q2 + 4Q AVC = 𝑇𝑉𝐶 𝑄 = 2Q + 4 AFC = 𝑇𝐹𝐶 𝑄= 16𝑄 ATC = 2Q + 16𝑄 +4 MC = 4Q + 4 b,
Ta có: tổng doanh thu TR = P × Q = ( 120 – 2Q ) × Q = 120Q – 2Q2 Ta có: MR = 120 – 4Q
Để xác định doanh thu tối đa của hang thì MR = 0  120 – 4Q = 0  Q = 30 => TR = 1800
Vậy doanh thu tối đa của hãng là 1800 c, Lợi nhuận (π):
π=TR−TC=(120Q−2Q^2)−(2Q^2+4Q+16)
π=−4Q^2+116Q−16
Để tối đa hóa lợi nhuận, lấy đạo hàm của π theo QQ và đặt bằng 0: Dπ/dQ=−8Q+116=0 8Q=116 Q=14.5
Thay Q=14.5 vào hàm lợi nhuận: π=−4(14.5)2+116×14.5−16 π=−4×210.25+1682−16 π=−841+1682−16=825
Vậy lợi nhuận tối đa là 825. d,
Câu nói này sai. Doanh thu tối đa xảy ra khi Q=30Q , nhưng lợi nhuận tối đa xảy ra khi
Q=14.5. Như vậy, doanh thu tối đa không trùng với lợi nhuận tối đa vì lợi nhuận không
chỉ phụ thuộc vào doanh thu mà còn phụ thuộc vào chi phí. Lợi nhuận tối đa đạt được khi
chi phí biên (MC) bằng doanh thu biên (MR), không phải khi doanh thu tối đa. e,
Khi chính phủ đánh một mức thuế t = 2 trên mỗi đơn vị sản phẩm bán ra làm đường cung
giảm và dịch chuyển sang trái, đường cầu không đổi.
MCt = MC + t = 4Q + 4 + 2 = 4Q + 6 TCt = TC + 2Q = 2Q2 + 6Q + 16
- Giải phương trình: MCt = MR <=> 4Q + 6 = 120 - 4Q <=> 8Q = 114 <=> Qt = 14,25
=> Pt = 120 - 2 x 14,25 = 91,5
-Tổng doanh thu mới: TRt = Pt x Qt = 91,5 x 14,25 = 1 303,875
-Tổng chi phí mới: TCt = 2Q2 + 6Q + 16 = 2 x 14,252 + 6 x 14,25 + 16 = 507,625
-Lợi nhuận tối đa sau thuế: π = TRt - TCt = 1 303,875 - 507,625 = 796,25 Bài 5:
a. Hàm cầu:𝑄𝐷=148 − 5 × 𝑃
Thay giá bán P = 18 vào phương trình đường cầu, ta có: 𝑄𝐷=148 − 5 × 18 =58
Doanh thu của hãng tại giá bán P = 18 là
𝑇𝑅 = 𝑃 × 𝑄 = 18 ×58 =1044 b, Khi giá P=20: QD=148−5(20)=48 Doanh thu mới: TR=20×48=960
Doanh thu giảm từ 1044 ( khi P=18) xuống 960 (khi P = 20). vì thế tăng giá làm giảm
doanh thu. Vậy dự định tăng giá để tăng doanh thu là sai. c, • Khi giá P= 22 : QD= 148-5P = 148−5(22)=38
• Lợi nhuận :
Π= QD × ( P- ATC)= 38× (22- 20)= 76
• Nhận xét : Với P= 22 thì hãng đang có lợi nhuận . Vì vậy hãng có thể tăng giá sản
phẩm để tăng lợi nhuận . Nhưng cũng nên cân nhắc việc tăng giá sản phẩm sao
cho hợp lí vì khi tăng giá sản phẩm thì lượng cầu cũng đang giảm Bài 6
a. Sản lượng cân bằng tiêu dùng xảy ra khi và chỉ khi: S = I  - 30 + 0.4YD = 50  YD = 200
Vậy sản lượng cân bằng tiêu dùng là YD = 200
b. Tổng tiêu dùng: C = YD – S Khi YD = 200 ta có: S = - 30 + 0.4 x 200 = 50
Vậy tiêu dùng C = YD – S = 200 – 50 = 150
Sản lượng cân bằng của nền kinh tế là: Y = C + I = 150 + 50 = 200
c. Sản lượng cân bằng tiêu dùng xảy ra khi và chỉ khi:
S = I <=> - 30 + 0.4YD = 70 => YD = 250
sản lượng cân bằng tiêu dùng là YD = 250
Vậy sản lượng cân bằng tiêu dùng tăng 50
Tổng tiêu dùng: C = YD – S Khi YD = 250 ta có: S = - 30 + 0.4 x 250 = 70
Vậy tiêu dùng C = YD – S = 250 – 70 = 180
Sản lượng cân bằng của nền kinh tế là: Y = C + I = 180+ 70 = 250
Sản lượng cân bằng của nền kinh tế tăng: 250-200 = 50 d.
1. Xác định hàm tiêu dùng và hàm tổng cầu
Trong nền kinh tế giản đơn, thu nhập khả dụng (YDYD) bằng tổng thu nhập (YY), vì
không có thuế và chi tiêu chính phủ. Hàm tiết kiệm được cho là: S=−30+0.4YS = -30 + 0.4Y
Ta có mối quan hệ giữa tiêu dùng và tiết kiệm:
Y=C+S⇒C=Y−SY = C + S \Rightarrow C = Y - S
Thay S=−30+0.4YS = -30 + 0.4Y vào phương trình trên:
C=Y−(−30+0.4Y)=30+0.6YC = Y - (-30 + 0.4Y) = 30 + 0.6Y Vậy hàm tiêu dùng là: C=30+0.6YC = 30 + 0.6Y
Tổng cầu trong nền kinh tế giản đơn là:
AD=C+I=(30+0.6Y)+IAD = C + I = (30 + 0.6Y) + I Với I=50I = 50, ta có:
AD=30+0.6Y+50=80+0.6YAD = 30 + 0.6Y + 50 = 80 + 0.6Y
2. Xác định sản lượng cân bằng
Sản lượng cân bằng xảy ra khi tổng cung bằng tổng cầu, tức là: Y=ADY = AD
Thay biểu thức của ADAD vào phương trình trên: Y=80+0.6YY = 80 + 0.6Y Giải phương trình:
Y−0.6Y=80Y - 0.6Y = 80 0.4Y=800.4Y = 80 Y=200Y = 200
Vậy sản lượng cân bằng ban đầu là 200.
3. Phân tích tác động của sự gia tăng đầu tư
Giả sử đầu tư tăng thêm ΔI=20\Delta I = 20, khi đó hàm tổng cầu mới là:
AD′=80+20+0.6Y=100+0.6YAD' = 80 + 20 + 0.6Y = 100 + 0.6Y
Xác định sản lượng cân bằng mới:
Y=100+0.6YY = 100 + 0.6Y 0.4Y=1000.4Y = 100 Y=250Y = 250
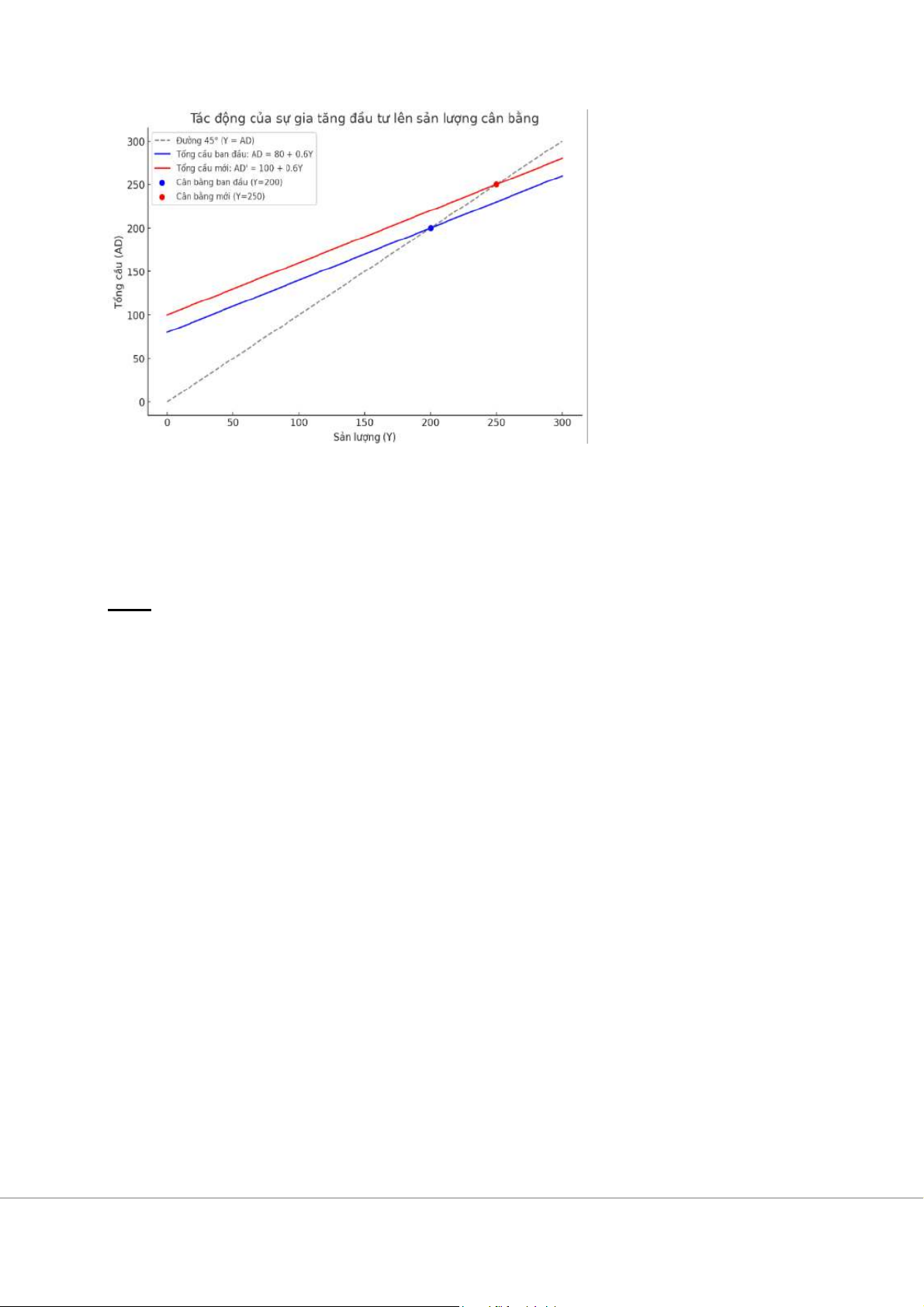
Vậy khi đầu tư tăng thêm 20, sản lượng cân bằng tăng từ 200 lên 250. 4. Đồ thị minh họa
Trục tung biểu diễn tổng cầu (AD) và trục hoành biểu diễn sản lượng (Y).
Vẽ đường tổng cung AS là đường 45 độ.
Vẽ đường tổng cầu ban đầu AD = 80 + 0.6Y. Giao điểm của AD và AS là sản lượng cân bằng ban đầu Y = 200.
Vẽ đường tổng cầu mới AD' = AD + ΔI. Đường AD' song song với AD và nằm phía trên.
Giao điểm của AD' và AS là sản lượng cân bằng mới Y'.
Sản lượng cân bằng mới Y' lớn hơn sản lượng cân bằng ban đầu Y. NHÓM 6 Bài 7
a. Tính sản lượng cân bằng của nền kinh tế và vẽ đồ thị đường tổng cầu
Ở trạng thái cân bằng, sản lượng (Y) thỏa mãn: Y = C + I Thay hàm C vào: Y = 340 + 0,8Y + 820 Y = 1160 + 0,8Y Chuyển vế: Y - 0,8Y = 1160 0,2Y = 1160 Y = 1160/0,2 = 5800
Vậy sản lượng cân bằng Y=5800.
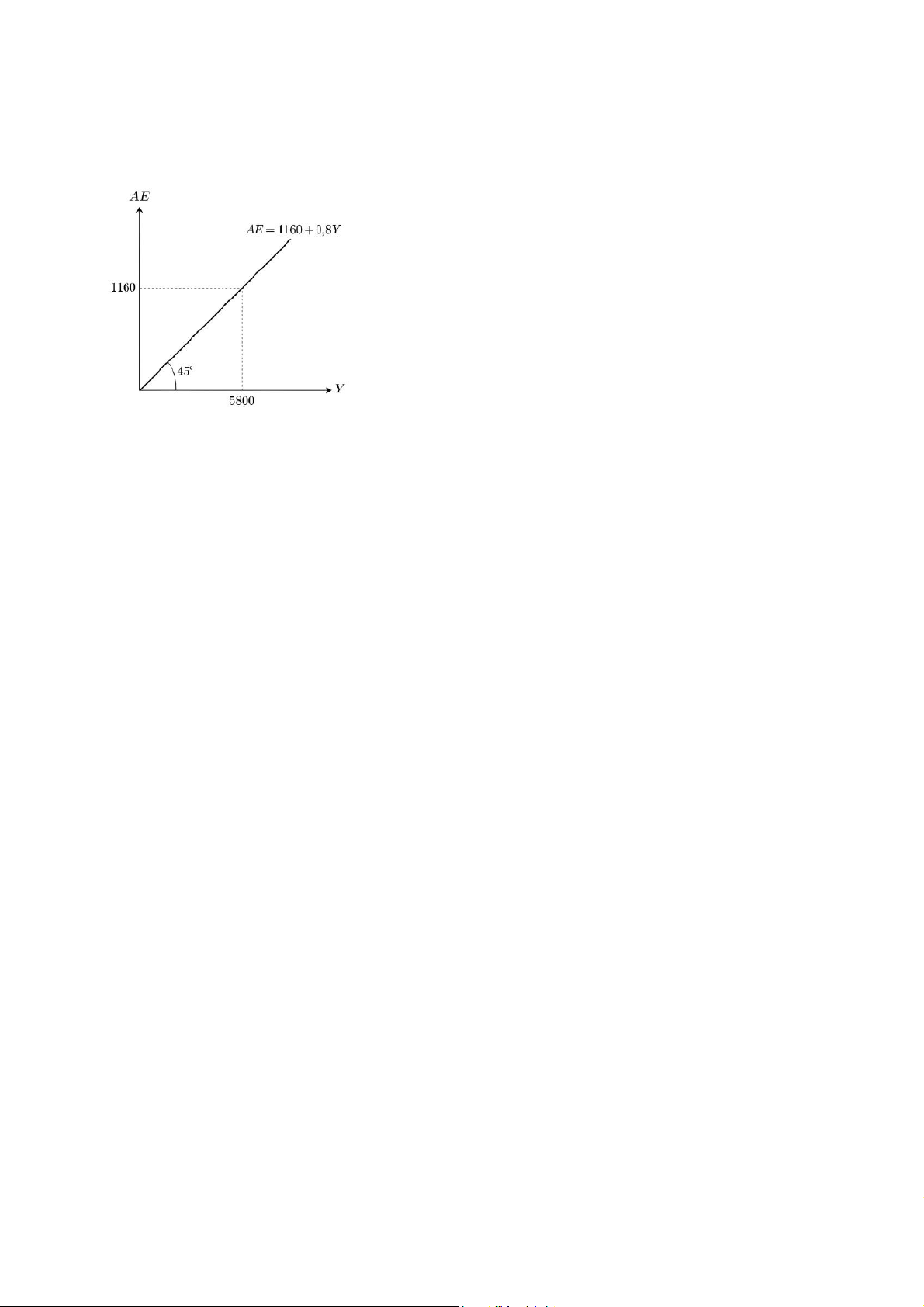
Vẽ đồ thị tổng cầu: Đường tổng cầu:
AE=C+l = (340 + 0,8Y) +820 = 1160 + 0,8Y
Đồ thị là đường thẳng có hệ số góc 0,8 và tung độ gốc 1160.
b. Từ 7.a ta đã tính được sản lượng cân bằng: Y = 5800 Hàm tiêu dùng: C= 340 + 0,8Y Thay Y=5800 vào hàm C C=340+0,8×5800 C=340+4640 C=4980
Vậy mức tiêu dùng (C) = 4980.
Mức tiết kiệm (S) được tính bằng: S = Y – C S=5800−4980 S=820
Vậy mức tiết kiệm (S) = 820. c.
• Thay đổi sản lượng cân bằng:
AE1= 𝐶 + 𝐼 + MPC.Y
Sản lượng đạt cân bằng  AE1 = Y
 𝐶 + 𝐼 + MPC.Y =Y  Y01= 1
1−𝑀𝑃𝐶( 𝐶 + 𝐼 )
Khi đầu tư tăng thêm một lượng 90 thì AE1’= 𝐶 + (𝐼+90) + MPC.Y  Y01’= 1
1−𝑀𝑃𝐶( 𝐶 + 𝐼 + 90) Δ𝑌 = Y01’ -Y01 = 1
1−𝑀𝑃𝐶( 𝐶 + 𝐼 + 90) - 1
1−𝑀𝑃𝐶( 𝐶 + 𝐼 ) = 1 1−𝑀𝑃𝐶 .90 = 1 1−0,8 .90 = 450
• Thay đổi mức tiêu dùng của cư dân : C= 𝐶  + MPC.Y C’= 𝐶 + MPC.Y’  Δ𝐶 = 𝐶′− 𝐶
= 𝐶  + MPC.Y’ – ( 𝐶  + MPC.Y) = MPC . Δ𝑌 = 0,8 . 450 = 360
d. Theo bài ra ta có : 𝐶 = 340 + 0,8𝑌 𝐼 = 820
Sản lượng đã tính ở ý a : 𝑌 = 5800
Mà ta lại có : 𝑌thực tế =6000 Suy ra : 𝑌thực tế > 𝑌∗
→ Hiện tượng ngoài dự kiến là hàng tồn kho tăng. Giải thích:
Sản lượng thực tế lớn hơn tổng cầu, nên doanh nghiệp không bán hết hàng, dẫn đến hàng
tồn kho ngoài dự kiến tăng lên.