BÀI TẬP ĐỒ HOẠ MÁY TÍNH Đà nẵng, 09/05/2023
2.1. Bài tập tính toán đồ hoạ máy tính: xa ya za 21 01 57 xb yb zb 23 03 55 xc yc zc 33 09 59 xD yD zD 35 15 65
1) Cho hai điểm A (xa, ya), B (xb, yb). Tìm phương trình của đường thẳng đi qua 2
điểm AB. Tự chọn các tọa độ cụ thể. Cho A (21, 1); B (23, 3)
= (2, 2) -> vecto pháp tuyến = (-2, 2)
-> Phương trình của đường thẳng cần tìm là:
(AB): -2x + 2y + c = 0 đi qua A (21,1) ->(AB): -2x+2y+40 = 0
2) Cho ba điểm A (xa, ya), B (xb, yb), C (xc, yc). Tự chọn các giá trị và tìm phương
trình đường tròn đi qua 3 điểm này.
Cho A (21, 1); B (23, 3),C(33,9).
Gọi I là tâm đường tròn ngoại tiếp tam giác ABC
Gọi M (22, 2) là trung điểm AB
Gọi N (27, 5) là trung điểm AC
Gọi d1 là đường trung trực của AB-> = (2, 2) là vecto pháp tuyến của d1
Gọi d2 là đường trung trực của AC -> = (12, 8) là vecto pháp tuyến của d2
d1: 2x +2y +c = 0 qua M (22, 2) -> d1: 2x+2y-48 = 0 (1)
d2: 12x + 8y+c = 0 qua N (27, 5) -> d2: 12x+8y-364 = 0 (2)
Từ (1) và (2) -> -> -> I (43, -19) R = IA = = 2
->(I): (x−43)2 + (y+19) = 884 2
3) Cho tam giác ABC với A (xa, ya), B xb, yb), C (xc, yc). Tự chọn các giá trị và xác
định tâm đường tròn ngoại tiếp, tâm đường tròn nội tiếp, giao điểm 3 đường cao,
giao điểm 3 đường trung tuyến, giao điểm 3 đường phân giác.
Cho A (21, 1); B (23, 3),C(33,9).
+ Tâm đường tròn ngoại tiếp
Gọi I là tâm đường tròn ngoại tiếp tam giác ABC
Gọi M (28, 6) là trung điểm BC
Gọi N (27,5) là trung điểm AC
Gọi d1 là đường trung trực BC -> VTPT: = (, 6)
Gọi d2 là đường trung trực AC -> VTPT: = (12, 8)
->d1 = 10x +6y+ c = 0 qua M -> d1: 10x += 0 (1)
d2 = 12x +8y + c = 0 qua N -> d2: 12x +8y -364= 0 (2) Từ (1), (2) -> -> I ()
+ Tâm đường tròn nội tiếp và giao điểm 3 đường phân giác AB = , AC =
Gọi AD là đường phân giác góc BAC, D ∈ BC, D (x, y) = -> = .
-> -> -> D (24.64, 3.98)
Gọi J là tâm đường trong nội tiếp tam giác ABC ->J
∈ AD, BJ là phân giác góc ABC, J (x, y) = (1.64, 0.98) -> BD =
Ta có: = -> = . -> = -5 -> -> -> J (24.03) + Giao điểm 3 đường cao
Gọi d1: qua A và vuông góc với BC 3
-> d1 = 10x +6y+ c = 0 qua A -> d1: 10x +6y-216 =0 (1)
Gọi d2: qua B và vuông góc AC
->d2 = 12x +8y + c = 0 qua B -> d2: 12x +8y -300 = 0 (2)
Gọi H là trực tâm tam giác ABC Từ (1), (2) -> -> ->H (-9, 51)
+ Giao điểm 3 đường trung tuyến
Gọi G là trọng tâm tam giác ABC
xG = = , yG =13/3= -> G (,13/3)
4) Cho hai đường thẳng AB, CD cắt nhau, có A (xa, ya), B (xb, yb), C (xc, yc), D (xd,
yd). Xác định giao điểm nếu có của hai đường thẳng này.
Cho A (21, 1); B (23, 3),C(33,9),D(35,15). = (2, 2) -> = (-2, 2) = (2, 6) -> = (-6,2)
->(AB): -2x+2y+c = 0 qua B -> (AB): -2x+2y+40 = 0 (1)
->(AC): -6x +2y+ c = 0 qua C -> (AC): -6x +2y+36 = 0 (2) Từ (1), (2) -> ->
-> Có giao điểm tại toạ độ có x = -1, y = -21
5) Cho đường tròn tâm O (xc, yc), bán kính R và điểm P (x, y) ngoài đường tròn.
Xác định khoảng cách ngắn nhất giữa P và đường tròn.
Cho O (33,9), R = 2, P (36, 13) ->PO = = 5
Khoảng cách ngắn nhất: PO – R = 5 – 2 = 3
6) Cho đường thẳng AB có A (xa, ya, za), B (xb, yb, zb). Tìm khoảng cách từ điểm
P (xc, yc, zc) đến đoạn thẳng AB.
A (21,1,57), B (23,3,55) -> = (2,2,-2) (AB) 4 P (33,9,59)
Gọi H là hình chiếu từ P lên AB, H ∈ AB ->H (21+2t, 1+2t, 57-2t) = (2t-12, 2t-8, -2t-2)
. = 0 -> t -2 + t-3 + t-4 = 0 -> t = 11.54 ->H (44.08,24.08,33.92) PH = = 33.29 7),8),10)
Cho A (21,1,57), B (23,3,55), C (33,9,59) = (2,2,-2), = (12, 8,2)
Vecto pháp tuyến: = , ]= (20, -28 , -8)
->(ABC): 20x-28y-8z +d = 0 qua A ->(ABC): 20x-28y-8z -64 = 0 Cho P (35,15,65)
Khoảng cách từ P đến mặt phẳng (ABC) dP/(ABC)= =
9) Cho vector v(xa, ya, za). Viết công thức chuẩn hóa vector v để có chiều dài đơn vị (= 1)
_ Cho v(21, 1, 57), |v| = = là độ dài vecto v Chuẩn hoá: = = ( , , ) Code: Struct Vector {float x,y,z;} Vector ChuanHoa (Vector a){
float c = sqrt (pow (a.x,2) + pow (a.y,2) + pow (a.z,2)); Vector b; b.x = a.x/c; 5 b.y = a.y/c; b.z = a.z/c; return b; } 6
2.2. Bài tập các phép biến đổi đồ họa 1) Model Transformation Pobj = ( 21, 1, 57, 1 )
Phép tịnh tiến: theo vecto T(dx, d , d y z) = (1,4,6) MT = =
Phép quay 1 trục (ux , uy , uz )= (1,2,3) một góc 45 trong không gian 3D : [MR]u = c= cos α , S=sin α [MR]u=
Ma trận biến đổi: M = MT . [MR] = u =>Pworld = M.Pobj = 2) View Transformation
e(4,4,4) , c(0,1,4), up(0,1,0) n= = = () u= = (0,0,-1) v= u.n = () Mview = . = Pcam = Mview . Pworld = . =
3) Projection Transformation MProj = = = > Pproj =Mproj . Pcam =
4) Normalized Device Coordinate Pndc = =
5) ViewPort Transformation M1 = Ma trận Viewport M2 = 7
= > Pscreen = M2.Pndc = => Pscreen = ( 45.3645 ; 50.0116 )
2.3. Bài tập đường, mặt cong tham số: Mã SV thứ nhất u 102210157 0.57
1) Cho đường cong Bézier có n + 1 = 4 đỉnh điều khiển P0 = (10, 0), P1 = (20, 30),
P2= (50, 40), P3 = (80, 0). Tính tọa độ (Cx, Cy) của một điểm C(u) trên đường cong
ứngvới tham số u ∈ [0, 1].
Xét đường cong Bézier có n + 1 = 4 đỉnh điều khiển P0, P1, P2, P3:
Phương trình của đường cong như sau C(u) = (1-u)3P + 3u(1-u)2 2 3 0 P1 + 3u (1-u)P + u 2 P3 Với u = 0.57, ta được:
C (0.57) = (1-0.57) x (10, 0) + 3x0.57(1-0.57) 3
2x(20, 30) + 3x0.57 (1-0.57)x(50, 2 40) +0.57 x(80,0) 3 = (42.89014, 26.25021)
->C (x, y) = (42.89014, 26.25021)
2) Cho đường cong B-spline đồng nhất (uniform) có n + 1 = 4 đỉnh điều khiển P0 =
(0, 10), P1 = (10, 40), P2 = (40, 40), P3 = (50, 0) có bậc p =3. Tính tọa độ (Cx, Cy) của
điểm C(u) trên đường cong ứng với tham số tự chọn u ∈ [0, 1]
Phương trình biểu diễn đường cong B-spline bậc 3 (p = 3) đồng nhất có 4 đỉnh
điều khiển P0, P1, P2, P3: C(u)=
C(u)= N0,3(u)P0 + N1,3(u)P1 + N2,3(u)P2 + N3,3(u)P3
Với các hàm cơ sở Ni,3(u) được xác định (u = 0.57): N 3 0,3(u) = (1-u) = 0.01325 N 3 2
1,3(u) = (3u -6u + 4) = 0.43436 8 N 3
2,3(u) = (-3u +3u2 + 1) = 0.23652 N3,3(u) = u = 0.03087 3
->C(u) = 0.01325x(0, 10) + 0.43436x(10, 40) + 0.23652 x(40, 40) + 0.03087 x (50, 0) = (15.3479,26.9677)
->C (x, y) = (15.3479,26.9677)
3) Cho đường cong B-spline không đồng nhất có n + 1 = 4 đỉnh điều khiển P0 =
(10,0), P1 = (20, 30), P2 = (50, 40), P3 = (80, 0), bậc p = 2, vector nút U = {0, 0, 0,
0.5,1, 1, 1}.Tính tọa độ (Cx, Cy) của điểm C(u) trên đường cong ứng với tham số u ∈[0, 1].
Triển khai phương trình đường cong B-spline: C(u)= C(u) = N0,2(u)P + N 0 1,2(u)P + N 1 2,2(u)P + N 2 3,2(u)P (1) 3
Với k = 2, i = 0... (3+2-2), u = 0.57 N0,2(u) == 0.0196 (2) N1,2(u) = = 0.3306 (3) N 2 3
2,2(u) = =0.6498, ∀ u ∈ [u , u ) (4) N 2 3
3,2(u) = 0, ∀ u ∈ [u , u ) (5)
Từ (1), (2), (3), (4), (5), ta được:
C(u) = 0.0196x (10, 0) + 0.3306 x (20, 30) + 0.6498 x (50, 40) = (39.298,35.91) ->C(x, y) = (39.298,35.91)
2.4. Bài tập thuật toán cơ bản vẽ đường 1) A(21;1) và B(25;9) Ta có
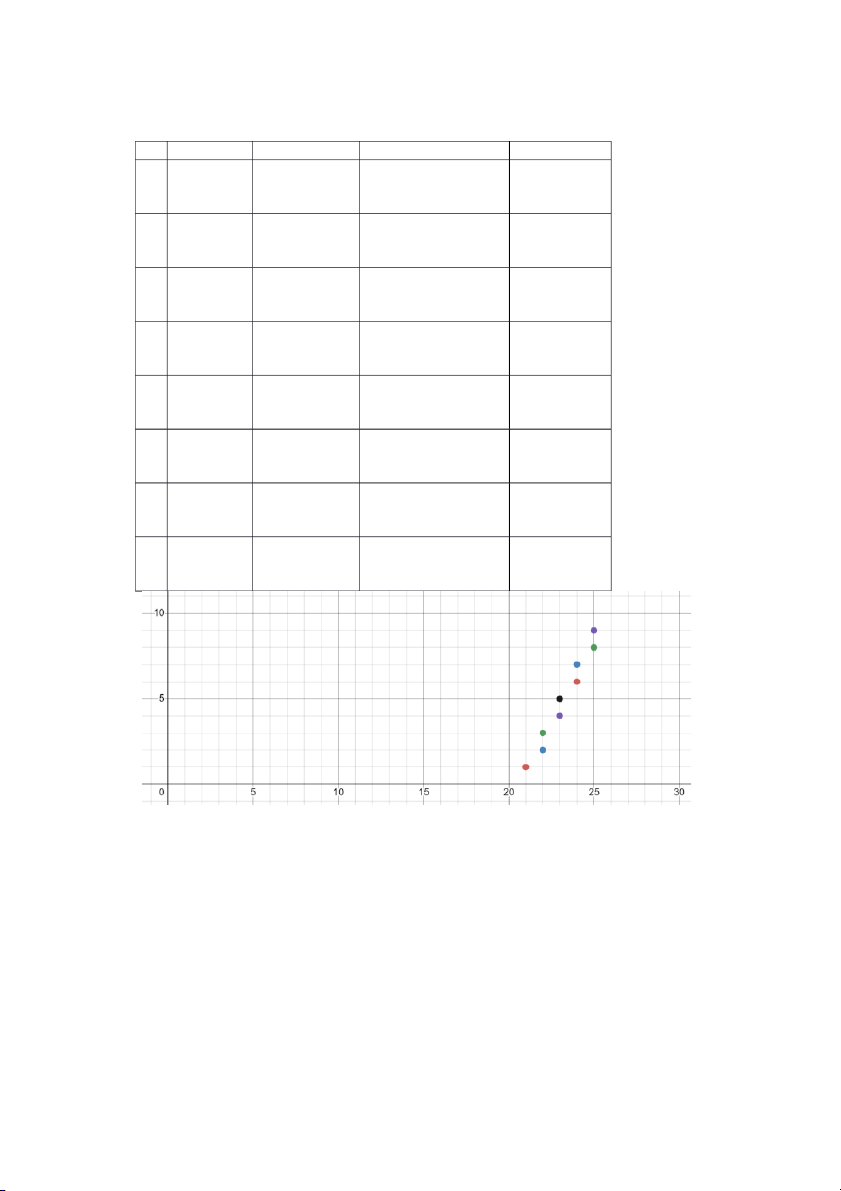
x=4, y=8. Hệ số góc m=2, p= 2 x- y. Ta có bảng: k pk = pk-1 Kiểm tra pk Tính toán (xk,yk) 9 0 p= (2*dx)-dy 21;1 1 0 p>=0 x1 =x1+1 22;2 y1 = y1+1 p= p+(2*dx)-(2*dy) 2 -8 p<0 x2 = x2 22;3 y2 = y2+1 P = p+2*dx 3 0 p>=0 x3 =x3+1 23;4 y3 = y3+1 p= p+(2*dx)-(2*dy) 4 -8 p<0 x4 = x4 23;5 y4 = y4+1 p = p+2*dx 5 0 p>=0 x5 =x5+1 24;6 y5 = y5+1 p= p+(2*dx)-(2*dy) 6 -8 p<0 x6 = x6 24;7 y6 = y6+1 p = p+2*dx 7 0 p>=0 x7 =x7+1 25;8 y7 = y7+1 p= p+(2*dx)-(2*dy) 8 -8 p<0 x8 = x8 25;9 y8 = y8+1 p = p+2*dx
Các điểm tọa độ nguyên theo thuật toán Bersenham 2) A(21;1) và B(25;9) 10 Ta có x=4, y=8. Ta có bảng: k pk = pk-1 Kiểm tra Tính toán (xk,y ) k pk 0 p = (2*dy)-dx = 8 21;1 1 8 p>=0 x1 =x1 21;2 y1 = y1+1 p=p+2(dx-dy) 2 0 p>=0 x2 =x2 21;3 y2 = y2+1 p=p+2(dx-dy) 3 -8 p<0 x3 = x3+1 22;3 y3 = y3 p= p+2*dy 4 8 p>=0 x4 =x4 22;4 y4 = y4+1 p=p+2(dx-dy) 5 0 p>=0 x5 =x5 22;5 y5 = y5+1 p=p+2(dx-dy) 6 -8 p<0 x6 = x6+1 23;5 y6 = y6 p= p+2*dy 7 8 p>=0 x7 =x7 23;6 y7 = y7+1 p=p+2(dx-dy) 8 0 p>=0 x8 =x8 23;7 y8 = y8+1 p=p+2(dx-dy) 9 -8 p<0 x9 = x9+1 24;7 y9 = y9 p= p+2*dy 10 8 p>=0 x10 =x10 24;8 y10 = y10+1 p=p+2(dx-dy) 11 0 p>=0 x11 =x11 24;9 y11 = y11+1 p=p+2(dx-dy) 12 -8 p<0 x12 = x12+1 25;9 y12 = y12 p= p+2*dy 11
Các điểm tọa độ nguyên theo thuật toán MidPoint
3) tâm O(21,1) và bán kính R=10
B1: Gán tọa độ điểm khởi đầu là (x0 ; y0) = (0;10) B2: P = 1 – R = -9; P 0 = P k 0 B3: P = -9 <0 => x k k+1 = xk + 1 = 1 yk+1 = yk =10
Pk+1 = Pk +2xk+1+3 = -9+2+3= -4
Do tâm là (21;1) nên xplot = 21; yplot =11 k pk Kiểm tra pk Tính toán (xk;yk) 0 p=1-10=9 (21;11) 1 -9 p<0 x=x-1 (20;11) y=y p=p+2*x+3 2 34 p>0 x=x-1 (19;12) y=y+1 p=p+2*x-2*y+5 3 53 p>0 x=x-1 (18;13) y=y+1 p=p+2*x-2*y+5 4 68 p>0 x=x-1 (17;14) y=y+1 p=p+2*x-2*y+5 5 79 p>0 x=x-1 (16;15) y=y+1 p=p+2*x-2*y+5 12 6 86 p>0 x=x-1 (15;16) y=y+1 p=p+2*x-2*y+5
Kết quả các điểm được tạo ra với các cung 45 : Quadrant-1 Quadrant-2 Quadrant-3 Quadrant-4 (X,Y) (-X,Y) (-X,-Y) (X,-Y) (21,11) (-21,11) (-21,-11) (21,-11) (20,11) (-20,11) (-20,-11) (20,-11) (19,12) (-19,12) (-19,-12) (19,-12) (18,13) (-18,13) (-18,-13) (18,-13) (17,14) (-17,14) (-17,-14) (17,-14) (16,15) (-16,15) (-16,-15) (16,-15) (15,16) (-15,16) (-15,-16) (15,-16) (16,15) (-16,15) (-16,-15) (16,-15) (15,16) (-15,16) (-15,-16) (15,-16) (14,17) (-14,17) (-14,-17) (14,-17) (13,18) (-13,18) (-13,-18) (13,-18) (12,19) (-12,19) (-12,-19) (12,-19) (11,20) (-11,20) (-11,-20) (11,-20) (11,21) (-11,21) (-11,-21) (11,-21) 13