Bài tập phương trình chứa căn – Lê Văn Đoàn

Phương trình căn thức lớp 10 Ths. Lê Văn Đoàn Dang 1. Ph P ng trirnh h cn n c ba b n B  ≥ 0   B  ≥ 0  A B  = ⇔  . A = B ⇔ . 2  A  = B  A  = B  
Phương pháp tổng quát : (nếu không thuộc hai dạng trên)
 Bước 1. Đặt điều kiện cho căn có nghĩa.
 Bước 2. Chuyển vế sao cho hai vế không âm.
 Bước 3. Bình phương hai vế để đưa về một trong các dạng trên. BA B I ITÂP P AP P DUNG N Bà B i à 1 . 1
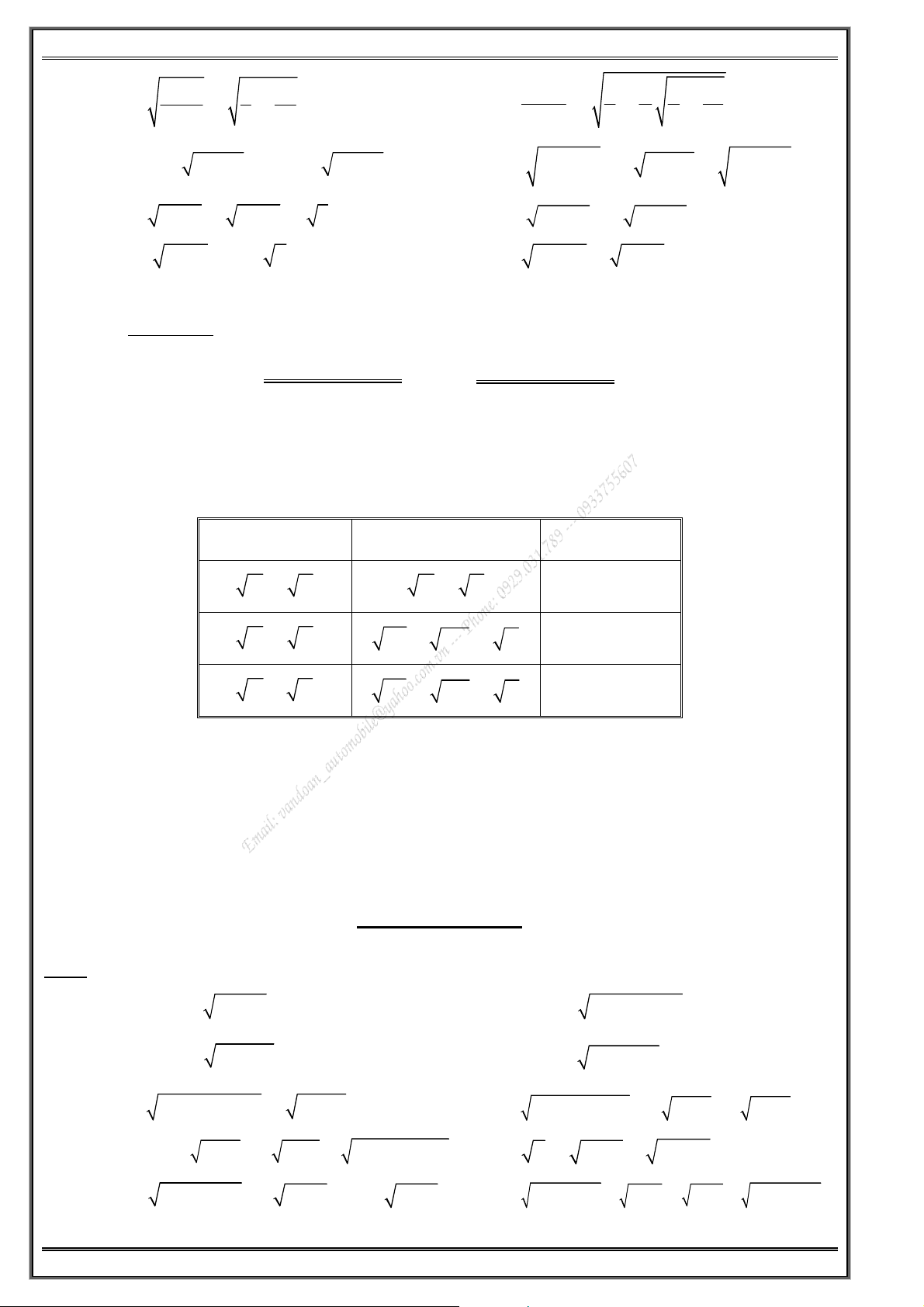
Giải các phương trình sau a/ 2x − 3 = x − 3 . b/ 5x + 10 = 8 − x . c/ x − 2x − 5 = 4 . d/ 2 x + x − 12 = 8 − x . e/ x − 2 = 4 − x . f/ 2 3x − 9x + 1 = x − 2 . g/ 2 3x − 9x + 1 = x − 2 . h/ 2 x − 3x − 10 = x − 2 . i/ x − 2x + 7 = 4 . j/ x + x − 1 = 13 . k/ x − x − 1 = 3 . l/ 2 x − 3x − 1 = 2x − 7 . m/ 2 x + 3x = 3x − 1 . n/ 2 x − 9x + 1 = x − 2 . o/ 2x − 2x − 1 = 7 . p/ 3 − x = 3x − 5 . q/ x − 4x − 3 = 2 . r/ 2 x − 1 = x − 1. s/ 2 x − 2 = x − 4x + 3 . t/ 2 x − 3x + 2 = 2x − 1 . u/ 2 x − + 4x − 3 = 2x − 5 . v/ 2 5 − x = x − 1 . x/ 2 3x + 5x + 1 + 1 = 4x . y/ 2 2 x − 2x + 1 = x − 2x + 1. Bà B i à 2 . 2 Giải các phương trình a/ 2 x + x + 7 = 7 . b/ 2 x − + 4x − 3 = 2x − 5 . c/ 16x + 17 = 8x − 23 . d/ 2 x − + 4x + 2 = 2x . e/ 2 x − 6x + 6 = 2x − 1 . f/ 2 x − 1 = x + 1 . g/ 2 4 − x = x + 2 . h/ 2 4 − x = x + 2 . Bà B i à 3 . 3
Giải các phương trình sau a/ 2 x + 2x + 4 = 2 − x . b/ 2 x − 3x = 2x − 1 . c/ 2 2 2x − 2x + 4 = x − x + 2 . d/ 2 x − 3x − 2 = x − 3 . Bà B i à 4 . 4
Giải các phương trình sau
"Cần cù bù thông minh…………" Page - 1 - Ths. Lê Văn Đoàn
Phương trình căn thức lớp 10 a/ 2x + 1 = 2 + x − 3 . b/ 3x + 4 − x − 3 = 3 . c/ x − 3 − x + 2 = 5 . d/ 2x + 1 = 4 − x − 3 . e/ 5x − 1 = 3x − 2 + 2x + 2 . f/ 3x + 1 − 4x − 3 = 5x + 4 . g/ x + 1 − x − 1 = 1 . h/ 3x + 7 − x + 1 = 2 . i/ 2 2 x + 9 − x − 7 = 2 . j/ 2 2
3x + 5x + 8 − 3x + 5x + 1 = 1. k/ 2x + 3 + 2x + 2 = 1 . l/ x + 4 − 2x − 6 = 1 . m/ 3x + 7 − x + 1 = 2 . n/ 11 − x − x − 1 = 2 . o/ 2 2 x + 9 − x + 7 = 2 . p/ x + x − 5 = 5 . q/ 3x − 5 + 2x + 3 = x + 2 .
r/ x − 2 + x − 1 = 2x − 3 . s/ x + 3 − 7 − x = 2x − 8 . t/ 2 − x = 7 − x − 3 − − 2x . u/ 5x − 1 = 3x − 2 − 2x − 1 .
v/ 5x − 1 − x − 1 = 2x − 4 . x/ x + 2 − 2x − 3 = 3x − 5 .
y/ x + 4 − 1 − x = 1 − 2x . Bà B i à 5 . 5
Giải các phương trình sau a/ 1 + x − 1 = 6 − x .
b/ 5x − 1 − 3x − 2 − x − 1 = 0 . c/ x + x + 1 = x + 2 . d/ 3x + 1 = 8 − x + 1 . e/ 3x − 3 − 5 − x = 2x − 4 . f/ x + 9 = 5 − 2x + 4 . Dang 2. Ph P ng trirnh h cn n s dung đ đ t ân phu h t = f x , t ≥ 0
Loại 1. af (x) + b (x)  ( ) + c = 0 ⇔  . 2 a  t  + bt + c = 0 
Loại 2. f (x) + g(x) + f (x).g(x) = h(x) . Đặt t = f (x) + g(x) .
Loại 3. Đặt ẩn phụ đưa về hệ phương trình : f (x) + g(x) = h(x).
● Đặt u = f (x), v = g(x) với u, v ≥ 0 .
● Đưa phương trình trên về hệ phương trình với hai ẩn là u và v.
Ta có thể giải dạng tổng quát dạng : n ( ) m f x + g(x) = a, (a = cons ) t . Page - 2 -
"All the flower of tomorrow are in the seeks of today……"
Phương trình căn thức lớp 10 Ths. Lê Văn Đoàn BA B I ITÂP P AP P DUNG N Bà B i à 6 . 6
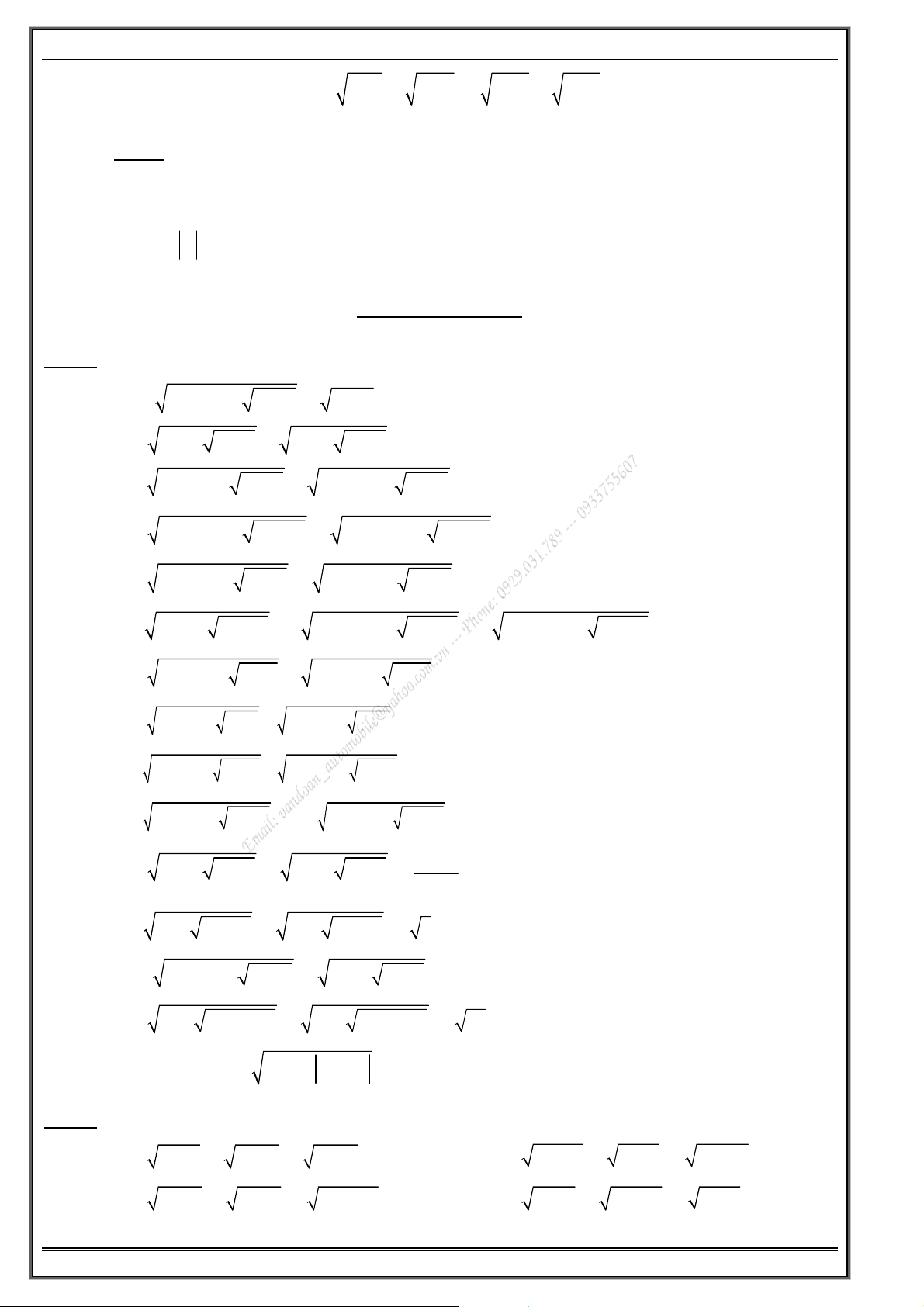
Giải các phương trình sau a/ 2 2
x − 6x + 9 = 4 x − 6x + 6 . b/ ( − )( − ) 2 x 3 8 x + 26 = x − + 11x . c/ ( + )( + ) 2 x 4 x 1 − 3 x + 5x + 2 = 6 . d/ ( + )( − ) 2 x 5 2 x = 3 x + 3x . e/ 2 2 x + x + 11 = 31 . f/ 2
x − 2x + 8 − 4 (4 − x)(x + ) 2 = 0 . g/ 2 2
4x − 12x − 5 4x − 12x + 11 = 0 . h/ 2 x + 4x − 3 2 + x + 4 = 0 . 1 1 i/ 2 4x + + 2x − − 6 = 0 . j/ 2 2 x − x + x − x + 9 = 3 . 2 x x k/ 2 2
x + 2 x − 3x + 11 = 3x + 4 . l/ 2 x − 3x − 10 + 3 x (x + ) 3 = 0 . m/ 2 2
x + 3x − 18 + 4 x + 3x − 6 = 0 . n/ 2 2
2x − x + 6x − 12x + 7 = 0 . o/ ( + )( + ) 2 x 4 x 1 − 3 x + 5x + 2 = 0 . p/ ( − )2 2 x 3 + 3x − 22 = x − 3x + 7 . q/ 2 2 x + 1 − 7 x + 1 + 10 = 0 . r/ 2 2
2x − 8x + 12 = x − 4x − 6 . Bà B i à 7 . 7
Giải các phương trình sau
a/ x + 3 + 6 − x = 3 + (x + ) 3 (6 − x) . b/ 2x 3 + + x 1 + =3x 2 + (2x+ ) 3 (x+ ) 1 1 − 6.
c/ x − 1 + 3 − x − (x − ) 1 (3 − x) = 1 .
d/ 7 − x + 2 + x − (7 − x)(2 + x) = 3 . e/ x + 1 + 4 − x + (x + ) 1 (4 − x) = 5 . f/ 2 3x −2 + x 1
− = 4x −9 +2 3x −5x +2 . 2 g/ 2 1 + x − x = x + 1 − x . h/ 2 x + 9 − x = x − + 9x + 9 . 3 i/ 2 2
x + 17 − x + x 17 − x = 9 . j/ x 1 − + x +3 +2 (x− ) 1 (x + ) 3 = 4 −2x . k/ 2
x + 4 + x − 4 = 2x −12 + 2 x −16 . l/ 2 2x+3 + x 1 + =3x 2 + 2x 5 + x+3 1 − 6. m/ 2 3x 2 − + x 1 − = 4x−9 +2 3x −5x +2 . n/ 2 2 2 3x +6x 1 + 6 + x +2x =2 x +2x +4 . Bà B i à 8 . 8
Giải các phương trình sau 3x − 1 x a/ 2 = + 1. b/ 3 x + 7 − x = 1 . x 3x − 1 3
c/ 3 2 − x = 1 − x − 1 . d/ x + 3 − x = 1 . 16x x − 1 5 e/ 3 3 x + 2 = 3 3x − 2 . f/ 5 5 + = . x − 1 16x 2
"Cần cù bù thông minh…………" Page - 3 - Ths. Lê Văn Đoàn
Phương trình căn thức lớp 10 2x 1 1 3 + x 1 1 4 2 g/ 3 3 + + = 2 . h/ = + + . x + 1 2 2x 2 3x 9 x 9 x 2 2 2 2 4 i/ x + 4 − x = 2 + 3x 4 − x . j/ 4 ( + ) 2 4 2 1 x + 3 1 − x + (1 − x) = 0 . k/ 4 4 5 − x + 4 − x = 2 . l/ 3
2 3x − 2 + 3 6 − 5x − 8 = 0 . m/ 3 x + 3 = 1 + x . n/ 3 3 x + 34 − x − 3 = 1 . Dang 3. Đ Đ a avê ph p ng trirnh h tich c sô (nhom, m liên n hiêp, …)
● Đoán nhận một nghiệm của phương trình để định hướng đưa về phương trình tích số hoặc nhân liên hiệp.
● Cần chú ý đến các cách biến đổi về tích và nhân liên hiệp Biểu thức Biểu thức liên hiệp Tích A ± B A A − B ∓ B 3 3 3 2 3 3 A + B A + B A − AB + B 3 3 A − B 3 2 3 3 − A + AB + A B B ● f (x) 2
= ax + bx + c = a (x − x x − x với x f x = 0 . 1 )( 2 )
1 và x2 là hai nghiệm của ( )
∗ u + v = 1 + uv ⇔ (u − ) 1 (v − ) 1 = 0 .
∗ au + bv = ab + vu ⇔ (u − b)(v − a) = 0
● Cần lưu ý đến các hằng đẳng thức (kết hợp đồng nhất thức) BA B I ITÂP P AP P DUNG N Bà B i à 9 . 9
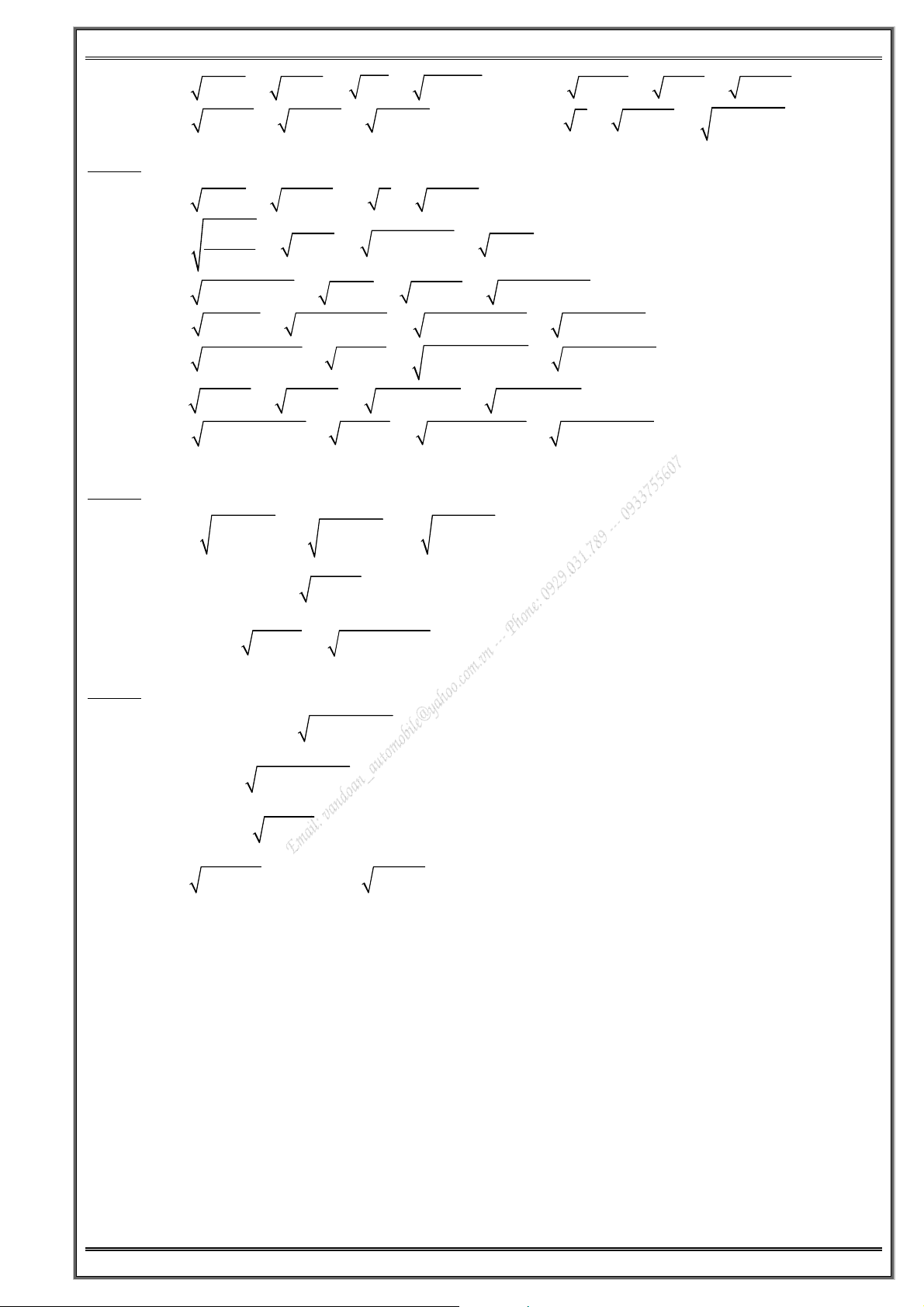
Giải các phương trình sau a/ ( − ) 2 2 x 3 x + 4 = x − 9 . b/ ( − ) 2 x 3 x − 5x + 4 = 2x − 6 . c/ ( + ) 2 2 x 3 10 − x = x − x − 12 . d/ ( + ) 2 x 1
16x + 17 = 8x − 15x − 23 . e/ 2 2
2x + 8x + 6 + x − 1 = 2x + 2 . f/ 2
x +10x +21 = 3 x +3 +2 x +7 −6 . g/ 2 x +2 7 − x = 2 x −1 + x − + 8x −7 +1. h/ 2 x + x + 1 − x + x = x . i/ 2
x − x − 2 − 2 x − 2 + 2 = x + 1 . j/ 2 2 x 3 − x 2 + + x 3 + = x 2 − + x 2 + x 3 − . Page - 4 -
"All the flower of tomorrow are in the seeks of today……"
Phương trình căn thức lớp 10 Ths. Lê Văn Đoàn k/ ( − ) + ( + ) 2 x x 1 x x 2 = 2 x . l/ 2 2 2 x 8 − x 1 + 5 + x 2 + x 1 − 5 = x 9 − x 1 + 8. m/ 2 3 2x + 5x − 1 = 7 x − 1 . n/ 2 2x − 1 + x − 3x + 1 = 0 . 2 x o/ − 3x − 2 = 1 − x . p/ 3 3 3 2
x + 1 + x + 2 = 1 + x + 3x + 2 . 3x − 2 q/ 3 3 2 3 3 2 x + 1 + x = x + x + x . r/ 2
x + 3 +2x x +1 = 2x + x + 4x + 3 . 4x s/ x + 3 + = 4 x . t/ + + ( + ) 2 x 1 2 x 1 =x 1 − + 1−x +3 1−x . x + 3 Bà B i à 1 0 1 .
0 Giải phương trình x + 3 4 1 3 a/ 4x + 1 − 3x − 2 = . b/ − = . 5 2 2 x x + x + x x − x + x 1 1 3 1 c/ − = . d/ x + x + 1 = . x 1 − 1 − x 1 + 1 − x x 5 4 1 3 e/ 2 x + 1 − x = . f/ − = . 2 2 x + 1 2 2 x x + x + x x − x + x g/ ( + ) = ( + ) − + . h/ = ( + ) − + . ( )2 2 4 x 1 2x 10 1 3 2x ( )2 2 2x x 9 2 9 2x 40 3x i/ 2 x + x + 16 = . j/ = 3x + 1 − 1 . 2 x + 16 3x + 10 3x − 2 k/ 2x + 4 − 2 2 − x = . l/ 1 + x − 1 1 − x + 1 = 2x . ( )( ) 3 3 m/ 2
3x + 1 − 6 − x + 3x − 14x − 8 = 0 . n/ 2 3 x − 1 + x = x − 2 . 6x − 4 o/ 2 2 x + 12 + 5 = 3x + x + 5 . p/ 2x + 4 − 2 2 − x = . 2 x + 4 Dang 4. S du d ng hng đ đ ng thc cđ đ a vê ph p ng trirnh c ba b n Loại 1. 3 3 3 A + B = C ( ) ∗ 3 3 Ta có ( ) 3 3 3 ∗ ⇔ + = 3 3 3 A B C ⇔ A + B + 3 AB A + B = C ∗ ∗ ( ) ( ) ( ) ( ) Thay 3 3 3 A + B = C vào (∗ ) ∗ , ta được: (∗ ) 3 ∗ ⇔ A + B + 3 ABC = C . f (x)+ h(x) = g(x)+ k(x)
Loại 2. f (x) + g(x) = h(x) + k(x) với f (x).h(x) = g(x).k(x) 
"Cần cù bù thông minh…………" Page - 5 - Ths. Lê Văn Đoàn
Phương trình căn thức lớp 10
● Biến đổi về dạng: f (x) − h(x) = k(x) − g(x) .
● Bình phương, giải phương trình hệ quả.
Loại 3. Căn trong căn
Sử dụng hẳng đẳng thức + ± = ( ± )2 2 2 a b 2ab a b nhưng lưu ý A  khi A ≥ 0 A  = 
. Đưa về phương trình căn cơ bản. A  khi A < 0  BA B I ITÂP P AP P DUNG N Bà B i à 1 1 1 .
1 Giải phương trình
a/ 2 x + 2 + 2 x + 1 − x + 1 = 4 .
b/ x + 2 x − 1 − x − 2 x − 1 = 2 − .
c/ x − 1 − 2 x − 2 − x + 2 + 4 x − 2 + 3 = 0
d/ 2x − 4 + 2 2x − 5 + 2x + 4 + 6 2x − 5 = 14 .
e/ x + 5 − 4 x + 1 + x + 2 − 2 x + 1 = 1 .
f/ 2x − 2 2x − 1 − 2 2x + 3 − 4 2x − 1 + 3 2x + 8 − 6 2x − 1 = 4 .
g/ x + 3 − 4 x −1 + x + 8 − 6 x −1 = 1. h/ x 8 + 6 − x 1 − − x+3+4 x 1 − 5 + =0. i/ 2x 4 − 2 − 2x 5 − − 2x 4 + 6 + 2x 5 − 4 + 0 = . j/ 2x 2 − 2 + 2x 3 − =4+ 2x 6 − 6 − 2x 3 − . x + 3
k/ x + 2 x − 1 + x − 2 x − 1 = . 2
l/ x + 2x − 1 + x − 2x − 1 = 2 .
m/ x − 3 − 2 x − 4 + x − 2 x − 1 = 1 .
n/ x + 14x − 49 + x − 14x − 49 = 14 .
o/ 21x − 63 + 7 10 − 4 3x − 9 = 0 . Bà B i à 1 2 1 .
2 Giải phương trình a/ 3 3 3 x + 1 + x + 2 + x + 3 = 0 . b/ 3 3 3
2x − 1 + x − 1 = 3x − 2 . c/ 3 3 3 x + 5 + x + 6 = 2x + 11 . d/ 3 3 3 x + 1 + 3x + 1 = x − 1 . Page - 6 -
"All the flower of tomorrow are in the seeks of today……"
Phương trình căn thức lớp 10 Ths. Lê Văn Đoàn e/ 3 3 3 2 3 2 x + 2 + x + 1 = 2x + 2x + 1 . f/ 3 3 3
2x − 1 + x − 1 + 3x − 2 = 0 . g/ 3 3 3 2x + 1 + 2x + 2 + 2x + 3 = 0 3 3 . h/ 3 x + 2x − 3 = 12(x − ) 1 . Bà B i à 1 3 1 .
3 Giải phương trình
a/ x + 3 + 3x + 1 = 2 x + 2x + 2 . 3 x + 1 b/ 2
+ x + 1 = x − x + 1 + x + 3 . x + 3 c/ 2 2
x − 3x + 2 + x + 3 = 6x − 2 + x + 2x − 3 . d/ 2 2 2 2
2x − 1 + x − 3x − 2 = 2x + 2x + 3 + x − x + 2 . e/ 2 2 2 2 3x − 5x + 1 − x − 2 =
3 x − x − 1 − x − 3x + 4 . ( ) f/ 2 2 2 2
x + 2 + x + 7 = x + x + 3 + x + x + 8 . g/ 2 2 2 2
3x − 7x + 3 − x − 2 = 3x − 5x − 1 − x − 3x + 4 . Bà B i à 1 4 1 .
4 Giải phương trình 2 2 a/ 3 ( + ) − ( 2 − ) 3 3 4 x 2 7 4 x + 3. (2 − x) = 0 . b/ ( 2 + ) 3 2 x 2 = 5 x + 1 . c/ 2 2 4 2 x + 3 x − 1 = x − x + 1 . Bà B i à 1 5 1 .
5 Giải phương trình (đặt ẩn phụ không hoàn toàn) a/ 2 + ( − ) 2 x 2 x 1 x + x + 1 − x + 2 = 0 . b/ ( + ) 2 2 x 1 x − 2x + 3 = x + 1 . c/ ( − ) 2 2 4x 1 x + 1 = 2x + 2x + 1 . d/ 2 2 x + 12 + 5 = 3x + x + 5 .
Ngoa i ca!ch giải thông th ng ̉ trên, ta co n mô#t sô! phng pha!p giải kha!c
• Phng pha!p đa!nh gia! du ng ca!c bâ!t đ̉ng th!c c bản : BĐT Cauchy, BĐT Bunhiacopxki, BĐT hi nh ho#c, ……
• Phng pha!p l#ng gia!c ho!a
• Phng pha!p khảo sa!t ha m sô! • ……………
"Cần cù bù thông minh…………" Page - 7 -