Bài tập thực hành Tích phân - Công nghệ thông tin | Trường Đại học Khoa học Tự nhiên, Đại học Quốc gia Thành phố Hồ Chí Minh

Bài tập . f có là đơn ánh, toàn ánh không. Giải thích?
i. f : R → R được định nghĩa bởi f(x) = 2−3x,∀x ∈ R.
ii. f : Z → Z được định nghĩa bởi f(n) = n
2 +n,∀x ∈ Z.
iii. f : R → R được định nghĩa bởi f(x) = 2x
2 +3,∀x ∈ R. Tài liệu được sưu tầm giúp bạn tham khảo, ôn tập và đạt kết quả cao trong kì thi sắp tới. Mời bạn đọc đón xem !

11 6 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Máy tính và công nghệ thông tin

Trường: Trường Đại học Khoa học tự nhiên, Đại học Quốc gia Thành phố Hồ Chí Minh

Thông tin:

18 trang 1 tháng trước

Tác giả:

Profile Phạm Thị Huyền
Th cự hành Vi tích phân 1B
Ngày 12 tháng 9 năm 2017
cuu duong than cong . com
M cụ l cụ
1 Dãy số và ánh xạ 3
2 Hàm số 5
2.1 Gi iớ h nạ hàm số.....................................................................................5
3 Đ oạ hàm và ngứ d ngụ 8
3.1 Đ oạ hàm hàm h p,ợ hàm nẩ ..................................................................8
3.2 Ph ngươ trình ti pế tuy nế .......................................................................9
3.3 X pấ xỉ tuy nế tính.................................................................................10
3.4 Các đ nhị lý giá trị trung bình.............................................................11
3.5 ngỨ d ngụ tính gi iớ h nạ ......................................................................11
3.6 Khai tri nể Taylor; Maclaurin................................................................12
4 Tích phân và ngứ d ngụ 13
5 Chu iỗ hàm 14
Tài li uệ tham kh oả 14
2
1.1
Dãy số
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
1.2
Ánh xạ
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
cuu duong than cong . com
–
Ch ngươ 1
Dãy số và ánh xạ
1.1 Dãy số
Bài t pậ 1. Tìm gi iớ h nạ c aủ dãy số sau:
1 1
lim (
+
).
n→∞
2n n
Bài t pậ 2. Tìm gi iớ h nạ c aủ dãy số sau:
cos
2
n sin
2
n
lim .
n→∞
n
Bài t pậ 3. Tìm gi iớ h nạ c aủ dãy số sau:
c) lim (−1)
n
n
+
1
.
n→∞
d)
lim
n
2
n !
.
n→∞
n
n
1.2 Ánh xạ
Bài t pậ 4.
f có là đ nơ ánh, toàn ánh không. Gi iả thích?
i. f : R → R đ cượ đ nhị nghĩa b iở f (x) = 2 − 3x, ∀x ∈ R.
ii. f : Z → Z đ cượ đ nhị nghĩa b iở f (n) = n
2
+ n, ∀x ∈ Z.
iii. f : R → R đ cượ đ nhị nghĩa b iở f (x) = 2x
2
+ 3, ∀x ∈ R.
3
x−3
1.2. ÁNH XẠ CH NGƯƠ 1. DÃY SỐ VÀ ÁNH XẠ
n
+
1
iv. f : N → N đ cượ đ nhị nghĩa b iở f (x) =
n
2
,
n uế n lẻ
2
, n uế n ch nẵ
v.
Cho A
=
R \ {3}, B
=
R \ {1}. f : A → B đ cượ đ nhị nghĩa b iở f
(
x
)
=
x−
2
.
4
cuu duong than cong . com
cuu duong than cong . com
–
Ch ngươ 2
Hàm số
2.1 Gi iớ h nạ hàm số
Bài t pậ 5. Tính các gi iớ h nạ sau:
(10 + h)
2
− 100
√
100 + h
−
10
a)
lim
h→0
c) lim
h
1
1
2017 x
b)
lim
h→0
d)
lim
h
√
1
+
t
−
√
1
−
t
x→−2017 2017 +
x
e)
lim
2
−
√
x
t→0 t
f)
lim
√
1
–
1
x→4
8x − x
3
(x + h)
3
x
3
g)
lim .
t→0
t
1 + t
t
h→0
h
Bài t pậ 6. Sử d ngụ đ nhị lý k pẹ chỉ ra
lim
(
x
2
cos 20πx
) =
0.
x→0
Bài t pậ 7. Sử d ngụ đ nhị lý k pẹ chỉ ra
lim
,
x
3
+ x
2
sin
π
= 0.
x→0 x
Bài t pậ 8. N u ế 4x − 9 ≤ f
(
x
)
≤ x
2
− 4x
+
7 v i ớ x ≥ 0. Tìm lim
x
→
4
f
(
x
)
.
Bài t pậ 9. N uế 2x ≤ g
(
x
)
≤ x
4
− x
2
+
2 v i m i ớ ọ x. Tìm lim
x
→
1
g
(
x
)
.
5
cuu duong than cong . com
g
(
x
) =
0
n uế
x
= 1
−
−
−
− −
−
2.1. GI IỚ H NẠ HÀM SỐ CH NGƯƠ 2.
HÀM SỐ
Bài t pậ 10. Ch ngứ minh r ngằ
lim
x→0
+
√
x[1 + sin
2
(2π/x)] = 0.
Bài t pậ 11. Tìm gi iớ h nạ sau n uế t nồ t i:ạ
a)
lim
x
−
1
b)
lim
7 −| x |
x→
1
−
|x
3
−
x
2
|
c)
lim
1
−
1
x→−7 3x
+
2
x→0
+
x |x|
Bài t pậ 12. Cho
x
2
− 1 n uế x < 1
2x
−
x
2
n uế 1 < x ≤ 2
x
3
− 5x + 4 n uế x > 2.
Tìm các gi iớ h nạ sau n uế t nồ t iạ
i.
lim
g
(
x
)
ii.
lim
g
(
x
)
iii. g
(
1
)
x→
1
−
x→1
+
iv. lim g(x) v.
lim g(x) vi. lim g(x)
x→2
−
x→2
+
x→2
Bài t pậ 13. Ch ngứ minh các kh ngằ đ nhị sau b ngằ đ nhị nghĩa δ, ε.
a) lim(20 3x) =
1
x→7
b)
lim
x→2
x
2
x 6
= 4
x
−
3
c)
lim
(
x
2
2x 3
) =
4
x→1
Bài t pậ 14. Từ đồ thị c aủ hàm số g cho bên d i,ướ tìm các kho ngả mà hàm số
g liên t c.ụ
Bài t p 15.ậ Hãy xác đ nhị f
(
2
)
sao cho m iỗ hàm số có gián đo nạ khử
đ cượ
trở thành liên t cụ t iạ 2.
–
a)
f
(
x
)
=
x
2
− x
−
2
x
−
2
x
3
8
b) f (x) =
x
2
−
4
6
cuu duong than cong . com
f (x) =
√
a) f (x) =
√
3
−
≤
CH NGƯƠ 2.
HÀM SỐ 2.1.
GI IỚ H NẠ HÀM SỐ
Hình 2.1: hình nhả c aủ bài 14
Bài t pậ 16. Ch ngứ minh r ngằ f liên t cụ trên (−∞, ∞) v iớ f đ nhị b iở
x
2
n uế x < 1
x n uế x ≥ 1.
Bài t pậ 17. Ch ngứ minh các hàm số sau liên t cụ trên R
x
3
+ 1 n uế x < 1
x + 3 n uế x ≥ 1.
sin(x/2 + cos x) n uế x < π/2
cos(x/2 + sin x − 1) n uế x ≥ π/2.
Bài t pậ 18. Tìm giá trị c aủ c sao cho hàm số sau liên t cụ trên (−∞, ∞):
c
2
x
2
+ 2cx n uế x < 1
f
(
x
) =
4x
−
cx n uế x ≥ 1.
Bài t pậ 19. Tìm giá trị c aủ a, b sao cho hàm số sau liên t cụ trên (−∞, ∞):
x
4
−1
x−1
n uế x < 1
f (x) =
ax
2
bx + 4 n uế 1 x < 2
3x + a − b
n uế
x ≥ 2.
7
b
)
f
(
x
)
=
cuu duong than cong . com
dx
Ch ngươ 3
Đ oạ hàm và ngứ d ngụ
3.1 Đ oạ hàm hàm h p,ợ hàm nẩ
Bài t pậ 20. Giả sử g có đ oạ hàm c pấ hai trên R và xét f
(
x
) =
sin
(
xg
(
e
x
))
.
Tính f
(
2
)
theo g, g
′
và g
′′
.
Bài t pậ 21. Tính y
′′
khi bi tế 9x
2
+
y
2
=
9.
Bài t pậ 22. Tính y
′′
khi bi tế
√
x +
√
y = 1.
Bài t pậ 23. Tìm công th cứ chính xác c aủ
dy
(dùng công th cứ hàm n)ẩ bi t:ế
(a) x
3
+ y
3
= 1.,
(b) 2
√
x +
√
y = 3.
(c)
x
2
+
xy
−
y
2
=
4,
(d) 2x
3
+ x
2
y − xy
3
=
2,
(e) x
4
(x + y) = y
2
(3x − y),
(f) y
5
+ x
2
y
3
= 1 + x
4
y,
(g) y cos x = x
2
+ y
2
,
(h) cos(xy) = 1 + sin y.
Bài t pậ 24. Giả sử y =
√
2x + 1, trong đó x và y là nh ngữ hàm theo t.
1.
Giả sử
dx
=
3, tìm
dy
khi x
=
4.
dt dt
2.
Giả sử
dy
=
5, tìm
dx
khi x
=
12.
dt dt
Bài t pậ 25. Giả sử 4x
2
+ y
2
= 9, trong đó x và y là nh ngữ hàm theo t.
1.
Giả sử
dy
=
1
, tìm
dx
khi x
=
2 và y
=
2
√
5.
dt
3
dt
3
2.
Giả sử
dx
=
3, tìm
dy
khi x
=
−2 và y
=
2
√
5.
dt dt
3
8
cuu duong than cong . com
CH NGƯƠ 3. Đ OẠ HÀM VÀ NGỨ
DỤ3
N
.2
G
.
PH NGƯƠ TRÌNH TI PẾ
TUY NẾ
Hình 3.1: Hình bài t pậ 28
Bài t pậ 26. Bi tế x
2
+
y
2
+
z
2
=
9,
dx
=
5,
dy
=
4, tìm
dz
khi
(
x, y, z
) = (
2, 2,
1
)
.
dt dt dt
Bài t pậ 27. Hai chi c xe b t đ u di chuy n t cùng m t đi m. M t chi cế ắ ầ ể ừ ộ ể ộ ế
đi về phía nam v iớ t cố độ 60 mi/h và chi cế còn l iạ di chuy nế về phía tây
v iớ t c đ 25 mi/h. Kho ng cách gi a hai chi c xe tăng lên m c nào haiố ộ ả ữ ế ở ứ
gi sau ờ đó?
Bài t pậ 28. M t chi c thuy n đ c kéo vào m t b n tàu b ng m t s iộ ế ề ượ ộ ế ằ ộ ợ
dây g nắ vào mũi thuy nề và đi qua m tộ ròng r cọ trên b nế tàu, mà nó cao
h nơ 1 m so v iớ mũi thuy n.ề N uế s iợ dây đ cượ kéo vào v iớ t cố độ 1 m/s,
thuy nề ti n g n đ n b n tàu nhanh nh th nào khi nó cách b n tàu 8ế ầ ế ế ư ế ế
m?
Bài t pậ 29. Vào bu iổ tr a,ư tàu A cách 100 km về phía tây c aủ tàu B. Tàu A
di chuy nể về phía nam v iớ t cố độ 35 km/h và tàu B di chuy nể về phía
b cắ v i t c đ 25 km/h. Kho ng cách gi a hai tàu thay đ i nhanh nhớ ố ộ ả ữ ổ ư
th nào vào lúc 4:00 PM?ế
3.2 Ph ngươ trình ti pế tuy nế
Bài t pậ 30. Hãy tìm ph ng trình ti p tuy n v i đ th m i hàm s t iươ ế ế ớ ồ ị ỗ ố ạ
giá tr ị x
0
cho tr c.ướ
(a) f (x) = x
2
, x
0
= 3.
(b)
f
(
x
)
=
x
x
2
+2
, x
0
= 1.
Bài t pậ 31. Vi t ph ng trình ti p tuy n c a đ th c a đ th hàm s ế ươ ế ế ủ ồ ị ủ ồ ị ố y đ c ượ
cho b i bi u th cở ể ứ
x
3
+ y
3
= 6xy
t iạ đi mể
(
3, 3
)
.
Bài t pậ 32. Vi t ph ng trình ti p tuy n c a đ th c a đ th hàm s ế ươ ế ế ủ ồ ị ủ ồ ị ố y đ c ượ
cho b i bi u th cở ể ứ
t iạ đi mể
(
3,
−4
)
.
x
2
+ y
2
= 25
9
2 4
x+
2
cuu duong than cong . com
1
(d) .
3.3. X PẤ XỈ TUY NẾ TÍNH CH NGƯƠ 3. Đ OẠ HÀM VÀ NGỨ D NGỤ
Bài t pậ 33. Vi t ph ng trình ti p tuy n c a đ th c a đ th hàm s ế ươ ế ế ủ ồ ị ủ ồ ị ố y đ cượ
cho b i bi u th cở ể ứ
t i đi mạ ể
π
,
π
.
y sin(2x) = x cos(2y)
Bài t pậ 34. Vi t ph ng trình ti p tuy n c a đ th c a đ th hàm s ế ươ ế ế ủ ồ ị ủ ồ ị ố y đ cượ
cho b i bi u th cở ể ứ
t iạ đi mể
(
π,
π
)
.
sin(x + y) = 2x − 2y
Bài t pậ 35. Tìm ph ng trình c a đ ng ti p tuy n v i đ ng cong t i đi mươ ủ ườ ế ế ớ ườ ạ ể
có t a đ cho tr c.ọ ộ ướ
1. y = 4x − 3x
2
, (2,
−4).
2. y = x
3
− 3x + 1, (2,
3).
3. y =
√
x, (1, 1).
4. y =
2
x+
1
, (1, 1).
Bài t pậ 36. (a) Tìm hệ số góc c aủ ti pế tuy nế t iớ đ ngườ cong y
=
đi mể x = a
(b)
Tìm ph ngươ trình c aủ ti pế tuy nế t iạ các đi mể
(
1, 1
)
và
(
4,
1/2
)
.
√
x
t iạ
(c)
Vẽ đồ thị c aủ đ ngườ cong và cả hai ti pế tuy nế trên m tộ màn
hình chung.
Tìm độ d cố hệ số
3.3 X pấ xỉ tuy nế tính
Bài t pậ 37. Hãy tính g nầ đúng các giá trị sau b ngằ x pấ xỉ tuy nế tính.
(a)
(
1.999
)
4
.
(b)
(sin 1
◦
.
1
4.002
(e)
tan
(
44
◦
)
.
(c)
√
3
1001.
(f)
√
99, 8.
Bài t pậ 38. (i) X pấ xỉ f b ngằ đa th cứ Taylor b cậ n t iạ a.
(ii)
Sử d ngụ B tấ đ ngẳ th cứ Taylor để cướ l ngượ độ chính xác c aủ x pấ
xỉ
f (x) ≈ T
n
(x) khi x n mằ trong đo nạ cho tr c.ướ
10
6 3
cuu duong than cong . com
3
8 8
−
–
x
CH NGƯƠ 3. Đ OẠ HÀM VÀ
Ứ
N
3.
G
4.
D
C
Ụ
Á
N
CG
Đ NHỊ
LÝ GIÁ TRỊ TRUNG BÌNH
(iii)
Ki mể tra k tế qu ph nả ầ
(
b
)
b ngằ đồ thị c aủ |R
n
(
x
)
|.
Th cự hi nệ các công vi cệ trên cho m iỗ hàm số sau ngứ v iớ a, n và đo n ạ
cho tr c.ướ
(a) f (x) =
√
x, a = 4, n = 2, 4 ≤ x ≤ 4.2.
(b) f (x) = x
−
2
, a = 1, n = 2, 0.9 ≤ x ≤ 1.1.
(c) f (x) = x
2/3
, a = 1, n = 3, 0.8 ≤ x ≤ 1.2.
(d) f (x) = sin x, a =
π
, n = 4, 0 ≤ x ≤
π
.
3.4 Các đ nhị lý giá trị trung bình
Bài t p 39. ậ Hãy ki m tra hàm s th a mãn ba gi thi t c a Đ nh lý Rolleể ố ỏ ả ế ủ ị
trên đo nạ cho tr c.ướ Sau đó, tìm t tấ cả các số c th aỏ mãn k tế lu nậ c aủ
đ nh lý Rolle.ị
(a) f (x) = 5 − 12x + 3x
2
, [1,
3].
(b)
f
(
x
) =
x
3
−
x
2
−
6x
+
2,
[
0, 3
]
.
(c) f (x) =
√
x −
1
x, [0, 9].
(d) f (x) = cos(2x),
h
π
,
7
π
i
.
Bài t pậ 40. Cho f
(
x
) = (
x
3
)
−
2
. Ch ng t r ng không t n t i ứ ỏ ằ ồ ạ c
(
1, 4
)
sao cho f
(
4
)
f
(
1
) =
f
′
(
x
)(
4 1
)
. T i sao đi u này không mâu thu n v iạ ề ẫ ớ
Đ nh lý Rolle?ị
Bài t pậ 41. Hãy ki mể tra r ngằ hàm số thoả mãn ba giả thi tế c aủ Đ nhị lý
giá trị trung bình trên kho ngả cho tr c.ướ Sau đó tìm t tấ cả các số c thoả
mãn k t lu n c a Đ nh lý giá tr trung bình.ế ậ ủ ị ị
(a) f (x) =
√
3
x, [0, 1].
(b) f (x) =
1
, [1, 3].
Bài t pậ 42. Ch ngứ tỏ r ngằ ph ngươ trình x
3
− 15x
+
c
=
0
=
0 có nhi uề
nh t m t nghi m trong đo n ấ ộ ệ ạ
[
−2, 2
]
v i m i s th c ớ ọ ố ự c.
3.5 ngỨ d ngụ đ oạ hàm tính gi iớ h nạ (quy t cắ
l’Hospital)
Bài t pậ 43. Tính
11
–
x
2
−
cuu duong than cong . com
–
x
3.6. KHAI TRI NỂ TAYLOR; MA
C
H
A
Ư
U
Ơ
R
N
I
N
G
3. Đ OẠ HÀM VÀ NGỨ
D NGỤ
(a)
lim
x→0
e
2x
1
,
x
(d)
lim
x→∞
1 +
1
,
x
(b)
lim
ln
x
,
(e)
lim
1
−
1
,
x→∞
x
x→1
+
ln n x − 1
(c)
lim
x
,
−x
(f)
lim
tan x e
x
1
.
x
2
x→−∞
e
x→0
1
−
e
3.6 Khai tri nể Taylor; Maclaurin
Bài t pậ 44. Tìm khai tri nể Maclaurin c aủ các hàm số sau.
(a)
f (x) = (1 − x)
−
2
,
(b) f (x) = ln(1 +
x),
(c) f (x) = sin(πx),
(d) f (x) = e
−
2
x
,
(e) f (x) = x cos x.
Bài t pậ 45. Tìm khai tri nể Taylor c aủ các hàm số sau quanh đi mể a t ng ươ
ng.ứ
(a) f (x) = x
4
− 3x
2
+ 1, a
= 1.
(b) f (x) = x − x
3
, a = −2.
(c) f (x) = ln x, a = 2.
(d)
f
(
x
) =
1
, a
=
3.
x
(e)
f
(
x
) =
e
2
x
, a
=
3 .
π
(f)
f
(
x
) =
sin x, a
=
2
.
(g) f (x) = cos x, a = π.
(h) f (x) =
√
x, a = 16.
Bài t pậ 46. (a) Tìm các đa th cứ Taylor đ nế b cậ 6 c aủ f (x) = cos x quanh
a
=
0. Vẽ đồ thị f và các đa th cứ này trên cùng đồ th .ị
(b)
Đánh giá f và nh ngữ đa th cứ này t iạ x
=
π
,
π
, π.
4 2
(c)
Bình lu nậ sự h iộ tụ c aủ các đa th cứ này về f .
Bài t pậ 47. Tìm đa th cứ Taylor T
3
(
x
)
cho hàm f
(
x
) =
1
quanh a
=
2. Vẽ f
và
T
3
(
x
)
trên cùng đồ th .ị
12
Ch ngươ 4
Tích phân và ngứ d ngụ
Bài t pậ 48.
13
Ch ng 5 ươ
Chu iỗ hàm
Bài t pậ 49.
14
| 1/18
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Thực hành Vi tích phân 1B

Ngày 12 tháng 9 năm 2017

Mục lục

  1. Dãy số và ánh xạ 3

1.1

Dãy số

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3

1.2

Ánh xạ

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3

  1. Hàm số 5
    1. Giới hạn hàm số 5

cuu duong than cong . com

  1. Đạo hàm và ứng dụng 8
    1. Đạo hàm hàm hợp, hàm ẩn 8
    2. Phương trình tiếp tuyến 9
    3. Xấp xỉ tuyến tính 10
    4. Các định lý giá trị trung bình 11
    5. Ứng dụng tính giới hạn 11
    6. Khai triển Taylor; Maclaurin 12
  2. Tích phân và ứng dụng 13
  3. Chuỗi hàm 14

Tài liệu tham khảo 14

2

Chương 1

Dãy số và ánh xạ

Dãy số

Bài tập 1. Tìm giới hạn của dãy số sau:

1 1

cuu duong than cong . com

lim ( + ).

n→∞ 2n n

Bài tập 2. Tìm giới hạn của dãy số sau:

cos2 n sin2 n

–

lim .

n→∞ n

Bài tập 3. Tìm giới hạn của dãy số sau:

  1. lim (−1)n n + 1 .

n→∞

  1. lim

n2

n! .

n→∞ nn

Ánh xạ

Bài tập 4. f có là đơn ánh, toàn ánh không. Giải thích?

      1. f : R → R được định nghĩa bởi f (x) = 2 − 3x, ∀x ∈ R.
      2. f : Z → Z được định nghĩa bởi f (n) = n2 + n, ∀x ∈ Z.
      3. f : R → R được định nghĩa bởi f (x) = 2x2 + 3, ∀x ∈ R.

3

1.2. ÁNH XẠ CHƯƠNG 1. DÃY SỐ VÀ ÁNH XẠ

n + 1

      1. f : N → N được định nghĩa bởi f (x) =  n 2

, nếu n lẻ

 2 , nếu n chẵn

      1. Cho A = R \ {3}, B = R \ {1}. f : A → B được định nghĩa bởi f (x) = x−2.

cuu duong than cong . com

x−3

4

Chương 2 Hàm số

Giới hạn hàm số

Bài tập 5. Tính các giới hạn sau:

(10 + h)2 − 100

cuu duong than cong . com

√100 + h − 10

      1. lim

h→0

c) lim

h

1 1

+

2017 x

      1. lim

h→0

  1. lim

h

√1 + t − √1 − t

x→−2017 2017 + x

  1. lim 2 − √x

t→0 t

  1. lim √ 1

– 1

x→4 8x − x3

(x + h)3 x3

–

  1. lim .

t→0 t

1 + t t

h→0 h

Bài tập 6. Sử dụng định lý kẹp chỉ ra

lim(x2 cos 20πx) = 0.

x→0

Bài tập 7. Sử dụng định lý kẹp chỉ ra

lim ,x3 + x2 sin π = 0.

x→0 x

Bài tập 8. Nếu 4x − 9 ≤ f (x) ≤ x2 − 4x + 7 với x ≥ 0. Tìm limx→4 f (x).

Bài tập 9. Nếu 2x ≤ g(x) ≤ x4 − x2 + 2 với mọi x. Tìm limx→1 g(x).

5

    1. GIỚI HẠN HÀM SỐ CHƯƠNG 2. HÀM SỐ

Bài tập 10. Chứng minh rằng

lim

x→0+

√x[1 + sin2(2π/x)] = 0.

Bài tập 11. Tìm giới hạn sau nếu tồn tại:

      1. lim

x − 1

      1. lim

7 −|x|

x→1− |x3 − x2|

      1. lim 1 − 1

x→−7 3x + 2

x→0+ x |x|

Bài tập 12. Cho

x2 − 1 nếu x < 1

2x − x2 nếu 1 < x ≤ 2

cuu duong than cong . com

g(x) = 0 nếu x = 1

x3 − 5x + 4 nếu x > 2.

Tìm các giới hạn sau nếu tồn tại

i. lim g(x) ii. lim g(x) iii. g(1)

x→1− x→1+

iv. lim g(x) v. lim g(x) vi. lim g(x)

x→2−

x→2+

x→2

Bài tập 13. Chứng minh các khằng định sau bằng định nghĩa δ, ε.

        1. lim(20 3x) = 1

− −

x→7

        1. lim

x→2

x2 x 6

= 4

− −

x − 3

        1. lim(x2 2x 3) = 4

− − −

x→1

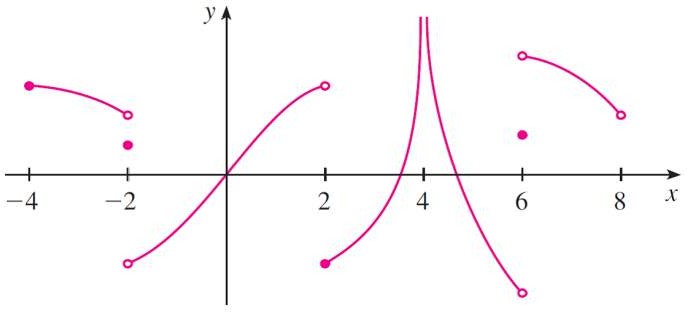
Bài tập 14. Từ đồ thị của hàm số g cho bên dưới, tìm các khoảng mà hàm số

g liên tục.

Bài tập 15. Hãy xác định f (2) sao cho mỗi hàm số có gián đoạn khử được

trở thành liên tục tại 2. a)

f (x) =

x2 − x − 2

x − 2

x3 8

b) f (x) = x2 − 4

–

6

CHƯƠNG 2. HÀM SỐ 2.1. GIỚI HẠN HÀM SỐ

Hình 2.1: hình ảnh của bài 14

Bài tập 16. Chứng minh rằng f liên tục trên (−∞, ∞) với f định bởi

x2 nếu x < 1

cuu duong than cong . com



f (x) = √

 x nếu x ≥ 1.

Bài tập 17. Chứng minh các hàm số sau liên tục trên R

x3 + 1 nếu x < 1



a) f (x) = √

 x + 3 nếu x ≥ 1.

sin(x/2 + cos x) nếu x < π/2

b) f (x) = 

cos(x/2 + sin x − 1) nếu x ≥ π/2.

Bài tập 18. Tìm giá trị của c sao cho hàm số sau liên tục trên (−∞, ∞):



c2x2 + 2cx nếu x < 1

f (x) =

 3

4x − cx nếu x ≥ 1.

Bài tập 19. Tìm giá trị của a, b sao cho hàm số sau liên tục trên (−∞, ∞):

x4−1

 x−1

nếu x < 1

f (x) = ax2 bx + 4 nếu 1 x < 2

 − ≤

3x + a − b nếu x ≥ 2.

7

Chương 3

Đạo hàm và ứng dụng

Đạo hàm hàm hợp, hàm ẩn

Bài tập 20. Giả sử g có đạo hàm cấp hai trên R và xét f (x) = sin(xg(ex)).

Tính f (2) theo g, g′ và g′′.

cuu duong than cong . com

Bài tập 21. Tính y′′ khi biết 9x2 + y2 = 9.

Bài tập 22. Tính y′′ khi biết √x + √y = 1.

Bài tập 23. Tìm công thức chính xác của dy (dùng công thức hàm ẩn) biết:

dx

      1. x3 + y3 = 1.,
      2. 2 √x + √y = 3.
      3. x2 + xy − y2 = 4,
      4. 2x3 + x2y − xy3 = 2,
      5. x4(x + y) = y2(3x − y),
      6. y5 + x2y3 = 1 + x4y,
      7. y cos x = x2 + y2,
      8. cos(xy) = 1 + sin y.

Bài tập 24. Giả sử y = √2x + 1, trong đó x và y là những hàm theo t.

  1. Giả sử dx = 3, tìm dy khi x = 4.

dt dt

  1. Giả sử dy = 5, tìm dx khi x = 12.

dt dt

Bài tập 25. Giả sử 4x2 + y2 = 9, trong đó x và y là những hàm theo t.

  1. Giả sử dy = 1, tìm dx khi x = 2 và y = 2 √5.

dt 3 dt 3

  1. Giả sử dx = 3, tìm dy khi x = −2 và y = 2 √5.

dt dt 3

8

CHƯƠNG 3. ĐẠO HÀM VÀ ỨNG DỤ3N.2G. PHƯƠNG TRÌNH TIẾP TUYẾN

Hình 3.1: Hình bài tập 28

Bài tập 26. Biết x2 + y2 + z2 = 9, dx = 5, dy = 4, tìm dz khi (x, y, z) = (2, 2, 1).

dt dt dt

Bài tập 27. Hai chiếc xe bắt đầu di chuyển từ cùng một điểm. Một chiếc đi về phía nam với tốc độ 60 mi/h và chiếc còn lại di chuyến về phía tây với tốc độ 25 mi/h. Khoảng cách giữa hai chiếc xe tăng lên ở mức nào hai giờ sau đó?

Bài tập 28. Một chiếc thuyền được kéo vào một bến tàu bằng một sợi dây gắn vào mũi thuyền và đi qua một ròng rọc trên bến tàu, mà nó cao hơn 1 m so với mũi thuyền. Nếu sợi dây được kéo vào với tốc độ 1 m/s, thuyền tiến gần đến bến tàu nhanh như thế nào khi nó cách bến tàu 8 m?

Bài tập 29. Vào buổi trưa, tàu A cách 100 km về phía tây của tàu B. Tàu A di chuyển về phía nam với tốc độ 35 km/h và tàu B di chuyển về phía bắc với tốc độ 25 km/h. Khoảng cách giữa hai tàu thay đổi nhanh như thế nào vào lúc 4:00 PM?

cuu duong than cong . com

Phương trình tiếp tuyến

Bài tập 30. Hãy tìm phương trình tiếp tuyến với đồ thị mỗi hàm số tại giá trị x0 cho trước.

      1. f (x) = x2, x0 = 3.
      2. f (x) =

x x2+2

, x0 = 1.

Bài tập 31. Viết phương trình tiếp tuyến của đồ thị của đồ thị hàm số y được cho bởi biểu thức

x3 + y3 = 6xy

tại điểm (3, 3).

Bài tập 32. Viết phương trình tiếp tuyến của đồ thị của đồ thị hàm số y được cho bởi biểu thức

tại điểm (3, −4).

x2 + y2 = 25

9

    1. XẤP XỈ TUYẾN TÍNH CHƯƠNG 3. ĐẠO HÀM VÀ ỨNG DỤNG

Bài tập 33. Viết phương trình tiếp tuyến của đồ thị của đồ thị hàm số y được cho bởi biểu thức

tại điểm π , π .

2

4

y sin(2x) = x cos(2y)

Bài tập 34. Viết phương trình tiếp tuyến của đồ thị của đồ thị hàm số y được cho bởi biểu thức

tại điểm (π, π).

sin(x + y) = 2x − 2y

Bài tập 35. Tìm phương trình của đường tiếp tuyến với đường cong tại điểm có tọa độ cho trước.

      1. y = 4x − 3x2, (2, −4).
      2. y = x3 − 3x + 1, (2, 3).
      3. y = √x, (1, 1).
      4. y = 2x+1, (1, 1).

x+2

Bài tập 36. (a) Tìm hệ số góc của tiếp tuyến tới đường cong y =

cuu duong than cong . com

1

điểm x = a

  1. Tìm phương trình của tiếp tuyến tại các điểm (1, 1) và (4, 1/2).

√x tại

  1. Vẽ đồ thị của đường cong và cả hai tiếp tuyến trên một màn hình chung.

Tìm độ dốc hệ số

Xấp xỉ tuyến tính

Bài tập 37. Hãy tính gần đúng các giá trị sau bằng xấp xỉ tuyến tính.

      1. (1.999)4.
      2. (sin 1◦.

1

4.002

(d) .

  1. tan(44◦).

√3 1001.

  1. √99, 8.

Bài tập 38. (i) Xấp xỉ f bằng đa thức Taylor bậc n tại a.

  1. Sử dụng Bất đẳng thức Taylor để ước lượng độ chính xác của xấp xỉ

f (x) ≈ Tn(x) khi x nằm trong đoạn cho trước.

10

CHƯƠNG 3. ĐẠO HÀM VÀ ỨN3.G4. DCỤÁNCGĐỊNH LÝ GIÁ TRỊ TRUNG BÌNH

  1. Kiểm tra kết quả phần (b) bằng đồ thị của |Rn(x)|.

Thực hiện các công việc trên cho mỗi hàm số sau ứng với a, n và đoạn cho trước.

    1. f (x) = √x, a = 4, n = 2, 4 ≤ x ≤ 4.2.
    2. f (x) = x−2, a = 1, n = 2, 0.9 ≤ x ≤ 1.1.
    3. f (x) = x2/3, a = 1, n = 3, 0.8 ≤ x ≤ 1.2.
    4. f (x) = sin x, a = π, n = 4, 0 ≤ x ≤ π .

6

3

Các định lý giá trị trung bình

Bài tập 39. Hãy kiểm tra hàm số thỏa mãn ba giả thiết của Định lý Rolle trên đoạn cho trước. Sau đó, tìm tất cả các số c thỏa mãn kết luận của định lý Rolle.

cuu duong than cong . com

      1. f (x) = 5 − 12x + 3x2, [1, 3].
      2. f (x) = x3 − x2 − 6x + 2, [0, 3].
      3. f (x) = √x − 1 x, [0, 9].
      4. f (x) = cos(2x), hπ , 7πi.

3

8

8

Bài tập 40. Cho f (x) = (x 3)−2. Chứng tỏ rằng không tồn tại c (1, 4) sao cho f (4) f (1) = f ′(x)(4 1). Tại sao điều này không mâu thuẫn với Định lý Rolle?

− −

– ∈

Bài tập 41. Hãy kiểm tra rằng hàm số thoả mãn ba giả thiết của Định lý giá trị trung bình trên khoảng cho trước. Sau đó tìm tất cả các số c thoả mãn kết luận của Định lý giá trị trung bình.

  1. f (x) = √3 x, [0, 1].
  2. f (x) = 1, [1, 3].

x

Bài tập 42. Chứng tỏ rằng phương trình x3 − 15x + c = 0 = 0 có nhiều nhất một nghiệm trong đoạn [−2, 2] với mọi số thực c.

Ứng dụng đạo hàm tính giới hạn (quy tắc l’Hospital)

Bài tập 43. Tính

11

3.6. KHAI TRIỂN TAYLOR; MACHAƯUƠRNING 3. ĐẠO HÀM VÀ ỨNG DỤNG

  1. lim

x→0

e2x 1

,

–

x

lim

x→∞

1 + 1 ,

x

x

  1. lim ln x ,
  2. lim 1 − 1 ,

x→∞ x

x→1+ ln n x − 1

  1. lim x ,

2

−x

lim

tan x ex 1

.

− −

x2

x→−∞ e

x→0

1 − e

Khai triển Taylor; Maclaurin

Bài tập 44. Tìm khai triển Maclaurin của các hàm số sau.

      1. f (x) = (1 − x)−2,
      2. f (x) = ln(1 + x),
      3. f (x) = sin(πx),
      4. f (x) = e−2x,
      5. f (x) = x cos x.

Bài tập 45. Tìm khai triển Taylor của các hàm số sau quanh điểm a tương ứng.

cuu duong than cong . com

  1. f (x) = x4 − 3x2 + 1, a = 1.
  2. f (x) = x − x3, a = −2.
  3. f (x) = ln x, a = 2.
  4. f (x) = 1 , a = 3.

–

x

  1. f (x) = e2x, a = 3 .

π

  1. f (x) = sin x, a = 2 .
  2. f (x) = cos x, a = π.
  3. f (x) = √x, a = 16.

Bài tập 46. (a) Tìm các đa thức Taylor đến bậc 6 của f (x) = cos x quanh

a = 0. Vẽ đồ thị f và các đa thức này trên cùng đồ thị.

    1. Đánh giá f và những đa thức này tại x = π, π, π.

4 2

    1. Bình luận sự hội tụ của các đa thức này về f .

Bài tập 47. Tìm đa thức Taylor T3(x) cho hàm f (x) = 1 quanh a = 2. Vẽ f và

x

T3(x) trên cùng đồ thị.

12

Chương 4

Tích phân và ứng dụng

Bài tập 48.

13

Chương 5 Chuỗi hàm

Bài tập 49.

14