

































Preview text:
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU MỤC LỤC Phần I
Đại số - Trang 3 Chương 1
Số hữu tỉ. Số thực Trang 5 BỬU Chủ đề 1
Số hữu tỉ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 G Chủ đề 2
Tỉ lệ thức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 AN Chủ đề 3
Số thực. Căn bậc hai . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14 QU Chương 2
Hàm số và đồ thị Trang 17 TẠ Chủ đề 1
Tỉ lệ thuận . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17 Chủ đề 2
Tỉ lệ nghịch . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20 THPT - Chủ đề 3
Hàm số - Đồ thị hàm số y = ax (a 6= 0) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23 G 0976071956 Phần II
Hình học - Trang 27 DŨN MATH.ND Chương 1
Đường thẳng vuông góc. Đường thẳng song song Trang 29 GỌC Chủ đề 1
Hai góc đối đỉnh . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29 N Chủ đề 2 ? ĐườngLớp TO vuông ÁN góc. THẦ Đường Y trung DŨNG trực . . . . . . . ?
. . . . . . . . . . . . . . . . . . . . . . . . 30 Chủ đề 3
Hai đường thẳng song song . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33 Chủ đề 4
Từ vuông góc đến song song . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40 GUYỄN N Chương 2 Tam giác Trang 45 Chủ đề 1
Tổng ba góc của một tam giác . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45 Thầy Chủ đề 2
Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47 Chủ đề 3
Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh . 48 Chủ đề 4
Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc . . 51 Chủ đề 5
Ôn tập học kỳ 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 1 of 56 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng Thầy N GUYỄN N GỌC DŨN G 0976071956 - THPT MATH.ND TẠ QU ? Lớp TOÁN THẦY DŨNG ? AN G BỬU Page 2 of 56
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? BỬU G PHẦN AN QU I TẠ THPT - G ĐẠI SỐ 0976071956 DŨN MATH.ND GỌC N ? Lớp TOÁN THẦY DŨNG ? GUYỄN N Thầy 3 Thầy N GUYỄN N GỌC DŨN G 0976071956 - THPT MATH.ND TẠ QU ? Lớp TOÁN THẦY DŨNG ? AN G BỬU 1
Số hữu tỉ. Số thực Chương Hình vuông đơn vị
Đường chéo bao nhiêu? Học số vô tỉ
Sẽ hiểu thêm nhiều. Trọng tâm chương: BỬU G
• Cộng, trừ, nhân, chia số hữu tỷ và số thập phân. AN
• Lũy thừa của số hữu tỷ. QU • Tỉ lệ thức. TẠ • Căn bậc hai. • Tìm x. THPT - G
| Chủ đề 1. Số hữu tỉ 0976071956 DŨN A
KIẾN THỨC CẦN NHỚ MATH.ND
a Các công thức cộng, trừ, nhân, chia số hữu tỉ: GỌC a a c •
+ c = a + c; • − = a − c; N b b b b b b a c ? Lớp TOÁN THẦY DŨNG a ?d • · = a · c ; • : c = a · = a · d. b d b · d b d b c b · c
b Các công thức lũy thừa của số hữu tỉ GUYỄN N
• an · am = an+m;
• an : am = an−m;
• (an)m = an·m; a n
• (a · b)n = an · bn; • = an . b bn Thầy B BÀI TẬP
! Sai một bài chép phạt 20 lần!!!
Dạng 1. Cộng, trừ, nhân, chia số hữu tỉ và số thập phân
d Bài 1. Thực hiện phép tính (nhớ bước quy đồng nhé) 5 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng 1 5 1 3 5 4 1 1 1 1 a ; b + ; c + ; d + ; e ; 2 − 2 2 4 − 9 7 3 10 6 − 4 3 5 −1 3 2 3 −7 −1 2 f ; g + ; h + ; i + −5; j + ; 4 − 6 2 4 3 4 15 9 2 3 21 −11 2 −2 11 1 k ; l + −1; m + −11; n 2 + −3 ; o ; 36 − 30 3 6 15 30 8 30 − 2 1 1 1 3 1 4 Thầy −1 −5 p ; q ; r 0 ; t + . 21 − 28 −22 − 34 , 5 − 4
s 5 − 0, 4; 9 7
d Bài 2. Thực hiện phép tính (chia là nhân nghịch đảo nhé) N 8 5 7 8 36 7 −2 −9 5 −3 GUYỄN a ; b ; c ; d ; e ; 10 · 11 5 · 3 35 · 54 3 · 4 3 · 10 −3 4 3 3 Å −4ã 2 −7 −5 3 f ; g : ; h ; i 1 ; j : ; 4 · 9 − 20 4
−3, 5 · 21 3 · 3 2 −4 Å 2ã Å 4ã 13 3 2 5 93 7 53 5 N k −8 : −2 ;l − : ; m ; n ; o : ; GỌC 5 5 10 5 5 · 4 4 · 5 4 7 −8 1 2 Å−3ã −5 3 1 Å 4ã p ; q ; r : ; s 1 t 4 : ; 15 · 14 5 · 4 2 4
, 25 : (−3, 5); 5 −25 DŨN 1 1 2 3 u 1 v : −5 ; w 4
17 · 124 · (−5, 1); 3 7 · 4
· (−3, 15) · 2, 5. G
d Bài 3. Thực hiện phép tính 0976071956 - 3 1 3 5 2 2 8 3 a 0 + ; b ; c + ; THPT , 25 − 4 3 4 − 6 − 3 3 − 15 10 MATH.ND 2 1 2 14 3 1 3 d 1 + 1 + 2; e 1 + ; f + ; 5 3 3 − 9 8 − 5 40 TẠ −4 3 5 2 9 7 3 1 g + h + ; i + ; QU 7 14 − 2; ? Lớp TO 6 ÁN 9 − THẦ 18 Y DŨNG ? 12 8 − 4 2 5 1 1 Å 1 1 ã 1 Å 1 1ã AN j + ; k + ; l ; 3 − 6 12 2 − 3 10 12 − 6 − 4 G 15 Å 1 5ã 1 −1 1 1 1 1 3 17 27 m ; n + + ; o + + ; BỬU 7 − 2 − 2 2 − 3 23 6 3 − 7 2 3 − 7
d Bài 4. Thực hiện phép tính 1 3 Å ã 2 3 Å−9ã 3 2 Å−3ã a + : −6 ; b + : ; c + ; 2 4 7 5 5 7 5 5 · 4 13 3 2 5 1 1 1 9 3 2 3 Å 3ã 15 13 d − : + ; e 7 ; f + : + ; 10 5 5 · 4
3 · 24 − 73 · 111 − 2 5 5 − 2 26 · 15 93 7 53 5 Å 3ã Å1 ã 5 1 5 1 g : ; h 0 ; i ; 4 · 5 − 4 7
, 5 − 4 · 5 − 0,4
6 · 173 − 6 · 473 11 11 4 Å−3ã 3 1 Å−1ã j k 3 : ; l + : ;
25 · (−24, 8) − 25 · 75, 2; − 15 4 4 4 3 Page 6 of 56
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU 2 1 3 1 Å−3ã 1 m 8 : 4 o + : ; 3 3 − 10;
n −1, 25 · (−4, 1) · 8 + 0, 2; 4 4 2 − 3 2 3 Å 9 ã 1 1 2 2 Å −3ã 3 1 1 3 p + : ; q + : ; r ; 5 5 − 10 − 3 7 7 3 − 7
5 · 173 − 323 · 5 7 8 5 15 Å 4 3ã 6 Å 5 2ã Å 3 7 ã Å 9 ã s + : ; t : + : u 9 : 5 : ; 21 21 6 − 9 9 − 5 5 9 − 5 4
, 2 + 3, 4 · 224 −116 6;5 Å −5 4ã 2018 Å 3 4ã 2018 v + : + : ; 9 7 2017 7 − 9 2017 BỬU
d Bài 5. Thực hiện phép tính G 2 3 −7 −1 2 21 −11 a + ; b + −5 ; c + ; d ; AN 3 4 15 9 2 3 36 − 30 2 −2 11 1 QU e + −1; f + −11 ; g 2 + −3 ; h ; 3 6 15 30 8 30 − 2 TẠ 1 −1 1 1 3 1 i ; j ; k 0 ; l ; −2 , 5 − 21 − 28 2 − 34 4 5 − 0, 4 Å ã THPT −5 4 3 3 −4 2 −7 m + ; n : ; o ; p 1 ; −
−3, 5 · - 9 7 20 4 21 3 · 3 G −5 3 Å 2ã Å 4ã 13 3 2 5 q : ; r : ; s : ; t ; −8 −2 − 2 −4 0976071956 5 5 10 5 5 · 4 Å ã DŨN 93 7 1 3 −6 −1 1 u ; v + : ; w 1 − , 25 : − 0, 25; 4 · 5 2 MA 4 TH.ND 7 2 − 3 13 3 −2 5 3 1 Å 4 3ã 6 5 2 6 x − : + ; y 0 ; z : + : .
, 5 − · GỌC 10 5 5 · 4 4 5 − 0, 4 9 − 5 5 9 − 5 5 N
d Bài 6. Thực hiện ? Lớp phép tính TO một ÁN cách THẦ hợp lý Y DŨNG ? Å −5ã 7 Å 11 ã Å 1ã Å 15ã 38 a A = b ; 11 · 15 · · (−30); B = − · − · −5 6 19 45 Å ã Å ã Å ã Å ã GUYỄN −5 3 13 3 2 9 3 3 c C = · + − · ; d D = 2 : − ; N 9 11 18 11 15 · 17 · 32 17 4 22 23 13 5 2 8 5 2 e E = + f + ; 3 − 35 3 − 35 − 2;
F = 13 · 7 3 · 7 − 3 Thầy 515 −2017 515 −1 2 Å−2ã 2 2 g G = + ; h : : ; 2019 · 2018 2019 · 2018 H = 53 7 − 73 7 15 15 19 15 2 6 Å−5 6ã 41 Å 1 1ã i I = + + + ; j + + + ; 34 17 34 − 117 3 J = 57 6 7 7 −6 7 1 1 3 17 27 1 1 1 9 3 k K = + + ; l . 3 − 7 2 3 − 7
L = 73 · 211 − 73 · 111 − 2
d Bài 7. Tìm x, biết (chuyển vế thì phải đổi dấu nhé)
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 7 of 56 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng 2 3 4 1 1 a x − = −5; b = ; c = ; 5 2 x + 5 15 x − 15 10 5 5 1 −2
d x + 0, 25 = ; e = ; f ; 4 x + 6 3 15 − x = −3 10 2 4 7 13 1 7 g − ; h ; i 3 = ; 3x = 15
− 19x = −24 x − 4 5 3 1 5 3 9 Thầy j 2x − = ; k 1 + 3 l + ; 4 2 x = −5; 8 8x = 2 2 2 3 1 1 4 3 1 2 m + ; n = ; o + ; N 3 9x = 4 2x − 3 9 4 4x = 5 GUYỄN 2 3 1 4 4 −2 5 p + ; q = −3; r + ; 5 5x = 4 5x − 35 5 5 6x = −4 15 1 2 18 5 3 2 4
s 1, 5x − 2 ; t ; u = ;
3x = 1, 5 − 3
5 − 4x = −1 6 5x − 7 5 N 2 7 5 2 1 3 5 2 1 GỌC v + : ; w + : ; x : = ; 3 4 x = 6 3 3 x = 5 7 x − 5 3 16 1 4 1 1 y x : + = ; z + = 1. 7 8 3 3 x : 3 DŨN
d Bài 8. Tìm x, biết 13 Å 3 ã 5 G a + + = ; b (2 c (8 20 5 x 6
, 4 − 3x) · 0, 5 = 0, 9;
, 8x − 50) : 0, 4 = 51; 0976071956 - Å 2x ã 2 11 Å 5ã 2 2 1 5 THPT d : ( ; e = ; f + (2 ; 3 − 3 −10) = 5 15 − x − 7 − 3 3 6 x + 2) = 6 MATH.ND Å 5 ã 5 15 Å 3 ã 4 3 11 1 g · = − ; h x − : = − ; i ; T 12 − x 7 36 14 21 4
5 − (0, 35 + x) = 12 Ạ Å ã Å ã Å ã QU 7 11 3 5 1 3 1 2 j + = ; k = 1; l = 1 ; 18 x
− 12 −?4 Lớp TO 4 − ÁN x + THẦ 3 Y DŨNG−? 4 − x + 2 3 AN
d Bài 9. Tìm x, biết (A · B = 0 thì A = 0 hoặc B = 0) G Å 3ã Å18 4 ã Å 1ã a x − = 0; b 5 = 0;
5 · 5 − 5x x x − 3 BỬU Å 1ã Å 3ã Å 5ã Å 5ã c x + = 0; d = 0; 4 x − 7 x + 3 · x − 4 Å 3 9 ã Å ã e 1 : = 0; f (2 4x − 16 · , 5 + −3 5 x
, 4 − 3x) · 0, 5 = 0; Å 2x ã Å 3 ã Å 5 ã g h 5 = 0;
3 − 3 · (−10 + 2x) = 0;
x − 14 · x + 12 Å 1 ã Å 2ã Å −2 ã Å 1ã i x : = 0; j 3 = 0.
3 − 3 · x − 5 15 − x · x − 4
d Bài 10. Tìm x, biết Page 8 of 56
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU 2 5 3 4 1 1 a = ; b = ; c = ; x − x + x − 5 2 5 15 15 10 5 5 1 −2 3
d |x + 0, 25| = ; e = ; f = ; 4 x + 6 3 15 − x 10 2 4 7 13 1 7 g = ; h = ; i 3 = ; − − x − 3x 15 19x 24 4 5 3 1 j 2 = . x − 4 2 d BỬU
Bài 11. Tìm x, biết 1 1 1 3 1 5 4 7 1 G a 2 · + = ; b + = ; c = 1 ; x + x − − 4 3 2 7 − x 2 7 7 4 2 AN 5 1 1 3 4 2 d = ; e = ; − − x +
f |x − 1, 5| = 2; 18 − x 2 5 5 − 5 5 QU 3 1 TẠ g = ; i 8 x +
h |2x − 1| + 1 = 4;
− |1 − 3x| = 3; 4 2 2 2 1 3 5 2 1 5 3 2 j = ; k = ; l = ; x − − x − THPT 3 − 3x − 2 4 2 3 4 7 − 5 3 - 5 3 1 1 5 7
m |3, 3 − x| − 5, 7 = −2, 7; n = + ; o = ; x + −2 − G 6 2 3 2 6 − x 3 0976071956 13 9 7 1 2 1 3 1 p : = ; q 3 = 1; r = ; x − x + − −2x + − DŨN 7 49 9 2 3 5 5 2 MATH.ND
Dạng 2. Lũy thừa của số hữu tỉ
d Bài 1. Tính các lũy thừa sau GỌC Å ã2 Å ã0 Å ã2 Å ã3 N 3 −15 −1 −1 a − ; b ; c ; d ; 2 ? Lớp TO 7 ÁN THẦY DŨNG 2 ? 2 Å 2017ã0 Å 3ã2
e (−0, 5)2; f − ; g ; h ( 2018 4 −0, 25)4; GUYỄN Å ã3 Å ã0 N 2 1 i 2 ; j ; k 20160; l (3 5 − 3 , 6)2; Å −1ã2 Å 2ã2 Å −7ã3 Å 1ã3 Thầy m ; n ; o ; p 2 . 12 − 5 3 3 A C
d Bài 2. Thực hiện phép tính (nhớ kỹ · = C nhé) B A B Å −1ã2 Å 1ã3 1 Å 3ã2 1 3 a : ; b : + 2
· | + 8| − −2 −
| − 0, 25| − − 16 2 4 4 · 20170; 2 5 Å 2ã3 7 Å 29 7 ã Å 2017ã0 c 3 ; d ( : ; · , 6 : 2 −0, 5)2 + ·10− − 3 − 6 5 2 30 − 15 2018
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 9 of 56 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng 8 Å 1ã2 3 −1 Å 1ã2 e + 3 −7 ; f 2 ; 3 − 3 − − − 3 2 − 12 3 Å 2 ã Å 2ã2 Å 2 1 ã Å 1ã2 1 −5 g 1 + 1 ; h + ;
3 − 0, 25 · −5 − 5 3 − 2 − 3 − 12 18 −2 1 32 Å 2 14ã Å5 4ã2 i + −3 ; j 1 + : ; 5 − 2 5 − 20 3 − 9 6 − 5 Thầy Å 3ã2 2 1 Å 11 5ã 1 Å3 2ã2 k 1 − : + ; l + 17 ; 2 − · − − 3 2 12 − 9 18 2 − 3 Å ã2 Å ã N 1 3 1 7
m 2 · 32 + (−2015)0 − ; n 1 + 5 ; − −
· − − − GUYỄN 3 4 8 16 −1 Å 1 3ã2 −1 Å 1ã0 o + : −5 ; p + 5 − 2 4 − − 20160; 8 3 3 7 1
Å −2ã5 Å−2ã4 Å −2 3ã2 12 11 N q + 5 : 11 + : ; r + ; 10 2 5 5 3 4 · 5 − 5 GỌC Å −4ã35 Å3ã36 Å 3ã2
63 · 7 − 63 · 12 s + −2 −9 : t . 3 · 4 3 · 4 − −2
63 · (53 − 52) Å −15ã0 DŨN ; 7 A C
d Bài 3. Rút gọn rồi tính (nhớ kỹ · = C nhé) G B A B 0976071956 - 211 · 92 324 · 93 65 · 32 810 · 163 a ; b ; c ; d ; THPT 35 · 162 272 · 85 43 · 93 414 · 323 104 · 272
35 · 158MATH.ND811 · 915 611 · 910 e ; f ; g ; h ; 64 · 153 (25 · 27)4 632 85 · 330 TẠ 27 · 272 43 · 86 10500 · 51515 529 · (−27)30 i ; j ; k ; l ; QU 162 · 81 222 251008 1530 ? Lớp TOÁN THẦY DŨNG · 8166 ? · 362 4913 · 84 815 · 910 415 · 219 8111 · 317 AN m ; n ; o ; p ; 1413 · 712 411 · 622 1612 2710 · 915 G 410 · 87 910 · 277 88 · 496 (−3)28 · 2510 q ; r ; s ; t . 240 340 1414 · 210 1519 · 273 BỬU A C
d Bài 4. Rút gọn rồi tính (nhớ kỹ · = C nhé) B A B 106 · 33 165 · 321
258 · 164 · 319 54 · 184 a ; b ; c ; d ; 252 · 65 · 52 127 · 185 · 81 48 · 276 · 516 125 · 95 · 16 814 · 155 · 52 82 · 95 Å 1 ã2016 532 · 1043 e ; f ( ; h ; 27
−0, 3)2·5− g · 272015; 7 · 59 39 · 43 27 1611 · 12525 1511 · 57 · 92 35 · 158 Å 5ã4 Å6ã3 454 · 55 i ; j ; k ; l ; 5 − · 18 · 276 (25 · 27)4 6 5 273 · 254 2714 318 · 244 286 · 76 Å 9 ã6 Å14ã7 m ; n ; o ; p . 3 · 12 · 916 184 · 95 27 · 987 14 9 Page 10 of 56
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
d Bài 5. Tìm x, biết Å 1ã2 Å ã2 Å 1ã2 Å −2ã2 Å 1 ã2 9 a 3 −3 x − = ; b 2 = ; c = ; 5 25 x − 3 9 3 − x 25 16 1
d (5 − x)2 = 25;
e (3x + 1)2 = 25;
f (6 − x)2 − = ; 5 25 Å 1ã2 25 Å 3 ã2 16 g 2x − = ; h (5 i = 0; 2 16
− x)3 − 125 = 0; 5 − 2x − 25 BỬU Å 3ã3 1 64 · 16 G j x − = ; k 2x+1 = ; l 53x−2 = 625; 5 27 28 AN Å 2ãx−2 8 Å 2ãx Å 8 ã2
m 3x+1 − 2 = 52; n = ; o = ; QU 5 125 3 27 TẠ 64 · 16 p 51−x = 125; q 3x+4 = 2710; r 2x+1 = ; 28 THPT - 26 · 92 s x = ;
t 33x + 33x+2 = 7290; 64 · 8 G 0976071956 DŨN
| Chủ đề 2. Tỉ lệ thức MATH.ND A
KIẾN THỨC CẦN NHỚ GỌC N
a Nếu a = c thì ad = bc (tích chéo bằng nhau); b d ? Lớp TOÁN THẦY DŨNG ?
b Nếu a = c thì b d GUYỄN a d d • = b; • = c ; • = b. N c d b a c a
(hoán vị theo đường chéo) Thầy
c Dãy tỉ số bằng nhau:
• Từ a = c ta suy ra a = c = a + c = a − c (có thể áp dụng cho dãy nhiều b d b d b + d b − d tỉ số);
• Khi nói a, b, c tỉ lệ với các số 2; 3; 7 thì nghĩa là a = b = c và cũng viết là 2 3 7
a : b : c = 2 : 3 : 7.
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 11 of 56 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng B BÀI TẬP
Dạng 1. Tìm x
d Bài 1. Tìm x, y, z (hoặc a, b, c) biết (nhớ tích chéo bằng nhau nhé) 2x − 1 5 15 x − 1, 2 4 a = −2; b = ; c = ; −5 9 x 24 3 5 Thầy 3 4 −6z + 4 4 − x 27 d = x − 2; e = −2; f = ; 4 8 −9 9 30 −5 x 7 4 g = −25; h = −2; i = x ; N 12 6 3 + 4y 9 x 9 GUYỄN 0, 2 x 3 x 15 j = −8; k = ; l = ; 2 x 49 7 −16 20 2x − 1 7 m =
= −6z + 4 = −2. −5 3 + 4y −9 9 N
d Bài 2. Tìm x, y, z (hoặc a, b, c) biết GỌC x a = y và 6 7
x + y = −39;
b x : y = 5 : (−3) và x − y = −16;
c x : 15 = y : 12 và x − y = 30;
d x : 17 = y : 13 và x − y = 40; DŨN x e
= y và x + y = 12;
f x : y = 5 : (−3) và x − y = −16; −3 5 G x g = y và 20 15 y − x = 20; 0976071956
h x : 2 = y : (−5) và x − y = 14; - THPT x2 x 7 i = y2 và j = và 9 16 x2 + y2 = 100; x − y = −16; MATH.NDy 3 x x k
= y và x + y = −12; l
= y và x − y = 6; T 10 4 5 Ạ −7 2x 3y 4z x QU m = = và + = 49; n = y = z và + 3 4 5 x ? Lớp
y + z TOÁN THẦ 5 Y DŨNG 4 7 x ?y − z = 10; x x AN o = y = z và p = y = z và 5 4 7
x + y + z = 10; 15 8 4
x + y + z = 54; G 1 2 3 x q r = y = z và
2x = 3y = 4z và x + y − z = 26; 5 2 7
x + y + z = 28; BỬU a x s = b = c và t = y = z và 5 6 7
a + b − c = 44; 6 5 7
x + y − z = 28; x x u = y = z và v = y = z và 2 5 6
x − y + z = 24; 12 16 15 x − y = −8.
d Bài 3. Tìm x, y, z (hoặc a, b, c) biết x x a = y và 2 b = y và 2 9 4
x + y = −66; 25 45 x − y = 15; x + 5 3 x c
= y − 7 = z và d = y = z và 2 4 3 5
x + y − 3z = 8; 3 4 5
x − y − 3z = 26; a e = b = c và 2 f 5 3 2 5
a + b − c = 24;
x = 3y và 2x − y = 3. Page 12 of 56
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
d Bài 4. Tìm x, y, z (hoặc a, b, c) biết a x a
= b; b = c và b
= y ; y = z và 3 4 5 6
a + b − c = 22; 5 4 7 8 x − y + z = 7; x a c
= y ; y = z và d
= b; b = c và 7 9 4 2
x − y + z = 10; 5 4 3 2
a − b + c = 55; x x e
= y ; y = z và 3 f
= y ; y = z và 3 2 7 5
x − 7y + 5z = 30; 5 4 7 8
x − y + z = 78. Dạng 2. Toán đố
d Bài 1. Ba lớp 7A, 7B, 7C trồng được 150 cây xanh. Biết rằng số cây của mỗi lớp trồng BỬU
được theo tỉ lệ 3; 5; 7. Tính số cây của mỗi lớp đã trồng. G
d Bài 2. Ba góc của tam giác tỉ lệ với 3; 4; 5. Tìm số đo mỗi góc của tam giác. AN
d Bài 3. Ba góc của tam giác tỉ lệ với 3; 5; 7. Tìm số đo mỗi góc của tam giác. d QU
Bài 4. Hưởng ứng tinh thần “Tương thân tương ái", chia sẻ mất mát với đồng bào miền
Trung bị lũ lụt. Nhà trường đã phát động phong trào quyên góp tiền cứu trợ đồng bào miền TẠ
Trung, số tiền quyên góp được của các khối 6; 7; 8; 9 lần lượt tỉ lệ với 2; 3; 4; 6. Hãy tính
số tiền đóng góp được của toàn trường, biết rằng số tiền đóng góp của khối 7 nhiều hơn số THPT
tiền đóng góp của khối 6 là 2 triệu đồng. -
d Bài 5. Học sinh của ba lớp 7 cần phải trồng và chăm sóc 27 cây xanh. Lớp 7A có 36 học G
sinh, lớp 7B có 32 học sinh, lớp 7C có 40 học sinh. Hỏi mỗi lớp phải trồng và chăm sóc bao 0976071956
nhiêu cây xanh, biết rằng số cây xanh tỉ lệ với số học sinh. DŨN
d Bài 6. Ba bạn An, Bình, C MA ông đã TH.ND
góp kế hoạch nhỏ một số kg giấy vụn, biết số kg giấy
mỗi bạn đã góp lần lượt tỉ lệ với 2 : 3 : 4 và số kg giấy bạn Bình đã góp ít hơn bạn Công 2 GỌC
kg. Tìm số kg giấy mỗi bạn đã góp. N
d Bài 7. Một ô tô đi ? từ Lớp thành TO phố ÁN Hồ ChíTHẦ Minh Y đến DŨNG
Vũng Tàu. ?Cùng lúc đó một xe máy đi
từ Vũng Tàu đến thành phố Hồ Chí Minh. Sau 50 phút hai xe gặp nhau. Vận tốc của ô tô và
vận tốc của xe máy tỉ lệ với 6; 4. Vận tốc ô tô lớn hơn vận tốc xe máy 30 km/giờ. GUYỄN
a Tính vận tốc xe máy, vận tốc xe ô tô; N
b Tính quãng đường từ thành phố Hồ Chí Minh đến Vũng Tàu. d Thầy
Bài 8. Hưởng ứng phong trào quyên góp sách giáo khoa cho thư viện để ủng hộ, giúp
đỡ các bạn học sinh có hoàn cảnh khó khăn, hai lớp 7A, 7B đã quyên góp số sách lần lượt
tỉ lệ với 6; 8. Tính số sách giáo khoa mỗi lớp quyên góp, biết số sách đóng góp của lớp 7B
nhiều hơn 7A là 14 quyển.
d Bài 9. Ba lớp 7A, 7B, 7C ở một trường quyên góp được 156 quyển sách cũ tặng các bạn
học sinh có hoàn cảnh khó khăn. Tìm số quyển sách mỗi lớp quyên góp được, biết số sách
của mỗi lớp quyên góp được tỉ lệ với 2; 3; 7.
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 13 of 56 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng
d Bài 10. Sau một tháng tổng tiền điện phải trả của ba hộ sử dụng là 540 000 đồng. Biết
rằng số tiền điện tiêu thụ của ba hộ tỉ lệ với 5; 8; 14. Tính số tiền điện mỗi hộ phải trả.
d Bài 11. Kết thúc hội thi học sinh thiết kế sản phẩm học tập có ứng dụng công nghệ
thông tin của trường Tân Bình. Ban tổ chức nhận được 180 sản phẩm của bốn khối 6, 7, 8,
9. Biết số sản phẩm của bốn khối 6, 7, 8, 9 tỉ lệ với các số 2; 5; 4; 7. Hỏi mỗi khối đã gửi về
cho ban tổ chức bao nhiêu sản phẩm? Thầy
d Bài 12. Một giá sách có ba loại sách Toán, Văn, Anh. Biết số sách Toán, Văn, Anh tỉ lệ với
9; 4; 5 và số sách Toán nhiều hơn số sách Anh là 20 cuốn sách. Tính số sách mỗi loại có N GUYỄN trên giá sách đó?
d Bài 13. Một trường tiểu học có số học sinh các khối lớp 3; 4; 5 lần lượt tỉ lệ với 3; 4; 5.
Biết số học sinh khối lớp 3 ít hơn số học sinh khối lớp 5 là 64 em. Tìm số học sinh của mỗi khối? N GỌC
d Bài 14. Số học sinh các lớp 7A, 7B, 7C lần lượt tỉ lệ với 4; 5; 7. Biết tổng số học sinh của
ba lớp là 240 em. Tính số học sinh mỗi lớp?
d Bài 15. Tìm chu vi của một hình chữ nhật. Biết rằng hai cạnh tỉ lệ với 2; 3 và chiều dài DŨN hơn chiều rộng là 18 m. d G
Bài 16. Ba lớp 7A, 7B, 7C quyên góp được 1200 quyển tập để hưởng ứng phong trào giúp
các bạn miền Trung đến lớp sau 0976071956
cơn bão. Biết rằng số tập quyển góp của ba lớp 7A, 7B, 7C - THPT
lần lượt tỉ lệ với 7; 8; 9. Tìm số tập của mỗi lớp đã quyên góp? d MATH.ND
Bài 17. Tìm số học sinh của hai lớp 7C và 7D. Biết rằng số học sinh của lớp 7C nhiều 5 T
hơn số học sinh của lớp 7D là 9 học sinh và tỉ số học sinh của hai lớp 7C và 7C là . Ạ 4 d QU
Bài 18. Số học sinh giỏi ba lớp 7A, 7B, 7C lần lượt tỉ lệ với 2; 3; 5. Tìm số học sinh giỏi ? Lớp TOÁN THẦY DŨNG ?
mỗi lớp biết số học sinh giỏi lớp 7C nhiều hơn lớp 7B là 10 học sinh. AN
d Bài 19. Sơ kết học kỳ 1, số học sinh giỏi các khối 6, 7, 8, 9 tỉ lệ với 6; 5; 4; 3. Biết tổng số G
học sinh giỏi của hai khối 6 và khối 9 là 540 học sinh. Tính số học sinh giỏi mỗi khối. BỬU
d Bài 20. Tính số học sinh của lớp 6C và lớp 6D biết số học sinh lớp 6D nhiều hơn số học 7
sinh lớp 6C là 12 học sinh và tỉ số học sinh của lớp 6C và lớp 6D là . 9
| Chủ đề 3. Số thực. Căn bậc hai A
KIẾN THỨC CẦN NHỚ Page 14 of 56
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU √ √ … 9 3 Å 3ã2 9 a 4 = 2 vì 22 = 4; b 9 = 3 vì 32 = 9; c = vì = . 25 5 5 25 B BÀI TẬP d Bài 1. Tính … 81 √ √ … 25 … 1 a ; b 0 c 121 d ; e ; 100 , 49; 36 81 BỬU √ … 4 √ √ … 16 G f 64; g ; h 25; i 144; j ; 49 9 … … … … AN 9 √ 1 7 36 k ; l 0 m ; n 2 ; o ; 64 , 81; 81 9 49 QU √ … 49 √ p p p (−4)2; q
(1, 6 − 0, 7)2; r 62 + 82; s ; t 15 − 6. TẠ 16 d Bài 2. Tính … √ √ … THPT 81 25 a 0, 49 + 93; b 121 − 0, 25 + ; - 100 − 36 … G 1 Å 1ã2 5 1 Å 1ã3 1 √ c : + 15 ; d + 64 81 − 3 9 · −
− | − 0, 25|; 0976071956 5 2 4 · ñ… ô DŨN Å 1ã3 1 √ 4 Å 1ã2 27 4 e + 100 f + : ; 3 5 · − | − 2|; MATH.ND 49
− 3 · 7 − 3 7 √ … 1 Å 1ã2 5 Å 7ã0 −4 GỌC g 25 − 812 : 169; h : + 18 ; 81 − 3 9 · − 9 − 45 N … Å ? Lớp ã2 TOÁN THẦY√ DŨNG … ? 25 5 2 16 1 i + ; j 144 + ; 9 − − − 5 · −5 6 3 9 3 5 3 √ … 9 … 1 √ p k 1 + 81 + ; l
(−2)2 − 5 · + 0, 81; GUYỄN 6 18 · 64 25 N … 1 … 36 Å −2ã2 3 … 7 p m
(−4)2 − 3 · + ; n + 2 ; 9 49 3 · 8 9 Thầy d Bài 3. Tính … 25 −1 Å 1ã5 Å3ã2 Å 3ã3 2 1 …81 a + 1 : ; b + ; 36 − − 24 2 2 2 5 − 2 25 Å 2ã2 … 49 √ c 1 −3 − + + p(1 d 0 5
, 6 − 0, 7)2; , 25; 5 16 − 3 −4 … 1 Å −1ã2 √ 1 e : ( ; f 62 + 82 : + 0 9 −4)2 − 144 2 − 6 , 4;
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 15 of 56 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng √ … 9 √ √ √ g 20160 p ·
16 − 2 · (−2)2 − 8 · ; h 64 25 + 100; 16 − √ … 1 √ √ √ i 0, 5 · 100 − ; j 3 400 225 + 64; 4 · − … 4 √ √ √ k + −1 l 16 + 64 169; 9 − (−2016)0; − 3 Thầy √ … 9 Å ã2 2 Å −1ã2 15 − 6 m + −3 −1 : ; n 4 + ; 25 − · 4 5 3 2 4 … … N √ 1 1 −1 9 Å −2ã2 o 0, 5 · 100 − p + ; − GUYỄN
4 − | − 5| + (−1)4; 3 6 4 − 5 Å −5ã2 … 1 q + 8 + ( 7 · 16 −1)2014; N GỌC DŨN G 0976071956 - THPT MATH.ND TẠ QU ? Lớp TOÁN THẦY DŨNG ? AN G BỬU Page 16 of 56
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? 2
Hàm số và đồ thị Chương
Bạn cần định vị? Cũng chẳng khó gì.
Hoành độ, tung độ Con số thần kì! Trọng tâm chương: BỬU G
• Biết nhận diện các đại lượng tỉ lệ thuận, tỉ lệ nghịch và các yếu tố liên quan. AN
• Biết trình bày và giải các bài toán về đại lượng tỉ lệ thuận, tỉ lệ nghịch. QU
• Biết vẽ đồ thị hàm số y = ax. TẠ
| Chủ đề 1. Tỉ lệ thuận THPT - A
KIẾN THỨC CẦN NHỚ G a
• Nếu y = kx thì 0976071956
ta nói y tỉ lệ thuận với x theo hệ số tỉ lệ k và x tỉ lệ thuận với 1 DŨN
y theo hệ số tỉ lệ . k
• Hệ số tỉ lệ k được MA tính TH.ND
theo công thức k = y : x. GỌC
b Nếu hai đại lượng y và x tỉ lệ thuận với nhau thì N • y1 = y2 ? = yLớp 3 = . . . TO (= k ÁN ). THẦY DŨNG ? x1 x2 x3
• x1 = y1 , x1 = y1 , . . . x2 y2 x3 y3 GUYỄN N B BÀI TẬP Thầy
Dạng 1. Xác định các yếu tố về đại lượng tỉ lệ thuận
d Bài 1. Các giá trị tương ứng của hai đại lượng x và y được cho trong bảng sau, hỏi chúng
có tỉ lệ thuận với nhau không? x −1 3 −5 6 10 x 1 2 4 7 8 a b y 2 −6 10 −12 −20 y 3 6 12 20 24
d Bài 2. Các giá trị tương ứng của hai đại lượng u và v được cho trong bảng sau: 17 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng u −1 −2 2 −15 4 v 2, 5 5 5 3, 75 −10
Hỏi hai đại lượng u và v có tỉ lệ thuận với nhau hay không? Vì sao?
d Bài 3. Cho biết x và y là hai đại lượng tỉ lệ thuận. Thầy
a Điền số thích hợp vào các ô trống sau: x
x1 = 0, 25 x2 = 2 x4 = 5 N y y1 = 1 y3 = 13 y5 = 30, 4 GUYỄN
b y tỉ lệ thuận với x theo hệ số tỉ lệ nào? Viết công thức.
c x tỉ lệ thuận với y theo hệ số tỉ lệ nào? Viết công thức. N 1
d Bài 4. Cho biết y tỉ lệ thuận với x theo hệ số tỉ lệ . Hỏi x tỉ lệ thuận với y theo hệ số tỉ GỌC 2 lệ nào?
d Bài 5. Cho biết hai đại lượng y và x tỉ lệ thuận với nhau. Nếu x = 5 thì y = −4. Viết công DŨN
thức liện hệ giữa hai đại lượng y và x. 3 4
d Bài 6. Cho biết y tỉ lệ thuận với x theo hệ số tỉ lệ . Tính giá trị của . 4
y khi x = −8; x = 9 G
d Bài 7. Cho biết y tỉ lệ thuận 0976071956
với x theo hệ số tỉ lệ −3. Tính giá trị của x khi y = −2; - THPT y = 1, 5. d MATH.ND
Bài 8. Cho biết x và y là hai đại lượng tỉ lệ thuận. Hãy điền số thích hợp vào ô trống T trong bảng sau: Ạ QU x x1 = −6 x3 = −5 x5 = 6, 5 ? Lớp TOÁN THẦY DŨNG ? y
y2 = −1, 1 y3 = 1 y4 = 0, 8 AN
d Bài 9. Cho x và y là hai đại lượng tỉ lệ thuận. Gọi x1, x2 là hai giá trị của x; gọi y1, y2 là G
hai giá trị tương ứng của y. Biết x1 = 6, x2 = 12 và y2 − y1 = 4. Tính y1 và y2. BỬU
d Bài 10. Cho biết 2 đại lượng x và y tỉ lệ thuận với nhau và khi x = −4 thì y = −8.
a Tìm hệ số tỉ lệ k.
b Hãy biểu diễn y theo x. 1 2
c Tìm y biết x = − . d Tìm . 2
x biết y = −3
d Bài 11. Cho biết 2 đại lượng x và y tỉ lệ thuận với nhau và khi x = 4 thì y = −16.
a Tìm hệ số tỉ lệ k.
b Hãy biểu diễn y theo x. 1 2
c Tìm y biết x = . d Tìm . 2 x biết y = 3 Page 18 of 56
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU 3
d Bài 12. Cho y tỉ lệ thuận với x theo hệ số tỉ lệ k = − . 4
a Hãy biểu diễn y theo x.
b Hỏi x tỉ lệ thuận với y theo hệ số tỉ lệ nào?
Dạng 2. Toán đố về tỉ lệ thuận
d Bài 1. 5 m dây đồng nặng 43 kg. Hỏi 10 m dây đồng như thế nặng bao nhiêu kg?
d Bài 2. Một cốc nước đựng 600 g nước biển có chứa 20 g muối. Hỏi 10 kg nước biển chứa BỬU bao nhiêu kg muối? G
d Bài 3. Cứ 100 kg thóc thì cho 60 kg gạo. Muốn có 90 kg gạo thì cần bao nhiêu kg thóc? d AN
Bài 4. Có 36 m vải may được 9 bộ quần áo. Hỏi có 60 m vải thì may được bao nhiêu bộ quần áo như thế? QU
d Bài 5. Một đoạn dây thép dài 1 mét có khối lượng 25 g. Để bán 30 m dây thép, người ta TẠ
cần phải cân cho khách bao nhiêu gam?
d Bài 6. Mua 6 gói kẹo thì hết 45 000 đồng. Khi đó với 60 000 đồng thì mua được mấy gói THPT kẹo như thế? - d G
Bài 7. Cho biết 5 người làm cỏ một cánh đồng hết 8 giờ. Hỏi 16 người làm cỏ cánh đồng
hết bao nhiêu giờ? (biết 0976071956
năng suất mỗi người như nhau) DŨN
d Bài 8. Trong 10 ml nước muối sinh lý có 90 ml mước natri clorua. Một công ty dược
muốn sản xuất 100 lít nước m MA uối TH.ND
sinh lý thì cần bao nhiêu kg muối natri clorua.
d Bài 9. Hai nền nhà hình chữ nhật có chiều dài bằng nhau. Nền nhà thứ nhất có chiều GỌC
rộng 5 m, nền nhà thứ hai có chiều rộng 6 m. Để lát nền nhà thứ nhất người ta dùng 600 N viên gạch hình ? vuông. Lớp Hỏi TO phải ÁN dùng bao THẦ nhiêu Y viên DŨNG gạch cùng ?
loại để lát nền nhà thứ hai?
d Bài 10. Một công nhân may trong 5 giờ được 20 cái áo. Hỏi trong 8 giờ người đó may được bao nhiêu cái áo? GUYỄN N
d Bài 11. Cứ xay xát 50 kg thóc thì được 36 kg gạo. Hỏi nếu xay xát 175 kg thóc thì được bao nhiêu kg gạo?
Dạng 3. Các bài toán chia tỉ lệ áp dụng dãy tỉ số bằng nhau Thầy
d Bài 1. Ba bạn An, Bình, Châu ủng hộ phong trào Kế hoạch nhỏ của Liên đội trường với
tổng số tiền là 660 000 đồng. Tìm số tiền mà mỗi bạn đóng góp, biết chúng tỉ lệ thuận với 5; 7; 8.
d Bài 2. Ba đơn vị kinh doanh góp vốn theo tỉ lệ 3 : 4 : 6. Hỏi mỗi đơn vị được chia bao
nhiêu tiền nếu tổng số tiền lãi là 650 triệu đồng và tiền lãi được chia theo tỉ lệ thuận với số tiền đóng góp?
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 19 of 56 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng
d Bài 3. Trong một buổi làm từ thiện giúp người nghèo trong quận, học sinh khối 6 đã góp
một số tiền nhiều hơn khối 9 là 500 000 đồng. Tính tổng số tiền đóng góp của trường học
đó. Biết số tiền đóng góp của khối 6; 7; 8; 9 lần lượt tỉ lệ thuận với 8; 7; 9; 6.
d Bài 4. Trước khi bán, người ta đã phân loại gạo thành ba loại: loại I, loại II, loại III có
khối lượng tỉ lệ với các số 1; 2; 3. Tính số gạo mỗi loại trong 3 tấn gạo. Thầy
d Bài 5. Học sinh của ba lớp 7 cần phải trồng và chăm sóc 30 cây xanh. Lớp 7A có 45 học
sinh, lớp 7B có 50 học sinh, lớp 7C có 55 học sinh. Hỏi mỗi lớp phải trồng và chăm sóc bao
nhiêu cây xanh, biết rằng số cây xanh phải trồng tỉ lệ thuận với số học sinh? N GUYỄN
d Bài 6. Tam giác ABC có số đo các góc A, B, C tỉ lệ với 1; 2; 6. Tính số đo các góc của tam giác ABC.
d Bài 7. Học sinh của ba lớp 7 cần phải trồng và chăm sóc 21 cây xanh. Lớp 7A có 35 học N
sinh, lớp 7B có 30 học sinh, lớp 7C có 40 học sinh. Hỏi mỗi lớp phải trồng và chăm sóc bao GỌC
nhiêu cây xanh, biết rằng số cây xanh tỉ lệ với số học sinh.
d Bài 8. Chia số 440 thành ba số tỉ lệ với 0, 4; 0, 6 và 1, 2. Tìm 3 số đó? DŨN
d Bài 9. Học sinh của ba lớp 7 cần phải trồng và chăm sóc 27 cây xanh. Lớp 7A có 40 học
sinh, lớp 7B có 32 học sinh, lớp 7C có 36 học sinh. Hỏi mỗi lớp phải trồng và chăm sóc bao
nhiêu cây xanh, biết rằng số cây xanh tỉ lệ với số học sinh. G 0976071956 -
d Bài 10. Chia số 330 thành ba số tỉ lệ với 0, 4; 0, 6 và 1, 2. Tìm 3 số đó? THPT MATH.ND
| Chủ đề 2. Tỉ lệ nghịch TẠ QU A
KIẾN THỨC CẦN ? Lớp NHỚ TOÁN THẦY DŨNG ? AN a
• Nếu y = k (hoặc xy = k) thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ k và x x G
tỉ lệ nghịch với y theo hệ số tỉ lệ k. BỬU
• Hệ số tỉ lệ k được tính theo công thức k = x · y.
b Nếu hai đại lượng y và x tỉ lệ thuận với nhau thì
• x1y1 = x2y2 = x3y3 = . . . (= k).
• x1 = y2 , x1 = y3 , . . . x2 y1 x3 y1 B BÀI TẬP
Dạng 1. Xác định các yếu tố về đại lượng tỉ lệ nghịch Page 20 of 56
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
d Bài 1. Cho biết x và y là hai đại lượng tỉ lệ nghịch. Điền các số thích hợp vào ô trống trong bảng sau x2 = x x1 = 0,5 x5 = 4 x6 = 6 −1,2 y y3 = 3 y4 = −2 y5 = 1,5
d Bài 2. Các giá trị tương ứng của x và y được cho trong bảng sau BỬU x x1 = −2 x2 = −1 x3 = 4 x4 = 8 G y y1 = −8 y2 = −16 y3 = 4 y4 = 2 AN
Hai đại lượng x và y có tỉ lệ nghịch với nhau hay không? Vì sao? QU
d Bài 3. Cho biết x và y là hai đại lượng tỉ lệ nghịch. Điền các số thích hợp vào ô trống trong bảng sau TẠ x x1 = −20 x2 = −12 x3 = 2 x4 = 3 x5 = 4 x6 = 5 THPT y y - 2 = −5 y6 = 10 G
d Bài 4. Cho biết x và y là hai đại lượng tỉ lệ nghịch. Điền các số thích hợp vào ô trống trong bảng sau 0976071956 DŨN x x1 MA = −9 TH.ND x2 = −1 x4 = 3 y y2 = −27 y3 = 27 GỌC d N
Bài 5. Các giá trị tương ứng của x và y được cho trong bảng sau ? Lớp TOÁN THẦY DŨNG ? x x1 = 2 x2 = 3 x3 = 5 x4 = 6 y y1 = 15 y2 = 10 y3 = 6 y4 = 5 GUYỄN N
Hai đại lượng x và y có tỉ lệ nghịch với nhau hay không? Vì sao?
d Bài 6. Cho biết hai đại lượng x và y tỉ lệ nghịch với nhau và khi x = 4, 2 thì y = 15. Hãy
biểu diễn x theo y. Thầy
d Bài 7. Cho x và y là hai đại lượng tỉ lệ nghịch với nhau. Vẽ lại bảng sau rồi điền các số thích hợp vào ô trống: x −9 −5 2 y −10 −30 1
d Bài 8. Cho x và y tỉ lệ nghịch với nhau theo hệ số tỉ lệ k = . 2
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 21 of 56 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng 1
a Hãy biểu diễn y theo x.
b Tính giá trị của y khi x = − . 16
d Bài 9. Cho biết hai đại lượng x và y tỉ lệ nghịch với nhau và khi x = 8 thì y = 15.
a Tìm hệ số tỉ lệ k.
b Hãy biểu diễn y theo x.
c Tính giá trị của y khi x = 6, x = 10. Thầy
d Bài 10. Cho hai đại lượng x và y tỉ lệ nghịch với nhau theo hệ số tỉ lệ k = 16. N 1
a Hãy biểu diễn y theo x.
b Tính giá trị của y khi x = − . GUYỄN 4
d Bài 11. Cho biết hai đại lượng x và y tỉ lệ nghịch với nhau và khi x = 2 thì y = 9.
a Tìm hệ số tỉ lệ k. N GỌC
b Hãy biểu diễn y theo x.
c Tính giá trị của y khi x1 = −2, x2 = 1, x3 = 3, x4 = 8. DŨN
d Bài 12. Cho biết hai đại lượng x và y tỉ lệ nghịch với nhau và khi x = 4 thì y = 9.
a Tìm hệ số tỉ lệ k. G 0976071956 -
b Hãy biểu diễn y theo x. THPT
c Tính giá trị của y khi x MATH.ND
1 = −9, x2 = −6, x3 = 3, x4 = 12, x5 = 36. TẠ
Dạng 2. Toán đố về tỉ lệ nghịch QU
d Bài 1. Một ô tô chạy ? từ Lớp A đến TO B vớiÁN vận THẦ tốc 60 Y DŨNG
km/h thì hết 2, ?5giờ. Lúc từ B về A, xe
chạy với vận tốc 50 km/h thì mất bao lâu? AN
d Bài 2. Để hoàn thành một công việc cần 12 người làm trong 10 ngày. Nếu muốn làm G
xong sớm 2 ngày thì cần bao nhiêu người (với năng suất như nhau)? BỬU
d Bài 3. Biết 3 học sinh khi làm vệ sinh lớp học hết 3 phút. Hỏi 5 học sinh (cùng năng suất)
sẽ làm vệ sinh lớp học hết bao nhiêu phút?
d Bài 4. Biết 20 công nhân cùng làm một công việc thì hết 6 giờ. Hỏi nếu có thêm 4 công
nhân nữa cùng làm thì sẽ xong sớm hơn được mấy giờ?
d Bài 5. Một ô tô chạy từ A đến B với vận tốc 70 km/h thì hết 3 giờ. Hỏi một ô tô khác
chạy từ A đến B với vận tốc bằng 1, 2 lần ô tô trước thì hết bao nhiêu giờ?
d Bài 6. Để làm một công việc trong 8 giờ cần 35 công nhân. Nếu có 40 công nhân thì
công việc được hoàn thành trong mấy giờ? Page 22 of 56
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
d Bài 7. Một tổ sản xuất giày của nhà máy A có 20 công nhân (với năng suất làm việc
như nhau) cùng làm một kiện hàng trong 60 ngày. Do tính chất công việc nên nhà máy đã
chuyển 8 công nhân sang khâu khác làm việc. Hỏi số công nhân còn lại sẽ cùng nhau xong
kiện hàng trên trong bao nhiêu ngày?
Dạng 3. Các bài toán chia tỉ lệ áp dụng dãy tỉ số bằng nhau
d Bài 1. Tìm 3 số a, b, c biết a, b, c tỉ lệ nghịch với 2; 3; 4 theo thứ tự và a + b − c = 21.
d Bài 2. Tìm độ dài ba cạnh của tam giác biết chu vi tam giác là 62 cm và độ dài ba cạnh
tỉ lệ nghịch với 2; 3; 5. BỬU
d Bài 3. Một ô tô chạy từ A đến B với vận tốc 50 km/h rồi chạy từ B về A với vận tốc 40 G
km/h. Cả đi lẫn về mất 4 giờ 30 phút. Tính thời gian đi và thời gian về? AN
d Bài 4. Một ô tô đi từ A đến B với vận tốc 60 km/h và đi từ B về A với vận tốc 48 km/h. QU
Cả đi lẫn về mất 13 giờ 30 phút. Tính độ dài quãng đường AB. d TẠ
Bài 5. Hãy chia số 470 thành ba phần tỉ lệ nghịch với 3; 4; 5.
d Bài 6. Chia số 200 thành ba phần tỉ lệ nghịch với 7; 4; 2. 1 2 THPT
d Bài 7. Chi số 116 thành ba phần tỉ lệ nghịch với ; và 3. - 2 5
d Bài 8. Ba người An, Bình, Phúc mua tất cả 5, 75 m vải để may áo cỡ như nhau. Số mét G
vải mà An, Bình, Phúc đã mua lần lượt tỉ lệ nghịch với 0, 8; 0, 9 và 1, 2. Hỏi mỗi người đã 0976071956 mua mấy mét vải? DŨN
d Bài 9. Chia số 7576 thành baMATH.ND
phần tỉ lệ nghịch với: 2 5 3 a 4; 7; 6. b ; ; . GỌC 3 6 8 N
d Bài 10. Ba đội máy cày, cài trên ba cánh đồng có cùng diện tích. Đội I cày xong cánh ? Lớp TOÁN THẦY DŨNG ?
đồng trong 8 ngày; đội II cày xong trong 9 ngày; đội III cày xong trong 12 ngày. Hỏi mỗi
đội có bao nhiêu máy cày, biết rằng cả ba đội có 69 máy cày (giả sử năng suất mỗi máy cày là như nhau). GUYỄN N
d Bài 11. Để phục vụ cho việc in tài liệu học tập môn Toán cho học sinh khối 7, ba xưởng
in dành ra tổng cộng 12 máy in (cùng năng suất), và mỗi xưởng được giao in số lượng sách
như nhau. Xưởng thứ nhất in xong trong 4 ngày, xưởng thứ hai in xong trong 6 ngày, xưởng Thầy
thứ ba in xong trong 12 ngày. Hỏi mỗi xưởng có bao nhiêu máy in để phục vụ công tác này?
| Chủ đề 3. Hàm số - Đồ thị hàm số y = ax (a 6= 0) Å −1ã
d Bài 1. Cho hàm số y = f(x) = −4x2 + x − 5. Tính f(−2); f . 2
d Bài 2. Cho hàm số y = f(x) = x3 − 4x. Tính f(0); f(−2).
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 23 of 56 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng Å 1ã
d Bài 3. Cho hàm số y = f(x) = 4x2 − 7. Tính f ; 2 f (3).
d Bài 4. Cho hàm số y = f(x) = −2x2 + 3. Tính f(−1); f(2).
d Bài 5. Vẽ đồ thị hàm số y = x.
d Bài 6. Vẽ đồ thị hàm số y = −x. Thầy
d Bài 7. Vẽ đồ thị hàm số y = 2x.
d Bài 8. Vẽ đồ thị hàm số y = −1 2 x. N
d Bài 9. Vẽ trên cùng một hệ trục tọa độ, đồ thị của các hàm số sau: GUYỄN a y = 3x;
b y = 0, 5x.
d Bài 10. Vẽ trên cùng một hệ trục tọa độ, đồ thị của các hàm số sau: N 1
a y = −2x;
b y = −1 GỌC 3x.
d Bài 11. Vẽ trên cùng một hệ trục tọa độ, đồ thị của các hàm số sau: 3
a y = 2, 5x; b y = − DŨN 4x.
d Bài 12. Điểm nào dưới đây thuộc đồ thị hàm số y = −3x: G
a A(1; −3);
b B(3; 0976071956 −6); c C(0; 0); d D(2; 3). - THPT
d Bài 13. Điểm nào dưới đây thuộc đồ thị hàm số y = 2x: MATH.ND a A(1; 2); b B(2; 3); c C(0; 4); d D(3; 6). TẠ 2 QU
d Bài 14. Điểm nào dưới đây thuộc đồ thị hàm số y = − ? Lớp TOÁN THẦY DŨNG 3x: ? AN a A(1; 2);
b B(3; −2);
c C(6; −4); d D(0; 3). G 2 d Bài 15.
a Vẽ đồ thị hàm số y = − 3x. BỬU Å 2ã
b Cho biết tọa độ các điểm A(−3; 2), B 1; , 3
C(6; 0). Bằng phép tính hãy xác định xem
điểm nào thuộc đồ thị hàm số và biểu diễn các điểm đó trên hệ trục tọa độ.
d Bài 16. Đồ thị của hàm số y = ax đi qua điểm M(−4; 6). Tính hệ số a.
d Bài 17. Đồ thị của hàm số y = ax đi qua điểm M(5; 2). Tính hệ số a.
d Bài 18. Đồ thị của hàm số y = ax đi qua điểm M(6; −4). Tính hệ số a.
d Bài 19. Cho hàm số: y = f(x) = 8x2˘3.
a Tính f (2), f (−3); Page 24 of 56
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
b Tìm x khi f (x) = 13.
d Bài 20. Biết đồ thị hàm số y = mx đi qua điểm M(2; −1).
a Tìm hệ số m.
b Vẽ đồ thị hàm số trên với hệ số m tìm được ở câu a.
d Bài 21. Một gia đình lắp đặt mạng Internet. Hình thức trả tiền được xác định bởi hàm số
sau: T = 500a + 45000. Trong đó: T là số tiền nhà đó phải trả hàng tháng, a (tính bằng giờ) BỬU
là thời gian truy cập Internet trong một tháng. Hãy tính số tiền nhà đó phải trả nếu sử dụng 50 giờ trong một tháng? G
d Bài 22. Năm 1832 nhà bác học người Bỉ là Adolphe Quetelet đã đưa ra chỉ số BMI để đo AN
độ gầy hay béo của cơ thể như sau: BMI = W , với H2 QU
W : khối lượng của một người tính bằng kilogam. TẠ
H: chiều cao của người đó đo bằng mét.
Tổ chức y tế thế giới WHO đã đưa ra tiêu chuẩn như sau: THPT - BMI < 18, 5 : gầy G
18, 5 ≤ BMI ≤ 25 : bình thường 0976071956 25 < BMI ≤ 30 : dư cân DŨN 30 < BMI : béo phì MATH.ND
Bạn Quân có chiều cao của bạn là 1, 6 mét và cân nặng 60 kg. Em hãy kiểm tra chỉ số BMI
của bạn Quân và cho biết bạn có bị béo phì không? GỌC N ? Lớp TOÁN THẦY DŨNG ? GUYỄN N Thầy
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 25 of 56 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng Thầy N GUYỄN N GỌC DŨN G 0976071956 - THPT MATH.ND TẠ QU ? Lớp TOÁN THẦY DŨNG ? AN G BỬU Page 26 of 56
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? BỬU G PHẦN AN QU II TẠ THPT - G HÌNH HỌC 0976071956 DŨN MATH.ND GỌC N ? Lớp TOÁN THẦY DŨNG ? GUYỄN N Thầy 27 Thầy N GUYỄN N GỌC DŨN G 0976071956 - THPT MATH.ND TẠ QU ? Lớp TOÁN THẦY DŨNG ? AN G BỬU 1
Đường thẳng vuông góc. Đường thẳng Chương song song Trọng tâm chương: • Hai góc đối đỉnh.
• Đường trung trực của đoạn thẳng. Vẽ đường thẳng vuông góc. BỬU G
• Hai đường thẳng song song, phân biệt được các loại góc (so le trong, đồng vị,. . . ) AN
• Từ vuông góc đến song song. QU
| Chủ đề 1. Hai góc đối đỉnh TẠ A
KIẾN THỨC CẦN NHỚ THPT
• Hai góc kề bù thì có tổng bằng 180◦; - G
• Hai góc đối đỉnh thì bằng nhau. 0976071956
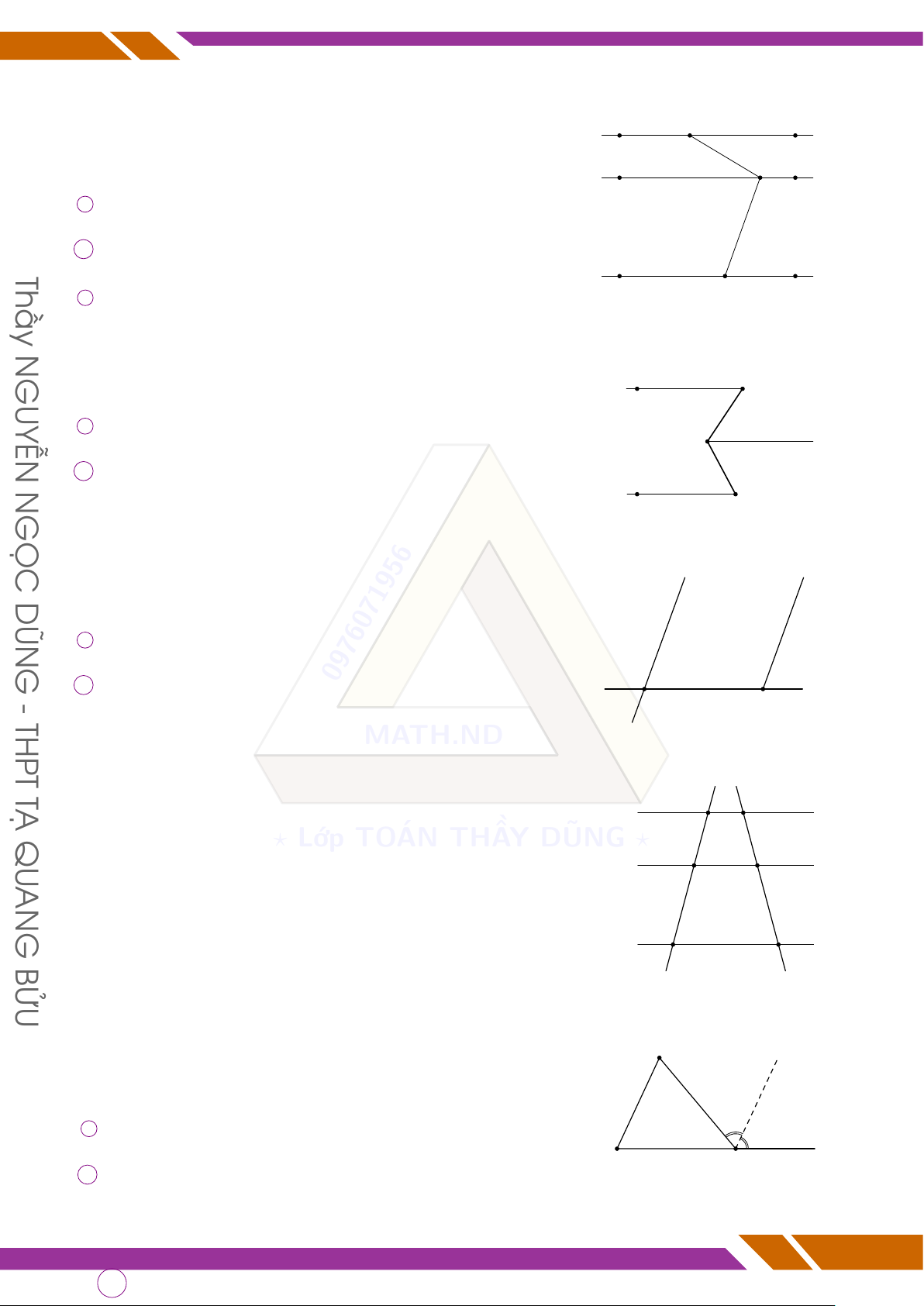
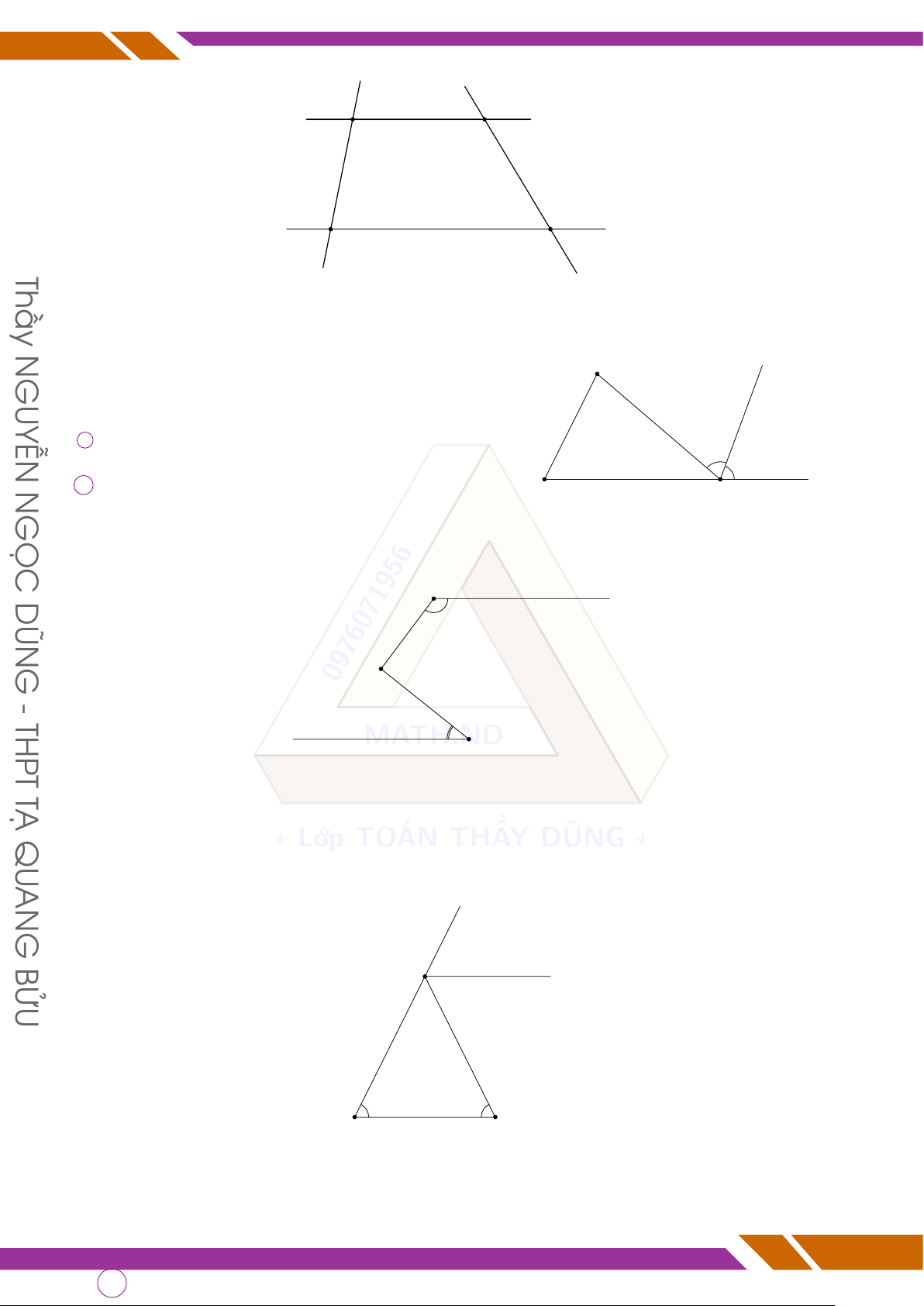
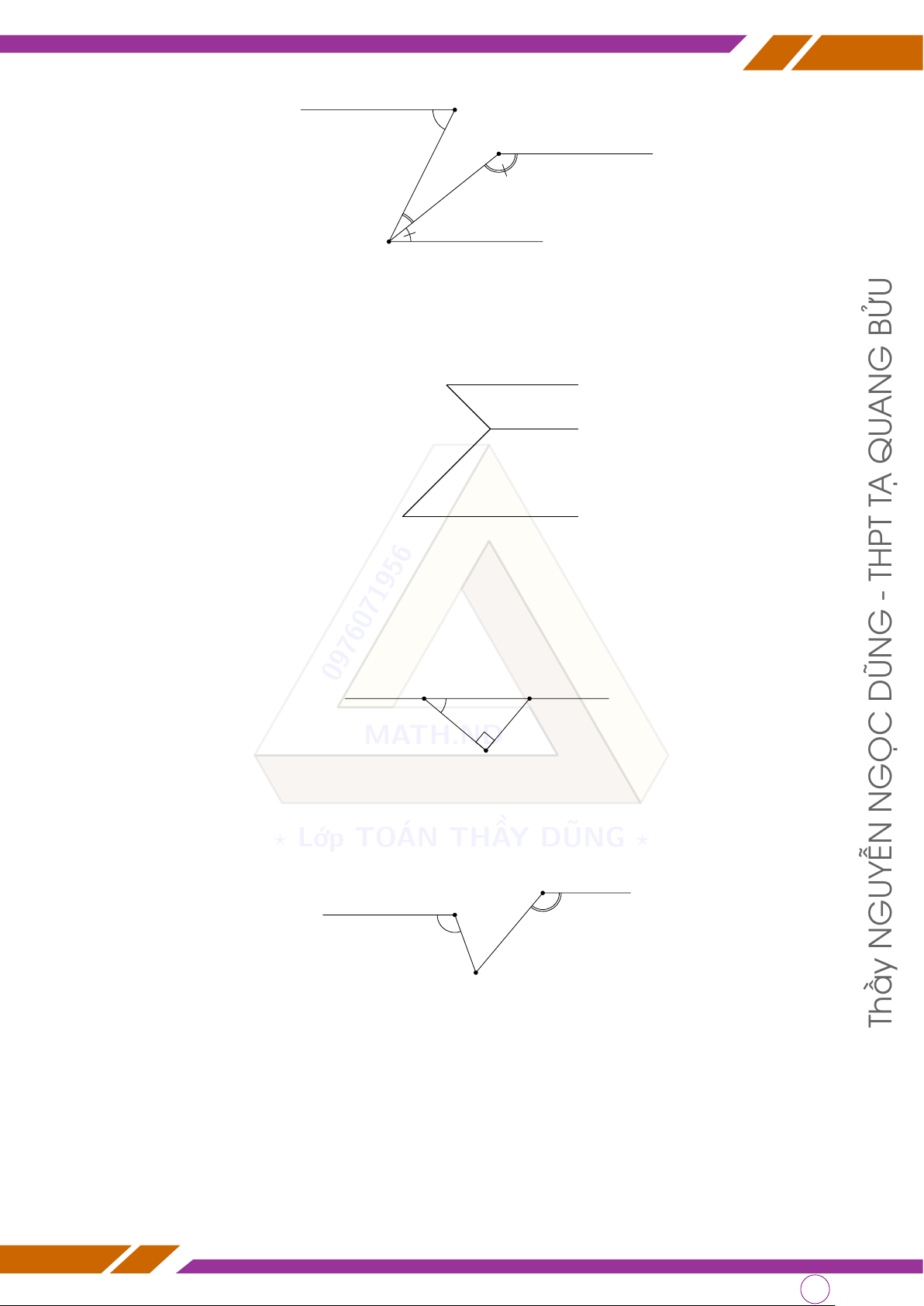
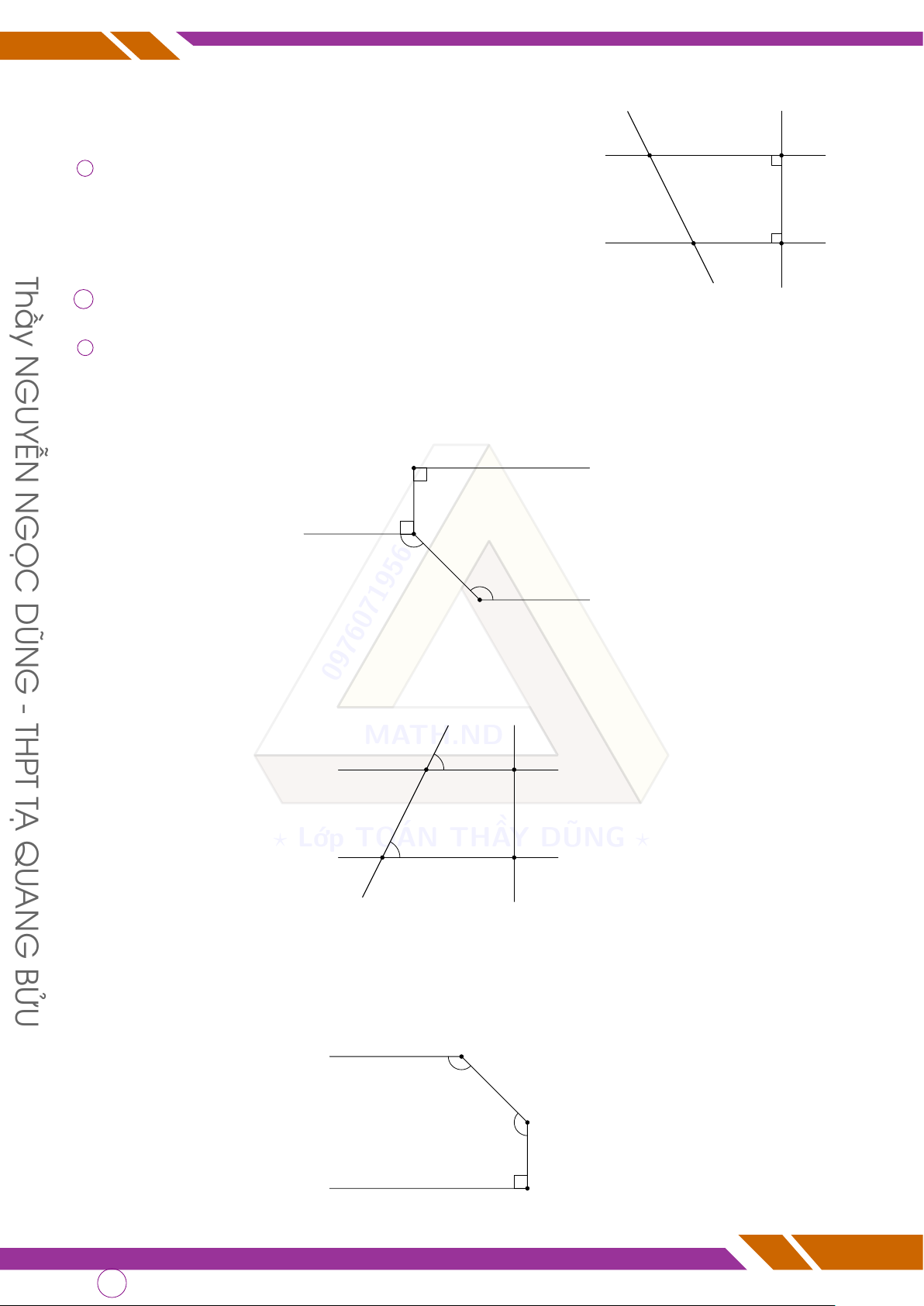
• Tia phân giác là tia chia đôi góc thành hai góc bằng nhau và bằng một nửa góc ban DŨN đầu. MATH.ND GỌC B BÀI TẬP N d Bài 1. Hình nào ? dưới Lớp đây TO có cặp ÁN góc THẦ đối đỉnh.Y DŨNG Gọi tên các ?
cặp góc đối đỉnh ấy. E M M B 4 3 1 2 P 2 1 GUYỄN 1 2 A Q N C D
d Bài 2. Vẽ hai đường thẳng aa0 và bb0 cắt nhau tại A. Hãy viết tên các cặp góc đối đỉnh. Thầy
d Bài 3. Hai đường thẳng cắt nhau tại I sao cho một trong các góc đỉnh I có số đo 124◦. Vẽ
hình và tính số đo các góc tại đỉnh I. d Bài 4. Vẽ góc [
xOy = 65◦. Vẽ tia Ox0 là tia đối của tia Ox, tia Oy0 là tia đối của tia Oy. Tính số đo các góc \ x0Oy0, \ x0Oy và \ xOy0. d Bài 5. Vẽ góc [
xOy có số đo 75◦. Vẽ tia Ox0 là tia đối của tia Ox, tia Oy0 là tia đối của tia
Oy. Tính số đo các góc \ x0Oy0, \ x0Oy và \ xOy0. 29 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng
d Bài 6. Vẽ hai đường thẳng xy và x0y0 cắt nhau tại O. Cho \
xOx0 = 60◦. Hãy tính số đo của \ x0Oy và [ yOy0. d Bài 7. Cho hình vẽ sau: E B
a Kể tên các cặp góc đối đỉnh? A Thầy b Cho [
BAC = 38◦, tính số đo góc [ EAD. C D d Bài 8. Vẽ góc [
xOy có số đo 80◦. Vẽ góc \
x0Oy0 đối đỉnh với góc [
xOy (Ox và Ox0 là hai tia N
đối nhau). Vẽ tia phân giác Ot của góc \
x0Oy0. Tính số đo của góc [ x0Ot? GUYỄN
d Bài 9. Vẽ hai đường thẳng cắt nhau sao cho trong các góc tạo thành có một góc 47◦. Tính số đo các góc còn lại.
d Bài 10. Hai đường thẳng AB và CD cắt nhau tại O tạo thành bốn góc. Tính số đo của N GỌC
bốn góc ấy, biết rằng [ AOD − \ BOD = 30◦.
d Bài 11 (?). Cho góc [
AOB có OM là tia phân giác. Gọi OA0 là tia đối của tia OA, OB0 là
tia đối của tia OB, ON là tia phân giác của \
A0OB0. Chứng tỏ rằng \ AOM = \ A0ON. DŨN
| Chủ đề 2. Đường vuông góc. Đường trung trực G 0976071956 - THPT A
KIẾN THỨC CẦN NHỚ MATH.ND
• Đường trung trực của đoạn thẳng là đường vuông góc với đoạn thẳng đó tại trung T điểm. Ạ QU ? Lớp TOÁN THẦY DŨNG ? B BÀI TẬP AN
d Bài 1. Trên đường thẳng xy lấy theo thứ tự ba điểm A, B, C sao cho AB = 4 cm, BC = 6 G
cm. Vẽ đường trung trực n của đoạn thẳng AB và đường trung trực m của đoạn thẳng BC. BỬU
d Bài 2. Vẽ hình theo cách diễn đạt bằng lời sau, vẽ trên cùng một hình:
Cho ba điểm M, N, P không thẳng hàng sao cho MN = 6 cm.
- Vẽ đường thẳng a là đường trung trực của đoạn thẳng MN;
- Qua điểm N, vẽ đường thẳng b vuông góc với đường thẳng MP;
d Bài 3. Cho ba điểm A, B, C không thẳng hàng.
- Vẽ đường thẳng đi qua A và vuông góc với BC;
- Vẽ đường trung trực của đoạn thẳng AC. Page 30 of 56
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
d Bài 4. Vẽ hình theo cách diễn đạt bằng lời sau, vẽ trên cùng một hình: - Vẽ \ HAK nhọn và \
mAn là góc đối đỉnh với \ HAK.
- Vẽ HB vuông góc với AK tại B.
- Vẽ đường thẳng c là đường trung trực của BH.
d Bài 5. Vẽ hình theo cách diễn đạt bằng lời sau: - Vẽ góc [
xOy có số đo bằng 60◦. BỬU G
- Lấy điểm A trên tia Ox (A khác O) rồi vẽ đường thẳng d1 vuông góc với tia Ox tại A. AN
- Lấy điểm B trên tia Oy (B khác O) rồi vẽ đường thẳng d2 vuông góc với tia Oy tại B. QU
- Gọi giao điểm của d1 và d2 là C. TẠ
d Bài 6. Cho đoạn thẳng AB = 6 cm. Hãy vẽ đường trung trực d của đoạn thẳng AB (có kí hiệu đầy đủ). THPT
d Bài 7. Vẽ hình theo cách diễn đạt bằng lời sau: -
- Cho đường thẳng m và điểm A nằm ngoài đường thẳng m. Vẽ đường thẳng d0 đi qua G
A và vuông góc với m 0976071956 tại B. DŨN
- Vẽ đường thẳng n là đường trung trực của AB. MATH.ND
d Bài 8. Vẽ hình theo phát biểu sau: Cho [
xOy = 50◦, vẽ Ot là tia phân giác của [ xOy. Trên GỌC
tia Ot lấy điểm A sao cho OA = 3 cm, vẽ đường trung trực d của OA. N d Bài 9. Vẽ hình ? theo Lớp cách TO diễn đạÁN t sau: THẦY DŨNG ? - Vẽ [ xOy = 60◦; GUYỄN
- Trên tia Ox lấy điểm M sao cho OM = 4 cm; N
- Vẽ đường trung trực h của OM, trên h lấy điểm N sao cho N nằm trong góc [ xOy;
- Qua N vẽ đường thẳng n vuông góc với Oy tại I. Thầy
d Bài 10. Vẽ hình theo cách diễn đạt sau: Vẽ góc ”
zIt có số đo bằng 45◦. Lấy điểm B bất kỳ nằm trong góc ”
zIt và điểm C nằm trên
cạnh Iz sao cho IC = 4 cm.
a Vẽ đường trung trực m của đoạn thẳng IC;
b Qua điểm C vẽ đường thẳng d vuông góc với cạnh It tại K.
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 31 of 56 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng
d Bài 11. Vẽ hình theo cách diễn đạt sau: - Vẽ góc [
xOy = 60◦. Trên tia Ox lấy điểm M sao cho OM = 4 cm.
- Vẽ đường trung trực h của đoạn thẳng OM, trên h lấy điểm N sao cho N nằm trong góc [ xOy. Thầy
- Qua N vẽ đường thẳng n vuông góc với tia Oy tại P.
d Bài 12. Vẽ hình theo cách diễn đạt sau: N
Vẽ đoạn thẳng BC dài 4 cm. Vẽ đường thẳng d1 là đường trung trực của đoạn BC. Trên d1 GUYỄN
lấy một điểm A bất kỳ (A /∈ BC). Qua A vẽ d2 vuông góc với d1.
d Bài 13. Vẽ hình theo cách diễn đạt sau, vẽ trên cùng một hình:
- Vẽ tam giác ABC. Vẽ đường thẳng a đi qua A và vuông góc với BC. N GỌC
- Vẽ đường thẳng b đi qua C và vuông góc với BC.
- Gọi M là giao điểm của đường thẳng a và BC. Vẽ đường thẳng c là đường trung trực DŨN
của đoạn thẳng AM. d G Bài 14. Cho y ‘
xAy = 80◦ và điểm M như 0976071956
hình vẽ. Hãy vẽ lại hình và vẽ tiếp - THPT theo yêu cầu sau đây: MATH.ND
- Vẽ qua điểm M đường thẳng d vuông góc với tia Ay. M TẠ
- Vẽ đường thẳng t là đường trung trực của đoạn thẳng AM. QU A x - Vẽ \ x0Ay0 đối đỉnh ? với Lớp ‘ xAy. TO Tính ÁN số đo THẦ \ x0Ay0. Y DŨNG ? AN
d Bài 15. Vẽ trên cùng một hình theo cách diễn đạt sau: G
- Lấy ba điểm A, B, C không thẳng hàng, vẽ góc [ BAC. BỬU
- Vẽ đường trung trực a của đoạn thẳng AB.
- Vẽ đường thẳng m vuông góc với AC tại C. - Vẽ góc \
HAQ đối đỉnh với góc [ BAC.
d Bài 16 (?). Cho góc bẹt [
AOB. Trên một nửa mặt phẳng bờ AB vẽ các tia OC và OD sao 1 cho \ AOC = 60◦; \ BOD = \
2AOC. Chứng tỏ rằng hai tia OC và OD vuông góc với nhau.
d Bài 17 (?). Cho hai góc [ xOy và \
yOx0 kề bù, vẽ Ot và Ot0 lần lượt là tia phân giác của [ xOy và \
yOx0. Chứng minh rằng tia Ot vuông góc với tia Ot0. Page 32 of 56
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
d Bài 18. Cho xy là đường trung trực của đoạn thẳng AB. Trên tia đối của tia AB lấy điểm
C, trên tia đối của tia BA lấy điểm D sao cho BD = AC. Vì sao xy là đường trung trực của CD?
d Bài 19. Cho hai góc kề bù AOM và BOM trong đó \
AOM = 50◦. Vẽ tia ON ở trong góc
BOM sao cho ON ⊥ OM. Tính số đo góc BON.
| Chủ đề 3. Hai đường thẳng song song BỬU G A
KIẾN THỨC CẦN NHỚ AN
a Nếu một đường thẳng cắt hai đường thẳng song song thì: QU
• Hai góc so le trong bằng nhau; b A 2 TẠ
• Hai góc đồng vị bằng nhau; 1
• Hai góc trong cùng phía bù nhau. a 1 THPT B - c A1 = c B1 (hai góc so le trong) G a k b Ñ c A2 = c B1 (hai góc đồng vị) c A2 + c B1 = 0976071956
180◦ (hai góc trong cùng phía). DŨN
b Để chứng minh hai đường MATH.ND
thẳng song song, ta chứng minh một trong các ý sau: GỌC
• Hai góc so le trong bằng nhau; N • Hai góc ? đồng Lớp vị TO bằng nhaÁN u; THẦY DŨNG ?
• Hai góc trong cùng phía có tổng bằng 180◦. GUYỄN
c Tính chất bắc cầu: N c a k b Ñ a k c. b Thầy b k c a B BÀI TẬP
Dạng 1. Xác định các loại góc d Bài 1.
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 33 of 56 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng
Cho hình vẽ bên, điền vào chỗ trống c M - Góc so le trong với a 4 3 c
N1 là . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 2 - Góc đồng vị với b 1 2 c
N2 là . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . N
- Góc trong cùng phía với ”
M1 là . . . . . . . . . . . . . . . . . . . . . . . . . . Thầy
d Bài 2. Xem hình rồi điền vào chỗ trống vị trí các cặp góc trong các câu sau: N E D GUYỄN a [ EBC và \
BCG là một cặp góc . . . . . . . . . . . . . . . . . . . . H B A C b [ ABF và [
EBC là một cặp góc . . . . . . . . . . . . . . . . . . . . . c \ DCB và \
HCD là một cặp góc . . . . . . . . . . . . . . . . . . . . N GỌC F G d [ F BC và \
GCB là một cặp góc . . . . . . . . . . . . . . . . . . . . e [ ABF và \
BCG là một cặp góc . . . . . . . . . . . . . . . . . . . . DŨN d Bài 3. G
Xem hình rồi điền vào chỗ 0976071956
trống vị trí các cặp góc trong các - THPT câu sau: B 1 A MATH.ND 2 1 2 a c A1 và c
A2 là hai góc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . TẠ b c A1 và c
B2 là hai góc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . QU ? Lớp TOÁN THẦY DŨNG ? c c A1 và c
B1 là hai góc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . AN G d Bài 4. BỬU
Cho hình vẽ, hãy điền vào chỗ trống thích hợp các câu sau: c A3 4 a c B1 và c
B3 là một cặp góc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . a 2 1 b c B2 và c
A2 là một cặp góc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B 3 4 c 2 c B3 và c
A2 là một cặp góc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . b 1 d c B4 và c
A2 là một cặp góc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . d Bài 5. Page 34 of 56
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
Cho hình vẽ, hãy điền vào chỗ trống thích hợp các câu sau: c A 2 a 3 c A1 và c
B2 là một cặp góc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . a 1 4 b c A1 và c
B3 là một cặp góc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B 3 2 c 1 c A1 và c
B1 là một cặp góc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . b 4 d c B3 và c
B4 là một cặp góc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . e c B2 và c
B4 là một cặp góc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . BỬU
Dạng 2. Hai đường thẳng song song G d Bài 1. Cho hình vẽ sau. Biết c c A1 = 45◦, c B1 = 135◦. AN a Tính A c B a QU 2. 1 TẠ
b Đường thẳng a có song song với đường thẳng b không? Vì sao? 1 2 b B THPT d - Bài 2. Cho hình vẽ sau, biết \ aMP = 110◦; \ MPb = 70◦. G a M N 1
a Chứng minh MN k PQ.0976071956 110◦ DŨN 70◦ 3 b Cho 1 c
N1 = 50◦. Tính c Q1; c Q2.MATH.ND b 2 P Q d GỌC
Bài 3. Cho hình vẽ sau, tính số đo góc c D1. N ? Lớp TOÁN A THẦY DŨNG C 100◦ ? 70◦ GUYỄN N 70◦ 1 2 B D Thầy d Bài 4. Cho hình vẽ, biết c B1 = 135◦; c E1 = 45◦. a B1 M 1 a Tính số đo c
B2. Chứng minh a k b. 3 b Tính số đo 1 1 c B3; c E2; c E3. b 2E N
c Biết 2 · ” M1 = 3 · c N1. Tính số đo ” M1; c N1.
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 35 of 56 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng d Bài 5.
Cho hình vẽ sau. Biết AD k CF; BE k AD; \ DMN = 32◦; A M D [ NPF = 58◦. B E N
a BE có song song với CF không? Vì sao? b Tính \ MNB. Thầy C F
c Chứng tỏ MN ⊥ NP. P N d Bài 6. GUYỄN
Cho hình vẽ bên, biết AB k Dx k CE, \
BDC = 115◦; “ C = 45◦. A B a Tính số đo góc [ xDC. x D N b Tính số đo góc b B. GỌC E C d Bài 7. DŨN Cho hình bên dưới, biết x y c A2 = 70◦, b B = 110◦. a Tính số đo c A1. G 0976071956 -
b Chứng tỏ rằng Ax k By. 1 110◦ 2 THPT A B 70◦ MATH.ND d Bài 8. TẠ
Cho hình vẽ sau. Biết a k b k c; [ BAD = 120◦; [
DEB = 60◦. Tính số A D a QU đo các góc [ aDe, [ ABE, c C1?, Lớp c F1. TOÁN THẦY DŨNG ? B E b AN G C F c BỬU 1 1 d Bài 9.
Cho hình vẽ, biết rằng tia Cx là tia phân giác của [ ACy. Chứng A tỏ rằng x a Cx k AB; 65◦ 50◦ B C y
b Tính số đo của b A. d Bài 10. Page 36 of 56
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
Cho hình vẽ bên, biết AB k CD, y b A = 40◦, “ C = 30◦. Tính A B số đo \
AOC (học sinh phải vẽ đúng số đo những góc đã cho). O C D x d Bài 11.
Cho hình dưới, chứng tỏ rằng A x 45◦ BỬU a Ax k By; y G 135◦ 75◦ b Cz k By. B AN 30◦ z C QU
d Bài 12 (? Giữa kỳ 1, THPT Chuyên Trần Đại Nghĩa 2016 - 2017). TẠ
Cho hình vẽ sau, biết rằng DE song song với AB, A B 60◦ F [ ECF = 40◦, [ CF G = 100◦, [ BAC = 60◦. G 100◦ THPT D E a Tính số đo góc [ DEC; - 40◦ G
b Chứng minh rằng DE k FG. 0976071956 C DŨN d Bài 13. Cho [
xOy = 120◦. Lấy điểm A trên tia Ox. Trên nửa mặt phẳng bờ Ox có chứa
tia Oy, vẽ tia At sao cho ‘ OAt = MA 60◦. TH.ND GỌC
a Chứng minh At k Oy. N ? Lớp TOÁN THẦY DŨNG ?
b Gọi On, Am lần lượt là hai tia phân giác của các góc [ xOy, ‘
xAt. Chứng minh On k Am. L GUYỄN Lời giải N a Ta có: ‘
OAt = 60◦. Suy ra ‘ xAt = 120◦. Suy ra At k Oy. Thầy b Ta có: [ xOn = 60◦, \ xAm = 60◦. Suy ra On k Am.
d Bài 14. Tìm x trong hình vẽ sau?
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 37 of 56 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng 100◦ A C 135◦ B 80◦ D x Thầy d Bài 15. N x GUYỄN
Cho hình vẽ sau, biết rằng tia Cx là tia phân giác A
của góc ACy. Chứng tỏ rằng: a Cx k AB; 65◦ N 50◦
b Tính số đo của góc A. GỌC B C y
d Bài 16. Cho hình vẽ sau, biết AB k EF. Tính số đo [ ACE. DŨN A x 120◦ G C 0976071956 - THPT MATH.ND 30◦ y E TẠ d QU
Bài 17. Cho hình vẽ sau, biết b B = “
C và Ay k BC. Chứng tỏ rằng tia Ay là tia phân giác ? Lớp TOÁN THẦY DŨNG ? của [ CAx. AN x G BỬU y A B C
d Bài 18. Cho hình vẽ sau, biết [ ABy = 60◦; [ BAC = 20◦; [ CAx = 40◦; ‘
ACt = 140◦. Chứng tỏ Ct k By. Page 38 of 56
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU y B 60◦ C t 140◦ 20◦ 40◦ x A
d Bài 19 (?). Cho hình vẽ: BỬU G x A 45◦ 135◦ y AN 75◦B QU 30◦ z TẠ C
Chứng minh rằng Ax k By k Cz. THPT -
d Bài 20 (?). Cho hình vẽ sau, biết [ DAB = 40◦; [
DBA = 90◦. Tính số đo góc [ ADB. G 0976071956 A D x DŨN 40 ◦ MATH.ND B GỌC N
d Bài 21 (?). Cho ? hình Lớp vẽ sa TO u, biết ÁN AB k THẦ DE; Y [ ABC DŨNG = 110◦; ? [
CDE = 130◦. Tính góc [ BCD. D E A B 130◦ GUYỄN 110◦ N C Thầy d Bài 22. Cho góc [
xOy. Lấy điểm A trên tia Ox, điểm B trên tia Oy. Vẽ ra ngoài góc [ xOy
các tia Am và Bn song song với nhau thỏa mãn \
OAm = 30◦ và [
OBn = 60◦. Chứng tỏ rằng Ox ⊥ Oy. d Bài 23. Cho góc \
MON có số đo bằng 70◦. Lấy điểm A trên tia OM, điểm B trên tia ON.
Vẽ các tia Ax và By ở trong góc \ MON sao cho \
MAx = 30◦ và [
NBy = 40◦. Chứng tỏ rằng Ax k By.
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 39 of 56 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng
| Chủ đề 4. Từ vuông góc đến song song A
KIẾN THỨC CẦN NHỚ
• Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song song với nhau. Thầy d a ⊥ d b N Ñ a k b. GUYỄN b ⊥ d a
• Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông N GỌC
góc với đường còn lại. d d ⊥ b b DŨN Ñ d ⊥ a. a k b a G 0976071956 - THPT MATH.ND B BÀI TẬP TẠ d Bài 1. QU
Cho hình vẽ sau. Biết a c ? ⊥ c Lớp , b ⊥ c TO ; c A1 ÁN
= 47◦. THẦY DŨNG ?b A 1 AN
a Đường thẳng a có song song với đường thẳng b không? Vì sao? G a B 1 2 BỬU b Tính c B1 và c B2. d Bài 2.
Cho hình vẽ sau, biết c A1 = 115◦. a A C a Vì sao a k b. 1 b Tính c B1. b 1 3 B D d Bài 3. Page 40 of 56
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU Cho hình vẽ sau, biết c c D1 = c
C1. Chứng tỏ c ⊥ b. a A D 1 b 1 B C d Bài 4. Cho hình vẽ sau. P R 1
a Chứng minh PR k QS. BỬU 1 b Cho c R G
1 = 50◦. Tính số đo các góc [ PRS, [ RSQ, “ S1. Q S AN d Bài 5.
Cho hình vẽ sau. Biết m ⊥ k, n ⊥ k; c D1 = 45◦. k QU m D A 1 a TẠ
Giải thích vì sao có thể kết luận m k n? n 1
b Tính số đo các góc 2 c C1 và c C2. C B THPT -
d Bài 6. Cho hình vẽ sau: G B 0976071956D N x y DŨN MATH.ND A 60◦ 50◦ GỌC C M N ? Lớp TOÁN THẦY DŨNG ? Hãy tìm x, y. d Bài 7. GUYỄN
Cho hình vẽ sau (học sinh phải vẽ hình đúng số đo góc đã N a A D 45◦ cho).
a Chứng minh a k b. b Thầy B C 45◦
b Chứng minh AB ⊥ b.
c Kẻ At là tia phân giác của [
BAD. Chứng minh At k DC.
d Kẻ Az là tia phân giác của [
aAB. Chứng minh Az ⊥ DC.
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 41 of 56 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng d Bài 8. Xem hình vẽ sau a A C
a Điền vào chỗ trống: • [
CAB và B3 là cặp góc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . b 4 3 • [ CAB và B Thầy
3 là cặp góc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B1 2 D
b Chứng minh AC k BD. N c Cho biết [
CAB = 67◦. Tính số đo các góc c B1, c B2. GUYỄN
d Bài 9. Cho hình vẽ sau, biết AB ⊥ AD, CD ⊥ AD, [
CDE = 130◦ và b
E = 130◦. Chứng minh rằng AB k EF. A B N GỌC C D 130◦ 130◦ DŨN E F G
d Bài 10. Cho hình vẽ sau, biết 0976071956 c A1 = c B1 và c C1 = c
C2. Chứng minh rằng m ⊥ b. - THPT n m MATH.ND a A 1 C T 1 2 Ạ QU ? Lớpb TOÁN 1 THẦY DŨNG ? AN B D G d BỬU
Bài 11. Cho hình vẽ sau, biết MN ⊥ NP, \ ABM = \
BMN = 135◦. Chứng minh rằng AB k NP. A B 135◦ M 135◦ P N Page 42 of 56
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
d Bài 12. Cho tam giác ABC có b B = “
C. Tia phân giác của góc [
BAC cắt BC tại D. Vẽ tia
Ay nằm trong nửa mặt phẳng bờ AB có chứa điểm C sao cho Ay k BC. Chứng minh rằng Ay ⊥ AD.
d Bài 13 (Đề 1 tiết, THCS Trường Chinh, Tân Bình 2016 - 2017). Cho góc nhọn \ mOn và điểm
H thuộc tia Om. Vẽ tia Hx song song với tia On và nằm ngoài góc mOn. Vẽ tia Oy và Ht
lần lượt là phân giác của \ mOn và \
xHm. Chứng minh rằng Oy ⊥ Ht.
d Bài 14. Cho hai đường thẳng a, b song song với nhau, một cát tuyến d cắt a, b lần lượt tại
A và B. Vẽ tia Ax, By theo thứ tự là tia phân giác của [ aAB và [
bBA. Chứng minh Ax ⊥ By. BỬU G AN QU TẠ THPT - G 0976071956 DŨN MATH.ND GỌC N ? Lớp TOÁN THẦY DŨNG ? GUYỄN N Thầy
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 43 of 56 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng Thầy N GUYỄN N GỌC DŨN G 0976071956 - THPT MATH.ND TẠ QU ? Lớp TOÁN THẦY DŨNG ? AN G BỬU Page 44 of 56
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? 2 Tam giác Chương
Châu thổ sông Hồng Có hình tam giác Một thảm lúa vàng Mênh mông bát ngát Trọng tâm chương: BỬU G
• Nhớ tính chất tổng ba góc trong một tam giác, góc ngoài tam giác. AN
• Biết chứng minh hai tam giác bằng nhau dựa vào ba trường hợp. QU
• Chứng minh các yếu tố hình học dựa vào tam giác bằng nhau. TẠ
| Chủ đề 1. Tổng ba góc của một tam giác THPT
d Bài 1. Tìm số đo x trong các hình vẽ sau: - G A G x x 0976071956 DŨN MATH.ND 55◦ 40◦ 122◦ m B C 55◦ GỌC H I N Hình a)
? Lớp TOÁN THẦY DŨNG ?Hình b)
d Bài 2. Cho 4ABC. a Biết b A = 45◦, b
B = 80◦. Tính “ C. b Biết b A = 60◦ và b B − “
C = 10◦. Tính b B, “ C. GUYỄN N
d Bài 3. Tính số đo góc x ở các hình sau 30◦ Thầy 90◦ x x 55◦ x 40◦ 50◦ x Hình a) Hình b) Hình c)
d Bài 4. Tính số đo các góc x, y ở các hình dưới 45 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng D y A 40◦40◦ 60◦ 40◦ x 70◦ x y E K B D C Thầy Hình a) Hình b) N GUYỄN
d Bài 5. Tính số đo các góc của các tam giác sau: A D 2x 3x N GỌC x 2x 3x B C E F DŨN Hình a) Hình b) G
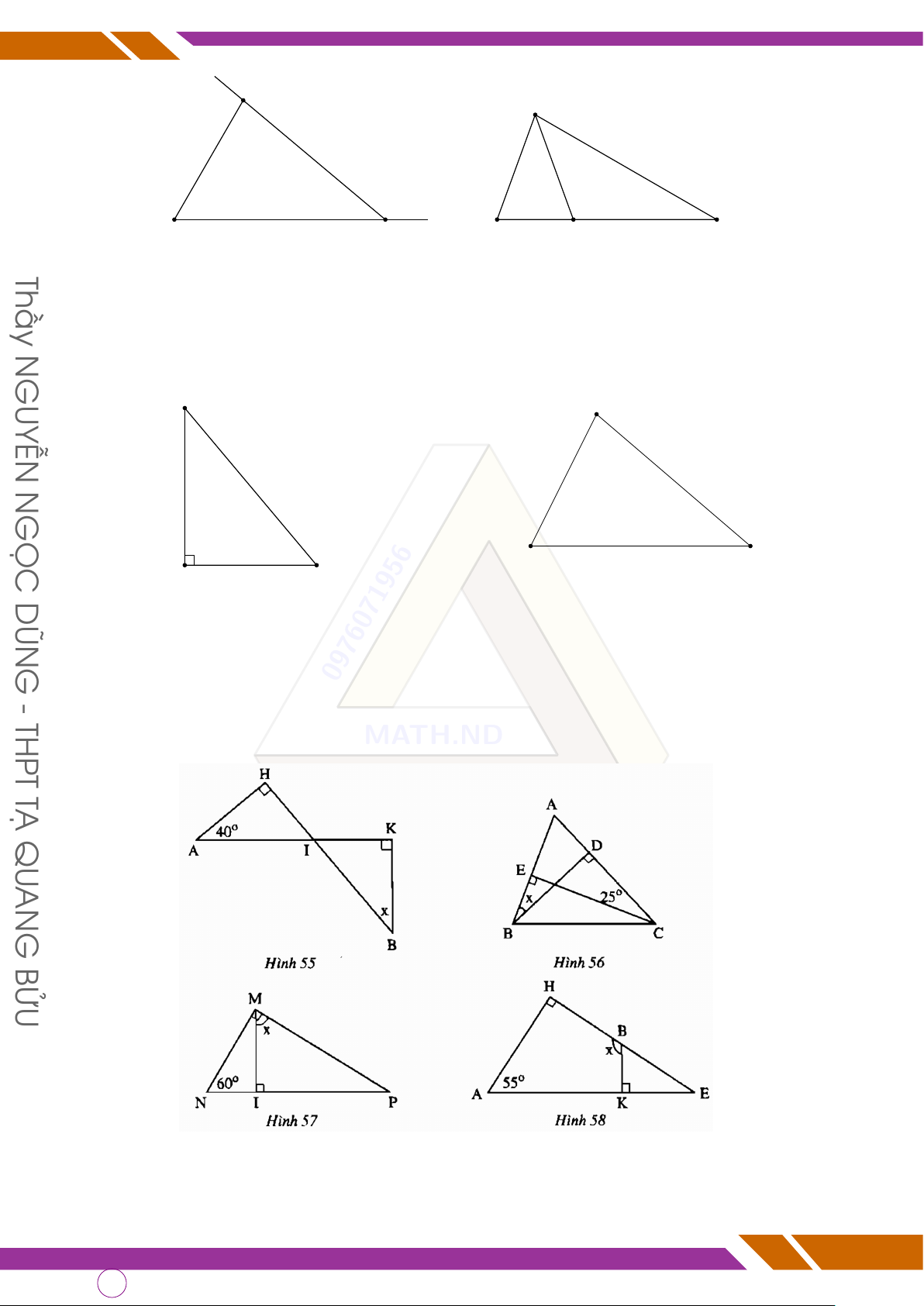
d Bài 6. Tính số đo x ở các 0976071956 hình 55, 56, 57, 58. - THPT MATH.ND TẠ QU ? Lớp TOÁN THẦY DŨNG ? AN G BỬU Page 46 of 56
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
| Chủ đề 2. Trường hợp bằng nhau thứ nhất của tam
giác: cạnh - cạnh - cạnh
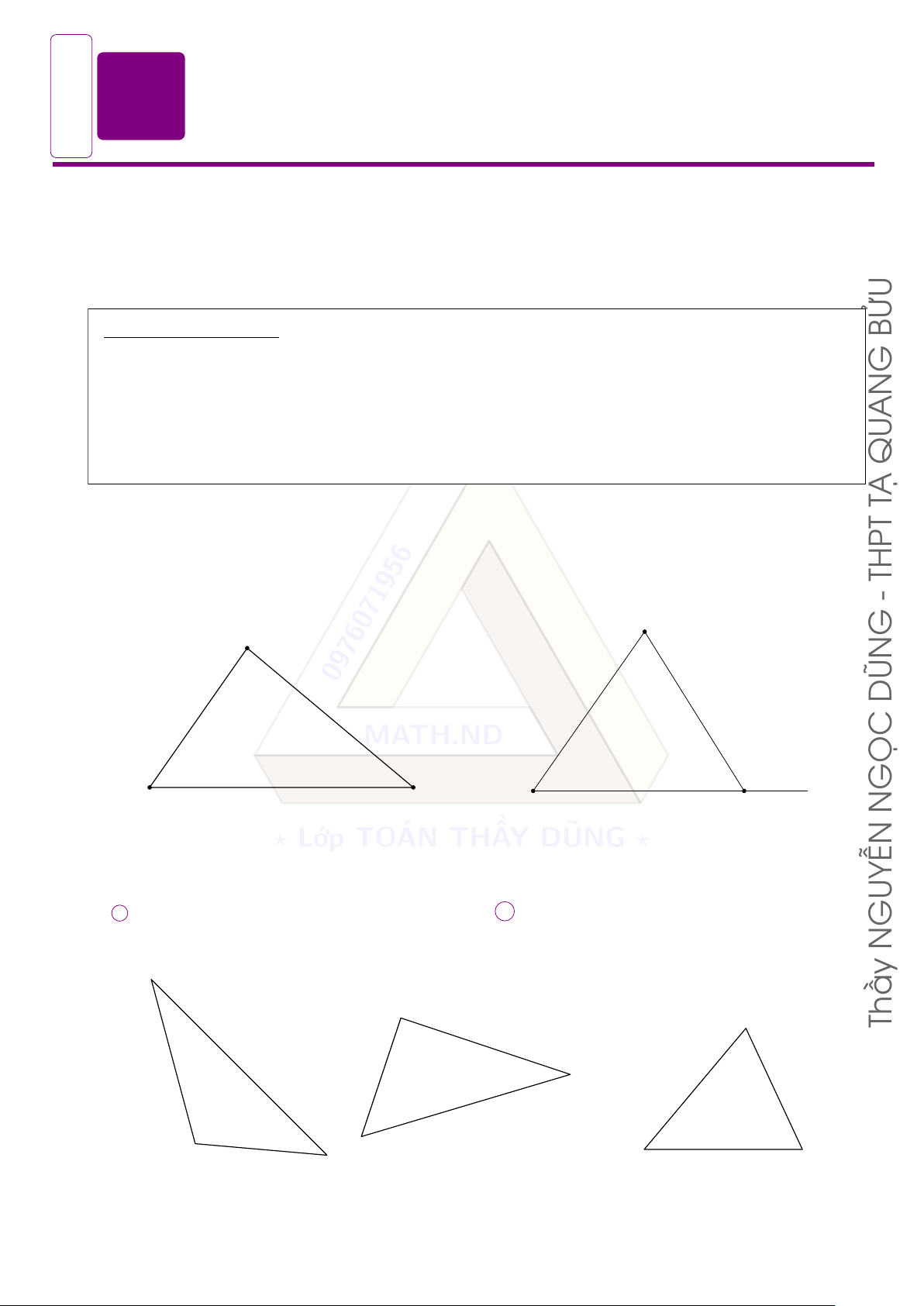
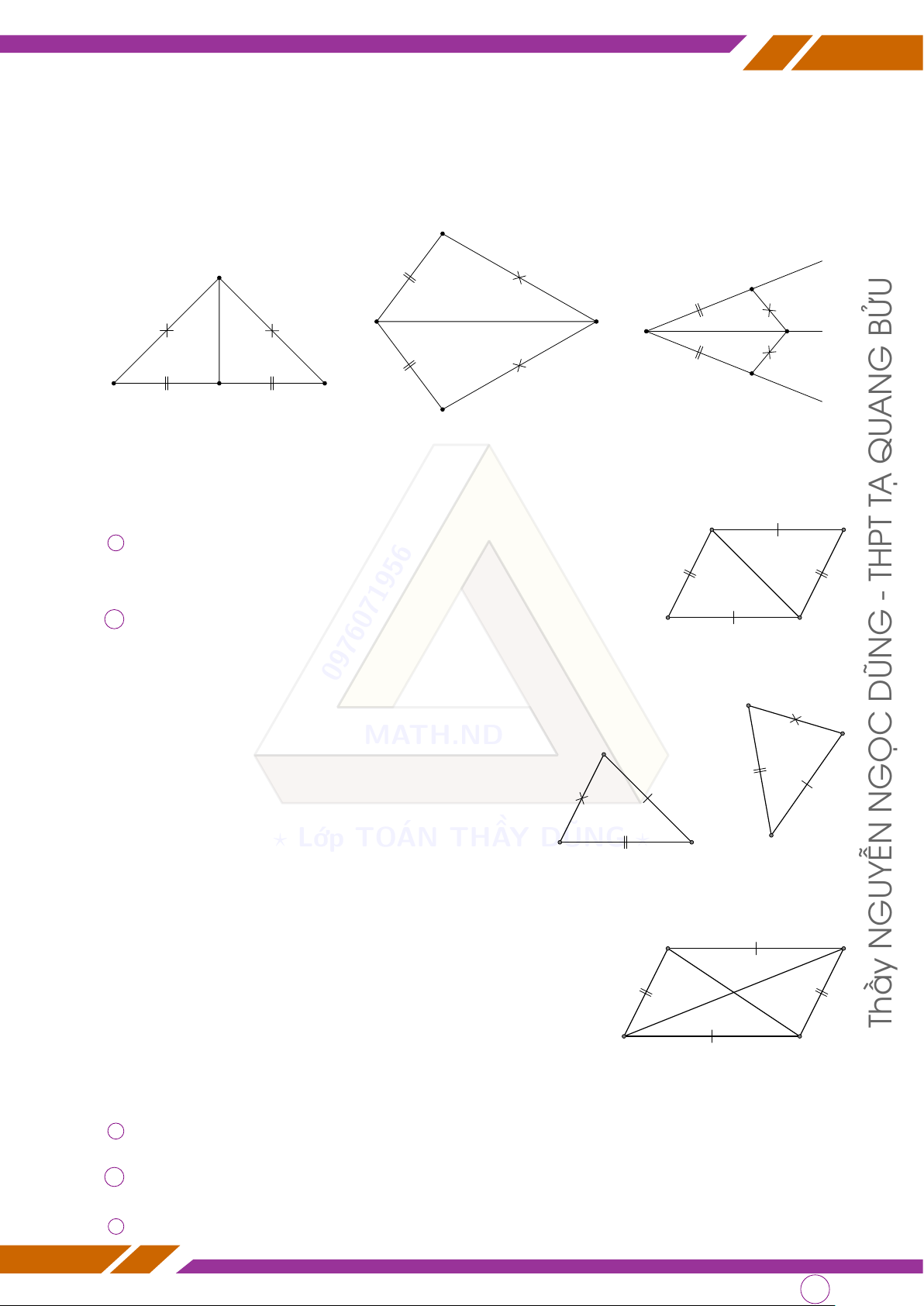
d Bài 1. Chứng minh các tam giác sau bằng nhau: A x A A O B C t BỬU C G B C B y M c) AN a) D b) QU d Bài 2. TẠ A B
a Cho hình vẽ, chứng tỏ rằng hai tam giác 4ABC và 4ADC bằng nhau. THPT - b Cho biết b
B = 60◦, tính góc D. D C G d Bài 3. 0976071956
Chứng minh hai tam giác trong hình vẽ sau bằng M DŨN
nhau, từ đó tính số đo các góc N MA của 4 TH.ND MNP. A 55◦ GỌC N ? Lớp TOÁN THẦY DŨNG 80◦ ? B C P d Bài 4. GUYỄN
Cho hình vẽ bên, chứng minh rằng 4ADC = 4CBA và A B N 4ABD = 4CDB. Thầy D C
d Bài 5. Cho 4ABC có AB = AC, M là trung điểm của BC.
a Chứng minh 4AMB = 4AMC.
b Chứng minh AM là tia phân giác của [ BAC.
c Chứng minh AM vuông góc với BC.
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 47 of 56 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng
d Bài 6. Cho 4ABC có AB = AC, M là trung điểm của BC. a Chứng minh b B = “ C.
b Chứng minh AM là tia phân giác của [ BAC. Thầy
c Chứng minh AM là đường trung trực của BC. N d Bài 7. Cho góc ‘
xAy. Lấy A làm tâm vẽ đường tròn bán kính r, cắt Ax tại B, cắt Ay tại GUYỄN
D. Lần lượt lấy B và D làm tâm vẽ hai đường tròn cũng có bán kính bằng r, hai đường tròn
này cắt nhau tại C (C khác A). Chứng minh
a AC là tia phân giác của ‘ xAy. N GỌC b AD k BC. DŨN
c BD là tia phân giác của [ BAC. G d AC ⊥ DB. 0976071956 - THPT
d Bài 8 (?). Cho tam giác ABC. Vẽ đoạn thẳng AD vuông góc với AB (D và C nằm khác
phía đối với AB), AD = AB. Vẽ đoạn MATH.ND
thẳng AE vuông góc với AC (E và B nằm khác phía đối
với AC), AE = AC. Biết rằng DE = BC. Tính [ BAC. TẠ QU ? Lớp TOÁN THẦY DŨNG ? | AN
Chủ đề 3. Trường hợp bằng nhau thứ hai của tam
giác: cạnh - góc - cạnh G
BỬU A KIẾN THỨC CẦN NHỚ
Xét 4ABC và 4A0B0C0 có A A0 AB = A0B0 b A = “ A0 AC = A0C0 B B0 C C0
Ñ 4ABC = 4A0B0C0 (c.g.c). Page 48 of 56
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU B BÀI TẬP
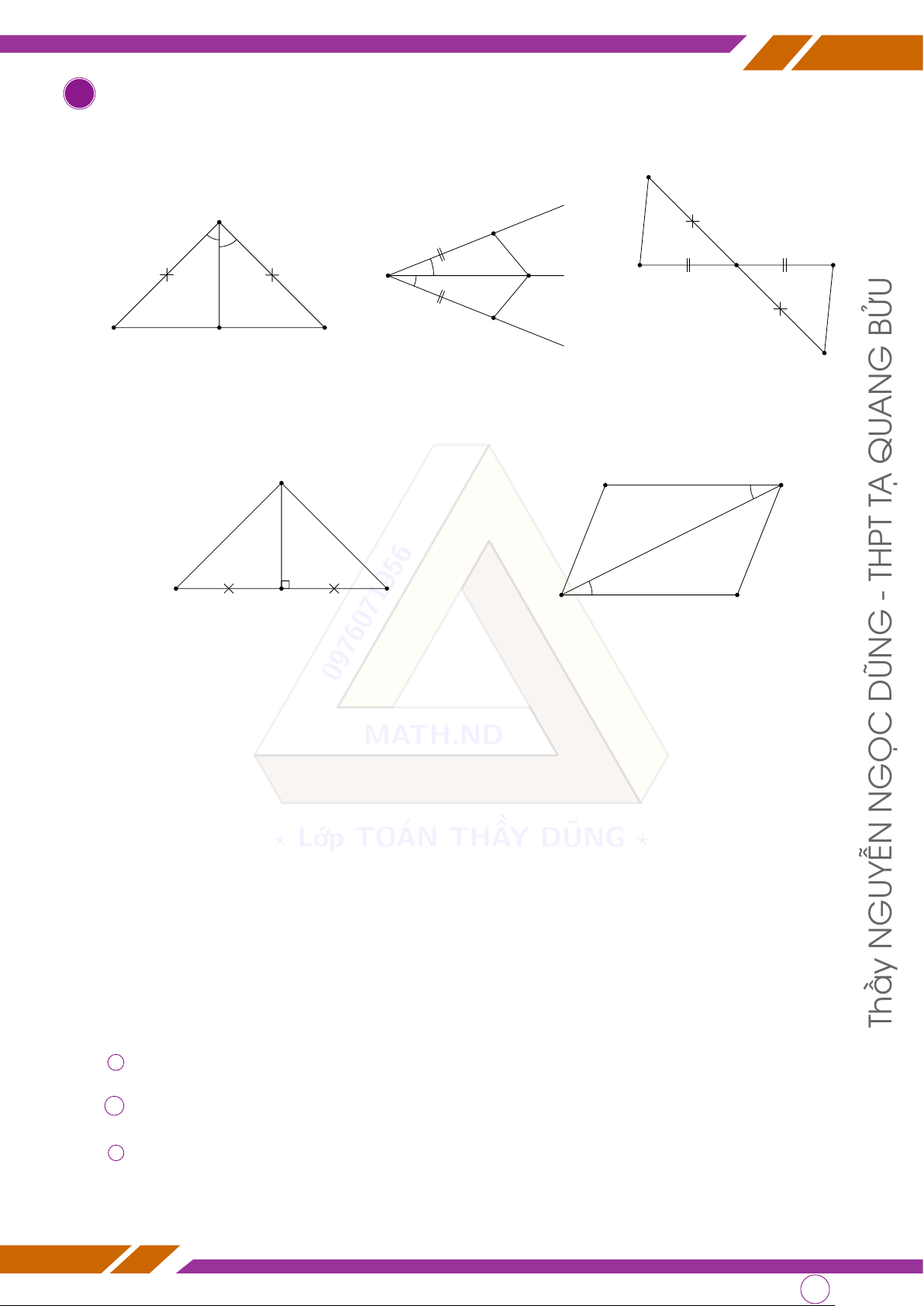
d Bài 1. Chứng minh các tam giác sau bằng nhau: A x A A M C O t B C B C B y BỬU M a) b) D G c) AN
d Bài 2. Chứng minh các tam giác sau bằng nhau QU A A D TẠ THPT B C - M B C a) G b)
d Bài 3. Cho 4ABC có AB 0976071956
= AC, gọi AM là tia phân giác của góc bA (M thuộc BC). Chứng
minh 4ABM = 4ACM. DŨN
d Bài 4. Cho 4ABC có AB = MA AC, TH.ND
gọi AM là tia phân giác của góc bA (M thuộc BC). Chứng
minh M là trung điểm của BC. GỌC
d Bài 5. Cho 4ABC có M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao N cho MA = MD. ? Chứng Lớp minh TO 4AB ÁN M = 4 THẦ DCM. Y DŨNG ?
d Bài 6. Cho 4ABC có M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao
cho MA = MD. Chứng minh AB k CD. GUYỄN d N
Bài 7. Cho 4ABC có D là trung điểm của AC. Trên tia đối của tia DB lấy điểm E sao
cho DB = DE. Chứng minh BC k AE.
d Bài 8. Cho 4ABC có AB = AC, gọi AM là tia phân giác của góc b
A (M thuộc BC). Thầy
a Chứng minh M là trung điểm của cạnh BC.
b Chứng minh AM ⊥ BC.
c Trên tia AM lấy điểm K sao cho MA = MK. Chứng minh AB = CK và AB k CK.
d Bài 9. Cho 4ABC có M là trung điểm của cạnh BC. Trên tia đối của tia MA lấy điểm D
sao cho MA = MD.
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 49 of 56 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng
a Chứng minh 4ABM = 4DCM.
b Chứng minh AB k CD.
c Chứng minh AC = BD và AC k BD.
d Bài 10. Cho 4ABC có M là trung điểm của cạnh AC. Trên tia đối của tia MB lấy điểm Thầy
D sao cho MB = MD.
a Chứng minh 4AMB = 4CMD. N GUYỄN
b Chứng minh AB k CD.
c Chứng minh AD = BC và AD k BC.
d Bài 11. Cho 4ABC vuông tại A; trên tia đối của tia CA lấy điểm D sao cho C là trung N
điểm của AD; trên tia đối của tia CB lấy điểm E sao cho C là trung điểm của BE. Chứng GỌC minh
a 4ABC = 4DEC và CD ⊥ DE. DŨN
b 4BCD = 4ECA. G c BD k AE. 0976071956 - THPT
d Bài 12. Cho 4ABC vuông tại A có K là trung điểm của BC. Trên tia đối của tia KA lấy
điểm D sao cho KD = KA. MATH.ND T
a Chứng minh AB = CD. Ạ QU
b Chứng minh AC k ?
BD.Lớp TOÁN THẦY DŨNG ? AN c Tính [ DCA. G 1
d Chứng minh AK = 2BC. BỬU d Bài 13. Cho [
xOy nhọn. Trên tia Ox lần lượt lấy điểm A và B (khác O), trên tia Oy lấy
điểm C và D sao cho OA = OC, OB = OD.
a Chứng minh 4OAD = 4OCB. b Chứng minh [ CAD = [ ACB.
c Chứng minh AC k BD.
d Bài 14. Cho 4ABC, có b
A = 90◦. Trên cạnh BC lấy điểm E sao cho BE = AB. Tia phân
giác của bB cắt AC tại D. Page 50 of 56
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
a Chứng minh rằng AD = ED; b Tính số đo [ BED.
d Bài 15 (?). Cho 4ABC, có b B = 2“
C. Trên tia đối của tia CB lấy điểm K sao cho AB = CK.
Tia phân giác của bB cắt AC tại D, trên tia đối của tia BD lấy điểm E sao cho AC = BE.
Chứng minh rằng AK = AE.
d Bài 16 (?). Cho tam giác ABC có AB = AC. Trên cạnh AB, AC lần lượt lấy các điểm
M, N sao cho AM = AN. Gọi I là giao điểm của BN và CM. Chứng minh rằng
a BN = CM;
b 4BMC = 4CNB; BỬU
c 4BIM = 4CIN;
d AI là tia phân giác của góc [ BAC. G AN
| Chủ đề 4. Trường hợp bằng nhau thứ ba của tam QU
giác: góc - cạnh - góc TẠ A
KIẾN THỨC CẦN NHỚ A A0 THPT
Xét 4ABC và 4A0B0C0 có - b B = “ B0 G BC = B0C0 “ C = c C0 0976071956 B B0 C C0
Ñ 4ABC = 4A0B0C0 (g.c.g) DŨN MATH.ND B BÀI TẬP GỌC N
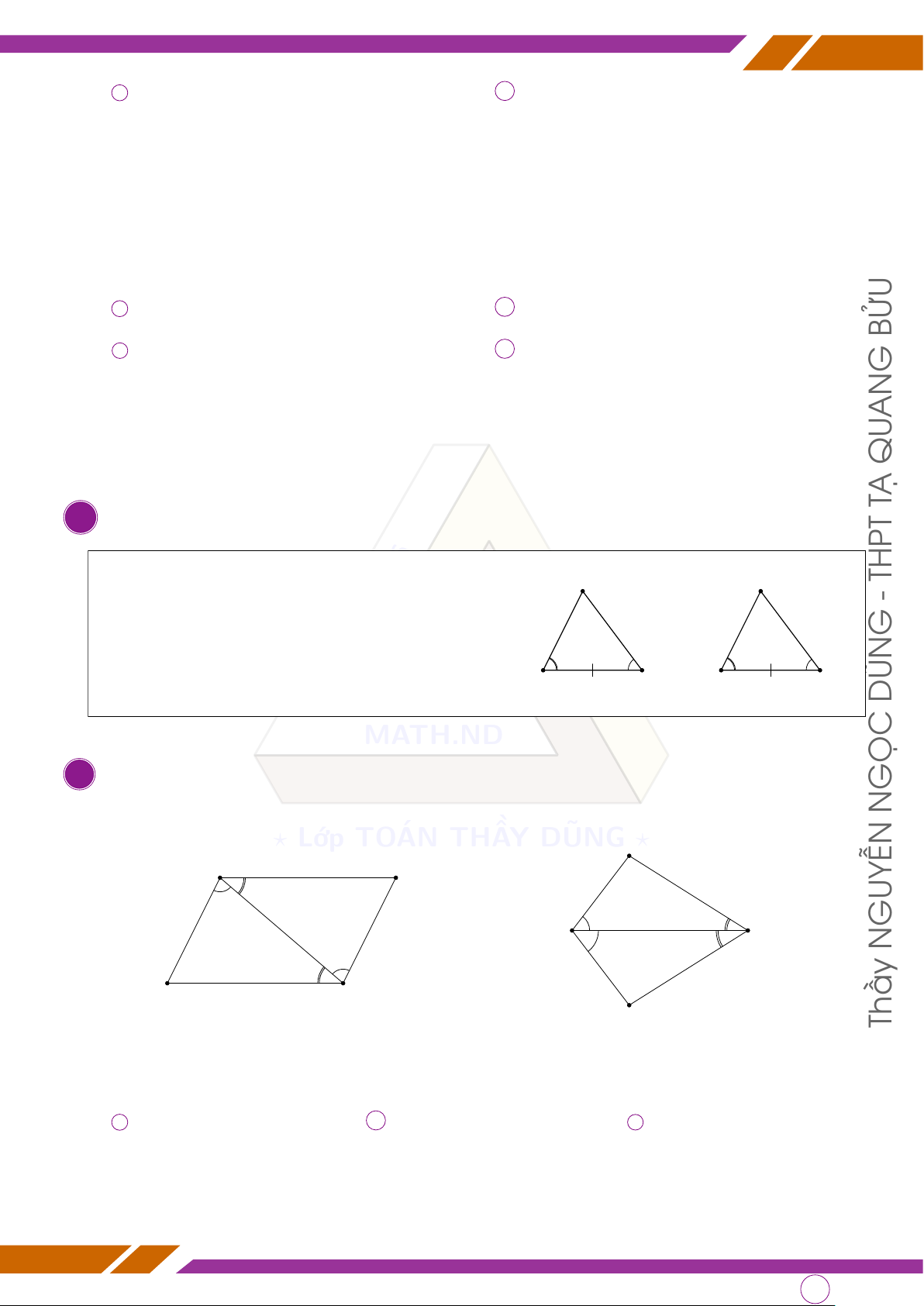
d Bài 1. Chứng minh các tam giác sau bằng nhau
? Lớp TOÁN THẦY DŨNGA? A D GUYỄN O C N B C B Thầy
d Bài 2. Cho 4ABC, gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao
cho MA = MD. Chứng minh
a 4AMB = 4DMC; b AB k CD;
c AC = BD.
d Bài 3. Cho 4ABC vuông tại A, trên tia đối của tia CA lấy điểm D sao cho C là trung
điểm của AD; trên tia đối của tia CB lấy điểm E sao cho C là trung điểm của BE. Chứng minh
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 51 of 56 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng
a 4ABC = 4DEC và CD ⊥ DE;
b 4BCD = 4ECA; c BD k AE.
d Bài 4. Cho 4ABC nhọn (AB < AC). Gọi D; E lần lượt là trung điểm của AB; AC. Trên
tia đối của tia ED lấy điểm F sao cho ED = EF. Chứng minh Thầy
a 4AED = 4CEF;
b AD = CF; AD k CF;
c 4BDC = 4FCD; DE k BC. N
d Bài 5. Cho 4DEF (DE < DF). Gọi I là trung điểm của EF. Trên tia đối của tia ID lấy GUYỄN
điểm M sao cho IM = ID. Chứng minh
a 4DEI = 4MFI;
b DE = MF; ‘ IDE = [
IMF , từ đó suy ra DE k MF; N GỌC
c DF = ME; 4DEF = 4MFE.
d Bài 6. Cho 4MND. Gọi D là trung điểm của MN, E là trung điểm của MP. Trên tia DŨN
đối của tia EN lấy điểm F sao cho EF = EN, trên tia đối của tia DP lấy điểm G sao cho
DG = DP. Chứng minh G
a 4DMG = 4DNP; 0976071956
b MF = PN và MF k PN;
c M là trung điểm của GF. - THPT
d Bài 7. Cho góc xOy, vẽ tia phân giác Ot của góc đó. Trên tia Ox lấy điểm A, trên tia Oy
lấy điểm B sao cho OA = OB, MA trên tia TH.ND
Ot lấy điểm C. Gọi D là giao điểm của AB và Ot. Chứng minh TẠ QU
a 4AOC = 4BOC;
b OC là tia phân giác của [ ACB; ? Lớp TOÁN THẦY DŨNG ? AN
c 4ODA = 4ODB; d AB ⊥ OC. G
d Bài 8. Cho 4ABC vuông tại A, M là trung điểm của AB. Trên tia đối của tia MC lấy
điểm N sao cho MN = MC. Chứng minh BỬU
a AN = BC; b BN ⊥ AB; c AC k BN.
d Bài 9. Cho 4ABC có M, N lần lượt là trung điểm của AC và AB. Trên tia đối của tia
MB lấy điểm D sao cho MD = MB. Trên tia đối của tia NC lấy điểm E sao cho NE = NC. Chứng minh
a 4AMD = 4CMB; b AE k BC;
c A là trung điểm của DE.
d Bài 10. Cho 4ABC, M thuộc BC. Gọi I là trung điểm của AM. Trên tia đối của tia IB
lấy điểm E sao cho IE = IB. Chứng minh Page 52 of 56
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
a AE = BM; b AE k BC;
c Gọi F là giao điểm của CI và AE. Chứng minh I là trung điểm của CF.
d Bài 11. Cho góc xOy khác góc bẹt. Lấy các điểm A; B thuộc tia Ox sao cho OA < OB.
Lấy các điểm C; D thuộc tia Oy sao cho OC = OA; OD = OB. Gọi E là giao điểm của AD
và BC. Chứng minh
a AD = BC;
b 4EAB = 4ECD; BỬU G
c OE là tia phân giác của góc xOy. AN
d Bài 12. Cho 4PQR có M là trung điểm của QR. Trên tia đối của tia MP lấy điểm S sao cho MS = MP. QU
a Chứng minh PQ = RS và PQ k RS. TẠ
b Chứng minh PR = QS và PR k QS. THPT
d Bài 13. Cho 4ABC vuông tại A có K là trung điểm của BC. Trên tia đối của tia KA lấy -
điểm D sao cho KD = KA. G
a Chứng minh AB = CD;0976071956
b Chứng minh AC k BD; DŨN 1 c Tính [ DCA;
MATH.NDd Chứng minh AK = 2BC.
d Bài 14. Cho 4MNP có MN = NP, gọi NA là tia phân giác của góc “
N (A thuộc MP). GỌC N
a Chứng minh A là trung điểm của cạnh MP. ? Lớp TOÁN THẦY DŨNG ?
b Chứng minh NA ⊥ MP.
c Trên tia NA lấy điểm K sao cho AK = AN. Chứng minh NM = PK và NM k PK. GUYỄN N
| Chủ đề 5. Ôn tập học kỳ 1 Thầy A BÀI TẬP CƠ BẢN
d Bài 1. Cho 4ABC có AB = AC, M là trung điểm của BC. a Chứng minh b B = “ C.
b Chứng minh AM là tia phân giác của [ BAC.
c Chứng minh AM ⊥ BC.
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 53 of 56 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng
d Bài 2. Cho 4ABC có AB = AC, gọi AM là tia phân giác của góc A (M thuộc BC).
a Chứng minh M là trung điểm của cạnh BC.
b Chứng minh AM ⊥ BC.
c Trên tia AM lấy điểm K sao cho MA = MK. Chứng minh AB = CK và AB k CK. Thầy
d Bài 3. Cho 4ABC có M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MA = MD. N
a Chứng minh 4ABM = 4DCM. GUYỄN
b Chứng minh AB k CD.
c Chứng minh AC = BD và AC k BD. N d GỌC
Bài 4. Cho 4ABC, gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao
cho MA = MD. Chứng minh
a 4AMB = 4DMC. DŨN b AB k CD. G
c AC = BD. 0976071956 - THPT
d Bài 5. Cho 4ABC vuông tại A, trên tia đối của tia CA lấy điểm D sao cho C là trung
điểm AD; trên tia đối của tia CB MA lấy TH.ND
điểm E sao cho C là trung điểm BE. Chứng minh TẠ
a 4ABC = 4DEC và CD ⊥ DE. QU
b 4BCD = 4ECA. ? Lớp TOÁN THẦY DŨNG ? AN c BD k AE. G
d Bài 6. Cho 4ABC nhọn (AB < AC); Cho D, E lần lượt là trung điểm của AB và AC. Trên BỬU
tia đối của tia ED lấy điểm F sao cho ED = EF. Chứng minh
a 4AED = 4CEF.
b AD = CF và AD k CF.
c 4BDC = 4FCD và DE k BC.
d Bài 7. Cho 4ABC, M thuộc BC. Gọi I là trung điểm của AM, trên tia đối của tia IB lấy
điểm E sao cho IE = IB. Chứng minh
a AE = BM; Page 54 of 56
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU b AE k BC;
c Gọi F là giao điểm của CI và AE. Chứng minh I là trung điểm của CF.
d Bài 8. Cho 4ABC vuông tại A có K là trung điểm của BC. Trên tia đối của tia KA lấy
điểm D sao cho KD = KA.
a Chứng minh AB = CD.
b Chứng minh AC k BD. BỬU c Tính [ DCA. G 1
d Chứng minh AK = 2BC. AN QU B BÀI TẬP NÂNG CAO d TẠ
Bài 1 (Đề thi HKI, PGD quận 6, năm 2016 - 2017). Cho 4ABC có AB = AC, gọi M là
trung điểm của đoạn thẳng BC. THPT
a Chứng minh 4AMB = 4AMC; -
b Chứng minh AM là tia phân giác của góc [
BAC và AM ⊥ BC; G
c Gọi I là trung điểm 0976071956
của đoạn thẳng AC. Trên tia đối của tia IM, lấy điểm D sao cho DŨN
ID = IM. Tính số đo góc \ ADC. MATH.ND
d Bài 2 (Đề thi HKI, PGD quận 3, năm 2014 - 2015). Cho Tam giác ABC vuông tại A. Gọi
M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA. GỌC N
a Tính số đo của ? Lớp [ ABC khi TO [ ACB ÁN = 40◦; THẦY DŨNG ?
b Chứng minh 4AMB = 4EMC và AB k EC;
c Từ C kẻ đường thẳng d song song với AE. Kẻ EK vuông góc với d tại K. Chứng minh GUYỄN \ KEC N = [ BCA.
d Bài 3 (Đề thi HKI, PGD quận 1, năm 2015 - 2016). Cho tam giác ABC có AB = AC. Gọi
D là trung điểm của BC. Thầy
a Chứng minh rằng 4ABD = 4ACD và AD là tia phân giác của góc [ BAC;
b Vẽ DM ⊥ AB tại M. Trên cạnh AC lấy điểm N sao cho AN = AM. Chứng minh rằng
4ADM = 4ADN và DN ⊥ AC;
c Gọi K là trung điểm của đoạn thẳng CN. Trên tia đối của tia KD lấy điểm E sao cho
KE = KD. Chứng minh M, E, N thẳng hàng.
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 55 of 56 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng
d Bài 4 (Đề thi HKI, PGD quận 9, năm 2016 - 2017). Cho tam giác ABC có góc [ BAC = 90◦
(AB < AC). Tia phân giác của góc B cắt cạnh AC tại D, trên cạnh BC lấy điểm E sao cho BE = AB.
a Chứng minh 4ABD = 4EBD;
b Chứng minh BD ⊥ AE; Thầy
c Trên tia đối của tia AB lấy điểm K sao cho BK = BC. Chứng minh ba điểm K, D, E thẳng hàng. N GUYỄN
d Bài 5 (Đề thi HKI, PGD quận 12, năm 2015 - 2016). Cho tam giác ABC vuông tại A, có
M là trung điểm của AB. Trên tia CM lấy điểm K sao cho M là trung điểm của CK.
a Chứng minh 4MBK = 4MAC; N GỌC
b Chứng minh AK k BC;
c Qua B kẻ đường thẳng vuông góc với BC cắt tia CA tại I. Kẻ AH vuông góc với BC (H
thuộc BC), tia AH cắt tia KB tại D. Chứng minh AI = BD. DŨN
d Bài 6 (Đề thi HKI, THPT Chuyên Trần Đại Nghĩa, năm 2014 - 2015). Cho 4ABC nhọn, vẽ G
đường thẳng xy qua A và song song với BC. Từ B vẽ BD vuông góc với AC tại D, BD cắt
xy tại E. Trên tia BC lấy điểm F0976071956 - sao cho BF = AE. THPT
a Chứng minh rằng EF = AB MA và EF TH.ND k AB; T
b Từ F vẽ FK vuông góc với BE ở K. Chứng minh FK = AD; Ạ QU
c Gọi I là trung điểm của KD. Chứng minh ba điểm A, I, F thẳng hàng; ? Lớp TOÁN THẦY DŨNG ? AN
d Gọi M là trung điểm của đoạn AB, MI cắt EF tại N. Chứng minh N là trung điểm của EF . G BỬU Page 56 of 56
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
Document Outline
- I Đại số
- Số hữu tỉ. Số thực
- Số hữu tỉ
- Tỉ lệ thức
- Số thực. Căn bậc hai
- Hàm số và đồ thị
- Tỉ lệ thuận
- Tỉ lệ nghịch
- Hàm số - Đồ thị hàm số y=ax (a=0)
- II Hình học
- Đường thẳng vuông góc. Đường thẳng song song
- Hai góc đối đỉnh
- Đường vuông góc. Đường trung trực
- Hai đường thẳng song song
- Từ vuông góc đến song song
- Tam giác
- Tổng ba góc của một tam giác
- Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh
- Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh
- Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc
- Ôn tập học kỳ 1
- Đường thẳng vuông góc. Đường thẳng song song
- Số hữu tỉ. Số thực







