Bài tập Toán 9 học kì 1 – Trần Quốc Nghĩa

Tài liệu gồm 104 trang được biên soạn bởi thầy Trần Quốc Nghĩa tóm tắt lý thuyết, phương pháp giải toán và tuyển chọn các bài tập Toán 9 giai đoạn học kì 1 giúp học sinh tự rèn luyện. Mời bạn đọc đón xem.

42 21 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 9

Môn: Toán 9

Thông tin:

104 trang 8 tháng trước

Tác giả:

Profile Hà Việt Anh
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 104
Mục lục
Phần 0. Ôn tập ................................................................................................ 1
Biểu diễn nghiệm trên trục số ................................................................... 1
Phương trình chứa dấu giá trị tuyệt đối .................................................... 2
Bất phương trình tích, thương. Bất phương trình bậc hai. Bất phương trình
chứa dấu giá trị tuyệt đối. ......................................................................... 4
Phần 1. Đại số ................................................................................................. 9
Chương 1 CĂN BẬC HAI – CĂN BẬC BA............................................... 9
A - Căn bậc hai ........................................................................................ 9
B - Căn thức bậc hai. Hằng đẳng thức
2
A | A|
.................................... 12
C - Khai phương một tích. Nhân các căn thức bậc hai. ........................... 17
D - Khai phương một thương. C hia các căn thức bậc hai ....................... 17
E - Biến đổi đơn giản căn thức bậc hai ................................................... 23
F - Rút gọn biểu thức có chứa căn thức bậc hai ...................................... 29
G - Căn bậc ba ....................................................................................... 33
H - Ôn tập chương 1............................................................................... 34
Chương 2 HÀM SỐ BẬC NHẤT ............................................................. 41
A - Nhắc lại và bổ sung các khái niệm về hàm số .................................... 41
B - Hàm số bậc nhất y = ax + b (a
0) .................................................. 45
C - Hệ số góc của đường thẳng y = ax + b (a
0) .................................. 45
D - Ôn tập chương 2............................................................................... 53
Phần 2. Hình học .......................................................................................... 57
Chương 1 HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG............. 57
A - Một số hệ thức về cạnh và đường cao trong tam giác vuông .............. 57
B - Tỉ số lượng giác của góc nhọn .......................................................... 62
C - Bảng lượng giác và máy tính bỏ túi................................................... 66
D - Hệ thức giữa các cạnh và các góc trong một tam giác vuông ............ 67
E - Ôn tập chương 1 ............................................................................... 69
Chương 2 ĐƯỜNG TRÒN ....................................................................... 73
A - Sự xác định đường tròn. Tính chất đối xứng của đường tròn ............ 73
B - Đường kính và dây cung của đường tròn ........................................... 76
C - Liên hệ giữa dây và khoảng cách từ tâm đến dây .............................. 78
D - Các công thức về
vuông cân tam giác đều và nửa tam giác đều ...... 81
E - Vị trí tương đối của đường thẳng và đường tròn. Dấu hiệu nhận biết
tiếp tuyến của đường tròn. Tính chất của hai tiếp tuyến cắt nhau...... 82
F - Đường tròn nội tiếp – bàng tiếp tam giác .......................................... 89
G - Vị trí tương đối của hai đường tròn .................................................. 91
H - Ôn tập chương 2............................................................................... 94
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 1
Phần 0. Ôn tập
Biểu diễn tập nghiệm BPT trên trục số
Thông thường một bất phương trình có vô số nghiệm nên không thể kiệt
kê hết được. Người ta chọn cách thể hiện tập nghiệm bằng cách biểu diễn
trên trục số (phần không bị xóa). Sau đây là các trường hợp thường gặp:
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
Chú ý: Tại a, biểu diễn ngoặc vuông “[, ]” tức trong tập nghiệm có
x = a, còn ngược lại biểu diễn ngoặc đơn “(, )” khi x = a không
thuộc tập nghiệm.
O.1 Biểu diễn các tập nghiệm sau lên trục số:
a)
S {x / x 5}
b)
S {x / x 2}
c)
S {x / x 1}
d)
S {x / x 1}
e)
S {x / 1 x 2}
f)
S {x / x 2 hoac x 1}
a
(
{x / a < x < b}
b
)
O
x
(vô số nghiệm)
a
[
{x / a ≤ x ≤ b}
b
]
O
x
R (vô số nghiệm)
a
)
{x / x < a hoặc x > b}
b
(
a
]
{x / x ≤ a hoặc x ≥ b}
b
[
b
)
{ x / x b}
b
]
{ x / x b}
a
(
{ x / x a }
a
[
{ x / x a }
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 104
Mục lục
Phần 0. Ôn tập ................................................................................................ 1
Biểu diễn nghiệm trên trục số ................................................................... 1
Phương trình chứa dấu giá trị tuyệt đối .................................................... 2
Bất phương trình tích, thương. Bất phương trình bậc hai. Bất phương trình
chứa dấu giá trị tuyệt đối. ......................................................................... 4
Phần 1. Đại số ................................................................................................. 9
Chương 1 CĂN BẬC HAI – CĂN BẬC BA............................................... 9
A - Căn bậc hai ........................................................................................ 9
B - Căn thức bậc hai. Hằng đẳng thức
2
A | A|
.................................... 12
C - Khai phương một tích. Nhân các căn thức bậc hai. ........................... 17
D - Khai phương một thương. C hia các căn thức bậc hai ....................... 17
E - Biến đổi đơn giản căn thức bậc hai ................................................... 23
F - Rút gọn biểu thức có chứa căn thức bậc hai ...................................... 29
G - Căn bậc ba ....................................................................................... 33
H - Ôn tập chương 1............................................................................... 34
Chương 2 HÀM SỐ BẬC NHẤT ............................................................. 41
A - Nhắc lại và bổ sung các khái niệm về hàm số .................................... 41
B - Hàm số bậc nhất y = ax + b (a
0) .................................................. 45
C - Hệ số góc của đường thẳng y = ax + b (a
0) .................................. 45
D - Ôn tập chương 2............................................................................... 53
Phần 2. Hình học .......................................................................................... 57
Chương 1 HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG............. 57
A - Một số hệ thức về cạnh và đường cao trong tam giác vuông .............. 57
B - Tỉ số lượng giác của góc nhọn .......................................................... 62
C - Bảng lượng giác và máy tính bỏ túi................................................... 66
D - Hệ thức giữa các cạnh và các góc trong một tam giác vuông ............ 67
E - Ôn tập chương 1 ............................................................................... 69
Chương 2 ĐƯỜNG TRÒN ....................................................................... 73
A - Sự xác định đường tròn. Tính chất đối xứng của đường tròn ............ 73
B - Đường kính và dây cung của đường tròn ........................................... 76
C - Liên hệ giữa dây và khoảng cách từ tâm đến dây .............................. 78
D - Các công thức về
vuông cân tam giác đều và nửa tam giác đều ...... 81
E - Vị trí tương đối của đường thẳng và đường tròn. Dấu hiệu nhận biết
tiếp tuyến của đường tròn. Tính chất của hai tiếp tuyến cắt nhau...... 82
F - Đường tròn nội tiếp – bàng tiếp tam giác .......................................... 89
G - Vị trí tương đối của hai đường tròn .................................................. 91
H - Ôn tập chương 2............................................................................... 94
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 1
Phần 0. Ôn tập
Biểu diễn tập nghiệm BPT trên trục số
Thông thường một bất phương trình có vô số nghiệm nên không thể kiệt
kê hết được. Người ta chọn cách thể hiện tập nghiệm bằng cách biểu diễn
trên trục số (phần không bị xóa). Sau đây là các trường hợp thường gặp:
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
Chú ý: Tại a, biểu diễn ngoặc vuông “[, ]” tức trong tập nghiệm có
x = a, còn ngược lại biểu diễn ngoặc đơn “(, )” khi x = a không
thuộc tập nghiệm.
O.1 Biểu diễn các tập nghiệm sau lên trục số:
a)
S {x / x 5}
b)
S {x / x 2}
c)
S {x / x 1}
d)
S {x / x 1}
e)
S {x / 1 x 2}
f)
S {x / x 2 hoac x 1}
a
(
{x / a < x < b}
b
)
O
x
(vô số nghiệm)
a
[
{x / a ≤ x ≤ b}
b
]
O
x
R (vô số nghiệm)
a
)
{x / x < a hoặc x > b}
b
(
a
]
{x / x ≤ a hoặc x ≥ b}
b
[
b
)
{ x / x b}
b
]
{ x / x b}
a
(
{ x / x a }
a
[
{ x / x a }
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 2
Phương trình chứa dấu giá trị tuyệt đối
Dạng 1: A = B (1) (với B là một số thực không chứa biến)
Nếu B < 0 : phương trình vô nghiệm
Nếu B > 0 : (1)
A = B hoặc A = – B
Dạng 2: A = B (2) (với B là một biểu thức có chứa biến)
Cách 1: Dùng định nghĩa bỏ dấu giá trị tuyệt đối:
Nếu A
0
x … (*)
(2)
A = B
x = … (đem nghiệm này so với điều kiện (*) nếu
thỏa thì lấy)
Chú ý: Trường hợp phương trình A = B có VSN thì phương trình
(2) có nghiệm là (*).
Nếu A < 0
x … (**)
(2)
– A = B
x = … (đem nghiệm này so với điều kiện (**) nếu
thỏa thì lấy)
Chú ý: Trường hợp ph/trình – A = B có VSN thì phương trình (2)
có nghiệm là (**).
Vậy nghiệm của phương trình là: (lấy nghiệm của hai trường hợp trên).
Cách 2: Dùng công thức:
B 0
A B
A B
A B
Dạng 3: A = B
A = B
A = B hoặc A = – B
(giải hai phương trình này tìm nghiệm nếu có).
Dạng 4:
A + B + … + N= 0 (1)
A 0 ( a )
B 0 (b )
...
N 0 ( n )
Nghiệm của (1) là nghiệm chung của các phương trình (a), (b), … (n).
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 103
c) Gọi O là trung điểm của AH. Chứng minh OOIM là hình thang cân.
d) G là trọng tâm của ABC. So sánh diện tích của AOG và AHG.
2.148 Cho nửa đường tròn tâm O, đường kính AB. Trên nửa mặt phẳng bờ AB
chứa nửa đường tròn, kẻ tia tiếp tuyến Ax. Từ M trên Ax, kẻ tiếp tuyến
MC tới nửa đường tròn (C (O)). Đường thẳng BC cắt tia Ax tại D.
a) Chứng minh: MA = MD.
b) Kẻ CH AB, BM cắt CH tại I. Chứng minh: I là trung điểm của CH.
c) Kẻ tia Oy OM, tia này cắt MC tại N. Chứng minh: NB là tiếp tuyến
của nửa (O).
2.149 Cho hai đường tròn (O) và (O) tiếp xúc ngoài nhau tại A. Bán kính của
(O) là R = 5cm, bán kính của (O) là r = 3cm. Một đường thẳng qua A
hợp với OO một góc 30
0
cắt (O) tại B, cắt đường tròn (O) tại C.
a) Chứng minh:
AO'C
=
AOB
và OC // OB.
b) Chứng minh: tiếp tuyến của (O) tại B và tiếp tuyến của (O) tại C song
song với nhau.
c) Tiếp tuyến của (O) tại C cắt đường thẳng OO tại D. Tính CD và OD.
d) Đường thẳng CD cắt đường thẳng BO tại E. Tính diện tích ABE.
2.150 Cho đường tròn (O; R) đường kính AB. Lấy điểm C ngoài đường tròn sao
cho B là trung điểm của OC. Từ C vẽ hai tiếp tuyến CM, CN đến (O) với
M, N là hai tiếp điểm.
a) Chứng minh: AMN cân. Tính CM và AM theo R.
b) Chứng minh: tứ giác AMCN là hình thoi. Tính S
AMCN
theo R.
c) Gọi I là trung điểm của CM. Đường thẳng AI cắt OM tại K.
Chứng minh: K là trung điểm của AI.
d) Tính diện tích AKB theo R.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 2
Phương trình chứa dấu giá trị tuyệt đối
Dạng 1: A = B (1) (với B là một số thực không chứa biến)
Nếu B < 0 : phương trình vô nghiệm
Nếu B > 0 : (1)
A = B hoặc A = – B
Dạng 2: A = B (2) (với B là một biểu thức có chứa biến)
Cách 1: Dùng định nghĩa bỏ dấu giá trị tuyệt đối:
Nếu A
0
x … (*)
(2)
A = B
x = … (đem nghiệm này so với điều kiện (*) nếu
thỏa thì lấy)
Chú ý: Trường hợp phương trình A = B có VSN thì phương trình
(2) có nghiệm là (*).
Nếu A < 0
x … (**)
(2)
– A = B
x = … (đem nghiệm này so với điều kiện (**) nếu
thỏa thì lấy)
Chú ý: Trường hợp ph/trình – A = B có VSN thì phương trình (2)
có nghiệm là (**).
Vậy nghiệm của phương trình là: (lấy nghiệm của hai trường hợp trên).
Cách 2: Dùng công thức:
B 0
A B
A B
A B
Dạng 3: A = B
A = B
A = B hoặc A = – B
(giải hai phương trình này tìm nghiệm nếu có).
Dạng 4:
A + B + … + N= 0 (1)
A 0 ( a )
B 0 (b )
...
N 0 ( n )
Nghiệm của (1) là nghiệm chung của các phương trình (a), (b), … (n).
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 103
c) Gọi O là trung điểm của AH. Chứng minh OOIM là hình thang cân.
d) G là trọng tâm của ABC. So sánh diện tích của AOG và AHG.
2.148 Cho nửa đường tròn tâm O, đường kính AB. Trên nửa mặt phẳng bờ AB
chứa nửa đường tròn, kẻ tia tiếp tuyến Ax. Từ M trên Ax, kẻ tiếp tuyến
MC tới nửa đường tròn (C (O)). Đường thẳng BC cắt tia Ax tại D.
a) Chứng minh: MA = MD.
b) Kẻ CH AB, BM cắt CH tại I. Chứng minh: I là trung điểm của CH.
c) Kẻ tia Oy OM, tia này cắt MC tại N. Chứng minh: NB là tiếp tuyến
của nửa (O).
2.149 Cho hai đường tròn (O) và (O) tiếp xúc ngoài nhau tại A. Bán kính của
(O) là R = 5cm, bán kính của (O) là r = 3cm. Một đường thẳng qua A
hợp với OO một góc 30
0
cắt (O) tại B, cắt đường tròn (O) tại C.
a) Chứng minh:
AO'C
=
AOB
và OC // OB.
b) Chứng minh: tiếp tuyến của (O) tại B và tiếp tuyến của (O) tại C song
song với nhau.
c) Tiếp tuyến của (O) tại C cắt đường thẳng OO tại D. Tính CD và OD.
d) Đường thẳng CD cắt đường thẳng BO tại E. Tính diện tích ABE.
2.150 Cho đường tròn (O; R) đường kính AB. Lấy điểm C ngoài đường tròn sao
cho B là trung điểm của OC. Từ C vẽ hai tiếp tuyến CM, CN đến (O) với
M, N là hai tiếp điểm.
a) Chứng minh: AMN cân. Tính CM và AM theo R.
b) Chứng minh: tứ giác AMCN là hình thoi. Tính S
AMCN
theo R.
c) Gọi I là trung điểm của CM. Đường thẳng AI cắt OM tại K.
Chứng minh: K là trung điểm của AI.
d) Tính diện tích AKB theo R.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 102
2.144 Cho 2 đường tròn ngoài nhau (O; R) và (O; r) với R > r, AB là tiếp tuyến
chung ngoài (A là là tiếp điểm trên (O), B là tiếp điểm trên (O)). Từ O
vẽ OC OA.
a) Chứng tỏ ABOC là hình chữ nhật.
b) Chứng tỏ OC là tiếp tuyến của đường tròn tâm O bán kính R = R – r.
c) Suy ra cách dựng đường t/tuyến chung ngoài AB khi cho trước 2
đường tròn (O; R) và (O; r).
d) Tương tự, dựng tiếp tuyến chung trong của 2 đường tròn (O; R) và
(O; r).
e) Tính độ dài của tiếp tuyến chung ngoài và tiếp tuyến chung trong và
khoảng cách hai tâm d = OO theo hai bán kính.
2.145 Cho đường tròn (O; R) và điểm I cố định với OI = R/2. AB là dây cung
quay quanh I.
a) Tìm vị trí C, D của A (hay B) tương ứng lúc độ dài IA (hay IB) dài
nhất, ngắn nhất.
b) Chứng tỏ tập hợp các trung điểm M của dây cung AB là một đường
tròn, tìm tâm và bán kính đường tròn này.
c) Gọi EF là vị trí giới hạn của dây cung AB lúc M tiến dần đến I. C/m:
i. EF CD.
ii. EF là độ dài ngắn nhất của dây cung AB và CD là độ dài lớn nhất
của AB.
d) Chứng minh CEF đều, tính chu vi và diện tích tam giác này theo R.
2.146 Cho (O; R) và (O; R) tiếp xúc ngoài nhau tại E. Gọi AB là tiếp tuyến
chung ngoài của hai đường tròn (A (O), B (O)).
a) Tính diện tích tứ giác AOOB theo R và R.
b) Gọi D là điểm đối xứng của A qua O. C/minh: B, E, D thẳng hàng.
c) Xác định vị trí tương đối của hai đường thẳng AB và đường tròn
đường kính OO.
2.147 Cho ABC có 3 góc nhọn. Đường tròn tâm I đường kính BC cắt AB tại F,
cắt AC tại E, BE cắt CF tại H.
a) Trong ABC điểm H gọi là gì ?
b) Gọi K là điểm đối xứng của H qua I và M là điểm đối xứng của H qua
BC. Chứng minh 5 điểm A, B, K, M, C cùng thuộc một đường tròn.
Xác định tâm và bán kính của đường tròn này.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 3
Dạng 5: Phương trình có chứa nhiều dấu giá trị tuyệt đối:
Tìm giá trị của ăn để biểu thức trong dấu giá trị tuyệt đối bằng 0. Các
giá trị này khi biểu diễn lên trục số sẽ chia trục số thành nhiều khoảng
giá trị của ẩn.
Cho ẩn lấy giá trị trên từng khoảng, trên từng khoảng đó dấu của biểu
thức bên trong dấu giá trị tuyệt đối sẽ âm hoặc dương. Dựa vào đó mà
bỏ dấu trị tuyệt đối.
Giải phương trình, giá trị tìm được phải nằm trong khoảng đang xét
mới nhận làm nghiệm.
Nghiệm của phương trình là tất cả các nghiệm vừa tìm được trên từng
khoảng.
O.2 Giải các phương trình sau:
1. a) x – 5 = 3 b) 2x – 5 = 4
c) x + 6 = 1 d) 3 – 7x = 0
e) x – 5 = 2 f) 8x – 5x = 2
2. a) x 7 = 2x + 3 b) x + 4 = 2x – 5
c) x + 3 = 3x – 1 d) 9 + x = 2x
e) 3x – 1 = 3x + 2 f) x + 6 = 2x + 9
3. a) 2x – 3 = 2x – 3 b) 5x – 4 = 4 – 5x
c) 2x + 3 = 2x + 2 d) 5x – 3 = 5x – 5
e) x
2
– 3x + 3 = x
2
+ 3x – 1 f) x
2
– 9 = x
2
– 9
4. a) 5x 3x – 2 = 0 b) x – 5x + 2x 3 = 0
e) 3 – x+ x
2
– (4 + x)x = 0 f) (x – 1)
2
+ x + 21 x
2
– 13 = 0
5. a) 2 – x=2x – 3 b) x + 3 = 5 – x
c) 2x – 1 = 2 – 3x d) 2x = x(x – 2)
e) x(x + 1) = 3 – x f) 3x – 12x + 3 = 0
6
*
. a) x – 1+2 x = 3 b) x + 3+x – 5 = 3x – 1
c) x 2x – 1 + 3x – 2 = 4 d) x – 1+x+2+x – 3 = 14
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 102
2.144 Cho 2 đường tròn ngoài nhau (O; R) và (O; r) với R > r, AB là tiếp tuyến
chung ngoài (A là là tiếp điểm trên (O), B là tiếp điểm trên (O)). Từ O
vẽ OC OA.
a) Chứng tỏ ABOC là hình chữ nhật.
b) Chứng tỏ OC là tiếp tuyến của đường tròn tâm O bán kính R = R – r.
c) Suy ra cách dựng đường t/tuyến chung ngoài AB khi cho trước 2
đường tròn (O; R) và (O; r).
d) Tương tự, dựng tiếp tuyến chung trong của 2 đường tròn (O; R) và
(O; r).
e) Tính độ dài của tiếp tuyến chung ngoài và tiếp tuyến chung trong và
khoảng cách hai tâm d = OO theo hai bán kính.
2.145 Cho đường tròn (O; R) và điểm I cố định với OI = R/2. AB là dây cung
quay quanh I.
a) Tìm vị trí C, D của A (hay B) tương ứng lúc độ dài IA (hay IB) dài
nhất, ngắn nhất.
b) Chứng tỏ tập hợp các trung điểm M của dây cung AB là một đường
tròn, tìm tâm và bán kính đường tròn này.
c) Gọi EF là vị trí giới hạn của dây cung AB lúc M tiến dần đến I. C/m:
i. EF CD.
ii. EF là độ dài ngắn nhất của dây cung AB và CD là độ dài lớn nhất
của AB.
d) Chứng minh CEF đều, tính chu vi và diện tích tam giác này theo R.
2.146 Cho (O; R) và (O; R) tiếp xúc ngoài nhau tại E. Gọi AB là tiếp tuyến
chung ngoài của hai đường tròn (A (O), B (O)).
a) Tính diện tích tứ giác AOOB theo R và R.
b) Gọi D là điểm đối xứng của A qua O. C/minh: B, E, D thẳng hàng.
c) Xác định vị trí tương đối của hai đường thẳng AB và đường tròn
đường kính OO.
2.147 Cho ABC có 3 góc nhọn. Đường tròn tâm I đường kính BC cắt AB tại F,
cắt AC tại E, BE cắt CF tại H.
a) Trong ABC điểm H gọi là gì ?
b) Gọi K là điểm đối xứng của H qua I và M là điểm đối xứng của H qua
BC. Chứng minh 5 điểm A, B, K, M, C cùng thuộc một đường tròn.
Xác định tâm và bán kính của đường tròn này.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 3
Dạng 5: Phương trình có chứa nhiều dấu giá trị tuyệt đối:
Tìm giá trị của ăn để biểu thức trong dấu giá trị tuyệt đối bằng 0. Các
giá trị này khi biểu diễn lên trục số sẽ chia trục số thành nhiều khoảng
giá trị của ẩn.
Cho ẩn lấy giá trị trên từng khoảng, trên từng khoảng đó dấu của biểu
thức bên trong dấu giá trị tuyệt đối sẽ âm hoặc dương. Dựa vào đó mà
bỏ dấu trị tuyệt đối.
Giải phương trình, giá trị tìm được phải nằm trong khoảng đang xét
mới nhận làm nghiệm.
Nghiệm của phương trình là tất cả các nghiệm vừa tìm được trên từng
khoảng.
O.2 Giải các phương trình sau:
1. a) x – 5 = 3 b) 2x – 5 = 4
c) x + 6 = 1 d) 3 – 7x = 0
e) x – 5 = 2 f) 8x – 5x = 2
2. a) x 7 = 2x + 3 b) x + 4 = 2x – 5
c) x + 3 = 3x – 1 d) 9 + x = 2x
e) 3x – 1 = 3x + 2 f) x + 6 = 2x + 9
3. a) 2x – 3 = 2x – 3 b) 5x – 4 = 4 – 5x
c) 2x + 3 = 2x + 2 d) 5x – 3 = 5x – 5
e) x
2
– 3x + 3 = x
2
+ 3x – 1 f) x
2
– 9 = x
2
– 9
4. a) 5x 3x – 2 = 0 b) x – 5x +  2x 3 = 0
e) 3 – x+ x
2
– (4 + x)x = 0 f) (x – 1)
2
+ x + 21 x
2
– 13 = 0
5. a) 2 – x=2x – 3 b) x + 3 = 5 – x
c) 2x – 1 = 2 – 3x d) 2x = x(x – 2)
e) x(x + 1) = 3 – x f) 3x – 12x + 3 = 0
6
*
. a) x – 1+2 x = 3 b) x + 3+x – 5 = 3x – 1
c) x 2x – 1 + 3x – 2 = 4 d) x – 1+x+2+x – 3 = 14
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 4
Bất phương trình tích, thương. Bất phương trình bậc hai.
Bất phương trình chứa dấu giá trị tuyệt đối.
1. Bất phương trình tích
Dạng 1.
A( x ).B( x ) 0
A( x ) 0
B( x ) 0
hoặc
A( x ) 0
B( x ) 0
A( x ).B( x ) 0
A( x ) 0
B( x ) 0
hoặc
A( x ) 0
B( x ) 0
Dạng 2.
A( x ).B( x ) 0
A( x ) 0
B( x ) 0
hoặc
A( x ) 0
B( x ) 0
A( x ).B( x ) 0
A( x ) 0
B( x ) 0
hoặc
A( x ) 0
B( x ) 0
2. Bất phương trình thương
Dạng 1.
A( x )
0
B( x )
A( x ) 0
B( x ) 0
hoặc
A( x ) 0
B( x ) 0
A( x )
0
B( x )
A( x ) 0
B( x ) 0
hoặc
A( x ) 0
B( x ) 0
Dạng 2.
A( x )
0
B( x )
A( x ) 0
B( x ) 0
hoặc
A( x ) 0
B( x ) 0
A( x )
0
B( x )
A( x ) 0
B( x ) 0
hoặc
A( x ) 0
B( x ) 0
3. Bất phương trình chứa dấu giá trị tuyệt đối
x a
a x a
(với a ≥ 0)
x a
x a
hoặc
x a
(với a ≥ 0)
Một số bất phương trình đặc biệt:
|a| ≥ 0
a
R
|a| > 0
a ≠ 0
|a| ≤ 0
a = 0
|a| < 0
a
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 101
c) Đường tròn (K) cắt (O) tại E và F. Chứng tỏ IE, IF là hai tiếp tuyến
của (O). Suy ra cách dựng tiếp tuyến vẽ từ I đến (O).
d) Chứng tỏ: AB > CD OM < ON. Nói rõ vị trí tương đối của 2 cát
tuyến IAB và ICD lúc AB = CD.
e) Trường hợp dây cung AB = R
3
. Tính các góc và diện tích của
AOB theo R.
2.141 Cho đường tròn (O; R) có đường kính AB. AC và BD là hai dây cung
song song với nhau.
a) Chứng minh: AC = BD, suy ra CD là đường kính của (O).
b) Chứng tỏ ACBD là hình chữ nhật.
c) Chứng tỏ rằng nếu dây cung AC = R
2
thì ACBD là hình vuông và
ngược lại.
d) Tính diện tích ACBD trong trường hợp
BAC
= 30
0
.
2.142 Cho hai đường tròn (O; R) và (O; R) có R = 8, R = 6 và OO = 10.
a) Chứng tỏ (O; R) và (O; R) cắt nhau tại 2 điểm A và B và OOlà
đường trung trực của AB.
b) Chứng minh AO là tiếp tuyến của (O) và AO là tiếp tuyến của (O).
c) Gọi I là giao điểm OO và AB. Tính độ dài của IA, IO.
d) Xác định tâm và tính bán kính của đường tròn qua 4 điểm A, O, B, O.
e) Tìm điều kiện về bán kính của đường tròn (O) sao cho đường tròn này
không có điểm chung nào với (O; R).
2.143 Cho đường tròn (O; R) có đường kính AB, gọi (I) là đường tròn tâm I,
đường kính OA.
a) Chứng tỏ (O) và (I) tiếp xúc trong nhau.
b) Cho C là điểm bất kì (O) (C khác A, B), AC cắt (I) tại K. C/minh:
i. ABC và AOK vuông.
ii. K là trung điểm của AC và OK = BC/2
iii. IOK và OBC đồng dạng.
c) Gọi EF là đường kính của (O) qua K, chứng tỏ B, C, E, F là 4 đỉnh của
hình thang cân.
d) Cho
BOC
= 60
0
. Tính các cạnh, diện tích của ABC và của hình
thang cân BCEF.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 4
Bất phương trình tích, thương. Bất phương trình bậc hai.
Bất phương trình chứa dấu giá trị tuyệt đối.
1. Bất phương trình tích
Dạng 1.
A( x ).B( x ) 0
A( x ) 0
B( x ) 0
hoặc
A( x ) 0
B( x ) 0
A( x ).B( x ) 0
A( x ) 0
B( x ) 0
hoặc
A( x ) 0
B( x ) 0
Dạng 2.
A( x ).B( x ) 0
A( x ) 0
B( x ) 0
hoặc
A( x ) 0
B( x ) 0
A( x ).B( x ) 0
A( x ) 0
B( x ) 0
hoặc
A( x ) 0
B( x ) 0
2. Bất phương trình thương
Dạng 1.
A( x )
0
B( x )
A( x ) 0
B( x ) 0
hoặc
A( x ) 0
B( x ) 0
A( x )
0
B( x )
A( x ) 0
B( x ) 0
hoặc
A( x ) 0
B( x ) 0
Dạng 2.
A( x )
0
B( x )
A( x ) 0
B( x ) 0
hoặc
A( x ) 0
B( x ) 0
A( x )
0
B( x )
A( x ) 0
B( x ) 0
hoặc
A( x ) 0
B( x ) 0
3. Bất phương trình chứa dấu giá trị tuyệt đối
x a
a x a
(với a ≥ 0)
x a
x a
hoặc
x a
(với a ≥ 0)
Một số bất phương trình đặc biệt:
|a| ≥ 0
a
R
|a| > 0
a ≠ 0
|a| ≤ 0
a = 0
|a| < 0
a
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 101
c) Đường tròn (K) cắt (O) tại E và F. Chứng tỏ IE, IF là hai tiếp tuyến
của (O). Suy ra cách dựng tiếp tuyến vẽ từ I đến (O).
d) Chứng tỏ: AB > CD OM < ON. Nói rõ vị trí tương đối của 2 cát
tuyến IAB và ICD lúc AB = CD.
e) Trường hợp dây cung AB = R
3
. Tính các góc và diện tích của
AOB theo R.
2.141 Cho đường tròn (O; R) có đường kính AB. AC và BD là hai dây cung
song song với nhau.
a) Chứng minh: AC = BD, suy ra CD là đường kính của (O).
b) Chứng tỏ ACBD là hình chữ nhật.
c) Chứng tỏ rằng nếu dây cung AC = R
2
thì ACBD là hình vuông và
ngược lại.
d) Tính diện tích ACBD trong trường hợp
BAC
= 30
0
.
2.142 Cho hai đường tròn (O; R) và (O; R) có R = 8, R = 6 và OO = 10.
a) Chứng tỏ (O; R) và (O; R) cắt nhau tại 2 điểm A và B và OOlà
đường trung trực của AB.
b) Chứng minh AO là tiếp tuyến của (O) và AO là tiếp tuyến của (O).
c) Gọi I là giao điểm OO và AB. Tính độ dài của IA, IO.
d) Xác định tâm và tính bán kính của đường tròn qua 4 điểm A, O, B, O.
e) Tìm điều kiện về bán kính của đường tròn (O) sao cho đường tròn này
không có điểm chung nào với (O; R).
2.143 Cho đường tròn (O; R) có đường kính AB, gọi (I) là đường tròn tâm I,
đường kính OA.
a) Chứng tỏ (O) và (I) tiếp xúc trong nhau.
b) Cho C là điểm bất kì (O) (C khác A, B), AC cắt (I) tại K. C/minh:
i. ABC và AOK vuông.
ii. K là trung điểm của AC và OK = BC/2
iii. IOK và OBC đồng dạng.
c) Gọi EF là đường kính của (O) qua K, chứng tỏ B, C, E, F là 4 đỉnh của
hình thang cân.
d) Cho
BOC
= 60
0
. Tính các cạnh, diện tích của ABC và của hình
thang cân BCEF.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 100
b) Gọi (I) là đường tròn tâm I có đường kính AB, đường thẳng OI cắt
đường tròn (O) tại C và D, cắt đường tròn (I) tại E và F. Chứng tỏ C,
D, E và F cách đều A và B.
c) Chứng minh: AEBF là hình vuông.
d) So sánh 2 tích IE . IF và IC . ID
e) Biết OI = R/2, tính độ dài các cạnh và diện tích của ACD và hình
vuông AEBF theo R.
2.138 Cho đường tròn (O; R), H là điểm bên trong (O) (H khác O), CD là đường
kính qua H (HC > HD), AB là dây cung vuông góc với CD tại H.
a) Chứng tỏ CD là đường trung trực của AB.
b) Chứng minh:
CAD
=
CBD
= 90
0
.
c) Chứng minh: HA . HB = HC . HD theo 2 cách:
i. Dùng 2 tam giác đồng dạng.
ii. Dùng hệ thức lượng trong tam giác vuông.
d) Trường hợp OH = R/2, chứng minh ABC đều và cạnh có độ dài là
R
3
. Suy ra cách vẽ tam giác đều có 3 đỉnh nằm trên đường tròn
(O; R) cho trước.
2.139 Cho ABC vuông tại A có đường cao AH. Gọi I và K lần lượt là tâm của
2 đường tròn có đường kính HB và HC.
a) Chứng tỏ 2 đường tròn (I) và (K) tiếp xúc ngoài nhau và tiếp xúc trong
với đường tròn qua 3 điểm A, B, C.
b) Đường tròn (I) cắt AB tại D, đường tròn (K) cắt AC tại E. Chứng minh
ADHE là hình chữ nhật và AD . AB = AE . AC. Suy ra ABC đồng
dạng với AED.
c) Chứng tỏ tứ giác BDEC có các góc đối bù nhau.
d) Cho AH = 4 và HB = 3. Tính diện tích của tứ giác BDEC bằng 2 cách:
i. Diện tích của nhiều tam giác.
ii. Diện tích của 2 tam giác.
2.140 Từ điểm I ở ngoài đường tròn (O; R) vẽ 2 cát tuyến IAB và ICD (không
qua O). Gọi M, N lần lượt là 2 trung điểm của 2 dây cung AB, CD.
a) Chứng minh: OMAB, ONCD, OM + ON 2R, CD<2R, AB < 2R.
b) Chứng tỏ có 1 đường tròn qua 4 điểm O, I, M, N. Xác định tâm K của
đường tròn này.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 5
4. Bất phương trình bậc hai
a) Bất phương trình bậc hai là bất phương trình có các dạng:
(1): ax
2
+ bx + c > 0 (2): ax
2
+ bx + c ≥ 0
(3): ax
2
+ bx + c < 0 (4): ax
2
+ bx + c ≤ 0
(trong đó a, b, c là các số thực và a ≠ 0)
Một số bất phương trình đặc biệt:
a
2
≥ 0
a
R
a
2
> 0
a ≠ 0
a
2
≤ 0
a = 0
a
2
< 0
a
b) Cách giải:
Cách 1: Đưa về bất phương trình tích bằng cách phân tích vế trái
thành nhân tử.
Cách 2: Đưa về bất phương trình chứa dấu giá trị tuyệt đối:
2 2
X A
X A A X A
2 2
X A
X A X A
hoặc
X A
Cách 3: Xét dấu (Học ở lớp 10)
O.3 Giải các bất phương trình sau và biểu diễn nghiệm trên trục số:
a) x(x – 1) < 0 b) (x – 2)(x – 5) > 0 c) (x + 5)(7 – 2x) > 0
d) (2x + 1)(x – 3) < 0 e) x
2
– 6x < 0 f) (2 – x)(x + 3) > 0
g)
x 2
0
x 3
h)
x 2
0
x 5
i)
x 1
1
x 3
j)
2 x
1
3x 1
k)
x 1
0
x 2
l)
2
x 1
0
x 3
O.4 Giải các bất phương trình sau và biểu diễn nghiệm trên trục số:
a) x
2
– 4 < 0 b) x
2
+ x – 6 0 c) x
2
– x – 6 > 0
d) x
2
– 3x – 10 ≥ 0 e) x
2
– 6x < 0 f) –x
2
+ 4x – 3 0
g) x
2
– 10x + 16 ≥ 0 h) – x
2
+ 7x – 10 < 0 i) x
2
– 15x + 50 > 0
j) – x
2
+ 3x + 4 > 0 k) x
2
– 6x + 5 ≥ 0 l) x
2
– x – 20 0
m) x
2
– 6x + 8 < 0 n) – x
2
+ 12x – 32 > 0 o) x
2
+ 6x + 8 0
O.5 Giải các bất phương trình sau và biểu diễn nghiệm trên trục số:
a)
x 4
b)
x 7
c)
2x 1 3
d)
x 1 2
e)
2 x 3 x 6
f)
1 2x x 1
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 100
b) Gọi (I) là đường tròn tâm I có đường kính AB, đường thẳng OI cắt
đường tròn (O) tại C và D, cắt đường tròn (I) tại E và F. Chứng tỏ C,
D, E và F cách đều A và B.
c) Chứng minh: AEBF là hình vuông.
d) So sánh 2 tích IE . IF và IC . ID
e) Biết OI = R/2, tính độ dài các cạnh và diện tích của ACD và hình
vuông AEBF theo R.
2.138 Cho đường tròn (O; R), H là điểm bên trong (O) (H khác O), CD là đường
kính qua H (HC > HD), AB là dây cung vuông góc với CD tại H.
a) Chứng tỏ CD là đường trung trực của AB.
b) Chứng minh:
CAD
=
CBD
= 90
0
.
c) Chứng minh: HA . HB = HC . HD theo 2 cách:
i. Dùng 2 tam giác đồng dạng.
ii. Dùng hệ thức lượng trong tam giác vuông.
d) Trường hợp OH = R/2, chứng minh ABC đều và cạnh có độ dài là
R
3
. Suy ra cách vẽ tam giác đều có 3 đỉnh nằm trên đường tròn
(O; R) cho trước.
2.139 Cho ABC vuông tại A có đường cao AH. Gọi I và K lần lượt là tâm của
2 đường tròn có đường kính HB và HC.
a) Chứng tỏ 2 đường tròn (I) và (K) tiếp xúc ngoài nhau và tiếp xúc trong
với đường tròn qua 3 điểm A, B, C.
b) Đường tròn (I) cắt AB tại D, đường tròn (K) cắt AC tại E. Chứng minh
ADHE là hình chữ nhật và AD . AB = AE . AC. Suy ra ABC đồng
dạng với AED.
c) Chứng tỏ tứ giác BDEC có các góc đối bù nhau.
d) Cho AH = 4 và HB = 3. Tính diện tích của tứ giác BDEC bằng 2 cách:
i. Diện tích của nhiều tam giác.
ii. Diện tích của 2 tam giác.
2.140 Từ điểm I ở ngoài đường tròn (O; R) vẽ 2 cát tuyến IAB và ICD (không
qua O). Gọi M, N lần lượt là 2 trung điểm của 2 dây cung AB, CD.
a) Chứng minh: OMAB, ONCD, OM + ON 2R, CD<2R, AB < 2R.
b) Chứng tỏ có 1 đường tròn qua 4 điểm O, I, M, N. Xác định tâm K của
đường tròn này.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 5
4. Bất phương trình bậc hai
a) Bất phương trình bậc hai là bất phương trình có các dạng:
(1): ax
2
+ bx + c > 0 (2): ax
2
+ bx + c ≥ 0
(3): ax
2
+ bx + c < 0 (4): ax
2
+ bx + c ≤ 0
(trong đó a, b, c là các số thực và a ≠ 0)
Một số bất phương trình đặc biệt:
a
2
≥ 0
a
R
a
2
> 0
a ≠ 0
a
2
≤ 0
a = 0
a
2
< 0
a
b) Cách giải:
Cách 1: Đưa về bất phương trình tích bằng cách phân tích vế trái
thành nhân tử.
Cách 2: Đưa về bất phương trình chứa dấu giá trị tuyệt đối:
2 2
X A
X A A X A
2 2
X A
X A X A
hoặc
X A
Cách 3: Xét dấu (Học ở lớp 10)
O.3 Giải các bất phương trình sau và biểu diễn nghiệm trên trục số:
a) x(x – 1) < 0 b) (x – 2)(x – 5) > 0 c) (x + 5)(7 – 2x) > 0
d) (2x + 1)(x – 3) < 0 e) x
2
– 6x < 0 f) (2 – x)(x + 3) > 0
g)
x 2
0
x 3
h)
x 2
0
x 5
i)
x 1
1
x 3
j)
2 x
1
3x 1
k)
x 1
0
x 2
l)
2
x 1
0
x 3
O.4 Giải các bất phương trình sau và biểu diễn nghiệm trên trục số:
a) x
2
– 4 < 0 b) x
2
+ x – 6 0 c) x
2
– x – 6 > 0
d) x
2
– 3x – 10 ≥ 0 e) x
2
– 6x < 0 f) –x
2
+ 4x – 3 0
g) x
2
– 10x + 16 ≥ 0 h) – x
2
+ 7x – 10 < 0 i) x
2
– 15x + 50 > 0
j) – x
2
+ 3x + 4 > 0 k) x
2
– 6x + 5 ≥ 0 l) x
2
– x – 20 0
m) x
2
– 6x + 8 < 0 n) – x
2
+ 12x – 32 > 0 o) x
2
+ 6x + 8 0
O.5 Giải các bất phương trình sau và biểu diễn nghiệm trên trục số:
a)
x 4
b)
x 7
c)
2x 1 3
d)
x 1 2
e)
2 x 3 x 6
f)
1 2x x 1
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 6
O.6 CMR: các bất phương trình sau đây vô nghiệm:
a) x
2
+ 1 < 1 b) x
2
+ 2x < 2x c) x
2
– 2x + 3 < 2x + 3
d) x
2
+ 2x + 2 0 e) 4x
2
4x + 5 0 f) x
2
+ x + 1 0
O.7 CMR: mọi số thực x đều là nghiệm của các bất phương trình sau:
a) 2x
2
4x + 5 > 0 b) 3x
2
+ 2x + 1 0 c) x
2
+ 6x 10 < 0
d) x
2
+ 3x 3 < 0 e)
2
x 4x 5
0
2
f)
2
2
6 2x x
0
x 1
O.8 Tìm giá trị nhỏ nhất của các biểu thức sau:
a) A = 2x
2
+ 20x – 43 b) B = x
2
+ 2x + 2
c) C = x
2
– x +1 d) D = 4x
2
+ 4x + 3
e) E = x
2
– 20x + 101 f) F = x
2
+ xy + y
2
+ 1
g) G = (x – 3)(x + 5) + 40 h) H = (x – 2)(x + 4) – 10
O.9 Tìm giá trị nhỏ nhất của các biểu thức sau:
a) A = – 2x
2
+ 5x – 17 b) B = – x
2
+ 4x – 5
c) C = – 4x
2
– 4x – 2 d) D = – 6 – 8x – 16x
2
e) E = – 3x
2
+ 12x – 11 f) F = – 2x
2
+ 5x – 17
O.10 Tìm giá trị nhỏ nhất hoặc giá trị lớn nhất của các biểu thức sau:
a) A =
2
6
2x 3
b) B =
2
1
x 2x 6
c) C =
2
7
10x x 3
d) D =
2
24
x 2x 3
e) E =
2
21
x 4x 5
f) F =
2
2013
x 6x 11
O.11 Tìm giá trị nguyên của biến x để tại đó giá trị của mỗi biểu thức sau là
một số nguyên:
a)
2
x 3
b)
3
x 2
c)
3 2
3x 4x x 1
x 4
d)
2
3x x 1
3x 2
O.12 Chứng minh rằng:
a)
3
2
x 2 x 8x 7
1 0
x 1 2x 2 2x 2
(x 1, x – 1)
b)
2 2 2
2
1 x x 3x 14x 3
1 0
x x 3 x 3x
(x 0, x – 3)
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 99
2.133 Cho đoạn thẳng AB. Trên nửa mặt phẳng bờ AB kẻ hai tia bất kì Ax và
By song song với nhau. Một đường tròn tâm M tiếp xúc với AB tại C, với
Ax tại D, với By tại E.
a) Nêu cách dựng đường tròn tâm M.
b) Chứng minh: AD + BE không phụ thuộc vào vị trí của Ax và By.
c) Chứng minh: E, M, D thẳng hàng.
d) Chứng minh: M thuộc một đường tròn cố định khi Ax và By thay đổi.
2.134 Cho hai đường tròn (O ; R) và (O; R) tiếp xúc ngoài tại A. Gọi BC là
tiếp tuyến chung ngoài của hai đường tròn (B (O)).
a) Chứng minh:
BAC
= 90
0
.
b) Gọi D là điểm đối xứng của C qua O. C/minh: B, A, D thẳng hàng.
c) Chứng minh: BC là tiếp tuyến của đường tròn đường kính OO.
d) Chứng minh: BC = 2
RR'
.
2.135 Cho hai đường tròn (O) và (O) cắt nhau ở A và B. Gọi C và lần lượt là
điểm đối xứng của A qua O và O. Một đường thẳng (d) bất kì qua A cắt
(O) và (O) tại M và N.
a) Chứng minh: C, B, D thẳng hàng.
b) AC cắt (O) tại E, AD cắt (O) tại F. Chứng minh: C, D, E, F cùng
thuộc một đường tròn.
c) Chứng minh: trung trực của MN luôn đi qua trung điểm của CD khi
(d) thay đổi. Suy ra trung điểm của MN luôn di động trên một đường
tròn cố định.
d) Định vị trí của đường thẳng (d) để MN có độ dài lớn nhất.
2.136 Cho nửa đường tròn tâm O đường kính AB. Gọi M là điểm bất kì thuộc
nửa đường tròn, H là chân đường vuông góc kẻ từ M đến AB. Vẽ đường
tròn (M ; MH). Kẻ các tiếp tuyến AC, BD với đường tròn tâm M (C, D là
các tiếp điểm khác H).
a) Chứng minh: C, M, D thẳng hàng và CD là tiếp tuyến của (O).
b) Chứng minh: Khi M di chuyển trên AB thì tổng AC + BD không đổi.
c) Giả sử CD và AB cắt nhau tại I. Chứng minh: OH . OI không đổi.
2.137 Cho đường tròn (O; R) và điểm I trong (O) (I khác O).
a) Hãy vẽ dây cung AB qua I và nhận I làm trung điểm.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 6
O.6 CMR: các bất phương trình sau đây vô nghiệm:
a) x
2
+ 1 < 1 b) x
2
+ 2x < 2x c) x
2
– 2x + 3 < 2x + 3
d) x
2
+ 2x + 2 0 e) 4x
2
4x + 5 0 f) x
2
+ x + 1 0
O.7 CMR: mọi số thực x đều là nghiệm của các bất phương trình sau:
a) 2x
2
4x + 5 > 0 b) 3x
2
+ 2x + 1 0 c) x
2
+ 6x 10 < 0
d) x
2
+ 3x 3 < 0 e)
2
x 4x 5
0
2
f)
2
2
6 2x x
0
x 1
O.8 Tìm giá trị nhỏ nhất của các biểu thức sau:
a) A = 2x
2
+ 20x – 43 b) B = x
2
+ 2x + 2
c) C = x
2
– x +1 d) D = 4x
2
+ 4x + 3
e) E = x
2
– 20x + 101 f) F = x
2
+ xy + y
2
+ 1
g) G = (x – 3)(x + 5) + 40 h) H = (x – 2)(x + 4) – 10
O.9 Tìm giá trị nhỏ nhất của các biểu thức sau:
a) A = – 2x
2
+ 5x – 17 b) B = – x
2
+ 4x – 5
c) C = – 4x
2
– 4x – 2 d) D = – 6 – 8x – 16x
2
e) E = – 3x
2
+ 12x – 11 f) F = – 2x
2
+ 5x – 17
O.10 Tìm giá trị nhỏ nhất hoặc giá trị lớn nhất của các biểu thức sau:
a) A =
2
6
2x 3
b) B =
2
1
x 2x 6
c) C =
2
7
10x x 3
d) D =
2
24
x 2x 3
e) E =
2
21
x 4x 5
f) F =
2
2013
x 6x 11
O.11 Tìm giá trị nguyên của biến x để tại đó giá trị của mỗi biểu thức sau là
một số nguyên:
a)
2
x 3
b)
3
x 2
c)
3 2
3x 4x x 1
x 4
d)
2
3x x 1
3x 2
O.12 Chứng minh rằng:
a)
3
2
x 2 x 8x 7
1 0
x 1 2x 2 2x 2
(x 1, x – 1)
b)
2 2 2
2
1 x x 3x 14x 3
1 0
x x 3 x 3x
(x 0, x – 3)
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 99
2.133 Cho đoạn thẳng AB. Trên nửa mặt phẳng bờ AB kẻ hai tia bất kì Ax và
By song song với nhau. Một đường tròn tâm M tiếp xúc với AB tại C, với
Ax tại D, với By tại E.
a) Nêu cách dựng đường tròn tâm M.
b) Chứng minh: AD + BE không phụ thuộc vào vị trí của Ax và By.
c) Chứng minh: E, M, D thẳng hàng.
d) Chứng minh: M thuộc một đường tròn cố định khi Ax và By thay đổi.
2.134 Cho hai đường tròn (O ; R) và (O; R) tiếp xúc ngoài tại A. Gọi BC là
tiếp tuyến chung ngoài của hai đường tròn (B (O)).
a) Chứng minh:
BAC
= 90
0
.
b) Gọi D là điểm đối xứng của C qua O. C/minh: B, A, D thẳng hàng.
c) Chứng minh: BC là tiếp tuyến của đường tròn đường kính OO.
d) Chứng minh: BC = 2
RR'
.
2.135 Cho hai đường tròn (O) và (O) cắt nhau ở A và B. Gọi C và lần lượt là
điểm đối xứng của A qua O và O. Một đường thẳng (d) bất kì qua A cắt
(O) và (O) tại M và N.
a) Chứng minh: C, B, D thẳng hàng.
b) AC cắt (O) tại E, AD cắt (O) tại F. Chứng minh: C, D, E, F cùng
thuộc một đường tròn.
c) Chứng minh: trung trực của MN luôn đi qua trung điểm của CD khi
(d) thay đổi. Suy ra trung điểm của MN luôn di động trên một đường
tròn cố định.
d) Định vị trí của đường thẳng (d) để MN có độ dài lớn nhất.
2.136 Cho nửa đường tròn tâm O đường kính AB. Gọi M là điểm bất kì thuộc
nửa đường tròn, H là chân đường vuông góc kẻ từ M đến AB. Vẽ đường
tròn (M ; MH). Kẻ các tiếp tuyến AC, BD với đường tròn tâm M (C, D là
các tiếp điểm khác H).
a) Chứng minh: C, M, D thẳng hàng và CD là tiếp tuyến của (O).
b) Chứng minh: Khi M di chuyển trên AB thì tổng AC + BD không đổi.
c) Giả sử CD và AB cắt nhau tại I. Chứng minh: OH . OI không đổi.
2.137 Cho đường tròn (O; R) và điểm I trong (O) (I khác O).
a) Hãy vẽ dây cung AB qua I và nhận I làm trung điểm.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 98
2.129 Cho đường tròn (O ; R) và đường thẳng xy cố định ở ngoài (O). Từ điểm
M bất kì trên xy kẻ hai tiếp tuyến MB, MC đến đường tròn (O) (B, C là
các tiếp điểm).
a) Xác định tâm O của đường tròn đi qua M, B, O, C.
b) Chứng minh: (O) luôn đi qua một điểm cố định H khác O.
c) Dây cung BC cắt OH tại I vad cắt OM tại K.
Chứng minh: OI.OH = OK.OM = R
2
. Suy ra khi M thay đổi trên xy thì
BC luôn đi qua một điểm cố định.
2.130 Cho nửa đường tròn (O) đường kính AB = 2R và một điểm M bất kì trên
nửa đường tròn (M khác A, B). Đường thẳng (d) tiếp xúc với nửa đường
tròn tại M và cắt trung trực của đoạn AB tại I. Đường tròn (I) tiếp xúc với
AB cắt đường thẳng (d) tại C và D (D nằm trong góc BÔM).
a) Chứng minh: OC, OD là các tia phân giác của các góc AÔM và BÔM.
b) Chứng minh: CA và DB vuông góc với AB.
c) Chứng minh: AC . BD = R
2
.
d) AM cắt BD tại F, BM cắt AC tại E. Chứng minh: S
ABM
= S
EFM
.
e) Xác định vị trí của M sao cho diện tích hình thang ABCD nhỏ nhất.
2.131 Cho đường tròn (O) và dây BC cố định. Điểm A di động trên cung lớn
BC. Gọi M là trung điểm của dây AC. Vẽ đường kính BD của (O).
a) Chứng minh: M thuộc một đường tròn cố định. Xác định tâm I của
đường tròn này.
b) Gọi K là trung điểm của BC, đường tròn (I) cắt CD tại J.
Chứng minh: K, I, J thẳng hàng.
c) Gọi H là hình chiếu của M trên AB, chứng tỏ đường thẳng HM luôn đi
qua trung điểm của dây CD khi A thay đổi.
d) C/minh: khi A di động thì H luôn di động trên một đường tròn cố định.
2.132 Cho đường tròn (O ; R) và đường thẳng (d) cắt đường tròn tại E, F. Từ
điểm A bất kì trên (d) và ở ngoài đường tròn (O), vẽ các tiếp tuyến AB,
AC đến đường tròn (O) (B, C là các tiếp điểm). Gọi H là trung điểm của
EF và BC cắt OA, OH lần lượt tại I, K. Chứng minh:
a) 5 điểm A, B, C, O, H thuộc một đường tròn.
b) OI . OA = OH . OK = R
2
.
c) Khi A thay đổi, đường thẳng BC luôn đi qua một điểm cố định.
d) I luôn thuộc một đường tròn cố định khi A thay đổi.
e) KE, KF là các tiếp tuyến của (O; R).
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 7
O.13 Chứng minh rằng:
a)
2
2
2
x 1 x 1 2 1
: 1 1
x x x 1 x
(x 0, x – 1)
b)
2
2 2
x x 3x x 3 x
1
x 3 2x 3 x 3x x 9
(x 0, x 3, x –3/2)
c)
2
2 2 2
1 x x x 1
1
x 1 x 1 x 2x 1 x 1
(x 1)
d)
2 2 2
x x 6 2x 6 x
: 1
x 36 x 6x x 6x 6 x
(x 0 và x 6)
O.14 Phân tích các đa thức sau thành nhân tử:
1) a)
2
x 4x 12
b)
2
6x 7x 1
c)
2
2x 4x 6
d)
2
2x 10x 8
e)
2
10x 4x 6
f)
2
x 2x 15
2. a)
4 2
2x x 6
b)
4 2
x 6x 8
c)
4 2
x 5x 14
d)
4 2
4x 7x 3
e)
4 2
6x 7x 2
f)
4 2
x 8x 15
3. a)
x 5 x 6
b)
x 9 x 18
c)
3x 5 x 8
d)
2x 3 x 5
e)
4x x 3
f)
x 2 x 3
O.15 Cho biểu thức:
2 2
3
x 6 1 10 x
: x 2
x 4x 6 3x x 2 x 2
a) Tìm điều kiện xác định của biểu thức. Rút gọn biểu thức.
b) Tìm giá trị của x để giá trị của biểu thức có giá trị dương.
O.16 Cho biểu thức:
2
x 2 2 2 4x x 3x 1
3 :
3x x 1 x 1 3x
a) Tìm điều kiện xác định của biểu thức. Rút gọn biểu thức.
b) Tìm giá trị của x để giá trị của biểu thức có giá trị âm.
O.17 Cho biểu thức:
2
2 2
2
x
2x 1 x 1
x 1
x
x x x 1
x x 1
a) Tìm điều kiện xác định của biểu thức. Rút gọn biểu thức.
b) Tìm giá trị của x để giá trị của biểu thức có giá trị dương.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 98
2.129 Cho đường tròn (O ; R) và đường thẳng xy cố định ở ngoài (O). Từ điểm
M bất kì trên xy kẻ hai tiếp tuyến MB, MC đến đường tròn (O) (B, C là
các tiếp điểm).
a) Xác định tâm O của đường tròn đi qua M, B, O, C.
b) Chứng minh: (O) luôn đi qua một điểm cố định H khác O.
c) Dây cung BC cắt OH tại I vad cắt OM tại K.
Chứng minh: OI.OH = OK.OM = R
2
. Suy ra khi M thay đổi trên xy thì
BC luôn đi qua một điểm cố định.
2.130 Cho nửa đường tròn (O) đường kính AB = 2R và một điểm M bất kì trên
nửa đường tròn (M khác A, B). Đường thẳng (d) tiếp xúc với nửa đường
tròn tại M và cắt trung trực của đoạn AB tại I. Đường tròn (I) tiếp xúc với
AB cắt đường thẳng (d) tại C và D (D nằm trong góc BÔM).
a) Chứng minh: OC, OD là các tia phân giác của các góc AÔM và BÔM.
b) Chứng minh: CA và DB vuông góc với AB.
c) Chứng minh: AC . BD = R
2
.
d) AM cắt BD tại F, BM cắt AC tại E. Chứng minh: S
ABM
= S
EFM
.
e) Xác định vị trí của M sao cho diện tích hình thang ABCD nhỏ nhất.
2.131 Cho đường tròn (O) và dây BC cố định. Điểm A di động trên cung lớn
BC. Gọi M là trung điểm của dây AC. Vẽ đường kính BD của (O).
a) Chứng minh: M thuộc một đường tròn cố định. Xác định tâm I của
đường tròn này.
b) Gọi K là trung điểm của BC, đường tròn (I) cắt CD tại J.
Chứng minh: K, I, J thẳng hàng.
c) Gọi H là hình chiếu của M trên AB, chứng tỏ đường thẳng HM luôn đi
qua trung điểm của dây CD khi A thay đổi.
d) C/minh: khi A di động thì H luôn di động trên một đường tròn cố định.
2.132 Cho đường tròn (O ; R) và đường thẳng (d) cắt đường tròn tại E, F. Từ
điểm A bất kì trên (d) và ở ngoài đường tròn (O), vẽ các tiếp tuyến AB,
AC đến đường tròn (O) (B, C là các tiếp điểm). Gọi H là trung điểm của
EF và BC cắt OA, OH lần lượt tại I, K. Chứng minh:
a) 5 điểm A, B, C, O, H thuộc một đường tròn.
b) OI . OA = OH . OK = R
2
.
c) Khi A thay đổi, đường thẳng BC luôn đi qua một điểm cố định.
d) I luôn thuộc một đường tròn cố định khi A thay đổi.
e) KE, KF là các tiếp tuyến của (O; R).
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 7
O.13 Chứng minh rằng:
a)
2
2
2
x 1 x 1 2 1
: 1 1
x x x 1 x
(x 0, x – 1)
b)
2
2 2
x x 3x x 3 x
1
x 3 2x 3 x 3x x 9
(x 0, x 3, x –3/2)
c)
2
2 2 2
1 x x x 1
1
x 1 x 1 x 2x 1 x 1
(x 1)
d)
2 2 2
x x 6 2x 6 x
: 1
x 36 x 6x x 6x 6 x
(x 0 và x 6)
O.14 Phân tích các đa thức sau thành nhân tử:
1) a)
2
x 4x 12
b)
2
6x 7x 1
c)
2
2x 4x 6
d)
2
2x 10x 8
e)
2
10x 4x 6
f)
2
x 2x 15
2. a)
4 2
2x x 6
b)
4 2
x 6x 8
c)
4 2
x 5x 14
d)
4 2
4x 7x 3
e)
4 2
6x 7x 2
f)
4 2
x 8x 15
3. a)
x 5 x 6
b)
x 9 x 18
c)
3x 5 x 8
d)
2x 3 x 5
e)
4x x 3
f)
x 2 x 3
O.15 Cho biểu thức:
2 2
3
x 6 1 10 x
: x 2
x 4x 6 3x x 2 x 2
a) Tìm điều kiện xác định của biểu thức. Rút gọn biểu thức.
b) Tìm giá trị của x để giá trị của biểu thức có giá trị dương.
O.16 Cho biểu thức:
2
x 2 2 2 4x x 3x 1
3 :
3x x 1 x 1 3x
a) Tìm điều kiện xác định của biểu thức. Rút gọn biểu thức.
b) Tìm giá trị của x để giá trị của biểu thức có giá trị âm.
O.17 Cho biểu thức:
2
2 2
2
x
2x 1 x 1
x 1
x
x x x 1
x x 1
a) Tìm điều kiện xác định của biểu thức. Rút gọn biểu thức.
b) Tìm giá trị của x để giá trị của biểu thức có giá trị dương.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 8
O.18 Cho biểu thức:
2
2
1 2x x 2x 24 12x
4 2x 3x 6 12 3x 6 13x
a) Tìm điều kiện xác định của biểu thức. Rút gọn biểu thức.
b) Tìm giá trị của x để giá trị của biểu thức có giá trị dương.
O.19 Cho biểu thức:
2
x 2 2 2 4x x 3x 1
3 :
3x x 1 x 1 3x
a) Tìm điều kiện xác định của biểu thức. Rút gọn biểu thức.
b) Tìm giá trị của x để giá trị của biểu thức có giá trị âm.
O.20 Cho biểu thức:
3 2
4x 6x 8x
2x 1
a) Tìm điều kiện xác định của biểu thức. Rút gọn biểu thức.
b) Tìm giá trị của x để giá trị của biểu thức có giá trị không âm.
O.21 Cho biểu thức:
2
8 2x
x x 20
a) Tìm điều kiện xác định của biểu thức. Rút gọn biểu thức.
b) Tìm giá trị của x để giá trị của biểu thức có giá trị âm.
O.22 Cho biểu thức:
2 2
x x 4
M 4 3
x 2 x
a) Tìm điều kiện xác định của biểu thức M. Rút gọn M.
b) Tìm x để biểu thức M đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó.
O.23 Cho biểu thức:
2 2 2
(x 2) x x 6x 4
N 1
x x 2 x
a) Tìm điều kiện xác định của biểu thức N. Rút gọn N.
b) Tìm x để biểu thức N đạt giá trị lớn nhất. Tìm giá trị lớn nhất đó.
2 2 2
( A B ) A 2AB B
2 2 2
( A B ) A 2AB B
2 2
A B ( A B )( A B )
3 3 2 2 3
( A B ) A 3A B 3AB B
3 3 2 2 3
( A B ) A 3A B 3AB B
3 3 2 2
A B ( A B )( A AB B )
3 3 2 2
A B ( A B )( A AB B )
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 97
c) C luôn luôn thuộc một đường tròn cố định khi B thay đổi.
2.125 Cho đường tròn (O ; R) AB. Vẽ dây CD của (O) vuông góc với OA tại
trung điểm của M của OA. Gọi E là trung điểm của BC.
d) Chứng minh: O, M, C, E cùng thuộc một đường tròn.
a) Tính BC theo R.
b) Tiếp tuyến tại B của (O) cắt OE tại N. C/m: NC là tiếp tuyến của (O).
c) Chứng minh: NA chia MC hai phần bằng nhau.
d) Chứng minh: MA
2
+ MB
2
+ MC
2
+ MD
2
= 4R
2
.
2.126 Cho ABC có
A
= 90
0
, (AB < AC) nội tiếp (O ; R), có đường cao AH.
Gọi M là trung điểm AC.
a) Chứng minh: A, M, O, H cùng thuộc một đường tròn. Xác định tâm I
của đường tròn này.
b) Chứng minh: (O) và (I) tiếp xúc nhau.
c) Đường tròn (I) cắt AB tại N. Chứng minh: I, M, N thẳng hàng.
2.127 Cho đường tròn (O; R) đường kính AB. Lấy điểm M (O). Gọi P, Q theo
thứ tự là hình chiếu của M trên AB và tiếp tuyến Ax của (O). gọi I là
trung điểm của của PQ.
a) Chứng minh: A, I, M thẳng hàng. Suy ra I thuộc một đường tròn cố
định và tính theo R bán kính của đường tròn này.
b) Tiếp tuyến tại M của (O) cắt tiếp tuyến Ax ở N. Chứng minh: O, I, N
thẳng hàng và MA là phân giác các góc OMQ, NMP.
c) Đường trung trực của đường kính AB cắt MB tại K.
Chứng minh: NK = R.
d) Xác định vị trí của M để AMN đều.
2.128 Cho đường tròn (O; R) đường kính AB. Lấy điểm C ngoài đường tròn sao
cho B là trung điểm của OC. Từ C vẽ hai tiếp tuyến CM và CN đến
đường tròn (O) (M, N là các tiếp điểm).
a) Chứng minh: AMN là tam giác cân. Tính CM và AM theo R.
b) Chứng minh: tứ giác AMCN là hình thoi. Tính S
AMCN
theo R.
c) Gọi I là trung điểm của CM, AI cắt OM tại K. Chứng minh: K là trung
điểm của AI.
d) Tính diện tích AKB theo R.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 8
O.18 Cho biểu thức:
2
2
1 2x x 2x 24 12x
4 2x 3x 6 12 3x 6 13x
a) Tìm điều kiện xác định của biểu thức. Rút gọn biểu thức.
b) Tìm giá trị của x để giá trị của biểu thức có giá trị dương.
O.19 Cho biểu thức:
2
x 2 2 2 4x x 3x 1
3 :
3x x 1 x 1 3x
a) Tìm điều kiện xác định của biểu thức. Rút gọn biểu thức.
b) Tìm giá trị của x để giá trị của biểu thức có giá trị âm.
O.20 Cho biểu thức:
3 2
4x 6x 8x
2x 1
a) Tìm điều kiện xác định của biểu thức. Rút gọn biểu thức.
b) Tìm giá trị của x để giá trị của biểu thức có giá trị không âm.
O.21 Cho biểu thức:
2
8 2x
x x 20
a) Tìm điều kiện xác định của biểu thức. Rút gọn biểu thức.
b) Tìm giá trị của x để giá trị của biểu thức có giá trị âm.
O.22 Cho biểu thức:
2 2
x x 4
M 4 3
x 2 x
a) Tìm điều kiện xác định của biểu thức M. Rút gọn M.
b) Tìm x để biểu thức M đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó.
O.23 Cho biểu thức:
2 2 2
(x 2) x x 6x 4
N 1
x x 2 x
a) Tìm điều kiện xác định của biểu thức N. Rút gọn N.
b) Tìm x để biểu thức N đạt giá trị lớn nhất. Tìm giá trị lớn nhất đó.
2 2 2
( A B ) A 2AB B
2 2 2
( A B ) A 2AB B
2 2
A B ( A B )( A B )
3 3 2 2 3
( A B ) A 3A B 3AB B
3 3 2 2 3
( A B ) A 3A B 3AB B
3 3 2 2
A B ( A B )( A AB B )
3 3 2 2
A B ( A B )( A AB B )
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 97
c) C luôn luôn thuộc một đường tròn cố định khi B thay đổi.
2.125 Cho đường tròn (O ; R) AB. Vẽ dây CD của (O) vuông góc với OA tại
trung điểm của M của OA. Gọi E là trung điểm của BC.
d) Chứng minh: O, M, C, E cùng thuộc một đường tròn.
a) Tính BC theo R.
b) Tiếp tuyến tại B của (O) cắt OE tại N. C/m: NC là tiếp tuyến của (O).
c) Chứng minh: NA chia MC hai phần bằng nhau.
d) Chứng minh: MA
2
+ MB
2
+ MC
2
+ MD
2
= 4R
2
.
2.126 Cho ABC có
A
= 90
0
, (AB < AC) nội tiếp (O ; R), có đường cao AH.
Gọi M là trung điểm AC.
a) Chứng minh: A, M, O, H cùng thuộc một đường tròn. Xác định tâm I
của đường tròn này.
b) Chứng minh: (O) và (I) tiếp xúc nhau.
c) Đường tròn (I) cắt AB tại N. Chứng minh: I, M, N thẳng hàng.
2.127 Cho đường tròn (O; R) đường kính AB. Lấy điểm M (O). Gọi P, Q theo
thứ tự là hình chiếu của M trên AB và tiếp tuyến Ax của (O). gọi I là
trung điểm của của PQ.
a) Chứng minh: A, I, M thẳng hàng. Suy ra I thuộc một đường tròn cố
định và tính theo R bán kính của đường tròn này.
b) Tiếp tuyến tại M của (O) cắt tiếp tuyến Ax ở N. Chứng minh: O, I, N
thẳng hàng và MA là phân giác các góc OMQ, NMP.
c) Đường trung trực của đường kính AB cắt MB tại K.
Chứng minh: NK = R.
d) Xác định vị trí của M để AMN đều.
2.128 Cho đường tròn (O; R) đường kính AB. Lấy điểm C ngoài đường tròn sao
cho B là trung điểm của OC. Từ C vẽ hai tiếp tuyến CM và CN đến
đường tròn (O) (M, N là các tiếp điểm).
a) Chứng minh: AMN là tam giác cân. Tính CM và AM theo R.
b) Chứng minh: tứ giác AMCN là hình thoi. Tính S
AMCN
theo R.
c) Gọi I là trung điểm của CM, AI cắt OM tại K. Chứng minh: K là trung
điểm của AI.
d) Tính diện tích AKB theo R.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 96
c) Chứng minh: 4 điểm I, O, M, B cùng thuộc một đường tròn.
2.120 Cho hai đường tròn (O) và (O) tiếp xúc ngoài A. Kẻ tiếp tuyến chung
ngoài DE, D (O), E (O). Kẻ tiếp tuyến chung trong tại A, cắt DE ở I.
Gọi M là giao điểm của OI và AD, N là giao điểm của OI và AE.
a) Tứ giác AMIN là hình gì ? Vì sao ?
b) Chứng minh: IM . IO = IN . IO
c) Chứng minh: OO là tiếp tuyến của đường tròn có đường kính là DE.
d) Biết OA = 5cm, OA = 3,2cm. Tính DE.
2.121 Cho ABC vuông tại A (AB < AC) nội tiếp đường tròn (O) có đường
kính BC. Kẻ dây AD vuông góc với BC. Gọi E là giao điểm của DB và
CA. Qua E kẻ đường thẳng vuông góc với BC, cắt BC ở H, cắt AB ở F.
Chứng minh:
a) EBF cân. b) HAF cân. c) HA là tiếp tuyến của (O).
2.122 Cho (O) đường kính AB, điểm C nằm giữa A và O. Vẽ đường tròn (O) có
đường kính CB.
a) Hai đường tròn (O) và (O) có vị trí tương đối như thế nào với nhau ?
b) Kẻ dây DE của đường tròn (O) vuông góc với AC tại trung điểm H
của AC. Tứ giác ADCE là hình gì ? Vì sao ?
c) Gọi K là giao điểm của DB và (O). Chứng minh: ba điểm E, C, K
thẳng hàng.
d) Chứng minh: KH là tiếp tuyến của (O).
2.123 Cho hai đường tròn (O; R) và (O; R) tiếp xúc ngoài tại A (R > R). Vẽ
các đường kính AOB, AOC. Dây DE của đường tròn (O) vuông góc với
BC tại trung điểm K của BC.
a) Chứng minh: tứ giác BDCE là hình thoi.
b) Gọi I là giao điểm của EC và đường tròn (O). Chứng minh: ba điểm D,
A, I thẳng hàng.
c) Chứng minh: KI là tiếp tuyến của (O).
2.124 Cho đường tròn (O; R) và tiếp tuyến xy tại điểm A cố định trên đường
tròn. Từ điểm B tùy ý trên (O) (khác A), kẻ BH xy. Đường phân giác
trong của góc AÔB cắt BH tại C và cắt xy tại M. Chứng minh:
a) BA là tia phân giác của OBH.
b) MB là tiếp tuyến của (O; R).
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 9
Phần 1. Đại số
Chương 1
CĂN BẬC HAI – CĂN BẬC BA
A - Căn bậc hai
1. Định nghĩa: Căn bậc hai của số a không âm là số x sao cho x
2
= a.
2. Ký hiệu:
a > 0:
a
: Căn bậc hai của số a
a
: Căn bậc hai âm của số a
a = 0:
0 0
3. Chú ý: Với a
0:
2 2
( a ) ( a ) a
4. Căn bậc hai số học:
Với a
0: số
a
được gọi là CBHSH của a
Phép khi phương là phép toán tìm CBHSH của số a không âm.
5. So sánh các CBHSH: Với a
0, b
0:
a b a b
1.1 Điền vào ô trống trong bảng sau:
x 11 12 13 14 15 16 17 18 19 20
x
2
1.2 Tìm căn bậc hai số học rồi suy ra căn bậc hai của các số sau:
a) 121 b) 144 c) 169 d) 225
e) 256 f) 324 g) 361 h) 400
i) 0,01 j) 0,04 k) 0,49 l) 0,64
m) 0,25 n) 0,81 o) 0,09 p) 0,16
1.3 Tính:
a)
0,09
b)
16
c)
0,25. 0,16
d)
( 4).( 25)
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 96
c) Chứng minh: 4 điểm I, O, M, B cùng thuộc một đường tròn.
2.120 Cho hai đường tròn (O) và (O) tiếp xúc ngoài A. Kẻ tiếp tuyến chung
ngoài DE, D (O), E (O). Kẻ tiếp tuyến chung trong tại A, cắt DE ở I.
Gọi M là giao điểm của OI và AD, N là giao điểm của OI và AE.
a) Tứ giác AMIN là hình gì ? Vì sao ?
b) Chứng minh: IM . IO = IN . IO
c) Chứng minh: OO là tiếp tuyến của đường tròn có đường kính là DE.
d) Biết OA = 5cm, OA = 3,2cm. Tính DE.
2.121 Cho ABC vuông tại A (AB < AC) nội tiếp đường tròn (O) có đường
kính BC. Kẻ dây AD vuông góc với BC. Gọi E là giao điểm của DB và
CA. Qua E kẻ đường thẳng vuông góc với BC, cắt BC ở H, cắt AB ở F.
Chứng minh:
a) EBF cân. b) HAF cân. c) HA là tiếp tuyến của (O).
2.122 Cho (O) đường kính AB, điểm C nằm giữa A và O. Vẽ đường tròn (O) có
đường kính CB.
a) Hai đường tròn (O) và (O) có vị trí tương đối như thế nào với nhau ?
b) Kẻ dây DE của đường tròn (O) vuông góc với AC tại trung điểm H
của AC. Tứ giác ADCE là hình gì ? Vì sao ?
c) Gọi K là giao điểm của DB và (O). Chứng minh: ba điểm E, C, K
thẳng hàng.
d) Chứng minh: KH là tiếp tuyến của (O).
2.123 Cho hai đường tròn (O; R) và (O; R) tiếp xúc ngoài tại A (R > R). Vẽ
các đường kính AOB, AOC. Dây DE của đường tròn (O) vuông góc với
BC tại trung điểm K của BC.
a) Chứng minh: tứ giác BDCE là hình thoi.
b) Gọi I là giao điểm của EC và đường tròn (O). Chứng minh: ba điểm D,
A, I thẳng hàng.
c) Chứng minh: KI là tiếp tuyến của (O).
2.124 Cho đường tròn (O; R) và tiếp tuyến xy tại điểm A cố định trên đường
tròn. Từ điểm B tùy ý trên (O) (khác A), kẻ BH xy. Đường phân giác
trong của góc AÔB cắt BH tại C và cắt xy tại M. Chứng minh:
a) BA là tia phân giác của OBH.
b) MB là tiếp tuyến của (O; R).
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 9
Phần 1. Đại số
Chương 1
CĂN BẬC HAI – CĂN BẬC BA

A - Căn bậc hai
1. Định nghĩa: Căn bậc hai của số a không âm là số x sao cho x
2
= a.
2. Ký hiệu:
a > 0:
a
: Căn bậc hai của số a
a
: Căn bậc hai âm của số a
a = 0:
0 0
3. Chú ý: Với a
0:
2 2
( a ) ( a ) a
4. Căn bậc hai số học:
Với a
0: số
a
được gọi là CBHSH của a
Phép khi phương là phép toán tìm CBHSH của số a không âm.
5. So sánh các CBHSH: Với a
0, b
0:
a b a b
1.1 Điền vào ô trống trong bảng sau:
x 11 12 13 14 15 16 17 18 19 20
x
2
1.2 Tìm căn bậc hai số học rồi suy ra căn bậc hai của các số sau:
a) 121 b) 144 c) 169 d) 225
e) 256 f) 324 g) 361 h) 400
i) 0,01 j) 0,04 k) 0,49 l) 0,64
m) 0,25 n) 0,81 o) 0,09 p) 0,16
1.3 Tính:
a)
0,09
b)
16
c)
0,25. 0,16
d)
( 4).( 25)
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 10
e)
25
4
f)
0405
166
,
g) 490360 ,,
1.4 Trong các số sau, số nào có căn bậc hai:
a) 5 b) 1,5 c) 0,1 d) 9
1.5 Trong các biểu thức sau, biểu thức nào có căn bậc hai:
a) (x – 4)(x – 6) + 1 b) (3 – x)(x – 5) – 4
c) x
2
+ 6x – 9 d) 5x
2
+ 8x – 4
e) x(x – 1)(x + 1)(x + 2) + 1 f) x
2
+ 20x + 101
1.6 So sánh hai số sau (không dùng máy tính):
a) 1 và 2 b) 2 và 3 c) 6 và 41
d) 7 và 47 e) 2 và 12 f) 1 và 3 1
g) 2 31 và 10 h) 3 và 12 i) 5 và 29
j) 2 5 và 19 k) 3 và 2 l) 32 và 23
m) 2 + 6 và 5 n) 7 – 2 2 và 4 o) 15 + 8 và 7
p) 1437 và 6– 15 q) 12617 và 99
1.7 Dùng kí hiệu viết nghiệm của các phương trình đưới đây, sau đó dùng
máy tính để tính chính xác nghiệm với 3 chữ số thập phân.
a) x
2
= 2 b) x
2
= 3 c) x
2
= 3,5 d) x
2
= 4,12
e) x
2
= 5 f) x
2
= 6 g) x
2
= 2,5 h) x
2
= 5
1.8 Giải các phương trình sau:
a) x
2
= 25 b) x
2
= 30,25 c) x
2
= 5
d) x
2
– 3 = 2 e) x
2
5 = 0 f) x
2
+ 5 = 2
g) x
2
= 3 h) 2x
2
+3 2 =2 3 i) (x – 1)
2
= 1
9
16
j) x
2
= (1 – 3 )
2
k) x
2
= 27 – 10 2 l) x
2
+ 2x =3 –2 3
1.9 Giải phương trình:
a) x = 3 b) x = 5 c)
x
= 0 d) x = 2
1.10 Trong các số:
2
7)( ,
2
7)( ,
2
7 ,
2
7)( thì số nào là căn bậc
hai số học của 49 ?
1.11 Cho hai số dương a và b. Chứng minh rằng:
a) Nếu a > b thì ba b) Nếu ba thì a > b
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 95
2.116 Cho đường tròn tâm O đường kính AB, điểm M thuộc đường tròn. Gọi N
là điểm đối xứng với A qua M. BN cắt đường tròn ở C. Gọi E là giao
điểm của AC và BM.
a) Chứng minh: NE AB.
b) Gọi F là điểm đối xứng với E qua M. Chứng minh: FA là tiếp tuyến
của (O).
c) Chứng minh: FN là tiếp tuyến của đường tròn (B; BA).
2.117 Cho đường tròn (O; R) đường kính AB và (d) la tiếp tuyến của (O) tại A.
M là điểm di động trên (d). Kẻ tiếp tuyến MC đến (O) (C là tiếp điểm
khác A). Tia BC cắt (d) tại K và kẻ CH vuông góac với AB tại H.
a) Chứng minh: OM // BK.
b) BM cắt CH tại I. Chứng minh: I là trung điểm của CH.
c) Gọi N là trực tâm của AMC. Chứng minh: tứ giác AOCN là hình
bình hành. Từ đó suy ra N di động trên đường cố định, chỉ rõ đường cố
định đó ?
d) Cho OM = 2R. Chứng minh: AMC đều và tính AM, S
AMC
theo R.
2.118 Cho đường tròn (O ; R) và hai điểm A, B thuộc đường tròn. Tiếp tuyến tại
A và B của (O) cắt nhau tại C. Tia CO cắt (O) tại E và F (E OC). Gọi I
là trung điểm của AB.
a) Cho biết
AOB
= 120
0
.
i. Tính OI theo R và chứng minh I thuộc một đường thẳng cố định
khi A, B di động trên (O) sao cho
AOB
luôn có số đo bằng 120
0
.
ii. Lấy K AC (AK < AC). Vẽ đường tròn đường kính OK cắt cung
AB của (O) tại M (M khác A). Tia KM cắt BC tại H. Chứng minh:
KH là tiếp tuyến của (O).
iii. Lấy T AB sao cho
KOT
= 60
0
(A, T nằm khác phía đối với OK).
Chứng minh: O, T, H thẳng hàng.
b) Chứng minh: EI . FC = FI . EC.
2.119 Cho đường tròn (O; R) đường kính AB và dây AC = R. Vẽ đường kính
CD của (O).
a) Tính theo R độ dài đoạn AD và S
ACD
.
b) Gọi xy là tiếp tuyến tại B của (O). Tia AC và AD cắt xy tại E và F.
Gọi M là trung điểm của EF, đường thẳng (d) qua C và song song với
AM. Đoạn thẳng AM cắt CD tại I. Chứng minh: (d) tiếp xúc (O).
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 10
e)
25
4
f)
0405
166
,
g) 490360 ,,
1.4 Trong các số sau, số nào có căn bậc hai:
a) 5 b) 1,5 c) 0,1 d) 9
1.5 Trong các biểu thức sau, biểu thức nào có căn bậc hai:
a) (x – 4)(x – 6) + 1 b) (3 – x)(x – 5) – 4
c) x
2
+ 6x – 9 d) 5x
2
+ 8x – 4
e) x(x – 1)(x + 1)(x + 2) + 1 f) x
2
+ 20x + 101
1.6 So sánh hai số sau (không dùng máy tính):
a) 1 và 2 b) 2 và 3 c) 6 và 41
d) 7 và 47 e) 2 và 12 f) 1 và 3 1
g) 2 31 và 10 h) 3 và 12 i) 5 và 29
j) 2 5 và 19 k) 3 và 2 l) 32 và 23
m) 2 + 6 và 5 n) 7 – 2 2 và 4 o) 15 + 8 và 7
p) 1437 và 6– 15 q) 12617 và 99
1.7 Dùng kí hiệu viết nghiệm của các phương trình đưới đây, sau đó dùng
máy tính để tính chính xác nghiệm với 3 chữ số thập phân.
a) x
2
= 2 b) x
2
= 3 c) x
2
= 3,5 d) x
2
= 4,12
e) x
2
= 5 f) x
2
= 6 g) x
2
= 2,5 h) x
2
= 5
1.8 Giải các phương trình sau:
a) x
2
= 25 b) x
2
= 30,25 c) x
2
= 5
d) x
2
– 3 = 2 e) x
2
5 = 0 f) x
2
+ 5 = 2
g) x
2
= 3 h) 2x
2
+3 2 =2 3 i) (x – 1)
2
= 1
9
16
j) x
2
= (1 – 3 )
2
k) x
2
= 27 – 10 2 l) x
2
+ 2x =3 –2 3
1.9 Giải phương trình:
a) x = 3 b) x = 5 c)
x
= 0 d) x = 2
1.10 Trong các số:
2
7)( ,
2
7)( ,
2
7 ,
2
7)( thì số nào là căn bậc
hai số học của 49 ?
1.11 Cho hai số dương a và b. Chứng minh rằng:
a) Nếu a > b thì ba b) Nếu ba thì a > b
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 95
2.116 Cho đường tròn tâm O đường kính AB, điểm M thuộc đường tròn. Gọi N
là điểm đối xứng với A qua M. BN cắt đường tròn ở C. Gọi E là giao
điểm của AC và BM.
a) Chứng minh: NE AB.
b) Gọi F là điểm đối xứng với E qua M. Chứng minh: FA là tiếp tuyến
của (O).
c) Chứng minh: FN là tiếp tuyến của đường tròn (B; BA).
2.117 Cho đường tròn (O; R) đường kính AB và (d) la tiếp tuyến của (O) tại A.
M là điểm di động trên (d). Kẻ tiếp tuyến MC đến (O) (C là tiếp điểm
khác A). Tia BC cắt (d) tại K và kẻ CH vuông góac với AB tại H.
a) Chứng minh: OM // BK.
b) BM cắt CH tại I. Chứng minh: I là trung điểm của CH.
c) Gọi N là trực tâm của AMC. Chứng minh: tứ giác AOCN là hình
bình hành. Từ đó suy ra N di động trên đường cố định, chỉ rõ đường cố
định đó ?
d) Cho OM = 2R. Chứng minh: AMC đều và tính AM, S
AMC
theo R.
2.118 Cho đường tròn (O ; R) và hai điểm A, B thuộc đường tròn. Tiếp tuyến tại
A và B của (O) cắt nhau tại C. Tia CO cắt (O) tại E và F (E OC). Gọi I
là trung điểm của AB.
a) Cho biết
AOB
= 120
0
.
i. Tính OI theo R và chứng minh I thuộc một đường thẳng cố định
khi A, B di động trên (O) sao cho
AOB
luôn có số đo bằng 120
0
.
ii. Lấy K AC (AK < AC). Vẽ đường tròn đường kính OK cắt cung
AB của (O) tại M (M khác A). Tia KM cắt BC tại H. Chứng minh:
KH là tiếp tuyến của (O).
iii. Lấy T AB sao cho
KOT
= 60
0
(A, T nằm khác phía đối với OK).
Chứng minh: O, T, H thẳng hàng.
b) Chứng minh: EI . FC = FI . EC.
2.119 Cho đường tròn (O; R) đường kính AB và dây AC = R. Vẽ đường kính
CD của (O).
a) Tính theo R độ dài đoạn AD và S
ACD
.
b) Gọi xy là tiếp tuyến tại B của (O). Tia AC và AD cắt xy tại E và F.
Gọi M là trung điểm của EF, đường thẳng (d) qua C và song song với
AM. Đoạn thẳng AM cắt CD tại I. Chứng minh: (d) tiếp xúc (O).
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 94
2.112 Cho (O; R) và (O; r) ở ngoài nhau. AB là một trong các tiếp tuyến chung
ngoài, EF là một trong các tiếp tuyến chung trong (A và E thuộc đường
tròn (O)). EF cắt AB tại C.
a) Chứng minh: OC OC.
b) Chứng minh: AC . BC = R.r
c) Tính AB, EF theo R, r và OO = d.
2.113 Cho hai đường tròn (O) và (O) cắt nhau tại A và B. Dây AC của đường
tròn (O) tiếp xúc với đường tròn (O) tại A. Dây AD của đường tròn (O)
tiếp xúc với đường tròn (O) tại A. Gọi K là điểm đối xứng với A qua
trung điểm của I của OO, E là điểm đối xứng với A qua B. Chứng minh:
a) AB KB
b) Bốn điểm A, C, E, D nằm trên một đường tròn.
H - Ôn tập chương 2
2.114 Cho ABC vuông tại A có
B
= 60
0
và BC = 2a. Vẽ đường kính AB và
đường tròn (F) đường kính AC. Hai đường tròn này cắt nhau tại điểm thứ
hai là H.
a) Chứng minh: B, H, C thẳng hàng.
b) Chứng minh: AC tiếp xúc (E) và EF AH tại K.
c) Tính theo a diện tích AKF.
d) Gọi M là trung điểm của BC. Chứng minh: A, E, H, M, F cùng thuộc
một đường tròn.
2.115 Cho đoạn thẳng AB, điểm C nằm giữa A và B. Vẽ về một phía của AB
các nửa đường tròn có đường kính theo thứ tự là AB, AC và CB. Đường
vuông góc với AB tại C cắt nửa đường tròn lớn tại D. DA, DB cắt nửa
đường tròn có đường kính AC, CB theo thứ tự tại M, N.
a) Tứ giác DMCN là hình gì ? Vì sao ?
b) Chứng minh: DM . DA = DN . DB
c) Chứng minh: MN là tiếp tuyến chung của nửa đường tròn có đường
kính AC và CB.
d) Điểm C ở vị trí nào trên AB thì MN có độ dài lớn nhất ?
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 11
1.12 Cho số dương a. Chứng minh rằng:
a) Nếu a > 1 thì ba b) Nếu a < 1 thì ba
1.13 Cho số dương a. Chứng minh rằng:
a) Nếu a > 1 thì a > a b) Nếu a < 1 thì a < a
1.
a b b a
2.
a b
a c
b c
3.
a b a c b c
(cộng 2 vế với c)
a c b a b c
(cộng 2 vế với – c)
a b a b 0
(cộng 2 vế với – b)
a b a b 0
(cộng 2 vế với – b)
4.
a b
a c b d
c d
5.
a b a.c b.c
(nếu c > 0: giữ nguyên chiều)
a b a.c b.c
(nếu c < 0: đổi chiều)
6.
a b 0
a.c b.d
c d 0
7.
n n *
a b 0 a b ( n )
8.
1 1
a b 0
a b
Một số tính chất bất đẳng thức
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 94
2.112 Cho (O; R) và (O; r) ở ngoài nhau. AB là một trong các tiếp tuyến chung
ngoài, EF là một trong các tiếp tuyến chung trong (A và E thuộc đường
tròn (O)). EF cắt AB tại C.
a) Chứng minh: OC OC.
b) Chứng minh: AC . BC = R.r
c) Tính AB, EF theo R, r và OO = d.
2.113 Cho hai đường tròn (O) và (O) cắt nhau tại A và B. Dây AC của đường
tròn (O) tiếp xúc với đường tròn (O) tại A. Dây AD của đường tròn (O)
tiếp xúc với đường tròn (O) tại A. Gọi K là điểm đối xứng với A qua
trung điểm của I của OO, E là điểm đối xứng với A qua B. Chứng minh:
a) AB KB
b) Bốn điểm A, C, E, D nằm trên một đường tròn.
H - Ôn tập chương 2
2.114 Cho ABC vuông tại A có
B
= 60
0
và BC = 2a. Vẽ đường kính AB và
đường tròn (F) đường kính AC. Hai đường tròn này cắt nhau tại điểm thứ
hai là H.
a) Chứng minh: B, H, C thẳng hàng.
b) Chứng minh: AC tiếp xúc (E) và EF AH tại K.
c) Tính theo a diện tích AKF.
d) Gọi M là trung điểm của BC. Chứng minh: A, E, H, M, F cùng thuộc
một đường tròn.
2.115 Cho đoạn thẳng AB, điểm C nằm giữa A và B. Vẽ về một phía của AB
các nửa đường tròn có đường kính theo thứ tự là AB, AC và CB. Đường
vuông góc với AB tại C cắt nửa đường tròn lớn tại D. DA, DB cắt nửa
đường tròn có đường kính AC, CB theo thứ tự tại M, N.
a) Tứ giác DMCN là hình gì ? Vì sao ?
b) Chứng minh: DM . DA = DN . DB
c) Chứng minh: MN là tiếp tuyến chung của nửa đường tròn có đường
kính AC và CB.
d) Điểm C ở vị trí nào trên AB thì MN có độ dài lớn nhất ?
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 11
1.12 Cho số dương a. Chứng minh rằng:
a) Nếu a > 1 thì ba b) Nếu a < 1 thì ba
1.13 Cho số dương a. Chứng minh rằng:
a) Nếu a > 1 thì a > a b) Nếu a < 1 thì a < a
1.
a b b a
2.
a b
a c
b c
3.
a b a c b c
(cộng 2 vế với c)
a c b a b c
(cộng 2 vế với – c)
a b a b 0
(cộng 2 vế với – b)
a b a b 0
(cộng 2 vế với – b)
4.
a b
a c b d
c d
5.
a b a.c b.c
(nếu c > 0: giữ nguyên chiều)
a b a.c b.c
(nếu c < 0: đổi chiều)
6.
a b 0
a.c b.d
c d 0
7.
n n *
a b 0 a b ( n )
8.
1 1
a b 0
a b
Một số tính chất bất đẳng thức
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 12
B - Căn thức bậc hai. Hằng đẳng thức
2
A A
1. Căn thức bậc hai:
Nếu A là một biểu thức đại số thì
A
gọi là căn thức bậc hai của A.
A được gọi là biểu thức lấy căn hay biểu thức dưới dấu căn.
A
các định (có nghĩa) khi A
0
Chú ý:
a) Điều kiện có nghĩa của một số biểu thức:
A(x) là một đa thức
A(x) luôn có nghĩa.
A( x )
B( x )
có nghĩa
B(x)
0
A( x )
có nghĩa
A(x)
0
1
A( x )
có nghĩa
A(x) > 0
b) Với M > 0, ta có:
2 2
X M X M M X M
2 2
X M X M X M
hoặc
X M
2. Hằng đẳng thức
2
( A) A
Định lí: Với mọi số a, ta có:
2
a khi a 0
a a
a khi a 0
Chú ý: Tổng quát, với A là một biểu thức đại số, ta cũng có:
2
A khi A 0
A A
A khi A 0
1.14 Tìm x để biểu thức sau có nghĩa:
1. a) 3x2 b) x5
c) 7x3 d) 7x3
e)
3
x
f) x5
g) x4 h)
2
x1
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 93
b) Gọi I là giao điểm của BC và OO. Tính OI.
2.107 Cho (O; 48cm) và (O; 14cm), khoảng cách tâm là d = 50cm.
a) Chứng minh: (O) và (O) cắt nhau tại A và B.
b) Tính
OAA'
.
c) Tính AB.
2.108 Cho ABC vuông tại A, có AB = a, BC = 2a. Các đường tròn đường kính
AB, AC cắt nhau tại điểm thứ hai là D.
a) Chứng minh: B, C, D thẳng hàng.
b) Gọi E và F lần lượt là điểm đối xứng của D qua AB và AC.
Chứng minh: E, A, F thẳng hàng.
c) Tính theo a khoảng cách từ trung điểm O của BC đến EF.
d) Tính theo a diện tích tứ giác BCEF.
2.109 Cho đường tròn tâm O đường kính AB. Đường thẳng (d) tiếp xúc với nửa
đường tròn tại C. Gọi D và E theo thứ tự là hình chiếu của A và B trên
(d). Chứng minh:
a) C là trung điểm của DE.
b) (A; AD) và (B; BE) tiếp xúc ngoài nhau tại một điểm H thuộc đường
kính AB.
2.110 Cho ABC vuông tại A. Vẽ các đường tròn (O) và (I) đi qua A và tiếp
xúc với BC tại các điểm B và C. Gọi M là trung điểm của BC. Chứng
minh:
a) Các đường tròn (O) và (I) tiếp xúc với nhau.
b) AM là tiếp tuyến chung của hai đường tròn (O) và (I).
c) OMI vuông.
d) BC là tiếp tuyến của đường tròn ngoại tiếp OMI.
2.111 Cho (O; R) và (O; r) tiếp xúc ngoài tại A. Gọi BC là tiếp tuyến chung
ngoài của hai đường tròn (B(O), C(O)). Tiếp tuyến chung trong của
(O) và (O) cắt BC tại I.
a) Chứng tỏ các góc
BAC
và
OIO'
là góc vuông.
b) Kẻ đường kính BD của (O). Chứng minh ba điểm A, C, D thẳng hàng.
c) Tính theo R và r độ dài BC, BA, CA.
d) Kẻ đường kính CE của (O). Chứng minh: S
ABC
= S
ADE
.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 12
B - Căn thức bậc hai. Hằng đẳng thức
2
A A
1. Căn thức bậc hai:
Nếu A là một biểu thức đại số thì
A
gọi là căn thức bậc hai của A.
A được gọi là biểu thức lấy căn hay biểu thức dưới dấu căn.
A
các định (có nghĩa) khi A
0
Chú ý:
a) Điều kiện có nghĩa của một số biểu thức:
A(x) là một đa thức
A(x) luôn có nghĩa.
A( x )
B( x )
có nghĩa
B(x)
0
A( x )
có nghĩa
A(x)
0
1
A( x )
có nghĩa
A(x) > 0
b) Với M > 0, ta có:
2 2
X M X M M X M
2 2
X M X M X M
hoặc
X M
2. Hằng đẳng thức
2
( A) A
Định lí: Với mọi số a, ta có:
2
a khi a 0
a a
a khi a 0
Chú ý: Tổng quát, với A là một biểu thức đại số, ta cũng có:
2
A khi A 0
A A
A khi A 0
1.14 Tìm x để biểu thức sau có nghĩa:
1. a) 3x2 b) x5
c) 7x3 d) 7x3
e)
3
x
f) x5
g) x4 h)
2
x1
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 93
b) Gọi I là giao điểm của BC và OO. Tính OI.
2.107 Cho (O; 48cm) và (O; 14cm), khoảng cách tâm là d = 50cm.
a) Chứng minh: (O) và (O) cắt nhau tại A và B.
b) Tính
OAA'
.
c) Tính AB.
2.108 Cho ABC vuông tại A, có AB = a, BC = 2a. Các đường tròn đường kính
AB, AC cắt nhau tại điểm thứ hai là D.
a) Chứng minh: B, C, D thẳng hàng.
b) Gọi E và F lần lượt là điểm đối xứng của D qua AB và AC.
Chứng minh: E, A, F thẳng hàng.
c) Tính theo a khoảng cách từ trung điểm O của BC đến EF.
d) Tính theo a diện tích tứ giác BCEF.
2.109 Cho đường tròn tâm O đường kính AB. Đường thẳng (d) tiếp xúc với nửa
đường tròn tại C. Gọi D và E theo thứ tự là hình chiếu của A và B trên
(d). Chứng minh:
a) C là trung điểm của DE.
b) (A; AD) và (B; BE) tiếp xúc ngoài nhau tại một điểm H thuộc đường
kính AB.
2.110 Cho ABC vuông tại A. Vẽ các đường tròn (O) và (I) đi qua A và tiếp
xúc với BC tại các điểm B và C. Gọi M là trung điểm của BC. Chứng
minh:
a) Các đường tròn (O) và (I) tiếp xúc với nhau.
b) AM là tiếp tuyến chung của hai đường tròn (O) và (I).
c) OMI vuông.
d) BC là tiếp tuyến của đường tròn ngoại tiếp OMI.
2.111 Cho (O; R) và (O; r) tiếp xúc ngoài tại A. Gọi BC là tiếp tuyến chung
ngoài của hai đường tròn (B(O), C(O)). Tiếp tuyến chung trong của
(O) và (O) cắt BC tại I.
a) Chứng tỏ các góc
BAC
và
OIO'
là góc vuông.
b) Kẻ đường kính BD của (O). Chứng minh ba điểm A, C, D thẳng hàng.
c) Tính theo R và r độ dài BC, BA, CA.
d) Kẻ đường kính CE của (O). Chứng minh: S
ABC
= S
ADE
.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 92
2.99 Cho (O) và (O) cắt nhau tại A và B. Gọi I là trung điểm của OO. Qua A
vẽ đường thẳng vuông góc với IA, cắt (O) và (O) tại C và D (khác A).
Chứng minh: AC = AD.
2.100 Cho hai đường tròn (O) và (O) tiếp xúc ngoài nhau tại A. Vẽ hai đường
kính AOB và AOC Gọi DE là tiếp tuyến chung của hai đường tròn,
D (O), E (O). Gọi M là giao điểm của BD và CE.
a) Tính
DAE
.
b) Tứ giác ADME là hình gì ? Vì sao ?
c) Chứng minh: MA là tiếp tuyến chung của hai đường tròn.
2.101 Cho hai đường tròn (O) và (O) cắt nhau tại A và B, trong đó O nằm trên
(O). Kẻ đường kính OOC của đường tròn (O).
a) Chứng minh: CA, CB là các tiếp tuyến của (O).
b) Đường vuông góc với AO tại O cắt CB ở I. Đường vuông góc với
AC tại C cắt đường thẳng OB ở K. Chứng minh O, I, K thẳng hàng.
2.102 Cho hai đường tròn đồng tâm O. Gọi AB là dây bất kì của đường tròn
nhỏ. Đường thẳng AB cắt đường tròn lớn ở C và D (A nằm giữa B và C).
So sánh AC và BD.
2.103 Cho I là trung điểm của của đọan thẳng AB. Vẽ các đường tròn (I; IA) và
(B; BA).
a) Xét vị trí tương đối của hai đường tròn (I) và (B).
b) Đường thẳng qua A cắt các đường tròn (I) và (B) theo thứ tự tại M và
N. So sánh AM và MN.
2.104 Cho hai đường tròn (O) và (O) tiếp xúc ngoài tại A. Gọi CD là tiếp tuyến
chung ngoài của hai đường tròn (C (O), D (O)).
a) Tính
CAD
. b) Tính CD biết OA = 4,5cm và OA = 2cm.
2.105 Cho hai đường tròn đồng tâm O. Một đường tròn (O) cắt đường tròn nhỏ
tại A và B, cắt đường tròn lớn tại C và D. Chứng minh rằng AB // CD.
2.106 Cho đường tròn (O; 3cm) và đường tròn (O; 1cm) tiếp xúc ngoài nhau tại
A. Vẽ hai bán kính OB và OC song song với nhau và thuộc cùng một nửa
mặt phẳng có bờ OO.
a) Tính
BAC
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 13
i)
6x
5
2
j)
2
x
2
k)
x1
1
l)
3x
4
m)
2
x4
n)
2
x3
o)
1x2x
2
P)
2
x 2x 1
2. a) 5x4x
2
b)
2
x 2x 2
c)
2
1
4x 12x 9
d)
1xx
1
2
e)
15x8x
1
2
f)
20x7x3
1
2
3. a) 9x3x
2
b)
5
x
1
2x
c) x25
9x
2
2
d) x84x2
e)
2
x9
1x
x4
f)
2x24x
2
4. a) ))(( 3x1x b)
3x
4
c)
x5
x2
d)
x 1
x 2
1.15 Tính
a) 5
4
2)( b) 4
6
3)(
c) 5
8
5)( d)
2
4040 ),(,
e)
2
10 ),( f)
2
30 ),(
g)
2
31 ),( h) 2
4
2)( + 3
8
2)(
1.16 Chứng minh rằng:
a)
2
25549 )( b) 25549
c)
2
747823 )( d)
17 12 2 2 2 3
1.17 Rút gọn biểu thức:
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 92
2.99 Cho (O) và (O) cắt nhau tại A và B. Gọi I là trung điểm của OO. Qua A
vẽ đường thẳng vuông góc với IA, cắt (O) và (O) tại C và D (khác A).
Chứng minh: AC = AD.
2.100 Cho hai đường tròn (O) và (O) tiếp xúc ngoài nhau tại A. Vẽ hai đường
kính AOB và AOC Gọi DE là tiếp tuyến chung của hai đường tròn,
D (O), E (O). Gọi M là giao điểm của BD và CE.
a) Tính
DAE
.
b) Tứ giác ADME là hình gì ? Vì sao ?
c) Chứng minh: MA là tiếp tuyến chung của hai đường tròn.
2.101 Cho hai đường tròn (O) và (O) cắt nhau tại A và B, trong đó O nằm trên
(O). Kẻ đường kính OOC của đường tròn (O).
a) Chứng minh: CA, CB là các tiếp tuyến của (O).
b) Đường vuông góc với AO tại O cắt CB ở I. Đường vuông góc với
AC tại C cắt đường thẳng OB ở K. Chứng minh O, I, K thẳng hàng.
2.102 Cho hai đường tròn đồng tâm O. Gọi AB là dây bất kì của đường tròn
nhỏ. Đường thẳng AB cắt đường tròn lớn ở C và D (A nằm giữa B và C).
So sánh AC và BD.
2.103 Cho I là trung điểm của của đọan thẳng AB. Vẽ các đường tròn (I; IA) và
(B; BA).
a) Xét vị trí tương đối của hai đường tròn (I) và (B).
b) Đường thẳng qua A cắt các đường tròn (I) và (B) theo thứ tự tại M và
N. So sánh AM và MN.
2.104 Cho hai đường tròn (O) và (O) tiếp xúc ngoài tại A. Gọi CD là tiếp tuyến
chung ngoài của hai đường tròn (C (O), D (O)).
a) Tính
CAD
. b) Tính CD biết OA = 4,5cm và OA = 2cm.
2.105 Cho hai đường tròn đồng tâm O. Một đường tròn (O) cắt đường tròn nhỏ
tại A và B, cắt đường tròn lớn tại C và D. Chứng minh rằng AB // CD.
2.106 Cho đường tròn (O; 3cm) và đường tròn (O; 1cm) tiếp xúc ngoài nhau tại
A. Vẽ hai bán kính OB và OC song song với nhau và thuộc cùng một nửa
mặt phẳng có bờ OO.
a) Tính
BAC
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 13
i)
6x
5
2
j)
2
x
2
k)
x1
1
l)
3x
4
m)
2
x4
n)
2
x3
o)
1x2x
2
P)
2
x 2x 1
2. a) 5x4x
2
b)
2
x 2x 2
c)
2
1
4x 12x 9
d)
1xx
1
2
e)
15x8x
1
2
f)
20x7x3
1
2
3. a) 9x3x
2
b)
5
x
1
2x
c) x25
9x
2
2
d) x84x2
e)
2
x9
1x
x4
f)
2x24x
2
4. a) ))(( 3x1x b)
3x
4
c)
x5
x2
d)
x 1
x 2
1.15 Tính
a) 5
4
2)( b) 4
6
3)(
c) 5
8
5)( d)
2
4040 ),(,
e)
2
10 ),( f)
2
30 ),(
g)
2
31 ),( h) 2
4
2)( + 3
8
2)(
1.16 Chứng minh rằng:
a)
2
25549 )( b) 25549
c)
2
747823 )( d)
17 12 2 2 2 3
1.17 Rút gọn biểu thức:
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 14
1. a)
2
(4 3 2)
b)
2
(2 5)
c)
2
24 )( d)
2
3232 )(
e)
2
32 )( f)
2
52 )(
g)
22
2313 )()( h)
22
1552 )()(
2. a)
6 2 5
b)
7 4 3
c)
12 6 3
d)
17 12 2
e)
22 12 2
f)
10 4 6
g)
5526
26112
h)
53
53
53
53
3. a) 3324 b) 232611
c) 2462611 d) 34133611
e) 381943 )( f)
2
74
728
g)
5526
26112
h)
53
53
53
53
4. a) 32426 b) 3413326
c) 34710483 d)
23 6 10 4 3 2 2
5. a)
5x
5x
2
b)
2
x
2x22x
2
2
1.18 Rút gọn biểu thức sau (loại bỏ dấu căn và dấu trị tuyệt đối):
1. a) x2x9
2
với x < 0 b)
2
x2
với x 0
c)
2
2x3 )( với x < 2 d)
2
x2
5x với x < 0
e) x3x25
2
với x 0 f)
24
x3x9 với x bất kỳ
g)
2
xx8164x với x > 4
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 91
G - Vị trí tương đối của hai đường tròn
2.94 Cho (O; 5cm) và điểm O sao cho OO = 7cm. Với giá trị nào của R thì
(O; R):
a) Cắt đường tròn (O)
b) Tiếp xúc với (O)
c) Không có điểm chung với (O) ?
2.95 Cho (O; R) và điểm I cách O một khoảng d < R. Với giá trị nào của r thì
đường tròn (I; r) tiếp xúc với (O; R) ?
2.96 Cho hai đường tròn (O) và (O) tiếp xúc ngoài nhau tại A. Đường thẳng
bất kì qua A cắt (O) và (O) theo thứ tự tại B và C. Chứng minh rằng các
tiếp tuyến tại B và C song với nhau.
2.97 Cho (O; 30cm) và (O ; 40cm) cắt nhau tại A và B. Biết AB = 48cm.
Chứng minh: OO là đường trung trực của AB. Tính khoảng cách OO
2.98 Cho hai đường tròn (O) và (O) cắt nhau tại A và B. Kẻ các đường kính
AOC và AOD. Chứng minh ba điểm C, B, D thẳng hàng và AB CD.
1. Vị trí tương đối của hai đường tròn:
Cho (O ; R) và (O; r) với R > r và OO = d.
(O) và (O) cắt nhau
R – r < d < R + r
(O) và (O) tiếp xúc ngoài
d = R + r
(O) và (O) tiếp xúc trong
d = R – r
(O) và (O) ở ngoài nhau
d > R + r
(O) và (O) đựng nhau
d < R – r
(O) và (O) đồng tâm
d = 0
2. Tính chất đường nối tâm:
a. Nếu hai đường tròn cắt nhau thì hai giao điểm đối xứng với nhau
qua đường nối tâm, tức là đường nối tâm là đường trung trực của
dây chung.
b. Nếu hai đường tròn tiếp xúc nhau thì tiếp điểm nằm trên đường
nối tâm.
c. Tiếp tuyến chung của hai đường tròn là đường thẳng tiếp xúc với
cả hai đường tròn. Có hai loại: tiếp tuyến chung trong (cắt đoạn
nối tâm) và tiếp tuyến chung ngoài (không cắt đoạn nối tâm).
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 14
1. a)
2
(4 3 2)
b)
2
(2 5)
c)
2
24 )( d)
2
3232 )(
e)
2
32 )( f)
2
52 )(
g)
22
2313 )()( h)
22
1552 )()(
2. a)
6 2 5
b)
7 4 3
c)
12 6 3
d)
17 12 2
e)
22 12 2
f)
10 4 6
g)
5526
26112
h)
53
53
53
53
3. a) 3324 b) 232611
c) 2462611 d) 34133611
e) 381943 )( f)
2
74
728
g)
5526
26112
h)
53
53
53
53
4. a) 32426 b) 3413326
c) 34710483 d)
23 6 10 4 3 2 2
5. a)
5x
5x
2
b)
2
x
2x22x
2
2
1.18 Rút gọn biểu thức sau (loại bỏ dấu căn và dấu trị tuyệt đối):
1. a) x2x9
2
với x < 0 b)
2
x2
với x 0
c)
2
2x3 )( với x < 2 d)
2
x2
5x với x < 0
e) x3x25
2
với x 0 f)
24
x3x9 với x bất kỳ
g)
2
xx8164x với x > 4
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 91
G - Vị trí tương đối của hai đường tròn
2.94 Cho (O; 5cm) và điểm O sao cho OO = 7cm. Với giá trị nào của R thì
(O; R):
a) Cắt đường tròn (O)
b) Tiếp xúc với (O)
c) Không có điểm chung với (O) ?
2.95 Cho (O; R) và điểm I cách O một khoảng d < R. Với giá trị nào của r thì
đường tròn (I; r) tiếp xúc với (O; R) ?
2.96 Cho hai đường tròn (O) và (O) tiếp xúc ngoài nhau tại A. Đường thẳng
bất kì qua A cắt (O) và (O) theo thứ tự tại B và C. Chứng minh rằng các
tiếp tuyến tại B và C song với nhau.
2.97 Cho (O; 30cm) và (O ; 40cm) cắt nhau tại A và B. Biết AB = 48cm.
Chứng minh: OO là đường trung trực của AB. Tính khoảng cách OO
2.98 Cho hai đường tròn (O) và (O) cắt nhau tại A và B. Kẻ các đường kính
AOC và AOD. Chứng minh ba điểm C, B, D thẳng hàng và AB CD.
1. Vị trí tương đối của hai đường tròn:
Cho (O ; R) và (O; r) với R > r và OO = d.
(O) và (O) cắt nhau
R – r < d < R + r
(O) và (O) tiếp xúc ngoài
d = R + r
(O) và (O) tiếp xúc trong
d = R – r
(O) và (O) ở ngoài nhau
d > R + r
(O) và (O) đựng nhau
d < R – r
(O) và (O) đồng tâm
d = 0
2. Tính chất đường nối tâm:
a. Nếu hai đường tròn cắt nhau thì hai giao điểm đối xứng với nhau
qua đường nối tâm, tức là đường nối tâm là đường trung trực của
dây chung.
b. Nếu hai đường tròn tiếp xúc nhau thì tiếp điểm nằm trên đường
nối tâm.
c. Tiếp tuyến chung của hai đường tròn là đường thẳng tiếp xúc với
cả hai đường tròn. Có hai loại: tiếp tuyến chung trong (cắt đoạn
nối tâm) và tiếp tuyến chung ngoài (không cắt đoạn nối tâm).
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 90
c)
1 2 3
1 1 1 1
r h h h
(với h
1
, h
2
, h
3
là các đường cao của ABC)
2.89 Cho tam giác ABC vuông tại A có đường cao AH. Đường tròn (O; r),
(O; r
1
), (O; r
2
) theo thứ tự là đường tròn nội tiếp các ABC, ABH,
ACH. Chứng minh rằng:
a) AB + AC – BC = 2r. b) R + r
1
+ r
2
= AH. c)
2 2 2
1 2
r r r
2.90 Cho ABC có BC = a, CA = b, AB = c và đường tròn bàng tiếp trong góc
A tiếp xúc với BC tại D, tiếp xúc với phần kéo dài của AC và AB tại E và
F. Tính theo a, b, c độ dài AE, BD, CD.
2.91 Cho ABC có I là tâm đường tròn nội tiếp và O là tâm đường tròn bàng
tiếp trong góc A. gọi D và F lần lượt là tiếp điểm của (I) và (O) trên BC.
Chứng minh rằng BD = CF.
2.92 Tính cạnh huyền của một tam giác vuông, biết r là bán kính đường tròn
nội tiếp và R là bán kính đường tròn bàng tiếp trong góc vuông.
2.93 Cho ABC đường cao AH. Gọi E và F lần lượt là các điểm đối xứng của
H qua AB và AC. Đường thẳng EF cắt AB ở I và cắt AC ở K. C/m:
a) A là tâm đường tròn bàng tiếp HIK.
b) BK và CI là các đường cao của ABC.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 15
2. a) A = a2a4a41
2
b) B = 1x29x12x4
2
c) C =
25x10x
x
5
2
d) D =
1x2x
1
x
1x
2
2
)(
e) E =
3
x
9x6x
2
f) F = 16x8xx
242
1.19 Chứng tỏ:
2
2x24x22x )( với x 2
Áp dụng rút gọn biểu thức sau:
4x22x4x22x với x 2
1.20 Rút gọn biểu thức sau (loại bỏ dấu căn và dấu trị tuyệt đối):
a) 4x4x với x 4
b) 3x22x với x 3
c) 1x2x1x2x với x 1
d)
x 2 x 1 x 2 x 1
với x 0
1.21 Với giá trị nào của a và b thì:
a)
ab
1
bab2a
1
22
? b) )()( b1a1b2ba
22
?
1.22 So sánh hai số sau (không dùng máy tính):
a) 9 và 6 + 2 2 b) 2 + 3 và 3
c) 16 và 9 + 4 5 d) 311 và 2
1.23 Rút gọn rồi tính giá trị của biểu thức:
a)
2
A 9x 12x 4 1 3x
tại
1
x
3
b)
2
B 2x 6x 2 9
tại
x 3 2
1.24 Giải phương trình:
a)
2
x9 = 2x + 1 b)
7x
4
c) 1x39x6x
2
d)
7x
2
e) 8x
2
f)
5x4x41
2
g)
9x
4
h)
2
(x 2) 2x 1
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 90
c)
1 2 3
1 1 1 1
r h h h
(với h
1
, h
2
, h
3
là các đường cao của ABC)
2.89 Cho tam giác ABC vuông tại A có đường cao AH. Đường tròn (O; r),
(O; r
1
), (O; r
2
) theo thứ tự là đường tròn nội tiếp các ABC, ABH,
ACH. Chứng minh rằng:
a) AB + AC – BC = 2r. b) R + r
1
+ r
2
= AH. c)
2 2 2
1 2
r r r
2.90 Cho ABC có BC = a, CA = b, AB = c và đường tròn bàng tiếp trong góc
A tiếp xúc với BC tại D, tiếp xúc với phần kéo dài của AC và AB tại E và
F. Tính theo a, b, c độ dài AE, BD, CD.
2.91 Cho ABC có I là tâm đường tròn nội tiếp và O là tâm đường tròn bàng
tiếp trong góc A. gọi D và F lần lượt là tiếp điểm của (I) và (O) trên BC.
Chứng minh rằng BD = CF.
2.92 Tính cạnh huyền của một tam giác vuông, biết r là bán kính đường tròn
nội tiếp và R là bán kính đường tròn bàng tiếp trong góc vuông.
2.93 Cho ABC đường cao AH. Gọi E và F lần lượt là các điểm đối xứng của
H qua AB và AC. Đường thẳng EF cắt AB ở I và cắt AC ở K. C/m:
a) A là tâm đường tròn bàng tiếp HIK.
b) BK và CI là các đường cao của ABC.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 15
2. a) A = a2a4a41
2
b) B = 1x29x12x4
2
c) C =
25x10x
x
5
2
d) D =
1x2x
1
x
1x
2
2
)(
e) E =
3
x
9x6x
2
f) F = 16x8xx
242
1.19 Chứng tỏ:
2
2x24x22x )( với x 2
Áp dụng rút gọn biểu thức sau:
4x22x4x22x với x 2
1.20 Rút gọn biểu thức sau (loại bỏ dấu căn và dấu trị tuyệt đối):
a) 4x4x với x 4
b) 3x22x với x 3
c) 1x2x1x2x với x 1
d)
x 2 x 1 x 2 x 1
với x 0
1.21 Với giá trị nào của a và b thì:
a)
ab
1
bab2a
1
22
? b) )()( b1a1b2ba
22
?
1.22 So sánh hai số sau (không dùng máy tính):
a) 9 và 6 + 2 2 b) 2 + 3 và 3
c) 16 và 9 + 4 5 d) 311 và 2
1.23 Rút gọn rồi tính giá trị của biểu thức:
a)
2
A 9x 12x 4 1 3x
tại
1
x
3
b)
2
B 2x 6x 2 9
tại
x 3 2
1.24 Giải phương trình:
a)
2
x9 = 2x + 1 b)
7x
4
c) 1x39x6x
2
d)
7x
2
e) 8x
2
f)
5x4x41
2
g)
9x
4
h)
2
(x 2) 2x 1
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 16
i)
2
x 6x 9 5
j)
2
4x 12x 9 x 3
k)
2 2
4x 4x 1 x 2x 1
l)
2 2
4x 12x 9 9x 24x 16
1.25 Phân tích thành hân tử:
a) x
2
– 7 b) x
2
3 c) x
2
– 2 13 x + 13
d) x
2
– 3 e) x
2
– 2 2 x + 2 f) x
2
+ 2 5 x + 5
1.26 Với n là số tự nhiên, chứng minh:
2222
n1nn1n )()(
Viết đẳng thức trên khi n là 1; 2; 3; 4; 5; 6; 7.
1.27 Cho ba số a, b, c khác 0 và a + b + c = 0. Chứng minh rằng:
2 2 2
1 1 1 1 1 1
a b c a b c
1.28 Tính:
2
2
2
2013 2013
1 2013
2014 2014
.
1.29 Chứng minh bất đẳng thức Côsi (Cauchy):
x + y 2 xy
Dấu “ = ” xảy ra khi nào ?
Áp dụng: Chứng minh rằng với x, y, z là các số dương, ta có:
zx
1
yz
1
xy
1
z
1
y
1
x
1
Một chủ doanh nghiệp đi về quê chơi cùng 1 người bạn l
à dân toán.
Họ thấy một đàn bò rất lớn trên một đồng cỏ.
Anh doanh nghi
ệp nói:
- Nhi
ều b
ò quá, tôi ch
ưa bao giờ thấy nhiều thế n
ày, có l
ẽ phải
hàng nghìn con.
Anh b
ạn toán học trả lời :
-
Đúng đấy,
có c
ả thẩy 2428 con.
- 'Tr
ời, l
àm sao mà anh l
ại đếm được nhanh thế?
- Anh ch
ủ DN hỏi.
Anh toán h
ọc trả lời:
-
À, tôi đếm tất cả chân rồi chia cho 4 l
à xong!
Chuyện vui Toán học: Câu chuyện số 1
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 89
F - Đường tròn nội tiếp – bàng tiếp tam giác
2.84 Cho ABC vuông cân tại A nội tiếp (O; R). Gọi (I; r) là đường tròn nội
tiếp ABC. Tính độ dài AB và r theo R.
2.85 Cho ABC đều có cạnh 8cm.
a) Tính bán kính đường tròn (I) nội tiếp ABC.
b) Một tiếp tuyến của (I) cắt AB, AC theo thứ tự ở M và N.
Cho biết MN = 3cm. Tính S
ABC
.
2.86 Từ một điểm A ở bên ngoài đường tròn (O) kẻ hai tiếp tuyến AB, AC đến
đường tròn (O). OA cắt (O) tại I. Chứng minh rằng I là tâm đường tròn
nội tiếp của ABC.
2.87 Cho (I; r) nội tiếp ABC vuông tại A. Các tiếp điểm trên AC, AB theo
thứ tự là D, E.
a) Tứ giác ADOE là hình gì ? Vì sao ?
b) Tính chu vi và diện tích tứ giác ADOE theo r.
c) Gọi R là bán kính đường tròn ngoại tiếp ABC.
Chứng minh: AB + AC = 2(R + r).
2.88 Cho đường tròn (I ; r) nội tiếp ABC. Gọi D, E, F lần lượt là hình chiếu
của I trên các cạnh BC, CA, AB. Cho BC = a, AC = b, AB = c. Chứng
minh:
a) S = p.r (với S là diện tích và p là nửa chu vi của ABC)
b) AE = p – a; BF = p – b; CD = p – c.
1. a. Đường tròn tiếp xúc với ba cạnh của
gọi là đường tròn nội
tiếp tam giác.
b. Tâm đường tròn nội tiếp tam giác là giao điểm các đường phân
giác trong của tam giác.
2. a. Đường tròn tiếp xúc với một cạnh của tam giác và các phần kéo
dài của hai cạnh kia gọi là đường tròn bàng tiếp của tam giác.
b. Tâm của đường tròn bàng tiếp của tam giác là giao điểm của
phân giác trong và hai phân giác ngoài của hai góc còn lại.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 16
i)
2
x 6x 9 5
j)
2
4x 12x 9 x 3
k)
2 2
4x 4x 1 x 2x 1
l)
2 2
4x 12x 9 9x 24x 16
1.25 Phân tích thành hân tử:
a) x
2
– 7 b) x
2
3 c) x
2
– 2 13 x + 13
d) x
2
– 3 e) x
2
– 2 2 x + 2 f) x
2
+ 2 5 x + 5
1.26 Với n là số tự nhiên, chứng minh:
2222
n1nn1n )()(
Viết đẳng thức trên khi n là 1; 2; 3; 4; 5; 6; 7.
1.27 Cho ba số a, b, c khác 0 và a + b + c = 0. Chứng minh rằng:
2 2 2
1 1 1 1 1 1
a b c a b c
1.28 Tính:
2
2
2
2013 2013
1 2013
2014 2014
.
1.29 Chứng minh bất đẳng thức Côsi (Cauchy):
x + y 2 xy
Dấu “ = ” xảy ra khi nào ?
Áp dụng: Chứng minh rằng với x, y, z là các số dương, ta có:
zx
1
yz
1
xy
1
z
1
y
1
x
1
Một chủ doanh nghiệp đi về quê chơi cùng 1 người bạn l
à dân toán.
Họ thấy một đàn bò rất lớn trên một đồng cỏ.
Anh doanh nghi
ệp nói:
- Nhi
ều b
ò quá, tôi ch
ưa bao giờ thấy nhiều thế n
ày, có l
ẽ phải
hàng nghìn con.
Anh b
ạn toán học trả lời :
-
Đúng đấy,
có c
ả thẩy 2428 con.
- 'Tr
ời, l
àm sao mà anh l
ại đếm được nhanh thế?
- Anh ch
ủ DN hỏi.
Anh toán h
ọc trả lời:
-
À, tôi đếm tất cả chân rồi chia cho 4 l
à xong!
Chuyện vui Toán học: Câu chuyện số 1
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 89
F - Đường tròn nội tiếp – bàng tiếp tam giác
2.84 Cho ABC vuông cân tại A nội tiếp (O; R). Gọi (I; r) là đường tròn nội
tiếp ABC. Tính độ dài AB và r theo R.
2.85 Cho ABC đều có cạnh 8cm.
a) Tính bán kính đường tròn (I) nội tiếp ABC.
b) Một tiếp tuyến của (I) cắt AB, AC theo thứ tự ở M và N.
Cho biết MN = 3cm. Tính S
ABC
.
2.86 Từ một điểm A ở bên ngoài đường tròn (O) kẻ hai tiếp tuyến AB, AC đến
đường tròn (O). OA cắt (O) tại I. Chứng minh rằng I là tâm đường tròn
nội tiếp của ABC.
2.87 Cho (I; r) nội tiếp ABC vuông tại A. Các tiếp điểm trên AC, AB theo
thứ tự là D, E.
a) Tứ giác ADOE là hình gì ? Vì sao ?
b) Tính chu vi và diện tích tứ giác ADOE theo r.
c) Gọi R là bán kính đường tròn ngoại tiếp ABC.
Chứng minh: AB + AC = 2(R + r).
2.88 Cho đường tròn (I ; r) nội tiếp ABC. Gọi D, E, F lần lượt là hình chiếu
của I trên các cạnh BC, CA, AB. Cho BC = a, AC = b, AB = c. Chứng
minh:
a) S = p.r (với S là diện tích và p là nửa chu vi của ABC)
b) AE = p – a; BF = p – b; CD = p – c.
1. a. Đường tròn tiếp xúc với ba cạnh của
gọi là đường tròn nội
tiếp tam giác.
b. Tâm đường tròn nội tiếp tam giác là giao điểm các đường phân
giác trong của tam giác.
2. a. Đường tròn tiếp xúc với một cạnh của tam giác và các phần kéo
dài của hai cạnh kia gọi là đường tròn bàng tiếp của tam giác.
b. Tâm của đường tròn bàng tiếp của tam giác là giao điểm của
phân giác trong và hai phân giác ngoài của hai góc còn lại.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 88
2.83 Cho đường tròn (O; R) tiếp xúc với đường thẳng xy tại A. Trên tia Oz
song song với đường thẳng xy lấy điểm I. Từ I vẽ các tiếp tuyến với (O)
cắt xy tại E và F.
a) Chứng minh: I là tâm đường tròn ngoại tiếp OEF.
b) Cho OI = R
2
, tính chu vi IEF.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 17
C - Khai phương một tích. Nhân các căn thức bậc hai.
D - Khai phương một thương. C hia các căn thức bậc hai
1. Với A
0, B
0:
AB A B
2. Với A
0, B > 0:
A A
B
B
1.30 Tính:
1. a) 64090 ., b)
24
72 ).( c) 360112 .,
d)
42
32 . e) 8045. f) 4875.
g) 4690 ,. h) 41452 ,.,
2. a) 637. b) 483052 .., c) 4640 ,.,
d) 51572 ,.., e) 4010. f) 455.
g) 1352. h) 162.2
3. a)
22
1213 b)
22
817 c)
22
108117
d)
22
312313 e)
22
2386 ,, f)
22
218821 ,,
g) 2562751095146
22
.,,
4. a) 3232 . b) 32233223 .
c)
2
2323 )( d) )).(( 321321
5. a)
169
9
b)
144
25
c)
16
9
1
d)
81
7
2 e) 00250, f) 91663 ,.,
6. a)
18
2
b)
735
15
c)
500
12500
d)
53
5
32
6
.
e)
23
2300
f)
50
512
,
,
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 88
2.83 Cho đường tròn (O; R) tiếp xúc với đường thẳng xy tại A. Trên tia Oz
song song với đường thẳng xy lấy điểm I. Từ I vẽ các tiếp tuyến với (O)
cắt xy tại E và F.
a) Chứng minh: I là tâm đường tròn ngoại tiếp OEF.
b) Cho OI = R
2
, tính chu vi IEF.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 17
C - Khai phương một tích. Nhân các căn thức bậc hai.
D - Khai phương một thương. C hia các căn thức bậc hai
1. Với A
0, B
0:
AB A B
2. Với A
0, B > 0:
A A
B
B
1.30 Tính:
1. a) 64090 ., b)
24
72 ).( c) 360112 .,
d)
42
32 . e) 8045. f) 4875.
g) 4690 ,. h) 41452 ,.,
2. a) 637. b) 483052 .., c) 4640 ,.,
d) 51572 ,.., e) 4010. f) 455.
g) 1352. h) 162.2
3. a)
22
1213 b)
22
817 c)
22
108117
d)
22
312313 e)
22
2386 ,, f)
22
218821 ,,
g) 2562751095146
22
.,,
4. a) 3232 . b) 32233223 .
c)
2
2323 )( d) )).(( 321321
5. a)
169
9
b)
144
25
c)
16
9
1
d)
81
7
2 e) 00250, f) 91663 ,.,
6. a)
18
2
b)
735
15
c)
500
12500
d)
53
5
32
6
.
e)
23
2300
f)
50
512
,
,
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 18
7. a) 010
9
4
5
16
9
1 ,.. b)
164
124165
22
c)
22
22
384457
76149
d) 40441211441 ,.,,.,
8. a)
3
35273122
b)
2
85032
1.31 Tính:
1. a) 5261528 b) 1821972217
c) 24932212 d) 549180229
e) 27474 f) 23116116
g)
8 2 15 7 2 10
h)
10 2 21 9 2 14
i)
8 3 7 4 7
j)
5 21 5 21
k)
9 3 5 9 3 5
l)
( 10 2) 4 6 2 5
2. a) ))(( 3413324 b) 232623 ))((
c) 5321053 ))(( d) 154610154 ))((
e) 532154154
f) 22222284 ..
g) )).().(( 21232123245
h)
2 3. 2 2 3 . 2 2 2 3 . 2 2 2 3
3*.
A 7 5 2 7 4 1
ĐS:
2( 7 1)
A
2
5
B 4 3 6 3 15 3
2
ĐS:
6
B
2
Với m, n > 0 thỏa m + n = A và m . n = B
ta có:
2
)nm(n.m2nmB2A
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 87
c) Gọi H là giao đểm của AO và MN. Chứng minh: OH . OA = R
2
.
2.78 Cho đường tròn (O) đường kính BC và 1 điểm A nằm trên đường tròn (A
khác B và C). Qua O, kẻ tia Ox song song với AC, tia Ox cắt AB tại D.
a) Chứng minh: OD AB và từ đó suy ra D là trung điểm của AB.
b) Tiếp tuyến tại B của (O) cắt tia Ox tại E.
Chứng minh: EA cũng là tiếp tuyến của (O)
c) Tia CA cắt tia BE tại F. Chứng minh: tia CE đi qua trung điểm I của
của đường cao AH của ABC.
2.79 Cho đường tròn (O; R) đường kính AB. Từ trung điểm I của bán kính OB
vẽ dây cung CD vuông góc với OB.
a) So sánh IC và ID.
b) Tiếp tuyến tại C của (O) cắt đường thẳng AB tại M. Chứng minh:
i) COM = DOM. ii) MD là tiếp tuyến của (O) .
c) Tính độ dài đoạn MC theo R.
2.80 Cho (O ; 3cm) và điểm A sao cho OA = 5cm. Kẻ cac tiếp tuyến AB, AC
với đường tròn (B, C là hai tiếp điểm). Gọi H là giao điểm của AO và BC.
a) Tính độ dài OH.
b) Qua điểm M bắt kì thuộc cung nhỏ BC, kẻ tiếp tuyến với đường tròn,
cắt AB, AC theo thứ tự tại D và E. Tính chi vi ADE.
2.81 Cho ABC vuông tại A, đường cao AH. Vẽ đường tròn (A; AH). Kẻ các
tiếp tuyến BD, CE với đường tròn (D, E là các tiếp điểm khác H). C/m:
a) Ba điểm D, A, E thẳng hàng.
b) DE tiếp xúc với đường tròn đường kính BC.
2.82 Cho (O ; R), và điểm A sao cho OA = R
2
, kẻ các tiếp tuyến AB, AC
với (O). (B, C là các tiếp điểm). Qua điểm M bắt kì thuộc cung nhỏ BC,
kẻ tiếp tuyến với đường tròn, cắt AB, AC theo thứ tự tại D và E.
a) Tứ giác ABOC là hình gì ? Vì sao ?
b) Tính số đo góc
DOE
.
c) Đoạn OA cắt (O) tại K. Chứng minh: K là tâm đường tròn nội tiếp
ABC. Tính bán kính của đường tròn này.
d) Tính độ dài BK theo R.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 18
7. a) 010
9
4
5
16
9
1 ,.. b)
164
124165
22
c)
22
22
384457
76149
d) 40441211441 ,.,,.,
8. a)
3
35273122
b)
2
85032
1.31 Tính:
1. a) 5261528 b) 1821972217
c) 24932212 d) 549180229
e) 27474 f) 23116116
g)
8 2 15 7 2 10
h)
10 2 21 9 2 14
i)
8 3 7 4 7
j)
5 21 5 21
k)
9 3 5 9 3 5
l)
( 10 2) 4 6 2 5
2. a) ))(( 3413324 b) 232623 ))((
c) 5321053 ))(( d) 154610154 ))((
e) 532154154
f) 22222284 ..
g) )).().(( 21232123245
h)
2 3. 2 2 3 . 2 2 2 3 . 2 2 2 3
3*.
A 7 5 2 7 4 1
ĐS:
2( 7 1)
A
2
5
B 4 3 6 3 15 3
2
ĐS:
6
B
2
Với m, n > 0 thỏa m + n = A và m . n = B
ta có:
2
)nm(n.m2nmB2A
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 87
c) Gọi H là giao đểm của AO và MN. Chứng minh: OH . OA = R
2
.
2.78 Cho đường tròn (O) đường kính BC và 1 điểm A nằm trên đường tròn (A
khác B và C). Qua O, kẻ tia Ox song song với AC, tia Ox cắt AB tại D.
a) Chứng minh: OD AB và từ đó suy ra D là trung điểm của AB.
b) Tiếp tuyến tại B của (O) cắt tia Ox tại E.
Chứng minh: EA cũng là tiếp tuyến của (O)
c) Tia CA cắt tia BE tại F. Chứng minh: tia CE đi qua trung điểm I của
của đường cao AH của ABC.
2.79 Cho đường tròn (O; R) đường kính AB. Từ trung điểm I của bán kính OB
vẽ dây cung CD vuông góc với OB.
a) So sánh IC và ID.
b) Tiếp tuyến tại C của (O) cắt đường thẳng AB tại M. Chứng minh:
i) COM = DOM. ii) MD là tiếp tuyến của (O) .
c) Tính độ dài đoạn MC theo R.
2.80 Cho (O ; 3cm) và điểm A sao cho OA = 5cm. Kẻ cac tiếp tuyến AB, AC
với đường tròn (B, C là hai tiếp điểm). Gọi H là giao điểm của AO và BC.
a) Tính độ dài OH.
b) Qua điểm M bắt kì thuộc cung nhỏ BC, kẻ tiếp tuyến với đường tròn,
cắt AB, AC theo thứ tự tại D và E. Tính chi vi ADE.
2.81 Cho ABC vuông tại A, đường cao AH. Vẽ đường tròn (A; AH). Kẻ các
tiếp tuyến BD, CE với đường tròn (D, E là các tiếp điểm khác H). C/m:
a) Ba điểm D, A, E thẳng hàng.
b) DE tiếp xúc với đường tròn đường kính BC.
2.82 Cho (O ; R), và điểm A sao cho OA = R
2
, kẻ các tiếp tuyến AB, AC
với (O). (B, C là các tiếp điểm). Qua điểm M bắt kì thuộc cung nhỏ BC,
kẻ tiếp tuyến với đường tròn, cắt AB, AC theo thứ tự tại D và E.
a) Tứ giác ABOC là hình gì ? Vì sao ?
b) Tính số đo góc
DOE
.
c) Đoạn OA cắt (O) tại K. Chứng minh: K là tâm đường tròn nội tiếp
ABC. Tính bán kính của đường tròn này.
d) Tính độ dài BK theo R.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 86
a) Chu vi MPQ không phụ thuộc vào vị trí điểm M.
b)
BOC 2DOE
. c) DE <
1
(AB AC)
2
2.74 Cho đường tròn (O; 5cm) có đường kính AB và dây cung CD. Kéo dài
AB và CD cắt nhau tại M. Gọi N là trung điểm của dây cung CD.
a) Chứng minh: MNO là tam giác vuông.
b) Tiếp tuyến tại B của (O) cắt đường thẳng CD tại Q.
Chứng minh: MN . MQ = MO . MB
c) Tia ON cắt (O) tại E. Tính độ dài dây cung EC nếu độ dài dây cung
CD = 6 cm
2.75 Cho nửa đường tròn (O ; R) đường kính AB. Gọi Ax, By là các tia vuông
góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ
AB). Gọi D là điểm bất kì thuộc nửa đường tròn. Tiếp tuyến tại D cắt Ax
và By theo thứ tự tại M và N.
a) Tứ giác AMNB là hình gì ? Vì sao ?
b) Tính số đo góc MÔN.
c) Chứng minh: MN = AM + BN.
d) Chứng minh: AM . BN = R
2
.
e) Đường tròn đường kính MN tiếp xúc với AB tại O.
f) AN và BM cắt nhau tại Q, DQ cắt AB tại H.
Chứng minh: DQ AB và QH = QD.
g) Tìm vị trí của D để tứ giác AMNB có chu vi nhỏ nhất.
h) Cho R = 2cm. Tìm vị trí của M và N để chu vi tứ giác AMNB có chu
vi bằng 14cm.
2.76 Cho đường tròn (O; R) đường kính AB và 1 là điểm C nằm trên đường
tròn. Đường thẳng song song với AC kẻ từ O cắt tiếp tuyến tại C của (O)
tại D. Chứng minh:
a)
COD BOD
. b) DB cũng là tiếp tuyến tại B của (O).
c) AC . OD = 2R
2
.
2.77 Cho đường tròn (O; R) và một điểm A nằm ngoài (O). Từ A kẻ hai tiếp
tuyến AM, AN của (O) (M, N là hai tiếp điểm).
a) AMN là gì ? Vì sao ?
b) Đường thẳng vuông góc với OM tại O cắt đường thẳng AN tại P.
Chứng minh: AP = PO.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 19
C 1 2 5 5 11 5 2
ĐS:
2( 5 1)
C
2
1 2 27 2 38 5 3 2
D
3 2 4
ĐS:
D 1
E 5 2 2 2 2 2 1 2 1
ĐS:
E 2
1.32 Phân tích thành tích số:
a) 6321 b) 3310556
1.33 Rút gọn biểu thức sau (loại bỏ dấu căn và dấu trị tuyệt đối):
1. a)
2
x360, với x < 0 b)
24
)x3(x với x 3
c)
2
x14827 )(. với x > 1 d)
24
yxx
yx
1
)(.
a, b > 0
e)
2
3x4 ).( với x 3 f)
2
2x9 ).( với x < 2
g)
22
)1x.(x với x > 0 h)
22
1xx )( với x < 0
i)
8
x3
3
x2
. với x 0 j)
x
52
x13 với x > 0
k) x3x45.x5 với x bất kỳ l)
22
x18020x3 .,)( , x
2. a)
y7
y63
3
với y > 0 b)
5
3
x3
x48
với x > 0
c)
m20
mn45
2
với m > 0, n > 0 d)
66
64
yx128
yx16
với x < 0 và y 0
e)
4
2
y
x
y
x
với x > 0, y 0 f)
2
4
2
y4
x
y2
với y < 0
g)
6
2
y
x25
xy5
với x < 0, y > 0 h)
84
33
yx
16
yx20 , với x 0, y 0
i)
42
2
yx
3
xy với x < 0, y 0 j)
48
3x27
2
)(
với x > 3
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 86
a) Chu vi MPQ không phụ thuộc vào vị trí điểm M.
b)
BOC 2DOE
. c) DE <
1
(AB AC)
2
2.74 Cho đường tròn (O; 5cm) có đường kính AB và dây cung CD. Kéo dài
AB và CD cắt nhau tại M. Gọi N là trung điểm của dây cung CD.
a) Chứng minh: MNO là tam giác vuông.
b) Tiếp tuyến tại B của (O) cắt đường thẳng CD tại Q.
Chứng minh: MN . MQ = MO . MB
c) Tia ON cắt (O) tại E. Tính độ dài dây cung EC nếu độ dài dây cung
CD = 6 cm
2.75 Cho nửa đường tròn (O ; R) đường kính AB. Gọi Ax, By là các tia vuông
góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ
AB). Gọi D là điểm bất kì thuộc nửa đường tròn. Tiếp tuyến tại D cắt Ax
và By theo thứ tự tại M và N.
a) Tứ giác AMNB là hình gì ? Vì sao ?
b) Tính số đo góc MÔN.
c) Chứng minh: MN = AM + BN.
d) Chứng minh: AM . BN = R
2
.
e) Đường tròn đường kính MN tiếp xúc với AB tại O.
f) AN và BM cắt nhau tại Q, DQ cắt AB tại H.
Chứng minh: DQ AB và QH = QD.
g) Tìm vị trí của D để tứ giác AMNB có chu vi nhỏ nhất.
h) Cho R = 2cm. Tìm vị trí của M và N để chu vi tứ giác AMNB có chu
vi bằng 14cm.
2.76 Cho đường tròn (O; R) đường kính AB và 1 là điểm C nằm trên đường
tròn. Đường thẳng song song với AC kẻ từ O cắt tiếp tuyến tại C của (O)
tại D. Chứng minh:
a)
COD BOD
. b) DB cũng là tiếp tuyến tại B của (O).
c) AC . OD = 2R
2
.
2.77 Cho đường tròn (O; R) và một điểm A nằm ngoài (O). Từ A kẻ hai tiếp
tuyến AM, AN của (O) (M, N là hai tiếp điểm).
a) AMN là gì ? Vì sao ?
b) Đường thẳng vuông góc với OM tại O cắt đường thẳng AN tại P.
Chứng minh: AP = PO.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 19
C 1 2 5 5 11 5 2
ĐS:
2( 5 1)
C
2
1 2 27 2 38 5 3 2
D
3 2 4
ĐS:
D 1
E 5 2 2 2 2 2 1 2 1
ĐS:
E 2
1.32 Phân tích thành tích số:
a) 6321 b) 3310556
1.33 Rút gọn biểu thức sau (loại bỏ dấu căn và dấu trị tuyệt đối):
1. a)
2
x360, với x < 0 b)
24
)x3(x với x 3
c)
2
x14827 )(. với x > 1 d)
24
yxx
yx
1
)(.
a, b > 0
e)
2
3x4 ).( với x 3 f)
2
2x9 ).( với x < 2
g)
22
)1x.(x với x > 0 h)
22
1xx )( với x < 0
i)
8
x3
3
x2
. với x 0 j)
x
52
x13 với x > 0
k) x3x45.x5 với x bất kỳ l)
22
x18020x3 .,)( , x
2. a)
y7
y63
3
với y > 0 b)
5
3
x3
x48
với x > 0
c)
m20
mn45
2
với m > 0, n > 0 d)
66
64
yx128
yx16
với x < 0 và y 0
e)
4
2
y
x
y
x
với x > 0, y 0 f)
2
4
2
y4
x
y2
với y < 0
g)
6
2
y
x25
xy5
với x < 0, y > 0 h)
84
33
yx
16
yx20 , với x 0, y 0
i)
42
2
yx
3
xy với x < 0, y 0 j)
48
3x27
2
)(
với x > 3
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 20
k)
2
yx
xy
yx
)(
)(
với x < y, y < 0
l)
2
2
y
x4x129
với x >1,5 và y<0
1.34 Chứng minh:
a) 13232 )()( b) 8179179 .
c)
( 2014 2013)
.
( 2014 2013)
=1
d) 9622212322
2
)()(
1.35 Rút gọn các biểu thức sau:
1. a)
2832
146
b)
432
168632
2. a)
1x2x
1x2x
với x 0 b)
4
2
1x
1y2y
1y
1x
)(
)(
,x1,y1,y>0
1.36 Rút gọn rồi tính giá trị của các biểu thức sau:
1. a)
22
x9x614 )( tại x = 2
b) )( b44ba9
22
tại a = 2, b = 3
2. a)
2x
x2x
8x4
23
tại x = 2
b)
3x
1x
x3
2x
2
2
4
)(
)(
(với x < 3) tại x = 0,5
1.37 So sánh hai số sau (không dùng máy tính):
a) 2 + 3 và 10 b) 3 + 2và 62
c) 16 và 1715. d) 8 và 15 + 17
1.38 So sánh
2012 2014
và 2.
2013
1.39 Giải phương trình:
1. a) 8x16 b) 5x4
c) 061x2x4
2
)( d) 21x1x9 )(
e) 35x f) 210x
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 85
c) EF cắt OM tại K và cắt OI tại H. C/minh: OM . OK = OH . OI = R
2
.
2.67 Cho ABC vuông tại A (AB < AC) có đường cao AH. Vẽ đường tròn tâm
B, bán kính BA, đường tròn này cắt AH tại điểm thứ hai là D.
a) Chứng minh: CD tiếp xúc với đường tròn (B ; BA).
b) Gọi I là đối xứng của B qua AH, đường thẳng AI cắt CD tại E. Chứng
minh: A, H, E, C cùng thuộc một đường tròn. Suy ra AB là tiếp tuyến
của đường tròn này.
2.68 Cho đường tròn đường kính AB. Gọi C là điểm bắt kì trên đường tròn và
H là hình chiếu của C trên AB. Từ A và B kẻ các tiếp tuyến AD và BE
đến đường tròn (C ; CH). Chứng minh:
a) D, C, E thẳng hàng.
b) DE là tiếp tuyến của đường tròn đường kính BC.
c) Xác định vị trí của điểm C để diện tích tứ giác ABED lớn nhất.
2.69 Cho góc xÔy, điểm A thuộc tia Ox. Dựng (I) tiếp xúc với Ox tại A và có
tâm I nằm trên Oy.
2.70 Cho đường tròn (O) và đường thẳng d không giao nhau. Dựng tiếp tuyến
của đường tròn (O) sao cho tiếp tuyến đó song song với d.
2.71 Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến
AM, AN với đường tròn (M, N là hai tiếp điểm).
a) Chứng minh: OA MN.
b) Vẽ đường kính NOC. Chứng minh: MC // AO.
c) Tính độ dài các cạnh của AMN biết OM = 3cm, OA = 5cm.
2.72 Cho đường tròn tâm O đường kính AB và một điểm C nằm trên đường
tròn (C khác A và B). Gọi D là trung điểm của AC.
a) Tính số đo ODA và chứng tỏ rằng OD song song với BC.
b) Tiếp tuyến tại A của (O) cắt tia OD tại E. Chứng minh: EC là tiếp
tuyến của (O).
c) Đường thẳng BC cắt tiếp tuyến tại A của (O) tại điểm M.
d) Chứng minh rằng OE là trung tuyến của AOM.
2.73 Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ tiếp tuyến
AB, AC với đường tròn (B và C là hai tiếp điểm). Qua điểm M thuộc
cung nhỏ BC, kẻ tiếp tuyến với đường tròn, tiếp tuyến này cắt AB và AC
lần lượt tại D và E. Chứng minh rằng
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 20
k)
2
yx
xy
yx
)(
)(
với x < y, y < 0
l)
2
2
y
x4x129
với x >1,5 và y<0
1.34 Chứng minh:
a) 13232 )()( b) 8179179 .
c)
( 2014 2013)
.
( 2014 2013)
=1
d) 9622212322
2
)()(
1.35 Rút gọn các biểu thức sau:
1. a)
2832
146
b)
432
168632
2. a)
1x2x
1x2x
với x 0 b)
4
2
1x
1y2y
1y
1x
)(
)(
,x1,y1,y>0
1.36 Rút gọn rồi tính giá trị của các biểu thức sau:
1. a)
22
x9x614 )( tại x = 2
b) )( b44ba9
22
tại a = 2, b = 3
2. a)
2x
x2x
8x4
23
tại x = 2
b)
3x
1x
x3
2x
2
2
4
)(
)(
(với x < 3) tại x = 0,5
1.37 So sánh hai số sau (không dùng máy tính):
a) 2 + 3 và 10 b) 3 + 2và 62
c) 16 và 1715. d) 8 và 15 + 17
1.38 So sánh
2012 2014
và 2.
2013
1.39 Giải phương trình:
1. a) 8x16 b) 5x4
c) 061x2x4
2
)( d) 21x1x9 )(
e) 35x f) 210x
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 85
c) EF cắt OM tại K và cắt OI tại H. C/minh: OM . OK = OH . OI = R
2
.
2.67 Cho ABC vuông tại A (AB < AC) có đường cao AH. Vẽ đường tròn tâm
B, bán kính BA, đường tròn này cắt AH tại điểm thứ hai là D.
a) Chứng minh: CD tiếp xúc với đường tròn (B ; BA).
b) Gọi I là đối xứng của B qua AH, đường thẳng AI cắt CD tại E. Chứng
minh: A, H, E, C cùng thuộc một đường tròn. Suy ra AB là tiếp tuyến
của đường tròn này.
2.68 Cho đường tròn đường kính AB. Gọi C là điểm bắt kì trên đường tròn và
H là hình chiếu của C trên AB. Từ A và B kẻ các tiếp tuyến AD và BE
đến đường tròn (C ; CH). Chứng minh:
a) D, C, E thẳng hàng.
b) DE là tiếp tuyến của đường tròn đường kính BC.
c) Xác định vị trí của điểm C để diện tích tứ giác ABED lớn nhất.
2.69 Cho góc xÔy, điểm A thuộc tia Ox. Dựng (I) tiếp xúc với Ox tại A và có
tâm I nằm trên Oy.
2.70 Cho đường tròn (O) và đường thẳng d không giao nhau. Dựng tiếp tuyến
của đường tròn (O) sao cho tiếp tuyến đó song song với d.
2.71 Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến
AM, AN với đường tròn (M, N là hai tiếp điểm).
a) Chứng minh: OA MN.
b) Vẽ đường kính NOC. Chứng minh: MC // AO.
c) Tính độ dài các cạnh của AMN biết OM = 3cm, OA = 5cm.
2.72 Cho đường tròn tâm O đường kính AB và một điểm C nằm trên đường
tròn (C khác A và B). Gọi D là trung điểm của AC.
a) Tính số đo ODA và chứng tỏ rằng OD song song với BC.
b) Tiếp tuyến tại A của (O) cắt tia OD tại E. Chứng minh: EC là tiếp
tuyến của (O).
c) Đường thẳng BC cắt tiếp tuyến tại A của (O) tại điểm M.
d) Chứng minh rằng OE là trung tuyến của AOM.
2.73 Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ tiếp tuyến
AB, AC với đường tròn (B và C là hai tiếp điểm). Qua điểm M thuộc
cung nhỏ BC, kẻ tiếp tuyến với đường tròn, tiếp tuyến này cắt AB và AC
lần lượt tại D và E. Chứng minh rằng
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 84
2.58 Cho ABC cân tại A, có O là trung điểm của BC và BC = 2a. Đường tròn
(O) tiếp xúc với AB, AC lần lượt tại H và K. Qua D trên cung nhỏ HK, kẻ
tiếp tuyến với (O) cắt AB và AC ở M và N.
a) Chứng minh: A, H, O, K cùng thuộc một đường tròn.
b) Chứng minh: MÔN = ABC.
c) Tính tích BM . CN theo a.
d) Định vị trí của MN sao cho BM + CN đạt giá trị nhỏ nhất.
2.59 Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Dùng thước và
compa, hãy dựng các điểm B và C thuộc đường tròn (O) sao cho AB và
AC là các tiếp tuyến của đường tròn (O).
2.60 Cho điểm A nằm trên đường thẳng d, điểm B nằm ngoài đường thẳng d.
Dựng đường tròn (O) đi qua A và B, nhận đường thẳng d làm tiếp tuyến.
2.61 Cho ABC vuông tại A. Vẽ đường tròn (B ; BA) và đường tròn (C ; CA),
chúng cắt nhau tại điểm D (khác A). C/minh CD là tiếp tuyến của (B).
2.62 Cho ABC cân tại A, các đường cao AD và BE cắt nhau tại H. Vẽ đường
tròn (O) có đường kính AH. Chứng minh:
a) Điểm E nằm trên đường tròn (O).
b) DE là tiếp tuyến của đường tròn (O).
2.63 Cho điểm M trên (O; R) đường kính AB. Gọi H là trung điểm của BM,
OH cắt (O) tại I và cắt tiếp tuyến tại B của (O) ở điểm D. Gọi N là hình
chiếu của I trên AM. Chứng minh: NI và DM là các tiếp tuyến của (O).
2.64 Cho đường tròn (O ; R) đường kính AB. Một tiếp tuyến tại M của (O) cắt
hai tiếp tuyến Ax, By theo thứ tự tại C và D. Chứng minh: đường tròn
đường kính CD tiếp xúc với AB.
2.65 Trên tiếp tuyến tại A của (O; R) lấy điểm B với AB = R. Từ A kẻ đường
vuông góc với OB tại H, cắt (O) tại C. OB cắt cung nhỏ AC tại I.
a) Chứng minh: AC là tiếp tuyến của đường tròn (O).
b) Tính theo R độ dài BH, IH và AI.
2.66 Từ điểm I bên ngoài (O; R) vẽ hai cát tuyến IAB và ICD (không qua tâm
O). Gọi M và N lần lượt là trung điểm của hai dây AB và CD.
a) Chứng minh: O, I, M, N cùng thuộc một đường tròn.
b) Đường tròn (OIMN) cắt (O) tại E và F. Chứng minh: IE, IF là hai tiếp
tuyến của (O).
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 21
g) 51x2 h) 12x54
2. a)
5xx4
2
b) 1x23x
2
)(
c) 6x3 d) 211x7 )(
3. a) 050x2 . b) 08x2
1.40 Giải các phương trình:
a) 2
1x
3x2
và 2
1x
3x2
b) 3
1x
3x4
và 3
1x
3x4
1.41 Cho hai biểu thức: 3x2xA . và ))(( 3x2xB
a) Tìm x để A có nghĩa. Tìm x để B có nghĩa.
b) Với giá trị nào của x thì B có nghĩa còn A không có nghĩa.
c) Với giá trị nào của x thì A = B.
1.42 Cho hai biểu thức: và
3x
3x2
A
3x
3x2
B
.
a) Tìm x để A có nghĩa. Tìm x để B có nghĩa.
b) Với giá trị nào của x thì B có nghĩa còn A không có nghĩa.
c) Với giá trị nào của x thì A = B.
1.43 Cho
2
51
bvaø
2
51
a
. Tính a
2
+ b
2
và a
5
+ a
5
.
1.44 Cho 52104bvaø52104a .
Tính a
2
+ b
2
và ab. Suy ra giá trị của a + b.
1.45 Thực hiện phép tính:
a)
A 12 3 7 12 3 7
b)
7 5 7 5
B 3 2 2
7 11
c)
C 8 2 10 2 5 8 2 10 2 5
1.46 Rút gọn rồi tính giá trị của biểu thức sau:
2
A 10a 12a 10 36
với x =
2 5
x
5 2
1.47 Cho hai số a và b với a > 0, b > 0. Chứng minh: baba .
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 84
2.58 Cho ABC cân tại A, có O là trung điểm của BC và BC = 2a. Đường tròn
(O) tiếp xúc với AB, AC lần lượt tại H và K. Qua D trên cung nhỏ HK, kẻ
tiếp tuyến với (O) cắt AB và AC ở M và N.
a) Chứng minh: A, H, O, K cùng thuộc một đường tròn.
b) Chứng minh: MÔN = ABC.
c) Tính tích BM . CN theo a.
d) Định vị trí của MN sao cho BM + CN đạt giá trị nhỏ nhất.
2.59 Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Dùng thước và
compa, hãy dựng các điểm B và C thuộc đường tròn (O) sao cho AB và
AC là các tiếp tuyến của đường tròn (O).
2.60 Cho điểm A nằm trên đường thẳng d, điểm B nằm ngoài đường thẳng d.
Dựng đường tròn (O) đi qua A và B, nhận đường thẳng d làm tiếp tuyến.
2.61 Cho ABC vuông tại A. Vẽ đường tròn (B ; BA) và đường tròn (C ; CA),
chúng cắt nhau tại điểm D (khác A). C/minh CD là tiếp tuyến của (B).
2.62 Cho ABC cân tại A, các đường cao AD và BE cắt nhau tại H. Vẽ đường
tròn (O) có đường kính AH. Chứng minh:
a) Điểm E nằm trên đường tròn (O).
b) DE là tiếp tuyến của đường tròn (O).
2.63 Cho điểm M trên (O; R) đường kính AB. Gọi H là trung điểm của BM,
OH cắt (O) tại I và cắt tiếp tuyến tại B của (O) ở điểm D. Gọi N là hình
chiếu của I trên AM. Chứng minh: NI và DM là các tiếp tuyến của (O).
2.64 Cho đường tròn (O ; R) đường kính AB. Một tiếp tuyến tại M của (O) cắt
hai tiếp tuyến Ax, By theo thứ tự tại C và D. Chứng minh: đường tròn
đường kính CD tiếp xúc với AB.
2.65 Trên tiếp tuyến tại A của (O; R) lấy điểm B với AB = R. Từ A kẻ đường
vuông góc với OB tại H, cắt (O) tại C. OB cắt cung nhỏ AC tại I.
a) Chứng minh: AC là tiếp tuyến của đường tròn (O).
b) Tính theo R độ dài BH, IH và AI.
2.66 Từ điểm I bên ngoài (O; R) vẽ hai cát tuyến IAB và ICD (không qua tâm
O). Gọi M và N lần lượt là trung điểm của hai dây AB và CD.
a) Chứng minh: O, I, M, N cùng thuộc một đường tròn.
b) Đường tròn (OIMN) cắt (O) tại E và F. Chứng minh: IE, IF là hai tiếp
tuyến của (O).
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 21
g) 51x2 h) 12x54
2. a)
5xx4
2
b) 1x23x
2
)(
c) 6x3 d) 211x7 )(
3. a) 050x2 . b) 08x2
1.40 Giải các phương trình:
a) 2
1x
3x2
và 2
1x
3x2
b) 3
1x
3x4
và 3
1x
3x4
1.41 Cho hai biểu thức: 3x2xA . và ))(( 3x2xB
a) Tìm x để A có nghĩa. Tìm x để B có nghĩa.
b) Với giá trị nào của x thì B có nghĩa còn A không có nghĩa.
c) Với giá trị nào của x thì A = B.
1.42 Cho hai biểu thức: và
3x
3x2
A
3x
3x2
B
.
a) Tìm x để A có nghĩa. Tìm x để B có nghĩa.
b) Với giá trị nào của x thì B có nghĩa còn A không có nghĩa.
c) Với giá trị nào của x thì A = B.
1.43 Cho
2
51
bvaø
2
51
a
. Tính a
2
+ b
2
và a
5
+ a
5
.
1.44 Cho 52104bvaø52104a .
Tính a
2
+ b
2
và ab. Suy ra giá trị của a + b.
1.45 Thực hiện phép tính:
a)
A 12 3 7 12 3 7
b)
7 5 7 5
B 3 2 2
7 11
c)
C 8 2 10 2 5 8 2 10 2 5
1.46 Rút gọn rồi tính giá trị của biểu thức sau:
2
A 10a 12a 10 36
với x =
2 5
x
5 2
1.47 Cho hai số a và b với a > 0, b > 0. Chứng minh: baba .
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 22
Áp dụng: So sánh 925 và 925
1.48 Cho hai số a và b với a > b > 0. Chứng minh: baba .
Áp dụng: So sánh 925 và 925
1.49 Với n là số tự nhiên, chứng minh:
11n21n2n1n
22
2
)()(
Viết đẳng thức trên khi n là 1; 2; 3; 4.
1.50 Cho hai số a 0, b 0. Chứng minh:
a)
a b
ab
2
b)
2
ba
2
ba
1.51 Chứng minh:
a) 3 là số vô tỉ. b) 5 2 và 3 + 2 đều là số vô tỉ.
1.52 Giải các bất phương trình sau và biểu diễn nghiệm trên trục số:
a) 2x b) 3x
Có 2 ngu
ời bạn đang đi ch
ơi trên khinh khí c
ầu (KKC), họ bị lạc
hướng nên phải hạ thấp xuống để hỏi đường.
Khi th
ấy một anh ở dưới, một người hỏi :
-
"Chúng tôi đang ở đâu đấy?".
Anh chàng dư
ới đất trả lời:
-
"Các anh đang ở tr
ên m
ột cái KK
C".
Người trên KKC hỏi tiếp:
- "Anh là dân Toán à?".
-
"Đúng rồi".
Nguời bạn kia ngạc nhiên hỏi:
- "Sao anh bi
ết người ta l
à dân toán?".
Anh b
ạn này bảo:
- "Thì
đấy, họ trả lời bao giờ cũng rất chính xác, nhưng l
ại
không giúp được g
ì c
ả!''
Chuyện vui Toán học: Câu chuyện số 2
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 83
2.52 Cho đường tròn (O; 2cm). Một đường thẳng đi qua điểm A nằm bên
ngoài đường tròn và cắt đường tròn tại B và C, trong đó AB = BC. Kẻ
đường kính COD. Tính AD.
2.53 Cho hình thang ABCD (
0
A D 90
), AB = 4cm, BC= 13cm, CD = 9cm.
a) Tính độ dài AD.
b) Chứng minh rằng AD tiếp xúc với đường tròn có đường kính là BC.
2.54 Cho (O; R), bán kính OA, dây CD là đường trung trực của OA.
a) Tứ giác OCAD là hình gì ? Vì sao ?
b) Kẻ tiếp tuyến với đường tròn tại C, tiếp tuyến này cắt đường thẳng OA
tại I. Tính CI.
2.55 Cho nửa đường tròn tâm O, đường kính AB. Qu điểm C thuộc nửa đường
tròn, kẻ tiếp tuyến d của đường tròn. Gọi E và F lần lượt là chân các
đường vuông góc kẻ từ A và B đến d. Gọi H là chân đường vuông góc kẻ
từ C đến AB. Chứng minh rằng:
a) CE = CF. b) AC là tia phân giác của
BAE
. c) CH
2
= AE . BF
2.56 Cho đường tròn (O ; R) có đường kính AB và hai tiếp tuyến Ax, By. Một
tiếp tuyến khác tại điểm M cắt Ax ở C và cắt By ở D.
a) Chứng minh: CD = AC + BD.
b) Chứng minh: COD vuông.
c) Chứng minh: AB
2
= 4AC . BD.
d) AM cắt OC tại I, BM cắt OD tại K. Tứ giác OIMK là hình gì ? Định vị
trí của M để OIMK là hình vuông.
e) AM cắt By tại F, BM cắt Ax tại E. Chứng minh:
i. C là trung điểm của AE ii) S
ABM
= S
EFM
.
2.57 Cho đường tròn (O ; R) và đoạn thẳng OA = 2R. Từ A kẻ hai tiếp tuyến
AB, AC đến đường tròn (O).
a) Chứng minh: OA là đường trung trực của đoạn thẳng BC.
b) Chứng minh: ABC đều.
c) Tính theo R độ dài BC và diện tích ABC.
d) Đoạn OA cắt (O) tại D. Tứ giác OBDI là hình gì ? Vì sao ?
e) BO cắt AC kéo dài tại I. Tính theo R độ dài các cạnh của ABI.
f) Từ O kẻ đường vuông góc với OC cắt AB tại K. Tính khoảng cách từ
K đến OA.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 22
Áp dụng: So sánh 925 và 925
1.48 Cho hai số a và b với a > b > 0. Chứng minh: baba .
Áp dụng: So sánh 925 và 925
1.49 Với n là số tự nhiên, chứng minh:
11n21n2n1n
22
2
)()(
Viết đẳng thức trên khi n là 1; 2; 3; 4.
1.50 Cho hai số a 0, b 0. Chứng minh:
a)
a b
ab
2
b)
2
ba
2
ba
1.51 Chứng minh:
a) 3 là số vô tỉ. b) 5 2 và 3 + 2 đều là số vô tỉ.
1.52 Giải các bất phương trình sau và biểu diễn nghiệm trên trục số:
a) 2x b) 3x
Có 2 ngu
ời bạn đang đi ch
ơi trên khinh khí c
ầu (KKC), họ bị lạc
hướng nên phải hạ thấp xuống để hỏi đường.
Khi th
ấy một anh ở dưới, một người hỏi :
-
"Chúng tôi đang ở đâu đấy?".
Anh chàng dư
ới đất trả lời:
-
"Các anh đang ở tr
ên m
ột cái KK
C".
Người trên KKC hỏi tiếp:
- "Anh là dân Toán à?".
-
"Đúng rồi".
Nguời bạn kia ngạc nhiên hỏi:
- "Sao anh bi
ết người ta l
à dân toán?".
Anh b
ạn này bảo:
- "Thì
đấy, họ trả lời bao giờ cũng rất chính xác, nhưng l
ại
không giúp được g
ì c
ả!''
Chuyện vui Toán học: Câu chuyện số 2
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 83
2.52 Cho đường tròn (O; 2cm). Một đường thẳng đi qua điểm A nằm bên
ngoài đường tròn và cắt đường tròn tại B và C, trong đó AB = BC. Kẻ
đường kính COD. Tính AD.
2.53 Cho hình thang ABCD (
0
A D 90
), AB = 4cm, BC= 13cm, CD = 9cm.
a) Tính độ dài AD.
b) Chứng minh rằng AD tiếp xúc với đường tròn có đường kính là BC.
2.54 Cho (O; R), bán kính OA, dây CD là đường trung trực của OA.
a) Tứ giác OCAD là hình gì ? Vì sao ?
b) Kẻ tiếp tuyến với đường tròn tại C, tiếp tuyến này cắt đường thẳng OA
tại I. Tính CI.
2.55 Cho nửa đường tròn tâm O, đường kính AB. Qu điểm C thuộc nửa đường
tròn, kẻ tiếp tuyến d của đường tròn. Gọi E và F lần lượt là chân các
đường vuông góc kẻ từ A và B đến d. Gọi H là chân đường vuông góc kẻ
từ C đến AB. Chứng minh rằng:
a) CE = CF. b) AC là tia phân giác của
BAE
. c) CH
2
= AE . BF
2.56 Cho đường tròn (O ; R) có đường kính AB và hai tiếp tuyến Ax, By. Một
tiếp tuyến khác tại điểm M cắt Ax ở C và cắt By ở D.
a) Chứng minh: CD = AC + BD.
b) Chứng minh: COD vuông.
c) Chứng minh: AB
2
= 4AC . BD.
d) AM cắt OC tại I, BM cắt OD tại K. Tứ giác OIMK là hình gì ? Định vị
trí của M để OIMK là hình vuông.
e) AM cắt By tại F, BM cắt Ax tại E. Chứng minh:
i. C là trung điểm của AE ii) S
ABM
= S
EFM
.
2.57 Cho đường tròn (O ; R) và đoạn thẳng OA = 2R. Từ A kẻ hai tiếp tuyến
AB, AC đến đường tròn (O).
a) Chứng minh: OA là đường trung trực của đoạn thẳng BC.
b) Chứng minh: ABC đều.
c) Tính theo R độ dài BC và diện tích ABC.
d) Đoạn OA cắt (O) tại D. Tứ giác OBDI là hình gì ? Vì sao ?
e) BO cắt AC kéo dài tại I. Tính theo R độ dài các cạnh của ABI.
f) Từ O kẻ đường vuông góc với OC cắt AB tại K. Tính khoảng cách từ
K đến OA.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 82
E - Vị trí tương đối của đường thẳng và đường tròn
Dấu hiệu nhận biết tiếp tuyến của đường tròn
Tính chất của hai tiếp tuyến cắt nhau
2.49 Trên mặt phẳng tọa độ cho điểm I(–3 ; 2). Nếu vẽ đường tròn tâm I bán
kính bằng 2 thì đường tròn đó có vị trí tương đối như thế nào đối với cac
trục tọa độ ?
2.50 Cho đường thẳng a. Tâm I của tất cả các đường tròn có bán kính 5cm và
tiếp xúc với đường thẳng a nằm trên đường nào ?
2.51 Cho điểm A cách đường thẳng xy là 12cm. Vẽ đường tròn (A ; 13cm).
a) Chứng minh đường tròn (A) có hai giao điểm với đường thẳng xy.
b) Gọi hai giao điểm nói trên là B và C. Tính độ dài BC.
1.
Cho đư
ờng tr
òn (O ; R),
đư
ờng thẳng cách O một khoảng d.
d > R
a và (O) không có điểm chung
d = R
a và (O) tiếp xúc nhau (có một điểm chung)
d < R
a và (O) cắt nhau (có hai điểm chung)
2. Tiếp tuyến của đường tròn là đường thẳng cí điểm chung duy nhất với
đường tròn (điểm chung đó gọi là tiếp điểm)
a. Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó
vuông góc với bán kính đi qua tiếp điểm.
b. Nếu một đường thẳng đi qua một điểm của đường tròn và vuông
góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp
tuyến của đường tròn.
3. Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì:
a. Điểm đó cách đều hai tiếp điểm.
b. Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai
tiếp tuyến.
c. Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai
bán kính đi qua tiếp điểm.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 23
E - Biến đổi đơn giản căn thức bậc hai
1. Đưa thừa số ra ngoài dấu căn:
2
A B khi A 0
A B A B ( B 0 )
A B khi A 0
2. Đưa thừa số vào trong dấu căn:
Với A
0, ta có:
2
A B A B ( B 0 )
Với A < 0, ta có:
2
A B A B ( B 0 )
3. Khử mẫu của biểu thức dưới dấu căn:
2
A A.B A.B
B B B
với A.B
0, B
0
4. Trục căn thức ở mẫu:
Phân tích tử và mẫu thành nhân tử tồi rút gọn cho nhân tử chung chứa
căn thức (nếu có).
Trường hợp mẫu là biểu thức dạng tích các căn thức và các số:
A A C
( B 0;C 0 )
B.C
B C
Nếu mẫu là một biểu thức dạng tổng có chứa căn, nhân tử và mẫu với
biểu thức liên hợp của mẫu:
2
C C( A B )
A B
A B
với A
0 , A
B
2
C C( A B )
A B
A B
với A
0, B
0, A
B
2
1.53 Đưa nhân tử ra ngoài dấu căn:
1. a) 54 b) 108
c) 0,1
20000
d) 0,05 28800
2. a)
2
x7 với x>0 b)
4
y48
c)
3
x25 với x > 0 d)
2
y8 với y > 0
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 82
E - Vị trí tương đối của đường thẳng và đường tròn
Dấu hiệu nhận biết tiếp tuyến của đường tròn
Tính chất của hai tiếp tuyến cắt nhau
2.49 Trên mặt phẳng tọa độ cho điểm I(–3 ; 2). Nếu vẽ đường tròn tâm I bán
kính bằng 2 thì đường tròn đó có vị trí tương đối như thế nào đối với cac
trục tọa độ ?
2.50 Cho đường thẳng a. Tâm I của tất cả các đường tròn có bán kính 5cm và
tiếp xúc với đường thẳng a nằm trên đường nào ?
2.51 Cho điểm A cách đường thẳng xy là 12cm. Vẽ đường tròn (A ; 13cm).
a) Chứng minh đường tròn (A) có hai giao điểm với đường thẳng xy.
b) Gọi hai giao điểm nói trên là B và C. Tính độ dài BC.
1.
Cho đư
ờng tr
òn (O ; R),
đư
ờng thẳng cách O một khoảng d.
d > R
a và (O) không có điểm chung
d = R
a và (O) tiếp xúc nhau (có một điểm chung)
d < R
a và (O) cắt nhau (có hai điểm chung)
2. Tiếp tuyến của đường tròn là đường thẳng cí điểm chung duy nhất với
đường tròn (điểm chung đó gọi là tiếp điểm)
a. Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó
vuông góc với bán kính đi qua tiếp điểm.
b. Nếu một đường thẳng đi qua một điểm của đường tròn và vuông
góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp
tuyến của đường tròn.
3. Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì:
a. Điểm đó cách đều hai tiếp điểm.
b. Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai
tiếp tuyến.
c. Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai
bán kính đi qua tiếp điểm.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 23
E - Biến đổi đơn giản căn thức bậc hai
1. Đưa thừa số ra ngoài dấu căn:
2
A B khi A 0
A B A B ( B 0 )
A B khi A 0
2. Đưa thừa số vào trong dấu căn:
Với A
0, ta có:
2
A B A B ( B 0 )
Với A < 0, ta có:
2
A B A B ( B 0 )
3. Khử mẫu của biểu thức dưới dấu căn:
2
A A.B A.B
B B B
với A.B
0, B
0
4. Trục căn thức ở mẫu:
Phân tích tử và mẫu thành nhân tử tồi rút gọn cho nhân tử chung chứa
căn thức (nếu có).
Trường hợp mẫu là biểu thức dạng tích các căn thức và các số:
A A C
( B 0;C 0 )
B.C
B C
Nếu mẫu là một biểu thức dạng tổng có chứa căn, nhân tử và mẫu với
biểu thức liên hợp của mẫu:
2
C C( A B )
A B
A B
với A
0 , A
B
2
C C( A B )
A B
A B
với A
0, B
0, A
B
2
1.53 Đưa nhân tử ra ngoài dấu căn:
1. a) 54 b) 108
c) 0,1
20000
d) 0,05 28800
2. a)
2
x7 với x>0 b)
4
y48
c)
3
x25 với x > 0 d)
2
y8 với y > 0
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 24
1.54 Đưa nhân tử vào trong dấu căn:
1. a) 53 b) 25
c) 22 d) 23
2. a) xy
3
2
b) 5x với x 0
c) 13x với x < 0 d)
x
2
x với x > 0
1.55 So sánh hai số sau (không dùng máy tính):
a) 33 và 12 b) 20 và 53
c) 54
3
1
và 150
5
1
d) 6
2
1
và
2
1
6
e)
2573
5
và
13
3
f) 2829vaø2930
g)
2012 2014
và
2 2013
h)
2014 2013
và
2013 2012
1.56 Sắp xếp theo thứ tự tăng dần:
a)
2 5
, 62 , 29 , 53 b)
3 6
,
3 3
,
4 7
, 142
1.57 Rút gọn các biểu thức sau:
1. a) 3004875 b) 8507298 ,
c) a49a16a9 (a 0) d)
b b b
160 2 40 3 90
(b0)
2. a) 5032218423 b) 108752274485
c) 454803202125 d) 1121753632282
3. a) 603532 )( b) 25055225 )(
c) 212771228 )( d) 22311111899 )(
4. a)
2 40 12 2 75 3 5 48
b)
2 80 3 2 5 3 3 20 3
5. a) ))(( xx1x1 b) ))(( 4x2x2x
c) ))(( xyyxyx d) ))(( yxyxyx
2
6. a) ))(( x2xx2x4 b) ))(( y2x3yx2
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 81
D - Các công thức về tam giác vuông cân
tam giác đều và nửa tam giác đều
2.46 Tính bán kính đường tròn ngoại tiếp:
a) Tam giác vuông cân có cạnh góc vuông bằng a.
b) Tam giác đều cạnh bằng a.
2.47 Cho đường tròn (O ; R) có hai bán kính OA, OB với góc AÔB = 120
0
.
Đường cao OI của AOB cắt (O) tại C.
a) Chứng tỏ tứ giác OACB là hình thoi.
b) Kẻ đường kính CD của (O). Chứng tỏ ABD đều.
2.48 Cho đường tròn (O ; R) có hai bán kính OA, OB vuông góc với nhau. Tia
phân giác của AÔB cắt (O) ở C. Lấy điểm bất kì trên cung BC và hạ
đường vuông góc DH xuống OA, đường này cắt OC ở E.
a) Tính theo R khoảng cách từ C đến OA.
b) Chứng minh: HD
2
+ HE
2
không đổi khi D thay đổi.
1.
Tam giác vuông cân
:
Cho
ABC vuông cân tại A:
BC = AB.
2
= a.
2
BC
AB AC
2
2. Tam giác đều:
Cho
ABC đều cạnh a, chiều cao h, diện tích S.
a 3
h
2
;
2h 3
a
3
;
2
a 3
S
4
3. Nửa tam giác đều:
ABC: Â = 90
0
,
B
= 60
0
,
C
= 30
0
AB =
BC
2
; AC =
BC 3
2
;
AC = AB.
3
;
2
BC 3
S
8
A
B
C
H
a
h
C
B
A
a
h
B
A
a
C
a
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 24
1.54 Đưa nhân tử vào trong dấu căn:
1. a) 53 b) 25
c) 22 d) 23
2. a) xy
3
2
b) 5x với x 0
c) 13x với x < 0 d)
x
2
x với x > 0
1.55 So sánh hai số sau (không dùng máy tính):
a) 33 và 12 b) 20 và 53
c) 54
3
1
và 150
5
1
d) 6
2
1
và
2
1
6
e)
2573
5
và
13
3
f) 2829vaø2930
g)
2012 2014
và
2 2013
h)
2014 2013
và
2013 2012
1.56 Sắp xếp theo thứ tự tăng dần:
a)
2 5
, 62 , 29 , 53 b)
3 6
,
3 3
,
4 7
, 142
1.57 Rút gọn các biểu thức sau:
1. a) 3004875 b) 8507298 ,
c) a49a16a9 (a 0) d)
b b b
160 2 40 3 90
(b0)
2. a) 5032218423 b) 108752274485
c) 454803202125 d) 1121753632282
3. a) 603532 )( b) 25055225 )(
c) 212771228 )( d) 22311111899 )(
4. a)
2 40 12 2 75 3 5 48
b)
2 80 3 2 5 3 3 20 3
5. a) ))(( xx1x1 b) ))(( 4x2x2x
c) ))(( xyyxyx d) ))(( yxyxyx
2
6. a) ))(( x2xx2x4 b) ))(( y2x3yx2
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 81
D - Các công thức về tam giác vuông cân
tam giác đều và nửa tam giác đều
2.46 Tính bán kính đường tròn ngoại tiếp:
a) Tam giác vuông cân có cạnh góc vuông bằng a.
b) Tam giác đều cạnh bằng a.
2.47 Cho đường tròn (O ; R) có hai bán kính OA, OB với góc AÔB = 120
0
.
Đường cao OI của AOB cắt (O) tại C.
a) Chứng tỏ tứ giác OACB là hình thoi.
b) Kẻ đường kính CD của (O). Chứng tỏ ABD đều.
2.48 Cho đường tròn (O ; R) có hai bán kính OA, OB vuông góc với nhau. Tia
phân giác của AÔB cắt (O) ở C. Lấy điểm bất kì trên cung BC và hạ
đường vuông góc DH xuống OA, đường này cắt OC ở E.
a) Tính theo R khoảng cách từ C đến OA.
b) Chứng minh: HD
2
+ HE
2
không đổi khi D thay đổi.
1.
Tam giác vuông cân
:
Cho
ABC vuông cân tại A:
BC = AB.
2
= a.
2
BC
AB AC
2
2. Tam giác đều:
Cho
ABC đều cạnh a, chiều cao h, diện tích S.
a 3
h
2
;
2h 3
a
3
;
2
a 3
S
4
3. Nửa tam giác đều:
ABC: Â = 90
0
,
B
= 60
0
,
C
= 30
0
AB =
BC
2
; AC =
BC 3
2
;
AC = AB.
3
;
2
BC 3
S
8
A
B
C
H
a
h
C
B
A
a
h
B
A
a
C
a
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 80
a) Chứng minh:
AMBN
1
S AB. MN
2
b) Định vị trí của MN để diện tích tứ giác AMBN lớn nhất.
2.43 Cho đường tròn (O) và dây BC cố định. Điểm A di chuyển trên cung lớn
BC. Gọi M là trung điểm của AC và H là hình chiếu của M trên AB. Kẻ
CD BC. Chứng minh:
a) B, O, D thẳng hàng. b) MH luôn đi qua một điểm cố định.
2.44 Cho hình vuông ABCD cạnh a, O là giao điểm của hai đường chéo. Gọi
M là trung điểm của OB, N là trung điểm của CD.
a) Xác định tâm và bán kính đường tròn ngoại tiếp ABN.
b) Gọi K là tâm đường tròn ngoại tiếp AON và E là trung điểm của ON.
Chứng minh: KIE và AND đồng dạng.
c) Tính bán kính đường tròn ngoại tiếp AON.
d) Chứng minh
AMN
= 90
0
và AN > MD.
2.45 Cho đường tròn (O) và hai điểm A, B nằm bên trong đường tròn và không
cùng thuộc một đường kính. Dựng hai dây song song và bằng nhau sao
cho điểm A nằm trên một dây, điểm B nằm trên dây còn lại.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 25
7. a)
22
x21x5
1
x
2
2
)(
với x > 0,5
b)
2
yx3
yx
2
2
22
)(
với x, y > 0 và x y
1.58 Rút gọn các biểu thức sau:
a)
1 1
5 20 5
5 2
b)
1
4,5 12,5
2
c)
20 45 3 18 72
d)
20 45 3 18 72
e)
2
6 5 120
f)
1 2
72 5 4,5 2 2 27
3 3
g)
28 2 3 7 7 84
h)
1 1
48 2 75 54 5 1
2 3
1.59 Rút gọn các biểu thức sau (biết a > 0, b > 0):
a) a92ab362a253a5
23
b) ba81b5ab9ab2ba123ab64
3333
c)
3
a300
5
2
a2
5,13
aa75a32
1.60 Thực hiện các phép tính sau:
1. a)
3424
64213
b)
21217
223
c)
3363
31269
d)
25
245
e)
2353
25
f)
526
343
2. a)
2
32
A
b)
2
356
B
c)
230
158
C
3. a)
452
525
13
515
b)
13
13
13
13
c)
230
275
4818
1282
d)
132
33
132
33
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 80
a) Chứng minh:
AMBN
1
S AB. MN
2
b) Định vị trí của MN để diện tích tứ giác AMBN lớn nhất.
2.43 Cho đường tròn (O) và dây BC cố định. Điểm A di chuyển trên cung lớn
BC. Gọi M là trung điểm của AC và H là hình chiếu của M trên AB. Kẻ
CD BC. Chứng minh:
a) B, O, D thẳng hàng. b) MH luôn đi qua một điểm cố định.
2.44 Cho hình vuông ABCD cạnh a, O là giao điểm của hai đường chéo. Gọi
M là trung điểm của OB, N là trung điểm của CD.
a) Xác định tâm và bán kính đường tròn ngoại tiếp ABN.
b) Gọi K là tâm đường tròn ngoại tiếp AON và E là trung điểm của ON.
Chứng minh: KIE và AND đồng dạng.
c) Tính bán kính đường tròn ngoại tiếp AON.
d) Chứng minh
AMN
= 90
0
và AN > MD.
2.45 Cho đường tròn (O) và hai điểm A, B nằm bên trong đường tròn và không
cùng thuộc một đường kính. Dựng hai dây song song và bằng nhau sao
cho điểm A nằm trên một dây, điểm B nằm trên dây còn lại.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 25
7. a)
22
x21x5
1
x
2
2
)(
với x > 0,5
b)
2
yx3
yx
2
2
22
)(
với x, y > 0 và x y
1.58 Rút gọn các biểu thức sau:
a)
1 1
5 20 5
5 2
b)
1
4,5 12,5
2
c)
20 45 3 18 72
d)
20 45 3 18 72
e)
2
6 5 120
f)
1 2
72 5 4,5 2 2 27
3 3
g)
28 2 3 7 7 84
h)
1 1
48 2 75 54 5 1
2 3
1.59 Rút gọn các biểu thức sau (biết a > 0, b > 0):
a) a92ab362a253a5
23
b) ba81b5ab9ab2ba123ab64
3333
c)
3
a300
5
2
a2
5,13
aa75a32
1.60 Thực hiện các phép tính sau:
1. a)
3424
64213
b)
21217
223
c)
3363
31269
d)
25
245
e)
2353
25
f)
526
343
2. a)
2
32
A
b)
2
356
B
c)
230
158
C
3. a)
452
525
13
515
b)
13
13
13
13
c)
230
275
4818
1282
d)
132
33
132
33
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 26
e)
13
2
13
2
f)
113
3
113
3
g)
32
61
12
122
13
432
h)
)()( 235212
5
235212
5
4. a)
71032
6
7411
1
b)
8410
1
608
1
14012
1
c)
21210
4
1027
3
57
2
23
1
1.61 Chứng minh các số sau đây là số nguyên:
a)
16
66
23
2233
A
b)
116
63
12
26
4
16
15
B
c) 32
13
22323232
C
1.62 Chứng minh các số sau đây là số dương:
a)
2 3 2 3
A
2 2 3 2 2 3
b)
23 2 3 2
B
2 14 5 3 2 14 5 3
1.63 Chứng tỏ rằng các số sau là số hữu tỉ:
a)
2 2
7 5 7 5
b)
7 5 7 5
7 5 7 5
1.64 Các số sau đây có căn bậc hai không ?
a)
3 1 3 1
A 1 : 2
2 2
2 2 2 2
1 1
3 3
C
2 2 2 2
1 1
3 3
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 79
2.34 Cho đường tròn (O), hai dây AB và CD (AB = CD) cắt nhau tại I nằm bên
trong đường tròn. Chứng minh:
a) OI là tia phân giác của một trong hai góc tạo bởi hai dây AB và CD.
b) I chia AB, CD thành các đoạn thẳng bằng nhau từng đôi một.
2.35 Cho đường tròn (O), dây AB bất kỳ không đi qua tâm. Trên cung nhỏ AB
lấy hai điểm phân biệt C, D sao cho D nằm trên cung nhỏ AC và
AD = BC. Chứng minh: CD // AB.
2.36 Cho đường tròn (O; 5cm), hai dây AB, CD (AB // CD), biết AB = 8cm,
CD = 6cm. Tính khoảng cách giữa hai dây.
2.37 Cho đường tròn (O) và điểm I nằm bên trong đường tròn. Vẽ dây
AB OI tại I. Chứng minh rằng AB là dây cung ngắn hơn mọi dây cung
khác đi qua I.
2.38 Cho ABC nội tiếp trong đường tròn (O) có
A B C
. Gọi OH, OI, OK
lần lượt là khoảng cách từ O đến BC, AC và AB. So sánh các độ dài OH,
OI, OK.
2.39 Cho đường tròn (O), các bán kính OA, OB. Trên cung nhỏ AB lấy các
điểm M và N sao cho AM = BN. Gọi C là giao điểm của các đường thẳng
AM và BN. Chứng minh rằng:
a) OC là tia phân giác của
AOB
. b) OC AB.
2.40 Cho (O; R) và một điểm A cố định với OA = R/2. Một dây cung MN
quay quanh A.
a) Chứng minh: trung điểm của MN thuộc một đường tròn cố định.
b) Xác định vị trí của MN để độ dài MN ngắn nhất ? Dài nhất ? Tính độ
dài ngắn nhất, dài nhất đó của MN.
2.41 Cho ABC vuông tại A, M là điểm di động trên cạnh huyền BC. Gọi (O)
là đường tròn đường kính AM.
a) Chứng minh: (O) luôn đi qua hai điểm cố định.
b) (O) cắt AB, AC lần lượt tại E và F. Định vị trí của M sao cho độ dài
EF nhỏ nhất.
2.42 Cho đường tròn (O) và dây AB cố định. M và N là hai điểm di động lần
lượt trên cung lớn và cung nhỏ AB.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 26
e)
13
2
13
2
f)
113
3
113
3
g)
32
61
12
122
13
432
h)
)()( 235212
5
235212
5
4. a)
71032
6
7411
1
b)
8410
1
608
1
14012
1
c)
21210
4
1027
3
57
2
23
1
1.61 Chứng minh các số sau đây là số nguyên:
a)
16
66
23
2233
A
b)
116
63
12
26
4
16
15
B
c) 32
13
22323232
C
1.62 Chứng minh các số sau đây là số dương:
a)
2 3 2 3
A
2 2 3 2 2 3
b)
23 2 3 2
B
2 14 5 3 2 14 5 3
1.63 Chứng tỏ rằng các số sau là số hữu tỉ:
a)
2 2
7 5 7 5
b)
7 5 7 5
7 5 7 5
1.64 Các số sau đây có căn bậc hai không ?
a)
3 1 3 1
A 1 : 2
2 2
2 2 2 2
1 1
3 3
C
2 2 2 2
1 1
3 3
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 79
2.34 Cho đường tròn (O), hai dây AB và CD (AB = CD) cắt nhau tại I nằm bên
trong đường tròn. Chứng minh:
a) OI là tia phân giác của một trong hai góc tạo bởi hai dây AB và CD.
b) I chia AB, CD thành các đoạn thẳng bằng nhau từng đôi một.
2.35 Cho đường tròn (O), dây AB bất kỳ không đi qua tâm. Trên cung nhỏ AB
lấy hai điểm phân biệt C, D sao cho D nằm trên cung nhỏ AC và
AD = BC. Chứng minh: CD // AB.
2.36 Cho đường tròn (O; 5cm), hai dây AB, CD (AB // CD), biết AB = 8cm,
CD = 6cm. Tính khoảng cách giữa hai dây.
2.37 Cho đường tròn (O) và điểm I nằm bên trong đường tròn. Vẽ dây
AB OI tại I. Chứng minh rằng AB là dây cung ngắn hơn mọi dây cung
khác đi qua I.
2.38 Cho ABC nội tiếp trong đường tròn (O) có
A B C
. Gọi OH, OI, OK
lần lượt là khoảng cách từ O đến BC, AC và AB. So sánh các độ dài OH,
OI, OK.
2.39 Cho đường tròn (O), các bán kính OA, OB. Trên cung nhỏ AB lấy các
điểm M và N sao cho AM = BN. Gọi C là giao điểm của các đường thẳng
AM và BN. Chứng minh rằng:
a) OC là tia phân giác của
AOB
. b) OC AB.
2.40 Cho (O; R) và một điểm A cố định với OA = R/2. Một dây cung MN
quay quanh A.
a) Chứng minh: trung điểm của MN thuộc một đường tròn cố định.
b) Xác định vị trí của MN để độ dài MN ngắn nhất ? Dài nhất ? Tính độ
dài ngắn nhất, dài nhất đó của MN.
2.41 Cho ABC vuông tại A, M là điểm di động trên cạnh huyền BC. Gọi (O)
là đường tròn đường kính AM.
a) Chứng minh: (O) luôn đi qua hai điểm cố định.
b) (O) cắt AB, AC lần lượt tại E và F. Định vị trí của M sao cho độ dài
EF nhỏ nhất.
2.42 Cho đường tròn (O) và dây AB cố định. M và N là hai điểm di động lần
lượt trên cung lớn và cung nhỏ AB.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 78
C - Liên hệ giữa dây và khoảng cách từ tâm đến dây
2.27 Cho đường tròn tâm O bán kính 5cm, dây AB = 8cm.
a) Tính khoảng cách từ tâm O đến dây AB.
b) Gọi I là điểm thuộc dây AB sao cho AI = 1cm. Kẻ dây CD đi qua I và
vuông góc với AB. Chứng minh CD = AB.
2.28 Cho đường tròn tâm O bán kính 25cm, dây AB = 40cm. Vẽ dây CD song
song với AB và có khoảng cách đến AB bằng 22cm. Tính độ dài dây CD.
2.29 Cho đường tròn (O), điểm A nằm bên trong đường tròn. Vẽ dây BC OA
tại A. Vẽ dây EF bất kỳ đi qua A và không vuông góc với OA. So sánh
BC và EF .
2.30 Cho đường tròn tâm O có các dây cung AB và CD bằng nhau và vuông
góc với nhau tại I. Biết IC = 2cm, ID = 14cm. Tính khoảng cách từ O đến
mỗi dây.
2.31 Cho (O) có các dây cung AB và CD bằng nhau, các tia AB và CD cắt
nhau tại E nằm nên ngoài đường tròn. Gọi H và K lần lượt là trung điểm
của của AB và CD. Chứng minh:
a) EH = EK b) EA = EC.
2.32 Cho đường tròn (O), dây AB và CD (AB < CD) cắt nhau tại K nằm bên
ngoài đường tròn. Đường tròn (O ; OK) cắ KA và BC lần lượt tạo M và
N. So sánh KM và KN.
2.33 Cho đường tròn (O), dây AB và CD (AB > CD) cắt nhau tại M. Gọi H và
K lần lượt là trung điểm của AB và CD. So sánh MH và MK (Chú ý: xét 2
trường hợp của điểm M).
1.
Trong m
ột đ
ư
ờng tr
òn:
a. Hai dây bằng nhau thì cách đều tâm.
b. Hai dây cách đều tâm thì bằng nhau.
2. Trong hai dây của một đường tròn:
a. Dây nào lớn hơn thì dây đó gần tâm hơn.
b. Dây nào gần tâm hơn thì dây đó lớn hơn.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 27
b)
25
1
5
5
31
26
B
:
c)
2 2 2 5 1
C
3 12
3 3 6
1.65 Tìm x biết:
a) 35x25 b) 12x3
c) 162x4 d) 10x2
1.66 Giải các phương trình sau:
1. a)
2 3x 4 3x 27 3 3x
b)
3 2x 5 8x 7 18x 28
2. a)
2
b)
2
x 4 2 x 2 0
1.67 Khử mẫu của các biểu thức dưới dấu căn (giả thiết rằng các biểu thức đã
cho có nghĩa):
a)
600
1
;
540
11
;
50
3
;
98
5
;
27
31
2
)(
b)
b
a
ab ;
a
b
b
a
;
2
b
1
b
1
;
b36
a9
3
;
xy
2
xy3
c)
3
2
;
5
x
2
;
x
3
;
7
x
x
2
2
;
xy
2
xy3
1.68 Trục căn thức ở mẫu của các biểu thức sau (giả thiết rằng các biểu thức đã
cho có nghĩa):
a)
10
5
;
33
1
;
52
5
;
25
222
;
yb
yby
b)
13
3
;
13
2
;
32
32
;
b3
b
;
1p2
p
c)
13
3
;
710
3
;
yx
1
;
ba
ab
2
.
d)
2
35
;
325
26
;
104
5102
;
2263
329
.
e)
123
1
;
235
1
.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 78
C - Liên hệ giữa dây và khoảng cách từ tâm đến dây
2.27 Cho đường tròn tâm O bán kính 5cm, dây AB = 8cm.
a) Tính khoảng cách từ tâm O đến dây AB.
b) Gọi I là điểm thuộc dây AB sao cho AI = 1cm. Kẻ dây CD đi qua I và
vuông góc với AB. Chứng minh CD = AB.
2.28 Cho đường tròn tâm O bán kính 25cm, dây AB = 40cm. Vẽ dây CD song
song với AB và có khoảng cách đến AB bằng 22cm. Tính độ dài dây CD.
2.29 Cho đường tròn (O), điểm A nằm bên trong đường tròn. Vẽ dây BC OA
tại A. Vẽ dây EF bất kỳ đi qua A và không vuông góc với OA. So sánh
BC và EF .
2.30 Cho đường tròn tâm O có các dây cung AB và CD bằng nhau và vuông
góc với nhau tại I. Biết IC = 2cm, ID = 14cm. Tính khoảng cách từ O đến
mỗi dây.
2.31 Cho (O) có các dây cung AB và CD bằng nhau, các tia AB và CD cắt
nhau tại E nằm nên ngoài đường tròn. Gọi H và K lần lượt là trung điểm
của của AB và CD. Chứng minh:
a) EH = EK b) EA = EC.
2.32 Cho đường tròn (O), dây AB và CD (AB < CD) cắt nhau tại K nằm bên
ngoài đường tròn. Đường tròn (O ; OK) cắ KA và BC lần lượt tạo M và
N. So sánh KM và KN.
2.33 Cho đường tròn (O), dây AB và CD (AB > CD) cắt nhau tại M. Gọi H và
K lần lượt là trung điểm của AB và CD. So sánh MH và MK (Chú ý: xét 2
trường hợp của điểm M).
1.
Trong m
ột đ
ư
ờng tr
òn:
a. Hai dây bằng nhau thì cách đều tâm.
b. Hai dây cách đều tâm thì bằng nhau.
2. Trong hai dây của một đường tròn:
a. Dây nào lớn hơn thì dây đó gần tâm hơn.
b. Dây nào gần tâm hơn thì dây đó lớn hơn.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 27
b)
25
1
5
5
31
26
B
:
c)
2 2 2 5 1
C
3 12
3 3 6
1.65 Tìm x biết:
a) 35x25 b) 12x3
c) 162x4 d) 10x2
1.66 Giải các phương trình sau:
1. a)
2 3x 4 3x 27 3 3x
b)
3 2x 5 8x 7 18x 28
2. a)
2
x 9 3 x 3 0
b)
2
x 4 2 x 2 0
1.67 Khử mẫu của các biểu thức dưới dấu căn (giả thiết rằng các biểu thức đã
cho có nghĩa):
a)
600
1
;
540
11
;
50
3
;
98
5
;
27
31
2
)(
b)
b
a
ab ;
a
b
b
a
;
2
b
1
b
1
;
b36
a9
3
;
xy
2
xy3
c)
3
2
;
5
x
2
;
x
3
;
7
x
x
2
2
;
xy
2
xy3
1.68 Trục căn thức ở mẫu của các biểu thức sau (giả thiết rằng các biểu thức đã
cho có nghĩa):
a)
10
5
;
33
1
;
52
5
;
25
222
;
yb
yby
b)
13
3
;
13
2
;
32
32
;
b3
b
;
1p2
p
c)
13
3
;
710
3
;
yx
1
;
ba
ab
2
.
d)
2
35
;
325
26
;
104
5102
;
2263
329
.
e)
123
1
;
235
1
.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 28
1.69 Phân tích thành nhân tử:
a) 1aabab b)
2233
xyyxyx
1.70 Giải phương trình:
a) 213x2 b) 351x c) 322x3
1.71 Giải các bất phương trình sau và biểu diễn nghiệm trên trục số:
a) 32x b) 32x
1.72 Với n là số tự nhiên, chứng minh:
n1n
1
n1n
Áp dụng tính:
34
1
23
1
12
1
1.73 Cho các biểu thức :
2524
1
43
1
32
1
21
1
A
;
24
1
3
1
2
1
1
1
B
a) Tính giá trị của A. b) Chứng minh rằng B > 8.
1.74 Rút gọn các biểu thức sau:
a)
n1n
1
43
1
32
1
21
1
A
b)
2524
1
43
1
32
1
21
1
B
Đ
ừng lo lắng về khó khăn của bạn trong toán học, tôi
đ
ảm bảo với bạn rằng những khó khăn toán học của tôi
còn gấp bội.
Do not worry about your difficulties in Mathematics.
I can assure you mine are still greater.
Albert Einstein
Danh ngôn học tập
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 77
b) Cho nửa đường tròn tâm O, đường kính AB. Trên AB lấy các điểm M,
N sao cho AM = BN. Qua M và N kẻ các đường thẳng song song với
nhau, chúng cắt nửa đường tròn lần lượt tại C và D.
Chứng minh: MC CD và ND CD.
2.25 Cho đường tròn (O ; R) và điểm M nằm bên trong đường tròn.
a) Hãy nêu cách dựng AB nhận M làm trung điểm.
b) Tính AB, biết R = 5cm, OM = 1,4cm.
2.26 Cho đường tròn (O), điểm A nằm bên trong đường tròn, điểm B nằm bên
ngoài đường tròn sao cho trung điểm I của AB nằm bên trong đường
tròn.Vẽ dây CD OI tại I. Tứ giác ACBD là hình gì ? Vì sao ?
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 28
1.69 Phân tích thành nhân tử:
a) 1aabab b)
2233
xyyxyx
1.70 Giải phương trình:
a) 213x2 b) 351x c) 322x3
1.71 Giải các bất phương trình sau và biểu diễn nghiệm trên trục số:
a) 32x b) 32x
1.72 Với n là số tự nhiên, chứng minh:
n1n
1
n1n
Áp dụng tính:
34
1
23
1
12
1
1.73 Cho các biểu thức :
2524
1
43
1
32
1
21
1
A
;
24
1
3
1
2
1
1
1
B
a) Tính giá trị của A. b) Chứng minh rằng B > 8.
1.74 Rút gọn các biểu thức sau:
a)
n1n
1
43
1
32
1
21
1
A
b)
2524
1
43
1
32
1
21
1
B
Đ
ừng lo lắng về khó khăn của bạn trong toán học, tôi
đ
ảm bảo với bạn rằng những khó khăn toán học của tôi
còn gấp bội.
Do not worry about your difficulties in Mathematics.
I can assure you mine are still greater.
Albert Einstein
Danh ngôn học tập
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 77
b) Cho nửa đường tròn tâm O, đường kính AB. Trên AB lấy các điểm M,
N sao cho AM = BN. Qua M và N kẻ các đường thẳng song song với
nhau, chúng cắt nửa đường tròn lần lượt tại C và D.
Chứng minh: MC CD và ND CD.
2.25 Cho đường tròn (O ; R) và điểm M nằm bên trong đường tròn.
a) Hãy nêu cách dựng AB nhận M làm trung điểm.
b) Tính AB, biết R = 5cm, OM = 1,4cm.
2.26 Cho đường tròn (O), điểm A nằm bên trong đường tròn, điểm B nằm bên
ngoài đường tròn sao cho trung điểm I của AB nằm bên trong đường
tròn.Vẽ dây CD OI tại I. Tứ giác ACBD là hình gì ? Vì sao ?
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 76
B - Đường kính và dây cung của đường tròn
2.19 Cho đường tròn (O) có bán kính OA = 3cm. Dây BC của đường tròn
vuông góc với OA tại trung điểm của OA. Tính BC.
2.20 Cho ABC, các đường cao BD và CE. Chứng minh:
a) Bốn điểm B, E, D và C cùng nằm trên một đường tròn.
b) DE < BC.
2.21 a) Cho đường tròn (O) đường kính AB, dây CD không cắt đường kính
AB. Gọi H và K lần lượt là hình chiếu của A và B trên CD. Chứng
minh: CH = DK.
b) Cho đường tròn (O) đường kính AB, dây CD cắt đường kính AB tại I.
Gọi H và K lần lượt là hình chiếu của A và B trên CD. Chứng minh:
CH = DK.
2.22 Tứ giác ABCD có
0
B D 90
.
a) Chứng minh: bốn điểm A, B, C, D cùng nằm trên một đường tròn.
b) So sánh AC và BD. Nếu AB = CD thì tứ giác ABCD là hình gì ?
2.23 Cho đường tròn (O) có đường kính AD = 2R. Vẽ cung tròn tâm D bán
kính R, cung này cắt đường tròn (O) ở B và C.
a) Tứ giác OBDC là hình gì ? Vì sao ?
b) Tính các góc CBD, CBO, OBA.
c) Chứng minh: ABC đều.
2.24 a) Cho nửa đường tròn tâm O, đường kính AB, dây CD. Các đường
vuông góc với CD tại C và D tương ứng cắt AB ở M và N.
Chứng minh: AM = BN.
1.
Trong các dây c
ủa một đ
ư
ờng tr
òn, dây l
ớn nhất l
à đư
ờng kính. Từ đó
suy ra nếu AB là một dây cung bất kì của (O ; R) thì AB
2R.
2. a. Trong một đường tròn, đường kính vuông góc với một dây thì đi
qua trung điểm của dây ấy.
b. Trong một đường tròn, đường kính đi qua trung điểm của một dây
không đi qua tâm thì vuông góc với dây ấy.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 29
F - Rút gọn biểu thức có chứa căn thức bậc hai
Cho x
0, y
0. Ta có các công thức biến đổi sau:
1.
2
x ( x )
;
3
x x ( x )
2.
x x x( x 1)
3.
x y y x xy( x y )
4.
x y ( x y )( x y )
5.
2
x 2 xy y ( x y )
6.
3 3
x x y y ( x ) ( y ) ( x y )( x xy y )
1.75 Chứng minh các đẳng thức sau:
a) 1xx
1x
1x
3
với x > 0, x 1
b)
yx
xy
yxxyyx
))((
với x, y > 0
1.76 Rút gọn:
a)
x 2 3x 3
A
x x 3 3
với x 0
b)
x x y y
B
x y
với x 0, y 0 và x y
c)
a b 2 ab a b
C
a b a b
(với a 0, b 0, a b)
d)
( a 1)(a ab)( a b)
D
(a b)(a a a)
(với a > 0, b 0, a b)
e)
2
a 1 1
E :
a a a a a a
(với a > 0)
f)
x y xy xy 1
F :
x y
x y x y
(với x 0, y 0, x y)
g)
x y x y
G
xy y xy x xy
(với xy 0, x y)
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 76
B - Đường kính và dây cung của đường tròn
2.19 Cho đường tròn (O) có bán kính OA = 3cm. Dây BC của đường tròn
vuông góc với OA tại trung điểm của OA. Tính BC.
2.20 Cho ABC, các đường cao BD và CE. Chứng minh:
a) Bốn điểm B, E, D và C cùng nằm trên một đường tròn.
b) DE < BC.
2.21 a) Cho đường tròn (O) đường kính AB, dây CD không cắt đường kính
AB. Gọi H và K lần lượt là hình chiếu của A và B trên CD. Chứng
minh: CH = DK.
b) Cho đường tròn (O) đường kính AB, dây CD cắt đường kính AB tại I.
Gọi H và K lần lượt là hình chiếu của A và B trên CD. Chứng minh:
CH = DK.
2.22 Tứ giác ABCD có
0
B D 90
.
a) Chứng minh: bốn điểm A, B, C, D cùng nằm trên một đường tròn.
b) So sánh AC và BD. Nếu AB = CD thì tứ giác ABCD là hình gì ?
2.23 Cho đường tròn (O) có đường kính AD = 2R. Vẽ cung tròn tâm D bán
kính R, cung này cắt đường tròn (O) ở B và C.
a) Tứ giác OBDC là hình gì ? Vì sao ?
b) Tính các góc CBD, CBO, OBA.
c) Chứng minh: ABC đều.
2.24 a) Cho nửa đường tròn tâm O, đường kính AB, dây CD. Các đường
vuông góc với CD tại C và D tương ứng cắt AB ở M và N.
Chứng minh: AM = BN.
1.
Trong các dây c
ủa một đ
ư
ờng tr
òn, dây l
ớn nhất l
à đư
ờng kính. Từ đó
suy ra nếu AB là một dây cung bất kì của (O ; R) thì AB
2R.
2. a. Trong một đường tròn, đường kính vuông góc với một dây thì đi
qua trung điểm của dây ấy.
b. Trong một đường tròn, đường kính đi qua trung điểm của một dây
không đi qua tâm thì vuông góc với dây ấy.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 29
F - Rút gọn biểu thức có chứa căn thức bậc hai
Cho x
0, y
0. Ta có các công thức biến đổi sau:
1.
2
x ( x )
;
3
x x ( x )
2.
x x x( x 1)
3.
x y y x xy( x y )
4.
x y ( x y )( x y )
5.
2
x 2 xy y ( x y )
6.
3 3
x x y y ( x ) ( y ) ( x y )( x xy y )
1.75 Chứng minh các đẳng thức sau:
a) 1xx
1x
1x
3
với x > 0, x 1
b)
yx
xy
yxxyyx
))((
với x, y > 0
1.76 Rút gọn:
a)
x 2 3x 3
A
x x 3 3
với x 0
b)
x x y y
B
x y
với x 0, y 0 và x y
c)
a b 2 ab a b
C
a b a b
(với a 0, b 0, a b)
d)
( a 1)(a ab)( a b)
D
(a b)(a a a)
(với a > 0, b 0, a b)
e)
2
a 1 1
E :
a a a a a a
(với a > 0)
f)
x y xy xy 1
F :
x y
x y x y
(với x 0, y 0, x y)
g)
x y x y
G
xy y xy x xy
(với xy 0, x y)
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 30
h)
3 3
a b a b
H
a b
a b
(với a 0, b 0, a b)
i)
2
( x y) 4 xy
x y
I
x y x y
(với x 0, y 0, x y)
j)
x 1 x 1 x 1
J : 1
x 1 x 1 x 1
(với x > 0, x 1)
k)
x 1 1 2
K :
x 1
x 1 x x 1 x
(với x > 0, x 1)
l)
a 2 a 2 1
L 1
a 1
a 2 a 1 a
(với a > 0, a 1)
m)
x 1 2 x 2 5 x
M
4 x
x 2 x 2
(với x 0, x 4)
n)
2
x x y y x y
N xy
x y
x y
(với x 0, y 0, x y)
o)
2
a b b a a a b b a b
O :
a b a b a b
(với a 0, b 0, a b)
p)
2x 1 x x x 1
P x
x x 1 x x 1 x 1
(với x 0, x 1)
q)
x y x y
x xy
Q :
1 xy
1 xy 1 xy
(với x > 0, y > 0, xy 1)
r)
2
x x y y x y y x
R : x y
x y x y
(với x 0, y 0, x y)
s)
x 1 x 1 x x 2x 4 x 8
S
x 4
x 4 x 4 x
(với x > 0, x 4)
t)
x x 2x 28 x 4 x 8
T
x 3 x 4 x 1 4 x
(với x 0, x 16
1.77 Cho 1xx29xx216
22
.
Tính
22
xx29xx216A
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 75
2.14 Cho ABC cân tại A, nội tiếp đường tròn (O). Đường cao AH cắt đường
tròn (O) ở D.
a) Chứng minh: AD là đường kính của đường tròn (O).
b) Tính
ACD
.
c) Cho BC = 24cm, AC = 20cm. Tính AH và bán kính của (O).
2.15 Cho ABC có đường cao AH. Từ một điểm M bất kỳ trên cạnh BC, kẻ
MD AB và ME AC. Chứng minh: năm điểm A, D, H, M và E cùng
nằm trên một đường tròn.
2.16 Cho ABC. Điểm I di động trên cạnh BC. Gọi D, E lần lượt là hình chiếu
của I trên AB và AC. Lấy M đối xứng với A qua D, lấy N đối xứng với A
qua E. Chứng minh:
a) I là tâm đường tròn đi qua ba điểm A, M, N.
b) Đường tròn (I) nói trên đi qua một điểm cố định khác A.
2.17 Cho ABC nhọn có ba đỉnh thuộc đường tròn (O ; R). Gọi H là trực tâm
của ABC. Vẽ đường kính AD.
a) Tứ giác BHCD là hình gì ? Vì sao ?
b) Gọi I là trung điểm của BC. Chứng minh: AH = 2OI.
c) Gọi G là trọng tâm của ABC. Chứng minh: O, H, G thẳng hàng.
d) So sánh diện tích của hai tam giác AHG và AOG.
2.18 Ba đường cao AD, BE, CF của ABC gặp nhau tại H. Gọi I, K, L lần lượt
là trung điểm của AB, BC, CA và M, N, P lần lượt là trung điểm của HA,
HB, HC. Chứng minh:
a) Các tứ giác INPL và MLKN là các hình chữ nhật.
b) 9 điểm D, E, F, L, I, K, M, N và P cùng nằm trên một đường tròn.
(đường tròn Euler)
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 30
h)
3 3
a b a b
H
a b
a b
(với a 0, b 0, a b)
i)
2
( x y) 4 xy
x y
I
x y x y
(với x 0, y 0, x y)
j)
x 1 x 1 x 1
J : 1
x 1 x 1 x 1
(với x > 0, x 1)
k)
x 1 1 2
K :
x 1
x 1 x x 1 x
(với x > 0, x 1)
l)
a 2 a 2 1
L 1
a 1
a 2 a 1 a
(với a > 0, a 1)
m)
x 1 2 x 2 5 x
M
4 x
x 2 x 2
(với x 0, x 4)
n)
2
x x y y x y
N xy
x y
x y
(với x 0, y 0, x y)
o)
2
a b b a a a b b a b
O :
a b a b a b
(với a 0, b 0, a b)
p)
2x 1 x x x 1
P x
x x 1 x x 1 x 1
(với x 0, x 1)
q)
x y x y
x xy
Q :
1 xy
1 xy 1 xy
(với x > 0, y > 0, xy 1)
r)
2
x x y y x y y x
R : x y
x y x y
(với x 0, y 0, x y)
s)
x 1 x 1 x x 2x 4 x 8
S
x 4
x 4 x 4 x
(với x > 0, x 4)
t)
x x 2x 28 x 4 x 8
T
x 3 x 4 x 1 4 x
(với x 0, x 16
1.77 Cho 1xx29xx216
22
.
Tính
22
xx29xx216A
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 75
2.14 Cho ABC cân tại A, nội tiếp đường tròn (O). Đường cao AH cắt đường
tròn (O) ở D.
a) Chứng minh: AD là đường kính của đường tròn (O).
b) Tính
ACD
.
c) Cho BC = 24cm, AC = 20cm. Tính AH và bán kính của (O).
2.15 Cho ABC có đường cao AH. Từ một điểm M bất kỳ trên cạnh BC, kẻ
MD AB và ME AC. Chứng minh: năm điểm A, D, H, M và E cùng
nằm trên một đường tròn.
2.16 Cho ABC. Điểm I di động trên cạnh BC. Gọi D, E lần lượt là hình chiếu
của I trên AB và AC. Lấy M đối xứng với A qua D, lấy N đối xứng với A
qua E. Chứng minh:
a) I là tâm đường tròn đi qua ba điểm A, M, N.
b) Đường tròn (I) nói trên đi qua một điểm cố định khác A.
2.17 Cho ABC nhọn có ba đỉnh thuộc đường tròn (O ; R). Gọi H là trực tâm
của ABC. Vẽ đường kính AD.
a) Tứ giác BHCD là hình gì ? Vì sao ?
b) Gọi I là trung điểm của BC. Chứng minh: AH = 2OI.
c) Gọi G là trọng tâm của ABC. Chứng minh: O, H, G thẳng hàng.
d) So sánh diện tích của hai tam giác AHG và AOG.
2.18 Ba đường cao AD, BE, CF của ABC gặp nhau tại H. Gọi I, K, L lần lượt
là trung điểm của AB, BC, CA và M, N, P lần lượt là trung điểm của HA,
HB, HC. Chứng minh:
a) Các tứ giác INPL và MLKN là các hình chữ nhật.
b) 9 điểm D, E, F, L, I, K, M, N và P cùng nằm trên một đường tròn.
(đường tròn Euler)
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 74
2.4 Chứng minh định lí sau:
a) Tâm của đường tròn ngoại tiếp
vuông là trung điểm của cạnh huyền.
b) Nếu một
có một cạnh là đường kính của đường tròn ngoại tiếp thì
đó là
vuông.
2.5 Cho hình vuông ABCD, O là giao điểm của hai đường chéo,
OA 2
cm. Vẽ đường tròn tâm A bán kính 2cm. Hãy xác định vị trí của
năm điểm A, B, C, D, O so với đường tròn
2.6 Cho ABC nhọn. Vẽ (O) có đường kính BC, nó cắt các cạnh AB, AC
theo thứ tự ở D và E.
a) Chứng minh: CD AB và BE AC.
b) Gọi K là giao điểm của BE và CD. Chứng minh: AK BC.
2.7 Cho tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi M, N, P,
Q lần lượt là trung điểm của AB, BC, CD và DA. C/m: bốn điểm M, N, P
và Q cùng nằm trên một đường tròn.
2.8 Cho ABC đều. Gọi M, N, P lần lượt là trung điểm của AB, BC, CA.
Chứng minh rằng bốn điểm B, C, P và M cùng nằm trên một đường tròn.
2.9 Cho ABC đều có độ dài cạnh là a (cm). Tính bán kính của đường tròn
ngoại tiếp ABC.
2.10 Cho (O ; 4cm) có hai đường kính AB và CD vuông góc với nhau. Dây
AM của (O) cắt bán kính OC tại I. Cho biết OI = 3cm. Tính AM và đường
cao MH của AMB.
2.11 Cho hình vuông ABCD cạnh a.
a) Chứng minh: bốn đỉnh A, B, C và D của hình vuông trên cùng nằm
trên một đường tròn.
b) Xác định tâm và bán kính của đường tròn đó.
2.12 Cho ABC cân tại A, BC = 12cm, đường cao AH = 4cm. Tính bán kính
của đường tròn ngoại tiếp ABC.
2.13 Cho ABC cân tại A, đường cao BE. Gọi D, F lần lượt là trung điểm của
BC và AB.
a) Chứng minh: 4 điểm A, B, D và E cùng nằm trên một đường tròn.
b) Chứng minh: C không thuộc đường tròn trên.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 31
1.78 Rút gọn các biểu thức sau:
a)
a
b
b
a
ab
b
a
với a > 0 và b > 0
b)
81
mx4mx8m4
xx21
m
2
2
với m > 0 và x > 1
1.79 Rút gọn rồi so sánh giá trị của biểu thức sau với 1:
1a2a
1a
:
1a
1
aa
1
M
với a > 0 và a 1
1.80 Giải các phương trình sau:
1. a) 645x9
3
4
x5320x4
b) 1x6
9
1x
2
15
25x25
c) 45x45x9
3
1
20x4
d) 1x164x49x916x16 .
2. a)
1xx1
2
b)
2x4x4x
2
c) x27x2
2
d) 2x3x4x
2
e)
0x24x
2
f)
1x24x4x
2
g) 1x)1x)(4x2( h)
2x1x4x2
2
.
3. a) x459x2 b)
1x1x2
c) 3x3x d) x3xx
2
e) 1x1x3x
2
f) 3x43x2
2
g) 3x6xx
2
h) 3x2x4x9
2
.
4. a) 54x4x
b) 21x2x1x2x
c) 12x67x2x42x
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 74
2.4 Chứng minh định lí sau:
a) Tâm của đường tròn ngoại tiếp
vuông là trung điểm của cạnh huyền.
b) Nếu một
có một cạnh là đường kính của đường tròn ngoại tiếp thì
đó là
vuông.
2.5 Cho hình vuông ABCD, O là giao điểm của hai đường chéo,
OA 2
cm. Vẽ đường tròn tâm A bán kính 2cm. Hãy xác định vị trí của
năm điểm A, B, C, D, O so với đường tròn
2.6 Cho ABC nhọn. Vẽ (O) có đường kính BC, nó cắt các cạnh AB, AC
theo thứ tự ở D và E.
a) Chứng minh: CD AB và BE AC.
b) Gọi K là giao điểm của BE và CD. Chứng minh: AK BC.
2.7 Cho tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi M, N, P,
Q lần lượt là trung điểm của AB, BC, CD và DA. C/m: bốn điểm M, N, P
và Q cùng nằm trên một đường tròn.
2.8 Cho ABC đều. Gọi M, N, P lần lượt là trung điểm của AB, BC, CA.
Chứng minh rằng bốn điểm B, C, P và M cùng nằm trên một đường tròn.
2.9 Cho ABC đều có độ dài cạnh là a (cm). Tính bán kính của đường tròn
ngoại tiếp ABC.
2.10 Cho (O ; 4cm) có hai đường kính AB và CD vuông góc với nhau. Dây
AM của (O) cắt bán kính OC tại I. Cho biết OI = 3cm. Tính AM và đường
cao MH của AMB.
2.11 Cho hình vuông ABCD cạnh a.
a) Chứng minh: bốn đỉnh A, B, C và D của hình vuông trên cùng nằm
trên một đường tròn.
b) Xác định tâm và bán kính của đường tròn đó.
2.12 Cho ABC cân tại A, BC = 12cm, đường cao AH = 4cm. Tính bán kính
của đường tròn ngoại tiếp ABC.
2.13 Cho ABC cân tại A, đường cao BE. Gọi D, F lần lượt là trung điểm của
BC và AB.
a) Chứng minh: 4 điểm A, B, D và E cùng nằm trên một đường tròn.
b) Chứng minh: C không thuộc đường tròn trên.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 31
1.78 Rút gọn các biểu thức sau:
a)
a
b
b
a
ab
b
a
với a > 0 và b > 0
b)
81
mx4mx8m4
xx21
m
2
2
với m > 0 và x > 1
1.79 Rút gọn rồi so sánh giá trị của biểu thức sau với 1:
1a2a
1a
:
1a
1
aa
1
M
với a > 0 và a 1
1.80 Giải các phương trình sau:
1. a) 645x9
3
4
x5320x4
b) 1x6
9
1x
2
15
25x25
c) 45x45x9
3
1
20x4
d) 1x164x49x916x16 .
2. a)
1xx1
2
b)
2x4x4x
2
c) x27x2
2
d) 2x3x4x
2
e)
0x24x
2
f)
1x24x4x
2
g) 1x)1x)(4x2( h)
2x1x4x2
2
.
3. a) x459x2 b)
1x1x2
c) 3x3x d) x3xx
2
e) 1x1x3x
2
f) 3x43x2
2
g) 3x6xx
2
h) 3x2x4x9
2
.
4. a) 54x4x
b) 21x2x1x2x
c) 12x67x2x42x
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 32
d) 225x232x5x232x .
5. a) 7x3x5x3x
22
b) 4x5x28x5x5
22
c) 6x3x25x3x22
22
d) 33x3x29x3x2
22
1.81 Chứng minh đẳng thức sau:
2. a)
3
1
2x6:x6
3
x2
x
6
x
với x > 0
b) 1
a1
a1
a
a1
aa1
2
với a > 0 và a 1
c) a
bab2a
ba
b
ba
22
42
2
với a + b > 0 và b 0
1.82 Cho biểu thức:
x4
x52
2x
x2
2x
1x
P
a) Rút gọn P nếu x 0 và x 4.
b) Tìm x để P = 2.
1.83 Cho biểu thức:
1a
2a
2a
1a
:
a
1
1a
1
Q
a) Chứng tỏ rằng Q xác định với a > 0, a 4 và a 1.
b) Tìm giá trị của a để Q dương.
1.84 Cho biểu thức:
6x5x
1x
3
2x
1x
3x
2x
Q
a) Tìm điều kiện xác định và rút gọn Q.
b) Tìm các giá trị của x để Q < 1.
c) Tìm các giá trị của x Z sao cho 2Q Z.
1.85 Với 3 số a, b, c không âm. Chứng minh:
cabcabcba
Hãy mở rộng kết quả trên cho trường hợp 4 số, 5 số không âm.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 73
Chương 2
ĐƯỜNG TRÒN
A - Sự xác định đường tròn.
Tính chất đối xứng của đường tròn
2.1 Cho hình chữ nhật ABCD.
a) Chứng minh rằng bốn điểm A, B, C và D cùng thuộc một đường tròn.
b) Cho AB = 10cm và BC = 6cm. Tính bán kính của đường tròn trên.
2.2 Cho hình thang cân ABCD. Chứng minh rằng bốn điểm A, B, C và D
nằm trên một đường tròn.
2.3 Trong mặt phẳng tọa độ Oxy, hãy xác định vị trí của mỗi điểm A(1 ; –1),
B(2 ; 1) và C(–
3
;
3
) với đường tròn tâm O bán kính 2 (với O là gốc
tọa độ).
1.
T
ập hợp các điểm M cách đều điểm O cho tr
ư
ớc một khoảng không đổi
bằng R là đường tròn tâm O bán kính R. Kí hiệu (O ; R) hoặc (O).
OM = R
M
(O ; R)oooo
2. a. Qua 3 điểm không thẳng hàng, ta vẽ được một và chỉ một đường
tròn.
b. Đường tròn qua 3 đỉnh của một tam giác gọi là đường tròn ngoại
tiếp tam giác đó. Khi đó tam giác được gọi là nội tiếp đường tròn.
Tâm của đường tròn này là giao điểm của hai hay ba đường trung
trực của tam giác đó.
3. a. Tâm của đường tròn ngoại tiếp
vuông là trung điểm cạnh huyền.
b. Nếu một tam giác có một cạnh là đường kính của đường tròn ngoại
tiếp thì tam giác đó là tam giác vuông.
4. Đường tròn là hình có tâm đối xứng. Đó là tâm của đường tròn đó.
5. Đường tròn có vô số trục đối xứng, đó là bất kì đường kính nào của
đường tròn.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 32
d) 225x232x5x232x .
5. a) 7x3x5x3x
22
b) 4x5x28x5x5
22
c) 6x3x25x3x22
22
d) 33x3x29x3x2
22
1.81 Chứng minh đẳng thức sau:
2. a)
3
1
2x6:x6
3
x2
x
6
x
với x > 0
b) 1
a1
a1
a
a1
aa1
2
với a > 0 và a 1
c) a
bab2a
ba
b
ba
22
42
2
với a + b > 0 và b 0
1.82 Cho biểu thức:
x4
x52
2x
x2
2x
1x
P
a) Rút gọn P nếu x 0 và x 4.
b) Tìm x để P = 2.
1.83 Cho biểu thức:
1a
2a
2a
1a
:
a
1
1a
1
Q
a) Chứng tỏ rằng Q xác định với a > 0, a 4 và a 1.
b) Tìm giá trị của a để Q dương.
1.84 Cho biểu thức:
6x5x
1x
3
2x
1x
3x
2x
Q
a) Tìm điều kiện xác định và rút gọn Q.
b) Tìm các giá trị của x để Q < 1.
c) Tìm các giá trị của x Z sao cho 2Q Z.
1.85 Với 3 số a, b, c không âm. Chứng minh:
cabcabcba
Hãy mở rộng kết quả trên cho trường hợp 4 số, 5 số không âm.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 73
Chương 2
ĐƯỜNG TRÒN

A - Sự xác định đường tròn.
Tính chất đối xứng của đường tròn
2.1 Cho hình chữ nhật ABCD.
a) Chứng minh rằng bốn điểm A, B, C và D cùng thuộc một đường tròn.
b) Cho AB = 10cm và BC = 6cm. Tính bán kính của đường tròn trên.
2.2 Cho hình thang cân ABCD. Chứng minh rằng bốn điểm A, B, C và D
nằm trên một đường tròn.
2.3 Trong mặt phẳng tọa độ Oxy, hãy xác định vị trí của mỗi điểm A(1 ; –1),
B(2 ; 1) và C(–
3
;
3
) với đường tròn tâm O bán kính 2 (với O là gốc
tọa độ).
1.
T
ập hợp các điểm M cách đều điểm O cho tr
ư
ớc một khoảng không đổi
bằng R là đường tròn tâm O bán kính R. Kí hiệu (O ; R) hoặc (O).
OM = R
M
(O ; R)oooo
2. a. Qua 3 điểm không thẳng hàng, ta vẽ được một và chỉ một đường
tròn.
b. Đường tròn qua 3 đỉnh của một tam giác gọi là đường tròn ngoại
tiếp tam giác đó. Khi đó tam giác được gọi là nội tiếp đường tròn.
Tâm của đường tròn này là giao điểm của hai hay ba đường trung
trực của tam giác đó.
3. a. Tâm của đường tròn ngoại tiếp
vuông là trung điểm cạnh huyền.
b. Nếu một tam giác có một cạnh là đường kính của đường tròn ngoại
tiếp thì tam giác đó là tam giác vuông.
4. Đường tròn là hình có tâm đối xứng. Đó là tâm của đường tròn đó.
5. Đường tròn có vô số trục đối xứng, đó là bất kì đường kính nào của
đường tròn.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 72
1.88 Cho ABC đều, gọi O là trung điểm của cạnh BC,
0
xOy 60
có cạnh
Ox, Oy luôn cắt AB, AC tại M và N. Chứng minh :
a) OBM NOC suy ra OB
2
= BM . CN
b) OBM ONM suy ra MO, NO lần lượt là tia phân giác
BMN
và
CNM
.
c) BM . CN =
1
4
BC
2
.
1.89 Cho ABC cân tại A có H là trung điểm của BC. Gọi I là hình chiếu của
H lên cạnh AC và O là trung điểm của HI. Chứng minh :
a) BIC AOH b) AO BI
1.90 Cho ABC cân tại A có đường cao AH, BK. Chứng minh :
2 2 2
1 1 1
BK BC 4AH
.
3 - Giải bài toán:
Th
ực hiện lời giải m
à b
ạn đ
ã
đề ra.
B
ạn có nghĩ rằng các bước là đúng?
B
ạn có thể chứng minh nó đú
ng?
4 - Khai thác bài toán:
B
ạn có nghĩ ra một hướng khác để giải b
ài toán? L
ời giải có
ng
ắn hơn, đặc sắc hơn.
B
ạn đ
ã áp d
ụng cách giải đó cho bài toán nào chưa?
B
ạn có thể áp dụng bài toán này để giải các b
ài toán khác
đ
ã bi
ết?
(H
ết)
Giải bài toán như thế nào? – Phần 4
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 33
G - Căn bậc ba
1. Định nghĩa:
Căn bậc ba của một số a là số x sao cho x
3
= a
2. Tính chất:
a)
3 3
a b a b
b)
3 3 3
ab a. b
c) Với b
0, ta có
3
3
3
a a
b
b
1.86 Tính:
a)
3
512 ;
3
729 ;
3
064,0 ;
3
216,0 ;
3
008,0 .
b)
3
343 ;
3
027,0 ;
3
331,1 ;
3
512,0 ;
3
125 .
1.87 So sánh:
a) 5 và
3
123 b)
3
65 và
3
56
c)
3
32 và
3
23 d) 33 và
3
13333
1.88 Giải các phương trình sau:
a) 5,1x
3
b) 9,05x
3
1.89 Giải các bất phương trình sau và biểu diễn nghiệm trên trục số:
a)
2x
3
b) 5,1x
3
1.90 Chứng minh rằng với a, b kất kỳ thì:
a) aa
3 3
b)
aa
3
3
c)
3
3 3
baba
Trong cách học, phải lấy tự học làm cốt.
H
ồ Chí Minh
Danh ngôn học tập
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 72
1.88 Cho ABC đều, gọi O là trung điểm của cạnh BC,
0
xOy 60
có cạnh
Ox, Oy luôn cắt AB, AC tại M và N. Chứng minh :
a) OBM NOC suy ra OB
2
= BM . CN
b) OBM ONM suy ra MO, NO lần lượt là tia phân giác
BMN
và
CNM
.
c) BM . CN =
1
4
BC
2
.
1.89 Cho ABC cân tại A có H là trung điểm của BC. Gọi I là hình chiếu của
H lên cạnh AC và O là trung điểm của HI. Chứng minh :
a) BIC AOH b) AO BI
1.90 Cho ABC cân tại A có đường cao AH, BK. Chứng minh :
2 2 2
1 1 1
BK BC 4AH
.
3 - Giải bài toán:
Th
ực hiện lời giải m
à b
ạn đ
ã
đề ra.
B
ạn có nghĩ rằng các bước là đúng?
B
ạn có thể chứng minh nó đú
ng?
4 - Khai thác bài toán:
B
ạn có nghĩ ra một hướng khác để giải b
ài toán? L
ời giải có
ng
ắn hơn, đặc sắc hơn.
B
ạn đ
ã áp d
ụng cách giải đó cho bài toán nào chưa?
B
ạn có thể áp dụng bài toán này để giải các b
ài toán khác
đ
ã bi
ết?
(H
ết)
Giải bài toán như thế nào? – Phần 4
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 33
G - Căn bậc ba
1. Định nghĩa:
Căn bậc ba của một số a là số x sao cho x
3
= a
2. Tính chất:
a)
3 3
a b a b
b)
3 3 3
ab a. b
c) Với b
0, ta có
3
3
3
a a
b
b
1.86 Tính:
a)
3
512 ;
3
729 ;
3
064,0 ;
3
216,0 ;
3
008,0 .
b)
3
343 ;
3
027,0 ;
3
331,1 ;
3
512,0 ;
3
125 .
1.87 So sánh:
a) 5 và
3
123 b)
3
65 và
3
56
c)
3
32 và
3
23 d) 33 và
3
13333
1.88 Giải các phương trình sau:
a) 5,1x
3
b) 9,05x
3
1.89 Giải các bất phương trình sau và biểu diễn nghiệm trên trục số:
a)
2x
3
b) 5,1x
3
1.90 Chứng minh rằng với a, b kất kỳ thì:
a) aa
3 3
b)
aa
3
3
c)
3
3 3
baba
Trong cách học, phải lấy tự học làm cốt.
H
ồ Chí Minh
Danh ngôn học tập
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 34
H - Ôn tập chương 1
1.91 Tính giá trị của các biểu thức sau bằng cách biến đổi, rút gọn thích hợp:
a)
25 16 196
81 49 9
b)
1 14 34
3 2 2
16 25 81
c)
640 34,3
567
d)
2 2
21,6. 810. 11 5
1.92 Rút gọn các biểu thức sau:
a)
4,032.10238
b)
2 2
0,2 ( 10) .3 2 ( 3 5)
c)
8
1
15
8
:
5
4
5
4
3
1
2
3
2
1
2
1
d)
422
)1(5)3(2)32(2
e) 3242)32(
2
f) 612336615
g)
10:50245032005
h) 1281812226
i)
26
4813332
j)
2
12:1
210
2
1027
1
k)
232
232
:)16(5
l)
13
2
:
22102
62230102
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 71
1.82 Cho ABC vuông tại A, đường cao AH. Kẻ HE AB tại E và HF AC
tại F. Chứng minh:
a)
2
2
AB HB
AC HC
và
3
3
AB BE
AC CF
. b) BC = AB.sinC + AC.cosB.
c) AH
3
=BC.BE.CF=BC.AE.AF. d) AH
2
= AB.AC.sinB.cosB.
e) AH = BC.sinB.cosB. f)
BE CH CF BH AH BC
g) Cho AH = 4 cm; BC = 10 cm. Tính S
BEFC
.
1.83 Cho ABC nhọn (AB > AC) có đường cao AH và đường trung tuyến
AM. Chứng minh:
a)
cotB cotC
tanMAH
2
b)
HAC HC
tan
2 AH AC
1.84 Cho ABC cân tại A, đường cao AH. Biết AB = 10cm, AH = 8cm.
a) Tính BC và diện tích ABC.
b) Gọi I là trung điểm của AC. Qua A vẽ đường thẳng song song với BC
cắt đường thẳng HI tại K. Chứng minh: AKCH là hình chữ nhật.
c) Đường thẳng BI cắt AH tại G và cắt CK tại M. Cmrằng :
i. BGH BMC ii. BG . BC = BM . BH
d) Chứng minh : BG
2
+ AH
2
= AC
2
+ GH
2
.
1.85 Cho hình thang ABCD (
0
A D 90
). Gọi M là trung điểm của AD. Kẻ
MK BC tại K. Biết AB = 9cm, BC = 25cm, CD = 16cm.
a) Tính AD, MB, MC.
b) Chứng minh : MBC vuông tại M.
c) Tính MK và diện tích MKC.
1.86 Các đường cao của ABC có ba góc nhọn cắt nhau tại H. Trên các đoạn
HB, HC lấy điểm M và N sao cho
0
AMC ANB 90
.
Chứng minh : AM = AN.
1.87 Cho tam giác nhọn ABC. Chứng minh:
a)
cotA.cotB cotB.cotC cotC.cotA 1
b)
tanA tanB tanC tanA.tanB.tan C
c)
ABC
1
S AB.AC.sinA
2
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 34
H - Ôn tập chương 1
1.91 Tính giá trị của các biểu thức sau bằng cách biến đổi, rút gọn thích hợp:
a)
25 16 196
81 49 9
b)
1 14 34
3 2 2
16 25 81
c)
640 34,3
567
d)
2 2
21,6. 810. 11 5
1.92 Rút gọn các biểu thức sau:
a)
4,032.10238
b)
2 2
0,2 ( 10) .3 2 ( 3 5)
c)
8
1
15
8
:
5
4
5
4
3
1
2
3
2
1
2
1
d)
422
)1(5)3(2)32(2
e) 3242)32(
2
f) 612336615
g)
10:50245032005
h) 1281812226
i)
26
4813332
j)
2
12:1
210
2
1027
1
k)
232
232
:)16(5
l)
13
2
:
22102
62230102
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 71
1.82 Cho ABC vuông tại A, đường cao AH. Kẻ HE AB tại E và HF AC
tại F. Chứng minh:
a)
2
2
AB HB
AC HC
và
3
3
AB BE
AC CF
. b) BC = AB.sinC + AC.cosB.
c) AH
3
=BC.BE.CF=BC.AE.AF. d) AH
2
= AB.AC.sinB.cosB.
e) AH = BC.sinB.cosB. f)
BE CH CF BH AH BC
g) Cho AH = 4 cm; BC = 10 cm. Tính S
BEFC
.
1.83 Cho ABC nhọn (AB > AC) có đường cao AH và đường trung tuyến
AM. Chứng minh:
a)
cotB cotC
tanMAH
2
b)
HAC HC
tan
2 AH AC
1.84 Cho ABC cân tại A, đường cao AH. Biết AB = 10cm, AH = 8cm.
a) Tính BC và diện tích ABC.
b) Gọi I là trung điểm của AC. Qua A vẽ đường thẳng song song với BC
cắt đường thẳng HI tại K. Chứng minh: AKCH là hình chữ nhật.
c) Đường thẳng BI cắt AH tại G và cắt CK tại M. Cmrằng :
i. BGH BMC ii. BG . BC = BM . BH
d) Chứng minh : BG
2
+ AH
2
= AC
2
+ GH
2
.
1.85 Cho hình thang ABCD (
0
A D 90
). Gọi M là trung điểm của AD. Kẻ
MK BC tại K. Biết AB = 9cm, BC = 25cm, CD = 16cm.
a) Tính AD, MB, MC.
b) Chứng minh : MBC vuông tại M.
c) Tính MK và diện tích MKC.
1.86 Các đường cao của ABC có ba góc nhọn cắt nhau tại H. Trên các đoạn
HB, HC lấy điểm M và N sao cho
0
AMC ANB 90
.
Chứng minh : AM = AN.
1.87 Cho tam giác nhọn ABC. Chứng minh:
a)
cotA.cotB cotB.cotC cotC.cotA 1
b)
tanA tanB tanC tanA.tanB.tan C
c)
ABC
1
S AB.AC.sinA
2
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 70
1.77 Cho ABC có
0
A 90
, AB = 15cm, AC = 20cm, đường cao AH.
a) Tính độ dài BC, AH, BH.
b) Gọi D là điểm đối xứng của B qua H. Vẽ hình bình hành ADCE.
Chứng minh: ABCE là hình thang cân.
c) Tính diện tích hình thang cân ABCE.
1.78 Cho ABC có đường cao AH. Từ H vẽ HM AB tại M, HN AC tại N.
Biết HA = 15cm, HC = 36cm, BC = 56cm.
a) Tính AB, AC.
b) Chứng minh: AB.AM = AC.AN và ABC ANM.
c) Chứng minh: AB.AM = AC.BN
d) Chứng minh: ABN ACM.
1.79 Cho ABC vuông tại A, đường cao AH.
a) Biết 3AB = 2AC. Tính
sinACB
,
tanACB
.
b) Vẽ đường phân giác CK của AHC. Biết AH = 2,4 cm; BH = 1,8 cm.
Tính CH, AC, CK,
cosHCK
.
c) Lấy M BC. Kẻ ME AB tại E và MF AC tại F. Chứng minh
MB.MC = EA.EB + FE.FC
1.80 Cho ABC vuông tại A, đường cao AH. Đường thẳng vuông góc với AC
tại C cắt tia AH tại D.
a) Chứng minh: BC.CH = AD.AH = AB.CD.
b) Chứng minh:
2
ABC CAD
S S .tan ACB
c) Kẻ HE AB tại E. Chứng minh BE = BC.cos
3
B.
d) Chứng minh:
2
2
AB .AC
EH
BC
.
e) Gọi F là hình chiếu của H lên AC. C/m:
2
BEFC ABC
S S .(1 tan ACE)
f) Biết
AB 3
AC 4
và AH = 12 cm. Tính AB, AC, BH, KH.
1.81 Cho tam giác nhọn ABC có ba đường cao AD, BE, CF cắt nhau tại H.
Chứng minh:
a) EF = AH.sinA
b)
HBC HAC
HAB
S S
S
tanA tanB tanC
c)
2 2 2
DEF ABC
S (1 cos A cos B cos C).S
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 35
m)
21139
625)62049)(625(
n) 521028521028
o) 154)610)(154(
p) 53)210)(35(
1.93 Phân tích thành nhân tử (với x, y, a, b dương và a > b)
a) 3 +
x
+ 9 – x b) xy + y
x
+
x
+ 1
c) aybxbyxa d)
22
baba
1.94 Rút gọn rồi tính giá trị của các biểu thức sau:
a)
2
a4a129a9 với a = 9
b) 4m4m
2
m
m
3
1
2
với m < 0
c) a4a25a101
2
với a =
2
d) 1x6x9x4
2
với x = 3
1.95 Rút gọn các biểu thức sau:
a) A =
x 2 1 10 x
: x 2
x 4
2 x x 2 x 2
b) B =
yx
y2
yx:xy
yx
yyxx
c) C =
x x 3 2 x x 2
1 :
1 x x 2 3 x x 5 x 6
d) D =
2 2
a x a x
2 a 2 a
x x
với a > 0, x > 0.
1.96 Giải các phương trình sau:
a) x15
3
1
11x15x15
3
5
b)
15
8
5x7
1x3
c) 3)1x2(
2
d) 3x48x2
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 70
1.77 Cho ABC có
0
A 90
, AB = 15cm, AC = 20cm, đường cao AH.
a) Tính độ dài BC, AH, BH.
b) Gọi D là điểm đối xứng của B qua H. Vẽ hình bình hành ADCE.
Chứng minh: ABCE là hình thang cân.
c) Tính diện tích hình thang cân ABCE.
1.78 Cho ABC có đường cao AH. Từ H vẽ HM AB tại M, HN AC tại N.
Biết HA = 15cm, HC = 36cm, BC = 56cm.
a) Tính AB, AC.
b) Chứng minh: AB.AM = AC.AN và ABC ANM.
c) Chứng minh: AB.AM = AC.BN
d) Chứng minh: ABN ACM.
1.79 Cho ABC vuông tại A, đường cao AH.
a) Biết 3AB = 2AC. Tính
sinACB
,
tanACB
.
b) Vẽ đường phân giác CK của AHC. Biết AH = 2,4 cm; BH = 1,8 cm.
Tính CH, AC, CK,
cosHCK
.
c) Lấy M BC. Kẻ ME AB tại E và MF AC tại F. Chứng minh
MB.MC = EA.EB + FE.FC
1.80 Cho ABC vuông tại A, đường cao AH. Đường thẳng vuông góc với AC
tại C cắt tia AH tại D.
a) Chứng minh: BC.CH = AD.AH = AB.CD.
b) Chứng minh:
2
ABC CAD
S S .tan ACB
c) Kẻ HE AB tại E. Chứng minh BE = BC.cos
3
B.
d) Chứng minh:
2
2
AB .AC
EH
BC
.
e) Gọi F là hình chiếu của H lên AC. C/m:
2
BEFC ABC
S S .(1 tan ACE)
f) Biết
AB 3
AC 4
và AH = 12 cm. Tính AB, AC, BH, KH.
1.81 Cho tam giác nhọn ABC có ba đường cao AD, BE, CF cắt nhau tại H.
Chứng minh:
a) EF = AH.sinA
b)
HBC HAC
HAB
S S
S
tanA tanB tanC
c)
2 2 2
DEF ABC
S (1 cos A cos B cos C).S
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 35
m)
21139
625)62049)(625(
n) 521028521028
o) 154)610)(154(
p) 53)210)(35(
1.93 Phân tích thành nhân tử (với x, y, a, b dương và a > b)
a) 3 +
x
+ 9 – x b) xy + y
x
+
x
+ 1
c) aybxbyxa d)
22
baba
1.94 Rút gọn rồi tính giá trị của các biểu thức sau:
a)
2
a4a129a9 với a = 9
b) 4m4m
2
m
m
3
1
2
với m < 0
c) a4a25a101
2
với a =
2
d) 1x6x9x4
2
với x = 3
1.95 Rút gọn các biểu thức sau:
a) A =
x 2 1 10 x
: x 2
x 4
2 x x 2 x 2
b) B =
yx
y2
yx:xy
yx
yyxx
c) C =
x x 3 2 x x 2
1 :
1 x x 2 3 x x 5 x 6
d) D =
2 2
a x a x
2 a 2 a
x x
với a > 0, x > 0.
1.96 Giải các phương trình sau:
a) x15
3
1
11x15x15
3
5
b)
15
8
5x7
1x3
c) 3)1x2(
2
d) 3x48x2
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 36
1.97 Chứng minh các đẳng thức sau:
1. a)
2 3 6 216 1
1,5
3
8 2 6
b)
14 7 15 5 1
: 2
1 2 1 3 7 5
c) 63232
d)
2
2
4 4
8
(2 5)
(2 5)
e) 2
2
3
4
3
2
26
2
3
2
3
4
3
2
26
2
3
2. a)
a b b a 1
: a b
ab a b
(với a, b > 0 và a 0)
b)
a a a a
1 1 1 a
a 1 a 1
(với a > 0 và a 1)
c)
a b a b 2b 2 b
b a
2 a 2 b 2 a 2 b a b
(với a, b > 0 và a b
d)
a a a a
1 1 1 a
a 1 a 1
(với a, b > 0 và a b)
1.98 Tìm x nguyên để
x 1
x 3
nhận giá trị nguyên.
1.99 a) Chứng tỏ:
2
)24x(4x4x
b) Tìm điều kiện xác định và rút gọn:
4x4x4x4xA
1.100 Cho các biểu thức:
1xxA
và
1x4xB
a) Tìm điều kiện xác định của A và B.
b) Chứng tỏ A 1 và B 5
c) Tìm x để A = 1, B = 2.
1.101 Tìm giá trị lớn nhất của biểu thức:
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 69
E - Ôn tập chương 1
1.71 Cho ABD có AB = 15cm, AD = 20cm, BD = 25cm. Vẽ AM BD.
a) Chứng minh : ABD vuông. Tính AM, BM, MD.
b) Kẻ tia Bx // AD, vẽ AM BD cắt Bx tại C. C/m : AB
2
= AD.BC
c) Kẻ CE AD cắt BD tại I. Chứng minh : BM
2
= MI . MD.
d) Chứng minh : S
AMB
= S
MCD
.
1.72 Cho ABC vuông tại A, đường cao AH. Kẻ HD AB, HE AC,
AK DE. Gọi I là giao điểm của AH và DE, biết AI
2
= AD . AE.
Chứng minh : AI
2
= DE . AK.
1.73 Cho ABC, một đường thẳng song song BC cắt AB tại D, cắt AC tại E
thỏa điều kiện DC
2
= BC . DE.
a) Chứng minh : DEC CDB.
b) Chứng minh : AD
2
= AC . AE và AC
2
= AB . AD
1.74 Cho ABC có 3 góc nhọn. Các đường cao AD, BE, CF cắt nhau tại H.
Chứng minh :
a) AF.AB = AH.AD = AE.AC b) DH.DA = DB.DC
c) BF.BA = BH. BE = BD.BC d) HB.HE = HC.HF = HA.HD
e) BH.BE + CH.CF = BC
2
f) DB.DC = DH.DA
1.75 Cho ABC. Gọi M là trung điểm của BC, N là trung điểm của AC. Các
đường trung trực của cạnh BC và AC cắt nhau tại O. Gọi H là trực tâm và
G là trọng tâm của ABC. Chứng minh:
a) AHB MON.
b) AHG MOG.
c) Ba điểm H, G, O thẳng hàng. (đường thẳng Euler)
1.76 Cho ABC vuông tại A, đường cao AH. Biết BC = 5cm;
BH = 1,8cm. Gọi M là trung điểm của BC, đường trung trực của BC cắt
AC tại D.
a) Tính AB, AH.
b) Tính tỉ số diện tích của DMC và ABC.
c) Chứng minh : AC . DC =
1
2
BC
2
.
d) Tính diện tích tứ giác ADMB.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 36
1.97 Chứng minh các đẳng thức sau:
1. a)
2 3 6 216 1
1,5
3
8 2 6
b)
14 7 15 5 1
: 2
1 2 1 3 7 5
c) 63232
d)
2
2
4 4
8
(2 5)
(2 5)
e) 2
2
3
4
3
2
26
2
3
2
3
4
3
2
26
2
3
2. a)
a b b a 1
: a b
ab a b
(với a, b > 0 và a 0)
b)
a a a a
1 1 1 a
a 1 a 1
(với a > 0 và a 1)
c)
a b a b 2b 2 b
b a
2 a 2 b 2 a 2 b a b
(với a, b > 0 và a b
d)
a a a a
1 1 1 a
a 1 a 1
(với a, b > 0 và a b)
1.98 Tìm x nguyên để
x 1
x 3
nhận giá trị nguyên.
1.99 a) Chứng tỏ:
2
)24x(4x4x
b) Tìm điều kiện xác định và rút gọn:
4x4x4x4xA
1.100 Cho các biểu thức:
1xxA
và
1x4xB
a) Tìm điều kiện xác định của A và B.
b) Chứng tỏ A 1 và B 5
c) Tìm x để A = 1, B = 2.
1.101 Tìm giá trị lớn nhất của biểu thức:
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 69
E - Ôn tập chương 1
1.71 Cho ABD có AB = 15cm, AD = 20cm, BD = 25cm. Vẽ AM BD.
a) Chứng minh : ABD vuông. Tính AM, BM, MD.
b) Kẻ tia Bx // AD, vẽ AM BD cắt Bx tại C. C/m : AB
2
= AD.BC
c) Kẻ CE AD cắt BD tại I. Chứng minh : BM
2
= MI . MD.
d) Chứng minh : S
AMB
= S
MCD
.
1.72 Cho ABC vuông tại A, đường cao AH. Kẻ HD AB, HE AC,
AK DE. Gọi I là giao điểm của AH và DE, biết AI
2
= AD . AE.
Chứng minh : AI
2
= DE . AK.
1.73 Cho ABC, một đường thẳng song song BC cắt AB tại D, cắt AC tại E
thỏa điều kiện DC
2
= BC . DE.
a) Chứng minh : DEC CDB.
b) Chứng minh : AD
2
= AC . AE và AC
2
= AB . AD
1.74 Cho ABC có 3 góc nhọn. Các đường cao AD, BE, CF cắt nhau tại H.
Chứng minh :
a) AF.AB = AH.AD = AE.AC b) DH.DA = DB.DC
c) BF.BA = BH. BE = BD.BC d) HB.HE = HC.HF = HA.HD
e) BH.BE + CH.CF = BC
2
f) DB.DC = DH.DA
1.75 Cho ABC. Gọi M là trung điểm của BC, N là trung điểm của AC. Các
đường trung trực của cạnh BC và AC cắt nhau tại O. Gọi H là trực tâm và
G là trọng tâm của ABC. Chứng minh:
a) AHB MON.
b) AHG MOG.
c) Ba điểm H, G, O thẳng hàng. (đường thẳng Euler)
1.76 Cho ABC vuông tại A, đường cao AH. Biết BC = 5cm;
BH = 1,8cm. Gọi M là trung điểm của BC, đường trung trực của BC cắt
AC tại D.
a) Tính AB, AH.
b) Tính tỉ số diện tích của DMC và ABC.
c) Chứng minh : AC . DC =
1
2
BC
2
.
d) Tính diện tích tứ giác ADMB.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 68
1.67 Cho ABC vuông tại B, dựng tam giác ACD (B và D nằm khắc phía đối
với AC). Biết
0
ACB 54
,
0
ACD 74
, AC = 8cm, AD = 9,6 cm. Hãy
tính: AB và
ADC
.
1.68 Cho ABC vuông ở A, đường cao AH. Biết HB = 2cm, HC = 64cm. Tính
B
,
C
.
1.69 Cho ABC có BC = 12cm,
0
B 60
,
0
C 40
.
a) Tính chiều cao CH và AC. b) Tính S
ABC
.
1.70 Một con thuyền với vận tốc thực 2km/h vượt qua một khúc sông nước
chảy mạnh mất 5 phút. Biết rằng đường đi của con thuyền tạo với bờ một
góc 70
0
. Từ đó đã có thể tính được chiều rộng của khúc sông ? Nếu có thể
hãy tính chính xác đến mét.
2 - Tìm tòi lời giải bài toán:
B
ạn đ
ã g
ặp b
à
i toán nào tương tự thế này chưa? Hay ở một dạng hơi
khác?
B
ạn có biết một định lý, một bài toán liên quan đến b
ài toán này
không?
Hãy xét k
ỹ cái chưa biết, v
à th
ử nhớ xem có b
ài toán nào có cùng cái
chưa biết không?
Đây là bài toán mà bạn đ
ã có l
ần giải n
ó r
ồi, bạn có thể áp dụng
được g
ì
ở nó? Phương pháp? Kết quả? Hay phải đưa thêm yếu tố phụ
vào m
ới áp dụng được?
Hãy xét k
ỹ các khái niệm có trong b
ài toán và n
ếu cần h
ãy quay v
ề
các định nghĩa.
N
ếu bạn chưa giải được b
ài toán này, hãy th
ử giải một b
ài toán ph
ụ
d
ễ hơn có liên quan, một trường hợp riêng, tương tự, tổng quát hơn?
Hãy gi
ữ lại một phần giả thiết khi đó ẩn được xác định đến chừng
m
ực n
ào? T
ừ các điều đó bạn có thể rút ra được điều g
ì có ích cho
vi
ệc giải b
ài toán? V
ới giả thiết n
ào thì b
ạn có thể giải được b
ài toán
này?
B
ạn đ
ã t
ận dụng hết giả thiết của bài toán chưa?
(Xem ti
ếp ở trang
72)
Giải bài toán như thế nào? – Phần 3
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 37
a) A =
1xx
1
b) B =
21xx4
2
c) C = x6x91
2
d) D =
x42x
1.102 Tìm giá trị nhỏ nhất của biểu thức:
a) A =
2x4x4
2
b) B = 5x4x2
2
c) P =
21x
3
x
d) Q = x – 2
2x
.
1.103 Cho biểu thức:
2
x
4
1x4x4
A
2
. Chứng tỏ A = 0,5 với x 0,5.
1.104 Cho
222222
baa
b
:
ba
a
1
ba
a
Q
với a > b > 0
a) Rút gọn Q
b) Tìm giá trị của Q khi a = 3b.
1.105 Cho biểu thức:
ab
abba
ba
ab4)ba(
A
2
a) Tìm điều kiện để A có nghĩa.
b) Khi A có nghĩa, chứng tỏ giá trị A không phụ thuộc vào a.
1.106 Cho biểu thức:
x
x1
x1
1xx
x
1x
1x2
Q
3
3
với x 0 và x 1
a) Rút gọn Q.
b) Tìm giá trị của x để Q = 3.
1.107 Cho biểu thức:
x
1
x3x
1x3
:
x9
9x
x3
x
C với x 0 và x 9.
a) Rút gọn C
b) Tìm giá trị của x để C < 1.
1.108 Cho biểu thức: yyx5x6A
2
.
a) Phân tích biểu thức A thành nhân tử.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 68
1.67 Cho ABC vuông tại B, dựng tam giác ACD (B và D nằm khắc phía đối
với AC). Biết
0
ACB 54
,
0
ACD 74
, AC = 8cm, AD = 9,6 cm. Hãy
tính: AB và
ADC
.
1.68 Cho ABC vuông ở A, đường cao AH. Biết HB = 2cm, HC = 64cm. Tính
B
,
C
.
1.69 Cho ABC có BC = 12cm,
0
B 60
,
0
C 40
.
a) Tính chiều cao CH và AC. b) Tính S
ABC
.
1.70 Một con thuyền với vận tốc thực 2km/h vượt qua một khúc sông nước
chảy mạnh mất 5 phút. Biết rằng đường đi của con thuyền tạo với bờ một
góc 70
0
. Từ đó đã có thể tính được chiều rộng của khúc sông ? Nếu có thể
hãy tính chính xác đến mét.
2 - Tìm tòi lời giải bài toán:
B
ạn đ
ã g
ặp b
à
i toán nào tương tự thế này chưa? Hay ở một dạng hơi
khác?
B
ạn có biết một định lý, một bài toán liên quan đến b
ài toán này
không?
Hãy xét k
ỹ cái chưa biết, v
à th
ử nhớ xem có b
ài toán nào có cùng cái
chưa biết không?
Đây là bài toán mà bạn đ
ã có l
ần giải n
ó r
ồi, bạn có thể áp dụng
được g
ì
ở nó? Phương pháp? Kết quả? Hay phải đưa thêm yếu tố phụ
vào m
ới áp dụng được?
Hãy xét k
ỹ các khái niệm có trong b
ài toán và n
ếu cần h
ãy quay v
ề
các định nghĩa.
N
ếu bạn chưa giải được b
ài toán này, hãy th
ử giải một b
ài toán ph
ụ
d
ễ hơn có liên quan, một trường hợp riêng, tương tự, tổng quát hơn?
Hãy gi
ữ lại một phần giả thiết khi đó ẩn được xác định đến chừng
m
ực n
ào? T
ừ các điều đó bạn có thể rút ra được điều g
ì có ích cho
vi
ệc giải b
ài toán? V
ới giả thiết n
ào thì b
ạn có thể giải được b
ài toán
này?
B
ạn đ
ã t
ận dụng hết giả thiết của bài toán chưa?
(Xem ti
ếp ở trang
72)
Giải bài toán như thế nào? – Phần 3
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 37
a) A =
1xx
1
b) B =
21xx4
2
c) C = x6x91
2
d) D =
x42x
1.102 Tìm giá trị nhỏ nhất của biểu thức:
a) A =
2x4x4
2
b) B = 5x4x2
2
c) P =
21x
3
x
d) Q = x – 2
2x
.
1.103 Cho biểu thức:
2
x
4
1x4x4
A
2
. Chứng tỏ A = 0,5 với x 0,5.
1.104 Cho
222222
baa
b
:
ba
a
1
ba
a
Q
với a > b > 0
a) Rút gọn Q
b) Tìm giá trị của Q khi a = 3b.
1.105 Cho biểu thức:
ab
abba
ba
ab4)ba(
A
2
a) Tìm điều kiện để A có nghĩa.
b) Khi A có nghĩa, chứng tỏ giá trị A không phụ thuộc vào a.
1.106 Cho biểu thức:
x
x1
x1
1xx
x
1x
1x2
Q
3
3
với x 0 và x 1
a) Rút gọn Q.
b) Tìm giá trị của x để Q = 3.
1.107 Cho biểu thức:
x
1
x3x
1x3
:
x9
9x
x3
x
C với x 0 và x 9.
a) Rút gọn C
b) Tìm giá trị của x để C < 1.
1.108 Cho biểu thức: yyx5x6A
2
.
a) Phân tích biểu thức A thành nhân tử.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 38
b) Tính giá trị của A khi
2 b
x , y
3
4 7
.
1.109 Cho biểu thức:
21x
3
x
B
.
a) Tìm điều kiện xác định của B.
b) Rút gọn B.
c) Tính giá trị của B khi x = 10 – 56
d) Tìm giá trị nhỏ nhất của B.
1.110 Cho biểu thức:
3x
xx6
C
.
a) Tìm điều kiện xác định của C.
b) Rút gọn B.
c) Tìm giá trị lớn nhất của C.
1.111 Cho biểu thức:
1x
xx
x1x
1
x1x
1
P
3
.
a) Tìm điều kiện xác định của P.
b) Rút gọn P.
c) Tính giá trị của P khi
729
53
x
d) Giải phương trình : P = 16.
1.112 Cho biểu thức:
1xxxx
x2
1x
1
:
1x
x
1Q .
a) Tìm điều kiện xác định của Q.
b) Rút gọn Q.
c) Tính giá trị của Q khi x = 4 + 32
d) Giải bất phương trình : Q > 1.
1.113 Cho biểu thức: 1
a
aa2
1aa
aa
A
2
.
a) Rút gọn A.
b) Biết a > 0, hãy so sánh A vớiA
c) Tìm a để A = 2
d) Tìm giá trị nhỏ nhất của A.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 67
D - Hệ thức giữa các cạnh và các góc
trong một tam giác vuông
1. Các hệ thức:
1) b = a.sinB = a.cosC
2) c = a.sinC = a.cosB
3) b = c.tanB = c.cotC
4) c = b.tanC =b.cotB
2. Giải tam giác vuông:
Giải tam giác vuông là tìm tất cả các yếu tố còn lại của một tam giác
vuông khi biết trước hai yếu tố (trong đó có ít nhất một yếu tố về cạnh và
không kể góc vuông).
1.61 Giải tam giác vuông ABC biết rằng  = 90
0
và :
a) b = 10 cm,
0
C 30
; b) c = 10 cm,
0
C 45
;
c) a = 20 cm,
0
B 35
; d) c = 21 cm, b = 18 cm;
1.62 Cho ABC nhọn có đường cao AH và đường trung tuyến AM. Biết
0
B 57
, AB = 9 cm, AC = 12 cm. Giải tam giác ABC và tính AM.
1.63 Một cây cột đèn cao 7m có bóng trên mặt đất dài 4m. Hãy tính góc của tia
sáng mặt trời tạo với mặt đất.
1.64 Cho ABC có đường cao AH. Biết AB = 25 cm,
0
B 70
,
0
C 50
. Tính
độ dài AH và BC (làm tròn đến chữ số thập phân thứ hai)
1.65 Một khúc sông rộng khoảng 250m. Một chiếc đò chèo qua sông bị dòng
nước đẩy xiên nên phải chèo khoảng 320m mới sang đươực bờ bên kia.
Hỏi dòng nước đã đẩy chiếc đò lệch đi một góc bằng bao nhiêu ?
1.66 Cho ABC, trong đó AB = 11 cm,
0
ABC 38
,
0
ACB 30
. Gọi điểm N
là chân của đường vuông góc kẻ từ A đến cạnh BC. Hãy tính: AN và AC.
A
B
C
a
c
b
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 38
b) Tính giá trị của A khi
2 b
x , y
3
4 7
.
1.109 Cho biểu thức:
21x
3
x
B
.
a) Tìm điều kiện xác định của B.
b) Rút gọn B.
c) Tính giá trị của B khi x = 10 – 56
d) Tìm giá trị nhỏ nhất của B.
1.110 Cho biểu thức:
3x
xx6
C
.
a) Tìm điều kiện xác định của C.
b) Rút gọn B.
c) Tìm giá trị lớn nhất của C.
1.111 Cho biểu thức:
1x
xx
x1x
1
x1x
1
P
3
.
a) Tìm điều kiện xác định của P.
b) Rút gọn P.
c) Tính giá trị của P khi
729
53
x
d) Giải phương trình : P = 16.
1.112 Cho biểu thức:
1xxxx
x2
1x
1
:
1x
x
1Q .
a) Tìm điều kiện xác định của Q.
b) Rút gọn Q.
c) Tính giá trị của Q khi x = 4 + 32
d) Giải bất phương trình : Q > 1.
1.113 Cho biểu thức: 1
a
aa2
1aa
aa
A
2
.
a) Rút gọn A.
b) Biết a > 0, hãy so sánh A vớiA
c) Tìm a để A = 2
d) Tìm giá trị nhỏ nhất của A.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 67
D - Hệ thức giữa các cạnh và các góc
trong một tam giác vuông
1. Các hệ thức:
1) b = a.sinB = a.cosC
2) c = a.sinC = a.cosB
3) b = c.tanB = c.cotC
4) c = b.tanC =b.cotB
2. Giải tam giác vuông:
Giải tam giác vuông là tìm tất cả các yếu tố còn lại của một tam giác
vuông khi biết trước hai yếu tố (trong đó có ít nhất một yếu tố về cạnh và
không kể góc vuông).
1.61 Giải tam giác vuông ABC biết rằng  = 90
0
và :
a) b = 10 cm,
0
C 30
; b) c = 10 cm,
0
C 45
;
c) a = 20 cm,
0
B 35
; d) c = 21 cm, b = 18 cm;
1.62 Cho ABC nhọn có đường cao AH và đường trung tuyến AM. Biết
0
B 57
, AB = 9 cm, AC = 12 cm. Giải tam giác ABC và tính AM.
1.63 Một cây cột đèn cao 7m có bóng trên mặt đất dài 4m. Hãy tính góc của tia
sáng mặt trời tạo với mặt đất.
1.64 Cho ABC có đường cao AH. Biết AB = 25 cm,
0
B 70
,
0
C 50
. Tính
độ dài AH và BC (làm tròn đến chữ số thập phân thứ hai)
1.65 Một khúc sông rộng khoảng 250m. Một chiếc đò chèo qua sông bị dòng
nước đẩy xiên nên phải chèo khoảng 320m mới sang đươực bờ bên kia.
Hỏi dòng nước đã đẩy chiếc đò lệch đi một góc bằng bao nhiêu ?
1.66 Cho ABC, trong đó AB = 11 cm,
0
ABC 38
,
0
ACB 30
. Gọi điểm N
là chân của đường vuông góc kẻ từ A đến cạnh BC. Hãy tính: AN và AC.
A
B
C
a
c
b
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 66
C - Bảng lượng giác và máy tính bỏ túi
1.55 Dùng bảng lượng giác hoặc máy tính bỏ túi để tính các tỉ số lượng giác
sau đây:
a) sin40
0
12 b) cos52
0
54 c) tan63
0
36 d) cot25
0
18
e) sin39
0
13 f) cos52
0
18 g) tan13
0
20 h) cot10
0
17
i) sin70
0
13 j) cos25
0
32 k) tan43
0
10 l) cot32
0
15
1.56 Dùng bảng lượng giác hoặc máy tính bỏ túi để tính số đo của góc x (làm
tròn kết quả đến phút):
a) sinx 0,2368 b) cosx 0,6224
c) tanx 2,154 d) cotx 3,163
e) sinx 0,5446 f) cosx 0,4444
g) tanx 1,1111 h) cotx 0,7813
i) sinx 0,3495 j) cosx 0,5427
1.57 So sánh các tỉ số lượng giác (không dùng bảng và máy tính):
a) sin20
0
và sin70
0
b) cos25
0
và cos63
0
15’
c) tan73
0
20’ và tg45
0
d) cot2
0
và cot37
0
40’
e) tan45
0
và cos45
0
f) cot32
0
và cos32
0
g) tan25
0
và sin25
0
h) cot60
0
và sin30
0
1.58 Không dùng bảng và máy tính hãy, tính:
a)
0
0
sin25
cos65
b) tan58
0
– cot32
0
1.59 Hãy sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần (không dùng
bảng và máy tính).
a) sin78
0
, cos14
0
, sin47
0
, cos87
0
b) tan73
0
, cot25
0
, tan62
0
, cot38
0
1.60 Hãy sắp xếp các tỉ số lượng giác sau theo thứ tự giảm dần (không dùng
bảng và máy tính).
a) tan42
0
, tan56
0
, cot3
0
, cot18
0
b) sin13
0
, cos47
0
, tan46
0
, cot2
0
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 39
1.114 Cho biểu thức:
1
a1
3
:a1
a1
3
B
2
.
a) Tìm điều kiện xác định của B.
b) Rút gọn B.
c) Tính giá trị của B khi
32
3
a
d) Tìm giá trị của a để :
BB
.
1.115 Cho biểu thức:
222222
baa
b
:1
ba
a
ba
a
M
.
a) Rút gọn M.
b) Tìm giá trị của M nếu
2
3
b
a
c) Tìm điều kiện của a, b để M < 1.
1.116 Cho biểu thức:
2
x1
1x2x
2x
1x
2x
P
2
.
a) Tìm điều kiện xác định của P.
b) Rút gọn P.
c) Tính giá trị lớn nhất của P.
d) Chứng minh: nếu 0 < x < 1 thì P > 0.
1.117 Cho biểu thức:
x3
1x2
2x
3x
6x5x
9x2
Q
.
a) Tìm điều kiện xác định của Q.
b) Rút gọn Q.
c) Tìm các giá trị của x để Q < 1
d) Tìm x Z sao cho Q Z.
1.118 Cho biểu thức:
yx
xyyx
:
xy
yx
yx
yx
Q
2
33
.
a) Tìm điều kiện xác định của Q. b) Rút gọn Q.
c) So sánh Q với Q d) Chứng minh Q 0.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 66
C - Bảng lượng giác và máy tính bỏ túi
1.55 Dùng bảng lượng giác hoặc máy tính bỏ túi để tính các tỉ số lượng giác
sau đây:
a) sin40
0
12 b) cos52
0
54 c) tan63
0
36 d) cot25
0
18
e) sin39
0
13 f) cos52
0
18 g) tan13
0
20 h) cot10
0
17
i) sin70
0
13 j) cos25
0
32 k) tan43
0
10 l) cot32
0
15
1.56 Dùng bảng lượng giác hoặc máy tính bỏ túi để tính số đo của góc x (làm
tròn kết quả đến phút):
a) sinx 0,2368 b) cosx 0,6224
c) tanx 2,154 d) cotx 3,163
e) sinx 0,5446 f) cosx 0,4444
g) tanx 1,1111 h) cotx 0,7813
i) sinx 0,3495 j) cosx 0,5427
1.57 So sánh các tỉ số lượng giác (không dùng bảng và máy tính):
a) sin20
0
và sin70
0
b) cos25
0
và cos63
0
15’
c) tan73
0
20’ và tg45
0
d) cot2
0
và cot37
0
40’
e) tan45
0
và cos45
0
f) cot32
0
và cos32
0
g) tan25
0
và sin25
0
h) cot60
0
và sin30
0
1.58 Không dùng bảng và máy tính hãy, tính:
a)
0
0
sin25
cos65
b) tan58
0
– cot32
0
1.59 Hãy sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần (không dùng
bảng và máy tính).
a) sin78
0
, cos14
0
, sin47
0
, cos87
0
b) tan73
0
, cot25
0
, tan62
0
, cot38
0
1.60 Hãy sắp xếp các tỉ số lượng giác sau theo thứ tự giảm dần (không dùng
bảng và máy tính).
a) tan42
0
, tan56
0
, cot3
0
, cot18
0
b) sin13
0
, cos47
0
, tan46
0
, cot2
0
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 39
1.114 Cho biểu thức:
1
a1
3
:a1
a1
3
B
2
.
a) Tìm điều kiện xác định của B.
b) Rút gọn B.
c) Tính giá trị của B khi
32
3
a
d) Tìm giá trị của a để :
BB
.
1.115 Cho biểu thức:
222222
baa
b
:1
ba
a
ba
a
M
.
a) Rút gọn M.
b) Tìm giá trị của M nếu
2
3
b
a
c) Tìm điều kiện của a, b để M < 1.
1.116 Cho biểu thức:
2
x1
1x2x
2x
1x
2x
P
2
.
a) Tìm điều kiện xác định của P.
b) Rút gọn P.
c) Tính giá trị lớn nhất của P.
d) Chứng minh: nếu 0 < x < 1 thì P > 0.
1.117 Cho biểu thức:
x3
1x2
2x
3x
6x5x
9x2
Q
.
a) Tìm điều kiện xác định của Q.
b) Rút gọn Q.
c) Tìm các giá trị của x để Q < 1
d) Tìm x Z sao cho Q Z.
1.118 Cho biểu thức:
yx
xyyx
:
xy
yx
yx
yx
Q
2
33
.
a) Tìm điều kiện xác định của Q. b) Rút gọn Q.
c) So sánh Q với Q d) Chứng minh Q 0.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 40
1.119 Cho biểu thức:
x1
2x
2x
1x
2xx
3x9x3
M
.
a) Tìm ĐKXĐ và rút gọn M b) Tìm x Z sao cho M Z.
1.120 Cho biểu thức:
x3
3x2
x1
2x3
3x2x
11x15
P
.
a) Tìm điều kiện xác định của P b) Rút gọn P.
c) Giải phương trình P =
2
1
d) So sánh P với
3
2
.
1.121 Cho biểu thức:
3x
3x2
2x
3x
6xx
x9
:1
9x
x3x
Q .
a) Tìm ĐKXĐ và rút gọn Q b) Tìm x để Q < 1.
1.122 Cho biểu thức:
1xx
2
1xx
3
1x
1
M
.
a) Rút gọn M. b) Chứng minh: M 1.
1.123 Cho biểu thức:
1xx
xx
1xx
xx
N
22
.
Hãy rút gọn A = 1 – 1xN .
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 65
1.49 Cho ABC có đường cao AH. Biết HB = 20cm, HC = 21cm,
0
B 45
.
Tính AC.
1.50 a) Cho cos = 0,8. Hãy tìm sin, tan, cot.
b) Cho tan =
3
4
. Hãy tìm sin, cos, cot.
c) Cho cot =
7
3
. Hãy tìm sin, cos, tan.
1.51 Biết tanB = 2. Tính :
sinB cosB
A
sinB cosB
2sin cos
B
3sin 4cos
2 2
C sin 2sin .cos 3cos
2 2
sin sin .cos cos
D
2sin .cos
1.52 Biết
2
sin
5
. Tính
2tan 10cos
M
5cos 4cot
1.53 Hãy tìm cos và tan, nếu:
a)
3
sin
5
b)
40
sin
41
1.54 Hãy tìm sin và cos, nếu:
a)
1
tan
3
b)
3
cot
4
1 - Tìm hiểu bài toán:
Đâu là ẩn? đâu l
à d
ữ kiện? đâu là đi
ều kiện? có thể thỏa
mãn
điều kiện b
ài
toán? đi
ều kiện có đủ để xác định ẩn? Hay
là th
ừa, hay c
òn thi
ếu? Hay có mâu thuẫn?
V
ẽ h
ình.
S
ki
ện, dữ kiện th
ành công th
ức được không? Phân biệt r
õ các
ph
ần của điều kiện.
(Xem ti
ếp ở trang 6
8)
Giải bài toán như thế nào? – Phần 2
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 40
1.119 Cho biểu thức:
x1
2x
2x
1x
2xx
3x9x3
M
.
a) Tìm ĐKXĐ và rút gọn M b) Tìm x Z sao cho M Z.
1.120 Cho biểu thức:
x3
3x2
x1
2x3
3x2x
11x15
P
.
a) Tìm điều kiện xác định của P b) Rút gọn P.
c) Giải phương trình P =
2
1
d) So sánh P với
3
2
.
1.121 Cho biểu thức:
3x
3x2
2x
3x
6xx
x9
:1
9x
x3x
Q .
a) Tìm ĐKXĐ và rút gọn Q b) Tìm x để Q < 1.
1.122 Cho biểu thức:
1xx
2
1xx
3
1x
1
M
.
a) Rút gọn M. b) Chứng minh: M 1.
1.123 Cho biểu thức:
1xx
xx
1xx
xx
N
22
.
Hãy rút gọn A = 1 – 1xN .
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 65
1.49 Cho ABC có đường cao AH. Biết HB = 20cm, HC = 21cm,
0
B 45
.
Tính AC.
1.50 a) Cho cos = 0,8. Hãy tìm sin, tan, cot.
b) Cho tan =
3
4
. Hãy tìm sin, cos, cot.
c) Cho cot =
7
3
. Hãy tìm sin, cos, tan.
1.51 Biết tanB = 2. Tính :
sinB cosB
A
sinB cosB
2sin cos
B
3sin 4cos
2 2
C sin 2sin .cos 3cos
2 2
sin sin .cos cos
D
2sin .cos
1.52 Biết
2
sin
5
. Tính
2tan 10cos
M
5cos 4cot
1.53 Hãy tìm cos và tan, nếu:
a)
3
sin
5
b)
40
sin
41
1.54 Hãy tìm sin và cos, nếu:
a)
1
tan
3
b)
3
cot
4
1 - Tìm hiểu bài toán:
Đâu là ẩn? đâu l
à d
ữ kiện? đâu là đi
ều kiện? có thể thỏa
mãn
điều kiện b
ài
toán? đi
ều kiện có đủ để xác định ẩn? Hay
là th
ừa, hay c
òn thi
ếu? Hay có mâu thuẫn?
V
ẽ h
ình.
S
ử dụng các kí hiệu thích hợp, có thể biểu diễn các điều
ki
ện, dữ kiện th
ành công th
ức được không? Phân biệt r
õ các
ph
ần của điều kiện.
(Xem ti
ếp ở trang 6
8)
Giải bài toán như thế nào? – Phần 2
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 64
1.41 Tính giá trị của x (làm tròn đến chữ số thập phân thứ 3) trong mỗi trường
hợp sau. Biết tanB 1,072; cosE 0,188.
1.42 Cho MNP vuông ở M, đường cao MQ chia cạnh huyền NP thành hai
đoạn NQ = 3, PQ = 6. Hãy so sánh cotN và cotP. Tỉ số nào lớn hơn và lớn
hơn bao nhiêu lần.
1.43 Biến đổi tỉ số lượng giác của các góc sau đây thành tỉ số lượng giác của
các góc nhỏ hơn 45
0
:
sin60
0
, cos75
0
, sin52
0
30, cot82
0
, tan80
0
.
1.44 Dựng góc nhọn , biết:
a)
2
sin
3
b) cos = 0,5 c)
3
tan
4
d)
3
cot
2
1.45 Sử dụng định nghĩa các tỉ số lượng giác của một góc nhọn để chứng minh
rằng: Với góc nhọn tùy ý, ta có:
a) sin < 1, cos < 1
b)
sin
tan
cos
,
cos
cot
sin
, tan . cot = 1
c) sin
2
+ cos
2
= 1
1.46 Cạnh huyền của một tam giác vuông có một góc bằng 60
0
là 8. Hãy tìm
độ dài của cạnh đối diện với góc 60
0
.
1.47 Cạnh góc vuông kề với góc 60
0
của một tam giác vuông bằng 3. Hãy tìm
cạnh huyền và cạnh góc vuông còn lại (sử dụng bảng lượng giác của các
góc đặc biệt).
1.48 Đường cao BD của tam giác nhọn ABC bằng 6, đoạn thẳng AD bằng 5.
a) Tính diện tích ABD.
b) Tính AC, dùng các thông tin sau đây nếu cần:
3
sin
5
,
4
cosC
5
.
A
B
63
( a )
x
C
D
F
E
(b )
16
x
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 41
Chương 2
HÀM SỐ BẬC NHẤT
A - Nhắc lại và bổ sung các khái niệm về hàm số
2.1 Hãy biểu diễn các điểm sau trên cùng một mặt phẳng tọa độ:
A(0 ; –3) B(2 ; 0) C(1 ; 3) D(–2 ; 4) F(–3 ; –2)
G(2 ; –4) H(0 ;
2
) I(–
3
; 0) J(–
2
;
3
) K(–
2
;–
3
).
2.2 Trong các bảng sau ghi các giá trị tương ứng của x và y. Bảng nào xác
định y là hàm số của x ? Vì sao ?
x 1 2 4 5 7 8 x 3 4 3 5 8
y 3 5 9 11 15 17 y 6 8 4 8 16
2.3 a) Cho hàm số y = f(x) =
2
5
x.
Tính: f(–2) ; f(–1) ; f(0) ; f
1
2
; f(1); f(2); f(3)
b) Cho hàm số y = g(x) =
2
5
x + 3
1. Hàm số f từ tập hợp số X đến tập hợp số Y là một qui tắc cho tương ứng
mỗi giá trị x
X với một và chỉ một giá trị y
Y mà ta kí hiệu f(x), x là
biến số, y = f(x) là giá trị của hàm số tại x.
2. Cho hàm số y = f(x) xác định với mọi x thuộc R.
Xét hai giá trị bất kì x
1
, x
2
R:
x
1
< x
2
f(x
1
) < f(x
2
) : hàm số đồng biến trên R.
x
1
< x
2
f(x
1
) > f(x
2
) : hàm số nghịch biến trên R.
3. Đồ thị của hàm số y = f(x) là tập hợp các điểm M(x ; y) trên mặt phẳng
tọa độ thỏa y = f(x).
Gọi (C) là đồ thị của hàm số f, ta có:
A(x
A
; y
A
)
(C)
y
A
= f(x
A
).
B(x
B
; y
B
)
(C)
y
B
f(x
B
).
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 64
1.41 Tính giá trị của x (làm tròn đến chữ số thập phân thứ 3) trong mỗi trường
hợp sau. Biết tanB 1,072; cosE 0,188.
1.42 Cho MNP vuông ở M, đường cao MQ chia cạnh huyền NP thành hai
đoạn NQ = 3, PQ = 6. Hãy so sánh cotN và cotP. Tỉ số nào lớn hơn và lớn
hơn bao nhiêu lần.
1.43 Biến đổi tỉ số lượng giác của các góc sau đây thành tỉ số lượng giác của
các góc nhỏ hơn 45
0
:
sin60
0
, cos75
0
, sin52
0
30, cot82
0
, tan80
0
.
1.44 Dựng góc nhọn , biết:
a)
2
sin
3
b) cos = 0,5 c)
3
tan
4
d)
3
cot
2
1.45 Sử dụng định nghĩa các tỉ số lượng giác của một góc nhọn để chứng minh
rằng: Với góc nhọn tùy ý, ta có:
a) sin < 1, cos < 1
b)
sin
tan
cos
,
cos
cot
sin
, tan . cot = 1
c) sin
2
+ cos
2
= 1
1.46 Cạnh huyền của một tam giác vuông có một góc bằng 60
0
là 8. Hãy tìm
độ dài của cạnh đối diện với góc 60
0
.
1.47 Cạnh góc vuông kề với góc 60
0
của một tam giác vuông bằng 3. Hãy tìm
cạnh huyền và cạnh góc vuông còn lại (sử dụng bảng lượng giác của các
góc đặc biệt).
1.48 Đường cao BD của tam giác nhọn ABC bằng 6, đoạn thẳng AD bằng 5.
a) Tính diện tích ABD.
b) Tính AC, dùng các thông tin sau đây nếu cần:
3
sin
5
,
4
cosC
5
.
A
B
63
( a )
x
C
D
F
E
(b )
16
x
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 41
Chương 2
HÀM SỐ BẬC NHẤT

A - Nhắc lại và bổ sung các khái niệm về hàm số
2.1 Hãy biểu diễn các điểm sau trên cùng một mặt phẳng tọa độ:
A(0 ; –3) B(2 ; 0) C(1 ; 3) D(–2 ; 4) F(–3 ; –2)
G(2 ; –4) H(0 ;
2
) I(–
3
; 0) J(–
2
;
3
) K(–
2
;–
3
).
2.2 Trong các bảng sau ghi các giá trị tương ứng của x và y. Bảng nào xác
định y là hàm số của x ? Vì sao ?
x 1 2 4 5 7 8 x 3 4 3 5 8
y 3 5 9 11 15 17 y 6 8 4 8 16
2.3 a) Cho hàm số y = f(x) =
2
5
x.
Tính: f(–2) ; f(–1) ; f(0) ; f
1
2
; f(1); f(2); f(3)
b) Cho hàm số y = g(x) =
2
5
x + 3
1. Hàm số f từ tập hợp số X đến tập hợp số Y là một qui tắc cho tương ứng
mỗi giá trị x
X với một và chỉ một giá trị y
Y mà ta kí hiệu f(x), x là
biến số, y = f(x) là giá trị của hàm số tại x.
2. Cho hàm số y = f(x) xác định với mọi x thuộc R.
Xét hai giá trị bất kì x
1
, x
2
R:
x
1
< x
2
f(x
1
) < f(x
2
) : hàm số đồng biến trên R.
x
1
< x
2
f(x
1
) > f(x
2
) : hàm số nghịch biến trên R.
3. Đồ thị của hàm số y = f(x) là tập hợp các điểm M(x ; y) trên mặt phẳng
tọa độ thỏa y = f(x).
Gọi (C) là đồ thị của hàm số f, ta có:
A(x
A
; y
A
)
(C)
y
A
= f(x
A
).
B(x
B
; y
B
)
(C)
y
B
f(x
B
).
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 42
Tính: g(–2); g(–1); g(0); g
1
2
; g(1); g(2); g(3)
c) Có nhận xét gì về giá trị của hai hàm số đã cho ở trên khi biến x lấy
cùng một giá trị ?
2.4 Cho hàm số y = f(x) =
3
4
x.
Tính : f(–3) ; f(–2) ; f(–1) ; f (0) ; f
1
2
; f(a) ; f(a + 1)
2.5 Cho hàm số y = f(x) =
2
5
x + 3.
a) Tính giá trị tương ứng của y theo các giá trị của x rồi điền vào bảng:
x – 2 –1,5
– 1 –0,5
0 0,5 1 1,5 2
y =
5
2
x + 3
b) Hàm số đã cho là hàm đồng biến hay nghịch biến ? Vì sao ?
2.6 Cho hai hàm số y = 3x và y = – 3x.
a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của hai hàm số đã cho.
b) Trong hai hàm số trên, hàm số nào đồng biến ? Hàm số nào nghịch
biến ? Vì sao ?
2.7 Cho hai hàm số y = x và y = 0,25x.
a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của hai hàm số đã cho.
b) Đường thẳng song song với trục Ox và cắt trục Oy tại điểm có tung độ
là 4 lần lượt cắt các đường thẳng y = x và y = 0,25x tại A và B. Tìm
tọa độ của các điểm A, B và tính chu vi, diện tích của OAB theo đơn
vị đo trên các trục tọa độ là xentimét.
2.8 Cho hai hàm số y = 2x và y = 2x + 3.
a) Tính giá trị y tương ứng của mỗi hàm số theo giá trị của biến x rồi điền
vào bảng sau:
x – 2,25
–1,5 – 1 0 1 1,5 2,25
y = 2x
y = 2x + 3
b) Có nhận xét gì về các giá trị tương ứng của hai hàm số khi biến x lấy
cùng một giá trị ?
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 63
4. Một số hệ thức giữa các tỉ số lượng giác của một góc nhọn:
Cho góc nhọn
, ta có:
1)
2 2
sin cos 1
2)
sin
tan
cos
3)
cos
cot
sin
4) tan
.cot
= 1
5. So sánh các tỉ số lượng giác:
Khi góc nhọn
tăng dần thì sin
và tan
tăng, còn cos
và cot
giảm
Với cùng một góc nhọn
thì: sin
< tan
; cos
< cot
.
1.34 Cho ABC vuong tại A, đường cao AH. Tính các tỉ số lượng giác của các
góc B từ đó suy ra các tỉ số lượng giác của góc C, nếu biết:
a) AB = 16cm; BC = 12 cm b) AB = 13 cm; BH = 5 cm
c) BH = 16 cm; CH = 9 cm d) AB = 6 cm; AC = 8 cm
1.35 Lập tỉ số lượng giác của góc 34
0
bằng cách vẽ một tam giác vuông có một
góc nhọn 34
0
.
1.36 Cho ABC vuông tại C, trong đó AC = 0,90m, BC = 1,20m. Tính các tỉ
số lượng giác của góc B, từ đó suy ra các tỉ số lượng giác của góc A.
1.37 Cho hình bên:
Biết
3
tan
4
. Hãy tính:
a) Cạnh AC.
b) Cạnh BC.
1.38 Cho ABC vuông tại A,
0
B 30
, BC = 8cm. Hãy tính cạnh AB (làm tròn
đến chữ số thập phân thứ ba). Biết cos30
0
0,866.
1.39 Cho ABC vuông tại A, Chứng minh rằng:
AC sinB
AB sinC
.
1.40 Cho ABC vuông tại A. Kẻ đường cao AH. Tính sinB, sinC, biết:
a) AB = 13cm, BH = 5cm. b) BH = 3cm, CH = 4cm.
A
B
C
6 cm
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 42
Tính: g(–2); g(–1); g(0); g
1
2
; g(1); g(2); g(3)
c) Có nhận xét gì về giá trị của hai hàm số đã cho ở trên khi biến x lấy
cùng một giá trị ?
2.4 Cho hàm số y = f(x) =
3
4
x.
Tính : f(–3) ; f(–2) ; f(–1) ; f (0) ; f
1
2
; f(a) ; f(a + 1)
2.5 Cho hàm số y = f(x) =
2
5
x + 3.
a) Tính giá trị tương ứng của y theo các giá trị của x rồi điền vào bảng:
x – 2 –1,5
– 1 –0,5
0 0,5 1 1,5 2
y =
5
2
x + 3
b) Hàm số đã cho là hàm đồng biến hay nghịch biến ? Vì sao ?
2.6 Cho hai hàm số y = 3x và y = – 3x.
a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của hai hàm số đã cho.
b) Trong hai hàm số trên, hàm số nào đồng biến ? Hàm số nào nghịch
biến ? Vì sao ?
2.7 Cho hai hàm số y = x và y = 0,25x.
a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của hai hàm số đã cho.
b) Đường thẳng song song với trục Ox và cắt trục Oy tại điểm có tung độ
là 4 lần lượt cắt các đường thẳng y = x và y = 0,25x tại A và B. Tìm
tọa độ của các điểm A, B và tính chu vi, diện tích của OAB theo đơn
vị đo trên các trục tọa độ là xentimét.
2.8 Cho hai hàm số y = 2x và y = 2x + 3.
a) Tính giá trị y tương ứng của mỗi hàm số theo giá trị của biến x rồi điền
vào bảng sau:
x – 2,25
–1,5 – 1 0 1 1,5 2,25
y = 2x
y = 2x + 3
b) Có nhận xét gì về các giá trị tương ứng của hai hàm số khi biến x lấy
cùng một giá trị ?
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 63
4. Một số hệ thức giữa các tỉ số lượng giác của một góc nhọn:
Cho góc nhọn
, ta có:
1)
2 2
sin cos 1
2)
sin
tan
cos
3)
cos
cot
sin
4) tan
.cot
= 1
5. So sánh các tỉ số lượng giác:
Khi góc nhọn
tăng dần thì sin
và tan
tăng, còn cos
và cot
giảm
Với cùng một góc nhọn
thì: sin
< tan
; cos
< cot
.
1.34 Cho ABC vuong tại A, đường cao AH. Tính các tỉ số lượng giác của các
góc B từ đó suy ra các tỉ số lượng giác của góc C, nếu biết:
a) AB = 16cm; BC = 12 cm b) AB = 13 cm; BH = 5 cm
c) BH = 16 cm; CH = 9 cm d) AB = 6 cm; AC = 8 cm
1.35 Lập tỉ số lượng giác của góc 34
0
bằng cách vẽ một tam giác vuông có một
góc nhọn 34
0
.
1.36 Cho ABC vuông tại C, trong đó AC = 0,90m, BC = 1,20m. Tính các tỉ
số lượng giác của góc B, từ đó suy ra các tỉ số lượng giác của góc A.
1.37 Cho hình bên:
Biết
3
tan
4
. Hãy tính:
a) Cạnh AC.
b) Cạnh BC.
1.38 Cho ABC vuông tại A,
0
B 30
, BC = 8cm. Hãy tính cạnh AB (làm tròn
đến chữ số thập phân thứ ba). Biết cos30
0
0,866.
1.39 Cho ABC vuông tại A, Chứng minh rằng:
AC sinB
AB sinC
.
1.40 Cho ABC vuông tại A. Kẻ đường cao AH. Tính sinB, sinC, biết:
a) AB = 13cm, BH = 5cm. b) BH = 3cm, CH = 4cm.
A
B
C
6 cm
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 62
B - Tỉ số lượng giác của góc nhọn
1. Định nghĩa:
1.
doi AB
sin
huyen BC
2.
ke AC
cos
huyen BC
3.
doi AB
tan
ke AC
4.
ke AC
cot
doi AB
2. Tỉ số lượng giác của hai góc phụ nhau (có tổng số đo bằng 90
0
):
1) sin
= cos
2) cos
= sin
3) tan
= cot
4) cot
= tan
3. Bảng tỉ số lượng giác của các góc đặc biệt:
30
0
45
0
60
0
sin
2
1
2
2
3
2
cos
3
2
2
2
2
1
tan
3
3
1
3
cot
3
1
3
3
A
B
C
A
B
C
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 43
2.9 Cho hàm số y = f(x) = 5x.
Cho x hai giá trị bất kì x
1
, x
2
sao cho x
1
< x
2
. Hãy chứng minh f(x
1
) < f(x
2
)
rồi rút ra kết luận hàm số đã cho đồng bến trên R.
2.10 Cho hàm số y = f(x) = – 2x.
Cho x hai giá trị bất kì x
1
, x
2
sao cho x
1
< x
2
. Hãy chứng minh f(x
1
) > f(x
2
)
rồi rút ra kết luận hàm số đã cho nghịch bến trên R.
2.11 Cho hàm số y = f(x) = –
2
5
x + 3 với x R. Chứng minh rằng hàm số
nghịch biến trên R.
2.12 Chứng minh hàm số y = 2x – 1 đồng biến trên R.
2.13 Cho hàm số y = f(x) =
x
.
a) Tìm ĐKXĐ và chứng minh rằng hàm số đồng biến với ĐKXĐ đó.
b) Trong các điểm A(4 ; 2), B(2 ; 1), C(9 ; –3), D(8 ; 2
2
) điểm nào
thuộc và điểm nào không thuộc đồ thị của hàm số trên ?
2.14 Tìm điều kiện xác định của các hàm số sau:
a) y = – x + 5 b) y = 2x
2
c) y = 3 d) y =
2
x 1
x 2x 3
e)
2
3 x
y
7x 10 x
f)
5 x
y
x 1
g)
y x 2x 1
h)
y x 5 3 x
i)
y 2 x 2 1 x
j) y =
2
x 3x 2
2.15 Cho hàm số y = f(x) =
2
x 3x 2
.
a) Tìm ĐKXĐ của hàm số.
b) Hãy so sánh f
5
4
và f
7
4
.
c) Tìm x, biết f(x) =
1
2
2.16 Cho hàm số y = f(x) =
x 1
x 1
.
a) Tìm ĐKXĐ của hàm số.
b) Tính f(4 – 2
3
); f(a
2
) với a < –1.
c) Tìm giá trị x để f(x) =
3
d) Tìm giá trị x để f(x) = f(x
2
).
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 62
B - Tỉ số lượng giác của góc nhọn
1. Định nghĩa:
1.
doi AB
sin
huyen BC
2.
ke AC
cos
huyen BC
3.
doi AB
tan
ke AC
4.
ke AC
cot
doi AB
2. Tỉ số lượng giác của hai góc phụ nhau (có tổng số đo bằng 90
0
):
1) sin
= cos
2) cos
= sin
3) tan
= cot
4) cot
= tan
3. Bảng tỉ số lượng giác của các góc đặc biệt:
30
0
45
0
60
0
sin
2
1
2
2
3
2
cos
3
2
2
2
2
1
tan
3
3
1
3
cot
3
1
3
3
A
B
C
A
B
C
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 43
2.9 Cho hàm số y = f(x) = 5x.
Cho x hai giá trị bất kì x
1
, x
2
sao cho x
1
< x
2
. Hãy chứng minh f(x
1
) < f(x
2
)
rồi rút ra kết luận hàm số đã cho đồng bến trên R.
2.10 Cho hàm số y = f(x) = – 2x.
Cho x hai giá trị bất kì x
1
, x
2
sao cho x
1
< x
2
. Hãy chứng minh f(x
1
) > f(x
2
)
rồi rút ra kết luận hàm số đã cho nghịch bến trên R.
2.11 Cho hàm số y = f(x) = –
2
5
x + 3 với x R. Chứng minh rằng hàm số
nghịch biến trên R.
2.12 Chứng minh hàm số y = 2x – 1 đồng biến trên R.
2.13 Cho hàm số y = f(x) =
x
.
a) Tìm ĐKXĐ và chứng minh rằng hàm số đồng biến với ĐKXĐ đó.
b) Trong các điểm A(4 ; 2), B(2 ; 1), C(9 ; –3), D(8 ; 2
2
) điểm nào
thuộc và điểm nào không thuộc đồ thị của hàm số trên ?
2.14 Tìm điều kiện xác định của các hàm số sau:
a) y = – x + 5 b) y = 2x
2
c) y = 3 d) y =
2
x 1
x 2x 3
e)
2
3 x
y
7x 10 x
f)
5 x
y
x 1
g)
y x 2x 1
h)
y x 5 3 x
i)
y 2 x 2 1 x
j) y =
2
x 3x 2
2.15 Cho hàm số y = f(x) =
2
x 3x 2
.
a) Tìm ĐKXĐ của hàm số.
b) Hãy so sánh f
5
4
và f
7
4
.
c) Tìm x, biết f(x) =
1
2
2.16 Cho hàm số y = f(x) =
x 1
x 1
.
a) Tìm ĐKXĐ của hàm số.
b) Tính f(4 – 2
3
); f(a
2
) với a < –1.
c) Tìm giá trị x để f(x) =
3
d) Tìm giá trị x để f(x) = f(x
2
).
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 44
2.17 Cho hai hàm số y = f(x) = 6x
2
và y = g(x) = 5x.
a) Hãy chứng tỏ f(–x) = f(x) và g(–x) = – g(x).
b) Tìm số a sao cho f(a) = g(a)
2.18 Cho 2 hàm số
2
y f(x) x 4
và
2
y g(x) x 4
.
Hãy tính f
1
a
a
+ g
1
a
a
với a > 0.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 61
a) AB.AD = AC.AE b)
2
2
AB BH
AC CH
c)
3
3
AB BD
AC CE
d)
3
AH BC.BD.CE
e) Biết BC = 10 cm, AH = 4 cm. Tính HB, HC và S
ADHE
, S
BDEC
.
1.32 Cho hình vuông ABCD, M là điểm nằm giữa B và C. Đường thẳng AM
cắt đường thẳng DB, DC lần lượt tại I và N. Chứng minh:
a) IB
2
+ ID
2
= 2IA
2
. b)
2 2 2
1 1 1
AB AM AN
1.33 Cho ABC. Từ một điểm M bất kỳ trong tam giác kẻ MD BC,
ME AC, MF AB.
Chứng minh rằng: BD
2
+ CE
2
+ AF
2
= DC
2
+ EA
2
+ FB
2
.
G. Polya là m
ột nh
à Toán h
ọc, nhà sư ph
ạm nổi
ti
ếng người Mỹ, nếu bạn l
à m
ột ngư
ời quan tâm
nhi
ều đến Toán học cũng như các vấn đề li
ên quan
ch
ắc hẳn bạn đ
ã t
ừng đọc qua ho
ặc ghe nói đến
b
ộ sách 3 quyển của ông đư
ợc dịch ra tiếng Việt
- Ba trong s
ố hững tác phẩm tâm huyết nhất của ông b
àn v
ề quá
trình gi
ải Toán, sáng tạo, t
ìm tòi các v
ấn đề Toán "Giải b
ài toán
như thế n
ào?", "Sáng t
ạo Toán học" v
à "Toán h
ọc v
à nh
ững s
uy
lu
ận có lý".
Đây là bài viết tóm lư
ợc những ý chính trong quyển
sách "Gi
ải bài toán như thế n
ào?" - c
ũng cần nói th
êm
ở đây rằng
t
ừ "Giải bài toán" theo G. Polya không đơn thuần chỉ dừn
g l
ại ở
vi
ệc t
ìm ra
đáp số, như nhiều học sinh thậm chí cả sinh vi
ên v
ẫn
thường hay hiểu,
"Gi
ải b
ài toán"
ở đây bao quát to
àn b
ộ quá tr
ình
suy ng
ẫm, t
ìm tòi l
ời giải cũng như l
ý gi
ải nguy
ên nhân phát sinh
bài toán, và cu
ối c
ùng là phát tri
ển b
ài toán v
ừa làm đư
ợc, hoặc ít
ra nêu ra nh
ững hướng đi mới trên cơ sở đ
ã hi
ểu nguồn gốc từ đâu
bài toán phát sinh.
(Xem ti
ếp ở trang 65)
Giải bài toán như thế nào? – Phần 1
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 44
2.17 Cho hai hàm số y = f(x) = 6x
2
và y = g(x) = 5x.
a) Hãy chứng tỏ f(–x) = f(x) và g(–x) = – g(x).
b) Tìm số a sao cho f(a) = g(a)
2.18 Cho 2 hàm số
2
y f(x) x 4
và
2
y g(x) x 4
.
Hãy tính f
1
a
a
+ g
1
a
a
với a > 0.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 61
a) AB.AD = AC.AE b)
2
2
AB BH
AC CH
c)
3
3
AB BD
AC CE
d)
3
AH BC.BD.CE
e) Biết BC = 10 cm, AH = 4 cm. Tính HB, HC và S
ADHE
, S
BDEC
.
1.32 Cho hình vuông ABCD, M là điểm nằm giữa B và C. Đường thẳng AM
cắt đường thẳng DB, DC lần lượt tại I và N. Chứng minh:
a) IB
2
+ ID
2
= 2IA
2
. b)
2 2 2
1 1 1
AB AM AN
1.33 Cho ABC. Từ một điểm M bất kỳ trong tam giác kẻ MD BC,
ME AC, MF AB.
Chứng minh rằng: BD
2
+ CE
2
+ AF
2
= DC
2
+ EA
2
+ FB
2
.
G. Polya là m
ột nh
à Toán h
ọc, nhà sư ph
ạm nổi
ti
ếng người Mỹ, nếu bạn l
à m
ột ngư
ời quan tâm
nhi
ều đến Toán học cũng như các vấn đề li
ên quan
ch
ắc hẳn bạn đ
ã t
ừng đọc qua ho
ặc ghe nói đến
b
ộ sách 3 quyển của ông đư
ợc dịch ra tiếng Việt
- Ba trong s
ố hững tác phẩm tâm huyết nhất của ông b
àn v
ề quá
trình gi
ải Toán, sáng tạo, t
ìm tòi các v
ấn đề Toán "Giải b
ài toán
như thế n
ào?", "Sáng t
ạo Toán học" v
à "Toán h
ọc v
à nh
ững s
uy
lu
ận có lý".
Đây là bài viết tóm lư
ợc những ý chính trong quyển
sách "Gi
ải bài toán như thế n
ào?" - c
ũng cần nói th
êm
ở đây rằng
t
ừ "Giải bài toán" theo G. Polya không đơn thuần chỉ dừn
g l
ại ở
vi
ệc t
ìm ra
đáp số, như nhiều học sinh thậm chí cả sinh vi
ên v
ẫn
thường hay hiểu,
"Gi
ải b
ài toán"
ở đây bao quát to
àn b
ộ quá tr
ình
suy ng
ẫm, t
ìm tòi l
ời giải cũng như l
ý gi
ải nguy
ên nhân phát sinh
bài toán, và cu
ối c
ùng là phát tri
ển b
ài toán v
ừa làm đư
ợc, hoặc ít
ra nêu ra nh
ững hướng đi mới trên cơ sở đ
ã hi
ểu nguồn gốc từ đâu
bài toán phát sinh.
(Xem ti
ếp ở trang 65)
Giải bài toán như thế nào? – Phần 1
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 60
b) Kẻ Bx // AC cắt AH ở D. Tính HD và c/m: AB
2
= AC . BD.
c) Kẻ DE AC (E AC), DE cắt BC ở F. C/minh: BH
2
= HF . HC
d) Chứng minh: S
ABH
= S
CDH
. (Không cần tính diện tích)
1.27 Cho ABC vuông ở A có AB = 12cm, AC = 16cm.
a) Tính độ dài trung tuyến AM.
b) Kẻ đường cao AH. Tính chu vi ABH.
c) Tia phân giác của góc AMB và góc AMC cắt AB, AC lần lượt ở D và
E. Chứng minh: ABC và ADE đồng dạng.
d) Tính: S
BDEC
và S
DME
.
1.28 Cho ABC vuông tại A, đường cao AD. Đặt BC = a, AB = c, AC = b,
AD = h.
a) Chứng minh rằng số đo độ dài h; b + c; a + h là độ dài ba cạnh của
một tam giác vuông.
b) Chứng minh: EA.EB + FE.FB = DB.DC
c) C/minh hệ thức trên đúng với mọi vị trí của D bất kì trên cạnh BC.
d) Kẻ DE AB tại E, DF AC tại F. Chứng minh rằng:
2
2 2
b c
AE
b c
và
2
2 2
bc
AF
b c
e) Chứng minh rằng:
3
3
BF c
CF b
1.29 Cho hình thang ABCD (AB // CD) có AB = 4cm, CD = 9cm, BD = 5cm,
AC = 12cm.
a) Qua B kẻ đường thẳng song song với AC, cắt DC ở E. Tính
DBE
.
b) Tính diện tích hình thang ABCD.
1.30 Cho tam giác ABC vuông ở A, đường cao AH. Kẻ HD AB, HE AC,
AK DE (D AB, E AC, K DE). Gọi I là giao điểm của AH và
DE. Biết AI
2
= AD.AE.
a) Chứng minh: AI
2
= DE.AK.
b) Tính
AIK
. Tính các góc của ABC.
c) AK cắt BC ở N. Chứng minh: N là trung điểm của BC.
1.31 Cho ABC vuông tại A (AB < AC) với đường cao AH. Gọi D và E lần
lượt là hình chiếu của H trên AB và AC. Chứng minh:
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 45
B - Hàm số bậc nhất y = ax + b (a 0)
C - Hệ số góc của đường thẳng y = ax + b (a 0)
2.19 Trong các hàm số sau, hàm số nào là hàm số bậc nhất ? Hãy xác định các
hệ số a, b của chúng và xét xem hàm số bậc nhất đó đồng biến hay nghịch
biến ?
a) y = 1 – 5x b) y = – 0,5x
c) y =
2
(x – 1) +
3
d) y = 2x
2
+ 3
e) y =
3
x –
2
(2 – x) f) y = 3 – 0,5x
g) y = –1,5x h) y = 5 – 2x
2
1. Hàm số bậc nhất là hàm số được cho bởi công thức y = ax + b, trong đó
a, b là các số cho trước và a
0.
2. Hàm số bậc nhất xác định với mọi x
R và có tính chất sau:
Đồng biến trên R khi a > 0.
Nghịch biến trên R khi a < 0.
3. Đồ thị của hàm số y = ax + b (a
0) là một đường thẳng:
Cắt trục tung tại điểm có tung độ bằng b. (b gọi là tung độ gốc của
đường thẳng)
Song song với đường thẳng y = ax, nếu b
0, trùng với đường thẳng
y = ax nếu b = 0.
4. Để vẽ đồ thị của hàm số y = ax + b ta chỉ cần xác định dược hai điểm
phân biệt nào đó thuộc đồ thị rồi vẽ đường thẳng đi qua hai điểm đó. Ta
thường xác định hai điểm đặc biệt là giao điểm của đồ thị với hai trục
tọa độ.
5. Hệ số a của đường thẳng y = ax + b gọi là hệ số góc của đường thẳng.
Còn b được gọi là tung độ gốc của đường thẳng.
6. Cho 2 đường thẳng: (d) : y =ax + b và (d
) : y = a
x + b
(với a, a
0):
(d)
(d
)
a = a
và b = b
(d) // (d
)
a = a
và b
b
(d) cắt (d
)
a
a
(d)
(d
)
a . a
= –1
(d) cắt (d
) tại một điểm trên trục tung
a
a
và b = b
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 60
b) Kẻ Bx // AC cắt AH ở D. Tính HD và c/m: AB
2
= AC . BD.
c) Kẻ DE AC (E AC), DE cắt BC ở F. C/minh: BH
2
= HF . HC
d) Chứng minh: S
ABH
= S
CDH
. (Không cần tính diện tích)
1.27 Cho ABC vuông ở A có AB = 12cm, AC = 16cm.
a) Tính độ dài trung tuyến AM.
b) Kẻ đường cao AH. Tính chu vi ABH.
c) Tia phân giác của góc AMB và góc AMC cắt AB, AC lần lượt ở D và
E. Chứng minh: ABC và ADE đồng dạng.
d) Tính: S
BDEC
và S
DME
.
1.28 Cho ABC vuông tại A, đường cao AD. Đặt BC = a, AB = c, AC = b,
AD = h.
a) Chứng minh rằng số đo độ dài h; b + c; a + h là độ dài ba cạnh của
một tam giác vuông.
b) Chứng minh: EA.EB + FE.FB = DB.DC
c) C/minh hệ thức trên đúng với mọi vị trí của D bất kì trên cạnh BC.
d) Kẻ DE AB tại E, DF AC tại F. Chứng minh rằng:
2
2 2
b c
AE
b c
và
2
2 2
bc
AF
b c
e) Chứng minh rằng:
3
3
BF c
CF b
1.29 Cho hình thang ABCD (AB // CD) có AB = 4cm, CD = 9cm, BD = 5cm,
AC = 12cm.
a) Qua B kẻ đường thẳng song song với AC, cắt DC ở E. Tính
DBE
.
b) Tính diện tích hình thang ABCD.
1.30 Cho tam giác ABC vuông ở A, đường cao AH. Kẻ HD AB, HE AC,
AK DE (D AB, E AC, K DE). Gọi I là giao điểm của AH và
DE. Biết AI
2
= AD.AE.
a) Chứng minh: AI
2
= DE.AK.
b) Tính
AIK
. Tính các góc của ABC.
c) AK cắt BC ở N. Chứng minh: N là trung điểm của BC.
1.31 Cho ABC vuông tại A (AB < AC) với đường cao AH. Gọi D và E lần
lượt là hình chiếu của H trên AB và AC. Chứng minh:
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 45
B - Hàm số bậc nhất y = ax + b (a 0)
C - Hệ số góc của đường thẳng y = ax + b (a 0)
2.19 Trong các hàm số sau, hàm số nào là hàm số bậc nhất ? Hãy xác định các
hệ số a, b của chúng và xét xem hàm số bậc nhất đó đồng biến hay nghịch
biến ?
a) y = 1 – 5x b) y = – 0,5x
c) y =
2
(x – 1) +
3
d) y = 2x
2
+ 3
e) y =
3
x –
2
(2 – x) f) y = 3 – 0,5x
g) y = –1,5x h) y = 5 – 2x
2
1. Hàm số bậc nhất là hàm số được cho bởi công thức y = ax + b, trong đó
a, b là các số cho trước và a
0.
2. Hàm số bậc nhất xác định với mọi x
R và có tính chất sau:
Đồng biến trên R khi a > 0.
Nghịch biến trên R khi a < 0.
3. Đồ thị của hàm số y = ax + b (a
0) là một đường thẳng:
Cắt trục tung tại điểm có tung độ bằng b. (b gọi là tung độ gốc của
đường thẳng)
Song song với đường thẳng y = ax, nếu b
0, trùng với đường thẳng
y = ax nếu b = 0.
4. Để vẽ đồ thị của hàm số y = ax + b ta chỉ cần xác định dược hai điểm
phân biệt nào đó thuộc đồ thị rồi vẽ đường thẳng đi qua hai điểm đó. Ta
thường xác định hai điểm đặc biệt là giao điểm của đồ thị với hai trục
tọa độ.
5. Hệ số a của đường thẳng y = ax + b gọi là hệ số góc của đường thẳng.
Còn b được gọi là tung độ gốc của đường thẳng.
6. Cho 2 đường thẳng: (d) : y =ax + b và (d
) : y = a
x + b
(với a, a
0):
(d)
(d
)
a = a
và b = b
(d) // (d
)
a = a
và b
b
(d) cắt (d
)
a
a
(d)
(d
)
a . a
= –1
(d) cắt (d
) tại một điểm trên trục tung
a
a
và b = b
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 46
i) y +
2
= x –
3
j) y =
1
x
k) y =
2x 1
3
l) y =
5 x 2
.
2.20 Cho các hàm số y = (m – 2)x + 3 và y = (m + 1) + 5. Tìm các giá trị của
m để mỗi hàm số:
a) Là hàm số bậc nhất
b) Là hàm số nghịch biến
c) Là hàm số đồng biến.
2.21 Một hình chữ nhật có các kích thước là 15cm và 25cm. Người ta tăng
thêm mỗi kích thước của hình đó thêm x (cm) được hình chữ nhật mới có
chu vi là y (cm). Hãy lập công thức tính y theo x.
2.22 Một hình chữ nhật có các kích thước là 30cm và 40cm. Người ta giảm bớt
mỗi kích thước của hình đó x (cm). Gọi S và P thứ tự là diện tích và chu
vi của hình chữ nhật mới theo x.
a) Hỏi rằng các đại lượng S và P có phải là hàm số bậc nhất của x không?
Vì sao ?
b) Tính giá trị tương ứng của P khi x nhận các giá trị (tính theo đợ vị cm)
sau: 0; 1; 1,5; 2,5; 3,5.
2.23 Chứng minh rằng hàm số bậc nhất y = ax + b đồng biến khi a > 0 và
nghịch biến khi a < 0.
2.24 Cho hàm số y = ax + 5. Tìm hệ số a, biết rằng khi x = 1 thì y = 2.
2.25 Với giá trị nào của m thì hàm số sau là hàm số bậc nhất ?
a) y =
5 m
(x – 1) b) y =
m 1
m 1
x + 3,5 c) y =
1
m 2
x –
3
4
2.26 Cho hàm số y = (1 –
5
)x – 1.
a) Hàm số trên là đồng biến hay nghịch biến trên R? Vì sao ?
b) Tính giá trị của y khi x = 1 +
5
c) Tính giá trị của x khi y =
5
.
2.27 Cho hàm số y = (3 –
2
)x + 1.
a) Hàm số trên là đồng biến hay nghịch biến trên R? Vì sao ?
b) Tính giá trị của y khi x nhận các giá trị: 0; 1;
2
; 3 +
2
; 3 –
2
c) Tính giá trị của x khi y nhận các giá trị: 0; 1; 8; 2 +
2
; 2 –
2
.
2.28 Tìm trên mặt phẳng tọa độ tất cả các điểm :
a) Có tung độ bằng 6; b) Có hoành độ bằng – 3 ;
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 59
1.16 Cho hình chữ nhật ABCD. Đường phân giác của
B
cắt đường chéo AC
thành hai đoạn
2
4 m
7
và
5
5 m
7
. Tính các kích thước của hình chữ nhật.
1.17 Cho ABC vuông tại A, vẽ đường cao AH. Chu vi của ABH là 30cm và
ACH là 40cm. Tính chu vi của ABC.
1.18 Cho ABC vuông tại A có cạnh AB = 6cm và AC = 8cm. Các đường
phân giác trong và ngoài của góc B cắt đường thẳng AC lần lượt tại M và
N. Tính các đoạn thẳng AM và AN.
1.19 Cho ABC vuông ở A, AB = 30cm, AC = 40cm, đường cao AH, trung
tuyến AM.
a) Tính BH, HM, MC. b) Tính AH.
1.20 Cho ABC vuông ở A, đường cao AH. Gọi M, N theo thứ tự là trung
điểm của AB, AC. Biết HM = 15cm, HN = 20cm. Tính HB, HC, AH.
1.21 Cho ABC cân ở A, đường cao BK. Biết AK = 7cm, KC = 2cm.
Tính BC.
1.22 Cho ABC vuông ở A có AC = 20cm, chiều cao AH = 12cm. Tính diện
tích ABC.
1.23 Cho hình vuông ABCD, gọi I là một điểm nằm giữa A và B. Tia DI và tia
cắt CB cắt nhau ở K. Qua D kẻ đường thẳng vuông góc với DI để đường
thẳng BC tại M.
a) Chứng minh: IDM cân.
b) Chứng minh:
2 2
1 1
DI DK
không đổi khi I di chuyển trên cạnh AB.
1.24 Cho hình thang vuông ABCD (
0
A D 90
) có hai đường chéo AC và
BD vuông góc với nhau tại H. Biết HD = 18 cm, HB = 8 cm. tính diện
tích hình thang ABCD.
1.25 Cho ABC cân tại A, kẻ đường cao AH và CK. Biết AH = 7,5 cm;
CK = 12 cm. Tính BC, AB.
1.26 Cho ABC có đường cao AH (H nằm giữa B và C). AH = 12cm,
HB = 9cm, BC = 25cm.
a) Chứng minh: ABC vuông tại A.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 46
i) y +
2
= x –
3
j) y =
1
x
k) y =
2x 1
3
l) y =
5 x 2
.
2.20 Cho các hàm số y = (m – 2)x + 3 và y = (m + 1) + 5. Tìm các giá trị của
m để mỗi hàm số:
a) Là hàm số bậc nhất
b) Là hàm số nghịch biến
c) Là hàm số đồng biến.
2.21 Một hình chữ nhật có các kích thước là 15cm và 25cm. Người ta tăng
thêm mỗi kích thước của hình đó thêm x (cm) được hình chữ nhật mới có
chu vi là y (cm). Hãy lập công thức tính y theo x.
2.22 Một hình chữ nhật có các kích thước là 30cm và 40cm. Người ta giảm bớt
mỗi kích thước của hình đó x (cm). Gọi S và P thứ tự là diện tích và chu
vi của hình chữ nhật mới theo x.
a) Hỏi rằng các đại lượng S và P có phải là hàm số bậc nhất của x không?
Vì sao ?
b) Tính giá trị tương ứng của P khi x nhận các giá trị (tính theo đợ vị cm)
sau: 0; 1; 1,5; 2,5; 3,5.
2.23 Chứng minh rằng hàm số bậc nhất y = ax + b đồng biến khi a > 0 và
nghịch biến khi a < 0.
2.24 Cho hàm số y = ax + 5. Tìm hệ số a, biết rằng khi x = 1 thì y = 2.
2.25 Với giá trị nào của m thì hàm số sau là hàm số bậc nhất ?
a) y =
5 m
(x – 1) b) y =
m 1
m 1
x + 3,5 c) y =
1
m 2
x –
3
4
2.26 Cho hàm số y = (1 –
5
)x – 1.
a) Hàm số trên là đồng biến hay nghịch biến trên R? Vì sao ?
b) Tính giá trị của y khi x = 1 +
5
c) Tính giá trị của x khi y =
5
.
2.27 Cho hàm số y = (3 –
2
)x + 1.
a) Hàm số trên là đồng biến hay nghịch biến trên R? Vì sao ?
b) Tính giá trị của y khi x nhận các giá trị: 0; 1;
2
; 3 +
2
; 3 –
2
c) Tính giá trị của x khi y nhận các giá trị: 0; 1; 8; 2 +
2
; 2 –
2
.
2.28 Tìm trên mặt phẳng tọa độ tất cả các điểm :
a) Có tung độ bằng 6; b) Có hoành độ bằng – 3 ;
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 59
1.16 Cho hình chữ nhật ABCD. Đường phân giác của
B
cắt đường chéo AC
thành hai đoạn
2
4 m
7
và
5
5 m
7
. Tính các kích thước của hình chữ nhật.
1.17 Cho ABC vuông tại A, vẽ đường cao AH. Chu vi của ABH là 30cm và
ACH là 40cm. Tính chu vi của ABC.
1.18 Cho ABC vuông tại A có cạnh AB = 6cm và AC = 8cm. Các đường
phân giác trong và ngoài của góc B cắt đường thẳng AC lần lượt tại M và
N. Tính các đoạn thẳng AM và AN.
1.19 Cho ABC vuông ở A, AB = 30cm, AC = 40cm, đường cao AH, trung
tuyến AM.
a) Tính BH, HM, MC. b) Tính AH.
1.20 Cho ABC vuông ở A, đường cao AH. Gọi M, N theo thứ tự là trung
điểm của AB, AC. Biết HM = 15cm, HN = 20cm. Tính HB, HC, AH.
1.21 Cho ABC cân ở A, đường cao BK. Biết AK = 7cm, KC = 2cm.
Tính BC.
1.22 Cho ABC vuông ở A có AC = 20cm, chiều cao AH = 12cm. Tính diện
tích ABC.
1.23 Cho hình vuông ABCD, gọi I là một điểm nằm giữa A và B. Tia DI và tia
cắt CB cắt nhau ở K. Qua D kẻ đường thẳng vuông góc với DI để đường
thẳng BC tại M.
a) Chứng minh: IDM cân.
b) Chứng minh:
2 2
1 1
DI DK
không đổi khi I di chuyển trên cạnh AB.
1.24 Cho hình thang vuông ABCD (
0
A D 90
) có hai đường chéo AC và
BD vuông góc với nhau tại H. Biết HD = 18 cm, HB = 8 cm. tính diện
tích hình thang ABCD.
1.25 Cho ABC cân tại A, kẻ đường cao AH và CK. Biết AH = 7,5 cm;
CK = 12 cm. Tính BC, AB.
1.26 Cho ABC có đường cao AH (H nằm giữa B và C). AH = 12cm,
HB = 9cm, BC = 25cm.
a) Chứng minh: ABC vuông tại A.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 58
1.4 Đường cao của một tam giác vuông chia cạnh huyền thành hai đoạn thẳng
có độ dài là 1 và 2. Hãy tính các cạnh của vuông này.
1.5 Một tam giác vuông có cạnh huyền là 5, còn đường cao ứng với cạnh
huyền là 2. Hãy tính cạnh nhỏ nhất của tam giác vuông này.
1.6 Cho một tam giác vuông. Biết tỉ số hai cạnh góc vuông là 3 : 4 và cạnh
huyền là 125cm. Tính độ dài các cạnh của tam giác vuông và hình chiếu
của cạnh góc vuông trên cạnh huyền.
1.7 Cho tam giác ABC vuông tại A. Biết
AB 5
AC 6
, đường cao AH = 30 cm.
Tính BH, HC.
1.8 Cho tam giác ABC vuông tại A. Biết
AB 3
AC 7
, đường cao AH = 42 cm.
Tính BH, HC.
1.9 Cho h.vuông ABCD có độ dài cạnh là a. Tính độ dài đường chéo theo a.
1.10 Hãy tính đường cao của tam giác đều cạnh a.
1.11 Cho ABC cân tại A. Gọi H là hình chiếu của B trên cạnh AC. Tính cạnh
đáy BC của tam giác, biết rằng AH = 7, HC = 2.
1.12 Hãy tìm tam giác vuông trong các tam giác có độ dài 3 cạnh sau:
a) IJ = 6 JK = 10 KI = 8;
b) RS = 7 ST = 24 TR = 25;
c) AB =
1
3
BC =
1
4
AC =
1
5
;
d) MN = 6,5 ML = 3,3 LN = 5,6.
1.13 Cho tam giác có độ dài các cạnh là 5, 12, 13. Tìm góc của tam giác đối
diện với cạnh có độ dài 13.
1.14 Trong tam giác ABC, biết AB = 10cm, BC = 17cm. Vẽ đường cao BD
với D thuộc cạnh AC và BD = 8cm. Tính AC.
1.15 Cho ABC, đường cao AH.
a) Cho AH = 16, BH = 25. Tính AB, AC, BC, CH.
b) Cho AB = 12, BH = 6. Tính AH, AC, BC, CH.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 47
c) Có tung độ bằng 0 ; d) Có hoành độ bằng 0 ;
e) Có hoành độ và tung độ bằng nhau ;
f) Có hoành độ và tung độ đối nhau.
2.29 Cho hai điểm A(x
A
; y
A
) và B(x
B
; y
B
). Chứng minh công thức tính
khoảng cách giữa hai điẩm A và B là :
2 2
B A B A
AB (x x ) (y y )
Áp dụng : Tính khoảng cách giữa hai điểm, biết rằng:
a) A(1 ; 1) và B(5 ; 4) b. M(–2 ; 2) và B(3 ; 5)
2.30 a) Vẽ đồ thị của các hàm số y = x +
3
và y = 2x +
3
trên cùng một
mặt phẳng tọa độ.
b) Gọi giao điểm của đường thẳng y = x +
3
với trục Oy, Ox theo thứ
tự là A, B và giao điểm của đường thẳng y = 2x +
3
với các trục Oy,
Ox theo thứ tự là C, D. Tính các góc của ABC (dùng máy tính bỏ túi)
2.31 a) Vẽ đồ thị của các hàm số y = x + 1 và y = –x + 3 trên cùng một mặt
phẳng tọa độ.
b) Hai đường thẳng trên cắt nhau tại C và cát trục Ox theo thứ tự tại A và
B. Tìm toạ độ các điểm A, B, C.
c) Tính chu vi và diện tích ABC (đơn vị các trục là xentimét)
2.32 a) Vẽ trên cùng hệ trục tọa độ Oxy đồ thị của các hàm số sau:
y = 2x ; y = 2x + 5 ; y = –
2
3
x và y = –
2
3
x + 5
b) Bốn đường thẳng trên cắt nhau tạo thành tứ giác OABC (O là gốc tọa
độ). Tứ giác OABC có phải là hình bình hành không ? Vì sao ?
2.33 Cho hàm số y = (m – 3)x
a) Với giá trị nào của m thì hàm số đồng biến ? Nghịch biến ?
b) Xác định giá trị của m để đồ thị của hàm số đi qua điểm A(1 ; 2).
c) Xác định giá trị của m để đồ thị của hàm số đi qua điểm B(1 ; –2).
d) Vẽ đồ thị của hàm số ứng với giá trị của m tìm được ở các câu b và c.
2.34 Cho hàm số y = ax + 3 có đồ thị (d) cắt trục hoành tại điểm A có hoành
độ bằng 3.
a) Tìm giá trị của a.
b) Xét tính biến thiên (đồng biến hay nghịch biến) của hàm số.
c) Gọi B là giao điểm của (d) với trục tung. Tính khoảng cách từ O đến
AB.
2.35 Cho hàm số y = (a – 1)x + a.
a) Xác định giá trị của a để đồ thị của hàm số cắt trục tung tại điểm có
tung độ bằng
2
+ 1
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 58
1.4 Đường cao của một tam giác vuông chia cạnh huyền thành hai đoạn thẳng
có độ dài là 1 và 2. Hãy tính các cạnh của vuông này.
1.5 Một tam giác vuông có cạnh huyền là 5, còn đường cao ứng với cạnh
huyền là 2. Hãy tính cạnh nhỏ nhất của tam giác vuông này.
1.6 Cho một tam giác vuông. Biết tỉ số hai cạnh góc vuông là 3 : 4 và cạnh
huyền là 125cm. Tính độ dài các cạnh của tam giác vuông và hình chiếu
của cạnh góc vuông trên cạnh huyền.
1.7 Cho tam giác ABC vuông tại A. Biết
AB 5
AC 6
, đường cao AH = 30 cm.
Tính BH, HC.
1.8 Cho tam giác ABC vuông tại A. Biết
AB 3
AC 7
, đường cao AH = 42 cm.
Tính BH, HC.
1.9 Cho h.vuông ABCD có độ dài cạnh là a. Tính độ dài đường chéo theo a.
1.10 Hãy tính đường cao của tam giác đều cạnh a.
1.11 Cho ABC cân tại A. Gọi H là hình chiếu của B trên cạnh AC. Tính cạnh
đáy BC của tam giác, biết rằng AH = 7, HC = 2.
1.12 Hãy tìm tam giác vuông trong các tam giác có độ dài 3 cạnh sau:
a) IJ = 6 JK = 10 KI = 8;
b) RS = 7 ST = 24 TR = 25;
c) AB =
1
3
BC =
1
4
AC =
1
5
;
d) MN = 6,5 ML = 3,3 LN = 5,6.
1.13 Cho tam giác có độ dài các cạnh là 5, 12, 13. Tìm góc của tam giác đối
diện với cạnh có độ dài 13.
1.14 Trong tam giác ABC, biết AB = 10cm, BC = 17cm. Vẽ đường cao BD
với D thuộc cạnh AC và BD = 8cm. Tính AC.
1.15 Cho ABC, đường cao AH.
a) Cho AH = 16, BH = 25. Tính AB, AC, BC, CH.
b) Cho AB = 12, BH = 6. Tính AH, AC, BC, CH.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 47
c) Có tung độ bằng 0 ; d) Có hoành độ bằng 0 ;
e) Có hoành độ và tung độ bằng nhau ;
f) Có hoành độ và tung độ đối nhau.
2.29 Cho hai điểm A(x
A
; y
A
) và B(x
B
; y
B
). Chứng minh công thức tính
khoảng cách giữa hai điẩm A và B là :
2 2
B A B A
AB (x x ) (y y )
Áp dụng : Tính khoảng cách giữa hai điểm, biết rằng:
a) A(1 ; 1) và B(5 ; 4) b. M(–2 ; 2) và B(3 ; 5)
2.30 a) Vẽ đồ thị của các hàm số y = x +
3
và y = 2x +
3
trên cùng một
mặt phẳng tọa độ.
b) Gọi giao điểm của đường thẳng y = x +
3
với trục Oy, Ox theo thứ
tự là A, B và giao điểm của đường thẳng y = 2x +
3
với các trục Oy,
Ox theo thứ tự là C, D. Tính các góc của ABC (dùng máy tính bỏ túi)
2.31 a) Vẽ đồ thị của các hàm số y = x + 1 và y = –x + 3 trên cùng một mặt
phẳng tọa độ.
b) Hai đường thẳng trên cắt nhau tại C và cát trục Ox theo thứ tự tại A và
B. Tìm toạ độ các điểm A, B, C.
c) Tính chu vi và diện tích ABC (đơn vị các trục là xentimét)
2.32 a) Vẽ trên cùng hệ trục tọa độ Oxy đồ thị của các hàm số sau:
y = 2x ; y = 2x + 5 ; y = –
2
3
x và y = –
2
3
x + 5
b) Bốn đường thẳng trên cắt nhau tạo thành tứ giác OABC (O là gốc tọa
độ). Tứ giác OABC có phải là hình bình hành không ? Vì sao ?
2.33 Cho hàm số y = (m – 3)x
a) Với giá trị nào của m thì hàm số đồng biến ? Nghịch biến ?
b) Xác định giá trị của m để đồ thị của hàm số đi qua điểm A(1 ; 2).
c) Xác định giá trị của m để đồ thị của hàm số đi qua điểm B(1 ; –2).
d) Vẽ đồ thị của hàm số ứng với giá trị của m tìm được ở các câu b và c.
2.34 Cho hàm số y = ax + 3 có đồ thị (d) cắt trục hoành tại điểm A có hoành
độ bằng 3.
a) Tìm giá trị của a.
b) Xét tính biến thiên (đồng biến hay nghịch biến) của hàm số.
c) Gọi B là giao điểm của (d) với trục tung. Tính khoảng cách từ O đến
AB.
2.35 Cho hàm số y = (a – 1)x + a.
a) Xác định giá trị của a để đồ thị của hàm số cắt trục tung tại điểm có
tung độ bằng
2
+ 1
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 48
b) Xác định giá trị của a để đồ thị của hàm số cắt trục hoành tại điểm có
hoành độ –
3
c) Vẽ đồ thị của hàm số ứng với a tìm được ở câu a). Tính khoảng cách
từ gốc tọa độ đến đường thẳng đó.
2.36 Cho hàm số y = (m
2
– 5m)x + 3.
a) Với giá trị nào của m thì hàm số là hàm số bậc nhất ?
b) Với giá trị nào của m thì hàm số nghịch biến ?
c) Xác định m khi đồ thị của hàm số qua điểm A(1 ; –3).
2.37 Cho hàm số y = (a – 1)x + a.
a) Xác định giá trị của a để đồ thị của hàm số cắt trục tung tại điểm có
tung độ bằng 2.
b) Xác định giá trị của a để đồ thị của hàm số cắt trục hoành tại điểm có
hoành độ bằng –3.
c) Vẽ đồ thị của hai hàm số ứng với giá trị của a vừa tìm được ở các câu
a và b trên cùng hệ trục tọa độ Oxy và tìm giao điểm của hai đường
thẳng vừa vẽ được.
2.38 a) Vẽ đồ thị của các hàm số y = x và y = 2x + 2 trên cùng một mặt phẳng
tọa độ.
b) Gọi A là giao điểm của hai đồ thị của hàm số nói trên, tìm tọa độ của
điểm A.
c) Vẽ qua điểm B(0 ; 2) một đường thẳng song song với Ox, cắt đường
thẳng y = x tại C. Tìm tọa độ của điểm C rồi tính diện tích ABC (đơn
vị các trục là xentimét)
2.39 a) Biết rằng với x = 4 thì hàm số y = 3x + b có giá trị là 11. Tìm b. Vẽ đồ
thị của hàm số với giá trị của b vừa tìm được.
b) Biết rằng đồ thị của hàm số của hàm số y = ax + 5 đi qua điểm
A(–1 ; 3). Tìm a. Vẽ đồ thị của hàm số với giá trị của a vừa tìm được.
2.40 Vẽ đồ thị của hàm số y =
5
x +
5
bằng thước thẳng và compa.
2.41 a) Vẽ trên cùng hệ trục tọa độ Oxy đồ thị của các hàm số sau:
(d
1
) : y = x (d
2
) : y = 2x (d
3
) : y = – x + 3
b) Đường thẳng (d
3
) cắt các đường thẳng (d
1
), (d
2
) theo thứ tự tại A, B.
Tìm tọa độ các điểm A, B và tính diện tích OAB.
2.42 Hãy chỉ ra ba cặp đường thẳng cắt nhau và các cặp đường thẳng song
song với nhau :
a) y = –2x + 3 ; b) y = x + 2 ; c) y = 0,5x – 3
d) y = x – 3 ; e) y = 1,5x – 1 ; f) y = 0,5x + 3
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 57
Phần 2. Hình học
Chương 1
HỆ THỨC LƯỢNG
TRONG TAM GIÁC VUÔNG
A - Một số hệ thức về cạnh và đường cao
trong tam giác vuông
1)
2 2 2
BC AB AC
2)
2
AC CH.BC
3)
2
AB BH.BC
4)
2
AH HB.HC
5)
AH .BC AB.AC
6)
2 2 2
1 1 1
AH AC AB
1) a
2
= b
2
+ c
2
2) b
2
= a.b
3) c
2
= a.c
4) h
2
= b.c
5) h.a = b.c
6)
2 2 2
1 1 1
h b c
1.1 Cho tam giác ABC vuông tại A có đường cao AH. Trong các đoạn thẳng
sau: AB, AC, BC, AH, BH, CH hãy tính độ dài các đoạn thẳng còn lại
nếu biết:
a) AB = 15cm; BC = 25 cm b) BH = 18 cm; CH = 32 cm
c) AB = 6 cm; BH = 3,6 cm d) AC = 12 cm; AH = 7,2 cm
e) AH = 7,2 cm; CH = 9,6 cm f) BC = 25cm; AH = 12cm (AB<AC)
1.2 Cho tam giác ABC vuông tại A có đường cao AH và đường phân giác
AD (D BC). Biết DB = 15 cm, CD = 20 cm. Tính AH, AD (làm tròn
đến chữ số thập phân thứ hai).
1.3 Cạnh huyền của một tam giác vuông lớn hơn một cạnh góc vuông là 1cm,
còn tổng của hai cạnh góc vuông lớn hơn cạnh huyền 4cm. Hãy tính các
cạnh của tam giác vuông này.
A
B
H
C
a
c
b
c'
b'
h
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 48
b) Xác định giá trị của a để đồ thị của hàm số cắt trục hoành tại điểm có
hoành độ –
3
c) Vẽ đồ thị của hàm số ứng với a tìm được ở câu a). Tính khoảng cách
từ gốc tọa độ đến đường thẳng đó.
2.36 Cho hàm số y = (m
2
– 5m)x + 3.
a) Với giá trị nào của m thì hàm số là hàm số bậc nhất ?
b) Với giá trị nào của m thì hàm số nghịch biến ?
c) Xác định m khi đồ thị của hàm số qua điểm A(1 ; –3).
2.37 Cho hàm số y = (a – 1)x + a.
a) Xác định giá trị của a để đồ thị của hàm số cắt trục tung tại điểm có
tung độ bằng 2.
b) Xác định giá trị của a để đồ thị của hàm số cắt trục hoành tại điểm có
hoành độ bằng –3.
c) Vẽ đồ thị của hai hàm số ứng với giá trị của a vừa tìm được ở các câu
a và b trên cùng hệ trục tọa độ Oxy và tìm giao điểm của hai đường
thẳng vừa vẽ được.
2.38 a) Vẽ đồ thị của các hàm số y = x và y = 2x + 2 trên cùng một mặt phẳng
tọa độ.
b) Gọi A là giao điểm của hai đồ thị của hàm số nói trên, tìm tọa độ của
điểm A.
c) Vẽ qua điểm B(0 ; 2) một đường thẳng song song với Ox, cắt đường
thẳng y = x tại C. Tìm tọa độ của điểm C rồi tính diện tích ABC (đơn
vị các trục là xentimét)
2.39 a) Biết rằng với x = 4 thì hàm số y = 3x + b có giá trị là 11. Tìm b. Vẽ đồ
thị của hàm số với giá trị của b vừa tìm được.
b) Biết rằng đồ thị của hàm số của hàm số y = ax + 5 đi qua điểm
A(–1 ; 3). Tìm a. Vẽ đồ thị của hàm số với giá trị của a vừa tìm được.
2.40 Vẽ đồ thị của hàm số y =
5
x +
5
bằng thước thẳng và compa.
2.41 a) Vẽ trên cùng hệ trục tọa độ Oxy đồ thị của các hàm số sau:
(d
1
) : y = x (d
2
) : y = 2x (d
3
) : y = – x + 3
b) Đường thẳng (d
3
) cắt các đường thẳng (d
1
), (d
2
) theo thứ tự tại A, B.
Tìm tọa độ các điểm A, B và tính diện tích OAB.
2.42 Hãy chỉ ra ba cặp đường thẳng cắt nhau và các cặp đường thẳng song
song với nhau :
a) y = –2x + 3 ; b) y = x + 2 ; c) y = 0,5x – 3
d) y = x – 3 ; e) y = 1,5x – 1 ; f) y = 0,5x + 3
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 57
Phần 2. Hình học
Chương 1
HỆ THỨC LƯỢNG
TRONG TAM GIÁC VUÔNG

A - Một số hệ thức về cạnh và đường cao
trong tam giác vuông
1)
2 2 2
BC AB AC
2)
2
AC CH.BC
3)
2
AB BH.BC
4)
2
AH HB.HC
5)
AH .BC AB.AC
6)
2 2 2
1 1 1
AH AC AB
1) a
2
= b
2
+ c
2
2) b
2
= a.b
3) c
2
= a.c
4) h
2
= b.c
5) h.a = b.c
6)
2 2 2
1 1 1
h b c
1.1 Cho tam giác ABC vuông tại A có đường cao AH. Trong các đoạn thẳng
sau: AB, AC, BC, AH, BH, CH hãy tính độ dài các đoạn thẳng còn lại
nếu biết:
a) AB = 15cm; BC = 25 cm b) BH = 18 cm; CH = 32 cm
c) AB = 6 cm; BH = 3,6 cm d) AC = 12 cm; AH = 7,2 cm
e) AH = 7,2 cm; CH = 9,6 cm f) BC = 25cm; AH = 12cm (AB<AC)
1.2 Cho tam giác ABC vuông tại A có đường cao AH và đường phân giác
AD (D BC). Biết DB = 15 cm, CD = 20 cm. Tính AH, AD (làm tròn
đến chữ số thập phân thứ hai).
1.3 Cạnh huyền của một tam giác vuông lớn hơn một cạnh góc vuông là 1cm,
còn tổng của hai cạnh góc vuông lớn hơn cạnh huyền 4cm. Hãy tính các
cạnh của tam giác vuông này.
A
B
H
C
a
c
b
c'
b'
h
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 56
2.89 a) Cho các điểm M(–1 ; – 2), N(–2 ; –4), P(2 ; –3), Q(3 ; –4,5). Tìm tọa
độ của các điểm M’, N’, P’ và Q’ lần lượt là các điểm dối xứng với
các điểm M, N, P và Q qua trục Ox.
b) Vẽ đồ thị của hàm số y = x ; và y = x + 1 .
c) Tìm tọa độ giao điểm của các hàm số trên. Từ đó suy ra phương trình
x = x + 1 có một nghiệm duy nhất.
2.90 Vẽ đồ thị của các hàm số sau:
a) y = x – 1 b) y = 1 – x + 2x + 3 c) y = x +
2
x
x
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 49
2.43 Trong các đường thẳng sau, đường nào song song với nhau, đường nào
vuông góc với nhau ?
a) y = 1,5x + 2 ; b) y =
1
2
x – 3 ; c) y = 5 – x
d) y =
x 1
2
; e) y = –x + 4 ; f) y = 2x – 1.
2.44 Cho hai hàm số bậc nhất y = mx + 3 và y = (2m + 1)x – 5. Tìm m để đồ
thị của các hàm số là:
a) Hai đường thẳng song song với nhau.
b) Hai đường thẳng cắt nhau.
c) Hai đường thẳng vuông góc với nhau.
2.45 Cho hai hàm số bậc nhất y = 2x + 3k và y = (2m + 1)x + 2k – 3. Tìm giá
trị của m và k để đồ thị của các hàm số là:
a) Hai đường thẳng song song với nhau.
b) Hai đường thẳng cắt nhau.
c) Hai đường thẳng trùng nhau.
2.46 Cho hai hàm số bậc nhất (d
1
) : y = (2 – m
2
)x + m – 5 và
(d
2
) : y = mx + 3m – 7. Tìm giá trị của m để đồ thị của các hàm số là:
a) Hai đường thẳng song song với nhau.
b) Hai đường thẳng cắt nhau.
c) Hai đường thẳng vuông góc với nhau.
2.47 Cho hàm số y = ax – 3. Hãy xác định hệ số a trong mỗi trường hợp sau :
a) Đồ thị của hàm số song song với đường thẳng y = – 2x.
b) Khi x = 2 thì hàm số có giá trị y = 7.
c) Cắt trục tung tại điểm có tung độ bằng – 1.
d) Cắt trục hoành tại điểm có hoành độ 3 – 1.
e) Đồ thị của hàm số cắt đường thẳng y = 2x – 1 tại điểm có hoành độ
bằng 2.
f) Đồ thị của hàm số cắt đường thẳng y = –3x + 2 tại điểm có tung độ
bằng 5.
2.48 Cho hàm số y = 2x + b. Hãy xác định hệ số b trong mỗi trường hợp sau :
a) Đồ thị của hàm số cắt trục tung tại điểm có tung độ bằng 3.
b) Đồ thị của hàm số đã cho đi qua điểm A(1 ; 5).
2.49 a) Vẽ đồ thị của các hàm số y =
2
3
x + 2 và y =
3
2
x + 2 trên cùng một
mặt phẳng tọa độ.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 56
2.89 a) Cho các điểm M(–1 ; – 2), N(–2 ; –4), P(2 ; –3), Q(3 ; –4,5). Tìm tọa
độ của các điểm M’, N’, P’ và Q’ lần lượt là các điểm dối xứng với
các điểm M, N, P và Q qua trục Ox.
b) Vẽ đồ thị của hàm số y = x ; và y = x + 1 .
c) Tìm tọa độ giao điểm của các hàm số trên. Từ đó suy ra phương trình
x = x + 1 có một nghiệm duy nhất.
2.90 Vẽ đồ thị của các hàm số sau:
a) y = x – 1 b) y = 1 – x + 2x + 3 c) y = x +
2
x
x
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 49
2.43 Trong các đường thẳng sau, đường nào song song với nhau, đường nào
vuông góc với nhau ?
a) y = 1,5x + 2 ; b) y =
1
2
x – 3 ; c) y = 5 – x
d) y =
x 1
2
; e) y = –x + 4 ; f) y = 2x – 1.
2.44 Cho hai hàm số bậc nhất y = mx + 3 và y = (2m + 1)x – 5. Tìm m để đồ
thị của các hàm số là:
a) Hai đường thẳng song song với nhau.
b) Hai đường thẳng cắt nhau.
c) Hai đường thẳng vuông góc với nhau.
2.45 Cho hai hàm số bậc nhất y = 2x + 3k và y = (2m + 1)x + 2k – 3. Tìm giá
trị của m và k để đồ thị của các hàm số là:
a) Hai đường thẳng song song với nhau.
b) Hai đường thẳng cắt nhau.
c) Hai đường thẳng trùng nhau.
2.46 Cho hai hàm số bậc nhất (d
1
) : y = (2 – m
2
)x + m – 5 và
(d
2
) : y = mx + 3m – 7. Tìm giá trị của m để đồ thị của các hàm số là:
a) Hai đường thẳng song song với nhau.
b) Hai đường thẳng cắt nhau.
c) Hai đường thẳng vuông góc với nhau.
2.47 Cho hàm số y = ax – 3. Hãy xác định hệ số a trong mỗi trường hợp sau :
a) Đồ thị của hàm số song song với đường thẳng y = – 2x.
b) Khi x = 2 thì hàm số có giá trị y = 7.
c) Cắt trục tung tại điểm có tung độ bằng – 1.
d) Cắt trục hoành tại điểm có hoành độ 3 – 1.
e) Đồ thị của hàm số cắt đường thẳng y = 2x – 1 tại điểm có hoành độ
bằng 2.
f) Đồ thị của hàm số cắt đường thẳng y = –3x + 2 tại điểm có tung độ
bằng 5.
2.48 Cho hàm số y = 2x + b. Hãy xác định hệ số b trong mỗi trường hợp sau :
a) Đồ thị của hàm số cắt trục tung tại điểm có tung độ bằng 3.
b) Đồ thị của hàm số đã cho đi qua điểm A(1 ; 5).
2.49 a) Vẽ đồ thị của các hàm số y =
2
3
x + 2 và y =
3
2
x + 2 trên cùng một
mặt phẳng tọa độ.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 50
b) Một đường thẳng song song với trục hoành Ox, cắt trục tung Oy tại
điểm có tung độ bằng 1, cắt các đường thẳng trên theo thứ tự tại M
và N. Tìm tọa độ hai điểm M và N.
2.50 Tìm hệ số a của hàm số y = ax + 1, biết khi x = 1 +
2
thì y = 3 +
2
.
2.51 Xác định hàm số y = ax + b biết đồ thị của hàm số cắt trục tung tại điểm
có tung độ bằng 3 và cắt trục hoành tại điểm có hoành độ bằng –2.
2.52 Trên mặt phẳng tọa độ Oxy cho hai điểm A(1 ; 2), B(3 ; 4).
a) Tìm hệ số a của đường thẳng đi qua A và B.
b) Xác định hàm số biết đồ thị của nó là đường thẳng đi qua A và B.
2.53 Cho đường thẳng (d) : y = (k + 1)x + k. Tìm k để đường thẳng (d):
a) Đi qua gốc tọa độ.
b) Cắt trục tung tại điểm có tung độ bằng 1 –
2
.
c) Song song với đường thẳng y = ( 3+ 1)x + 3
2.54 Xét đường thẳng (d) : y = (2m – 1)x – m + 3. Định m để đường thẳng (d):
a) Đi qua gốc tọa độ.
b) Đi qua A(2 ; 3)
c) Cắt đường thẳng y = 3x + 7 tại một điểm trên trục tung
d) Song song với đường thẳng y = 5x + 3
e) Vuông góc với đường thẳng y = 2x – 1.
2.55 Cho các đường thẳng: (d
1
) : y = 3x + 1 và (d
2
) : y =
1
4
x – 2
a) Viết phương trình đường thẳng (d
3
) qua M(4 ; –5) và song song với
đường thẳng (d
1
)
b) Viết phương trình đường thẳng (d
4
) qua N(3 ; 2) và vuông góc với
đường thẳng (d
2
).
c) Viết phương trình đường thẳng (d
5
) qua hai điểm M và N.
2.56 Đường thẳng (d) cắt trục hoành tại điểm A có hoành độ là –4 và cắt trục
tung tại điểm B có tung độ là –3.
a) Xác định phương trình đường thẳng (d).
b) Viết phương trình đường cao CH của ABC với C( –1 ; –1)
2.57 Cho hai điểm A(5 ; 1) và B(–1 ; 5) trong hệ tọa độ vuông góc Oxy. Chứng
minh AOB vuông cân. Tính chu vi và diện tích của AOB.
2.58 Chứng minh rằng khi m thay đổi, đồ thị của hàm số sau luôn đi qua một
điểm cố định. Hãy xác định tọa độ của điểm cố định đó.
a) y = (m – 2)x + 3 b) y = mx + (2m + 1)
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 55
c) ABC là tam giác gì ?
d) Tìm tọa độ hình chiếu của A trên BC.
2.84 Trong mặt phẳng Oxy cho ba điểm A(–5 ; –1), B(–1 ; 4) và C(3 ; 2).
a) Vẽ ABC.
b) Viết phương trình các đường thẳng chứa các cạnh của tam giác.
c) Qua A kẻ đường thẳng song song với BC. Qua B kẻ đường thẳng
vuông góc với BC. Xác định tọa độ giao điểm D của hai đường thẳng
đó.
2.85 a) Vẽ đồ thị của các hàm số sau trên cùng một mặt phẳng tọa độ :
(d
1
): y = 3x + 6 (d
2
): y = 2x + 4 (d
3
): y = x + 2 (d
1
): y = 0,5x + 1
b) Tính góc giữa các đường thẳng trên với trục Ox.
c) Có nhận xét gì về độ dốc của các đường thẳng trên.
2.86 a) Vẽ đồ thị của các hàm số sau trên cùng một mặt phẳng tọa độ :
(d
1
) : y = 2x – 2 (d
2
) : y = 2x
3
4
(d
3
) : y =
3
1
x + 3
b) Gọi giao điểm các đường thẳng (d
3
) với hai đường thẳng (d
1
) và (d
2
)
lần lượt tại A và B. Tìm tọa độ của các điểm A và B.
c) Tính khoảng cách giữa hai điểm A và B.
2.87 a) Vẽ đồ thị của các hàm số (d
1
) : y = 0,5x + 2 và (d
2
) : y = 5 – 2x.
b) Gọi giao điểm các đường thẳng (d
1
) và (d
2
) với trục hoành lần lượt tại
A và B. gọi giao điểm của hai đường thẳng đó là C. Tìm tọa độ của
các điểm A, B và C.
c) Tính độ dài các đoạn thẳng AB, AC và BC (đơn vị trên các trục là cm)
(làm tròn đến chữ số thập phân thứ hai).
d) Tính các góc tạo bởi các đường thẳng trên với trục Ox (làm tròn đến
phút).
2.88 a) Vẽ đồ thị của các hàm số (d
1
) : y = 2x , (d
2
) : y = 0,5x và
(d
3
) : y = –x + 6.
b) Gọi giao điểm các đường thẳng (d
3
) với hai đường thẳng (d
1
) và (d
2
)
lần lượt tại A và B. Tìm tọa độ của các điểm A và B.
c) Tính các góc của OAB.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 50
b) Một đường thẳng song song với trục hoành Ox, cắt trục tung Oy tại
điểm có tung độ bằng 1, cắt các đường thẳng trên theo thứ tự tại M
và N. Tìm tọa độ hai điểm M và N.
2.50 Tìm hệ số a của hàm số y = ax + 1, biết khi x = 1 +
2
thì y = 3 +
2
.
2.51 Xác định hàm số y = ax + b biết đồ thị của hàm số cắt trục tung tại điểm
có tung độ bằng 3 và cắt trục hoành tại điểm có hoành độ bằng –2.
2.52 Trên mặt phẳng tọa độ Oxy cho hai điểm A(1 ; 2), B(3 ; 4).
a) Tìm hệ số a của đường thẳng đi qua A và B.
b) Xác định hàm số biết đồ thị của nó là đường thẳng đi qua A và B.
2.53 Cho đường thẳng (d) : y = (k + 1)x + k. Tìm k để đường thẳng (d):
a) Đi qua gốc tọa độ.
b) Cắt trục tung tại điểm có tung độ bằng 1 –
2
.
c) Song song với đường thẳng y = ( 3+ 1)x + 3
2.54 Xét đường thẳng (d) : y = (2m – 1)x – m + 3. Định m để đường thẳng (d):
a) Đi qua gốc tọa độ.
b) Đi qua A(2 ; 3)
c) Cắt đường thẳng y = 3x + 7 tại một điểm trên trục tung
d) Song song với đường thẳng y = 5x + 3
e) Vuông góc với đường thẳng y = 2x – 1.
2.55 Cho các đường thẳng: (d
1
) : y = 3x + 1 và (d
2
) : y =
1
4
x – 2
a) Viết phương trình đường thẳng (d
3
) qua M(4 ; –5) và song song với
đường thẳng (d
1
)
b) Viết phương trình đường thẳng (d
4
) qua N(3 ; 2) và vuông góc với
đường thẳng (d
2
).
c) Viết phương trình đường thẳng (d
5
) qua hai điểm M và N.
2.56 Đường thẳng (d) cắt trục hoành tại điểm A có hoành độ là –4 và cắt trục
tung tại điểm B có tung độ là –3.
a) Xác định phương trình đường thẳng (d).
b) Viết phương trình đường cao CH của ABC với C( –1 ; –1)
2.57 Cho hai điểm A(5 ; 1) và B(–1 ; 5) trong hệ tọa độ vuông góc Oxy. Chứng
minh AOB vuông cân. Tính chu vi và diện tích của AOB.
2.58 Chứng minh rằng khi m thay đổi, đồ thị của hàm số sau luôn đi qua một
điểm cố định. Hãy xác định tọa độ của điểm cố định đó.
a) y = (m – 2)x + 3 b) y = mx + (2m + 1)
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 55
c) ABC là tam giác gì ?
d) Tìm tọa độ hình chiếu của A trên BC.
2.84 Trong mặt phẳng Oxy cho ba điểm A(–5 ; –1), B(–1 ; 4) và C(3 ; 2).
a) Vẽ ABC.
b) Viết phương trình các đường thẳng chứa các cạnh của tam giác.
c) Qua A kẻ đường thẳng song song với BC. Qua B kẻ đường thẳng
vuông góc với BC. Xác định tọa độ giao điểm D của hai đường thẳng
đó.
2.85 a) Vẽ đồ thị của các hàm số sau trên cùng một mặt phẳng tọa độ :
(d
1
): y = 3x + 6 (d
2
): y = 2x + 4 (d
3
): y = x + 2 (d
1
): y = 0,5x + 1
b) Tính góc giữa các đường thẳng trên với trục Ox.
c) Có nhận xét gì về độ dốc của các đường thẳng trên.
2.86 a) Vẽ đồ thị của các hàm số sau trên cùng một mặt phẳng tọa độ :
(d
1
) : y = 2x – 2 (d
2
) : y = 2x
3
4
(d
3
) : y =
3
1
x + 3
b) Gọi giao điểm các đường thẳng (d
3
) với hai đường thẳng (d
1
) và (d
2
)
lần lượt tại A và B. Tìm tọa độ của các điểm A và B.
c) Tính khoảng cách giữa hai điểm A và B.
2.87 a) Vẽ đồ thị của các hàm số (d
1
) : y = 0,5x + 2 và (d
2
) : y = 5 – 2x.
b) Gọi giao điểm các đường thẳng (d
1
) và (d
2
) với trục hoành lần lượt tại
A và B. gọi giao điểm của hai đường thẳng đó là C. Tìm tọa độ của
các điểm A, B và C.
c) Tính độ dài các đoạn thẳng AB, AC và BC (đơn vị trên các trục là cm)
(làm tròn đến chữ số thập phân thứ hai).
d) Tính các góc tạo bởi các đường thẳng trên với trục Ox (làm tròn đến
phút).
2.88 a) Vẽ đồ thị của các hàm số (d
1
) : y = 2x , (d
2
) : y = 0,5x và
(d
3
) : y = –x + 6.
b) Gọi giao điểm các đường thẳng (d
3
) với hai đường thẳng (d
1
) và (d
2
)
lần lượt tại A và B. Tìm tọa độ của các điểm A và B.
c) Tính các góc của OAB.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 54
2.78 Cho đường thẳng (d) : y = (1 – 4m)x + m – 2. Tìm giá trị của m để đường
thẳng (d):
a) Đi qua gốc tọa độ.
b) Tạo với trục Ox một góc nhọn ? Góc tù ?
c) Cắt trục tung tại một điểm có tung độ bằng 1,5.
d) Cắt trục hoành tại một điểm có hoành độ bằng 0,5.
2.79 Cho đường thẳng (d) : y = (m – 2)x + n (m 2). Tìm giá trị của m và n
để đường thẳng (d):
a) Đi qua hai điểm A(–1 ; 2), B(3 ; –4).
b) Cắt trục tung tại một điểm có tung độ bằng 1 –
2
và cắt trục hoành
tại một điểm có hoành độ bằng 2 +
2
.
c) Cắt đường thẳng : –2y + x – 3 = 0.
d) Song song với đường thẳng : 3x + 2y = 1.
e) Trùng với đường thẳng : y – 2x + 3 = 0.
2.80 Cho hai đường thẳng :
(d
1
) : y = (m
2
– 1)x + m + 2 và (d
2
) : y = (5 – m)x + 2m + 5.
Tìm m để hai đường thẳng trên song song với nhau.
2.81 Cho đường thẳng: (d) : y = (2m – 1)x + m – 2. Tìm m để đường thẳng (d):
a) Đi qua điểm A(1 ; 6).
b) Song song với đường thẳng 2x + 3y – 5 = 0.
c) Vuông góc với đường thẳng x + 2y + 1 = 0.
d) Không đi qua điểm B(
1
2
; 1)
e) Luôn đi qua một điểm cố định.
2.82 Tìm m để ba đường thẳng sau đồng qui:
a) (d
1
) : y = 2x – 1, (d
2
) : 3x + 5y = 8, (d
3
) : (m + 8)x – 2my = 3m
b) (d
1
) : y = –x + 1, (d
2
) : y = x – 1, (d
3
) : (m + 1)x – (m – 1)y = m + 1
c) (d
1
) : y = 2x – m, (d
2
) : y = –x + 2m, (d
3
) : mx – (m – 1)y = 2m – 1
2.83 Trên hệ trục tọa độ vuông góc Oxy cho ABC mà ba cạnh AB, BC, CA
của nó lần lượt nằm trên ba đường thẳng sau:
(d
1
) : y = x + 3, (d
2
) : x – 5y = – 7 (d
3
) : y = 5 – x.
a) Vẽ các đường thẳng AB, BC, CA trên cùng hệ trục tọa độ.
b) Tìm tọa độ ba đỉnh của ABC.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 51
2.59 Cho hai đường thẳng (d
1
): y = mx – 2m – 1, (d
2
): y = (m + 2)x + 1 – 2m
a) Khi (d
1
) (d
2
), hãy xác định tọa độ giao điểm của mỗi đường thẳng
với các trục tọa độ.
b) Chứng minh rằng khi m thay đổi, mỗi đường thẳng nói trên luôn đi
qua một điểm cố định.
2.60 Xác định hàm số trong mỗi trường hợp sau, biết đồ thị của hàm số là
đường thẳng đi qua gốc tọa độ :
a) Đi qua điểm A(3 ; 2);
b) Có hệ số góc bằng
3
;
c) Song song với đường thẳng y = 3x + 1.
2.61 Cho hàm số bậc nhất y = ax + 3.
a) Xác định hệ số góc a, biết rằng đồ thị của hàm số đi qua điểm A(2 ; 6).
b) Vẽ đồ thị của hàm số ứng với giá trị của a vừa tìm được.
2.62 Cho hàm số y = –2x + 3 (d).
a) Vẽ đồ thị của hàm số.
b) Tính góc tạo bởi đường thẳng (d) và trục Ox (làm tròn đến phút).
2.63 Xác định hàm số bậc nhất y = ax + b trong mỗi trường hợp sau :
a) a = 2 và đồ thị của hàm số cắt trục hoành tại điểm có hoành độ bằng
1,5.
b) a = 3 và đồ thị của hàm số đi qua điểm A(2 ; 2)
c) Đồ thị của hàm số song song với đường thẳng y =
3
x và đi qua điểm
B(1 ;
3
+ 5).
2.64 a) Vẽ đồ thị của các hàm số y =
1
2
x + 2 và y = – x + 2 trên cùng một mặt
phẳng tọa độ.
b) Gọi giao điểm của hai đường thẳng trên với trục hoành theo thứ tự là
A, B và gọi giao điểm của hai đường thẳng đó là C. Tính các góc của
ABC (làm tròn đến độ).
c) Tính chu vi và diện tích của ABC (đơn vị đo trên các trục tọa độ là
xentimét)
2.65 a) Vẽ đồ thị của các hàm số: y = x + 1; y =
1
3
x +
3
; y =
3
x –
3
.
b) Gọi , , lần lượt là các góc tạo bởi các đường thẳng trên và trục Ox.
CMR: tan = 1, tan =
1
3
, an =
3
. Tính số đo các góc , , .
2.66 a) Tìm hệ số góc của đường thẳng đi qua gốc tọa độ và qua điểm A(2 ; 1)
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 54
2.78 Cho đường thẳng (d) : y = (1 – 4m)x + m – 2. Tìm giá trị của m để đường
thẳng (d):
a) Đi qua gốc tọa độ.
b) Tạo với trục Ox một góc nhọn ? Góc tù ?
c) Cắt trục tung tại một điểm có tung độ bằng 1,5.
d) Cắt trục hoành tại một điểm có hoành độ bằng 0,5.
2.79 Cho đường thẳng (d) : y = (m – 2)x + n (m 2). Tìm giá trị của m và n
để đường thẳng (d):
a) Đi qua hai điểm A(–1 ; 2), B(3 ; –4).
b) Cắt trục tung tại một điểm có tung độ bằng 1 –
2
và cắt trục hoành
tại một điểm có hoành độ bằng 2 +
2
.
c) Cắt đường thẳng : –2y + x – 3 = 0.
d) Song song với đường thẳng : 3x + 2y = 1.
e) Trùng với đường thẳng : y – 2x + 3 = 0.
2.80 Cho hai đường thẳng :
(d
1
) : y = (m
2
– 1)x + m + 2 và (d
2
) : y = (5 – m)x + 2m + 5.
Tìm m để hai đường thẳng trên song song với nhau.
2.81 Cho đường thẳng: (d) : y = (2m – 1)x + m – 2. Tìm m để đường thẳng (d):
a) Đi qua điểm A(1 ; 6).
b) Song song với đường thẳng 2x + 3y – 5 = 0.
c) Vuông góc với đường thẳng x + 2y + 1 = 0.
d) Không đi qua điểm B(
1
2
; 1)
e) Luôn đi qua một điểm cố định.
2.82 Tìm m để ba đường thẳng sau đồng qui:
a) (d
1
) : y = 2x – 1, (d
2
) : 3x + 5y = 8, (d
3
) : (m + 8)x – 2my = 3m
b) (d
1
) : y = –x + 1, (d
2
) : y = x – 1, (d
3
) : (m + 1)x – (m – 1)y = m + 1
c) (d
1
) : y = 2x – m, (d
2
) : y = –x + 2m, (d
3
) : mx – (m – 1)y = 2m – 1
2.83 Trên hệ trục tọa độ vuông góc Oxy cho ABC mà ba cạnh AB, BC, CA
của nó lần lượt nằm trên ba đường thẳng sau:
(d
1
) : y = x + 3, (d
2
) : x – 5y = – 7 (d
3
) : y = 5 – x.
a) Vẽ các đường thẳng AB, BC, CA trên cùng hệ trục tọa độ.
b) Tìm tọa độ ba đỉnh của ABC.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 51
2.59 Cho hai đường thẳng (d
1
): y = mx – 2m – 1, (d
2
): y = (m + 2)x + 1 – 2m
a) Khi (d
1
) (d
2
), hãy xác định tọa độ giao điểm của mỗi đường thẳng
với các trục tọa độ.
b) Chứng minh rằng khi m thay đổi, mỗi đường thẳng nói trên luôn đi
qua một điểm cố định.
2.60 Xác định hàm số trong mỗi trường hợp sau, biết đồ thị của hàm số là
đường thẳng đi qua gốc tọa độ :
a) Đi qua điểm A(3 ; 2);
b) Có hệ số góc bằng
3
;
c) Song song với đường thẳng y = 3x + 1.
2.61 Cho hàm số bậc nhất y = ax + 3.
a) Xác định hệ số góc a, biết rằng đồ thị của hàm số đi qua điểm A(2 ; 6).
b) Vẽ đồ thị của hàm số ứng với giá trị của a vừa tìm được.
2.62 Cho hàm số y = –2x + 3 (d).
a) Vẽ đồ thị của hàm số.
b) Tính góc tạo bởi đường thẳng (d) và trục Ox (làm tròn đến phút).
2.63 Xác định hàm số bậc nhất y = ax + b trong mỗi trường hợp sau :
a) a = 2 và đồ thị của hàm số cắt trục hoành tại điểm có hoành độ bằng
1,5.
b) a = 3 và đồ thị của hàm số đi qua điểm A(2 ; 2)
c) Đồ thị của hàm số song song với đường thẳng y =
3
x và đi qua điểm
B(1 ;
3
+ 5).
2.64 a) Vẽ đồ thị của các hàm số y =
1
2
x + 2 và y = – x + 2 trên cùng một mặt
phẳng tọa độ.
b) Gọi giao điểm của hai đường thẳng trên với trục hoành theo thứ tự là
A, B và gọi giao điểm của hai đường thẳng đó là C. Tính các góc của
ABC (làm tròn đến độ).
c) Tính chu vi và diện tích của ABC (đơn vị đo trên các trục tọa độ là
xentimét)
2.65 a) Vẽ đồ thị của các hàm số: y = x + 1; y =
1
3
x +
3
; y =
3
x –
3
.
b) Gọi , , lần lượt là các góc tạo bởi các đường thẳng trên và trục Ox.
CMR: tan = 1, tan =
1
3
, an =
3
. Tính số đo các góc , , .
2.66 a) Tìm hệ số góc của đường thẳng đi qua gốc tọa độ và qua điểm A(2 ; 1)
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 52
b) Tìm hệ số góc của đường thẳng đi qua gốc tọa độ và điểm B(1 ; –2)
c) Vẽ đồ thị của các hàm số với hệ số góc vừa tìm được ở các câu a và b
trên cùng một mặt phẳng tọa độ và chứng tỏ rằng hai đường thẳng đó
vuông góc với nhau.
2.67 Cho hai đường thẳng (d) : y = ax + b và (d) y = ax + b.
Chứng minh rằng: Trên cùng một mặt phẳng tọa độ, hai đường thẳng (d)
và (d’) vuông góc với nhau khi và chỉ khi a .a’ = –1.
2.68 a) Vẽ đồ thị của các hàm số (d
1
) : y = x và (d
2
) : y = 0,5x.
b) Vẽ đường thẳng (d) song song với Ox và cắt trục tung tại điểm có tung
độ bằng 2, và cắt các đường thẳng trên theo thứ tự tại D và E. Tìm tọa
độ của các điểm D và E. Tính chu vi và diện tích của ODE.
2.69 a) Vẽ đồ thị của các hàm số (d
1
) : y = –2x và (d
2
) : y = 0,5x.
b) Qua điểm K(0 ; 2) vẽ đường thẳng (d) song song với Ox. Đường thẳng
(d) cắt đường thẳng (d
1
) và (d
2
) lần lượt tại A và B. Tìm tọa độ của các
điểm A và B.
c) Hãy chứng tỏ rằng AÔB = 90
0
.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 53
D - Ôn tập chương 2
2.70 Cho hàm số y = f(x) =
2 x 2 1 x
a) Tìm điều kiện xác định của hàm số.
b) Tìm tọa độ giao điểm của đồ thị hàm số với trục tung và trục hoành.
c) So sánh f(–
2
) và f(–1,5).
2.71 Với giá trị nào của m thì hàm số bậc nhất sau đồng biến ?
a) y = (m – 1)x + 3 b) y = (m + 6)x – 7
2.72 Với những giá trị nào của k thì các hàm số bậc nhất nghịch biến ?
a) y = (5 – k)x + 1 b) y = (–k + 9)x + 100.
2.73 Với giá trị nào của m thì đồ thị của các hàm số cắt nhau tại một điểm trên
trục tung ?
a) y = 2x + (3 + m) và y = 3x + (5 – m)
b) y = 12x + (5 – m) và y = 3x + (3 + m)
2.74 Tìm các giá trị của a để hai đường thẳng sau y = (a – 1)x + 2 (a
1) và
y = (3 – a)x + 1 (a
3) song song với nhau.
2.75 Xác định k để hai đường thẳng sau đây trùng nhau:
y = kx + (m – 2) (k
0) và y = (5 – k)x + (4 – m) (k
5)
2.76 Cho hai hàm số bậc nhất y = (k + 1)x + 3 và y = (3 – 2k)x + 1.
a) Với giá trị nào của k thì đồ thị của hai hàm số của hai hàm số là hai
đường thẳng song song với nhau ?
b) Với giá trị nào của k thì đồ thị của hai hàm số là hai đường thẳng cắt
nhau ?
c) Hai đường thẳng nói trên có thể trùng nhau được không ? Vì sao ?
2.77 Cho hàm số y = (2m – 1)x với
2
1
m .
a) Với giá trị nào của m thì hàm số đồng biến ? Nghịch biến ?
b) Tìm giá trị của m để đồ thị của hàm số đi qua điểm A(–0,5; 1,5).
c) Vẽ đồ thị của hàm số với giá trị m vừa tìm được ở câu b).
d) Đồ thị vừa vẽ có quan hệ như thế nào với các đường thẳng sau:
(d
1
): 3x + y = 1 ; (d
2
): 3y – x – 12 = 0.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 52
b) Tìm hệ số góc của đường thẳng đi qua gốc tọa độ và điểm B(1 ; –2)
c) Vẽ đồ thị của các hàm số với hệ số góc vừa tìm được ở các câu a và b
trên cùng một mặt phẳng tọa độ và chứng tỏ rằng hai đường thẳng đó
vuông góc với nhau.
2.67 Cho hai đường thẳng (d) : y = ax + b và (d) y = ax + b.
Chứng minh rằng: Trên cùng một mặt phẳng tọa độ, hai đường thẳng (d)
và (d’) vuông góc với nhau khi và chỉ khi a .a’ = –1.
2.68 a) Vẽ đồ thị của các hàm số (d
1
) : y = x và (d
2
) : y = 0,5x.
b) Vẽ đường thẳng (d) song song với Ox và cắt trục tung tại điểm có tung
độ bằng 2, và cắt các đường thẳng trên theo thứ tự tại D và E. Tìm tọa
độ của các điểm D và E. Tính chu vi và diện tích của ODE.
2.69 a) Vẽ đồ thị của các hàm số (d
1
) : y = –2x và (d
2
) : y = 0,5x.
b) Qua điểm K(0 ; 2) vẽ đường thẳng (d) song song với Ox. Đường thẳng
(d) cắt đường thẳng (d
1
) và (d
2
) lần lượt tại A và B. Tìm tọa độ của các
điểm A và B.
c) Hãy chứng tỏ rằng AÔB = 90
0
.
Bài tập Toán 9 Học kì 1
Gv: Trần Quốc Nghĩa Trang 53
D - Ôn tập chương 2
2.70 Cho hàm số y = f(x) =
2 x 2 1 x
a) Tìm điều kiện xác định của hàm số.
b) Tìm tọa độ giao điểm của đồ thị hàm số với trục tung và trục hoành.
c) So sánh f(–
2
) và f(–1,5).
2.71 Với giá trị nào của m thì hàm số bậc nhất sau đồng biến ?
a) y = (m – 1)x + 3 b) y = (m + 6)x – 7
2.72 Với những giá trị nào của k thì các hàm số bậc nhất nghịch biến ?
a) y = (5 – k)x + 1 b) y = (–k + 9)x + 100.
2.73 Với giá trị nào của m thì đồ thị của các hàm số cắt nhau tại một điểm trên
trục tung ?
a) y = 2x + (3 + m) và y = 3x + (5 – m)
b) y = 12x + (5 – m) và y = 3x + (3 + m)
2.74 Tìm các giá trị của a để hai đường thẳng sau y = (a – 1)x + 2 (a
1) và
y = (3 – a)x + 1 (a
3) song song với nhau.
2.75 Xác định k để hai đường thẳng sau đây trùng nhau:
y = kx + (m – 2) (k
0) và y = (5 – k)x + (4 – m) (k
5)
2.76 Cho hai hàm số bậc nhất y = (k + 1)x + 3 và y = (3 – 2k)x + 1.
a) Với giá trị nào của k thì đồ thị của hai hàm số của hai hàm số là hai
đường thẳng song song với nhau ?
b) Với giá trị nào của k thì đồ thị của hai hàm số là hai đường thẳng cắt
nhau ?
c) Hai đường thẳng nói trên có thể trùng nhau được không ? Vì sao ?
2.77 Cho hàm số y = (2m – 1)x với
2
1
m .
a) Với giá trị nào của m thì hàm số đồng biến ? Nghịch biến ?
b) Tìm giá trị của m để đồ thị của hàm số đi qua điểm A(–0,5; 1,5).
c) Vẽ đồ thị của hàm số với giá trị m vừa tìm được ở câu b).
d) Đồ thị vừa vẽ có quan hệ như thế nào với các đường thẳng sau:
(d
1
): 3x + y = 1 ; (d
2
): 3y – x – 12 = 0.
| 1/104
| | Tải xuống

Có thể bạn quan tâm:

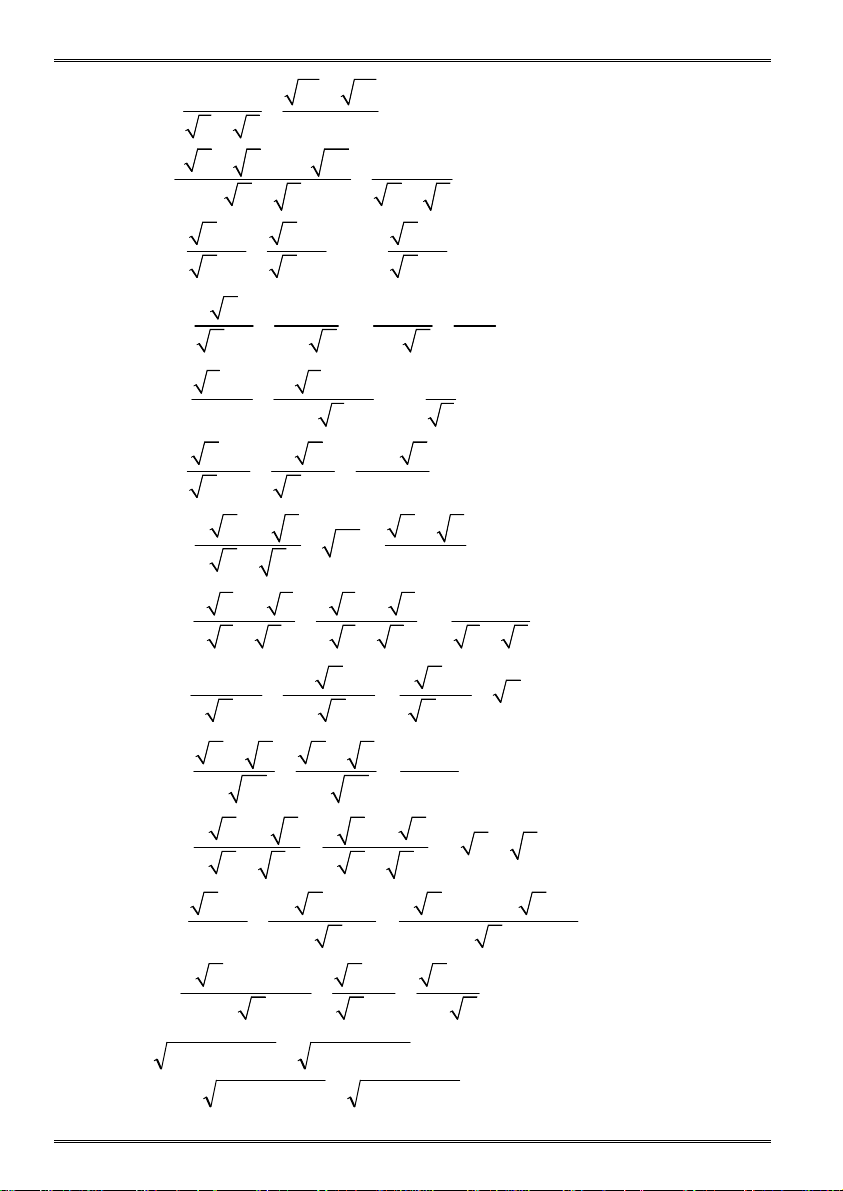
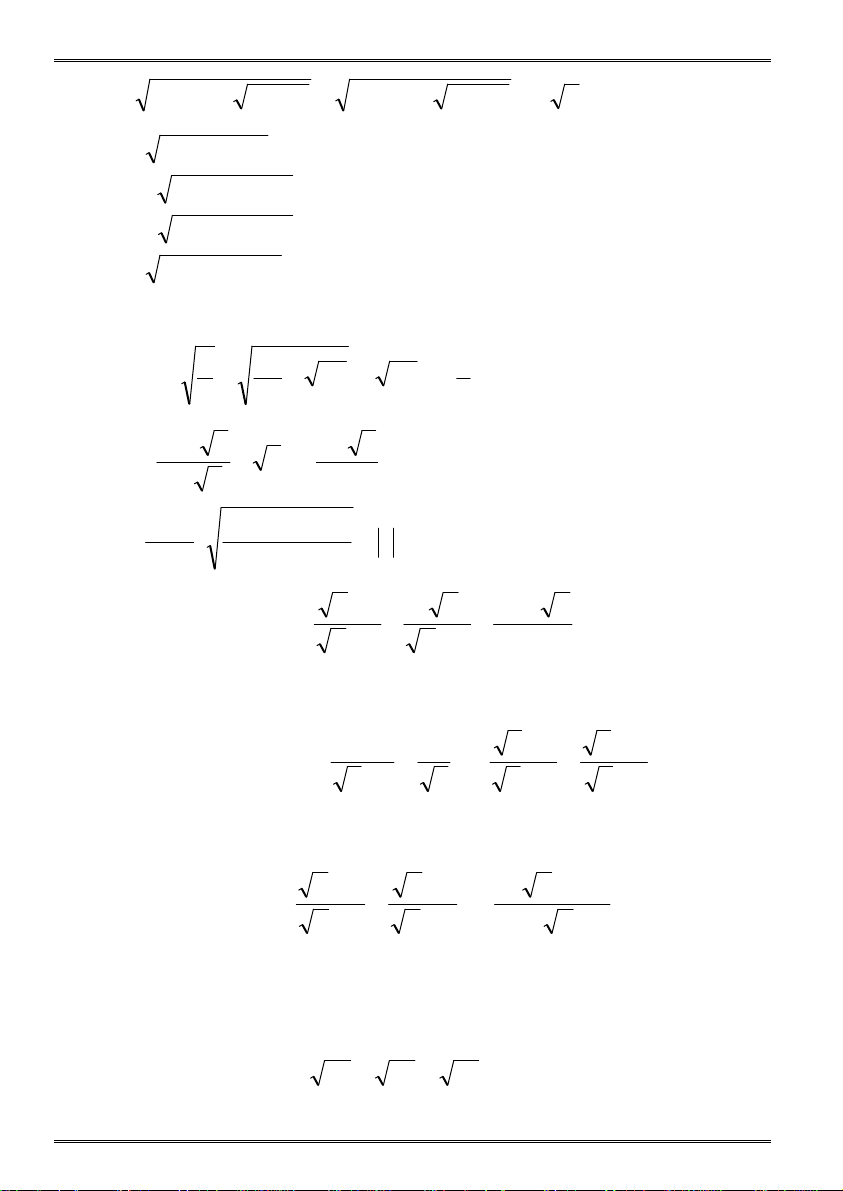
Preview text:

Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1 Mục lục Phần 0. Ôn tập
Phần 0. Ôn tập ................................................................................................ 1
Biểu diễn nghiệm trên trục số ................................................................... 1
Biểu diễn tập nghiệm BPT trên trục số
Phương trình chứa dấu giá trị tuyệt đối .................................................... 2
Bất phương trình tích, thương. Bất phương trình bậc hai. Bất phương trình
chứa dấu giá trị tuyệt đối. ......................................................................... 4
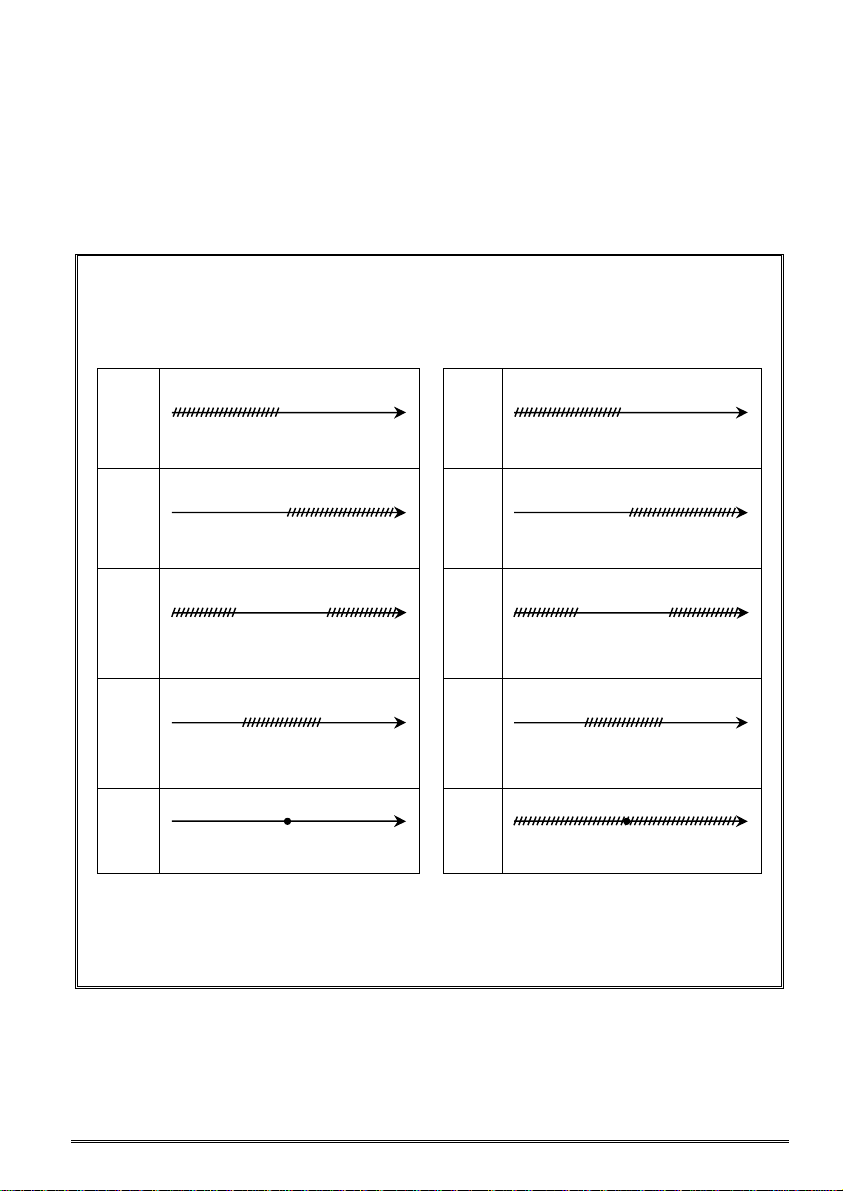
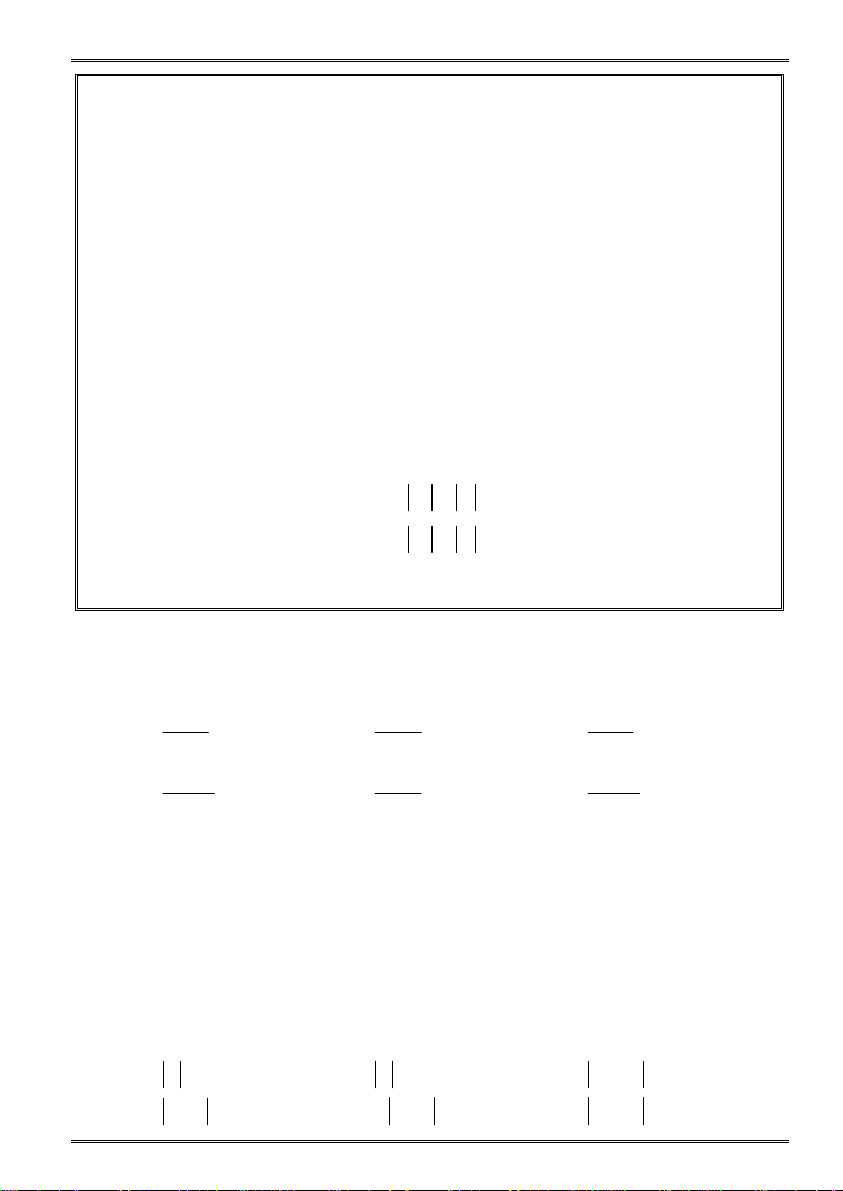
Thông thường một bất phương trình có vô số nghiệm nên không thể kiệt
Phần 1. Đại số ................................................................................................. 9
kê hết được. Người ta chọn cách thể hiện tập nghiệm bằng cách biểu diễn
Chương 1 CĂN BẬC HAI – CĂN BẬC BA............................................... 9
trên trục số (phần không bị xóa). Sau đây là các trường hợp thường gặp:
A - Căn bậc hai ........................................................................................ 9 a a
B - Căn thức bậc hai. Hằng đẳng thức 2 A |
A | .................................... 12 [ (
C - Khai phương một tích. Nhân các căn thức bậc hai. ........................... 17 (1) (2)
D - Khai phương một thương. C hia các căn thức bậc hai ....................... 17 { x / x a } { x / x a }
E - Biến đổi đơn giản căn thức bậc hai ................................................... 23
F - Rút gọn biểu thức có chứa căn thức bậc hai ...................................... 29 b b ] )
G - Căn bậc ba ....................................................................................... 33 (3) (4)
H - Ôn tập chương 1............................................................................... 34 { x / x b } { x / x b }
Chương 2 HÀM SỐ BẬC NHẤT ............................................................. 41 a b a b
A - Nhắc lại và bổ sung các khái niệm về hàm số .................................... 41 [ ] ( )
B - Hàm số bậc nhất y = ax + b (a  0) .................................................. 45 (5) (6)
C - Hệ số góc của đường thẳng y = ax + b (a  0) .................................. 45
{x / a ≤ x ≤ b}
{x / a < x < b}
D - Ôn tập chương 2............................................................................... 53 a b a b
Phần 2. Hình học .......................................................................................... 57 ] [ ) (
Chương 1 HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG............. 57 (7) (8)
A - Một số hệ thức về cạnh và đường cao trong tam giác vuông .............. 57
{x / x ≤ a hoặc x ≥ b}
{x / x < a hoặc x > b}
B - Tỉ số lượng giác của góc nhọn .......................................................... 62
C - Bảng lượng giác và máy tính bỏ túi................................................... 66 O O
D - Hệ thức giữa các cạnh và các góc trong một tam giác vuông ............ 67 (9) (10)
x  R (vô số nghiệm)
x   (vô số nghiệm)
E - Ôn tập chương 1 ............................................................................... 69
Chương 2 ĐƯỜNG TRÒN ....................................................................... 73
Chú ý: Tại a, biểu diễn ngoặc vuông “[, ]” tức trong tập nghiệm có
A - Sự xác định đường tròn. Tính chất đối xứng của đường tròn ............ 73
B - Đường kính và dây cung của đường tròn ........................................... 76
x = a, còn ngược lại biểu diễn ngoặc đơn “(, )” khi x = a không
C - Liên hệ giữa dây và khoảng cách từ tâm đến dây .............................. 78
thuộc tập nghiệm.
D - Các công thức về vuông cân tam giác đều và nửa tam giác đều ...... 81
E - Vị trí tương đối của đường thẳng và đường tròn. Dấu hiệu nhận biết
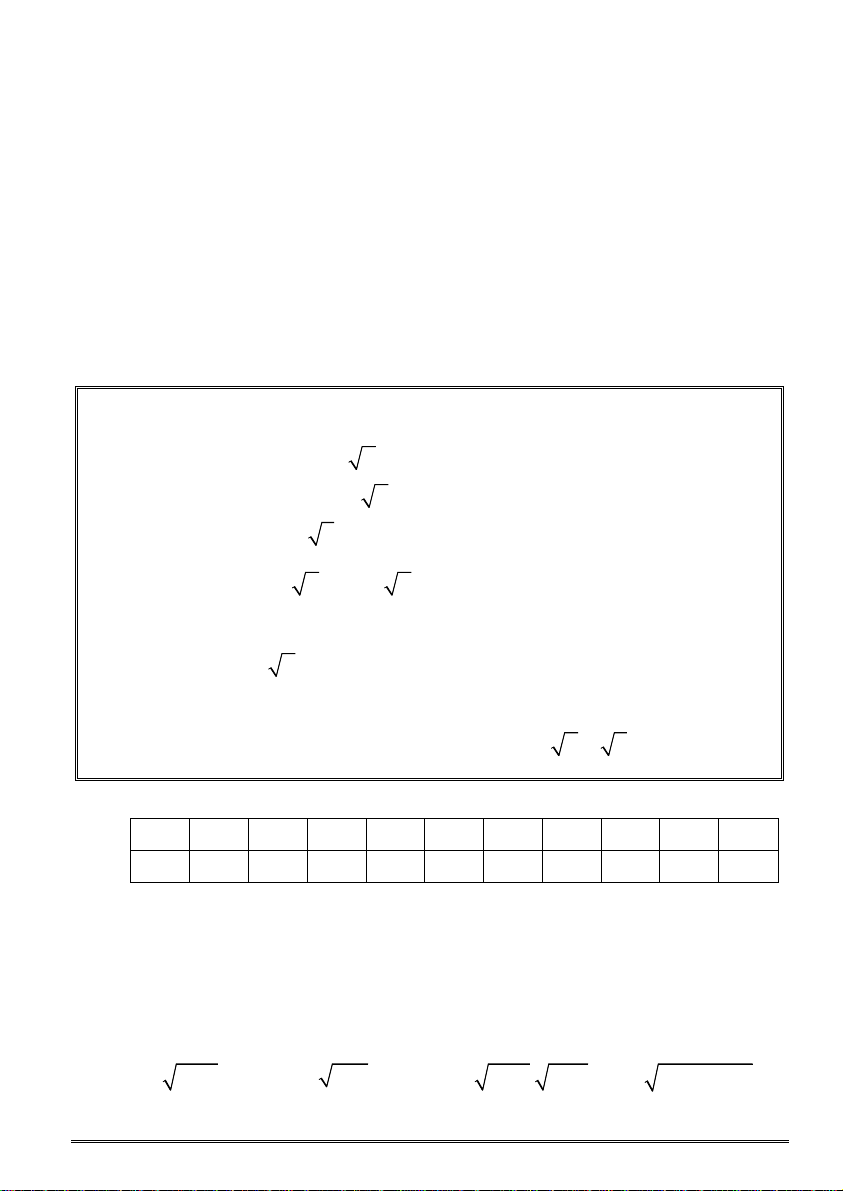
O.1 Biểu diễn các tập nghiệm sau lên trục số:
tiếp tuyến của đường tròn. Tính chất của hai tiếp tuyến cắt nhau...... 82 a) S  {x / x  5} b) S  {x / x  2  } c) S  {x / x  1}
F - Đường tròn nội tiếp – bàng tiếp tam giác .......................................... 89 d) S  {x / x  1  } e) S  {x / 1   x  2}
G - Vị trí tương đối của hai đường tròn .................................................. 91
H - Ôn tập chương 2............................................................................... 94 f) S  {x / x  2  hoac x  1} Gv: Trần Quốc Nghĩa Trang 104 Gv: Trần Quốc Nghĩa Trang 1 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1 Mục lục Phần 0. Ôn tập
Phần 0. Ôn tập ................................................................................................ 1
Biểu diễn nghiệm trên trục số ................................................................... 1
Biểu diễn tập nghiệm BPT trên trục số
Phương trình chứa dấu giá trị tuyệt đối .................................................... 2
Bất phương trình tích, thương. Bất phương trình bậc hai. Bất phương trình
chứa dấu giá trị tuyệt đối. ......................................................................... 4
Thông thường một bất phương trình có vô số nghiệm nên không thể kiệt
Phần 1. Đại số ................................................................................................. 9
kê hết được. Người ta chọn cách thể hiện tập nghiệm bằng cách biểu diễn
Chương 1 CĂN BẬC HAI – CĂN BẬC BA............................................... 9
trên trục số (phần không bị xóa). Sau đây là các trường hợp thường gặp:
A - Căn bậc hai ........................................................................................ 9 a a
B - Căn thức bậc hai. Hằng đẳng thức 2 A |
A | .................................... 12 [ (
C - Khai phương một tích. Nhân các căn thức bậc hai. ........................... 17 (1) (2)
D - Khai phương một thương. C hia các căn thức bậc hai ....................... 17 { x / x a } { x / x a }
E - Biến đổi đơn giản căn thức bậc hai ................................................... 23
F - Rút gọn biểu thức có chứa căn thức bậc hai ...................................... 29 b b ] )
G - Căn bậc ba ....................................................................................... 33 (3) (4)
H - Ôn tập chương 1............................................................................... 34 { x / x b } { x / x b }
Chương 2 HÀM SỐ BẬC NHẤT ............................................................. 41 a b a b
A - Nhắc lại và bổ sung các khái niệm về hàm số .................................... 41 [ ] ( )
B - Hàm số bậc nhất y = ax + b (a  0) .................................................. 45 (5) (6)
C - Hệ số góc của đường thẳng y = ax + b (a  0) .................................. 45
{x / a ≤ x ≤ b}
{x / a < x < b}
D - Ôn tập chương 2............................................................................... 53 a b a b
Phần 2. Hình học .......................................................................................... 57 ] [ ) (
Chương 1 HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG............. 57 (7) (8)
A - Một số hệ thức về cạnh và đường cao trong tam giác vuông .............. 57
{x / x ≤ a hoặc x ≥ b}
{x / x < a hoặc x > b}
B - Tỉ số lượng giác của góc nhọn .......................................................... 62
C - Bảng lượng giác và máy tính bỏ túi................................................... 66 O O
D - Hệ thức giữa các cạnh và các góc trong một tam giác vuông ............ 67 (9) (10)
x  R (vô số nghiệm)
x   (vô số nghiệm)
E - Ôn tập chương 1 ............................................................................... 69
Chương 2 ĐƯỜNG TRÒN ....................................................................... 73
Chú ý: Tại a, biểu diễn ngoặc vuông “[, ]” tức trong tập nghiệm có
A - Sự xác định đường tròn. Tính chất đối xứng của đường tròn ............ 73
B - Đường kính và dây cung của đường tròn ........................................... 76
x = a, còn ngược lại biểu diễn ngoặc đơn “(, )” khi x = a không
C - Liên hệ giữa dây và khoảng cách từ tâm đến dây .............................. 78
thuộc tập nghiệm.
D - Các công thức về vuông cân tam giác đều và nửa tam giác đều ...... 81
E - Vị trí tương đối của đường thẳng và đường tròn. Dấu hiệu nhận biết
O.1 Biểu diễn các tập nghiệm sau lên trục số:
tiếp tuyến của đường tròn. Tính chất của hai tiếp tuyến cắt nhau...... 82 a) S  {x / x  5} b) S  {x / x  2  } c) S  {x / x  1}
F - Đường tròn nội tiếp – bàng tiếp tam giác .......................................... 89 d) S  {x / x  1  } e) S  {x / 1   x  2}
G - Vị trí tương đối của hai đường tròn .................................................. 91
H - Ôn tập chương 2............................................................................... 94 f) S  {x / x  2  hoac x  1} Gv: Trần Quốc Nghĩa Trang 104 Gv: Trần Quốc Nghĩa Trang 1 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
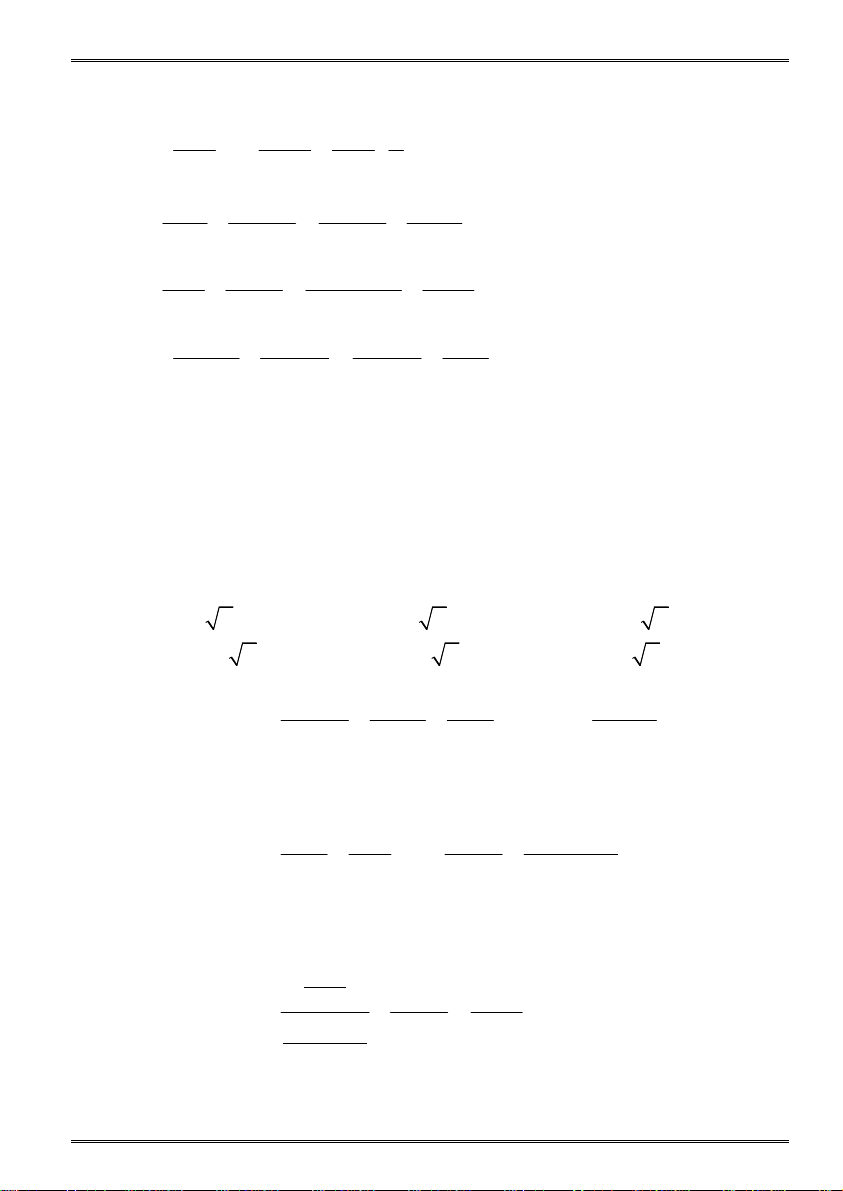
Phương trình chứa dấu giá trị tuyệt đối
c) Gọi O là trung điểm của AH. Chứng minh OOIM là hình thang cân.
d) G là trọng tâm của ABC. So sánh diện tích của AOG và AHG. 
2.148 Cho nửa đường tròn tâm O, đường kính AB. Trên nửa mặt phẳng bờ AB
Dạng 1: A = B (1)
(với B là một số thực không chứa biến)
chứa nửa đường tròn, kẻ tia tiếp tuyến Ax. Từ M trên Ax, kẻ tiếp tuyến
Nếu B < 0 : phương trình vô nghiệm
MC tới nửa đường tròn (C  (O)). Đường thẳng BC cắt tia Ax tại D.
Nếu B > 0 : (1)  A = B hoặc A = – B a) Chứng minh: MA = MD.
Dạng 2: A = B (2)
(với B là một biểu thức có chứa biến)
b) Kẻ CH  AB, BM cắt CH tại I. Chứng minh: I là trung điểm của CH.
Cách 1: Dùng định nghĩa bỏ dấu giá trị tuyệt đối:
c) Kẻ tia Oy  OM, tia này cắt MC tại N. Chứng minh: NB là tiếp tuyến
Nếu A  0  x … (*) của nửa (O).
(2)  A = B  x = … (đem nghiệm này so với điều kiện (*) nếu
2.149 Cho hai đường tròn (O) và (O) tiếp xúc ngoài nhau tại A. Bán kính của thỏa thì lấy)
(O) là R = 5cm, bán kính của (O) là r = 3cm. Một đường thẳng qua A
Chú ý: Trường hợp phương trình A = B có VSN thì phương trình
(2) có nghiệm là (*).
hợp với OO một góc 300 cắt (O) tại B, cắt đường tròn (O) tại C.
Nếu A < 0  x … (**) a) Chứng minh:  AO 'C =  AOB và OC // OB.
(2)  – A = B  x = … (đem nghiệm này so với điều kiện (**) nếu
b) Chứng minh: tiếp tuyến của (O) tại B và tiếp tuyến của (O) tại C song thỏa thì lấy) song với nhau.
Chú ý: Trường hợp ph/trình – A = B có VSN thì phương trình (2)
c) Tiếp tuyến của (O) tại C cắt đường thẳng OO tại D. Tính CD và OD. có nghiệm là (**).
d) Đường thẳng CD cắt đường thẳng BO tại E. Tính diện tích ABE.
Vậy nghiệm của phương trình là: (lấy nghiệm của hai trường hợp trên).
2.150 Cho đường tròn (O; R) đường kính AB. Lấy điểm C ngoài đường tròn sao
Cách 2: Dùng công thức:
cho B là trung điểm của OC. Từ C vẽ hai tiếp tuyến CM, CN đến (O) với B 0
M, N là hai tiếp điểm.
A B   A B
a) Chứng minh: AMN cân. Tính CM và AM theo R.
 A  B 
b) Chứng minh: tứ giác AMCN là hình thoi. Tính SAMCN theo R.
c) Gọi I là trung điểm của CM. Đường thẳng AI cắt OM tại K.
Dạng 3: A = B
Chứng minh: K là trung điểm của AI.
A = B A = B hoặc A = – B
d) Tính diện tích AKB theo R.
(giải hai phương trình này tìm nghiệm nếu có). Dạng 4: A 0 ( a )  B 0 ( b )
A + B + … + N= 0 (1)   ...  N 0 ( n )
Nghiệm của (1) là nghiệm chung của các phương trình (a), (b), … (n). Gv: Trần Quốc Nghĩa Trang 2 Gv: Trần Quốc Nghĩa Trang 103 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
Phương trình chứa dấu giá trị tuyệt đối
c) Gọi O là trung điểm của AH. Chứng minh OOIM là hình thang cân.
d) G là trọng tâm của ABC. So sánh diện tích của AOG và AHG. 
2.148 Cho nửa đường tròn tâm O, đường kính AB. Trên nửa mặt phẳng bờ AB
Dạng 1: A = B (1)
(với B là một số thực không chứa biến)
chứa nửa đường tròn, kẻ tia tiếp tuyến Ax. Từ M trên Ax, kẻ tiếp tuyến
Nếu B < 0 : phương trình vô nghiệm
MC tới nửa đường tròn (C  (O)). Đường thẳng BC cắt tia Ax tại D.
Nếu B > 0 : (1)  A = B hoặc A = – B a) Chứng minh: MA = MD.
Dạng 2: A = B (2)
(với B là một biểu thức có chứa biến)
b) Kẻ CH  AB, BM cắt CH tại I. Chứng minh: I là trung điểm của CH.
Cách 1: Dùng định nghĩa bỏ dấu giá trị tuyệt đối:
c) Kẻ tia Oy  OM, tia này cắt MC tại N. Chứng minh: NB là tiếp tuyến
Nếu A  0  x … (*) của nửa (O).
(2)  A = B  x = … (đem nghiệm này so với điều kiện (*) nếu
2.149 Cho hai đường tròn (O) và (O) tiếp xúc ngoài nhau tại A. Bán kính của thỏa thì lấy)
(O) là R = 5cm, bán kính của (O) là r = 3cm. Một đường thẳng qua A
Chú ý: Trường hợp phương trình A = B có VSN thì phương trình
(2) có nghiệm là (*).
hợp với OO một góc 300 cắt (O) tại B, cắt đường tròn (O) tại C.
Nếu A < 0  x … (**) a) Chứng minh:  AO 'C =  AOB và OC // OB.
(2)  – A = B  x = … (đem nghiệm này so với điều kiện (**) nếu
b) Chứng minh: tiếp tuyến của (O) tại B và tiếp tuyến của (O) tại C song thỏa thì lấy) song với nhau.
Chú ý: Trường hợp ph/trình – A = B có VSN thì phương trình (2)
c) Tiếp tuyến của (O) tại C cắt đường thẳng OO tại D. Tính CD và OD. có nghiệm là (**).
d) Đường thẳng CD cắt đường thẳng BO tại E. Tính diện tích ABE.
Vậy nghiệm của phương trình là: (lấy nghiệm của hai trường hợp trên).
2.150 Cho đường tròn (O; R) đường kính AB. Lấy điểm C ngoài đường tròn sao
Cách 2: Dùng công thức:
cho B là trung điểm của OC. Từ C vẽ hai tiếp tuyến CM, CN đến (O) với B 0
M, N là hai tiếp điểm.
A B   A B
a) Chứng minh: AMN cân. Tính CM và AM theo R.
 A  B 
b) Chứng minh: tứ giác AMCN là hình thoi. Tính SAMCN theo R.
c) Gọi I là trung điểm của CM. Đường thẳng AI cắt OM tại K.
Dạng 3: A = B
Chứng minh: K là trung điểm của AI.
A = B A = B hoặc A = – B
d) Tính diện tích AKB theo R.
(giải hai phương trình này tìm nghiệm nếu có). Dạng 4: A 0 ( a )  B 0 ( b )
A + B + … + N= 0 (1)   ...  N 0 ( n )
Nghiệm của (1) là nghiệm chung của các phương trình (a), (b), … (n). Gv: Trần Quốc Nghĩa Trang 2 Gv: Trần Quốc Nghĩa Trang 103 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
2.144 Cho 2 đường tròn ngoài nhau (O; R) và (O; r) với R > r, AB là tiếp tuyến
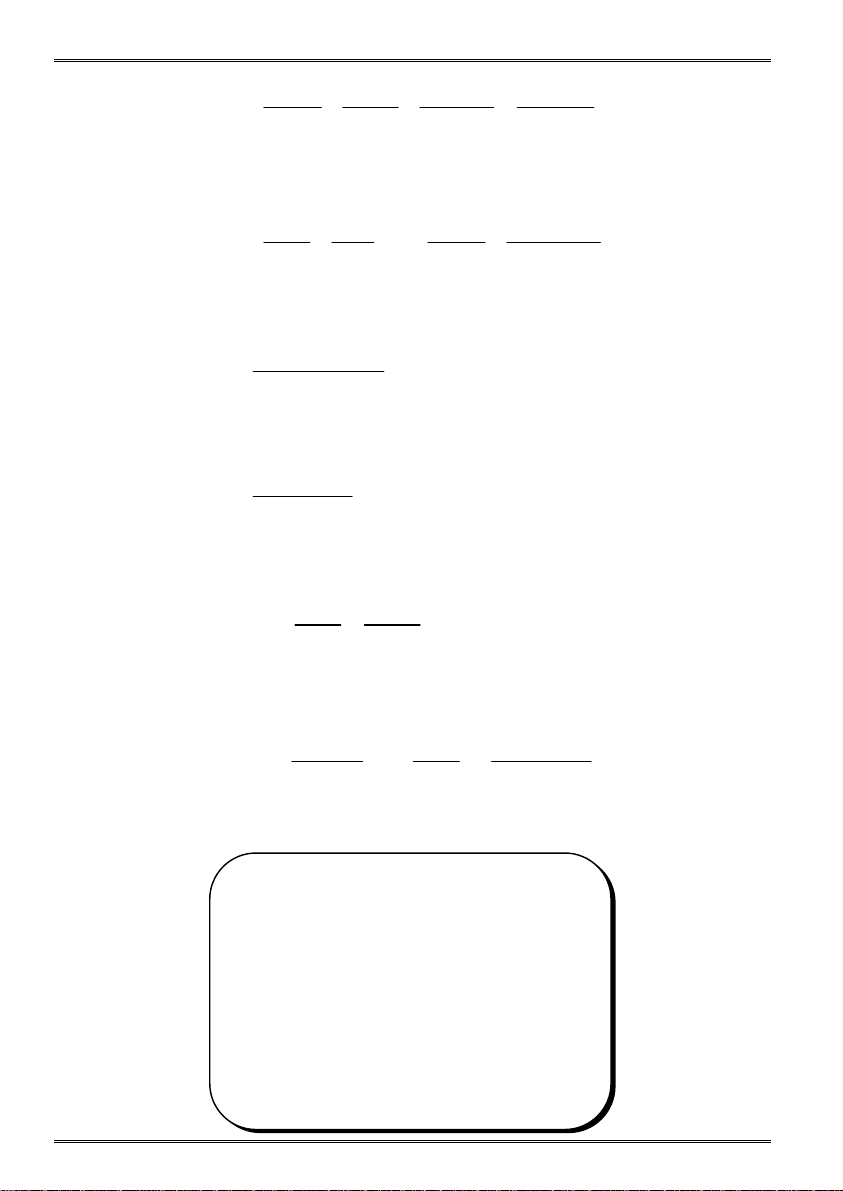
Dạng 5: Phương trình có chứa nhiều dấu giá trị tuyệt đối:
chung ngoài (A là là tiếp điểm trên (O), B là tiếp điểm trên (O)). Từ O vẽ OC  OA.
Tìm giá trị của ăn để biểu thức trong dấu giá trị tuyệt đối bằng 0. Các
a) Chứng tỏ ABOC là hình chữ nhật.
giá trị này khi biểu diễn lên trục số sẽ chia trục số thành nhiều khoảng giá trị của ẩn.
b) Chứng tỏ OC là tiếp tuyến của đường tròn tâm O bán kính R = R – r.
c) Suy ra cách dựng đường t/tuyến chung ngoài AB khi cho trước 2
Cho ẩn lấy giá trị trên từng khoảng, trên từng khoảng đó dấu của biểu
đường tròn (O; R) và (O; r).
thức bên trong dấu giá trị tuyệt đối sẽ âm hoặc dương. Dựa vào đó mà
d) Tương tự, dựng tiếp tuyến chung trong của 2 đường tròn (O; R) và
bỏ dấu trị tuyệt đối. (O; r).
Giải phương trình, giá trị tìm được phải nằm trong khoảng đang xét
e) Tính độ dài của tiếp tuyến chung ngoài và tiếp tuyến chung trong và
mới nhận làm nghiệm.
khoảng cách hai tâm d = OO theo hai bán kính.
Nghiệm của phương trình là tất cả các nghiệm vừa tìm được trên từng
2.145 Cho đường tròn (O; R) và điểm I cố định với OI = R/2. AB là dây cung khoảng. quay quanh I.
a) Tìm vị trí C, D của A (hay B) tương ứng lúc độ dài IA (hay IB) dài
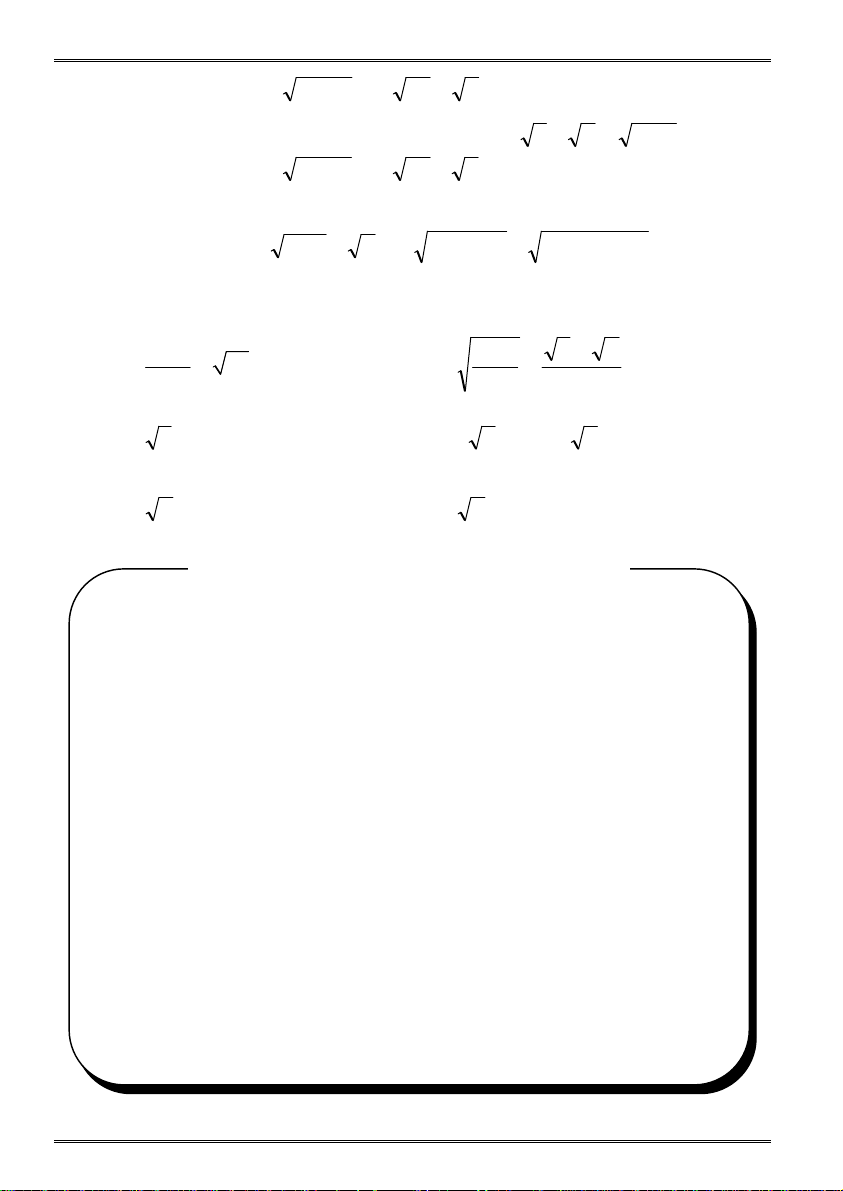
O.2 Giải các phương trình sau: nhất, ngắn nhất. 1. a) x – 5 = 3 b) 2x – 5 = 4
b) Chứng tỏ tập hợp các trung điểm M của dây cung AB là một đường c) x + 6 = 1 d) 3 – 7x = 0
tròn, tìm tâm và bán kính đường tròn này. e) x – 5 =  2 f) 8x – 5x = 2
c) Gọi EF là vị trí giới hạn của dây cung AB lúc M tiến dần đến I. C/m: 2. a) x  7 = 2x + 3 b) x + 4 = 2x – 5 i. EF  CD. c) x + 3 = 3x – 1 d) 9 + x = 2x
ii. EF là độ dài ngắn nhất của dây cung AB và CD là độ dài lớn nhất của AB. e) 3x – 1 = 3x + 2 f) x + 6 = 2x + 9
d) Chứng minh CEF đều, tính chu vi và diện tích tam giác này theo R.
3. a) 2x – 3 = 2x – 3 b) 5x – 4 = 4 – 5x
2.146 Cho (O; R) và (O; R) tiếp xúc ngoài nhau tại E. Gọi AB là tiếp tuyến c) 2x + 3 = 2x + 2 d) 5x – 3 = 5x – 5
chung ngoài của hai đường tròn (A  (O), B  (O)).
e) x2 – 3x + 3 =  x2 + 3x – 1 f) x2 – 9 = x2 – 9
a) Tính diện tích tứ giác AOOB theo R và R.
4. a) 5x  3x – 2 = 0
b) x – 5x +  2x 3 = 0
b) Gọi D là điểm đối xứng của A qua O. C/minh: B, E, D thẳng hàng.
e) 3 – x+ x2 – (4 + x)x = 0
f) (x – 1)2 + x + 21 x2 – 13 = 0
c) Xác định vị trí tương đối của hai đường thẳng AB và đường tròn
5. a) 2 – x=2x – 3 b) x + 3 = 5 – x đường kính OO.
c) 2x – 1 = 2 – 3x
d) 2x = x(x – 2)
2.147 Cho ABC có 3 góc nhọn. Đường tròn tâm I đường kính BC cắt AB tại F,
e) x(x + 1) = 3 – x
f) 3x – 12x + 3 = 0
cắt AC tại E, BE cắt CF tại H.
6*. a) x – 1+2  x = 3
b) x + 3+x – 5 = 3x – 1
a) Trong ABC điểm H gọi là gì ?
b) Gọi K là điểm đối xứng của H qua I và M là điểm đối xứng của H qua
c) x  2x – 1 + 3x – 2 = 4
d) x – 1+x+2+x – 3 = 14
BC. Chứng minh 5 điểm A, B, K, M, C cùng thuộc một đường tròn.
Xác định tâm và bán kính của đường tròn này. Gv: Trần Quốc Nghĩa Trang 102 Gv: Trần Quốc Nghĩa Trang 3 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
2.144 Cho 2 đường tròn ngoài nhau (O; R) và (O; r) với R > r, AB là tiếp tuyến
Dạng 5: Phương trình có chứa nhiều dấu giá trị tuyệt đối:
chung ngoài (A là là tiếp điểm trên (O), B là tiếp điểm trên (O)). Từ O vẽ OC  OA.
Tìm giá trị của ăn để biểu thức trong dấu giá trị tuyệt đối bằng 0. Các
a) Chứng tỏ ABOC là hình chữ nhật.
giá trị này khi biểu diễn lên trục số sẽ chia trục số thành nhiều khoảng giá trị của ẩn.
b) Chứng tỏ OC là tiếp tuyến của đường tròn tâm O bán kính R = R – r.
c) Suy ra cách dựng đường t/tuyến chung ngoài AB khi cho trước 2
Cho ẩn lấy giá trị trên từng khoảng, trên từng khoảng đó dấu của biểu
đường tròn (O; R) và (O; r).
thức bên trong dấu giá trị tuyệt đối sẽ âm hoặc dương. Dựa vào đó mà
d) Tương tự, dựng tiếp tuyến chung trong của 2 đường tròn (O; R) và
bỏ dấu trị tuyệt đối. (O; r).
Giải phương trình, giá trị tìm được phải nằm trong khoảng đang xét
e) Tính độ dài của tiếp tuyến chung ngoài và tiếp tuyến chung trong và
mới nhận làm nghiệm.
khoảng cách hai tâm d = OO theo hai bán kính.
Nghiệm của phương trình là tất cả các nghiệm vừa tìm được trên từng
2.145 Cho đường tròn (O; R) và điểm I cố định với OI = R/2. AB là dây cung khoảng. quay quanh I.
a) Tìm vị trí C, D của A (hay B) tương ứng lúc độ dài IA (hay IB) dài
O.2 Giải các phương trình sau: nhất, ngắn nhất. 1. a) x – 5 = 3 b) 2x – 5 = 4
b) Chứng tỏ tập hợp các trung điểm M của dây cung AB là một đường c) x + 6 = 1 d) 3 – 7x = 0
tròn, tìm tâm và bán kính đường tròn này. e) x – 5 =  2 f) 8x – 5x = 2
c) Gọi EF là vị trí giới hạn của dây cung AB lúc M tiến dần đến I. C/m: 2. a) x  7 = 2x + 3 b) x + 4 = 2x – 5 i. EF  CD. c) x + 3 = 3x – 1 d) 9 + x = 2x
ii. EF là độ dài ngắn nhất của dây cung AB và CD là độ dài lớn nhất của AB. e) 3x – 1 = 3x + 2 f) x + 6 = 2x + 9
d) Chứng minh CEF đều, tính chu vi và diện tích tam giác này theo R.
3. a) 2x – 3 = 2x – 3 b) 5x – 4 = 4 – 5x
2.146 Cho (O; R) và (O; R) tiếp xúc ngoài nhau tại E. Gọi AB là tiếp tuyến c) 2x + 3 = 2x + 2 d) 5x – 3 = 5x – 5
chung ngoài của hai đường tròn (A  (O), B  (O)).
e) x2 – 3x + 3 =  x2 + 3x – 1 f) x2 – 9 = x2 – 9
a) Tính diện tích tứ giác AOOB theo R và R.
4. a) 5x  3x – 2 = 0
b) x – 5x +  2x 3 = 0
b) Gọi D là điểm đối xứng của A qua O. C/minh: B, E, D thẳng hàng.
e) 3 – x+ x2 – (4 + x)x = 0
f) (x – 1)2 + x + 21 x2 – 13 = 0
c) Xác định vị trí tương đối của hai đường thẳng AB và đường tròn
5. a) 2 – x=2x – 3 b) x + 3 = 5 – x đường kính OO.
c) 2x – 1 = 2 – 3x
d) 2x = x(x – 2)
2.147 Cho ABC có 3 góc nhọn. Đường tròn tâm I đường kính BC cắt AB tại F,
e) x(x + 1) = 3 – x
f) 3x – 12x + 3 = 0
cắt AC tại E, BE cắt CF tại H.
6*. a) x – 1+2  x = 3
b) x + 3+x – 5 = 3x – 1
a) Trong ABC điểm H gọi là gì ?
b) Gọi K là điểm đối xứng của H qua I và M là điểm đối xứng của H qua
c) x  2x – 1 + 3x – 2 = 4
d) x – 1+x+2+x – 3 = 14
BC. Chứng minh 5 điểm A, B, K, M, C cùng thuộc một đường tròn.
Xác định tâm và bán kính của đường tròn này. Gv: Trần Quốc Nghĩa Trang 102 Gv: Trần Quốc Nghĩa Trang 3 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
c) Đường tròn (K) cắt (O) tại E và F. Chứng tỏ IE, IF là hai tiếp tuyến
Bất phương trình tích, thương. Bất phương trình bậc hai.
của (O). Suy ra cách dựng tiếp tuyến vẽ từ I đến (O).
d) Chứng tỏ: AB > CD  OM < ON. Nói rõ vị trí tương đối của 2 cát
tuyến IAB và ICD lúc AB = CD.
Bất phương trình chứa dấu giá trị tuyệt đối.
e) Trường hợp dây cung AB = R 3 . Tính các góc và diện tích của AOB theo R.
1. Bất phương trình tích
2.141 Cho đường tròn (O; R) có đường kính AB. AC và BD là hai dây cung  A( x ) 0A( x ) 0 song song với nhau. Dạng 1.
A( x ).B( x ) 0   hoặc B( x )   0 B( x )   0
a) Chứng minh: AC = BD, suy ra CD là đường kính của (O).
b) Chứng tỏ ACBD là hình chữ nhật.  A( x ) 0A( x ) 0
A( x ).B( x ) 0   hoặc B( x )
c) Chứng tỏ rằng nếu dây cung AC = R 2 thì ACBD là hình vuông và  0 B( x )   0 ngược lại.  A( x ) 0A( x ) 0 Dạng 2.
A( x ).B( x ) 0   hoặc
d) Tính diện tích ACBD trong trường hợp  BAC = 300. B( x )   0 B( x )   0A( x ) 0A( x ) 0
2.142 Cho hai đường tròn (O; R) và (O; R) có R = 8, R = 6 và OO = 10.
A( x ).B( x ) 0   hoặc B( x )
a) Chứng tỏ (O; R) và (O; R) cắt nhau tại 2 điểm A và B và OOlà  0 B( x )   0
đường trung trực của AB.
2. Bất phương trình thương
b) Chứng minh AO là tiếp tuyến của (O) và AO là tiếp tuyến của (O). A( x )A( x ) 0A( x ) 0
c) Gọi I là giao điểm OO và AB. Tính độ dài của IA, IO. Dạng 1. 0   hoặc B( x ) B( x )   0 B( x )   0
d) Xác định tâm và tính bán kính của đường tròn qua 4 điểm A, O, B, O.
e) Tìm điều kiện về bán kính của đường tròn (O) sao cho đường tròn này A( x )A( x ) 0A( x ) 00   hoặc
không có điểm chung nào với (O; R). B( x ) B( x )   0 B( x )   0
2.143 Cho đường tròn (O; R) có đường kính AB, gọi (I) là đường tròn tâm I, A( x )A( x ) 0A( x ) 0 Dạng 2. 0   hoặc đường kính OA. B( x ) B( x )   0 B( x )   0
a) Chứng tỏ (O) và (I) tiếp xúc trong nhau. A( x )A( x ) 0A( x ) 00
b) Cho C là điểm bất kì  (O) (C khác A, B), AC cắt (I) tại K. C/minh:  hoặc B( x ) B( x )   0 B( x )   0 i. ABC và AOK vuông.
3. Bất phương trình chứa dấu giá trị tuyệt đối
ii. K là trung điểm của AC và OK = BC/2
iii. IOK và OBC đồng dạng.
x a  a x a (với a ≥ 0)
c) Gọi EF là đường kính của (O) qua K, chứng tỏ B, C, E, F là 4 đỉnh của
x a x  a hoặc x a (với a ≥ 0) hình thang cân.
Một số bất phương trình đặc biệt: d) Cho 
BOC = 600. Tính các cạnh, diện tích của ABC và của hình
 |a| ≥ 0  a  R
 |a| > 0  a ≠ 0 thang cân BCEF.
 |a| ≤ 0  a = 0
 |a| < 0  a   Gv: Trần Quốc Nghĩa Trang 4 Gv: Trần Quốc Nghĩa Trang 101 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
c) Đường tròn (K) cắt (O) tại E và F. Chứng tỏ IE, IF là hai tiếp tuyến
Bất phương trình tích, thương. Bất phương trình bậc hai.
của (O). Suy ra cách dựng tiếp tuyến vẽ từ I đến (O).
d) Chứng tỏ: AB > CD  OM < ON. Nói rõ vị trí tương đối của 2 cát
tuyến IAB và ICD lúc AB = CD.
Bất phương trình chứa dấu giá trị tuyệt đối.
e) Trường hợp dây cung AB = R 3 . Tính các góc và diện tích của AOB theo R.
1. Bất phương trình tích
2.141 Cho đường tròn (O; R) có đường kính AB. AC và BD là hai dây cung  A( x ) 0A( x ) 0 song song với nhau. Dạng 1.
A( x ).B( x ) 0   hoặc B( x )   0 B( x )   0
a) Chứng minh: AC = BD, suy ra CD là đường kính của (O).
b) Chứng tỏ ACBD là hình chữ nhật.  A( x ) 0A( x ) 0
A( x ).B( x ) 0   hoặc B( x )
c) Chứng tỏ rằng nếu dây cung AC = R 2 thì ACBD là hình vuông và  0 B( x )   0 ngược lại.  A( x ) 0A( x ) 0 Dạng 2.
A( x ).B( x ) 0   hoặc
d) Tính diện tích ACBD trong trường hợp  BAC = 300. B( x )   0 B( x )   0A( x ) 0A( x ) 0
2.142 Cho hai đường tròn (O; R) và (O; R) có R = 8, R = 6 và OO = 10.
A( x ).B( x ) 0   hoặc B( x )
a) Chứng tỏ (O; R) và (O; R) cắt nhau tại 2 điểm A và B và OOlà  0 B( x )   0
đường trung trực của AB.
2. Bất phương trình thương
b) Chứng minh AO là tiếp tuyến của (O) và AO là tiếp tuyến của (O). A( x )A( x ) 0A( x ) 0
c) Gọi I là giao điểm OO và AB. Tính độ dài của IA, IO. Dạng 1. 0   hoặc B( x ) B( x )   0 B( x )   0
d) Xác định tâm và tính bán kính của đường tròn qua 4 điểm A, O, B, O.
e) Tìm điều kiện về bán kính của đường tròn (O) sao cho đường tròn này A( x )A( x ) 0A( x ) 00   hoặc
không có điểm chung nào với (O; R). B( x ) B( x )   0 B( x )   0
2.143 Cho đường tròn (O; R) có đường kính AB, gọi (I) là đường tròn tâm I, A( x )A( x ) 0A( x ) 0 Dạng 2. 0   hoặc đường kính OA. B( x ) B( x )   0 B( x )   0
a) Chứng tỏ (O) và (I) tiếp xúc trong nhau. A( x )A( x ) 0A( x ) 00
b) Cho C là điểm bất kì  (O) (C khác A, B), AC cắt (I) tại K. C/minh:  hoặc B( x ) B( x )   0 B( x )   0 i. ABC và AOK vuông.
3. Bất phương trình chứa dấu giá trị tuyệt đối
ii. K là trung điểm của AC và OK = BC/2
iii. IOK và OBC đồng dạng.
x a  a x a (với a ≥ 0)
c) Gọi EF là đường kính của (O) qua K, chứng tỏ B, C, E, F là 4 đỉnh của
x a x  a hoặc x a (với a ≥ 0) hình thang cân.
Một số bất phương trình đặc biệt: d) Cho 
BOC = 600. Tính các cạnh, diện tích của ABC và của hình
 |a| ≥ 0  a  R
 |a| > 0  a ≠ 0 thang cân BCEF.
 |a| ≤ 0  a = 0
 |a| < 0  a   Gv: Trần Quốc Nghĩa Trang 4 Gv: Trần Quốc Nghĩa Trang 101 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
b) Gọi (I) là đường tròn tâm I có đường kính AB, đường thẳng OI cắt
4. Bất phương trình bậc hai
đường tròn (O) tại C và D, cắt đường tròn (I) tại E và F. Chứng tỏ C,
D, E và F cách đều A và B.
a) Bất phương trình bậc hai là bất phương trình có các dạng:
c) Chứng minh: AEBF là hình vuông.
(1): ax2 + bx + c > 0
(2): ax2 + bx + c ≥ 0
d) So sánh 2 tích IE . IF và IC . ID
(3): ax2 + bx + c < 0
(4): ax2 + bx + c ≤ 0
e) Biết OI = R/2, tính độ dài các cạnh và diện tích của ACD và hình
(trong đó a, b, c là các số thực và a ≠ 0) vuông AEBF theo R.
Một số bất phương trình đặc biệt:
2.138 Cho đường tròn (O; R), H là điểm bên trong (O) (H khác O), CD là đường
 a2 ≥ 0  a  R
 a2 > 0  a ≠ 0
kính qua H (HC > HD), AB là dây cung vuông góc với CD tại H.  a2 ≤ 0  a = 0
 a2 < 0  a  
a) Chứng tỏ CD là đường trung trực của AB.
b) Cách giải: b) Chứng minh:  CAD =  CBD = 900.
Cách 1: Đưa về bất phương trình tích bằng cách phân tích vế trái
c) Chứng minh: HA . HB = HC . HD theo 2 cách: thành nhân tử.
i. Dùng 2 tam giác đồng dạng.
Cách 2: Đưa về bất phương trình chứa dấu giá trị tuyệt đối:
ii. Dùng hệ thức lượng trong tam giác vuông.  2 2
X A X A   A X A
d) Trường hợp OH = R/2, chứng minh ABC đều và cạnh có độ dài là  2 2
X A X A X   A hoặc X A
R 3 . Suy ra cách vẽ tam giác đều có 3 đỉnh nằm trên đường tròn (O; R) cho trước.
Cách 3: Xét dấu (Học ở lớp 10)
2.139 Cho ABC vuông tại A có đường cao AH. Gọi I và K lần lượt là tâm của
O.3 Giải các bất phương trình sau và biểu diễn nghiệm trên trục số:
2 đường tròn có đường kính HB và HC. a) x(x – 1) < 0 b) (x – 2)(x – 5) > 0 c) (x + 5)(7 – 2x) > 0
a) Chứng tỏ 2 đường tròn (I) và (K) tiếp xúc ngoài nhau và tiếp xúc trong
d) (2x + 1)(x – 3) < 0 e) x2 – 6x < 0 f) (2 – x)(x + 3) > 0
với đường tròn qua 3 điểm A, B, C. x  2 x  2 x 1 g)  0 h)  0 i)  1
b) Đường tròn (I) cắt AB tại D, đường tròn (K) cắt AC tại E. Chứng minh x  3 x  5 x  3
ADHE là hình chữ nhật và AD . AB = AE . AC. Suy ra ABC đồng 2  x x  1 2 x  1 j)  1  k)  0 l)  0 dạng với AED. 3x 1 x  2 x  3
c) Chứng tỏ tứ giác BDEC có các góc đối bù nhau.
O.4 Giải các bất phương trình sau và biểu diễn nghiệm trên trục số:
d) Cho AH = 4 và HB = 3. Tính diện tích của tứ giác BDEC bằng 2 cách: a) x2 – 4 < 0 b) x2 + x – 6  0 c) x2 – x – 6 > 0
i. Diện tích của nhiều tam giác. d) x2 – 3x – 10 ≥ 0 e) x2 – 6x < 0 f) –x2 + 4x – 3  0
ii. Diện tích của 2 tam giác. g) x2 – 10x + 16 ≥ 0 h) – x2 + 7x – 10 < 0 i) x2 – 15x + 50 > 0
2.140 Từ điểm I ở ngoài đường tròn (O; R) vẽ 2 cát tuyến IAB và ICD (không j) – x2 + 3x + 4 > 0 k) x2 – 6x + 5 ≥ 0 l) x2 – x – 20  0
qua O). Gọi M, N lần lượt là 2 trung điểm của 2 dây cung AB, CD. m) x2 – 6x + 8 < 0 n) – x2 + 12x – 32 > 0 o) x2 + 6x + 8  0
a) Chứng minh: OMAB, ONCD, OM + ON  2R, CD<2R, AB < 2R.
O.5 Giải các bất phương trình sau và biểu diễn nghiệm trên trục số:
b) Chứng tỏ có 1 đường tròn qua 4 điểm O, I, M, N. Xác định tâm K của đường tròn này. a) x  4 b) x  7 c) 2x 1  3 d) x 1  2 e) 2 x  3  x  6 f) 1 2x  x 1 Gv: Trần Quốc Nghĩa Trang 100 Gv: Trần Quốc Nghĩa Trang 5 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
b) Gọi (I) là đường tròn tâm I có đường kính AB, đường thẳng OI cắt
4. Bất phương trình bậc hai
đường tròn (O) tại C và D, cắt đường tròn (I) tại E và F. Chứng tỏ C,
D, E và F cách đều A và B.
a) Bất phương trình bậc hai là bất phương trình có các dạng:
c) Chứng minh: AEBF là hình vuông.
(1): ax2 + bx + c > 0
(2): ax2 + bx + c ≥ 0
d) So sánh 2 tích IE . IF và IC . ID
(3): ax2 + bx + c < 0
(4): ax2 + bx + c ≤ 0
e) Biết OI = R/2, tính độ dài các cạnh và diện tích của ACD và hình
(trong đó a, b, c là các số thực và a ≠ 0) vuông AEBF theo R.
Một số bất phương trình đặc biệt:
2.138 Cho đường tròn (O; R), H là điểm bên trong (O) (H khác O), CD là đường
 a2 ≥ 0  a  R
 a2 > 0  a ≠ 0
kính qua H (HC > HD), AB là dây cung vuông góc với CD tại H.  a2 ≤ 0  a = 0
 a2 < 0  a  
a) Chứng tỏ CD là đường trung trực của AB.
b) Cách giải: b) Chứng minh:  CAD =  CBD = 900.
Cách 1: Đưa về bất phương trình tích bằng cách phân tích vế trái
c) Chứng minh: HA . HB = HC . HD theo 2 cách: thành nhân tử.
i. Dùng 2 tam giác đồng dạng.
Cách 2: Đưa về bất phương trình chứa dấu giá trị tuyệt đối:
ii. Dùng hệ thức lượng trong tam giác vuông.  2 2
X A X A   A X A
d) Trường hợp OH = R/2, chứng minh ABC đều và cạnh có độ dài là  2 2
X A X A X   A hoặc X A
R 3 . Suy ra cách vẽ tam giác đều có 3 đỉnh nằm trên đường tròn (O; R) cho trước.
Cách 3: Xét dấu (Học ở lớp 10)
2.139 Cho ABC vuông tại A có đường cao AH. Gọi I và K lần lượt là tâm của
O.3 Giải các bất phương trình sau và biểu diễn nghiệm trên trục số:
2 đường tròn có đường kính HB và HC. a) x(x – 1) < 0 b) (x – 2)(x – 5) > 0 c) (x + 5)(7 – 2x) > 0
a) Chứng tỏ 2 đường tròn (I) và (K) tiếp xúc ngoài nhau và tiếp xúc trong
d) (2x + 1)(x – 3) < 0 e) x2 – 6x < 0 f) (2 – x)(x + 3) > 0
với đường tròn qua 3 điểm A, B, C. x  2 x  2 x 1 g)  0 h)  0 i)  1
b) Đường tròn (I) cắt AB tại D, đường tròn (K) cắt AC tại E. Chứng minh x  3 x  5 x  3
ADHE là hình chữ nhật và AD . AB = AE . AC. Suy ra ABC đồng 2  x x  1 2 x  1 j)  1  k)  0 l)  0 dạng với AED. 3x 1 x  2 x  3
c) Chứng tỏ tứ giác BDEC có các góc đối bù nhau.
O.4 Giải các bất phương trình sau và biểu diễn nghiệm trên trục số:
d) Cho AH = 4 và HB = 3. Tính diện tích của tứ giác BDEC bằng 2 cách: a) x2 – 4 < 0 b) x2 + x – 6  0 c) x2 – x – 6 > 0
i. Diện tích của nhiều tam giác. d) x2 – 3x – 10 ≥ 0 e) x2 – 6x < 0 f) –x2 + 4x – 3  0
ii. Diện tích của 2 tam giác. g) x2 – 10x + 16 ≥ 0 h) – x2 + 7x – 10 < 0 i) x2 – 15x + 50 > 0
2.140 Từ điểm I ở ngoài đường tròn (O; R) vẽ 2 cát tuyến IAB và ICD (không j) – x2 + 3x + 4 > 0 k) x2 – 6x + 5 ≥ 0 l) x2 – x – 20  0
qua O). Gọi M, N lần lượt là 2 trung điểm của 2 dây cung AB, CD. m) x2 – 6x + 8 < 0 n) – x2 + 12x – 32 > 0 o) x2 + 6x + 8  0
a) Chứng minh: OMAB, ONCD, OM + ON  2R, CD<2R, AB < 2R.
O.5 Giải các bất phương trình sau và biểu diễn nghiệm trên trục số:
b) Chứng tỏ có 1 đường tròn qua 4 điểm O, I, M, N. Xác định tâm K của đường tròn này. a) x  4 b) x  7 c) 2x 1  3 d) x 1  2 e) 2 x  3  x  6 f) 1 2x  x 1 Gv: Trần Quốc Nghĩa Trang 100 Gv: Trần Quốc Nghĩa Trang 5 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
O.6 CMR: các bất phương trình sau đây vô nghiệm:
2.133 Cho đoạn thẳng AB. Trên nửa mặt phẳng bờ AB kẻ hai tia bất kì Ax và a) x2 + 1 < 1 b) x2 + 2x < 2x
c) x2 – 2x + 3 <  2x + 3
By song song với nhau. Một đường tròn tâm M tiếp xúc với AB tại C, với d) x2 + 2x + 2  0 e) 4x2  4x + 5  0 f) x2 + x + 1  0 Ax tại D, với By tại E.
O.7 CMR: mọi số thực x đều là nghiệm của các bất phương trình sau:
a) Nêu cách dựng đường tròn tâm M. a) 2x2  4x + 5 > 0 b) 3x2 + 2x + 1  0 c)  x2 + 6x  10 < 0
b) Chứng minh: AD + BE không phụ thuộc vào vị trí của Ax và By. 2 x  4x  5 2 6   2x  x
c) Chứng minh: E, M, D thẳng hàng. d)  x2 + 3x  3 < 0 e)  0 f)  0
d) Chứng minh: M thuộc một đường tròn cố định khi Ax và By thay đổi. 2 2 x 1
O.8 Tìm giá trị nhỏ nhất của các biểu thức sau:
2.134 Cho hai đường tròn (O ; R) và (O; R) tiếp xúc ngoài tại A. Gọi BC là a) A = 2x2 + 20x – 43 b) B = x2 + 2x + 2
tiếp tuyến chung ngoài của hai đường tròn (B  (O)). c) C = x2 – x +1 d) D = 4x2 + 4x + 3 a) Chứng minh:  BAC = 900. e) E = x2 – 20x + 101 f) F = x2 + xy + y2 + 1
b) Gọi D là điểm đối xứng của C qua O. C/minh: B, A, D thẳng hàng. g) G = (x – 3)(x + 5) + 40
h) H = (x – 2)(x + 4) – 10
c) Chứng minh: BC là tiếp tuyến của đường tròn đường kính OO.
O.9 Tìm giá trị nhỏ nhất của các biểu thức sau:
d) Chứng minh: BC = 2 RR ' . a) A = – 2x2 + 5x – 17 b) B = – x2 + 4x – 5
2.135 Cho hai đường tròn (O) và (O) cắt nhau ở A và B. Gọi C và lần lượt là c) C = – 4x2 – 4x – 2 d) D = – 6 – 8x – 16x2 e) E = – 3x2 + 12x – 11 f) F = – 2x2 + 5x – 17
điểm đối xứng của A qua O và O. Một đường thẳng (d) bất kì qua A cắt (O) và (O) tại M và N.
O.10 Tìm giá trị nhỏ nhất hoặc giá trị lớn nhất của các biểu thức sau:
a) Chứng minh: C, B, D thẳng hàng. 6 1 a) A = b) B =
b) AC cắt (O) tại E, AD cắt (O) tại F. Chứng minh: C, D, E, F cùng 2 2  x  3 2 x  2x  6
thuộc một đường tròn. 7 2  4 c) C = d) D =
c) Chứng minh: trung trực của MN luôn đi qua trung điểm của CD khi 2 10x  x  3 2 x  2x  3
(d) thay đổi. Suy ra trung điểm của MN luôn di động trên một đường 21 2013 e) E = f) F = tròn cố định. 2 x  4x  5 2 x  6x  11
d) Định vị trí của đường thẳng (d) để MN có độ dài lớn nhất.
O.11 Tìm giá trị nguyên của biến x để tại đó giá trị của mỗi biểu thức sau là
2.136 Cho nửa đường tròn tâm O đường kính AB. Gọi M là điểm bất kì thuộc một số nguyên:
nửa đường tròn, H là chân đường vuông góc kẻ từ M đến AB. Vẽ đường 2 3 3 2 3x  4x  x 1 2 3x  x  1 a) b) c) d)
tròn (M ; MH). Kẻ các tiếp tuyến AC, BD với đường tròn tâm M (C, D là x  3 x  2 x  4 3x  2 các tiếp điểm khác H).
O.12 Chứng minh rằng:
a) Chứng minh: C, M, D thẳng hàng và CD là tiếp tuyến của (O). 3 x  2  x  8x  7
b) Chứng minh: Khi M di chuyển trên AB thì tổng AC + BD không đổi. a)  1   0   (x  1, x  – 1) 2
c) Giả sử CD và AB cắt nhau tại I. Chứng minh: OH . OI không đổi. x 1 2x  2 2x  2   2 2 2 1  x  x  3x 14x  3
2.137 Cho đường tròn (O; R) và điểm I trong (O) (I khác O). b)  1   0   (x  0, x  – 3) 2 x x  3 x  3x
a) Hãy vẽ dây cung AB qua I và nhận I làm trung điểm.   Gv: Trần Quốc Nghĩa Trang 6 Gv: Trần Quốc Nghĩa Trang 99 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
O.6 CMR: các bất phương trình sau đây vô nghiệm:
2.133 Cho đoạn thẳng AB. Trên nửa mặt phẳng bờ AB kẻ hai tia bất kì Ax và a) x2 + 1 < 1 b) x2 + 2x < 2x
c) x2 – 2x + 3 <  2x + 3
By song song với nhau. Một đường tròn tâm M tiếp xúc với AB tại C, với d) x2 + 2x + 2  0 e) 4x2  4x + 5  0 f) x2 + x + 1  0 Ax tại D, với By tại E.
O.7 CMR: mọi số thực x đều là nghiệm của các bất phương trình sau:
a) Nêu cách dựng đường tròn tâm M. a) 2x2  4x + 5 > 0 b) 3x2 + 2x + 1  0 c)  x2 + 6x  10 < 0
b) Chứng minh: AD + BE không phụ thuộc vào vị trí của Ax và By. 2 x  4x  5 2 6   2x  x
c) Chứng minh: E, M, D thẳng hàng. d)  x2 + 3x  3 < 0 e)  0 f)  0
d) Chứng minh: M thuộc một đường tròn cố định khi Ax và By thay đổi. 2 2 x 1
O.8 Tìm giá trị nhỏ nhất của các biểu thức sau:
2.134 Cho hai đường tròn (O ; R) và (O; R) tiếp xúc ngoài tại A. Gọi BC là a) A = 2x2 + 20x – 43 b) B = x2 + 2x + 2
tiếp tuyến chung ngoài của hai đường tròn (B  (O)). c) C = x2 – x +1 d) D = 4x2 + 4x + 3 a) Chứng minh:  BAC = 900. e) E = x2 – 20x + 101 f) F = x2 + xy + y2 + 1
b) Gọi D là điểm đối xứng của C qua O. C/minh: B, A, D thẳng hàng. g) G = (x – 3)(x + 5) + 40
h) H = (x – 2)(x + 4) – 10
c) Chứng minh: BC là tiếp tuyến của đường tròn đường kính OO.
O.9 Tìm giá trị nhỏ nhất của các biểu thức sau:
d) Chứng minh: BC = 2 RR ' . a) A = – 2x2 + 5x – 17 b) B = – x2 + 4x – 5
2.135 Cho hai đường tròn (O) và (O) cắt nhau ở A và B. Gọi C và lần lượt là c) C = – 4x2 – 4x – 2 d) D = – 6 – 8x – 16x2 e) E = – 3x2 + 12x – 11 f) F = – 2x2 + 5x – 17
điểm đối xứng của A qua O và O. Một đường thẳng (d) bất kì qua A cắt (O) và (O) tại M và N.
O.10 Tìm giá trị nhỏ nhất hoặc giá trị lớn nhất của các biểu thức sau:
a) Chứng minh: C, B, D thẳng hàng. 6 1 a) A = b) B =
b) AC cắt (O) tại E, AD cắt (O) tại F. Chứng minh: C, D, E, F cùng 2 2  x  3 2 x  2x  6
thuộc một đường tròn. 7 2  4 c) C = d) D =
c) Chứng minh: trung trực của MN luôn đi qua trung điểm của CD khi 2 10x  x  3 2 x  2x  3
(d) thay đổi. Suy ra trung điểm của MN luôn di động trên một đường 21 2013 e) E = f) F = tròn cố định. 2 x  4x  5 2 x  6x  11
d) Định vị trí của đường thẳng (d) để MN có độ dài lớn nhất.
O.11 Tìm giá trị nguyên của biến x để tại đó giá trị của mỗi biểu thức sau là
2.136 Cho nửa đường tròn tâm O đường kính AB. Gọi M là điểm bất kì thuộc một số nguyên:
nửa đường tròn, H là chân đường vuông góc kẻ từ M đến AB. Vẽ đường 2 3 3 2 3x  4x  x 1 2 3x  x  1 a) b) c) d)
tròn (M ; MH). Kẻ các tiếp tuyến AC, BD với đường tròn tâm M (C, D là x  3 x  2 x  4 3x  2 các tiếp điểm khác H).
O.12 Chứng minh rằng:
a) Chứng minh: C, M, D thẳng hàng và CD là tiếp tuyến của (O). 3 x  2  x  8x  7
b) Chứng minh: Khi M di chuyển trên AB thì tổng AC + BD không đổi. a)  1   0   (x  1, x  – 1) 2
c) Giả sử CD và AB cắt nhau tại I. Chứng minh: OH . OI không đổi. x 1 2x  2 2x  2   2 2 2 1  x  x  3x 14x  3
2.137 Cho đường tròn (O; R) và điểm I trong (O) (I khác O). b)  1   0   (x  0, x  – 3) 2 x x  3 x  3x
a) Hãy vẽ dây cung AB qua I và nhận I làm trung điểm.   Gv: Trần Quốc Nghĩa Trang 6 Gv: Trần Quốc Nghĩa Trang 99 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
2.129 Cho đường tròn (O ; R) và đường thẳng xy cố định ở ngoài (O). Từ điểm
O.13 Chứng minh rằng:
M bất kì trên xy kẻ hai tiếp tuyến MB, MC đến đường tròn (O) (B, C là 2 2        các tiếp điểm). x 1 x 1 2 1 a) :  1  1    (x  0, x  – 1) 2  
a) Xác định tâm O của đường tròn đi qua M, B, O, C.  x  x x 1   x 
b) Chứng minh: (O) luôn đi qua một điểm cố định H khác O. 2 x x  3x  x  3 x  b)   
 1 (x  0, x  3, x  –3/2)
c) Dây cung BC cắt OH tại I vad cắt OM tại K.  2 2  x  3 2x  3  x  3x x  9 
Chứng minh: OI.OH = OK.OM = R2. Suy ra khi M thay đổi trên xy thì 2 1 x  x  x 1 
BC luôn đi qua một điểm cố định. c)     1  (x   1) 2  2 2  x 1 x 1  x  2x 1 x 1 
2.130 Cho nửa đường tròn (O) đường kính AB = 2R và một điểm M bất kì trên  x x  6  2x  6 x
nửa đường tròn (M khác A, B). Đường thẳng (d) tiếp xúc với nửa đường d)  :   1   (x  0 và x   6) 2 2  2  x  36 x  6x  x  6x 6  x
tròn tại M và cắt trung trực của đoạn AB tại I. Đường tròn (I) tiếp xúc với
AB cắt đường thẳng (d) tại C và D (D nằm trong góc BÔM).
O.14 Phân tích các đa thức sau thành nhân tử:
a) Chứng minh: OC, OD là các tia phân giác của các góc AÔM và BÔM. 1) a) 2 x  4x 12 b) 2 6x  7x 1 c) 2 2x  4x  6
b) Chứng minh: CA và DB vuông góc với AB. d) 2 2x  10x  8 e) 2 10x  4x  6 f) 2 x  2x 15
c) Chứng minh: AC . BD = R2.
d) AM cắt BD tại F, BM cắt AC tại E. Chứng minh: S 2. a) 4 2 2x  x  6 b) 4 2 x  6x  8 c) 4 2 x  5x 14 ABM = SEFM.
e) Xác định vị trí của M sao cho diện tích hình thang ABCD nhỏ nhất. d) 4 2 4x  7x  3 e) 4 2 6x  7x  2 f) 4 2 x  8x  15
2.131 Cho đường tròn (O) và dây BC cố định. Điểm A di động trên cung lớn 3. a) x  5 x  6 b) x  9 x  18 c) 3x  5 x  8
BC. Gọi M là trung điểm của dây AC. Vẽ đường kính BD của (O). d) 2  x  3 x  5 e) 4  x  x  3 f) x  2 x  3
a) Chứng minh: M thuộc một đường tròn cố định. Xác định tâm I của đường tròn này. 2 2  x 6 1   10  x 
b) Gọi K là trung điểm của BC, đường tròn (I) cắt CD tại J.
O.15 Cho biểu thức:   : x  2   3    x  4x 6  3x x  2 x  2    
Chứng minh: K, I, J thẳng hàng.
a) Tìm điều kiện xác định của biểu thức. Rút gọn biểu thức.
c) Gọi H là hình chiếu của M trên AB, chứng tỏ đường thẳng HM luôn đi
b) Tìm giá trị của x để giá trị của biểu thức có giá trị dương.
qua trung điểm của dây CD khi A thay đổi. 2
d) C/minh: khi A di động thì H luôn di động trên một đường tròn cố định.  x  2 2  2  4x x  3x 1
O.16 Cho biểu thức:   3 :     3x x  1  x  1 3x
2.132 Cho đường tròn (O ; R) và đường thẳng (d) cắt đường tròn tại E, F. Từ
a) Tìm điều kiện xác định của biểu thức. Rút gọn biểu thức.
điểm A bất kì trên (d) và ở ngoài đường tròn (O), vẽ các tiếp tuyến AB,
b) Tìm giá trị của x để giá trị của biểu thức có giá trị âm.
AC đến đường tròn (O) (B, C là các tiếp điểm). Gọi H là trung điểm của
EF và BC cắt OA, OH lần lượt tại I, K. Chứng minh:  x  2
a) 5 điểm A, B, C, O, H thuộc một đường tròn.  2x 1   x 1
O.17 Cho biểu thức: x 1     b) OI . OA = OH . OK = R2. 2 2 x x  x x 1    
c) Khi A thay đổi, đường thẳng BC luôn đi qua một điểm cố định. 2  x  x 1 
d) I luôn thuộc một đường tròn cố định khi A thay đổi.
a) Tìm điều kiện xác định của biểu thức. Rút gọn biểu thức.
e) KE, KF là các tiếp tuyến của (O; R).
b) Tìm giá trị của x để giá trị của biểu thức có giá trị dương. Gv: Trần Quốc Nghĩa Trang 98 Gv: Trần Quốc Nghĩa Trang 7 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
2.129 Cho đường tròn (O ; R) và đường thẳng xy cố định ở ngoài (O). Từ điểm
O.13 Chứng minh rằng:
M bất kì trên xy kẻ hai tiếp tuyến MB, MC đến đường tròn (O) (B, C là 2 2        các tiếp điểm). x 1 x 1 2 1 a) :  1  1    (x  0, x  – 1) 2  
a) Xác định tâm O của đường tròn đi qua M, B, O, C.  x  x x 1   x 
b) Chứng minh: (O) luôn đi qua một điểm cố định H khác O. 2 x x  3x  x  3 x  b)   
 1 (x  0, x  3, x  –3/2)
c) Dây cung BC cắt OH tại I vad cắt OM tại K.  2 2  x  3 2x  3  x  3x x  9 
Chứng minh: OI.OH = OK.OM = R2. Suy ra khi M thay đổi trên xy thì 2 1 x  x  x 1 
BC luôn đi qua một điểm cố định. c)     1  (x   1) 2  2 2  x 1 x 1  x  2x 1 x 1 
2.130 Cho nửa đường tròn (O) đường kính AB = 2R và một điểm M bất kì trên  x x  6  2x  6 x
nửa đường tròn (M khác A, B). Đường thẳng (d) tiếp xúc với nửa đường d)  :   1   (x  0 và x   6) 2 2  2  x  36 x  6x  x  6x 6  x
tròn tại M và cắt trung trực của đoạn AB tại I. Đường tròn (I) tiếp xúc với
AB cắt đường thẳng (d) tại C và D (D nằm trong góc BÔM).
O.14 Phân tích các đa thức sau thành nhân tử:
a) Chứng minh: OC, OD là các tia phân giác của các góc AÔM và BÔM. 1) a) 2 x  4x 12 b) 2 6x  7x 1 c) 2 2x  4x  6
b) Chứng minh: CA và DB vuông góc với AB. d) 2 2x  10x  8 e) 2 10x  4x  6 f) 2 x  2x 15
c) Chứng minh: AC . BD = R2.
d) AM cắt BD tại F, BM cắt AC tại E. Chứng minh: S 2. a) 4 2 2x  x  6 b) 4 2 x  6x  8 c) 4 2 x  5x 14 ABM = SEFM.
e) Xác định vị trí của M sao cho diện tích hình thang ABCD nhỏ nhất. d) 4 2 4x  7x  3 e) 4 2 6x  7x  2 f) 4 2 x  8x  15
2.131 Cho đường tròn (O) và dây BC cố định. Điểm A di động trên cung lớn 3. a) x  5 x  6 b) x  9 x  18 c) 3x  5 x  8
BC. Gọi M là trung điểm của dây AC. Vẽ đường kính BD của (O). d) 2  x  3 x  5 e) 4  x  x  3 f) x  2 x  3
a) Chứng minh: M thuộc một đường tròn cố định. Xác định tâm I của đường tròn này. 2 2  x 6 1   10  x 
b) Gọi K là trung điểm của BC, đường tròn (I) cắt CD tại J.
O.15 Cho biểu thức:   : x  2   3    x  4x 6  3x x  2 x  2    
Chứng minh: K, I, J thẳng hàng.
a) Tìm điều kiện xác định của biểu thức. Rút gọn biểu thức.
c) Gọi H là hình chiếu của M trên AB, chứng tỏ đường thẳng HM luôn đi
b) Tìm giá trị của x để giá trị của biểu thức có giá trị dương.
qua trung điểm của dây CD khi A thay đổi. 2
d) C/minh: khi A di động thì H luôn di động trên một đường tròn cố định.  x  2 2  2  4x x  3x 1
O.16 Cho biểu thức:   3 :     3x x  1  x  1 3x
2.132 Cho đường tròn (O ; R) và đường thẳng (d) cắt đường tròn tại E, F. Từ
a) Tìm điều kiện xác định của biểu thức. Rút gọn biểu thức.
điểm A bất kì trên (d) và ở ngoài đường tròn (O), vẽ các tiếp tuyến AB,
b) Tìm giá trị của x để giá trị của biểu thức có giá trị âm.
AC đến đường tròn (O) (B, C là các tiếp điểm). Gọi H là trung điểm của
EF và BC cắt OA, OH lần lượt tại I, K. Chứng minh:  x  2
a) 5 điểm A, B, C, O, H thuộc một đường tròn.  2x 1   x 1
O.17 Cho biểu thức: x 1     b) OI . OA = OH . OK = R2. 2 2 x x  x x 1    
c) Khi A thay đổi, đường thẳng BC luôn đi qua một điểm cố định. 2  x  x 1 
d) I luôn thuộc một đường tròn cố định khi A thay đổi.
a) Tìm điều kiện xác định của biểu thức. Rút gọn biểu thức.
e) KE, KF là các tiếp tuyến của (O; R).
b) Tìm giá trị của x để giá trị của biểu thức có giá trị dương. Gv: Trần Quốc Nghĩa Trang 98 Gv: Trần Quốc Nghĩa Trang 7 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1 2  1  2x x 2x  24 12x
c) C luôn luôn thuộc một đường tròn cố định khi B thay đổi.
O.18 Cho biểu thức:     2  4  2x 3x  6 12  3x 6  13x  
2.125 Cho đường tròn (O ; R) AB. Vẽ dây CD của (O) vuông góc với OA tại
a) Tìm điều kiện xác định của biểu thức. Rút gọn biểu thức.
trung điểm của M của OA. Gọi E là trung điểm của BC.
b) Tìm giá trị của x để giá trị của biểu thức có giá trị dương.
d) Chứng minh: O, M, C, E cùng thuộc một đường tròn. 2 a) Tính BC theo R.  x  2 2  2  4x x  3x 1
O.19 Cho biểu thức:   3 :   
b) Tiếp tuyến tại B của (O) cắt OE tại N. C/m: NC là tiếp tuyến của (O).  3x x  1  x  1 3x
c) Chứng minh: NA chia MC hai phần bằng nhau.
a) Tìm điều kiện xác định của biểu thức. Rút gọn biểu thức.
d) Chứng minh: MA2 + MB2 + MC2 + MD2 = 4R2.
b) Tìm giá trị của x để giá trị của biểu thức có giá trị âm.  3 2 4x  6x  8x
2.126 Cho ABC có A = 900, (AB < AC) nội tiếp (O ; R), có đường cao AH.
O.20 Cho biểu thức: 2x 1 Gọi M là trung điểm AC.
a) Tìm điều kiện xác định của biểu thức. Rút gọn biểu thức.
a) Chứng minh: A, M, O, H cùng thuộc một đường tròn. Xác định tâm I
b) Tìm giá trị của x để giá trị của biểu thức có giá trị không âm. của đường tròn này.
b) Chứng minh: (O) và (I) tiếp xúc nhau. 8  2x
O.21 Cho biểu thức:
c) Đường tròn (I) cắt AB tại N. Chứng minh: I, M, N thẳng hàng. 2 x  x  20
a) Tìm điều kiện xác định của biểu thức. Rút gọn biểu thức.
2.127 Cho đường tròn (O; R) đường kính AB. Lấy điểm M  (O). Gọi P, Q theo
b) Tìm giá trị của x để giá trị của biểu thức có giá trị âm.
thứ tự là hình chiếu của M trên AB và tiếp tuyến Ax của (O). gọi I là 2 2 trung điểm của của PQ. x  x  4 
O.22 Cho biểu thức: M    4  3  
a) Chứng minh: A, I, M thẳng hàng. Suy ra I thuộc một đường tròn cố x  2 x  
định và tính theo R bán kính của đường tròn này.
a) Tìm điều kiện xác định của biểu thức M. Rút gọn M.
b) Tiếp tuyến tại M của (O) cắt tiếp tuyến Ax ở N. Chứng minh: O, I, N
b) Tìm x để biểu thức M đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó.
thẳng hàng và MA là phân giác các góc OMQ, NMP. 2 2 2 (x  2)  x  x  6x  4
c) Đường trung trực của đường kính AB cắt MB tại K.
O.23 Cho biểu thức: N   1     x x  2 x Chứng minh: NK = R.  
d) Xác định vị trí của M để AMN đều.
a) Tìm điều kiện xác định của biểu thức N. Rút gọn N.
b) Tìm x để biểu thức N đạt giá trị lớn nhất. Tìm giá trị lớn nhất đó.
2.128 Cho đường tròn (O; R) đường kính AB. Lấy điểm C ngoài đường tròn sao
cho B là trung điểm của OC. Từ C vẽ hai tiếp tuyến CM và CN đến  2 2 2
( A B ) A 2 AB B
đường tròn (O) (M, N là các tiếp điểm).  2 2 2
( A B ) A 2 AB B
a) Chứng minh: AMN là tam giác cân. Tính CM và AM theo R.  2 2
A B ( A B )( A B )
b) Chứng minh: tứ giác AMCN là hình thoi. Tính SAMCN theo R.  3 3 2 2 3
( A B ) A 3A B 3AB B
c) Gọi I là trung điểm của CM, AI cắt OM tại K. Chứng minh: K là trung điểm của AI.  3 3 2 2 3
( A B ) A 3A B 3AB B
d) Tính diện tích AKB theo R.  3 3 2 2
A B ( A B )( A AB B ) 3 3 2 2
A B ( A B )( A AB B ) Gv: Trần Quốc Nghĩa Trang 8 Gv: Trần Quốc Nghĩa Trang 97 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1 2  1  2x x 2x  24 12x
c) C luôn luôn thuộc một đường tròn cố định khi B thay đổi.
O.18 Cho biểu thức:     2  4  2x 3x  6 12  3x 6  13x  
2.125 Cho đường tròn (O ; R) AB. Vẽ dây CD của (O) vuông góc với OA tại
a) Tìm điều kiện xác định của biểu thức. Rút gọn biểu thức.
trung điểm của M của OA. Gọi E là trung điểm của BC.
b) Tìm giá trị của x để giá trị của biểu thức có giá trị dương.
d) Chứng minh: O, M, C, E cùng thuộc một đường tròn. 2 a) Tính BC theo R.  x  2 2  2  4x x  3x 1
O.19 Cho biểu thức:   3 :   
b) Tiếp tuyến tại B của (O) cắt OE tại N. C/m: NC là tiếp tuyến của (O).  3x x  1  x  1 3x
c) Chứng minh: NA chia MC hai phần bằng nhau.
a) Tìm điều kiện xác định của biểu thức. Rút gọn biểu thức.
d) Chứng minh: MA2 + MB2 + MC2 + MD2 = 4R2.
b) Tìm giá trị của x để giá trị của biểu thức có giá trị âm.  3 2 4x  6x  8x
2.126 Cho ABC có A = 900, (AB < AC) nội tiếp (O ; R), có đường cao AH.
O.20 Cho biểu thức: 2x 1 Gọi M là trung điểm AC.
a) Tìm điều kiện xác định của biểu thức. Rút gọn biểu thức.
a) Chứng minh: A, M, O, H cùng thuộc một đường tròn. Xác định tâm I
b) Tìm giá trị của x để giá trị của biểu thức có giá trị không âm. của đường tròn này.
b) Chứng minh: (O) và (I) tiếp xúc nhau. 8  2x
O.21 Cho biểu thức:
c) Đường tròn (I) cắt AB tại N. Chứng minh: I, M, N thẳng hàng. 2 x  x  20
a) Tìm điều kiện xác định của biểu thức. Rút gọn biểu thức.
2.127 Cho đường tròn (O; R) đường kính AB. Lấy điểm M  (O). Gọi P, Q theo
b) Tìm giá trị của x để giá trị của biểu thức có giá trị âm.
thứ tự là hình chiếu của M trên AB và tiếp tuyến Ax của (O). gọi I là 2 2 trung điểm của của PQ. x  x  4 
O.22 Cho biểu thức: M    4  3  
a) Chứng minh: A, I, M thẳng hàng. Suy ra I thuộc một đường tròn cố x  2 x  
định và tính theo R bán kính của đường tròn này.
a) Tìm điều kiện xác định của biểu thức M. Rút gọn M.
b) Tiếp tuyến tại M của (O) cắt tiếp tuyến Ax ở N. Chứng minh: O, I, N
b) Tìm x để biểu thức M đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó.
thẳng hàng và MA là phân giác các góc OMQ, NMP. 2 2 2 (x  2)  x  x  6x  4
c) Đường trung trực của đường kính AB cắt MB tại K.
O.23 Cho biểu thức: N   1     x x  2 x Chứng minh: NK = R.  
d) Xác định vị trí của M để AMN đều.
a) Tìm điều kiện xác định của biểu thức N. Rút gọn N.
b) Tìm x để biểu thức N đạt giá trị lớn nhất. Tìm giá trị lớn nhất đó.
2.128 Cho đường tròn (O; R) đường kính AB. Lấy điểm C ngoài đường tròn sao
cho B là trung điểm của OC. Từ C vẽ hai tiếp tuyến CM và CN đến  2 2 2
( A B ) A 2 AB B
đường tròn (O) (M, N là các tiếp điểm).  2 2 2
( A B ) A 2 AB B
a) Chứng minh: AMN là tam giác cân. Tính CM và AM theo R.  2 2
A B ( A B )( A B )
b) Chứng minh: tứ giác AMCN là hình thoi. Tính SAMCN theo R.  3 3 2 2 3
( A B ) A 3A B 3AB B
c) Gọi I là trung điểm của CM, AI cắt OM tại K. Chứng minh: K là trung điểm của AI.  3 3 2 2 3
( A B ) A 3A B 3AB B
d) Tính diện tích AKB theo R.  3 3 2 2
A B ( A B )( A AB B ) 3 3 2 2
A B ( A B )( A AB B ) Gv: Trần Quốc Nghĩa Trang 8 Gv: Trần Quốc Nghĩa Trang 97 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
c) Chứng minh: 4 điểm I, O, M, B cùng thuộc một đường tròn.
2.120 Cho hai đường tròn (O) và (O) tiếp xúc ngoài A. Kẻ tiếp tuyến chung Phần 1. Đại số
ngoài DE, D  (O), E  (O). Kẻ tiếp tuyến chung trong tại A, cắt DE ở I.
Gọi M là giao điểm của OI và AD, N là giao điểm của OI và AE.
a) Tứ giác AMIN là hình gì ? Vì sao ? Chương 1
b) Chứng minh: IM . IO = IN . IO
CĂN BẬC HAI – CĂN BẬC BA
c) Chứng minh: OO là tiếp tuyến của đường tròn có đường kính là DE. 
d) Biết OA = 5cm, OA = 3,2cm. Tính DE. A - Căn bậc hai
2.121 Cho ABC vuông tại A (AB < AC) nội tiếp đường tròn (O) có đường
kính BC. Kẻ dây AD vuông góc với BC. Gọi E là giao điểm của DB và
CA. Qua E kẻ đường thẳng vuông góc với BC, cắt BC ở H, cắt AB ở F.
1. Định nghĩa: Căn bậc hai của số a không âm là số x sao cho x2 = a. Chứng minh:
2. Ký hiệu:  a > 0: 
a : Căn bậc hai của số a a) EBF cân. b) HAF cân.
c) HA là tiếp tuyến của (O).
a : Căn bậc hai âm của số a
2.122 Cho (O) đường kính AB, điểm C nằm giữa A và O. Vẽ đường tròn (O) có đường kính CB.
a = 0: 0 0
a) Hai đường tròn (O) và (O) có vị trí tương đối như thế nào với nhau ?
3. Chú ý: Với a  0: 2   2 ( a ) (
a ) a
b) Kẻ dây DE của đường tròn (O) vuông góc với AC tại trung điểm H
của AC. Tứ giác ADCE là hình gì ? Vì sao ?
4. Căn bậc hai số học:
c) Gọi K là giao điểm của DB và (O). Chứng minh: ba điểm E, C, K
Với a  0: số a được gọi là CBHSH của a thẳng hàng.
 Phép khi phương là phép toán tìm CBHSH của số a không âm.
d) Chứng minh: KH là tiếp tuyến của (O).
5. So sánh các CBHSH: Với a  0, b  0: a b a b
2.123 Cho hai đường tròn (O; R) và (O; R) tiếp xúc ngoài tại A (R > R). Vẽ
các đường kính AOB, AOC. Dây DE của đường tròn (O) vuông góc với 1.1
Điền vào ô trống trong bảng sau:
BC tại trung điểm K của BC. x 11 12 13 14 15 16 17 18 19 20
a) Chứng minh: tứ giác BDCE là hình thoi. x2
b) Gọi I là giao điểm của EC và đường tròn (O). Chứng minh: ba điểm D, A, I thẳng hàng. 1.2
Tìm căn bậc hai số học rồi suy ra căn bậc hai của các số sau: a) 121 b) 144 c) 169 d) 225
c) Chứng minh: KI là tiếp tuyến của (O). e) 256 f) 324 g) 361 h) 400
2.124 Cho đường tròn (O; R) và tiếp tuyến xy tại điểm A cố định trên đường i) 0,01 j) 0,04 k) 0,49 l) 0,64
tròn. Từ điểm B tùy ý trên (O) (khác A), kẻ BH  xy. Đường phân giác m) 0,25 n) 0,81 o) 0,09 p) 0,16
trong của góc AÔB cắt BH tại C và cắt xy tại M. Chứng minh: 1.3 Tính:
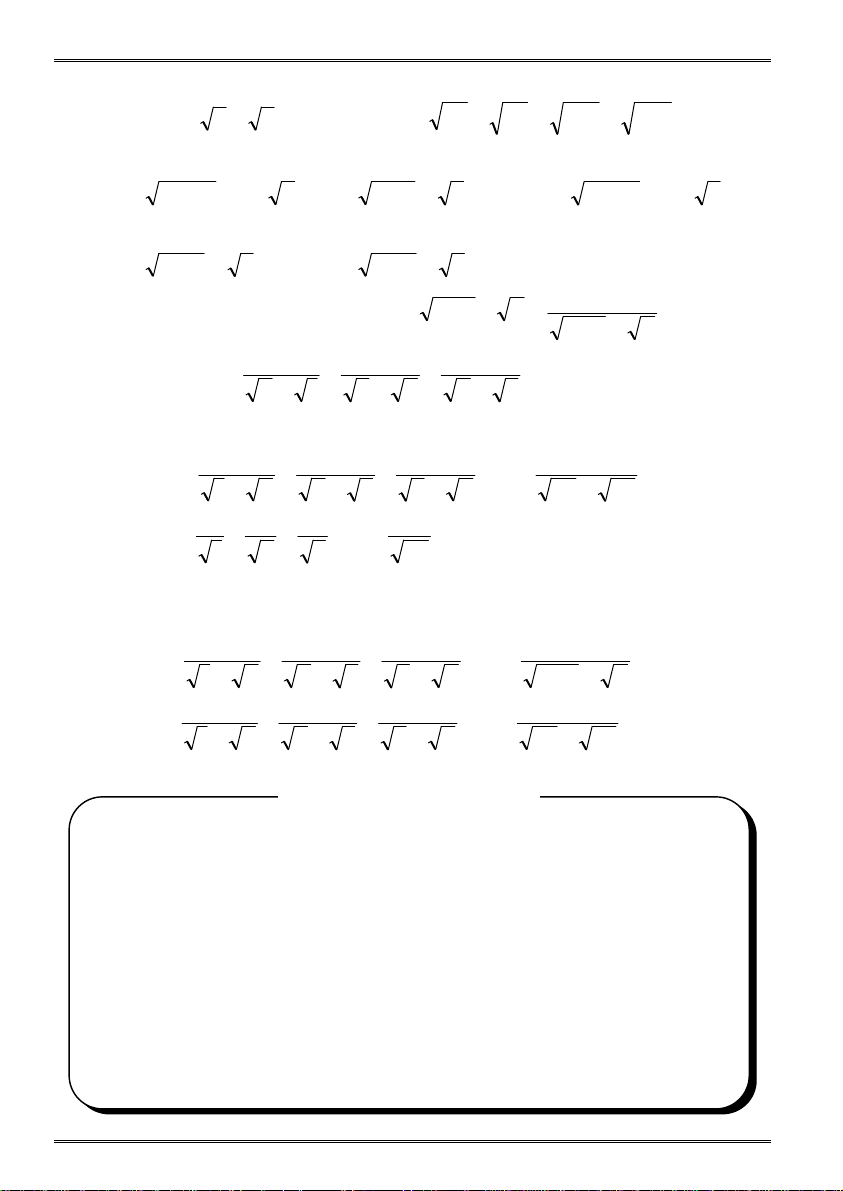
a) BA là tia phân giác của OBH. a) 0, 09 b) 16  c) 0, 25. 0,16 d) ( 4  ).( 2  5)
b) MB là tiếp tuyến của (O; R). Gv: Trần Quốc Nghĩa Trang 96 Gv: Trần Quốc Nghĩa Trang 9 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
c) Chứng minh: 4 điểm I, O, M, B cùng thuộc một đường tròn.
2.120 Cho hai đường tròn (O) và (O) tiếp xúc ngoài A. Kẻ tiếp tuyến chung Phần 1. Đại số
ngoài DE, D  (O), E  (O). Kẻ tiếp tuyến chung trong tại A, cắt DE ở I.
Gọi M là giao điểm của OI và AD, N là giao điểm của OI và AE.
a) Tứ giác AMIN là hình gì ? Vì sao ? Chương 1
b) Chứng minh: IM . IO = IN . IO
CĂN BẬC HAI – CĂN BẬC BA
c) Chứng minh: OO là tiếp tuyến của đường tròn có đường kính là DE. 
d) Biết OA = 5cm, OA = 3,2cm. Tính DE. A - Căn bậc hai
2.121 Cho ABC vuông tại A (AB < AC) nội tiếp đường tròn (O) có đường
kính BC. Kẻ dây AD vuông góc với BC. Gọi E là giao điểm của DB và
CA. Qua E kẻ đường thẳng vuông góc với BC, cắt BC ở H, cắt AB ở F.
1. Định nghĩa: Căn bậc hai của số a không âm là số x sao cho x2 = a. Chứng minh:
2. Ký hiệu:  a > 0: 
a : Căn bậc hai của số a a) EBF cân. b) HAF cân.
c) HA là tiếp tuyến của (O).
a : Căn bậc hai âm của số a
2.122 Cho (O) đường kính AB, điểm C nằm giữa A và O. Vẽ đường tròn (O) có đường kính CB.
a = 0: 0 0
a) Hai đường tròn (O) và (O) có vị trí tương đối như thế nào với nhau ?
3. Chú ý: Với a  0: 2   2 ( a ) (
a ) a
b) Kẻ dây DE của đường tròn (O) vuông góc với AC tại trung điểm H
của AC. Tứ giác ADCE là hình gì ? Vì sao ?
4. Căn bậc hai số học:
c) Gọi K là giao điểm của DB và (O). Chứng minh: ba điểm E, C, K
Với a  0: số a được gọi là CBHSH của a thẳng hàng.
 Phép khi phương là phép toán tìm CBHSH của số a không âm.
d) Chứng minh: KH là tiếp tuyến của (O).
5. So sánh các CBHSH: Với a  0, b  0: a b a b
2.123 Cho hai đường tròn (O; R) và (O; R) tiếp xúc ngoài tại A (R > R). Vẽ
các đường kính AOB, AOC. Dây DE của đường tròn (O) vuông góc với 1.1
Điền vào ô trống trong bảng sau:
BC tại trung điểm K của BC. x 11 12 13 14 15 16 17 18 19 20
a) Chứng minh: tứ giác BDCE là hình thoi. x2
b) Gọi I là giao điểm của EC và đường tròn (O). Chứng minh: ba điểm D, A, I thẳng hàng. 1.2
Tìm căn bậc hai số học rồi suy ra căn bậc hai của các số sau: a) 121 b) 144 c) 169 d) 225
c) Chứng minh: KI là tiếp tuyến của (O). e) 256 f) 324 g) 361 h) 400
2.124 Cho đường tròn (O; R) và tiếp tuyến xy tại điểm A cố định trên đường i) 0,01 j) 0,04 k) 0,49 l) 0,64
tròn. Từ điểm B tùy ý trên (O) (khác A), kẻ BH  xy. Đường phân giác m) 0,25 n) 0,81 o) 0,09 p) 0,16
trong của góc AÔB cắt BH tại C và cắt xy tại M. Chứng minh: 1.3 Tính:
a) BA là tia phân giác của OBH. a) 0, 09 b) 16  c) 0, 25. 0,16 d) ( 4  ).( 2  5)
b) MB là tiếp tuyến của (O; R). Gv: Trần Quốc Nghĩa Trang 96 Gv: Trần Quốc Nghĩa Trang 9 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1 4 6 16
2.116 Cho đường tròn tâm O đường kính AB, điểm M thuộc đường tròn. Gọi N e) f) g) 0 3 , 6  0,49 25 5 0
là điểm đối xứng với A qua M. BN cắt đường tròn ở C. Gọi E là giao ,04 điểm của AC và BM. 1.4
Trong các số sau, số nào có căn bậc hai: a) Chứng minh: NE  AB. a) 5 b) 1,5 c)  0,1 d)  9
b) Gọi F là điểm đối xứng với E qua M. Chứng minh: FA là tiếp tuyến 1.5
Trong các biểu thức sau, biểu thức nào có căn bậc hai: của (O). a) (x – 4)(x – 6) + 1 b) (3 – x)(x – 5) – 4
c) Chứng minh: FN là tiếp tuyến của đường tròn (B; BA). c)  x2 + 6x – 9 d)  5x2 + 8x – 4
2.117 Cho đường tròn (O; R) đường kính AB và (d) la tiếp tuyến của (O) tại A.
e) x(x – 1)(x + 1)(x + 2) + 1 f) x2 + 20x + 101
M là điểm di động trên (d). Kẻ tiếp tuyến MC đến (O) (C là tiếp điểm 1.6
So sánh hai số sau (không dùng máy tính):
khác A). Tia BC cắt (d) tại K và kẻ CH vuông góac với AB tại H. a) 1 và 2 b) 2 và 3 c) 6 và 41 a) Chứng minh: OM // BK. d) 7 và 47 e) 2 và 2  1 f) 1 và 3  1
b) BM cắt CH tại I. Chứng minh: I là trung điểm của CH. g) 2 31 và 10 h) 3 và 12 i) 5 và  29
c) Gọi N là trực tâm của AMC. Chứng minh: tứ giác AOCN là hình
bình hành. Từ đó suy ra N di động trên đường cố định, chỉ rõ đường cố j) 2 5 và 19 k) 3 và 2 l) 2 3 và 3 2 định đó ? m) 2 + 6 và 5 n) 7 – 2 2 và 4 o) 15 + 8 và 7
d) Cho OM = 2R. Chứng minh: AMC đều và tính AM, SAMC theo R. p) 37  14 và 6– 15 q) 17  26  1 và 99
2.118 Cho đường tròn (O ; R) và hai điểm A, B thuộc đường tròn. Tiếp tuyến tại 1.7 Dùng kí hiệu
viết nghiệm của các phương trình đưới đây, sau đó dùng
A và B của (O) cắt nhau tại C. Tia CO cắt (O) tại E và F (E  OC). Gọi I
máy tính để tính chính xác nghiệm với 3 chữ số thập phân. là trung điểm của AB. a) x2 = 2 b) x2 = 3 c) x2 = 3,5 d) x2 = 4,12 a) Cho biết  AOB = 1200. e) x2 = 5 f) x2 = 6 g) x2 = 2,5 h) x2 = 5
i. Tính OI theo R và chứng minh I thuộc một đường thẳng cố định 1.8
Giải các phương trình sau:
khi A, B di động trên (O) sao cho 
AOB luôn có số đo bằng 1200. a) x2 = 25 b) x2 = 30,25 c) x2 = 5
ii. Lấy K  AC (AK < AC). Vẽ đường tròn đường kính OK cắt cung d) x2 – 3 = 2 e) x2  5 = 0 f) x2 + 5 = 2
AB của (O) tại M (M khác A). Tia KM cắt BC tại H. Chứng minh: 9 g) x2 = 3 h) 2x2+3 2 =2 3 i) (x – 1)2 = 1
KH là tiếp tuyến của (O). 16
iii. Lấy T  AB sao cho  j) x2 = (1 – 3 )2 k) x2 = 27 – 10 2 l) x2 + 2x =3 –2 3
KOT = 600 (A, T nằm khác phía đối với OK).
Chứng minh: O, T, H thẳng hàng. 1.9
Giải phương trình:
b) Chứng minh: EI . FC = FI . EC. a) x = 3 b) x = 5 c) x = 0 d) x = 2
2.119 Cho đường tròn (O; R) đường kính AB và dây AC = R. Vẽ đường kính 1.10 Trong các số: 2 ( 7  ) , 2 ( 7  ) , 2  7 ,  2 ( 7
 ) thì số nào là căn bậc CD của (O).
hai số học của 49 ?
a) Tính theo R độ dài đoạn AD và SACD .
b) Gọi xy là tiếp tuyến tại B của (O). Tia AC và AD cắt xy tại E và F.
1.11 Cho hai số dương a và b. Chứng minh rằng:
Gọi M là trung điểm của EF, đường thẳng (d) qua C và song song với a) Nếu a > b thì a  b b) Nếu a  b thì a > b
AM. Đoạn thẳng AM cắt CD tại I. Chứng minh: (d) tiếp xúc (O). Gv: Trần Quốc Nghĩa Trang 10 Gv: Trần Quốc Nghĩa Trang 95 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1 4 6 16
2.116 Cho đường tròn tâm O đường kính AB, điểm M thuộc đường tròn. Gọi N e) f) g) 0 3 , 6  0,49 25 5 0
là điểm đối xứng với A qua M. BN cắt đường tròn ở C. Gọi E là giao ,04 điểm của AC và BM. 1.4
Trong các số sau, số nào có căn bậc hai: a) Chứng minh: NE  AB. a) 5 b) 1,5 c)  0,1 d)  9
b) Gọi F là điểm đối xứng với E qua M. Chứng minh: FA là tiếp tuyến 1.5
Trong các biểu thức sau, biểu thức nào có căn bậc hai: của (O). a) (x – 4)(x – 6) + 1 b) (3 – x)(x – 5) – 4
c) Chứng minh: FN là tiếp tuyến của đường tròn (B; BA). c)  x2 + 6x – 9 d)  5x2 + 8x – 4
2.117 Cho đường tròn (O; R) đường kính AB và (d) la tiếp tuyến của (O) tại A.
e) x(x – 1)(x + 1)(x + 2) + 1 f) x2 + 20x + 101
M là điểm di động trên (d). Kẻ tiếp tuyến MC đến (O) (C là tiếp điểm 1.6
So sánh hai số sau (không dùng máy tính):
khác A). Tia BC cắt (d) tại K và kẻ CH vuông góac với AB tại H. a) 1 và 2 b) 2 và 3 c) 6 và 41 a) Chứng minh: OM // BK. d) 7 và 47 e) 2 và 2  1 f) 1 và 3  1
b) BM cắt CH tại I. Chứng minh: I là trung điểm của CH. g) 2 31 và 10 h) 3 và 12 i) 5 và  29
c) Gọi N là trực tâm của AMC. Chứng minh: tứ giác AOCN là hình
bình hành. Từ đó suy ra N di động trên đường cố định, chỉ rõ đường cố j) 2 5 và 19 k) 3 và 2 l) 2 3 và 3 2 định đó ? m) 2 + 6 và 5 n) 7 – 2 2 và 4 o) 15 + 8 và 7
d) Cho OM = 2R. Chứng minh: AMC đều và tính AM, SAMC theo R. p) 37  14 và 6– 15 q) 17  26  1 và 99
2.118 Cho đường tròn (O ; R) và hai điểm A, B thuộc đường tròn. Tiếp tuyến tại 1.7 Dùng kí hiệu
viết nghiệm của các phương trình đưới đây, sau đó dùng
A và B của (O) cắt nhau tại C. Tia CO cắt (O) tại E và F (E  OC). Gọi I
máy tính để tính chính xác nghiệm với 3 chữ số thập phân. là trung điểm của AB. a) x2 = 2 b) x2 = 3 c) x2 = 3,5 d) x2 = 4,12 a) Cho biết  AOB = 1200. e) x2 = 5 f) x2 = 6 g) x2 = 2,5 h) x2 = 5
i. Tính OI theo R và chứng minh I thuộc một đường thẳng cố định 1.8
Giải các phương trình sau:
khi A, B di động trên (O) sao cho 
AOB luôn có số đo bằng 1200. a) x2 = 25 b) x2 = 30,25 c) x2 = 5
ii. Lấy K  AC (AK < AC). Vẽ đường tròn đường kính OK cắt cung d) x2 – 3 = 2 e) x2  5 = 0 f) x2 + 5 = 2
AB của (O) tại M (M khác A). Tia KM cắt BC tại H. Chứng minh: 9 g) x2 = 3 h) 2x2+3 2 =2 3 i) (x – 1)2 = 1
KH là tiếp tuyến của (O). 16
iii. Lấy T  AB sao cho  j) x2 = (1 – 3 )2 k) x2 = 27 – 10 2 l) x2 + 2x =3 –2 3
KOT = 600 (A, T nằm khác phía đối với OK).
Chứng minh: O, T, H thẳng hàng. 1.9
Giải phương trình:
b) Chứng minh: EI . FC = FI . EC. a) x = 3 b) x = 5 c) x = 0 d) x = 2
2.119 Cho đường tròn (O; R) đường kính AB và dây AC = R. Vẽ đường kính 1.10 Trong các số: 2 ( 7  ) , 2 ( 7  ) , 2  7 ,  2 ( 7
 ) thì số nào là căn bậc CD của (O).
hai số học của 49 ?
a) Tính theo R độ dài đoạn AD và SACD .
b) Gọi xy là tiếp tuyến tại B của (O). Tia AC và AD cắt xy tại E và F.
1.11 Cho hai số dương a và b. Chứng minh rằng:
Gọi M là trung điểm của EF, đường thẳng (d) qua C và song song với a) Nếu a > b thì a  b b) Nếu a  b thì a > b
AM. Đoạn thẳng AM cắt CD tại I. Chứng minh: (d) tiếp xúc (O). Gv: Trần Quốc Nghĩa Trang 10 Gv: Trần Quốc Nghĩa Trang 95 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
2.112 Cho (O; R) và (O; r) ở ngoài nhau. AB là một trong các tiếp tuyến chung
1.12 Cho số dương a. Chứng minh rằng:
ngoài, EF là một trong các tiếp tuyến chung trong (A và E thuộc đường a) Nếu a > 1 thì a  b b) Nếu a < 1 thì a  b
tròn (O)). EF cắt AB tại C.
1.13 Cho số dương a. Chứng minh rằng:
a) Chứng minh: OC  OC.
a) Nếu a > 1 thì a > a
b) Nếu a < 1 thì a < a
b) Chứng minh: AC . BC = R.r
c) Tính AB, EF theo R, r và OO = d.
2.113 Cho hai đường tròn (O) và (O) cắt nhau tại A và B. Dây AC của đường
tròn (O) tiếp xúc với đường tròn (O) tại A. Dây AD của đường tròn (O)
tiếp xúc với đường tròn (O) tại A. Gọi K là điểm đối xứng với A qua
Một số tính chất bất đẳng thức
trung điểm của I của OO, E là điểm đối xứng với A qua B. Chứng minh:
1. a b b a a) AB  KB
b) Bốn điểm A, C, E, D nằm trên một đường tròn. a b 2.   a c b c  H - Ôn tập chương 2
3. a b a c b c (cộng 2 vế với c)
 a c b a b c (cộng 2 vế với – c)
2.114 Cho ABC vuông tại A có B = 600 và BC = 2a. Vẽ đường kính AB và
 a b a b 0 (cộng 2 vế với – b)
đường tròn (F) đường kính AC. Hai đường tròn này cắt nhau tại điểm thứ hai là H.
 a b a b 0 (cộng 2 vế với – b)
a) Chứng minh: B, H, C thẳng hàng. a b
b) Chứng minh: AC tiếp xúc (E) và EF  AH tại K. 4.
  a c b d c d
c) Tính theo a diện tích AKF.
5. a b a.c b.c (nếu c > 0: giữ nguyên chiều)
d) Gọi M là trung điểm của BC. Chứng minh: A, E, H, M, F cùng thuộc một đường tròn.
a b a.c b.c (nếu c < 0: đổi chiều)
2.115 Cho đoạn thẳng AB, điểm C nằm giữa A và B. Vẽ về một phía của AB
a b 0  6.
  a.c b.d
các nửa đường tròn có đường kính theo thứ tự là AB, AC và CB. Đường
c d 0
vuông góc với AB tại C cắt nửa đường tròn lớn tại D. DA, DB cắt nửa 7. n n *
a b 0 a b ( n  )
đường tròn có đường kính AC, CB theo thứ tự tại M, N.
a) Tứ giác DMCN là hình gì ? Vì sao ? 1 1
8. a b 0  
b) Chứng minh: DM . DA = DN . DB a b
c) Chứng minh: MN là tiếp tuyến chung của nửa đường tròn có đường kính AC và CB.
d) Điểm C ở vị trí nào trên AB thì MN có độ dài lớn nhất ? Gv: Trần Quốc Nghĩa Trang 94 Gv: Trần Quốc Nghĩa Trang 11 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
2.112 Cho (O; R) và (O; r) ở ngoài nhau. AB là một trong các tiếp tuyến chung
1.12 Cho số dương a. Chứng minh rằng:
ngoài, EF là một trong các tiếp tuyến chung trong (A và E thuộc đường a) Nếu a > 1 thì a  b b) Nếu a < 1 thì a  b
tròn (O)). EF cắt AB tại C.
1.13 Cho số dương a. Chứng minh rằng:
a) Chứng minh: OC  OC.
a) Nếu a > 1 thì a > a
b) Nếu a < 1 thì a < a
b) Chứng minh: AC . BC = R.r
c) Tính AB, EF theo R, r và OO = d.
2.113 Cho hai đường tròn (O) và (O) cắt nhau tại A và B. Dây AC của đường
tròn (O) tiếp xúc với đường tròn (O) tại A. Dây AD của đường tròn (O)
tiếp xúc với đường tròn (O) tại A. Gọi K là điểm đối xứng với A qua
Một số tính chất bất đẳng thức
trung điểm của I của OO, E là điểm đối xứng với A qua B. Chứng minh:
1. a b b a a) AB  KB
b) Bốn điểm A, C, E, D nằm trên một đường tròn. a b 2.   a c b c  H - Ôn tập chương 2
3. a b a c b c (cộng 2 vế với c)
 a c b a b c (cộng 2 vế với – c)
2.114 Cho ABC vuông tại A có B = 600 và BC = 2a. Vẽ đường kính AB và
 a b a b 0 (cộng 2 vế với – b)
đường tròn (F) đường kính AC. Hai đường tròn này cắt nhau tại điểm thứ hai là H.
 a b a b 0 (cộng 2 vế với – b)
a) Chứng minh: B, H, C thẳng hàng. a b
b) Chứng minh: AC tiếp xúc (E) và EF  AH tại K. 4.
  a c b d c d
c) Tính theo a diện tích AKF.
5. a b a.c b.c (nếu c > 0: giữ nguyên chiều)
d) Gọi M là trung điểm của BC. Chứng minh: A, E, H, M, F cùng thuộc một đường tròn.
a b a.c b.c (nếu c < 0: đổi chiều)
2.115 Cho đoạn thẳng AB, điểm C nằm giữa A và B. Vẽ về một phía của AB
a b 0  6.
  a.c b.d
các nửa đường tròn có đường kính theo thứ tự là AB, AC và CB. Đường
c d 0
vuông góc với AB tại C cắt nửa đường tròn lớn tại D. DA, DB cắt nửa 7. n n *
a b 0 a b ( n  )
đường tròn có đường kính AC, CB theo thứ tự tại M, N.
a) Tứ giác DMCN là hình gì ? Vì sao ? 1 1
8. a b 0  
b) Chứng minh: DM . DA = DN . DB a b
c) Chứng minh: MN là tiếp tuyến chung của nửa đường tròn có đường kính AC và CB.
d) Điểm C ở vị trí nào trên AB thì MN có độ dài lớn nhất ? Gv: Trần Quốc Nghĩa Trang 94 Gv: Trần Quốc Nghĩa Trang 11 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
b) Gọi I là giao điểm của BC và OO. Tính OI.
B - Căn thức bậc hai. Hằng đẳng thức 2 A  A
2.107 Cho (O; 48cm) và (O; 14cm), khoảng cách tâm là d = 50cm.
a) Chứng minh: (O) và (O) cắt nhau tại A và B.
1. Căn thức bậc hai: b) Tính  OAA ' .
Nếu A là một biểu thức đại số thì A gọi là căn thức bậc hai của A. c) Tính AB.
A được gọi là biểu thức lấy căn hay biểu thức dưới dấu căn.
A các định (có nghĩa) khi A  0
2.108 Cho ABC vuông tại A, có AB = a, BC = 2a. Các đường tròn đường kính 
AB, AC cắt nhau tại điểm thứ hai là D. Chú ý:
a) Chứng minh: B, C, D thẳng hàng.
a) Điều kiện có nghĩa của một số biểu thức:
b) Gọi E và F lần lượt là điểm đối xứng của D qua AB và AC.
A(x) là một đa thức  A(x) luôn có nghĩa.
Chứng minh: E, A, F thẳng hàng. A( x ) có nghĩa  B(x)  0
c) Tính theo a khoảng cách từ trung điểm O của BC đến EF. B( x )
d) Tính theo a diện tích tứ giác BCEF.  A( x ) có nghĩa  A(x)  0
2.109 Cho đường tròn tâm O đường kính AB. Đường thẳng (d) tiếp xúc với nửa 1
đường tròn tại C. Gọi D và E theo thứ tự là hình chiếu của A và B trên có nghĩa  A(x) > 0 A( x ) (d). Chứng minh:
b) Với M > 0, ta có:
a) C là trung điểm của DE.  2 2
b) (A; AD) và (B; BE) tiếp xúc ngoài nhau tại một điểm H thuộc đường
X M X M  M X M kính AB.  2 2
X M X M X  M hoặc X M
2.110 Cho ABC vuông tại A. Vẽ các đường tròn (O) và (I) đi qua A và tiếp
2. Hằng đẳng thức 2
( A ) A
xúc với BC tại các điểm B và C. Gọi M là trung điểm của BC. Chứng minh: a khi a 0
Định lí: Với mọi số a, ta có: 2 a a  
a) Các đường tròn (O) và (I) tiếp xúc với nhau. a khi a   0
b) AM là tiếp tuyến chung của hai đường tròn (O) và (I).
Chú ý: Tổng quát, với A là một biểu thức đại số, ta cũng có: c) OMI vuông.  A khi A 0
d) BC là tiếp tuyến của đường tròn ngoại tiếp OMI. 2 A A   A khi A   0
2.111 Cho (O; R) và (O; r) tiếp xúc ngoài tại A. Gọi BC là tiếp tuyến chung
1.14 Tìm x để biểu thức sau có nghĩa:
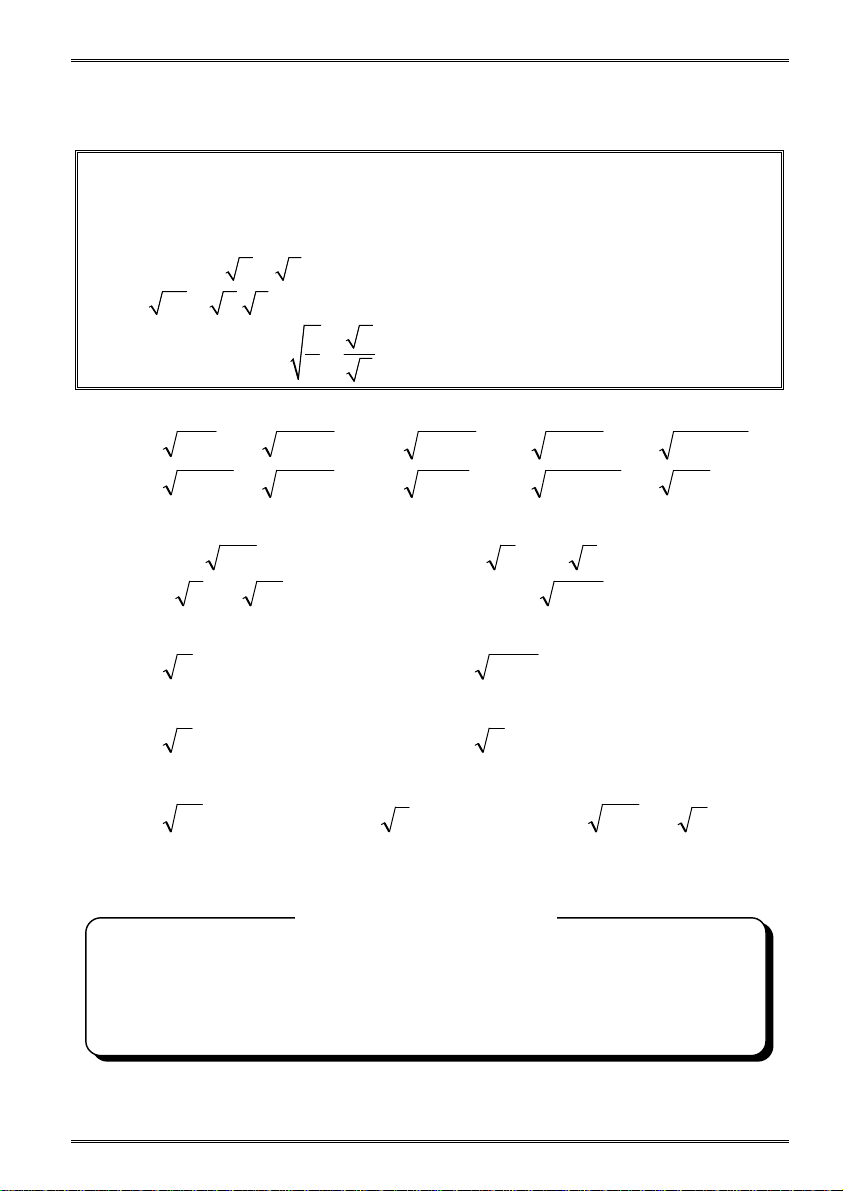
ngoài của hai đường tròn (B(O), C(O)). Tiếp tuyến chung trong của 1. a)  2x  3 b)  x 5
(O) và (O) cắt BC tại I. c)  x 3  7 d) x 3  7 a) Chứng tỏ các góc  BAC và  OIO ' là góc vuông. x
b) Kẻ đường kính BD của (O). Chứng minh ba điểm A, C, D thẳng hàng. e) f)  x 5 3
c) Tính theo R và r độ dài BC, BA, CA.
d) Kẻ đường kính CE của (O). Chứng minh: SABC = SADE. g) 4  x h) 2 1  x Gv: Trần Quốc Nghĩa Trang 12 Gv: Trần Quốc Nghĩa Trang 93 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
b) Gọi I là giao điểm của BC và OO. Tính OI.
B - Căn thức bậc hai. Hằng đẳng thức 2 A  A
2.107 Cho (O; 48cm) và (O; 14cm), khoảng cách tâm là d = 50cm.
a) Chứng minh: (O) và (O) cắt nhau tại A và B.
1. Căn thức bậc hai: b) Tính  OAA ' .
Nếu A là một biểu thức đại số thì A gọi là căn thức bậc hai của A. c) Tính AB.
A được gọi là biểu thức lấy căn hay biểu thức dưới dấu căn.
A các định (có nghĩa) khi A  0
2.108 Cho ABC vuông tại A, có AB = a, BC = 2a. Các đường tròn đường kính 
AB, AC cắt nhau tại điểm thứ hai là D. Chú ý:
a) Chứng minh: B, C, D thẳng hàng.
a) Điều kiện có nghĩa của một số biểu thức:
b) Gọi E và F lần lượt là điểm đối xứng của D qua AB và AC.
A(x) là một đa thức  A(x) luôn có nghĩa.
Chứng minh: E, A, F thẳng hàng. A( x ) có nghĩa  B(x)  0
c) Tính theo a khoảng cách từ trung điểm O của BC đến EF. B( x )
d) Tính theo a diện tích tứ giác BCEF.  A( x ) có nghĩa  A(x)  0
2.109 Cho đường tròn tâm O đường kính AB. Đường thẳng (d) tiếp xúc với nửa 1
đường tròn tại C. Gọi D và E theo thứ tự là hình chiếu của A và B trên có nghĩa  A(x) > 0 A( x ) (d). Chứng minh:
b) Với M > 0, ta có:
a) C là trung điểm của DE.  2 2
b) (A; AD) và (B; BE) tiếp xúc ngoài nhau tại một điểm H thuộc đường
X M X M  M X M kính AB.  2 2
X M X M X  M hoặc X M
2.110 Cho ABC vuông tại A. Vẽ các đường tròn (O) và (I) đi qua A và tiếp
2. Hằng đẳng thức 2
( A ) A
xúc với BC tại các điểm B và C. Gọi M là trung điểm của BC. Chứng minh: a khi a 0
Định lí: Với mọi số a, ta có: 2 a a  
a) Các đường tròn (O) và (I) tiếp xúc với nhau. a khi a   0
b) AM là tiếp tuyến chung của hai đường tròn (O) và (I).
Chú ý: Tổng quát, với A là một biểu thức đại số, ta cũng có: c) OMI vuông.  A khi A 0
d) BC là tiếp tuyến của đường tròn ngoại tiếp OMI. 2 A A   A khi A   0
2.111 Cho (O; R) và (O; r) tiếp xúc ngoài tại A. Gọi BC là tiếp tuyến chung
1.14 Tìm x để biểu thức sau có nghĩa:
ngoài của hai đường tròn (B(O), C(O)). Tiếp tuyến chung trong của 1. a)  2x  3 b)  x 5
(O) và (O) cắt BC tại I. c)  x 3  7 d) x 3  7 a) Chứng tỏ các góc  BAC và  OIO ' là góc vuông. x
b) Kẻ đường kính BD của (O). Chứng minh ba điểm A, C, D thẳng hàng. e) f)  x 5 3
c) Tính theo R và r độ dài BC, BA, CA.
d) Kẻ đường kính CE của (O). Chứng minh: SABC = SADE. g) 4  x h) 2 1  x Gv: Trần Quốc Nghĩa Trang 12 Gv: Trần Quốc Nghĩa Trang 93 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
2.99 Cho (O) và (O) cắt nhau tại A và B. Gọi I là trung điểm của OO. Qua A  5 2 i) j)
vẽ đường thẳng vuông góc với IA, cắt (O) và (O) tại C và D (khác A). x2  6 2 x Chứng minh: AC = AD. 1 4 k) l)
2.100 Cho hai đường tròn (O) và (O) tiếp xúc ngoài nhau tại A. Vẽ hai đường  1  x x  3
kính AOB và AOC Gọi DE là tiếp tuyến chung của hai đường tròn, m) 2 4x n) 2  x 3
D  (O), E  (O). Gọi M là giao điểm của BD và CE. o) x2  2x  1 P) 2 x  2x 1  a) Tính DAE . 2. a)  x2  4x  5 b) 2 x  2x  2
b) Tứ giác ADME là hình gì ? Vì sao ? 1 1
c) Chứng minh: MA là tiếp tuyến chung của hai đường tròn. c) d) 2 4x 12x  9 x2  x  1
2.101 Cho hai đường tròn (O) và (O) cắt nhau tại A và B, trong đó O nằm trên 1 1 e) f)
(O). Kẻ đường kính OOC của đường tròn (O). x2  x 8  15 x 3 2  x 7  20
a) Chứng minh: CA, CB là các tiếp tuyến của (O). 2 1
b) Đường vuông góc với AO tại O cắt CB ở I. Đường vuông góc với 3. a) x  3  x  9 b) x  2  x  5
AC tại C cắt đường thẳng OB ở K. Chứng minh O, I, K thẳng hàng. 2 c)  5  2x d) 2x  4  8  x 2
2.102 Cho hai đường tròn đồng tâm O. Gọi AB là dây bất kì của đường tròn x  9
nhỏ. Đường thẳng AB cắt đường tròn lớn ở C và D (A nằm giữa B và C). 4  x e) 2  9  x f) x2  4  2 x  2 So sánh AC và BD. x  1
2.103 Cho I là trung điểm của của đọan thẳng AB. Vẽ các đường tròn (I; IA) và 4 4. a) (x  ) 1 (x  ) 3 b) (B; BA). x  3
a) Xét vị trí tương đối của hai đường tròn (I) và (B). 2  x x 1 c) d)
b) Đường thẳng qua A cắt các đường tròn (I) và (B) theo thứ tự tại M và 5  x x  2 N. So sánh AM và MN. 1.15 Tính
2.104 Cho hai đường tròn (O) và (O) tiếp xúc ngoài tại A. Gọi CD là tiếp tuyến a) 5 4 ( 2  ) b)  4 6 ( 3  )
chung ngoài của hai đường tròn (C  (O), D  (O)). c) 5 8 ( 5  ) d) 2  0,4 ( 0  ,4) a) Tính  CAD .
b) Tính CD biết OA = 4,5cm và OA = 2cm. e) 2 (0 1 , ) f) 2 ( 0  3 , )
2.105 Cho hai đường tròn đồng tâm O. Một đường tròn (O) cắt đường tròn nhỏ
tại A và B, cắt đường tròn lớn tại C và D. Chứng minh rằng AB // CD. g) 2  ( 1  3 , ) h) 2 4 ( 2  ) + 3 8 ( 2  )
2.106 Cho đường tròn (O; 3cm) và đường tròn (O; 1cm) tiếp xúc ngoài nhau tại
1.16 Chứng minh rằng:
A. Vẽ hai bán kính OB và OC song song với nhau và thuộc cùng một nửa a) 2 9  4 5  ( 5  2) b) 9  4 5  5  2  mặt phẳng có bờ OO. c) 2 23  8 7  (4  7) d) 17 12 2  2 2  3 a) Tính  BAC
1.17 Rút gọn biểu thức: Gv: Trần Quốc Nghĩa Trang 92 Gv: Trần Quốc Nghĩa Trang 13 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
2.99 Cho (O) và (O) cắt nhau tại A và B. Gọi I là trung điểm của OO. Qua A  5 2 i) j)
vẽ đường thẳng vuông góc với IA, cắt (O) và (O) tại C và D (khác A). x2  6 2 x Chứng minh: AC = AD. 1 4 k) l)
2.100 Cho hai đường tròn (O) và (O) tiếp xúc ngoài nhau tại A. Vẽ hai đường  1  x x  3
kính AOB và AOC Gọi DE là tiếp tuyến chung của hai đường tròn, m) 2 4x n) 2  x 3
D  (O), E  (O). Gọi M là giao điểm của BD và CE. o) x2  2x  1 P) 2 x  2x 1  a) Tính DAE . 2. a)  x2  4x  5 b) 2 x  2x  2
b) Tứ giác ADME là hình gì ? Vì sao ? 1 1
c) Chứng minh: MA là tiếp tuyến chung của hai đường tròn. c) d) 2 4x 12x  9 x2  x  1
2.101 Cho hai đường tròn (O) và (O) cắt nhau tại A và B, trong đó O nằm trên 1 1 e) f)
(O). Kẻ đường kính OOC của đường tròn (O). x2  x 8  15 x 3 2  x 7  20
a) Chứng minh: CA, CB là các tiếp tuyến của (O). 2 1
b) Đường vuông góc với AO tại O cắt CB ở I. Đường vuông góc với 3. a) x  3  x  9 b) x  2  x  5
AC tại C cắt đường thẳng OB ở K. Chứng minh O, I, K thẳng hàng. 2 c)  5  2x d) 2x  4  8  x 2
2.102 Cho hai đường tròn đồng tâm O. Gọi AB là dây bất kì của đường tròn x  9
nhỏ. Đường thẳng AB cắt đường tròn lớn ở C và D (A nằm giữa B và C). 4  x e) 2  9  x f) x2  4  2 x  2 So sánh AC và BD. x  1
2.103 Cho I là trung điểm của của đọan thẳng AB. Vẽ các đường tròn (I; IA) và 4 4. a) (x  ) 1 (x  ) 3 b) (B; BA). x  3
a) Xét vị trí tương đối của hai đường tròn (I) và (B). 2  x x 1 c) d)
b) Đường thẳng qua A cắt các đường tròn (I) và (B) theo thứ tự tại M và 5  x x  2 N. So sánh AM và MN. 1.15 Tính
2.104 Cho hai đường tròn (O) và (O) tiếp xúc ngoài tại A. Gọi CD là tiếp tuyến a) 5 4 ( 2  ) b)  4 6 ( 3  )
chung ngoài của hai đường tròn (C  (O), D  (O)). c) 5 8 ( 5  ) d) 2  0,4 ( 0  ,4) a) Tính  CAD .
b) Tính CD biết OA = 4,5cm và OA = 2cm. e) 2 (0 1 , ) f) 2 ( 0  3 , )
2.105 Cho hai đường tròn đồng tâm O. Một đường tròn (O) cắt đường tròn nhỏ
tại A và B, cắt đường tròn lớn tại C và D. Chứng minh rằng AB // CD. g) 2  ( 1  3 , ) h) 2 4 ( 2  ) + 3 8 ( 2  )
2.106 Cho đường tròn (O; 3cm) và đường tròn (O; 1cm) tiếp xúc ngoài nhau tại
1.16 Chứng minh rằng:
A. Vẽ hai bán kính OB và OC song song với nhau và thuộc cùng một nửa a) 2 9  4 5  ( 5  2) b) 9  4 5  5  2  mặt phẳng có bờ OO. c) 2 23  8 7  (4  7) d) 17 12 2  2 2  3 a) Tính  BAC
1.17 Rút gọn biểu thức: Gv: Trần Quốc Nghĩa Trang 92 Gv: Trần Quốc Nghĩa Trang 13 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1 1. a) 2 (4  3 2) b) 2 (2  5)
G - Vị trí tương đối của hai đường tròn c) 2 (4  2 ) d) 2 2 3  (2  3) e) 2 (2  3) f) 2 (2  5)
1. Vị trí tương đối của hai đường tròn:
Cho (O ; R) và (O; r) với R > r và OO = d. g) 2 2 ( 3  1)  ( 3  2) h) 2 2 (2  5)  ( 5  1)
(O) và (O) cắt nhau
 R – r < d < R + r
(O) và (O) tiếp xúc ngoài  d = R + r 2. a) 6  2 5 b) 7  4 3
(O) và (O) tiếp xúc trong  d = R – r  c) 12  6 3 d) 17  12 2
(O) và (O) ở ngoài nhau  d > R + r
(O) và (O) đựng nhau  d < R – r e) 22 12 2 f) 10  4 6
(O) và (O) đồng tâm  d = 0 2  11  6 2 3  5 3  5
2. Tính chất đường nối tâm: g) h)  6
a. Nếu hai đường tròn cắt nhau thì hai giao điểm đối xứng với nhau  2 5  5 3  5 3  5
qua đường nối tâm, tức là đường nối tâm là đường trung trực của dây chung. 3. a) 4  2 3  3 b) 11  6 2  3  2
b. Nếu hai đường tròn tiếp xúc nhau thì tiếp điểm nằm trên đường c) 11  6 2  6  4 2 d) 11 6 3  13  4 3 nối tâm.
c. Tiếp tuyến chung của hai đường tròn là đường thẳng tiếp xúc với 4  7 e) ( 3  4) 19  8 3 f) 8  2 7
cả hai đường tròn. Có hai loại: tiếp tuyến chung trong (cắt đoạn 2
nối tâm) và tiếp tuyến chung ngoài (không cắt đoạn nối tâm). 2  11  6 2 3  5 3  5 g) h)  6  2 5  5 3  5 3  5
2.94 Cho (O; 5cm) và điểm O sao cho OO = 7cm. Với giá trị nào của R thì (O; R): a) Cắt đường tròn (O) 4. a) 6  2 4  2 3 b) 6  2 3  13  4 3 b) Tiếp xúc với (O) c) 3  48  10 7  4 3 d) 23  6 10  4 3  2 2
c) Không có điểm chung với (O) ?
2.95 Cho (O; R) và điểm I cách O một khoảng d < R. Với giá trị nào của r thì x2  5 x2  2 2x  2 5. a) b)
đường tròn (I; r) tiếp xúc với (O; R) ? x  5 x2  2
2.96 Cho hai đường tròn (O) và (O) tiếp xúc ngoài nhau tại A. Đường thẳng
1.18 Rút gọn biểu thức sau (loại bỏ dấu căn và dấu trị tuyệt đối):
bất kì qua A cắt (O) và (O) theo thứ tự tại B và C. Chứng minh rằng các 1. a) 9x2  2x với x < 0 b) 2 2 x với x  0
tiếp tuyến tại B và C song với nhau. c) 2 3 (x  2) với x < 2 d) 2 2 x  5x với x < 0
2.97 Cho (O; 30cm) và (O ; 40cm) cắt nhau tại A và B. Biết AB = 48cm. e) 2 x 5 2  x 3 với x  0 f) 4 2 9x  x 3 với x bất kỳ
Chứng minh: OO là đường trung trực của AB. Tính khoảng cách OO g) 2 x  4  16  x 8  x với x > 4
2.98 Cho hai đường tròn (O) và (O) cắt nhau tại A và B. Kẻ các đường kính
AOC và AOD. Chứng minh ba điểm C, B, D thẳng hàng và AB  CD. Gv: Trần Quốc Nghĩa Trang 14 Gv: Trần Quốc Nghĩa Trang 91 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1 1. a) 2 (4  3 2) b) 2 (2  5)
G - Vị trí tương đối của hai đường tròn c) 2 (4  2 ) d) 2 2 3  (2  3) e) 2 (2  3) f) 2 (2  5)
1. Vị trí tương đối của hai đường tròn:
Cho (O ; R) và (O; r) với R > r và OO = d. g) 2 2 ( 3  1)  ( 3  2) h) 2 2 (2  5)  ( 5  1)
(O) và (O) cắt nhau
 R – r < d < R + r
(O) và (O) tiếp xúc ngoài  d = R + r 2. a) 6  2 5 b) 7  4 3
(O) và (O) tiếp xúc trong  d = R – r  c) 12  6 3 d) 17  12 2
(O) và (O) ở ngoài nhau  d > R + r
(O) và (O) đựng nhau  d < R – r e) 22 12 2 f) 10  4 6
(O) và (O) đồng tâm  d = 0 2  11  6 2 3  5 3  5
2. Tính chất đường nối tâm: g) h)  6
a. Nếu hai đường tròn cắt nhau thì hai giao điểm đối xứng với nhau  2 5  5 3  5 3  5
qua đường nối tâm, tức là đường nối tâm là đường trung trực của dây chung. 3. a) 4  2 3  3 b) 11  6 2  3  2
b. Nếu hai đường tròn tiếp xúc nhau thì tiếp điểm nằm trên đường c) 11  6 2  6  4 2 d) 11 6 3  13  4 3 nối tâm.
c. Tiếp tuyến chung của hai đường tròn là đường thẳng tiếp xúc với 4  7 e) ( 3  4) 19  8 3 f) 8  2 7
cả hai đường tròn. Có hai loại: tiếp tuyến chung trong (cắt đoạn 2
nối tâm) và tiếp tuyến chung ngoài (không cắt đoạn nối tâm). 2  11  6 2 3  5 3  5 g) h)  6  2 5  5 3  5 3  5
2.94 Cho (O; 5cm) và điểm O sao cho OO = 7cm. Với giá trị nào của R thì (O; R): a) Cắt đường tròn (O) 4. a) 6  2 4  2 3 b) 6  2 3  13  4 3 b) Tiếp xúc với (O) c) 3  48  10 7  4 3 d) 23  6 10  4 3  2 2
c) Không có điểm chung với (O) ?
2.95 Cho (O; R) và điểm I cách O một khoảng d < R. Với giá trị nào của r thì x2  5 x2  2 2x  2 5. a) b)
đường tròn (I; r) tiếp xúc với (O; R) ? x  5 x2  2
2.96 Cho hai đường tròn (O) và (O) tiếp xúc ngoài nhau tại A. Đường thẳng
1.18 Rút gọn biểu thức sau (loại bỏ dấu căn và dấu trị tuyệt đối):
bất kì qua A cắt (O) và (O) theo thứ tự tại B và C. Chứng minh rằng các 1. a) 9x2  2x với x < 0 b) 2 2 x với x  0
tiếp tuyến tại B và C song với nhau. c) 2 3 (x  2) với x < 2 d) 2 2 x  5x với x < 0
2.97 Cho (O; 30cm) và (O ; 40cm) cắt nhau tại A và B. Biết AB = 48cm. e) 2 x 5 2  x 3 với x  0 f) 4 2 9x  x 3 với x bất kỳ
Chứng minh: OO là đường trung trực của AB. Tính khoảng cách OO g) 2 x  4  16  x 8  x với x > 4
2.98 Cho hai đường tròn (O) và (O) cắt nhau tại A và B. Kẻ các đường kính
AOC và AOD. Chứng minh ba điểm C, B, D thẳng hàng và AB  CD. Gv: Trần Quốc Nghĩa Trang 14 Gv: Trần Quốc Nghĩa Trang 91 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1 1 1 1 1 2 2 c)    (với h 2. a) A = 1  a 4  4a  a 2
b) B = 4x  12x  9  2x  1
1, h2, h3 là các đường cao của ABC) r h h h 1 2 3 5  x 2 x  1 c) C = d) D = (x  1) 
2.89 Cho tam giác ABC vuông tại A có đường cao AH. Đường tròn (O; r), x2  10x  25 x2  2x  1
(O; r1), (O; r2) theo thứ tự là đường tròn nội tiếp các ABC, ABH, x2  6x  9 2 4 2 ACH. Chứng minh rằng: e) E = f) F = x  x  x 8  16 x  3 a) AB + AC – BC = 2r. b) R + r1 + r2 = AH. c) 2 2 2 r  r  r 1 2 1.19 Chứng tỏ: 2
x  2 2x  4  ( 2  x  2 ) với x  2
2.90 Cho ABC có BC = a, CA = b, AB = c và đường tròn bàng tiếp trong góc
Áp dụng rút gọn biểu thức sau:
A tiếp xúc với BC tại D, tiếp xúc với phần kéo dài của AC và AB tại E và
F. Tính theo a, b, c độ dài AE, BD, CD.
x  2 2x  4  x  2 2x  4 với x  2
1.20 Rút gọn biểu thức sau (loại bỏ dấu căn và dấu trị tuyệt đối):
2.91 Cho ABC có I là tâm đường tròn nội tiếp và O là tâm đường tròn bàng
tiếp trong góc A. gọi D và F lần lượt là tiếp điểm của (I) và (O) trên BC. a) x  4 x  4 với x  4 Chứng minh rằng BD = CF. b) x  2  2 x  3 với x  3
2.92 Tính cạnh huyền của một tam giác vuông, biết r là bán kính đường tròn c)
x  2 x  1  x  2 x  1 với x  1
nội tiếp và R là bán kính đường tròn bàng tiếp trong góc vuông. d)
x  2 x 1  x  2 x  1 với x  0
2.93 Cho ABC đường cao AH. Gọi E và F lần lượt là các điểm đối xứng của
1.21 Với giá trị nào của a và b thì:
H qua AB và AC. Đường thẳng EF cắt AB ở I và cắt AC ở K. C/m: 1 1 2 2
a) A là tâm đường tròn bàng tiếp HIK. a)  ? b) a (b  2b  ) 1  ( a 1 b) ? 2 2 b  a a  2ab  b
b) BK và CI là các đường cao của ABC.
1.22 So sánh hai số sau (không dùng máy tính): a) 9 và 6 + 2 2 b) 2 + 3 và 3 c) 16 và 9 + 4 5 d) 11  3 và 2
1.23 Rút gọn rồi tính giá trị của biểu thức: 1 a) 2
A  9x 12x  4  1  3x tại x  3 b) 2 B  2x  6x 2  9 tại x  3 2
1.24 Giải phương trình: a) 2 9x = 2x + 1 b) x4  7 c) x2  6x  9  x 3  1 d) x2  7 e) x2   8 f) 1  4x  4x2  5 g) x4  9 h) 2 (x  2)  2x  1 Gv: Trần Quốc Nghĩa Trang 90 Gv: Trần Quốc Nghĩa Trang 15 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1 1 1 1 1 2 2 c)    (với h 2. a) A = 1  a 4  4a  a 2
b) B = 4x  12x  9  2x  1
1, h2, h3 là các đường cao của ABC) r h h h 1 2 3 5  x 2 x  1 c) C = d) D = (x  1) 
2.89 Cho tam giác ABC vuông tại A có đường cao AH. Đường tròn (O; r), x2  10x  25 x2  2x  1
(O; r1), (O; r2) theo thứ tự là đường tròn nội tiếp các ABC, ABH, x2  6x  9 2 4 2 ACH. Chứng minh rằng: e) E = f) F = x  x  x 8  16 x  3 a) AB + AC – BC = 2r. b) R + r1 + r2 = AH. c) 2 2 2 r  r  r 1 2 1.19 Chứng tỏ: 2
x  2 2x  4  ( 2  x  2 ) với x  2
2.90 Cho ABC có BC = a, CA = b, AB = c và đường tròn bàng tiếp trong góc
Áp dụng rút gọn biểu thức sau:
A tiếp xúc với BC tại D, tiếp xúc với phần kéo dài của AC và AB tại E và
F. Tính theo a, b, c độ dài AE, BD, CD.
x  2 2x  4  x  2 2x  4 với x  2
1.20 Rút gọn biểu thức sau (loại bỏ dấu căn và dấu trị tuyệt đối):
2.91 Cho ABC có I là tâm đường tròn nội tiếp và O là tâm đường tròn bàng
tiếp trong góc A. gọi D và F lần lượt là tiếp điểm của (I) và (O) trên BC. a) x  4 x  4 với x  4 Chứng minh rằng BD = CF. b) x  2  2 x  3 với x  3
2.92 Tính cạnh huyền của một tam giác vuông, biết r là bán kính đường tròn c)
x  2 x  1  x  2 x  1 với x  1
nội tiếp và R là bán kính đường tròn bàng tiếp trong góc vuông. d)
x  2 x 1  x  2 x  1 với x  0
2.93 Cho ABC đường cao AH. Gọi E và F lần lượt là các điểm đối xứng của
1.21 Với giá trị nào của a và b thì:
H qua AB và AC. Đường thẳng EF cắt AB ở I và cắt AC ở K. C/m: 1 1 2 2
a) A là tâm đường tròn bàng tiếp HIK. a)  ? b) a (b  2b  ) 1  ( a 1 b) ? 2 2 b  a a  2ab  b
b) BK và CI là các đường cao của ABC.
1.22 So sánh hai số sau (không dùng máy tính): a) 9 và 6 + 2 2 b) 2 + 3 và 3 c) 16 và 9 + 4 5 d) 11  3 và 2
1.23 Rút gọn rồi tính giá trị của biểu thức: 1 a) 2
A  9x 12x  4  1  3x tại x  3 b) 2 B  2x  6x 2  9 tại x  3 2
1.24 Giải phương trình: a) 2 9x = 2x + 1 b) x4  7 c) x2  6x  9  x 3  1 d) x2  7 e) x2   8 f) 1  4x  4x2  5 g) x4  9 h) 2 (x  2)  2x  1 Gv: Trần Quốc Nghĩa Trang 90 Gv: Trần Quốc Nghĩa Trang 15 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1 i) 2 x  6x  9  5 j) 2 4x 12x  9  x  3
F - Đường tròn nội tiếp – bàng tiếp tam giác k) 2 2 4x  4x 1  x  2x  1 l) 2 2
4x 12x  9  9x  24x  16
1.25 Phân tích thành hân tử: a) x2 – 7 b) x2  3 c) x2 – 2 13 x + 13
1. a. Đường tròn tiếp xúc với ba cạnh của  gọi là đường tròn nội
tiếp tam giác. d) x2 – 3 e) x2 – 2 2 x + 2 f) x2 + 2 5 x + 5
b. Tâm đường tròn nội tiếp tam giác là giao điểm các đường phân
1.26 Với n là số tự nhiên, chứng minh:
giác trong của tam giác. 2 2 2 2
(n  1)  n  (n  1)  n
2. a. Đường tròn tiếp xúc với một cạnh của tam giác và các phần kéo
dài của hai cạnh kia gọi là đường tròn bàng tiếp của tam giác.
Viết đẳng thức trên khi n là 1; 2; 3; 4; 5; 6; 7.
b. Tâm của đường tròn bàng tiếp của tam giác là giao điểm của
1.27 Cho ba số a, b, c khác 0 và a + b + c = 0. Chứng minh rằng:
phân giác trong và hai phân giác ngoài của hai góc còn lại. 1 1 1 1 1 1      2 2 2 a b c a b c
2.84 Cho ABC vuông cân tại A nội tiếp (O; R). Gọi (I; r) là đường tròn nội
tiếp ABC. Tính độ dài AB và r theo R. 2 2013 2013 1.28 Tính: 2 1 2013   . 2 2014 2014
2.85 Cho ABC đều có cạnh 8cm.
a) Tính bán kính đường tròn (I) nội tiếp ABC.
1.29 Chứng minh bất đẳng thức Côsi (Cauchy):
b) Một tiếp tuyến của (I) cắt AB, AC theo thứ tự ở M và N. x + y  2 xy
Cho biết MN = 3cm. Tính SABC.
Dấu “ = ” xảy ra khi nào ?
Áp dụng: Chứng minh rằng với x, y, z là các số dương, ta có:
2.86 Từ một điểm A ở bên ngoài đường tròn (O) kẻ hai tiếp tuyến AB, AC đến 1 1 1 1 1 1
đường tròn (O). OA cắt (O) tại I. Chứng minh rằng I là tâm đường tròn      x y z xy yz zx nội tiếp của ABC.
Chuyện vui Toán học: Câu chuyện số 1
2.87 Cho (I; r) nội tiếp ABC vuông tại A. Các tiếp điểm trên AC, AB theo thứ tự là D, E.
Một chủ do anh nghiệp đi về quê chơi cùng 1 người bạn là dân toán.
a) Tứ giác ADOE là hình gì ? Vì sao ?
Họ thấy một đàn bò rất lớn trên một đồng cỏ.
b) Tính chu vi và diện tích tứ giác ADOE theo r. Anh doanh nghiệp nói:
c) Gọi R là bán kính đường tròn ngoại tiếp ABC.
- Nhiều bò quá, tôi chưa bao giờ thấy nhiều thế này, có lẽ phải
Chứng minh: AB + AC = 2(R + r). hàng nghìn con.
Anh bạn toán học trả lời :
2.88 Cho đường tròn (I ; r) nội tiếp ABC. Gọi D, E, F lần lượt là hình chiếu
của I trên các cạnh BC, CA, AB. Cho BC = a, AC = b, AB = c. Chứng
- Đúng đấy, có cả thẩy 2428 con. minh:
- 'Trời, làm sao mà anh lại đếm được nhanh thế? - Anh chủ DN hỏi. a) S = p.r
(với S là diện tích và p là nửa chu vi của ABC) Anh toán học trả lời:
b) AE = p – a; BF = p – b; CD = p – c.
- À, tôi đếm tất cả chân rồi chia cho 4 là xong! Gv: Trần Quốc Nghĩa Trang 16 Gv: Trần Quốc Nghĩa Trang 89 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1 i) 2 x  6x  9  5 j) 2 4x 12x  9  x  3
F - Đường tròn nội tiếp – bàng tiếp tam giác k) 2 2 4x  4x 1  x  2x  1 l) 2 2
4x 12x  9  9x  24x  16
1.25 Phân tích thành hân tử: a) x2 – 7 b) x2  3 c) x2 – 2 13 x + 13
1. a. Đường tròn tiếp xúc với ba cạnh của  gọi là đường tròn nội
tiếp tam giác. d) x2 – 3 e) x2 – 2 2 x + 2 f) x2 + 2 5 x + 5
b. Tâm đường tròn nội tiếp tam giác là giao điểm các đường phân
1.26 Với n là số tự nhiên, chứng minh:
giác trong của tam giác. 2 2 2 2
(n  1)  n  (n  1)  n
2. a. Đường tròn tiếp xúc với một cạnh của tam giác và các phần kéo
dài của hai cạnh kia gọi là đường tròn bàng tiếp của tam giác.
Viết đẳng thức trên khi n là 1; 2; 3; 4; 5; 6; 7.
b. Tâm của đường tròn bàng tiếp của tam giác là giao điểm của
1.27 Cho ba số a, b, c khác 0 và a + b + c = 0. Chứng minh rằng:
phân giác trong và hai phân giác ngoài của hai góc còn lại. 1 1 1 1 1 1      2 2 2 a b c a b c
2.84 Cho ABC vuông cân tại A nội tiếp (O; R). Gọi (I; r) là đường tròn nội
tiếp ABC. Tính độ dài AB và r theo R. 2 2013 2013 1.28 Tính: 2 1 2013   . 2 2014 2014
2.85 Cho ABC đều có cạnh 8cm.
a) Tính bán kính đường tròn (I) nội tiếp ABC.
1.29 Chứng minh bất đẳng thức Côsi (Cauchy):
b) Một tiếp tuyến của (I) cắt AB, AC theo thứ tự ở M và N. x + y  2 xy
Cho biết MN = 3cm. Tính SABC.
Dấu “ = ” xảy ra khi nào ?
Áp dụng: Chứng minh rằng với x, y, z là các số dương, ta có:
2.86 Từ một điểm A ở bên ngoài đường tròn (O) kẻ hai tiếp tuyến AB, AC đến 1 1 1 1 1 1
đường tròn (O). OA cắt (O) tại I. Chứng minh rằng I là tâm đường tròn      x y z xy yz zx nội tiếp của ABC.
Chuyện vui Toán học: Câu chuyện số 1
2.87 Cho (I; r) nội tiếp ABC vuông tại A. Các tiếp điểm trên AC, AB theo thứ tự là D, E.
Một chủ do anh nghiệp đi về quê chơi cùng 1 người bạn là dân toán.
a) Tứ giác ADOE là hình gì ? Vì sao ?
Họ thấy một đàn bò rất lớn trên một đồng cỏ.
b) Tính chu vi và diện tích tứ giác ADOE theo r. Anh doanh nghiệp nói:
c) Gọi R là bán kính đường tròn ngoại tiếp ABC.
- Nhiều bò quá, tôi chưa bao giờ thấy nhiều thế này, có lẽ phải
Chứng minh: AB + AC = 2(R + r). hàng nghìn con.
Anh bạn toán học trả lời :
2.88 Cho đường tròn (I ; r) nội tiếp ABC. Gọi D, E, F lần lượt là hình chiếu
của I trên các cạnh BC, CA, AB. Cho BC = a, AC = b, AB = c. Chứng
- Đúng đấy, có cả thẩy 2428 con. minh:
- 'Trời, làm sao mà anh lại đếm được nhanh thế? - Anh chủ DN hỏi. a) S = p.r
(với S là diện tích và p là nửa chu vi của ABC) Anh toán học trả lời:
b) AE = p – a; BF = p – b; CD = p – c.
- À, tôi đếm tất cả chân rồi chia cho 4 là xong! Gv: Trần Quốc Nghĩa Trang 16 Gv: Trần Quốc Nghĩa Trang 89 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
2.83 Cho đường tròn (O; R) tiếp xúc với đường thẳng xy tại A. Trên tia Oz
C - Khai phương một tích. Nhân các căn thức bậc hai.
song song với đường thẳng xy lấy điểm I. Từ I vẽ các tiếp tuyến với (O) cắt xy tại E và F.
D - Khai phương một thương. C hia các căn thức bậc hai
a) Chứng minh: I là tâm đường tròn ngoại tiếp OEF.
b) Cho OI = R 2 , tính chu vi IEF.
1. Với A  0, B  0: AB A B A A
2. Với A  0, B > 0: B B 1.30 Tính: 1. a) 0,09.64 b) 4 2 2 .( 7  ) c) 12 1 , .360 d) 2 4 2 3 . e) 45 8 . 0 f) 75 4 . 8 g) 90.6,4 h) 2 5 , 1 . 4,4 2. a) 7. 63 b) 2,5. 30. 48 c) 0,4. 6,4 d) 2,7. 5. 1 5 , e) 10. 40 f) 5. 45 g) 52. 13 h) 2. 162 3. a) 2 2 13  12 b) 2 2 17  8 c) 2 2 117 108 d) 2 2 313  312 e) 2 2 6 8 ,  3 2 , f) 2 2 21 8 ,  18 2 , g) 146 52 ,  109 52 ,  27.256 4. a) 2  3 . 2  3 b) 3 2  2 3 . 3 2  2 3 c) 2 ( 3  2  3  2 )
d) (1  2  3).(1  2  3) 9 25 9 5. a) b) c) 1 169 144 16 7 d) 2 e) 0,0025 f) 3 6 , 1 . 6,9 81 2 15 12500 6. a) b) c) 18 735 500 5 6 2300 12 5 , d) e) f) 3 5 2 3 . 23 0 5 , Gv: Trần Quốc Nghĩa Trang 88 Gv: Trần Quốc Nghĩa Trang 17 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
2.83 Cho đường tròn (O; R) tiếp xúc với đường thẳng xy tại A. Trên tia Oz
C - Khai phương một tích. Nhân các căn thức bậc hai.
song song với đường thẳng xy lấy điểm I. Từ I vẽ các tiếp tuyến với (O) cắt xy tại E và F.
D - Khai phương một thương. C hia các căn thức bậc hai
a) Chứng minh: I là tâm đường tròn ngoại tiếp OEF.
b) Cho OI = R 2 , tính chu vi IEF.
1. Với A  0, B  0: AB A B A A
2. Với A  0, B > 0: B B 1.30 Tính: 1. a) 0,09.64 b) 4 2 2 .( 7  ) c) 12 1 , .360 d) 2 4 2 3 . e) 45 8 . 0 f) 75 4 . 8 g) 90.6,4 h) 2 5 , 1 . 4,4 2. a) 7. 63 b) 2,5. 30. 48 c) 0,4. 6,4 d) 2,7. 5. 1 5 , e) 10. 40 f) 5. 45 g) 52. 13 h) 2. 162 3. a) 2 2 13  12 b) 2 2 17  8 c) 2 2 117 108 d) 2 2 313  312 e) 2 2 6 8 ,  3 2 , f) 2 2 21 8 ,  18 2 , g) 146 52 ,  109 52 ,  27.256 4. a) 2  3 . 2  3 b) 3 2  2 3 . 3 2  2 3 c) 2 ( 3  2  3  2 )
d) (1  2  3).(1  2  3) 9 25 9 5. a) b) c) 1 169 144 16 7 d) 2 e) 0,0025 f) 3 6 , 1 . 6,9 81 2 15 12500 6. a) b) c) 18 735 500 5 6 2300 12 5 , d) e) f) 3 5 2 3 . 23 0 5 , Gv: Trần Quốc Nghĩa Trang 88 Gv: Trần Quốc Nghĩa Trang 17 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1 9 4 1652 1242
c) Gọi H là giao đểm của AO và MN. Chứng minh: OH . OA = R2. 7. a) 1 .5 .0,01 b) 16 9 164
2.78 Cho đường tròn (O) đường kính BC và 1 điểm A nằm trên đường tròn (A 2 2 149  76
khác B và C). Qua O, kẻ tia Ox song song với AC, tia Ox cắt AB tại D. c) d) 1,44.1,21  1,44 0 . ,4 2 2 457  384
a) Chứng minh: OD  AB và từ đó suy ra D là trung điểm của AB.
b) Tiếp tuyến tại B của (O) cắt tia Ox tại E. 2 12  3 27  5 3 32  50  8
Chứng minh: EA cũng là tiếp tuyến của (O) 8. a) b) 3 2
c) Tia CA cắt tia BE tại F. Chứng minh: tia CE đi qua trung điểm I của 1.31 Tính:
của đường cao AH của ABC.
2.79 Cho đường tròn (O; R) đường kính AB. Từ trung điểm I của bán kính OB
Với m, n > 0 thỏa m + n = A và m . n = B
vẽ dây cung CD vuông góc với OB. ta có: 2
A 2 B m n 2 m n
. ( m n ) a) So sánh IC và ID.
b) Tiếp tuyến tại C của (O) cắt đường thẳng AB tại M. Chứng minh: 1. a) 8  2 15  6  2 5 b) 17  2 72  19  2 18 i) COM = DOM.
ii) MD là tiếp tuyến của (O) .
c) Tính độ dài đoạn MC theo R. c) 12  2 32  9  4 2 d) 29  2 180  9  4 5
2.80 Cho (O ; 3cm) và điểm A sao cho OA = 5cm. Kẻ cac tiếp tuyến AB, AC e) 4  7  4  7  2 f) 6  11  6  11  3 2
với đường tròn (B, C là hai tiếp điểm). Gọi H là giao điểm của AO và BC. g) 8  2 15  7  2 10 h) 10  2 21  9  2 14 a) Tính độ dài OH. i) 8  3 7  4  7 j) 5  21  5  21
b) Qua điểm M bắt kì thuộc cung nhỏ BC, kẻ tiếp tuyến với đường tròn,
cắt AB, AC theo thứ tự tại D và E. Tính chi vi ADE. k) 9  3 5  9  3 5
l) ( 10  2) 4  6  2 5
2.81 Cho ABC vuông tại A, đường cao AH. Vẽ đường tròn (A; AH). Kẻ các 2. a) (4  2 3)(13  4 ) 3 b) ( 3  2)( 6  2 ) 3  2
tiếp tuyến BD, CE với đường tròn (D, E là các tiếp điểm khác H). C/m:
a) Ba điểm D, A, E thẳng hàng. c) 3 (  5)( 10  2 ) 3  5
d) (4  15)( 10  6 ) 4  15
b) DE tiếp xúc với đường tròn đường kính BC. e)
4  15  4  15  2 3  5
2.82 Cho (O ; R), và điểm A sao cho OA = R 2 , kẻ các tiếp tuyến AB, AC f)
4  8. 2  2  2 . 2  2  2
với (O). (B, C là các tiếp điểm). Qua điểm M bắt kì thuộc cung nhỏ BC,
kẻ tiếp tuyến với đường tròn, cắt AB, AC theo thứ tự tại D và E.
g) (5  4 2 ).(3  2 1  2 ).(3  2 1  2 )
a) Tứ giác ABOC là hình gì ? Vì sao ? h)
2  3 . 2  2  3 . 2  2  2  3 . 2  2  2  3 b) Tính số đo góc  DOE .
c) Đoạn OA cắt (O) tại K. Chứng minh: K là tâm đường tròn nội tiếp 2( 7 1 ) 3*. A  7  5  2 7  4 1 ĐS: A
ABC. Tính bán kính của đường tròn này. 2
d) Tính độ dài BK theo R. 5 6 B  4  3  6 3  15  3  ĐS: B  2 2 Gv: Trần Quốc Nghĩa Trang 18 Gv: Trần Quốc Nghĩa Trang 87 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1 9 4 1652 1242
c) Gọi H là giao đểm của AO và MN. Chứng minh: OH . OA = R2. 7. a) 1 .5 .0,01 b) 16 9 164
2.78 Cho đường tròn (O) đường kính BC và 1 điểm A nằm trên đường tròn (A 2 2 149  76
khác B và C). Qua O, kẻ tia Ox song song với AC, tia Ox cắt AB tại D. c) d) 1,44.1,21  1,44 0 . ,4 2 2 457  384
a) Chứng minh: OD  AB và từ đó suy ra D là trung điểm của AB.
b) Tiếp tuyến tại B của (O) cắt tia Ox tại E. 2 12  3 27  5 3 32  50  8
Chứng minh: EA cũng là tiếp tuyến của (O) 8. a) b) 3 2
c) Tia CA cắt tia BE tại F. Chứng minh: tia CE đi qua trung điểm I của 1.31 Tính:
của đường cao AH của ABC.
2.79 Cho đường tròn (O; R) đường kính AB. Từ trung điểm I của bán kính OB
Với m, n > 0 thỏa m + n = A và m . n = B
vẽ dây cung CD vuông góc với OB. ta có: 2
A 2 B m n 2 m n
. ( m n ) a) So sánh IC và ID.
b) Tiếp tuyến tại C của (O) cắt đường thẳng AB tại M. Chứng minh: 1. a) 8  2 15  6  2 5 b) 17  2 72  19  2 18 i) COM = DOM.
ii) MD là tiếp tuyến của (O) .
c) Tính độ dài đoạn MC theo R. c) 12  2 32  9  4 2 d) 29  2 180  9  4 5
2.80 Cho (O ; 3cm) và điểm A sao cho OA = 5cm. Kẻ cac tiếp tuyến AB, AC e) 4  7  4  7  2 f) 6  11  6  11  3 2
với đường tròn (B, C là hai tiếp điểm). Gọi H là giao điểm của AO và BC. g) 8  2 15  7  2 10 h) 10  2 21  9  2 14 a) Tính độ dài OH. i) 8  3 7  4  7 j) 5  21  5  21
b) Qua điểm M bắt kì thuộc cung nhỏ BC, kẻ tiếp tuyến với đường tròn,
cắt AB, AC theo thứ tự tại D và E. Tính chi vi ADE. k) 9  3 5  9  3 5
l) ( 10  2) 4  6  2 5
2.81 Cho ABC vuông tại A, đường cao AH. Vẽ đường tròn (A; AH). Kẻ các 2. a) (4  2 3)(13  4 ) 3 b) ( 3  2)( 6  2 ) 3  2
tiếp tuyến BD, CE với đường tròn (D, E là các tiếp điểm khác H). C/m:
a) Ba điểm D, A, E thẳng hàng. c) 3 (  5)( 10  2 ) 3  5
d) (4  15)( 10  6 ) 4  15
b) DE tiếp xúc với đường tròn đường kính BC. e)
4  15  4  15  2 3  5
2.82 Cho (O ; R), và điểm A sao cho OA = R 2 , kẻ các tiếp tuyến AB, AC f)
4  8. 2  2  2 . 2  2  2
với (O). (B, C là các tiếp điểm). Qua điểm M bắt kì thuộc cung nhỏ BC,
kẻ tiếp tuyến với đường tròn, cắt AB, AC theo thứ tự tại D và E.
g) (5  4 2 ).(3  2 1  2 ).(3  2 1  2 )
a) Tứ giác ABOC là hình gì ? Vì sao ? h)
2  3 . 2  2  3 . 2  2  2  3 . 2  2  2  3 b) Tính số đo góc  DOE .
c) Đoạn OA cắt (O) tại K. Chứng minh: K là tâm đường tròn nội tiếp 2( 7 1 ) 3*. A  7  5  2 7  4 1 ĐS: A
ABC. Tính bán kính của đường tròn này. 2
d) Tính độ dài BK theo R. 5 6 B  4  3  6 3  15  3  ĐS: B  2 2 Gv: Trần Quốc Nghĩa Trang 18 Gv: Trần Quốc Nghĩa Trang 87 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
a) Chu vi MPQ không phụ thuộc vào vị trí điểm M. 2( 5 1 ) C  1 2 5 5 11  5  2 ĐS: C  1 2 b)   BOC  2DOE . c) DE < (AB  AC) 2
2.74 Cho đường tròn (O; 5cm) có đường kính AB và dây cung CD. Kéo dài
1  2 27 2  38  5  3 2 D 
ĐS: D 1
AB và CD cắt nhau tại M. Gọi N là trung điểm của dây cung CD. 3 2  4
a) Chứng minh: MNO là tam giác vuông.  
b) Tiếp tuyến tại B của (O) cắt đường thẳng CD tại Q. E  5  2 2 2  2  2 1 2 1  
ĐS: E 2
Chứng minh: MN . MQ = MO . MB  
c) Tia ON cắt (O) tại E. Tính độ dài dây cung EC nếu độ dài dây cung
1.32 Phân tích thành tích số: CD = 6 cm a) 1  2  3  6 b) 6  55  10  33
2.75 Cho nửa đường tròn (O ; R) đường kính AB. Gọi Ax, By là các tia vuông
1.33 Rút gọn biểu thức sau (loại bỏ dấu căn và dấu trị tuyệt đối):
góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ 4
AB). Gọi D là điểm bất kì thuộc nửa đường tròn. Tiếp tuyến tại D cắt Ax 1. a) 2 0 3 , 6x với x < 0 b) 2 x 3 (  x) với x  3
và By theo thứ tự tại M và N. 1 c) 2 27.48 1 (  x) với x > 1 d) 4 2 . x (x  y) a, b > 0
a) Tứ giác AMNB là hình gì ? Vì sao ? x  y b) Tính số đo góc MÔN. e) 2 4.(x  3) với x  3 f) 2 9.(x  2) với x < 2
c) Chứng minh: MN = AM + BN. 2 2
d) Chứng minh: AM . BN = R2. g) 2 x .(x  ) 1 với x > 0 h) 2 x (x 1) với x < 0
e) Đường tròn đường kính MN tiếp xúc với AB tại O. 2x x 3 52 i) . với x  0 j) 13x với x > 0
f) AN và BM cắt nhau tại Q, DQ cắt AB tại H. 3 8 x
Chứng minh: DQ  AB và QH = QD. k) x 5 . 4 x 5  x 3 với x bất kỳ l) 2 2 3 (  x)  0,2. 180x , x
g) Tìm vị trí của D để tứ giác AMNB có chu vi nhỏ nhất.
h) Cho R = 2cm. Tìm vị trí của M và N để chu vi tứ giác AMNB có chu 63y 3 3 4 x 8 vi bằng 14cm. 2. a) với y > 0 b) với x > 0 7y 5 x 3
2.76 Cho đường tròn (O; R) đường kính AB và 1 là điểm C nằm trên đường 45mn2 4 6 16x y
tròn. Đường thẳng song song với AC kẻ từ O cắt tiếp tuyến tại C của (O) c) với m > 0, n > 0 d) với x < 0 và y  0 6 6 tại D. Chứng minh: 20m 128x y a)   COD  BOD .
b) DB cũng là tiếp tuyến tại B của (O). 2 x x 4 x e)  với x > 0, y  0 f) 2 2y  với y < 0 c) AC . OD = 2R2. 4 y y 2 4y
2.77 Cho đường tròn (O; R) và một điểm A nằm ngoài (O). Từ A kẻ hai tiếp 2 2 x 5 16 g) x 5 y 3 3 0 2 , x y  với x  0, y  0
tuyến AM, AN của (O) (M, N là hai tiếp điểm).  với x < 0, y > 0 h) 6 y 4 8 x y
a) AMN là  gì ? Vì sao ? 3 27(x  3 2 )
b) Đường thẳng vuông góc với OM tại O cắt đường thẳng AN tại P. i) 2 xy  với x < 0, y  0 j) với x > 3 2 4 Chứng minh: AP = PO. x y 48 Gv: Trần Quốc Nghĩa Trang 86 Gv: Trần Quốc Nghĩa Trang 19 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
a) Chu vi MPQ không phụ thuộc vào vị trí điểm M. 2( 5 1 ) C  1 2 5 5 11  5  2 ĐS: C  1 2 b)   BOC  2DOE . c) DE < (AB  AC) 2
2.74 Cho đường tròn (O; 5cm) có đường kính AB và dây cung CD. Kéo dài
1  2 27 2  38  5  3 2 D 
ĐS: D 1
AB và CD cắt nhau tại M. Gọi N là trung điểm của dây cung CD. 3 2  4
a) Chứng minh: MNO là tam giác vuông.  
b) Tiếp tuyến tại B của (O) cắt đường thẳng CD tại Q. E  5  2 2 2  2  2 1 2 1  
ĐS: E 2
Chứng minh: MN . MQ = MO . MB  
c) Tia ON cắt (O) tại E. Tính độ dài dây cung EC nếu độ dài dây cung
1.32 Phân tích thành tích số: CD = 6 cm a) 1  2  3  6 b) 6  55  10  33
2.75 Cho nửa đường tròn (O ; R) đường kính AB. Gọi Ax, By là các tia vuông
1.33 Rút gọn biểu thức sau (loại bỏ dấu căn và dấu trị tuyệt đối):
góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ 4
AB). Gọi D là điểm bất kì thuộc nửa đường tròn. Tiếp tuyến tại D cắt Ax 1. a) 2 0 3 , 6x với x < 0 b) 2 x 3 (  x) với x  3
và By theo thứ tự tại M và N. 1 c) 2 27.48 1 (  x) với x > 1 d) 4 2 . x (x  y) a, b > 0
a) Tứ giác AMNB là hình gì ? Vì sao ? x  y b) Tính số đo góc MÔN. e) 2 4.(x  3) với x  3 f) 2 9.(x  2) với x < 2
c) Chứng minh: MN = AM + BN. 2 2
d) Chứng minh: AM . BN = R2. g) 2 x .(x  ) 1 với x > 0 h) 2 x (x 1) với x < 0
e) Đường tròn đường kính MN tiếp xúc với AB tại O. 2x x 3 52 i) . với x  0 j) 13x với x > 0
f) AN và BM cắt nhau tại Q, DQ cắt AB tại H. 3 8 x
Chứng minh: DQ  AB và QH = QD. k) x 5 . 4 x 5  x 3 với x bất kỳ l) 2 2 3 (  x)  0,2. 180x , x
g) Tìm vị trí của D để tứ giác AMNB có chu vi nhỏ nhất.
h) Cho R = 2cm. Tìm vị trí của M và N để chu vi tứ giác AMNB có chu 63y 3 3 4 x 8 vi bằng 14cm. 2. a) với y > 0 b) với x > 0 7y 5 x 3
2.76 Cho đường tròn (O; R) đường kính AB và 1 là điểm C nằm trên đường 45mn2 4 6 16x y
tròn. Đường thẳng song song với AC kẻ từ O cắt tiếp tuyến tại C của (O) c) với m > 0, n > 0 d) với x < 0 và y  0 6 6 tại D. Chứng minh: 20m 128x y a)   COD  BOD .
b) DB cũng là tiếp tuyến tại B của (O). 2 x x 4 x e)  với x > 0, y  0 f) 2 2y  với y < 0 c) AC . OD = 2R2. 4 y y 2 4y
2.77 Cho đường tròn (O; R) và một điểm A nằm ngoài (O). Từ A kẻ hai tiếp 2 2 x 5 16 g) x 5 y 3 3 0 2 , x y  với x  0, y  0
tuyến AM, AN của (O) (M, N là hai tiếp điểm).  với x < 0, y > 0 h) 6 y 4 8 x y
a) AMN là  gì ? Vì sao ? 3 27(x  3 2 )
b) Đường thẳng vuông góc với OM tại O cắt đường thẳng AN tại P. i) 2 xy  với x < 0, y  0 j) với x > 3 2 4 Chứng minh: AP = PO. x y 48 Gv: Trần Quốc Nghĩa Trang 86 Gv: Trần Quốc Nghĩa Trang 19 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1 xy
c) EF cắt OM tại K và cắt OI tại H. C/minh: OM . OK = OH . OI = R2. k) (x  y)  với x < y, y < 0 2 (x  y)
2.67 Cho ABC vuông tại A (AB < AC) có đường cao AH. Vẽ đường tròn tâm 2 9  12x  4x
B, bán kính BA, đường tròn này cắt AH tại điểm thứ hai là D. l)
với x >1,5 và y<0 2 y
a) Chứng minh: CD tiếp xúc với đường tròn (B ; BA).
b) Gọi I là đối xứng của B qua AH, đường thẳng AI cắt CD tại E. Chứng
1.34 Chứng minh:
minh: A, H, E, C cùng thuộc một đường tròn. Suy ra AB là tiếp tuyến a) (2  3) (2  3)  1 b) 9  17. 9  17  8 của đường tròn này.
c) ( 2014  2013) . ( 2014  2013) =1
2.68 Cho đường tròn đường kính AB. Gọi C là điểm bắt kì trên đường tròn và d) 2 2 ( 3  2)  1 (  2 2 2 )  2 6  9
H là hình chiếu của C trên AB. Từ A và B kẻ các tiếp tuyến AD và BE
1.35 Rút gọn các biểu thức sau:
đến đường tròn (C ; CH). Chứng minh: 6 a) D, C, E thẳng hàng.  14 2  3  6  8  16 1. a) b)
b) DE là tiếp tuyến của đường tròn đường kính BC. 2 3  28 2  3  4
c) Xác định vị trí của điểm C để diện tích tứ giác ABED lớn nhất. x  2 x  1 2 x  1 (y  2 y  1)
2.69 Cho góc xÔy, điểm A thuộc tia Ox. Dựng (I) tiếp xúc với Ox tại A và có 2. a) với x  0 b) ,x1,y1,y>0 x  2 x  1 4 y  1 (x  1) tâm I nằm trên Oy.
1.36 Rút gọn rồi tính giá trị của các biểu thức sau:
2.70 Cho đường tròn (O) và đường thẳng d không giao nhau. Dựng tiếp tuyến
của đường tròn (O) sao cho tiếp tuyến đó song song với d. 1. a) 2 2 4 1 (  6x  9x ) tại x =  2
2.71 Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến b) 9a2 (b2  4  4b) tại a = 2, b =  3
AM, AN với đường tròn (M, N là hai tiếp điểm). x3  2x2 a) Chứng minh: OA  MN. 2. a) 4x  8  tại x =  2 x  2
b) Vẽ đường kính NOC. Chứng minh: MC // AO.
c) Tính độ dài các cạnh của AMN biết OM = 3cm, OA = 5cm. (x  2 4 ) x2  1 b) 
(với x < 3) tại x = 0,5 (3  x 2 ) x  3
2.72 Cho đường tròn tâm O đường kính AB và một điểm C nằm trên đường
tròn (C khác A và B). Gọi D là trung điểm của AC.
1.37 So sánh hai số sau (không dùng máy tính):
a) Tính số đo ODA và chứng tỏ rằng OD song song với BC. a) 2 + 3 và 10 b) 3 + 2và 2  6
b) Tiếp tuyến tại A của (O) cắt tia OD tại E. Chứng minh: EC là tiếp c) 16 và 15. 17 d) 8 và 15 + 17 tuyến của (O).
c) Đường thẳng BC cắt tiếp tuyến tại A của (O) tại điểm M.
1.38 So sánh 2012  2014 và 2. 2013
d) Chứng minh rằng OE là trung tuyến của AOM.
1.39 Giải phương trình:
2.73 Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ tiếp tuyến 1. a) 16x  8 b) 4x  5
AB, AC với đường tròn (B và C là hai tiếp điểm). Qua điểm M thuộc c)
4(x2  2x  1)  6  0 d) 9(x 1)x  21
cung nhỏ BC, kẻ tiếp tuyến với đường tròn, tiếp tuyến này cắt AB và AC
lần lượt tại D và E. Chứng minh rằng e) x  5  3 f) x  10  2  Gv: Trần Quốc Nghĩa Trang 20 Gv: Trần Quốc Nghĩa Trang 85 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1 xy
c) EF cắt OM tại K và cắt OI tại H. C/minh: OM . OK = OH . OI = R2. k) (x  y)  với x < y, y < 0 2 (x  y)
2.67 Cho ABC vuông tại A (AB < AC) có đường cao AH. Vẽ đường tròn tâm 2 9  12x  4x
B, bán kính BA, đường tròn này cắt AH tại điểm thứ hai là D. l)
với x >1,5 và y<0 2 y
a) Chứng minh: CD tiếp xúc với đường tròn (B ; BA).
b) Gọi I là đối xứng của B qua AH, đường thẳng AI cắt CD tại E. Chứng
1.34 Chứng minh:
minh: A, H, E, C cùng thuộc một đường tròn. Suy ra AB là tiếp tuyến a) (2  3) (2  3)  1 b) 9  17. 9  17  8 của đường tròn này.
c) ( 2014  2013) . ( 2014  2013) =1
2.68 Cho đường tròn đường kính AB. Gọi C là điểm bắt kì trên đường tròn và d) 2 2 ( 3  2)  1 (  2 2 2 )  2 6  9
H là hình chiếu của C trên AB. Từ A và B kẻ các tiếp tuyến AD và BE
1.35 Rút gọn các biểu thức sau:
đến đường tròn (C ; CH). Chứng minh: 6 a) D, C, E thẳng hàng.  14 2  3  6  8  16 1. a) b)
b) DE là tiếp tuyến của đường tròn đường kính BC. 2 3  28 2  3  4
c) Xác định vị trí của điểm C để diện tích tứ giác ABED lớn nhất. x  2 x  1 2 x  1 (y  2 y  1)
2.69 Cho góc xÔy, điểm A thuộc tia Ox. Dựng (I) tiếp xúc với Ox tại A và có 2. a) với x  0 b) ,x1,y1,y>0 x  2 x  1 4 y  1 (x  1) tâm I nằm trên Oy.
1.36 Rút gọn rồi tính giá trị của các biểu thức sau:
2.70 Cho đường tròn (O) và đường thẳng d không giao nhau. Dựng tiếp tuyến
của đường tròn (O) sao cho tiếp tuyến đó song song với d. 1. a) 2 2 4 1 (  6x  9x ) tại x =  2
2.71 Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến b) 9a2 (b2  4  4b) tại a = 2, b =  3
AM, AN với đường tròn (M, N là hai tiếp điểm). x3  2x2 a) Chứng minh: OA  MN. 2. a) 4x  8  tại x =  2 x  2
b) Vẽ đường kính NOC. Chứng minh: MC // AO.
c) Tính độ dài các cạnh của AMN biết OM = 3cm, OA = 5cm. (x  2 4 ) x2  1 b) 
(với x < 3) tại x = 0,5 (3  x 2 ) x  3
2.72 Cho đường tròn tâm O đường kính AB và một điểm C nằm trên đường
tròn (C khác A và B). Gọi D là trung điểm của AC.
1.37 So sánh hai số sau (không dùng máy tính):
a) Tính số đo ODA và chứng tỏ rằng OD song song với BC. a) 2 + 3 và 10 b) 3 + 2và 2  6
b) Tiếp tuyến tại A của (O) cắt tia OD tại E. Chứng minh: EC là tiếp c) 16 và 15. 17 d) 8 và 15 + 17 tuyến của (O).
c) Đường thẳng BC cắt tiếp tuyến tại A của (O) tại điểm M.
1.38 So sánh 2012  2014 và 2. 2013
d) Chứng minh rằng OE là trung tuyến của AOM.
1.39 Giải phương trình:
2.73 Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ tiếp tuyến 1. a) 16x  8 b) 4x  5
AB, AC với đường tròn (B và C là hai tiếp điểm). Qua điểm M thuộc c)
4(x2  2x  1)  6  0 d) 9(x 1)x  21
cung nhỏ BC, kẻ tiếp tuyến với đường tròn, tiếp tuyến này cắt AB và AC
lần lượt tại D và E. Chứng minh rằng e) x  5  3 f) x  10  2  Gv: Trần Quốc Nghĩa Trang 20 Gv: Trần Quốc Nghĩa Trang 85 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
2.58 Cho ABC cân tại A, có O là trung điểm của BC và BC = 2a. Đường tròn g) 2x 1  5 h) 4  x 5  12
(O) tiếp xúc với AB, AC lần lượt tại H và K. Qua D trên cung nhỏ HK, kẻ 2 2
tiếp tuyến với (O) cắt AB và AC ở M và N. 2. a) 4x  x  5 b) (x  3)  2x  1
a) Chứng minh: A, H, O, K cùng thuộc một đường tròn. c) x 3  6 d) 7(x  1)  21 b) Chứng minh: MÔN = ABC.
c) Tính tích BM . CN theo a. 3. a) 2 x .  50  0 b) 2  x  8  0
d) Định vị trí của MN sao cho BM + CN đạt giá trị nhỏ nhất.
1.40 Giải các phương trình:
2.59 Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Dùng thước và 2x  3 2x  3 4x  3 4x  3 a)  2 và  2 b)  3 và  3
compa, hãy dựng các điểm B và C thuộc đường tròn (O) sao cho AB và x  1 x  1 x  1 x  1
AC là các tiếp tuyến của đường tròn (O).
1.41 Cho hai biểu thức: A 
x  2. x  3 và B  (x  2)(x  ) 3
2.60 Cho điểm A nằm trên đường thẳng d, điểm B nằm ngoài đường thẳng d.
a) Tìm x để A có nghĩa. Tìm x để B có nghĩa.
Dựng đường tròn (O) đi qua A và B, nhận đường thẳng d làm tiếp tuyến.
b) Với giá trị nào của x thì B có nghĩa còn A không có nghĩa.
c) Với giá trị nào của x thì A = B.
2.61 Cho ABC vuông tại A. Vẽ đường tròn (B ; BA) và đường tròn (C ; CA),
chúng cắt nhau tại điểm D (khác A). C/minh CD là tiếp tuyến của (B). 2x  3 2x  3
1.42 Cho hai biểu thức: và A  B  . x  3 x  3
2.62 Cho ABC cân tại A, các đường cao AD và BE cắt nhau tại H. Vẽ đường
a) Tìm x để A có nghĩa. Tìm x để B có nghĩa.
tròn (O) có đường kính AH. Chứng minh:
b) Với giá trị nào của x thì B có nghĩa còn A không có nghĩa.
a) Điểm E nằm trên đường tròn (O).
c) Với giá trị nào của x thì A = B.
b) DE là tiếp tuyến của đường tròn (O). 1  5 1  5
2.63 Cho điểm M trên (O; R) đường kính AB. Gọi H là trung điểm của BM, 1.43 Cho a  vaø b 
. Tính a2 + b2 và a5 + a5. 2 2
OH cắt (O) tại I và cắt tiếp tuyến tại B của (O) ở điểm D. Gọi N là hình
chiếu của I trên AM. Chứng minh: NI và DM là các tiếp tuyến của (O). 1.44 Cho a 
4  10  2 5 vaø b  4  10  2 5 .
Tính a2 + b2 và ab. Suy ra giá trị của a + b.
2.64 Cho đường tròn (O ; R) đường kính AB. Một tiếp tuyến tại M của (O) cắt
hai tiếp tuyến Ax, By theo thứ tự tại C và D. Chứng minh: đường tròn
1.45 Thực hiện phép tính:
đường kính CD tiếp xúc với AB.
a) A  12  3 7  12  3 7
2.65 Trên tiếp tuyến tại A của (O; R) lấy điểm B với AB = R. Từ A kẻ đường 7  5  7  5 b) B   3  2 2
vuông góc với OB tại H, cắt (O) tại C. OB cắt cung nhỏ AC tại I. 7  11
a) Chứng minh: AC là tiếp tuyến của đường tròn (O).
b) Tính theo R độ dài BH, IH và AI.
c) C  8  2 10  2 5  8  2 10  2 5
2.66 Từ điểm I bên ngoài (O; R) vẽ hai cát tuyến IAB và ICD (không qua tâm
1.46 Rút gọn rồi tính giá trị của biểu thức sau:
O). Gọi M và N lần lượt là trung điểm của hai dây AB và CD. 2 5
a) Chứng minh: O, I, M, N cùng thuộc một đường tròn. 2
A  10a 12a 10  36 với x = x   5 2
b) Đường tròn (OIMN) cắt (O) tại E và F. Chứng minh: IE, IF là hai tiếp tuyến của (O).
1.47 Cho hai số a và b với a > 0, b > 0. Chứng minh: a  b  a  b . Gv: Trần Quốc Nghĩa Trang 84 Gv: Trần Quốc Nghĩa Trang 21 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
2.58 Cho ABC cân tại A, có O là trung điểm của BC và BC = 2a. Đường tròn g) 2x 1  5 h) 4  x 5  12
(O) tiếp xúc với AB, AC lần lượt tại H và K. Qua D trên cung nhỏ HK, kẻ 2 2
tiếp tuyến với (O) cắt AB và AC ở M và N. 2. a) 4x  x  5 b) (x  3)  2x  1
a) Chứng minh: A, H, O, K cùng thuộc một đường tròn. c) x 3  6 d) 7(x  1)  21 b) Chứng minh: MÔN = ABC.
c) Tính tích BM . CN theo a. 3. a) 2 x .  50  0 b) 2  x  8  0
d) Định vị trí của MN sao cho BM + CN đạt giá trị nhỏ nhất.
1.40 Giải các phương trình:
2.59 Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Dùng thước và 2x  3 2x  3 4x  3 4x  3 a)  2 và  2 b)  3 và  3
compa, hãy dựng các điểm B và C thuộc đường tròn (O) sao cho AB và x  1 x  1 x  1 x  1
AC là các tiếp tuyến của đường tròn (O).
1.41 Cho hai biểu thức: A 
x  2. x  3 và B  (x  2)(x  ) 3
2.60 Cho điểm A nằm trên đường thẳng d, điểm B nằm ngoài đường thẳng d.
a) Tìm x để A có nghĩa. Tìm x để B có nghĩa.
Dựng đường tròn (O) đi qua A và B, nhận đường thẳng d làm tiếp tuyến.
b) Với giá trị nào của x thì B có nghĩa còn A không có nghĩa.
c) Với giá trị nào của x thì A = B.
2.61 Cho ABC vuông tại A. Vẽ đường tròn (B ; BA) và đường tròn (C ; CA),
chúng cắt nhau tại điểm D (khác A). C/minh CD là tiếp tuyến của (B). 2x  3 2x  3
1.42 Cho hai biểu thức: và A  B  . x  3 x  3
2.62 Cho ABC cân tại A, các đường cao AD và BE cắt nhau tại H. Vẽ đường
a) Tìm x để A có nghĩa. Tìm x để B có nghĩa.
tròn (O) có đường kính AH. Chứng minh:
b) Với giá trị nào của x thì B có nghĩa còn A không có nghĩa.
a) Điểm E nằm trên đường tròn (O).
c) Với giá trị nào của x thì A = B.
b) DE là tiếp tuyến của đường tròn (O). 1  5 1  5
2.63 Cho điểm M trên (O; R) đường kính AB. Gọi H là trung điểm của BM, 1.43 Cho a  vaø b 
. Tính a2 + b2 và a5 + a5. 2 2
OH cắt (O) tại I và cắt tiếp tuyến tại B của (O) ở điểm D. Gọi N là hình
chiếu của I trên AM. Chứng minh: NI và DM là các tiếp tuyến của (O). 1.44 Cho a 
4  10  2 5 vaø b  4  10  2 5 .
Tính a2 + b2 và ab. Suy ra giá trị của a + b.
2.64 Cho đường tròn (O ; R) đường kính AB. Một tiếp tuyến tại M của (O) cắt
hai tiếp tuyến Ax, By theo thứ tự tại C và D. Chứng minh: đường tròn
1.45 Thực hiện phép tính:
đường kính CD tiếp xúc với AB.
a) A  12  3 7  12  3 7
2.65 Trên tiếp tuyến tại A của (O; R) lấy điểm B với AB = R. Từ A kẻ đường 7  5  7  5 b) B   3  2 2
vuông góc với OB tại H, cắt (O) tại C. OB cắt cung nhỏ AC tại I. 7  11
a) Chứng minh: AC là tiếp tuyến của đường tròn (O).
b) Tính theo R độ dài BH, IH và AI.
c) C  8  2 10  2 5  8  2 10  2 5
2.66 Từ điểm I bên ngoài (O; R) vẽ hai cát tuyến IAB và ICD (không qua tâm
1.46 Rút gọn rồi tính giá trị của biểu thức sau:
O). Gọi M và N lần lượt là trung điểm của hai dây AB và CD. 2 5
a) Chứng minh: O, I, M, N cùng thuộc một đường tròn. 2
A  10a 12a 10  36 với x = x   5 2
b) Đường tròn (OIMN) cắt (O) tại E và F. Chứng minh: IE, IF là hai tiếp tuyến của (O).
1.47 Cho hai số a và b với a > 0, b > 0. Chứng minh: a  b  a  b . Gv: Trần Quốc Nghĩa Trang 84 Gv: Trần Quốc Nghĩa Trang 21 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
Áp dụng: So sánh 25  9 và 25  9
2.52 Cho đường tròn (O; 2cm). Một đường thẳng đi qua điểm A nằm bên
ngoài đường tròn và cắt đường tròn tại B và C, trong đó AB = BC. Kẻ
1.48 Cho hai số a và b với a > b > 0. Chứng minh: a  b  a  b .
đường kính COD. Tính AD.
Áp dụng: So sánh 25  9 và 25  9
2.53 Cho hình thang ABCD (   0
A  D  90 ), AB = 4cm, BC= 13cm, CD = 9cm.
1.49 Với n là số tự nhiên, chứng minh: a) Tính độ dài AD.  2 n  1  n   2 ( n  1 2 )  (2n  1 2 )  1
b) Chứng minh rằng AD tiếp xúc với đường tròn có đường kính là BC.
Viết đẳng thức trên khi n là 1; 2; 3; 4.
2.54 Cho (O; R), bán kính OA, dây CD là đường trung trực của OA.
1.50 Cho hai số a  0, b  0. Chứng minh:
a) Tứ giác OCAD là hình gì ? Vì sao ? a  b a  b a  b
b) Kẻ tiếp tuyến với đường tròn tại C, tiếp tuyến này cắt đường thẳng OA a)  ab b)  2 2 2 tại I. Tính CI.
1.51 Chứng minh:
2.55 Cho nửa đường tròn tâm O, đường kính AB. Qu điểm C thuộc nửa đường a) 3 là số vô tỉ.
b) 5 2 và 3 + 2 đều là số vô tỉ.
tròn, kẻ tiếp tuyến d của đường tròn. Gọi E và F lần lượt là chân các
1.52 Giải các bất phương trình sau và biểu diễn nghiệm trên trục số:
đường vuông góc kẻ từ A và B đến d. Gọi H là chân đường vuông góc kẻ a) x  2 b) x  3
từ C đến AB. Chứng minh rằng:  a) CE = CF.
b) AC là tia phân giác của BAE . c) CH2 = AE . BF
Chuyện vui Toán học: Câu chuyện số 2
Có 2 nguời bạn đang đi chơi trên khinh khí cầu (KKC), họ bị lạc
2.56 Cho đường tròn (O ; R) có đường kính AB và hai tiếp tuyến Ax, By. Một
tiếp tuyến khác tại điểm M cắt Ax ở C và cắt By ở D.
hướng nên phải hạ thấp xuống để hỏi đường.
a) Chứng minh: CD = AC + BD.
Khi thấy một anh ở dưới, một người hỏi :
b) Chứng minh: COD vuông.
- "Chúng tôi đang ở đâu đấy?".
c) Chứng minh: AB2 = 4AC . BD.
Anh chàng dưới đất trả lời:
d) AM cắt OC tại I, BM cắt OD tại K. Tứ giác OIMK là hình gì ? Định vị
- "Các anh đang ở trên một cái KKC".
trí của M để OIMK là hình vuông.
Người trên KKC hỏi tiếp:
e) AM cắt By tại F, BM cắt Ax tại E. Chứng minh:
i. C là trung điểm của AE ii) SABM = SEFM.
- "Anh là dân Toán à?". - "Đúng rồi".
2.57 Cho đường tròn (O ; R) và đoạn thẳng OA = 2R. Từ A kẻ hai tiếp tuyến
AB, AC đến đường tròn (O).
Nguời bạn kia ngạc nhiên hỏi:
a) Chứng minh: OA là đường trung trực của đoạn thẳng BC.
- "Sao anh biết người ta là dân toán?".
b) Chứng minh: ABC đều. Anh bạn này bảo:
c) Tính theo R độ dài BC và diện tích ABC.
- "Thì đấy, họ trả lời bao giờ cũng rất chính xác, nhưng lại
d) Đoạn OA cắt (O) tại D. Tứ giác OBDI là hình gì ? Vì sao ?
không giúp được gì cả!'
e) BO cắt AC kéo dài tại I. Tính theo R độ dài các cạnh của ABI.
f) Từ O kẻ đường vuông góc với OC cắt AB tại K. Tính khoảng cách từ K đến OA. Gv: Trần Quốc Nghĩa Trang 22 Gv: Trần Quốc Nghĩa Trang 83 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
Áp dụng: So sánh 25  9 và 25  9
2.52 Cho đường tròn (O; 2cm). Một đường thẳng đi qua điểm A nằm bên
ngoài đường tròn và cắt đường tròn tại B và C, trong đó AB = BC. Kẻ
1.48 Cho hai số a và b với a > b > 0. Chứng minh: a  b  a  b .
đường kính COD. Tính AD.
Áp dụng: So sánh 25  9 và 25  9
2.53 Cho hình thang ABCD (   0
A  D  90 ), AB = 4cm, BC= 13cm, CD = 9cm.
1.49 Với n là số tự nhiên, chứng minh: a) Tính độ dài AD.  2 n  1  n   2 ( n  1 2 )  (2n  1 2 )  1
b) Chứng minh rằng AD tiếp xúc với đường tròn có đường kính là BC.
Viết đẳng thức trên khi n là 1; 2; 3; 4.
2.54 Cho (O; R), bán kính OA, dây CD là đường trung trực của OA.
1.50 Cho hai số a  0, b  0. Chứng minh:
a) Tứ giác OCAD là hình gì ? Vì sao ? a  b a  b a  b
b) Kẻ tiếp tuyến với đường tròn tại C, tiếp tuyến này cắt đường thẳng OA a)  ab b)  2 2 2 tại I. Tính CI.
1.51 Chứng minh:
2.55 Cho nửa đường tròn tâm O, đường kính AB. Qu điểm C thuộc nửa đường a) 3 là số vô tỉ.
b) 5 2 và 3 + 2 đều là số vô tỉ.
tròn, kẻ tiếp tuyến d của đường tròn. Gọi E và F lần lượt là chân các
1.52 Giải các bất phương trình sau và biểu diễn nghiệm trên trục số:
đường vuông góc kẻ từ A và B đến d. Gọi H là chân đường vuông góc kẻ a) x  2 b) x  3
từ C đến AB. Chứng minh rằng:  a) CE = CF.
b) AC là tia phân giác của BAE . c) CH2 = AE . BF
Chuyện vui Toán học: Câu chuyện số 2
Có 2 nguời bạn đang đi chơi trên khinh khí cầu (KKC), họ bị lạc
2.56 Cho đường tròn (O ; R) có đường kính AB và hai tiếp tuyến Ax, By. Một
tiếp tuyến khác tại điểm M cắt Ax ở C và cắt By ở D.
hướng nên phải hạ thấp xuống để hỏi đường.
a) Chứng minh: CD = AC + BD.
Khi thấy một anh ở dưới, một người hỏi :
b) Chứng minh: COD vuông.
- "Chúng tôi đang ở đâu đấy?".
c) Chứng minh: AB2 = 4AC . BD.
Anh chàng dưới đất trả lời:
d) AM cắt OC tại I, BM cắt OD tại K. Tứ giác OIMK là hình gì ? Định vị
- "Các anh đang ở trên một cái KKC".
trí của M để OIMK là hình vuông.
Người trên KKC hỏi tiếp:
e) AM cắt By tại F, BM cắt Ax tại E. Chứng minh:
i. C là trung điểm của AE ii) SABM = SEFM.
- "Anh là dân Toán à?". - "Đúng rồi".
2.57 Cho đường tròn (O ; R) và đoạn thẳng OA = 2R. Từ A kẻ hai tiếp tuyến
AB, AC đến đường tròn (O).
Nguời bạn kia ngạc nhiên hỏi:
a) Chứng minh: OA là đường trung trực của đoạn thẳng BC.
- "Sao anh biết người ta là dân toán?".
b) Chứng minh: ABC đều. Anh bạn này bảo:
c) Tính theo R độ dài BC và diện tích ABC.
- "Thì đấy, họ trả lời bao giờ cũng rất chính xác, nhưng lại
d) Đoạn OA cắt (O) tại D. Tứ giác OBDI là hình gì ? Vì sao ?
không giúp được gì cả!'
e) BO cắt AC kéo dài tại I. Tính theo R độ dài các cạnh của ABI.
f) Từ O kẻ đường vuông góc với OC cắt AB tại K. Tính khoảng cách từ K đến OA. Gv: Trần Quốc Nghĩa Trang 22 Gv: Trần Quốc Nghĩa Trang 83 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
E - Vị trí tương đối của đường thẳng và đường tròn
E - Biến đổi đơn giản căn thức bậc hai
Dấu hiệu nhận biết tiếp tuyến của đường tròn
1. Đưa thừa số ra ngoài dấu căn: A B khi A 0 2   A B A B   ( B 0 )  A B khi A 0
Tính chất của hai tiếp tuyến cắt nhau 
2. Đưa thừa số vào trong dấu căn:
Với A  0, ta có: 2 A B A B ( B 0 )
1. Cho đường tròn (O ; R), đường thẳng cách O một khoảng d.
d > R  a và (O) không có điểm chung
Với A < 0, ta có:   2 A B A B ( B 0 )
d = R  a và (O) tiếp xúc nhau (có một điểm chung)
3. Khử mẫu của biểu thức dưới dấu căn:
d < R  a và (O) cắt nhau (có hai điểm chung) A A.B A.B
2. Tiếp tuyến của đường tròn là đường thẳng cí điểm chung duy nhất với  
với A.B  0, B  0 2 B B B
đường tròn (điểm chung đó gọi là tiếp điểm)
a. Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó
4. Trục căn thức ở mẫu:
vuông góc với bán kính đi qua tiếp điểm.
Phân tích tử và mẫu thành nhân tử tồi rút gọn cho nhân tử chung chứa
b. Nếu một đường thẳng đi qua một điểm của đường tròn và vuông
căn thức (nếu có).
góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp
tuyến của đường tròn.
Trường hợp mẫu là biểu thức dạng tích các căn thức và các số:
3. Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì: A A C
( B 0;C 0 )
a. Điểm đó cách đều hai tiếp điểm. B C B.C
b. Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai
Nếu mẫu là một biểu thức dạng tổng có chứa căn, nhân tử và mẫu với tiếp tuyến.
biểu thức liên hợp của mẫu:
c. Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai
bán kính đi qua tiếp điểm. C C( A  B )
với A  0 , A  B2 A B A 2 B
2.49 Trên mặt phẳng tọa độ cho điểm I(–3 ; 2). Nếu vẽ đường tròn tâm I bán C C( A  B )
kính bằng 2 thì đường tròn đó có vị trí tương đối như thế nào đối với cac
với A  0, B  0, A  B2 A B A B trục tọa độ ?
2.50 Cho đường thẳng a. Tâm I của tất cả các đường tròn có bán kính 5cm và
1.53 Đưa nhân tử ra ngoài dấu căn:
tiếp xúc với đường thẳng a nằm trên đường nào ? 1. a) 54 b) 108
2.51 Cho điểm A cách đường thẳng xy là 12cm. Vẽ đường tròn (A ; 13cm). c) 0,1 20000 d)  0,05 28800
a) Chứng minh đường tròn (A) có hai giao điểm với đường thẳng xy. 2. a) 2 7x với x>0 b) 4 4 y 8
b) Gọi hai giao điểm nói trên là B và C. Tính độ dài BC. c) 3 25x với x > 0 d) 2 y 8 với y > 0 Gv: Trần Quốc Nghĩa Trang 82 Gv: Trần Quốc Nghĩa Trang 23 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
E - Vị trí tương đối của đường thẳng và đường tròn
E - Biến đổi đơn giản căn thức bậc hai
Dấu hiệu nhận biết tiếp tuyến của đường tròn
1. Đưa thừa số ra ngoài dấu căn: A B khi A 0 2   A B A B   ( B 0 )  A B khi A 0
Tính chất của hai tiếp tuyến cắt nhau 
2. Đưa thừa số vào trong dấu căn:
Với A  0, ta có: 2 A B A B ( B 0 )
1. Cho đường tròn (O ; R), đường thẳng cách O một khoảng d.
d > R  a và (O) không có điểm chung
Với A < 0, ta có:   2 A B A B ( B 0 )
d = R  a và (O) tiếp xúc nhau (có một điểm chung)
3. Khử mẫu của biểu thức dưới dấu căn:
d < R  a và (O) cắt nhau (có hai điểm chung) A A.B A.B
2. Tiếp tuyến của đường tròn là đường thẳng cí điểm chung duy nhất với  
với A.B  0, B  0 2 B B B
đường tròn (điểm chung đó gọi là tiếp điểm)
a. Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó
4. Trục căn thức ở mẫu:
vuông góc với bán kính đi qua tiếp điểm.
Phân tích tử và mẫu thành nhân tử tồi rút gọn cho nhân tử chung chứa
b. Nếu một đường thẳng đi qua một điểm của đường tròn và vuông
căn thức (nếu có).
góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp
tuyến của đường tròn.
Trường hợp mẫu là biểu thức dạng tích các căn thức và các số:
3. Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì: A A C
( B 0;C 0 )
a. Điểm đó cách đều hai tiếp điểm. B C B.C
b. Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai
Nếu mẫu là một biểu thức dạng tổng có chứa căn, nhân tử và mẫu với tiếp tuyến.
biểu thức liên hợp của mẫu:
c. Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai
bán kính đi qua tiếp điểm. C C( A  B )
với A  0 , A  B2 A B A 2 B
2.49 Trên mặt phẳng tọa độ cho điểm I(–3 ; 2). Nếu vẽ đường tròn tâm I bán C C( A  B )
kính bằng 2 thì đường tròn đó có vị trí tương đối như thế nào đối với cac
với A  0, B  0, A  B2 A B A B trục tọa độ ?
2.50 Cho đường thẳng a. Tâm I của tất cả các đường tròn có bán kính 5cm và
1.53 Đưa nhân tử ra ngoài dấu căn:
tiếp xúc với đường thẳng a nằm trên đường nào ? 1. a) 54 b) 108
2.51 Cho điểm A cách đường thẳng xy là 12cm. Vẽ đường tròn (A ; 13cm). c) 0,1 20000 d)  0,05 28800
a) Chứng minh đường tròn (A) có hai giao điểm với đường thẳng xy. 2. a) 2 7x với x>0 b) 4 4 y 8
b) Gọi hai giao điểm nói trên là B và C. Tính độ dài BC. c) 3 25x với x > 0 d) 2 y 8 với y > 0 Gv: Trần Quốc Nghĩa Trang 82 Gv: Trần Quốc Nghĩa Trang 23 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
1.54 Đưa nhân tử vào trong dấu căn:
D - Các công thức về tam giác vuông cân 1. a) 3 5 b)  5 2 c) 2 2 d) 3 2
tam giác đều và nửa tam giác đều 2 2. a)  xy b) x 5 với x  0 3
1. Tam giác vuông cân: C 2
Cho ABC vuông cân tại A: c) x 13 với x < 0 d) x với x > 0 x BC = AB. 2 = a. 2 a BC
1.55 So sánh hai số sau (không dùng máy tính): AB AC A 2 A a B a) 3 3 và 12 b) 20 và 3 5 1 1 1 1 2. Tam giác đều: c) 54 và 150 d) 6 và 6
Cho ABC đều cạnh a, chiều cao h, diện tích S. a h 3 5 2 2 a 3 2h 3 2 a 3 5 3 h ; a ; S e) và f) 30  29 vaø 29  28 2 3 4 3 7  5 2 13 B H C
3. Nửa tam giác đều: C g) 2012  2014 và 2 2013
ABC: Â = 900, B = 600, C = 300 h)
2014  2013 và 2013  2012 BC BC 3 AB = ; AC = ; a
1.56 Sắp xếp theo thứ tự tăng dần: h 2 2 a) 2 5 , 2 6 , 29 , 3 5 b) 3 6 , 3 3 , 4 7 , 2 14 2 BC 3 AC = AB. 3 ; S
1.57 Rút gọn các biểu thức sau: 8 A B 1. a) 75  48  300 b) 98  72  0 5 , 8
2.46 Tính bán kính đường tròn ngoại tiếp: c) 9a  16a  49a (a  0) d)
160b  2 40b  3 90b (b0)
a) Tam giác vuông cân có cạnh góc vuông bằng a.
2. a) 3 2  4 18  2 32  50
b) 5 48  4 27  2 75  108
b) Tam giác đều cạnh bằng a. c)
125  2 20  3 80  4 45 d) 2 28  2 63  3 175  112
2.47 Cho đường tròn (O ; R) có hai bán kính OA, OB với góc AÔB = 1200. 3. a) (2 3  5) 3  60 b) (5 2  2 5) 5  250
Đường cao OI của AOB cắt (O) tại C.
a) Chứng tỏ tứ giác OACB là hình thoi.
c) ( 28  12  7 ) 7  2 21 d) ( 99  18  11) 11  3 22
b) Kẻ đường kính CD của (O). Chứng tỏ ABD đều. 4. a) 2 40 12  2
75  3 5 48 b) 2 80 3  2 5 3  3 20 3
2.48 Cho đường tròn (O ; R) có hai bán kính OA, OB vuông góc với nhau. Tia
phân giác của AÔB cắt (O) ở C. Lấy điểm bất kì trên cung BC và hạ
5. a) (1  x )(1  x  x)
b) ( x  2)(x  2 x  4)
đường vuông góc DH xuống OA, đường này cắt OC ở E.
c) ( x  y )(x  y  xy )
d) (x  y )(x2  y  x y )
a) Tính theo R khoảng cách từ C đến OA.
b) Chứng minh: HD2 + HE2 không đổi khi D thay đổi.
6. a) (4 x  2x )( x  2x ) b) (2 x  y )(3 x  2 y ) Gv: Trần Quốc Nghĩa Trang 24 Gv: Trần Quốc Nghĩa Trang 81 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
1.54 Đưa nhân tử vào trong dấu căn:
D - Các công thức về tam giác vuông cân 1. a) 3 5 b)  5 2 c) 2 2 d) 3 2
tam giác đều và nửa tam giác đều 2 2. a)  xy b) x 5 với x  0 3
1. Tam giác vuông cân: C 2
Cho ABC vuông cân tại A: c) x 13 với x < 0 d) x với x > 0 x BC = AB. 2 = a. 2 a BC
1.55 So sánh hai số sau (không dùng máy tính): AB AC A 2 A a B a) 3 3 và 12 b) 20 và 3 5 1 1 1 1 2. Tam giác đều: c) 54 và 150 d) 6 và 6
Cho ABC đều cạnh a, chiều cao h, diện tích S. a h 3 5 2 2 a 3 2h 3 2 a 3 5 3 h ; a ; S e) và f) 30  29 vaø 29  28 2 3 4 3 7  5 2 13 B H C
3. Nửa tam giác đều: C g) 2012  2014 và 2 2013
ABC: Â = 900, B = 600, C = 300 h)
2014  2013 và 2013  2012 BC BC 3 AB = ; AC = ; a
1.56 Sắp xếp theo thứ tự tăng dần: h 2 2 a) 2 5 , 2 6 , 29 , 3 5 b) 3 6 , 3 3 , 4 7 , 2 14 2 BC 3 AC = AB. 3 ; S
1.57 Rút gọn các biểu thức sau: 8 A B 1. a) 75  48  300 b) 98  72  0 5 , 8
2.46 Tính bán kính đường tròn ngoại tiếp: c) 9a  16a  49a (a  0) d)
160b  2 40b  3 90b (b0)
a) Tam giác vuông cân có cạnh góc vuông bằng a.
2. a) 3 2  4 18  2 32  50
b) 5 48  4 27  2 75  108
b) Tam giác đều cạnh bằng a. c)
125  2 20  3 80  4 45 d) 2 28  2 63  3 175  112
2.47 Cho đường tròn (O ; R) có hai bán kính OA, OB với góc AÔB = 1200. 3. a) (2 3  5) 3  60 b) (5 2  2 5) 5  250
Đường cao OI của AOB cắt (O) tại C.
a) Chứng tỏ tứ giác OACB là hình thoi.
c) ( 28  12  7 ) 7  2 21 d) ( 99  18  11) 11  3 22
b) Kẻ đường kính CD của (O). Chứng tỏ ABD đều. 4. a) 2 40 12  2
75  3 5 48 b) 2 80 3  2 5 3  3 20 3
2.48 Cho đường tròn (O ; R) có hai bán kính OA, OB vuông góc với nhau. Tia
phân giác của AÔB cắt (O) ở C. Lấy điểm bất kì trên cung BC và hạ
5. a) (1  x )(1  x  x)
b) ( x  2)(x  2 x  4)
đường vuông góc DH xuống OA, đường này cắt OC ở E.
c) ( x  y )(x  y  xy )
d) (x  y )(x2  y  x y )
a) Tính theo R khoảng cách từ C đến OA.
b) Chứng minh: HD2 + HE2 không đổi khi D thay đổi.
6. a) (4 x  2x )( x  2x ) b) (2 x  y )(3 x  2 y ) Gv: Trần Quốc Nghĩa Trang 24 Gv: Trần Quốc Nghĩa Trang 81 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1 1 2 a) Chứng minh: S  AB . MN 7. a) 2 2 x 5 1 (  2x) với x > 0,5 AMBN 2 2x  1
b) Định vị trí của MN để diện tích tứ giác AMBN lớn nhất. 2 3(x  y 2 ) b)
với x, y > 0 và x  y 2 2
2.43 Cho đường tròn (O) và dây BC cố định. Điểm A di chuyển trên cung lớn x  y 2
BC. Gọi M là trung điểm của AC và H là hình chiếu của M trên AB. Kẻ
1.58 Rút gọn các biểu thức sau: CD  BC. Chứng minh: 1 1 1 a) B, O, D thẳng hàng.
b) MH luôn đi qua một điểm cố định. a) 5  20  5 b)  4,5  12,5 5 2 2
2.44 Cho hình vuông ABCD cạnh a, O là giao điểm của hai đường chéo. Gọi c) 20  45  3 18  72 d) 20  45  3 18  72
M là trung điểm của OB, N là trung điểm của CD. 1 2
a) Xác định tâm và bán kính đường tròn ngoại tiếp ABN. e)   2 6 5  120 f) 72  5  4,5 2  2 27 3 3
b) Gọi K là tâm đường tròn ngoại tiếp AON và E là trung điểm của ON. 1 1
Chứng minh: KIE và AND đồng dạng.
g)  28  2 3  7  7  84 h) 48  2 75  54  5 1 2 3
c) Tính bán kính đường tròn ngoại tiếp AON.
1.59 Rút gọn các biểu thức sau (biết a > 0, b > 0): d) Chứng minh  AMN = 900 và AN > MD. a) 5 a  3 2 a 5 3  2 36ab2  2 9a
2.45 Cho đường tròn (O) và hai điểm A, B nằm bên trong đường tròn và không b) 64ab3  3 12a3b3  2ab a 9 b  5b 8 a 1 3b
cùng thuộc một đường kính. Dựng hai dây song song và bằng nhau sao
cho điểm A nằm trên một dây, điểm B nằm trên dây còn lại. 13 5 , 2 c) 3 2 a 3  7 a 5  a  30 a 0 2a 5
1.60 Thực hiện các phép tính sau: 13 2  4 6 3  2 2 9 6  12 3 1. a) b) c) 24  4 3 17  12 2 3 6  3 3 45  2 5  2 3  4 3 d) e) f) 5  2 3 5  3 2 6  2  5 2  3 6  35 8  15 2. a) A  b) B  c) C  2 2 30  2 15  5 5  2 5 3  1 3  1 3. a)  b)  3  1 2 5  4 3  1 3  1 2 8  12 5  27 3  3 3  3 c)  d)  18  48 30  2 2 3  1 2 3  1 Gv: Trần Quốc Nghĩa Trang 80 Gv: Trần Quốc Nghĩa Trang 25 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1 1 2 a) Chứng minh: S  AB . MN 7. a) 2 2 x 5 1 (  2x) với x > 0,5 AMBN 2 2x  1
b) Định vị trí của MN để diện tích tứ giác AMBN lớn nhất. 2 3(x  y 2 ) b)
với x, y > 0 và x  y 2 2
2.43 Cho đường tròn (O) và dây BC cố định. Điểm A di chuyển trên cung lớn x  y 2
BC. Gọi M là trung điểm của AC và H là hình chiếu của M trên AB. Kẻ
1.58 Rút gọn các biểu thức sau: CD  BC. Chứng minh: 1 1 1 a) B, O, D thẳng hàng.
b) MH luôn đi qua một điểm cố định. a) 5  20  5 b)  4,5  12,5 5 2 2
2.44 Cho hình vuông ABCD cạnh a, O là giao điểm của hai đường chéo. Gọi c) 20  45  3 18  72 d) 20  45  3 18  72
M là trung điểm của OB, N là trung điểm của CD. 1 2
a) Xác định tâm và bán kính đường tròn ngoại tiếp ABN. e)   2 6 5  120 f) 72  5  4,5 2  2 27 3 3
b) Gọi K là tâm đường tròn ngoại tiếp AON và E là trung điểm của ON. 1 1
Chứng minh: KIE và AND đồng dạng.
g)  28  2 3  7  7  84 h) 48  2 75  54  5 1 2 3
c) Tính bán kính đường tròn ngoại tiếp AON.
1.59 Rút gọn các biểu thức sau (biết a > 0, b > 0): d) Chứng minh  AMN = 900 và AN > MD. a) 5 a  3 2 a 5 3  2 36ab2  2 9a
2.45 Cho đường tròn (O) và hai điểm A, B nằm bên trong đường tròn và không b) 64ab3  3 12a3b3  2ab a 9 b  5b 8 a 1 3b
cùng thuộc một đường kính. Dựng hai dây song song và bằng nhau sao
cho điểm A nằm trên một dây, điểm B nằm trên dây còn lại. 13 5 , 2 c) 3 2 a 3  7 a 5  a  30 a 0 2a 5
1.60 Thực hiện các phép tính sau: 13 2  4 6 3  2 2 9 6  12 3 1. a) b) c) 24  4 3 17  12 2 3 6  3 3 45  2 5  2 3  4 3 d) e) f) 5  2 3 5  3 2 6  2  5 2  3 6  35 8  15 2. a) A  b) B  c) C  2 2 30  2 15  5 5  2 5 3  1 3  1 3. a)  b)  3  1 2 5  4 3  1 3  1 2 8  12 5  27 3  3 3  3 c)  d)  18  48 30  2 2 3  1 2 3  1 Gv: Trần Quốc Nghĩa Trang 80 Gv: Trần Quốc Nghĩa Trang 25 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1 2 2 3 3
2.34 Cho đường tròn (O), hai dây AB và CD (AB = CD) cắt nhau tại I nằm bên e)  f)  3
trong đường tròn. Chứng minh:  1 3  1 3  1  1 3  1  1
a) OI là tia phân giác của một trong hai góc tạo bởi hai dây AB và CD. 2 3  4 2 2  1 1  6 5 5 g)   h) 
b) I chia AB, CD thành các đoạn thẳng bằng nhau từng đôi một. 3  1 2  1 2  3 12(2 5  3 2 ) 12(2 5  3 2 )
2.35 Cho đường tròn (O), dây AB bất kỳ không đi qua tâm. Trên cung nhỏ AB 1 6
lấy hai điểm phân biệt C, D sao cho D nằm trên cung nhỏ AC và 4. a)  11  4 7 32  10 7
AD = BC. Chứng minh: CD // AB. 1 1 1
2.36 Cho đường tròn (O; 5cm), hai dây AB, CD (AB // CD), biết AB = 8cm, b)   12  140 8  60 10  84
CD = 6cm. Tính khoảng cách giữa hai dây. 1 2 3 4
2.37 Cho đường tròn (O) và điểm I nằm bên trong đường tròn. Vẽ dây c)    3  2 7  5 7  2 10 10  2 21
AB  OI tại I. Chứng minh rằng AB là dây cung ngắn hơn mọi dây cung khác đi qua I.
1.61 Chứng minh các số sau đây là số nguyên: 3 3  2 2 6  6
2.38 Cho ABC nội tiếp trong đường tròn (O) có   
A  B  C . Gọi OH, OI, OK a) A   3  2 6  1
lần lượt là khoảng cách từ O đến BC, AC và AB. So sánh các độ dài OH,  15 4 12  OI, OK. b) B      6  1  1  6  1 6  2 3  6 
2.39 Cho đường tròn (O), các bán kính OA, OB. Trên cung nhỏ AB lấy các
điểm M và N sao cho AM = BN. Gọi C là giao điểm của các đường thẳng
2 3  2 3  2  3  2 2 c) C   2 3
AM và BN. Chứng minh rằng: 3  1
a) OC là tia phân giác của  AOB . b) OC  AB.
1.62 Chứng minh các số sau đây là số dương:
2.40 Cho (O; R) và một điểm A cố định với OA = R/2. Một dây cung MN 2  3 2  3 a) A   2 2 2 2 1   1 quay quanh A. 2  2  3 2  2  3 3 3 C 
a) Chứng minh: trung điểm của MN thuộc một đường tròn cố định. 23 2 3 2 2 2 2 2 b) B  
b) Xác định vị trí của MN để độ dài MN ngắn nhất ? Dài nhất ? Tính độ 1   1 2  14  5 3 2  14  5 3 3 3
dài ngắn nhất, dài nhất đó của MN.
1.63 Chứng tỏ rằng các số sau là số hữu tỉ:
2.41 Cho ABC vuông tại A, M là điểm di động trên cạnh huyền BC. Gọi (O) 2 2 7  5 7  5
là đường tròn đường kính AM. a)  b)  7  5 7  5 7  5 7  5
a) Chứng minh: (O) luôn đi qua hai điểm cố định.
b) (O) cắt AB, AC lần lượt tại E và F. Định vị trí của M sao cho độ dài
1.64 Các số sau đây có căn bậc hai không ? EF nhỏ nhất.  3 1   3 1  a) A  1  :   2 
2.42 Cho đường tròn (O) và dây AB cố định. M và N là hai điểm di động lần 2   2     
lượt trên cung lớn và cung nhỏ AB. Gv: Trần Quốc Nghĩa Trang 26 Gv: Trần Quốc Nghĩa Trang 79 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1 2 2 3 3
2.34 Cho đường tròn (O), hai dây AB và CD (AB = CD) cắt nhau tại I nằm bên e)  f)  3
trong đường tròn. Chứng minh:  1 3  1 3  1  1 3  1  1
a) OI là tia phân giác của một trong hai góc tạo bởi hai dây AB và CD. 2 3  4 2 2  1 1  6 5 5 g)   h) 
b) I chia AB, CD thành các đoạn thẳng bằng nhau từng đôi một. 3  1 2  1 2  3 12(2 5  3 2 ) 12(2 5  3 2 )
2.35 Cho đường tròn (O), dây AB bất kỳ không đi qua tâm. Trên cung nhỏ AB 1 6
lấy hai điểm phân biệt C, D sao cho D nằm trên cung nhỏ AC và 4. a)  11  4 7 32  10 7
AD = BC. Chứng minh: CD // AB. 1 1 1
2.36 Cho đường tròn (O; 5cm), hai dây AB, CD (AB // CD), biết AB = 8cm, b)   12  140 8  60 10  84
CD = 6cm. Tính khoảng cách giữa hai dây. 1 2 3 4
2.37 Cho đường tròn (O) và điểm I nằm bên trong đường tròn. Vẽ dây c)    3  2 7  5 7  2 10 10  2 21
AB  OI tại I. Chứng minh rằng AB là dây cung ngắn hơn mọi dây cung khác đi qua I.
1.61 Chứng minh các số sau đây là số nguyên: 3 3  2 2 6  6
2.38 Cho ABC nội tiếp trong đường tròn (O) có   
A  B  C . Gọi OH, OI, OK a) A   3  2 6  1
lần lượt là khoảng cách từ O đến BC, AC và AB. So sánh các độ dài OH,  15 4 12  OI, OK. b) B      6  1  1  6  1 6  2 3  6 
2.39 Cho đường tròn (O), các bán kính OA, OB. Trên cung nhỏ AB lấy các
điểm M và N sao cho AM = BN. Gọi C là giao điểm của các đường thẳng
2 3  2 3  2  3  2 2 c) C   2 3
AM và BN. Chứng minh rằng: 3  1
a) OC là tia phân giác của  AOB . b) OC  AB.
1.62 Chứng minh các số sau đây là số dương:
2.40 Cho (O; R) và một điểm A cố định với OA = R/2. Một dây cung MN 2  3 2  3 a) A   2 2 2 2 1   1 quay quanh A. 2  2  3 2  2  3 3 3 C 
a) Chứng minh: trung điểm của MN thuộc một đường tròn cố định. 23 2 3 2 2 2 2 2 b) B  
b) Xác định vị trí của MN để độ dài MN ngắn nhất ? Dài nhất ? Tính độ 1   1 2  14  5 3 2  14  5 3 3 3
dài ngắn nhất, dài nhất đó của MN.
1.63 Chứng tỏ rằng các số sau là số hữu tỉ:
2.41 Cho ABC vuông tại A, M là điểm di động trên cạnh huyền BC. Gọi (O) 2 2 7  5 7  5
là đường tròn đường kính AM. a)  b)  7  5 7  5 7  5 7  5
a) Chứng minh: (O) luôn đi qua hai điểm cố định.
b) (O) cắt AB, AC lần lượt tại E và F. Định vị trí của M sao cho độ dài
1.64 Các số sau đây có căn bậc hai không ? EF nhỏ nhất.  3 1   3 1  a) A  1  :   2 
2.42 Cho đường tròn (O) và dây AB cố định. M và N là hai điểm di động lần 2   2     
lượt trên cung lớn và cung nhỏ AB. Gv: Trần Quốc Nghĩa Trang 26 Gv: Trần Quốc Nghĩa Trang 79 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1  6  2 5  1
C - Liên hệ giữa dây và khoảng cách từ tâm đến dây b) B     :  1 3 5  5  2   2 2 2 5 1 c) C    
1. Trong một đường tròn: 3 3 3 12 6
a. Hai dây bằng nhau thì cách đều tâm.
b. Hai dây cách đều tâm thì bằng nhau.
1.65 Tìm x biết: a) 25x  35 b) 3 x  12
2. Trong hai dây của một đường tròn:
a. Dây nào lớn hơn thì dây đó gần tâm hơn. c) 4x  162 d) 2 x  10
b. Dây nào gần tâm hơn thì dây đó lớn hơn.
1.66 Giải các phương trình sau:
1. a) 2 3x  4 3x  27  3 3x
b) 3 2x  5 8x  7 18x  28
2.27 Cho đường tròn tâm O bán kính 5cm, dây AB = 8cm.
a) Tính khoảng cách từ tâm O đến dây AB. 2. a) 2 x  9  3 x  3  0 b) 2 x  4  2 x  2  0
b) Gọi I là điểm thuộc dây AB sao cho AI = 1cm. Kẻ dây CD đi qua I và
1.67 Khử mẫu của các biểu thức dưới dấu căn (giả thiết rằng các biểu thức đã
vuông góc với AB. Chứng minh CD = AB. cho có nghĩa):
2.28 Cho đường tròn tâm O bán kính 25cm, dây AB = 40cm. Vẽ dây CD song 1 11 3 5 1 (  3 2 ) a) ; ; ; ;
song với AB và có khoảng cách đến AB bằng 22cm. Tính độ dài dây CD. 600 540 50 98 27
2.29 Cho đường tròn (O), điểm A nằm bên trong đường tròn. Vẽ dây BC  OA a a b 1 1 a 9 3 2 b) ab ; ;  ; ; x 3 y 2
tại A. Vẽ dây EF bất kỳ đi qua A và không vuông góc với OA. So sánh b b a b b 36b xy BC và EF . 2 x2 3 2 x2 2 c) ; ; ; x  ; x 3 y
2.30 Cho đường tròn tâm O có các dây cung AB và CD bằng nhau và vuông 3 5 x 7 xy
góc với nhau tại I. Biết IC = 2cm, ID = 14cm. Tính khoảng cách từ O đến
1.68 Trục căn thức ở mẫu của các biểu thức sau (giả thiết rằng các biểu thức đã mỗi dây. cho có nghĩa):
2.31 Cho (O) có các dây cung AB và CD bằng nhau, các tia AB và CD cắt 5 1 5 2 2  2 y  b y a) ; ; ; ;
nhau tại E nằm nên ngoài đường tròn. Gọi H và K lần lượt là trung điểm 10 3 3 2 5 5 2 b y
của của AB và CD. Chứng minh: 3 2 2  3 b p a) EH = EK b) EA = EC. b) ; ; ; ; 3  1 3  1 2  3 3  b 2 p 1
2.32 Cho đường tròn (O), dây AB và CD (AB < CD) cắt nhau tại K nằm bên 3 3 1 a 2 b
ngoài đường tròn. Đường tròn (O ; OK) cắ KA và BC lần lượt tạo M và c) ; ; ; . 3  1 10  7 x  y a  b N. So sánh KM và KN. 5  3 26 2 10  5 9  2 3
2.33 Cho đường tròn (O), dây AB và CD (AB > CD) cắt nhau tại M. Gọi H và d) ; ; ; . 2 5  2 3 4  10 3 6  2 2
K lần lượt là trung điểm của AB và CD. So sánh MH và MK (Chú ý: xét 2 1 1
trường hợp của điểm M). e) ; . 3  2  1 5  3  2 Gv: Trần Quốc Nghĩa Trang 78 Gv: Trần Quốc Nghĩa Trang 27 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1  6  2 5  1
C - Liên hệ giữa dây và khoảng cách từ tâm đến dây b) B     :  1 3 5  5  2   2 2 2 5 1 c) C    
1. Trong một đường tròn: 3 3 3 12 6
a. Hai dây bằng nhau thì cách đều tâm.
b. Hai dây cách đều tâm thì bằng nhau.
1.65 Tìm x biết: a) 25x  35 b) 3 x  12
2. Trong hai dây của một đường tròn:
a. Dây nào lớn hơn thì dây đó gần tâm hơn. c) 4x  162 d) 2 x  10
b. Dây nào gần tâm hơn thì dây đó lớn hơn.
1.66 Giải các phương trình sau:
1. a) 2 3x  4 3x  27  3 3x
b) 3 2x  5 8x  7 18x  28
2.27 Cho đường tròn tâm O bán kính 5cm, dây AB = 8cm.
a) Tính khoảng cách từ tâm O đến dây AB. 2. a) 2 x  9  3 x  3  0 b) 2 x  4  2 x  2  0
b) Gọi I là điểm thuộc dây AB sao cho AI = 1cm. Kẻ dây CD đi qua I và
1.67 Khử mẫu của các biểu thức dưới dấu căn (giả thiết rằng các biểu thức đã
vuông góc với AB. Chứng minh CD = AB. cho có nghĩa):
2.28 Cho đường tròn tâm O bán kính 25cm, dây AB = 40cm. Vẽ dây CD song 1 11 3 5 1 (  3 2 ) a) ; ; ; ;
song với AB và có khoảng cách đến AB bằng 22cm. Tính độ dài dây CD. 600 540 50 98 27
2.29 Cho đường tròn (O), điểm A nằm bên trong đường tròn. Vẽ dây BC  OA a a b 1 1 a 9 3 2 b) ab ; ;  ; ; x 3 y 2
tại A. Vẽ dây EF bất kỳ đi qua A và không vuông góc với OA. So sánh b b a b b 36b xy BC và EF . 2 x2 3 2 x2 2 c) ; ; ; x  ; x 3 y
2.30 Cho đường tròn tâm O có các dây cung AB và CD bằng nhau và vuông 3 5 x 7 xy
góc với nhau tại I. Biết IC = 2cm, ID = 14cm. Tính khoảng cách từ O đến
1.68 Trục căn thức ở mẫu của các biểu thức sau (giả thiết rằng các biểu thức đã mỗi dây. cho có nghĩa):
2.31 Cho (O) có các dây cung AB và CD bằng nhau, các tia AB và CD cắt 5 1 5 2 2  2 y  b y a) ; ; ; ;
nhau tại E nằm nên ngoài đường tròn. Gọi H và K lần lượt là trung điểm 10 3 3 2 5 5 2 b y
của của AB và CD. Chứng minh: 3 2 2  3 b p a) EH = EK b) EA = EC. b) ; ; ; ; 3  1 3  1 2  3 3  b 2 p 1
2.32 Cho đường tròn (O), dây AB và CD (AB < CD) cắt nhau tại K nằm bên 3 3 1 a 2 b
ngoài đường tròn. Đường tròn (O ; OK) cắ KA và BC lần lượt tạo M và c) ; ; ; . 3  1 10  7 x  y a  b N. So sánh KM và KN. 5  3 26 2 10  5 9  2 3
2.33 Cho đường tròn (O), dây AB và CD (AB > CD) cắt nhau tại M. Gọi H và d) ; ; ; . 2 5  2 3 4  10 3 6  2 2
K lần lượt là trung điểm của AB và CD. So sánh MH và MK (Chú ý: xét 2 1 1
trường hợp của điểm M). e) ; . 3  2  1 5  3  2 Gv: Trần Quốc Nghĩa Trang 78 Gv: Trần Quốc Nghĩa Trang 27 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
1.69 Phân tích thành nhân tử:
b) Cho nửa đường tròn tâm O, đường kính AB. Trên AB lấy các điểm M, a) ab  b a  a  1 b) 3 3 2 2 x  y  x y  xy
N sao cho AM = BN. Qua M và N kẻ các đường thẳng song song với
nhau, chúng cắt nửa đường tròn lần lượt tại C và D.
1.70 Giải phương trình:
Chứng minh: MC  CD và ND  CD. a) 2x  3  1  2 b) x  1  5  3 c) x 3  2  2  3
2.25 Cho đường tròn (O ; R) và điểm M nằm bên trong đường tròn.
1.71 Giải các bất phương trình sau và biểu diễn nghiệm trên trục số:
a) Hãy nêu cách dựng AB nhận M làm trung điểm. a) x  2  3 b) x  2  3
b) Tính AB, biết R = 5cm, OM = 1,4cm. 1
1.72 Với n là số tự nhiên, chứng minh: n  1  n 
2.26 Cho đường tròn (O), điểm A nằm bên trong đường tròn, điểm B nằm bên n  1  n
ngoài đường tròn sao cho trung điểm I của AB nằm bên trong đường 1 1 1 Áp dụng tính:  
tròn.Vẽ dây CD  OI tại I. Tứ giác ACBD là hình gì ? Vì sao ? 2  1 3  2 4  3
1.73 Cho các biểu thức : 1 1 1 1 A       ; 1  2 2  3 3  4 24  25 1 1 1 1 B       1 2 3 24 a) Tính giá trị của A.
b) Chứng minh rằng B > 8.
1.74 Rút gọn các biểu thức sau: 1 1 1 1 a) A       1  2 2  3 3  4 n  1  n 1 1 1 1 b) B       1  2 2  3 3  4 24  25 Danh ngôn học tập Đừng l
o lắng về khó khăn của bạn trong toán học, tôi
đảm bảo với bạn rằng những khó khăn toán học của tôi còn gấp bội.
Do not worry about your difficulties in Mathematics.
I can assure you mine are still greater. Albert Einstein Gv: Trần Quốc Nghĩa Trang 28 Gv: Trần Quốc Nghĩa Trang 77 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
1.69 Phân tích thành nhân tử:
b) Cho nửa đường tròn tâm O, đường kính AB. Trên AB lấy các điểm M, a) ab  b a  a  1 b) 3 3 2 2 x  y  x y  xy
N sao cho AM = BN. Qua M và N kẻ các đường thẳng song song với
nhau, chúng cắt nửa đường tròn lần lượt tại C và D.
1.70 Giải phương trình:
Chứng minh: MC  CD và ND  CD. a) 2x  3  1  2 b) x  1  5  3 c) x 3  2  2  3
2.25 Cho đường tròn (O ; R) và điểm M nằm bên trong đường tròn.
1.71 Giải các bất phương trình sau và biểu diễn nghiệm trên trục số:
a) Hãy nêu cách dựng AB nhận M làm trung điểm. a) x  2  3 b) x  2  3
b) Tính AB, biết R = 5cm, OM = 1,4cm. 1
1.72 Với n là số tự nhiên, chứng minh: n  1  n 
2.26 Cho đường tròn (O), điểm A nằm bên trong đường tròn, điểm B nằm bên n  1  n
ngoài đường tròn sao cho trung điểm I của AB nằm bên trong đường 1 1 1 Áp dụng tính:  
tròn.Vẽ dây CD  OI tại I. Tứ giác ACBD là hình gì ? Vì sao ? 2  1 3  2 4  3
1.73 Cho các biểu thức : 1 1 1 1 A       ; 1  2 2  3 3  4 24  25 1 1 1 1 B       1 2 3 24 a) Tính giá trị của A.
b) Chứng minh rằng B > 8.
1.74 Rút gọn các biểu thức sau: 1 1 1 1 a) A       1  2 2  3 3  4 n  1  n 1 1 1 1 b) B       1  2 2  3 3  4 24  25 Danh ngôn học tập Đừng l
o lắng về khó khăn của bạn trong toán học, tôi
đảm bảo với bạn rằng những khó khăn toán học của tôi còn gấp bội.
Do not worry about your difficulties in Mathematics.
I can assure you mine are still greater. Albert Einstein Gv: Trần Quốc Nghĩa Trang 28 Gv: Trần Quốc Nghĩa Trang 77 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
B - Đường kính và dây cung của đường tròn
F - Rút gọn biểu thức có chứa căn thức bậc hai
1. Trong các dây của một đường tròn, dây lớn nhất là đường kính. Từ đó
Cho x  0, y  0. Ta có các công thức biến đổi sau:
suy ra nếu AB là một dây cung bất kì của (O ; R) thì AB  2R. 1. 2 x ( x ) ; 3 x x ( x )
2. a. Trong một đường tròn, đường kính vuông góc với một dây thì đi 2. x x x( x 1 )
qua trung điểm của dây ấy.
3. x y y x xy( x y )
b. Trong một đường tròn, đường kính đi qua trung điểm của một dây
không đi qua tâm thì vuông góc với dây ấy.
4. x y ( x y )( x y ) 5.     2 x 2 xy y ( x y )
2.19 Cho đường tròn (O) có bán kính OA = 3cm. Dây BC của đường tròn 6.   3 3 x x y y ( x ) ( y ) ( x y )( x  xy y )
vuông góc với OA tại trung điểm của OA. Tính BC.
2.20 Cho ABC, các đường cao BD và CE. Chứng minh:
1.75 Chứng minh các đẳng thức sau:
a) Bốn điểm B, E, D và C cùng nằm trên một đường tròn. x3  1 b) DE < BC. a)
 x  x  1 với x > 0, x  1 x  1
2.21 a) Cho đường tròn (O) đường kính AB, dây CD không cắt đường kính (x y  y x )( x  y )
AB. Gọi H và K lần lượt là hình chiếu của A và B trên CD. Chứng b)  x  y với x, y > 0 xy minh: CH = DK.
b) Cho đường tròn (O) đường kính AB, dây CD cắt đường kính AB tại I.
1.76 Rút gọn:
Gọi H và K lần lượt là hình chiếu của A và B trên CD. Chứng minh: x  2 3x  3 a) A  với x  0 CH = DK. x x  3 3 x x  y y
2.22 Tứ giác ABCD có   0 B  D  90 . b) B 
với x  0, y  0 và x  y
a) Chứng minh: bốn điểm A, B, C, D cùng nằm trên một đường tròn. x  y
b) So sánh AC và BD. Nếu AB = CD thì tứ giác ABCD là hình gì ? a  b  2 ab a  b c) C  
(với a  0, b  0, a  b)
2.23 Cho đường tròn (O) có đường kính AD = 2R. Vẽ cung tròn tâm D bán a  b a  b
kính R, cung này cắt đường tròn (O) ở B và C. ( a 1)(a  ab)( a  b) d) D 
(với a > 0, b  0, a  b)
a) Tứ giác OBDC là hình gì ? Vì sao ? (a  b)(a a  a)
b) Tính các góc CBD, CBO, OBA. a 1 1 e) E  : (với a > 0)
c) Chứng minh: ABC đều. 2 a a  a  a a  a
2.24 a) Cho nửa đường tròn tâm O, đường kính AB, dây CD. Các đường  x  y xy  xy  1 f)
(với x  0, y  0, x  y)
vuông góc với CD tại C và D tương ứng cắt AB ở M và N. F     :  x y x y    x  y   Chứng minh: AM = BN. x y x  y g) G    (với xy  0, x  y) xy  y xy  x xy Gv: Trần Quốc Nghĩa Trang 76 Gv: Trần Quốc Nghĩa Trang 29 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
B - Đường kính và dây cung của đường tròn
F - Rút gọn biểu thức có chứa căn thức bậc hai
1. Trong các dây của một đường tròn, dây lớn nhất là đường kính. Từ đó
Cho x  0, y  0. Ta có các công thức biến đổi sau:
suy ra nếu AB là một dây cung bất kì của (O ; R) thì AB  2R. 1. 2 x ( x ) ; 3 x x ( x )
2. a. Trong một đường tròn, đường kính vuông góc với một dây thì đi 2. x x x( x 1 )
qua trung điểm của dây ấy.
3. x y y x xy( x y )
b. Trong một đường tròn, đường kính đi qua trung điểm của một dây
không đi qua tâm thì vuông góc với dây ấy.
4. x y ( x y )( x y ) 5.     2 x 2 xy y ( x y )
2.19 Cho đường tròn (O) có bán kính OA = 3cm. Dây BC của đường tròn 6.   3 3 x x y y ( x ) ( y ) ( x y )( x  xy y )
vuông góc với OA tại trung điểm của OA. Tính BC.
2.20 Cho ABC, các đường cao BD và CE. Chứng minh:
1.75 Chứng minh các đẳng thức sau:
a) Bốn điểm B, E, D và C cùng nằm trên một đường tròn. x3  1 b) DE < BC. a)
 x  x  1 với x > 0, x  1 x  1
2.21 a) Cho đường tròn (O) đường kính AB, dây CD không cắt đường kính (x y  y x )( x  y )
AB. Gọi H và K lần lượt là hình chiếu của A và B trên CD. Chứng b)  x  y với x, y > 0 xy minh: CH = DK.
b) Cho đường tròn (O) đường kính AB, dây CD cắt đường kính AB tại I.
1.76 Rút gọn:
Gọi H và K lần lượt là hình chiếu của A và B trên CD. Chứng minh: x  2 3x  3 a) A  với x  0 CH = DK. x x  3 3 x x  y y
2.22 Tứ giác ABCD có   0 B  D  90 . b) B 
với x  0, y  0 và x  y
a) Chứng minh: bốn điểm A, B, C, D cùng nằm trên một đường tròn. x  y
b) So sánh AC và BD. Nếu AB = CD thì tứ giác ABCD là hình gì ? a  b  2 ab a  b c) C  
(với a  0, b  0, a  b)
2.23 Cho đường tròn (O) có đường kính AD = 2R. Vẽ cung tròn tâm D bán a  b a  b
kính R, cung này cắt đường tròn (O) ở B và C. ( a 1)(a  ab)( a  b) d) D 
(với a > 0, b  0, a  b)
a) Tứ giác OBDC là hình gì ? Vì sao ? (a  b)(a a  a)
b) Tính các góc CBD, CBO, OBA. a 1 1 e) E  : (với a > 0)
c) Chứng minh: ABC đều. 2 a a  a  a a  a
2.24 a) Cho nửa đường tròn tâm O, đường kính AB, dây CD. Các đường  x  y xy  xy  1 f)
(với x  0, y  0, x  y)
vuông góc với CD tại C và D tương ứng cắt AB ở M và N. F     :  x y x y    x  y   Chứng minh: AM = BN. x y x  y g) G    (với xy  0, x  y) xy  y xy  x xy Gv: Trần Quốc Nghĩa Trang 76 Gv: Trần Quốc Nghĩa Trang 29 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1 3 3 a  b a  b
2.14 Cho ABC cân tại A, nội tiếp đường tròn (O). Đường cao AH cắt đường h) H  
(với a  0, b  0, a  b) tròn (O) ở D. a  b a  b
a) Chứng minh: AD là đường kính của đường tròn (O). 2 ( x  y)  4 xy x  y i) I  
(với x  0, y  0, x  y) b) Tính  ACD . x  y x  y
c) Cho BC = 24cm, AC = 20cm. Tính AH và bán kính của (O).  x  1 x 1   x 1  j) J     : 1   (với x > 0, x  1) 
2.15 Cho ABC có đường cao AH. Từ một điểm M bất kỳ trên cạnh BC, kẻ x 1 x 1   x 1        
MD  AB và ME  AC. Chứng minh: năm điểm A, D, H, M và E cùng  x 1   1 2  k) K 
nằm trên một đường tròn.    :    (với x > 0, x  1)  x 1 x  x     1  x x 1
2.16 Cho ABC. Điểm I di động trên cạnh BC. Gọi D, E lần lượt là hình chiếu  a  2 a  2   1 
của I trên AB và AC. Lấy M đối xứng với A qua D, lấy N đối xứng với A l) L     1   (với a > 0, a  1)  a 1 a 2 a 1        a  qua E. Chứng minh:
a) I là tâm đường tròn đi qua ba điểm A, M, N. x  1 2 x 2  5 x m) M    (với x  0, x  4)
b) Đường tròn (I) nói trên đi qua một điểm cố định khác A. x  2 x  2 4  x 2 
2.17 Cho ABC nhọn có ba đỉnh thuộc đường tròn (O ; R). Gọi H là trực tâm x x  y y   x  y  n) N    xy  
(với x  0, y  0, x  y) 
của ABC. Vẽ đường kính AD. x  y   x y      
a) Tứ giác BHCD là hình gì ? Vì sao ? 2  a b  b a a a  b b   a  b 
b) Gọi I là trung điểm của BC. Chứng minh: AH = 2OI. o) O     : 
 (với a  0, b  0, a  b)  a b a b       a  b 
c) Gọi G là trọng tâm của ABC. Chứng minh: O, H, G thẳng hàng. 
d) So sánh diện tích của hai tam giác AHG và AOG. 2x  1 x   x x 1  p) P       x  (với x  0, x  1)  x x 1 x x 1   x 1         
2.18 Ba đường cao AD, BE, CF của ABC gặp nhau tại H. Gọi I, K, L lần lượt
là trung điểm của AB, BC, CA và M, N, P lần lượt là trung điểm của HA,  x  y x  y  x  xy q) Q     :
(với x > 0, y > 0, xy  1) HB, HC. Chứng minh:  1 xy 1  xy  1  xy  
a) Các tứ giác INPL và MLKN là các hình chữ nhật.    
b) 9 điểm D, E, F, L, I, K, M, N và P cùng nằm trên một đường tròn. r)    
(với x  0, y  0, x  y)     2 x x y y x y y x R : x y x  y x  y
(đường tròn Euler)    x 1 x 1  x x  2x  4 x  8 s) S      (với x > 0, x  4)  x 4 x 4 x 4     x   x x  2x  28 x  4 x  8 t) T    (với x  0, x  16 x  3 x  4 x 1 4  x
1.77 Cho 16  2x  x2  9  2x  x2  1 . Tính 2 2
A  16  2x  x  9  2x  x Gv: Trần Quốc Nghĩa Trang 30 Gv: Trần Quốc Nghĩa Trang 75 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1 3 3 a  b a  b
2.14 Cho ABC cân tại A, nội tiếp đường tròn (O). Đường cao AH cắt đường h) H  
(với a  0, b  0, a  b) tròn (O) ở D. a  b a  b
a) Chứng minh: AD là đường kính của đường tròn (O). 2 ( x  y)  4 xy x  y i) I  
(với x  0, y  0, x  y) b) Tính  ACD . x  y x  y
c) Cho BC = 24cm, AC = 20cm. Tính AH và bán kính của (O).  x  1 x 1   x 1  j) J     : 1   (với x > 0, x  1) 
2.15 Cho ABC có đường cao AH. Từ một điểm M bất kỳ trên cạnh BC, kẻ x 1 x 1   x 1        
MD  AB và ME  AC. Chứng minh: năm điểm A, D, H, M và E cùng  x 1   1 2  k) K 
nằm trên một đường tròn.    :    (với x > 0, x  1)  x 1 x  x     1  x x 1
2.16 Cho ABC. Điểm I di động trên cạnh BC. Gọi D, E lần lượt là hình chiếu  a  2 a  2   1 
của I trên AB và AC. Lấy M đối xứng với A qua D, lấy N đối xứng với A l) L     1   (với a > 0, a  1)  a 1 a 2 a 1        a  qua E. Chứng minh:
a) I là tâm đường tròn đi qua ba điểm A, M, N. x  1 2 x 2  5 x m) M    (với x  0, x  4)
b) Đường tròn (I) nói trên đi qua một điểm cố định khác A. x  2 x  2 4  x 2 
2.17 Cho ABC nhọn có ba đỉnh thuộc đường tròn (O ; R). Gọi H là trực tâm x x  y y   x  y  n) N    xy  
(với x  0, y  0, x  y) 
của ABC. Vẽ đường kính AD. x  y   x y      
a) Tứ giác BHCD là hình gì ? Vì sao ? 2  a b  b a a a  b b   a  b 
b) Gọi I là trung điểm của BC. Chứng minh: AH = 2OI. o) O     : 
 (với a  0, b  0, a  b)  a b a b       a  b 
c) Gọi G là trọng tâm của ABC. Chứng minh: O, H, G thẳng hàng. 
d) So sánh diện tích của hai tam giác AHG và AOG. 2x  1 x   x x 1  p) P       x  (với x  0, x  1)  x x 1 x x 1   x 1         
2.18 Ba đường cao AD, BE, CF của ABC gặp nhau tại H. Gọi I, K, L lần lượt
là trung điểm của AB, BC, CA và M, N, P lần lượt là trung điểm của HA,  x  y x  y  x  xy q) Q     :
(với x > 0, y > 0, xy  1) HB, HC. Chứng minh:  1 xy 1  xy  1  xy  
a) Các tứ giác INPL và MLKN là các hình chữ nhật.    
b) 9 điểm D, E, F, L, I, K, M, N và P cùng nằm trên một đường tròn. r)    
(với x  0, y  0, x  y)     2 x x y y x y y x R : x y x  y x  y
(đường tròn Euler)    x 1 x 1  x x  2x  4 x  8 s) S      (với x > 0, x  4)  x 4 x 4 x 4     x   x x  2x  28 x  4 x  8 t) T    (với x  0, x  16 x  3 x  4 x 1 4  x
1.77 Cho 16  2x  x2  9  2x  x2  1 . Tính 2 2
A  16  2x  x  9  2x  x Gv: Trần Quốc Nghĩa Trang 30 Gv: Trần Quốc Nghĩa Trang 75 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1 2.4 Chứng minh định lí sau:
1.78 Rút gọn các biểu thức sau:
a) Tâm của đường tròn ngoại tiếp  vuông là trung điểm của cạnh huyền. a a b a)  ab   với a > 0 và b > 0
b) Nếu một  có một cạnh là đường kính của đường tròn ngoại tiếp thì  b b a đó là  vuông. m 4m  m 8 x  4mx2 b)  với m > 0 và x > 1 2.5
Cho hình vuông ABCD, O là giao điểm của hai đường chéo, 1 2x  x2 81
OA  2 cm. Vẽ đường tròn tâm A bán kính 2cm. Hãy xác định vị trí của
1.79 Rút gọn rồi so sánh giá trị của biểu thức sau với 1:
năm điểm A, B, C, D, O so với đường tròn  1 1  a 1 M     : với a > 0 và a  1 2.6
Cho ABC nhọn. Vẽ (O) có đường kính BC, nó cắt các cạnh AB, AC  a  a a 1 a  2 a 1 theo thứ tự ở D và E.
1.80 Giải các phương trình sau:
a) Chứng minh: CD  AB và BE  AC. 4
b) Gọi K là giao điểm của BE và CD. Chứng minh: AK  BC. 1. a) 4x  20  3 5  x  9x  45  6 3 2.7
Cho tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi M, N, P, 15 x 1
Q lần lượt là trung điểm của AB, BC, CD và DA. C/m: bốn điểm M, N, P b) 2 x 5  25   6  x 1 2 9
và Q cùng nằm trên một đường tròn. 1 4x  20  9x  45  x  5 2.8
Cho ABC đều. Gọi M, N, P lần lượt là trung điểm của AB, BC, CA. c)  4 3
Chứng minh rằng bốn điểm B, C, P và M cùng nằm trên một đường tròn. d)
16x  16  9x  9  4x  4  16  x 1 . 2.9
Cho ABC đều có độ dài cạnh là a (cm). Tính bán kính của đường tròn 2 ngoại tiếp ABC. 2. a) 1  x  x  1 b) x2  4x  4  x  2 c) 2x2  7  2  x d) x2  4x  3  x  2
2.10 Cho (O ; 4cm) có hai đường kính AB và CD vuông góc với nhau. Dây
AM của (O) cắt bán kính OC tại I. Cho biết OI = 3cm. Tính AM và đường e) x2  4  2  x  0 f) x2  4x  4  2x  1 cao MH của AMB. g) 2 ( x  ) 4 (x  ) 1  x  1 h)
2x2  4x  1  x  2 .
2.11 Cho hình vuông ABCD cạnh a. 3. a) 2x  9  5  4x b) 2x  1  x  1
a) Chứng minh: bốn đỉnh A, B, C và D của hình vuông trên cùng nằm trên một đường tròn. c) x  3  x  3 d) x2  x  3  x
b) Xác định tâm và bán kính của đường tròn đó. e) x2  x 3  1  x  1 f) 2x2  3  4x  3
2.12 Cho ABC cân tại A, BC = 12cm, đường cao AH = 4cm. Tính bán kính g) x2  x  6  x  3 h) 9x2  4x  2x  3 .
của đường tròn ngoại tiếp ABC. 4. a) x  4 x  4  5
2.13 Cho ABC cân tại A, đường cao BE. Gọi D, F lần lượt là trung điểm của BC và AB. b)
x  2 x  1  x  2 x  1  2
a) Chứng minh: 4 điểm A, B, D và E cùng nằm trên một đường tròn. c)
x  2  4 x  2  x  7  6 x  2  1
b) Chứng minh: C không thuộc đường tròn trên. Gv: Trần Quốc Nghĩa Trang 74 Gv: Trần Quốc Nghĩa Trang 31 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1 2.4 Chứng minh định lí sau:
1.78 Rút gọn các biểu thức sau:
a) Tâm của đường tròn ngoại tiếp  vuông là trung điểm của cạnh huyền. a a b a)  ab   với a > 0 và b > 0
b) Nếu một  có một cạnh là đường kính của đường tròn ngoại tiếp thì  b b a đó là  vuông. m 4m  m 8 x  4mx2 b)  với m > 0 và x > 1 2.5
Cho hình vuông ABCD, O là giao điểm của hai đường chéo, 1 2x  x2 81
OA  2 cm. Vẽ đường tròn tâm A bán kính 2cm. Hãy xác định vị trí của
1.79 Rút gọn rồi so sánh giá trị của biểu thức sau với 1:
năm điểm A, B, C, D, O so với đường tròn  1 1  a 1 M     : với a > 0 và a  1 2.6
Cho ABC nhọn. Vẽ (O) có đường kính BC, nó cắt các cạnh AB, AC  a  a a 1 a  2 a 1 theo thứ tự ở D và E.
1.80 Giải các phương trình sau:
a) Chứng minh: CD  AB và BE  AC. 4
b) Gọi K là giao điểm của BE và CD. Chứng minh: AK  BC. 1. a) 4x  20  3 5  x  9x  45  6 3 2.7
Cho tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi M, N, P, 15 x 1
Q lần lượt là trung điểm của AB, BC, CD và DA. C/m: bốn điểm M, N, P b) 2 x 5  25   6  x 1 2 9
và Q cùng nằm trên một đường tròn. 1 4x  20  9x  45  x  5 2.8
Cho ABC đều. Gọi M, N, P lần lượt là trung điểm của AB, BC, CA. c)  4 3
Chứng minh rằng bốn điểm B, C, P và M cùng nằm trên một đường tròn. d)
16x  16  9x  9  4x  4  16  x 1 . 2.9
Cho ABC đều có độ dài cạnh là a (cm). Tính bán kính của đường tròn 2 ngoại tiếp ABC. 2. a) 1  x  x  1 b) x2  4x  4  x  2 c) 2x2  7  2  x d) x2  4x  3  x  2
2.10 Cho (O ; 4cm) có hai đường kính AB và CD vuông góc với nhau. Dây
AM của (O) cắt bán kính OC tại I. Cho biết OI = 3cm. Tính AM và đường e) x2  4  2  x  0 f) x2  4x  4  2x  1 cao MH của AMB. g) 2 ( x  ) 4 (x  ) 1  x  1 h)
2x2  4x  1  x  2 .
2.11 Cho hình vuông ABCD cạnh a. 3. a) 2x  9  5  4x b) 2x  1  x  1
a) Chứng minh: bốn đỉnh A, B, C và D của hình vuông trên cùng nằm trên một đường tròn. c) x  3  x  3 d) x2  x  3  x
b) Xác định tâm và bán kính của đường tròn đó. e) x2  x 3  1  x  1 f) 2x2  3  4x  3
2.12 Cho ABC cân tại A, BC = 12cm, đường cao AH = 4cm. Tính bán kính g) x2  x  6  x  3 h) 9x2  4x  2x  3 .
của đường tròn ngoại tiếp ABC. 4. a) x  4 x  4  5
2.13 Cho ABC cân tại A, đường cao BE. Gọi D, F lần lượt là trung điểm của BC và AB. b)
x  2 x  1  x  2 x  1  2
a) Chứng minh: 4 điểm A, B, D và E cùng nằm trên một đường tròn. c)
x  2  4 x  2  x  7  6 x  2  1
b) Chứng minh: C không thuộc đường tròn trên. Gv: Trần Quốc Nghĩa Trang 74 Gv: Trần Quốc Nghĩa Trang 31 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1 d)
x  2  3 2x  5  x  2  3 2x  5  2 2 . Chương 2 ĐƯỜNG TRÒN 5. a) x2  x 3  5  x2  x 3  7  b) 5 x2  x 5  28  x2  x 5  4
A - Sự xác định đường tròn. c) 2 2x 2  x 3  5  2x2  x 3  6 d) 2x2  x 3  9  2x2  x 3  33
Tính chất đối xứng của đường tròn
1.81 Chứng minh đẳng thức sau:  6 2x  1 2. a)  x    6x  : 6x  2  với x > 0
1. Tập hợp các điểm M cách đều điểm O cho trước một khoảng không đổi x 3  3  
bằng R là đường tròn tâm O bán kính R. Kí hiệu (O ; R) hoặc (O). 2  1 a a   1 a 
OM = R  M  (O ; R)oooo b)   a     1  với a > 0 và a  1 1 a   1 a     
2. a. Qua 3 điểm không thẳng hàng, ta vẽ được một và chỉ một đường tròn. a  b a2b4 c) 
 a với a + b > 0 và b  0
b. Đường tròn qua 3 đỉnh của một tam giác gọi là đường tròn ngoại b2 a2  2ab  b2
tiếp tam giác đó. Khi đó tam giác được gọi là nội tiếp đường tròn.
Tâm của đường tròn này là giao điểm của hai hay ba đường trung x 1 2 x 2  5 x
trực của tam giác đó.
1.82 Cho biểu thức: P    x  2 x  2 4  x
3. a. Tâm của đường tròn ngoại tiếp  vuông là trung điểm cạnh huyền.
a) Rút gọn P nếu x  0 và x  4.
b. Nếu một tam giác có một cạnh là đường kính của đường tròn ngoại b) Tìm x để P = 2.
tiếp thì tam giác đó là tam giác vuông.  1 1   a  1 a  2 
4. Đường tròn là hình có tâm đối xứng. Đó là tâm của đường tròn đó.
1.83 Cho biểu thức: Q   :       
5. Đường tròn có vô số trục đối xứng, đó là bất kì đường kính nào của  a  1 a   a  2 a  1  đường tròn.
a) Chứng tỏ rằng Q xác định với a > 0, a  4 và a  1.
b) Tìm giá trị của a để Q dương. x  2 x  1 x  1 2.1 Cho hình chữ nhật ABCD.
1.84 Cho biểu thức: Q    3 x  3 x  2 x  5 x  6
a) Chứng minh rằng bốn điểm A, B, C và D cùng thuộc một đường tròn.
a) Tìm điều kiện xác định và rút gọn Q.
b) Cho AB = 10cm và BC = 6cm. Tính bán kính của đường tròn trên.
b) Tìm các giá trị của x để Q <  1. 2.2
Cho hình thang cân ABCD. Chứng minh rằng bốn điểm A, B, C và D
c) Tìm các giá trị của x  Z sao cho 2Q  Z.
nằm trên một đường tròn.
1.85 Với 3 số a, b, c không âm. Chứng minh: 2.3
Trong mặt phẳng tọa độ Oxy, hãy xác định vị trí của mỗi điểm A(1 ; –1),
a  b  c  ab  bc  ca
B(2 ; 1) và C(– 3 ; 3 ) với đường tròn tâm O bán kính 2 (với O là gốc
Hãy mở rộng kết quả trên cho trường hợp 4 số, 5 số không âm. tọa độ). Gv: Trần Quốc Nghĩa Trang 32 Gv: Trần Quốc Nghĩa Trang 73 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1 d)
x  2  3 2x  5  x  2  3 2x  5  2 2 . Chương 2 ĐƯỜNG TRÒN 5. a) x2  x 3  5  x2  x 3  7  b) 5 x2  x 5  28  x2  x 5  4
A - Sự xác định đường tròn. c) 2 2x 2  x 3  5  2x2  x 3  6 d) 2x2  x 3  9  2x2  x 3  33
Tính chất đối xứng của đường tròn
1.81 Chứng minh đẳng thức sau:  6 2x  1 2. a)  x    6x  : 6x  2  với x > 0
1. Tập hợp các điểm M cách đều điểm O cho trước một khoảng không đổi x 3  3  
bằng R là đường tròn tâm O bán kính R. Kí hiệu (O ; R) hoặc (O). 2  1 a a   1 a 
OM = R  M  (O ; R)oooo b)   a     1  với a > 0 và a  1 1 a   1 a     
2. a. Qua 3 điểm không thẳng hàng, ta vẽ được một và chỉ một đường tròn. a  b a2b4 c) 
 a với a + b > 0 và b  0
b. Đường tròn qua 3 đỉnh của một tam giác gọi là đường tròn ngoại b2 a2  2ab  b2
tiếp tam giác đó. Khi đó tam giác được gọi là nội tiếp đường tròn.
Tâm của đường tròn này là giao điểm của hai hay ba đường trung x 1 2 x 2  5 x
trực của tam giác đó.
1.82 Cho biểu thức: P    x  2 x  2 4  x
3. a. Tâm của đường tròn ngoại tiếp  vuông là trung điểm cạnh huyền.
a) Rút gọn P nếu x  0 và x  4.
b. Nếu một tam giác có một cạnh là đường kính của đường tròn ngoại b) Tìm x để P = 2.
tiếp thì tam giác đó là tam giác vuông.  1 1   a  1 a  2 
4. Đường tròn là hình có tâm đối xứng. Đó là tâm của đường tròn đó.
1.83 Cho biểu thức: Q   :       
5. Đường tròn có vô số trục đối xứng, đó là bất kì đường kính nào của  a  1 a   a  2 a  1  đường tròn.
a) Chứng tỏ rằng Q xác định với a > 0, a  4 và a  1.
b) Tìm giá trị của a để Q dương. x  2 x  1 x  1 2.1 Cho hình chữ nhật ABCD.
1.84 Cho biểu thức: Q    3 x  3 x  2 x  5 x  6
a) Chứng minh rằng bốn điểm A, B, C và D cùng thuộc một đường tròn.
a) Tìm điều kiện xác định và rút gọn Q.
b) Cho AB = 10cm và BC = 6cm. Tính bán kính của đường tròn trên.
b) Tìm các giá trị của x để Q <  1. 2.2
Cho hình thang cân ABCD. Chứng minh rằng bốn điểm A, B, C và D
c) Tìm các giá trị của x  Z sao cho 2Q  Z.
nằm trên một đường tròn.
1.85 Với 3 số a, b, c không âm. Chứng minh: 2.3
Trong mặt phẳng tọa độ Oxy, hãy xác định vị trí của mỗi điểm A(1 ; –1),
a  b  c  ab  bc  ca
B(2 ; 1) và C(– 3 ; 3 ) với đường tròn tâm O bán kính 2 (với O là gốc
Hãy mở rộng kết quả trên cho trường hợp 4 số, 5 số không âm. tọa độ). Gv: Trần Quốc Nghĩa Trang 32 Gv: Trần Quốc Nghĩa Trang 73 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
1.88 Cho ABC đều, gọi O là trung điểm của cạnh BC,  0 xOy  60 có cạnh G - Căn bậc ba
Ox, Oy luôn cắt AB, AC tại M và N. Chứng minh :
a) OBM  NOC suy ra OB2 = BM . CN
1. Định nghĩa:
b) OBM  ONM suy ra MO, NO lần lượt là tia phân giác  BMN và
Căn bậc ba của một số a là số x sao cho x3 = a  CNM .
2. Tính chất: 1 3 3 c) BM . CN = BC2. a) a b a b 4 b) 33 3 ab a . b
1.89 Cho ABC cân tại A có H là trung điểm của BC. Gọi I là hình chiếu của 3 a a
c) Với b  0, ta có 3
H lên cạnh AC và O là trung điểm của HI. Chứng minh : 3 b b a) BIC  AOH b) AO  BI 1.86 Tính:
1.90 Cho ABC cân tại A có đường cao AH, BK. Chứng minh : a) 3 512 ; 3  729 ; 3 0 , 0 64 ; 3 2 , 0 16 ; 3  0 , 0 08 . 1 1 1   . b) 3  343 ; 3 0 , 0 27 ; 3 3 , 1 31 ; 3  5 , 0 12 ; 3 125 . 2 2 2 BK BC 4AH 1.87 So sánh: a) 5 và 3 123 b) 3 5 6 và 3 6 5 c) 3 2 3 và 3 23 d) 33 và 3 3 1333
Giải bài toán như thế nào? – Phần 4
1.88 Giải các phương trình sau: 3 - Giải bài toán: a) 3 x   5 , 1 b) 3 x  5  9 , 0
Thực hiện lời giải mà bạn đã đề ra.
1.89 Giải các bất phương trình sau và biểu diễn nghiệm trên trục số: 3 3
Bạn có nghĩ rằng các bước là đúng? a) x  2 b) x   5 , 1
Bạn có thể chứng minh nó đúng?
1.90 Chứng minh rằng với a, b kất kỳ thì: 3 3 3 3 3 3 4 - Khai thác bài toán: a) a  a b)  a   a c) 3 a b  a b
Bạn có nghĩ ra một hướng khác để giải bài toán? Lời giải có
ngắn hơn, đặc sắc hơn. Danh ngôn học tập
Bạn đã áp dụng cách giải đó cho bài toán nào chưa?
Trong cách học, phải lấy tự học làm cốt.
Bạn có thể áp dụng bài toán này để giải các bài toán khác đã biết? Hồ Chí Minh (Hết) Gv: Trần Quốc Nghĩa Trang 72 Gv: Trần Quốc Nghĩa Trang 33 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
1.88 Cho ABC đều, gọi O là trung điểm của cạnh BC,  0 xOy  60 có cạnh G - Căn bậc ba
Ox, Oy luôn cắt AB, AC tại M và N. Chứng minh :
a) OBM  NOC suy ra OB2 = BM . CN
1. Định nghĩa:
b) OBM  ONM suy ra MO, NO lần lượt là tia phân giác  BMN và
Căn bậc ba của một số a là số x sao cho x3 = a  CNM .
2. Tính chất: 1 3 3 c) BM . CN = BC2. a) a b a b 4 b) 33 3 ab a . b
1.89 Cho ABC cân tại A có H là trung điểm của BC. Gọi I là hình chiếu của 3 a a
c) Với b  0, ta có 3
H lên cạnh AC và O là trung điểm của HI. Chứng minh : 3 b b a) BIC  AOH b) AO  BI 1.86 Tính:
1.90 Cho ABC cân tại A có đường cao AH, BK. Chứng minh : a) 3 512 ; 3  729 ; 3 0 , 0 64 ; 3 2 , 0 16 ; 3  0 , 0 08 . 1 1 1   . b) 3  343 ; 3 0 , 0 27 ; 3 3 , 1 31 ; 3  5 , 0 12 ; 3 125 . 2 2 2 BK BC 4AH 1.87 So sánh: a) 5 và 3 123 b) 3 5 6 và 3 6 5 c) 3 2 3 và 3 23 d) 33 và 3 3 1333
Giải bài toán như thế nào? – Phần 4
1.88 Giải các phương trình sau: 3 - Giải bài toán: a) 3 x   5 , 1 b) 3 x  5  9 , 0
Thực hiện lời giải mà bạn đã đề ra.
1.89 Giải các bất phương trình sau và biểu diễn nghiệm trên trục số: 3 3
Bạn có nghĩ rằng các bước là đúng? a) x  2 b) x   5 , 1
Bạn có thể chứng minh nó đúng?
1.90 Chứng minh rằng với a, b kất kỳ thì: 3 3 3 3 3 3 4 - Khai thác bài toán: a) a  a b)  a   a c) 3 a b  a b
Bạn có nghĩ ra một hướng khác để giải bài toán? Lời giải có
ngắn hơn, đặc sắc hơn. Danh ngôn học tập
Bạn đã áp dụng cách giải đó cho bài toán nào chưa?
Trong cách học, phải lấy tự học làm cốt.
Bạn có thể áp dụng bài toán này để giải các bài toán khác đã biết? Hồ Chí Minh (Hết) Gv: Trần Quốc Nghĩa Trang 72 Gv: Trần Quốc Nghĩa Trang 33 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
1.82 Cho ABC vuông tại A, đường cao AH. Kẻ HE  AB tại E và HF  AC
H - Ôn tập chương 1 tại F. Chứng minh: 2 AB HB 3 AB BE
1.91 Tính giá trị của các biểu thức sau bằng cách biến đổi, rút gọn thích hợp: a)  và  . b) BC = AB.sinC + AC.cosB. 2 AC HC 3 AC CF 25 16 196 1 14 34 a)   b) 3  2  2 c) AH3=BC.BE.CF=BC.AE.AF. d) AH2 = AB.AC.sinB.cosB. 81 49 9 16 25 81 640  34,3 e) AH = BC.sinB.cosB.
f) BE CH  CF BH  AH BC c) d) 2 2 21,6. 810. 11  5 567
g) Cho AH = 4 cm; BC = 10 cm. Tính SBEFC.
1.92 Rút gọn các biểu thức sau:
1.83 Cho ABC nhọn (AB > AC) có đường cao AH và đường trung tuyến a)  8  3 2  10  . 2  3 , 0 4  AM. Chứng minh:   cot B  cot C HAC HC b) 2 2 0, 2 ( 1  0) .3  2 ( 3  5) a) tan MAH  b) tan  2 2 AH  AC  1 1 3 1 4 4  8 1 c)     :
1.84 Cho ABC cân tại A, đường cao AH. Biết AB = 10cm, AH = 8cm.  2 2 2 3 5 5  15 8  
a) Tính BC và diện tích ABC.
b) Gọi I là trung điểm của AC. Qua A vẽ đường thẳng song song với BC d) 2 2 4 2 ( 2  ) 3  ( 2  ) 3  5 ( ) 1
cắt đường thẳng HI tại K. Chứng minh: AKCH là hình chữ nhật. e) 2 (  3)2  2 4  2 3
c) Đường thẳng BI cắt AH tại G và cắt CK tại M. Cmrằng : i. BGH  BMC ii. BG . BC = BM . BH f) 15  6 6  33  12 6
d) Chứng minh : BG2 + AH2 = AC2 + GH2.
g) 5 200  3 450  2 50 : 10
1.85 Cho hình thang ABCD (   0
A  D  90 ). Gọi M là trung điểm của AD. Kẻ h) 6  2 2  12  18  128
MK  BC tại K. Biết AB = 9cm, BC = 25cm, CD = 16cm. a) Tính AD, MB, MC. 2 3  3  13  48
b) Chứng minh : MBC vuông tại M. i) 6  2
c) Tính MK và diện tích MKC.  1 2 
1.86 Các đường cao của ABC có ba góc nhọn cắt nhau tại H. Trên các đoạn j)    1 :  2  2 1  10  2 7  2 10   
HB, HC lấy điểm M và N sao cho   0 AMC  ANB  90 . Chứng minh : AM = AN. 2 3  2 k) 5( 6  ) 1 :
1.87 Cho tam giác nhọn ABC. Chứng minh: 2 3  2
a) cot A.cot B  cot B.cot C  cot C.cot A  1 2 10  30  2 2  6 2
b) t anA  tan B  tan C  t anA.tan B.tan C l) : 2 10  2 2 3  1 1 c) S  AB.AC.sin A ABC 2 Gv: Trần Quốc Nghĩa Trang 34 Gv: Trần Quốc Nghĩa Trang 71 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
1.82 Cho ABC vuông tại A, đường cao AH. Kẻ HE  AB tại E và HF  AC
H - Ôn tập chương 1 tại F. Chứng minh: 2 AB HB 3 AB BE
1.91 Tính giá trị của các biểu thức sau bằng cách biến đổi, rút gọn thích hợp: a)  và  . b) BC = AB.sinC + AC.cosB. 2 AC HC 3 AC CF 25 16 196 1 14 34 a)   b) 3  2  2 c) AH3=BC.BE.CF=BC.AE.AF. d) AH2 = AB.AC.sinB.cosB. 81 49 9 16 25 81 640  34,3 e) AH = BC.sinB.cosB.
f) BE CH  CF BH  AH BC c) d) 2 2 21,6. 810. 11  5 567
g) Cho AH = 4 cm; BC = 10 cm. Tính SBEFC.
1.92 Rút gọn các biểu thức sau:
1.83 Cho ABC nhọn (AB > AC) có đường cao AH và đường trung tuyến a)  8  3 2  10  . 2  3 , 0 4  AM. Chứng minh:   cot B  cot C HAC HC b) 2 2 0, 2 ( 1  0) .3  2 ( 3  5) a) tan MAH  b) tan  2 2 AH  AC  1 1 3 1 4 4  8 1 c)     :
1.84 Cho ABC cân tại A, đường cao AH. Biết AB = 10cm, AH = 8cm.  2 2 2 3 5 5  15 8  
a) Tính BC và diện tích ABC.
b) Gọi I là trung điểm của AC. Qua A vẽ đường thẳng song song với BC d) 2 2 4 2 ( 2  ) 3  ( 2  ) 3  5 ( ) 1
cắt đường thẳng HI tại K. Chứng minh: AKCH là hình chữ nhật. e) 2 (  3)2  2 4  2 3
c) Đường thẳng BI cắt AH tại G và cắt CK tại M. Cmrằng : i. BGH  BMC ii. BG . BC = BM . BH f) 15  6 6  33  12 6
d) Chứng minh : BG2 + AH2 = AC2 + GH2.
g) 5 200  3 450  2 50 : 10
1.85 Cho hình thang ABCD (   0
A  D  90 ). Gọi M là trung điểm của AD. Kẻ h) 6  2 2  12  18  128
MK  BC tại K. Biết AB = 9cm, BC = 25cm, CD = 16cm. a) Tính AD, MB, MC. 2 3  3  13  48
b) Chứng minh : MBC vuông tại M. i) 6  2
c) Tính MK và diện tích MKC.  1 2 
1.86 Các đường cao của ABC có ba góc nhọn cắt nhau tại H. Trên các đoạn j)    1 :  2  2 1  10  2 7  2 10   
HB, HC lấy điểm M và N sao cho   0 AMC  ANB  90 . Chứng minh : AM = AN. 2 3  2 k) 5( 6  ) 1 :
1.87 Cho tam giác nhọn ABC. Chứng minh: 2 3  2
a) cot A.cot B  cot B.cot C  cot C.cot A  1 2 10  30  2 2  6 2
b) t anA  tan B  tan C  t anA.tan B.tan C l) : 2 10  2 2 3  1 1 c) S  AB.AC.sin A ABC 2 Gv: Trần Quốc Nghĩa Trang 34 Gv: Trần Quốc Nghĩa Trang 71 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1 1.77 Cho ABC có  0
A  90 , AB = 15cm, AC = 20cm, đường cao AH. 5
(  2 6)(49  20 6)  5  2 6
a) Tính độ dài BC, AH, BH. m) 9 3  11 2
b) Gọi D là điểm đối xứng của B qua H. Vẽ hình bình hành ADCE.
Chứng minh: ABCE là hình thang cân. n)
8  2 10  2 5  8  2 10  2 5
c) Tính diện tích hình thang cân ABCE. o) (4  15)( 10  6) 4  15
1.78 Cho ABC có đường cao AH. Từ H vẽ HM  AB tại M, HN  AC tại N.
Biết HA = 15cm, HC = 36cm, BC = 56cm. p) ( 5  ) 3 ( 10  2) 3  5 a) Tính AB, AC.
1.93 Phân tích thành nhân tử (với x, y, a, b dương và a > b)
b) Chứng minh: AB.AM = AC.AN và ABC  ANM. a) 3 + x + 9 – x b) xy + y x + x + 1
c) Chứng minh: AB.AM = AC.BN 2
d) Chứng minh: ABN  ACM. c) xa  by  bx  ay d) 2 a  b  a  b
1.79 Cho ABC vuông tại A, đường cao AH.
1.94 Rút gọn rồi tính giá trị của các biểu thức sau: a) Biết 3AB = 2AC. Tính  sin ACB ,  tan ACB . a) 2
 9a  9  12a  4a với a =  9
b) Vẽ đường phân giác CK của AHC. Biết AH = 2,4 cm; BH = 1,8 cm. m 3 b) 1 
m 2  4m  4 với m < 0 Tính CH, AC, CK,  cosHCK . m  2
c) Lấy M  BC. Kẻ ME  AB tại E và MF  AC tại F. Chứng minh c) 1  10a  2 a 5 2  a 4 với a = 2 MB.MC = EA.EB + FE.FC d) 4x 
9x2  6x  1 với x =  3
1.80 Cho ABC vuông tại A, đường cao AH. Đường thẳng vuông góc với AC
1.95 Rút gọn các biểu thức sau: tại C cắt tia AH tại D.  x 2 1   10  x 
a) Chứng minh: BC.CH = AD.AH = AB.CD. a) A =     : x  2     x 4 2 x x 2        x  2  b) Chứng minh: 2  S  S .tan ACB A  BC C  AD   
c) Kẻ HE  AB tại E. Chứng minh BE = BC.cos3B. x x y y 2 y b) B =   xy  : x  y  2   AB .AC x  y x  y d) Chứng minh: EH  .   2 BC  x   x  3 2  x x  2  c) C = 1   :    
e) Gọi F là hình chiếu của H lên AC. C/m: 2  S  S .(1 tan ACE)     BEFC ABC 1  x x  2 3  x x  5 x  6     AB 3 f) Biết 
và AH = 12 cm. Tính AB, AC, BH, KH. 2 2 a  x a  x AC 4 d) D =  2 a 
 2 a với a > 0, x > 0. x x
1.81 Cho tam giác nhọn ABC có ba đường cao AD, BE, CF cắt nhau tại H. Chứng minh:
1.96 Giải các phương trình sau: a) EF = AH.sinA 5 1 3 x  1 8 a) 15x  1 x 5  11  15x b)  S S S 3 3 7 x  5 15 b) HBC HAC HAB   t anA t anB t anC c) 2 ( x  ) 1 2  3 d) 2  x  8  4x  3 c) 2 2 2 S
 (1 cos A  cos B  cos C).S DEF ABC Gv: Trần Quốc Nghĩa Trang 70 Gv: Trần Quốc Nghĩa Trang 35 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1 1.77 Cho ABC có  0
A  90 , AB = 15cm, AC = 20cm, đường cao AH. 5
(  2 6)(49  20 6)  5  2 6
a) Tính độ dài BC, AH, BH. m) 9 3  11 2
b) Gọi D là điểm đối xứng của B qua H. Vẽ hình bình hành ADCE.
Chứng minh: ABCE là hình thang cân. n)
8  2 10  2 5  8  2 10  2 5
c) Tính diện tích hình thang cân ABCE. o) (4  15)( 10  6) 4  15
1.78 Cho ABC có đường cao AH. Từ H vẽ HM  AB tại M, HN  AC tại N.
Biết HA = 15cm, HC = 36cm, BC = 56cm. p) ( 5  ) 3 ( 10  2) 3  5 a) Tính AB, AC.
1.93 Phân tích thành nhân tử (với x, y, a, b dương và a > b)
b) Chứng minh: AB.AM = AC.AN và ABC  ANM. a) 3 + x + 9 – x b) xy + y x + x + 1
c) Chứng minh: AB.AM = AC.BN 2
d) Chứng minh: ABN  ACM. c) xa  by  bx  ay d) 2 a  b  a  b
1.79 Cho ABC vuông tại A, đường cao AH.
1.94 Rút gọn rồi tính giá trị của các biểu thức sau: a) Biết 3AB = 2AC. Tính  sin ACB ,  tan ACB . a) 2
 9a  9  12a  4a với a =  9
b) Vẽ đường phân giác CK của AHC. Biết AH = 2,4 cm; BH = 1,8 cm. m 3 b) 1 
m 2  4m  4 với m < 0 Tính CH, AC, CK,  cosHCK . m  2
c) Lấy M  BC. Kẻ ME  AB tại E và MF  AC tại F. Chứng minh c) 1  10a  2 a 5 2  a 4 với a = 2 MB.MC = EA.EB + FE.FC d) 4x 
9x2  6x  1 với x =  3
1.80 Cho ABC vuông tại A, đường cao AH. Đường thẳng vuông góc với AC
1.95 Rút gọn các biểu thức sau: tại C cắt tia AH tại D.  x 2 1   10  x 
a) Chứng minh: BC.CH = AD.AH = AB.CD. a) A =     : x  2     x 4 2 x x 2        x  2  b) Chứng minh: 2  S  S .tan ACB A  BC C  AD   
c) Kẻ HE  AB tại E. Chứng minh BE = BC.cos3B. x x y y 2 y b) B =   xy  : x  y  2   AB .AC x  y x  y d) Chứng minh: EH  .   2 BC  x   x  3 2  x x  2  c) C = 1   :    
e) Gọi F là hình chiếu của H lên AC. C/m: 2  S  S .(1 tan ACE)     BEFC ABC 1  x x  2 3  x x  5 x  6     AB 3 f) Biết 
và AH = 12 cm. Tính AB, AC, BH, KH. 2 2 a  x a  x AC 4 d) D =  2 a 
 2 a với a > 0, x > 0. x x
1.81 Cho tam giác nhọn ABC có ba đường cao AD, BE, CF cắt nhau tại H. Chứng minh:
1.96 Giải các phương trình sau: a) EF = AH.sinA 5 1 3 x  1 8 a) 15x  1 x 5  11  15x b)  S S S 3 3 7 x  5 15 b) HBC HAC HAB   t anA t anB t anC c) 2 ( x  ) 1 2  3 d) 2  x  8  4x  3 c) 2 2 2 S
 (1 cos A  cos B  cos C).S DEF ABC Gv: Trần Quốc Nghĩa Trang 70 Gv: Trần Quốc Nghĩa Trang 35 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
1.97 Chứng minh các đẳng thức sau:
E - Ôn tập chương 1  2 3  6 216  1 1. a)      1  ,5  8 2 3   6  
1.71 Cho ABD có AB = 15cm, AD = 20cm, BD = 25cm. Vẽ AM  BD.  14  7 15  5  1
a) Chứng minh : ABD vuông. Tính AM, BM, MD. b)    :  2   1 2 1 3    7  5  
b) Kẻ tia Bx // AD, vẽ AM  BD cắt Bx tại C. C/m : AB2 = AD.BC
c) Kẻ CE  AD cắt BD tại I. Chứng minh : BM2 = MI . MD. c) 2  3  2  3  6
d) Chứng minh : SAMB = SMCD. 4 4 d)   8 2
1.72 Cho ABC vuông tại A, đường cao AH. Kẻ HD  AB, HE  AC, 2 (2  5) (2  5)
AK  DE. Gọi I là giao điểm của AH và DE, biết AI2 = AD . AE.  3 2 3   3 2 3  Chứng minh : AI2 = DE . AK. e)   6  2   4     6  2   4     2  2 3 2   2 3 2     
1.73 Cho ABC, một đường thẳng song song BC cắt AB tại D, cắt AC tại E a b  b a 1
thỏa điều kiện DC2 = BC . DE. 2. a) :
 a  b (với a, b > 0 và a  0) ab a  b
a) Chứng minh : DEC  CDB. 
b) Chứng minh : AD2 = AC . AE và AC2 = AB . AD a  a   a  a  b) 1    1 
  1  a (với a > 0 và a  1)  a 1   a 1       
1.74 Cho ABC có 3 góc nhọn. Các đường cao AD, BE, CF cắt nhau tại H. Chứng minh : a  b a  b 2b 2 b c)   
(với a, b > 0 và a  b a) AF.AB = AH.AD = AE.AC b) DH.DA = DB.DC 2 a  2 b 2 a  2 b b  a a  b c) BF.BA = BH. BE = BD.BC d) HB.HE = HC.HF = HA.HD  a  a   a  a  d) 1    1 
  1  a (với a, b > 0 và a  b) e) BH.BE + CH.CF = BC2 f) DB.DC = DH.DA  a 1   a 1       
1.75 Cho ABC. Gọi M là trung điểm của BC, N là trung điểm của AC. Các x 1
đường trung trực của cạnh BC và AC cắt nhau tại O. Gọi H là trực tâm và
1.98 Tìm x nguyên để
nhận giá trị nguyên.
G là trọng tâm của ABC. Chứng minh: x  3 a) AHB  MON. 1.99 a) Chứng tỏ: 2
x  4 x  4  ( x  4  2) b) AHG  MOG.
b) Tìm điều kiện xác định và rút gọn:
c) Ba điểm H, G, O thẳng hàng. (đường thẳng Euler)
A  x  4 x  4  x  4 x  4
1.76 Cho ABC vuông tại A, đường cao AH. Biết BC = 5cm;
BH = 1,8cm. Gọi M là trung điểm của BC, đường trung trực của BC cắt
1.100 Cho các biểu thức:
A  x  x  1 và B  x  4  x  1 AC tại D.
a) Tìm điều kiện xác định của A và B. a) Tính AB, AH.
b) Chứng tỏ A  1 và B  5
b) Tính tỉ số diện tích của DMC và ABC. c) Tìm x để A = 1, B = 2. 1
1.101 Tìm giá trị lớn nhất của biểu thức: c) Chứng minh : AC . DC = BC2. 2
d) Tính diện tích tứ giác ADMB. Gv: Trần Quốc Nghĩa Trang 36 Gv: Trần Quốc Nghĩa Trang 69 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
1.97 Chứng minh các đẳng thức sau:
E - Ôn tập chương 1  2 3  6 216  1 1. a)      1  ,5  8 2 3   6  
1.71 Cho ABD có AB = 15cm, AD = 20cm, BD = 25cm. Vẽ AM  BD.  14  7 15  5  1
a) Chứng minh : ABD vuông. Tính AM, BM, MD. b)    :  2   1 2 1 3    7  5  
b) Kẻ tia Bx // AD, vẽ AM  BD cắt Bx tại C. C/m : AB2 = AD.BC
c) Kẻ CE  AD cắt BD tại I. Chứng minh : BM2 = MI . MD. c) 2  3  2  3  6
d) Chứng minh : SAMB = SMCD. 4 4 d)   8 2
1.72 Cho ABC vuông tại A, đường cao AH. Kẻ HD  AB, HE  AC, 2 (2  5) (2  5)
AK  DE. Gọi I là giao điểm của AH và DE, biết AI2 = AD . AE.  3 2 3   3 2 3  Chứng minh : AI2 = DE . AK. e)   6  2   4     6  2   4     2  2 3 2   2 3 2     
1.73 Cho ABC, một đường thẳng song song BC cắt AB tại D, cắt AC tại E a b  b a 1
thỏa điều kiện DC2 = BC . DE. 2. a) :
 a  b (với a, b > 0 và a  0) ab a  b
a) Chứng minh : DEC  CDB. 
b) Chứng minh : AD2 = AC . AE và AC2 = AB . AD a  a   a  a  b) 1    1 
  1  a (với a > 0 và a  1)  a 1   a 1       
1.74 Cho ABC có 3 góc nhọn. Các đường cao AD, BE, CF cắt nhau tại H. Chứng minh : a  b a  b 2b 2 b c)   
(với a, b > 0 và a  b a) AF.AB = AH.AD = AE.AC b) DH.DA = DB.DC 2 a  2 b 2 a  2 b b  a a  b c) BF.BA = BH. BE = BD.BC d) HB.HE = HC.HF = HA.HD  a  a   a  a  d) 1    1 
  1  a (với a, b > 0 và a  b) e) BH.BE + CH.CF = BC2 f) DB.DC = DH.DA  a 1   a 1       
1.75 Cho ABC. Gọi M là trung điểm của BC, N là trung điểm của AC. Các x 1
đường trung trực của cạnh BC và AC cắt nhau tại O. Gọi H là trực tâm và
1.98 Tìm x nguyên để
nhận giá trị nguyên.
G là trọng tâm của ABC. Chứng minh: x  3 a) AHB  MON. 1.99 a) Chứng tỏ: 2
x  4 x  4  ( x  4  2) b) AHG  MOG.
b) Tìm điều kiện xác định và rút gọn:
c) Ba điểm H, G, O thẳng hàng. (đường thẳng Euler)
A  x  4 x  4  x  4 x  4
1.76 Cho ABC vuông tại A, đường cao AH. Biết BC = 5cm;
BH = 1,8cm. Gọi M là trung điểm của BC, đường trung trực của BC cắt
1.100 Cho các biểu thức:
A  x  x  1 và B  x  4  x  1 AC tại D.
a) Tìm điều kiện xác định của A và B. a) Tính AB, AH.
b) Chứng tỏ A  1 và B  5
b) Tính tỉ số diện tích của DMC và ABC. c) Tìm x để A = 1, B = 2. 1
1.101 Tìm giá trị lớn nhất của biểu thức: c) Chứng minh : AC . DC = BC2. 2
d) Tính diện tích tứ giác ADMB. Gv: Trần Quốc Nghĩa Trang 36 Gv: Trần Quốc Nghĩa Trang 69 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
1.67 Cho ABC vuông tại B, dựng tam giác ACD (B và D nằm khắc phía đối 1 a) A = b) B = 4x  x 2  21 với AC). Biết  0 ACB  54 ,  0
ACD  74 , AC = 8cm, AD = 9,6 cm. Hãy x  x  1 tính: AB và  ADC . c) C = 1   9x 2  6x d) D = x  2  4  x
1.68 Cho ABC vuông ở A, đường cao AH. Biết HB = 2cm, HC = 64cm. Tính
1.102 Tìm giá trị nhỏ nhất của biểu thức:  2 2 B ,  C . a) A = 4x  4x  2 b) B = 2x  4x  5 x  3
1.69 Cho ABC có BC = 12cm,  0 B  60 ,  0 C  40 . c) P = d) Q = x – 2 x  2 . x  1  2
a) Tính chiều cao CH và AC. b) Tính SABC. 4x2  4x  1
1.70 Một con thuyền với vận tốc thực 2km/h vượt qua một khúc sông nước
1.103 Cho biểu thức: A 
. Chứng tỏ A = 0,5 với x  0,5.
chảy mạnh mất 5 phút. Biết rằng đường đi của con thuyền tạo với bờ một 4x  2
góc 700. Từ đó đã có thể tính được chiều rộng của khúc sông ? Nếu có thể a  a  b
hãy tính chính xác đến mét. 1.104 Cho Q   1   : với a > b > 0 2 2  2 2  2 2 a  b  a  b  a  a  b
Giải bài toán như thế nào? – Phần 3 a) Rút gọn Q
2 - Tìm tòi lời giải bài toán:
b) Tìm giá trị của Q khi a = 3b.
Bạn đã gặp bài toán nào tương tự thế này chưa? Hay ở một dạng hơi ( a  b)2  4 ab a b  b a khác?
1.105 Cho biểu thức: A   a  b ab
Bạn có biết một định lý, một bài toán liên quan đến bài toán này
a) Tìm điều kiện để A có nghĩa. không?
b) Khi A có nghĩa, chứng tỏ giá trị A không phụ thuộc vào a.
Hãy xét kỹ cái chưa biết, và thử nhớ xem có bài toán nào có cùng cái chưa biết không?
1.106 Cho biểu thức:
Đây là bài toán mà bạn đã có lần giải nó rồi, bạn có thể áp dụng   2x  1 x  3  1  x
được gì ở nó? Phương pháp? Kết quả? Hay phải đưa thêm yếu tố phụ Q        x 
với x  0 và x  1 3 
vào mới áp dụng được?    x  1 x  x  1  1  x 
Hãy xét kỹ các khái niệm có trong bài toán và nếu cần hãy quay về a) Rút gọn Q. các định nghĩa.
b) Tìm giá trị của x để Q = 3.
Nếu bạn chưa giải được bài toán này, hãy thử giải một bài toán phụ
1.107 Cho biểu thức:
dễ hơn có liên quan, một trường hợp riêng, tương tự, tổng quát hơn?
Hãy giữ lại một phần giả thiết khi đó ẩn được xác định đến chừng  x x  9   3 x  1 1  C     :   
mực nào? Từ các điều đó bạn có thể rút ra được điều gì có ích cho   
với x  0 và x  9. 3  x 9  x x  3 x x
việc giải bài toán? Với giả thiết nào thì bạn có thể giải được bài toán     này? a) Rút gọn C
b) Tìm giá trị của x để C <  1.
Bạn đã tận dụng hết giả thiết của bài toán chưa? 2
(Xem tiếp ở trang 72) 
1.108 Cho biểu thức: A  6x  x 5 y  y .
a) Phân tích biểu thức A thành nhân tử. Gv: Trần Quốc Nghĩa Trang 68 Gv: Trần Quốc Nghĩa Trang 37 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
1.67 Cho ABC vuông tại B, dựng tam giác ACD (B và D nằm khắc phía đối 1 a) A = b) B = 4x  x 2  21 với AC). Biết  0 ACB  54 ,  0
ACD  74 , AC = 8cm, AD = 9,6 cm. Hãy x  x  1 tính: AB và  ADC . c) C = 1   9x 2  6x d) D = x  2  4  x
1.68 Cho ABC vuông ở A, đường cao AH. Biết HB = 2cm, HC = 64cm. Tính
1.102 Tìm giá trị nhỏ nhất của biểu thức:  2 2 B ,  C . a) A = 4x  4x  2 b) B = 2x  4x  5 x  3
1.69 Cho ABC có BC = 12cm,  0 B  60 ,  0 C  40 . c) P = d) Q = x – 2 x  2 . x  1  2
a) Tính chiều cao CH và AC. b) Tính SABC. 4x2  4x  1
1.70 Một con thuyền với vận tốc thực 2km/h vượt qua một khúc sông nước
1.103 Cho biểu thức: A 
. Chứng tỏ A = 0,5 với x  0,5.
chảy mạnh mất 5 phút. Biết rằng đường đi của con thuyền tạo với bờ một 4x  2
góc 700. Từ đó đã có thể tính được chiều rộng của khúc sông ? Nếu có thể a  a  b
hãy tính chính xác đến mét. 1.104 Cho Q   1   : với a > b > 0 2 2  2 2  2 2 a  b  a  b  a  a  b
Giải bài toán như thế nào? – Phần 3 a) Rút gọn Q
2 - Tìm tòi lời giải bài toán:
b) Tìm giá trị của Q khi a = 3b.
Bạn đã gặp bài toán nào tương tự thế này chưa? Hay ở một dạng hơi ( a  b)2  4 ab a b  b a khác?
1.105 Cho biểu thức: A   a  b ab
Bạn có biết một định lý, một bài toán liên quan đến bài toán này
a) Tìm điều kiện để A có nghĩa. không?
b) Khi A có nghĩa, chứng tỏ giá trị A không phụ thuộc vào a.
Hãy xét kỹ cái chưa biết, và thử nhớ xem có bài toán nào có cùng cái chưa biết không?
1.106 Cho biểu thức:
Đây là bài toán mà bạn đã có lần giải nó rồi, bạn có thể áp dụng   2x  1 x  3  1  x
được gì ở nó? Phương pháp? Kết quả? Hay phải đưa thêm yếu tố phụ Q        x 
với x  0 và x  1 3 
vào mới áp dụng được?    x  1 x  x  1  1  x 
Hãy xét kỹ các khái niệm có trong bài toán và nếu cần hãy quay về a) Rút gọn Q. các định nghĩa.
b) Tìm giá trị của x để Q = 3.
Nếu bạn chưa giải được bài toán này, hãy thử giải một bài toán phụ
1.107 Cho biểu thức:
dễ hơn có liên quan, một trường hợp riêng, tương tự, tổng quát hơn?
Hãy giữ lại một phần giả thiết khi đó ẩn được xác định đến chừng  x x  9   3 x  1 1  C     :   
mực nào? Từ các điều đó bạn có thể rút ra được điều gì có ích cho   
với x  0 và x  9. 3  x 9  x x  3 x x
việc giải bài toán? Với giả thiết nào thì bạn có thể giải được bài toán     này? a) Rút gọn C
b) Tìm giá trị của x để C <  1.
Bạn đã tận dụng hết giả thiết của bài toán chưa? 2
(Xem tiếp ở trang 72) 
1.108 Cho biểu thức: A  6x  x 5 y  y .
a) Phân tích biểu thức A thành nhân tử. Gv: Trần Quốc Nghĩa Trang 68 Gv: Trần Quốc Nghĩa Trang 37 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1 2 b
b) Tính giá trị của A khi x   , y  . 3 4  7
D - Hệ thức giữa các cạnh và các góc x  3
1.109 Cho biểu thức: B  . x  1  2
trong một tam giác vuông
a) Tìm điều kiện xác định của B. b) Rút gọn B.
1. Các hệ thức:
c) Tính giá trị của B khi x = 10 – 56 A
d) Tìm giá trị nhỏ nhất của B. 1) b = a.sinB = a.cosC 6 2) c = a.sinC = a.cosB  x  x c b
1.110 Cho biểu thức: C  . 3) b = c.tanB = c.cotC x  3 4) c = b.tanC =b.cotB
a) Tìm điều kiện xác định của C. B a C b) Rút gọn B.
c) Tìm giá trị lớn nhất của C.
2. Giải tam giác vuông:
Giải tam giác vuông là tìm tất cả các yếu tố còn lại của một tam giác 1 1 x3  x
vuông khi biết trước hai yếu tố (trong đó có ít nhất một yếu tố về cạnh và
1.111 Cho biểu thức: P    .
không kể góc vuông). x  1  x x 1  x x  1
a) Tìm điều kiện xác định của P.
1.61 Giải tam giác vuông ABC biết rằng  = 900 và : b) Rút gọn P. 53 a) b = 10 cm,  0 C  30 ; b) c = 10 cm,  0 C  45 ;
c) Tính giá trị của P khi x  9  2 7 c) a = 20 cm,  0 B  35 ; d) c = 21 cm, b = 18 cm;
d) Giải phương trình : P = 16.
1.62 Cho ABC nhọn có đường cao AH và đường trung tuyến AM. Biết  x   1 2 x   0
B  57 , AB = 9 cm, AC = 12 cm. Giải tam giác ABC và tính AM.
1.112 Cho biểu thức: Q  1   :        .
x  1  x 1 x x  x  x 1
1.63 Một cây cột đèn cao 7m có bóng trên mặt đất dài 4m. Hãy tính góc của tia
a) Tìm điều kiện xác định của Q.
sáng mặt trời tạo với mặt đất. b) Rút gọn Q.
c) Tính giá trị của Q khi x = 4 + 2 3
1.64 Cho ABC có đường cao AH. Biết AB = 25 cm,  0 B  70 ,  0 C  50 . Tính
d) Giải bất phương trình : Q > 1.
độ dài AH và BC (làm tròn đến chữ số thập phân thứ hai) a2  a 2a  a
1.65 Một khúc sông rộng khoảng 250m. Một chiếc đò chèo qua sông bị dòng
1.113 Cho biểu thức: A    1.
nước đẩy xiên nên phải chèo khoảng 320m mới sang đươực bờ bên kia. a  a  1 a
Hỏi dòng nước đã đẩy chiếc đò lệch đi một góc bằng bao nhiêu ? a) Rút gọn A.
b) Biết a > 0, hãy so sánh A vớiA
1.66 Cho ABC, trong đó AB = 11 cm,  0 ABC  38 ,  0 ACB  30 . Gọi điểm N c) Tìm a để A = 2
là chân của đường vuông góc kẻ từ A đến cạnh BC. Hãy tính: AN và AC.
d) Tìm giá trị nhỏ nhất của A. Gv: Trần Quốc Nghĩa Trang 38 Gv: Trần Quốc Nghĩa Trang 67 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1 2 b
b) Tính giá trị của A khi x   , y  . 3 4  7
D - Hệ thức giữa các cạnh và các góc x  3
1.109 Cho biểu thức: B  . x  1  2
trong một tam giác vuông
a) Tìm điều kiện xác định của B. b) Rút gọn B.
1. Các hệ thức:
c) Tính giá trị của B khi x = 10 – 56 A
d) Tìm giá trị nhỏ nhất của B. 1) b = a.sinB = a.cosC 6 2) c = a.sinC = a.cosB  x  x c b
1.110 Cho biểu thức: C  . 3) b = c.tanB = c.cotC x  3 4) c = b.tanC =b.cotB
a) Tìm điều kiện xác định của C. B a C b) Rút gọn B.
c) Tìm giá trị lớn nhất của C.
2. Giải tam giác vuông:
Giải tam giác vuông là tìm tất cả các yếu tố còn lại của một tam giác 1 1 x3  x
vuông khi biết trước hai yếu tố (trong đó có ít nhất một yếu tố về cạnh và
1.111 Cho biểu thức: P    .
không kể góc vuông). x  1  x x 1  x x  1
a) Tìm điều kiện xác định của P.
1.61 Giải tam giác vuông ABC biết rằng  = 900 và : b) Rút gọn P. 53 a) b = 10 cm,  0 C  30 ; b) c = 10 cm,  0 C  45 ;
c) Tính giá trị của P khi x  9  2 7 c) a = 20 cm,  0 B  35 ; d) c = 21 cm, b = 18 cm;
d) Giải phương trình : P = 16.
1.62 Cho ABC nhọn có đường cao AH và đường trung tuyến AM. Biết  x   1 2 x   0
B  57 , AB = 9 cm, AC = 12 cm. Giải tam giác ABC và tính AM.
1.112 Cho biểu thức: Q  1   :        .
x  1  x 1 x x  x  x 1
1.63 Một cây cột đèn cao 7m có bóng trên mặt đất dài 4m. Hãy tính góc của tia
a) Tìm điều kiện xác định của Q.
sáng mặt trời tạo với mặt đất. b) Rút gọn Q.
c) Tính giá trị của Q khi x = 4 + 2 3
1.64 Cho ABC có đường cao AH. Biết AB = 25 cm,  0 B  70 ,  0 C  50 . Tính
d) Giải bất phương trình : Q > 1.
độ dài AH và BC (làm tròn đến chữ số thập phân thứ hai) a2  a 2a  a
1.65 Một khúc sông rộng khoảng 250m. Một chiếc đò chèo qua sông bị dòng
1.113 Cho biểu thức: A    1.
nước đẩy xiên nên phải chèo khoảng 320m mới sang đươực bờ bên kia. a  a  1 a
Hỏi dòng nước đã đẩy chiếc đò lệch đi một góc bằng bao nhiêu ? a) Rút gọn A.
b) Biết a > 0, hãy so sánh A vớiA
1.66 Cho ABC, trong đó AB = 11 cm,  0 ABC  38 ,  0 ACB  30 . Gọi điểm N c) Tìm a để A = 2
là chân của đường vuông góc kẻ từ A đến cạnh BC. Hãy tính: AN và AC.
d) Tìm giá trị nhỏ nhất của A. Gv: Trần Quốc Nghĩa Trang 38 Gv: Trần Quốc Nghĩa Trang 67 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
C - Bảng lượng giác và máy tính bỏ túi  3   3 
1.114 Cho biểu thức: B   1  a :   1    . 2   1  a   1  a 
1.55 Dùng bảng lượng giác hoặc máy tính bỏ túi để tính các tỉ số lượng giác
a) Tìm điều kiện xác định của B. b) Rút gọn B. sau đây: a) sin40012 b) cos52054 c) tan63036 d) cot25018 3
c) Tính giá trị của B khi a  e) sin39013 f) cos52018 g) tan13020 h) cot10017 2  3 i) sin70013 j) cos25032 k) tan43010 l) cot32015
d) Tìm giá trị của a để : B  B .
1.56 Dùng bảng lượng giác hoặc máy tính bỏ túi để tính số đo của góc x (làm a  a  b
tròn kết quả đến phút):
1.115 Cho biểu thức: M     1 : . 2 2  2 2  2 2 a  b  a  b  a  a  b a) sinx  0,2368 b) cosx  0,6224 a) Rút gọn M. c) tanx  2,154 d) cotx  3,163 a 3 e) sinx  0,5446 f) cosx  0,4444
b) Tìm giá trị của M nếu  b 2 g) tanx  1,1111 h) cotx  0,7813
c) Tìm điều kiện của a, b để M < 1. i) sinx  0,3495 j) cosx  0,5427  x  2 x  2  1 x2 
1.57 So sánh các tỉ số lượng giác (không dùng bảng và máy tính):
1.116 Cho biểu thức: P        . a) sin200 và sin700 b) cos250 và cos63015’ x  1 x  2 x  1 2   c) tan73020’ và tg450 d) cot20 và cot37040’
a) Tìm điều kiện xác định của P. e) tan450 và cos450 f) cot320 và cos320 b) Rút gọn P. g) tan250 và sin250 h) cot600 và sin300
c) Tính giá trị lớn nhất của P.
d) Chứng minh: nếu 0 < x < 1 thì P > 0.
1.58 Không dùng bảng và máy tính hãy, tính: 0 2 x  9 x  3 2 x  1 sin 25 a) b) tan580 – cot320
1.117 Cho biểu thức: Q    . 0 cos 65 x  5 x  6 x  2 3  x
a) Tìm điều kiện xác định của Q.
1.59 Hãy sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần (không dùng b) Rút gọn Q.
bảng và máy tính).
c) Tìm các giá trị của x để Q < 1
a) sin780, cos140, sin470, cos870
b) tan730, cot250, tan620, cot380
d) Tìm x  Z sao cho Q  Z.
1.60 Hãy sắp xếp các tỉ số lượng giác sau theo thứ tự giảm dần (không dùng
1.118 Cho biểu thức:
bảng và máy tính). 2  x  y
x3  y3   x  y   xy  
a) tan420, tan560, cot30, cot180
b) sin130, cos470, tan460, cot20 Q   : .  x  y y  x  x  y  
a) Tìm điều kiện xác định của Q. b) Rút gọn Q. c) So sánh Q với Q d) Chứng minh Q  0. Gv: Trần Quốc Nghĩa Trang 66 Gv: Trần Quốc Nghĩa Trang 39 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
C - Bảng lượng giác và máy tính bỏ túi  3   3 
1.114 Cho biểu thức: B   1  a :   1    . 2   1  a   1  a 
1.55 Dùng bảng lượng giác hoặc máy tính bỏ túi để tính các tỉ số lượng giác
a) Tìm điều kiện xác định của B. b) Rút gọn B. sau đây: a) sin40012 b) cos52054 c) tan63036 d) cot25018 3
c) Tính giá trị của B khi a  e) sin39013 f) cos52018 g) tan13020 h) cot10017 2  3 i) sin70013 j) cos25032 k) tan43010 l) cot32015
d) Tìm giá trị của a để : B  B .
1.56 Dùng bảng lượng giác hoặc máy tính bỏ túi để tính số đo của góc x (làm a  a  b
tròn kết quả đến phút):
1.115 Cho biểu thức: M     1 : . 2 2  2 2  2 2 a  b  a  b  a  a  b a) sinx  0,2368 b) cosx  0,6224 a) Rút gọn M. c) tanx  2,154 d) cotx  3,163 a 3 e) sinx  0,5446 f) cosx  0,4444
b) Tìm giá trị của M nếu  b 2 g) tanx  1,1111 h) cotx  0,7813
c) Tìm điều kiện của a, b để M < 1. i) sinx  0,3495 j) cosx  0,5427  x  2 x  2  1 x2 
1.57 So sánh các tỉ số lượng giác (không dùng bảng và máy tính):
1.116 Cho biểu thức: P        . a) sin200 và sin700 b) cos250 và cos63015’ x  1 x  2 x  1 2   c) tan73020’ và tg450 d) cot20 và cot37040’
a) Tìm điều kiện xác định của P. e) tan450 và cos450 f) cot320 và cos320 b) Rút gọn P. g) tan250 và sin250 h) cot600 và sin300
c) Tính giá trị lớn nhất của P.
d) Chứng minh: nếu 0 < x < 1 thì P > 0.
1.58 Không dùng bảng và máy tính hãy, tính: 0 2 x  9 x  3 2 x  1 sin 25 a) b) tan580 – cot320
1.117 Cho biểu thức: Q    . 0 cos 65 x  5 x  6 x  2 3  x
a) Tìm điều kiện xác định của Q.
1.59 Hãy sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần (không dùng b) Rút gọn Q.
bảng và máy tính).
c) Tìm các giá trị của x để Q < 1
a) sin780, cos140, sin470, cos870
b) tan730, cot250, tan620, cot380
d) Tìm x  Z sao cho Q  Z.
1.60 Hãy sắp xếp các tỉ số lượng giác sau theo thứ tự giảm dần (không dùng
1.118 Cho biểu thức:
bảng và máy tính). 2  x  y
x3  y3   x  y   xy  
a) tan420, tan560, cot30, cot180
b) sin130, cos470, tan460, cot20 Q   : .  x  y y  x  x  y  
a) Tìm điều kiện xác định của Q. b) Rút gọn Q. c) So sánh Q với Q d) Chứng minh Q  0. Gv: Trần Quốc Nghĩa Trang 66 Gv: Trần Quốc Nghĩa Trang 39 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1 x 3   9x  3 x  1 x  2
1.49 Cho ABC có đường cao AH. Biết HB = 20cm, HC = 21cm, 0 B  45 .
1.119 Cho biểu thức: M    . x  x  2 x  2 1  x Tính AC.
a) Tìm ĐKXĐ và rút gọn M
b) Tìm x  Z sao cho M  Z.
1.50 a) Cho cos = 0,8. Hãy tìm sin, tan, cot. 15 x  11 3 x  2 2 x  3 3
1.120 Cho biểu thức: P    . b) Cho tan =
. Hãy tìm sin, cos, cot. x  2 x  3 1  x 3  x 4
a) Tìm điều kiện xác định của P b) Rút gọn P. 7 c) Cho cot =
. Hãy tìm sin, cos, tan. 1 2 3 c) Giải phương trình P = d) So sánh P với . 2 3
1.51 Biết tanB = 2. Tính :
1.121 Cho biểu thức: sin B  cos B 2sin   cos A  B   x  3 x   9  x x  3 2 x  3  sin B  cos B 3sin   4cos  Q    1 :         . 2 2 sin   sin .  co s   cos   x  9   x  x  6 x  2 x  3  2 2 C  sin   2sin .  cos  3cos  D 
a) Tìm ĐKXĐ và rút gọn Q b) Tìm x để Q < 1. 2sin .  cos  1 3 2 2 2 tan  10cos
1.122 Cho biểu thức: M    . 1.52 Biết sin   . Tính M  x  1 x x  1 x  x  1 5 5cos   4cot  a) Rút gọn M. b) Chứng minh: M  1.
1.53 Hãy tìm cos và tan, nếu: x2  x x2  x 3 40
1.123 Cho biểu thức: N   . a) sin   b) sin   x  x  1 x  x  1 5 41
Hãy rút gọn A = 1 – N  x  1 .
1.54 Hãy tìm sin và cos, nếu: 1 3 a) tan   b) cot   3 4
Giải bài toán như thế nào? – Phần 2 1 - Tìm hiểu bài toán:
Đâu là ẩn? đâu là dữ kiện? đâu là điều kiện? có thể thỏa
mãn điều kiện bài toán? điều kiện có đủ để xác định ẩn? Hay
là thừa, hay còn thiếu? Hay có mâu thuẫn? Vẽ hình.
Sử dụng các kí hiệu thích hợp, có thể biểu diễn các điều
kiện, dữ kiện thành công thức được không? Phân biệt rõ các
phần của điều kiện.
(Xem tiếp ở trang 68)  Gv: Trần Quốc Nghĩa Trang 40 Gv: Trần Quốc Nghĩa Trang 65 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1 x 3   9x  3 x  1 x  2
1.49 Cho ABC có đường cao AH. Biết HB = 20cm, HC = 21cm, 0 B  45 .
1.119 Cho biểu thức: M    . x  x  2 x  2 1  x Tính AC.
a) Tìm ĐKXĐ và rút gọn M
b) Tìm x  Z sao cho M  Z.
1.50 a) Cho cos = 0,8. Hãy tìm sin, tan, cot. 15 x  11 3 x  2 2 x  3 3
1.120 Cho biểu thức: P    . b) Cho tan =
. Hãy tìm sin, cos, cot. x  2 x  3 1  x 3  x 4
a) Tìm điều kiện xác định của P b) Rút gọn P. 7 c) Cho cot =
. Hãy tìm sin, cos, tan. 1 2 3 c) Giải phương trình P = d) So sánh P với . 2 3
1.51 Biết tanB = 2. Tính :
1.121 Cho biểu thức: sin B  cos B 2sin   cos A  B   x  3 x   9  x x  3 2 x  3  sin B  cos B 3sin   4cos  Q    1 :         . 2 2 sin   sin .  co s   cos   x  9   x  x  6 x  2 x  3  2 2 C  sin   2sin .  cos  3cos  D 
a) Tìm ĐKXĐ và rút gọn Q b) Tìm x để Q < 1. 2sin .  cos  1 3 2 2 2 tan  10cos
1.122 Cho biểu thức: M    . 1.52 Biết sin   . Tính M  x  1 x x  1 x  x  1 5 5cos   4cot  a) Rút gọn M. b) Chứng minh: M  1.
1.53 Hãy tìm cos và tan, nếu: x2  x x2  x 3 40
1.123 Cho biểu thức: N   . a) sin   b) sin   x  x  1 x  x  1 5 41
Hãy rút gọn A = 1 – N  x  1 .
1.54 Hãy tìm sin và cos, nếu: 1 3 a) tan   b) cot   3 4
Giải bài toán như thế nào? – Phần 2 1 - Tìm hiểu bài toán:
Đâu là ẩn? đâu là dữ kiện? đâu là điều kiện? có thể thỏa
mãn điều kiện bài toán? điều kiện có đủ để xác định ẩn? Hay
là thừa, hay còn thiếu? Hay có mâu thuẫn? Vẽ hình.
Sử dụng các kí hiệu thích hợp, có thể biểu diễn các điều
kiện, dữ kiện thành công thức được không? Phân biệt rõ các
phần của điều kiện.
(Xem tiếp ở trang 68)  Gv: Trần Quốc Nghĩa Trang 40 Gv: Trần Quốc Nghĩa Trang 65 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
1.41 Tính giá trị của x (làm tròn đến chữ số thập phân thứ 3) trong mỗi trường Chương 2
hợp sau. Biết tanB  1,072; cosE  0,188. HÀM SỐ BẬC NHẤT A E 16 D  x 63 x
A - Nhắc lại và bổ sung các khái niệm về hàm số B ( a ) C ( b ) F
1.42 Cho MNP vuông ở M, đường cao MQ chia cạnh huyền NP thành hai
1. Hàm số f từ tập hợp số X đến tập hợp số Y là một qui tắc cho tương ứng
đoạn NQ = 3, PQ = 6. Hãy so sánh cotN và cotP. Tỉ số nào lớn hơn và lớn
mỗi giá trị x  X với một và chỉ một giá trị y  Y mà ta kí hiệu f(x), x là hơn bao nhiêu lần.
biến số, y = f(x) là giá trị của hàm số tại x.
2. Cho hàm số y = f(x) xác định với mọi x thuộc R.
1.43 Biến đổi tỉ số lượng giác của các góc sau đây thành tỉ số lượng giác của
Xét hai giá trị bất kì x1, x2  R:
các góc nhỏ hơn 450:
x1 < x2  f(x1) < f(x2) : hàm số đồng biến trên R.
sin600, cos750, sin52030, cot820, tan800.
x1 < x2  f(x1) > f(x2) : hàm số nghịch biến trên R.
1.44 Dựng góc nhọn , biết:
3. Đồ thị của hàm số y = f(x) là tập hợp các điểm M(x ; y) trên mặt phẳng 2 3 3
tọa độ thỏa y = f(x). a) sin   b) cos = 0,5 c) tan   d) cot  
Gọi (C) là đồ thị của hàm số f, ta có: 3 4 2
A(xA ; yA)  (C)  yA = f(xA).
1.45 Sử dụng định nghĩa các tỉ số lượng giác của một góc nhọn để chứng minh
B(xB ; yB)  (C)  yB  f(xB).
rằng: Với góc nhọn  tùy ý, ta có:
a) sin < 1, cos < 1 2.1
Hãy biểu diễn các điểm sau trên cùng một mặt phẳng tọa độ: sin  cos  A(0 ; –3) B(2 ; 0) C(1 ; 3) D(–2 ; 4) F(–3 ; –2) b) tan   , cot   , tan . cot = 1 cos  sin  G(2 ; –4) H(0 ; 2 ) I(– 3 ; 0) J(– 2 ; 3 ) K(– 2 ;– 3 ). c) sin2 + cos2 = 1 2.2
Trong các bảng sau ghi các giá trị tương ứng của x và y. Bảng nào xác
1.46 Cạnh huyền của một tam giác vuông có một góc bằng 600 là 8. Hãy tìm
định y là hàm số của x ? Vì sao ?
độ dài của cạnh đối diện với góc 600. x 1 2 4 5 7 8 x 3 4 3 5 8
1.47 Cạnh góc vuông kề với góc 600 của một tam giác vuông bằng 3. Hãy tìm y 3 5 9 11 15 17 y 6 8 4 8 16
cạnh huyền và cạnh góc vuông còn lại (sử dụng bảng lượng giác của các 2 góc đặc biệt). 2.3 a) Cho hàm số y = f(x) = x. 5
1.48 Đường cao BD của tam giác nhọn ABC bằng 6, đoạn thẳng AD bằng 5.  1 
Tính: f(–2) ; f(–1) ; f(0) ; f ; f(1); f(2); f(3) a) Tính diện tích ABD.    2  3 4
b) Tính AC, dùng các thông tin sau đây nếu cần: sin   , cos C  . 2 b) Cho hàm số y = g(x) = x + 3 5 5 5 Gv: Trần Quốc Nghĩa Trang 64 Gv: Trần Quốc Nghĩa Trang 41 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
1.41 Tính giá trị của x (làm tròn đến chữ số thập phân thứ 3) trong mỗi trường Chương 2
hợp sau. Biết tanB  1,072; cosE  0,188. HÀM SỐ BẬC NHẤT A E 16 D  x 63 x
A - Nhắc lại và bổ sung các khái niệm về hàm số B ( a ) C ( b ) F
1.42 Cho MNP vuông ở M, đường cao MQ chia cạnh huyền NP thành hai
1. Hàm số f từ tập hợp số X đến tập hợp số Y là một qui tắc cho tương ứng
đoạn NQ = 3, PQ = 6. Hãy so sánh cotN và cotP. Tỉ số nào lớn hơn và lớn
mỗi giá trị x  X với một và chỉ một giá trị y  Y mà ta kí hiệu f(x), x là hơn bao nhiêu lần.
biến số, y = f(x) là giá trị của hàm số tại x.
2. Cho hàm số y = f(x) xác định với mọi x thuộc R.
1.43 Biến đổi tỉ số lượng giác của các góc sau đây thành tỉ số lượng giác của
Xét hai giá trị bất kì x1, x2  R:
các góc nhỏ hơn 450:
x1 < x2  f(x1) < f(x2) : hàm số đồng biến trên R.
sin600, cos750, sin52030, cot820, tan800.
x1 < x2  f(x1) > f(x2) : hàm số nghịch biến trên R.
1.44 Dựng góc nhọn , biết:
3. Đồ thị của hàm số y = f(x) là tập hợp các điểm M(x ; y) trên mặt phẳng 2 3 3
tọa độ thỏa y = f(x). a) sin   b) cos = 0,5 c) tan   d) cot  
Gọi (C) là đồ thị của hàm số f, ta có: 3 4 2
A(xA ; yA)  (C)  yA = f(xA).
1.45 Sử dụng định nghĩa các tỉ số lượng giác của một góc nhọn để chứng minh
B(xB ; yB)  (C)  yB  f(xB).
rằng: Với góc nhọn  tùy ý, ta có:
a) sin < 1, cos < 1 2.1
Hãy biểu diễn các điểm sau trên cùng một mặt phẳng tọa độ: sin  cos  A(0 ; –3) B(2 ; 0) C(1 ; 3) D(–2 ; 4) F(–3 ; –2) b) tan   , cot   , tan . cot = 1 cos  sin  G(2 ; –4) H(0 ; 2 ) I(– 3 ; 0) J(– 2 ; 3 ) K(– 2 ;– 3 ). c) sin2 + cos2 = 1 2.2
Trong các bảng sau ghi các giá trị tương ứng của x và y. Bảng nào xác
1.46 Cạnh huyền của một tam giác vuông có một góc bằng 600 là 8. Hãy tìm
định y là hàm số của x ? Vì sao ?
độ dài của cạnh đối diện với góc 600. x 1 2 4 5 7 8 x 3 4 3 5 8
1.47 Cạnh góc vuông kề với góc 600 của một tam giác vuông bằng 3. Hãy tìm y 3 5 9 11 15 17 y 6 8 4 8 16
cạnh huyền và cạnh góc vuông còn lại (sử dụng bảng lượng giác của các 2 góc đặc biệt). 2.3 a) Cho hàm số y = f(x) = x. 5
1.48 Đường cao BD của tam giác nhọn ABC bằng 6, đoạn thẳng AD bằng 5.  1 
Tính: f(–2) ; f(–1) ; f(0) ; f ; f(1); f(2); f(3) a) Tính diện tích ABD.    2  3 4
b) Tính AC, dùng các thông tin sau đây nếu cần: sin   , cos C  . 2 b) Cho hàm số y = g(x) = x + 3 5 5 5 Gv: Trần Quốc Nghĩa Trang 64 Gv: Trần Quốc Nghĩa Trang 41 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1  1 
Tính: g(–2); g(–1); g(0); g   ; g(1); g(2); g(3)
4. Một số hệ thức giữa các tỉ số lượng giác của một góc nhọn:  2 
Cho góc nhọn , ta có:
c) Có nhận xét gì về giá trị của hai hàm số đã cho ở trên khi biến x lấy sin cùng một giá trị ? 1) 2  2 sin cos  1 2) tan cos 3 2.4 Cho hàm số y = f(x) = x. co s 4 3) cot  4) tan.cot = 1 sin  1  Tính : f(–3) ;
f(–2) ; f(–1) ; f (0) ; f   ; f(a) ; f(a + 1)
5. So sánh các tỉ số lượng giác:  2 
Khi góc nhọn  tăng dần thì sin và tan tăng, còn cos và cot 2 2.5 Cho hàm số y = f(x) = x + 3. giảm 5
Với cùng một góc nhọn  thì: sin < tan; cos < cot.
a) Tính giá trị tương ứng của y theo các giá trị của x rồi điền vào bảng: x – 2 –1,5 – 1 –0,5 0 0,5 1 1,5 2
1.34 Cho ABC vuong tại A, đường cao AH. Tính các tỉ số lượng giác của các 2
góc B từ đó suy ra các tỉ số lượng giác của góc C, nếu biết: y = x + 3 5 a) AB = 16cm; BC = 12 cm b) AB = 13 cm; BH = 5 cm c) BH = 16 cm; CH = 9 cm d) AB = 6 cm; AC = 8 cm
b) Hàm số đã cho là hàm đồng biến hay nghịch biến ? Vì sao ?
1.35 Lập tỉ số lượng giác của góc 340 bằng cách vẽ một tam giác vuông có một 2.6
Cho hai hàm số y = 3x và y = – 3x. góc nhọn 340.
a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của hai hàm số đã cho.
b) Trong hai hàm số trên, hàm số nào đồng biến ? Hàm số nào nghịch
1.36 Cho ABC vuông tại C, trong đó AC = 0,90m, BC = 1,20m. Tính các tỉ biến ? Vì sao ?
số lượng giác của góc B, từ đó suy ra các tỉ số lượng giác của góc A. 2.7
Cho hai hàm số y = x và y = 0,25x.
1.37 Cho hình bên: C
a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của hai hàm số đã cho.
b) Đường thẳng song song với trục Ox và cắt trục Oy tại điểm có tung độ 3 Biết tan   . Hãy tính:
là 4 lần lượt cắt các đường thẳng y = x và y = 0,25x tại A và B. Tìm 4
tọa độ của các điểm A, B và tính chu vi, diện tích của OAB theo đơn a) Cạnh AC.
vị đo trên các trục tọa độ là xentimét. b) Cạnh BC. A 6 cm B 2.8
Cho hai hàm số y = 2x và y = 2x + 3.  0
a) Tính giá trị y tương ứng của mỗi hàm số theo giá trị của biến x rồi điền
1.38 Cho ABC vuông tại A, B  30 , BC = 8cm. Hãy tính cạnh AB (làm tròn vào bảng sau:
đến chữ số thập phân thứ ba). Biết cos300  0,866. x – 2,25 –1,5 – 1 0 1 1,5 2,25 AC sin B
1.39 Cho ABC vuông tại A, Chứng minh rằng:  . y = 2x AB sin C y = 2x + 3
1.40 Cho ABC vuông tại A. Kẻ đường cao AH. Tính sinB, sinC, biết: a) AB = 13cm, BH = 5cm. b) BH = 3cm, CH = 4cm.
b) Có nhận xét gì về các giá trị tương ứng của hai hàm số khi biến x lấy cùng một giá trị ? Gv: Trần Quốc Nghĩa Trang 42 Gv: Trần Quốc Nghĩa Trang 63 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1  1 
Tính: g(–2); g(–1); g(0); g   ; g(1); g(2); g(3)
4. Một số hệ thức giữa các tỉ số lượng giác của một góc nhọn:  2 
Cho góc nhọn , ta có:
c) Có nhận xét gì về giá trị của hai hàm số đã cho ở trên khi biến x lấy sin cùng một giá trị ? 1) 2  2 sin cos  1 2) tan cos 3 2.4 Cho hàm số y = f(x) = x. co s 4 3) cot  4) tan.cot = 1 sin  1  Tính : f(–3) ;
f(–2) ; f(–1) ; f (0) ; f   ; f(a) ; f(a + 1)
5. So sánh các tỉ số lượng giác:  2 
Khi góc nhọn  tăng dần thì sin và tan tăng, còn cos và cot 2 2.5 Cho hàm số y = f(x) = x + 3. giảm 5
Với cùng một góc nhọn  thì: sin < tan; cos < cot.
a) Tính giá trị tương ứng của y theo các giá trị của x rồi điền vào bảng: x – 2 –1,5 – 1 –0,5 0 0,5 1 1,5 2
1.34 Cho ABC vuong tại A, đường cao AH. Tính các tỉ số lượng giác của các 2
góc B từ đó suy ra các tỉ số lượng giác của góc C, nếu biết: y = x + 3 5 a) AB = 16cm; BC = 12 cm b) AB = 13 cm; BH = 5 cm c) BH = 16 cm; CH = 9 cm d) AB = 6 cm; AC = 8 cm
b) Hàm số đã cho là hàm đồng biến hay nghịch biến ? Vì sao ?
1.35 Lập tỉ số lượng giác của góc 340 bằng cách vẽ một tam giác vuông có một 2.6
Cho hai hàm số y = 3x và y = – 3x. góc nhọn 340.
a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của hai hàm số đã cho.
b) Trong hai hàm số trên, hàm số nào đồng biến ? Hàm số nào nghịch
1.36 Cho ABC vuông tại C, trong đó AC = 0,90m, BC = 1,20m. Tính các tỉ biến ? Vì sao ?
số lượng giác của góc B, từ đó suy ra các tỉ số lượng giác của góc A. 2.7
Cho hai hàm số y = x và y = 0,25x.
1.37 Cho hình bên: C
a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của hai hàm số đã cho.
b) Đường thẳng song song với trục Ox và cắt trục Oy tại điểm có tung độ 3 Biết tan   . Hãy tính:
là 4 lần lượt cắt các đường thẳng y = x và y = 0,25x tại A và B. Tìm 4
tọa độ của các điểm A, B và tính chu vi, diện tích của OAB theo đơn a) Cạnh AC.
vị đo trên các trục tọa độ là xentimét. b) Cạnh BC. A 6 cm B 2.8
Cho hai hàm số y = 2x và y = 2x + 3.  0
a) Tính giá trị y tương ứng của mỗi hàm số theo giá trị của biến x rồi điền
1.38 Cho ABC vuông tại A, B  30 , BC = 8cm. Hãy tính cạnh AB (làm tròn vào bảng sau:
đến chữ số thập phân thứ ba). Biết cos300  0,866. x – 2,25 –1,5 – 1 0 1 1,5 2,25 AC sin B
1.39 Cho ABC vuông tại A, Chứng minh rằng:  . y = 2x AB sin C y = 2x + 3
1.40 Cho ABC vuông tại A. Kẻ đường cao AH. Tính sinB, sinC, biết: a) AB = 13cm, BH = 5cm. b) BH = 3cm, CH = 4cm.
b) Có nhận xét gì về các giá trị tương ứng của hai hàm số khi biến x lấy cùng một giá trị ? Gv: Trần Quốc Nghĩa Trang 42 Gv: Trần Quốc Nghĩa Trang 63 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1 2.9 Cho hàm số y = f(x) = 5x.
B - Tỉ số lượng giác của góc nhọn
Cho x hai giá trị bất kì x1, x2 sao cho x1 < x2. Hãy chứng minh f(x1) < f(x2)
rồi rút ra kết luận hàm số đã cho đồng bến trên R.
2.10 Cho hàm số y = f(x) = – 2x.
1. Định nghĩa:
Cho x hai giá trị bất kì x1, x2 sao cho x1 < x2. Hãy chứng minh f(x1) > f(x2)
rồi rút ra kết luận hàm số đã cho nghịch bến trên R. doi AB 1. sin   huyen BC 2
2.11 Cho hàm số y = f(x) = –
x + 3 với x  R. Chứng minh rằng hàm số A 5 ke AC 2. co s  
nghịch biến trên R. huyen BC
2.12 Chứng minh hàm số y = 2x – 1 đồng biến trên R. doi AB 3. tan  
2.13 Cho hàm số y = f(x) = x . ke AC
a) Tìm ĐKXĐ và chứng minh rằng hàm số đồng biến với ĐKXĐ đó. ke AC B C 4. cot   
b) Trong các điểm A(4 ; 2), B(2 ; 1), C(9 ; –3), D(8 ; 2 2 ) điểm nào doi AB
thuộc và điểm nào không thuộc đồ thị của hàm số trên ?
2. Tỉ số lượng giác của hai góc phụ nhau (có tổng số đo bằng 900):
2.14 Tìm điều kiện xác định của các hàm số sau: a) y = – x + 5 b) y = 2x2 1) sin = cos A x 1 c) y = 3 d) y = 2 x  2x  3 2) cos = sin 3  x 5  x 3) tan = cot e) y  f) y  2 7x 10  x x 1 4) cot = tan B C g) y  x  2x 1 h) y  x  5  3  x i) y  2  x  2 1  x j) y = 2 x  3x  2
3. Bảng tỉ số lượng giác của các góc đặc biệt:
2.15 Cho hàm số y = f(x) = 2 x  3x  2 .
a) Tìm ĐKXĐ của hàm số. 300 450 600  5   7 
b) Hãy so sánh f   và f  . 1 3  4   4  sin 2 2 2 2 1 c) Tìm x, biết f(x) = 3 2 1 2 cos 2 2 2 x  1
2.16 Cho hàm số y = f(x) = . 3 x 1 tan 1 3 3
a) Tìm ĐKXĐ của hàm số.
b) Tính f(4 – 2 3 ); f(a2) với a < –1. 3 cot 3 1 3
c) Tìm giá trị x để f(x) = 3
d) Tìm giá trị x để f(x) = f(x2). Gv: Trần Quốc Nghĩa Trang 62 Gv: Trần Quốc Nghĩa Trang 43 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1 2.9 Cho hàm số y = f(x) = 5x.
B - Tỉ số lượng giác của góc nhọn
Cho x hai giá trị bất kì x1, x2 sao cho x1 < x2. Hãy chứng minh f(x1) < f(x2)
rồi rút ra kết luận hàm số đã cho đồng bến trên R.
2.10 Cho hàm số y = f(x) = – 2x.
1. Định nghĩa:
Cho x hai giá trị bất kì x1, x2 sao cho x1 < x2. Hãy chứng minh f(x1) > f(x2)
rồi rút ra kết luận hàm số đã cho nghịch bến trên R. doi AB 1. sin   huyen BC 2
2.11 Cho hàm số y = f(x) = –
x + 3 với x  R. Chứng minh rằng hàm số A 5 ke AC 2. co s  
nghịch biến trên R. huyen BC
2.12 Chứng minh hàm số y = 2x – 1 đồng biến trên R. doi AB 3. tan  
2.13 Cho hàm số y = f(x) = x . ke AC
a) Tìm ĐKXĐ và chứng minh rằng hàm số đồng biến với ĐKXĐ đó. ke AC B C 4. cot   
b) Trong các điểm A(4 ; 2), B(2 ; 1), C(9 ; –3), D(8 ; 2 2 ) điểm nào doi AB
thuộc và điểm nào không thuộc đồ thị của hàm số trên ?
2. Tỉ số lượng giác của hai góc phụ nhau (có tổng số đo bằng 900):
2.14 Tìm điều kiện xác định của các hàm số sau: a) y = – x + 5 b) y = 2x2 1) sin = cos A x 1 c) y = 3 d) y = 2 x  2x  3 2) cos = sin 3  x 5  x 3) tan = cot e) y  f) y  2 7x 10  x x 1 4) cot = tan B C g) y  x  2x 1 h) y  x  5  3  x i) y  2  x  2 1  x j) y = 2 x  3x  2
3. Bảng tỉ số lượng giác của các góc đặc biệt:
2.15 Cho hàm số y = f(x) = 2 x  3x  2 .
a) Tìm ĐKXĐ của hàm số. 300 450 600  5   7 
b) Hãy so sánh f   và f  . 1 3  4   4  sin 2 2 2 2 1 c) Tìm x, biết f(x) = 3 2 1 2 cos 2 2 2 x  1
2.16 Cho hàm số y = f(x) = . 3 x 1 tan 1 3 3
a) Tìm ĐKXĐ của hàm số.
b) Tính f(4 – 2 3 ); f(a2) với a < –1. 3 cot 3 1 3
c) Tìm giá trị x để f(x) = 3
d) Tìm giá trị x để f(x) = f(x2). Gv: Trần Quốc Nghĩa Trang 62 Gv: Trần Quốc Nghĩa Trang 43 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
2.17 Cho hai hàm số y = f(x) = 6x2 và y = g(x) = 5x. 2 AB BH 3 AB BD
a) Hãy chứng tỏ f(–x) = f(x) và g(–x) = – g(x). a) AB.AD = AC.AE b)  c)  2 AC CH 3 AC CE
b) Tìm số a sao cho f(a) = g(a) d) 3 AH  BC.BD.CE 2.18 Cho 2 hàm số 2 y  f (x)  x  4 và 2 y  g(x)  x  4 .
e) Biết BC = 10 cm, AH = 4 cm. Tính HB, HC và SADHE, SBDEC.  1   1 
1.32 Cho hình vuông ABCD, M là điểm nằm giữa B và C. Đường thẳng AM Hãy tính f a    + g a    với a > 0.
cắt đường thẳng DB, DC lần lượt tại I và N. Chứng minh:  a   a  1 1 1 a) IB2 + ID2 = 2IA2. b)   2 2 2 AB AM AN
1.33 Cho ABC. Từ một điểm M bất kỳ trong tam giác kẻ MD  BC, ME  AC, MF  AB.
Chứng minh rằng: BD2 + CE2 + AF2 = DC2 + EA2 + FB2.
Giải bài toán như thế nào? – Phần 1
G. Polya là một nhà Toán học, nhà sư phạm nổi
tiếng người Mỹ, nếu bạn là một người quan tâm
nhiều đến Toán học cũng như các vấn đề liên quan
chắc hẳn bạn đã từng đọc qua hoặc ghe nói đến
bộ sách 3 quyển của ông được dịch ra tiếng Việt
- Ba trong số hững tác phẩm tâm huyết nhất của ông bàn về quá
trình giải Toán, sáng tạo, tìm tòi các vấn đề Toán "Giải bài toán
như thế nào?", "Sáng tạo Toán học" và "Toán học và những suy luận có lý".
Đây là bài viết tóm lược những ý chính trong quyển
sách "Giải bài toán như thế nào?" - cũng cần nói thêm ở đây rằng
từ "Giải bài toán" theo G. Polya không đơn thuần chỉ dừng lại ở
việc tìm ra đáp số, như nhiều học sinh thậm chí cả sinh viên vẫn
thường hay hiểu, "Giải bài toán" ở đây bao quát toàn bộ quá trình
suy ngẫm, tìm tòi lời giải cũng như lý giải nguyên nhân phát sinh
bài toán, và cuối cùng là phát triển bài toán vừa làm được, hoặc ít
ra nêu ra những hướng đi mới trên cơ sở đã hiểu nguồn gốc từ đâu bài toán phát sinh.
(Xem tiếp ở trang 65)  Gv: Trần Quốc Nghĩa Trang 44 Gv: Trần Quốc Nghĩa Trang 61 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
2.17 Cho hai hàm số y = f(x) = 6x2 và y = g(x) = 5x. 2 AB BH 3 AB BD
a) Hãy chứng tỏ f(–x) = f(x) và g(–x) = – g(x). a) AB.AD = AC.AE b)  c)  2 AC CH 3 AC CE
b) Tìm số a sao cho f(a) = g(a) d) 3 AH  BC.BD.CE 2.18 Cho 2 hàm số 2 y  f (x)  x  4 và 2 y  g(x)  x  4 .
e) Biết BC = 10 cm, AH = 4 cm. Tính HB, HC và SADHE, SBDEC.  1   1 
1.32 Cho hình vuông ABCD, M là điểm nằm giữa B và C. Đường thẳng AM Hãy tính f a    + g a    với a > 0.
cắt đường thẳng DB, DC lần lượt tại I và N. Chứng minh:  a   a  1 1 1 a) IB2 + ID2 = 2IA2. b)   2 2 2 AB AM AN
1.33 Cho ABC. Từ một điểm M bất kỳ trong tam giác kẻ MD  BC, ME  AC, MF  AB.
Chứng minh rằng: BD2 + CE2 + AF2 = DC2 + EA2 + FB2.
Giải bài toán như thế nào? – Phần 1
G. Polya là một nhà Toán học, nhà sư phạm nổi
tiếng người Mỹ, nếu bạn là một người quan tâm
nhiều đến Toán học cũng như các vấn đề liên quan
chắc hẳn bạn đã từng đọc qua hoặc ghe nói đến
bộ sách 3 quyển của ông được dịch ra tiếng Việt
- Ba trong số hững tác phẩm tâm huyết nhất của ông bàn về quá
trình giải Toán, sáng tạo, tìm tòi các vấn đề Toán "Giải bài toán
như thế nào?", "Sáng tạo Toán học" và "Toán học và những suy luận có lý".
Đây là bài viết tóm lược những ý chính trong quyển
sách "Giải bài toán như thế nào?" - cũng cần nói thêm ở đây rằng
từ "Giải bài toán" theo G. Polya không đơn thuần chỉ dừng lại ở
việc tìm ra đáp số, như nhiều học sinh thậm chí cả sinh viên vẫn
thường hay hiểu, "Giải bài toán" ở đây bao quát toàn bộ quá trình
suy ngẫm, tìm tòi lời giải cũng như lý giải nguyên nhân phát sinh
bài toán, và cuối cùng là phát triển bài toán vừa làm được, hoặc ít
ra nêu ra những hướng đi mới trên cơ sở đã hiểu nguồn gốc từ đâu bài toán phát sinh.
(Xem tiếp ở trang 65)  Gv: Trần Quốc Nghĩa Trang 44 Gv: Trần Quốc Nghĩa Trang 61 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
b) Kẻ Bx // AC cắt AH ở D. Tính HD và c/m: AB2 = AC . BD.
c) Kẻ DE  AC (E  AC), DE cắt BC ở F. C/minh: BH2 = HF . HC
B - Hàm số bậc nhất y = ax + b (a  0)
d) Chứng minh: SABH = SCDH. (Không cần tính diện tích)
C - Hệ số góc của đường thẳng y = ax + b (a  0)
1.27 Cho ABC vuông ở A có AB = 12cm, AC = 16cm.
a) Tính độ dài trung tuyến AM.
b) Kẻ đường cao AH. Tính chu vi ABH.
1. Hàm số bậc nhất là hàm số được cho bởi công thức y = ax + b, trong đó
c) Tia phân giác của góc AMB và góc AMC cắt AB, AC lần lượt ở D và
a, b là các số cho trước và a  0.
E. Chứng minh: ABC và ADE đồng dạng.
2. Hàm số bậc nhất xác định với mọi x  R và có tính chất sau: d) Tính: SBDEC và SDME.
Đồng biến trên R khi a > 0.
1.28 Cho ABC vuông tại A, đường cao AD. Đặt BC = a, AB = c, AC = b,
Nghịch biến trên R khi a < 0. AD = h.
3. Đồ thị của hàm số y = ax + b (a  0) là một đường thẳng:
a) Chứng minh rằng số đo độ dài h; b + c; a + h là độ dài ba cạnh của
Cắt trục tung tại điểm có tung độ bằng b. (b gọi là tung độ gốc của một tam giác vuông. đường thẳng)
b) Chứng minh: EA.EB + FE.FB = DB.DC
Song song với đường thẳng y = ax, nếu b  0, trùng với đường thẳng
c) C/minh hệ thức trên đúng với mọi vị trí của D bất kì trên cạnh BC. y = ax nếu b = 0.
d) Kẻ DE  AB tại E, DF  AC tại F. Chứng minh rằng:
4. Để vẽ đồ thị của hàm số y = ax + b ta chỉ cần xác định dược hai điểm 2 b c 2 bc
phân biệt nào đó thuộc đồ thị rồi vẽ đường thẳng đi qua hai điểm đó. Ta AE  và AF  2 2
thường xác định hai điểm đặc biệt là giao điểm của đồ thị với hai trục b  c 2 2 b  c tọa độ. 3 BF c e) Chứng minh rằng: 
5. Hệ số a của đường thẳng y = ax + b gọi là hệ số góc của đường thẳng. 3 CF b
Còn b được gọi là tung độ gốc của đường thẳng.
1.29 Cho hình thang ABCD (AB // CD) có AB = 4cm, CD = 9cm, BD = 5cm,
6. Cho 2 đường thẳng: (d) : y =ax + b và (d) : y = ax + b(với a, a  0): AC = 12cm. (d)  (d) a = a và b = b
a) Qua B kẻ đường thẳng song song với AC, cắt DC ở E. Tính DBE .  (d) // (d) a = a và b  b
b) Tính diện tích hình thang ABCD.  (d) cắt (d) a  a (d)  (d) a . a= –1
1.30 Cho tam giác ABC vuông ở A, đường cao AH. Kẻ HD  AB, HE  AC,
(d) cắt (d) tại một điểm trên trục tung  a  a và b = b
AK  DE (D  AB, E  AC, K  DE). Gọi I là giao điểm của AH và
DE. Biết AI2 = AD.AE.
2.19 Trong các hàm số sau, hàm số nào là hàm số bậc nhất ? Hãy xác định các a) Chứng minh: AI2 = DE.AK.
hệ số a, b của chúng và xét xem hàm số bậc nhất đó đồng biến hay nghịch  biến ?
b) Tính AIK . Tính các góc của ABC. a) y = 1 – 5x b) y = – 0,5x
c) AK cắt BC ở N. Chứng minh: N là trung điểm của BC. c) y = 2 (x – 1) + 3 d) y = 2x2 + 3
1.31 Cho ABC vuông tại A (AB < AC) với đường cao AH. Gọi D và E lần e) y = 3 x – 2 (2 – x) f) y = 3 – 0,5x
lượt là hình chiếu của H trên AB và AC. Chứng minh: g) y = –1,5x h) y = 5 – 2x2 Gv: Trần Quốc Nghĩa Trang 60 Gv: Trần Quốc Nghĩa Trang 45 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
b) Kẻ Bx // AC cắt AH ở D. Tính HD và c/m: AB2 = AC . BD.
c) Kẻ DE  AC (E  AC), DE cắt BC ở F. C/minh: BH2 = HF . HC
B - Hàm số bậc nhất y = ax + b (a  0)
d) Chứng minh: SABH = SCDH. (Không cần tính diện tích)
C - Hệ số góc của đường thẳng y = ax + b (a  0)
1.27 Cho ABC vuông ở A có AB = 12cm, AC = 16cm.
a) Tính độ dài trung tuyến AM.
b) Kẻ đường cao AH. Tính chu vi ABH.
1. Hàm số bậc nhất là hàm số được cho bởi công thức y = ax + b, trong đó
c) Tia phân giác của góc AMB và góc AMC cắt AB, AC lần lượt ở D và
a, b là các số cho trước và a  0.
E. Chứng minh: ABC và ADE đồng dạng.
2. Hàm số bậc nhất xác định với mọi x  R và có tính chất sau: d) Tính: SBDEC và SDME.
Đồng biến trên R khi a > 0.
1.28 Cho ABC vuông tại A, đường cao AD. Đặt BC = a, AB = c, AC = b,
Nghịch biến trên R khi a < 0. AD = h.
3. Đồ thị của hàm số y = ax + b (a  0) là một đường thẳng:
a) Chứng minh rằng số đo độ dài h; b + c; a + h là độ dài ba cạnh của
Cắt trục tung tại điểm có tung độ bằng b. (b gọi là tung độ gốc của một tam giác vuông. đường thẳng)
b) Chứng minh: EA.EB + FE.FB = DB.DC
Song song với đường thẳng y = ax, nếu b  0, trùng với đường thẳng
c) C/minh hệ thức trên đúng với mọi vị trí của D bất kì trên cạnh BC. y = ax nếu b = 0.
d) Kẻ DE  AB tại E, DF  AC tại F. Chứng minh rằng:
4. Để vẽ đồ thị của hàm số y = ax + b ta chỉ cần xác định dược hai điểm 2 b c 2 bc
phân biệt nào đó thuộc đồ thị rồi vẽ đường thẳng đi qua hai điểm đó. Ta AE  và AF  2 2
thường xác định hai điểm đặc biệt là giao điểm của đồ thị với hai trục b  c 2 2 b  c tọa độ. 3 BF c e) Chứng minh rằng: 
5. Hệ số a của đường thẳng y = ax + b gọi là hệ số góc của đường thẳng. 3 CF b
Còn b được gọi là tung độ gốc của đường thẳng.
1.29 Cho hình thang ABCD (AB // CD) có AB = 4cm, CD = 9cm, BD = 5cm,
6. Cho 2 đường thẳng: (d) : y =ax + b và (d) : y = ax + b(với a, a  0): AC = 12cm. (d)  (d) a = a và b = b
a) Qua B kẻ đường thẳng song song với AC, cắt DC ở E. Tính DBE .  (d) // (d) a = a và b  b
b) Tính diện tích hình thang ABCD.  (d) cắt (d) a  a (d)  (d) a . a= –1
1.30 Cho tam giác ABC vuông ở A, đường cao AH. Kẻ HD  AB, HE  AC,
(d) cắt (d) tại một điểm trên trục tung  a  a và b = b
AK  DE (D  AB, E  AC, K  DE). Gọi I là giao điểm của AH và
DE. Biết AI2 = AD.AE.
2.19 Trong các hàm số sau, hàm số nào là hàm số bậc nhất ? Hãy xác định các a) Chứng minh: AI2 = DE.AK.
hệ số a, b của chúng và xét xem hàm số bậc nhất đó đồng biến hay nghịch  biến ?
b) Tính AIK . Tính các góc của ABC. a) y = 1 – 5x b) y = – 0,5x
c) AK cắt BC ở N. Chứng minh: N là trung điểm của BC. c) y = 2 (x – 1) + 3 d) y = 2x2 + 3
1.31 Cho ABC vuông tại A (AB < AC) với đường cao AH. Gọi D và E lần e) y = 3 x – 2 (2 – x) f) y = 3 – 0,5x
lượt là hình chiếu của H trên AB và AC. Chứng minh: g) y = –1,5x h) y = 5 – 2x2 Gv: Trần Quốc Nghĩa Trang 60 Gv: Trần Quốc Nghĩa Trang 45 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1 1  i) y + 2 = x – 3 j) y =
1.16 Cho hình chữ nhật ABCD. Đường phân giác của B cắt đường chéo AC x 2 5 2x 1
thành hai đoạn 4 m và 5 m . Tính các kích thước của hình chữ nhật. k) y = l) y = 5 x  2 . 7 7 3
1.17 Cho ABC vuông tại A, vẽ đường cao AH. Chu vi của ABH là 30cm và
2.20 Cho các hàm số y = (m – 2)x + 3 và y = (m + 1) + 5. Tìm các giá trị của  m để mỗi h
ACH là 40cm. Tính chu vi của ABC. àm số: a) Là hàm số bậc nhất
1.18 Cho ABC vuông tại A có cạnh AB = 6cm và AC = 8cm. Các đường
b) Là hàm số nghịch biến
phân giác trong và ngoài của góc B cắt đường thẳng AC lần lượt tại M và
c) Là hàm số đồng biến.
N. Tính các đoạn thẳng AM và AN.
2.21 Một hình chữ nhật có các kích thước là 15cm và 25cm. Người ta tăng
thêm mỗi kích thước của hình đó thêm x (cm) được hình chữ nhật mới có
1.19 Cho ABC vuông ở A, AB = 30cm, AC = 40cm, đường cao AH, trung
chu vi là y (cm). Hãy lập công thức tính y theo x. tuyến AM.
2.22 Một hình chữ nhật có các kích thước là 30cm và 40cm. Người ta giảm bớt a) Tính BH, HM, MC. b) Tính AH.
mỗi kích thước của hình đó x (cm). Gọi S và P thứ tự là diện tích và chu
1.20 Cho ABC vuông ở A, đường cao AH. Gọi M, N theo thứ tự là trung
vi của hình chữ nhật mới theo x.
điểm của AB, AC. Biết HM = 15cm, HN = 20cm. Tính HB, HC, AH.
a) Hỏi rằng các đại lượng S và P có phải là hàm số bậc nhất của x không? Vì sao ?
1.21 Cho ABC cân ở A, đường cao BK. Biết AK = 7cm, KC = 2cm.
b) Tính giá trị tương ứng của P khi x nhận các giá trị (tính theo đợ vị cm) Tính BC. sau: 0; 1; 1,5; 2,5; 3,5.
1.22 Cho ABC vuông ở A có AC = 20cm, chiều cao AH = 12cm. Tính diện
2.23 Chứng minh rằng hàm số bậc nhất y = ax + b đồng biến khi a > 0 và nghịch biến khi a < 0. tích ABC.
2.24 Cho hàm số y = ax + 5. Tìm hệ số a, biết rằng khi x = 1 thì y = 2.
1.23 Cho hình vuông ABCD, gọi I là một điểm nằm giữa A và B. Tia DI và tia
2.25 Với giá trị nào của m thì hàm số sau là hàm số bậc nhất ?
cắt CB cắt nhau ở K. Qua D kẻ đường thẳng vuông góc với DI để đường m  1 1 3 thẳng BC tại M. a) y = 5  m (x – 1) b) y = x + 3,5 c) y = x – m 1 m  2 4 a) Chứng minh: IDM cân. 1 1
2.26 Cho hàm số y = (1 – 5 )x – 1. b) Chứng minh: 
không đổi khi I di chuyển trên cạnh AB. 2 2 DI DK
a) Hàm số trên là đồng biến hay nghịch biến trên R? Vì sao ?
b) Tính giá trị của y khi x = 1 + 5
1.24 Cho hình thang vuông ABCD (   0
A  D  90 ) có hai đường chéo AC và
c) Tính giá trị của x khi y = 5 .
BD vuông góc với nhau tại H. Biết HD = 18 cm, HB = 8 cm. tính diện tích hình thang ABCD.
2.27 Cho hàm số y = (3 – 2 )x + 1.
a) Hàm số trên là đồng biến hay nghịch biến trên R? Vì sao ?
1.25 Cho ABC cân tại A, kẻ đường cao AH và CK. Biết AH = 7,5 cm;
b) Tính giá trị của y khi x nhận các giá trị: 0; 1; 2 ; 3 + 2 ; 3 – 2 CK = 12 cm. Tính BC, AB.
c) Tính giá trị của x khi y nhận các giá trị: 0; 1; 8; 2 + 2 ; 2 – 2 .
1.26 Cho ABC có đường cao AH (H nằm giữa B và C). AH = 12cm,
2.28 Tìm trên mặt phẳng tọa độ tất cả các điểm : HB = 9cm, BC = 25cm. a) Có tung độ bằng 6;
b) Có hoành độ bằng – 3 ;
a) Chứng minh: ABC vuông tại A. Gv: Trần Quốc Nghĩa Trang 46 Gv: Trần Quốc Nghĩa Trang 59 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1 1  i) y + 2 = x – 3 j) y =
1.16 Cho hình chữ nhật ABCD. Đường phân giác của B cắt đường chéo AC x 2 5 2x 1
thành hai đoạn 4 m và 5 m . Tính các kích thước của hình chữ nhật. k) y = l) y = 5 x  2 . 7 7 3
1.17 Cho ABC vuông tại A, vẽ đường cao AH. Chu vi của ABH là 30cm và
2.20 Cho các hàm số y = (m – 2)x + 3 và y = (m + 1) + 5. Tìm các giá trị của  m để mỗi h
ACH là 40cm. Tính chu vi của ABC. àm số: a) Là hàm số bậc nhất
1.18 Cho ABC vuông tại A có cạnh AB = 6cm và AC = 8cm. Các đường
b) Là hàm số nghịch biến
phân giác trong và ngoài của góc B cắt đường thẳng AC lần lượt tại M và
c) Là hàm số đồng biến.
N. Tính các đoạn thẳng AM và AN.
2.21 Một hình chữ nhật có các kích thước là 15cm và 25cm. Người ta tăng
thêm mỗi kích thước của hình đó thêm x (cm) được hình chữ nhật mới có
1.19 Cho ABC vuông ở A, AB = 30cm, AC = 40cm, đường cao AH, trung
chu vi là y (cm). Hãy lập công thức tính y theo x. tuyến AM.
2.22 Một hình chữ nhật có các kích thước là 30cm và 40cm. Người ta giảm bớt a) Tính BH, HM, MC. b) Tính AH.
mỗi kích thước của hình đó x (cm). Gọi S và P thứ tự là diện tích và chu
1.20 Cho ABC vuông ở A, đường cao AH. Gọi M, N theo thứ tự là trung
vi của hình chữ nhật mới theo x.
điểm của AB, AC. Biết HM = 15cm, HN = 20cm. Tính HB, HC, AH.
a) Hỏi rằng các đại lượng S và P có phải là hàm số bậc nhất của x không? Vì sao ?
1.21 Cho ABC cân ở A, đường cao BK. Biết AK = 7cm, KC = 2cm.
b) Tính giá trị tương ứng của P khi x nhận các giá trị (tính theo đợ vị cm) Tính BC. sau: 0; 1; 1,5; 2,5; 3,5.
1.22 Cho ABC vuông ở A có AC = 20cm, chiều cao AH = 12cm. Tính diện
2.23 Chứng minh rằng hàm số bậc nhất y = ax + b đồng biến khi a > 0 và nghịch biến khi a < 0. tích ABC.
2.24 Cho hàm số y = ax + 5. Tìm hệ số a, biết rằng khi x = 1 thì y = 2.
1.23 Cho hình vuông ABCD, gọi I là một điểm nằm giữa A và B. Tia DI và tia
2.25 Với giá trị nào của m thì hàm số sau là hàm số bậc nhất ?
cắt CB cắt nhau ở K. Qua D kẻ đường thẳng vuông góc với DI để đường m  1 1 3 thẳng BC tại M. a) y = 5  m (x – 1) b) y = x + 3,5 c) y = x – m 1 m  2 4 a) Chứng minh: IDM cân. 1 1
2.26 Cho hàm số y = (1 – 5 )x – 1. b) Chứng minh: 
không đổi khi I di chuyển trên cạnh AB. 2 2 DI DK
a) Hàm số trên là đồng biến hay nghịch biến trên R? Vì sao ?
b) Tính giá trị của y khi x = 1 + 5
1.24 Cho hình thang vuông ABCD (   0
A  D  90 ) có hai đường chéo AC và
c) Tính giá trị của x khi y = 5 .
BD vuông góc với nhau tại H. Biết HD = 18 cm, HB = 8 cm. tính diện tích hình thang ABCD.
2.27 Cho hàm số y = (3 – 2 )x + 1.
a) Hàm số trên là đồng biến hay nghịch biến trên R? Vì sao ?
1.25 Cho ABC cân tại A, kẻ đường cao AH và CK. Biết AH = 7,5 cm;
b) Tính giá trị của y khi x nhận các giá trị: 0; 1; 2 ; 3 + 2 ; 3 – 2 CK = 12 cm. Tính BC, AB.
c) Tính giá trị của x khi y nhận các giá trị: 0; 1; 8; 2 + 2 ; 2 – 2 .
1.26 Cho ABC có đường cao AH (H nằm giữa B và C). AH = 12cm,
2.28 Tìm trên mặt phẳng tọa độ tất cả các điểm : HB = 9cm, BC = 25cm. a) Có tung độ bằng 6;
b) Có hoành độ bằng – 3 ;
a) Chứng minh: ABC vuông tại A. Gv: Trần Quốc Nghĩa Trang 46 Gv: Trần Quốc Nghĩa Trang 59 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1 1.4
Đường cao của một tam giác vuông chia cạnh huyền thành hai đoạn thẳng c) Có tung độ bằng 0 ;
d) Có hoành độ bằng 0 ;
có độ dài là 1 và 2. Hãy tính các cạnh của  vuông này.
e) Có hoành độ và tung độ bằng nhau ;
f) Có hoành độ và tung độ đối nhau. 1.5
Một tam giác vuông có cạnh huyền là 5, còn đường cao ứng với cạnh
2.29 Cho hai điểm A(x
huyền là 2. Hãy tính cạnh nhỏ nhất của tam giác vuông này.
A ; yA) và B(xB ; yB). Chứng minh công thức tính
khoảng cách giữa hai điẩm A và B là : 2 2
AB  (x  x )  (y  y ) B A B A 1.6
Cho một tam giác vuông. Biết tỉ số hai cạnh góc vuông là 3 : 4 và cạnh
Áp dụng : Tính khoảng cách giữa hai điểm, biết rằng:
huyền là 125cm. Tính độ dài các cạnh của tam giác vuông và hình chiếu a) A(1 ; 1) và B(5 ; 4) b. M(–2 ; 2) và B(3 ; 5)
của cạnh góc vuông trên cạnh huyền.
2.30 a) Vẽ đồ thị của các hàm số y = x + 3 và y = 2x + 3 trên cùng một AB 5 1.7
Cho tam giác ABC vuông tại A. Biết  , đường cao AH = 30 cm. mặt phẳng tọa độ. AC 6
b) Gọi giao điểm của đường thẳng y = x + 3 với trục Oy, Ox theo thứ Tính BH, HC.
tự là A, B và giao điểm của đường thẳng y = 2x + 3 với các trục Oy, AB 3
Ox theo thứ tự là C, D. Tính các góc của ABC (dùng máy tính bỏ túi) 1.8
Cho tam giác ABC vuông tại A. Biết  , đường cao AH = 42 cm. AC 7
2.31 a) Vẽ đồ thị của các hàm số y = x + 1 và y = –x + 3 trên cùng một mặt Tính BH, HC. phẳng tọa độ.
b) Hai đường thẳng trên cắt nhau tại C và cát trục Ox theo thứ tự tại A và 1.9
Cho h.vuông ABCD có độ dài cạnh là a. Tính độ dài đường chéo theo a.
B. Tìm toạ độ các điểm A, B, C.
1.10 Hãy tính đường cao của tam giác đều cạnh a.
c) Tính chu vi và diện tích ABC (đơn vị các trục là xentimét)
1.11 Cho ABC cân tại A. Gọi H là hình chiếu của B trên cạnh AC. Tính cạnh
2.32 a) Vẽ trên cùng hệ trục tọa độ Oxy đồ thị của các hàm số sau:
đáy BC của tam giác, biết rằng AH = 7, HC = 2. 2 2 y = 2x ; y = 2x + 5 ; y = – x và y = – x + 5 3 3
1.12 Hãy tìm tam giác vuông trong các tam giác có độ dài 3 cạnh sau:
b) Bốn đường thẳng trên cắt nhau tạo thành tứ giác OABC (O là gốc tọa a) IJ = 6 JK = 10 KI = 8;
độ). Tứ giác OABC có phải là hình bình hành không ? Vì sao ? b) RS = 7 ST = 24 TR = 25;
2.33 Cho hàm số y = (m – 3)x 1 1 1 c) AB = BC = AC = ;
a) Với giá trị nào của m thì hàm số đồng biến ? Nghịch biến ? 3 4 5
b) Xác định giá trị của m để đồ thị của hàm số đi qua điểm A(1 ; 2). d) MN = 6,5 ML = 3,3 LN = 5,6.
c) Xác định giá trị của m để đồ thị của hàm số đi qua điểm B(1 ; –2).
d) Vẽ đồ thị của hàm số ứng với giá trị của m tìm được ở các câu b và c.
1.13 Cho tam giác có độ dài các cạnh là 5, 12, 13. Tìm góc của tam giác đối
2.34 Cho hàm số y = ax + 3 có đồ thị (d) cắt trục hoành tại điểm A có hoành
diện với cạnh có độ dài 13. độ bằng 3.
1.14 Trong tam giác ABC, biết AB = 10cm, BC = 17cm. Vẽ đường cao BD a) Tìm giá trị của a.
với D thuộc cạnh AC và BD = 8cm. Tính AC.
b) Xét tính biến thiên (đồng biến hay nghịch biến) của hàm số.
c) Gọi B là giao điểm của (d) với trục tung. Tính khoảng cách từ O đến
1.15 Cho ABC, đường cao AH. AB.
a) Cho AH = 16, BH = 25. Tính AB, AC, BC, CH.
2.35 Cho hàm số y = (a – 1)x + a.
b) Cho AB = 12, BH = 6. Tính AH, AC, BC, CH.
a) Xác định giá trị của a để đồ thị của hàm số cắt trục tung tại điểm có tung độ bằng 2 + 1 Gv: Trần Quốc Nghĩa Trang 58 Gv: Trần Quốc Nghĩa Trang 47 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1 1.4
Đường cao của một tam giác vuông chia cạnh huyền thành hai đoạn thẳng c) Có tung độ bằng 0 ;
d) Có hoành độ bằng 0 ;
có độ dài là 1 và 2. Hãy tính các cạnh của  vuông này.
e) Có hoành độ và tung độ bằng nhau ;
f) Có hoành độ và tung độ đối nhau. 1.5
Một tam giác vuông có cạnh huyền là 5, còn đường cao ứng với cạnh
2.29 Cho hai điểm A(x
huyền là 2. Hãy tính cạnh nhỏ nhất của tam giác vuông này.
A ; yA) và B(xB ; yB). Chứng minh công thức tính
khoảng cách giữa hai điẩm A và B là : 2 2
AB  (x  x )  (y  y ) B A B A 1.6
Cho một tam giác vuông. Biết tỉ số hai cạnh góc vuông là 3 : 4 và cạnh
Áp dụng : Tính khoảng cách giữa hai điểm, biết rằng:
huyền là 125cm. Tính độ dài các cạnh của tam giác vuông và hình chiếu a) A(1 ; 1) và B(5 ; 4) b. M(–2 ; 2) và B(3 ; 5)
của cạnh góc vuông trên cạnh huyền.
2.30 a) Vẽ đồ thị của các hàm số y = x + 3 và y = 2x + 3 trên cùng một AB 5 1.7
Cho tam giác ABC vuông tại A. Biết  , đường cao AH = 30 cm. mặt phẳng tọa độ. AC 6
b) Gọi giao điểm của đường thẳng y = x + 3 với trục Oy, Ox theo thứ Tính BH, HC.
tự là A, B và giao điểm của đường thẳng y = 2x + 3 với các trục Oy, AB 3
Ox theo thứ tự là C, D. Tính các góc của ABC (dùng máy tính bỏ túi) 1.8
Cho tam giác ABC vuông tại A. Biết  , đường cao AH = 42 cm. AC 7
2.31 a) Vẽ đồ thị của các hàm số y = x + 1 và y = –x + 3 trên cùng một mặt Tính BH, HC. phẳng tọa độ.
b) Hai đường thẳng trên cắt nhau tại C và cát trục Ox theo thứ tự tại A và 1.9
Cho h.vuông ABCD có độ dài cạnh là a. Tính độ dài đường chéo theo a.
B. Tìm toạ độ các điểm A, B, C.
1.10 Hãy tính đường cao của tam giác đều cạnh a.
c) Tính chu vi và diện tích ABC (đơn vị các trục là xentimét)
1.11 Cho ABC cân tại A. Gọi H là hình chiếu của B trên cạnh AC. Tính cạnh
2.32 a) Vẽ trên cùng hệ trục tọa độ Oxy đồ thị của các hàm số sau:
đáy BC của tam giác, biết rằng AH = 7, HC = 2. 2 2 y = 2x ; y = 2x + 5 ; y = – x và y = – x + 5 3 3
1.12 Hãy tìm tam giác vuông trong các tam giác có độ dài 3 cạnh sau:
b) Bốn đường thẳng trên cắt nhau tạo thành tứ giác OABC (O là gốc tọa a) IJ = 6 JK = 10 KI = 8;
độ). Tứ giác OABC có phải là hình bình hành không ? Vì sao ? b) RS = 7 ST = 24 TR = 25;
2.33 Cho hàm số y = (m – 3)x 1 1 1 c) AB = BC = AC = ;
a) Với giá trị nào của m thì hàm số đồng biến ? Nghịch biến ? 3 4 5
b) Xác định giá trị của m để đồ thị của hàm số đi qua điểm A(1 ; 2). d) MN = 6,5 ML = 3,3 LN = 5,6.
c) Xác định giá trị của m để đồ thị của hàm số đi qua điểm B(1 ; –2).
d) Vẽ đồ thị của hàm số ứng với giá trị của m tìm được ở các câu b và c.
1.13 Cho tam giác có độ dài các cạnh là 5, 12, 13. Tìm góc của tam giác đối
2.34 Cho hàm số y = ax + 3 có đồ thị (d) cắt trục hoành tại điểm A có hoành
diện với cạnh có độ dài 13. độ bằng 3.
1.14 Trong tam giác ABC, biết AB = 10cm, BC = 17cm. Vẽ đường cao BD a) Tìm giá trị của a.
với D thuộc cạnh AC và BD = 8cm. Tính AC.
b) Xét tính biến thiên (đồng biến hay nghịch biến) của hàm số.
c) Gọi B là giao điểm của (d) với trục tung. Tính khoảng cách từ O đến
1.15 Cho ABC, đường cao AH. AB.
a) Cho AH = 16, BH = 25. Tính AB, AC, BC, CH.
2.35 Cho hàm số y = (a – 1)x + a.
b) Cho AB = 12, BH = 6. Tính AH, AC, BC, CH.
a) Xác định giá trị của a để đồ thị của hàm số cắt trục tung tại điểm có tung độ bằng 2 + 1 Gv: Trần Quốc Nghĩa Trang 58 Gv: Trần Quốc Nghĩa Trang 47 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
b) Xác định giá trị của a để đồ thị của hàm số cắt trục hoành tại điểm có hoành độ – 3 Phần 2. Hình học
c) Vẽ đồ thị của hàm số ứng với a tìm được ở câu a). Tính khoảng cách
từ gốc tọa độ đến đường thẳng đó.
2.36 Cho hàm số y = (m2 – 5m)x + 3. Chương 1
a) Với giá trị nào của m thì hàm số là hàm số bậc nhất ?
b) Với giá trị nào của m thì hàm số nghịch biến ? HỆ THỨC LƯỢNG
c) Xác định m khi đồ thị của hàm số qua điểm A(1 ; –3). TRONG TAM GIÁC VUÔNG
2.37 Cho hàm số y = (a – 1)x + a. 
a) Xác định giá trị của a để đồ thị của hàm số cắt trục tung tại điểm có tung độ bằng 2.
A - Một số hệ thức về cạnh và đường cao
b) Xác định giá trị của a để đồ thị của hàm số cắt trục hoành tại điểm có hoành độ bằng –3. trong tam giác vuông
c) Vẽ đồ thị của hai hàm số ứng với giá trị của a vừa tìm được ở các câu
a và b trên cùng hệ trục tọa độ Oxy và tìm giao điểm của hai đường thẳng vừa vẽ được. 1) 2 2 2
BC AB AC 1) a2 = b2 + c2
2.38 a) Vẽ đồ thị của các hàm số y = x và y = 2x + 2 trên cùng một mặt phẳng A 2) 2 AC CH .BC 2) b2 = a.b tọa độ. 3) c2 = a.c c
b) Gọi A là giao điểm của hai đồ thị của hàm số nói trên, tìm tọa độ của 3) 2 AB BH .BC b h
4) h2 = b.c điểm A. 4) 2 AH HB.HC c' b' 5) h.a = b.c
c) Vẽ qua điểm B(0 ; 2) một đường thẳng song song với Ox, cắt đường
5) AH .BC AB.AC B H a C 1 1 1
thẳng y = x tại C. Tìm tọa độ của điểm C rồi tính diện tích ABC (đơn 1 1 1 6)   6)   2 2 2 h b c
vị các trục là xentimét) 2 2 2 AH AC AB
2.39 a) Biết rằng với x = 4 thì hàm số y = 3x + b có giá trị là 11. Tìm b. Vẽ đồ 1.1
Cho tam giác ABC vuông tại A có đường cao AH. Trong các đoạn thẳng
thị của hàm số với giá trị của b vừa tìm được.
sau: AB, AC, BC, AH, BH, CH hãy tính độ dài các đoạn thẳng còn lại
b) Biết rằng đồ thị của hàm số của hàm số y = ax + 5 đi qua điểm nếu biết:
A(–1 ; 3). Tìm a. Vẽ đồ thị của hàm số với giá trị của a vừa tìm được. a) AB = 15cm; BC = 25 cm b) BH = 18 cm; CH = 32 cm
2.40 Vẽ đồ thị của hàm số y = 5 x + 5 bằng thước thẳng và compa. c) AB = 6 cm; BH = 3,6 cm d) AC = 12 cm; AH = 7,2 cm
2.41 a) Vẽ trên cùng hệ trục tọa độ Oxy đồ thị của các hàm số sau: e) AH = 7,2 cm; CH = 9,6 cm
f) BC = 25cm; AH = 12cm (AB(d1) : y = x (d2) : y = 2x (d3) : y = – x + 3 1.2
Cho tam giác ABC vuông tại A có đường cao AH và đường phân giác
b) Đường thẳng (d3) cắt các đường thẳng (d1), (d2) theo thứ tự tại A, B.
AD (D  BC). Biết DB = 15 cm, CD = 20 cm. Tính AH, AD (làm tròn
Tìm tọa độ các điểm A, B và tính diện tích OAB.
đến chữ số thập phân thứ hai).
2.42 Hãy chỉ ra ba cặp đường thẳng cắt nhau và các cặp đường thẳng song song với nhau : 1.3
Cạnh huyền của một tam giác vuông lớn hơn một cạnh góc vuông là 1cm, a) y = –2x + 3 ; b) y = x + 2 ; c) y = 0,5x – 3
còn tổng của hai cạnh góc vuông lớn hơn cạnh huyền 4cm. Hãy tính các d) y = x – 3 ; e) y = 1,5x – 1 ; f) y = 0,5x + 3
cạnh của tam giác vuông này. Gv: Trần Quốc Nghĩa Trang 48 Gv: Trần Quốc Nghĩa Trang 57 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
b) Xác định giá trị của a để đồ thị của hàm số cắt trục hoành tại điểm có hoành độ – 3 Phần 2. Hình học
c) Vẽ đồ thị của hàm số ứng với a tìm được ở câu a). Tính khoảng cách
từ gốc tọa độ đến đường thẳng đó.
2.36 Cho hàm số y = (m2 – 5m)x + 3. Chương 1
a) Với giá trị nào của m thì hàm số là hàm số bậc nhất ?
b) Với giá trị nào của m thì hàm số nghịch biến ? HỆ THỨC LƯỢNG
c) Xác định m khi đồ thị của hàm số qua điểm A(1 ; –3). TRONG TAM GIÁC VUÔNG
2.37 Cho hàm số y = (a – 1)x + a. 
a) Xác định giá trị của a để đồ thị của hàm số cắt trục tung tại điểm có tung độ bằng 2.
A - Một số hệ thức về cạnh và đường cao
b) Xác định giá trị của a để đồ thị của hàm số cắt trục hoành tại điểm có hoành độ bằng –3. trong tam giác vuông
c) Vẽ đồ thị của hai hàm số ứng với giá trị của a vừa tìm được ở các câu
a và b trên cùng hệ trục tọa độ Oxy và tìm giao điểm của hai đường thẳng vừa vẽ được. 1) 2 2 2
BC AB AC 1) a2 = b2 + c2
2.38 a) Vẽ đồ thị của các hàm số y = x và y = 2x + 2 trên cùng một mặt phẳng A 2) 2 AC CH .BC 2) b2 = a.b tọa độ. 3) c2 = a.c c
b) Gọi A là giao điểm của hai đồ thị của hàm số nói trên, tìm tọa độ của 3) 2 AB BH .BC b h
4) h2 = b.c điểm A. 4) 2 AH HB.HC c' b' 5) h.a = b.c
c) Vẽ qua điểm B(0 ; 2) một đường thẳng song song với Ox, cắt đường
5) AH .BC AB.AC B H a C 1 1 1
thẳng y = x tại C. Tìm tọa độ của điểm C rồi tính diện tích ABC (đơn 1 1 1 6)   6)   2 2 2 h b c
vị các trục là xentimét) 2 2 2 AH AC AB
2.39 a) Biết rằng với x = 4 thì hàm số y = 3x + b có giá trị là 11. Tìm b. Vẽ đồ 1.1
Cho tam giác ABC vuông tại A có đường cao AH. Trong các đoạn thẳng
thị của hàm số với giá trị của b vừa tìm được.
sau: AB, AC, BC, AH, BH, CH hãy tính độ dài các đoạn thẳng còn lại
b) Biết rằng đồ thị của hàm số của hàm số y = ax + 5 đi qua điểm nếu biết:
A(–1 ; 3). Tìm a. Vẽ đồ thị của hàm số với giá trị của a vừa tìm được. a) AB = 15cm; BC = 25 cm b) BH = 18 cm; CH = 32 cm
2.40 Vẽ đồ thị của hàm số y = 5 x + 5 bằng thước thẳng và compa. c) AB = 6 cm; BH = 3,6 cm d) AC = 12 cm; AH = 7,2 cm
2.41 a) Vẽ trên cùng hệ trục tọa độ Oxy đồ thị của các hàm số sau: e) AH = 7,2 cm; CH = 9,6 cm
f) BC = 25cm; AH = 12cm (AB(d1) : y = x (d2) : y = 2x (d3) : y = – x + 3 1.2
Cho tam giác ABC vuông tại A có đường cao AH và đường phân giác
b) Đường thẳng (d3) cắt các đường thẳng (d1), (d2) theo thứ tự tại A, B.
AD (D  BC). Biết DB = 15 cm, CD = 20 cm. Tính AH, AD (làm tròn
Tìm tọa độ các điểm A, B và tính diện tích OAB.
đến chữ số thập phân thứ hai).
2.42 Hãy chỉ ra ba cặp đường thẳng cắt nhau và các cặp đường thẳng song song với nhau : 1.3
Cạnh huyền của một tam giác vuông lớn hơn một cạnh góc vuông là 1cm, a) y = –2x + 3 ; b) y = x + 2 ; c) y = 0,5x – 3
còn tổng của hai cạnh góc vuông lớn hơn cạnh huyền 4cm. Hãy tính các d) y = x – 3 ; e) y = 1,5x – 1 ; f) y = 0,5x + 3
cạnh của tam giác vuông này. Gv: Trần Quốc Nghĩa Trang 48 Gv: Trần Quốc Nghĩa Trang 57 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
2.89 a) Cho các điểm M(–1 ; – 2), N(–2 ; –4), P(2 ; –3), Q(3 ; –4,5). Tìm tọa
2.43 Trong các đường thẳng sau, đường nào song song với nhau, đường nào
độ của các điểm M’, N’, P’ và Q’ lần lượt là các điểm dối xứng với vuông góc với nhau ?
các điểm M, N, P và Q qua trục Ox. 1 a) y = 1,5x + 2 ; b) y = x – 3 ; c) y = 5 – x
b) Vẽ đồ thị của hàm số y = x ; và y = x + 1 . 2
c) Tìm tọa độ giao điểm của các hàm số trên. Từ đó suy ra phương trình x  1 d) y = ; e) y = –x + 4 ; f) y = 2x – 1.
x  = x + 1  có một nghiệm duy nhất. 2
2.44 Cho hai hàm số bậc nhất y = mx + 3 và y = (2m + 1)x – 5. Tìm m để đồ
2.90 Vẽ đồ thị của các hàm số sau:
thị của các hàm số là: 2 x
a) Hai đường thẳng song song với nhau. a) y = x – 1 
b) y = 1 – x  + 2x + 3  c) y = x + x
b) Hai đường thẳng cắt nhau.
c) Hai đường thẳng vuông góc với nhau.
2.45 Cho hai hàm số bậc nhất y = 2x + 3k và y = (2m + 1)x + 2k – 3. Tìm giá
trị của m và k để đồ thị của các hàm số là:
a) Hai đường thẳng song song với nhau.
b) Hai đường thẳng cắt nhau.
c) Hai đường thẳng trùng nhau.
2.46 Cho hai hàm số bậc nhất (d1) : y = (2 – m2)x + m – 5 và
(d2) : y = mx + 3m – 7. Tìm giá trị của m để đồ thị của các hàm số là:
a) Hai đường thẳng song song với nhau.
b) Hai đường thẳng cắt nhau.
c) Hai đường thẳng vuông góc với nhau.
2.47 Cho hàm số y = ax – 3. Hãy xác định hệ số a trong mỗi trường hợp sau :
a) Đồ thị của hàm số song song với đường thẳng y = – 2x.
b) Khi x = 2 thì hàm số có giá trị y = 7.
c) Cắt trục tung tại điểm có tung độ bằng – 1.
d) Cắt trục hoành tại điểm có hoành độ 3 – 1.
e) Đồ thị của hàm số cắt đường thẳng y = 2x – 1 tại điểm có hoành độ bằng 2.
f) Đồ thị của hàm số cắt đường thẳng y = –3x + 2 tại điểm có tung độ bằng 5.
2.48 Cho hàm số y = 2x + b. Hãy xác định hệ số b trong mỗi trường hợp sau :
a) Đồ thị của hàm số cắt trục tung tại điểm có tung độ bằng 3.
b) Đồ thị của hàm số đã cho đi qua điểm A(1 ; 5). 2 3
2.49 a) Vẽ đồ thị của các hàm số y = x + 2 và y =  x + 2 trên cùng một 3 2 mặt phẳng tọa độ. Gv: Trần Quốc Nghĩa Trang 56 Gv: Trần Quốc Nghĩa Trang 49 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
2.89 a) Cho các điểm M(–1 ; – 2), N(–2 ; –4), P(2 ; –3), Q(3 ; –4,5). Tìm tọa
2.43 Trong các đường thẳng sau, đường nào song song với nhau, đường nào
độ của các điểm M’, N’, P’ và Q’ lần lượt là các điểm dối xứng với vuông góc với nhau ?
các điểm M, N, P và Q qua trục Ox. 1 a) y = 1,5x + 2 ; b) y = x – 3 ; c) y = 5 – x
b) Vẽ đồ thị của hàm số y = x ; và y = x + 1 . 2
c) Tìm tọa độ giao điểm của các hàm số trên. Từ đó suy ra phương trình x  1 d) y = ; e) y = –x + 4 ; f) y = 2x – 1.
x  = x + 1  có một nghiệm duy nhất. 2
2.44 Cho hai hàm số bậc nhất y = mx + 3 và y = (2m + 1)x – 5. Tìm m để đồ
2.90 Vẽ đồ thị của các hàm số sau:
thị của các hàm số là: 2 x
a) Hai đường thẳng song song với nhau. a) y = x – 1 
b) y = 1 – x  + 2x + 3  c) y = x + x
b) Hai đường thẳng cắt nhau.
c) Hai đường thẳng vuông góc với nhau.
2.45 Cho hai hàm số bậc nhất y = 2x + 3k và y = (2m + 1)x + 2k – 3. Tìm giá
trị của m và k để đồ thị của các hàm số là:
a) Hai đường thẳng song song với nhau.
b) Hai đường thẳng cắt nhau.
c) Hai đường thẳng trùng nhau.
2.46 Cho hai hàm số bậc nhất (d1) : y = (2 – m2)x + m – 5 và
(d2) : y = mx + 3m – 7. Tìm giá trị của m để đồ thị của các hàm số là:
a) Hai đường thẳng song song với nhau.
b) Hai đường thẳng cắt nhau.
c) Hai đường thẳng vuông góc với nhau.
2.47 Cho hàm số y = ax – 3. Hãy xác định hệ số a trong mỗi trường hợp sau :
a) Đồ thị của hàm số song song với đường thẳng y = – 2x.
b) Khi x = 2 thì hàm số có giá trị y = 7.
c) Cắt trục tung tại điểm có tung độ bằng – 1.
d) Cắt trục hoành tại điểm có hoành độ 3 – 1.
e) Đồ thị của hàm số cắt đường thẳng y = 2x – 1 tại điểm có hoành độ bằng 2.
f) Đồ thị của hàm số cắt đường thẳng y = –3x + 2 tại điểm có tung độ bằng 5.
2.48 Cho hàm số y = 2x + b. Hãy xác định hệ số b trong mỗi trường hợp sau :
a) Đồ thị của hàm số cắt trục tung tại điểm có tung độ bằng 3.
b) Đồ thị của hàm số đã cho đi qua điểm A(1 ; 5). 2 3
2.49 a) Vẽ đồ thị của các hàm số y = x + 2 và y =  x + 2 trên cùng một 3 2 mặt phẳng tọa độ. Gv: Trần Quốc Nghĩa Trang 56 Gv: Trần Quốc Nghĩa Trang 49 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
b) Một đường thẳng song song với trục hoành Ox, cắt trục tung Oy tại c) ABC là tam giác gì ?
điểm có tung độ bằng 1, cắt các đường thẳng trên theo thứ tự tại M
d) Tìm tọa độ hình chiếu của A trên BC.
và N. Tìm tọa độ hai điểm M và N.
2.84 Trong mặt phẳng Oxy cho ba điểm A(–5 ; –1), B(–1 ; 4) và C(3 ; 2).
2.50 Tìm hệ số a của hàm số y = ax + 1, biết khi x = 1 + 2 thì y = 3 + 2 . a) Vẽ ABC.
2.51 Xác định hàm số y = ax + b biết đồ thị của hàm số cắt trục tung tại điểm
b) Viết phương trình các đường thẳng chứa các cạnh của tam giác.
có tung độ bằng 3 và cắt trục hoành tại điểm có hoành độ bằng –2.
c) Qua A kẻ đường thẳng song song với BC. Qua B kẻ đường thẳng
2.52 Trên mặt phẳng tọa độ Oxy cho hai điểm A(1 ; 2), B(3 ; 4).
vuông góc với BC. Xác định tọa độ giao điểm D của hai đường thẳng
a) Tìm hệ số a của đường thẳng đi qua A và B. đó.
b) Xác định hàm số biết đồ thị của nó là đường thẳng đi qua A và B.
2.85 a) Vẽ đồ thị của các hàm số sau trên cùng một mặt phẳng tọa độ :
2.53 Cho đường thẳng (d) : y = (k + 1)x + k. Tìm k để đường thẳng (d):
(d1): y = 3x + 6 (d2): y = 2x + 4 (d3): y = x + 2 (d1): y = 0,5x + 1 a) Đi qua gốc tọa độ.
b) Tính góc giữa các đường thẳng trên với trục Ox.
b) Cắt trục tung tại điểm có tung độ bằng 1 – 2 .
c) Có nhận xét gì về độ dốc của các đường thẳng trên.
c) Song song với đường thẳng y = ( 3 + 1)x + 3
2.86 a) Vẽ đồ thị của các hàm số sau trên cùng một mặt phẳng tọa độ :
2.54 Xét đường thẳng (d) : y = (2m – 1)x – m + 3. Định m để đường thẳng (d): 4 1 a) Đi qua gốc tọa độ.
(d1) : y = 2x – 2 (d2) : y =  x  2 (d3) : y = x + 3 3 3 b) Đi qua A(2 ; 3)
c) Cắt đường thẳng y = 3x + 7 tại một điểm trên trục tung
b) Gọi giao điểm các đường thẳng (d3) với hai đường thẳng (d1) và (d2)
d) Song song với đường thẳng y = 5x + 3
lần lượt tại A và B. Tìm tọa độ của các điểm A và B.
e) Vuông góc với đường thẳng y = 2x – 1.
c) Tính khoảng cách giữa hai điểm A và B. 1
2.87 a) Vẽ đồ thị của các hàm số (d
2.55 Cho các đường thẳng: (d
1) : y = 0,5x + 2 và (d2) : y = 5 – 2x.
1) : y = 3x + 1 và (d2) : y =  x – 2 4
b) Gọi giao điểm các đường thẳng (d1) và (d2) với trục hoành lần lượt tại
a) Viết phương trình đường thẳng (d3) qua M(4 ; –5) và song song với
A và B. gọi giao điểm của hai đường thẳng đó là C. Tìm tọa độ của đường thẳng (d1) các điểm A, B và C.
b) Viết phương trình đường thẳng (d4) qua N(3 ; 2) và vuông góc với
c) Tính độ dài các đoạn thẳng AB, AC và BC (đơn vị trên các trục là cm) đường thẳng (d2).
c) Viết phương trình đường thẳng (d
(làm tròn đến chữ số thập phân thứ hai). 5) qua hai điểm M và N.
d) Tính các góc tạo bởi các đường thẳng trên với trục Ox (làm tròn đến
2.56 Đường thẳng (d) cắt trục hoành tại điểm A có hoành độ là –4 và cắt trục phút).
tung tại điểm B có tung độ là –3.
a) Xác định phương trình đường thẳng (d).
2.88 a) Vẽ đồ thị của các hàm số (d1) : y = 2x , (d2) : y = 0,5x và
b) Viết phương trình đường cao CH của ABC với C( –1 ; –1) (d3) : y = –x + 6.
2.57 Cho hai điểm A(5 ; 1) và B(–1 ; 5) trong hệ tọa độ vuông góc Oxy. Chứng
b) Gọi giao điểm các đường thẳng (d3) với hai đường thẳng (d1) và (d2)
minh AOB vuông cân. Tính chu vi và diện tích của AOB.
lần lượt tại A và B. Tìm tọa độ của các điểm A và B.
2.58 Chứng minh rằng khi m thay đổi, đồ thị của hàm số sau luôn đi qua một
c) Tính các góc của OAB.
điểm cố định. Hãy xác định tọa độ của điểm cố định đó. a) y = (m – 2)x + 3 b) y = mx + (2m + 1) Gv: Trần Quốc Nghĩa Trang 50 Gv: Trần Quốc Nghĩa Trang 55 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
b) Một đường thẳng song song với trục hoành Ox, cắt trục tung Oy tại c) ABC là tam giác gì ?
điểm có tung độ bằng 1, cắt các đường thẳng trên theo thứ tự tại M
d) Tìm tọa độ hình chiếu của A trên BC.
và N. Tìm tọa độ hai điểm M và N.
2.84 Trong mặt phẳng Oxy cho ba điểm A(–5 ; –1), B(–1 ; 4) và C(3 ; 2).
2.50 Tìm hệ số a của hàm số y = ax + 1, biết khi x = 1 + 2 thì y = 3 + 2 . a) Vẽ ABC.
2.51 Xác định hàm số y = ax + b biết đồ thị của hàm số cắt trục tung tại điểm
b) Viết phương trình các đường thẳng chứa các cạnh của tam giác.
có tung độ bằng 3 và cắt trục hoành tại điểm có hoành độ bằng –2.
c) Qua A kẻ đường thẳng song song với BC. Qua B kẻ đường thẳng
2.52 Trên mặt phẳng tọa độ Oxy cho hai điểm A(1 ; 2), B(3 ; 4).
vuông góc với BC. Xác định tọa độ giao điểm D của hai đường thẳng
a) Tìm hệ số a của đường thẳng đi qua A và B. đó.
b) Xác định hàm số biết đồ thị của nó là đường thẳng đi qua A và B.
2.85 a) Vẽ đồ thị của các hàm số sau trên cùng một mặt phẳng tọa độ :
2.53 Cho đường thẳng (d) : y = (k + 1)x + k. Tìm k để đường thẳng (d):
(d1): y = 3x + 6 (d2): y = 2x + 4 (d3): y = x + 2 (d1): y = 0,5x + 1 a) Đi qua gốc tọa độ.
b) Tính góc giữa các đường thẳng trên với trục Ox.
b) Cắt trục tung tại điểm có tung độ bằng 1 – 2 .
c) Có nhận xét gì về độ dốc của các đường thẳng trên.
c) Song song với đường thẳng y = ( 3 + 1)x + 3
2.86 a) Vẽ đồ thị của các hàm số sau trên cùng một mặt phẳng tọa độ :
2.54 Xét đường thẳng (d) : y = (2m – 1)x – m + 3. Định m để đường thẳng (d): 4 1 a) Đi qua gốc tọa độ.
(d1) : y = 2x – 2 (d2) : y =  x  2 (d3) : y = x + 3 3 3 b) Đi qua A(2 ; 3)
c) Cắt đường thẳng y = 3x + 7 tại một điểm trên trục tung
b) Gọi giao điểm các đường thẳng (d3) với hai đường thẳng (d1) và (d2)
d) Song song với đường thẳng y = 5x + 3
lần lượt tại A và B. Tìm tọa độ của các điểm A và B.
e) Vuông góc với đường thẳng y = 2x – 1.
c) Tính khoảng cách giữa hai điểm A và B. 1
2.87 a) Vẽ đồ thị của các hàm số (d
2.55 Cho các đường thẳng: (d
1) : y = 0,5x + 2 và (d2) : y = 5 – 2x.
1) : y = 3x + 1 và (d2) : y =  x – 2 4
b) Gọi giao điểm các đường thẳng (d1) và (d2) với trục hoành lần lượt tại
a) Viết phương trình đường thẳng (d3) qua M(4 ; –5) và song song với
A và B. gọi giao điểm của hai đường thẳng đó là C. Tìm tọa độ của đường thẳng (d1) các điểm A, B và C.
b) Viết phương trình đường thẳng (d4) qua N(3 ; 2) và vuông góc với
c) Tính độ dài các đoạn thẳng AB, AC và BC (đơn vị trên các trục là cm) đường thẳng (d2).
c) Viết phương trình đường thẳng (d
(làm tròn đến chữ số thập phân thứ hai). 5) qua hai điểm M và N.
d) Tính các góc tạo bởi các đường thẳng trên với trục Ox (làm tròn đến
2.56 Đường thẳng (d) cắt trục hoành tại điểm A có hoành độ là –4 và cắt trục phút).
tung tại điểm B có tung độ là –3.
a) Xác định phương trình đường thẳng (d).
2.88 a) Vẽ đồ thị của các hàm số (d1) : y = 2x , (d2) : y = 0,5x và
b) Viết phương trình đường cao CH của ABC với C( –1 ; –1) (d3) : y = –x + 6.
2.57 Cho hai điểm A(5 ; 1) và B(–1 ; 5) trong hệ tọa độ vuông góc Oxy. Chứng
b) Gọi giao điểm các đường thẳng (d3) với hai đường thẳng (d1) và (d2)
minh AOB vuông cân. Tính chu vi và diện tích của AOB.
lần lượt tại A và B. Tìm tọa độ của các điểm A và B.
2.58 Chứng minh rằng khi m thay đổi, đồ thị của hàm số sau luôn đi qua một
c) Tính các góc của OAB.
điểm cố định. Hãy xác định tọa độ của điểm cố định đó. a) y = (m – 2)x + 3 b) y = mx + (2m + 1) Gv: Trần Quốc Nghĩa Trang 50 Gv: Trần Quốc Nghĩa Trang 55 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
2.78 Cho đường thẳng (d) : y = (1 – 4m)x + m – 2. Tìm giá trị của m để đường
2.59 Cho hai đường thẳng (d1): y = mx – 2m – 1, (d2): y = (m + 2)x + 1 – 2m thẳng (d):
a) Khi (d1)  (d2), hãy xác định tọa độ giao điểm của mỗi đường thẳng a) Đi qua gốc tọa độ.
với các trục tọa độ.
b) Tạo với trục Ox một góc nhọn ? Góc tù ?
b) Chứng minh rằng khi m thay đổi, mỗi đường thẳng nói trên luôn đi
qua một điểm cố định.
c) Cắt trục tung tại một điểm có tung độ bằng 1,5.
d) Cắt trục hoành tại một điểm có hoành độ bằng 0,5.
2.60 Xác định hàm số trong mỗi trường hợp sau, biết đồ thị của hàm số là
đường thẳng đi qua gốc tọa độ :
2.79 Cho đường thẳng (d) : y = (m – 2)x + n (m  2). Tìm giá trị của m và n a) Đi qua điểm A(3 ; 2); để đường thẳng (d):
b) Có hệ số góc bằng 3 ;
a) Đi qua hai điểm A(–1 ; 2), B(3 ; –4).
c) Song song với đường thẳng y = 3x + 1.
b) Cắt trục tung tại một điểm có tung độ bằng 1 – 2 và cắt trục hoành
2.61 Cho hàm số bậc nhất y = ax + 3.
tại một điểm có hoành độ bằng 2 + 2 .
a) Xác định hệ số góc a, biết rằng đồ thị của hàm số đi qua điểm A(2 ; 6).
c) Cắt đường thẳng : –2y + x – 3 = 0.
b) Vẽ đồ thị của hàm số ứng với giá trị của a vừa tìm được.
d) Song song với đường thẳng : 3x + 2y = 1.
2.62 Cho hàm số y = –2x + 3 (d).
e) Trùng với đường thẳng : y – 2x + 3 = 0.
a) Vẽ đồ thị của hàm số.
b) Tính góc tạo bởi đường thẳng (d) và trục Ox (làm tròn đến phút).
2.80 Cho hai đường thẳng :
2.63 Xác định hàm số bậc nhất y = ax + b trong mỗi trường hợp sau :
(d1) : y = (m2 – 1)x + m + 2 và (d2) : y = (5 – m)x + 2m + 5.
a) a = 2 và đồ thị của hàm số cắt trục hoành tại điểm có hoành độ bằng
Tìm m để hai đường thẳng trên song song với nhau. 1,5.
2.81 Cho đường thẳng: (d) : y = (2m – 1)x + m – 2. Tìm m để đường thẳng (d):
b) a = 3 và đồ thị của hàm số đi qua điểm A(2 ; 2) a) Đi qua điểm A(1 ; 6).
c) Đồ thị của hàm số song song với đường thẳng y = 3 x và đi qua điểm
b) Song song với đường thẳng 2x + 3y – 5 = 0. B(1 ; 3 + 5).
c) Vuông góc với đường thẳng x + 2y + 1 = 0. 1 1
2.64 a) Vẽ đồ thị của các hàm số y =
x + 2 và y = – x + 2 trên cùng một mặt
d) Không đi qua điểm B(  ; 1) 2 2 phẳng tọa độ.
e) Luôn đi qua một điểm cố định.
b) Gọi giao điểm của hai đường thẳng trên với trục hoành theo thứ tự là
A, B và gọi giao điểm của hai đường thẳng đó là C. Tính các góc của
2.82 Tìm m để ba đường thẳng sau đồng qui:
ABC (làm tròn đến độ).
a) (d1) : y = 2x – 1, (d2) : 3x + 5y = 8, (d3) : (m + 8)x – 2my = 3m
c) Tính chu vi và diện tích của ABC (đơn vị đo trên các trục tọa độ là
b) (d1) : y = –x + 1, (d2) : y = x – 1, (d3) : (m + 1)x – (m – 1)y = m + 1 xentimét)
c) (d1) : y = 2x – m, (d2) : y = –x + 2m, (d3) : mx – (m – 1)y = 2m – 1 1
2.83 Trên hệ trục tọa độ vuông góc Oxy cho ABC mà ba cạnh AB, BC, CA
2.65 a) Vẽ đồ thị của các hàm số: y = x + 1; y = x + 3 ; y = 3 x – 3 . 3
của nó lần lượt nằm trên ba đường thẳng sau:
b) Gọi , ,  lần lượt là các góc tạo bởi các đường thẳng trên và trục Ox.
(d1) : y = x + 3, (d2) : x – 5y = – 7 (d3) : y = 5 – x. 1
a) Vẽ các đường thẳng AB, BC, CA trên cùng hệ trục tọa độ. CMR: tan = 1, tan =
, an = 3 . Tính số đo các góc , , . 3
b) Tìm tọa độ ba đỉnh của ABC.
2.66 a) Tìm hệ số góc của đường thẳng đi qua gốc tọa độ và qua điểm A(2 ; 1) Gv: Trần Quốc Nghĩa Trang 54 Gv: Trần Quốc Nghĩa Trang 51 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
2.78 Cho đường thẳng (d) : y = (1 – 4m)x + m – 2. Tìm giá trị của m để đường
2.59 Cho hai đường thẳng (d1): y = mx – 2m – 1, (d2): y = (m + 2)x + 1 – 2m thẳng (d):
a) Khi (d1)  (d2), hãy xác định tọa độ giao điểm của mỗi đường thẳng a) Đi qua gốc tọa độ.
với các trục tọa độ.
b) Tạo với trục Ox một góc nhọn ? Góc tù ?
b) Chứng minh rằng khi m thay đổi, mỗi đường thẳng nói trên luôn đi
qua một điểm cố định.
c) Cắt trục tung tại một điểm có tung độ bằng 1,5.
d) Cắt trục hoành tại một điểm có hoành độ bằng 0,5.
2.60 Xác định hàm số trong mỗi trường hợp sau, biết đồ thị của hàm số là
đường thẳng đi qua gốc tọa độ :
2.79 Cho đường thẳng (d) : y = (m – 2)x + n (m  2). Tìm giá trị của m và n a) Đi qua điểm A(3 ; 2); để đường thẳng (d):
b) Có hệ số góc bằng 3 ;
a) Đi qua hai điểm A(–1 ; 2), B(3 ; –4).
c) Song song với đường thẳng y = 3x + 1.
b) Cắt trục tung tại một điểm có tung độ bằng 1 – 2 và cắt trục hoành
2.61 Cho hàm số bậc nhất y = ax + 3.
tại một điểm có hoành độ bằng 2 + 2 .
a) Xác định hệ số góc a, biết rằng đồ thị của hàm số đi qua điểm A(2 ; 6).
c) Cắt đường thẳng : –2y + x – 3 = 0.
b) Vẽ đồ thị của hàm số ứng với giá trị của a vừa tìm được.
d) Song song với đường thẳng : 3x + 2y = 1.
2.62 Cho hàm số y = –2x + 3 (d).
e) Trùng với đường thẳng : y – 2x + 3 = 0.
a) Vẽ đồ thị của hàm số.
b) Tính góc tạo bởi đường thẳng (d) và trục Ox (làm tròn đến phút).
2.80 Cho hai đường thẳng :
2.63 Xác định hàm số bậc nhất y = ax + b trong mỗi trường hợp sau :
(d1) : y = (m2 – 1)x + m + 2 và (d2) : y = (5 – m)x + 2m + 5.
a) a = 2 và đồ thị của hàm số cắt trục hoành tại điểm có hoành độ bằng
Tìm m để hai đường thẳng trên song song với nhau. 1,5.
2.81 Cho đường thẳng: (d) : y = (2m – 1)x + m – 2. Tìm m để đường thẳng (d):
b) a = 3 và đồ thị của hàm số đi qua điểm A(2 ; 2) a) Đi qua điểm A(1 ; 6).
c) Đồ thị của hàm số song song với đường thẳng y = 3 x và đi qua điểm
b) Song song với đường thẳng 2x + 3y – 5 = 0. B(1 ; 3 + 5).
c) Vuông góc với đường thẳng x + 2y + 1 = 0. 1 1
2.64 a) Vẽ đồ thị của các hàm số y =
x + 2 và y = – x + 2 trên cùng một mặt
d) Không đi qua điểm B(  ; 1) 2 2 phẳng tọa độ.
e) Luôn đi qua một điểm cố định.
b) Gọi giao điểm của hai đường thẳng trên với trục hoành theo thứ tự là
A, B và gọi giao điểm của hai đường thẳng đó là C. Tính các góc của
2.82 Tìm m để ba đường thẳng sau đồng qui:
ABC (làm tròn đến độ).
a) (d1) : y = 2x – 1, (d2) : 3x + 5y = 8, (d3) : (m + 8)x – 2my = 3m
c) Tính chu vi và diện tích của ABC (đơn vị đo trên các trục tọa độ là
b) (d1) : y = –x + 1, (d2) : y = x – 1, (d3) : (m + 1)x – (m – 1)y = m + 1 xentimét)
c) (d1) : y = 2x – m, (d2) : y = –x + 2m, (d3) : mx – (m – 1)y = 2m – 1 1
2.83 Trên hệ trục tọa độ vuông góc Oxy cho ABC mà ba cạnh AB, BC, CA
2.65 a) Vẽ đồ thị của các hàm số: y = x + 1; y = x + 3 ; y = 3 x – 3 . 3
của nó lần lượt nằm trên ba đường thẳng sau:
b) Gọi , ,  lần lượt là các góc tạo bởi các đường thẳng trên và trục Ox.
(d1) : y = x + 3, (d2) : x – 5y = – 7 (d3) : y = 5 – x. 1
a) Vẽ các đường thẳng AB, BC, CA trên cùng hệ trục tọa độ. CMR: tan = 1, tan =
, an = 3 . Tính số đo các góc , , . 3
b) Tìm tọa độ ba đỉnh của ABC.
2.66 a) Tìm hệ số góc của đường thẳng đi qua gốc tọa độ và qua điểm A(2 ; 1) Gv: Trần Quốc Nghĩa Trang 54 Gv: Trần Quốc Nghĩa Trang 51 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
b) Tìm hệ số góc của đường thẳng đi qua gốc tọa độ và điểm B(1 ; –2)
c) Vẽ đồ thị của các hàm số với hệ số góc vừa tìm được ở các câu a và b
D - Ôn tập chương 2
trên cùng một mặt phẳng tọa độ và chứng tỏ rằng hai đường thẳng đó vuông góc với nhau.
2.70 Cho hàm số y = f(x) = 2  x  2 1  x
2.67 Cho hai đường thẳng (d) : y = ax + b và (d) y = ax + b.
Chứng minh rằng: Trên cùng một mặt phẳng tọa độ, hai đường thẳng (d)
a) Tìm điều kiện xác định của hàm số.
và (d’) vuông góc với nhau khi và chỉ khi a .a’ = –1.
b) Tìm tọa độ giao điểm của đồ thị hàm số với trục tung và trục hoành.
2.68 a) Vẽ đồ thị của các hàm số (d
c) So sánh f(– 2 ) và f(–1,5).
1) : y = x và (d2) : y = 0,5x.
b) Vẽ đường thẳng (d) song song với Ox và cắt trục tung tại điểm có tung
2.71 Với giá trị nào của m thì hàm số bậc nhất sau đồng biến ?
độ bằng 2, và cắt các đường thẳng trên theo thứ tự tại D và E. Tìm tọa a) y = (m – 1)x + 3 b) y = (m + 6)x – 7
độ của các điểm D và E. Tính chu vi và diện tích của ODE.
2.69 a) Vẽ đồ thị của các hàm số (d
2.72 Với những giá trị nào của k thì các hàm số bậc nhất nghịch biến ?
1) : y = –2x và (d2) : y = 0,5x.
b) Qua điểm K(0 ; 2) vẽ đường thẳng (d) song song với Ox. Đường thẳng a) y = (5 – k)x + 1 b) y = (–k + 9)x + 100.
(d) cắt đường thẳng (d1) và (d2) lần lượt tại A và B. Tìm tọa độ của các
2.73 Với giá trị nào của m thì đồ thị của các hàm số cắt nhau tại một điểm trên điểm A và B. trục tung ?
c) Hãy chứng tỏ rằng AÔB = 900. a) y = 2x + (3 + m) và y = 3x + (5 – m) b) y = 12x + (5 – m) và y = 3x + (3 + m)
2.74 Tìm các giá trị của a để hai đường thẳng sau y = (a – 1)x + 2 (a  1) và
y = (3 – a)x + 1 (a  3) song song với nhau.
2.75 Xác định k để hai đường thẳng sau đây trùng nhau:
y = kx + (m – 2) (k  0) và y = (5 – k)x + (4 – m) (k  5)
2.76 Cho hai hàm số bậc nhất y = (k + 1)x + 3 và y = (3 – 2k)x + 1.
a) Với giá trị nào của k thì đồ thị của hai hàm số của hai hàm số là hai
đường thẳng song song với nhau ?
b) Với giá trị nào của k thì đồ thị của hai hàm số là hai đường thẳng cắt nhau ?
c) Hai đường thẳng nói trên có thể trùng nhau được không ? Vì sao ? 1
2.77 Cho hàm số y = (2m – 1)x với m  . 2
a) Với giá trị nào của m thì hàm số đồng biến ? Nghịch biến ?
b) Tìm giá trị của m để đồ thị của hàm số đi qua điểm A(–0,5; 1,5).
c) Vẽ đồ thị của hàm số với giá trị m vừa tìm được ở câu b).
d) Đồ thị vừa vẽ có quan hệ như thế nào với các đường thẳng sau:
(d1): 3x + y = 1 ; (d2): 3y – x – 12 = 0. Gv: Trần Quốc Nghĩa Trang 52 Gv: Trần Quốc Nghĩa Trang 53 Bài tập Toán 9 Học kì 1 Bài tập Toán 9 Học kì 1
b) Tìm hệ số góc của đường thẳng đi qua gốc tọa độ và điểm B(1 ; –2)
c) Vẽ đồ thị của các hàm số với hệ số góc vừa tìm được ở các câu a và b
D - Ôn tập chương 2
trên cùng một mặt phẳng tọa độ và chứng tỏ rằng hai đường thẳng đó vuông góc với nhau.
2.70 Cho hàm số y = f(x) = 2  x  2 1  x
2.67 Cho hai đường thẳng (d) : y = ax + b và (d) y = ax + b.
Chứng minh rằng: Trên cùng một mặt phẳng tọa độ, hai đường thẳng (d)
a) Tìm điều kiện xác định của hàm số.
và (d’) vuông góc với nhau khi và chỉ khi a .a’ = –1.
b) Tìm tọa độ giao điểm của đồ thị hàm số với trục tung và trục hoành.
2.68 a) Vẽ đồ thị của các hàm số (d
c) So sánh f(– 2 ) và f(–1,5).
1) : y = x và (d2) : y = 0,5x.
b) Vẽ đường thẳng (d) song song với Ox và cắt trục tung tại điểm có tung
2.71 Với giá trị nào của m thì hàm số bậc nhất sau đồng biến ?
độ bằng 2, và cắt các đường thẳng trên theo thứ tự tại D và E. Tìm tọa a) y = (m – 1)x + 3 b) y = (m + 6)x – 7
độ của các điểm D và E. Tính chu vi và diện tích của ODE.
2.69 a) Vẽ đồ thị của các hàm số (d
2.72 Với những giá trị nào của k thì các hàm số bậc nhất nghịch biến ?
1) : y = –2x và (d2) : y = 0,5x.
b) Qua điểm K(0 ; 2) vẽ đường thẳng (d) song song với Ox. Đường thẳng a) y = (5 – k)x + 1 b) y = (–k + 9)x + 100.
(d) cắt đường thẳng (d1) và (d2) lần lượt tại A và B. Tìm tọa độ của các
2.73 Với giá trị nào của m thì đồ thị của các hàm số cắt nhau tại một điểm trên điểm A và B. trục tung ?
c) Hãy chứng tỏ rằng AÔB = 900. a) y = 2x + (3 + m) và y = 3x + (5 – m) b) y = 12x + (5 – m) và y = 3x + (3 + m)
2.74 Tìm các giá trị của a để hai đường thẳng sau y = (a – 1)x + 2 (a  1) và
y = (3 – a)x + 1 (a  3) song song với nhau.
2.75 Xác định k để hai đường thẳng sau đây trùng nhau:
y = kx + (m – 2) (k  0) và y = (5 – k)x + (4 – m) (k  5)
2.76 Cho hai hàm số bậc nhất y = (k + 1)x + 3 và y = (3 – 2k)x + 1.
a) Với giá trị nào của k thì đồ thị của hai hàm số của hai hàm số là hai
đường thẳng song song với nhau ?
b) Với giá trị nào của k thì đồ thị của hai hàm số là hai đường thẳng cắt nhau ?
c) Hai đường thẳng nói trên có thể trùng nhau được không ? Vì sao ? 1
2.77 Cho hàm số y = (2m – 1)x với m  . 2
a) Với giá trị nào của m thì hàm số đồng biến ? Nghịch biến ?
b) Tìm giá trị của m để đồ thị của hàm số đi qua điểm A(–0,5; 1,5).
c) Vẽ đồ thị của hàm số với giá trị m vừa tìm được ở câu b).
d) Đồ thị vừa vẽ có quan hệ như thế nào với các đường thẳng sau:
(d1): 3x + y = 1 ; (d2): 3y – x – 12 = 0. Gv: Trần Quốc Nghĩa Trang 52 Gv: Trần Quốc Nghĩa Trang 53