Bài tập toán lớp 7 giá trị của một biểu thức đại số ( có lời giải chi tiết )

Tổng hợp toàn bộ Bài tập  toán lớp 7 giá trị của một biểu thức đại số  ( có lời giải chi tiết) gồm lí thuyết và được biên soạn gồm 5 trang. Các bạn tham khảo và ôn tập kiến thức đầy đủ cho kì thi sắp tới. Chúc các bạn đạt kết quả cao nhé và đạt được thành tích bạn đã kì vọng !!!

41 21 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 7: Biểu thức đại số và đa thức một biến (KNTT)

Môn: Toán 7

Thông tin:

5 trang 9 tháng trước

Tác giả:

Profile Hiền Trần
Trang 1
GIÁ TRỊ CỦA MỘT BIỂU THỨC ĐẠI SỐ
I. TM TT L THUYT
Khi thay các biến trong một biểu thức đại số bằng những số đã cho, ta được một biểu
thức đại số. Kết quả nhận được khi thực hiện các phép tính trong biểu thức đại số đó gọi
là giá trị của biểu thức đại số tại các giá trị cho trước của các biến.
II. BÀI TẬP
Bài 1: Tính giá trị của các biểu thức sau:
Biểu thức
Giá trị biểu thức tại
x3
5
x
2
2x =
1,5x =-
2
2x 5x 3-+
( )
( )
2
4x 3 x 2 2x- + +
Bài 2: Tính giá trị của các biểu thức sau tại
1
, 1.
2
xy==
a)
2
2 3 5A x x= - +
b)
22
2 3 .B x xy y= - +
Giải:
1
2
x =
nên
............x =
hoặc
............x =
1.y =
nên
......y =
hoặc
......y =
a) Với
............x =
ta có
A =
…………………………………………………………………..
Với
............x =
ta có
A =
…………………………………………………………………..
b) Với
............x =
;
............y =
ta có
B =
…………………………………………………..
………………………………………………………………………………………………….
Với
............x =
;
............y =
ta có
B =
…………………………………………………..
………………………………………………………………………………………………….
Với
............x =
;
............y =
ta có
B =
…………………………………………………..
………………………………………………………………………………………………….
Trang 2
Với
............x =
;
............y =
ta có
B =
…………………………………………………..
………………………………………………………………………………………………….
Bài 3: Một mảnh vườn hình chữ nhật có chiều dài
x
(m), chiều rộng
y
(m). Người ta
mở một lối đi xung quanh vườn (thuộc đất của vườn) rộng
z
(m)
( )
, 2zxy>
.
a) Tính diện tích đất làm đường đi theo
, , .x y z
b) Tính diện tích đất dành làm đường đi biết
50; 30; 2x y z= = =
c) Tìm chiều dài và chiều rộng miếng đất biết diện tích dành làm đường là
2
384m
,
chiều rộng đường đi là 2m và chiều dài hơn chiều rộng 12m.
………………………………………………………………………………….
………………………………………………………………………………….
………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
Trang 3
………………………………………………………………………………………………….
………………………………………………………………………………………………….
Bài 4: Tính giá trị của biểu thức sau biết rằng
1 0.xy+ + =
( ) ( )
2 2 2 2
2( ) 3.D x x y y x y x y x y= + - + + - + + +
……………………………………………………………………………………………
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
Bài 5: Cho
2xyz =
và
0xyz+ + =
. Tính giá trị của biểu thức
( )( )( )
.M x y y z x z= + + +
……………………………………………………………………………………………
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
Bài 6: Tìm giá trị nhỏ nhất của các biểu thức sau:
a)
( )
2
5 7 2000A x y= - + - +
b)
6
4
2
2019
7
B x y
æö
÷
ç
÷
= + - -
ç
÷
ç
÷
ç
èø
……………………………………………………………………………………………
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
……………………………………………………………………………………………
………………………………………………………………………………………………….
………………………………………………………………………………………………….
Trang 4
………………………………………………………………………………………………….
HDG
Bài 1:
Biểu thức
Giá trị biểu thức tại
x3
5
x
2
2x =
1,5x =-
2
2x 5x 3-+
( )
( )
2
4x 3 x 2 2x- + +
Bài 2: Tại
1
x
2
Tính được
2
1 1 1 3 1 3
2 3. 5 2. 5 5 1 5 4
2 2 4 2 2 2
A
æö
÷
ç
÷
= - + = - + = - + = - + =
ç
÷
ç
÷
ç
èø
Tại
1
x
2

tính được
2
1 1 1 3 1 3
2 3. 5 2. 5 5 2 5 7
2 2 4 2 2 2
A
æ ö æ ö
÷÷
çç
÷÷
= - - - + = + + = + + = + =
çç
÷÷
çç
÷÷
çç
è ø è ø
b) Tại
1
2
x =
,
1y =
tính được
0B =
Tại
1
2
x =-
,
1y =
tính được
3B =
Tại
1
2
x =
,
1y =-
tính được
3B =
Tại
1
2
x =-
,
1y =-
tính được
0B =
Bài 3: a) Diện tích mảnh vườn ban đầu là:
2
()xy m
Sau khi mở một lối đi xung quanh vườn (thuộc đất của vườn) rộng
z( )m
thì mảnh vườn còn
lại có chiều dài là
2 ( )x z m-
, chiều rộng là
y 2 ( )zm-
nên mảnh vườn lúc sau có diện tích là
( )( )
2
2z 2z ( )x y m--
Vậy diện tích đất làm đường đi là:
( )( ) ( )
2 2 2
2 2z 2xz 2 4z 2z 4z ( )xy x z y xy xy yz x y m- - - = - + + - = + -
b) Với
50; 30; 2x y z= = =
thì diện tích đất dành làm đường đi là:
( )
22
2 2 50 30 4 2 304 ( )m× × + - × =
c) Vì diện tích dành làm đường là
2
384m
, chiều rộng đường đi là 2m nên ta có:
( )
2
2 2 4 2 384 100x y x y× × + - × = Û + =
(1)
Vì chiều dài hơn chiều rộng 12m nên ta có:
12xy-=
(2)
Trang 5
Từ (1) và (2) suy ra:
( )
100 12 : 2 56 ( / )x t m= + =
và
100 56 44 ( / )y t m= - =
Vậy mảnh vườn ban đầu có chiều dài là 56m, chiều rộng là 44m.
Bài 4
Từ
10xy+ + =
suy ra
1xy+ = -
. Thay
1xy+ = -
vào biểu thức
D
ta được:
2 2 2 2
.( 1) y .( 1) .y 2.( 1) 3D x x= - - - + + - +
2 2 2 2
y y 2 3 1xx= - + + - - + =
Bài 5
0xyz+ + =
nên
x y z+ = -
,
y z x+ = -
,
x z y+ = -
. Thay các giá trị này vào biểu thức
M
ta được:
( )( )( ) xyz 2M z x y= - - - = - = -
Bài 6:
Ta có :
( )
2
5 0,xx- ³ "
và
7 0,yy- ³ "
nên
( )
2
5 7 2000 2000 ,A x y x y= - + - + ³ "
Dấu
""=
xảy ra khi:
5 0 5
7 0 7
xx
yy
ìì
ïï
- = =
ïï
Û
íí
ïï
- = =
ïï
îî
Vậy giá trị nhỏ nhất của biểu thức A là 2000 khi
5; y 7x ==
.
b) Ta có :
4
0,xx³"
và
6
2
0,
7
yy
æö
÷
ç
÷
- ³ "
ç
÷
ç
÷
ç
èø
nên
6
4
2
2019 2019, ,
7
B x y x y
æö
÷
ç
÷
= + - - ³ - "
ç
÷
ç
÷
ç
èø
Dấu
""=
xảy ra khi:
0
2
7
x
y
ì
ï
=
ï
ï
ï
í
ï
=
ï
ï
ï
î
Vậy giá trị nhỏ nhất của biểu thức B là
2019-
khi
2
0; y
7
x ==
.
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

GIÁ TRỊ CỦA MỘT BIỂU THỨC ĐẠI SỐ
I. TÓM TẮT LÝ THUYẾT
 Khi thay các biến trong một biểu thức đại số bằng những số đã cho, ta được một biểu
thức đại số. Kết quả nhận được khi thực hiện các phép tính trong biểu thức đại số đó gọi
là giá trị của biểu thức đại số tại các giá trị cho trước của các biến.  II. BÀI TẬP
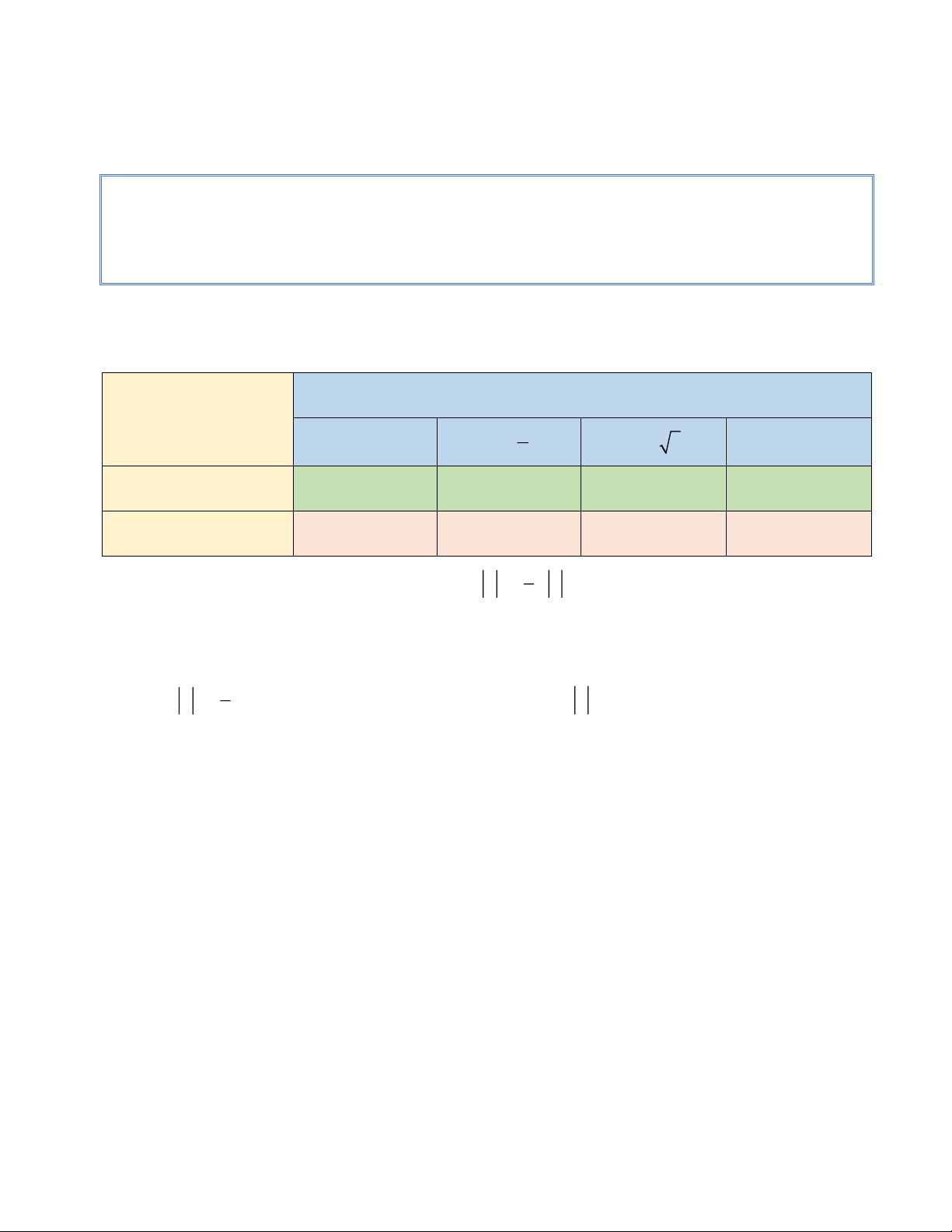
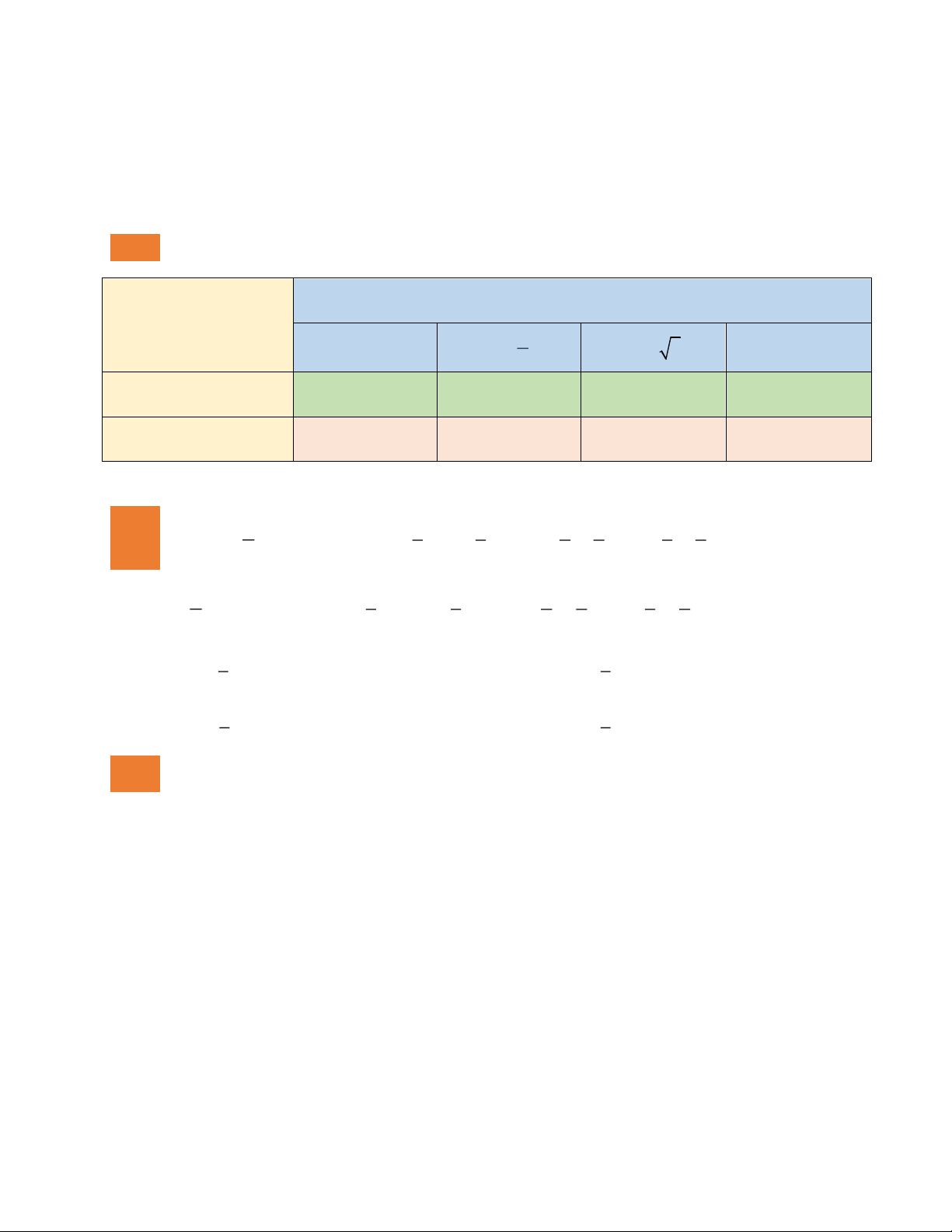
Bài 1: Tính giá trị của các biểu thức sau:
Giá trị biểu thức tại Biểu thức 5 x  3  x  x = 2 x = - 1, 5 2 2 2x - 5x + 3 ( - )( 2 4x 3 x + 2x + ) 2 1
Bài 2: Tính giá trị của các biểu thức sau tại x = , y = 1. 2 a) 2
A = 2x - 3x + 5 b) 2 2
B = 2x - 3xy + y . Giải:  1 x =
nên x = ............ hoặc x = ............
y = 1.nên y = ...... hoặc y = ...... 2 a) Với x = ............ ta có A =
………………………………………………………………….. Với x = ............ ta có A =
………………………………………………………………….. b) Với x = ............ ; y = ............ ta có B =
…………………………………………………..
………………………………………………………………………………………………….
 Với x = ............; y = ............ ta có B = …………………………………………………..
………………………………………………………………………………………………….
 Với x = ............; y = ............ ta có B = …………………………………………………..
…………………………………………………………………………………………………. Trang 1
 Với x = ............; y = ............ ta có B = …………………………………………………..
………………………………………………………………………………………………….
Bài 3: Một mảnh vườn hình chữ nhật có chiều dài x (m), chiều rộng y (m). Người ta
mở một lối đi xung quanh vườn (thuộc đất của vườn) rộng z (m) (x,y > 2z).
a) Tính diện tích đất làm đường đi theo x, y, z.
b) Tính diện tích đất dành làm đường đi biết x = 50; y = 30; z = 2
c) Tìm chiều dài và chiều rộng miếng đất biết diện tích dành làm đường là 2 384 m ,
chiều rộng đường đi là 2m và chiều dài hơn chiều rộng 12m.
………………………………………………………………………………….
………………………………………………………………………………….
………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
…………………………………………………………………………………………………. Trang 2
………………………………………………………………………………………………….
………………………………………………………………………………………………….
Bài 4: Tính giá trị của biểu thức sau biết rằng x + y + 1 = 0. 2
D = x (x + y ) 2
- y (x + y ) 2 2
+ x - y + 2(x + y ) + 3.
 ……………………………………………………………………………………………
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
Bài 5: Cho xyz = 2 và x + y + z = 0 . Tính giá trị của biểu thức M = (x + y )(y + z )(x + z ).
 ……………………………………………………………………………………………
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
Bài 6: Tìm giá trị nhỏ nhất của các biểu thức sau: 6 æ 2ö ç ÷ a) A = (x - )2 5 + y - 7 + 2000 b) 4 B = x + y ç - ÷ - 2019 ç ÷ çè 7÷ ø
 ……………………………………………………………………………………………
………………………………………………………………………………………………….
………………………………………………………………………………………………….
………………………………………………………………………………………………….
 ……………………………………………………………………………………………
………………………………………………………………………………………………….
…………………………………………………………………………………………………. Trang 3
…………………………………………………………………………………………………. HDG Bài 1:
Giá trị biểu thức tại Biểu thức 5 x  3  x  x = 2 x = - 1, 5 2 2 2x - 5x + 3 ( - )( 2 4x 3 x + 2x + ) 2 2 1 1 æ ö ç ÷ 1 1 3 1 3 Bài 2: Tại x 
Tính được A = 2ç ÷ - 3. + 5 = 2. - + 5 = - + 5 = - 1 + 5 = 4 ç ÷ 2 çè2÷ø 2 4 2 2 2 2 1 æ 1ö æ 1ö ç ÷ ç ÷ 1 3 1 3
Tại x   tính được A = 2 - ç ÷ - 3. - ç ÷+ 5 = 2. + + 5 = + + 5 = 2 + 5 = 7 ç ÷ ç ÷ ç ÷ 2 è 2ø çè 2÷ø 4 2 2 2 1 1 b)  Tại x =
, y = 1 tính được B = 0  Tại x = -
, y = 1 tính được B = 3 2 2 1 1  Tại x =
, y = - 1 tính được B = 3  Tại x = -
, y = - 1 tính được B = 0 2 2
Bài 3: a) Diện tích mảnh vườn ban đầu là: 2 xy (m )
Sau khi mở một lối đi xung quanh vườn (thuộc đất của vườn) rộng z(m ) thì mảnh vườn còn
lại có chiều dài là x - 2z (m ) , chiều rộng là y- 2z (m ) nên mảnh vườn lúc sau có diện tích là (x - )(y - ) 2 2z 2z (m )
Vậy diện tích đất làm đường đi là:
xy - (x - z )(y - ) 2 = xy - xy + + yz - = (x + y) 2 2 2 2z 2xz 2 4z 2z - 4z (m )
b) Với x = 50;y = 30;z = 2 thì diện tích đất dành làm đường đi là: × ( × + ) 2 2 2 2 50 30 - 4 2 × = 304 (m )
c) Vì diện tích dành làm đường là 2
384m , chiều rộng đường đi là 2m nên ta có: × ( × x + y ) 2 2 2 - 4 2
× = 384 Û x + y = 100 (1)
Vì chiều dài hơn chiều rộng 12m nên ta có: x - y = 12 (2) Trang 4
Từ (1) và (2) suy ra: x = (100 + 12): 2 = 56 (t / m ) và y = 100 - 56 = 44 (t / m)
Vậy mảnh vườn ban đầu có chiều dài là 56m, chiều rộng là 44m. Bài 4
Từ x + y + 1 = 0 suy ra x + y = - 1. Thay x + y = - 1 vào biểu thức D ta được: 2 2 2 2
D = x .(- 1) - y .(- 1) + x . y + 2.(- 1) + 3 2 2 2 2
= - x + y + x - y - 2 + 3 = 1 Bài 5
x + y + z = 0 nên x + y = - z , y + z = - x , x + z = - y . Thay các giá trị này vào biểu thức
M ta được: M = (- z)(- x )(- y) = - xyz = - 2 Bài 6: Ta có : (x - )2 5
³ 0, " x và y - 7 ³ 0, " y nên A = (x - )2 5
+ y - 7 + 2000 ³ 2000 " x,y ìï x - 5 = 0 ìï x = 5 Dấu ï ï " = " xảy ra khi: í Û í ï y - 7 = 0 ï y = 7 ïî ïî
Vậy giá trị nhỏ nhất của biểu thức A là 2000 khi x = 5; y = 7 . 6 æ 6 2ö æ 2ö b) Ta có : 4 ç ÷ ç ÷
x ³ 0, " x và y ç - ÷ ³ 0, " y 4 ç ÷
nên B = x + y ç -
÷ - 2019 ³ - 2019, " x,y ç ç ÷ è 7 ÷ ø çè 7 ÷ ø ìï x = 0 ï Dấu ï " = " xảy ra khi: í 2 ï y = ïïî 7 2
Vậy giá trị nhỏ nhất của biểu thức B là - 2019 khi x = 0; y = . 7 Trang 5