





































Preview text:
CHUÛ ÑEÀ GIÔÙI HAÏN 4. Baøi 01
GIÔÙI HAÏN CUÛA DAÕY SOÁ
I GIỚI HẠN HỮU HẠN CỦA DÃY SỐ – 1. Định nghĩa Định nghĩa 1
Ta nói dãy số (u có giới hạn là 0 khi n dần tới dương vô cực, nếu u có thể n ) n
nhỏ hơn một số dương bé tuỳ ý, kể từ một số hạng nào đó trở đi.
Kí hiệu: lim u = 0 hay u → 0 khi n → + . ∞ n n n→+∞ Định nghĩa 2
Ta nói dãy số (v có giới hạn là a (hay v dần tới a ) khi n → + , ∞ nếu n ) n
lim (v − a) = 0. n n→+∞
Kí hiệu: lim v = a hay v → a khi n → + . ∞ n n n→+∞
2. Một vài giới hạn đặc biệt a) 1 lim = 0; 1 lim
= 0 với k nguyên dương; n→+∞ n k n→+∞ n b) lim n
q = 0 nếu q < 1; n→+∞
c) Nếu u = c ( c là hằng số) thì lim u = lim c = c. n n n→+∞ n→+∞
Chú ý: Từ nay về sau thay cho lim u = a ta viết tắt là lim u = a . n n n→+∞
II ĐỊNH LÝ VỀ GIỚI HẠN HỮU HẠN – Định lí 1
a) Nếu lim u = a và lim v = b thì n n
• lim(u + v = a + b
• lim(u −v = a −b n n ) n n ) u a
• lim(u .v ) = . a b • lim n
= (nếu b ≠ 0 ). n n v b n lim u = a b) Nếu u = a n thì lim n . u ≥ 0, ∀n n a ≥ 0
III TỔNG CỦA CẤP SỐ NHÂN LÙI VÔ HẠN –
Cấp số nhân vô hạn (u có công bội q , với q <1 được gọi là cấp số nhân lùi vô n ) hạn.
Tổng của cấp số nhân lùi vô hạn: u 1
S = u + u + u +…+ u +…= q <1 . 1 2 3 n ( ) 1−q
IV GIỚI HẠN VÔ CỰC – 1. Định nghĩa
• Ta nói dãy số (u có giới hạn là +∞ khi n → +∞ , nếu u có thể lớn hơn một n ) n
số dương bất kì, kể từ một số hạng nào đó trở đi.
Kí hiệu: lim u = +∞ hay u → +∞ khi n → + . ∞ n n
• Dãy số (u có giới hạn là −∞ khi n → +∞ , nếu lim( u − = +∞ n ) n ) .
Kí hiệu: lim u = −∞ hay u → −∞ khi n → + . ∞ n n
Nhận xét: u = +∞ ⇔ lim( u − ) = − . ∞ n n
2. Một vài giới hạn đặc biệt
Ta thừa nhận các kết quả sau a) lim k
n = +∞ với k nguyên dương; b) lim n
q = +∞ nếu q > 1 . 3. Định lí 2 a) Nếu u
lim u = a và limv = ±∞ thì lim n = 0 . n n vn b) Nếu u
lim u = a > 0 , limv = 0 và v > 0, ∀n > 0 thì lim n = + . ∞ n n n vn
c) Nếu lim u = +∞ và lim v = a > 0 thì lim u .v = + . ∞ n n n n
CÂU HỎI V= B=I TẬP TRẮC NGHIỆM 11
NGUYỄN PHÚ KHÁNH HUỲNH ĐỨC KHÁNH –
Đăng ký mua trọn bộ trắc nghiệm 11 FILE WORD
Liên hệ tác giả HUỲNH ĐỨC KHÁNH 0975120189 –
https://www.facebook.com/duckhanh0205 Khi mua có sẵn File đề riêng;
File đáp án riêng để thuận tiện cho việc in ấn dạy học
CÂU HỎI TRẮC NGHIỆM
Vấn đề 1. DÃY SỐ DẠNG PHÂN THỨC
Câu 1. Kết quả của giới hạn sin 5n lim −2 bằng: 3n A. −2. B. 3. C. 0. D. 5. 3 Lời giải. Ta có sin 5n 1 n 0 ≤ ≤ , mà 1 lim = 0 nên sin 5 lim = 0, do đó 3n n n 3n sin 5n lim
− 2 = −2. Chọn A. 3n
Nhận xét : Có thể dùng MTCT để tính (có thể chính xác hoặc gần đúng) giới hạn như
sau (các bài sau có thể làm tương tự) : sin 5 Nhập ( X )−2. 3X
Bấm CALC và nhập 9999999999 (một số dòng MTCT khi bấm nhiều số « 9 » thì nó
báo lỗi, khi đó ta cần bấm ít số « 9 » hơn.
Bấm « = » ta được kết quả (có thể gần đúng), sau đó chọn đáp án có giá trị gần
đúng với kết quả hiện trên MTCT. 1 −2 k n n cos
Câu 2. Có bao nhiêu số tự nhiên chẵn 1 k để lim n = . 2n 2 A. 0. B. 1. C. 4. D. Vô số.
Lời giải. Ta có n−2 n sin 2n 1 n sin 2n = − . 2n 2 n 1 k n cos
Điều kiện bài toán trở thành lim n = 0. n Ta có 1 lim cos
= cos 0 = 1 nên bài toán trở thành tìm k sao cho n k k 1 n − k 2 lim = lim n = 0 ⇔
−1 < 0 ⇔ k < 2 → không tồn tại k (do k nguyên * k∈ℕ , k=3 n 2 l
dương và chẵn). Chọn A.
Câu 3. Kết quả của giới hạn
3 sin n + 4 cos n lim bằng: n +1 A. 1. B. 0. C. 2. D. 3. Lời giải. Ta có 3sin n + 4 cos n 7 7 3sin n + 4 cos n 0 ≤ ≤ ≤ → 0 → lim = 0. Chọn B. n +1 n +1 n n +1
Câu 4. Kết quả của giới hạn n cos 2n lim 5 − bằng: 2 n +1 A. 4. B. 1 . C. 5. D. −4. 4 Lời giải. Ta có n cos 2n n 1 n cos 2n n cos 2n 0 ≤ ≤ ≤ → 0 → lim = 0 → lim 5 − = 5. Chọn C. 2 2 2 2 n +1 n +1 n n +1 n +1
Câu 5. Kết quả của giới hạn n 2 π 3 lim n sin − 2n là: 5 A. − . ∞ B. −2. C. 0. D. + . ∞ Lời giải. Ta có nπ 1 sin n 2 3 3 π limn sin 2n lim n − = . − 2. Vì 5 n 5 3 3 l im n = +∞ l im n = +∞ 1 sin n 3 π π → π → lim n n . − 2 = − . 1 sin n 1 1 sin ∞ 0 ≤ . ≤ → 0 l im . − 2 = −2 < 0 n 5 n 5 n n 5 Chọn A. n
Câu 6. Giá trị của giới hạn (− ) 1 lim 4 + bằng: n +1 A. 1. B. 3. C. 4. D. 2. n n n Lời giải. −1 1 1 −1 −1 Ta có ( ) ( ) ( ) 0 ≤ ≤ ≤ → 0 → lim = 0 → lim4 + = 4. n +1 n +1 n n +1 n +1 Chọn C. n Câu 7. −1 Cho hai dãy số 1 (u và (v có ( ) u = và v =
. Khi đó lim (u + v n n ) n ) n ) n 2 n +1 n 2 n + 2 có giá trị bằng: A. 3. B. 0. C. 2. D. 1. 1 1 0 ≤ u ≤ ≤ → 0 n 2
Lời giải. Ta có n +1 n
→ lim u = lim v = 0 → lim u + v = n n ( n n ) 0. 1 1 0 ≤ v ≤ ≤ → 0 n 2 n + 2 n Chọn B.
Chú ý : Cho P(n), Q(n) lần lượt là các đa thức bậc ,
m k theo biến n : P(x) m m 1 = a n + a
n − +⋯+ a n + a a = / 0 m m 1 − 1 0 ( m ) Q(n) k k 1
= b n + b n − +⋯+ b n + b b = / 0 k k 1 − 1 0 ( k ) m m Khi đó P(n) a n P n a n lim = lim m , viết tắt ( ) m ∼
, ta có các trường hợp sau : Q(n) k b n Q(n) k b n k k Nếu P n
« bậc tử » < « bậc mẫu ( m < k ) thì ( ) lim = 0. Q(n) Nếu P n a
« bậc tử » = « bậc mẫu ( m = k ) thì ( ) lim m = . Q(n) bk P n + ∞ khi a b > 0
Nếu « bậc tử » > « bậc mẫu ( m > k ) thì ( ) lim m k = . Q(n)
−∞ khi a b < 0 m k
Để ý rằng nếu P(n), Q(n) có chứa « căn » thì ta vẫn tính được bậc của nó. Cụ thể m k n tì có bậc là k 1
. Ví dụ n có bậc là 3 4 ,
n có bậc là 4 ,... n 2 3
Trong các bài sau ta có thể dùng dấu hiệu trên để chỉ ra kết quả một cách nhanh chóng !
Câu 8. Giá trị của giới hạn 3 − lim là: 2 4n −2n +1 A. 3 − . B. − . ∞ C. 0. D. −1. 4 3 − Lời giải. 2 Ta có −3 0 lim = lim n = = 0. Chọn C. 2 4n − 2n +1 2 1 4 4 − + 2 n n
Giải nhanh : Dạng « bậc tử » < « bậc mẫu » nên kết quả bằng 0. 2
Câu 9. Giá trị của giới hạn n + 2n lim bằng: 3 n + 3n −1 A. 2. B. 1. C. 2 . D. 0. 3 1 2 2 + Lời giải. 2 Ta có n + 2n 0 lim = lim n n = = 0. Chọn D. 3 n + 3n 1 3 1 − 1 1+ − 2 3 n n
Giải nhanh : Dạng « bậc tử » < « bậc mẫu » nên kết quả bằng 0. 3
Câu 10. Giá trị của giới hạn 3n − 2n +1 lim là: 4 4n + 2n +1 A. + . ∞ B. 0. C. 2 . D. 3 . 7 4 3 2 1 3 − + Lời giải. 2 4 Ta có 3n − 2n +1 0 lim = lim n n
n = = 0. Chọn B. 4 4n + 2n +1 2 1 4 4 + + 3 4 n n
Giải nhanh : Dạng « bậc tử » < « bậc mẫu » nên kết quả bằng 0.
Câu 11. Giá trị của giới hạn n n +1 lim bằng: n2 + 2 A. 3 . B. 2. C. 1. D. 0. 2 1 1 + 2 Lời giải. Ta có n n +1 n n 0 lim = lim = = 0. Chọn D. n2 + 2 2 1 1+ 2 n
Giải nhanh n n +1 n n 1 : ∼ = → 0. 2 2 n + 2 n n
Câu 12. Cho hai dãy số v (u và (v có 1 u = và 2 v =
. Khi đó lim n có giá n ) n ) n n +1 n n + 2 un trị bằng: A. 1. B. 2. C. 0. D. 3. 1 1+ Lời giải. Ta có v n +1 1 lim n = lim = lim
n = =1. Chọn A. u n + 2 2 1 n 1+ n Giải nhanh n + n : 1 ∼ =1. n + 2 n Câu 13. Cho dãy số an + (u với 4 u =
trong đó a là tham số thực. Để dãy số (u n ) n ) n 5n + 3
có giới hạn bằng 2 , giá trị của a là:
A. a = 10. B. a = 8. C. a = 6. D. a = 4. 4 a + Lời giải. Ta có an + 4 a lim = lim = lim n u = . Khi đó n 5n + 3 3 5 5 + n a lim u = 2 ⇔ = 2 ⇔ a = 10 → Chọn A. n 5 Giải nhanh an + an a : 4 2 ∼ ∼ = ⇔ a = 10. 5n + 3 5n 5 Câu 14. Cho dãy số n + b (u với 2 u =
trong đó b là tham số thực. Để dãy số (u n ) n ) n 5n + 3
có giới hạn hữu hạn, giá trị của b là:
A. b là một số thực tùy ý. B. b = 2. C. không tồn tại . b D. b = 5. b 2 + Lời giải. Ta có 2n + b 2 lim = lim = lim n u = b ∀ ∈ ℝ → Chọn A. n ( ) 5n + 3 3 5 5 + n Giải nhanh n + b n : 2 2 2 ∼ =
với mọi b ∈ ℝ. 5n + 3 5n 5 2
Câu 15. Tính giới hạn n + n + 5 L = lim . 2 2n +1 A. 3 L = . B. 1 L = . C. L = 2. D. L = 1. 2 2 1 5 2 1+ + Lời giải. 2 Ta có n + n + 5 1 = lim = lim n n L = → Chọn B. 2 2n +1 1 2 2 + 2 n 2 2
Giải nhanh: n + n +5 n 1 ∼ = . 2 2 2n +1 2n 2 2 Câu 16. Cho dãy số 4n + n + 2 (u với u =
. Để dãy số đã cho có giới hạn bằng 2 , n ) n 2 an + 5
giá trị của a là: A. a = −4. B. a = 4. C. a = 3. D. a = 2. 1 2 2 4 + + Lời giải. 2 4n + n + 2 4 2 = lim = lim = lim n n u = a =
/ 0 ⇔ a = 2. Chọn D. n 2 ( ) an + 5 5 a a + 2 n 2 2 Giải nhanh 4n + n + 2 4n 4 : 2 ∼ ∼ = ⇔ a = 2. 2 2 an + 5 an a 2 3
Câu 17. Tính giới hạn n −3n L = lim . 3 2n + 5n − 2 A. 3 L = − . B. 1 L = . C. 1 L = . D. L = 0. 2 5 2 1 2 3 −3 Lời giải. n −3n −3 = lim = lim n L = → Chọn A. 3 2n + 5n − 2 5 2 2 2 + − 2 3 n n 2 3 3
Giải nhanh: n −3n −3n 3 ∼ = − . 3 3 2n + 5n − 2 2n 2 2 4
Câu 18. Tìm tất cả các giá trị của tham số 5n − 3an a để L = lim > 0. (1−a) 4 n + 2n +1
A. a ≤ 0;a ≥1.
B. 0 < a <1.
C. a < 0; a >1.
D. 0 ≤ a <1. 5 2 4 −3a − − Lời giải. 2 5n 3an 3a a < 0 = lim = lim n L = > 0 ⇔ . Chọn C. (1−a) 4 n + 2n +1 2 1 ( − a a > 1 a) (1 ) 1 − + + 3 4 n n ( 3 2n − n )( 2 3n + ) 1
Câu 19. Tính giới hạn L = lim . (2n − ) 1 ( 4 n −7) A. 3 L = − . B. L = 1. C. L = 3. D. L = + . ∞ 2 Lời giải. Ta có 2 1 2 1 3 2 − + − ( 3 n n + 2n − n )( 2 3n + ) 1 . 3 1 3 2 2 2 2 1 n n n n −1.3 3 L = lim = lim = lim = = − . (2n − ) 1 ( 4 n − 7) 1 7 1 7 2.1 2 4 n2 − . n 1 − 2 − 1 − 4 4 n n n n Chọn A. ( 3 2n − n )( 2 3n + ) 3 2 1 Giải nhanh: n − .3n 3 ∼ = − . (2n− ) 1 ( 4 n − 7) 4 2 . n n 2 ( 2 n + 2n)( 3 2n + ) 1 (4n + ) 5
Câu 20. Tính giới hạn L = lim . ( 4 n −3n − ) 1 ( 2 3n −7) A. L = 0. B. L = 1. C. 8 L = . D. L = + . ∞ 3 2 1 5 + + ( 2 + n + 2n)( 3 2n + ) 1 (4n + ) 1 2 4 3 5 Lời giải. n n n 1.2.4 8 L = lim = lim = = . ( 4 n −3n − ) 1 ( 2 3n − 7) 3 1 7 1.3 3 1 − − 3 − 3 4 2 n n n Chọn C. ( 2 n + 2n)( 3 2n + ) 1 (4n + ) 2 3 5 Giải nhanh: n .2n .4n 8 ∼ = . ( 4 n −3n − ) 1 ( 2 3n − 7) 4 2 n .3n 3 3
Câu 21. Tính giới hạn n +1 L = lim . 3 n + 8 A. 1 L = . B. L = 1. C. 1 L = . D. L = + . ∞ 2 8 1 1+ 3 3 Lời giải. n +1 1 n L = lim = lim = = 1 → Chọn B. 3 3 n + 8 8 1 3 1+ n 3 3
Giải nhanh: n +1 n ∼ = 1. 3 3 n + 8 n 3
Câu 22. Kết quả của giới hạn n − 2n lim là: 2 1−3n A. 1 − . B. + . ∞ C. − . ∞ D. 2 . 3 3 2 3 2 n 1 − 3 1− 2 Lời giải. 2 n − 2n n lim = lim = lim . n n . Ta có 2 1−3n 1 1 2 n −3 −3 2 2 n n l im n = +∞ 2 2 3 1− 2 n − − 2 1 n n 2 1 →im = lim . n Chọn C. n = −∞ → 2 l im = − < 0 1−3 1 n 1 −3 3 2 −3 n 2 n 3 3
Giải nhanh n −2n n 1 : ∼ = − n →− . ∞ 2 2 1−3n −3n 3 3
Câu 23. Kết quả của giới hạn 2n + 3n lim là: 2 4n + 2n +1 A. 3 . B. + . ∞ C. 0 D. 5. 4 7 2 3 2 n + 3 3 + 3 2 Lời giải. 2 2n + 3n n lim = lim = lim . n n . Ta có 2 4n + 2n +1 2 1 2 1 2 n 4 4 + + + + 2 2 n n n n l im n = +∞ 2 2 3 + 3 2 2n + + 3 3 n n 2 3 →im = lim . n = + . Chọn B. n ∞ 2 l im = > 0 4n + 2n +1 2 1 2 1 4 4 + + 2 4 + + n n 2 n n 3 3 Giải nhanh 2n + 3n 3n 3 : ∼ = .n →+ . ∞ 2 2 4n + 2n +1 4n 4 4
Câu 24. Kết quả của giới hạn 3n − n lim là: 4n −5 A. 0. B. + . ∞ C. − . ∞ D. 3 . 4 3 4 3 n −1 4 −1 3 Lời giải. 3 3n − n n 3 lim = lim = lim . n n . Ta có 4n −5 5 5 n4 4 − − n n 3 l im n = +∞ 3 4 −1 3 3 3 −1 n − n 3 n 3 → lim = l lim n . = − . 1 ∞ Chọn C. l im n = − < 0 4n −5 5 4 5 4 − 4 − n n 4 4
Giải nhanh 3n−n n − 1 : 3 ∼ = − .n →− . ∞ 4n −5 4n 4
Câu 25. Trong các giới hạn sau đây, giới hạn nào bằng 0? 3 2 3 2 4 A. 3 + 2n 2n −3 2n − 3n 2n −3n lim . B. lim . C. lim . D. lim . 2 2n −1 3 −2n − 4 2 −2n −1 4 2 −2n + n
Lời giải. Theo dấu hiệu ở đã nêu ở phần Chú ý trên thì ta chọn giới hạn nào rơi vào
trường hợp « bậc tử » < « bậc mẫu » ! 3 3 + 2n lim
= +∞ : « bậc tử » > « bậc mẫu » và a b = 2.2 = 4 > 0. 2 2n −1 m k 2 2n −3 lim
= 0 : « bậc tử » < « bậc mẫu ». Chọn B. 3 −2n − 4 3 2n −3n lim
= +∞ : « bậc tử » > « bậc mẫu » và a b = − − > n k ( ) 3 ( . 2) 0. 2 −2n −1 2 4 2n −3n −3 3 a − lim = =
: « bậc tử » = « bậc mẫu » và 3 3 m = = . 4 2 −2n + n −2 2 b −2 2 k
Câu 26. Dãy số nào sau đây có giới hạn bằng 1 − ? 3 2 4 3 2 3 2 B. n − 2n n − + 2n −1 n −3n n − + 2n −5 u = . A. u = . C. u = . D. u = . n 2 3n + 5 n 3 2 3n + 2n −1 n 3 2 9n + n −1 n 3 3n + 4n − 2
Lời giải. Ta chọn đáp án dạng « bậc tử » = « bậc mẫu » và a b > 0. Chọn C. m k 2 3 n −3n −3 1 lim u = lim = = − . n 3 2 9n + n −1 9 3
Câu 27. Dãy số nào sau đây có giới hạn là +∞? 2 2 2 A. 1+ n n − 2 n − 2n 1+ 2n u = . B. u = . C. u = . D. . n 5n + 5 n 3 5n + 5n n 2 5n + 5n 2 5n + 5n
Lời giải. Ta chọn đáp án dạng « bậc tử » > « bậc mẫu » với a b > 0. Chọn A. m k l im n = +∞ 1 2 +1 1 2 1+ n +1 lim = lim = lim . n u n = +∞ vì 2 a 1 . n n 5n + 5 5 l im m = = > 0 5 + 5 b 5 n 5 k + n
Các đáp án còn lại đều rơi vào trường hợp « bậc tử » ≤ « bậc mẫu » nên cho kết quả hữa hạn.
Câu 28. Dãy số nào sau đây có giới hạn là −∞? 3 2 4 2 A. 1+ 2n n + 2n −1 2n −3n n − 2n . B. u = . C. u = . D. u = . 2 5n + 5n n 3 n − + 2n n 2 3 n + 2n n 5n +1
Lời giải. Ta chọn đáp án dạng « bậc tử » = « bậc mẫu » và a b < 0. Chọn C. m k 2 4 2n −3n u =
: « bậc tử » > « bậc mẫu » và a b = −3.2 = −6 < 0 → lim u = − . ∞ n 2 3 n + 2n m k n Chú ý + ∞ khi a > 0 : (i) lim( m m 1 − n a n a n ⋯+ a n + a + + = . m n 1 − 1 0 ) −∞ khi a < 0 n
(ii) Giả sử q > max{ q : i =1;2 ; … m thì i } a khi q <1 0 lim( . n n n a q a q ⋯+ a q + a + + = +
∞ khi a > 0, q >1. m m 1 1 0 )
−∞ khi a <0, q >1
Ta dùng « dấu hiệu nhanh » này để đưa ra kết quả nhanh chóng cho các bài sau.
Câu 29. Tính giới hạn L = ( 2
lim 3n + 5n − ) 3 . A. L = 3. B. L = − . ∞ C. L = 5. D. L = + . ∞ 2 l im n = +∞ Lời giải. L lim( 5 3 2 3n 5n ) 2 3 lim n = + − = 2 + − = +∞ vì . 5 3 2 n n l im2 + − = 2 > 0 2 n n Chọn D. Giải nhanh : 2 2
3n + 5n −3 ∼ 3n → + . ∞
Câu 30. Có bao nhiêu giá trị nguyên của tham số a thuộc khoảng (−10;10) để L = ( n− ( 2 a − ) 3 lim 5 3 2 n ) = −∞ . A. 19. B. 3. C. 5. D. 10. Lời giải. Ta có lim (5n 3( 5 2 a 2) 3 n ) 3 lim n − − = −3( 2
a − 2 = −∞ 2 ) n 5 lim ⇔ −3( 2 a − 2) 2
= a −2 < 0 ⇔ − 2 < a < 2 →a = −1; 0; 1. Chọn B. 2 a , a ( 10;10) n ∈ ∈ − ℤ
Câu 31. Tính giới hạn ( 4 2
lim 3n + 4n − n + ) 1 . A. L = 7. B. L = − . ∞ C. L = 3. D. L = + . ∞ Lời giải. Ta có 4 l im n = +∞ lim( 4 1 1 4 2
3n + 4n − n + ) 4 1 = lim n 3 + − + = +∞ vì . 4 1 1 2 3 4 n n n l im 3 + − + = 3 > 0 2 3 4 n n n Chọn D. Giải nhanh : 4 2 4
3n + 4n − n +1 ∼ 3n →+ . ∞ Câu 32. Cho dãy số 2 n
(u với u = 2 + + +
Mệnh đề nào sau đây đúng ? n ( 2) ... ( 2) . n ) A. lim u = − . ∞ B. 2 lim u = . n n 1− 2 C. lim u = + . ∞
D. Không tồn tại lim u . n n Lời giải. Vì ( )2 n 2, 2
, … ,( 2) lập thành cấp số nhân có u = 2 = q nên 1 n 1−( 2) n a = 2− 2 > 0 u = 2. = − − → u = +∞ vì . Chọn C. n (2 2) ( 2) 1 lim n 1− 2 q = 2 >1 1 3 n +1+ +...+
Câu 33. Giá trị của giới hạn 2 2 2 lim bằng: 2 n +1 A. 1. B. 1. C. 1 . D. 1 . 8 2 4 Lời giải. + Ta có 1 3 n 1 1 n(n ) 1 +1+ +...+ = (1+ 2 +⋯+ n) = . . Do đó 2 2 2 2 2 2 1 3 n +1+ +...+ 2 n + n 1 2 2 2 lim = lim =
(“bậc tử” = “bậc mẫu”). Chọn D. 2 2 n +1 4n + 4 4
Câu 34. Giá trị của giới hạn 1 2 n −1 lim + +... + bằng: 2 2 2 n n n A. 0. B. 1. C. 1 . D. 1. 3 2 Lời giải. 1 2 n −1 1 1 n −1 1+ n −1 Ta có ( )( ) 2 n − n + +...+ = 1+ 2 +⋯+ n −1 = . = . 2 2 2 2 ( ) 2 2 n n n n n 2 2n Do đó 2 1 2 n −1 n − n 1 lim + +... + = lim = . Chọn C. 2 2 2 2 n n n 2n 2 + + +⋯+ + Câu 35. 1 3 5 2n 1 Giá trị của giới hạn ( ) lim bằng: 2 3 n + 4 A. 0. B. 1. C. 2 . D. 1. 3 3 Lời giải. n 1+ 2n −1 Ta có ( ) 1+ 3 + 5 + ( ⋯ 2n − ) 2 1 = = n nên 2 1 + 3+ 5 +⋯+(2n + ) 2 1 n 1 lim = lim = → Chọn B. 2 2 3 n + 4 3 n + 4 3
Câu 36. Giá trị của giới hạn 1 1 1 lim + +... + là: 1.2 2.3 n (n + ) 1 A. 1 . B. 1. C. 0. D. − . ∞ 2 Lời giải. Ta có 1 1 1 1 1 1 1 1 1 lim + +...+ = lim 1 − + − +⋯+ − = lim 1 − = 1. 1 .2 2.3 n (n + ) 1 2 2 3 n n +1 n +1 Chọn B.
Câu 37. Giá trị của giới hạn 1 1 1 lim + +... + bằng: 1.3 3.5 (2n − ) 1 (2n + ) 1 A. 1 . B. 1 . C. 1. D. 2. 2 4
Lời giải. Với mọi 1 1 1 1 * k ∈ ℕ thì = − , do đó (2k − ) 1 (2k + ) 1 2 2k −1 2k +1 1 1 1 1 1 1 1 1 1 lim + +...+ = lim 1 − + − + − 1 .3 3.5 (2n− ) 1 (2n + ) 1 2 3 3 5 2n −1 2n +1 1 1 1 = lim 1 − = . 2 2n +1 2 Chọn A.
Câu 38. Giá trị của giới hạn 1 1 1 lim ...... + + + bằng: 1.4 2.5 n(n ) 3 + A. 11. B. 2. C. 1. D. 3 . 18 2 Lời giải. Ta có 1 1 1 1 1 1 1 1 1 1 1 + +......+ = 1 − + − + − +⋯+ − 1.4 2.5 n(n + ) 3 3 4 2 5 3 6 n n + 3 1 1 1 1 1 1 1 1 = 1 ⋯ + + + + − + + +⋯+ 3 2 3 n 4 5 6 n + 3 1 1 1 1 1 1 = 1 + + − − − 3 2 3 n +1 n + 2 n + 3 1 1 1 1 1 1 = − − − 3 6 n +1 n + 2 n + 3 Do đó 1 1 1 1 1 1 1 1 1 11 lim + +......+ = lim Chọn A. − − − = . 1 .4 2.5 n (n + ) 3 3 6 n +1 n + 2 n + 3 8 2 2 2
Câu 39. Giá trị của giới hạn 1 + 2 +... + n lim bằng: n( 2 n + ) 1 A. 4. B. 1. C. 1 . D. 1. 2 3 3 2 Lời giải.
2n −3n + n n n −1 2n +1 Đặt ( )( ) P(n) = = thì ta có 6 6 2 2 2 2
1 + 2 + 3 +⋯+ n = (P(2)− P( ) 1 )+(P( )
3 − P(2))+⋯+(P(n + ) 1 − P(n)) n(n + ) 1 (2n + ) 3 = P(n + ) 1 − P( ) 1 = 6 2 2 2 + + + n n n +1 2n + 3 Do đó 1 2 ... ( )( ) 2 1 lim = lim = = . Chọn D. n( 2 n + ) 1 6n( 2 n + ) 1 6 3 1 u = n
Câu 40. Cho dãy số có giới hạn 2
(u xác định bởi . Tính lim u . n ) 1 n u = , n ≥ 1 n 1 + 2 −u n
A. lim u = −1. B. lim u = 0. C. 1 lim u = . D. lim u =1. n n n 2 n
Lời giải. Giả sử limu = a thì ta có n a = / 2 a = / 2 1 1 a lim u lim = = = ⇔ ⇔
⇔ a = 1. Chọn D. n 1 + 2 −u 2 − a a − a = a − a + = n (2 ) 2 1 2 1 0 u = 2 1
Câu 41. Cho dãy số có giới hạn (u xác định bởi u +1 . Tính lim u . n ) n u = , n ≥ 1 n n 1 + 2 A. lim u =1. B. lim u = 0. C. lim u = 2. D. lim u = + . ∞ n n n n
Lời giải. Giả sử limu = a thì ta có n u +1 a +1 a = lim u = lim n = ⇔ a = 1 → Chọn A. n 1 + 2 2 2
Câu 42. Kết quả của giới hạn 9n − n +1 lim bằng: 4n − 2 A. 2 . B. 3 . C. 0. D. 3. 3 4 1 1 9 − + 2 2 Lời giải. 9n − n +1 3 n n lim = lim = → Chọn B. 4n − 2 2 4 4 − n 2 2
Giải nhanh: 9n −n +1 9n 3 ∼ = . 4n − 2 4n 4 2
Câu 43. Kết quả của giới hạn n − + 2n +1 lim bằng: 4 3n + 2 A. 2 − . B. 1 . C. 3 − . D. 1 − . 3 2 3 2 2 1 2 −1+ + Lời giải. 2 n − + 2n +1 1 lim = lim n n = − → Chọn C. 4 3n + 2 2 3 3 + 4 n 2 2 Giải nhanh n − + 2n +1 n − 1 : ∼ = − . 4 4 3n + 2 3 3 n
Câu 44. Kết quả của giới hạn 2n + 3 lim là: 2n + 5 A. 5 . B. 5. C. + . ∞ D. 1. 2 7 3 2 + Lời giải. 2n + 3 2 n lim = lim = = 1. Chọn D. 5 2n + 5 2 2 + n
Giải nhanh: 2n +3 2n ∼ = 1. 2n + 5 2n
Câu 45. Kết quả của giới hạn n +1 − 4 lim bằng: n +1 + n A. 1. B. 0. C. −1. D. 1 . 2 1 1 4 + − 2 Lời giải. n +1 − 4 0 n n n lim = lim = = 0 → Chọn B. n +1 + n 1 1 1 + +1 2 n n
Giải nhanh: n +1−4 n 1 ∼ = → 0. n +1 + n n n 2 Câu 46. Biết rằng n n 1 π + + lim = a sin + . b Tính 3 3
S = a + b . 2 4 n − n − 2 A. S =1. B. S = 8. C. S = 0. D. S = −1. 1 1+ 1+ 2 2 Lời giải. Ta có n + n +1 n 1+ 1 π lim = lim = = 2 2 sin 2 n − n − 2 1 2 1 4 1− − n n a = 2 2 → →S = 8 → Chọn B. b = 0
Câu 47. Kết quả của giới hạn 10 lim là: 4 2 n + n +1 A. + . ∞ B. 10. C. 0. D. − . ∞ 10 Lời giải. 2 10 0 lim = lim n = = 0. Chọn C. 4 2 n + n +1 1 1 1 1+ + 2 4 n n Giải nhanh: 10 10 10 ∼ = → 0. 2 4 2 4 + +1 n n n n
Câu 48. Kết quả của giới hạn 2n + 2 lim (n + ) 1 là: 4 2 n + n −1 A. + . ∞ B. 1. C. 0. D. − . ∞ Lời giải. 2n + 2 2(n + )3 1 lim(n + ) 1 = lim
= 0 (“bậc tử” < “bậc mẫu”). Chọn C. 4 2 4 2 n + n −1 n + n −1 Giải nhanh: 2n + 2 2n 2 (n + ) 1 ∼ . n = → 0. 4 2 4 n + n −1 n n 3 3 2 Câu 49. Biết rằng an + 5n −7 lim
= b 3 + c với a, b, c là các tham số. Tính giá trị 2 3n − n + 2 của biểu thức a + c P = . 3 b
A. P = 3. B. 1 P = . C. P = 2. D. 1 P = . 3 2 5 7 3 a + − 3 3 2 3 3 3 Lời giải. Ta có an + 5n −7 n n b a lim = lim = = 3 2 3n − n + 2 1 2 3 3 3 − + 2 n n b 3 a = 1 b 3 c = + ⇒
3 ⇒ P = . Chọn B. 3 c = 0
Câu 50. Kết quả của giới hạn 5 5 2
lim 200 − 3n + 2n là: A. + . ∞ B. 1. C. 0. D. − . ∞ Lời giải. Ta có l im n = +∞ 200 2 5 5 2 5 lim
200 −3n + 2n = lim n −3 + = −∞ vì 200 2 . 5 3 n n 5 5 l im −3 + = − 3 < 0 5 3 n n Chọn D. Giải nhanh: 5 5 2 5 5 5
200 −3n + 2n ∼ −3n = − 3.n →− . ∞
Vấn đề 2. DÃY SỐ CHỨA CĂN THỨC
Câu 51. Giá trị của giới hạn lim( n +5 − n +1) bằng: A. 0. B. 1. C. 3. D. 5.
Lời giải. n +5 − n +1 ∼ n − n = 0
→ nhân lượng liên hợp : ( n+ − n+ ) 4 lim 5 1 = lim = 0 → Chọn A. n + 5 + n +1
Câu 52. Giá trị của giới hạn ( 2 lim
n − n +1 − n) là: A. 1 − . B. 0. C. 1. D. − . ∞ 2 Lời giải. 2 2
n − n +1 − n ∼ n − n = 0
→ nhân lượng liên hợp : 1 −1+ n − + lim( 1 1 2 − +1− )= lim = lim n n n n = − → Chọn A. 2 n − n +1 1 1 2 + n 1− + +1 2 n n Giải nhanh n − +1 n − 1 : 2
n − n +1 − n = ∼ = − . 2 2 2
n − n +1 + n n + n
Câu 53. Giá trị của giới hạn ( 2 2 lim
n −1 − 3n + 2 ) là: A. −2. B. 0. C. − . ∞ D. + . ∞ Lời giải. lim( 1 2 2 2
n −1 − 3n + 2)= limn 1− − 3+ = −∞ vì 2 2 n n 1 2 lim n = + , ∞ lim 1− − 3+
=1− 3 < 0. Chọn C. 2 2 n n Giải nhanh : 2 2 2 2
n −1 − 3n + 2 ∼ n − 3n = (1− 3)n →− . ∞
Câu 54. Giá trị của giới hạn ( 2 2 lim
n + 2n − n − 2n ) là: A. 1. B. 2. C. 4. D. + . ∞ Lời giải. 2 2 2 2
n + 2n − n − 2n ∼ n − n = 0
→ nhân lượng liên hợp : n lim( 4 4 2 2
n + 2n − n − 2n )= lim = lim = 2. Chọn B. 2 2
n + 2n + n − 2 2 2 n 1+ + 1− n n Giải nhanh 4n 4n : 2 2
n + 2n − n − 2n = ∼ = 2. 2 2 2 2
n + 2n + n − 2n n + n
Câu 55. Có bao nhiêu giá trị của a để ( 2 2 2 lim
n + a n − n +(a + 2)n +1)= 0. A. 0. B. 2. C. 1. D. 3. Lời giải. 2 2 2
n + a n − n +(a + ) 2 2
2 n +1 ∼ n − n = 0
→ nhân lượng liên hợp: 2
a − a − 2 n −1 Ta có lim( 2 2 2
n + a n − n +(a + 2)n +1) ( ) = lim 2 2
n + n + n +1 1 2
a − a − 2 − 2 a − a − 2 a = −1 = lim n = = 0 ⇔ . Chọn B. 1 1 2 b = 2 1 1 + + + 2 n n
Câu 56. Giá trị của giới hạn ( 2 2 lim
2n − n +1 − 2n −3n + 2 ) là: A. 0. B. 2 . C. − . ∞ D. + . ∞ 2 Lời giải. 2 2 2 2
2n − n +1 − 2n −3n + 2 ∼ 2n − 2n = 0
→ nhân lượng liên hợp : n − lim( 2 1 2 2
2n − n +1 − 2n − 3n + 2)= lim 2 2
2n − n +1 + 2n − 3n + 2 1 2 − 1 = lim n = . 1 1 3 2 2 2 − + + 2 − + 2 2 n n n n Chọn B. Giải nhanh : 2n −1 2n 1 2 2
2n − n +1 − 2n −3n + 2 = ∼ = . 2 2 2 2
2n − n +1 + 2n −3n + 2 2n + 2 2 n
Câu 57. Giá trị của giới hạn ( 2 2 lim
n + 2n −1 − 2n + n ) là: A. −1. B. 1− 2. C. − . ∞ D. + . ∞
Lời giải. Giải nhanh : 2 2 2 2
n + 2n −1 − 2n + n ∼ n − 2n = (1− 2)n →− . ∞ Cụ thể 2 1 1 : lim( 2 2
n + 2n −1 − 2n + n ) = lim . n 1+ − − 2 + = −∞ vì 2 n n n 2 1 1 lim n = + , ∞ lim 1+ −
− 2 + = 1− 2 < 0 → Chọn C. 2 n n n
Câu 58. Có bao nhiêu giá trị nguyên của a thỏa ( 2 2 lim
n − 8n − n + a ) = 0 . A. 0. B. 2. C. 1. D. Vô số. Lời giải. Nếu 2 2 2
n −8n − n + a ∼ n − n = 0
→ nhân lượng liên hợp : 2 2 2a −8 n Ta có a − lim ( 2 8 2 2
n −8n − n + a ) ( ) = lim = lim 2 n + n + n 1 1+ +1 n 2
= a − 4 = 0 ⇔ a = ±2. Chọn B.
Câu 59. Giá trị của giới hạn ( 2 lim
n − 2n + 3 − n) là: A. −1. B. 0. C. 1. D. + . ∞ Lời giải. 2 2
n − 2n + 3 − n ∼ n − n = 0
→ nhân lượng liên hợp : 3 −2 + − n + lim( 2 3 2 − 2 + 3 − )= lim = lim n n n n = −1 → Chọn A. 2 n − 2n + 3 2 3 + n 1− + +1 2 n n Giải nhanh −2n + 3 −2n : 2
n − 2n + 3 − n = ∼ = −1. 2 2
n − 2n + 3 + n n + n
Câu 60. Cho dãy số (u với 2 2
u = n + an + 5 − n +1 , trong đó a là tham số thực. n ) n
Tìm a để lim u = −1. n A. 3. B. 2. C. −2. D. −3. Lời giải : 2 2 2 2
n + an + 5 − n +1 ∼ n − n = 0
→ nhân lượng liên hợp : an + −1 = lim u = lim
n + an + − n + = n ( 4 2 2 5 1) lim 2 2
n + an + 5 + n +1 4 a + a = lim n = ⇔ a = −2. a 5 1 2 1+ + + 1+ 2 2 n n n Chọn C. Giải nhanh : an + 4 an a 2 2
−1 ∼ n + an + 5 − n +1 = ∼ = ⇔ a = −2. 2 2 2 2 2
n + an + 5 + n +1 n + n
Câu 61. Giá trị của giới hạn lim(3 3 3 3
n +1 − n + 2 ) bằng: A. 3. B. 2. C. 0. D. 1. Lời giải. 3 3 3 3 3 3 3 3
n +1 − n + 2 ∼ n − n = 0
→ nhân lượng liên hợp : − lim( 1 3 3 3 3
n +1 − n + 2) = lim = 0. → Chọn C. 3 (n + )2 3 3 3 3 3 3 1
+ n +1. n + 2 + ( 3 n + 2)
Câu 62. Giá trị của giới hạn (3 2 3 lim
n − n + n) là: A. 1. B. + . ∞ C. 0. D. 1. 3 Lời giải. 3 2 3 3 3
n − n + n ∼ n − + n = 0
→ nhân lượng liên hợp : 2 n lim( 1 1 3 2 3
n − n + n)= lim = lim = . ( 2 3 n − n )2 2 3 2 3 2 3 3 1 1
− n n − n + n 3 3 −1 − −1 +1 n n Chọn A. 2 2 Giải nhanh n n 1 : 3 2 3
n − n + n = ∼ = . ( 2 3 − )2 3 6 3 3 2 3 2 3 2 3 3 n − n n − + n n n
− n n − n + n
Câu 63. Giá trị của giới hạn (3 3 2 lim
n − 2n − n) bằng: A. 1. B. 2 − . C. 0. D. 1. 3 3 Lời giải. 3 3 2 3 3
n − 2n − n ∼ n − n = 0
→ nhân lượng liên hợp : 2 − n − lim( 2 2 2 3 3 2
n − 2n − n)= lim = lim = − . ( 3 2 n − 2n )2 2 3 3 2 2 3 3 + . n n − 2 2 2 n + n 3 3 1− + 1− +1 n n Chọn B. 2 2 Giải nhanh −2n −2n 2 : 3 3 2
n − 2n − n = ∼ = − . ( 3 2 − )2 3 6 3 3 2 3 3 2 2 3 3 n + . 2 + . − 2 n n + n n n n n n + n
Câu 64. Giá trị của giới hạn lim n ( n 1 n 1) + − − là: A. −1. B. + . ∞ C. 0. D. 1.
Lời giải. n ( n+1− n− ) 1 ∼
n ( n − n) = 0
→ nhân lượng liên hợp :
n ( n + − n− ) 2 n 2 lim 1 1 = lim = lim = 1 → Chọn D. n +1 + n −1 1 1 1+ + 1− n n Giải nhanh n n
: n ( n + − n− ) 2 2 1 1 = ∼ = 1. n +1 + n −1 n + n
Câu 65. Giá trị của giới hạn lim n ( n 1 n ) + − bằng: A. 0. B. 1 . C. 1. D. 1 . 2 3 4
Lời giải. n ( n+1− n) ∼ n( n − n)= 0 → nhân lượng liên hợp :
n ( n + − n) n 1 1 lim 1 = lim = lim = → Chọn B. n +1 + n 1 2 1+ +1 n Giải nhanh n n
: n ( n + − n) 1 1 = ∼ = . n +1 2 + n n + n
Câu 66. Giá trị của giới hạn n ( 2 2 lim
n +1 − n − 3) bằng: A. −1. B. 2. C. 4. D. + . ∞
Lời giải. n( 2 2
n + − n − ) ∼ n( 2 2 1 3
n − n )= 0
→ nhân lượng liên hợp : n lim n( 4 4 2 2
n +1 − n −3)= lim = lim = 2 → Chọn B. 2 2 n +1 + n −3 1 3 1+ + 1− 2 2 n n Giải nhanh 4n 4n : n( 2 2
n +1 − n −3)= ∼ = 2. 2 2 2 2 n +1 + n −3 n + n
Câu 67. Giá trị của giới hạn n ( 2 2 lim
n + n +1 − n + n − 6 ) là: A. 7 −1. B. 3. C. 7 . D. + . ∞ 2
Lời giải. n( 2 2
n + n + − n + n − ) ∼ n( 2 2 1 6
n − n )= 0
→ nhân lượng liên hợp : n lim n( 7 2 2
n + n +1 − n + n − 6)= lim 2 2
n + n +1 + n + n − 6 7 7 = lim = . 1 1 1 6 2 1+ + + 1+ − 2 2 n n n n Chọn C. Giải nhanh 7n 7n 7 : n( 2 2
n + n +1 − n + n − 6) = ∼ = . 2 2 2 2 2
n + n +1 + n + n − 6 n + n
Câu 68. Giá trị của giới hạn 1 lim là: 2 2 n + 2 − n + 4 A. 1. B. 0. C. − . ∞ D. + . ∞ Lời giải. 2 2 2 2
n + 2 − n + 4 ∼ n − n = 0
→ nhân lượng liên hợp : 1 1 lim = lim − + + + = − + + + = −∞ 2 ( 1 2 4 2 2 n 2 n 4 ) lim . n 1 1 2 2 2 2 2 + 2 − + 4 n n n n vì 1 2 4 lim n = + , ∞ lim − 1+ + 1 + = −1< 0 → Chọn C. 2 2 2 n n Giải nhanh : 1 1 = − + + + ∼ − + = − →−∞ 2 ( 1 2 2 n 2 n 4 ) ( 2 2 n n n . 2 ) 2 2 n + 2 − n + 4 2
Câu 69. Giá trị của giới hạn
9n − n − n + 2 lim là: 3n − 2 A. 1. B. 0. C. 3. D. + . ∞ Lời giải. 2 2
9n − n − n + 2 ∼ 9n = 3n = / 0 → giải nhanh : 2 2
9n − n − n + 2 9n ∼ = 1 → Chọn A. 3n − 2 3n 1 1 2 9 − − + 2 2 Cụ thể
9n − n − n + 2 9 n n n : lim = lim = = 1. 3n − 2 2 3 3− n
Câu 70. Giá trị của giới hạn 1 lim là: 3 3 n +1 − n A. 2. B. 0. C. − . ∞ D. + . ∞ Lời giải. 3 3 3 3
n +1 − n ∼ n − n = 0
→ nhân lượng liên hợp : lim( 1 3 3 n +1 − n)= lim = 0 → Chọn B. 3 (n + )2 3 3 3 2 1 + n n +1 + n
Vấn đề 3. DÃY SỐ CHỨA H=M LŨY THỪA n+2
Câu 71. Kết quả của giới hạn 2 −5 lim bằng: 3n + 2.5n A. 25 − . B. 5 . C. 1. D. 5 − . 2 2 2 n+2 n+2
Lời giải. Giải nhanh 2−5 −5 25 : ∼ = − → Chọn A. 3n + 2.5n 2.5n 2 n 1 2 − 25 n+2 Cụ thể 2 − 5 5 25 : lim = lim = − . 3n + 2.5n n 3 2 + 2 5 n n 1 +
Câu 72. Kết quả của giới hạn 3 − 2.5 lim bằng: n 1 2 + + 5n A. −15. B. −10. C. 10. D. 15. n n 1 + n 1 +
Lời giải. Giải nhanh 3 −2.5 −2.5 : ∼ = −10 → Chọn B. n 1 2 + + 5n 5n n 3 −10 n n 1 + Cụ thể 3 − 2.5 5 : lim = lim = −10. n 1 2 + + 5n n 2 2. +1 5 n n 1 +
Câu 73. Kết quả của giới hạn 3 − 4.2 −3 lim là: 3.2n + 4n A. 0. B. 1. C. − . ∞ D. + . ∞ 1 n n n+ n
Lời giải. Giải nhanh 3 −4.2 −3 3 3 : ∼ = → 0. Chọn A. 3.2n + 4n 4n 4 n n n 3 1 1 −8. −3. n n 1 + Cụ thể 3 − 4.2 −3 4 2 4 0 : lim = lim = = 0. 3.2n + 4n n 1 1 3. +1 2 n
Câu 74. Kết quả của giới hạn 3 −1 lim bằng: 2n − 2.3n +1 A. −1. B. 1 − . C. 1 . D. 3 . 2 2 2 n n
Lời giải. Giải nhanh − : 3 1 3 1 ∼ = − → Chọn B. 2n − 2.3n +1 −2.3n 2 n 1 1− n Cụ thể 3 −1 3 1 : lim = lim = − . 2n − 2.3n +1 n n 2 1 2 − 2 + 3 3 ( n 5) n 1 + 2 −2 +1 Câu 75. Biết rằng 2n + 3 a 5 lim + = + c với a, , b c ∈ . ℤ Tính giá + n + ( )n 1 2 n −1 5.2 5 −3 b trị của biểu thức 2 2 2
S = a + b + c . A. S = 26. B. S = 30. C. S = 21. D. S = 31.
Lời giải. Giải nhanh : ( n n + a = 5) n 1 1 2 −2 +1 n + ( 5 2 3 ) 2 2n 1 5 ∼ 2 2 b + + = + = + → = 5. n+ n+ − 5.2n +( 5) 1 2 n 1 −3 ( 5) 1 2 n 5 5 c = 2 Vậy 2 2 2
S = 1 + 5 + 2 = 30. Chọn B. n n 2 1 n 3 ( ) n 1 + 1− 2. − + + + + 2 2 5 2 1 Cụ thể : 2 2n 3 5 5 lim + + = lim n + n+ n n − 5.2n + ( 5) 1 2 n 1 1 −3 2 1 1− 5. + 5 −. 2 5 5 n 1 5 = + 2 = + 2. 5 5 n n 2n
Câu 76. Kết quả của giới hạn π + 3 + 2 lim là: n n 2 n+2 3π −3 + 2 A. 1. B. 1. C. + . ∞ D. 1 . 3 4 n n 2n n n n n
Lời giải. Giải nhanh: π +3 + 2 π + 3 + 4 4 1 = ∼ = → Chọn D. n n 2 n+2 3π −3 + 2 3 n π −3n + 4.4n 4.4n 4 n n π 3 + +1 n n 2n Cụ thể π + 3 + 2 4 4 1 : lim = lim = . n n 2 n+2 3π −3 + 2 n n π 3 4 3. −3. + 4 4 4
Câu 77. Kết quả của giới hạn n lim 3n − 5 là: A. 3. B. − 5. C. − . ∞ D. + . ∞
Lời giải. Giải nhanh n : Vì 3 > 5 nên 3n 5 ∼ 3n − →+ . ∞ Chọn D. l im3n = +∞ n Cụ thể n n : 5 lim 3n − 5 = lim3n 1 − = +∞ vì . 5 3 lim1 − =1> 0 3
Câu 78. Kết quả của giới hạn ( 4 n 1
lim 3 .2 + −5.3n ) là: A. 2 . B. −1. C. − . ∞ D. 1. 3 3
Lời giải. Giải nhanh : 4 n 1
3 .2 + −5.3n ∼ −5.3n = −∞ (−5 < 0). → Chọn C. l im3n = +∞ n Cụ thể 2 : lim( 4 n 1
3 .2 + −5.3n ) = lim3n 1 62. n
−5 = −∞ vì . 2 3 l im 1 62.
−5 = −5 < 0 3 n n 1 +
Câu 79. Kết quả của giới hạn 3 − 4.2 −3 lim là: 3.2 + 4n n A. 0. B. 1. C. − . ∞ D. + . ∞ 1 n n n+ n
Lời giải. Giải nhanh 3 −4.2 −3 3 3 : ∼ = → 0. Chọn A. 3.2 + 4n 4n n 4 n n 1 + 1 n n+ n n 1 + Cụ thể 3 − 4.2 −3 8.3 3 3 − 4.2 −3 : 0 ≤ ≤ = 24. → 0 → lim = 0. 3.2n + 4n 4n 4 3.2n + 4n n 1 +
Câu 80. Kết quả của giới hạn 2 + 3n +10 lim là: 2 3n − n + 2 A. + . ∞ B. 2 . C. 3 . D. − . ∞ 3 2 n → 0 n n Lời giải. n n −1 n − 2 Ta có n 2 n k n 3 ( )( ) 3 2 = C ⇒ 2 C ≥ = ⇒ . ∑ ∼ Khi đó: n n 6 6 2n k =0 → +∞ 2 n 2n n lim = +∞ n 1 2 n 2 + 3. +10. n 1 2 + + 3n +10 2n 2n 2 n lim = lim . = +∞ vì n 1 + + . 2 2 2 3. 10. 3n − n + 2 1 2 n n 3− + 2 2 2 2 n lim = > 0 n 1 2 3 3− + 2 n n Chọn A. n n 1 +
Câu 81. Tìm tất cả giá trị nguyên của 4 + 2 1
a thuộc (0;2018) để 4 lim ≤ . 3n + 4n+a 1024 A. 2007. B. 2008. C. 2017. D. 2016. n n 1 + n
Lời giải. Giải nhanh: 4 + 2 4 1 1 4 a 10 4 ∼ = ≤
⇔ 2 ≥ 1024 = 2 ⇔ a ≥ 10. n n+2 3 + 4 4n+a 2a 1024
Mà a ∈(0;2018) và a ∈ ℤ nên a ∈ {10;2017} → có 2008 giá trị . a Chọn B. n 1 1+ 2. n n 1 + Cụ thể 4 + 2 2 1 1 1 : 4 lim = lim = = = . 4 3n + 4n+a n a a 3 4 (2a a )2 2 + 4 4 2 n Câu 82. n + 2n −1
Kết quả của giới hạn ( ) lim + bằng: 3n −1 3n A. 2 . B. −1. C. 1. D. 1 − . 3 3 3 2 n 2 n Lời giải. n + 2 −1 n n + 2 −1 Ta có ( ) n ( ) lim + = lim + lim . Ta có 3 n −1 3n 3 n −1 3n 2 1 + 2 n + 2n 1 n l im = lim = 3 n −1 1 n 2 3 − n + 2n (− ) 1 1 3 ⇒ lim + = . Chọn C. n 3 n −1 3n 3 (− )n n 1 n 1 (− ) 1 0 ≤ ≤ → 0 ⇒ lim = 0 3n 3 3n n Câu 83. 3 n + −1 cos 3n
Kết quả của giới hạn ( ) lim bằng: n −1 A. 3 . B. 3. C. 5. D. −1. 2 n n Lời giải. 3 n +(− ) 1 cos 3n 3n (− ) 1 cos 3n lim = lim + Ta có . : n −1 n −1 n 3n 3 l im = = 3 n 1 1 n 3 n +(− ) 1 cos 3n − ⇒ lim = 3. (− )n n 1 cos 3n 1 (− ) 1 cos 3n n −1 0 ≤ ≤ → 0 ⇒ lim = 0 n −1 n −1 n −1 Chọn B. 2
Câu 84. Có bao nhiêu giá trị nguyên của an −1 1
a thuộc (0;20) sao cho lim 3 + − 2 3 + n 2n là một số nguyên. A. 1. B. 3. C. 2. D. 4. 1 2 a − 2 an −1 lim = lim n = a 2 2 3 + n 3 Lời giải. Ta có an −1 1 +1 2 ⇒ lim 3 + − = 3 + a. 2 n 3 + n 2n n 1 1 lim = lim = 0 2n 2 a (0;20), a ℤ Ta có ∈ ∈ → a ∈ {1;6;1 } 3 . Chọn B. a +3 ∈ ℤ
Câu 85. Kết quả của giới hạn lim 2.3n −n + 2 là: A. 0. B. 2. C. 3. D. + . ∞ n Lời giải. Ta có n 1 lim
2.3n − n + 2 = lim 3n . 2 − + 2. . Vì 3n 3 lim 3n = +∞ l im 3n = +∞ n n n 2 n 0 ≤ ≤ = = → 0 ⇒ lim = 0 n → , n 2 3 C n n n − n − n ( ) n 1 1 1 3 lim 2 − + 2. = 2 > 0 3n 3 2 n 1 lim = 0 3
do đó lim 2.3n −n + 2 = + . ∞ Chọn D.
Vấn đề 4. TỔNG CỦA CẤP SỐ NHÂN LÙI VÔ HẠN
Câu 86. Tổng của một cấp số nhân lùi vô hạn bằng 2 , tổng của ba số hạng đầu tiên
của cấp số nhân bằng 9 . Số hạng đầu u của cấp số nhân đó là: 4 1 A. 9 u = 3. B. u = 4. C. u = . D. u = 5. 1 1 1 2 1
Lời giải. Gọi q là công bội của cấp số nhân, ta có : u 1 1 = 2 u = 2 1− q q = − 1 ( ) 1 − q 2 ⇔ ⇔ . 9 Chọn A. 3 1− q 9 2 ( 3 1− q ) 1 = S = u . = u = 2 1 + = 3 4 1 3 1 1− q 4 2 Câu 87. Tính tổng 1 1 1 S = 9 + 3 +1+ + +⋯+ +⋯ . −3 3 9 3n A. 27 S = . B. S =14. C. S =16. D. S =15. 2 Lời giải. Ta có 1 1 1 1 1 1 1 1 27 S = 9 + 3 +1+ + +⋯+ +⋯ = 9 1 + + + +⋯+ + ⋯ = 9 = . n 3 − 2 4 n 1 3 9 3 3 3 3 3 − 1 2 1 − 1 CSN lvh: u 1 = , q= 3 1 3 Chọn A. Câu 88. Tính tổng 1 1 1 1 S = 2 1 + + + +⋯+ + ⋯ . 2 4 8 2n A. S = 2 +1. B. S = 2. C. S = 2 2. D. 1 S = . 2 Lời giải. Ta có 1 1 1 1 1 S = 2 1 + + + +⋯+ + ⋯ = 2 = 2 2. Chọn C. 2 4 8 2n 1 1 − 1 CSN lv : h u 1 = , q= 2 1 2 n Câu 89. Tính tổng 2 4 2 S = 1+ + +⋯+ +⋯ . 3 9 3n A. S = 3. B. S = 4. C. S = 5. D. S = 6. Lời giải. Ta có 2 n 2 4 2n 2 2 2 1 S = 1+ + +⋯+ +⋯ = 1 ⋯ + + + + +⋯= 3. Chọn A. 3 9 3n 3 3 = 3 2 1− 2 3 CSN lv : h u 1 = , q= 1 3 n+ Câu 90. 1 1 1 −1
Tổng của cấp số nhân vô hạn ( ) 1 ,− , ,..., ,... bằng: n 1 2 6 18 2.3 − A. 3 . B. 8. C. 2 . D. 3. 4 3 3 8 Lời giải. Ta có : n+ n+ − − 1 1 1 ( ) 1 1 1 1 1 ( ) 1 1 1 1 3 S = − + +⋯+ +⋯ = 1 − + +⋯+ = = . Chon D. n 1 − 2 n 1 2 6 18 2.3 2 3 3 3 − 2 1 8 1 + 1 CSN lvh:u 1 = , q=− 3 1 3 Câu 91. Tính tổng 1 1 1 1 1 1 S
= − + − +... + − +... . 2 3 4 9 2n 3n A. 1. B. 2 . C. 3 . D. 1 . 3 4 2 Lời giải. Ta có 1 1 1 1 1 1 S = − + − +... + − +... 2 3 4 9 2n 3n 1 1 1 1 1 1 1 1 1 1 = 2 3 + +⋯+ + ⋯ − + +⋯+ +⋯ = − = 1− = . 2 4 2n 3 9 3n 1 1 2 2 1− 1− 1 1 CSN lvh: u =q= CSN lv : 2 3 1 h u =q= 1 2 3 Chọn D. 2 n
Câu 92. Giá trị của giới hạn
1+ a + a +... + a lim
a < 1, b < 1 bằng: 2 n ( )
1+ b + b +... + b A. −b − a 0. B. 1 . C. 1 . D. Không tồn tại. 1− a 1− b Lời giải. Ta có 2 1+ + +... n a a
+ a là tổng n +1 số hạng đầu tiên của cấp số nhân với 1. 1 n a + 1 n a + − − 2 n ( 1 ) 1
số hạng đầu là 1 và công bội là a , nên 1+ a + a +...+ a = = . 1− a 1− a 1 1 n b + 1 n b + − − 2 n ( 1 ) 1
Tương tự: 1+ b +b +...+ b = = . 1− b 1−b n 1 1− a + 2 n n 1 + Do đó
1+ a + a +... + a 1−b 1− a 1 1 −b lim = lim −a = lim . =
a < 1, b < 1 . 2 n n 1 + n 1 + ( )
1+ b + b +... + b 1−b 1− a 1−b 1− a 1−b Chọn B. Câu 93. Rút gọn 2 4 6 2 S = 1+ cos + cos + cos +⋯+ cos n x x x
x +⋯ với cos x ≠ ±1. A. 1 1 2 S = sin x. B. 2 S = cos x. C. S = . D. S = . 2 sin x 2 cos x Lời giải. Ta có 1 1 2 4 6 2
S = 1+ cos x + cos x + cos x +⋯+ cos n x +⋯ = = . Chọn C. 2 2 1− cos x sin x 2 CSN lvh: u 1 = , q=cos x 1 Câu 94. Rút gọn 2 4 6 = − + − +⋯+(− )n 2 1 sin sin sin 1 .sin n S x x x
x +⋯ với sin x ≠ ±1. A. 1 2 S = sin x. B. 2 S = cos x. C. S = . D. 2 S = tan x. 2 1+ sin x Lời giải. Ta có n 1 2 4 6
S = 1−sin x + sin x −sin x +⋯+(− ) 2 1 .sin n x +⋯ = . Chọn C. 2 1+ s n i x 2 CSN lvh: u 1 = , q=−sin x 1 Câu 95. Thu gọn 2 3 π
S = 1− tan α + tan α tan α − +… với 0 α < < . 4 A. 1 α α S = . B. cos S = . C. tan S = . D. 2 S tan . α = 1− tan α π 1+ tan α 2 sin α + 4 Lời giải. Ta có π tan α ∈ (0; ) 1 với mọi α ∈ 0; , do đó 4 1 cos α cos α 2 3
S = 1− tan α + tan α − tan α +… = = = . Chọn B. 1+ tan α sin α + cos α π CSN lv : h u 1 = , q=−tan 1 α 2 sin α + 4 Câu 96. Cho ,
m n là các số thực thuộc (−1; ) 1 và các biểu thức: 2 3
M = 1+ m + m + m +⋯ 2 3
N = 1+ n + n + n +⋯ 2 2 3 3
A = 1+ mn + m n + m n +⋯
Khẳng định nào dưới đây đúng? A. MN MN A = . B. A = . M + N −1 M + N +1 C. 1 1 1 A = + − . D. 1 1 1 A = + + . M N MN M N MN 1 1 M = m = 1−
Lời giải. Ta có 1 − m M ⇒ , khi đó 1 1 N = n = 1− 1 n − N 1 1 MN A = = = . Chọn A. 1− mn 1 1 M + N −1 1− 1 − 1 − M N
Câu 97. Số thập phân vô hạn tuần hoàn 0,5111⋯ được biểu diễn bởi phân số tối giản
a . Tính tổng T = a + .b b A. 17. B. 68. C. 133. D. 137. Lời giải. Ta có −2 −3 0,5111⋯ = 0,5 +10 +10
+⋯+10−n +⋯ Dãy số 2 − 3
10 ;10− ;...;10−n ;... là một cấp số nhân lùi vô hạn có số hạng đầu bằng −2 u 10 1 −2
u = 10 , công bội bằng −1 q = 10 nên 1 S = = = . 1 −1 1− q 1−10 90 46 23 a = 23 Vậy 0,5111... 0,5 S = + = = →
→T = a + b = 68. Chọn B. 90 45 b = 45
Câu 98. Số thập phân vô hạn tuần hoàn A = 0,353535... được biểu diễn bởi phân số
tối giản a . Tính T = a . b b A. 3456. B. 3465. C. 3645. D. 3546. Lời giải. Ta có 35 2 35 35 35 a = 35 10 A 0, 353535... 0, 35 0, 0035 ... ... = = + + = + + = = ⇒ ⇒ T = 3465. . 2 4 10 10 1 99 b = 99 1 − 2 10 Chọn B.
Câu 99. Số thập phân vô hạn tuần hoàn B = 5,231231... được biểu diễn bởi phân số
tối giản a . Tính T = a − . b b A. 1409. B. 1490. C. 1049. D. 1940. Lời giải. Ta có
B = 5, 231231... = 5 + 0, 231+ 0, 000231+... 231 3 231 231 231 1742 a =1742 10 5 ... 5 5 = + + + = + = + = → ⇒ T = 1409 3 6 10 10 1 999 333 b = 333 1 − 3 10 Chọn A.
Câu 100. Số thập phân vô hạn tuần hoàn 0,17232323… được biểu diễn bởi phân số tối
giản a . Khẳng định nào dưới đây đúng? b A. 15 a −b > 2 . B. 14 a −b > 2 . C. 13 a −b > 2 . D. 12 a −b > 2 . Lời giải. Ta có 1 1 1 0,17232323… = 0,17 + 23 + + ⋯ 4 6 8 1 0 10 10 1 17 17 23 1706 853 10000 = + 23. = + = = . 100 1 100 100.99 9900 4950 1−100 a = 853 12 13 →
⇒ 2 < T = 4097 < 2 . b = 4950 Chọn D. Baøi 02
GIÔÙI HAÏN CUÛA HAØM SOÁ
I GIỚI HẠN HỮU HẠN CỦA H M SỐ TẠI MỘT ĐIỂM – 1. Định nghĩa Định nghĩa 1
Cho khoảng K chứa điểm x và hàm số y = f (x) xác định trên K hoặc trên 0 K \ {x . 0 }
Ta nói hàm số y = f (x) có giới hạn là số L khi x dần tới x nếu với dãy số (x n ) 0
bất kì, x ∈ K \ x và x → x , ta có f (x → L n ) . n { 0 } n 0
Kí hiệu: lim f (x)= L hay f (x)→ L khi x → x . 0 x →x0
Nhận xét: lim x = x ; lim c = c với c là hằng số. 0 x →x0 x →x0
2. Định lí về giới hạn hữu hạn Định lí 1
a) Giả sử lim f (x)= L và lim g(x)= M . Khi đó: x →x0 x →x0
• lim f (x)+ g (x) = L + M ; x →x 0
• lim f (x)− g (x) = L − M ; x →x 0
• lim f (x).g (x) = . L M ; x →x 0 f (x ) L • lim = (nếu M ≠ 0 ).
x →x0 g (x ) M
b) Nếu f (x)≥ 0 và lim f (x)= L , thì L ≥ 0 và lim f (x) = L. x →x0 x →x0 3. Giới hạn một bên Định nghĩa 2
• Cho hàm số y = f (x) xác định trên (x ;b . 0 )
Số L được gọi là giới hạn bên phải của hàm số y = f (x) khi x → x nếu với dãy 0
số (x bất kì, x < x < b và x → x , ta có f (x → L n ) . n ) 0 n n 0
Kí hiệu: lim f (x) = . L x x + → 0
• Cho hàm số y = f (x) xác định trên (a; x . 0 )
Số L được gọi là giới hạn bên trái của hàm số y = f (x) khi x → x nếu với dãy số 0
(x bất kì, a < x < x và x → x , ta có f (x → L n ) . n ) n 0 n 0
Kí hiệu: lim f (x) = . L x x − → 0 Định lí 2
lim f (x ) = L ⇔ lim f (x ) = lim f (x ) = . L x x + − → 0 x →x0 x →x0
II GIỚI HẠN HỮU HẠN CỦA H M SỐ TẠI VÔ CỰC – Định nghĩa 3
a) Cho hàm số y = f (x) xác định trên (a;+∞).
Ta nói hàm số y = f (x) có giới hạn là số L khi x → +∞ nếu với dãy số (x bất n )
kì, x > a và x → +∞ , ta có f (x → L n ) . n n
Kí hiệu: lim f (x)= . L x →+∞
b) Cho hàm số y = f (x) xác định trên (− ; ∞ a).
Ta nói hàm số y = f (x) có giới hạn là số L khi x → −∞ nếu với dãy số (x bất n )
kì, x < a và x → −∞ , ta có f (x → L n ) . n n
Kí hiệu: lim f (x)= . L x →−∞ Chú ý:
a) Với c, k là hằng số và k nguyên dương, ta luôn có: c c
lim c = c; lim c = c; lim = 0; lim = 0. k k x →+∞ x →−∞ x →+∞ x x →−∞ x
b) Định lí 1 về giới hạn hữu hạn của hàm số khi x → x vẫn còn đúng khi 0
x → +∞ hoặc x → −∞ . n
III GIỚI HẠN VÔ CỰC CỦA H M SỐ – 1. Giới hạn vô cực Định nghĩa 4
Cho hàm số y = f (x) xác định trên (a;+∞).
Ta nói hàm số y = f (x) có giới hạn là −∞ khi x → +∞ nếu với dãy số (x bất n )
kì, x > a và x → +∞ , ta có f (x → −∞ n ) . n n
Kí hiệu: lim f (x) = − . ∞ x →+∞
Nhận xét: lim f (x)= +∞ ⇔ lim (− f (x)) = − . ∞ x →+∞ x →+∞
2. Một vài giới hạn đặc biệt a) lim k
x = +∞ với k nguyên dương. x →+∞ neáu k chaün b) k +∞ lim x = . x→−∞ −∞ neáu k leû
3. Một vài quy tắc về giới hạn vô cực
a) Quy tắc tìm giới hạn của tích f (x).g(x)
lim f (x ) = L lim g (x )
lim f (x ) g (x ) x → x 0 x → x0 x → x0 +∞ +∞ L > 0 −∞ −∞ +∞ −∞ L < 0 −∞ +∞
b) Quy tắc tìm giới hạn của thương f (x) g (x ) f (x )
lim f (x ) = L lim g (x )
Dấu của g (x) lim x → x0 x → x0
x → x0 g (x ) L ±∞ Tùy ý 0 + +∞ L > 0 − −∞ 0 + −∞ L < 0 − +∞
CÂU HỎI TRẮC NGHIỆM
CÂU HỎI TRẮC NGHIỆM
Vấn đề 1. DÃY SỐ CÓ GIỚI HẠN HỮU HẠN
Câu 1. Giá trị của giới hạn lim( 2 3x + 7x +1 ) 1 là: x →2 A. 37. B. 38. C. 39. D. 40. Lời giải. lim( 2 3x + 7x +1 ) 2 1 = 3.2 + 7.2 +11 = 37 → Chọn A. x→2
Câu 2. Giá trị của giới hạn 2 lim x − 4 là: x → 3 A. 0. B. 1. C. 2. D. 3.
Lời giải. lim x −4 = ( 3)2 2 − 4 = 1 → Chọn B. x→ 3
Câu 3. Giá trị của giới hạn 1 2 lim x sin là: x →0 2 A. 1 sin . B. + . ∞ C. − . ∞ D. 0. 2 Lời giải. Ta có 1 1 2 lim x sin = 0.sin = 0 → Chọn D. x→0 2 2 2
Câu 4. Giá trị của giới hạn x −3 lim là: 3 x → 1 − x + 2 A. 1. B. −2. C. 2. D. 3 − . 2 2 2 Lời giải. x − 3 (− ) 1 −3 lim = = −2 → Chọn B. 3 x→− x + 2 (− )3 1 1 + 2 3
Câu 5. Giá trị của giới hạn x − x lim là: x → (2x − ) 1 ( 4 1 x − ) 3 A. 1. B. −2. C. 0. D. 3 − . 2 3 3 Lời giải. x − x 1−1 lim = = 0 → Chọn C. x→ (2x − ) 1 ( 4 x − ) 3 (2.1− ) 1 ( 4 1 1 − ) 3
Câu 6. Giá trị của giới hạn x −1 lim là: 4 x → 1 − x + x −3 A. 3 − . B. 2 . C. 3 . D. 2 − . 2 3 2 3 Lời giải. x −1 −1−1 Ta có 2 lim = = − → Chọn D. 4
x→−1 x + x − 3 1−1−3 3 2
Câu 7. Giá trị của giới hạn 3x +1 − x lim là: x → 1 − x −1 A. 3 − . B. 1 . C. 1 − . D. 3 . 2 2 2 2 2 Lời giải. Ta có 3x +1 − x 3 +1 +1 3 lim = = − → Chọn A. x→−1 x −1 −1−1 2 2
Câu 8. Giá trị của giới hạn 9x − x lim là: x → (2x − ) 1 ( 4 3 x − ) 3 A. 1 . B. 5. C. 1 . D. 5. 5 5 2 2 Lời giải. 9x − x 9.3 −3 1 lim = = → Chọn C. x→ (2x − ) 1 ( 4 x − ) 3 (2.3− ) 1 ( 4 3 3 − ) 3 5 2
Câu 9. Giá trị của giới hạn x − x +1 3 lim là: 2 x →2 x + 2x A. 1 . B. 1 . C. 1. D. 1 . 4 2 3 5 2 2 Lời giải. x − x +1 2 − 2 +1 1 3 lim = = → Chọn B. 2 2 x→2 x + 2x 2 + 2.2 2 3 2
Câu 10. Giá trị của giới hạn
3x − 4 − 3x − 2 lim là: x →2 x +1 A. 3 − . B. 2 − . C. 0. D. + . ∞ 2 3 3 2 3 Lời giải. Ta có:
3x − 4 − 3x − 2 12 − 4 − 6 − 2 0 lim = = = 0 → Chọn C. x→2 x +1 3 3
Vấn đề 2. GIỚI HẠN MỘT BÊN
Câu 11. Kết quả của giới hạn x −15 lim là: x 2+ → x − 2 A. − . ∞ B. + . ∞ C. 15 − . D. 1. 2 lim (x −1 ) 5 = −13 < 0 Lời giải. Vì + → x −15 x 2 → lim = − . ∞ Chọn A. lim (x −2) x→2
= 0 & x − 2 > 0, ∀x > 2 + x − 2 x →2+
Câu 12. Kết quả của giới hạn x + 2 lim là: x 2+ → x − 2 A. − . ∞ B. + . ∞ C. 15 − .
D. Không xác định. 2
lim x + 2 = 2 > 0 Lời giải. + → x + 2 x 2 → lim = + . ∞ Chọn B. x→2+ lim
x − 2 = 0 & x − 2 > 0, x ∀ > 2 x − 2 x →2+ Câu 13. 3x + 6
Kết quả của giới hạn lim là: + x ( → −2) x + 2 A. − . ∞ B. 3. C. + . ∞
D. Không xác định.
Lời giải. Ta có x + 2 = x + 2 với mọi x > −2, do đó : 3x + 6 3 x + 2 3(x + 2) lim = lim = lim = lim 3 = 3 → Chọn B. + + + + x ( → − ) 2 x + 2 x ( → 2 − ) x + 2 x ( → − ) 2 x + 2 x ( → − ) 2
Câu 14. Kết quả của giới hạn 2 − x lim là: − 2 x →2 2x −5x + 2 A. − . ∞ B. + . ∞ C. 1 − . D. 1. 3 3 Lời giải. Ta có 2 − x 2 − x 1 1 lim = lim = lim = − . Chọn C. − 2 x 2 x 2 2x −5x + 2
− (2 − x )(1− 2x ) x 2− → → → 1− 2x 3 2
Câu 15. Kết quả của giới hạn x +13x + 30 lim là: x 3+ →− (x +3)( 2 x + ) 5 A. −2. B. 2. C. 0. D. 2 . 15
Lời giải. Ta có x +3> 0 với mọi x > −3, nên: 2 x +13x + 30 (x + ) 3 (x +10) x + 3.(x +10) −3+ 3(−3+ 7) lim = lim = lim = = 0 . x 3+ ( + + →− x + ) 3 ( 2 x + ) x→ 3 5 − (x + ) 3 ( 2 x + ) 2 x→ 3 5 − x + 5 (− )2 3 + 5 Chọn C. 2x víi x < 1 Câu 16. Cho hàm số f (x ) = 1 − x
. Khi đó lim f (x ) là: + x 1 → 2 3x 1 víi x 1 + ≥ A. + . ∞ B. 2. C. 4. D. − . ∞
Lời giải. lim f (x) 2 2
= lim 3x +1 = 3.1 +1 = 2 → Chọn B. x 1+ x 1+ → → 2 x +1 víi Câu 17. x < 1
Cho hàm số f (x) = 1− x
. Khi đó lim f (x) là: − x 1 →
2x − 2 víi x ≥1 A. + . ∞ B. −1. C. 0. D. 1. 2 2 lim + = − ( x ) 1 2 Lời giải. x +1 lim f (x) = lim = +∞ vì x 1 → . Chọn A. x 1− x 1− → → 1− x lim
(1− x) = 0 & 1− x > 0 (∀x < ) 1 x 1− → 2 Câu 18. víi Cho hàm số x −3 x ≥ 2 f (x) =
. Khi đó lim f (x) là: x −1 víi x < 2 x →2 A. −1. B. 0. C. 1. D. Không tồn tại.
lim f (x)= lim − = + + ( 2 x ) 3 1
Lời giải. Ta có x→2 x→2
⇒ lim f (x) = lim f (x) = 1 ⇒ lim f (x) = 1. lim f
(x) = lim (x − ) x→2+ x→2− x→2 1 = 1 x →2− x→2− Chọn C. Câu 19. Cho hàm số
x − 2 + 3 víi x ≥ 2 f (x) =
. Tìm a để tồn tại lim f (x). a x −1 víi x < 2 x →2 A. a = 1. B. a = 2. C. a = 3. D. a = 4.
lim f (x) = lim (ax − ) 1 = 2a −1
Lời giải. Ta có x→2− x→2− . lim f (x) = lim − + = + + ( x 2 ) 3 3 x →2 x→2
Khi đó lim f (x) tồn tại ⇔ lim f (x)= lim f (x) ⇔ 2a−1= 3 ⇔ a = 2. Chọn B. x→2 x 2− x 2+ → → 2
x − 2x +3 víi x > 3 Câu 20. Cho hàm số f (x) = 1 víi
x = 3. Khẳng định nào dưới đây sai? 2 3 −2x víi x < 3
A. lim f (x)= 6.
B. Không tồn tại lim f (x). x 3+ → x→3
C. lim f (x)= 6.
D. lim f (x)= −15. x 3− → x 3− →
lim f (x)= lim x − x + = + + ( 2 2 ) 3 6
Lời giải. Ta có x→3 x→3
→ lim f (x) ≠ lim f (x) lim f (x) = lim x→ x→ − x = − − − ( 2 3 2 ) 3+ 3 15 − x→3 x→3
→ không tồn tại giới hạn khi x → 3.
Vậy chỉ có khẳng định C sai. Chọn C.
Vấn đề 3. GIỚI HẠN TẠI VÔ CỰC
Câu 21. Giá trị của giới hạn ( 3 lim x − x + ) 1 là: x →−∞ A. 1. B. − . ∞ C. 0. D. + . ∞ 3 lim x = −∞ x→−∞ Lời giải. lim ( 1 1 3 x x ) 3 1 lim x − + = −1 + = +∞ vì . 2 3 1 1 x→−∞ x→−∞ x x lim −1 + = −1 < 0 2 3 x→−∞ x x Chọn D. Giải nhanh: 3 x − x + khi ∼ (− ) 3 1 1 x →+∞ x → − . ∞
Câu 22. Giá trị của giới hạn ( 3 2 lim
x + 2x + 3 x ) là: x →−∞ A. 0. B. + . ∞ C. 1. D. −∞ . Lời giải. Ta có lim ( 3 2 3 2 x 2x 3 x ) lim ( 3 2 x 2x 3x ) 3 lim x + + = − + − = −1 + − = + . ∞ Chọn B. 2 x →−∞ x →−∞ x →−∞ x x Giải nhanh: 3 3 2
x + 2x + 3 x khi ∼ x → +∞ x → − . ∞
Câu 23. Giá trị của giới hạn ( 2 lim x +1 + x) là: x →+∞ A. 0. B. + . ∞ C. 2 −1. D. −∞ .
Lời giải. Giải nhanh: 2 2 x → +∞ : x +1 + x . Chọn B. ∼
x + x = 2x → +∞
Đặt x làm nhân tử chung: lim x = +∞ x→+∞ lim ( 1 2
x +1 + x) = lim x 1+ +1 = +∞ vì . 2 1 x→+∞ x→+∞ x lim 1+ +1 = 2 > 0 + 2 x →2 x
Câu 23. Giá trị của giới hạn (3 3 2 lim
3x −1 + x + 2) là: x →+∞ A. 3 3 +1. B. + . ∞ C. 3 3 −1. D. −∞ .
Lời giải. Giải nhanh: 3 3 2 3 3 2 x → +∞ x − + x + ∼ x + x = (3 : 3 1 2 3 3 + ) 1 x → + . ∞ Chọn B.
Đặt x làm nhân tử chung: lim ( 1 2 3 3 2 3x −1 + x + 2) 3 = lim x 3− + 1+ = +∞ vì 3 2 x→+∞ x→+∞ x x lim x = +∞ x→+∞ . 1 2 3 3 lim 3− + 1+ = 3 +1> 0 3 2 x→+∞ x x
Câu 25. Giá trị của giới hạn x + + là: →+∞ ( 2 lim 4x 7x 2x x ) A. 4. B. − . ∞ C. 6. D. +∞ .
Lời giải. Giải nhanh: x → +∞ x( 2
x + x + x) ∼ x ( 2 x + x) 2 : 4 7 2 4 2 = 4x → + . ∞ Chọn D. Đặt 2
x làm nhân tử chung: 2 lim x = +∞ x→+∞ lim x + + = + + = +∞ vì . 7 →+∞ ( 7 2 4x 7x 2x) 2 lim x 4 2 x x→+∞ x lim 4 + + 2 = 4 > 0 x→+∞ x
Vấn đề 4. DẠNG VÔ ĐỊNH 0 0 3
Câu 26. Giá trị của giới hạn x −8 lim là: 2 x →2 x − 4 A. 0. B. + . ∞ C. 3.
D. Không xác định. 3 2 2 Lời giải. Ta có x −8
(x − 2)(x + 2x + 4) x + 2x + 4 12 lim = lim = lim = = 3 2 x →2 x →2 x →2 x − 4 (x − 2)(x + 2) x + 2 4 Chọn C. 5
Câu 27. Giá trị của giới hạn x +1 lim là: 3 x → 1 − x +1 A. 3 − . B. 3. C. 5 − . D. 5. 5 5 3 3 1 (x + ) 1 ( 4 3 2 5
x − x + x − x x + + ) 4 3 2 1 Lời giải.
x − x + x − x +1 5 lim = lim = lim = . 3 x →− x +1 x →− (x + ) 1 ( 2 1 1 x − x + ) 2 x →−1 1 x − x +1 3 Chọn D. 3 Câu 28. Biết rằng 2x + 6 3 lim = a 3 + . b Tính 2 2 a + b . 2 x →− 3 3− x A. 10. B. 25. C. 5. D. 13. 2 2 3 3 (x + 3)( 2 x − 3x + ) 3 2( 2 3 x − 3x x + + ) 3
Lời giải. Ta có lim = lim = lim 2 x →− 3 x →− 3 3− x ( 3−x)( 3 + x) x →− 3 3 − x
2 (− 3)2 − 3.(− 3)+3 18 a = 3 2 2 3 3 = = = →
⇒ a + b = 10 . Chọn A. 3 −(− 3) 2 3 b = 1 2
Câu 29. Giá trị của giới hạn −x − x + 6 lim là: 2 x → 3 − x + 3x A. 1. B. 2 . C. 5. D. 3. 3 3 3 5 2 Lời giải. −x − x + 6 (x + ) 3 (x −2) x − 2 −3−2 5 lim = lim = lim = = . Chọn C. 2 x → 3 − x →−3 x + 3x x (x + ) x → 3 3 − x −3 3
Câu 30. Giá trị của giới hạn 3− x lim là: x →3− 3 27 − x A. 1. B. 0. C. 5. D. 3. 3 3 5
Lời giải. Ta có 3− x > 0 với mọi x < 3, do đó: 3− x 3− x lim = lim x 3− 3 x →3− → 27 − x (3− x)( 2 9 + 3x + x ) 3− x 3−3 = lim = = 0. Chọn B. x →3− 2 2 9 + 3x + x 9 + 3.3 + 3 ( 2 21 x π + )7 21 1− 2x π −
Câu 31. Giá trị của giới hạn lim là: x →0 x 21 21 21 21 A. 2π 2π 2π 1 2π − − . B. − . C. − . D. . 7 9 5 7 Lời giải. Ta có ( 2 21 x + )7 21 1− 2x − ( 2 21 x π π π + )(7 1−2x − ) 21 1 2π lim = lim + lim x = − . Chọn A. x →0 x →0 x →0 x x 7 2
Câu 32. Giá trị của giới hạn
x + x − x lim là: + 2 x →0 x A. 0. B. − . ∞ C. 1. D. + . ∞
x + x − x ( 2 2
x + x )− x Lời giải. Ta có 1 lim = lim = lim = +∞ + 2 x 0 x 0+ 2 x + → → x ( 2
x + x + x ) x→0 2 x + x + x vì 1> 0 ; lim + + = và 2
x + x + x > 0 với mọi x > 0. Chọn D. + → ( 2x x x 0 x 0 ) 3
Câu 33. Giá trị của giới hạn x −1 lim là: x 1 → 3 4x + 4 −2 A. −1. B. 0. C. 1. D. + . ∞ 3 (x −1) 4x + 4 + 2 4x + 4 + 4 3 ( ) x −1 ( 2 3 )
Lời giải. Ta có lim = lim x 1 → 3 x 1 4x + 4 − 2 → (4x + 4 −8)(3 2 3 x + x + ) 1 3 (4x + 4) ( 2 3 + 2 4x + 4 + 4) 12 = lim = = 1. Chọn C. x 1 → (3 2 3 x + x + ) 12 4 1 3
Câu 34. Giá trị của giới hạn
2 1+ x − 8 − x lim là: x →0 x A. 5 . B. 13 . C. 11. D. 13 − . 6 12 12 12 3 3 Lời giải. Ta có
2 1+ x − 8 − x 2 1+ x − 2 2 − 8 − x lim = lim + x →0 x →0 x x x 2 1 1 13 = lim + = 1+ = . Chọn B. x →0 3 x +1 +1 3
4 + 2 8 − x + (8− x)2 12 12 3 Câu 35. Biết rằng ax +1 − 1−bx
b > 0, a + b = 5 và lim
= 2 . Khẳng định nào dưới x →0 x đây sai?
A. 1< a < 3. B. b >1. C. 2 2 a + b > 10.
D. a −b < 0. 3 3 Lời giải. Ta có ax +1 − 1−bx ax +1 −1 1− 1−bx lim = lim + x →0 x →0 x x x ax bx = lim + x →0 3 ( + ) ( 2 3 + + + ) x(1+ 1 1 1 1 − x x x x ) a b a b = lim + = + = 2. x →0 3 ( + ) ( 2 3 + + + ) (1+ 1 1 1 1 − x x x ) 3 2 a + b = 5 Vậy ta được: a + b = 5 a b ⇔
⇔ a = 3, b = 2 → Chọn A. + = 2 2 a + 3b = 12 3 2
Vấn đề 5. DẠNG VÔ ĐỊNH ∞ ∞ 2
Câu 36. Kết quả của giới hạn 2x + 5x −3 lim là: 2
x →−∞ x + 6x + 3 A. −2. B. + . ∞ C. 3. D. 2 . 5 3 2 2 + − Lời giải. 2 Ta có 2x + 5x − 3 lim = lim x
x = 2 . Chọn D. 2
x →−∞ x + 6x + 3 x →+∞ 6 3 1+ + 2 x x 2 2 Giải nhanh 2x + 5x −3 2x
: khi x → −∞ thì : ∼ = 2. 2 2 x + 6x + 3 x 3 2
Câu 37. Kết quả của giới hạn 2x + 5x −3 lim là: 2 x →−∞ x + 6x + 3 A. −2. B. + . ∞ C. − . ∞ D. 2 . 5 3 3 2 2 + − Lời giải. 3 Ta có: 2x + 5x −3 lim = lim . x x x = − . ∞ Chọn C. 2 x →−∞ x + 6x + 3 x →−∞ 6 3 1+ + 2 x x 3 2 3 Giải nhanh 2x + 5x −3 2x
: khi x → −∞ thì : ∼ = 2x → − . ∞ 2 2 x + 6x + 3 x 3 2
Câu 38. Kết quả của giới hạn 2x −7x +11 lim là: 6 5
x →−∞ 3x + 2x −5 A. −2. B. + . ∞ C. 0. D. − . ∞ 2 7 11 3 2 − + Lời giải. 3 4 6 Ta có: 2x −7x +11 0 lim = lim x x
x = = 0. Chọn C. 6 5
x →−∞ 3x + 2x − 5 x →−∞ 2 5 3 3 + − 6 x x 3 2 3 Giải nhanh 2x −7x +11 2x 2 1
: khi x → −∞ thì : ∼ = . → 0. 6 5 6 3 3x + 2x −5 3x 3 x
Câu 39. Kết quả của giới hạn 2x −3 lim là: x →−∞ 2 x +1 − x A. −2. B. + . ∞ C. 3. D. −1 .
Lời giải. Khi x → −∞ thì 2 2 2 x = −x → x +1 − x ∼
x − x = −x − x = −2x = / 0 3 2 − 2x −3
→ chia cả tử và mẫu cho x , ta được lim = lim x = −1 . x →−∞ 2 x +1 x − x →−∞ 1 − 1+ −1 2 x Chọn D.
Câu 40. Biết rằng (2−a)x −3 có giới hạn là +∞ khi x → +∞ (với a là tham số). 2 x +1 − x
Tính giá trị nhỏ nhất của 2
P = a − 2a + 4. A. P = 1. B. P = 3. C. P = 4. D. P = 5. min min min min
Lời giải. Khi x → +∞ thì 2 2 2 x = x → x +1 − x ∼
x − x = x − x = 0
→ Nhân lượng liên hợp: 2 a x 3 − − Ta có ( ) 3 1 lim = lim ( ( 2−a)x − ) 3 x + + x = x − a − + + x →+∞ x →+∞ ( 2 1 ) 2 lim 2 1 1 . 2 2 +1 x →+∞ x x x − x 2 lim x = +∞ x→+∞ 2 − a x −3 Vì ( ) ⇒ lim 1 = +∞ x →+∞ 2 lim 1+ +1 = 4 > 0 x +1 − x 2 x →+∞ x 3 lim ⇔ 2 − a
− = 2 −a > 0 ⇒ a < 2 . x →+∞ x Giải nhanh 2x −3
: ta có x → +∞ → 2 x +1 − x = (
( −a)x − )( 2 x + + x ) . ∼ ( − a) x ( 2 2 3 1 2 .
x + x )= 2(2−a)x → +∞ ⇔ a < 2 Khi đó 2
P = a − 2a + 4 = (a − )2
1 + 3 ≥ 3, P = 3 ⇔ a = 1 < 2 ⇒ P = 3. Chọn B. i m n 2
Câu 41. Kết quả của giới hạn 4x − x +1 lim là: x →−∞ x +1 A. −2. B. −1. C. −2. D. + . ∞ 2 2
Lời giải. Giải nhanh: khi 4x − x +1 4x −2x x → −∞ → Chọn C. ∼ = = −2. x +1 x x 1 1 − 4 − + 2 2 Cụ thể: 4x − x +1 x x − 4 lim = lim = = −2. x →−∞ x +1 x →−∞ 1 1 1+ x 2
Câu 42. Kết quả của giới hạn
4x − 2x +1 + 2 − x lim là: x →+∞ 2
9x −3x + 2x A. 1 − . B. + . ∞ C. − . ∞ D. 1 . 5 5
Lời giải. Giải nhanh : khi 2 2
4x − 2x +1 + 2 − x 4x − x 2x − x 1 x → +∞ → Chọn D. ∼ = = . 2 2 3x + 2x 5
9x −3x + 2x 9x + 2x 2 1 2 4 − + + −1 2 2 Cụ thể
4x − 2x +1 + 2 − x x x x 1 : lim = lim = . x →+∞ 2 9x −3x + 2 x x →+∞ 3 5 9 − + 2 x 2 Câu 43. Biết rằng
4x − 2x +1 + 2 − x L = lim
> 0 là hữu hạn (với a,b là tham số). x →−∞ 2
ax −3x + bx
Khẳng định nào dưới đây đúng. A. a ≥ 0. B. 3 L = − C. 3 L = D. b > 0. a + b b − a
Lời giải. Ta phải có 2
ax −3x > 0 trên ( ;α −∞ ) ⇔ a ≥ 0. Ta có 2 2 x → −∞
→ 4x −2x +1 + 2 − x ∼
4x − x = −3x = / 0. 2
Như vậy xem như “tử” là một đa thức bậc 1. Khi đó
4x − 2x +1 + 2 − x lim > 0 khi x →−∞ 2
ax −3x + bx và chỉ khi 2
ax −3x + bx là đa thức bậc 1. Ta có 2 2
ax −3x + bx ∼
ax + bx = (− a +b)x → − a + b = / 0. 2
Khi đó 4x −2x +1 + 2 − x −3x 3 ∼ =
= L > 0 ⇔ b − a > 0 ⇒ b > a. 2
ax −3x + bx
(− a +b)x b− a Chọn B. 3 3 2
Câu 44. Kết quả của giới hạn x + 2x +1 lim là: x →−∞ 2 2x +1 A. 2 . B. 0. C. 2 − . D. 1. 2 2 3 3 2 3 3
Lời giải. Giải nhanh: x + 2x +1 x x 1 x → −∞ → Chọn C. ∼ = = − . 2 2 2x +1 2x − 2x 2 2 1 3 1+ + 3 3 2 3 Cụ thể: x + 2x +1 x x 1 lim = lim = − . x →−∞ 2 2x +1 x →−∞ 1 2 − 2 + 2 x
Câu 45. Tìm tất cả các giá trị của a để + + là + . ∞ →−∞ ( 2 lim 2x 1 ax x ) A. a > 2. B. a < 2. C. a > 2. D. a < 2.
Lời giải. Giải nhanh: 2 2 x → −∞ → 2x +1 + ax ∼ 2x + x
= − 2x + ax = (a − 2)x → +∞ ⇔ a − 2 < 0 ⇔ a < 2. Chọn B. Cụ thể: vì 1 lim x = −∞ nên lim x + + ax = x − + + a = +∞ x →−∞ ( 2 2 1 ) lim 2 x →−∞ 2 x →−∞ x 1 ⇔ lim − 2 +
+ a = a − 2 < 0 ⇔ a < 2. 2 x →−∞ x
Vấn đề 6. DẠNG VÔ ĐỊNH ∞−∞
Câu 46. Giá trị của giới hạn ( 3 2
lim 2x − x ) là: x →−∞ A. 1. B. + . ∞ C. −1. D. −∞ .
Lời giải. Giải nhanh : 3 2 3 x → −∞ → 2x − x Chọn D. ∼ 2x → − . ∞ 3 lim x = −∞ x→−∞ Cụ thể: lim ( 1 3 2 2x x ) 3 lim x − = 2 − = −∞ vì . 1 x →−∞ x →−∞ x lim 2 − = 2 > 0 x→−∞ x
Câu 47. Giá trị của giới hạn 1 1 lim − là: − 2
x →2 x − 2 x − 4 A. − . ∞ B. + . ∞ C. 0. D. 1. Lời giải. Ta có 1 1 x + 2 −1 x +1 lim − = lim = lim = −∞ − 2 − 2 − 2 x →2 x − − →2 x − →2 x 2 x 4 x 4 x − 4 Vì lim (x + ) 1 = 3 > 0; lim − = và 2
x − 4 < 0 với mọi x ∈ (−2;2). Chọn A. − − ( 2 x 4) 0 x →2 x →2 Câu 48. Biết rằng a b
a + b = 4 và lim −
hữu hạn. Tính giới hạn 3 x 1 →
1− x 1− x b a L = lim − . 3 x 1 → 1− x 1− x A. 1. B. 2. C. 1. D. −2. 2 2 Lời giải. Ta có a b
a + ax + ax −b
a + ax + ax −b lim − = lim = lim . 3 3 x → 1− x 1 x − x → 1 x − x → (1− x)( 2 1 1 1 1+ x + x ) Khi đó a b lim − hữu hạn 2 ⇔ 1+ . a 1+ .
a 1 −b = 0 ⇔ 2a −b = −1. 3 x 1 →
1− x 1− x + = Vậy ta có a b 4 a = 1 a b ⇔ ⇒ L = −lim − 3 x 1 2
a −b = −1 b = 3 →
1− x 1− x 2 x + x − 2 −(x + 2) = −lim = −lim = 1 . Chọn C. x → (1− x )( 2 1 1+ x + x ) 2 x 1 → 1+ x + x
Câu 49. Giá trị của giới hạn ( 2 lim
1+ 2x − x) là: x →+∞ A. 0. B. + . ∞ C. 2 −1. D. −∞ . Lời giải. Ta có lim ( 1 2
1+ 2x − x) = lim x + 2 −1 = +∞ 2 x →+∞ x →+∞ x Vì 1 lim x = + ; ∞ lim
+ 2 −1 = 2 −1 > 0. Chọn B. 2 x →+∞ x →+∞ x Giải nhanh : 2 2 x → +∞ → 1+ 2x − x ∼
2x − x = 2x − x = ( 2 − ) 1 x → + . ∞
Câu 50. Giá trị của giới hạn + − là: →+∞ ( 2 lim x 1 x x ) A. 0. B. + . ∞ C. 1 . D. −∞ . 2 Lời giải. 2 2 x → +∞ → x +1 − x Nhân lượng liên hợp. ∼
x − x = x − x = 0 → Giải nhanh: 1 1 1 2 x → +∞ → x +1 − x = Chọn A. ∼ = → 0. 2 2 2 +1 x x + x x + x 1 Cụ thể: lim x x + − x = = = = x →+∞ ( 1 0 2 1 ) lim lim 0. x →+∞ 2 x +1 x + x →+∞ 1 2 1+ +1 2 x Câu 51. Biết rằng + + =
+ Tính S = 5a + . b →−∞ ( 2 lim 5x 2x x 5) a 5 . b x A. S =1. B. S = −1. C. S = 5. D. S = −5. Lời giải: 2 2 x → −∞
→ 5x + 2x + x 5 ∼
5x + x 5 = − 5x + x 5 = 0
→ Nhân lượng liên hợp: Giải nhanh: 2 x → −∞
→ 5x + 2x + x 5 2x 2x 2x 1 = ∼ = = − . 2 2
5x + 2x + x 5 5x − x 5 −2 5x 5 Cụ thể: Ta có x lim x + x + x = x →−∞ ( 2 2 5 2 5) lim x →−∞ 2
5x + 2x + x 5 1 2 2 1 1 a = − lim 5 = = = − = − →
5 ⇒ S = −1. Chọn A. x →−∞ 2 2 5 5 5 − − 5 + + 5 b = 0 x
Câu 52. Giá trị của giới hạn + − + là: →+∞ ( 2 2 lim x 3x x 4x x ) A. 7 . B. 1 − . C. + . ∞ D. − . ∞ 2 2 Lời giải. Khi 2 2 2 2 x → +∞
→ x + 3x − x + 4x ∼ x − x = 0
→ Nhân lượng liên hợp: Giải nhanh: 2 2 x → +∞
→ x + 3x − x + 4x −x −x −x 1 = Chọn B. ∼ = = − . 2 2 2 2 2x 2
x + 3x + x + 4x x + x Cụ thể: + − + = →+∞ ( 2 2 lim x 3x x 4x x ) −x −1 1 lim = lim = − . x →+∞ 2 2
x + 3x + x + 4 x x →+∞ 3 4 2 1+ + 1+ x x
Câu 53. Giá trị của giới hạn (3 3 2 lim
3x −1 + x + 2) là: x →−∞ A. 3 3 +1. B. + . ∞ C. 3 3 −1. D. −∞ .
Lời giải. Giải nhanh: 3 3 2 3 3 2 x → −∞ → x − + x + Chọn D. ∼ x + x = (3 3 1 2 3 3 − ) 1 x → − . ∞ Cụ thể: lim ( 1 2 3 3 2 3x −1 + x + 2) 3 = lim x 3− − 1+ = −∞ 3 2 x →−∞ x →−∞ x x Vì 1 2 3 3 lim x = − , ∞ lim 3− − 1+ = 3 −1> 0. 3 2 x →−∞ x →−∞ x x
Câu 54. Giá trị của giới hạn + − − là: →+∞ ( 2 3 3 2 lim x x x x x ) A. 5 . B. + . ∞ C. −1. D. −∞ . 6 Lời giải. Khi 2 3 3 2 2 3 3 x → +∞
→ x + x − x − x ∼
x −− x = x − x = 0
→ Nhân lượng liên hợp: Giải nhanh: 2 3 3 2 + − − = ( 2 + − )+( 3 3 2 x x x x x x x
x − x − x ) 2 2 x x x x = + ∼ + 2 2 3 x +1 + x + −1 + ( 3 3 − )2 2 2 3 3 6 6 3 1 x + x
x + x x + x x x x x 1 1 5 = + =
(x → +∞). Chọn A. 2 3 6 Cụ thể: + − − = + − + − − →+∞ ( 2 3 3 2 x x x x ) →+∞ ( 2 3 3 2 lim lim x x x x x x x x ) 2 x x 1 1 5 = lim + = + = . x →+∞ 2 2 3 x + + x x + x x −1 + ( 3 2 3 6 1 3 x − )2 3 1
Câu 55. Giá trị của giới hạn (3 3 lim
2x −1 − 2x +1) là: x →+∞ A. 0. B. + . ∞ C. −1. D. −∞ . Lời giải. 3 3 3 3 x → +∞
→ 2x −1 − 2x +1 nhân lượng liên hợp: ∼
2x − 2x = 0 → Giải nhanh: 3 3
2x −1 − 2x +1 = −2 −2 −2 Chọn A. ∼ = → 0. 3 (2x − )2 3 1
+ 4x −1 − (2x + )2 3 2 3 2 3 2 3 2 3 2 1
4x + 4x + 4x 3 4x Cụ thể: − lim ( 2 3 3
2x −1 − 2x +1) = lim = 0. x →+∞ x →+∞ (2x − )2 3 1 + (2x − ) 1 (2x + ) 1 + (2x + )2 3 3 1
Vấn đề 7. DẠNG VÔ ĐỊNH 0.∞
Câu 56. Kết quả của giới hạn 1 lim x 1 − là: x →0 x A. + . ∞ B. −1. C. 0. D. +∞ . Lời giải. Ta có 1 lim x 1 − = lim (x − )
1 = 0 −1 = −1. Chọn B. x →0 x →0 x
Câu 57. Kết quả của giới hạn x lim (x −2) là: + 2 x →2 x − 4 A. 1. B. + . ∞ C. 0. D. −∞ . Lời giải. Ta có x x − 2. x 0. 2 lim (x − 2) = lim = = 0 . Chọn C. + 2 x 2 x 2 x − 4 + → → x + 2 2
Câu 58. Kết quả của giới hạn 2x +1 lim x là: 3 2 x →+∞ 3x + x + 2 A. 2 . B. 6 . C. + . ∞ D. −∞ . 3 3
Lời giải. Giải nhanh: 2x +1 2x 6 1 6 1 6 x → +∞ → x Chọn B. ∼ x. = .x. = .x. = . 3 2 2 2 3x + x + 2 3x 3 3 x 3 x 1 2 2 + Cụ thể: 2x +1 x 2x +1 ( ) 6 lim = lim = lim x x = . 3 2 3 2 x →+∞ 3x + x + 2 x →+∞ 3x + x + 2 x →+∞ 1 2 3 3 + + 3 x x
Câu 59. Kết quả của giới hạn 1 2 lim x sin π x − là: 2 x →0 x A. 0 . B. −1 . C. . π D. + . ∞ Lời giải. Ta có 1 2 lim x sin π x − = lim( 2
x sin πx −1 = −1. Chọn B. 2 ) x →0 x →0 x
Câu 60. Kết quả của giới hạn x lim + là: + ( 3 x ) 1 2 x ( → − ) 1 x −1 A. 3. B. + . ∞ C. 0. D. −∞ . Lời giải. Với x
x ∈ (−1;0) thì x +1> 0 và > 0 . x −1 Do đó x x lim + = + − + + ( 3 x ) 1 lim (x ) 1 + ( 2 x x 1 2 ) x ( → − ) 1 x −1 x ( → − ) 1 (x − ) 1 (x + ) 1 x = lim x +1 − + = . Chọn C. + ( 2 x x ) 1 0 x ( → − ) 1 x −1 Baøi 03
HAØM SOÁ LIEÂN TUÏC
I H M SỐ LIÊN TỤC TẠI MỘT ĐIỂM – Định nghĩa 1
Cho hàm số y = f (x) xác định trên khoảng K và x ∈ K. 0
Hàm số y = f (x) được gọi là liên tục tại x nếu lim f (x)= f (x . 0 ) 0 x →x0
II H M SỐ LIÊN TỤC TRÊN MỘT KHOẢNG – Định nghĩa 2
Hàm số y = f (x) được gọi là liên tục trên một khoảng nếu nó liên tục tại mọi điểm của khoảng đó.
Hàm số y = f (x) được gọi là liên tục trên đoạn [a;b] nếu nó liên tục trên khoảng (a;b) và
lim f (x) = f (a), lim f (x) = f (b). x a+ x b− → →
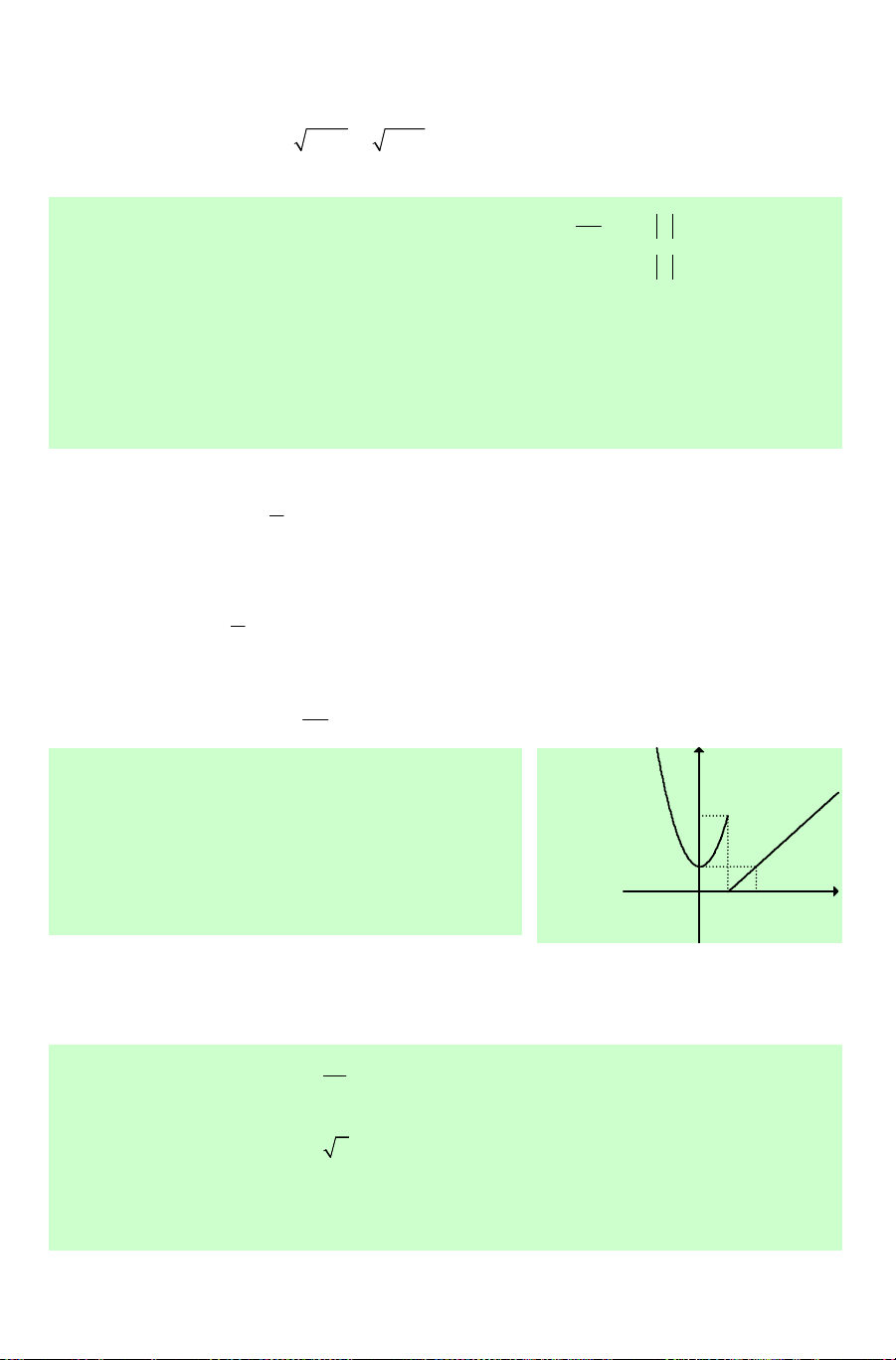
Nhận xét: Đồ thị của hàm số liên tục trên một khoảng là một ' đường liền ' trên khoảng đó. y y x a b a x O O b
Hàm số liên tục trên khoảng (a;b) Hàm số không liên tục trên khoảng (a;b)
III MỘT SỐ ĐỊNH LÍ CƠ BẢN – Định lí 1
a) Hàm số đa thức liên tục trên toàn bộ tập số thực ℝ .
b) Hàm số phân thức hữu tỉ và hàm số lượng giác liên tục trên từng khoảng xác định của chúng. Định lí 2
Giả sử y = f (x) và y = g(x) là hai hàm số liên tục tại điểm x . Khi đó: 0
a) Các hàm số y = f (x)+ g(x) , y = f (x)− g(x) và y = f (x).g(x) liên tục tại x ; 0
b) Hàm số f (x) liên tục tại x nếu g(x ≠ 0 . 0 ) g (x ) 0 Định lí 3
Nếu hàm số y = f (x) liên tục trên đoạn [a;b] và f (a). f (b)< 0, thì tồn tại ít nhất
một điểm c ∈(a;b) sao cho f (c) = 0 .
Định lí 3 có thể phát biểu theo một dạng khác như sau:
Nếu hàm số y = f (x) liên tục trên đoạn [a;b] và f (a). f (b)< 0, thì phương trình
f (x) = 0 có ít nhất một nghiệm nằm trong khoảng (a;b) .
CÂU HỎI TRẮC NGHIỆM
Vấn đề 1. XÉT TÍNH LIÊN TỤC CỦA H M SỐ Câu 1. Hàm số 1
f (x) = 3− x + liên tục trên: x + 4 A. [−4;3]. B. [−4; ) 3 . C. (−4;3]. D. [− ; ∞ −4]∪[3;+∞). −
Lời giải. Điều kiện: 3 x ≥ 0 x > −4 TXD ⇔ → D = (−4; ] 3
→ hàm số liên tục trên x + 4 > 0 x ≤ −3 (−4; )
3 . Xét tại x = 3, ta có 1 1
lim f (x) = lim 3− x + = = f ( ) 3
→ Hàm số liên tục trái tại x = 3. x 3− x 3− → → x + 4 7
Vậy hàm số liên tục trên (−4; ] 3 . Chọn C. 3 Câu 2. Hàm số
x + x cos x + sin x f (x) = liên tục trên: 2 sin x + 3 A. [−1; ] 1 . B. [1;5]. C. 3 − ; +∞ . D. . ℝ 2
Lời giải. Vì 2sin x +3 =/ 0 với mọi TXD x ∈ ℝ → D = ℝ
→ Hàm số liên tục trên . ℝ Chọn D. 2 Câu 3. Cho hàm số x −3x + 2
f (x) xác định và liên tục trên ℝ với f (x ) = với mọi x −1 x = / 1. Tính f ( ) 1 . A. 2. B. 1. C. 0. D. −1.
Lời giải. Vì f (x) liên tục trên ℝ nên suy ra 2 x −3x + 2 f ( )
1 = lim f (x) = lim
= lim(x − 2) = −1. Chọn D. x 1 → x 1 → x 1 x −1 → Câu 4. Cho hàm số x + 3 − 3− x
f (x) xác định và liên tục trên [−3; ] 3 với f (x ) = x
với x ≠ 0 . Tính f (0). A. 2 3 . B. 3 . C. 1. D. 0. 3 3
Lời giải. Vì f (x) liên tục trên [−3; ] 3 nên suy ra x + 3 − 3− x 2 1
f (0) = lim f (x) = lim = lim = . Chọn B. x→0 x→0 x→0 x x + 3 + 3− x 3 Câu 5. Cho hàm số x
f (x) xác định và liên tục trên (−4;+∞) với f (x ) = x + 4 − 2
với x ≠ 0 . Tính f (0). A. 0. B. 2. C. 4. D. 1.
Lời giải. Vì f (x) liên tục trên (−4;+∞) nên suy ra x
f (0) = lim f (x) = lim = lim( x + 4 + ) 2 = 4. Chọn C. x→0 x→0 x→0 x + 4 − 2
Vấn đề 2. H M SỐ LIÊN TỤC TẠI MỘT ĐIỂM 2
x − x −2
Câu 6. Tìm giá trị thực của tham số khi x ≠ 2
m để hàm số f (x) = x − 2 liên m khi x = 2 tục tại x = 2. A. m = 0. B. m =1. C. m = 2. D. m = 3.
Lời giải. Tập xác định: D = ℝ , chứa x = 2 . Theo giả thiết thì ta phải có 2 x − x − 2
m = f (2) = lim f (x) = lim = lim(x + ) 1 = 3. Chọn D. x→2 x→2 x→2 x − 2 3 2
x − x + 2x −2
Câu 7. Tìm giá trị thực của tham số khi x ≠ 1
m để hàm số f (x) = x −1 3 x +m khi x = 1
liên tục tại x = 1. A. m = 0. B. m = 2. C. m = 4. D. m = 6.
Lời giải. Hàm số xác định với mọi x ∈ ℝ . Theo giả thiết ta phải có
x − x + x − (x − ) 1 ( 2 3 2 x + 2 2 2 ) 3 + m = f ( )
1 = lim f (x) = lim = lim = lim( 2
x + 2) = 3 ⇔ m = 0. x 1 → x 1 → x 1 → x 1 x −1 x −1 → Chọn A. x −1
Câu 8. Tìm giá trị thực của tham số khi x ≠ 1
k để hàm số y = f (x) = x −1 liên
k +1 khi x =1 tục tại x = 1. A. 1 k = . B. k = 2. C. 1 k = − . D. k = 0. 2 2
Lời giải. Hàm số f (x) có TXĐ: D =[0;+∞). Điều kiện bài toán tương đương với Ta có: x −1 1 1 1 k +1 = y ( ) 1 = lim y = lim = lim =
⇔ k = − . Chọn C. x 1 → x 1 → x 1 x −1 → x +1 2 2 3− x khi x ≠ 3
Câu 9. Biết rằng hàm số
f (x) = x +1 − 2
liên tục tại x = 3 (với m là m khi x = 3
tham số). Khẳng định nào dưới đây đúng?
A. m ∈(−3;0). B. m ≤−3. C. m ∈[0; ) 5 .
D. m ∈[5;+∞).
Lòi giải. Hàm số f (x) có tập xác định là (−1;+ )
∞ . Theo giả thiết ta phải có (3− x) x ( x+1+ − ) 2 3 m = f ( )
3 = lim f (x) = lim = lim = −lim( x +1 + ) 2 = −4. x→3 x→3 x→3 x→3 x +1 − 2 x −3 Chọn B. 1 2
Câu 10. Tìm giá trị thực của tham số x sin khi x ≠ 0
m để hàm số f (x ) = x liên m khi x = 0 tục tại x = 0.
A. m ∈(−2;− )
1 . B. m ≤ −2.
C. m ∈[−1;7).
D. m ∈[7;+∞).
Lời giải. Với mọi x =/ 0 ta có 1 0 ≤ f (x) 2 2 = x sin
≤ x → 0 khi x → 0
→ lim f (x) = 0. x x→0
Theo giải thiết ta phải có: m = f (0)= lim f (x)= 0. Chọn C. x→0 tan x Câu 11. Biết rằng sin x khi x ≠ 0 lim
= 1. Hàm số f (x) = x liên tục trên khoảng x→0 x 0 khi x = 0 nào sau đây? A. π π π π 0; . B. − ; ∞ . C. − ; . D. (− ; ∞ +∞). 2 4 4 4
Lời giải. Tập xác định: π π 3π
π π π 3π
D = ℝ ∖ + k ℤ ⋯ π | k ∈ = + kπ; + kπ = ∪ − ; ∪ + ∪⋯ ∪ 2 ℤ 2 2 2 2 2 2 k∈ Ta có tan x sin x 1 1 lim f (x) = lim = lim . = 1. = 1 = / 0 = f (0)
→ f (x) không liên x→0 x→0 x→0 x x cos x cos 0
tục tại x = 0. Chọn A. Câu 12. Biết rằng sin x lim
= 1. Tìm giá trị thực của tham số m để hàm số x→0 x sin πx khi x 1 f (x ) ≠ = x −1
liên tục tại x = 1. m khi x = 1 A. m . π = − B. m . π =
C. m = −1. D. m =1.
Lời giải. Tập xác định D = .
ℝ Điều kiện bài toán tương đương với sin π x m = f ( )
1 = lim f (x ) =lim x 1 → x 1 → x −1 sin ( π x π π − + )
−sin π(x − ) 1 sin π(x − ) 1 = lim = lim = lim ( π − ). ( ) * . x 1 → x 1 → x 1 x −1 x −1 → π (x − ) 1 Đặt t π = (x − )
1 thì t → 0 khi x → 1. Do đó (*) trở thành: sin t m = lim( π − ). = − . π Chọn A. t →0 t Câu 13. Biết rằng sin x lim
= 1. Tìm giá trị thực của tham số m để hàm số x→0 x 1 + cos x khi x π ≠ f (x) = (x π − )2 liên tục tại x . π = m khi x π = A. π π m = . B. m = − . C. 1 m = . D. 1 m = − . 2 2 2 2
Lời giải. Hàm số xác định với mọi x ∈ ℝ . Điều kiện củz bài toán trở thành: 2 x π x x 2 π 2 2 sin − sin 2 cos − 1+ cos x 2 2 1
m = f (π) = f (x) 2 2 2 lim = lim = lim = lim = lim * 2 2 2 ( ) x π → x π → ( − ) x π → ( − ) x π → ( − ) 2 x π → x x x x π π π π − 2 2 2 Đặt x π 1 sin t 1 1 t = −
→ 0 khi x → 1. Khi đó (*) trở thành: 2 m = lim = .1 = . 2 2 t →0 2 t 2 2 Chọn C. 3 khi x = −1 4 Câu 14. Hàm số x + x f (x ) =
khi x ≠ −1, x ≠ 0 liên tục tại: 2 x + x 1 khi x = 0
A. mọi điểm trừ x = 0, x =1.
B. mọi điểm x ∈ . ℝ
C. mọi điểm trừ x = −1.
D. mọi điểm trừ x = 0.
Lời giải. Hàm số y = f (x) có TXĐ: D = ℝ .
Dễ thấy hàm số y = f (x) liên tục trên mỗi khoảng (− ; ∞ − ) 1 ,(−1;0) và (0;+∞) .
(i) Xét tại x = −1, ta có x(x + ) 1 ( 2 4 x − x x x + + ) 1 lim f (x) = lim = lim = lim ( 2
x − x +1 = 3 = f −1 . 2 ) ( ) x→−1 x→ 1 − x→ 1 x + x − x(x + ) x→ 1 1 −
→ hàm số y = f (x) liên tục tại x = −1 .
(ii) Xét tại x = 0 , ta có x(x + ) 1 ( 2 4 x − x x x + + ) 1 lim f (x) = lim = lim = lim( 2
x − x +1 = 1 = f 0 . 2 ) ( ) x→0 x→0 x→0 x + x x(x + ) x→0 1
→ hàm số y = f (x) liên tục tại x = 0 . Chọn B. 0 ,5 khi x = −1
Câu 15. Số điểm gián đoạn của hàm số x (x + ) 1 f (x ) =
khi x ≠ −1, x ≠ 1 là: 2 x −1 1 khi x = 1 A. 0. B. 1. C. 2. D. 3.
Lời giải. Hàm số y = f (x) có TXĐ D = ℝ . Hàm số x (x + ) 1 f (x ) =
liên tục trên mỗi khoảng (− ; ∞ − ) 1 , (−1; ) 1 và (1;+ ) ∞ . 2 x −1 (i) Xét tại x(x + ) 1 x 1
x = −1 , ta có lim f (x) = lim = lim = = f (− ) 1 → Hàm số 2 x→−1 x→ 1 − x→−1 x −1 x −1 2
liên tục tại x = −1. x(x + ) 1 x
lim f (x)= lim = lim = +∞ + + 2 (ii) Xét tại x 1 → x 1 → x 1 x −1 + → x −1 x = 1 , ta có
→ Hàm số y = f (x) x(x + ) 1 x
lim f (x) = lim = lim = −∞ − − 2 x 1 → x 1 → x 1 x −1 − → x −1
gián đoạn tại x = 1. Chọn B.
Vấn đề 3. H M SỐ LIÊN TỤC TRÊN MỘT KHOẢNG
Câu 16. Có bao nhiêu giá trị thực của tham số m để hàm số 2 2 m x khi x ≤ 2 f (x ) = liên tục trên ℝ ? (
1−m)x khi x > 2 A. 2. B. 1. C. 0. D. 3.
Lời giải. TXĐ: D = ℝ . Hàm số liên tục trên mỗi khoảng (− ; ∞ 2); (2;+∞) .
Khi đó f (x) liên tục trên ℝ ⇔ f (x) liên tục tại x = 2
⇔ lim f (x) = f (2) ⇔ lim f (x) = lim f (x) = f (2). (*) x 2 x 2+ x 2− → → → f (2) 2 = 4m m = −1 Ta có
lim f (x)= lim (1−m)x = 2(1−m) →(*) 2
⇔ 4m = 2(1− m) ⇔ 1 . x→2+ x →2+ m = f (x) 2 2 2 2 lim = lim m x = 4m x →2− x →2− Chọn A.
Câu 17. Biết rằng hàm số x khi x ∈ [0;4] f (x) =
tục trên [0;6]. Khẳng định nào 1
+ m khi x ∈ (4;6] sau đây đúng? A. m < 2.
B. 2 ≤ m < 3.
C. 3 < m < 5. D. m ≥ 5.
Lời giải. Dễ thấy f (x) liên tục trên mỗi khoảng (0;4) và (4;6) . Khi đó hàm số liên
tục trên đoạn [0;6] khi và chỉ khi hàm số liên tục tại x = 4, x = 0, x = 6 .
lim f (x)= f (0) x→0+
Tức là ta cần có lim f (x)= f (6) . (*) x→6−
lim f (x)= lim f (x)= f (4) x →4− x →4+ lim f (x) = lim x = 0 x→0+ x →0+ • ; f (0)= 0 = 0
lim f (x) = lim (1+ m) = 1+ m x 6− x 6 • − → → ; f (6)=1+m lim f (x) = lim x = 2 x→4− x →4−
• lim f (x) = lim (1+ m) = 1+ m ; x→4+ x →4+
f (4)=1+m
Khi đó (*) trở thành 1+m = 2 ⇔ m =1< 2. Chọn A. 2
x −3x + 2 khi x ≠ 1
Câu 18. Có bao nhiêu giá trị của tham số a để hàm số f (x) = x −1 a khi x = 1 liên tục trên . ℝ A. 1. B. 2. C. 0. D. 3.
Lời giải. Hàm số f (x) liên tục trên (− ; ∞ ) 1 và (1;+ )
∞ . Khi đó hàm số đã cho liên
tục trên ℝ khi và chỉ khi nó liê tục tại x = 1, tức là ta cần có
lim f (x) = f ( )
1 ⇔ lim f (x) = lim f (x) = f ( ) 1 . (*) x 1 x 1+ x 1− → → →
x −2 khi x >1
lim f (x) = lim (2 − x) = 1 Ta có − − f (x) x 1 → x 1 a khi x 1 → = = → →(*) không tỏa mãn lim f
(x) = lim (x −2) = −1 2 − x khi x < 1 x 1+ → x 1+ → với mọi a ∈ .
ℝ Vậy không tồn tại giá trị a thỏa yêu cầu. Chọn C. 2 x −1 Câu 19. Biết rằng khi x ≠ 1 f (x) = x −1
liên tục trên đoạn [0; ] 1 (với a là tham a khi x = 1
số). Khẳng định nào dưới đây về giá trị a là đúng?
A. a là một số nguyên.
B. a là một số vô tỉ. C. a > 5.
D. a < 0.
Lời giải. Hàm số xác định và liên tục trên [0; )
1 . Khi đó f (x) liên tục trên [0; ] 1 khi
và chỉ khi lim f (x) = f ( ) 1 . (*) x 1− → f ( ) 1 = a Ta có 2 x → − (*) ⇔ a = 4. 1 Chọn A.
lim f (x) = lim = lim (x + ) 1 + = − − − ( x ) 1 4 x 1 → x 1 → x 1 x 1 → − x −1
Câu 20. Xét tính liên tục của hàm số khi x < 1
f (x) = 2 − x −1 . Khẳng định nào − 2x khi x ≥ 1 dưới đây đúng?
A. f (x) không liên tục trên . ℝ
B. f (x) không liên tục trên (0;2).
C. f (x) gián đoạn tại x =1.
D. f (x) liên tục trên . ℝ
Lời giải. Dễ thấy hàm số liên tục trên (− ; ∞ ) 1 và (1;+ ) ∞ .
f ( )1=−2
Ta có lim f (x)= lim (−2x)= −2
→ f (x) liên tục tại x = 1. x 1+ → x 1+ → x −1 lim f (x) = lim = lim − − + = − − − − ( 2 x ) 1 2 x 1 → x 1 → x 1 2 x 1 → − −
Vậy hàm số f (x) liên tục trên . ℝ Chọn D. 2
x −5x + 6
Câu 21. Tìm giá trị nhỏ nhất của khi x > 3
a để hàm số f (x) = 4x −3 − x liên tục 2 1 a x khi x 3 − ≤ tại x = 3 . A. 2 − . B. 2 . C. 4 − . D. 4 . 3 3 3 3
Lời giải. Điều kiện bài toán trở thành: lim f (x)= lim f (x)= f (3). (*) x 3+ x 3− → → f ( ) 2 3 = 1−3a 2 (x −2) − + ( 4x −3 5 6 + x x x )
Ta có lim f (x)= lim = lim = −3 x→3+ x →3+ x →3 4x −3 − x + 1− x
lim f (x)= lim − = − − − ( 2 1 a x ) 3 1 3a . x →3 x →3 2 2 →(*) ⇔ a = ± → a = − . Chọn A. min 3 3 3 3x + 2 −2 khi x > 2
Câu 22. Tìm giá trị lớn nhất của
a để hàm số f (x) x − 2 = liên tục 1 2 a x + khi x ≤ 2 4 tại x = 2. A. a = 3. B. a = 0. C. a = 1. D. a = 2. max max max max
Lời giải. Ta cần có lim f (x)= lim f (x) = f (2). (*) x 2+ x 2− → → 7 f (2) 2 = 2a − 4 3 Ta có 3x + 2 − 2 1
lim f (x)= lim =
→(*) ⇔ a = ±1 → a = 1. Chọn C. max x→2+ x →2+ x − 2 4 1 7 lim f (x) 2 2 = lim a x + = 2a − x →2− x →2− 4 4 1
−cos x khi x ≤ 0
Câu 23. Xét tính liên tục của hàm số f (x) =
. Khẳng định nào sau x +1 khi x > 0 đây đúng?
A. f (x) liên tục tại x = 0.
B. f (x) liên tục trên (− ; ∞ ) 1 .
C. f (x) không liên tục trên . ℝ
D. f (x) gián đoạn tại x =1.
Lời giải. Hàm số xác định với mọi x ∈ ℝ .
Ta có f (x) liên tục trên (− ; ∞ 0) và (0;+∞). f (0)=1
Mặt khác lim f (x)= lim (1−cos x)=1−cos0 = 0
→ f (x) gián đoạn tại x = 0. x→0− x →0− lim f
(x) = lim x +1 = 0 +1 = 1 x →0+ x →0+ Chọn C. π x
Câu 24. Tìm các khoảng liên tục của hàm số cos khi x ≤ 1 f (x) = 2 . Mệnh đề nào x −1 khi x > 1 sau đây là sai?
A. Hàm số liên tục tại x = −1.
B. Hàm số liên tục trên các khoảng (− , ∞ − ) 1 ; (1;+∞).
C. Hàm số liên tục tại x = 1.
D. Hàm số liên tục trên khoảng (−1, ) 1 .
Lời giải. Ta có f (x) liên tục trên (− ; ∞ − ) 1 , (−1; ) 1 , (1;+∞). π f (− ) 1 = cos − = 0 • Ta có 2
→ f (x ) gián đoạn tại x = −1. Chọn A.
lim f (x)= lim (x − ) 1 = −2 − − x ( → − ) 1 x ( → − ) 1 π f ( ) 1 = cos = 0 2
• Ta có lim f (x ) = lim (x − ) 1 = 0
→ f (x) liên tục tại x = 1. x 1+ → x 1+ → π x lim f (x) = lim cos = 0 x 1− → x 1− → 2
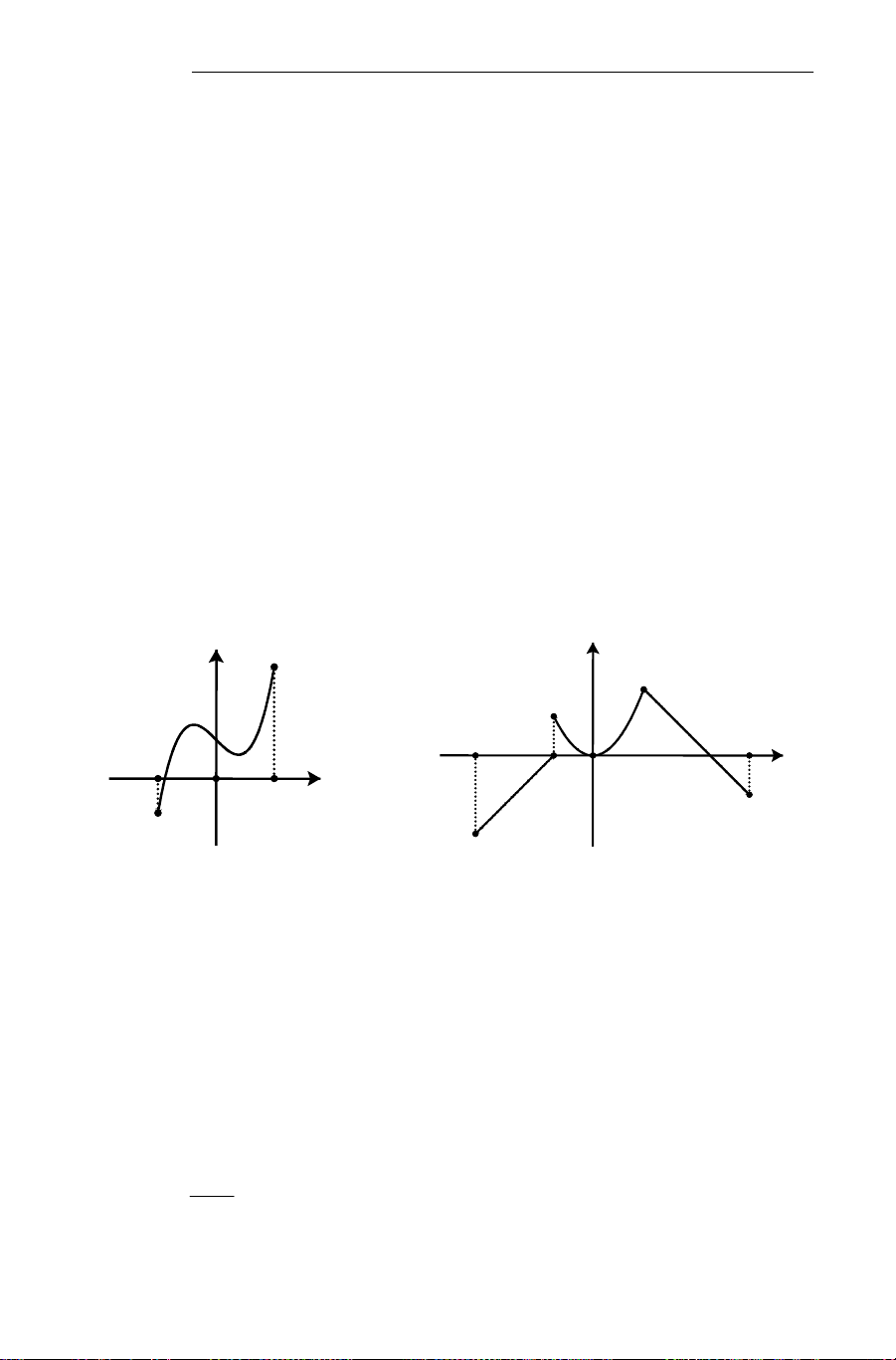
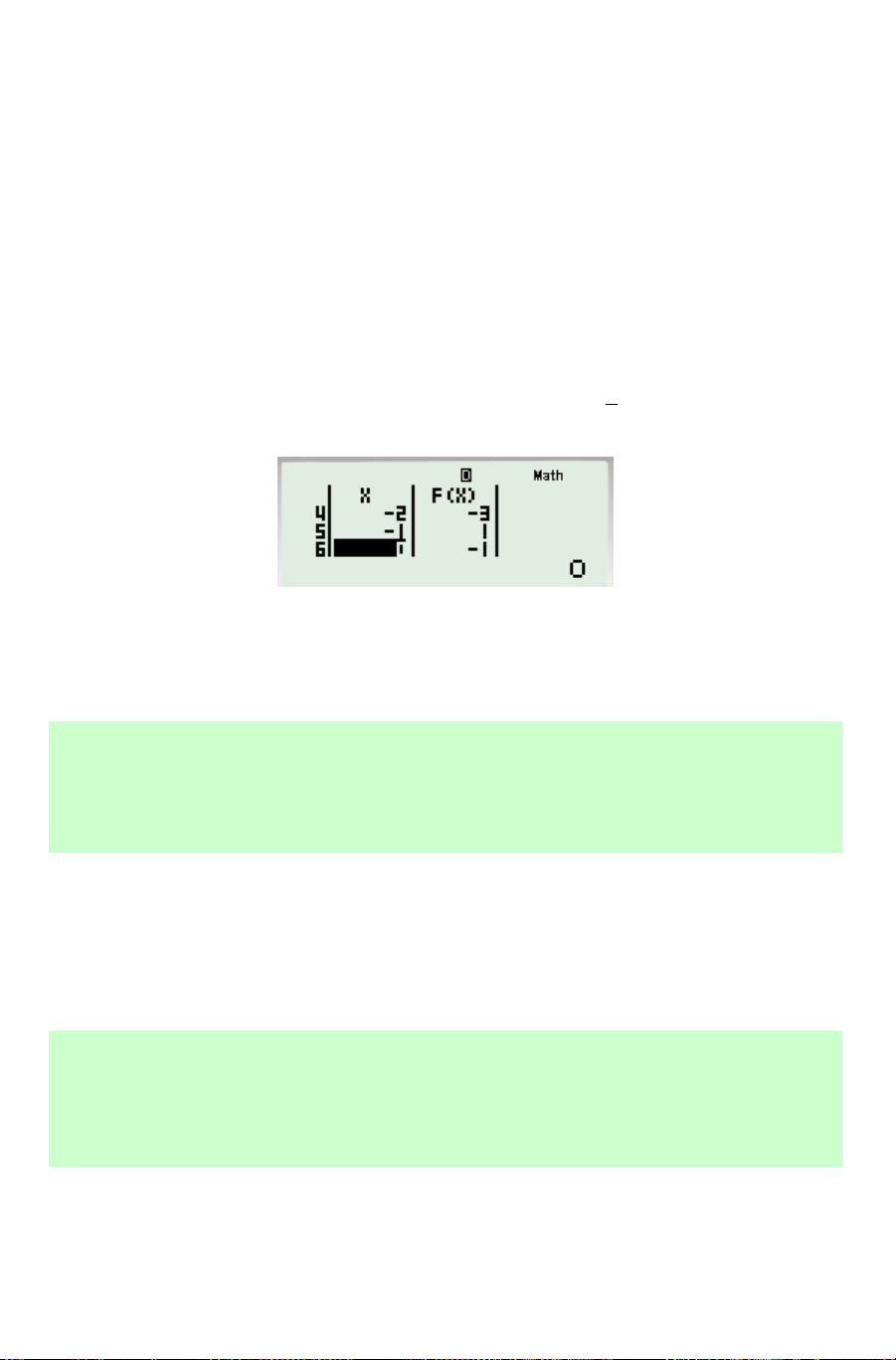
Câu 25. Hàm số f (x) có đồ thị như hình bên y
không liên tục tại điểm có hoành độ là bao nhiêu? 3 A. x = 0. B. x = 1. 1 x C. x = 2. O 1 2 D. x = 3.
Lời giải. Dễ thấy tại điểm có hoành độ x = 1 đồ thị của hàm số bị ' đứt ' nên hàm số
không liên tục tại đó.
Cụ thể: lim f (x)= 0 =/ 3 = lim f (x) nên f (x) gián đoạn tại x =1. Chọn B. x 1+ x 1− → → 2 x
khi x < 1, x ≠ 0 x Câu 26. Cho hàm số f (x) 0 = khi x = 0
. Hàm số f (x) liên tục tại: x khi x ≥1
A. mọi điểm thuộc ℝ .
B. mọi điểm trừ x = 0 .
C. mọi điểm trừ x = 1.
D. mọi điểm trừ x = 0 và x = 1.
Lời giải. Hàm số y = f (x) có TXĐ: D = ℝ .
Dễ thấy hàm số y = f (x) liên tục trên mỗi khoảng (− ; ∞ 0),(0; ) 1 và (1;+ ) ∞ . f (0)= 0 2 Ta có x
lim f (x)= lim = lim x = 0
→ f (x) liên tục tại x = 0. x→0− x →0− x →0 x − 2 x
lim f (x) = lim = lim x = 0 x→0+ x →0+ x →0 x + f ( ) 1 = 1 2 Ta có x
lim f (x)= lim = lim x = 1
→ f (x) liên tục tại x = 1. x 1− → x 1− → x 1 x − →
lim f (x)= lim x =1 x 1+ → x 1+ →
Vậy hàm số y = f (x) liên tục trên ℝ . Chọn A. 2 x −1
khi x < 3, x ≠ 1 x −1 Câu 27. Cho hàm số f (x) = 4 khi x = 1
. Hàm số f (x) liên tục tại: x +1 khi x ≥ 3
A. mọi điểm thuộc ℝ .
B. mọi điểm trừ x = 1.
C. mọi điểm trừ x = 3 .
D. mọi điểm trừ x = 1 và x = 3 .
Lời giải. Hàm số y = f (x) có TXĐ: D = ℝ .
Dễ thấy hàm số y = f (x) liên tục trên mỗi khoảng (− ; ∞ ) 1 ,(1; ) 3 và (3;+∞) . f ( ) 1 = 4 Ta có 2 − gián đoạn tại 1 → f (x x ) x = 1.
lim f (x)= lim = lim (x + ) 1 = 2 x 1 → x 1 → x 1 x −1 → f ( ) 3 = 2 Ta có 2 − gián đoạn tại 1 → f (x x ) x = 3.
lim f (x)= lim = lim (x + ) 1 = 4 x 3− x 3− x 3 x −1 − → → → Chọn D. 2
x khi x < 0
Câu 28. Số điểm gián đoạn của hàm số h(x) 2
= x +1 khi 0 ≤ x ≤ 2 là: 3
x −1 khi x > 2 A. 1. B. 2. C. 3. D. 0.
Lời giải. Hàm số y = h(x) có TXĐ: D = ℝ .
Dễ thấy hàm số y = h(x) liên tục trên mỗi khoảng (− ; ∞ 0),(0;2) và (2;+∞) . h (0) = 1 Ta có
→ f (x) không liên tục tại x = 0 .
lim h(x) = lim 2x = 0 x 0− x 0− → → h (2) = 5
Ta có lim h(x)= lim + = →
liên tục tại x = 2 . − − ( 2 x ) 1 5 f (x) x→2 x →2
lim h(x)= lim (3x− )1=5 x →2+ x →2+ Chọn A. 2
x + x khi x <1 Câu 29. Tính tổng
S gồm tất cả các giá trị m để hàm số f (x) 2 = khi x = 1 2 m
x +1 khi x > 1
liên tục tại x = 1. A. S = −1. B. S = 0. C. S =1. D. S = 2.
Lời giải. Hàm số xác định với mọi x ∈ ℝ .
Điều kiện bài toán trở thành lim f (x)= lim f (x)= f ( ) 1 . (*) x 1+ x 1− → → f ( ) 1 = 2
Ta có lim f (x) = lim + = + → ⇔ + = + + ( 2 m x ) 2 1 m 1 (*) 2 m 1 2 x 1 → x 1 →
lim f (x)= lim + = − − ( 2 x x ) 2 x 1 → x 1 → ⇔ m = ±1
→S = 0. Chọn B. −
x cos x khi x < 0 2 Câu 30. Cho hàm số x f (x) =
khi 0 ≤ x < 1. Hàm số f (x) liên tục tại: 1 + x 3 x khi x ≥ 1
A. mọi điểm thuộc x ∈ . ℝ
B. mọi điểm trừ x = 0.
C. mọi điểm trừ x = 1.
D. mọi điểm trừ x = 0; x = 1.
Lời giải. Hàm số y = f (x) có TXĐ: D = ℝ .
Dễ thấy f (x) liên tục trên mỗi khoảng (− ; ∞ 0),(0; ) 1 và (1;+ ) ∞ .
f (0)=0
Ta có lim f (x)= lim (−x cos x) = 0
→ f (x) liên tục tại x = 0 . x→0− x →0− 2 x
lim f (x)= lim = 0 x→0+ x →0+ 1+ x f ( )1=1 2 Ta có x 1
lim f (x)= lim =
→ f (x) không liên tục tại x = 1 . x 1− → x 1− → 1+ x 2
lim f (x) 3 = lim x = 1 + x 1+ x 1 → → Chọn C.
Vấn đề 5. SỐ NGHIỆM CỦA PHƯƠNG TRÌNH TRÊN MỘT KHOẢNG
Câu 31. Cho hàm số f (x) 3
= −4x + 4x −1. Mệnh đề nào sau đây là sai?
A. Hàm số đã cho liên tục trên . ℝ
B. Phương trình f (x)= 0 không có nghiệm trên khoảng (− ; ∞ ) 1 .
C. Phương trình f (x)= 0 có nghiệm trên khoảng (−2;0). D. Phương trình
f (x) = 0 có ít nhất hai nghiệm trên khoảng 1 −3; . 2
Lời giải. (i) Hàm f (x) là hàm đa thức nên liên tục trên ℝ → A đúng. f (− ) 1 = −1< 0 (ii) Ta có
→ f (x) = 0 có nghiệm x trên (−2; ) 1 , mà 1 f (−2) = 23 > 0 (−2;− ) 1 ⊂ (−2;0) ⊂ (− ; ∞ ) 1 → B sai và C đúng → Chọn B.
f (0) = −1< 0 (iii) Ta có → f (x) = 0 1 1
có nghiệm x thuộc 1 0;
. Kết hợp với (1) suy 2 f = > 0 2 2 2 ra 1
f (x) = 0 có các nghiệm x , x thỏa: −3 < x < −1< 0 < x < → D đúng. 1 2 1 2 2
Câu 32. Cho phương trình 4 2
2x −5x + x +1 = 0. Mệnh đề nào sau đây là đúng?
A. Phương trình không có nghiệm trong khoảng (−1; ) 1 .
B. Phương trình không có nghiệm trong khoảng (−2;0).
C. Phương trình chỉ có một nghiệm trong khoảng (−2; ) 1 .
D. Phương trình có ít nhất hai nghiệm trong khoảng (0;2).
Lời giải. Hàm số f (x) 4 2
= 2x −5x + x +1 là hàm đa thức có tập xác định là ℝ nên liên tục trên ℝ . Ta có f (0) =1 (i) ⇒ f (− ) 1 . f (0) < 0
→ f (x) = 0 có ít nhất một nghiệm x thuộc (−1;0). 1 f (− ) 1 = −3 f (0) =1 (ii) ⇒ f (0). f ( ) 1 < 0
→ f (x) = 0 có ít nhất một nghiệm x thuộc (0; ) 1 . 2 f ( ) 1 = −1 f ( ) 1 = −1 (iii) ⇒ f ( ) 1 . f (2) < 0
→ f (x) = 0 có ít nhất một nghiệm x thuộc (1;2). 3 f (2) = 15
Vậy phương trình f (x)= 0 đã cho có các nghiệm x , x , x thỏa 1 2 3
−1 < x < 0 < x <1 < x < 2 → Chọn D. 1 2 3 Câu 33. Cho hàm số 3
f (x ) = x −3x −1 . Số nghiệm của phương trình f (x) = 0 trên ℝ là: A. 0. B. 1. C. 2. D. 3.
Lời giải. Hàm số f (x) 3
= x −3x −1 là hàm đa thức có tập xác định là ℝ nên liên tục
trên ℝ . Do đó hàm số liên tục trên mỗi khoảng (−2;− ) 1 , (−1;0), (0;2). Ta có f (−2) = −3 •
⇒ f (−2) f (− ) 1 < 0 →( )
1 có ít nhất một nghiệm thuộc (−2;− ) 1 . f (− ) 1 = 1 f (− ) 1 = 1 • ⇒ f (− ) 1 f (0) < 0 →( )
1 có ít nhất một nghiệm thuộc (−1;0). f (0) = −1 f (2) = 1 •
⇒ f (2) f (0)< 0 →( )
1 có ít nhất một nghiệm thuộc (0;2). f (0) = −1 Như vậy phương trình ( )
1 có ít nhất ba thuộc khoảng (−2;2) . Tuy nhiên phương
trình f (x)= 0 là phương trình bậc ba có nhiều nhất ba nghiệm. Vậy phương trình
f (x) = 0 có đúng nghiệm trên . ℝ Chọn D.
Cách CASIO. (i) Chọn MODE 7 (chức năng TABLE) và nhập: 3
F ( X ) = X − 3X −1.
(ii) Ấn “=” và tiếp tục nhập: Start ↔ −5 (có thể chọn số nhỏ hơn).
End ↔ 5 (có thể chọn số lớn hơn).
Step ↔1 (có thể nhỏ hơn, ví dụ 1 ). 2
(iii) Ấn “=” ta được bảng sau:
Bên cột X ta cần chọn hai giá trị a và b (a < b) sao cho tương ứng bên cột F(X )
nhận các giá trị trái dấu, khi đó phương trình có nghiệm (a;b). Có bao nhiêu cặp số
a, b như thế sao cho khác khoảng (a;b) rời nhau thì phương trình f (x) = 0 có bấy nhiêu nghiệm.
Câu 34. Cho hàm số f (x) liên tục trên đoạn [−1;4] sao cho f (− )
1 = 2 , f (4) = 7 . Có
thể nói gì về số nghiệm của phương trình f (x) = 5 trên đoạn [−1;4]: A. Vô nghiệm.
B. Có ít nhất một nghiệm.
C. Có đúng một nghiệm.
D. Có đúng hai nghiệm.
Lời giải. Ta có f (x)= 5 ⇔ f (x)−5 = 0 . Đặt g(x)= f (x)−5. Khi đó g(− ) 1 = f (− ) 1 −5 = 2 − 5 = −3 ⇒ g (− ) 1 g (4) < 0. g
(4) = f (4)−5 = 7 −5 = 2
Vậy phương trình g(x) = 0 có ít nhất một nghiệm thuộc khoảng (1;4) hay phương
trình f (x) = 5 có ít nhất một nghiệm thuộc khoảng (1;4) . Chọn B.
Câu 35. Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc khoảng (−10;10) để phương trình 3 2
x −3x +(2m −2)x + m −3 = 0 có ba nghiệm phân biệt x , x , x thỏa 1 2 3
mãn x < −1< x < x ? 1 2 3 A. 19. B. 18. C. 4. D. 3.
Lời giải. Xét hàm số f (x) 3 2
= x −3x +(2m −2)x + m −3 liên tục trên ℝ .
● Giả sử phương trình có ba nghiệm phân biệt x , x , x sao cho x < −1 < x < x . 1 2 3 1 2 3
Khi đó f (x)= (x − x x − x x − x . 1 )( 2 )( 3 ) Ta có f (− ) 1 = (−1− x −1− x
−1− x > 0 (do x < −1 < x < x ). 1 )( 2 )( 3 ) 1 2 3 Mà f (− ) 1 = m − −5 nên suy ra m
− −5 > 0 ⇔ m < −5.
● Thử lại: Với m < −5 , ta có
▪ lim f (x ) = −∞ nên tồn tại a < −1 sao cho f (a) < 0 . ( ) 1 x →−∞
▪ Do m < −5 nên f (− ) 1 = m − −5 > 0 . (2)
▪ f (0) = m −3 < 0 . ( ) 3
▪ lim f (x ) = +∞ nên tồn tại b > 0 sao cho f (b) > 0 . (4) x →+∞ Từ ( )
1 và (2) , suy ra phương trình có nghiệm thuộc khoảng (− ; ∞ − ) 1 ; Từ (2) và ( ) 3 ,
suy ra phương trình có nghiệm thuộc khoảng (−1;0) ; Từ ( ) 3 và (4) , suy ra phương
trình có nghiệm thuộc khoảng (0;+∞).
Vậy khi m < −5 thỏa mãn m∈
ℤ→ m ∈ {−9;−8;−7;−6}. Chọn C. m ( ∈ 1 − 0;10)




