Bài tập trắc nghiệm quan hệ song song trong không gian (có lời giải)

Bài tập trắc nghiệm quan hệ song song trong không gian có lời giải và đáp án được phân thành các dạng toán sau:xác định giao tuyến giũa hai mặt phẳng; xác định giao điểm của đường thẳng và mặt phẳng; tìm thiết diện của hình chóp và khối chóp; chứng minh hai đường thảng song song trong không gian; thiết diện qua một đường thẳng và song song với một đường thẳng cho trước; tính góc giữa hai đường thẳng ….Bài tập được viết dưới dạng PDF gồm 46 trang. Các bạn xem và tải về ở dưới.

138 69 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 4: Quan hệ song song trong không gian (KNTT)

Môn: Toán 11

Thông tin:

47 trang 9 tháng trước

Tác giả:

Profile Thùy Dương (H)
Trang 1
BÀI TẬP TRẮC NGHIỆM ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG
GIAN.QUAN HỆ SONG SONG
A. LÝ THUYẾT
I. ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG
1. Mặt phẳng
Mặt bảng, mặt bàn, mặt nước hồ yên lặng cho ta hình ảnh một phần của mặt phẳng. Mặt phẳng không có
bề dày và không có giới hạn.
Để kí hiệu mặt phẳng, ta thường dùng các chữ cái in hoa hoặc chữ cái Hy Lạp đặt trong dấu ngoặc (). Ví
dụ như mặt phẳng …
Để biểu diễn mặt phẳng, ta thường dùng hình bình hành hoặc một miền góc và ghi tên của mặt phẳng vào
một góc của hình biểu diễn.
Đường thẳng và mặt phẳng là tập hợp các điểm. Do đó,
- Nếu điểm thuộc đường thẳng , ta kí hiệu và đôi khi còn nói rằng đường thẳng đi qua
điểm .
- Nếu điểm thuộc mặt phẳng , ta kí hiệu và đôi khi còn nói rằng mặt phẳng đi qua
điểm .
- Nếu đường thẳng chứ trong mặt phẳng , ta kí hiệu và đôi khi còn nói rằng mặt phẳng
đi qua (hoặc chứa) đường thẳng .
2. Quy tắc để vẽ hình biểu diễn của một hình trong không gian
- Hình biểu diễn của một đường thẳng là một đường thẳng, của đoạn thẳng là đoạn thẳng.
- Hình biểu diễn của hai đường thẳng song song là hai đường thẳng song song, của hai đường thẳng cắt
nhau là hai đường thẳng cắt nhau. Hai đoạn thẳng song song và bằng nhau thì phải được vẽ song song và
bằng nhau. Trung điểm của một đoạn thẳng phải được lấy ngay tại điểm chính giữa của đoạn thẳng đó.
- Hình biểu diễn phải giữ nguyên quan hệ thuộc giữa điểm và đường thẳng.
- Dùng nét vẽ liền để biểu diễn cho đường nhìn thấy và nét đứt đoạn biểu diễn cho đường bị che khuất.
3. Các tính chất thừa nhận của hình học không gian
- Tính chất 1: Có một và chỉ một đường thẳng đi qua hai điểm phân biệt.
- Tính chất 2: Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng.
Như vậy, một mặt phẳng trong không gian có thể được xác định bởi một trong các cách thức sau:
- Mặt phẳng đó đi qua 3 điểm không thẳng hàng . Kí hiệu là mp .
- Mặt phẳng đó đi qua một đường thẳng và một điểm không thuộc đường thẳng . Kí hiệu: ;
mp .
- Mặt phẳng đó đi qua hai đường thẳng cắt nhau và . Kí hiệu, mp .
- Mặt phẳng đó đi qua hai đường thẳng song song , .
- Tính chất 3: Trong không gian có ít nhất bốn điểm không cùng thuộc bất cứ mặt phẳng nào.
- Tính chất 4: Trong không gian, hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường
thẳng chung duy nhất chứa tất cả các điểm chung của hai mặt phẳng đó.
- Tính chất 5: Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường
thẳng đều thuộc mặt phẳng đó.
( ) ( ) ( ) ( )
,,,PQ
ab
P
P
A
a
AaÎ
a
A
A
( )
a
( )
A
a
Î
( )
a
A
a
( )
a
( )
a
a
,,ABC
( )
ABC
a
A
a
(,)Aa
mp(ABC)
A
B
C
mp(A;a)
a
A
mp(a,b)
b
a
b
a
a
b
( )
,ab
a
b
Trang 2
- Tính chất 6: Trong mỗi mặt phẳng của không gian, các kết quả đã biết của hình học phẳng đều đúng.
3.Vị trí tương đối của các đường thẳng và mặt phẳng trong không gian
a) Vị trí tương đối của một đường thẳng và một mặt phẳng
Cho đường thẳng và một mặt phẳng . Có thể xãy ra các khả năng sau:
- Đường thẳng và mặt phẳng không có điểm chung. Trong trường hợp này ta nói
đường thẳng song song với mặt phẳng , kí hiệu .
- Đường thẳng và mặt phẳng có đúng một điểm chung. Trong trường hợp này ta
nói ta nói đường thẳng cắt mặt phẳng tại , kí hiệu:
- Đường thẳng và mặt phẳng có nhiều hơn một điểm chung.Trường hợp
này ta nói đường thẳng nằm trong mặt phẳng ta kí hiệu: hay
.
b) Vị trí tương đối của hai mặt phẳng:
Cho hai mặt phẳng phân biệt và . Có thể xảy ra một trong các khả năng
sau:
- Hai mặt phẳng và không có điểm chung. Trong trường hợp này ta nói
các mặt phẳng và song song với nhau, kí hiệu .
- Hai mặt phẳng và có ít nhất một điểm chung. Trong trường hợp này ta
nói các mặt phẳng và có phần chung là một đường thẳng, giả sử đường
thẳng đó là , ta kí hiệu .
Đường thẳng được gọi là giao tuyến của hai mặt phẳng. Như vậy, việc xác định giao tuyến của hai mặt
phẳng tương ứng với việc xác định hai điểm cùng thuộc đồng thời hai mặt phẳng phân biệt đó. Ngoài ra,
nếu biết được rằng ba điểm phân biệt cùng thuộc đồng thời hai mặt phẳng thì ba điểm đó phải nằm trên
một được thẳng.
c) Vị trí tương đối của hai đương thẳng: Cho hai đường thẳng phân biệt và . Có thể xảy ra một
trong các khả năng sau:
- Các đường thẳng và cùng thuộc một mặt phẳng. Khi đó và hoặc cắt nhau tại một điểm hoạc
song song với nhau.
- Các đương thẳng và không cùng nằm trong bất kì một mặt phẳng nào. Trong trường hợp này ta nói
các đường thẳng và chéo nhau.
4. Hình chóp và hình tứ diện
d
( )
a
d
( )
a
d
( )
a
( )
//d
a
d
( )
a
d
( )
a
A
( ) { }
dA
a
Ç=
d
( )
a
d
( )
a
( )
d
a
Ì
( )
d
a
É
( )
a
( )
b
( )
a
( )
b
( )
a
( )
b
( ) ( )
//
ab
( )
a
( )
b
( )
a
( )
b
d
( ) ( )
d
ab
Ç=
d
a
b
a
b
a
b
a
b
a
b
A
b
a
α
d
α
d
A
α
d
β
α
α
β
Trang 3
1. Hình chóp:
Trong mặt phẳng , cho đa giác lồi .Lấy điểm nằrm ngoài mặt phẳng . Lần lượt nối với
các đỉnh để được n tam giác .Hình gồm đa giác và n tam giác
và gọi là hình chóp và được kí hiệu là
Ta gọi S là đỉnh, đa giác là mặt đáy, tam giác gọi là một mặt bên của hình
chóp, Các đoạn thẳng gọi là các cạnh bên, các cạnh của đa giác là các cạnh đáy của hình
chóp.
-Cách gọi tên: Hình chóp + tên đa giác.
- Ví dụ: hình chóp tam giác, hình chóp tứ giác….
Lưu ý: Hình chóp có đáy là đa giác đều, các cạnh bên bằng nhaulaf hình chóp đa giác đều.
b) tứ diện:
Tứ diện là hình được thành lập từ bốn điểm không đồng phẳng .Các điểm là các đỉnh
của tứ diện, các tam giác được gọi là các mặt của tứ diện đối diện với các đỉnh
và các đoạn thẳng gọi là các cạnh của tứ diện . Trong đó các cặp cạnh
và , và DB, và thường được gọi là các cặp cạnh đối của tứ diện.
B. CÁC DẠNG BÀI TOÁN VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG
DẠNG 1: XÁC ĐỊNH GIAO TUYẾN GIŨA HAI MẶT PHẲNG
Phương pháp: Để tìm giao tuyến của hai mặt phẳng và ta tiến hành đi tìm hai điểm thuộc cả hai
mặt phẳng và .
Lưu ý:
Một điểm chung của hai mặt phẳng và thường tìm được bằng cách: Chọn một mặt phẳng
sao cho các giao tuyến của và với có thể dựng được ngay. Giao điểm của (
trong ) là điểm chung cần tìm.
Ta thường chứng minh ba điểm thẳng hàng bằng cách chứng minh ba điểm đó thuộc giao tuyến của hai
mặt phẳng.
+ Ta cũng có thể chứng minh bà đường thẳng đồng quy bằng cách:
Cách 1: Hai trong ba đường thẳng ấy cắt nhau và lần lượt nằm trong hai mặt phẳng nhận đường thứ ba
làm giao tuyến.
Cách 2: Tìm một đoạn thẳng trên một đường thẳng nào đó. Chứng minh hai đường thẳng còn lại
chia đoạn theo cùng một tỉ số đại số.
DẠNG 2: XÁC ĐỊNH GIAO ĐIỂM CỦA ĐƯỜNG THẲNG VÀ MẶT PHẲNG .
Phương pháp:
Mặt đáy
cạnh đáy
cạnh bên
Mặt bên
D
C
B
A
S
A
5
A
4
A
3
A
2
A
1
S
S
A
3
A
2
A
1
( )
a
12
...
n
AA A
S
( )
a
S
12
,,...,
n
AA A
12 23 1
,,...,
n
SA A SA A SA A
12
,,...,
n
AA A
12 23 1
,,...,
n
SA A SA A SA A
12
....
n
SAA A
12
,,...,
n
AA A
12 23 1
,,...,
n
SA A SA A SA A
12
,,...,
n
SA SA SA
12
...
n
AA A
ABCD
,,,ABCD
,,,ABCD
,,,BCD ACD A BD ABC
,,,ABCD
,,,,,AB BC CD DA CA BD
AB
CD
AC
AD
BC
( )
a
( )
b
( )
a
( )
b
( )
a
( )
b
( )
g
12
,DD
( )
a
( )
b
( )
g
I
12
,DD
( )
g
AB
AB
D
( )
a
Trang 4
+ Nếu phát hiện ra một đường thẳng trong mặt phẳng cắt tại thì chính là giao điểm của
với mặt phẳng .
+ Nếu chưa phát hiện ra đường thẳng thì ta dựng bằng cách: Chọn một mặt phẳng chứa sao
cho giao tuyến của và có thể dựng được ngay, giao tuyến đó chính là đường thẳng cần tìm.
Hai định lí quan trọng thường dùng:
Định lí Ceva: Cho tam giác . Các điểm khác và theo thứ tự thuộc các đường
thẳng . Khi đó các đường thẳng hoặc đồng quy hoặc đôi một song song khi và
chỉ khi
Định lí Menelaus : Cho tam giác . Các điểm khác và theo thứ tự thuộc các
đường thẳng . Khi đó các điểm thẳng hàng khi và chỉ khi .
DẠNG 3: BÀI TOÁN DỰNG THIẾT DIỆN
Cho trước khối đa diện và mặt phẳng . Nếu có điểm chung với thì sẽ cắt một số mặt
của theo các đoạn thẳng. Phần mặt phẳng giới hạn bởi các đoạn đó thường là một đa giác, gọi là
mặt cắt ( còn gọi là thiết diện) giữa và .
Chú ý:
+ Đỉnh của thiết diện là giao điểm của với các cạnh của . Cạnh của thiết diện là các đoạn giao
tuyến của với các mặt của . Do đó thực chất của việc dựng thiết diện là bài toán dựng giao điểm
giữa đường thẳng và mặt phẳng và dựng giao tuyến giữa hai mặt phẳng.
+ Do mỗi cạnh của thiết diện là đoạn giao tuyến của mặt phẳng với một mặt của . Do đó số cạnh
nhiều nhất mà thiết diện có thể có chính là số mặt của .
- Đối với hình chóp tam giác ( hoặc tứ diện), thiết diện của nó cắt bởi mặt phẳng chỉ có thể là tam
giác hoặc tứ giác ( ở đay ta quy ước không xét các trường hợp suy biến khi thiết diện là một mặt hoặc một
cạnh của hình chóp).
-Đối với hình chóp tứ giác, thiết diện của nó chỉ có thể là tam giác, tứ giác hoặc ngũ giác.
Các bài toán liên quan đến thiết diện gồm các dạng:
+ Dựng thiết diện.
+ Xác định hình dạng thiết diện.
+ tính diện tích thiết diện.
+ Tính tỉ số thể tích hai phần do thiết diện phân chia khối thể tích đã cho ( sẽ được trình bày trong Công
phá toán tập 3).
Ví dụ 1: Cho hình chóp có đáy là một hình bình hành tâm . Gọi và lần lượt là trung
điểm của và . Gọi là mặt phẳng qua 3 điểm .
a) Tìm các giao tuyến của và ; và .
b) Tìm giao điểm của đường thẳng với mặt phẳng và giao điểm của đường
thẳng với mặt phẳng .
c) Xác định các giao tuyến của mặt phẳng với mặt phẳng và mặt phẳng .
Từn đó suy ra thiết diện của hình chóp cắt bởi .
d) Xác định các giao điểm của các đường thẳng , với . Chứng minh rằng
thẳng hàng.
Lời giải::
d
( )
a
D
I
I
D
( )
a
d
d
( )
g
D
( )
g
( )
a
d
ABC
,,MNP
,,ABC
,,BC CA AB
,,AM BN CP
.. 1
MB NC PA
MC NA PB
=-
ABC
,,MNP
,,ABC
,,BC CA AB
,,MNP
.. 1
MB NC PA
MC NA PB
=
T
( )
a
( )
a
T
( )
a
T
( )
a
T
( )
a
( )
a
T
( )
a
T
( )
a
T
T
( )
a
.S ABCD
O
M
N
SA
SC
()P
,,MNB
( )
P
( )
SAB
( )
P
( )
SBC
I
SO
( )
P
K
SD
()P
()P
()SAD
()SCD
()BMN
,EF
DA
DC
()P
,,EBF
Trang 5
a) Ta có:
Lại có
Từ (1) và (2) suy ra
Ta có :
Từ (3) và (4) suy ra
.
Tương tự ta cũng suy ra
.
b) Trong mặt phẳng , gọi là giao
điểm của với
Ta có :
là giao điểm của với .
Trong mặt phẳng , gọi là giao điểm của với . Ta có :
. Suy ra chính là giao điểm của với .
c) Ta có : .
Ta lại có : .
Như vậy tứ giác là thiết diện của hình chóp cắt bởi mặt phẳng .
d) Trong mặt phẳng , gọi . Ta có: nên .
Vậy chính là giao điểm của với .
Trong mặt phẳng gọi .
Ta có nên ,
,
Suy ra ba điểm cùng nằm trên giao tuyến của hai mặt phẳng và . Do
đó ba điểm thẳng hàng.
Ví dụ 2: Cho tứ diện và các điểm lần lượt thuộc các cạnh sao cho
không song song với . đồng phẳng khi :
A. B.
C. D. .
Đáp án A.
Lời giải:.
+ Giả sử cùng thuộc mặt phẳng .
Nếu cắt tại thì là điểm chung của các mặt phẳng , nên
cũng đi qua
Áp dụng định lí cho các tam giác ta được :
( ) ( )( )
,1MSASA SAB M SABÎÌÞÎ
( ) ( )
2MBMNÎ
( ) ( )( )
3MSAB BMNÎÇ
( ) ( )( )
4BSAB BMNÎÇ
( ) ( )
BM SAB BMN=Ç
( ) ( )
BM SAB BMN=Ç
( )
SAC
I
SO
MN
( ) ( )
,IMNMN BMN I BMN IÎÌÞÎÞ
SO
( )
SBD
K
BI
SD
( ) ( )
,KBIBI BMN K BMNÎÌ ÞÎ
K
SD
( )
( )
( ) ( )
KBMN
K BMN SAD
K SAD
Î
ì
ï
ÞÎ Ç
í
Î
ï
î
( ) ( )
MBMN SDCÎÇ
BMKN
.S ABCD
( )
SAD
{ }
EMKAD=Ç
( )
MK BMNÌ
( )
EBMNÎ
E
AD
( )
SDC
{ }
FNKCD=Ç
( )
NK BMNÌ
( )
FBMNÎ
( )
( )
( ) ( )
EBMN
E BMN ABCD
E ABCD
Î
ì
ï
ÞÎ Ç
í
Î
ï
î
( )
( )
( ) ( )
B BMN
B BMN ABCD
B ABCD
Î
ì
ï
ÞÎ Ç
í
Î
ï
î
,,BEF
( )
ABCD
,,BEF
ABCD
,,,MNPQ
,,,AB BC CD DA
MN
AC
,,,MNPQ
... 1
AM BN CP DQ
BM CN DP AQ
=
... 1
BM CN CP DQ
AM BN DP AQ
=
... 1
BM CN DP DQ
AM BN CP AQ
=
... 1
AM BN DP AQ
BM CN CP DQ
=
,,,MNPQ
( )
a
MN
AC
K
K
( ) ( )
, ABC
a
( )
ADC
PQ
.K
Menelaus
,ABC ADC
I
O
A
B
C
D
S
E
M
N
K
F
Trang 6
;
Nhận xét :
Trường hợp song song với thì ví dụ trên vẫn đúng.
+ Liệu trường hợp ngược lại, có thì có đồng phẳng hay
không ?
Câu trả lời là trường hợp ngược là ví dụ vẫn đúng. Ta sẽ cùng chứng minh nhé :
Trong mặt phẳng , cắt tại thì các điểm đồng phẳng.
Theo ví dụ 2 ta có: . Ví dụ được chứng minh.
+ Ví dụ này có thể được mở rộng đối với các điểm bất kì trên các đường thẳng
như sau :
đồng phẳng khi và chỉ khi ( khẳng định này dôi khi còn
được gọi là định lí Menelaus mở rộng trong không gian)
Ví dụ 3: Cho hình chóp và là điểm thuộc mặt bên . lần lượt là trung điểm của
. Thiết diện của hình chóp cắt bởi là :
A. Tam giác. B. Tứ giác. C. Ngũ giác. D. Lục giác.
Đáp án C.
Lời giải: :
Trong mặt phẳng , gọi lần lượt là giao điểm của với
Dễ thấy thiết diện là hình lập phương bị cắt bởi mặt phẳng là ngũ giác .
Vậy đáp án đúng là C.
b) Theo cách dựng ta có là trung điểm của . Do đó
Suy ra :
Do
Tương tự ta có :
Do đó :
Diện tích thiết diện là :
Do hai tam giác vuông và bằng nhau (c.g.c) nên Vậy tam giác cân tại
Gọi là trung điểm của
Ta có :
Diện tích của bằng :
.. 1
AM BN CK
BM CN AK
=
.. 1
AK CP DQ
CK DP AQ
=
... 1
AM BN CP DQ
BM CN DP AQ
Þ=
MN
AC
... 1
AM BN CP DQ
BM CN DP AQ
=
,,,MNPQ
( )
ACD
KO
AD
Q
¢
,,,MNPQ
¢
... 1
AM BN CP AQ
BM CN DP D Q
¢
=
¢
DQ DQ
QQ
AQ AQ
¢
¢
Þ=Þº
¢
,,,MNPQ
,,,AB BC CD DA
,,,MNPQ
¢
... 1
AM BN CP DQ
BM
CN DP AQ
=
.S ABCD
E
()SCD
,EF
( )
EFG
( )
ABCD
,IH
FG
( )
a
MNGFE
E
'BB
''
2
a
BF BP CQ===
232 133
EF= , .
22 344
aaMBPB
PE QF PQ CN CD a
NC PC
== Þ= = =Þ= =
( )
( ) ( )
( )
' ' / /( ' ')
'' //
('')
ABB A DCC D
KE ABB A KE NG
NG DCC D
a
a
ì
ï
=Ç Þ
í
ï
=Ç
î
//MN FG
22
11
,
99
QGF
PME
PQN QNP
S
S
PE QE
SPQ SPQ
æö æö
== ==
ç÷ ç÷
èø èø
( )
7
.
9
MNGFE PNQ PEM QFG PNQ
SSSS S=- + =
NCP
NCQ
.NQ NP=
NPQ
.N
I
PQ
22
22 22
55 45 18 3
,.
416164
aaaaa
PN PC CN NI PN PI=+= =-= -=
NPQ
22
196 76
..
216 16
NPQ MNGFE
aa
S NI PQ S==Þ=
Trang 7
Vậy đáp án đúng là B.
Câu 23. Đáp án D.
Trong mặt phẳng , dựng đường thẳng qua , song song với cắt theo thứ
tự tại .
Trong mặt phẳng dựng đường thẳng qua song song với cắt theo
thứ tự tại Ta có :
Áp dụng định lý Thales ta có :
Từ đây sauy ra
Theo cách dựng ta suy ra :
Từ (1) và (2)
Vậy luôn song song với mặt phẳng cố định, mặt phẳng đó là
Ví dụ 4. Cho hình chóp S.ABC. Gọi M, N lần lượt là trung điểm của SA và BC. P là điểm nằm trên
cạnh AB sao cho . Gọi Q là giao điểm của SC với mặt phẳng . Tính
A. . B. . C. . D. .
Lời giải:
Đáp án A.
Trong mặt phẳng , gọi
Khi đó Q chính là giao điểm của SC với EM.
Áp dụng địnhlý Menelaus vào tam giác ABC ta có:
Áp dụng địnhlý Menelaus vào tam giác SAC ta có:
()ABCD
M
BC
'',' 'AB C D
,EF
(''' '),ABCD
N
''BC
'',' 'AB C D
,.KI
''
.
'' '
BM C N BM C N
BD C A BD NA
=Þ=
'K '
// '.
'K 'N
BCNMBBE
KE BB
AAMDEA
===Þ
//( ' ') (1).KE BCC B
/ /( ' ') (2).EF BCC B
( ) ( )
( )
( )
// ' '
// ' ' .
//
EFIK BCC B
MN BCC B
MN EFIK
ì
ï
ÞÞ
í
ï
î
MN
(BCC'B')
( )
MNP
SQ
SC
1
3
1
6
1
2
2
3
( )
ABC
E NP AC=Ç
.. 1 2
AP BN CE CE
PB NC EA EA
=Þ =
11
.. 1
23
AM SQ CE SQ SQ
MS QC EA QC SC
=Þ = Þ =
Trang 8
Ví dụ 5. Cho tứ diện ABCD. Gọi tương ứng là trọng tâm của các tam giác BCD, ACD,
ABD và ABC. Chứng minh rằng đồng quy tại điểm G và ta có:
Lời giải:
Lưu ý: Điểm G được gọi là trọng tâm tứ diện ABCD
Gọi M là trung điểm CD. Theo tính chất trọng tâm ta có: và
Trong mặt phẳng , gọi G là giao điểm của
Theo định lý Thales ta có:
Tương tự ta có:
Từ và suy ra G, G’, G” trùng nhau, tức là đồng quy tại điểm G và
ta có :
Bài tập tương tự: Cho tứ diện . Gọi tương ứng là các trung điểm của
. Chứng minh rằng đòng quy tại một điểm và điểm đồng
quy chính là trọng tâm của tứ diện
C. BÀI TẬP RÈN LUYỆN KỸ NĂNG
Câu 1. Trong các mệnh đề sau mệnh đề nào sai?
A. Dùng nét đứt biểu diễn cho đường bị che khuất.
B. Hình biểu diễn của đường thẳng là đường thẳng.
C. Hình biểu diễn phải giữ nguyên qua hệ thuộc giữa điểm và đường thẳng..
D. Hình biểu diễn của hai đường cắt nhau có thể là hai đường song song.
Câu 2. Trong các hình vẽ sau hình nào có thể là hình biểu diễn của một hình tứ diện? (Chọn câu đúng
nhất)
111 1
,,,ABCD
11 1 1
,,,AA BB CC DD
11 1 1
3
4
AG BG CG DG
AA BB CC DD
== = =
11
11
1
//
3
MA MB
AB AB
MB MA
==Þ
11
1
3
AB
AB
=
( )
AMB
11
,BB AA
( )
111
1
13
1
34
AG AB
AG
GA AB AA
==Þ=
( )
11
1
1
1
'3
',
4
2
"3
'' ' ,
4
AG
G CC AA
AA
AG
GDDAA
AA
ì
=Ç =
ï
ï
í
ï
=Ç =
ï
î
( )
1
( )
2
11 1 1
,,,AA BB CC DD
11 1 1
3
4
AG BG CG DG
AA BB CC DD
== = =
ABCD
,,, , ,IJEFKH
,,,,,AB CD AC BD AD BC
,,IJ EF KH
G
ABCD
Trang 9
A. . B. .
C. . D.
Câu 3. Hình nào sau đây vẽ đúng quy tắc?
A. . B. .
C. . D.
Câu 4. Cho hình chóp có đáy là hình thang, đáy lớn gấp đôi đáy nhỏ , là
trung điểm của đoạn . Hình vẽ nào sau đây vẽ đúng quy tắc?
A. . B. . C. . D.
Câu 5. Một hình không gian có hình chiếu đứng (nhìn từ trước vào (có thể nhìn từ sau) để từ hình 3D
chuyển sang hình 2D) hình chiếu bằng (nhìn từ trên xuống) có thể nhìn từ dưới lên)), hình
chiếu cạnh (từ trái sang (có thể nhìn từ phải sang)) lần lượt được thể hiện như sau:
( )
I
( )
II
( )
III
( )
IV
( ) ( )
,.III
( ) ( ) ( ) ( )
,, ,IIIIIIIV
( ) ( ) ( )
,,IIIIII
( )
.I
.S ABCD
ABCD
AB
CD
E
AB
Trang 10
Hãy vẽ hình biểu diễn của hình đó?
A. . B. .
C. . D.
Câu 6. Mệnh đề nào sau đây đúng?
A. Qua ba điểm xác định một và chỉ một mặt phẳng.
B. Qua ba điểm phân biệt xác định một và chỉ một mặt phẳng.
C. Qua ba điểm phân biệt không thẳng hàng xác định hai mặt phẳng phân biệt.
D. Qua ba điểm phân biệt không thẳng hàng xác định một và chỉ một mặt phẳng.
Câu 7. Xét các mệnh đề sau đây:
Có một và chỉ một đường thẳng đi qua hai điểm phân biệt.
Có một và chỉ một mặt phẳng đi qua ba điểm phân biệt.
Tồn tại bốn điểm không cùng thuộc một mặt phẳng.
Nếu hai mặt phẳng có một điểm chung thì chúng còn có duy nhất một điểm chung khác
nữa.
Số mệnh đề sai trong các mệnh đề trên là:
A. 3. B. 1. C. 2. D. 4.
Câu 8. Cho điểm phân biệt trong không gian .Biết rằng bốn điểm bất kỳ trong điểm đã
cho cùng thuộc một mặt phẳng. Khẳng định nào sau đây đúng?
A. Tất cả điểm thuộc cùng một mặt phẳng.
B. Có đúng điểm thuộc cùng một mặt phẳng.
C. Có đúng điểm thuộc cùng một mặt phẳng.
D. Không tồn tại mặt phẳng nào chứa tất cả điểm.
Câu 9. Trong các mệnh đề sau mệnh đề nào đúng?
A. Có đúng hai mặt phẳng cắt nhau theo một đường thẳng cho trước..
B. Hai mặt phẳng có một điểm chung duy nhất.
C. Hai mặt phẳng cùng chứa hai cạnh của một tam giác thì trùng nhau..
D. Có đúng hai mặt phẳng phân biệt đi qua ba điểm phân biệt..
Câu 10. Cho tứ giác lồi và điểm không thuộc mặt phẳng . Có bao nhiêu mặt phẳng
qua và hai trong số bốn điểm
A. 3. B. 4. C. 5. D. 6.
Câu 11. Cho năm điểm phân biệt trong đó không có bốn điểm nào cùng nằm trên một mặt
phẳng. Hỏi có bao nhiêu mặt phẳng tạo bởi ba trong năm điểm đã cho ?
( )
I
( )
II
( )
III
( )
IV
n
( )
4n >
n
n
1n -
2n -
n
ABCD
S
( )
ABCD
S
,,, ?ABCD
,,, ,ABCDE
Trang 11
A. 6. B. 10. C. 60. D. 8.
Câu 12. Cho đường thẳng phân biệt đồng quy tại O trong đó không có ba đường thẳng
nào cùng năm trên một mặt phẳng. Có bao nhiêu mặt phẳng đi qua hai trong số đường thẳng
trên?
A. . B. . C. . D. .
Câu 13. Cho mặt phẳng và hai đường thẳng cắt nhau cùng nằm trong mặt phẳng . Gọi A
là một điểm thuộc đường thẳng nhưng không thuộc đường thẳng và là một điểm nằm
ngoài . Khẳng định nào sau đây đúng:
A. và chéo nhau. B.
và song song .
C. và cắt nhau. D. và trùng nhau.
Câu 14. Cho tứ diện lần lượt là trung điểm của và . Khẳng định nào sau đây
đúng?
A.
song song . B.
trùng nhau. C. cắt nhau D. chéo nhau
Câu 15. Cho hình chóp có đáy là một tứ giác ( không song song ). Gọi là
trung điểm của , là điểm nằm trên cạnh sao cho là giao điểm của
và . Cặp đường thẳng nào sau đây cắt nhau:
A. và . B. và . C. và D. và .
Câu 16. Cho bốn điểm không cùng nằm trong một mặt phẳng. Trên lần lượt lấy các
điểm và sao cho cắt tại . Điểm không thuộc mặt phẳng nào sau đây:
A. . B. . C.
. D. .
Câu 17. Cho tứ diện . Gọi lần lượt là trung điểm của . Khi đó và là
hai đường thẳng:
A. Chéo nhau. B. Có hai điểm chung. C. Song song D. Cắt nhau
Câu 18. Cho tứ diện . Gọi là trung điểm cạnh là điểm thuộc cạnh sao cho
là một điểm thuộc miền trong của tam giác . Mệnh đề nào sau đây là
mệnh đề đúng?
A. Mặt phẳng chứa đường thẳng
B. Mặt phẳng đi qua giao điểm của hai đường thẳng và .
C. Mặt phẳng đi qua điểm .
D. Mặt phẳng chứa đường thẳng .
Câu 19. Ba điểm phân biệt cùng thuộc hai mặt phẳng phân biệt thì :
A. Cùng thuộc một đường tròn B. Cùng thuộc một đường thẳng
C. Cùng thuộc một eliP D. Cùng thuộc một tam giác.
Câu 20. Cho hình chóp có đáy là hình thang ( là đáy lớn, là đáy nhỏ). Khẳng
định nào sau đây sai:
A. Hình chóp có bốn mặt bên..
B. Giao tuyến của hai mặt phẳng và là trong đó là một điểm thuộc mặt
phẳng .
C. Giao tuyến của hai mặt phẳng và là trong đó là giao điểm của hai
đường thẳng và
D. Giao tuyến của hai mặt phẳng và là trong đó là giao điểm của và
.
Câu 21. Cho hình chóp có đáy là một tứ giác ( không song song ). Gọi M là
trung điểm của là điểm nằm trên cạnh sao cho là giao điểm của
( )
3,nn n³Î•
n
( )
!
22!
n
n -
( )
!
2!
n
n -
!
2
n
!n
( )
a
,ab
( )
a
a
b
P
( )
a
PA
b
PA
b
PA
b
PA
b
,,ABCD I J
AD
BC
,AJ BI
,AJ BI
,AJ BI
,AJ BI
SABCD
ABCD
AB
CD
M
SD
N
SB
2,SN NB O=
AC
BD
SO
AD
MN
SO
MN
SC
SA
BC
,,,ABCD
M
N
MN
BD
I
I
( )
ACD
( )
BCD
( )
CMN
( )
ABD
ABCD
,MN
BC
MN
ABCD
M
,AC N
AD
2.AN ND O=
BCD
( )
OMN
AB
( )
OMN
MN
CD
( )
OMN
A
( )
OMN
CD
.S ABCD
ABCD
AB
CD
.S ABCD
( )
SAB
( )
SCD
SK
K
( )
ABCD
( )
SAC
( )
SBD
SO
O
AC
BD
( )
SAD
( )
SBC
SI
I
AD
BC
.S ABCD
ABCD
AB
CD
,SD N
SB
2,SN NB O=
AC
Trang 12
và . Giả sử đường thẳng là giao tuyến của và . Nhận xét nào sau đây là
sai:N
A. cắt . B. cắt . C. cắt . D. cắt .
Câu 22. Cho hình chóp có đáy là hình bình hành .Mặt phẳng di
động chứa đường thẳng và cắt các đoạn lần lượt tại . Mặt phẳng di
động chứa đường thẳng và cắt lần lượt tại là giao điểm của là
giao điểm của . Xét các mệnh đề sau:
Đường thẳng luôn đi qua một điểm cố định..
Đường thẳng luôn đi qua một điểm cố định.
Đường thẳng luôn đi qua một điểm cố dịnh.
Có bao nhiêu mệnh đề đúng?
A. . B. . C.
. D. .
Câu 23. Cho tứ diện đều có các cạnh bằng . Gọi là trung điểm , là điểm thuộc
cạnh sao cho là điểm thuộc cạnh sao cho . Tính độ dài
đoạn giao tuyến của mặt phẳng với mặt phẳng của hình chóp theo .
A. . B. . C. . D. .
Câu 24. Cho tứ diện nằm trên đoạn sao cho là điểm nằm trên sao cho
. Gọi là giao điểm của và . Giao tuyến của hai mặt phẳng và
là:
A. trong đó thuộc sao cho
B. trong đó thuộc sao cho
C. trong đó thuộc sao cho
D. trong đó thuộc sao cho
Câu 25. Cho tứ diện có là các đường phân giác trong của
tam giác . Giao tuyến của hai mặt phẳng và là:
A. trong đó thuộc sao cho
B. trong đó thuộc sao cho
C. trong đó thuộc sao cho
D. trong đó thuộc sao cho
Câu 26. Cho hình chóp có đáy là hình bình hành tâm . Gọi lần lượt là
trung điểm của và . Gọi là giao điểm của với . Tính
A. . B. . C. . D. .
BD
d
( )
SAB
( )
SCD
d
CD
d
MN
d
AB
d
SO
.S ABCD
ABCD
( )
//BC AD
( )
P
AB
,SC SD
,EF
( )
Q
CD
,SA SB
,.GHI
,;AE BF J
,CG DH
( )
1
EF
( )
2
GH
( )
3
IJ
0
1
2
3
ABCD
a
E
AB
F
BC
2,BF FC G=
CD
2CG GD=
( )
EFG
( )
ACD
ABCD
a
19
15
a
141
30
a
34 15 3
15
a +
34 15 3
15
a -
,ABCD E
BC
3,BC EC F=
BD
3CD DF=
G
BF
DE
( )
ACG
( )
ABD
AH
H
BD
4BH HD=-
!!! " !!! "
AH
H
BD
1
4
BH HD=
!!! " !!! "
AH
H
BD
4BH HD=
!!! " !!!"
AH
H
BD
1
4
BH HD=-
!!! " !!! "
SABC
,,.,,AB c BC a AC b AD BE CF== =
ABC
( )
SBE
( )
SCF
SI
I
AD
bc
AI ID
a
+
=
!! " !!"
SI
I
AD
bc
AI ID
a
+
=-
!! " !!"
SI
I
AD
a
AI ID
bc
=
+
!! " !!"
SI
I
AD
a
AI ID
bc
-
=
+
!! " !!"
.S ABCD
ABCD
O
,,MNP
SO
H
SC
( )
MNP
?
SH
SC
1
3
1
4
3
4
2
3
Trang 13
Câu 27. Cho hình chóp có đáy là hình bình hành. Gọi lần lượt là trung điểm
của và . Trên đường thẳng lấy điểm sao cho là trung điểm . Gọi là
giao điểm của với mặt phẳng . Tính
A. . B. . C. . D. .
Câu 28. Cho tứ diện lần lượt thuộc đoạn Gọi là giao điểm của và .
Gọi là giao điểm của với . Mệnh đề nào sau đây đúng?
A. . B. .
C. . D. .
Câu 29. Cho hình chóp lần lượt là trung điểm của . Gọi là giao điểm của
với là giao điểm của với . Tính ?
A. . B. . C. D. .
Câu 30. Cho hình chóp có đáy là hình bình hành. Một mặt phẳng cắt các cạnh
bên tương ứng tại các điểm . Gọi .
Mệnh đề nào sau đây đúng?
A. . B. .
C.
. D. .
Câu 31. Cho hình chóp có đáy là hình bình hành tâm . Gọi lần lượt là các
điểm nằm trên cạnh sao cho . Gọi là điểm trên cạnh sao
cho . là giao điểm của với . Tính
A. . B. . C. . D. .
Câu 32. Cho tứ diện . là điểm thuộc đoạn sao cho là các đei63m thuộc
đường thẳng sao cho là các điểm thuộc đường thẳng
sao cho thuộc tia đối của tia sao cho là trung điểm của .
Trong các mệnh đề sau, mệnh đề nào đúng?
A. Bốn điểm đồng phẳng B. Bốn điểm đồng phẳng.
C. Bốn điểm đồng phẳng. D. Bốn điểm đồng phẳng.
Câu 33. Cho tứ diện là điểm thuộc đường thẳng sao cho
là các điểm thuộc đường thẳng sao cho
là các điểm thuộc đường thẳng sao cho
là các điểm nằm trên đường thẳng sao cho
. Bốn điểm nào dưới đây lập nên một tứ diện?
A. . B. . C. . D. .
Câu 34. Cho tứ diện có lần lượt là trung điểm của và là điểm thuộc cạnh
( không là trung điểm ).
.S ABCD
ABCD
,MN
AD
CD
DS
P
D
SP
R
SB
()MNP
?
SR
SB
1
3
1
4
3
4
2
5
,,SABC E F
,.AC AB
K
BE
CF
D
( )
SAK
BC
6
AK BK CK
KD KE KF
++³
6
AK BK CK
KD KE KF
++£
6
AK BK CK
KD KE KF
++>
6
AK BK CK
KD KE KF
++<
.,,SABCD DM
,BC AD
E
( )
SBM
,AC F
( )
SCM
AB
MF ME
CM ME BM ME
+
--
1
2
1
2
1
3
.S ABCD
ABCD
( )
a
,,,SA SB SC SD
,,,EFGH
,IACBDJEGSI=Ç =Ç
SA SC SB SD
SE SG SF SH
+=+
2
SA SC SI
SE SG SJ
+³
SA SC SB SD
SE SG SF SH
+>+
2
SB SD SI
SF SH SJ
+³
.S ABCD
ABCD
O
,MN
21
,
32
BM NC
MA BN
==
P
SD
1
5
PD
PS
=
J
SO
( )
MNP
?
SJ
SO
10
11
1
11
3
4
5
2
ABCD
E
AB
2.,EA EB F G=
BC
5, 5.,FC FB GC GB H I==-
!!!" !!!" !!!" !!!"
CD
5, 5,HC HD ID IC J=- =-
!!!" !!! " !!" !!"
DA
D
AJ
,, ,EFH J
,,,EFI J
,, ,EGH I
,,,EGI J
,,ABCD E U
AB
2,5 4.,EA EB UA UB F G=- =
!! !" !!!" !! !" !!!"
BC
5, 2.,FC FB GC GB H I==-
!!!" !!!" !!!" !!!"
CD
5, 5.,HC HD ID IC J K=- =
!!!" !!! " !!" !!"
DA
2, 5JA JD KD KA==
!!" !! !" !!!" !!!"
,, ,EFH J
,,,EGI K
,, ,UGHJ
,,,UFIK
ABCD
,MN
P
BC
P
BC
Trang 14
a) Thiết diện của tứ diện bị cắt bởi là:
A. Tam giác B. Tứ giác C. Ngũ giác. D. Lục giác.
b) Gọi là giao điểm của với là giao điểm của với . Mệnh đề nào
sau đây đúng?
A. . B. . C. . D. .
Câu 35. Cho hình chóp có đáy là hình bình hành, là trung điểm của lần
lượt là các điểm thuộc cạnh . Thiết diện của hình chóp cắt bởi là:
A. Tam giác B. Tứ giác C. Ngũ giác. D. Lục giác.
Câu 36. Cho hình chóp có đáy là hình thang với đáy lớn là trung điểm của
cạnh là các điểm thuộc cạnh ( không là trung điểm của ). Thiết diện
của hình chóp cắt bởi mặt phẳng là:
A. Tam giác B. Tứ giác C. Ngũ giác. D. Lục giác.
Câu 37. Cho hình chóp với đáy là đa giác lồi Trên tia đối của tia
lấy điểm là các điểm nằm trên cạnh . Thiết diện của hình chóp cắt bởi
mặt phẳng là:
A. Đa giác cạnh. B. Đa giác cạnh. C. Đa giác cạnh. D. Đa giác cạnh.
Câu 38. Cho hình chóp có đáy là hình bình hành, E là điểm thuộc cạnh bên SD sao
cho . F là trọng tâm tam giác là điểm thay đổi trên cạnh BC. Thiết diện cắt
bởi mặt phẳng là:
A. Tam giác B. Tứ giác C. Ngũ giác. D. Lục giác.
Câu 39. Cho hình chóp có đáy là hình thang với đáy lớn AD, E là một điểm thuộc
mặt bên . F, G lần lượt là các điểm thuộc cạnh AB và SB. Thiết diện của hình chóp
cắt bởi mặt phẳng có thể là:
A. Tam giác, tứ giác . B. Tứ giác, ngũ giác. C. Tam giác, ngũ giác. D. Ngũ giác.
Câu 40. Cho hình chóp là trung điểm của thuộc SC sao cho là một
điểm thuộc miền trong tam giác . Thiết diện của hình chóp cắt bởi mặt phẳng là:
A. Tam giác, tứ giác . B. Tứ giác, ngũ giác. C. Tam giác, ngũ giác. D. Ngũ giác.
Câu 41. Cho hình tứ diện có tất cả các cạnh bằng . Gọi M, N lần lượt là trung điểm của CA,
CB. P là điểm trên cạnh BD sao cho . Diện tích S thiết diện của tứ diện bị
cắt bởi là:
A. . B. . C. . D. .
Câu 42. Cho tứ diện có cạnh bằng a. Trên tia đối của các tia CB, DA lần lượt lấy các điểm E, F
sao cho . Gọi M là trung điểm của đoạn AB. Diện tích S thiết diện của tứ diện
cắt bởi mặt phẳng là:
A. . B. . C. . D. .
Câu 43. Cho hình chóp có đáy là hình bình hành. Gọi M, N, P lần lượt là trung điểm
của AB, AD, SC. Gọi Q là giao điểm của SD với . Tính
A. . B. . C. . D. .
Câu 44. Cho hình chóp có đáy là hình bình hành tâm O. Gọi M, N , P lần lượt là
trung điểm của AB, AD và SO. Gọi H là giao điểm của SC với . Tính
( )
MNP
Q
( )
MNP
,AD I
MN
PQ
2
MNPQ MPN
SS=
2
MNPQ MPQ
SS=
4
MNPQ MPI
SS=
4
MNPQ PIN
SS=
.S ABCD
ABCD
E
,,SA F G
( )
MNP
.S ABCD
ABCD
,AD E
,,SA F G
,SC AB
F
SC
( )
EFG
12
...
n
SA A A
( )
12
... 3, .
n
AA A n n³Î•
1
AS
12
,,...
n
BB B
2
,
n
SA SA
( )
12n
BB B
2n -
1n -
n
1n +
.S ABCD
ABCD
3SD SE=
,SAB G
( )
EFG
.S ABCD
ABCD
( )
SCD
.S ABCD
( )
EFG
.,S ABCD E
,SB F
32,SF SC G=
!! !" !! !"
SAD
( )
EFG
ABCD
6a
2BP PD=
ABCD
( )
MNP
2
5 51
4
a
S =
2
5147
4
a
S =
2
5147
2
a
S =
2
5 51
2
a
S =
ABCD
,CE a DF a==
ABCD
( )
MEF
2
33
18
a
S =
2
3
a
S =
2
6
a
S =
2
33
9
a
S =
.S ABCD
ABCD
( )
MNP
?
SQ
SD
1
3
1
4
3
4
2
3
.S ABCD
ABCD
( )
MNP
?
SH
SC
Trang 15
A. . B. . C. . D. .
Câu 45. Cho hình chóp có đáy là hình bình hành. Gọi M, N lần lượt là trung điểm của
AD và CD. Trên đường thẳng DS lấy điểm P sao cho D là trung điểm của SP. Gọi R là giao
điểm của SB với mặt phẳng . Tính
A. . B. . C. . D. .
1
3
1
4
3
4
2
3
SABCD
ABCD
( )
MNP
?
SR
SB
1
3
1
4
3
4
2
5
Trang 16
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1. Đáp án D.
Câu 2. Đáp án B.
Câu 3. Đáp án A.
Câu 4. Đáp án A.
Theo quy tắc vẽ hình, các đoạn thẳng song song được vẽ bằng các đoạn thẳng song song nên
đáp án D bị loại. Trung điểm được vẽ ở chính giữa đoạn nên ý C bị loại. Nét khuất được vẽ bởi
nét đứt đoạn, nét với góc nhìn này với đáp án B thì hoặc AB đứt đoạn hoặc SC, SD đứt đoạn.
Do đó chỉ có đáp án A đúng.
Câu 5. Đáp án C.
Hình A, B, D sai khi vẽ các đường không nhìn thấy bằng nét liền.
Câu 6. Đáp án D.
- Đáp án A, B sai, các em có thể lấy ví dụ ba điểm phân biệt , thẳng hàng , thì có vô số
mặt phẳng đi qua ba điểm đó.
- Đáp án C sai, vì theo tính chất thừa nhận, ba điểm phân biệt không thẳng hàng có duy nhất
một mp đi qua ba điểm.
Câu 7. Đáp án B.
Theo các tính chất thừa nhận, ta thấy (I), (II), (III) đúng và nếu hai mp có 1 điểm chung thì
chúng còn vô số điểm chung khác nữa. Điều đó đồng nghĩa với nhận xét (IV) là sai. Như vậy
có 1 quy tắc sai.
Câu 8. Đáp án A.
- Nếu điểm đã cho cùng thuộc một đường thẳng thì hiển nhiên điểm thuộc cùng 1 mp. Do
đó loại được đáp án B, C, D.
- Nếu điểm đã cho không cùng thuộc một đường thẳng thì trong chúng phải có 3 điểm không
thẳng hàng. Khi đó ba điểm này xác định 1 mp, kí hiệu là mp . Lấy một điểm trong
điểm còn lại thì theo giả thiết điểm đó phải thuộc mp . Suy ra tất cả các điểm đã cho cùng
thuộc 1 mp.
Câu 9. Đáp án C.
Một đường thẳng cho trước có vô số mp đi q ua.
Hai mp đã có 1 điểm chung thì có vô số điểm chung khác nữa. Còn có trường hợp 2 mp không
có điểm chung nào.
Có duy nhất 1 mp đi qua ba điểm phân biệt. Như vậy ta chọn ý C.
Câu 10. Đáp án D.
Số cách chọn 2 trong 4 điểm là .
Vậy có 6 mp đi qua và 2 trong 4 điểm .
Câu 11. Đáp án B.
Chọn 3 trong 5 điểm trên sẽ tạo nên 1 mp. Do đó, số mp tạo bởi 3 trong 5 điểm trên là .
Câu 12. Đáp án A.
Hai đường thẳng phân biệt cắt nhau tại xác định 1 mp . Nên số các mp chứa 2 trong
đường thẳng trên là .
Câu 13. Đáp án A .
Dễ thấy không trùng nhau.
Giả sử không chéo nhau, khi đó hoặc song song hoặc cắt nhau. Lúc đó, theo cách
xác định 1 mp, ta thấy cùng thuộc 1 mp . Các mp đều chứa đường thẳng
và đi qua điểm ở ngoài nên 2 mp trùng nhau. Suy ra điểm phải thuộc mp
(Vô lý). Như vậy chéo nhau.
Câu 14. Đáp án D.
Giả sử đồng phẳng, suy ra đồng phẳng do đó cùng thuộc 1 mp (vô
lý).
,,ABC
n
n
n
( )
P
3n -
( )
P
,,,ABCD
2
4
6C =
S
,,,ABCD
O
n
( )
2
!
22!
n
n
C
n
=
-
,PA b
,PA b
,PA b
,PA b
( )
b
( ) ( )
,
ab
b
A
b
( ) ( )
,
ab
P
( )
a
,PA b
,AJ BI
,AJ BI
,,,ABCD
Trang 17
Do đó không đồng phẳng, do đó chéo nhau. Chọn đáp án D.
Câu 15. Đáp án B.
Giả sử cắt nhau. Khi đó đồng phẳng, suy ra thuộc mp (Vô lý).
Đáp án A bị loại.
Giả sử cắt . Khi đó và đồng phẳng, suy ra thuộc (vô lý). Do đó
đáp án C bị loại.
Giả sử cắt . Khi đó đồng phẳng. Suy ra, thuộc mp (vô lý). Đáp án
D bị loại. cùng nằm trong mp , không song song và trùng nhau.
Câu 16. Đáp án A.
Do là giao điểm của và nên thuộc các mp chứa và các mp chứa . Do đó
thuộc
Giả sử thuộc khi đó thuộc (vô lý).
Câu 17. Đáp án A.
Giả sử đồng phẳng. Do đó lần lượt thuộc đường thẳng nên cũng
thuộc mp đó. Như vậy đồng phẳng(vô lý). Như vậy đáp án B, C, D không thỏa mãn.
Câu 18. Đáp án A.
Gọi là giao điểm của và CD. Khi đó thuộc . Vậy đáp án A đúng.
Giả sử chứa đường thẳng . Khi đó cùng thuộc mp . Suy ra
cùng thuộc mp (vô lý). Đáp án B không thỏa mãn.
Giả sử đi qua điểm . Do lần lượt thuộc các đường thẳng nên
thuộc mp . Như vậy 2 mp trùng nhau. Suy ra thuộc mp (vô
lý). Vậy đáp án C bị loại.
Tương tự ta cũng dễ dàng suy ra đáp án D bị loại.
Câu 19. Đáp án B.
Giao tuyến của 2mp phân biệt là 1 đường thẳng, nên ba điểm phân biệt cùng thuộc 2 mp phân
biệt sẽ nằm trên giao tuyến của 2mp phân biệt.
Câu 20. Đáp án B.
Hiển nhiên hình chóp có 4 mặt bên nên đáp án A đúng.
Ta thấy giao tuyến của 2mp là , là điểm thuộc cả hai mp do đó
. tương tự ta cũng chứng minh được . Như vậy thuộc cả hai đường thẳng
(vô lý do song song). Do vậy đáp án B sai.
Do đó thuộc giao tuyến của hai mp .
,AJ BI
,AJ BI
O
A
D
B
C
S
M
N
S
( )
ABCD
MN
SC
MN
SC
C
( )
SBD
SA
BC
,SA BC
S
( )
ABCD
,MN SO
( )
SBD
I
MN
BD
I
MN
BD
I
( ) ( ) ( )
,,.BCD CM N ABD
I
( )
ACD
B
( )
ACD
,MN BC
,DA
,MC NB
,DA
,,,ABCD
I
MN
I
AB
,OB
,OB
( )
ACD
A
,DC
,AN AM
,DC
( ) ( )
,OCD AMN
B
( )
ACD
.S ABCD
( ) ( )
,SAB ABCD
AB
K
KCDÎ
K
( )
( )
.
.
OAC O SAC
OBD O SBD
ÎÞÎ
ÎÞÎ
O
( ) ( )
,SAC SBD
Trang 18
Tương tự ta cũng dễ thấy .
Như vậy đáp án C,D đúng.
Câu 21. Đáp án B.
Gọi . Ta có:
Lại có
Do đó
Vậy cắt .
Giả sử cắt . Khi đó thuộc mp . Suy ra thuộc (vô lý). Vậy không
cắt . Đáp án B sai.
Câu 22. Đáp án D.
Trong mp , gọi . Khi đó cố định.
Như vậy: cùng nằm trên hai mp và , do đó ba điểm thẳng hàng.
Vậy đường thẳng luôn đi qua một điểm cố định .
Tương tự, ta có cùng nằm trên hai mp và ,do đó thẳng hàng.
Vậy các đường thẳng luôn đi qua một điểm cố định .
( ) ( )
SI SA D SBC=Ç
I
O
A
D
B
C
S
M
N
I AB CD=Ç
( ) ( )
( ) ( )
( ) ( )
,
,
I AB AB SAB I SAB
I SAB SCD
I CD CD SCD I SCD
ÎÌÞÎ
ì
ï
ÞÎ Ç
í
ÎÌÞÎ
ï
î
( ) ( )
.SSAB SCDÎÇ
( ) ( )
.SI SAB SCD=Ç
.d SI޺
d
,,AB CD SO
d
MN
M
( )
SAB
D
( )
SAB
d
MN
J
I
E
H
M
O
A
D
B
C
S
F
G
( )
ABCD
;MABCDOACBD=Ç = Ç
,MO
,,EFM
( )
P
( )
SCD
,,EFM
EF
M
,,GH M
( )
Q
( )
SAB
,,GH M
GH
M
Trang 19
Do .
Tương tự ta cũng có
Do đó ba điểm thẳng hàng. Vậy luôn đi qua điểm cố định .
Vậy ta chọn đáp án D.
Câu 23. Đáp án A.
Trong mp , gọi .
Trong mp , gọi .
Khi đó .
Áp dụng định lý Menelaus cho tam giác với ba điểm thẳng hàng ta có:
Áp dụng định lý Menelaus cho tam giác với ba điểm thẳng hàng ta có:
Áp dụng định lý cosin vào tam giác ta có:
Câu 24. Đáp án C.
Trong , gọi .
Dễ thấy thuộc đoạn nên cùng hướng.
Do đó đáp án A, D bị loại.
Áp dụng định lý Ceva trong tam giác với đồng quy ta có:
( )
( )
( ) ( )
I AE SAC
I SAC SBD
I BF SBD
ÎÌ
ì
ï
ÞÎ Ç
í
ÎÌ
ï
î
( ) ( ) ( ) ( )
;JSAC SBDOSAC SBDÎÇ ÎÇ
,,IJO
IJ
O
B
I
D
C
A
E
F
G
H
( )
BCD
I FG BD=Ç
( )
ADB
H IE AD=Ç
( ) ( )
HG EFG ACD=Ç
BCD
,,IGF
1
.. 1
4
ID FB GC ID
IB FC GD IB
=Þ =
ABD
,H,EI
1
.. 1
45
HD EA IB HD a
HD
HA EB ID HA
=Þ = Þ =
HDG
222 0
222 2
2..cos60
19 19
25 9 15 225 15
HG HD DG DH DG
aaa a
HG a
=+-
=+-= Þ =
G
F
E
H
B
D
C
A
( )
BCD
H CG BD=Ç
H
BD
,BH HD
!!!" !!! "
BCD
,,BF DE CH
Trang 20
Do cùng hướng nên .
Câu 25. Đáp án A.
Do thuộc đoạn nên cùng hướng. Do đó B, D bị loại.
là phân giác trong của tam giác nên theo tính chất đường phân giác ta có:
Ta có: là phân giác trong của tam giác nên theo tính chất đường phân giác ta có:
Do đó:
Câu 26. Đáp án B.
Trong mp , gọi . Dễ thấy .
Do là đường trung bình của tam giác nên là trung điểm AO. Suy ra và
là đường trung bình của tam giác . Do đó .
Áp dụng định lý Thales ta có:
Câu 27. Đáp án D.
Trong mp , gọi .
Dễ thấy .
Do là đường trung bình của tam giác nên là trung điểm DO. Suy ra .
Áp dụng định lý Menelaus vào taam giác ta có :
Câu 28. Đáp án A.
1
.. 12.2. 1 4
4
EB FC HD HD HD
BH DH
EC FD HB HB HB
=Þ =Þ = Þ =
,BH HD
!!!" !!! "
4BH HD=
!!! " !!! "
I
E
D
F
B
A
C
S
I
AD
,AI ID
!!" !!"
AD
ABC
BD AB c ac
BD
DC AC b b c
==Þ=
+
BI
ABD
IA BA b c b c
IA ID
ID BD a a
++
== Þ=
bc
AI ID
a
+
=
!! " !!"
( )
ABCD
I MN AO=Ç
H PO SC=Ç
MN
ABD
I
1
4
AI
AC
=
PI
OSA
//IH SA
1
.
4
SH AI
SD AC
==
()ABCD
,IBDMNOACBD=Ç =Ç
R IP SB=Ç
MN
ABD
I
1
3
DI
IB
=
SBD
12
.. 1 .2.1
33
BR PS BI BR SR
RS PD ID RS SB
=Þ =Þ =
Trang 21
Nếu K trùng với trọng tâm G thì . Do đó C, D bị loại.
Ta có
Áp dụng định lý bất đẳng thức Cauchy ta có:
Câu 29. Đáp án A.
Ta có :
.
Tương tự ta cũng chứng minh được:
Và
Từ (1,2,3) suy ra
Câu 30. Đáp án A.
K
E
D
F
B
A
C
S
6
AK BK CK
KD KE KF
++=
1
KBC KAC
KAB
ABC ABC ABC
SS
S
DK EK FK
DA EB FC S S S
++= + + =
9
96
DK EK FK DA EB FC
DA EB FC DK EK FK
DA EB FC AK BK CK
DK EK FK KD KE KF
æöæö
++ ++ ³
ç÷ç÷
èøèø
Þ++³Þ++³
M
E
D
F
B
A
C
S
CBM ABM CBM ABM CBM
ABM
AME CME AME CME AME
SSSSS
S
BM BD BF
ME S S S S S CD FA
++
=== = =+
+
( )
11
BF BM BM ME
AF ME ME
-
Þ= -=
( )
12
CM CE CD CE CM CM MF
MF AE BD AE MF MF
-
=+Þ= -=
( )
13
AM AE AF
MD CE BF
==+
1
MF ME
CM M F BM ME
+=
--
Trang 22
Xét trường hợp đặc biệt lần lượt là trung điểm của SA, SB, SC, SD. Khi đó ta dễ
dàng loại được đáp án D.
Dựng
Theo định lý Thales, ta có:
Suy ra:
Như vậy, ý B bị loại.
Tương tự, ta chứng minh được
Từ đây ta thấy ngay ý C bị loại và A là đáp án A là đáp án
lựa chọn.
Chú ý: Cho tam giác ABC. Gọi O là trung điểm AC, M, N
là hai điểm nằm trên cạnh AB, AC. MN cắt BO tại I. Khi đó: .
Câu 31. Đáp án A.
Theo chú ý câu 30 ta có:
.
E
J
I
C
D
S
B
A
F
G
H
,,,EFGH
( ) ( )
// , //AT EG T SI CK EG KESIÎ
,; 1
SA ST SC SK IT IA
SE SJ SG SJ IK IC
====
2
SA SC ST SK SI IT SI IK SI
SE SG SJ SJ SJ
+-++
+= = =
2.
SB SD SI
SF SH SJ
+=
2BA BC BO
BM BN BI
+=
J
I
O
C
D
S
B
A
M
N
K
53 2 1 1
442
22 2 2
BA BC BO BO OI OI
BM BN BI BI BO OD
+=+=Þ =Þ=Þ=Þ=
S
C
K
E
G
T
Trang 23
Áp dụng định lý Menelaus trong tam giác ta có:
Câu 32. Đáp án A.
Dựa vào nhận xét ví dụ 2, ta có:
nên đồng phẳng.
nên không đồng phẳng.
nên không đồng phẳng.
nên không đồng phẳng.
Câu 33. Đáp án D.
Dựa vào nhận xét ví dụ 2, ta có:
nên đồng phẳng.
nên đồng phẳng.
nên đồng phẳng.
nên không đồng phẳng. Do đó 4 điểm này
lập nên 1 tứ diện.
Câu 34. Đáp án B, A.
a)Do tứ diện ABCD có 4 mặt nên thiết diện không thể là ngũ giác hay lục giác. Nó chỉ có thể là
tam giác hoặc tứ giác.
SOD
10
.. 1 10
11
IO PD JS JS SJ
ID PS JO JO SO
=Þ = Þ =
B
A
J
C
F
I
D
E
H
( )
11
.. . 2..5.1
52
AE BF CH DJ
BE CF DH AJ
=- - =
,, ,EFH J
111 1
... 2...
552 25
AE BF CI DJ
BE CF DI AJ
æö
=- =
ç÷
èø
,,,EFI J
( )
11
.. . 2. .5. 1
52
AE BG CH DJ
BE CG DH AJ
æö
=- - - =-
ç÷
èø
,, ,EGH J
1111
... 2. ..
55225
AE BG CI DJ
BE CG DI AJ
æöæö
=- - =
ç÷ç÷
èøèø
,,,EGI J
( )
11
.. . 2..5.1
52
AE BF CH DJ
BE CF DH AJ
=- - =
,, ,EFH J
( )
11
... 2. .5.1
25
AE BG CI DK
CG
BE DI AK
æö
=- - =
ç÷
èø
,G, ,KEI
( )
41 1
.. . . .5.1
52 2
AU BG CH DJ
BU CG DH AJ
æö
=- - =
ç÷
èø
U, G, ,HJ
( )
41 1 4
... ..5.
55 5 25
AU BF CI DK
BU CF DI AK
æö
==
ç÷
èø
U, F, I, K
j
I
B
D
C
A
M
Q
N
P
Trang 24
Trong mp , gọi (P không phải là trung điểm đoạn BC nên MP cắt AC)
Trong mp , gọi
Do nên
Ta có:
Suy ra thiết diện cần tìm là tứ giác
Ta chọn đáp án B.
b)Áp dụng ví dụ 11, do đồng phẳng nên
(Do M, N lần lượt là trung điểm của AB, CD) . Từ đây suy ra
Giả sử . Khi đó ta suy ra
Suy ra
Do J là trung điểm của PQ.
Ta có:
Chứng minh tương tự ta cũng có:
Từ (1,2,3) suy ra . Điều này dẫn đến M, N, J thẳng hàng. Như vậy I trùng J.
Điều này suy ra .
Chọn đáp án A.
Câu 35. Đáp án C.
Trong mp , gọi
Trong mp , gọi
Trong mp , gọi .
( )
ABC
K MP AC=Ç
( )
ACD
QKN AD=Ç
( )
QKN MNPÎÌ
( )
QMNP AD=Ç
( ) ( )
( ) ( )
( ) ( )
( ) ( )
MNP ABD MQ
MNP ABC MP
MNP BCD PN
MNP ACD NQ
Ç=
ì
ï
Ç=
ï
í
Ç=
ï
ï
Ç=
î
,,,MNPQ
.. . 1 . 1
AM BP CN DQ BP DQ
BM CP DN AQ CP AQ
=Þ =
.
BP AQ
CP DQ
=
,BP k PC AQ kQD==
!!!" !!!" !!!" !!!"
( )
( )
1BP AQ k CP QD+=- +
!!!" !!!" !!!" !!!"
( )
22
MJ MB BP PJ
MJ AQ BP
MJ MA AQ QJ
ì
=++
ï
Þ=+
í
=++
ï
î
!!!" !!!" !!!" !! !"
!!!" !!!" !!!"
!!!" !!!" !!!" !! !"
( )
23NJ CP DQ=+
!!!" !!!" !!! "
MJ k NJ=-
!!!" !!!"
2
MNPQ MPN
SS=
H
K
I
O
C
D
S
B
A
F
E
G
J
( )
ABCD
;IFGABKFGAD=Ç =Ç
( )
SAB
H IE SB=Ç
( )
SAD
J EK SD=Ç
Trang 25
Ta có:
Do đó ngũ giác EHFGJ là thiết diện của hình chóp cắt bởi
Câu 36. Đáp án C.
Trong mp , Gọi
Trong mp , Gọi
Trong mp , Gọi
Khi đó ta có:
Do đó ngũ giác EKFHG là thiết diện của hình chóp cắt bởi
Câu 37. Đáp án D.
Trong mặt phẳng gọi là giao điểm của với .
Trong mặt phẳng gọi là giao điểm của với .
Trong mặt phẳng gọi là giao điểm của với .
Trong mặt phẳng , gọi là giao điểm của với .
( ) ( )
( ) ( )
( ) ( )
( ) ( )
( ) ( )
,EFG ABCD FG
EFG SCD GJ
EFG SAD JE
EFG SAB HE
EFG SBC HF
Ç=
Ç=
Ç=
Ç=
Ç=
( )
EFG
J
H
I
S
B
D
A
C
G
E
F
K
( )
SAC
I EF AC=Ç
( )
ABCD
,HIGBCJIGAB=Ç =Ç
( )
SAD
K JE SD=Ç
( ) ( )
( ) ( )
( ) ( )
( ) ( )
( ) ( )
,EFG ABCD GH
EFG SCD KF
EFG SAD EK
EFG SAB GE
EFG SBC HF
Ç=
ì
ï
Ç=
ï
ï
Ç=
í
ï
Ç=
ï
ï
Ç=
î
( )
EFG
C
1
C
2
O
k
I
k
B
1
B
2
B
k
B
n
A
n
A
k
A
2
A
1
S
2
C
12
BB
12
AA
n
C
1 n
BB
1 n
AA
( )
12
...
n
AA A
k
O
( )
3, 4, ..., 1kn=-
1 k
AA
2 n
AA
( )
2 n
SA A
k
I
( )
3, 4, ..., 1kn=-
k
SO
2 n
BB
Trang 26
Trong mặt phẳng , gọi là giao điểm của với .
Do nên là giao điểm của với mặt phẳng
.
Vậy thiết diện của hình chóp cắt bởi là đa giác .
Câu 38. Đáp án C.
Cách 1:
Gọi là trung điểm của , khi đó , , thẳng hàng.
Trong mặt phẳng , gọi là giao điểm của với . Khi đó
.
Trong mặt phẳng , gọi là giao điểm của với . Ta thấy thuộc nên
thuộc . Trong , gọi là giao điểm của với . Trong mặt phẳng ,
gọi là giao điểm của với .
Trong mặt phẳng , gọi là giao điểm của với . Trong mặt phẳng ,
gọi là giao điểm của với .
Ta có: .
Vậy ngũ giác là thiết diện của hình chóp cắt bởi .
Chú ý: Mấu chốt của ví dụ trên là việc dựng được điểm là giao điểm của với
(thông qua việc dựng giao tuyến của mặt phẳng với mặt phẳng ). Có
thể dựng thiết diện trên bằng nhiều cách với việc dựng giao điểm (khác ) của một trong
các đường thẳng ; hoặc với một mặt của hình chóp. Sau đây, tôi xin trình bày cách
hai, điểm mấu chốt là xác định giao điểm của với mặt phẳng .
Cách 2:
k
B
( )
3, 4, ..., 1kn=-
k
SA
1 k
BI
( )
112kk n
BBI BBBÎÌ
k
B
k
SA
( )
3, 4, ..., 1kn=-
( )
12n
BB B
( )
12n
BB B
22
...
nn
CB BC
G
F
H
N
L
M
D
C
B
A
I
K
E
J
S
M
AB
S
F
M
( )
ABCD
I
MG
AD
( ) ( )
SI SM G SAD=Ç
( )
SMG
J
FG
SI
J
FG
J
( )
EFG
( )
SAD
K
JE
SA
( )
SAB
L
KF
AB
( )
ABCD
H
LG
CD
( )
SCD
N
EH
SC
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
( ) ( )
;
;
EFG ABCD LG EFG SBC GN
EFG SCD NE EFG SAD EK
EFG SAB KL
Ç= Ç=
ì
ï
Ç= Ç=
í
ï
Ç=
î
LGNEK
( )
EFG
J
FG
( )
SAD
SI
( )
SFG
( )
SAD
,,EFG
GE
EF
( )
ABCD
Trang 27
Trong mặt phẳng , gọi là giao điểm của với .
Trong mặt phẳng , gọi là giao điểm của với , .
Trong mặt phẳng , gọi là giao điểm của với .
Trong mặt phẳng , gọi là giao điểm của với .
Ta có: .
Vậy ngũ giác là thiết diện của hình chóp cắt bởi .
Câu 39. Đáp án B.
Trong mặt phẳng , gọi là giao điểm của và . Trong mặt phẳng , gọi
là giao điểm của và .
Xét các trường hợp sau:
Trường hợp 1:
Trong mặt phẳng , cắt tại và cắt đoạn tại .
Ta có nên là giao điểm của với ,
nên là giao điểm của với .
G
F
H
N
L
M
D
C
B
A
P
K
E
S
P
EF
MD
( )
ABCD
,HL
,PG
CD
AB
( )
SAB
K
LF
SA
( )
SCD
N
EH
SC
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
( ) ( )
;
;
EFG ABCD LG EFG SBC GN
EFG SCD NE EFG SAD EK
EFG SAB KL
Ç= Ç=
ì
ï
Ç= Ç=
í
ï
Ç=
î
LGNEK
( )
EFG
( )
ABCD
H
AB
CD
( )
SAB
I
FG
SH
J
G
C
A
D
H
S
B
F
I
K
E
( )
SCD
IE
SC
J
CD
K
( )
ÎÌJIE EFG
J
( )
EFG
SC
( )
ÎÌKIE EFG
K
( )
EFG
CD
Trang 28
Ta có
Suy ra tứ giác là thiết diện của hình chóp cắt bởi .
Trường hợp 2:
Trong mặt phẳng , cắt tại và cắt đoạn tại (cắt tại một điểm nằm
ngoài đoạn ).
Trong mặt phẳng :
Nếu song song với thì ta có: . Gọi là giao điểm của với .
Áp dụng định lí Menelaus vào các tam giác và ta có
. Điều này chỉ xảy ra khi thuộc đoạn (vô
lí)
Do vây cắt , giả sử tại .
Trong mặt phẳng , gọi là giao điểm của với .
Ta có
Suy ra ngũ giác là thiết diện của hình chóp cắt bởi .
Vậy thiết diện của hình chóp cắt bởi mặt phẳng hoặc là tứ giác hoặc là ngũ
giác.
Câu 40. Đáp án B.
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
;
;
Ç= Ç=
ì
ï
í
Ç= Ç=
ï
î
EFG ABCD FK EFG SAB FG
EFG SBC GJ EFG SCD JK
KFGJ
( )
EFG
M
L
J
G
C
A
D
H
S
B
F
I
K
E
( )
SCD
IE
SC
J
SD
K
CD
CD
( )
SBC
GJ
BC
SS
BG CJ
GJ
=
T
IE
CD
SBH
SCH
SS
.. 1 ..
FB IH G TC IH J FB TC
FH IS GB TH IS JC FH TH
== Þ =
T
CD
GJ
BC
L
( )
ABCD
M
LF
AD
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
( ) ( )
;
;
Ç= Ç=
ì
ï
Ç= Ç=
í
ï
Ç=
î
EFG ABCD FM EFG SAB FG
EFG SBC GJ EFG SCD JK
EFG SAD KM
KJGFM
( )
EFG
.S ABCD
( )
EFG
Trang 29
Trong mặt phẳng , gọi là giao điểm của với . Trong mặt phẳng , gọi
là giao điểm của với . Trong mặt phẳng , gọi là giao điểm của với
. Trong mặt phẳng , gọi là giáo điểm của với .
Trong mặt phẳng , có hai khả năng xảy ra như sau:
Trường hợp 1: cắt đoạn tại .
Trong mặt phẳng , gọi là giao điểm của với . Trong mặt phẳng ,
gọi là giao điểm của với .
Ta có
Trường hợp này , ngũ giác là thiết diện của hình chóp cắt bởi .
Trường hợp 2: cắt tại ( không cắt đoạn ).
( )
SBC
J
EF
BC
( )
SAD
I
SG
AD
( )
ABCD
N
IJ
CD
( )
SIJ
K
JG
SN
( )
SCD
FK
CD
P
G
R
J
I
Q
P
K
N
F
E
D
C
B
A
S
( )
ABCD
Q
JP
AD
( )
SAD
R
QG
SA
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
( ) ( )
;
;
Ç= Ç=
ì
ï
Ç= Ç=
í
ï
Ç=
î
EFG ABCD PQ EFG SAD QR
EFG SAB RE EFG SBC EF
EFG SCD FP
REFPQ
.S ABCD
( )
EFG
FK
SD
H
FK
CD
Trang 30
Trong mặt phẳng , gọi là giao điểm của với ( không thể cắt đoạn
vì giả sử ngược lại cắt cạnh tại , khi đó sẽ cắt cạnh (vô lí vì đã
cắt cạnh )).
Khi đó
Trường hợp này, tứ giác là thiết diện của hình chóp cắt bởi .
Câu 41. Đáp án A.
Trong mặt phẳng , gọi là giao điểm của với .
Trong mặt phẳng , gọi là giao điểm của và . Suy ra là giao điểm của
với . Khi đó, tứ giác là thiết diện của tứ diện cắt bởi mặt phẳng .
Trong tam giác ta có là trọng tâm của tam giác suy ra là trung điểm của .
Trong tam giác có là trọng tâm của tam giác nên .
Ta có .
Suy ra là hình thang với đáy lớn .
Ta có: Áp dụng định lí cosin trong tam giác ta có:
.
Tương tự ta cũng tính được .
Dễ thấy là hình thang cân. Do đó:
.
Câu 42. Đáp án C.
G
M
J
I
H
P
K
N
F
E
D
C
B
A
S
( )
SAD
M
HG
SA
HG
AD
HG
AD
O
JO
CD
( )
EFG
,SC SD
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
;
;
Ç= Ç=
ì
ï
í
Ç= Ç=
ï
î
EFG SCD FH EFG SAD MH
EFG SAB ME EFG SBC EF
MEFH
( )
EFG
( )
BCD
I
NP
CD
( )
ACD
Q
AD
MI
Q
AD
( )
MNP
MNPQ
( )
MNP
BCI
P
D
CI
ACI
Q
2
//
3
IP IQ
PQ MN
IN IM
==Þ
MNPQ
MN
4, 3 , 2.AQ a AM a MN PQ a=== =
MAQ
222 02222
2..cos6016 912 13 13MQ AM AQ AM AQ a a a a MQ a=+- =+-=Þ=
13NP a=
MNPQ
( )
2
2
2
2
551
24
MN PQ
MN PQ MQ
a
S
-
æö
+-
ç÷
èø
==
Trang 31
Trong mặt phẳng , gọi là giao điểm
của với .
Trong mặt phẳng , gọi là giao điểm
của và .
Ta có: .
Do đó tam giác là thiết diện của tứ diện
cắt bởi .
Dễ thấy lần lượt là trọng tâm của các tam
giác và .
Ta có: .
Xét hai tam giác và có chung, nên hai
tam giác này bằng nhau. Suy ra . Vậy tam giác cân tại .
Áp dụng định lí cosin trong tam giác :
.
Gọi là trung điểm của đoạn . Ta có .
Suy ra: .
Diện tích thiết diện là: .
Câu 43. Đáp án C.
Trong mặt phẳng , gọi là giao điểm của với và là trung điểm của
.Dễ thấy chính là giao điểm của với .
Ta có: Áp dụng Thales ta có: .
Suy ra là trung điểm .
là đường trung bình của tam giác ta có: .
là đường trung bình của tam giác ta có: .
Từ đó suy ra: .
Câu 44. Đáp án B.
Trong mặt phẳng , gọi là giao điểm của với .
Dễ thấy chính là giao điểm của với .
Do là đường trung bình của tam giác nên là trung điểm . Suy ra và
là đường trung bình của tam giác . Do đó: .
Áp dụng định lí Thales ta có: .
Câu 45. Đáp án D.
( )
ABC
H
ME
AC
( )
ABD
K
MF
AD
( ) ( )
( ) ( )
( ) ( )
MEF ABC MH
MEF ABD MK
MEF ACD HK
Ç=
ì
ï
Ç=
í
ï
Ç=
î
MHK
( )
MEF
,HK
ABE
ABF
2
3
a
AH AK HK===
AMH
AMK
AM
∑
∑
0
2
60 ,
3
a
MAH MAK AH AK== ==
MH MK=
MHK
M
AMH
22
22
222 0
2 13 13
2 .cos 60
2 3 3 36 6
aaaa a
MH AM AH AMAH MH
æö æ ö
=+- =+ -=Þ=
ç÷ ç ÷
èø è ø
I
HK
MI HK^
22 2
222
13
36 9 4 2
aa a a
MI MH HI MI=-=-=Þ=
MHK
2
112
...
22326
aa a
SMIHK===
( )
ABCD
E
MN
DC
F
CD
Q
PE
SD
.ME BC=
11
22
ND ED
EF EF
MF EF
==Þ=
D
EF
PQ
EPF
1
2
DQ
PF
=
PF
CSD
3
4
4
SD SQ
DQ SD
=Þ =
( )
ABCD
I
MN
AO
H
PO
SC
MN
ABD
I
AO
1
4
AI
AC
=
PI
OSA
//IH SA
1
4
SH AI
SD AC
==
K
H
D
C
B
F
E
A
M
Trang 32
Trong mặt phẳng , gọi .
Dễ thấy chính là giao điểm của với .
Do là đường trung bình của tam giác nên là trung điểm . Suy ra .
Áp dụng định lí Menelaus vào tam giác ta có:
( )
ABCD
,IBDMNOACBD=Ç =Ç
R
IP
SB
MN
ABD
I
DO
1
3
DI
IB
=
SBD
132
.. 1 .2.1
325
BR PS BI BR BR SR
RS PD ID RS RS SB
=Þ =Þ = Þ =
Trang 33
ĐƯỜNG THẲNG SONG SONG VỚI ĐƯỜNG THẲNG
A. LÝ THUYẾT
1. Định nghĩa
Trong phần vị trí tương đối của hai đường thẳng trong không gian, ta biết rằng hai đường thẳng phân biệt
bất kì hoặc chéo nhau hoặc song song hoặc cắt nhau. Nếu hai đường thẳng phân biệt đồng phẳng và
không cắt nhau thì ta nói hai đường thẳng đó song song với nhau.
Định nghĩa:
Hai đường thẳng phân biệt trong không gian được gọi là song song với nhau, kí hiệu nếu
chúng đồng phẳng và không cắt nhau.
2. Tính chất
Định lí 1: Trong không gian cho đường thẳng và điểm nằm ngoài . Lúc đó tồn tại duy nhất một
đường thẳng và và song song với đường thẳng d.
Chú ý:
Định lí này cho ta thêm một cách xác định đường thẳng trong không gian: đó là đường thẳng đi qua một
điểm và song song với một đường thẳng cho trước không chứa điểm đó. Kết hợp với định lí 2 dưới đây
cho ta một cách để xác định giao tuyến của hai mặt phẳng.
Định lí 2 ( Về giao tuyến của ba mặt phẳng):
Nếu ba mặt phẳng phân biệt đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng
quy hoặc đôi một song song với nhau.
Hệ quả:
Nếu hai mặt phẳng phân biệt chứa hai đường thẳng song song thì giao tuyến của chúng ( nếu có) cũng
song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
Đến đây ta có thể bổ sung một phương pháp tìm giao tuyến của hai mặt phẳng:
Bước 1: Chỉ ra hai mặt phẳng lần lượt chứa hai đường thẳng song song .
Bước 2: Tìm một điểm chung của hai mặt phẳng
Bước 3: Khi đó
Định lí 3:
Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.
Như vậy, cho hai đường thẳng phân biệt thỏa mãn
3. Góc giữa hai đường thẳng trong không gian
a) Định nghĩa
Góc giữa hai đường thẳng và trong không là góc giữa hai đường thẳng và cùng đi
qua một điểm và lần lượt song song với và .
b. Phương pháp tính góc giữa hai đường thẳng trong không gian
Bước 1: Dựng góc
- Tìm trên hình vẽ xem góc giữa hai đường thẳng có sẵn không?
- Nếu không có sẵn thì ta tiến hành:
+ Chọn một điểm O bất kì trong không gian.
+ Qua O dựng đường thẳng . Góc nhọn hay góc vuông tọc bởi chính là góc giữa và
.
Lưu ý:
+ Ta thường lấy điểm O thuộc một trong hai đường thẳng và .
,ab
//ab
A
d
A
d
a
A
b
c
a
γ
β
α
b
c
a
γ
β
α
A
( ) ( )
,
ab
,ab
M
( ) ( )
// //Mx a b
ab
Ç=
//
//
//
ab
ab
bc
ì
Þ
í
î
a
b
'a
'b
a
b
,aabb
¢¢
!!
,ab
¢¢
a
b
a
b
Trang 34
+ Chọn O sao cho góc giữa là góc của một tam giác mà độ dài các cạnh của nó đã biết hoặc có thể
tính dễ dàng
Bước 2: Tính góc
Dùng hệ thức lượng trong tam giác, tỉ số lượng giác hay định lí cosin, sin. Trường hợp góc giữa hai
đường thẳng và bằng ta nói .
B. DẠNG TOÁN VỀ ĐƯỜNG THẲNG SONG SONG VỚI ĐƯỜNG THẲNG
DẠNG 1. CHỨNG MINH HAI ĐƯỜNG THẢNG SONG SONG TRONG KHÔNG GIAN
Phương pháp chung: Để chứng minh hai đường thẳng song song trong không gian ta sẽ sử dụng một
trong các sách sau:
+ Cách 1: Chứng minh hai đường thẳng đồng phẳng, sau đó áp dụng các phương pháp chứng minh song
song trong hình học phẳng như tính chất đường trung bình, định lí Thales đảo, tính chất song song của
hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ 3…
+ Cách 2: Sử dụng tính chất bắc cầu: Chứng minh hai đường thẳng phân biệt cùng song song với đường
thẳng thứ ba.
+ Cách 3: Áp dụng định lí về giao tuyến của ba mặt phẳng.
Ví dụ 1. Cho tứ diện . Gọi lần lượt là trọng tâm của các tam giác . Đường thẳng
song song với đường thẳng:
A. trong đó là trung điểm . B. .
C. . D. .
Lời giải:
Đáp án D.
Cách 1: ( Đưa về cùng mặt phẳng và vận dụng kiến thức hình học phẳng)
Gọi là trung điểm của . Ta có nên suy ra và đồng phẳng.
Do lần lượt là trọng tâm của các tam giác nên ta có: . Suy ra
.
Cách 2: ( Sử dụng tính chất bắc cầu)
Gọi lần lượt là trung điểm của và . Suy ra (1).
Do lần lượt là trọng tâm của các tam giác nên ta có: . Suy ra
(2).
Từ (1) và (2) suy ra .
Cách 3: (Sử dụng định lí giao tuyến của 3 mặt phẳng).
Có lẽ trong ví dụ này cách này hơi dài, song chúng tôi vẫn sẽ trình bày ở đây, để các bạn có thể
hiểu và vận dụng cách 3 hợp lí trong các ví dụ khác.
Dễ thấy, bốn điểm , , , đồng phẳng.
Ta có: .
Ví dụ 2. Cho hình bình hành . Gọi , , là các đường thẳng song song với nhau lần lượt
đi qua , , và nằm về một phía của mặt phẳng , đồng thời không nằm trong mặt
phẳng . Một mặt phẳng đi qua và cắt , , lần lượt tại , , với
, . Khi đó bằng:
A. . B. . C. . D. .
Lời giải:
Đáp án D.
,ab
¢¢
a
b
0
90
ab^
ABCD
,IJ
,ABC ABD
IJ
CM
M
BD
AC
DB
CD
E
AB
ICE
JDE
Î
ì
í
Î
î
IJ
CD
,IJ
,ABC ABD
1
3
EI EJ
EC ED
==
,MN
BD
BC
MN CD!
,IJ
,ABC ABD
2
3
AI AJ
AN AM
==
IJ MN!
D
C
I
J
( ) ( )
( ) ( )
( ) ( )
DCIJ AMN IJ
DCIJ BCD CD
IJ CD MN
AMN BCD MN
MN CD
Ç=
ì
ï
Ç=
ï
Þ
í
Ç=
ï
ï
î
!!
!
ABCD
Bx
Cy
Dz
B
C
D
( )
ABCD
( )
ABCD
A
Bx
Cy
Dz
B
¢
C
¢
D
¢
2BB
¢
=
4DD
¢
=
CC
¢
3
4
5
6
Trang 35
Gọi là tâm của hình bình hành . là
trung điểm của .
Do , song song với nhau nên là
hình thang và là đường trung bình của hình
thang đó. Suy ra .
Mặt khác song song với (vì cùng song
song với ) nên có bốn điểm , , ,
đồng phẳng.
Giao tuyến của hai mặt phẳng với
là . Lại có thuộc ,
thuộc . Do đó , , thẳng hàng. Từ đây dễ dàng suy ra, là trung điểm đoạn
. Do vậy, .
Nhận xét: Ta có bài toán tổng quát cho bài toán này như sau:
Cho hình bình hành . Gọi , , , là các đường thẳng song song với nhau lần
lượt đi qua , , , đồng thời không nằm trong mặt phẳng . Một mặt phẳng cắt
, , , lần lượt tại , , , . Khi đó là hình bình hành và
.
Do đó khi biết 3 trong 4 đối tượng , , , ta sẽ dễ dàng tính được đối tượng
còn lại.
Ví dụ 3. Cho hình bình hành tâm . Gọi , , , là các đường thẳng song song với
nhau lần lượt đi qua , , , và nằm về một phía của mặt phẳng , đồng thời
không nằm trong mặt phẳng . Một mặt phẳng di động cắt , , , lần
lượt tại , , , sao cho ( có độ dài cho trước). Mặt
phẳng luôn đi qua điểm cố định . Mệnh đề nào sau đây đúng?
A. nằm trên đường thẳng song song với và .
B. nằm trên đường thẳng song song với và .
C. nằm trên đường thẳng song song với và .
D. nằm trên đường thẳng song song với và .
Lời giải:
Đáp án B.
Theo ví dụ 2, ta có : nên .
Bài tập tương tự: Cho tam giác . Ở về một phía của , người ta kẻ các đường
thẳng song song lần lượt lấy trên các điểm .
a) và lần lượt là trung điểm . Chứng minh rằng song song với .
b) và lần lượt là trọng tâm của tam giác và . Chứng minh rằng
song song với .
Ví dụ 4. Cho hình chóp có đáy là hình bình hành. Các điểm thứ tự thuộc các
đoạn và sao cho . Gọi I là giao điểm của và
a) Chứng minh rằng .
b) Qua M kẻ ( P là điểm trên ). Chứng minh rằng .
Lời giải:
O
ABCD
I
BD
¢¢
Bx
Dz
BDD B
¢¢
OI
3
2
BB DD
IO
¢¢
+
==
OI
CC
¢
DD
¢
C
C
¢
O
I
( )
AB D
¢¢
AC
¢
I
( )
AB D
¢¢
I
A
I
C
¢
I
AC
¢
26CC OI
¢
==
ABCD
At
Bx
Cy
Dz
A
B
C
D
( )
ABCD
At
Bx
Cy
Dz
A
¢
B
¢
C
¢
D
¢
ABCD
¢¢¢¢
AA CC BB DD
¢¢¢ ¢
+=+
AA
¢
BB
¢
CC
¢
DD
¢
ABCD
O
At
Bx
Cy
Dz
A
B
C
D
( )
ABCD
( )
ABCD
( )
a
At
Bx
Cy
Dz
A
¢
B
¢
C
¢
D
¢
AA CC BB DD a
¢¢¢ ¢
+++ =
O
( )
a
I
I
O
At
2
a
OI =
I
O
At
4
a
OI =
I
O
At
3
2
a
OI =
I
O
At
OI a=
''2 '''' 'AA CC OI BB AA CC BB DD a+==++++ =
4
a
OI =
ABC
( )
ABC
,,.Ax By Cz
,,Ax By C z
', ', 'ABC
M
'M
,''AB A B
'MM
'CC
G
'G
ABC
'''ABC
'GG
'CC
.S ABCD
ABCD
,MN
BC
SD
1
2
MB NS
MC ND
==
MD
.AB
//MN SI
//MN CD
BD
//MP SB
Trang 36
S
B
C
D
A
N
M
F
E
a) Ta có
Trong tam giác có
b) Ta có
Trong tam giác có
DẠNG 2. TÌM GIAO TUYẾN CỦA HAI MẶT PHẲNG (cách 2). THIẾT DIỆN QUA MỘT ĐƯỜNG
THẲNG VÀ SONG SONG VỚI MỘT ĐƯỜNG THẲNG CHO TRƯỚC.
•
Tìm giao tuyến của hai mặt phẳng (cách 2)
Để tìm giao tuyến của hai mặt phẳng chứa hai đường thẳng a và b song song, ta tìm:
+ Một điểm chung của hai mặt phẳng đó.
+ Giao tuyến của hai mặt phẳng là đường thẳng qua điểm chung và song song với a và b ( hoặc
trùng với một trong hai đường thẳng đó).
Ví dụ 1. Cho hình chóp có đáy là hình chữ nhật. .
Gọi lần lượt là trung điểm của và . là điểm tùy ý trên cạnh ( không trùng với
)
a) Xác định giao tuyến của các mặt phẳng và ; và .
b) Xác định giao tuyến của các mặt phẳng và . Từ đó suy ra giao điểm N
của và . Chứng minh rằng là hình thang cân.
Lời giải:
a) Ta có
Tương tự
b) Do lần lượt là trung điểm của nên là đường trung bình của tam giác
. Do đó (1)
Ta có (2)
Gọi là giao điểm của với . Ta có:
.
Từ (1) và (2) suy ra . Suy ra là hình thang.
1
//
2
IM MB
BI CD
MD MC
Þ==
SDI
1
// .
2
SN IM
MN SI
ND MD
æö
==Þ
ç÷
èø
1
//
2
BP MB
MP AB
PD MC
Þ= =
SBD
1
// .
2
BP SN
NP SB
PD ND
==Þ
.S ABCD
ABCD
,3SA SB a SC SD a== = =
,EF
SA
SB
M
BC
,BC
( )
SAB
( )
SCD
( )
SAD
( )
SBC
( )
MEF
( )
ABCD
AD
( )
MEF
MNEF
S
B
C
D
A
N
M
F
E
( ) ( )
( ) ( )
( ) ( )
// // .
// , ,
S SAB SCD
SAB SCD Sx AB CD
AB CD AB SAB CD SCD
ÎÇ
ì
ï
ÞÇ =
í
ÌÌ
ï
î
( ) ( )
( ) ( )
( ) ( )
// // .
// , ,
S SAB SBC
SAD SBC Sy AD BC
AD BC AD SAD BC SBC
ÎÇ
ì
ï
ÞÇ=
í
ÌÌ
ï
î
,EF
,SA SB
EF
SAB
1
// , /
2
EF AB EF AB=
( ) ( )
( ) ( )
( ) ( )
// , ,
// //
EF AB EF MEF AB ABCD
MEF ABCD Mt AB CD
M MEF ABCD
ÌÌ
ì
ï
ÞÇ =
í
ÎÇ
ï
î
N
Mt
AD
( ) ( )
{ } ( )
,,NMtMt MEFAB ABCD
NADMEF
MAD
ÎÌ Ì
ì
ï
Þ=Ç
í
Î
ï
î
1
// ,
2
EF MN EF AB MN=<
MNEF
Trang 37
Dễ thấy vậy
là hình thang cân.
Thiết diện qua một đường thẳng và song song với một đường thẳng cho trước
Được xác dịnh bằng cách phối hợp hai cách xác định giao tuyến đã biết:
Cách 1: Tìm hai điểm chung của hai mặt phẳng.
Cách 2: Tìm một điểm chung và phương ( song song với một đường thẳng cho trước) của giao
tuyến.
Ví dụ 2. Cho tứ diện . Gọi lần lượt là trung điểm của và , Gọi E là điểm trên cạnh
với . Thiết diện tạo bởi mặt phẳng và tứ diện là:
A. Tam giác .
B. Tứ giác với là điểm bất kì trên cạnh .
C. Hình bình hành với là điểm bất kì trên cạnh mà .
D. Hình thang với là điểm bất kì trên cạnh và .
Lời giải:
Trong mặt phẳng , Gọi là giao điểm của đường thẳng qua , song song với
.
Ta có
Vậy tứ giác là thiết diện của hình chóp cắt bởi .
Lại có
Suy ra tứ giác là hình thang .
Ví dụ 3. Cho hình chóp , đáy là hình bình hành. Gọi M là trung điểm của SA. Thiết
diện của mặt phẳng với hình chóp là hình gì?
A. Tam giác. B. Hình bình hành.
C. Hình thang. D. Hình thoi.
Lời giải:
Đáp án C.
Gọi là trung điểm của . Do , .
Như vậy suy ra thuộc mặt phẳng .
Ta có:
Vậy tứ giác là thiết diện của hình chóp bị cắt bởi mặt phẳng .
Kết hợp với , suy ra là hình thang.
DẠNG 3: GÓC GIỮA HAI ĐƯỜNG THẲNG
Ví dụ 1. Cho tứ diện có , , . Xét các khẳng định sau:
a. Cosin của góc giữa hai đường thẳng và bằng .
b. Cosin của góc giữa hai đường thẳng và bằng .
∑
∑
( )
(..) . .SAD SBC c c c SAD SBC EAN FBM c g c FM END=D Þ = ÞD =D Þ=
MNEF
ABCD
,MN
AB
AC
CD
3ED EC=
( )
MNE
ABCD
MNE
MNEF
F
BD
MNEF
F
BD
//EF BC
MNEF
F
BD
//EF BC
( )
BCD
F
E
BC
BD
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
;
;
MNE ABC MN MNE BCD EF
MNE ABD MF MNE ACD NE
Ç= Ç=
ì
ï
í
Ç= Ç=
ï
î
MNEF
( )
MNE
( ) ( )
( ) ( )
( ) ( )
// .
//
MNE ABC MN
MNE BCD EF
EF MN
MCD ABC BC
BC MN
Ç=
ì
ï
Ç=
ï
Þ
í
Ç=
ï
ï
î
MNEF
( )
EF MN>
.S ABCD
ABCD
.S ABCD
N
SB
//MN AB
//AB CD
//MN CDÞ
N
( ) ( )
( ) ( )
( ) ( )
( ) ( )
MCD SAD MD
MCD SAB MN
MCD SBC NC
MCD ABCD CD
Ç=
ì
ï
Ç=
ï
í
Ç=
ï
ï
Ç=
î
MNCD
//MN CD
MNCD
ABCD
AB CD a==
AC BD b==
AD BC c==
AB
CD
AC
BD
22
2
ac
b
-
Trang 38
B
D
C
A
F
G
E
c. Cosin của góc giữa hai đường thẳng và bằng .
Trong các khẳng định trên có bao nhiêu khẳng định đúng?
A. . B. . C. . D. .
Lời giải:
Đáp án C.
Gọi , , lần lượt là trung điểm của , , .
Ta có: , , suy ra góc giữa hai đường thẳng và .
Ta có: .
Do nên .
Suy ra cân tại . Vậy
.
Xét tam giác có:
.
Vì .
Vậy cosin của góc giữa hai đường thẳng và bằng .
Tương tự ta cũng suy ra cosin của góc giữa và bằng .
Nhận xét: Từ ví dụ này, ta còn suy ra được một trong ba giá trị ;
; bằng tổng hai giá trị còn lại. Cũng từ ví dụ này ta còn suy ra
được với tứ diện đều thì góc giữa các cặp cạnh đối diện luôn bằng
C. BÀI TẬP RÈN LUYỆN KỸ NĂNG
Câu 1. Cho hai đường thẳng và chéo nhau. Mệnh đề nào sau đây đúng?
A. Tồn tại hai đường thẳng , song song với nhau, mỗi đường đều cắt cả và .
B. Không thể tồn tại hai đường thẳng , phân biệt mỗi đường đều cắt cả và .
C. Không thể tồn tại một đường thẳng cắt cả và .
D. Cả ba câu trên đều sai.
Câu 2. Nếu ba mặt phẳng phân biệt đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy
A. Đôi một cắt nhau. B. Đồng quy.
C. Hoặc đồng quy hoặc đôi một song song. D. Đôi một song song.
Câu 3. Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng
(nếu có) sẽ:
A. Song song với hai đường thẳng đó.
B. Song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
C. Trùng với một trong hai đường thẳng đó.
D. Cắt một trong hai đường thẳng đó.
Câu 4. Cho hai đường thẳng và chéo nhau. Xét hai đường thẳng , mà mỗi đường thẳng đều
cắt cả và , cắt tại , cắt tại ( không trùng với ). Khi đó hai đường
thẳng và :
A. Cắt nhau. B. Trùng nhau.
AD
BC
22
2
ba
c
-
0
1
2
3
E
F
G
AC
BC
AD
//EF AB
//EG CD
AB
CD
22 2222
2
2424
AB AC BC a b c
AF
++
=-=-
( )
..ABC DBC c c cD=D
AF DF=
AFDD
F
222
22
2
abc
FG AD FG FA AG
+-
^Þ= - =
EFG
∑
22222
2
cos
2.
EF EG FG c b
FEG
EF EG a
+- -
==
∑
( )
∑
( )
∑
22
2
0,90cos,cos
oo
bc
EF EG EF EG FEG
a
-
££Þ ==
AB
CD
AC
BD
22
2
ac
b
-
( )
2
cos ,aABCD
( )
2
cos ,bACBD
( )
2
cos ,cADBC
ABCD
90
o
a
b
c
d
a
b
c
d
a
b
a
b
a
b
p
q
a
b
p
a
M
q
a
N
M
N
p
q
Trang 39
C. Song song với nhau. D. Hoặc chéo nhau hoặc cắt nhau.
Câu 5. Hai đường thẳng cùng song song với đường thẳng thứ ba thì hai đường thẳng đó:
A. Song song. B. Trùng nhau.
C. Chéo nhau. D. Hoặc song song hoặc trùng nhau.
Câu 6. Giả sử , , là ba mặt phẳng cắt nhau theo ba giao tuyến phân biệt , , . Trong
đó: , , .
Trong các mệnh đề sau, mệnh đề nào sai?
A. và cắt nhau hoặc song song với nhau.
B. Ba giao tuyến , , đồng quy hoặc đôi một cắt nhau.
C. Nếu và song song với nhau thì và không thể cắt nhau, cũng vậy, và không
thể cắt nhau.
D. Ba giao tuyến , , đồng quy hoặc đôi một song song.
Câu 7. Cho hình chóp có đáy là hình bình hành. Khi đó giao tuyến của hai mặt phẳng
và là đường thẳng :
A. Đi qua . B. Đi qua điểm và song song với .
C. Đi qua điểm và song song với . D. Đi qua điểm và song song với .
Câu 8. Giả sử có ba đường thẳng , , trong đó và . Hãy chọn câu đúng:
A. Nếu mặt phẳng không trùng với mặt phẳng thì và chéo nhau.
B. Nếu mặt phẳng trùng với mặt phẳng thì ba đường thẳng , , song song
với nhau từng đôi một.
C. Dù cho hai mặt phẳng và có trùng nhau hay không, ta vẫn có .
D. Cả ba câu trên đều sai.
Câu 9. Cho hai đường thẳng , . Hai đường thẳng này sẽ nằm ở một trong các trường hợp:
(1) Hai đường thẳng phân biệt trong không gian.
(2) Hai đường thẳng phân biệt trong mặt phẳng.
(3) là giao tuyến của và , là giao tuyến của và , trong đó , ,
là ba mặt phẳng khác nhau từng đôi một.
Tương ứng với mỗi trường hợp trên, số các khả năng có thể xảy ra giữa và lần lượt là:
A. 3, 2, 2. B. 3, 2, 3. C. 2, 3, 2. D. 3, 2, 1.
Câu 10. Xét hình bên dưới:
Các cạnh của hình hộp nằm trên các đường thẳng , , như hình vẽ:
(1) Đường thẳng và đường thẳng cùng nằm trên một mặt phẳng.
(2) Có một mặt phẳng qua hai đường thẳng và .
(3) Có một mặt phẳng qua hai đường thẳng và .
Trong ba câu trên:
A. Chỉ có (1) và (2) đúng. B. Chỉ có (1) và (3) đúng.
C. Chỉ có (2) và (3) đúng. D. Cả ba câu trên đều đúng.
Câu 11. Cho hình chóp có đáy là hình thang đáy lớn là . Gọi M là trung điểm của
, là giao điểm của cạnh và mặt phẳng . Mệnh đề nào sau đây đúng?
A. và cắt nhau. B. và chéo nhau.
C. và cắt nhau. D. và song song với nhau.
Câu 12. Cho tứ diện . Gọi lần lượt là trung điểm của các cạnh .
Mệnh đề nào sau đây sai?
( )
P
( )
Q
( )
R
a
b
c
( ) ( )
aP R=Ç
( ) ( )
bQ R=Ç
( ) ( )
cP Q=Ç
a
b
a
b
c
a
b
a
c
b
c
a
b
c
SABCD
( )
SBC
( )
SAD
d
S
S
AB
S
AD
S
AC
a
b
c
//ba
c/ /a
( )
,ab
( )
,ca
b
c
( )
,ab
( )
,ca
a
b
c
( )
,ab
( )
,ca
b/ / c
a
b
a
( )
P
( )
R
b
( )
Q
( )
R
( )
P
( )
Q
( )
R
a
b
a
c
b
a
b
c
a
b
a
c
b
c
.S ABCD
ABCD
CD
SA
N
SB
MN
SD
MN
CD
MN
SC
MN
CD
ABCD
,,,MNPQ
,,,AB AD CD BC
Trang 40
A. chéo nhau. B. và .
C. là hình bình hành. D. và .
Câu 13. Cho hình chóp với đáy là hình bình hành. Gọi lần lượt là trung
điểm của các cạnh . Đường thẳng nào sau đây không song song với đường
thẳng ?
A. . B. . C. . D. .
Câu 14. Cho hình chóp với đáy là hình bình hành. Gọi lần lượt là
trung điểm của các cạnh . Các điểm nào sau đây không đồng phẳng?
A. . B. . C. . D. .
Câu 15. Cho hình chóp với đáy là hình thang với đáy và
. Gọi lần lượt là trọng tâm các tam giác và . Mặt phẳng
cắt lần lượt tại . Mặt phẳng cắt lần lượt tại . Gọi
là giao điểm của và , là giao điểm của và . Trong các mệnh đề dưới đây,
có bao nhiêu mệnh đề sai?
1) và song song với nhau.
2) và song song với nhau.
3) .
4)
A. . B. . C. . D. .
Câu 16. Cho tứ diện . Gọi lần lượt là trung điểm của . là điểm trên đoạn
sao cho , là giao điểm của và . Giao tuyến của hai mặt phẳng
và song song với đường thẳng?
A. . B. . C. . D. .
Câu 17. Cho tứ diện . Gọi lần lượt là trung điểm của . Giao tuyến của hai mặt
phẳng và là:
A. Đường thẳng đi qua và . B. Đường thẳng đi qua và .
C. Đường thẳng đi qua và . D. Đường thẳng .
Câu 18. Cho hình chóp , là một điểm nằm trong tam giác . Các đường thẳng qua
song song với cắt các mặt phẳng lần lượt tại .
a) có giá trị không đổi bằng bao nhiêu khi di động trong tam giác
?
A. . B. . C. . D. .
b) nhận giá trị lớn nhất. Khi đó vị trí của trong tam giác là:
A. Trực tâm . B. Trọng tâm .
C. Tâm ngoại tiếp . D. Tâm nội tiếp .
Câu 19. Cho hình chóp với đáy là hình bình hành tâm . Mặt phẳng di động đi
qua và cắt lần lượt tại .
a) Tứ giác là hình gì?
A. Hình bình hành. B. Hình thang.
C. Hình thoi. D. Tứ giác lồi có các cặp cạnh đối cắt nhau.
b) Giao điểm của hai đường thẳng và luôn chạy trên đường thẳng cố định:
,MP NQ
MN PQ∥
MN PQ=
MNPQ
MN BD∥
1
2
MN BD=
.S ABCD
ABCD
,,,MNPQ
,,,SA SB SC SD
MN
AB
CD
PQ
SC
.A BCD
ABCD
,,,,,MNPQRS
,,,,,AC BD AB CD AD BC
,,,MPRQ
,,,MRSN
,,,PQRS
,,,MPQN
.S ABCD
ABCD
AD
BC
( )
AD a BC b=> =
,IJ
SAD
SBC
( )
ADJ
,SB SC
,MN
( )
BCI
,SA SD
,PQ
E
AM
PB
F
CQ
DN
MN
PQ
MN
EF
( )
2
5
EF a b=+
( )
1
4
EF a b=+
4
1
2
3
ABCD
,IJ
,AC BC
K
BD
2KB KD=
F
AD
( )
IJK
( )
SAD
( )
IJK
AJ
BI
IJ
CI
ABCD
,IJ
( )
AIJ
( )
ACD
d
A
d BC∥
d
A
d BD∥
d
A
dCD∥
AB
.S ABC
M
ABC
M
,,SA SB SC
( ) ( ) ( )
,,SBC SAC SAB
,,ABC
¢¢¢
MA MB MC
SA SB SC
¢¢ ¢
++
M
ABC
1
3
1
2
1
2
3
..
MA MB MC
SA SB SC
¢¢ ¢
M
ABC
ABCD
ABCD
ABCD
ABCD
.S ABCD
ABCD
O
( )
a
AB
,SC SD
,MN
ABMN
AM
BN
Trang 41
A. . B. Đường thẳng đi qua .
C. Đường thẳng đi qua , song song với . D. Đường thẳng đi qua , song song với .
c) Giao điểm của hai đường thẳng và luôn chạy trên đường thẳng cố định:
A. . B. Đường thẳng đi qua .
C. Đường thẳng đi qua , song song với . D. Đường thẳng đi qua , song song với .
d) Tính ?
A. . B. . C. . D. .
Câu 20. Cho tứ diện . Gọi là trọng tâm tam giác và là điểm nằm bên trong tam giác
. Đường thẳng qua và song song với lần lượt cắt các mặt phẳng
tại .
a) Khi di động trong tam giác , đại lượng không đổi và bằng:
A. . B. . C. . D. .
b) Xác định vị trí của để đạt giá trị lớn nhất?
A. là trực tâm tam giác . B. là tâm ngoại tiếp tam giác .
C. là trọng tâm tam giác . D. là tâm ngoại tiếp tam giác .
Câu 21. Cho hình chóp có đáy là hình vuông cạnh , tâm . Mặt bên là tam
giác đều và . Gọi là đường thẳng qua và song song với .
a) Giao điểm của đường thẳng với mặt phẳng chạy trên đường thẳng:
A. Qua và song song với . B. Qua và song song với
C. . D. .
b) Diện tích thiết diện của hình chóp cắt bởi là:
A. . B. . C. . D. .
Câu 22. Cho hình chóp có đáy là hình vuông cạnh , tâm . Mặt bên là tam
giác đều, . Gọi lần lượt là trung điểm của . là điểm trên cạnh
. Mặt phẳng cắt tại .
a) là hình gì?
A. Tứ giác lồi có các cặp cạnh đối cắt nhau. B. Hình thoi.
C. Hình thang cân. D. Hình bình hành.
b) Đặt . Tìm theo để diện tích tứ giác đạt giá trị nhỏ nhất?
A. . B. . C. . D. .
Câu 23. Cho hình chóp có đáy là hình thang có cạnh đáy và . Gọi lần
lượt là trung điểm của các cạnh . là trọng tâm của tam giác . Thiết diện của
hình chóp cắt bởi là một tứ giác. Tìm điều kiện của để thiết diện đó
là hình bình hành?
A. . B. . C. . D. .
Câu 24. Cho tứ diện . Gọi lần lượt là trung điểm của các cạnh . là một điểm trên
cạnh ( khác ). Tìm điều kiện của tứ diện và điểm sao cho thiết diện của
hình chóp cắt bởi là hình thoi?
A. . B. .
C. . D. .
Câu 25. Số đo góc giữa hai đường thẳng bằng thì hai đường thẳng đó:
SO
S
S
AB
S
AD
AN
BM
SO
S
S
AB
S
AD
AB BC
MN SK
-
0
1
2
1
3
2
3
ABCD
G
BCD
M
BCD
M
GA
( ) ( ) ( )
,,ABC ACD ADB
,,PQR
M
BCD
MP MQ MR
GA
++
1
2
3
4
M
..MP MQ MR
M
BCD
M
BCD
M
BCD
M
BCD
.S ABCD
ABCD
a
O
( )
SAB
∑
90SAD =°
Dx
D
SC
I
Dx
( )
SAB
S
AB
S
AD
SO
SD
.S ABCD
( )
AIC
2
7
8
a
2
7
4
a
2
7
2
a
2
7
16
a
.S ABCD
ABCD
a
O
( )
SAB
3SC SD a==
,HK
,SA SB
M
AD
( )
HKM
BC
N
( )
0AM x x a=££
x
a
0
a
2
a
4
a
.S ABCD
ABCD
AB
CD
,IJ
,AD BC
G
SAB
.S ABCD
( )
IJG
3AB CD=
2AB CD=
2CD AB=
3CD AB=
ABCD
,IJ
E
AD
E
,AD
ABCD
E
( )
IJE
,AB CD EA ED==-
!! !" !!!"
,AD BC EA ED==-
!! !" !!!"
,2AB CD EA ED==-
!! !" !!!"
,2AD BC EA ED==-
!! !" !!!"
0°
Trang 42
A. Song song. B. Chéo nhau.
C. Trùng nhau. D. Song song hoặc trùng nhau.
Câu 26. Bạn Tùng Chi xác định góc giữa hai đường thẳng trong không gian như sau:
Bước 1: Lấy điểm bất kì. Qua dựng đường thẳng song song với . Trên đường thẳng
lấy điểm khác .
Bước 2: Dựng đường thẳng song song với song song với . Trên đường thẳng lấy điểm
khác .
Bước 3: Góc giữa hai đường thẳng và chính là góc .
Hỏi bạn Tùng Chi có làm đúng không, nếu sai thì sai ở bước nào?
A. Bước 1. B. Bước 2. C. Bước 3. D. Bạn làm đúng.
Câu 27. Cho ba đường thẳng sao cho . Khi đó góc giữa hai đường thẳng và
bằng:
A. . B. . C. . D. .
Câu 28. Cho hình chóp có các tam giác , đều cạnh , là trung điểm của .
Tính số đo của góc giữa hai đường thẳng và biết rằng .
A. . B. . C. . D. .
Câu 29. Cho hình chóp có đáy là hình vuông cạnh , .
Gọi lần lượt là trung điểm của các đoạn . Tính cosin của góc giữa hai đường
thẳng và .
A. . B. . C. . D. .
Câu 30. Cho hình chóp có đáy là hình chữ nhật với . Các
tam giác vuông tại . Tính cosin của góc giữa hai đường thẳng và .
A. . B. . C. . D. .
Câu 31. Cho tứ diện có . Tính số đo của góc giữa hai đường
thẳng và ?
A.
. B.
. C. . D. .
Câu 32. Cho tứ diện có . Gọi là trung
điểm của đoạn . Tính cosin của góc giữa hai đường thẳng và .
A. . B. . C. . D. .
HƯỚNG DẪN GIẢI
Câu 1. Đáp án D.
! Đáp án A sai. Giả sử cắt lần lượt tại , cắt lần lượt tại . Suy ra
đồng phẳng, hay đồng phẳng, vô lí.
! Đáp án B, C sai, chúng ta có thể dễ dàng thấy một ví dụ là tứ diện có và đếu
cắt hai đường thẳng chéo nhau và .
Câu 2. Đáp án C.
Câu 3. Đáp án B.
Câu 4. Đáp án D.
Câu 5. Đáp án D.
Câu 6. Đáp án B.
Câu 7. Đáp án C.
Câu 8. Đáp án D.
,ab
O
O
m
a
m
A
O
n
b
m
B
O
a
b
∑
AOB
,,abc
,abb c^∥
a
c
90°
60°
45°
30°
.A BCD
ABC
ABD
a
E
CD
AD
BC
∑
90AEB =°
90°
60°
45°
30°
.S ABCD
ABCD
2a
∑
∑
,90SA a ASB SAD===°
,EF
,AB BC
SE
DF
7
5
2
5
1
5
3
5
.S ABCD
ABCD
,3, 3AB a AD a SA a== =
,,SAB SAC SAD
A
SC
BD
8
130
4
130
3
2
1
5
ABCD
5, AC 7, 57 , 9AB BD CD=== =
BC
AD
30°
45°
60°
90°
ABCD
∑
∑ ∑
,60,90AB AC AD a BAC BAD CAD=== = =° =°
E
BC
AB
ED
5
5
5
10
25
5
1
2
c
,ab
,AB
d
,ab
,CD
,,,ABCD
,ab
ABCD
AB
CD
AD
BC
Trang 43
! Đáp án A sai vì nếu và không trùng nhau thì đôi một phân biệt. theo tính
chất bắc cầu suy ra .
! Đáp án B, C sai, vì ta có thể lấy ví dụ .
Câu 9. Đáp án B.
! Trường hợp có thể xảy ra giữa hai đường thẳng là chéo nhau, song song, cắt nhau.
! Trường hợp có thể là song song, cắt nhau.
! Trường hợp có thể là song song, cắt nhau hoặc trùng nhau.
Như vậy, tương ứng với mối trường hợp, số các khả năng có thể xảy ra giữa là .
Câu 10. Đáp án C.
Nhìn vào hình vẽ, ta thấy chéo nhau, nên không có mặt phẳng nào chứa cả . Do đó
sai. Vậy đáp án A, B, C sai.
Đường thẳng cắt nhau, xác định duy nhất một mặt phẳng chứa cả hai đường. Đáp án
đúng.
Đường thẳng cắt nhau, xác định duy nhất một mặt phẳng chứa cả hai đường. Đáp án
đúng.
Câu 11. Đáp án D.
Ta có: .
Câu 12. Đáp án A.
Do lần lượt là trung điểm của nên .
Do lần lượt là trung điểm của nên .
Suy ra , do đó đồng phẳng. Do đó không thể chéo nhau.
Câu 13. Đáp án D.
Do là đường trung bình của tam giác nên .
Tương tự, do là đường trung bình của tam giác nên .
là hình bình hành nên . Do đó: và .
không song song với vì giả sử ngược lại thì và trùng nhau (vô lí).
Câu 14. Đáp án A.
Do lần lượt là trung điểm của nên ,
, . Do đó đồng phẳng; đồng phẳng;
đồng phẳng.
( )
,ab
( )
,ca
,,abc
bc∥
bcº
( )
1
,ab
( )
2
( )
3
,ab
3, 2, 3
,ab
,ab
( )
1
,ac
( )
2
,bc
( )
3
( ) ( )
( ) ( )
,
AB CD
AB SAB CD MCD MN CD
MN SAB MCD
ì
ï
ÌÌÞ
í
ï
=Ç
î
∥
∥
N
M
D
C
A
B
S
,MN
1
,
2
MN BD MN BD=∥
,PQ
,CD CB
1
,
2
PQ BD PQ BD=∥
MN PQ∥
,,,MNPQ
,MP NQ
MN
SAB
MN AB∥
PQ
SCD
PQ CD∥
ABCD
AB CD∥
PQ MN∥
MN CD∥
MN
SC
SC
CD
,,,,,MNPQRS
,,,,,AC BD AB CD AD BC
MR CD SN∥∥
PS AC RQ∥∥
MP BC NQ∥∥
,,,MRSN
,,,PQRS
,,,MPQN
Trang 44
không đồng phẳng vì giả sử ngược lại thì sẽ thuộc mặt phẳng , suy ra
thuộc mặt phẳng (vô lí).
Câu 15. Đáp án B.
Ta có , suy ra .
Do .
Ta có: , suy ra .
Do .
Từ đó suy ra và song song với nhau.
Ta có: .
Suy ra . Gọi là giao điểm của với .
Do .
Theo định lý Thalet ta có: . Do song song với nên theo định lý
Thalet ta có : .
Tương tự ta cũng có: .
Từ đây suy ra .
Câu 16. Đáp án C.
Ta có: .
,,,MPRQ
P
( )
ACD
B
( )
ACD
( )
ISADÎ
( ) ( )
ISAD BCIÎÇ
( ) ( )
( ) ( )
,
SAD BCI PQ
AD SAD BC BCI PQ AD BC
AD BC
Ç=
ì
ï
ÌÌÞ
í
ï
î
∥∥
∥
( )
JSBCÎ
( ) ( )
JSBC ADJÎÇ
( ) ( )
( ) ( )
,
SBC ADJ MN
BC SBC AD ADJ MN AD BC
AD BC
Ç=
ì
ï
ÌÌÞ
í
ï
î
∥∥
∥
MN
PQ
( ) ( )
( ) ( )
( ) ( )
EF ADNM BCQP
AD ADNM ABCD
EF AD
BC ABCD BCQP
AD BC
=Ç
ì
ï
=Ç
ï
Þ
í
=Ç
ï
ï
î
∥
∥
EF MN∥
K
CP
EF
EF EK KF=+
2
3
SP SM
PM AB
SA SB
== Þ ∥
22
35
PE PE
EB PB
=Þ =
EK
BC
22
55
PE EK
EK b
PB BC
==Þ=
2553322
.
3335535
QF QC PQ
FK PQ AD a
FC FC FK
=Þ =Þ =Þ = = =
( )
2
5
EF a b=+
( ) ( )
( ) ( )
,
SAD IJK FK
AD SAD IJ IJK FK IJ
AD IJ
Ç=
ì
ï
ÌÌÞ
í
ï
î
∥
∥
Trang 45
Dễ dàng chứng minh được các đường thẳng còn lại không song song với .
Câu 17. Đáp án C.
Do lần lượt là trung điểm của nên là đường trung bình của tam giác .
Suy ra .
Ta có: .
Câu 18. Đáp án C, B.
a) Do nên bốn điểm này nằm trong cùng mặt phẳng. Giả sử là giao điểm của mặt
phẳng này với . Khi đó thẳng hàng và ta có: .
Tương tự ta có: . Vậy . Vậy đáp án đúng là .
b) Ap dụng bất đẳng thức Cauchy ta có :
.
Dầu bằng xảy ra khi và chỉ khi: .
Điều này chỉ xảy ra khi là trọng tâm tam giác . Vậy đáp án đúng là B.
Câu 19. Đáp án B, A, D, A.
a) Ta có : . Do đó là hình thang. Do
nên không thể là hình bình hành, hinh thoi. Vậy đáp án đúng là B.
FK
,IJ
IJ
BCD
IJ CD∥
( ) ( )
( ) ( )
( ) ( )
,,IJ CD IJ AIJ CD ACD
AIJ ACD At CD
AAIJ ACD
ÌÌ
ì
ï
ÞÇ =
í
ÎÇ
ï
î
∥
∥
MA SA
¢
∥
E
BC
MBC
ABC
S
MA ME
SA EA S
¢
==
,
MAC
MAB
ABC ABC
S
S
MB MC
SB S SC S
¢¢
==
1
MA MB MC
SA SB SC
¢¢ ¢
++ =
3
1
3.. ..
27
MA MB MC MA MB MC MA MB MC
SA SB SC SA SB SC SA SB SC
¢¢ ¢ ¢¢¢ ¢¢¢
++ ³ Þ £
MAC MAB MBC
MA MB MC
SSS
SA SB SC
¢¢ ¢
==Þ==
M
ABC
( ) ( )
( ) ( )
( ) ( )
MN ABM SCD
AB ABM ABCD
MN AB
CD ABCD SCD
CD AB
=Ç
ì
ï
=Ç
ï
Þ
í
=Ç
ï
ï
î
∥
∥
ABMN
MN AB<
ABMN
Trang 46
b) Gọi . Vậy đáp án đúng là A.
c) Gọi .
Giao tuyến của hai mặt phẳng và là đường thẳng qua và song song với .
Vậy đáp án đúng là D.
d) Do nên .
Do nên .
Từ và suy ra . Vậy đáp án đúng là A.
Câu 20. Đáp án C, C.
a) Trong mặt phẳng , gọi .
Qua kẻ . Trong (đây chính là giao điểm của với )
Tương tự .
Ta có : .
Theo định lý Thalet ta có : . Do đó : .
Chứng minh tương tự ta có : .
Vậy đáp án đúng là C.
b) Áp dụng bất đẳng thức Cauchy ta có : .
Vậy giá trị lớn nhất của bằng . Dấu bằng xảy ra khi và chỉ khi
. Điều này xảy ra khi là trọng tâm tam giác . Vậy đáp án đúng là C.
Câu 21. Đáp án A, A.
( )
( )
( ) ( )
I SAC
I AM BN I SO SAC SBD
I SBD
Î
ì
ï
=ÇÞ ÞÎ= Ç
í
Î
ï
î
( )
( )
( ) ( )
I SAD
K AN BM I SAD SBC
I SBC
Î
ì
ï
=Ç Þ ÞÎ Ç
í
Î
ï
î
( )
SAD
( )
SBC
S
AD
MN AB∥
( )
1
AB BM
MN MK
=
SK BC∥
( )
2
CB MB
SK MK
=
( )
1
( )
2
0
AB BC
MN SK
-=
( )
BCD
,,IMGBCJMGCDKMGBD=Ç =Ç =Ç
M
Mx GA∥
( )
:AIJ Mx AI PÇ=
Mx
( )
ABC
,Mx AK R Mx AJ QÇ= Ç=
3
MIC MIC MIB MBC MBC
MIB
GIC GIB GIC GIB GBC BCD
SSSSS
S
IM
IG S S S S S S
+
=== = =
+
IM MP
IG GA
=
3
MBC
BCD
S
MP
GA S
=
3
3
,3
MCD
MBD
BCD BCD
S
S
MQ MR MP MQ MR
GA S GA S GA
++
==Þ =
3
3
..
3
MP MQ MR
MP MQ MR GA
++
æö
£=
ç÷
èø
..MP MQ MR
3
GA
MP MQ MR==
M
BCD
Trang 47
a) Do nên hai đường thẳng này cùng nằm trong mặt phẳng .
Lại có, hai mặt phẳng và có là điểm chung, nên giao tuyến là
đường thẳng đi qua và song song với . Vậy thuộc giao tuyến này.
Vậy đáp án đúng là A.
b) Gọi là giao điểm của và . Suy ra thiết diện của hình chóp cắt bởi mặt phẳng
là tam giác .
Ta có là hình thang nên và . Suy ra và . Điều này
suy ra là hình bình hành. Khi đó .
Mặt khác, .
Xét tam giác có : .
Ta có : .
Diện tích thiết diện là : .
Vậy đáp án đúng là A.
Câu 22. Đáp án C, A.
a) Ta có :
.
Ta lại có: .
Dx SC∥
( )
SCD
( )
SAB
( )
SCD
D
AB CD∥
S
AB
I
E
SD
IC
( )
AIC
ACE
SIDC
SI CD=
SI CD∥
SI AB=
SI AB∥
SIDC
AI SB a==
2
2
2
a
AC SD a AE== Þ =
IAC
( )
22222
2442CI AC AI AE a CI a=+-=Þ=
∑ ∑
2
22
222
2
2
37
2
cos sin
2. 2 4 4
a
aa
AE AC CE
CAE CAE
AC AE a
+-
+-
===Þ=
∑
2
11277
. .sin 2. .
22248
aa
S AC AE CAE a===
( ) ( )
( ) ( )
( ) ( ) ( )
,,
1
KH AB KH HKM AB ABCD
HKM ABCD MN AB HK
M HKM ABCD
ÌÌ
ì
ï
ÞÇ =
í
ÎÇ
ï
î
∥
∥∥
( )
∑
∑
..SAD SB C c c c SAD SBCD=D Þ =
| 1/47
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


BÀI TẬP TRẮC NGHIỆM ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG
GIAN.QUAN HỆ SONG SONG A. LÝ THUYẾT
I. ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG 1. Mặt phẳng
Mặt bảng, mặt bàn, mặt nước hồ yên lặng cho ta hình ảnh một phần của mặt phẳng. Mặt phẳng không có
bề dày và không có giới hạn.
Để kí hiệu mặt phẳng, ta thường dùng các chữ cái in hoa hoặc chữ cái Hy Lạp đặt trong dấu ngoặc (). Ví
dụ như mặt phẳng (P),(Q),(a ),(b ) …
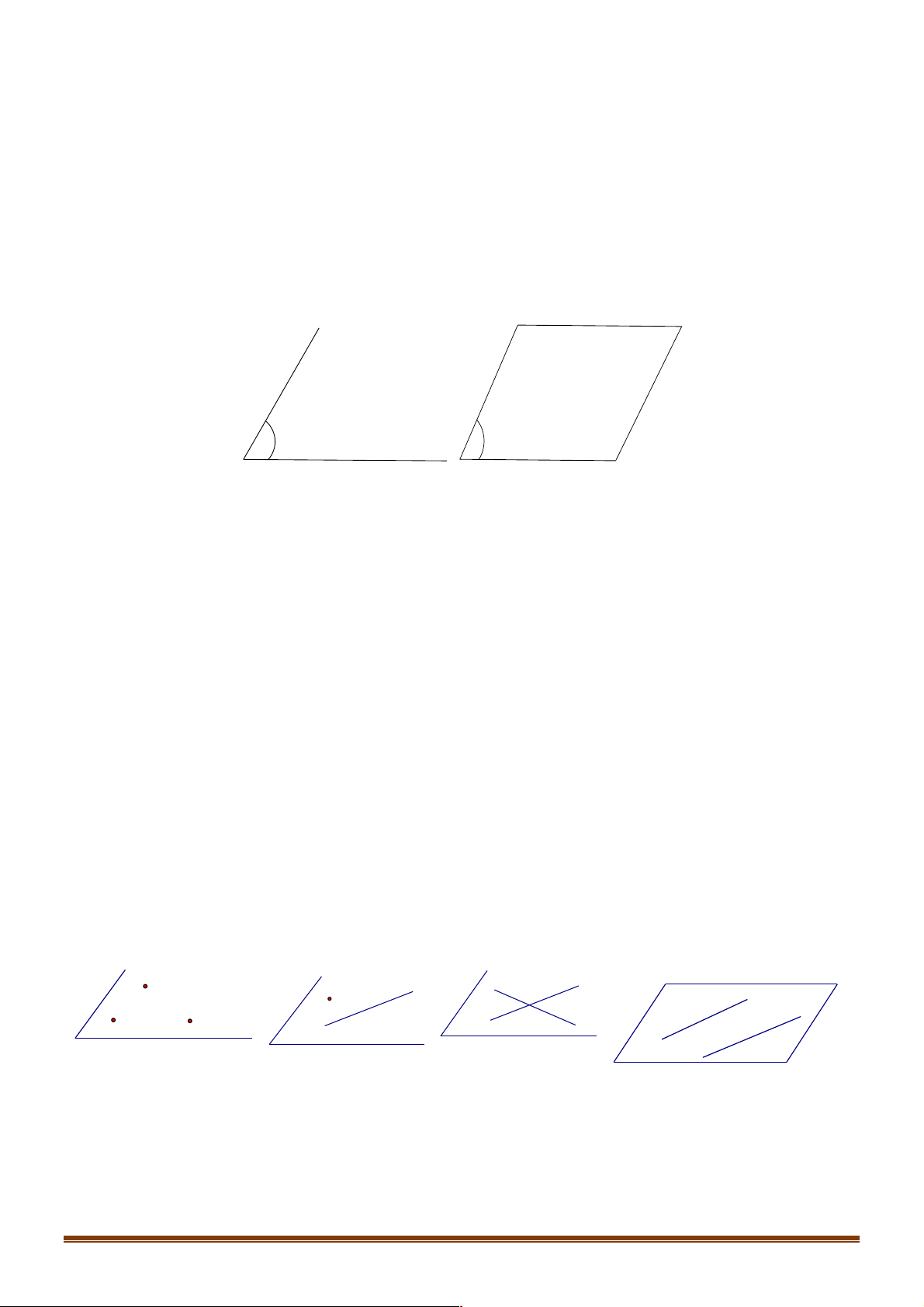
Để biểu diễn mặt phẳng, ta thường dùng hình bình hành hoặc một miền góc và ghi tên của mặt phẳng vào
một góc của hình biểu diễn. P P
Đường thẳng và mặt phẳng là tập hợp các điểm. Do đó,
- Nếu điểm A thuộc đường thẳng a , ta kí hiệu AÎ a và đôi khi còn nói rằng đường thẳng a đi qua điểm A .
- Nếu điểm A thuộc mặt phẳng (a ), ta kí hiệu AÎ(a ) và đôi khi còn nói rằng mặt phẳng (a ) đi qua điểm A .
- Nếu đường thẳng a chứ trong mặt phẳng (a ), ta kí hiệu a Ì (a ) và đôi khi còn nói rằng mặt phẳng
(a) đi qua (hoặc chứa) đường thẳng a.
2. Quy tắc để vẽ hình biểu diễn của một hình trong không gian
- Hình biểu diễn của một đường thẳng là một đường thẳng, của đoạn thẳng là đoạn thẳng.
- Hình biểu diễn của hai đường thẳng song song là hai đường thẳng song song, của hai đường thẳng cắt
nhau là hai đường thẳng cắt nhau. Hai đoạn thẳng song song và bằng nhau thì phải được vẽ song song và
bằng nhau. Trung điểm của một đoạn thẳng phải được lấy ngay tại điểm chính giữa của đoạn thẳng đó.
- Hình biểu diễn phải giữ nguyên quan hệ thuộc giữa điểm và đường thẳng.
- Dùng nét vẽ liền để biểu diễn cho đường nhìn thấy và nét đứt đoạn biểu diễn cho đường bị che khuất.
3. Các tính chất thừa nhận của hình học không gian
- Tính chất 1: Có một và chỉ một đường thẳng đi qua hai điểm phân biệt.
- Tính chất 2: Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng.
Như vậy, một mặt phẳng trong không gian có thể được xác định bởi một trong các cách thức sau:
- Mặt phẳng đó đi qua 3 điểm không thẳng hàng ,
A B,C . Kí hiệu là mp ( ABC).
- Mặt phẳng đó đi qua một đường thẳng a và một điểm A không thuộc đường thẳng a . Kí hiệu: ; mp ( , A a) . B A b a a A C a b mp(ABC) mp(A;a) mp(a,b)
- Mặt phẳng đó đi qua hai đường thẳng cắt nhau a và b . Kí hiệu, mp ( , a b).
- Mặt phẳng đó đi qua hai đường thẳng song song a , b .
- Tính chất 3: Trong không gian có ít nhất bốn điểm không cùng thuộc bất cứ mặt phẳng nào.
- Tính chất 4: Trong không gian, hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường
thẳng chung duy nhất chứa tất cả các điểm chung của hai mặt phẳng đó.
- Tính chất 5: Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường
thẳng đều thuộc mặt phẳng đó. Trang 1
- Tính chất 6: Trong mỗi mặt phẳng của không gian, các kết quả đã biết của hình học phẳng đều đúng.
3.Vị trí tương đối của các đường thẳng và mặt phẳng trong không gian
a) Vị trí tương đối của một đường thẳng và một mặt phẳng
Cho đường thẳng d và một mặt phẳng (a). Có thể xãy ra các khả năng sau: d
- Đường thẳng d và mặt phẳng (a ) không có điểm chung. Trong trường hợp này ta nói
đường thẳng d song song với mặt phẳng (a ), kí hiệu d / / (a) . α d
- Đường thẳng d và mặt phẳng (a )có đúng một điểm chung. Trong trường hợp này ta
nói ta nói đường thẳng d cắt mặt phẳng (a ) tại A , kí hiệu: d Ç(a ) = { } A A α
- Đường thẳng d và mặt phẳng (a ) có nhiều hơn một điểm chung.Trường hợp
này ta nói đường thẳng d nằm trong mặt phẳng (a )ta kí hiệu: d Ì (a ) hay d (a) É d . α
b) Vị trí tương đối của hai mặt phẳng:
Cho hai mặt phẳng phân biệt (a ) và (b ) . Có thể xảy ra một trong các khả năng sau: α
- Hai mặt phẳng (a ) và (b )không có điểm chung. Trong trường hợp này ta nói
các mặt phẳng (a ) và (b )song song với nhau, kí hiệu (a ) / /(b ) . β
- Hai mặt phẳng (a ) và (b )có ít nhất một điểm chung. Trong trường hợp này ta α
nói các mặt phẳng (a ) và (b )có phần chung là một đường thẳng, giả sử đường
thẳng đó là d , ta kí hiệu (a ) Ç(b ) = d . β
Đường thẳng d được gọi là giao tuyến của hai mặt phẳng. Như vậy, việc xác định giao tuyến của hai mặt
phẳng tương ứng với việc xác định hai điểm cùng thuộc đồng thời hai mặt phẳng phân biệt đó. Ngoài ra,
nếu biết được rằng ba điểm phân biệt cùng thuộc đồng thời hai mặt phẳng thì ba điểm đó phải nằm trên một được thẳng.
c) Vị trí tương đối của hai đương thẳng: Cho hai đường thẳng phân biệt a và b . Có thể xảy ra một trong các khả năng sau:
- Các đường thẳng a và b cùng thuộc một mặt phẳng. Khi đó a và b hoặc cắt nhau tại một điểm hoạc song song với nhau.
- Các đương thẳng a và b không cùng nằm trong bất kì một mặt phẳng nào. Trong trường hợp này ta nói
các đường thẳng a và b chéo nhau. a A b
4. Hình chóp và hình tứ diện Trang 2 S S cạnh bên S Mặt bên A A D A1 A5 1 B A4 A3 cạnh đáy C
A2 Mặt đáy A3 A2 1. Hình chóp:
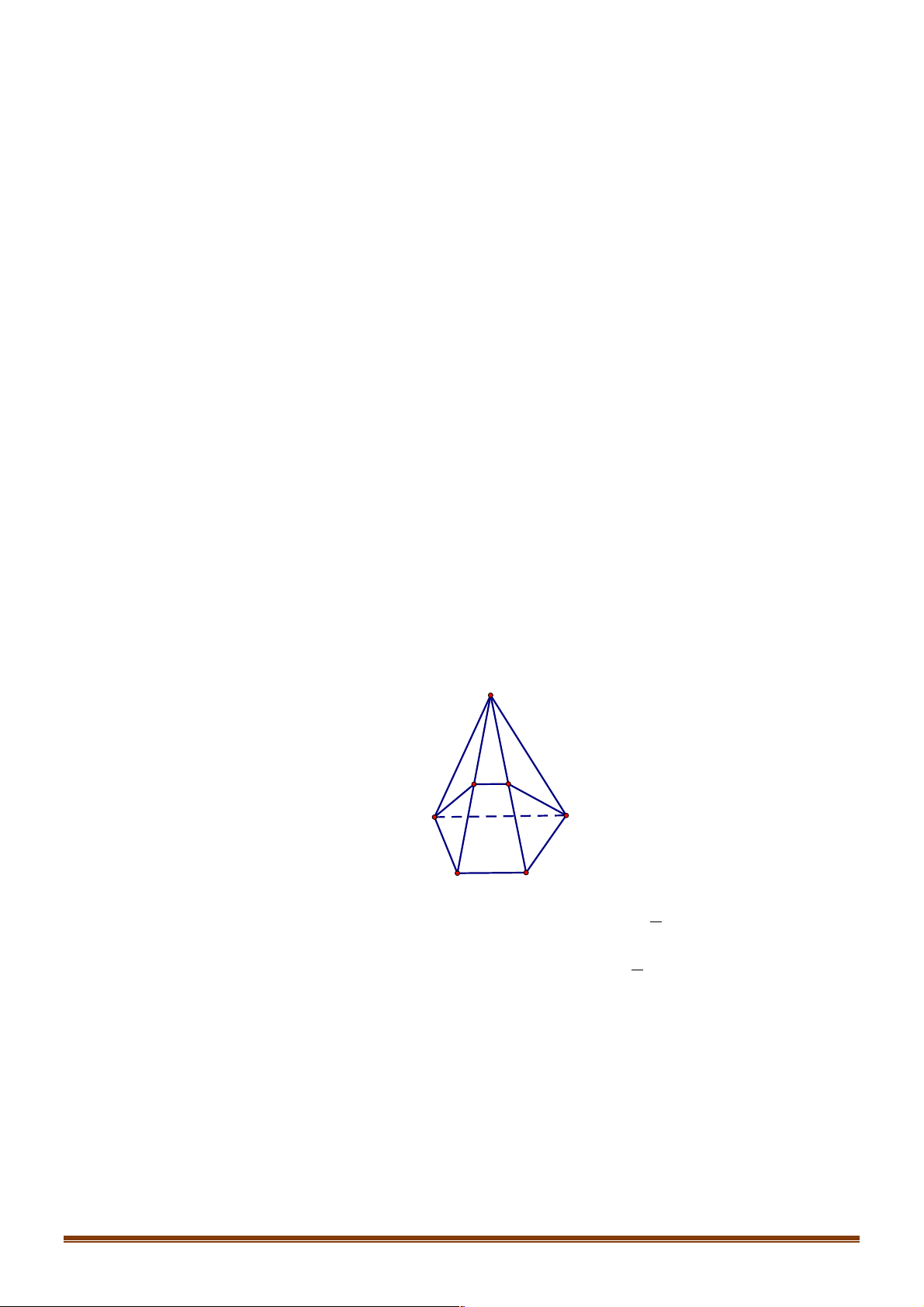
Trong mặt phẳng (a ) , cho đa giác lồi A A ...A .Lấy điểm S nằrm ngoài mặt phẳng(a ) . Lần lượt nối S với 1 2 n
các đỉnh A , A ,..., A để được n tam giác SA A ,SA A ,..., SA A .Hình gồm đa giác A , A ,..., A và n tam giác 1 2 n 1 2 2 3 n 1 1 2 n
SA A ,SA A ,...,SA A và gọi là hình chóp và được kí hiệu là S.A A ...A 1 2 2 3 n 1 1 2 n
Ta gọi S là đỉnh, đa giác A , A ,..., A là mặt đáy, tam giác SA A ,SA A ,..., SA A gọi là một mặt bên của hình 1 2 n 1 2 2 3 n 1
chóp, Các đoạn thẳng SA ,SA ,...,SA gọi là các cạnh bên, các cạnh của đa giác A A ...A là các cạnh đáy của hình 1 2 n 1 2 n chóp.
-Cách gọi tên: Hình chóp + tên đa giác.
- Ví dụ: hình chóp tam giác, hình chóp tứ giác….
Lưu ý: Hình chóp có đáy là đa giác đều, các cạnh bên bằng nhaulaf hình chóp đa giác đều. b) tứ diện:
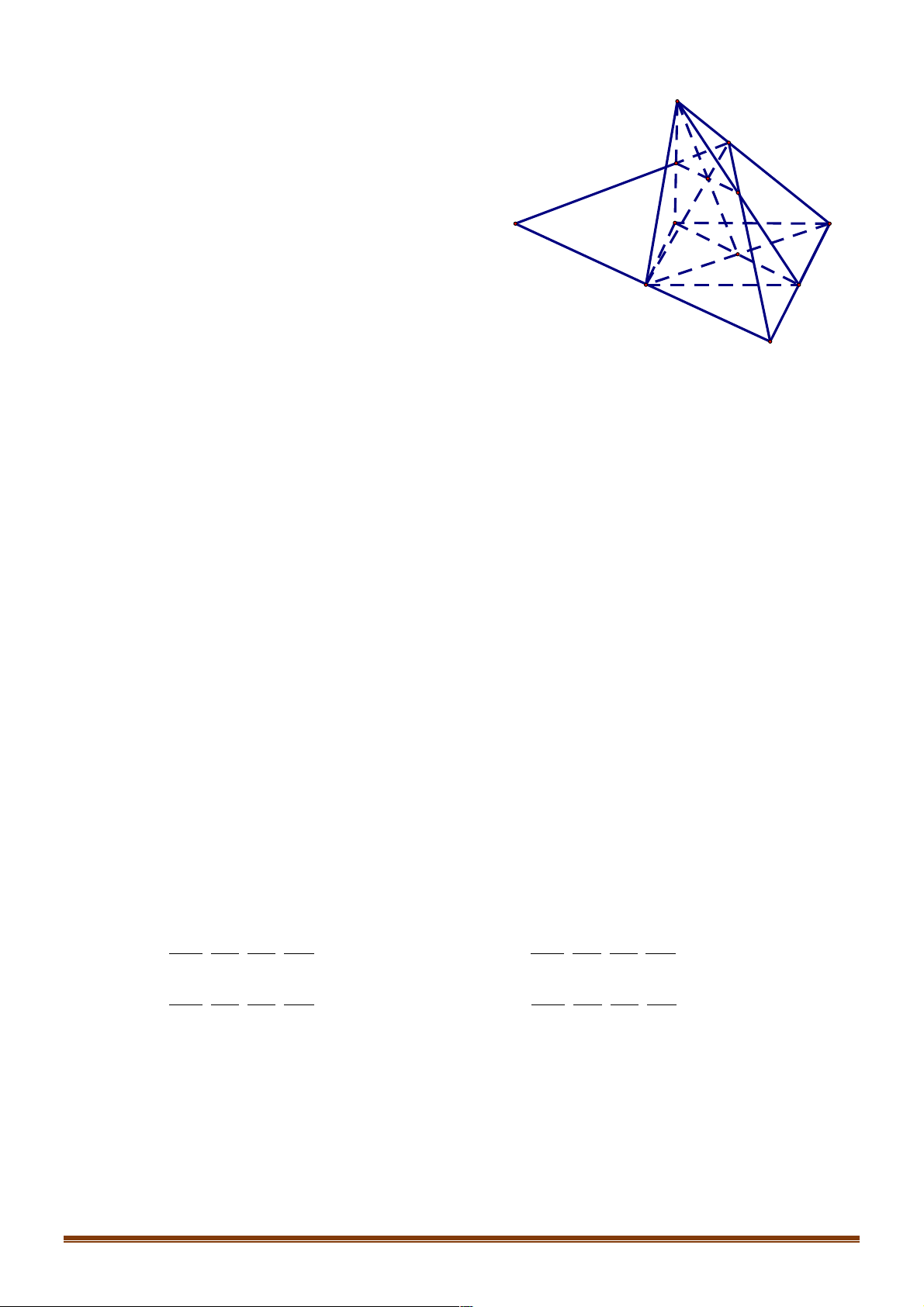
Tứ diện ABCD là hình được thành lập từ bốn điểm không đồng phẳng , A ,
B C,D .Các điểm , A ,
B C,D là các đỉnh
của tứ diện, các tam giác BC , D AC , D A ,
BD ABCđược gọi là các mặt của tứ diện đối diện với các đỉnh ,
A B,C, D và các đoạn thẳng , AB BC,C , D D , A C ,
A BD gọi là các cạnh của tứ diện . Trong đó các cặp cạnh AB
và CD , AC và DB, AD và BC thường được gọi là các cặp cạnh đối của tứ diện.
B. CÁC DẠNG BÀI TOÁN VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG
DẠNG 1: XÁC ĐỊNH GIAO TUYẾN GIŨA HAI MẶT PHẲNG
Phương pháp: Để tìm giao tuyến của hai mặt phẳng (a ) và (b ) ta tiến hành đi tìm hai điểm thuộc cả hai mặt phẳng (a ) và (b ) . Lưu ý:
Một điểm chung của hai mặt phẳng (a ) và (b ) thường tìm được bằng cách: Chọn một mặt phẳng (g )
sao cho các giao tuyến D , D của (a ) và (b ) với (g )có thể dựng được ngay. Giao điểm I của D ,D ( 1 2 1 2
trong (g )) là điểm chung cần tìm.
Ta thường chứng minh ba điểm thẳng hàng bằng cách chứng minh ba điểm đó thuộc giao tuyến của hai mặt phẳng.
+ Ta cũng có thể chứng minh bà đường thẳng đồng quy bằng cách:
Cách 1: Hai trong ba đường thẳng ấy cắt nhau và lần lượt nằm trong hai mặt phẳng nhận đường thứ ba làm giao tuyến.
Cách 2: Tìm một đoạn thẳng AB trên một đường thẳng nào đó. Chứng minh hai đường thẳng còn lại
chia đoạn AB theo cùng một tỉ số đại số.
DẠNG 2: XÁC ĐỊNH GIAO ĐIỂM CỦA ĐƯỜNG THẲNG D VÀ MẶT PHẲNG (a ) .
Phương pháp: Trang 3
+ Nếu phát hiện ra một đường thẳng d trong mặt phẳng (a ) cắt D tại I thì I chính là giao điểm của D với mặt phẳng (a ) .
+ Nếu chưa phát hiện ra đường thẳng d thì ta dựng d bằng cách: Chọn một mặt phẳng (g ) chứa D sao
cho giao tuyến của (g ) và (a ) có thể dựng được ngay, giao tuyến đó chính là đường thẳng d cần tìm.
Hai định lí quan trọng thường dùng:
Định lí Ceva: Cho tam giác ABC . Các điểm M , N, P khác ,
A B,C và theo thứ tự thuộc các đường thẳng BC,C ,
A AB . Khi đó các đường thẳng AM , BN,CP hoặc đồng quy hoặc đôi một song song khi và MB NC PA chỉ khi . . = - 1 MC NA PB
Định lí Menelaus : Cho tam giác ABC . Các điểm M , N, P khác ,
A B,C và theo thứ tự thuộc các MB NC PA
đường thẳng BC,C ,
A AB . Khi đó các điểm M , N, P thẳng hàng khi và chỉ khi . . =1 . MC NA PB
DẠNG 3: BÀI TOÁN DỰNG THIẾT DIỆN
Cho trước khối đa diện T và mặt phẳng (a ) . Nếu (a )có điểm chung với T thì (a ) sẽ cắt một số mặt
của T theo các đoạn thẳng. Phần mặt phẳng (a ) giới hạn bởi các đoạn đó thường là một đa giác, gọi là
mặt cắt ( còn gọi là thiết diện) giữa T và (a ). Chú ý:
+ Đỉnh của thiết diện là giao điểm của (a ) với các cạnh của T . Cạnh của thiết diện là các đoạn giao
tuyến của (a ) với các mặt của T . Do đó thực chất của việc dựng thiết diện là bài toán dựng giao điểm
giữa đường thẳng và mặt phẳng và dựng giao tuyến giữa hai mặt phẳng.
+ Do mỗi cạnh của thiết diện là đoạn giao tuyến của mặt phẳng (a ) với một mặt của T . Do đó số cạnh
nhiều nhất mà thiết diện có thể có chính là số mặt của T .
- Đối với hình chóp tam giác ( hoặc tứ diện), thiết diện của nó cắt bởi mặt phẳng (a ) chỉ có thể là tam
giác hoặc tứ giác ( ở đay ta quy ước không xét các trường hợp suy biến khi thiết diện là một mặt hoặc một cạnh của hình chóp).
-Đối với hình chóp tứ giác, thiết diện của nó chỉ có thể là tam giác, tứ giác hoặc ngũ giác.
Các bài toán liên quan đến thiết diện gồm các dạng: + Dựng thiết diện.
+ Xác định hình dạng thiết diện.
+ tính diện tích thiết diện.
+ Tính tỉ số thể tích hai phần do thiết diện phân chia khối thể tích đã cho ( sẽ được trình bày trong Công phá toán tập 3).
Ví dụ 1: Cho hình chóp S.ABCD có đáy là một hình bình hành tâm O . Gọi M và N lần lượt là trung
điểm của SA và SC . Gọi (P) là mặt phẳng qua 3 điểm M , N, B .
a) Tìm các giao tuyến của (P) và (SAB) ; (P) và (SBC .)
b) Tìm giao điểm I của đường thẳng SO với mặt phẳng (P) và giao điểm K của đường
thẳng SD với mặt phẳng (P) .
c) Xác định các giao tuyến của mặt phẳng (P) với mặt phẳng (SAD) và mặt phẳng (SCD) .
Từn đó suy ra thiết diện của hình chóp cắt bởi (BMN) .
d) Xác định các giao điểm E, F của các đường thẳng DA , DC với (P) . Chứng minh rằng
E, B, F thẳng hàng.
Lời giải:: Trang 4 a) Ta có: S M ÎS ,
A SA Ì (SAB) Þ M Î(SAB)( ) 1
Lại có M Î(BMN ) (2) K Từ (1) và (2) suy ra M
M Î(SAB)Ç(BMN )( ) 3 I N
Ta có : BÎ(SAB)Ç(BMN )(4) A D E Từ (3) và (4) suy ra
BM = (SAB)Ç(BMN ) . O Tương tự ta cũng suy ra B C
BM = (SAB)Ç(BMN ) .
b) Trong mặt phẳng (SAC), gọi I là giao F
điểm của SO với MN Ta có :
I ÎMN, MN Ì (BMN ) Þ I Î(BMN ) Þ I là giao điểm của SO với (BMN ).
Trong mặt phẳng (SBD), gọi K là giao điểm của BI với SD . Ta có :
K Î BI, BI Ì (BMN ) Þ K Î(BMN ) . Suy ra K chính là giao điểm của SD với (BMN ) . ìK Î ï (BMN ) c) Ta có : í
Þ K Î(BMN ) Ç(SAD) . ïK Î î (SAD)
Ta lại có : M Î(BMN)Ç(SDC) .
Như vậy tứ giác BMKN là thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (BMN ) .
d) Trong mặt phẳng (SAD), gọi { }
E = MK Ç AD. Ta có: MK Ì (BMN ) nên E Î(BMN ) .
Vậy E chính là giao điểm của AD với (BMN ) .
Trong mặt phẳng (SDC) gọi {F} = NK ÇCD .
Ta có NK Ì (BMN )nên F Î(BMN ) , ìE Î ï (BMN ) ìB Î ï (BMN ) í
Þ E Î(BMN ) Ç( ABCD), í
Þ B Î(BMN ) Ç( ABCD) ïE Î î ( ABCD) ïB Î î ( ABCD)
Suy ra ba điểm B, E, F cùng nằm trên giao tuyến của hai mặt phẳng (BMN ) và ( ABCD) . Do
đó ba điểm B, E, F thẳng hàng.
Ví dụ 2: Cho tứ diện ABCD và các điểm M , N, ,
P Q lần lượt thuộc các cạnh AB, BC,CD, DA sao cho
MN không song song với AC . M , N, ,
P Qđồng phẳng khi : AM BN CP DQ BM CN CP DQ A. . . . = 1 B. . . . = 1 BM CN DP AQ AM BN DP AQ BM CN DP DQ AM BN DP AQ C. . . . = 1 D. . . . = . 1 AM BN CP AQ BM CN CP DQ Đáp án A.
Lời giải:.
+ Giả sử M , N, ,
P Q cùng thuộc mặt phẳng (a ) .
Nếu MN cắt AC tại K thì K là điểm chung của các mặt phẳng (a ),( ABC) ,( ADC) nên
PQ cũng đi qua K.
Áp dụng định lí Menelaus cho các tam giác ABC, ADC ta được : Trang 5 AM BN CK AK CP DQ AM BN CP DQ . . = 1 ; . . =1 Þ . . . = 1 BM CN AK CK DP AQ BM CN DP AQ Nhận xét :
Trường hợp MN song song với AC thì ví dụ trên vẫn đúng. AM BN CP DQ
+ Liệu trường hợp ngược lại, có . . . = 1 thì M , N, ,
P Q có đồng phẳng hay BM CN DP AQ không ?
Câu trả lời là trường hợp ngược là ví dụ vẫn đúng. Ta sẽ cùng chứng minh nhé :
Trong mặt phẳng ( ACD), KO cắt AD tại Q¢ thì các điểm M , N, P,Q ¢đồng phẳng. AM BN CP AQ¢ DQ¢ DQ Theo ví dụ 2 ta có: . . . =1 Þ =
Þ Q º Q¢. Ví dụ được chứng minh. BM CN DP DQ¢ AQ¢ AQ
+ Ví dụ này có thể được mở rộng đối với các điểm M , N, ,
P Q bất kì trên các đường thẳng
AB, BC,CD, DA như sau : AM BN CP DQ
M , N, P,Q¢ đồng phẳng khi và chỉ khi . . . =
1 ( khẳng định này dôi khi còn BM CN DP AQ
được gọi là định lí Menelaus mở rộng trong không gian)
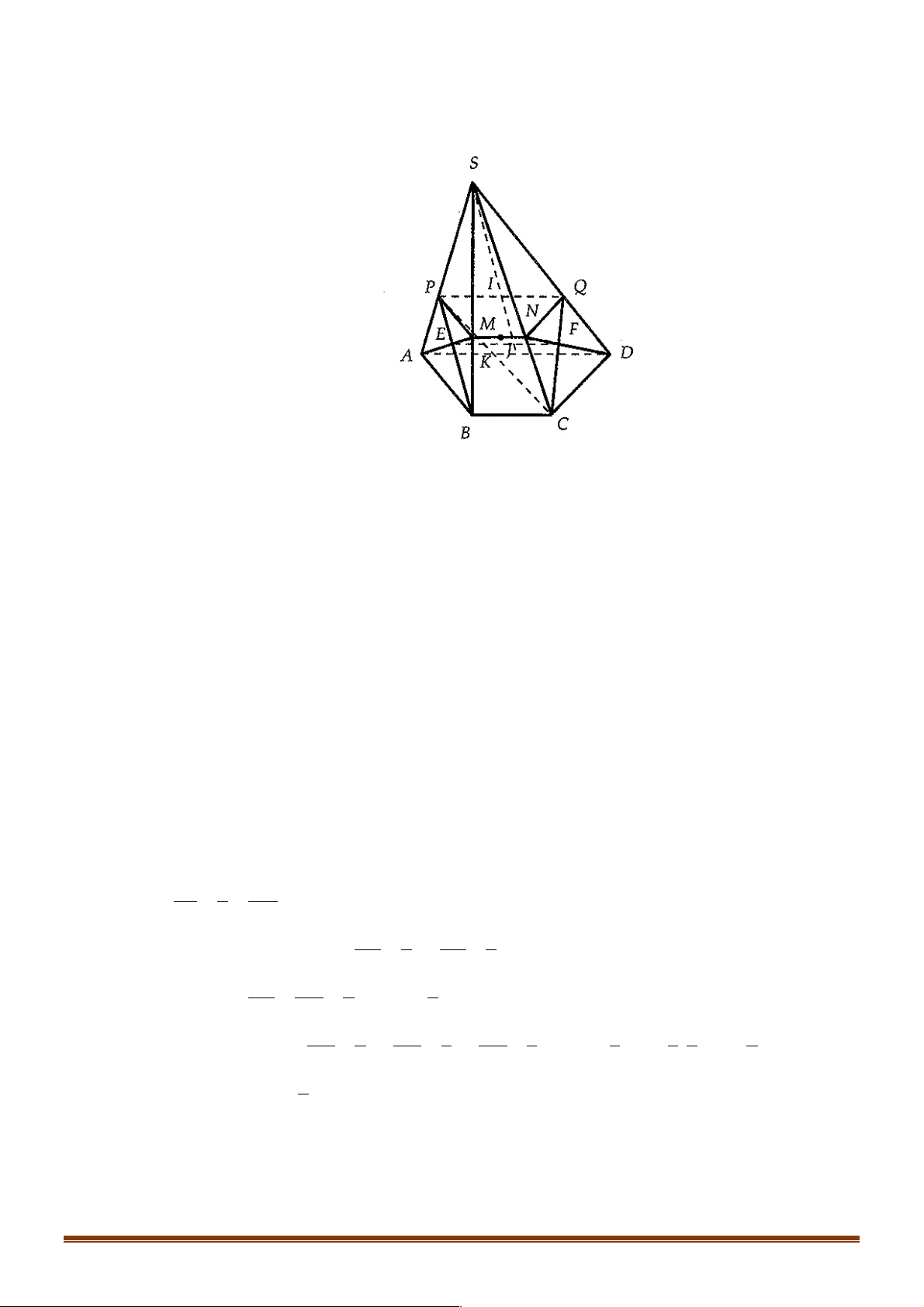
Ví dụ 3: Cho hình chóp S.ABCD và E là điểm thuộc mặt bên (SCD) . E, F lần lượt là trung điểm của
AB, AD . Thiết diện của hình chóp cắt bởi (EFG) là : A. Tam giác. B. Tứ giác. C. Ngũ giác. D. Lục giác. Đáp án C.
Lời giải: :
Trong mặt phẳng ( ABCD) , gọi I, H lần lượt là giao điểm của FG với BC,CD
Dễ thấy thiết diện là hình lập phương bị cắt bởi mặt phẳng (a ) là ngũ giác MNGFE . Vậy đáp án đúng là C. a
b) Theo cách dựng ta có E là trung điểm của BB '. Do đó B ' F = BP = = C 'Q 2 a 2 3a 2 MB PB 1 3 3
Suy ra : PE = QF = EF= Þ PQ = , = = Þ CN = CD = . a 2 2 NC PC 3 4 4 (
ì ABB ' A') / /(DCC 'D') ï
Do íKE = (a ) Ç ( ABB ' A') Þ KE / /NG ïNG = î (a )Ç(DCC 'D')
Tương tự ta có : MN / /FG 2 2 S æ PE ö 1 S æ QE ö PME QGF 1 Do đó : = = , = = ç ÷ ç ÷ S è PQ ø 9 S è PQ ø 9 PQN QNP
Diện tích thiết diện là : S = S - S + S = S MNGFE PNQ ( PEM QFG) 7 . 9 PNQ
Do hai tam giác vuông NCP và NCQ bằng nhau (c.g.c) nên NQ = .
NP Vậy tam giác NPQ cân tại
N. Gọi I là trung điểm của PQ 2 2 5a 5 45a 18a 3a a Ta có : 2 2 2 2
PN = PC + CN =
, NI = PN - PI = - = . 4 16 16 4
Diện tích của NPQ bằng : 2 2 1 9a 6 7a 6 S = NI.PQ = Þ S = . NPQ 2 16 MNGFE 16 Trang 6 Vậy đáp án đúng là B. Câu 23. Đáp án D.
Trong mặt phẳng (ABCD) , dựng đường thẳng qua M , song song với BC cắt A' B ',C ' D ' theo thứ
tự tại E, F .
Trong mặt phẳng (A' B 'C ' D '), dựng đường thẳng qua N song song với B 'C ' cắt A' B ',C ' D ' theo BM C ' N BM C ' N
thứ tự tại K , I .Ta có : = Þ = . BD C ' A' BD NA'
Áp dụng định lý Thales ta có : B 'K C ' N MB BE = = = Þ KE / /BB '. A'K A'N MD EA
Từ đây sauy ra KE / /(BCC ' B ') (1).
Theo cách dựng ta suy ra : EF / /(BCC ' B ') (2). ( ì EFIK ï ) / /(BCC 'B') Từ (1) và (2) Þ í
Þ MN / / (BCC 'B'). ïMN / / î (EFIK )
Vậy MN luôn song song với mặt phẳng cố định, mặt phẳng đó là (BCC'B') Ví dụ 4.
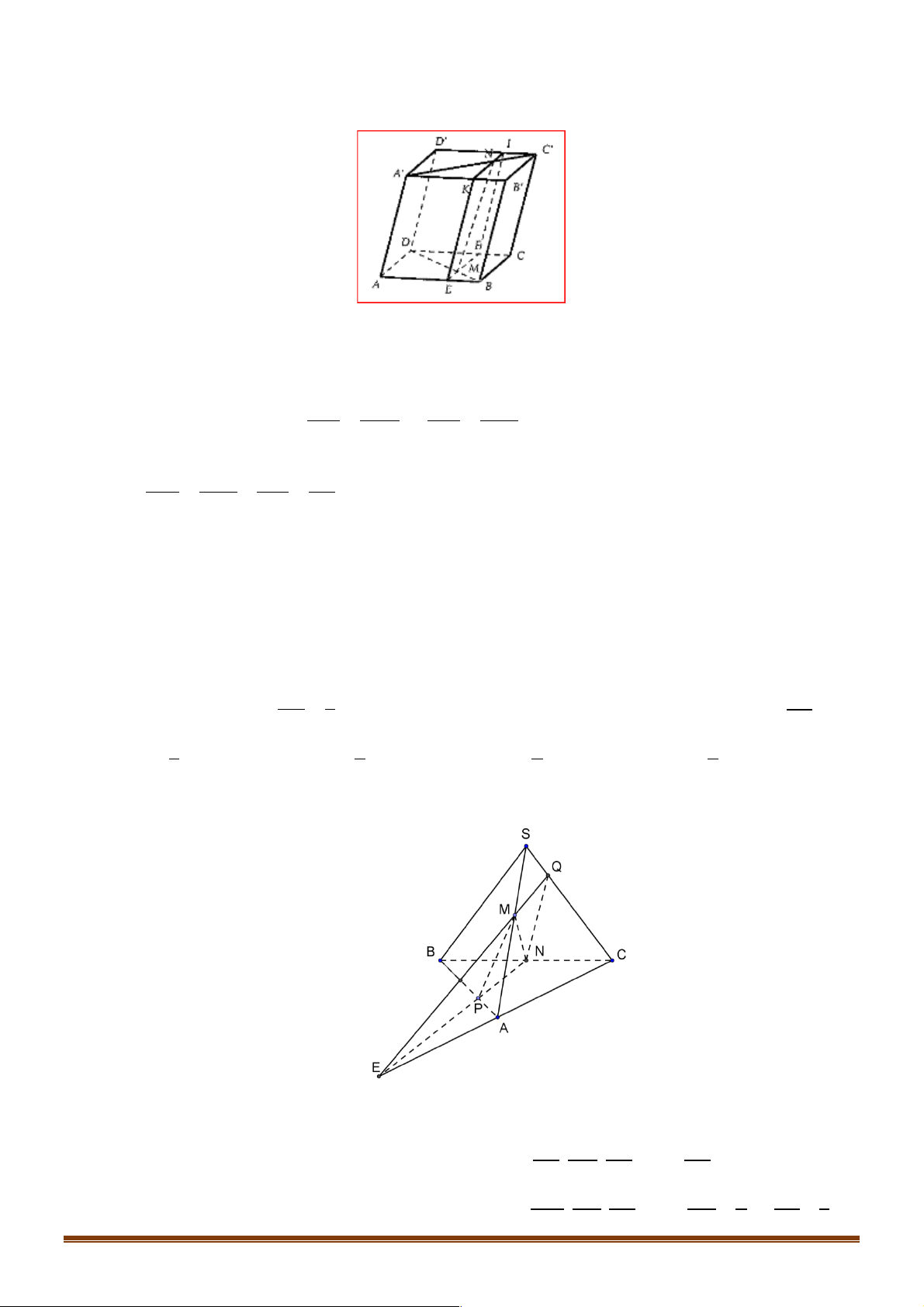
Cho hình chóp S.ABC. Gọi M, N lần lượt là trung điểm của SA và BC. P là điểm nằm trên AP 1 SQ cạnh AB sao cho
= . Gọi Q là giao điểm của SC với mặt phẳng (MNP) . Tính AB 3 SC 1 1 1 2 A. . B. . C. . D. . 3 6 2 3 Lời giải: Đáp án A.
Trong mặt phẳng ( ABC) , gọi E = NP Ç AC
Khi đó Q chính là giao điểm của SC với EM. AP BN CE CE
Áp dụng địnhlý Menelaus vào tam giác ABC ta có: . . =1Þ = 2 PB NC EA EA AM SQ CE SQ 1 SQ 1
Áp dụng địnhlý Menelaus vào tam giác SAC ta có: . . =1Þ = Þ = MS QC EA QC 2 SC 3 Trang 7 Ví dụ 5.
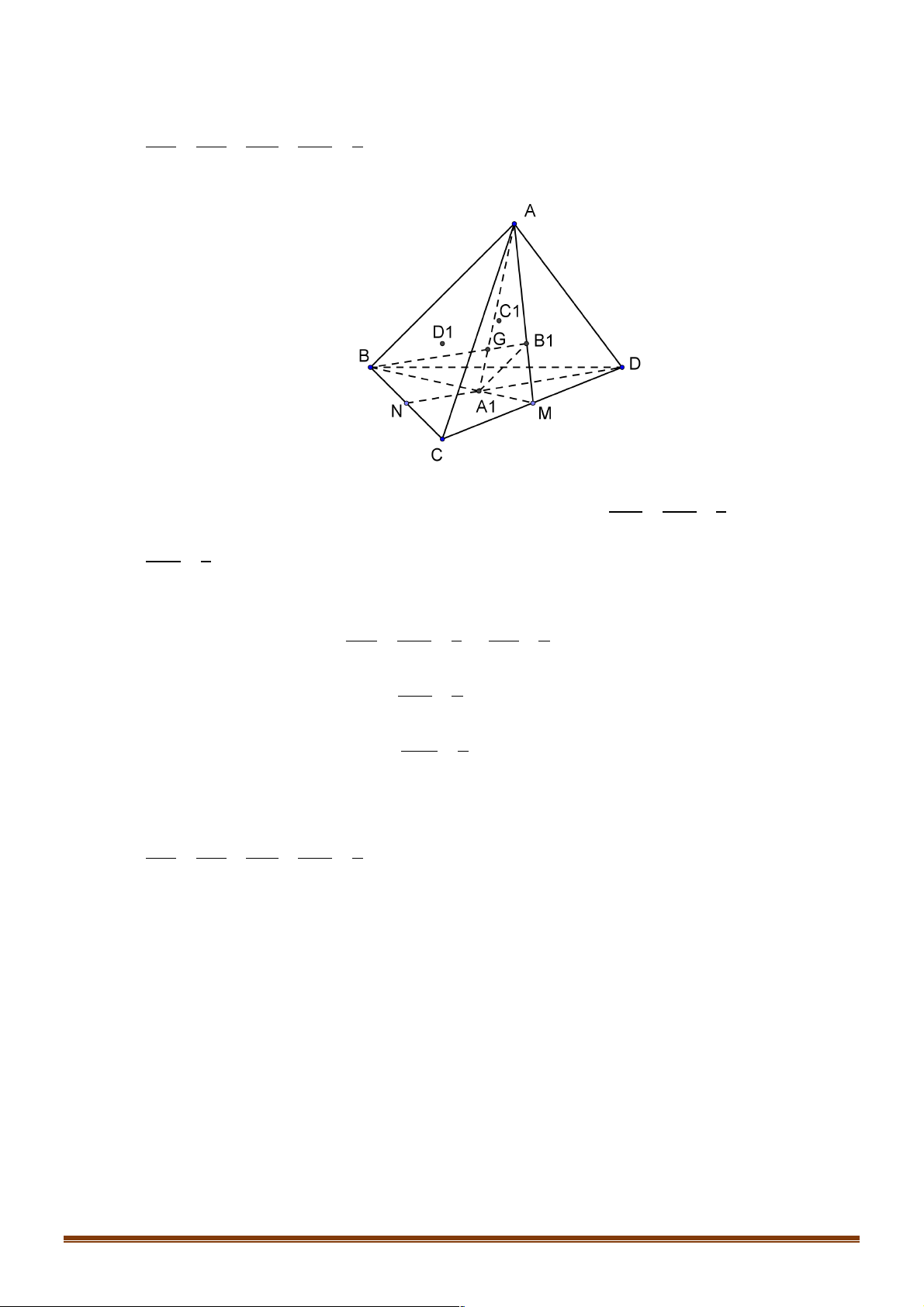
Cho tứ diện ABCD. Gọi A , B ,C , D tương ứng là trọng tâm của các tam giác BCD, ACD, 1 1 1 1
ABD và ABC. Chứng minh rằng AA , BB ,CC , DD đồng quy tại điểm G và ta có: 1 1 1 1 AG BG CG DG 3 = = = = AA BB CC DD 4 1 1 1 1 Lời giải:
Lưu ý: Điểm G được gọi là trọng tâm tứ diện ABCD MA MB 1
Gọi M là trung điểm CD. Theo tính chất trọng tâm ta có: 1 1 =
= Þ A B / / AB và 1 1 MB MA 3 A B 1 1 1 = AB 3
Trong mặt phẳng ( AMB) , gọi G là giao điểm của BB , AA 1 1 A G A B 1 AG 3
Theo định lý Thales ta có: 1 1 1 = = Þ = ( )1 GA AB 3 AA 4 1 ì AG ' 3
G ' = CC Ç AA , = ï 1 1 ï AA 4 Tương tự ta có: 1 í (2) AG" 3 G
ï '' = DD'Ç AA , = 1 ï AA 4 î 1 Từ ( )
1 và (2) suy ra G, G’, G” trùng nhau, tức là AA , BB ,CC , DD đồng quy tại điểm G và 1 1 1 1 ta có : AG BG CG DG 3 = = = = AA BB CC DD 4 1 1 1 1
Bài tập tương tự: Cho tứ diện ABCD . Gọi I, J , E, F, K, H tương ứng là các trung điểm của
AB,CD, AC, , BD ,
AD BC . Chứng minh rằng IJ, EF, KH đòng quy tại một điểm và điểm đồng
quy chính là trọng tâm G của tứ diện ABCD
C. BÀI TẬP RÈN LUYỆN KỸ NĂNG
Câu 1. Trong các mệnh đề sau mệnh đề nào sai?
A. Dùng nét đứt biểu diễn cho đường bị che khuất.
B. Hình biểu diễn của đường thẳng là đường thẳng.
C. Hình biểu diễn phải giữ nguyên qua hệ thuộc giữa điểm và đường thẳng..
D. Hình biểu diễn của hai đường cắt nhau có thể là hai đường song song.
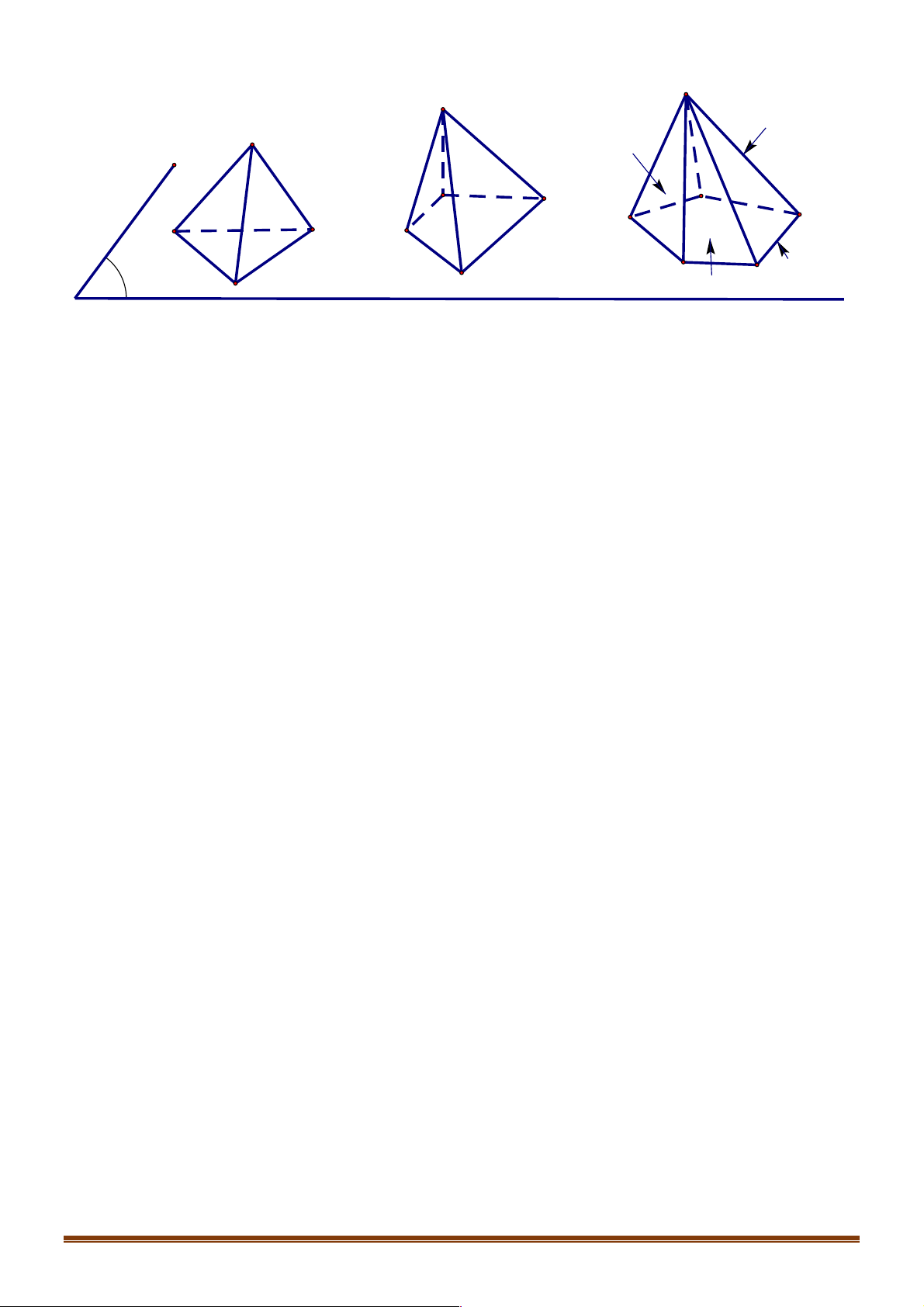
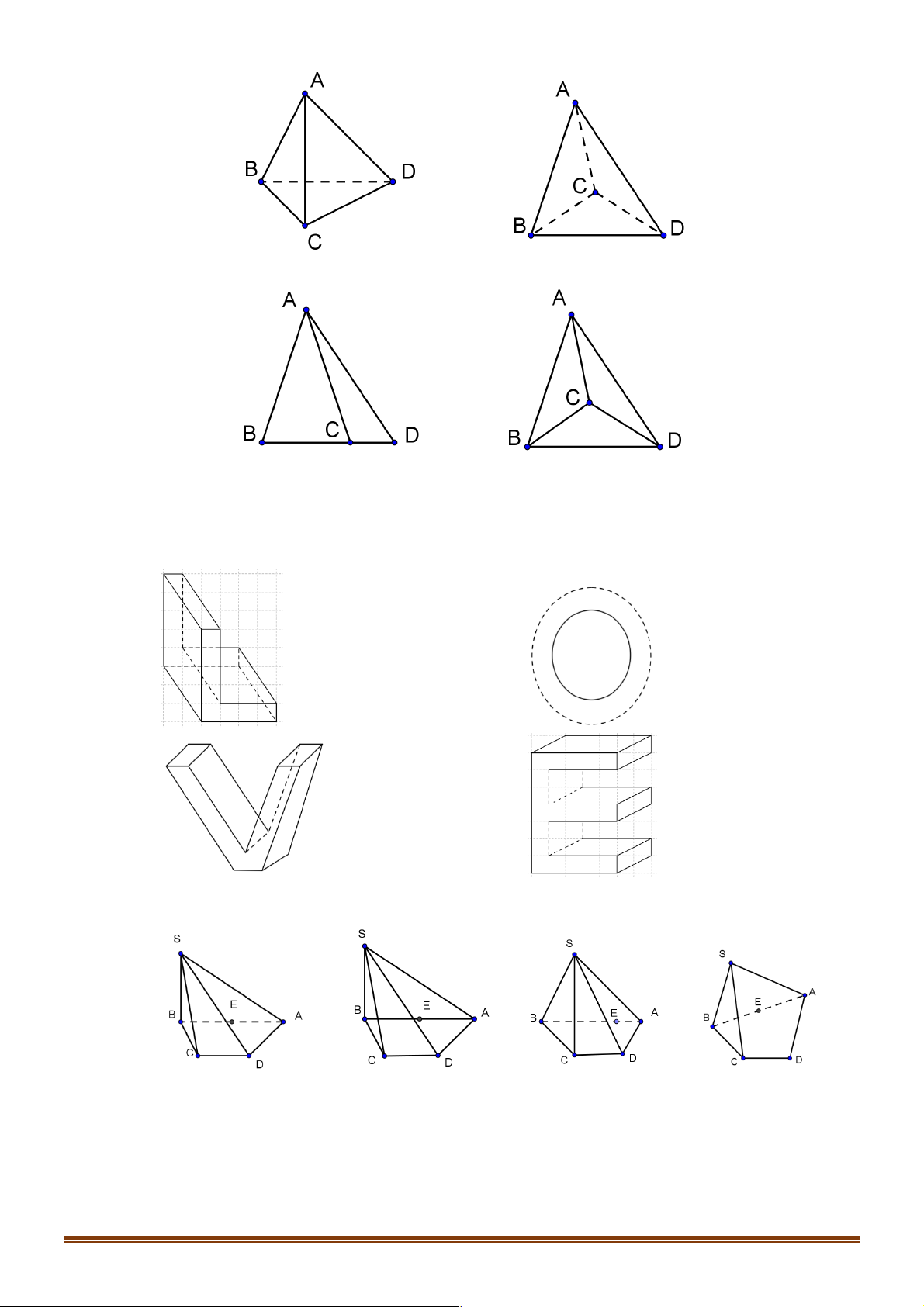
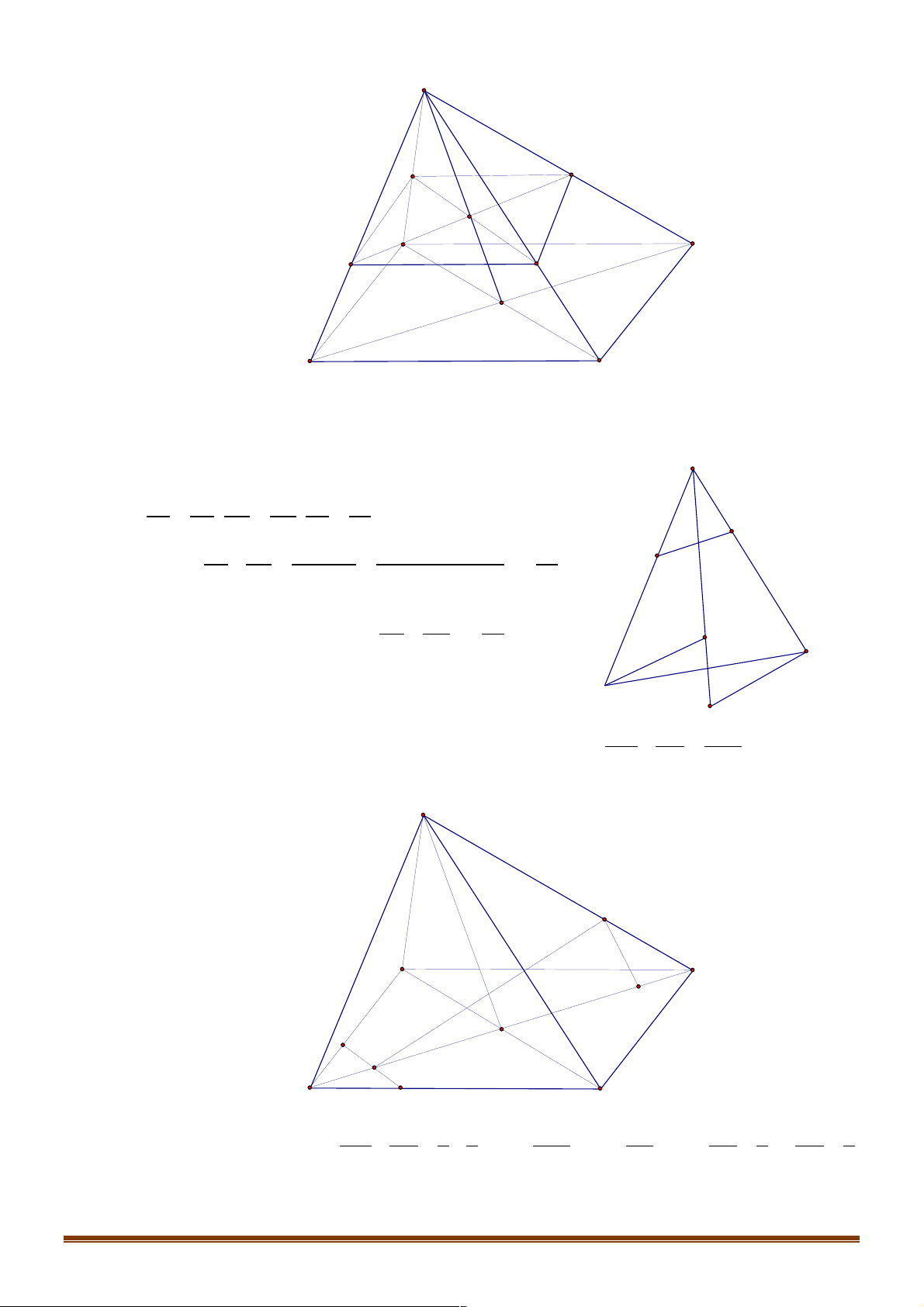
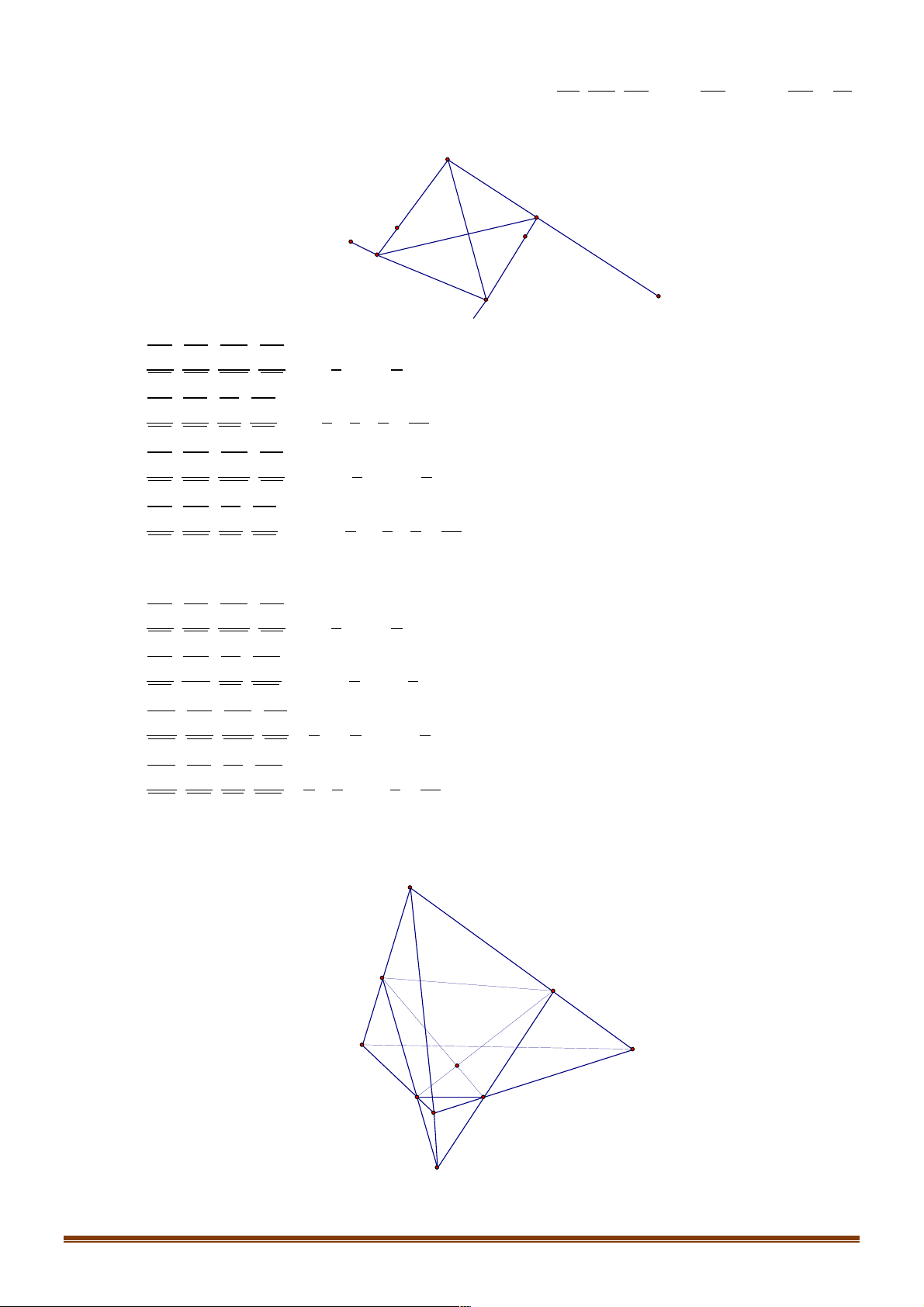
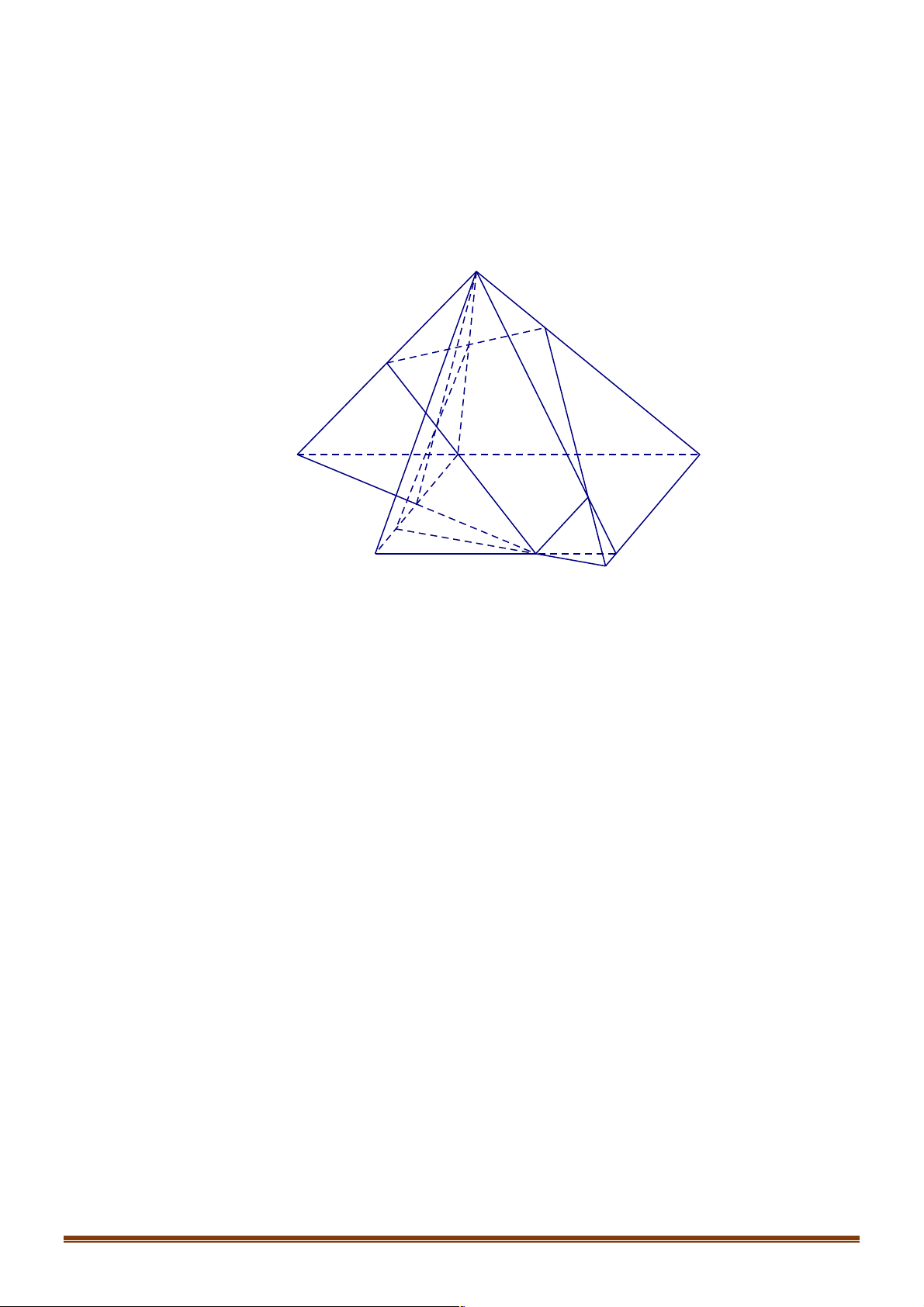
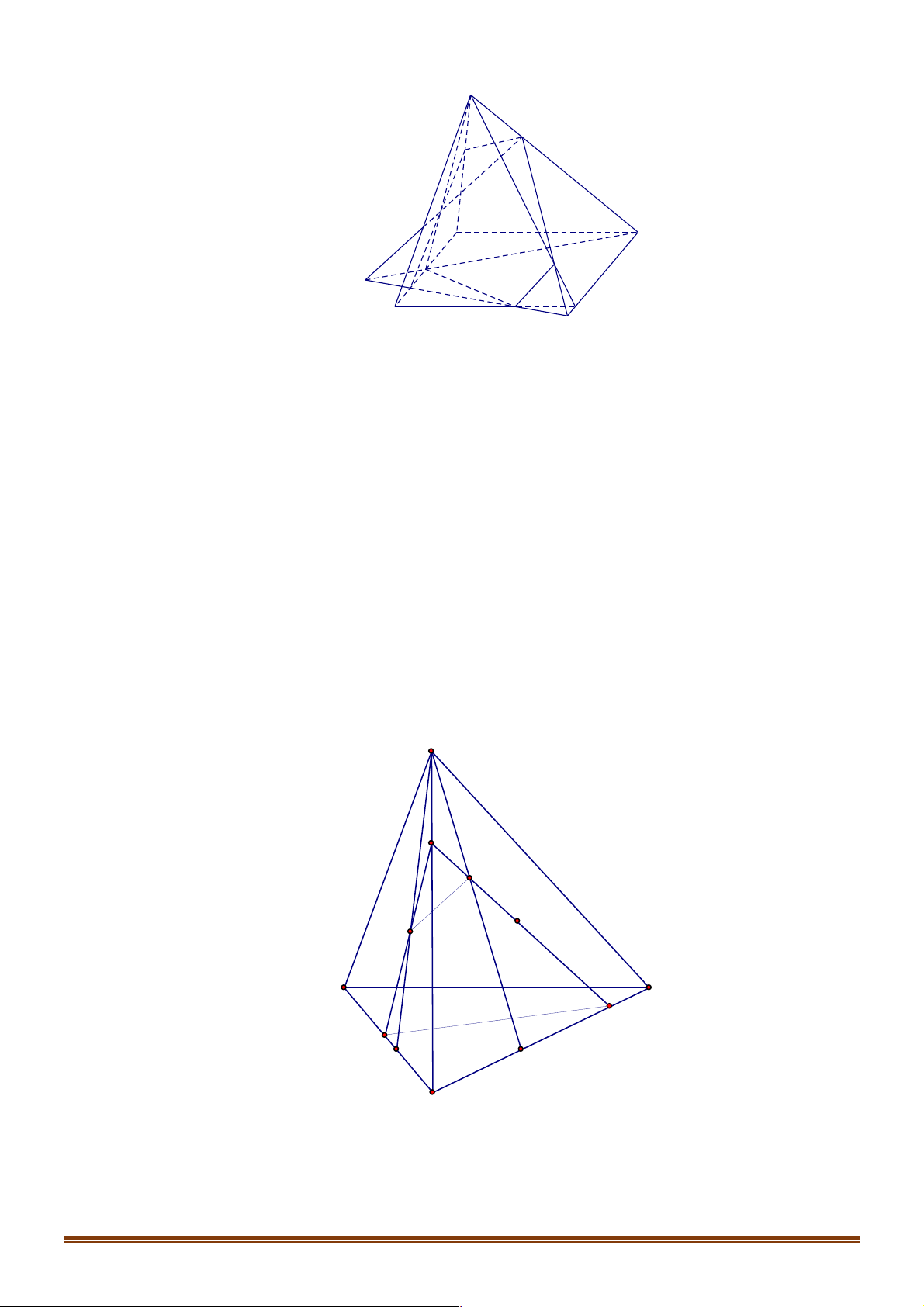
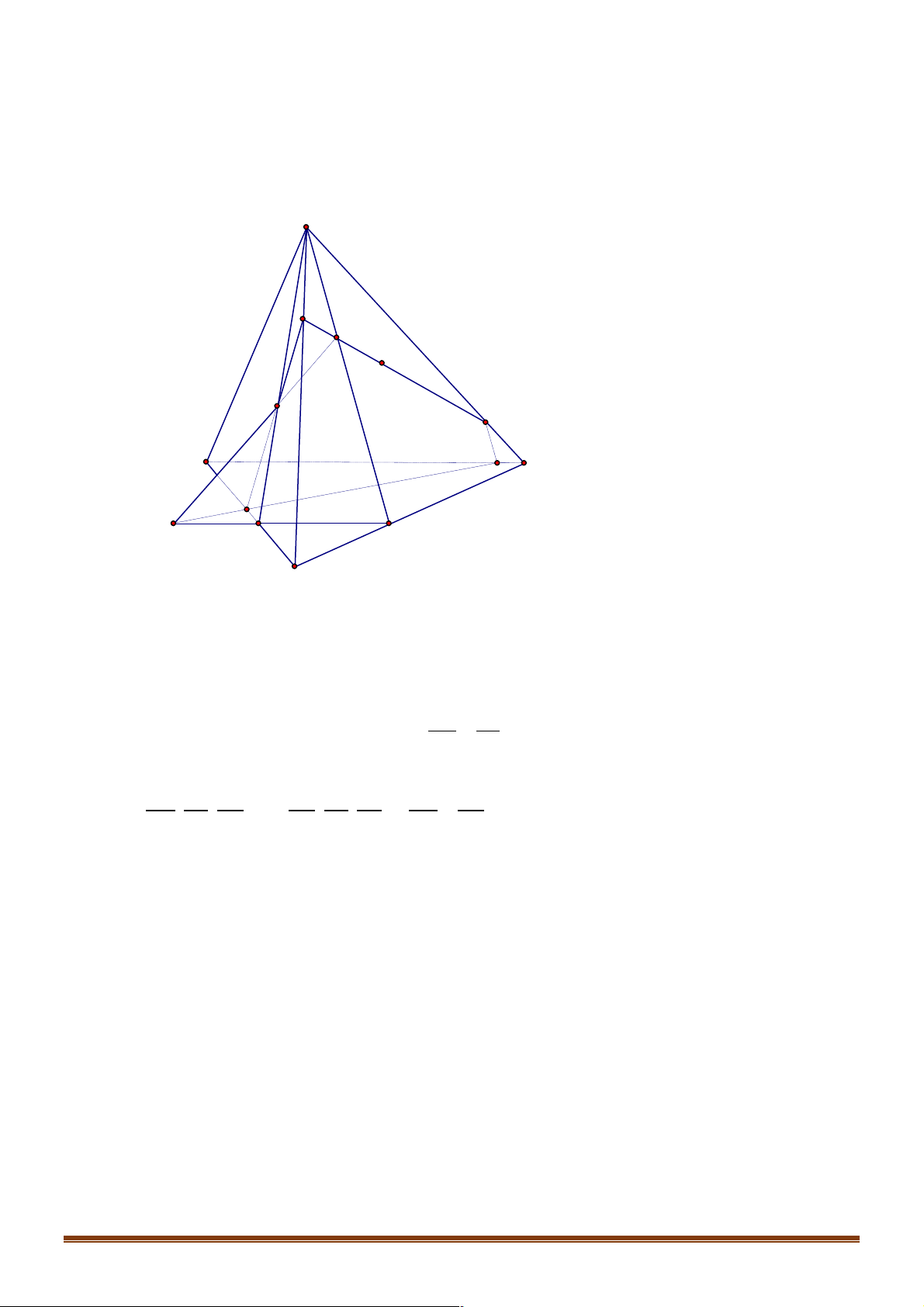
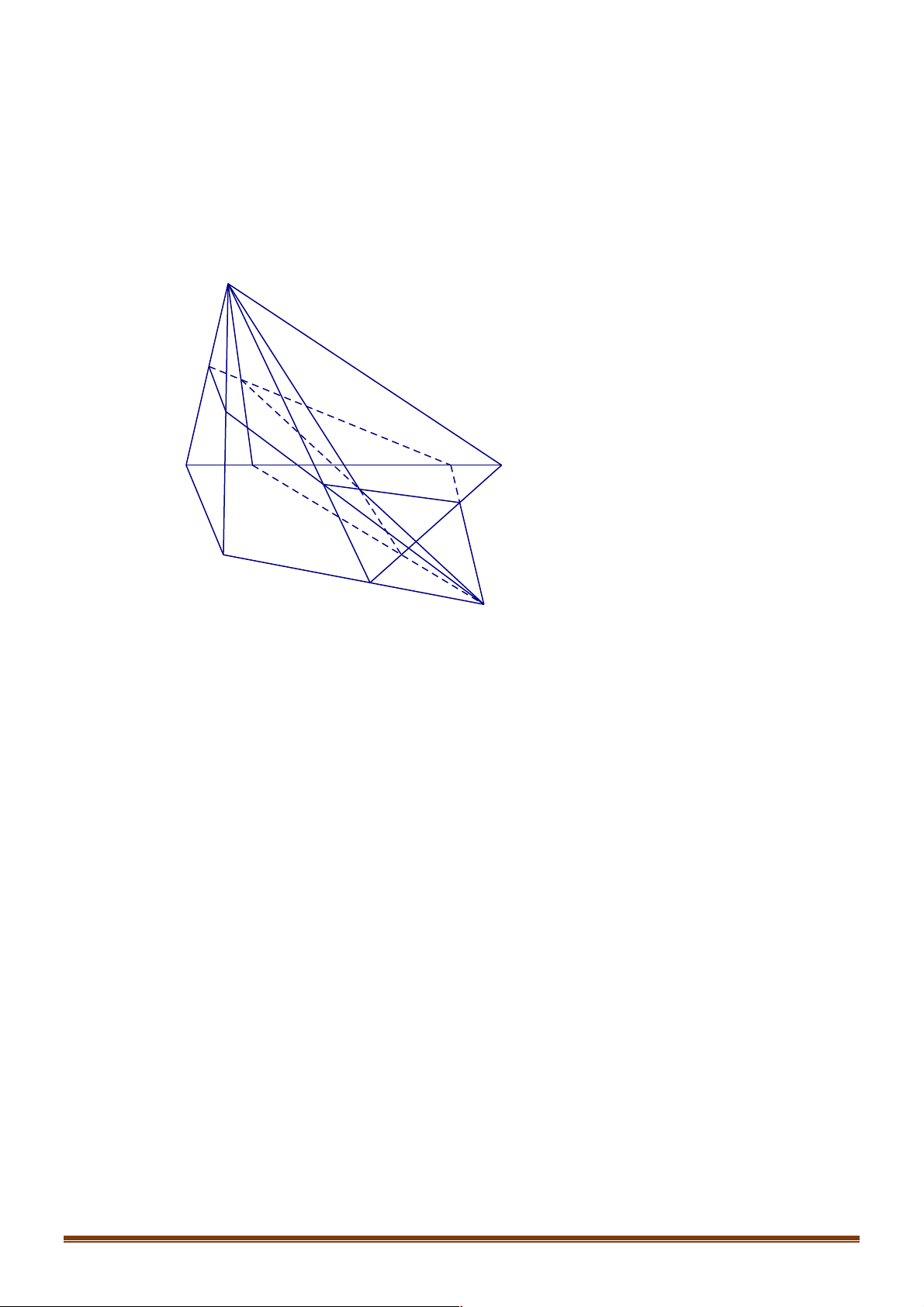
Câu 2. Trong các hình vẽ sau hình nào có thể là hình biểu diễn của một hình tứ diện? (Chọn câu đúng nhất) Trang 8 (I) (II ) (III) (IV )
A. (I ),(II ) ..
B. (I ),(II ),(III ),(IV ) .
C. (I ),(II ),(III ). D. (I ).
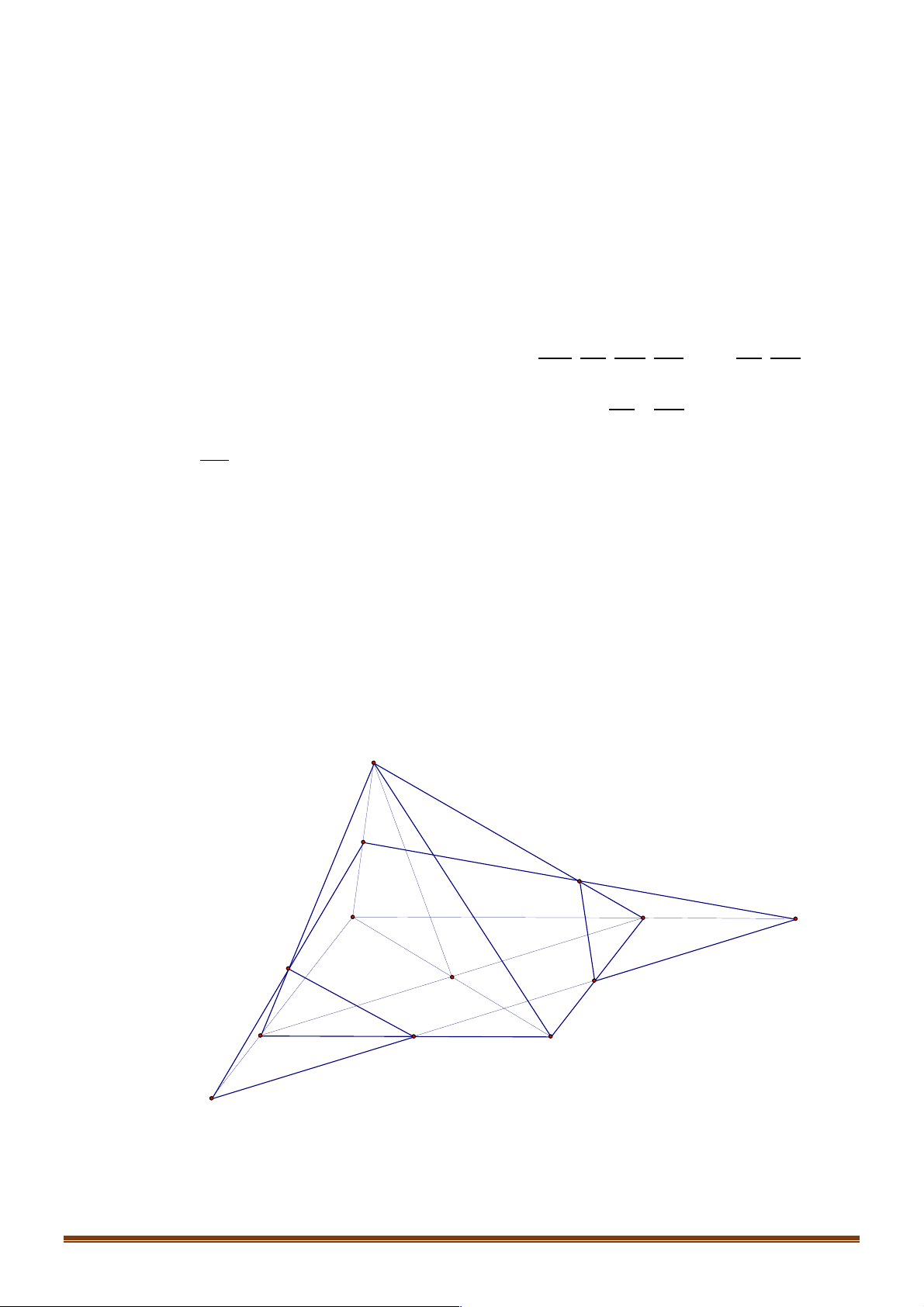
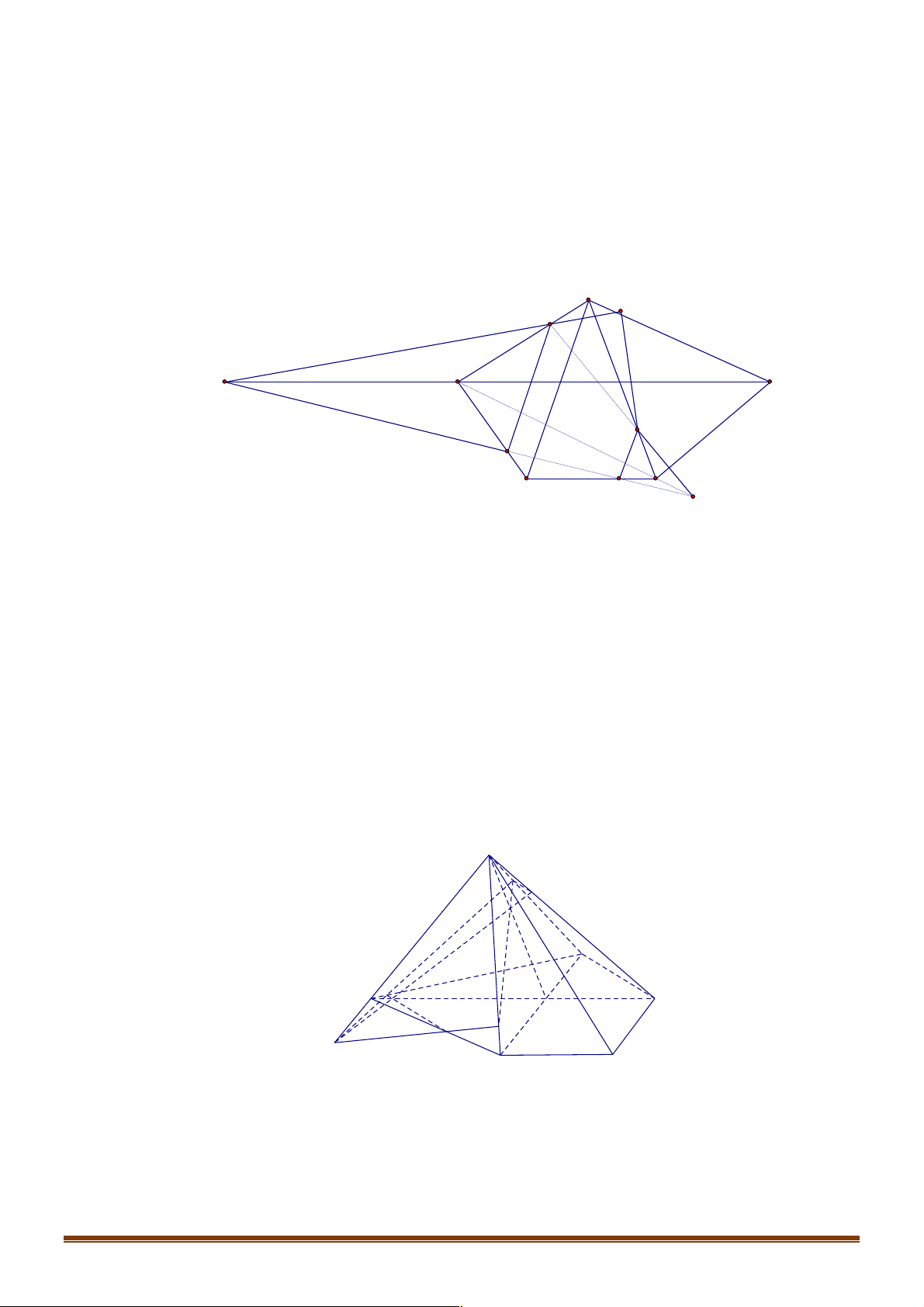
Câu 3. Hình nào sau đây vẽ đúng quy tắc? A. . B. . C. . D.
Câu 4. Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AB gấp đôi đáy nhỏ CD , E là
trung điểm của đoạn AB . Hình vẽ nào sau đây vẽ đúng quy tắc? A. . B. . C. . D.
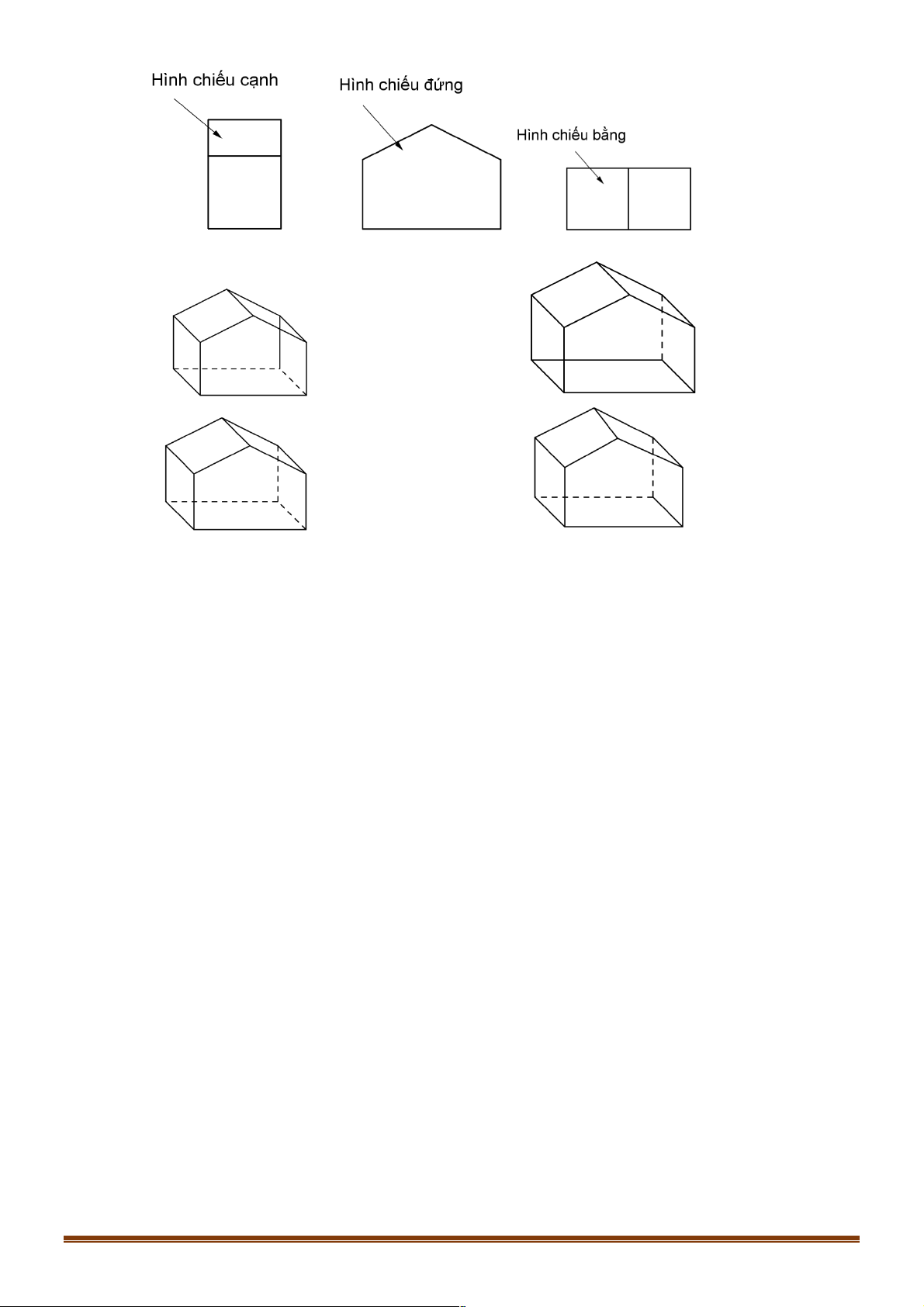
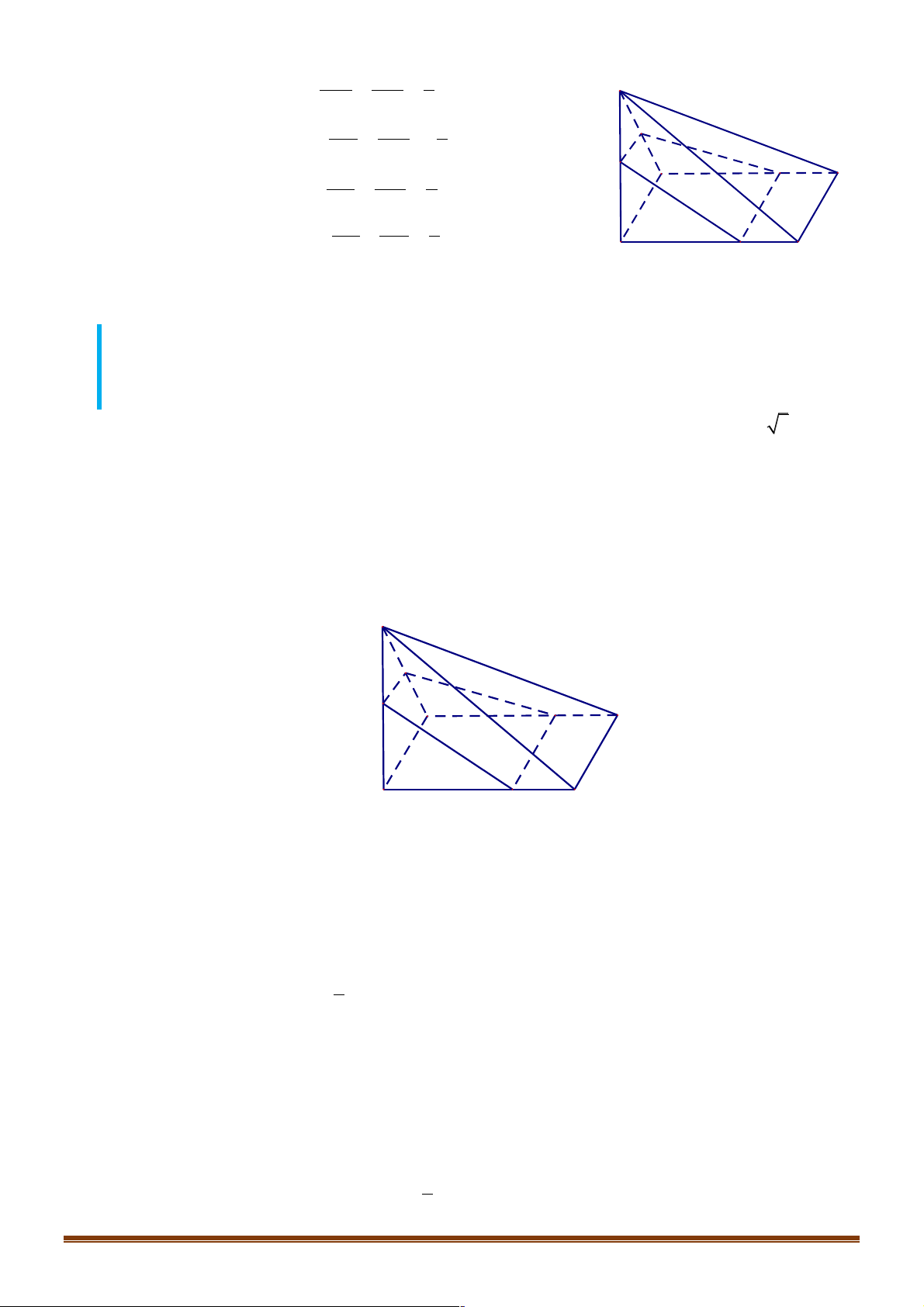
Câu 5. Một hình không gian có hình chiếu đứng (nhìn từ trước vào (có thể nhìn từ sau) để từ hình 3D
chuyển sang hình 2D) hình chiếu bằng (nhìn từ trên xuống) có thể nhìn từ dưới lên)), hình
chiếu cạnh (từ trái sang (có thể nhìn từ phải sang)) lần lượt được thể hiện như sau: Trang 9
Hãy vẽ hình biểu diễn của hình đó? A. . B. . C. . D.
Câu 6. Mệnh đề nào sau đây đúng?
A. Qua ba điểm xác định một và chỉ một mặt phẳng.
B. Qua ba điểm phân biệt xác định một và chỉ một mặt phẳng.
C. Qua ba điểm phân biệt không thẳng hàng xác định hai mặt phẳng phân biệt.
D. Qua ba điểm phân biệt không thẳng hàng xác định một và chỉ một mặt phẳng.
Câu 7. Xét các mệnh đề sau đây:
(I) Có một và chỉ một đường thẳng đi qua hai điểm phân biệt.
(II ) Có một và chỉ một mặt phẳng đi qua ba điểm phân biệt.
(III) Tồn tại bốn điểm không cùng thuộc một mặt phẳng.
(IV ) Nếu hai mặt phẳng có một điểm chung thì chúng còn có duy nhất một điểm chung khác nữa.
Số mệnh đề sai trong các mệnh đề trên là: A. 3. B. 1. C. 2. D. 4.
Câu 8. Cho n điểm phân biệt trong không gian (n > 4) .Biết rằng bốn điểm bất kỳ trong n điểm đã
cho cùng thuộc một mặt phẳng. Khẳng định nào sau đây đúng?
A. Tất cả n điểm thuộc cùng một mặt phẳng.
B. Có đúng n -1 điểm thuộc cùng một mặt phẳng.
C. Có đúng n - 2 điểm thuộc cùng một mặt phẳng.
D. Không tồn tại mặt phẳng nào chứa tất cả n điểm.
Câu 9. Trong các mệnh đề sau mệnh đề nào đúng?
A. Có đúng hai mặt phẳng cắt nhau theo một đường thẳng cho trước..
B. Hai mặt phẳng có một điểm chung duy nhất.
C. Hai mặt phẳng cùng chứa hai cạnh của một tam giác thì trùng nhau..
D. Có đúng hai mặt phẳng phân biệt đi qua ba điểm phân biệt..
Câu 10. Cho tứ giác lồi ABCD và điểm S không thuộc mặt phẳng ( ABCD) . Có bao nhiêu mặt phẳng
qua S và hai trong số bốn điểm ,
A B,C, D? A. 3. B. 4. C. 5. D. 6.
Câu 11. Cho năm điểm , A , B C, ,
D E phân biệt trong đó không có bốn điểm nào cùng nằm trên một mặt
phẳng. Hỏi có bao nhiêu mặt phẳng tạo bởi ba trong năm điểm đã cho ? Trang 10 A. 6. B. 10. C. 60. D. 8.
Câu 12. Cho n (n ³ 3,nΕ ) đường thẳng phân biệt đồng quy tại O trong đó không có ba đường thẳng
nào cùng năm trên một mặt phẳng. Có bao nhiêu mặt phẳng đi qua hai trong số n đường thẳng trên? n! n! n! A. . B. . C. . D. n .! 2(n - 2)! (n-2)! 2
Câu 13. Cho mặt phẳng (a ) và hai đường thẳng a,b cắt nhau cùng nằm trong mặt phẳng (a ) . Gọi A
là một điểm thuộc đường thẳng a nhưng không thuộc đường thẳng b và P là một điểm nằm
ngoài (a ). Khẳng định nào sau đây đúng:
A. PA và b chéo nhau.
B. PA và b song song .
C. PA và b cắt nhau.
D. PA và b trùng nhau.
Câu 14. Cho tứ diện ABCD, I, J lần lượt là trung điểm của AD và BC . Khẳng định nào sau đây đúng?
A. AJ, BI song song . B. AJ, BI trùng nhau. C. AJ, BI cắt nhau D. AJ, BI chéo nhau
Câu 15. Cho hình chóp SABCD có đáy ABCD là một tứ giác ( AB không song song CD ). Gọi M là
trung điểm của SD , N là điểm nằm trên cạnh SB sao cho SN = 2NB,O là giao điểm của
AC và BD . Cặp đường thẳng nào sau đây cắt nhau:
A. SO và AD .
B. MN và SO .
C. MN và SC
D. SA và BC .
Câu 16. Cho bốn điểm ,
A B,C, D không cùng nằm trong một mặt phẳng. Trên AB, AD lần lượt lấy các
điểm M và N sao cho MN cắt BD tại I . Điểm I không thuộc mặt phẳng nào sau đây: A. ( ACD). B. (BCD). C. (CMN ) . D. ( ABD).
Câu 17. Cho tứ diện ABCD . Gọi M , N lần lượt là trung điểm của CD, AB . Khi đó BC và MN là hai đường thẳng: A. Chéo nhau.
B. Có hai điểm chung. C. Song song D. Cắt nhau
Câu 18. Cho tứ diện ABCD . Gọi M là trung điểm cạnh AC, N là điểm thuộc cạnh AD sao cho AN = 2N .
D O là một điểm thuộc miền trong của tam giác BCD . Mệnh đề nào sau đây là mệnh đề đúng?
A. Mặt phẳng (OMN ) chứa đường thẳng AB
B. Mặt phẳng (OMN ) đi qua giao điểm của hai đường thẳng MN và CD.
C. Mặt phẳng (OMN ) đi qua điểm A .
D. Mặt phẳng (OMN )chứa đường thẳng CD .
Câu 19. Ba điểm phân biệt cùng thuộc hai mặt phẳng phân biệt thì :
A. Cùng thuộc một đường tròn
B. Cùng thuộc một đường thẳng
C. Cùng thuộc một eliP
D. Cùng thuộc một tam giác.
Câu 20. Cho hình chóp S.ABCD có đáy là hình thang ABCD ( AB là đáy lớn, CD là đáy nhỏ). Khẳng định nào sau đây sai:
A. Hình chóp S.ABCD có bốn mặt bên..
B. Giao tuyến của hai mặt phẳng (SAB) và (SCD) là SK trong đó K là một điểm thuộc mặt phẳng ( ABCD) .
C. Giao tuyến của hai mặt phẳng (SAC) và (SBD) là SO trong đó O là giao điểm của hai
đường thẳng AC và BD
D. Giao tuyến của hai mặt phẳng (SAD) và (SBC) là SI trong đó I là giao điểm của AD và BC .
Câu 21. Cho hình chóp S.ABCD có đáy ABCD là một tứ giác ( AB không song song CD ). Gọi M là
trung điểm của SD, N là điểm nằm trên cạnh SB sao cho SN = 2NB,O là giao điểm của AC Trang 11
và BD . Giả sử đường thẳng d là giao tuyến của (SAB) và (SCD) . Nhận xét nào sau đây là sai:N
A. d cắt CD .
B. d cắt MN .
C. d cắt AB .
D. d cắt SO .
Câu 22. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành (BC / / AD) .Mặt phẳng (P) di
động chứa đường thẳng AB và cắt các đoạn SC, SD lần lượt tại E, F . Mặt phẳng (Q) di
động chứa đường thẳng CD và cắt ,
SA SB lần lượt tại G, H.I là giao điểm của AE, BF; J là
giao điểm của CG, DH . Xét các mệnh đề sau: ( )
1 Đường thẳng EF luôn đi qua một điểm cố định..
(2) Đường thẳng GH luôn đi qua một điểm cố định.
(3) Đường thẳng IJ luôn đi qua một điểm cố dịnh.
Có bao nhiêu mệnh đề đúng? A. 0 . B. 1. C. 2 . D. 3 .
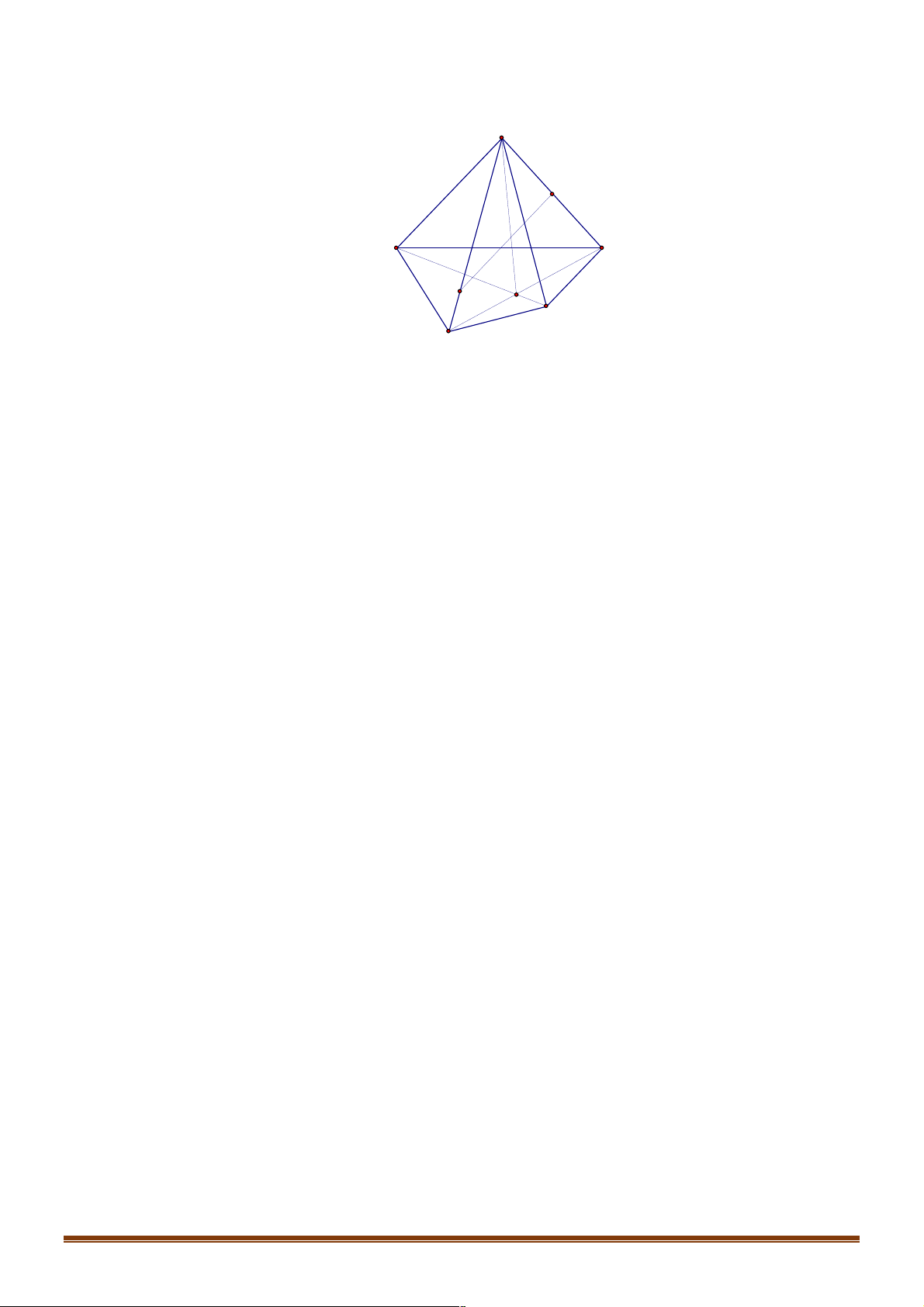
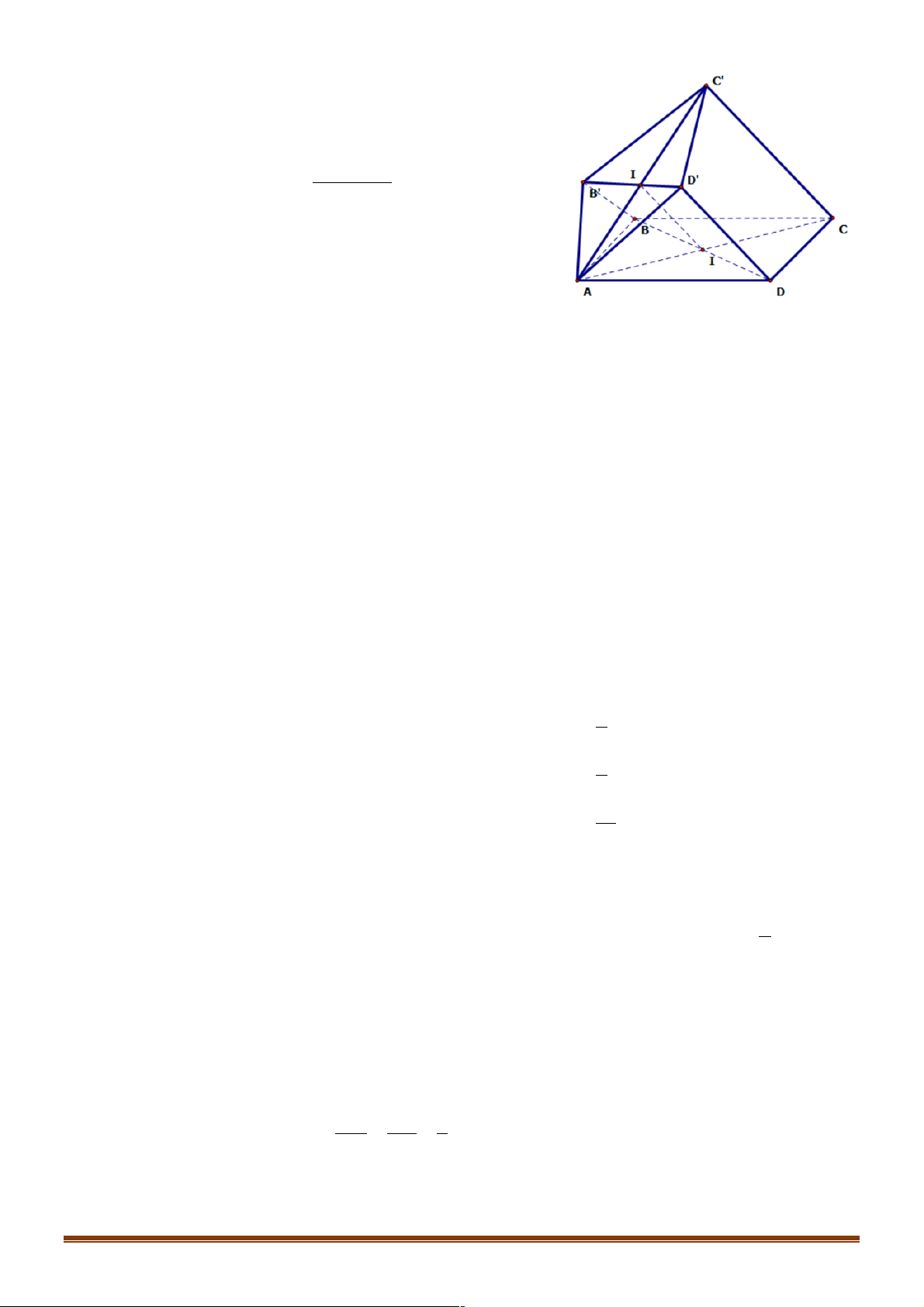
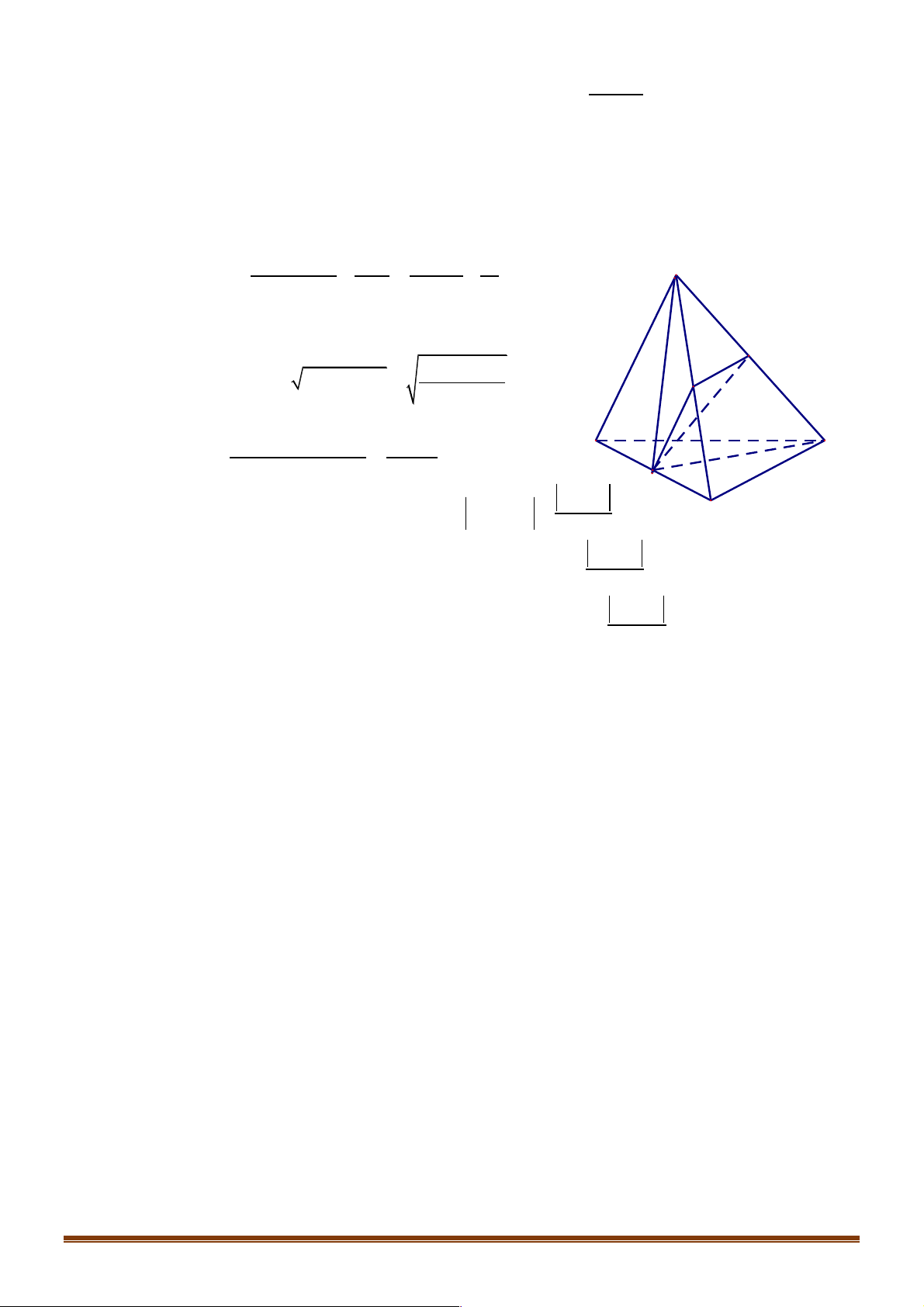
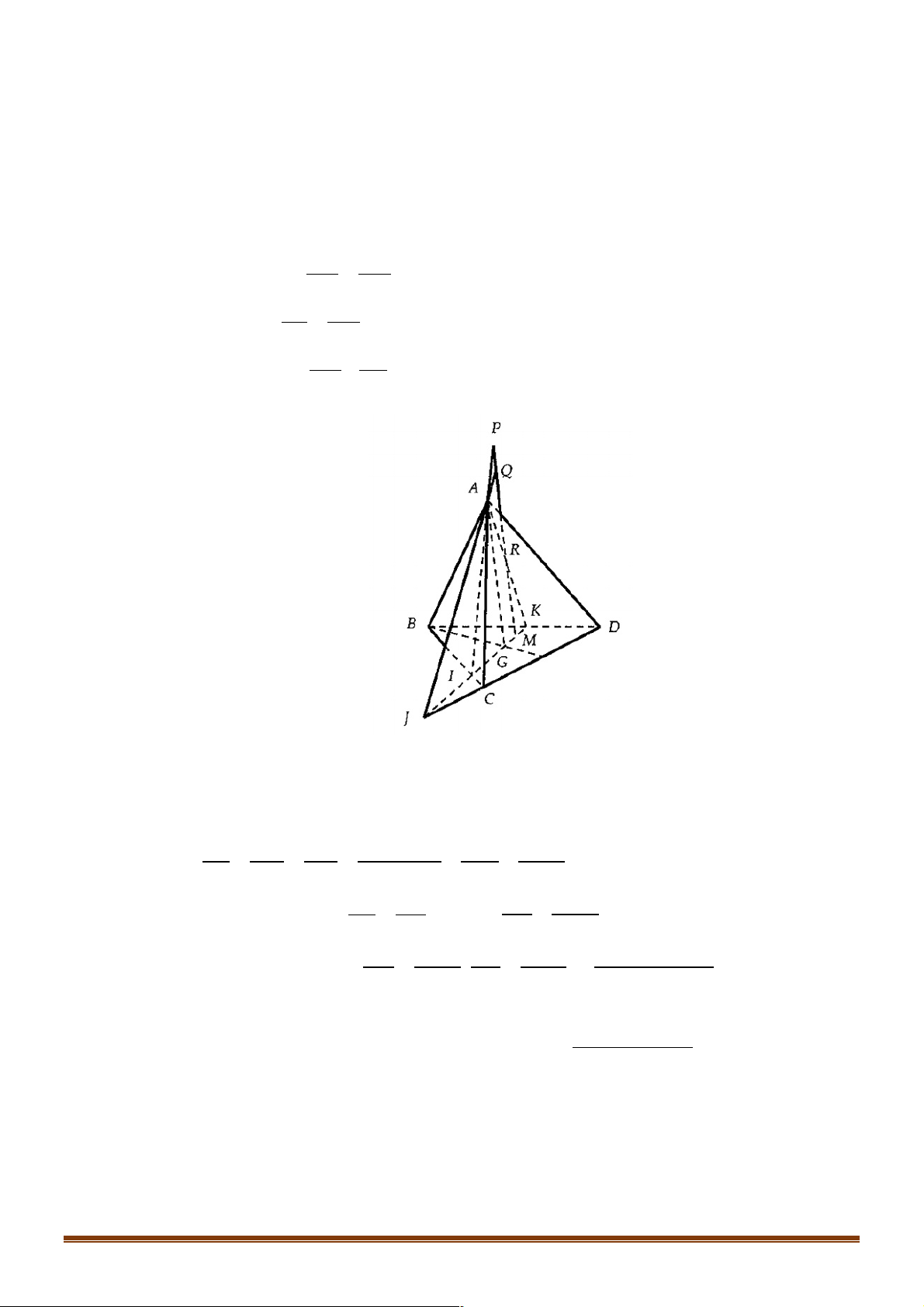
Câu 23. Cho tứ diện đều ABCD có các cạnh bằng a . Gọi E là trung điểm AB , F là điểm thuộc
cạnh BC sao cho BF = 2FC,G là điểm thuộc cạnh CD sao cho CG = 2GD . Tính độ dài
đoạn giao tuyến của mặt phẳng (EFG) với mặt phẳng ( ACD) của hình chóp ABCD theo a . 19 a 141 a 34 +15 3 a 34 -15 3 A. a. B. . C. . D. . 15 30 15 15
Câu 24. Cho tứ diện ABCD, E nằm trên đoạn BC sao cho BC = 3EC, F là điểm nằm trên BD sao cho
CD = 3DF . Gọi G là giao điểm của BF và DE . Giao tuyến của hai mặt phẳng ( ACG) và (ABD) là: !!!" !!!"
A. AH trong đó H thuộc BD sao cho BH = 4 - HD !!!" 1 !!!"
B. AH trong đó H thuộc BD sao cho BH = HD 4 !!!" !!!"
C. AH trong đó H thuộc BD sao cho BH = 4HD !!!" 1 !!!"
D. AH trong đó H thuộc BD sao cho BH = - HD 4
Câu 25. Cho tứ diện SABC có AB = ,
c BC = a, AC = . b ,
AD BE,CF là các đường phân giác trong của
tam giác ABC . Giao tuyến của hai mặt phẳng (SBE) và (SCF ) là: !!" b + c !!"
A. SI trong đó I thuộc AD sao cho AI = ID a !!" b + c !!"
B. SI trong đó I thuộc AD sao cho AI = - ID a !!" a !!"
C. SI trong đó I thuộc AD sao cho AI = ID b + c !!" -a !!"
D. SI trong đó I thuộc AD sao cho AI = ID b + c
Câu 26. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Gọi M , N, P lần lượt là SH
trung điểm của AB, AD và SO . Gọi H là giao điểm của SC với (MNP) . Tính ? SC 1 1 3 2 A. . B. . C. . D. . 3 4 4 3 Trang 12
Câu 27. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M , N lần lượt là trung điểm
của AD và CD . Trên đường thẳng DS lấy điểm P sao cho D là trung điểm SP . Gọi R là SR
giao điểm của SB với mặt phẳng (MNP) . Tính ? SB 1 1 3 2 A. . B. . C. . D. . 3 4 4 5
Câu 28. Cho tứ diện SABC, E, F lần lượt thuộc đoạn AC, .
AB Gọi K là giao điểm của BE và CF .
Gọi D là giao điểm của (SAK ) với BC . Mệnh đề nào sau đây đúng? AK BK CK AK BK CK A. + + ³ 6. B. + + £ 6. KD KE KF KD KE KF AK BK CK AK BK CK C. + + > 6. D. + + < 6. KD KE KF KD KE KF
Câu 29. Cho hình chóp S.ABC , D ,
D M lần lượt là trung điểm của BC, AD . Gọi E là giao điểm của ( MF ME
SBM ) với AC, F là giao điểm của (SCM ) với AB . Tính + ?
CM - ME BM - ME 1 1 A. 1. B. 2 . C. D. . 2 3
Câu 30. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Một mặt phẳng (a ) cắt các cạnh bên ,
SA SB, SC, SD tương ứng tại các điểm E, F, G, H . Gọi I = AC Ç BD, J = EG Ç SI .
Mệnh đề nào sau đây đúng? SA SC SB SD SA SC SI A. + = + . B. + ³ 2 . SE SG SF SH SE SG SJ SA SC SB SD SB SD SI C. + > + . D. + ³ 2 . SE SG SF SH SF SH SJ
Câu 31. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Gọi M , N lần lượt là các BM 2 NC 1
điểm nằm trên cạnh AB, AD sao cho = ,
= . Gọi P là điểm trên cạnh SD sao MA 3 BN 2 PD 1 SJ cho
= . J là giao điểm của SO với (MNP) . Tính ? PS 5 SO 10 1 3 5 A. . B. . C. . D. . 11 11 4 2
Câu 32. Cho tứ diện ABCD . E là điểm thuộc đoạn AB sao cho EA = 2 .
EB F,G là các đei63m thuộc !!!" !!!" !!!" !!!"
đường thẳng BC sao cho FC = 5FB,GC = 5 - G .
B H , I là các điểm thuộc đường thẳng CD !!!" !!!" !!" !!" sao cho HC = 5 - HD, ID = 5
- IC, J thuộc tia đối của tia DA sao cho D là trung điểm của AJ .
Trong các mệnh đề sau, mệnh đề nào đúng?
A. Bốn điểm E, F, H, J đồng phẳng
B. Bốn điểm E, F, I, J đồng phẳng.
C. Bốn điểm E,G, H, I đồng phẳng.
D. Bốn điểm E,G, I, J đồng phẳng.
Câu 33. Cho tứ diện ABC ,
D E,U là điểm thuộc đường thẳng AB sao cho !!!" !!!" !!!" !!!" EA = 2
- EB, 5UA = 4U .
B F,G là các điểm thuộc đường thẳng BC sao cho !!!" !!!" !!!" !!!"
FC = 5FB, GC = 2 - G .
B H , I là các điểm thuộc đường thẳng CD sao cho !!!" !!!" !!" !!" HC = 5
- HD, ID = 5IC.J, K là các điểm nằm trên đường thẳng DA sao cho !!" !!!" !!!" !!!"
JA = 2JD, KD = 5KA . Bốn điểm nào dưới đây lập nên một tứ diện?
A. E, F, H, J .
B. E,G, I, K .
C. U ,G, H , J .
D. U, F, I, K .
Câu 34. Cho tứ diện ABCD có M , N lần lượt là trung điểm của AB,CD và P là điểm thuộc cạnh BC
( P không là trung điểm BC ). Trang 13
a) Thiết diện của tứ diện bị cắt bởi (MNP) là: A. Tam giác B. Tứ giác C. Ngũ giác. D. Lục giác.
b) Gọi Q là giao điểm của (MNP) với AD, I là giao điểm của MN với PQ . Mệnh đề nào sau đây đúng? A. S = 2S . B. S = 2S . C. . S = 4S D. S = 4S . MNPQ MPN MNPQ MPQ MNPQ MPI MNPQ PIN
Câu 35. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, E là trung điểm của , SA F,G lần
lượt là các điểm thuộc cạnh BC,CD . Thiết diện của hình chóp cắt bởi (MNP) là: A. Tam giác B. Tứ giác C. Ngũ giác. D. Lục giác.
Câu 36. Cho hình chóp S.ABCD có đáy ABCD là hình thang với đáy lớn AD, E là trung điểm của cạnh ,
SA F,G là các điểm thuộc cạnh SC, AB ( F không là trung điểm của SC ). Thiết diện
của hình chóp cắt bởi mặt phẳng (EFG) là: A. Tam giác B. Tứ giác C. Ngũ giác. D. Lục giác.
Câu 37. Cho hình chóp SA A ...A với đáy là đa giác lồi A A ...A n ³ 3,nΕ . 1 2 n ( ) Trên tia đối của tia 1 2 n
A S lấy điểm B , B ,...B là các điểm nằm trên cạnh SA , SA . Thiết diện của hình chóp cắt bởi 1 1 2 n 2 n mặt phẳng (B B B 1 2 n ) là:
A. Đa giác n - 2 cạnh. B. Đa giác n -1 cạnh. C. Đa giác n cạnh.
D. Đa giác n +1 cạnh.
Câu 38. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, E là điểm thuộc cạnh bên SD sao
cho SD = 3SE . F là trọng tâm tam giác SAB,G là điểm thay đổi trên cạnh BC. Thiết diện cắt
bởi mặt phẳng (EFG) là: A. Tam giác B. Tứ giác C. Ngũ giác. D. Lục giác.
Câu 39. Cho hình chóp S.ABCD có đáy ABCD là hình thang với đáy lớn AD, E là một điểm thuộc
mặt bên (SCD) . F, G lần lượt là các điểm thuộc cạnh AB và SB. Thiết diện của hình chóp
S.ABCD cắt bởi mặt phẳng (EFG) có thể là:
A. Tam giác, tứ giác . B. Tứ giác, ngũ giác. C. Tam giác, ngũ giác. D. Ngũ giác. !!!" !!!"
Câu 40. Cho hình chóp S.ABCD, E là trung điểm của SB, F thuộc SC sao cho 3SF = 2SC, G là một
điểm thuộc miền trong tam giác SAD . Thiết diện của hình chóp cắt bởi mặt phẳng (EFG) là:
A. Tam giác, tứ giác . B. Tứ giác, ngũ giác. C. Tam giác, ngũ giác. D. Ngũ giác.
Câu 41. Cho hình tứ diện ABCD có tất cả các cạnh bằng 6a . Gọi M, N lần lượt là trung điểm của CA,
CB. P là điểm trên cạnh BD sao cho BP = 2PD . Diện tích S thiết diện của tứ diện ABCD bị cắt bởi (MNP) là: 2 5a 51 2 5a 147 2 5a 147 2 5a 51 A. S = . B. S = . C. S = . D. S = . 4 4 2 2
Câu 42. Cho tứ diện ABCD có cạnh bằng a. Trên tia đối của các tia CB, DA lần lượt lấy các điểm E, F
sao cho CE = a, DF = a . Gọi M là trung điểm của đoạn AB. Diện tích S thiết diện của tứ diện
ABCD cắt bởi mặt phẳng (MEF ) là: 2 a 33 2 a 2 a 2 a 33 A. S = . B. S = . C. S = . D. S = . 18 3 6 9
Câu 43. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm SQ
của AB, AD, SC. Gọi Q là giao điểm của SD với (MNP) . Tính ? SD 1 1 3 2 A. . B. . C. . D. . 3 4 4 3
Câu 44. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N , P lần lượt là SH
trung điểm của AB, AD và SO. Gọi H là giao điểm của SC với (MNP) . Tính ? SC Trang 14 1 1 3 2 A. . B. . C. . D. . 3 4 4 3
Câu 45. Cho hình chóp SABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của
AD và CD. Trên đường thẳng DS lấy điểm P sao cho D là trung điểm của SP. Gọi R là giao SR
điểm của SB với mặt phẳng (MNP) . Tính ? SB 1 1 3 2 A. . B. . C. . D. . 3 4 4 5 Trang 15
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1. Đáp án D. Câu 2. Đáp án B. Câu 3. Đáp án A. Câu 4. Đáp án A.
Theo quy tắc vẽ hình, các đoạn thẳng song song được vẽ bằng các đoạn thẳng song song nên
đáp án D bị loại. Trung điểm được vẽ ở chính giữa đoạn nên ý C bị loại. Nét khuất được vẽ bởi
nét đứt đoạn, nét với góc nhìn này với đáp án B thì hoặc AB đứt đoạn hoặc SC, SD đứt đoạn.
Do đó chỉ có đáp án A đúng. Câu 5. Đáp án C.
Hình A, B, D sai khi vẽ các đường không nhìn thấy bằng nét liền. Câu 6. Đáp án D.
- Đáp án A, B sai, các em có thể lấy ví dụ ba điểm ,
A B,C phân biệt , thẳng hàng , thì có vô số
mặt phẳng đi qua ba điểm đó.
- Đáp án C sai, vì theo tính chất thừa nhận, ba điểm phân biệt không thẳng hàng có duy nhất một mp đi qua ba điểm. Câu 7. Đáp án B.
Theo các tính chất thừa nhận, ta thấy (I), (II), (III) đúng và nếu hai mp có 1 điểm chung thì
chúng còn vô số điểm chung khác nữa. Điều đó đồng nghĩa với nhận xét (IV) là sai. Như vậy có 1 quy tắc sai. Câu 8. Đáp án A.
- Nếu n điểm đã cho cùng thuộc một đường thẳng thì hiển nhiên n điểm thuộc cùng 1 mp. Do
đó loại được đáp án B, C, D.
- Nếu n điểm đã cho không cùng thuộc một đường thẳng thì trong chúng phải có 3 điểm không
thẳng hàng. Khi đó ba điểm này xác định 1 mp, kí hiệu là mp (P) . Lấy một điểm trong n - 3
điểm còn lại thì theo giả thiết điểm đó phải thuộc mp (P) . Suy ra tất cả các điểm đã cho cùng thuộc 1 mp. Câu 9. Đáp án C.
Một đường thẳng cho trước có vô số mp đi q ua.
Hai mp đã có 1 điểm chung thì có vô số điểm chung khác nữa. Còn có trường hợp 2 mp không có điểm chung nào.
Có duy nhất 1 mp đi qua ba điểm phân biệt. Như vậy ta chọn ý C. Câu 10. Đáp án D.
Số cách chọn 2 trong 4 điểm , A B,C, D 2 là C = 6 4 .
Vậy có 6 mp đi qua S và 2 trong 4 điểm ,
A B,C, D . Câu 11. Đáp án B.
Chọn 3 trong 5 điểm trên sẽ tạo nên 1 mp. Do đó, số mp tạo bởi 3 trong 5 điểm trên là 3 C = 10. 5 Câu 12. Đáp án A.
Hai đường thẳng phân biệt cắt nhau tại O xác định 1 mp . Nên số các mp chứa 2 trong n n! đường thẳng trên là 2 C = . n 2(n - 2)! Câu 13. Đáp án A . Dễ thấy ,
PA b không trùng nhau. Giả sử ,
PA b không chéo nhau, khi đó ,
PA b hoặc song song hoặc cắt nhau. Lúc đó, theo cách xác định 1 mp, ta thấy ,
PA b cùng thuộc 1 mp (b ) . Các mp (a ),(b ) đều chứa đường thẳng b
và đi qua điểm A ở ngoài b nên 2 mp (a ),(b )trùng nhau. Suy ra điểm P phải thuộc mp (a ) (Vô lý). Như vậy , PA b chéo nhau. Câu 14. Đáp án D.
Giả sử AJ , BI đồng phẳng, suy ra AJ , BI đồng phẳng do đó ,
A B,C, D cùng thuộc 1 mp (vô lý). Trang 16
Do đó AJ , BI không đồng phẳng, do đó AJ , BI chéo nhau. Chọn đáp án D. Câu 15. Đáp án B. S N A D M O C B
Giả sử SO, AD cắt nhau. Khi đó SO, ADđồng phẳng, suy ra S thuộc mp ( ABCD) (Vô lý). Đáp án A bị loại.
Giả sử MN cắt SC . Khi đó MN và SC đồng phẳng, suy ra C thuộc (SBD) (vô lý). Do đó đáp án C bị loại.
Giả sử SA cắt BC . Khi đó ,
SA BC đồng phẳng. Suy ra, S thuộc mp ( ABCD) (vô lý). Đáp án
D bị loại. MN, SO cùng nằm trong mp (SBD), không song song và trùng nhau. Câu 16. Đáp án A.
Do I là giao điểm của MN và BD nên I thuộc các mp chứa MN và các mp chứa BD . Do đó
I thuộc (BCD),(CMN),( ABD).
Giả sử I thuộc ( ACD) khi đó B thuộc ( ACD) (vô lý). Câu 17. Đáp án A.
Giả sử MN, BC đồng phẳng. Do đó D, A lần lượt thuộc đường thẳng MC, NB nên D, A cũng thuộc mp đó. Như vậy ,
A B,C, D đồng phẳng(vô lý). Như vậy đáp án B, C, D không thỏa mãn. Câu 18. Đáp án A.
Gọi I là giao điểm của MN và CD. Khi đó I thuộc (OMN ). Vậy đáp án A đúng.
Giả sử (OMN ) chứa đường thẳng AB . Khi đó O, B cùng thuộc mp( AMN ) . Suy ra O, B
cùng thuộc mp ( ACD) (vô lý). Đáp án B không thỏa mãn.
Giả sử (MNO) đi qua điểm A . Do D,C lần lượt thuộc các đường thẳng AN, AM nên D,C
thuộc mp ( AMN ) . Như vậy 2 mp (OCD),( AMN) trùng nhau. Suy ra B thuộc mp( ACD) (vô
lý). Vậy đáp án C bị loại.
Tương tự ta cũng dễ dàng suy ra đáp án D bị loại. Câu 19. Đáp án B.
Giao tuyến của 2mp phân biệt là 1 đường thẳng, nên ba điểm phân biệt cùng thuộc 2 mp phân
biệt sẽ nằm trên giao tuyến của 2mp phân biệt. Câu 20. Đáp án B.
Hiển nhiên hình chóp S.ABCD có 4 mặt bên nên đáp án A đúng.
Ta thấy giao tuyến của 2mp (SAB),( ABCD) là AB , K là điểm thuộc cả hai mp do đó
K Î AB . tương tự ta cũng chứng minh được K ÎCD . Như vậy K thuộc cả hai đường thẳng
AB,CD (vô lý do AB,CD song song). Do vậy đáp án B sai.
O Î AC Þ O Î(SAC).
O Î BD Þ O Î(SBD).
Do đó O thuộc giao tuyến của hai mp (SAC),(SBD) . Trang 17
Tương tự ta cũng dễ thấy SI = (SAD)Ç(SBC) .
Như vậy đáp án C,D đúng. Câu 21. Đáp án B. S N A D M O C B I
Gọi I = AB Ç CD . Ta có:
ìI Î AB, AB Ì ï
(SAB) Þ I Î(SAB) í
Þ I Î(SAB) Ç(SCD)
ïI ÎCD,CD Ì î
(SCD) Þ I Î(SCD)
Lại có S Î(SAB)Ç(SCD).
Do đó SI = (SAB)Ç(SCD). Þ d º SI.
Vậy d cắt AB,CD, SO .
Giả sử d cắt MN . Khi đó M thuộc mp (SAB) . Suy ra D thuộc (SAB) (vô lý). Vậy d không
cắt MN . Đáp án B sai. Câu 22. Đáp án D. S F G I A E D H J O B C M
Trong mp ( ABCD) , gọi M = AB ÇC ;
D O = AC Ç BD . Khi đó M ,O cố định.
Như vậy: E, F, M cùng nằm trên hai mp (P) và (SCD) , do đó ba điểm E, F, M thẳng hàng.
Vậy đường thẳng EF luôn đi qua một điểm cố định M .
Tương tự, ta có G, H, M cùng nằm trên hai mp (Q) và (SAB) ,do đó G, H, M thẳng hàng.
Vậy các đường thẳng GH luôn đi qua một điểm cố định M . Trang 18 ìI Î AE Ì ï (SAC) Do í
Þ I Î(SAC) Ç(SBD) . ïI Î BF Ì î (SBD)
Tương tự ta cũng có J Î(SAC)Ç(SBD);OÎ(SAC)Ç(SBD)
Do đó ba điểm I, J,O thẳng hàng. Vậy IJ luôn đi qua điểm cố định O . Vậy ta chọn đáp án D. Câu 23. Đáp án A. A E H B D I F G C
Trong mp (BCD) , gọi I = FG Ç BD .
Trong mp ( ADB) , gọi H = IE Ç AD .
Khi đó HG = (EFG)Ç( ACD) .
Áp dụng định lý Menelaus cho tam giác BCD với ba điểm I,G, F thẳng hàng ta có: ID FB GC ID 1 . . =1Þ = IB FC GD IB 4
Áp dụng định lý Menelaus cho tam giác ABD với ba điểm I, H, E thẳng hàng ta có: HD EA IB HD 1 a . . =1Þ = Þ HD = HA EB ID HA 4 5
Áp dụng định lý cosin vào tam giác HDG ta có: 2 2 2 0
HG = HD + DG - 2DH. . DG cos 60 2 2 2 2 a a a 19a 19 = + - = Þ HG = a 25 9 15 225 15 Câu 24. Đáp án C. A B H D G E F C
Trong (BCD) , gọi H = CG Ç BD . !!!" !!!"
Dễ thấy H thuộc đoạn BD nên BH , HD cùng hướng.
Do đó đáp án A, D bị loại.
Áp dụng định lý Ceva trong tam giác BCD với BF, DE,CH đồng quy ta có: Trang 19 EB FC HD HD HD 1 . . =1Þ 2.2. =1Þ = Þ BH = 4DH EC FD HB HB HB 4 !!!" !!!" !!!" !!!"
Do BH , HD cùng hướng nên BH = 4HD . Câu 25. Đáp án A. S B F A I D E C !!" !!"
Do I thuộc đoạn AD nên AI , ID cùng hướng. Do đó B, D bị loại.
AD là phân giác trong của tam giác ABC nên theo tính chất đường phân giác ta có: BD AB c ac = = Þ BD = DC AC b b + c
Ta có: BI là phân giác trong của tam giác ABD nên theo tính chất đường phân giác ta có: IA BA b + c b + c = = Þ IA = ID ID BD a a !!" b + c !!" Do đó: AI = ID a Câu 26. Đáp án B.
Trong mp ( ABCD) , gọi I = MN Ç AO . Dễ thấy H = PO Ç SC . AI 1
Do MN là đường trung bình của tam giác ABD nên I là trung điểm AO. Suy ra = và AC 4
PI là đường trung bình của tam giác OSA . Do đó IH / /SA . SH AI 1
Áp dụng định lý Thales ta có: = = . SD AC 4 Câu 27. Đáp án D.
Trong mp (ABCD) , gọi I = BD Ç MN,O = AC Ç BD .
Dễ thấy R = IP Ç SB . DI 1
Do MN là đường trung bình của tam giác ABD nên I là trung điểm DO. Suy ra = . IB 3
Áp dụng định lý Menelaus vào taam giác SBD ta có : BR PS BI BR 1 SR 2 . . =1Þ .2. =1Þ = RS PD ID RS 3 SB 3 Câu 28. Đáp án A. Trang 20 S B F A K D E C AK BK CK
Nếu K trùng với trọng tâm G thì + +
= 6 . Do đó C, D bị loại. KD KE KF DK EK FK S S S Ta có KBC KAC KAB + + = + + =1 DA EB FC S S S ABC ABC ABC
Áp dụng định lý bất đẳng thức Cauchy ta có:
æ DK EK FK öæ DA EB FC ö + + + + ³ 9 ç ÷ç ÷
è DA EB FC øè DK EK FK ø DA EB FC AK BK CK Þ + + ³ 9 Þ + + ³ 6 DK EK FK KD KE KF Câu 29. Đáp án A. S B F A M D E C BM S S S + S S + S BD BF Ta có : ABM CBM ABM CBM ABM CBM = = = = = + ME S S S + S S CD FA AME CME AME CME AME BF BM BM - ME Þ = -1 = ( )1 . AF ME ME CM CE CD CE CM CM - MF
Tương tự ta cũng chứng minh được: = + Þ = -1 = (2) MF AE BD AE MF MF AM AE AF Và 1 = = + (3) MD CE BF MF ME Từ (1,2,3) suy ra + = 1 CM - MF BM - ME Câu 30. Đáp án A. Trang 21 S E H J D F A G I B C
Xét trường hợp đặc biệt E, F,G, H lần lượt là trung điểm của SA, SB, SC, SD. Khi đó ta dễ
dàng loại được đáp án D.
Dựng AT / /EG(T ÎSI ),CK / /EG(KESI ) S
Theo định lý Thales, ta có: SA ST SC SK IT IA = , = ; = = 1 SE SJ SG SJ IK IC G SA SC ST + SK
SI - IT + SI + IK SI E Suy ra: + = = = 2 SE SG SJ SJ SJ Như vậy, ý B bị loại. SB SD SI
Tương tự, ta chứng minh được + = 2 . T SF SH SJ C
Từ đây ta thấy ngay ý C bị loại và A là đáp án A là đáp án lựa chọn. K
Chú ý: Cho tam giác ABC. Gọi O là trung điểm AC, M, N BA BC 2BO
là hai điểm nằm trên cạnh AB, AC. MN cắt BO tại I. Khi đó: + = . BM BN BI Câu 31. Đáp án A. S D A J K M O I B N C BA BC 5 3 2BO BO OI 1 OI 1 Theo chú ý câu 30 ta có: + = + = 4 Þ = 4 Þ = 2 Þ = Þ = BM BN 2 2 BI BI BO 2 OD 2 . Trang 22 IO PD JS JS SJ 10
Áp dụng định lý Menelaus trong tam giác SOD ta có: . . =1Þ =10 Þ = ID PS JO JO SO 11 Câu 32. Đáp án A. A E D F B H J C I
Dựa vào nhận xét ví dụ 2, ta có: AE BF CH DJ 1 = - (- ) 1 . . .
2. . 5 . = 1 nên E, F, H, J đồng phẳng. BE CF DH AJ 5 2 AE BF CI DJ 1 æ 1 ö 1 1 . . . = 2 - . . . =
nên E, F, I, J không đồng phẳng. ç ÷ BE CF DI AJ 5 è 5 ø 2 25 AE BG CH DJ æ 1 ö = - - ç ÷ (- ) 1 . . . 2. . 5 . = 1
- nên E,G, H, J không đồng phẳng. BE CG DH AJ è 5 ø 2 AE BG CI DJ æ 1 ö æ 1 ö 1 1 . . . = 2 - . - . . =
nên E,G, I, J không đồng phẳng. ç ÷ ç ÷ BE CG DI AJ è 5 ø è 5 ø 2 25 Câu 33. Đáp án D.
Dựa vào nhận xét ví dụ 2, ta có: AE BF CH DJ 1 = - (- ) 1 . . .
2. . 5 . = 1 nên E, F, H, J đồng phẳng. BE CF DH AJ 5 2 AE BG CI DK æ 1 ö = - - ç ÷ ( ) 1 . . . 2.
. 5 . =1 nên E,G, I, K đồng phẳng. BE CG DI AK è 2 ø 5 AU BG CH DJ 4 æ 1 ö = - ç ÷ (- ) 1 . . . . . 5 . =
1 nên U,G, H, J đồng phẳng. BU CG DH AJ 5 è 2 ø 2 AU BF CI DK 4 æ 1 ö = ç ÷ ( ) 1 4 . . . . . 5 . =
nên U, F, I, K không đồng phẳng. Do đó 4 điểm này BU CF DI AK 5 è 5 ø 5 25 lập nên 1 tứ diện.
Câu 34. Đáp án B, A. A M Q B D j I P N C
a)Do tứ diện ABCD có 4 mặt nên thiết diện không thể là ngũ giác hay lục giác. Nó chỉ có thể là tam giác hoặc tứ giác. Trang 23
Trong mp ( ABC) , gọi K = MP Ç AC (P không phải là trung điểm đoạn BC nên MP cắt AC)
Trong mp ( ACD) , gọi Q = KN Ç AD
Do QÎ KN Ì (MNP) nên Q = (MNP) Ç AD (
ì MNP) Ç( ABD) = MQ ( ï
ï MNP) Ç( ABC) = MP Ta có: í (MNP ï )Ç(BCD) = PN ( ï MNP î )Ç(ACD) = NQ
Suy ra thiết diện cần tìm là tứ giác MPNQ . Ta chọn đáp án B. AM BP CN DQ BP DQ
b)Áp dụng ví dụ 11, do M , N, ,
P Q đồng phẳng nên . . . =1Þ . = 1 BM CP DN AQ CP AQ BP AQ
(Do M, N lần lượt là trung điểm của AB, CD) . Từ đây suy ra = . CP DQ BP !!!" !!!" !!!" !!!" Giả sử
= k . Khi đó ta suy ra BP = k PC, AQ = kQD PC !!!" !!!" !!!" !!!"
Suy ra BP + AQ = -k (CP + QD)( ) 1
Do J là trung điểm của PQ. !!!" !!!" !!!" !!!"
ìïMJ = MB + BP + PJ !!!" !!!" !!!"
Ta có: í!!!" !!!" !!!" !!!" Þ 2MJ = AQ + BP(2)
ïîMJ = MA+ AQ + QJ !!!" !!!" !!!"
Chứng minh tương tự ta cũng có: 2NJ = CP + DQ(3) !!!" !!!"
Từ (1,2,3) suy ra MJ = k
- NJ . Điều này dẫn đến M, N, J thẳng hàng. Như vậy I trùng J. Điều này suy ra S = 2S . MNPQ MPN Chọn đáp án A. Câu 35. Đáp án C. S E J K D A H O G B F C I
Trong mp ( ABCD) , gọi I = FG Ç A ;
B K = FG Ç AD
Trong mp (SAB) , gọi H = IE Ç SB
Trong mp (SAD) , gọi J = EK Ç SD . Trang 24
(EFG)Ç( ABCD) = FG,
(EFG)Ç(SCD) = GJ
Ta có: (EFG) Ç(SAD) = JE
(EFG)Ç(SAB) = HE
(EFG)Ç(SBC) = HF
Do đó ngũ giác EHFGJ là thiết diện của hình chóp cắt bởi (EFG) Câu 36. Đáp án C. S K E J D A F G B H C I
Trong mp (SAC) , Gọi I = EF Ç AC
Trong mp ( ABCD) , Gọi H = IG Ç BC, J = IG Ç AB
Trong mp (SAD) , Gọi K = JE Ç SD (
ì EFG) Ç( ABCD) = GH, ( ï
ï EFG) Ç(SCD) = KF ï Khi đó ta có: (
í EFG) Ç(SAD) = EK (
ï EFG)Ç(SAB) = GE ï(ïEFG î )Ç(SBC) = HF
Do đó ngũ giác EKFHG là thiết diện của hình chóp cắt bởi (EFG) Câu 37. Đáp án D. S Bn Bk Ik An C1 A1 A O k k B2 C2 B1 A2
Trong mặt phẳng (SA A C B B A A 1 2 ) gọi là giao điểm của với . 2 1 2 1 2
Trong mặt phẳng (SA A C B B A A 1 n ) gọi là giao điểm của với . n 1 n 1 n
Trong mặt phẳng ( A A ...A
O (k = 3,4,...,n - ) 1 A A A A 1 2 n ) gọi là giao điểm của với . k 1 k 2 n
Trong mặt phẳng (SA A
I (k = 3,4,...,n - ) 1 SO B B 2 n ) , gọi là giao điểm của với . k k 2 n Trang 25
Trong mặt phẳng (SA A
B (k = 3,4,...,n - ) 1 SA B I 1 k ) , gọi là giao điểm của với . k k 1 k
Do B Î B I Ì B B B B
SA (k = 3,4,...,n - ) 1 k 1 k
( 1 2 n) nên là giao điểm của với mặt phẳng k k (B B B 1 2 n ) .
Vậy thiết diện của hình chóp cắt bởi (B B B C B ...B C 1 2 n ) là đa giác . 2 2 n n Câu 38. Đáp án C. Cách 1: S E J K F I A D N M L G C B H
Gọi M là trung điểm của AB , khi đó S , F , M thẳng hàng.
Trong mặt phẳng ( ABCD), gọi I là giao điểm của MG với AD . Khi đó
SI = (SMG)Ç(SAD).
Trong mặt phẳng (SMG), gọi J là giao điểm của FG với SI . Ta thấy J thuộc FG nên J
thuộc (EFG). Trong (SAD), gọi K là giao điểm của JE với SA. Trong mặt phẳng (SAB),
gọi L là giao điểm của KF với AB .
Trong mặt phẳng ( ABCD), gọi H là giao điểm của LG với CD . Trong mặt phẳng (SCD) ,
gọi N là giao điểm của EH với SC . (
ì EFG) Ç( ABCD) = LG;(EFG) Ç(SBC) = GN ï Ta có: (
í EFG) Ç(SCD) = NE;(EFG) Ç(SAD) = EK . ( ï EFG î )Ç(SAB) = KL
Vậy ngũ giác LGNEK là thiết diện của hình chóp cắt bởi (EFG). Chú ý:
Mấu chốt của ví dụ trên là việc dựng được điểm J là giao điểm của FG với
(SAD) (thông qua việc dựng giao tuyến SI của mặt phẳng (SFG) với mặt phẳng (SAD)). Có
thể dựng thiết diện trên bằng nhiều cách với việc dựng giao điểm (khác E, F,G ) của một trong
các đường thẳng EF, FG; hoặc GE với một mặt của hình chóp. Sau đây, tôi xin trình bày cách
hai, điểm mấu chốt là xác định giao điểm của EF với mặt phẳng ( ABCD). Cách 2: Trang 26 S E K F A D N M P L G C B H
Trong mặt phẳng (SMD), gọi P là giao điểm của EF với M D .
Trong mặt phẳng ( ABCD), gọi H, L là giao điểm của P,G với CD, AB .
Trong mặt phẳng (SAB), gọi K là giao điểm của LF với SA.
Trong mặt phẳng (SCD), gọi N là giao điểm của EH với SC . (
ì EFG) Ç( ABCD) = LG;(EFG) Ç(SBC) = GN ï Ta có: (
í EFG) Ç(SCD) = NE;(EFG) Ç(SAD) = EK . ( ï EFG î )Ç(SAB) = KL
Vậy ngũ giác LGNEK là thiết diện của hình chóp cắt bởi (EFG). Câu 39. Đáp án B.
Trong mặt phẳng ( ABCD), gọi H là giao điểm của AB và CD . Trong mặt phẳng (SAB), gọi
I là giao điểm của FG và SH .
Xét các trường hợp sau: Trường hợp 1: S I J E G A D K F B C H
Trong mặt phẳng (SCD) , IE cắt SC tại J và cắt đoạn CD tại K .
Ta có J Î IE Ì (EFG) nên J là giao điểm của (EFG) với SC ,
K Î IE Ì (EFG) nên K là giao điểm của (EFG) với CD. Trang 27 (
ìï EFG)Ç( ABCD) = FK; (EFG)Ç(SAB) = FG Ta có í (
ïî EFG) Ç(SBC) = GJ; (EFG) Ç(SCD) = JK
Suy ra tứ giác KFGJ là thiết diện của hình chóp cắt bởi (EFG). Trường hợp 2: S I J E G K A M D F L B C H
Trong mặt phẳng (SCD) , IE cắt SC tại J và cắt đoạn SD tại K (cắt CD tại một điểm nằm ngoài đoạn CD ).
Trong mặt phẳng (SBC) : BG CJ
Nếu GJ song song với BC thì ta có: =
. Gọi T là giao điểm của IE với CD . S G S J
Áp dụng định lí Menelaus vào các tam giác SBH và SCH ta có FB IH S G TC IH JS FB TC . . =1 = . . Þ =
. Điều này chỉ xảy ra khi T thuộc đoạn CD (vô FH IS GB TH IS JC FH TH lí)
Do vây GJ cắt BC , giả sử tại L .
Trong mặt phẳng (ABCD) , gọi M là giao điểm của LF với AD . (
ì EFG) Ç( ABCD) = FM; (EFG) Ç(SAB) = FG ï Ta có (
í EFG) Ç(SBC) = GJ; (EFG) Ç(SCD) = JK ( ï EFG)Ç(SAD) = î KM
Suy ra ngũ giác KJGFM là thiết diện của hình chóp cắt bởi (EFG) .
Vậy thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (EFG) hoặc là tứ giác hoặc là ngũ giác. Câu 40. Đáp án B. Trang 28
Trong mặt phẳng (SBC) , gọi J là giao điểm của EF với BC . Trong mặt phẳng (SAD ), gọi
I là giao điểm của SG với AD . Trong mặt phẳng (ABCD) , gọi N là giao điểm của IJ với
CD . Trong mặt phẳng (SIJ) , gọi K là giáo điểm của JG với SN .
Trong mặt phẳng (SCD) , có hai khả năng xảy ra như sau:
Trường hợp 1: FK cắt đoạn CD tại P . S R G E Q D A I K F P B N C J
Trong mặt phẳng (ABCD) , gọi Q là giao điểm của JP với AD . Trong mặt phẳng (SAD ),
gọi R là giao điểm của QG với SA . (
ì EFG) Ç( ABCD) = P ;
Q (EFG) Ç(SAD) = QR ï Ta có (
í EFG) Ç(SAB) = RE; (EFG) Ç(SBC ) = EF ( ï EFG)Ç(SCD) = î FP
Trường hợp này , ngũ giác REFPQ là thiết diện của hình chóp S.ABCD cắt bởi (EFG).
Trường hợp 2: FK cắt SD tại H ( FK không cắt đoạn CD ). Trang 29 S M G H E K I D A F P B N C J
Trong mặt phẳng (SAD) , gọi M là giao điểm của HG với SA ( HG không thể cắt đoạn AD
vì giả sử ngược lại HG cắt cạnh AD tại O , khi đó JO sẽ cắt cạnh CD (vô lí vì (EFG) đã
cắt cạnh SC,SD )). (
ìï EFG)Ç(SCD) = FH; (EFG)Ç(SAD) = MH Khi đó í (
ïî EFG) Ç(SAB) = ME; (EFG) Ç(SBC) = EF
Trường hợp này, tứ giác MEFH là thiết diện của hình chóp cắt bởi (EFG).
Câu 41. Đáp án A.
Trong mặt phẳng (BCD), gọi I là giao điểm của NP với CD.
Trong mặt phẳng ( ACD), gọi Q là giao điểm của AD và MI . Suy ra Q là giao điểm của
AD với (MNP). Khi đó, tứ giác MNPQ là thiết diện của tứ diện cắt bởi mặt phẳng (MNP).
Trong tam giác BCI ta có P là trọng tâm của tam giác suy ra D là trung điểm của CI . QA
Trong tam giác ACI có Q là trọng tâm của tam giác nên = 2. QD IP IQ 2 Ta có = = Þ PQ / /MN . IN IM 3
Suy ra MNPQ là hình thang với đáy lớn MN .
Ta có: AQ = 4a, AM = 3a = MN, PQ = 2 .
a Áp dụng định lí cosin trong tam giác MAQ ta có: 2 2 2 0 2 2 2 2
MQ = AM + AQ - 2AM.A .
Q cos 60 =16a + 9a -12a =13a Þ MQ = a 13.
Tương tự ta cũng tính được NP = a 13.
Dễ thấy MNPQ là hình thang cân. Do đó: 2 ( + ) æ - 2 MN PQ ö MN PQ MQ - ç ÷ 2 è 2 ø 5a 51 S = = . 2 4
Câu 42. Đáp án C. Trang 30
Trong mặt phẳng ( ABC), gọi H là giao điểm A
của ME với AC .
Trong mặt phẳng ( ABD), gọi K là giao điểm
của MF và AD . (
ì MEF ) Ç( ABC) = MH M ï Ta có: (
í MEF ) Ç( ABD) = MK . K ( ï MEF î )Ç( ACD) = HK H
Do đó tam giác MHK là thiết diện của tứ diện cắt bởi (MEF ). B F D
Dễ thấy H , K lần lượt là trọng tâm của các tam C
giác ABE và ABF . E 2a
Ta có: AH = AK = HK = . 3 2a
Xét hai tam giác AMH và AMK có AM chung, ∑ ∑ 0
MAH = MAK = 60 , AH = AK = nên hai 3
tam giác này bằng nhau. Suy ra MH = MK . Vậy tam giác MHK cân tại M .
Áp dụng định lí cosin trong tam giác AMH : 2 2 2 2 æ a ö æ 2a ö a 13a a 13 2 2 2 0
MH = AM + AH - 2AMAH.cos 60 = + - = Þ MH = . ç ÷ ç ÷ è 2 ø è 3 ø 3 36 6
Gọi I là trung điểm của đoạn HK . Ta có MI ^ HK . 2 2 2 13a a a a Suy ra: 2 2 2
MI = MH - HI = - = Þ MI = . 36 9 4 2 2 1 1 2a a a
Diện tích thiết diện MHK là: S = MI.HK = . . = . 2 2 3 2 6
Câu 43. Đáp án C.
Trong mặt phẳng ( ABCD), gọi E là giao điểm của MN với DC và F là trung điểm của
CD .Dễ thấy Q chính là giao điểm của PE với SD . ND ED Ta có: ME = 1 1
BC. Áp dụng Thales ta có: = = Þ EF = EF . MF EF 2 2
Suy ra D là trung điểm EF . DQ
PQ là đường trung bình của tam giác EPF 1 ta có: = . PF 2 PF DS
là đường trung bình của tam giác CSD ta có: = 2. PF SD SQ 3 Từ đó suy ra: = 4 Þ = . DQ SD 4 Câu 44. Đáp án B.
Trong mặt phẳng ( ABCD), gọi I là giao điểm của MN với AO.
Dễ thấy H chính là giao điểm của PO với SC . AI 1
Do MN là đường trung bình của tam giác ABD nên I là trung điểm AO . Suy ra = và AC 4
PI là đường trung bình của tam giác OSA. Do đó: IH / /SA. SH AI 1
Áp dụng định lí Thales ta có: = = . SD AC 4
Câu 45. Đáp án D. Trang 31
Trong mặt phẳng ( ABCD), gọi I = BD Ç MN,O = AC Ç BD.
Dễ thấy R chính là giao điểm của IP với SB . DI 1
Do MN là đường trung bình của tam giác ABD nên I là trung điểm DO . Suy ra = . IB 3
Áp dụng định lí Menelaus vào tam giác SBD ta có: BR PS BI BR 1 BR 3 SR 2 . . =1Þ .2. =1Þ = Þ = RS PD ID RS 3 RS 2 SB 5 Trang 32
ĐƯỜNG THẲNG SONG SONG VỚI ĐƯỜNG THẲNG A. LÝ THUYẾT 1. Định nghĩa
Trong phần vị trí tương đối của hai đường thẳng trong không gian, ta biết rằng hai đường thẳng phân biệt
bất kì hoặc chéo nhau hoặc song song hoặc cắt nhau. Nếu hai đường thẳng phân biệt đồng phẳng và
không cắt nhau thì ta nói hai đường thẳng đó song song với nhau. Định nghĩa:
Hai đường thẳng phân biệt a,b trong không gian được gọi là song song với nhau, kí hiệu a / /b nếu
chúng đồng phẳng và không cắt nhau. 2. Tính chất A
Định lí 1: Trong không gian cho đường thẳng d và điểm A nằm ngoài d . Lúc đó tồn tại duy nhất một
đường thẳng a và A và song song với đường thẳng d. Chú ý:
Định lí này cho ta thêm một cách xác định đường thẳng trong không gian: đó là đường thẳng đi qua một
điểm và song song với một đường thẳng cho trước không chứa điểm đó. Kết hợp với định lí 2 dưới đây
cho ta một cách để xác định giao tuyến của hai mặt phẳng.
Định lí 2 ( Về giao tuyến của ba mặt phẳng): β β c γ c γ b b A a a α α
Nếu ba mặt phẳng phân biệt đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng
quy hoặc đôi một song song với nhau. Hệ quả:
Nếu hai mặt phẳng phân biệt chứa hai đường thẳng song song thì giao tuyến của chúng ( nếu có) cũng
song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
Đến đây ta có thể bổ sung một phương pháp tìm giao tuyến của hai mặt phẳng:
Bước 1: Chỉ ra hai mặt phẳng (a ),(b ) lần lượt chứa hai đường thẳng song song a,b.
Bước 2: Tìm một điểm chung M của hai mặt phẳng
Bước 3: Khi đó (a )Ç(b ) = Mx / /a / /b Định lí 3:
Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau. ìa / /b
Như vậy, cho hai đường thẳng phân biệt thỏa mãn í Þ a / /b b î / /c
3. Góc giữa hai đường thẳng trong không gian a) Định nghĩa
Góc giữa hai đường thẳng a và b trong không là góc giữa hai đường thẳng a 'và b ' cùng đi
qua một điểm và lần lượt song song với a và b .
b. Phương pháp tính góc giữa hai đường thẳng trong không gian
Bước 1: Dựng góc
- Tìm trên hình vẽ xem góc giữa hai đường thẳng có sẵn không?
- Nếu không có sẵn thì ta tiến hành:
+ Chọn một điểm O bất kì trong không gian.
+ Qua O dựng đường thẳng a¢ ! a, b¢ ! b. Góc nhọn hay góc vuông tọc bởi a ,¢b¢ chính là góc giữa a và b . Lưu ý:
+ Ta thường lấy điểm O thuộc một trong hai đường thẳng a và b . Trang 33
+ Chọn O sao cho góc giữa a ,¢b¢ là góc của một tam giác mà độ dài các cạnh của nó đã biết hoặc có thể tính dễ dàng Bước 2: Tính góc
Dùng hệ thức lượng trong tam giác, tỉ số lượng giác hay định lí cosin, sin. Trường hợp góc giữa hai
đường thẳng a và b bằng 0
90 ta nói a ^ b.
B. DẠNG TOÁN VỀ ĐƯỜNG THẲNG SONG SONG VỚI ĐƯỜNG THẲNG
DẠNG 1. CHỨNG MINH HAI ĐƯỜNG THẢNG SONG SONG TRONG KHÔNG GIAN
Phương pháp chung: Để chứng minh hai đường thẳng song song trong không gian ta sẽ sử dụng một trong các sách sau:
+ Cách 1: Chứng minh hai đường thẳng đồng phẳng, sau đó áp dụng các phương pháp chứng minh song
song trong hình học phẳng như tính chất đường trung bình, định lí Thales đảo, tính chất song song của
hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ 3…
+ Cách 2: Sử dụng tính chất bắc cầu: Chứng minh hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba.
+ Cách 3: Áp dụng định lí về giao tuyến của ba mặt phẳng.
Ví dụ 1. Cho tứ diện ABCD . Gọi I, J lần lượt là trọng tâm của các tam giác ABC, ABD . Đường thẳng
IJ song song với đường thẳng:
A. CM trong đó M là trung điểm BD. B. AC . C. DB . D. CD . Lời giải: Đáp án D.
Cách 1: ( Đưa về cùng mặt phẳng và vận dụng kiến thức hình học phẳng) ìI ÎCE
Gọi E là trung điểm của AB . Ta có í
nên suy ra IJ và CD đồng phẳng. îJ Î DE EI EJ 1
Do I, J lần lượt là trọng tâm của các tam giác ABC, ABD nên ta có: = = . Suy ra EC ED 3 IJ ! CD.
Cách 2: ( Sử dụng tính chất bắc cầu)
Gọi M , N lần lượt là trung điểm của BD và BC . Suy ra MN ! CD (1). AI AJ 2
Do I, J lần lượt là trọng tâm của các tam giác ABC, ABD nên ta có: = = . Suy ra AN AM 3 IJ ! MN (2).
Từ (1) và (2) suy ra IJ ! CD.
Cách 3: (Sử dụng định lí giao tuyến của 3 mặt phẳng).
Có lẽ trong ví dụ này cách này hơi dài, song chúng tôi vẫn sẽ trình bày ở đây, để các bạn có thể
hiểu và vận dụng cách 3 hợp lí trong các ví dụ khác.
Dễ thấy, bốn điểm D , C , I , J đồng phẳng. (
ì DCIJ ) Ç( AMN ) = IJ ( ï
ï DCIJ ) Ç(BCD) = CD Ta có: í
Þ IJ ! CD ! MN . (
ï AMN ) Ç(BCD) = MN ï îMN ! CD Ví dụ 2.
Cho hình bình hành ABCD . Gọi Bx , Cy, Dz là các đường thẳng song song với nhau lần lượt
đi qua B , C , D và nằm về một phía của mặt phẳng ( ABCD), đồng thời không nằm trong mặt
phẳng ( ABCD). Một mặt phẳng đi qua A và cắt Bx , Cy, Dz lần lượt tại B¢, C¢ , D¢ với
BB¢ = 2 , DD¢ = 4. Khi đó CC¢ bằng: A. 3 . B. 4 . C. 5 . D. 6 . Lời giải: Đáp án D. Trang 34
Gọi O là tâm của hình bình hành ABCD . I là trung điểm của B D ¢ ¢ .
Do Bx , Dz song song với nhau nên BDD B ¢ ¢ là
hình thang và OI là đường trung bình của hình BB¢ + DD¢ thang đó. Suy ra IO = = . 3 2
Mặt khác OI song song với CC¢ (vì cùng song
song với DD¢ ) nên có bốn điểm C , C¢ , O , I đồng phẳng.
Giao tuyến của hai mặt phẳng ( AB D ¢ ¢) với
(ACC¢) là AC¢. Lại có I thuộc (AB D ¢ ¢), I
thuộc ( ACC¢). Do đó A , I , C¢ thẳng hàng. Từ đây dễ dàng suy ra, I là trung điểm đoạn
AC¢. Do vậy, CC¢ = 2OI = 6 .
Nhận xét: Ta có bài toán tổng quát cho bài toán này như sau:
Cho hình bình hành ABCD . Gọi At , Bx , Cy, Dz là các đường thẳng song song với nhau lần
lượt đi qua A , B , C , D đồng thời không nằm trong mặt phẳng ( ABCD). Một mặt phẳng cắt
At , Bx , Cy, Dz lần lượt tại A¢, B¢, C¢ , D¢ . Khi đó A¢B C ¢ D
¢ ¢ là hình bình hành và
AA¢ + CC¢ = BB¢ + DD¢ .
Do đó khi biết 3 trong 4 đối tượng AA¢ , BB¢ , CC¢ , DD¢ ta sẽ dễ dàng tính được đối tượng còn lại. Ví dụ 3.
Cho hình bình hành ABCD tâm O . Gọi At , Bx , Cy, Dz là các đường thẳng song song với
nhau lần lượt đi qua A , B , C , D và nằm về một phía của mặt phẳng ( ABCD), đồng thời
không nằm trong mặt phẳng ( ABCD). Một mặt phẳng (a ) di động cắt At , Bx , Cy, Dz lần
lượt tại A¢, B¢, C¢ , D¢ sao cho AA¢ + CC¢ + BB¢ + DD¢ = a ( O có độ dài cho trước). Mặt
phẳng (a ) luôn đi qua điểm cố định I . Mệnh đề nào sau đây đúng? a
A. I nằm trên đường thẳng O song song với At và OI = . 2 a
B. I nằm trên đường thẳng O song song với At và OI = . 4 3a
C. I nằm trên đường thẳng O song song với At và OI = . 2
D. I nằm trên đường thẳng O song song với At và OI = a . Lời giải: Đáp án B. a
Theo ví dụ 2, ta có : AA'+ CC ' = 2OI = BB '+ AA'+ CC '+ BB '+ DD ' = a nên OI = . 4
Bài tập tương tự: Cho tam giác ABC . Ở về một phía của ( ABC), người ta kẻ các đường thẳng song song , Ax By,C .
z lần lượt lấy trên Ax, By,Cz các điểm A', B ',C .'
a) M và M ' lần lượt là trung điểm AB, A' B '. Chứng minh rằng MM ' song song với CC '.
b) G và G ' lần lượt là trọng tâm của tam giác ABC và A' B 'C ' . Chứng minh rằng GG ' song song với CC '. Ví dụ 4.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Các điểm M , N thứ tự thuộc các MB NS 1
đoạn BC và SD sao cho =
= . Gọi I là giao điểm của MD và . AB MC ND 2
a) Chứng minh rằng MN / /SI .
b) Qua M kẻ MN / /CD ( P là điểm trên BD ). Chứng minh rằng MP / /SB . Lời giải: Trang 35 IM MB 1 S
a) Ta có BI / /CD Þ = = MD MC 2 SN IM æ 1 E ö
Trong tam giác SDI có = = Þ MN / /SI. ç ÷ ND MD è 2 ø F N D A BP MB 1
b) Ta có MP / / AB Þ = = PD MC 2 BP SN 1
Trong tam giác SBD có = = Þ NP / /S . B PD ND 2 B M C
DẠNG 2. TÌM GIAO TUYẾN CỦA HAI MẶT PHẲNG (cách 2). THIẾT DIỆN QUA MỘT ĐƯỜNG
THẲNG VÀ SONG SONG VỚI MỘT ĐƯỜNG THẲNG CHO TRƯỚC. •
Tìm giao tuyến của hai mặt phẳng (cách 2)
Để tìm giao tuyến của hai mặt phẳng chứa hai đường thẳng a và b song song, ta tìm:
+ Một điểm chung của hai mặt phẳng đó.
+ Giao tuyến của hai mặt phẳng là đường thẳng qua điểm chung và song song với a và b ( hoặc
trùng với một trong hai đường thẳng đó).
Ví dụ 1. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. SA = SB = a, SC = SD = a 3 .
Gọi E, F lần lượt là trung điểm của SA và SB . M là điểm tùy ý trên cạnh BC ( không trùng với B,C )
a) Xác định giao tuyến của các mặt phẳng (SAB) và (SCD); (SAD)và (SBC).
b) Xác định giao tuyến của các mặt phẳng (MEF ) và ( ABCD). Từ đó suy ra giao điểm N
của AD và (MEF ). Chứng minh rằng MNEF là hình thang cân. Lời giải: S E F N D A B M C ìS Î ï (SAB)Ç(SCD) a) Ta có í
Þ (SAB) Ç(SCD) = Sx / / AB / / . CD
ïAB / /CD, AB Ì î
(SAB),CD Ì (SCD) ìS Î ï (SAB)Ç(SBC) Tương tự í
Þ (SAD) Ç(SBC) = Sy / / AD / /BC ïAD BC AD Ì î
(SAD) BC Ì (SBC) . / / , ,
b) Do E, F lần lượt là trung điểm của ,
SA SB nên EF là đường trung bình của tam giác SAB 1
. Do đó EF / / AB, EF / = AB (1) 2
ìEF / / AB, EF Ì ï
(MEF), AB Ì (ABCD) Ta có í
Þ (MEF ) Ç( ABCD) = Mt / / AB / /CD (2) ïM Î î (MEF)Ç( ABCD)
Gọi N là giao điểm của Mt với AD . Ta có:
ìïN ÎMt,Mt Ì (MEF), AB Ì ( ABCD) í
Þ{N} = ADÇ(MEF). ïîM Î AD 1
Từ (1) và (2) suy ra EF / /MN, EF = AB < MN . Suy ra MNEF là hình thang. 2 Trang 36 Dễ thấy ∑ ∑ SA D D = SB D C( . c . c )
c Þ SAD = SBC Þ E D AN = F
D BM ( .cg.c) Þ FM = EN vậy
MNEF là hình thang cân.
Thiết diện qua một đường thẳng và song song với một đường thẳng cho trước
Được xác dịnh bằng cách phối hợp hai cách xác định giao tuyến đã biết:
Cách 1: Tìm hai điểm chung của hai mặt phẳng.
Cách 2: Tìm một điểm chung và phương ( song song với một đường thẳng cho trước) của giao tuyến. Ví dụ 2.
Cho tứ diện ABCD . Gọi M , N lần lượt là trung điểm của AB và AC , Gọi E là điểm trên cạnh
CD với ED = 3EC . Thiết diện tạo bởi mặt phẳng (MNE) và tứ diện ABCD là:
A. Tam giác MNE .
B. Tứ giác MNEF với F là điểm bất kì trên cạnh BD .
C. Hình bình hành MNEF với F là điểm bất kì trên cạnh BD mà EF / /BC .
D. Hình thang MNEF với F là điểm bất kì trên cạnh BD và EF / /BC . Lời giải:
Trong mặt phẳng (BCD), Gọi F là giao điểm của đường thẳng qua E , song song BC với BD . ( ì MNE ï
)Ç(ABC) = MN;(MNE)Ç(BCD) = EF Ta có í ( ï MNE î
)Ç(ABD) = MF;(MNE)Ç(ACD) = NE
Vậy tứ giác MNEF là thiết diện của hình chóp cắt bởi (MNE). (
ì MNE) Ç( ABC) = MN ( ï
ï MNE) Ç(BCD) = EF Lại có í Þ EF / /MN. (
ï MCD) Ç( ABC) = BC ï îBC / /MN
Suy ra tứ giác MNEF là hình thang (EF > MN ). Ví dụ 3.
Cho hình chóp S.ABCD , đáy ABCD là hình bình hành. Gọi M là trung điểm của SA. Thiết
diện của mặt phẳng (MCD) với hình chóp S.ABCD là hình gì? A. Tam giác. B. Hình bình hành. C. Hình thang. D. Hình thoi. Lời giải: Đáp án C.
Gọi N là trung điểm của SB . Do MN / / AB , AB / /CD Þ MN / /CD .
Như vậy suy ra N thuộc mặt phẳng (MCD). (
ì MCD) Ç(SAD) = MD ( ï
ï MCD) Ç(SAB) = MN Ta có: í (MCD ï )Ç(SBC) = NC ( ï MCD î )Ç( ABCD) = CD
Vậy tứ giác MNCD là thiết diện của hình chóp bị cắt bởi mặt phẳng (MCD).
Kết hợp với MN / /CD , suy ra MNCD là hình thang.
DẠNG 3: GÓC GIỮA HAI ĐƯỜNG THẲNG
Ví dụ 1. Cho tứ diện ABCD có AB = CD = a , AC = BD = b , AD = BC = c . Xét các khẳng định sau: 2 2 b - c
a. Cosin của góc giữa hai đường thẳng AB và CD bằng . 2 a 2 2 a - c
b. Cosin của góc giữa hai đường thẳng AC và BD bằng . 2 b Trang 37 2 2 b - a
c. Cosin của góc giữa hai đường thẳng AD và BC bằng . 2 c
Trong các khẳng định trên có bao nhiêu khẳng định đúng? A. 0 . B. 1. C. 2 . D. 3 . Lời giải: Đáp án C.
Gọi E , F , G lần lượt là trung điểm của AC , BC , AD .
Ta có: EF / / AB , EG / /CD , suy ra góc giữa hai đường thẳng AB và CD . 2 2 2 2 2 2 AB + AC BC a + b c A Ta có: 2 AF = - = - . 2 4 2 4 Do ABC D = D
D BC ( .c .cc) nên AF = DF . Suy ra AFD D cân tại F . Vậy G 2 2 2 a + b - c 2 2
FG ^ AD Þ FG = FA - AG = . E 2 Xét tam giác EFG có:
EF + EG - FG c - b B D ∑ 2 2 2 2 2 cos FEG = = . 2 2EF.EG a F 2 2 b - c Vì o ∑ 0 £ (EF,EG) o ∑
£ 90 Þ cos(EF,EG) ∑ = cos FEG = . C 2 a 2 2 b - c
Vậy cosin của góc giữa hai đường thẳng AB và CD bằng . 2 a 2 2 a - c
Tương tự ta cũng suy ra cosin của góc giữa AC và BD bằng . 2 b
Nhận xét: Từ ví dụ này, ta còn suy ra được một trong ba giá trị 2 a cos( A , B CD); 2
b cos( AC, BD); 2 c cos( A ,
D BC) bằng tổng hai giá trị còn lại. Cũng từ ví dụ này ta còn suy ra
được với tứ diện đều ABCD thì góc giữa các cặp cạnh đối diện luôn bằng 90o
C. BÀI TẬP RÈN LUYỆN KỸ NĂNG
Câu 1. Cho hai đường thẳng a và b chéo nhau. Mệnh đề nào sau đây đúng?
A. Tồn tại hai đường thẳng c , d song song với nhau, mỗi đường đều cắt cả a và b .
B. Không thể tồn tại hai đường thẳng c , d phân biệt mỗi đường đều cắt cả a và b .
C. Không thể tồn tại một đường thẳng cắt cả a và b .
D. Cả ba câu trên đều sai.
Câu 2. Nếu ba mặt phẳng phân biệt đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy
A. Đôi một cắt nhau. B. Đồng quy.
C. Hoặc đồng quy hoặc đôi một song song.
D. Đôi một song song.
Câu 3. Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) sẽ:
A. Song song với hai đường thẳng đó.
B. Song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
C. Trùng với một trong hai đường thẳng đó.
D. Cắt một trong hai đường thẳng đó.
Câu 4. Cho hai đường thẳng a và b chéo nhau. Xét hai đường thẳng p , q mà mỗi đường thẳng đều
cắt cả a và b , p cắt a tại M , q cắt a tại N ( M không trùng với N ). Khi đó hai đường
thẳng p và q : A. Cắt nhau. B. Trùng nhau. Trang 38
C. Song song với nhau.
D. Hoặc chéo nhau hoặc cắt nhau.
Câu 5. Hai đường thẳng cùng song song với đường thẳng thứ ba thì hai đường thẳng đó: A. Song song. B. Trùng nhau. C. Chéo nhau.
D. Hoặc song song hoặc trùng nhau.
Câu 6. Giả sử (P), (Q), (R) là ba mặt phẳng cắt nhau theo ba giao tuyến phân biệt a , b , c . Trong
đó: a = (P) Ç(R), b = (Q) Ç(R), c = (P) Ç(Q).
Trong các mệnh đề sau, mệnh đề nào sai?
A. a và b cắt nhau hoặc song song với nhau.
B. Ba giao tuyến a , b , c đồng quy hoặc đôi một cắt nhau.
C. Nếu a và b song song với nhau thì a và c không thể cắt nhau, cũng vậy, b và c không thể cắt nhau.
D. Ba giao tuyến a , b , c đồng quy hoặc đôi một song song.
Câu 7. Cho hình chóp SABCD có đáy là hình bình hành. Khi đó giao tuyến của hai mặt phẳng (SBC)
và (SAD) là đường thẳng d : A. Đi qua S .
B. Đi qua điểm S và song song với AB .
C. Đi qua điểm S và song song với AD .
D. Đi qua điểm S và song song với AC .
Câu 8. Giả sử có ba đường thẳng a , b , c trong đó b / /a và c/ /a. Hãy chọn câu đúng:
A. Nếu mặt phẳng ( ,
a b) không trùng với mặt phẳng ( ,c
a ) thì b và c chéo nhau.
B. Nếu mặt phẳng ( ,
a b) trùng với mặt phẳng ( ,c
a ) thì ba đường thẳng a , b , c song song
với nhau từng đôi một.
C. Dù cho hai mặt phẳng ( , a b) và ( ,c
a ) có trùng nhau hay không, ta vẫn có b/ / c.
D. Cả ba câu trên đều sai.
Câu 9. Cho hai đường thẳng a , b . Hai đường thẳng này sẽ nằm ở một trong các trường hợp:
(1) Hai đường thẳng phân biệt trong không gian.
(2) Hai đường thẳng phân biệt trong mặt phẳng.
(3) a là giao tuyến của (P) và (R), b là giao tuyến của (Q) và (R), trong đó (P), (Q),
(R) là ba mặt phẳng khác nhau từng đôi một.
Tương ứng với mỗi trường hợp trên, số các khả năng có thể xảy ra giữa a và b lần lượt là: A. 3, 2, 2. B. 3, 2, 3. C. 2, 3, 2. D. 3, 2, 1.
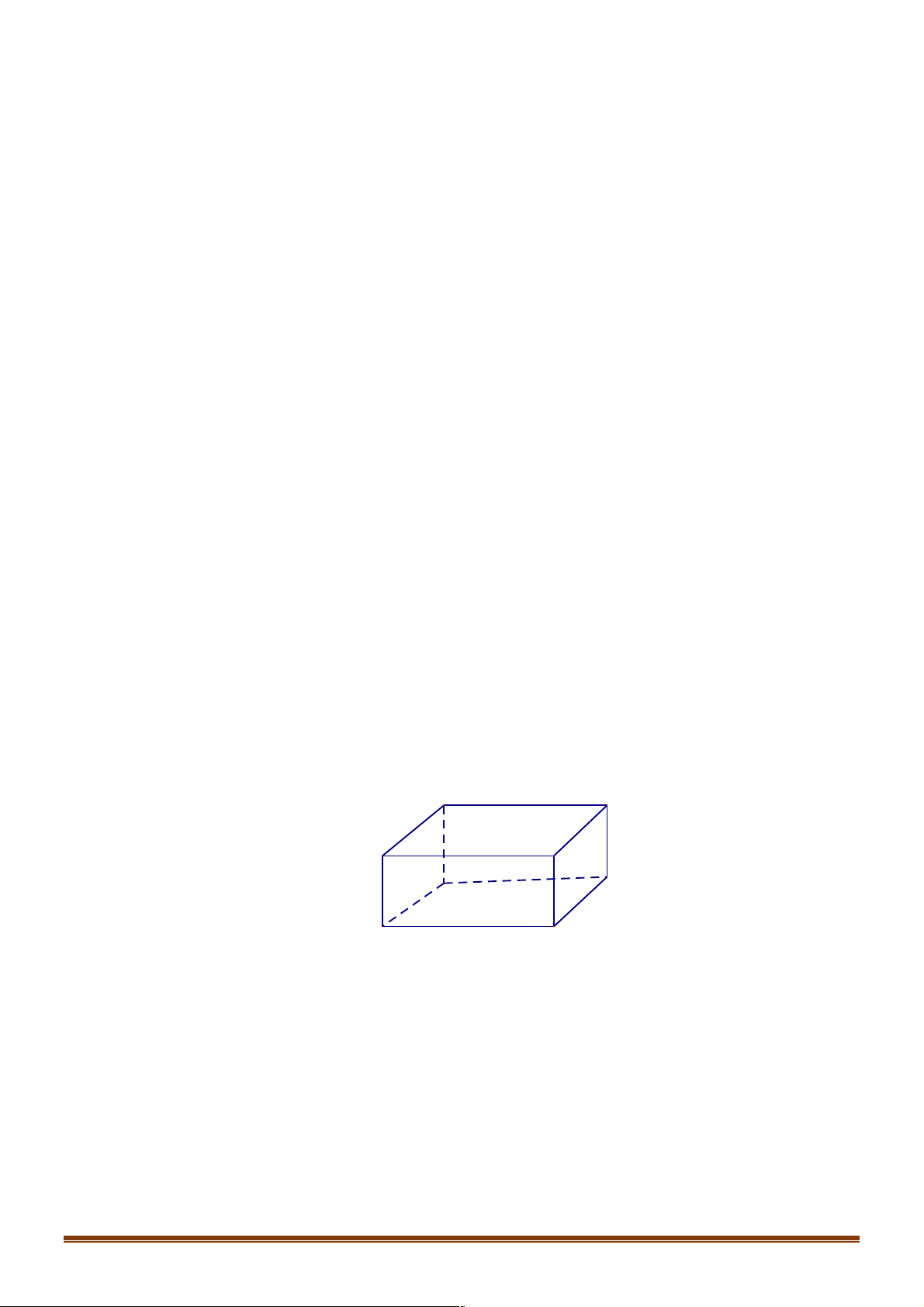
Câu 10. Xét hình bên dưới: c a b
Các cạnh của hình hộp nằm trên các đường thẳng a , b , c như hình vẽ:
(1) Đường thẳng a và đường thẳng b cùng nằm trên một mặt phẳng.
(2) Có một mặt phẳng qua hai đường thẳng a và c .
(3) Có một mặt phẳng qua hai đường thẳng b và c . Trong ba câu trên:
A. Chỉ có (1) và (2) đúng.
B. Chỉ có (1) và (3) đúng.
C. Chỉ có (2) và (3) đúng.
D. Cả ba câu trên đều đúng.
Câu 11. Cho hình chóp S.ABCD có đáy ABCD là hình thang đáy lớn là CD . Gọi M là trung điểm của
SA , N là giao điểm của cạnh SB và mặt phẳng (MCD). Mệnh đề nào sau đây đúng?
A. MN và SD cắt nhau.
B. MN và CD chéo nhau.
C. MN và SC cắt nhau.
D. MN và CD song song với nhau.
Câu 12. Cho tứ diện ABCD . Gọi M , N, ,
P Q lần lượt là trung điểm của các cạnh , AB , AD C , D BC .
Mệnh đề nào sau đây sai? Trang 39
A. MP, NQ chéo nhau. B. MN P
∥ Q và MN = PQ. 1
C. MNPQ là hình bình hành. D. MN BD ∥ và MN = BD. 2
Câu 13. Cho hình chóp S.ABCD với đáy ABCD là hình bình hành. Gọi M , N, ,
P Q lần lượt là trung điểm của các cạnh ,
SA SB, SC, SD. Đường thẳng nào sau đây không song song với đường thẳng MN ? A. AB . B. CD . C. PQ. D. SC .
Câu 14. Cho hình chóp .
A BCD với đáy ABCD là hình bình hành. Gọi M , N, P,Q, R, S lần lượt là
trung điểm của các cạnh AC, , BD AB,C , D ,
AD BC. Các điểm nào sau đây không đồng phẳng?
A. M , P, R,Q .
B. M , R, S, N .
C. P,Q, R, S . D. M , , P , Q N .
Câu 15. Cho hình chóp S.ABCD với đáy ABCD là hình thang với đáy AD và BC
(AD = a > BC = b). Gọi I, J lần lượt là trọng tâm các tam giác SAD và SBC . Mặt phẳng (ADJ ) cắt ,
SB SC lần lượt tại M , N . Mặt phẳng (BCI ) cắt ,
SA SD lần lượt tại P,Q . Gọi E
là giao điểm của AM và PB , F là giao điểm của CQ và DN . Trong các mệnh đề dưới đây,
có bao nhiêu mệnh đề sai?
1) MN và PQ song song với nhau.
2) MN và EF song song với nhau. 2
3) EF = (a + b). 5 1
4) EF = (a + b) 4 A. 4 . B. 1. C. 2 . D. 3 .
Câu 16. Cho tứ diện ABCD . Gọi I, J lần lượt là trung điểm của AC, BC . K là điểm trên đoạn BD
sao cho KB = 2KD , F là giao điểm của AD và (IJK ). Giao tuyến của hai mặt phẳng (SAD)
và (IJK ) song song với đường thẳng? A. AJ . B. BI . C. IJ . D. CI .
Câu 17. Cho tứ diện ABCD . Gọi I, J lần lượt là trung điểm của BC, BD. Giao tuyến của hai mặt
phẳng ( AIJ ) và ( ACD) là:
A. Đường thẳng d đi qua A và d BC ∥ .
B. Đường thẳng d đi qua A và d BD ∥ .
C. Đường thẳng d đi qua A và d C ∥ D .
D. Đường thẳng AB .
Câu 18. Cho hình chóp S.ABC , M là một điểm nằm trong tam giác ABC . Các đường thẳng qua M song song với ,
SA SB, SC cắt các mặt phẳng (SBC),(SAC),(SAB) lần lượt tại A ,¢ B ,¢C¢.
MA¢ MB¢ MC¢ a) + +
có giá trị không đổi bằng bao nhiêu khi M di động trong tam giác SA SB SC ABC ? 1 1 2 A. . B. . C. 1. D. . 3 2 3
MA¢ MB¢ MC¢ b) . .
nhận giá trị lớn nhất. Khi đó vị trí của M trong tam giác ABC là: SA SB SC
A. Trực tâm ABC D .
B. Trọng tâm ABC D .
C. Tâm ngoại tiếp ABC D .
D. Tâm nội tiếp ABC D .
Câu 19. Cho hình chóp S.ABCD với đáy ABCD là hình bình hành tâm O . Mặt phẳng (a ) di động đi
qua AB và cắt SC, SD lần lượt tại M , N .
a) Tứ giác ABMN là hình gì? A. Hình bình hành. B. Hình thang. C. Hình thoi.
D. Tứ giác lồi có các cặp cạnh đối cắt nhau.
b) Giao điểm của hai đường thẳng AM và BN luôn chạy trên đường thẳng cố định: Trang 40 A. SO .
B. Đường thẳng đi qua S .
C. Đường thẳng đi qua S , song song với AB . D. Đường thẳng đi qua S , song song với AD .
c) Giao điểm của hai đường thẳng AN và BM luôn chạy trên đường thẳng cố định: A. SO .
B. Đường thẳng đi qua S .
C. Đường thẳng đi qua S , song song với AB . D. Đường thẳng đi qua S , song song với AD . AB BC d) Tính - ? MN SK 1 1 2 A. 0 . B. . C. . D. . 2 3 3
Câu 20. Cho tứ diện ABCD . Gọi G là trọng tâm tam giác BCD và M là điểm nằm bên trong tam giác
BCD . Đường thẳng qua M và song song với GA lần lượt cắt các mặt phẳng
(ABC),(ACD),(ADB) tại , P , Q R.
MP + MQ + MR
a) Khi M di động trong tam giác BCD , đại lượng không đổi và bằng: GA A. 1. B. 2 . C. 3 . D. 4 .
b) Xác định vị trí của M để . MP .
MQ MR đạt giá trị lớn nhất?
A. M là trực tâm tam giác BCD .
B. M là tâm ngoại tiếp tam giác BCD .
C. M là trọng tâm tam giác BCD .
D. M là tâm ngoại tiếp tam giác BCD .
Câu 21. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , tâm O . Mặt bên (SAB) là tam giác đều và ∑
SAD = 90° . Gọi Dx là đường thẳng qua D và song song với SC .
a) Giao điểm I của đường thẳng Dx với mặt phẳng (SAB) chạy trên đường thẳng:
A. Qua S và song song với AB .
B. Qua S và song song với AD C. SO . D. SD .
b) Diện tích thiết diện của hình chóp S.ABCD cắt bởi ( AIC) là: 2 a 7 2 a 7 2 a 7 2 a 7 A. . B. . C. . D. . 8 4 2 16
Câu 22. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , tâm O . Mặt bên (SAB) là tam
giác đều, SC = SD = a 3 . Gọi H , K lần lượt là trung điểm của ,
SA SB. M là điểm trên cạnh
AD . Mặt phẳng (HKM ) cắt BC tại N .
a) HKNM là hình gì?
A. Tứ giác lồi có các cặp cạnh đối cắt nhau. B. Hình thoi. C. Hình thang cân. D. Hình bình hành.
b) Đặt AM = x (0 £ x £ a). Tìm x theo a để diện tích tứ giác HKNM đạt giá trị nhỏ nhất? a a A. 0 . B. a . C. . D. . 2 4
Câu 23. Cho hình chóp S.ABCD có đáy ABCD là hình thang có cạnh đáy AB và CD . Gọi I, J lần
lượt là trung điểm của các cạnh ,
AD BC . G là trọng tâm của tam giác SAB . Thiết diện của
hình chóp S.ABCD cắt bởi (IJG) là một tứ giác. Tìm điều kiện của AB,CD để thiết diện đó là hình bình hành?
A. AB = 3CD .
B. AB = 2CD .
C. CD = 2AB .
D. CD = 3AB .
Câu 24. Cho tứ diện ABCD . Gọi I, J lần lượt là trung điểm của các cạnh BC, BD. E là một điểm trên
cạnh AD ( E khác ,
A D). Tìm điều kiện của tứ diện ABCD và điểm E sao cho thiết diện của
hình chóp cắt bởi (IJE)là hình thoi? !!!" !!!" !!!" !!!"
A. AB = CD, EA = -ED.
B. AD = BC, EA = -ED . !!!" !!!" !!!" !!!"
C. AB = CD, EA = 2 - ED .
D. AD = BC, EA = -2ED.
Câu 25. Số đo góc giữa hai đường thẳng bằng 0° thì hai đường thẳng đó: Trang 41 A. Song song. B. Chéo nhau. C. Trùng nhau.
D. Song song hoặc trùng nhau.
Câu 26. Bạn Tùng Chi xác định góc giữa hai đường thẳng a,b trong không gian như sau:
Bước 1: Lấy điểm O bất kì. Qua O dựng đường thẳng m song song với a . Trên đường thẳng
m lấy điểm A khác O .
Bước 2: Dựng đường thẳng n song song với song song với b . Trên đường thẳng m lấy điểm B khác O .
Bước 3: Góc giữa hai đường thẳng a và b chính là góc ∑ AOB.
Hỏi bạn Tùng Chi có làm đúng không, nếu sai thì sai ở bước nào? A. Bước 1. B. Bước 2. C. Bước 3. D. Bạn làm đúng.
Câu 27. Cho ba đường thẳng a,b, c sao cho a∥ ,
b b ^ c . Khi đó góc giữa hai đường thẳng a và c bằng: A. 90° . B. 60° . C. 45°. D. 30° .
Câu 28. Cho hình chóp .
A BCD có các tam giác ABC , ABD đều cạnh a , E là trung điểm của CD .
Tính số đo của góc giữa hai đường thẳng AD và BC biết rằng ∑ AEB = 90°. A. 90° . B. 60° . C. 45°. D. 30° .
Câu 29. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a , ∑ ∑ SA = ,
a ASB = SAD = 90°.
Gọi E, F lần lượt là trung điểm của các đoạn AB, BC. Tính cosin của góc giữa hai đường
thẳng SE và DF . 7 2 1 3 A. . B. . C. . D. . 5 5 5 5
Câu 30. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, AD = 3a, SA = a 3 . Các tam giác SA ,
B SAC, SAD vuông tại A . Tính cosin của góc giữa hai đường thẳng SC và BD . 8 4 3 1 A. . B. . C. . D. . 130 130 2 5
Câu 31. Cho tứ diện ABCD có AB = 5, AC = 7, BD = 57,CD = 9. Tính số đo của góc giữa hai đường
thẳng BC và AD ? A. 30° . B. 45°. C. 60° . D. 90° .
Câu 32. Cho tứ diện ABCD có ∑ ∑ ∑
AB = AC = AD = ,
a BAC = BAD = 60 ,
° CAD = 90°. Gọi E là trung
điểm của đoạn BC . Tính cosin của góc giữa hai đường thẳng AB và ED . 5 5 2 5 1 A. . B. . C. . D. . 5 10 5 2 HƯỚNG DẪN GIẢI Câu 1. Đáp án D.
Đáp án A sai. Giả sử c cắt a,b lần lượt tại ,
A B , d cắt a,b lần lượt tại C, D . Suy ra ,
A B,C, D đồng phẳng, hay a,b đồng phẳng, vô lí.
Đáp án B, C sai, chúng ta có thể dễ dàng thấy một ví dụ là tứ diện ABCD có AB và CD đếu
cắt hai đường thẳng chéo nhau AD và BC . Câu 2. Đáp án C. Câu 3. Đáp án B. Câu 4. Đáp án D. Câu 5. Đáp án D. Câu 6. Đáp án B. Câu 7. Đáp án C. Câu 8. Đáp án D. Trang 42 Đáp án A sai vì nếu ( , a b) và ( ,c
a ) không trùng nhau thì a,b,c đôi một phân biệt. theo tính
chất bắc cầu suy ra b c ∥ .
Đáp án B, C sai, vì ta có thể lấy ví dụ b º c . Câu 9. Đáp án B. Trường hợp ( )
1 có thể xảy ra giữa hai đường thẳng a,blà chéo nhau, song song, cắt nhau.
Trường hợp (2) có thể là song song, cắt nhau.
Trường hợp (3) có thể là song song, cắt nhau hoặc trùng nhau.
Như vậy, tương ứng với mối trường hợp, số các khả năng có thể xảy ra giữa a,b là 3, 2,3. Câu 10. Đáp án C.
Nhìn vào hình vẽ, ta thấy a,b chéo nhau, nên không có mặt phẳng nào chứa cả a,b. Do đó ( ) 1
sai. Vậy đáp án A, B, C sai.
Đường thẳng a,c cắt nhau, xác định duy nhất một mặt phẳng chứa cả hai đường. Đáp án (2) đúng. Đường thẳng ,
b c cắt nhau, xác định duy nhất một mặt phẳng chứa cả hai đường. Đáp án (3) đúng. Câu 11. Đáp án D. ìAB CD ∥ ï
Ta có: íAB Ì (SAB),CD Ì (MCD) Þ MN CD ∥ . ïMN = (SAB)Ç î (MCD) Câu 12. Đáp án A. S M N D C A B 1
Do M , N lần lượt là trung điểm của AB, AD nên MN B
∥ D, MN = BD. 2 1
Do P,Q lần lượt là trung điểm của CD,CB nên PQ BD ∥ , PQ = BD. 2 Suy ra MN P
∥ Q, do đó M , N, ,
P Q đồng phẳng. Do đó MP, NQ không thể chéo nhau. Câu 13. Đáp án D.
Do MN là đường trung bình của tam giác SAB nên MN∥AB .
Tương tự, do PQ là đường trung bình của tam giác SCD nên PQ C ∥ D.
ABCD là hình bình hành nên AB C
∥ D . Do đó: PQ M ∥ N và MN C ∥ D .
MN không song song với SC vì giả sử ngược lại thì SC và CD trùng nhau (vô lí). Câu 14. Đáp án A.
Do M , N, P,Q, R, S lần lượt là trung điểm của AC, , BD AB,C , D , AD BC nên MR C ∥ D SN ∥ , PS AC ∥ RQ ∥ , MP B ∥ C NQ ∥
. Do đó M , R, S, N đồng phẳng; P,Q, R, S đồng phẳng; M , , P , Q N đồng phẳng. Trang 43
M , P, R,Q không đồng phẳng vì giả sử ngược lại thì P sẽ thuộc mặt phẳng ( ACD), suy ra B
thuộc mặt phẳng ( ACD) (vô lí). Câu 15. Đáp án B.
Ta có I Î(SAD), suy ra I Î(SAD)Ç(BCI ). (
ì SAD) Ç(BCI ) = PQ ï
Do íAD Ì (SAD), BC Ì (BCI ) Þ PQ∥AD B ∥ C . ïAD BC î ∥
Ta có: J Î(SBC), suy ra J Î(SBC)Ç( ADJ ). (
ì SBC) Ç( ADJ ) = MN ï
Do íBC Ì (SBC), AD Ì ( ADJ ) Þ MN∥AD BC ∥ . ïAD BC î ∥
Từ đó suy ra MN và PQ song song với nhau.
ìEF = ( ADNM ) Ç(BCQP) ï
ïAD = ( ADNM ) Ç( ABCD) Ta có: í Þ EF∥AD .
ïBC = ( ABCD) Ç(BCQP) ï îAD BC ∥ Suy ra EF M
∥ N . Gọi K là giao điểm của CP với EF EF = EK + KF . SP 2 SM Do = = Þ PM AB ∥ . SA 3 SB PE 2 PE 2
Theo định lý Thalet ta có: = Þ
= . Do EK song song với BC nên theo định lý EB 3 PB 5 PE EK 2 2 Thalet ta có : = = Þ EK = b. PB BC 5 5 QF 2 QC 5 PQ 5 3 3 2 2 Tương tự ta cũng có: = Þ = Þ
= Þ FK = PQ = . AD = a. FC 3 FC 3 FK 3 5 5 3 5 2
Từ đây suy ra EF = (a + b). 5 Câu 16. Đáp án C. (
ì SAD) Ç(IJK ) = FK ï
Ta có: íAD Ì (SAD), IJ Ì (IJK ) Þ FK I ∥ J . ïAD I ∥ J î Trang 44
Dễ dàng chứng minh được các đường thẳng còn lại không song song với FK . Câu 17. Đáp án C.
Do I, J lần lượt là trung điểm của BC, BD nên IJ là đường trung bình của tam giác BCD . Suy ra IJ C ∥ D . ìIJ C ∥ D, IJ Ì ï
( AIJ ),CD Ì (ACD) Ta có: í
Þ ( AIJ ) Ç( ACD) = At C ∥ D. ïAÎ î (AIJ )Ç(ACD)
Câu 18. Đáp án C, B. a) Do MA¢ SA ∥
nên bốn điểm này nằm trong cùng mặt phẳng. Giả sử E là giao điểm của mặt MA¢ ME S
phẳng này với BC . Khi đó ,
A M , E thẳng hàng và ta có: MBC = = . SA EA SABC MB¢ S MC¢ S
MA¢ MB¢ MC¢ Tương tự ta có: MAC = , MAB = . Vậy + + = . V 1 ậy đáp án đúng là . SB S SC S SA SB SC ABC ABC
b) Ap dụng bất đẳng thức Cauchy ta có :
MA¢ MB¢ MC¢
MA¢ MB¢ MC¢
MA¢ MB¢ MC¢ 1 3 + + ³ 3 . . Þ . . £ . SA SB SC SA SB SC SA SB SC 27 MA¢ MB¢ MC¢
Dầu bằng xảy ra khi và chỉ khi: = = Þ S = S = S . MAC MAB MBC SA SB SC
Điều này chỉ xảy ra khi M là trọng tâm tam giác ABC . Vậy đáp án đúng là B.
Câu 19. Đáp án B, A, D, A.
ìMN = ( ABM ) Ç(SCD) ï
ïAB = ( ABM ) Ç( ABCD) a) Ta có : í
Þ MN∥AB. Do đó ABMN là hình thang. Do MN < AB C
ï D = ( ABCD) Ç(SCD) CD ï î ∥AB
nên ABMN không thể là hình bình hành, hinh thoi. Vậy đáp án đúng là B. Trang 45 ìI Î ï (SAC)
b) Gọi I = AM Ç BN Þ í
Þ I Î SO = (SAC)Ç(SBD). Vậy đáp án đúng là A. ïI Î î (SBD) ìI Î ï (SAD)
c) Gọi K = AN Ç BM Þ í
Þ I Î(SAD) Ç(SBC) . ïI Î î (SBC)
Giao tuyến của hai mặt phẳng (SAD) và (SBC) là đường thẳng qua S và song song với AD. Vậy đáp án đúng là D. AB BM
d) Do MN∥AB nên = ( ) 1 . MN MK CB MB Do SK BC ∥ nên = (2). SK MK AB BC Từ ( ) 1 và (2) suy ra -
= 0. Vậy đáp án đúng là A. MN SK
Câu 20. Đáp án C, C.
a) Trong mặt phẳng (BCD), gọi I = MG Ç BC, J = MG ÇC ,
D K = MG Ç BD. Qua M kẻ Mx G
∥ A. Trong ( AIJ ): Mx Ç AI = P(đây chính là giao điểm của Mx với ( ABC))
Tương tự Mx Ç AK = R, Mx Ç AJ = Q . IM S S S + S S 3S Ta có : MIC MIB MIC MIB MBC MBC = = = = = . IG S S S + S S S GIC GIB GIC GIB GBC BCD IM MP MP S
Theo định lý Thalet ta có : = 3 . Do đó : MBC = . IG GA GA SBCD MQ 3S MR 3S
MP + MQ + MR
Chứng minh tương tự ta có : MCD = , MBD = Þ = 3. GA S GA S GA BCD BCD Vậy đáp án đúng là C. 3
æ MP + MQ + MR ö
b) Áp dụng bất đẳng thức Cauchy ta có : 3 M . P M . Q MR £ = GA . ç ÷ è 3 ø
Vậy giá trị lớn nhất của . MP . MQ MR bằng 3
GA . Dấu bằng xảy ra khi và chỉ khi
MP = MQ = MR. Điều này xảy ra khi M là trọng tâm tam giác BCD. Vậy đáp án đúng là C.
Câu 21. Đáp án A, A. Trang 46 a) Do Dx SC ∥
nên hai đường thẳng này cùng nằm trong mặt phẳng (SCD).
Lại có, hai mặt phẳng (SAB) và (SCD) có D là điểm chung, AB C
∥ D nên giao tuyến là
đường thẳng đi qua S và song song với AB . Vậy I thuộc giao tuyến này. Vậy đáp án đúng là A.
b) Gọi E là giao điểm của SD và IC . Suy ra thiết diện của hình chóp cắt bởi mặt phẳng
(AIC) là tam giác ACE .
Ta có SIDC là hình thang nên SI = CD và SI C
∥ D . Suy ra SI = AB và SI∥AB . Điều này
suy ra SIDC là hình bình hành. Khi đó AI = SB = a . a 2
Mặt khác, AC = SD = a 2 Þ AE = . 2
Xét tam giác IAC có : 2 CI = ( 2 2 AC + AI ) 2 2 2
- 4AE = 4a Þ CI = 2a. 2 a 2 2 2 2 2 + 2a - a
AE + AC - CE 3 7 Ta có : ∑ 2 ∑ cosCAE = = = Þ sin CAE = . 2 2AC.AE 2a 4 4 a a
Diện tích thiết diện là : ∑ 2 1 1 2 7 7
S = AC.AE.sin CAE = a 2. . = . 2 2 2 4 8 Vậy đáp án đúng là A.
Câu 22. Đáp án C, A. a) Ta có :
ìKH∥AB, KH Ì ï
(HKM ), AB Ì (ABCD) í
Þ (HKM ) Ç( ABCD) = MN∥AB H ∥ K ( ) 1 . ïM Î î (HKM )Ç( ABCD) Ta lại có: SA D D = SB D C(c c c) ∑ ∑
. . Þ SAD = SBC . Trang 47