Thông tin
Hỏi đáp

Bài tập trắc nghiệm Toán 7

Tài liệu gồm 125 trang, tuyển tập các bài tập trắc nghiệm Toán 7 (Đại số 7 và Hình học 7) theo chuyên đề, có đáp án và lời giải chi tiết.

Chủ đề:

Tài liệu chung Toán 7 231 tài liệu

Môn:

Toán 7 2.1 K tài liệu

Thông tin:

125 trang 10 tháng trước

Tác giả:

Kim Oanh

docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Bài tập trắc nghiệm Toán 7

Tài liệu gồm 125 trang, tuyển tập các bài tập trắc nghiệm Toán 7 (Đại số 7 và Hình học 7) theo chuyên đề, có đáp án và lời giải chi tiết.

53 27 lượt tải Tải xuống

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

hần I. HƯỚNG DẪN LÀM BÀI TẬP TRẮC NGHIỆM

những thay đổi trong tính chất và phương pháp thi trong năm học này nên việc ôn

tập cũng phải thay đổi. Hình thức thi trắc nghiệm sẽ là phổ biến trong các môn thi. Để đáp ứng

một bài thi trắc nghiệm cần phải đạt được 4 mức độ kiến thức:

1. Nhận biết

*Nhận biết có thể được hiểu là học sinh nêu hoặc nhận ra các khái niệm, nội dung, vấn đề đã

học khi được yêu cầu

*Các hoạt động tươn

g ứng với cấp độ nhận biết là: nhận dạng, đối chiếu, chỉ ra…

*Các động từ tương ứng với cấp độ nhận biết là: xác định, liệt kê, đối chiếu hoặc gọi tên, giới

thiệu, chỉ ra…nhận thức được những kiến thức đã nên trong sách giáo khoa

Học

sinh nhớ được (Bản chất) những khái niệm cơ bản của chủ đề và có thể nêu hoặc nhận ra

các khái niệm khi được yêu cầu. Đây là bậc thấp của nhận thức, khi học sinh kể tên, nêu lại,

nhớ lại một sự kiên, hiện tượng. Chẳng hạn ở mực độ này, học sinh chỉ cần có kiến thức về

hàm số bậc nhất để thay tọa độ điểm vào phương trình đường thẳng để tìm ra tọa độ điểm phù

hợp.

Ví dụ 1: Cho hai số nguyên x, y và

0y 

. Nếu x, y trái dấu thì số hữu tỉ



0a 

0a 

0a 

D. Cả B và

C sai

Đáp án C

Ví dụ 2: Cặp số hữu tỉ nào dưới dây bằng nhau?



và

2

và

Đáp án A

Ví dụ 3: Biểu đồ dân

số Việt Nam qua tổng điều tra trong thế kỉ

XX (đơn vị của các cột là triệu người)

Chon câu trả lời sai

. Năm 19

21 số dân của nước ta là 16 triệu người

. Năm 19

60 số dân của nước ta là 30 nghìn người

C. Năm 19

80 số dân của nước ta là 66 triệu người

D. Năm 19

99 số dân của nước ta là 76 triệu người

999

980

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Đáp án C

. Thông

hiểu

*Học sinh hiểu các khái niệm cơ bản, có khả năng diễn đạt được kiến thức đã học

theo

hiểu của mình và có thể sử dụng khi câu hỏi được đặt ra tương tự hoặc gần với các ví dụ học

sinh đã được học trên lớp.

*Các hoạt động tương ứng với cấp độ thông hiểu là: diễn giải, kể lại, viết lại, lấy đượ

ví dụ theo các hiểu của mình.

*Các động từ tương ứng với cấp độ thông hiểu có thể là: Tóm tắt, giải thích, mô tả,

sánh (đơn

giản), phân biệt, trình bày lại, viết lại, minh họa, hình dung, chứng tỏ, chuyển đổi…

Học sinh hiểu các khái niệm cơ bản và có thể sử dụng khi câu hỏi được đặt ra gần với

các ví dụ học sinh đã được học trên lớp.

Ví dụ 1. Cho đoạn thẳng AB dài 8cm. Lấy điểm M trên đoạn thẳng AB sao cho

6AM 

cm.

Đường thẳng d là đường trung trực của MB, d cắt MB tại K. Khẳng định nào dưới đây sai?

B cm



. B.

A cm



. C.

d AB

. D.

/ /d AB

Ví dụ 2. Có bao

nhiêu số



thỏa mã

3 5 3 0



  

. Không

có

. B. Có một

số

. C. Có hai

số

. D. Có ba số.

Ví

dụ 3. Theo dõi các bạn nghỉ học ở từng buổi trong một tháng, bạn lớp trưởng ghi lại như

0 0 0 1 0 3 2 0 3 0 1 0 1

1 0 0 1 0 0 1 2 2 2 0 1 0

Dấu hiệu ở đây là

gì?

. Tổng số lượt học

sinh nghỉ học cả tháng

B. Là các số 0, 1, 2,

C. Số học sinh nghỉ học trong mỗi buổi.

D. Mỗi thá

ng học có 26 buổi

Đáp án C

. Vận dụng

*Học

sinh vượt qua cấp độ hiểu đơn thuần và có thể sử dụng, xử lý các khái niệm của

chủ đề trong các tình huống tương tự nhưng không hoàn toàn giống nhau như tình huống đã

gặp trên lớp. Học sinh có khả năng sử dụng kiến thức, kĩ năng đã học trong những tình huống

cụ thể, tình huống tương tự nhưng không hoàn toàn giống như tình huống đã học trên lớp

(thực hiện nhiệm vụ quen thuộc nhưng mới hơn thông thường) .

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

*Các

hoạt động tương ứng với vận dụng ở cấp độ thấp là: xây dựng mô hình, phỏng

vấn, trình bày, tiến hành thí nghiệm, xây dựng các phân loại, áp dụng quy tắc (định lý, định

luật, mệnh đề…), sắm vai và đảo vai trò….

*Các động từ tương ứng với vận dụng ở cấp độ thấp có thể là: thực hiện, giải quyết

minh

họa, tính toán, diễn dịch, bày tỏ, áp dụng, phân loại, sửa đổi, đưa vào thực tế, chứng

minh, ước tính, vận hành, …

Học sinh vượt qua cấp độ hiểu đơn thuần và có thể áp dụng các khái niệm của chủ đề

trong các tình huống tương tự trên lớp để giải quyết một tình huống cụ thể trong thực tế hoặc

học sinh cá khả năng sử dụng các khái niệm cơ bản để giải quyết một vấn đề mới chưa từng

được học hoặc trải nghiệm trước đấy, nhưng có thể giải quyết bằng kỹ năng, kiến thức và thái

độ đã được học tập và rèn luyện. Các vấn đề này tương tự như các tình huống thực tế học sinh

sẽ gặp ngoài môi trương.

Ví dụ 1. Tìm



thỏa mãn

1 2

x x



  



. B.





. C.





. D.

0x 

Đáp án A

Ví dụ 2. Giá trị của biểu thức

x y xy





tại



và

1y 



bằng

. B.



. C.

. D.

Đáp án A

Ví dụ 3. Cho

/ /a b

và



100

A B 

(hình vẽ bên) .

Số đo góc



bằng:

. B.

. D.

Đáp án D

. Vận dụng ở mức độ cao hơn

Học

sinh có khả năng sử dụng các khái niệm cơ bản để giải quyết một vấn đề mới hoặc

không quen thuộc, chưa từng được học hoặc trải nghiệm trước đây, nhưng có thể giải quyết

bằng các kỹ năng và kiến thức đã được dạy ở mức độ tương đương. Những vấn đề này tương

tự như các tình huống thực tế học sinh sẽ gặp ngoài môi trường lớp học.

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Ở mức độ này học

sinh phải xác định được những thành tố trong 1 tổng thể và mối quan

hệ qua lạị giữa chúng, phát biểu ý kiến cá nhân và bảo vệ được ý kiến đó về 1 sự kiện, hiện

tượng hay nhân vật lịch sử nào đó.

Ví dụ 1. Cho

/ /a b

như hình vẽ bên.

Số đo góc x bằng:

150

. B.

. D.

Đáp án C

Ví

dụ 2. Cho hai đa thức

 

4 3 2

2 5P x x x x x   

và

 

4 3 2

6 2

Q x x x x x

    

, gọi

     

x P x Q x





. Hỏi đa thức

 

có bao nhiêu nghiệm?

. B.

. C.

. D.

Đáp án C

Ví dụ 3. Cho





Hỏi có bao nhiêu nghiệm x để H có giá trị nguyên?

. B.

. C.

. D.

Đáp án A

Ở bài

thi trắc nghiệm thường sẽ là những bài yêu cầu giải nhanh và không qua rườm rà,

yêu cầu kiến thức rộng và bao quát hơn. Nếu như các em đang theo phương pháp “chậm và

chắc” thì bạn phải đổi ngay từ “chậm” thành “nhanh”. Giải nhanh chính là chìa khóa để bạn có

được điểm cao ở môn thi trắc nghiệm. Với các bài thi nặng về lý thuyết thì sẽ yêu cầu ghi nhớ

nhiều hơn, các em nên chú trọng phần liên hệ.

Ngoài việc sử dụng kiến thức để làm bài thi, các em có thể vận dụng thêm các phương

pháp sau đây:

- Phương pháp phỏng đoán: Dựa vào kiến thức đã học, đưa ra phỏng đoán để tiết kiệm

thời gian làm bài.

- Phương pháp loại trừ:

Một khi các em không có cho mình mottj đáp án thực sự chính xác thì phương pháp loại

trừ cũng là một các hữu hiệu giúp bạn tìm ra câu trả lời đúng. Mỗi câu hỏi thường có 4 đáp án,

các đáp án cũng thường không khác nhau nhiều lắm về nội dung, tuy nhiên vẫn có cơ sở để

các em dùng phương án loại trừ bằng “mẹo” của mình cộng thêm chút may mắn nữa. Tháy vì

đi tìm đáp án đứng, bạn hãy thử tìm phương án sai… đó cũng là một cách hay và loại trừ càn

nhiều phương án càng tốt.

30°

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Khi

các em không còn đủ cơ sở để loại trừ nữa thì hãy dùng cách phỏng đoán, nhận

thấy phương án nào khả thi thi hơn và đủ tin cậy hơn thì khoanh vào phiếu trả lời. Đó là cách

cuối cùng dành cho các em.

Thi trắc nghiệm nhằm mục đích vừa đảm bảo hiểu rộng kiến thức vừa đảm bảo thời

gian nên các em cần phải phân bố thời gian cho hợp lý nhất.

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Chủ đề 1. BỐN

PHÉP TOÁN TRÊN TẬP SỐ HỮU TỈ

1. Một số vấn đề cần ôn tập

Số hữu tỉ là số viết được dưới dạng phân số

với

, ; 0

a b Z b

 

Tập hợp cá

c số hữu tỉ được kí hiệu là Q.

Cộng và trừ số hữu tỉ:

Cho hai số hữu tỉ

: ;

a b

y x y



 

, , 0

b m Z m





b a b

x y

m m



   

;

b a b

x y

m m



   

Nhân và chia hai số hữu tỉ:

Cho hai số hữu tỉ

: ;

v u v



 

, , ; , 0

b c d Z b d





c ac

b d bd



Nếu

0v 

thì

: .

a c a d ad

d b c bc



 

Số hữu tỉ

0x 

có số nghịc

h đảo là

Tính chất: Cho c

ác số hữu tỉ

y z

. Ta có:

Tính chất giao hoán:

;

. .

y y x x y y x



  

Tính chất kết hợp:

       

;

. . . .

y z x y z x y z x y z



    

Tính chất cộng với số 0:

x o o x xx   

Tính chất n

hân với số 1:

x x



Tính chất n

hân với 0:

0. 0



Tính chất p

hân phối của phép nhân đối với phép cộng:

 

. .

y z x y x z



 

Một số ph

ép toán hay sử dụng:

;

y x y x y x y

z z z z z z







  

, với

0z 

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

. 0















   

. . .

x y x y x y    

Chú ý kh

ông có tính chất:

 

: : :

x y x z x y z  

2. Ví dụ

Ví dụ 1 (Nhận biết) . T

ính



4 1

9 3









2 .3

,5 : 2

 

 

 

Giải:

7 6 7 13

11 11 11



  

Nhận xét: Hai số hữu tỉ

và

là hai phân số có cùng mẫu, nên áp dụng ngay phép

toán cộng và trừ số hữu tỉ để giải.

4 1 11 4 1 15 1 5 1 5 1 4

9 3 9 3 9 3 3 3 3 3





         

Nhận

xét: Với câu này tuy xuất hiện nhiều số hữu tỉ song ta thực hiện phép tính theo tuần

tự vẫn giải được.

Ngoài ra nếu ta chưa phát hiện

9 3



thì

ta có thể quy đồng và giải tiếp như cách giả

câu c.

. MSC=B

CNN

 

;11

10.11 110

1 2 11 20 11 20 9

11 10 11 110 110 110 110



     

Nhận

xét: Trong câu này ta nên đưa về phép tính hai số hữu tỉ viết dưới dạng phân số,

song hai phân số này không cùng mẫu số nên ta tìm bội số chung nhỏ nhất của chúng rồi áp

dụng phép toán.

2.2.3



2.2.2



, MSC=BCN

 

2.2.3.2



BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

3 13 19 26 57 26 57 83

8 12 8 24 24 24 24



     

Nhận xét: Câu này

giải hoàn toàn tương tự câu c ở trên.

2 8.2 16

5 3.5 15



 



3 14 9 14.9 126

.3 . 21

3 2 3 2 3.2 6



  

8 6 3 6.3 18 9

5 3 5 8 5.8 40 20



  

3 1 11 1 4 1.4 4 2

0,5: 2 : .

2 4 2 11 2.11 22 11





    





 

Nhận xét: Nhìn chung các phép nhân và chia ta chỉ cần áp dụng đúng công thức mà

không phải tìm bội số chung nhỏ nhất.

Ví dụ 2 (Thông hiểu) . Thực hiện phép tính.

1 6 1 1 1

3 6 5 2 3 6



  



  

   

   

2 1 5

1 1

3 3 3

 

   

    

   

 

   

 

5 1 1 1

3. :

6 5 10 4

 

 

  

 

 

 

 

1 1 3

10.

: 1

2 3 5

1 2 3 5 7

3 4 2 6



  



 



  



  



   



  



  



  

1 1 1 1 1 1

100 1000 10000 100000 1000000

E 

    

Giải:

Lưu ý trước khi

giải ví dụ 2:

Thứ nhất: nắm vững quy tắc và thứ tự thực hiện các phép tính.

Thứ hai: quy tắc bỏ dấu ngoặc

Nếu bỏ dấu ngoặc có dấu “+” đằng trước thì dấu các số hạng trong ngoặc vẫn giữ nguyên

Nếu bỏ dấu ngoặc có dấu “-” đằng trước thì ta phải đổi dấu tất cả các số hạng trong

ngoặc.

1 6 1 1 1 2 1 6 1 2 1

: . :

6 5 2 3 6 6 6 5 2 6 6



      



      

       

       

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

1 6 1 2 1 3 6 1 1

: . :

5 2 6 6 5 2 6







      



  



      



      

5 1 1 3.5 1

: .6

6 2 6 6.5 2



  

3 15 3 15 12

5 5 5 5





    

2 1 5 2 3 1 5 2 3 1 5

1 1 1 1

3 3 3 3 3 3 3 3 3

 

 

           

            

         

 

           

 

1 4 1 4 1 4 3

1 1 1 1 1 1 0

3 3 3 3 3

    

   

            



  

   

5 1 1 1 5 1 2 5 5 1 2 5

3. : 3. : 3. :

6 5 10 4 6 5 20 20 6 5 20

     



     

       

     

     

     

     

5 1 7 5 1 20 5 4

3. : 3. . 3.

6 5 20 6 5 7 6 7

 

     

     

 

 

   

     

 

24 11 11

42 42 14





  



 



  

   

2 1 1 3 4 5 1 5 3

10.

: 1 10. :

2 3 5 10 10 3 5 5

2 3 5 7 3 4 3 15 7

1 : 1

3 4 2 6 6 6 4 6 6



      



    



      



      





      



      

       



      

4 5 1 5 3 1 1 8

10 1 5

10. : 10. :

10 3 5 10 3 5

10 3 8

3 4 3 15 7 7 3 22 14 9 11

1 : 1 : 1

4 6 6 4 6 12 12 3

  

       



 



       

       

  

 



          



    

           

           

5 24 5 29

3.8

24 24 24 24

5 3 5 5 44

9 11

. 1 1

: 1

12 11 44 44 44

12 3

 

    

   



 

  



 

 

   

9 29

29 . 44

39 29 44 319

4 24

: .

5 44 39

24 44 24 39 24.39 234



 

  

      

 

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

1 1 1 1 1

100 1000 10000 100000 1000000

E 

    

,1 0,01 0,001 0,0001 0,00001 0,000001



    

,1 0,01 0,001 0,0001 0,000011

,1 0,001 0,0001 0,000111 0,1 0,01 0,001111

0,1 0,011111 0,111111



   



     

  

Ví dụ 3 (Vận dụng) . Thực hiện phép

tính bằng cách hợp lý

5 6 1 7

7 6 3



  

2 8 7 3

0,25

3 4 2



   

1 16 10

11 5 5 11







 

 

 

1 5 5 1 5

3 5 3 3 5 3

   



  

   

   

Giải:

Nhận xét: Trong v

í dụ này ta phải sử dụng các tính chất để nhóm các số hữu tỉ mà dễ tính được

giá trị sau khi nhóm. Sâu đây là bài giải, các bạn xem và tìm ra tính chất đã được sử dụng để

làm bài tập này

6 1 7 5 1 6 7 5 1 6 7 2 6 7

7 6 3 6 6 7 3 6 7 3 3 7 3





  



            



  

   

7 6 2 7 6 6 21 6 27

3 7 3 7 7 7 7 7





  

         

   

   

8 7 3 5 8 1 7 3 5 8 1 7 3

0,25

3 3 4 2 3 3 4 4 2 3 4 2



   



           



  

   

6 3 3 3 3 3

1 1 0 1

4 2 2 2 2 2

  

 



             





 

1 16 10 10 1 16 10 1 16 10 15

. . . . .

5 5 11 11 5 5 11 5 11 5

   



      

     



      



      

11 11



1 1 5 5 1 5 1 1 5 1 5 1 1 5 1 3

: : : .

3 5 3 3 5 3 3 5 3 5 3 3 5 3 5 5

 

         

           

         

 

         

 

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

1 5 1 1 3 1 5 3 4 3 4

. 0 . .

3 3 5 5 5 3 5 3 5 5

 

   

     

      

     

 

     

 

Ví dụ 4 (vận dụng và

vận dụng cao) . Tìm số hữu tỉ x biết:

)

 

2 5







 





 



x x

 









 

: (3 )

5 3





2016

008

5 3 2

x x





 

Giải:

)

12 12 5 12 5 12 17

1 1

5 5 5 5 5

x x x x x



           

Kết luận:



)

2 5 2 5 5 2

1 1

7 7 7 7 7

x x

 



         





 

1 1 0

7 7

x x x

 



       





 

Kết luận:

0x 

)

3 3 5 3 6 3.6 9

: .

2 2 6 2 5 2.5 5

x x x x x

        

Kết luận:



x x

 



  

 

 

hoặc

 

0x



hoặc

 

Kết luận:

0x 

hoặc





   

11 19 11 19 11 6

2 : (3 ) : 3 2 : 3

3 5 3 5 3 3

x x x

       

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

   

11 6 19 5 19 5 19 3 19.3

3 : 3 3 : 3 . 3

3 5 3 5 3 5 5 5.5

x x x x





        

57 57 57 1 19

3 : 3 .

25 25 3 25

x x x x       

Kết luận:

x 

     

2016

2016 1 1 1

100

8 2016 . 2016 . 2016 .

3 2 5 3 2

x x

x x x





       

   

1 1

2016

. 2016 . 0

5 3 2

x x

 



    

 

 

 

1 1 1

2016 . 0

3 2

 

    





 

. Dễ thấy

1 1

5 3 2



 

nên

2016 0x  

hay

2016x  

Kết luận:

2016x  

Lưu ý: Tron

g câu này nhiều học sinh nhằm

       

2016

016 : 5 2016 :3 2016 : 5 3

5 3

x x x





      

Dẫn đến tì

m sai kết quả.

. Câu hỏi trắc n

ghiệm

Câu 1. Câu nói nào dưới đây đúng?

A. Các số

đều là số hữa tỉ.

B. Số 0 k

hông phải là số hữu tỉ

C. Số hữu tỉ x có số nghịch đảo là

. Các số hữu tỉ đều b

iểu diễn được trên trục số

Câu 2. Kết quả phép tính

1 1

8 6 3









 

 

là.

. B.

. C.

. D.



BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Câu 3. Kết quả ph

ép tính

1 1 1

2 3

3 2 3



    



    



    



    

là.

. B.

. C.

4

. D.

Câu 4. Số



là kết quả của phép tín

h nào dưới đây?

2 8



. B.

8 4



. C.

8 4



. D.

2 8



Câu 5. C

ho biết

2 :











 

, tìm số hữu tỉ x:

. B.

128

. C.

. D.

Câu 6. Tr

ong các phân số sau, phân số nào biểu diễn số hữu tỉ

,125

. B.

. C.

. D.

125

Câu 7. C

ho hai số nguyên

và

0y 

. Nếu

trái dấu t

hì số hữu tỉ



0a 

. B.

. C.

0a 

. D. Cả B và

C sai

Câu 8. Các cặp số hữu tỉ nào dưới đây bằng nhau?



và

. B.

và

. C.

và

. D.

và

Câu 9. Số hữu tỉ nào

sau đây nằm giữa



và

. B.

. C.



. D.



Câu 10. Chọn đáp án sai: Các số nguyên

,x y

mà

x y



là:

, 1



. B.

, 3



  

3, 2x y 

. D.

0x y 

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Câu 11. Câu nói

nào dưới đây sai

. Số 9 là

một số tự nhiên

. B. Số -2 là

một số nguyên âm

C. Số



là một số hữu tỉ. D. Số 0 là

một số hữu tỉ dương

Câu 12. T

ính giá trị của

1 1 1

...

1.2 2.3 3.4 2017.2018

H 

   

2016

2017

H 

. B.

2017

2018

H 

201

H 

. D.

201

H 

Câu 13. T

ìm



, biết

  

2 4 0



 

3 2x  

. B.

2 3x  

2x 

. D.

3x 



Câu 14. Có bao n

hiêu số nguyên dương x thỏa mãn

  

3 7 2 0



 

số. B.

số. C.

số. D.

số.

Câu 15. Trong các câu sau, câu nào sai?

. Số hữu tỉ â

m nhỏ hơn số hữu tỉ dương

B. Số tự nhiê

n lớn hơn số hữu tỉ âm

C. Số ngu

yên âm không phải là số hữu tỉ

D. Số hữu tỉ

không l

à số hữu tỉ dương cũng không là số hữu tỉ âm

Câu 16. Trong các câu sau, câu nào đúng?

. Phép cộng luôn

luôn thực hiện được trong tập hợp số tự nhiên

B. Phép trừ lu

ôn luôn thực hiện được trong tập hợp số tự nhiên

C. Phép ch

ia luôn luôn thực hiện được trong tập hợp số hữu tỉ

D. Phép n

hân không luôn luôn thực hiện được trong tập hợp số hữu tỉ

MA TRẬN CÂU HỎI TNKQ CHỦ ĐỀ 1

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Mức độ

Chủ đề

Nhận biết

(câu)

Thông hiểu

(Câu)

Vận dụng (câu)

Thấp Cao

1 2, 4, 7, 8, 11 1, 3, 5, 6, 15 9, 10, 16 12, 13, 14

Chủ đề 2. SO S

ÁNH HAI SỐ HỮU TỈ

. Một số phương

pháp thường gặp

Với hai số hữu tỉ bất kỳ

ta luôn c

ó: hoặc



hoặc



hoặc



Phương pháp 1: So sánh với số 0: số hữu tỉ dương lớn hơn số hữu tỉ âm.

Phương pháp

2: Đưa hai số hữu tỉ về dạng phân số có cùng mẫu số hoặc cùng tử số.

Phương pháp 3: Làm xuất hiện một số hữu tỉ trung gian để so sánh.

Phương pháp

4: Sử dụng công thức:

Cho

0b 

, nếu

a b

thì

a a







, nếu

a b

thì

a a







Cho

, 0



, nếu



thì

a c c

b d d



 



2. Ví dụ

Ví dụ 1 (Nhận

biết) . So sánh các cặp số hữu tỉ sau:

và

9

và



và



và

Giải:

. Có



và





nên





(ta đã sử dụng phương pháp 1)

. Có



và



. Vì



và



nên



hay



(ta đã sử dụng

phương pháp 2: Đưa hai số hữu tỉ về dạng phân số có cùng mẫu số) .

. Có

16 32



. Vì



và



nên

32 32



hay

32 16



BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

(ta đã sử dụng

phương pháp 2: Đưa hai số hữu tỉ về dạng phân số có cùng tử số)

d. Có

,6 1



 

. Vì

9 8  

và

8 0

nên





hay



 

Suy ra





(ta sử dụng phương pháp 3: Làm xuất hiện một số

1

)

e. Vì



và



nên

7 7



hay





Vì

32 34

và

17 0

nên

17 17



hay



. Suy r

7 17



(ta sử dụng p

hương pháp 3: Làm xuất hiện một số

)

Chú ý: để ý

hơn ít nữa ta thấy







f. Áp dụng công thức ở phương pháp 4: Cho

0b 

, nếu

a b

thì

b b







Vì



và



nên

20 1

1 31 1







hay



Ví dụ 2 (T

hông hiểu) . Hãy viết ba số hữu tủ xen giữa



và



Giải: Sử dụn

g công thức ở phương pháp 4:

Cho

, 0



, nếu



thì

a c c

b d d







Ta có

1 1

 



nên có

1 2 1

11 6

  







nên có

3 1

17 6



 

 





nên có

4 1

23 6



 



Vậy

2 3 4 1

11 17 23 6



   



  

Ví dụ 3 (Vận dụng) . Viết lại các số hữu tỉ sa

u theo thứ tự lớn dần?

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

9 25 3 9

, , ,

8 12 7 7



Giải:

Vì





và



nên





Vì



và



nên

7 7



hay



Vì

9 8

và

8 0

nên

8 8



hay



. Vậy

7 8



Vì



và



nên

9 9



Vì



và



nên



hay



Vì

25 24

và

12 0

nên



hay



. Vậy



Kết luận: cá

c số hữu tỉ sau theo thứ tự tăng dần là

3 9 9 25

, , ,

7 8 7 12



Ví dụ 4 (b

ài 5 trang 8 SGK Toán 7 tập 1) (Vận dụng cao) .

Giả sử

,y ( , , , 0)

a b

x a b m Z m

   

và



. Hãy

chứng tỏ rằng nếu chọ

a b





thì

có

z y



Giải:

Ta có

b a b

m m m



  

nên

2x y z 

Mà



nên

x x y



 

hay



hay

x z

 

Mặt khác

x y

nên

x y y y  

hay



hay

z y

 

Từ

 

và

 

suy ra

z y



(điều phải chứng minh)

. Câu hỏi trắc n

ghiệm

Câu 1. Kết quả phép tính

1 5 7

3 2 4

















là

. Khẳng định nào dưới đây đúng?

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7



. B.

0a 

. C.

4a 



. D.

4a 



Câu 2. S

o sánh nào dưới đây đúng





. B.



. C.



. D.

101





Câu 3. Cặp số hữu tỉ nào dưới đây bằng nhau



và

2

. B.

và

. C.

và

. D.

và

Câu 4. Cá

c số hữu tỉ

5 7 3 18

;

; ; ;

1 9 5 5 13



ược sắp xếp theo thứ tự lớn dần là

5 18 7 3

;

; ; ;

11 9 13 5 5



. B.

5 3 18 7

;

; ; ;

9 11 5 13 5



5 3 18 7

;

; ; ;

11 9 5 13 5



. D.

5 3 7 18

;

; ; ;

9 11 5 5 13



Câu 5. C

ó bao nhiêu phân số có mẫu số bằng

, lớn hơn



và nhỏ hơn



số. B.

số. C.

số. D.

số.

Câu 6. C

ó bao nhiêu phân số có tử số bằng

, lớn hơn

và nhỏ h

ơn

số B.

số C.

số D.

số

Câu 7. C

ho các số có quy luật

1 5 25 125

;

; ;

8 8 8

   

. Số tiếp th

eo của các số là

625



. B.

225



525



. D.

575



Câu

8. Cho các tích sau

15 7



   





  



  

9 14

5 17 23



     





    





    

4 3 4 5

. ... .

13 13 13 13 13



 

         



         



        

. Khẳng định nào dưới

đây đúng?

3 1

H H H 

. B.

2 3

H H H 

2 1

H H H 

. D.

1 3

H H H 

Câu 9. Tì

m hai số hữu tỉ

và

sao cho

y x y x y



 

, trong đ

0y 

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7





và

1y 

. B.





và

1y 





và

1y 

. D.



và.

Câu

10. Bình và Công mua quà tặng sinh nhật bạn An. Giá một cái bánh là

300000

đồng,

Bình mua

cái

bánh này. Một thùng nước ngọt giá

250

000

đồn

g, Công mua nửa thùng nướ

này. Hỏi bạn nào m

ua hết nhiều tiền hơn?

. Bình m

ua hết nhiều nước hơn

. B. Công

mua hết nhiều tiền hơn

C. Hai bạn

nhiều như nhau

. D. Không

xác định được ai mua nhiều

MA TRẬN CÂU

HỎI TNKQ CHỦ ĐỀ 2

Mức độ

Chủ đề

Nhận biết

(câu)

Thông hiểu

(câu)

Vận dụng (câu)

Thấp Cao

,2,3

,8,9,10

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Chủ đề 3. GIÁ

TRỊ TUYỆT ĐỐI CỦA MỘT SỐ HỮU TỈ

1. Một số vấn đề cần ôn tập

Giá trị tuyệt đối của số hữu tỉ

, kí hiệu

, là khoảng cách từ điểm

tới điểm

trên trực số.

Ta có:

 

x x



















Nhận xét: Với mọi

Q y Q



ta luôn có

0, , , ,

x x x x x x x x x      

. ,

x y x y



(phép chia

với điều kiên

0y 

)

y x y x y x y



    

x y x y  

khi

. 0x y 

. Ví dụ

Ví dụ 1 (Nhận biết) . Tìm

, biết



,76

x 







1 29

4 6

x 



Giải:

x 



vì



 

0.7

6 0,76 0,76



    

, vì

,76 0





3 3

5 5





     

 

 

, vì





1 29 33 58 33 58 25

6 12 12 12 12



     

Nên

25 25 25

12 12

 

 

   

 

 

, vì





Ví dụ 2 (T

hông hiểu) . Tìm



, biết:

1,2

 

0,3







3 2





BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Giải:

Nhận xét: dạng bài

toán tìm

để

 

x B



, ta thực hiện

như sau

Vì

 



nên

Khi

0B 

, sẽ không có

giá trị

Khi

0B 

, giá trị

phải thỏa

mãn

 



Khi

0B 

, giá trị

phải thỏa

mãn

 

x B





hoặc

 

x B



Vì

, 1,2 0



 

, nên không có số hữu tỉ

thỏa mãn





b. Vì

,3 0





, nên có

hai giá trị thỏa mãn là

,3; 0,3



 





hay

5 5





hay

0 3





hay



Có hai giá

trị thỏa mãn là

;

x x

  

d. Giá trị

phải thỏa mãn





hoặc



 

Khi

3 2





có

2 3





hay

6 6





hay





hay



Khi

  

có

  

hay





hay





Kết luận: có

hai giá trị thỏa mãn là

;





Ví dụ 3 (Vận dụng) . Tìm



, biết:

2 2 3

x x



  

 

3 6

x x





Giải:

Vì

2 0





và





nên

2 2 0



  

, do đó

x 

hay

0x 

Khi

ta có

3 2 2 3x x x   

hay

4x  

(không

thỏa mãn

0x 

)

. Vậy không có giá trị



thỏa mãn đề bài

Vì

 

2 3 0,

x x

 

nên

x 

hay

0x 

Khi

0x 

ta có

 

3 6

x x





Nếu

0x 

thì

 

2.0 3 6.0





(đúng)

Nếu

0x 

thì ta có

3 6

x 



hay

6 3

x 



hay



(thỏa mãn

0x 

)

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Kết luận:



Nhận xét: trong ví dụ này có nhiều học sinh nhầm như sau.

 

3 6 2 3 6 2 3

x x x x x



       

Giải: như vậy dẫn đến thiếu giá trị cho

Ví dụ 4 (Vận dụng và vận dụng cao) . Tìm giá trị nhỏ nhất của các biểu thức sau

a. Vì

1 0

 

nên

1 3 3

   

1 3 3

   

khi

1x 

Vậy

đạt giá trị nhỏ nhất là

3

khi

1x 

b. Ta có

2018



 

(vì tính chất

b a b



 

)

Hay

1, 1B B 

khi

  

17 2018 0



 

(xảy ra được,

chẳng hạn

2017x 

)

Vậy

đạt giá trị nhỏ nhất là

khi

  

2017 2018 0

x x

  

c. Ta có

0, 2 2

x x



   

Nên

2 3 0 2 3

x x x x



        

hay

5C 

5C 

khi xảy ra đồng thời

0, 2 2

x x



   

và



 

tức

1x 

Vậy

đạt giá trị nhỏ nhất là

khi

1x 

Nhận

xét: Câu này là một bài toán khó, yêu cầu người giải: bài tập phải vận dụng linh hoạt các

công thức đã biết và phải còn khéo léo triệt tiêu

hợp lý

trên cơ sở

0C 

. Câu hỏi trắc n

ghiệm

Câu 1. Cho

14 5

3 2

x  

. Tính



. B.



. C.



. D.



Câu 2. Gi

á trị nào của

dưới đây thỏa

mãn

2 3 9 2x x  





. B.



. C.

0x 

. D.

6x 

Câu 3. Có bao nhiêu số



thỏa mãn

3 5 3 0



  

. Không

có

. B. Có một

số

. C. Có hai

số

. D. Có ba số.

Câu 4. Câ

u nói nào dưới đây sai?

A. Không có số hữu tỉ

nào thỏa mãn

5 2



 

B. Có đún

g một số hữu tỉ

thỏa mãn

19 0





C. Chỉ có

hai số hữu tỉ

thỏa mãn

7 12 8

 

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

D. Chỉ có

hai số hữu tỉ

thỏa mãi

2 1 6



 

Câu 5. C





thì

0x 

. B.

0x 

. C.

0x 

. D.

0x 

Câu 6. C





và



. Tính

giá trị của biểu thức

H x y 





. B.





. C.



. D.



Câu 7. C

Q y Q



thỏa mãn

y y x



 

. Kết luận nào sau đây đúng

0x 

và

0y 

. B.

0x 

và

0y 

0x 

và

0y 

. D.

0x 

và

0y 

Câu 8. C

Q y Q



thỏa mãn

x y x y  

. Kết luận nà

o sau đây đúng

và

trái dấu. B.

và

cùng dấu.

và

cùng dư

ơng

. D.

và

cùng âm.

Câu 9. Tì

m giá trị nhỏ nhất của

3 4



 

đạt giá t

rị nhỏ nhất là

. B.

đạt giá

trị nhỏ nhất là

3

đạt giá t

rị nhỏ nhất là

. D.

đạt giá t

rị nhỏ nhất là

4

Câu 10. T

ìm giá trị lớn nhất của



 

đạt giá t

rị lớn nhất là

. B.

đạt giá

trị lớn nhất là

đạt giá trị lớn nhất là

. D.

đạt giá trị lớn nhất là

Câu 11. Tìm

x Q

thỏa mãn

1 2

x x



  







0x 

Câu 12. Hỏi có ba

o nhiêu giá trị



thỏa mãn

 

x x





A. Có một

giá trị B

. Có hai

giá trị

. Có ba g

iá trị D

. Có bốn

giá trị

MA TRẬN CÂU

HỎI TNKQ CHỦ ĐỀ 3

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Mức độ

Chủ đề

Nhận biết

(câu)

Thông h

iểu

(câu)

Vận dụng (câu)

Thấp Cao

,5,6,7

,3,4,9,10

,11

Chủ đề 4. LŨY

THỪA CỦA MỘT SỐ HỮU TỈ

. Một số vấn đề cần

ôn tập

Lũy thừa với số mũ tự nhiên:

. . ...a

a a a a





 

a Q n N

 

Các công thức: Cho

b Q,n ,

Q N m N



  

, : a

n m n m n m n

a a a a







(với phép

chia:

0b 

)

 

1 0

a a





 

, không tồn tại số

Với

, 1



 

, nếu

a a

thì



2. Ví dụ

Ví dụ 1 (Nhận b

iết) . Viết các biểu thức số sau dưới dạng lũy thừa của một số hữu tỉ.

2 .8

36 : 6

2 .9

 

8 7

0,25 .16 56.8



Giải:

Phương ph

áp: sử dụng các công thức ở trên để đưa biểu thức số về dạng

 

6 3.3 6 3 6 3 6 9

2 .8 2 .8 2 .8 8 8



   

 

10 2 10 2.8 10 16 10 6

36 : 6 6 : 6 6 : 6 6 6



   

 

9 9

9 10 9 9 9

9 2 9 9 9

2 .9

2.9

2 .9 2 .9 .9 18 18

3 3 .3 9.3 3 3 3

 



    

 

 

 

   

8 7

7 2 3 2.8 3.7

1 1

0,25 .16 56.8 . 4 7.8. 2 .4 7.2

4 4

 

    

 

 

 

21 16 4 3 21 2 24 24 3 24 27

7.2 .2 4 7.2 2 7.2 8.2 2 2



 

       

Ví dụ 2 (T

hông hiểu) . Tính giá trị của các biểu thức sau:

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

3 .

 



 

 

1 1

16 4

   



   

   

5 5 6

.5 10

3.5





 

,25 .2 6

2 16







Giải:

Phương pháp: Biến đổi các lũy thừa về dạng các lũy thừa có cùng cơ số hoặc cùng số mũ hoặc

cùng cả số mũ và cơ số, sau đó sử dụng các công thức để rút gọn

 

19 19 19 18

1 3

. 3 . 3 3









   





 

28 2.15 28 30 28 2

1 1 1 1 1 1 1

: :

16 4 4 4 4 4 16



           

    

           

           

 

5 6 5 5 5

5 5 5 5

2.5

10.10

2 .5 10 10 10.10 9.10 10

3.5 3.5 3.5 3.5 5



  

 



      





 

 

5 4

0,25 .2 6

2 .2 6 1

2 16 2 2 1 2





  

 

Ví dụ 3 (Vận dụng) . Tìm số tự nhiê

, biết

8 1



 







2 .3 36



n



Giải

5 3 5 8

1 2 1

2 .2 2 2 2 8

32 2 2

n n





        

Kết luận:

8n 

   

 

         

2 1 2

5 5 5 5 5 5

n n





             



   

5 5 3

     

Kết luận:

3n 

 

.3 36 2.3 6 6 6 2

n n



     

Kết luận

2n 

5 5 0

1 6 6

6 :3 96. 1 32 1 2 .2 1 2

96 3.3 3

n n n



 

        

 

 

0 5



    

(số thự nhiên luôn lớn hơn hoặc bằng

, không thỏa mãn)

Kết luận: k

hông có giá trị

thỏa mã

n đề bài.

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Ví dụ 4: (Vận dụng ca

o) . Chứng minh

 

5.2 8



chia hết cho

 

28 2018 2017

3 .13 9

chia hết cho

Giải:

a. Ta có

 

14 5 14 3 14 3.5 14 15 14 14 14

5.2 8 5.2 2 5.2 2 5.2 2 5.2 2.2 3.2

         

 

2 7

3.2 4. 2 3.4

  

chia hết

cho

chia

hết cho

và

 

3,4 1

UCLN



Nên

 

5.2 8



chia hết cho

(đpc

)

2028

2018 2017 10 2018 2018 2016 10 2018 2018 2016

.13 9 3 .13 9.9 3 .3 .13 9.9





   

 

018

5 2016 2 2018 2016

3 3.13 9.9 3 .39 9.9

   

2018 2016 4 2018 2016

.39 9.9 9.9 .39 9.9



 

Vì

2018 2016

,39 ,9.9

đều là n

hững số có chữ số hàng đơn vị là

Nên

2018

9.9

.39

và

2016

9.9

đều những số c

ó chữ số hàng đơn vị là

Suy ra

4 2018 2016

9.9

.39 9.9



có chữ số hàng

đơn vị là 0.

Tức là

 

18 2018 2017

3 .13 9

chia hết c

(đpcm)

Nhận xét: tr

ong bài này ta cần ghi nhớ kết quả sau:

Tất cả số có chữ số tận cùng là

;1;5;6

, khi

nâng lũy thừa với số mũ nguyên dương cho ta chữ

số tận cùng giữu nguyên.

Các số có chữ số tận cùng là:

, khi nân

g lũy thừa với số mũ chẵn cho ta chữ số tận cùng là

khi nâng lũ

y thừa với số mũ lẻ cho ta chữ số tận cùng

Các

số có chữ số tận cùng là:

, khi

nâng lũy thừa với số mũ chẵn cho ta chữ số tận cùng là

khi nâng lũy thừa với số mũ lẻ cho ta chữ số tận cùng

Các số có c

hữ số tận cùng còn lại ta sẽ thêm bớt đề xuất hiện một trong các số đã nói ở trên.

. Câu hỏi trắc n

ghiệm

Câu 1. Viết số

 

0,125

dưới dạng lũy thừa của cơ số

là:

 

. B.

 

. C.

 

. D.

 

Câu 2. Viết số

dưới dạng lũy thừa có

số mũ là

. B.

. C.

. D.

Câu 3. Tr

ong các khẳng định sau khẳng định nào sai.

 



là một

số âm

. B.

 



là một

số dương.

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7





. D.

0 0

Câu 4. Tì

m số nguyên dương

thỏa mãn

5 625

3 81

 



 

 

2n 

. B.

3n 

. C.

4n 

. D.

5n 

Câu 5. C

ó bao nhiêu số hữu tỉ

thỏa mãn



. 1 số. B.

số. C.

số. D.

số.

Câu 6. Tìm số hữu tỉ

thỏa mãn

 

125

x 







. B.





. C.



. D.



Câu 7. C

ho số

5 10



. Tìm số các chữ số của

chữ số. B.

chữ số. C.

chữ số. D.

chữ số.

Câu 8. C

ho hai số



10b



. Khẳng định

nào dưới đây đúng?

a b

. B.

a b

. C.

a b

. D.

2b a

Câu 9. C

ho hai số



20b



. Khẳng định

nào dưới đây đúng?

a b

. B.

a b

. C.



. D.

Câu 10. Cho hai

số

32 223

, 3

b 

. Khẳng định

nào dưới đây đúng?

a b

. B.

a b

. C.

a b

. D.

3 2a b

Câu 11. Cho

 

5 10

3 15 3

. 0,5 3.2

.2 2 : 2







. Khẳng định nào dưới

đây đúng?



. B.



. C.



. D.

1E 

Câu 12. Cho

 

4 7 8

2.6 6

2 9 2.3 3





 

. Khẳng định nào dưới

đây đúng?

8F 

. B.

6F 

. C.

8F 

. D.



BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Câu 13. Cho

4 9

8 8

.9 2.6

.3 6 .20







. Khẳng định nào dưới

đây đúng?



. B.



. C.

0F 

. D.

3F 



Câu 14. T

ìm số tự nhiên

thỏa mãn

n



để

 



chia hết cho

19n 

. B.

18n 

. C.

17n 

. D.

16n 

Câu 15. Cho số

9 5 10

2 .5





. Khẳn

g định nào dưới đây đúng?

có chữ số tận cùng

bằng

. B.

110A

có chữ số tận cùng bằng

. D.

1000A

Câu 16. Có bao n

hiêu số hữu tỉ

thỏa mãn

x

số B.

số C.

số D.

số.

MA TRẬN CÂU

HỎI TNKQ CHỦ ĐỀ 4

Mức độ

Chủ đề

Nhận biết

(câu)

Thông hiểu

(câu)

Vận dụng (câu)

Thấp Cao

,2,3,4,5,6,16

,9,11,12,13

,10

,15

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Chủ đề 5. TỈ LỆ THỨC. TÍN

H CHẤT CỦA DÃY SỐ TỈ SỐ BẰNG NHAU

. Một số vấn đề cần

ôn tập

Tỉ lệ thức là đẳng thức của hai tỉ số

Tỉ lệ thức

a c



còn được viết

: :a b c d

Các số

, ,

b c d

được gọi là các số hàng của tỉ lệ thức

và

gọi là n

goại tỉ (số hạng ngoài)

và

gọi là trung tỉ (số hạng trong)

Tính chất:

Nếu

b d



thì

ad bc

Nếu

ad bc

và

, , , 0

a b c d



thì ta có các

tỉ lệ thức

, , ,

c a b d c d b

d c d b a c a

   

Tính chất của dãy tỉ số bằng nhau:

Từ tỉ lệ thức

a c



ta suy ra

a c a c a c

d b d b d

 



 





(giả thiết các

tỉ số đều có nghĩa)

Từ dãy tỉ số bằng nhau

a c e

b d f

 

ta suy ra

a c e a c e a c e

b d f b d f b d f

   

   

   

(giả thiết cá

c tỉ số đều có ý nghĩa)

Khi có dãy

tỉ số

2 3 5

b c



ta nói

các số

b c

tỉ lệ với

;3;5

Ta cũng viết

: : 2 : 3:5a b c 

2. Ví dụ

Ví dụ 1 (nhận b

iết) . Tìm số hữu tỉ

biết:

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

,1: 0,2 : 0,06

x

 

 









 









Giải:

,1: 0,2 : 0,06 0,2. 0,1.0,06



     

0,06

0,2.x 0,06 x 0,03

0,2



       



Vậy

0,03x 

là giá trị cần tì

   

2 2

12 . 3 36 6

x x x x





       



suy ra

6x 

hoặc

6x 



là giá trị cần tìm

   

2 .7 3 .3 7 14 9 3 7 3 9 14

x x x x x



            





   

thỏa mãn

3x 

Vậy





là giá trị cần tìm.

Chú ý: ta có

thẻ giải bài này như sau:

3 2 3 2 3 2 3

7 3 7 3 7 3 7

x x x x x x



      

     

 

Do vậy

 

5 2 1

.2 3.1 2 4 3 2 3 4

3 10 3 2

x x x





          





   

(thỏa mãn

3x 

)

Vậy





là giá trị cần tìm.

Ví dụ 2: (Thông hiểu) Một mảnh đất hình chữ nhật có tỉ số giữa chiều dài và chiều rộng bằng

. Tính diện

tích mảnh đất này biết rằng chu vi của mảnh đất bằng 28m?

Giải:

Gọi chiều dài. chiều rộng của mảnh đất lần lượt là x, y (m) (x, y > 0)

Do tỉ số giữa chiều dài và chiều rộng bằng

nên

có



hay

4 3



Do chu vi của mản

h đất bằng 28 m nên có 2x +2y = 28 hay x + y =14

Áp dụng tính chất của dãy tỉ số bằng nhau có:

4 3 4 3 7

y x y





  



BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Suy ra

8, 2 6

x y



    

(thử lại các gía

trị ta tấy thỏa mãn

)

Vậy mảnh

đất hình chữ nhật có chiều dài 8m và chiều rộng 6m

Ví dụ 3: (Thông hiểu) Số học sinh giỏi của lớp &A, 7B, 7C tỉ lệ với cá số 4; 3; 5. Biết rằng

tổng số học sinh giỏi của hai lớp 7A và 7C nhiều hơn số học sinh giỏi của lớp 7B là 30. Hỏi

mỗi lớp có bao nhiêu hc sinh giỏi?

Giải:

Gọi số học sinh giỏi của lớp 7A, 7B, 7C lần lượt là x, y, z (

,x y z 



)

Do x, y, z tỉ lệ với các số 4; 3; 5 nên

3 5

y z

 

Tổng số học si

nh giỏi của hai lớp 7A và 7C nhiều hơn số học sinh giỏi của lớp 7B là 30 nên có

x+z –y =30.

Áp dụng tính chất của dãy tỉ số bằng nhau có:

3 5 4 3 5 6

x y z x y z

 

    





Suy ra

20; 5 15; 5 25

3 5

y z

x y y



       

Vậy số học

sinh của lớp 7A là 20 bạn; 7B là 15 bạn; 7C là 25 bạn.

Ví dụ 4: (Vận dụng và vận dụng cao) . Giả thiết cá tỉ số đều có nghĩa

a. Cho



. Chứng minh rằn

b c a

a b c a





 

b. Cho tỉ lệ t

hức

a c



. Chứng minh rằng

17 2017 2017

2017 2017 2017

(

)

(

)

c a c

b d b d

 



 

Giải:

Nhận

xét: Trong VD này, mỗi câu đều có nhiều cách giải khác nhau, song tôi xin trình b một

cách được cho là phù hợp nhất của bài toán.

a. Từ



có

a c



Áp dụn

g tính cất có

a c a c c a

a b a a b

 

 







Suy ra

a b c a

b c a

 





(điều phải c

hứng minh)

b. Đặt



suy ra a =kb; c

=kd

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

17 2017 2017 2017 2017 2017 2017 2017 2017 2017 2017

17 2017 2017 2017 2017 2017 2017 2017

(

) ( ) . . .( )a c kb kd k b k d k b d

d b d b d b d



  

   

   

17 2017 2017 2017 2017

17 2017 2017 2017

(

) ( ) [k.(b+d)] ( )

( ) ( ) ( ) ( )

a c kb kd k b d

d b d b d b d

  

   

   

Từ đó suy ra

17 2017 2017

2017 2017 2017

( )

(

)

a c a c

b d b d

 



 

(điều phải chứng minh)

. Câu hỏi trắc n

ghiệm

Câu 1. Thay tỉ số (1, 2; 1, 35) bằng tỉ số giữa các số nguyên

. 50: 81 B. 9: 8 C. 5: 8 D. 1: 10

Câu 2: T

hay tỉ số

2 8

2 :













bằng tỉ số giữa các số nguyên

A. 7: 10 B. 10: 7 C. 128: 35 D. 35: 128 .

Câu 3: Cho tỉ lệ thức



. kết luận nào

dưới đây đúng?

. 8 và

là trung tỉ của

tỉ lệ thức B

. 9 và

là ngoại tỉ của

tỉ lệ thứ

C. 8 và

là ngoại tỉ của

tỉ lệ thức D

. Cả A, B, C đều

sai

Câu 4: Tỉ số nào t

rong các cặp tỉ số sau lập được tỉ lệ thức?

. .

: 3 và 0, 3: 5 B. 6: 5 và

: 3

. 6: 8 và

0, 3: 0, 5 D

. 0, 3: 2, 7 và 1, 71: 1

5, 39

Câu 5: Các số nào sau đây lập được các tỉ lệ thức?

. 1; 3; 5; 15 B. 2; 4; 7;

. -3; 2; 5;

9 D

. -5; -3; 1

5; 17

Câu 6: Tìm x trong tỉ lệ thức sau

6 2 3

: 1 :

5 3 2







 

 

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

A. x = 6 B. x =

C. x =

D. x =15

Câu 7: Tì

m ba số x, y, z biết rằng:

3 5

x y z

 

và xyz =

240

. x = 1, y

= 2, z = 3 B

. x = -4, y

= -6, z = -10

. x = 4, y

= 6, z = 10 D

. x = 2, y

= 3, z = 5

Câu 8. Tìm ba số x, y, z biết rằng:



;



và x + y - z = 9

. x = 3, y

= 4, z = -2 B

. x = 6, y

= 8, z = 5

. x = -6, y = -8, z =

-23 D

. x = -6, y

= 8, z = 5

Câu 9. Cho hai số x, y thỏa mãn 3x = 2y và y – x = 4. Tính H =

2 2

y x

. H = -80 B. H = 80 C. H = -4 D. H = 4

Câu

10. Một mảnh đất hình chữ nhật có tỉ số giữa chiều rộng và chiều dài bằng

. Tính chu

vi mảnh đất này biết rằng diện tích của mảnh đất bằng 144

A. 60m B. 30m C. 72m D. 144m

Câu 11. Một tam giác có các cạnh của tam giác tỉ lệ với các số 3; 4; 6 và hiệu giữa cạnh lớn

nhất và nhỏ nhất bằng 6. Độ dài các cạnh của tam giác này là:

. 6; 8; 12 B. 12; 16; 24 C. 3; 4; 6 D. 18; 20; 24

Câu 12. Chọn đá

p án đúng. Từ tỉ lệ thức

(

, , , 0)

a b c d





ta su

y ra

c b



b d



a d



d c



Câu

13. Có 16 tờ giấy bạc loại 2000đ, 5000đ và 10000đ. Trị giá mỗi loại tiền trên đều bằng

nhau. Vậy số tờ giấy bạc loại 2000đ, 5000đ và 10000đ theo thứ tự là:

. 2; 4; 10 B. 10; 4; 2 C. 9; 5; 2 D. 8; 6; 2

Câu 14. Cho

a b c

  

và

3 4

b c



. Tìm giá trị của

b c











C. H =12 D.



Câu 15: Cho tỉ lệ thức

165

, khẳng địn

h nào dưới đây đúng?

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7



a c

b d







3 2 3

5 2 5

b c d







c a

d b







(giả thiết cá

c tỉ số đều có nghĩa)

Câu 16: Cho ba số a, b, c thỏa mãn abc

0. 0, 0; 0

abc a b b c a c

      

và

b c

c c a a b

 



 

. Tính giá t

rị của





A. H = -1 B. H =

C. H =1 D. H = 2

MA TRẬN CÂU HỎI TNKQ TRONG CÁC CHỦ ĐỀ

Mức dộ chủ đề Nhận biết (câu)

Thông hiểu

(câu)

Vận dụng (câu)

Thấp Cao

5 1, 2, 3, 4, 5, 6, 9 7, 8, 11, 12, 13 14, 16 15

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Chủ đề 6. SỐ T

HẬP PHÂN HỮU HẠN VÀ SỐ THẬP PHÂN VÔ HẠN TUẦN HOÀN

LÀM TRÒN SỐ

1. Một số vấn đề cần ôn tập

- Nếu một phân số tối giản với mẫu dương mà mẫu không có ước nguyên tố khác 2 và 5 thì

phân số đó viết được dưới dạng số thập phân hữu hạn.

- Nếu

một phân số tối giản với mẫu dương mà mẫu có ước nguyên tố khác 2 và 5 thì phân số

đó viết được dưới dạng

số thập phân vô hạn tuần hoàn

Mỗi

số hữu tỉ được biểu diễn bởi một số thập phân hữu hạn hoặc vô hạn tuần hoàn. Ngược lại,

mỗi số thập phân

hữu hạn hoặc vô hạn tuần hoàn biểu diễn một số hữu tỉ.

Chú ý:

1 1 1

,(1), 0,(01), 0,(001),...

99 999



 

2. Ví dụ:

Ví

dụ 1: (Nhận biết) : Giải thích tại sao phân số

150



viết được

dưới dạng số thập phân hữu

hạn rồi viết số thập phân này.

Giải:

150





, mẫu

2.5



không

có ước nguyên tố khác 2 và 5. Nên phân số



viết

đượ

dưới dạng số thập ph

ân hữu hạn

Ta có:

,18

150







Ví

dụ 2: (Thông hiểu) : Giải thích tại sao phân số

112

viết

được dưới dạng số thập phân vô

hạn tuần hoàn, viết số

112

dưới

dạng số thập phân khi đã làm tròn đến chữ số thập phân thứ

tư sau dấu phẩy.

Giải:

112



, mẫu

2 .7



có

ước nguyên tố 7 khác 2 và 5. Nên phân số

112

viết

được

dưới dạng số thập phân vô hạn tuần hoàn

Ta có:

0,17(857142)

112



suy ra

0,1786

112



Ví dụ 3: (Thôn

g hiểu) : Cho biết 1 in – sơ

2,54cm

. Do vậy 42 in- sơ

2,54.42cm

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Vậy đường ch

éo màn hình khoảng 107 cm.

Ví dụ 4: (Thông hiểu và vận dụng) . Viết các số thập phân sau dưới dạng phân số tối giản

a. 0, 258 b

. 0, (12) c. 0, 1 (6)

Giải

1 12 4

,(12) 0,(01).12 .12

99 33



  

c. Nhận

xét: Trong câu này ta cần vận dụng linh hoạt hơn để có thể đưa về bài toán giống ở

câu b

,(6) 1 0,(6) 1 0,(6) 1 1

,1(6) .6.0,(1)

10 10 10 10 10

1 6 1 9 6 9 6 15 1

10 9 90 90 90 90 6





    



      

3. Câu hỏi t

rắc nghiệm

Câu 1. Viết số thập phân 0, 52 dưới dạng phân số tối giản là

100

6,5

12,5

Câu 2. P

hân số nào dưới đây viết được dưới dạng số thập phân vô hạn tuần hoàn?

165

2292

100

165

Câu 3. Phân số nào dưới đây viết được dưới dạng số thập phân hữu hạn?

160

Câu 4. Số 2, 3 (1

5) được viết dưới dạng hỗn số là:

165

2292

100

165

Câu 5. Viết số

dưới dạng số thập

phân

. 0, 25 B. 0, 2 (5) C. 0, (25) D. 0, (025)

Câu 6. Kết quả là

m tròn số 0, 7125 đến chữ số thập phân thứ 3 là:

A. 0, 712 B. 0, 713 C. 0, 710 D. 0, 700

Câu 7. Là

m tròn số 674 đến hàng chục là:

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

A. 670 B. 680 C. 770 D. 780

Câu 8. Thực

hiện phép tính 13: 27 rồi làm tròn đến chữ số thập phân thứ hai được kết quả là:

. 0, 50 B. 0, 49 C. 0, 47 D. 0, 48

Câu

9. Có bao nhiêu phân số tối giản có mẫu khác 1, biết rằng tích cảu từ vầ mẫu bằng 1260

và phân số này có thể viết được dưới dạng số thập phân hữu hạn?

A. 1 phân số B. 2 phân số C. 3 phân số D. 4 phân số

Câu 10. Cho



, có bao nhiêu số nguyên tố x có một chữ số để A viết được dưới dạng số

thập phân hữu hạn?

A. 4 số B. 3 số C. 2 số D.. 1 số

Câu 11. Kết quả phép tính 0, (432) +0, (567) bằng:

. 1 B. 2 C. 3 D. 4

Câu

12. Chữ số thập phân thứ 100 sau dấu phẩy của phân số

(viết dưới dạng số thập phân)

là chữ số nào?

A. chữ số 2 B. chữ số 5 C. chữ số 7 D. chữ số 8

Câu 13. Tính giá trị của

16 25 100 50

2 5 10 3

P    

P 





P 

D..





Câu 14. T

rong các số sau, số nào viết được dưới dạng số thập phân vô hạn tuần hoàn?

. 10 B.



Câu 15. T

rong các số sau, số nào là số hữu tỉ âm?



C. 3 D.

Câu 16. Xét các khẳng

định sau:

(I)

















là một

số hữu tỉ âm (II

)















là một

số hữu tỉ âm

Chọn câu trả lời đúng:

. Chỉ (I) đúng B. Chỉ (II) đúng

. Cả (I) và (II) đều đúng D. Cả (I) và (II) cùng sai

MA TRẬN CÂU HỎI TNKQ TRONG CÁC CHỦ ĐỀ

Mức dộ chủ

đề

Nhận biết

(câu)

Thông hiểu (câu)

Vận dụng (câu)

Thấp Cao

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

1, 2, 3, 6, 7, 8,

13, 14, 15,

4, 5, 11 10, 12 9

Chủ đề 7. SỐ V

Ô TỈ. KHÁI NIỆM VỀ CĂN BẬC HAI. SỐ THỰC

. Một số vấn đề cần

ôn tập

- Số vô tỉ là số viết được dưới dạng số thập phân vô hạn không tuần hoàn

Căn bậc hai

của một số a không âm là số x sao cho

x a

Số dương a c

ó đúng hai căn bậc hai, một số dương kí hiệu là

và một

số âm kí hiệu là



Số 0 chỉ có

một căn bậc hai là số 0, ta cũng viết



Chú ý: không đượ viết

9 3 

Số hữu tỉ vầ số vô tỉ được gọi chung là số thực.

Mỗi

số thực được biểu diễn bởi một điểm trên trục số. Ngược lại, mỗi điểm trên trục số đều

biểu diễn

một số thực.

2. Ví dụ:

Ví dụ 1:

(Nhận biết) Thực hiện phép tính bẳng cách hợp lý:

( 5) ( 8)

9 81

10 15 2 10

 

   

4 1 16 7

3 5

49 49 5 441

B 

 

Giải:

2 2

( 5) ( 8)

9 81 25 3 9 64

10 15 2 10 10 15 2 10

5 1 9 8 1 9 1 4 1 9 1 4

10 5 2 10 2 2 5 5 2 5

8 5

4 1 3

2 5

a A

 

       

 

   

         

   

   



      

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

4 1 16 7 1 2 1 4 7

. . . . .

5 5.7 3 7 5 5.21

49 49 5 441

b B      

2 7 4 1 2 7 4 1 9 4

. .

21 21 7 5 21 7 5 21 7

3 4 1 3 4 1 7 1 1

. . . .1

5 7 7 5 7 5 7 5 5

 





    



     



    

 

     







 

     

 

 

Ví dụ 2 (Thông

hiểu) : Chứng minh các số sau là những số vô tỉ:

. 5 . 9 5

a b 

Giải:

a. Nhận

xét: trong bài toán này giải trực tiếp không thể biến đổi được, nên ta sẽ giải gián tiế

bằng phương

pháp chứng minh phản chứ

Giả sử

là số hữu tỉ nên có



trong đó

; 0

b b



 

và

là phân số tối giản

5 5

a a



   

5a 

lại có 5 là số nguyê

n tố và

a  

nên

5a

, đặt a =5k,

k  

Khi a = 5k, có

 

2 2 2 2

5 5 25 5 5k b k b b k

    

Lập luận tươg

ntự trên suy ra

5b

Suy ra phâ

n số

không là phân số tối giản (mâu thuẫn giả thiết)

Từ đóy suy ra

là số vô

tỉ (điều phải chứng minh)

b. Coi

a



, giả sử



là số hữu tỉ nên a cũng là số hữu tỉ

2 2

5 9 5 9 5

a a       

Vì a là số hữu

tỷ =>

cũng là số hữu tỉ

cũng là số hữu tỉ (điều này sai v

là số vô tỉ, chứng minh t

rên)

Từ đó suy ra



là số vô

tỉ (điều phải chứng minh)

Nhận xét: Qua bài toán này, ta ghi nhớ kết quả sau: nếu có số tự nhiên a không phải là số

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

chính phương thì

là số vô tỉ. Nếu số tự nhiên a là số chính phương thì

là số tự nhiên.

Ví dụ 3 (Vận dụng) Tìm giá trị lớn nhất của:

a. I =

7 2 3x 

b. H =



Giải:

Phương

pháp: để tìm GTLN của M, ta phải tìm một sô thuwcjr (không chứa x) để



và ở

đây xảy ra đượcM =r k

hi x bằng bao nhiêu.

a. Vì





nên

3 0



 

, suy ra

2 3 7



 

hay

7I 

I =7 khi





hay x =3.



nên





, suy ra

7 7





hay



H =

khi

3 3

 

hay x =0

Kết luận: h đạt giá trị lớn nhất là

khi và chỉ khi x =0

Ví dụ 4 (Vận dụng cao) . Cho H =



với



. Tìm

x



để H có giá

trị nguyên

b. Tìm



để H có giá

trị nguyên

Giải:

a. Khi x là số tự nhiên thì

hoặc là số tự nhiên (nếu x là số chính phương) hoặc là số vô tỉ

(nếu x không phải là số chính phương) . Để





là

số nguyên thì

phải

là số tự

nhiên và

 



phải là ước của 7

Do đó chỉ xảy ra





(vì ước của 7 là -7; -1; 1; 7

và





)

Suy ra



hay x =16

Kết luận x =

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

b. Ta có:





, theo ví dụ 3

thì

7 7





. Hay





Do H có giá trị nguyên nên H = 1 hoặc H = 2

Xét H =1

1 3 7 4 16

x x x

        



Xét H =2

 

7 1

2 2 3 7 2 6 7 2 1

x x x x

           



Kết luận:

;



3. Câu hỏi trắc n

ghiệm

Câu 1: Trong các số sau đây, số nào không có căn bậc hai?

. . -2 B.

C. 0 D. 0, 3

Câu 2: P

hát biểu nào dưới đây đúng?

A. Số dương 2 chỉ có một căn bậc hai B.

là một số thực

C. Số

là một số v

ô tỉ D.

là một số vô tỉ

Câu 3: P

hát biểu nào dưới đây sai?

A. Số 19 là một số tự nhiên B. Số -2 là một số nguyên âm

C. Số

là một số v

ô tỉ D.

là một số vô tỉ

Câu 4: Số nào dưới

đây số vô tỉ?

144

B. 0, (121) C. 0, 0100

100011… D



Câu 5: Trong các số sau đây, số nào bằng

16 2



4 9

23 625



  

81 25

1 2 1 2



 

Câu 6: Số dương 9

có hai căn bậc hai là

9 3  

và

9 3



 

và



BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Câu 7: Nếu



thì x bằng:

. x = -2 B. x =2 C.. x = -16 D. x = 16

Câu 8: Nếu



thì

bằng:

81x  

9x 

x 

81x 

Câu 9: P

hép tính nào dưới đây đúng:

100





 



 





Câu 10: H

ãy tính

 



 

16 16  

 

16 4  

 

16 4 

 

16 16 

Câu 11: Chọn câu

trả lời đúng: nếu a là số vô tỉ thì:

. a cũng là

số tự nhiên B

. a cũng là

số nguyên

. a cũng là

số hữu tỉ D

. a cũng là

số thực

Câu 12: Phát biểu nào dưới đây sai?

. Số vô tỉ là số viết đợc dưới dạng

số thập phân vô hạn không tuần hoàn

. Số hữu tỉ và số vô

tỉ được gọi chung là số thực

C. Chỉ có số 0 không phải số hữu tỉ dương và cũng không là số hữu tỉ âm.

D. Mỗi điểm trên t

rục số đều biểu diễn một số hữu tỉ

Câu 13: Giá trị lớn nhất của



 

là:

. 7 B. 6 C. 5 D. 0

Câu 14: Sắp xếp c

ác số sau theo thứ ự từ nhỏ đến lớn

;2; ; 10;10





; 5;2; ;10





;2; 5; ; ;10





10;2; 5; ; ;10





10;2; ; 5; ;10





Câu 15: Cho





. Hỏi có

bao nhiêu số nguyên x và x < 100 để H có giá trị nguyên?

A. 2 B

. 3 C. 4 D. 50

Câu 16:

Cho





Hỏi có ba

o nhiêu số nguyên x để H có giá trị nguyên?

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

A. 2 B. 3 C. 5 D. 6

MA TRẬN CÂU

HỎI TNKQ TRONG CÁC CHỦ ĐỀ 7

Mức dộ chủ

đề

Nhận biết

(câu)

Thông hiểu (câu)

Vận dụng (câu)

Thấp Cao

1, 2, 3, 4, 6, 9,

10, 11

5, 7, 8, 12,

13, 14 15 16

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Chủ đề 8. ĐẠI

LƯỢNG TỈ LỆ THUẬN. ĐẠI LƯỢNG TỈ LỆ NGHỊCH

. Một số vấn đề cần

ôn tập

Nếu đại lượng

liên hệ với đại lượng

theo công thức

y kx

(với

là hằng số

khác

) thì ta nói

tỉ lệ thuận với

theo hệ số tỉ lệ

Nếu

tỉ lệ thuận

với

theo

hệ số tỉ lệ

(với

0k 

) thì

tỉ lệ thuận

với

theo

hệ

số tỉ lệ là

và ta nói hai đại lượng đó tỉ lệ thuận với nhau.

Giả sử

và

tỉ lệ thuận

với nhau:



(với

là

hằng số khác

)

. Khi đó, với

mỗi

giá trị

2 3

, , , ...

x x x

khác

của

có một giá trị tương ứng

1 2 2 3 3

, , , ...

y kx y kx y kx

  

của

và luôn

có:

1 2 3

...

x x

   

1 1 1 2 2

2 2 3 3 3 3

; ; ;...

x y x y x y

  

Nếu

đại lượng

liên

hệ với đại lượng

theo

công thức



hay

y a



(với

là

hằng số khác

) thì ta nói hai đại lượng đó tỉ lệ nghịch với nhau.

Giả sử

và

tỉ lệ n

ghịch với nhau:



(với

là

hằng số khác

)

. Khi đó, vớ

mỗi

giá trị

2 3

, , , ...

x x x

khác

của

có một giá trị tương ứng

2 3

1 2 3

, ,...

a a

y y

x x x

  

của

và luôn có:

1 2 2 3 3

...x y x y x y a   

31 2 1 2

2 1 3 1 3 2

;

; ;...

x y x x

x y x y x y

  

2. Ví dụ

Ví

dụ 1 (Nhận biết) . Cho

và

là

hai đại lượng tỉ lệ thuận biết

1 2

x x

 

à hai giá trị

tương ứng

y y

 

. Tìm hệ số tỉ lệ của

đối với

Giải

và

là hai đại lượng tỉ lệ thuận nên giả sử

y kx

 



Từ

y y

 

có

kx kx

 

hay

 

x x





thay

x x

 

ta tìm được

10k 

Kết luận: hệ số tỉ lệ của

đối với

là

10k 

Ví

dụ 2 (Thông hiểu) . Cho

và

là

hai đại lượng tỉ lệ nghịch với nhau khi

nhận

các giá

trị

2; 3

x x

 

thì tổn

g các giá trị tương ứng của

là

Hãy

biểu diễn

theo

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Giải

và

là hai đại lượng tỉ lệ nghịch nên giả sử



Từ giả thiết có



và

y y

 

Suy ra

25 5 25.6 30

2 3 6

a a a

a a



      

Kết luận: biểu diễn của

theo

là



Ví dụ 3 (Vận

dụng) . Một ô tô đi từ A đến B với vận tốc

km/h và

từ B trở về A với vận tốc

km/h. Thời

gian cả đi lẫn về là

giờ

phút. Tính

thời gian đi, thời gian về và độ dài

quãng đường AB.

Giải

và

là thời

gian đi và thời gian về (giờ,

0, 0x y 

) .

Thời gian

cả đi lẫn về là

giờ

phút, nên c

x y 

hay

x y

 

Thời

gian và vận tốc đi trên một đoạn đường là hai đại lượng tỉ lệ nghịch, nên ta có



hay

x y



Theo tính c

hất của dãy tỉ số bằng nhau ta có

: 7

3 4 3 4 4

y x y



   



Suy ra



hay

 

hay



Kết luận: t

hời gian đi là

giờ, thời gian

về là

phút, độ dà

i quãng đường AB bằng

km.

Nhận xét: đây

là một bài toán về đại lượng tỉ lệ nghịch, mà quãng đường chính là hệ số tỉ lệ

Trong bài giải ta nên sử dụng tính chất của dãy tỉ số bằng nhau để giải cho gọn.

Ví dụ 4 (Vận dụng cao) . Hỏi trên một chiếc đồng hồ khi kim giờ quay được một vòng thì

kim phút, kim giây quay được bao nhiêu vòng?

Giải

Ta đã biết

giờ

60

phút,

phút

60

giây.

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Do đó

khi kim giờ đi được

giờ thì ki

m phút đi được

vòng, vậy trên

mặt chiếc đồng

hồ khi kim giờ quay được

vòng (tức

là kim giờ đi được

giờ) th

ì kim phút quay được

1.12



(vòng) .

Kim

phút đi được

phú

t thì kim giây đi được

vòng, vậy

trên mặt chiếc đồng hồ khi

kim phút quay được

òng (tức là kim phút đi được

phút

hay kim giờ đi được

giờ) t

hì

kim giây quay được (vòng) . Nên kim phút quay được

vòng

thì kim giây quay được

.60 720



(vòng) .

Kết

luận: trên mặt chiếc đồng hồ khi kim giờ quay được

vòng

thì kim phút quay

được

vòng và

kim giây quay được

vòng.

Nhận

xét: đây là một bài toán về đại lượng tỉ lệ thuận. Nếu gọi

, , zx y

theo

thứ tự là

số vòng quay của kim giờ, kim phút, kim giây trong cùng một thời gian thì

12 , 60 , 720 .y x z y z x  

. Câu hỏi trắc nghiệm

Câu 1. Các giá trị tương ứng của hai đại lượng

và

được

cho trong các bảng dưới đây, hỏi

bảng nào thể hiện hai đại lượng

và

tỉ lệ thuận

với nhau

 



 



 



 



 



 



 



 

Câu

2. Các giá trị tương ứng của hai đại lượng

và

được

cho trong các bảng dưới đây, hỏi

bảng nào thể hiện hai đại lượng

và

tỉ lệ nghịc

h với nhau?

 



 

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7



 



 



 



 



 



 



 



Câu 3. Hai đại lượng

và

tỉ lệ nghịch. Giá trị của

và

trong ô sau là:



12, 12

y x

 

. B.

12, 12

y x

  

12, 12

y x

  

. D.

1, 1

y x

 

Câu

5. Cho biết hai đại lượng

và

tỉ lệ thuận

với nhau, khi

3x 

thì

2y 

. Hỏi

tỉ lệ

thuận với

theo tỉ lệ

bằng



. B.



. C.

3k 

. D.

2k 

Câu

6. Cho biết hai đại lượng

và

tỉ lệ thuận

với nhau, khi

5x 

thì

3y 

. Hỏi

tỉ lệ

thuận với

theo tỉ lệ

bằng



. B.

3k 

. C.

5k 

. D.



Câu

7. Cho biết hai đại lượng

và

tỉ lệ ng

hịch với nhau, với



. Hỏi

hai đại

lượng

và

tỉ lệ nghịch

với nhau theo hệ số tỉ lệ

bằng

2k 

. B.



. C.



. D.



Câu 8. K

hẳng định nào dưới đây thể hiện hai đại lượng tỉ lệ thuận với nhau?

. Chiều d

ài và chiều rộng của hình chữ nhật có diện tích cho trước

B. Năng s

uất lao động và thời gian để làm xong một công việc

C. Vận tốc

và thời gian khi đi trên cùng quãng đường

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

D. Chu vi

và bán kính của một đường tròn

Câu 9. Cho biết

tỉ lệ thuận với

theo hệ số tỉ lệ

tỉ lệ thuận với

theo hệ số tỉ lệ

 



thì

tỉ lệ thuận với

theo hệ số tỉ lệ bằng

. B.

. C.

. D. Cả ba

câu A; B; C đều sai

Câu

10. Chọn câu trả lời đúng. Các máy bơm có cùng công suất bơm nước vào cùng một bể

chứa thì

. Số lượng

máy bơm tỉ lệ thuận với thời gian bơm đầy bể chứa

B. Thời g

ian bơm đầy bể chứa không tỉ lệ với số máy bơm

C. Số lượng

máy bơm tỉ lệ nghịch với thời gian bơm đầy bể chứa

D. Thời g

ian bơm đầy bể chứa tỉ lệ thuận với công suất máy bơm

Câu 11. Đại lượng

tỉ lệ thuận với đại lượn

nếu

x ky

. B.



với hằng số

0k 

. D.



Câu 12. Công thức n

ào dưới đây thể hiện

và

là hai đại lượn

g tỉ lệ nghịch



. B.



. C.





Câu 13. Đại lượng

tỉ lệ thuận với đại lượn

theo hệ số tỉ lệ

khi



. B.



. C.







Câu 14. Đại lượng

tỉ lệ thuận với đại lượn

theo hệ số tỉ lệ

khi

3xy 

. B.



. C.



y x



Câu

15. Cho bốn số

; ; ;a b c d

. Biết

rằng

: 2 : 3a b 

;

: 4 : 5b c 

;

: 6 : 7c d 

. T

hế thì

: : :a b c d

bằng

:12 :15:13

. B.

: 24 :32 :35

4 :12 : 6 : 7

16 : 24 : 30 : 35

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Câu

16. Chia số

thành

ba phần tỉ lệ nghịch với

:3: 4

thì

số nhỏ nhất trong ba số được

chia là

. B.

. C.

MA TRẬN CÂU

HỎI TNKQ CHỦ ĐỀ 8

Mức độ

Chủ đề

Nhận biết (câu) Thông h

iểu (câu)

Vận dụng (câu)

Thấp Cao

3; 4; 5; 6; 7; 12;

13; 14

1; 2; 8; 11 9; 10; 15 16

Chủ đề 9. HÀ

M SỐ. ĐỒ THỊ CỦA HÀM SỐ



 



. Một số vấn đề cần

ôn tập

Nếu đại lượng

phụ thuộc

vào đại lượng thay đối

sao

cho với mỗi giá trị của

luôn

xác định được chỉ một giá trị tương ứng của

thì

được

gọi là hàm số của

và

gọi

là biến số (gọi tắt l

à biến)

Nếu

thay đổi mà

không thay đổi thì

được gọi là hàm hằng.

Đồ thị của

hàm số

 

y f x

là

tập hợp tất cả các điểm biểu diễn các cặp giá trị tương

ứng

 

trên mặt phẳng tọa độ.

Đồ thị hàm

số

   

f x ax a



 

là một đ

ường thẳng đi qua gốc tọa độ.

Để vẽ đồ thị hàm

số

 

ax a





, ta

chỉ cần vẽ một đường thẳng đi qua hai điểm là

 

; 0

và

 

;

2. Ví dụ

Ví dụ 1 (Nhận

biết) . Cho hàm số



có đồ thị là

 

a. Tìm tọa

độ của ba điểm bất kỳ thuộc đồ thị là

 

b. Điểm

 

;

M x y

thuộc đồ thị

 

có tung độ



Tìm hoành độ

Giải

. Để tìm

tọa độ của ba điểm bất kỳ trên

 

, rất

đơn giản ta chỉ cần cho biến số

giá trị

bất kì để tìm ra

, từ đó tìm ra tọa độ của ba

điểm thuộc đồ thị là

 

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Chọn

1x 

suy ra

3y 

Chọn

1x 



suy ra

3y 



Chọn

3x 

suy ra

1y 

Kết luận: tọa độ của ba điểm bất kỳ thuộc

 

là

     

; 3 , 1; 3 , 3;1

B C



. Điểm

 

;M x y

thuộc đồ thị

 

, nên có



, lại có



Suy ra















hay

x 

hay



Kết luận:



Ví

dụ 2 (Thông hiểu) . Vẽ trên cùng mặt phẳng tọa độ

đồ thị của

hai hàm số





và



Giải

Hai

hàm số trong bài này có đồ thị là hai

đường thẳng đi qua gốc tọa độ, nên để vẽ chúng ta cần

chọn thêm mỗi đồ thị một điểm nữa không phải là gốc

tọa độ, đường thẳng đi qua điểm đó và gốc tọa độ là

đồ thị cần vẽ.

Với hàm số





, nếu

chọn

1x 

thì

2y 



, nên

 

; 2



thuộc đồ thị của

hàm số này.

Vẽ hệ trục tọa độ

và

xác định điểm

 

1; 2



, đường thẳng

là đồ thị của hàm số





Với hàm số



, nếu chọn

2x 

thì

1y 

, nên

 

thuộc đồ thị của hàm số này.

Vẽ hệ trục

tọa độ

Oxy

và

xác định điểm

 

, đường

thẳng

là

đồ thị của hàm số

y x



Ví

dụ 3 (Vận dụng) . Tìm

để đồ thị của hàm số

x m



 

đi qua điểm

;

2 3















Với giá trị

tìm được, hỏi đồ thị của hàm số nà

y có cắt được trục hoành không?

y=-2x

-1

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Giải

Điểm

;

2 3



 

 

 

thuộc

đồ thị của hàm số



 

nên

thay





và





vào hàm số ta được

1 1 1 1 1 1

2 2 2

3 2 3 4 3 4

m m m

   

 

         

 

 

3 1

12 24



 



  

Khi





hàm số

x m



 

trở thành





 

Rõ

ràng



 

nên

0y 

, nên

các điểm thuộc đồ thị đều có tung độ âm.

Mà

các điểm th

uộc trục hoành đều có tung độ bằng

Nên khi





đồ thị của

hàm số này không cắt được trục hoành

Ví dụ 4 (Vận dụng cao) . Trong mặt phẳng tọa độ

, cho hàm số





. Gọi

 

;M x y

là điểm thuộc đồ thị của hàm số, s

ao cho

0 0





. Tín

h giá trị của

 

4 2

x y



Giải

 

;M x y

là điểm thuộc đồ thị của hàm số





, nên thay

x x y y 

vào

hàm số ta có





Lại có

3 3 3 3

0 0 0 0 0 0

1 1

56 56 56

2 8

x y x x x x



 

       

 

 

3 3 3

0 0

0 0 0 0

8.56

7 8.56 64 4

8 7

x x x x





        

Với



ta được

 

Giá trị của

 

4 2

0 0

2 4.4 2. 2 64 32 32



     

. Câu hỏi trắc n

ghiệm

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Cho

phương án

, ,

B C D

trong

mỗi câu hỏi, khoanh tròn vào phương án trả lời đúng

trong mỗi câu sau.

Câu 1. Bảng giá trị tương ứng nào dưới đây thể hiện đại lượng

là hàm số của đại lượng

Bảng 1

2

1

2

4

Bảng 2

1

Bảng 3

2

1

2

6

3

Bảng 4

3

6

10

6

A. Bảng 1. B. Bảng 2. C. Bảng 3. D. Bảng 4.

Câu 2. Cho hàm số

 

5 1

y f x x

  

kết quả nào dưới

đây đúng

216

. B.

. C.

. D.

Câu 2. C

ho hàm số

 

3 ,y f x x

  

kết quả nào dưới đây sai?











 

. B.







 

 

. C.

 





. D.

 



 

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Câu

5. Tìm tọa độ các điểm

, ,

N P Q

trong hình

bên

       

; 3 , 3; 4 , 2; 0 , 0; 2

N P Q



       

; 4 , 4; 3 , 2; 0 , 0; 2

N P Q



       

; 3 , 3; 4 , 0; 2 , 2; 0

N P Q



       

; 4 , 4; 3 , 0; 2 , 2; 0

N P Q



Câu 6. Điểm nào dưới đây thuộc đồ thị hàm số

y x





; 4















. B.

 

. C.

;















. D.

 

; 2

Câu 7. Trong các điểm sau:

 

9 3 1 1

;

1 , ; , ; , 3; 2

4 2 6 9

A B C D

    

     



     

     

; điểm nào thuộc

không thuộc đồ thị của hàm số



. Điểm A. B. Điểm B. C. Điểm C. D. Điểm D.

Câu 8. Đường thẳng

ở hình bên là đồ thị

của hàm số



, xác định hệ số

0a 



0a 



Câu 9. Đường thẳng

ở hình

bên là đồ thị

của hàm số



, xác định hệ số



. B.







. D.





2 3

-2

-1

1 1

-3 -2

-1

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Câu 10. Một điểm bất

kì trên trục hoành có tung độ bằng:

A. Hoành độ. B.

. C.

. D.

1

Câu 11. Một điểm bất kì trên trục tung có hoành độ bằng:

. Tung độ. B.

. C.

. D.

1

Câu 12. T

rong mặt phẳng tọa độ

, khẳng định

nào dưới đây sai?

. Những điểm thuộc

góc phần tư thứ I có hoành độ dương và tung độ dương

B. Những điểm thuộc góc phần tư thứ III có hoành độ âm và tung độ âm.

C. Những điểm thuộc

góc phần tư thứ II có hoành độ âm và tung độ dương

D. Những điểm thuộc

góc phần tư thứ IV có tung độ dương

Câu

13. Trong mặt phẳng tọa độ

, cho

bốn điểm

       

; 2 , 2; 5 , 2; 2 , 9; 5

B C D



Các đoạn thẳng song song với trục hoành là:

và

. B.

và

. C.

và

. D.

Câu

14. Trong mặt phẳng tọa độ

, cho

bốn điểm

       

; 2 , 0; 5 , 0;12 , 9; 8

B C D



Đoạn thẳng

song song với trục tung là:

và

. B.

và

. C.

và

. D.

Câu

15. Trong mặt phẳng tọa độ

, cho

bốn điểm

       

; 2 , 2; 0 , 2; 2 , 3; 0

B C D



 

Hỏi tứ giác

là hình gì?

là hình

bình hành

. B.

là hình

chữ nhật

là hình

thoi

. D.

là hình

vuông

Câu

16. Trong mặt phẳng tọa độ

, cho

hàm số

y x





. Gọi

 

;M x y

là

điểm thuộc đồ

thị của hàm số, sao cho

0 0





. Tính giá trị của

 

x y



5

. B.

. C.

. D.

MA TRẬN CÂU HỎI TNKQ CHỦ ĐỀ 9

Mức độ

Chủ đề

Nhận biết (câu) Thông h

iểu (câu)

Vận dụng (câu)

Thấp Cao

9 1; 2; 3; 4; 5 6; 7; 8; 9; 10; 11 12; 13; 14 15; 16

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Chủ đề 10. THỐNG K

. Một số vấn đề cần

ôn tập

Thu thập số liệu về vấn đề được quan tâm, các số liệu được ghi lại trong một bảng, gọi

là bảng số liệu thống k

ê ban đầu.

Vấn

đề hay hiện tượng mà người điều tra quan tâm tìm hiểu gọi là dấu hiệu (thường kí

hiệu bằng cá

c chữ cái in hoa

,...

) . Mỗi đơn

vị trong dấu hiệu là một đơn vị điều tra.

Ứng

với mỗi đơn vị điều tra có một số liệu, số liệu đó gọi là một giá trị của dấu hiệu

(thường

được kí hiệu là

)

. Số tất cả các giá trị (không nhất thiết khác nhau) của dấu hiệu

bằng số các

đơn vị điều tra (thường được kí hiệu là

) .

Số lần

xuất hiện của một giá trị trong dãy giá trị của dấu hiệu được gọi là tần số của

giá trị đó (t

hường được kí hiệu là

) .

Số trung bình cộng là giá trị trung bình của dấu hiệu (thường được kí hiệu là

) . Số

trung

bình cộng thường được dùng làm “đại diện” cho dấu hiệu, đặc biệt là khi muốn so sánh

các dấu hiệu

cùng loại.

Mốt của dấu hiệu là giá trị có tần số lớn nhất trong bảng tần số, kí hiệu

2. Ví dụ

Khi điều

tra về điểm kiểm tra học kỳ 2 môn toán của

học si

nh lớp 7A được kết quả

như sau:

a. Dấu hiệu ở đây là gì? Hãy nêu các giá trị khác nhau của dấu hiệu.

b. Lập

bảng tần số, tính điểm trung bình bài kiểm tra của lớp 7A (làm tròn đến chữ số

thập phân thứ nhất) .

. Tìm mốt

của dấu hiệu

d. Vẽ biểu

đồ đoạn thẳng

Giải

. Dấu hiệu

là điểm kiểm tra học kỳ 2 môn toán của

học sinh lớp 7A.

Các giá trị khác nha

u của dấu hiệu:

4, 5, 6, 7, 8, 9,10

. Bảng tần

số

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Giá trị

 

Tần số

 

40N 

Điểm trung bình bài kiểm tra của lớp 7A

4.2

5.5 6.6 7.6 8.12 9.6 10.3



    





. Mốt của

dấu hiệu

là



. Biểu đồ đoạn thẳng ở hình bê

3. Câu hỏi trắc n

ghiệm

Câu 1. Chọn câu trả lời sai.

. Số các g

iá trị (không nhất thiết khác nhau) của dấu hiệu đúng bằng số các đơn vị điều tra

B. Các số l

iệu thu thập được khi điều tra về một dấu hiệu gọi là số liệu thống kê.

. Tần số của một

giá trị là số các đơn vị điều tra

D. Số lần

xuất hiện của một giá trị trong dãy giá trị của dấu hiệu là tần số của giá trị đó

Sử dụng dữ kiện sau để giải câu 2, câu 3, câu 4, câu 5

Biểu đồ dân số Việt Nam qua tổng điều tra trong thế kỉ XX

(đơn vị của các cột là triệu người) .

Câu 2. Chọn câu trả lời sai.

. Năm 19

21 số dân của nước ta là

triệu người.

B. Năm 19

60 số dân của nước ta là

nghìn người.

C. Năm 19

90 số dân của nước ta là

triệu người.

D. Năm 19

99 số dân của nước ta là

triệu người.

Câu 3. Từ năm 1980 đến năm 1999, dân số nước ta tăng

thêm bao nhiêu?

triệu người. B.

triệu người.

triệu người. D.

triệu người.

765

4321

1999

198

921

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Câu 4. Nă

m 1999, dân số nước ta là bao nhiêu?

triệu người. B.

nghìn người.

triệu người. D.

triệu người.

Câu 5. Sa

u bao nhiêu năm (kể từ năm 1960) thì dân số nước ta tăng thêm

triệu người?

. Sau

năm. B. Sau

năm.

C. Sau

năm. D. Sau

năm.

Sử dụng bảng thống kê ban đầu, hãy trả lời các câu 6, câu 7, câu 8, câu 9, câu 10

Khi điều tra về số bộ quần áo quyên góp vì người nghèo của các lớp 7 trong trường,

người điều tra lập bảng dưới đây:

Lớp 7A 7B 7C 7D 7E 7G

Số bộ quần áo

Câu 6. Dấu hiệu cần tì

m hiểu ở bảng trên là:

A. Số các lớp 7 trong trường.

B. Số bộ quần áo

quyên góp vì người nghèo của các lớp 7

C. Cả A và

B đều đúng

D. Cả A và

B đều sai

Câu 7. Tr

ong bảng trên có bao nhiêu đơn vị điều tra?

. Có

đơn vị điều tra. B. Có

đơn vị điều tra.

C. Cả A và

B đều đúng

. D. Cả A và

B đều sai

Câu 8. Câ

u nói nào dưới đây sai?

A. Mỗi lớp trong bảng trên là một đơn vị điều ta.

B. Trong bảng trên

có

đơn vị điều tra.

C. Lớp 7

D quyên góp được nhiều bộ quần áo nhất

D. Mốt tro

ng bảng trên là

Câu 9. Số các giá t

rị của dấu hiệu ở bảng trên là:

. B.

. C.

. D.

Câu 10. Số các giá trị khác nhau của dấu hiệu ở bảng trên là:

. B.

. C.

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Sử dụng

bảng này, hãy trả lời các câu 11, câu 12, câu 13, câu 14

Theo dõi các bạn nghỉ học ở từng buổi trong một tháng, bạn lớp trưởng ghi lại như sau:

Câu 11. Có bao n

hiêu buổi học trong tháng đó?

buổi. B.

buổi. C.

buổi. D.

buổi.

Câu 12. Dấu hiệu ở đâ

y là gì?

. Tổng số lượt học

sinh nghỉ học cả tháng

B. Là các số

,1,2,3

C. Số học

sinh nghỉ học trong mỗi buổi

. Một thá

ng học 26 buổi

Câu 13. Số buổi có nhiều học sinh nghỉ học nhất là

Câu 14. Tần số b

uổi không có bạn nào nghỉ học là

Câu 15. Chọn khẳng định đúng nhất. Số trung bình cộng

. Không

được dùng làm “đại diện” cho dấu hiệu

B. Thường được

dùng làm “đại diện” cho dấu hiệu

C. Không

dùng để so sánh các dấu hiệu cùng loại

D. Cả A, B, C trả lời đều sai.

Câu 16. Điểm thi đua trong các tháng của một năm học của lớp

được cho trong bảng sau:

Tháng 9 10 11 12 1 2 3 4 5

Điểm 8 9 10 9 8 8 9 7 9

Tính điểm

trung bình

 

(làm tròn đến chữ số thập phân thứ nhất) và mốt

 

8,6, 8

X M

 

8,5, 9

X M

 

8,5, 8

X M

 

8,6, 9

X M

 

MA TRẬN CÂU

HỎI TNKQ CHỦ ĐỀ 10

Mức độ

Chủ đề

Nhận biết (câu) Thông hiểu (câu)

Vận dụng (câu)

Thấp Cao

, 3, 4, 5,11,13,14

, 6, 7, 8, 9,10,12,15

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Chủ đề 11. KHÁI

NIỆM VỀ BIỂU THỨC ĐẠI SỐ - GIÁ TRỊ CỦA MỘT BIỂU THỨC ĐẠI SỐ

1. Một số vấn đề cần ôn tập

Biểu thức đại số là biểu thức gồm các số, các kí hiệu phép toán cộng, trừ, nhân, chia, nâng

lên lũy thừa và

các chữ (đại diện cho các số) .

Khi

thực hiện các phép toán trên các chữ, ta có thể áp dụng những tính chất, quy tắc phép

toán như tr

ên các số.

Để tính giá trị của một biểu thức đại số tại những giá trị cho trước của các biến, ta thay các

giá trị cho t

rước đó vào biểu thức rồi thực hiện các phép tính.

2. Ví dụ

Ví

dụ 1. (Nhận biết) . Viết biểu thức đại số biểu thị tổng các lũy thừa bậc ba của ba số tự

nhiên liên tiếp, có chữ số đầu tiên là

( ).

a a

 

Và tính tổng đó khi

2a 

Giải:

Ba của ba số tự nhiên l

iên tiếp là

1, 2.

a a



Tổng các lũ

y thừa bậc ba của ba số tự nhiên liên tiếp là

3 3

(

1) ( 2)

a a   

Khi

2a 

, tổng các lũy thừa bậc ba của ba số tự nhiên liên tiếp bằng:

3 3

(2 1) (2 2) 8 27 64 99



      

Ví

dụ 2. (Thông hiểu) . Một người lái xe máy với vận tốc

/v km h

. Viết

biểu thức đại số biểu

thị quãng đường đi được của người lái xe trong khoảng thời gian t giờ. Tính quãng đường đi

được khi

45 /h, 1v km t 

giờ 20 phút.

Giải:

Biểu thức đại số biểu thị quãng đường đi được là v t (km)

t = 1 giờ 20 phút hay



giờ hay



giờ.

Quãng đường

đi được khi

45 /h, 1v km t 

giờ 20 phút l

45. 60 ( ).



Ví dụ 3. (Thông hiểu) . Dùng ngôn ngữ “tổng”, “hiệu”, “tích”, “bình phương” để đọc các biểu

thức sau

10x 

(

)



  

y x y





Giải:

a. Hiệu của

x và 10

. Tích của

x và y

. Bình phươ

ng của tổng x và y

. Tích của tổng x

và y với hiệu của x và y

Ví dụ 4 (Vận dụng) . Bạn X điều khiển chiếc xe đạp chạy từ nhà mình, với vận tốc

12 /km h

giờ kể từ khi

bạn X đi, bố bạn X điều khiển chiếc xe máy cũng chạy từ nhà, với vận tốc

36 /km h

. Tính

quãng đường đi được của bạn X trong khoảng thời gian t giờ. Khi

3t 

giờ, bố

bạn X đi được

bao xa và cho nhận xét?

Giải:

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Bạn

X điều khiển chiếc xe đạp vận tốc

12 /km h

trong

khoảng thời gian t giờ sẽ đi được

quãng đường là

12 ( )t km

Nếu

bạn X đi t (giờ)

(



thì

bố bạn X đi

 



giờ. Do

vậy quãng đường bố bạn X đi

được là

36( 2) ( )t km

Khi

3t 

giờ, bố bạn

X đi được

36.(3 2) 36 ( )km 

Khi

3t 

giờ, bạn X đ

i được

12.3 36 ( )km

Nhận

xét: Sau khi bạn X đi được 3 giờ thì bố bạn X sẽ gặp được bạn tại một địa điểm cách

nhà 36 km.

3. Câu hỏi trắc nghiệm

Câu 1. Câu nói nào dưới đây đúng. Biểu thức đại số biểu thị

. Tổng của a và b l

à ab

. Diện tíc

h của một tam giác đều cạnh a là 3a

C. Diện tích hình vuông cạnh a là 4a

. Tổng của bình p

hương của a và b là

2 2



Câu 2. Một ca nô chạy trên sông với vận tốc thực

35 /km h

(nếu dòng nước yên lặng), giả sử

vận tốc dòng nước là

/x km h

( 35)



. Viết biểu thức đại số biểu thị vận tốc ca nô chạy xuôi

dòng.

(35 ) /x km h

(35 ) /x km h

( 35) /x km h

35 /x km h

Câu

3. Một bác công nhân được hưởng mức lương x đồng trong một tháng. Do bác công nhân

có nhiều sáng kiến để tăng năng suất lao động, nên trong năm nay bác được thưởng thêm

đồng. Hỏi bác công nhân nhận được bao nhiêu tiền trong năm (biết một năm có 12 tháng

lương) ?

A. xm đồng B.

(

)



đồng

(

)



đồng D.

(

12 )



đồng

Câu

4. Viết biểu thức đại số biểu thị thời gian đi của một xe máy trên quãng đường 120 k

với vận tốc x km/h.

(

120 : )

giờ B.

120x

giờ C.

(

:120)

giờ D.

x

giờ

Câu 5. Biểu thức đại

số biểu diễn hai số tự nhiên chẵn liên tiếp là:

2k 2

và

2 ( )

k k



12k 

và

2 ( )

k k



và

2 2 ( )

k k

  

và

2 1 ( )

k k

 

Câu 6. Biểu thức đại

số biểu thị bình phương của một tổng hai chữ số a và b là

a b



(

)



Câu

7. Biểu thức đại số biểu thị diện tích hình thang có đáy lớn a (m), đáy bé b (cm) và đường

cao h (m) là

(

)

(

)

b h



(

0,01 )

(

)

b h



( ) ( )a b h m



(

)

(

c )

b h



BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Câu

8. Nền nhà hình chữ nhật có chiều dài 6x (m) và chiều rộng 3y (m) . Dùng gạch lát nền

hình vuông cạnh 30 (cm) để lát nền nhà này. Số gạch cần dùng là:

2xy

viên B.

6xy

viên C.

20xy

viên D.

200xy

viên

Câu 9.

Một vòi nước chảy vào bể nước, mỗi phút được x lít nước. Cùng lúc một vòi khác chảy

từ bể ra, mỗi phút lượng nước chảy ra bằng

lượng

nước chảy vào. Biểu thị số nước có thêm

trong bể sau khi đồng thời mở cả hai vòi trên trong a phút.

lít B.

lít C.

2ax

lít D.

lít

Câu 10. Giá trị của biểu thức

2 1

x x



 

tại





bằng:



B. 0 C.

2

Câu 11. Giá trị của

biểu thức

x y xy





tại



và

1y 



bằng:



Câu 12. Giá trị của

biểu thức

3 4

x y z



 

tại

, 1

x y



  

và



là:



MA TRẬN CÂU

HỎI TNKQ CHỦ ĐỀ 11

Mức độ

Chủ đề

Nhận biết (câu) Thông hiểu (câu)

Vận dụng (câu)

Thấp Cao

1, 2, 6, 7,10

3, 4, 5,11

9,12

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Chủ đề 12. ĐƠ

N THỨC. ĐƠN THỨC ĐỒNG DẠNG

. Một số vấn đề cần

ôn tập

Đơn thức là biểu thức đại số chỉ gồm một số, hoặc một biến, hoặc một tích giữa các số và

các biến. Số 0 được gọi

là đơn thức không.

Đơn

thức thu gọn là đơn thức chỉ gồm tích của một số với các biến, mà mỗi biến đã được

nâng lên lũy thừa với số mũ nguyên dương. Số nói trên gọi là hệ số, phần còn lại gọi là phần

biến của đ

ơn thức thu gọn.

Bậc

của đơn thức có hệ số khác 0 là tổng số mũ của tất cả các biến trong đơn thức đó. Số

thực khác 0 là đ

ơn thức bậc không. Số 0 được coi là đơn thức không có bậc.

Để nhân hai

đơn thức, ta nhân các hệ số với nhau và nhân các phần biến với nhau.

Hai đơn thức đồng dạng là hai đơn thức có hệ số khác 0 và có cùng phần biến.

Để cộng (ha

y trừ) các đơn thức đồng dạng, ta cộng (hay trừ) các hệ số với nhau và giữ

nguyên phần biến.

2. Ví dụ

Ví

dụ 1 (Nhận biết) . Tính tích của hai đơn thức



và



sau đó tìm bậc của

đơn thức thu

được

Giải:

Tích của hai đơn thức



và



là

  

   

2 2 5 2 2

5 2 3 6 3

3 13 3 13

. .

5 9 5 9

13 13

. . .

15 15

xy z x yz xy z x yz

x x y y z z x y z

   

     



     

     

 

Đơn

thức thu được có biến x có số mũ là 3, biến y có số mũ là 6, biến z có số mũ là 3. Nên

ta có bậc của đơn thức thu được là 12.

Ví dụ 2 (Thông hiểu) . Tính tổng:

2 2 2 2 3 2

1 1 7 1 5

12 3 2 3 4 6

y xy x y xy x x y





  

  

   

   

Giải:

Ta có

 

2 3 2

1 1 1 1

. . .

3 2 3 2 6

y x y x x y y x y



  

 

   

   

 

2 2 2 3 2

2 2 2 2 3 2 3 2

2 3 2 3 2

7 1 7 1 7

. .

3 4 3 4 12

7 1 1 7 1 5 7 1 7 5

12 3 2 3 4 6 12 6 12 6

7 7 1 5

(0 1)

12 12 6 6

xy x x x y x y

y xy x y xy x x y x y

y x y x y

  

   

 

   

   

 

     

      

     

     

 

   

      

   

 

   

 

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Ví dụ 3 (Thông

hiểu) . Tính giá trị của đơn thức

y z

tại

0,1; 8x y 

và





Giải:

Thay

,1 , 8



 

và





vào đơn

thức ta được

3 2

1 1 1 1 1 1 16

. .8 . .64.

2 2 10 3 20 27 135

xy z

  

 

  

 

 

Ví dụ 4 (Vận dụng) . Tìm x để giá trị của đơn thức

bằng

tại



Giải:

Đơn thức

bằng

tại



nê

n ta có:

3 3 3

1 1 16 1 1 16 1 16 16 1

. . :

4 5 25 4 25 25 100 25 25 100

x x x x

 

      

 

 

.100

64 4

x x



    

Kết luận:

4x 

. Câu hỏi trắc n

ghiệm

Câu 1. Trong các biểu thức sau, biểu thức nào là đơn thức?

(

1 )



2x y

(

)

z t



2 5

Câu 2. Tr

ong các biểu thức sau, biểu thức nào không là đơn thức?

( )x y z

y xz















2 3

y z

D. 0.

Câu 3. Biểu thức nào

dưới đây là đơn thức thu gọn

  

2 3

xy x z

y xz

 











x y

Câu 4. Đ

ơn thức nào dưới đây là không đơn thức thu gọn?

y xz

 











Câu 5. Bậc của đ

ơn thức

2 3

là:

. 1 B. 3 C. 4 D. 7.

Câu 6. Tíc

h của hai đơn thức

và

 

x y xz



có phần hệ số là:

8

4

D. 7.

Câu 7. Tíc

h của hai đơn thức

 

x y



và















là đơn thức

có bậc bằng:

. 4 B. 5 C. 7 D. 8.

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Câu 8. Viết đơn thức

 

2 2 3

xy x y xy

 

thành đơn thức thu gọn.



Câu 9. Cặp đơn thứcnào dưới đây là hai đơn thức đồng dạng?

và



và

x y

và



và

x y

Câu 10. Khẳng định nà

o sau đây là sai?

và



là hai đơn t

hức đồng dạng



và

3 2

. .y

là hai đơn t

hức đồng dạng

và

 

5 3

2 3

x y x y

 

là hai đơn thức đồng dạng

và

là hai đơn thức

đồng dạ

Câu 11. T

ính tổng

3 3

x x







 









15x

Câu 12. T

ính tổng

3 2 3

2 1 4

2 3 2 3

xy y xy xy







   

 

 



MA TRẬN CÂU

HỎI TNKQ CHỦ ĐỀ 12

Mức độ

Chủ đề

Nhận biết (câu) Thông hiểu (câu) Vận dụng (câu)

Thấp Cao

12 1, 2, 3, 4, 5, 6 7, 8, 9, 10,

11 12

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Chủ đề 13. ĐA THỨC

. Một số vấn đề cần ôn tập

Đa thức là một tổng của những đơn thức. Mỗi đơn thức trong tổng gọi là một hạng tử của đa

thức đó.

Chú ý: Mỗi đơn thức được coi là một đa thức.

Nếu đa thức có những hạng tử là đơn thức đồng dạng (gọi tắt là hạng tử đồng dạng) thì ta

thu gọn các hạng tử đồng dạng để được một đa thức không còn hai hạng tử nào đồng dạng, ta

gọi đó là dạng thu gọn của đa thức.

Bậc của đa thức là bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức đó. Số 0

được gọi là đa thức không và nó không có bậc.

Muốn cộng hai đa thức ta thực hiện các bước:

Viết các hạng tử của hai đa thức đó cùng với dấu của chúng.

Thu gọn các

hạng tử đồng dạng

Muốn trừ ha

i đa thức ta nên thực hiện các bước

Viết các hạn

g tử của đa thức thứ nhất cùng với dấu của chúng

Viết tiếp các hạng tử của đa thức tứ hai với dấu ngược lại.

- Thu gọn các

ạng tử đồng dạng.

2. Ví dụ

Ví dụ 1 (Nhận

biết) . Tính giá trị của đa thức

2 3

x y x y xy y z



   

tại

x y

  

và

2z 

Giải:

Thay

x y

  

và

2z 

vào đa thức ta

có

1 1 1

1 2

2 4 4

       

Ví dụ 2 (Vận dụng) . Cho hai đa

thức

xy xy x



 

và

xy y xy





 

Tính M + N và M – N.

Giải:

3 2 3

2 3

N xy xy x xy y xy









     





 

3 2 3 2 2 3 3

1 1 1

2 3 3 2

xy x xy y xy xy xy xy xy x y



  



          



  

   

3 3 2 3 3

1 2 3

1 1

3 2 3 2

xy x y xy xy x y



  



        



  

   

2 3 2 3 2 3 2 3

1 1 1

2 3 2 3

N xy xy x xy y xy xy xy x xy y xy









           





 

2 3 3 2 3 3

1 1 1

1 1

3 2 3 2

y xy xy xy x y xy xy x y



      



          



      

       

2 3 3

xy xy x y

   

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

3. Câu hỏi trắc n

ghiệm

Câu 1. Tất cả các hạng tử của đa thức

2 3x y xy

 

là:

2 2

2 ; ; 3x y xy

2 2

2 ; y ; 3x xy



2 2

2 ;x y

2 2

2 ; y



Câu

2. Trong siêu thị, giá mít là

(đ/kg) và

giá cam là y (đ/kg) . Biểu thức biểu thị số tiền

mua 3 kg mít và 2 kg cam là

A. Một đơn thức B. Một đơn thức thu gọn

. Một đa

thức D

. Cả A, B và C đều sa

Câu 3. Bậc của đa thức

8 7 2 3

x y x y



  

bằng:

. 2 B. 5 C. 7 D. 8

Câu 4. Th

u gọn đa thức

 

2 2 2

2 :x y x y xy



ta được

y xy



y xy



2 3 2

y x y



2 2

y x y



Câu 5. Gi

á trị của đa thức

tại





bằng



Câu 6. C

ho hai đa thức

M x y xy

   

và

2 2 2

N x y xy

   

. Tính M+N bằng:

N x y



 

N x y



 

N x y



  

N x y



  

Câu 7. C

ho hai đa thức

x y xy



  

và

2 2

x y xy



  

. Tính M – N

bằng:

N x y



 

N x y



  

2 2

2 4

N x y xy



   

N xy



  

Câu 8. Tìm đa thức

, biết

 

2 2 2

P x y xy x y

     

x xy



 

1x 

y xy



  

1P y xy   

Câu 9. Tìm đa thức Q, biết

 

2 2 2 2

Q x y xy x y

     

x xy



 

y xy



 

y xy



 

x xy



 

Câu 10. T

ìm đa thức P, biết

 

2 2 2 2

1 1.

P x x y xy xy x y xy

       

x xy



 

x xy





2 2

x xy x y xy



   

2 2

x xy x y xy



   

Câu 11. T

ìm đa thức Q, biết

 

4 3 2 2 3 2

yx .Q x y xy y xy xy x y x x      

4 2

x y xy x



  

4 2

x y xy x



 

4 2

x y xy x



 

4 2

x y xy x



  

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Câu

12. Cho hai đa thức

2 1E x y xy   

và

2 2

F x y xy

  

. Khẳng

định nào dưới đây

sai?



luôn lu

ôn dương B



luôn lu

ôn dương

C. Cả A và B đều đúng D. Cả A và B đều sai.

MA TRẬN CÂU

HỎI TNKQ CHỦ ĐỀ 13

Mức độ

Nhận biết (câu) Thông hiểu (câu)

Vận dụng (câu)

Chủ đề Thấp Cao

13 1, 2, 3, 4, 5 6, 7, 8, 9, 10, 11 12

Chủ đề 14. ĐA THỨC

MỘT BIẾN

. Một số vấn đề cần

ôn tập

Đa thức một biến là tổng hợp của những đơn thức của cùng một biến. Mỗi số được coi là

một đa thức một biến.

Bậc

của đa thức một biến (khác đa thức không, đã thu gọn) là số mũ lớn nhất của biến trong

trong đa thức đ

ó.

Hệ số cao n

hất là hệ số của số hạng có bậc cao nhất.

Hệ số tự do là

số hạng không chứa biến.

Để cộng hoặc trừ hai đ

a thức một biến, ta có thể thực hiện theo cách sau:

Cách 1: Thực hiện theo cách cộng, trừ đa thức đã học ở bài trước.

Cách

2: Sắp xếp các hạng tử của hai đa thức theo cùng lúy thừa giảm (hoặc tăng) của biến,

rồi

đặt phép tính theo cột dọc tương ứng như cộng, trừ các số (chú ý đặt các đơn thức đồng

dạng dạng ở cùng

một cột) .

Nếu x= a, đa thức P (x) có giá trị bằng 0 thì ta nói a (hoặc x=a) là một nghiệm của đa thức

đó.

2. Ví dụ

Ví

dụ 1: (Thông hiểu) . Cho các đa thức

 

3 2

2 3 1P x x x x   

và

 

3 2

2 3.

Q x x x

  

Tìm

đa thức R (x), sao cho

(

) ( ) ( )

x P x Q x





. Từ đó tìm ng

hiệm của R (x

) .

Giải:

   

2 3 2

( ) ( ) ( ) 2 3 1 2 3

R x P x Q x x x x x x

        

   

2 3 2 3 3 2 2

2 3 1 2 3 2 2 3 1 3

x x x x x x x x x x

             

x



(

) 0 3 4 0 3 4

x x x x



        

Kết luận:

(

) 3 4

x x





và nghiệm của

(

)

là





Ví

dụ 2 (Vận dụng cao) . Cho các đa thức

(

) ax

x bx c



 

, biết

(0) , ( 1)P P

    

và

(

2)P





. Chứng minh

rằng

(

3)P





và

(

6 6 )a b



 

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Giải

(0) ,P c

mà

(0) ,

 

nên

c 



(

1) ,

a b c



  

mà

(

1)P



 

và

c 



nên

(

)

b Z





, suy ra

 

2a b



 

và

 

4a b



 

(

2) 4 2 ,

a b c



 

mà

(

2)P





và

c 



, nên

 

2a b



 

suy ra

 

4a b



 

Ta có:

     

9 3 8 4 , (3)

a b c a b a b c P



      

là tổng của

các số nguyên nên

(

3)P





có

6 6 (4 2 ) (2 2 ) (4 2 ) (4 4 ), (6 6 )a b a b a b a b a b a b         

là tổng và hiệu của các

số nguyên nên

 

6a b



 

(điều phải chứng minh)

. Câu hỏi trắc n

ghiệm

Câu 1. Thu gọn và sắp xếp các hạng tử của đa thức

2 2

(

) 3 2 3

x x x x x



   

theo

lũy thừ

giảm của biến.

( ) 3 2 2

A x x x x    

( ) 2 2 3A x x x x   

2 2

( ) 3 2 3

A x x x x x

    

( ) 3 2 2A x x x x    

Câu

2. Thu gọn và sắp xếp các hạng tử của đa thức

2 3

B( ) 5 2

x x x x x

    

theo

lũy thừa

tăng của biến.

( ) 2 5 2

x x x



  

( ) 5 2

x x x



  

(

) 2 5

x x x x



   

( ) 2 5 2

x x x



   

Câu 3. Đa thức

(

) 5 6 12

x x x x



  

có hệ số cao nhất là:

12

B. 3 C. 5 D. 6

Câu 4. Đa thức

(

) 5 6 12

x x x x



  

có hệ số tự do là:

12

B. 3 C. 5 D. 6

Câu 5. Đa

thức

3 2

( ) 5 2 6 1

x x x x



   

có hệ số lũy thừa bậc 4 là:

A. 5 B. 1 C. 0 D. -2

Câu 6. Đa thức bậc 6 một biến có hai hạng tử mà hệ số cao nhất là 5, hệ số tự do là -1. Đó là

đa thức

x 

x 

Câu 7. C

ho hai đa thức

(

x) x 2

x x



  

và

(

) 2

x x x x



  

. Tính

(

) ( )

x Q x



( ) ( ) 3P x Q x x x    

( ) ( ) 3 2 3

P x Q x x x x

    

(

) ( ) 2 3

x Q x x x x



   

(

) ( ) 3 2 3

x Q x x x x



   

Câu 8. C

ho hai đa thức

4 3

(

x) x 2

x x



  

và

3 3 2

(

) 2 2

x x x x x



  

. tính

(

) ( )

x Q x



4 3 2

(

) ( ) 2 3 2

x Q x x x x x



    

3 2

(

) ( ) 3 3 2

x Q x x x x



    

3 2

(

) ( ) 3 3 2

x Q x x x x



   

3 2

(

) ( ) 3 3 2

x Q x x x x



   

Câu 9. Tìm đa thức A (x), biết

3 2

(

) ( 3 2) 2 2

x x x x x x



     

3 2

(

)

x x x x x



   

(

)

x x x x



  

(

)

x x x x



 

(

) 5

x x x x



 

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Câu 10. T

ìm đa thức B (x), biết

2 3

2 ( ) 2x x x B x x x    

3 2

( )

B x x x x   

3 2

( )

B x x x x  

3 2

( )

B x x x x  

3 2

( ) 4B x x x x x   

Câu

11. Cho các đa thức

2 2

( ) 2 2; ( ) 9; ( ) 3

P x x Q x x R x x

     

Cả ba đa thức trên có tấ

cả bao nhiêu

nghiệm

A. 1 B. 2 C. 3 D. 4

Câu 12. Cho hai đa thức

3 3 2

(

) 5; ( ) 1

x x x Q x ax x



    

(a là

hằng số). Tìm a để

(

) ( )

x Q x



la một đa thức bậc 3

1a 

1a 

0a 

0a 

Câu 13. Cho biết

3 2

2 3 0x x  

. Tính giá trị của

(

) 5 10 15 1

x x x x



   

(

) 0



(

) 1



(

) 5





(

) 6





Câu 14. Số nào dưới đây là nghiệm của đa

thức

(

) 20

x x x x



 

1x 



1x 





Câu

15. Cho hai đa thức

3 2 4 3 2

(

) 2 5 ; ( ) 6 2

x x x x x Q x x x x x



       

gọi

(

) ( ) ( )

x P x Q x





. Hỏi đa thức

(

)

có bao nhiêu nghiệm

A.1 B.2 C.3 D.4

Câu 16. Cho đa thức

( )

P x ax bx c  

trong

đó a, b, c là các hằng số thỏa mãn

3 4 6 0a b c  

. Tính

(1) 2 (0,5)

P P



(

1) 2 (0,5) 0





(

1) 2 (0,5) 3





(

1) 2 (0,5) 4





(

1) 2 (0,5) 6





MA TRẬN CÂU

HỎI TNKQ CHỦ ĐỀ 14

Mức độ Nhận biết (câu) Thông hiểu (câu) Vận dụng (câu)

Chủ đề Thấp Cao

14 1, 2, 3, 4,

5, 6, 14 7, 8, 9, 10, 11, 13 12 15, 16

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Chủ đề 15. ĐƯỜNG

THẲNG VUÔNG GÓC. ĐƯỜNG THẲNG SONG SONG

. Kiến thức cần

nhớ

Hai góc đối đỉnh: là hai góc mà mỗi cạnh của góc này là

tia

đối của một cạnh của góc kia.

Tính chất: Hai góc đối đỉnh thì bằng nhau.

Hình bên: Hai góc





đối

đỉnh, suy ra





O O

. Hai

góc



và



đối đỉnh, suy ra

 



Hai đường thẳng vuông góc: Hai đường thẳng xx’ và

yy’ cắt nhau và trong các góc tạo thành có một góc vuông được

gọi là hai đường thẳng vuông góc. Kí hiệu

' 'xx yy

- Tính chất: Có một và chỉ một đường thẳng a’ đi qua

điểm O và vuông góc với đường thẳng acho trước.

- Đường thẳng trung trực của đoạn thẳng: đường thẳng

vuông góc với đoạn thẳng tại trung điểm của nó được gọi là

đường trung trực của đoạn thẳng ấy.

Khi xy là đường trung trực của đoạn thẳng AB ta cũng

nói: hai điểm A và B đối xứng nhau qua đường thẳng xy

c) Góc so le trong, góc đồng vị

đường thẳng c cắt hai đường thẳng a và b tại hai điểm A, B

tạo thành 4 góc đỉnh A, 4 góc đỉnh B (như hình bên)

- Hai góc



và



, cũng

như hai góc



và



được

gọi

là hai góc so le trong

- Bốn cặp góc



và





và





và





và



được gọi là các

cặp góc đồng vị

Tính chất: Nếu đường thẳng c cắt hai đường thảng a và b, trong các góc được tạo thành,

có một cặp góc so le trong bằng nhau thì hai góc so le trong còn lại bằng nhau và hai góc đồng

vị bang nhau.

Dấu hiệu nhận biết hai đường thẳng song song: Nếu đường thẳng c cắt hai đườ

thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau (hoặc một cặp góc

đồng vị bằng nhau) thì a và b song song với nhau.

Kí hiệu:

a b

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Tiên đề Ơ – clit: Qua một điểm ở ngoài đường thẳng, chỉ có một đường thẳng song

song với đường thẳng đó.

Tính chất của hai đường thẳng song song: Nếu một đường thẳng cắt hai đường thẳng

song song thì:

Hai góc so le trong bằng nhau; Hai góc đồng vị bằng nhau; Hai góc trong cùng phía bù

nhau.

g) Quan hêj giữa tính vuông góc và tính song song:

Hai

đường thẳng phân biệt cùng vuông góc vơi một

đường thẳng thứ ba thì chúng song song với nhau.

Một đường thẳng vuông góc với một trong hai đường

thẳng song song thì nó cũng vuông góc với đường thẳng kia

h) Ba đường thẳng song song:

Hai

đường thẳng phân biệt cùng song song với đường

thẳng thứ ba thì chúng song song với nhau.

Khi ba đường thẳng

2 3

, ,d d d

song

song với nhau

từng đôi một, ta nói ba đường thẳng ấy song song với nhau

và kí hiệu

2 3

d d d 

. Một số ví dụ

Ví dụ 1 (

Nhận biết). cho hình vẽ bên. Tính số đo góc



Giải:



70xAD xBC  

, hai

góc



xAD

và



xBC

ở vị trí

đồng

vị, suy ra



Ta có



và



(đánh dấu trên hình) là hai góc trong cùng phía bù nhau.

Suy ra









và



lại là hai góc đối đỉnh. Vậy







Ví dụ 2 (Thông hiểu). Cho hình bên, E thuộcđoạn FM. Chứng minh:



EM EFG EGF





Giải:

Ta có



180GEF GEM  

và



EF EFG EGF



  

, suy

140°

70°

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7



EM EFG EGF





(đpcm)

Nhận

xét: Đây là tính chất: “góc ngoài của tam giác bằng tổng

hai góc trong không bù với nó”

VÍ dụ 3 (Vận dụng). Cho hình vẽ bên. Chứng minh



Giải:

Kẻ tia

t Mx



(như

hình). Suy ra



60MNt  

(vì



NMx

và



MNt

là

hai góc trong cùng phía bù nhau). Mà



 



80 20 20

MNP PNt PNt NPy

        

Mà hai góc



và



NPy

là

hai góc ở vị trí so le trong.

Suy ra

t Py



Mà

t Mx



, hai

đường thẳng Mx và Py là hai đường

thẳng phân biệt.

Theo tính chất suy ra:



Ví dụ 4 (

Vận dụng cao). Cho định lý:

“Nếu hai góc nhọn



xOy

và



' ' 'x O y

có

'; ' '

x O x Oy O y



thì



' ' 'xOy x O y



a) Viết giả t

hiết và kiết luận cho định lý trên

b) Chúng

minh định lý trên.

Giải:

Giả thiết



xOy

và



' ' 'x O y

là hai g

óc nhọn.

' '; ' 'Ox O x Oy O y 

Kết luận



' ' 'xOy x O y



b) Vẽ đường thẳng OO’ và chứng minh với hình vẽ trên

Vì

O x



, nên hai

góc đồng vị bằng nhau:



2 2



Vì

y O y



, nên hai

góc đồng vị bằng nhau:







Suy ra







1 2 1

O O O



 

hay



' ' 'xOy x O y



20°

0°

120°

0°

20°

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Chú

ý: Trong bài này có thể vị trí tia

;

' '; ; ' '

x O x Oy O y

ở những

vị trí khác nhau thì

cách trình bày vẫn tương tự và ra kết quả



' ' 'xOy x O y



Đó là định lý “Hai góc nhọn có cạnh tương ứng song song thì bằng nhau”.

3. Câu hỏi trắc nghiệm

Câu 1. Cho hai đường thẳng xx’ và yy’ cắt nhau tại O, Biết



' 50

xOy

 

. Số đo của

góc



'x Oy

bằng:



Câu 2. Cho

hai đường thẳng xx’và yy’ cắt nhau tại O, biết



' ' 140

xOy x Oy

  

. Số đo

góc



xOy

bằng:



Câu 3. Khẳng định nào sau đây đúng?

. Hai góc

bằng nhau thì đối đỉnh

. Hai góc

đối đỉnh thì bằng nhau

. Hai tia p

hân giác của hai góc đối đỉnh trùng nhau

. Hai góc

đối đỉnh là hai góc mà mỗi cạnh của góc nay là tia trùng của một cạnh của góc k

Câu 4. Hai đường thẳng cắt nhau thì:

. Tạo thàn

h hai góc đối đỉnh B

. Tạo thàn

h hai cặp góc đối đỉnh

. Tạo thàn

h ba cặp góc đối đỉnh D

. Tạo thàn

h bốn cặp góc đối đỉnh

Câu 5. Cho hai đường thẳng xy và x’y’ cắt nhau tại O, biết



' 80xOx  

. Gọi Ot là tia phân giác của

góc



'yOy

. Số đo góc



tOy

bằng:

55

80

110

40

Câu 6. Hai đường thẳng xx’ v

à yy’ cắt nhau tại O. Chúng được gọi là đường vuông góc khi:



xOy

 



' 180xOx  



' 90

x Oy

 

D. A và C

đều đúng

Câu 7. Khẳng định nào sau đây đúng?

. Hai đường

thẳng cắt nhau thì vuông góc

. Hai đường

thẳng vuông góc chỉ tạo thành một góc vuông

C. Hai đường thẳng vuông góc thì mỗi đường thẳng là phân giác của một góc bẹt

. Hai đường

thẳng vuông góc chỉ tạo thành một cặp góc đối đỉnh

Câu 8. Có bao nhiêu đường thẳng đi qua điểm O và vuông góc với đường thảng a cho trước?

A. 1 B. 2 C. 4 D. Vô số

Câu 9. Đường thẳng xy là trung trực của đoạn thẳng AB nếu:

A. xy đi qua trung điểm của AB

. xy vuôn

g góc với AB

. xy vuôn

g góc với AB tại trung điểm của AB

. xy cắt AB

Câu 10. Khẳng địn

h nào dưới đây sai:

. Hai đường

thẳng cắt nhau thì vuông góc

. Hai góc

đối đỉnh thì bằng nhau

. Hai đường

thẳng vuông góc thì cắt nhau

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

D. Hai đường

thẳng vuông góc tạo thành hai cặp góc vuông đối đỉnh

Câu 11. Cho đoạn thẳng AB dài

. Lấy

điểm M trên cạnh AB sao cho

M cm



. Đường

thẳng

d là trung trực của MB, d cắt MB tại K. Khẳng định nào dưới đây sai

B cm



5KA



d AB



Câu 12. Đường

thẳng c cắt hai đường thẳng a và b như hình. Có bao

nhiêu cặp góc so le trong?

A. 0 B. 1

C. 2 D. 4

Câu 13. Đường thẳng c cắt hai đường thẳng a và b(như hình vẽ câu

12). Có bao nhiêu cặp góc đồng vị?

A. 0 B. 1 C. 2 D. 4

Câu 14. Đường thẳng cắt hai đường thẳng a và b tai A và B tạo thành bốn

góc đỉnh A và bốn góc đỉnh B được đánh số như hình vẽ. Khẳng

định nào dưới đây đúng nhất?

. Hai góc



và



được gọi là hai góc

so le trong

. Hai góc



và



được gọi là hai gó

c so le trong

. Cả A và

B đều đúng

. Cả A và

B đều sai

Câu 15. Đường thẳng cắt hai đường thẳng a và b tai A và B tạo thành bốn góc đỉnh A và bốn góc

đỉnh B được đánh số (như hình vẽ câu 14). Xét các khẳng định dưới đây:

(I). Hai góc



và



được gọi là hai góc đồng vị

(II). Hai góc



và



được gọi là hai góc đồng vị

(III). Hai góc



và



được gọi là hai góc đồng vị

(IV). Hai góc



và



được gọi là hai góc đồng vị

Số các khẳng định đúng là:

. 1 B. 2 C. 3 D. 4

Câu 16. Đường

thẳng c cắt hai đường thẳng a và b như hình. Khi đó

trên hình vẽ ta có:

. Hai cặp

góc trong cùng phía

. Bốn cặp

góc so le trong

C. Hai cặp góc đồng vị

D. Cả A, B và C đều sai

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Câu 17. Hình bên c



A B

  

. Tìm khẳng định sa





 







 



A B

  





180

A B

  

Câu 18. Phát biểu b

ào dưới đây đúng?

A. Hai đường thẳng phân biệt thì song song

. Hai đường

thẳng không song song là hai đường thẳng không có điểm chung

. Hai đường

thẳng song song là hai đường thẳng không có điểm chung

. Hai đường

thẳng vuông góc là hai đường thẳng song song

Câu 19. Qua một điểm ở ngoài một đường thẳng, có bao nhiêu đường thẳng song song với đường

thẳng đó:

. Không

có B

. Chỉ có

một C

. Có ít n

hất một D

. Có vô

số

Câu 20. Tìm các đường thẳng song song trong các hình vẽ sau:



Câu 21. Tìm các đườn

g thẳng song song trong các hình vẽ sau:



x y

m n

u v

40°

45°

0°

30°

2 1

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Câu 22. Phát biểu n

ào dưới đây đúng?

. Hai đường

thẳng không cắt nhau thì song song

. Hai đường

thẳng không có điểm chung thì song song

C. Nếu hai đường thẳng vuông góc thì cắt nhau và ngược lại

. Nếu hai

đường thẳng cắt nhau thì có một cặp góc đối đỉnh

Câu 23. Chọn câu trả lời đúng:

Cho một đường thẳng các hai đường thẳng song song.

Xét các khẳng định sau:

(I). Hai góc so le trong bằng nhau

(II). Hai góc đồng vị bằng nhau

(III). Hai góc trong cùng phía bù nhau

. Chỉ có (

I) đúng B

. Chỉ có (

II) đúng

C. Có (I) và (II) đúng D. Cả (I), (II) và (III) đều đúng

Câu 24. Cho một đường thẳng cắt hai đường thẳng song song. Khi đó số cặp góc so le trong bằng

nhau được tạo ra là:

. 0 B. 1 C. 2 D. 3

Câu 25. Cho một đường

thẳng cắt hai đường thẳng song song. Khi đó số cặp góc đồng vị bằng nhau

được tạo ra là:

. 4 B. 3 C. 2 D. 1

Câu 26. Cho

một đường thẳng cắt hai đường thẳng song song. Khi đó số cặp góc trong cùng phía

bù nhau được tạo ra là:

. 1 B. 2 C. 3 D. 4

Câu 27. Cho

b

, số đo góc x t

rên hình vẽ bằng:

45

90

35

80

Câu 28. Cho

a b

, số đo góc x t

rên hình vẽ bằng:

35

0

5

0

Câu 29. Cho hình

vẽ bên, để

a b

thì số đo góc

x bằng:

20

0

80

Câu 30. Cho

b

và



00A B  

(hình vẽ b

ên). Số đo góc



bằng:

35°

45°

120°

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

10

0

5

0

Câu 31. Cho

b

và



0A B  

(hình vẽ b

ên). Số đo góc



bằng:

0

30

0

5

Câu 32. Cho

a b

và



1 1

B

(hình vẽ b

ên). Số đo góc



bằng:

0

5

Câu 33. Cho

a b

như hình vẽ bên.

Số đo góc x bằng:

0

50

0

Câu 34. Cho

b

như hình vẽ bên.

Số đo góc x bằng:

150

90

0

Câu 35. Cho

a b

như hình vẽ bên.

Số đo góc x bằng:

0

20

50

Câu 36. Cho ba đườn

g thẳng phân biệt a, b, c. Hai đường thẳng a và b song song với nhau khi:

. a và b c

ùng vuông góc với c B

. a và b c

ùng cắt với c

. a vuôn

g góc với c D

. b vuôn

g góc với c

Câu 37. Cho hai đường thẳng a và b song song với nhau. Nếu đường thẳng c vuông góc với đường

thẳng a thì:

c b

c b

c b

D. Đáp án

khác.

Câu 38. Phát biểu nào dưới đây đúng:

. Nếu

hai đường thẳng cùng song song với một đường thẳng thứ ba thì chúng song song vớ

nhau.

B. Nếu hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì chúng song song với

nhau

C. Nếu

hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng

song

song với

nhau

40°

120°

30°

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

D. Nếu

hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì chúng vuông góc vớ

nhau.

Câu 39. Cho

b

và

y

như hình vẽ b

ên. Tính số đo góc x.

0

20

50

Câu 40. Cho

BC

, nếu đường thẳng m song so

ng với BC và

cắt cạnh AB thì

m AC

m AC

C. m cắt cạn

h AC D

. m khôn

g cắt cạnh AC

Câu 41. Tìm số đo góc x ở hình bên:

0

30

Câu 42. Tìm số đo

góc x ở hình bên:

0

20

50

Câu 43. Tìm số đo

góc x ở hình bên:

30

60

0

20

Câu 44. Tìm số đo

góc x ở hình bên:

0

100

130

Câu 45. Viết

giả thiết kết luận cho định lý: “ Nếu một đường thẳng vuông góc với một trong hai

đường thẳng song song thì nó vuông góc với đường thẳng kia”

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Giả thiết

a c b



Kết luận



Giả thiết

b c a



Kết luận

c b



Giả thiết

,c b a b

 

Kết luận



Giả thiết

c b



Kết luận

b c a



Câu 46. Cho hình

vẽ bên. Phát biểu nào dưới đây sai?

. Hai

đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song

song với nhau

. Một

đường thẳng vuông góc với một trong hai đường thẳng

song song thì nó cũng vuông góc với đường thẳng kia

. Hai

đường thẳng cùng vuông góc với một đường thẳng thứ

ba thì chúng song song hoặc trùng nhau

. Hai

đường thẳng cùng vuông góc với một đường thẳng thứ

ba thì chúng vuông góc với nhau

MA TRẬN CÂU HỎI TNKQ CHỦ ĐỀ 15

Mức độ Nhận biết (câu) Thông hiểu (câu) Vận dụng (câu)

Chủ đề Thấp Cao

15 1, 2, 3, 4, 5, 6, 7, 8, 9, 12, 13,

14, 15, 16,

19, 20, 21, 23, 24,

25, 26, 27, 28, 29, 37

5, 7, 10, 11, 17, 18,

22, 30, 31, 32, 36,

38, 40, 43, 45

33, 39,

42, 44, 46

34, 55

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Chủ đề 16. T

AM GIÁC

. Kiến thức cần

nhớ

a) Tổng ba

góc của một tam giác

 Tổng ba góc của một tam giác bằng

180

 Tam giác vuông là tam giác có một góc vuông

 Trong tam giác vuông hai, góc nhọn phụ nhau

 Góc ngoài của một tam giác là góc kề bù với một góc của tam giác ấy. mỗi góc

ngoiaf

của một tam giác bằng tổng của hai góc trong không kề với nó.

b) Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các

góc

tương ứng bằng

nha. Kí hiệu:

' ' 'ABC A B C  

Người ta q

ui ước khi kí hiệu sự bằng nhau của hai tam giác, các chữ cái chỉ tên các đỉnh

tương ứng được viết theo cùng thứ tự.

c) Ba trường hợp bằn

g nhau của tam giác

Nếu

BC

và

' 'A B C

có:

'; ' '; ' 'AB A B AC A C BC B C  

thì

' 'ABC A B C  

(c. c. c

)

Nếu

BC

và

' 'A B C

có:



' '; '; ' 'AB A B B B BC B C  

thì

' 'ABC A B C  

(c. g. c

)

Nếu

BC

và

' 'A B C

có:



' '; '; 'AB A B A A B B  

thì

' 'ABC A B C  

(g. c. g)

d) Tam giác

cân là tam giác có hai cạnh bằng nhau

Tam giác cân ABC có

( )AB AC

, ta

gọi AB và AC là các

cạnh bên, BC là cạnh đáy,



và



là

các góc ở đáy,



là

góc ở

đỉnh.

BC

có

B AC

còn được

gọi là

BC

cân tại A

Tính chất:

Trong một

tam giác cân, hai góc ở đáy bằng nhau.

Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.

Tam giác vuông cân là tam giác vuông có hai cạnh góc vuông bằng nhau.

Tam giác đều là tam giác có ba cạnh bằng nhau.

Hệ quả: Trong một tam giác dều, mỗi góc bằng 60

Nếu một ta

m giác có ba góc bằng nhau thì tam giác đó là tam giác đều.

Nếu một tam giác cân có một góc bằng 60

thì tam giác đ

ó là tam giác đều.

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Định lý Py-ta-go: Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng c

ác

bình phương

của hai cạnh góc vuông

Định

lý Py-ta-go đảo: Nếu một tam giác có bình phương của một cạnh bằng tổng các bình

phương của hai cạnh kia thì tam giác đó là tam giác vuông.

f) Các trường

hợp bằng nhau của tam giác vuông

- Nếu

hai cạnh góc vuông của tam giác vuông này bằng hai cạ

góc

vuông của tam giác vuông kia thì hai tam giác vuông đ

bằng nhau. (theo trườn

g hợp cạnh – góc – cạnh)

- Nếu

một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam

giác vuông này bằng một cạnh góc vuông và một góc nhọn kề với

cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng

nhau. (g. c. g)

- Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằ

với

cạnh huyền và một góc nhọn của tam giác vuông kia thì hai

tam giác vuông đó bằng nhau. (theo trường hợp g. c. g)

- Trường hợp bằng nhau về cạnh huyền và cạnh góc vuông: Nếu

cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng

cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai

tam giác vuông đó bằng nhau

2. Một số ví dụ

Ví dụ 1 (N

hận biết). Hai đoạn thẳng AB và CD cắt nhau tại trung điểm O của mỗi đoạn thẳng.

Chứng minh AC // BD.

Giải:

Giả thiết

 

AB CD O

 

OA OB



OC OD



Kết luận AC // BD

Có:



, , OA OB OC OD AOC DOC  

(đối đỉnh)

Suy ra

AC OBD  

(cạnh – góc – cạnh)

Suy ra



AC OBD

hay



AC ABD

, mà hai

góc



và



ABD

ở vị trí so le tr

ong,

nên AC // BD.

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Ví

dụ 2 (Thông hiểu). Cho tam giác ABC vuông tại A, có

B AC

Qua

A kẻ đường thẳng

xy (B, C nằm cùng phía đối với xy). Kẻ

D xy

tại D, kẻ

E xy

tại E. Chứng minh:

AD ACE  

E BD CE 

Giải:

Giả thiết

ABC



vuông tại

AB AC



;A xy



B và C nằm cùng

phía xy

BD xy



tại D,

CE xy



tại E

Kết luận

AD ACE



 

DE BD CE

 

a) Có



 



90 , 90

ABD DAB DAB CAE   

uy ra



ABD CAE

(cùng

phụ góc



DAB

Lại

có

B AC

Vậy

AD ACE  

(trường

hợp cạnh huyền – góc nhọn của hai tam giác

vuông)

Vì

AD ACE  

nên

AD CE AE BD 

D CE AE AD DE    

(vì A nằm

giữa D và E)

Ví dụ 3 (Vận dụng). Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên

tia đối của tia CB lấy điểm E sao cho



AD CAE

. Kẻ B

H vuông góc với AD tại H, kẻ CK

vuông góc với AE tại K. Chứng minh rằng:

D CE

H CK

Gọi I là giao điểm của hai đường thẳng HB và CK. Chứng minh rằng AI là tia phân giác

của góc



BAC

Giải:

a) Có



BD BAC ACB 

(tính chất góc ngoài của tam giác)



ACE CAB ABC 

(tính chất góc ngoài của tam giác)

Mà



CB ABC

(vì

BC

cân

tại A) suy ra



BD ACE

lại

có



BAD CAE ABD ACE    

(g-c-g)

BD CE 

b) Do

BD ACE  

nên

D CE

và



DB KEC

Mà hai tam

giác

DB

và

EC

là ha

i tam giác vuông

(cạnh huyền – góc nhọn). Suy ra:

H CK

c) Ta có:



IBC HBD

(đối đỉnh)



ICB KCE

(đối đỉnh)

Mà



BD KCE

(vì chứng minh trên

DB KEC  

)

. Suy

ra:



BC ICB IBC  

cân tại I

,IB IC 

lại có

B AC

(giả thiết)

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Suy ra

BI ACI  

(cạnh- cạnh- cạn

 

AI CAI 

Do đó AI l

à tia phân giác của góc



Ví dụ 4 (Vận dụng cao). Cho tam giác ABC vuông tại A, kẻ

H BC

tại H.

Trên tia đối của tia HA lấy điểm D sao cho

.HD HA

a) Chứng minh rằng:

HB DHB  

b) Chứng minh rằng:

D CD

c) Cho



BC 

Tính số đo

góc



Giải:

a) Hai tam g

iác

HB

và

HB

có:

HB chung,

,HA HD



HA BHD 

Suy ra

.AHB DHB  

b) Có:





A

(cùng phụ



) mà





D

(vì

.AHB DHB  

) nên



D

(1)

Lại có:

HDC HAC  

(tương tự chứn

g minh câu a). Suy ra





C

(2)

Từ (1) và (2) su

y ra:





D

, mà









1 1 2

0 90 90 .

o o

C D D BDC      

Tức là:

D CD

BC

vuông tại

A có





0 30

BC C  

(hai g

óc nhọn phụ nhau)

Mà











1 1 2

C C ACD C C    

. Câu hỏi trắc n

ghiệm

Câu 1. Cho

ABC

, chọn đáp

án đúng trong các đáp án sau

 



B C  

 



B C  

 



B C  

 



B C  

Câu 2. C

ABC

vuông tại A. Khẳng định nào dưới

đây sai:



C A 



C 



A 



C 

Câu

3. Cho

BC

có

góc



BCx

là

góc ngoài tại đỉnh C của

BC

. Khẳng

định nào dưới đây

sai:





Cx A





Cx B



 

Cx A B 



 

Cx A B 

Câu 4. C

BC

, tìm số đo

x ở hình bên:

x 

Câu 5. C

BC

, tìm số đo

x, y ở hình bên:

0 , 100

y 

100 , 100

x y 

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

0 , 100

y 

0 , 110

y 

Câu 6. Tì

m góc x trên hình sau để AB // CD.

x 

Câu

7. Cho

BC

vuông

tại A,



B 

Tia

phân giác của góc . . … cắt AB ở D. Số đo góc



bằng:

120

Câu 8. Cho

BC

biết

 

45 , 30

A B 

Góc n

goài tại đỉnh C có số đo bằng:

105

Câu 9. Tr

ong hình vẽ bên, cho

BC

có MN //

BC. Tìm số đo góc



Câu 10. Khẳng định nà

o dưới đây sai?

. Một ta

m giác có thể có nhiều nhất một góc tù

B. Một ta

m giác có thể có nhiều nhất một góc vuông

C. Một ta

m giác có thể có ba góc nhọn

D. Trong

một tam giác vuông, hai góc nhọn bù nhau

Câu 11. T

ìm số đo x trong hình vẽ sau:

Câu 12. Tổng các

góc ngoài của một tam giác bằng:

Câu 13. Cho

BC

có



C

và



B 

. Khi đó số đo góc



bằng

Câu

14. Cho

BC MNP  

có

cm, 3 cm, 4 cmAB AC PN  

. Tính

chu vi tam giác

NP

A. 4, 5 cm B. 9 cm C. 7 cm D. 6 cm

Câu 15. Cho

ABC MNP  

Khẳng định nào dưới đ

ây đúng?



BC MNP



BC MPN

B MP

C MP

Câu 16. Cho

BC MNP  

biết

cmAC 

Cạn

h nào của

NP

có độ dài

bằng 5cm

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

. Không

có cạnh nào

Câu 17. Cho

BC MNP  

biết



A 

và



B 

Số đo góc



bằng:

Câu 18. Cho hai tam giác

ABC

và

EF

có:

B DE

AC DF

BC EF

và



,A D



, B E C F 

Cách viết

nào dưới đây đúng?

ABC DEF  

ABC DFE  

BC EFD  

D. Cả A, B, C đều

đúng

Câu 19. T

ìm số đo góc



trên hình vẽ bên:

Câu 20. Chọn câu

trả lời đúng:

. Nếu ba cạnh của t

am giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau

B. Nếu ba góc của tam giác này bằng ba góc của tam giác kia thì hai tam giác đó bằng nhau.

C. Cả A và

B đều đúng

D. Cả A và

B đều sai

Câu 21. Trên hình vẽ bên, có bao nhiêu cặp tam giác bằng nhau

theo trường hợp cạnh – cạnh – cạnh?

. 1 B. 2

C. 3 D. 4

Câu

22. Tính góc



BAC

trong

hình vẽ bên và cho biết AD có

song song với BC không?



120

BAC 

và AD /

/ BC



AC 

và AD /

/ BC



120

BAC 

và AD k

hông song song BC



AC 

và AD k

hông song song BC

Câu

23. Cho hai tam giác

BC

và

EF

có

, AB DE AC DF 

. Tìm đ

iều kiện để

ABC DEF  

theo trường hợp cạnh

– cạnh – cạnh

C DE

C EF

B DF

Câu 24. Cho hìn

h bên, xét các khẳng định

(I). “AD là t

ia phân giác của góc



”

(II). ”BC là

tia phân giác củagóc



ABD

”

Chọn câu trả lời đ

úng:

. Chỉ có (

I) đúng. B

. Chỉ có (

II) đúng

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

C. Cả (I) và

(II) đều đúng. D. Cả (I) và (II) đều sai

Câu

25. Cho hai tam giác

ABC

và

EF

có:



, AB DE ABC DEF 

. Tìm điều

kiện để

BC DEF  

theo trường hợp cạnh

– góc – cạnh.

C DF

C EF



ACB DFE

D. Tất cả đều sai.

Câu

26. Cho hình vẽ bên. Tìm điều kiện để

BC AFE  

theo

trường hợp cạnh –góc – cạnh.



CB AFE

C EF

C AE

C AF

Câu

27. Cho hình vẽ bên, số cặp giác bằng nhau trên hình theo

trương hợp góc-cạnh-góc là:

. 0 B. 1

. 2 D. 3

Câu

28. Cho hình vẽ bên, số cặp tam giác bằng nhau trên hình

là:

. 0 B. 1

. 2 D. 3

Câu 29. Cho hìn

h bên, xét các khẳng định:

(I).

BC EF

(II).

d BC

Chọn câu trả lời đ

úng:

. Chỉ có (

I) đúng. B

. Chỉ có

(II) đúng

C. Cả (I) và

(II) đều đúng. D

. Cả (I) và

(II) đều sai

Câu 30. Cho hìn

h vẽ bên và có



, , AB AC BD EC ABC ACB  

Xét các khẳn

g định sau:

(I).

BD ACE  

(II).

BE ACD  

Chọn câu trả lời đ

úng:

. Chỉ có (

I) đúng. B

. Chỉ có (

II) đúng

C. Cả (I) và (II) đều đúng. D. Cả (I) và (II) đều sai.

Câu 31. Cho

BC

và

EF

có



, A D B E 

Để

BC DEF  

theo trường hợp góc-cạnh-

góc phải thêm điều kiện nào sau đây?

B DE

C DF

C EF



ACB DFE

Câu

32. Cho hình vẽ bên biết



BE ACF

Cần

thêm điều kiện gì để

ABE ACF  

theo trường hợp góc-cạnh-góc.

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7



EB AFC

B AC

BE CF

AF AC

Câu 33. Cho

BC

, tia phân giác của góc



cắt BC tại D, trên tia AC lấy điểm Esao cho

.AB AE

Hỏi

BD AED  

theo trường hợp

nào?

A. Cạnh-cạnh-cạnh B. Cạnh-góc-cạnh

. Góc-cạn

h-góc D. Góc-góc-góc

Câu 34. Trường hợp nào dưới đây thể hiện sai các trường hợp bằng nhau của hai tam giác?

. Cạnh-cạnh-cạnh B. Cạnh-g

óc-cạnh

. Góc-cạn

h-góc D

. Góc-góc-góc

Câu 35. Phát biểu

nào dưới đây đúng?

. Hai

góc và một cạnh của tam giác này bằng với hai góc và một cạnh của tam giác kia

thì

hai tam giác

đó bằng nhau

B. Hai

cạnh và một góc của tam giác này bằng với hai cạnh và một góc của tam giác kia

thì

hai tam giác đó bằng nhau.

C. Ba góc của tam

giác này bằng ba góc của tam giác kia thì hai tam giác đó bằng nhau

D. Ba cạnh

của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau

Câu 36. Giả thiết

nào dưới đây không suy ra được







, , .A M B N C P  

, , AB MN AC MP BC NP  





, , AB MN AC MP A M   D.







, , A M B N AB MN  

Câu 37. Cho hình vẽ saucó





1 1 1

B C D  

Khẳng địn

h nào dưới đây sai?

ID BIC  

CB BDA  

BCD ADC  

IAB ICD  

Câu 38. Cho hìn

h bên, tính độ dài đoạn thẳng CD:

. 1cm B. 2cm

. 3cm D. Đáp án

khác

Câu 39. Cho

BC

cân tại A, có



A

Tính số đo góc



A. 120

B. 30

C. 20

D. 80

Câu 40. Cho

BC

biết

3 , 5 , 3AB cm BC cm AC cm  

. Tìm

khẳng định đúng



BC BCA



BC CAB



ACB CAB



BAC BCA

Câu 41. Khẳng định nà

o dưới đây là sai?

. Tam giác

cân có một góc 60

là tam

giác đều

B. Tam giác vuông có một góc nhọn bằng 45

là tam giác vuông cân.

. Trong ta

m giác vuông cạnh huyền là cạnh có độ dài lớn nhất.

BÀI TẬ

P TRẮC NGHIỆM TOÁN 7

D. Tam giác cân kh

ông thể là tam giác tù.

Câu 42. Cho

C

biết

, 5 , 13AB cm BC cm AC cm  

Khi đó ABC là tam giá

A. đều B. vuông tại A C. vuông tại B D. vuông tại C

Câu 43. Cho

C

cân tại A, phân giác trong của

góc



cắt cạnh BC t

ại D.

Khẳng định nào dưới đây sai?

A. Đường thẳng AD là trung trực của cạnh BC



C CAD 

B ADC  



C ADC 

Câu 44. Cho hình bên.

Tính độ dài đoạn thẳng BD.

A. 2cm B. 3cm C. 4cm D. 5cm

Câu 45. Trong các phương án sau, phương án nào chứa hình có hai tam giác vuông không

bằng nhau

A. B

C. D.

Câu 46.

Một cầu trượt có mô hình như hình vẽ bên. Đường đi lên đỉnh trượt là đoạn

5CA

m

các đo

ạn thẳng

4 ,

5 , 1 .CH m BH m BD m  

Bạn An

đứng trên đỉnh A của cầu trượt và trượt xuống đến vị trí D thì dừng lại. Hỏi quãng

đường trượt ABD của An dài khoảng bao nhiêu mét? (Chọn kết quả chính xác nhất trong bốn

đáp án sau)

A. 6m B. 7m

C. 8m D. 9m

TRẬN CÂU HỎI

TNKQ CHỦ ĐỀ 16

Mức độ

Nhận biết(câu) Thông hiểu(câu)

Vận dụng

Chủ đề Thấp Cao

1, 2, 3, 6, 8, 14,

15, 16, 17, 18,

23, 25, 31, 34,

36, 39, 40

4, 7, 10, 11, 12,

13, 19, 20, 21, 24,

26, 27, 32, 33, 35,

41, 42, 45.

5, 9, 22, 28,

29, 30, 43,

44, 46

37, 38

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Chủ đề 1

7. QUAN HỆ GIỮA CÁC YẾU TỐ TRONG TAM GIÁC - CÁC ĐƯỜNG

ĐỒNG QUY CỦA TAM GIÁC

. Kiến thức cần

nhớ

. Quan hệ góc và cạn

h đối diện trong một tam giác

Định lý 1: Trong một tam giác, góc đối diện với cạnh lớn hơn

là góc lớn hơn.

Định lý 2: Trong một tam giác, cạnh đối diện với góc lớn hơn

là cạnh lớn hơn.

b. Quan hệ đường vuông góc và đường xiên, đường xiên và hình chiếu

Khái niệm: Từ điểm A không nằm trên đường thẳng d, kẻ một đường thẳng vuông góc với d

tại H, trên d lấy điểm B không trùng với điểm H. Khi đó:

Đoạn thẳng AH gọi là đoạn vuông góc hay đường vuông góc kẻ từ điểm A đến đường thẳng d,

điểm H gọi là chân của đường vuông góc hay hình chiếu của điểm A lên đường thẳng d.

Đoạn thẳng AB gọi là một đường xiên kẻ từ điểm A đến đường thẳng d.

Đoạn thẳng HB gọi là hình chiếu của đường xiên AB trên đường thẳng d.

Định lý 1. Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài một đường

thẳng đến đường thẳng đó, đường vuông góc là đường ngắn nhất.

Định lý 2: Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng

đó:

Đường xiên nào có hình chiếu lớn hơn thì lớn hơn.

Đường xiên nào lớn hơn thì có hình chiếu lớn hơn.

Nếu hai đường xiên bằng nhau thì hai hình chiếu bằng nhau, và ngược lại nếu hai hình chiếu

bằng nhau thì hai đường xiên bằng nhau.

. Quan hệ giữa ba cạn

h của một tam giác, bất đẳng thức tam giác

Định

lý: Trong một tam giác, tổng độ dài hai cạnh bất kỳ bao giờ cũng lớn hơn độ dài cạnh

còn lại.

Hệ quả: Trong một tam giác, hiệu độ dài hai cạnh bất kỳ bao giờ cũng nhỏ hơn độ dài cạnh

còn lại.

Chẳng hạn, trong

ABC

, với cạnh BC ta c

ó:

AB AC BC AB AC   

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Lưu ý: khi

xét độ dài ba đoạn thẳng có thảo mãn bất đẳng thức tam giác hay không, ta chỉ cần

so sánh độ dài lớn nhất với tổng hai độ dài còn lại, hoặc so sánh độ dài nhỏ nhất với hiệu hai

độ dài còn lại.

. Tính chất ba đườn

g trung tuyến của tam giác

Đường trung tuyến của tam giác: Đoạn thẳng nối đỉnh A của tam

giác ABC với trung điểm M của cạnh BC gọi là đường trung tuyến

(xuất phát từ đỉnh A hoặc ứng với cạnh BC) của



Đôi

khi, đường thẳng AM cũng gọi là đường trung tuyến của



Mỗi tam g

iác có ba đường trung tuyến.

Định lý: Ba đường trung tuyến của 1 tam giác cùng đi qua 1 điểm.

Điểm đó cách đỉnh một khoảng bằng

độ dài

đường trung tuyến

đi qua đỉnh ấy.

Ba đường trung tuyến đồng quy tại điểm G. Điểm G gọi là trọng

tâm của

ABC

. Tính chất

tia phân giác của một góc

Định lý thuận: Điểm nằm trên tia phân giác của một góc thì cách

đều hai cạnh của góc đó.

Định lý đảo: Điểm nằm bên trong một góc và cách đều hai cạnh của

góc thì nằm trên tia phân giác của góc đó.

. Tính chất

ba đường phân giác của tam giác

Đường phân giác của tam giác: Trong



, tia phân giác của góc

A cắt cạnh BC tại điểm M. Khi đó đoạn thẳng AM được gọi là

đường phân giác (xuất phát từ đỉnh A) của



Đôi

khi ta cũng gọi đường thẳng AM là đường phân giác của



. Mỗi tam

giác có ba đường phân giác.

Chú ý: Trong một tam giác cân, đường phân giác xuất phát từ đỉnh đối diện với đáy đồng thời

là đường trung tuyến ứng với cạnh đáy.

Định lý: Ba đường phân giác của một tam giác cùng đi qua một điểm. Điểm này cách đều ba

cạnh của tam giác đó.

. Tính chất

đường trung trực của một đoạn thẳng

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Định

lý thuận: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai đầu mút

của đoạn thẳng đó.

Định lý đảo: Điểm cách đều hai đầu mút của một đoạn thẳng thì nằm trên đường trung trực

của đoạn thẳng đó.

Nhận xét: Tập hợp các điểm cách đều hai đầu mút của một đoạn thẳng là đường trung trực của

đoạn thẳng đó.

h. Tính chất ba đường trung trực của tam giác.

Đường trung trực của tam giác: trong một tam giác, đường trung trực của

mỗi cạnh gọi là đường trung trực của tam giác đó. Mỗi tam giác có 3

đường trung trực/

Trong một tam giác cân, đường trung trực của cạnh đáy đồng thời là

đường trung tuyến ứng với cạnh đáy.

Định lý: Ba đường trung trực của tam giác cùng đi qua 1 điểm. Điểm này cách đều 3 đỉnh của

tam giác đó.

Chú ý: Vì giao điểm O của ba đường trung trực của



cách đều ba đỉnh của tam giác đó

nên có một đường tròn tâm O đi qua ba đỉnh A, B, C.

k. Tính chất ba đường cao của tam giác.

Đường

cao của tam giác: Trong một tam giác, đoạn vuông góc kẻ từ

một đỉnh đến đường thẳng chứa cạnh đối diện gọi là đường cao của

tam giác đó.

Mỗi tam giác có ba đường cao.

Hình vẽ bên đoạn thẳng AI là một đường cao của

ABC

. Ta

cũng nói AI là đường cao xuất

phát từ đỉnh A (của



Đôi khi ta cũng gọi đường thẳng

AI là một đường cao của



Tính chất: Ba đường

cao của một tam giác cùng đi qua 1 điểm.

Tính chất của tam giác cân: Trong tam giác cân, đường trung tuyến ứng với cạnh đáy đồng

thời là đường phân giác, đường trung tuyển và đường cao cùng xuất phát từ đỉnh đối diện với

cạnh đó.

Nhận xét: Trong một tam giác, nếu hai trong bốn loại đường (đường trung tuyến, đường phân

giác, đường cao cũng xuất phát từ một đỉnh và đường trung trực ứng với cạnh đối diện của

đỉnh này) trùng nhau thì tam giác đó là tam giác cân.

Đặc biệt: Trong tam giác đều, trọng tâm, trực tâm, điểm cách đều ba đỉnh, điểm nằm trong tam

giác và cách đều ba cạnh là bốn điểm trùng nhau.

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

2. Một số ví dụ:

Ví

dụ 1 (Nhận biết). Chứng minh nếu tam giác vuông có một góc nhọn bằng

thì

cạnh góc

vuông đối diện với nó bằng nửa cạnh huyền.

Giải:

Trên tia CB, lấy điểm D sao cho CD=CA.



vuông

tại

và



30A



suy



cân

và có góc





nên tam giá

CAD

đều

AC DA DC  

Suy ra



0 0

60 90 30DAC DAB DAC

    



có



30DAB DBA

 

nên



cân tại D.

Suy ra

DA DB

Suy ra

C DA DB DC



 

do đó:

C AC



(dpcm).

Nhận xét: Trên đây là một cách giải, bạn đọc có thể giải bằng những cách

khác. Chẳn hạn như sau, trên tia đối của tia AC, lấy điểm E sao cho

AE=AC và chứng minh cho EC=BC.

Ví dụ 2 (Thông hiểu). Cho hình vẽ bên:

a) Chứng minh

I AB



b) Cho



40A



tính số đo g

óc



B ,

ID DIE

Giải:



có

hai đường cao AD và BE cắt nhau tại I nên I là

trực tâm của



Vậy

I AB



(tính chất).

BEC

vuông

tại E, có





, suy





(hai

góc nhọn của tam

giác

vuông phụ nhau).

Góc



B ,

ID DIE

bù nhau nên





Ví

dụ 3 (Vận dụng thấp). Cho



vuông

tại A có đường trung tuyến AM. Trên tia đối

của tia MA lấy điểm D sao cho

D MA



a. Tính số đo góc



ABD

b. Chứng minh:

BC BAD



 

c. So sánh độ dài A

M và BC

Giải:

Giả thiết



vuông

tại A, đường trung tuyến

60°

30°

60°

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

AM. D th

uộc tia đối MA

Kết luận



ABD

ABC BAD  

c. So sánh

độ dài AM và BC

a) Dễ thấy

 



. . ,MCA MBD

MAC MDB c g c AC BD     

Hai góc



MCA,MBD

ở vị trí so

le trong bằng nhau nên

/ /AC BD

Mà

 

AC AB gt AB BD  

hay



BD 90



,ABC BAD 

có cạnh AB

chung



   

ABD 90 ,AC BD

BAC cmt cmt

  

 

BC BAD c g c



  

c) Từ câu b suy ra:

C AD



mà



nên



Nhận xét: Trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh

huyền.

Ví dụ 4 (Vận dụng cao). Cho

ABC

vuông

tại A, tia phân giác của góc B cắt AC tại D, kẻ

E BC



tại E. Đường

thẳng ED cắt BA tại F. Chứng minh:

BD EBD



 

F DC



D DC



Gỉa thiết



vuông

tại A, BD là tia phân

giác

góc B,

DE BC

tại E. ED cắt BA tại F

Kết luận a)

BD EBD



 

F DC



AD DC

Giải:

a) Hai

BD EBD



là

hai tam giác vuông có chung cạnh huyên BD và góc nhọ



ABD EBD

nên

ABD EBD  

(cạnh huyền-gó

c nhọn)

b) Từ

BD EBD



 

suy



BAD BDE

. Mà



DF EDC



(đối

đỉnh) và



BDF BDA ADF 

và



DC BDE EDC





Suy ra



DC BDF



Hai

DF BDC



có



BDC BDF



, BD chung,



DBF DBC



Suy ra:

 

DF BDC g c g



 

F DC





(dpcm).

c) Trong tam

giác ADF có:



AD DC



 

Lại có:



90A DF DC AD DC

    

(dpcm).

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Nhận

xét: Bài toán này sẽ trở nên khó hơn khi trong đề bài bỏ câu b mà chỉ hỏi câu c.

Do đó khi gặp tình huống đề chỉ có câu c mà không có câu b, ta không so sánh trực tiếp

được nên phải nghĩ đến so sánh AD với một cạnh khác, mà cạnh này bằng DC. Lúc đó

trên hình vẽ và phán đoán ta sẽ suy ra phải so sánh AD với DF.

. Câu hỏi trắc n

ghiệm

Câu 1. C



biết

, 3 , 4

B cm BC cm CA cm



 

. So sá

nh các góc của



 



A B C 

 



B A C 



A C B 



 

C A B 

Câu 2. So sánh các cạnh của



biết rằng

 

50 ; 70

A B 

B BC CA



B AC BC



B BC CA





C AB CA



Câu 3. C



biết

, 5 , 6

B cm BC cm CA cm



 

. Góc

lớn nhất của



là:



 



B C



Câu 4. Cho

ABC

biết

 

60 ; 80

A B 

. Cạnh nào của

ABC

là cạnh nhỏ nhất?

A. CA B. CB C. AB D. Cả B và C đều sai

Câu 5: Trong một tam giác, đối diện với cạnh nhỏ nhất là góc có đặc điểm gì?

. Nhọn B. Vuông C. Tù D. Bẹt

Câu

6: Cho



biết

, 5 , 3

B cm BC cm CA cm



 

. So

sánh

các

góc của

ABC

 



B C





 



A B C 

 



B C





 



B C





Câu 7. C

ho hình vẽ bên, biết

AB BD

. Khẳng địn

h nào sau đây đúng?



BAD BCA





BAC BCA





AC BCA





DB DAC



Câu 8. Cho



biết rằng:

 

20 ; 50

A B 

. Xét các khẳng định sau:

(I)



là một tam giác tù

(II)



có cạnh

lớn nhất là AB

(III)



có cạnh

nhỏ nhất là BC

Số khẳng

định đúng ở trên là

A. 0 B. 1 C. 2 D. 3

Câu 9. C



vuông tại

A biết

5 , 13AB cm BC cm 

. So sánh các

góc của





 

B A





C A



 



B A C 



 

C A B 

Câu 10. Cho



biết

 

30 ; 60

A B 

. So sánh các cạnh của



B BC CA



B AC BC



AB BC CA 

BC AB CA 

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Câu 11. Cho



biết



90 ;

A AB AC

 

. Khẳng định nào dưới đây đúng?

B BC



3BC AB







AB CA

Câu 12. Cho hình vẽ bên và

B AC



. Xét các khẳng định sau

và chọn đáp

án đúng

(I) “

C AD



”

(II) “



CB ACD



”

. Chỉ có (I) đúng

. Chỉ có (

II) đúng

. Chỉ có (

I) và (II) đều đúng

. Cả có (I)

và (II) đều sai

Câu 13. Cho hình vẽ bên và

B AC



. Khẳng định

nào sau đây đúng?



BC ADB



AB AD



DB CAD



D. Tất cả đều sai

Câu

14. Cho

ABC

có

AB AC

ở hìn

h bên. Khẳng định nào sau đây

đúng?

B DC



B DC



DB DC



ABC ACB



Câu 15. Cho hìn

h vẽ bên, khẳng định nào sau đây đúng?

AC AE CF 

C AE CF





AC AE CF 

D. Cả A, B, C đều sai

Câu 16. Cho



có



70 ; 50

o o

ABC ACB 

. Gọi

H là chân

đường vuông góc hạ từ B. Khẳng định nào sau đây đúng?

B HC



B HC



B HC





BAC



Câu 17. Cho



, gọi H là

chân đường vuông góc hạ từ A. Khẳng định nào sau đây đúng?

B AC



B AC



B AC





BC ACB



Câu

18. Cho



có



30 ; 70

ABC ACB 

. Gọi

H là chân đường vuông góc hạ từ B.

Khẳng định nào sau đây đúng?

A HC



A HC



A HC



D. Không

so sánh được

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Câu

19. Cho



vuông

tại A, trên cạnh AB lấy điểm E, trên cạnh AC lấy điểm F. So sánh

độ dài các cạnh EF, BF, BC.

F<BC=BF

F BF BC



EF BC BF 

F BF



Câu 20. Cho



vuông tại A, biết

B cm



, trên đường thẳng AB lấy hai điểm E và F

sao cho

, 5

E cm AF cm



. So sánh

CA, CB, CE và CF

A CE CF CB



 

A CB CF CE



 

A CE CB CF



 

A CF CE CB



 

Câu

21. Cho



biết

0 , 12

MP cm NP cm



 

. Trên

đường thẳng NP lấy điểm K

sao cho

K cm



. Hỏi có ba

o nhiêu điểm K thỏa mãn?

. 0 B. 1 C. 2 D. 3

Câu

22. Cho



có

 

100 ; 40

A B 

. Gọi

H là chân đường vuông góc hạ từ A đến BC

So sánh H

B và HC

B HC



B HC



B HC



D. Không

so sánh được

Câu 23. Cho



. Gọi

H là chân đường vuông góc hạ từ A đến BC, biết

B HC



. Khẳng

định nào sa

u đây đúng?



BC ACB





BC ACB





BC ACB





BC BAC



Câu

24. Cho



, biết



60 , 30

B C 

. Trên

đường thẳng BC lấy điểm M, N sao

cho

M CN 

. So sánh

AB, AM, AN

B AM AN





N AB AM



B AM AN



B AN AM



Câu 25. Cho

ABC

biết

5 , 12 , 13AB cm BC cm CA cm  

. Trên đường thẳng BC lấy các

điểm I, J, K sao cho

I AJ AK



. So sánh BI, BJ, B

BI BJ BK 

BI BK BJ 

J BK BI



J BI BK



Câu 26. Bộ ba độ dài n

ào dưới đây là độ dài ba cạnh của một tam giác?

,3 ,2

cm cm

,3 ,5

cm cm

,6 ,4

m cm cm

,8 ,9

cm cm

Câu

27. Cho



biết

, 8

B cm CA cm



. Hỏi

cạnh BC có thể nhận độ dài (cm) nào sau

đây?

. 4 B. 9 C. 12 D. 13

Câu

28. Cho



biết

, 1

B cm BC cm



. Hỏi

cạnh AC có thể nhận độ dài (cm) nào sau

đây?

A. 1 B. 8 C. 9 D. 10

Câu 29. Tính chu vi của một tam giác cân có độ dài hai cạnh của nó là 2cm và 6cm.

A. 14cm B. 10cm C. 8cm D. 5cm

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Câu

30. Cho



có

độ dài các cạnh là các số nguyên (đơn vị cm). Biết

,A 10

B cm C cm



. Hỏi độ dà

i cạnh BC có thể nhận được bao nhiêu giá trị?

. 8 giá trị B. 9 giá trị C. 10 giá trị D. 11 giá trị

Câu

31. Cho



biết

4 ,B 4 , 5AB cm C cm CA cm  

. Gọi M là trung điểm của AC. Độ

dài đoạn thẳng BM bằng

A. 14m B. 1. 5cm C. 2cm D. 2. 5cm

Câu 32. Cho



có đườn

g trung tuyến AM và trọng tâm G. Kết quả nào dưới đây sai?

G AM



M AM



G GM



A AM



Câu 33. Cho

ABC

có trọng

tâm G. Khẳng định nào sau đây đúng?

G cm



G cm



G cm



M cm



Câu 34. Cho

ABC

có trọng tâm G và

8BG cm

. Đường trung tuyến BM. Khẳng định nào

sau đây đú

ng?

M cm



M cm



24C

G cm



B cm



Câu 35. Cho

ABC

có trọng

tâm G. Khẳng định nào sau đây đúng?

A. AG cắt BC tại M thỏa mãn

MB MC



A GB GC



cắt

tại trung điểm của

. D.

/ /BG AC

Câu

36. Cho



cân

tại

có

0 , 16

B cm BC cm



. Tính

độ dài đường trung tuyến

của



Câu 37. Cho

ABC

có

6AB BC AC cm  

. Gọi

là trọng tâm

ABC

. Tính

, , .GA GB GC

2 3GA GB GC cm

  

3GA GB GC cm

  

3 3

GA GB GC cm

  

GA GB GC cm

  

Câu

38. Cho



có

C cm



. Trên

tia đối của tia

lấy

điểm

sao

cho

D BA



. Gọi

là trọng tâ



. Kết quả nào dưới đây

đúng.

, 3

B cm GC cm



, 6

B cm GC cm



B GC cm



D. Cả

B C

đều sai.

Câu 39. Cho hìn

h vẽ bên. Tính tỉ số

Câu 40. Cho hìn

h vẽ bên. Tính tỉ số

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Câu

41. Cho



vuông

tại

. Gọi

là

trọng tâm



biết

G cm



, Tính

độ dài

24c

Câu

42. Cho



là

một tam giác đều có trọng tâm

. Đường

trung tuyến

M cm



Tính độ dài

và

B GC cm



B GC cm



B GC cm



B GC cm



Câu

43. Cho góc



xOy

khác

góc bẹt. Gọi tia

là

tia phân giác của góc



xOy

là

điểm trên

tia

(

không

trùng

). Vẽ

vuông

góc

tại

vuông

góc

tại

. Khẳng

định

nào dưới đây sai?

B AC



B OC



A OB OC





AO CAO



Câu

44. Cho



biết



30BAC



và

B AC AM



à tia phân giác của góc



. Số đo

góc



BAM

là.

Câu 45. Xét các khẳng định sau và chọn câu trả lời đúng nhất.

(I). “ Điểm

nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó. ”

(II). “ Điểm nằm bên trong một góc và cách đều hai cạnh của góc thì nằm trên tia phân giác

của góc đó. ”

. Chỉ có (

I) đúng. B

. Chỉ có (

II) đúng

C. Cả (I) và

(II) đều đúng

. D. Cả (I) và

(II) đều sai

Câu 46. Cho



cân

tại

, biết



50A



. Gọi

là

điểm nằm trong tam giác và cách đều ba

cạnh của tam giác này. Tính số đo



Câu

47. Cho



biết



60 , 80

ABC BAC 

. Gọi

là

điểm nằm trong tam giác và cách

đều ba cạnh của tam giác này. Tính số đo



Câu

48. Cho



biết



60 , 80

BAC ACB 

. Gọi

là

điểm nằm trong tam giác và cách

đều ba cạnh của tam giác này. Tính số đo góc



AIB

Câu

49. Cho



biết



0 0

70 , 60

ABC ACB 

. Tia

phân giác góc



BAC

cắt

tại

, qua

kẻ đường thẳng son

g song với

và cắt

tại

. Tín

h số đo góc



BNM

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

Câu 50. Cho đường thẳng

. Gọi

là một điểm nằm trên đường trung trực của đoạn thẳng

và

M cm



. Tính đọ dài đ

oạn

N cm



N cm



N cm



N cm



Câu 51. Cho đoạn thẳng

và

là hai điểm thuộc đường trung trực của

sao cho

, 7

M QN



. Gọi

là giao điểm của

và

. So sán

và

P IQ



P IQ



P IQ



D. Không so sánh được.

Câu

52. Cho



, gọi

là

giao điểm của hai đường trung trực của hai cạnh

và

Biết

A cm



. Tính đọ dài

12cm

4cm

6cm

8cm

Câu

53. Cho



cân

tại

, gọi

là

điểm cách đều ba đỉnh của



và

góc



30OBA



Tính số đo

góc



Câu 54. Cho các phát biểu:

(I) . Ba đường trung tuyến của tam giác đồng quy

(II) . Ba đường p

hân giác của tam giác đồng quy

(III) . Ba đường trung trực của tam giác đồng quy.

(IV) . Ba đường ca

o của tam giác đồng quy

Số các phát

biểu đúng là:

Câu 55. T

rong một tam giác, trực tâm là giao điểm của ba đường gì?

A. Trung trực B. Phân giác C. Trung tuyến D. Đường cao

Câu 56. Giao điểm của ba đường trung tuyến trong một tam giác gọc là gì?

A. Điểm cách đều ba đỉnh của tam giác đó B. Trọng tâm

. Điểm các

h đều ba cạnh của tam giác đó D

. Trực tâm

Câu 57. Cho



vuông tại

. Trực tâm của



là điểm nào

. Điểm

B. Điểm

C. Điểm

D. Không

có trực tâm

Câu 58. Cho



nhọn

có



50ACB



, Gọi

là

trực tâm



. Khẳng

định nào dưới

đây sai?

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

100









 

AC HBC



 



B C



Câu 59.

Trong



có trọn

g tâm, điểm cách đều ba đỉnh, điểm cách đều ba cạnh trùng nhau.

Hỏi



có đặc điểm gì?



vuông B.



cân C.



đều D. là tam g

iác thường

Câu 60. Cho

ABC

cân tại

. Gọi

là trực tâm của tam giác và góc





. Xét hai

khẳng định sau:

(I).



là tam giác vuông cân. (II).



là tam giác đều.

Chọn câu trả lời đúng

. Chỉ có (

I) đúng. B

. Chỉ có (

II) đúng

C. Cả (I) và

(II) đều đúng

. D. Cả (I) và

(II) đều sai

MA TRẬN CÂU

HỎI TNKQ CHỦ ĐỀ 17

Mức độ

Nhận biết

(câu)

Thông hiểu

(câu)

Vận dụng (câu)

Chủ

đề

Thấp Cao

1, 2, 3, 4, 10, 11,

17, 22, 26, 31, 32,

35, 38, 39, 40, 44,

45, 50, 52, 54, 55,

56, 57

5, 6, 8, 9, 12, 14,

15, 16, 18, 23, 24,

27, 28, 29, 33, 34,

36, 41, 43, 46, 47,

48, 51, 53, 59

7, 13,

19, 25,

30, 37,

42, 49,

20, 21,

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

101

hần II. MỘT SỐ ĐỀ MINH HỌA KIỂM TRA

Đề 1

KIỂM TR

A 45 PHÚT ĐẠI SỐ CHƯƠNG 1

Câu 1. Kết quả phép tính

5 11 2

6 6 3





bằng.

2

Câu 2. Kết quả ph

ép tính

3 9 4

2 10 5



 

bằng



Câu 3. So sánh các số

5 7 7

;

3 2 3

7 7

2 3



7 7

3 2



7 5

2 3



5 7

3 3



Câu 4. Cặp số hữu tỉ n

ào dưới đây bằng nhau:

và



và

Câu 5. C





. Tính

: (I):

x 

(II):

" "

 

Chọn câu trả lời đ

úng:

. Chỉ có (

I) đúng. B

. Chỉ có (

II) đúng

C. Cả (I) và (II) đều đúng. D. Cả (I) và (II) đều sai.

Câu 6. P

hát biểu nào dưới đây đúng?



khi

0x 



khi

0x 





khi

0x 





khi

0x 

Câu 7: Tí

nh giá trị của biểu thức

.12

 



 

 

P 





P 

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

102

Câu 8: Viết số

dưới dạng lũy thừa số mũ là

(

3 )

Câu 9: Th

ay tỉ số

 

1,2 :1,4

bằn

g tỉ số giữa các số nguyên

10 : 4

12 :10

7 : 6

6: 7

Câu 10: Tỉ số nào trong các tỉ số sau lập được tỉ lệ thức?

và

:12

và

: 2

và

(

4) : 2



và

: 2

Câu 11: V

iết số thập phân vô hạn tuần hoàn 3, (3) dưới dạng phân số tối giản

Câu 12: Cho phâ

n số

. Viết phân số đó dưới

dạng số thập phân



,(6)



,67



Câu 13: Kết quả p

hép tính

1 1 1

2 2

  

1



Câu 14: T

rong các số sau, số nào là số hữu tỉ ?

Câu 15: T

rong các số sau đây, số nào không có căn bặc hai ?



Câu 16: Phép tín

h nào nào dưới đây đúng ?

5 5



5 25



 

5 5



 

5 5





Câu 17: Phép tín

(

100)



bằng

( 100) 100

  

. B.

( 100) 10  

(

100) 100





. D.

(

100) 10





BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

103

Câu 18: Phát biểu

nào dưới đây sai ?

. Chỉ có

số 0 không là số hữu tỉ dương cũng không là số hữu tỉ âm

. Số vô tỉ là số viết được dưới dạng

số thập phân hữu hạn hoặc vô hạn

. Số hữu tỉ l

à số viết được dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn

. Có những

điểm trên trục số không biểu diễn cho số thực nào ?

Câu 19: Tìm số hữu tỉ

biết



 









Câu 20: T

rong các phân số sau, phân số nào bằng phân số



Câu 21: G

iá trị nào của

thỏa mãn

1 1 1



 



Câu 22: T

ìm số tự nhiên

thỏa mã



4n 

5n 

6n 

7n 

Câu 23: Kết quả phép tính

2 8.2

4.2



B. 2 C.

Câu 24: Chọn đá

p án đúng. Từ tỉ lệ thức

(

, , , 0)

a b c d





ta su

y ra



Câu 25: T

rong các phân số sau, phân số nào viết được dưới dạng số thập phân vô hạn tuần

hoàn ?

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

104

Câu 26: Cho



thì

bằng:

4x 

16x 

16x  

256x 

Câu 27: Cho





. Hỏi có bao nhiêu giá trị của

để H có giá trị là số nguyên ?

. 0 B. 1 C. 2 D. 3

Câu 28: G

iá trị nhỏ nhất của

1 1

H x

  

bằng ?

. 0 B. 1 C. -1 D. 2

Câu 29: Có bao n

hiêu số hữu tỉ

thỏa mãn



 

. 0 B. 1 C. 2 D. 3

Câu 30: Có bao nhiêu phân số có mẫu là 6, lớn hơn

và nhỏ hơ

. 2 B. 3 C. 4 D. 5

MA TRẬN CÂU

HỎI TNKQ TRONG ĐỀ 1

Mức độ

Đề KT

Nhận biết (câu)

Thông hiểu

(câu)

Vận dụng

Thấp Cao

45’, Đại,

Chương I

1, 2, 4, 6, 7, 8, 9, 12,

13, 14, 15,

16, 17,

20,

3, 10, 11, 18, 19,

21, 24, 25, 26,

22, 23,

28, 29

27, 30

Tổng 15 câu Tổng 9 câu Tổng 4 câu Tổng 2 câu

ĐỀ 2:

KIỂM TRA 45’ ĐẠI SỐ CHƯƠNG 2

Câu 1:

tỉ lệ thuận với

theo hệ số tỉ lệ

( 0)

k k



cách viết nào dưới đây đúng ?



Câu 2:

tỉ lệ thuận

với

theo hệ số tỉ lệ

a(a 0)

, cách viết nào dưới đâ

y đúng ?

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

105



y a



Câu 3: Ha

i đại lượng

và

tỉ lệ thuận. Giá t

rị

trong bảng

sau bằng bao nhiêu ?



 



 



 

Câu 4: Ha

i đại lượng

và

tỉ lệ nghịch. Giá trị

trong bảng sau bằng bao nhiêu ?



Câu 5: C

ho hàm số

(

)y f x



. Tính

(

12)

(12)



(12) 6



(12) 24



(12) 10



Câu 6: Tì

m tọa độ

và

trong hình

(1;3), (2; 3)

A B



(3;1), ( 3;2)

A B



(1;3), ( 3;2)

A B



(3;1), (3; 2)

A B



Câu 7: C

ho hàm số



. Đồ thị của

hàm số này là

y =

-3

y =

-2

y =

-3

y =

...

C D.

...

-3

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

106

Câu 8: Tr

ong mặt phẳng

cho hai

điểm

(

2;1)

và

(

1;1)



. Khẳng địn

h nào sau đây đúng

. AB cắt trục hoàn

. B. AB khô

ng vuông góc trục tung

C. AB son

g song với trục hoành

. D. AB son

g song với trục tung

Câu

9: Các giá trị tương ứng của hai đại lương tương

và

được

cho trong các bảng sau,

bảng nào thể hiện được hai đại lượng

và

tỉ lệ thuận với

nhau ?



 



 



 



 



. . .



 

Câu

10: Các giá trị tương ứng của hai đại lương tương

và

được

cho trong các bảng sau,

bảng nào thể hiện được hai đại lượng

và

tỉ lệ nghịch với nhau ?



 



 



 



 



BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

107

Câu

11: Trong mặt phẳng

cho

một hàm số có đồ thị

như hình sau:

Hỏi đồ thị đó là hàm số nào ?











Câu 12: Cho hàm

số

(

) 1

f x x



 

. Kết quả nào dưới đây đúng ?

(0) 1

 

(



(0) 0



(





Câu 13: Cho hàm

số

(

)

f x x



 

. Kết quả nào

dưới đây sai ?

(

0) 0



(

)













 

 

(

1) 0





Câu

14: Bảnggiá trị tương ứng tương nào dưới đây thể hiện đại lượng

là

hàm số của đại

lượng

2

1

2

1

2

1

2

Câu 15: Cho hàm

số



có đồ thị là

đường thẳng đi qua điểm

(

2;3)

. Tìm hệ số

2a 

3a 



Câu 16: Đ

iểm nào dưới đây thuộc đồ thị của hàm số



-1

-2

-3

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

108

(1; )



(2; )



(3; 1)



(1; )

Câu 17: Đ

iểm nào dưới đây không thuộc đồ thị của hàm số





; 2)



(

3;2)



(

1; )

(

1; )

D 

Câu 18: N

hững điểm thuộc trục hoành có đặc điểm

. Tung độ khác 0. B. Tung độ bằng 0

C. Hoành

độ bằng 1

. D. Trùng đ

iểm

(

0;0)

Câu 19: Những điểm thuộc trục tung có đặc điểm

. Hoành

độ khác 0

. B. Tung độ khác 1. .

C. Hoành độ bằng 0 D. Trùng điểm

(0;0)

Câu

20: Cho biết hai đại lượng

và

tỉ lệ thuận

với nhau, biết khi

3x 

1y 



. Hỏi

tỉ lệ thuận

với

theo hệ số tỉ lệ

là bao nhiê

u ?

3k  





3k 



Câu

21: Hai đại lượng

và

tỉ lệ nghịch

với nhau, biết khi





thì



. Hỏi

tỉ lệ

thuận với

theo hệ số tỉ lệ

là bao nhiêu ?









a 



a 

Câu

22: Hai đại lượng

và

tỉ lệ t

huận với nhau, biết khi

10x 

thì

2y 

. Hỏi

tỉ lệ

thuận với

theo hệ số tỉ lệ

là bao nhiêu ?

20k 



5k 

k 

Câu 23: T

ìm

để đồ thị của hàm số

x m





đi qua điểm

1 1

(

; )

3 2



Câu 24: Công thức n

ào dưới đây thể hiện

và

là hai đại lượng tỉ lệ n

ghịch ?

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

109

1 2

x y





Câu

25: Biết

tỉ lệ th

uận với

theo

hệ số tỉ lệ

tỉ lệ t

huận với

theo

hệ số tỉ lệ

( , 0)

b a b



. Hỏi

tỉ lệ thuận với

theo hệ số tỉ lệ bằng

bao nhiêu ?

Câu 26: Đường thẳn

ở hình sau

là đồ thụ của hàm số



. Xác định



3a 

2a 

Câu

27: Đồ thị của hàm số



là

đường thẳng thuộc góc phần tư thứ hai và thứ tư. Kết quả

nào sau đây đúng ?

0a 

0a 

0a 

D. Tất cả đều sai

Câu 28: T

rong các điểm sau, điểm nào thuộc vào đồ thị của hàm số

mx m





(

1;0)



(

1;1)



(

1;2)



(

1; 1)



Câu 29: Chọn câu

trả lời sai ?

Các máy bơm có cùng công suất bơm nước vào cùng một bể chứa là

A. Số lượng máy bơm tỉ lệ nghịch với thời gian bơm đầy bể

. Số lượng

máy bơm tỉ lệ thuận với thời gian bơm đầy bể

C. Thời gian bơm đầy bể chứa không tỉ lệ thuận với số lượng máy bơm.

D. Công s

uất máy bơm tỉ lệ nghịch với thời goan bơm đầy bể

Câu 30: Trong mặt phẳng

cho bốn điểm

(0;1)

(1;0)

(0; 1)



và

( 1;0)



. Hỏi tứ

giác

BCD

là hình gì ?

A. Hình bình hành. B. Hình thoi.

-1

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

110

C. HÌnh chữ n

hật

. D. Hình v

uông

MA TRẬN CÂU

HỎI TNKQ TRONG ĐỀ 2

Mức độ

Đề KT

Nhận biết (câu)

Thông hiểu

(câu)

Vận dụng

Thấp Cao

45’, Đại,

Chương 2

1, 2, 3, 4, 5, 6, 7, 12,

14, 15, 18,

19, 20,

21, 22

8, 9, 10, 11, 13,

16, 17, 23, 24,

25, 27,

29, 20

Tổng 15 câu Tổng 10 câu Tổng 3 câu Tổng 2 câu

ĐỀ 3

KIỂM T

RA HỌC KÌ 1

Câu 1: Kết quả phép tính

3 5

2 3

 

bằng

Câu 2: Kết quả phép tính

10 10 11

. :10

13 13 3







 





bằng

143

000



Câu 3: Xé

t hai phát biểu sau:

3 11

(

) :

2 6



3 11

(

) :

2 6



Chọn câu trả lời đ

úng.

. Chi có (

I) đúng. B

. Chỉ có (

II) đúng

C. Cả (I) và

(II) đều đúng

. D. Cả (I) và

(II) đều sai

Câu 4: Tìm số nguyên

để

11 13



A. 2 B. 1 C. 4 D. 3

Câu 5: Viết số

dưới dạng lũy thừa của một số hữu tỉ.

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

111

Câu 6: Khẳng địn

h nào dưới đây là đúng ?

0 0

. B.

(

0,1)



là một số dương.

( 0,3)



là một số âm. D.

6 3

( 0,2) (0,04)

 

Câu 7: Th

ay tỉ số

,2 :1,6

bằn

g tỉ số giữa các số nguyên

6: 25

3:8

: 4

Câu 8: Kh

i các số

, ,a b c

tỉ lệ với các số

1,6,8

. Cách viết nào dưới đây

đúng ?

: : 1: 6 :8a b c 

. B.

1: 6:8



( : ) 1: 6 :8

b c



. D.

(

a : b) : c (1: 6) :8



Câu

9: Thực hiện phép tính

:11

rồi

làm tròn đến chữ số thập phân thứ nhất nhận được kết

quả:

2,2

2,3

2,7

2,0

Câu 10: Trong các số sau, số nào có đúng hai căn bậc hai khác nhau ?



2

Câu 11: T

hực hiện phép tính

25 9 1

3 3 3

 

bằng:



Câu 12: Nếu

tỉ lệ thuận với

theo hệ số

. Cách

viết nào dưới đây đúng ?

( 0)

y kx k

 

( 0)

x ky k

 



x k





Câu

13: Cho biết hai đại lượng

và

tỉ lệ nghịch

với nhau, khi



thì

y 

. Hỏi

hai

đại lượng

và

tỉ lệ nghịch với nhau theo hệ số tỉ lệ bằng bao nhiêu ?

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

112

Câu

14: Bảnggiá trị tương ứng tương nào dưới đây thể hiện đại lượng

là

hàm số của đại

lượng

Bản

g 1

Câu 15: Tọa độ của cá

c điêm

và

ở hình

sau là

M(1;3), (2; 4)



(3;1), ( 4;2)

A B



M( 4;2), (3;1)



M(4; 2), (3;1)



Câu 16: Cặp số hữu tỉ nào dưới đây không bằng nhau ?



và



. B.

3

và



và

. D.



và



Câu 17: Tìm số hữu tỉ

biết

1 1 1

3 4













 



Câu 18: Có bao n

hiêu số hữu tỉ

thỏa mãn



. Không có số nào. B. Chỉ có 1 số.

C. Có 2 số. D. Có 3 số.

Câu 19: T

ìm số tự nhiên

thỏa mãn



1n 

4n 

5n 

32n 

-1

-4

-2

-3

Bảng

-3 5 8 8

1 3 -7 5

Bảng

-1 0 3 3

1 2 -3 1

Bảng 2

-2 -1 -1 3

2 5 1 3

Bảng4

-3 -2 1 3

1 0 2 1

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

113

Câu 20: Một thửa ruộng hình chữ nhật có tỉ số giữa chiều dài và chiều rộng bằng

. Tính

diện tích thửa ruộng này, biết chu vi của nó bằng

2400m

400

1200m

240m

Câu 21: Phân số nào d

ưới đây viết được số thập phân vô hạn tuần hoàn ?

Câu 22: T

rong các khằng định sau, khẳng định nào sai ?

A. Số 12 là số tự nhiên. B. Số

là một số hữu tỉ.

C. Số 0, 1

211005…là một số thực

. D. Số

là một số vô tỉ.

Câu

23: Cho biếtc

tỉ lệ thuận

với

theo

hệ số tỉ lệ

tỉ lệ thuận

với

theo

hệ số tỉ lệ

( , 0)

b a b



. Hỏi

tỉ lệ thuận với

theo hệ số tỉ lệ bằng

bao nhiêu ?

Câu 24: Ch biết

1 2 3 4 ... 19 20 210      

. Tính

2 4 6 8 ... 38 40     

. 210 B. 420 C. 630 D. 105

Câu 25. Các số hữu tỉ

3 2 5 11

; ; ; ;

10 3 3 5



được sắp xếp t

heo thứ tự giảm dần là:

1 5 2 3 3

;

; ; ;

3 3 13 10



1 5 2 3 3

;

; ; ;

3 3 10 13



11 2 3 3

; ; ; ;

5 3 10 13



11 2 3 3

; ; ; ;

5 3 13 10



Câu 26. Khẳng định nà

o dưới đây đúng?

 

64 3



chia hết

cho 3 B

 

64 3



chia hết

cho 5

 

64 3



chia hết

cho 9 D

 

64 3



chia hết

cho 10

Câu 27. Cho ba số dương a, b, c thỏa mãn

2 2

b c

b c a b c a b c

 



    

. Tính giá trị

của biểu thức:

c a c a b

b c



 



 

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

114

A. H = 2 B. H = 6 C. H =

D. H =

Câu 28. Chữ sô thập

phân thứ 2019 sau dấu phẩy của phân số

(viết

dưới dạng thập phân

là như thế nào?

. 2. B. 3 C. 5 D. 7

Câu 29. Cho hai

đường thẳng xx’ và yy’ cắt nhau tại O như hình vẽ. Biết xOy’ = 45

. Tính số

đo

B. 45

C. 135

D. 180

Câu 30. Cho hai

đường thẳng a và b có a // b như hình vẽ. Tìm số đo góc x trên hình vẽ.

. 120

B. 60

C. 30

D. 150

Câu 31. Cho hình vẽ. Tìm số đo góc x để a // b

. 90

B. 60

C. 30

D. 120

Câu 32. Chọn câu

trả lời đúng. Cho tam giác ABC, có:

 



B C



 

 



B C



 

 



B C



 

 



B C



 

45°

30°

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

115

Câu 33. Cho tam giác ABC biết

 

50 , 70

A B 

. Góc ngoài tại đỉnh C có số đo bằng:

A. 20

B. 60

C. 100

D. 120

Câu 34. T

ìm số đo góc x trên hình sau

A. 40

B. 50

C. 130

D. 140

Câu 35. Cho

BC MNP



 

, biết AB = 2cm, BC = 5cm, A

C = 4cm. Chu vi



bằng:

. 11cm B. 5, 5cm C. 9cm D. 6cm

Câu 36. Cho hai

tam giác ABC và DEF có AB = DE,



B E

. Để

BC DEF



 

theo trương

hợp canh - góc - cạnh phải thêm điều kiện nào dưới đây





 

A B

C. AC = DF D. BC = EF

Câu 37. Cho tam giác ABC, có MN // BC và các góc như hình vẽ. Tính số đo



BAC

A. 30

B. 70

C. 60

D. 50

Câu 38. Cho hìn

h vẽ. Khẳng định nào dưới đây sai?

. AB = AC B. BD = D

. AB > AC D.





Câu 39. Cho tam

giác ABC vuông ở A, biết





. Tia phân giá

c của góc B cắt AC tại

. Số đo



BDC

bằng:

40°

120°

50°

30°

40°

30°

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

116

A. 30

B. 60

C. 15

D. 105

Câu 40. Cho hìn

h vẽ sau khẳng định nào dưới đây sai?

AID BIC  

AB ICD



 

ACB BDA  

CD ADC



 

MA TRẬN CÂU

HỎI TNKQ ĐỀ 5

Mức độ

Nhận biết (câu) Thông hiểu

(câu)

Vận dụng (câu)

Thấp Cao

Học kỳ 1

1; 3; 4; 5;

6; 7; 8;

10 ; 11; 12; 13;

14; 15; 21; 22;

29; 30; 31; 32;

33; 35; 36

2; 9; 16; 17; 18;

19; 25; 34; 37;

20; 23; 24; 27;

26; 28; 40

Tổng 22 Tổng 10 Tổng 5 Tổng 3

ĐỀ 4

KIỂM TR

A HỌC KỲ 2

Câu 1. Điểm nào dưới đây thuộc đồ thị hàm số



. (3; 1) B.

 









 











D. (-2; 2)

Câu 2. Khi điều tra điểm kiểm tra của một tổ trong lớp, giáo viên thu được kết quả điểm trong

bảng sau:

8 7 9 8 8

10 8 8 8 9

Điểm trung bình của tổ này là:

. 6, 8 B. 8. 3 C. 7, 0 D. 7, 1

Câu

3. Viết biểu thức đại số biểu thị chu vi của một hình chữ nhật có chiều dài và chiều rộng

là a, b

A. a - b B. ab C. a + b D. 2(a + b)

Câu 4. Viết biểu thức đại số biểu thị quảng đường đi được của một xe máy với vận tốc v

(km/h) trong khoảng thời gian t

A. vt B. v + t C. v - t D.

Câu 5. Gi

á trị của biểu thức P =



tại

;

x y

  

bằng:

0°20°

20°

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

117



145



C. -2 D.

143



Câu 6. Biểu thức nào

dưới đây được gọi là đơn thức?

A. 2x + y B. x - y C. (xy + z)t D. xyx

Câu 7. Bậc của đ

ơn thức

là:

A. 6 B. 2 C. 3 D. 4

Câu 8. Thu gọn biểu thức

y x





ta được:

A. 8x

+ y B. y C.



Câu 9. Tất cả các hạng tử của đa thức

2 3x y xy

 

là:

. 2x

B. 2x

;y;3xy C. 2x

;-y;3xy D. 2x

;3xy

Câu 10. Cho hai

đa thức M = x

+ y

- xy; N = x

- y

+ xy. Tính M + N bằng:

. 2x

+ 2y

B. 2x

+ 2y

– xy C. x

+ xy D. 2x

Câu 11. Cho đa t

hức M = xy + x

- 1. Tìm đ

a thức P biết M - P = x

- 1

. x

-1 B. -xy C. xy D. 2xy

Câu 12. T

hu gọn và sắp xếp các hạng tử của đa thức A(x) = x

+ x

- x

+ 2x

-1

A. A(x) = x

+ x

- x

-1 B. A(x) = x

- x

+ x

-1

. A(x) = x

+ 3x

- x

D. A(x) = x

+ 3x

- x

-1

Câu 13. Đa thức B(x)

= 10x

- 2x

+ 2x + 12

có hệ số cao nhất là:

. 10 B. 12 C. -2 D. 4

Câu 14. Đa thức một

biến Q(x) = x

- x có bao nhiêu nghiệm?

. 0 B. 1 C. 2 D. 3

Câu 15. Số nào dưới đ

ây là nghiệm của đa thức 4x

- 4x + 1 = 0?

. 0 B. 2 C. -2 D.

Câu 16. Đường thẳn

g OA ở hình bên là đồ thị của hàm số y = ax. Xác định hệ số a.

A. a =



B. a =

C. a = 3 D. a = -3

Câu 17. Khi điều

tra về cỡ áo của một lớp ta thu được kết quả số áo thể hiện trong bảng sau:

35 36 35 38 35 36 35 39 39 40

42 35 37 36 36 36 35 37 38 35

40 42 35 36 38 40 38 42 40 39

37 35 36 36 35 36 35 36 35 36

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

118

Tìm mốt

của dấu hiệu

. M

= 35 B. M

= 36 C. M

= 11 D. M

= 12

Câu 18. Viết biểu

thức đại số biểu thị tổng các lũy thừa bậc 3 của hai số tự nhiên liên tiếp

 

1 ( )a a a N

  

 

2 ( )a a a N

  

 

( )

a a N



 

 

( )

a a N



 

Câu 19. Biểu thức nà

o sau đây là đơn thức thu gọn?

A. xy(x

y) B. (2x

)(

yx) C. x

ỹ D. x

Câu 20. Cặp đơ

n thức nào sau đây là hai đơn thức đồng dạng?

A. 2x

y và 2xy

B. 2xy

x và

C. 2xy và

D. xyx và

Câu 21. T

ích của hai đơn thức (2x

y) và

x là một đơ

n thức có bậc bằng:

. 3 B. 6 C. 8 D. 9

Câu 22. Giả sử một

quyển vở là x (đồng/quyển) và giá của một hộp bút là y (đồng/quyển).

Biểu thức biểu thị số tiền mua hai quyển vở và ba cái bút là:

. Một đa

thức B

. Một đ

ơn thức

. Một đ

ơn thức thu gọn D

. Cả A, B, C đều

sai

Câu 23. Giá trị của đa thức: M = x

+ y – x

y tại x =

và y =

bằng:



Câu 24. Cho hai

đa thức P(x) = x

– x

+ x; Q(

x) = x

– 2x

. Gọi đa t

hức R(x) được xác định

bởi

R(x) = P(x) – Q(x). R(x) có bao nhiêu nghiệm?

. 0 B. 1 C. 2 D. 3

Câu 25. Đa thức P(x)

= 2x

– 4x

+ x – 1 – x

+ x

có hệ số của

lũy thừa bậc 4 là:

. 2 B. -5 C. -4 D. 4

Câu 26. Cho đa t

hức bậc 5 một biến có hai hạng tử mà hệ số cao nhất là 2, hệ số tự do là 128.

Hỏi đa thức này có bao nhiêu nghiệm?

. 0 B. 1 C. 2 D. 3

Câu 27. T

ìm tất cả các số hữu tỉ x để giá trị của đa thức 2x

y – y bằng

tại y =

là:

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

119



C. 0 D.

;



Câu 28. Cho đa t

hức P(x) = ax

+ bx + c. Tro

ng đó a, b, c là các hằng số thỏa mãn

b c

1 2 3



và a

0

. Tính

   

2 3 1

P P

 

A. -6 B. -15 C. 6 D. 15

Câu 29. So sánh

các cạnh của tam giác ABC biết

 

100 ; 40

A B 

. AB = AC > BC B. AB = AC < BC

. AB = A

C = BC D

. AB > A

C = BC

Câu 30. Cho tam giác ABC có AB > AC, gọi D là chân đường vuông góc hạ từ A đến BC.

Khẳng định nào sau đây đúng?

. DB = D

C B

. DB < D

C C

. DB > D

C D



ABC ACB



Câu 31. Cho tam

giác ABC có trung tuyến AM và trọng tâm G. Kết quả nào dưới đây sai?

A. AG =

AM B. GM =

GA C. GA =

MG D. MB =

Câu 32. Cho tam giác ABC biết

 

50 ; 60

A B 

. Gọi I

nằm trong tam giác và cách đều ba

cạnh của tam giác này. Tính số đo góc BIC.

. 70

B. 130

C. 65

D. 115

Câu 33. Cho tam giác ABC, gọi I là giao điểm của hai đường trung trực của hai cạnh AB và

AC. Kết quả nào dưới đây đúng?

. IA > IB

> IC B

. IA = IB

= IC

. IA < IB

< IC D

. Không

so sánh đơcj IA, IB, IC

Câu 34. Trong một tam giác, giao điểm của ba đường cao gọi là:

A. Điểm cách đều 3 đỉnh của tam giác này B. Trọng tâm

. Điểm các

h đều 3 cạnh của tam giác này D. Trực tâm

Câu 35. Cho tam giác ABC cân tại A, gọi G là trọng tâm của tam giác ABC và





Khi đó



là:

. Tam giác

ABC vuông cân tại A B

. Tam giá

c đều

C. Tam giác cân tại A D. Tam giác tù

Câu 36. Cho đoạn thẳng PQ, gọi A và B là hai điểm thuộc đường trung trực của đoạn PQ sao

cho AP = 6cm, BQ = 8cm. Gọi I là giao điểm của PQ và AB. So sánh IA và IB.

A. IA = IB B. IA > IB C. IA < IB D. Không so sánh được

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

120

Câu 37. Chu vi của một tam giác câ

n biết độ dài hai cạnh của nó là 3cm và 8cm là:

. 14cm B. 7cm C. 19cm D. 11cm

Câu 38. Cho hìn

h bên. Tính độ dài đoạn CD

. 8 cm

. 4 cm

. 10 cm

. 6 cm

Câu 39. Cho tam

giác ABC là tam giác vuông cân tại A. Biết BC = 12cm. Gọi G là trọng tâm

của tam giác ABC. Tính GB.

D. 4cm

Câu

40. Cho tam giác ABC biết AB = 2cm, AC = 6cm. Cạnh BC có độ dài là một số nguyên

đơn vị xentimet. Hỏi độ dài cạnh BC có thể nhận được bao nhiêu giá trị?

. 3 giá trị B. 4 giá trị C. 5 giá trị D. 6 giá trị

MA TRẬN CÂU

HỎI TNKQ ĐỀ 6

Mức độ

Nhận biết (câu) Thông hiểu

(câu)

Vận dụng (câu)

Thấp Cao

Học kỳ 2

1; 2; 3; 4;

5; 6; 7;

8; 9; 10 ; 11; 12;

13; 14; 15; 16;

17; 20; 23; 25;

29; 30; 31; 33;

34; 36

11; 17; 18; 21;

22; 24; 32; 35;

26; 27; 38; 39 28; 40

Tổng 25 Tổng 9 Tổng 4 Tổng 2

10cm

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

121

Phần 3

GIẢI MỘT SỐ ĐỀ K

IỂM TRA

ĐÁP ÁN CHỦ ĐỀ 1

Câu 1 2 3 4 5 6 7 8

Đáp án D D C B A B C D

Câu 1 2 3 4 5 6 7 8

Đáp án A C D B A C C A

ĐÁP ÁN CHỦ ĐỀ 2

Câu 1 2 3 4 5 6 7 8 9 10

Đáp án

C D A B B C A A D B

ĐÁP ÁN

CHỦ ĐỀ 3

Câu 1 2 3 4 5 6

Đáp án D B A D C B

Câu 1 2 3 4 5 6

Đáp án A B D B A C

ĐÁP ÁN

CHỦ ĐỀ 4

Câu 1 2 3 4 5 6 7 8

Đáp án A B D C B D C A

Câu 1 2 3 4 5 6 7 8

Đáp án D C B A B C B C

ĐÁP ÁN CHỦ ĐỀ 5

Câu 1 2 3 4 5 6 7 8

Đáp án A B C D A B C B

Câu 1 2 3 4 5 6 7 8

Đáp án B A A D B C C D

ĐÁP ÁN

CHỦ ĐỀ 6

Câu 1 2 3 4 5 6 7 8

Đáp án C D B A C B A D

Câu 1 2 3 4 5 6 7 8

Đáp án C B A D B D A B

ĐÁP ÁN

CHỦ ĐỀ 7

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

122

Câu 1 2 3 4 5 6 7 8

Đáp án A B C C B A D D

Câu 1 2 3 4 5 6 7 8

Đáp án A D D D B C B A

ĐÁP ÁN

CHỦ ĐỀ 8

Câu 1 2 3 4 5 6 7 8

Đáp án A A A A B D C D

Câu 9 10 11 12 13 14 15 16

Đáp án B C C B B C D C

ĐÁP ÁN

CHỦ ĐỀ 9

Câu 1 2 3 4 5 6 7 8

Đáp án D B A C A C D B

Câu 9 10 11 12 13 14 15 16

Đáp án B B B D C D B D

ĐÁP ÁN CHỦ ĐỀ 10

Câu 1 2 3 4 5 6 7 8

Đáp án C B D A C B A D

Câu 9 10 11 12 13 14 15 16

Đáp án D B C C B C B D

ĐÁP ÁN

CHỦ ĐỀ 11

Câu 1 2 3 4 5 6

Đáp án D B D A C D

Câu 7 8 9 10 11 12

Đáp án B D A B A D

ĐÁP ÁN

CHỦ ĐỀ 12

Câu 1 2 3 4 5 6

Đáp án D A D B D C

Câu 7 8 9 10 11 12

Đáp án D A C D A B

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

123

ĐÁP ÁN

CHỦ ĐỀ 13

Câu 1 2 3 4 5 6

Đáp án B C D A D A

Câu 7 8 9 10 11 12

Đáp án B C D A B C

ĐÁP ÁN

CHỦ ĐỀ 14

Câu 1 2 3 4 5 6 7 8

Đáp án B D C A C B A B

Câu 9 10 11 12 13 14 15 16

Đáp án B C C B B D C A

ĐÁP ÁN CHỦ ĐỀ 15

Câu 1 2 3 4 5 6

Đáp án B C B B D D

Câu 7 8 9 10 11 12 13 14 15 16

Đáp

án

C A C A B D D C D A

Câu 17 18 19 20 21 22 23 24 25 26

Đáp

án

B C B D A B D C A B

Câu 27 28 29 30 31 32 33 34 35 36

Đáp

án

C C C D D B C C B A

Câu 37 38 39 40 41 42 43 44 45 46

Đáp

án

B C B C B A C D B D

ĐÁP ÁN

CHỦ ĐỀ 16

Câu 1 2 3 4 5 6

Đáp án C D C D A B

Câu 7 8 9 10 11 12 13 14 15 16

Đáp

án

A C D D D B A B A C

Câu 17 18 19 20 21 22 23 24 25 26

Đáp B A B A C A B A B C

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

124

án

BCâu 27 28 29 30 31 32 33 34 35 36

Đáp án

C D C C A B B D D A

Câu 37 38 39 40 41 42 43 44 45 46

Đáp án

D C D A D C D C D B

ĐÁP ÁN

CHỦ ĐỀ 17

Câu 1 2 3 4 5 6 7 8 9 10

Đáp án

C D B C A D B C A D

Câu 11 12 13 14 15 16 17 18 19 20

Đáp

án

C A B A C A B B B A

Câu 21 22 23 24 25 26 27 28 29 30

Đáp

án

C A B D A D B C A B

Câu 31 32 33 34 35 36 37 38 39 40

Đáp

án

D D A B C D A B A B

Câu 41 42 43 44 45 46 47 48 49 50

Đáp

án

D B C A C B B D D A

Câu 51 52 53 54 55 56 57 58 59 60

Đáp

án

C A B D D B A D C B

ĐÁP ÁN

ĐỀ KIỂM TRA 45 PHÚT ĐẠI SỐ CHƯƠNG I

Câu 1 2 3 4 5 6 7 8 9 10

Đáp

án

A B B D A C C A D B

Câu 11 12 13 14 15 16 17 18 19 20

Đáp

án

C C D C A A C D B D

Câu 21 22 23 24 25 26 27 28 29 30

BÀ

I TẬP TRẮC NGHIỆM TOÁN 7

125

Đáp

án

A C B D B D B C B B

ĐÁP ÁN

ĐỀ KIỂM TRA 45 PHÚT ĐẠI SỐ CHƯƠNG II

Câu 1 2 3 4 5 6 7 8 9 10

Đáp án A C B D A B A C B C

Câu 11 12 13 14 15 16 17 18 19 20

Đáp án D D C C D D C B B B

Câu 21 22 23 24 25 26 27 28 29 30

Đáp án A C B B D A B A B D

ĐÁP ÁN ĐỀ KIỂM TRA HỌC KỲ I

Câu 1 2 3 4 5 6 7 8 9 10

Đáp án B D B A C D C A B C

Câu 11 12 13 14 15 16 17 18 19 20

Đáp án D A A D B C A C C A

Câu 21 22 23 24 25 26 27 28 29 30

Đáp án C D A B A B B D B C

Câu 31 32 33 34 35 36 37 38 39 40

Đáp án A B D C A D B C D B

ĐÁP ÁN

ĐỀ KIỂM TRA HỌC KỲ II

Câu 1 2 3 4 5 6 7 8 9 10

Đáp án C B D A D D D D C D

Câu 11 12 13 14 15 16 17 18 19 20

Đáp án C D A C D B A C D A

Câu 21 22 23 24 25 26 27 28 29 30

Đáp án D A A C B B D B B C

Câu 31 32 33 34 35 36 37 38 39 40

Đáp án C D B D B C C D B A

Bấm Tải xuống để xem toàn bộ.

| 1/125

| | Tải xuống

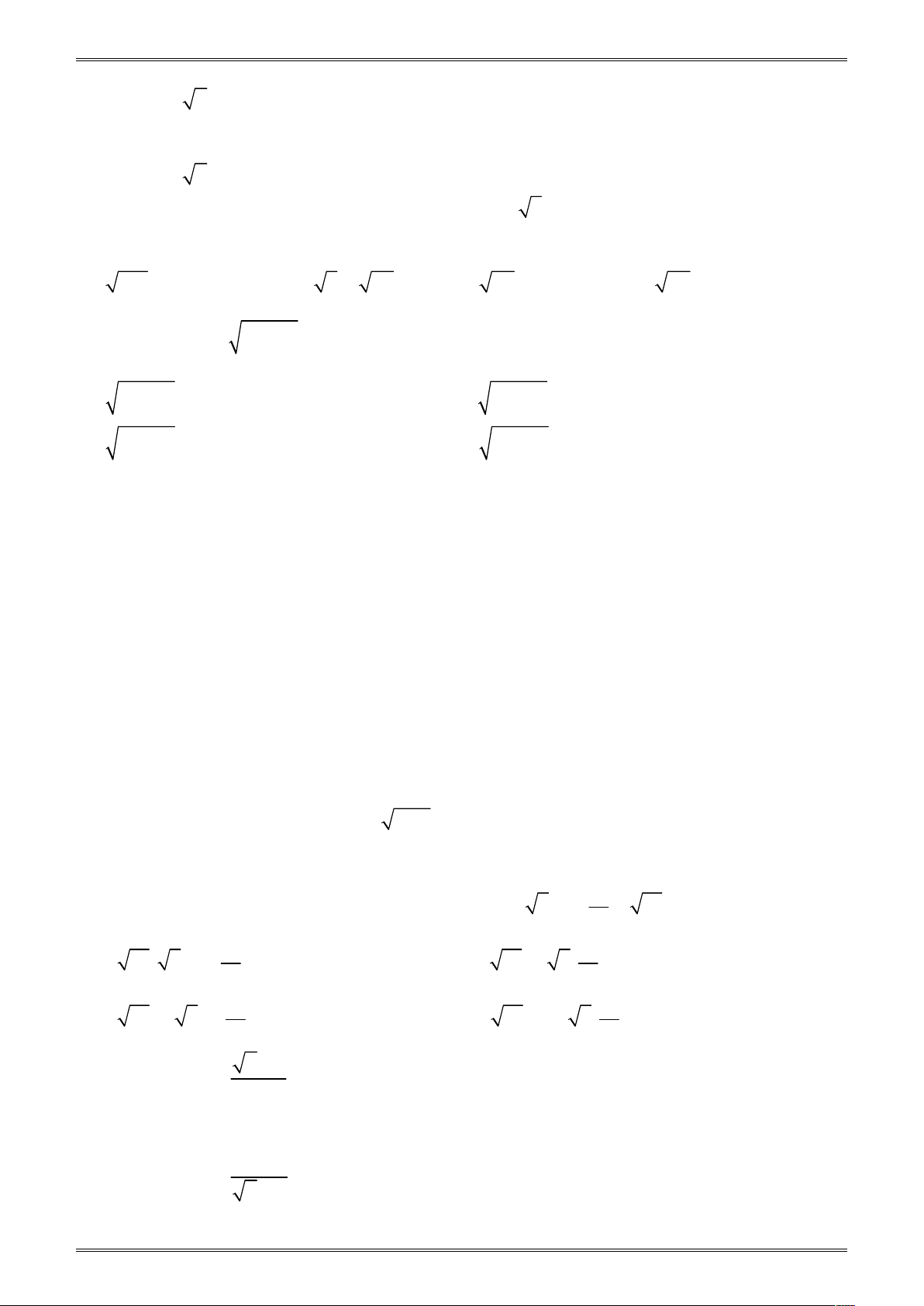
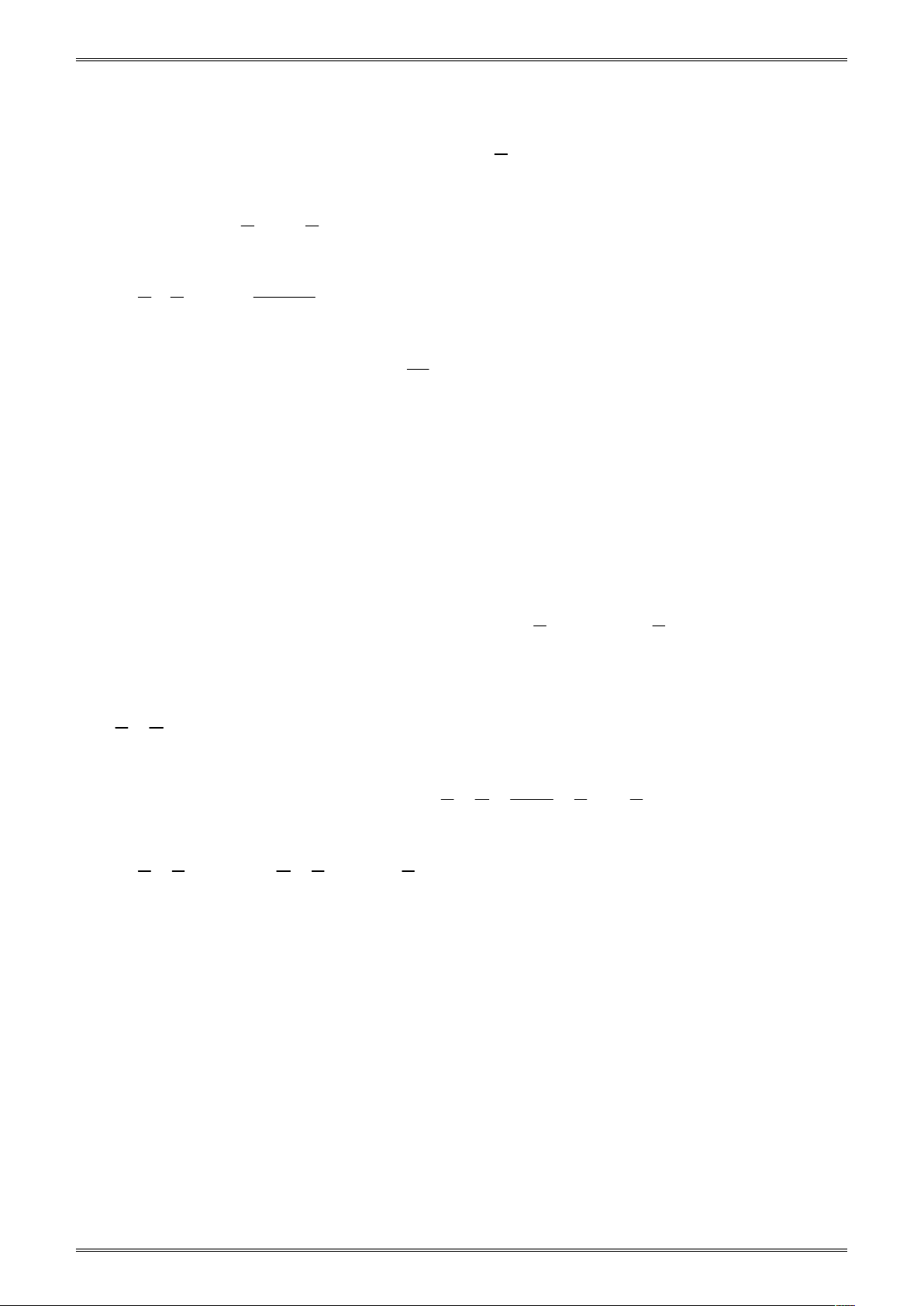
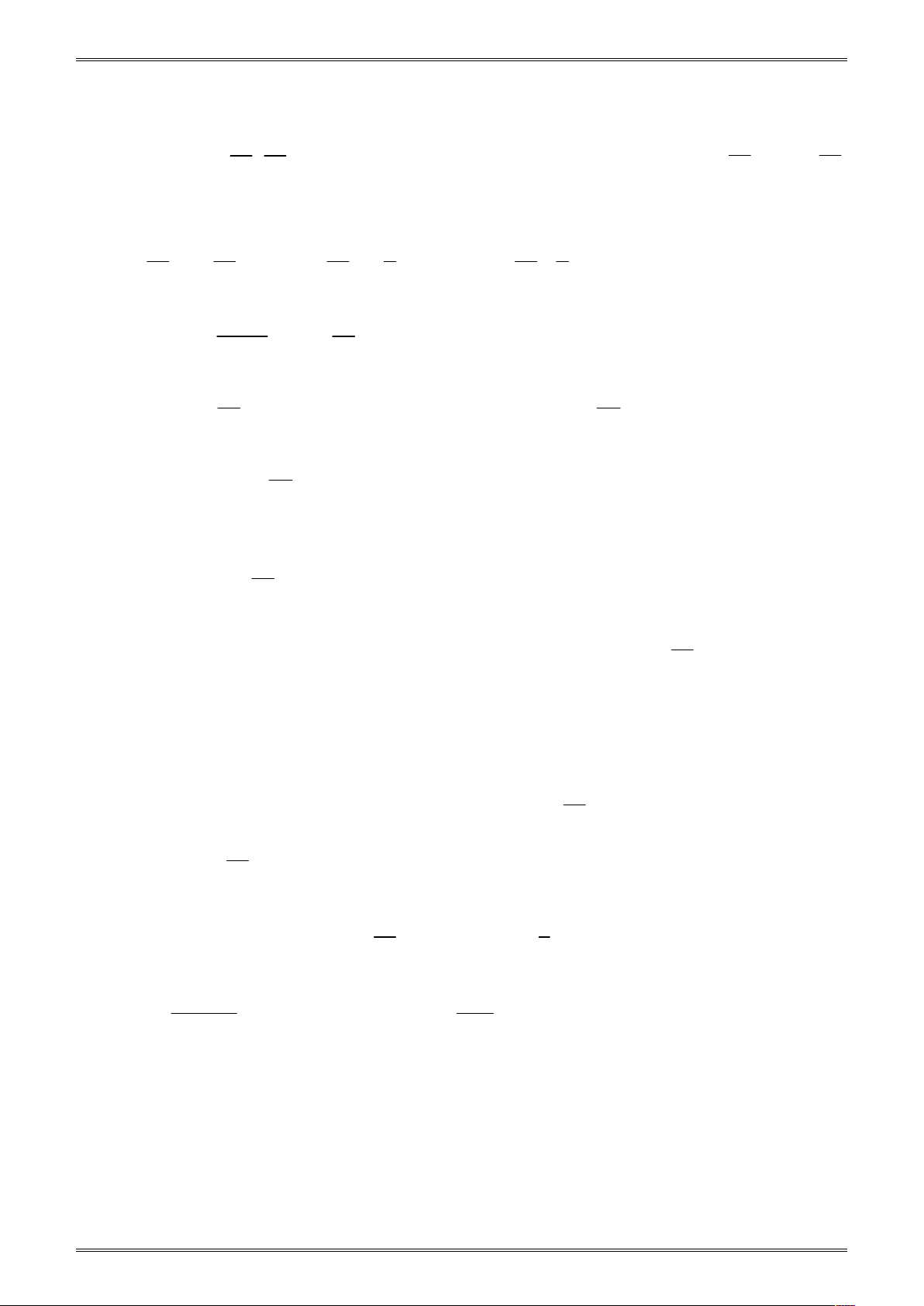
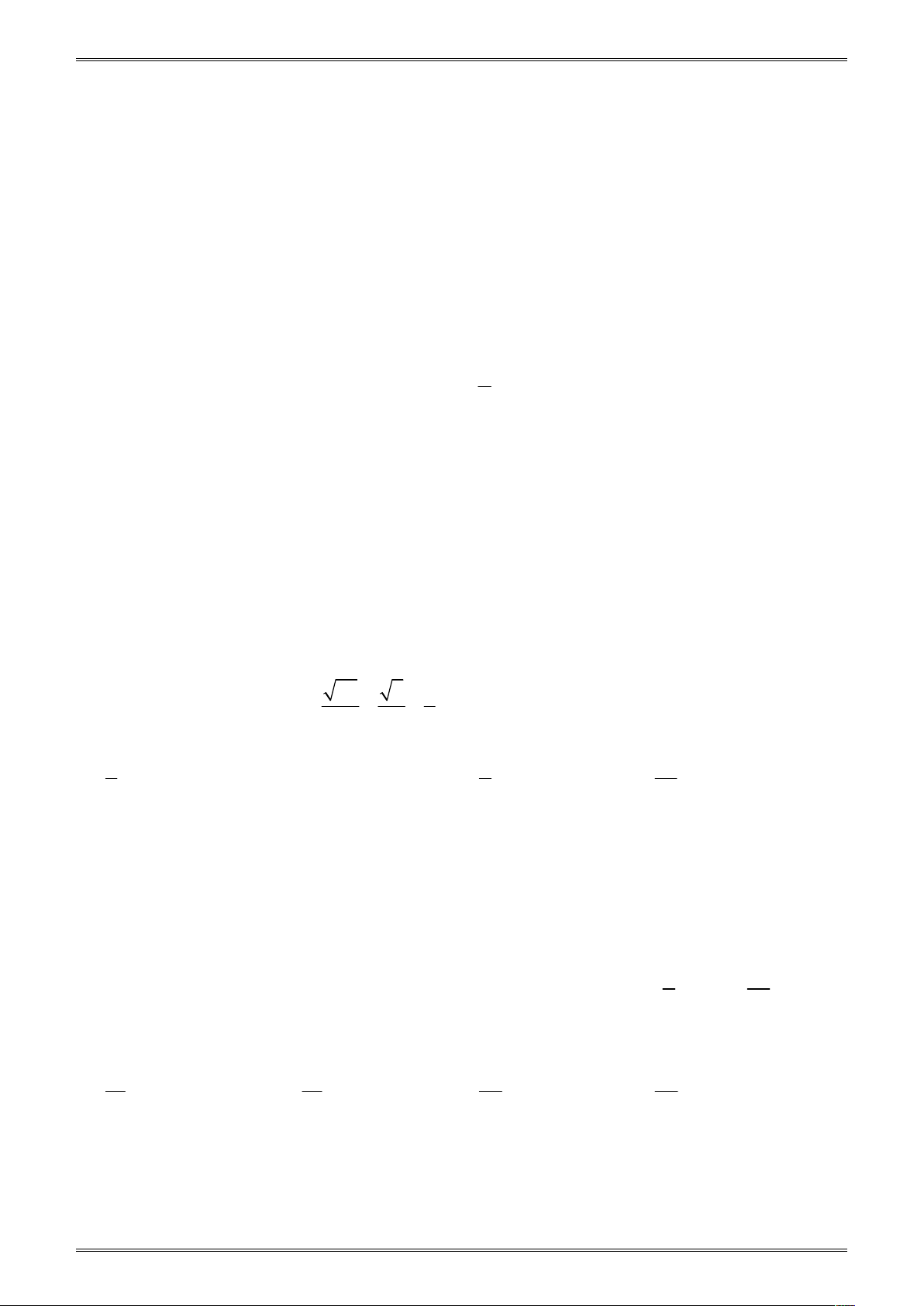
Preview text:

BÀI TẬP TRẮC NGHIỆM TOÁN 7
Phần I. HƯỚNG DẪN LÀM BÀI TẬP TRẮC NGHIỆM
Do những thay đổi trong tính chất và phương pháp thi trong năm học này nên việc ôn
tập cũng phải thay đổi. Hình thức thi trắc nghiệm sẽ là phổ biến trong các môn thi. Để đáp ứng
một bài thi trắc nghiệm cần phải đạt được 4 mức độ kiến thức: 1. Nhận biết
*Nhận biết có thể được hiểu là học sinh nêu hoặc nhận ra các khái niệm, nội dung, vấn đề đã học khi được yêu cầu.
*Các hoạt động tương ứng với cấp độ nhận biết là: nhận dạng, đối chiếu, chỉ ra…
*Các động từ tương ứng với cấp độ nhận biết là: xác định, liệt kê, đối chiếu hoặc gọi tên, giới
thiệu, chỉ ra…nhận thức được những kiến thức đã nên trong sách giáo khoa.
Học sinh nhớ được (Bản chất) những khái niệm cơ bản của chủ đề và có thể nêu hoặc nhận ra
các khái niệm khi được yêu cầu. Đây là bậc thấp của nhận thức, khi học sinh kể tên, nêu lại,
nhớ lại một sự kiên, hiện tượng. Chẳng hạn ở mực độ này, học sinh chỉ cần có kiến thức về
hàm số bậc nhất để thay tọa độ điểm vào phương trình đường thẳng để tìm ra tọa độ điểm phù hợp. x
Ví dụ 1: Cho hai số nguyên x, y và y  0 . Nếu x, y trái dấu thì số hữu tỉ a  . y A. a  0 B. a  0 C. a  0 D. Cả B và C sai Đáp án C
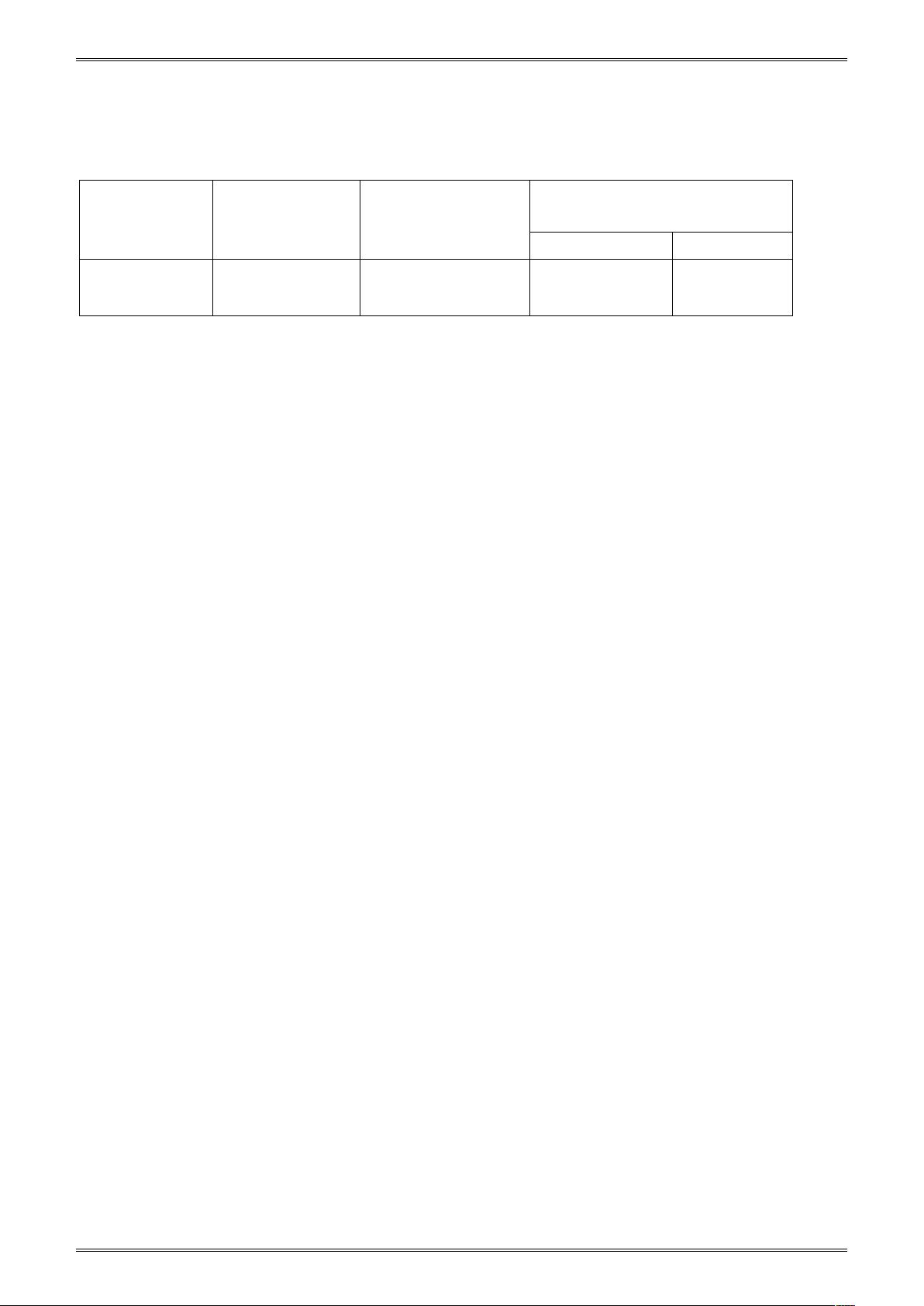
Ví dụ 2: Cặp số hữu tỉ nào dưới dây bằng nhau? 12  3 10 9 6 12 5 7 A. và B. và C. và D. và 8 2  11 10 8 15 7 5 Đáp án A 76 66
Ví dụ 3: Biểu đồ dân số Việt Nam qua tổng điều tra trong thế kỉ
XX (đơn vị của các cột là triệu người) 54 Chon câu trả lời sai
A. Năm 1921 số dân của nước ta là 16 triệu người 30
B. Năm 1960 số dân của nước ta là 30 nghìn người 16
C. Năm 1980 số dân của nước ta là 66 triệu người
D. Năm 1999 số dân của nước ta là 76 triệu người 1921 1960 1980 1990 1999 1
BÀI TẬP TRẮC NGHIỆM TOÁN 7 Đáp án C 2. Thông hiểu
*Học sinh hiểu các khái niệm cơ bản, có khả năng diễn đạt được kiến thức đã học theo
ý hiểu của mình và có thể sử dụng khi câu hỏi được đặt ra tương tự hoặc gần với các ví dụ học
sinh đã được học trên lớp.
*Các hoạt động tương ứng với cấp độ thông hiểu là: diễn giải, kể lại, viết lại, lấy được
ví dụ theo các hiểu của mình.
*Các động từ tương ứng với cấp độ thông hiểu có thể là: Tóm tắt, giải thích, mô tả, so
sánh (đơn giản), phân biệt, trình bày lại, viết lại, minh họa, hình dung, chứng tỏ, chuyển đổi…
Học sinh hiểu các khái niệm cơ bản và có thể sử dụng khi câu hỏi được đặt ra gần với
các ví dụ học sinh đã được học trên lớp.
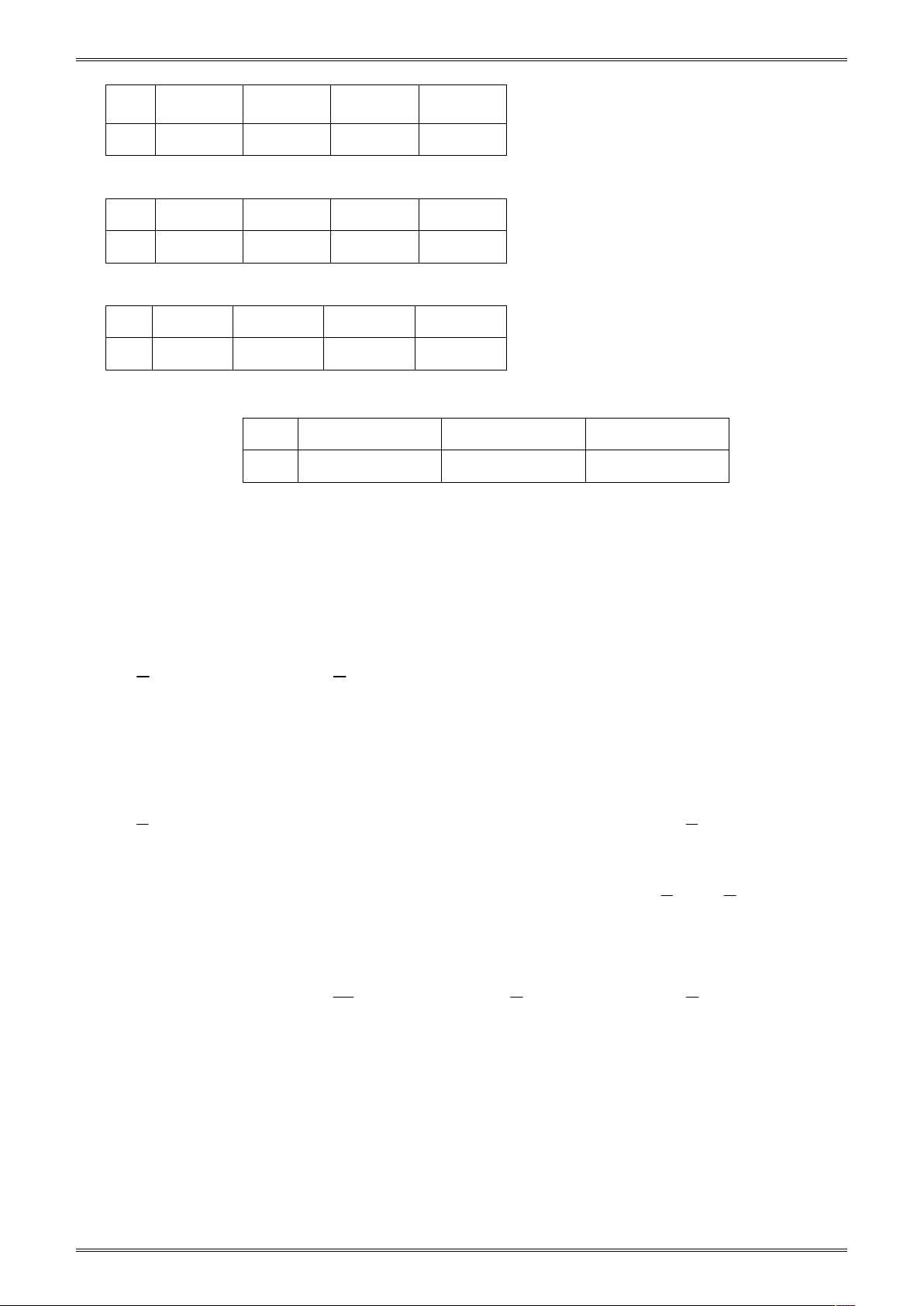
Ví dụ 1. Cho đoạn thẳng AB dài 8cm. Lấy điểm M trên đoạn thẳng AB sao cho AM  6 cm.
Đường thẳng d là đường trung trực của MB, d cắt MB tại K. Khẳng định nào dưới đây sai? A. KB  1cm . B. KA  7cm . C. d  AB . D. d / / AB .
Ví dụ 2. Có bao nhiêu số x  Q thỏa mãn 2x  3  5  3x  0 ? A. Không có. B. Có một số. C. Có hai số. D. Có ba số.
Ví dụ 3. Theo dõi các bạn nghỉ học ở từng buổi trong một tháng, bạn lớp trưởng ghi lại như sau: 0 0 0 1 0 3 2 0 3 0 1 0 1 1 0 0 1 0 0 1 2 2 2 0 1 0
Dấu hiệu ở đây là gì?
A. Tổng số lượt học sinh nghỉ học cả tháng.. B. Là các số 0, 1, 2, 3.
C. Số học sinh nghỉ học trong mỗi buổi.
D. Mỗi tháng học có 26 buổi. Đáp án C 3. Vận dụng
*Học sinh vượt qua cấp độ hiểu đơn thuần và có thể sử dụng, xử lý các khái niệm của
chủ đề trong các tình huống tương tự nhưng không hoàn toàn giống nhau như tình huống đã
gặp trên lớp. Học sinh có khả năng sử dụng kiến thức, kĩ năng đã học trong những tình huống
cụ thể, tình huống tương tự nhưng không hoàn toàn giống như tình huống đã học trên lớp
(thực hiện nhiệm vụ quen thuộc nhưng mới hơn thông thường) . 2
BÀI TẬP TRẮC NGHIỆM TOÁN 7
*Các hoạt động tương ứng với vận dụng ở cấp độ thấp là: xây dựng mô hình, phỏng
vấn, trình bày, tiến hành thí nghiệm, xây dựng các phân loại, áp dụng quy tắc (định lý, định
luật, mệnh đề…), sắm vai và đảo vai trò….
*Các động từ tương ứng với vận dụng ở cấp độ thấp có thể là: thực hiện, giải quyết,
minh họa, tính toán, diễn dịch, bày tỏ, áp dụng, phân loại, sửa đổi, đưa vào thực tế, chứng
minh, ước tính, vận hành, …
Học sinh vượt qua cấp độ hiểu đơn thuần và có thể áp dụng các khái niệm của chủ đề
trong các tình huống tương tự trên lớp để giải quyết một tình huống cụ thể trong thực tế hoặc
học sinh cá khả năng sử dụng các khái niệm cơ bản để giải quyết một vấn đề mới chưa từng
được học hoặc trải nghiệm trước đấy, nhưng có thể giải quyết bằng kỹ năng, kiến thức và thái
độ đã được học tập và rèn luyện. Các vấn đề này tương tự như các tình huống thực tế học sinh
sẽ gặp ngoài môi trương.
Ví dụ 1. Tìm x  Q thỏa mãn x  2  x 1  2x . 3 3 1  A. x  . B. x   . C. x  . D. x  0 . 2 2 2 Đáp án A 1
Ví dụ 2. Giá trị của biểu thức 3 5
Q  x y  2xy tại x  và y  1  bằng 3 17 17  19 A. . B. . C. . D. 1 . 27 27 27 Đáp án A
Ví dụ 3. Cho a / /b và   0
A  B  100 (hình vẽ bên) . 1 1 A 1 a Số đo góc  A bằng: 1 A. 0 10 . B. 0 90 1 b C. 0 45 . D. 0 50 . B Đáp án D
4. Vận dụng ở mức độ cao hơn
Học sinh có khả năng sử dụng các khái niệm cơ bản để giải quyết một vấn đề mới hoặc
không quen thuộc, chưa từng được học hoặc trải nghiệm trước đây, nhưng có thể giải quyết
bằng các kỹ năng và kiến thức đã được dạy ở mức độ tương đương. Những vấn đề này tương
tự như các tình huống thực tế học sinh sẽ gặp ngoài môi trường lớp học. 3
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Ở mức độ này học sinh phải xác định được những thành tố trong 1 tổng thể và mối quan
hệ qua lạị giữa chúng, phát biểu ý kiến cá nhân và bảo vệ được ý kiến đó về 1 sự kiện, hiện
tượng hay nhân vật lịch sử nào đó.
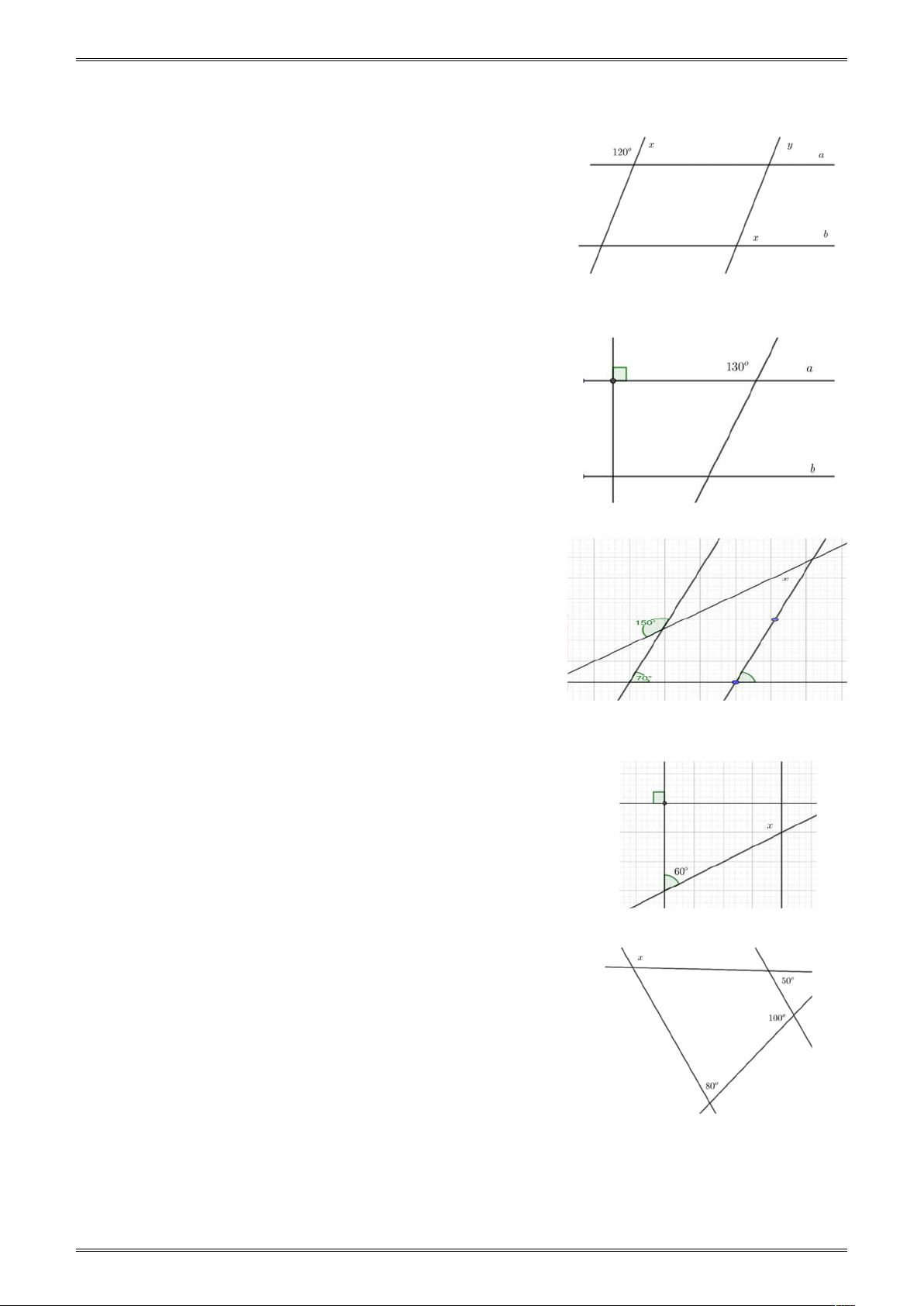
Ví dụ 1. Cho a / /b như hình vẽ bên. Số đo góc x bằng: a 30° A. 0 150 . B. 0 90 C. 0 60 . D. 0 30 . Đáp án C b x
Ví dụ 2. Cho hai đa thức P  x 4 3 2
 x  2x  x  5x và Q  x 4 3 2
 x  x  x  6x  2 , gọi
H  x  P  x  Q  x . Hỏi đa thức H  x có bao nhiêu nghiệm? A. 1 . B. 2 . C. 3. D. 4 . Đáp án C 9
Ví dụ 3. Cho H 
Hỏi có bao nhiêu nghiệm x để H có giá trị nguyên? x  2 A. 2 . B. 3. C. 5 . D. 6 . Đáp án A
Ở bài thi trắc nghiệm thường sẽ là những bài yêu cầu giải nhanh và không qua rườm rà,
yêu cầu kiến thức rộng và bao quát hơn. Nếu như các em đang theo phương pháp “chậm và
chắc” thì bạn phải đổi ngay từ “chậm” thành “nhanh”. Giải nhanh chính là chìa khóa để bạn có
được điểm cao ở môn thi trắc nghiệm. Với các bài thi nặng về lý thuyết thì sẽ yêu cầu ghi nhớ
nhiều hơn, các em nên chú trọng phần liên hệ.
Ngoài việc sử dụng kiến thức để làm bài thi, các em có thể vận dụng thêm các phương pháp sau đây:
- Phương pháp phỏng đoán: Dựa vào kiến thức đã học, đưa ra phỏng đoán để tiết kiệm thời gian làm bài. - Phương pháp loại trừ:
Một khi các em không có cho mình mottj đáp án thực sự chính xác thì phương pháp loại
trừ cũng là một các hữu hiệu giúp bạn tìm ra câu trả lời đúng. Mỗi câu hỏi thường có 4 đáp án,
các đáp án cũng thường không khác nhau nhiều lắm về nội dung, tuy nhiên vẫn có cơ sở để
các em dùng phương án loại trừ bằng “mẹo” của mình cộng thêm chút may mắn nữa. Tháy vì
đi tìm đáp án đứng, bạn hãy thử tìm phương án sai… đó cũng là một cách hay và loại trừ càn
nhiều phương án càng tốt. 4
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Khi các em không còn đủ cơ sở để loại trừ nữa thì hãy dùng cách phỏng đoán, nhận
thấy phương án nào khả thi thi hơn và đủ tin cậy hơn thì khoanh vào phiếu trả lời. Đó là cách
cuối cùng dành cho các em.
Thi trắc nghiệm nhằm mục đích vừa đảm bảo hiểu rộng kiến thức vừa đảm bảo thời
gian nên các em cần phải phân bố thời gian cho hợp lý nhất. 5
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Chủ đề 1. BỐN PHÉP TOÁN TRÊN TẬP SỐ HỮU TỈ
1. Một số vấn đề cần ôn tập a
Số hữu tỉ là số viết được dưới dạng phân số
với a,b  Z;b  0 b
Tập hợp các số hữu tỉ được kí hiệu là Q.
Cộng và trừ số hữu tỉ: a b
Cho hai số hữu tỉ x, y : x  ; y 
a,b,m  Z,m  0 m m a b a  b a b a  b x  y    ; x  y    m m m m m m
Nhân và chia hai số hữu tỉ: a c
Cho hai số hữu tỉ u, v : u  ;v 
a,b,c,d  Z; , b d  0 b d a c ac . u v  .  b d bd a c a d ad
Nếu v  0 thì u : v  :  .  b d b c bc 1
Số hữu tỉ x  0 có số nghịch đảo là x
Tính chất: Cho các số hữu tỉ x, y, z . Ta có:
Tính chất giao hoán: x  y  y  ; x . x y  . y x
Tính chất kết hợp:  x  y  z  x   y  z; . x y.z  . x  . y z 
Tính chất cộng với số 0: x  o  o  x  xx
Tính chất nhân với số 1: .1
x  1.x  x Tính chất nhân với 0: .0 x  0.x  0
Tính chất phân phối của phép nhân đối với phép cộng: .
x  y  z  . x y  . x z x  y x y x  y x y
Một số phép toán hay sử dụng:   ;   , với z  0 z z z z z z 6
BÀI TẬP TRẮC NGHIỆM TOÁN 7  x  0 .
x y  0   y  0    . x y   . x y  . x  y
Chú ý không có tính chất: x : y  x : z  x :  y  z 2. Ví dụ
Ví dụ 1 (Nhận biết) . Tính 6 7 11 4 1 2 1 3 a.  b.   c. 0,1  d. 1  2 11 11 9 9 3 11 12 8 8  2 8 3 6 8  3  e. . f. 2 .3 g. : h. 0,5 : 2   3 5 3 2 5 3  4  Giải: 6 7 6  7 13 a.    11 11 11 11 6 7
Nhận xét: Hai số hữu tỉ và
là hai phân số có cùng mẫu, nên áp dụng ngay phép 11 11
toán cộng và trừ số hữu tỉ để giải. 11 4 1 11  4 1 15 1 5 1 5 1 4 b.           9 9 3 9 3 9 3 3 3 3 3
Nhận xét: Với câu này tuy xuất hiện nhiều số hữu tỉ song ta thực hiện phép tính theo tuần tự vẫn giải được. 15 5
Ngoài ra nếu ta chưa phát hiện 
thì ta có thể quy đồng và giải tiếp như cách giải 9 3 câu c. c. MSC=BCNN 10;  11 =10.11  110 2 1 2 11 20 11  20 9  0,1        11 10 11 110 110 110 110
Nhận xét: Trong câu này ta nên đưa về phép tính hai số hữu tỉ viết dưới dạng phân số,
song hai phân số này không cùng mẫu số nên ta tìm bội số chung nhỏ nhất của chúng rồi áp dụng phép toán.
d. 12  2.2.3 , 8  2.2.2 , MSC=BCNN 12;8 = 2.2.3.2  24 7
BÀI TẬP TRẮC NGHIỆM TOÁN 7 1 3 13 19 26 57 26  57 83 1  2       12 8 12 8 24 24 24 24
Nhận xét: Câu này giải hoàn toàn tương tự câu c ở trên. 8  2 8.2  16  e. .   3 5 3.5 15 8 3 14 9 14.9 126 f. 2 .3  .    21 3 2 3 2 3.2 6 6 8 6 3 6.3 18 9 g. :  .    5 3 5 8 5.8 40 20  3  1 11 1 4 1.4 4 2 h. 0,5 : 2  :  .       4  2 4 2 11 2.11 22 11
Nhận xét: Nhìn chung các phép nhân và chia ta chỉ cần áp dụng đúng công thức mà
không phải tìm bội số chung nhỏ nhất.
Ví dụ 2 (Thông hiểu) . Thực hiện phép tính.  1 1  6 1  1 1   2  1  5  a. A   .  :      b. B  1   1       3 6  5 2  3 6   3  3   3   2 1  1  3  10.   : 1  5 1      1 1   5 2  3  5 c. C  3.  :      d. D  6 5 10 4      1 2 3   5 7    :  1      2 3 4   2 6  1 1 1 1 1 1 e. E       10 100 1000 10000 100000 1000000 Giải:
Lưu ý trước khi giải ví dụ 2:
Thứ nhất: nắm vững quy tắc và thứ tự thực hiện các phép tính.
Thứ hai: quy tắc bỏ dấu ngoặc
Nếu bỏ dấu ngoặc có dấu “+” đằng trước thì dấu các số hạng trong ngoặc vẫn giữ nguyên
Nếu bỏ dấu ngoặc có dấu “-” đằng trước thì ta phải đổi dấu tất cả các số hạng trong ngoặc.  1 1  6 1  1 1   2 1  6 1  2 1  a. A   .  :    .  :           3 6  5 2  3 6   6 6  5 2  6 6  8
BÀI TẬP TRẮC NGHIỆM TOÁN 7  2 1  6 1  2 1   3  6 1  1   .  :  .  :          6  5 2  6   6  5 2  6  3 5 1 1 3.5 1  .  :   .6 6 6 2 6 6.5 2 3 3 15 3 15 12    3     5 5 5 5 5  2  1  5   2 3  1 5   2  3   1  5  b. B  1   1     1   1               3  3   3   3 3  3 3   3   3   1    4   1  4 1   4 3   1   1  1  1  1 1  0      3   3  3 3 3 3  5 1  1 1   5 1  2 5   5 1  2  5  c. C  3.  :   3.  :   3.  :          6 5 10 4 6 5 20 20 6 5 20            5 1  7   5 1 20   5 4   3.  :  3.  .  3.     6 5 20   6 5 7   6 7          35  24   11  11  3.  3.       42   42  14  2 1  1  3   4 5  1  5 3  10.   : 1 10.   :           5 2  3  5   10 10  3  5 5 d. D     1 2 3   5 7   3 4 3   15 7    :  1   :  1          2 3 4   2 6   6 6 4   6 6   4  5  1  5  3   1   1  8  1  0 1 5 10.  : 10.  :          .  10  3  5   10  3  5  10 3 8     3  4 3   15  7   7 3   22   14 9   11  : 1  : 1  : 1              6 4   6   6 4   6   12 12   3  1.5 5 24 5 29 1   1      3.8 24 24 24 24      14  9  11 5 3 5 5 44 : 1 . 1 1     12  3 12 11 44 44 44 29 29   29 39  29  44   29  . 44   319 24 24     :  .   . 5  44 39  24 44 24 39 24.39 234 44 44 9
BÀI TẬP TRẮC NGHIỆM TOÁN 7 1 1 1 1 1 1 e. E       10 100 1000 10000 100000 1000000
 0,1  0, 01  0, 001  0, 0001  0, 00001  0, 000001
 0,1  0, 01  0, 001 0, 0001  0, 000011
 0,1  0, 001 0, 0001 0, 000111  0,1  0, 01 0, 001111
 0,1  0, 011111  0,111111
Ví dụ 3 (Vận dụng) . Thực hiện phép tính bằng cách hợp lý 5 6 1 7 2 8 7 3 a. A    
b. B  1  0, 25    6 7 6 3 3 3 4 2 10  1   16 10  1 1  5  5 1  5 c. C  .  .   d. D   :   :     11  5  5 11  3 5  3  3 5  3 Giải:
Nhận xét: Trong ví dụ này ta phải sử dụng các tính chất để nhóm các số hữu tỉ mà dễ tính được
giá trị sau khi nhóm. Sâu đây là bài giải, các bạn xem và tìm ra tính chất đã được sử dụng để làm bài tập này 5 6 1 7  5 1  6 7  5 1  6 7 2 6 7 a. A                   6 7 6 3  6 6  7 3  6  7 3 3 7 3  2 7  6  2  7  6 6 21 6 27       3          3 3  7  3  7 7 7 7 7 2 8 7 3  5 8   1 7  3 5  8 1 7 3
b. B  1  0, 25                3 3 4 2  3 3   4 4  2 3 4 2 3  6 3 3 3  3  3      1    1     1   0  1    3 4 2 2 2  2 2  10  1   16 10 10  1  16  10  1  16  10  15  c. C  .  .  .   .  .         11  5  5 11 11  5 5  11  5  11  5  10 30  .3  11 11  1 1  5  5 1  5  1 1   5 1  5  1 1 5 1  3 d. D   :   :     :     .            3 5  3  3 5  3  3 5   3 5  3   3 5 3 5  5 10
BÀI TẬP TRẮC NGHIỆM TOÁN 7  1 5   1 1  3  1 5  3 4 3 4     .   0 .  .         3 3   5 5  5   3  5 3 5 5
Ví dụ 4 (vận dụng và vận dụng cao) . Tìm số hữu tỉ x biết: 12  2  5 a) x   1 b) 1  x     5  7  7 5 3  11  c) x  d) x x   0   6 2  4  19 11 x  2016 x  2016 x e) 2  : (3x)  f)   1008 5 3 5 3 2 Giải: 12 12 5 12 5 12 17 a) x   1  x  1   x    x   x  5 5 5 5 5 5 17 Kết luận: x  . 5  2  5 2 5 5 2 b) 1  x    x   1   x  1      7  7 7 7 7 7  5 2   x  1  
 x  11  x  0    7 7 
Kết luận: x  0 . 5 3 3 5 3 6 3.6 9 c) x   x  :  x  .  x   x  6 2 2 6 2 5 2.5 5 9 Kết luận: x  5  11  11 11 d) x x   0  x  0   hoặc x 
 0  x  0 hoặc x    4  4 4 11
Kết luận: x  0 hoặc x   . 4 19 11 19 11 19 11 6 e) 2  : (3x)   : 3x   2  : 3x   5 3 5 3 5 3 3 11
BÀI TẬP TRẮC NGHIỆM TOÁN 7 19 11 6 19 5 19 5 19 3 19.3  : 3x  
: 3x   3x  :  3x  .  3x  5 3 5 3 5 3 5 5 5.5 57 57 57 1 19  3x   x  : 3  x  .  x  25 25 25 3 25 19 Kết luận: x  . 25 x  2016 x  2016 x 1 1 1 f)  
1008   x  2016.   x  2016.   x  2016. 5 3 2 5 3 2  1 1  1   x  2016.      x  2016.  0  5 3  2  1 1 1 1 1 1    x  2016.    0   . Dễ thấy  
 0 nên x  2016  0 hay x  20  16 .  5 3 2  5 3 2 Kết luận: x  20  16
Lưu ý: Trong câu này nhiều học sinh nhằm x  2016 x  2016 
  x  2016 : 5   x  2016 : 3   x  2016 : 5  3 . 5 3
Dẫn đến tìm sai kết quả. 3. Câu hỏi trắc nghiệm
Câu 1. Câu nói nào dưới đây đúng? a A. Các số đều là số hữa tỉ. b
B. Số 0 không phải là số hữu tỉ. 1
C. Số hữu tỉ x có số nghịch đảo là . x
D. Các số hữu tỉ đều biểu diễn được trên trục số.  3   1 1
Câu 2. Kết quả phép tính 2.  :   là.  8  6 3 5 1 3 1  A. . B. . C. . D. . 4 2 4 4 12
BÀI TẬP TRẮC NGHIỆM TOÁN 7  1 1   1   1 
Câu 3. Kết quả phép tính 1     2   3       là.  2 3   2   3  8 4 A. . B. 4 . C. 4  . D. . 3 3 3  Câu 4. Số
là kết quả của phép tính nào dưới đây? 8 1 1 1  1 1 1 1 1 A.  . B.  . C.  . D.   . 2 8 8 4 8 4 2 8  3  9 Câu 5. Cho biết : 2 : x    , tìm số hữu tỉ x:  8  8 2 27 27 3 A. . B. . C. . D. ? 3 128 32 2
Câu 6. Trong các phân số sau, phân số nào biểu diễn số hữu tỉ 0,125 1 1 1 1 A. . B. . C. . D. 4 8 16 125 x
Câu 7. Cho hai số nguyên x, y và y  0 . Nếu x, y trái dấu thì số hữu tỉ a  y 1 A. a  0 . B. . C. a  0 . D. Cả B và C sai 8
Câu 8. Các cặp số hữu tỉ nào dưới đây bằng nhau? 3  6 1 11 A. và . B. 0, 4 và . C. 0,1 và 10 . D. và 0,5 . 5 10 4 22 1 1
Câu 9. Số hữu tỉ nào sau đây nằm giữa  và 4 2 3 5 5 2 A. . B. . C.  . D.  8 8 8 3 x y
Câu 10. Chọn đáp án sai: Các số nguyên x, y mà  là: 2 3
A. x  1, y  1. B. x  2  , y  3  .
C. x  3, y  2 . D. x  y  0 13
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Câu 11. Câu nói nào dưới đây sai
A. Số 9 là một số tự nhiên.
B. Số -2 là một số nguyên âm. 10  C. Số là một số hữu tỉ.
D. Số 0 là một số hữu tỉ dương. 11 1 1 1 1
Câu 12. Tính giá trị của H     ...  . 1.2 2.3 3.4 2017.2018 2016 2017 A. H  . B. H  . 2017 2018 2018 2019 C. H  . D. H  . 2019 2018
Câu 13. Tìm x  Q , biết  x  32x  4  0 A. 3   x  2 . B. 2   x  3 . C. x  2 . D. x  3  .
Câu 14. Có bao nhiêu số nguyên dương x thỏa mãn 5x  37  2x  0 ? A. 1 số. B. 2 số. C. 3số. D. 4 số.
Câu 15. Trong các câu sau, câu nào sai?
A. Số hữu tỉ âm nhỏ hơn số hữu tỉ dương.
B. Số tự nhiên lớn hơn số hữu tỉ âm.
C. Số nguyên âm không phải là số hữu tỉ.
D. Số hữu tỉ 0 không là số hữu tỉ dương cũng không là số hữu tỉ âm.
Câu 16. Trong các câu sau, câu nào đúng?
A. Phép cộng luôn luôn thực hiện được trong tập hợp số tự nhiên.
B. Phép trừ luôn luôn thực hiện được trong tập hợp số tự nhiên.
C. Phép chia luôn luôn thực hiện được trong tập hợp số hữu tỉ.
D. Phép nhân không luôn luôn thực hiện được trong tập hợp số hữu tỉ
MA TRẬN CÂU HỎI TNKQ CHỦ ĐỀ 1 14
BÀI TẬP TRẮC NGHIỆM TOÁN 7 Mức độ Nhận biết Thông hiểu Vận dụng (câu) Chủ đề (câu) (Câu) Thấp Cao 1 2, 4, 7, 8, 11 1, 3, 5, 6, 15 9, 10, 16 12, 13, 14 .
Chủ đề 2. SO SÁNH HAI SỐ HỮU TỈ
1. Một số phương pháp thường gặp
Với hai số hữu tỉ bất kỳ x, y ta luôn có: hoặc x  y hoặc x  y hoặc x  y .
Phương pháp 1: So sánh với số 0: số hữu tỉ dương lớn hơn số hữu tỉ âm.
Phương pháp 2: Đưa hai số hữu tỉ về dạng phân số có cùng mẫu số hoặc cùng tử số.
Phương pháp 3: Làm xuất hiện một số hữu tỉ trung gian để so sánh.
Phương pháp 4: Sử dụng công thức: a a 1 a a 1
Cho b  0 , nếu a  b thì 
, nếu a  b thì  . b b 1 b b 1 a c a a  c c
Cho b  0, d  0 , nếu  thì   . b d b b  d d 2. Ví dụ
Ví dụ 1 (Nhận biết) . So sánh các cặp số hữu tỉ sau: 2 7 5 7 32 16 a. và b. và c. và 11 9  6 9 9 5 9  16 32 20 21 d. 0  , 6 và e. và f. và 8 7 17 31 32 Giải: 2 7 2 7 a. Có  0 và  0 nên 
(ta đã sử dụng phương pháp 1) 11 9  11 9  5 15 7 14 15 14 5 7 b. Có  và 
. Vì 15  14 và 18  0 nên  hay  6 18 9 18 18 18 6 9
(ta đã sử dụng phương pháp 2: Đưa hai số hữu tỉ về dạng phân số có cùng mẫu số) . 16 32 32 32 32 16 c. Có 
. Vì 32  0 và 9  10 nên  hay  5 10 9 10 9 5 15
BÀI TẬP TRẮC NGHIỆM TOÁN 7
(ta đã sử dụng phương pháp 2: Đưa hai số hữu tỉ về dạng phân số có cùng tử số) 9  8  9  d. Có 0  , 6  1  . Vì 9   8  và 8  0 nên  hay  1  . 8 8 8 9  Suy ra 0  , 6 
(ta sử dụng phương pháp 3: Làm xuất hiện một số 1  ) 8 16 14 6 
e. Vì 16  14 và 7  0 nên  hay  2 7 7 7 32 34 32 16 32
Vì 32  34 và 17  0 nên  hay  2 . Suy ra  17 17 17 7 17
(ta sử dụng phương pháp 3: Làm xuất hiện một số 2 ) 16  32
Chú ý: để ý hơn ít nữa ta thấy  2 7 17 a a 1
f. Áp dụng công thức ở phương pháp 4: Cho b  0 , nếu a  b thì  b b 1 20 20 1 20 21
Vì 31  0 và 20  31 nên  hay  . 31 311 31 32 1  1 
Ví dụ 2 (Thông hiểu) . Hãy viết ba số hữu tủ xen giữa và . 5 6
Giải: Sử dụng công thức ở phương pháp 4: a c a a  c c
Cho b  0, d  0 , nếu  thì   b d b b  d d Ta có 1  1  1  2  1  nên có   5 6 5 11 6 2  1 2  3  1  nên có   11 6 11 17 6 3  1  3  4  1  nên có   17 6 17 23 6 1  2  3  4  1 Vậy     . 5 11 17 23 6
Ví dụ 3 (Vận dụng) . Viết lại các số hữu tỉ sau theo thứ tự lớn dần? 16
BÀI TẬP TRẮC NGHIỆM TOÁN 7 11  9 25 3 9 , , , , 9 8 12 7 7 Giải: 11  3 11  3 Vì  0 và  0 nên  9 7 9 7 3 7 3 Vì 3  7 và 7  0 nên  hay  1 7 7 7 9 8 9 3 9 Vì 9  8 và 8  0 nên  hay  1. Vậy  8 8 8 7 8 9 9 Vì 8  7 và 9  0 nên  8 7 9 14 9 Vì 9  14 và 7  0 nên  hay  2 7 7 7 25 24 25 9 25
Vì 25  24 và 12  0 nên  hay  2 . Vậy  12 12 12 7 12 11  3 9 9 25
Kết luận: các số hữu tỉ sau theo thứ tự tăng dần là , , , , . 9 7 8 7 12
Ví dụ 4 (bài 5 trang 8 SGK Toán 7 tập 1) (Vận dụng cao) . a b a  b Giả sử x  , y 
(a,b, m  Z , m  0) và x  y . Hãy chứng tỏ rằng nếu chọn z  thì ta m m 2m
có x  z  y Giải: a b a  b
Ta có x  y   
nên x  y  2z m m m
Mà x  y nên x  x  x  y hay 2x  2z hay x  z   1
Mặt khác x  y nên x  y  y  y hay 2z  2 y hay z  y 2 Từ  
1 và 2 suy ra x  z  y (điều phải chứng minh) . 3. Câu hỏi trắc nghiệm  1 1 5  7
Câu 1. Kết quả phép tính   .  
là a . Khẳng định nào dưới đây đúng?  6 3 2  4 17
BÀI TẬP TRẮC NGHIỆM TOÁN 7 7 A. a  . B. a  0 . C. a  4  . D. a  4  . 2
Câu 2. So sánh nào dưới đây đúng 9  7  11 11 79 77 101 7  A.  . B.  . C.  . D.  . 2 2 5 6 5 4 37 3
Câu 3. Cặp số hữu tỉ nào dưới đây bằng nhau 12  3 10 9 6 12 5 7 A. và . B. và . C. và . D. và . 8 2  11 10 8 15 7 5 5  5  7 3 18 Câu 4. Các số hữu tỉ ; ; ; ;
được sắp xếp theo thứ tự lớn dần là 11 9 5 5 13 5  5  18 7 3 5  5  3 18 7 A. ; ; ; ; . B. ; ; ; ; . 11 9 13 5 5 9 11 5 13 5 5  5  3 18 7 5  5  3 7 18 C. ; ; ; ; . D. ; ; ; ; . 11 9 5 13 5 9 11 5 5 13 6  2 
Câu 5. Có bao nhiêu phân số có mẫu số bằng 7 , lớn hơn và nhỏ hơn 7 5 A. 2 số. B. 3 số. C. 4 số. D. 5 số. 5 7
Câu 6. Có bao nhiêu phân số có tử số bằng 6 , lớn hơn và nhỏ hơn 7 5 A. 6 số B. 7 số C. 8 số D. 9 số 1  5  2  5 12  5
Câu 7. Cho các số có quy luật ; ; ;
. Số tiếp theo của các số là 8 8 8 8 625  225  525  575  A. . B. C. . D. . 8 8 8 8  23    12    3    9   14   Câu 8. Cho các tích sau H  . , H  . . , 1     2        15   7   5   17    23   5    4    3    4   5  H  . . ... .
. Khẳng định nào dưới đây đúng? 3          
 13   13   13   13   13 
A. H  H  H .
B. H  H  H . 2 3 1 1 2 3
C. H  H  H .
D. H  H  H . 3 2 1 2 1 3
Câu 9. Tìm hai số hữu tỉ x và y sao cho x  y  .
x y  x : y , trong đó y  0 . 18
BÀI TẬP TRẮC NGHIỆM TOÁN 7 1  1  A. x  và y  1. B. x  và y  1  . 2 2 1 1 C. x  và y  1. D. x  và. 2 2
Câu 10. Bình và Công mua quà tặng sinh nhật bạn An. Giá một cái bánh là 300 000 đồng, 1
Bình mua cái bánh này. Một thùng nước ngọt giá 250 000 đồng, Công mua nửa thùng nước 3
này. Hỏi bạn nào mua hết nhiều tiền hơn?
A. Bình mua hết nhiều nước hơn.
B. Công mua hết nhiều tiền hơn.
C. Hai bạn nhiều như nhau.
D. Không xác định được ai mua nhiều.
MA TRẬN CÂU HỎI TNKQ CHỦ ĐỀ 2 Mức độ Nhận biết Thông hiểu Vận dụng (câu) Chủ đề (câu) (câu) Thấp Cao 2 1, 2,3 7,8,9,10 4,5 6 19
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Chủ đề 3. GIÁ TRỊ TUYỆT ĐỐI CỦA MỘT SỐ HỮU TỈ
1. Một số vấn đề cần ôn tập
Giá trị tuyệt đối của số hữu tỉ x , kí hiệu x , là khoảng cách từ điểm x tới điểm 0 trên trực số. x   x  0
Ta có: x  x   x  0 
Nhận xét: Với mọi x  Q, y  Q ta luôn có 2 2
x  0, x  x , x  x, x  x, x  x x x .
x y  x . y , 
(phép chia với điều kiên y  0 ) y y
x  y  x  y , x  y  x  y
x  y  x  y khi . x y  0 . 2. Ví dụ
Ví dụ 1 (Nhận biết) . Tìm x , biết 11 3 11 29 a. x  b. x  0  , 76 c. x  5  d. x   10 5 4 6 Giải: 11 11 11 a. x   , vì  0 10 10 10 b. x  0.7  6    0  , 76  0,76 , vì 0  , 76  0 3  3  3 3 c. x  5    5   5   , vì 5   0 5  5  5 5 11 29 33 58 33  58 25  d. x       4 6 12 12 12 12 25   25   25 25  Nên x       , vì  0 12  12  12 12
Ví dụ 2 (Thông hiểu) . Tìm x  Q , biết: 3 1 1 a. x  1  , 2 b. x  0,3 c. 2  x  d. x   5 3 2 20
BÀI TẬP TRẮC NGHIỆM TOÁN 7 Giải:
Nhận xét: dạng bài toán tìm x để A x  B , ta thực hiện như sau:
Vì A x  0 nên
Khi B  0 , sẽ không có giá trị x .
Khi B  0 , giá trị x phải thỏa mãn A x  0 .
Khi B  0 , giá trị x phải thỏa mãn A x  B hoặc A x  B a. Vì x  0, 1
 , 2  0 , nên không có số hữu tỉ x thỏa mãn x  1  , 2
b. Vì x  0,3  0 , nên có hai giá trị thỏa mãn là x  0,3; x  0  ,3 3 10 3 10  3 7 c. x  2  hay x   hay x  hay x  5 5 5 5 5 7 7
Có hai giá trị thỏa mãn là x  ; x   . 5 5 1 1 1 1
d. Giá trị x phải thỏa mãn x   hoặc x    3 2 3 2 1 1 1 1 3 2 3  2 1 Khi x   có x   hay x   hay x  hay x  3 2 2 3 6 6 6 6 1 1 1 1 3   2 5  Khi x    có x    hay x  hay x  3 2 2 3 6 6 1 5 
Kết luận: có hai giá trị thỏa mãn là x  ; x  . 6 6
Ví dụ 3 (Vận dụng) . Tìm x  Q , biết:
a. 3x  2  x  2  3x B. x 2x  3  6x Giải:
a. Vì 3x  2  0 và x  2  0 nên 3x  2  x  2  0 , do đó 3x  0 hay x  0
Khi ta có 3x  2  x  2  3x hay x  4
 (không thỏa mãn x  0 ) . Vậy không có giá trị x  Q thỏa mãn đề bài
Vì x 2x  3  0, nên 6x  0 hay x  0
Khi x  0 ta có x 2x  3  6x
Nếu x  0 thì 02.0  3  6.0 (đúng) 3
Nếu x  0 thì ta có 2x  3  6 hay 2x  6  3 hay x 
(thỏa mãn x  0 ) 2 21
BÀI TẬP TRẮC NGHIỆM TOÁN 7 3
Kết luận: x  0, x  2
Nhận xét: trong ví dụ này có nhiều học sinh nhầm như sau. 3
x 2x  3  6x  2x  3  6  2x  3  x  2
Giải: như vậy dẫn đến thiếu giá trị cho x .
Ví dụ 4 (Vận dụng và vận dụng cao) . Tìm giá trị nhỏ nhất của các biểu thức sau
a. Vì x 1  0 nên x 1  3  3
 , x 1  3  3  khi x  1
Vậy A đạt giá trị nhỏ nhất là 3  khi x  1.
b. Ta có x  2018  2018  x (vì tính chất a  b  a  b )
Hay B  1, B  1 khi  x  2017 x  2018  0 (xảy ra được, chẳng hạn x  2017 )
Vậy B đạt giá trị nhỏ nhất là 1 khi  x  20172018  x  0
c. Ta có x 1  0, x  2  2  x ,
Nên x 1  x  2  x  3  0  2  x  x  3 hay C  5
C  5 khi xảy ra đồng thời x 1  0, x  2  2  x và x  3  x  3 tức x  1
Vậy C đạt giá trị nhỏ nhất là 5 khi x  1.
Nhận xét: Câu này là một bài toán khó, yêu cầu người giải: bài tập phải vận dụng linh hoạt các
công thức đã biết và phải còn khéo léo triệt tiêu x hợp lý trên cơ sở C  0 . 1. Câu hỏi trắc nghiệm 5 14 5 Câu 1. Cho x   : . Tính x 3 3 2 15 6 3 A. x  . B. x  0 . C. x  . D. x  . 2 5 15
Câu 2. Giá trị nào của x dưới đây thỏa mãn 2x  3  9  2x ? 3  3 A. x  . B. x  . C. x  0 . D. x  6 . 2 2
Câu 3. Có bao nhiêu số x  Q thỏa mãn 2x  3  5  3x  0 ? A. Không có. B. Có một số. C. Có hai số. D. Có ba số.
Câu 4. Câu nói nào dưới đây sai?
A. Không có số hữu tỉ x nào thỏa mãn 9x  5  2  .
B. Có đúng một số hữu tỉ x thỏa mãn 13x 19  0 .
C. Chỉ có hai số hữu tỉ x thỏa mãn 7x 12  8 . 22
BÀI TẬP TRẮC NGHIỆM TOÁN 7
D. Chỉ có hai số hữu tỉ x thỏa mãi 3x  2 1  6x .
Câu 5. Cho x  x  0 thì A. x  0 . B. x  0 . C. x  0 . D. x  0 . 7  5 Câu 6. Cho x  và y 
. Tính giá trị của biểu thức 2
H  3x  y 8 4 1  1 17  11 17 A. H  . B. H  . C. H  . D. H  . 16 16 16 16
Câu 7. Cho x  Q, y  Q thỏa mãn x  y  y  x . Kết luận nào sau đây đúng
A. x  0 và y  0 .
B. x  0 và y  0 .
C. x  0 và y  0 .
D. x  0 và y  0 .
Câu 8. Cho x  Q, y  Q thỏa mãn x  y  x  y . Kết luận nào sau đây đúng.
A. x và y trái dấu.
B. x và y cùng dấu.
C. x và y cùng dương.
D. x và y cùng âm.
Câu 9. Tìm giá trị nhỏ nhất của H  2x  3  4 .
A. H đạt giá trị nhỏ nhất là 2 .
B. H đạt giá trị nhỏ nhất là 3 
C. H đạt giá trị nhỏ nhất là 9 .
D. H đạt giá trị nhỏ nhất là 4  .
Câu 10. Tìm giá trị lớn nhất của H  8  x  6 .
A. H đạt giá trị lớn nhất là 15 .
B. H đạt giá trị lớn nhất là 8
C. H đạt giá trị lớn nhất là 6 .
D. H đạt giá trị lớn nhất là 1 /
Câu 11. Tìm x  Q thỏa mãn x  2  x 1  2x 3 3 1  A. x  B. x   C. x  D. x  0 2 2 2
Câu 12. Hỏi có bao nhiêu giá trị x  Q thỏa mãn x  x  2  x ? A. Có một giá trị B. Có hai giá trị C. Có ba giá trị D. Có bốn giá trị.
MA TRẬN CÂU HỎI TNKQ CHỦ ĐỀ 3 23
BÀI TẬP TRẮC NGHIỆM TOÁN 7 Mức độ Nhận biết Thông hiểu Vận dụng (câu) Chủ đề (câu) (câu) Thấp Cao 3 1,5, 6, 7 2,3, 4,9,10 8,11 12
Chủ đề 4. LŨY THỪA CỦA MỘT SỐ HỮU TỈ
1. Một số vấn đề cần ôn tập
Lũy thừa với số mũ tự nhiên: n a  . a . a ... a a *  
 a Q, n  N  . n Các công thức: Cho * *
a  Q, b  Q, n  N , m  N m . n mn  , m : an mn a a a a  a
(với phép chia: b  0 ) n 1 0 a  , a  a  , không tồn tại số 0 0 n  1 0 a
Với a  0, a  1  , nếu m n
a  a thì m  n . 2. Ví dụ
Ví dụ 1 (Nhận biết) . Viết các biểu thức số sau dưới dạng lũy thừa của một số hữu tỉ. 9 10 2 .9 a. 9 6 2 .8 b. 8 10 36 : 6 c. d.  4 8 7 0, 25 .16  56.8 11 3 Giải:
Phương pháp: sử dụng các công thức ở trên để đưa biểu thức số về dạng n a a.    3 9 6 3.3 6 3 6 36 9 2 .8 2 .8 2 .8  8  8 b.   8 8 10 2 10 2.8 10 16 10  6 36 : 6 6 : 6  6 : 6  6  6 9. 2 .9 2 .9 .9  9 9 2 .9  2.99 9 9 10 9 9 9 18  18  c. 9       6 11 9 2 9 9 9   3 3 .3 9.3 3 3  3  4 8 7 4  1  1 d. 0, 25 8 7 .16  56.8  .    2 4   7.8. 3 2  2.8 3.7  .4  7.2 4  4  4 16
4  7.2 .2  4   7.2   2 12 3 21 16 4 3 21 2 24 24 324 27  7.2  8.2  2  2 = 4 4
Ví dụ 2 (Thông hiểu) . Tính giá trị của các biểu thức sau: 24
BÀI TẬP TRẮC NGHIỆM TOÁN 7 9 15 28  1   1   1  a. 19 A  3 .  b. B  :      9   16   4  5 5 6 2 .5 10 0,254 9 .2  6 c. C  d. D  5 3.5 5 2 16 Giải:
Phương pháp: Biến đổi các lũy thừa về dạng các lũy thừa có cùng cơ số hoặc cùng số mũ hoặc
cùng cả số mũ và cơ số, sau đó sử dụng các công thức để rút gọn 9 19  1  1 3 a. 19 19 19 18 A  3 .  3 .   3   3   9  9  9  2 3 9 15 28 2.15 28 3028 2  1   1   1   1   1   1  1 b. B  :  :                 16   4   4   4   4   4  16 5 5 6 2 .5 10 2.55 5 5 5 5 5 10.10 10 10.10 9.10   10  c. C      3   96  5 5 5 5   3.5 3.5 3.5 3.5  5  0,254 9 8  9 .2  6 2 .2  6 1 d. D    5 4 2 16 2 2   1 2
Ví dụ 3 (Vận dụng) . Tìm số tự nhiên n , biết n 8 1  5   n n 1 a.  b.  5  c. 2 .3 n n  36 d. 1 6 : 3  2n 32 25 96 Giải 3 8 1 2 1 a. n 3 5 n 35 8     2  2 .2  2  2  2  n  8 n n 5 2 32 2 2 Kết luận: n  8  n n 5    5   n 1 2 n 12 b.  5    5   5   5  5   5   5 2           25  5  
  n   3 5 5  n  3 Kết luận: n  3 n c. n n     2 n 2 2 .3 36 2.3
 6  6  6  n  2 Kết luận n  2 n  1 6n n n  6  d. 1 5 n n5 0 6 : 3   96.  1  32
 1  2 .2  1  x  2   96 3.3n  3 
 n  5  0  n  5
 (số thự nhiên luôn lớn hơn hoặc bằng 0 , không thỏa mãn)
Kết luận: không có giá trị n thỏa mãn đề bài. 25
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Ví dụ 4: (Vận dụng cao) . Chứng minh a.  14 5
5.2  8  chia hết cho 12 b.  2028 2018 2017 3 .13  9  chia hết cho 10 Giải: a. Ta có     5 14 5 14 3 14 3.5 14 15 14 14 14 5.2 8 5.2 2  5.2  2
 5.2  2  5.2  2.2  3.2    7 14 2 7 3.2 4. 2  3.4 Do 3chia hết cho 3, 7
4 chia hết cho 4 và UCLN 3, 4  1 Nên  14 5
5.2  8  chia hết cho 12 (đpcm) b. 2028 2018 2017 102018 2018 2016 10 2018 2018 2016 3 .13  9  3 .13  9.9  3 .3 .13  9.9       5 2018 2.5 2016 2 2018 2016 3 3.13 9.9 3 .39  9.9 5 2018 2016 4 2018 2016 9 .39  9.9  9.9 .39  9.9 Vì 4 2018 2016 9 ,39 ,9.9
đều là những số có chữ số hàng đơn vị là 1 . Nên 4 2018 9.9 .39 và 2016 9.9
đều những số có chữ số hàng đơn vị là 9 . Suy ra 4 2018 2016 9.9 .39  9.9
có chữ số hàng đơn vị là 0. Tức là  2018 2018 2017 3 .13  9 chia hết cho 10 (đpcm)
Nhận xét: trong bài này ta cần ghi nhớ kết quả sau:
Tất cả số có chữ số tận cùng là 0;1;5;6 , khi nâng lũy thừa với số mũ nguyên dương cho ta chữ
số tận cùng giữu nguyên.
Các số có chữ số tận cùng là: 4 , khi nâng lũy thừa với số mũ chẵn cho ta chữ số tận cùng là 6 ,
khi nâng lũy thừa với số mũ lẻ cho ta chữ số tận cùng 4 .
Các số có chữ số tận cùng là: 9 , khi nâng lũy thừa với số mũ chẵn cho ta chữ số tận cùng là 1 ,
khi nâng lũy thừa với số mũ lẻ cho ta chữ số tận cùng 9 .
Các số có chữ số tận cùng còn lại ta sẽ thêm bớt đề xuất hiện một trong các số đã nói ở trên. 3. Câu hỏi trắc nghiệm Câu 1. Viết số  5
0,125 dưới dạng lũy thừa của cơ số 0,5 là: A.  15 0,5 . B.  10 0,5 . C.  8 0,5 . D.  7 0,5 . Câu 2. Viết số 20
2 dưới dạng lũy thừa có số mũ là 5 A. 5 8 . B. 5 16 . C. 5 32 . D. 5 64 .
Câu 3. Trong các khẳng định sau khẳng định nào sai. A.  9 0, 7 là một số âm. B.  10 0,9 là một số dương. 26
BÀI TẬP TRẮC NGHIỆM TOÁN 7 1  1 C. 9 : 2  . D. 0 0  0 . 10 2 2 n  5  625
Câu 4. Tìm số nguyên dương n thỏa mãn    .  3  81 A. n  2 . B. n  3 . C. n  4 . D. n  5 . n x
Câu 5. Có bao nhiêu số hữu tỉ x thỏa mãn  32 ? 8 A. 1 số. B. 2 số. C. 3số. D. 4 số.
Câu 6. Tìm số hữu tỉ x thỏa mãn  x  3 8 2 1  . 125 7  3  3 7 A. x  . B. x  . C. x  . D. x  . 10 10 10 10 Câu 7. Cho số 15 10
a  2 .5 . Tìm số các chữ số của a . A. 10 chữ số. B. 11 chữ số. C. 12 chữ số. D. 13 chữ số. Câu 8. Cho hai số 10 a  50 , 20
b  10 . Khẳng định nào dưới đây đúng? A. a  b . B. a  b . C. a  b . D. b  2a . Câu 9. Cho hai số 50 a  100 , 100 b  20
. Khẳng định nào dưới đây đúng? A. a  b . B. a  b . C. 100 a  2 .b . D. 100 2 .a . Câu 10. Cho hai số 332 223 a  2 ,b  3
. Khẳng định nào dưới đây đúng? A. a  b . B. a  b . C. a  b . D. 3a  2b . 2 .0,55 15 10  3.2 Câu 11. Cho E 
. Khẳng định nào dưới đây đúng? 11 3 15 3 2 .2  2 : 2 1 1 1 A. E  . B. E  . C. E  . D. E  1. 5 3 2 7 8 2.6  6 Câu 12. Cho F 
. Khẳng định nào dưới đây đúng? 5 2  4 7 8 9  2.3  3  A. F  8 . B. F  6 . C. 2 F  8 . D. F  10 . 27
BÀI TẬP TRẮC NGHIỆM TOÁN 7 5 4 9 4 .9  2.6 Câu 13. Cho G 
. Khẳng định nào dưới đây đúng? 10 8 8 2 .3  6 .20 1 1 A. F  . B. F  . C. F  0 . D. F  3  . 3 3
Câu 14. Tìm số tự nhiên n thỏa mãn 16  n  19 để  10 n   1 chia hết cho 10 . A. n  19 . B. n  18 . C. n  17 . D. n  16 . Câu 15. Cho số 9 5 10
A  10  2 .5 . Khẳng định nào dưới đây đúng?
A. A có chữ số tận cùng bằng 5 . B. A 11  0 .
C. A có chữ số tận cùng bằng 2 . D. A 10  00 . 11 x
Câu 16. Có bao nhiêu số hữu tỉ x thỏa mãn 9  x ? 25 A. 1 số B. 2 số C. 3 số D. 4 số.
MA TRẬN CÂU HỎI TNKQ CHỦ ĐỀ 4 Mức độ Nhận biết Thông hiểu Vận dụng (câu) Chủ đề (câu) (câu) Thấp Cao 4 1, 2,3, 4,5, 6,16 8,9,11,12,13 7,10 14,15 28
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Chủ đề 5. TỈ LỆ THỨC. TÍNH CHẤT CỦA DÃY SỐ TỈ SỐ BẰNG NHAU
1. Một số vấn đề cần ôn tập
Tỉ lệ thức là đẳng thức của hai tỉ số a c Tỉ lệ thức 
còn được viết a : b  c : d b d Các số a, ,
b c, d được gọi là các số hàng của tỉ lệ thức
a và d gọi là ngoại tỉ (số hạng ngoài)
b và c gọi là trung tỉ (số hạng trong) Tính chất: a c Nếu  thì ad  bc b d
Nếu ad  bc và a, ,
b c, d  0 thì ta có các tỉ lệ thức a c a b d c d b  ,  ,  ,  b d c d b a c a
Tính chất của dãy tỉ số bằng nhau: a c a c a  c a  c Từ tỉ lệ thức  ta suy ra   
(giả thiết các tỉ số đều có nghĩa) b d b d b  d b  d a c e
Từ dãy tỉ số bằng nhau   ta suy ra b d f a c e
a  c  e
a  c  e     b d f
b  d  f
b  d  f
(giả thiết các tỉ số đều có ý nghĩa) a b c Khi có dãy tỉ số   ta nói các số a, ,
b c tỉ lệ với 2;3;5 . 2 3 5
Ta cũng viết a : b : c  2 : 3 : 5 . 2. Ví dụ
Ví dụ 1 (nhận biết) . Tìm số hữu tỉ x biết: 29
BÀI TẬP TRẮC NGHIỆM TOÁN 7 x 3 x  2 3 a. 0  ,1: x  0  , 2 : 0, 06 b.   x  0 c.   x  3 12  x 3  x 7 Giải: a. 0
 ,1: x  0, 2 : 0, 06  0  , 2.x  0  ,1.0, 06 0  , 06  0  , 2.x  0  , 06  x   x  0, 03 . 0  , 2
Vậy x  0, 03 là giá trị cần tìm. x 3  b.   .
x x  12. 3   2 2 2
 x  36  x  6 12  x
suy ra x  6 hoặc x  6  là giá trị cần tìm x  2 3 c. 
  x  2.7  3  x.3  7x 14  9  3x  7x  3x  9 14 3  x 7 1   10x  5   x  thỏa mãn x  3 2 1  Vậy x  là giá trị cần tìm. 2
Chú ý: ta có thẻ giải bài này như sau: x  2 3 x  2 3  x x  2 3  x
x  2  3  x       3  x 7 3 7 3 7 3  7 x  2 5 x  2 1 Do vậy   
  x  2.2  3.1  2x  4  3  2x  3  4 3 10 3 2 1   2x  1   x  (thỏa mãn x  3) 2 1  Vậy x  là giá trị cần tìm. 2
Ví dụ 2: (Thông hiểu) Một mảnh đất hình chữ nhật có tỉ số giữa chiều dài và chiều rộng bằng
4 . Tính diện tích mảnh đất này biết rằng chu vi của mảnh đất bằng 28m? 3 Giải:
Gọi chiều dài. chiều rộng của mảnh đất lần lượt là x, y (m) (x, y > 0) 4 x 4 x y
Do tỉ số giữa chiều dài và chiều rộng bằng nên có  hay  3 y 3 4 3
Do chu vi của mảnh đất bằng 28 m nên có 2x +2y = 28 hay x + y =14 x y x  y 14
Áp dụng tính chất của dãy tỉ số bằng nhau có:     2 4 3 4  3 7 30
BÀI TẬP TRẮC NGHIỆM TOÁN 7 x y Suy ra  2  x  8,
 2  y  6 (thử lại các gía trị ta tấy thỏa mãn) 4 3
Vậy mảnh đất hình chữ nhật có chiều dài 8m và chiều rộng 6m
Ví dụ 3: (Thông hiểu) Số học sinh giỏi của lớp &A, 7B, 7C tỉ lệ với cá số 4; 3; 5. Biết rằng
tổng số học sinh giỏi của hai lớp 7A và 7C nhiều hơn số học sinh giỏi của lớp 7B là 30. Hỏi
mỗi lớp có bao nhiêu hc sinh giỏi? Giải:
Gọi số học sinh giỏi của lớp 7A, 7B, 7C lần lượt là x, y, z ( *
x , y, z   ) x y z
Do x, y, z tỉ lệ với các số 4; 3; 5 nên   4 3 5
Tổng số học sinh giỏi của hai lớp 7A và 7C nhiều hơn số học sinh giỏi của lớp 7B là 30 nên có x+z –y =30. x y z
x  y  z 30
Áp dụng tính chất của dãy tỉ số bằng nhau có:      5 4 3 5 4  3  5 6 x y z Suy ra  5  x  20;  5  y  15;  5  y  25 4 3 5
Vậy số học sinh của lớp 7A là 20 bạn; 7B là 15 bạn; 7C là 25 bạn.
Ví dụ 4: (Vận dụng và vận dụng cao) . Giả thiết cá tỉ số đều có nghĩa a  b c  a a. Cho 2
a  bc . Chứng minh rằng  a  b c  a a c 2017 2017 2017 a  c (a  c) b. Cho tỉ lệ thức  . Chứng minh rằng  b d 2017 2017 2017 b  d (b  d ) Giải:
Nhận xét: Trong VD này, mỗi câu đều có nhiều cách giải khác nhau, song tôi xin trình b một
cách được cho là phù hợp nhất của bài toán. a c a c a  c c  a a. Từ 2 a  bc có  Áp dụng tính cất có    b a b a b  a a  b a  b c  a Suy ra 
(điều phải chứng minh) a  b c  a a c b. Đặt 
 k suy ra a =kb; c =kd b d 31
BÀI TẬP TRẮC NGHIỆM TOÁN 7 2017 2017 2017 2017 2017 2017 2017 2017 2017 2017 2017 a  c (kb)  (kd ) k .b  k .d k .(b  d ) 2017     k 2017 2017 2017 2017 2017 2017 2017 2017 b  d b  d b  d b  d 2017 2017 2017 2017 2017 (a  c) (kb  kd ) [k.(b+d)] k (b  d ) 2017     k 2017 2017 2017 2017 (b  d ) (b  d ) (b  d ) (b  d ) 2017 2017 2017 a  c (a  c) Từ đó suy ra 
(điều phải chứng minh) 2017 2017 2017 b  d (b  d ) 3. Câu hỏi trắc nghiệm:
Câu 1. Thay tỉ số (1, 2; 1, 35) bằng tỉ số giữa các số nguyên A. 50: 81 B. 9: 8 C. 5: 8 D. 1: 10  2 8  Câu 2: Thay tỉ số 2 : 
 bằng tỉ số giữa các số nguyên  7 5  A. 7: 10 B. 10: 7 C. 128: 35 D. 35: 128 . 1 3 8 Câu 3: Cho tỉ lệ thức 5 
. kết luận nào dưới đây đúng? 9 8 2 5 8 1 A. 8 và 2
là trung tỉ của tỉ lệ thức
B. 9 và 3 là ngoại tỉ của tỉ lệ thức 5 5 8 C. 8 và 2
là ngoại tỉ của tỉ lệ thức D. Cả A, B, C đều sai. 5
Câu 4: Tỉ số nào trong các cặp tỉ số sau lập được tỉ lệ thức? 2 1 A. . 1 : 3 và 0, 3: 5 B. 6: 5 và 2 : 3 3 5 C. 6: 8 và 0, 3: 0, 5
D. 0, 3: 2, 7 và 1, 71: 15, 39
Câu 5: Các số nào sau đây lập được các tỉ lệ thức? A. 1; 3; 5; 15 B. 2; 4; 7; 9 C. -3; 2; 5; 9 D. -5; -3; 15; 17  1  6 2 3
Câu 6: Tìm x trong tỉ lệ thức sau .x :  1 :    5  5 3 2 32
BÀI TẬP TRẮC NGHIỆM TOÁN 7 20 8 A. x = 6 B. x = C. x = D. x =15 3 9 x y z
Câu 7: Tìm ba số x, y, z biết rằng:   và xyz = 240 2 3 5 A. x = 1, y = 2, z = 3 B. x = -4, y = -6, z = -10 C. x = 4, y = 6, z = 10 D. x = 2, y = 3, z = 5 x y y z
Câu 8. Tìm ba số x, y, z biết rằng:  ;  và x + y - z = 9 2 4 8 5 A. x = 3, y = 4, z = -2 B. x = 6, y = 8, z = 5 C. x = -6, y = -8, z = -23 D. x = -6, y = 8, z = 5
Câu 9. Cho hai số x, y thỏa mãn 3x = 2y và y – x = 4. Tính H = 2 2 y  x A. H = -80 B. H = 80 C. H = -4 D. H = 4 1
Câu 10. Một mảnh đất hình chữ nhật có tỉ số giữa chiều rộng và chiều dài bằng . Tính chu 4
vi mảnh đất này biết rằng diện tích của mảnh đất bằng 144 2 m A. 60m B. 30m C. 72m D. 144m
Câu 11. Một tam giác có các cạnh của tam giác tỉ lệ với các số 3; 4; 6 và hiệu giữa cạnh lớn
nhất và nhỏ nhất bằng 6. Độ dài các cạnh của tam giác này là: A. 6; 8; 12 B. 12; 16; 24 C. 3; 4; 6 D. 18; 20; 24 a c
Câu 12. Chọn đáp án đúng. Từ tỉ lệ thức  (a, ,
b c, d  0) ta suy ra: b d c b b d a d d c A.  B.  C.  D.  d a c a c b b a
Câu 13. Có 16 tờ giấy bạc loại 2000đ, 5000đ và 10000đ. Trị giá mỗi loại tiền trên đều bằng
nhau. Vậy số tờ giấy bạc loại 2000đ, 5000đ và 10000đ theo thứ tự là: A. 2; 4; 10 B. 10; 4; 2 C. 9; 5; 2 D. 8; 6; 2 a b c
a  2b  c
Câu 14. Cho a  b  c  0 và  
. Tìm giá trị của H  2 3 4
a  b  c 3 4 1 A. H  B. H  C. H =12 D. H  4 3 12 56
Câu 15: Cho tỉ lệ thức 1
, khẳng định nào dưới đây đúng? 165 33
BÀI TẬP TRẮC NGHIỆM TOÁN 7 a d a a  2c 2a  3b 2c  3d c c  3a A.  B.  C.  D.  c b b b  2d 2a  5b 2c  5d d d  3b
(giả thiết các tỉ số đều có nghĩa)
Câu 16: Cho ba số a, b, c thỏa mãn abc abc  0.a  b  0,b  c  0; a  c  0 và a b c b  c  
. Tính giá trị của H  b  c c  a a  b a 1 A. H = -1 B. H = C. H =1 D. H = 2 2
MA TRẬN CÂU HỎI TNKQ TRONG CÁC CHỦ ĐỀ Thông hiểu Vận dụng (câu) Mức dộ chủ đề Nhận biết (câu) (câu) Thấp Cao 5 1, 2, 3, 4, 5, 6, 9 7, 8, 11, 12, 13 14, 16 15 34
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Chủ đề 6. SỐ THẬP PHÂN HỮU HẠN VÀ SỐ THẬP PHÂN VÔ HẠN TUẦN HOÀN LÀM TRÒN SỐ
1. Một số vấn đề cần ôn tập
- Nếu một phân số tối giản với mẫu dương mà mẫu không có ước nguyên tố khác 2 và 5 thì
phân số đó viết được dưới dạng số thập phân hữu hạn.
- Nếu một phân số tối giản với mẫu dương mà mẫu có ước nguyên tố khác 2 và 5 thì phân số
đó viết được dưới dạng số thập phân vô hạn tuần hoàn.
Mỗi số hữu tỉ được biểu diễn bởi một số thập phân hữu hạn hoặc vô hạn tuần hoàn. Ngược lại,
mỗi số thập phân hữu hạn hoặc vô hạn tuần hoàn biểu diễn một số hữu tỉ. 1 1 1 Chú ý:  0, (1),  0, (01),  0, (001),... 9 99 999 2. Ví dụ: 27 
Ví dụ 1: (Nhận biết) : Giải thích tại sao phân số
viết được dưới dạng số thập phân hữu 150
hạn rồi viết số thập phân này. Giải: 27  9  27   , mẫu 2
50  2.5 không có ước nguyên tố khác 2 và 5. Nên phân số viết được 150 50 150
dưới dạng số thập phân hữu hạn 27  Ta có:  0  ,18 150 20
Ví dụ 2: (Thông hiểu) : Giải thích tại sao phân số
viết được dưới dạng số thập phân vô 112 20
hạn tuần hoàn, viết số
dưới dạng số thập phân khi đã làm tròn đến chữ số thập phân thứ 112 tư sau dấu phẩy. 20 5 20 Giải:  , mẫu 2
28  2 .7 có ước nguyên tố 7 khác 2 và 5. Nên phân số viết được 112 28 112
dưới dạng số thập phân vô hạn tuần hoàn 20 20 Ta có:  0,17(857142) suy ra  0,1786 112 112
Ví dụ 3: (Thông hiểu) : Cho biết 1 in – sơ  2,54cm . Do vậy 42 in- sơ  2,54.42cm 35
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Vậy đường chéo màn hình khoảng 107 cm.
Ví dụ 4: (Thông hiểu và vận dụng) . Viết các số thập phân sau dưới dạng phân số tối giản a. 0, 258 b. 0, (12) c. 0, 1 (6) Giải 1 12 4 b. 0, (12)  0, (01).12  .12   99 99 33
c. Nhận xét: Trong câu này ta cần vận dụng linh hoạt hơn để có thể đưa về bài toán giống ở câu b 1, (6) 1 0, (6) 1 0, (6) 1 1 0,1(6)       .6.0, (1) 10 10 10 10 10 10 1 6 1 9 6 9  6 15 1   .      10 10 9 90 90 90 90 6 3. Câu hỏi trắc nghiệm
Câu 1. Viết số thập phân 0, 52 dưới dạng phân số tối giản là: 52 26 13 6,5 A. B. C. D. 100 50 25 12,5
Câu 2. Phân số nào dưới đây viết được dưới dạng số thập phân vô hạn tuần hoàn? 3 52 2292 54 A. B. 2 C. D. 1 8 165 100 165
Câu 3. Phân số nào dưới đây viết được dưới dạng số thập phân hữu hạn? 7 17 5 13 A. B. C. D. 6 160 18 14
Câu 4. Số 2, 3 (15) được viết dưới dạng hỗn số là: 52 2292 54 52 A. 2 B. C. 2 D. 1 165 100 165 165 25 Câu 5. Viết số
dưới dạng số thập phân 99 A. 0, 25 B. 0, 2 (5) C. 0, (25) D. 0, (025)
Câu 6. Kết quả làm tròn số 0, 7125 đến chữ số thập phân thứ 3 là: A. 0, 712 B. 0, 713 C. 0, 710 D. 0, 700
Câu 7. Làm tròn số 674 đến hàng chục là: 36
BÀI TẬP TRẮC NGHIỆM TOÁN 7 A. 670 B. 680 C. 770 D. 780
Câu 8. Thực hiện phép tính 13: 27 rồi làm tròn đến chữ số thập phân thứ hai được kết quả là: A. 0, 50 B. 0, 49 C. 0, 47 D. 0, 48
Câu 9. Có bao nhiêu phân số tối giản có mẫu khác 1, biết rằng tích cảu từ vầ mẫu bằng 1260
và phân số này có thể viết được dưới dạng số thập phân hữu hạn? A. 1 phân số B. 2 phân số C. 3 phân số D. 4 phân số 35 Câu 10. Cho A 
, có bao nhiêu số nguyên tố x có một chữ số để A viết được dưới dạng số 2.x thập phân hữu hạn? A. 4 số B. 3 số C. 2 số D.. 1 số
Câu 11. Kết quả phép tính 0, (432) +0, (567) bằng: A. 1 B. 2 C. 3 D. 4 1
Câu 12. Chữ số thập phân thứ 100 sau dấu phẩy của phân số
(viết dưới dạng số thập phân) 7 là chữ số nào? A. chữ số 2 B. chữ số 5 C. chữ số 7 D. chữ số 8 16 25 100 50
Câu 13. Tính giá trị của P     2 5 10 3 38 3  8 62 4  6 A. P  B. P  C. P  D.. P  3 3 3 3
Câu 14. Trong các số sau, số nào viết được dưới dạng số thập phân vô hạn tuần hoàn? 15 25  6 A. 10 B. C. D. 3 2 9
Câu 15. Trong các số sau, số nào là số hữu tỉ âm? 1  2 1 A. B. C. 3 D. 3 5 2
Câu 16. Xét các khẳng định sau:  5    1  (I)  3 
 là một số hữu tỉ âm (II)  9 
 là một số hữu tỉ âm  2   3 
Chọn câu trả lời đúng: A. Chỉ (I) đúng B. Chỉ (II) đúng
C. Cả (I) và (II) đều đúng D. Cả (I) và (II) cùng sai
MA TRẬN CÂU HỎI TNKQ TRONG CÁC CHỦ ĐỀ Mức dộ chủ Nhận biết Vận dụng (câu) Thông hiểu (câu) đề (câu) Thấp Cao 37
BÀI TẬP TRẮC NGHIỆM TOÁN 7 1, 2, 3, 6, 7, 8, 6 4, 5, 11 10, 12 9 13, 14, 15, 15
Chủ đề 7. SỐ VÔ TỈ. KHÁI NIỆM VỀ CĂN BẬC HAI. SỐ THỰC
1. Một số vấn đề cần ôn tập
- Số vô tỉ là số viết được dưới dạng số thập phân vô hạn không tuần hoàn.
Căn bậc hai của một số a không âm là số x sao cho 2 x  a
Số dương a có đúng hai căn bậc hai, một số dương kí hiệu là a và một số âm kí hiệu là  a
Số 0 chỉ có một căn bậc hai là số 0, ta cũng viết 0  0
Chú ý: không đượ viết 9  3 
Số hữu tỉ vầ số vô tỉ được gọi chung là số thực.
Mỗi số thực được biểu diễn bởi một điểm trên trục số. Ngược lại, mỗi điểm trên trục số đều
biểu diễn một số thực. 2. Ví dụ:
Ví dụ 1: (Nhận biết) Thực hiện phép tính bẳng cách hợp lý: 2 2 ( 5  ) 9 81 ( 8  ) a) A     10 15 2 10 1 4 1 16 7 b) B  .  .  5 49 3 49 5 5 441 Giải: 2 2 ( 5  ) 9 81 (8) 25 3 9 64 . a A         10 15 2 10 10 15 2 10 5 1 9 8  1 9   1 4  1 9 1 4               10 5 2 10  2 2   5 5  2 5 8  5    4  1  3  2 5 38
BÀI TẬP TRẮC NGHIỆM TOÁN 7 1 4 1 16 7 1 2 1 4 7 . b B  .  .   .  .  5 49 3 49 5 5 441 5.7 3 7 5 5.21 1  2 7  4  1  2  7 4  1  9 4   .    .   .         5  21 21 7 5   21 7  5  21 7  1  3 4  1 3  4 1 7 1 1  .   .  .  .1    5  7 7  5 7 5 7 5 5
Ví dụ 2 (Thông hiểu) : Chứng minh các số sau là những số vô tỉ: . a 5 . b 9  5 Giải:
a. Nhận xét: trong bài toán này giải trực tiếp không thể biến đổi được, nên ta sẽ giải gián tiếp
bằng phương pháp chứng minh phản chứng a a
Giả sử 5 là số hữu tỉ nên có 5 
trong đó a,b  ;  b  0 và là phân số tối giản b b 2 a a 2 2 5   5   a  5b 2 b b 2
a 5 lại có 5 là số nguyên tố và a   nên a5 , đặt a =5k, k  
Khi a = 5k, có  k 2 2 2 2 2 2 5
 5b  25k  5b  b  5k
Lập luận tươg ntự trên suy ra b5 a Suy ra phân số
không là phân số tối giản (mâu thuẫn giả thiết) b
Từ đóy suy ra 5 là số vô tỉ (điều phải chứng minh)
b. Coi 9  5  a , giả sử 9  5 là số hữu tỉ nên a cũng là số hữu tỉ 2 2
9  5  a  9  5  a  9  a  5
Vì a là số hữu tỷ => 2
a cũng là số hữu tỉ
=> 5 cũng là số hữu tỉ (điều này sai vì 5 là số vô tỉ, chứng minh trên)
Từ đó suy ra 9  5 là số vô tỉ (điều phải chứng minh)
Nhận xét: Qua bài toán này, ta ghi nhớ kết quả sau: nếu có số tự nhiên a không phải là số 39
BÀI TẬP TRẮC NGHIỆM TOÁN 7
chính phương thì a là số vô tỉ. Nếu số tự nhiên a là số chính phương thì a là số tự nhiên.
Ví dụ 3 (Vận dụng) Tìm giá trị lớn nhất của: 7 a. I = 7  2 x  3 b. H = x  3 Giải:
Phương pháp: để tìm GTLN của M, ta phải tìm một sô thuwcjr (không chứa x) để M  r và ở
đây xảy ra đượcM =r khi x bằng bao nhiêu. a. Vì x  3  0 nên 2 
x  3  0 , suy ra 7  2 x  3  7 hay I  7
I =7 khi x  3  0 hay x =3. 7 7 7
b. x  0 nên x  3  3, suy ra  hay H  x  3 3 3 7 H =
khi x  3  3 hay x =0 3 7
Kết luận: h đạt giá trị lớn nhất là khi và chỉ khi x =0 3 7
Ví dụ 4 (Vận dụng cao) . Cho H = với x  0 x  3
a. Tìm x   để H có giá trị nguyên.
b. Tìm x  Q để H có giá trị nguyên Giải:
a. Khi x là số tự nhiên thì x hoặc là số tự nhiên (nếu x là số chính phương) hoặc là số vô tỉ 7
(nếu x không phải là số chính phương) . Để H  là số nguyên thì x phải là số tự x  3
nhiên và  x  3  phải là ước của 7
Do đó chỉ xảy ra x  3  7 (vì ước của 7 là -7; -1; 1; 7 và x  3  3)
Suy ra x  4 hay x =16 Kết luận x =16 40
BÀI TẬP TRẮC NGHIỆM TOÁN 7 7 7 7 7 b. Ta có:  0 , theo ví dụ 3 thì  . Hay 0  H  x  3 x  3 3 3
Do H có giá trị nguyên nên H = 1 hoặc H = 2 7 Xét H =1   1  x  3  7 
x  4  x  16 x  3 7 1 Xét H =2 
 2  2 x  3  7  2 x  6  7  2 x  1 x  x  3 4 1 Kết luận: x  ; x  16 4 3. Câu hỏi trắc nghiệm
Câu 1: Trong các số sau đây, số nào không có căn bậc hai? 1 A. . -2 B. C. 0 D. 0, 3 3
Câu 2: Phát biểu nào dưới đây đúng? 2
A. Số dương 2 chỉ có một căn bậc hai B. là một số thực 3 11 C. Số là một số vô tỉ D. 5 là một số vô tỉ 14
Câu 3: Phát biểu nào dưới đây sai?
A. Số 19 là một số tự nhiên
B. Số -2 là một số nguyên âm 2 C. Số là một số vô tỉ D. 2 là một số vô tỉ 7
Câu 4: Số nào dưới đây số vô tỉ? 2  A. 144 B. 0, (121) C. 0, 0100100011… D. 3 1
Câu 5: Trong các số sau đây, số nào bằng ? 2 4  9 4  9 81  25 4 A. B. C. D. 16  2 2 23  625 1 21 2 9
Câu 6: Số dương 9 có hai căn bậc hai là A.  9  3  và 9  3 B. 2 9  3 C.  9  81  và 9  81 D. 9  3 41
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Câu 7: Nếu x  4 thì x bằng: A. x = -2 B. x =2 C.. x = -16 D. x = 16 Câu 8: Nếu x  4 thì 2 x bằng: A. 2 x  8  1 B. 2 x  9 C. 2 x  3 D. 2 x  81
Câu 9: Phép tính nào dưới đây đúng: A. 100  10 B.  5  5  C. 9   3  D. 9  3 Câu 10: Hãy tính  2 16  A.  2 16  16  B.  2 16  4  C.  2 16  4 D.  2 16  16
Câu 11: Chọn câu trả lời đúng: nếu a là số vô tỉ thì:
A. a cũng là số tự nhiên B. a cũng là số nguyên C. a cũng là số hữu tỉ D. a cũng là số thực
Câu 12: Phát biểu nào dưới đây sai?
A. Số vô tỉ là số viết đợc dưới dạng số thập phân vô hạn không tuần hoàn
B. Số hữu tỉ và số vô tỉ được gọi chung là số thực
C. Chỉ có số 0 không phải số hữu tỉ dương và cũng không là số hữu tỉ âm.
D. Mỗi điểm trên trục số đều biểu diễn một số hữu tỉ
Câu 13: Giá trị lớn nhất của H  6  x 1 là: A. 7 B. 6 C. 5 D. 0 13
Câu 14: Sắp xếp các số sau theo thứ ự từ nhỏ đến lớn: 5; 2; ;  10;10 4 13 13 A.  10; 5; 2; ;10 B.  10; 2; 5; ; ;10 4 4 13 13 C.  10; 2; 5; ; ;10 D.  10; 2; ; 5; ;10 4 4 x  5 Câu 15: Cho H 
. Hỏi có bao nhiêu số nguyên x và x < 100 để H có giá trị nguyên? 3 A. 2 B. 3 C. 4 D. 50 9 Câu 16: Cho H 
Hỏi có bao nhiêu số nguyên x để H có giá trị nguyên? x  2 42
BÀI TẬP TRẮC NGHIỆM TOÁN 7 A. 2 B. 3 C. 5 D. 6
MA TRẬN CÂU HỎI TNKQ TRONG CÁC CHỦ ĐỀ 7 Mức dộ chủ Nhận biết Vận dụng (câu) Thông hiểu (câu) đề (câu) Thấp Cao 1, 2, 3, 4, 6, 9, 7 5, 7, 8, 12, 13, 14 15 16 10, 11 43
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Chủ đề 8. ĐẠI LƯỢNG TỈ LỆ THUẬN. ĐẠI LƯỢNG TỈ LỆ NGHỊCH
1. Một số vấn đề cần ôn tập
Nếu đại lượng y liên hệ với đại lượng x theo công thức y  kx (với k là hằng số
khác 0 ) thì ta nói y tỉ lệ thuận với x theo hệ số tỉ lệ k .
Nếu y tỉ lệ thuận với x theo hệ số tỉ lệ k (với k  0 ) thì x tỉ lệ thuận với y theo hệ 1 số tỉ lệ là
và ta nói hai đại lượng đó tỉ lệ thuận với nhau. k
Giả sử y và x tỉ lệ thuận với nhau: y  kx (với k là hằng số khác 0 ) . Khi đó, với
mỗi giá trị x , x , x , ... khác 0 của x ta có một giá trị tương ứng y  kx , y  kx , y  kx , ... 1 2 3 1 1 2 2 3 3
của y và luôn có: y y y x y x y x y 1 2 3    ...  k 1 1 1 1 2 2  ;  ;  ;... x x x x y x y x y 1 2 3 2 2 3 3 3 3 a
Nếu đại lượng y liên hệ với đại lượng x theo công thức y 
hay xy  a (với a là x
hằng số khác 0 ) thì ta nói hai đại lượng đó tỉ lệ nghịch với nhau. a
Giả sử y và x tỉ lệ nghịch với nhau: y 
(với a là hằng số khác 0 ) . Khi đó, với x a a a
mỗi giá trị x , x , x , ... khác 0 của x ta có một giá trị tương ứng y  , y  , y  ,... 1 2 3 1 2 3 x x x 1 2 3
của y và luôn có: x y x y x y
x y  x y  x y  ...  a 1 2 1 3 2 3  ;  ;  ;... 1 1 2 2 3 3 x y x y x y 2 1 3 1 3 2 2. Ví dụ
Ví dụ 1 (Nhận biết) . Cho x và y là hai đại lượng tỉ lệ thuận biết x  x  5 và hai giá trị 1 2
tương ứng y  y  50 . Tìm hệ số tỉ lệ của y đối với x . 1 2 Giải
x và y là hai đại lượng tỉ lệ thuận nên giả sử y  kx k  0 .
Từ y  y  50 có kx  kx  50 hay k  x  x  50 thay x  x  5 ta tìm được k  10 . 1 2  1 2 1 2 1 2
Kết luận: hệ số tỉ lệ của y đối với x là k  10 .
Ví dụ 2 (Thông hiểu) . Cho x và y là hai đại lượng tỉ lệ nghịch với nhau khi x nhận các giá
trị x  2; x  3 thì tổng các giá trị tương ứng của y là 25. Hãy biểu diễn y theo x . 1 2 44
BÀI TẬP TRẮC NGHIỆM TOÁN 7 Giải a
x và y là hai đại lượng tỉ lệ nghịch nên giả sử y  . x a a
Từ giả thiết có y  , y 
và y  y  25 1 2 2 3 1 2 a a 3a  2a Suy ra   25 
 25  5a  25.6  a  30 2 3 6 30
Kết luận: biểu diễn của y theo x là y  . x
Ví dụ 3 (Vận dụng) . Một ô tô đi từ A đến B với vận tốc 60 km/h và từ B trở về A với vận tốc
80 km/h. Thời gian cả đi lẫn về là 1 giờ 45 phút. Tính thời gian đi, thời gian về và độ dài quãng đường AB. Giải
x và y là thời gian đi và thời gian về (giờ, x  0, y  0 ) . 3 7
Thời gian cả đi lẫn về là 1 giờ 45 phút, nên có x  y  1 hay x  y  . 4 4
Thời gian và vận tốc đi trên một đoạn đường là hai đại lượng tỉ lệ nghịch, nên ta có 60x  80 y x y hay  . 4 3 x y x  y 7 1
Theo tính chất của dãy tỉ số bằng nhau ta có    : 7  . 4 3 4  3 4 4 x 1 y 1 3 Suy ra  hay x  1,  hay y  4 4 3 4 4
Kết luận: thời gian đi là 1 giờ, thời gian về là 45 phút, độ dài quãng đường AB bằng 60 km.
Nhận xét: đây là một bài toán về đại lượng tỉ lệ nghịch, mà quãng đường chính là hệ số tỉ lệ a .
Trong bài giải ta nên sử dụng tính chất của dãy tỉ số bằng nhau để giải cho gọn.
Ví dụ 4 (Vận dụng cao) . Hỏi trên một chiếc đồng hồ khi kim giờ quay được một vòng thì
kim phút, kim giây quay được bao nhiêu vòng? Giải
Ta đã biết 1 giờ  60 phút, 1 phút  60 giây. 45
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Do đó khi kim giờ đi được 1 giờ thì kim phút đi được 1 vòng, vậy trên mặt chiếc đồng
hồ khi kim giờ quay được 1 vòng (tức là kim giờ đi được 12 giờ) thì kim phút quay được 1.12  12 (vòng) .
Kim phút đi được 1 phút thì kim giây đi được 1 vòng, vậy trên mặt chiếc đồng hồ khi
kim phút quay được 1 vòng (tức là kim phút đi được 60 phút hay kim giờ đi được 1 giờ) thì
kim giây quay được (vòng) . Nên kim phút quay được 12 vòng thì kim giây quay được 12.60  720 (vòng) .
Kết luận: trên mặt chiếc đồng hồ khi kim giờ quay được 1 vòng thì kim phút quay
được 12 vòng và kim giây quay được 720 vòng.
Nhận xét: đây là một bài toán về đại lượng tỉ lệ thuận. Nếu gọi x, y, z theo thứ tự là
số vòng quay của kim giờ, kim phút, kim giây trong cùng một thời gian thì
y  12x, z  60 y, z  720 . x 3. Câu hỏi trắc nghiệm
Câu 1. Các giá trị tương ứng của hai đại lượng x và y được cho trong các bảng dưới đây, hỏi
bảng nào thể hiện hai đại lượng x và y tỉ lệ thuận với nhau A. x x  2  x  2 x  3 x  5 1 2 3 4 y y  6 y  6  y  9  y  15  1 2 3 4 B. x x  2  x  2 x  3 x  5 1 2 3 4 y y  6 y  6 y  9  y  15 1 2 3 4 C. x x  2 x  2 x  3 x  5 1 2 3 4 y y  6 y  6 y  9  y  15 1 2 3 4 D. x x  2  x  2 x  3 x  5 1 2 3 4 y y  6 y  6  y  9  y  15  1 2 3 4
Câu 2. Các giá trị tương ứng của hai đại lượng x và y được cho trong các bảng dưới đây, hỏi
bảng nào thể hiện hai đại lượng x và y tỉ lệ nghịch với nhau? A. x x  2  x  2 x  3 x  6 1 2 3 4 y y  3 y  3  y  2  y  1  1 2 3 4 46
BÀI TẬP TRẮC NGHIỆM TOÁN 7 B. x x  6 x  2  x  3 x  10 1 2 3 4 y y  6 y  6 y  9  y  15 1 2 3 4 C. x x  2  x  2 x  3 x  5 1 2 3 4 y y  6 y  6  y  9  y  15  1 2 3 4 D. x x  2 x  2 x  3 x  5 1 2 3 4 y
y  6 y  6 y  9  y  15 1 2 3 4
Câu 3. Hai đại lượng x và y tỉ lệ nghịch. Giá trị của y và x trong ô sau là: 1 3 x x  2 1 y y y  3 y  2 1 2 3
A. y  12, x  12 . B. y  1  2, x  12 . 1 3 1 3
C. y  12, x  12  .
D. y  1, x  1. 1 3 1 3
Câu 5. Cho biết hai đại lượng y và x tỉ lệ thuận với nhau, khi x  3 thì y  2 . Hỏi y tỉ lệ
thuận với x theo tỉ lệ k bằng 3 2 A. k  . B. k  . C. k  3. D. k  2 . 2 3
Câu 6. Cho biết hai đại lượng y và x tỉ lệ thuận với nhau, khi x  5 thì y  3 . Hỏi x tỉ lệ
thuận với y theo tỉ lệ k bằng 3 5 A. k  . B. k  3. C. k  5 . D. k  . 5 3 3 5
Câu 7. Cho biết hai đại lượng y và x tỉ lệ nghịch với nhau, với x  , y  . Hỏi hai đại 5 6
lượng x và y tỉ lệ nghịch với nhau theo hệ số tỉ lệ k bằng 9 2 5 A. k  2 . B. k  . C. k  . D. k  . 10 5 2
Câu 8. Khẳng định nào dưới đây thể hiện hai đại lượng tỉ lệ thuận với nhau?
A. Chiều dài và chiều rộng của hình chữ nhật có diện tích cho trước.
B. Năng suất lao động và thời gian để làm xong một công việc.
C. Vận tốc và thời gian khi đi trên cùng quãng đường. 47
BÀI TẬP TRẮC NGHIỆM TOÁN 7
D. Chu vi và bán kính của một đường tròn.
Câu 9. Cho biết y tỉ lệ thuận với x theo hệ số tỉ lệ a , x tỉ lệ thuận với z theo hệ số tỉ lệ b ,
a, b  0 thì y tỉ lệ thuận với z theo hệ số tỉ lệ bằng a b A. . B. ab . C. .
D. Cả ba câu A; B; C đều sai. b a
Câu 10. Chọn câu trả lời đúng. Các máy bơm có cùng công suất bơm nước vào cùng một bể chứa thì
A. Số lượng máy bơm tỉ lệ thuận với thời gian bơm đầy bể chứa.
B. Thời gian bơm đầy bể chứa không tỉ lệ với số máy bơm.
C. Số lượng máy bơm tỉ lệ nghịch với thời gian bơm đầy bể chứa.
D. Thời gian bơm đầy bể chứa tỉ lệ thuận với công suất máy bơm.
Câu 11. Đại lượng y tỉ lệ thuận với đại lượng x nếu k A. x  ky . B. y  . x 1
C. y  kx với hằng số k  0 . D. y  . x
Câu 12. Công thức nào dưới đây thể hiện x và y là hai đại lượng tỉ lệ nghịch x y x 3 A.  . B.  . C. x  2 y
D. y  x  5 . 2 3 2 y
Câu 13. Đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ 9 khi A. x  9 y . B. y  9x . C. xy  9
D. x  y  9 . 1
Câu 14. Đại lượng x tỉ lệ thuận với đại lượng y theo hệ số tỉ lệ khi 3 1 1 A. xy  3 . B. xy  . C. x  3y D. y  x . 3 3 Câu 15. Cho bốn số ; a ; b ;
c d . Biết rằng a : b  2 : 3 ; b : c  4 : 5 ; c : d  6 : 7 . Thế thì
a : b : c : d bằng A. 8 :12 :15 :13 . B. 16 : 24 : 32 : 35 . C. 4 :12 : 6 : 7 D. 16 : 24 : 30 : 35 . 48
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Câu 16. Chia số 104 thành ba phần tỉ lệ nghịch với 2 : 3 : 4 thì số nhỏ nhất trong ba số được chia là A. 12 . B. 21 . C. 24 D. 48.
MA TRẬN CÂU HỎI TNKQ CHỦ ĐỀ 8 Mức độ Vận dụng (câu) Nhận biết (câu) Thông hiểu (câu) Chủ đề Thấp Cao 3; 4; 5; 6; 7; 12; 8 1; 2; 8; 11 9; 10; 15 16 13; 14
Chủ đề 9. HÀM SỐ. ĐỒ THỊ CỦA HÀM SỐ y  ax a  0
1. Một số vấn đề cần ôn tập
Nếu đại lượng y phụ thuộc vào đại lượng thay đối x sao cho với mỗi giá trị của x ta
luôn xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x và x gọi
là biến số (gọi tắt là biến)
Nếu x thay đổi mà y không thay đổi thì y được gọi là hàm hằng.
Đồ thị của hàm số y  f  x là tập hợp tất cả các điểm biểu diễn các cặp giá trị tương ứng  ;
x y trên mặt phẳng tọa độ.
Đồ thị hàm số y  f  x  ax a  0 là một đường thẳng đi qua gốc tọa độ.
Để vẽ đồ thị hàm số y  ax a  0 , ta chỉ cần vẽ một đường thẳng đi qua hai điểm là
O 0; 0 và A1; a . 2. Ví dụ 3
Ví dụ 1 (Nhận biết) . Cho hàm số y 
có đồ thị là C  x
a. Tìm tọa độ của ba điểm bất kỳ thuộc đồ thị là C  . 9
b. Điểm M  x ; y
thuộc đồ thị C  có tung độ y  . Tìm hoành độ x . 0 0  0 2 0 Giải
a. Để tìm tọa độ của ba điểm bất kỳ trên C  , rất đơn giản ta chỉ cần cho biến số x ba giá trị
bất kì để tìm ra y , từ đó tìm ra tọa độ của ba điểm thuộc đồ thị là C  : 49
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Chọn x  1 suy ra y  3 Chọn x  1  suy ra y  3 
Chọn x  3 suy ra y  1
Kết luận: tọa độ của ba điểm bất kỳ thuộc C  là A1; 3, B  1
 ;  3, C 3;  1 . 3 9
b. Điểm M  x ; y thuộc đồ thị C  , nên có y  , lại có y  0 0  0 x 0 2 0  9  2 2 Suy ra x  3 :
hay x  3. hay x  . 0   0 0  2  9 3 2 Kết luận: x  . 0 3
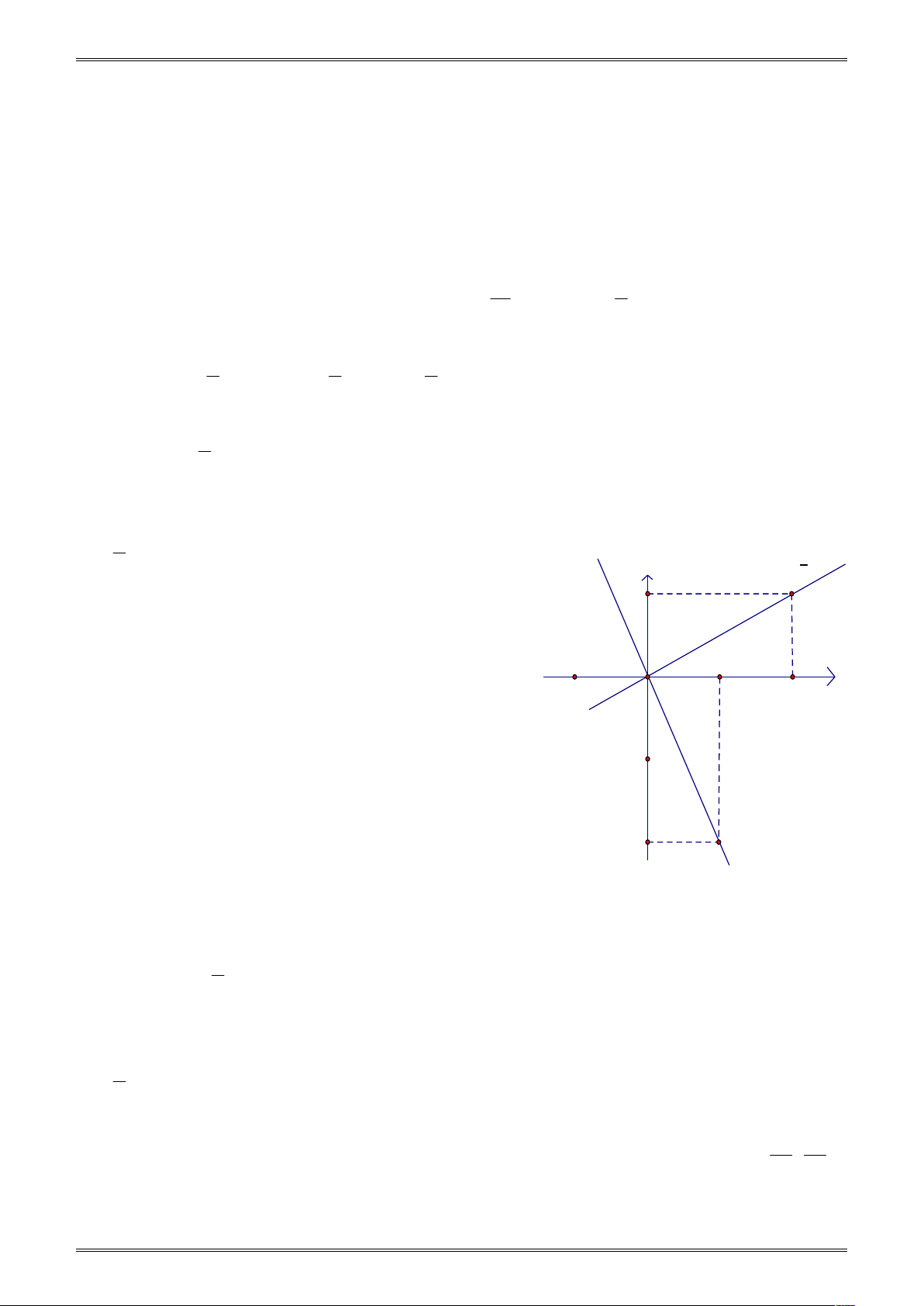
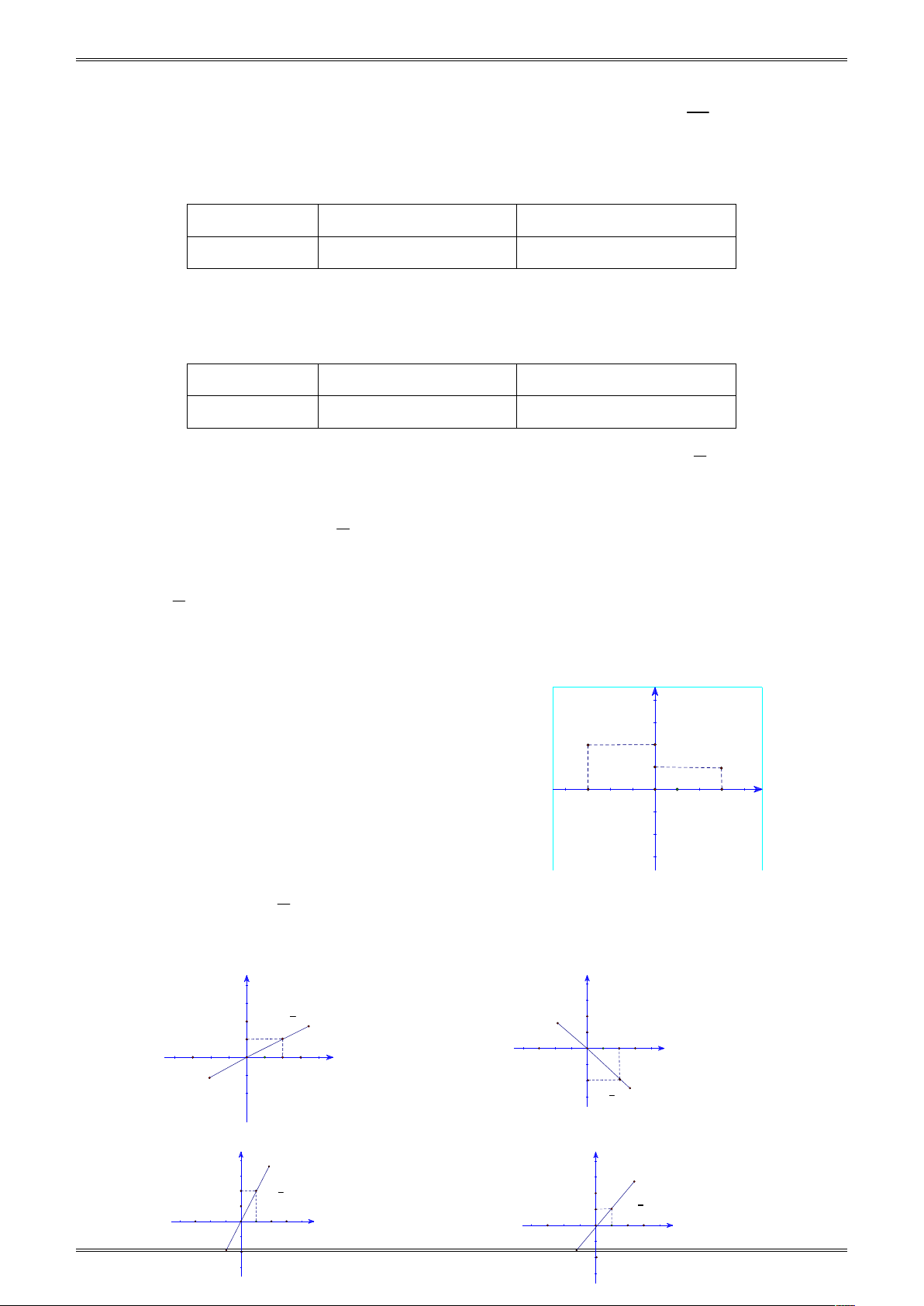
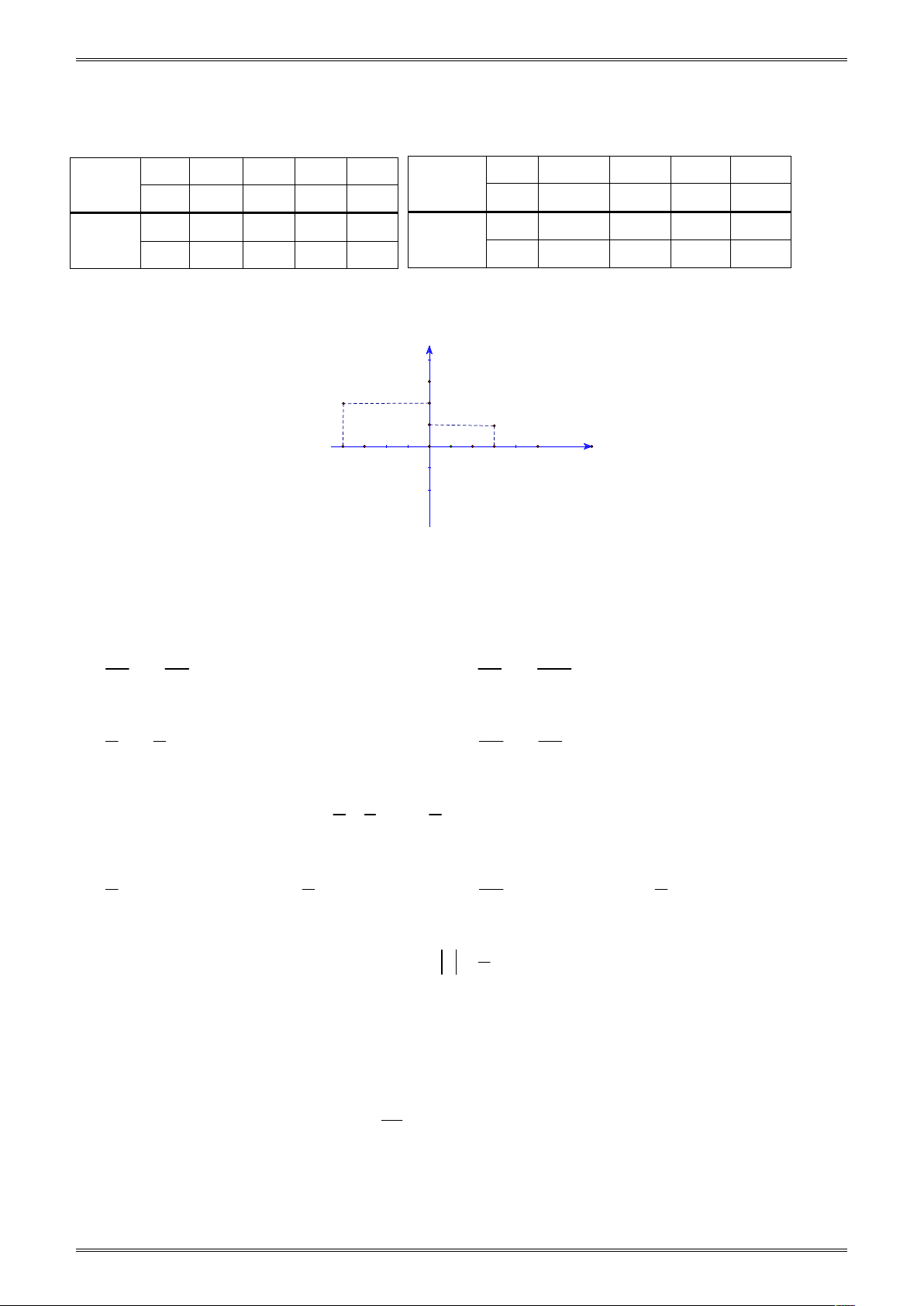
Ví dụ 2 (Thông hiểu) . Vẽ trên cùng mặt phẳng tọa độ Oxy đồ thị của hai hàm số y  2  x và 1 y  x . 1 2 y= x 2 1 Giải N
Hai hàm số trong bài này có đồ thị là hai -1 1
đường thẳng đi qua gốc tọa độ, nên để vẽ chúng ta cần O 2
chọn thêm mỗi đồ thị một điểm nữa không phải là gốc
tọa độ, đường thẳng đi qua điểm đó và gốc tọa độ là đồ thị cần vẽ. -1 Với hàm số y  2
 x , nếu chọn x  1 thì y  2
 , nên M 1;  2 thuộc đồ thị của hàm số này. M -2 y=-2x
Vẽ hệ trục tọa độ Oxy và xác định điểm
M 1;  2 , đường thẳng OM là đồ thị của hàm số y  2  x . 1 Với hàm số y 
x , nếu chọn x  2 thì y  1, nên N 2; 
1 thuộc đồ thị của hàm số này. 2
Vẽ hệ trục tọa độ Oxy và xác định điểm N 2; 
1 , đường thẳng ON là đồ thị của hàm số 1 y  x . 2  1  1  
Ví dụ 3 (Vận dụng) . Tìm m để đồ thị của hàm số 2
y  x  2m đi qua điểm M ; .    2 3 
Với giá trị m tìm được, hỏi đồ thị của hàm số này có cắt được trục hoành không? 50
BÀI TẬP TRẮC NGHIỆM TOÁN 7 Giải  1  1   1  1  Điểm M ; 
 thuộc đồ thị của hàm số 2
y    2m, nên thay x  và y   2 3  2 3 vào hàm số ta được 2 1   1   1  1 1  1    2m   
 2m  2m     3  2  3 4 3 4 4   3 1   2m   m  12 24 1  2 Khi m  , hàm số 2
y  x  2m trở thành 2 y  x  24 24 2  Rõ ràng 2 x 
 0 nên y  0 , nên các điểm thuộc đồ thị đều có tung độ âm. Mà 24
các điểm thuộc trục hoành đều có tung độ bằng 0. 1 Nên khi m 
đồ thị của hàm số này không cắt được trục hoành. 24 1 
Ví dụ 4 (Vận dụng cao) . Trong mặt phẳng tọa độ Oxy , cho hàm số y 
x . Gọi M  x ; y 0 0  2
là điểm thuộc đồ thị của hàm số, sao cho 3 3
x  y  56 . Tính giá trị của  2 4 4x  2 y 0 0  0 0 Giải 1 
M  x ; y là điểm thuộc đồ thị của hàm số y 
x , nên thay x  x , y  y vào 0 0  2 0 0 1 hàm số ta có y  x . 0 0 2 3  1   1 Lại có 3 3 3 3 3
x  y  56  x  x  56  x  x  56 0 0 0  0  0 0  2  8 3 3 8x  x 8.56 0 0 3 3 3 
 56  7x  8.56  x 
 x  64  x  4 0 0 0 0 8 7
Với x  4 ta được y  2  0 0
Giá trị của 4x  2y   4.4  2. 2  4 2 4 2  64  32  32 . 0 0 3. Câu hỏi trắc nghiệm 51
BÀI TẬP TRẮC NGHIỆM TOÁN 7 Cho phương án ,
A B, C, D trong mỗi câu hỏi, khoanh tròn vào phương án trả lời đúng trong mỗi câu sau.
Câu 1. Bảng giá trị tương ứng nào dưới đây thể hiện đại lượng y là hàm số của đại lượng x Bảng 1 x 2  1  2  3 y 4 1 4  9 Bảng 2 x 1  1  2 3 y 7 8 7 7 Bảng 3 x 2  1  2  5 y 6  3  6 15 Bảng 4 x 6 3  6 10 y 6  10  6  3 A. Bảng 1. B. Bảng 2. C. Bảng 3. D. Bảng 4. 5 1
Câu 2. Cho hàm số y  f  x  x  , kết quả nào dưới đây đúng 6 8 216 10 2 3 A. . B. . C. . D. . 5 3 3 2
Câu 2. Cho hàm số y  f  x 2
 3  x , kết quả nào dưới đây sai?  1  11  1  26 A. f    . B. f    . C. f  2    7 . D. f 3  6  .  2  4  3  9 52
BÀI TẬP TRẮC NGHIỆM TOÁN 7
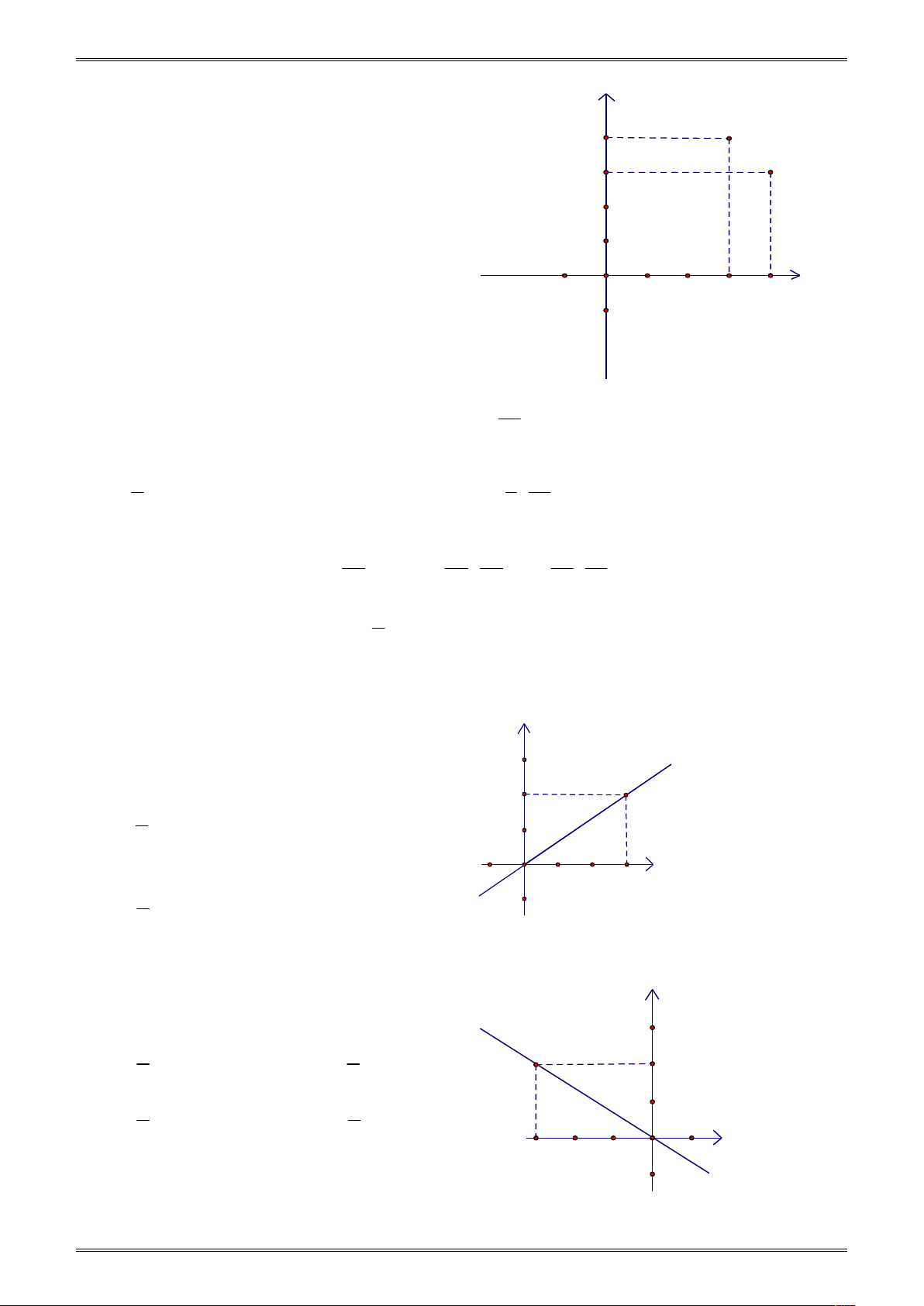
Câu 5. Tìm tọa độ các điểm M , N , P, Q y trong hình bên N 4
A. M 4; 3, N 3; 4, P  2
 ; 0, Q 0;  2 . M 3
B. M 3; 4, N 4; 3, P  2
 ; 0, Q 0;  2 . 2
C. M 4; 3, N 3; 4, P 0;  2, Q 2; 0 . 1
D. M 3; 4, N 4; 3, P 0;  2, Q 2; 0 . -2 -1 O 1 2 3 4 x -1 1 
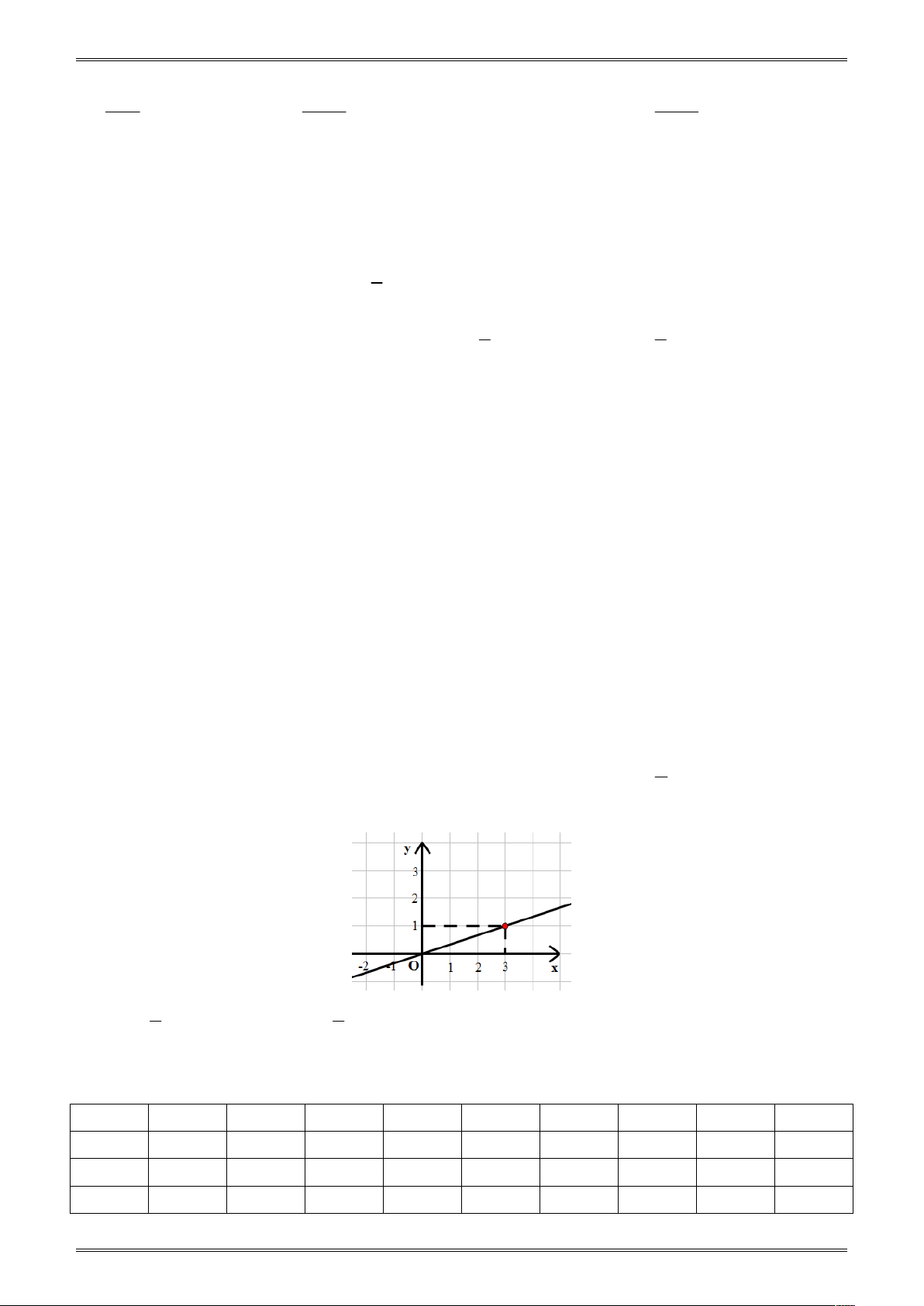
Câu 6. Điểm nào dưới đây thuộc đồ thị hàm số y  x . 2  1   1 1   A. A ;  4   . B. B 2;  1 . C. C ;   . D. D 4; 2 .  2   3 6   3    9  3    1  1  
Câu 7. Trong các điểm sau: A ; 1 , B ; , C ; , D      
3;  2 ; điểm nào thuộc  2   4 2   6 9  2
không thuộc đồ thị của hàm số y  x . 3 A. Điểm A. B. Điểm B. C. Điểm C. D. Điểm D.
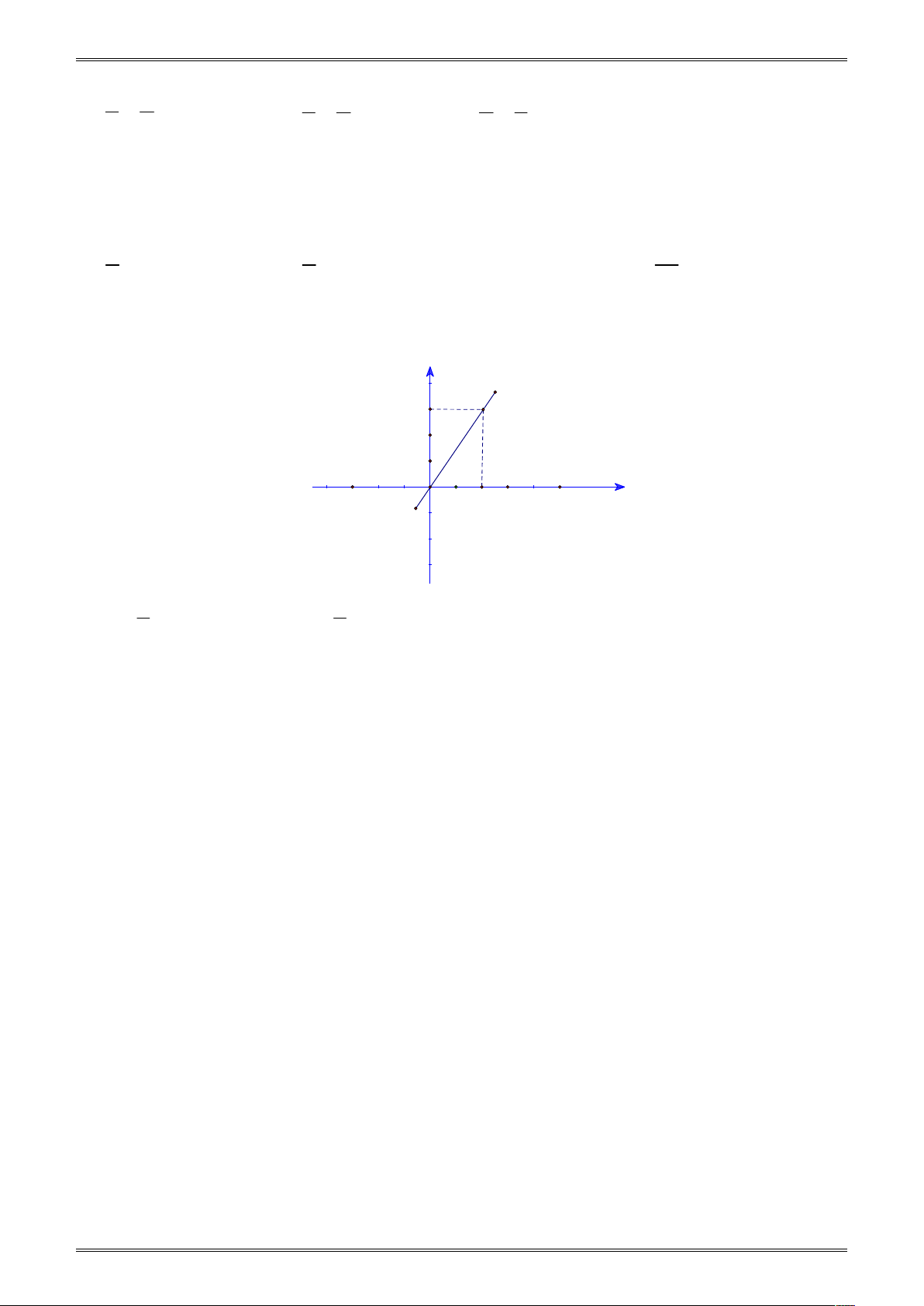
Câu 8. Đường thẳng OA ở hình bên là đồ thị y
của hàm số y  ax , xác định hệ số a 3 A. a  0 . A 2 2 B. a  . 1 3 C. a  0 . -1 O 1 2 3 x 3 D. a  . -1 2
Câu 9. Đường thẳng OB ở hình bên là đồ thị y
của hàm số y  ax , xác định hệ số 3 2 2 B A. a  . B. a   . 2 3 3 3 3 1 C. a  . D. a   . 2 2 -3 -2 -1 O 1 x -1 53
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Câu 10. Một điểm bất kì trên trục hoành có tung độ bằng: A. Hoành độ. B. 0 . C. 1 . D. 1  .
Câu 11. Một điểm bất kì trên trục tung có hoành độ bằng: A. Tung độ. B. 0 . C. 1 . D. 1  .
Câu 12. Trong mặt phẳng tọa độ Oxy , khẳng định nào dưới đây sai?
A. Những điểm thuộc góc phần tư thứ I có hoành độ dương và tung độ dương.
B. Những điểm thuộc góc phần tư thứ III có hoành độ âm và tung độ âm.
C. Những điểm thuộc góc phần tư thứ II có hoành độ âm và tung độ dương.
D. Những điểm thuộc góc phần tư thứ IV có tung độ dương.
Câu 13. Trong mặt phẳng tọa độ Oxy , cho bốn điểm A1; 2, B  2  ; 5, C  2
 ; 2, D 9; 5 .
Các đoạn thẳng song song với trục hoành là: A. AB và CD . B. AD và BC . C. AC và BD . D. AB .
Câu 14. Trong mặt phẳng tọa độ Oxy , cho bốn điểm A9; 2, B 0;  5, C 0; 12, D 9;  8 .
Đoạn thẳng song song với trục tung là: A. AB và CD . B. AD và BC . C. AC và BD . D. AD .
Câu 15. Trong mặt phẳng tọa độ Oxy , cho bốn điểm A1; 2, B 2; 0, C  2
 ;  2, D 3; 0 .
Hỏi tứ giác ABCD là hình gì?
A. ABCD là hình bình hành.
B. ABCD là hình chữ nhật.
C. ABCD là hình thoi.
D. ABCD là hình vuông. 1 
Câu 16. Trong mặt phẳng tọa độ Oxy , cho hàm số y 
x . Gọi M  x ; y là điểm thuộc đồ 0 0  3 13
thị của hàm số, sao cho 3 3 x  y  . Tính giá trị của  2 2 x  y 0 0  0 0 4 5 A. 5  . B. 1 . C. 2 . D. . 2
MA TRẬN CÂU HỎI TNKQ CHỦ ĐỀ 9 Mức độ Vận dụng (câu) Nhận biết (câu) Thông hiểu (câu) Chủ đề Thấp Cao 9 1; 2; 3; 4; 5 6; 7; 8; 9; 10; 11 12; 13; 14 15; 16 54
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Chủ đề 10. THỐNG KÊ
1. Một số vấn đề cần ôn tập
Thu thập số liệu về vấn đề được quan tâm, các số liệu được ghi lại trong một bảng, gọi
là bảng số liệu thống kê ban đầu.
Vấn đề hay hiện tượng mà người điều tra quan tâm tìm hiểu gọi là dấu hiệu (thường kí
hiệu bằng các chữ cái in hoa X , Y ,... ) . Mỗi đơn vị trong dấu hiệu là một đơn vị điều tra.
Ứng với mỗi đơn vị điều tra có một số liệu, số liệu đó gọi là một giá trị của dấu hiệu
(thường được kí hiệu là x ) . Số tất cả các giá trị (không nhất thiết khác nhau) của dấu hiệu
bằng số các đơn vị điều tra (thường được kí hiệu là N ) .
Số lần xuất hiện của một giá trị trong dãy giá trị của dấu hiệu được gọi là tần số của
giá trị đó (thường được kí hiệu là n ) .
Số trung bình cộng là giá trị trung bình của dấu hiệu (thường được kí hiệu là X ) . Số
trung bình cộng thường được dùng làm “đại diện” cho dấu hiệu, đặc biệt là khi muốn so sánh
các dấu hiệu cùng loại.
Mốt của dấu hiệu là giá trị có tần số lớn nhất trong bảng tần số, kí hiệu M . 0 2. Ví dụ
Khi điều tra về điểm kiểm tra học kỳ 2 môn toán của 40 học sinh lớp 7A được kết quả như sau: 8 8 8 8 9 5 5 4 6 7 10 8 9 6 7 8 8 8 9 7 6 5 8 10 8 6 9 4 10 9 7 5 8 7 6 9 5 6 7 8
a. Dấu hiệu ở đây là gì? Hãy nêu các giá trị khác nhau của dấu hiệu.
b. Lập bảng tần số, tính điểm trung bình bài kiểm tra của lớp 7A (làm tròn đến chữ số thập phân thứ nhất) .
c. Tìm mốt của dấu hiệu.
d. Vẽ biểu đồ đoạn thẳng. Giải
a. Dấu hiệu là điểm kiểm tra học kỳ 2 môn toán của 40 học sinh lớp 7A.
Các giá trị khác nhau của dấu hiệu: 4, 5, 6, 7, 8, 9, 10 . b. Bảng tần số 55
BÀI TẬP TRẮC NGHIỆM TOÁN 7 Giá trị  x 4 5 6 7 8 9 10 Tần số n 2 5 6 6 12 6 3 N  40
Điểm trung bình bài kiểm tra của lớp 7A
4.2  5.5  6.6  7.6  8.12  9.6 10.3 12 X   7,3 . 11 40 10
c. Mốt của dấu hiệu là M  8 . 9 0 8
d. Biểu đồ đoạn thẳng ở hình bên. 7 6 5 4 3 2 1 3. Câu hỏi trắc nghiệm O 1 2 3 4 5 6 7 8 9 10
Câu 1. Chọn câu trả lời sai.
A. Số các giá trị (không nhất thiết khác nhau) của dấu hiệu đúng bằng số các đơn vị điều tra.
B. Các số liệu thu thập được khi điều tra về một dấu hiệu gọi là số liệu thống kê.
C. Tần số của một giá trị là số các đơn vị điều tra.
D. Số lần xuất hiện của một giá trị trong dãy giá trị của dấu hiệu là tần số của giá trị đó.
Sử dụng dữ kiện sau để giải câu 2, câu 3, câu 4, câu 5
Biểu đồ dân số Việt Nam qua tổng điều tra trong thế kỉ XX 76
(đơn vị của các cột là triệu người) . 66
Câu 2. Chọn câu trả lời sai. 54
A. Năm 1921 số dân của nước ta là 16 triệu người.
B. Năm 1960 số dân của nước ta là 30 nghìn người.
C. Năm 1990 số dân của nước ta là 66 triệu người. 30
D. Năm 1999 số dân của nước ta là 76 triệu người.
Câu 3. Từ năm 1980 đến năm 1999, dân số nước ta tăng 16 thêm bao nhiêu? A. 60 triệu người. B. 46 triệu người. 1921 1960 1980 1990 1999 C. 16 triệu người. D. 22 triệu người. 56
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Câu 4. Năm 1999, dân số nước ta là bao nhiêu? A. 76 triệu người. B. 76 nghìn người. C. 66 triệu người. D. 16 triệu người.
Câu 5. Sau bao nhiêu năm (kể từ năm 1960) thì dân số nước ta tăng thêm 36 triệu người? A. Sau 10 năm. B. Sau 20 năm. C. Sau 30 năm. D. Sau 40 năm.
Sử dụng bảng thống kê ban đầu, hãy trả lời các câu 6, câu 7, câu 8, câu 9, câu 10
Khi điều tra về số bộ quần áo quyên góp vì người nghèo của các lớp 7 trong trường,
người điều tra lập bảng dưới đây: Lớp 7A 7B 7C 7D 7E 7G Số bộ quần áo 75 80 90 100 80 90
Câu 6. Dấu hiệu cần tìm hiểu ở bảng trên là:
A. Số các lớp 7 trong trường.
B. Số bộ quần áo quyên góp vì người nghèo của các lớp 7. C. Cả A và B đều đúng. D. Cả A và B đều sai.
Câu 7. Trong bảng trên có bao nhiêu đơn vị điều tra?
A. Có 6 đơn vị điều tra.
B. Có 1 đơn vị điều tra. C. Cả A và B đều đúng. D. Cả A và B đều sai.
Câu 8. Câu nói nào dưới đây sai?
A. Mỗi lớp trong bảng trên là một đơn vị điều ta.
B. Trong bảng trên có 6 đơn vị điều tra.
C. Lớp 7D quyên góp được nhiều bộ quần áo nhất.
D. Mốt trong bảng trên là 100 .
Câu 9. Số các giá trị của dấu hiệu ở bảng trên là: A. 1 . B. 4 . C. 5 . D. 6 .
Câu 10. Số các giá trị khác nhau của dấu hiệu ở bảng trên là: A. 1 . B. 4 . C. 5 . 0 D. 6 . 57
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Sử dụng bảng này, hãy trả lời các câu 11, câu 12, câu 13, câu 14
Theo dõi các bạn nghỉ học ở từng buổi trong một tháng, bạn lớp trưởng ghi lại như sau: 0 0 1 0 3 2 0 3 0 1 0 1 1 0 0 1 0 0 1 2 2 2 0 1 0
Câu 11. Có bao nhiêu buổi học trong tháng đó? A. 15 buổi. B. 30 buổi. C. 26 buổi. D. 22 buổi.
Câu 12. Dấu hiệu ở đây là gì?
A. Tổng số lượt học sinh nghỉ học cả tháng B. Là các số 0,1, 2,3
C. Số học sinh nghỉ học trong mỗi buổi
D. Một tháng học 26 buổi
Câu 13. Số buổi có nhiều học sinh nghỉ học nhất là: A. 1 B. 2 C. 3 D. 4
Câu 14. Tần số buổi không có bạn nào nghỉ học là A. 0 B. 12 C. 13 D. 14
Câu 15. Chọn khẳng định đúng nhất. Số trung bình cộng
A. Không được dùng làm “đại diện” cho dấu hiệu.
B. Thường được dùng làm “đại diện” cho dấu hiệu.
C. Không dùng để so sánh các dấu hiệu cùng loại.
D. Cả A, B, C trả lời đều sai.
Câu 16. Điểm thi đua trong các tháng của một năm học của lớp 7G được cho trong bảng sau: Tháng 9 10 11 12 1 2 3 4 5 Điểm 8 9 10 9 8 8 9 7 9
Tính điểm trung bình  X 7 (làm tròn đến chữ số thập phân thứ nhất) và mốt M0 
A. X  8, 6, M  8
B. X  8,5, M  9 o o
C. X  8,5, M  8
D. X  8, 6, M  9 o o
MA TRẬN CÂU HỎI TNKQ CHỦ ĐỀ 10 Mức độ Vận dụng (câu) Nhận biết (câu) Thông hiểu (câu) Chủ đề Thấp Cao 10 2, 3, 4, 5, 11, 13, 14 1, 6, 7, 8, 9, 10, 12, 15 16 58
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Chủ đề 11. KHÁI NIỆM VỀ BIỂU THỨC ĐẠI SỐ - GIÁ TRỊ CỦA MỘT BIỂU THỨC ĐẠI SỐ
1. Một số vấn đề cần ôn tập
Biểu thức đại số là biểu thức gồm các số, các kí hiệu phép toán cộng, trừ, nhân, chia, nâng
lên lũy thừa và các chữ (đại diện cho các số) .
Khi thực hiện các phép toán trên các chữ, ta có thể áp dụng những tính chất, quy tắc phép toán như trên các số.
Để tính giá trị của một biểu thức đại số tại những giá trị cho trước của các biến, ta thay các
giá trị cho trước đó vào biểu thức rồi thực hiện các phép tính. 2. Ví dụ
Ví dụ 1. (Nhận biết) . Viết biểu thức đại số biểu thị tổng các lũy thừa bậc ba của ba số tự
nhiên liên tiếp, có chữ số đầu tiên là a (a  ). Và tính tổng đó khi a  2 . Giải:
Ba của ba số tự nhiên liên tiếp là a, a 1, a  2.
Tổng các lũy thừa bậc ba của ba số tự nhiên liên tiếp là: 3 3 3
a  (a 1)  (a  2)
Khi a  2 , tổng các lũy thừa bậc ba của ba số tự nhiên liên tiếp bằng: 3 3 3
2  (2 1)  (2  2)  8  27  64  99
Ví dụ 2. (Thông hiểu) . Một người lái xe máy với vận tốc v km / h . Viết biểu thức đại số biểu
thị quãng đường đi được của người lái xe trong khoảng thời gian t giờ. Tính quãng đường đi
được khi v  45k /
m h, t  1 giờ 20 phút. Giải:
Biểu thức đại số biểu thị quãng đường đi được là v t (km) 1 4
t = 1 giờ 20 phút hay t  1 giờ hay t  giờ. 3 3 4
Quãng đường đi được khi v  45k /
m h, t  1 giờ 20 phút là 45.  60 (km). 3
Ví dụ 3. (Thông hiểu) . Dùng ngôn ngữ “tổng”, “hiệu”, “tích”, “bình phương” để đọc các biểu thức sau a. x 10 b. xy c. 2 (x  y)
d.  x  y x  y Giải: a. Hiệu của x và 10 b. Tích của x và y
c. Bình phương của tổng x và y
d. Tích của tổng x và y với hiệu của x và y
Ví dụ 4 (Vận dụng) . Bạn X điều khiển chiếc xe đạp chạy từ nhà mình, với vận tốc 12 / km h .
Sau 2 giờ kể từ khi bạn X đi, bố bạn X điều khiển chiếc xe máy cũng chạy từ nhà, với vận tốc 36k /
m h . Tính quãng đường đi được của bạn X trong khoảng thời gian t giờ. Khi t  3 giờ, bố
bạn X đi được bao xa và cho nhận xét? Giải: 59
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Bạn X điều khiển chiếc xe đạp vận tốc12 /
km h trong khoảng thời gian t giờ sẽ đi được
quãng đường là 12t (km)
Nếu bạn X đi t (giờ) (t  2) thì bố bạn X đi t  2 giờ. Do vậy quãng đường bố bạn X đi
được là 36(t  2) (km)
Khi t  3 giờ, bố bạn X đi được 36.(3  2)  36 (km)
Khi t  3 giờ, bạn X đi được 12.3  36 (km)
Nhận xét: Sau khi bạn X đi được 3 giờ thì bố bạn X sẽ gặp được bạn tại một địa điểm cách nhà 36 km. 3. Câu hỏi trắc nghiệm
Câu 1. Câu nói nào dưới đây đúng. Biểu thức đại số biểu thị A. Tổng của a và b là ab
B. Diện tích của một tam giác đều cạnh a là 3a
C. Diện tích hình vuông cạnh a là 4a
D. Tổng của bình phương của a và b là 2 2 a  b
Câu 2. Một ca nô chạy trên sông với vận tốc thực 35 /
km h (nếu dòng nước yên lặng), giả sử
vận tốc dòng nước là x k /
m h (x  35) . Viết biểu thức đại số biểu thị vận tốc ca nô chạy xuôi dòng.
A. (35  x) k / m h
B. (35  x) k / m h
C. (x  35) k / m h D. 35x k / m h
Câu 3. Một bác công nhân được hưởng mức lương x đồng trong một tháng. Do bác công nhân
có nhiều sáng kiến để tăng năng suất lao động, nên trong năm nay bác được thưởng thêm m
đồng. Hỏi bác công nhân nhận được bao nhiêu tiền trong năm (biết một năm có 12 tháng lương) ? A. xm đồng
B. (x  m) đồng
C. (x  m) đồng
D. (12x  m) đồng
Câu 4. Viết biểu thức đại số biểu thị thời gian đi của một xe máy trên quãng đường 120 km với vận tốc x km/h. A. (120 : x) giờ B. 120x giờ C. (x :120) giờ D. 120  x giờ
Câu 5. Biểu thức đại số biểu diễn hai số tự nhiên chẵn liên tiếp là:
A. 2k  2 và 2k (k  )
B. 2k 1 và 2k (k  )
C. 2k và 2k  2 (k  )
D. 2k và 2k 1 (k  )
Câu 6. Biểu thức đại số biểu thị bình phương của một tổng hai chữ số a và b là: A. 2 2 a b B. a  b C. 2 2 a  b D. 2 (a  b)
Câu 7. Biểu thức đại số biểu thị diện tích hình thang có đáy lớn a (m), đáy bé b (cm) và đường cao h (m) là
(a  b)h
(a  0, 01b)h A. 2 (m ) B. 2 (m ) 2 2
(a  b)h C. 2
(a  b)h (m ) D. 2 (c m ) 2 60
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Câu 8. Nền nhà hình chữ nhật có chiều dài 6x (m) và chiều rộng 3y (m) . Dùng gạch lát nền
hình vuông cạnh 30 (cm) để lát nền nhà này. Số gạch cần dùng là: A. 2xy viên B. 6xy viên C. 20xy viên D. 200xy viên
Câu 9. Một vòi nước chảy vào bể nước, mỗi phút được x lít nước. Cùng lúc một vòi khác chảy 1
từ bể ra, mỗi phút lượng nước chảy ra bằng
lượng nước chảy vào. Biểu thị số nước có thêm 2
trong bể sau khi đồng thời mở cả hai vòi trên trong a phút. ax ax A. lít B. ax lít C. 2ax lít D. lít 2 3 1 
Câu 10. Giá trị của biểu thức 2
P  3x  2x 1 tại x  bằng: 3 4  2 A. B. 0 C. 2  D. 3 3 1
Câu 11. Giá trị của biểu thức 3 3
Q  x y  2xy tại x  và y  1  bằng: 3 17 17  19 A. B. C. D. 1 27 27 27 1  1
Câu 12. Giá trị của biểu thức 3 3 4
R  x  y  2z tại x 
, y  1và z  là: 2 2 5  9 9  11 A. B. C. D. 8 8 8 8
MA TRẬN CÂU HỎI TNKQ CHỦ ĐỀ 11 Mức độ Vận dụng (câu) Nhận biết (câu) Thông hiểu (câu) Chủ đề Thấp Cao 11 1, 2, 6, 7, 10 3, 4, 5, 11 9, 12 8 61
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Chủ đề 12. ĐƠN THỨC. ĐƠN THỨC ĐỒNG DẠNG
1. Một số vấn đề cần ôn tập
Đơn thức là biểu thức đại số chỉ gồm một số, hoặc một biến, hoặc một tích giữa các số và
các biến. Số 0 được gọi là đơn thức không.
Đơn thức thu gọn là đơn thức chỉ gồm tích của một số với các biến, mà mỗi biến đã được
nâng lên lũy thừa với số mũ nguyên dương. Số nói trên gọi là hệ số, phần còn lại gọi là phần
biến của đơn thức thu gọn.
Bậc của đơn thức có hệ số khác 0 là tổng số mũ của tất cả các biến trong đơn thức đó. Số
thực khác 0 là đơn thức bậc không. Số 0 được coi là đơn thức không có bậc.
Để nhân hai đơn thức, ta nhân các hệ số với nhau và nhân các phần biến với nhau.
Hai đơn thức đồng dạng là hai đơn thức có hệ số khác 0 và có cùng phần biến.
Để cộng (hay trừ) các đơn thức đồng dạng, ta cộng (hay trừ) các hệ số với nhau và giữ nguyên phần biến. 2. Ví dụ 3  13 
Ví dụ 1 (Nhận biết) . Tính tích của hai đơn thức 5 xy z và 2 2
x yz , sau đó tìm bậc của 5 9 đơn thức thu được Giải: 3  13  Tích của hai đơn thức 5 xy z và 2 2 x yz là 5 9  3    1  3   3  13  5 2 2  xy z . x yz  .       5 xy z  2 2 x yz   5   9   5 9  13   13 2 . x x  5 y .y  2 . z z  3 6 3  x y z 15 15
Đơn thức thu được có biến x có số mũ là 3, biến y có số mũ là 6, biến z có số mũ là 3. Nên
ta có bậc của đơn thức thu được là 12.
Ví dụ 2 (Thông hiểu) . Tính tổng: 7 1  1   7   1 5 3 2 2 2 2 3 2 x y  xy x y  xy x  x y     12 3  2   3  4 6 Giải: 1  1   1 1  1 Ta có 2 xy x y  .     2 . x x  . y y  3 2  x y 3  2   3 2  6  7   1  7  1  7 2 2 xy x  .     2 . x x  2 3 2 y  x y  3  4  3 4  12 7 1  1   7   1 5  7 1 7  5 3 2 2 2 2 3 2  3 2 x y  xy x y  xy x  x y     x y       12 3  2   3  4 6  12 6 12 6   7 7    1 5  3 2 3 2 3 2    
x y  (0 1)x y  x y     12 12 6 6      62
BÀI TẬP TRẮC NGHIỆM TOÁN 7 1 1 
Ví dụ 3 (Thông hiểu) . Tính giá trị của đơn thức 2 3
xy z tại x  0,1; y  8 và z  . 2 3 Giải: 1 1  Thay x  0,1 
, y  8 và z  vào đơn thức ta được 10 3 3 1 1 1  1   1 1  16  2 3 2 xy z  . .8 .  .64.    2 2 10  3  20 27 135 1 16 1
Ví dụ 4 (Vận dụng) . Tìm x để giá trị của đơn thức 3 2 x y bằng tại y  . 4 25 5 Giải: 1 16 1 Đơn thức 3 2 x y bằng tại y  nên ta có: 4 25 5 2 1  1  16 1 1 16 1 16 16 1 3 3 3 3 x .   x .   x   x  :   4  5  25 4 25 25 100 25 25 100 16 3 3  x 
.100  x  64  x  4 25 Kết luận: x  4 3. Câu hỏi trắc nghiệm
Câu 1. Trong các biểu thức sau, biểu thức nào là đơn thức? A. 3 (1  x)x B. x  2 y
C. (xy  z)t D. 2 5 3xy z .
Câu 2. Trong các biểu thức sau, biểu thức nào không là đơn thức?  1 
A. (x  y)z B. 2 2x  y xz   C. 2 3 xy z D. 0.  3 
Câu 3. Biểu thức nào dưới đây là đơn thức thu gọn  1  x 2 y A.  2  2 3 xy x z  B. 2 2x  y xz   C. . D. 3 x . y  3  y 3
Câu 4. Đơn thức nào dưới đây là không đơn thức thu gọn?  1  A. 3 3 3x yz B. 2 2x  y xz   C. 3 2x zt D. 3 x . y  3  1
Câu 5. Bậc của đơn thức 2 3 x yzx là: 3 A. 1 B. 3 C. 4 D. 7. 1
Câu 6. Tích của hai đơn thức 3
xy và x  y 2 8
xz có phần hệ số là: 2 1 A. B. 8  C. 4  D. 7. 2  2  
Câu 7. Tích của hai đơn thức x  3 2  y  và 2 2 2x y 
 là đơn thức có bậc bằng:  5  A. 4 B. 5 C. 7 D. 8. 63
BÀI TẬP TRẮC NGHIỆM TOÁN 7 Câu 8. Viết đơn thức 2 xy  2 2 2  x y 3
  xy thành đơn thức thu gọn. A. 4 4 12x y B. 4 4 1  2x y C. 6 4 12x y D. 4 6 12x y
Câu 9. Cặp đơn thứcnào dưới đây là hai đơn thức đồng dạng? 6 A. 4 4 12x y và 4 6 12x y B. 4 4 1  2x y và 6 12x y 6 C. 6 4 12x y và 6 4 2  x y D. 4 6 12x y và 6 12x y
Câu 10. Khẳng định nào sau đây là sai? A. 4 4 x y và 4 4
x y là hai đơn thức đồng dạng B. 5 12  x y và 3 2
15x .x . y là hai đơn thức đồng dạng C. 7 4 5x y và 2  x y   5 3 2
3 x y là hai đơn thức đồng dạng D. 4 6 12x y và 4 5
12x y là hai đơn thức đồng dạng  1  Câu 11. Tính tổng 3 3 3
3x  5x   x    2  15 7 A. 3 x B. 3 15x C. 3 x D. 3 7x 2 2 1  2  1  4 Câu 12. Tính tổng 3 3 2 3 xy  xy   y xy  xy .   2 3  2  3 2 1 A. 3 xy B. 3 xy C. 3 xy D. 3 xy . 3 3
MA TRẬN CÂU HỎI TNKQ CHỦ ĐỀ 12 Mức độ Nhận biết (câu) Thông hiểu (câu) Vận dụng (câu) Chủ đề Thấp Cao 12 1, 2, 3, 4, 5, 6 7, 8, 9, 10, 11 12 64
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Chủ đề 13. ĐA THỨC
1. Một số vấn đề cần ôn tập
Đa thức là một tổng của những đơn thức. Mỗi đơn thức trong tổng gọi là một hạng tử của đa thức đó.
Chú ý: Mỗi đơn thức được coi là một đa thức.
Nếu đa thức có những hạng tử là đơn thức đồng dạng (gọi tắt là hạng tử đồng dạng) thì ta
thu gọn các hạng tử đồng dạng để được một đa thức không còn hai hạng tử nào đồng dạng, ta
gọi đó là dạng thu gọn của đa thức.
Bậc của đa thức là bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức đó. Số 0
được gọi là đa thức không và nó không có bậc.
Muốn cộng hai đa thức ta thực hiện các bước:
- Viết các hạng tử của hai đa thức đó cùng với dấu của chúng.
- Thu gọn các hạng tử đồng dạng.
Muốn trừ hai đa thức ta nên thực hiện các bước:
- Viết các hạng tử của đa thức thứ nhất cùng với dấu của chúng.
- Viết tiếp các hạng tử của đa thức tứ hai với dấu ngược lại.
- Thu gọn các hạng tử đồng dạng. 2. Ví dụ
Ví dụ 1 (Nhận biết) . Tính giá trị của đa thức 1 3 2 3
P  x y  x y  2xy  2 y  z tại x  1  , y  và z  2 2 Giải: 1 1 1 1 1 Thay x  1  , y 
và z  2 vào đa thức ta có P    1   2   2 2 2 4 4
Ví dụ 2 (Vận dụng) . Cho hai đa thức 1 1  2 3 M  xy  xy  x và 2 3 N  xy  y  . xy 2 3 Tính M + N và M – N. Giải: 1  1 2 3 2 3 
M  N  xy  xy  x 
xy  y  xy   2  3  1 1  1   1 2 3 2 3 2 2  3 3  xy  xy  x 
xy  y  xy  xy  xy 
xy  xy  x  y     2 3  3   2   1   1  2 3 2 3 3 2 3 3  1  xy 
1 xy  x  y  xy 
xy  x  y      3   2  3 2 1  1   1 1 2 3 2 3 2 3 2 3
M  N  xy  xy  x 
xy  y  xy  xy  xy  x 
xy  y  xy   2  3  2 3  1   1   1   1 2 2 3 3 2  3 3  xy  xy 
xy  xy  x  y  1  xy 
1 xy  x  y          3   2   3   2  4 1 2 3 3  xy 
xy  x  y . 3 2 65
BÀI TẬP TRẮC NGHIỆM TOÁN 7 3. Câu hỏi trắc nghiệm
Câu 1. Tất cả các hạng tử của đa thức 2 2
2x  y  3xy là: A. 2 2
2x ; y ; 3xy B. 2 2 2x ;  y ; 3xy C. 2 2 2x ; y D. 2 2 2x ;  y
Câu 2. Trong siêu thị, giá mít là x (đ/kg) và giá cam là y (đ/kg) . Biểu thức biểu thị số tiền mua 3 kg mít và 2 kg cam là A. Một đơn thức
B. Một đơn thức thu gọn C. Một đa thức D. Cả A, B và C đều sai
Câu 3. Bậc của đa thức 8 7 2 3
M  x  y  x y 1 bằng: A. 2 B. 5 C. 7 D. 8
Câu 4. Thu gọn đa thức  4 2 2 2
x y  2x y  : xy ta được A. 3 x y  2xy B. 3 x y  2xy C. 6 2 3 2 x y  x y D. 3 2 2 x y  x y 1 
Câu 5. Giá trị của đa thức 3
3x y tại x  2, y  bằng 2 7  5  13 3 A. B. C. D. 2 2 2 2 Câu 6. Cho hai đa thức 2 2
M  x  y  xy  2 và 2 2
N  2x  2 y  xy  2 . Tính M+N bằng: A. 2 2
M  N  3x  y B. 4 4
M  N  3x  y C. 2 2
M  N  x  3y D. 2 2
M  N  x  3y Câu 7. Cho hai đa thức 2 2
M  x  y  xy  2 và 2 2
N  2x  2 y  xy  2 . Tính M – N bằng: A. 2 2
M  N  x  3y B. 2 2
M  N  x  3y C. 2 2
M  N  3x  y  2xy  4 D. M  N  2  xy  4
Câu 8. Tìm đa thức P , biết P   2 2
x  y  xy  2 2  x  y 1 A. 3
P  2x  xy 1 B. x 1 C. 2 P  2
 y  xy 1
D. P   y  xy 1
Câu 9. Tìm đa thức Q, biết Q   2 2
x  y  xy 2 2
 x  y 1. A. 2
Q  2x  xy 1 B. 2
Q  2 y  xy 1 C. 2
Q  2 y  xy 1 D. 2
Q  2x  xy 1
Câu 10. Tìm đa thức P, biết P   3 2 2
x  x y  xy  xy   2 2
1  x y  xy 1. A. 3
P  x  xy B. 3
P  x  xy C. 3 2 2
P  x  xy  2x y  2xy D. 3 2 2
P  x  xy  2x y  2xy
Câu 11. Tìm đa thức Q, biết Q   2 4 3 2 2
x y  xy  y xy  xy  3 2
 x y  x yx  . x A. 2 4 2
Q  x y  xy  x B. 2 4 2
Q  x y  xy  x C. 2 4 2
Q  x y  xy  x D. 2 4 2
Q  x y  xy  x 66
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Câu 12. Cho hai đa thức 2 2
E  x y  2xy 1 và 2 2
F  2x y  xy  2 . Khẳng định nào dưới đây sai?
A. F  E luôn luôn dương
B. F  E luôn luôn dương C. Cả A và B đều đúng D. Cả A và B đều sai.
MA TRẬN CÂU HỎI TNKQ CHỦ ĐỀ 13 Mức độ Vận dụng (câu) Nhận biết (câu) Thông hiểu (câu) Chủ đề Thấp Cao 13 1, 2, 3, 4, 5 6, 7, 8, 9, 10, 11 12
Chủ đề 14. ĐA THỨC MỘT BIẾN
1. Một số vấn đề cần ôn tập
Đa thức một biến là tổng hợp của những đơn thức của cùng một biến. Mỗi số được coi là
một đa thức một biến.
Bậc của đa thức một biến (khác đa thức không, đã thu gọn) là số mũ lớn nhất của biến trong trong đa thức đó.
Hệ số cao nhất là hệ số của số hạng có bậc cao nhất.
Hệ số tự do là số hạng không chứa biến.
Để cộng hoặc trừ hai đa thức một biến, ta có thể thực hiện theo cách sau:
Cách 1: Thực hiện theo cách cộng, trừ đa thức đã học ở bài trước.
Cách 2: Sắp xếp các hạng tử của hai đa thức theo cùng lúy thừa giảm (hoặc tăng) của biến,
rồi đặt phép tính theo cột dọc tương ứng như cộng, trừ các số (chú ý đặt các đơn thức đồng
dạng dạng ở cùng một cột) .
Nếu x= a, đa thức P (x) có giá trị bằng 0 thì ta nói a (hoặc x=a) là một nghiệm của đa thức đó. 2. Ví dụ
Ví dụ 1: (Thông hiểu) . Cho các đa thức P  x 3 2
 x  2x  3x 1 và Q  x 3 2
 x  2x  3. Tìm
đa thức R (x), sao cho R(x)  P(x)  Q(x) . Từ đó tìm nghiệm của R (x) . Giải:
R x  P x  Q x   3 2
x  x  x     3 2 ( ) ( ) ( ) 2 3 1
x  2x  3 3 2 3 2
 x  x  x   x  x    3 3
x  x    2 2 2 3 1 2 3
2x  2x   3x 1 3  3x  4 . 4
R(x)  0  3x  4  0  3x  4   x   3 4
Kết luận: R(x)  3x  4 và nghiệm của R(x) là x   3
Ví dụ 2 (Vận dụng cao) . Cho các đa thức 2
P(x)  ax  bx  c , biết P(0)  ,  P( 1  )   và
P(2)   . Chứng minh rằng P(3)   và (6a  6b)   . 67
BÀI TẬP TRẮC NGHIỆM TOÁN 7 Giải
P(0)  c, mà P(0)  , nên c   . P( 1
 )  a  b  c, mà P( 1
 )   và c   nên (a  b)  Z , suy ra 2a  2b   và 4a  4b   .
P(2)  4a  2b  c, mà P(2)   và c   , nên 4a  2b   suy ra 8a  4b   Ta có:
P 3  9a  3b  c  8a  4b  a  b  c, P(3) là tổng của các số nguyên nên P(3)  
Ta có 6a  6b  (4a  2b)  (2a  2b)  (4a  2b)  (4a  4b), (6a  6b) là tổng và hiệu của các
số nguyên nên 6a  6b   (điều phải chứng minh) . 3. Câu hỏi trắc nghiệm
Câu 1. Thu gọn và sắp xếp các hạng tử của đa thức 3 2 2 (
A x)  x  3x  2x  x  3 theo lũy thừa giảm của biến. A. 2 3 ( A x)  3
  2x  2x  x B. 3 2 (
A x)  x  2x  2x  3 C. 3 2 2 (
A x)  x  3x  2x  x  3 D. 2 3 ( A x)  3
  2x  x  2x
Câu 2. Thu gọn và sắp xếp các hạng tử của đa thức 3 2 3
B(x)  x  5x  x  x  2 theo lũy thừa tăng của biến. A. 3 2
B(x)  2x  5x  x  2 B. 3 2
B(x)  x  5x  x  2 C. 2 3 B(x)  2
  x  5x  x D. 2 3 B(x)  2
  x  5x  2x Câu 3. Đa thức 3 2
C(x)  5x  x  6x 12 có hệ số cao nhất là: A. 12  B. 3 C. 5 D. 6 Câu 4. Đa thức 3 2
C(x)  5x  x  6x 12 có hệ số tự do là: A. 12  B. 3 C. 5 D. 6 Câu 5. Đa thức 4 3 2
P(x)  5x  2x  6x  x 1 có hệ số lũy thừa bậc 4 là: A. 5 B. 1 C. 0 D. -2
Câu 6. Đa thức bậc 6 một biến có hai hạng tử mà hệ số cao nhất là 5, hệ số tự do là -1. Đó là đa thức A. 3 6x 1 B. 6 5x 1 C. 3 6x 1 D. 6 5x 1 1 11 Câu 7. Cho hai đa thức 3 2 P(x)  x 
 x  2x và 2 3
Q(x)  x  2x 
 x . Tính P(x)  Q(x) 4 4 5 A. 3
P(x)  Q(x)  x  x  3 B. 3 2
P(x)  Q(x)  3x  2x  3x  2 C. 3 2
P(x)  Q(x)  x  2x  x  3 D. 3 2
P(x)  Q(x)  3
 x  2x  3x Câu 8. Cho hai đa thức 3 4 3
P(x)  x  x  x  2 và 2 3 3 2
Q(x)  x  x  2x  2x . tính P(x)  Q(x) . A. 5 4 3 2
P(x)  Q(x)  2x  x  x  3x  2 B. 4 3 2
P(x)  Q(x)  x  3x  3x  2 C. 4 3 2
P(x)  Q(x)  x  3x  3x  2 D. 4 3 2
P(x)  Q(x)  x  3x  3x  2
Câu 9. Tìm đa thức A (x), biết 4 3 2 (
A x)  (x  3x  2)  x  x  2x  2 A. 4 3 2 (
A x)  x  x  x  x B. 4 2 (
A x)  x  x  x C. 4 2 (
A x)  x  x  x D. 4 2 (
A x)  x  x  5x 68
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Câu 10. Tìm đa thức B (x), biết 5 2 3
x  2x  x  B(x)  x  2x A. 5 3 2
B(x)  x  x  x B. 5 3 2
B(x)  x  x  x C. 5 3 2
B(x)  x  x  x D. 5 3 2
B(x)  x  x  x  4x Câu 11. Cho các đa thức 2 2
P(x)  2x  2; Q(x)  x  9; R(x)  x  3 . Cả ba đa thức trên có tất cả bao nhiêu nghiệm A. 1 B. 2 C. 3 D. 4 Câu 12. Cho hai đa thức 3 3 2
P(x)  x  x  5;Q(x)  ax  x 1 (a là hằng số). Tìm a để
P(x)  Q(x) la một đa thức bậc 3 A. a 1 B. a  1 C. a  0 D. a  0 Câu 13. Cho biết 3 2
x  2x  3  0 . Tính giá trị của 4 3 H (x)  5
 x 10x 15x 1 A. H (x)  0 B. H (x)  1 C. H (x)  5  D. H (x)  6 
Câu 14. Số nào dưới đây là nghiệm của đa thức 5 3
P(x)  20x  x  x 1 1 A. x  1  B. x  1 C. x  D. x  2 2 Câu 15. Cho hai đa thức 4 3 2 4 3 2
P(x)  x  2x  x  5x;Q(x)  x  x  x  6x  2 , gọi
H (x)  P(x)  Q(x) . Hỏi đa thức H (x) có bao nhiêu nghiệm A.1 B.2 C.3 D.4 Câu 16. Cho đa thức 2
P(x)  ax  bx  c trong đó a, b, c là các hằng số thỏa mãn
3a  4b  6c  0 . Tính P(1)  2P(0, 5)
A. P(1)  2P(0, 5)  0
B. P(1)  2P(0, 5)  3
C. P(1)  2P(0, 5)  4
D. P(1)  2P(0, 5)  6
MA TRẬN CÂU HỎI TNKQ CHỦ ĐỀ 14 Mức độ Nhận biết (câu) Thông hiểu (câu) Vận dụng (câu) Chủ đề Thấp Cao 14 1, 2, 3, 4, 5, 6, 14 7, 8, 9, 10, 11, 13 12 15, 16 69
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Chủ đề 15. ĐƯỜNG THẲNG VUÔNG GÓC. ĐƯỜNG THẲNG SONG SONG 1. Kiến thức cần nhớ
a) Hai góc đối đỉnh: là hai góc mà mỗi cạnh của góc này là tia
đối của một cạnh của góc kia. 2O 3 1
Tính chất: Hai góc đối đỉnh thì bằng nhau. 4 Hình bên: Hai góc  O và 
O đối đỉnh, suy ra   O  O . Hai 1 3 1 3 góc  O và 
O đối đỉnh, suy ra   O  O 2 4 2 4
b) Hai đường thẳng vuông góc: Hai đường thẳng xx’ và y'
yy’ cắt nhau và trong các góc tạo thành có một góc vuông được x x'
gọi là hai đường thẳng vuông góc. Kí hiệu xx '  yy ' y
- Tính chất: Có một và chỉ một đường thẳng a’ đi qua
điểm O và vuông góc với đường thẳng acho trước. x
- Đường thẳng trung trực của đoạn thẳng: đường thẳng
vuông góc với đoạn thẳng tại trung điểm của nó được gọi là A
đường trung trực của đoạn thẳng ấy. y
Khi xy là đường trung trực của đoạn thẳng AB ta cũng
nói: hai điểm A và B đối xứng nhau qua đường thẳng xy
c) Góc so le trong, góc đồng vị
đường thẳng c cắt hai đường thẳng a và b tại hai điểm A, B c
tạo thành 4 góc đỉnh A, 4 góc đỉnh B (như hình bên) a 2 1 - Hai góc  A và 
B , cũng như hai góc  A và  B được gọi 3 4 A 3 1 4 2 là hai góc so le trong 2 1 - Bốn cặp góc  A và  B ,  A và  B ,  A và  B ,  A và  B b 1 1 2 2 3 3 4 4 3 4 B
được gọi là các cặp góc đồng vị
Tính chất: Nếu đường thẳng c cắt hai đường thảng a và b, trong các góc được tạo thành,
có một cặp góc so le trong bằng nhau thì hai góc so le trong còn lại bằng nhau và hai góc đồng vị bang nhau.
d) Dấu hiệu nhận biết hai đường thẳng song song: Nếu đường thẳng c cắt hai đường
thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau (hoặc một cặp góc
đồng vị bằng nhau) thì a và b song song với nhau.
Kí hiệu: a  b 70
BÀI TẬP TRẮC NGHIỆM TOÁN 7
e) Tiên đề Ơ – clit: Qua một điểm ở ngoài đường thẳng, chỉ có một đường thẳng song
song với đường thẳng đó.
f) Tính chất của hai đường thẳng song song: Nếu một đường thẳng cắt hai đường thẳng song song thì:
Hai góc so le trong bằng nhau; Hai góc đồng vị bằng nhau; Hai góc trong cùng phía bù nhau.
g) Quan hêj giữa tính vuông góc và tính song song: c
Hai đường thẳng phân biệt cùng vuông góc vơi một a
đường thẳng thứ ba thì chúng song song với nhau.
Một đường thẳng vuông góc với một trong hai đường b
thẳng song song thì nó cũng vuông góc với đường thẳng kia
h) Ba đường thẳng song song:
Hai đường thẳng phân biệt cùng song song với đường
thẳng thứ ba thì chúng song song với nhau. d1
Khi ba đường thẳng d , d , d song song với nhau d2 1 2 3
từng đôi một, ta nói ba đường thẳng ấy song song với nhau d3
và kí hiệu d  d  d 1 2 3 2. Một số ví dụ
Ví dụ 1 (Nhận biết). cho hình vẽ bên. Tính số đo góc  C b 1 a x A Giải: B 70° 70°    
Do xAD  xBC  70 , hai góc xAD và xBC ở vị trí đồng 1 C D y
vị, suy ra a  b . 2 140° Ta có  C và 
D (đánh dấu trên hình) là hai góc trong cùng phía bù nhau. 2 Suy ra  C  40 .  C và 
C lại là hai góc đối đỉnh. Vậy  C  40 2 1 2 1   
Ví dụ 2 (Thông hiểu). Cho hình bên, E thuộcđoạn FM. Chứng minh: GEM  EFG  EGF Giải: M  
Ta có GEF  GEM  180 E    và
GEF  EFG  EGF  180 , suy ra F G 71
BÀI TẬP TRẮC NGHIỆM TOÁN 7   
GEM  EFG  EGF (đpcm)
Nhận xét: Đây là tính chất: “góc ngoài của tam giác bằng tổng
hai góc trong không bù với nó” M x 120°
VÍ dụ 3 (Vận dụng). Cho hình vẽ bên. Chứng minh Mx  Py . Giải: 80° N 
Kẻ tia Nt  Mx (như hình). Suy ra MNt  60 (vì y 20° P  NMx 
và MNt là hai góc trong cùng phía bù nhau). Mà    
MNP  80  PNt  20  PNt  NPy  20 M x 120° 
Mà hai góc PNt và 
NPy là hai góc ở vị trí so le trong.
Suy ra Nt  Py 80° t N
Mà Nt  Mx , hai đường thẳng Mx và Py là hai đường y 20° P thẳng phân biệt.
Theo tính chất suy ra: Mx  Py
Ví dụ 4 (Vận dụng cao). Cho định lý: “Nếu hai góc nhọn  xOy và 
x 'O ' y ' có Ox  O ' x ';Oy  O ' y ' thì  
xOy  x 'O ' y '
a) Viết giả thiết và kiết luận cho định lý trên.
b) Chúng minh định lý trên. Giải: y a) 1 2 x O Giả thiết  y' xOy và 
x 'O ' y ' là hai góc nhọn. 2
Ox  O ' x ';Oy  O ' y ' 1 x' O' Kết luận  
xOy  x 'O ' y '
b) Vẽ đường thẳng OO’ và chứng minh với hình vẽ trên
Vì Ox  O ' x ' , nên hai góc đồng vị bằng nhau:   O  O ' 2 2
Vì Oy  O ' y ' , nên hai góc đồng vị bằng nhau:   O  O ' 1 1 Suy ra    
O  O  O '  O ' hay  
xOy  x 'O ' y ' 2 1 2 1 72
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Chú ý: Trong bài này có thể vị trí tia O ;
x O ' x ';Oy;O ' y ' ở những vị trí khác nhau thì
cách trình bày vẫn tương tự và ra kết quả  
xOy  x 'O ' y ' .
Đó là định lý “Hai góc nhọn có cạnh tương ứng song song thì bằng nhau”. 3. Câu hỏi trắc nghiệm
Câu 1. Cho hai đường thẳng xx’ và yy’ cắt nhau tại O, Biết 
xOy '  50 . Số đo của góc  x 'Oy bằng: A. 140 B. 50 C. 40 D. 130
Câu 2. Cho hai đường thẳng xx’và yy’ cắt nhau tại O, biết  
xOy  x 'Oy '  140 . Số đo góc  xOy bằng: A. 140 B. 40 C. 70 D. 180
Câu 3. Khẳng định nào sau đây đúng?
A. Hai góc bằng nhau thì đối đỉnh
B. Hai góc đối đỉnh thì bằng nhau
C. Hai tia phân giác của hai góc đối đỉnh trùng nhau
D. Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc nay là tia trùng của một cạnh của góc kia
Câu 4. Hai đường thẳng cắt nhau thì:
A. Tạo thành hai góc đối đỉnh
B. Tạo thành hai cặp góc đối đỉnh
C. Tạo thành ba cặp góc đối đỉnh
D. Tạo thành bốn cặp góc đối đỉnh 
Câu 5. Cho hai đường thẳng xy và x’y’ cắt nhau tại O, biết xOx '  80 . Gọi Ot là tia phân giác của góc 
yOy '. Số đo góc  tOy bằng: A. 55 B. 80 C. 110 D. 40
Câu 6. Hai đường thẳng xx’ và yy’ cắt nhau tại O. Chúng được gọi là đường vuông góc khi:    A. xOy  90 B. xOx '  180
C. x 'Oy  90 D. A và C đều đúng
Câu 7. Khẳng định nào sau đây đúng?
A. Hai đường thẳng cắt nhau thì vuông góc
B. Hai đường thẳng vuông góc chỉ tạo thành một góc vuông
C. Hai đường thẳng vuông góc thì mỗi đường thẳng là phân giác của một góc bẹt
D. Hai đường thẳng vuông góc chỉ tạo thành một cặp góc đối đỉnh
Câu 8. Có bao nhiêu đường thẳng đi qua điểm O và vuông góc với đường thảng a cho trước? A. 1 B. 2 C. 4 D. Vô số
Câu 9. Đường thẳng xy là trung trực của đoạn thẳng AB nếu:
A. xy đi qua trung điểm của AB
B. xy vuông góc với AB
C. xy vuông góc với AB tại trung điểm của AB
D. xy cắt AB
Câu 10. Khẳng định nào dưới đây sai:
A. Hai đường thẳng cắt nhau thì vuông góc
B. Hai góc đối đỉnh thì bằng nhau
C. Hai đường thẳng vuông góc thì cắt nhau 73
BÀI TẬP TRẮC NGHIỆM TOÁN 7
D. Hai đường thẳng vuông góc tạo thành hai cặp góc vuông đối đỉnh
Câu 11. Cho đoạn thẳng AB dài 8cm . Lấy điểm M trên cạnh AB sao cho AM  6cm . Đường thẳng
d là trung trực của MB, d cắt MB tại K. Khẳng định nào dưới đây sai A. KB  1cm B. KA  5cm C. d  AB D. d  AB c
Câu 12. Đường thẳng c cắt hai đường thẳng a và b như hình. Có bao a
nhiêu cặp góc so le trong? A A. 0 B. 1 C. 2 D. 4 b B
Câu 13. Đường thẳng c cắt hai đường thẳng a và b(như hình vẽ câu
12). Có bao nhiêu cặp góc đồng vị? A. 0 B. 1 C. 2 D. 4
Câu 14. Đường thẳng cắt hai đường thẳng a và b tai A và B tạo thành bốn c
góc đỉnh A và bốn góc đỉnh B được đánh số như hình vẽ. Khẳng a 2 1
định nào dưới đây đúng nhất? 3 4 A A. Hai góc  A và 
B được gọi là hai góc so le trong 3 1 2 B. Hai góc  A và 
B được gọi là hai góc so le trong 1 4 2 b 3 4 B C. Cả A và B đều đúng D. Cả A và B đều sai
Câu 15. Đường thẳng cắt hai đường thẳng a và b tai A và B tạo thành bốn góc đỉnh A và bốn góc
đỉnh B được đánh số (như hình vẽ câu 14). Xét các khẳng định dưới đây: (I). Hai góc  A và 
B được gọi là hai góc đồng vị 1 1 (II). Hai góc  A và 
B được gọi là hai góc đồng vị 2 2 (III). Hai góc  A và 
B được gọi là hai góc đồng vị 3 3 (IV). Hai góc  A và 
B được gọi là hai góc đồng vị 4 4
Số các khẳng định đúng là: A. 1 B. 2 C. 3 D. 4
Câu 16. Đường thẳng c cắt hai đường thẳng a và b như hình. Khi đó c trên hình vẽ ta có: a
A. Hai cặp góc trong cùng phía
B. Bốn cặp góc so le trong C. Hai cặp góc đồng vị b D. Cả A, B và C đều sai 74
BÀI TẬP TRẮC NGHIỆM TOÁN 7 Câu 17. Hình bên có  
A  B  50 . Tìm khẳng định sai 3 1 c    
A. A  B  130
B. A  B  50 2 1 a 4 2 1 4     3 A4
C. A  B  50
D. A  B  180 1 1 4 1 2 b 1 3 B 4
Câu 18. Phát biểu bào dưới đây đúng?
A. Hai đường thẳng phân biệt thì song song
B. Hai đường thẳng không song song là hai đường thẳng không có điểm chung
C. Hai đường thẳng song song là hai đường thẳng không có điểm chung
D. Hai đường thẳng vuông góc là hai đường thẳng song song
Câu 19. Qua một điểm ở ngoài một đường thẳng, có bao nhiêu đường thẳng song song với đường thẳng đó: A. Không có B. Chỉ có một C. Có ít nhất một D. Có vô số m n t c u p a 40° x 40° v b y
Câu 20. Tìm các đường thẳng song song trong các hình vẽ sau: c a 45° 45° b A. a  b B. x  y C. m  n D. u  v
Câu 21. Tìm các đường thẳng song song trong các hình vẽ sau: u z x 30° 100° v y t A. a  b B. x  y C. m  n D. u  v 75
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Câu 22. Phát biểu nào dưới đây đúng?
A. Hai đường thẳng không cắt nhau thì song song
B. Hai đường thẳng không có điểm chung thì song song
C. Nếu hai đường thẳng vuông góc thì cắt nhau và ngược lại
D. Nếu hai đường thẳng cắt nhau thì có một cặp góc đối đỉnh
Câu 23. Chọn câu trả lời đúng:
Cho một đường thẳng các hai đường thẳng song song.
Xét các khẳng định sau:
(I). Hai góc so le trong bằng nhau
(II). Hai góc đồng vị bằng nhau
(III). Hai góc trong cùng phía bù nhau A. Chỉ có (I) đúng B. Chỉ có (II) đúng C. Có (I) và (II) đúng
D. Cả (I), (II) và (III) đều đúng
Câu 24. Cho một đường thẳng cắt hai đường thẳng song song. Khi đó số cặp góc so le trong bằng nhau được tạo ra là: A. 0 B. 1 C. 2 D. 3
Câu 25. Cho một đường thẳng cắt hai đường thẳng song song. Khi đó số cặp góc đồng vị bằng nhau được tạo ra là: A. 4 B. 3 C. 2 D. 1
Câu 26. Cho một đường thẳng cắt hai đường thẳng song song. Khi đó số cặp góc trong cùng phía
bù nhau được tạo ra là: A. 1 B. 2 C. 3 D. 4 c
Câu 27. Cho a  b , số đo góc x trên hình vẽ bằng: a x? A. 45 B. 90 C. 135 D. 180 135° b c
Câu 28. Cho a  b , số đo góc x trên hình vẽ bằng: x? a A. 135 B. 90 C. 45 D. 0 45° b c
Câu 29. Cho hình vẽ bên, để a  b thì số đo góc x bằng: a A. 120 B. 30 120° C. 60 D. 180 x? b
Câu 30. Cho a  b và  
A  B  100 (hình vẽ bên). Số đo góc  A bằng: A 1 a 1 1 1 1 b B 76
BÀI TẬP TRẮC NGHIỆM TOÁN 7 c A. 10 B. 90 A a C. 45 D. 50 2 1
Câu 31. Cho a  b và  
A  B  50 (hình vẽ bên). Số đo góc  B bằng: 1 1 1 1 b A. 90 B. 130 B C. 50 D. 65 c 1 a
Câu 32. Cho a  b và  
A  2B (hình vẽ bên). Số đo góc  B bằng: A 1 1 1 A. 30 B. 60 1 b C. 90 D. 45 B b Câu 33. Cho 40°
a  b như hình vẽ bên. Số đo góc x bằng: A. 40 B. 150 x C. 70 D. 30 120° a a
Câu 34. Cho a  b như hình vẽ bên. Số đo góc x bằng: 30° A. 150 B. 90 C. 60 D. 30 b x
Câu 35. Cho a  b như hình vẽ bên.
Số đo góc x bằng: A. 30 B. 60 C. 120 D. 150
Câu 36. Cho ba đường thẳng phân biệt a, b, c. Hai đường thẳng a và b song song với nhau khi:
A. a và b cùng vuông góc với c
B. a và b cùng cắt với c
C. a vuông góc với c
D. b vuông góc với c
Câu 37. Cho hai đường thẳng a và b song song với nhau. Nếu đường thẳng c vuông góc với đường thẳng a thì: A. c  b B. c  b C. c  b D. Đáp án khác.
Câu 38. Phát biểu nào dưới đây đúng:
A. Nếu hai đường thẳng cùng song song với một đường thẳng thứ ba thì chúng song song với nhau.
B. Nếu hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
C. Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng song song với nhau. 77
BÀI TẬP TRẮC NGHIỆM TOÁN 7
D. Nếu hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì chúng vuông góc với nhau.
Câu 39. Cho a  b và x  y như hình vẽ bên. Tính số đo góc x. A. 30 B. 60 C. 120 D. 150 Câu 40. Cho A
 BC , nếu đường thẳng m song song với BC và cắt cạnh AB thì A. m  AC B. m  AC
C. m cắt cạnh AC
D. m không cắt cạnh AC
Câu 41. Tìm số đo góc x ở hình bên: A. 30 B. 50 C. 90 D. 130
Câu 42. Tìm số đo góc x ở hình bên: A. 30 B. 60 C. 120 D. 150
Câu 43. Tìm số đo góc x ở hình bên: A. 30 B. 60 C. 90 D. 120
Câu 44. Tìm số đo góc x ở hình bên: A. 50 B. 80 C. 100 D. 130
Câu 45. Viết giả thiết kết luận cho định lý: “ Nếu một đường thẳng vuông góc với một trong hai
đường thẳng song song thì nó vuông góc với đường thẳng kia” 78
BÀI TẬP TRẮC NGHIỆM TOÁN 7 A. Giả thiết
c  a, c  b Kết luận a  b B. Giả thiết
a  b, c  a Kết luận c  b C. Giả thiết
c  b, a  b Kết luận c  b D. Giả thiết c  b Kết luận
a  b, c  a
Câu 46. Cho hình vẽ bên. Phát biểu nào dưới đây sai?
A. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau
B. Một đường thẳng vuông góc với một trong hai đường thẳng
song song thì nó cũng vuông góc với đường thẳng kia
C. Hai đường thẳng cùng vuông góc với một đường thẳng thứ
ba thì chúng song song hoặc trùng nhau
D. Hai đường thẳng cùng vuông góc với một đường thẳng thứ
ba thì chúng vuông góc với nhau
MA TRẬN CÂU HỎI TNKQ CHỦ ĐỀ 15 Mức độ Nhận biết (câu) Thông hiểu (câu) Vận dụng (câu) Chủ đề Thấp Cao 15
1, 2, 3, 4, 5, 6, 7, 8, 9, 12, 13, 5, 7, 10, 11, 17, 18, 33, 39, 34, 55
14, 15, 16, 19, 20, 21, 23, 24, 22, 30, 31, 32, 36, 42, 44, 46 25, 26, 27, 28, 29, 37 38, 40, 43, 45 79
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Chủ đề 16. TAM GIÁC 1. Kiến thức cần nhớ
a) Tổng ba góc của một tam giác 
Tổng ba góc của một tam giác bằng 180 
Tam giác vuông là tam giác có một góc vuông 
Trong tam giác vuông hai, góc nhọn phụ nhau 
Góc ngoài của một tam giác là góc kề bù với một góc của tam giác ấy. mỗi góc ngoiaf
của một tam giác bằng tổng của hai góc trong không kề với nó.
b) Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc
tương ứng bằng nha. Kí hiệu: A  BC  A  ' B 'C '
Người ta qui ước khi kí hiệu sự bằng nhau của hai tam giác, các chữ cái chỉ tên các đỉnh
tương ứng được viết theo cùng thứ tự.
c) Ba trường hợp bằng nhau của tam giác Nếu A  BC và A
 ' B 'C ' có: AB  A' B '; AC  A'C '; BC  B 'C ' thì A  BC  A
 ' B 'C ' (c. c. c) Nếu A  BC và A
 ' B 'C ' có:  
AB  A' B '; B  B '; BC  B 'C ' thì A  BC  A
 ' B 'C ' (c. g. c) Nếu A  BC và A
 ' B 'C ' có:    
AB  A' B '; A  A'; B  B ' thì A  BC  A
 ' B 'C ' (g. c. g)
d) Tam giác cân là tam giác có hai cạnh bằng nhau
Tam giác cân ABC có ( AB  AC) , ta gọi AB và AC là các 
cạnh bên, BC là cạnh đáy, 
B và C là các góc ở đáy,  A là góc ở đỉnh. A
 BC có AB  AC còn được gọi là A
 BC cân tại A Tính chất:
Trong một tam giác cân, hai góc ở đáy bằng nhau.
Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.
Tam giác vuông cân là tam giác vuông có hai cạnh góc vuông bằng nhau.
Tam giác đều là tam giác có ba cạnh bằng nhau.
Hệ quả: Trong một tam giác dều, mỗi góc bằng 60o.
Nếu một tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều.
Nếu một tam giác cân có một góc bằng 60o thì tam giác đó là tam giác đều. 80
BÀI TẬP TRẮC NGHIỆM TOÁN 7
e) Định lý Py-ta-go: Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các
bình phương của hai cạnh góc vuông.
Định lý Py-ta-go đảo: Nếu một tam giác có bình phương của một cạnh bằng tổng các bình
phương của hai cạnh kia thì tam giác đó là tam giác vuông.
f) Các trường hợp bằng nhau của tam giác vuông:
- Nếu hai cạnh góc vuông của tam giác vuông này bằng hai cạnh
góc vuông của tam giác vuông kia thì hai tam giác vuông đó
bằng nhau. (theo trường hợp cạnh – góc – cạnh).
- Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam
giác vuông này bằng một cạnh góc vuông và một góc nhọn kề với
cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. (g. c. g)
- Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng
với cạnh huyền và một góc nhọn của tam giác vuông kia thì hai
tam giác vuông đó bằng nhau. (theo trường hợp g. c. g)
- Trường hợp bằng nhau về cạnh huyền và cạnh góc vuông: Nếu
cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng
cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai
tam giác vuông đó bằng nhau. 2. Một số ví dụ
Ví dụ 1 (Nhận biết). Hai đoạn thẳng AB và CD cắt nhau tại trung điểm O của mỗi đoạn thẳng. Chứng minh AC // BD. Giải:
AB  CD    O Giả thiết OA  OB OC  OD Kết luận AC // BD Có:  
OA  OB, OC  OD, AOC  DOC (đối đỉnh) Suy ra O  AC  O
 BD (cạnh – góc – cạnh)     
Suy ra OAC  OBD hay BAC  ABD , mà hai góc BAC và 
ABD ở vị trí so le trong, nên AC // BD. 81
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Ví dụ 2 (Thông hiểu). Cho tam giác ABC vuông tại A, có AB  AC . Qua A kẻ đường thẳng
xy (B, C nằm cùng phía đối với xy). Kẻ BD  xy tại D, kẻ
CE  xy tại E. Chứng minh: a) B  AD  A  CE
b) DE  BD  CE Giải: A
 BC vuông tại A, AB  AC Giả thiết
A  xy; B và C nằm cùng phía xy.
BD  xy tại D, CE  xy tại E a) B  AD  A  CE Kết luận
b) DE  BD  CE   a) Có   o     90 ,   90o ABD DAB DAB CAE
. Suy ra ABD  CAE (cùng phụ góc  DAB ).
Lại có: AB  AC . Vậy B  AD  A
 CE (trường hợp cạnh huyền – góc nhọn của hai tam giác vuông). b) Vì B  AD  A
 CE nên AD  CE, AE  BD c)
 BD  CE  AE  AD  DE (vì A nằm giữa D và E).
Ví dụ 3 (Vận dụng). Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên  
tia đối của tia CB lấy điểm E sao cho BAD  CAE . Kẻ BH vuông góc với AD tại H, kẻ CK
vuông góc với AE tại K. Chứng minh rằng: a) BD  CE b) BH  CK
c) Gọi I là giao điểm của hai đường thẳng HB và CK. Chứng minh rằng AI là tia phân giác  của góc BAC . Giải:   
a) Có ABD  BAC  ACB (tính chất góc ngoài của tam giác)   
ACE  CAB  ABC (tính chất góc ngoài của tam giác)    
Mà ACB  ABC (vì A
 BC cân tại A) suy ra ABD  ACE , lại có  
BAD  CAE  A  BD  A  CE (g-c-g)  BD  CE   b) Do A  BD  A
 CE nên BD  CE và HDB  KEC . Mà hai tam giác H  DB và K
 EC là hai tam giác vuông
(cạnh huyền – góc nhọn). Suy ra: BH  CK.    
c) Ta có: IBC  HBD (đối đỉnh) ICB  KCE (đối đỉnh)    
Mà HBD  KCE (vì chứng minh trên H  DB  K
 EC ). Suy ra: IBC  ICB  I  BC cân tại I
 IB  IC, lại có AB  AC (giả thiết) 82
BÀI TẬP TRẮC NGHIỆM TOÁN 7   Suy ra A  BI  A
 CI (cạnh- cạnh- cạnh)  BAI  CAI . 
Do đó AI là tia phân giác của góc BAC .
Ví dụ 4 (Vận dụng cao). Cho tam giác ABC vuông tại A, kẻ AH  BC tại H.
Trên tia đối của tia HA lấy điểm D sao cho HD  H . A
a) Chứng minh rằng: A  HB  D  HB
b) Chứng minh rằng: BD  CD   c) Cho 60o ABC 
. Tính số đo góc ACD . Giải: a) Hai tam giác A  HB và D  HB có:
HB chung, HA  HD,     90o BHA BHD . Suy ra A  HB  D  H . B b) Có:  
C  A (cùng phụ  A ) mà  
A  D (vì A  HB  D  H . B ) nên   C  D (1) 2 1 2 1 1 2 1 Lại có: H  DC  H
 AC (tương tự chứng minh câu a). Suy ra   C  C 2 1 (2) Từ (1) và (2) suy ra:  
C  D , mà   o   o    90    90   90 . o D C D D BDC 1 1 2 1 1 2
Tức là: BD  C . D c) A
 BC vuông tại A có  o   60   30o ABC C (hai góc nhọn phụ nhau) 2 Mà           60o C C ACD C C 2 1 1 2 . 3. Câu hỏi trắc nghiệm Câu 1. Cho A
 BC , chọn đáp án đúng trong các đáp án sau:       A.    100o A B C B.    180o A B C       C.    180o A B C D.    100o A B C Câu 2. Cho A
 BC vuông tại A. Khẳng định nào dưới đây sai:        
A. B  C  A B.   90o B C C. 90o A  D.   90o B C  Câu 3. Cho A
 BC có góc BCx là góc ngoài tại đỉnh C của A
 BC . Khẳng định nào dưới đây sai:     A. BCx  A B. BCx  B      
C. BCx  A  B
D. BCx  A  B Câu 4. Cho A
 BC , tìm số đo x ở hình bên: A. 100o x  B. 80o x  C. 90o x  D. 40o x  Câu 5. Cho A
 BC , tìm số đo x, y ở hình bên: A.
 70o,  100o x y o o
B. x  100 , y  100 83
BÀI TẬP TRẮC NGHIỆM TOÁN 7 C o o
. x  30 , y  100 D.
 70o,  110o x y
Câu 6. Tìm góc x trên hình sau để AB // CD. A. 30o x  B. 60o x  C. 90o x  D. 120o x   Câu 7. Cho A  BC vuông tại A, 30o B 
. Tia phân giác của góc . . … cắt AB ở D. Số đo góc  BCD bằng: A. 30o B. 60o C. 90o D. 120o Câu 8. Cho A  BC biết  o   45 ,  30o A B
. Góc ngoài tại đỉnh C có số đo bằng: A. 30o B. 45o C. 75o D. 105o 
Câu 9. Trong hình vẽ bên, cho A
 BC có MN // BC. Tìm số đo góc BAC . A. 95o B. 45o C. 135o D. 85o
Câu 10. Khẳng định nào dưới đây sai?
A. Một tam giác có thể có nhiều nhất một góc tù.
B. Một tam giác có thể có nhiều nhất một góc vuông.
C. Một tam giác có thể có ba góc nhọn.
D. Trong một tam giác vuông, hai góc nhọn bù nhau.
Câu 11. Tìm số đo x trong hình vẽ sau: A. 130o B. 80o C. 50o D. 30o
Câu 12. Tổng các góc ngoài của một tam giác bằng: A. 180o B. 360o C. 720o D. 90o     Câu 13. Cho A
 BC có A  5C và 60o B 
. Khi đó số đo góc C bằng A. 20o B. 30o C. 60o D. 90o Câu 14. Cho A  BC  M
 NP có AB  2 cm, AC  3 cm, PN  4 cm . Tính chu vi tam giác M  NP A. 4, 5 cm B. 9 cm C. 7 cm D. 6 cm Câu 15. Cho A  BC  M
 NP . Khẳng định nào dưới đây đúng?     A. ABC  MNP B. ABC  MPN C. AB  MP D. BC  MP Câu 16. Cho A  BC  M
 NP biết AC  5 cm . Cạnh nào của M
 NP có độ dài bằng 5cm. 84
BÀI TẬP TRẮC NGHIỆM TOÁN 7 A. PN B. MN C. MP D. Không có cạnh nào   Câu 17. Cho A  BC  M  NP biết 40o A  và 70o B  . Số đo góc  P bằng: A. 40o B. 70o C. 20o D. 50o
Câu 18. Cho hai tam giác A  BC và D
 EF có: AB  DE , AC  DF , BC  EF và   A  D,    
B  E, C  F . Cách viết nào dưới đây đúng? A. A  BC  D  EF B. A  BC  D  FE C. A  BC  E  FD D. Cả A, B, C đều đúng. 
Câu 19. Tìm số đo góc ABC trên hình vẽ bên: A. 20o B. 40o C. 80o D. 120o
Câu 20. Chọn câu trả lời đúng:
A. Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
B. Nếu ba góc của tam giác này bằng ba góc của tam giác kia thì hai tam giác đó bằng nhau. C. Cả A và B đều đúng. D. Cả A và B đều sai.
Câu 21. Trên hình vẽ bên, có bao nhiêu cặp tam giác bằng nhau
theo trường hợp cạnh – cạnh – cạnh? A. 1 B. 2 C. 3 D. 4 
Câu 22. Tính góc BAC trong hình vẽ bên và cho biết AD có song song với BC không?  A. 120o BAC  và AD // BC  B. 60o BAC  và AD // BC  C. 120o BAC  và AD không song song BC.  D. 30o BAC  và AD không song song BC.
Câu 23. Cho hai tam giác A  BC và D
 EF có AB  DE, AC  DF . Tìm điều kiện để A  BC  D
 EF theo trường hợp cạnh – cạnh – cạnh. A. BC  DE B. BC  EF C. AC  EF D. AB  DF .
Câu 24. Cho hình bên, xét các khẳng định: 
(I). “AD là tia phân giác của góc BAC ”
(II). ”BC là tia phân giác củagóc  ABD ”
Chọn câu trả lời đúng: A. Chỉ có (I) đúng. B. Chỉ có (II) đúng. 85
BÀI TẬP TRẮC NGHIỆM TOÁN 7
C. Cả (I) và (II) đều đúng.
D. Cả (I) và (II) đều sai.
Câu 25. Cho hai tam giác A  BC và D  EF có:  
AB  DE, ABC  DEF . Tìm điều kiện để A  BC  D
 EF theo trường hợp cạnh – góc – cạnh. A. AC  DF B. BC  EF   C. ACB  DFE D. Tất cả đều sai.
Câu 26. Cho hình vẽ bên. Tìm điều kiện để A  BC  A  FE theo
trường hợp cạnh –góc – cạnh.   A. ACB  AFE B. AC  EF C. AC  AE D. BC  AF
Câu 27. Cho hình vẽ bên, số cặp giác bằng nhau trên hình theo
trương hợp góc-cạnh-góc là: A. 0 B. 1 C. 2 D. 3
Câu 28. Cho hình vẽ bên, số cặp tam giác bằng nhau trên hình là: A. 0 B. 1 C. 2 D. 3
Câu 29. Cho hình bên, xét các khẳng định: (I). BC  EF
(II). d  BC
Chọn câu trả lời đúng: A. Chỉ có (I) đúng. B. Chỉ có (II) đúng.
C. Cả (I) và (II) đều đúng.
D. Cả (I) và (II) đều sai.  
Câu 30. Cho hình vẽ bên và có AB  AC, BD  EC, ABC  ACB
Xét các khẳng định sau: (I). A  BD  A  CE (II). A  BE  A  CD
Chọn câu trả lời đúng: A. Chỉ có (I) đúng. B. Chỉ có (II) đúng.
C. Cả (I) và (II) đều đúng.
D. Cả (I) và (II) đều sai. Câu 31. Cho A  BC và D  EF có    
A  D, B  E . Để A  BC  D
 EF theo trường hợp góc-cạnh-
góc phải thêm điều kiện nào sau đây? A. AB  DE B. AC  DF   C. BC  EF D. ACB  DFE  
Câu 32. Cho hình vẽ bên biết ABE  ACF . Cần thêm điều kiện gì để A  BE  A
 CF theo trường hợp góc-cạnh-góc. 86
BÀI TẬP TRẮC NGHIỆM TOÁN 7   A. AEB  AFC B. AB  AC C. BE  CF D. AF  AC  Câu 33. Cho A
 BC , tia phân giác của góc BAC cắt BC tại D, trên tia AC lấy điểm Esao cho
AB  AE. Hỏi A  BD  A
 ED theo trường hợp nào? A. Cạnh-cạnh-cạnh B. Cạnh-góc-cạnh C. Góc-cạnh-góc D. Góc-góc-góc
Câu 34. Trường hợp nào dưới đây thể hiện sai các trường hợp bằng nhau của hai tam giác? A. Cạnh-cạnh-cạnh B. Cạnh-góc-cạnh C. Góc-cạnh-góc D. Góc-góc-góc
Câu 35. Phát biểu nào dưới đây đúng?
A. Hai góc và một cạnh của tam giác này bằng với hai góc và một cạnh của tam giác kia thì
hai tam giác đó bằng nhau.
B. Hai cạnh và một góc của tam giác này bằng với hai cạnh và một góc của tam giác kia thì
hai tam giác đó bằng nhau.
C. Ba góc của tam giác này bằng ba góc của tam giác kia thì hai tam giác đó bằng nhau.
D. Ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
Câu 36. Giả thiết nào dưới đây không suy ra được A.      
A  M , B  N , C  . P
B. AB  MN , AC  MP, BC  NP      
C. AB  MN , AC  MP, A  M
D. A  M , B  N , AB  MN
Câu 37. Cho hình vẽ saucó    
A  B  C  D 1 1 1 1 .
Khẳng định nào dưới đây sai? A. A  ID  B  IC B. A  CB  B  DA C. B  CD  A  DC D. I  AB  I  CD
Câu 38. Cho hình bên, tính độ dài đoạn thẳng CD: A. 1cm B. 2cm C. 3cm D. Đáp án khác   Câu 39. Cho A
 BC cân tại A, có C  4A. Tính số đo góc B . A. 120o B. 30o C. 20o D. 80o Câu 40. Cho A
 BC biết AB  3cm, BC  5cm, AC  3cm . Tìm khẳng định đúng:     A. ABC  BCA B. ABC  CAB     C. ACB  CAB D. BAC  BCA.
Câu 41. Khẳng định nào dưới đây là sai?
A. Tam giác cân có một góc 60o là tam giác đều.
B. Tam giác vuông có một góc nhọn bằng 45o là tam giác vuông cân.
C. Trong tam giác vuông cạnh huyền là cạnh có độ dài lớn nhất. 87
BÀI TẬP TRẮC NGHIỆM TOÁN 7
D. Tam giác cân không thể là tam giác tù. Câu 42. Cho A
 BC biết AB  12cm, BC  5cm, AC  13cm . Khi đó ABC là tam giác: A. đều B. vuông tại A C. vuông tại B D. vuông tại C Câu 43. Cho A
 BC cân tại A, phân giác trong của góc 
A cắt cạnh BC tại D.
Khẳng định nào dưới đây sai?  
A. Đường thẳng AD là trung trực của cạnh BC B.   90o ABC CAD   C. A  DB  A  DC D.   180o ABC ADC
Câu 44. Cho hình bên. Tính độ dài đoạn thẳng BD. A. 2cm B. 3cm C. 4cm D. 5cm
Câu 45. Trong các phương án sau, phương án nào chứa hình có hai tam giác vuông không bằng nhau A. B. C. D.
Câu 46. Một cầu trượt có mô hình như hình vẽ bên. Đường đi lên đỉnh trượt là đoạn CA  5m ,
các đoạn thẳng CH  4m, BH  5m, BD  1 . m
Bạn An đứng trên đỉnh A của cầu trượt và trượt xuống đến vị trí D thì dừng lại. Hỏi quãng
đường trượt ABD của An dài khoảng bao nhiêu mét? (Chọn kết quả chính xác nhất trong bốn đáp án sau) A. 6m B. 7m C. 8m D. 9m
MA TRẬN CÂU HỎI TNKQ CHỦ ĐỀ 16 Mức độ Vận dụng Nhận biết(câu) Thông hiểu(câu) Chủ đề Thấp Cao 1, 2, 3, 6, 8, 14, 4, 7, 10, 11, 12, 5, 9, 22, 28, 15, 16, 17, 18, 13, 19, 20, 21, 24, 16 29, 30, 43, 37, 38 23, 25, 31, 34, 26, 27, 32, 33, 35, 44, 46 36, 39, 40 41, 42, 45. 88
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Chủ đề 17. QUAN HỆ GIỮA CÁC YẾU TỐ TRONG TAM GIÁC - CÁC ĐƯỜNG ĐỒNG QUY CỦA TAM GIÁC 1. Kiến thức cần nhớ
a. Quan hệ góc và cạnh đối diện trong một tam giác A
Định lý 1: Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn.
Định lý 2: Trong một tam giác, cạnh đối diện với góc lớn hơn d H B là cạnh lớn hơn.
b. Quan hệ đường vuông góc và đường xiên, đường xiên và hình chiếu
Khái niệm: Từ điểm A không nằm trên đường thẳng d, kẻ một đường thẳng vuông góc với d
tại H, trên d lấy điểm B không trùng với điểm H. Khi đó:
Đoạn thẳng AH gọi là đoạn vuông góc hay đường vuông góc kẻ từ điểm A đến đường thẳng d,
điểm H gọi là chân của đường vuông góc hay hình chiếu của điểm A lên đường thẳng d.
Đoạn thẳng AB gọi là một đường xiên kẻ từ điểm A đến đường thẳng d.
Đoạn thẳng HB gọi là hình chiếu của đường xiên AB trên đường thẳng d.
Định lý 1. Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài một đường
thẳng đến đường thẳng đó, đường vuông góc là đường ngắn nhất.
Định lý 2: Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó:
Đường xiên nào có hình chiếu lớn hơn thì lớn hơn.
Đường xiên nào lớn hơn thì có hình chiếu lớn hơn.
Nếu hai đường xiên bằng nhau thì hai hình chiếu bằng nhau, và ngược lại nếu hai hình chiếu
bằng nhau thì hai đường xiên bằng nhau.
c. Quan hệ giữa ba cạnh của một tam giác, bất đẳng thức tam giác.
Định lý: Trong một tam giác, tổng độ dài hai cạnh bất kỳ bao giờ cũng lớn hơn độ dài cạnh còn lại.
Hệ quả: Trong một tam giác, hiệu độ dài hai cạnh bất kỳ bao giờ cũng nhỏ hơn độ dài cạnh còn lại. Chẳng hạn, trong A
 BC , với cạnh BC ta có: AB  AC  BC  AB  AC 89
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Lưu ý: khi xét độ dài ba đoạn thẳng có thảo mãn bất đẳng thức tam giác hay không, ta chỉ cần
so sánh độ dài lớn nhất với tổng hai độ dài còn lại, hoặc so sánh độ dài nhỏ nhất với hiệu hai độ dài còn lại.
d. Tính chất ba đường trung tuyến của tam giác A
Đường trung tuyến của tam giác: Đoạn thẳng nối đỉnh A của tam
giác ABC với trung điểm M của cạnh BC gọi là đường trung tuyến
(xuất phát từ đỉnh A hoặc ứng với cạnh BC) của A  BC .
Đôi khi, đường thẳng AM cũng gọi là đường trung tuyến của B M C A  BC .
Mỗi tam giác có ba đường trung tuyến.
Định lý: Ba đường trung tuyến của 1 tam giác cùng đi qua 1 điểm. A 2
Điểm đó cách đỉnh một khoảng bằng
độ dài đường trung tuyến 3 N P G đi qua đỉnh ấy.
Ba đường trung tuyến đồng quy tại điểm G. Điểm G gọi là trọng B M C tâm của A  BC .
e. Tính chất tia phân giác của một góc x
Định lý thuận: Điểm nằm trên tia phân giác của một góc thì cách K
đều hai cạnh của góc đó. M t
Định lý đảo: Điểm nằm bên trong một góc và cách đều hai cạnh của O
góc thì nằm trên tia phân giác của góc đó. H y
f. Tính chất ba đường phân giác của tam giác
Đường phân giác của tam giác: Trong A
 BC , tia phân giác của góc A
A cắt cạnh BC tại điểm M. Khi đó đoạn thẳng AM được gọi là
đường phân giác (xuất phát từ đỉnh A) của A  BC .
Đôi khi ta cũng gọi đường thẳng AM là đường phân giác của A  BC
. Mỗi tam giác có ba đường phân giác. B M C
Chú ý: Trong một tam giác cân, đường phân giác xuất phát từ đỉnh đối diện với đáy đồng thời
là đường trung tuyến ứng với cạnh đáy.
Định lý: Ba đường phân giác của một tam giác cùng đi qua một điểm. Điểm này cách đều ba cạnh của tam giác đó.
g. Tính chất đường trung trực của một đoạn thẳng. 90
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Định lý thuận: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.
Định lý đảo: Điểm cách đều hai đầu mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.
Nhận xét: Tập hợp các điểm cách đều hai đầu mút của một đoạn thẳng là đường trung trực của đoạn thẳng đó.
h. Tính chất ba đường trung trực của tam giác. d A
Đường trung trực của tam giác: trong một tam giác, đường trung trực của
mỗi cạnh gọi là đường trung trực của tam giác đó. Mỗi tam giác có 3 đường trung trực/ B M C
Trong một tam giác cân, đường trung trực của cạnh đáy đồng thời là
đường trung tuyến ứng với cạnh đáy.
Định lý: Ba đường trung trực của tam giác cùng đi qua 1 điểm. Điểm này cách đều 3 đỉnh của tam giác đó.
Chú ý: Vì giao điểm O của ba đường trung trực của A
 BC cách đều ba đỉnh của tam giác đó
nên có một đường tròn tâm O đi qua ba đỉnh A, B, C.
k. Tính chất ba đường cao của tam giác. A
Đường cao của tam giác: Trong một tam giác, đoạn vuông góc kẻ từ
một đỉnh đến đường thẳng chứa cạnh đối diện gọi là đường cao của tam giác đó. B I C
Mỗi tam giác có ba đường cao.
Hình vẽ bên đoạn thẳng AI là một đường cao của A
 BC . Ta cũng nói AI là đường cao xuất
phát từ đỉnh A (của A  BC ).
Đôi khi ta cũng gọi đường thẳng AI là một đường cao của A  BC .
Tính chất: Ba đường cao của một tam giác cùng đi qua 1 điểm.
Tính chất của tam giác cân: Trong tam giác cân, đường trung tuyến ứng với cạnh đáy đồng
thời là đường phân giác, đường trung tuyển và đường cao cùng xuất phát từ đỉnh đối diện với cạnh đó.
Nhận xét: Trong một tam giác, nếu hai trong bốn loại đường (đường trung tuyến, đường phân
giác, đường cao cũng xuất phát từ một đỉnh và đường trung trực ứng với cạnh đối diện của
đỉnh này) trùng nhau thì tam giác đó là tam giác cân.
Đặc biệt: Trong tam giác đều, trọng tâm, trực tâm, điểm cách đều ba đỉnh, điểm nằm trong tam
giác và cách đều ba cạnh là bốn điểm trùng nhau. 91
BÀI TẬP TRẮC NGHIỆM TOÁN 7 2. Một số ví dụ:
Ví dụ 1 (Nhận biết). Chứng minh nếu tam giác vuông có một góc nhọn bằng 0 30 thì cạnh góc
vuông đối diện với nó bằng nửa cạnh huyền. Giải: B
Trên tia CB, lấy điểm D sao cho CD=CA. 30°   D Do A
 BC vuông tại Avà 0
ABC  30 suy ra C
 AD cân và có góc 0 C  60 nên tam giác C
 AD đều  AC  DA  DC .  60° 0  0  A C Suy ra 0
DAC  60  DAB  90  DAC  30 A  BD   có 0
DAB  DBA  30 nên A  BD cân tại D. Suy ra DA  DB
Suy ra AC  DA  DB  DC B
do đó: BC  2AC (dpcm). 30°
Nhận xét: Trên đây là một cách giải, bạn đọc có thể giải bằng những cách
khác. Chẳn hạn như sau, trên tia đối của tia AC, lấy điểm E sao cho
AE=AC và chứng minh cho EC=BC. 60° E A C
Ví dụ 2 (Thông hiểu). Cho hình vẽ bên:
a) Chứng minh CI  AB .    A b) Cho 0
ACB  40 tính số đo góc B ID, DIE ? E Giải: I a) A
 BC có hai đường cao AD và BE cắt nhau tại I nên I là trực tâm của A  BC .
Vậy CI  AB (tính chất). B D C   b) B
 EC vuông tại E, có 0 ECB  40 , suy ra 0
ECB  50 (hai góc nhọn của tam giác vuông phụ nhau).  Góc  
B ID, DIE bù nhau nên 0 DIE  140
Ví dụ 3 (Vận dụng thấp). Cho A
 BC vuông tại A có đường trung tuyến AM. Trên tia đối
của tia MA lấy điểm D sao cho MD  M . A B C a. Tính số đo góc  ABD b. Chứng minh: A  BC  B  AD . M
c. So sánh độ dài AM và BC. Giải: A D Giả thiết A
 BC vuông tại A, đường trung tuyến 92
BÀI TẬP TRẮC NGHIỆM TOÁN 7 AM. D thuộc tia đối MA Kết luận a.  ABD ? b. A  BC  B  AD .
c. So sánh độ dài AM và BC.
a) Dễ thấy MAC  MDB c g c   . .
 AC  BD, MCA  MBD . Hai góc  
MCA, MBD ở vị trí so le trong bằng nhau nên AC / / BD . 
Mà AC  AB  gt   AB  BD hay 0 ABD  90 .
b) ABC, BAD có cạnh AB chung.   0
ABD  BAC  90 cmt , AC  BD cmt   A  BC  B  AD  . c g.c 1 1
c) Từ câu b suy ra: BC  AD mà AM  AD nên AM  BC . 2 2
Nhận xét: Trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
Ví dụ 4 (Vận dụng cao). Cho A
 BC vuông tại A, tia phân giác của góc B cắt AC tại D, kẻ
DE  BC tại E. Đường thẳng ED cắt BA tại F. Chứng minh: a) A  BD  E
 BD b) DF  DC c) AD  DC B Gỉa thiết A
 BC vuông tại A, BD là tia phân giác góc B,
DE  BC tại E. ED cắt BA tại F E Kết luận a) A  BD  E  BD b) DF  DC A C D c) AD  DC K Giải: a) Hai ABD, E
 BD là hai tam giác vuông có chung cạnh huyên BD và góc nhọn  
ABD  EBD nên A  BD  E
 BD (cạnh huyền-góc nhọn).   b) Từ A  BD  E  BD suy ra   BAD  BDE . Mà
ADF  EDC (đối đỉnh) và        
BDF  BDA  ADF và BDC  BDE  EDC. Suy ra BDC  BDF .    
Hai BDF , BDC có BDC  BDF , BD chung, DBF  DBC . Suy ra: B  DF  B  DC  g. .
c g   DF  DC (dpcm).  c) Trong tam giác ADF có: 0
A  90  AD  DC  Lại có: 0
A  90  DF  DC  AD  DC (dpcm). 93
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Nhận xét: Bài toán này sẽ trở nên khó hơn khi trong đề bài bỏ câu b mà chỉ hỏi câu c.
Do đó khi gặp tình huống đề chỉ có câu c mà không có câu b, ta không so sánh trực tiếp
được nên phải nghĩ đến so sánh AD với một cạnh khác, mà cạnh này bằng DC. Lúc đó
trên hình vẽ và phán đoán ta sẽ suy ra phải so sánh AD với DF. 3. Câu hỏi trắc nghiệm: Câu 1. Cho A
 BC biết AB  2cm, BC  3cm,CA  4cm . So sánh các góc của A  BC            
A. A  B  C
B. B  A  C
C. A  C  B
D. C  A  B
Câu 2. So sánh các cạnh của A
 BC biết rằng  o   50 ;  70o A B :
A. AB  BC  CA
B. AB  AC  BC
C. AB  BC  CA
D. BC  AB  CA Câu 3. Cho A
 BC biết AB  3cm, BC  5cm,CA  6cm . Góc lớn nhất của A  BC là:       A. A B. B C. C
D. A  B  C Câu 4. Cho A  BC biết  o   60 ;  80o A B . Cạnh nào của A
 BC là cạnh nhỏ nhất? A. CA B. CB C. AB D. Cả B và C đều sai
Câu 5: Trong một tam giác, đối diện với cạnh nhỏ nhất là góc có đặc điểm gì? A. Nhọn B. Vuông C. Tù D. Bẹt Câu 6: Cho A
 BC biết AB  3cm, BC  5cm,CA  3cm . So sánh các A góc của A  BC .   
A. A  B  C   
B. A  B  C   
C. A  B  C B D C   
D. A  B  C
Câu 7. Cho hình vẽ bên, biết AB  BD . Khẳng định nào sau đây đúng?     A. BAD  BCA B. BAC  BCA     C. BAC  BCA D. ADB  DAC Câu 8. Cho A
 BC biết rằng:  o   20 ;  50o A B
. Xét các khẳng định sau: (I) A
 BC là một tam giác tù (II) A
 BC có cạnh lớn nhất là AB (III) A
 BC có cạnh nhỏ nhất là BC.
Số khẳng định đúng ở trên là: A. 0 B. 1 C. 2 D. 3 Câu 9. Cho A
 BC vuông tại A biết AB  5cm, BC  13cm . So sánh các góc của A  BC      
A. C  B  A
B. B  C  A      
C. B  A  C
D. C  A  B Câu 10. Cho A  BC biết  o   30 ;  60o A B
. So sánh các cạnh của A  BC .
A. AB  BC  CA
B. AB  AC  BC
C. AB  BC  CA
D. BC  AB  CA 94
BÀI TẬP TRẮC NGHIỆM TOÁN 7 Câu 11. Cho A
 BC biết   90o A
; AB  AC . Khẳng định nào dưới đây đúng? A. AB  BC B. 2 2 BC  3AB   C.   45o B C D. AB  CA
Câu 12. Cho hình vẽ bên và AB  AC . Xét các khẳng định sau và chọn đáp án đúng: A (I)
“ AC  AD ”   (II)
“ ACB  ACD ” A. Chỉ có (I) đúng B. Chỉ có (II) đúng
C. Chỉ có (I) và (II) đều đúng B C D
D. Cả có (I) và (II) đều sai
Câu 13. Cho hình vẽ bên và AB  AC . Khẳng định nào sau đây đúng? A   A. ABC  ADB B. AB  AD   C. ADB  CAD D. Tất cả đều sai Câu 14. Cho A
 BC có AB  AC ở hình bên. Khẳng định nào sau đây B A D C đúng? A. DB  DC B. DB  DC C. DB  DC   B D C D. ABC  ACB
Câu 15. Cho hình vẽ bên, khẳng định nào sau đây đúng? A
A. AC  AE  CF
B. AC  AE  CF
C. AC  AE  CF D. Cả A, B, C đều sai F B E D C Câu 16. Cho A  BC có  o   70 ;  50o ABC ACB . Gọi H là chân
đường vuông góc hạ từ B. Khẳng định nào sau đây đúng? A. HB  HC B. HB  HC  C. HB  HC D. 70o BAC  Câu 17. Cho A
 BC , gọi H là chân đường vuông góc hạ từ A. Khẳng định nào sau đây đúng? A. AB  AC B. AB  AC   C. AB  AC D. ABC  ACB Câu 18. Cho A  BC có  o   30 ;  70o ABC ACB
. Gọi H là chân đường vuông góc hạ từ B.
Khẳng định nào sau đây đúng? A. HA  HC B. HA  HC C. HA  HC D. Không so sánh được 95
BÀI TẬP TRẮC NGHIỆM TOÁN 7 Câu 19. Cho A
 BC vuông tại A, trên cạnh AB lấy điểm E, trên cạnh AC lấy điểm F. So sánh
độ dài các cạnh EF, BF, BC.
A. EFB. EF  BF  BC
C. EF  BC  BF D. EF  BF Câu 20. Cho A
 BC vuông tại A, biết AB  10cm , trên đường thẳng AB lấy hai điểm E và F
sao cho AE  3cm, AF  5cm . So sánh CA, CB, CE và CF.
A. CA  CE  CF  CB
B. CA  CB  CF  CE
C. CA  CE  CB  CF
D. CA  CF  CE  CB Câu 21. Cho M
 NP biết MN  MP  10cm, NP  12cm . Trên đường thẳng NP lấy điểm K
sao cho MK  9cm . Hỏi có bao nhiêu điểm K thỏa mãn? A. 0 B. 1 C. 2 D. 3 Câu 22. Cho A  BC có  o   100 ;  40o A B
. Gọi H là chân đường vuông góc hạ từ A đến BC. So sánh HB và HC. A. HB  HC B. HB  HC C. HB  HC D. Không so sánh được Câu 23. Cho A
 BC . Gọi H là chân đường vuông góc hạ từ A đến BC, biết HB  HC . Khẳng định nào sau đây đúng?     A. ABC  ACB B. ABC  ACB     C. ABC  ACB D. ABC  BAC Câu 24. Cho A  BC , biết  o   60 ,  30o B C
. Trên đường thẳng BC lấy điểm M, N sao cho AB CM  CN  . So sánh AB, AM, AN. 2
A. AB  AM  AN
B. AN  AB  AM
C. AB  AM  AN
D. AB  AN  AM Câu 25. Cho A
 BC biết AB  5cm, BC  12cm,CA  13cm . Trên đường thẳng BC lấy các
điểm I, J, K sao cho AI  AJ  AK . So sánh BI, BJ, BK.
A. BI  BJ  BK
B. BI  BK  BJ
C. BJ  BK  BI
D. BJ  BI  BK
Câu 26. Bộ ba độ dài nào dưới đây là độ dài ba cạnh của một tam giác?
A. 1cm,3cm, 2cm B. 1 ,
cm 3cm,5cm
C. 2cm, 6cm, 4cm
D. 6cm,8cm,9cm Câu 27. Cho A
 BC biết AB  4cm,CA  8cm . Hỏi cạnh BC có thể nhận độ dài (cm) nào sau đây? A. 4 B. 9 C. 12 D. 13 Câu 28. Cho A
 BC biết AB  9cm, BC  1cm . Hỏi cạnh AC có thể nhận độ dài (cm) nào sau đây? A. 1 B. 8 C. 9 D. 10
Câu 29. Tính chu vi của một tam giác cân có độ dài hai cạnh của nó là 2cm và 6cm. A. 14cm B. 10cm C. 8cm D. 5cm 96
BÀI TẬP TRẮC NGHIỆM TOÁN 7 Câu 30. Cho A
 BC có độ dài các cạnh là các số nguyên (đơn vị cm). Biết
AB  5cm, A C  10cm . Hỏi độ dài cạnh BC có thể nhận được bao nhiêu giá trị? A. 8 giá trị B. 9 giá trị C. 10 giá trị D. 11 giá trị Câu 31. Cho A
 BC biết AB  4cm, BC  4cm,CA  5cm . Gọi M là trung điểm của AC. Độ
dài đoạn thẳng BM bằng: A. 14m B. 1. 5cm C. 2cm D. 2. 5cm Câu 32. Cho A
 BC có đường trung tuyến AM và trọng tâm G. Kết quả nào dưới đây sai? 2 1 1 A. AG  AM B. GM  AM C. AG  2GM D. GA  AM 3 3 3 Câu 33. Cho A
 BC có trọng tâm G. Khẳng định nào sau đây đúng? A. AG  4cm B. BG  4cm C. CG  4cm D. GM  12cm Câu 34. Cho A
 BC có trọng tâm G và BG  8cm . Đường trung tuyến BM. Khẳng định nào sau đây đúng? 16 A. GM  12cm B. BM  12cm C. CG  24cm D. GB  cm 3 Câu 35. Cho A
 BC có trọng tâm G. Khẳng định nào sau đây đúng? 2
A. AG cắt BC tại M thỏa mãn MB  MC
B. GA  GB  GC 3
C. CG cắt AB tại trung điểm của AB . D. BG / / AC Câu 36. Cho A
 BC cân tại Acó AB  10cm, BC  16cm . Tính độ dài đường trung tuyến AM của A  BC . A. 8cm B. 2cm C. 9cm D. 6cm Câu 37. Cho A
 BC có AB  BC  AC  6cm . Gọi G là trọng tâm A  BC . Tính , GA GB,GC.
A. GA  GB  GC  2 3cm
B. GA  GB  GC  3cm 3 3 3
C. GA  GB  GC  cm
D. GA  GB  GC  cm 2 2 Câu 38. Cho A
 BC có BC  9cm . Trên tia đối của tia BA lấy điểm D sao cho BD  BA . Gọi
G là trọng tâm A
 CD . Kết quả nào dưới đây đúng.
A. GB  6cm,GC  3cm
B. GB  3cm,GC  6cm
C. GB  GC  4,5cm D. Cả ,
A B,C đều sai. GB A
Câu 39. Cho hình vẽ bên. Tính tỉ số . GN 1 N A. 2 B. G 2 1 C. D. 3 B M C 3 BP
Câu 40. Cho hình vẽ bên. Tính tỉ số . A BC 1 A. 2 B. N M G 2 B P C 97
BÀI TẬP TRẮC NGHIỆM TOÁN 7 1 2 C. D. 3 3 Câu 41. Cho A
 BC vuông tại A. Gọi G là trọng tâm A
 BC biết AG  4cm , Tính độ dài BC . A. 24cm B. 6cm C. 16cm D. 12cm Câu 42. Cho A
 BC là một tam giác đều có trọng tâm G . Đường trung tuyến AM  3cm .
Tính độ dài GB và GC .
A. GB  GC  3cm
B. GB  GC  2cm C. GB  GC  1cm D. GB  GC  4,5cm Câu 43. Cho góc 
xOy khác góc bẹt. Gọi tia Oz là tia phân giác của góc 
xOy . Alà điểm trên
tia Oz ( Akhông trùng O ). Vẽ AB vuông góc Ox tại B , AC vuông góc Oy tại C . Khẳng định nào dưới đây sai?   A. AB  AC B. OB  OC
C. OA  OB  OC D. BAO  CAO  Câu 44. Cho A  BC biết 0
BAC  30 và AB  AC, AM là tia phân giác của góc  A . Số đo góc  BAM là. A. 0 15 B. 0 30 C. 0 60 D. 0 180
Câu 45. Xét các khẳng định sau và chọn câu trả lời đúng nhất.
(I). “ Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó. ”
(II). “ Điểm nằm bên trong một góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó. ” A. Chỉ có (I) đúng. B. Chỉ có (II) đúng.
C. Cả (I) và (II) đều đúng.
D. Cả (I) và (II) đều sai.  Câu 46. Cho A
 BC cân tại A, biết 0
A  50 . Gọi I là điểm nằm trong tam giác và cách đều ba 
cạnh của tam giác này. Tính số đo BIC . A. 0 130 B. 0 115 C. 0 65 D. 0 50 Câu 47. Cho A  BC biết  0  0
ABC  60 , BAC  80 . Gọi I là điểm nằm trong tam giác và cách 
đều ba cạnh của tam giác này. Tính số đo ICA . A. 0 40 B. 0 20 C. 0 30 D. 0 80 Câu 48. Cho A  BC biết  0  0
BAC  60 , ACB  80 . Gọi I là điểm nằm trong tam giác và cách
đều ba cạnh của tam giác này. Tính số đo góc  AIB . A. 0 110 B. 0 65 C. 0 140 D. 0 130  Câu 49. Cho A  BC biết  0  0
ABC  70 , ACB  60 . Tia phân giác góc BAC cắt BC tại M , qua M 
kẻ đường thẳng song song với AC và cắt AB tại N . Tính số đo góc BNM . 98
BÀI TẬP TRẮC NGHIỆM TOÁN 7 A. 0 130 B. 0 70 C. 0 60 D. 0 50
Câu 50. Cho đường thẳng MN . Gọi I là một điểm nằm trên đường trung trực của đoạn thẳng
MN và IM  8cm . Tính đọ dài đoạn IN . A. IN  8cm B. IN  4cm C. IN  16cm D. IN  3cm
Câu 51. Cho đoạn thẳng MN . P và Q là hai điểm thuộc đường trung trực của MN sao cho
PM  6,QN  7 . Gọi I là giao điểm của MN và PQ . So sánh IP và IQ . A. IP  IQ B. IP  IQ C. IP  IQ D. Không so sánh được. Câu 52. Cho A
 BC , gọi I là giao điểm của hai đường trung trực của hai cạnh AB và AC .
Biết IA  12cm . Tính đọ dài IB . A. 12cm B. 4cm C. 6cm D. 8cm  Câu 53. Cho A
 BC cân tại A, gọi O là điểm cách đều ba đỉnh của A  BC và góc 0 OBA  30 . 
Tính số đo góc OCA . A. 0 20 B. 0 30 C. 0 60 D. 0 70
Câu 54. Cho các phát biểu: (I)
. Ba đường trung tuyến của tam giác đồng quy. (II)
. Ba đường phân giác của tam giác đồng quy. (III)
. Ba đường trung trực của tam giác đồng quy. (IV)
. Ba đường cao của tam giác đồng quy.
Số các phát biểu đúng là: A. 1 B. 2 C. 3 D. 4
Câu 55. Trong một tam giác, trực tâm là giao điểm của ba đường gì? A. Trung trực B. Phân giác C. Trung tuyến D. Đường cao
Câu 56. Giao điểm của ba đường trung tuyến trong một tam giác gọc là gì?
A. Điểm cách đều ba đỉnh của tam giác đó B. Trọng tâm
C. Điểm cách đều ba cạnh của tam giác đó D. Trực tâm Câu 57. Cho A
 BC vuông tại A. Trực tâm của A
 BC là điểm nào A. Điểm A B. Điểm B C. Điểm C D. Không có trực tâm  Câu 58. Cho A  BC nhọn có 0
ACB  50 , Gọi H là trực tâm A
 BC . Khẳng định nào dưới đây sai? 99
BÀI TẬP TRẮC NGHIỆM TOÁN 7        A. 0 AHB  130 B. 0 HBC  40 C. HAC  HBC
D. A  B  C Câu 59. Trong A
 BC có trọng tâm, điểm cách đều ba đỉnh, điểm cách đều ba cạnh trùng nhau. Hỏi A
 BC có đặc điểm gì? A. A  BC vuông B. A  BC cân C. A  BC đều D. là tam giác thường  Câu 60. Cho A
 BC cân tại A. Gọi H là trực tâm của tam giác và góc 0 BHA  30 . Xét hai khẳng định sau: (I). A
 BC là tam giác vuông cân. (II). A
 BC là tam giác đều.
Chọn câu trả lời đúng A. Chỉ có (I) đúng. B. Chỉ có (II) đúng.
C. Cả (I) và (II) đều đúng.
D. Cả (I) và (II) đều sai.
MA TRẬN CÂU HỎI TNKQ CHỦ ĐỀ 17 Mức độ Vận dụng (câu) Nhận biết Thông hiểu Chủ (câu) (câu) Thấp Cao đề 1, 2, 3, 4, 10, 11, 5, 6, 8, 9, 12, 14, 7, 13, 17, 22, 26, 31, 32, 15, 16, 18, 23, 24, 19, 25, 20, 21, 17 35, 38, 39, 40, 44, 27, 28, 29, 33, 34, 30, 37, 58 45, 50, 52, 54, 55, 36, 41, 43, 46, 47, 42, 49, 56, 57 48, 51, 53, 59 60 100
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Phần II. MỘT SỐ ĐỀ MINH HỌA KIỂM TRA Đề 1
KIỂM TRA 45 PHÚT ĐẠI SỐ CHƯƠNG 1 5 11 2
Câu 1. Kết quả phép tính   bằng. 6 6 3 14 7 A. 2 B. 2  C. D. 3 3 1 3 9 4
Câu 2. Kết quả phép tính    : 2 bằng 5 2 10 5 1 1 13 13 A. B.  C. D.  5 5 5 5 5 7 7 Câu 3. So sánh các số ; ; 3 2 3 5 7 7 5 7 7 7 7 5 7 5 7 A.   B.   C.   D.   3 2 3 3 3 2 3 2 3 2 3 3
Câu 4. Cặp số hữu tỉ nào dưới đây bằng nhau: 1 1 8 16 2 1 5 3 A. và B. và C. và  D. và 4 2 10 20 6 3 20 12 5 6 1 1 Câu 5. Cho x  
. Tính x : (I): " x  " (II): " x   " 7 7 7 7
Chọn câu trả lời đúng: A. Chỉ có (I) đúng. B. Chỉ có (II) đúng.
C. Cả (I) và (II) đều đúng.
D. Cả (I) và (II) đều sai.
Câu 6. Phát biểu nào dưới đây đúng?
A. x  x khi x  0
B. x  x khi x  0
C. x  x khi x  0
D. x  x khi x  0 5  1 
Câu 7: Tính giá trị của biểu thức 4 P  .12    12  1 A. P  12 B. P  1  2 C. P  D. 9 P  12 12 101
BÀI TẬP TRẮC NGHIỆM TOÁN 7 Câu 8: Viết số 30
3 dưới dạng lũy thừa số mũ là 10 A. 10 27 B. 20 10 (3 ) C. 10 3 D. 10 6
Câu 9: Thay tỉ số 1, 2 :1, 4 bằng tỉ số giữa các số nguyên A. 10 : 4 B. 12 :10 C. 7 : 6 D. 6 : 7
Câu 10: Tỉ số nào trong các tỉ số sau lập được tỉ lệ thức? A. 12 : 5 và 5 :12 B. 8 : 6 và 4 : 3 C. 1: 2 và 2 : 3 D. (4) : 2 và 4 : 2
Câu 11: Viết số thập phân vô hạn tuần hoàn 3, (3) dưới dạng phân số tối giản 1 10 3 A. B. 3 C. D. 3 3 10 11 Câu 12: Cho phân số
. Viết phân số đó dưới dạng số thập phân 3 11 11 11 11 A.  3,7 B.  3,6 C.  3, (6) D.  3,67 3 3 3 3 4 1 1 1
Câu 13: Kết quả phép tính    3 2 9 2 1  1 A. 1  B. C. D. 1 3 3
Câu 14: Trong các số sau, số nào là số hữu tỉ ? A. 5 B. 2 C. 9 D. 3
Câu 15: Trong các số sau đây, số nào không có căn bặc hai ? 11 A. 1  0 B. 0 C. 1 D. 5
Câu 16: Phép tính nào nào dưới đây đúng ? A. 25  5 B.  25  2  5 C. 2  5  5  D. 2  5  5 Câu 17: Phép tính 2 (100) bằng A. 2 (100)  100 . B. 2 (100)  10 . C. 2 (100)  100 . D. 2 (100)  10 . 102
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Câu 18: Phát biểu nào dưới đây sai ?
A. Chỉ có số 0 không là số hữu tỉ dương cũng không là số hữu tỉ âm
B. Số vô tỉ là số viết được dưới dạng số thập phân hữu hạn hoặc vô hạn
C. Số hữu tỉ là số viết được dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn
D. Có những điểm trên trục số không biểu diễn cho số thực nào ? 5
Câu 19: Tìm số hữu tỉ x, biết x  2  1  2 5 3 5 3 A. x  B. x  C. x   D. x   3 5 3 5 12
Câu 20: Trong các phân số sau, phân số nào bằng phân số 5 12 24 12 24 A. B. C.  D. 10 5 10 10
Câu 21: Giá trị nào của x thỏa mãn 2x 1  1  1? 1 1  A. B. 1 C. 0 D. 2 2 1 1
Câu 22: Tìm số tự nhiên n thỏa mãn  2n 64 A. n  4 B. n  5 C. n  6 D. n  7 8 5 2  8.2
Câu 23: Kết quả phép tính 7 5 2  4.2 1 8 A. B. 2 C. D. 1 2 7 a c
Câu 24: Chọn đáp án đúng. Từ tỉ lệ thức  (a, ,
b c, d  0) ta suy ra b d a c a d a b c d A.  B.  C.  D.  b d b c d c a b
Câu 25: Trong các phân số sau, phân số nào viết được dưới dạng số thập phân vô hạn tuần hoàn ? 103
BÀI TẬP TRẮC NGHIỆM TOÁN 7 1 2 5 1 A. B. C. D. 5 3 2 4
Câu 26: Cho x  16 thì x bằng: A. x  4 B. x  16 C. x  16  D. x  256 x Câu 27: Cho H 
. Hỏi có bao nhiêu giá trị của x để H có giá trị là số nguyên ? x  1 A. 0 B. 1 C. 2 D. 3
Câu 28: Giá trị nhỏ nhất của H  x 1 1 bằng ? A. 0 B. 1 C. -1 D. 2
Câu 29: Có bao nhiêu số hữu tỉ x thỏa mãn x  2  x ? A. 0 B. 1 C. 2 D. 3 1 5
Câu 30: Có bao nhiêu phân số có mẫu là 6, lớn hơn và nhỏ hơn ? 5 6 A. 2 B. 3 C. 4 D. 5
MA TRẬN CÂU HỎI TNKQ TRONG ĐỀ 1 Mức độ Thông hiểu Vận dụng Nhận biết (câu) Đề KT (câu) Thấp Cao
1, 2, 4, 6, 7, 8, 9, 12, 3, 10, 11, 18, 19, 22, 23, 45’, Đại, 13, 14, 15, 16, 17, 27, 30 21, 24, 25, 26, 28, 29 Chương I 20, Tổng 15 câu Tổng 9 câu Tổng 4 câu Tổng 2 câu ĐỀ 2:
KIỂM TRA 45’ ĐẠI SỐ CHƯƠNG 2
Câu 1: y tỉ lệ thuận với x theo hệ số tỉ lệ k (k  0) cách viết nào dưới đây đúng ? 1 A. y  kx B. x  ky C. xy  k D. y  kx
Câu 2: y tỉ lệ thuận với x theo hệ số tỉ lệ a(a  0) , cách viết nào dưới đây đúng ? 104
BÀI TẬP TRẮC NGHIỆM TOÁN 7 1 A. y  ax B. x  ay C. xy  a D. y  ax
Câu 3: Hai đại lượng x và y tỉ lệ thuận. Giá trị x trong bảng sau bằng bao nhiêu ? 1 x x x  2 1 2 y y  8  y  4 1 2 A. x  4 B. x  4  C. x  8 D. x  8  1 1 1 1
Câu 4: Hai đại lượng x và y tỉ lệ nghịch. Giá trị y trong bảng sau bằng bao nhiêu ? 12 x x  3 x  6 1 2 y y  1 y 1 2 1 A. y  3 B. y  12 C. y  2 D. y  2 2 2 2 2 2
Câu 5: Cho hàm số y  f (x)  . Tính f (12) x 1 A. f (12)  B. f (12)  6 C. f (12)  24 D. f (12)  10 6
Câu 6: Tìm tọa độ A và B trong hình sau: A. ( A 1;3), B(2; 3  ) y B B. (3 A ;1), B( 3  ; 2) 2 A 1 C. ( A 1;3), B( 3  ; 2) -3 0 3 1 x D. (3 A ;1), B(3; 2)  1
Câu 7: Cho hàm số y 
x . Đồ thị của hàm số này là 2 y y 1 y = x 2 2 2 1 1 B -3 0 A 3 1 x -3 0 3 1 x ... ... -2 1 y = x 2 y y 1 2 y = x 2 2 1 1 y = x 1 2 -3 0 C 3 1 x D. -3 0 3 1 x -2 .. 105 -2
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Câu 8: Trong mặt phẳng Oxy cho hai điểm (
A 2;1) và B(1;1) . Khẳng định nào sau đây đúng
A. AB cắt trục hoành.
B. AB không vuông góc trục tung.
C. AB song song với trục hoành.
D. AB song song với trục tung.
Câu 9: Các giá trị tương ứng của hai đại lương tương x và y được cho trong các bảng sau,
bảng nào thể hiện được hai đại lượng x và y tỉ lệ thuận với nhau ? x x  2 x  4 x  6 x  12 1 2 3 4 A. y y  6 y  3 y  2 y  1 1 2 3 4 x x  2  x  0 x  2 x  10 1 2 3 4 B. y y  1  y  0 y  1 y  5 1 2 3 4 x x  1 x  3 x  1  x  2  1 2 3 4 C. y y  1 y  2 y  1 y  2 1 2 3 4 x x  2 x  3 x  1  x  2 1 2 3 4 D. y . . . y  2 y  1 y  2  2 3 4
Câu 10: Các giá trị tương ứng của hai đại lương tương x và y được cho trong các bảng sau,
bảng nào thể hiện được hai đại lượng x và y tỉ lệ nghịch với nhau ? x x  1 x  2 x  3 x  5 1 2 3 4 A. y y  10 y  5  y  3 y  2 1 2 3 4 x x  8 x  6 x  3 x  1 1 2 3 4 B. y y  1 y  2 y  3 y  1 1 2 3 4 x x  2  x  2 x  4 x  1  6 1 2 3 4 C. y y  16 y  16 y  8  y  2 1 2 3 4 x x  16 x  8 x  4 x  1 1 2 3 4 D. 1 y y  8 y  4 y  2 y  1 2 3 4 2 106
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Câu 11: Trong mặt phẳng Oxy cho một hàm số có đồ thị y như hình sau: 2
Hỏi đồ thị đó là hàm số nào ? 1 A. y  5x B. y  5x -3 0 1 2 3 4 5 x -1 1 1 -2 C. y   x D. y  x 5 5 1
Câu 12: Cho hàm số y  f (x) 
x 1 . Kết quả nào dưới đây đúng ? 2 1 1 A. f (0)  1 B. f (1)  C. f (0)  0 D. f ( 1  )  2 2 Câu 13: Cho hàm số 2
y  f (x)  x . Kết quả nào dưới đây sai ? 1 1   1  1  A. f (0)  0 B. f ( )  C. f    D. f (1)  0 2 4  3  9
Câu 14: Bảnggiá trị tương ứng tương nào dưới đây thể hiện đại lượng y là hàm số của đại lượng x ? x 2  1  1 2  A. y 2 1 2  3 x 2  1  0 3 B. B. y 2 1 0 2 x 2  1 2  1 C. y 2 2 3 3 x 1  2 3 2 D. y 5 2  2  3
Câu 15: Cho hàm số y  ax có đồ thị là đường thẳng đi qua điểm M (2;3) . Tìm hệ số a 2 3 A. a  2 B. a  3 C. a  D. a  3 2 1
Câu 16: Điểm nào dưới đây thuộc đồ thị của hàm số y  x ? 3 107
BÀI TẬP TRẮC NGHIỆM TOÁN 7 1  2  1 A. ( A 1; ) B. B(2; ) C. C(3; 1) D. D(1; ) 3 3 3 2
Câu 17: Điểm nào dưới đây không thuộc đồ thị của hàm số y   x ? 3 2 2 A. A(3; 2) B. B(3; 2) C. C(1; ) D. D( 1  ; ) 3 3
Câu 18: Những điểm thuộc trục hoành có đặc điểm A. Tung độ khác 0. B. Tung độ bằng 0 . C. Hoành độ bằng 1.
D. Trùng điểm O(0; 0) .
Câu 19: Những điểm thuộc trục tung có đặc điểm A. Hoành độ khác 0. B. Tung độ khác 1. . C. Hoành độ bằng 0
D. Trùng điểm O(0;0) .
Câu 20: Cho biết hai đại lượng x và y tỉ lệ thuận với nhau, biết khi x  3 thì y  1. Hỏi y
tỉ lệ thuận với x theo hệ số tỉ lệ k là bao nhiêu ? 1 1 A. k  3  B. k   C. k  3 D. k  3 3 2  9
Câu 21: Hai đại lượng x và y tỉ lệ nghịch với nhau, biết khi x  thì y  . Hỏi x tỉ lệ 3 8
thuận với y theo hệ số tỉ lệ a là bao nhiêu ? 3 3 16 27 A. a   B. a   C. a   D. a  4 8 27 16
Câu 22: Hai đại lượng x và y tỉ lệ thuận với nhau, biết khi x  10 thì y  2 . Hỏi x tỉ lệ
thuận với y theo hệ số tỉ lệ k là bao nhiêu ? 1 1 A. k  20 B. k  C. k  5 D. k  5 20 1 1
Câu 23: Tìm m để đồ thị của hàm số y  x  m đi qua điểm M ( ; ) 3 2 1 1  1 1 A. B. C. D. 6 6 3 2
Câu 24: Công thức nào dưới đây thể hiện x và y là hai đại lượng tỉ lệ nghịch ? 108
BÀI TẬP TRẮC NGHIỆM TOÁN 7 x y x 3 x 1 A.  B.  C.  D. y  1  x 1 2 2 y y 2
Câu 25: Biết y tỉ lệ thuận với x theo hệ số tỉ lệ a , x tỉ lệ thuận với z theo hệ số tỉ lệ
b (a,b  0) . Hỏi z tỉ lệ thuận với y theo hệ số tỉ lệ bằng bao nhiêu ? a b 1 A. B. C. ab D. b a ab
Câu 26: Đường thẳng OA ở hình sau là đồ thụ của hàm số y  ax . Xác định a y A 3 2 1 -1 0 1 2 x -1 3 2 A. a  B. a  C. a  3 D. a  2 2 3
Câu 27: Đồ thị của hàm số y  ax là đường thẳng thuộc góc phần tư thứ hai và thứ tư. Kết quả nào sau đây đúng ? A. a  0 B. a  0 C. a  0 D. Tất cả đều sai
Câu 28: Trong các điểm sau, điểm nào thuộc vào đồ thị của hàm số y  mx  m A. A(1;0) B. B(1;1) C. C(1; 2) D. D(1; 1)
Câu 29: Chọn câu trả lời sai ?
Các máy bơm có cùng công suất bơm nước vào cùng một bể chứa là
A. Số lượng máy bơm tỉ lệ nghịch với thời gian bơm đầy bể
B. Số lượng máy bơm tỉ lệ thuận với thời gian bơm đầy bể
C. Thời gian bơm đầy bể chứa không tỉ lệ thuận với số lượng máy bơm.
D. Công suất máy bơm tỉ lệ nghịch với thời goan bơm đầy bể.
Câu 30: Trong mặt phẳng Oxy cho bốn điểm A(0;1) , B(1;0) , C(0; 1) và D( 1  ; 0) . Hỏi tứ
giác ABCD là hình gì ? A. Hình bình hành. B. Hình thoi. 109
BÀI TẬP TRẮC NGHIỆM TOÁN 7 C. HÌnh chữ nhật. D. Hình vuông.
MA TRẬN CÂU HỎI TNKQ TRONG ĐỀ 2 Mức độ Thông hiểu Vận dụng Nhận biết (câu) Đề KT (câu) Thấp Cao 1, 2, 3, 4, 5, 6, 7, 12, 8, 9, 10, 11, 13, 25, 27, 45’, Đại, 14, 15, 18, 19, 20, 16, 17, 23, 24, 29, 20 28 Chương 2 21, 22 26 Tổng 15 câu Tổng 10 câu Tổng 3 câu Tổng 2 câu ĐỀ 3 KIỂM TRA HỌC KÌ 1 1 3 5
Câu 1: Kết quả phép tính   bằng 2 2 3 8 1 1 8 A. B. C. D. 3 3 6 6  1 10 10 11 
Câu 2: Kết quả phép tính .  . :10   bằng  3 13 13 3  3 100 1000 10 A. B. C.  D.  143 39 39 39
Câu 3: Xét hai phát biểu sau: 3 11 3 11 (I ) :  (II ) :  2 6 2 6
Chọn câu trả lời đúng. A. Chi có (I) đúng. B. Chỉ có (II) đúng.
C. Cả (I) và (II) đều đúng.
D. Cả (I) và (II) đều sai. 11 13
Câu 4: Tìm số nguyên x để  x  6 6 A. 2 B. 1 C. 4 D. 3 6 48 Câu 5: Viết số
dưới dạng lũy thừa của một số hữu tỉ. 18 2 A. 6 24 B. 6 8 C. 6 6 D. 12 24 110
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Câu 6: Khẳng định nào dưới đây là đúng ? A. 0 0  0 . B. 7 ( 0
 ,1) là một số dương. C. 8 ( 0  ,3) là một số âm. D. 6 3 ( 0  , 2)  (0,04) .
Câu 7: Thay tỉ số 5, 2 :1, 6 bằng tỉ số giữa các số nguyên A. 16 : 25 B. 13 : 8 C. 13 : 4 D. 7 :1
Câu 8: Khi các số a,b, c tỉ lệ với các số 1, 6,8 . Cách viết nào dưới đây đúng ? a
A. a : b : c  1: 6 : 8 . B. : c  1: 6 : 8 . b
C. a : (b : c)  1: 6 : 8 .
D. (a : b) : c  (1: 6) : 8 .
Câu 9: Thực hiện phép tính 25 :11 rồi làm tròn đến chữ số thập phân thứ nhất nhận được kết quả: A. 2, 2 B. 2,3 C. 2, 7 D. 2, 0
Câu 10: Trong các số sau, số nào có đúng hai căn bậc hai khác nhau ? A. 1  0 B. 2  C. 2 D. 0 25 9 1
Câu 11: Thực hiện phép tính   bằng: 3 3 3 5 1 1  A. B. 2 C. D. 3 6 6
Câu 12: Nếu y tỉ lệ thuận với x theo hệ số k . Cách viết nào dưới đây đúng ?
A. y  kx (k  0)
B. x  ky (k  0) C. xy  k
D. y  x  k 4 20
Câu 13: Cho biết hai đại lượng x và y tỉ lệ nghịch với nhau, khi x  thì y  . Hỏi hai 5 3
đại lượng x và y tỉ lệ nghịch với nhau theo hệ số tỉ lệ bằng bao nhiêu ? 16 3 3 25 A. B. C. D. 3 16 25 3 111
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Câu 14: Bảnggiá trị tương ứng tương nào dưới đây thể hiện đại lượng y là hàm số của đại lượng x ? Bảng x -3 5 8 8 x -2 -1 -1 3 Bảng 2 1 y 1 3 -7 5 y 2 5 1 3 A. Bảng x -1 0 3 3 x -3 -2 1 3 Bảng4 Bản 3 y 1 2 -3 1 y 1 0 2 1 g 1
Câu 15: Tọa độ của các điêm M và N ở hình sau là y 3 N 2 1 M -4 -3 -2 -1 O 1 2 3 4 x -1 A. M(1;3), N (2; 4)  B. (3
A ;1), B(4; 2) C. M( 4
 ; 2), N (3;1) D. M(4; 2),  N (3;1)
Câu 16: Cặp số hữu tỉ nào dưới đây không bằng nhau ? 3 9 4 1  2 A. và . B. và . 5 5 3 9 5 2 9 3 C. và . D. và . 2 5 6 2  1 1  1
Câu 17: Tìm số hữu tỉ x biết  : x     2 3  4 2 3 2 3 A. B. C. D. 3 2 3 4 5
Câu 18: Có bao nhiêu số hữu tỉ x thỏa mãn x  ? 9 A. Không có số nào. B. Chỉ có 1 số. C. Có 2 số. D. Có 3 số. 2n
Câu 19: Tìm số tự nhiên n thỏa mãn  2 16 A. n  1 B. n  4 C. n  5 D. n  32 112
BÀI TẬP TRẮC NGHIỆM TOÁN 7 3
Câu 20: Một thửa ruộng hình chữ nhật có tỉ số giữa chiều dài và chiều rộng bằng . Tính 2
diện tích thửa ruộng này, biết chu vi của nó bằng 200m . A. 2 2400m B. 2400m C. 2 1200m D. 2 240m
Câu 21: Phân số nào dưới đây viết được số thập phân vô hạn tuần hoàn ? 3 61 25 23 A. B. C. D. 5 10 3 2
Câu 22: Trong các khằng định sau, khẳng định nào sai ? 11
A. Số 12 là số tự nhiên. B. Số là một số hữu tỉ. 3
C. Số 0, 1211005…là một số thực. D. Số 25 là một số vô tỉ.
Câu 23: Cho biếtc y tỉ lệ thuận với x theo hệ số tỉ lệ a , x tỉ lệ thuận với z theo hệ số tỉ lệ
b (a,b  0) . Hỏi z tỉ lệ thuận với y theo hệ số tỉ lệ bằng bao nhiêu ? 1 a b A. B. ab C. D. ab b a
Câu 24: Ch biết 1 2  3  4  ... 19  20  210 . Tính 2  4  6  8  ...  38  40 A. 210 B. 420 C. 630 D. 105 3  3  2 5 11 Câu 25. Các số hữu tỉ ; ; ; ;
được sắp xếp theo thứ tự giảm dần là: 13 10 3 3 5 11 5 2 3  3  11 5 2 3  3  A. ; ; ; ; B. ; ; ; ; 5 3 3 13 10 5 3 3 10 13 5 11 2 3  3  5 11 2 3  3  C. ; ; ; ; D. ; ; ; ; 3 5 3 10 13 3 5 3 13 10
Câu 26. Khẳng định nào dưới đây đúng? A.  7 16 64  3  chia hết cho 3 B.  7 16 64  3  chia hết cho 5 C.  7 16 64  3  chia hết cho 9 D.  7 16 64  3  chia hết cho 10 a b c
Câu 27. Cho ba số dương a, b, c thỏa mãn   . Tính giá trị
2a  b  c
a  2b  c
a  b  2c b  c a  c a  b
của biểu thức: H    a b c 113
BÀI TẬP TRẮC NGHIỆM TOÁN 7 1 1 A. H = 2 B. H = 6 C. H = D. H = 4 3 25
Câu 28. Chữ sô thập phân thứ 2019 sau dấu phẩy của phân số
(viết dưới dạng thập phân 11 là như thế nào? A. 2. B. 3 C. 5 D. 7
Câu 29. Cho hai đường thẳng xx’ và yy’ cắt nhau tại O như hình vẽ. Biết xOy’ = 454. Tính số đo xOy y x' 45° x y' A. 0 0 B. 450 C. 1350 D. 1800
Câu 30. Cho hai đường thẳng a và b có a // b như hình vẽ. Tìm số đo góc x trên hình vẽ. c a 30° b x A. 1200 B. 600 C. 300 D. 1500
Câu 31. Cho hình vẽ. Tìm số đo góc x để a // b x? a b c A. 900 B. 600 C. 300 D. 1200
Câu 32. Chọn câu trả lời đúng. Cho tam giác ABC, có:       A. 0
A  B  C  180 B. 0
A  B  C  180       C. 0
A  B  C  360
D. A  B  C  180 114
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Câu 33. Cho tam giác ABC biết  0  0
A  50 , B  70 . Góc ngoài tại đỉnh C có số đo bằng: A. 200 B. 600 C. 1000 D. 1200
Câu 34. Tìm số đo góc x trên hình sau: x? a 40° b A. 400 B. 500 C. 1300 D. 1400 Câu 35. Cho A  BC  M
 NP , biết AB = 2cm, BC = 5cm, AC = 4cm. Chu vi M  NP bằng: A. 11cm B. 5, 5cm C. 9cm D. 6cm
Câu 36. Cho hai tam giác ABC và DEF có AB = DE,  
B  E . Để A  BC  D  EF theo trương
hợp canh - góc - cạnh phải thêm điều kiện nào dưới đây     A. C  F B. A  B C. AC = DF D. BC = EF 
Câu 37. Cho tam giác ABC, có MN // BC và các góc như hình vẽ. Tính số đo BAC . A 50° M N 120° B C A. 300 B. 700 C. 600 D. 500
Câu 38. Cho hình vẽ. Khẳng định nào dưới đây sai? A 30° 30° 40° 40° D B C A. AB = AC B. BD = DC  C. AB > AC D. 0 BDC  140 
Câu 39. Cho tam giác ABC vuông ở A, biết 0
ACB  60 . Tia phân giác của góc B cắt AC tại 
D. Số đo BDC bằng: 115
BÀI TẬP TRẮC NGHIỆM TOÁN 7 A. 300 B. 600 C. 150 D. 1050
Câu 40. Cho hình vẽ sau khẳng định nào dưới đây sai? A. A  ID  B  IC D C B. I  AB  I  CD 20° 20° C. A  CB  B  DA I D. B  CD  A  DC 20° 20° A B
MA TRẬN CÂU HỎI TNKQ ĐỀ 5 Mức độ Nhận biết (câu) Thông hiểu Vận dụng (câu) KT (câu) Thấp Cao 1; 3; 4; 5; 6; 7; 8; 10 ; 11; 12; 13; 2; 9; 16; 17; 18; 20; 23; 24; 27; 14; 15; 21; 22; 19; 25; 34; 37; 26; 28; 40 Học kỳ 1 38 29; 30; 31; 32; 39 33; 35; 36 Tổng 22 Tổng 10 Tổng 5 Tổng 3 ĐỀ 4 KIỂM TRA HỌC KỲ 2 1
Câu 1. Điểm nào dưới đây thuộc đồ thị hàm số y  x 3  2   1  A. (3; 1) B. 2;   C. 1  ;   D. (-2; 2)  3   3 
Câu 2. Khi điều tra điểm kiểm tra của một tổ trong lớp, giáo viên thu được kết quả điểm trong bảng sau: 8 7 9 8 8 10 8 8 8 9
Điểm trung bình của tổ này là: A. 6, 8 B. 8. 3 C. 7, 0 D. 7, 1
Câu 3. Viết biểu thức đại số biểu thị chu vi của một hình chữ nhật có chiều dài và chiều rộng là a, b. A. a - b B. ab C. a + b D. 2(a + b)
Câu 4. Viết biểu thức đại số biểu thị quảng đường đi được của một xe máy với vận tốc v
(km/h) trong khoảng thời gian t. v A. vt B. v + t C. v - t D. t 1 1
Câu 5. Giá trị của biểu thức P = 3 2
x y  2 tại x  ; y   bằng: 2 3 116
BÀI TẬP TRẮC NGHIỆM TOÁN 7 1  7 1  45 1  43 A. B. C. -2 D. 9 72 72
Câu 6. Biểu thức nào dưới đây được gọi là đơn thức? A. 2x + y B. x - y C. (xy + z)t D. xyx3
Câu 7. Bậc của đơn thức 2 2xy z là: A. 6 B. 2 C. 3 D. 4 1
Câu 8. Thu gọn biểu thức 2 2
3x  y  x ta được: 3 8 8 A. 8x2 + y B. y C. 2 x D. 2 x  y 3 3
Câu 9. Tất cả các hạng tử của đa thức 2
2x  y  3xy là: A. 2x2 B. 2x2;y;3xy C. 2x2;-y;3xy D. 2x2;3xy
Câu 10. Cho hai đa thức M = x2 + y2 - xy; N = x2 - y2 + xy. Tính M + N bằng: A. 2x2 + 2y2 B. 2x2 + 2y2 – xy C. x2 + xy D. 2x2
Câu 11. Cho đa thức M = xy + x2 - 1. Tìm đa thức P biết M - P = x2 - 1 A. x2 -1 B. -xy C. xy D. 2xy
Câu 12. Thu gọn và sắp xếp các hạng tử của đa thức A(x) = x5 + x3 - x2 + 2x3 -1 A. A(x) = x5 + x3 - x2 -1 B. A(x) = x5 - x3 + x2 -1 C. A(x) = x5 + 3x3 - x2 D. A(x) = x5 + 3x3 - x2 -1
Câu 13. Đa thức B(x) = 10x4 - 2x2 + 2x + 12 có hệ số cao nhất là: A. 10 B. 12 C. -2 D. 4
Câu 14. Đa thức một biến Q(x) = x2 - x có bao nhiêu nghiệm? A. 0 B. 1 C. 2 D. 3
Câu 15. Số nào dưới đây là nghiệm của đa thức 4x2 - 4x + 1 = 0? 1 A. 0 B. 2 C. -2 D. 2
Câu 16. Đường thẳng OA ở hình bên là đồ thị của hàm số y = ax. Xác định hệ số a. 1 1 A. a =  B. a = C. a = 3 D. a = -3 3 3
Câu 17. Khi điều tra về cỡ áo của một lớp ta thu được kết quả số áo thể hiện trong bảng sau: 35 36 35 38 35 36 35 39 39 40 42 35 37 36 36 36 35 37 38 35 40 42 35 36 38 40 38 42 40 39 37 35 36 36 35 36 35 36 35 36 117
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Tìm mốt M0 của dấu hiệu A. M0 = 35 B. M0 = 36 C. M0 = 11 D. M0 = 12
Câu 18. Viết biểu thức đại số biểu thị tổng các lũy thừa bậc 3 của hai số tự nhiên liên tiếp A. a  3 3
1  a (a  N )
B. a  a  3 3 2 (a  N )
C. a  a  3 3 1 (a  N ) D. a  3 3 2
 a (a  N )
Câu 19. Biểu thức nào sau đây là đơn thức thu gọn? 1 A. xy(x2y) B. (2x2)( yx) C. x2ỹ D. x3y2 3
Câu 20. Cặp đơn thức nào sau đây là hai đơn thức đồng dạng? 7 A. 2x3y và 2xy3 B. 2xy2x và x2y2 3 C. 2xy và xy2 D. xyx và x3y2x 1
Câu 21. Tích của hai đơn thức (2x2y) và x3y2x là một đơn thức có bậc bằng: 8 A. 3 B. 6 C. 8 D. 9
Câu 22. Giả sử một quyển vở là x (đồng/quyển) và giá của một hộp bút là y (đồng/quyển).
Biểu thức biểu thị số tiền mua hai quyển vở và ba cái bút là: A. Một đa thức B. Một đơn thức
C. Một đơn thức thu gọn D. Cả A, B, C đều sai 1 1
Câu 23. Giá trị của đa thức: M = x2 + y – xy tại x = và y = bằng: 5 2 11 11 16 11 A. B. C. D.  25 50 25 50
Câu 24. Cho hai đa thức P(x) = x3 – x2 + x; Q(x) = x3 – 2x2. Gọi đa thức R(x) được xác định bởi
R(x) = P(x) – Q(x). R(x) có bao nhiêu nghiệm? A. 0 B. 1 C. 2 D. 3
Câu 25. Đa thức P(x) = 2x5 – 4x4 + x – 1 – x4 + x2 có hệ số của lũy thừa bậc 4 là: A. 2 B. -5 C. -4 D. 4
Câu 26. Cho đa thức bậc 5 một biến có hai hạng tử mà hệ số cao nhất là 2, hệ số tự do là 128.
Hỏi đa thức này có bao nhiêu nghiệm? A. 0 B. 1 C. 2 D. 3 7 1
Câu 27. Tìm tất cả các số hữu tỉ x để giá trị của đa thức 2x2y – y bằng tại y = là: 4 2 118
BÀI TẬP TRẮC NGHIỆM TOÁN 7 3 3 3 3 A. B.  C. 0 D. ;  2 2 2 2 a b c
Câu 28. Cho đa thức P(x) = ax2 + bx + c. Trong đó a, b, c là các hằng số thỏa mãn   1 2 3 P  2    3P   1 và a  0 . Tính a A. -6 B. -15 C. 6 D. 15
Câu 29. So sánh các cạnh của tam giác ABC biết  0  0
A  100 ; B  40 . A. AB = AC > BC B. AB = AC < BC C. AB = AC = BC D. AB > AC = BC
Câu 30. Cho tam giác ABC có AB > AC, gọi D là chân đường vuông góc hạ từ A đến BC.
Khẳng định nào sau đây đúng?   A. DB = DC B. DB < DC C. DB > DC D. ABC  ACB
Câu 31. Cho tam giác ABC có trung tuyến AM và trọng tâm G. Kết quả nào dưới đây sai? 2 1 1 A. AG = AM B. GM = GA C. GA = MG D. MB = MC 3 2 3
Câu 32. Cho tam giác ABC biết  0  0
A  50 ; B  60 . Gọi I nằm trong tam giác và cách đều ba
cạnh của tam giác này. Tính số đo góc BIC. A. 700 B. 1300 C. 650 D. 1150
Câu 33. Cho tam giác ABC, gọi I là giao điểm của hai đường trung trực của hai cạnh AB và
AC. Kết quả nào dưới đây đúng? A. IA > IB > IC B. IA = IB = IC C. IA < IB < IC
D. Không so sánh đơcj IA, IB, IC
Câu 34. Trong một tam giác, giao điểm của ba đường cao gọi là:
A. Điểm cách đều 3 đỉnh của tam giác này B. Trọng tâm
C. Điểm cách đều 3 cạnh của tam giác này D. Trực tâm 
Câu 35. Cho tam giác ABC cân tại A, gọi G là trọng tâm của tam giác ABC và 0 GAC  30 . Khi đó A  BC là:
A. Tam giác ABC vuông cân tại A B. Tam giác đều C. Tam giác cân tại A D. Tam giác tù
Câu 36. Cho đoạn thẳng PQ, gọi A và B là hai điểm thuộc đường trung trực của đoạn PQ sao
cho AP = 6cm, BQ = 8cm. Gọi I là giao điểm của PQ và AB. So sánh IA và IB. A. IA = IB B. IA > IB C. IA < IB D. Không so sánh được 119
BÀI TẬP TRẮC NGHIỆM TOÁN 7
Câu 37. Chu vi của một tam giác cân biết độ dài hai cạnh của nó là 3cm và 8cm là: A. 14cm B. 7cm C. 19cm D. 11cm B
Câu 38. Cho hình bên. Tính độ dài đoạn CD 6cm 10cm A. 8 cm B. 4 cm C A C. 10 cm 10cm D. 6 cm D
Câu 39. Cho tam giác ABC là tam giác vuông cân tại A. Biết BC = 12cm. Gọi G là trọng tâm
của tam giác ABC. Tính GB. A. 10cm B. 2 10cm C. 3 10cm D. 4cm
Câu 40. Cho tam giác ABC biết AB = 2cm, AC = 6cm. Cạnh BC có độ dài là một số nguyên
đơn vị xentimet. Hỏi độ dài cạnh BC có thể nhận được bao nhiêu giá trị? A. 3 giá trị B. 4 giá trị C. 5 giá trị D. 6 giá trị
MA TRẬN CÂU HỎI TNKQ ĐỀ 6 Mức độ Nhận biết (câu) Thông hiểu Vận dụng (câu) KT (câu) Thấp Cao 1; 2; 3; 4; 5; 6; 7; 8; 9; 10 ; 11; 12; 11; 17; 18; 21; 13; 14; 15; 16; 22; 24; 32; 35; 26; 27; 38; 39 28; 40 Học kỳ 2 17; 20; 23; 25; 37 29; 30; 31; 33; 34; 36 Tổng 25 Tổng 9 Tổng 4 Tổng 2 120
BÀI TẬP TRẮC NGHIỆM TOÁN 7 Phần 3
GIẢI MỘT SỐ ĐỀ KIỂM TRA ĐÁP ÁN CHỦ ĐỀ 1 Câu 1 2 3 4 5 6 7 8 Đáp án D D C B A B C D Câu 1 2 3 4 5 6 7 8 Đáp án A C D B A C C A ĐÁP ÁN CHỦ ĐỀ 2 Câu 1 2 3 4 5 6 7 8 9 10 Đáp án C D A B B C A A D B ĐÁP ÁN CHỦ ĐỀ 3 Câu 1 2 3 4 5 6 Đáp án D B A D C B Câu 1 2 3 4 5 6 Đáp án A B D B A C ĐÁP ÁN CHỦ ĐỀ 4 Câu 1 2 3 4 5 6 7 8 Đáp án A B D C B D C A Câu 1 2 3 4 5 6 7 8 Đáp án D C B A B C B C ĐÁP ÁN CHỦ ĐỀ 5 Câu 1 2 3 4 5 6 7 8 Đáp án A B C D A B C B Câu 1 2 3 4 5 6 7 8 Đáp án B A A D B C C D ĐÁP ÁN CHỦ ĐỀ 6 Câu 1 2 3 4 5 6 7 8 Đáp án C D B A C B A D Câu 1 2 3 4 5 6 7 8 Đáp án C B A D B D A B ĐÁP ÁN CHỦ ĐỀ 7 121
BÀI TẬP TRẮC NGHIỆM TOÁN 7 Câu 1 2 3 4 5 6 7 8 Đáp án A B C C B A D D Câu 1 2 3 4 5 6 7 8 Đáp án A D D D B C B A ĐÁP ÁN CHỦ ĐỀ 8 Câu 1 2 3 4 5 6 7 8 Đáp án A A A A B D C D Câu 9 10 11 12 13 14 15 16 Đáp án B C C B B C D C ĐÁP ÁN CHỦ ĐỀ 9 Câu 1 2 3 4 5 6 7 8 Đáp án D B A C A C D B Câu 9 10 11 12 13 14 15 16 Đáp án B B B D C D B D ĐÁP ÁN CHỦ ĐỀ 10 Câu 1 2 3 4 5 6 7 8 Đáp án C B D A C B A D Câu 9 10 11 12 13 14 15 16 Đáp án D B C C B C B D ĐÁP ÁN CHỦ ĐỀ 11 Câu 1 2 3 4 5 6 Đáp án D B D A C D Câu 7 8 9 10 11 12 Đáp án B D A B A D ĐÁP ÁN CHỦ ĐỀ 12 Câu 1 2 3 4 5 6 Đáp án D A D B D C Câu 7 8 9 10 11 12 Đáp án D A C D A B 122
BÀI TẬP TRẮC NGHIỆM TOÁN 7 ĐÁP ÁN CHỦ ĐỀ 13 Câu 1 2 3 4 5 6 Đáp án B C D A D A Câu 7 8 9 10 11 12 Đáp án B C D A B C ĐÁP ÁN CHỦ ĐỀ 14 Câu 1 2 3 4 5 6 7 8 Đáp án B D C A C B A B Câu 9 10 11 12 13 14 15 16 Đáp án B C C B B D C A ĐÁP ÁN CHỦ ĐỀ 15 Câu 1 2 3 4 5 6 Đáp án B C B B D D Câu 7 8 9 10 11 12 13 14 15 16 Đáp C A C A B D D C D A án Câu 17 18 19 20 21 22 23 24 25 26 Đáp B C B D A B D C A B án Câu 27 28 29 30 31 32 33 34 35 36 Đáp C C C D D B C C B A án Câu 37 38 39 40 41 42 43 44 45 46 Đáp B C B C B A C D B D án ĐÁP ÁN CHỦ ĐỀ 16 Câu 1 2 3 4 5 6 Đáp án C D C D A B Câu 7 8 9 10 11 12 13 14 15 16 Đáp A C D D D B A B A C án Câu 17 18 19 20 21 22 23 24 25 26 Đáp B A B A C A B A B C 123
BÀI TẬP TRẮC NGHIỆM TOÁN 7 án A BCâu 27 28 29 30 31 32 33 34 35 36 Đáp án C D C C A B B D D A Câu 37 38 39 40 41 42 43 44 45 46 Đáp án D C D A D C D C D B ĐÁP ÁN CHỦ ĐỀ 17 Câu 1 2 3 4 5 6 7 8 9 10 Đáp án C D B C A D B C A D Câu 11 12 13 14 15 16 17 18 19 20 Đáp C A B A C A B B B A án Câu 21 22 23 24 25 26 27 28 29 30 Đáp C A B D A D B C A B án Câu 31 32 33 34 35 36 37 38 39 40 Đáp D D A B C D A B A B án Câu 41 42 43 44 45 46 47 48 49 50 Đáp D B C A C B B D D A án Câu 51 52 53 54 55 56 57 58 59 60 Đáp C A B D D B A D C B án
ĐÁP ÁN ĐỀ KIỂM TRA 45 PHÚT ĐẠI SỐ CHƯƠNG I Câu 1 2 3 4 5 6 7 8 9 10 Đáp A B B D A C C A D B án Câu 11 12 13 14 15 16 17 18 19 20 Đáp C C D C A A C D B D án Câu 21 22 23 24 25 26 27 28 29 30 124
BÀI TẬP TRẮC NGHIỆM TOÁN 7 Đáp A C B D B D B C B B án
ĐÁP ÁN ĐỀ KIỂM TRA 45 PHÚT ĐẠI SỐ CHƯƠNG II Câu 1 2 3 4 5 6 7 8 9 10 Đáp án A C B D A B A C B C Câu 11 12 13 14 15 16 17 18 19 20 Đáp án D D C C D D C B B B Câu 21 22 23 24 25 26 27 28 29 30 Đáp án A C B B D A B A B D
ĐÁP ÁN ĐỀ KIỂM TRA HỌC KỲ I Câu 1 2 3 4 5 6 7 8 9 10 Đáp án B D B A C D C A B C Câu 11 12 13 14 15 16 17 18 19 20 Đáp án D A A D B C A C C A Câu 21 22 23 24 25 26 27 28 29 30 Đáp án C D A B A B B D B C Câu 31 32 33 34 35 36 37 38 39 40 Đáp án A B D C A D B C D B
ĐÁP ÁN ĐỀ KIỂM TRA HỌC KỲ II Câu 1 2 3 4 5 6 7 8 9 10 Đáp án C B D A D D D D C D Câu 11 12 13 14 15 16 17 18 19 20 Đáp án C D A C D B A C D A Câu 21 22 23 24 25 26 27 28 29 30 Đáp án D A A C B B D B B C Câu 31 32 33 34 35 36 37 38 39 40 Đáp án C D B D B C C D B A 125