lOMoARcPSD| 45473628 Phần tự luận
Bài 1: Cho một mẫu số liệu về thu nhập (Y đơn vị tính: triệu đồng/tháng), thâm
niên giảng dạy (X: số năm) và giới tính (Z, trong đó Z=0 nếu là giáo viên nữ và Z
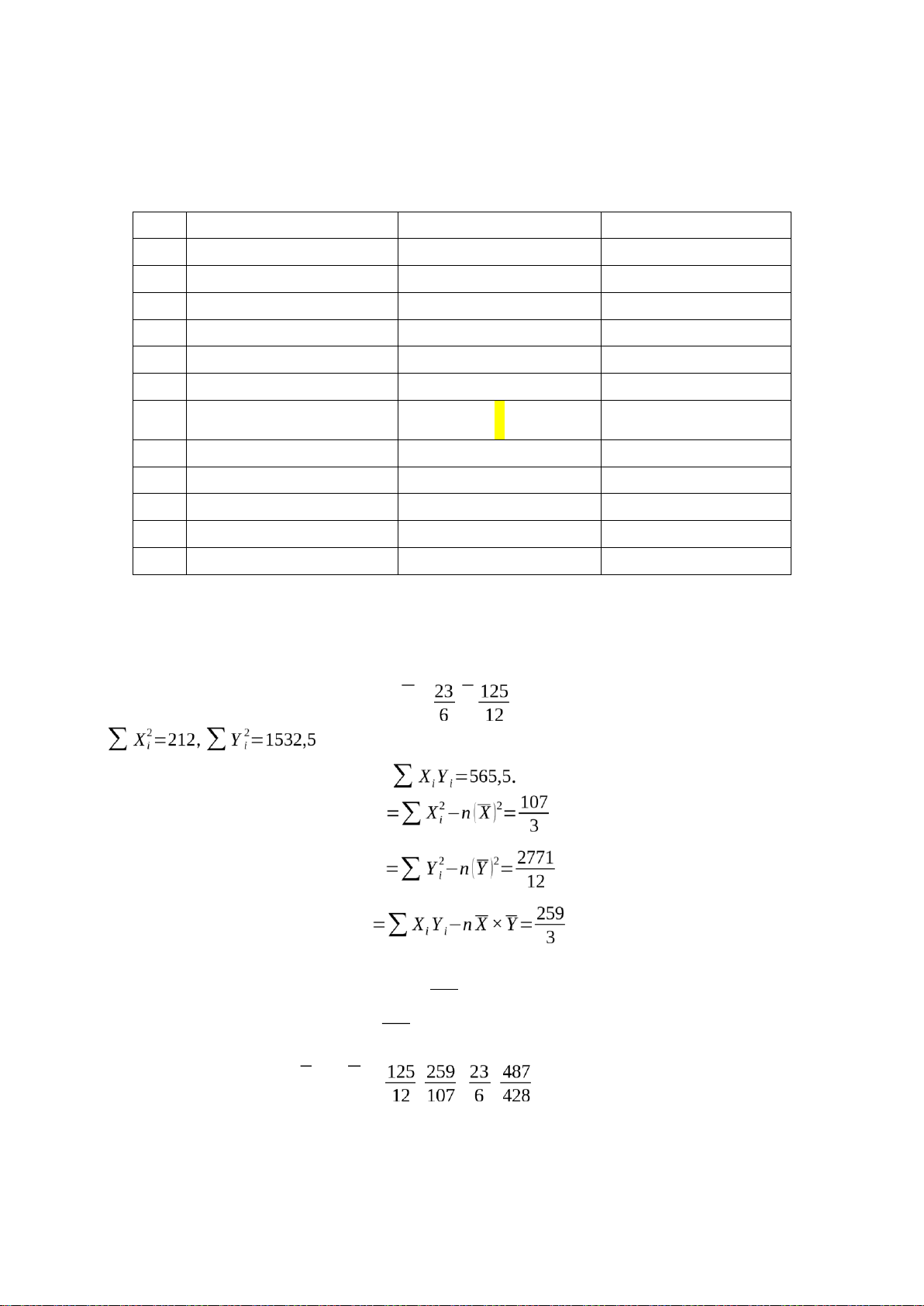
= 1 nếu là giáo viên nam) của một số giáo viên sau: STT Y X Z 1 4.5 3 0 2 6.5 2 0 3 10 3 1 4 9 3 1 5 14 5 0 6 4 1 0 7 16 6 1 8 11 4 0 9 14 5 1 10 18 7 1 11 6 2 1 12 12 5 0 Câu 1: a) N = 12 X= ,Y= SXX SYY SXY SXY 259 β^2= SXX=107=2,420560748
β^1=Y−β^2 X= − × = =1,137850467 lOMoARcPSD| 45473628
Y^ i=1,137850467+2,420560748Xi Ý nghĩa:
β^1=1,137850467 có ý nghĩa khi giảng viên mới vào nghề có mức thu nhập trung bình
đạt 1,137850467 triệu đồng/tháng.
β^2=2,420560748 Khi thâm niên giảng dạy tăng thêm 1 năm, thu nhập bình quân của
giảng viên tăng 2,420560748triệu đồng/tháng. SYY = 277112 b) TSS =
ESS = ( β^2)2×SXX=2,4205607482 × 1073 =208,9750779 σ^ = = =2,14416 n−2 10 Se SXX
Ta có: n =12; Se(β^2)=0,245187 β^2=2,420560748
t (n−2) =t100,025=2,228
Khoảng tin cậy 95% cho hệ số β2:
[β^2−t (n−2 )
×Se(β^2);β^2+t( n−2) ×Se( β^2)]
= [2,420560748−2,228×0,245187;2,420560748+2,228×0,245187] = [1,874250; 2,966871]
Vậy khi thâm niên giảng dạy tăng thêm 1 năm, thu nhập bình quân tăng từ 1,874250
đến 2,966871 triệu đồng/tháng với mức độ tin cậy 95%.
c) Khi thâm niên giảng dạy là 20 năm, ước lượng điểm thu nhập của giảng viênlà:
Y^ 0=1,137850467+2,420560748×20=49,54906543 triệu đồng/tháng lOMoARcPSD| 45473628 √ Se 0 n S XX
Ta có khoảng dự báo 95% của E(Y|X) là:
[Y^0−t (n−2)
×Se(Y^0);Y^0+t ( n−2 ) ×Se(Y^ 0)]
¿> [ 49,54906543−2,228×3,986330;49,54906543+2,228×3,986330 ]
¿> [ 40,667522;58,430609]
Vậy khi giảng viên có thâm niên 20 năm thì dự báo mức thu nhập bình quân nằm
trong khoảng từ 40,667522 triệu đồng/tháng đến 58,430609 triệu đồng/tháng với độ tin cậy 95%. d)
Kiểm định giả thiết H0 :β2=3và đối thiết H1: β2 ≠3
Se(β^2)=0,245187 β^2=2,420560748
t (n−2) =t100,025=2,228
Trị thống kê: t=Se( β^2) = 0,245187 =−2,363 |t|=2,363>2,228 Bác bỏ H , chấp nhận H 0 1
Với mức ý nghĩa 5%, khi giảng viên có thêm 1 năm kinh nghiệm, thu nhập bình
quân tăng khác 3 triệu đồng/tháng. Câu 2:
lnY^ i=1,2541+0,8082ln Xi
a) Ý nghĩa: hệ số hồi quy LnXi là 0,8082 có ý nghĩa khi thâm niên giảng dạy tăngthêm
1% thì thu nhập bình quân của giảng viên tăng 0,8082% trong điều kiện các yếu tố khác không đổi.
b) Có thể sử dụng R2 để so sánh mức độ phù hợp với mẫu dữ liệu của MH1 và MH2 lOMoARcPSD| 45473628
Hệ số xác định có thể được sử dụng để so sánh mức độ giải thích của các mô
hình hồi quy khác nhau cho cùng một tập dữ liệu. Trong trường hợp này, tập dữ liệu
giữa MH1 và MH2 trùng khớp nên có thể sử dụng để so sánh mức độ phù hợp của mô hình. Câu 3:
a) β^1=Se(β^1)×t 1=1,4840×0,5896=0,8750 β^2=Se(β^2)×t2=0,4064×5,7514=2,3374
β^3=Se(β^3)×t3=2,1699×0,5890=1,2781
β^4=Se( β^4)×t4=0,5283×(−0,0514 )=−0,0272 R2/(4−1) 0,9235/3 F=(
1−R2)/(n−4)=(1−0,9235)/8=32,2069
b) Y^i=0,8750+2,3374 Xi+1,2781Zi−0,0272 Xi Zi c)
Kiểm định giả thiết H0 :β4=0và H1: β4≠0
P-value = 0,9603 > 0,05 => Chấp nhận H0
Với mức ý nghĩa 5% hệ số hồi quy trước biến XZ không có ý nghĩa thống kê. d)
Kiểm định giả thiết H0 :β2=3và đối thiết H1: β2 ≠3 Se(β^2)=0,4064 β^2=2,3374
t (n−2) =t100,025=2,228
Trị thống kê: t=Se( β^2) = 0,4064 =−1,6304 |t|=1,6304<2,228 Chấp nhận H0
Với mức ý nghĩa 5%, khi giảng viên có thêm 1 năm kinh nghiệm, thu nhập bình
quân tăng 3 triệu đồng/tháng. Bài 2: lOMoARcPSD| 45473628
a) β^1=Se(β^1)×t 1=6,3516×18,7217=118,9127
β^2=Se(β^2)×t2=1,0960×(−7,2152)=−7,9079
β^3=Se(β^3)×t3=0,6832×2,7263=1,8646
^SALESi=118,9127−7,9079 PRIC Ei+1,8646 ADVERT i
b) Với độ tin cậy 95%, ước lượng giá trị cá biệt của Sale khi Price bằng
USD12và Advert bằng USD8000 1 (12)
Khi Price = 12, Advert = 8 => X 0= 8
^SALE S0=118,9127−7,9079×12+1,8646×8=38,9347
σ^ 2=4,88612=23,873973 t220,025=2,074 6,79
Se(SALE0−SALE^0)
0,01 Ta có khoảng dự báo 95% của E(Y|X) là: [ ) ^SALE
×Se(S ALE0−^SALE0);^SALE0+t ] 0−t ( n−3 )
(n−3 ) ×Se(SALE0−^SALE0
¿> [38,9347−2,074 ×9,3929;38,9347+2,074×9,3929]¿> [19,4538;58,4156 ]
Vậy dự báo giá trị cá biệt của Sale khi Price bằng USD12 và Advert bằng USD8000
nằm trong khoảng từ 19,4538 nghìn đến 58,4156 nghìn với độ tin cậy 95%.
Bài 3: Người ta cho rằng chi tiêu cho mặt hàng A (Y: ngàn đồng/tháng) không chỉ
phụ thuộc vào thu nhập của người tiêu dùng (X: triệu đồng/tháng) mà còn phụ
thuộc vào giới tính của người đó (D = 1 nếu là nam; D = 0 nếu là nữ). Với số liệu
của một mẫu có kích thước n = 20 người ta đã ước lượng mô hình sau:
a) Ước lượng hệ số hồi quy ở độ tin cậy 95%
+) Khoảng tin cậy 95% của β1 Ta có:
n =20; Se(β^1)=20,23; β^2=90,44 lOMoARcPSD| 45473628
t (n−4 )=t160,025=2,120
Khoảng tin cậy 95% cho hệ số β1:
β^1−t(αn−4 ) ×Se(β^1);β^1+t( n−4 ) ×Se( β^1)] 2
⇔ [ 90,44−20,23×2,120;90,44+20,23×2,120 ]
⇔ [ 47,5524;133,3276]
Vậy khi không có thu nhập và không xét giới tính, chi tiêu bình quân cho mặt hàng A
nằm trong khoảng từ 47,5524 đến 133,3276 ngàn đồng/tháng với mức độ tin cậy 95%.
+) Khoảng tin cậy 95% của β2 Ta có: n =20; Se(β^2)=10,31; β^2=38,92
t (n−4)=t160,025=2,120
Khoảng tin cậy 95% cho hệ số β2:
β^2−t(αn−4 ) ×Se( β^2);β^2+t( n−4 ) ×Se( β^2)] 2
⇔ [38,92−10,31×2,120;38,92+10,31×2,120 ]
⇔ [17,0628;60,7772]
Vậy khi không xét giới tính, khi thu nhập tăng thêm 1 triệu đồng/tháng thì chi tiêu bình
quân cho mặt hàng A tăng trong khoảng từ 17,0628 đến 60,7772 ngàn đồng/tháng với mức độ tin cậy 95%.
+) Khoảng tin cậy 95% của β3 Ta có:
n =20; Se(β^3)=4,25; β^3=−8,41
t (n−4 )=t160,025=2,120
Khoảng tin cậy 95% cho hệ số β3:
β^3−t(αn−4 ) ×Se( β^3);β^3+t (n−4 ) ×Se( β^3)] 2
⇔ [−8,41−4,25×2,120;−8,41+4,25×2,120] lOMoARcPSD| 45473628
⇔ [−17,42;0,6000 ]
Vậy khi thu nhập không đổi, chi tiêu bình quân cho mặt hàng A của nam thấp hơn nữ
từ 0,6 đến 17,42 ngàn đồng/tháng với mức độ tin cậy 95%. +) Khoảng tin cậy 95% của
β4 Ta có: n =20; Se(β^4)=1,81; β^4=−6,53
t (n−4 )=t160,025=2,120
Khoảng tin cậy 95% cho hệ số β4:
β^4−t (αn−4 ) ×Se (β^4);β^4+t ( n−4) ×Se(β^4)] 2
⇔ [−6,53−1,81×2,120;−6,53+1,81×2,120]
⇔ [−10,3672;−2,6928]
Vậy khi thu nhập tăng 1 triệu đồng/tháng, chi tiêu bình quân cho mặt hàng A của nam
thấp hơn nữ từ 2,6928 đến 10,3672 ngàn đồng/tháng với mức độ tin cậy 95%. b)
+) Kiểm định giả thiết H0 :β3=0và đối thiết H1: β3 ≠0 Se(β^3)=4,25 β^3=−8,41
t (n−4 )=t160,025=2,120 β^3 −8,41 Trị thống kê: t= ^ = 4,25 =−1,9788 Se( β3) |t|=1,9788<2,120 Chấp nhận H0
Với mức ý nghĩa 5%, chi tiêu về loại hàng A của nam và nữ là giống nhau trong điều
kiện thu nhập không đổi.
+) Kiểm định giả thiết H0 :β4=0và đối thiết H1: β4≠0 Se(β^4)=1,81 β^4=−6,53
t (n−4)=t160,025=2,120 lOMoARcPSD| 45473628 β^4 −6,53 Trị thống kê: t=
Se( β^4)= 1,81 =−3,6077 |t|=3,6077>2,120 Bác bỏ H , chấp nhận H 0 1
Với mức ý nghĩa 5%, khi thu nhập thay đổi, chi tiêu về loại hàng A của nam và nữ là khác nhau.
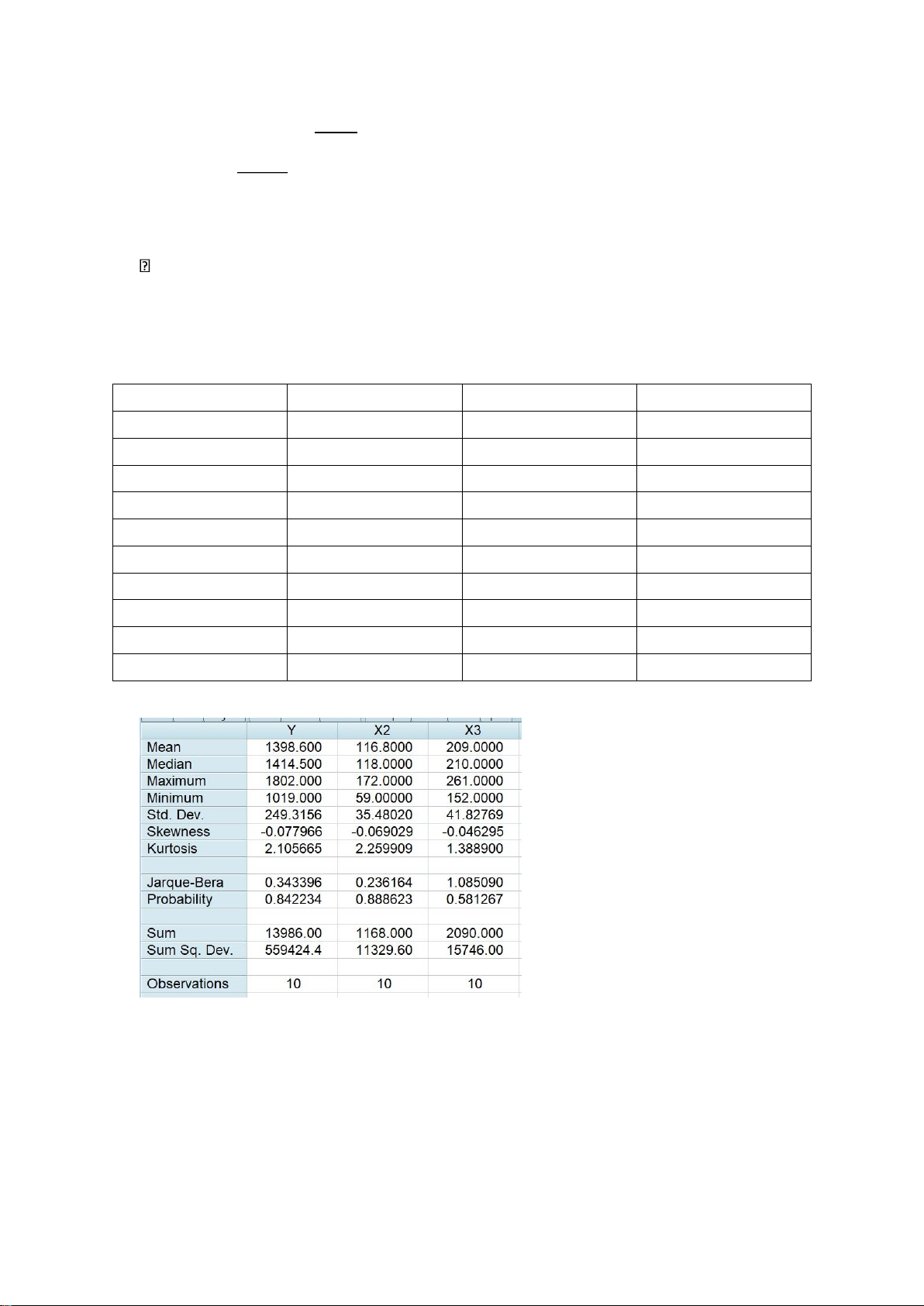
Phần thực hành EVIEWS STT Y X2 X3 1 1268 103 181 2 1491 105 247 3 1058 59 192 4 1628 161 238 5 1019 71 152 6 1802 172 261 7 1607 140 258 8 1284 119 161 9 1389 117 172 10 1440 121 228 a) Thống kê mô tả
b) Bảng ma trận hiệp phương sai và hệ số tương quan lOMoARcPSD| 45473628
c) Bảng ma trận hiệp phương sai của các hệ số hồi quy d) Dependent Variable: Y Method: Least Squares Date: 06/17/24 Time: 22:30 Sample: 1 10 Included observations: 10 Variable Coefficient Std. Error t-Statistic Prob. C 348.1606 77.14508 4.513063 0.0028 X2 4.795553 0.567656 8.447996 0.0001 X3 2.346023 0.481512 4.872200 0.0018 R-squared 0.974090 Mean dependent var 1398.600 Adjusted R-squared 0.966687 S.D. dependent var 249.3156 S.E. of regression
45.50476 Akaike info criterion 10.71684 Sum squared resid 14494.79 Schwarz criterion 10.80761 Log likelihood
-50.58418 Hannan-Quinn criter. 10.61726 F-statistic 131.5821 Durbin-Watson stat 2.246589 Prob(F-statistic) 0.000003
Hàm hồi quy mẫu của Y theo X2 và X3.
Y^i=348,1606+4,795553 X2+2,346023 X3 e) Wald Test: Equation: Untitled Test Statistic Value df Probability t-statistic 2.042672 7 0.0804 F-statistic 4.172508 (1, 7) 0.0804 Chi-square 4.172508 1 0.0411
Null Hypothesis: C(2)+2*C(3)=8 Null Hypothesis Summary: Normalized Restriction (= 0) Value Std. Err. lOMoARcPSD| 45473628 -8 + C(2) + 2*C(3) 1.487599 0.728261
Restrictions are linear in coefficients.
Kiểm định giả thiết H0 :β2+2 β3=8và đối thiết H1: β2+2 β3≠8 Từ
bảng kết quả eviews, ta có: P-value = 0,0804 > 0,05 Chấp nhận H0
Với mức ý nghĩa 5%, khi chi phí chào hàng tăng 1 triệu đồng/tháng và chi phí quảng
cáo tăng 2 triệu đồng/tháng, doanh số bán hàng bình quân tăng 8 triệu đồng/tháng.
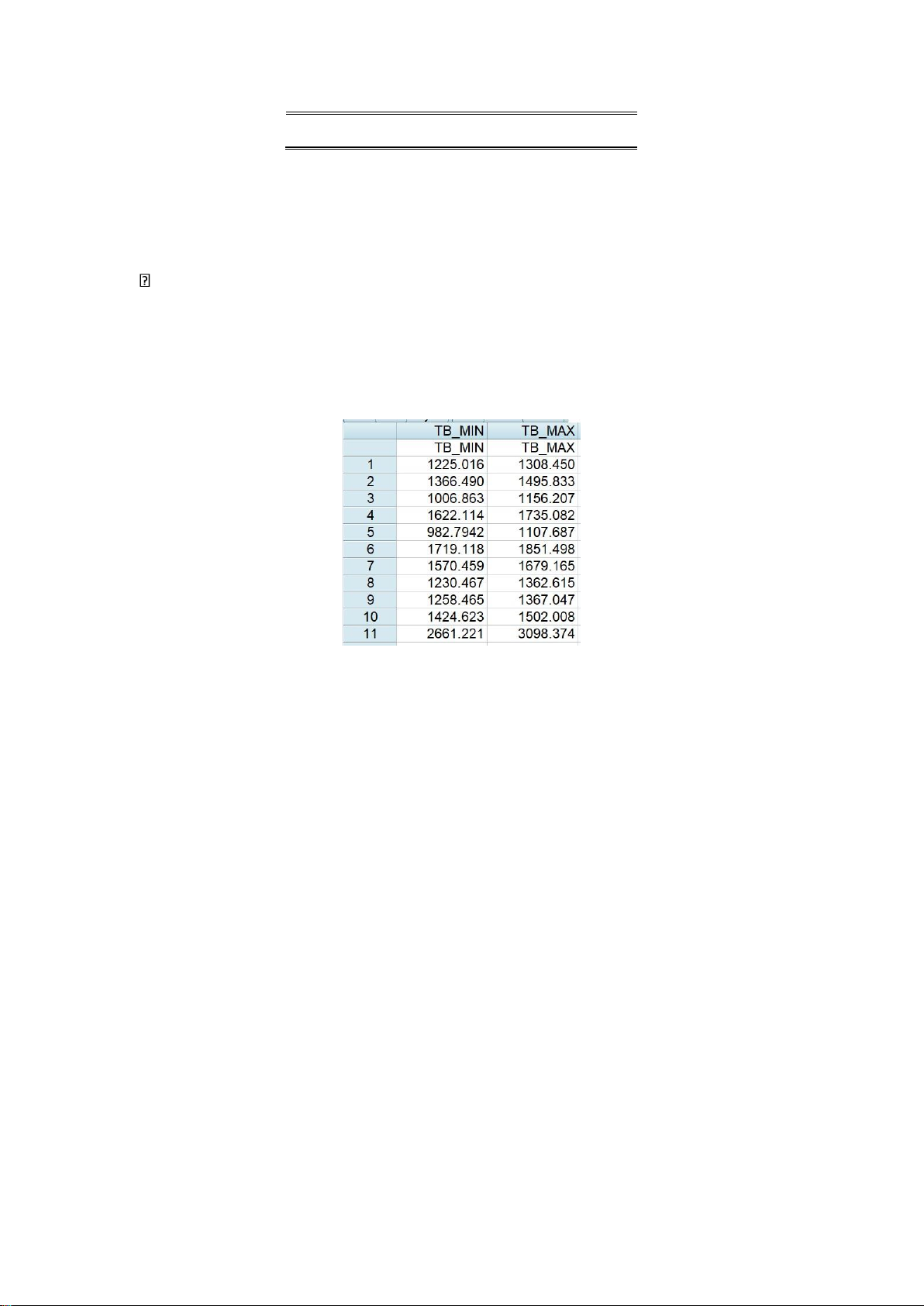
f) Ở độ tin cậy 95%, dự báo doanh số bán hàng trung bình khi chi phí chào hàng là 320
triệu đồng/tháng và chi phí quảng cáo 425 triệu đồng/tháng.
Dự báo doanh số bán hàng trung bình khi chi phí chào hàng là 320 triệu đồng/tháng và
chi phí quảng cáo 425 triệu đồng/tháng nằm trong khoảng 2661,221 đến 3098,374 triệu đồng/tháng.