










Preview text:
ÐÁP ÁN
Ngành đào tạo: ÐIÖN TƯ – VIỄN THÔNG
HÖ đào tạo : ÐẠI HỌC
Môn học : LÝ THUYẾT THÔNG TIN Mã số 411 LTT 340A Số ÐVHT: 4
PHẦN 1: LÝ THUYẾT THÔNG TIN
C©u 1: (1 điễm): Ðịnh nghĩa lưọng thông tin riêng Idé bất dịnh) của mét biến
ngấu nhiên. Xác dịnh các dơn vị do
- Ðịnh nghĩa lượng thông tin riêng (độ bất định)
Lượng thông tin riêng là độ bất định tiềm năng chứa trong một biến cố ngau nhiên xk . Ký hiÖu Ix k Ix k klnpxk - Các đơn vị đo k 1 Ix (nat) k lnpxk k 1
I x log p x (bít) ln2 k 2 k k 1
I x lgpx (hart) ln10 k k 1 nat = 1,443 bít 1 hart = 3,322 bít
C©u 2: (1 điễm) Ðịnh nghĩa entropy của nguồn ròi rạc
Entropy của nguồn tin rời rạc A là trung bình thống kê của lượng thông tin
riêng của các tin thuộc A Ký hiÖu: H 1 A
H1 AM Iai a A 1 a2 . . as
pa1 pa2 . . pas s 0 pa i 1 pa i 1 i1 s' H (bít)
1 A pai log pai i1 http://www.ebook.edu.vn 1
C©u 3: (1 điễm) Nêu các tính chất của entropy của nguồn ròi rạc
Các tính chất của H1A - Khi pa k 1, pai
0 với i k thì H1 A H1 A 0 min
- Một nguồn tin rời rạc gồm s dấu đồng xác suất cho entropy cực đại. Ta có H 1 A logs max
- Entropy của nguồn rời rạc là một đại lượng giới nội 0 H 1 a logs
C©u 4: (1 điễm) Ðịnh nghĩa khả năng thông qua kênh ròi rạc, nêu các tính chất?
- Ðịnh nghĩa: Khả năng thông qua của kênh rời rạc là giá trị cực đại của lượng
thông tin chéo trung bình truyền qua kênh trong một đơn vị thời gian lấy theo
mọi khả năng có thễ có của nguồn tin A. C' '
max I A,B vk max IA, B (bps) A A - Các tính chất: + C' 0
C' 0 khi A và B là độc lËp (kênh bị đứt) + C' v logs k
C' v logs khi kênh không nhiÔu k
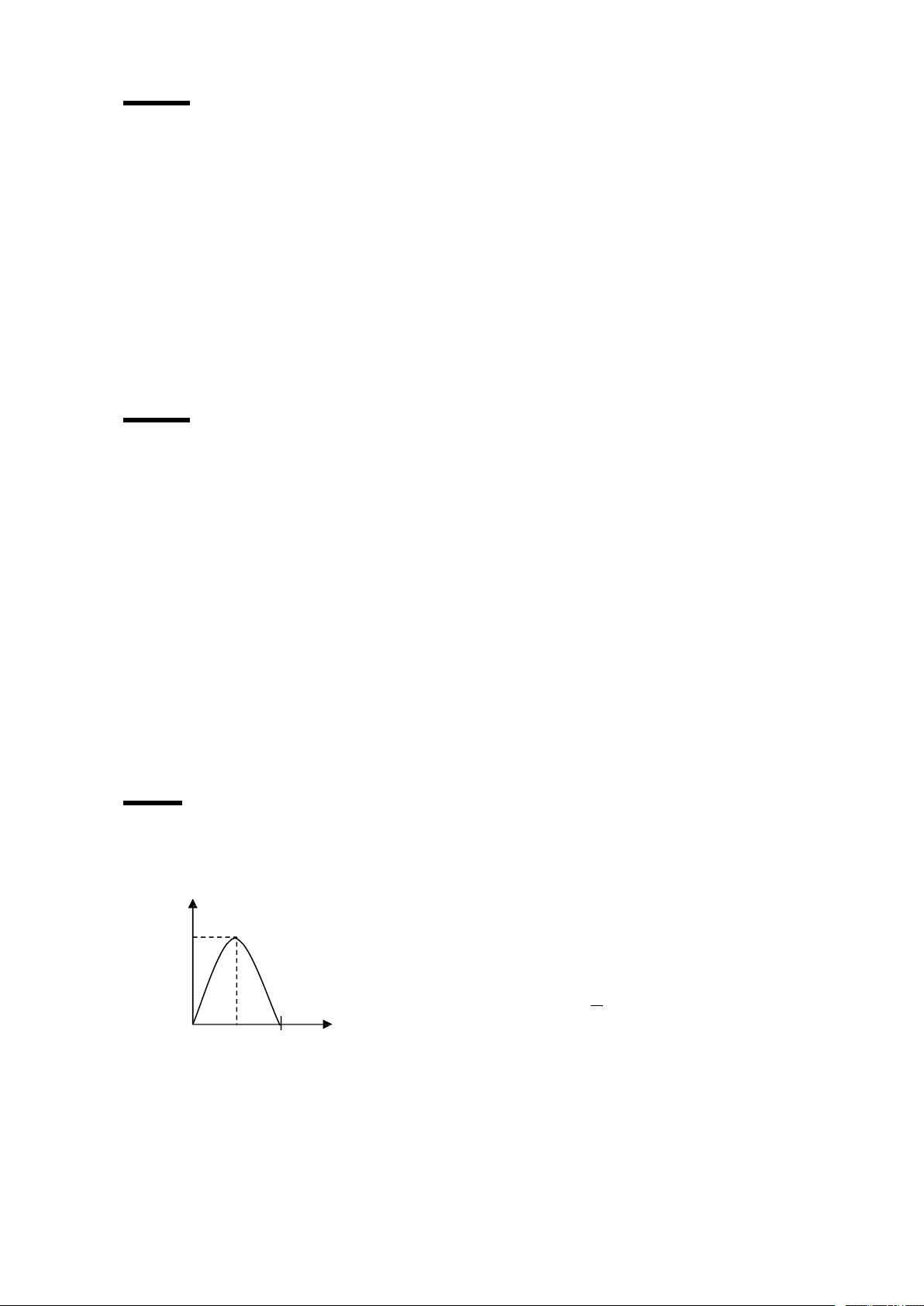
C©u 5: (2 điễm) Entropy của nguồn ròi rạc nhị phân. ý nghĩa của aơn vị do bít?
- Entropy của nguồn rời rạc nhị phân. a A 1 a2 H A (bits) 1 p 1 p 1
H1A plogp 1 plog1 p max Khi p 1 p 1 p 2 0,5 1 H A H A 1bit 1 1 max
- ý nghĩa: 1 bít là lượng thông tin riêng trung bình chứa trong một biến cố của
một nguồn rời rạc 2 phân đồng xác suất. http://www.ebook.edu.vn 2
C©u 6: (2 điễm) Xác dịnh hai trạng thái cực doan của kênh ròi rạc. - Kênh bị đứt:
Các nguồn tin A và B ở hai đầu thu và phát là độc lËp. pa i bj pai pb j ai pai pa i bj pai pbj Ta có: HA b j HA HA B HA
NhËn xét: Lượng thông tin tỗn hao trung bình đúng bằng entropy của
nguồn. Kênh không thễ truyền tin được - Kênh không nhiÔu: AB pa k bk 1 HA b k 0 HA B 0
NhËn xét: Lượng thông tin tỗn hao trên kênh bằng 0
C©u 7: (2 điễm) Entropy có diều kiÖn HA B: dịnh nghĩa và nêu các tính chất
- Ðịnh nghĩa: Entropy có điều kiÖn về 1 trường tin A khi đã rõ trường tin B được
xác định theo công thức sau: s t
HA B pa b ibj log pai j i1 j1 - Các tính chất:
+ HAB HA HB A HB HA B
+ 0 HA B HA
+ HAB HA HB
C©u 8: (2 điễm) Lưọng thông tin chéo trung bình truyền qua kênh ròi rạc: dịnh nghĩa và tính chất - Ðịnh nghĩa:
IA, B M Ia ,b i j với Ia log p i , bj a i bj pa i http://www.ebook.edu.vn 3 s t pa i bj IA,B pa ibj log i1 j1 pa i
IA, B HA HA B HB HB A - Tính chất: + IA, B 0 + IA, B HA
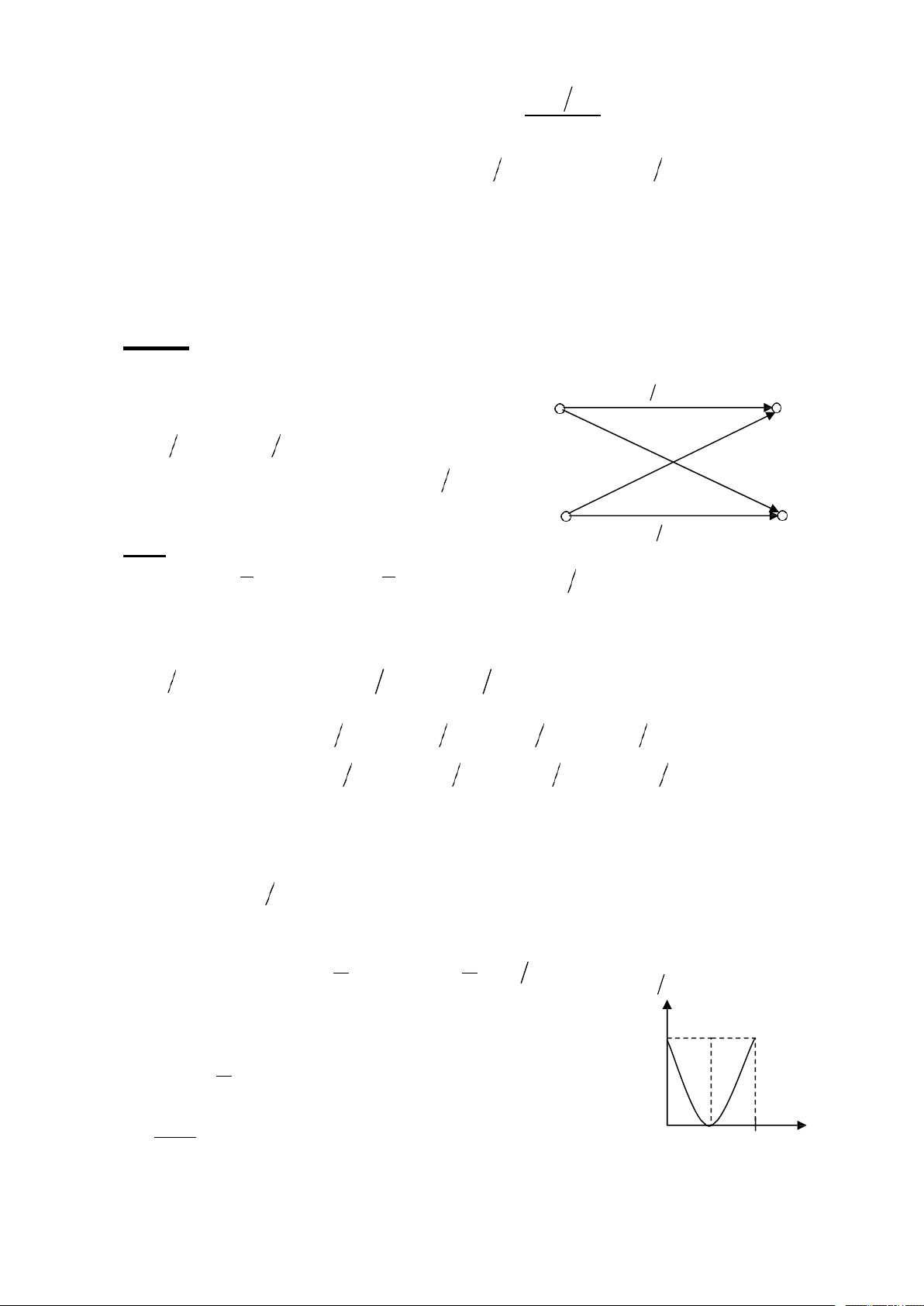
C©u 9: (3 điễm) Cho kênh dối xúng nhị phân sau pa 1 p A B
pb1 a2 pd pa 2 1 p a1 b1 pb 1 a2 pb2 a1 ps 1 pd p p s s
Cho tốc dé truyền tin của kênh v k 1 T
Tính khả năng thông qua C' của kênh này. a2 b2
pb2 a1 pd Giải:
Ta có C' 1 max IA,B 1 max HB HB A T A T A Trong đó: 2 t
HB A pa a log pb i pbj i j ai i1 j1 pa
1 pb1 a1 log pb1 a1 pb2 a1 logpb2 a1 pa
2 pb1 a2 log pb1 a2 pb2 a2 logpb2 a2 p1 p s log1 ps
pslogps 1 pps logps 1 ps log1 ps p s log ps 1 ps log1 ps
Ta thấy HB A không phụ thuộc vào xác suất tiên nghiÖm của các tin thuộc nguồn A. Do đó:
C' 1 max HB 1 HB A T A T C' C'max
Ta có maxHB HB log2 1bit A max 1 ' C 1 khi p max T s 0 (kênh không nhiÔu) C' p 1 p '
s log ps 1 ps log1 ps s 0,5 1 Cmax http://www.ebook.edu.vn 4
C©u 10: (3 điễm) A chọn ngấu nhiên mét trong các số tù 0 dến 7. Tính số câu
hỏi trung bình tối thiểu mà B cần d¾t cho A dể xác dịnh dưọc số mà A dã chọn.
Nêu thu¾t toán hỏi? Giả sŭ A dã chọn số 3, hãy d¾t các câu hỏi cần thiết?
Ðộ bất định của số được chọn ngau nhiên: Ia log1 3bit i logpai 8
Ðễ tìm được số đã chọn của A, B phải đÆt các câu hỏi cho A đễ thu được đủ
một lượng thông tin cần thiết là 3 bít.
Mői câu hỏi của B (dạng lựa chọn) có thễ xem là nguồn rời rạc nhị phân, bởi
vËy lượng thông tin nhËn được sau mői câu trả lời tương ứng là:
HB plogp 1 plog1 p Với p
: xác suất nhËn câu trả lời đúng
1 p : xác suất nhËn câu trả lời sai Iai
VËy số câu hỏi cần thiết n là : n HB Iai
Số câu hỏi trung bình tối thiễu là: n min HBmax HB khi p 1 p 1 max 2 3bit n 3 lần hỏi min 1bit
Giả sử A chọn số B. Các câu hỏi b có thễ đÆt cho A là:
- Câu 1 - Số A chọn lớn hơn 3? Trả lời: Sai
- Câu 2 - Số A chọn lớn hơn 1? Trả lời: Ðúng
- Câu 3 - Số A chọn lớn hơn 2? Trả lời: Sai VËy số A chọn là 3
C©u 11: (4 điễm) Mét thiết bị vô tuyến diÖn gồm 16 khối có dé tin c¾y như nhau
và dưọc mắc nối tiếp. Ta sŭ aṇng mét thiết bị do dể do tín hiÖu ra của các khối.
Giả sŭ có mét khối nào dó bị hỏng. Hãy tính số lần do trung bình tối thiểu dể tìm
dưọc khối bị hỏng. Nêu thu¾t toán do? Giả sŭ khối hỏng là khối thú 6, tìm vị trí
các diểm do cần thiết?
Theo giả thiết độ bất định của khối hỏng là: Ia log 1 i logpai 4bit 16
Lượng thông tin nhËn được sau mői phép đo:
HB plogp 1 plog1 p http://www.ebook.edu.vn 5 Với p : xác suất có tín hiÖu
1 p : xác suất không có tín hiÖu
Ðễ xác định được khối hỏng (khử hết độ bất định) số phép đo cần thiết n là: Ia n i min HBmax
HB max khi p 1 p 12 HB 1bit max n 4bit 4 lần đo min 1bit
Ðễ nmin thuËt toán đo phải đảm bảo HB max Mői lần đo phải đo ở 1
điễm giữa của các khối cần xác định nhằm đảm bảo p 1 p . 2
Giả sử khối hỏng là khối 6. Các phép đo cần thiết là:
- Lần 1: Ðo ở đầu ra khối 8: Không có tín hiÖu, khối hỏng nằm trong các khối từ 1 8.
- Lần 2: Ðo ở đầu ra khối 4: Không có tín hiÖu, khối hỏng nằm trong các khối từ 5 8.
- Lần 3: Ðo ở đầu ra khối 6: Không có tín hiÖu, khối hỏng nằm trong khối 5 hoÆc 6.
- Lần 4: Ðo ở đầu ra khối 5: Có tín hiÖu. VËy khối hỏng là khối 6
C©u 12: (4 điễm) Trong bé tú lơ khơ 52 quân Ikhông kể făng teo), A rút ra mét
quân bài bất kỳ. Tính số câu hỏi trung bình tối tiểu mà B cần d¾t cho A dể xác
dịnh dưọc quân bài mà A dã rút. Nêu thu¾t toán hỏi? Giả sŭ A rút ra 7 quân rô,
hãy nêu các câu hỏi cần thiết?
Ðộ bất định về quân bài mà A đã rút: Ia log 1 i logpai 6bit 52
Giả sử B đÆt cho A câu hỏi dạng lựa chọn, khi đó lượng thông tin nhËn được
sau mői câu trả lời của A là:
HB plogp 1 plog1 p Với p
: xác suất nhËn câu trả lời là đúng
1 p : xác suất nhËn câu trả lời là sai Iai
Số câu hỏi cần thiết đễ xác định được quân bài A đã rút là: n HB http://www.ebook.edu.vn 6
Ta thấy n min khi HB max HB HB 1bit khi p 1 p 1 max 2 log52 bit
Số câu hỏi trung bình tối thiễu là: n 6 lần min 1bit 1
ThuËt toán phải đảm bảo p 1 p . 2
Giả sử A rút ra 7 rô. Các câu hỏi cần thiết có thễ như sau:
- Câu 1: Quân A rút là quân đỏ? Ðúng
- Câu 2: Quân A rút là quân cơ? Sai
- Câu 3: Quân A rút có giá trị 7? Ðúng (giả sử J = 11, Q = 12, K = 13, At=1)
- Câu 4: Quân A rút có giá trị 3? Sai
- Câu 5: Quân A rút có giá trị 5? Sai
- Câu 6: Quân A rút là 6 rô? Sai VËy quân A rút là 7 rô
C©u 13 :(4 diểm) Trong 27 dồng xu có 1 dồng xu giả nhẹ hơn. Ðể tìm dưọc
dồng xu giả ngưòi ta sŭ aṇng mét cân dĩa thăng bằng. Hãy tính số lần cân
trung bình tối thiểu dể xác dịnh dưọc dồng xu giả. Nêu thu¾t toán cân ?
Theo giả thiết độ bất định chứa trong sự kiÖn đồng xu giả là :
I(xi) = - log p(xi) = - log 1/27 = log 27 bit
Khi sử dụng cân đĩa thăng bằng, sau mői lần cân các sự kiÖn có thễ có là :
- Cân thăng bằng với xác suất p
- Cân lÖch trái với xác suất q
- Cân lÖch phải với xác suất 1-p-q
Lượng thông tin nhËn được sau mői lần cân :
H(B) = -plog p – qlog q – (1-p-q)log (1-p-q)
Ðễ xác định được đồng xu giả tỗng lượng thông tin nhËn được sau các lần cân
phải không nhỏ hơn độ bất định của đông xu giả. Như vËy số lần cân cần thiết là : n = I(xi)/H(B)
Ðễ n có giá trị nhỏ nhất thì H(B) phải đạt giá trị cực đại.
Ta có H(B) = H(B)max= log 3 khi p = q = 1-p-q = 1/3.
Khi đó nmin= I(xi)/H(B)max = log27/log 3 = 3 lần cân.
ThuËt toán cân như sau( đảm bảo p = q = 1-p-q )
- Lần 1 : Chia 27 đồng xu thành 3 phần, mői phần có 9 đồng xu. Lấy 2 phần
bất kỳ đÆt lên mői bàn cân 1 phần . Nếu cân thăng bằng thì đồng xu giả http://www.ebook.edu.vn 7
nằm trong 9 đồng xu chưa cân. Ngược lại, tuỳ theo cân lÖch trái hay lÖch
phải ta cũng xác định được phần có chứa đồng xu giả.
- Lần 2 : Chia 9 đồng có chứa đồng xu giả thành 3 phần như nhau, mői phần
có 3 đồng xu. ÐÆt 2 phần bất kỳ lên 2 bàn cân. Kết quả của phép cân sẽ
giúp ta xác định được 3 đồng xu có chứa đông xu giả.
- Lần 3 : Lấy 2 đồng xu bất kỳ trong 3 đồng xu có chứa đồng xu giả đÆt lên
2 đĩa cân. Sau lần cân này ta sẽ xác định được đồng xu giả.
C©u 14 : I2 diểm) Tính entropie của trưòng sự kiÖn dồng thòi ?
Xét 2 trường sự kiÖn A và B sau : a A i i 1,0 B bj j1,t pa pb i j
Khi đó, trường sự kiÖn đồng thời C A.B là : C a ibj pa i,j, i 1,0, j1,t ipbj
Theo định nghĩa, entropie của trường sự kiÖn đồng thời được xác định như sau : s t
HC pa ibj log paibj i1 j1
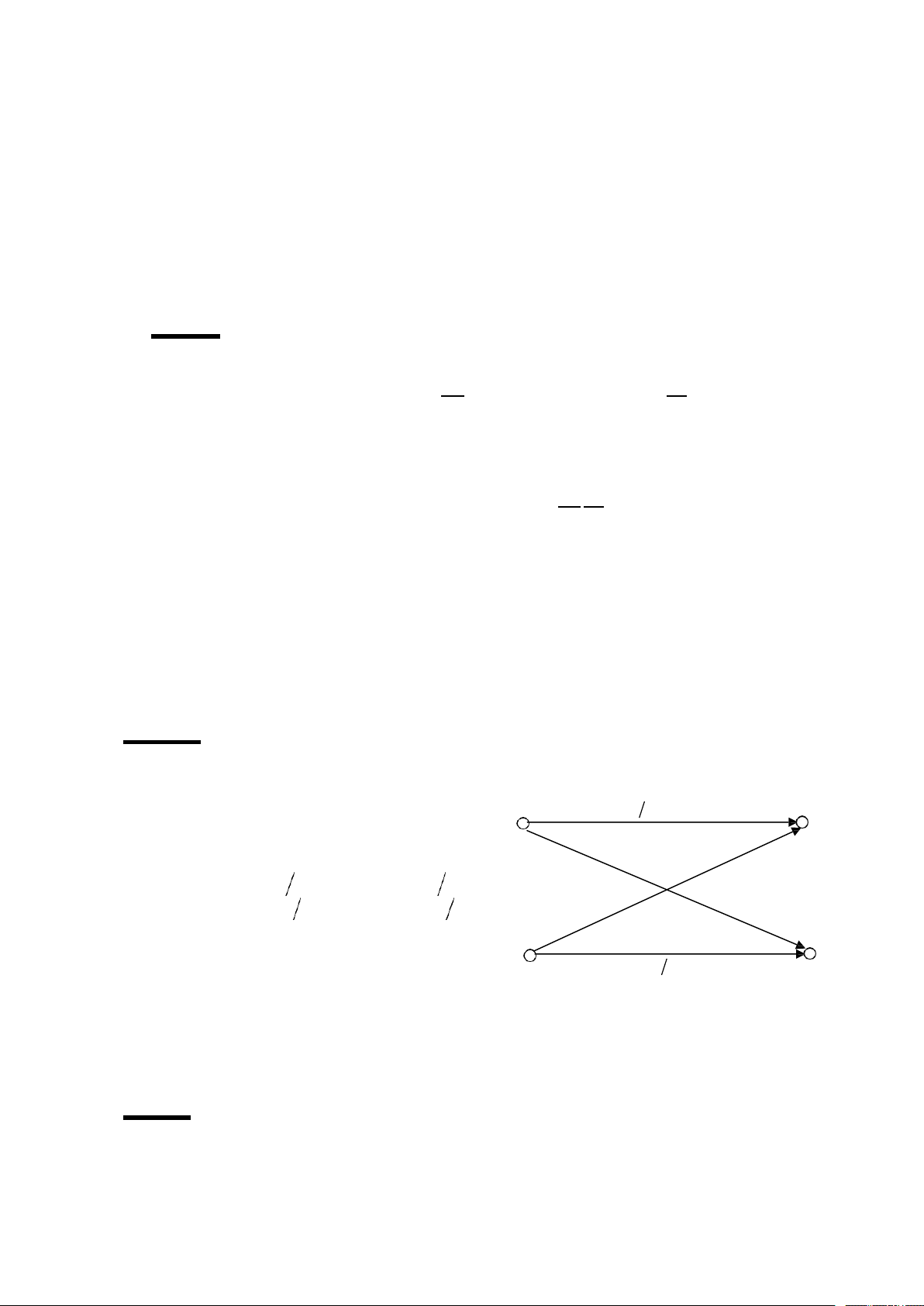
C©u 15: I2 diểm) Cho kênh nhị phân dối xúng không nhó sau Ihình vẽ).
Hãy tính phân bố xác suất của các tin ỏ dầu ra?
Biết rằng pIa1)=p ; pIa2)=1-p. A pb B 1 a2 pd a
Theo công thức xác suất đầy đủ ta có: 1 b1 pb 1 pa1 .pb1 a1 pa2 .pb1 a2
pb pa .pb a pa .pb a pS pS 2 1 2 1 2 2 2 1 pb1 a2
pb2 a1 pd b2
PHẦN 2: LÝ THUYẾT M∙ HOÁ
C©u 1: (1 điễm): Ðịnh nghĩa dé aài trung bình của tù mã ? Phát biểu dịnh lý mã
hoá thú nhất của Shannon?
Xét phép mã hoá các tin rời rạc sau: a ni i i http://www.ebook.edu.vn 8 ai nii A V pa i pai
- Ðịnh nghĩa: Ðộ dài trung bình của từ mã là kỳ vọng của đại lượng ngau nhiên ni s n pai ni i1
- Ðịnh lý mã hoá thứ nhất của Shannon (đối với mã nhị phân)
Luôn luôn có thễ xây dựng được một phép mã hoá các tin rời rạc có hiÖu quả
mà độ dài trung bình của từ mã có thễ nhỏ tuỳ ý, nhưng không nhỏ hơn
entropie xác định bởi các đÆc tính thống kê của nguồn n H 1 A
C©u 2: (1 điễm) Nêu nguyên tắc l¾p mã tiết kiÖm?
Từ định lý mã hoá thứ 1 của Shannon: s s
n pai ni H1A pai logpai i1 i1 1 ta có: n i log pa i
Nguyên tắc: Các tin có xác suất xuất hiÖn lớn được mã hoá bằng các từ mã có
độ dài nhỏ và ngược lại các tin có xác suất xuất hiÖn nhỏ được mã hoá bằng các từ mã có độ dài lớn.
C©u3: (1 điễm) Trọng số của tù mã: dịnh nghĩa và tính chất?
- Ðịnh nghĩa trọng số của từ mã: Wni i
Trọng số của 1 từ mã là số các dấu mã khác không chứa trong từ mã - Tính chất: + 0 Wni i 1 + Wn n i j dni ,n j
C©u 4: (1 điễm) Nêu các dịnh lý quy dịnh khả năng phát hiÖn sai và khả năng sŭa sai của mét bé mã?
- Ðịnh lý về khả năng phát hiÖn sai:
Mã đều nhị phân có độ thừa với khoảng cách Hamming d0 1 có khả năng
phát hiÖn t sai thoả mãn điều kiÖn t d0 1.
- Ðịnh lý về khả năng sửa sai: http://www.ebook.edu.vn 9
Mã đều nhị phân có độ thừa với khoảng cách Hamming d0 3 có khả năng
sửa được t sai thoả mãn điều kiÖn: t d 1 0
. Trong đó x ký hiÖu phần 2 nguyên của số x.
C©u 5: (2 điễm) Khoảng cách mã: dịnh nghĩa, tính chất? Ðịnh nghĩa khoảng cách mã tối thiểu? - Ðịnh nghĩa:
Khoảng cách giữa hai từ mã n và n là số các dấu mã khác nhau về giá i j
trị tính theo cùng một thứ tự giữa 2 từ mã này. Ví dụ: 7 0 1 1 0 1 0 0 i 7 1 0 1 0 0 1 1 j * * * * * d7i ,7 j 5 - Tính chất: + dni ,n j 0 dn khi n n i ,n j 0 i j + dni ,n j n
+ Tính chất tam giác: dni,n j dnj,n k dni,n k
Ðịnh nghĩa khoảng cách mã tối thiễu:
d0= min d( ian, jan) với mọi i,j
C©u 6: (2 điễm) Cho mã xyclic V- n - k có da thúc sinh gx=1+x + x3
n =7, k =4. Hãy thiết l¾p ma tr¾n sinh và ma tr¾n kiểm tra của mã này?
Cho ma trËn sinh G. 1 x x3 11 0100 0
x x2 x4 0 1 10 10 0 G=
x2 x3 x5 0 0 1 1 0 1 0 x3 x4 x6 0 0 0 1 1 0 1 Ma trËn kiễm tra H : Ta có : hx x7 1 x4 x2 x 1 gx http://www.ebook.edu.vn 10 x7 1 x3 x 1
x7 x5 x4 x4 x2 x 1 x5 x4 1 x5 x3 x2 x4 x3 x2 1 x4 x2 x x3 x 1 x3 x 1 0
h*X XdeghxhX1 x4 x3 x2 1 h* x x.h*x H . . . . . . . . . xr1.h* x
1 x2 x3 x4 1011100
H x x3 x4 x5 01 0111 0
x2 x4 x5 x6 001 0111 Ta có G.HT 0
C©u 7: (2 điễm) hãy thiết l¾p tù mã hÖ thống của bé mã xyclic I7,4) có da thúc
sinh gx =1+x + x3 tương úng vói da thúc thông tin a x = x + x3 . ISŭ aṇng thu¾t toán 4 bưóc).
- Bước 1: ax = x + x3
- Bước 2: Nâng bËc axxn-k x3 xx74 x6 x4 - Bước 3: Chia tính dư: x6 x4 x3 x 1 x6 x4 x3 x3 1 x3 x3 x 1 rx x 1
- Bước 4: Thiết lËp từ mã f(x)
f x axxnk rx
f x x6 x4 x 1 1 1 0 0 1 0 1
x6. . . . . . . . . . . . . . . . . . . . . . . . . . . 6 http://www.ebook.edu.vn 11
C©u 8: (2 điễm) Cho phân tích x7 +1 như sau
x7 +1= 1+ x1 x x31 x2 x3
Hãy nêu tất cả các mã xyclic có thể có trên vành Z 2 x x7 + 1 . TT Ða thức sinh g(x) Mã (n, k) d0 1 1+ x 7,6 2 2 1+ x + x3 7,4 3 3 1+ x2 + x3 7,4 3 4 1+ x + x2 + x4 7,3 4 5 1+ x2 + x3 + x4 7,3 4 6 6 7,1 7 xi i=0 7 1 7,7 1
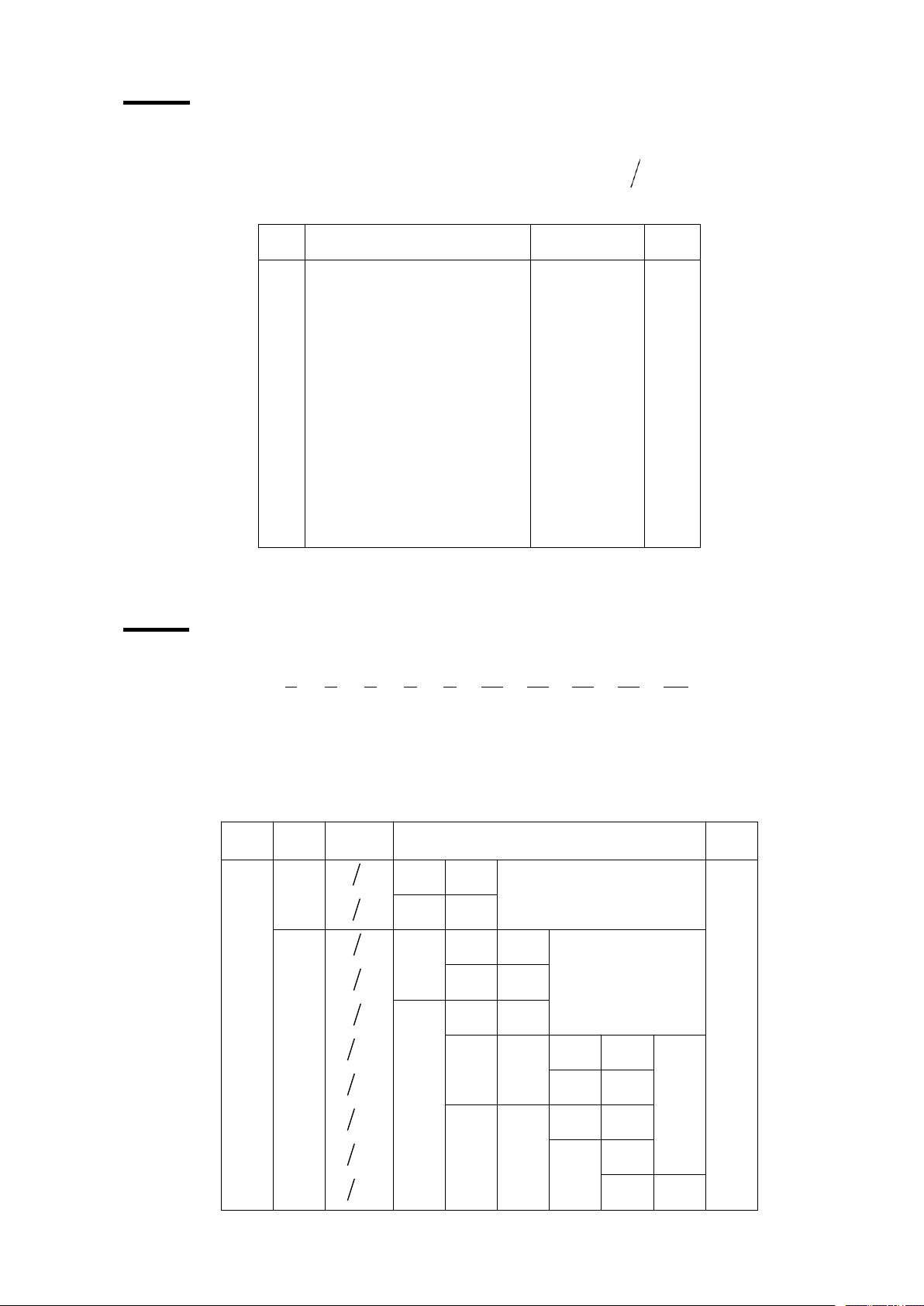
C©u 9: (4 điễm) Hãy thực hiÖn mã hoá Shannon – Fano cho nguồn ròi rạc A sau: a a a a a a a a a a 1 2 3 4 5 6 7 8 9 10
A= 1 1 1 1 1 1 1 1 1 1 4 4
8 8 8 32 32 32 64 64
Ðánh giá hiÖu quả của phép mã hoá này?
Hãy giải mã cho aãy bít nh¾n dưọc có aạng: 101100111010101… TT a Từ mã ni i pa n i i i 1 a 1 4 0 0 2 1 2 a 0 1 2 2 1 4 3 a 1 8 1 0 0 3 3 4 a 1 0 1 4 1 8 3 5 a5 1 8 1 1 0 3 6 a6 1 32 1 1 1 0 0 5 7 a7 1 32 1 1 1 0 1 5 8 a8 1 32 1 1 1 1 0 5 9 a9 1 64 1 1 1 1 1 0 6 10 a10 1 64 1 1 1 1 1 1 6 http://www.ebook.edu.vn 12 - Ðánh giá hiÖu quả: 10 n
pa n 2.2.1 3.3.1 3.5. 1 2.6. 1 i i 4 8 32 64 i1 9 15 6 1 2.25 dấu 8 32 32 32 10
H A pa log 1 2.1.log43.1log8 3. 1 log32 2. 1 log64 1 i pa 4 8 32 64 i1 i 2.25 bit 32 n H
1 A phép mã hoá là tối ưu
- Giải mã cho dãy bít nhËn sau:
1 0 1 1 0 0 1 1 1 0 1 0 1 0 1 . . a4 a3 a8 a4 a2
C©u 10: (4 điễm) Giả sŭ tù mã nh¾n dưọc của mã xyclic I7,3) vói da thúc sinh
gx =1+x+ x2 + x4 có aạng sau v x = x6 + x5 + x4 + x3 + x2 . Hãy sŭ aṇng
thu¾t toán chia aịch vòng dể tìm dưọc tù mã dã phát, biết rằng mã I7, 3) này có a0 = 4.
- Bước 1: Chia v(x) cho g(x)
x6 x5 x4 x3 x2 x3 x 1 x6 x4 x3 x2 x2 x x5 x5 x3 x2 x 0 r x x3 x2 x
- Bước 2: Wr x 3 t d 1 4 1 1,5 0
2 2
- Bước 3: (lần 1) x.vx x6 x5 x4 x3 1
x6 x5 x4 x3 1 x3 x 1 x6 x4 x3 x2 x2 x x5 x2 1 x5 x3 x2 x 1 r x x3 x 1 Wr
1 x 3 t 1 Bước 3 http://www.ebook.edu.vn 13
- Bước 3: (lần 2): x2.vx x6 x5 x4 x 1
x6 x5 x4 x 1 x3 x 1 x6 x4 x3 x2 x2 x x5 x3 x2 x 1 x5 x3 x2 x r2 x 1 Wr 2 x 1 t - Bước 4: ^ 2 x x6 x5 x4 x f x x2vx r x2 x2 ^ 6 4 3 2
f x x x x x 0011101 * Sai ở x5 đã được sửa
C©u 11: (3 điễm) Hãy xác dịnh t¾p tất cả các tù mã của bé mã xyclic I7, 3) có da
thúc sinh gx =1+ x2 + x3 + x4.
Cho mã xyclic (7, 3) có gx =1+ x2 + x3 + x4 ma trËn sinh:
1 x2 x3 x4 1011100
G x x3 x4 x5 0101110
x2 x4 x5 x6 001 0111
TËp 2k 23 8 từ mã, trong đó 7 từ mã khác không là tËp các tỗ hợp tuyến
tính các hàng của ma trËn G gx =1+ x2 + x3 + x4 1 0 1 1 1 0 0
xgx x x3 x4 x5 0 1 0 1 1 1 0
x2gx x2 x4 x5 x6 0 0 1 0 1 1 1
1 xgx 1 x x2 x5 1 1 1 0 0 1 0
1x2gx 1x3 x5 x6 1 0 0 1 0 1 1
x x2gx xx2 x3 x6 0 111 0 0 1
1x x2gx 1 x x4 x6 1 1 0 0 1 0 1 http://www.ebook.edu.vn 14
C©u 12: (3 điễm) Phát biểu và chúng minh giói hạn Hamming? Ðịnh nghĩa mã hoàn thiÖn? - Giới hạn Hamming.
Với mã tuyến tính (n, k), điều kiÖn cần đễ sử được t sai là: t n Ci 2nk i0
Chứng minh: Số các kiễu sai có trọng số i là Cin t
Số các kiễu sai có trọng số t là: C0 C1 . . Ct Ci n n n n i0
Số các trạng thái khác nhau của các dấu kiễm tra là: 2r 2nk
Ðễ sửa được sai, mői trạng thái của các dấu kiễm tra chỉ được gán tối đa cho 1 kiễu sai. t
VËy đễ sửa được tất cả các kiễu sai có trọng số t ta có: i C 2nk n i0
- Ðịnh nghĩa mã hoàn thiÖn.
Mã hoàn thiÖn là mã (n, k, d) đạt được giới hạn Hamming Ví dụ: Mã (7, 4) có d = 3 d 1 Ta có : t 1 2
C0 C1 274 23 8 7 7 1 7 8
VËy mã (7, 4) là 1 mã hoàn thiÖn.
C©u 13: I4 diểm) Cho phân tích của x15+1 như sau :
X15+1=I1+x)I1+x+x2)I1+x+x4)I1+x3+x4)I1+x+x2+x3+x4)
Hãy nêu tất cả các mã xyclic có dé aài 15 trên vành Z2[x]/x15+1? ÐÆt g X 1 X g X 1 X X2 1 2 g 3 X 1 X X4 g 4 X 1 X3 X4 http://www.ebook.edu.vn 15 TT Ða thức sinh Mã (n,k) 1 g 1 X (15,14) 2 g 2 X (15,13) 3 g 3 X (15,11) 4 g 4 X (15,11) 5 g 5 X (15,11) 6 g1.g2 (15,12) 7 g1.g3 (15,10) 8 g1.g4 (15,10) 9 g1.g5 (15,10) 10 g2.g3 (15,9) 11 g 2.g4 (15,9) 12 g2.g5 (15,9) 13 g3.g4 (15,7) 14 g3.g5 (15,7) 15 g4.g5 (15,7) 16 g1.g2.g3 (15,8) 17 g1.g2.g4 (15,8) 18 g1.g2.g5 (15,8) 19 g2.g3.g4 (15,5) 20 g2.g3.g5 (15,5) 21 g1.g3.g4 (15,6) 22 g1.g3.g5 (15,6) 23 g1.g4.g5 (15,6) 24 g2.g4.g5 (15,5) 25 g3.g4.g5 (15,3) 26 g (15,4) 1.g2.g3.g4 27 g1.g2.g3.g5 (15,4) 28 g1.g2.g4.g5 (15,4) 29 g2.g3.g4.g5 (15,1) 30 g1.g3.g4.g5 (15,2) 31 1 (15,15) http://www.ebook.edu.vn 16
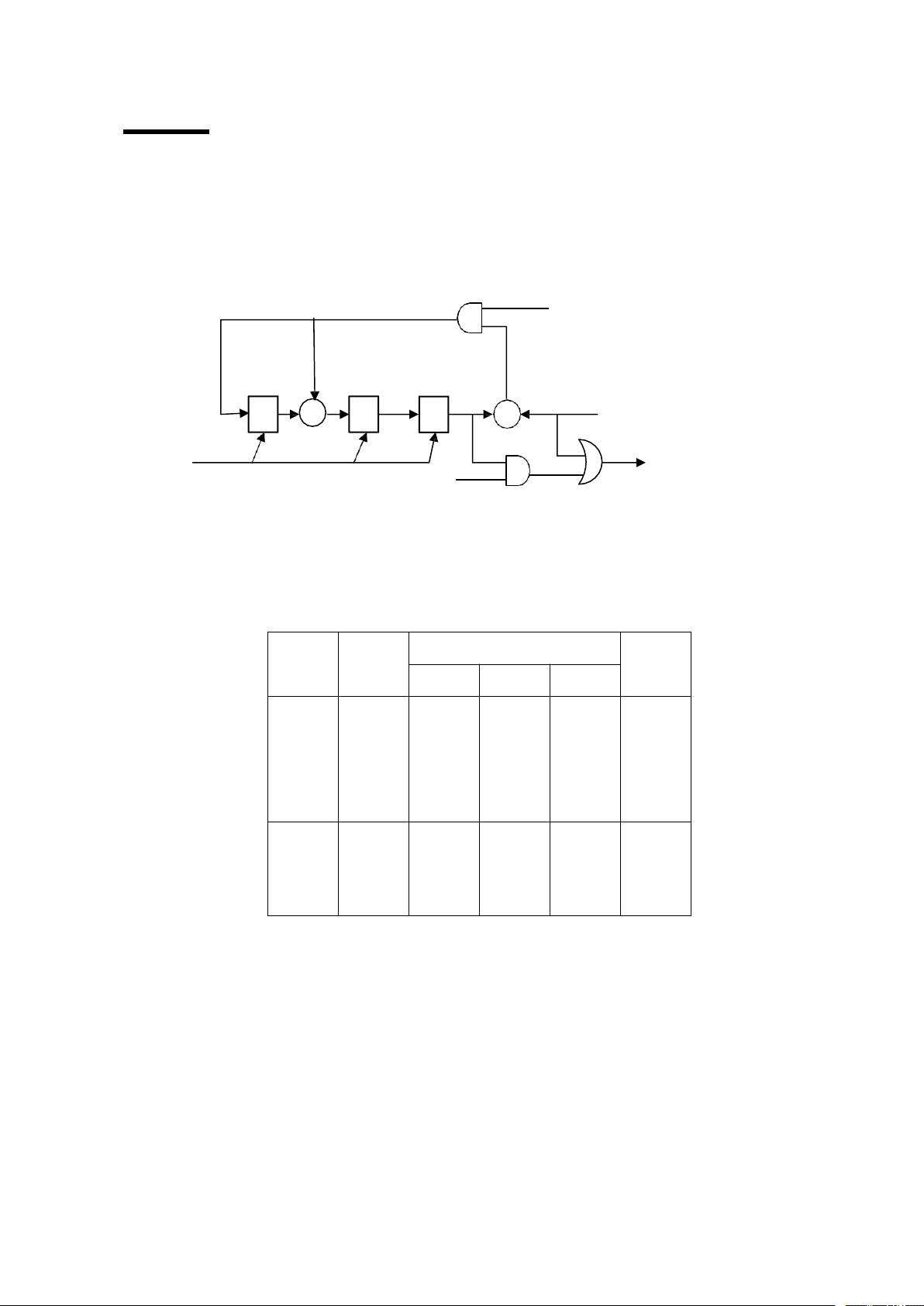
C©u 14:(3 diểm) Mô tả sơ dồ chúc năng thiết bị mã hoá theo phương pháp chia
cho mã xyclic hÖ thống I7,4) có da thúc sinh gIx)=1+x+x3. Tìm tù mã dầu ra của
thiết bị này khi da thúc thông tin dầu vào aIx)=1+x3.
Mã (7, 4) có gX 1 X X3 V1 1 4 Vµo 1 + 2 3 + RA 1 7 5 7 V2 a X 1 X3 aX.xnk X6 X3 Xung Trạng thái các ô nhớ Vào Ra nhịp 1 2 1 1 1 1 1 0 1 2 0 0 1 1 0 3 0 1 1 1 0 4 1 0 1 1 1 5 0 0 0 1 1 6 0 0 0 0 1 7 0 0 0 0 0
Từ mã ra 0 1 1 1 0 0 1 X X2 X3 X6 http://www.ebook.edu.vn 17
C©u 15: I2 diểm) Mô tả vành da thúc vói 2 phép toán céng và nhân các da thúc theo moaulo xn+1
Vành đa thức: Z2 xn 1 n1
f X fixi ; deg f X n 1 ; fi GF2 i0 n1 n1
Phép cộng: aX aixi ; bX bixi i0 i0 n1
cX aX bX ci xi trong đó ci ai bi mod2 i0
Phép nhân: a X.bX a X.bXmod Xn 1 Ta có Xi.Xj Xi jmodn http://www.ebook.edu.vn 18
Document Outline
- PHẦN 1: LÝ THUYẾT THÔNG TIN
- PHẦN 2: LÝ THUYẾT M∙ HOÁ


