Bài Thảo Luận Học Phần Lập Trình Python: Dự Đoán Khả Năng Vay Vốn Bằng Decision | Đại học Thương Mại

lOMoAR cPSD| 45315597
TRƯỜNG ĐẠI HỌC THƯƠNG MẠI KHOA: HTTTKT & TMĐT
--------------------------------------------------- BÀI THẢO LUẬN HỌC PHẦN LẬP TRÌNH PYTHON ĐỀ TÀI:
SỬ DỤNG PHƯƠNG PHÁP DECISION TREE
ĐỂ DỰ ĐOÁN KHẢ NĂNG VAY VỐN
Giảng viên hướng dẫn: Th.S Đỗ Thị Thanh Tâm Mã lớp học phần: 242_INFO4511_08
Nhóm thực hiện: 07 lOMoAR cPSD| 45315597 LỜI CẢM ƠN
Lời đầu tiên, nhóm 7 chúng em xin được gửi lời cảm ơn tới Ban Giám hiệu Trường
Đại học Thương mại cùng toàn thể các cán bộ Khoa Hệ thống thông tin kinh tế và
Thương mại điện tử đã tạo điều kiện thuận lợi để sinh viên có cơ hội tiếp cận với tri thức
mới, được học tập và rèn luyện trong một môi trường hiện đại, năng động và đầy cảm hứng.
Chúng em xin bày tỏ lòng biết ơn sâu sắc tới cô Đỗ Thị Thanh Tâm - giảng viên
học phần “Lập trình Python”, người đã tận tình hướng dẫn, hỗ trợ và đồng hành cùng
chúng em trong suốt quá trình thực hiện đề tài. Nhờ sự chỉ bảo nhiệt tình, sự quan tâm
và định hướng sát sao của cô, chúng em không chỉ nắm bắt được những kiến thức quan
trọng về lập trình, mà còn phát triển tư duy logic, kỹ năng làm việc nhóm và khả năng
giải quyết vấn đề một cách khoa học và sáng tạo. Một lần nữa, chúng em xin gửi tới cô
lời cảm ơn trân trọng và chân thành nhất.
Học phần “Lập trình Python” đã thực sự mở ra một cánh cửa mới trong hành trình
học tập và phát triển bản thân của chúng em. Đây chính là nền tảng vững chắc để nhóm
có thể tiếp tục học hỏi, sáng tạo và ứng dụng vào các lĩnh vực chuyên môn sau này. Tuy
nhiên, do thời gian có hạn và kinh nghiệm thực tiễn còn chưa nhiều, sản phẩm của nhóm
không tránh khỏi những thiếu sót nhất định. Kính mong cô và các bạn trong lớp đóng
góp ý kiến để nhóm 7 có thể rút kinh nghiệm, chỉnh sửa và hoàn thiện đề tài một cách tốt hơn trong tương lai.
Nhóm 7 chúng em xin chân thành cảm ơn! Thân ái! Nhóm 7 2 lOMoAR cPSD| 45315597 MỤC LỤC
LỜI CẢM ƠN ................................................................................................................ 2
MỤC LỤC ...................................................................................................................... 3
BẢNG PHÂN CÔNG NHIỆM VỤ TỪNG THÀNH VIÊN ....................................... 4
LỜI MỞ ĐẦU ................................................................................................................ 5
I. ĐẶT VẤN VỀ ............................................................................................................. 5
1. Tầm quan trọng ...................................................................................................... 5
2. Mục tiêu nghiên cứu .............................................................................................. 6
3. Phương pháp tiếp cận ............................................................................................ 6
II. LÝ THUYẾT VỀ PHƯƠNG PHÁP DECISION TREE ....................................... 8
1. Khái niệm ............................................................................................................... 8
2. Cấu trúc của Cây Quyết định ................................................................................ 9
3. Phân loại Cây Quyết định .................................................................................... 10
3.1. Cây phân loại (Classification tree) ............................................................... 10
3.2. Cây hồi quy (Regressive Tree) ...................................................................... 16
4. Quy trình xây dựng cây quyết định ..................................................................... 19
5. Ưu điểm và nhược điểm của phương pháp Decision Tree ................................ 20
5.1. Ưu điểm ......................................................................................................... 20
5.2. Nhược điểm ................................................................................................... 20
6. Ứng dụng của phương pháp Decision Tree ........................................................ 21
III. MÔ TẢ BÀI TOÁN .............................................................................................. 22
IV. MÔ TẢ DỮ LIỆU .................................................................................................. 22
V. DÙNG NGÔN NGỮ PYTHON ĐỂ GIẢI QUYẾT BÀI TOÁN ......................... 25
VI. MỞ RỘNG PHƯƠNG PHÁP DECISION TREE ............................................. 25
KẾT LUẬN .................................................................................................................. 26 3 lOMoAR cPSD| 45315597
DANH MỤC TÀI LIỆU THAM KHẢO ................................................................... 26
DANH MỤC HÌNH ẢNH ........................................................................................... 27
BẢNG PHÂN CÔNG NHIỆM VỤ TỪNG THÀNH VIÊN ST Mã sinh viên Họ và tên Nhiệm vụ T 1 24D190152 Nguyễn Thị Thúy Hiền
Làm nội dung các phần: Lời cảm
ơn + Lời mở đầu + Kết luận + phần
I + mục 8: Trực quan hóa cây quyết định + làm Word. 2 24D190162
Nguyễn Hoàng Hải Linh Làm nội dung các mục 4, 5, 6 phần II 3 24D190170 Nguyễn Thị Hồng
Làm nội dung mục 4, 5, 6, 7 phần Nhung
V + mục 1, 2, 3, 4 phần VI, làm Word. 4 24D190171 Lê Hồng Phong
Làm nội dung mục 5, 6, 7, 8 phần VI + làm slide PPT 5 24D190174 Nguyễn Thị Mỹ Tâm
Làm nội dung mục 1, 2, 3 phần II 6 24D190185 Lê Hải Yến
Làm nội dung mục III, IV + mục 1, 2, 3 phần V 4 lOMoAR cPSD| 45315597 LỜI MỞ ĐẦU
Trong bối cảnh nền kinh tế không ngừng phát triển và hội nhập, nhu cầu vay vốn
của người dân và doanh nghiệp ngày càng trở nên phổ biến nhằm phục vụ các mục tiêu
tiêu dùng, đầu tư và phát triển kinh doanh. Tuy nhiên, việc đánh giá khả năng vay vốn
của khách hàng vẫn là một bài toán quan trọng và đầy thách thức đối với các tổ chức tín
dụng. Theo báo cáo của Ngân hàng Nhà nước Việt Nam, tổng dư nợ tín dụng năm 2020
đạt hơn 9 triệu tỷ đồng, tăng 12,13% so với năm 2019 cho thấy tín dụng là một kênh tài
chính thiết yếu trong nền kinh tế. Mặc dù vậy, tỷ lệ nợ xấu vẫn là một vấn đề đáng lo
ngại, với mức trung bình khoảng 1,7 - 2; đòi hỏi các ngân hàng cần có những phương
pháp phân tích và dự báo hiệu quả hơn trong việc xét duyệt hồ sơ vay vốn. Trong bối
cảnh đó, các mô hình học máy (Machine Learning) đang ngày càng được ứng dụng rộng
rãi trong lĩnh vực tài chính - ngân hàng, đặc biệt là trong việc hỗ trợ ra quyết định tín
dụng. Một trong những phương pháp đơn giản nhưng hiệu quả cao là Decision Tree -
cây quyết định. Phương pháp này không chỉ giúp trực quan hóa quá trình phân loại khách
hàng mà còn cung cấp những tiêu chí rõ ràng và dễ hiểu cho các nhà quản lý tín dụng.
Đề tài “Sử dụng phương pháp Decision Tree để dự đoán khả năng vay vốn của khách
hàng” là một đề tài mang ý nghĩa thực tiễn và khoa học cao. Đề tài nhằm mục đích
nghiên cứu, xây dựng và thử nghiệm một mô hình dự đoán dựa trên thuật toán cây quyết
định, sử dụng dữ liệu thực tế về đặc điểm cá nhân và tài chính của khách hàng. Thông
qua đề tài này, nhóm có cơ hội tiếp cận với quy trình khai phá dữ liệu, vận dụng kiến
thức về học máy, đồng thời rèn luyện kỹ năng phân tích và lập trình để giải quyết một
bài toán cụ thể trong lĩnh vực tài chính - ngân hàng. I. ĐẶT VẤN VỀ 1. Tầm quan trọng
Dự đoán khả năng vay vốn của khách hàng là một bước quan trọng trong quy trình
thẩm định tín dụng của các tổ chức tài chính. Việc dự đoán chính xác không chỉ giúp
giảm thiểu rủi ro nợ xấu mà còn góp phần tối ưu hóa hiệu quả cho vay, nâng cao chất
lượng danh mục tín dụng và đảm bảo tính bền vững trong hoạt động kinh doanh của ngân hàng.
Trong bối cảnh nhu cầu vay vốn ngày càng tăng, đặc biệt là với sự phát triển của
các dịch vụ tài chính số, việc áp dụng các phương pháp dự đoán hiện đại dựa trên dữ
liệu ngày càng trở nên cấp thiết. Một hệ thống dự đoán hiệu quả giúp các tổ chức tài 5 lOMoAR cPSD| 45315597
chính đưa ra quyết định nhanh chóng, công bằng và minh bạch hơn, đồng thời cải thiện
trải nghiệm khách hàng và giảm tải cho nhân viên thẩm định.
Đề tài không chỉ góp phần làm rõ vai trò thiết yếu của việc dự đoán khả năng vay
vốn mà còn giúp nhóm nghiên cứu ứng dụng kiến thức học thuật vào thực tiễn. Qua đó,
nhóm có cơ hội tiếp cận với tư duy dữ liệu, kỹ năng phân tích và các công cụ công nghệ
hiện đại, phục vụ cho nhu cầu học tập và định hướng nghề nghiệp sau này.
2. Mục tiêu nghiên cứu
Mục tiêu của đề tài là tìm ra một cách tiếp cận phù hợp để dự đoán khả năng vay
vốn của khách hàng thông qua việc áp dụng thuật toán Decision Tree. Nhóm hướng đến
việc xây dựng một mô hình có thể hỗ trợ các tổ chức tài chính trong quá trình đánh giá
hồ sơ vay một cách nhanh chóng và có căn cứ rõ ràng. Bên cạnh đó, đề tài còn nhằm
xác định những yếu tố ảnh hưởng lớn nhất đến quyết định cho vay, từ đó giúp quá trình
xét duyệt trở nên hiệu quả và minh bạch hơn. Ngoài mục tiêu ứng dụng thực tế, nhóm
cũng muốn thông qua đề tài này để áp dụng các kiến thức về lập trình Python, xử lý dữ
liệu và học máy đã được học, từ đó củng cố kỹ năng thực hành và rèn luyện tư duy logic
trong việc giải quyết bài toán thực tế.
3. Phương pháp tiếp cận
Trong nghiên cứu này, nhóm lựa chọn sử dụng phương pháp Decision Tree để dự
đoán khả năng vay vốn của khách hàng. Đây là một trong những thuật toán học máy phổ
biến, được ứng dụng rộng rãi trong các bài toán phân loại nhờ vào khả năng xây dựng
mô hình đơn giản nhưng hiệu quả. Phương pháp này không chỉ giúp dự đoán một cách
chính xác, mà còn dễ dàng giải thích các yếu tố tác động đến quyết định cho vay, điều
này rất quan trọng trong lĩnh vực tài chính, nơi các quyết định phải được minh bạch và có cơ sở rõ ràng.
Cây quyết định (Decision Tree) được triển khai trong môi trường Visual Studio, sử
dụng thư viện Pandas để xử lý và phân tích dữ liệu. Một trong những lợi ích lớn nhất
của phương pháp này là khả năng phân tích và trực quan hóa các yếu tố ảnh hưởng đến
kết quả dự đoán. Một ưu điểm nữa của Decision Tree là tính dễ dàng trong việc điều
chỉnh và tối ưu mô hình, từ đó giúp cải thiện độ chính xác của dự đoán. Mặc dù phương
pháp này có thể bị ảnh hưởng bởi một số yếu tố như quá khớp dữ liệu (overfitting),
nhưng nếu được điều chỉnh đúng cách, Decision Tree có thể trở thành công cụ mạnh mẽ
giúp cải thiện hiệu quả của quá trình xét duyệt vay vốn. Chính vì vậy, việc áp dụng 6 lOMoAR cPSD| 45315597
phương pháp này không chỉ cung cấp dự đoán chính xác mà còn giúp tạo ra một hệ
thống minh bạch và dễ hiểu trong quá trình ra quyết định vay vốn. 7 lOMoAR cPSD| 45315597
II. LÝ THUYẾT VỀ PHƯƠNG PHÁP DECISION TREE 1. Khái niệm
Trong nghiên cứu và ứng dụng khoa học, quá trình quan sát, phân tích và ra quyết
định thường dựa trên việc xây dựng và trả lời các câu hỏi. Từ nền tảng này, trong lĩnh
vực học máy (Machine Learning), một mô hình được phát triển dựa trên cơ chế tổ chức
các câu hỏi theo cấu trúc phân cấp dạng cây, được gọi là mô hình Cây Quyết định (Decision Tree).
Cây Quyết định, về bản chất, là một đồ thị có hướng được thiết kế để hỗ trợ quá
trình ra quyết định. Cụ thể, nó biểu diễn các lựa chọn và kết quả tiềm năng thông qua
cấu trúc phân nhánh. Để minh họa cho điều này ta xét ví dụ sau: giả sử một học sinh cần
xây dựng chiến lược lựa chọn ngành học dựa trên kết quả thi tốt nghiệp trung học phổ
thông, việc ra quyết định có thể được mô hình hóa thông qua một chuỗi các tiêu chí phân nhánh: -
Nếu tổng điểm ba môn đạt trên 28,5, học sinh sẽ đăng ký vào ngành Công nghệ Thông tin (CNTT). -
Ngược lại, nếu tổng điểm ba môn nhỏ hơn hoặc bằng 28,5, cơ hội vẫn tồn tại nếu
điểm môn Toán đủ cao, do điểm Toán được áp dụng hệ số nhân 2. Cụ thể, học sinh sẽ
tiếp tục chọn ngành CNTT nếu điểm Toán đạt 10. -
Trong các trường hợp còn lại, học sinh sẽ đăng ký vào ngành Kỹ thuật Điện tử và Viễn thông (KTĐTVT). -
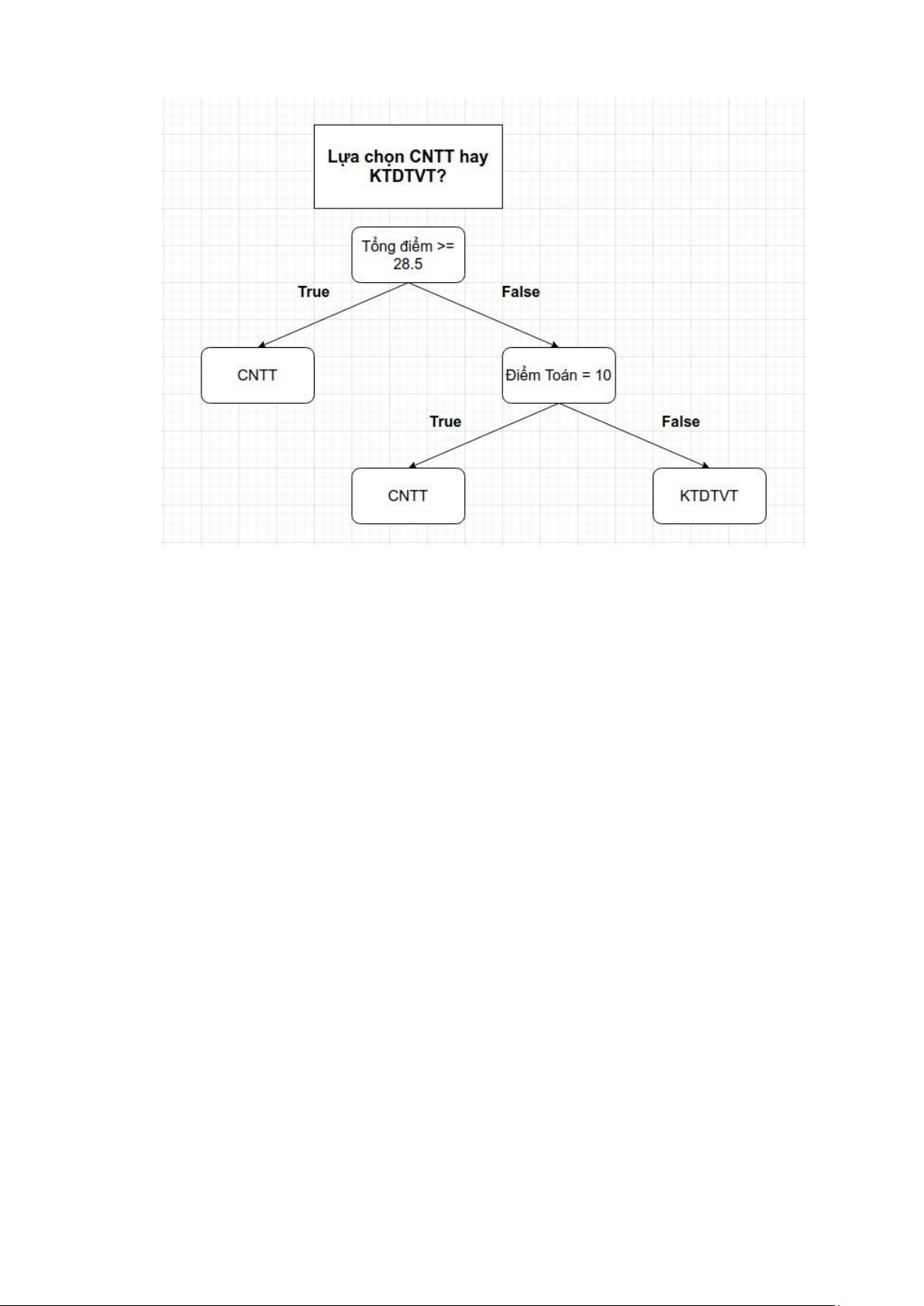
Tập hợp các câu hỏi và lựa chọn của bạn có thể ở trên được khái quát thành một cây quyết định: 8 lOMoAR cPSD| 45315597
Hình 1 : Ví dụ về mô hình Cây quyết định
Cây quyết định ở sơ đồ trên còn được gọi là cây quyết định nhị phân vì một câu
hỏi chỉ có hai phương án là True hoặc False. Trên thực tế có thể có những dạng cây
quyết định khác nhiều hơn hai phương án cho một câu hỏi.
2. Cấu trúc của Cây Quyết định
Cấu trúc cây phân cấp bắt đầu từ một câu hỏi chính, được gọi là node, phân nhánh
thành các kết quả khả thi khác nhau, bao gồm:
- Node gốc (Root Node): Điểm khởi đầu, đại diện cho toàn bộ tập dữ liệu.
- Nhánh (Branches): Các đường kết nối giữa các node, biểu thị luồng chuyển tiếp từ
một quyết định sang quyết định tiếp theo.
- Node nội (Internal Nodes): Các điểm ra quyết định, dựa trên các đặc trưng đầu vào.
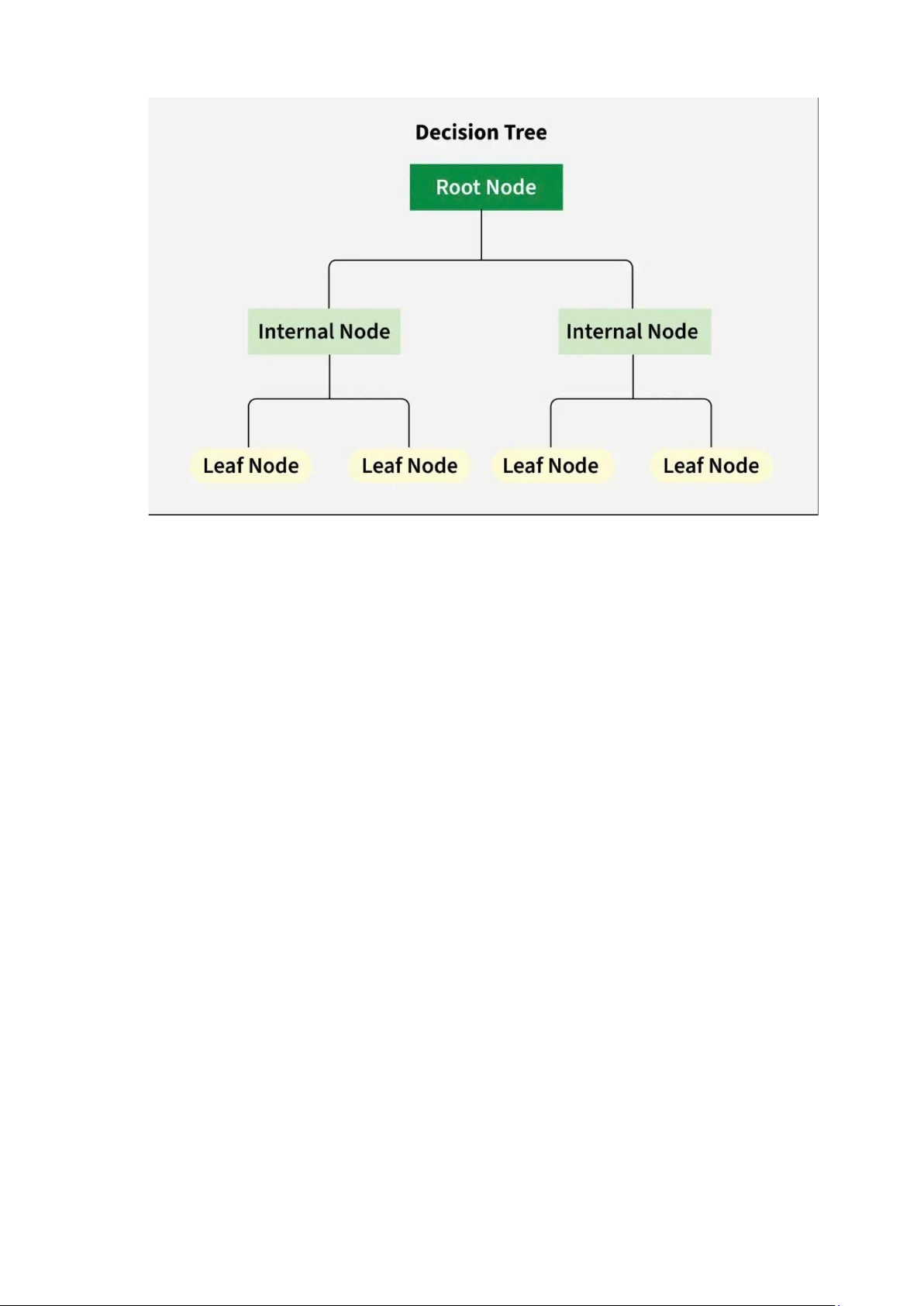
- Node lá (Leaf Nodes): Các node cuối cùng ở cuối mỗi nhánh, biểu thị kết quả hoặc dự đoán cuối cùng. 9 lOMoAR cPSD| 45315597
Hình 2: Cấu trúc của Cây Quyết định
3. Phân loại Cây Quyết định
Cây quyết định được phân thành hai loại chính dựa trên bản chất của biến mục
tiêu: cây phân loại (classification tree), dùng cho biến mục tiêu rời rạc, và cây hồi quy
(regression tree), dùng cho biến mục tiêu liên tục.
3.1. Cây phân loại (Classification tree)
Cây phân loại (Classification Tree) là một mô hình học máy thuộc nhóm thuật toán
cây quyết định, được thiết kế để dự đoán biến mục tiêu định tính (rời rạc) dựa trên tập
hợp các quan sát đầu vào. Mô hình này biểu diễn quá trình ra quyết định dưới dạng một
cấu trúc cây phân cấp, trong đó các quyết định được tổ chức thành các node và nhánh,
dẫn đến các nhãn lớp cụ thể tại các node lá. Ví dụ, trong ví dụ ở phần “Khái niệm cây
quyết định”, cây có thể dự đoán các nhãn như "phù hợp" hoặc "không phù hợp" (như
trong trường hợp được đề cập), hoặc các nhãn khác như "có bệnh"/"không bệnh" trong
chẩn đoán y khoa. Biến mục tiêu trong cây phân loại luôn là một biến phân loại
(categorical), tức là thuộc một tập hợp hữu hạn các giá trị rời rạc, phân biệt với cây hồi
quy (dự đoán biến liên tục).
Quá trình xây dựng cây phân loại dựa trên kỹ thuật phân vùng đệ quy nhị phân,
một phương pháp lặp chia tập dữ liệu thành các tập con nhỏ hơn tại mỗi node của cây.
Cụ thể, tại mỗi node, một đặc trưng (feature) và một ngưỡng (threshold) được chọn để
phân tách dữ liệu thành hai tập con (thường dựa trên điều kiện nhị phân, ví dụ: 10 lOMoAR cPSD| 45315597
"True"/"False" hoặc "lớn hơn"/"nhỏ hơn"). Quá trình này được thực hiện đệ quy, tiếp
tục chia các tập con trên mỗi nhánh cho đến khi đạt một tiêu chí dừng, chẳng hạn như:
- Tất cả mẫu trong node thuộc cùng một lớp (node thuần khiết).
- Đạt giới hạn độ sâu tối đa của cây (max_depth).
- Số mẫu tại node nhỏ hơn ngưỡng tối thiểu (min_samples_split).
- Không còn cải thiện đáng kể trong tiêu chí phân tách (ví dụ: Gini Index hoặc Entropy).
Để chọn đặc trưng và ngưỡng tối ưu tại mỗi node, cây phân loại sử dụng các tiêu
chí sau đây: a) Entropy
Entropy là thuật ngữ thuộc Nhiệt động lực học, là thước đo của sự biến đổi, hỗn
loạn hoặc ngẫu nhiên. Năm 1948, Shannon đã mở rộng khái niệm Entropy sang lĩnh vực
nghiên cứu, thống kê với công thức như sau:
Với một phân phối xác suất của một biến rời rạc x có thể nhận n giá trị khác nhau x1, x2, …, xn.
Giả sử rằng xác suất để x nhận các giá trị này là pi = p (x = xi).
Ký hiệu phân phối này là p = (p1, p2, …, pn). Entropy của phân phối này được định nghĩa là: n
H ( p )=−∑ pi log(pi) i=1 Trong đó:
- H(p): Đây là giá trị Entropy của tập dữ liệu, thường được ký hiệu là H(S) trong các tài
liệu về Decision Tree (trong đó S là tập dữ liệu) - pi là xác suất hoặc tỷ lệ của lớp i trong tập dữ liệu.
- log(pi): Là logarit cơ số 2 của xác suất pi, thường dùng trong lý thuyết thông tin (log
cơ số 2 vì Entropy được đo bằng bit).
- n: Số lượng lớp trong tập dữ liệu
- Khi tất cả mẫu trong một node thuộc cùng một lớp (ví dụ: 100% mẫu thuộc lớp
"CNTT"), Entropy bằng 0, biểu thị trạng thái thuần khiết hoàn toàn, không có sự không
chắc chắn (tinh khiết nhất)
- Khi các lớp phân bố đồng đều (ví dụ: 50% "CNTT" và 50% "KTĐTVT"), Entropy đạt
giá trị tối đa, phản ánh mức độ hỗn loạn cao nhất (vẩn đục nhất) Để hiểu được hàm
Entropy, ta có 2 ví dụ sau:
VD1: Giả sử bạn tung một đồng xu, entropy sẽ được tính như sau:
H (p) = - [0.5 log2(0.5) + 0.5 log2 (0.5)] = 1 11 lOMoAR cPSD| 45315597
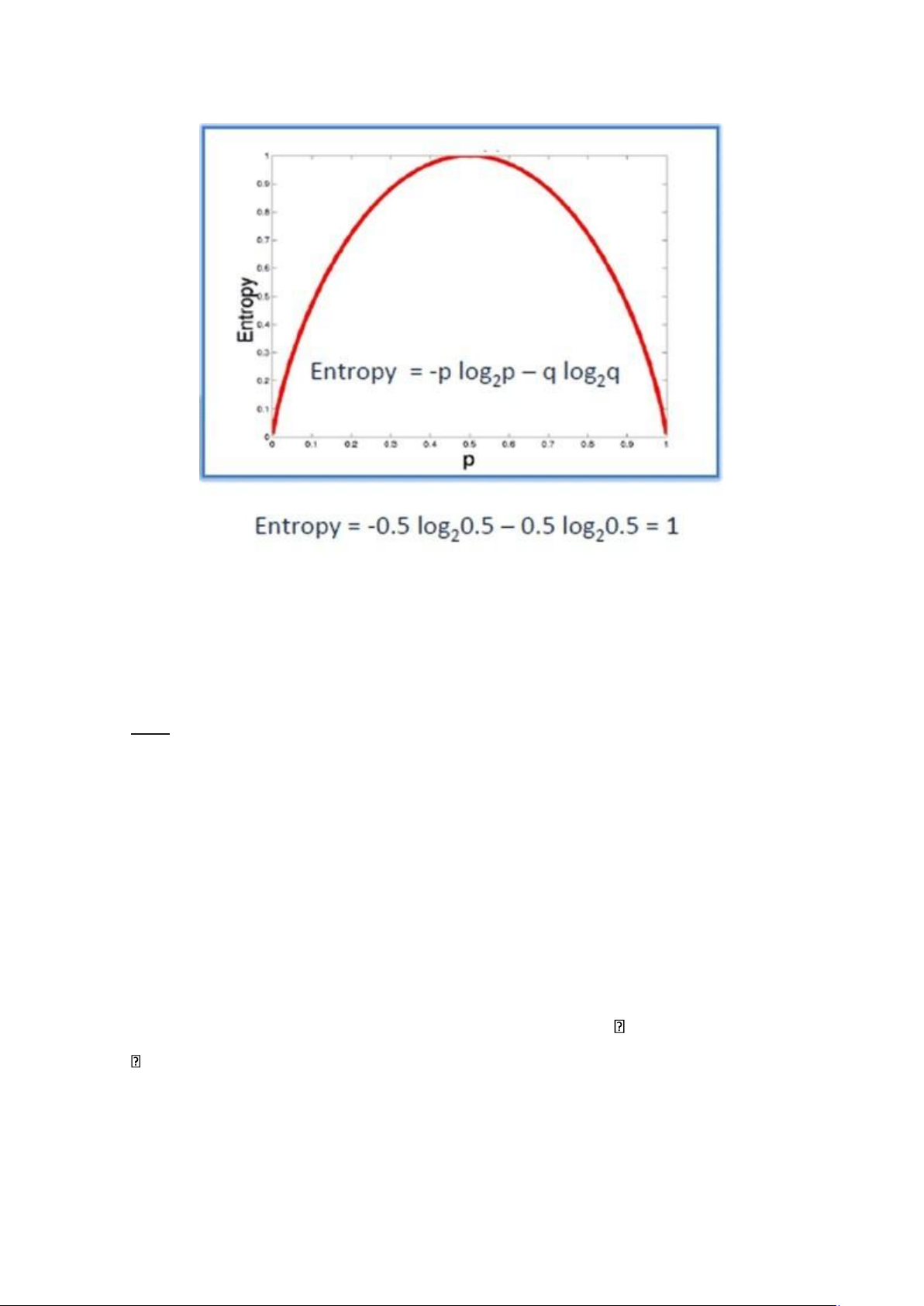
Dưới đây là hình vẽ biểu diễn sự thay đổi của hàm Entropy:
Hình 3: Sự thay đổi của hàm Entropy với n = 2
Ta có thể thấy rằng, Entropy đạt tối đa khi xác suất xảy ra của hai lớp bằng nhau.
- P tinh khiết: pi = 0 hoặc pi = 1
- P vẩn đục: pi = 0.5, khi đó hàm Entropy đạt đỉnh cao nhất
VD2: Giả sử bạn có tập dữ liệu với 100 ngày. Trong đó có 60 ngày “có mưa” và 40 ngày
“không mưa”. Hãy tính Entropy.
Phân tích bài toán:
- Tổng số mẫu: 100 ngày
- Lớp "có mưa": 60 ngày, tỷ lệ p1 = 0.6
- Lớp "không mưa": 40 ngày, tỷ lệ p2 = 0.4 - Số lớp: n = 2
Entropy sẽ được tính như sau:
H(p) = - [0.6 log2 (0.6) + 0.4 log2 (0.4)]  0.971
 Giá trị Entropy ≈ 0.971 (gần 1) cho thấy tập dữ liệu có mức độ không chắc chắn cao,
vì phân bố lớp không quá chênh lệch (60% "có mưa", 40% "không mưa"). b) Information Gain
Information Gain là thước đo dựa trên mức giảm của Entropy khi tập dữ liệu được
phân tách theo một đặc trưng (attribute). Trong quá trình xây dựng cây quyết định, thuật 12 lOMoAR cPSD| 45315597
toán ưu tiên lựa chọn đặc trưng mang lại Information Gain cao nhất tại mỗi node để tối
ưu hóa việc phân tách dữ liệu.
Quy trình xác định các node trong cây quyết định được thực hiện bằng cách tính
Information Gain cho từng đặc trưng tại mỗi node, theo các bước sau:
Bước 1: Tính toán hệ số Entropy của biến mục tiêu S có N phần tử với Nc phần tử thuộc lớp c cho trước: C N N ∑ H C =1 N log N ¿
Bước 2: Tính hàm số Entropy tại mỗi thuộc tính: với thuộc tính x, các điểm dữ liệu trong
S được chia ra K child node S1, S2, …, SK với số điểm trong mỗi child node lần lượt là m1, m2, …, mK, ta có: K m H ( )=∑= N ( k) k 1
Bước 3: Chỉ số Gain Information được tính bằng:
G ( x,S )=H ( S)−H(x, S)
Với ví dụ 2 ở trên, ta tính được chỉ số Gain Information thông qua các bước sau:
Dữ liệu bài toán:
- Tập dữ liệu S: 100 ngày
- Lớp “có mưa”: 60 ngày (p1 = 0.6, Ncó mưa = 60)
- Lớp “không có mưa”: 40 ngày (p2 = 0.4, Nkhông mưa = 40) - Số lớp: C = 2
- Đặc trưng giả định: “Độ ẩm” với 2 giá trị phân tách (Cao/ Thấp)
• Tập con S1: (Độ ẩm Cao, m1 = 50) 40 ngày “có mưa” (80%), 10 ngày “không mưa” (20%)
• Tập con S2: (Độ ẩm Thấp, m2 = 50) 20 ngày “có mưa” (40%), 30 ngày “không mưa” (60 %)
Bước 1: Tính hệ số Entropy của tập dữ liệu gốc S H
Bước 2: Tính hàm số Entropy tại các thuộc tính đặc trưng “Độ ẩm” - Tập con S1: 13 lOMoAR cPSD| 45315597
• Tỷ lệ: 80% có mưa (40/50 = 0.8), 20% không mưa (10/50 = 0.2)
• Entropy: H (S1)=−[0.8log2( 0.8)+0.2log2]≈0.722 - Tập con S2:
• Tỷ lệ: 40% có mưa (20/50 = 0.4), 60% không mưa (30/50 = 0.6)
• Entropy: H (S2)=−[0.4log2 (0.4 )+0.6log2( 0.6)] ≈0.971 - Entropy trung bình có trọng số: H = N k 100 100 ×0.971=0.8465 k 1
Bước 3: Tính Gain Information
G (Độ ẩm, S) = H(S) – H (Độ ẩm, S) = 0.971 – 0.8465 = 0.1245
Trong lĩnh vực học máy, cây phân loại (Classification Tree) được xây dựng dựa
trên các thuật toán tối ưu hóa việc phân tách dữ liệu, nhằm dự đoán nhãn lớp một cách
hiệu quả. Các thuật toán tiêu biểu áp dụng Classification Tree bao gồm:
- Thuật toán ID3 (Iterative Dichotomiser 3)
Thuật toán ID3 (Iterative Dichotomiser 3) là một thuật toán học máy thuộc nhóm
cây quyết định, được sử dụng để xây dựng cây phân loại (Classification Tree) cho các
bài toán phân loại với biến mục tiêu rời rạc. ID3 chọn các đặc trưng tối ưu để phân tách
dữ liệu dựa trên Entropy và Information Gain, nhằm tạo ra một cây quyết định đơn giản
và hiệu quả. Được phát triển bởi J. Ross Quinlan vào năm 1986, ID3 là tiền đề cho các
thuật toán cải tiến như C4.5 và CART.
Đặc điểm của thuật toán ID3:
• ID3 sử dụng Entropy để đo lường độ không chắc chắn của tập dữ liệu và Information
Gain để đánh giá mức giảm Entropy khi phân tách theo một đặc trưng. Đặc trưng với
Information Gain cao nhất được chọn tại mỗi node.
• Phân tách đệ quy nhị phân: Thuật toán chia tập dữ liệu thành các tập con dựa trên giá
trị của đặc trưng được chọn, lặp lại đệ quy cho đến khi đạt tiêu chí dừng.
• Chỉ xử lý đặc trưng phân loại: ID3 được thiết kế cho các đặc trưng rời rạc
(categorical). Nếu đặc trưng là liên tục (numerical), cần tiền xử lý để rời rạc hóa (discretization). 14 lOMoAR cPSD| 45315597
• Dễ overfitting: ID3 có xu hướng tạo cây sâu, học cả nhiễu trong dữ liệu, đặc biệt với
tập dữ liệu nhỏ hoặc nhiều đặc trưng.
• ID3 không tích hợp cơ chế cắt tỉa (pruning), dẫn đến cây phức tạp hơn so với các
thuật toán sau này như C4.5.
Cách thức hoạt động của thuật toán ID3: ID3 xây dựng cây quyết định thông qua các bước sau:
Bước 1: Tính Entropy của tập dữ liệu gốc
Bước 2: Tính Gain Information cho mỗi đặc trưng
Bước 3: Phân tách dữ liệu (Chia tập dữ liệu thành các tập con dựa trên giá trị của đặc
trưng được chọn (mỗi giá trị tạo một nhánh)).
Bước 4: Lặp lại đệ quy
Áp dụng các bước trên cho mỗi tập con, trừ đặc trưng đã sử dụng, cho đến khi:
• Node thuần khiết (Entropy = 0).
• Không còn đặc trưng để phân tách.
• Số mẫu tại node quá nhỏ.
Bước 5: Gán nhãn cho node lá (Node lá được gán nhãn lớp chiếm đa số trong tập con tương ứng). - Thuật toán C4. 5
Thuật toán C4.5 là thuật toán cải tiến của ID3.
Trong thuật toán ID3, Information Gain được sử dụng làm độ đo. Tuy nhiên,
phương pháp này lại ưu tiên những thuộc tính có số lượng lớn các giá trị mà ít xét tới
những giá trị nhỏ hơn. Do vậy, để khắc phục nhược điểm trên, ta sử dụng độ đo Gain
Ratio (trong thuật toán C4.5) như sau:
Đầu tiên, ta chuẩn hoá Information Gain với trị thông tin phân tách (Split information): Information gain Gain Ratio= Spit information
Trong đó Split Information được tính như sau: n
Split Info=−∑ Di log2 Di i=1
Giả sử chúng ta phân chia biến thành n nút con và Di đại diện cho số lượng bản ghi
thuộc nút đó. Do đó, hệ số Gain Ratio sẽ xem xét được xu hướng phân phối khi chia cây. 15 lOMoAR cPSD| 45315597
Ngoài ID3, C4. 5 ta còn có một số thuật toán khác cũng sử dụng Classification Tree như:
- Thuật toán CHAID: tạo cây quyết định bằng cách sử dụng thống kê chi-square để xác
định các phân tách tối ưu. Các biến mục tiêu đầu vào có thể là số (liên tục) hoặc phân loại.
- Thuật toán C&R: sử dụng phân vùng đệ quy để chia cây. Tham biến mục tiêu có thể
dạng số hoặc phân loại. - MARS - Conditional Inference Trees
3.2. Cây hồi quy (Regressive Tree)
Cây hồi quy (Regressive Tree hoặc Regression Tree) là một mô hình học máy thuộc
nhóm thuật toán cây quyết định, được thiết kế để dự đoán biến mục tiêu liên tục
(numerical) thay vì biến rời rạc như trong cây phân loại.
Cây hồi quy hoạt động bằng cách chia không gian đặc trưng thành các vùng dựa
trên các ngưỡng của đặc trưng, tối ưu hóa một tiêu chí như tổng bình phương sai số
(Mean Squared Error - MSE) hoặc tổng sai số tuyệt đối (Mean Absolute Error - MAE).
Thuật toán này được giới thiệu trong công trình của Breiman và cộng sự (1984) và là
nền tảng cho các phương pháp như CART (Classification and Regression Tree). Dưới
đây là chi tiết các tiêu chí phân tách chính của thuật toán cây hồi quy:
a) Tổng bình phương sai số (Mean Squared Error – MSE)
MSE là trung bình của bình phương sai số giữa dự đoán và thực tế. Công thức này
đặc biệt hữu ích khi cần đặt trọng số nhiều hơn vào các sai số lớn, vì việc bình phương
sẽ làm tăng sự chênh lệch của các sai số lớn so với sai số nhỏ.
Với định nghĩa trên ta có thể hiểu MSE đơn giản như sau: Nếu ta có giá trị thực tế
là 3 và giá trị dự đoán là 5, sai số bình phương sẽ là (3 – 5)2 = 4. Tương tự, nếu ta dự
đoán giá trị là 7 trong khi giá trị thực tế là 10, sai số bình phương sẽ là (7 – 10)2 = 9.
MSE sẽ lấy trung bình của tất cả các sai số bình phương như vậy. Công thức: n MSE ¿¿ với:
- yi là giá trị thực của mẫu i n 16 lOMoAR cPSD| 45315597
- ^y là giá trị trung bình của các mẫu trong tập con (^y yi)
- n là số mẫu trong tập con
MSE là chỉ số nên lựa chọn khi muốn nhấn mạnh các sai số lớn. Điều này giúp làm
nổi bật các điểm dữ liệu ngoại lai.
b) Tổng sai số tuyệt đối (Mean Absolute Error – MAE)
MAE là một trong những matrics đơn giản và trực quan nhất, phản ánh trung bình
độ lệch tuyệt đối giữa giá trị dự đoán và giá trị thực tế. MAE cung cấp một cái nhìn
không thiên vị về sai số trung bình mà mô hình tạo hình, giúp đánh giá chất lượng dự
đoán trong các tình huống thực tế.
Với định nghĩa trên thì MAE có thể được hiểu đơn giản như sau: Nếu ta có giá trị
thực tế là 3 và giá trị dự đoán là 5, sai số tuyệt đối sẽ là |3 – 5| = 2. Tương tự, nếu dự
đoán giá trị là 7 trong khi giá trị thực tế là 10, sai số tuyệt đối sẽ là |7 – 10| = 3. MAE sẽ
lấy trung bình của tất cả các sai số tuyệt đối như vậy. Công thức: n MAE ¿ yi−y^∨¿
MAE là sai số được sử dụng khi muốn dự đoán sai số trung bình mà không quan
tâm đến việc nó có phải là sai số lớn hay không.
Các thuật toán tiêu biểu sử dụng Regressive Tree bao gồm: Thuật toán CART
CART là một thuật toán dự đoán được sử dụng trong Học máy (Machine Learning),
cho phép giải thích cách giá trị của biến mục tiêu (target variable) có thể được dự đoán
dựa trên các yếu tố khác. Đây là một cấu trúc cây quyết định, trong đó mỗi nhánh được
phân tách dựa trên một biến dự đoán (predictor variable), và mỗi nút lá chứa dự đoán cho biến mục tiêu.
Thuật ngữ CART được dùng như một khái niệm tổng quát bao gồm hai loại cây quyết định chính:
• Cây phân loại (Classification Trees): Được sử dụng để xác định “lớp” mà biến mục
tiêu có khả năng cao thuộc về, khi biến này là biến rời rạc (danh mục).
• Cây hồi quy (Regression Trees): Được sử dụng để dự đoán giá trị của biến mục tiêu liên tục. 17 lOMoAR cPSD| 45315597
Các bước chính của thuật toán CART:
Bước 1: Xác định điểm phân chia tốt nhất cho từng thuộc tính đầu vào, dựa trên tiêu chí:
• Gini impurity cho phân loại
• Giảm dư phương sai (Residual Reduction)
Bước 2: Chọn điểm phân chia tối ưu trong số các điểm vừa tìm được
Bước 3: Chia tập dữ liệu tại nút hiện tại thành 2 dựa trên điểm phân phối tối ưu Bước
4: Lặp lại đệ quy quá trình phân chia cho các nhánh con cho đến khi:
• Đạt điều kiện dừng (số lượng mẫu nhỏ, độ sâu tối đa, …)
• Không còn phân chia nào mang lại cải thiện rõ rệt
Bước 5: Tỉa cây (pruning) để tránh quá khớp, sử dụng một trong các kỹ thuật như:
• Tỉa theo độ phức tạp chi phí (Cost Complexity Pruning)
• Tỉa theo thông tin thu được (Information Gain Pruning) Cách hoạt động của thuật toán CART:
• Tìm điểm phân chia tốt nhất cho từng thuộc tính đầu vào
• Xác định điểm phân chia “tốt nhất” trong số các điểm vừa tìm được
• Phân chia thuộc tính được chọn theo điểm phân chia tốt nhất đó
• Lặp lại quá trình cho đến khi thỏa mãn điều kiện dừng, ví dụ như đạt số lượng lá tối
đa hoặc không còn cách phân chia tối ưu nào nữa.
Gini là chỉ số được sử dụng trong bài toán phân loại của CART, tính bằng tổng
bình phương xác suất của từng lớp. Nó đại diện cho xác suất một phần tử bị phân loại
sai nếu được chọn ngẫu nhiên, dựa trên xác suất của từng lớp.
Giá trị của chỉ số Gini nằm trong khoảng từ 0 đến 1:
• Gini = 0: Tập dữ liệu hoàn toàn thuần khiết (chỉ có một lớp).
• Gini gần 1: Dữ liệu có độ hỗn hợp cao, nhiều lớp phân bổ đều. Công thức: n Gini=1−∑¿¿ i=1
Trong đó pi là xác suất phần tử thuộc lớp i
Ngoài thuật toán CART, một số thuật toán cũng sử dụng Regressive Tree như: - M5 và M5' (M5 Prime)
- Gradient Boosted Regression Trees (GBRT/GBM) - Random Forest Regression 18 lOMoAR cPSD| 45315597
4. Quy trình xây dựng cây quyết định
Bước 1: Phân tách dữ liệu - Lựa chọn nút gốc
• Quá trình bắt đầu với toàn bộ tập dữ liệu.
• Thuộc tính (tính năng) tốt nhất để phân tách được chọn dựa trên tiêu chí như độ tạp
chất Gini, Entropy hoặc Sai số bình phương trung bình (MSE) (đối với hồi quy).
- Chia tách tập dữ liệu
• Tính năng được chọn sẽ chia tập dữ liệu thành các tập hợp con.
• Việc phân chia được lựa chọn để tối đa hóa lượng thông tin thu được (tức là giảm tạp
chất càng nhiều càng tốt).
Bước 2: Tạo nhánh và tập con
• Mỗi tập hợp con tạo thành một nhánh dẫn đến các nút con.
• Quá trình này tiếp tục theo cách đệ quy, chọn tính năng tốt nhất ở mỗi bước để phân chia dữ liệu sâu hơn.
Bước 3: Kiểm tra điều kiện dừng
- Việc chia tách dừng lại khi:
• Một nút trở nên thuần túy (tức là tất cả các mẫu đều thuộc cùng một lớp).
• Đã đạt đến giới hạn độ sâu được xác định trước.
• Số lượng mẫu tối thiểu trên mỗi nút quá nhỏ để có thể phân tách thêm.
Bước 4: Lặp lại trên các tập con
• Lặp lại các bước 1-3 cho từng tập con được tạo ra từ bước 2.
• Mỗi tập con được xử lý độc lập, trở thành một nhánh con trong cây quyết định.  Quá
trình này tiếp tục cho đến khi tất cả các nút đều trở thành nút lá hoặc thỏa mãn điều kiện dừng.
Bước 5: Cắt tỉa cây (tùy chọn)
• Cắt tỉa (pruning) là quá trình loại bỏ các nhánh không cần thiết để giảm độ phức tạp
của cây và tránh quá khớp (overfitting).
• Có hai loại cắt tỉa: 
Pre-pruning: Áp dụng các giới hạn trong quá trình xây dựng cây (ví dụ: max_depth, min_samples_split) 
Post-pruning: Xây dựng cây đầy đủ trước, sau đó loại bỏ các nhánh không cải
thiện đáng kể hiệu suất trên tập kiểm tra. 19 lOMoAR cPSD| 45315597
5. Ưu điểm và nhược điểm của phương pháp Decision Tree
5.1. Ưu điểm -
Cây quyết định dễ hiểu. Người ta có thể hiểu mô hình cây quyết định sau khi
được giải thích ngắn. -
Việc chuẩn bị dữ liệu cho một cây quyết định là cơ bản hoặc không cần thiết. Các
kỹ thuật khác thường đòi hỏi chuẩn hóa dữ liệu, cần tạo các biến phụ (dummy variable)
và loại bỏ các giá trị rỗng. -
Cây quyết định có thể xử lý cả dữ liệu có giá trị bằng số và dữ liệu có giá trị là
tên thể loại. Các kỹ thuật khác thường chuyên để phân tích các bộ dữ liệu chỉ gồm một
loại biến. Chẳng hạn, các luật quan hệ chỉ có thể dùng cho các biến tên, trong khi mạng
nơ-ron chỉ có thể dùng cho các biến có giá trị bằng số. -
Cây quyết định là một mô hình hộp trắng. Nếu có thể quan sát một tình huống
cho trước trong một mô hình, thì có thể dễ dàng giải thích điều kiện đó bằng logic
Boolean. Mạng nơ-ron là một ví dụ về mô hình hộp đen, do lời giải thích cho kết quả
quá phức tạp để có thể hiểu được. -
Có thể thẩm định một mô hình bằng các kiểm tra thống kê. Điều này làm cho ta
có thể tin tưởng vào mô hình. -
Cây quyết định có thể xử lý tốt một lượng dữ liệu lớn trong thời gian ngắn. Có
thể dùng máy tính cá nhân để phân tích các lượng dữ liệu lớn trong một thời gian đủ
ngắn để cho phép các nhà chiến lược đưa ra quyết định dựa trên phân tích của cây quyết định.
5.2. Nhược điểm -
Rủi ro quá khớp: Dữ liệu đào tạo có thể dễ dàng quá khớp, đặc biệt là nếu dữ liệu đào tạo quá sâu. -
Không ổn định với những thay đổi nhỏ: Những thay đổi nhỏ trong dữ liệu có thể
dẫn đến những cây hoàn toàn khác. -
Thiên vị đối với các tính năng có nhiều cấp độ hơn: Cây quyết định có thể thiên
vị đối với các tính năng có nhiều danh mục tập trung quá nhiều vào chúng trong quá
trình ra quyết định. Điều này có thể khiến mô hình bỏ lỡ các tính năng quan trọng khác
dẫn đến dự đoán kém chính xác hơn. -
Giới hạn trong việc phân chia theo trục: Gặp khó khăn khi xử lý các ranh giới
quyết định phức tạp hoặc chéo. 20