Bài thực hành môn Cấu trúc dữ liệu - Giải thuật | Học viện Công Nghệ Bưu Chính Viễn Thông

lOMoAR cPSD| 58457166
H Ọ C VI Ệ N CÔNG NGH Ệ BƯU CHÍNH VI Ễ N THÔNG BÀI TH Ự C HÀNH C
Ấ U TRÚC D Ữ LI Ệ U VÀ GI Ả I THU Ậ T
Giảng viên hướng dẫn :Phạm Ho àng Anh
Họ và tên sinh viên
: Nguyễn Duy Mạnh
Mã sinh viên
: B22DCDT 188 Lớp
: D22CQDT 04 - B Nhóm :18
Hà N ộ i – 05 / 2025 lOMoAR cPSD| 58457166 MỤC LỤC
Lời cảm ơn ................................................................... 3
Đề bài ........................................................................... 4
Bài làm ......................................................................... 5
➢ Câu 1 .................................................................... 5
➢ Câu 2 .................................................................... 6
➢ Câu 3 .................................................................... 10 ➢
Câu 4 .................................................................... 11
➢ Câu 5 .................................................................... 14
➢ Câu 6 .................................................................... 16
➢ Câu 7 .................................................................... 19 LỜI CẢM ƠN
Em xin gửi lời cảm ơn chân thành đến thầy vì những kiến thức
và sự hướng dẫn tận tâm mà thầy đã truyền đạt trong suốt kỳ học vừa
qua. Nhờ sự nhiệt huyết và phương pháp giảng dạy lôi cuốn của thầy,
em đã có thêm nhiều động lực và hứng thú với môn học này. Em cảm
nhận được sự tận tâm của thầy trong từng bài giảng, điều đó đã giúp
em có thêm quyết tâm để hoàn thành tốt bài thực hành này và đạt được kết quả tốt nhất.
Kính chúc thầy luôn mạnh khỏe và thành công trong sự nghiệp. lOMoAR cPSD| 58457166 Đề bài:
Bài 1. DSA03019 PHÂN SỐ ĐƠN VỊ CÁC MÔ HÌNH THUẬT TOÁN Giải thuật tham lam 2.
Bài 2. DSA06038 CẶP SỐ CÁC MÔ HÌNH THUẬT TOÁN Sắp xếp - Tìm kiếm 2
Bài 3. DSA07028 NHỊP CHỨNG KHOÁN CÁC CẤU TRÚC DỮ LIỆU CƠ BẢN Ngăn xếp 2
Bài 4. DSA04011 TÍCH HAI SỐ NHỊ PHÂN CÁC MÔ HÌNH THUẬT TOÁN Chia và trị
Bài 5. DSA09007 ĐƯỜNG ĐI THEO BFS TRÊN ĐỒ THỊ VÔ HƯỚNG CÁC MÔ
HÌNH THUẬT TOÁN Duyệt đồ thị 2
Bài 6. DSA09015 KIỂM TRA CHU TRÌNH TRÊN ĐỒ THỊ CÓ HƯỚNG CÁC
MÔ HÌNH THUẬT TOÁN Duyệt đồ thị 2
Bài 7. DSA10008 DIJKSTRA CÁC MÔ HÌNH THUẬT TOÁN Đồ thị nâng cao 3
*Tổng hợp code và lưu đồ của những bài TH:
https://github.com/tylenter/BaiThucHanh lOMoAR cPSD| 58457166
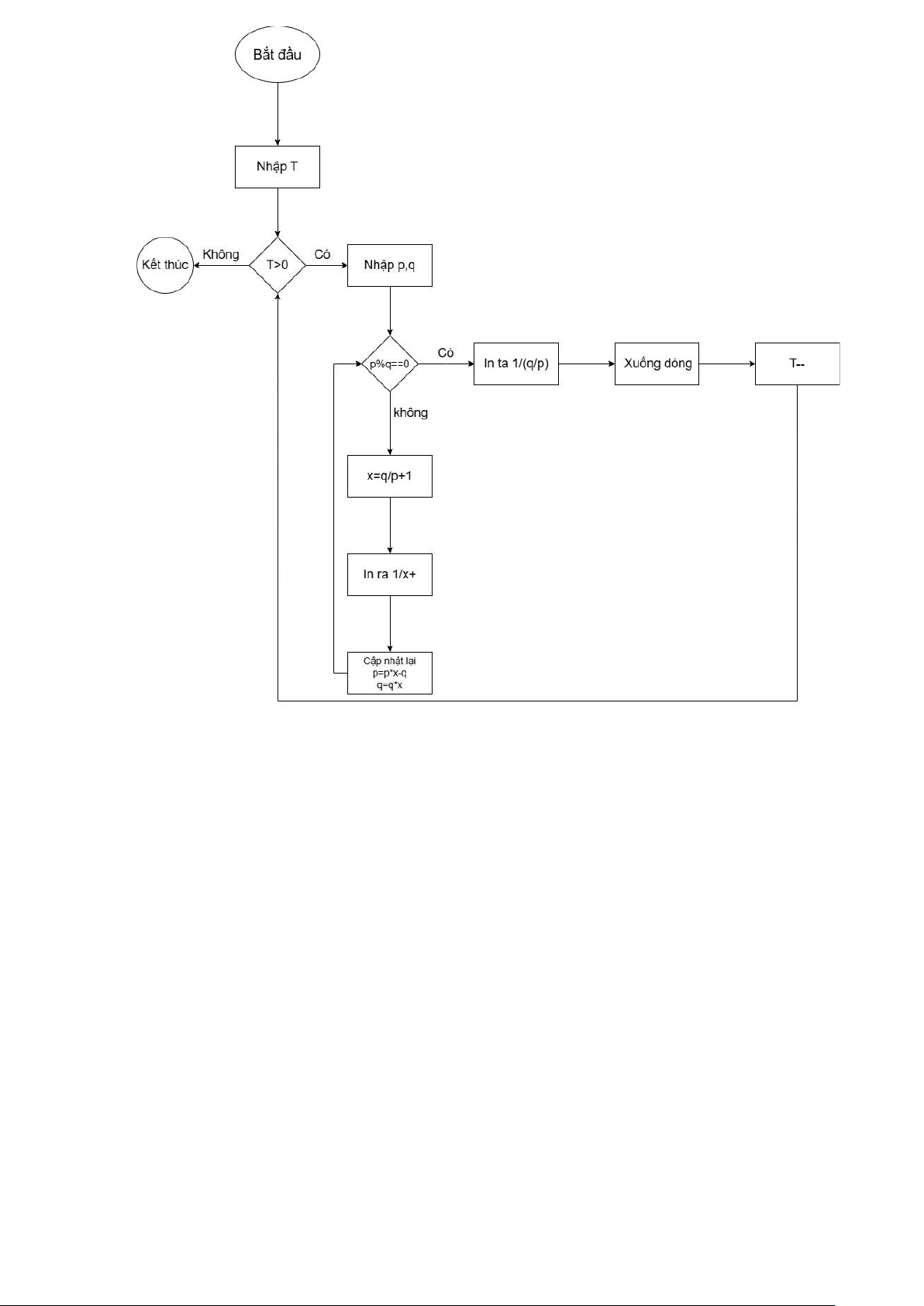
Bài 1. DSA03019 PHÂN SỐ ĐƠN VỊ CÁC MÔ HÌNH THUẬT TOÁN *Code: #include using namespace std; void testCase() { long
long p, q; cin >> p >> q; while (1) { if (q % p == 0) { cout << "1/" << q / p; return; } long long x = q / p + 1;
cout << "1/" << x << " + "; p = p * x - q; q *= x; } } int main() {
ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL); int T = 1; cin >> T; while (T--) { testCase(); cout << "\n"; } return 0; }
* Nêu ngắn gọn ý tưởng:
• Kiểm tra nếu q chia hết cho p, in ra 1 và dừng. Lấy x=, in ra 1
làm một phần của tổng. 𝑥
• Cập nhật phân số: p=p*x-q, q=q*x, lặp lại đến khi xong. Lưu đồ thuật toán: lOMoAR cPSD| 58457166
Bài 2. DSA06038 CẶP SỐ CÁC MÔ HÌNH THUẬT TOÁN Sắp xếp *Code: #include using namespace std;
long long merge(vector& arr, int left, int mid, int right) {
vector temp(right - left + 1); int i = left, j = mid + 1, k = 0; long long inv = 0;
while (i <= mid && j <= right) { if (arr[i] <= arr[j]) { temp[k++] = arr[i++]; } else { temp[k++] = arr[j++]; inv += (mid - i + 1); } } lOMoAR cPSD| 58457166 while (i <= mid) { temp[k++] = arr[i++]; } while (j <= right) { temp[k++] = arr[j++]; }
for (int p = 0; p < k; p++) { arr[left + p] = temp[p]; } return inv; }
long long _mergeSort(vector& arr, int left, int right) {
long long inv = 0; if (left < right) { int mid = left +
(right - left) / 2; inv += _mergeSort(arr, left, mid);
inv += _mergeSort(arr, mid + 1, right);
inv += merge(arr, left, mid, right); } return inv; }
long long count_inversions(vector& arr) { if (arr.empty()) return 0;
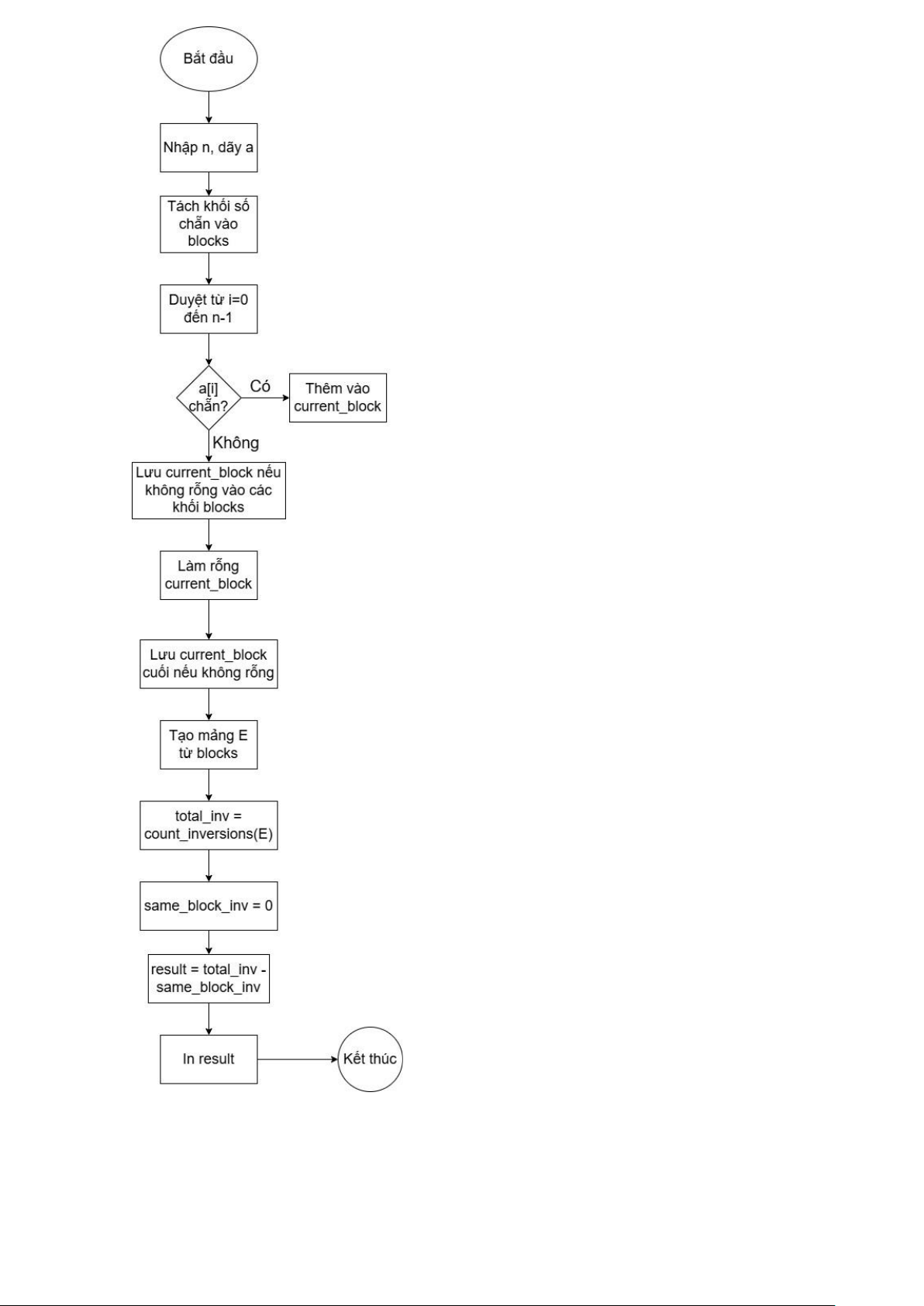
return _mergeSort(arr, 0, arr.size() - 1); } void testCase() { int n; cin >> n; vector a(n); for (int i
= 0; i < n; i++) { cin >> a[i]; } vector> blocks; vector current_block;
for (int i = 0; i < n; i++) { if (a[i] % 2 == 0) {
current_block.push_back(a[i]); } else {
if (!current_block.empty()) {
blocks.push_back(current_block); current_block.clear(); } } }
if (!current_block.empty()) {
blocks.push_back(current_block); } vector E;
for (const auto& block : blocks) {
E.insert(E.end(), block.begin(), block.end()); lOMoAR cPSD| 58457166 }
long long total_inv = count_inversions(E);
long long same_block_inv = 0; for (auto& block : blocks) {
same_block_inv += count_inversions(block); }
long long result = total_inv - same_block_inv; cout << result; } int main() {
ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL); testCase(); cout << "\n"; return 0; }
* Nêu ngắn gọn ý tưởng:
• Nhập dãy a kích thước n.
• Tách dãy thành các khối liên tiếp chứa số chẵn, phân cách bởi số lẻ.
• Tạo mảng E chứa tất cả số chẵn từ các khối theo thứ tự ban đầu.
• Tính tổng số nghịch đảo trong E bằng Merge Sort (count_inversions). Tính số nghịch
đảo trong từng khối chẵn riêng lẻ.
• Kết quả = tổng nghịch đảo trong E trừ đi nghịch đảo trong cùng khối. • In kết quả * Lưu đồ thuật toán: lOMoAR cPSD| 58457166
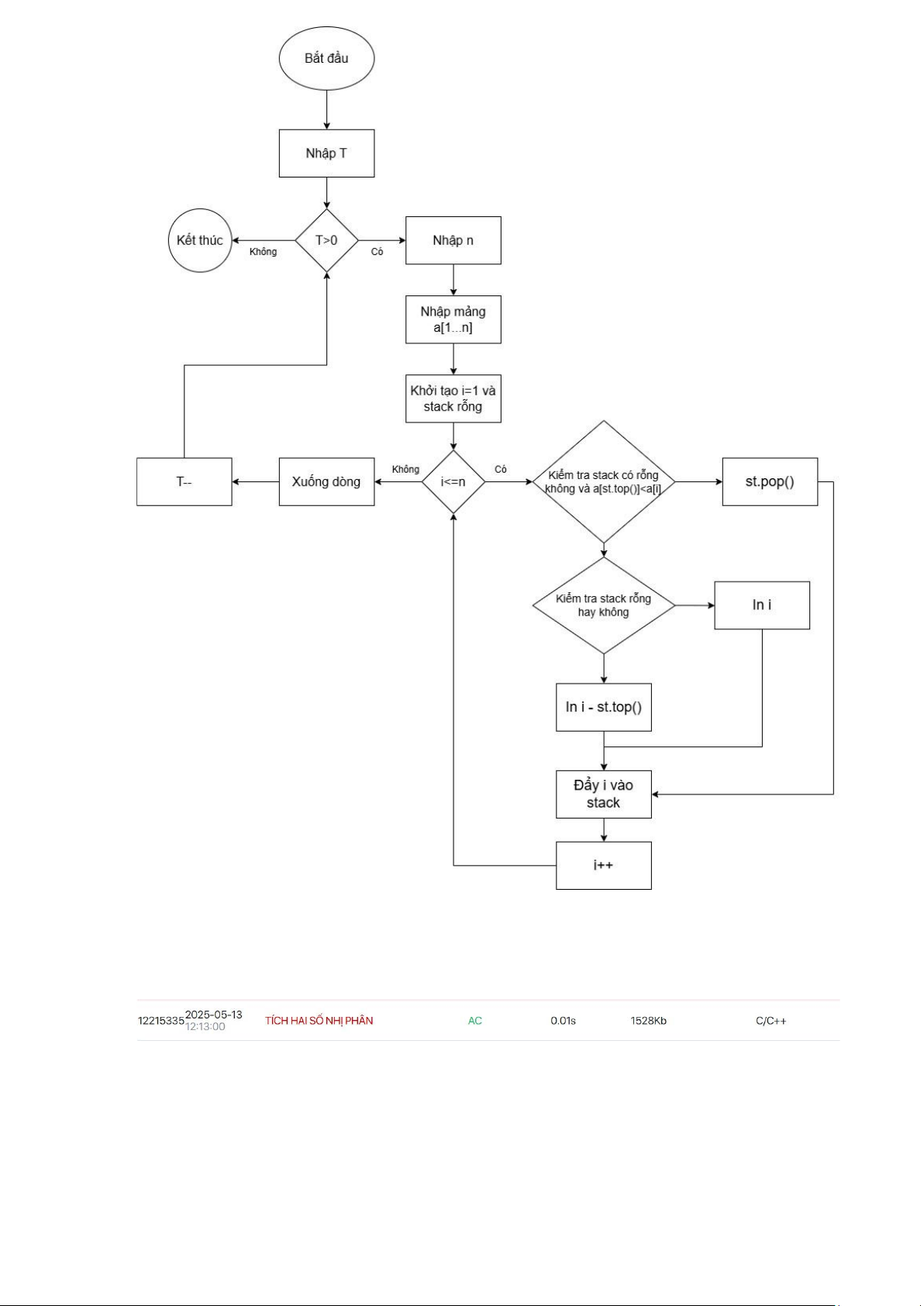
Bài 3. DSA07028 NHỊP CHỨNG KHOÁN CÁC CẤU TRÚC DỮ LIỆU CƠ BẢN Ngăn xếp 2 lOMoAR cPSD| 58457166 *Code: #include using namespace std; void testCase() { int n; cin >> n; int a[n + 1];
for (int i = 1; i <= n; ++i) { cin >> a[i]; } stack st;
for (int i = 1; i <= n; ++i) {
while (!st.empty() && a[st.top()] <= a[i]) { st.pop(); }
if (st.empty()) cout << i << " ";
else cout << i - st.top() << " "; st.push(i); } } int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL); int T = 1; cin >> T; while (T--) { testCase(); cout << "\n"; } return 0; }
* Nêu gắn gọn ý tưởng:
• Dùng stack lưu chỉ số các phần tử giảm dần (monotonic stack).
• Với mỗi i (1 đến n):
o Xóa các chỉ số trong stack mà a[st.top()] <= a[i] (để giữ stack giảm dần). o Nếu
stack rỗng, in i (không có phần tử lớn hơn bên trái).
o Nếu stack không rỗng, in i - st.top() (khoảng cách đến phần tử lớn hơn gần nhất). o Đẩy i vào stack.
• In ra khoảng cách cho mỗi a[i] trên một dòng. lOMoAR cPSD| 58457166
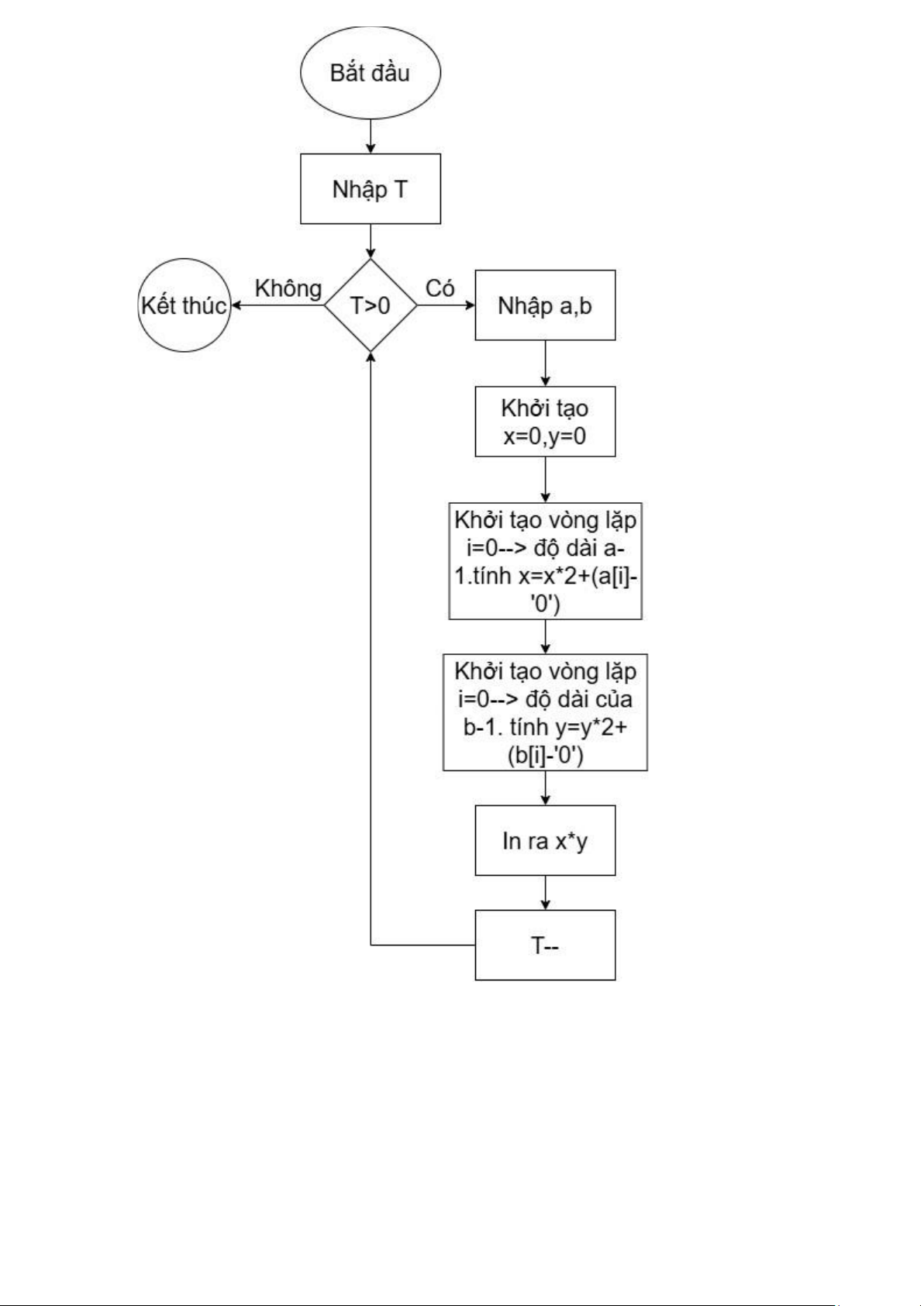
Bài 4. DSA04011 TÍCH HAI SỐ NHỊ PHÂN CÁC MÔ HÌNH THUẬT TOÁN Chia và trị *Code: #include using namespace std;
void testCase() { string a, b;
cin >> a >> b; long long x = 0, y lOMoAR cPSD| 58457166
= 0; for (int i = 0; i < a.length(); ++i) { x = x * 2 + (a[i] - '0'); }
for (int i = 0; i < b.length(); ++i) { y = y * 2 + (b[i] - '0'); } cout << x * y; } int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL); int T = 1; cin >> T; while (T--) { testCase(); cout << "\n"; } return 0; }
* Nêu ngắn gọn ý tưởng:
• Nhập hai chuỗi a và b (số nhị phân).
• Chuyển chuỗi a thành số thập phân x bằng cách: nhân x với 2 và cộng giá trị bit (a[i] - '0').
• Chuyển chuỗi b thành số thập phân y tương tự. Tính và in tích x * y.
• In tích của hai số nhị phân cho mỗi test case. lOMoAR cPSD| 58457166
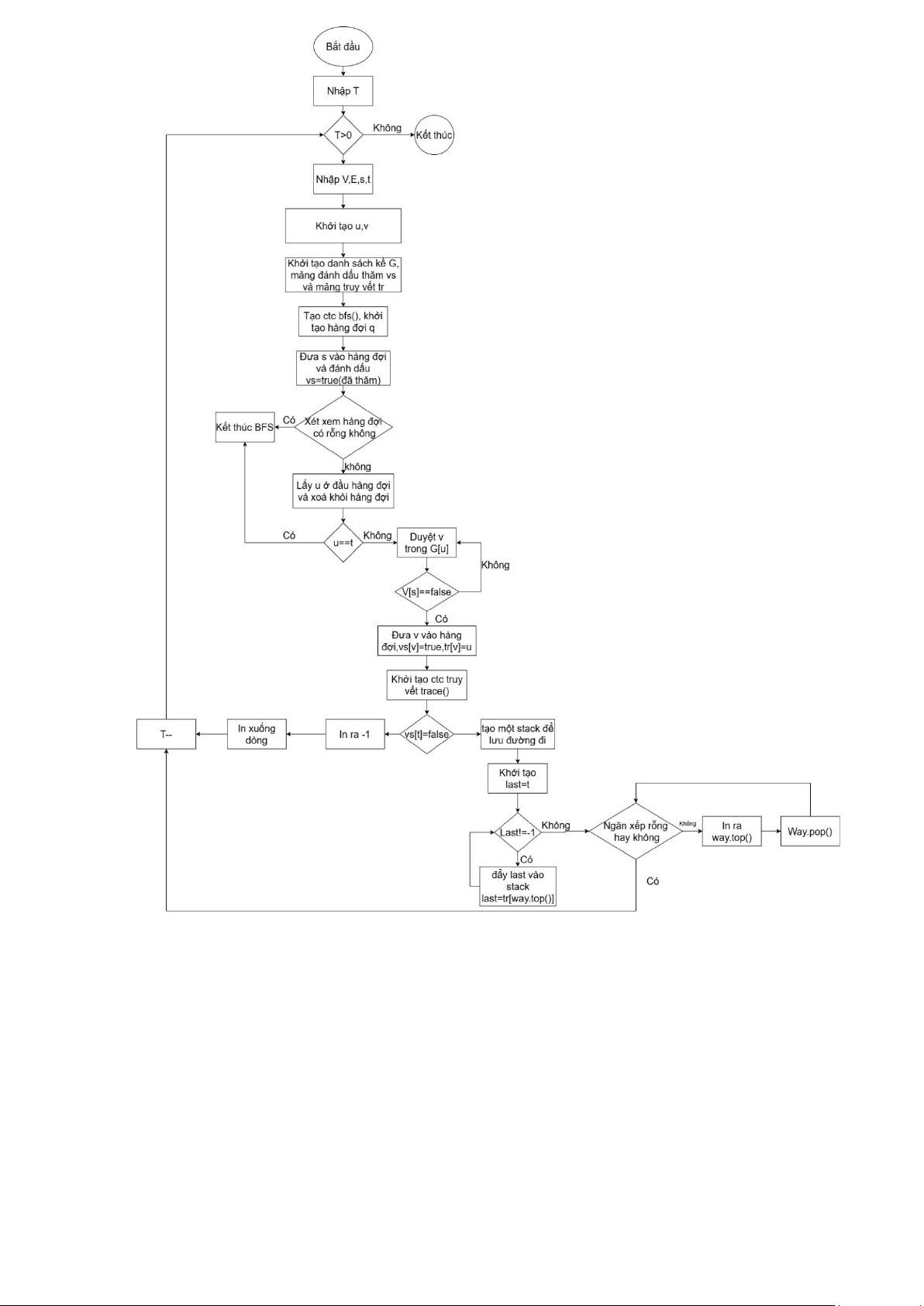
Bài 5. DSA09007 ĐƯỜNG ĐI THEO BFS TRÊN ĐỒ THỊ VÔ HƯỚNG CÁC MÔ
HÌNH THUẬT TOÁN Duyệt đồ thị 2 *Code: lOMoAR cPSD| 58457166 #include using namespace std; int V, E, s, t, u, v; vector> G; vector tr; // trace vector vs; // visit void bfs(int s) { queue q; q.push(s); vs[s] = true; while (!q.empty()) { u = q.front(); q.pop(); if (u == t) return; for (int v : G[u]) { if (vs[v] == false) { q.push(v); vs[v] = true; tr[v] = u; } } } } void trace() { if (vs[t] == false) { cout << -1; return; } stack way; int last = t; while (last != -1) { way.push(last); last = tr[way.top()]; } while (!way.empty()) {
cout << way.top() << " "; way.pop(); } }
void testCase() { cin >>
V >> E >> s >> t; G.clear(); G.resize(V + 1);
vs.clear(); vs.resize(V + 1, 0);
tr.clear(); tr.resize(V + 1, -1);
while (E--) { cin >> u >> v; G[u].push_back(v); G[v].push_back(u); lOMoAR cPSD| 58457166 } bfs(s); trace(); } int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL); int T = 1; cin >> T; while (T--) { testCase(); cout << "\n"; } return 0; }
* Nêu ngắn gọn ý tưởng:
• Nhập số đỉnh V, số cạnh E, đỉnh bắt đầu s, đỉnh kết thúc t. • Khởi tạo:
o Đồ thị G (danh sách kề).
o Mảng vs (đánh dấu đỉnh đã thăm).
o Mảng tr (lưu vết đường đi).
• Đọc E cạnh, thêm vào G (đồ thị vô hướng, thêm cả hai chiều). • Chạy BFS từ s:
o Dùng queue, đánh dấu đỉnh đã thăm, lưu cha của mỗi đỉnh trong tr.
o Dừng khi gặp t hoặc queue rỗng. • Truy vết:
o Nếu t chưa thăm (vs[t] = false), in -1 (không có đường đi).
o Ngược lại, dùng stack để truy ngược từ t về s qua tr, in đường đi.
• In đường đi ngắn nhất từ s đến t (hoặc -1 nếu không tồn tại). lOMoAR cPSD| 58457166
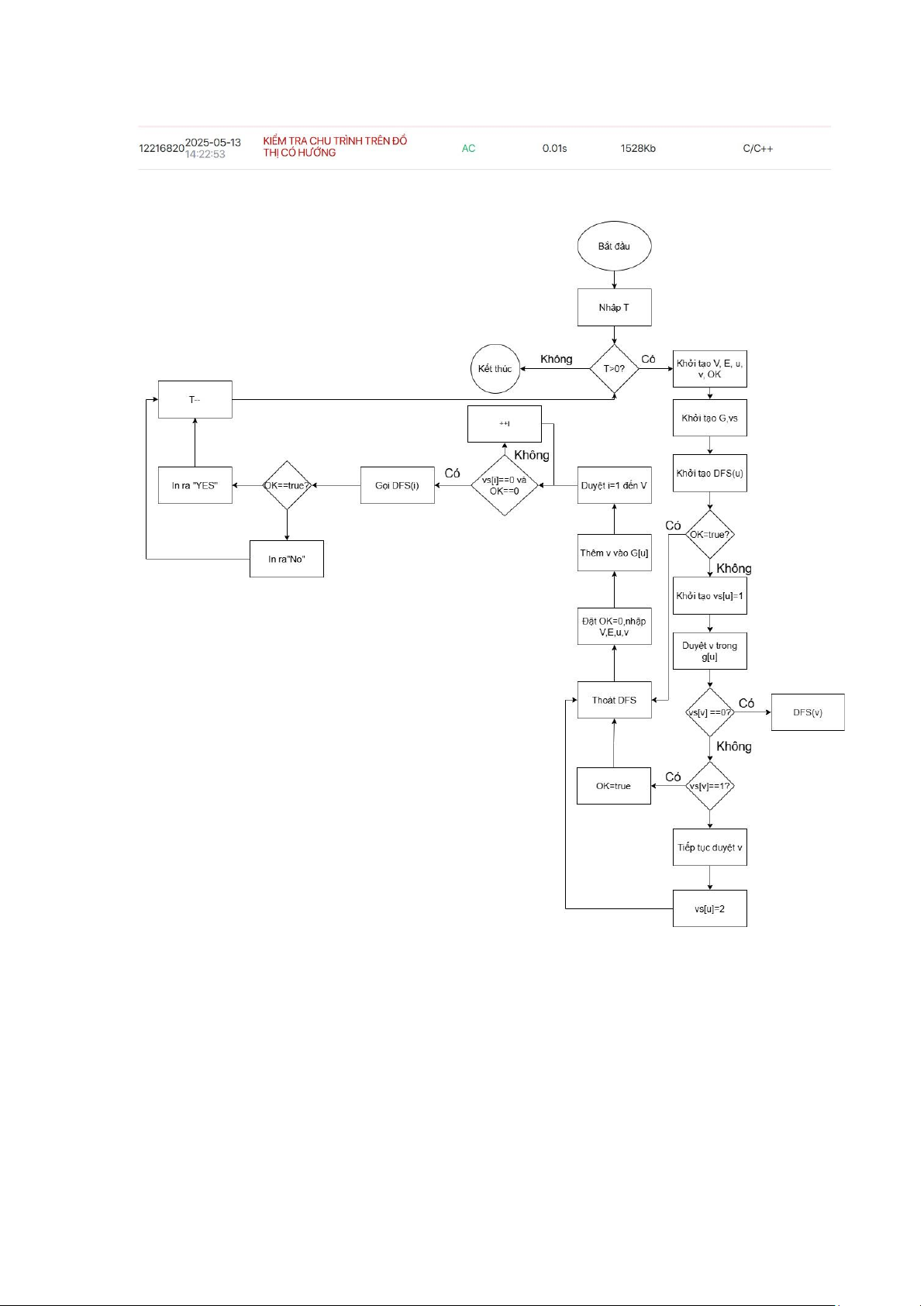
Bài 6. DSA09015 KIỂM TRA CHU TRÌNH TRÊN ĐỒ THỊ CÓ HƯỚNG *Code: #include using namespace std; int V, E, u, v, OK; vector> G; vector vs; void DFS(int u) { if (OK) return; lOMoAR cPSD| 58457166 vs[u] = 1; for (int v : G[u]) { if (vs[v] == 0) DFS(v); else if (vs[v] == 1) { OK = true; return; } } vs[u] = 2; } void TestCase() { OK
= 0; cin >> V >> E; G.assign(V + 1, {}); vs.assign(V + 1, 0); while (E--) { cin >> u >> v; G[u].push_back(v); }
for (int i = 1; i <= V; ++i) { if (!vs[i] && !OK) { DFS(i); } }
cout << (OK ? "YES" : "NO"); } int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL); int T; cin >> T; while (T--) { TestCase(); cout << endl; } return 0; }
* Nêu ngắn gọn ý tưởng:
• Nhập số đỉnh V, số cạnh E. • Khởi tạo:
o Đồ thị G (danh sách kề). o Mảng vs (trạng thái thăm: 0 = chưa thăm, 1 = đang
thăm, 2 = đã thăm). o Biến OK (đánh dấu tìm thấy chu trình).
• Đọc E cạnh, thêm vào G (đồ thị có hướng).
• Chạy DFS từ mỗi đỉnh chưa thăm:
o Đánh dấu đỉnh đang thăm (vs[u] = 1). o Duyệt các đỉnh kề:
▪ Nếu chưa thăm (vs[v] = 0), gọi đệ quy DFS.
▪ Nếu đang thăm (vs[v] = 1), phát hiện chu trình, đặt OK = true. lOMoAR cPSD| 58457166
o Sau khi duyệt xong, đánh dấu đỉnh đã thăm (vs[u] = 2).
• In "YES" nếu tìm thấy chu trình (OK = true), ngược lại in "NO".
• Xác định đồ thị có chu trình hay không. * Lưu đồ thuật toán:
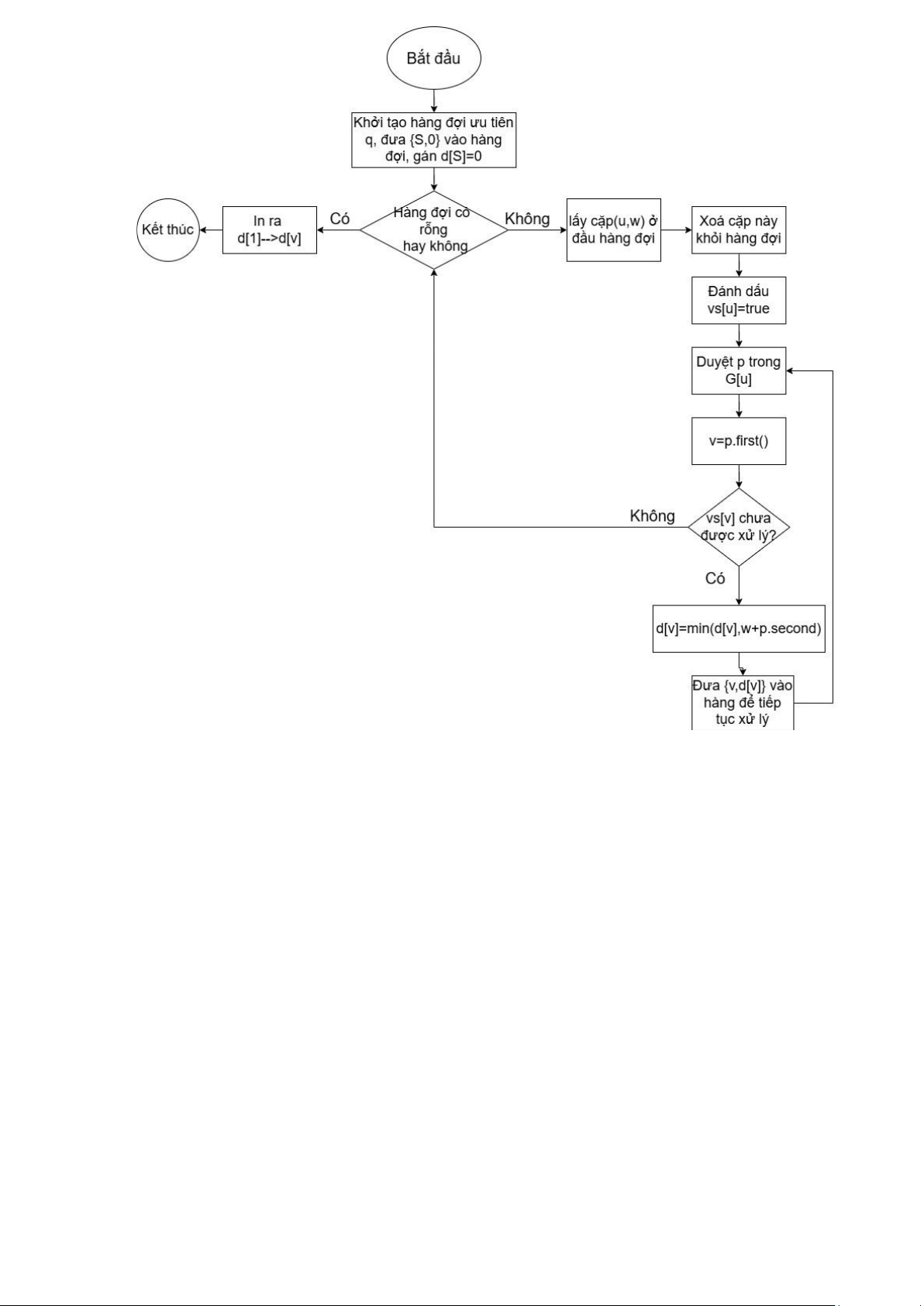
Bài 7. DSA10008 DIJKSTRA CÁC MÔ HÌNH THUẬT TOÁN *Code: #include #define ll long long #define II pair using namespace std; lOMoAR cPSD| 58457166 int V, E, S, u, v, w; vector> G; vector vs; vector d; struct cmp {
bool operator() (pair a, pair b) {
return a.second > b.second; } }; void Dijkstra(int S) { priority_queue, cmp> q;
q.push({S, 0}); d[S] = 0; while (!q.empty()) {
u = q.top().first, w = q.top().second;
q.pop(); vs[u] = true; for (II p : G[u]) { v = p.first; if (!vs[v]) {
d[v] = min(d[v], w + p.second); q.push({v, d[v]}); } } }
for (int i = 1; i <= V; ++i) {
cout << d[i] << " "; } } void TestCase() {
cin >> V >> E >> S; G.assign(V + 1, {}); vs.assign(V + 1, false); d.assign(V + 1, INT_MAX); while (E--) { cin >> u >> v >> w; G[u].push_back({v, w}); G[v].push_back({u, w}); } Dijkstra(S); } int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL); int T = 1; cin >> T; while (T--) { TestCase(); cout << endl; lOMoAR cPSD| 58457166 } return 0; }
* Nêu ngắn gọn ý tưởng:
• Nhập số đỉnh V, số cạnh E, đỉnh bắt đầu S. • Khởi tạo:
o Đồ thị G (danh sách kề, lưu cặp {đỉnh, trọng số}). o Mảng vs (đánh dấu đỉnh đã xử lý).
o Mảng d (khoảng cách ngắn nhất, ban đầu là INT_MAX).
• Đọc E cạnh (đỉnh u, v, trọng số w), thêm vào G (đồ thị vô hướng). • Chạy Dijkstra từ S:
o Dùng priority queue (ưu tiên khoảng cách nhỏ) để chọn đỉnh u có d[u] nhỏ nhất.
o Đánh dấu u đã xử lý, duyệt các đỉnh kề v:
▪ Nếu v chưa xử lý, cập nhật d[v] = min(d[v], d[u] + w(u,v)). ▪ Đẩy {v, d[v]} vào queue.
• In khoảng cách d[i] từ S đến mỗi đỉnh i.
• In khoảng cách ngắn nhất từ S đến tất cả đỉnh. * Lưu đồ thuật toán: lOMoAR cPSD| 58457166