


Preview text:
Dạng toàn phương
1. Khái niệm dạng toàn phương:
Định nghĩa: Dạng toàn phương n biến
là một hàm bậc hai dạng: với các hệ số
là các số thực và các biến là các biến thực. Nếu ta ký hiệu:
chú ý A là ma trận đối xứng.
Khi đó, ta có thể viết dạng toàn phương ở dạng ma trận sau:
Ma trận A được gọi là ma trận của dạng toàn phương. Vậy ma trận của dạng
toàn phương có dạng ma trận đối xứng.
ví dụ 1: Cho hàm bậc hai
. Rõ ràng, f(x) là dạng toàn
phương. Ma trận A có dạng:
Ví dụ 2: Cho hàm bậc hai . Rõ ràng, g(x) là
dạng toàn phương 3 biến. Ma trận A ccủa dạng toàn phương có dạng:
1.2 Dạng toàn phương
1.2 Dạng toàn phương chính tắc:
Một dạng toàn phương chính tắc là dạng toàn phương mà trong biểu thức
xác định không chứa các tích
mà chỉ chứa các số hạng bình phương
Nghĩa là: ma trận của dạng toàn phương là 1 ma trận chéo. Ví dụ:
là 1 dạng toàn phương chính tắc.
2. Đưa dạng toàn phương về dạng chính tắc:
2.1 Phương pháp ma trận trực giao:
Từ định nghĩa của dạng toàn phương chính tắc, ta thấy nếu chuyển ma trận
của dạng toàn phương về dạng ma trận chéo thì có nghĩa là ta sẽ chuyển
được dạng toàn phương về dạng toàn phương chính tắc.
Mặt khác, A là ma trận đối xứng nên ta có A luôn có n giá trị riêng thực, và
các VTR ứng với các giá trị riêng khác nhau đều trực giao với nhau. Khi đó,
nếu P là ma trận trực giao chéo hóa ma trận A và D là dạng chéo của A thì ta có: (trong đó
). Vậy có thể chuyển A về dạng chéo
, nghĩa là chuyển dạng toàn phương về dạng chính tắc. Định lý: Cho dạng toàn phương
, với A là ma trận vuông đối xứng cấp n với các giá trị riêng
và P là ma trận trực giao làm chéo hóa A:
Khi đó, bằng cách đổi biến
ta đưa dạng toàn phương về dạng chính tắc sau: Chứng minh: Thật vậy ta đặt : Ta có: Rõ ràng
Vậy ta chỉ cần chéo hóa trực giao ma trận A của dạng toàn phương và thực
hiện phép đổi biến, ta sẽ đưa về dạng toàn phương chính tắc.
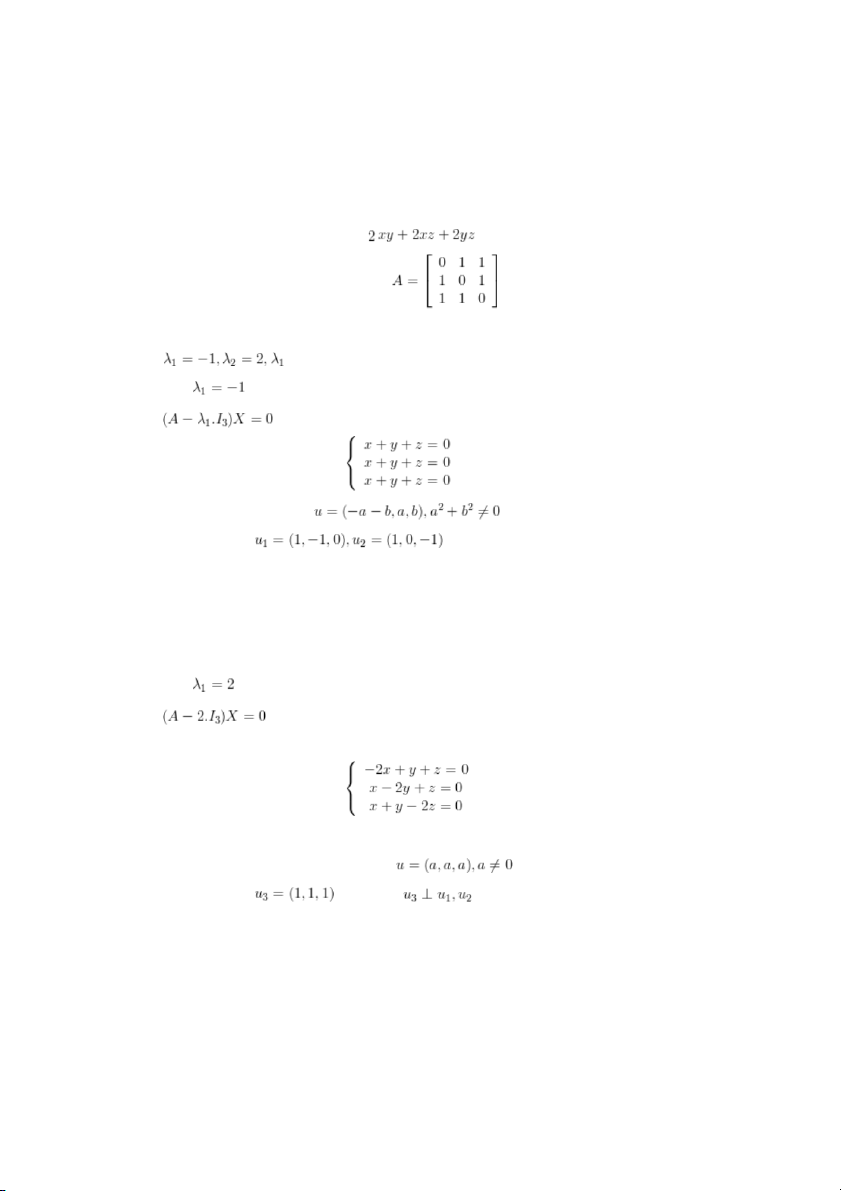
Ví dụ: Cho dạng toàn phương
Ma trận của dạng toàn phương là:
Giải phương trình đặc trưng của ma trận A, ta có ma trận A có 2 giá trị riêng là nghiệm kép. Với
Vectơ riêng ứng với GTR là nghiệm cũa hệ phương trình:
Hay ta có hệ phương trình: Từ đó : VTR có dạng: và ta có 2 VTR độc lập tuyến tính là:
Trực chuẩn hóa Gram – Schmidt hệ này ta được hệ trực chuẩn: Với
Vectơ riêng ứng với GTR là nghiệm cũa hệ phương trình:
Hay ta có hệ phương trình:
Giải hệ này ta được VTR có dạng: và ta có 1 VTR độc lập tuyến tính là: . Rõ ràng, Chuẩn hóa vectơ ta có:
Vậy dạng toàn phương chính tắc là: Và ma trận P có dạng:
Và công thức đổi biến là: Hay: Theo PVT




