Bài toán tối ưu | Trường Đại học Công nghệ thông tin, Đại học Quốc gia Thành phố Hồ Chí Minh

Chương 4: Bài toán tối ưu 4.3 Tối ưu lồi Nguyễn Văn Hợi
Trường Đại học Công nghệ Thông tin Bộ môn Toán - Lý 1 Nội dung
4.3.1 Các định nghĩa. ▶ Hàm lồi, tập lồi.
▶ Cách nhận biết hàm lồi.
4.3.2 Bài toán tối ưu lồi.
4.3.3 Điều kiện KKT 2
4.3.1 Các định nghĩa
Một bài toán tối ưu có ràng buộc thường được viết dưới dạng: minimize f (x) thỏa mãn: hi(x) = 0, i = 1, . . . , m gj(x) ≤ 0, j = 1, . . . , p, trong đó: • x ∈ n R là biến tối ưu. • f : n R → R là hàm mục tiêu. • h n i : R
→ R là hàm ràng buộc đẳng thức. • g n j : R
→ R là hàm ràng buộc bất đẳng thức.
Chú ý: Bài toán tìm giá trị lớn nhất của hàm số f (x) có thể được quy về bài toán
tìm giá trị nhỏ nhất của hàm số −f (x). 3
1. Tập xác định D: n
Là tập hợp các điểm mà tất cả các hàm R D (Tập xác định)
trong bài toán đều có nghĩa. (nơi các hàm có nghĩa) m p \ \ D = dom f ∩ dom hi ∩ dom gj, χ i=1 j=1 (Tập khả thi)
với domf là tập xác định của hàm f .
2. Tập khả thi χ:
3. Điểm tối ưu và giá trị tối ưu
Là tập hợp các điểm trong tập xác định
Điểm x∗ ∈ χ được gọi là điểm tối ưu nếu
thỏa mãn tất cả các ràng buộc.
f (x∗) đạt giá trị nhỏ nhất trên tập khả thi: ( ) hi(x) = 0, i = 1, . . . , m; χ = x ∈ D . f (x∗) ≤ f (x), ∀x ∈ χ. g j (x) ≤ 0, j = 1, . . . , p
Giá trị tương ứng f (x∗) được gọi là giá trị
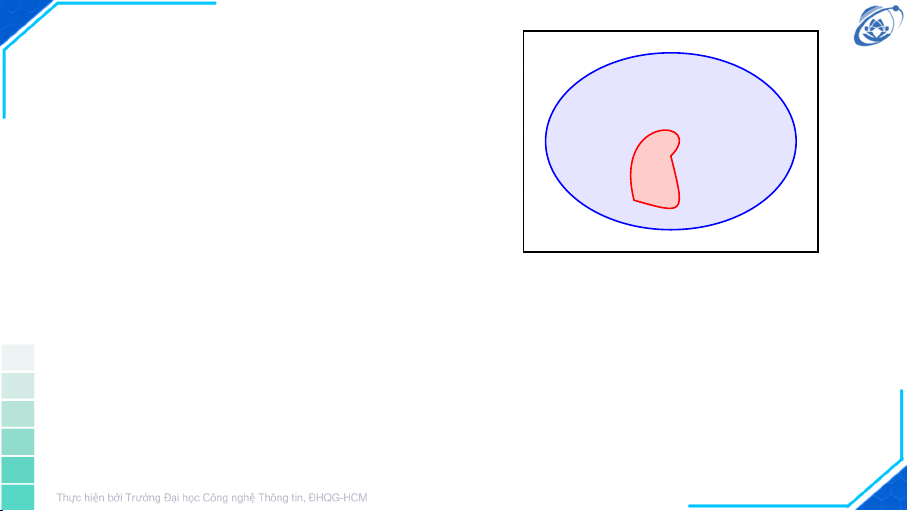
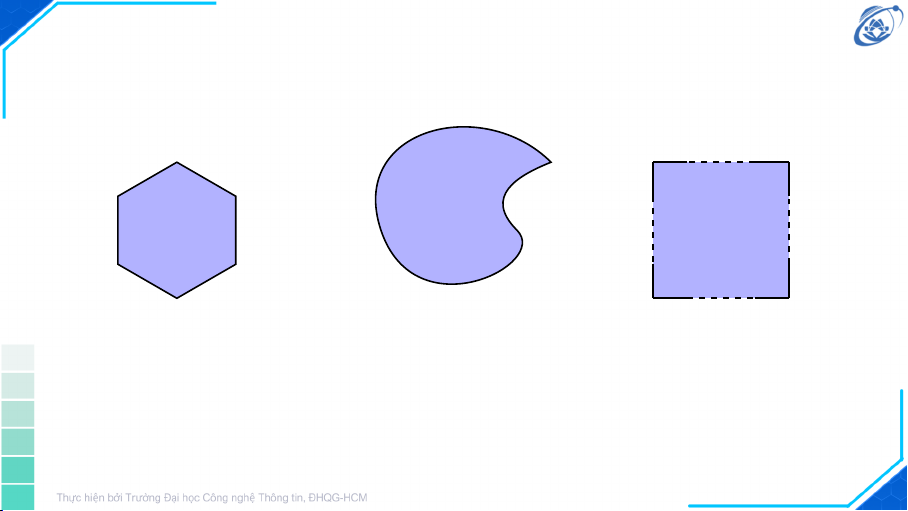
tối ưu của bài toán. 4 Tập lồi ❒ C ⊂ n
R là một tập lồi nếu và chỉ nếu với mọi x, y ∈ C và 0 ≤ α ≤ 1, αx + (1 − α)y ∈ C. x y x Tập lồi y Tập không lồi 5
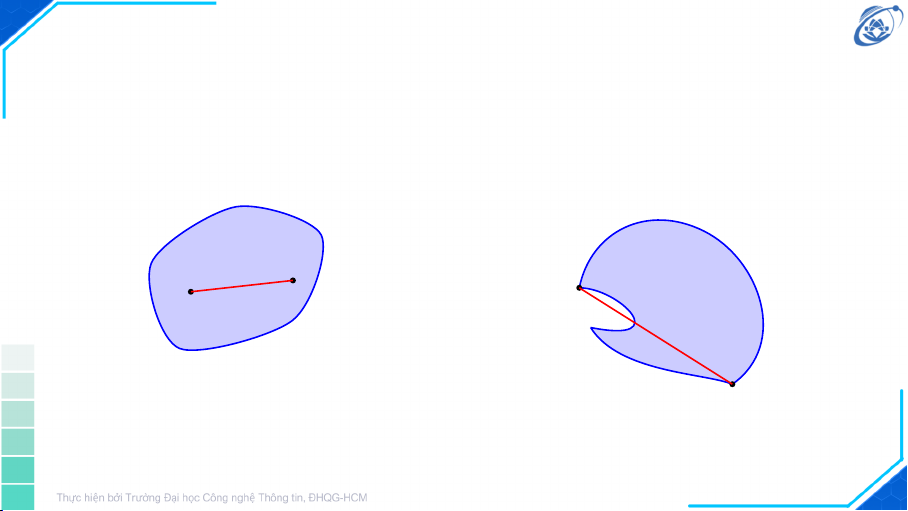
▲ Tập nào sau đây là tập lồi? Vì sao? (1) (2) (3) 6 Hàm lồi
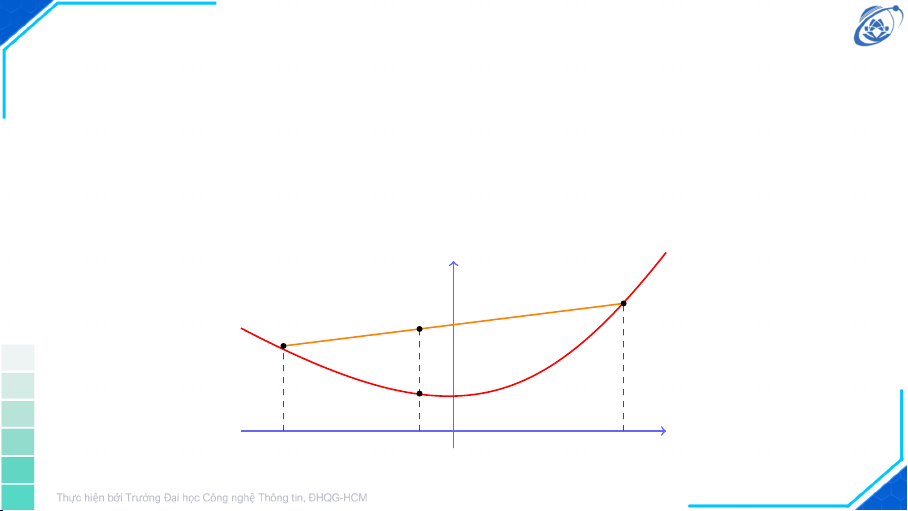
❒ Định nghĩa: Một hàm số f : Ω → R được gọi là hàm lồi nếu tập xác định Ω ⊆ n
R của nó là một tập lồi, và với mọi x1, x2 ∈ Ω, mọi α ∈ [0, 1], ta có f αx 1 + (1 − α)x2
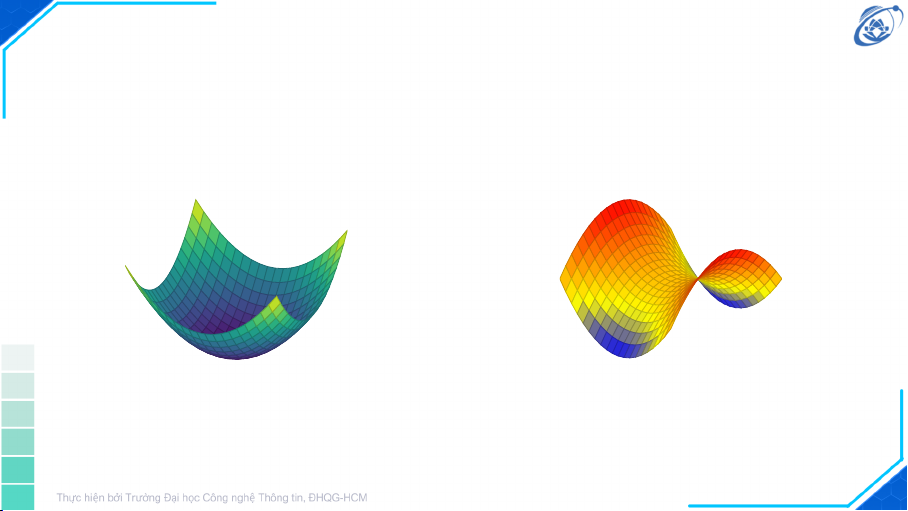
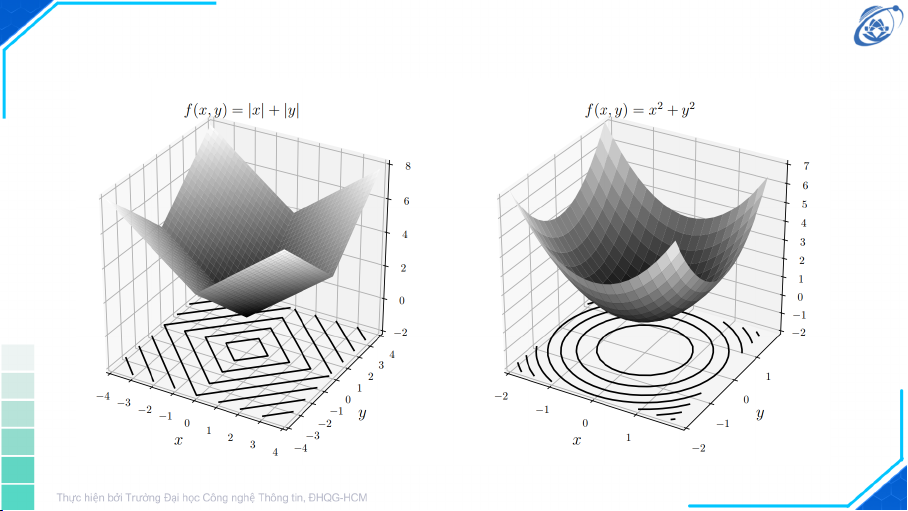
≤ αf (x1) + (1 − α)f (x2) f (x αf (x 2) 1) + (1 − α)f (x2) f (x1) f (αx1 + (1 − α)x2) x1 x2 αx1 + (1 − α)x2 7 Hàm lồi Hàm Không lồi f (x, y) = x2 + y2 f (x, y) = x2 − y2 8
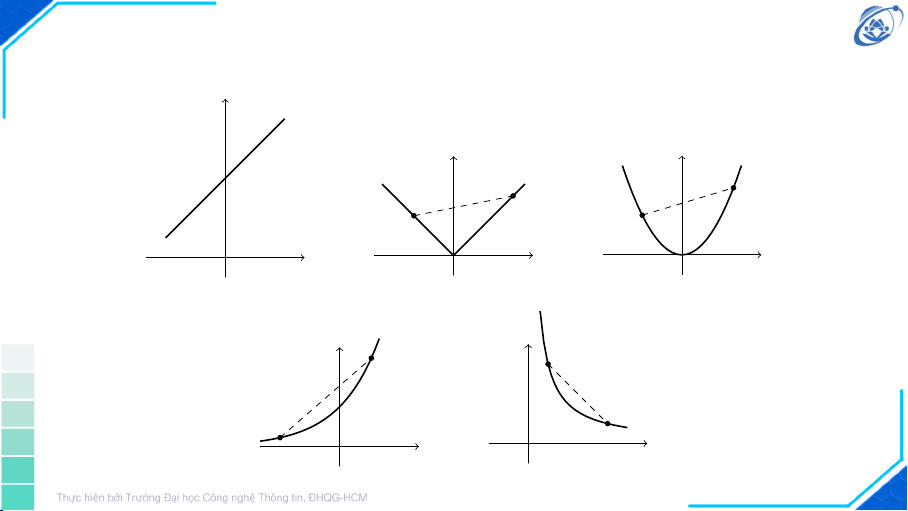
Một số ví dụ về hàm lồi y = ax + b y = |x| y = x2 y = ex y = x−1, x > 0 9 10 11 Ma trận con cấp k
❒ Định nghĩa: Một ma trận con cấp k: Mi
của ma trận A được tạo thành 1i2...ik
bằng cách chọn các hàng {i1, i2, . . . , ik} và cột {i1, i2, . . . , ik}. Định thức của chúng ký hiệu là Di . 1i2...ik
▲ Ví dụ: Xét ma trận A cấp 3 × 3: a  11 a12 a13 A = a  21 a22 a23 a31 a32 a33
Để tạo ma trận con M13, ta giữ lại các hàng và cột có chỉ số 1 và 3: a  11 a12 a13 chọn hàng/cột {1,3} a a
−−−−−−−−−−−→ 11 a13  21 a22 a23 a a 31 a33 31 a32 a33
Định thức con tương ứng là D13. 12
▲ Ví dụ: Cho ma trận 1 2 3 A = 4 5 0   . 7 8 9 Các định thức con Di : 1i2...ik
Cấp 1: (Hàng/cột {1}, {2}, {3}) D1 = 1 , D2 = 5 , D3 = 9 .
Cấp 2: (Hàng/cột {1, 2}, {1, 3}, {2, 3}) 1 2 1 3 5 0 D 12 = , D13 = , D23 = . 4 5 7 9 8 9
Cấp 3: Hàng/cột {1, 2, 3} 1 2 3 D 123 = 4 5 0 . 7 8 9 13 Trị riêng
❒ Định nghĩa: Cho ma trận vuông A cấp n × n. Một số thực λ được gọi là một trị
riêng của A nếu λ là nghiệm của phương trình det(A − λI) = 0,
với I là ma trận đơn vị cấp n.
▲ Ví dụ: Tìm các trị riêng của ma trận0 0 −2 A = 1 2 1 . 1 0 3 Xét phương trình 0 − λ 0 −2 det(A − λI) = 1 2 − λ 1
= (2 − λ)(λ2 − 3λ + 2) = 0. 1 0 3 − λ
Giải phương trình trên ta được λ = 2 và λ = 1. 14
Ma trận nửa xác định dương
❒ Định nghĩa: Cho một ma trận vuông đối xứng A cấp n. Ma trận A được gọi là
nửa xác định dương, ký hiệu A ⪰ 0, nếu zT Az ≥ 0, ∀z ∈ n R .
❑ Định lý 1 (Tiêu chuẩn định thức): Ma trận vuông đối xứng A cấp n là nửa xác
định dương nếu và chỉ nếu tất cả các định thức con Di ≥ 0. 1i2...ik
❑ Định lý 2 (Tiêu chuẩn trị riêng): Ma trận vuông đối xứng A cấp n là nửa xác
định dương nếu và chỉ nếu tất cả các trị riêng của A đều lớn hơn hoặc bằng không. 15
Điều kiện lồi cấp hai của hàm số
❒ Điều kiện lồi cấp hai: Cho Ω ⊂ n
R là một tập mở, lồi và f : Ω → R có đạo hàm
riêng cấp hai liên tục trên Ω. Khi đó f là hàm lồi nếu và chỉ nếu với mọi x ∈ Ω ma
trận Hessian H(x) là nửa xác định dương. Điều này có nghĩa là: zT H(x)z ≥ 0, ∀z ∈ n R .
Chú ý: Trong trường hợp f (x) hàm một biến xác định trên (a, b) ⊂ R, f (x) lồi trên
(a, b) nếu và chỉ nếu f ′′(x) ≥ 0 với mọi x ∈ (a, b).
Nhắc lại, ma trận Hessian H(x) (hoặc ký hiệu ∇2f (x)) được xây dựng như sau:  f f · · · f  x2 x x 1 1x2 1xn fx f · · · f 2x1 x2 x2xn  H(x) =  2 . . .   . . . .. .   . . .  fx f · · · f nx1 xnx2 x2 n với fx
là các đạo hàm riêng cấp hai của f . ixj 16
▲ Ví dụ: Xét hàm số f (x) = (x1 + x2)4. Ma trận Hessian: " # f f x 12(x H(x) = x2 1 + x2)2 12(x1 + x2)2 1 1x2 = . fx f 12(x 2x1 x2 1 + x2)2 12(x1 + x2)2 2
Ta kiểm tra tính lồi của hàm số f (x) thông qua kiểm tra tính nửa xác định dương
của ma trận Hessian. Ta sẽ tiến hành lần lượt bằng 3 cách:
Cách 1: Kiểm tra bằng định nghĩa. Với mọi z ∈ 2 R , ta xét 12(x z zT H(x)z = [z 1 + x2)2 12(x1 + x2)2 1 1 z2] = 12(x 12(x 1 +x2)2(z2 1 +2z1z2 +z2 2 ). 1 + x2)2 12(x1 + x2)2 z2
• Đưa về dạng tổng các bình phương zT H(x)z = 12(x 2
1 + x2)2(z1 + z2)2 ≥ 0, ∀z ∈ R .
• Suy ra H(x) là nửa xác định dương. Do đó, f (x) là hàm lồi. 17
Cách 2: Kiểm tra bằng định thức con. Ma trận Hessian: 12(x H(x) = 1 + x2)2 12(x1 + x2)2 . 12(x1 + x2)2 12(x1 + x2)2 Định thức con cấp 1:
D1 = 12(x1 + x2)2 ≥ 0, D2 = 12(x1 + x2)2 ≥ 0. Định thức con cấp 2: 12(x D 1 + x2)2 12(x1 + x2)2 12 = = 0 ≥ 0. 12(x1 + x2)2 12(x1 + x2)2
Suy ra H(x) là nửa xác định dương. Do đó, f (x) là hàm lồi. 18
Cách 3: Kiểm tra bằng trị riêng. Ma trận Hessian: 12(x H(x) = 1 + x2)2 12(x1 + x2)2 . 12(x1 + x2)2 12(x1 + x2)2
• Ta tìm các trị riêng của H(x). Xét phương trình det(H(x) − λI) = 0. Ta có 12(x det(H(x) − λI) = 1 + x2)2 − λ 12(x1 + x2)2
= λ[λ − 24(x1 + x2)2] = 0. 12(x1 + x2)2 12(x1 + x2)2 − λ • Các trị riêng là λ 2
1 = 0 ≥ 0 và λ2 = 24(x1 + x2)2 ≥ 0 với mọi (x1, x2) ∈ R .
• Vì tất cả các trị riêng đều không âm nên H(x) là nửa xác định dương. Do đó, f (x) là hàm lồi. 19
Khảo sát tính lồi của hàm số
▲ Ví dụ 1: f (x) = ex. Vì f ′′(x) = ex > 0 với mọi x ∈ R nên f (x) là hàm lồi.
▲ Ví dụ 2: f (x) = −8x2. Vì f ′′(x) = −16 < 0 với mọi x ∈ R nên f (x) không phải hàm lồi.
▲ Ví dụ 3: f (x1, x2) = 2x2 − 6x2. Thiết lập ma trận Hessian: 1 2 " # f f x 4 0 H(x) = x2 1 1x2 = . fx f 0 −12 2x1 x2 2 20