Bai2 CSLT update - Tài liệu tham khảo | Đại học Hoa Sen
Bai2 CSLT update - Tài liệu tham khảo | Đại học Hoa Sen và thông tin bổ ích giúp sinh viên tham khảo, ôn luyện và phục vụ nhu cầu học tập của mình cụ thể là có định hướng, ôn tập, nắm vững kiến thức môn học và làm bài tốt trong những bài kiểm tra, bài tiểu luận, bài tập kết thúc học phần, từ đó học tập tốt và có kết quả cao cũng như có thể vận dụng tốt những kiến thức mình đã học.
Môn: information technology (IT Sotfware) 30 tài liệu
Trường: Đại học Hoa Sen 4.8 K tài liệu
Tác giả:
Preview text:
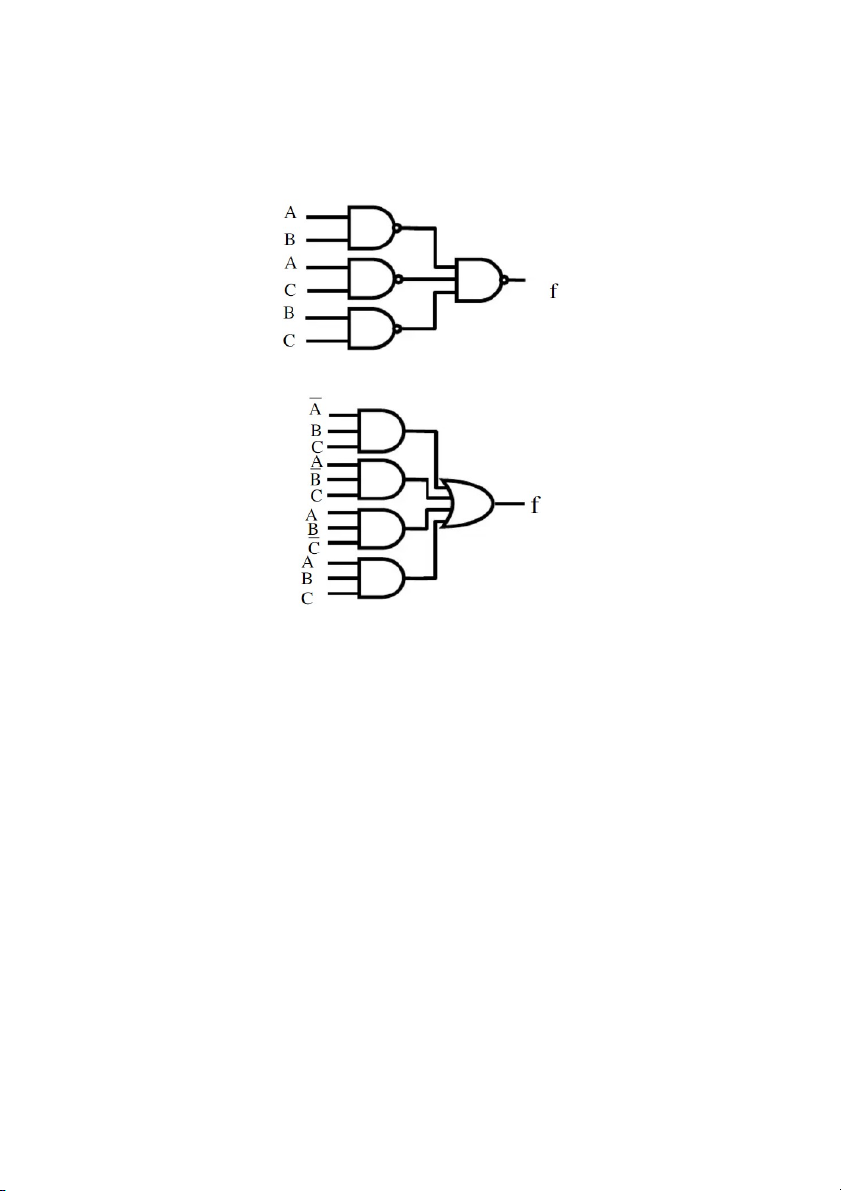
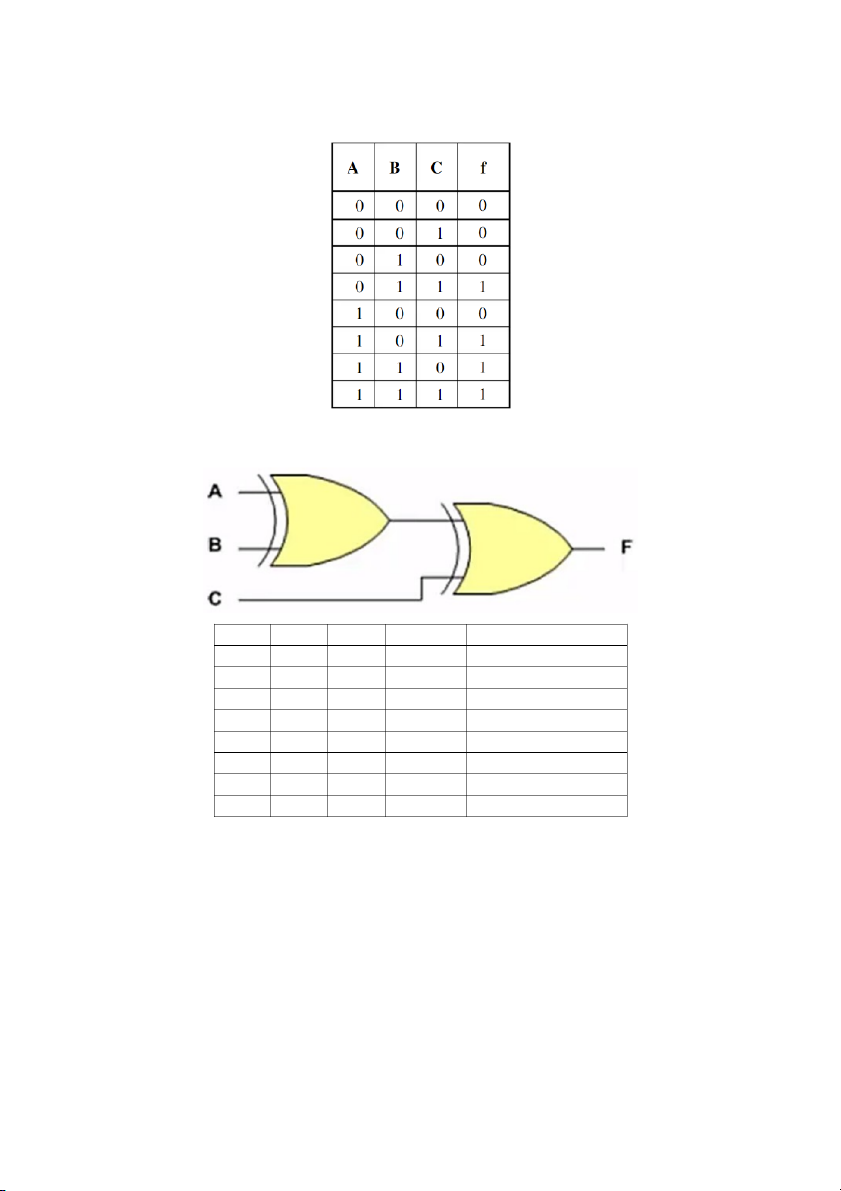
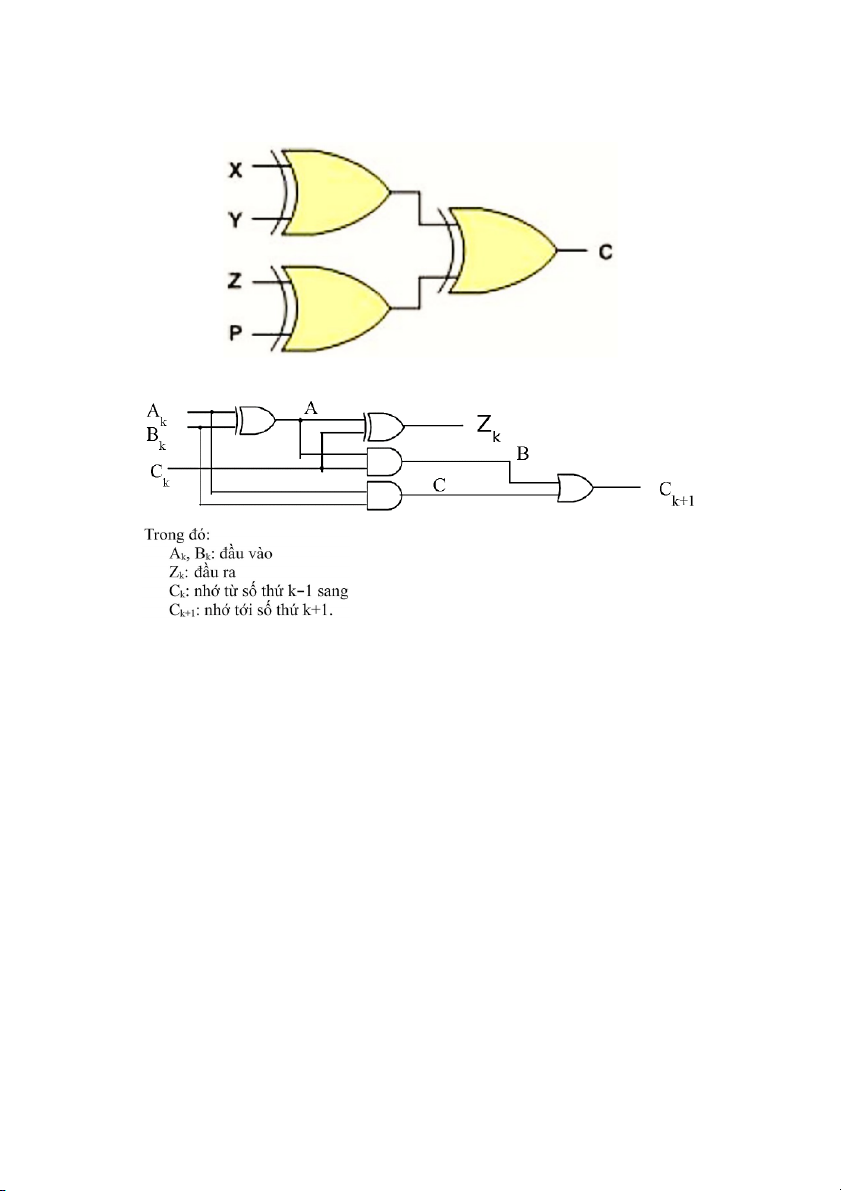
Bài 1. Hãy lập b n ả g chân tr ịcho m c ạ h sau: A. B. Đáp án: Bài 2. Ch n ứ g minh m c ạ h sau là m c ạ h l ẻ 3 đ u ầ vào (s ố bit 1 là l ẻ 🡺 đ u ầ ra là 1, ng c ượ l i ạ đ u ầ ra là 0) A B C xor(A, B) F = xor(C, xor(A, B) 0 0 0 0 0 0 0 1 0 1 0 1 0 1 1 0 1 1 1 0 1 0 0 1 1 1 0 1 1 0 1 1 0 0 0 1 1 1 0 1 Bài 3. Ch n ứ g minh m c ạ h sau là m c ạ h l ẻ 4 đ u ầ vào (s ố bit 1 là l ẻ 🡺 đ u ầ ra là 1, ng c ượ l i ạ đ u ầ ra là 0) Bài 4. Cho m c ạ h sau: CH N Ứ G MINH: A. N u
ế Ak = 0, Bk = 0, Ck = 0 🡺 Zk = 0 và Ck+1 = 0 B. N u
ế Ak = 0, Bk = 0, Ck = 1 🡺 Zk = 1 và Ck+1 = 0 C. N u
ế Ak = 0, Bk = 1, Ck = 0 🡺 Zk = 1 và Ck+1 = 0 D. N u
ế Ak = 0, Bk = 1, Ck = 1 🡺 Zk = 0 và Ck+1 = 1 E. N u
ế Ak = 1, Bk = 0, Ck = 0 🡺 Zk = 1 và Ck+1 = 0 F. N u
ế Ak = 1, Bk = 0, Ck = 1 🡺 Zk = 0 và Ck+1 = 1 G. N u
ế Ak = 1, Bk = 1, Ck = 0 🡺 Zk = 0 và Ck+1 = 1 H. N u
ế Ak = 1, Bk = 1, Ck = 1 🡺 Zk = 1 và Ck+1 = 1 Đáp án A: Bài 5. Ch n ứ g minh r n ằ g đây là m c ạ h AND 2 đ u ầ vào A, B, k t ế qu ả ra K. X = Y = Z = K = A B
NOR(A,B) NOR(A,X) NOR(B,Y) NOR(Y,Z) AND(A, B) 0 0 1 0 1 0 0 0 1 0 1 0 0 0 1 0 0 0 1 0 0 1 1 0 0 0 1 1