Bảng kí hiệu phần học kinh tế vĩ mô | Đại học Lao động - Xã hội

Bảng kí hiệu phần học kinh tế vĩ mô | Đại học Lao động - Xã hội với những kiến thức và thông tin bổ ích giúp sinh viên tham khảo, ôn luyện và phục vụ nhu cầu học tập của mình cụ thể là có định hướng, ôn tập, nắm vững kiến thức môn học và làm bài tốt trong những bài kiểm tra, bài tiểu luận, bài tập kết thúc học phần, từ đó học tập tốt và có kết quả cao cũng như có thể vận dụng tốt những kiến thức mình đã học vào thực tiễn cuộc sống

58 29 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Kinh tế vi mô (ViMO0523H)

Trường: Đại học Lao động - Xã hội

Thông tin:

2 trang 7 tháng trước

Tác giả:

Profile Nguyễn Vân
Ki
hiê
u
ĐN Công thc
P Gia -
Q Sn lưng -
P
d
Gia cu a.Q+b (a<0)
Q
d
Lưng cu C.P+d (c<0)
P
s
Gia cung a.Q+b (a>0)
Q
s
Lưng cung C.P+d (c>0)
t thuê Cô
#
ng v%o P đ( ra P m+i
s s
E
d
p
HS co d/n
c0a cu theo
gia
T3ng quat=
TH1: t8nh HSCD t:i 1đ c; th( =(Q
d
)’ .
p
TH2: t8nh HSCD khong A(P ) v%
1
;Q
1
B(P ;Q )
1 1
=.
E
d
i
HS co d/n
c0a cu theo
thu nhâ
#
p
T3ng quat=
TH1: t8nh HSCD t:i 1đ c; th( =(Q
d
)’ .
I
TH2: t8nh HSCD khong A(I ) v%
1
;Q
1
B(I ;Q )
1 1
=.
E
d
(
HS co d/n
chDo
T3ng quat=
TH1: t8nh HSCD t:i 1đ c; th( =(Q
x
)’ .
py
TH2: t8nh HSCD khong A(P ) v%
y
;Q
x
B(P ;Q )
y x
=.
I Thu nhâ
#
p Phương trHnh đưIng ngân sach:
x.P
x
+yP
y
=I (x,y sK lưng h%ng hLa)
Nguyên tOc
cân bPng li
8ch câ
#
n biên
= ==. . .
U Li 8ch
-
TU T3ng li 8ch =
(TU max → MU=0)
L Lao đô
#
ng
-
APL Năng suVt
TB
= (K cK đWnh)
APK = (L cK đWnh)
MPL Năng suVt
câ
#
n biên
== (Q)’ (K cK đWnh)
L
MP
K
= =(Q)’ (L cK đWnh)
K
TC T3ng chi ph8 =wL+rK
=FC+VC=ATC.Q
VC Chi phi biên
đ3i
=AVC.Q
(Q=0 →VC=0)
FC Chi ph8 cK
đWnh
=AFC.Q
AVC Chi ph8 biên
đ3i bHnh
quân
=
ATC
(AC)
T3ng chi ph8
bHnh quân
==AVC+AFC
AFC Chi ph8 cK
đWnh bHnh
quân
=
MC Chi ph8 câ
#
n
biên
==(TC)’
q
=
TR T3ng doanh
thu
=P.Q= a.Q
2
+bQ=AR.Q
AR Doanh thu
bHnh quân
=
MR Doanh thu
câ
#
n biên
==(TR)’
q
(MR=0 → tKi đa hLa doanh thu→E
d
b
=-
1)
(MR=MC → TKi đa hLa li nhuâ
#
n)
Li nhuâ
#
n =TR-TC
MU Li 8ch câ
#
n
biên
==(TU)’
q
()
K Tư bn
-
| 1/2
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

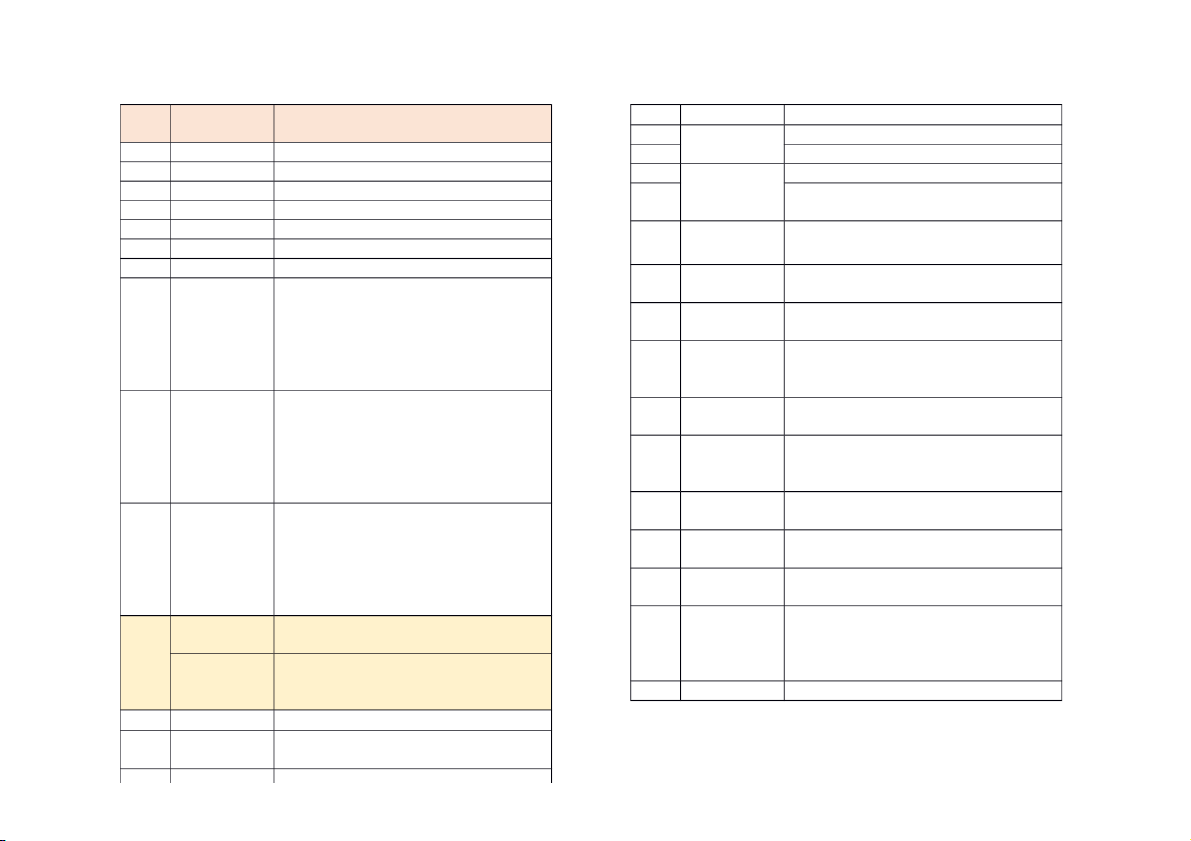
Ki ĐN Công thc L Lao đô #ng - hiê u APL Năng suVt = (K cK đWnh) P Gia - APK TB = (L cK đWnh) Q Sn lưng - MPL Năng suVt == (Q)’L (K cK đWnh) Pd Gia cu a.Q+b (a<0) MP câ #n biên = =(Q)’K (L cK đWnh) Qd Lưng cu C.P+d (c<0) K Ps Gia cung a.Q+b (a>0) TC T3ng chi ph8 =wL+rK Qs Lưng cung C.P+d (c>0) =FC+VC=ATC.Q t thuê Cô #ng v%o Ps đ( ra Ps m+i VC Chi phi biên =AVC.Q Edp HS co d/n T3ng quat= đ3i (Q=0 →VC=0) c0a cu theo
TH1: t8nh HSCD t:i 1đ c; th( =(Qd)’p. FC Chi ph8 cK =AFC.Q gia
TH2: t8nh HSCD khong A(P1;Q1) v% đWnh B(P1;Q1) AVC Chi ph8 biên = =. đ3i bHnh quân Edi HS co d/n T3ng quat= ATC T3ng chi ph8 ==AVC+AFC c0a cu theo
TH1: t8nh HSCD t:i 1đ c; th( =(Qd)’I. (AC) bHnh quân thu nhâ #p
TH2: t8nh HSCD khong A(I1;Q1) v% AFC Chi ph8 cK = B(I1;Q1) đWnh bHnh =. quân MC Chi ph8 câ #n ==(TC)’ Ed q = ( HS co d/n T3ng quat= biên chDo
TH1: t8nh HSCD t:i 1đ c; th( =(Qx)’py. TR T3ng doanh =P.Q= a.Q2+bQ=AR.Q
TH2: t8nh HSCD khong A(Py;Qx) v% thu B(Py;Qx) AR Doanh thu = =. bHnh quân MR Doanh thu ==(TR)’ I Thu nhâ #p
Phương trHnh đưIng ngân sach: q câ
(MR=0 → tKi đa hLa doanh thu→Ed x.P #n biên b=-
x+yPy=I (x,y sK lưng h%ng hLa) 1) Nguyên tOc = ==. . .
(MR=MC → TKi đa hLa li nhuâ cân bPng li #n) Li nhuâ #n =TR-TC 8ch câ #n biên U Li 8ch - TU T3ng li 8ch = (TU max → MU=0) MU Li 8ch câ #n ==(TU)’q () biên K Tư bn -