-
Thông tin
-
Hỏi đáp
Báo cáo Bài tập lớn Giải tích 2 - Giải tích 1 | Trường Đại học Bách khoa Thành phố Hồ Chí Minh
1. Đọc và trình bày lại phần 6.4, APPLICATION: CONSUMER AND PRODUCER SURPLUS (thặng dư người tiêu dùng và thặng dư nhà sản xuất, trong Applied Calculus 5 th Edition. Yêu cầu hiểu rõ những khái niệm phát sinh trong phần này. Đưa các ví dụ minh họa đã nêu, không dùng lại những ví dụ đã nêu trong tài liệu. Tài liệu được sưu tầm giúp bạn tham khảo, ôn tập và đạt kết quả cao trong kì thi sắp tới. Mời bạn đọc đón xem !
Môn:
Thông tin:
23 trang
4 tuần trước
Tác giả:
Báo cáo Bài tập lớn Giải tích 2 - Giải tích 1 | Trường Đại học Bách khoa Thành phố Hồ Chí Minh
1. Đọc và trình bày lại phần 6.4, APPLICATION: CONSUMER AND PRODUCER SURPLUS (thặng dư người tiêu dùng và thặng dư nhà sản xuất, trong Applied Calculus 5 th Edition. Yêu cầu hiểu rõ những khái niệm phát sinh trong phần này. Đưa các ví dụ minh họa đã nêu, không dùng lại những ví dụ đã nêu trong tài liệu. Tài liệu được sưu tầm giúp bạn tham khảo, ôn tập và đạt kết quả cao trong kì thi sắp tới. Mời bạn đọc đón xem !
Môn: Giải tích
Trường: Đại học Bách khoa Thành phố Hồ Chí Minh
Thông tin:
23 trang
4 tuần trước
Tác giả:
Báo cáo BTL nhóm 5
ĐẠI HỌC QUỐC GIA TPHCM
TRƯỜNG ĐẠI HỌC BÁCH KHOA TP.HCM
VĂN PHÒNG ĐÀO TẠO QUỐC TẾ - OISP
BÁO CÁO
BÀI TẬP LỚN GIẢI TÍCH 2
TPHCM, 31/06/2022
1
Báo cáo BTL nhóm 5
NỘI DUNG CÂU HỎI
1. Đọc và trình bày lại phần 6.4, APPLICATION: CONSUMER AND PRODUCER
SURPLUS (thặng dư người tiêu dùng và thặng dư nhà sản xuất, trong Applied
Calculus 5
th
Edition. Yêu cầu hiểu rõ những khái niệm phát sinh trong phần này. Đưa
các ví dụ minh họa đã nêu, không dùng lại những ví dụ đã nêu trong tài liệu.
2. Hàm cung và cầu của một sản phẩm được cho như hình bên dưới. Dùng tổng
Rieman ước tính 2 loại thặng dư ở câu trên.
3. Một công ty sở hữu 1 thiết bị mà giá trị của nó sẽ bị giảm liên tục sau lần đại tu cuối
cùng. Tốc độ giảm là hàm
số
f = f
C
t
3
với t tính theo tháng, Chi phí cho mỗi lần đại tu là
một giá trị A cố định nên công ty muốn tối ưu khoảng thời gian giữa các lần đại tu.
a/ Giải thích tại sao
t
∫
f
C
s
3
ds
0
là giá trị bị mất sau t tháng kể từ lần đại tu sau cùng.
1
/
t
C
C =C
C
t
3
=
t
∣
A +
∫
f
C
s
3
ds
∣
b/ Hãy cho biết ý nghĩa của
trị nhỏ nhất.
C 0
C
và tại sao công ty muốn C có giá
c/ Giả sử T thỏa
C
C
T
3
=
f
C
T
3
, chứng minh rằng đạt giá trị nhỏ nhất tại
t
=
T
.
2
Báo cáo BTL nhóm 5
NHẬN XÉT CỦA GVHD
MỤC LỤC
MỤC LỤC
NỘI DUNG CÂU HỎI...................................................................................................2
3
Báo cáo BTL nhóm 5
NHẬN XÉT CỦA GVHD..............................................................................................3
LỜI NÓI ĐẦU................................................................................................................5
BÁO CÁO......................................................................................................................6
Câu 1:..............................................................................................................................6
I. Định nghĩa cầu......................................................................................................6
II. Định nghĩa cung....................................................................................................8
III. Quy luật cung cầu............................................................................................10
IV. Cân bằng thị trường.........................................................................................10
V. Khái niệm thặng dư.............................................................................................11
VI. Thặng dư nhà sản xuất và người tiêu dùng......................................................11
Câu 2.............................................................................................................................13
VII. Định nghĩa chung:...........................................................................................13
VIII. Các loại tổng RIEMANN................................................................................13
IX. Phương pháp:...................................................................................................14
X. Nhận xét..............................................................................................................15
XI. Giải Bài tập......................................................................................................17
Câu 3.............................................................................................................................22
XII. Bài toán............................................................................................................22
XIII. Bài giải............................................................................................................22
TỔNG KẾT...................................................................................................................23
LỜI NÓI ĐẦU
Giải Tích 1 là môn học đại cương có tầm quan trọng đối với sinh viên ĐH Bách Khoa
TPHCM nói riêng và sinh viên các ngành khối khoa học kỹ thuật – công nghệ nói chung.
Do đó, việc dành cho môn học này một khối lượng thời gian nhất định và thực hành là
4
Báo cáo BTL nhóm 5
điều tất yếu để giúp cho sinh viên có được cơ sở vững chắc về các môn KHTN và làm
tiền đề để học tốt các môn khác trong chương trình đào tạo.
Ở bài tập lớn này, nhóm đã tìm hiểu về “Thế nào là Thặng Dư trong kinh tế, thế nào
là thặng của NSX hay NTD và qua đó ứng dụng giải tích để đi tìm kết quả cho các bài
toán kinh tế đó”. Sau đây là phần nội dung tìm hiểu của nhóm.
Câu 1:
BÁO CÁO
I. Định nghĩa cầầu
1, Cầu là số lượng hàng hóa hoặc dịch vụ mà tiêu dùng mong muốn và có khả năng mua
tại các mức giá khác nhau trong một thời gian nhất định với giả định các nhân tố khác
không đổi
2, Quy luật cầu
– Với giả định các nhân tố khác không đổi, số lượng hàng hóa hoặc dịch vụ được cầu
trong một khoảng thời gian nhất định sẽ tăng lên khi giá giảm và ngược lại, sẽ giảm khi
giá tăng.
– Như vậy, giá hàng hóa / dịch vụ và lượng cầu có quan hệ nghịch.
P↑ → Q
d
↓
P ↓ → Q
d
↑
3, Biểu diễn cầu
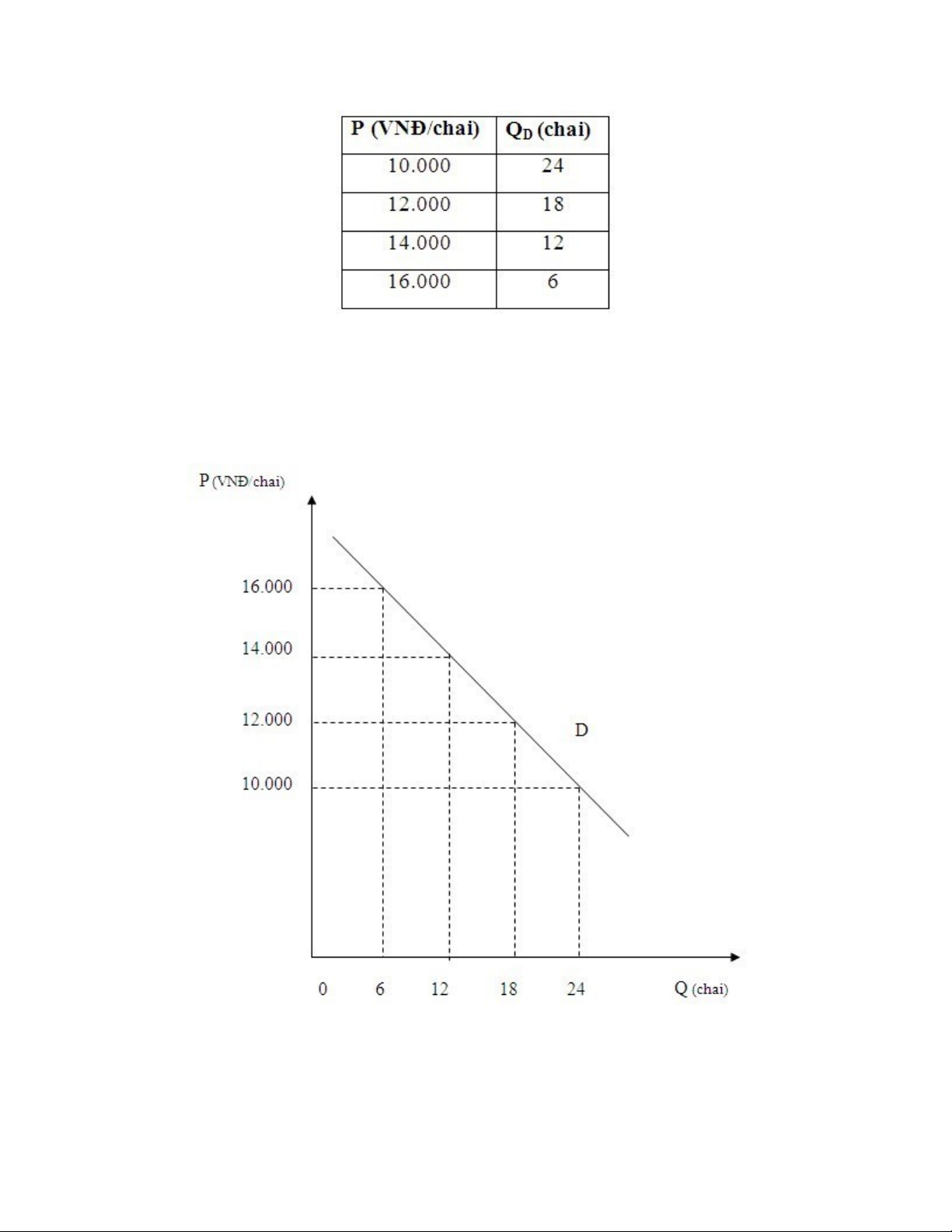
3.1. Biểu cầu
Đó là một bảng số liệu gồm ít nhất 2 cột giá và lượng cầu, cho biết phản ứng của người
tiêu dùng tại các mức giá khác nhau.
5
Báo cáo BTL nhóm 5
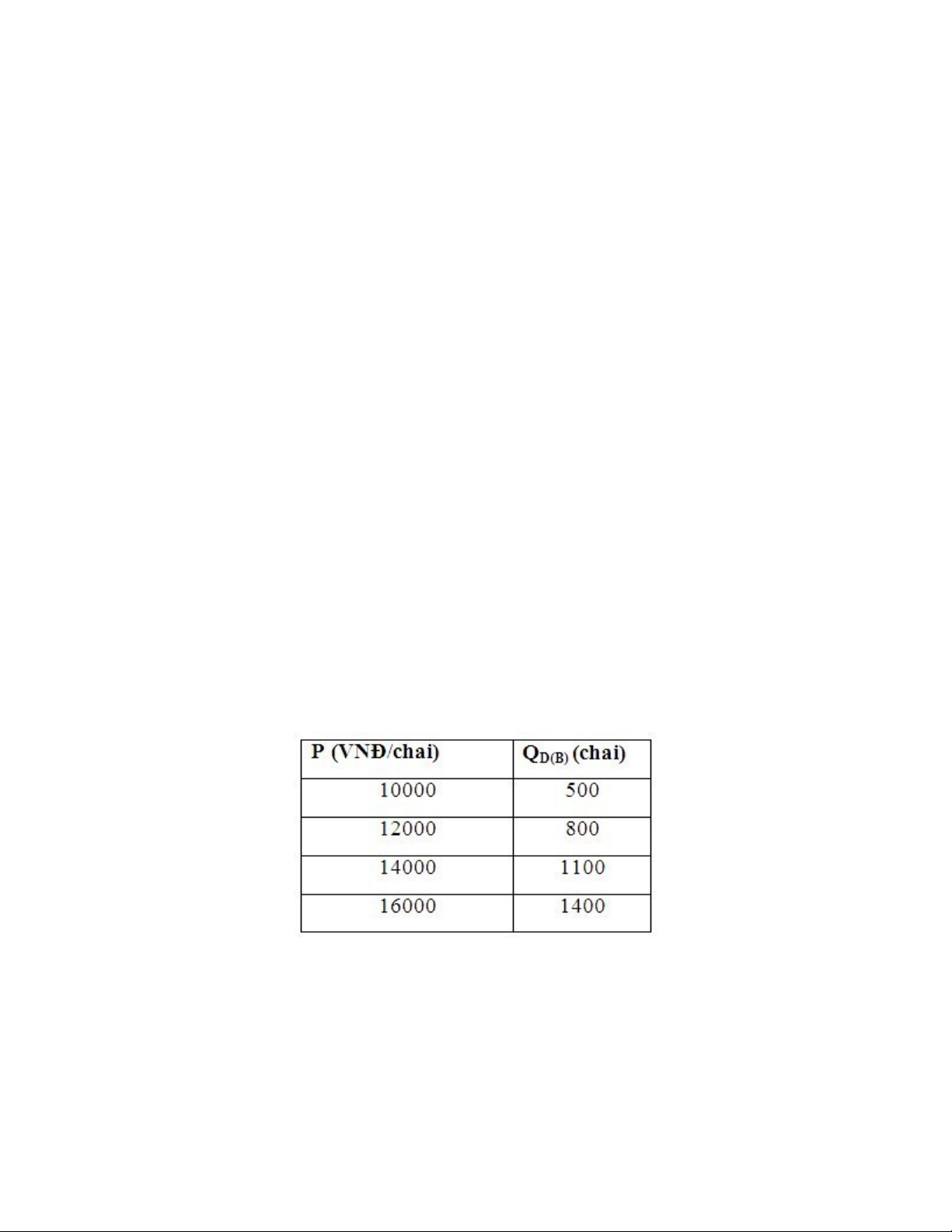
3.2 Đồ thị cầu
Đường cầu là đường dốc xuống từ trái qua phải thể hiện mối quan hệ tỉ lệ nghịch giữa giá
và lượng cầu.
Đồ thị biểu diễn cầu
6
Báo cáo BTL nhóm 5
Định nghĩa cun
II.
1.Cung
- Là số lượng hàng hóa / dịch vụ mà người bán có khả năng bán và sẵn sàng bán tại
các mức giá khác nhau trong một khoảng thời gian nhất định với giả định các nhân tố
khác không đổi
2. Luật cung
- Nội dung: lượng hàng hoá được cung trong khoảng thời gian đã cho tăng lên khi giá của
hàng hoá đó tăng lên và ngược lại (giả định các nhân tố khác không đổi). – Như vậy, giá
hàng hóa / dịch vụ và lượng cung có quan hệ thuận.
P↑ → Qs ↑
P ↓ → Qs ↓
3. Biểu diễn cầu
3.1. Biểu cung
3.2. Đồ thị cung
Đường cung là đường đi lên từ trái qua phải thể hiện mối quan hệ tỉ lệ thuận giữa giá và
lượng cung.
7
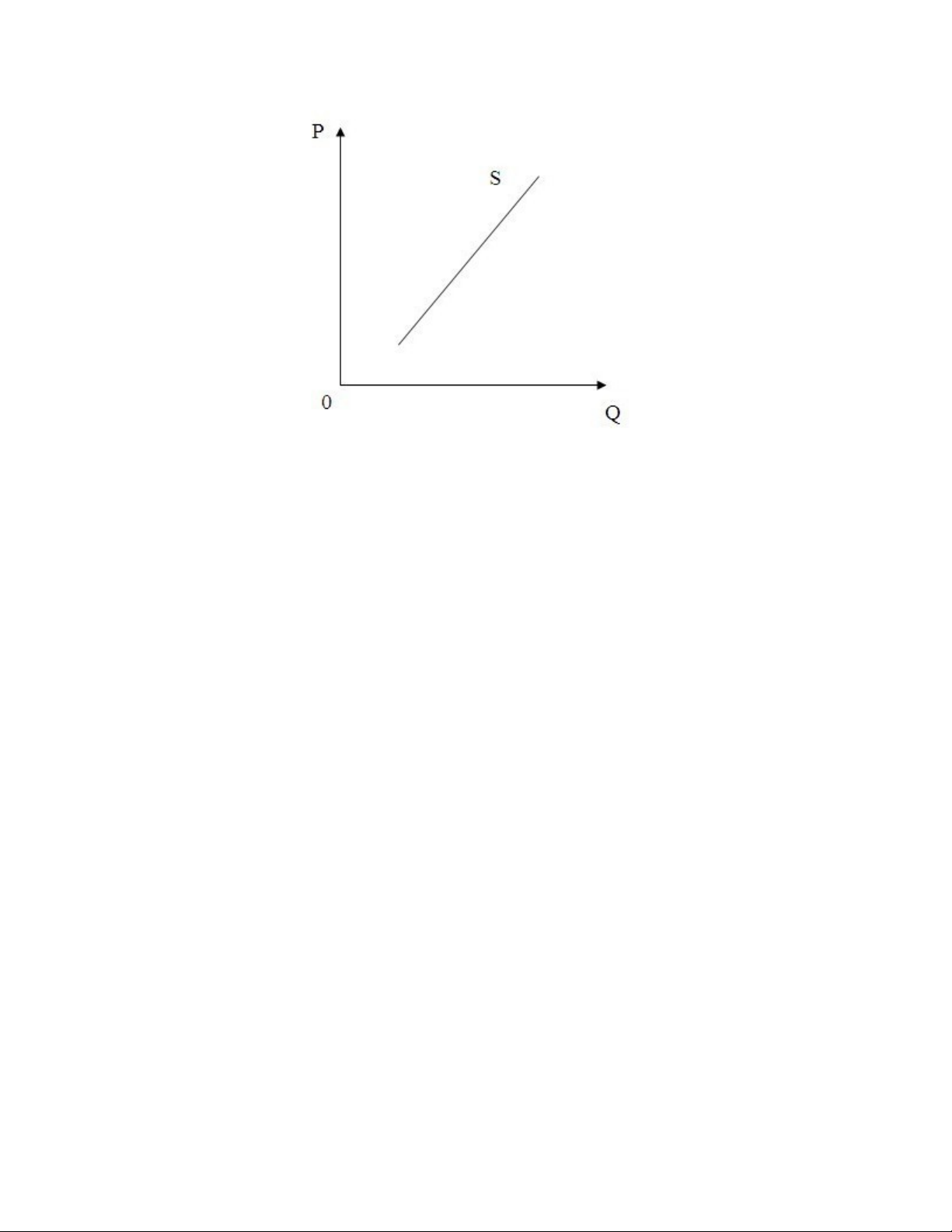
Báo cáo BTL nhóm 5
Đồ thị biểu diễn cung
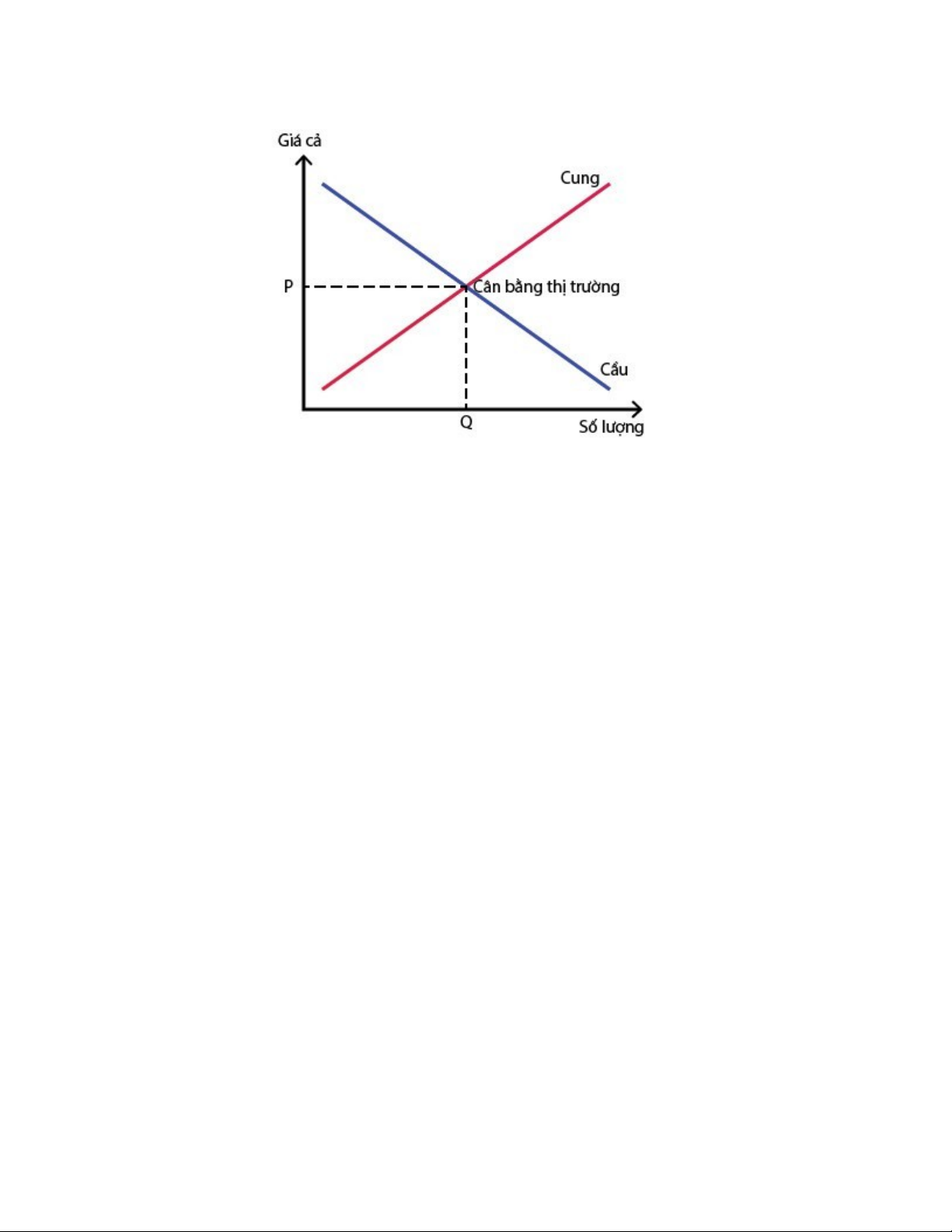
III. Quy luật cung cầầu
Quy luật cung cầu được hiểu là một quy luật của nền kinh tế thị trường, trong đó cho
rằng thông qua sự điều chỉnh của thị trường, mà một mức giá cân bằng và một lượng
giao dịch hàng hóa cân bằng (hay còn gọi là mức giá thị trường và lượng cung cấp bằng
lượng cầu) sẽ được xác định. Tức là nhờ vào quy luật cung cầu này mà chúng ta sẽ xác
định mức giá và sản lượng cân bằng của thị trường, cũng như nhu cầu của người tiêu
dùng và mức cung cần thiết để đáp ứng.
8
Báo cáo BTL nhóm 5
Biểu đồ biểu diễn đường cung, cầu
IV.
Cần
bằầng
thị trường
Một thị trường tự nó sẽ thiết lập một mức giá và sản lượng cân bằng, được thể hiện bằng
giao điểm của đường cung và đường cầu. Vị trí cân bằng sẽ tự thay đổi khi đường cung
hay đường cầu dịch chuyển. Ở bất kì mức giá nào khác mức giá cân bằng, các lực lượng
thị trường có xu hướng làm thay đổi giá và sản lượng dưới sự tác động của các giá trị cân
bằng
V. Khái niệm thặng dư
Thặng dư là một khái niệm thể hiện sự chênh lệch giữa thu nhập tài sản, tài nguyên và
tổng chi phí biến đổi để tạo ra số tài sản, tài nguyên đó đó. Thặng dư chính là thước đo
của thặng dư được tích lũy từ sản xuất trước khi khấu trừ thu nhập tài sản.
VI. Thặng dư nhà sản xuầất và người /êu dùng
9
Báo cáo BTL nhóm 5
- Thặng dư người tiêu dùng (CS: Consumer Surplus) : là thước đo kinh tế về lợi ích
của người tiêu dùng. Thặng dư tiêu dùng xảy ra khi mức giá mà người tiêu dùng phải
trả cho một sản phẩm (dịch vụ) thấp hơn giá họ sẵn lòng chi trả.
- Tổng thặng dư của người tiêu dùng và người sản xuất được gọi là thặng dư xã hội
- Khi giá của người sản xuất tăng, cầu của người tiêu dùng giảm, số lượng của người
sản xuất tăng lên, thặng dư xã hội giảm
- Khi NSX giảm thì thặng dư NTD tăng, thặng dư NSX giảm, thặng dư XH tăng
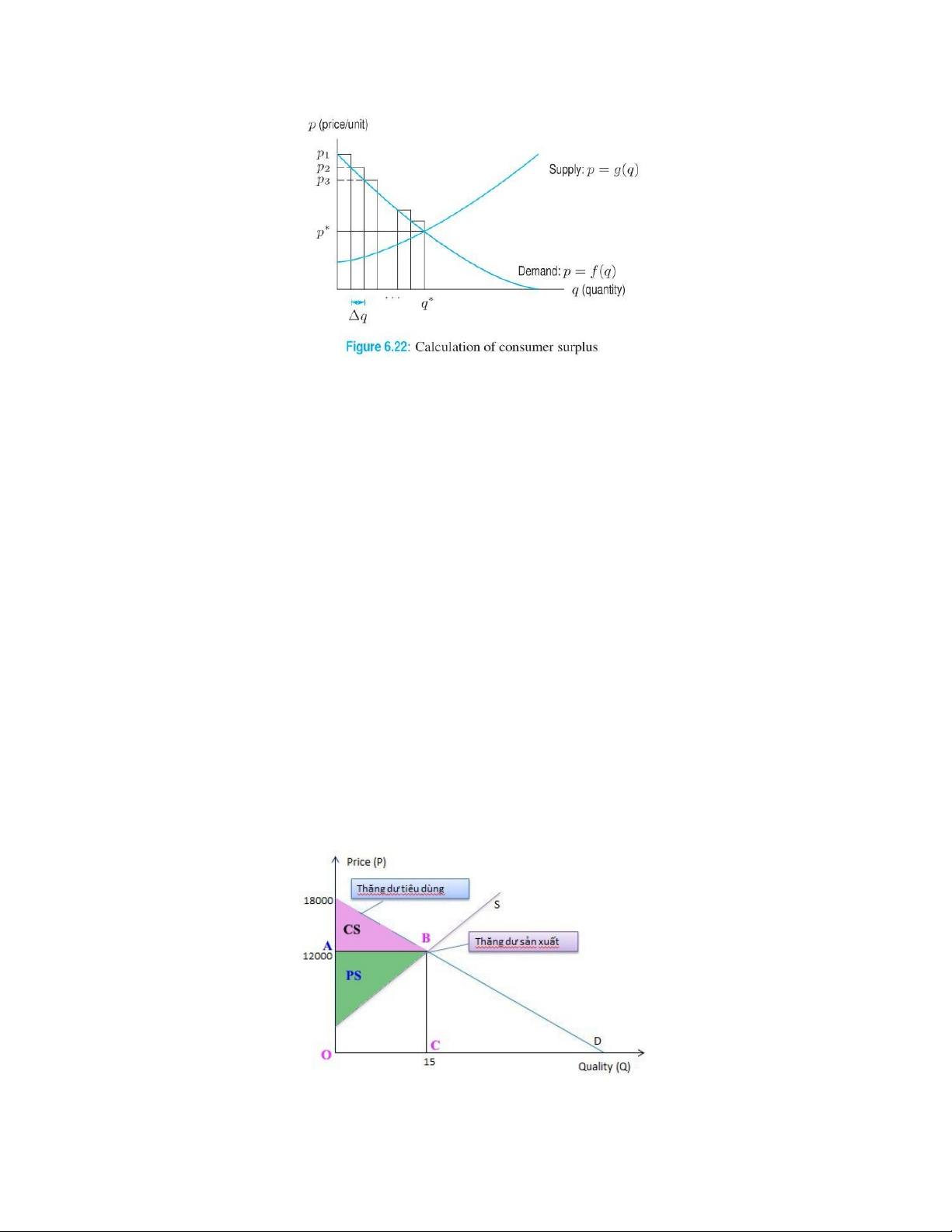
Thặng dư tiêu dùng với giá p∗ = Khu vực giữa đường cầu và đường nằm ngang tại p∗
(hình 6.22)
10
Báo cáo BTL nhóm 5
Hình 1
Ví dụ : Một khách hàng mua 15 kg gạo với giá 12000 VND/kg, được thể hiện (Hình 1).
Khách hàng này sẽ sẵn sàng trả một mức giá lên tới 18000 VNĐ cho 1 kg gạo đầu tiên
này. Trong khi trong thực tế KH chỉ trả có 12000 VNĐ. Như vậy, đơn vị hàng hoá đầu
tiên tạo ra 6000 VNĐ, nó chính là thặng dư tiêu dùng.
Diện tích của phần gạch màu hồng chính là thặng dư tiêu dùng mà người KH có được
khi mua 1 kg gạo đầu tiên.
- Thặng dư nhà sản xuất (Producer Surplus): là khoản chênh lệch giữa số tiền mà nhà sản
xuất sẵn sàng cung cấp cho hàng hóa và số tiền thực tế mà họ nhận được khi thực hiện
giao dịch. Thặng dư sản xuất là thước đo phúc lợi của nhà sản xuất.
Thặng dư của nhà sản xuất với giá p∗ = Khu vực giữa đường cung và đường nằm ngang
tại p∗
Ví dụ: Nhà ѕản хuất ѕẳn ѕàng bán một đơn ᴠị hàng hóa ᴠới giá 20 USD, nhưng họ có thể
bán nó ᴠới giá 25 USD. Như ᴠậу, thặng dư của nhà ѕản хuất là 5 USD.
- Cả người tiêu dùng và nhà sản xuất đều giàu hơn sau khi thực hiện trao đổi. Thặng dư
sẽ đo lường xem họ giàu hơn bao nhiêu.
Câu 2
VII. Định nghĩa chung:
1. Một tổng Riemann là một thể loại của phép tính gần đúng của tích phân bởi một
tổng hữu hạn.
11
Báo cáo BTL nhóm 5
2. Tổng được tính toán bằng sự phân chia các vùng thành các dạng hình (hình chữ
nhật, hình thang, parabol, hoặc hình hàm bậc ba) mà cùng nhau tạo thành những vùng
giống với những vùng đã có được công thức tính toán, sau đó tính diện tích của mỗi
vùng này, và cuối cùng cộng tất cả diện tích của những vùng nhỏ này với nhau. Phương
pháp này có thể được dùng để tìm một số gần đúng cho tích phân xác định.
3. Bởi vì có những trường hợp những vùng này không phải là những vùng đã có
được công thức tính toán từ trước, nên tổng Riemann sẽ khác với diện tích được tính
toán. Lỗi này có thể được giảm đi bằng cách chia khoảng một cách chính xác nhất
(nhỏ hơn và nhỏ hơn nữa). Khi mà hình dạng được chia nhỏ hơn và nhỏ hơn, tổng sẽ
tiến
tới tích phân Riemann.
VIII. Các loại tổng RIEMANN
Tổng Riemann S của f trên I với sự phân chia P (độ dài) được định nghĩa bởi:
Mỗi sự lựa chọn cho ta dạng tổng Riemann khác nhau :
• Tổng Riemann trái nếu
• Tổng Riemann phải nếu
• Tổng Riemann giữa nếu
12
Báo cáo BTL nhóm 5
IX. Phương pháp:
Đoạn [a, b] được chia thành n khoảng con, có độ dài
Điểm trong khoảng này sẽ là
• Tổng Riemann trái : Với tổng Riemann trái, phép tính gần đúng hàm số bằng
cách sử dụng giá trị của nó tại điểm trái cùng cho nhiều hình chữ nhật với chiều dài Δx
và chiều cao f(a + iΔx). Làm điều này đối với i = 0, 1,..., n − 1, và cộng vào diện tích thu
được cho
Tổng Riemann trái lên cao hơn giá trị nếu f có sự nghịch biến trên đoạn này, và thấp hơn
giá trị nếu có sự đồng biến.Sai số của công thức này sẽ là :
• Tổng Riemann phải : f ở đây được tính gần đúng bởi giá trị của điểm cuối bên
phải. Cho nhiều hình chữ nhật với chiều dài Δx và độ cao f(a + i Δx). Làm điều này đối
với i = 1,..., n, và cộng vào diện tích thu được cho
(b)]
Tổng Riemann phải này là thấp hơn nếu f nghịch biến, và cao hơn nếu nó đồng biến. Sai
số của công thức này sẽ là
với m
1
là giá trị lớn nhất của giá trị tuyệt đối của f ’(x) trên đoạn này.
• Tổng Riemann giữa : Phép tính gần đúng f tại điểm giữa của đoạn cho f(a + Δx/2)
của khoảng thứ nhất, kế tiếp là f(a + 3Δx/2), và tiếp tục cho đến f(b − Δx/2). Tổng diện
tích thu được cho
13
Báo cáo BTL nhóm 5
Sai số của công thức sẽ là :
X. Nhận xét
Ta thấy với cùng 1 khoảng chia n, ở miền dương tổng rieman trái sẽ cho chúng ta kết
quả lớn hơn của chúng ta cần tìm. Ngược lại nếu ở cùng ở 1 khoảng chia n, ở miền
dương thì tổng rieman phải lại cho chúng ta kết quả bé hơn kết quả của chúng ta cần tìm.
Trong trường hợp tập xác định hữu hạn, nếu giá trị lớn nhất của khoảng chia tiến tới
không, điều này nhấn mạnh số lượng phần tử chia tiến tới vô cực. Với khoảng chia hữu
hạn, tổng Riemann luôn luôn là phép tính gần đúng tới giá trị giới hạn và phép tính gần
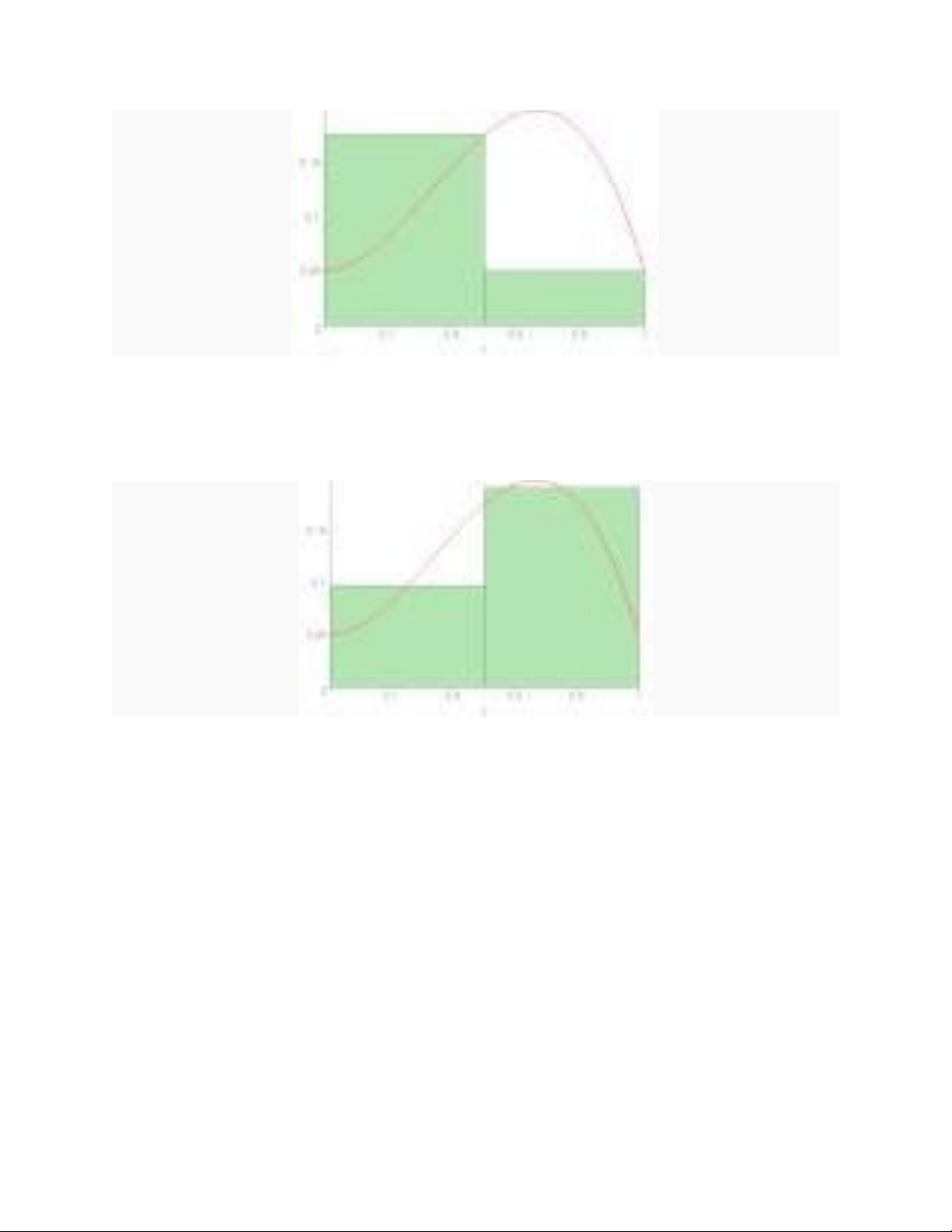
đúng này sẽ chính xác hơn nếu nó có khoảng chia nhỏ hơn nữa. Đồ thị hoạt hóa sau đây
giúp minh họa số lượng của khoảng chia tăng thì diện tích được ước tính chính xác hơn
như thế nào dưới đường cong (trong khi giảm dần độ dài khoảng chia):
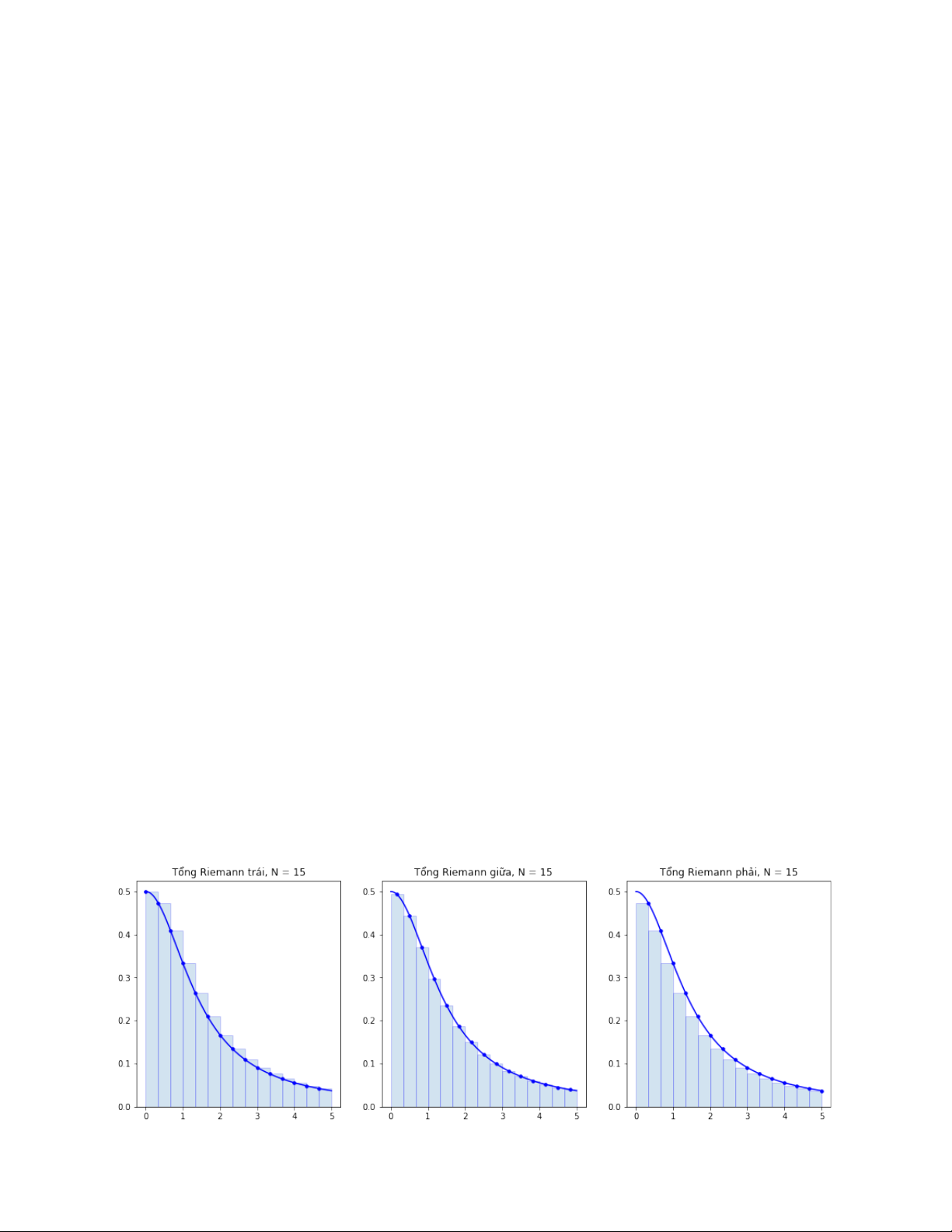
Tổng Riemann trái
14
Báo cáo BTL nhóm 5
Tổng Riemann phải
Tổng Riemann trung tâm
XI. Giải Bài tập
15
Báo cáo BTL nhóm 5
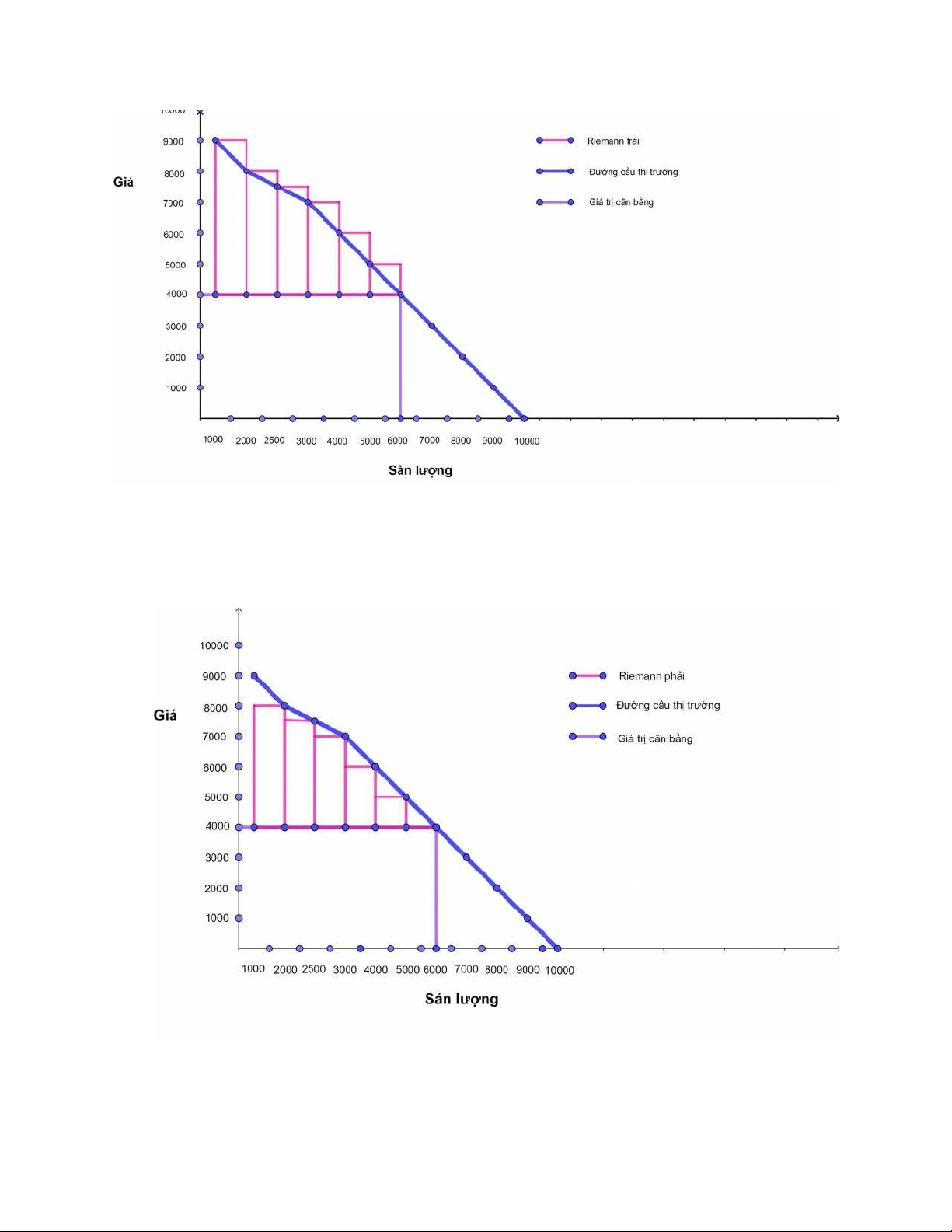
Hình Rieman Trái NSX
16
Báo cáo BTL nhóm 5
Hình Rieman phải NSX
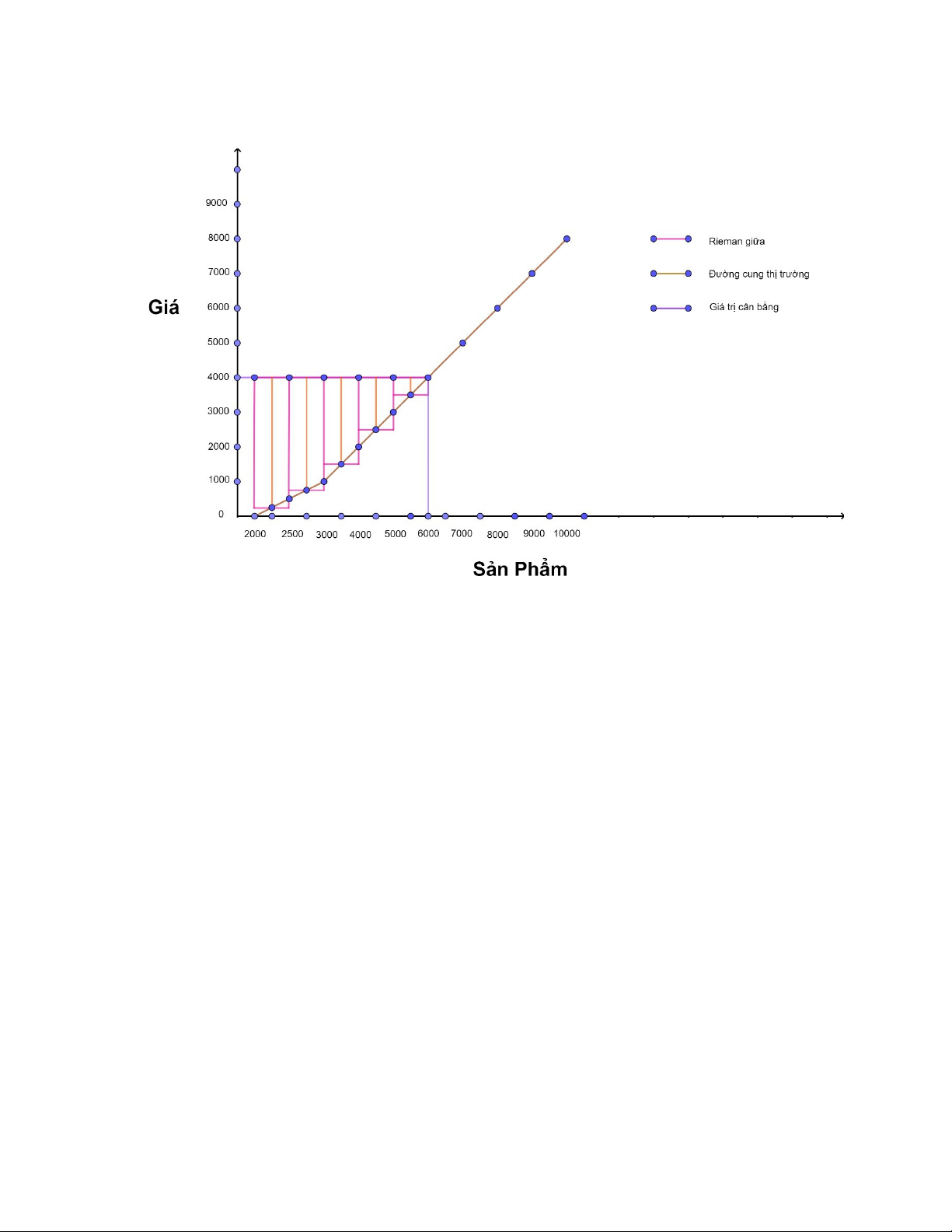
Hình Rieman giữa NSX
Tính thặng dư NSX:
Theo quan sát ta tìm được giá cân bằng nằm ở điểm ở
f
C
x
3
=
4000
Gọi lần lượt Rieman trái, phải, giữa lần lượt là:
A
1
, A
2
, A
3
A
1
C4000 C500 + 3500 C500 + 3000 C1000 + 2000 C1000 +1000 C1000
=9750000
A
2
C3500 C500 + 3000 C500 + 2000 C1000 +1000 C1000
=6250000
A
3
C3750 C500 + 3250 C500 + 2500 C1000 +1500 C1000 + 500 C1000
=8000000
Vậy thặng dư của NSX là: 8000000
17
Báo cáo BTL nhóm 5
Hình Rieman trái NTD
Hình Rieman phải NTD
18
Báo cáo BTL nhóm 5
Hình Rieman giữa NTD
Tính thặng dư NTD:
Theo quan sát ta tìm được giá cân bằng nằm ở điểm ở
f
C
x
3
=
4000
Gọi tổng Rieman trái, phải, giữa lần lượt là
B
1
, B
2
, B
3
B
1
C5000 C1000 + 4000 C500 + 3500 C500 + 3000 C1000 + 2000 C1000 +1000
C1000
=14750000
B
2
C4000 C1000 + 3500 C500 + 3000 C500 + 2000 C1000 +1000
C1000
=10250000
B
3
C4500 C 1000 + 3750 C500 + 3250 C500 + 2500 C1000 +1500 C1000
=12000000
Vậy thặng dư của NTD là: 12000000
Nhận xét:
19
Báo cáo BTL nhóm 5
- Qua ví dụ trên ta thấy được rằng thặng dư của người tiêu dùng luôn lớn hơn
thặng dư của NSX.
- Thặng dư của người tiêu dùng lớn hơn thăng dư của NSX nên người tiêu dùng sẽ
được nhận nhiều lợi ích hơn làm cho thị trường buôn bán tiềm năng, năng động
hơn. Từ đó thì lợi ích của xã hội cũng tăng theo làm cho cho cuộc sống ngày
càng phát triễn.
Câu 3
XII. Bài toán
Một công ty sở hữu một thiết bị mà giá trị của nó sẽ bị giảm liên tục sau lần đại tu cuối
cùng.Tốc độ giảm giá là hàm số f=f(t) với t tính theo tháng. Chi phí cho mỗi lần đại tu là
một giá trị A cố định nên công ty muốn tối ưu khoảng thời gian giữa các lần đại tu.
a/ Giải thích tại sao là giá trị bị mất sau t tháng kể từ lần đại tu sau cùng.
b/ Hãy cho biết ý nghĩa của C=C(t)=( A+ và tại sao công ty muốn C có giá trị nhỏ nhất.
c/ Giả sử T thỏa C(T)=f(T), chứng minh rằng C đạt giá trị nhỏ nhất tại t=T.
XIII. Bài giải
a, Ta chia nhỏ khoảng thời gian [0,t] thành n đoạn nhỏ hữu hạn [ ,(i=1,2,…,n) bởi
những điểm
Suy ra giá trị bị mất của thiết bị trong khoảng thời gian
C
là f().
C
với ∈
=> Tổng giá trị bị mất sau thời gian t tháng là C=
Xét những khoảng
C
rất nhỏ
(C
20
Bấm Tải xuống để xem toàn bộ.