Báo cáo bài tập lớn "Phép phân tích A=QR bằng phép biến đổi householder"

ĐẠI HỌC QUỐC GIA THÀNH PHỐ HỒ CHÍ MINH
TRƯỜNG ĐẠI HỌC BÁCH KHOA
BÁO CÁO BÀI TẬP LỚN
MÔN: ĐẠI SỐ TUYẾN TÍNH
ĐỀ TÀI 4: PHÉP PHÂN TÍCH A= QR
BẰNG PHÉP BIẾN ĐỔI HOUSEHOLDER
GIẢNG VIÊN HƯỚNG DẪN: ĐẶNG VĂN VINH LỚP:L06 NHÓM 1
TPHCM, NGÀY THÁNG NĂM i
ĐẠI HỌC QUỐC GIA THÀNH PHỐ HỒ CHÍ MINH
TRƯỜNG ĐẠI HỌC BÁCH KHOA
BÁO CÁO BÀI TẬP LỚN
MÔN: ĐẠI SỐ TUYẾN TÍNH
ĐỀ TÀI 4: PHÉP BIẾN ĐỔI A = QR
BẰNG PHÉP BIẾN ĐỔI HOUSEHOLDER LỚP: L06 NHÓM: 1
NĂM HỌC: 2021-2022 ii
ĐẠI HỌC QUỐC GIA THÀNH PHỐ HỒ CHÍ MINH
TRƯỜNG ĐẠI HỌC BÁCH KHOA
• DANH SÁCH THÀNH VIÊN:
STT HỌ VÀ TÊN MSSV 1 Cao Vũ An 2110688 2 Nguyễn Quốc Bảo 2112873 3 Vương Khuyến 2111571 4 Nguyễn Lê Thanh Minh 2114059 5 Phan An Nam 2114123 6 Ngô Nhật Thiên 2114860 7 Nguyễn Hữu Đạt 2113139 LỚP: L06 NHÓM: 1
NĂM HỌC 2021-2022 iii Mục lục
LỜI MỞ ĐẦU ...................................................................................................... v
ĐỀ TÀI ................................................................................................................. vi
I. Cơ sở lý thuyết của phép phân tích A = QR .................................................. 1
I.1. Định nghĩa ................................................................................................... 1
I.2. Phân tích: .................................................................................................... 1
I.3. Ví dụ ứng dụng ........................................................................................... 2
I.3.1. Ví dụ 1: .................................................................................................. 2
I.3.2. Ví dụ 2: .................................................................................................. 3
II. Xây dựng chương trình Matlab để biến đổi A=QR bằng biến đổi
Householder ......................................................................................................... 5
II.1. Tổng quan về Matlab ............................................................................... 5
II.2. Phần code ................................................................................................... 5
III. Ứng dụng của phép phân tích A = QR ........................................................ 7
TÀI LIỆU THAM KHẢO ................................................................................... 8 iv
LỜI MỞ ĐẦU
C uộc sống ngày càng phát triển, nhu cầu của con người ngày càng
phong phú, dẫn đến các thuật toán được đặt ra ngày càng nhiều
và được nghiên cứu để phục vụ cho khoa học kĩ thuật, ứng dụng
vào đời sống của con người. Có rất nhiều các thuật toán đã được
nghiên cứu thành công và đưa vào ứng dụng cho đời sống của con người.
Trong số đó phân rã A = QR đã được đem vào ứng dụng rất nhiều phục vụ
cho việc nghiên cứu khoa học. Phân tích A = QR thường được ứng dụng
trên máy học, chẳng hạn như việc tự động xóa một đối tượng khỏi hình
ảnh. Đồng thời nó cũng được sử dụng trong hệ thống xử lí tín hiệu và hệ
thống MIMO,… Phân rã QR có rất nhiều phép biến đổi khác nhau,như
biến đổi bằng trực giao hóa Gram Schmidt, phép biến đổi HouseHolder. Và
trong bài báo cáo này, nhóm xin được phép giới thiệu về “Phép phân tích A
= QR bằng phép biến đổi HOUSEHOLDER”. v ĐỀ TÀI
- Nêu cơ sở lý thuyết của phân tích A=QR
- Viết chương trinh dùng để phân tích A = QR bằng biến đổi Householder
- Tìm các ứng dụng của phân tích A = QR vi
I. Cơ sở lý thuyết của phép phân tích A = QR
I.1. Định nghĩa:
• Cho ma trận A ∈ Mmxn(ℝ) . Phân tích QR của ma trận A là biểu diễn A =
QR với Q là ma trận trực giao (QT=Q-1) và R là ma trận tam giác trên (rij=0, ∀i > j). I.2. Phân tích:
Ta dùng phép biến đổi Householder để tìm các ma trận Q và R sao cho Qn-1 .Qn-2 …Q1 .A = R Như vậy: A = (Qn-1 .Qn-2 … Q1)-1 .R
= (Q1)-1…(Qn-2)-1.(Qn-1)-1.R = (Q1)T…(Qn-2)T.(Qn-1)T.R = QR
Tích của các ma trận Householder Q = Q1.Q2…Qn-1
Không những đối xứng mà còn trực giao như mỗi ma trận Qk: QT.Q = (Q …Q …Q 1.Q2 n-1)T.(Q1.Q2 n-1) = I
Giả sử u ∈ Mnx1(ℝ) là vector khác không tuỳ ý,
khi đó hình chiếu vuông góc của vector v lên
không gian con F sinh bởi vector u là: pru(v) = .
Phép biến đổi là phép chiếu vuông góc của một
vector tuỳ ý lên không gian con sinh bởi vector u.
Vector v được phân tích thành v=a+b, với a là
hình chiếu vuông góc của v lên F bù vuông góc
và b là hình chiếu vuông góc của v lên F. Ta có: v = a + a = v - = Phép biến đổi:
là phép chiếu vuông góc của 1 vector lên không gian con F bù vuông góc. Ta có : = + .
Phép đối xứng qua F bù vuông góc là ( phép biến đổi này được gọi là phép biến đổi Householder).
Giả sử là cột thứ nhất của ma trận A 1
Ta cần tìm một ma trận trực giao P1 để P1A*1 =.
Ma trận P1 tương ứng với phép biến đổi trực giao nên nó bảo toàn độ dài vector.
Vậy độ dài của P1A*1 bằng độ dài của A*1. Do đó ta chọn P1A*1 = . Đặt vector = A*1, =. Khi đó = + = - . Đặt = = A*1 -
Dùng vector này tạo ra phép biến đổi Householder
P1 = và phép biến đổi này sẽ khử tất cả các phần tử trong cột thứ nhất của ma
trận A ngoại trừ phần tử đầu tiên.
I.3. Ví dụ ứng dụng:
I.3.1. Ví dụ 1: Cho ma trận .
Dùng phép biến đổi Householder tìm phân tích . Giải Tạo ra vector
Tìm phép biến đổi Householder để khử cột 1 của A: Khi đó Xét ma trận Tương tự như trên: Tạo ra vector Q ‘2 Khi đó Q’2 Đặt Q2 = Ta có Suy ra .
I.3.2. Ví dụ 2: Cho ma trận A = .
Dùng phép biến đổi Householder, tìm phân tích A=QR. Giải
Tạo ra vector u = A*1 - . e1 = ( -1; 1; 1; 1 )T. 2
Tìm phép biến đổi Householder để khử cột 1 của A: Q1 = = . Khi đó Q1 . A = . Xét ma trận A1 = .
Lặp lại các bước trên cho ma trận A1.
Tạo ra vector u = - . e1 = ( -6; 0; 6 )T.
Tìm phép biến đổi Householder để khử cột 1 của A1: Q’2 = = . Khi đó Q’2 . A1 = . Đặt Q2 = . Ta có Q2 . Q1 . A = = R. Suy ra A = . R = R = QR.
II. Xây dựng chương trình Matlab để biến đổi A=QR
bằng biến đổi Householder.
II.1. Tổng quan về Matlab:
- Matlab (viết tắt của Matrix Laborary) là một ngôn ngữ lập trình bậc
cao bốn thế hệ, môi trường để tính toán số học, trực quan và lập trình.
Được phát triển bởi MathWorks.
- Là phần mềm cung cấp môi trường tính toán số và lập trình, do công
ty MathWorks thiết kế. MATLAB cho phép tính toán số với ma trận, vẽ
đồ thị hàm số hay biểu đồ thông tin, thực hiện thuật toán, tạo các giao
diện người dùng và liên kết với những chương trình máy tính viết trên
nhiều ngôn ngữ lập trình khác.
-Nó có rất nhiều lệnh và hàm toán học nhằm hỗ trợ đắc lực cho bạn trong việc
tính toán, vẽ các hình vẽ, biểu đồ thông dụng và thực thi các phương pháp tính toán. 3
II.2. Phần code: • Phần code function [Q,R] = qrfactor(A) [m,n] = size(A); Q=eye(m); for k = 1:n z = A(k:m,k);
v = [ -sign(z(1))*norm(z) - z(1); -z(2:end) ]; v = v / sqrt(v'*v); for j = 1:n
A(k:m,j) = A(k:m,j) - v*( 2*(v'*A(k:m,j)) ); end for j = 1:m
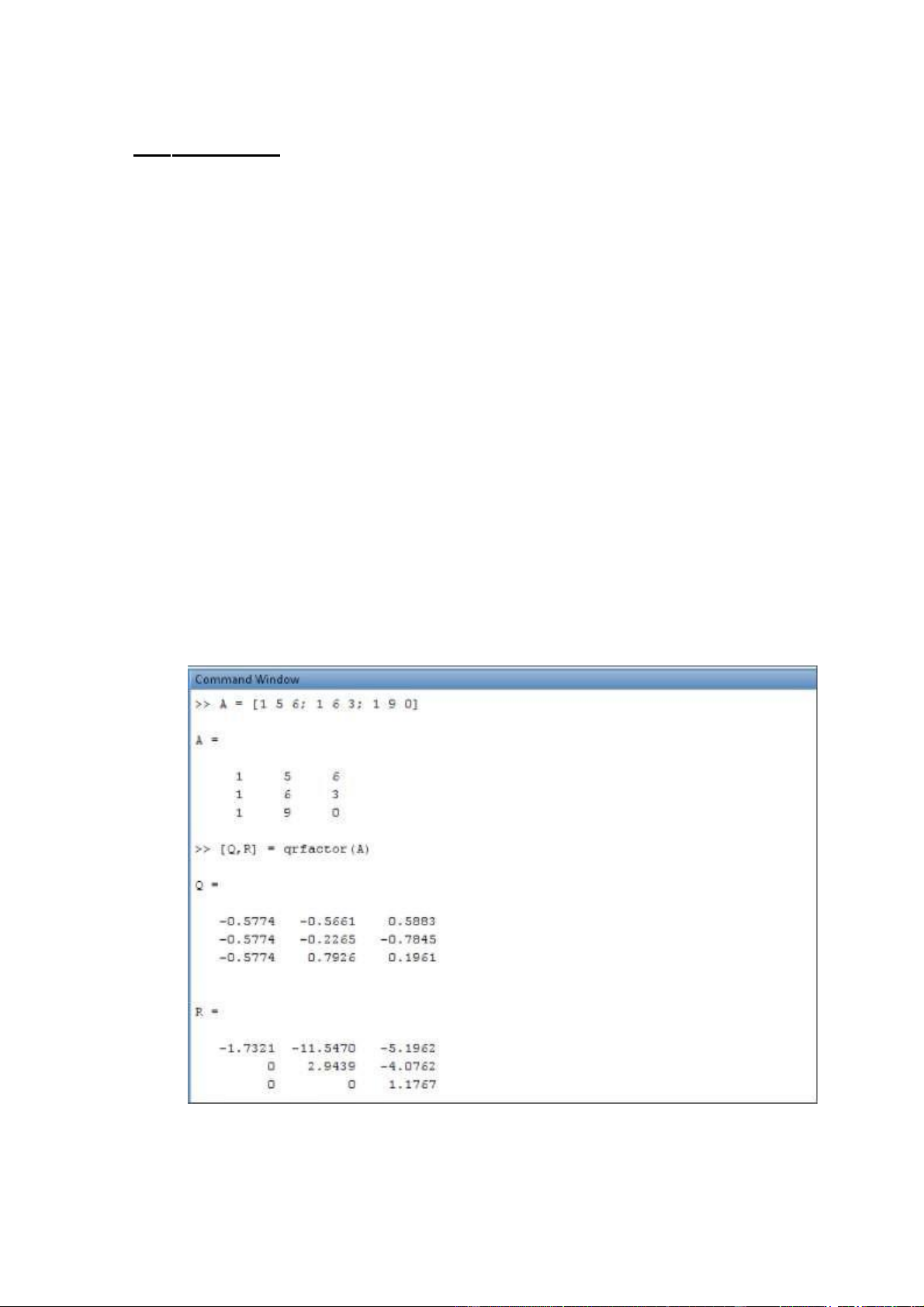
Q(k:m,j) = Q(k:m,j) - v*( 2*(v'*Q(k:m,j)) ); end end Q = Q'; R = triu(A); • Phần kết quả 4 • Giải thích code:
- [m,n] = size (A) : A là ma trận có m hàng và n cột ( ma trận cỡ m x n)
- Q = eye(m) : ma trận đơn vị cấp m - For k = 1:n … end
Vòng lặp được lặp lại từ 1 đến n lần
- z = A(k:m,k) : ma trận z = lấy các phần tử cột k từ vị trí k đến m của ma trận A - sign: dấu ma trận
- norm(v): độ dài vecto v tính theo tích vô hướng
- z(2:end): chọn phần tử cuối cùng hàng 2 của ma trận z
- sqrt(v’*v): căn bậc 2 của ( ma trận v chuyển vị nhận ma trận v)
- triu A: ma trận trên của A
III. Ứng dụng của phép phân tích A = QR •
Phân rã QR có thể hữu ích trong các ứng dụng học máy . Một ví dụ về
việc sử dụng phân rã QR trong học máy là tự động xóa một đối tượng
khỏi hình ảnh. Hãy tưởng tượng bạn muốn cắt hình ảnh của một chiếc ô tô
từ một video clip. Sử dụng những gì được gọi là phân rã giá trị đơn lẻ, nó
trở nên tương đối đơn giản. Nói tóm lại, bằng cách chia video thành các
khung hình riêng lẻ, chuyển các khung hình thành vectơ 1D và tạo ma
trận các vectơ tương ứng với mỗi hình ảnh, sau đó người ta có thể chạy
một phân tách giá trị duy nhất trên video. Sự phân hủy cho phép tách các
đối tượng nền trước khỏi không gian nền trong hình ảnh từ video một cách đơn giản. Ví dụ minh họa: 5
• Phân tách QR được sử dụng trong hệ thống xử lý tín hiệu và hệ thống MIMO.
• Phân hủy QR bằng đường chéo và ứng dụng để thiết kế mã cho trước.
• Phân tích phân biệt trọng số dựa trên hạt nhân với phân rã QR và ứng
dụng của nó để nhận dạng khuôn mặt.
• Một số lược đồ thủy vẫn mới dựa trên phân tích QR.
TÀI LIỆU THAM KHẢO
[1] Giáo trình đại số tuyến tính của thầy Đặng Văn Vinh, Trường Đại học
Bách Khoa TP.HCM
[2] Kernel-based weighted discriminant analysis with QR decomposition
and its application to face recognition - Jianqiang Gao
(https://dl.acm.org/doi/abs/10.5555/2064828.2064831)
[3] Implementation comparisons of the QR decomposition for MIMO
detection - Gabriel Luca Nazar, Christina Gimmler-Dumont, Norbert When
(https://www.researchgate.net/publication/220850919_Implementation_compari
sons_of_the_QR_decomposition_for_MIMO_detection)
[4] QR Decomposition and Machine Learning
(https://deepai.org/machine-learning-glossary-and-terms/qr-decomposition)
[5] Giáo trình matlab cơ bản – Trần Văn Chính 6