Báo cáo bài tập lớn: Tối ưu lập kế hoạch định tuyến nhân viên bảo trì môn Tối ưu lập kế hoạch | Trường Đại học Bách Khoa Hà Nội

TRƯỜNG ĐẠI HỌC BÁCH KHOA HÀ NỘI
BÁO CÁO BÀI TẬP LỚN
Định tuyến nhân viên bảo trì mạng
Sinh viên thực hiện: Bùi Trọng Đức 20200157 Lê Nam Khánh 20200316 Nguyễn Văn Nam 20200421 Đặng Tiến Đạt 20200133
Giảng viên hướng dẫn: TS. Bùi Quốc Trung Trường:
Công nghệ thông tin và Truyền thông HÀ NỘI, 12/2023 MỤC LỤC
CHƯƠNG 1. GIỚI THIỆU .................................................................................................................2
1.1 Phát biểu bài toán: ....................................................................................................................2
1.2 Phân công công việc .................................................................................................................2
CHƯƠNG 2. THUẬT TOÁN .............................................................................................................3
2.1 Back tracking with branch and bound .................................................................................3
2.2 Constraints programming ........................................................................................................4
2.2.1 Biến ............................................................................................................................................4
2.2.2 Ràng buộc.................................................................................................................................5
2.2.3 Hàm mục tiêu ..........................................................................................................................6
2.3 MIP ................................................................................................................................................6
2.3.1 Biến ............................................................................................................................................6
2.3.2 Ràng buộc.................................................................................................................................6
2.3.3 Hàm mục tiêu ..........................................................................................................................7
2.4 Tham lam .....................................................................................................................................7
2.4.1 Greedy 1 ...................................................................................................................................7
2.4.2 Greedy 2 ...................................................................................................................................8
2.5 Tìm kiếm cục bộ .........................................................................................................................8
2.5.1 Relocate operator ..................................................................................................................8
2.5.2 Swap operator .........................................................................................................................9
2.5.3 K-Exchange operator .............................................................................................................9
2.5.4 Cross operator ..................................................................................................................... 10
2.6 Tham lam kết hợp tìm kiếm cục bộ ................................................................................... 11
2.7 Giải thuật di truyền (GA) ...................................................................................................... 12
2.7.1 Mã hóa lời giải ..................................................................................................................... 12
2.7.2 Toán tử di truyền ................................................................................................................. 12
2.7.3 Tham số ................................................................................................................................. 12
2.8 Thuật toán di truyền có cải tiến (GGA) ............................................................................. 13
CHƯƠNG 3. KẾT QUẢ THỰC NGHIỆM .................................................................................... 13
3.1 Bộ dữ liệu .................................................................................................................................. 13
3.2 Các giải thuật chính xác ........................................................................................................ 13
3.3 Các giải thuật heuristic và meta-heuristic ........................................................................ 14
CHƯƠNG 4. KẾT LUẬN ................................................................................................................. 16 DANH MỤC HÌNH VẼ Hình 2.1
Ví dụ cho biểu diễn phương pháp quay lui. . . . . . . . . . . . . . . 4
Hình 2.2 Ví dụ cho relocate operator.
. . . . . . . . . . . . . . . . . . . . . . 10 Hình 2.3
Ví dụ cho swap operator. . . . . . . . . . . . . . . . . . . . . . . . . 10
Hình 2.4 Ví dụ cho relocate operator.
. . . . . . . . . . . . . . . . . . . . . . 11
Hình 2.5 Ví dụ cho relocate operator.
. . . . . . . . . . . . . . . . . . . . . . 12 Hình 2.6
Ví dụ biểu diễn của một các thể . . . . . . . . . . . . . . . . . . . . 13
Hình 2.7 Lai ghép thứ tự
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 Hình 2.8
Đột biến hoán điểm . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 Hình 3.1
Giá trị hàm mục tiêu của các thuật toán . . . . . . . . . . . . . . . . 17
Hình 3.2 Mức cải thiện của các heuristic và meta-heuristic so với Greedy 1 . 17 ii
DANH MỤC BẢNG BIỂU Bảng 1.1
Bảng phân công công việc . . . . . . . . . . . . . . . . . . . . . . . 3
Bảng 2.1 Tham số cho giải thuật di truyền.
. . . . . . . . . . . . . . . . . . . 14 Bảng 3.1
Kết quả của các giải thuật chính xác . . . . . . . . . . . . . . . . . . 15 Bảng 3.2
Kết quả của các giải thuật heuristic và meta-heuristic . . . . . . . . 16 lOMoAR cPSD| 59671932
CHƯƠNG 1. GIỚI THIỆU
1.1 Phát biểu bài toán:
Có N khách hàng 1,2,...,N cần được bảo trì mạng internet. Khách hàng i ở địa điểm i =
1,...,N. Việc bảo trì cho khách hàng i kéo dài d(i) đơn vị thời gian (s). Có K nhân viên kỹ
thuật ở trụ sở công ty (điểm 0) và có thời điểm bắt đầu làm việc là t0 = 0. Thời gian di
chuyển từ điểm i đến điểm j là t(i,j). Lập kế hoạch phân công nhân viên thực hiện bảo
trì cho các khách hàng sao cho thời gian làm việc nhiều nhất (thời gian di chuyển cộng
thời gian bảo trì) của một nhân viên nào đó là nhỏ nhất.
Lộ trình của nhân viên k được biểu diễn bằng một dãy các điểm r[0],r[1],r[2],...,r[Lk],
trong đó r[0] = r[Lk] = 0 (kho). Input
• Line 1: chứa N và K (1 ≤ N ≤ 1000,1 ≤ K ≤ 100)
• Line 2: chứa d(1),d(2),...,d(N) (1 ≤ d(i) ≤ 1000)
• Lines i + 3 (i = 0,1,2,...,N): chứa dòng thứ i của ma trận t
Output • Line 1: chứa K
• Lines 2k (k = 1,...,K): chứa số nguyên dương Lk
• Lines 2k + 1 (k = 1,2,...,K): chứa r[0],r[1],r[2],...,r[Lk] CHƯƠNG 1. GIỚI THIỆU
1.2 Phân công công việc Thành viên MSSV Công việc Bùi Trọng Đức 20200157
Tham lam kết hợp tìm kiếm cục
bộ, giải thuật di truyền có cải tiến Lê Nam Khánh 20200316
Thuật toán quay lui, các kĩ thuật tìm kiếm cục bộ Đặng Tiến Đạt 20200133 Thuật toán tham lam Nguyễn Văn Nam 20200421 Constraint programming, mixed integer programming
Bảng 1.1: Bảng phân công công việc 2 lOMoAR cPSD| 59671932
CHƯƠNG 2. THUẬT TOÁN 2.1
Back tracking with branch and bound
Ý tưởng: Sử dụng 2 mảng x và y để lưu thứ tự khách hàng được phục vụ. Trong đó,
• yk chỉ khách hàng đầu tiên được phụ vụ bởi nhân viên k, với k = 1,...,K. • xi chỉ khách
hàng sau được phục vụ sau khách hàng i, với i = 1,...N 1 1 3 4
2 0 5 0 4 5
Hình 2.1: Ví dụ cho biểu diễn phương pháp quay lui. Thuật toán:
• Sử dụng thuật toán quy lui để duyệt qua lân lượt các phần tử trong mảng Y với điều
kiện giá trị các phần tử tăng dần.
• Sau khi chọn xong phần tử thứ K thì duyệt qua mảng X theo thứ tự các khách hàng
được bảo trì từ các nhân viên.
• Sau khi nhân viên điểm 0 tức kho hàng. Thì chuyển qua xét nhân viên tiếp theo. 3 lOMoAR cPSD| 59671932
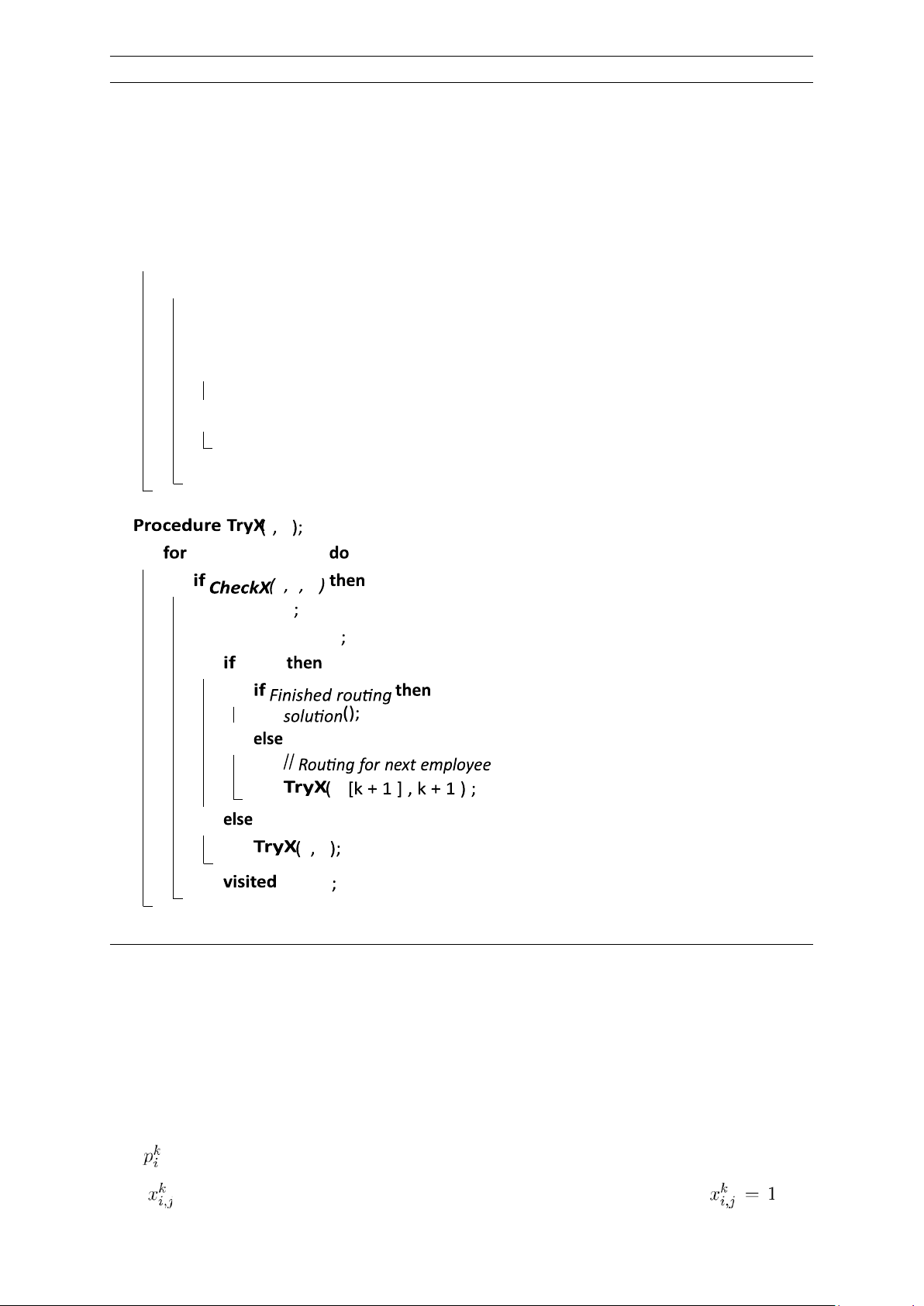
Algorithm 1: Quay lui nhánh cận
Input: Số nhân viên K, số khách hàng N, t, d
Output: Lịch trình tối ưu cho các nhân viên
Initialize arrays X, Y, and visited; Set fbest ← ∞;
Procedure TryY(k); for i ∈ {Y[k −
1],...,N} do if CheckY(i,
k) then Y[k] ← i;
visited[i] ← 1;
if k = K then
TryX(Y[first], first); //first chỉ nhân viên đầu tiên hoạt động else TryY(K + 1);
visited[i] ← 0; i k
v ∈{ 0 ,1 ,...,N } v i k
X [ i] ← v
visited [ v ] ← 1 v =0 Y v k [ v ] ← 0
Return Optimal routes as determined by X and Y ; 2.2
Constraints programming 2.2.1 Biến
• yk để chỉ trạng thái hoạt động của nhân viên k, nếu yk = 1 tức là nhân viên k hoạt
động, ngược lại, yk = 0 nhân viên k không hoạt động.
• để chỉ thứ tự của khách hàng thứ i trong hành trình của nhân viên k. •
chỉ cung (i,j) có thuộc hành trình của nhân viên k hay không. Nếu 4
Downloaded by Uc Lan (uehbsaxac464@gmail.com)
thì cung (i,j) thuộc hành trình của nhân viên k. Ngược lại, thì cung (i,j)
không thuộc hành trình của nhân viên k.
• max_work_time Thời gian làm việc lớn nhất của một nhân viên nào đó. 2.2.2 Ràng buộc
• Mỗi khách hàng chỉ được bảo trì bởi một nhân viên. K N
XXxki,j = 1,∀j = 1,...,N (2.1) k=1 i=0
• Đến và rời khỏi khách hàng bởi cùng một nhân viên. N N
Xxki,j = Xxkj,i,∀j = 0,...,N;k = 1,...,K (2.2) i=0 i=0
• Mỗi nhân viên bắt đầu từ 0 và kết thúc tại 0. N
Xxk0,j = yk,∀k = 1,...,K (2.3) j=1 N
Xxkj,0 = yk,∀k = 1,...,K (2.4) j=1
• Nhân viên cần di chuyển đến các khách hàng. (2.5)
• Loại bỏ sub-tour (Nếu cung (i,j) thuộc hành trình của nhân viên k thì khách hàng j
được bảo trì sau khách hàng i). Nếu,
(2.6) ∀i ̸= j;i = 0,...,N;j = 1,...,N;k = 1,...,K
• Để tối ưu thời gian chạy code, giả sử các nhân viên được sắp xếp sao cho nếu nhân
viên k hoạt động thì nhân viên k+1 cũng phải hoạt động (dồn tất cả nhân viên
không hoạt động lên đầu, để tránh trường hợp hoán vị).
yk ≤ yk+1,∀k = 1,...,K − 1 • Thời (2.7)
gian làm việc lớn nhất.
N N max_work_time ≥ XXxki,j × (dj +
ti,j),∀k = 1,...,K (2.8) i=0 j=0
• Miền giá trị của các biến.
xki,j ∈ {0,1}, (2.9)
∀i = 0,...,N;j = 0,...,N;k = 1,...,K
yk ∈ {0,1},∀k = 1,...,K (2.10) (2.11)
max_work_time ∈ {0,∞} (2.12) 2.2.3 Hàm mục tiêu
• Cực tiểu hóa max_work_time. 2.3 MIP 2.3.1 Biến
• yk để chỉ trạng thái hoạt động của nhân viên k, nếu yk = 1 tức là nhân viên k hoạt
động, ngược lại, yk = 0 nhân viên k không hoạt động.
• để chỉ thứ tự của khách hàng thứ i trong hành trình của nhân viên k. •
chỉ cung (i,j) có thuộc hành trình của nhân viên k hay không. Nếu thì
cung (i,j) thuộc hành trình của nhân viên k. Ngược lại, xki,j = 0 thì cung (i,j) không
thuộc hành trình của nhân viên k.
• max_work_time Thời gian làm việc lớn nhất của một nhân viên nào đó. 2.3.2 Ràng buộc
• Mỗi khách hàng chỉ được bảo trì bởi một nhân viên. K N
XXxki,j = 1,∀j = 1,...,N (2.13) k=1 i=0
• Đến và rời khỏi khách hàng bởi cùng một nhân viên. (2.14)
• Mỗi nhân viên bắt đầu từ 0 và kết thúc tại 0. N
Xxk0,j = yk,∀k = 1,...,K (2.15) j=1 (2.16)
• Nhân viên cần di chuyển đến các khách hàng. (2.17)
• Loại bỏ sub-tour (Nếu cung (i,j) thuộc hành trình của nhân viên k thì khách hàng j
được bảo trì sau khách hàng i).
(2.18) ∀i ̸= j;j =
1,...,N;i = 1,...,N;k = 1,...,K
• Để tối ưu thời gian chạy code, giả sử các nhân viên được sắp xếp sao cho nếu nhân
viên k hoạt động thì nhân viên k+1 cũng phải hoạt động (dồn tất cả nhân viên
không hoạt động lên đầu, để tránh trường hợp hoán vị).
yk ≤ yk+1,∀k = 1,...,K − 1 • Thời (2.19)
gian làm việc lớn nhất. N N (2.20)
max_work_time ≥ XXxki,j × (dj + ti,j),∀k = 1,...,K i=0 j=0
• Miền giá trị của các biến. (2.21)
∀i = 0,...,N;j = 0,...,N;k = 1,...,K
yk ∈ {0,1},∀k = 1,...,K (2.22) , (2.23)
max_work_time ∈ {0,∞} (2.24) 2.3.3 Hàm mục tiêu
• Cực tiểu hóa max_work_time. 2.4 Tham lam 2.4.1 Greedy 1
• Ý tưởng: Tập các khách hàng chưa được phục vụ được sắp xếp theo thứ tự tăng
dần về thời gian (thời gian di chuyển + thời gian bảo trì) so với công ty 0 ("gần").
Sau đó các khách hàng được thêm vào các tuyến của nhân viên sao cho làm giá
trị của hàm mục tiêu tăng ít nhất. Nếu không làm tăng giá trị hàm mục tiêu,
khách hàng được thêm vào tuyến của nhân viên đang có thời gian làm việc ngắn nhất.
• Sơ đồ giải thuật Algorithm 2: Greedy 1
P ← tập khách hàng;
Sắp xếp theo thứ tự "gần" công ty;
while P khác rỗng do
Lấy khách hàng đầu c trong P;
Q ← tập các nhân viên có hành trình làm tăng ít giá trị hàm mục tiêu nhất nếu thêm c vào hành trình;
Lựa chọn nhân viên k đang có thời gian làm việc nhỏ nhất trong Q;
Thêm c vào hành trình của k;
Loại bỏ c khỏi P; 2.4.2 Greedy 2
• Ý tưởng: Tại mỗi bước, mỗi nhân viên sẽ chọn khách hàng tốn ít thời gian nhất
để đi đến. Thứ tự chọn khách hàng của nhân viên được thực hiện lần lượt.
• Sơ đồ giải thuật Algorithm 3: Greedy 2
Khởi tạo hành trình của mỗi nhân viên bắt đầu tại 0; k ← 1;
while Tồn tại khách hàng chưa được phục vụ do
Lựa chọn khách hàng tốn ít thời gian nhất thêm vào hành trình của
k; k ← (k + 1)%K;
2.5 Tìm kiếm cục bộ
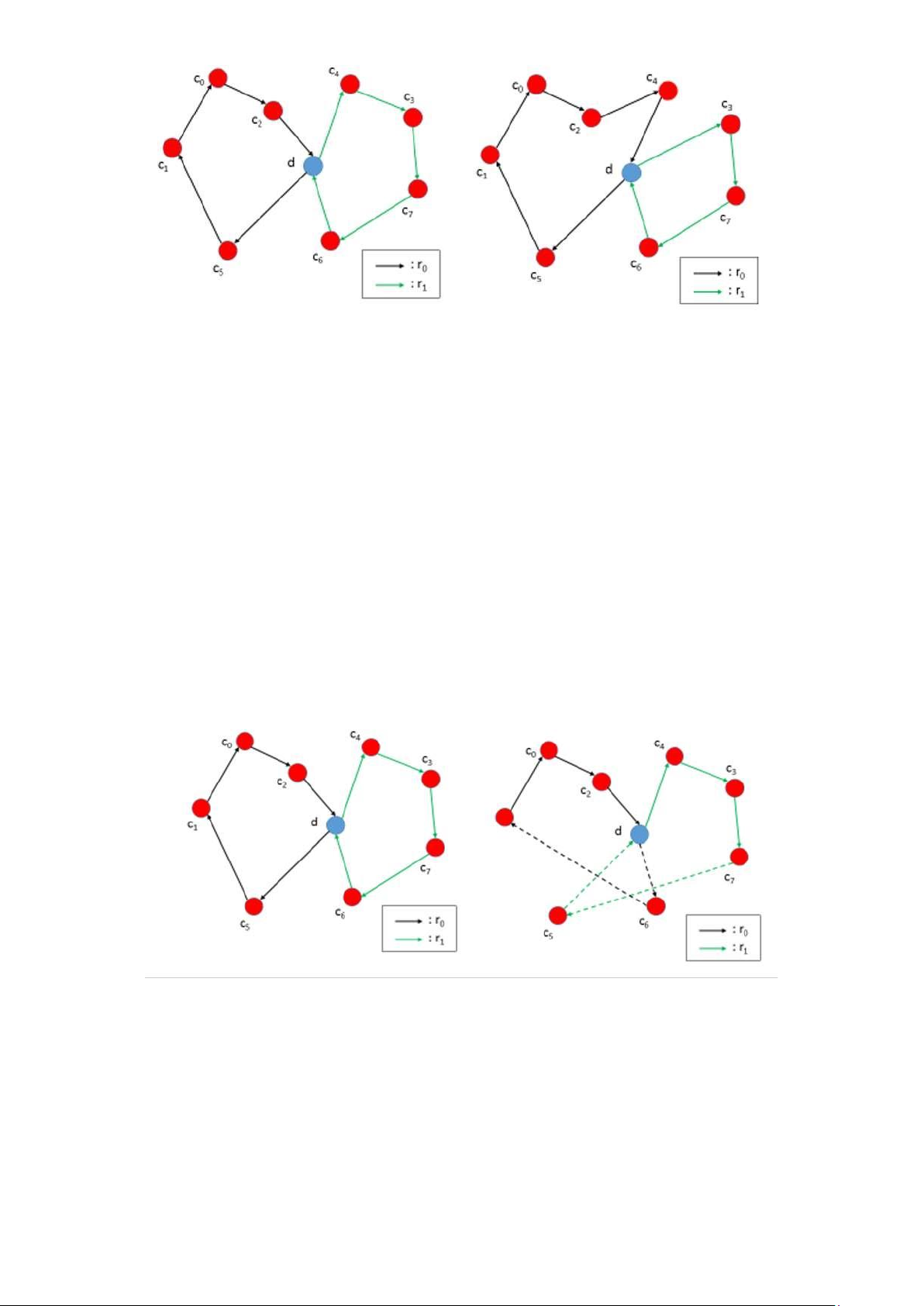
2.5.1 Relocate operator
Phép toán này bao gồm việc di chuyển một khách hàng từ một tuyến đường này
sang một tuyến đường khác. Cụ thể, khách hàng i từ tuyến đường r0 sẽ được loại bỏ
khỏi r0 và chèn vào tuyến đường r1 tại vị trí p, nơi mà r0 ≠ r1 và 0 ≤ p ≤ |r1|.
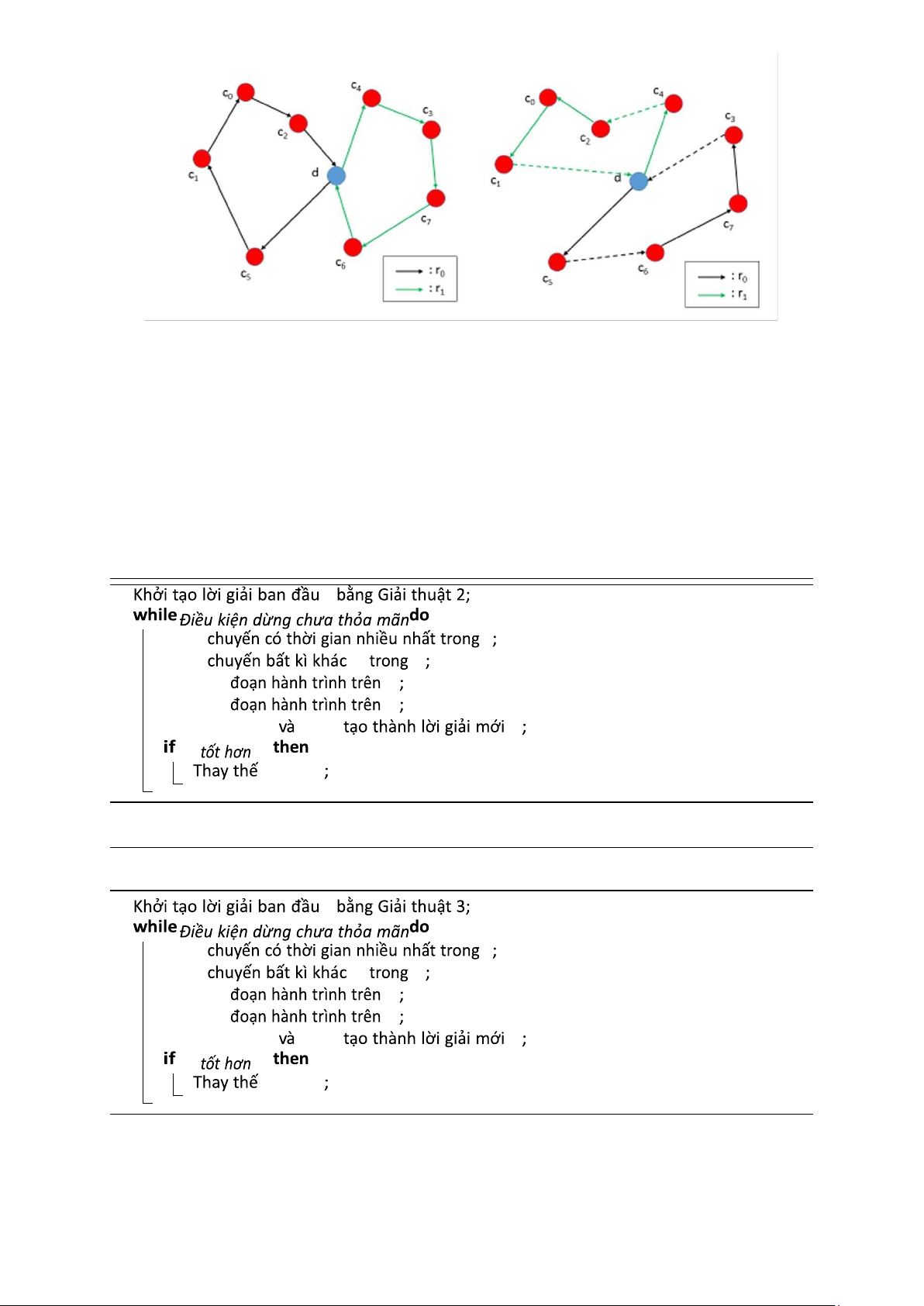
Ví dụ, trong Hình 2.3, khách hàng c4 được di chuyển từ tuyến đường r1 sang tuyến đường r0.
Hình 2.2: Ví dụ cho relocate operator. 2.5.2 Swap operator
Phép toán này bao gồm việc đổi chỗ hai khách hàng từ hai tuyến đường khác nhau.
Nó có thể được xem như một sự di chuyển kép, trong đó các khách hàng được chèn
vào vị trí tương ứng của nhau trong tuyến đường. Một cách chính thức hơn, khách
hàng ci tại vị trí pi trong tuyến đường r0 được di chuyển đến vị trí pj trong tuyến đường
r1, trong khi khách hàng cj tại vị trí pj trong tuyến đường r1 được di chuyển đến vị trí pi
trong tuyến đường r0.
Trong hình 2.3, khách hàng c6 từ tuyến đường r1 và khách hàng c5 từ tuyến đường r0
được đổi chỗ theo vị trí tương ứng của họ.
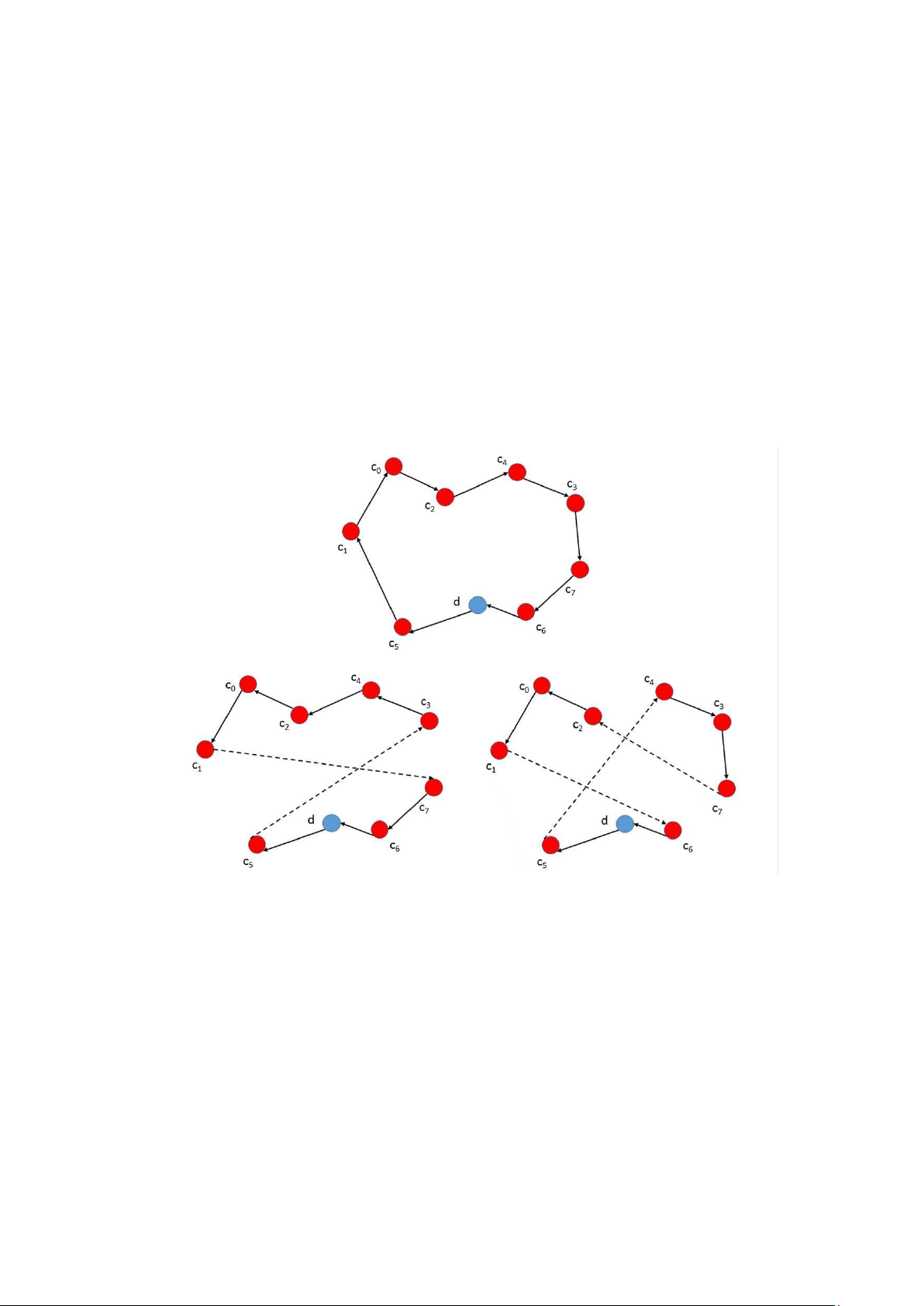
Hình 2.3: Ví dụ cho swap operator. 2.5.3 K-Exchange operator
Phép toán này, còn được gọi là k-opt, bao gồm việc loại bỏ k cạnh trong cùng một
tuyến đường và sau đó kết nối lại các đoạn đường còn lại bằng các cạnh khác. Kết quả
là, một số đoạn có thể được đảo ngược. Một cách chính thức, nó bao gồm việc loại bỏ
k cạnh mà các điểm cuối của chúng nằm ở các vị trí < p0p1 ...pk > trên tuyến đường. Mục
tiêu là kết nối lại các đoạn đường theo một trật tự khác nhau. Phép toán này có thể
được định nghĩa cho bất kỳ số lượng cạnh nào bắt đầu từ hai. Tuy nhiên, việc tính toán
tất cả các sự trao đổi có thể đòi hỏi rất nhiều tài nguyên. Vì vậy, phép toán thường được
giới hạn ở sự trao đổi 2-cạnh hoặc 3-cạnh.
Ví dụ về phép toán trao đổi 2-cạnh và trao đổi 3-cạnh được mô tả trong Hình 2.4.
Trong trường hợp đầu tiên, hai cạnh được loại bỏ với c1 và c7 là điểm cuối. Tuyến đường
kết quả là một tuyến đường mới chứa đoạn bắt đầu từ c1 và kết thúc ở c3 theo hình thức đảo ngược.
Trong trường hợp thứ hai, các cạnh này có c1, c4 và c6 là điểm cuối. Do đó, chúng ta
thu được hai đoạn đường bắt đầu từ c1 và c4 và kết thúc tại c2 và c7 tương ứng. Đoạn
thứ hai được theo dõi trước tiên theo cùng một trật tự. Sau đó, đoạn đầu tiên được
theo dõi theo trật tự đảo ngược.
Hình 2.4: Ví dụ cho relocate operator. 2.5.4 Cross operator
Phép toán này cắt hai tuyến đường khác nhau thành hai phần và tái cấu trúc chúng
bằng cách sử dụng các cạnh chéo. Một cách chính thức, nó trao đổi các đoạn từ tuyến
đường r1 và r2 bắt đầu từ khách hàng ci và cj tương ứng và kết thúc ở kho, nơi r1 = r2.
Hình 2.5: Ví dụ cho relocate operator. 2.6
Tham lam kết hợp tìm kiếm cục bộ
• Ý tưởng: Sử dụng Giải thuật 2 hoặc Giải thuật 3 để tạo ra lời giải ban đầu, sau đó
tiến hành tìm kiếm các lời giải láng giếng bằng việc hoán đổi một đoạn hành trình
của nhân viên đang có thời gian dài nhất cho một nhân viên khác bất kì.
• Sơ đồ giải thuật Algorithm 4: GLS1 S r 1 ← S r 2 ← r 1 S sub 1 ← r 1 sub 2 ← r 2
Hoán đổi sub 1 sub 2 S ′ S ′ S S bởi S ′ Algorithm 5: GLS2 S r 1 ← S r 2 ← r 1 S sub 1 ← r 1 sub 2 ← r 2
Hoán đổi sub 1 sub 2 S ′ S ′ S S bởi S ′ 2.7
Giải thuật di truyền (GA)
2.7.1 Mã hóa lời giải
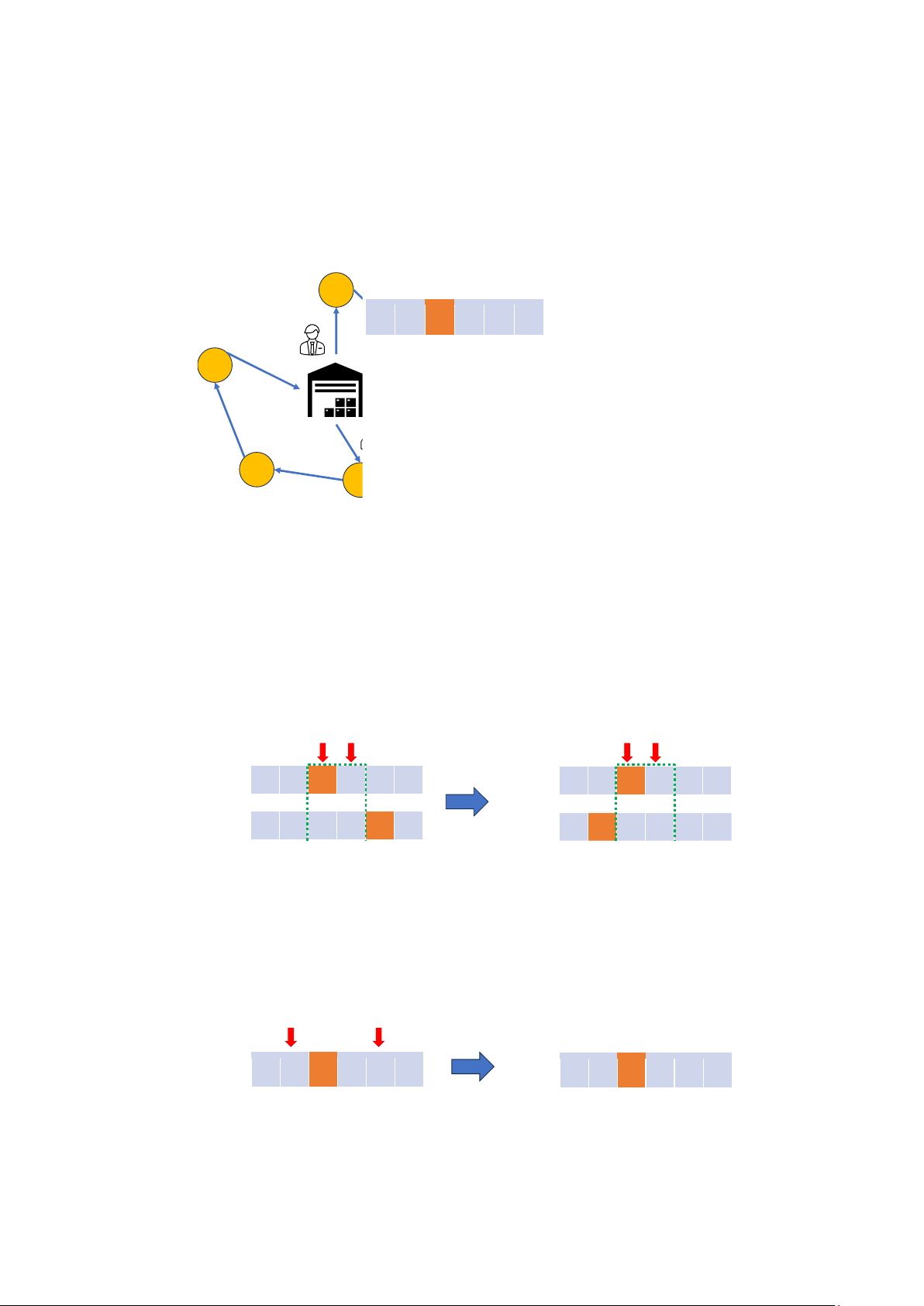
Mỗi cá thể được biểu diễn bởi một mảng có kích thước (N + K − 1) gồm các số từ 1
đến N + K − 1, trong đó, các số từ 1 đến N chỉ khách hàng, các số còn lại điểm ngăn cách
giữa các tuyến. Hình 2.6 minh hoạ cho một cá thể hợp lệ với N = 5,K = 2, cá thể tương
ứng với lời giải: 0 − 1 − 2 − 0 và 0 − 3 − 5 − 4 − 0. 1
1 2 6 3 5 4 4 5 3
Hình 2.6: Ví dụ biểu diễn của một các thể
2.7.2 Toán tử di truyền
Trong báo cáo này, hai toán tử di truyền được sử dụng là: lai ghép thứ tự và đột biến
đổi vị trí. Việc áp dụng hai toán tử này đảm bảo cá thể con sinh ra là một cá thể hợp lệ.
Hình 2.7 và 2.8 minh họa cho hai toán tử. Cha
1 2 6 3 5 4
5 4 6 3 2 1
1 5 3 4 6 2
2 6 3 4 5 1 1:Con 1: Cha 2:Con 2:
Hình 2.7: Lai ghép thứ tự Cha:
1 2 6 3 5 4 Con:
1 5 6 3 2 4
Hình 2.8: Đột biến hoán điểm 2.7.3 Tham số
Tham số của giải thuật được trình bày trong Bảng 2.1 Tham số Giá trị Kích thước quần thể 100 Số thế hệ 500 Tỉ lệ lai ghép 0.8 Tỉ lệ đột biến 0.1 Điều kiện dừng 50 Chọn cha mẹ Đấu tranh
Bảng 2.1: Tham số cho giải thuật di truyền. 2.8
Thuật toán di truyền có cải tiến (GGA)
Tại bước khởi tạo thay vì khởi tạo ngẫu nhiên hoàn toàn các cá thể, nhóm sử dụng
các heuristic để tạo ra một số cá thể cho vào quần thể ban đầu.
CHƯƠNG 3. KẾT QUẢ THỰC NGHIỆM 3.1 Bộ dữ liệu
Trong phần này, nhóm em tiến hành đánh giá các thuật toán đề xuất trên 22 bộ dữ liệu.
Trong đó mỗi bộ dữ liệu được đặt tên với dạng data_[Số khách hàng]_[Số nhân viên].
Ví dụ, data_5_2 tương ứng với 5 khách hàng và 2 nhân viên. Vị trí khách hàng được
sinh ngẫu nhiên theo phân phối đều ([−100,100] × [−100,100]). Thời gian di chuyển
giữa các khách hàng tỉ lệ thuận với khoảng cách giữa các khách hàng. Thời gian bảo trì
cho mỗi khách hàng được sinh ngẫu nhiên theo phân phối đều trong khoảng [50,1000]. 3.2
Các giải thuật chính xác
Bảng 3.1 trình bày kết quả của ba giải thuật chính xác với các bộ dữ liệu nhỏ.
Bộ dữ liệu Quay lui nhánh cận CP MIP Obj Time(s) Obj Time(s) Obj Time(s) data_5_2 360 0.002 360 0.0188 360 0.36 data_5_3 861 0.003 861 0.0187 861 0.86 data_10_2 540 207 540 17.70 540 219.28 data_10_3 1885 191 1885 13.68 1885 490.1 data_10_5 1193 98.95 1193 1.52 1193 707.5 data_15_3 ~ TL 3610 36381.6 ~ TL data_15_5 ~ TL 1785 9191.6 ~ TL data_15_7 ~ TL 1446 613.29 ~ TL
Bảng 3.1: Kết quả của các giải thuật chính xác 3.3
Các giải thuật heuristic và meta-heuristic
Các giải thuật chính xác cho lời giải tối ưu, tuy nhiên việc hạn chế về thời gian và tài
nguyên tính toán khiến cho các giải thuật này không còn khả thi với những bộ dữ liệu
lớn. Trong phần này, chúng em đánh giá hiệu quả của các thuật toán heuristic và meta-
heuristic được trình bài trong Phần 3. Kết quả được trình bày trong Bảng 3.2.
Để phân tích xu hướng của thuật toán cũng như sự phù hợp của các thuật toán trong
từng bộ dữ liệu. Nhóm em sử dụng kết quả của thuật toán Greedy 1 như một đường
cơ sở để tham chiếu cho các thuật toán còn lại. Mức cải thiện của thuật toán B so với
thuật toán A được đánh giá như sau: 100% (3.1)
trong đó, imp(B) là mức cải thiện của thuật toán B, v(.) là giá trị của lời giải.
CHƯƠNG 3. KẾT QUẢ THỰC NGHIỆM Bộ dữ liệu Greedy1 Greedy2 GLS1 GLS2 GA GGA
Obj Time(s) Obj Time(s) Obj Time(s) Obj Time(s) Obj Time(s) Obj Time(s) data_5_2 410 ~0 370 ~0 360 0.094 360 0.114 360 1.022 360 1.325 data_5_3 1098 0.001 1098 ~0 1029 0.081 1029 0.085 861 1.164 861 1.366 data_10_2 680 0.001 590 0.001 588 0.103 578 0.098 540 1.630 540 1.840 data_10_3
2468 0.001 2337 0.001 1970.8 0.097 1953.6 0.096 1885 1.804 1885 2.012 data_10_5 1560 0.001 1560 0.001 1283 0.1 1283 0.103 1193 2.216 1193 2.517 data_15_3
4053 0.001 3958 0.001 3721.4 0.121 3753.6 0.115 3675 2.617 3628 2.903 data_15_5
2249 0.001 2177 0.001 1807.8 0.111 1830 0.108 1785 3.078 1793 3.364 data_15_7
2026 0.001 2026 0.001 1452.6 0.112 1456.8 0.112 1453 3.617 1453 3.905 data_20_5
2637 0.001 2666 0.001 2298.8 0.128 2322.6 0.122 2284 4.249 2267 4.506 data_20_7
1739 0.001 1828 0.001 1368.8 0.122 1402.2 0.120 1408 4.787 1368 4.993 data_20_10 1944 0.001 1928 0.001 1679 0.126 1679 0.123 1679 5.702 1679 5.921 data_50_5
7405 0.002 7135 0.001 6601.8 0.324 6484.2 0.440 6865 15.13 6385 15.872 data_50_10
3178 0.001 3124 0.002 2611.2 0.194 2553.6 0.244 2739 17.8 2551 18.01 data_50_20
2137 0.002 2102 0.002 1740.6 0.193 1697 0.196 1793 23.9 1612 23.224 data_100_10 3310 0.01 3860 0.005 3242 0.384 3718 0.253 5390 54.3 3280 54.901
data_200_10 5130 0.025 4990 0.038 5018 0.567 4526 0.511 11610 186.2 4530 187.0 data_200_20 3710 0.03 3920 0.016 3554 0.415 3732 0.534
6530 204.505 3510 205.23
data_400_40 3560 0.086 3800 0.067 3436 0.798 3702 0.804 7000 610.27 3380 611.94
data_500_50 3540 0.122 4010 0.102 3492 0.953 3810 0.950 7080 925.89 3410 927.01
data_700_70 3500 0.249 3780 0.208 3450 1.39 3780 1.281
8160 1772.513 3410 1774.7
data_900_90 3580 0.404 3720 0.315 3472 1.944 3720 1.708 8570 2887.8 3490 2889.5
data_1000_100 3520 0.637 3910 0.472 3520 2.68 3718 2.280 8770 3546.8 3520 3549.1
Bảng 3.2: Kết quả của các giải thuật heuristic và meta-heuristic
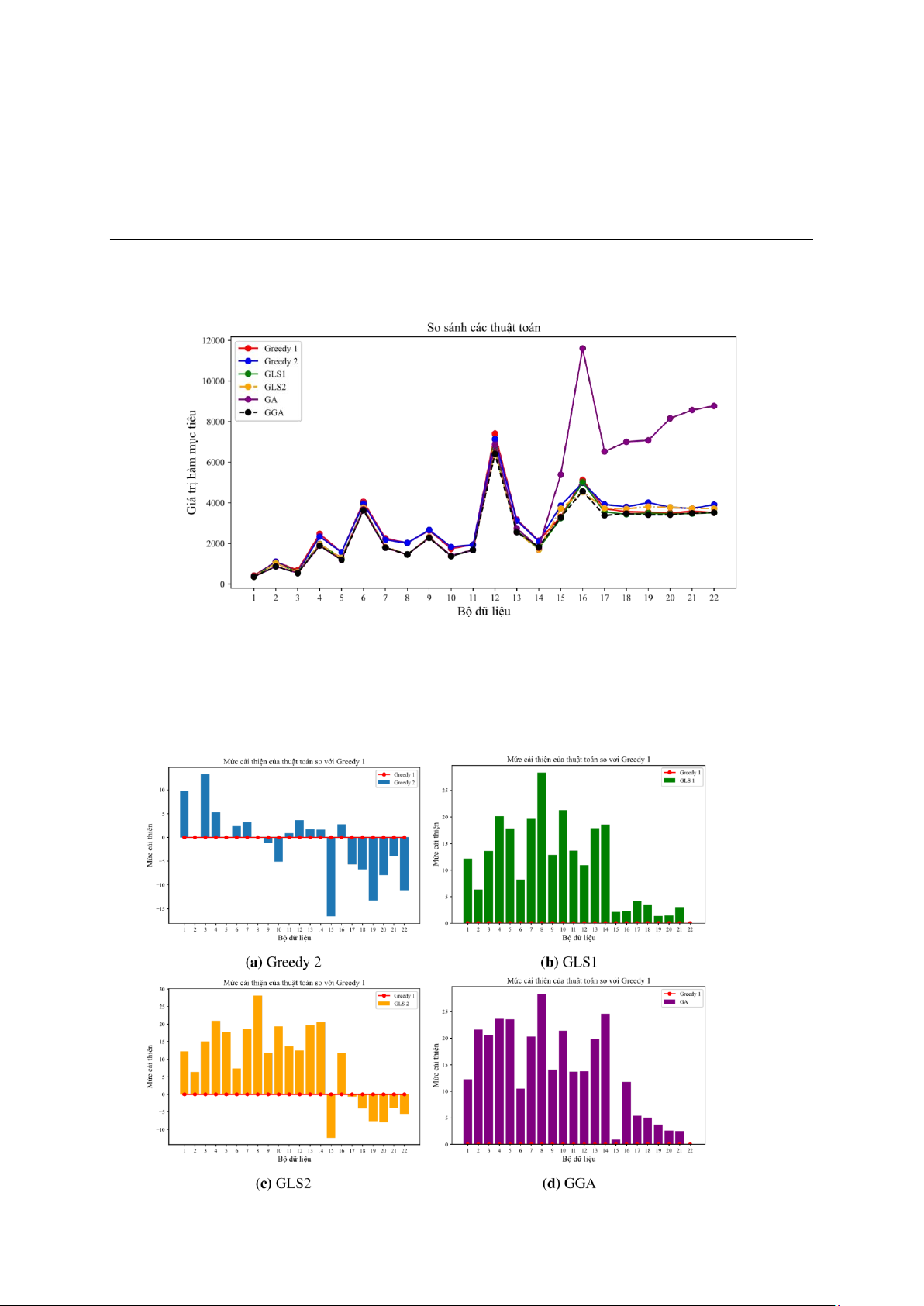
Như quan sát Bảng 3.2 và Hình 3.1 cho thấy, mức độ tối ưu của thuật toán bị ảnh
hưởng bởi số khách hàng và số nhân viên. Hình 3.2a chỉ ra rằng chiến lược chia đều các
khách hàng cho các nhân viên chỉ phù hợp và hiệu quả khi số lượng khách hàng ít, mật
độ thưa. Tuy nhiên, khi số lượng tăng lên, mật độ khách hàng lớn thì chiến lược này
không còn hiệu quả, lúc này thuật toán Greedy 1 cho thấy điểm trội của mình. Hình
3.2b và 3.2c cho thấy sự cải thiện rõ rệt khi các phép tìm kiếm cục bộ được kết hợp với
chiến lược tìm kiếm tham lam. Giải thuật di truyền (GA) cho thấy hiệu quả mạnh mẽ
đối với các bộ dữ liệu nhỏ khi tìm được các lời giải tối ưu, tuy nhiên khi số lượng khách
hàng và nhân viên tăng lên làm tăng kích thước của một gen dẫn đến hạn chế trong
việc khám phá không gian lời giải. Với giải thuật di truyền có cải tiến (GGA) (Hình 3.2d)
cho thấy hiệu quả trên hầu hết các bộ dữ liệu. Một mặt tối của GA đó là thời gian tính
toán để đưa ra lời, được chỉ ra ở Bảng 3.2.
CHƯƠNG 3. KẾT QUẢ THỰC NGHIỆM
Hình 3.1: Giá trị hàm mục tiêu của các thuật toán
Hình 3.2: Mức cải thiện của các heuristic và meta-heuristic so với Greedy 1
CHƯƠNG 4. KẾT LUẬN
Trong báo cáo này, nhóm em đã đưa ra nhiều cách tiếp cận khác nhau để giải bài toán
"Định tuyến nhân viên bảo trì mạng", đây là một vấn đề NP−hard và được áp dụng cho
nhiều trường hợp trong thực tiễn.
Đầu tiên, nhóm sử dụng phương pháp quay lui nhánh cận để giải bài toán trong
trường hợp bộ dữ liệu có kích thước nhỏ. Sau đó, nhóm đã mô hình hóa bài toán dưới
dạng Contraist programming và Mixed integer programming. Nhóm đã đề xuất các giải
thuật heuristic và meta-heuristic bao gồm: chiến lược tham lam, chiến lược tham lam
kết hợp với tìm kiếm cục bộ và giải thuật di truyền.
Trong phần thực nghiệm, nhóm xây dựng tập các bộ dữ liệu theo các kích thước khác
nhau để tiến hành phân tích và đánh giá các thuật toán đề xuất. Với các thuật toán
chính xác nhóm thống kê giá trị lời giải và thời gian của từng phương pháp trên các bộ
dữ liệu nhỏ. Tương tự, với các giải thuật heuristic và meta-heuristic được đánh giá trên
các bộ dữ liệu lớn với 30 lần chạy, kết quả thu được là giá trị trung bình của các lần
chạy. Các kết quả được trình bày trong các bảng và hình vẽ.