



Preview text:
lOMoAR cPSD| 59671932 0.1
Back tracking with branch and bound
Ý tưởng: Sử dụng 2 mảng x và y để lưu thứ tự khách hàng được phục vụ. Trong đó,
• yk chỉ khách hàng đầu tiên được phụ vụ bởi nhân viên k, với k = 1,...,K. • xi chỉ khách
hàng sau được phục vụ sau khách hàng i, với i = 1,...N 1 1 3 4
2 0 5 0 4 5
Hình 0.1: Ví dụ cho biểu diễn phương pháp quay lui. Thuật toán:
• Sử dụng thuật toán quy lui để duyệt qua lân lượt các phần tử trong mảng Y với
điều kiện giá trị các phần tử tăng dần.
• Sau khi chọn xong phần tử thứ K thì duyệt qua mảng X theo thứ tự các khách hàng
được bảo trì từ các nhân viên.
• Sau khi nhân viên điểm 0 tức kho hàng. Thì chuyển qua xét nhân viên tiếp theo.
Algorithm 1: Backtracking for Vehicle Routing Problem
Input: Cost matrix C, Number of vehicles K, Number of customers N
Output: Optimal routes for vehicles
Initialize arrays X, Y , and visited; Set fbest ← ∞;
Set initial routes in Y ; while not all
configurations tried do
Generate new configurations for Y ; for
k ∈ {1,2,...,K} do: TryY(k); for i ∈ Y do:
TryX(i, k where Y [k] = i); Update fbest if a better solution is found;
Procedure TryY(k); foreach i ∈
{0,1,...,N} do: lOMoAR cPSD| 59671932
if CheckY(i, k) then Y [k] ← i;
visited[i] ← 1; TryY(k + 1);
visited[i] ← 0;
Procedure TryX(i, k);
v ∈{ 0 , 1 ,...,N } v i k
X [ i] ← v
visited [ v ] ← 1 v k
visited [ v ] ← 0 X Y 2 0.2 Local search
0.2.1 Relocate operator
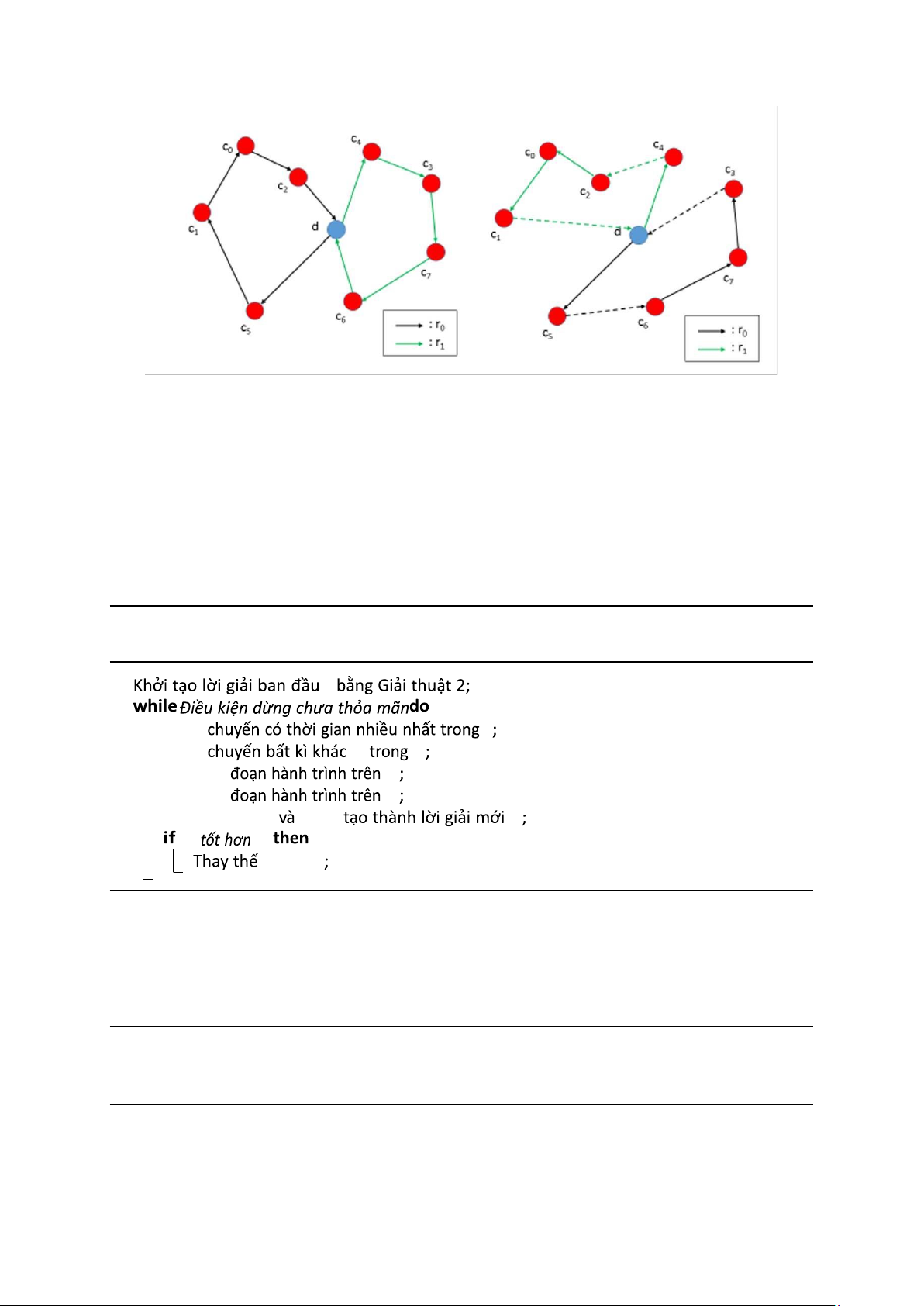
Phép toán này bao gồm việc di chuyển một khách hàng từ một tuyến đường này
sang một tuyến đường khác. Cụ thể, khách hàng i từ tuyến đường r0 sẽ được loại bỏ
khỏi r0 và chèn vào tuyến đường r1 tại vị trí p, nơi mà r0 ≠ r1 và 0 ≤ p ≤ |r1|.
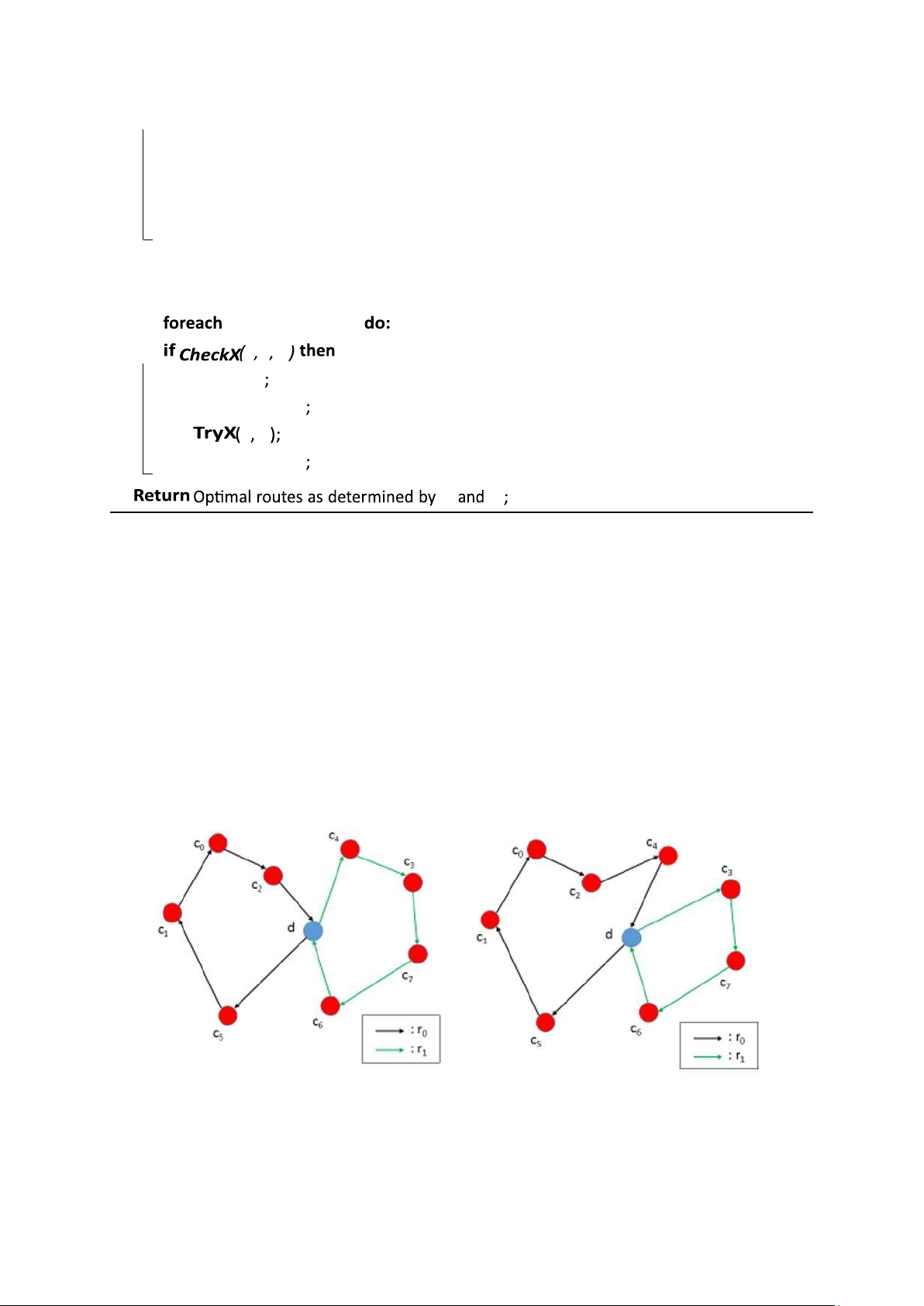
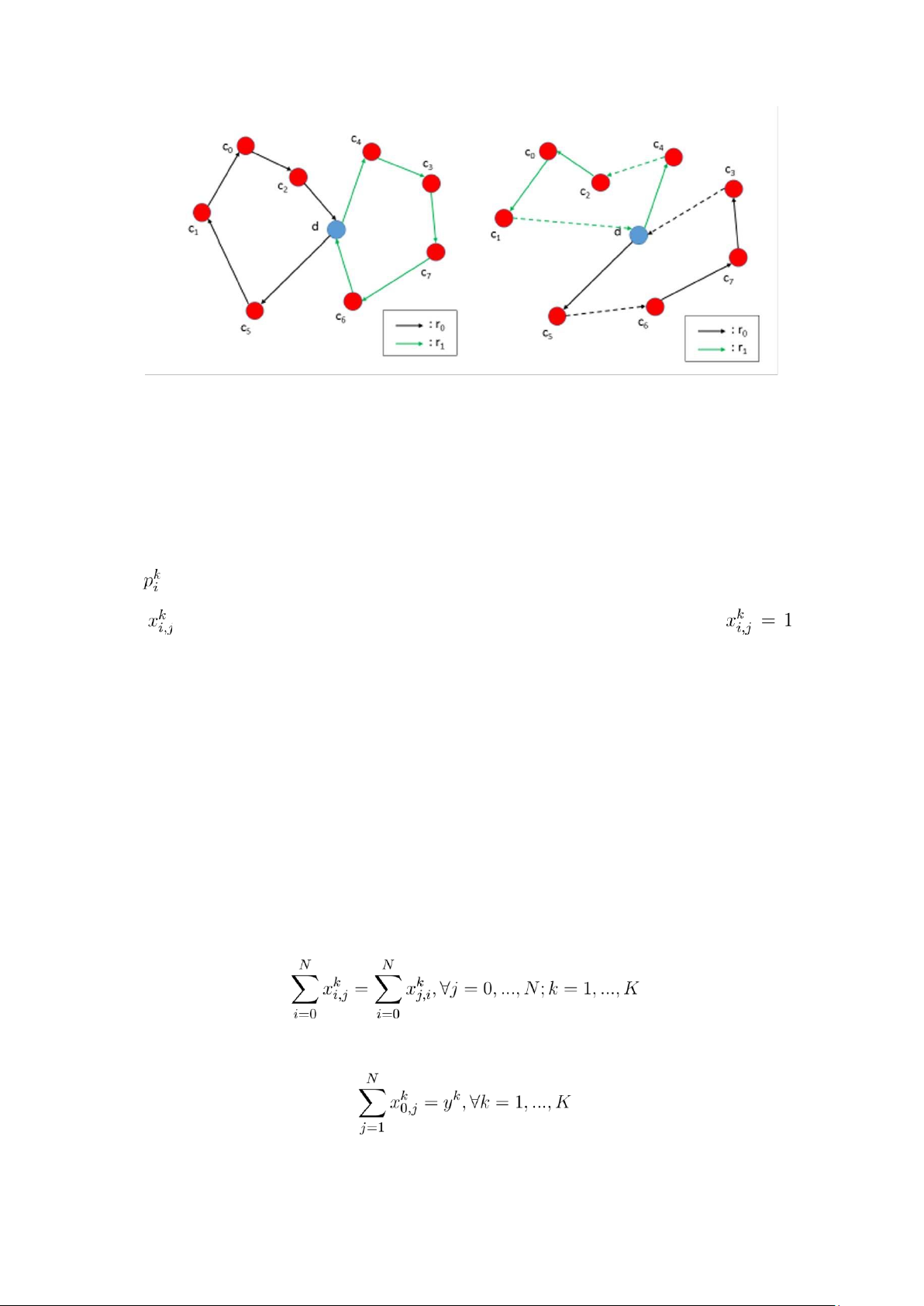
Ví dụ, trong Hình 0.7, khách hàng c4 được di chuyển từ tuyến đường r1 sang tuyến đường r0.
Hình 0.2: Ví dụ cho relocate operator. lOMoAR cPSD| 59671932 0.2.2 Swap operator
Phép toán này bao gồm việc đổi chỗ hai khách hàng từ hai tuyến đường khác nhau.
Nó có thể được xem như một sự di chuyển kép, trong đó các khách hàng được chèn
vào vị trí tương ứng của nhau trong tuyến đường. Một cách chính thức hơn, khách
hàng ci tại vị trí pi trong tuyến đường r0 được di chuyển đến vị trí pj trong tuyến đường
r1, trong khi khách hàng cj tại vị trí pj trong tuyến đường r1 được di chuyển đến vị trí pi
trong tuyến đường r0.
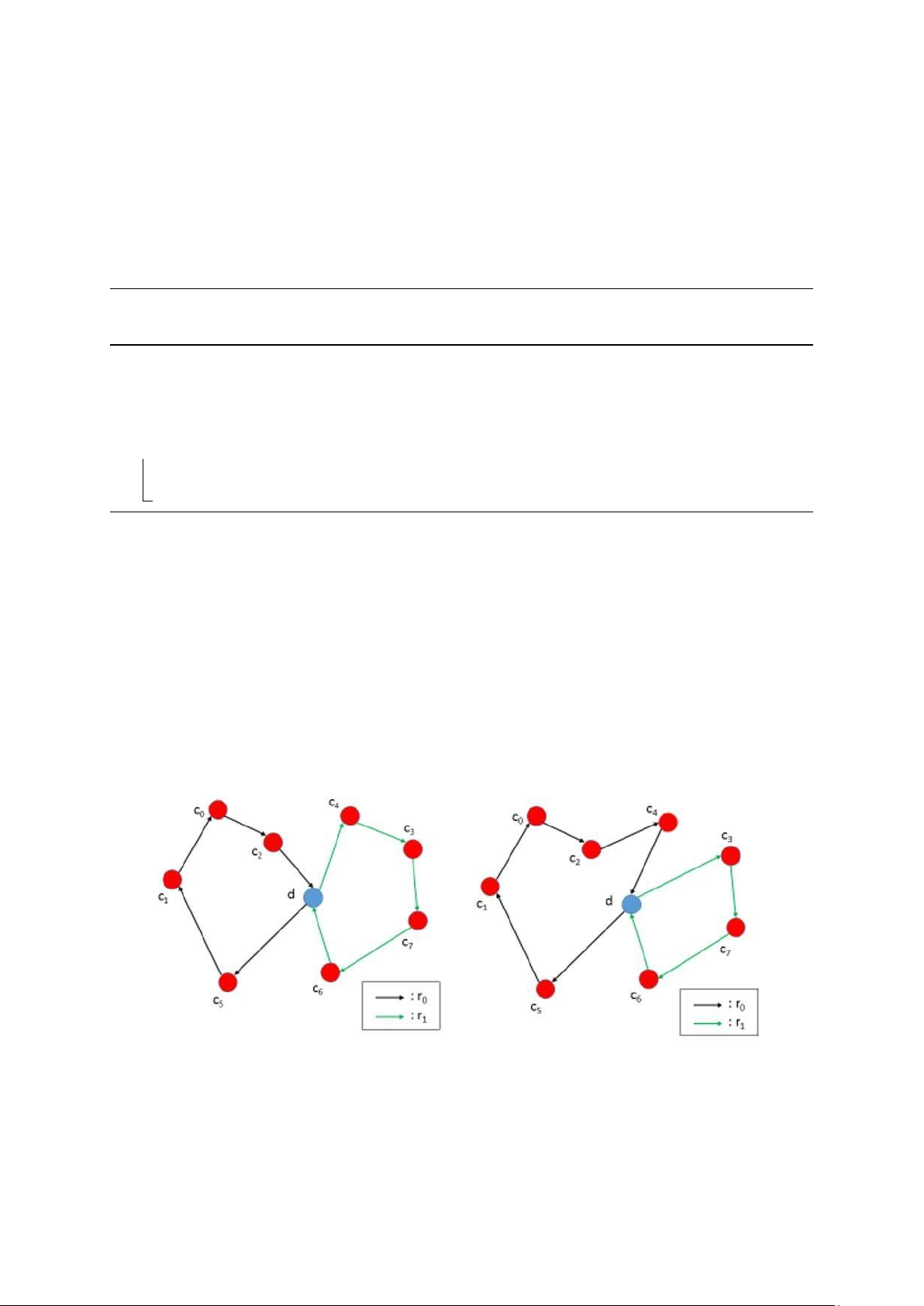
Trong hình 0.7, khách hàng c6 từ tuyến đường r1 và khách hàng c5 từ tuyến đường r0
được đổi chỗ theo vị trí tương ứng của họ.
Hình 0.3: Ví dụ cho swap operator. 0.2.3 K-Exchange operator
Phép toán này, còn được gọi là k-opt, bao gồm việc loại bỏ k cạnh trong cùng một
tuyến đường và sau đó kết nối lại các đoạn đường còn lại bằng các cạnh khác. Kết quả
là, một số đoạn có thể được đảo ngược. Một cách chính thức, nó bao gồm việc loại bỏ
k cạnh mà các điểm cuối của chúng nằm ở các vị trí < p0p1 ...pk > trên tuyến đường. Mục
tiêu là kết nối lại các đoạn đường theo một trật tự khác nhau. Phép toán này có thể
được định nghĩa cho bất kỳ số lượng cạnh nào bắt đầu từ hai. Tuy nhiên, việc tính toán
tất cả các sự trao đổi có thể đòi hỏi rất nhiều tài nguyên. Vì vậy, phép toán thường được
giới hạn ở sự trao đổi 2-cạnh hoặc 3-cạnh.
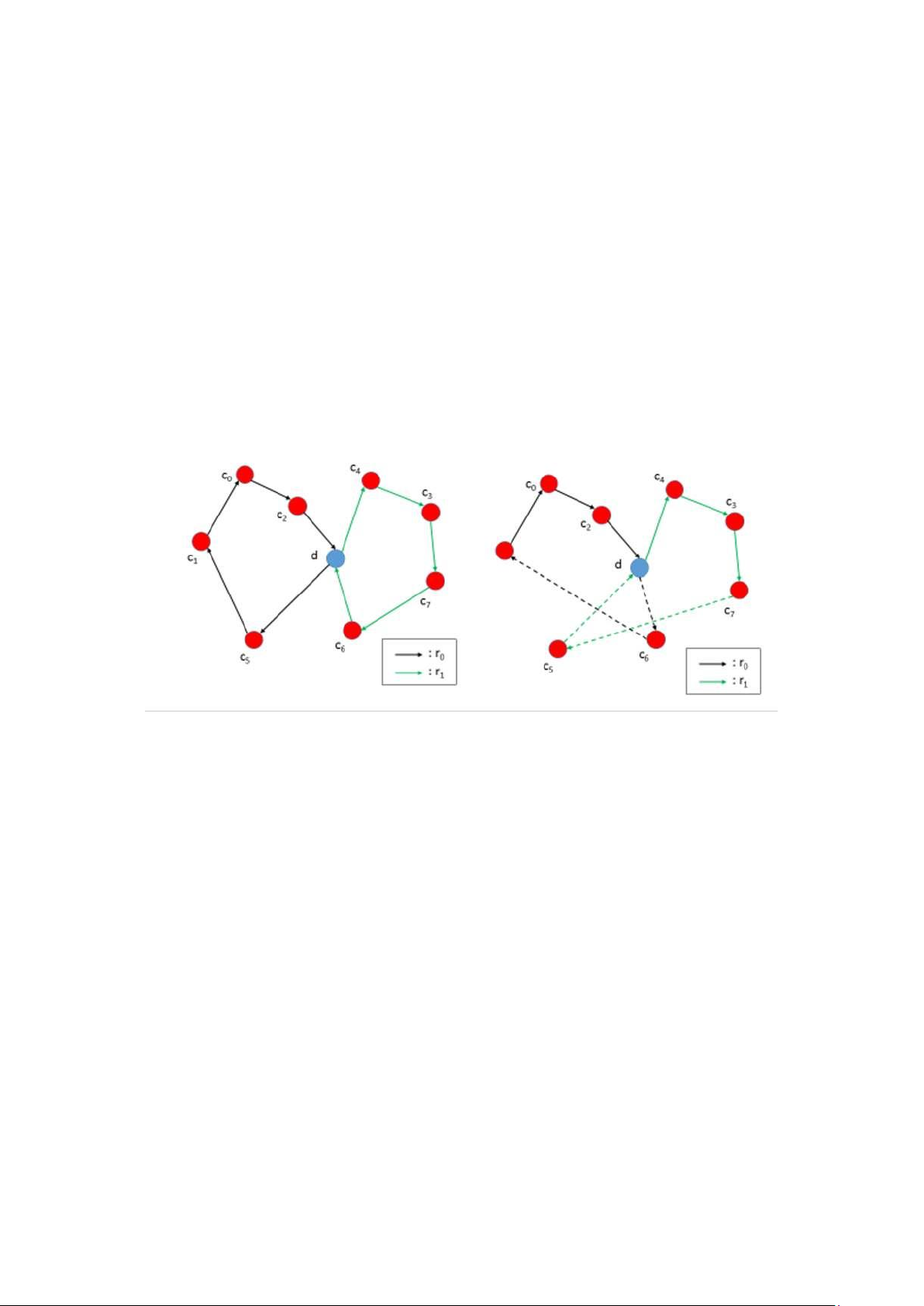
Ví dụ về phép toán trao đổi 2-cạnh và trao đổi 3-cạnh được mô tả trong Hình 0.8.
Trong trường hợp đầu tiên, hai cạnh được loại bỏ với c1 và c7 là điểm cuối. Tuyến đường lOMoAR cPSD| 59671932
kết quả là một tuyến đường mới chứa đoạn bắt đầu từ c1 và kết thúc ở c3 theo hình thức đảo ngược.
Trong trường hợp thứ hai, các cạnh này có c1, c4 và c6 là điểm cuối. Do đó, chúng ta
thu được hai đoạn đường bắt đầu từ c1 và c4 và kết thúc tại c2 và c7 tương ứng. Đoạn
thứ hai được theo dõi trước tiên theo cùng một trật tự. Sau đó, đoạn đầu tiên được
theo dõi theo trật tự đảo ngược.
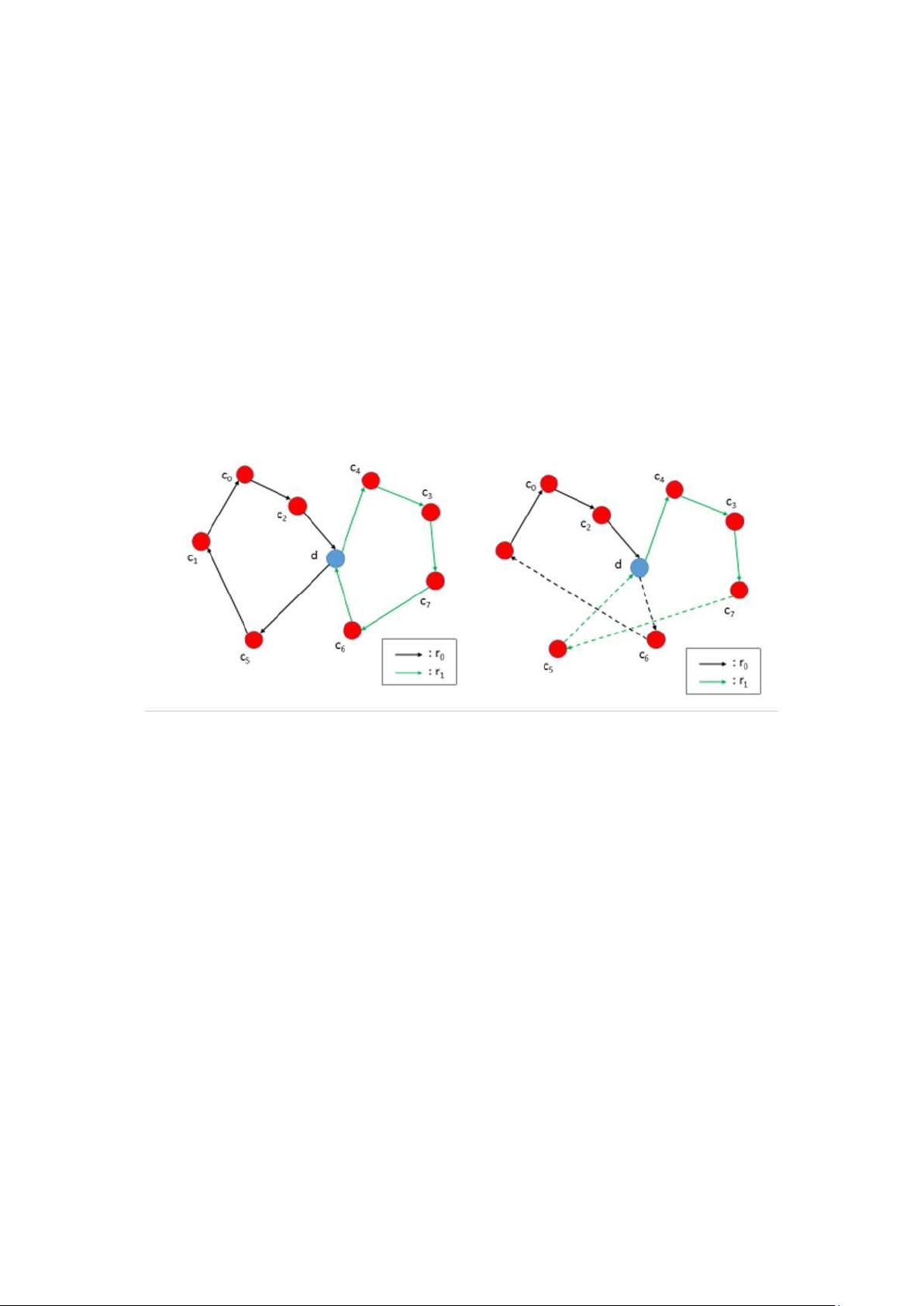
Hình 0.4: Ví dụ cho relocate operator. 0.2.4 Cross operator
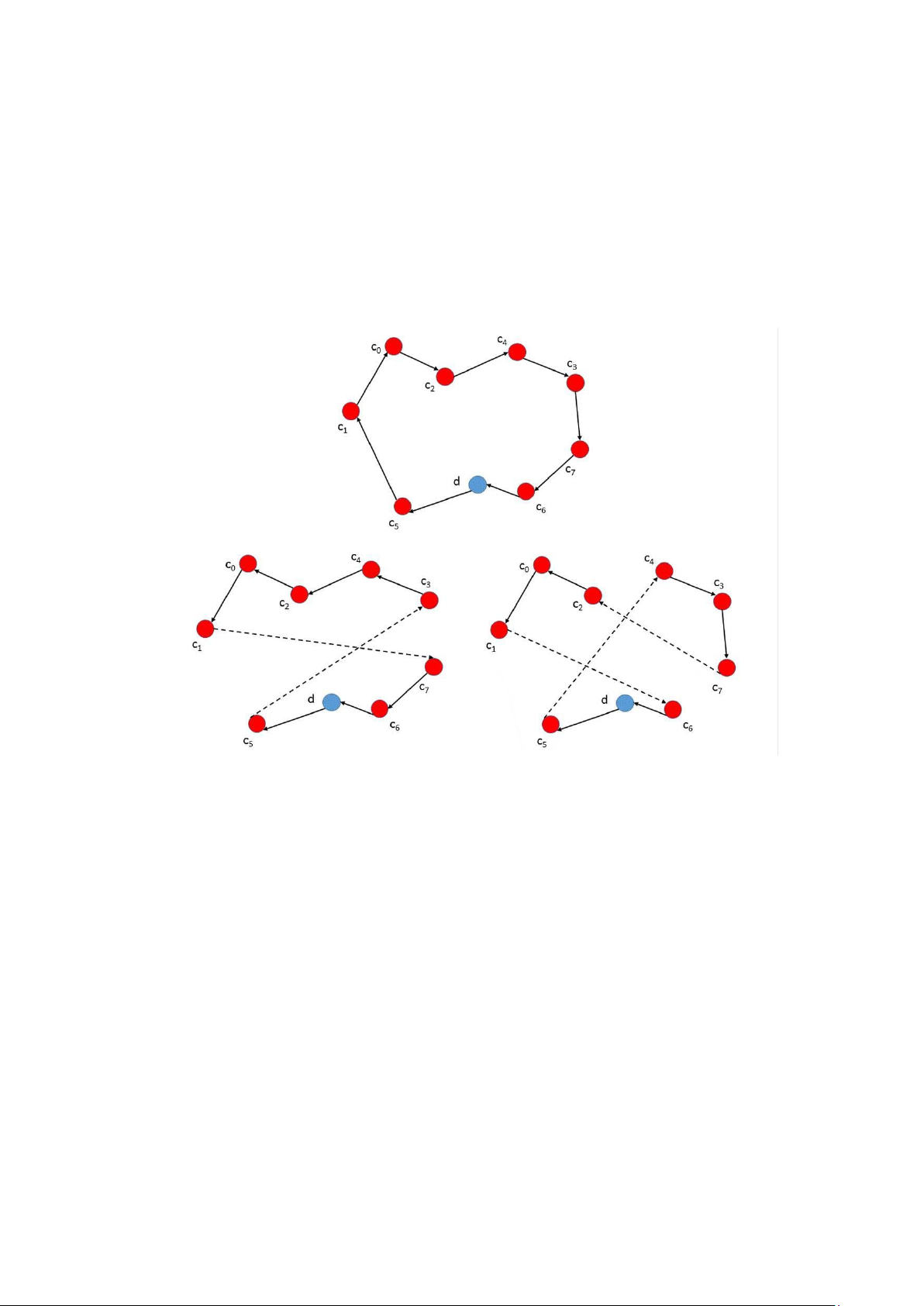
Phép toán này cắt hai tuyến đường khác nhau thành hai phần và tái cấu trúc chúng
bằng cách sử dụng các cạnh chéo. Một cách chính thức, nó trao đổi các đoạn từ tuyến
đường r1 và r2 bắt đầu từ khách hàng ci và cj tương ứng và kết thúc ở kho, nơi r1 = r2. lOMoAR cPSD| 59671932
Hình 0.5: Ví dụ cho relocate operator. 0.3
Constraints programming 0.3.1 Biến
• yk để chỉ trạng thái hoạt động của nhân viên k, nếu yk = 1 tức là nhân viên k hoạt
động, ngược lại, yk = 0 nhân viên k không hoạt động.
• để chỉ thứ tự của khách hàng thứ i trong hành trình của nhân viên k. •
chỉ cung (i,j) có thuộc hành trình của nhân viên k hay không. Nếu thì
cung (i,j) thuộc hành trình của nhân viên k. Ngược lại, xki,j = 0 thì cung (i,j) không
thuộc hành trình của nhân viên k.
• max_work_time Thời gian làm việc lớn nhất của một nhân viên nào đó. 0.3.2 Ràng buộc
• Mỗi khách hàng chỉ được bảo trì bởi một nhân viên. K N
XXxki,j = 1,∀j = 1,...,N (1) k=1 i=0
• Đến và rời khỏi khách hàng bởi cùng một nhân viên. (2)
• Mỗi nhân viên bắt đầu từ 0 và kết thúc tại 0. (3) N lOMoAR cPSD| 59671932
Xxkj,0 = yk,∀k = 1,...,K (4) j=1
• Nhân viên cần di chuyển đến các khách hàng.
xki,i = 0,∀i = 0,...,N;∀k = 1,...,K (5)
• Loại bỏ sub-tour (Nếu cung (i,j) thuộc hành trình của nhân viên k thì khách hàng j
được bảo trì sau khách hàng i). Nếu,
(6) ∀i ̸= j;i = 0,...,N;j = 1,...,N;k = 1,...,K
• Để tối ưu thời gian chạy code, giả sử các nhân viên được sắp xếp sao cho nếu nhân
viên k hoạt động thì nhân viên k+1 cũng phải hoạt động (dồn tất cả nhân viên
không hoạt động lên đầu, để tránh trường hợp hoán vị).
yk ≤ yk+1,∀k = 1,...,K − 1 • Thời (7)
gian làm việc lớn nhất. (8)
• Miền giá trị của các biến. , (9)
∀i = 0,...,N;j = 0,...,N;k = 1,...,K
yk ∈ {0,1},∀k = 1,...,K (10)
pki i ∈ {0,∞},∀i = 0,...,N;k = 1,...,K (11)
max_work_time ∈ {0,∞} (12) 0.3.3 Hàm mục tiêu
• Cực tiểu hóa max_work_time. 0.4 MIP 0.4.1 Biến
• yk để chỉ trạng thái hoạt động của nhân viên k, nếu yk = 1 tức là nhân viên k hoạt
động, ngược lại, yk = 0 nhân viên k không hoạt động.
• để chỉ thứ tự của khách hàng thứ i trong hành trình của nhân viên k. lOMoAR cPSD| 59671932 •
chỉ cung (i,j) có thuộc hành trình của nhân viên k hay không. Nếu thì
cung (i,j) thuộc hành trình của nhân viên k. Ngược lại,
thì cung (i,j) không
thuộc hành trình của nhân viên k.
• max_work_time Thời gian làm việc lớn nhất của một nhân viên nào đó. 0.4.2 Ràng buộc
• Mỗi khách hàng chỉ được bảo trì bởi một nhân viên. K N
XXxki,j = 1,∀j = 1,...,N (13) k=1 i=0
• Đến và rời khỏi khách hàng bởi cùng một nhân viên. (14)
• Mỗi nhân viên bắt đầu từ 0 và kết thúc tại 0. N
Xxk0,j = yk,∀k = 1,...,K (15) j=1 N
Xxkj,0 = yk,∀k = 1,...,K (16) j=1
• Nhân viên cần di chuyển đến các khách hàng. (17)
• Loại bỏ sub-tour (Nếu cung (i,j) thuộc hành trình của nhân viên k thì khách hàng j
được bảo trì sau khách hàng i).
(18) ∀i ̸= j;j = 1,...,N;i =
1,...,N;k = 1,...,K
• Để tối ưu thời gian chạy code, giả sử các nhân viên được sắp xếp sao cho nếu nhân
viên k hoạt động thì nhân viên k+1 cũng phải hoạt động (dồn tất cả nhân viên
không hoạt động lên đầu, để tránh trường hợp hoán vị).
yk ≤ yk+1,∀k = 1,...,K − 1 • Thời (19)
gian làm việc lớn nhất. lOMoAR cPSD| 59671932 (20)
• Miền giá trị của các biến. (21)
∀i = 0,...,N;j = 0,...,N;k = 1,...,K
yk ∈ {0,1},∀k = 1,...,K (22) , (23)
max_work_time ∈ {0,∞} (24) 0.4.3 Hàm mục tiêu
• Cực tiểu hóa max_work_time. 0.5 Tham lam 0.5.1 Greedy 1
• Ý tưởng: Tập các khách hàng chưa được phục vụ được sắp xếp theo thứ tự tăng
dần về thời gian (thời gian di chuyển + thời gian bảo trì) so với công ty 0 ("gần").
Sau đó các khách hàng được thêm vào các tuyến của nhân viên sao cho làm giá
trị của hàm mục tiêu tăng ít nhất. Nếu không làm tăng giá trị hàm mục tiêu,
khách hàng được thêm vào tuyến của nhân viên đang có thời gian làm việc ngắn nhất.
• Sơ đồ giải thuật
Algorithm 2: Greedy 1
P ← tập khách hàng;
Sắp xếp theo thứ tự "gần" công ty;
while P khác rỗng do
Lấy khách hàng đầu c trong P;
Q ← tập các nhân viên có hành trình làm tăng ít giá trị hàm mục tiêu nhất nếu thêm c vào hành trình;
Lựa chọn nhân viên k đang có thời gian làm việc nhỏ nhất trong Q;
Thêm c vào hành trình của k; lOMoAR cPSD| 59671932
Loại bỏ c khỏi P; 0.5.2 Greedy 2
• Ý tưởng: Tại mỗi bước, mỗi nhân viên sẽ chọn khách hàng tốn ít thời gian nhất
để đi đến. Thứ tự chọn khách hàng của nhân viên được thực hiện lần lượt.
• Sơ đồ giải thuật
Algorithm 3: Greedy 2
Khởi tạo hành trình của mỗi nhân viên bắt đầu tại 0; k ← 1;
while Tồn tại khách hàng chưa được phục vụ do
Lựa chọn khách hàng tốn ít thời gian nhất thêm vào hành trình của k;
k ← (k + 1)%K;
0.6 Tìm kiếm cục bộ
0.6.1 Relocate operator
Phép toán này bao gồm việc di chuyển một khách hàng từ một tuyến đường này
sang một tuyến đường khác. Cụ thể, khách hàng i từ tuyến đường r0 sẽ được loại bỏ
khỏi r0 và chèn vào tuyến đường r1 tại vị trí p, nơi mà r0 ̸= r1 và 0 ≤ p ≤ |r1|.
Ví dụ, trong Hình 0.7, khách hàng c4 được di chuyển từ tuyến đường r1 sang tuyến đường r0.
Hình 0.6: Ví dụ cho relocate operator. lOMoAR cPSD| 59671932 0.6.2 Swap operator
Phép toán này bao gồm việc đổi chỗ hai khách hàng từ hai tuyến đường khác nhau.
Nó có thể được xem như một sự di chuyển kép, trong đó các khách hàng được chèn
vào vị trí tương ứng của nhau trong tuyến đường. Một cách chính thức hơn, khách
hàng ci tại vị trí pi trong tuyến đường r0 được di chuyển đến vị trí pj trong tuyến đường
r1, trong khi khách hàng cj tại vị trí pj trong tuyến đường r1 được di chuyển đến vị trí pi
trong tuyến đường r0.
Trong hình 0.7, khách hàng c6 từ tuyến đường r1 và khách hàng c5 từ tuyến đường r0
được đổi chỗ theo vị trí tương ứng của họ.
Hình 0.7: Ví dụ cho swap operator. 0.6.3 K-Exchange operator
Phép toán này, còn được gọi là k-opt, bao gồm việc loại bỏ k cạnh trong cùng một
tuyến đường và sau đó kết nối lại các đoạn đường còn lại bằng các cạnh khác. Kết quả
là, một số đoạn có thể được đảo ngược. Một cách chính thức, nó bao gồm việc loại bỏ
k cạnh mà các điểm cuối của chúng nằm ở các vị trí < p0p1 ...pk > trên tuyến đường. Mục
tiêu là kết nối lại các đoạn đường theo một trật tự khác nhau. Phép toán này có thể
được định nghĩa cho bất kỳ số lượng cạnh nào bắt đầu từ hai. Tuy nhiên, việc tính toán
tất cả các sự trao đổi có thể đòi hỏi rất nhiều tài nguyên. Vì vậy, phép toán thường được
giới hạn ở sự trao đổi 2-cạnh hoặc 3-cạnh.
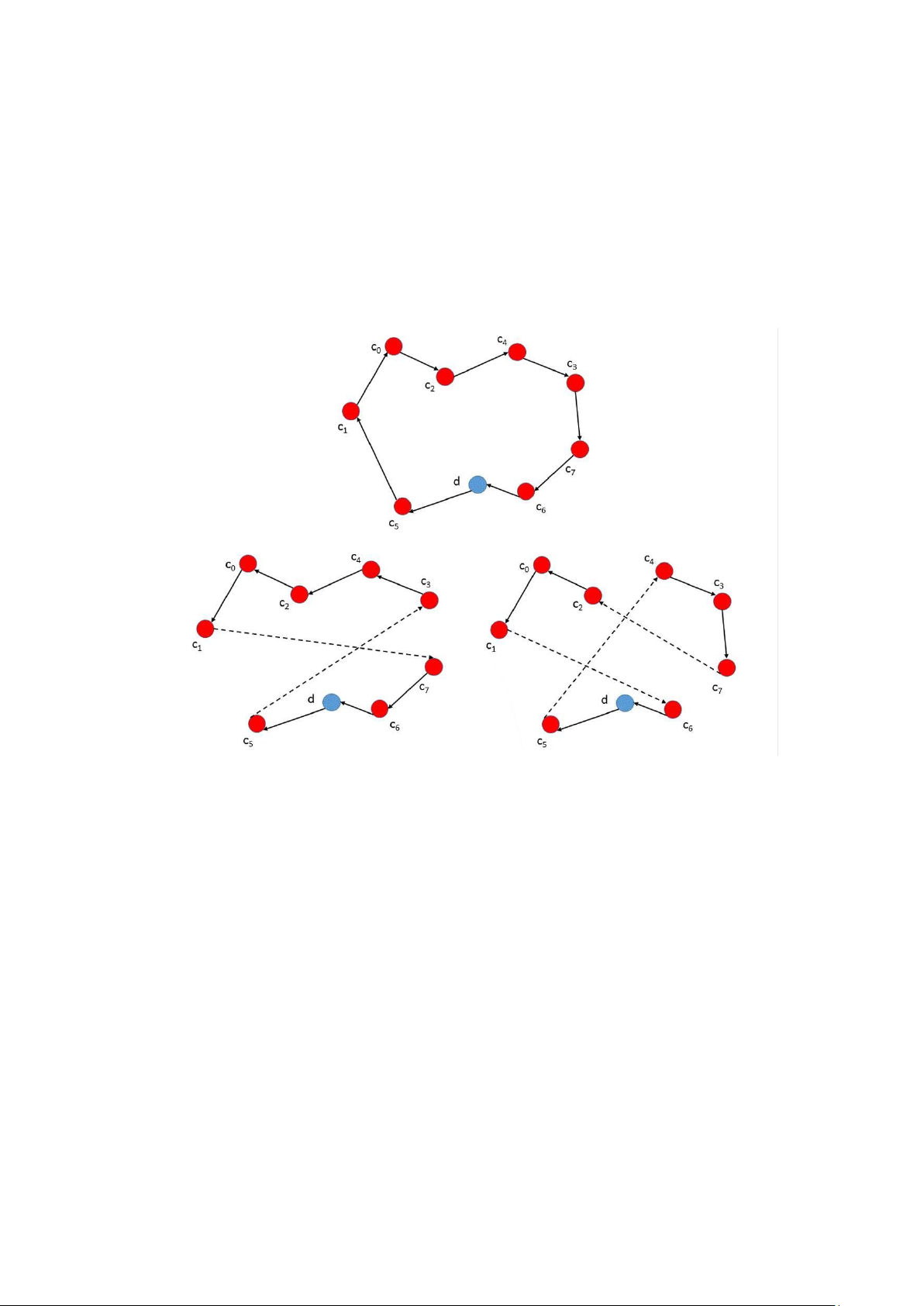
Ví dụ về phép toán trao đổi 2-cạnh và trao đổi 3-cạnh được mô tả trong Hình 0.8.
Trong trường hợp đầu tiên, hai cạnh được loại bỏ với c1 và c7 là điểm cuối. Tuyến đường lOMoAR cPSD| 59671932
kết quả là một tuyến đường mới chứa đoạn bắt đầu từ c1 và kết thúc ở c3 theo hình thức đảo ngược.
Trong trường hợp thứ hai, các cạnh này có c1, c4 và c6 là điểm cuối. Do đó, chúng ta
thu được hai đoạn đường bắt đầu từ c1 và c4 và kết thúc tại c2 và c7 tương ứng. Đoạn
thứ hai được theo dõi trước tiên theo cùng một trật tự. Sau đó, đoạn đầu tiên được
theo dõi theo trật tự đảo ngược.
Hình 0.8: Ví dụ cho relocate operator. 0.6.4 Cross operator
Phép toán này cắt hai tuyến đường khác nhau thành hai phần và tái cấu trúc chúng
bằng cách sử dụng các cạnh chéo. Một cách chính thức, nó trao đổi các đoạn từ tuyến
đường r1 và r2 bắt đầu từ khách hàng ci và cj tương ứng và kết thúc ở kho, nơi r1 = r2. lOMoAR cPSD| 59671932
Hình 0.9: Ví dụ cho relocate operator.
0.7 Tham lam kết hợp tìm kiếm cục bộ
• Ý tưởng: Sử dụng Giải thuật 2 hoặc Giải thuật 3 để tạo ra lời giải ban đầu, sau đó
tiến hành tìm kiếm các lời giải láng giếng bằng việc hoán đổi một đoạn hành trình
của nhân viên đang có thời gian dài nhất cho một nhân viên khác bất kì.
• Sơ đồ giải thuật
Algorithm 4: GLS1 S r 1 ← S r 2 ← r 1 S sub 1 ← r 1 sub 2 ← r 2
Hoán đổi sub 1 sub 2 S ′ S ′ S S bởi S ′ 0.8
Giải thuật di truyền (GA)
0.8.1 Mã hóa lời giải
Mỗi cá thể được biểu diễn bởi một mảng có kích thước (N + K − 1) gồm các số từ 1
đến N + K − 1, trong đó, các số từ 1 đến N chỉ khách hàng, các số còn lại điểm ngăn Algorithm 5: GLS2 lOMoAR cPSD| 59671932 S r 1 ← S r 2 ← r 1 S sub 1 ← r 1 sub 2 ← r 2
Hoán đổi sub 1 sub 2 S ′ S ′ S S bởi S ′
cách giữa các tuyến. Hình 0.10 minh hoạ cho một cá thể hợp lệ với N = 5,K = 2, cá thể
tương ứng với lời giải: 0 − 1 − 2 − 0 và 0 − 3 − 5 − 4 − 0. 1
1 2 6 3 5 4 4 5 3
Hình 0.10: Ví dụ biểu diễn của một các thể
0.8.2 Toán tử di truyền
Trong báo cáo này, hai toán tử di truyền được sử dụng là: lai ghép thứ tự và đột biến
đổi vị trí. Việc áp dụng hai toán tử này đảm bảo cá thể con sinh ra là một cá thể hợp lệ. Hình 0.11 và 0.12 minh
họa cho hai 1 2 6 3 5 4 toán
5 4 6 3 2 1 tử. Cha
1 5 3 4 6 2
2 6 3 4 5 1 1:Con 1: Cha 2:Con 2:
Hình 0.11: Lai ghép thứ tự Cha:
1 2 6 3 5 4 Con:
1 5 6 3 2 4
Hình 0.12: Đột biến hoán điểm lOMoAR cPSD| 59671932 0.8.3 Tham số
Tham số của giải thuật được trình bày trong Bảng 1 Tham số Giá trị Kích thước quần thể 100 Số thế hệ 500 Tỉ lệ lai ghép 0.8 Tỉ lệ đột biến 0.1 Điều kiện dừng 50 Chọn cha mẹ Đấu tranh
Bảng 1: Tham số cho giải thuật di truyền.



