lOMoARcPSD|47207367 lOMoARcPSD|47207367
ĐẠI HỌC QUỐC GIA TP. HỒ CHÍ
MINH TRƯỜNG ĐẠI HỌC BÁCH KHOA ···☼···
BÁO CÁO BÀI TẬP LỚN Môn: Giải tích
Giảng viên hướng dẫn: Lê Xuân Đại Lớp: L02 Nhóm: 6 Thành viên MSSV Vũ Xuân Chính 2210392 Nguyễn Phương Duy 2210526 Quách Thanh Điền 2210754 Đường Bảo Định 2210761 Nguyễn Phú Quý 2153760 lOMoARcPSD|47207367
Thành phố Hồ Chí Minh – 2022 Chủ đề 6 Thành viên nhóm Vũ Xuân Chính Nguyễn Phương Duy Quách Thanh Điền Đường Bảo Định Nguyễn Phú Quý lOMoARcPSD|47207367 Mục lục Đề bài 2 Cơ sở lý thuyết 3 Giải quyết bài toán 6
Bài 1: Bài toán sản xuất sản phẩm 6 a 6 b 7 c 8 d 10 e 11 f 11
Bài 2: Average rate of change and Relative change 12
Bài 3: Bài toán về thông lượng máu 16 a 16 b 17
Chú thích và tài liệu tham khảo 17 Đề bài lOMoARcPSD|47207367 Bài 1
Với x đơn vị nguyên liệu thô, nhà sản xuất tạo ra f (x) đơn vị sản phẩm. Nguyên
liệu thô được mua với giá w $/đơn vị và sản phẩm được bán ra với giá
p $/đơn vị. Số đơn vị nguyên liệu thô được sử dụng để lợi nhuận đạt
giá trị cao nhất ký hiệu làx¿.
a. Theo em, nhà sản xuất muốn f ’(x ) dương hay âm? Lý giải điều này.
b. Giải thích tại sao g(x )= pf (x) – wx là lợi nhuận thu được từ x đơn vị nguyên liệu thô.
c. Nếu f có đạo hàm tại x¿, tính f ’ (x¿).
d. Nếu f ’ ’(x¿) khác 0, giá trị của nó là âm hay dương.
e. Nếu nhà cung cấp nguyên liệu thô thay đổi w, ta có thể xem x¿ là hàm theo ¿ x
w, xác định dạng ddw và cho biết giá trị này dương hay âm?
f. Nếu w tăng, nhà sản xuất nên tăng hay giảm việc nhập nguyên liệu thô này? Bài 2
Đọc và trình bày lại phần 1.3, Average rate of change and Relative
change trong Applied Calculus – 5th Edition. Yêu cầu nêu được khái
niệm (định nghĩa), ý nghĩa, cách tính, so sánh 2 giá trị này. Cho ví dụ
minh họa 2 giá trị này, không dùng lại ví dụ của sách. Bài 3
Xét bài toán sau: Khi máu lưu thông trong mạch, lượng máu đi qua
một điểm cho trước trong một đơn vị thời gian (thông lượng) được
cho bởi công thức F=k R4 , trong đó R là bán kính của mạch máu.
a. Chứng minh rằng sự thay đổi tương đối củaF xấp xỉ 4 lần sự thay
đổi tương đối của R.
b. Nếu bán kính mạch máu tăng 5% thì ảnh hưởng như thế nào đến lưu lượng máu. Cơ sở lý thuyết
2.1 Các công cụ toán học được sử dụng
Việc giải các bài toán chủ yếu dựa vào kiến thức của chương Đạo
hàm và vi phân của hàm một biến số trong tài liệu Giáo trình Giải lOMoARcPSD|47207367
tích 1, có tham khảo một số nội dung trong Applied Calculus – 5th
Edition của Hughes-Hallett cùng một số tài liệu khác trên internet.
2.2 Định nghĩa đạo hàm của hàm một biến[1]
Cho hàm số y=f (x ) xác định trong lân cận của điểm x0. Giới hạn
(nếu có) của tỷ số f (x )– f(x0) được gọi là đạo hàm của hàm số y=f (x ) x – x0 tại ( x ) )
0 và được ký hiệu là f ’ (x0 , y ’ x0 hay dy . dx *Đạo hàm từ một phía
Tương tự như trên, ta có các định nghĩa về đạo hàm bên
trái và bên phải của y=f (x ) tại x0.
Định lý 1: Hàm số y=f (x ) có đạo hàm tại x0 khi và chỉ khi nó có
đạo hàm bên trái và bên phải tại x0 và chúng phải bằng nhau.
2.3 Đạo hàm của hàm hợp Định lý 2: Cho hàm số ( )
u=u(x) có đạo hàm hữu hạn u ’ x0 tại điểm x )
0 còn hàm số y=f (u) có đạo hàm hữu hạn f ’ (u0 tại điểm tương ứng ) u = 0
u (x0 thuộcE(u). Khi đó hàm hợp y=f (u)=f (u (x)) sẽ
có đạo hàm hữu hạn tại điểm x0 và luôn có đẳng thức sau:
y ’(x0 )= y ’(u0 ). u ’(x0 ) hay dy =dy .du dx du dx
2.4 Tính đơn điệu của hàm số
Định lý 3: Điều kiện đủ để hàm tăng nghiêm ngặt
Hàm f (x) khả vi trên (a , b) là hàm tăng trên khoảng (a , b) khi
thỏa mãn những điều kiện sau:
1. f ’(x )≥ 0 với mọi xthuộc (a , b) 2. )
f ’ (x )≢ 0 trên bất kỳ tập E con (a , b nào lOMoARcPSD|47207367
Định lý 4: Điều kiện để hàm khả vi có cực trị:
Nếu hàm số f (x) khả vi tại điểm x0và có cực trị (cực đại hoặc cực tiểu) tại điểm ( x )= 0 này thì f ’ x0 0.
2.5 Khảo sát cực trị và tính lồi, lõm của hàm số
Cho x0 là một cực trị của hàm số f ( x ) :
+Nếu f ’(x ) đổi dấu từ + sang – khi đi qua x0 thì hàm số đạt cực đại tại x0.
+Nếu f ’ (x ) đổi dấu từ – sang + khi đi qua x0 thì hàm số đạt cực tiểu tại x0.
+Nếuf ’ ’(x )>0trong khoảng (a , b) nào đó thì đồ thị hàm số lõm trong khoảng này.
+Nếu f ’ ’(x )<0 trong khoảng (a , b) nào đó thì đồ thị hàm số lồi trong khoảng này.
2.6 Vi phân của hàm số một biến số
Vi phân cấp 1 của hàm số )= (
y=f (x ) tại điểm x ) 0 là df ( x f ’ x0 dx.
2.7 Một số ký hiệu và quy ước ở Bài 1
x là số đơn vị nguyên liệu thô; f (x) là số đơn vị sản phẩm sản
xuất được từx đơn vị nguyên liệu thô.
w là giá nhập về của mỗi đơn vị nguyên liệu thô; p là giá bán của mỗi sản phẩm.
C (x) là chi phí nhậpx đơn vị nguyên liệu thô.
R(x )là doanh thu khi bán f (x) đơn vị sản phẩm.
Các đại lượng trên đều không âm.
2.8 Các câu lệnh Matlab được sử dụng lOMoARcPSD|47207367
clc; clear; close all; Các câu lệnh thiết lập màn hình syms
x; Khai báo biến symbolic x diff(f, n); Tính đạo hàm cấp n
của hàm f subs(f, x, n); Tính giá trị của hàm f tại x = n
x = input(‘ ’); Biến x nhận giá trị nhập vào từ bàn phím
fprintf(‘ %f’, x); In ra màn hình kết quả tính toán disp(‘
‘); in ra màn hình chuỗi ký tự
for i = a:b … end; câu lệnh lặp Giải quyết bài toán Bài 1
Theo đề bài, việc sản xuất ra sản phẩm sẽ bị chi phối bởi:
Lượng nguyên liệu thô đầu vào: x (đơn vị)
Sản lượng của sản phẩm:f (x) (đơn vị)
Giá thành sản phẩm: p ($/đơn vị)
Giá nguyên liệu thô: w ($/đơn vị)
Tổng doanh thu của sản phẩm: R(x )= pf (x) ($)
Tổng chi phí nhập nguyên liệu thô: C (x)=wx ($)
a. Khi lượng nguyên liệu thô x tăng lên, nhà sản xuất sẽ mong
muốn doanh thu R(x ) cũng tăng theo để có thể đạt lợi nhuận
cao hơn, bởi vì nếu f (x) là hàm giảm thì R(x ) cũng giảm trong
khi C (x) luôn tăng theo x, khi đó lợi nhuận của nhà sản xuất
sẽ ngày càng giảm khi sản xuất càng nhiều sản phẩm. lOMoARcPSD|47207367 x >30 f ’(x ) R(x )
Từ R(x )= pf (x) ⇒ R ’(x)= pf ’(x ). Để R(x ) tăng thì ta phải có R ’(x)>0, do đó f
’(x ) cũng > 0. Vậy nên nhà sản xuất sẽ mong muốn f ’(x ) có giá trị dương.
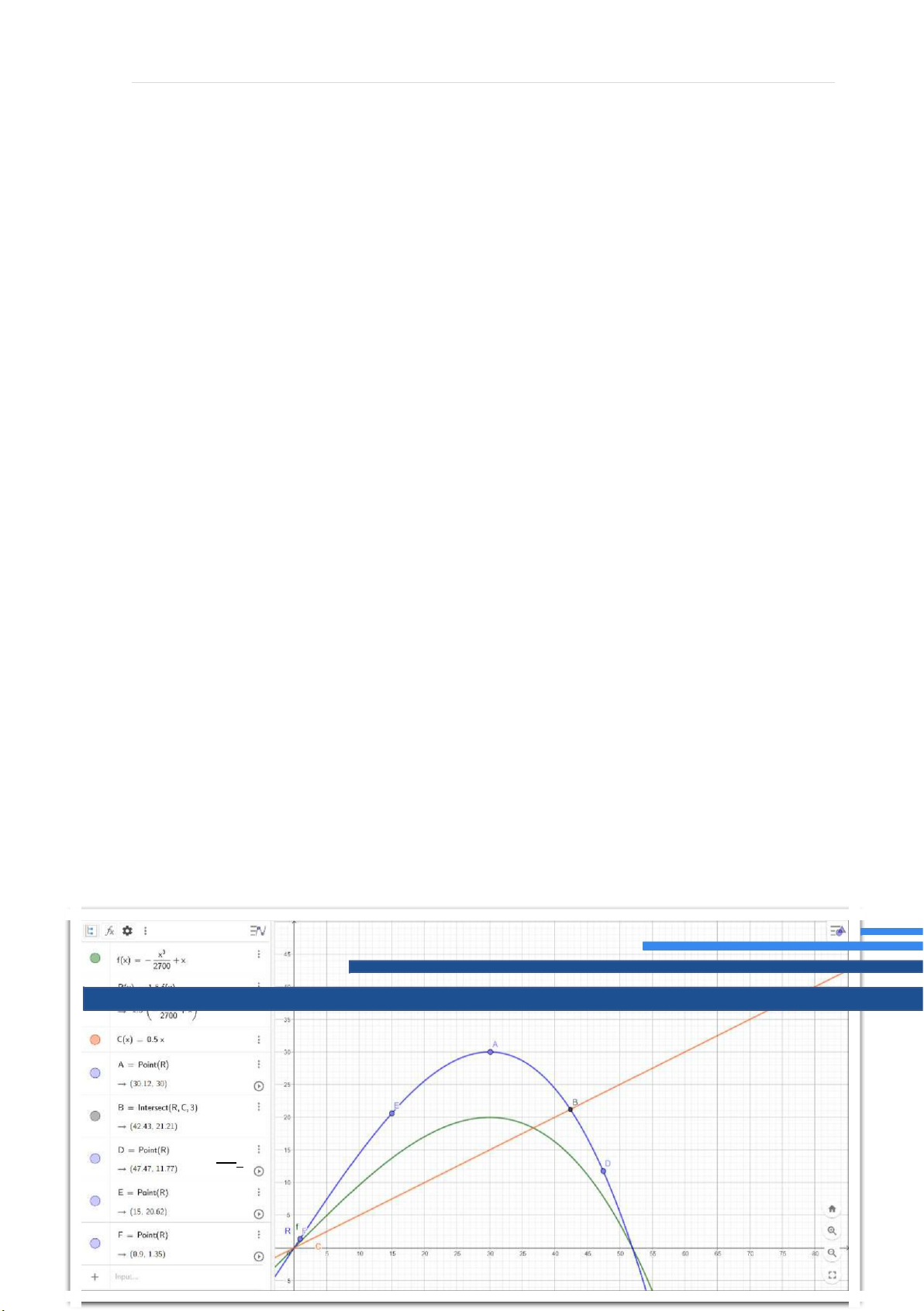
Ví dụ: Với f (x) = −x3 +x, p=1.5 , w=0.5 2700
Ta có f (x) = −x2 +1. Dễ dàng thấy rằng f ’ (x ) dương trên khoảng (0 , 30), 900
khi đó đường doanh thu R(x ) luôn ở trên C (x), ví dụ như tại cái
điểm F, E, A và còn có xu hướng tăng. Khi thì âm khiến cho
giảm dần, đến điểm B thì doanh
thu cân bằng với chi phí còn đến điểm D thì doanh thu đã thấp hơn cả chi phí.
b. Ta có lợi nhuận là hiệu số giữa doanh thu với chi phí, vậy nên nếu đặt ( ( ) (
g x )=R x )– C (x )= pf (x – wx thì g x )chính là lợi nhuận
thu được từ x đơn vị nguyên liệu thô. lOMoARcPSD|47207367
Code Matlab để tính g(x ) với f (x), p , w lấy từ ví dụ của câu a. syms x; for i = 1:5 x = input('x='); c = 0.5*x;
r = 1.5*(-x^3/2700 + x); g = r - c;
fprintf('g(x)=%f',g); disp(' '); end
Giá trị của g(x ) tại một số
giá trị x cho trước, trong ba
trường hợp đầu tiên g(x ) dương cho biết nếu sản
xuất từ x đơn vị nguyên liệu
thô thì nhà sản xuất sẽ có
lãi, ngược lại, ở hai trường
hợp còn lại tương ứng nhà sản xuất sẽ chịu lỗ
c. Với lợi nhuận được tính bằng công thức g(x )= pf (x) – wx, lấy đạo hàm hai vế theo ( )= (
x, ta được g ’ x pf ’ x )– w.
Đặt x0 là điểm cực đại của hàm g(x ) (nếu có). Lợi nhuận g(x ) chỉ có
thể đạt giá trị lớn nhất hoặc tại các điểm cực đại, hoặc tại biên x=0,
ngược lại max g(x ) sẽ không tồn tại. Tại điểm x¿ hàm f có đạo hàm
nên x¿ không phải là điểm biên x = 0 (do f ’ ¿ không tồn tại nên theo
định lý 1, f ’(0) không tồn tại)⇒x¿ = x0 với x0 là điểm cực đại mà tại đó g ( )
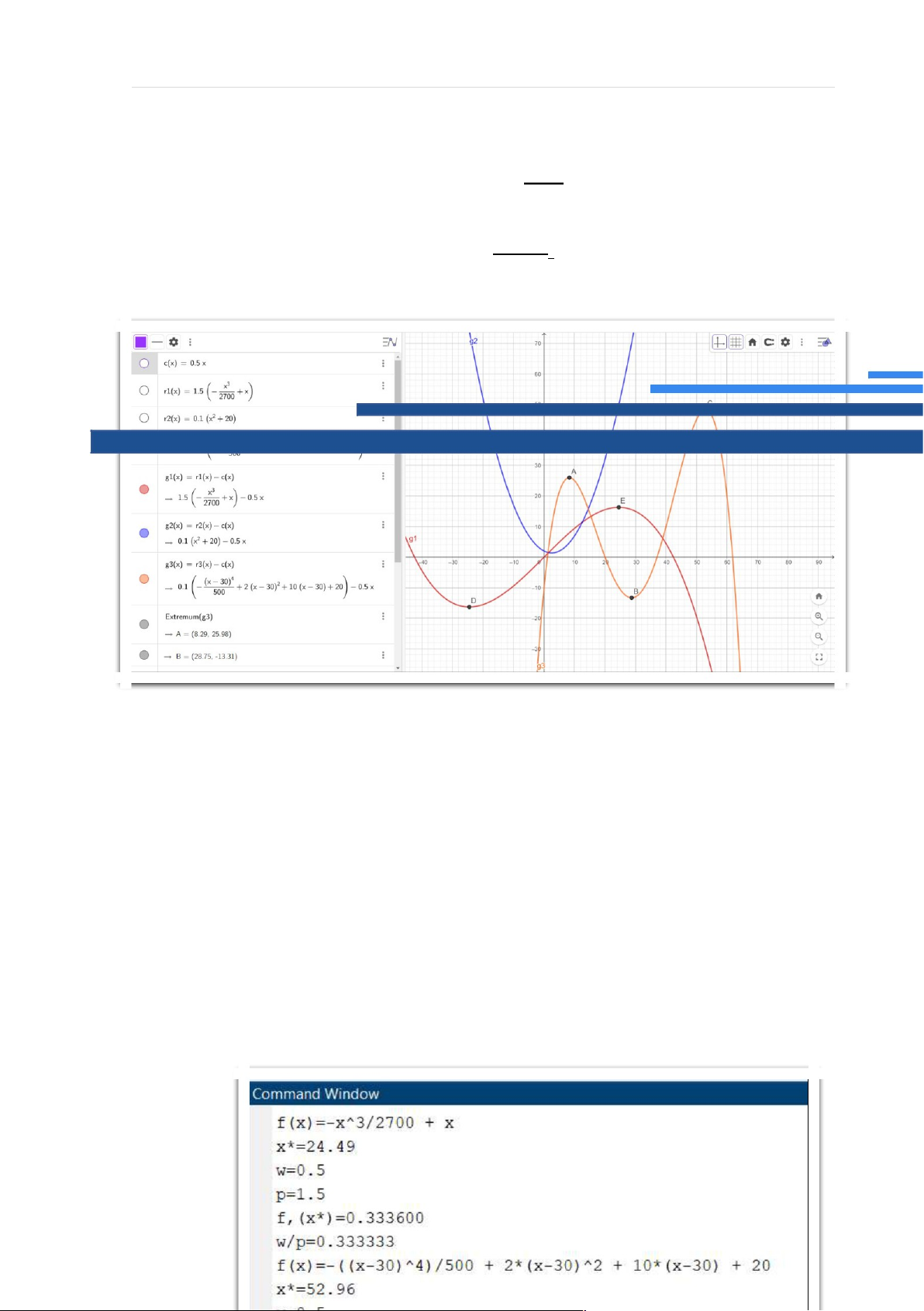
x0 đạt giá trị lớn nhất. Dog ’( x¿)=g ’ (x0 )=0 ⇒ pf ’( x¿)−w=0 ⇒ f ’ ( x¿ )= wp . lOMoARcPSD|47207367 Ví dụ: 3 Hàm g (x ) ( x) x 1
ứng với w=0.5 , p=1.5 và f 1
= – 2700 + x có x¿ ≈
24.49 Hàm g2 ( x)không có giá trị lớn nhất nên ta không xét Hàm (x−30) g 4
3 (x ) ứng với w=0.5 , p=0.1 và f 3 (x) ¿−
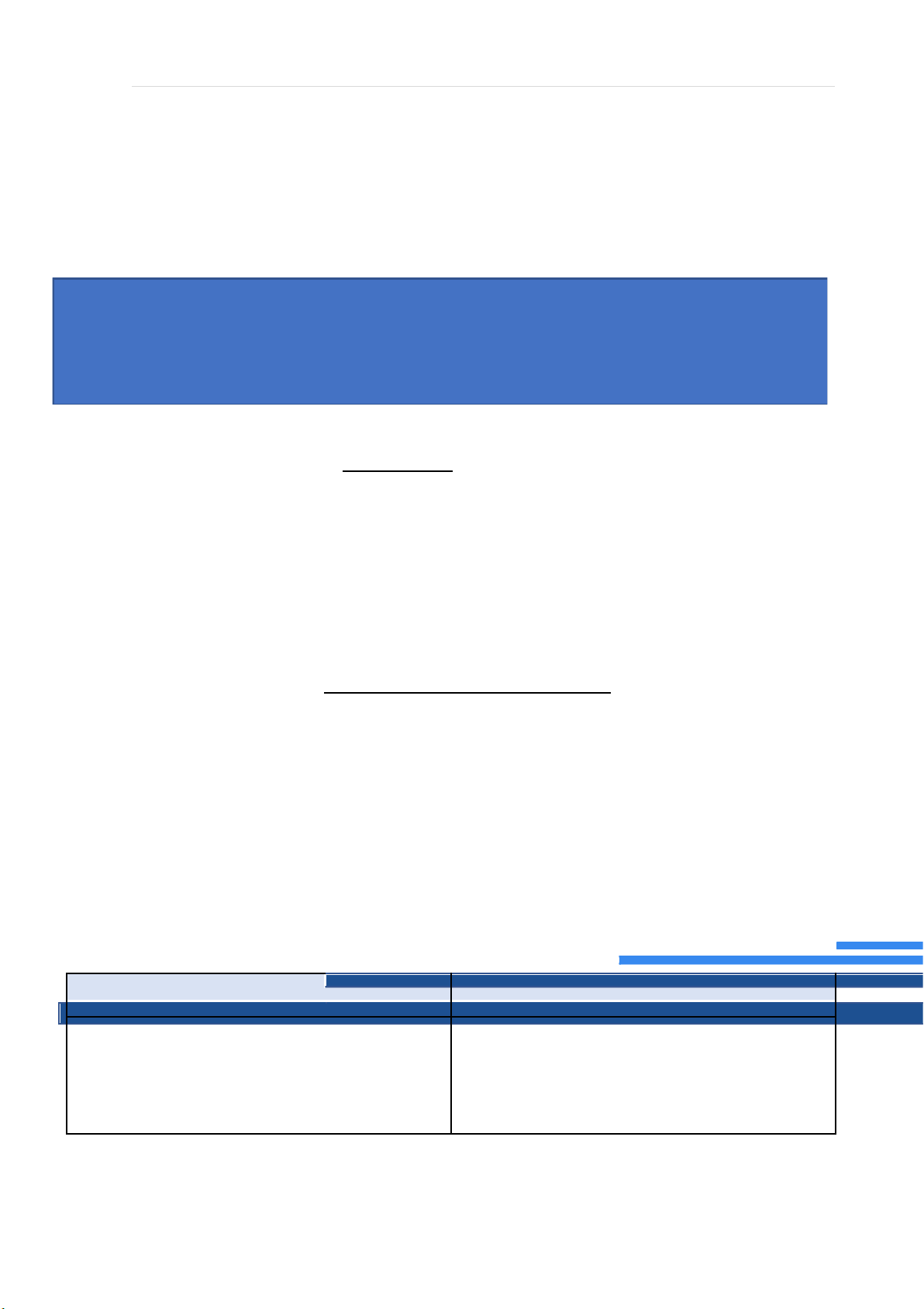
+2(x−30)2 +10(x−30)+20 có 500 x¿ ≈ 52.96 Code Matlab: syms x; for i = 1:2 f = input('f(x)='); n = input('x*='); w = input('w='); p = input('p=');
fprintf('f,(x*)=%f',subs(diff(f),x,n)); disp(' ');
fprintf('w/p=%f',w/p); disp(' '); end lOMoARcPSD|47207367
d. Từ câu c ta có x¿ là một điểm cực đại của hàm g(x )⇒g ’ (x) đổi dấu từ
dương sang âm khi đi qua điểm x¿. Lấy đạo hàm hai vế của phương
trình g ’( x)= pf ’(x )– w ta được g ’ ’ (x)= pf ’ ’ (x). Do f ’ ’(x¿) tồn tại nên g ’ ’(x¿)
tồn tại, đồng thời f ’ ’(x¿) và g ’ ’ (x¿) cùng dấu do p > 0. Mặt khác, g
’ ’(x¿) tồn tại nên hàm g ’( x) khả vi tại x¿ ⇒ g ’( x) liên tục tại x¿. Suy ra: lim ¿ x→ x
Vì f ’ ’(x¿)≠ 0 nên g ’ ’(x¿)≠ 0, giả sử g ’ ’(x)>0 trên một ¿−¿ g' ( x)= lim ¿ ¿
x →x¿ +¿ g ' (x)=g ' (x¿ )=0 ¿
khoảng nào đó chứa x¿, khi đó g ’( x) là hàm tăng. Bên
cạnh đó g ’( x) mang dấu dương ở bên trái điểm x¿ và
mang dấu âm ở bên phải điểm x¿ nên ta phải có: lim ¿
x→ x¿−¿ g ' (x)>0 lim ¿ ¿ (vô lý)
x→ x¿ +¿ g' ( x)<0 ¿
Vậy phải có g ’ ’( x¿ )<0⇒f ’ ’ (x¿)<0 hay f ’ ’(x¿) có giá trị âm. Ví dụ:
Tính f ’ ’(x¿) với hai ví dụ ở câu c: for i = 1:2
f = input('f(x)='); n = input('x*=');
fprintf('f' (x)=%f',subs(diff(f,2),x,n)); disp(' '); end lOMoARcPSD|47207367
e. Từ câu c ta có f ’(x¿)= wp , đạo hàm hai vế theo w ta được: d x¿ 1 1
f ' ' (x¿ ). = ⇒ d x¿ = dw p dw pf ' '(x¿)
Ví dụ: Với x¿= √w, ta có: d x¿ ¿ 1 f ' ( x¿ ) x¿2 f ' ' (x ¿ 2 x¿ dw √ 2 w = ) p = p 1 1 1 1 = ¿ ¿ = ¿ = pf ' ' (x ) 2 x 2 x 2√w p . p f. Do d x¿ 1 = ¿
< 0 với mọi w nên x¿ là hàm nghịch biến theo biến w dw pf ' ' (x)
trên tập xác định của nó. Giả sử ta đang ở mức lợi nhuận
cao nhất. Nếu giá nhập nguyên liệu thô w tăng thì x¿ sẽ giảm,
điều đó có nghĩa là cần phải giảm nhập nguyên liệu thô này
về còn đúng x¿ đơn vị thì sẽ lại thu được lợi nhuận tối đa g(x¿). \ 3 Sự thay đổi của = x
x¿ theo w : p 1.5 , f (x )=¿ – 2700 +x
D (w = 0.1), F (w = 0.5), H (w = 1.4) lOMoARcPSD|47207367 Bài 2[2]
Tỉ lệ thay đổi trung bình (Average Rate of Change) Khái niệm
Là tỷ số giữa sự thay đổi của đại lượng y và sự thay đổi
của đại lượng t, trong đó y là một hàm theo biến t. Cách tính
Với y=f (t ), tỷ lệ thay đổi trung bình của y giữa t=a và t=b được tính theo công thức: ∆ y
f (b)−f (a)
Tỷ lệ thay đổi trung bình = ∆ t = b−a
Tỷ lệ thay đổi trung bình giữa y1 (tại A) và y2 (tại B) chính là hệ
số góc hay độ dốc của cát tuyến đi qua A và B (=1)
Dễ thấy rằng nếu tỷ lệ thay đổi trung bình của một hàm là
hằng số thì hàm đó là tuyến tính. lOMoARcPSD|47207367
Đơn vị của tỉ lệ thay đổi trung bình là đơn vị của y/đơn vị của t.
Ví dụ: Nếu y (m) và t (s), đơn vị là m/s, nếu y (đ) và t (kg), đơn vị là đ/kg. Ý nghĩa
Tỷ lệ thay đổi trung bình được dùng để khảo sát sự thay đổi trung
bình của một đơn vị theo thời gian hoặc theo một đơn vị khác
Ví dụ 1: Một hồ cá khi mới thả có 1000 con cá giống, sau 24 tháng
số cá trong hồ chỉ còn 760 con. Tỷ lệ thay đổi trung bình của số
lượng cá trong hồ là 760−1000 24 = -10 (con/tháng).
Ví dụ 2: Nếu s là quãng đường đi được và t là thời gian di chuyển thì
tỷ lệ thay đổi trung bình của s theo t chính là tốc độ trung bình của
chuyển động. Giả sử quãng đường đi được của một chiếc xe là
100km và thời gian di chuyển là 4h thì tỷ lệ thay đổi trung bình của
quãng đường theo thời gian = tốc độ trung bình của chiếc xe = 1004 = 25 (km/h).
Độ thay đổi tương đối (Relative Change) Khái niệm:
Khi đại lượng P thay đổi một lượng P từ P0 sang P1 thì ta gọi
P là độ thay đổi tuyệt đối của P.
Độ thay đổi tương đối của P là tỷ số giữa độ thay đổi
tuyệt đối của P và P0. Cách tính
Độ thay đổi tương đối được tính bằng công thức: ∆ P P
Độ thay đổi tương đối = 1−P0 P0 = P0 lOMoARcPSD|47207367
Độ thay đổi tương đối là một số không thứ nguyên và
thường được biểu diễn dưới dạng phần trăm. Ý nghĩa:
Độ thay đổi tương đối được dùng để khảo sát sự ảnh hưởng của sự
thay đổi đối với vật thể khảo sát. Sự ảnh hưởng có thể tốt hoặc xấu.
Ví dụ 1: Tăng giá của một chiếc bút từ 15000 lên 20000, độ thay đổi
tương đối của giá bút là 20000 – 15000 15000 = 30%.
Ví dụ 2: Tỉ lệ thay đổi tương đương (hệ số co giãn): Biểu hiện
cho sự ảnh hưởng của sự thay đổi số lượng khi thay đổi giá,
thường được dùng cho toán kinh tế.
Độ co giãn = | Độthay đổi tương đươngcủa sảnlượng
Độ thay đổitương đươngcủa giá |
Ví dụ 3: Tốc độ tăng trưởng hàng năm của nền kinh tế một
quốc gia là 7% có nghĩa là độ thay đổi trung bình của giá trị
nền kinh tế của năm sau so với năm trước đó là 7%.
Tương quan giữa hai giá trị
Tỉ lệ thay đổi trung bình
Độ thay đổi tương đối
So sánh mức độ thay đổi của đại Dùng để so sánh mức độ thay
lượng này theo mức độ thay đổi đổi của một đại lượng với chính của đại lượng kia nó lOMoARcPSD|47207367
Dùng để khảo sát sự thay đổi Để đánh giá ảnh hưởng của sự
của một đại lượng đối với một thay đổi đối với đại lượng ban đại lượng khác đầu
Sự thay đổi dân số Việt Nam qua các giai đoạn (1921 – 2008)[3] Mức tăng Mức tăng Giai đoạn (nghìn người/năm) (%) 1921 - 1943 319,5 37,62% 1943 - 1951 56,1 2% 1951 - 1957 753 18,18% 1957 - 1976 1135,8 58,52% 1976 - 1985 1190,2 19,89% 1985 - 2008 1142,9 36,8% lOMoARcPSD|47207367 P a g e | 19 Bài 3
a. Từ bài 2, ta có sự thay đổi tương đối (relative change) của bán kính
R được định nghĩa: khiR thay đổi một lượng ∆ R thì độ thay đổi tương đối là: ∆ R dR r = R R = R
Khi F thay đổi một lượng ∆ F thì sự thay đổi tương đối của F là: ∆ F dF F' × dR F' × R ×dR F'×R dR F'×R r (*) F = ≈ = = = × = × rR F F F F × R F R F
Mặt khác: F = k × R4 ⇒ F ’=4 × k × R3 (**)
Từ (*) và (**), ta được: r F ≈ 4 × rR Code Matlab: syms R; for i = 1:2 k = input('k='); F = k*R^4; x = input('R0='); y = input('R1=');
fprintf('Độ thay đổ8i tương đổ;i cu8a R là rR = %f', (y - x)/x); disp(' ');
fprintf('Độ thay đổ8i tương đổ;i cu8a F là rF = %f',
(subs(F,R,y)-subs(F,R,x))/subs(F,R,x)); disp(' '); end
b. Vì r R = 5% nên theo chứng minh ở câu a, r F ≈ 4 × 5% = 20% lOMoARcPSD|47207367 P a g e | 20
Ta có thể phát biểu như sau:
Khi bán kính của mạch máu tăng lên 5% thì khi đó thông lượng
máu (lượng máu lưu thông trong mạch đi qua một điểm cho trước
trong một đơn vị thời gian) sẽ tăng lên khoảng 20% so với ban đầu.
Chú thích và tài liệu tham khảo Trích dẫn
[1] 2.2 – 2.6 Giáo trình giải tích 1, NXB. ĐHQG TP. HCM
[2] Applied Calculus – 5th Edition, Hughes-Hallett, NXB. WILEY
[3] [https://vneconomy.vn/dan-so-viet-nam-qua-cac-thoi-ky.htm]
Phần mềm được sử dụng:
Vẽ đồ thị: Geogebra Classical Tính toán: Matlab Mẫu bìa báo cáo:
[https://m.facebook.com/story.php?
story_fbid=pfbid0XFxHqfeQxkpVDSxELa9V2BqG83xTYhN55Rz
AME5DTTNLUF6CZXr7sJwDBnzt37WLl&id=106029178927680 &mibextid=qC1gEa] EN