KHOA KHOA HỌC ỨNG DỤNG

ĐẠI HỌC QUỐC GIA TP. HỒ CHÍ MINH

TRƯỜNG ĐẠI HỌC BÁCH KHOA

🙞······🙜

BÁO CÁO BÀI TẬP LỚN MÔN GIẢI TÍCH 1

GV hướng dẫn: TS. Huỳnh Thái Duy Phương

Đề tài số: 04

Lớp: L01

Nhóm: 04

Danh sách sinh viên thực hiện:

Thành phố Hồ Chí Minh, tháng 12, năm 2023

LỜI NÓI ĐẦU

Giải tích 1 là một trong những môn học nền tảng ở trình độ Đại học đóng góp một vai trò vô cùng quan trọng, tạo cơ sở để học và nghiên cứu các ngành kỹ thuật. Môn học được áp dụng phổ biến trong các lĩnh vực nghiên cứu và ứng dụng toán học:

• Hiểu rõ hơn về biến đổi và biến thiên: Giải tích giúp chúng ta hiểu rõ hơn về sự biến thiên của các đại lượng, như độ dốc, tốc độ, gia tốc và tỷ lệ thay đổi của chúng. Điều này cung cấp cho chúng ta cái nhìn sâu sắc về các quy luật tự nhiên và quá trình biến đổi trong thế giới thực.
• Ứng dụng trong khoa học và kỹ thuật: Giải tích là công cụ cơ bản trong nhiều lĩnh vực khoa học và kỹ thuật, bao gồm vật lý, hóa học, kỹ thuật điện, khoa học máy tính và nhiều lĩnh vực khác. Nó giúp mô hình hóa và phân tích các hiện tượng tự nhiên và xây dựng các mô hình toán học để giải quyết các vấn đề thực tế.
• Ứng dụng trong kinh tế và tài chính: Giải tích được áp dụng rộng rãi trong lĩnh vực kinh tế và tài chính để phân tích và dự đoán các xu hướng, tối ưu hóa quyết định và định giá tài sản. Các công cụ giải tích như vi phân và tích phân đóng vai trò quan trọng trong việc phân tích hàm số và tính toán các chỉ số kinh tế.
• Phát triển tư duy logic và khả năng giải quyết vấn đề: Học Giải tích đòi hỏi sự logic, quyết đoán và khả năng giải quyết vấn đề. Nó giúp phát triển tư duy phân tích và khả năng áp dụng các phương pháp toán học để giải quyết các vấn đề phức tạp.
• Đóng góp vào sự phát triển của toán học: Giải tích là một trong những lĩnh vực cơ bản và quan trọng nhất của toán học. Nó đã và đang đóng góp rất nhiều vào sự phát triển của toán học và mang lại những khám phá và ý tưởng mới cho ngành này.

Tóm lại, Giải tích không chỉ mang lại những kiến thức cơ bản về biến thiên và biến đổi, mà còn có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau. Nó cung cấp một cách tiếp cận toán học sâu sắc và phát triển tư duy logic và giải quyết vấn đề.

Nhóm 04 lớp L01 xin chân thành gửi lời cảm ơn sâu sắc đến Khoa Khoa học Ứng dụng nói chung và Thầy Hữu Thái Duy Phương nói riêng đã luôn cống hiến, giảng dạy hết mình để xây dựng môn học Giải tích 1, làm nền tảng cho bao thế hệ kỹ sư tài năng nước Việt Nam.

Trong quá trình viết bài báo cáo, chúng em cũng mắc ít nhiều sai sót cần có sự giúp đỡ từ phía giảng viên bộ môn. Đồng thời, cũng không thể thiếu tinh thần đoàn kết của các thành viên trong nhóm. Để hoàn thành được bài tập lớn này, không phải là công sức của riêng ai mà đó là sự nỗ lực của cả nhóm. Tuy có ít cơ hội được ngồi làm việc trực tiếp với nhau, nhưng các bạn trong nhóm vẫn tận tình giúp đỡ nhau qua những cuộc gặp gỡ trực tuyến, qua những dòng tin nhắn trao đổi, thảo luận và giải quyết những vấn đề chung của nhóm để có được bài báo cáo chỉn chu như ngày hôm nay.

Tuy vậy, do vẫn còn hạn chế về mặt kiến thức nên nhóm sẽ gặp phải những sai sót không đáng có. Nhóm luôn sẵn sàng tiếp nhận những ý kiến đóng góp và sửa chữa. Kính mong được nhận góp ý từ Thầy để giúp nhóm chúng em phát triển hơn.

Một lần nữa, chúng em - nhóm 04 lớp L01 - xin gửi lời cảm ơn sâu sắc nhất đến Thầy và xin chúc Thầy có nhiều sức khỏe, thành công trong sự nghiệp.

TÓM TẮT NỘI DUNG BÁO CÁO

Đề tài báo cáo

1. Thiết lập các phương trình vi phân mô tả sự lây lan dịch tễ.
2. Đưa ra ví dụ thực tế cụ thể để nêu rõ ý nghĩa nghiệm của phương trình.
3. Nhập n và hàm y  f(x) tho´a x  x(t) , viết đoạn code tìm yⁿ (đạo hàm cấp).

y  y(t)



Kiến thức cần có

• Sử dụng các kiến thức cơ bản trong Giải tích 1 (giải phương trình vi phân cấp 1, …).
• Có kiến thức cơ bản về lập trình trên phần mềm MATLAB.

Vận dụng

Những kiến thức, kinh nghiệm và ý nghĩa thực tế được rút ra trong quá trình nghiên cứu đề tài.

Đề mục Trang

LỜI NÓI ĐẦU .............................................................................................................................

LỜI CẢM ƠN ..............................................................................................................................

TÓM TẮT NỘI DUNG BÁO CÁO ............................................................................................

MỤC LỤC ...................................................................................................................................

Yêu cầu 1. Thiết lập các phương trình vi phân mô tả sự lây lan dịch tễ 1

• 1. Mô hình SIR 1
  2. Mô hình SIR được biểu diễn bằng hệ phương trình vi phân 2
  3. Ước tính số người đã nhiễm bệnh sau khi dịch bệnh kết thúc 2
  4. Ước lượng đỉnh dịch 3
  5. Các biến thể và mô hình phát triển 4

Yêu cầu 2. Đưa ra ví dụ thực tế cụ thể để nêu rõ ý nghĩa nghiệm của phương trình 5

• 1. Ví dụ 1 5
     1. Lời giải 5
     2. Ý nghĩa 5
  2. Ví dụ 2 6
     1. Lời giải 6
     2. Ý nghĩa 6

Yêu cầu 3. Viết đoạn code tìm đạo hàm cấp 7

• 1. Giới thiệu về phần mềm MATLAB 7
  2. Sơ đồ khối của chương trình 7
  3. Các lệnh được sử dụng trong chương trình 8
  4. Các khối lệnh được sử dụng trong chương trình 8
  5. Lập trình trên phần mềm MATLAB 9
     1. Đề bài 9
     2. Phần lập trình 9
     3. Màn hình kết quả 9

TÀI LIỆU THAM KHẢO ...........................................................................................................

Yêu cầu 1. Thiết lập các phương trình vi phân mô tả sự lây lan dịch tễ

Mô hình SIR

Mô hình SIR là một mô hình toán học trong epidemiology (dịch tễ học) được sử dụng để mô tả và dự đoán sự lan truyền của các bệnh truyền nhiễm trong một quần thể.

Cụ thể, SIR đại diện cho ba nhóm chính của quần thể:

• S (Susceptible): Những người trong nhóm này chưa mắc bệnh nhưng có thể mắc nếu tiếp xúc với người nhiễm bệnh.
• I (Infected): Những người trong nhóm này đã mắc bệnh và có khả năng lây nhiễm cho những người khác.
• R (Recovered/Removed): Những người trong nhóm này đã hồi phục hoặc bị loại bỏ khỏi quá trình lây nhiễm, có khả năng miễn dịch và không thể lây nhiễm nữa.

Mô hình SIR giả định rằng quá trình lây nhiễm diễn ra theo một số luật lệ cơ bản, bao gồm tỷ lệ tiếp xúc giữa những người khỏe mạnh và người nhiễm bệnh, tỷ lệ chuyển đổi từ người khỏe mạnh sang người nhiễm bệnh, và tỷ lệ hồi phục.

Một số biến thể của mô hình SIR bao gồm các yếu tố như tỉ lệ tử vong, sự gia tăng tự nhiên của dân số, việc áp dụng biện pháp kiểm soát (như cách ly, tiêm chủng), và thậm chí là sự biến đổi của bệnh dịch theo thời gian.

Mô hình SIR cung cấp một cách tiếp cận cơ bản nhưng hữu ích để hiểu và dự đoán sự lan truyền của các bệnh truyền nhiễm trong các quần thể, và nó đã được sử dụng rộng rãi trong việc đánh giá và lập kế hoạch phòng chống dịch bệnh.

Bài tập lớn môn Giải tích 1 Khóa K23 Trang 1/9

Mô hình SIR được biểu diễn bằng hệ phương trình vi phân

S^′ = − β SI.

N

I^′ = β SI − αI.

N

R^′ = αI.

Trong đó:

Β: là hệ số truyền nhiễm.

α: là hệ số hồi phục.

S^′, I^′, R′: là tốc độ biến đổi của các nhóm theo thời gian.

Xét t = 0 là thời điểm xuất hiện những người đầu tiên bị nhiễm bệnh: S(0) = S0, I(0) = I0, S0 + I0 = N.

Nhận thấy S(t) và R(t) là hàm đơn điệu theo t và bị chặn giữa 0 và N. Ta nhận được kết quả S và R hội tụ khi t → +∞. Do đó R^′ → 0, I → 0 và có thể hiểu rằng dịch luôn chấm dứt.

Ước tính số người đã nhiễm bệnh sau khi dịch bệnh kết thúc

Số lượng người từng bị bệnh ta ước lượng R_∞, giới hạn của R khi t → +∞.

I = R′

α

→ S^′ + β

Nα

R^′S = 0.

Ta nhân cho mỗi vế với ^β

exp (

Nα

R)sau đố lấy tích phân hai vế ta được:

β

S. exp (

Nα

R) = C (1)

Do R0 = 0 nên C = S0.

Ta cho t → +∞ và S_∞

= N − R_∞

→ (N − R_∞

β

. exp (

)

Nα

R) = S₀

Đặt về trái là F(R_∞). Ta có F là một hàm giảm. Với R_∞ → 0 → R_∞ ≤ 0 → S₀ = N − R₀ ≤ N. R_∞ → N → R_∞ ≤ N → S₀ = N − R₀ ≥ 0.

Suy ra, phương trình có nghiệm duy nhất nằm giữa 0 và N. Nghiệm này có thể tính xấp xỉ bằng phương pháp số.

Tổng kết: R_∞ cho ta biết tổng số người từng bị bệnh sau khi dịch bệnh chấm dứt.

Khóa K23

Bài tập lớn môn Giải tích 1 Trang 2/9

Ước lượng đỉnh dịch

Đỉnh dịch là thời điểm mà số người mắc bệnh đạt giá trị lớn nhất hay còn gọi là Imax. I giảm khi và chỉ khi S < N.

𝞀

I tăng khi và chỉ khi S > N.

𝞀

Với ρ = β (tỷ suất tái tạo cơ bản).

α

Nếu ρ < 1 → N > S → I luôn giản hay dịch bệnh sẽ không bùng phát.

𝞀

Nói cách khác, I_max = I0.

Nếu ρ > 1 và N < S

0

𝞀

→ I sẽ tăng cho đến khi S = N sau đó giảm.

𝞀

Khi đó, Imax khi và chỉ khi S = N .

𝞀

Thay giá trị này của S vào (1) ta được:

^N . exp (𝞀 R) = S → R = N ln S

₀ (

ρ).

𝞀 N 𝞀 N

0

Ta có I = N – S – R.

Suy ra, I

= N [1 − 1 − 1 S0

max

ln (ρ)].

𝞀 𝞀 N

Bài tập lớn môn Giải tích 1 Khóa K23 Trang 3/9

Các biến thể và mô hình phát triển

Khóa K23

Mô hình SIR đã là một công cụ quan trọng trong dịch tễ học và y tế công cộng, nhưng trong quá trình phát triển, nhiều biến thể và mô hình mở rộng hơn đã được tạo ra để cải thiện khả năng dự đoán và đáp ứng với các tình huống y tế phức tạp hơn.

Các biến thể và mô hình phát triển từ mô hình SIR bao gồm:

• Mô hình SEIR: Mở rộng từ SIR, mô hình này bao gồm một giai đoạn tiềm ẩn (Exposed) trước khi người nhiễm bệnh trở nên lây nhiễm. Điều này cho phép mô hình mô tả sự chuyển đổi từ khi mắc bệnh đến khi trở nên lây nhiễm.
• Mô hình SIRD: Thêm một phần tử 'Removed' được chia thành hai phần, một cho những người đã hồi phục và một cho những người đã qua đời, để mô tả sự biến đổi của dịch bệnh và tỷ lệ tử vong.
• Mô hình Agent-Based Models (ABM): Đây là một loại mô hình mô phỏng dựa trên đối tượng, mô phỏng từng cá nhân trong quần thể. ABM cho phép mô phỏng các chi tiết cụ thể hơn về hành vi cá nhân, tiếp xúc và phản ứng với biện pháp kiểm soát, giúp hiểu rõ hơn về sự lan truyền của bệnh.
• Mô hình mạng lưới (Network Models): Sử dụng để mô phỏng mối quan hệ giữa các cá nhân hoặc cộng đồng thông qua mạng lưới. Các mô hình này có thể áp dụng để phân tích sự lan truyền của bệnh trong các môi trường mạng lưới phức tạp như các mạng xã hội.
• Mô hình dự đoán sử dụng Machine Learning và AI: Các phương pháp học máy và trí tuệ nhân tạo được áp dụng để dự đoán sự lan truyền của dịch bệnh dựa trên dữ liệu lịch sử và các yếu tố biến đổi, giúp cải thiện khả năng dự đoán và quản lý dịch bệnh.

Những mô hình này cung cấp cái nhìn sâu hơn và linh hoạt hơn trong việc mô phỏng, dự đoán và đánh giá các biến đổi phức tạp của dịch bệnh trong y tế cộng đồng. Sự phát triển của các mô hình này làm gia tăng khả năng hiểu biết và quản lý trong việc ứng phó với các tình huống y tế khẩn cấp.

Bài tập lớn môn Giải tích 1 Trang 4/9

Yêu cầu 2. Đưa ra ví dụ thực tế cụ thể để nêu rõ ý nghĩa nghiệm của phương trình

Ví dụ 1

Tốc độ lây lan của một dịch bệnh tỷ lệ với số người nhiễm bệnh và số người không nhiễm bệnh. Ở một thị trần có 5000 người, vào lúc đầu tuần thì có 160 người mắc bệnh, đến cuối tuần thì con đã đạt 1200 người. Sau bao lâu thì 80% dân cư nhiễm bệnh?

(Gợi ý: x tỷ lệ với u và v tức là x-kuy)

Lời giải

Gọi y(t) là số người nhiễm bệnh theo t (ngày).

Suy ra ^dy là tốc dộ lây lan và 500  y(t) là số người chưa nhiễm bệnh.

dt

Vì ^dy tỷ lệ với y và 500  y(t) nên:

dt

dy  ky500  y  dy  kdt  1 ln y

 kt  C (tích phân hai vế)

dt y5000  y

5000

y  5000

Với y(0)  160

y(7)  1200



, ta có hệ:

1 ln | 160

| = 0K + C

C = 1

ln 4

5000

{

1

5000

160−5000

ln | 1200

1200−5000

| = 7K + C

 { 5000

K = 1

35000

121

ln 363

38

1 𝑦

𝑙𝑛 |

1

| = 𝑙𝑛

363

𝑡 +

1 4

𝑙𝑛

5000

𝑦 − 5000

35000 38

5000

121

Yêu cầu bài toán tương đương:

1

𝑙𝑛 |

5000

1

| = 𝑙𝑛

363

𝑡 +

1 4

𝑙𝑛

5000

5000 ∗ 80% − 5000

35000 38

5000

121

 t  14,9 (nga`y)

Ý nghĩa

Sau gần 14,9 ngày thì 80% dân cư nhiễm bệnh.

Bài tập lớn môn Giải tích 1 Khóa K23 Trang 5/9

Ví dụ 2

Trong một cộng đồng dân cư có n người, khi dịch cúm xuất hiện, tốc độ lây lan bệnh (tốc độ biến động số người mắc bệnh theo số ngày) tỷ lệ thuận với số người nhiễm bệnh và số người chưa nhiễm bệnh.

Giả sử cộng đồng có 2000 người và ban đầu có 1 người nhiễm bệnh, sau 20 ngày, số người mắc bệnh là 15.

Xác định số người nhiễm bệnh sau 2 tháng?

Lời giải

Gọi y(t) là số người nhiễm bệnh theo t (ngày).

Suy ra ^dy là tốc dộ lây lan và n  y(t) là số người chưa nhiễm bệnh với n  2000 .

dt

Vì ^dy tỷ lệ với y và 2000  y

dt

^dy = ky (2000 - y)  ^dy

nên:

= kdt  tích phân hai vế ta được ¹

ln | y

| = kt + C (1)

dt

Tại t  0, y  1

t  20, y  15



y(2000−y)

, ta có hệ:

2000

y−2000

¹ ln | 1

| = 0K + C

C = 1

ln 1

{2000 1−2000

 { 2000

1999

1

2000

ln | 15

15−2000

| = 20K + C

K = 1

40000

ln 5997

397

Thế C và K vào phương trình (1) ta được:

¹ ln | y

| = ¹

ln 5997 t + 1

ln 1

2000

y−2000

40000

397

2000

1999

Sau hai tháng t= 60 (ngày) ta được:

¹ ln | y

|= ¹

ln 5997.60+ ¹

ln 1

2000

y−2000

40000

397

2000

1999

 y  1266 (ngn6`i)

Ý nghĩa

Số người nhiễm bệnh sau 2 tháng là gần bằng 1266 người.

Khóa K23

Bài tập lớn môn Giải tích 1 Trang 6/9

Yêu cầu 3. Viết đoạn code tìm đạo hàm cấp

Giới thiệu về phần mềm MATLAB

• MATLAB (viết tắt của matrix laborary) là phần mềm cung cấp môi trường tính toán số và lập trình.
• Nó cho phép theo tác với ma trận, vẽ biểu đồ với hàm và số liệu, hiện thực thuật toán, tạo ra giao diện người dùng, bao gồm C, C++, Java và Fortan; phân tích dữ liệu, phát triển thuật toán, tạo các kiểu mẫu và ứng dụng.
• Nó là công cụ hỗ trợ đắc lực cho bạn trong việc tính toán, vẽ các hình, vẽ biểu đồ thông dụng cả thực thi các phương pháp tính toán.
• Trên nền tảng và các thuật toán có trong MATLAB, ta ứng dụng vào việc tạo một chương

trình tìm đạo hàm cấp (Phiên bản MATLAB được sử dụng).

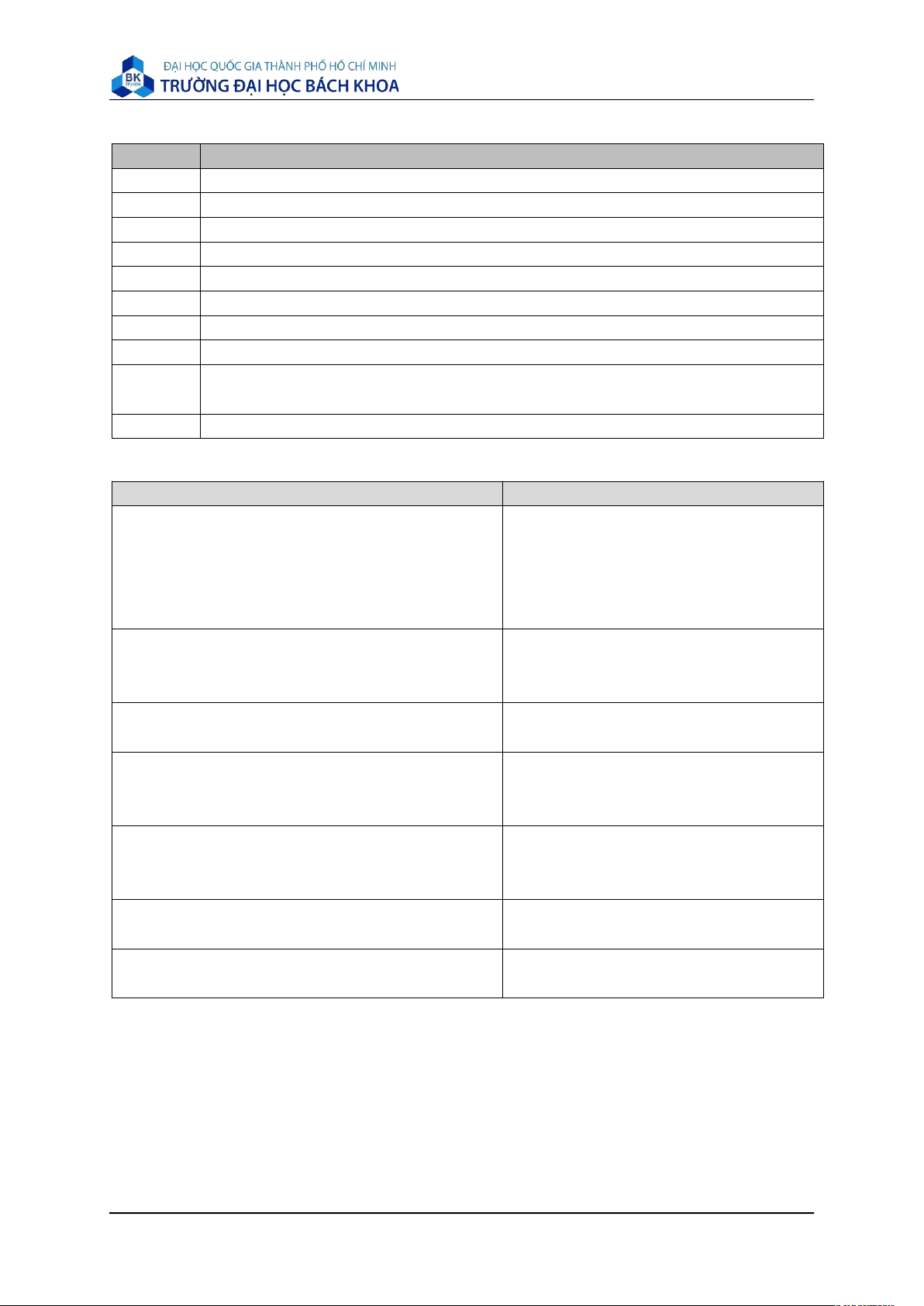
Sơ đồ khối của chương trình

Khai báo biến kí hiệu t và x

Nhập giá trị cho x(t) và y(t)

Nhập bậc của đạo hàm từ bàn phím

Tìm t theo x

Thay thế t tìm được vào phương trình y(t)

Tính đạo hàm bậc n của y theo x

Hiển thị giá trị của đạo hàm bậc n của y theo x

Bài tập lớn môn Giải tích 1 Khóa K23 Trang 7/9

Các lệnh được sử dụng trong chương trình

Các khối lệnh được sử dụng trong chương trình

Khóa K23

Bài tập lớn môn Giải tích 1 Trang 8/9

Lập trình trên phần mềm MATLAB

Đề bài

Nhập n và hàm y  f(x) tho´a x  x(t) , viết đoạn code tìm yⁿ (đạo hàm cấp)

y  y(t)



Phần lập trình

syms t x; % Khai báo biến ký hiệu t và x

% Nhập giá trị cho x(t) và y(t)

xt = input('Nhập phương trình x(t): '); yt = input('Nhập phương trình y(t): ');

n = input('Nhập bậc của đạo hàm cần tính: '); % Nhập bậc của đạo hàm từ bàn phím

% Tìm t theo x

t_x = solve(xt == x, t); t_x = simplify(t_x);

% Thay thế t tìm được vào phương trình y(t)

y_x = subs(yt, t, t_x);

% Tính đạo hàm bậc n của y theo x dy_dx = simplify(diff(y_x, x, n));

% Hiển thị giá trị của đạo hàm bậc n của y theo x

disp(['Giá trị của đạo hàm bậc ', num2str(n), ' của y theo x là:']); disp(dy_dx);

Màn hình kết quả

Bài tập lớn môn Giải tích 1 Khóa K23 Trang 9/9

TÀI LIỆU THAM KHẢO

1. Nguyễn Đình Huy, “Giáo trình Giải tích 1”, NXB ĐHQG, 2016.
2. Nguyễn Đình Huy, Nguyễn Quốc Lân, Nguyễn Bá Thi, Trần Lưu Cường, Đậu Thế Cấp, Huỳnh Bá Lân, “Lý thuyết chuỗi và phương trình vi phân”, NXB GD, 2006.
3. James Stewart – Thomson Brooks Cole, “Calculus early transcendentals”, 2008.
4. C. Henry Edwards, David E. Penney, David T. Calvis, “Differential Equations and

Boundary Value Problems. Computing and Modeling – Pearson”, 2014.