lOMoARcPSD|47207367 lOMoARcPSD|47207367
ĐẠI HỌC QUỐC GIA THÀNH PHỐ HỒ CHÍ MINH
TRƯỜNG ĐẠI HỌC BÁCH KHOA 
BÁO CÁO BÀI TẬP LỚN 2 XÁC SUẤT THỐNG KÊ
GVHD: Nguyễn Kiều Dung
Khoa Kỹ thuật hóa học – Nhóm 7 Danh sách thành viên: STT Họ và tên MSSV Lớp Kí tên 1
Trần Đức Hoàng Huy 1913558 L16 2
Thới Lê Nhật Bình 1912737 L16 3
Đặng Ngọc Tân 1912008 L04 4 Lê Tiến Anh 1910754 L13 5
Ngô Thị Phương Thùy 1915402 L16 6 Trần Song Khôi 1911433 L09 7 Lâm Thanh Ngân 1914273 L16 8 Phan Nguyên Minh 1911617 L09 9 Đinh Trung Hiếu 1911140 L09
Mã thứ tự báo cáo nhóm: B42 lOMoARcPSD|47207367 MỤC LỤC
Lời mở đầu.....................................................................................................................................................................2
Phần đề bài.....................................................................................................................................................................3
A. Phần chung.........................................................................................................................................................3
B. Phần riêng...........................................................................................................................................................4
Phần lời giải...................................................................................................................................................................6
A. Phần chung.........................................................................................................................................................6
1. Đọc dữ liệu....................................................................................................................................................6
2. Làm sạch dữ liệu (Data cleaning)....................................................................................................6
3. Làm rõ dữ liệu (Data visualization)................................................................................................7
4. Xây dựng các mô hình hồi quy tuyến tính (Fitting linear regression models)....12
5. Dự báo (Predictions)................................................................................................................................15 B. Phần riêng
1. Đọc dữ liệu....................................................................................................................................................17
2. Làm sạch dữ liệu (Data cleaning)....................................................................................................17
3. Làm rõ dữ liệu (Data visualization)................................................................................................17
4. Xây dựng các mô hình hồi quy tuyến tính (Fitting linear regression models)....27
5. Dự báo (Predictions)................................................................................................................................32 1 lOMoARcPSD|47207367 LỜI MỞ ĐẦU
Thống kê là nghiên cứu của tập hợp nhiều lĩnh vực khác nhau, bao gồm phân tích, giải
thích, trình bày và tổ chức dữ liệu. Trong thực tiễn, thống kê có rất nhiều ứng dụng vào
nhiều lĩnh vực khác nhau, đặc biệt rất cần thiết cho sinh viên các ngành khoa học, kỹ
thuật. Môn học Xác suất & thống kê cung cấp kiến thức cơ bản về lý thuyết, giới thiệu một
số hàm phân phối xác suất thông dụng, kiểm định giả thuyết, ước lượng khoảng tin cậy,
v.v…Thông qua thống kê, các dữ liệu thu thập được phân tích theo nhiều tiêu chí khác
nhau giúp người sử dụng có cái nhìn tổng quan về dữ liệu của họ, đưa ra được ước lượng
về tổng thể lớn hơn hay dự đoán mô hình và kiểm định lại giả thuyết theo các mức ý nghĩa khác nhau.
Trong riêng lĩnh vực Kỹ thuật Hóa học, rất nhiều nghiên cứu cần có các dữ liệu từ thực
nghiệm để nghiên cứu như tính chất của hợp chất, tính hiệu quả của sản phẩm, hiệu suất
phản ứng ở các điều kiện phản ứng khác nhau, v.v. Vì vậy tính ứng dụng của Xác suất &
thống kê trong Kỹ thuật Hóa học rất cao, là nền tảng, là tiền đề cho việc nghiên cứu.
Báo cáo của nhóm tập trung vào việc tìm hiểu hai phương pháp được sử dụng phổ
biến trong Thống kê là Phân tích phương sai và Hồi quy tuyến tính bội. Từ đó vận
dụng chúng vào việc xử lý tệp dữ liệu cho sẵn, đưa ra những giá trị thống kê mô tả,
đánh giá đặc điểm, tính chất của đối tượng thống kê, vẽ các đồ thị để có cái nhìn trực
quan,.v.v.bằng phần mềm R/Rstudio. 2 lOMoARcPSD|47207367 PHẦN ĐỀ BÀI A. PHẦN CHUNG
Tập tin “diem_so.csv” chứa thông tin về điểm toán của các em học sinh trung học
thuộc hai trường học ở Bồ Đào Nha. Các thuộc tính dữ liệu bao gồm điểm học sinh, nơi cư
trú, và một số hoạt động xã hội khác. Dữ liệu được thu thập bằng cách sử dụng báo cáo
của các trường và các kết quả khảo sát sinh viên. Dữ liệu gốc được cung cấp tại:
https://archive.ics.uci.edu/ml/datasets/student+performance.
Các biến chính trong bộ dữ liệu:
• G1: Điểm thi học kì 1.
• G2: Điểm thi học kì 2.
• G3: Điểm cuối khoá.
• studytime: Thời gian tự học trên tuần (1 – ít hơn 2 giờ, 2 – từ 2 đến 5 giờ, 3 – từ 5
đến 10 giờ, or 4 – lớn hơn 10 giờ).
• failures: số lần không qua môn (1,2,3, hoặc 4 chỉ nhiều hơn hoặc bằng 4 lần).
• absences: số lần nghỉ học.
• higher: Có muốn học cao hơn hay không (yes: có, no: không).
• age: Tuổi của học sinh. Câu hỏi:
1. Đọc dữ liệu: Hãy dùng lệnh read.csv() để đọc tệp tin.
2. Làm sạch dữ liệu (Data cleaning):
(a) Hãy trích ra một dữ liệu con đặt tên là new_DF chỉ bao gồm các biến chính mà
ta quan tâm như đã trình bày trong phần giới thiệu dữ liệu. Từ câu hỏi này về sau,
mọi yêu cầu xử lý đều dựa trên tập dữ liệu con new_DF này.
(b) Kiểm tra các dữ liệu bị khuyết trong tập tin. (Các câu lênh tham khảo: is.na(),
which(), apply()). Nếu có dữ liệu bị khuyết, hãy đề xuất phương pháp thay thế cho những
dữ liệu bị khuyết này.
3. Làm rõ dữ liệu (Data visualization):
(a) Đối với các biến liên tục, hãy tính các giá trị thống kê mô tả bao gồm: trung bình,
trung vị, độ lệch chuẩn, giá trị lớn nhất và giá trị nhỏ nhất. Xuất kết quả dưới dạng bảng.
(Hàm gợi ý: mean(), median(), sd(), min(), max() , apply(), as.data.frame(), rownames()).
(b) Đối với các biến phân loại, hãy lập một bảng thống kê số lượng cho từng chủng loại.
(c) Hãy dùng hàm hist() để vẽ đồ thị phân phối của biến G3.
(d) Hãy dùng hàm boxplot() vẽ phân phối của biến G3 cho từng nhóm phân loại của
biến studytime, failures, và biến higher.
(e) Dùng lệnh pairs() vẽ các phân phối của biến G3 lần lượt theo các biến G1,
G2, age và absences.
4. Xây dựng các mô hình hồi quy tuyến tính (Fitting linear regression models): 3 lOMoARcPSD|47207367
Chúng ta muốn khám phá rằng có những nhân tố nào và tác động như thế nào đến
điểm cuối khoá môn Toán của các em học sinh.
(a) Xét mô hình hồi quy tuyến tính bao gồm biến G3 là một biến phụ thuộc, và tất
cả các biến còn lại đều là biến độc lập. Hãy dùng lệnh lm() để thực thi mô hình hồi quy
tuyến tính bội.
(b) Dựa vào kết quả của mô hình hồi quy tuyến tính trên, những biến nào bạn sẽ
loại khỏi mô hình tương ứng với các mức tin cậy 5% và 1%?
(c) Xét 3 mô hình tuyến tính cùng bao gồm biến G3 là biến phụ thuộc nhưng:
• Mô hình M1 chứa tất cả các biến còn lại là biến độc lập.
• Mô hình M2 là loại bỏ biến higher từ M1.
• Mô hình M3 là loại bỏ biến failure từ M2.
Hãy dùng lệnh anova() để đề xuất mô hình hồi quy hợp lý hơn.
(d) Từ mô hình hồi quy hợp lý nhất từ câu (c) hãy suy luận sự tác động của các
biến lên điểm thi cuối kì.
(e) Từ mô hình hồi quy hợp lý nhất từ câu (c) hãy dùng lệnh plot() để vẽ đồ thị
biểu thị sai số hồi quy và giá trị dự báo. Nêu ý nghĩa và nhận xét.
5. Dự báo (Predictions):
(a) Trong dữ liệu của bạn, hãy tạo thêm biến đặt tên là evaluate, biến này biểu
diễn tỷ lệ đạt (G3 >= 10) hoặc không đạt (G3 < 10) của sinh viên trong điểm thi cuối
kì. Hãy thống kê tỷ lệ đạt/không đạt (Hàm gợi ý: cbind()).
(b) Xét mô hình hồi quy hợp lý nhất mà bạn đã chọn trong câu 4(c). Hãy lập một
bảng số liệu mới đặt tên là new_X bao gồm toàn bộ các biến độc lập trong mô hình
này, và dùng lênh predict() để đưa ra số liệu dự báo cho biến G3 phụ thuộc vào
new_X. Gọi kết quả dự báo này là biến pred_G3.
(c) Khảo sát độ chính xác trong kết quả dự báo của câu trên bằng cách lập một
bảng so sánh kết quả dự báo pred_G3 với kết quả thực tế của biến G3. Đạt Không đạt Quan sát Dự báo B. PHẦN RIÊNG
Tập tin “PRSA_Data_Wanshouxigong_20130301-20170228.csv” Bộ dữ liệu này bao
gồm dữ liệu về các chất ô nhiễm không khí hàng giờ từ 12 địa điểm giám sát chất lượng
không khí được kiểm soát trên toàn quốc. Dữ liệu chất lượng không khí được lấy từ
Trung tâm Giám sát Môi trường Thành phố Bắc Kinh. Dữ liệu khí tượng tại mỗi địa
điểm chất lượng không khí được khớp với trạm thời tiết gần nhất của Cục Khí tượng
Trung Quốc. Khoảng thời gian từ ngày 1 tháng 3 năm 2013 đến ngày 28 tháng 2 năm
2017. Dữ liệu bị thiếu được ký hiệu là NA. Dữ liệu gốc được cung cấp tại
https://archive.ics.uci.edu/ml/datasets/student+performance. 4 lOMoARcPSD|47207367
Các biến chính trong bộ dữ liệu:
• PM2.5: nồng độ PM2.5 (µg/m3)
• PM10: Nồng độ PM10 (µg/m3)
• CO: Nồng độ CO (µg/m3)
• TEMP: nhiệt độ (oC)
• PRES: áp suất (hPa)
• DEWP: nhiệt độ điểm sương (oC)
• RAIN: lượng mưa (mm) • wd: hướng gió
• WSPM: tốc độ gió (m/s) 5 lOMoARcPSD|47207367 PHẦN LỜI GIẢI A. PHẦN CHUNG 1. Đọc dữ liệu: Input:
diem_so<-read.csv("C:/Users/Huy Tran/Desktop/diem_so.csv",header=T) attach(diem_so)
→ Đọc tệp tin và lưu dữ liệu với tên là: "diem_so"
2. Làm sạch dữ liệu (Data cleaning): a. Trích dữ liệu: Input:
newDF<-data.frame(G1,G2,G3,studytime,failures,absences,higher,age)
→ Trích ra dữ liệu con đặt tên là new_DF bao gồm các biến chính. attach(new_DF)
→ Khai báo biến chính mà ta quan tâm, và để dữ liệu về sau được sử lí bằng
new_DF b. Kiểm tra các dữ liệu bị khuyết trong tập tin. Nếu có dữ liệu bị
khuyết, hãy đề xuất phương pháp thay thế cho những dữ liệu bị khuyết này.
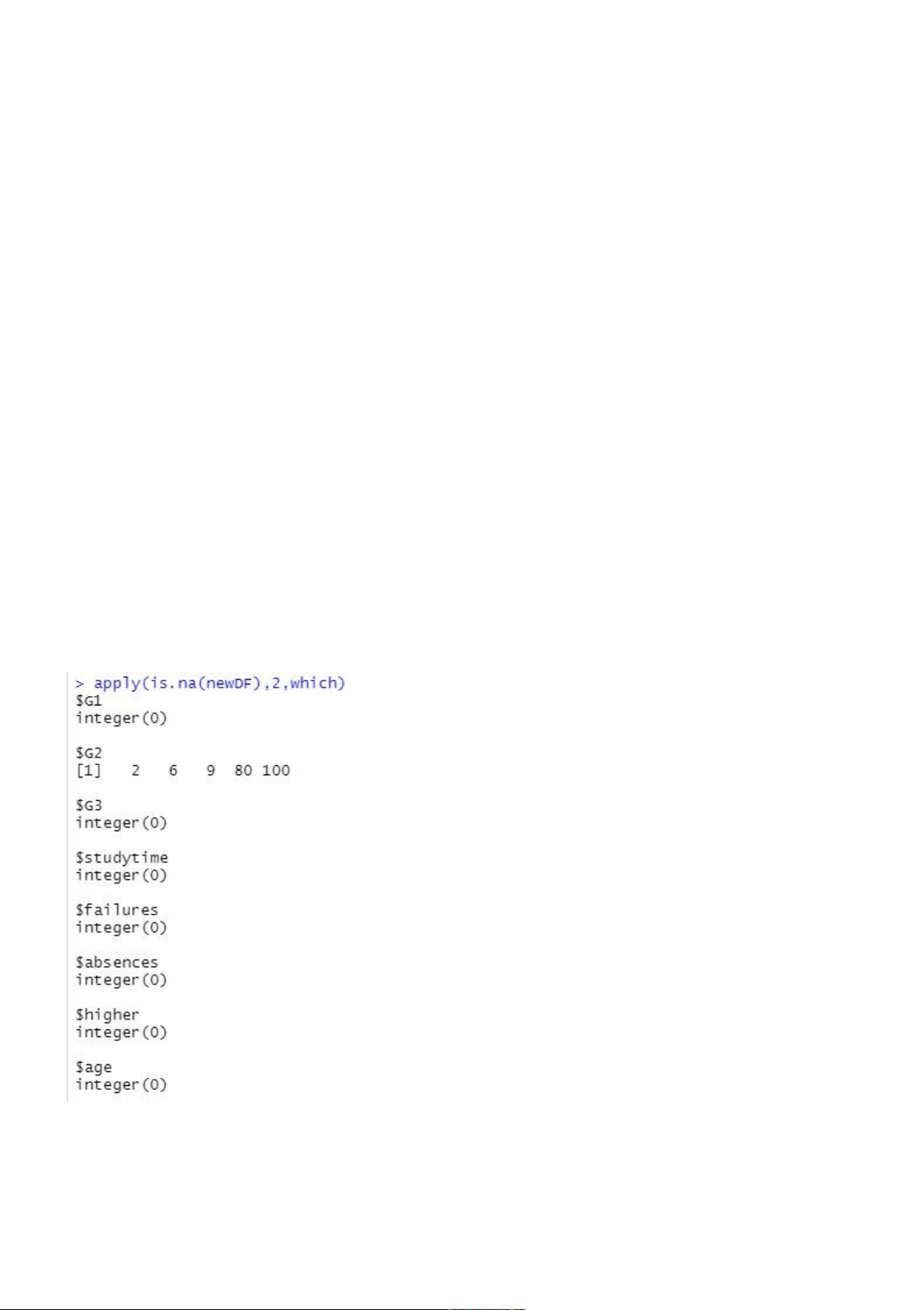
Input: apply(is.na(new_DF), 2 , which)
→ Kiểm tra và xuất ra giá trị khuyết của các biến trong dữ liệu new_DF. Output:
Dựa trên kết quả thu được, ta nhận thấy có 5 giá trị khuyết tại biến G2. Do đó, ta cần
xử đưa ra các phương pháp cho các giá trị khuyết đó.
Ta có các phương pháp xử lý các giá trị khuyết như sau: 6 lOMoARcPSD|47207367
– Phương pháp 01: Deletion(xoá): phương pháp này được dùng khi khi xác suất thiếu
biến là như nhau cho tất cả các quan sát.
– Phương pháp 02: Mean/ Mode/ Median Imputation: là một phương pháp để điền vào các
giá trị còn thiếu với các giá trị ước tính.
Ta sẽ chọn thay phương pháp xóa các quan sát mà bất kỳ biến nào bị thiếu. Input: new_DF=na.omit(new_DF)
→ Xóa các giá trị bị khuyết, mà gán lại new_DF mới.
3. Làm rõ dữ liệu ( Data visualization):
a. Đối với các biến liên tục, hãy tính các giá trị thống kê mô tả bao gồm:
trung binh, trung vị độ lệch chuẩn, giá trị lớn nhất và giá trị nhỏ nhất. Xuất
kết quả dưới dạng bảng. Input :
mean = apply(new_DF[,c(1,2,3,8)],2, mean)
→ Tính trung bình của các biến liên tục (G1, G2, G3, age) và lưu vào biến có tên là mean.
median = apply(new_DF[,c(1,2,3,8)],2, median)
→ Tính trung vị của các biến liên tục (G1, G2, G3, age) và lưu vào biến có tên là median.
sd = apply(new_DF[,c(1,2,3,8)],2, sd)
→ Tính độ lệch chuẩn của các biến liên tục (G1, G2, G3, age) và lưu vào biến có tên là sd.
max = apply(new_DF[,c(1,2,3,8)],2, max)
→ Tính giá trị lớn nhất của các biến liên tục (G1, G2, G3, age) và lưu vào biến có tên là max.
min = apply(new_DF[,c(1,2,3,8)],2, min)
→ Tính giá trị nhỏ nhất của các biến liên tục (G1, G2, G3, age) và lưu vào biến có tên là min.
des = cbind(mean,median,sd,max,min)
→ Tạo matrix thể hiện các giá trị thống kê mô tả cho các biến liên tục, lưu vào biến des. as.data.frame(des)
→ Chuyển matrix thành dạng bảng dữ liệu. Output: 7 lOMoARcPSD|47207367
b. Đối với các biến phân loại, hãy lập một bảng thống kê số lượng cho từng chủng loại. Input: table(failures)
→ Tạo bảng thống kê số lượng cho biến failures table(studytime)
→ Tạo bảng thống kê số lượng cho biến studytime. table(higher)
→ Tạo bảng thống kê số lượng cho biến higher. Output:
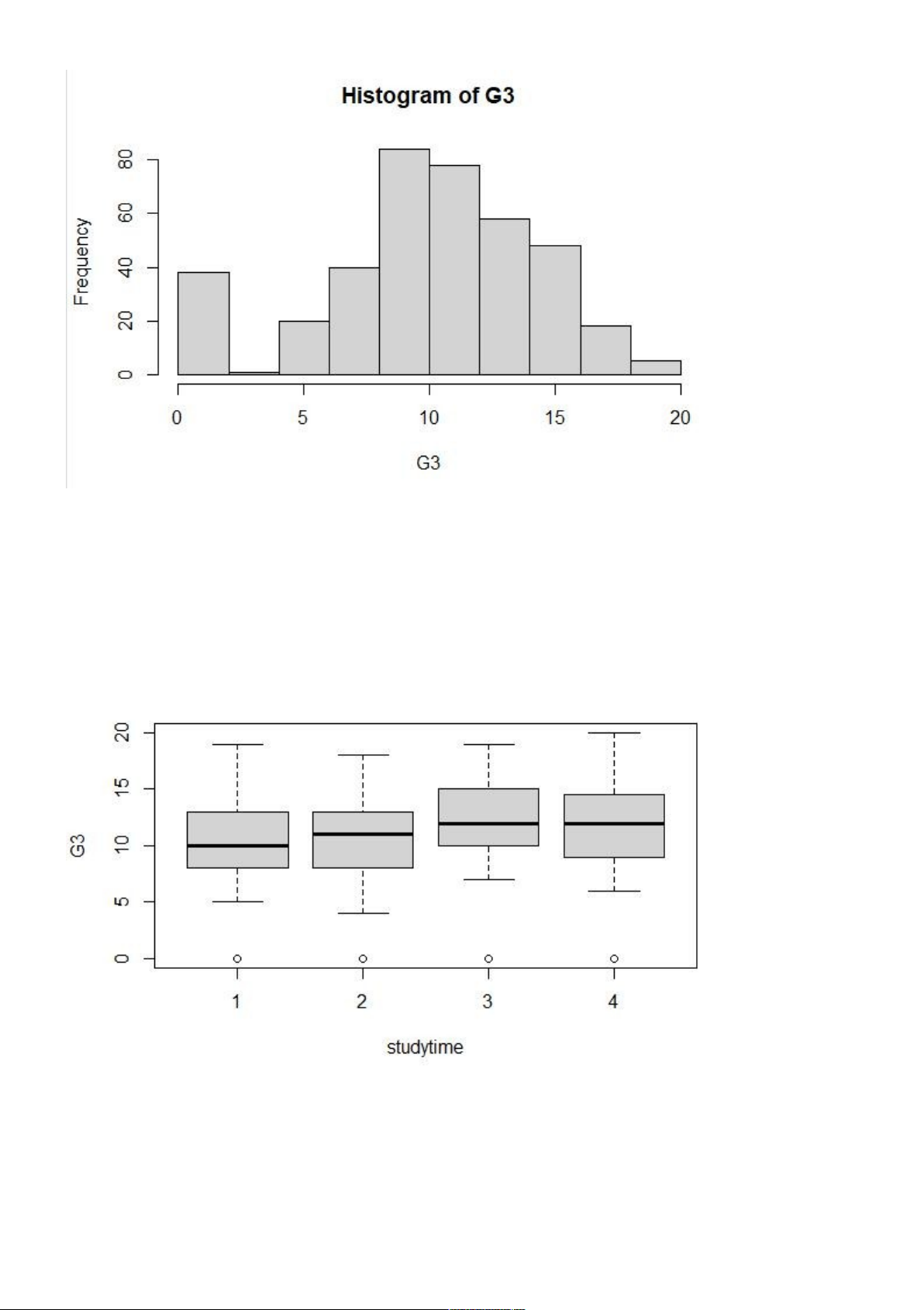
c. Vẽ đồ thị biểu diễn cho biến G3 Input: hist(G3)
→ Vẽ biểu đồ histogram cho biến G3. Output: 8 lOMoARcPSD|47207367
d. Dùng hàm boxplot() vẽ phân phối của biến G3 cho từng nhóm phân loại
của biến sutdytime, failures, và biến higher.
• Phân loại nhóm cho biến studytime Input : boxplot(G3 ~ studytime)
→ Vẽ biểu đồ Boxplot của biến G3 phân phối cho từng loại của biến studytime Output:
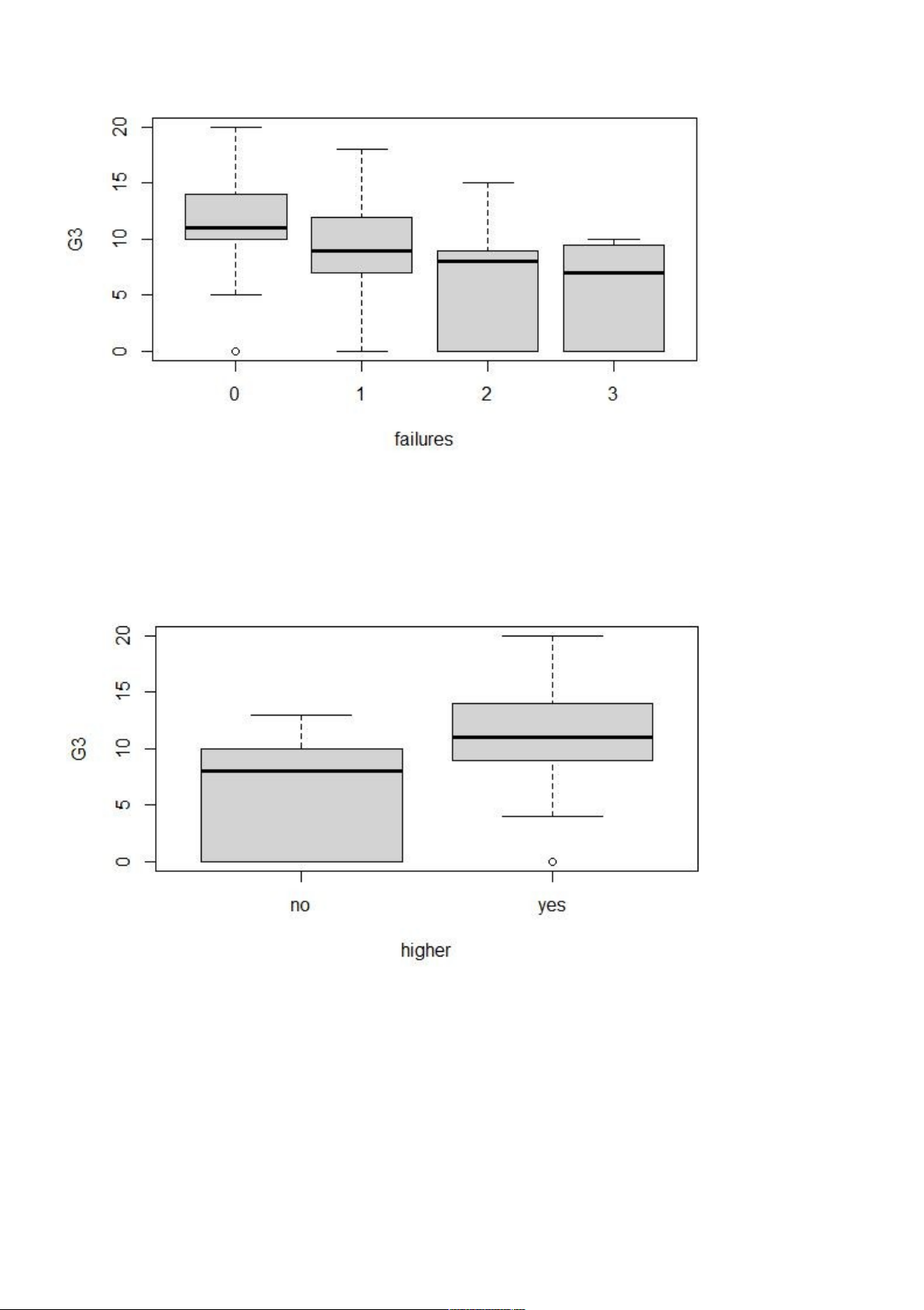
• Phân loại nhóm cho biến failures Input : boxplot(G3 ~ failures)
→ Vẽ biểu đồ Boxplot của biến G3 cho từng nhóm phân loại của biến failures 9 lOMoARcPSD|47207367 Output:
• Phân loại nhóm cho biến higher Input: boxplot(G3 ~ higher)
→ Vẽ biểu đồ Boxplot của biến G3 cho từng nhóm phân loại của biến higher Output:
e. Dùng lệnh pairs() vẽ các phân phối của biến G3 lần lượt cho các biến G1, G2, age và absences
• Phân phối biến G3 cho biến G1 Input: pairs(G3 ~ G1)
→ Vẽ các phân phối của biến G3 phân phối theo theo biến G1. Output: 10 lOMoARcPSD|47207367
• Phân phối biến G3 cho biến G2 Input: pairs(G3 ~ G2)
→ Vẽ các phân phối của biến G3 phân phối theo biến G2. Output:
• Phân phối biến G3 cho biến age Input: pairs(G3 ~ age)
→ Vẽ các phân phối của biến G3 phân phối theo biến age. Output: 11 lOMoARcPSD|47207367
• Phân phối biến G3 cho biến absences Input: pairs(G3 ~ absences)
→ Vẽ các phân phối của biến G3 phân phối theo biến absences. Output:
4. Xây dụng các mô hình hồi quy (Fitting linear regression models):
a. Xét mô hình hồi quy tuyến tính bao gồm biến G3 là một biến phụ thuộc, và
tất cả các biến còn lại đều là độc lập. Dùng lệnh lm() để thực thi mô hình hồi quy tuyến tính bội. Xét mô hình :
• G1: biến liên tục
• G2: biến liên tục
• G3: biến liên tục 12 lOMoARcPSD|47207367
• studytime: biến phân loại
• failures: biến phân loại
• absences: biến rời rạc
• higher: biến phân loại
• age: biến liên tục Input:
studytime = as.factor(studytime)
→ Thay biến studytime thành biến nhân
tố. failures = as.factor(failures)
→ Thay biến failures thành biến nhân
tố. higher = as.factor(higher)
→ Thay biến higher thành biến nhân tố.
m1 = lm(G3 ~ G1 + G2 + studytime + failures + absences + higher+ age) summary(m1)
→ Xây dựng mô hình hồi quy tuyến tính bội. Output:
b. Dựa vào kết quả của mô hình tuyến tính trên, những biến nào bạn sẽ loại
khỏi mô hình tương ứng với các mức tin cậy 5% và 1% ?
So sánh Pr(>|t|) với mức α cần xét, khi đó các biến bị loại khỏi mô hình ở
– Mức 5%: studytime2, studytime3, failures2, failures3, higheryes, age. 13 lOMoARcPSD|47207367
– Mức 1%: studytime2, studytime3, studytime4, failures2, failures3, higheryes, age.
c. Xét 3 mô hình tuyến tính cùng bao gồm biến G3 là biến phụ thuộc:
• Mô hình M1 chưa tất cả các biến còn lại là biến độc lập
→ Mô hình M1 là đáp án của câu (a)
• Mô hình M2 là loại bỏ biến higher từ M1 Input:
m2 = lm(G3 ~ G1 + G2 + studytime + failures + absences + age)
• Mô hình M3 là loại bỏ biến failures từ M2 Input:
m3 = lm(G3 ~ G1 + G2 + studytime + absences + age)
• Dùng anova() để đề xuất mô hình hồi quy hợp lý :
– Xét hai mô hình hồi quy M1 và M2 : Input: anova(m1,m2)
→ Phân tích phương sai cho hai mô hình tuyến tính m1, m2 Output: Lí luận:
Đặt giả thiết H0: hai mô hình bằng nhau
Đặt giả thiết H1: hai mô hình khác nhau
Nhìn vào kết quả ta thấy : 0.5386 > 0.05 nên ta kết luận rằng chấp nhận giả thiết H0.
Vậy 2 mô hình M1 và M2 là bằng nhau.
– Xét mô hình M1, M3 Input: anova(m1,m3)
→ Phân tích phương sai cho hai mô hình tuyến tính m1, m3. Output: Lí luận: 14 lOMoARcPSD|47207367
Đặt giả thiết H0: hai mô hình bằng nhau
Đặt giả thiết H1: hai mô hình khác nhau
Nhìn vào kết quả ta thấy : 0.03194 < 0.05 nên ta kết luận rằng bác bỏ giả thiết H0,
chấp nhận giả thiết H1.
Vậy hai mô hình M1 và M3 là khác nhau.
Kết luận: Chọn M2 vì M2 chứa nhiều biến tin cậy, ít biến không tin cậy
d. Từ mô hình hồi quy hợp lí nhất của câu c, suy luận sự tác động của các
biến điểm thi cuối kì.
Với mức alpha 5% các biến G1, G2, studytime4, failures1, absences tác động mạnh
đến điểm thi cuối kỳ G3.
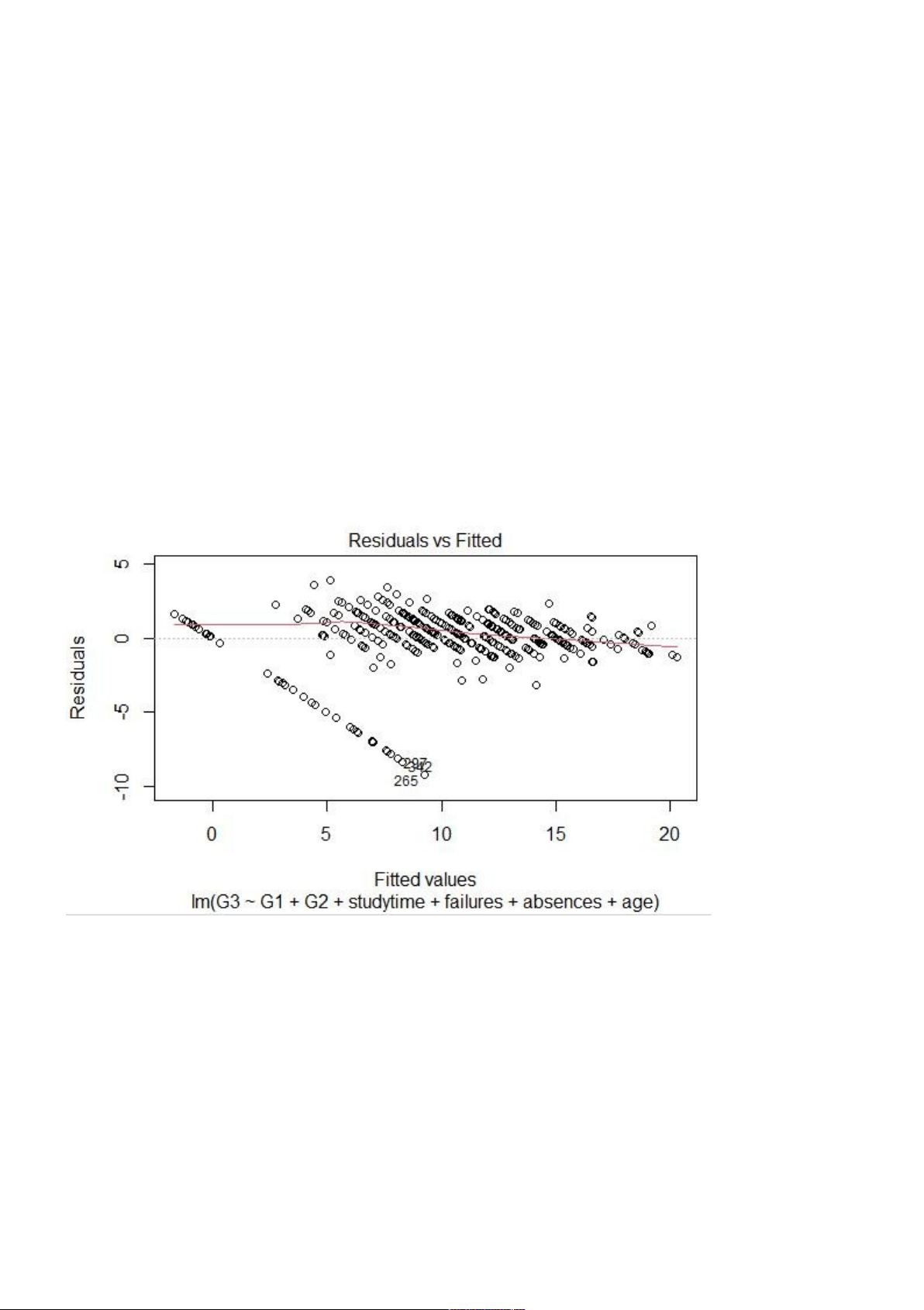
e. Từ mô hình hồi quy hợp lí nhất của câu c, dung lệnh plot() vẽ đồ thị biểu thị
sai số hồi quy và giá trị dự báo. Nêu ý nghĩa và nhận xét. Input: plot(m2, which = 1) Output:
Mức độ dao dộng của sai số và giá trị dự báo quanh giá trị 0. Mô hình hồi quy
tốt 5. Dự báo (Predictions) :
a. Trong dữ liệu của bạn, hãy tạo thêm biến đặt tên là evaluate, biến này biểu
diễn tỷ lệ đạt (G3 >= 10) hoặc không đạt (G3 < 10) của sinh viên trong điểm thi
cuối kì. Hãy thống kê tỷ lệ đạt/không đạt Input:
evaluate = prop.table(table(G3>=10))
→ Tính tỉ lệ đạt và lưu vào biến evaluate . evaluate 15 lOMoARcPSD|47207367
→ Hiển thị kết quả của biến evaluate Output:
b. Xét mô hình hồi quy hợp lý nhất mà bạn đã chọn trong câu 4c. Hãy lập một
bảng số liệu mới đặt tên là new_X bao gồm toàn bộ các biến độc lập trong mô
hình này, và dùng lênh predict() để đưa ra số liệu dự báo cho biến G3 phụ
thuộc vào new_X. Gọi kết quả dự báo này là biến pred_G3. Input:
New_X = data.frame(G1,G2,studytime,failures,absences,age)
→ Tạo một dữ liệu mới bao gồm các biến độc lập như ở mô hình m2 và đặt tên dữ liệu đó là New_X
New_X$pred_G3 = predict(m2,New_X)
→ Tính số liệu dự báo của biến G3 phụ thuộc vào dữ liệu New_X sau đó lưu kết
quả vào biến pred_G3, đồng thời thêm biến pred_G3 vào dữ liệu New_X. attach(New_X)
→ Thông báo cho phần mềm biết từ đây trở về sau mọi phép tính đều được thực
hiện trên dữ liệu New_X
evaluate_2 = prop.table(table(pred_G3>=10))
→ Tính tỉ lệ dự báo và lưu vào biến evaluate_2
c. Khảo sát độ chính xác trong kết quả dự báo của câu trên bằng cách lập một bảng
so sánh kết quả dự báo pred_G3 với kết quả thực tế của biến G3. Đạt Không đạt Quan sát Dự báo Input:
Ket_qua = cbind(evaluate,evaluate_2)
→ Kết quả thống kê tỷ lệ đạt vào không đạt đối với biến dự báo là
pred_G3 colnames(Ket_qua)=c("Quan sát","Dự báo")
→ Khai báo tên của cột Ket_qua
rownames(Ket_qua)=c("Không đạt","Đạt")
→ Khai báo tên của hàng Ket_qua t(Ket_qua)
→ Xuất kết quả dự báo Output: 16 lOMoARcPSD|47207367 B. PHẦN RIÊNG 1. Đọc dữ liệu: Input:
khong_khi = read.csv("C:/Users/Huy Tran/Desktop/khong_khi.csv",header=T) attach(khong_khi)
2. Làm sạch dữ liệu (Data
cleaning): a. Trích dữ liệu: Input:
new_DF = data.frame(PM2.5,PM10,O3,TEMP,PRES,DEWP,WSPM,wd) attach(new_DF)
b. Kiểm tra các dữ liệu bị khuyết trong tập tin. Nếu có dữ liệu bị khuyết, hãy
đề xuất phương pháp thay thế cho những dữ liệu bị khuyết này. Input:
apply(is.na(new_DF), 2 , which) new_DF=na.omit(new_DF)
3. Làm rõ dữ liệu ( Data visualization):
a. Đối với các biến liên tục, hãy tính các giá trị thống kê mô tả bao gồm:
trung binh, trung vị độ lệch chuẩn, giá trị lớn nhất và giá trị nhỏ nhất. Xuất
kết quả dưới dạng bảng. Input :
mean = apply(new_DF[,c(1,2,3,4,5,6,7)],2, mean)
median = apply(new_DF[,c(1,2,3,4,5,6,7)],2, median)
sd = apply(new_DF[,c(1,2,3,4,5,6,7)],2, sd)
max = apply(new_DF[,c(1,2,3,4,5,6,7)],2, max)
min = apply(new_DF[,c(1,2,3,4,5,6,7)],2, min)
des = cbind(mean,median,sd,max,min) as.data.frame(des) Output: 17 lOMoARcPSD|47207367
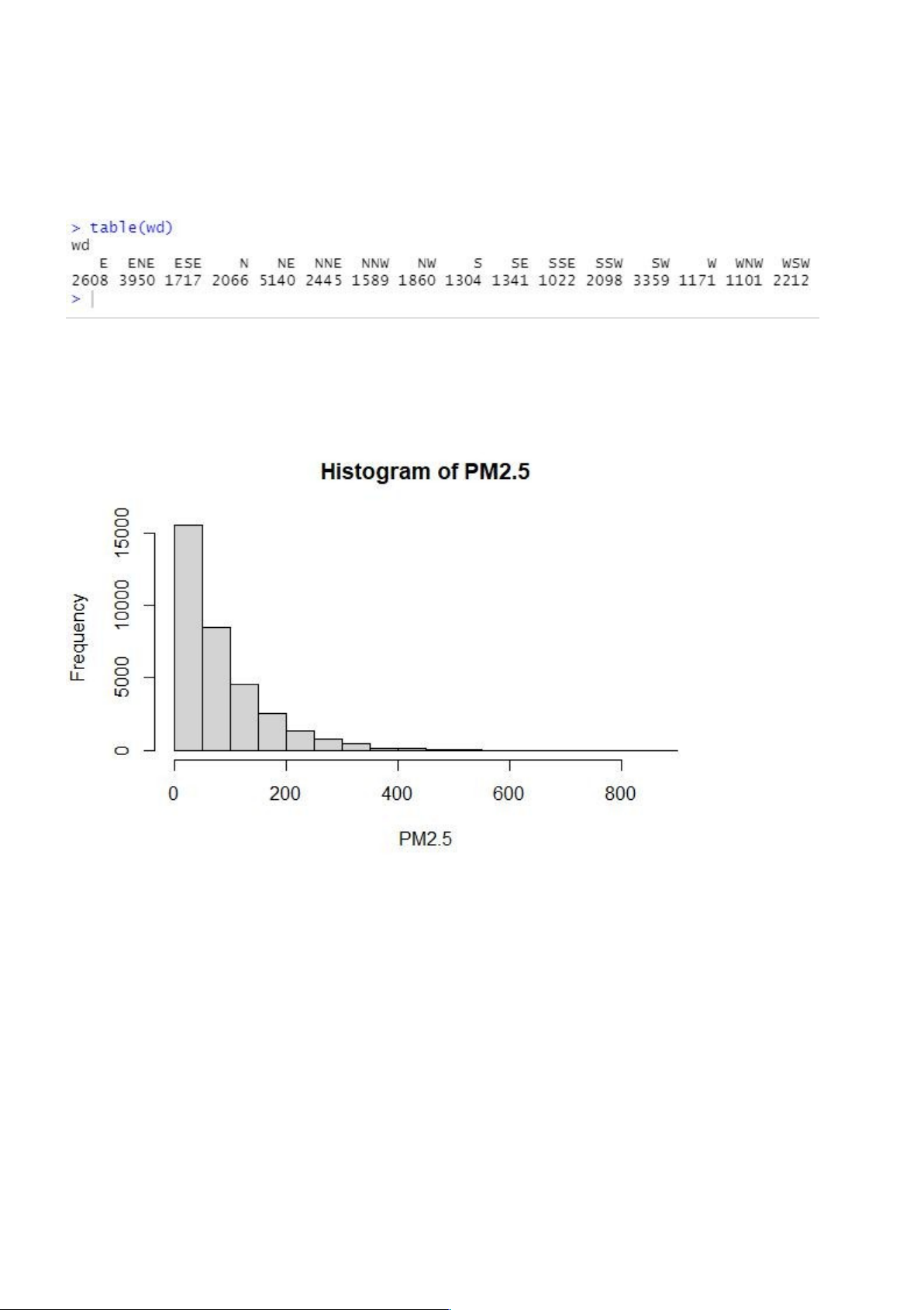
b. Đối với các biến phân loại, hãy lập một bảng thống kê số lượng cho từng chủng loại. Input: table(wd) Output:
c. Vẽ đồ thị biểu diễn cho biến PM2.5, PM10, O3 Input: hist(PM2.5) Output: Input: hist(PM10) Output: 18 lOMoARcPSD|47207367 Input: hist(O3) Output:
d. Dùng hàm boxplot() vẽ phân phối của biến PM2.5, PM10, O3 cho từng
nhóm phân loại của biến wd.
• Phân loại nhóm cho biến PM2.5 Input: boxplot(PM2.5 ~ wd) Output: 19