Báo cáo Chuyên đề: Game Cờ Caro bằng Giải thuật Minimax - Tổng quan AI | Đại học Điện lực

lOMoARcPSD| 59629529
TRƯỜNG ĐẠI HỌC ĐIỆN LỰC
KHOA CÔNG NGHỆ THÔNG TIN
BÁO CÁO CHUYÊN ĐỀ HỌC PHẦN
NHẬP MÔN TRÍ TUỆ NHÂN TẠO
Đ Ề TÀI:
XÂY DỰNG GAME CỜ CARO BẰNG GIẢI THUẬT MINIMAX
Sinh viên thực hiện
: TRẦN ĐỨC ANH
: TRIỆU HO À NG GIANG
Giảng viên hướng dẫn : NGÔ HO À NG HUY Ngành
: CÔNG NGHỆ THÔNG TIN Chuyên ngành
: CÔNG NGHỆ PHẦN MỀM Lớp
: D14CNPM 5 Khóa : 2019-2023
Hà Nội, tháng 8 năm 2022 lOMoAR cPSD| 59629529 PHIẾU CHẤM ĐIỂM Sinh viên thực hiện: STT Họ và tên Chữ ký Nhiệm vụ 1 TRẦN ĐỨC ANH Mã SV: 19810310381 2 TRIỆU HOÀNG GIANG Mã SV: 20810310548 3 Giảng viên chấm: Họ và tên Chữ ký Ghi chú Giảng viên chấm 1: lOMoAR cPSD| 59629529 Giảng viên chấm 2: lOMoARcPSD| 59629529 MỤC LỤC LỜI MỞ ĐẦU 5
CHƯƠNG 1: GIỚI THIỆU VỀ AI VÀ THUẬT TOÁN MINIMAX 5
1.1. GIỚI THIỆU VỀ TRÍ TUỆ NHÂN TẠO 5
1.2. GIỚI THIỆU VỀ KỸ THUẬT MINIMAX 9 1.3. KẾT LUẬN 11
CHƯƠNG 2: BÀI TOÁN CỜ CARO 12 2.1 BÀI TOÁN 12
2.2 GIẢI QUYẾT BÀI TOÁN 12 2.2.1. Ý tưởng 12
CHƯƠNG 3: ĐÁNH GIÁ THỬ NGIỆM 12
3. Cặt đặt với C# Winform 12 KẾT LUÂṆ 15
TÀI LIÊU THAM KḤ ẢO 17 lOMoARcPSD| 59629529 LỜI MỞ ĐẦU
Bài toán “Cờ Caro ” là một bài toán thú vị, tương đối kinh điển của thuật toán
Minimax – 1 thuật toán quan trọng và phổ biến trong Trí tuệ Nhân tạo. Cờ caro là
bài toán về việc chơi một ván cờ caro. Một mặt các ô vuông chúng ta điền vào đó
“x”và “o” tượng trưng cho hai bên và thi 1 trong 2 đội điền được 5 quân của mình thẳng hàng là Win.
Chính vì vây cḥúng em đã đi đến viêc ḷ ựa chọn đề tài “ÁP DỤNG THUẬT
TOÁN MINIMAX GIẢI QUYẾT BÀI TOÁN CỜ CARO” cho bài tâp lớn môn ̣
Nhập Môn Trí Tuệ Nhân Tạo . Chúng em vô cùng biết ơn Cô Nguyễn Thị Thanh
Tân , người trực tiếp giảng dạy, hướng dẫn nhiệt tình cho chúng em trong quá trình
nghiên cứu và thực hiện đề tài.
Mặc dù đề tài đã hoàn thành, nhưng chắc chắn vẫn không thể tránh khỏi
những thiếu sót, vì vậy chúng em mong muốn nhận được các ý kiến đóng góp của
các thầy cô để có thể hoàn thiện hơn nữa.
Chúng em xin chân thành cảm ơn!
CHƯƠNG 1: GIỚI THIỆU VỀ AI VÀ THUẬT TOÁN MINIMAX
1.1. GIỚI THIỆU VỀ TRÍ TUỆ NHÂN TẠO
1.1.1. Trí tuệ nhân tạo là gì ?
Để hiểu trí tuệ nhân tạo (artificial intelligence) là gì chúng ta bắt đầu với khái
niệm sự bay nhân tạo (flying machines), tức là cái máy bay.
Đã từ lâu, loài người mong muốn làm ra một cái máy mà có thể di chuyển
được trên không trung mà không phụ thuộc vào địa hình ở dưới mặt đất, hay nói
cách khác là máy có thể bay được. Không có gì ngạc nhiên khi những ý tưởng đầu
tiên làm máy bay là từ nghiên cứu cách con chim bay. Những chiếc máy biết bay
được thiết kế theo nguyên lý “vỗ cánh” như con chim chỉ có thể bay được quãng
đường rất ngắn và lịch sử hàng không thực sự sang một trang mới kể từ anh em nhà
Wright thiết kế máy bay dựa trên các nguyên lý của khí động lực học (aerodynamics). lOMoAR cPSD| 59629529
Các máy bay hiện nay, như đã thấy, có sức trở rất lớn và bay được quãng
đường có thể vòng quanh thế giới. Nó không nhất thiết phải có nguyên lý bay của
con chim nhưng vẫn bay được như chim (dáng vẻ), và còn tốt hơn chim.
Quay lại câu hỏi Trí tuệ nhân tạo là gì. Trí tuệ nhân tạo là trí thông minh của
máy do con người tạo ra. Ngay từ khi chiếc máy tính điện tử đầu tiên ra đời, các
nhà khoa học máy tính đã hướng đến phát hiển hệ thống máy tính (gồm cả phần
cứng và phần mềm) sao cho nó có khả năng thông minh như loài người. Mặc dù
cho đến nay, theo quan niệm của người viết, ước mơ này vẫn còn xa mới thành hiện
thực, tuy vậy những thành tựu đạt được cũng không hề nhỏ: chúng ta đã làm được
các hệ thống (phần mềm chơi cờ vua chạy trên siêu máy tinh GeneBlue) có thể
thắng được vua cờ thế giới; chúng ta đã làm được các phần mềm có thể chứng minh
được các bài toán hình học; v.v. Hay nói cách khác, trong một số lĩnh vực, máy tính
có thể thực hiện tốt hơn hoặc tương đương con người (tất nhiên không phải tất cả
các lĩnh vực). Đó chính là các hệ thống thông minh.
Có nhiều cách tiếp cận để làm ra trí thông minh của máy (hay là trí tuệ nhân
tạo), chẳng hạn là nghiên cứu cách bộ não người sản sinh ra trí thông minh của loài
người nhưthế nào rồi ta bắt chước nguyên lý đó, nhưng cũng có những cách khác
sử dụng nguyên lý hoàn toàn khác với cách sản sinh ra trí thông minh của loài
người mà vẫn làm ra cái máy thông minh như hoặc hơn người; cũng giống như máy
bay hiện nay bay tốt hơn con chim do nó có cơ chế bay không phải là giống như cơ chế bay của con chim.
Như vậy, trí tuệ nhân tạo ở đây là nói đến khả năng của máy khi thực hiện
các công việc mà con người thường phải xử lý; và khi dáng vẻ ứng xử hoặc kết quả
thực hiện của máy là tốt hơn hoặc tương đương với con người thì ta gọi đó là máy
thông minh hay máy đó có trí thông minh. Hay nói cách khác, đánh giá sự thông
minh của máy không phải dựa trên nguyên lý nó thực hiện nhiệm vụ đó có giống
cách con người thực hiện hay không mà dựa trên kết quả hoặc dáng vẻ ứng xử bên
ngoài của nó có giống với kết quả hoặc dáng vẻ ứng xử của con người hay không.
Các nhiệm vụ của con người thường xuyên phải thực hiện là: giải bài toán
(tìm kiếm, chứng minh, lập luận), học, giao tiếp, thể hiện cảm xúc, thích nghi với
môi trường xung quanh, v.v., và dựa trên kết quả thực hiện các nhiệm vụ đó để kết
luận rằng một ai đó có là thông minh hay không. Môn học Trí tuệ nhân tạo nhằm
cung cấp các phương pháp luận để làm ra hệ thống có khả năng thực hiện các
nhiệm vụ đó: giải toán, học, giao tiếp, v.v. bất kể cách nó làm có như con người
hay không mà là kết quả đạt được hoặc dáng vẻ bên ngoài như con người.
Trong môn học này, chúng ta sẽ tìm hiểu các phương pháp để làm cho máy
tính biết cách giải bài toán, biết cách lập luận, biết cách học, v.v. lOMoARcPSD| 59629529 1.1.2. Lịch sử
Vào năm 1943, Warren McCulioch và Walter Pitts bắt đầu thực hiện nghiên
cứu ba cơ sở lý thuyết cơ bản: triết học cơ bản và chức năng của các noron thần
kinh; phân tích các mệnh đề logic; và lý thuyết dự đoán của Turing. Các tác giả đã
nghiên cứu đề xuât mô hình noron nhân tạo, mỗi noron đặc trưng bởi hai trạng thái
“bật”, “tắt” và phát hiện mạng noron có khả năng học.
Thuật ngữ “Trí tuệ nhân tạo” (Artificial Intelligence - AI) được thiết lập bởi
John McCarthy tại Hội thảo đầu tiên về chủ đề này vào mùa hè năm 1956. Đồng
thời, ông cũng đề xuất ngôn ngữ lập trình Lisp – một trong những ngôn ngữ lập
trình hàm tiêu biểu, được sử dụng trong lĩnh vực AI. Sau đó, Alan Turing đưa ra
"Turing test" như là một phương pháp kiểm chứng hành vi thông minh.
Thập kỷ 60, 70 Joel Moses viết chương trình Macsyma - chương trình toán
học sử dụng cơ sở tri thức đầu tiên thành công. Marvin Minsky và Seymour Papert
đưa ra các chứng minh đầu tiên về giới hạn của các mạng nơ-ron đơn giản. Ngôn
ngữ lập trình logic Prolog ra đời và được phát triển bởi Alain Colmerauer. Ted
Shortliffe xây dựng thành công một số hệ chuyên gia đầu tiên trợ giúp chẩn đoán
trong y học, các hệ thống này sử dụng ngôn ngữ luật để biểu diễn tri thức và suy diễn.
Vào đầu những năm 1980, những nghiên cứu thành công liên quan đến AI
như các hệ chuyên gia (expert systems) – một dạng của chương trình AI mô phỏng
tri thức và các kỹ năng phân tích của một hoặc nhiều chuyên gia con người.
Vào những năm 1990 và đầu thế kỷ 21, AI đã đạt được những thành tựu to lớn
nhất, AI được áp dụng trong logic, khai phá dữ liệu, chẩn đoán y học và nhiều lĩnh
vực ứng dụng khác trong công nghiệp. Sự thành công dựa vào nhiều yếu tố: tăng
khả năng tính toán của máy tính, tập trung giải quyết các bài toán con cụ thể, xây
dựng các mối quan hệ giữa AI và các lĩnh vực khác giải quyết các bài toán tương
tự, và một sự chuyển giao mới của các nhà nghiên cứu cho các phương pháp toán
học vững chắc và chuẩn khoa học chính xác.
1.1.3. Lĩnh vực của AI ⮚ Lập luận, suy diễn tự động: Khái niệm lập luận (reasoning), và suy diễn lOMoAR cPSD| 59629529
(reference) được sử dụng rất phổ biến trong lĩnh vực AI. Lập luận là suy diễn
logic, dùng để chỉ một tiến trình rút ra kết luận (tri thức mới) từ những giả
thiết đã cho (được biểu diễn dưới dạng cơ sở tri thức). Như vậy, để thực hiện
lập luận người ta cần có các phương pháp lưu trữ cơ sở tri thức và các thủ
tục lập luận trên cơ sở tri thức đó.
⮚ Biểu diễn tri thức: Muốn máy tính có thể lưu trữ và xử lý tri thức thì cần có
các phương pháp biểu diễn tri thức. Các phương pháp biểu diễn tri thức ở
đây bao gồm các ngôn ngữ biểu diễn và các kỹ thuật xử lý tri thức. Một ngôn
ngữ biểu diễn tri thức được đánh giá là “tốt” nếu nó có tính biểu đạt cao và
các tính hiệu quả của thuật toán lập luận trên ngôn ngữ đó. Tính biểu đạt của
ngôn ngữ thể hiện khả năng biểu diễn một phạm vi rộng lớn các thông tin
trong một miền ứng dụng. Tính hiệu quả của các thuật toán lập luận thể hiện
chi phí về thời gian và không gian dành cho việc lập luận. Tuy nhiên, hai yếu
tố này dường như đối nghịch nhau, tức là nếu ngôn ngữ có tínhbiểu đạt cao
thì thuật toán lập luận trên đó sẽ có độ phức tạp lớn (tính hiệu quả thấp)và
ngược lại (ngôn ngữ đơn giản, có tính biểu đạt thấp thì thuật toán lập luận
trên đó sẽ có hiệu quả cao). Do đó, một thách thức lớn trong lĩnh vực AI là
xây dựng các ngôn ngữ biểu diễn tri thức mà có thể cân bằng hai yếu tố này,
tức là ngôn ngữ có tínhbiểu đạt đủ tốt (tùy theo từng ứng dụng) và có thể lập luận hiệu quả.
⮚ Lập kế hoạch: khả năng suy ra các mục đích cần đạt được đối với các nhiệm
vụ đưa ra, và xác định dãy các hành động cần thực hiện để đạt được mục đích đó.
⮚ Học máy: là một lĩnh vực nghiên cứu của AI đang được phát triển mạnh mẽ
và có nhiều ứng dụng trong các lĩnh vực khác nhau như khai phá dữ liệu, khám phá tri thức,… lOMoARcPSD| 59629529
⮚ Xử lý ngôn ngữ tự nhiên: là một nhánh của AI, tập trung vào các ứng dụng
trên ngôn ngữ của con người. Các ứng dụng trong nhận dạng tiếng nói, nhận
dạng chữ viết, dịch tự động, tìm kiếm thông tin,…
⮚ Hệ chuyên gia: cung cấp các hệ thống có khả năng suy luận để đưa ra những
kết luận. Các hệ chuyên gia có khả năng xử lý lượng thông tin lớn và cung
cấp các kết luận dựa trên những thông tin đó. Có rất nhiều hệ chuyên gia nổi
tiếng như các hệ chuyên gia y học MYCIN, đoán nhận cấu trúc phân tử từ
công thức hóa học DENDRAL, … ⮚ Robotics ⮚ …
1.2. GIỚI THIỆU VỀ KỸ THUẬT MINIMAX
Giải thuật Minimax là một thuật toán đệ quy lựa chọn bước đi kế tiếp trong một
trò chơi có hai người. Xét một trò chơi đối kháng trong đó hai người thay phiên đi
nước đi của mình như tic-tac-toe, cờ vua, cờ tướng, cờ caro, cờ vây… Khi chơi bạn
có thể khai triển hết không gian trạng thái nhưng khó khăn chủ yếu là bạn phải tính
toán được phản ứng và nước đi của đối thủ mình như thế nào? Cách xử lý đơn giản
là bạn giả sử đối thủ của bạn cũng sử dụng kiến thức về không gian trạng thái giống
bạn. Giải thuật Minimax áp dụng giả thuyết này để tìm kiếm không gian trạng thái của trò chơi. 1.2.1. Tư tưởng
Giải thuật Minimax là một thuật toán đệ quy lựa chọn bước đi kế tiếp trong
một trò chơi có hai người. Xét một trò chơi đối kháng trong đó hai người
thay phiên đi nước đi của mình như tic-tac-toe, cờ vua, cờ tướng, cờ caro, cờ
vây… Khi chơi bạn có thể khai triển hết không gian trạng thái nhưng khó
khăn chủ yếu là bạn phải tính toán được phản ứng và nước đi của đối thủ lOMoARcPSD| 59629529
mình như thế nào? Cách xử lý đơn giản là bạn giả sử đối thủ của bạn cũng sử
dụng kiến thức về không gian trạng thái giống bạn. Giải thuật Minimax áp
dụng giả thuyết này để tìm kiếm không gian trạng thái của trò chơi.
1.2.2. Một thuật toán minimax là một thuật toán đệ quy cho việc lựa chọn bước đi
kế tiếp trong một trò chơi có hai người chơi. Một giá trị được gán cho mỗi vị
trí hay một trạng thái của trò chơi. Giá trị này được tính toán bằng một hàm
tính giá trị vị trí và nó cho biết độ tốt nếu như một người chơi đạt được đến
đó. Người chơi sau đó đi một bước làm tối đa giá trị tối thiểu của vị trí là kết
quả từ tập hợp những bước đi có thể của đối thủ. Nếu đó là phiên A sẽ đi, A
sẽ cho một giá trị cho mỗi bước đi hợp pháp của anh ta. 1.2.3. Phương pháp
Hai đối thủ trong trò chơi được gọi là MIN và MAX luân phiên thay thế nhau đi.
MAX đại diện cho người quyết dành thắng lợi và cố gắng tối đa hóa ưu thế của
mình, ngược lại người chơi đại diện cho MIN lại cố gắng giảm điểm số của MAX
và cố gắng làm cho điểm số của mình càng âm càng tốt. Giả thiết đưa ra MIN và
MAX có kiến thức như nhau về không gian trạng thái trò chơi và cả hai đối thủ đều cố gắng như nhau.
Mỗi Node biểu diễn cho một trạng thái trên cây trò chơi. Node lá là Node chứa
trạng thái kết thúc của trò chơi.
Giải thuật Minimax thể hiện bằng cách định trị các Node trên cây trò chơi:
Node thuộc lớp MAX thì gán cho nó giá trị lớn nhất của con Node đó.
Node thuộc lớp MIN thì gán cho nó giá trị nhỏ nhất của con Node đó.
Từ các giá trị này người chơi sẽ lựa chọn cho mình nước đi tiếp theo hợp lý nhất.
1.2.4. Mô hình bài toán
Trong ví dụ sau đây của một trò chơi tổng bằng 0, khi A và B đi các bước cùng
một lúc, minh họa thuật toán minimax. Nếu như mỗi người chơi có 3 chọn lựa và
ma trận lợi cho A là:
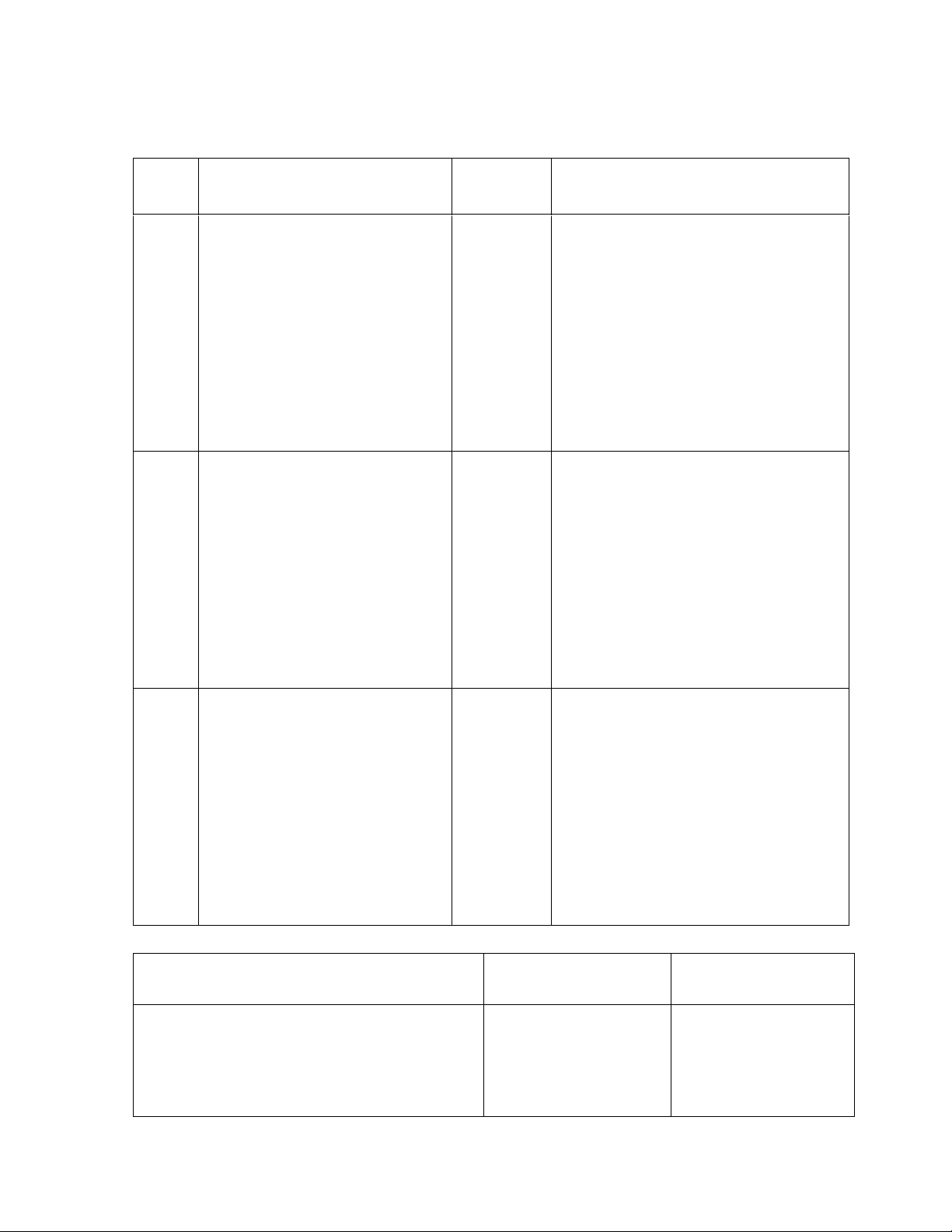
B chọn B1 B chọn B2 B chọn B3 A chọn A1 +3 -2 +2 lOMoARcPSD| 59629529 A chọn A2 -1 0 +4 A chọn A3 -4 -3 +1
Hình : minh họa thuật toán
Và B có ma trận lợi như nhau nhưng ngược dấu (i.e. nếu các lựa chọn là A1 và B1
thì B trả 3 cho A) sau đó lựa chọn minimax đơn giản cho A là A2 bởi vì kết quả
xấu nhất là sau khi phải trả 1, trong khi lựa chọn minimax đơn giản cho B là B2 bởi
vì kết quả xấu nhất là sau đó không phải trả gì cả. Tuy vậy, lời giải này là không ổn
định, bởi vì nếu B tin rằng A sẽ chọn A2 thì B sẽ chọn B1 để thắng 1; sau đó nếu A
tin rằng B sẽ chọn B1 thì A sẽ chọn A1 để thắng 3; và sau đó B sẽ chọn B2; và cuối
cùng cả hai người chơi sẽ nhận ra sự khó khăn của việc chọn lựa. Do đó một chiến
lược ổn định hơn là cần thiết.
Một số chọn lựa bị thống trị bởi những người khác và có thể bị loại bỏ: A sẽ không
chọn A3 bởi vì hoặc A1 hay A2 sẽ sinh ra một kết quả tốt hơn, bất kể là B chọn gì;
B sẽ không chọn B3 bởi vì B2 sẽ sinh ra kết quả tốt hơn, bất kể là A chọn cái gì.
A có thể tránh việc phải trả số lượng dự định (expected payment) hơn 1/3 bằng cách
chọn A1 với xác suất 1/6 và A2 với xác suất 5/6, bất kể là B đã chọn gì. B có thể
tính chắc phần lợi dự định (expected gain) ít nhất 1/3 bằng cách sử dụng một chiến
thuật ngẫu nhiên của việc chọn B1 với xác suất 1/3 và B2 với xác suất 2/3, bất kể là
A chọn gì. Những chiến lược minimax hỗn hợp bây giờ là ổn định và không thể nào cải tiến nữa. 1.3. KẾT LUẬN -
Ưu điểm: Tìm kiếm được mọi nước đi tiếp theo sau đó lựa chọn nước đi tốt
nhất, vì giải thuật có tính chất vét cạn nên không bỏ soát trạng thái. -
Nhược điểm: Đối với các trò chơi có không gian trạng thái lớn như caro, cờ
tướng… việc chỉ áp dụng giải thuật Minimax có lẽ không còn hiệu quả nữa do sự
bùng nổ tổ hợp quá lớn.
Giải thuật áp dụng nguyên lý vét cạn không tận dụng được thông tin của trạng thái
hiện tại để lựa chọn nước đi, vì duyệt hết các trạng thái nên tốn thời gian. lOMoARcPSD| 59629529
CHƯƠNG 2: BÀI TOÁN CỜ CARO 2.1 BÀI TOÁN
Giới thiệu đề tài “Game Caro” Game gồm có 2 người chơi, một người cầm quân X,
một người cầm quân O. Hai người chơi sẽ lần lượt đưa đánh quân tương ứng của
mình trên một bàn cờ MxN ô (thường thì M = N). Luật chơi: Quân X là quân được
đánh trước. Hai người chơi có thể đánh vào bất kỳ ô nào trên bàn cờ miễn là ô đó
chưa được đánh. Trò chơi kết thúc khi một trong hai người chơi có 3 quân thằng
hàng liên tiếp nhau (ngang, dọc hoặc chéo). Dưới đây là bàn cờ caro
2.2 GIẢI QUYẾT BÀI TOÁN 2.2.1. Ý tưởng
Có 2 người chơi là Min và Max. • Một chiến lược tối ưu là một chuỗi
các nước đi giúp đưa đến trạng thái đích mong muốn. • Chiến lược của MAX
bị ảnh hưởng ( phụ thuộc ) vào các nước đi của MIN –và ngược lại. • MAX
cần chọn một chiến lược giúp cực đại hóa giá trị của hàm mục tiêu – với giả
sử là MIN đi các nước đi tối ưu. • Chiến lược này được xác định bằng việc xét
các giá trị MINIMAX đối với mỗi nút trong cây biểu diễn trò chơi. • MAX
chọn các nước đi tương ứng với giá trị MINIMAX cực đại ( MIN chọn các
nước đi ứng với giá trị MINIMAX cực tiểu. b. Áp dụng vào game Caro: Người
chơi cầm quân X đóng vai trò như Max, người chơi cầm quân O đóng vai trò
như Min. Để quyết định nước đi tiếp theo, ta xây dựng một thủ tục đệ quy gồm
2 hàm max_value() để tìm nước đi tiếp theo cho quân X, min_value() để tìm
nước đi tiếp theo cho quân O. Để giảm thời gian của giải thuật đệ quy, ta giới
hạn độ sâu của giải thuật bằng 4. int max_value(state s, int
dept){ if(terminal_test() || dept >= 4) return eval(s); v = -; for(duyệt tất cả các
trạng thái con s’ của s){ v = max(v, min_value(s’, dept + 1)); } return v; } int
min_value(state s, int dept){ if(terminal_test() || dept >= 4 ) return eval(s); v =
+; for(duyệt tất cả các trạng thái con s’ của s){ v = min(v, max_value(s’, dept
+ 1)); } return v; } Hàm xác định trạng thái kết thúcterminal_test():
CHƯƠNG 3: ĐÁNH GIÁ THỬ NGIỆM
3. Cặt đặt với C# Winform
3.1 Giao diện khi chạy chương trình lOMoARcPSD| 59629529
Hình 1: Giao diện khi chạy chương trình
3.2:Giao diện khi bắt đầu chơi (sau khi bắt đầu chúng ta sẽ bắt đầu tích
vào những ô trống để chơi) lOMoARcPSD| 59629529
Hình 8: bàn cờ khi bắt đầu chơi
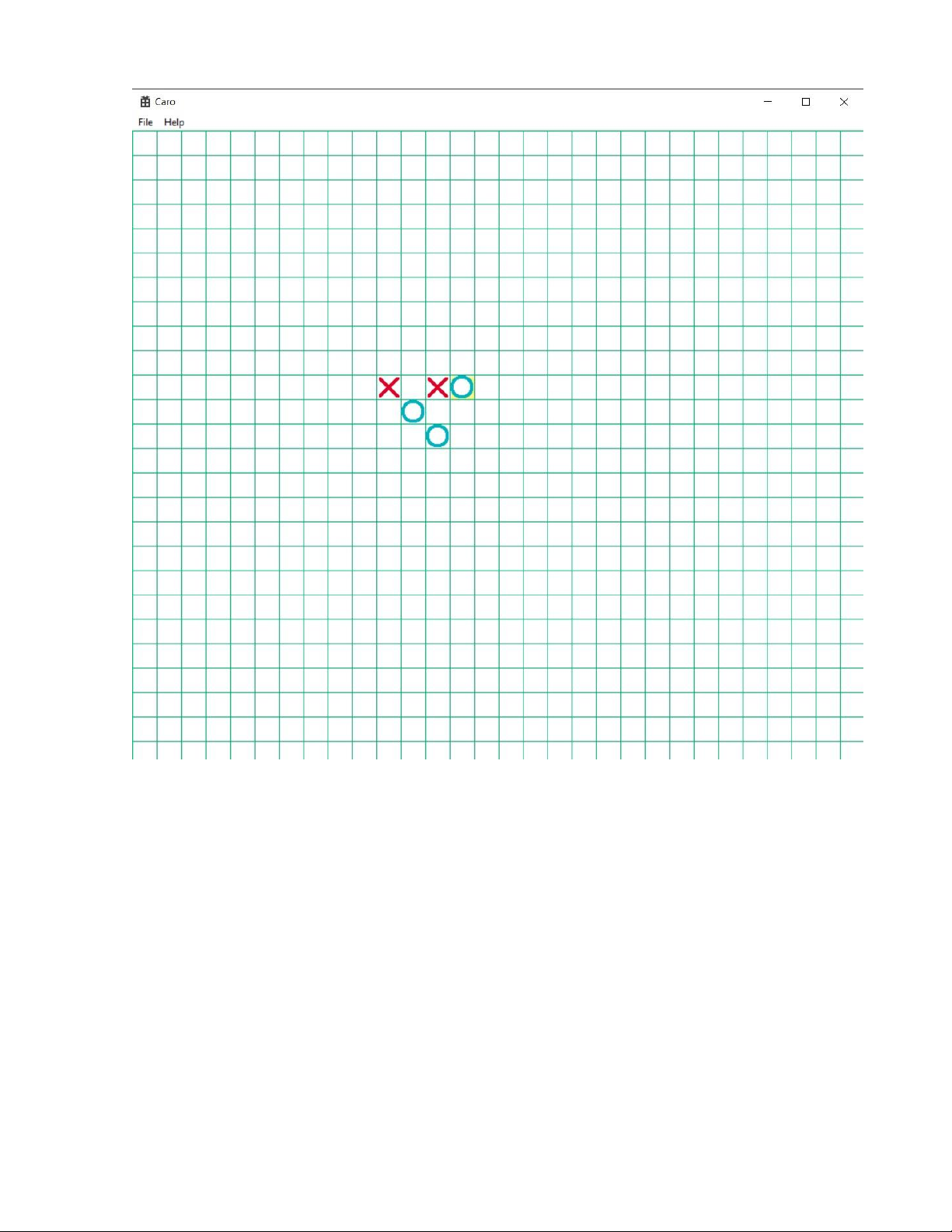
3. 3 Giao diện sau khi chơi ( chúng ta sẽ tích vào ô trống cho đến khi một
trong hai người hoặc máy hoàn thành 5 kí tự thẳng hàng và sau đó hệ thống
sẽ thông báo người thắng cuộc và hỏi xem chúng ta có muốn chơi ván mới không) lOMoARcPSD| 59629529
Hình 9: ván đấu kết thúc KẾT LUÂṆ
Với kiến thức hiện có của mình, chúng em đã hoàn thành các yêu cầu ở trên khi
tiến hành thực hiên đ ̣ ề tài “ÁP DỤNG THUẬT TOÁN MINIMAX GIẢI QUYẾT
BÀI TOÁN CỜ CARO”. Tuy nhiên, trong quá trình làm sẽ không tránh khỏi những
thiếu sót, hoặc cũng sẽ có những chỗ còn vướng mắc, chính vì vậy, chúng em mong
được sự góp ý giúp đỡ của thầy giáo, để bài này được hoàn thiện hơn !
Chúng em xin gửi lời cảm ơn chân thành tới giảng viên Nguyễn Thị Thanh Tân
là giảng viên giảng dạy môn Nhập môn Trí tuệ nhân tạo của lớp D14CNPM5 đã tận
tình hướng dẫn chúng em hoàn thành đề tài này! lOMoARcPSD| 59629529
Chúng em xin chân thành cảm ơn! lOMoARcPSD| 59629529
TÀI LIÊU THAM KḤ ẢO 1. Internet 2. Wikipedia (tài liệu)