Báo cáo Chuyên đề Môn Nhập Môn Học Máy Dự Đoán Bệnh Tim Mạch | Đại học Điện lực

lOMoARcPSD| 59629529
TRƯỜNG ĐẠI HỌC ĐIỆN LỰC
KHOA CÔNG NGHỆ THÔNG TIN
BÁO CÁO CHUYÊN ĐỀ HỌC PHẦN MÔN
NHẬP MÔN HỌC MÁY
SỬ DỤNG MÔ HÌNH MÁY VECTOR HỖ TRỢ (SVM) ĐỂ DỰ ĐOÁN
KHẢ NĂNG MẮC BỆNH TIM MẠCH
Sinh viên thực hiện : NGUYỄN HUY ANH NGUYỄN HỒNG TÌNH
Giảng viên hướng dẫn : VŨ VĂN ĐỊNH Ngành
: CÔNG NGHỆ THÔNG TIN Chuyên ngành
: CÔNG NGHỆ PHẦN MỀM Lớp : D16CNPM1
Hà Nội, tháng 5 năm 2024 lOMoARcPSD| 59629529 PHIẾU CHẤM ĐIỂM
Sinh viên thực hiện: Họ và tên Chữ ký Điểm Nguyễn Huy Anh Nguyễn Hồng Tình Giảng viên chấm: Họ và tên Chữ ký Ghi chú Giảng viên chấm 1 : Giảng viên chấm 2 : MỤC LỤC
LỜI NÓI ĐẦU .......................................................................................................... 1
CHƯƠNG 1: GIỚI THIỆU MÔ HÌNH SVM ....................................................... 1
1.1 Khái niệm về mô hình SVM ....................................................................... 1
1.2 Các bước thực hiện của mô hình SVM ...................................................... 2
1.3 Cách thức hoạt động của mô hình SVM .................................................... 3
1.4 Margin trong SVM ................................................................................... 10
1.5 Kết luận về thuật toán .............................................................................. 10 lOMoARcPSD| 59629529
CHƯƠNG 2: ỨNG DỤNG MÔ HÌNH SVM VÀO GIẢI QUYẾT BÀI
TOÁN ...................................................................................................................... 12
2.1 Giới thiệu bài toán .................................................................................... 12
2.2 Giải quyết bài toán.................................................................................... 12
2.2.1 Phân tích dữ liệu dataset .................................................................... 12
2.2.2 Áp dụng mô hình vào biến đổi dữ liệu ............................................... 14
2.2.2.1 Cột tuổi (age) ................................................................................. 15
2.2.2.2 Cột giới tính .................................................................................. 15
2.2.2.3 Cột loại đau ngực .......................................................................... 16
2.2.2.4 Cột huyết áp lúc nghỉ .................................................................... 16
2.2.2.5 Cột cholesterol .............................................................................. 17
2.2.2.6 Cột lượng đường trong máu ......................................................... 17
2.2.2.7 Cột kết quả điện tâm đồ lúc nghỉ ngơi ......................................... 18
2.2.2.8 Cột nhịp tim tối đa đạt được ........................................................ 18
2.2.2.9 Cột tập thể dục có gây đau thắt ngực không ............................... 19
2.2.2.10 Cột chênh lệch đoạn ST khi tập thể dục so với lúc nghỉ ........... 19
2.2.2.11 Cột độ dốc tại đỉnh của đoạn ST khi tập thể dục ...................... 20
2.2.2.12 Cột số lượng đoạn mạch chính ................................................... 20
2.2.2.13 Cột dấu hiệu của sóng ................................................................. 21
2.2.2.14 Cột chuẩn đoán ........................................................................... 21 lOMoARcPSD| 59629529 LỜI NÓI ĐẦU
Bệnh tim mạch là một trong những nguyên nhân gây tử vong hàng đầu trên
thế giới, ảnh hưởng đến sức khỏe và chất lượng cuộc sống con người: số người chết
hàng năm do bệnh tim mạch cao hơn bất kì nguyên nhân nào khác. Những người
mắc bệnh tim mạch hoặc có nguy cơ cao mắc bệnh tim mạch nếu được theo dõi và
phát hiện sớm sẽ làm giảm được tỉ lệ tử vong. Tuy nhiên, vấn đề là việc theo dõi và
giám sát bệnh nhân liên tục và xuyên suốt đòi hỏi nhiều thời gian, kinh nghiệm,
chuyên môn cao và nguồn nhân lực rất lớn.
Với sự phát triển vũ bão của công nghệ, nhất là trong lĩnh vực trí tuệ nhân tạo
AI, hiện nay người ta đã và đang liên tục phát triển các giải pháp của cac vấn đề
trong mọi lĩnh vực, trong đó có các giải pháp kết hợp AI để tăng khả năng điều trị
trong lĩnh vực y tế, một ví dụ cụ thể hơn đó là mô hình chẩn đoán khả năng mắc
bệnh tim dựa trên các số liệu theo dõi mà máy móc có thể tự động ghi nhận với tần
suất cao trong thời gian dài.
Qua những phân tích trên, chúng em quyết định chọn đề tài: “SỬ DỤNG MÔ
HÌNH MÁY VECTOR HỖ TRỢ (SVM) ĐỂ DỰ ĐOÁN KHẢ NĂNG MẮC
BỆNH TIM MẠCH” để làm báo cáo chuyên đề cuối môn.
Chúng em xin chân thành gửi lời cảm ơn đến các thầy cô giáo trong Trường
Đại học Điện Lực nói chung và các thầy cô trong Khoa Công nghệ thông tin nói
riêng đã tận tình giảng dạy, truyền đạt cho chúng em những kiến thức cũng như kinh
nghiệm quý báu trong suốt quá trình học. Đặc biệt, chúng em gửi lời cảm ơn đến
thầy Vũ Văn Định đã tận tình theo sát giúp đỡ, trực tiếp chỉ bảo, hướng dẫn trong
suốt quá trình nghiên cứu và học tập của chúng em.
CHƯƠNG 1: GIỚI THIỆU MÔ HÌNH SVM
1.1 Khái niệm về mô hình SVM
Support Vector Machine (SVM) hay Mô hình Máy Vector hỗ trợ là một
thuật toán giám sát, nó có thể sử dụng cho cả việc phân loại hoặc đệ quy. Tuy
nhiên nó được sử dụng chủ yếu cho việc phân loại. Trong thuật toán này, chúng
ta sẽ vẽ đồ thị dữ liệu là các điểm trong n chiều (ở đây n là số lượng các tính
năng hiện có) với giá trị của mỗi tính năng sẽ là một phần liên kết. Sau đó chúng
ta thực hiện tìm “đường bay” (hyper-plane) phân chia các lớp. Hyperplane có
thể hiểu đơn giản là một đường thẳng có thể phân chia các lớp ra hai phần riêng biệt. lOMoARcPSD| 59629529
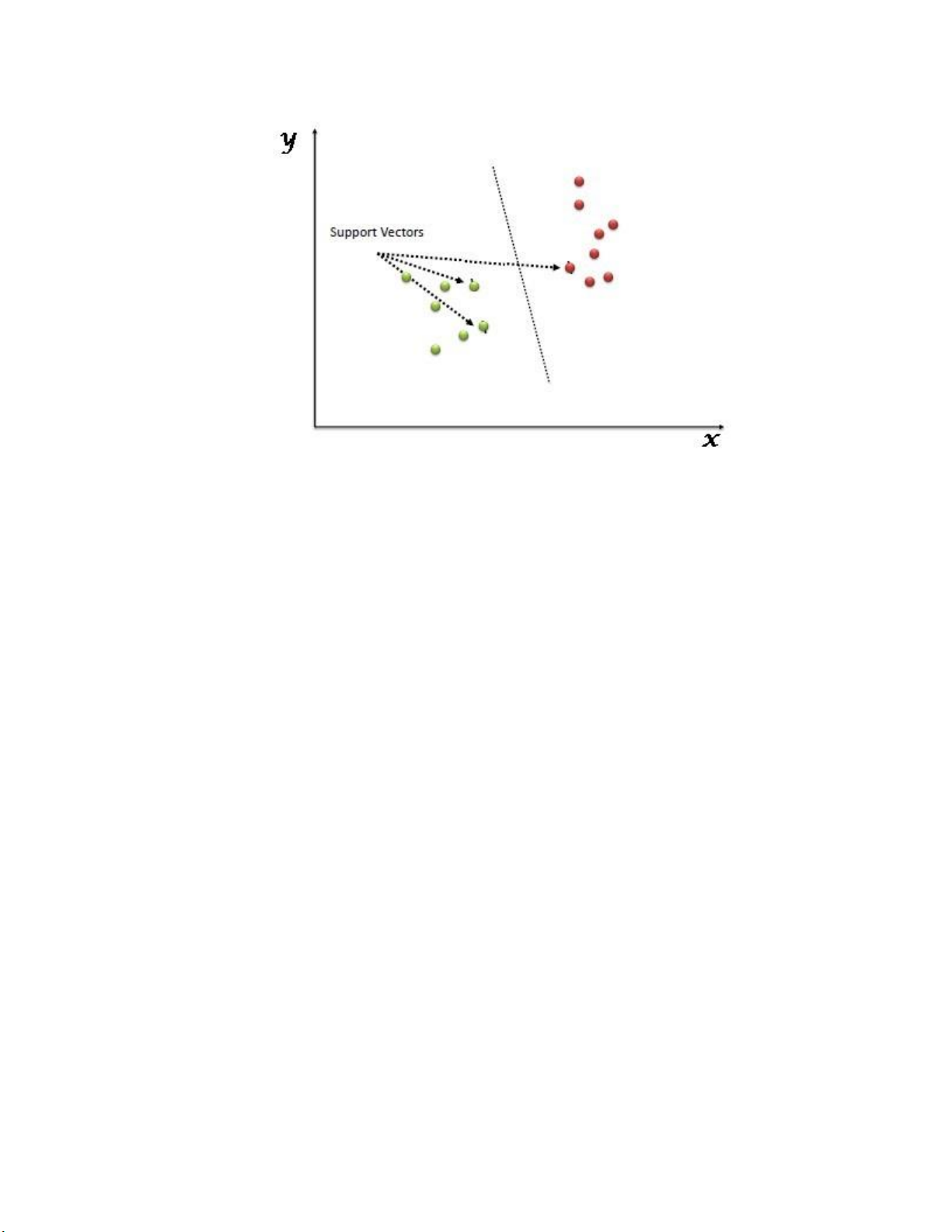
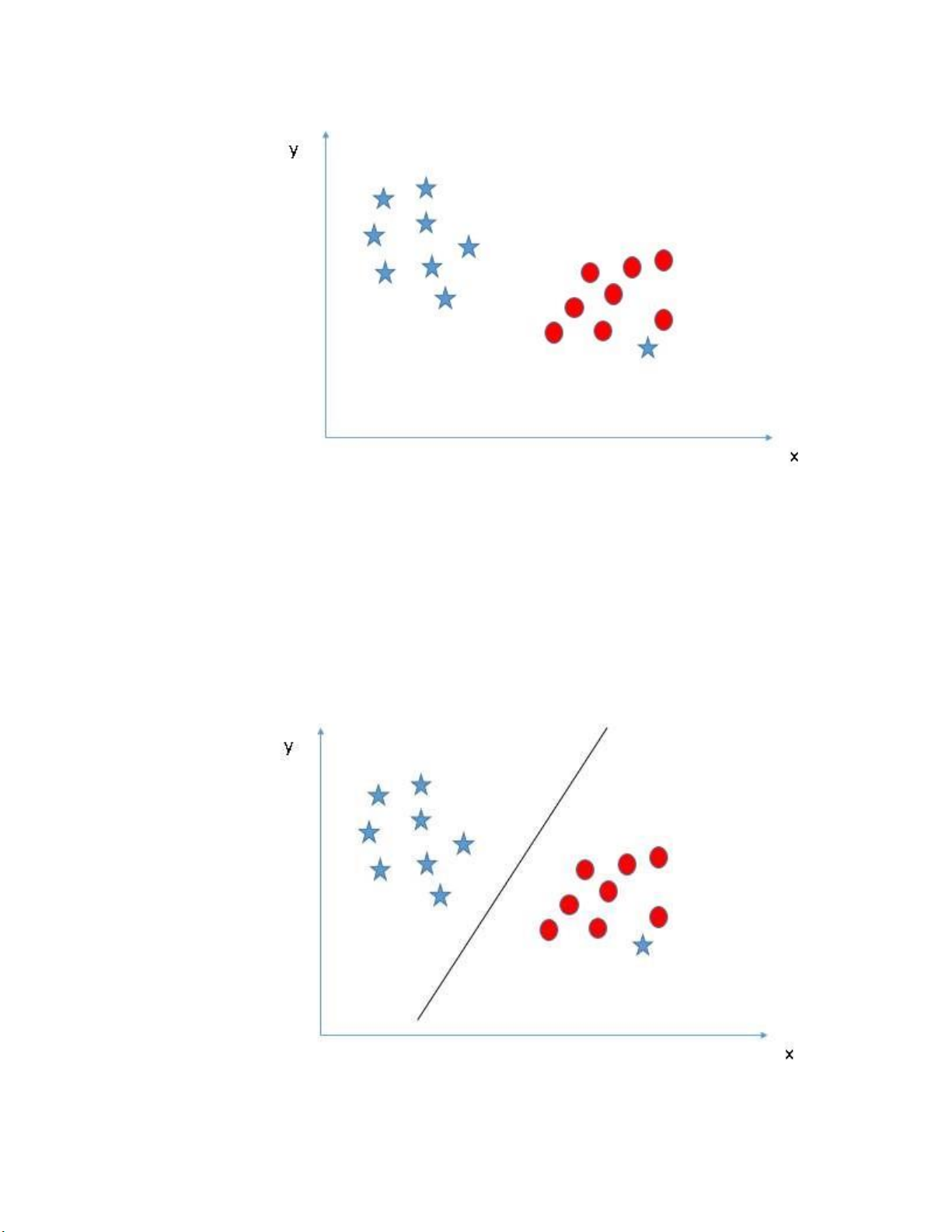
Hình 1.1 Biểu đồ Vector hỗ trợ (SVM) phân loại dữ liệu
Ví dụ, ở hình 1.1 mô tả một biểu đồ SVM được sử dụng để phân loại hai lớp dữ liệu khác nhau:
• Biểu đồ phân tán: Hình ảnh là một trục X và Y.
• Hai nhóm dữ liệu: Có hai nhóm dữ liệu rõ ràng được biểu diễn bằng các chấm màu đỏ và xanh lá.
• Đường biên quyết định: Một đường nét đứt biểu thị đường biên quyết định, tác
biệt hai nhóm dữ liệu này.
• Vector hỗ trợ: “Support Vectors” được gán nhãn trên ba chấm xanh lá gần
đường biên quyết định nhất, chỉ ra rằng những điểm này được sử dụng để xác
định vị trí và hướng của đường biên quyết định.
Tóm lại, Support Vector có thể hiểu một cách đơn giản là các đối tượng
trên đồ thị tọa độ quan sát, Support Vector Machine là một biên giới để chia
ranh giới giữa các lớp được tốt nhất.
1.2 Các bước thực hiện của mô hình SVM
Để thực hiện thuật toán của mô hình SVM, chúng ta thực hiện các bước sau:
- Xây dựng bài toán tối ưu cho SVM: Bài toán tối ưu của SVM nhằm tìm ra
vector trọng số (w) và hệ số dẫn (b) sao cho được tối ưu hóa một hàm mục
tiêu nhất định. Hàm mục tiêu thường là tối ưu hóa khoảng cách giữa các điểm
dữ liệu và lề phân tách, đồng thời giữ cho lề càng rộng càng tốt để các điểm
khác vẫn có thể được phân loại chính xác. lOMoARcPSD| 59629529
- Bài toán đối ngẫu cho SVM: SVM là một bài toán lồi, và nếu một bài toán lồi
thoả mãn tiêu chuẩn Slater, thì strong duality thoả mãn. Nếu strong duality
thoả mãn, nghiệm của bài toán chính là nghiệm của hệ điều kiện KKT (Karush-Kuhn-Tucker).
- Điều kiện KKT: Điều kiện KKT là một tập hợp các điều kiện cần thiết để một
bài toán tối ưu có nghiệm tối ưu. Trong SVM, điều kiện KKT bao gồm các
điều kiện về vector trọng số (w), hệ số dẫn (b), và các giá trị của hàm mục tiêu.
- Lập trình tìm nghiệm cho SVM: Có hai cách chính để tìm nghiệm cho SVM:
một là tính toán trực tiếp dựa trên công thức, và cách khác là sử dụng thư viện
sklearn. Cách sử dụng thư viện sklearn thường được ưa chuộng vì nó tiết kiệm thời gian và công sức.
- Sử dụng kernel: Kernel là một kỹ thuật quan trọng trong SVM, giúp mở rộng
không gian đặc trưng của dữ liệu, cho phép SVM giải quyết các bài toán phân
loại có Decision Boundary phức tạp.
- Chọn siêu tham số C: Siêu tham số C trong SVM đóng vai trò như một tham
số phạt, quyết định mức độ chấp nhận lỗi phân loại. Càng lớn giá trị C, SVM
càng bị phạt nặng khi thực hiện phân loại sai, dẫn đến việc lề phân tách càng
hẹp và càng ít vectơ hỗ trợ được sử dụng.
1.3 Cách thức hoạt động của mô hình SVM
Ở nội dung trước đã minh họa việc chia hyper-plane. Phần hiện tại sẽ làm rõ
vấn đề “Làm sao để vẽ - xác định đúng hyper-plane”. Việc xác định đúng
hyperplane sẽ đi theo các tiêu chí sau: • Quy tắc số 1:
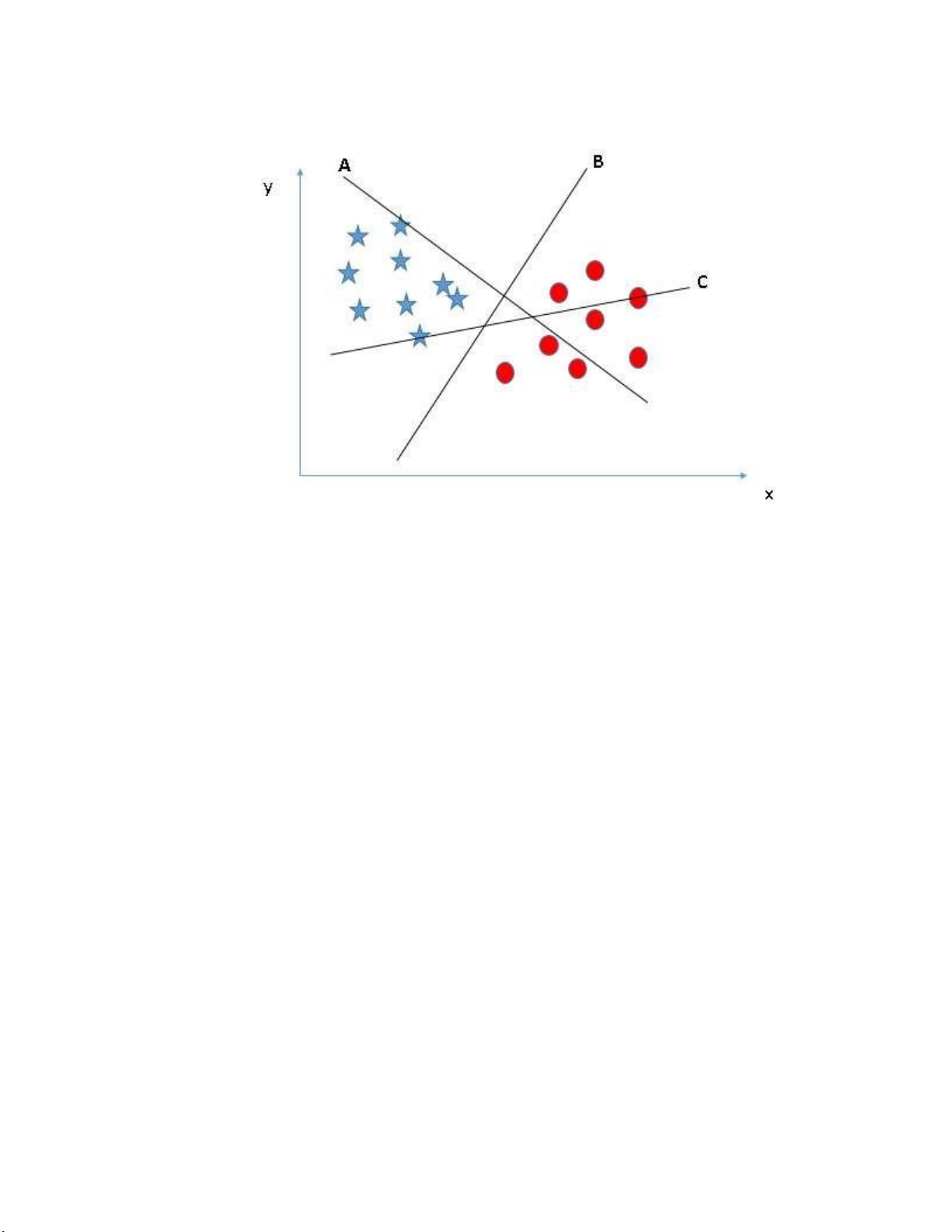
Ở đây chúng ta có 3 đường hyper-plane (A, B và C). lOMoARcPSD| 59629529
Hình 1.2 Biểu đồ SVM với đường phân cách B đúng
Ta xét từng đường phân cách như sau:
- Đường A và C: Không phân tách hiệu quả hai nhóm hình dạng vì một
số ngôi sao và hình tròn chồng lên nhau.
- Đường B: Phân tách hoàn hảo ngôi sao khỏi hình tròn, do đó ta chọn
đường B là một phân loại hiệu quả.
Do đó, quy tắc số một để chọn hyper-plane, chọn một hyper-plane để phân chia hai lớp tốt nhất. • Quy tắc số 2:
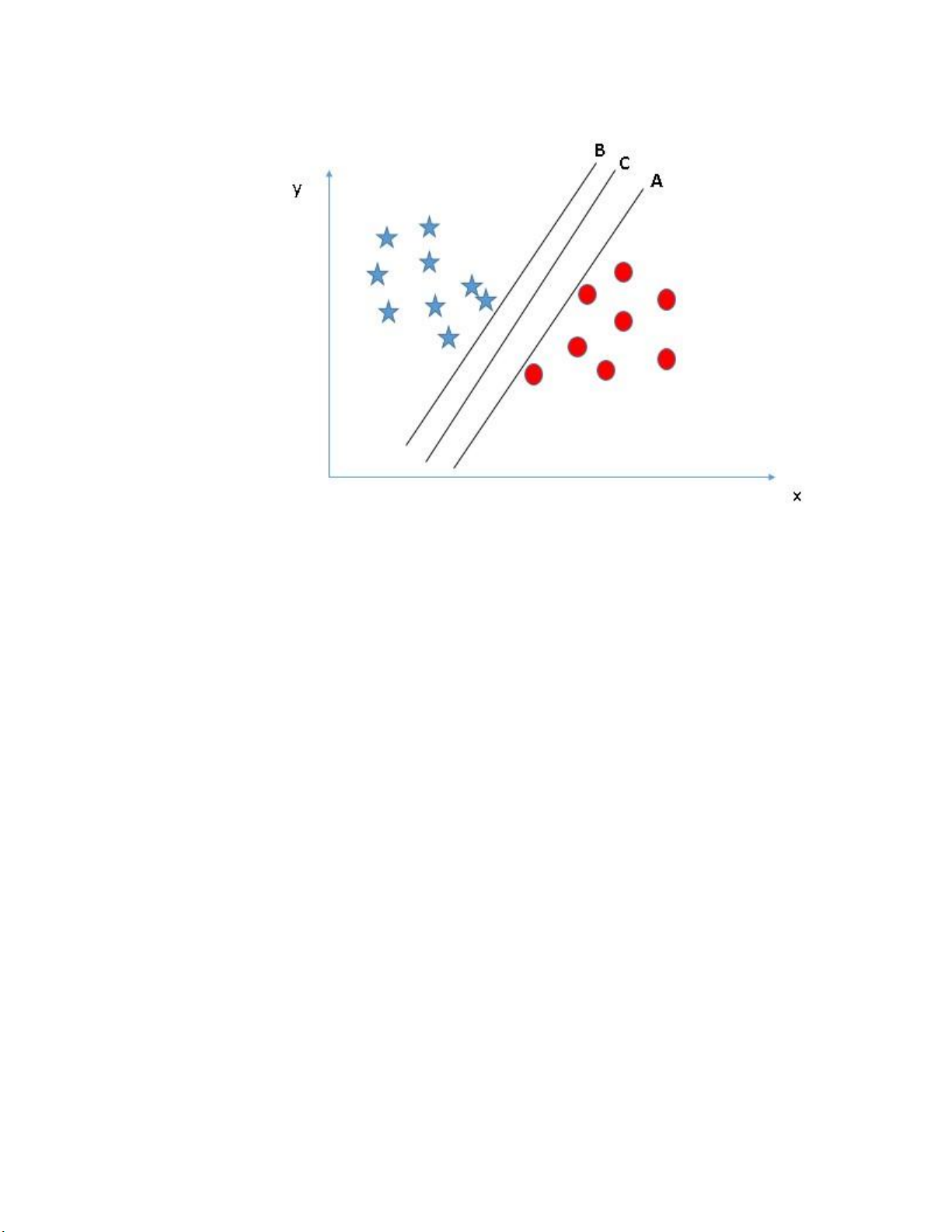
Hình ảnh bên dưới cũng mô tả ba đường hyper-plane (A, B và C).
Theo quy tắc số 1, chúng đều thỏa mãn. lOMoARcPSD| 59629529
Hình 1.3 Biểu đồ SVM với khoảng cách “Margin” từ các vector
hỗ trợ đến đường hyper-plane
Quy tắc thứ hai chính là xác định khoảng cách lớn nhất từ điểm gần
nhất của một lớp nào đó đến đường hyper-plane. Khoảng cách từ các điểm
này của mỗi lớp đến đường hyper-plane được gọi là “Margin”. Khoảng
cách “Margin” là yếu tố quan trọng trong việc xác định mô hình SVM,
giúp tối ưu hóa sự phân loại và đảm bảo độ chính xác cao. Đường hyper-
plane tối ưu sẽ là đường có “Margin” lớn nhất, tạo khoảng trống rõ ràng
giữa các lớp dữ liệu.
Xét hình 1.3, có thể thấy khoảng cách margin lớn nhất là đường C. Cần
nhớ nếu chọn sai đường hyper-plane có margin thấp hơn thì sau này khi
dữ liệu tăng lên thì sẽ sinh ra nguy cơ cao về việc xác định nhầm lớp cho dữ liệu. • Quy tắc số 3:
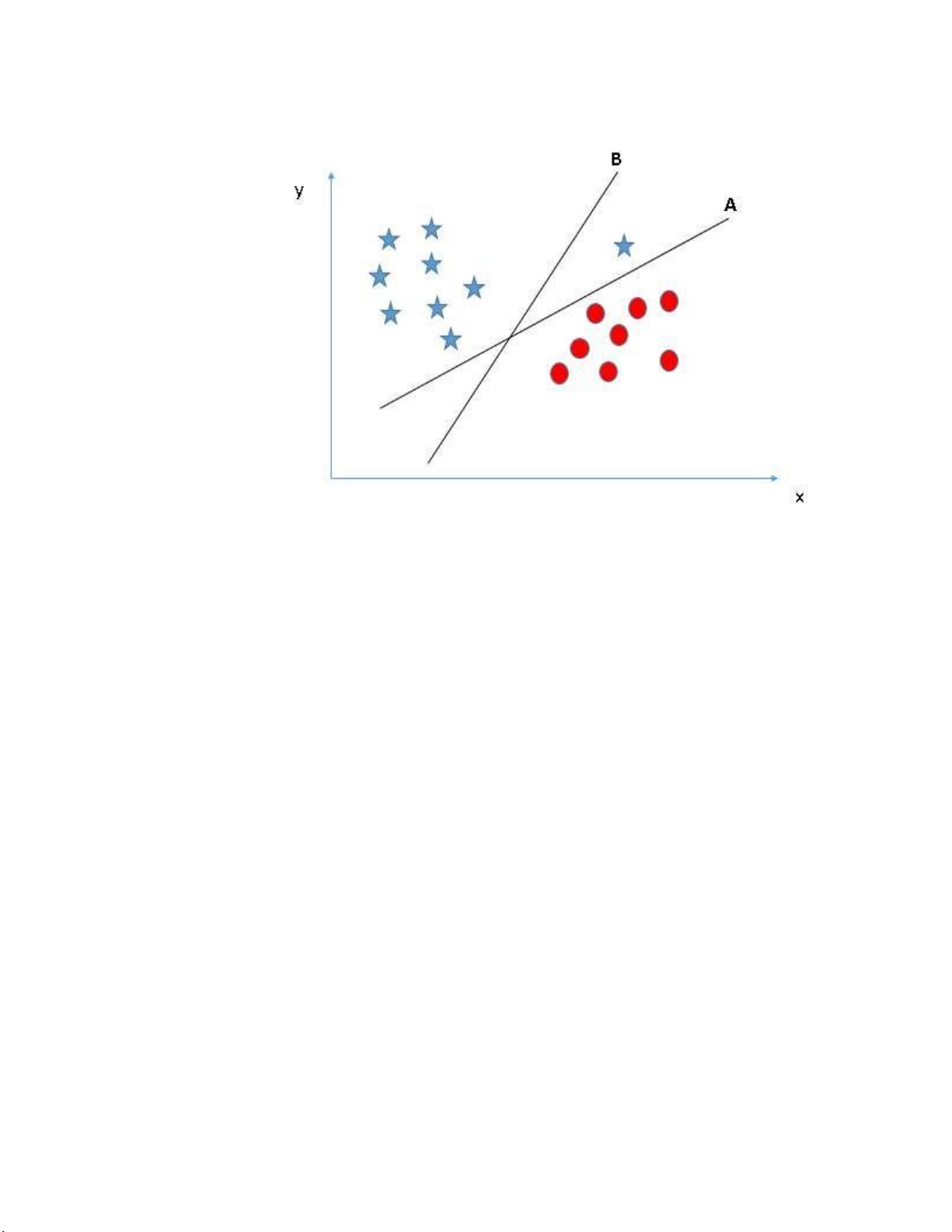
Chúng ta tiếp tục xét hình sau: lOMoARcPSD| 59629529
Hình 1.4 Biểu đồ SVM với đường phân cách A đúng giữa 2 lớp dữ liệu
Mặc dù đường B có margin lớn hơn đường A, nhưng nó không có sự
phân loại chính xác các điểm dữ liệu vì có sự chồng chéo giữa các lớp. Theo
nguyên tắc số 1, chúng ta cần chọn hyper-plane để phân chia các lớp riêng
biệt. Do đó, chúng ta chọn đường A vì nó không có sự chồng chéo và phân
loại dữ liệu một cách rõ ràng, tuân thủ theo nguyên tắc đầu tiên. • Quy tắc số 4:
Tiếp tục với hình bên dưới, câu hỏi đặt ra là chúng ta có thể phân loại
hai lớp trong trường hợp này không? Theo như mô tả, phần chỉ chứa các
điểm tròn có ngôi sao, cho nên ta không thể chia thành hai lớp riêng biệt
chỉ với một đường thẳng. lOMoARcPSD| 59629529
Hình 1.5 Biểu đồ SVM với một ngôi sao nằm bên vùng của hình tròn đỏ
Ở đây ta sẽ chấp nhận, một ngôi sao ở bên ngoài cuối được xem như
một ngôi sao phía ngoài hơn, SVM có khả năng mạnh trong việc chấp nhận
ngoại lệ bằng cách tìm ra hyper-plane có biên giới tối đa, cho phép một số
ngoại lệ mà không làm giảm hiệu suất phân loại tổng thể. Điều này giúp
SVM trở thành một công cụ linh hoạt và mạnh mẽ trong việc phân loại dữ liệu. lOMoARcPSD| 59629529
Hình 1.6 Biểu đồ SVM với đường phân cách và ngoại lệ được xác định Quy tắc số 5:
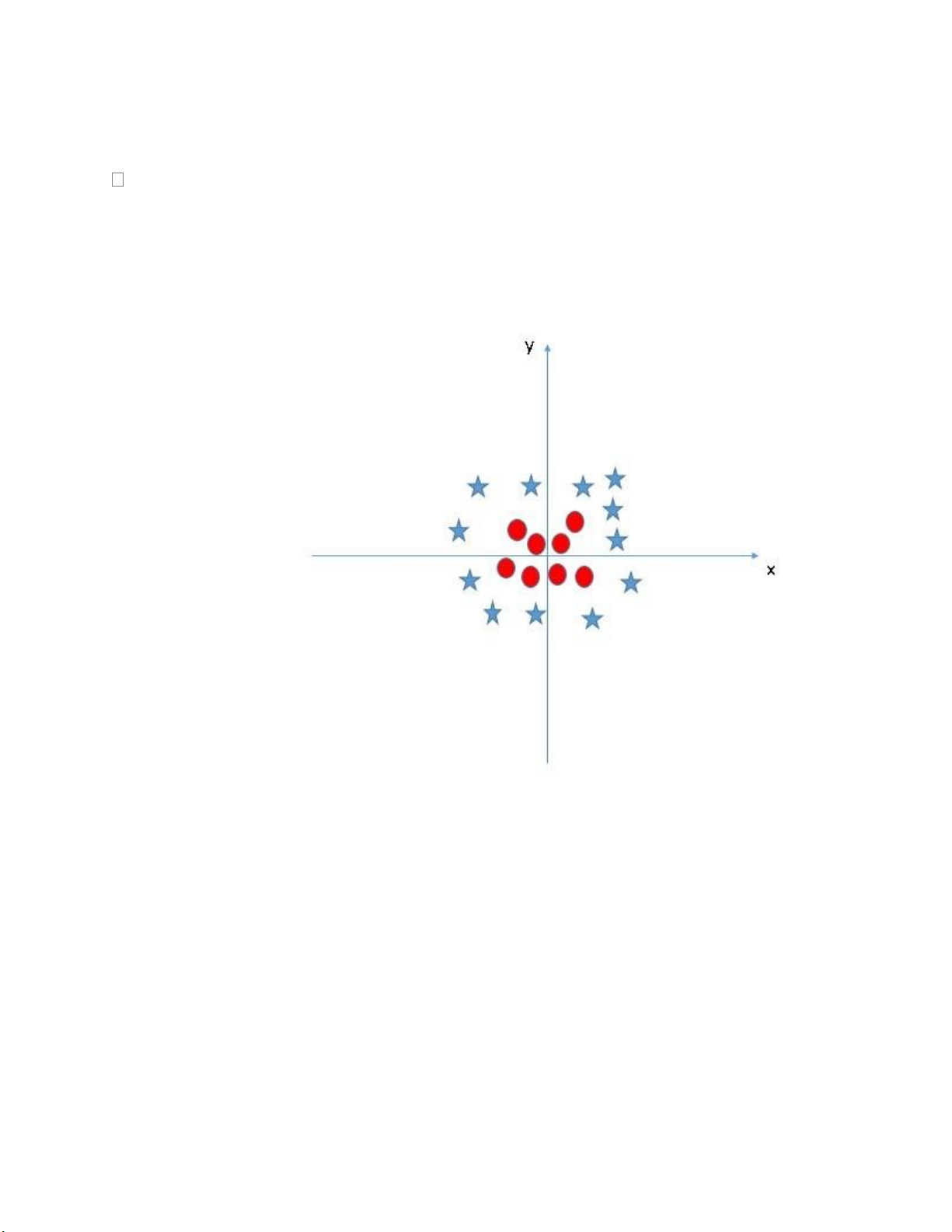
Trong trường hợp dưới đây, chúng ta không thể tìm ra một đường
hyper-plane tương đối để chia các lớp, vậy làm thế nào để SVM phân tách
dữ liệu thành hai lớp riêng biệt? Cho đến bây giờ chúng ta chỉ nhìn vào các
đường tuyến tính hyper-plane.
Hình 1.7 Biểu đồ SVM với dữ liệu không tách biệt tuyến tính
SVM có thể giải quyết được vấn đề này. Trong trường hợp này, chúng
ta thêm một tính năng mới là z = x^2 + y^2, biến đổi không gian dữ liệu
từ 2D (với trục x và y) thành 3D, (với trục x, y và z mới). Trong không
gian 3D này, các lớp dữ liệu có thể được phân tách một cách rõ ràng bởi
một siêu phẳng, giúp việc phân loại trở nên chính xác hơn. Bây giờ, dữ
liệu sẽ được biến đổi như sau: lOMoARcPSD| 59629529
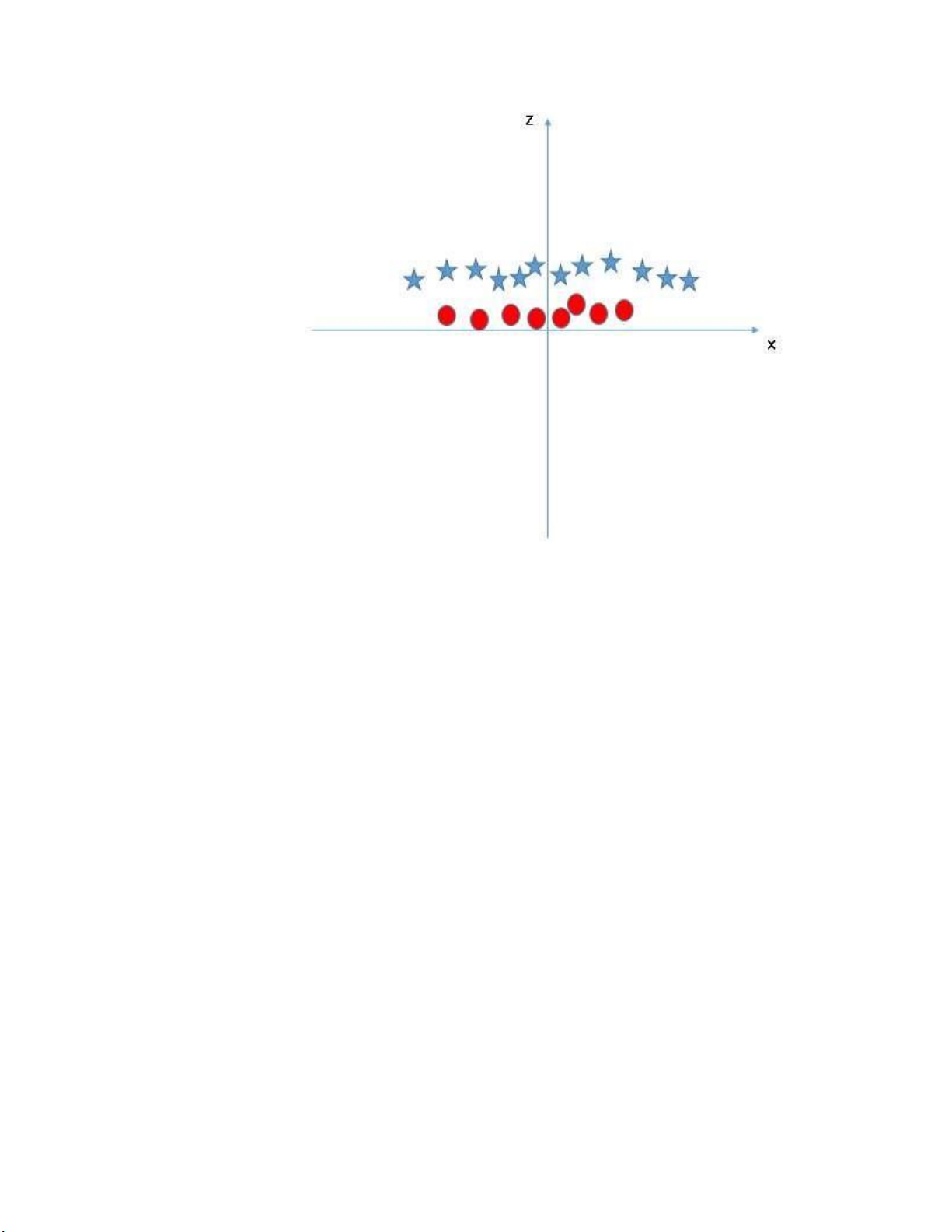
Hình 1.8 Biểu đồ SVM sau khi được biến đổi Trong
sơ đồ trên, các điểm cần xem xét là:
o Tất cả dữ liệu trên trục z sẽ là số dương vì nó là tổng bình phương x và y.
o Trên biểu đồ các điểm tròn đỏ xuất hiện gần trục x và y hơn, vì thế
z sẽ nhỏ hơn => nằm gần trục x hơn trong đồ thị (z,x).
Trong SVM, rất dễ dàng để có một siêu phẳng tuyến tính (linear hyper-
plane) để chia thành hai lớp. Câu hỏi được đặt ra là chúng ta có cần phải thêm
một tính năng phân chia này bằng tay hay không. SVM có một kĩ thuật được
gọi là kernel trick (kỹ thuật hạt nhân), đây là tính năng có không gian đầu vào
có chiều sâu thấm và biến đổi nó thành không gian có chiều cao hơn, nơi có
thể tìm được một phân loại siêu phẳng tốt hơn, giúp phân loại dễ dàng hơn.
Tức là nó không phân chia các vấn đề thành cac vấn đề riêng biệt, các tính
năng này được gọi là kernel. Nói một cách đơn giản nó thực hiện một số biến
đổi dữ liệu phức tạp, sau đó tìm ra quá trình tách dữ liệu dựa trên các nhãn
hoặc đầu ra mà chúng ta đã xác định trước.
Qua đó, SVM có thể giải quyết các vấn đề phân loại phức tạp mà không
cần phải can thiệp thủ công vào dữ liệu. lOMoARcPSD| 59629529 1.4 Margin trong SVM
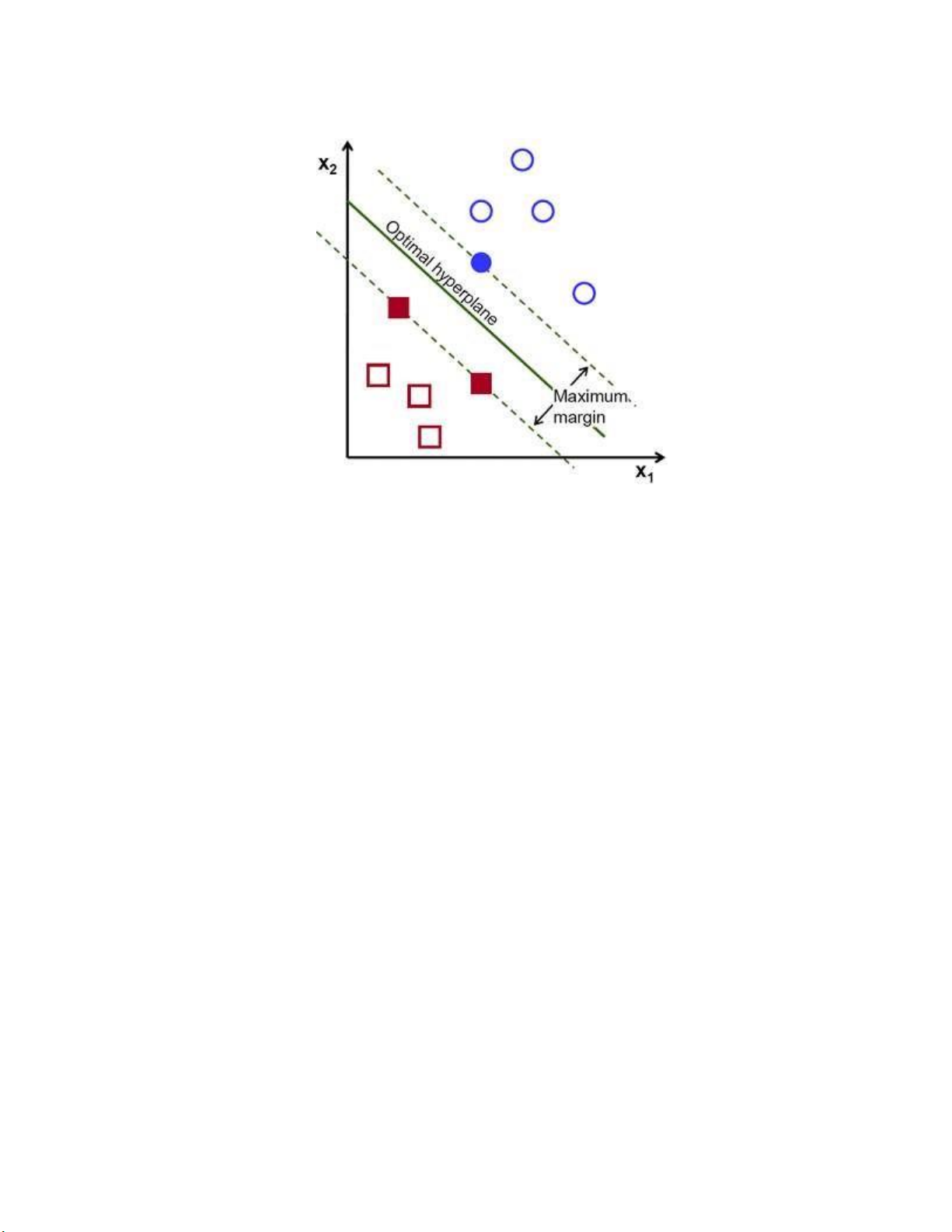
Hình 1.9 Margin trong SVM
Margin là khoảng cách giữa siêu phẳng đến 2 điểm dữ liệu gần nhất tương ứng
với các phân lớp. Trong ví dụ quả táo quả lê đặt trên mặt bán, margin chính là khoảng
cách giữa cây que và hai quả táo và lê gần nó nhất. Điều quan trọng ở đây đó là
phương pháp SVM luôn cố gắng cực đại hóa margin này, từ đó thu được một siêu
phẳng tạo khoảng cách xa nhất so với 2 quả táo và lê. Nhờ vậy, SVM có thể giảm
thiểu việc phân lớp sai (misclassification) đối với điểm dữ liệu mới đưa vào.
1.5 Kết luận về thuật toán
Là một kĩ thuật phân lớp khá phổ biến, SVM thể hiện được nhiều ưu điểm trong
số đó có việc tính toán hiệu quả trên các tập dữ liệu lớn. Có thể kể thêm một số ưu
điểm của phương pháp này như:
• Xử lý trên không gian số chiều cao: SVM là một công cụ tính toán hiệu quả trong
không gian chiều cao, trong đó đặc biệt áp dụng cho các bài toán phân loại văn
bản và phân tích quan điểm nơi chiều có thể cực kỳ lớn.
• Tiết kiệm bộ nhớ: Do chỉ có một tập hợp con của các điểm được sử dụng trong
quá trình huấn luyện và ra quyết định thực tế cho các điểm dữ liệu mới nên chỉ
có những điểm cần thiết mới được lưu trữ trong bộ nhớ khi ra quyết định.
• Tính linh hoạt - phân lớp thường là phi tuyến tính. Khả năng áp dụng Kernel mới
cho phép linh động giữa các phương pháp tuyến tính và phi tuyến tính từ đó khiến
cho hiệu suất phân loại lớn hơn. lOMoARcPSD| 59629529 Nhược điểm:
• Bài toán số chiều cao: Trong trường hợp số lượng thuộc tính (p) của tập dữ liệu
lớn hơn rất nhiều so với số lượng dữ liệu (n) thì SVM cho kết quả khá tồi.
• Chưa thể hiện rõ tính xác suất: Việc phân lớp của SVM chỉ là việc cố gắng tách
các đối tượng vào hai lớp được phân tách bởi siêu phẳng SVM. Điều này chưa
giải thích được xác suất xuất hiện của một thành viên trong một nhóm là như thế
nào. Tuy nhiên hiệu quả của việc phân lớp có thể được xác định dựa vào khái
niệm margin từ điểm dữ liệu mới đến siêu phẳng phân lớp mà chúng ta đã bàn luận ở trên.
Kết luận: SVM là một phương pháp hiệu quả cho bài toán phân lớp dữ liệu. Nó
là một công cụ đắc lực cho các bài toán về xử lý ảnh, phân loại văn bản, phân tích
quan điểm. Một yếu tố làm nên hiệu quả của SVM đó là việc sử dụng Kernel function
khiến cho các phương pháp chuyển không gian trở nên linh hoạt hơn. lOMoARcPSD| 59629529
CHƯƠNG 2: ỨNG DỤNG MÔ HÌNH SVM VÀO GIẢI QUYẾT BÀI TOÁN
2.1 Giới thiệu bài toán
Tệp dữ liệu là file mở rộng heart.csv. Trong tệp dữ liệu này có 14 cột và 1026 hàng gồm:
• Age: tuổi của từng bệnh nhân.
• Sex: giới tính của từng bệnh nhân.
• CP: loại đau ngực của từng bệnh nhân (chest pain type)
- Giá trị 0: đau ngực không điển hình (asymptomatic)
- Giá trị 1: đau ngực không phải do angina (non-anginal pain)
- Giá trị 3: đau ngực điển hình (typical angina)
• Trestbps: huyết áp nghỉ cảu bệnh nhân khi nhập viện (resting blood pressure, đơn vị là mm Hg).
• Chol: lượng cholesterol trong máu (đơn vị là mg/dl) Fbs: chỉ số đường huyết
sau khi nhịn ăn (fasting blood sugar).
• Restecg: kết quả điện tâm đồ nghỉ ngơi.
• Thalach: tốc độ nhịp tim tối đa của bệnh nhân.
• Exang: đau thắt ngực do tập thể dục.
• Oldpeak: sự giảm của đường cong ST trên đồ thị điện tâm đồ (ECG) khi bệnh
nhân tập thể dục so với khi nghỉ.
• Slope: độ dốc của đoạn ST trong quá trình tập luyện cao nhất.
• Ca: số lượng các đường dẫn chính.
• Thal: đại diện cho rối loạn máu.
• Target: xác định bệnh nhân có bị bệnh tim hay không.
2.2 Giải quyết bài toán
2.2.1 Phân tích dữ liệu dataset
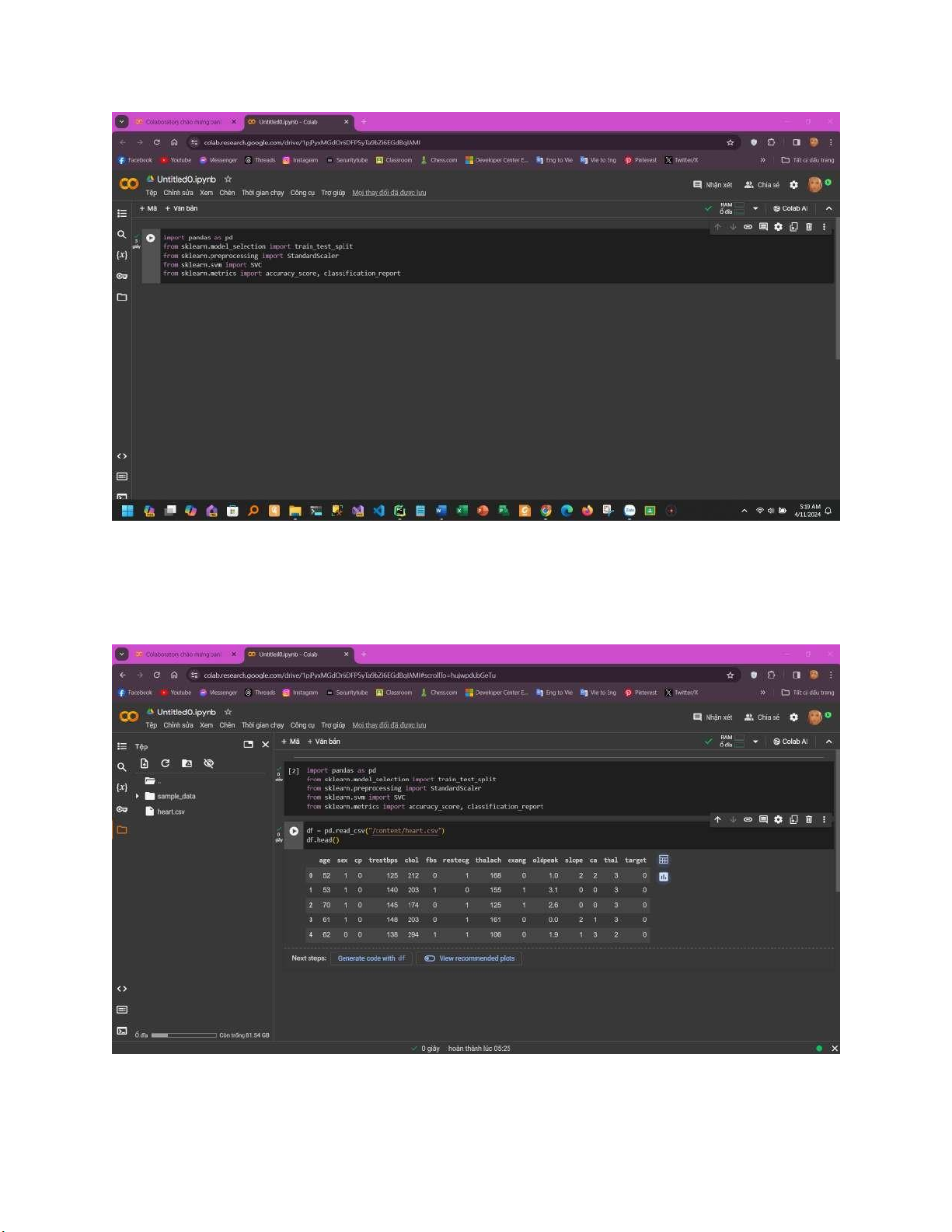
Chúng ta sẽ sử dụng một số thư viện cần thiết để xử lí và phân tích trực quan hóa dữ liệu: lOMoARcPSD| 59629529
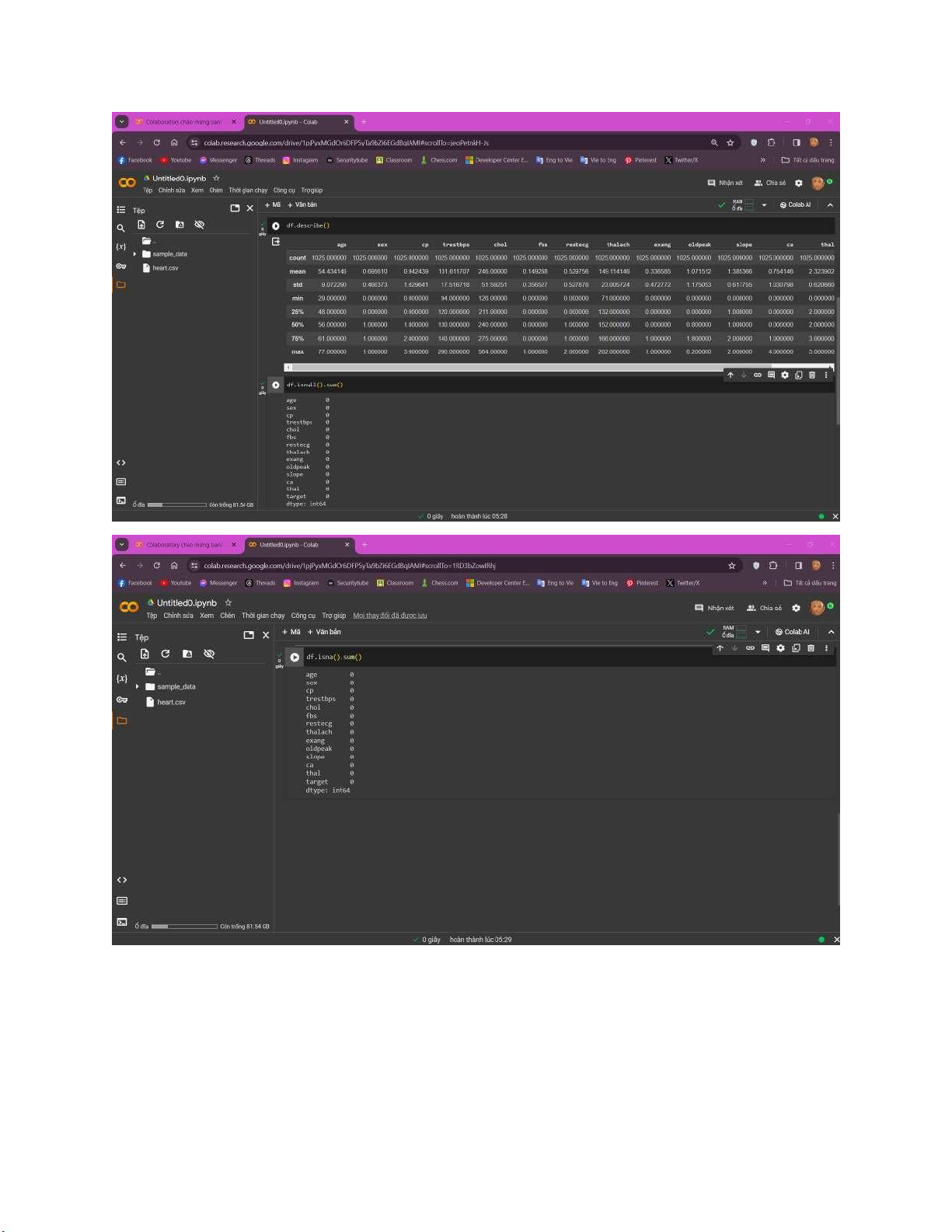
Tiếp theo chúng ta sẽ load tệp dữ liệu có đuôi .csv:
Để có thể xem tổng quát về dataset này ta có thể sử dụng các lệnh sau: lOMoARcPSD| 59629529
2.2.2 Áp dụng mô hình vào biến đổi dữ liệu
Ta sử dụng mô hình máy vector hỗ trợ (svm) để dự đoán khả năng mắc bệnh tim
mạch dựa trên giá trị các cột. Bây giờ chúng ta sẽ sử dụng hàm distplot() từ thư viện
Seaborn để vẽ các biểu đồ của các cột: lOMoARcPSD| 59629529
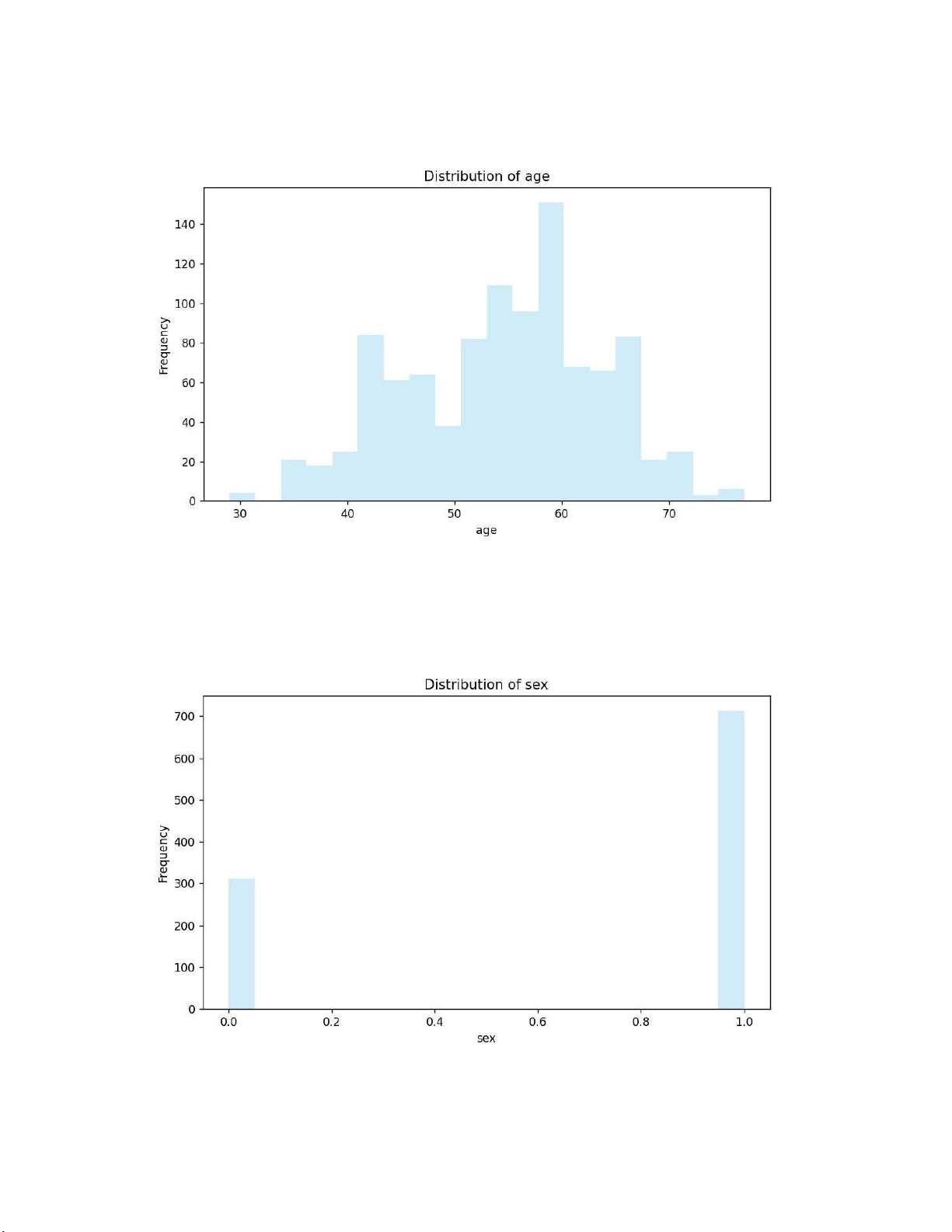
2.2.2.1 Cột tuổi (age)
=> Ta có thể thấy bệnh nhân chiếm đa số ở độ tuổi khoảng 60 tuổi.
2.2.2.2 Cột giới tính lOMoARcPSD| 59629529
=> Ở đây, dữ liệu ghi nhận số bệnh nhân nữ khoảng 301, số bệnh nhân nam là trên 700.
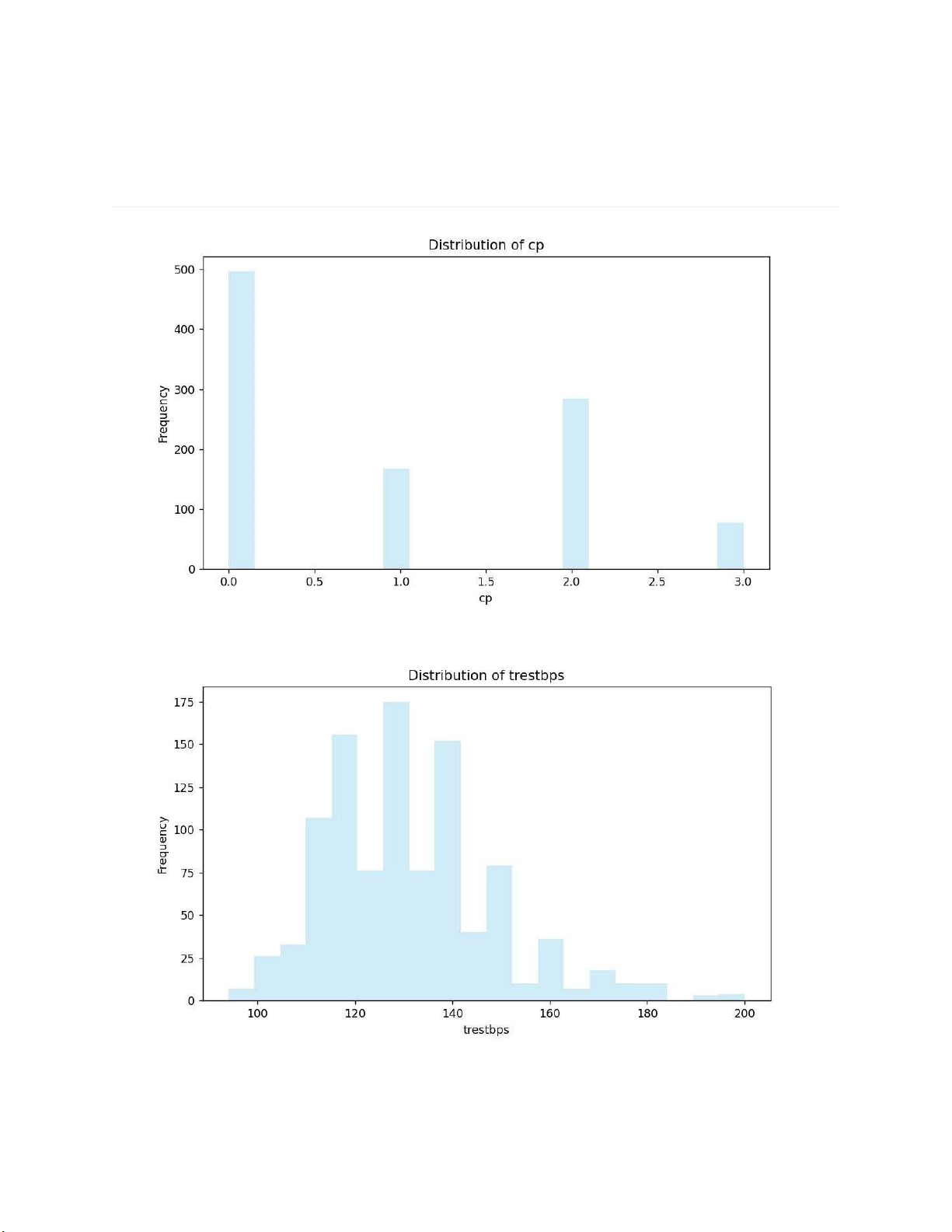
2.2.2.3 Cột loại đau ngực
2.2.2.4 Cột huyết áp lúc nghỉ