lOMoARcPSD|47207367 lOMoARcPSD|47207367
ĐẠI HỌC QUỐC GIA TP. HỒ CHÍ MINH
TRƯỜNG ĐẠI HỌC BÁCH KHOA
BÁO CÁO BÀI TẬP LỚN GIẢI TÍCH 1 ĐỀ TÀI 1 TÊN ĐỀ TÀI
Đạo hàm và tốc độ thay đổi LỚP: L24 Nhóm 1
GVHD: Thầy Đào Huy Cường TP.HCM 29/11/2023 1 lOMoARcPSD|47207367
DANH SÁCH THÀNH VIÊN VÀ CÔNG VIỆC Họ và tên MSSV Công việc Nguyễn Quý
2310120 Làm bài 39; kiểm tra bài 1, 2, 11, 12, Anh(nhóm trưởng)
17, 40, 41, 45, 47; dịch đề bài.
Mai Trần Thiên Ân 2310181 Làm bài 40, 41, 45, 47; kiểm tra phần lý thuyết. Đỗ Gia Bảo
2310214 Làm bài 1, 2, 11, 12, 17; kiểm tra phần lý thuyết. Nguyễn Thái Bảo
2310249 Tóm tắt lý thuyết, kiểm tra bản dịch đề bài. Nguyễn Vũ Thiên
2310302 Soạn thảo báo cáo, kiểm tra bản dịch Bình đề bài. 2 lOMoARcPSD|47207367 MỤC LỤC
Danh sách thành viên................................................................................................................................2
Mục lục..................................................................................................................................................................3
Lời cám ơn..........................................................................................................................................................4
I.Phần mở đầu.................................................................................................................................................5
II. Cơ sở lý thuyết.........................................................................................................................................6
III. Ứng dụng vào giải bài tập...........................................................................................................9
IV.Phần kết luận........................................................................................................................................23
Tài liệu tham khảo....................................................................................................................................24 3 lOMoARcPSD|47207367 Lời cảm ơn
Chúng em xin chân thành cám ơn Thầy Đào Huy Cường đã hướng dẫn chi tiết và giảng
dạy tận tình nhằm cung cấp kiến thức để giúp chúng em hoàn thành đề tài lần này.
Đồng thời, qua bài tập lần này chúng em còn rèn luyện được các kĩ năng làm
việc nhóm, tự giác trong công việc và kĩ năng giao tiếp nhằm nâng cao chất lượng
công việc, học hỏi, góp ý lẫn nhau để hoàn thành sản phẩm bài tập lớn Giải tích
đầu tiên của chúng em.
Mặc dù đã có những đầu tư nhất định trong quá trình làm bài song cũng khó có thể
tránh khỏi những sai sót, lỗi trình bày Vì vậy, nhóm 1 chúng em rất mong nhận được
những đóng góp từ Thầy và các bạn. Chúng em xin chân thành cảm ơn. 4 lOMoARcPSD|47207367 I.Phần mở đầu
Trong toán học, đạo hàm là một khái niệm vô cùng quan trọng và cơ bản. Nó được
sử dụng để xác định sự biến đổi của một hàm số tại một điểm cụ thể và cho biết độ
dốc của đường cong tại điểm đó. Đạo hàm giúp chúng ta hiểu rõ hơn về sự thay đổi
của hàm số và cung cấp nền tảng cho nhiều ứng dụng trong các lĩnh vực khác nhau.
Vai trò của đạo hàm không chỉ giới hạn trong lĩnh vực toán học mà còn rất quan
trọng trong các lĩnh vực khoa học tự nhiên, kỹ thuật, kinh tế, và xã hội. Ví dụ,
trong vật lý, đạo hàm được sử dụng để tính toán tốc độ và gia tốc của một vật thể
đang di chuyển. Trong kỹ thuật, nó hỗ trợ trong thiết kế và tối ưu hóa các hệ thống
phức tạp. Trong kinh tế, đạo hàm được dùng để tối ưu hóa sản xuất và đầu tư.
Phân tích hàm số thông qua đạo hàm giúp chúng ta xác định các điểm cực trị,
điểm biên giới, sự thay đổi độ dốc, và các đặc tính quan trọng khác của đồ thị hàm
số. Điều này giúp chúng ta hiểu rõ hơn về hàm số và làm cho các bài toán phức tạp
trở nên dễ dàng hơn trong việc nghiên cứu và ứng dụng.
Với tầm quan trọng vượt trội trong nhiều lĩnh vực, việc nắm vững khái niệm và
ứng dụng của đạo hàm là cực kỳ hữu ích và thiết thực, vậy nên mời Thầy và các bạn
cùng đi sâu vào đề tài bài tập lớn hôm nay của nhóm 1 “ Đạo hàm và tốc độ thay đổi” 5 lOMoARcPSD|47207367
II. Cơ sở lý thuyết TIẾP TUYẾN
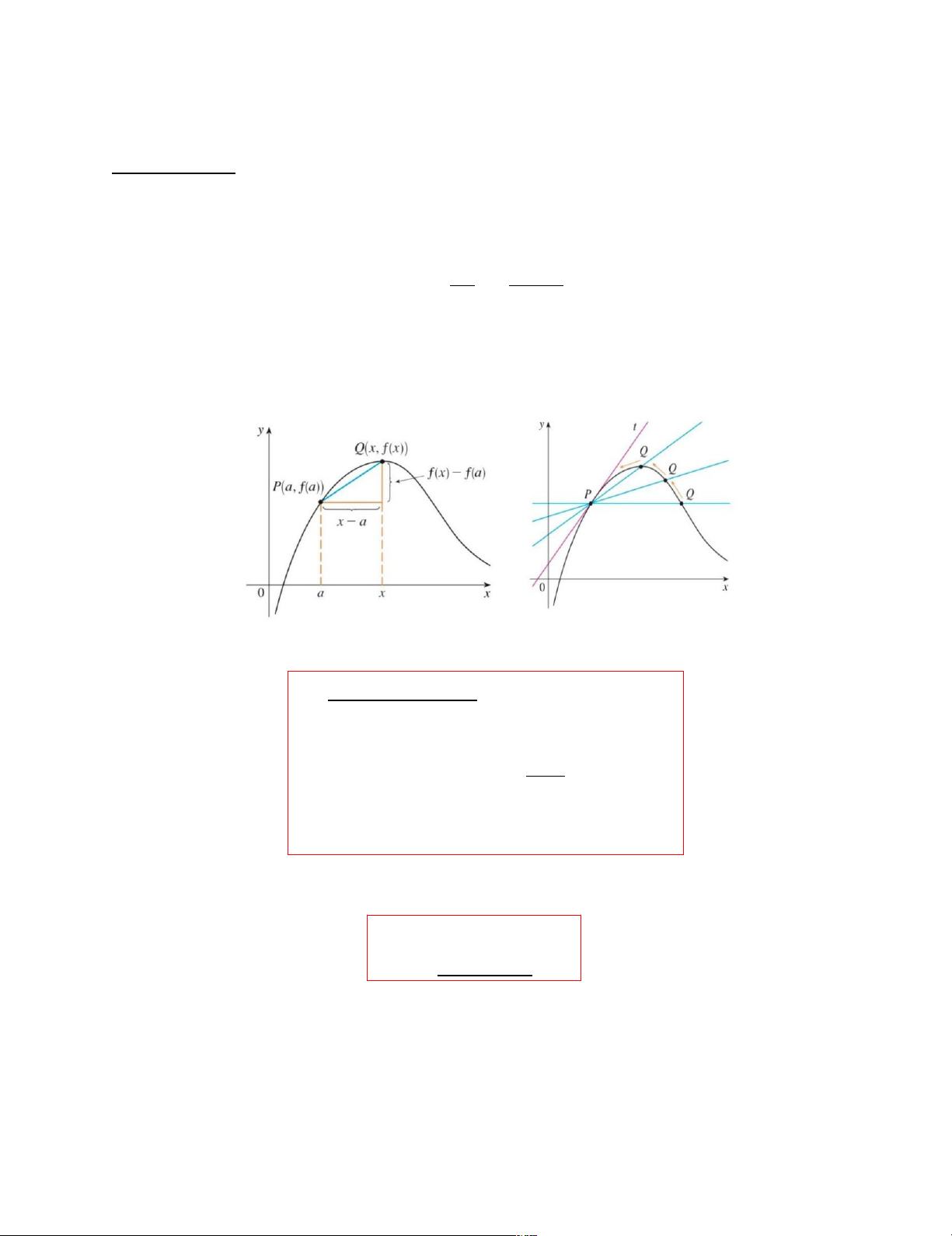
Nếu một đường cong C có phương trình y = f(x) và ta muốn tìm tiếp tuyến với C
tại điểm P(a, f(a)), thì ta sẽ xét một điểm Q(x, f(x)) gần đó, với x ≠ a , và tính độ dốc của cát tuyến PQ: mPQ = f(xx−a)−f(a)
Sau đó cho Q tiến đến P dọc theo đường cong C bằng cách cho x tiến đến a. Nếu
mPQ tiến đến một số m , thì ta định nghĩa tiếp tuyến t là đường thẳng qua P và có
độ dốc m. ( Điều này có nghĩa là tiếp tuyến là vị trí giới hạn của cát tuyến PQ khi Q
tiến đến P. (Xem Hình 1) HÌNH 1
1 ĐỊNH NGHĨA : Tiếp tuyến với đường
cong y = f(x) tại điểm P(a, f(a)) là đường
thẳng qua P với độ dốc m= ( )− ( ) − →
với điều kiện là giới hạn này tồn tại.
Có một biểu thức khác để tính độ dốc của tiếp tuyến đôi khi dễ sử dụng hơn. Nếu
đặt h = x- a, thì x = a + h thì độ dốc của cát tuyến PQ là: 2
mPQ= ( + )− ( )
VÍ DỤ 1: Tìm phương trình tiếp tuyến của parabol y = x2 tai điểm P(1, 1) 6 lim ( +ℎ)− ( ) ℎ→0 ℎ lOMoARcPSD|47207367
GIẢI Ở đây ta có a = 1 và f(x) = x2, do đó độ dốc là m= ( )− (1) = 2−1 −1 x→1 −1 →1 =lim lim (x− 1)(x+ 1) −1 lim →1 lim( + 1) = 1 + 1 = 2 = →1
Biết rằng phương trình đường thẳng qua điểm (xo, yo) và có hệ số góc m là y – yo = m(x
– x0), do đó phương trình tiếp tuyến tại điểm (1, 1) cần
tìm là: y - 1 = 2(x - 1) hay y = 2x – 1 VẬN TỐC
Tổng quát, giải sử một vật thể chuyển động trên một đường thẳng với phương
trình chuyển động là s = f(t), trong đó s là vị trí của vật đối với điểm gốc tại thời
điểm t. Hàm số f mô tả chuyển động gọi là hàm số vị trí của vật thể. Trong khoảng
thời gian từ t = a đến t = a + h, sự thay đổi vị trí là f(a + h) - f(a) . Vận tốc trung bình trong khoảng thời gian này là:
vận tốc trung bình = độ dời = f (a h) f (a) thời gian ℎ
Giờ giả sử ta tính các vận tốc trung bình trong những khoảng thời gian càng lúc
càng ngắn [a, a + h]. Nói cách khác, ta cho h tiến đến 0. Như trong ví dụ quả bóng
rơi, ta định nghĩa vận tốc (tốc đô tức thời) v(a) ở thời điểm t = a chính là giới hạn
của vận tốc trung bình ( + ) − ( ) 3 ( )3= → 3 ĐẠO HÀM
Ta thấy rằng cùng một dạng giới hạn xuất hiện khi tìm độ dốc của tiếp tuyến hay vận
tốc của vật thể. Thật ra, giới hạn dạng
xuất hiện bất cứ khi nào ta tính vận tốc biến thiên trong bất kỳ ngành khoa học
hoặc kỹ thuật, như vận tốc phản ứng trong hóa học hoặc chi phí cận biên(marginal)
trong kinh tế học. Vì dạng giới hạn này xảy ra quá phổ biến, nó đã được đặt cho
một tên và một kí hiệu đặc biệt. 7 lOMoARcPSD|47207367
4. ĐỊNH NGHĨA Đạo hàm của hàm số f tại số a, kí hiệu f '(a), ′ → ( + ) − ( ) là ( ) =
nếu giới hạn này tồn tại.
Ta định nghĩa tiếp tuyến của đường cong y = f(x) tại điểm P(a, f(a)) là đường
thẳng qua P và có độ dốc m cho bởi phương trình 1 hoặc 2. Theo định nghĩa 4, độ
dốc này chính là f '(a), ta có thể phát biểu như sau:
-Tiếp tuyến với y = f(x) tại(a, f(a)) là đường thẳng đi qua điểm (a, f(a)) và
có độ dốc là f'(a), đạo hàm của f tại a.
Nếu ta dùng dạng phương trình điểm-độ dốc của đường thẳng , ta có thể viết
phương trình tiếp tuyến của đường cong y = f(x) tại điểm (a, f(a))
y - f(a) = f '(a)(x - a) TỐC ĐỘ BIẾN
THIÊN Tỉ số biến thiên ∆ ( 2 ) − ( 1 ) ∆x = 2 − 1
Tốc độ biến thiên tức thời ) )
∆ →0l im ∆ ∆ = 2→ 1lim ( 2 − ( 1 2 1
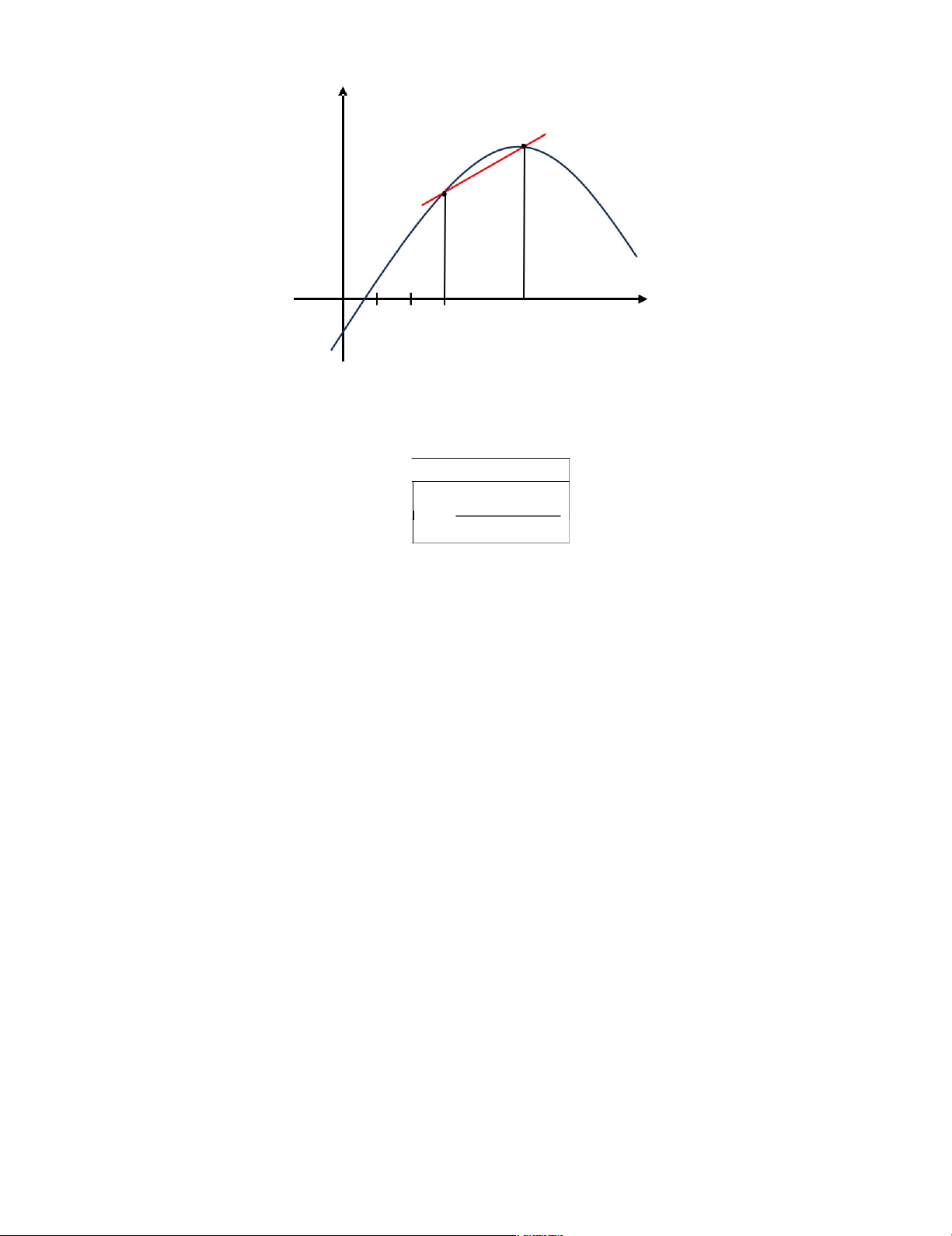
Ta nhận ra giới hạn này chính là đạo hàm f ' (x1), và cũng chính là độ dốc của
tiếp tuyến của đồ thị y = f(x) tại điểm có hoành độ là x1. Như vậy ta có ý nghĩa
thứ hai của đạo hàm .
-Đạo hàm f'(a) là tốc độ biến thiên tức thời của y = f(x) đối với x khi x = a
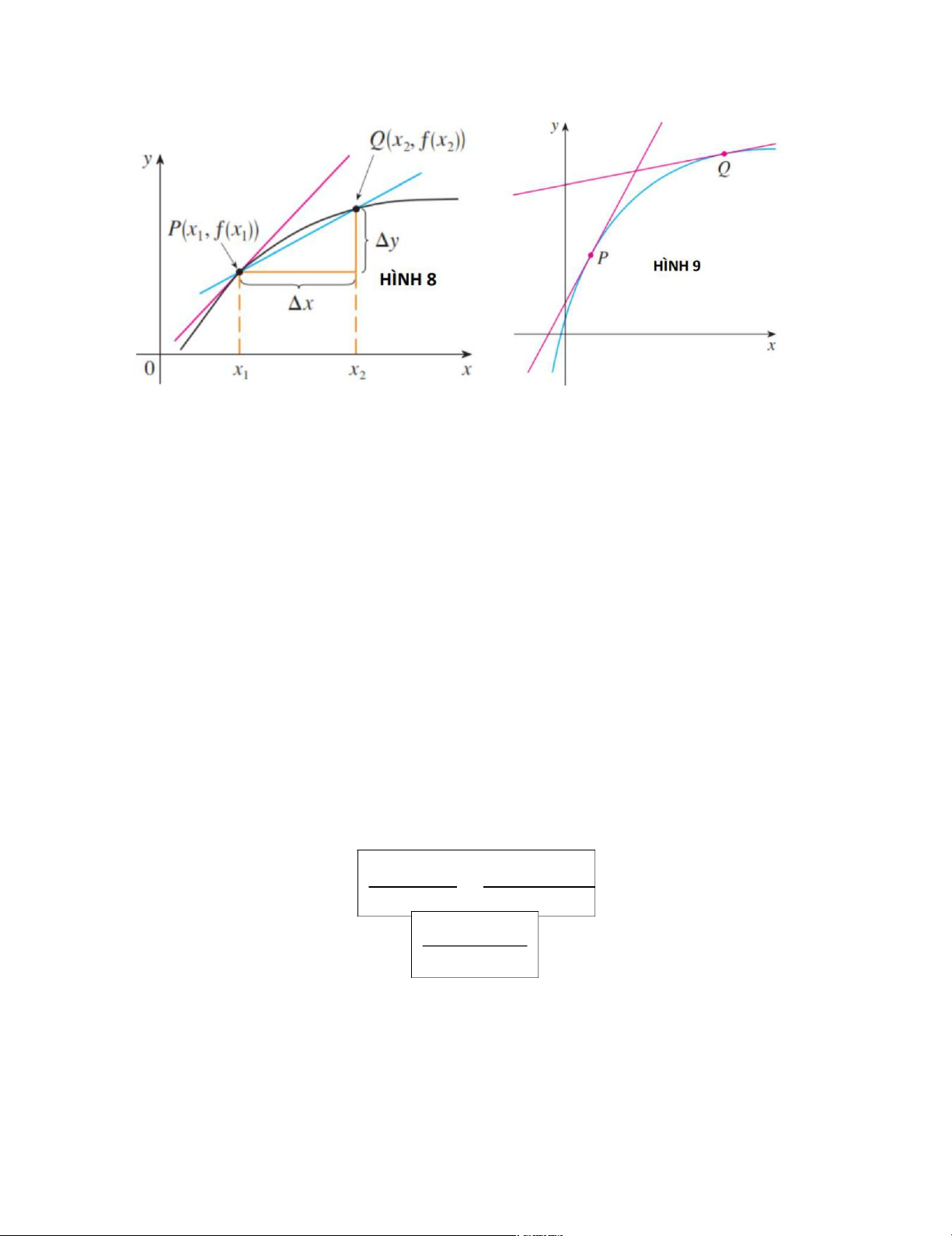
Như vậy khi đạo hàm lớn ( tức đường cong dốc như ở điểm P trong Hình 9 ), thì giá
trị y thay đổi nhanh. Khi đạo hàm nhỏ, đường cong tương đối dẹt (như ở Q trong
hình bên) thì giá trị y thay đổi chậm. 8 lOMoARcPSD|47207367
III. Ứng dụng vào giải bài tập
Bài 1: A curve has equation y = ƒ (x) .
(a) Write an expression for the slope of the secant line through the points P(3, ƒ (3)) and Q(x, ƒ(x)).
(b) Write an expression for the slope of the tangent line at P.
Dịch đề: Một đường cong có phương trình y = ƒ (x)
(a) Viết biểu thức hệ số góc của cát tuyến qua điểm P(3, ƒ (3)) và Q(x, ƒ(x)).
(b) Viết biểu thức hệ số góc của tiếp tuyến tại P. Giải ( , ( )) ( , ( )) là: (a)
- Phương trình chính tắc của đường cát tuyến đi qua hai điểm và −− ( ) = ( ) − ( )
- Suy ra, hệ số góc của đường cát tuyến đi qua hai điểm (3, (3)) ( ) − (3)3
và ( , ( )) là: 9 lOMoARcPSD|47207367 y ( , ( )) (3, (3)) 3 x
- Biểu thức độ dốc của tiếp tuyến của đường cong = ( ) tại điểm ( , ( )) là: (b) → lim ( ) ( ) −= ( ) (3, (3))
- Suy ra, hệ số góc đường tiếp tuyến của đường cong tại điểm là: →3lim ( ) − (3)3
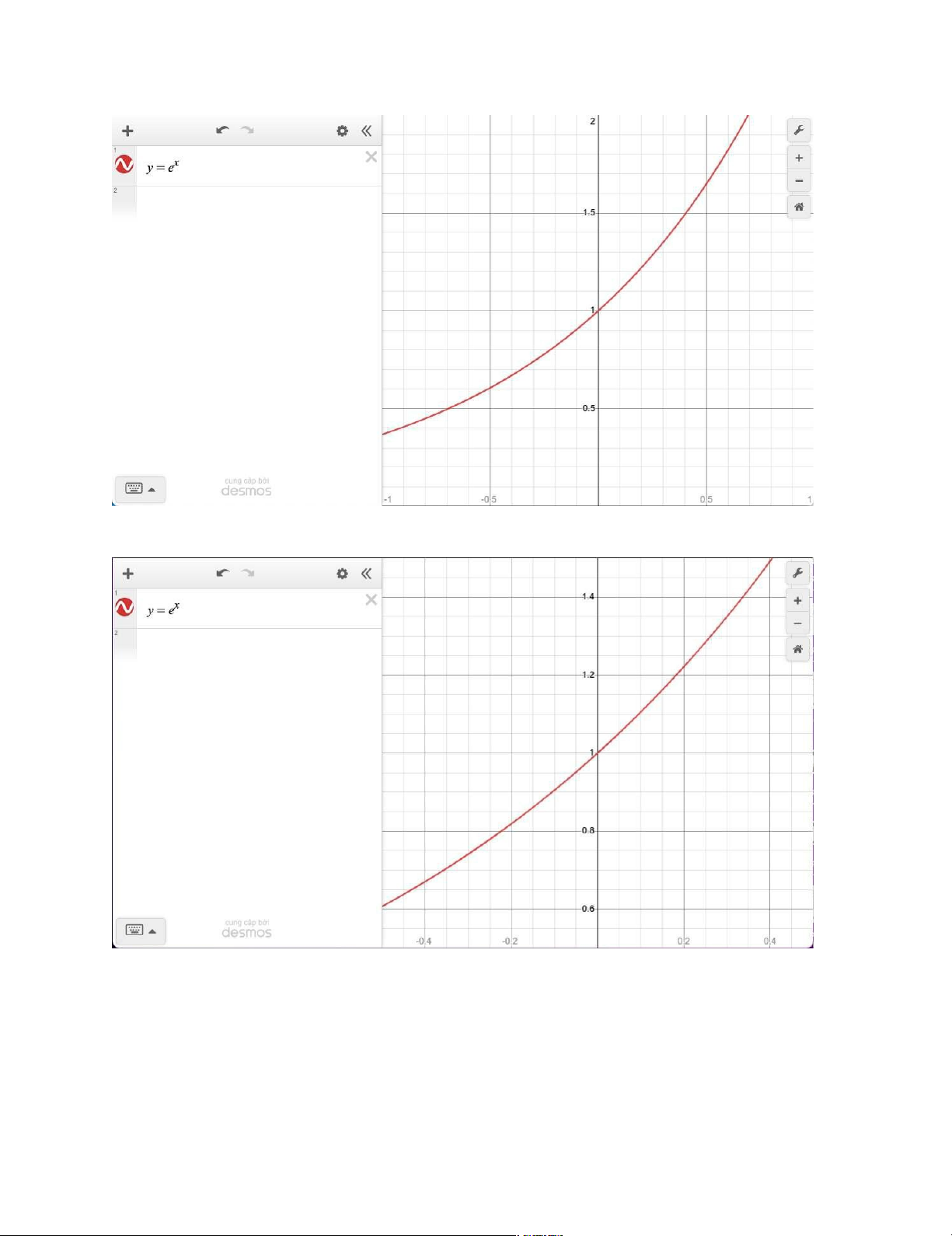
Bài 2: Graph the curve y = ex in the viewing rectangles [-1, 1] by [0, 2], [ -0.5, 0.5] by
[0.5, 1.5] and [-0.1, 0.1] by [0.9, 1.1]. What do you notice about the curve as you
zoom in toward the point (0, 1)?
Dịch đề: Vẽ đồ thị đường cong y = ex trong các cửa sổ xem [ -1, 1] x [0, 2], [-0.5,
0,5] x [0.5, 1.5] và [-0.1, 0.1] x [0.9, 1.1]. Bạn nhận thấy điều gì về đường cong khi
bạn phóng to về phía điểm (0, 1)? Giải
Sử dụng Desmos.com để vẽ đồ thị. - Đường cong y = ex
+ Cửa sổ xem [-1, 1] x [0, 2]: 10 lOMoARcPSD|47207367
+ Cửa sổ xem [-0.5, 0,5] x [0.5, 1.5]: 11 lOMoARcPSD|47207367
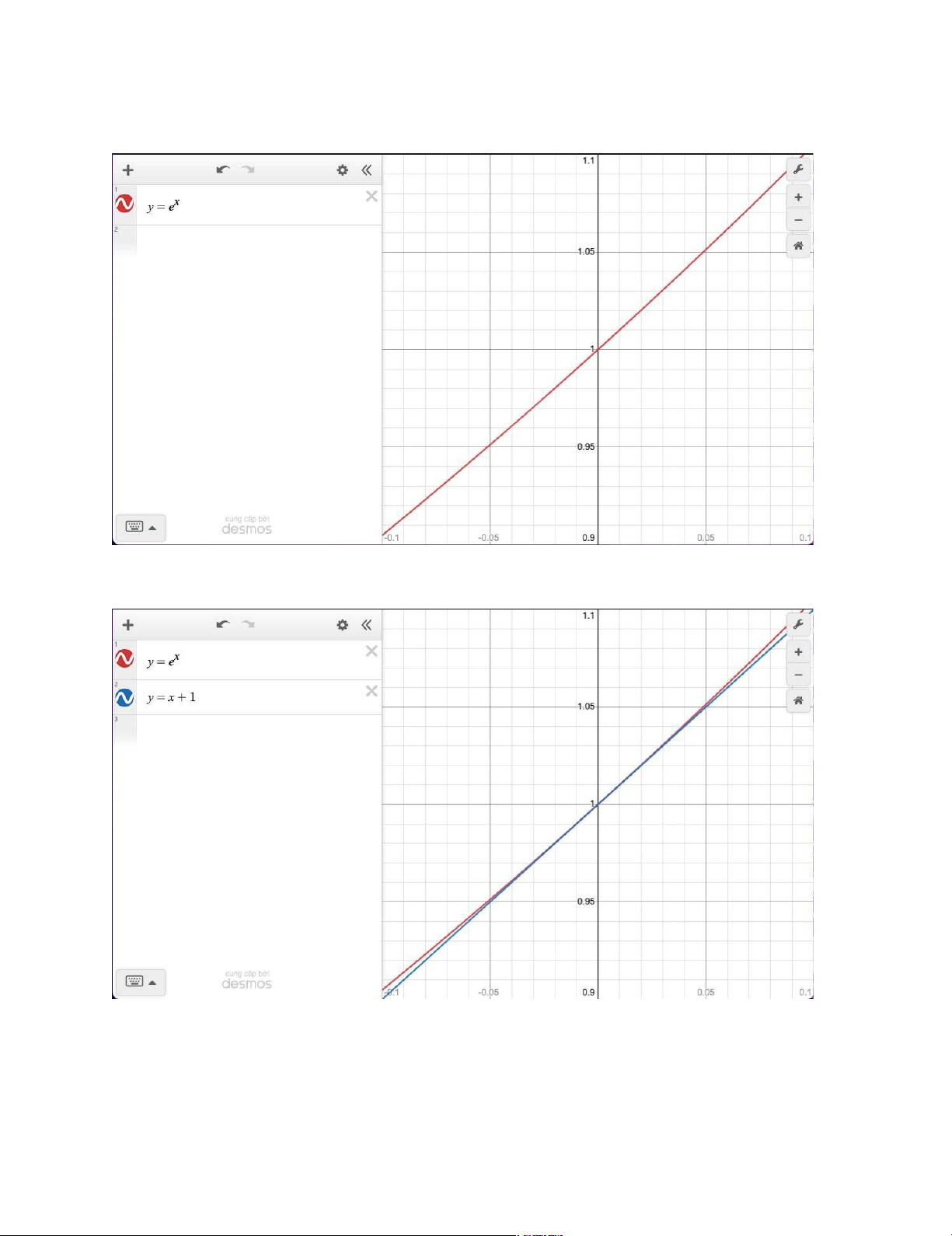
+ Cửa sổ xem [-0.1, 0.1] x [0.9, 1.1]:
- Nếu ta phóng to vào điểm (0,1) của đường cong = , đường cong trông như một đường thẳng
Nói cách khác, đường cong gần như không thể phân biệt được với đường
tiếp tuyến của nó tại điểm (0,1). = = + 1
- Ta so sánh giữa đường cong
(màu đỏ) và tiếp tuyến (màu xanh): 12 lOMoARcPSD|47207367 Bài 11:
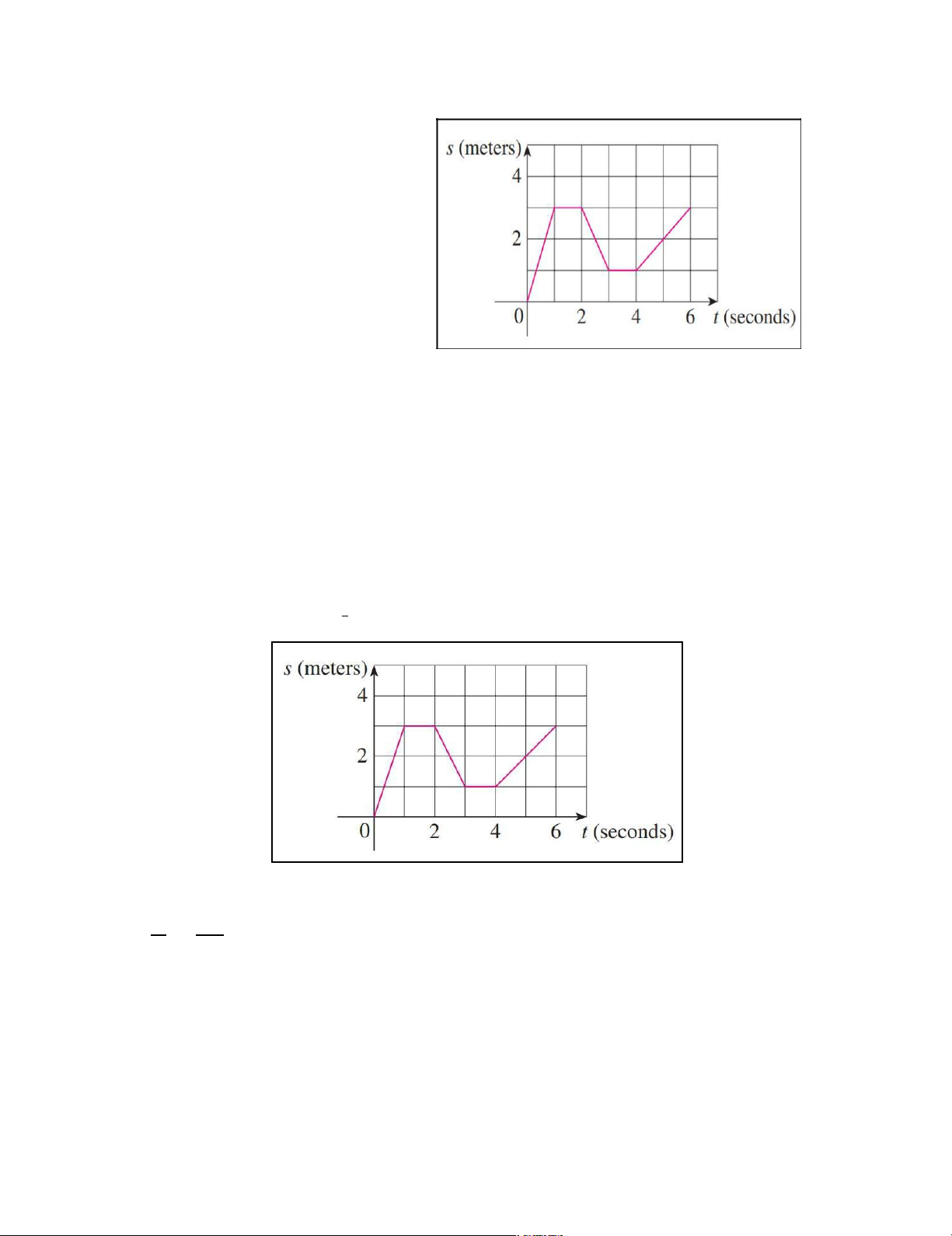
(a) A particle starts by moving to
the right along a horizontalline;
the graph of its position function is shown. When is the particle
moving to the right? Moving to the left? Standing still?
(b) Draw a graph of the velocity function.
Dịch đề: (a) Một hạt bắt đầu di chuyển sang phải dọc theo một đường nằm ngang,
đồ thị vị trí của hạt được cho bên dưới. Khi nào hạt đang chuyển động sang bên
phải? Đang chuyển động sang trái? Đang đứng yên?
(b) Vẽ đồ thị hàm số vận tốc. Giải (a) ∆
- Xét một hạt chuyển động theo phương ngang với chiều dương đi từ trái sang phải, trong khoảng thời gian Δt chất điểm dịch chuyển được độ dời Δs. = ∆ 0
- Trong khoảng < < 1
hạt đi từ vị trí = 0 tới vị trí = 3 ta có: = ∆ ∆ = − −
= 3 (m/s) =>hạt đi từ trái sang phải 13 lOMoARcPSD|47207367
- Trong khoảng 1 < < 2 hạt đứng yên tại vị trí = 3 - Trong khoảng 2< <3
hạt đi từ vị trí = 3
tới vị trí = 1 ta có: = ∆ − ∆ = − = −2 (m/s)
=> hạt đi từ phải sang trái
< 4 hạt đứng yên tại vị trí =
- Trong khoảng 3 < 1 - Trong khoảng 4< <6
hạt đi từ vị trí = 1
tới vị trí = 3 ta có: = ∆ − ∆ = − = 1 => (m/s)
hạt đi từ trái sang phải -Kết luận:
- Hạt sẽ đi sang phải khi hàm số vị trí của hạt tăng: 0< <1. và . . 1< <2
- Hạt sẽ đi sang trái khi hàm số vị trí của hạt giảm: 4< <6
tăng cũng không giảm: và 3< <4
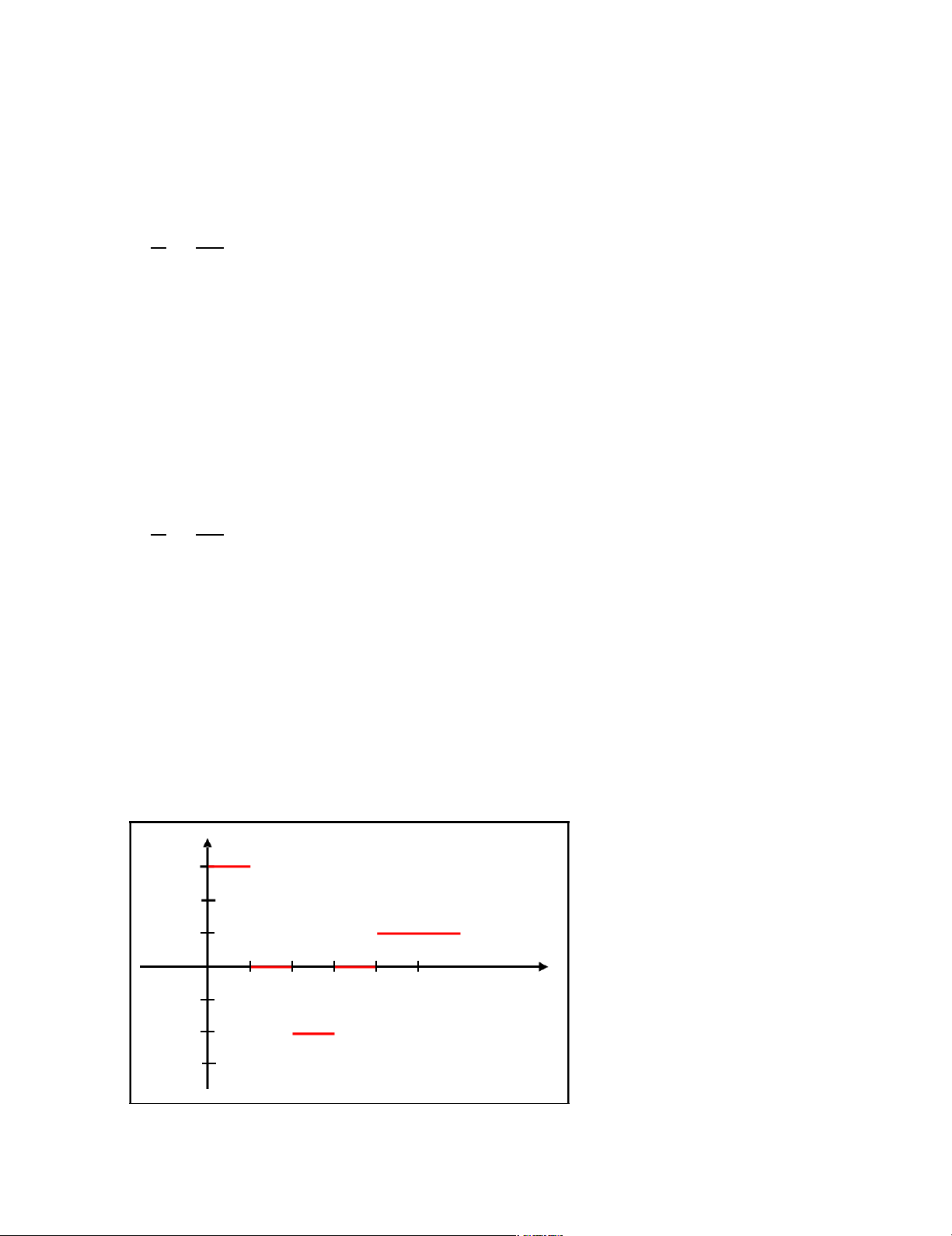
- Hạt sẽ đứng yên khi hàm số vị trí của hạt không 2< <3 (b)
- Đồ thị hàm vận tốc của hạt: ( / ) 1 0 ( ) 1 14 lOMoARcPSD|47207367
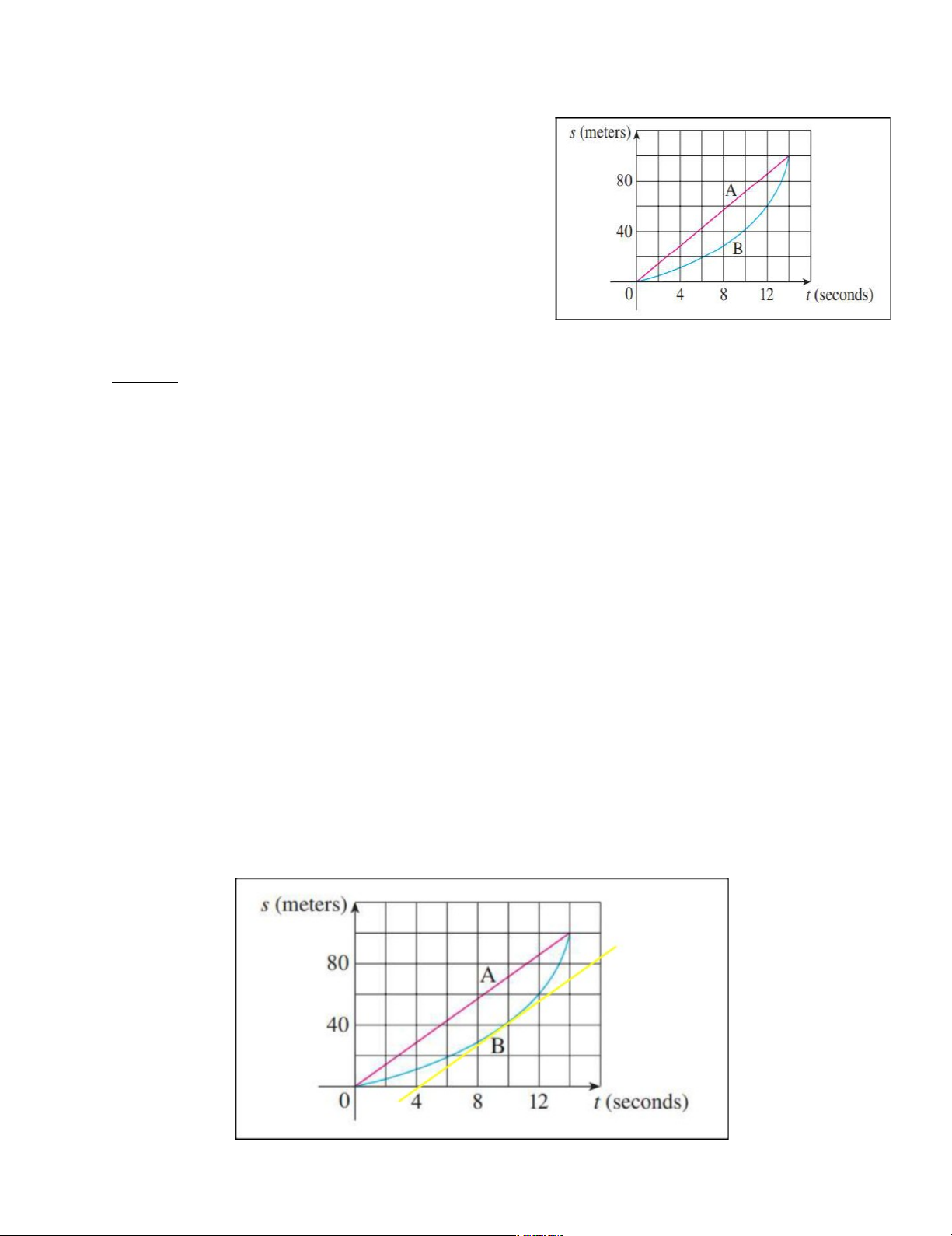
Bài 12: Shown are graphs of the position
functions of two runners, A and B, who run a
100-m race and finish in a tie.
(a) Describe and compare how the runners run the race.
(b) At what time is the distance between the runners the greatest?
(c) At what time do they have the same velocity?
Dịch đề: Đồ thị được cho sau đây là đồ thị hàm số vị trí của hai người chạy bộ, A
và B, họ hoà nhau trong cuộc đua 100 mét.
(a) Hãy mô tả và so sánh hai người đã chạy như thế nào trong cuộc đua.
(b) Vào lúc nào khoảng cách giữa 2 người này là lớn nhất?
(c) Vào lúc nào họ có cùng vận tốc? Giải (a)
- Người chạy bộ A chạy hết quãng đường với vận tốc không đổi.
- Người chạy bộ B ban đầu chạy chậm nhưng tăng tốc dần và đuổi kịp người chạy
bộ A vào giây thứ 14. (b)
- Khoảng cách giữa 2 người là độ chênh lệch tung độ giữa 2 điểm trên 2 đồ thị có
cùng hoành độ. Nhìn vào đồ thị ta có thể thấy vào khoảng giây thứ 10, khoảng
cách giữa hai người A và B sẽ là xa nhất vào khoảng 30m. (c) 15 lOMoARcPSD|47207367 ( ) ( )
- Gọi hàm vị trí và hàm vận tốc của người chạy bộ A lần lượt là và . ( )
- Gọi hàm vị trí và hàm vận tốc của người chạy bộ B lần lượt là và( ) .
- Ta có đạo hàm của hàm quãng đường là hàm vận tốc: của hàm ′ tại x = a. - Lại có
là hệ số góc tiếp tuyến ( ) = ( ) ′( ) ( ) tại t = b. + ( )
là hệ số góc tiếp tuyến của hàm ( ) - Suy ra: ( ) - Tại ( ) +
là hệ số góc tiếp tuyến của hàm tại t = a. ( )
góc của hai hàm số này bằng nhau => ( ) . (10) = (10)
thời điểm t = 10 ta thấy tiếp tuyến của
gần như song song với => hệ số
- Vậy ta có thể kết luận rằng vận tốc của cả hai người A và B bằng nhau vào khoảng giây thứ 10.
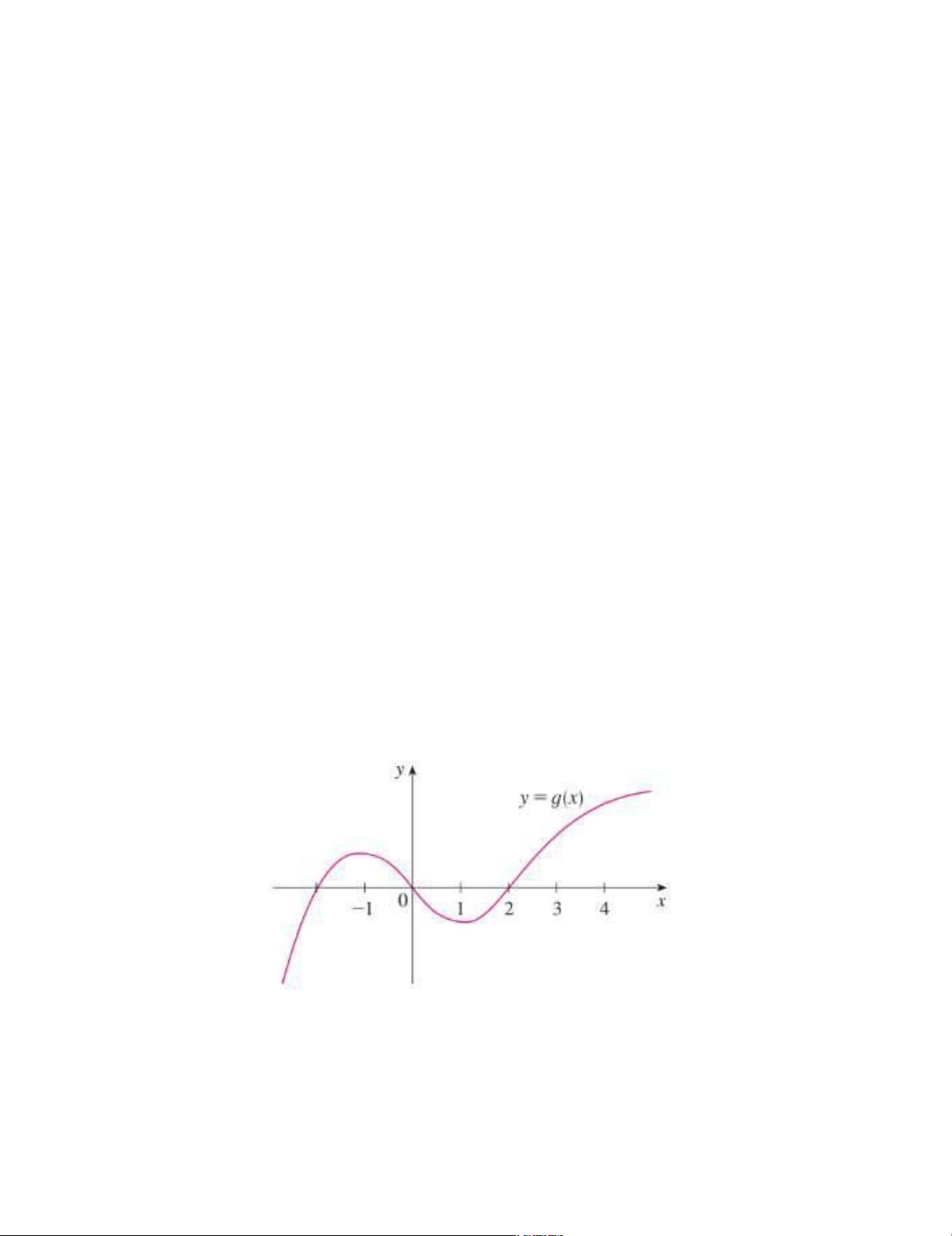
Bài 17: For the function t whose graph is given, arrange the following numbers in
increasing order and explain your reasoning: 0 g’(-2) g’(0) g’(2) g’(4)
Dịch đề: Với hàm số g có đồ thị được cho dưới đây, hãy sắp xếp những con số sau
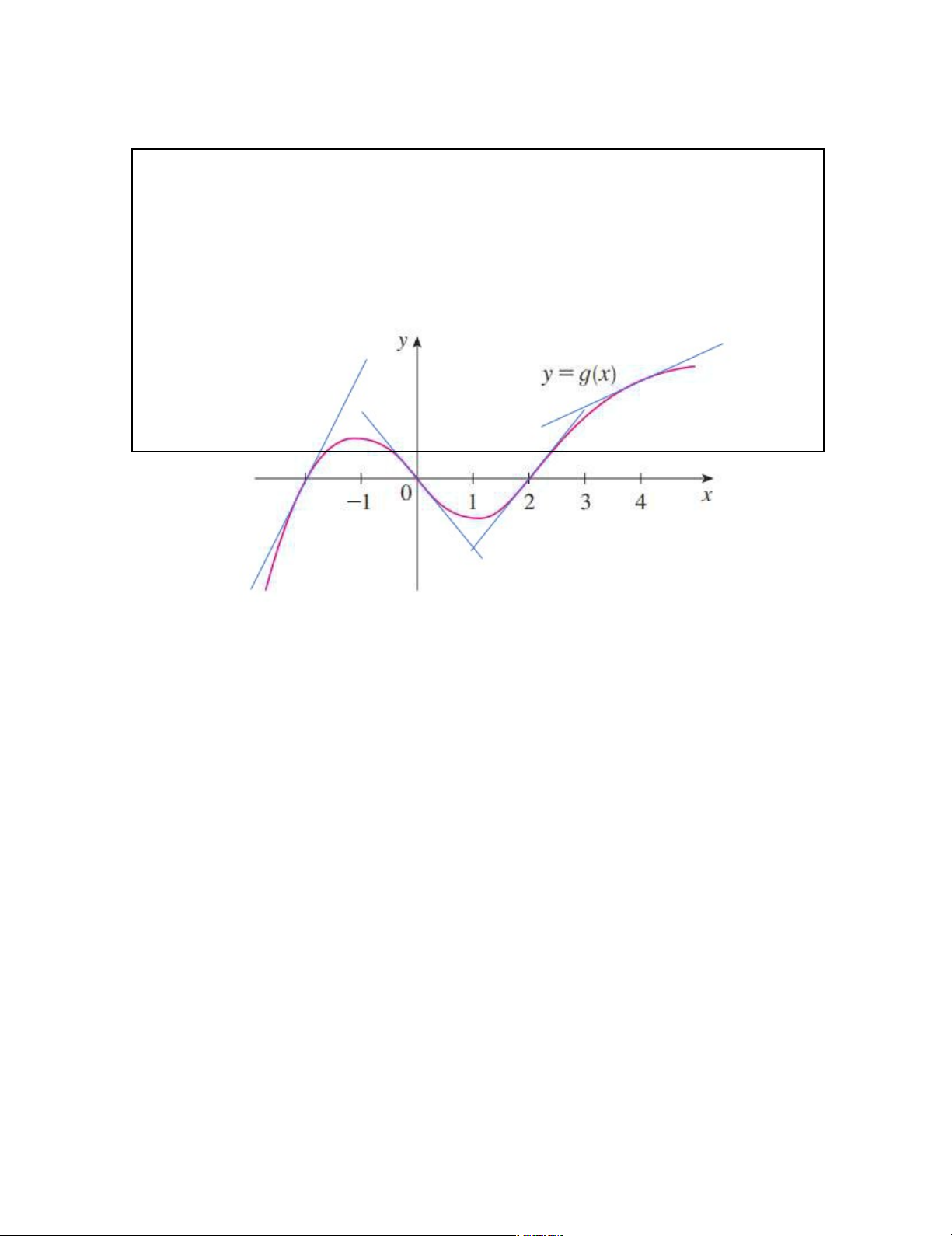
đây theo thứ tự tăng dần và giải thích lý do: 0 g’(-2) g’(0) g’(2) g’(4) 16 lOMoARcPSD|47207367 Giải (0 (−2) ) (2) ′(4) -Tại điểm ta ′ = 0 (0) < 0 -Tại điểm ta thấy hàm ( )
-Ta có các giá trị: 0 ′ ′ ′ = −2 ( ) ′(−2) > 0 thấy hàm số -Với đang giảm nên . ′ → , ta thấy hàm số (0)<0< (−2) ′ số đang tăng nên . ′ tiếp ′ (2) ( ) (2)>0 = 2 = 2 ′ ′ ′ = −2 nhưng góc tạo bởi -Với , ta thấy hàm số đang tăng tại nên ′ → (0)<0< (2) < (−′2) tuyến với trục tại điểm
lại nhỏ hơn tại điểm . tiếp (4) ( ) = 4 (4)>0 = 4 = 2 đang tăng tại nên nhưng góc tạo bởi
→ ′(0) < 0 < ′(4) < ′(2) < ′(−2) tuyến với trục tại điểm
lại nhỏ hơn tại điểm .
- Vậy ta có thứ tự tăng dần là: ′
(0 ) < 0 < ′(4) < ′(2) < ′(−2)
Bài 39: A warm can of soda is placed in a cold refrigerator. Sketch the graph of
the temperature of the soda as a function of time. Is the initial rate of change of
temperature greater or less than the rate of change after an hour?
Dịch đề: Một lon nước ngọt ấm được đặt trong một cái tủ lạnh đang lạnh. Hãy phác
hoạ đồ thị nhiệt độ của lon nước ngọt như một hàm số theo thời gian. Tốc độ thay
đổi ban đầu của nhiệt độ lớn hơn hay nhỏ hơn tốc độ thay đổi sau một giờ? Giải 17 lOMoARcPSD|47207367
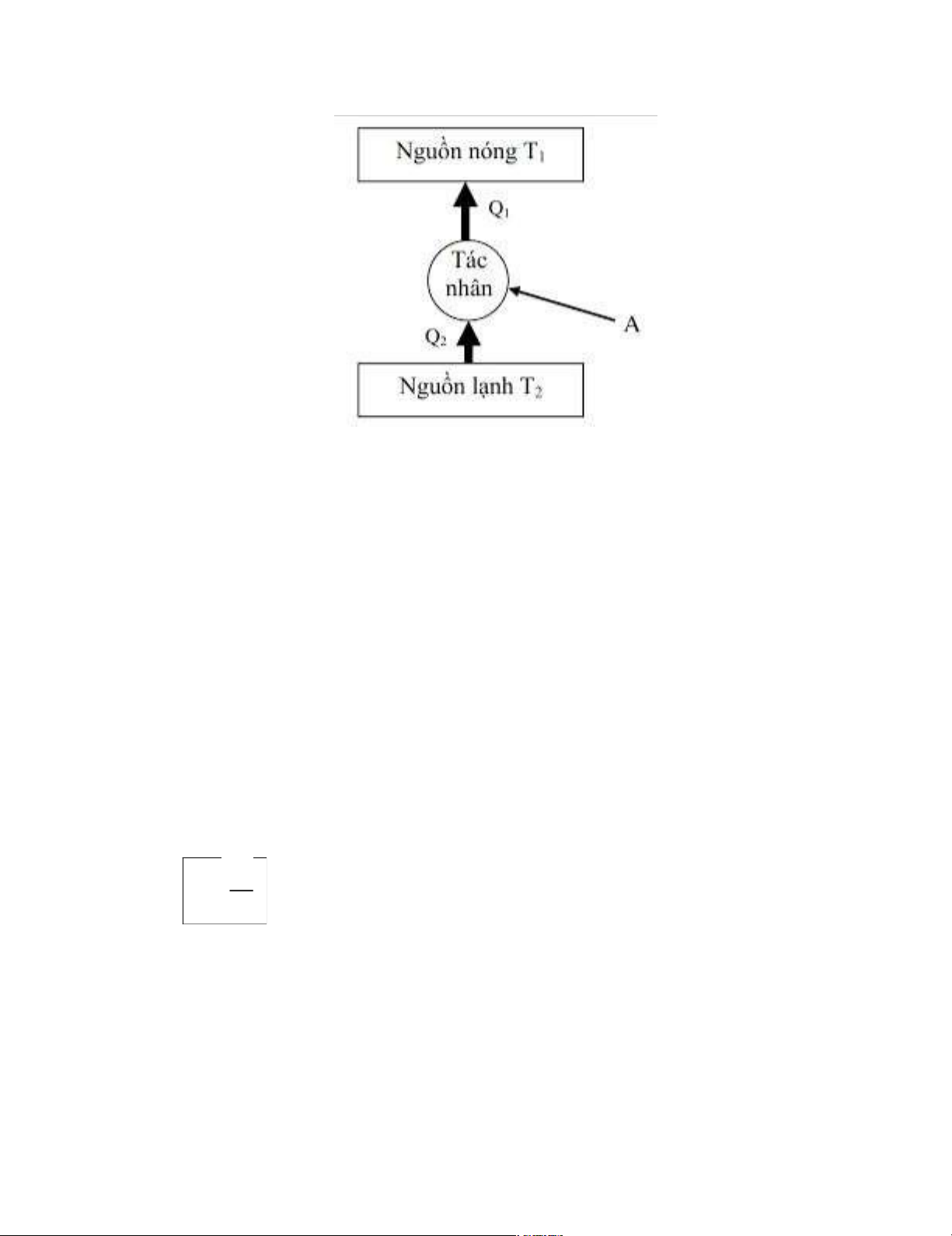
(Sơ đồ nguyên lí hoạt động của máy làm lạnh)
Hiểu theo cách đơn giản nhất, khi hoạt động, tủ lạnh sẽ nhận công của nguồn điện,
để chuyển nhiệt lượng bên trong tủ lạnh ra bên ngoài (môi trường nóng hơn).
Khi đặt một lon nước ngọt còn ấm vào tủ lạnh, lon nước sẽ truyền nhiệt lượng cho
không khí và các vật khác bên trong đó. Nhiệm vụ của tủ lạnh khi đó là liên tục lấy
nhiệt lượng của không khí bên trong tủ ra bên ngoài, khi không khí có nhiệt độ
thấp hơn các vật khác, nó lại nhận nhiệt từ các vật trong tủ và khi không khí đạt
mức nhiệt độ cài đặt nhiệt độ đó sẽ được giữ ổn định.
Giả sử lon nước làm bằng nhôm, ban đầu đang ở nhiệt độ T0, được đặt vào ngăn
mát ở 0 °C truyền cho tủ lạnh có công suất P và hệ số làm lạnh ε nhiệt lượng Q’ để
hạ nhiệt độ xuống nhiệt độ T.
Giả sử không khí trong ngăn mát nhận nhiệt lượng Q đúng bằng nhiệt lượng lon
nước toả ra, công suất của tủ lạnh để làm lạnh ngăn mát bằng k lần P (k<1) ta có
phương trình cân bằng nhiệt: Q=-Q’ ε = Q Ta có:
⇒Trong đó A = k.P.t là công mà tủ lạnh nhận được để làm lạnh ngăn mát theo thời gian t. Q = ε.k.P.t 18