Báo cáo giữa kỳ môn Lý thuyết mật mã | Trường Đại học Bách Khoa Hà Nội

ĐẠI HỌC BÁCH KHOA HÀ NỘI
Trường Điện – Điện tử Khoa Điện tử Báo cáo môn học:
Lý thuyết mật mã Nhóm 12
Thông 琀椀 n và nhiệm vụ từng thành viên:
1. Triệu Hoàng Quân (nhóm trưởng). Nhiệm vụ: tổng hợp thông 琀椀 n; 琀 m hiểu
cơ sở toán học lý thuyết mật mã, hệ mật vignere, hệ mật atbash; mô phỏng hệ thống truyền thông.
2. Nguyễn Minh Phúc. Nhiệm vụ: 琀 m hiểu cơ sở toán học lý thuyết mật mã, hệ mật
Hill, chuẩn mã hóa nâng cao AES.
3. Nguyễn Anh Tuấn. Nhiệm vụ: 琀 m hiểu cơ sở toán học lý thuyết mật mã, hệ mật
Caeser, hệ mật a 昀케 ne, hệ mật hiện đại RC4.
4. Đặng Hữu Công Hiếu. Nhiệm vụ: 琀 m hiểu cơ sở toán học lý thuyết mật mã, hệ
mật Playfair, hệ mật DES.
I. Cơ sở toán học của lý thuyết mật mã
1.1 Số học các số nguyên
Nghiên cứu về các 琀 nh chất của số nguyên, như 琀 nh chia hết, ước số chung,
bội số chung, số nguyên tố, thuật toán Euclide, thuật toán Euclide mở rộng, thuật
toán phân 琀 ch thừa số nguyên tố, thuật toán RSA, v.v.
• Tập hợp: Sử dụng các tập hợp số nguyên Z, số nguyên không âm 𝑍+với các phép toán cộng, trừ, nhân
• Cho hai số nguyên bất kỳ a và b , b > 1, ta luôn xác định được q và r sao cho (r là phần dư)
𝑎 = 𝑏 × 𝑞 + 𝑟, 0 < 𝑟 < 𝑏 • Ước chung lớn nhất 𝑑 = gcd(𝑎, 𝑏) • Số nguyên tố
Một số nguyên a > 1 được gọi là số nguyên tố, nếu a không có ước số nào
ngoài 1 và chính a; và a được gọi là hợp số nếu không phải là số nguyên tố
• Một số nguyên n > 1 bất kỳ đều có thể viết dưới dạng:
𝑛 = 𝑝1𝛼1. 𝑝2𝛼2 … 𝑝𝑘𝛼𝑘
Trong đó 𝑝1 , 𝑝2 , … , 𝑝𝑘 là các số nguyên tố khác nhau, 𝛼1, 𝛼2 , … , 𝛼𝑘 là các số mũ nguyên dương.
Đây là dạng khai triển chính tắc của n • Định lý:
Nếu 𝑏 > 0 và 𝑏 | 𝑎 thì 𝑔𝑐𝑑(𝑎 , 𝑏) = 𝑏
Nếu 𝑎 = 𝑏𝑞 + 𝑟 thì 𝑔𝑐𝑑(𝑎, 𝑏) = 𝑔𝑐𝑑(𝑏, 𝑟)
• Bội chung bé nhất m là bội số chung nhỏ nhất của a và b, và mọi bội số chung của
a và b đều là bội của m.
𝑚 = 𝑙𝑐𝑚(𝑎, 𝑏)
• Với hai số nguyên dương a và b bất kỳ ta có quan hệ
𝑙𝑐𝑚(𝑎, 𝑏). gcd(𝑎, 𝑏) = 𝑎. 𝑏
1.2 Đồng dư và phương trình đồng dư tuyến 琀 nh
Đồng dư theo modular: nghiên cứu về các phép toán và tính chất của các số dư khi
chia cho một số nguyên dương nào đó, như định lý số dư Trung Hoa, phương trình
đồng dư tuyến tính, phương trình đồng dư bậc hai, thặng dư thu gọn, phần tử
nguyên thủy, thuật toán Diffie-Hellman, thuật toán ElGamal, v.v. Đồng dư
• Cho số nguyên dương a và một số nguyŒn n, nếu phØp chia a cho n c kết
quả là r, thì ta nói đồng dư modulo n và ký hiệu l 𝑎 ≡ 𝑏 (𝑚𝑜𝑑 𝑛) Ví dụ: 17 ≡
3 (𝑚𝑜𝑑 7), ℎ𝑎𝑦 17 𝑐ℎ𝑖𝑎 𝑐ℎ𝑜 3 𝑑ư 7
• Hai số nguyên thuộc cùng một lớp tương đương khi và chỉ khi chúng cho
cùng một số dư nếu chia cho n.
Ví dụ: 68 và 39 là những số cùng lớp vì khi chia cho 29 đều dư 10.
• Mỗi lớp tương đương được đại diện bởi một số duy nhất trong tập hợp:
𝑍𝑛 = {0, 1, 2, 3, . . . . , 𝑛 − 1} là số dư chung khi chia cácsố trong lớp đó cho n.
𝑍25 = {0, 1, 2, 3, . . . . , 24}
• Cho 𝑎 ∈ 𝑍𝑛. Một số nguyŒn 𝑥 ∈ 𝑍𝑛 được gọi là nghịch đảo của a theo mod n , nếu
𝑎. 𝑥 ≡ 1 (𝑚𝑜𝑑 𝑛).
V dụ: a = 2 v x = 3 với n = 5 v 2.3 ≡ 1 (𝑚𝑜𝑑 5) • Nếu có
số x như vậy thì ta nói a là khả nghịch, và ký hiệu:
𝑥 𝑙à 𝑎−1𝑚𝑜𝑑 𝑛
Phương trình đồng dư tuyến 琀 nh
Phương trình đồng dư tuyến t nh c dạng 𝑎𝑥 ≡ 𝑏 (𝑚𝑜𝑑 𝑛).
Trong đó a, b, n là các số nguyên, n > 0, x là ẩn số
Hệ phương trình đồng dư tuyến 琀 nh
Cho k số nguyên dương đôi một nguyên tố cùng nhau 𝑛1, 𝑛2, … , 𝑛𝑘 v 𝑎1, 𝑎2, … , 𝑎𝑘
là k số nguyên tuỳ ý. Khi đó ta có hệ phương trình đồng dư tuyến t nh
𝑥 ≡ 𝑎1 (𝑚𝑜𝑑 𝑛1)
{𝑥 ≡ 𝑎2 (𝑚𝑜𝑑 𝑛2) …
𝑥 ≡ 𝑎𝑘 (𝑚𝑜𝑑 𝑛𝑘)
Có nghiệm duy nhất modulo 𝑛1. 𝑛2. … . 𝑛𝑘 Chứng minh định lý:
• Chứng minh sự duy nhất: Giả sử có hai nghiệm x, y dẫn đến
𝑥 ≡ 𝑦 (𝑚𝑜𝑑 𝑛𝑖), ∀ 𝑖 = 1,2, … , 𝑘
V 𝑛1, 𝑛2, … , 𝑛𝑘 đôi một nguyŒn tố cøng nhau nŒn 𝑥 ≡ 𝑦 (𝑚𝑜𝑑 𝑛1. 𝑛2. … . 𝑛𝑘). Tức
x và y cùng thuộc lớp thặng dư 𝑛1. 𝑛2. … . 𝑛𝑘
• Chứng minh sự tồn tại: Ta muốn viết các nghiệm như là một tổ hợp tuyến tính
của các số 𝑎1, 𝑎2, … , 𝑎𝑘 . Chẳng hạn như 𝑥 = 𝐴1𝑎1 + 𝐴2𝑎2 + ⋯ + 𝐴𝑘𝑎𝑘
Với các 𝐴𝑖 thoả mãn 𝐴𝑗 ≡ 0 (𝑚𝑜𝑑 𝑛𝑖) ∀, 𝑖 ≠ 𝑗 𝑣à 𝐴𝑖 ≡ 1 (𝑚𝑜𝑑 𝑛𝑖)
Thặng dư thu gọn và phần tử nguyên thuỷ
• Tập 𝒁𝒏 = { 0,1,2, … , 𝑛 − 1} thường được gọi là tập các thặng dư đầy đủ theo
mod n, vì mọi số nguyên bất kỳ đều có thể 琀 m được trong Zn một số đồng
dư với mình (theo 𝑚𝑜𝑑 𝑛 )
• Tập 𝒁𝒏 là đóng đối với các phép 琀 nh cộng, trừ và nhân theo 𝑚𝑜𝑑 𝑛, nhưng
không đóng đối với phép chia, vì phép chia cho 𝑎 theo 𝑚𝑜𝑑 𝑛 chỉ có thể thực
hiện được khi 𝑎 và 𝑛 nguyên tố với nhau, tức khi gcd( 𝑎 , 𝑛 ) = 1.
Thặng dư thu gọn
- Tập các thặng dư thu gọn theo 𝑚𝑜𝑑 𝑛 được định nghĩa là tập 𝑍𝑛 ∗ = {𝑎 ∈ 𝒁𝒏: gcd(𝑎
, 𝑛) = 1} , tức 𝒁𝒏 ∗ là tập con của 𝒁𝒏 bao gồm tất cả các phần tử nguyên tố với n. Vd :
• Tập thặng dư của mod 10 là Z10 ={1,2,3,4,5,6,7,8,9,11,12,13,14,15}. Trong đó
tập thặng dư thu gọn là tập các số thuộc Z nguyên tố với 10 : Z10* = {1,3,7,9,11,13}
• Số phần tử của tập là {𝜑 (10) = 6} được gọi là cấp 𝜑(𝑛) của nhóm.
Phần tử nguyên thủy
- Nếu 𝑝 là một số nguyên tố thì 𝒁𝒑 ∗ = {1,2, … , 𝑝 − 1}. Và khi đó ∀ 𝑏 ∈ 𝑍𝑝 ∗ ∶ 𝑏 𝑝−1 ≡ 1(𝑚𝑜𝑑 𝑝)
- Một phần tử 𝑔 ∈ 𝒁𝒏 ∗ có cấp 𝑚, nếu m là số nguyên dương bé nhất sao cho 𝑔𝑚
≡ 1(mod p) trong 𝒁 * n Vd : Cho Z *
10 = {1,3,7,9,11,13}, cấp của 7 là 3 vì 73 = 21 ≡ 1 mod (10) hay 21 đồng dư với 1 modulo 10
- Nếu 𝑏 có cấp 𝑝 − 1, tức 𝑝 − 1 là số mũ bé nhất thoả mãn công thức trên, thì các
phần tử 𝑏, 𝑏 2 , … . , 𝑏 𝑃−1 đều khác nhau và theo 𝑚𝑜𝑑 𝑝, chúng lập thành 𝒁𝒑 ∗ là
một nhóm cyclic ( nhóm được cấu thành từ các phần tử là lũy thừa của b ) và 𝑏
là một phần tử sinh, hay phần tử nguyên thuỷ của nhóm.
Vd : 7 là phần tử nguyên thủy của nhóm Z * 3 = {71, 72}
1.3 Phương trình đồng dư bậc hai và thặng dư bậc hai •
Phương trình đồng dư bậc hai có dạng: 𝑥2 ≡ 𝑎(𝑚𝑜𝑑 𝑛)
Trong đó n là một số nguyên dương, a là số nguyên với gcd(a,n) = 1, và x là ẩn số. •
Nếu phương trình có nghiệm thì a là thặng dư bậc 2 (mod n) •
Nếu phương trình vô nghiệm thì a là bất thặng dư bậc 2 (mod n)
Điều này được thực hiện bằng cách thử các giá trị của 𝑥 từ 0 đến n – 1 và kiểm tra
xem giá trị nào thỏa mãn phương trình 𝑥2 ≡ 𝑎(𝑚𝑜𝑑 𝑛)
Ví dụ, nếu muốn kiểm tra xem 7 có phải là thặng dư bậc hai modulo 11 hay không,
ta sẽ xem xét phương trình 𝑥2 ≡ 7(𝑚𝑜𝑑 11) Bằng cách thử các giá trị x từ 0 đến 10: 02 ≡ 0(𝑚𝑜𝑑 11) 12
≡ 1(𝑚𝑜𝑑 11) 22 ≡ 4(𝑚𝑜𝑑 11) 32 ≡ 9(𝑚𝑜𝑑 11) 42 ≡ 5(𝑚𝑜𝑑 11) 52 ≡ 3(𝑚𝑜𝑑 11) 62 ≡ 3(𝑚𝑜𝑑 11) 72 ≡ 5(𝑚𝑜𝑑 11) 82 ≡ 9(𝑚𝑜𝑑 11) 92 ≡ 4(𝑚𝑜𝑑 11) 102 ≡ 1(𝑚𝑜𝑑 11)
Ta thấy rằng không có số nguyên nào trong khoảng từ 0 đến 10 thỏa mãn phương trình 𝑥2
≡ 7(𝑚𝑜𝑑 11). Do đó 7 không phải là thặng dư bậc 2 modulo 11. •
Tập các số nguyên nguyên tố với 𝑛 được phân hoạch thành hai
tập con: tập 𝑄𝑛 các
thặng dư bậc hai 𝑚𝑜𝑑 𝑛 , và tập Qn các bất thặng dư mod n p−1 •
Tiêu chuẩn Euler: Số a là thặng dư bậc hai (mod p) nếu và chỉ
nếu a 2 1(mod p) •
Ký hiệu Legendre: p là một số nguyên tố lẻ, a 0 , ký hiệu Legendre ap được
định nghĩa như sau:
0 𝑘ℎ𝑖 𝑎 0 (𝑚𝑜𝑑 𝑝) • ap
= { −1 1, 𝑘ℎ𝑖 𝑎 , 𝑘ℎ𝑖 𝑎 Q Qp p •
a là thặng dư bậc hai mod p khi và chỉ khi ap =1 •
Với mọi a 0, ta có: ap =ap2−1(mod p) •
Ký hiệu Jacobi: nlà một số nguyên lẻ, a 0, ký hiệu Jacobi a
được định nghĩa n
như sau: Giả sử a có khải triển chính tắc thành thừa số nguyên tố là n p p= 1 1. 22...p nn thì: • an = pa1 1. pa2 2.... pak k • Tính chất: m1 = m2
o Nếu m m1 = 2(modn)thì n n o 2 = { 1 𝑘ℎ𝑖 n 1(𝑚𝑜𝑑 8) n − 1 𝑘ℎ𝑖 n 3(𝑚𝑜𝑑 8) o m m1. 2 = m1 . m2 n n n
o Nếu m và n đều là số lẻ thì: − m
, 𝑘ℎ𝑖 m 3(𝑚𝑜𝑑 4) 𝑣à n 3(𝑚𝑜𝑑 4) m = n n m
, 𝑘ℎ𝑖 m 1(𝑚𝑜𝑑 4) n 3(𝑚𝑜𝑑 4) { n
1.4 Xác suất và thuật toán xác suất
Trong phần này ta nghiên cứu về các khái niệm và công thức liên quan đến xác suất,
như không gian mẫu, biến cố, phép toán xác suất, xác suất có điều kiện, độc lập xác
suất, biến ngẫu nhiên, phân phối xác suất, kỳ vọng, phương sai, định lý giới hạn
trung tâm, thuật toán Monte Carlo, v.v.
- Biến cố: là một kết quả có thể xảy ra trong một phép thử ngẫu nhiên. Biến cố có
thể là đơn, hợp, phụ thuộc, độc lập, ....
- Không gian mẫu: là tập hợp tất cả các kết quả có thể xảy ra trong một phép thử
ngẫu nhiên. Kí hiệu Ω = {𝑠1, 𝑠2 … 𝑠𝑛}
- Biến ngẫu nhiên: là một hàm số gán một giá trị số cho mỗi kết quả trong không
gian mẫu. Biến ngẫu nhiên có thể là rời rạc hoặc liên tục, tùy thuộc vào giá trị
số có thể nhận được là hữu hạn hay vô hạn.
- Phân phối xác suất: là một quy tắc cho biết xác suất của mỗi giá trị hoặc khoảng
giá trị của một biến ngẫu nhiên. Phân phối xác suất có thể được biểu diễn bằng
bảng, công thức, đồ thị hoặc hàm mật độ xác suất. Có nhiều phân phối xác suất
thống kê cơ bản, như phân phối nhị thức, phân phối chuẩn, phân phối Poisson,...
Phân bố xác suất 𝑃 trên Ω được định nghĩa là một tập các số thực không âm 𝑃
= { 𝑝1, 𝑝2, … , 𝑝𝑛} có tổng ∑𝑝𝑖 = 1.
XÆc suất có điều kiện: là khả năng xảy ra của một biến cố A khi biết một biến cố B khác đã
xảy ra. Xác suất có điều kiện được ký hiệu là P(A|B) và được tính theo công thức: P(A B)=P(A∩B)/P(B)
Trong công thức trên, P(A ∩ B) là xác suất hợp của A và B, tức là xác suất của hai biến cố
cùng xảy ra. P(B) là xác suất của biến cố B. Xác suất có điều kiện có thể được hiểu như là
xác suất của A trong không gian mẫu mới, đã được thu hẹp lại bởi sự xảy ra của B.
II. CÁC HỆ MẬT CỔ ĐIỂN 2.1 Hệ mật mã Caeser
2.1.1 Giới thiệu:
Hệ mật mã Caeser còn được gọi l Mật mª dịch chuyển, l một trong những hệ mật mª cổ
điển đơn giản nhất và được biết đến nhiều nhất trong lịch sử. N hoạt động bằng cÆch dịch
chuyển mỗi k tự trong thông điệp một khoảng cố định theo bảng chữ cÆi. Trong lịch sử,
mật mª cộng hưởng được gọi l mật mª dịch chuyển. Julius Caeser đã sử dụng một hệ mật
mª cộng để liŒn lạc với các sĩ quan của m nh. V l do n y, cÆc hệ mật mª cộng đôi khi được
gọi l mật mã Caeser, Caeser đã sử dụng một kh a dịch chuyển là 3 cho các thông điệp của m nh.
2.1.2 Nguyên lý hoạt động
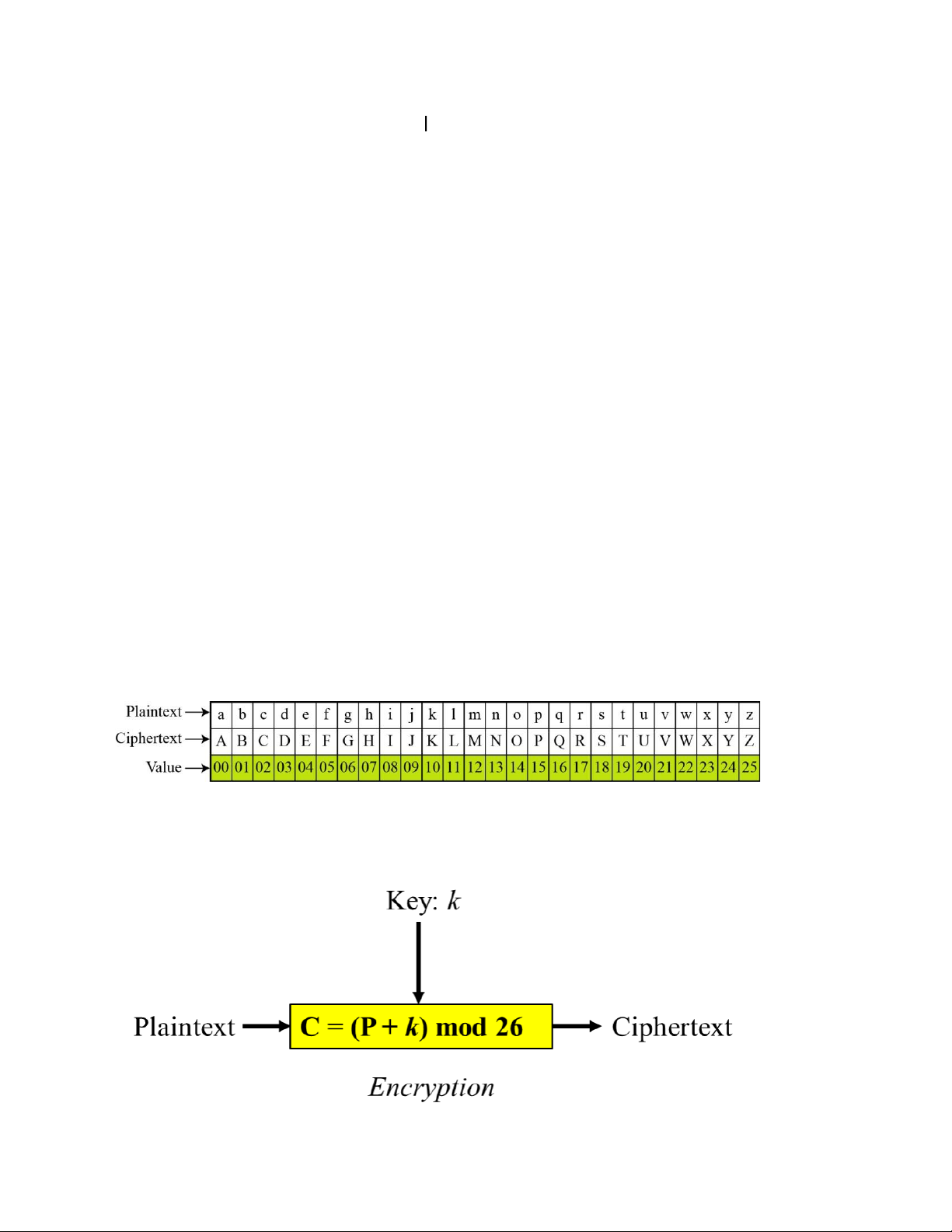
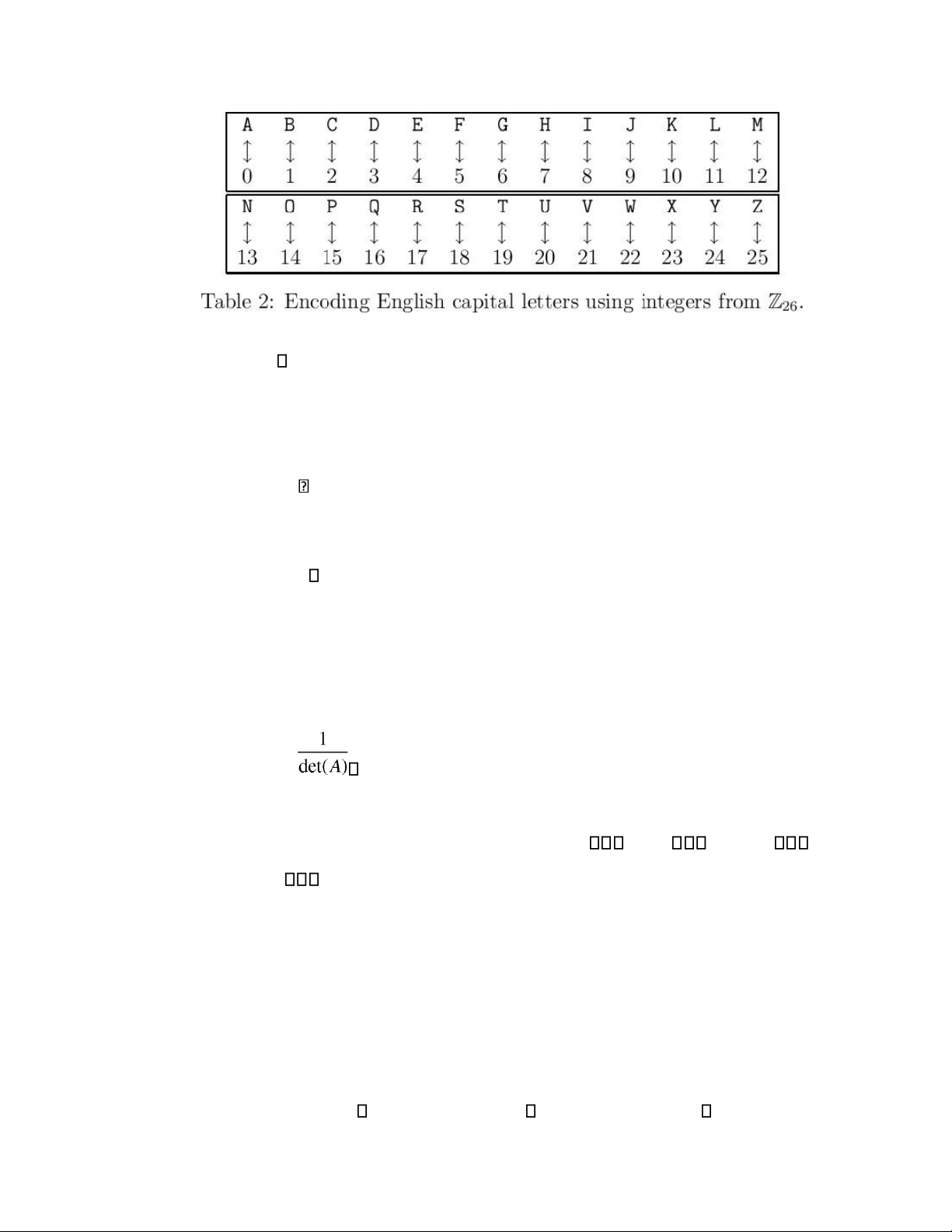
Để thực hiện được mª h a Caeser, trước tiŒn ta cần Ænh xạ cÆc k tự trong bảng th nh cÆc
chữ cÆi Latinh th nh cÆc số tương ứng từ 00 - 25
Plaintext and Ciphertex in Z26
Sau đó ta thự hiện quá trình mã hóa theo sơ đồ sau: =
Ở đây, khóa k l một số nguyŒn c giÆ trị thuộc tập Z26 0,1,2,...,25
VD: Mª h a bản tin P = “NGUYENANHTUAN” bằng mật mª cộng với kh a k=5 N → 13
Encryption: (13 + 05) mod 26 = 18 → S G → 06
Encryption: (06 + 05) mod 26 = 11 → L U → 20
Encryption: (20 + 05) mod 26 = 25 → Z Y → 24
Encryption: (24 + 05) mod 26 = 03 → D E → 04
Encryption: (04 + 05) mod 26 = 09 → J N → 13
Encryption: (13 + 05) mod 26 = 18 → S A → 00
Encryption: (00 + 05) mod 26 = 05 → F N → 13
Encryption: (13 + 05) mod 26 = 18 → S H → 07
Encryption: (07 + 05) mod 26 = 12 → M T → 19
Encryption: (19 + 05) mod 26 = 24 → Y U → 20
Encryption: (20 + 05) mod 26 = 25 → Z A → 00
Encryption: (00 + 05) mod 26 = 05 → F N → 13
Encryption: (13 + 05) mod 26 = 18 → S
C = “SLZDJSFSMYZFS”
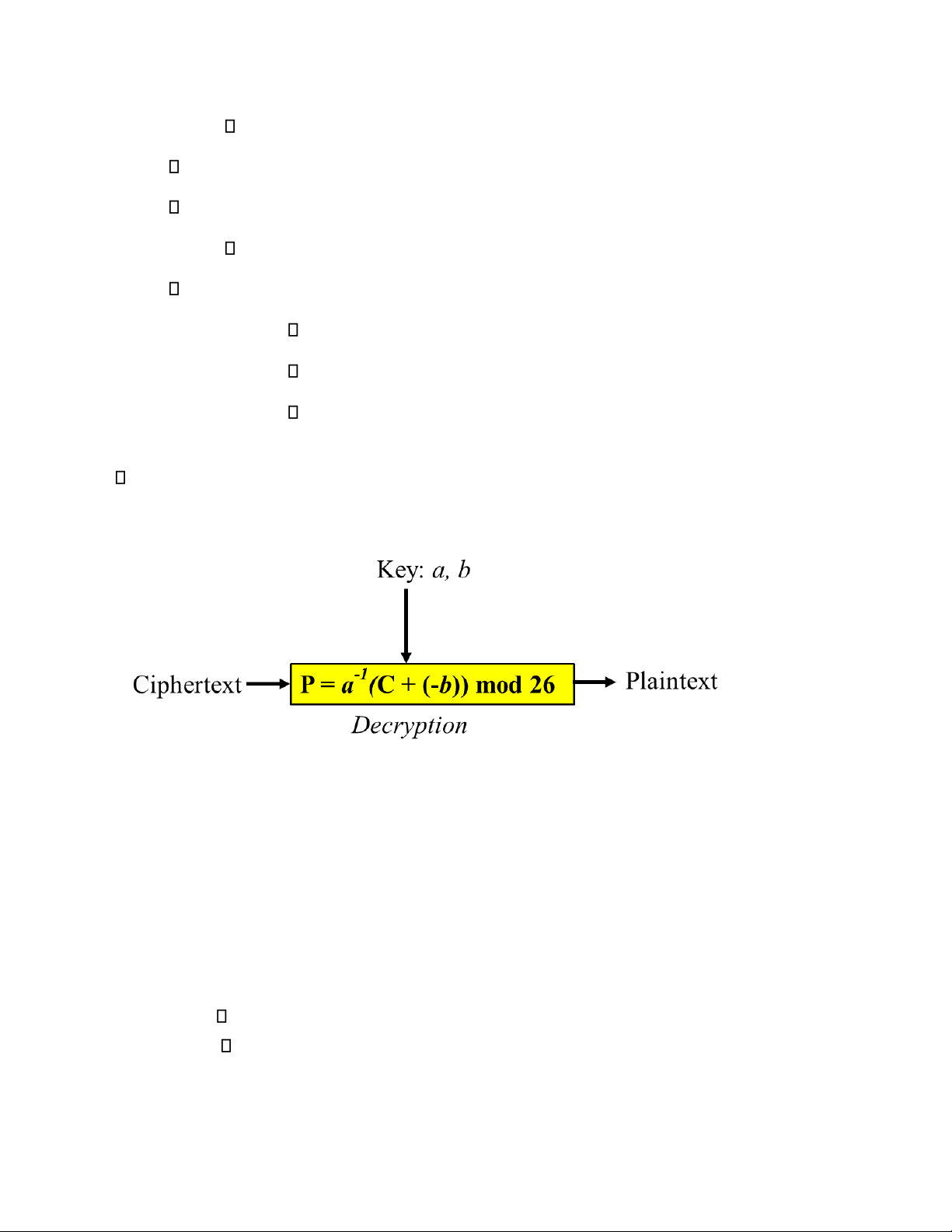
Để giải mª, ta thực hiện theo sơ đồ sau:
Trong c ng thức n y, −k l phần từ nghịch đảo cộng của k trong tập Z26:
(k+ −( k))mod26= 0
VD: Giả sử thu được ciphertext như ví dụ trŒn, biết kh a k =5. T m plaintext? k=5 − =k 21 S → 18
Dencryption: (18 + 21) mod 26 = 13 → N
L → 11 Dencryption: (11 + 21) mod 26 = 06 → G Z → 25
Dencryption: (25 + 21) mod 26 = 20 → U
D → 03 Dencryption: (03 + 21) mod 26 = 24 → Y J → 09
Dencryption: (09 + 21) mod 26 = 04 → E
S → 18 Dencryption: (18 + 21) mod 26 = 13 → N F → 05
Dencryption: (05 + 21) mod 26 = 00 → A S → 18
Dencryption: (18 + 21) mod 26 = 13 → N M → 12
Dencryption: (12 + 21) mod 26 = 07 → H Y → 24
Dencryption: (24 + 21) mod 26 = 19 → T
Z → 25 Dencryption: (25 + 21) mod 26 = 20 → U F → 05 Dencryption: (05 + 21) mod 26 = 00 → A S → 18
Dencryption: (18 + 21) mod 26 = 13 → N
P = “NGUYENANHTUAN” 2.1.3 Mô phỏng Mã hóa
def caesar_cipher_encrypt(text, shift): result = "" for char in text: if char.isalpha():
shifted = ord(char) - ord(’A’)
shifted = (shifted + shift) % 26
encrypted_char = chr(shifted + ord(’A’))
result += encrypted_char else: result += char return result plaintext = "NGUYENANHTUAN" shift_amount = 5
encrypted_text = caesar_cipher_encrypt(plaintext, shift_amount)
print("Mª h a Caesar:", encrypted_text) Giải mã
def caesar_cipher_decrypt(ciphertext, shift):
result = "" for char in ciphertext: if char.isalpha(): if char.islower(): x = ord(char) - ord(’a’)
decrypted_char = chr((x - shift) % 26 + ord(’a’))
result += decrypted_char else: x = ord(char) - ord(’A’)
decrypted_char = chr((x - shift) % 26 + ord(’A’))
result += decrypted_char else: result += char return result
ciphertext = "SLZDJSFSMYZFS" for i in range(26):
decrypted_text = caesar_cipher_decrypt(ciphertext, i)
print(f"Key = {i}: {decrypted_text}") 2.2 Hệ mật AFFINE 2.2.1 Giới thiệu
Mật mª Affine l một dạng mật mª thay thế døng một bảng chữ cái, trong đó mỗi
chữ cái được Ænh xạ tới một số, sau đó được mª h a th ng qua một h m bậc nhất c dạng y ax b= + .
2.2.2 Nguyên lý hoạt động
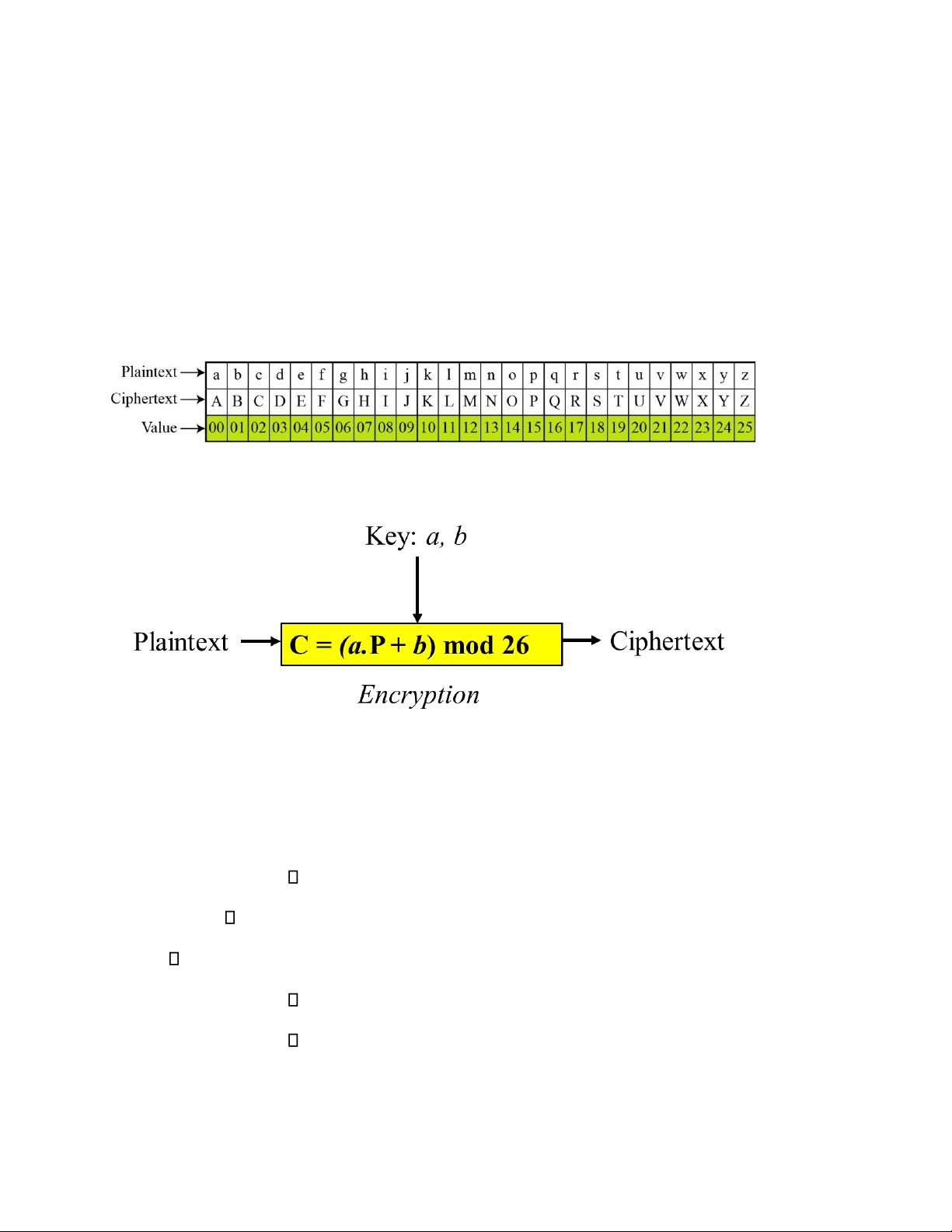
Để thực hiện mật mª h a Affine, trước tiŒn ta cần Ænh xạ cÆc k tự trong bảng chữ
cÆi Latinh th nh cÆc số tương ứng từ 00 - 25.
Plaintext and Ciphertex in Z26
Sau đó, thực hiện quá trình mã hóa theo sơ đồ sau:
Trong c ng thức n y, 2 kh a a v b l 2 số nguyŒn thuộc tập Z26, trong đó a v 26 l hai số
nguyŒn tố cøng nhau hay gcd( ,26)a =1
VD: Mª h a bản tin P = “NGUYENANHTUAN” bằng mật mª Affine với kh a a=17 v b=5 N → 13
Encryption: (17.13 + 05) mod 26 = 18 → S G → 06
Encryption: (17.06 + 05) mod 26 = 03 → D U → 20
Encryption: (17.20 + 05) mod 26 = 07 → H Y → 24
Encryption: (17.24 + 05) mod 26 = 23 → Y E → 04
Encryption: (17.04 + 05) mod 26 = 21 → V N → 13
Encryption: (17.13 + 05) mod 26 = 18 → S A → 00
Encryption: (17.00 + 05) mod 26 = 05 → F N → 13
Encryption: (17.13 + 05) mod 26 = 18 → S H → 07
Encryption: (17.07 + 05) mod 26 = 20 → U T → 19
Encryption: (17.19 + 05) mod 26 = 16 → Q U → 20
Encryption: (17.20 + 05) mod 26 = 07 → H A → 00
Encryption: (17.00 + 05) mod 26 = 05 → F N → 13
Encryption: (17.13 + 05) mod 26 = 18 → S
C = “SDHYVSFSUQHFS”
Để giải mª, ta thực hiện theo sơ đồ sau:
Ở đây, a−1 l phần tử nghịch đảo nh n của a v −b l phần tử nghịch đảo cộng của b
trong tập Z26: aa. −1mod26=1 v (b+ −( b))mod26= 0
Mật mª cộng l một trường hợp đặc biệt của mật mª Affine vớia=1
Mật mª nh n l một trường hợp đặc biệt của mật mª Affine với b=0
VD: Giải sử thu được ciphertext như ví dụ ở trŒn, biết kh a a=10 v b=5. T m plaintext? a=17 a−1 = 23
b= 05 − =b 21 S → 18
Dencryption: 23(18+21) mod 26 = 13 → N D → 03
Dencryption: 23(03+21) mod 26 = 06 → G H → 07
Dencryption: 23(07+21) mod 26 = 20 → U Y → 23
Dencryption: 23(23+21) mod 26 = 24 → Y V → 21
Dencryption: 23(21+21) mod 26 = 04 → E S → 18
Dencryption: 23(18+21) mod 26 = 13 → N F → 05
Dencryption: 23(05+21) mod 26 = 00 → A S → 18
Dencryption: 23(18+21) mod 26 = 13 → N U → 20
Dencryption: 23(20+21) mod 26 = 07 → H Q → 16
Dencryption: 23(16+21) mod 26 = 19 → T H → 07
Dencryption: 23(07+21) mod 26 = 20 → U F → 05
Dencryption: 23(05+21) mod 26 = 00 → A S → 18
Dencryption: 23(18+21) mod 26 = 13 → N
P = “NGUYENANHTUAN” 2.2.3 Mô phỏng Mã hóa
def affine_cipher_encrypt(plaintext, a, b): result = "" for char in plaintext: if char.isalpha(): if char.islower(): x = ord(char) - ord(’a’)
encrypted_char = chr(((a * x + b) % 26) + ord(’a’))
result += encrypted_char else: x = ord(char) - ord(’A’)
encrypted_char = chr(((a * x + b) % 26) + ord(’A’))
result += encrypted_char else: result += char return result plaintext = "NGUYENANHTUAN" a = 17 b = 5
encrypted_text = affine_cipher_encrypt(plaintext, a, b)
print("Mª h a Affine:", encrypted_text) Giải mã def mod_inverse(a, m): for i in range(m): if (a * i) % m == 1: return i return None
def affine_cipher_decrypt(ciphertext, a, b):
result = "" a_inv = mod_inverse(a, 26) if a_inv is None:
return "Kh ng thể giải mª với kh a n y." for char in ciphertext: if char.isalpha(): if char.islower(): x = ord(char) - ord(’a’)
decrypted_char = chr(((a_inv * (x - b)) % 26) + ord(’a’))
result += decrypted_char else: x = ord(char) - ord(’A’)
decrypted_char = chr(((a_inv * (x - b)) % 26) + ord(’A’))
result += decrypted_char else: result += char return result ciphertext = "SDHYVSFSUQHFS" a = 17 b = 5
decrypted_text = affine_cipher_decrypt(ciphertext, a, b) print("Giải mª Affine:", decrypted_text) 2.3 Hệ mật HILL
2.3.1 Lịch sử hình thành và phát triển :
Mật mã Hill được phát minh vào năm 1929 bởi Lester S. Hill. Đây là mật mã đa đồ
họa đầu 琀椀 ên trong đó việc thực tế là có thể hoạt động nhiều hơn 3 ký tự một lúc.
Mật mã Hill sử dụng modulo, nhân ma trận và nghịch đảo ma trận. Do đó, nó là mật
mã thiên về toán học nhiều hơn các loại mật mã khác.
2.3.2 Phương pháp mã hóa Hill :
a, Ma trận khả nghịch trên Z26 :
- Nếu ma trận A cấp m x m trên Z26 có det(A) ( định thức ) khả nghịch trên Z26 thì
bản thân ma trận A khả nghịch trên vành Z26.
 Det(A) 0 và Det(A) khả nghịch trên Z26 thì gcd[ det(A),26 ] = 1 thì khi đó ma
trận A khả nghịch trên Z26
- Vì ma trận A khả nghịch trên Z26 nên tồn tại 1 ma trận nghịch đảo của A trên Z26 là A-1
- Có 2 cách 琀 m ma trận nghịch đảo đã được học là :
• Sử dụng phần phụ đại số :
B1 : Tính det(A). Nếu det(A) = 0 thì không có ma trận nghịch đảo. Nếu
det(A) 0 thì có ma trận nghịch đảo.
B2 : Lập ma trận chuyển vị A’ ( các hàng của A chuyển thành các cột của A )
B3 : Lập ma trận phụ hợp của A’ : PA = (A’ij )nm với A’ij là phần bù đại số
của phần tử ở hàng i, cột j
B4 : Tính ma trận nghịch đảo theo công thức : A−1 =
=PA(det( ))A P−1 A
Chú ý : với ma trận vuông cấp 2 dạng A= a bc d thì PA = −dc − b a
• Sử dụng Gauss – Jordan : ít khi dùng trong mật mã Hill
b, Định nghĩa và cách dùng mật mã Hill :
Mật mã Hill là hệ mật trong đó P = C = (Z26 )m và K với P là tập các ma trận m x
m biểu diễn plain text, C là tập các ma trận m x m biểu diễn cipher text, K là
tập ác ma trận m x m khả nghịch trên Z26. p } c }
Với mỗi ma trận k K , ={p p1, 2,..., pm
P; ={c ,c ,...,c1 2 m C
Nếu các p và c ở dạng ma trận cột xác định : o Hàm mã hóa : eK(p) = K.p
o Hàm giải mã : dK(p) = K-1.c
Nếu các p và c ở dạng ma trận hàng xác định : o Hàm mã hóa : eK(p) = p.K
o Hàm giải mã : dK(c) = c.K-1
Trong đó K-1 là ma trận nghịch đảo của K. Tất cả các phép toán thực hiện trong Z26.
 Mã Hill thực hiện mã hóa một lần m kí tự bản rõ ( kí hiệu p1, p2,…, pm)
thay thế thành các kí tự trong bản mã ( kí hiệu c1, c2,…, cm).
 Việc thay thế này được thực hiện bằng m phương trình tuyến 琀 nh :
c1 = k11.p1 + k12.p2 + … + k1m.pm mod 26 c2
= k21.p1 + k22.p2 + … + k2m.pm mod 26
…………………………………………….
cm = km1.p1 + km2.p2 + … + kmm.pm mod 26
c, Ví dụ sử dụng mật mã Hill :
Cho đoạn văn bản rõ plain text là : P = NGUYENMINHPHUC.
a. Mã hóa đoạn văn bản trên bằng mật mã Hill với khóa key là K = HILL
b. Giải đoạn mã thu được ở câu a Bài làm : a. Mã hóa
Khóa K được viết dưới dạng ma trận vuông cấp 2 là : K = HI = 78 L L 11 11
Khóa K có kích thước 2x2 nên m=2 => chia bản rõ thành các đoạn có độ dài 2 kí tự
từ trái qua phải và mã hóa từng đoạn mã này :