BÁO CÁO MÔN THỐNG KÊ KINH DOANH - NHÓM 08 (TỰ LUẬN & TRẮC NGHIỆM) | Đại học Văn Lang

lOMoARcPSD| 61538472
ĐIỂM: (Phần này giảng viên ghi)
BÀI BÁO CÁO MÔN THỐNG KÊ KINH DOANH NHÓM: 08 STT MSSV
HỌ VÀ TÊN (Thứ tự ABC) Số điện thoại Điểm (10) Chữ ký 1.
2173401010391 Phạm Nguyễn Tú Anh 0767924932 10 2. 2273401150725 Ngô Xuân Mai 0762808080 10 3.
2273401151222 Trương Ngọc Thanh Tâm 0358510616 10 4.
2273401151281 Trần Kim Thảo 0943046806 10 5.
2273401151727 Huỳnh Thị Như Ý 0349694235 10 Nội dung làm bài: TŒn Tự luận Trắc nghiệm Excel Phạm Nguyễn Tú Anh c u 3,4 Tất cả b i 8,9 Ngô Xuân Mai c u 5,1 Tất cả b i 6,7 Trương Ngọc Thanh Tâm c u 1,2 Tất cả b i 8,9 Trần Kim Thảo c u 4,5 Tất cả b i 6,7 Huỳnh Thị Như Ý c u 2,3 Tất cả b i 8,9
• Họ và tên nhóm trưởng: Ngô Xuân Mai
• Địa chỉ email: mai.2273401150725@vanlanguni.vn PHẦN TỰ LUẬN:
B i 1: Cho X là biến ngẫu nhiên liên tục có hàm mật độ xác suất như sau: 𝑘 𝑓 Bài giải: a) Tìm k. Ta có: 𝑑𝑥 = 1 𝑘(𝑥2 + 1)𝑑𝑥 = 1 lOMoARcPSD| 61538472 𝑑𝑥 = 1 24𝑘 = 1 (=) 𝑘 =
b) Tìm kỳ vọng và phương sai của X. Ta có: Kỳ vọng: EX = 𝑑𝑥 => EX 𝑥(𝑥2 + 1)𝑑𝑥 = 𝑑𝑥 =
Phương sai: Var X = 𝐸𝑋2 − (𝐸𝑋)2 𝐸𝑋 𝑑𝑥 => 𝐸𝑋 + 1)𝑑𝑥 = 𝑑𝑥 = 2  Var X = − ( ) =
c) Tìm kỳ vọng và phương sai của (24X – mã số nhóm). Ta có: 𝑌 = 24𝑋 − 8
 Kỳ vọng: 𝐸𝑌 = 24𝐸𝑋 − 8 = 24 × − 8 =
 Var Y = Var (24X − 8) = 242 × 𝑉𝑎𝑟 𝑋 = 576 × = 337,8375
Bài 2: Cho X là biến ngẫu nhiên có phân phối chuẩn với X~N (45; 4 + mã số nhóm). Tính các xác suất sau:
Ta có: X~N (45;12) => 𝜇 = Bài giải: a) 𝑷 𝑃
= 𝜑(2,88) + 𝜑(0,86) = 0,4980 + 0,3051 = 0,8031 lOMoARcPSD| 61538472 b) 𝑷 𝟓𝟏, 𝟓𝟏) 𝑃 = 0,5 − 𝜑 = 0,5 − 𝜑 c) 𝑷 𝟓𝟎, 𝟖𝟖) 𝑃 d) 𝑷(|𝑿 − 𝝁| 𝑃(|𝑋 − 𝜇| = 2 × 0,3051 = 0,6102
Bài 3: Đường kính của một loại chi 琀椀 ết do một máy sản xuất tuân theo quy luật phân phối
chuẩn, với kỳ vọng là 20 mm và độ lệch chuẩn là 5 mm. Tính xác suất để lấy ngẫu nhiên một chi
琀椀 ết có đường kính trong khoảng (18 + mã số nhóm) mm đến (22 + mã số nhóm) mm. Bài giải: Ta có: X~N (20; 52) = 𝜑 − 𝜑(1,2) = 0,4772 – 0,3849 = 0,0923
Bài 4: Chiều cao của các sinh viên ở một trường đại học là biến ngẫu nhiên có phân phối chuẩn
với chiều cao trung bình là (158 + mã số nhóm) cm và độ lệch chuẩn là 7,5 cm. Nếu chọn ra 10%
sinh viên có chiều cao cao nhất thì chiều cao tối thiểu của sinh viên trong nhóm này là bao nhiêu? Bài giải:
= 158 + 8 =166; 𝜎 = 7,5 => X~N (166; 7,52)
Gọi a là chiều cao tối thiểu của sinh viên Ta c : P (X a)
= 10%= 0,1 => 0,5 − 𝜑(𝑎−166 ) = 0,1 7,5 lOMoARcPSD| 61538472 𝑎 − 166 (=) 𝜑() = 0,4 7,5 (=) 𝜑 (𝑎−166) = 𝜑( 1,28) 7,5  a= 175,6
Bài 5: Thời gian từ nhà đến trường của sinh viên A là một biến ngẫu nhiên T có phân phối chuẩn.
Biết 68% số ngày A đến trường mất hơn 20 phút và 9% số ngàn An đi mất hơn 30 phút. Bài giải:
a) Tính thời gian đến trường trung bình của sinh viên A và độ lệch 琀椀 êu chuẩn.
Gọi T là thời gian đi từ nhà đến trường của A. Ta có: 𝑇 ~ 𝑁 (𝑇 >
= 0,68 𝑣à 𝑃 (𝑇 >
• P(T>20) = 0,5 −𝜑 (20 − 𝜇) = 0,68 => 𝜑 ( 20 − 𝜇) = − 0,18 𝜎𝜎
 𝜑(−0,47) = − 0,18 => = − 0,47 (1) 𝜎
• P(T>30) = 0,5 – 𝜑 (
30 – 𝜇) = 0,09 => 𝜑 ( 30 – 𝜇 𝜎𝜎  𝜑 = 0,41 => 𝜎
b) Giả sử sinh viên A xuất phát từ nhà trước giờ học 26 phút. Tính xác suất để A bị muộn học. P(T > 26) = 0,5 − 𝜑 (
) = 0,5 − 𝜑(0,61) = 0,5 − 0,2291 = 0,2709 PHẦN TRẮC NGHIỆM Câu Phương
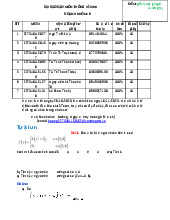
Giải chi 琀椀 ết Ghi chú án chọn 1. A 𝑛 = 10; 𝜎 = 0,9; Phạm vi sai số: 𝑧  1,96 × ± = 0,0882 ± 10 𝛼 =
 Từ 9,9118 đến 10,0882 ? Khoảng ước lượng lOMoARcPSD| 61538472 2. A Gọi x là số sinh viên cần 𝑛 205; 𝑓 = 0,82 khảo sát thêm 𝜀 = 3,4 %
𝛼 = 5% => 𝑧𝛼 = 𝑧0,025 = 1,96 Ta có: 𝜀 = 𝑧𝛼 × ; 𝑛 = 𝑛 2 + 𝑥
? thêm ít nhất bao nhiêu sinh viên 0,82 (1−0,82)  √ 3,4% = 1,96 205 + 𝑥  3. A Ta có: 𝑛 = = 0,9; 𝛼 = ? Khoảng ước lượng 𝜀 = 𝑡𝛼/2𝑛−1 ×
 Khoảng ước lượng: 10 ± 0,3916
 Từ 9,6084 đến 10,3916 4. D
Gọi 𝑝0 tỷ lệ trẻ em bị béo phì Đặt
𝑝0 = 0,33 => 𝑞0 = 0,67
giả thuyết 𝐻𝑜: 𝑝 = 0,33 đối với 𝑛 = 100; 𝑓 = 0,41 thuyết 𝐻
? Giá trị tiêu chuẩn kiểm định Ta có: 𝑧 = (𝑓 − 𝑝0) 5. A Giá trị trung bình:
Cho dãy số liệu: 6, 7, 8, 6, 5, 9. ? Giá trị trung bình = 6,8333 6. A Tỷ lệ cao hơn 165 cm =
𝑛 = 70 𝑐ó 45 > 165 𝑐𝑚 ? Tỷ lệ > 165 cm × 100% = 64,29% lOMoARcPSD| 61538472 7. A
Sử dụng máy tính giải các đặc trưng
Ta xét lượng trái cây có trọng của mẫu ta được:
lượng từ 200 gam đến 350 gam Giá trị trung bình: 𝑥
Biến ngẫu nhiên liên tục Độ lệch chuẩn: s=
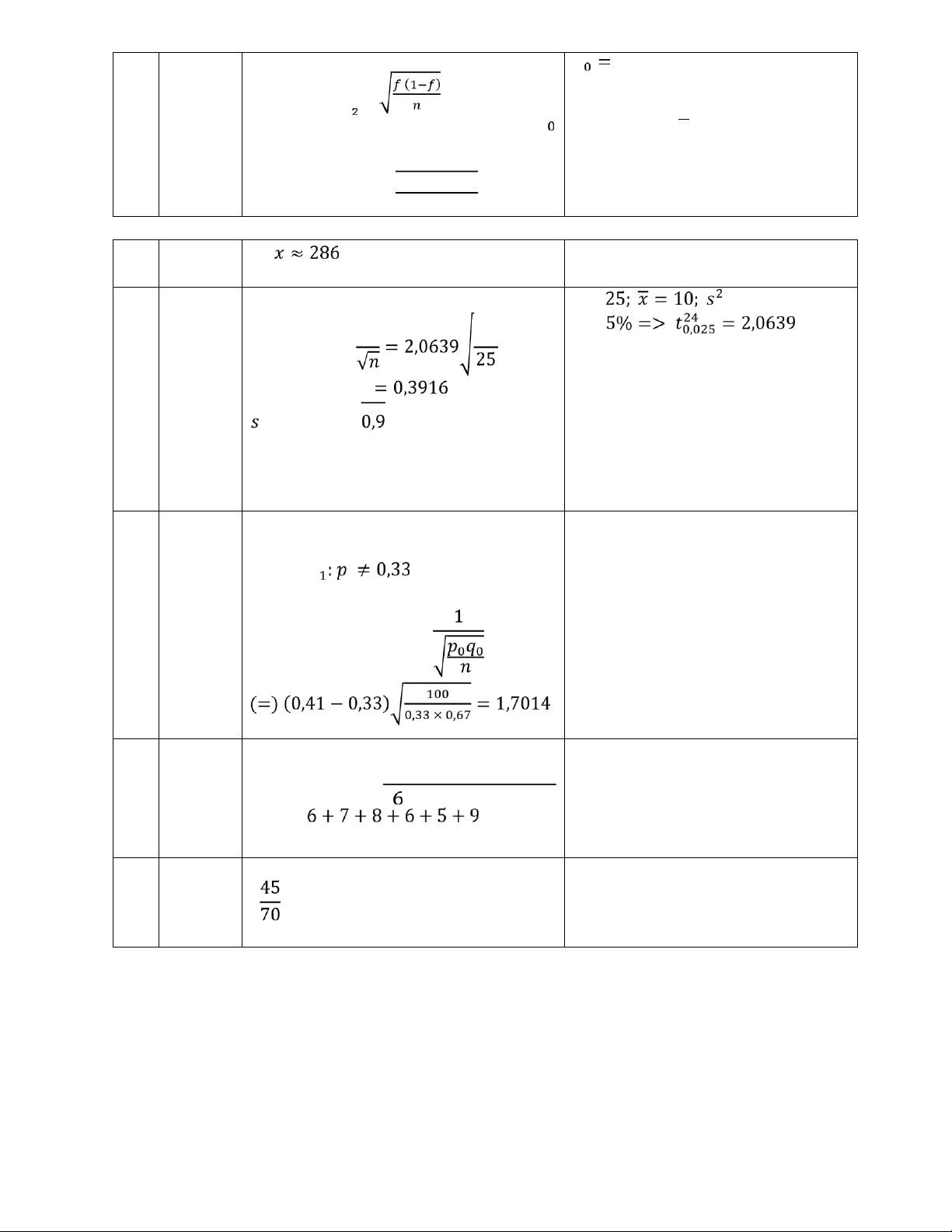
1 − 𝛼 = 95% => 𝑧𝛼 = 1,96 Ta có: 2 𝑠
Khoảng ước lượng = 𝑧 𝛼 × ±
Trọng 200 – 250 – 300 – 𝑥 lượng 250 300 350 (g) Số trái 40 80 55 5,5367 ±  n = 175
 Từ 273,8490 đến 284,7224 8. A Ta có:
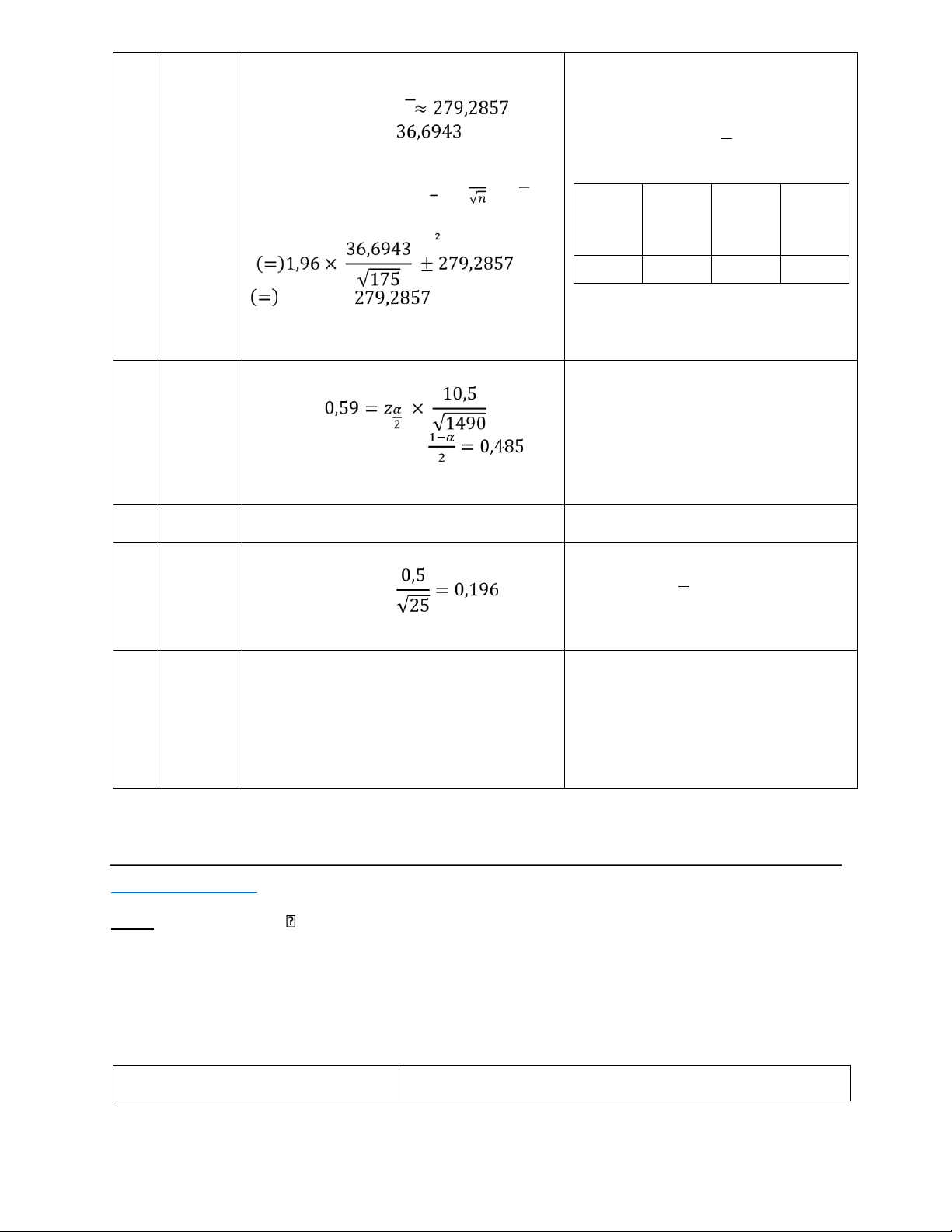
𝑛 = 1490; 𝑠 = 10,5; 𝜀 = 0,59 Độ tin cậy là 1 − 𝛼 = ?  𝑧𝛼 = 2,17 => 2  1 − 𝛼 = 97% 9. A Ta có: 𝑛 = 25; 𝜎 = 0,5;
𝛼 = 5% => 𝑧𝛼 = 𝑧0,025 = 1,96 2 𝜀 = 1,96 × 𝜀 =? 10. A
Sử dụng máy tính giải các đặc trưng
? trọng lượng trung bình và độ lệch của mẫu ta được: chuẩn về trọng lượng
Trọng lượng trung bình = 490,5932(g)
Độ lệch chuẩn = 5,9513 (g) PHẦN THỰC HÀNH
Bài 6. Sử dụng excel 琀 m bảng phân phối xác suất và vẽ đồ thị tương ứng cho biến ngẫu nhiên
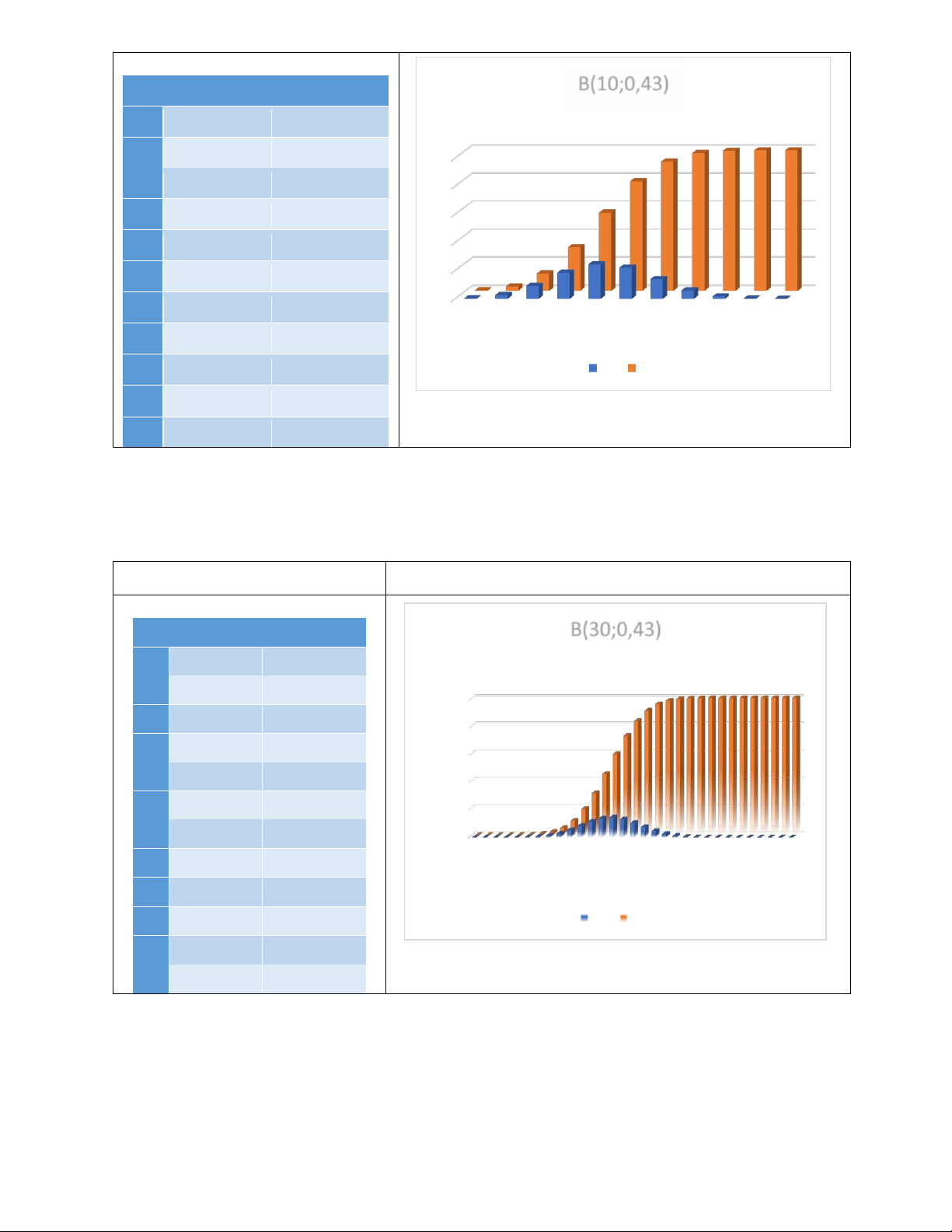
X có phân phối nhị thức với hai tham số n và p như sau: Bài làm: a) X ~ B(10; 0,43)
Bảng phân phối xác suất Hình minh họa lOMoARcPSD| 61538472 x f(x) F(x)’ B(10;0,43)
0 0,00362033 0,003620333 1 0,02731129 0,03093162 1 2 0,09271463 0,12364625 0 , 8 3 0,18651364 0,310159892 0 , 6 4 0,24623073 0,556390621 0 , 4 5 0,22290361 0,779294228 0 ,2 6 0,14012946 0,919423689 0 0 1 2 3 4 5 6 7 8 9 10 7 0,06040668 0,979830374 8 0,01708873 0,996919107 f(x) F(x)’ 9 0,00286478 0,999783885 10 0,00021611 1 b) X ~ B(30; 0,43)
Bảng phân phối xác suất Hình minh họa x f(x) F(x) B(30;0,43) 0 0,00000 0,00000 1 0,00000 0,00000 1,00000 2 0,00001 0,00001 0,80000 3 0,00008 0,00010 0,60000 4 0,00042 0,00052 0,40000 5 0,00165 0,00217 0,20000 … … … 0,00000 26 0,00000 1,00000
0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 27 0,00000 1,00000 28 0,00000 1,00000 f(x) F(x)’ 29 0,00000 1,00000 30 0,00000 1,00000 c) X ~ B(70; 0,43) lOMoARcPSD| 61538472
Bảng phân phối xác suất Hình minh họa x f(x) F(x)’ B(70;0,43) 0 8,1515E-18 8,15154E-18 1 4,3046E-16 4,3861E-16 1 2 1,1203E-14 1,16419E-14 0 , 8 3 1,9157E-13 2,03211E-13 0 , 6 4 2,4207E-12 2,62387E-12 0 , 4 5 2,4105E-11 2,67286E-11 0 , 2 … … … 0 65 1,0907E-18 1
0 4 8 12 16 20 24 28 32 36 40 44 48 52 56 60 64 68 66 6,2336E-20 1 67 2,8075E-21 1 f(x) F(x)’ 68 9,3438E-23 1 69 2,0431E-24 1 70 2,2019E-26 1 d) X ~ B(100; 0,43)
Bảng phân phối xác suất Hình minh họa x f(x) F(x)’ 0 3,868E-25 3,86799E-25 B(100;0,43) 1 2,918E-23 2,95664E-23 2 1,0896E-21 1,11919E-21 1 3 2,6852E-20 2,79712E-20 0 , 8 4 4,9123E-19 5,19198E-19 0 , 6 5 7,115E-18 7,63422E-18 0 , 4 … … … 0 , 2 95 6,8486E-29 1 0 96 2,6909E-30 1 97 8,371E-32 1 98 1,9331E-33 1 f(x) F(x)’ 99 2,9461E-35 1 100 2,2225E-37 1 e) X ~ B(300; 0,43) lOMoARcPSD| 61538472
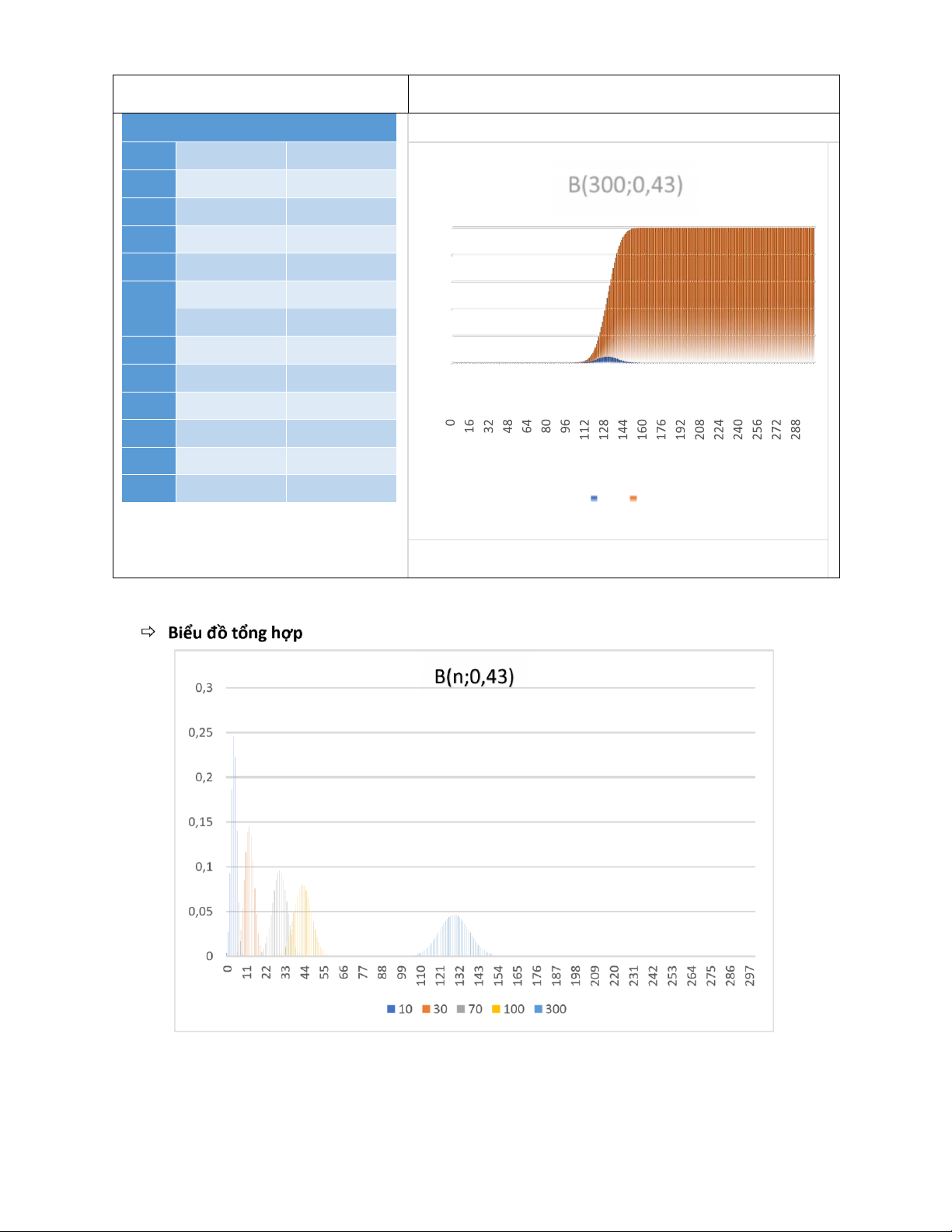
Bảng phân phối xác suất Hình minh họa x f(x) F(x)’ 0 5,78704E-74 5,78704E-74 1 1,3097E-71 1,31549E-71 B(300;0,43) 2 1,47709E-69 1,49024E-69 3 1,10687E-67 1,12177E-67 4 6,1999E-66 6,31208E-66 5 2,76886E-64 2,83198E-64 … … … 295 8,7992E-100 1 1 0,8 0,6 0,4 296 1,1213E-101 1 0,2 0 297 1,1392E-103 1 298 8,6519E-106 1 299 4,3658E-108 1 300 1,0978E-110 1 f(x) F(x)’ lOMoARcPSD| 61538472
Bài 7. Sử dụng excel 琀 m bảng phân phối xác suất và vẽ đồ thị tương ứng cho biến ngẫu
nhiên X có phân phối siêu bội với các tham số như sau Bài làm:
a. N = 18, M = 10, n = 5
Bảng phân phối xác suất Hình minh họa n P F(x) H(18,10,5) 0 0.006536 0.006536 1 1 0.081699 0.088235 2 0.294118 0.382353 0 , 5 3 0.392157 0.77451 4 0.196078 0.970588 0 0 1 2 3 4 5 5 0.029412 1 P F(x)
b. N = 38, M = 10, n = 5
Bảng phân phối xác suất Hình minh họa n P F(x) H(38,10,5) 0 0.1958 0.1958 1 0.407916 0.603715 1 2 0.293699 0.897414 0 , 8 3 0.090369 0.987783 0 , 6 4 0.011715 0.999498 0 , 4 5 0.000502 1 0 , 2 0 0 1 2 3 4 5 P F(x)
c. N = 78, M = 10, n = 5
Bảng phân phối xác suất Hình minh họa lOMoARcPSD| 61538472 n P F(x) H(78,10,5) 0 0.493775 0.493775 1 1 0.385762 0.879537 0 , 8 2 0.106826 0.986363 0 , 6 3 0 , 4 0.012949 0.999312 0 , 2 4 0.000676 0.999988 0 5 0 1 2 3 4 5 1.19E-05 1 P F(x)
d. N = 108m, M = 10, n = 5
Bảng phân phối xác suất Hình minh họa n P F(x) H(108,10,5) 0 0.609234 0.609234 1 1 0.324061 0.933295 0 , 8 2 0.061401 0.994696 0 , 6 3 0.005117 0.999813 0 , 4 4 0.000185 0.999998 0 , 2 5 2.26E-06 1 0 0 1 2 3 4 5 P F(x)
e. N = 208, M = 10, n = 5
Bảng phân phối xác suất Hình minh họa lOMoARcPSD| 61538472 n P F(x) H(208,10,5) 0 0.77972 0.77972 1 1 0.200959 0.980679 0 , 8 0 , 6 2 0.01855 0.999229 0 , 4 3 0.000757 0.999986 0 , 2 0 4 1.35E-05 1 0 1 2 3 4 5 P F(x) 5 8.15E-08 1
Bài 8. Sử dụng excel 琀 m bảng phân phối xác suất và vẽ đồ thị tương ứng cho biến ngẫu
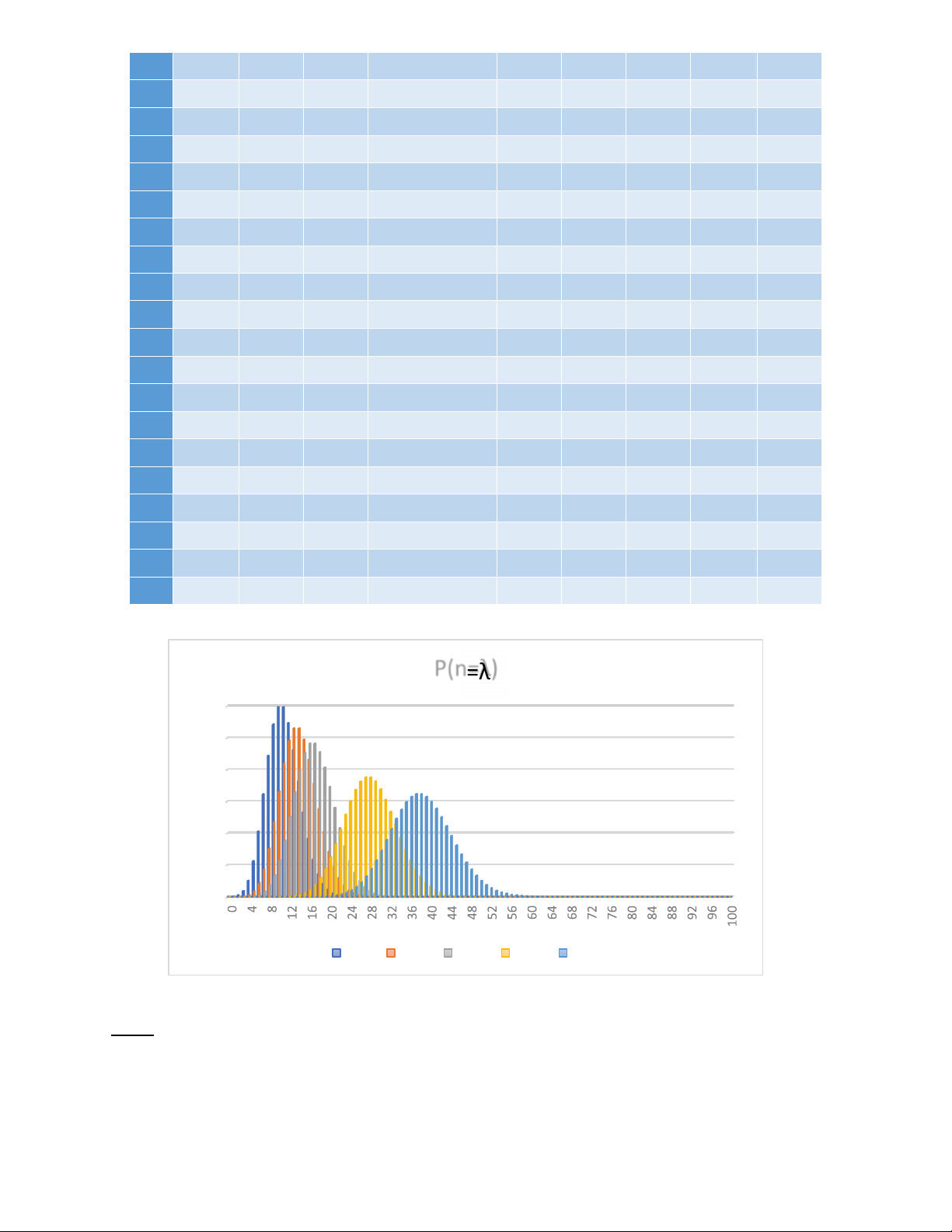
nhiên X có phân phối Poisson với tham số 𝜆 bằng Bài làm: λ 11 14 17 28 38 x P F(x) P2 F(x)2 P3 F(x)3 P4 F(x)4 P5 F(x)5 0
0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 1
0,0002 0,0002 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 2
0,0010 0,0012 0,0001 0,0001 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 3
0,0037 0,0049 0,0004 0,0005 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 4
0,0102 0,0151 0,0013 0,0018 0,0001 0,0002 0,0000 0,0000 0,0000 0,0000 5
0,0224 0,0375 0,0037 0,0055 0,0005 0,0007 0,0000 0,0000 0,0000 0,0000 6
0,0411 0,0786 0,0087 0,0142 0,0014 0,0021 0,0000 0,0000 0,0000 0,0000 7
0,0646 0,1432 0,0174 0,0316 0,0034 0,0054 0,0000 0,0000 0,0000 0,0000 8
0,0888 0,2320 0,0304 0,0621 0,0072 0,0126 0,0000 0,0000 0,0000 0,0000 9
0,1085 0,3405 0,0473 0,1094 0,0135 0,0261 0,0000 0,0000 0,0000 0,0000
10 0,1194 0,4599 0,0663 0,1757 0,0230 0,0491 0,0001 0,0001 0,0000 0,0000
11 0,1194 0,5793 0,0844 0,2600 0,0355 0,0847 0,0001 0,0002 0,0000 0,0000
12 0,1094 0,6887 0,0984 0,3585 0,0504 0,1350 0,0003 0,0006 0,0000 0,0000
13 0,0926 0,7813 0,1060 0,4644 0,0658 0,2009 0,0007 0,0013 0,0000 0,0000
14 0,0728 0,8540 0,1060 0,5704 0,0800 0,2808 0,0014 0,0027 0,0000 0,0000
15 0,0534 0,9074 0,0989 0,6694 0,0906 0,3715 0,0027 0,0054 0,0000 0,0000
16 0,0367 0,9441 0,0866 0,7559 0,0963 0,4677 0,0047 0,0101 0,0000 0,0000
17 0,0237 0,9678 0,0713 0,8272 0,0963 0,5640 0,0078 0,0179 0,0001 0,0001
18 0,0145 0,9823 0,0554 0,8826 0,0909 0,6550 0,0121 0,0300 0,0001 0,0002
19 0,0084 0,9907 0,0409 0,9235 0,0814 0,7363 0,0178 0,0478 0,0003 0,0005
20 0,0046 0,9953 0,0286 0,9521 0,0692 0,8055 0,0249 0,0727 0,0005 0,0010 lOMoARcPSD| 61538472
21 0,0024 0,9977 0,0191 0,9712 0,0560 0,8615 0,0332 0,1060 0,0009 0,0019
22 0,0012 0,9990 0,0121 0,9833 0,0433 0,9047 0,0423 0,1483 0,0016 0,0035
23 0,0006 0,9995 0,0074 0,9907 0,0320 0,9367 0,0515 0,1998 0,0026 0,0062
24 0,0003 0,9998 0,0043 0,9950 0,0226 0,9594 0,0601 0,2599 0,0042 0,0103
25 0,0001 0,9999 0,0024 0,9974 0,0154 0,9748 0,0673 0,3272 0,0063 0,0166
26 0,0000 1,0000 0,0013 0,9987 0,0101 0,9848 0,0725 0,3997 0,0092 0,0259
27 0,0000 1,0000 0,0007 0,9994 0,0063 0,9912 0,0752 0,4749 0,0130 0,0389
28 0,0000 1,0000 0,0003 0,9997 0,0038 0,9950 0,0752 0,5500 0,0176 0,0565
29 0,0000 1,0000 0,0002 0,9999 0,0023 0,9973 0,0726 0,6226 0,0231 0,0796
30 0,0000 1,0000 0,0001 0,9999 0,0013 0,9986 0,0677 0,6903 0,0293 0,1089
31 0,0000 1,0000 0,0000 1,0000 0,0007 0,9993 0,0612 0,7515 0,0359 0,1448
32 0,0000 1,0000 0,0000 1,0000 0,0004 0,9996 0,0535 0,8051 0,0426 0,1875
33 0,0000 1,0000 0,0000 1,0000 0,0002 0,9998 0,0454 0,8505 0,0491 0,2365
34 0,0000 1,0000 0,0000 1,0000 0,0001 0,9999 0,0374 0,8879 0,0549 0,2914
35 0,0000 1,0000 0,0000 1,0000 0,0000 1,0000 0,0299 0,9178 0,0596 0,3510
36 0,0000 1,0000 0,0000 1,0000 0,0000 1,0000 0,0233 0,9411 0,0629 0,4138
37 0,0000 1,0000 0,0000 1,0000 0,0000 1,0000 0,0176 0,9587 0,0646 0,4784
38 0,0000 1,0000 0,0000 1,0000 0,0000 1,0000 0,0130 0,9717 0,0646 0,5430
39 0,0000 1,0000 0,0000 1,0000 0,0000 1,0000 0,0093 0,9810 0,0629 0,6059 … … … … … … … … … … …
Biểu đồ minh họa: P(n= λ ) 0 12 , , 0 1 0 ,08 0 ,06 , 0 04 , 0 02 0 λ= 11 λ = 14 λ = 17 λ = 28 λ = 38
Bài 9. Chọn hai bộ số liệu, sử dụng excel, đặt câu hỏi và trình bày bài làm chi 琀椀 ết các câu sau: Bài làm: lOMoARcPSD| 61538472
Ta có mẫu số liệu được lấy trên h 琀琀 ps://www.pnj.com.vn/blog/gia-vang/ ngày 24/10/2023.
Giả sử số liệu tuân theo quy luật phân phối chuẩn. STT C ng ty
Loại vàng | ĐVT: 1.000đ/Chỉ GiÆ mua GiÆ bÆn 1. PNJ Vàng miếng SJC 999.9 6,990 7,065 2. PNJ Nhẫn Trơn PNJ 999.9 5,790 5,895 3. PNJ Vàng Kim Bảo 999.9 5,790 5,895 4. PNJ Vàng Phúc Lộc Tài 999.9 5,790 5,895 5. PNJ Vàng nữ trang 999.9 5,780 5,895 6. PNJ Vàng nữ trang 999 5,774 5,895 7. PNJ Vàng nữ trang 99 5,711 5,811 8. PNJ V ng 750 (18K) 4,270 4,410 9. PNJ V ng 585 (14K) 3,303 3,443 10. PNJ V ng 416 (10K) 2,313 2,453 11. PNJ Vàng miếng PNJ (999.9) 5,790 5,895 12. PNJ V ng 916 (22K) 5,328 5,895 13. PNJ V ng 650 (15.6K) 3,684 3,824 14. PNJ V ng 680 (16.3K) 3,860 4,000 15. PNJ V ng 610 (14.6K) 3,450 3,590 16. PNJ V ng 375 (9K) 2,073 2,213 17. PNJ V ng 333 (8K) 1,809 1,949
a. Tìm các đặc trưng cơ bản cho mỗi bộ số liệu đó. GiÆ mua GiÆ bÆn Mean 4,559117647 Mean 4,707235294 Standard Error 0,382470259 Standard Error 0,382419903 Median 5,328 Median 5,811 Mode 5,79 Mode 5,895 Standard Deviation 1,576965277 Standard Deviation 1,576757651 Sample Variance 2,486819485 Sample Variance 2,486164691 Kurtosis -1,060877067 Kurtosis -1,09777677 lOMoARcPSD| 61538472 Skewness -0,441802172 Skewness -0,474488316 Range 5,181 Range 5,116 Minimum 1,809 Minimum 1,949 Maximum 6,99 Maximum 7,065 Sum 77,505 Sum 80,023 Count 17 Count 17 Confidence Level (95,0%) 0,810800729 Confidence Level (95,0%) 0,810693978
b. Tìm khoảng 琀椀 n cậy cho trung bình.
Câu hỏi: Theo bộ số liệu trên, khoảng 琀椀 n cậy 95% cho giá vàng bán ra trung bình trong ngày
24/10/2023 nằm trong khoảng nào?
Theo bảng số liệu thống kê mô tả, ta có: 𝑥 = 4,7072
• Gọi là giá vàng trung bình bán ra của công ty • Với độ 琀椀 n cậy 95%,
ta có độ chính xác là = 0,8107
• Với độ 琀椀 n cậy 95%, khoảng ước lượng cần 琀 m là:
(𝑥 + 𝜀; 𝑥 − 𝜀) = (4,7072 − 0,8107; 4,7072 + 0,8107) = (3,8965; 5,5179)  Kết luận:
Khoảng 琀椀 n cậy 95% cho giá vàng trung bình bán ra trong ngày nằm trong khoảng từ
3,8965 (1000 VND/chỉ) đến 5,5179 (1000VND/chỉ).
c. Tìm khoảng 琀椀 n cậy cho tỷ lệ.
Câu hỏi: Theo bộ số liệu trên, khoảng 琀椀 n cậy 95% cho tỷ lệ loại PNJ có giá bán ra là 5,895
(1000VND/chỉ) nằm trong khoảng nào?
Theo bảng số liệu, ta có: n = 17, m = 7
• Gọi p là tỷ lệ loại PNJ có giá bán ra là 5,895 (1000VND/chỉ) của công ty. Tỷ lệ mẫu 𝑓 =
Với độ 琀椀 n cậy 1 − = 95% tra bảng 1 trong tài liệu 琀 m được: 𝑧𝛼 = 1,96 2 7 7 𝑓(1−𝑓) √ 17 (1− 17 ) Độ chính xác: 𝜀 = 𝑧 =1 ,96 × √ =0,2339 𝑛 17 𝛼 2
• Khoảng ước lượng cần 琀 m:
(𝑓 − 𝜀; 𝑓 + 𝜀) = ( − 0,2339; + 0,2339) = (0,1778; 0,6457) lOMoARcPSD| 61538472  Kết luận:
Khoảng 琀椀 n cậy 95% cho tỷ lệ loại PNJ có giá bán ra là 5,895 (1000VND/chỉ) nằm trong
khoảng từ 17,78% đến 64,57%
d. Kiểm định giả thuyết về trung bình.
Câu hỏi: Có báo cáo cho rằng giá vàng bán ra trung bình trong ngày 24 tháng 10 năm 2023 là
6,000 (1000VND/chỉ). Với mức ý nghĩa 5%, hãy cho nhận xét về báo cáo trên (yêu cầu: Lập mô
hình kiểm định, 琀 nh trị thống kê và cho kết luận).
Theo bảng số liệu thống kê mô tả, ta có: 𝑥 = 4,7072 và s = 0,382419903
• Gọi là giá vàng trung bình bán ra của công ty
Đặt 𝐻0: p = 6000 và 𝐻1: p ≠ 6000 Từ
𝛼 = 5% => 𝑡016,0,25 = 2,1199 • Trị thống kê: 𝑥 − 𝜇0 4,7072 − 6000 √ 𝑛 = √ 17 = −64642,36202 𝑡 = 𝑠 0,3824  Kết luận:
Vì |𝑡| = 64642,36202 > 𝑡016,0,25 = 2,1199 𝑛ê𝑛 𝑏á𝑐 𝑏ỏ 𝐻0.
Với mức ý nghĩa 5%, bác bỏ báo cáo trên.
e. Kiểm định giả thuyết về tỷ lệ.
Câu hỏi: Có báo cáo cho rằng tỷ lệ loại PNJ có giá bán ra là 5,895 (1000VND/chỉ) là 43%. Với mức
ý nghĩa 5%, hãy cho nhận xét về báo cáo trên (yêu cầu: Lập mô hình kiểm định, 琀 nh trị thống kê và cho kết luận).
Theo bảng số liệu, ta có: n = 17, m = 7
Gọi p là tỷ lệ loại PNJ có giá bán ra là 5,895 (1000VND/chỉ) của công ty PNJ Tỷ lệ mẫu 𝑓 =
Đặt 𝐻0: p = 43% và 𝐻1: p ≠ 43% Ta có: 𝑧𝛼 = 1,96 2
Trị thống kê: 𝑧 = (𝑓 − 𝑝0)  Kết luận:
Vì |𝑧| = 0,73 < 𝑧 𝛼 = 1,96 nên chưa đủ cơ sở để bác bỏ 𝐻0. Với mức ý nghĩa 5%, chưa 2 lOMoARcPSD| 61538472
đủ cơ sở để bác bỏ báo cáo trên.
f. So sánh hai trung bình của hai tổng thể.
Câu hỏi: Theo bộ số liệu trên, với mức ý nghĩa 5%, giá vàng trung bình mua vào so với giá vàng
trung bình bán ra có khác nhau không?
t-Test: Two-Sample Assuming Equal Variances GiÆ mua GiÆ bÆn 4,559117647 4,707235294 2,486819485 2,486164691 17 17 2,486492088 0 Mean 32 Variance Observations -0,273856294 Pooled Variance 0,392977532 Hypothesized Mean Difference df t Stat 1,693888748 P(T<=t) one-tail t Critical one-tail 0,785955064 P(T<=t) two-tail 2,036933343 t Critical two-tail
 Ta thấy rằng t Stat = - 0,273856294 và t Cri 琀椀 cal two-tail = 2,0369 nên giá vàng trung
bình mua vào khác với giá vàng trung bình bán ra.