ĐẠI HỌC QUỐC GIA HÀ NỘI
TRƯỜNG ĐẠI HỌC KHOA HỌC TỰ NHIÊN
BÁO CÁO THỰC HÀNH VẬT LÝ ĐẠI CƯƠNG 2
GIÁO VIÊN : NGUYỄN TỪ NIỆM SINH VIÊN: PHẠM HOÀNG AN MÃ SINH VIÊN :20002102
LỚP: KỸ THUẬT ĐIỆN TỬ VÀ TIN HỌC KHÓA :65
LỊCH THỰC HÀNH: SÁNG THỨ 4 TIẾT 1-4
HÀ NỘI, NĂM 2021
BÀI 1: SÓNG ĐỨNG TRÊN DÂY LECHER. 1. Mục đích.
Tạo sóng đứng trên dây Lecher với các trường hợp:
o Đầu cuối của dây Lecher đoản mạch. o Đầu
cuối của dâyLecher để hở.
o Đầu cuối của dây Lecher mắc với một điện
trở. Xác định bước sóng λ.
2. Cơ sở lý thuyết.
Năm 1890, E. Lecher đưa ra thí nghiệm về sự lan truyền của sóng điện
từ trên hai dây dẫn tiết diện tròn đặt song song với nhau (dây Lecher). Dây
Lecher được dùng rộng rãi để truyền sóng điện từ từ nơi phát đến nơi thu,
hoặc từ máy phát sóng điện từ tới các bức xạ sóng (anten).
Lý thuyết và thực nghiệm đều chứng tỏ rằngnếu khoảng cách b giữa
hai dây dẫn của dây Lecher là nhỏ so với bước sóng của sóng điện từ, thì
sóng điện từ có thể lan truyền dọc theo dây Lecher với vận tốc bằng: 𝑣 = Trong đó, 𝑐 =
: vận tốc lan truyền sóng điện từ trong chân không, ε
và μ lần lượt là hằng số điện môi và từ môi tương đối của môi trường xung
quanh. Nếu môi trường xung quanh là không khí thì 𝑣 ≈ 𝑐.
Khi sóng lan truyền trên dây Lecher rất dài, được coi là vô hạn, thì
sóng phản xạ từ các đầu cuối của dây nhỏ và có thể bỏ qua. Trong kỹ thuật
vô tuyến điện, người ta thường dùng dây Lecher có chiều dài cỡ một hoặc vài
bước sóng. Khi đó sóng phản xạ từ các đầu dây thể hiện rõ ràng. Sóng phản
xạ kết hợp với sóng tới và tạo thành sóng đứng trên dây.
Xét một đoạn dây Lecher một đầu được nuôi bởi một máy phát sóng
cao tần, đầu còn lại để hở hoặc đoản mạch, hoặc mắc với một điện trở
thuần.Khi một trường điện tần số cao được truyền vào vị trí x dây Lecher, một sóng điện áp: U = Uo. sin(ωt − kx) (1)
với: ω = 2𝜋.f: tần số góc, k = 2π/λ: số sóng,
lan truyền theo hướng x (từ trái qua phải) của đây. Tần số và bước sóng của
dây phù hợp với tần số và bước sóng của trường truyền.
2.1. Dây Lecher với đầu cuối đoản mạch
Nếu các dây của dây Lecher được đoản mạch ở đầu cuối, thì hiệu
điện thế U tại đó bằng không.Độ lệch pha giữa sóng tới và sóng phản xạ
là 180 o . Chọn gốc tọa độ O đặt ở đầu dây (điểm tiếp xúc giữa dây và
nguồn cao tần). Giả sử sóngđiện áp tới tại điểm có tọa độ x có dạng: U1 = Uo. sin(ωt − kx)
Khi đó sóng phản xạ tại điểm đó có dạng: U2 = − Uo. sin(ωt + kx)
Sóng tới kết hợp với sóng phản xạ tạo thành sóng đứng:
U = U1 + U2 = −2. Uo. sin(kx). cos(ωt) (2)
Điện áp giữa các dây được gắn liền với sự phân bố điện tích dọc theo dây.
Sự dao động của các điện tích này sinh ra một dòng điện I có dạng sóng truyền
trong dây.Tại đầu cuối của dây (đầu đoản mạch) luôn có dòng điện cố định chạy
qua.Vì vậy, không có sự thay đổi về pha giữa sóng tới và sóng phản xạ của cường
độ dòng điện. Nghĩa là, nếu phương trình của dòng tới có dạng: I1 = Io. sin(ωt − kx)
thì phương trình của dòng phản xạ có dạng:
I1 = Io. sin(ωt + kx) Phương trình
tổng hợp của I1& I2có dạng:
I = I1 + I2 = 2. Io. cos(kx). sin(ωt) (3)
Từ các phương trình (2) và (3) ta thấy rằng các vị trí nút sóng của sóng điện áp
tương ứng với các vị trí bụng sóng của sóng dòng điện và các vị trí bụng sóng của
sóng điện áp tương ứng với các vị trí nút sóng của sóng dòng điện. Vị trí của các nút điện áp là
x = 0, −λ/2, −λ, −3λ/2, … (4)
do đó, khoảng cách của chúng từ điểm đầu của dây là bội của λ/2. Sóng điện từ
đứng trên dây Lecher tương ứng với dòng điện I và điện tích (+,-) trên các dây được mô tả trên hình 1.
2.2. Dây Lecher với đầu cuối hở mạch
Trong trường hợp này, có một hiệu điện thế không đổi ở cuối dây
Lecher, tức là sóng điện áp tới và sóng điện áp phản xạ không có sự thay
đổi về pha. Trong khi đó, dòng điện ở đầu hở (đầu cuối) luôn luôn bằng
không, sóng dòng tới và sóng của dòng phản xạ lệch pha nhau 180 o . Do
đó các phương trình tổng hợp của điện áp, cũng như dòng điện của các
sóng tới và sóng phản xạ có dạng:
U = U1 + U2 = 2. Uo. cos kx. sinωt (5) Và
I = I1 + I2 = −2. Io. sinkx. cosωt (6)
Các phương trình này có thể thu được từ các phương trình (2) và (3)
bằng cách hoán đổi giữa U và I.
2.3. Dây Lecher có đầu cuối mắc với điện trở thuần
Sóng đứng không được hình thành nếu điểm cuối của dây Lecher
được nối với điện trở thuần.Trong trường hợp này, sóng dòng điện và
sóng điện áp tới không bị phản xạ ở điểm cuối của dây. XỬ LÝ SỐ LIỆU
a) Dây lecher với đầu cuối đoản mạch
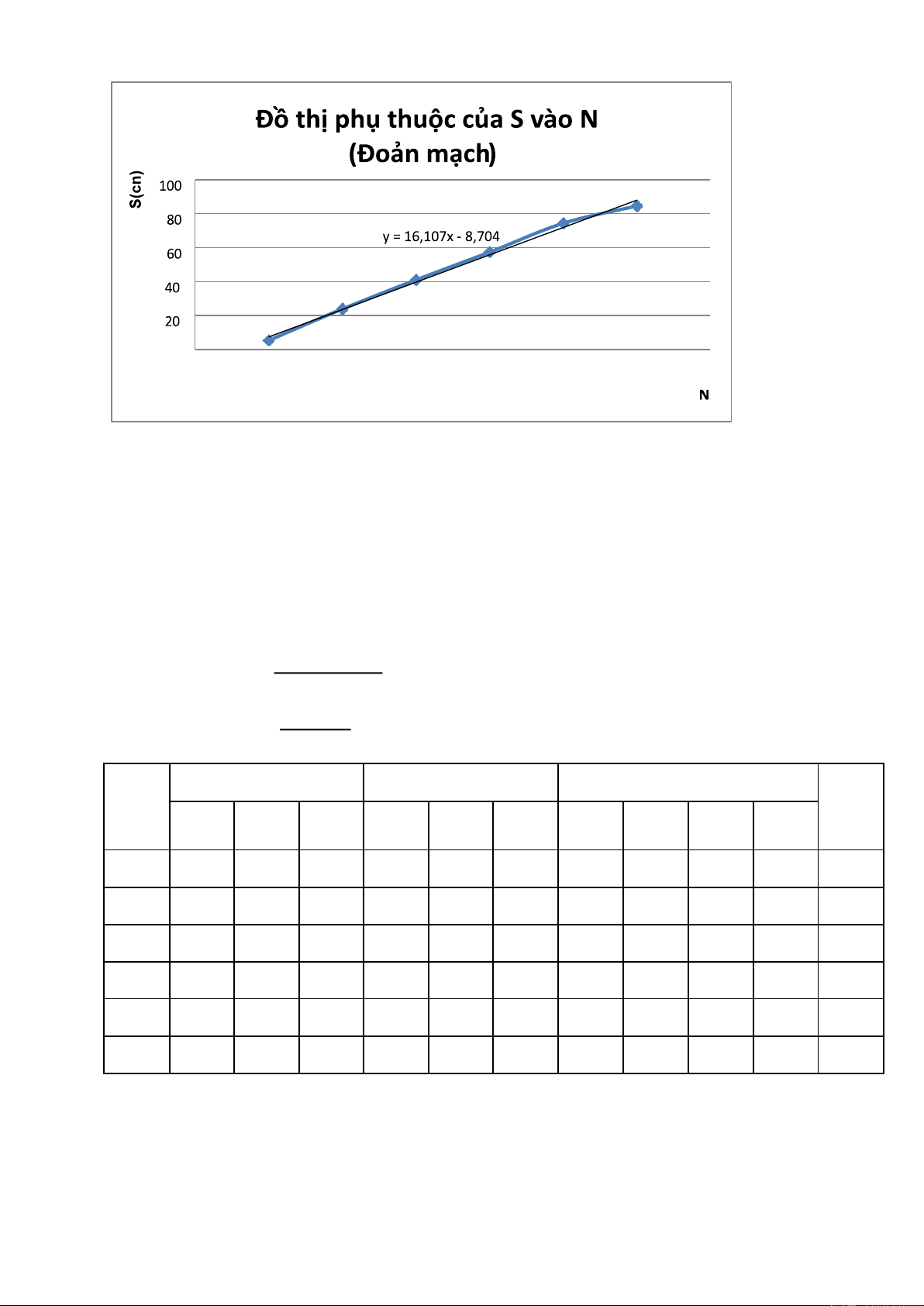
Bảng 2. Vị trí của các nút dòng và thế trên dây Lecher đoản mạch S1(cm) S2(cm) S=(S1+S2)/2(cm) Kiểu
N Lần Lần Lần Lần Lần Lần Lần 1 Lần 2 Lần 3 Stb (nút) 1 2 3 1 2 3 1 2.7 2.4 2.1 8.2 8.2 8.3 5.45 5.3 5.2 5.31 I 2 16.5 16.4 17.1 31.1 31.1 30.5 23.8 23.75 23.8 23.78 U 3 39.4 39.5 39.2 42.5
42.4 42.5 40.95 40.95 40.85 40.91 I 4 50.5 51.1 51.3 63.6 63.7 63.4 57.05 57.4 57.35 57.26 U 5 73 72.9 72.5 76 75.8 75.4 74.5 74.35 73.95 74.26 I 6 84.4 84.6 84.5 84.4 84.6 84.5 84.4 84.6 84.5 84.5 U 0 0 1 2 3 4 5 6 7
*Nhận xét : Khoảng cách giữa 2 nút điện áp U hoặc 2 nút dòng I =λ/2
U với I lệch pha pi/2(vuông pha)
==>khoảng cách giữa nút điện áp U và dòng I sẽ là λ/4 Y=16.107x – 8.704
16.107= λ/4  λ= 64.428 (cm)=0.64(m)
V= λ*f = 0,64*433.92*106 = 2.7*108 (m/s). λlt
= v/f = (3*108)/(433.92*106) = 0.69 (m). vlt = 3*108 (m/s). 8−2.7*108 3*10 Độ lệch chuẩn: 𝑉 = *100%=10% 3*10 0.69−0.64 8 Độ lệch chuẩn: λ = * 100% = 7,2% 0,69 S1(cm) S2(cm) S=(S1+S2)/2(cm) Kiểu N Lần Lần
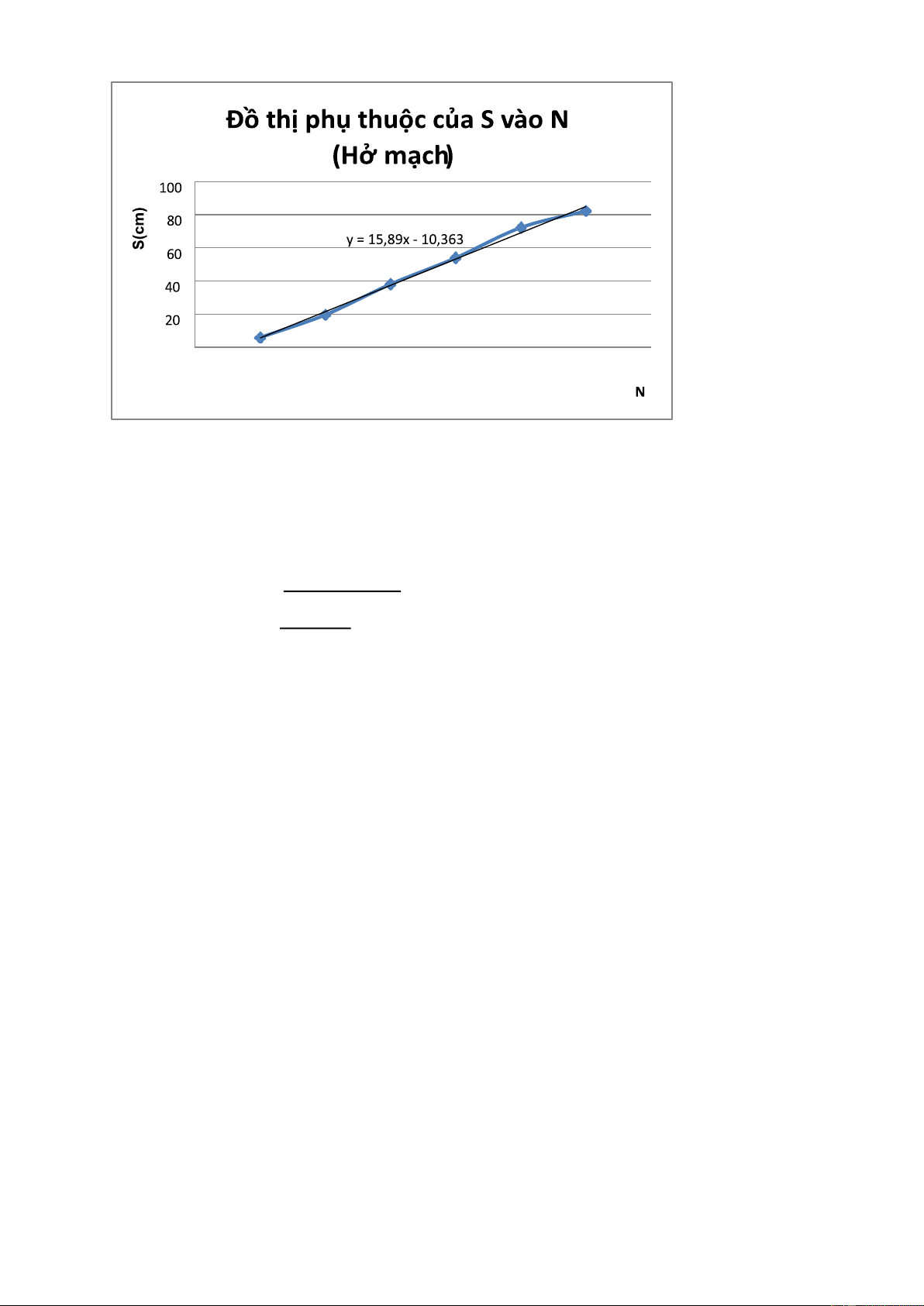
Lần 1 Lần 2 Lần 3 Lần 1 Lần 1 Lần 2 Lần 3 Stb (nút) 2 3 1 0 0 0 11.5 11.7 11.5 5.75 5.85 5.75 5.78 I 2 9.4 9.4 9.5 29.2 30 29.5 19.3 19.7 19.5 19.5 U 3 30.5 30.3 30.3 45.6 45.8 45.4 38.05 38.05 37.85 37.98 I 4 46.3 46.4 46.4 61.3 61.3 61.4 53.8 53.85 53.9 53.85 U 5 64.4 64.1 64.2 80.1 80.1 80.2 72.25 72.1 72.2 72.18 I 6 82.2 82.2 82.3 82.2 82.2 82.3 82.2 82.2 82.3 82.23 U 0 0 1 2 3 4 5 6 7
Y = 15.89x – 10.363  λ = 15.89*4 = 63.56 (cm) = 0.63 (m).
V = λ*f = 0.63*433.92*106 = 2.73*108 (m/s).
λlt = v/f = (3*108)/(433.92*106) = 0.69 (m). vlt = 3*108 (m/s). 8−2.73*108 3*10
Độ lệch chuẩn: 𝑉 = *100%=9% 3*10 0.69−0.63 8 Độ lệch chuẩn: λ = * 100% = 8,7% 0,69
BÀI 2: HIỆN TƯỢNG CẢM ỨNG ĐIỆN TỪ 1.Mục đích
- Khảo sát hiện tượng cảm ứng điện từ.
- Khảo sát sự phụ thuộc của suất điện động cảm ứng U xuất hiện cuộn
cảm đặt trong từ trường B vào:
• Tiết diện cuộn cảm A • Số vòng dây N1
• Biến thiên của cả ứng từ B theo thời gian ( thông qua biến thiên
của dòng điện qua cuộn solenoid theo thời gian dI/dt)
2.Tóm tắt lý thuyết
Khi đặt một khung dây dẫn điện tạo thành mạch điện kín vào trong trường có
cảm ứng từ B biến đổi theo thời gian , trong khung dây sẽ xuất hiện một dòng điện
cảm ứng từ B biến đổi theo thời gian . trong khung dây sẽ xuất hiện một dòng điện
cảm ứng ( hoặc suất điện động cảm ứng ) đó là hiện tượng cảm ứng điện từ Φ= 𝑁1.B.A
Trong đó, Φ: Là từ thông qua tiết diện A giới hjan bới vòng dây
A: Tiết diện của cuộn cảm B: Cảm ứng từ
𝑁1: Số vòng dây của cuộn cảm 𝑈 = − Định luât Faraday: 𝑑𝜱 hay U= -𝑁 𝑑𝐵 . 𝐴 (1) 𝑑𝑡 1 𝑑𝑡
Ngược lại khi có dòng điện I chạy qua vòng dây thì trong vòng dây sẽ
xuất hiện một từ trường .
Với cuộn Solenoid có số vòng dây 𝑁2, cảm ứng từ trong lòng cuộn dây đó là: 𝑁2 𝐵 = µ . 𝐼(2) 𝐿
Trong đó, 𝑁2: số vòng đây được quấn trên cuộn solenoid L: chiều dài ống dây
µ =˳ 4π10−7𝑉𝑠 𝐴/ m Do đó, 𝑁2
U=-µ .˳ . .𝐴 𝑁 𝑑𝐼 (3) 𝐿 1 𝑑𝑡
Biểu thức (3) thu được khi ta đặt cuộn cảm N1 có thiết diện A vào trong lòng cuộn N2
có chiều dài L với dòng điện I biến thiên theo thời gian chạy qua cuộn N2 (hình 1). Biểu
thức trên cho thấy suất điện động cảm ứng U tỷ lệ thuận với tiết diện cuộn cảm A, số
vòng dây của các cuộn cảm N1, N2 và tốc độ biến thiên dòng điện trong cuộn Solenoid dI/dt.
Trong bài thực hành này, ta sẽ tiến hành khảo sát hiện tượng cảm ứng của một cuộn
dây N1 đặt trong từ trường biến thiên của cuộn N2. Qua đó, khảo sát sự phụ thuộc của
suất điện động cảm ứng U xuất hiện trong cuộn cảm đặt trong từ trường biến thiên B
vào tiết diện cuộn cảm A, số vòng dây N1 và vào biến thiên của cảm ứng từ B theo
thời gian thông qua biến thiên của dòng điện qua cuộn solenoid theo thời gian dI/dt. XỬ LÝ SỐ LIỆU.
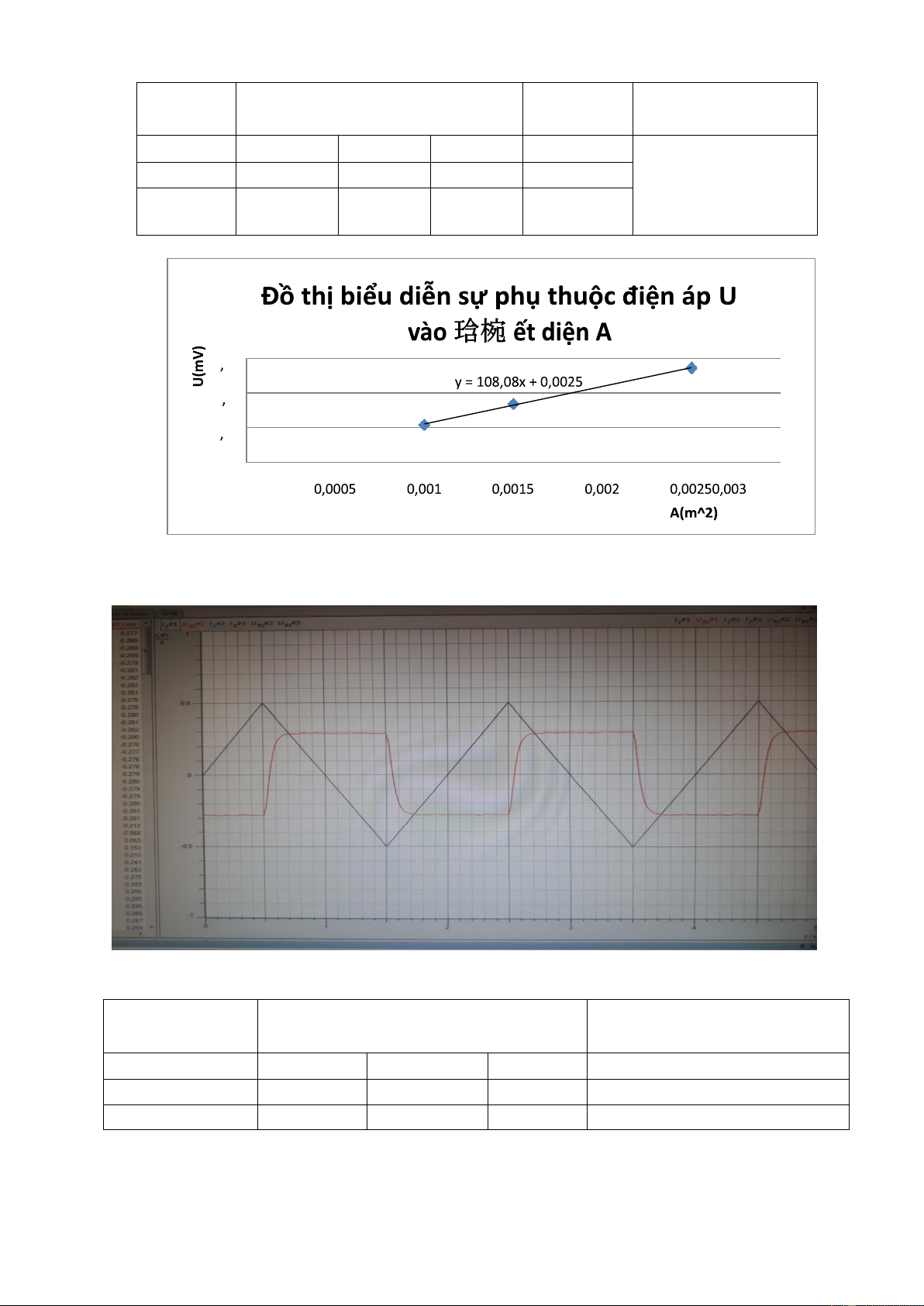
Bảng 2: Biên độ U theo tiết diện A của cuộn dây. A(m2) U(v) U T B ( m V ) 𝐼max 0,0025 0.271265 0.27168 0.27144 0.27146 I=2 0,0015 0.16801 0.1685 0.16846 0.168323 0,0010 0.108275 0.10781 0.10821 0.1081 5 T = 2s 0 3 0 2 0 1 0 0
Nhận xét: Ta thấy suất điện động cảm ứng U tỉ lệ thuận với số vòng N1 của cuộn dây theo hàm bậc nhất .
Đồ thị sự phụ thuộc của U(t) (màu đỏ) và I(t) (màu xanh).
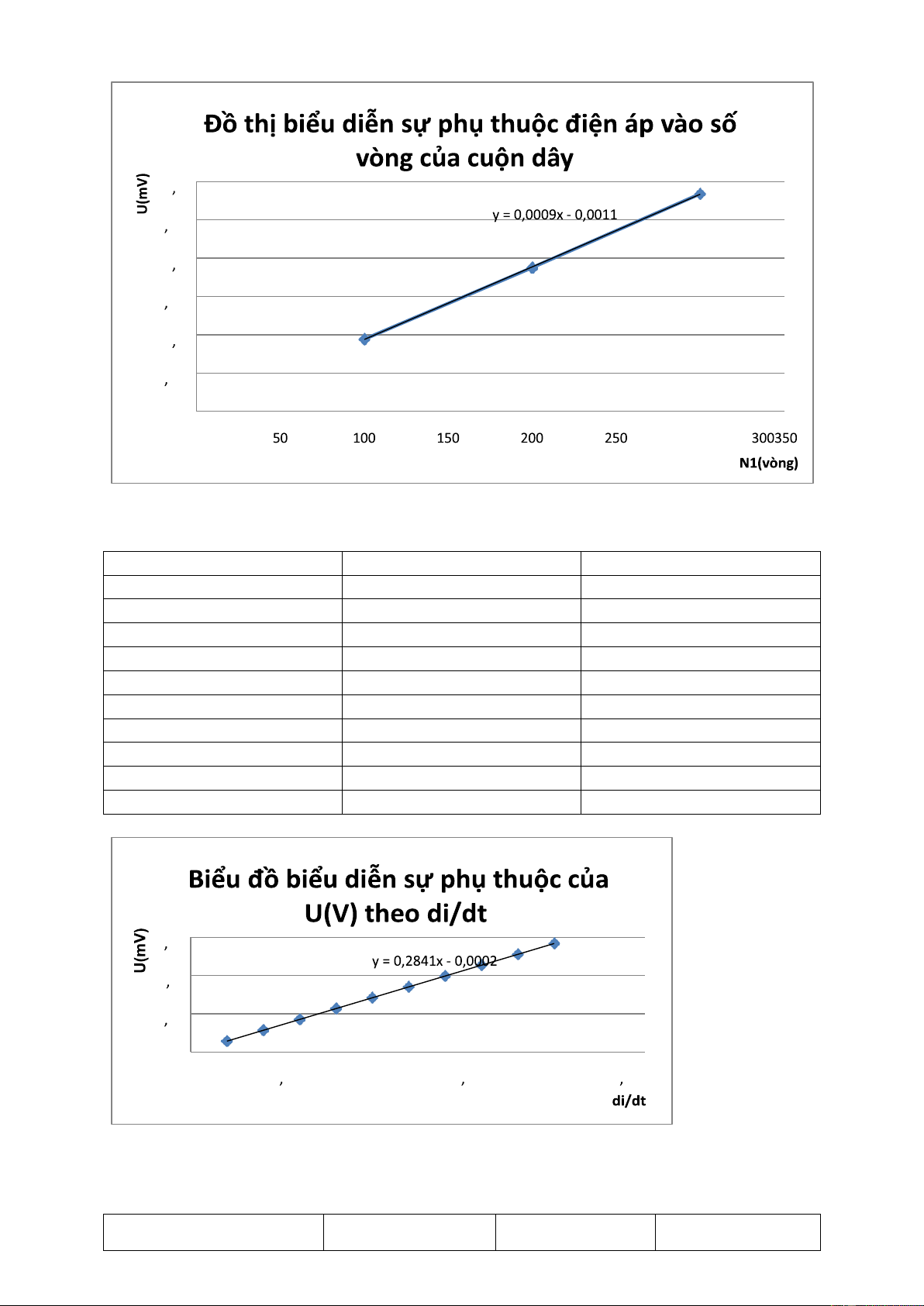
Bảng 3: Biên độ U theo tiết diện của N1 của cuộn dây. N1(vòng) U(v) Utb(mV) 300 0.28378 0.284055 0.283145 0.28391 200 0.18878 0.18905 0.18765 0.18765 100 0.094175 0.09423 0.09422 0.09422 0 3 0 25 0 2 0 15 0 1 0 05 0 0
Suất điện động cảm ứng tỉ lệ thuận với số vòng dây cuộn cảm.
Bảng4: Sự phụ thuộc của U(V) vào dI/dt (A/s). Imax( A) dI/dt U (V) 0.1 0.2 0.05651 0.2 0.4 0.113165 0.3 0.6 0.170915 0.4 0.8 0.22724 0.5 1.0 0.28337 0.6 1.2 0.340585 0.7 1.4 0.39731 0.8 1.6 0.454015 0.9 1.8 0.51129 1 2.0 0.568115
VỚI A = 0,0025 m2 và số vòng N1 = 300 vòng. 0 6 0 4 0 2 0 0 0 5 1 1 5 2 2 5
Suất điện động cảm ứng tỉ lệ thuận với tốc độ biến thiên dòng điện trong cuộn dI/dt.
Bảng: Hệ số góc của các đường thẳng U(A), U(N1), U(dI/dt). U(A) U(N1) U(dI/dt)
Hệ số góc thực nghiệm 108,8 0,0009 0,2841 Hệ số góc tính toán 110 0,000917 0,276
BÀI 3: . CHUYỂN ĐỘNG CỦA ĐIỆN TỬ TRONG ĐIỆN --TỪ TRƯỜNG, XÁC ĐỊNH e/m 1. Mục đích
• Khảo sát chuyển động của điện tử trong điện trường đều giữa hai bản tụ điện phẳng.
• Khảo sát chuyển động của điện tử trong từ trường tạo ra bởi cặp cuộn Helmholtz.
• Khảo sát chuyển động của điện tử trong khoảng không gian có đồng thời
điện trường và từ trường đồng nhất vuông góc với nhau. Bộ lọc vận tốc.
Xác định điện tích riêng e/m của điện tử.
2. Cơ sở lý thuyết
Trong bài thí nghiệm này, ống Thomson được sử dụng để khảo sát sự lệch
hướng của điện tử chuyển động trong điện trường cũng như từ trường và được sử
dụng làm bộ lọc vận tốc của các điện tử.
2.1.Sự chuyển động của điện tử trong điện trường
Xét một điện tích e chuyển động trong một điện trường đều nằm giữa hai bản tụ của
một tụ phẳng. Lực điện trường tác dụng lên vật: ̅*F→ = e. *E→ (1)
trong đó, e: là điện tích của vật,
E: là cường độ điện trường.
Phương trình chuyển động của điện tích có dạng: m. dv→ dt = e. * *E→(2)
với, m: khối lượng của điện tích, v:
vận tốc chuyển động của điện tích.
Chọn trục Oy theo phương của 𝐸→ và tại thời điểm t = 0, điện tích ở gốc O với vận
tốc v0 nằm trong mặt phẳng xOy. Khi đó, điện tích chỉ chuyển động trong mặt phẳng xOy.
Chiếu phương trình chuyển động (2) lần lượt xuống các trục Ox và Oy ta có: 𝑑2x m. dt2y2 = 0 (3) 𝑑 m. dt2 = eE (4)
Lấy tích phân 2 lần theo thời gian của (3) và (4) ta lần lượt được:
y = e. Ex = v. 𝑡20 + x. t (5). 𝑡 (6) 2m. v0y
Rút t từ biểu thức (5) thay vào biểu thức (6) ta có phương trình quỹ đạo của điện tích
chuyển động trong điện trường đều: e. E y = . x 2 + (tgφ). x (7) 2. m(v0. cosφ)2
trong đó, φ: là góc giữa vận tốc ban đầu v0 và trục Ox.
Như vậy, quỹ đạo của điện tích chuyển động trong điện trường đều là một đường
parabol. Nếu 𝜑 = 0 𝑜 , phương trình quỹ đạo của điện tích chuyển động trong điện
trường đều trở thành : e. E y = 2. m(v0. )2 (8)
Vì điện tử được gia tốc bởi 1 hiệu điện thế UA nên:m e. UA = v2 (9) 2
Rút v từ biểu thức (9) và thay vào phương trình (8) ta đươc: E y =. x 2 (10) 4UA
Với UP là hiệu điện thế đặt giữa hai bản tụ và d = 5,5 cm là khoảng cách giữa hai
bản tụ, do cấu trúc của ống Thomson, điện trường thực tế nhỏ hơn điện trường lý
thuyết và phải đưa vào một số hiệu chỉnh:
E thực tế = 0,75. Elý thuyết = UP (11) 0,75 . 𝑑
2.2.Sự chuyển động của điện tử trong từ trường.
Xét một điện tích e chuyển động với vận 𝑣→ trong từ trường 𝐵→ của cặp
Helmholtz và 𝑣→ vuông góc với 𝐵→. Khi đó từ trường 𝐵→→sẽ tác dụng lên điện tích e một lực Loren:
̅*F→ = e. [v* → *B→] (12)
Vì 𝑣→ vuông góc với 𝐵→ nên độ lớn của lực Loren là: F = e. v. 𝐵 (13)
Lực Loren có vai trò của lực hướng tâm làm cho điện tử chuyển động theo quỹ đạo tròn theo phương trình:
y = r − √𝑟2 − 𝑥2 (14) Bán kính của
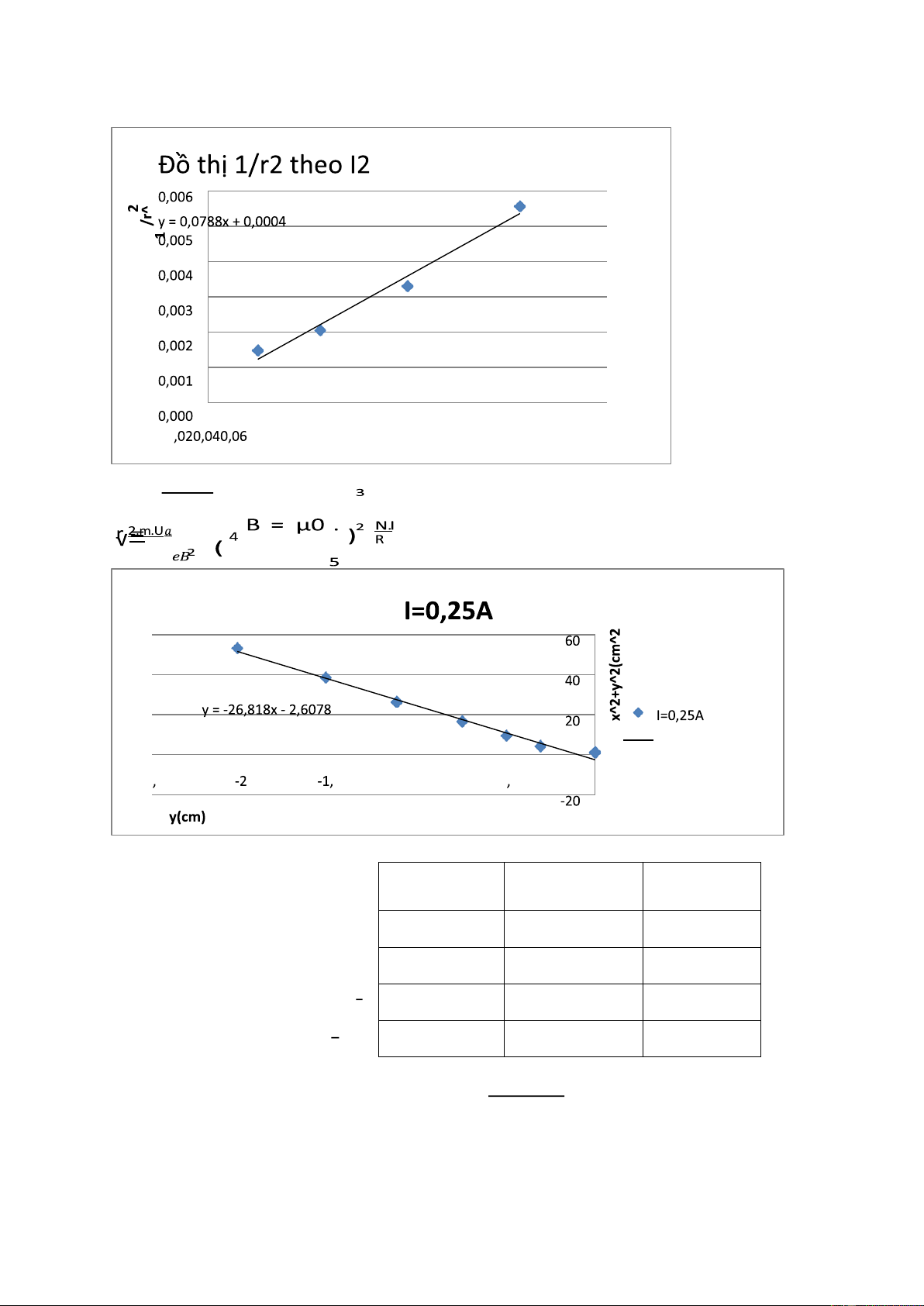
quỹ đạo r được xác định như sau: v2 v e. v. B = m.𝑟 hay e. B =m. 𝑟 (15)
Rút v từ biểu thức (8) và thay vào (15) ta được: 2. m. U𝑎 (16) r = √ 𝑒𝐵2
Biểu thức (16) cho biết bán kính quỹ đạo chuyển động của điện tử phụ thuộc hiệu
điện thế anot UA và từ trường B của cặp cuộn Helmholtz.
Từ trường tạo ra bởi cặp cuộn Helmholtz khi có dòng điện I chạy qua được xác định bởi: B = µ0 . ( 4 32 N. 5 I (17) ) R
với, 𝜇0=4π.10-7 (mT/A): độ từ thẩm của chân không,
N: số vòng dây của cuộn Helmholtz, R: bán kính cuộn Helmholtz.
Trong bài thí nghiệm này, N = 320 vòng và R = 6,7 cm. Từ
biểu thức (16), điện tích riêng e/m được xác định: 𝑒 2𝑈𝑎 = 2𝑟2 (18)
2.3.Sự chuyển động của điện tử trong khoảng không gian có đồng thời điện𝑚
𝐵 trường và từ trường đồng nhất vuông góc với nhau. Bộ lọc vận tốc.
Xét một điện tích chuyển động với vận tốc 𝑣→ trong điện trường 𝐸→ và từ
trường 𝐵→. Khi đó lực tổng hợp tác động lên điện tích là:
̅*F→ = e. *E→ + e. [*v*→*B*→] (19)
c. Cho chùm điện tử đi qua vùng có điện trường 𝐸→ và từ trường 𝐵→ đặt vuông góc
với nhau sao cho lực điện *F→ = e. *E→ cùng phương nhưng ngược chiều với lực từ
̅*F→ = e. [*v*→*B*→] . Bằng cách điều chỉnh điện trường và từ trường để độ lớn của
hai lực đó bằng nhau, nghĩa là: 𝐸
e. E = e. v. 𝐵 ℎ𝑎𝑦 𝑣 (20) = 𝐵
Thay biểu thức (20) vào biểu thức (9) được biểu thức tương đương sau: 𝑒 𝐸2 = 2 (21) XỬ LÝ SỐ LIỆU. 𝑚 2𝑈𝑎𝐵
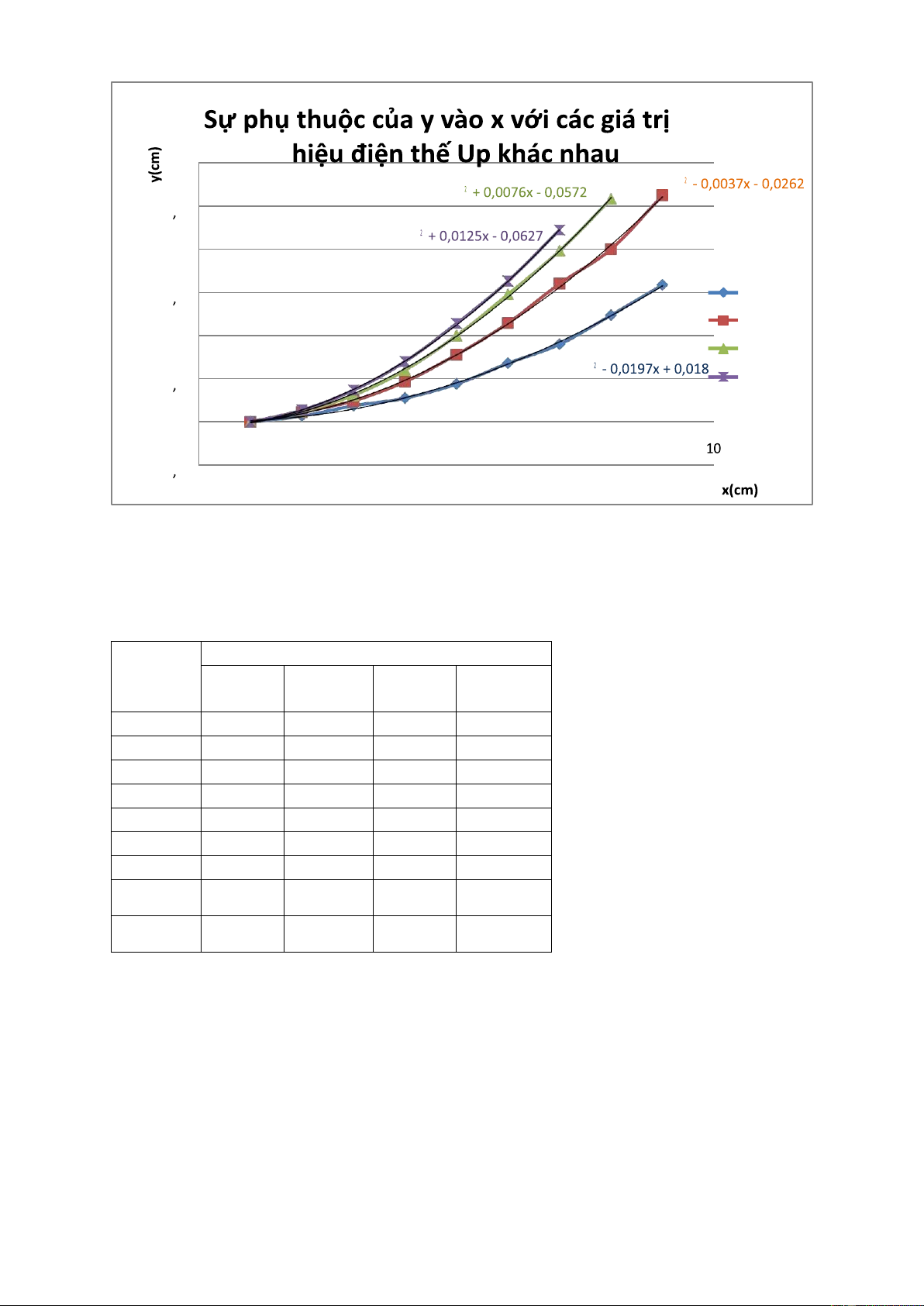
Bảng 2. Tọa độ (x,y) tương ứng trên quỹ đạo chuyển động của điện tử trong điện
trường với các hiệu điện thế Up khác nhau. y(cm) x(cm) Up = 2kV Up = 3kV Up = 4kV Up = 5kV 1 0 0 0 0 2 0,07 0,116 0,125 0,14 3 0,19 0,246 0,31 0,369 4 0,28 0,467 0,6 0,7 5 0,44 0,78 1 1,14 6 0,68 1,145 1,478 1,63 7 0,90 1,6 1,98 2,22 8 1,24 2 2,58 9 1,59 2,62 3 y = 0,0405x y = 0,0329x 2 5 y = 0,0449x 2 1 5 Up=2kV 1 Up=3kV y = 0,0214x Up=4kV 0 5 Up=5kV 0 0 2 4 6 8 -0 5
Nhận xét: Up càng tăng thì độ dốc của đồ thị cũng tăng theo do chịu tác dụng của
lực điện trường F=e.E mà 𝐸 = 𝑈  F=e. 𝑑
𝑑𝑈 ta thấy F tỉ lệ thuận với U
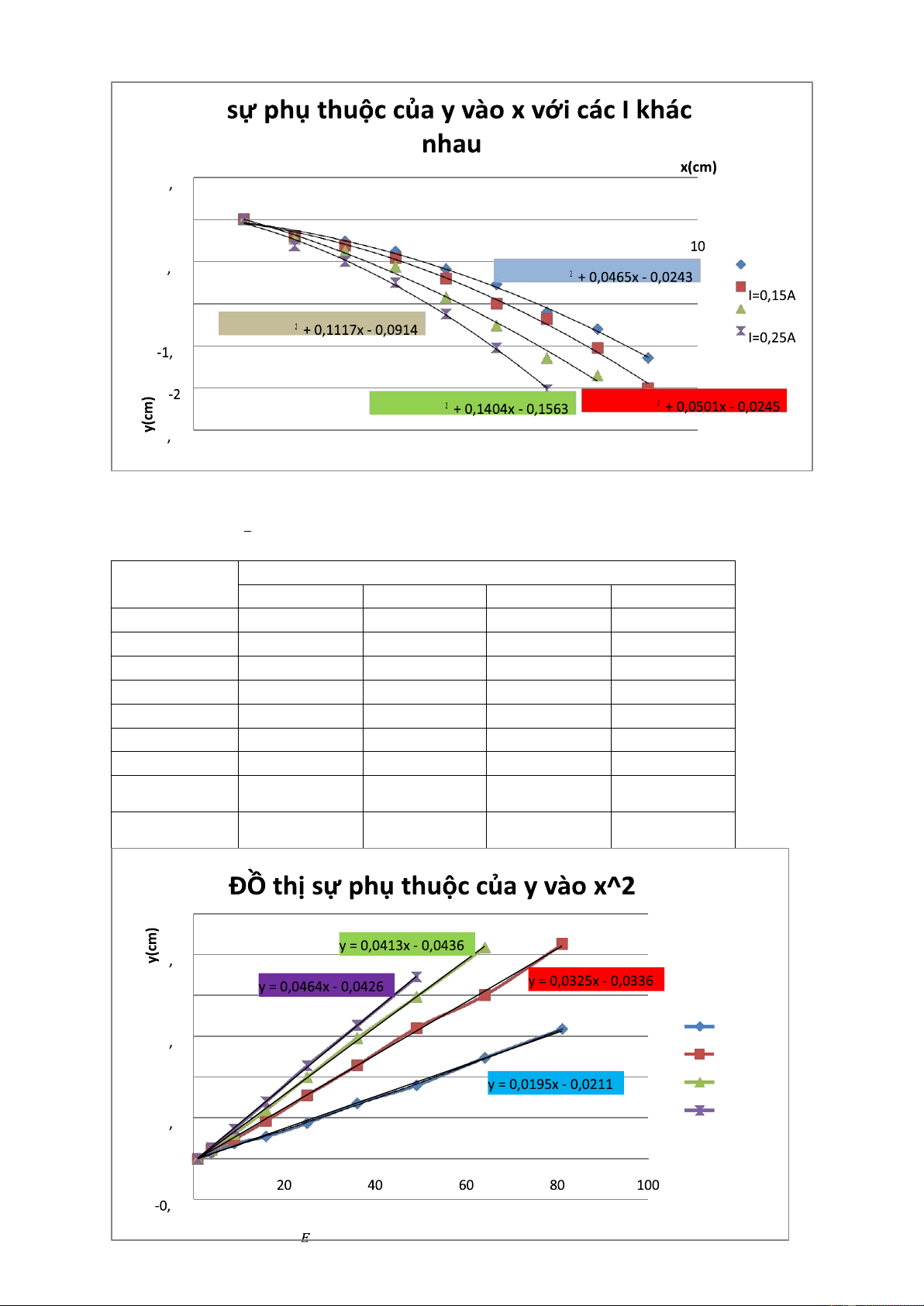
Bảng 3. Tọa độ (x,y) tương ứng trên quỹ đạo chuyển động của điện tử trong điện
trường với các dòng điện chạy trong cuộn Helmholzt khác nhau. y(cm) x(cm) I = 0,1 I= 0,15 I = 0,2 I = 0,25 A A A A 1 0 0 0 0 2 -0,19 -0,2 -0,225 -0,31 3 -0,26 -0,31 -0,38 -0,5 4 -0,38 -0,46 -0,56 -0,75 5 -0,59 -0,7 -0,92 -1,12 6 -0,77 -1 -1,26 -1,52 7 -1,1 -1,18 -1,64 -2,02 8 -1,3 -1,52 -1,85 9 -1,64 -2 0 5 0 0 2 4 6 8 -0 5 y = 0,0153x I=0,1A -1 I=0,2A y = 0,0267x 5 y = 0,0149x y = 0,0187x -2 5
Nhận xét : Ta thấy khi tăng I thì độ lệch của điện tử càng lớn do chịu tác dụng của
lực loren F=e.v.B mà cảm ứng từ B tỷ lệ thuận với cường độ dòng I
Theo CT: B=µ˳𝑁.𝐼 𝑘. 𝑅 y(cm) x 2(cm2) Up = 2kV Up = 3kV Up = 4kV Up = 5kV 1 0 0 0 0 4 0,07 0,116 0,125 0,14 9 0,19 0,246 0,31 0,369 16 0,28 0,467 0,6 0,7 25 0,44 0,78 1 1,14 36 0,68 1,145 1,478 1,63 49 0,90 1,6 1,98 2,22 64 1,24 2 2,58 81 1,59 2,62 3 2 5 2 1 5 Up=2kV Up=3kV 1 Up=4kV 0 5 Up=5kV 0 0 5 x^2(cm^2)
Hệ số góc đồ thị 𝛼 = 4𝑈𝑎
𝑡 𝑒𝑜ℎ 𝑐𝑡 (10)
𝐸 = 𝘢. 4Ua d=5.5cm =0.055m Etính toán =0.75.Up/d
Bảng 5:Điện trường giữa hai bản tụ Up = Up = Up = Đơn vị Up = 2kV 3kV 4kV 5kV E đo được 31,2 52 66,08 74,24 E tính kV/m toán 27,27 40,9 54,54 68,18
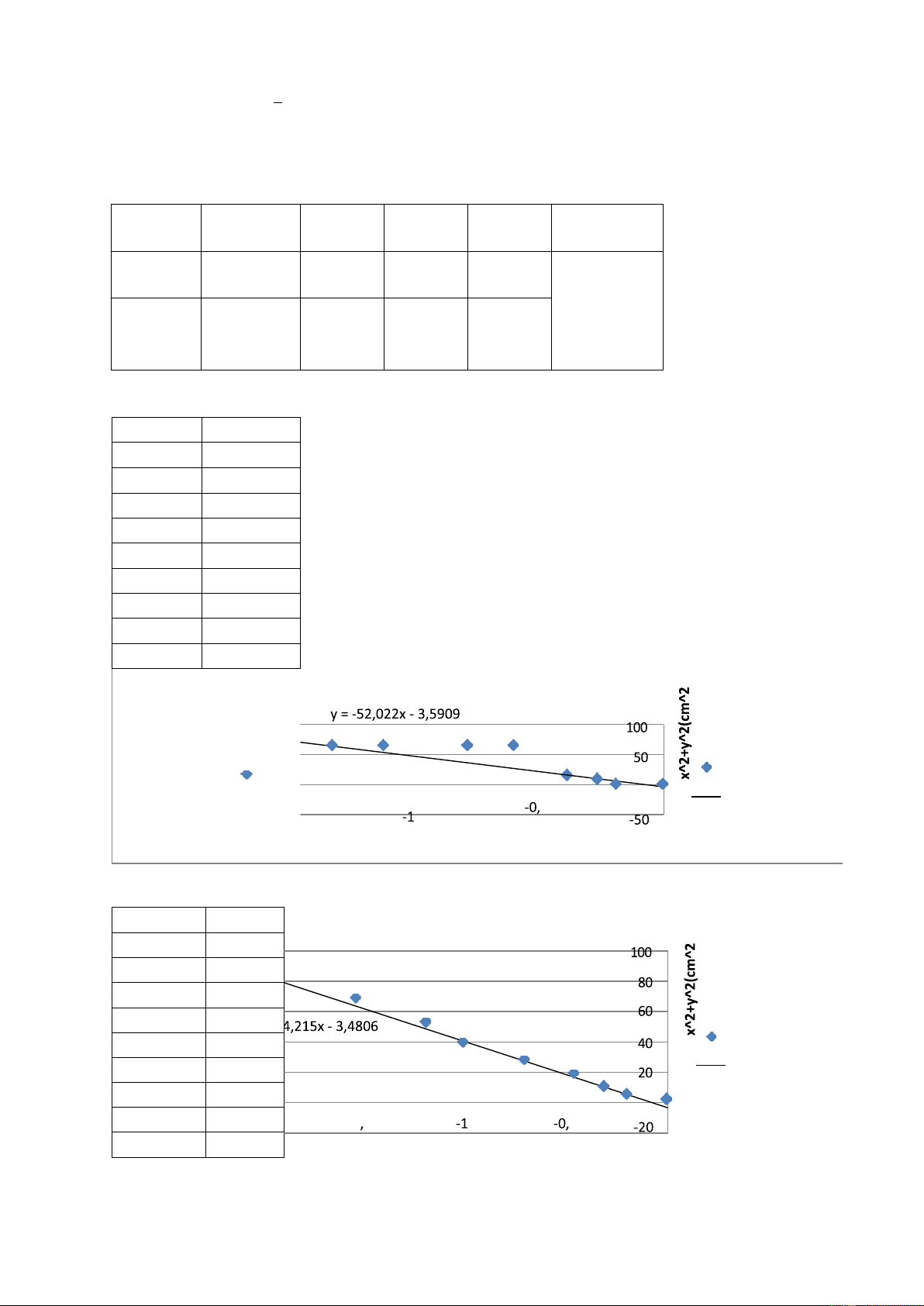
 Do sai số trong việc đo Y dẫn đến kết quả lệnh rất nhiều. Tính bán kính. x^2+y^2 y(cm) 1 0 4,0361 -0,19 9,0676 -0,26 16,1444 -0,38 25,348 -0,59 36,5929 -0,77 50,21 -1,1 65,69 -1,3 83,689 -1,64 I=0,1A 0 Linear (I=0,1A) 5 0 -I= 2 y(c 0,1 m) A -1,5
Nhận xét i=0,1A R=26,011 cm. x^2+y^2 y(cm) I=0,15A 1 0 4,04 -0,2 9,0961 -0,31 16,2116 -0,46 25,49 -0,7 I=0,15A 37 -1 Linear (I=0,15A) 50,3924 -1,18 0 66,3104 -1,52 0 -1 5 5 85 -2 -2,5 y(cm) -2
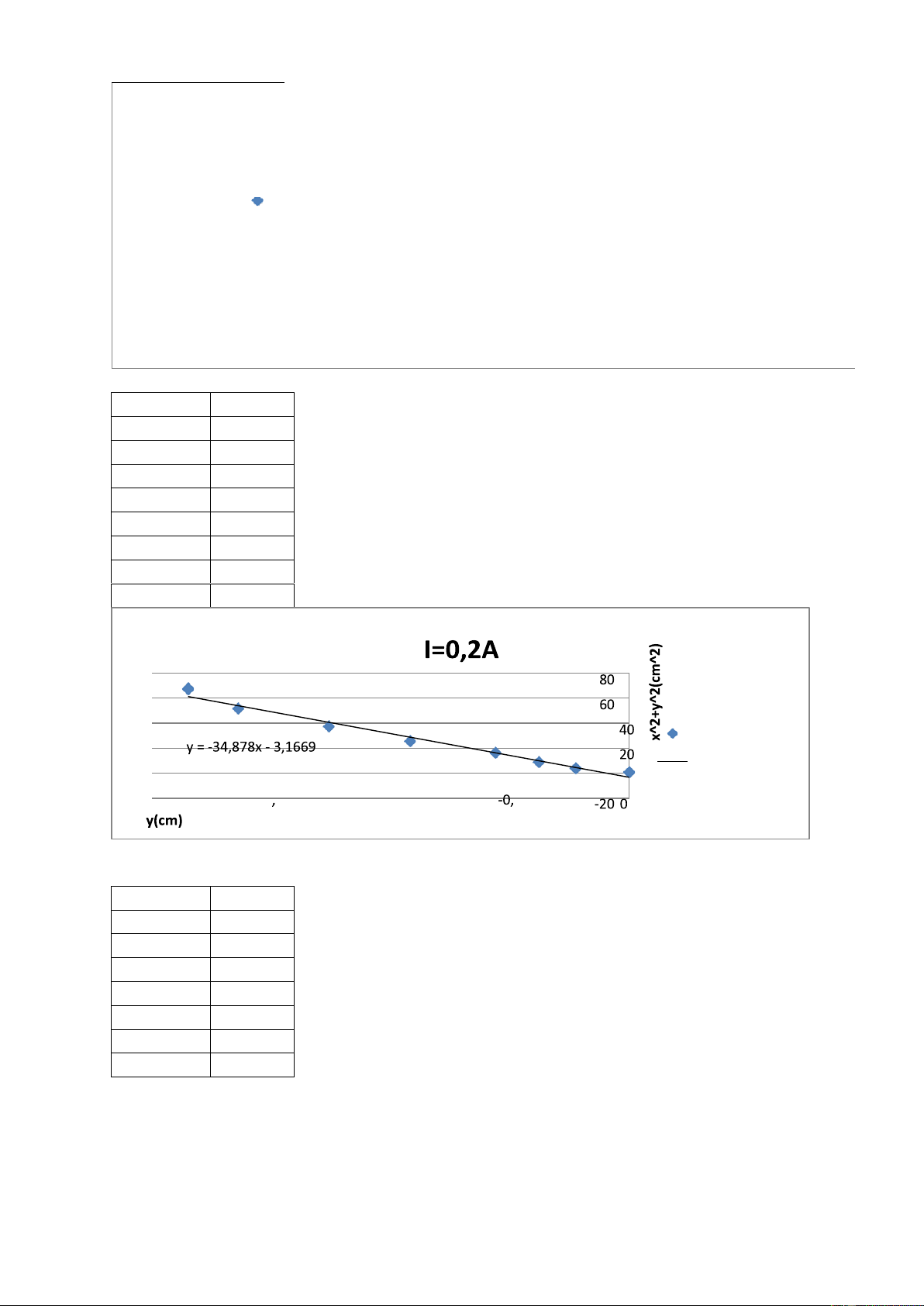
Nhận xét i=0,15A, R=21,0175 cm. x^2+y^2 y 1 0 4,050625 -0,225 9,1444 -0,38 16,3136 -0,56 25,8464 -0,92 37,5876 -1,26 51,6896 -1,64 67,4225 -1,85 I=0,2A Linear (I=0,2A) 0 -2 -1 5 -1 5
Nhận xét i=0,2A R=17,439 cm. x^2+y^2 y 1 0 4,0961 -0,31 9,25 -0,5 16,5625 -0,75 26,2544 -1,12 38,3104 -1,52 53,0804 -2,02 0 ,08 i^2 00
Nhận xét: Từ hệ số góc của phương trình ta tính được : với Linear (I=0,25A) 0 -2 5 5 -1 -0 5 0
Nhận xét i=0,25A R=13,409 cm. Ua(kV) I(A) 𝑟¯ ± ∆𝑟¯(cm) 4 0,1 26,011 4 0,15 22,1075 4 0,2 17,439 4 0,25 13,409
e/m =2,3585*1011(C/kg) e=1,6*10-19; me=9.1*10-31 ==>e/m ( lý
thuyết )=1.76*1011(C/kg) Độ lệch chuẩn là: ∆= 2,3585−1,76 * 100% = 34%. 1,76 BÀI 4: BIẾN THẾ. 1. Mục đích
• Khảo sát sự phụ thuộc của hiệu điện thế thứ cấp của một máy biến thế
không tải vào hiệu điện thế sơ cấp với các tỷ lệ số vòng dây giữa hai cuộn khác nhau.
• Khảo sát sự phụ thuộc của dòng điện thứ cấp của máy biến thế hoạt
động đoản mạch vào dòng điện sơ cấp với các tỷ lệ số vòng dây giữa hai cuộn khác nhau.
• Sự khác biệt giữa biến thế cô lập và một biến thế tự ngẫu.
• Đo hiệu điện thế và cường độ dòng điện trên cuộn thứ cấp của biến
thế “soft” và “hard” như hàm của trở tải.
• Xác định công suất đầu ra của máy biến thế trở tải theo dòng chạy trong cuộn thứ cấp.
• Khảo sát các đường sức từ trên biến thế “soft” và “hard”.
2. Cơ sở lý thuyết
Máy biến thế thông thường gồm có 2 cuộn dây cảm ứng liên kết với nhau thông qua
một lõi sắt (lõi biến thế).Lõi biến thế được ghép từ các bản mỏng được sơn lớp cách
điện hoặc được chế tạo từ những vật liệu từ mềm dẫn điện kém để giảm dòng
Foucault.Máy biến thế được sử dụng để thay đổi độ lớn hiệu điện thế của nguồn
điện xoay chiều mà không làm thay đổi giá trị tần số.
Các dây đầu vào được nối với cuộn sơ cấp, trong khi các dây đầu ra nối với
cuộn thứ cấp.Dòng điện xoay chiều trong cuộn dây sơ cấp gây ra từ thông biến thiên
chạy xung quanh lõi sắt từ.Từ thông biến thiên trong lõi sắt làm xuất hiện dòng điện
xoay chiều trong cuộn dây thứ cấp.
U2/U1 = N2/N1 (khi I2 = 0) (1) Đối
với máy biến thế lý tưởng không có tải,ta có:
Với U1, U2 lần lượt là hiệu điện thế của cuộn sơ cấp và thứ cấp; N1,
N2 lần lượt là số vòng dây của cuộn sơ cấp và thứ cấp.
Sự biến đổi dòng trong biến thế lý tưởnghoạt động đoản mạch tuân theo công thức sau: I2/I1 = N1/N2 (khi U2 = 0) (2)
Với I1, I2 lần lượt là dòng của cuộn sơ cấp và thứ cấp.
Trong bài thí nghiệm đối với phần này, hiệu điện thế và dòng điện biến đổi
được đo đối mới máy biến thế “soft” (cuộn sơ cấp và cuộn thứ cấp ở trên các phần
riêng biệt) không tải. Bên cạnh đó, biến thế cô lập và biến thế tự ngẫu được phân biệt.
Mối liên hệ giữa hiệu điện thế đầu vào U1 và hiệu điện thế đầu ra U2 của máy
biến thế ngoài phụ thuộc vào tỷ lệ số vòng dây N1: N2 của hai cuộn dây, còn phụ
thuộc vào trở tải. Hiệu điện thế U2 giảm với sự tăng dòng I2 trong cuộn thứ cấp do sự
sụt điện áp tăng trên điện trở nội của nguồn điện này (tức cuộn dây thứ cấp).
Ngoài ra, đặc trưng I - V của máy biến thế có trở tải cũng phụ thuộc vào thiết
kế vật lý của máy biến thế. Trong phần thí nghiệm này, mối liên hệ giữa hiệu điện thế
và dòng điện thứ cấp của máy biến thế có trở tải được khảo sát trong các trường
hợp cuộn sơ cấp và thứ cấp quấn:
• Phân bố đối xứng ở cả hai phần của lõi sắt (tỷ lệ cố định, biến thế “hard”)
• Quấn riêng biệt trên mỗi phần của lõi sắt (điện kháng cao, biến thế “soft”)
Trong cả hai trường hợp, các đường sức từ của máy biến thế được khảo sát
bằng cách sử dụng các mạt sắt trên tấm nhựa phẳng đặt bên trên biến thế. Công
suất đầu ra của hai kiểu biến thế (“hard” & “soft”) được xác định thông qua biểu thức
(giả sử tiêu hao thấp): P2 = U2.I2 (3) Như vậy, từ đường đặc trưng I – P có thể xác
định được công suất đầu ra cực đại. P2 = U2. I2 (3)
Như vậy, từ đường đặc trưng I – P có thể xác định được công suất đầu ra cực đại. XỬ LÝ SỐ LIỆU
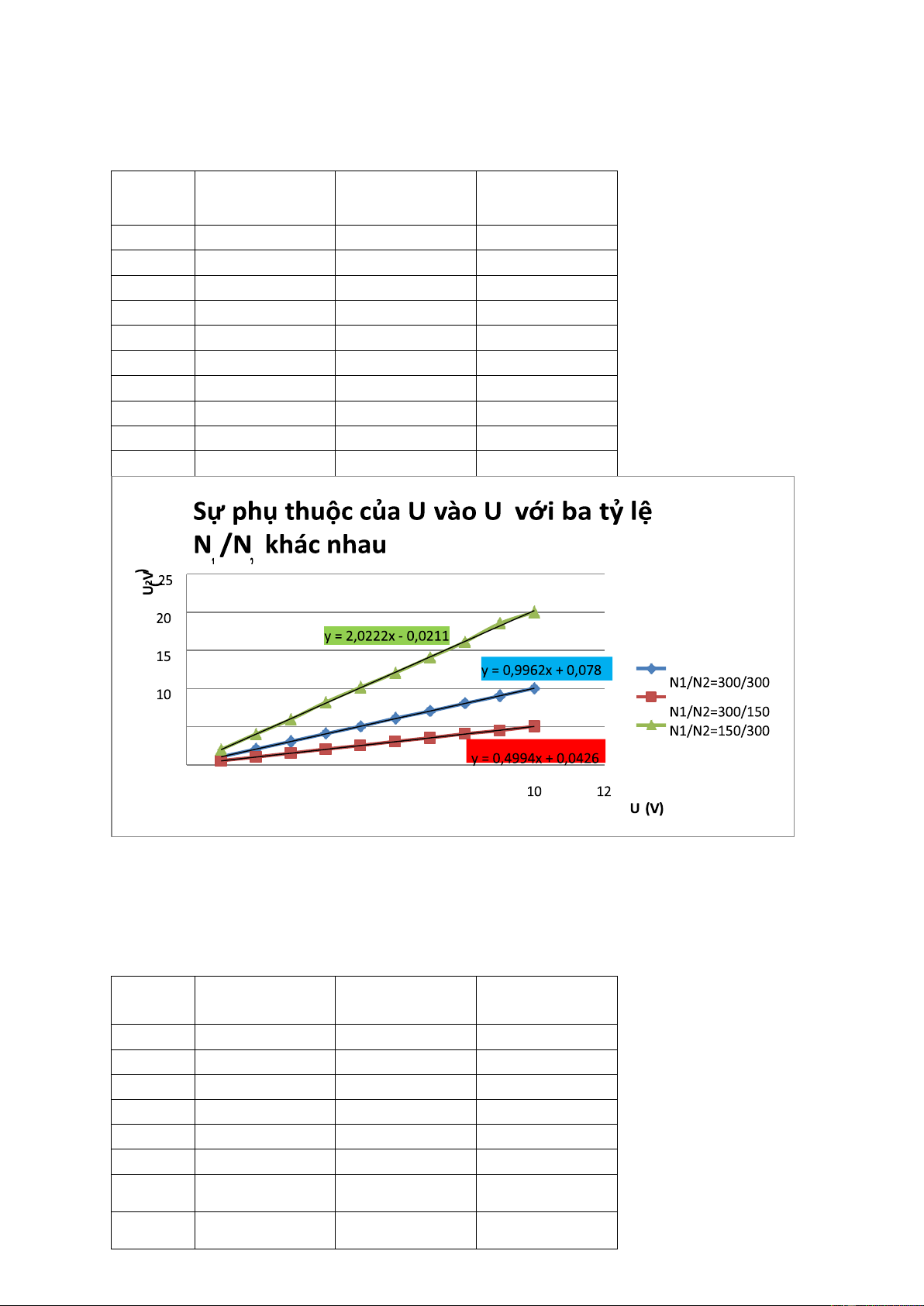
Bảng 2. Sự phụ thuộc của U2 vào U1 với các tỷ lệ N1/N2 khác nhau. U2 (V) với U2 (V) với U2 (V) với U N N N 1(V) 1/N2=300/300 1/N2=300/150 1/N2=150/300 1 1,061 0,541 2,001 2 2,061 1,026 4,030 3 3,070 1,536 5,950 4 4,080 2,055 8,180 5 5,050 2,536 10,140 6 6,100 3,062 12,040 7 7,040 3,538 14,060 8 8,041 4,060 16,100 9 9,030 4,500 18,501 10 10,040 5,040 20,010 2 1 5 0 0 2 4 6 8 1
Nhận xét: nhìn từ đồ thị ta thấy U1 và U2 tỷ lệ thuận với nhau theo hàm bậc nhất
(y=kx) và khi ta thay đổi số vòng dây trên mỗi cuộn thì U cũng thay đổi tuyến tính
U1/U2=N1/N2 ; U và N tỷ lệ thuận. Khi N2 là số vòng dây của cuộn thứ cấp nhỏ nhớ N1
là cuộn sơ cấp thì máy biến áp đó là máy hạ áp (U2Tương tự có (N2>N1) thì là máy tăng áp. (N2=N1) có hiệu điện thế không đổi
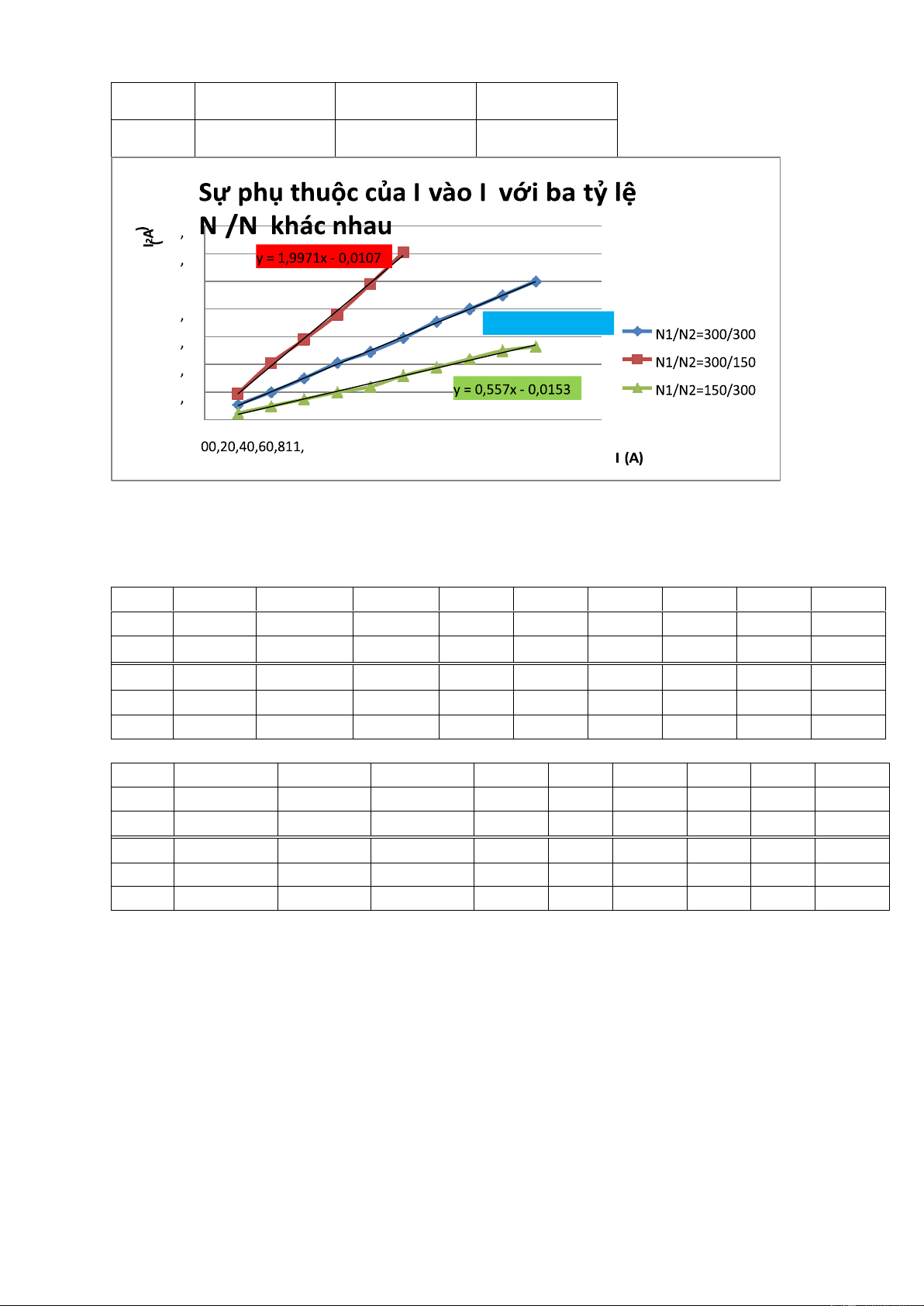
Bảng 3. Sự phụ thuộc của I2 vào I1 với các tỷ lệ N1/N2 khác nhau I2 (V) với I2 (V) với I2 (V) với I1(A)
N1/N2=300/300 N1/N2=300/150 N1/N2=150/300 0,1 0,11 0,19 0,05 0,2 0,2 0,41 0,1 0,3 0,3 0,58 0,15 0,4 0,41 0,76 0,2 0,5 0,49 0,98 0,24 0,6 0,59 1,21 0,32 0,7 0,71 0,38 0,8 0,8 0,44 0,9 0,9 0,5 1 1 0,53 2 1 1 4 1 2 1 2 1 0 8 y = 0,9945x + 0,00 4 0 6 0 4 0 2 0 2 1
Nhận xét: từ đồ thị ta thấy I1 và I2 tỉ lệ thuận với nhau theo hàm bậc nhất. Với I và N
tỉ lệ nghịch. Khi N1>N2 thì ta thấy I1càng cao tương ứng với hệ số góc càng lớn.
Bảng 4. Hiệu điện thế U2 tại các giá trị I2 khác nhau với biến thế “soft” I2(A) 0 0,04 0,08 0,13 0,17 0,22 0,26 0,3 0,33 U2(V) 4 3,99 3,79 3,6 3,47 3,36 3,11 2,9 2,65 P(W) 0 0,1596 0,3032 0,468 0,5899 0,7392 0,8086 0,87 0,8745 I2(A) 0,36 0,4 0,42 0,468 0,48 0,5 0,53 0,55 0,59 U2(V) 2,49 2,32 2,15 2 1,71 1,65 1,36 1,23 0,9 P(W) 0,8964 0,928 0,903 0,936 0,8208 0,825 0,7208 0,6765 0,531
Bảng 5.Hiệu điện thế U2 tại các giá trị I2 khác nhau với biến thế “hard” I2(A) 0 0,1 0,16 0,22 0,28 0,34 0,4 0,45 0,53 U2(V) 4,01 3,72 3,6 3,35 3,15 3,01 2,71 2,5 2,32 P(W) 0 0,372 0,576
0,737 0,882 1,0234 1,084 1,125 1,2296 I2(A) 0,58 0,62 0,7 0,75 0,8 0,86 0,93 1 1,05 U2(V) 2,18 2,05 1,8 1,63 1,47 1,24 1,1 0,78 0,66 P(W) 1,2644 1,271
1,26 1,2225 1,176 1,0664 1,023 0,78 0,693